UNIVERSUMS HISTORIA ENLIGT RELATERAD FYSIK OCH MATEMATIK | TGF2014a | 2014II18 | a BellDHARMA production | Senast uppdaterade version: 2018-12-27 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor ·

| Jordatmosfären | SlutgrafernaSAMBAND | SlutgrafernaGRAFER | SlutgrafernaPDAS | SlutgrafernaSAMBAND | JAGVH | VRF | ATFT

BlixtTGF2014a ........ GRUNDBEGREPPEN I MOLNBILDNINGENS TEKNISKA FYSIK — basbegreppen till

BlixtTGF2014b ........ BLIXTURLADDNINGENS FYSIK MED JORDSTRÖMMARNA OCH MOLNENS VATTENBILDNING

GRUNDBEGREPPEN i Molnbildningens Tekniska Fysik

ENLIGT RELATERAD FYSIK

MOTEF, molnbildningens tekniska fysik, inledning

Som nedan:: Jordatmosfärens massvolym (V) inom troposfären är (vad vi vet) konstant för molnbildningens tekniska fysik. Vi använder då förenklat Jordytan som en plan skiva med ytan 4·(pi)·(Rekvatorn=6,378 T6 M)² = 5,11 185 T14 M² med (troposfären) höjden ca 10 KM. Det ger oss en fast atmosfärisk referensvolym lika med V(tropos) = 5,1 T18 M³, figuren nedan. Den kan sedan användas i våra försök att, eventuellt, förstå detaljerna.

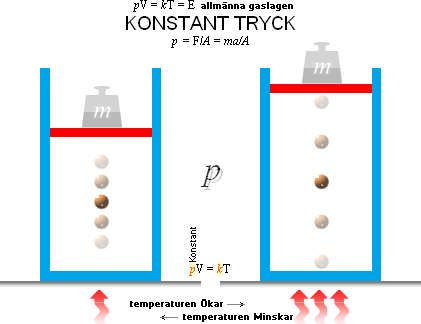
JORDATMOSFÄRENS KONSTANTA VOLYM

OCH MOLNBILDNINGENS TEKNISKA FYSIK — grunderna till blixturladdningens relaterbara fysik

Se även i JORDATMOSFÄRENS VOLYMKONSTANS [JAVK].

Primärformen

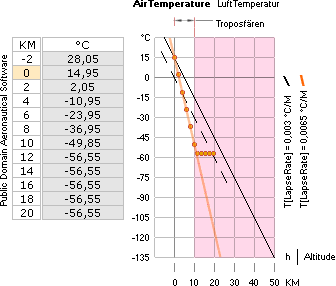
Solinstrålningen till den fasta (30%) och flytande (70%) Jordytan kan i netto förstås bilda en global medelmässig ekvivalent för hela Jordytan i formen av en plan fast/flytande materiell skiva, illustrationen nedan. Markskivan kan förstås ligga på en värmehäll som matas med konstant tillförd effekt (P=E/t) via Solens inverkan och som värmeläcker till den närmaste omgivande troposfären (höjd grovt max 10KM). Med den kontinuerligt tillförda Solvärmemängden och dess naturliga värmeläckning mot den yttre rymden, kan Jordatmosfärens olika komplicerade mer eller mindre globalt årsmedelfasta skiktbildningar förstås som anställda på Jordrotationen som blandare och Jordgravitationen som givare för lokala atmosfäriska fasta och fixa hydrostatiska tryck (p=F/A); Varje höjdnivå har sin särskilda fasta och fixa Tpρk-profil [JAGVH]. Men det är bara genom troposfären som temperaturen avtar entydigt med höjden (h), och därmed endast för det skiktet en termogravitellt bestämd hydrotemperaturvariation enligt E=Fh=mah=kT som ger

T/h=a/(k/m)=a/(Cp)_LUFT=0,0098°C/M, se ATFT.

Påenergi Q = Arbete W + Värmeläckning L [VRF], Relaterad Fysik — Illustration TermoRelFys

Solvärmen [Q] underhåller Jordatmosfäriska luftmasscirkulationer [W] som värmeläcker [L] genom Jordytmassans naturliga avsvalning från Solens markuppvärmning.

— Men i Modern Akademi är det svårt att hitta motsvarande referenser: läckfaktorn L finns inte med [VRF]. Det finns, relaterad fysik, heller ingen möjlighet att stänga av Q. Modern Akademi däremot, HELT i flera avseenden, baserar sin ”termodynamik” på just ”DåQärNoll”. I relaterad fysik finns heller inget sätt att RELATERA ”avsvalning är ARBETE” [WikipediaInternalEnergy] eftersom arbete, relaterad fysik [E=Fd, kraftvägen], definieras som orsaken till värmebildning [VLAFS], [HeatBASIC]. Alla dessa nu nämnda bidrar till en tydlig SPRÅKFÖRBISTRING — sambanden är OK men beskrivningen av deras innebörder är rena snurren [CentralAdia] — tydligen i regi av etablerad nomenklatur, speciellt i ämnet molnbildningens elementära fysik.

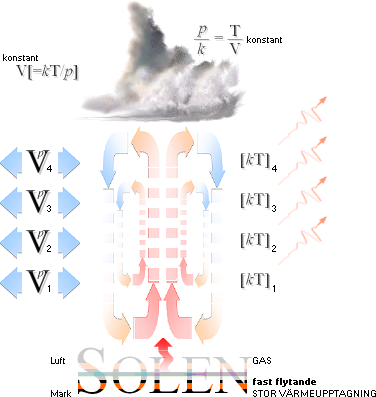
V[=kT/p]

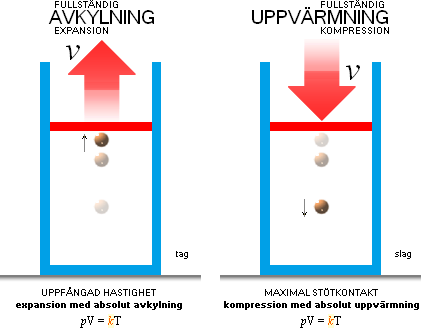
NOTERA figurens ”kT→konv. adiabat”: FlaskExpeditionen visar att isotermen pV=kT=konstant kan användas som HJÄLPSAMBAND [Hydrotransiten] för att rent experimentellt påvisa HUR markluft som förs uppåt genomgår expansion: »lägre tryck med högre höjd balanseras av större volym». »Argumentet» är samhörande [CentralAdia] [AdiabaticRef] med uppfattningen i modern akademi att ”expansionen förorsakar luften att avkylas” med »titelrubriken» ”adiabatic process”, ”adiabatic cooling”. Men hjälpsambandet är en isoterm (konstant temperatur) medan ”adiabatisk” i modern mening är något (helt) annat [FMadia] [MACadiaRef]. Det är f.ö. en av anledningarna varför grundbegreppen i molnbildningens fysik i etablerad nomenklatur blir ytterst krångliga (inte sällan kaotiska, »kraschiga») att navigera i [CitatPasco]. Därav noteringen.

— Se även vidare i AdiabatMAC, VRF, ATFT, VLAFS, om ej redan bekant.

Jordatmosfärens massvolym (V, inom troposfären) är konstant. Den är tydligen hydrostatiskt grundad genom Jordgravitationen [HydroTrycket] på ett ytterst stabilt, ytterst långsamt föränderligt etablerat fast medelglobalt skiktsystem tillsammans med Jordrotationen och Solvärmen. På allmänna gaslagens form kan den egenskapen skrivas V[=kT/p]=konstant. Varje atmosfäriskt skikt har REDAN en fast medelbaserad luftmassvolym [Slutgraferna]. Varje försök att ändra den statusen resulterar i en motsvarande strävan — reaktion — att återställa balansen.

Konvektionen, MOTEF, JAVK

Den fasta tillståndsgrunden med molnbildningens kretslopp eller KONVEKTIONEN i vår närmaste Jordatmosfär — klimatsfären eller troposfären — kan följaktligen förklaras med hjälp av ÄNDRINGSLAGARNA: aktion, reaktion och energi som underhåller flödet. Se utförligt i JAVK.

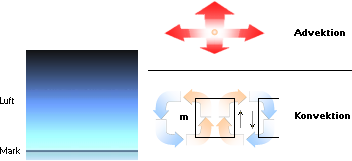
Illustrationen ovan höger ger en syntes av den cirkulerande eller konvekterande luften:

— Varm markluft stiger uppåt, lämnar ifrån sig sitt innehåll av vattenånga för molnbildning, och återvänder till marken igen för ytterligare uppvärmning och transport av vattenånga.

MOTEF, experimentella grunder — Inledning

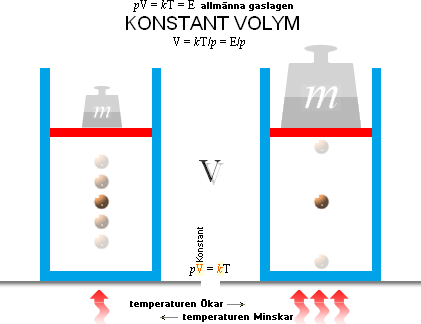
· FlaskExperimentet visar oss hur luftens massvolym (V), inom ett specifikt atmosfäriskt skikt, fungerar under den variabla temperaturens (T) inverkan — p/k=konstant=T/V;
varm markluft som — oberoende av atmosfäriskt skikt — exponeras för värmeläckning, dvs. avsvalning, genomgår volymminskning;

· JAVKbasic-experimentet fullständigar Flaskexperimentet med ett grovvärde för den fuktiga uppvärmda luftens naturliga avsvalningstakt, grovt 122°C/M/S;

· FlaskExpeditionen visar oss hur en innesluten lufts massvolym (V), i transport mellan olika specifika atmosfäriska skikt, fungerar under tryckets (p) inverkan — pV=energikonstant=kT;
isolerad markluft som exponeras för högre atmosfäriska skikt, genomgår volymökning;
— Men det förefaller vara en dålig analogi till den fria luftens konvektion där ingen avgränsning, här veterligt, finns utan istället en sammanhängande (komplicerad) vertikalpelare som genomtränger olika höjdskikt.
— Vi känner dock (här) inte till något annat samband med vars hjälp atmosfäriska tryckets avtagande med växande altitud (höjd över marken) ger motsvarande volymökande verkan — Se utförligt vidare i HydroTransiteringen. Formen för den moderna akademins ”adiabatiska gaslagen” (Poissons Ekvation), här MEKANISKA gaslagen, ansluter heller inte, se utförligt från EGoG och speciellt Exempel 2.

Figuren ovan (höger, klicka på bilden ovan för större) visar dessa detaljer i syntes med motsvarande nedanstående figurförklaring.

— Vi KANSKE skulle tro (Flaskexperimentet) att volymminskningen, associerad med temperaturminskningen i en markuppvärmd uppåtstigande luftbula eller luftpelare, skulle uppväga den förmodade volymökningen (Flaskexpeditionen) då luftbulan exponeras för de högre liggande atmosfäriska skiktens lägre hydrostatiska tryck (p). Så är emellertid INTE fallet [Slutgraferna]: tryckminskningen med växande höjd — pV=energikonstant=kT — och därmed volymökningen, avtar betydligt snabbare [Tabell hkT] än temperaturminskningen med växande höjd och dess masslufts åtföljande volymminskning (Flaskexperimentet) — p/k=konstant=T/V.

— Men det finns en (helt) annan aspekt i sammanhanget, svår att finna referenser för i nuvarande gratis webbutbud (Apr2014) och som delvis ändrar ovanstående »sämre odds» för Flaskexperimentets volymminskning.

— Nämligen, figuren nedan och föregående ovan med den centrala KONVEKTIONEN: aspekten med det rundgående omloppsslutna gasflödet i naturluften:

Värmeläckningen, VLbasic, kT-energin, MOTEF

Jordatmosfärens volymkonstant JAVK V[=kT/p=konstant] spärrar för fri massvolymexpansion [pV=kT=konstant] i de övre skikten och på samma sätt i de lägre skikten för massvolymunderskott. Massvolymöverskottet i de volymexpanderande övre skikten kan då förstås tvingas att återvända till markdelen via ett slutet flöde mark-luft-mark: en konvektion har etablerats. Konvektionen underhålls så länge Solvärmen påtvingar markluften kontinuerlig uppvärmning, och därmed inträde i högre skikt med lägre temperatur.

— Så länge någon överskottstemperatur finns kvar från den uppåtstigande markluften i en högre region, gäller den regionens specifika tryck (p) och fundamentala gaskonstant [k/(V=1M³)=p/T] på markrestluften, och därmed explicit för dennas motsvarande p/k=T/V, precis som i FlaskExperimentet.

— Differensen [Tabell hkT] i energikonstanterna [kT] mellan de olika skikten då den Soluppvärmda markluften stiger uppåt, ingår uppenbarligen integrerat i värmeflödet tillsammans med den naturliga VÄRMELÄCKNINGEN (Planckstrålningen).

EXPANSIONEN — pV=energikonstant=kT — som det markuppvärmda paketet upplever vid besök i de högre atmosfäriska, svalare, skikten är inte tillåten enligt JordHydrotryckets fasta atmosfäriska skiktsystems konstanta volym V[=kT/p]=konstant [JAVK]:

Vi söker också den meningen, eller en förklaring till varför den inte skulle gälla, i den omfattande etablerade litteraturen i ämnet. Men ännu (Apr2014) har ingen klargörande mening påträffats.

— Expansionen — Flaskepeditionen pV=energikonstant=kT — försöker ändra på systemet [JAVK] genom att försöka pressa in mera massvolym — den gästande markluften — än vad systemet är konstruerat för, och vilket inte går (Ändringslagarna). Samma princip »proklameras» av markskiktet: markskiktets specifika tillstånd håller i motsvarande grad på att förlora massvolym.

— REAKTIONEN på den Soluppvärmda uppåtstigande markluften SKULLE ALLTSÅ bli att ansatsen till massöverskott längre upp och ansatsen till massunderskott längre ner kopplar ett harmoniskt, balansåterställande, flödessystem, en KONVEKTION, som återställer ordningen.

— Samtidigt har den återvändande luften — i princip — lämnat ifrån sig sitt innehåll av vattenånga i någon nybildad molnbas, eller adderat mera till någon redan befintlig molnbas, och kan därmed återvända till marken igen för nytt transportuppdrag.

Se även i FETF för vidare.

HydroTransiten — från Inledningen

HYDROTRANSITERINGENS HJÄLPSAMBAND —

pV=energikonstant=kT

Om det etablerade Adiabatbegreppets korrumperade ställning i naturbeskrivningen

——————————————————————————————————

Se även omnämnande i förbigående i Förtydligande till allmänna gaslagen i Entropibegreppet

Luftändring med höjden (altituden) terminologiseras ofta i etablerade led som en s.k. ”adiabatisk tillståndsändringsprocess” [CentralAdia].

Efter genomgångarna i relaterad mening [VRF | EKoG | ATFT] måste den ordningen för atmosfärens del tydligen förstås som en hydrostatiskt betingad transiteringsprocess [HydroTransit]: hydrostatiskt betingad överföringsprocess mellan fasta värmegränsläckningsnivåer — på bekostnad av den Solenergiunderhållande luftkonvekterande processens värmeläckning [‡] — mellan olika atmosfäriska skikt;

Luften kan förstås DRAS eller DRIVAS konvekterande av Solenergin mellan fixt hydrostatiskt givna atmosfäriska skikt [MOTEF] med explicit individuellt specifika globalt medelbaserade INBÖRDES VARIERANDE pρkT-värden [Slutgraferna] [StandardAtmosphereData].

EV, EtableradVerifiering

Vi söker också den meningen, eller en förklaring till varför den inte skulle gälla, i den omfattande etablerade litteraturen i ämnet. Men ännu (Apr2014) har ingen klargörande mening påträffats.

pρkT-värdena kan beskrivas med olika IDEALISERADE hjälpsamband [‡] som alla mer eller mindre ansluter DIREKT till allmänna gaslagen, tillsammans med grundformen för hydrostatiska trycket.

Sambandsformen pV=energikonstant=kT [MOTEF] kan användas som ett provisorium för det experimentella påvisandet av hur en innesluten luftmängd beter sig, av princip, vid olika markhöjder [Flaskexpeditionen]. Den som är obefaren i termodynamikens begrepp kan med den enkla uppvisningen få den uppfattningen att sambandsformen — enligt etablerad nomenklatur — skulle sammanhänga med eller associera till den ofta i sådana Jordatmosfäriska sammanhang etablerat använda frasen ”adiabatisk process” [CentralAdia | AdiabaticRef] eller ”adiabatisk tillståndsändring” [FMadia].

Så är inte fallet. Sambandsformen beskriver en isoterm.

— Sambandsformen pV=energikonstant=kT [MOTEF] [Se även Allmänna Gaslagens Konstanter, AGKE och AGKK], även i etablerad nomenklatur, beskriver, associerar till och tillhör entydigt en isotermisk funktion: konstant temperatur (tillsammans med konstant fundamental gaskonstant k).

Anledningen varför den — egentligen helt oegentliga och för varierande altituder icke-användbara — fasta och fixa nivåatmosfäriska isotermen pV=kT »ändå fungerar» i Flaskexpeditionen ser vi konkret i utdraget till Tabell hkT: Medan temperaturminskningen mark-expeditionshöjd (4.300M) visar 90% behållning, visar motsvarande tryckreduktion 58% behållning: temperaturreduktionen är betydligt långsammare än tryckreduktionen, och den sistnämnda överväger därför och gör temperaturreduktionen ”redundant” (överflödig) — i princip samma som: »sambandet kan användas provisoriskt för altitudexperiment» efter som temperaturdelens reduktion i vilket fall kan bortses ifrån i förhållande till tryckändringen. Isotermen pV=kT är en hjälpfunktion.

Isotermen pV=energikonstant=kT figurerar, används och »pV-utnyttjas» (således) också generellt i den etablerade beskrivningen i samband med Jordatmosfären och dess luftcirkulation. MEN observera att den etablerade sammanhangsbeskrivningen i den användningen också (oftast) använder den etablerade frasen ”adiabatiska ändringar i temperatur” i samband med hela ämneskomplexet — och därmed en betydande komplikation i fattningen på ämnet generellt, sett enbart med de etablerade greppens hjälp:

@INTERNET Wikipedia Adiabatic process, Adiabatic heating and cooling [2014-04-25]

http://en.wikipedia.org/wiki/Adiabatic_process

”Adiabatic changes in temperature occur due to changes in pressure of a gas while not adding or subtracting any heat. In contrast, free expansion is an isothermal process for an ideal gas.”,

”Such temperature changes can be quantified using the ideal gas law, or the hydrostatic equation for atmospheric processes.”.

Termen ”free expansion” ansluter här till isotermen pV=kT i Allmänna Gaslagens Konstanter [AGKE]. Men termen ”adiabatic changes” besitter i relaterad mening ingen konsistent innebörd:

· ”Adiabatic changes in temperature occur . . . while not adding or subtracting any heat” verkar inte besitta någon annan saklig koppling till ämnet i etablerade korridorer — det faktum att termen ”adiabatic” alls används i etablerad beskrivning — än just (det berömda”) ”DåQärNoll” [CitatMACadia] i ”Termodynamikens första huvudsats”;

· I relaterad termofysik [VRF] existerar ingenting sådant som en ”avstängning” eller nollflöde av tillförd värmemängd (Q) [VLAFS]: Q=0 finns inte i naturboken; alla fysikens kroppar värmeläcker [HeatBasic]. Att alls, över huvud taget, använda eller bruka en fysikbeskrivning — utan klart och tydligt deklarerade meningar som förtydligar den inskränkta beskrivningsformen — som talar om ”processer där varken värme tillförs eller bortförs” [BKLadia] BLIR — resulterar — bara i en djupt vilseledande, missvisande, och uppenbart relaterbarligen direkt felaktig fysikbeskrivning; All tillståndsförändring bygger på arbete, och allt arbete sammanhänger med värmeöverföring [ÄNDRINGSLAGARNA | KONVEKTIONEN | VLAFS].

”Adiabatic changes in temperature” anspelar just på området [CentralAdia]

Volymändring som medför Temperaturändring — icke-isotermiska volymändringar [noAdia] —

med den etablerade ”sambandsformen DåQärNoll” som grund för termen ”adiabatic” (”Q=0”),

”expansion causes the parcel of air to cool”;

”Compression causes the temperature within the parcel to increase”

[CitatAdiaRef]

och det TROTS att volymändringens beskrivande grundfysik INTE uppvisar någon SÅDAN favoriserande bild [noAdia] för just icke-isotermiska volymändringar — de som sammanhänger med just temperaturändringar.

Ty:

— Också ett annat alternativ finns [AGKE], det isotermiska alternativet:

— Det isotermiska alternativet [AGKE] innefattar INTE temperaturändring VID volymändring — och som (i trängre mening — cylindriska inneslutningar) ansluter till Wikipediacitatets term ”free expansion”.

— Det isotermiska alternativet [AGKE] framhävs tydligen INTE — det göms istället undan — i den så tydligt FAVORISERADE etablerade beskrivningens förkärlek för ”temperaturändring med volymändring” i Jordatmosfäriska luftcirkulationens sammanhang, och det därmed associerade ”Termodynamikens första huvudsats”:s ”DåQärNoll”-Adiabat-tivoli.

MACadiaRef

Wikipediaartikeln på Isothermal process säger uttryckligen att

MODERN AKADEMI

————————————

isoterm ΔT = 0 ; Gäller även i relaterad fysik, se isotermiska volymändringar:

Q ≠ 0 ; Gäller även i relaterad fysik, se PåEnergin

————————————

adiabat ΔT ≠ 0 ; Adiabatbegreppet innefattar djupa oklarheter. Se från TILLÄMPNINGSEXEMPEL.

Q = 0 ; Förekommer inte i relaterad fysik. Se från ”då Q=0”.

————————————

För isotermen pV=kT i Flaskexpeditionens resultatfysik betyder det INOM MODERN AKADEMI uppenbarligen en KORRUPTION och ett PULSERANDE GODTYCKE mellan ”isoterm” och ”adiabat”: isotermen pV=kT [AGKK] [AGKE] används för att framhäva ”adiabaten” pV≠kT i alla beskrivande sammanhang med ”volymändring förorsakar temperaturändring” som figurerar mellan de olika Jordtroposfäriska skikten [AdiabaticRef].

Vi kan uppenbarligen inte, meningsfullt, använda en sådan referenskälla till någon meningsfull fysikbeskrivning [VRFsf].

— Saken förvärras ytterligare genom att det i relaterad värmefysik [VRF] inte finns något ”Q=0”. Tar vi, således, bort den delen från ovanstående moderna akademis gruppering, försvinner samtidigt HELA den etablerade användningen, beskrivningen och bruket av begreppet ”adiabatisk” EFTERSOM begreppet ”adiabatisk” JUST grundas på den matematiska behandlingsdelen i

”Termodynamikens första huvudsats”’s ”DåQärNoll” [FMadia]:

”while not adding or subtracting any heat”.

— ThankYouVeryMuch.

I andra ord:

— Vi kan inte, meningsfullt, tillskriva bruket av termen eller begreppet ”adiabatisk” någon som helst entydig, begripbar, rationell, logisk innebörd i fysikbeskrivningen. De entydigt beskrivande termerna är i sammanhanget isotermisk (volymändring) [AGKE], icke-isotermisk (volymändring), och dessa har ingen koppling till begreppet ”adiabatisk: som inte innefattar värmeöverföring [Q=0]”.

— I den motsvarande ”adiabatiska gaslagen” [i relaterad fysik, ENERGIKOMPLEXA GASLAGEN eller MEKANISKA gaslagen, exakt samma matematik] antar de värmekapacitiva ekvivalenterna allmänna gaslagens k-form pV=kT [pVT alla variabler], se särskilt jämförande RÄKNEEXEMPEL 1, samt inbegripet att inte heller ”adiabatiska gaslagen” kopplar Jordatmosfärens hydrostatik, RÄKNEEXEMPEL 2.

— Adiabattermen och adiabatbegreppet i etablerade led framstår alldeles tydligt med denna genomgång som, och om ingen annan beskrivande förklarande bild finns [EV], en högst korrumperad term och begrepp; Den korrupta delen grundas främst just på

”Termodynamikens första huvudsats”:s ”DåQärNoll”

och som sedan i här ej närmare klarlagd etablerad favorisering av

icke-isotermiska volymändringsprocesser [noAdia] framför isotermiska dito [AGKE]

framställer begreppet ADIABATISKA TILLSTÅNDSÄNDRINGAR [FMadia] i påståenden

att, som i citatutdraget ovan [AdiaRef],

stigande varmluft tappar temperatur på grund av volymexpansion [CentralAdia], och

sjunkande toppluft får ökad temperatur på grund av volymkompression.

— Det ser ut att vara hela sammansattheten i den etablerade formalian, och som här veterligt, ingen varken novis eller befaren förmår klargöra eller begripliggöra för en vanlig icke insatt människa — med användning av den etablerade nomenklaturen enbart.

— Jämför också »citatkaoset» närmast nedan i Bilmotorn. Här undviks därför HELT OCH HÅLLET termen och begreppet ”adiabatisk”. Vi använder och refererar här istället de VÄL relaterbara och härledbara sambandsformerna och deras innebörder i beskrivningssättet: isoterm resp. icke-isoterm, samt generellt värmerelaterad fysik [VRF | HeatBasic | ENERGIKOMPLEXA GASLAGEN | AllmännaGaslagen].

Bilmotorn

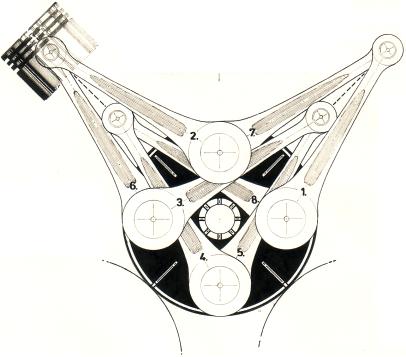
4-taktsotto · V8-motor · principer 1981 · Författarens arkiv

I MODERN AKADEMI menar man att begreppet adiabatisk sammanhänger med MEKANISK IHOPTRYCKNING — adiabatisk uppvärmning — och MEKANISK UTDRAGNING — adiabatisk kylning — av luftmassor i slutna behållare:

”Adiabatisk uppvärmning och kylning inträffar då trycket för en gas ändras.”, sv. Wikipedia, Adiabatisk process [2014-04-09].

— Samtidigt påstår man att

”Adiabatisk process (av grekiskans adiabatos, sluten, ogenomtränglig) är en termodynamisk process där ingen värme tillförs eller bortförs från en fluid.”, sv. Wikipedia, Adiabatisk process [2014-04-09]; fluid f.ö. lika med vätska eller gas.

— Adiabatisk — som inte innefattar ändring i temperatur — blir med dessa få exempel en omöjlig term — både INGEN och värme. Termen FÖREFALLER vara föremål för allmänt godtycke [»får endast användas av speciellt certifierade personer»], utan urskillning: Ingen vettig, konsistent, begripbar definition verkar finnas [»du måste använda ett efterhärmningsprotokoll»].

:

En kolv som IFALL DEN pressar ihop luften i en cylinder UTAN att tillföra luftvolymen någon nämnvärd temperaturändring [AGKE], kallas PÅ VISST SÄTT adiabatisk tillståndsändring — som INTE innefattar ändring i temperatur: trycket har ökat och volymen minskat utan att värme tillförts.

Men:

En kolv i en dieselmotor som (snabbt) pressar ihop luften i en cylinder [NoAdia] anses DÄREMOT tillföra luftvolymen VÄSENTLIG temperaturändring som får dieselbränslet att antändas, och kallas därmed OCKSÅ adiabatisk tillståndsändring — som innefattar ändring i temperatur:

”Dieselmotorer bygger på adiabatisk uppvärmning under kompressionsdelen av cykeln för att värma upp bränslet tillräckligt för att det skall kunna antändas.”, sv. Wikipedia, Adiabatisk process [2014-04-09].

— Vi kan inte anlita en sådan källa för att få fram begriplig konsistent rationell information:

Jämför FOCUS MATERIEN 1975 — fullt kaos råder:

”Adiabatiska tillståndsändringar är av särskilt intresse eftersom snabba tryck- och volymändringar är nära adiabatiska. Vid snabba ändringar hinner nämligen inget nämnvärt värmeutbyte ske mellan systemet och dess omgivning.”, [FMs322sp1m].

Jämför återigen kolven i bilmotorn ovan och de inbördes rakt motsatta påståendeformerna: ”den snabba kompressionen värmer”; ”den snabba kompression värmer inte”; bägge ”adiabatisk”.

— Vi kan inte anlita en sådan källa för att få fram begriplig konsistent rationell information:

Ytterligare exempel i AdiabaticCitat.

— Sambandsformen pV=energikonstant=kT är alltså med andra ord en HJÄLPFORM — ingen reguljär förklaringsform — till hur att förstå principen bakom det aktuella expeditionsresultatet, se FlaskExpeditionen. Jämför motsvarande etablerade beskrivningar som också intygar att adiabatformen (pV=konstant) är en förenkling:

Boston University — PDF-dokument

CHAPTER 5 – WATER IN THE ATMOSPHERE, Bruce T. Anderson, datumuppgift saknas

”Now we want to examine what

might cause air parcels to move; here we want to consider first just the movement of air parcels

in the vertical direction. To determine source of this movement, we have to determine how the

properties of an air parcel in motion change as the parcel is displaced from its original location.

A key assumption for this process is that there is no heat added or lost from the parcel during its

movement. This implies the parcel has to be displaced fast relative to heat conduction. The

assumption itself is called the Adiabatic assumption. It turns out that for many atmospheric

processes, the adiabatic assumption is fairly good. This assumption holds for two main reasons.

First, air is a poor conductor of heat so that, for an air parcel of reasonable size (larger than a

building), heating or cooling at the edges does not affect the internal properties of the parcel.

Second, many motions in the atmosphere occur relatively quickly - during convection, air parcels

rise and sink over the course of 20 minutes. Horizontally, air aloft flows at about 20-50m/s. As

such, an air parcel does not get much time to interact with changing conditions around it, again

precluding any heating or cooling from the surrounding environment.”.

Notera här citatkällans ”air is a poor conductor of heat”: Flaskexperimentets responstid på 20 sekunder MED PLASTMATERIALETS ISOLERANDE FUNKTION med JAVKbasic-experimentets kompletterande upplysning 122°C/M/S i den uppvärmda fuktiga luftens avsvalningstakt för att få se en märkbar volymminskning [15%] som följd av värmeläckning — är INTE direkt någon BRA indikator på STORT värmeLÄCKningsMOTSTÅND: uppvärmd [fuktig] luft SVALNAR — anpassar sig — [tydligen MYCKET] snabbt till omgivande värdluft.

— Påståendet i citatet att ”heating or cooling at the edges does not affect the internal properties” saknar referenser [i citatkällan]: Flaskexperimentet med stöd av JAVKbasic visar snarare, eller antyder i dess miniform, att luft inte alls får förstås analogt med ett fast materials STARKT INRE värmekonserverande egenskap [Flaskexperimentet MED en liten mängd ångvärmande vatten i flaskans botten och UTAN sådan skiljer i responstid för den observerbara volymändringen på ca 9ggr: över 3 minuter mot 20 sekunder, respektive]: ljushastigheten i luft avviker försumbart från ljushastighet i vakuum. Därmed får VÄRMELÄCKNINGEN i ett sådant glest partikelbefolkat medium som luft förstås starkt betingat av Planckstrålningens snabba [UT-]verkan: Gaspartiklarnas kollisionsförluster som medför temperatursänkning då ingen påfyllande Planckenergi E=hf finns närvarande att hålla temperaturen uppe på, kommer uppenbarligen HELT att styra avsvalningsprocessen. Det är här inte närmare känt varifrån, eller på bas av vilka observationer citatmeningen ska förstås relevant, och heller ingen annan [gratis tillgänglig webbkälla] verkar kunna fylla ut frågan med besvarande argument, och »Planckstrålningsargumentet» FÖREFALLER därför på visst sätt underminera citatmeningens åsyftning; »I själva verket sker luftavsvalningen inuti ett STORT luftpaket relativt snabbt» [EV]. Optiska mätningar på helt fri uppvärmd luft skulle kunna avgöra frågan; I väntan på att sådana kan hittas på webben intar tydligen det enkla köksexperimentets JAVKbasic-resultat en direkt experimentell referens som helt verkar utplåna ovanstående citatmenings hållning. ”Avsvalningshastighet för/hos luft” ger f.ö. noll på webbsökning [Apr2014].

@INTERNET Wikipedia Adiabatic process, Adiabatic heating and cooling [2014-04-09]

http://en.wikipedia.org/wiki/Adiabatic_process

”In practice, no process is truly adiabatic. Many processes rely on a large difference in time scales of the process of interest and the rate of heat dissipation across a system boundary, and thus are approximated by using an adiabatic assumption. There is always some heat loss, as no perfect insulators exist.”

— Det är f.ö. exceptionellt glädjande att få se den meningen från en etablerad källa: ”no perfect insulators exist”. Jämför ”DåQärNoll”. Exakt relaterad fysik.

Se även i LuftKonveNtionen, [NLA].

Möjligt att det finns, verkligen, mera upplysande (gratis tillgänglig) litteratur på webben (baserat på forskning) som kan göra rent hus med dessa (svåra, men avgörande) detaljer. Dock inget ännu upphittat. Eftersökning fortsätter.

ÄVEN om man räknar med att en uppåtstigande luftpelarens CENTRUM bibehåller sin T-form till något högre atmosfäriskt skikt, på grund av att centralen skyddas av omgivande delar som successivt matas av under uppstigningen — vårt idealt konstanta T i pV=kT — hamnar vi i den slutänden INTE i sambandsformen för flaskexpeditionens resultat utan snarare i sambandsformen för flaskexperimentet:

En kvarvarande (aktuella luftcentrumpelarens ev. rest) högre T-form i ett omgivande fast p-rum med sitt lägre t-värde visar att: Som T i restluften avtar (genom värmeläckning; WhyNotAdia, VLAFS, ATFT) MINSKAR restvolymen [‡]. Inte ökar: pV=kT. Det betyder »TRUBBEL I TEORIN» om man ENSIDIGT försöker hävda hjälpformens pV=kT status i hela komplexet.

Varför alltså Hjälpsambandet kan användas (pV) — och varför det inte ansluter (kT)

Eftersom temperaturen (T) i de atmosfäriska referensskikten avtar betydligt långsammare

[0,0065°C/M] än trycket (p), jämför Tabell hkT, har det SÅLEDES ingen betydelse för själva det experimentella påvisandet i den aktuella Flaskexpeditionen att T-värdet varierar vid nedstigningen (och därmed ORIKTIGT ansluter till hjälpsambandets form), nettoresultatet blir i vilket fall att en ursprungligt innesluten luftmassvolym avtar med avtagande höjd på kredit av att trycket ökar:

— Arbetskraften som bär den inneslutna volymen neråt marken (personen som bär utrustningen) ser till att den inneslutna flaskluftens gasbollar möter en tuffare yttre omgivning som tvingar flaskbollarna att samsas på allt mindre gasutrymme — gasbollarna påtvingas högre rörelseenergi på det nedbärande arbetets kredit — då flaskväggarna trycks ihop av det växande marktrycket, temperaturanpassningen till markdelen frånsett.

Svårigheten att anställa samma beskrivning för fri, kallare luft som via konvektion återvänder till den varmare marken från högre svalare delar är uppenbar därmed att ingen tvingande inneslutning existerar som tvingar luften att följa med. Det är, tydligen, bara den naturliga Solenergibaserade atmosfäriska konvektionskraften som kan styra den rörelsen, och den kräver en markkoppling som uppvisar ett visst (konvekterande) undertryck (luftmassunderskott från föregående uppstigande uppvärmda markluft) [JAVK]. I annat fall finns inget utrymme att inhysa den nedströmmande luften:

— »Den nedströmmande luften pressas (komprimeras) inte in i markdelen, den DRAS eller DRIVS (värmekonvekterar) in», [EV].

— Önskvärt att få se motsvarande beskrivning — eller orsaksförklaring som säger annat — i någon etablerad korridor. Ännu (Apr2014) inget upphittat.

EKoG, ENERGIKOMPLEXA GASLAGEN, VRF — Sambandets form — »AdiaTransformen», RelateratAdia — VTE, Värmekapacitiva Tillstånds Ekvivalenterna — relaterad fysik:

2014IV22

ENERGIKOMPLEXA GASLAGEN — i relaterad fysik

FRIHETSgradsGASLAGEN eller MEKANISKA GASLAGEN

——————————————————————————

konv. ”Adiabatiska gaslagen” eller Poissons ekvation|lag [‡]

Frihetsgradsekvivalenter som kopplar inbördes ändringar i pVT på konstant (k) värmekapacitet

EXTERNT MEKANISKT TILLSTÅNDSÄNDRANDE VOLYMÄNDRINGsARBETE via en entydigt arbetande mekanisk konstruktion med en cylindriskt innesluten gas

— som i volymändringens kraft påtvingas ändring i samtliga gasparametrar pVT med bevarad värmekapacitet (k) enligt

(pV/T)₀ = k = (pV/T)₁ : tillståndsekvivalenter på konstant värmekapacitet k

ALLMÄNNA GASLAGENS EKVIVALENTER FÖR FrihetsGradsGaslagen

FG, Gasbollar med olika frihetsgrader

ALLMÄNNA GASLAGEN [AGG-illustrationer] [AG-sambanden] har ingen direkt form för att uttrycka gasbollarnas s.k. frihetsgrader (här o):

— Beroende på hur gasbollarna är sammansatta — figuren ovan: enahanda atomer, eller molekyler med flera förenade atomer — finns olika fack för värme — tillförd PÅ-energi [VRF] — att leta sig in i, i gasbollens egenrum. Nämligen med möjligheten att lagra sig som rotationsenergi.

— Det betyder främst i temperatursammanhanget för allmänna gaslagens del, att

värme kan tillföras en gas utan att någon direkt temperaturhöjning iakttas

Nämligen att den värmematande och temperaturuppehållande strålbaserade Planckstrålningen E=hf till viss del och i en viss begränsad mening kommer att »gömma sig» i gasbollen i form av just rotationsenergi, och som sedan kan återvinnas i andra sammanhang.

— Eftersom — således — ingen direkt enhetlig form finns för kvantitetsbegreppet »energi» i samtliga möjliga fall med hänsyn till alla möjliga olika gasbollars sammansättning, kan vi heller INTE i en härledande ordning för ett SÅDANT sammanhang använda någon ENTYDIG ekvivalent energiassocierad koefficientform typ ”2=2” eller ”a=a” som utgångspunkt.

— I matematiken finns emellertid (redan) en utmärkt hjälpreda reserverad (för just sådana komplicerade sammanhang): metodidentifieraren eller mera konventionellt uttryckt den komplexa enheten i [Utförligt i DEN KOMPLEXA ALGEBRAN]

iRot

ROTATIONEN för i nämligen — y-enheten y=r=1 roterad +90° till negativa x-axeln — som ger ekvivalenta sambandsformen

i² = – 1 ;

Komplexa enhetens kvadrat — en första ordningens kvadrantrotation — transformerar gasbollarnas olika varierande frihetsgrader i bestämningen av gasens ekvivalenta tillståndsenergi:

kan — uppenbarligen, galant dessutom — användas som transformerande faktor för just gasbollarnas allmänna frihetsgrad:

o = i² = – 1 ;

–1 = o ; Frihetsgradens allmänna arbetstransform för allmänna gaslagens samband:

NOTERA att Wikipediaartikeln [Adiabatic process, Derivation] för sin del

INTE relaterar »den triviala sammansättningen» [här längre ner]

”–γpV = pV” till differentialformen ”–γp·dV = dp·V”:

Den godtyckliga [»KOMBINATORISKA»] differentieringen i Wikiartikeln, ”p·dV + V·dp” — och som således INTE klargör ekvivalenterna ”–γpV = pV” — GÖMMER därmed också BORT trivialformen ”–γpV = pV” — som uppenbarligen är den reala matematiska härledningsbasen i EKVIVALENTER — och därmed UNDANHÅLLER HÄRLEDNINGEN dess kärna:

”p·dV + V·dp” → ”–γpV = pV” → –γ = 1 → –1= γ: frihetsgradernas KOMPLEXA variabel iRot.

— I andra ord: UTGÅNGSPUNKTEN med ”according to the first law of thermodynamics” är IRRELEVANT [smörja].

— Den har uppenbarligen och relaterbarligen ingenting med saken att göra [‡].

Wikipediaartikeln som givit uppslaget till utvecklingarna här [Adiabatic process, Derivation [2014-04-15]] anger o-faktorn som 3 för enatomiga gaser (typ Argon), 5 för diatomiga (typ Syre, Kväve).

— Därmed finns full frihet för o-faktorn att associera VÄSENTLIGEN OLIKA energivärden för en och samma värmegrad, allt beroende på vilken typ av gas (och rotation) som energin arbetar på.

— o-faktorn kan då användas TILLSAMMANS med det allmänna uttrycket för gasbollens TryckVolymarbete E=pV enligt följande fullständigt relaterbara utvecklingar:

EKoGh, EKoG

–1 = o ;

–pV = opV ; E = pV = konstant:

–2pV = 2opV = opV + opV ;

–opV–2pV = opV = –pV(o+2) ;

opV = –pV(o+2) ;

pV = –pV(o+2)/o ; γ = (o+2)/o ; pdV = –Vdp/γ: Vidare i atmosfäriska värmeläcket.

γ = (o+2)/o ; = Cp/Cv = SpecificHeatPressureConstant/SHVolumeConstant

; För Cp och Cv; Se Wikipedia Specific heat, Thermodynamic relations and definition of heat capacity:

— Se även i CpMinusCv.

pV = –γpV ; Allmän differentiering — förberedande integrering:

dpV = –γdpV ; Optimal differentiering — vi utväljer ALLTID det mest passande på det dukade bordet:

dpV = –γpdV ; Division med pV:

dpV/pV = –γpdV/pV ;

dp/p = –γdV/V ; Efter integration; NOTERA LOG5 att Dn p/p0 = [1/p0][p/p0] = 1/p; ∫ dp/p =[medger p₀=1] p/p₀ :

ln(p/p₀) = – γ · ln(V/V₀) ; Logaritmlagarna:

= ln[(V/V₀)^–γ] ;

TRIVIALT gäller för alla funktionsranger i RELATERAD matematik: 1 = A/B = lnA / lnB = P^A / P^B = sinA / sin B osv.

— Logaritmiseringen lnA = lnB kan då utnyttjas på ekvivalenterna A = B.

— Jämför: e^a = A och e^b=B som ger a=lnA och b=lnB; är nu lnA=lnB gäller tydligen också att a=b och A=B:

Samtidigt blir vi oberoende av integralernas obestämda form (alla ln[x/X] är obestämda) eftersom logaritmrangen har eliminerats:

p/p₀ = (V/V₀)^–γ

= (V₀/V)^γ

= V₀^γ/V^γ ;

pV^γ = p₀V₀^γ = K ; konstant:

För att storheterna ska stämma mellan leden (V^γ → M³) måste en enhetsjustering göras:

— Vi noterar [2014-04-25] att en sådan transformation INTE omnämns eller ens antyds i Wikipediaartikeln:

pV^γ = (K → J/°K) · (1M³)^γ

p · V^γ/(1M³)^γ · 1M³ = K ; J/°K:

p · (V/1M³)^γ · 1M³ = K ; J/°K : Energikomplexa gaslagen, konv. ”adiabatiska gaslagen”

: Vi kan förenkla termformen med fetstil för METODEN V = V/1M³ med tillägg av en faktor 1M³, vilket ger det termenklare

pV^γ = K ; J/°K

”continuous formula for adiabatic heating and cooling”, Wikipedia Adiabatic process [2014-04-15]

”Any work (δW) done must be done at the expense of internal energy U, since no heat δQ is being supplied from the surroundings.”,

@INTERNET Wikipedia Adiabatic process [2014-04-09] — http://en.wikipedia.org/wiki/Adiabatic_process — se även i WikiAdia.

— Ovanstående citerade MAC-formalia således: Med påföljden att man i MAC anser att ”Q=0” eller ”δQ=0”, ”no heat is being supplied from the surroundings” och ”Derivation of continuous formula for adiabatic heating and cooling” sammanhänger med

”–1 = o”.

— Det finns tydligen, uppenbarligen, och relaterbarligen ingen sådan koppling i relaterad mening. Se härledningen från EKoGh, samt NOTERINGEN ovan till Wikipedias ”Derivation” i iRot, samt ANMÄRKNINGEN i VLA, och den klargörande satsbilden i VLAFS.

— Vi ser (här) återigen konkreta, tydligen fullständigt uttömmande väl relaterbara exempel, på hur två helt väsensskilda FÖRESTÄLLNINGSSÄTT (relaterat/primitivt) TNED/MAC använder samma matematiska formalia för tillfället att BESKRIVA likaledes tydligt VÄSENSSKILDA fysiksammanhang:

:

KONVENTIONELLT kallas sambandet pV^γ=K ovan för Poissons lag eller Adiabatiska gaslagen [Citat‡].

Se Wikipedia Adiabatic process, Derivation [2014-04-15].

EKoGT

Eftersom också allmänna gaslagen ger pV=kT=konstant kan vi substituera för att få fram en T-ekvivalent:

p = (1/V^γ)K ;

pV = V(1/V^γ)K

= kT ;

kT = V(1/V^γ)K ;

T = V(1/V^γ)K/k ; V justeras som ovan med V:

TV^γ–1 = K/k ; Ķ »k med cedilla»:

TV^γ–1 = Ķ ; °K/M³

Wikipediaartikeln använder f.ö. samma omvandlingstyp.

EKoGex, EKoGh

RÄKNEEXEMPEL 1:

— Wikipediaartikeln ger ett konkret räkneexempel via sambanden ovan, exakt samma sambandsformer, på vad man kallar ”adiabatic compression”:

en (γ=7/5=1,4)-kompression (kvävgas) i en cylinder från rumstemperatur;

V₀ = 0,001 M³ ;

V₀ = 0,001 = 1 t3 ;

p₀ = 100.000 Pa ;

γ = 7/5 = 1,4 ; Kvävgas:

p₀V₀^γ = K = (1 T5)(1 t3)^7/5 = 6,3096735 ;

V₁ = 0,0001 M³ ; V0 komprimeras 10ggr:

V₁ = 0,0001 = 1 t4;

p₁ = K/V₁^γ = [(1 T5)(1 t3)^7/5]/(1 t4)^7/5 = (1 T5)[(1 t3)/(1 t4)]^7/5

= 2.511.886,4 Pa = 25,118864 p₀ ;

Allmänna gaslagens Temperaturekvivalent:

T₀ = 300 °K = 26,85 °C ;

T₀V₀^γ–1 = Ķ = (300)(1 t3)^0,4 = 18,92872 ;

T₁ = Ķ/V₁^γ–1 = [(300)(1 t3)^0,4]/(1 t4)^0,4 = 753,56592 °K = 480,41592 °C ;

Allmänna gaslagen: KONTROLLRÄKNING AV RESULTATET [ingår inte i Wikipediaartikeln]:

(pV/T)₀ = k = (pV/T)₁ = (1 T5)(1 t3)/(300) = 1/3 J/KG°K = (2,5118864 T6)(1 t4)/(753,56592) ;

Värmekapacitiva [k] ekvivalenter till Allmänna gaslagen.

Däremot ser vi att pV=E-energierna INTE är lika stora före och efter:

(pV)₀ = (1 T5)(1 t3)

= 100 J ;

(pV)₁ = (~2,5 T5)(1 t4)

= 250 J ;

GasEkvivalenterna är värmekapacitiva — inte energiekvivalenter, inte värmeekvivalenter.

— VÄRME [150 J] HAR TILLFÖRTS GASEN under kompressionen.

:

De härledda sambandsformerna pV^γ=K och TV^γ–1=Ķ [Ķ »k-cedilla» (’KÅS’)] uttrycker tydligen VÄRMEKAPACITIVA EKVIVALENTER k (J/°K) genom ALLMÄNNA GASLAGENS pVT-variabler FÖR GASMOLEKYLER MED BESTÄMDA FRIHETSGRADER i cylindriska inneslutningar (»MEKANISKA gaslagen») och som kan sammanställas på allmänna gaslagens enkla energiformer (pV=kT=E) enligt

(pV/T)₀ = k = (pV/T)₁

Inget annat. Frihetsgradens faktor (gamma) γ = (o+2)/o = 1+2/o kan inte bli 1 — allmänna gaslagens idealt rena elementära form — på annat sätt än att frihetsgraden (o) går mot oändligt. Därmed kan heller inte allmänna gaslagen framställas i någon direkt motsvarande mening på den volymära exponentens samband. Jämför allmänna gaslagens motsvarande resultat: Väl får vi utgångsgruppens k=1/3 via (T5)(t3)/(300). Men beräkningen av p1 från V1=t4 via pV=(T5)(t3)=100 och som ger T6 motsvarar inte γ-gasens värden (2,5 T6) utan istället den fiktiva »oändliga frihetsgradsgasen» och dess »absolut lägsta» gasvärden. Emellertid gäller, som vi ser, likväl EKVIVALENS mellan alla erhållna faktorvärden sammantaget via fundamentala gaskonstanten (k) och dess värmekapacitet (J/°K).

EKoGex2, EKoGex1

RÄKNEEXEMPEL 2:

— Vi studerar en egentligen OTILLÅTEN HYDROSTATISK parallell — Jordatmosfärens olika höjdskikt inom troposfären — till (pV/T)₀ = k = (pV/T)₁ genom att anställa jämförelse på en bestämd utgångsvolym 1M³ vid marknivån. För exakt koll på värdeformerna till jämförelse använder vi här [PDAS] standardiserade internationella tabellvärden från Tabell hkT.

— Vi utgår från marknivåns

p₀ = 101.300 Pa och avancerar sedan till h=4.300M-nivåns lägre tryck

p₁ = 58.462 Pa. Vi antar marknivåns tabellvärde T₀=288,15 °K och får:

V₀ = 1 M³ ;

V₀ = 1 = 1 ;

p₀ = 101.300 Pa ;

γ = 7/5 = 1,4 ; Kvävgas:

p₀V₀^γ = K = (101.300)(1)^7/5 = 101.300 = p₁V₁^γ ;

p₁ = 58.462 Pa ;

V₁^γ = K/p₁ = (101.300)/(58.462) = 1,7327494 ;

V₁ = 1,4808994 ;

Allmänna gaslagens Temperaturekvivalent:

T₀ = 288,15 °K = 15 °C ;

T₀V₀^γ–1 = Ķ = (288,15)(1)^0,4 = 288,15 ;

T₁ = Ķ/V₁^γ–1 = [288,15]/(1,4808994)^0,4 = 246,26824 °K = -26,881756 °C ;

Tabell hkT visar -12,95°C — vilket visar och bevisar att sambandsformen INTE är direkt användbar:

Allmänna gaslagen: KONTROLLRÄKNING AV RESULTATET [ingår inte i Wikipediaartikeln]:

(pV/T)₀ = k₀ = 351,55301 J/KG°K ≠ k₁ = (pV/T)₁ = 353,47459 J/KG°K ;

ICKE-Värmekapacitiva [k] ekvivalenter till Allmänna gaslagen.

pV=E-energierna är heller INTE är lika stora före och efter:

(pV)₀ = (101300)(1)

= 101300 J ;

(pV)₁ = (58462)(1,4808994)

= 86576,34 J ;

GasEkvivalenterna gäller inte, är inte är värmekapacitiva — inte heller energiekvivalenter, inte värmeekvivalenter.

— VÄRME [14723,66 J] HAR BORTFÖRTS FRÅN GASEN under tryckminskningen — värmeläckning.

Exempelformen visar att ”adiabatiska gaslagen” (AG) INTE lämpar sig för jämförande Jordatmosfäriska hydrostatiska analogier.

— Men det visste vi ju redan från början, eftersom hydrostatiken är ett abstrakt begrepp för AG.

— Generellt: Det finns ingen separat, oberoende matematik för att BERÄKNA själva tillståndets ändring mellan två olika Jordatmosfäriska höjdskikt DÄRFÖR att varje skikt har sin specifika fasta fixa hydrostatiskt bestämda fysikprofil [Slutgraferna]: Jordgravitationen (gasmasskvarhållningen, analogt tryckändringen med höjden) tillsammans med Solenergin (markuppvärmningen) och Jordrotationen (”blandaren”) bestämmer den fysiktopografin; den är (globalmedelmässigt) fast och fix. Det är den man måste utgå ifrån och ta hänsyn till. Gaslagarna, som det ser ut, har således EXPLICT »ingenting där att skaffa», grymt sagt.

— SAMBANDSFORMERNA för Jordtroposfärens (internationellt) samlade fysikprofil (Tpρ) finns samlade i Slutgraferna.

GES, GammaExponentens samband

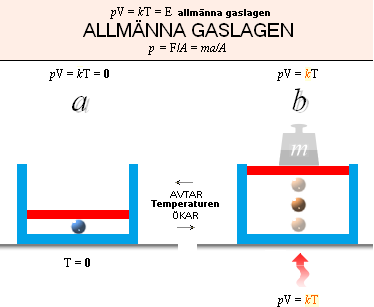
MEKANISKA gaslagen

Energikomplexa gaslagen (Konv. ”Adiabatiska gaslagen”) beskriver relaterat:

Ideal temperaturändring I ABSOLUT TIDSMÄSSIG SAMTIDIGHET MED volymändring och tryckändring:

en absolut faktortransformation, »omstuvning» inbördes mellan pVT-faktorerna,

(pV/T)₀ = k = (pV/T)₁

på en given gas’ frihetsgrad (iRot) och given värmekapacitet (k) [alt. värmekapaciTIVItet, se CpMinusCv]

— tydligen enligt exemplet INTE utan värmeutbyte:

en UPPENBART MASKINSTYRD

tryck- och temperaturomfördelning verkställd genom någon volymändrande anordning

som BEROENDE PÅ KONSTRUKTION KAN styra och reglera gaspartiklarnas rörelseenergier

på den konstruerade anordningen arbete = tillförda värme:

volymändring med absolut gaspartikelkontakt i fast cylindrisk gasinneslutning via separat arbetande rörlig kolv;

PMT

Parametertransformationen (pV/T)₀ = k = (pV/T)₁

— Vad betyder »Energikomplexa gaslagen» i sammanhanget? Den beskriver, uppenbarligen »en MEKANISK gaslag» [‡], samma som i ExpaKomp-figurerna (högra kolumnen), här sammanställt nedan vänster i en gemensam horisontell grupp:

Den korta versionen:

— ENDAST EN SPECIFIKT UTFORMAD MEKANISK KONSTRUKTION kan realisera »temperaturändring med volymändring»:

noAdia

— Det finns ingen obetingad temperaturändring med volymändring [‡]. ATT den typen SKULLE finnas är i ljuset av Allmänna Gaslagens Konstanter [AGK], och såvitt dessa är tillämpliga, tydligen en väl utbredd vanföreställning i etablerade korridorer — relaterbarligen med grund i det etablerade lärosystemets oförmåga att GENOMLYSA ämnets detaljer, om inget här är missat, och KLARGÖRA deras innebörd [”DåQärNoll”]. Skuldnotan står I SÅ FALL alldeles tydligt på den moderna akademins egenhändigt uppfunna fysikens räkning (ämnet är — ofta — OBEGRIPLIGT i etablerad skrift: en »djupturbulens» av akademiskt meriterade underförståddheter som kan döda vilken entusiast som helst); Isotermiska Alternativformen verkar inte ens omnämnas i etablerade verk (gör den det, sker det i så fall osynligt: eftersökt, ej upphittad). MAC uppehåller sig ensidigt vid den »adiabatiska» ”DåQärNoll”-ytterligheten, figurerna nedan vänster — speciellt tydligt i beskrivningarna som rör Jordatmosfärens luftcirkulation [CentralAdiaMAC].

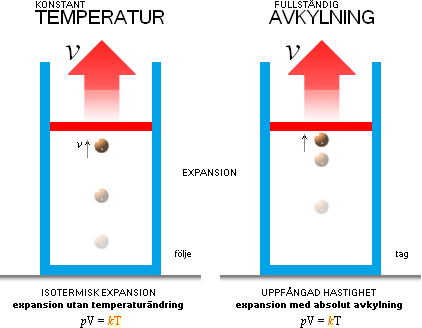
ICKE ISOTERMISK VOLYMÄNDRING, EKoG

ICKE ISOTERMISKA VOLYMÄNDRINGEN, figurerna nedan, är den raka motsatsen till det ISOTERMISKT VOLYMÄNDRANDE ALTERNATIVET [‡]. Icke isotermiska volymändringen åstadkommer en fullständig temperaturändring på det volymändrande arbetets bekostnad, förutsatt absolut mekanisk kontakt mellan anordningens volymändrande toppyta och den inneslutna gasens partiklar, enligt verkningssättets beskrivna villkorliga fysik.

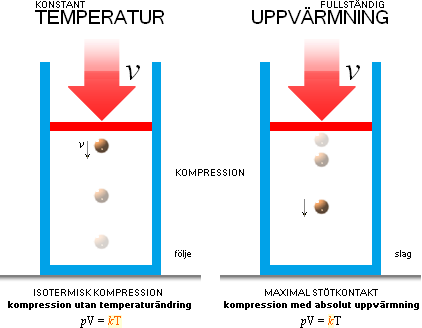
icke isotermisk EXPANSION — KOMPRESSION ——————————————————————— FULLSTÄNDIG temperaturändring pV = kT = E : (konv. ”adiabatisk tillståndsändring”) — Illustrationen till vänster sammanfattar ENA YTTERLIGHETSALTERNATIVET FÖR de MAXIMALT DIAMETRALT SKILDA tillståndssätten vid YTTRE FÖRORSAKAD expansion och kompression: — Gasens inneslutning påtvingas en volymär ändring som, utöver vidstående illustrerade alternativ, också kan yttra sig i en isotermisk (kT=konstant) ytterlighet. Se ExpaKomp för den ytterligheten, inkluderat figurbeskrivningen här till vänster, i mera sammansatt figur. Gasidealiseringen beskrivs i Figurförklaring. Fullständig avkylning (vänster): locket inväntar den annalkande gasbollen, och hämtar upp denna mjukt genom motsvarande mjuka lockacceleration så att gasbollens normala studs REDUCERAS HELT med lockets motsvarande hastighetsökning: — Locket har nu absorberat HELA gasbollens rörelseenergi, och gasbollen följer med i lockrörelsen, vilande relativt detta, ända tills locket börjar avstanna; sker den avstanningen också mjukt på lämpligt sätt, finns ingenting kvar åt gasbollen att avancera på: absolut nolltemperatur har uppnåtts. Dvs, total absolut avkylning. Fullständig uppvärmning (höger): locket inväntar den annalkande gasbollen, och accelererar upp mot denna med maximal sluthastighet precis då gasbollen touchar locket och börjar sin avstanningsprocess före återstudsen. Därmed pressas maximal rörelseenergi in i gasbollens ansvarsrum, och den kan svara med en motsvarande kraftigare studsenergi, analogt högre, tillförd rörelseenergin Ekin=mv^2/2. — Gasbollen har nu absorberat HELA lockets rörelseenergi, och temperaturen kommer därmed HELT att bestämmas av kraften i lockanslaget. Fullständig uppvärmning har uppnåtts.

Den villkorsformen betyder att inte vilken som helst volymändrande anordning automatiskt FÅR associeras med temperaturändring, eftersom NOLL temperaturändring garanteras med det isotermiska alternativet [‡]. Vilket som är vad, och graden av effektivitet, beror uppenbarligen på anordningens FUNKTION, utformning och verkningssätt. En motsvarande klargörande fysikbeskrivning i etablerad litteratur har eftersökts men ännu inte upphittats: man favoriserar, utan klargörande referenser, alternativet ovan vid ALL volymändring i samband med speciellt den Jordatmosfäriska molnbildningens fysik [CitatCentralAdia].

De härledda sambandsformerna med temperaturändring i »energikomplexa gaslagen» [Konv. ”Adiabatiska Gaslagen”] från

volymändring med absolut gaspartikelkontakt i fast cylindrisk gasinneslutning via separat arbetande rörlig kolv

pV^γ = K ; J/°K ; Energikomplexa gaslagen, konv. ”adiabatiska gaslagen”

TV^γ–1 = Ķ ; °K/M³

får alltså tydligen och relaterbarligen INTE uppfattas eller förstås som någon absolut föregiven fysikgrund:

— Sambandens härledning i relaterad mening [EKoGh] kopplar heller inte till den moderna akademins ”DåQärNoll” — f.ö. här ENDA kända grunden till den moderna akademins blotta idé [FMadia] i begreppet ”adiabatisk”. Den relaterbara härledningen inbegriper ENDAST en gas’ frihetsgrad (iRot) tillsammans med en elementär tryck·volym=energi-ekvivalent (E=pV), och frihetsgradens samhörande ekvivalens med gasens KONSTANTA värmekapaci(tivi)tet [k=E/T, J/°K]. Inget annat.

— Det ingår inga villkor i den relaterade härledningen [EKoGh] som kopplar till typ [FMadia] ”tillståndsändring där värme varken tillförs eller bortförs”. Den detaljen endast understryker [VRF] den värmerelaterade fysikens grund: Q=0 existerar inte i naturboken.

— Föreställningen om ”tillståndsändring där värme varken tillförs eller bortförs” i sambandsformen ovan grundas, tydligen, bara på omständigheten via ekvivalenterna [EKoG],

(pV/T)₀ = k = (pV/T)₁ : tillståndsekvivalenter på konstant värmekapacitet k

ALLMÄNNA GASLAGENS EKVIVALENTER FÖR FrihetsGradsGaslagen

och därmed en tydligt MEKANISK, cylindrisk, inneslutning: pVT-parametertransformation via en rörlig kolv, en mekaniskt anställd volymändring på en bestämd gas (γ) i en sluten cylinder: relaterat: MEKANISKA gaslagen.

— Situationen endast understryker det milt sagt »korrumperade» etablerade begreppet ”adiabatisk”. Se även i AdiaCitat.

— Den andra ytterligheten i volymändringens möjliga fysik, nämligen en isoterm [‡], visar just totala motsatsen till ovanstående: ingen som helst temperaturändring sker med volymändring, exakt samma volymändrande tekniska fysik, bägge fallen: innesluten cylinder med rörlig kolv [EV].

— Webben @INTERNET har (verkligen Apr2014) genomsökts på möjliga antydningar eller direkta beskrivningar från etablerade källverk som ansluter till det här nämnda förtydligandet mellan de bägge ytterligheterna, men ingenting har ännu (22Apr2014) upphittats.

— Så ska sambandsformernas pV^γ TV^γ–1 PRAKTISKA TILLÄMPNING som associerade med en temperaturändring tydligen tolkas på en SPECIFIKT ANPASSAD MEKANISK KONSTRUKTION (jämför Dieselmotorn) — och vilken temperaturändring följaktligen inte får förstås eller förväxlas obetingat med en volymändring [‡].

— Flertalet etablerade skriftställare verkar (EMELLERTID) ha anställt föreställningen om obetingad temperaturändring MED volymändring — speciellt i artiklar som berör Jordatmosfärens luftcirkulation [CentralAdia]. Vi bör känna till den detaljen, då den tydligen inte omnämns i etablerad skrift.

FETF, FLASKEXPEDITIONENS TILLÄMPADE FYSIKRESULTAT

FLASKEXPEDITIONENS TILLÄMPADE FYSIKRESULTAT PÅ MOLNBILDNINGENS GRUNDFYSIK

FLASKEXPEDITIONENS TILLÄMPADE FYSIKRESULTAT PÅ MOLNBILDNINGENS GRUNDFYSIK

ter sig på följande sätt enligt etablerade källverk [CentralAdia]:

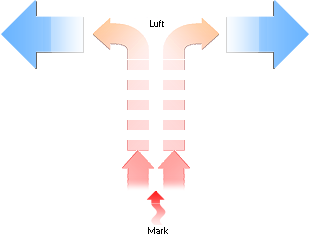
FlaskExpeditionens motsvarande Molnbildningsfysik.

— När markuppvärmd luft stiger uppåt kallare — trycklägre — atmosfäriska skikt, »ökar luftvolymen» — ENLIGT FLASKEXPEDITIONENS RESULTAT — och »på den vägen» — via [CentralAdia] ”adiabatiska gaslagen” — sjunker temperaturen.

I RELATERAD BESKRIVNING finns (främst) ETT huvudargument som talar emot den typen. Nämligen KONVEKTIONSARGUMENTET (molnbildningen SES inte överdrivet Heltäckande, utan uppenbart med tydliga mellanrum mellan nybildade molntappar — om nu Den iakttagelsen är relevant i sammanhanget):

— Varje (Jordtroposfäriskt) Jordatmosfäriskt skikt, med sin specifika [HydroTrycket] hydrostatiskt fasta och fixa Tpρk-profil [PDAS],

HELT baserad på Jordatmosfärens konstanta volym [JAVK] med Solen som enda underhållande LUFTKONVEKTIV energikälla i uppenbart smala vertikala spalter mellan höjdskikten och — som det DÅ får förstås — därmed i princip nollutrymme för explicita BREDBASERADE luftmassutbredningar INOM de skilda skikten,

UTESLUTER just en bredbaserad, luftmasseÄNDRING inom varje skikt: Istället ORSAKStvingas den markuppvärmda luftens markmassdeficit — på den uppåtträngande luftens luftmassexcess relativt de besökta skiktvärdarnas Tpρk-profiler — att SNARAST MÖJLIGT OMGÅENDE återvända KONVEKTIVT mot markdelen, enligt motsvarande illustrerade typform [VÄRMELÄCKNINGEN, kT-energin],

Fria luftens Molnbildningsfysik — i prövande framställning: Naturlig värmeläckning, med [HydroStyrd] konvektion på Solenergins räkning. Inget annat.

— FlaskExperimentets resultat som [i komplement från JAVKbasic] visar (och bevisar) luftens SNABBA temperaturanpassning, utpekar TILLSAMMANS med KONVEKTIONSARGUMENTET att luftens temperaturminskning med avtagande altitud snarare kan förstås och förklaras av NATURLIG VÄRMELÄCKNING på omgivande fasta hydrostatiska skikts fixa Tpρk-profil. Om så skulle vara fallet, framträder naturligt MÖJLIGEN (men här inte klart fastställd) en volymminskning [FlaskExperimentet] i netto, och förutsatt vi bortser ifrån YTTERDELARNA på ”den centrala luftpelaren” i dess (långsamma) uppstigning. Eller, möjligen att aspekterna eller ansatserna i volymutvidgning på grund av lägre tryck [FlaskExpeditionen] (Luftpelarens yttre regioner berörs främst) och volymminskning på grund av naturlig värmeläckning [FlaskExperimentet] (Luftpelarens inre regioner berörs) tar ut varandra — för den centrala molnbildningens räkning.

— [EV]: De yttre delarna i den markuppvärmda luftpelaren KAN uppföra sig som i FlaskExpeditionens fall, men BREDDFORMEN i den typutbredning i någon större omfattning HINDRAS av konvektionskrafterna som (snabbt) tvingar varje utbredningstendens i toppluften att DRAS åter mot markdelens motsvarande massunderskotts SUG (i ytterdelarna). Se även illustrationen i LuftKonventionen.

— Det vore VÄL önskvärt att få dessa antydningar KLART dementerade om de innehåller (här ej kända) oegentligheter. Webbsökningar i (det omfattande) ämnet har ännu (Apr2014) inte lämnat något avgörande klargörande bidrag på den punkten.

— De samband som finns redovisade i detta dokument säger heller i sig ingenting som utesluter ovan nämnda möjlighet.

Typbilden nedan FÖREFALLER utpeka ordningen:

Anblicken av molnformationer FÖREFALLER utpeka tydligt, klart och omisskänneligt en tydlig vertikalseparation mellan (nybildade) molnceller. Vi ser ingen tendens att molnpaketen försöker EXPANDERA IN I VARANDRA i aktuellt atmosfäriskt molnskikt — som vi kanske BORDE få se OM expansionsprincipen skulle vara den övervägande. Heller ser vi ingen tendens att molntapparna försöker förenas, vindstilla förutsatt.

Molnbilden ovan erinrar vad vi redan har »sett» vi otal tillfällen i Naturboken: Varje molntapp besitter sin egen unika VERTIKALSTAPEL där ackumulerande vattenånga kan förstås samlas genom ytterligare uppstigande uppvärmd markluft fortfarande utan expanderande versioner — eller att den bildade molntappen upplöser sig i takt med att Solen bränner på (under dagen), beroende på aktuella lokala atmosfäriska förhållanden.

— Vi ser heller ingen tendens att molntapparna skulle försöka pressa ihop sig eller gå ihop. Vi ser istället hur de flyter på lugnt och stillsamt i den närmaste himmelsregionen som fristående individuella paket med sin alldeles egna specifika individuella karaktär.

— Vi TROR oss därmed med dessa enkla iakttagelser ha visst berättigande i föreställningen att

uppåtstigande uppvärmd markluft uppvisar i sin nettofysik en energibalans som bevarar en vertikalt rak, icke breddexpanderande, uppåtstigande luftbula, och på vars räkning enskilda fristående molnbaser kan bildas utan att inkräkta på varandras vertikaldomäner:

— från den vertikala stapelns centrum kan vattenångan i luften bilda synliga molnbaser genom vattenångans kondensation, formering till mikroskopiska vattendroppar (och successivt större med allt mer tillströmmande uppåtstigande uppvärmd markluft), via luftbulans avsvalning uppåt genom de högre svalare atmosfäriska skikten, och så länge värmedifferenser finns

I modern akademi nämligen, intar man (kategoriskt) en hållning som INTE (riktigt) ansluter till ovanstående. Man menar, nämligen (kategoriskt), att uppstigande uppvärmd markluft EXPANDERAR ensidigt (via s.k. ”adiabatiska processer”. Se särskilt citat i CentralAdia).

— ATT det föreligger någon form av en expansion är helt klarlagt bortom varje tvivel enligt resultatet i FlaskExpeditionen. Alla typer av BALLONGEXPERIMENT ansluter också till den ordningen: (innesluten) markluft som tas uppåt i atmosfären expanderar. Att den delen däremot skulle spela någon avgörande roll i temperaturminskningen motsägs tydligen delvis av konvektionsargumentet [JAVK] med Jordatmosfärense konstanta volym och de hydrostatiskt fasta höjdskiktens fasta och fixa Tpρk-profiler [HydroTryckets Sambandsformer]. Därmed också den avgörande skillnaden mot Flaskexpeditionens förutsättningar: luftpelaren är INTE en innesluten avgränsad luftdomän »någon tar med sig uppåt eller neråt».

— Tills vidare klargöranden framkommer, måste vi tydligen räkna med den här antydda möjligheten, då ingen DIREKT argumentform finns som motsäger resultatbilden:

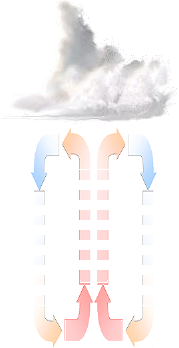
Varje molnbas garanteras sin egen individuella vattenbas OM den uppåtströmmande markuppvärmda luftens expansion i de övre skikten kopplar en ÅTERSTRÖMMANDE KONVEKTION som leder det övre atmosfäriska skiktets massöverskott tillbaka till markskiktets atmosfäriska massunderskott.

— Precis så länge Solvärmen fyller på med markvärmeenergin för uppströmningen, kan den konvektiva processen fortgå, och varje enskild molnbas kan därmed tillväxa i mängd bundet vatten.

— EXPANSIONEN AV DEN UPPTRANSPORTERADE MARKLUFTEN i det övre tunnare kallare atmosfäriska skiktet garanterar DÅ — och endast då — återströmningen av frisk ny markluft för ytterligare uppvärmning och transport av vattenånga till just DEN molnbasen — och ingen annan.

— Då stämmer Ekvationerna.

[EV]: Temperaturen i uppstigande uppvärmd markluft avtar inte på grund av någon ändring i volym eller tryck, utan på grund av att gasbollarna ALLTID »letar» efter minsta motståndets väg: största möjliga rörelsefrihet: vägen upp och ut mot de svalare atmosfäriska skikten. Då ingen motsvarande påfyllande energi finns till den rörelseenergi som gasbollarna tappar genom VÄRMELÄCKNINGEN (Planckstrålningen) på vägen ut mot de övre skikten, tappar också gasbollarna motsvarande värmegrad: temperatursänkningen är ett LÄCKFENOMEN, samma som »vanlig avsvalning» — och ansluter i så fall till viss del till [JAVKbasic] FlaskExperimentet: volymen avtar med (den förtätade) ångbildningen.

— Uppvärmning, transport, avsvalning. Solen underhåller energibasen för konvektionen: varmluft stiger, svalnar — inte avkyls av någon energikälla som utför arbete — och återvänder till marken, successivt återuppvärmd genom Solens försorg och dess markuppvärmande effekt.

MKonKonvek

MOLNBILDNINGEN KONTRA KONVEKTIONERNA

— Men vi behöver EGENTLIGEN inte bekymra oss (så mycket) i frågan om temperaturändringens detaljer om vi greppat principen med den KONVEKTIVA balans [JAVK] som krävs i samband med den uppåtstigande varma markluftens dynamiska koppling till sitt eget ursprung:

— Någonstans ifrån måste en påfyllning ske till markområdets massunderskott, och motsvarande uttömning ske ur det högre skiktets massöverskott: expansionen hos den varma uppåtstigande markluften i övre skiktet kan ske från utkanterna (med successiv avmatning inåt), så mycket det sedan finns kvar av vertikalstapeln av den uppåtströmmande varmluften på den konvektiva återströmningens räkning: så snart en TENDENS finns för expansion i någon övre atmosfärisk del, på grund av uppträngande varm markluft, sker omgående en motsvarande SUGANDE tendens från markdelen, och därmed strömmar expansionsdelen åter nedåt på den uppstigande varmluftens Soluppvärmda energiräkning: vertikalstapeln för just den molnbasen inte bara garanteras utan avgränsas av närliggande molnbasers motsvarande och samflödande nedåtkonvektioner i staplarnas utkanter.

— Hela ändamålet med den turbulensen blir så ENDAST att forsla upp vattenånga som kan bilda moln, för vidare transport.

Söker vi motsvarande uttömmande förklaringsgrunder i den konventionella hållningen, finns i varje fall här (Apr2014) ingen som helst upphittad beskrivning som ger motsvarande detaljerad upplysning, speciellt beträffande den avgörande konvektiva strömningen.

— Det ser ut som att det finns en heltäckande bild, men att den delen INTE (än) är välformulerad i etablerad litteratur.

Bildkälla: Författarens arkiv · 27 | 29Maj2010 Bild 71;13;81 RF2010:1UN · Nikon D90

MOLN kan tveklöst bilda de mest häpnadsväckande formationer. I varje fall det här författarämnet slutar ALDRIG att förstummas över och beundra målarmästarens ständiga himmelska underverk. Det har varit så för mig ända sedan barnsben, så långt tillbaka jag kan minnas. Lugnet och harmonin i dessa helt fantastiska formationer upphör tydligen aldrig att fascinera och inspirera. Sagoriken.

Studieexempel, molnbildning under 5 minuter

DEN RENT TEKNISKA ASPEKTEN förefaller uppenbar i ljuset av ovanstående rent visuellt observerade resultat:

Ingen bredexpansion.

— Molnbilderna ovan, och vad vi vet alla övriga, visar ingen överdriven tendens till BREDDEXPANDERANDE UTBREDNING;

— De seglar fram, samlade, i lugnt tempo, definitivt inget synbart expanderande, snarare tvärtom om Solen är framme.

— Molnformationer ses — oftast, i varje fall på våra nordliga breddgrader — som helt lugna och samlade närliggande himmelsobjekt som seglar fram i ytterst lugn takt — med samtidig ombildning DELS i tydliga tofsavdunstningar om Solen är framme, men (kolla noga på varma förmiddagar) även OMVÄXLANDE tydliga nybildningar, avdunstningar, återbildningar, och så vidare av molntappar som seglar förbi i lugn takt.

Foto BildSerie: E2 14Apr2014 — Molnformering — bildning, upplösning · Nikon D90 · BellDharma UNIVERSUMS HISTORIA

— Inom minuter (och kvartsminuter) ser man tydligt hur enstaka molntappar — här på en klar förmiddagshimmel Soltid omkr. kl 09:20 — ömsom byggs på och ömsom helt tycks upplösas, för att strax återbildas, osv.

— UPPFATTNINGEN att varje molntapp har någon form av SIN EGEN luftvattenångkopplande PROFIL — möjligen en vertikalstapel, på ett eller annat sätt — blir märkbar DÄRMED att ett och samma vertikalområde tycks ömsom upplösa (växelverkande varmluftstråk, avdunstning) och ömsom bilda (växelverkande kalluftstråk, kondensation) synlig vattenånga.

— Speciellt den större molntappen i mitten ses, faktiskt, delas upp i upplösningen på två separat skilda vertikalpelare med delvis upplösning/nybildning, om det nu är den beskrivningsformen som gäller.

— Hela serien ligger inom 09:21 till 09:26, alltså 5 minuter.

Den samlade formbilden (som beskriver processen) associerar i stort som just SAMMANHÄNGANDE vertikala rök- eller ångslingor [JAVKbasic] i vardagsrummet. Ingen direkt synbar breddspridning.

— Vi ser ingen tendens att molnen skulle sträva att EXPANDERA UTOM PÅ HÖJDEN, bilden nedan — vi kan se höjdexpansionsexempel i vita »rundbulliga» moln ibland om vi studerar rörelserna under några minuter mot klarblå himlar: starkt vita, höga molntoppar som ibland kan ses bulla upp sig på höjden, helt tydligt även inom tiotal sekunder.

Ingen bredexpansion.

Bildkälla: Författarens arkiv · 23Aug2010 Bild1 UN Moln · Nikon D90

JAVK, Jordatmosfärens volymkonstans

— Se även från MOLNBILDNINGENS TEKNISKA FYSIK, INLEDNING [MOTEF].

JORDATMOSFÄRENS KONSTANTA VOLYM

DET TREDJE ARGUMENTET — V[=kT/p] = konstant — energiförklaringen bakom Jordytsatmosfärens konvektion genom Ändringslagarna

Basic

Uppvärmd fuktig luft från något av kökets kärl med kokande vatten stiger RAKT uppåt DÄRFÖR att det är den enda tillgängliga ÖPPNINGEN för den högre temperaturens motsvarande större MEDELFRIVÄG för gaspartiklarna (uppvärmd luft+vattenånga) i deras framfart (v) där en MINDRE tyngdkraft verkar och därmed större rörelsefrihet [WhyNotAdia]: ingen iakttagen bredexpansion förekommer. Så: Varför skulle vattenavdunstningen från Jordytan [PrimärformenMOTEF] generellt fungera på annat sätt? Jämför CentralAdia. Det finns en konflikt här.

— Uppstigningshastigheten för fuktig varmluft (kökets kastruller) är ca 0,6 M/S — vi följer ångslingorna med blicken, övar in stigtakten, och använder ett av köksurens tickande sekunder för att mäta ut en motsvarande JÄMN höjdsträcka på en sekund. Vi markerar punkten, och mäter sträckan med måttband (10ggr för att vara helt säkra).

— Värmeavsvalningstakten hos uppstigande fuktig varmluft (kökets kastruller) är från kärlkanten i ett mätförsök (rumstemp. 24°C)

73°C nära vattennivån: mätinstrument, digital IR-termometer, Clas Ohlson [kat. 2012/2013s288, art.36-2286, 279:-]

35°C 30cM ovan vattennivån

29°C 60cM ovan vattennivån [aktuell omgivande rumstemperatur, 24°C]

——————————————————————————

IR-sensorn hålls lodrätt över mätnivån

grovt linjärt ca (73–29)°C/0,6M~73°C/M.

— Med stigtakten vid ”vackert vindstilla väder” 0,6 M/S ges en grov uppfattning om avsvalningstakten som 121,7(°C/M)/S. Med andra ord — jämför Flaskexperimentet (volymändring i innesluten tunn plastflaska märks först efter ca 20 S) — en ytterst snabb temperaturläckningsanpassning till aktuell hydroSITE för fri (fuktig) luft.

— Vi vet här inte närmare hur storleken på tvärsnittsytan i lodluftpelaren påverkar avsvalningstakten i pelarens centrum. Men vi kan ju, försöksvis, tillämpa lodtakten på horisontaltakten, vilket skulle ge grovt samma 122°C/MS: en (uppåtstigande, vid idealt vindstilla vackert väder) 122 meter grov luftpelare tappar 1,22°C per sekund horisontellt; Om luftpelaren får tappa max runt 10°C — och samtidigt har NÅGON vattenånga kvar (för molnbildning) — måste den i princip vara »runt 1,22 KM» (bredden eller höjden, vilketsom, grovt). Motsvarande basdata i molnbildningsfysikens elementa har eftersökts i den mest synliga gratis tillgängliga webblitteraturen, men inte hittats.

Editor2014IV29

OM nämligen värmeläckningstakten hos uppstigande markuppvärmd (fuktig) luft är SÅ snabb som visas av det enkla köksexperimentet ovan [121,7(°C/M)/S], blir det SVÅRT att få ihop det med den etablerade uppfattningen [CentralAdia] [AdiabaticRef] att ”expansion causes the parcel of air to cool”. Det enkla köksexperimentet utpekar snarare att den uppvärmda uppåtstigande varmluften avkyls — praktiskt taget omgående i takt med uppstigningen — genom NATURLIG VÄRMELÄCKNING [PrimärformenMOTEF] till den närmast omgivande hydrostatiska atomsfäriska nivån — samt med tillhörande luftmängds volymminskning i aktuellt hydrostatiskt fast atmosfäriskt skikt enligt det enkla FlaskExperimentet. Samt, att det citerade påståendet ENDAST tycks vara grundat på ”Termodynamikens första huvudsats” tillsammans med ”DåQärNoll” samt det isotermiska hjälpsambandet [FlaskExpeditionen] pV=kT=konstant för experimentellt påvisande av ”luften expanderar med lägre omgivande tryck”, speciellt tydligt relaterat i ”Adiabatiska gaslagen”.

— PROBLEMET [CentralAdia] med den moderna akademins etablerade [AdiabaticRef] beskrivningar i ämnet molnbildningens fysik, är att INGEN ANNAN REFERENS verkar finnas till ”adiabatisk (avkylning/uppvärmning)” än just det nyligen nämnda, främst ”DåQärNoll”. Relaterad värmefysik [VRF] [VLAFS], nämligen visar det sig, har inte dessa begrepp, och behöver dem inte heller, för att nå de aktuellt beskrivande sambanden. Det SKULLE innebära, att den etablerade molnbildningens rent retoriskt BESKRIVANDE fysik — sambanden är OK, men beskrivningarna vad de betyder är bedrövliga — verkligen inte är välformulerad. Den här framställningen är (bl.a.) ägnad att försöka klarlägga vad som gäller i naturboken genom jämförande citat, exempel och referenser.

V[=kT/p]

Jordatmosfärens volym är [vad vi vet] konstant. För troposfären med max höjd ca 10 KM gäller volymen 5,1 T18 M³. Den ändras inte med klimatsfärens (troposfärens) flöden av luft och vattenånga.

— På allmänna gaslagens form har den konstanta volymen (V) formen

V=kT/p=konstant. Fundamentala gaskonstanten (k) är fast och fix för varje region k/(V=1M³)=p/T — precis som i fallet med vårt vanliga marknära atmosfäriska skikt — och på samma sätt för alla andra atmosfäriska skikt — eller andra specifikt gasinnestängda domäner.

Genom Jordkroppens gravitation [HydroTrycket], i samspel med Solvärmen och Jordrotationen, besitter Jordatmosfären tydligen ett fast globalt medelmässigt Jordgravitellt[Hydrostatiskt]-Solvärmerelaterat atmosfäriskt system av olika dynamiskt samverkande skikt:

— Inom en begränsad del av atmosfären — troposfären (max runt 10 KM) eller klimatsfären — avtar alla Tpρk — temperatur (T) tryck (p) täthet (ρ, grek. rho), gaskonstant (k) — entydigt med växande höjd [Slutgraferna]:

h_{MAX 10 KM} → ∞ = Tpρk → 0

[EV]: Enbart på det hydrostatiska systemets räkning, dess bevarade TILLSTÅND på bestämd volym

— med gaslagens sätt att se saken V[=kT/p]: ingen volymändring tillåts [PrimärformMOTEF]

— kan Jordatmosfärens konvektion förklaras i PRINCIPIELL detalj, hur den uppkommer, bildas och underhålls i Troposfären (Jordens Klimatsfär). Nämligen på bekostnad av Solvärmen som energibas tillsammans med ÄNDRINGSLAGARNA [Newton3: ändringens ansats motsvarar tillståndets bevarande]:

KOKOVf, Konvektionen på konstant volym, förklaring. JAVK

Solppvärmd markluft med sin lägre täthet, högre temperatur och tryck [pV=kT] som tränger in i ett högre beläget atmosfäriskt skikt med lägre temperatur och tryck fungerar som en inträngande volymökande (eg. massökande) »bula» i det högre värdskiktet.

— Men konstanta volymformen V=kT/p=konstant tillåter ingenting sådant: Jordatmosfärens globalt medelbaserade hydrostatiskt bestämda SYSTEM bygger på konstant massvolym:

— Ansatsen, aktionsformen som ytterst återfaller på Solvärmen, att tränga ut det högre luftskiktets volyms fasta T/p-karaktär, analogt att bilda ett lokalt [massbaserat] övertryck — onaturligt tillstånd med större massinnehåll — via den uppåtstigande uppvärmda markluftbulan med sin specifika täthet, temperatur och tryck, motsvaras i markskiktet av en ansats, en reaktionsform att reducera markområdets volymforms fasta T/p-karaktär, analogt ansatsen att bilda ett undertryck — onaturligt tillstånd med mindre massinnehåll.

— Eller mera orsaksrelaterat till den markuppvärmande Solenergin. Den markuppvärmda luften (ACTION) skapar genom uppåtstigandet ett markluftunderskott i markskiktets hydrostatiska domän [PrimärformenMOTEF], och som resulterar (REACTION) i motsvarande SUG som bara kan återkopplas genom återvändande (kallare, avsvalnad) toppluft.

KOKOV, Konvektionen på konstant volym, KOKOVf

Uppåtträngande uppvärmd markluft initierar en AKTION som försöker tränga sig in på en ny högre atmosfärisk domän genom att tränga undan DESS naturliga tillstånd för att etablera SIN luftbulas egendomar. Markdelen svarar med motsatta REAKTIONEN: ett plötsligt massunderskott försöker rubba markskiktets balans. RESULTANTEN söker återställa balansen genom att bilda ett slutet flöde — en konvektion — med motsvarande nedåtströmmande luft från övre delens massöverskott till undre delens massunderskott. Därmed är energikretsen sluten.

— PRINCIPEN beskrivs också ungefärligen så i en del etablerade led, se t.ex.

Wikipedia [2014-04-09] på Atmospheric convection, Initiation,

http://en.wikipedia.org/wiki/Atmospheric_convection

”Associated with a thermal is a downward flow surrounding the thermal column.”.

— Bägge dessa ansatser — ansatsen att ändra tillståndet i både övre och undre skikten — kan i den allra närmaste lokala luftregionen förstås eftersträva att återställa balansen genom att bilda ett slutet konvektionsflöde, figuren ovan, och som underhålls så länge värmekällan är aktiv:

— Soluppvärmd markluft söker sig via den högre rörelseenergin på MINSTA MOTSTÅNDETS VÄGAR [VLbasic] mot områden med större rörelsefrihet = högre upp i atmosfären där trycket — och därmed statiska skikttemperaturen — är lägre: den uppvärmda markluften strömmar upp till och utbreder sig mot svalare glesare luftmassområden, och den ANSATSEN till ändring i det högre värdskiktet och motsvarande reaktion i markskiktet kompenseras genom motsvarande omvända, närmast lokalt kopplande, påtvingade flöden från högre till lägre för att återställa eller bevara massa/hydrotryckbalansen i de olika skikten. Hela processen har bara en enda energiagent att verkställa energiräkningen på via den uppvärmda markluften: Solvärmen [PrimärformenMOTEF].

MACadia, MOTEF

MAC:s adiabatiska luftfysik

Men trots en del principiella likheter i beskrivningssättet [KOKOV], framhäver man i modern akademi [MAC] en helt annan beskrivningsgrund för det uppvärmda, uppåtstigande markluftpaketet:

volymen ökar:

AdiabaticCitat, Wikipedia

@INTERNET Wikipedia, Adiabatic process, Adiabatic heating and cooling [2014-04-09]

http://en.wikipedia.org/wiki/Adiabatic_process

”When the pressure applied on a parcel of air decreases, the air in the parcel is allowed to expand; as the volume increases, the temperature falls and internal energy decreases.”.

Jämför den tillslutna luftflaskan som tas med till högre höjder: sambandsformen pV=kT=konstant är INTE den exakt beskrivande matematiska formen, men fungerar ändå därför att luften i flaskan fungerar på alldeles samma sätt som om den stannar kvar på marken och man sätter in flaskan i en vakuumtank och börjar suga ut luften omkring: det lägre omgivande trycket medför att flaskvolymen strävar att öka.

— Men Soluppvärmd uppåtstigande markluft har uppenbarligen ingenting gemensamt med en sluten innestängd luftmassa som utsätts för lägre omgivande tryck: Uppåtstigande markluften [KOKOV] bildar uppenbarligen en sammanhängande, inte avgränsad, vertikalpelare med sammankopplade konvektionsströmmar och vilken totalbild inte ingår i den slutna avgränsade flask- eller ballongluften: Jämförelsen med en innestängd avgränsad luftmassa är uppenbarligen inte rationell.

— pV=kT=konstant [HJÄLPSAMBANDET],

en isoterm, men vars liknelsemässiga molnbildningsfysik [CentralAdia] i etablerad molnbildningslitteratur [CentralAdia] istället framhävs som en s.k. ”adiabatisk tillståndsändring” [FMadia] eller ”adiabatisk process” där ”ΔT≠0”.

beskriver citatmeningens framhävda tryck-volymändring av princip — med minskat tryck följer ökad volym PÅ EN SAMBANDSGRUND pV=kT SOM INNEFATTAR KONSTANT TEMPERATUR ”ΔT=0” — samtidigt som själva FENOMENFORMEN (”volymökning orsakar temperaturminskning”) ”ΔT≠0” på andra ställen [MACadiaRef] framhävs som raka motsatsen:

— Begreppen ISOTERM och ADIABAT används uppenbarligen i etablerad litteratur pulserande underförstått godtyckligt, I DELVIS UPPENBARA MOTSATSFÖRHÅLLANDEN, utan närmare klargörande.

Det är den ena delen i kalasbutiken.

Del II

Den andra delen är den mest anmärkningsvärda:

— Genomgången [VRF] [VLA] [VLbasic] [VLAFS] [HeatBASIC] med speciellt den konventionellt benämnda s.k. ”adiabatiska gaslagen” har visat att det etablerade begreppet ”adiabatisk” helt förefaller baserat på typen ”DåΔQ|QärNoll” i ”Termodynamikens första huvudsats” [WikiAdiaGasRef].

:

I relaterad fysik existerar ingenting sådant som ”DåΔQärNoll” eller ”DåQärNoll”.

— Men hela den moderna akademins matematiska framställningssätt FÖREFALLER HELT tillägnat just den detaljen. Se särskild jämförande härledande genomgång i ”adiabatiska gaslagen”, om ej redan bekant.

Sett i relaterad fysik, med andra ord:

— Begreppet, termen och blotta föreställningen i modern akademi om ”adiabatisk” är ett djupt korrumperat, definitivt vilseledande, och absolut definitivt korkat (PRIMITIVT) begrepp som inte alls har i termodynamikens naturbok att göra.

— Det är INTE sambanden det hänger på, verkligen inte, utan SÄTTET att förstå och kunna relatera deras innebörd som saken gäller.

Rätta mig, absolut, om jag har fel.

Jämför speciellt molnbildningens (elementära) grunder från MOTEF.

Del III

Den tredje delen är den mest sorgliga:

Citatet framhäver alldeles tydligt sambandsformen pV=kT=konstant: ’pressure decreases, volume increases’. Men citatet framhäver också tydligt den mera anmärkningsvärda — definitivt enligt relaterad fysik (»grymt sammansatta») ”adiabatiska” — typen:

V→T [analogt p→T] [pVbasic] [WhyNotAdia]:

Modern akademi känner, uppenbarligen, inte till ordningen i massfysiken (pV→T→pV)

värmebildningens grunder från Planckstrålningens HÖGSTA frekvenser [NeutrinostrålningenBASIC] via fusionsgrunderna till Solenergin [TRYCKEKVATIONEN], vår närmaste absoluta värmekälla

och därmed heller inte MÖJLIGHETEN TILL SAMMANBLANDNING MED MOTSVARANDE I MATERIEFYSIKEN (den moderna akademins ”adiabatiska” begrepp)

V→T [analogt p→T]

och som inte gäller i naturboken, relaterad fysik [pVbasic].

— Det är den sorgliga delen i kalasbutiken. Med den relaterade fysikens mening således:

— Ingen seriöst menande tänkande människa kan undgå en medveten eller omedveten FÖRNIMMANDE NÄRVARO av naturens SAMTLIGA verksamheter, vare sig man kan formulera dem eller inte. Man är en del av dem, en produkt av dem.

— Meningen här betyder, då, endast att ovanstående ”p→T-lomplex” i modern akademi, och som uppenbarligen KAN förstås associerat med den tydligt korrumperade, irrationella, andemeningen i begreppet [Del II] ”adiabatisk” JUST är resultatet av ”en spontan (förvirrad) reflexion (som innefattar men inte förstår [Del III] massfysikens aspekter)”, och så utan penetrerad insikt, i ensidigt fasthållande vid en DOKTRIN ”Termodynamikens första huvudsats” förmenar en total FELAKTIG (primitiv) fysikbild typ ”adiabatiska gaslagen” PÅ PERFEKT MATEMATIK men med annan innebörd, EFTERSOM den medger det felaktiga [Del II] med ”DåΔQärNoll” eller ”DåQärNoll”.

— Resultatet totalt, blir en pulserande sammanblandning av allehanda ”godis” som virvlar omkring i den moderna akademins Termodynamiska Speceriaffär, och med speciell bekräftande citatmening som understryker studentens BERÄTTIGAT förvirrade uppsyn i ämnet.

— Men för all del. Visa att jag har fel. Ämnet är garanterat krävande, sammansatt, nödvändigtvis inte svårt i detaljerna, men trixigt att omfatta. Varenda detalj måste passa in. Annars är det kört.

— Enda energikällan bakom varmare luft som stiger uppåt i atmosfären är värmen från Solen: T→p, T→V: T driver hela systemet.

Inte V→T.

Tvivel finns inte.

— Föreställningen i modern akademi [CentralAdia] att det stigande luftpaketets temperatursänkning beror på något [WikiAdiaGasRef] ARBETE som utförs av luftpaketet PÅ den aktuella höjdSITE:ens hydrostatiska profil [PrimärformenMOTEF], raseras HELT av den relaterade fysikens sats för värmeläckningens arbetsfrihet [VLAFS]: värmeläckning, luftpaketets naturliga spontana TEMPERATURANPASSNING till aktuell höjdnivå (»SITE»), kan inte utföra arbete.

— Den detaljen bara understryks i härledningen till ”adiabatiska gaslagen”

[TILLÄMPNINGSEXEMPEL] [VRF] där det framkommer att den moderna akademins GREPP via ”Termodynamikens första huvudsats” med ”DåΔQärNoll” är irrationellt [noF], och i själva verket baseras på en KOMPLEX (iROT) frihetsgradsekvivalent (i²=–1=o) [EKoG], och som kan substitueras med en arbetsform (E=pV för en yttre mekanisk anordning med rörlig kolv i sluten cylinder, typ Dieselmotorns princip).

— Den förklaringen understryks ytterligare av det enkla köksexperimentet [JAVKbasic], komplementet till det enkla FlaskExperimentet, som visar och bevisar att uppvärmd fuktig luft stiger RAKT upp med (mycket) SNABB naturlig avkylningshastighet [122°C/M/S], utan observerad tendens till någon lokal volymökning; FlaskExperimentet bevisar istället motsatsen: volymminskning i lokal hydrostatisk SITE (»sajt»; domän, område) på befintlig fuktig varmluft som värmeläcker.

— KONVEKTIONSARGUMENTET visar dessutom att hydrostatiska balansen mellan de olika vertikala luftskikten kräver just en konvekterande sluten strömningsväg baserad på ÄNDRINGSLAGARNA med Solenergin som uteslutande enda pådrivande underhållande energikälla.

Jämför

MODERN AKADEMI:

»markluftpaketet ger ut sin högre markenergi i det högre luftskiktet genom att öka volymen».

RELATERAD FYSIK:

»markluftpaketet ger ut sin högre markenergi i det högre luftskiktet genom avsvalning».

— Volymen är konstant [JAVK].

— I FlaskExperimentet är beviset för »den uppvärmda markluftens energi» KRAFTEN SOM ÅSTADKOMMER flaskans volymminskning [den avtagande rörelseenergin hos gasbollarna, värmeläckaget, som ger ökad åtkomst för den omgivande luftens större lokala fasta tryck] då flaskluften svalnar till omgivningstemperaturen.

— Vi KAN förstå det som den lokala motsvarigheten till en anpassning i det mottagande högre atmosfäriska värdskiktets lägre egentemperatur.

— Så förefaller (Apr2014) den övergripande bilden beskriva inte bara ATT utan även HUR den etablerade beskrivningen i molnbildningens fysik definitivt INTE är välformulerad: Tydligt stora revor, hål och djupa avgrunder i begreppsbeskrivningen är uppenbara [AdiabatMAC].

WhyNotAdia, Aspekter på VÄRMELÄCKNINGEN — 2010VIII-2014IV | UniversumsHistoria BellDharma

Jordtroposfären: Det finns ännu ingen upphittad etablerad referens som kan beskriva eller förklara den närmaste vardagsatmosfärens detaljer på ett begripligt sammanhängande sätt [CitatAdia]. Vi är hänvisade till olika (internationella) standarder och tabellverk [PDAS] om vi vill försöka få en någotsånär sammanhängande bild av ämnesområdet (standard för internationell flygtrafik).

— Följande beskrivning utgår ifrån de mest synbarliga detaljerna, en del härledda samband, etablerade tabellverk med grundfysikaliska ordningar, och ger en totalbild från den utkikspunkten. Se inledningsvis närmast från MACadia.

aspekter på atmosfäriska VÄRMELÄCKNINGEN

VARFÖR ”adiabatisk tillståndsändring” INTE KAN ANVÄNDAS —

i samband med en förklaring till molnbildning enligt relaterad fysik

Om inget annat klargörande framkommer.

——————————————————————————————————

TERMODYNAMIKENS PRIMÄRA ENERGIEKVIVALENTER i relaterad fysik

För materiefysiken gäller:T→p — Temperaturen styr trycket: omvändningen gäller inte, se ORSAKEN TILL T INRYMS INTE I ALLMÄNNA GASLAGEN

E_k = 2(1M)ma = mv² = Fd = Mv₀²/2 = E_e · v₀/2c_z = pV = kT = hf = 2mw² ; Energiekvivalenterna

— I modern akademi finns ingen representation av eller för massfysiken [pVBasic] — man har ingen RELATERBAR GRUND till de skilda möjliga sätten T→pV=E [materiefysiken, Orsaken till T], alt. E=pV→T [massfysiken, se utförligt från PLANCKRINGEN och Strålningstrycket, om ej redan bekant]. Man möter [»följaktligen»] MAC-meningar av typen »temperaturen avtar på grund av att volymen ökar». Se AdiabatRefCitat.

— Men ÄR DU SÄKER PÅ ATT: kopplar den delen till T→p-komplexet?

— Det är ingen LÄTT sak att avgöra det — i ljuset av »den omedvetna MAC-nomenklaturen»: Människan i naturen är en fritt ASSOCIERANDE varelse som KÄNNER AV naturgrunderna, vare sig hon förstår dem eller inte, eller ens har en mening om någon FORMULERING i ämnet; Associationerna underförstått i olika formuleringar syns aldrig. Vi vet inte, bara att möjligheten finns. Vi kan ha det i bakhuvudet (om vi vill) så länge.

För varje (smalt) höjdavsnitt (h) över fasta Jordytan finns en viss temperatur (T), ett visst hydrostatiskt [‡] fast tryck (p), och en viss fast täthet (ρ, grek. rho) [Tabell hkT] [PrimärformenMOTEF].

Värmeläckningen:

— Genom Jordgravitationens koppling till variationerna i pρ (tryck, täthet [grek. rho]) kännetecknas också temperaturen (T) på varje höjd (h) av en viss bestämd Planckgenomströmningsekvivalent (E=hf=kT; f = T·k/h) [HeatBASIC] [Alla kroppar värmeläcker] och som kopplar hydrostatiskt till de bägge faktorerna tryck (p) och täthet (ρ, grek. rho).

— Det betyder, tydligen, att luft — med tillståndsvärden som hör till en viss h-region — som inträder i en annan h-region kommer att LEDAS — värmeläcka [VLAFS] — IN TILL den nya h-regionens T-fysik: Temperaturen i de olika h-skikten STYR (bestämmer hydrolokala temperaturkonstanten) — men kan inte påverkas av — tillståndsvariationerna mellan olika luftpaket som cirkulerar eller konvekterar mellan de skilda h-regionerna.

Markluft med en högre temperatur T som stiger upp till h ovanför marken där en lägre temperatur t råder, leds in till den högre h-regionens lägre t-värde:

Föreställningen att volymändring obetingat skulle sammanhänga med temperaturändring (konv. adiabatiska processer se CitatAdia) är inte välgrundad [MACadia] [noAdia].

— Grundfysiken med beskrivningen av isotermiska och icke-isotermiska volymändringar [AGKE] för cylindriskt inneslutna gaser visar att det finns just de två nämnda alternativen eller ytterligheterna. Beroende på den cylindriska inneslutningens konstruktion, hur den volymändrande kolvens rörelse utförs, kan volymändringen ske såväl helt utan (isoterm) temperaturändring som med (icke-isoterm). Ordet ”adiabatisk” används ofta för det icke-isoterma alternativet i etablerade led, men undviks här helt då det uppenbarligen kommit att associeras med en rent matematisk/algebraisk BEGREPPSFÖRBISTRANDE formalism. Se jämförande exempel [CentralAdia] och citat i AtmosAdiabatMAC, samt speciellt i ”Adiabatiska gaslagen” om ej redan bekant.

Temperaturens avtagande med höjden skulle då kunna förstås och förklaras inte på grund av någon ändring i volym eller tryck, utan på grund av att gasbollarna ALLTID »söker» minsta motståndets väg: största möjliga rörelsefrihet: Största rörelsefriheten finns otvetydigt på vägen upp och ut mot 1. den kallare rymden, 2. de svalare atmosfäriska skikten och 3. den svagare tyngdkraften. Då ingen motsvarande påfyllande energi finns tillgänglig till den rörelseenergi som gasbollarna så tappar genom VÄRMELÄCKNINGEN (Planckstrålningens avtagande [VLAFS]) på vägen ut mot de övre skikten och den svagare gravitationen, tappar också gasbollarna motsvarande värmegrad (ΔQ): temperatursänkningen kan förstås och förklaras som ett NATURLIGT LÄCKFENOMEN, samma som »vanlig avsvalning».

sammanstötningarna är just den allmänna orsaken till värmeläckning eller avsvalning: successiv avstanning sker om ingen påfyllande energistrålkälla finns som kontinuerligt matar varje gasboll med påfyllande, värmeuppehållande Planckenergi [VLAFS] [HeatBASIC]

— Variationer i tryck och volym som sådana i materiefysiken kan ALDRIG generera temperatur; det är ALLTID temperaturen, rörelseenergins upphovsbas [fusionerna (m→γ) — närmast Solen], som grundlägger — orsakar — ändringar i tryck och volym [pVBasic].

Bevis:

— Materiefysikens enda experimentellt bevisande gasinneslutning med anordning för volymreglering visar och bevisar den grundsatsens giltighet [pVBasic]: Det finns bara en positiv variabel (volymen V) att välja på med utgångspunkt från absoluta nollpunkten i allmänna gaslagens — materiefysikens — samband pV=kT=0=T; volymen (V). Trycket står redan på noll och har för övrigt ingen negativ innebörd i materiefysiken (negativa T-värden existerar inte i materiefysiken [man kan i själva verket inte ens nå exakta T=0°K]). Återstår V: Rent tekniskt kan V ökas på från T=0 genom att dra kolven i den slutna cylindern utåt och så öka volymen. Men den aktionen gör ingenting åt saken så länge den innestängda gasbollen saknar rörelseenergi: inget händer. Volymökningen gör inget åt saken [utom möjligheten att sänka T såvitt >0, se noAdia].

— Med absolutreferensen T=0 och den volymreglerande anordningen som enda materiell kandidat att försöka påverka T=0 till T>0, är det tydligt att materiefysiken inte kan generera T>0. Massfysiken däremot [TNED], med sin gravitation [PRIMÄRA HIMLAKROPPSBILDNINGEN] [GRUNDÄMNESBILDNINGEN], arbetar garanterat från T=0 på tryck över volym [STÄDETSolfysiken] [STJÄRNORNAS ALLMÄNNA TRYCKEKVATION]: fusioner genom höga g-tryck bildar i TNED den avgörande produkten från massdestruktionerna (m→γ) som värme och ljus: Planckstrålningen (E=hf). Den nivån är i orsakssammanhangen abstrakt för Materiefysiken.

— Först sedan den så bildade primära värmegrunden framträtt, kan olika processer i materiefysiken påverka, styra och reglera värmebildning, typ icke-isotermiska volymändringar [noAdia]. Det betyder i reda procedurtermer att materiefysiken ALLTID och uteslutande alltid, enbart, och därutöver inte alls, kan utföra typen

[pV_NUC] → T → [pV]_MAT; nukleärbaserad värmegrund som bas för regleringar — byggnader — inom materiefysiken. Omvändningen gäller inte.

(Följdsats: Ingen materiebaserad fysik kan åstadkomma nukleärbaserad värmegrund).

— NOTERA EMELLERTID ALTERNATIVEN med isotermiska och icke-isotermiska volymändringarna [AGKE] [noAdia]: I materiefysiken finns ingen ENTYDIG form för ändring av temperatur från ändring i volym. Medan isotermiska alternativet [AGKE] inte åstadkommer någon temperaturändring, gör det icke-isotermiska alternativet det: det finns ingen entydig form, utan allt beror på konstruktionen och sättet.

— Lägg dessutom till dessa detaljer omständigheterna i den moderna akademins värmelära med DåQärNoll kontra relaterad värmefysik [VRF] [NollQno], och därmed fördjupningarna i begreppet ”adiabatisk” [”Adiabatiska gaslagen”], och bilden av termodynamikens grunder i etablerad mening blir i stort sett en omöjlig uppgift att få ut något begripligt och konsistent, logiskt, ur. Sambanden är OK, men beskrivningen av deras innebörd är milt sagt en djup bedrövelse. Se även jämförande referenser i CitatAdia.

— Solstrålningens uppvärmning av markluften med T ger luftmolekylerna en viss rörelseenergi.

— ENDAST så länge Solvärmen fortsätter den energimatningen, bibehålls T;

ATFTrel, VarförINTE iModernLitteratur? [ATFT]

Jordgravitationens inbördes hydrostatiskt (globalt medelvärdes-) bestämt avtagande temperaturnivåer med växande höjd inom troposfärens höjdolika luftskikt, kopplar inte till hastigheten i kallningen hos uppåtstigande Solmarkuppvärmd luft:

— »HydroIsotermFallTakten», konv. eng. ”Dry Adiabatic Lapse Rate”

Förenklat med konstant tyngdkraftsacceleration räknat från Jordytan:

T/h = a/[k/m = Cp ~ 1000 J/KG°K för luft vid STP ] ; a standard = 9,81 M/S² vid Jordytan:

Γ_d ~ 0,0098°C/M ; Den rena hydrostatiskt luftbaserade FASTA temperaturVARIATIONStakten med varierande höjd:

— T/h-formen har uppenbarligen ingenting med Solen eller Solvärmen att göra: det finns bara specifika Jordkroppsparametrar med i bilden: termogravitella nivåkonstanter [F/k].

— Utan en klargörande, relaterad, översikt, kan man lätt får den uppfattningen att T/h-formen skulle sammanhänga med själva den uppåtstigande markuppvärmda luftens värmeläckningstemperaturfalltakt — »lapse rate», falltakt, hastigheten med vilken uppåtstigande uppvärmd markluft kallnar [CentralAdia | AdiabaticRef] . Det är tydligen inte så.

— VARIATIONER I uppåtstigande, kallnande, luft betigas av RÖRELSE (°C/M/S) medan VARIATIONER I hydrostatiken [termogravitella konstanter] betingas av TILLSTÅND (°C/M). Vi kan inte blanda ihop, eller ens jämföra, dessa bägge fysikaliskt skilda fenomenområden. Luften PASSERAR hydroskikten, eller DRAS/TRYCKS genom dessa.

— Jämför ”0,0098°C/M/8,03278t5S = 122°C/MS” från det enkla köksexperimentet i JAVKbasic:

— BARA OM varje °C/M i ett givet hydrostatiskt skikt avverkas på 8,03278t5S≈80µS av naturligt värmeläckande kallnande luft, kan vi postulera att »temperaturfalltakterna är identiska», analogt (med köksexperimentets resultat vid »vackert väder och vindstilla») 0,6M/S i den fuktiga luftstigningshastigheten, analogt för en vertikal luftpelare med höjden 1 KM, ca 1667 S eller nära 28 minuter.

— I andra ord;

— LUFTENS KALLNINGSTAKT har, verkligen, ingen DIREKT relaterbar koppling till hydroskiktens T-profiler, eftersom luften i sitt kallnande tydligen måste PASSERA dessa hydrostatiskt fasta isotermiska skikt [tills ingen temperaturdifferens i kallningen finns kvar att avverka någon mera höjd på].

— MarkEXPERIMENTskiktets grovt uppmätta värdeform för fuktig uppvärmd luft med kallningshastigheten 122°C/M/S i JAVKbasic bevisar hela komplexet.

samma som värmeläckagets absolut höjdrelaterade »Nu-Måste-Jag-Stanna-Värde»

är INTE LuftTemperaturens avtagande med altituden inom troposfären (grovt max 10 KM), analogt Jordytans luftbaserade värmeläckningshastighet ut till den omgivande rymden.

— Men det är ändå vad som framhävs — eller mera försiktigt uttryckt, vad som FÖREFALLER framhävas — i etablerad litteratur:

”.. 0,0098 °C/M” [AdiabaticRef].

— Här finns alltså ytterligare en uppmärksammad BRIST i relaterade sammanhang;

”expansion causes the parcel of air to cool at a set rate of 0.98°C per 100m”, [AdiabaticRef].

Jämför relaterad fysik — fortfarande till prövning [EV]:

— Den uppåtstigande luften KALLNAR med varmluftens EGEN värmeläckningshastighet [JAVKbasic] — en M/S-baserad fysikalisk storhet [122°C/M/S] — medan hydrotryckets fasta höjdprofiler besitter fasta STATISKT korrekta termogravitella isotermiska nivåkonstanter med höjdvariationskonstanten, det citerade, ”0,0098 °C/M”. Den sistnämnda delen är just STATISK. Inte Kinematisk: noll rörelse; T/h-formen kan INTE påföras någon som helst koppling till luftens avsvalningshastighet.

I andra ord:

— Termogravitella Hydrotryckets avtagande fasta T-värden med växande höjd

— altitudHYDROISOTERMERNA T/h=a/(k/m)_LUFT — är den nivå luftkallningen STANNAR PÅ vid aktuell höjd. Ingen »luftens avsvalningstakt».

Förtydligat, om inte redan bekant:

— När (således) den Soluppvärmda Jordmarkytans T-markluft med den högre rörelseenergin avancerar upp till h ovan marken med det lägre t-värdet, TAPPAR [VLAFS] luftmolekylerna samtidigt sin T-rörelseenergi som följd av NATURLIG VÄRMELÄCKNING:

— Varje atmosfärisk nivås fasta hydrostatisk bestämda temperatur är den nivåns lägsta läckgränsvärde för inkommande luft med högre temperatur:

— Den aktuella hydrostatiska nivån är alltså en nivåbaserad värmeekvivalent: F/k=ma/k=T/h.

— Vi HADE (alltså, också) kunnat göra det ännu enklare direkt i härledningen med:

E = kT = Fh = mah; T/h = ma/k = a/(k/m).

OM luft med ett högre T-värde befinner sig i en region med lägre t-värde, VÄRMELÄCKER nettoskillnaden i rörelseenergi — värme [kT-energin] — mellan T och t [VLAFS] ut i rymden (ovanför, uppåt mot kallare, täthetslägre regioner) på liknande sätt som luften ovanför det kokande vattnet i kastrullen svalnar (statiskt inom ett bestämt litet xyz-område, om värmetillförseln under kastrullen stängs av, eller per höjdmeter om vi följer ångpelaren uppåt): »differensvärmet» läcker utåt och fördelas på nivåerna [JAVKbasic];

Vartefter T-luftmolekylerna stöter samman med en viss medelhastighet via ett visst medelavstånd,

men att deras normala energiförluster vid T-kollisionerna som tidigare hela tiden kompenserades med den fasta värmekällans påfyllnad, nu saknar den detaljen,

tappar T-luften alltmer av sin ursprungliga T-rörelseenergi och inträder — antar — därmed h-regionens fasta t-nivå, eller så mycket av den som gäller med hänsyn till luftens PASSAGE genom aktuell höjdnivå.

— Ändringar mellan h-skikten kan inte beskrivas på den allmänna gaslagsformen.

— Ändringarna kan heller inte beskrivas på formen för ”adiabatiska gaslagen”; hydrostatiska variabler ingår inte där, som t.ex. att temperaturen avtar hydrostatiskt med höjden. Värdena man får kopplar inte, se EKoGex2.

— Ändringarna kan HELLER inte beskrivas VIA det konventionellt etablerade [CentralAdia | AdiabaticRef] ”Adiabatic lapse rate” 0,0098°C/M som någon förment luftens uppåtstigande avkylningstakt [ATFTrel].

— Allmänna gaslagen GÄLLER endast VID ett visst h-skikt och för en bestämd volym, inte mellan skilda h-skikt;

fundamentala gaskonstanten k gäller för en bestämd volym 1M³ som kvoten av lokalt tryck och temperatur:

k/[V=konstant=1M³] = p/T — k avtar med höjden över marken [k/k0]

— För övrigt finns bara en verksam faktor: värmeläckningen [ATFTrel]. Och den styrs tydligen INTE av T/h-formen, det konventionellt benämnda ”adiabatic cooling” [AdiabaticRef | CentralAdia].

— Alltså finns bara två sätt: tillståndsbeskrivning INOM ett visst skikt, samma som allmänna gaslagen, och VÄRMELÄCKNING generellt MELLAN godtyckliga skikt, vilket är en domän för Planckstrålningen [HeatBASIC | VLAFS].

Tillståndsformerna MELLAN olika h-skikt kan (alltså) inte tillämpas på allmänna gaslagens samband pV=kT, eftersom allmänna gaslagens samband pV=kT bara gäller i ett specifikt h-skikt: k-värdet avtar med höjden över marken.

— Jämför även ett rent TEORETISKT försök via pV=kT=konstant: Antar vi kT=konstant från marknivån via V=1M³ vid STP (kT=101.325 J) ställs vi inför Problemet med Volymfaktorn vid ett högre atmosfäriskt skikt: »Problemställningen är IRRATIONELL» därför att Jordatmosfären inbegriper ingenting sådant som en volymändringseffekt: »Tävlingen är inställd». Jordatmosfärens volym är KONSTANT.

— Inga gaslagar, inte alls över huvud taget, kan anställas i beräkningen av tillståndsändringar MELLAN olika atmosfäriska skikt — DÄRFÖR att Jordatmosfären styrs, regleras och fungerar på fasta fixa hydrostatiskt varierande grunder TILLSAMMANS med Solvärmen.

— Luftcirkulationen varmt-upp-avsvalning-ner-uppvärmning representerar DÅ enbart gaspartiklar som mobila flödesagenter i en sluten KONVEKTIV flödesväg som tydligen bara och enbart uteslutande DRAS igenom det hydrostatiska systemet av, via och från Solenergins markuppvärmande arbete.

— I praktiken, mellan de skilda h-skikten, blir det således I RELATERAD MENING varje h-skikts fasta och fixa specifika temperatur T(h) som styr eller BESTÄMMER rörelseenergins ändringar som ett lokalt undre temperaturläckgränsvärde för luft som FÖRS (nerifrån marken och uppåt) genom de olika h-regionerna — av Solenergin + Jordrotationen.

— För att vi — således meningsfullt — ska kunna utföra beräkningar MELLAN skilda h-skikt, måste vi veta varje h-skikts specifika tryck (p) och täthet (ρ, rho) vid h-skiktets specifika temperatur (T).

Vi kan få BRA KOLL på den delen genom att konsultera STANDARDISERADE ATMOSFÄRISKA TABELLER [Tabell hkT] [PDAStemp] [PDASatmo]. Med deras hjälp kan vi sedan — med vissa smärre avvikelser — »infoga standardvärden» tillsammans med enklare matematik [JAGVH] och därmed utföra »hyfsat överskådligt ANVÄNDBARA» beräkningar som kan orientera oss behjälpligt i uppfattningen om vissa praktiska sammanhang som berör [den klimatkopplande] Jordatmosfärens detaljer.

Generellt: Allmänna gaslagens fundamentala gaskonstant k i pV=kT gäller för ENDAST EN BESTÄMD VOLYM — k/(V=1M³)=p/T=101325 Pa vid STP.

— Jämförelser mellan olika h-skikts luftdelar måste likaledes ske med referens och i förhållande till just en bestämd volym [JAVK].

Det ansluter OCKSÅ UPPENBARLIGEN alldeles precis till hur Jordatmosfären GENERELLT arbetar tillsammans med Solenergin:

— Jordklimatets lokala värdevariationer arbetar på en bestämd (troposfärisk) volym [JAVK]: volymen är hela tiden densamma; volymen ändras inte.

Vi SER alltid tillståndsbeskrivningar generellt på en BESTÄMD avgränsad domän.

Frånsett HOLLYWOOD i dessa tider som försöker vänja publiken vid VISUELL JORDBÄVNINGSSTATUS så fort det blir ACTION: betala mera, se mindre → ge dem kreditkortet också, se ingenting.

— Se även i JORDATMOSFÄRENS KONSTANTA VOLYM.

VRF, värmetillståndets processbeskrivande relaterade fysik — TermoRelFys

— Termen system [IsoleratSYSTEM] används inte här i OBJEKTSBESKRIVNINGEN för fysikens processer därför att den termen INTE är tydligt relaterbar i någon beskrivande mening i fysiken: hela fysiken består av konkreta (synliga) kroppar som ständigt genomgår tillståndsförändringar: slutna byggnader, material, ämnen, inneslutningar och avgränsningar. Men gundbeskrivningen behöver å andra sidan inte heller inte ens baseras på kropparna, visar det sig:

I relaterad fysik (men inte i modern akademi) kan explicit ett direkt PROCESSBESKRIVANDE sätt användas för att uttrycka värmetillståndets fysik [Allmänna tillståndslagen], och som (här veterligt) inte förekommer i MAC:

tillgängligt material = befintlig G-massa + värmeOCHljus

:

Tillståndsändrande allmänna värmefysikaliska processen, eller

FUNKTIONEN — helt oberoende av »kropp» eller »system» — beskriver en mer RELATERBAR fysikbild, speciellt oberoende av det diffusa MAC-begreppet ”system”, och som (följaktligen därför heller) INTE innefattas i MAC-formalian (nämligen värmeläcket L) [ClausiusOriginal]:

total tillståndsändrande energi = utförande ändringsenergi + värmeläckage

Q = W + L

påenergi = arbete + värmeläck

Påenergin Q i det ljus- och värmeaktiva universumet kan inte stängas av (K-cellens värmefysik — det finns alltid någon aktiv ljuskälla verksam), och heller inte läckvärmet L: [VLAFS], alla fysikens kroppar värmeläcker. Däremot kan arbetet W pausa, avbrytas, eller helt upphöra, vilket kvarlämnar påenergin Q i form av värmeläckning L. Ett exempel är processen Solen, om vi väljer att se Solen från läckvärmets sida:

VLA, »värmeläckagets arbete», VRF, satsbild till prövning

Q = 0 + L ; Solen:

Fysikens processer summerar nollvärme:

0 = W – Q + L ;

0 = w + L ;

: Vi genomför nu en »KORKAD BESKRIVNING» för tillfället att få understryka detaljerna:

[Testa själv om du klarar det på kortare distans]:

:

»Läckvärmens arbetsform» w kan inte skrivas på någon POSITIV form typ w = L eftersom arbetets allmänna form är reserverad för

W = Q–L. »Läckvärmets arbetsform» måste istället skrivas på en NEGATIV PÅENERGI,

W – Q = w, som JUST garanterar att »läckvärmets arbetsform» blir NEGATIV:

Värmeläckning är inget arbete, eftersom arbete i relaterad mening definieras, förstås och beskrivs som orsaken till värmebildning: arbete = E=Fd = kraft över väg. Värmeläckning blir med den formalian tydligen »negativ kraft»: värmeläckning är icke-arbete: Kraftlöshet:

värmeläckning kan inte utföra arbete [VLAFS].

–L = w = pV = E = Fd = (F/A)Ad = pV: Absolutformen för »värmeläckagets arbete»

:

— w är ett arbete [pV] som INTE KAN utföras PÅ/AV något läckobjekts element [atomer, gaspartiklar].

ANMÄRKNING:

— Vi ser nu att vi hamnat i en direkt verbal ord- och begreppskonflikt: Hur vi än försöker med den erhållna w-formen, är vi inne på formuleringar som kräver typen »värmeläckning är arbete» och vilket fysiken I RELATERAD MENING [VLAFS] alldeles helt underbart tvärsäkert inte har utrymme för: arbete förknippas med värmebildning. Undantag existerar inte.

— Men utvecklingen har följande ändamål, nedan. Nämligen att visa hur man resonerar på motsvarande sätt i MAC, och hur den delen kopplar tillsammanhanget med ”adiabatiska gaslagen”:

— Speciellt ser vi här att w-formen blir samma som en [negativiserad] inre energi i Clausius original för värmetillståndets fysik, U = Q – W.

— Skillnaden är emellertid avsevärd: i MAC kan man sätta Q=0 medan den möjligheten inte finns i relaterad fysik:

PE, PåenerginRef, VLA

påenergin [TermoRelFys] Q i relaterad mening går inte att stänga av:

— Det finns ALLTID någon form av värmeaktivitet i ett ljusaktivt universum. En maskin som står tyst, avstängd i en maskinhall för natten, genomströmmas likväl av en Planckenergi i arbetshallens rumstemperatur: Q = L: vilande anordning. Varken påenergin Q eller läckvärmen L kan stängas av i den relaterade fysikens NATURLIGT PROCESSBESKRIVANDE mening och innebörd.

— Den beskrivningstypen används INTE i MAC.

TEadiaG, PE

TILLÄMPNINGSEXEMPEL — Poissons ekvation, eller

— ”adiabatiska gaslagen”:

Se utförligt relaterad härledning i EKoG

ISOTHERMAL AND ADIABATIC EXPANSION — Richard Fitzpatrick 2006-02-02 [2014-04-15]

http://farside.ph.utexas.edu/teaching/sm1/lectures/node53.html

” pV^γ = constant. (319)

This is the famous adiabatic gas law.”

;

UCL PHYSICS & ASTRONOMY — ADIABATIC PROCESS. POISSONS EQUATION [2014-04-15]

http://www.cmmp.ucl.ac.uk/~mls/Teaching/advanced_topics/Adiabatic_process.html

”PV^γ = const .

This equation is called the Poissons equation.”

Man undrar just hur mycket ansvar för missförstånd, missuppfattningar, svårigheter att FÖRSTÅ och kunna NAVIGERA I termodynamikens farvatten — värmeläran generellt — som den moderna akademins Q-begrepp, värmefallen relaterade nedan, har på sitt samvete. Därför att med ovanstående klargörande — som det FÖREFALLER att se ut — rätas alla frågetecken ut, dimmorna försvinner, och landskapet öppnar sig.

MACadia

— Den springande punktens kärna är, nämligen, begreppet adiabatisk [BKLadia] [FMadia] [WikiAdia] såsom — i etablerade kvarter [konv. från ”Termodynamikens första huvudsats”] — förknippat med utan tillförande eller bortförande av värme.

”En tillståndsändring kallas adiabatisk om värme varken tillförs eller bortförs, dvs. då ΔQ=0.”, [FMs322sp1mö];

— NOTERA relaterad värmefysik [VLAFS]: ΔQ betyder värmeläckagets minsta möjliga kvantitet, analogt värmeenergins minsta möjliga påfyllande kvantitet. Den kan inte elimineras. Därmed har det ingen betydelse om vi, här, använder ”ΔQ=0” eller ”Q=0” eftersom ingen av dem kan elimineras i relaterad fysik [VLAFS·6|8]. Se utförligt från VRF med referenser.

DåQärNoll, ANMÄRKNINGEN i VLA, MACadia, PE

”då ΔQ=0”. Se även relaterat i NollQno.

— Det påpekades just: som INTE den moderna akademins Q-begrepp, värmefallen, har på sitt samvete;

— Påenergin i relaterad fysik [‡] — den tillförande värmemängden, även i MAC — Q går inte att stänga av.

Jämför de olika skrivsätten:

Modern akademi (Clausius original — arbete som utförs AV en kropp):

Q = W + U

tillförd värmemängd = arbete + inre energi

Relaterad fysik:

Q = W + L

påenergi = arbete + värmeläck

Min genomsökning av det gratis tillgängliga webbmaterialet (Apr2014) har ännu inte hittat någon ANNAN motivgrund för meningsformen som ovan i citat ”en tillståndsändring kallas adiabatisk om värme varken tillförs eller bortförs” än JUST det citerade ”då ΔQ=0”.

— Ingen annan motivgrund verkar finnas.

— Därför, att om vi ser till den relaterade fysikens ENKLA härledningsform till den motsvarande ”adiabatiska gaslagen” — energikomplexa gaslagen eller enklare MEKANISKA GASLAGEN — och som vi här strax ska relatera närmare, visar samma räkneexempel [‡] som anges i Wkipediaartikeln i ämnet att tillståndsändringen (pV/T)₀=k=(pV/T)₁ (i detta aktuella exempel) INNEFATTAR värmetillförsel (150 J).

OM det finns personer som har svårt för att förlika sig med den fysikbild som visar en sluten cylinder med en rörlig kolv vars SAMMANPRESSANDE ARBETE = VÄRME inte anses vara ”tillförd energi” på den likväl betygade UPPVÄRMDA GASMASSANS kredit, då vet jag inte riktigt om det är lämpligt att vederbörande ALLS befinner sig i trafiken: vägen, väglaget, föraren, FORDONET. Viss risk för missbedömning föreligger [möjligheten att MISSA skillnaden mellan gas och broms: tillämpningen, i konkret situation].

— Dessutom avhandlar härledningsformen — exakt samma slutformalia som i MAC, men på den relaterade fysikens domäner, som ovan och vilket vi strax ska återkomma till — INTE, inte alls över huvud taget, någon ANNAN energiaspekt än en ekvivalent till en viss gas’ frihetsgrad: en energiekvivalent tillståndsform. Sambandsformen utmynnar (således) i en OMFÖRDELNING mellan faktorerna pVT genom den aktuella gasens konstanta värmekapacitet (k) som ovan enligt

(pV/T)₀ = k = (pV/T)₁

Med VOLYMÄNDRINGEN som bas för parametertransformationerna pVT dikterar sambandet tydligen en mekanisk gaslag som förutsätter en sluten cylinder med rörlig kolv:

där E=pV-energierna före (0) och efter (1) inte är ekvivalenta: värme tillförs (vid kompression) mellan tillstånden.

— I modern akademi skriver man nämligen INLEDNINGEN till sin ”adiabatiska gaslag” att

Modern akademi (Clausius original):

0 = W + U

tillförd värmemängd = arbete + inre energi

som ger

–U = W

och som tydligen motsvaras »i relaterad fysik» (vi är inte färdiga med prövningen än) av den här tidigare nämnda satsbilden [VLA]

–L = w = pV = E = Fd = (F/A)Ad = pV:

VLAE, TE

Värmeläckningens arbetsekvivalent (Se utförlig algebra i ATFTex):

— Genom att associera U|L med frihetsgraden (här o) som ger –oU|L, och sedan associera värmeläcket (»relaterat») eller inre energin (modern akademi) med temperaturens (T) arbetsform från allmänna gaslagen (pV=okT), som ger

–oU|L=W|w, analogt –opV=pV — eller DIREKT från energikomplexa gaslagen via komplexa enheten (som DIREKT substituerar rotationen för frihetsgraderna) i²=–1=o och därmed DIREKT –opV=pV med differentieringen –opdV=dpV eller –odpV=pdV vilket som passar således helt i OBEROENDE AV OVANSTÅENDE PÅENERGIRESONEMANG — får man slutformerna

pV^γ = K ; J/°K ; Energikomplexa gaslagen, konv. ”adiabatiska gaslagen”

”continuous formula for adiabatic heating and cooling”, Wikipedia Adiabatic process [2014-04-15]

”Any work (δW) done must be done at the expense of internal energy U, since no heat δQ is being supplied from the surroundings.”, exakt samma matematiska form

@INTERNET Wikipedia Adiabatic process [2014-04-09] — http://en.wikipedia.org/wiki/Adiabatic_process — se även i WikiAdia.

TV^γ–1 = Ķ ; °K/M³

Se ovan från VRF tillämpningsexempel — med fullständigt utförliga härledningen i Energikomplexa Gaslagen.

noF, VLA

”Värmeläckningens arbetsekvivalent” [VLA] är med andra ord och alldeles tydligen en irrationell form. Den har uppenbarligen ingenting med saken att göra — alldeles precis DET som formalian [ANMÄRKNINGEN i VLA] redan själv förklarat: omöjligheten i att associera värmeläckning med arbete. Och följaktligen: ”adiabatic” i citatet ovan skulle alltså i relaterad mening istället kunna vara:

MECHANIC:

Den Form, som tydligen HELT kan återföras på den komplexa enhetens ekvivalent [EKoG], i²=–1=o, är istället, uppenbarligen, en arbetsekvivalent (substitutionen med E=pV) till frihetsgraden (o) — pVT parametertransformation för värmekapacitet (k, J/°K) MED TILLHJÄLP AV EN YTTRE ANORDNINGS MEKANISKA ARBETE (rörlig kolv i sluten cylinder) [Dieselmotorn] — hos en gas, med motsvarande allmänna gaslagens ekvivalenter

(pV/T)₀ = k = (pV/T)₁ ; Mekaniska Gaslagen pV^γ = K ; TV^γ–1 = Ķ

Inget annat. Se den utförliga RENA härledningen i EKoG.

Inget spår av något

”en tillståndsändring där värme varken tillförs eller bortförs”

syns. Tvärtom.

— Exempelräkningen — samma som Wikipediaartikeln — visar entydigt ATT värmeenergi E=pV (150 J) tillförts under kompressionen.

— Vad som däremot syns — uppenbarligen — ALLDELES översvallande TYDLIGT är ”då ΔQ=0” — i den delens tydligt irrationella koppling till sambandsformen, den relaterade härledningen som ovan. Se f.ö. hela härledningen utförligt i EKoG.

Motsats- och Irrationalitets-NOMENKLATUREN i den moderna akademins lärosystem i ämnet ELEMENTÄR termodynamik är här alldeles övertydlig: Man använder tydligen en matematisk formalia för att beskriva sammanhang i fysken man uppenbarligen INTE förstår. Ingen människa kan uppenbarligen med vettet i behåll använda ett sådant lärosystem till något naturvetenskapligt uppbyggligt. Så återstår då enbart: naturerövring (naturvandalisering), herrefolksfasoner. Inget annat. Se facit: Fullständigt, totalt meningslös, naturvandaliserande, verksamhet.

Jämför:

”As the air parcel expands, it pushes on the air around it, doing work (thermodynamics). Since the parcel does work but gains no heat, it loses internal energy so that its temperature decreases”, [WikipediaInternalEnergy].

I relaterad fysik [HeatBASICS | VLAFS] kan värmeläckning INTE utföra arbete: allt utförande arbete sammanhänger med värmebildning. Undantag existerar inte.

Citatmeningen försöker tydligen övertyga läsaren om att den uppåtstigande markuppvärmda luftens naturliga VÄRMELÄCKNING [FlaskExperimentet] »ska förstås» analogt med ”adiabatic cooling”. Samt, att den typen av läromedel uppenbarligen ska associera till ”termodynamik”. Jämför satsen om värmeläckagets arbetsfrihet.

— Varför då, modern akademi, krångla till det i onödan: säg som det är: »Det är JAG som är Gud, och NI gör som JAG säger, annars ska NI bestraffas» [typ Loke 2012 i filmen Avengers: kneel before me!]. CentralAdia.

Arbetets förtydligande: Det enda relaterbara arbete som utförs PÅ ett atmosfäriskt skikts egna hydrostatiskt fasta och bestämda globalmedelbaserade Tpρk-profil [PrimärformenMOTEF] har bara Solenergin som kraftbas att återfalla på, dess underhållande arbete som verkställer KONVEKTION (vertikalt) i markdelen och ADVEKTION (horisontellt) i toppluften [CoriolisCellen].

KONVEKTION och ADVEKTION är de enda Solvärmeförorsakande atmosfäriska strömningsfenomen som finns inom Jordtroposfären. Alla andra strömningsfenomen — vindar, flöden, rörelser — följer av dessa bägge, tillsammans med Jordrotationen [BLANDAREN] och Jordgravitationen [HYDROTRYCKSGIVAREN].

Dvs., de cirkulerande (konvektiva) luftmassorna, i följd av Solenergins underhåll, utför — tydligen och uppenbarligen — alls inget arbete typ ”pushes on the air around it”, de DRAS/DRIVS uppenbarligen enbart cirkulerande runt [i smala vertikala staplar] via UPPVÄRMNING från markdelen (luftmassunderskott i markdelens atmosfäriska fasta tillstånd) med upptransport av vattenånga och sedan kraftlös, icke arbetande VÄRMELÄCKNING i luftdelen (luftmassöverskott i luftskiktens atmosfäriska fasta tillstånd: konvektion). Orsaken till den avgörande vertikalkonventionen kan bara vara just LUFTMASSUNDERSKOTT i markdelen som följd av Soluppvärmningen och därmed den tvunget stigande varmluften uppåt (lägre hydrotryck för den varmare luftens högre rörelseenergi) och därmed naturlig värmeläckning: markunderskottet skapar SUG — från Solvärmd markluft [PrimärformenMOTEF] — som DRAR motsvarande toppluft ÅTER; [EV].

Om inget — eller ingen — kan överbevisa mig att det finns något ANNAT ARGUMENT än just det nämnda ”då ΔQ=0” som är SJÄLVASTE ORSAKEN bakom det frekvent upprepade etablerade ”tillståndsändring där värme varken tillförs eller bortförs”, alltså helt enkelt grunden bakom och till det etablerade begreppet eller termen adiabatisk inom termodynamiken, då är det alldeles klart och tydligt att den frasdelen med denna avtäckning helt förlorat — aldrig haft — sin innebörd;

NollQno, ”då ΔQ=0”

Q=0 existerar inte i relaterad termofysik: ”tillståndsändring där värme varken tillförs eller bortförs” är ett föreställningssätt som HELT saknar fysikalisk grund och substans;

allt fysikaliskt arbete förorsakar tillståndsändring, och allt arbete förorsakar uppvärmning;

undantag existerar inte [HeatBASIC] [VLAFS];

”tillståndsändring där värme varken tillförs eller bortförs” finns inte i naturfysiken;

frasen är vilseledande, missledande, ologisk, irrationell, och uppenbarligen direkt felaktig;

I relaterad termofysik existerar varken ett ΔQ=0 eller ett Q=0 i någon som helst fysikalisk bemärkelse.

— Enda avställbara värmeformen i relaterad termofysik är arbetet (W). Inget annat.

Generellt finns ett etablerat speciellt citatställe som hjälper oss se hur man menar rent matematiskt i MAC i dessa sammanhang:

IsoThermalWiki

@INTERNET Wikipedia Isothermal process [2014-04-15]

http://en.wikipedia.org/wiki/Isothermal_process

”In other words, in an isothermal process, the value ΔT = 0 but Q ≠ 0, while in an adiabatic process, ΔT ≠ 0 but Q = 0.”

MAC:

————————————

isoterm ΔT = 0 ; Gäller även i relaterad fysik, se isotermiska volymändringar:

Q ≠ 0 ; Gäller även i relaterad fysik, se PåEnergin

————————————

adiabat ΔT ≠ 0 ; Adiabatbegreppet innefattar djupa oklarheter. Se från TILLÄMPNINGSEXEMPEL.

Q = 0 ; Förekommer inte i relaterad fysik. Se från ”då Q=0”.

————————————

Med den skrivningen blir det enklare att hänga med i relationsformerna till komplexet icke isotermiska volymändringar och isotermiska volymändringar som tydligen givit »speciellt fysikdjup» åt det etablerade begreppet adiabatisk. Vidare med jämförande citat i AtmosAdiabatMAC.

VRFsf

Sammanfattning VRF:

DE RELATERBARA FUNKTIONERNA för icke isotermiska volymändringar och isotermiska volymändringar illustrerar, tydligt, adiabatbegreppets (också tydligt, ypperligt sammansatta) språkförbistring med den ständiga strömmen exempel från etablerade korridorer, speciellt i ämnet Jordatmosfärens luftcirkulation.

— Det kanske också är betecknande för etymologin till ordet adiabatisk (från grekiskan) som betyder sluten, ogenomtränglig.

Den centrala förbistringen [CentralAdia]:

— Uppfattningen att VOLYMÄNDRING har en OBETINGAD FYSISK KOPPLING till TEMPERATURÄNDRING, och som populärt benämns adiabatisk tillståndsändring.

Se vidare jämförande exempel i AtmosAdiabatMAC, hur speciellt adiabattermen används i etablerade korridorer, och hur man (med den relaterbara framställningens referenser) kan förstå vad som menas i de olika beskrivningssätten — i ljuset av ovan genomgångna uppdaganden.

ATFT, Atmosfäriska hydrostatiska TemperaturFallTakt — missförstått begrepp: ”Atmosfäriska Värmeläcket”, konv. [dry] adiabatic lapse rate — från GammaReferensen

ATMOSFÄRISKA VÄRMELÄCKNINGEN

——————————————————————————————————————————————————

— TERMEN eller BEGREPPET ”adiabatisk” har i relaterad fysik innebörden MEKANISK eller HYDROSTATISK beroende på sambandsform,

”continuous formula for adiabatic heating and cooling”, MAC; [‡]

’continuous formula for MECHANIC heating and cooling’, TNED; VRF, EKoG

”Dry Adiabatic lapse rate”, MAC; Citatutdraget Wikipedia nedan i ATFTh

’Dry Hydrostatic lapse rate’, TNED; denna artikel, huvudtexten nedan från ATFThärledning

och vilka olikheter grundas på den moderna akademins ”adiabatisk tillståndsändring” från ”DåQärNoll” och som inte existerar i relaterad fysik [VRF] [HeatBASIC] [VLAFS.]: värmeläckning 1. kan inte stängas av och 2. kan inte utföra arbete och 3. ingår inte i den moderna akademins beskrivningar i ämnet [Clausius original].

ATFTh, härledningen utförligt

GAMMAREFERENSEN i utvecklingsexemplet [ENERGIKOMPLEXA GASLAGEN, utvecklingarna från i²=–1=o med substitutionen –pV=opV med vidare differentiering] [konv. ”adiabatiska gaslagen”] innehåller explicit en form

pdV = –Vdp/γ

som används i modern akademi för att ”härleda sambandet för Dry Adiabatic Lapse Rate” [DALR]. Se exv. Wikipedia Lapse rate, Dry adiabatic lapse rate [2014-04-15]. Artikeln använder för sin del ”first law of thermodynamics” med den här (nu) berömda formen för ”DåΔQ=0” för att komma fram till Γ_d=a/[k/m]. Wikipediaartikelns härledning i citat nedan:

”Since for adiabatic process:

PdV = – VdP / γ

the first law of thermodynamics can be written as

m cv dT – Vdp / γ = 0

Also since α = V/m and γ = cp/cv we can show that

cp dT – αdP = 0

where cp is the specific heat at constant pressure and α is the specific volume.

Assuming an atmosphere in hydrostatic equilibrium:[8]

dP = – ρgdz

where g is the standard gravity and ρ is the density. Combining these two equations to eliminate the pressure, one arrives at the result for the DALR, [9]

Γ_d = – dT/dz = g/cp = 9,8 °C / km ”

@INTERNET Wikipedia Lapse rate, Dry adiabatic lapse rate [2014-05-02]

http://en.wikipedia.org/wiki/Lapse_rate - Dry_adiabatic_lapse_rate

ANMÄRKNING:

— Det finns ingen egentlig anledning att DIREKT blanda in »hydrostatformen» hρa, då slutresultatet ovan nås direkt och mycket enklare enligt

E = Fh = mah = kT; T/h = (a=9,81 M/S²)/(k/m=Cp_LUFT~1000 J/KG°K) = 0,0098 °C/M

torrluftsbaserade altitudHYDROSTATISKA temperaturvariationstaktens TROPOSFÄRISKA konstant [gäller upp till max 10 KM, se PDAS]; variationerna i tyngdkraftsaccelerationen a över troposfären är försumbara, se TAI.

Vi studerar här en noggrann, fullständigt relaterad genomgång som visar och förklarar de skilda referenserna i MAC/TNED:

ATFTex, ATFTh

Från GAMMAREFERENSEN med beskrivningen i VLAE (MAC-härledningen till ”adiabatic gas law” i Wikipedia), utförligt relaterat i EKoG, visas här hur den IRRATIONELLA [ANMÄRKNINGEN i VLA med förtydligandet i noF] matematiska formen framträder. Vi fortsätter här från VLAE med Wikipediaartikelns beteckningar från ”First law of thermodynamics”, [Clausius original] och i utförligt jämförande värmedetaljer från VRF:

Allmänna gaslagen: pV = kT : momentana tillståndets BILD för en given gas med en given gaskonstant k:

: Anpassning relaterat: Q = W + L med Q=0 ger W = – L; vi ersätter L med konv. U:

dW = – dU ;

dW = – dU ;

= pdV ; Vi inför nu en faktor o associerad med U:

U = okT ; o, antal frihetsgrader: gasernas molekylära sammansättning: flera = större värmekapacitet:

pV = kT ; Allmänna gaslagen: o-faktorn tillämpad:

U = okT = opV ; Differentiering:

dU = okdT = dopV ;

dW = – dU ;

pdV = – dopV ; Notera här hur föregående led NU framstår som rent matematiskt svammel:

Se utförligt i NOLLFORMSALGEBRAN, differens- och differentialbegreppen, om ej redan bekant:

p(V/∞) = – (opV)/∞ ;

p(V) = – (opV) ;

pV = – opV ;

1 = – o ; Vad är det? Det är uppenbarligen grundformen som sambanden baseras på.

Enda TILLÅTNA matematiskt RELATERBARA GRUNDFORMEN att härleda en dylik »ekvivalent» på, är UPPENBARLIGEN via den komplexa imaginära enhetens komplexa ROTATION i²=–1=o;

–1 = i² = o ; Härifrån måste härledningen börja:

— Det detaljen ansluter också — exakt — till blotta innebörden som ovan i o: en ROTATIONSVARIABEL, se utförligt från EKoG.

— Och ALLTSÅ måste TVUNGET härledningen börja därifrån, och utöver den, eller vid sidan av den, eller utom DESS ekvivalent, inte alls: påtet med »dW=–dU» är uppenbarligen, ursäkta, rent matematiskt nonsens.

— Och fortsättningen blir, då som i EKoGh: exakt samma formalia i modern akademi — men där utan det här understrukna sammanhanget [MAC-grunden till övertrampet är ”DåQärNoll”]:

2pdV = – 2dopV ; Wikipediaartikeln [Adiabatic process, Derivation 2014-04-15] använder α = o/2:

= – do(pV + Vp) ; Här har vi full frihet att utveckla differentieringen efter alla till buds stående möjligheter:

= – o(pdV + Vdp) ;

–2pdV = o(pdV + Vdp) ;

= op dV + oVdp ;

–opdV – 2pdV = oVdp ;

p dV(–o – 2) = oVdp ;

–(o + 2)p dV = oVdp ; γ = (o+2)/o = 1+2/o :

pdV = –Vdp/γ ; Slutmålet nått: Se Gammareferensen.

— MAC-sättet — det ovan omnämnda fullständigt matematiskt relaterbara irrationella tilltaget — från dW=– dU — består, tydligen, i att via allmänna gaslagen

pV = kT

»arbetsformulera» också E=kT-faktorn på pV-form, genom att »trixa med kombinatoriska differentialer» typ som ovan

dW = – dU ;

= pdV ;

— Här har ”arbetet” pV »erhållit» digniteten av BÅDE egenenergin (E) för tryckvolym (E=pV) och energin (E) för värmegraden (T) med koefficienten (k), E=kT, via U-formen. Med andra ord — med upprinnelse i ”DåQärNoll” — med resultat i nämnda »smörja»

pV = – opV

och som »göms galant» med »kombinatorisk differentiering» (TYP: Byt ut registreringsskyltarna på Hyrbilen med JAGMIG [eng. IAMMEI] och testa hur långt du kommer innan du stoppas) enligt

p dV = – o dp V

så SÄKERT inget vanligt trottoarfolk hänger med.

— Därmed, på den erhållna Gammareferensens konto:

:

pV = kT = hρaV= h(m/V)aV = h(m)a ;

Atmosfäriska hydrotrycket p ska här egentligen skrivas negativt eftersom trycket avtar med växande höjd h. Vi frånser dock den delen här då sammanhanget i vilket fall är klart:

pdV = kdT = dhρaV= dh(m/V)aV = dh(m)a

= –Vdp / γ ; Gammareferensen som ovan;

Vi har nämligen också, se CpMinusCv, att

γ = Cp / Cv ;

Cp = γCv = k/m ; J/°K/KG Värmekapaciteten per KG betyder värmekapaciTIVItet [eng. specific heat].

k = m γ Cv ; Värmekapaciteten, J/°K:

pV = kT ; Allmänna gaslagen:

= m γ Cv T ;

pV/ γ = m Cv T ;

Eller som Wikipediaartikeln, citatet ovan, uttrycker saken (”enligt termodynamikens första huvudsats”) i differentialer:

”m cv dT – Vdp / γ = 0” ;

Vdp / γ = m cv dT ;

För själva härledningen till hur hydrostatiska lufttryckets temperaturSITE ändras med höjden över marken (upp till max ca 10 KM grovt)

— i modern akademi, eng. ”Dry Adiabatic Lapse Rate”, sv. TorrLuftsAdiabatiskaFallTakten [Wie | LiftedCon | Schlatter2009 s21ö | m.fl.]

— behöver vi alltså inte »krångla till det i onödan»; Vi kan DIREKT använda det ordinära matematikledets tillståndsvariabler från allmänna gaslagen enligt

pV = kT = hρaV= h(m/V)aV = h(m)a

för att ur andra och sista leden få

kT = h(m)a

med

T/h = a/(k/m)_LUFT

= (9,81 M/S²)/(Cp~1000 J/KG°K) ;

Γ_d ~ 0,0098 °C/M ; Γ grek. Gamma.

ATT vi SEDAN också via pV-formens differentialekvivalenter

pdV = kdT = dhρaV= dh(m/V)aV = dh(m)a

finner ekvivalens med Gammareferensens differentialform, som ovan,

pdV = –Vdp/γ

betyder emellertid INTE i relaterad fysik och matematik att DEN ekvivalenten kopplar till den moderna akademins ”adiabatisk”, typ den konventionellt benämnda s.k. ”adiabatiska gaslagen”, förtydligandet ovan [‡].

— Som framgår i härledningen [EkoGh] till den relaterade fysikens motsvarande benämning

FRIHETSgradsGASLAGEN — GES — MEKANISKA gaslagen

pV^γ = K ; J/°K: γ = (o+2)/o

pVT-parametertransformation för värmekapacitet (k, J/°K) MED TILLHJÄLP AV EN YTTRE ANORDNINGS MEKANISKA ARBETE (rörlig kolv i sluten cylinder) [Dieselmotorn] för en gas med given frihetsgrad, på motsvarande allmänna gaslagens ekvivalenter

(pV/T)₀ = k = (pV/T)₁ ; Energikomplexa gaslagen

finns ingen sådan koppling i relaterad fysik.

— Det betyder exakt samma samband i gruvligt skilda betydelser:

MAC:

pV^γ = K ; J/°K: γ = (o+2)/o

Adiabatic Gas Law, eller Poisson’s Equation

:

Γ_d ~ 0,0098 °C/M

Dry Adiabatic Lapse Rate

:

TNED:

pV^γ = K ; J/°K: γ = (o+2)/o

Energikomplexa gaslagen

:

Γ_d ~ 0,0098 °C/M

Hydrostatiskt fasta Temperaturnivåerna med varierande höjd — för torr luft, »Dry HYDROSTATIC lapse rate»

Eller mera komprimerat sammanställt:

MAC: Adiabatic Gas Law, eller Poisson’s Equation

pV^γ = K ; J/°K: γ = (o+2)/o

TNED: Energikomplexa gaslagen

:

MAC: Dry Adiabatic Lapse Rate

Γ_d ~ 0,0098 °C/M

TNED: Hydrostatiskt fasta Temperaturnivåerna med varierande höjd — för torr luft, »Dry HYDROSTATIC lapse rate»

ATFTsf, ATFTex

Eller kortare:

— I relaterad fysik existerar, av ovan redovisade skäl, ingen som helst koppling till det etablerade begreppet ”adiabatisk” och dess centralt upprinnande kärna ”DåQärNoll”, och därmed heller ingen substans i det etablerade begreppet ”adiabatisk” för de hydrostatiskt fasta och fixa temperaturnivåerna inom Jordtroposfären, och heller därmed inte deras etablerat påstådda STYRNING [CentralAdia] av den uppåtstigande uppvärmda markluftens AVKYLNING [ATFTrel].

— Sambanden är som sagt OK. Men beskrivningen av innebörden i MAC är, uppenbarligen, inkonsistent mot den relaterbara naturfysiken.

DABL, ATFTex

Därmed finns heller inte längre något spår kvar att relatera beträffande den moderna akademins etablerade begrepp ”adiabatisk”, här särskilt angående ”adiabatic lapse rate” [Wie | LiftedCon | Schlatter2009 s21ö | m.fl.]:

konv. (eng.) [dry] adiabatic lapse rate, sv. [atmosfäriska][torr-] adiabatiska [temperatur-] falltakten [här förk. ATFT, Atmosfäriska Temperatur Fall Takten].

— Som tidigare noterats [Jordatmosfären] [PDAS], gäller den entydiga Tpρ-reduktionen med växande höjd bara upp till max 10 KM grovt, alltså inom troposfären endast.

Jämför:

Missuppfattat:

— Det konventionellt benämnda Dry adiabatic lapse rate betyder motsvarande

luftens naturliga avsvalningstakt från Jordytans markskikt och uppåt via växande höjd eller altitud (h).

Relaterat:

— Det konventionellt benämnda Dry adiabatic lapse rate betyder motsvarande

Falltakten i Jordluftens hydrostatiskt fasta och bestämda temperaturnivåer från Jordytans markskikt och uppåt via växande höjd eller altitud (h) — med ordet, begreppet, eller TERMEN ”adiabatiskt” grundad på den moderna akademins ”DåQärNoll” i ”Termodynamikens första huvudsats”, och som saknar relaterbar fysisk substans, och därmed termen ”adiabatisk” att förstå som irrationell i relaterad fysik.

ATFTekv, ATFT

— Sambandsformen med HYDROISOTERMERNA T/h=a/(k/m)_LUFT framgår alltså direkt ur hydrotryckets grundform [ELLER som tidigare noterats med samma resultat enklare direkt från värmeenergins ekvivalent E=kT=mah; T/h=ma/k]:

— Vi använder då sambandet för hydrostatiska trycket (p=hρa) och allmänna gaslagen (pV=kT) enligt

p = hρa = h(m/V)a = kT/V ; De bägge sista leden ger ett hydrostatiskt volymOberoende:

T/h = (m/k)a ; Eller direkt från E=Fh=kT=mah som ger T/h=a/(k/m):

= a/[k/m = Cp ~ 1000 J/KG°K för luft vid STP ] ; a standard = 9,81 M/S² vid Jordytan:

För Cp ochCv, se särskilt CpMinusCv.

Se även Cp och Cv särskilt i

Wikipedia Specific heat, Thermodynamic relations and definition of heat capacity [2014-04-15],

http://en.wikipedia.org/wiki/Specific_heat

Cp är tryckbaserade (p) värmekapacitiviteten för luft [ca 1000 J/KG°K, ref. Karlebo HANDBOK s76 Tabell 4.2 Utg.12 Esselte 1977].

Γ_d ~ 0,0098 °C/M ; Konv. [dry] adiabatic lapse rate: Γ, grek. Gamma

Jordtroposfärens hydrostatiskt relaterade temperaturfalltakt räknat från marken och uppåt — till max 10 KM [PDAS]

Jämför PDAS standardiserade troposfärvärde: 0,0065 °C/M [luftfuktighetsbaserat]. Se vidare i k/m-stycket nedan [‡].

— Se även samma uppgift i SchlatterAtmosphere2009 Lapse Rate s21ö.

Hur vet vi att sambandsformen med HYDROISOTERMERNA T/h=a/(k/m)_LUFT INTE innehåller väsentligt förenklade former?

— MED REFERENS TILL en fast och bestämd referensvolym (1M³) — som dock INTE innesluter eller hindrar luftmassan, utan bara ser till hur denna förändras inom aktuella referensrummet — ändras både den givna fast markbaserad luftmassan (m) och gaskonstanten k med växande höjd (h) från marken: m avtar med avtagande täthet (ρ), och likaså fundamentala gaskonstanten k=p/T med konstant V=1M³. Se särskilt hur k-variationen ser ut i troposfären i k/k₀-grafen. Se även alla samlade i Slutgraferna.

RdivUref

Både PDAS tabellvärden och Slutgraferna som matchar dessa [PDAS p/ρT Tabell6 i Blixt2014.ods] visar att kvoten k/m uttrycker ett volymOberoende: k/m=pV/TρV=p/Tρ=R/U är en konstant — alla variabler till trots, hTpρk, och helt enligt Slutgrafernas samband och deras överensstämmelse med PDAS tabelldata:

k/m = p/Tρ

= konstant med T = (T₀ – h0,0065°C/M)

= R/U = (8314,9148 J/KG°K)/(28,952127)

= 287,1953 J/KG°K

~ 287,20 J/KG°K

; Konstant atmosfärisk värmekapacitivitetstal upp till10 KM

Sambandsformerna bakom detta resultat [PDAS standard] skulle motsvara en falltakt

Γ = 0,0341573°C/M — en betydande annorlunda värdeform än den ovan erhållna. Svaret ges i mer detalj:

— I SPECIFIC HEAT- tabellen på The Engineering Toolbox [2014-04-15]

http://www.engineeringtoolbox.com/specific-heat-capacity-gases-d_159.html

hittar vi igen det värdet i kolumnen INDIVIDUAL GAS CONSTANT för Air: Cp – Cv = 287 J/KG°K.

— FORMEN för k/m ovan är alltså i så fall EXPLICIT CpMINUSCv.

— Dessa detaljer faller [ännuApr2014, delvis] utanför den här framställningen: vi antar dem tills vidare — och konstaterar samtidigt att FLERA underförstådda parameterformer finns med i bilden [som grundlägger de etablerade tabellverken] men som inte explicit redovisas för oss.

Saken — HYDROISOTERMERNA T/h=a/(k/m)_LUFT — handlar tydligen inte om någon »värmeläckningstakt» från typ uppstigande luft, utan den temperatur som den uppåtstigande uppvärmda markluftens kallning (JAVKbasic) stannar VID för varje specifik höjdnivå, dock inom troposfären (max 10 KM);

Därmed är den konstanta differensen Cp – Cv = 287,20 J/KG°K bekräftad (eller stadfäst) inom varje specifikt JordTroposfäriskt Hydrostatiskt Temperaturområde — HYDROISOTERMERNA T/h=a/(k/m)_LUFT — för luftens del (U=28,952127) för samtliga tropoatmosfäriska tryckskikt.

— Men vilken INNEBÖRD har egentligen den sambandsformen — altitudHYDROISOTERMERNA T/h=a/(k/m)_LUFT?

— Därför att ÄVEN om vi tar bort Solen ur värmeekvationen, är det tydligt att sambandsformen fortfarande gäller som en fast egenskap för Jordkroppen, till och med och tydligen i härledningen, helt oberoende av Jordrotationens inverkan (»blandaren» som ger dag-nattAtmosfäriska medelglobala TroposfärKlimatsystemet).

— T/h-formen har uppenbarligen ingenting att göra med (Solen PÅ igen) den uppåtstigande luftens avsvalningstakt. T/h-formen är uppenbarligen bara ett fast »GALLER» som luften PASSERAR, mer eller mindre: en för varje specifik nivå fast omgivningstemperatur som luftkallningen i uppvägen kommer att stanna på lokalt och anpassa sig till.

— Med andra ord, samma PRINCIPIELLA OMGIVNING som gäller i det enkla köksexperimentet i JAVKbasic: verklig avsvalningstakt för uppvärmd fuktig uppåtstigande luft: 122°C/M/S. Det var något helt annat det.

TAI, tyngdkraftsaccelerationens inverkan

Tyngdkraftsaccelerationen (a=9,81 M/S² vid Jordytan) har i sig en högst marginell inverkan som variabel inom troposfärens område. Räknat med ekvatorsradien Re=6,378 T6 M som ideal sfärisk Jordradie och taget 10 KM upp ges respektive

a(Re) = Gm/(Re)² = (6,67 t11 JM/[KG]²)(5,975 T24 KG)/(6,378 T6 M)²

= 9,7970362 M/S² ;

a(Rh) = Gm/(Re+10.000M)²

= 9,7663869 M/S² ;

a_h/a_e = 0,9968715

~ 0,997 ; Förhållandet tyngdkraft tropopausen [h=10KM] och markytan

Den differensen är alldeles för liten för att ha någon praktiskt betydelse i de allmänna atmosfäriska grovräkningarna där globala årsmedelvärden i vilket fall uppvisar betydligt större variationer (minst flera procent).

— Med andra ord: atmosfäriska temperaturHYDROSTATISKA falltakten [AThFT] — inte den uppåtstigande markluftens kallningstakt (JAVKbasic) — FÖREFALLER, verkligen, baseras på en (för alla troposfäriskt meteorologiska, internationellt flygtekniska, praktiska ändamål nära exakt) konstant, icke föränderlig tillståndskonstant, T/h-formen. MEN, som däremot INTE har någon koppling till temperaturläckaget i uppstigande uppvärmd markluft [JAVKbasic | ATFTrel | VLAFS].

— En etablerad webbkälla (Apr2014) som klart uttrycker den detaljen eftersöks (här) löpande men har ännu ej påträffats.

JAGVH, JordAtmosfäriska Gastryckets Variation med Höjden — Sambandsformerna — Slutgraferna

GASTRYCKETS VARIATION ÖVER JORDYTAN

— inom troposfären

OM det finns någon »enkel sambandsform» som beskriver DEN NATURLIGA VARIATIONEN i ämnet Jordytans närmaste klimatsfär (troposfären) — vårt allmänna intresse för typ Blixturladdningens Fysik [molnbildningen, naturligtvis] — blir det mycket enklare att SEDAN, vidare, få en RENT PRAKTISKT FÖRANKRAD BILD och uppfattning för de vidare PRAKTISKA referenserna:

— Vi har — då — i varje fall NÅGON koll på vad vi håller på med. Följande genomgång har visat sig leda till en sådan översiktsbild. Jämförelser görs löpande med PDAS internationella atmosfäriska tabelldata.

HydroTrycket, JAGVH

Med hjälp av sambandet för hydrostatiskt tryck

Hydrostatiska trycket [Se även i Hydrostatiska tryckets elementära ekvation]

p = hρa från

p = F/A = ma/A = mah/Ah = mah/V = h(m/V)a = hρa , = h(m/[kT/p]=pm/kT)a = hp(U/RT)a

Jämför motsvarande konventionella grunduttryck i Schlatter2009 s8n.

beskriver tyngden (F) av en vätskepelare (gen. inkompressibelt medium) med höjden h över en yta (A) för en vätska med tätheten ρ och i ett Galileiskt kraftfält (rum med en och samma tyngdkraftsacceleration a överallt).

— Tangensformen dp/dh = ρa utpekar en variationsform som växer positivt [ / ] med växande h-värde: hydrostatiska trycket (p) växer positivt med vätskepelarens höjd (h).

— För ett motsvarande atmosfäriskt gastryck (hydrostatiska sambandet antaget utan vidare: gas är högeligen kompressibel, och därmed är vi redan från början, här, inne på vissa äventyr), räknat från marknivån, skulle istället p AVTA [ \ ] — dp/dh = –ρa — med växande h, så att vi får allt lägre tryckvärde (negativ tangensform) med växande höjd — vårt naturliga Jordatmosfäriska fall: ju längre ut från Jordytan, desto mindre gas kvarhålls av Jordgravitationen (a-värdet måste då också, egentligen, underkastas någon form av integration), och desto lägre tryck.

— Utvecklingarna nedan ansluter till en del redan etablerade exempel på webben (Apr2014), referenser ges längre ner, formalian är densamma men här i explicita noter.

— Med fortsättning från ovanstående grundgenomgång, samt tillsammans med allmänna gaslagen (pV=kT) — som också strängt taget bara gäller för ett begränsat homogeniserat gasområde, och därmed ytterligare en grov förenkling — ges följande samband:

Tryckvarianten, JAGVH

dp/dh = ρa ; Hydrostatiska tryckformens variant — trycket p avtar med växande h: negativ derivata:

;

pV = p(m/ρ) = kT = (ρV/U)R·T ; R allmänna [konv. universella] gaskonstanten = 8314,9148 (J/°K)/KG = k/Nu

; Notera också R-formen här mot den, se R* nedan, i modern akademi

p = (ρ/U)R·T ; Uluft = 28,952127

ρ = pU/RT ; ρ anger lokala [hydrostatiska idealt inkompressibla material-] gastätheten:

dp/dh = paU/RT ; aSTANDARDJordytan 9,81 M/S²

dp/p = aU/RT · dh ; Ua/R = 0,0341579 M^–1: Täthetsfaktorn helt eliminerad:

Se även utvecklingen till pSVP-sambandet i SVPintegralen — alldeles samma grundform och lösningstyp:

; Varianten dy/dx = y’ = f (x)(y) är en FOIVEVK

[en FörstaOrdningensInhomogenaVariant med EnVariabelKoefficient]

:

y’ + f (x)(y – A) = 0 ; FOIVEVK-varianten, allmän form: dy/dx = y’ = f (x)(A – y)

med differentialekvationen

dy/(y – A) = – f (x) · dx

med lösningen

ln (y – A) = – F(x)

och exponentformen

y = A + C e^–F(x)

med A=0, y=p och x=h; Här är emellertid f(h) en ÖPPEN fråga: flera olika sätt finns:

p = C e^–F(x) ; Koefficienten C får enheten Pascal och därmed en tryckkoefficient:

= p₀e^–F(x) ; F(x=h): p₀ gäller vid Jordytan — eller annan referensnivå under h:

–F(h) = – ∫ aU/RT · dh ;

För att 1/T-integralen ska fungera som bestämd integral måste T-formen ha fasonen (b±T/c)

— I annat fall urartar funktionen med obegränsat värde vid T=0;

= – aU/RT · h ; Integralens fullständiga lösning:

= – h · aU/RT

= – h · aU/R(b±T/c)

= eEXP ; e-exponenten:

BILDORIGINAL Apr2014 — Varken InternetExplorer, GoogleChrome eller MozillaFirefox webbläsarna förmår återge originalet: alla förvanskar originalet och gör det mer eller mindre oläsligt. Endast typen TimesNewRoman storlek 9 verkar ge likvärdiga presentationer:

p = p₀e^{–hUa/RT = –h(0,0341579)/T}

Hydrostatiskt [idealiserat grovt förenklade] atmosfäriska trycket från nivån p0

Förenklade tryckformen med fast T-värde

Sätts ett fast och bestämt T-värde in i °K lika med Ua-värdet 284,02036 i M/S³, som betyder T = 10,870365 °C, fås en enklare form

BILDORIGINAL Apr2014 — Varken InternetExplorer, GoogleChrome eller MozillaFirefox webbläsarna förmår återge originalet: alla förvanskar originalet och gör det mer eller mindre oläsligt. Endast typen TimesNewRoman storlek 9 verkar ge likvärdiga presentationer:

p = p₀e^–(h/R)(M/S²°K)

Tryckformen närmast ovan visar sig ha viss passande koppling till etablerade former, se inlagd jämförelse i Wikipedia, Atmosphere of Earth Mar2014.

— Vi ska här försöka ge en något mera med internationella atmosfäriska tabelldata [PDAS] överensstämmande matematisk form för atmosfären upp till 10 KM, och fortsätter därför (komprimerat) som följer.

Vi studerar först den öppna frågan om f (h):

— f (h) [»funktionen för h»] får uppenbarligen INTE avse tyngdkraftsaccelerationen a=Gm(R+h)^–2 som variabel (R fasta Jordradien); används integralformen för det fallet [–Gm(R+h)^–1] ges galna värden.

— Tyngdkraftsaccelerationen a ska — liksom i grundfallet ovan i hydrostatiska trycket p=hρa — tydligen avse EN bestämd referensnivå (markytan 9,81 M/S²).

Jordsfärens avplattning är 0,0034 [BAs173.Tabell10.1, ”(Re – Rp)/Rp” 0,0034, Re 6378 KM, Re ekvatorialradien Rp polradien]:

Re = 6,378 T6 M ; största: Jordradien vid ekvatorn — troposfären till 18 KM

Re/Rp – 1 = 0,0034 ;

Re/Rp = 1,0034 ; Förhållandet mellan Ekvatorial/Polradierna Jorden:

= (6,378 T6 M)/Rp ;

Rp = Re/1,0034

= 6,3563882 T6 M ; minsta: Polradien — troposfären till 10 KM

Re – Rp = 21.611,721 M ; Jordekvatorns radie är drygt 20 KM större är Polradien:

Motsvarande förhållande för idealt Jordsfäriska tyngdkraftsaccelerationen a:

a(Rp)/a(Re) = Gm(J)/Rp² / Gm(J)/Re² = (Re/Rp)² = (1,0034)² = 1,0068115 ~ 1,0068

Största a-skillnaden mellan max troposfärhöjd Rt=Re+18KM och minsta Jordradien Rp:

a(Rp)/a(Rt) = Gm(J)/Rp² / Gm(J)/Rt² = (Rt/Rp)² = (1,0062318)² = 1,0125024 ~ 1,0125

Resultatbild:

— ÄVEN om vi räknar internt med variationer i tyngdkraftsaccelerationen över hela troposfäriska intervallet, hela Jordlokalen totalt, blir skillnaden i de olika värdena som använder a-faktorn max 1,25% ~ 1,3%. Den differensen är alldeles för liten för att ha någon övergripande avgörande betydelse i grovräkningarna (i denna presentation) då lokala fluktuationer i troposfären i vilket fall (ofta) är betydligt större än enstaka procent (sett till dagliga och årliga variationer över olika regioner).

— Jämför uppgiften för »troposfärens utsträckning»: 10KM / 18 KM ~ 56%: Standard Atmosphere använder en [för våra nordligare regioner] internationellt fastställd (»normaliserad») atmosfärisk modellbild eller norm med nominella troposfärens övre gräns ca 10 KM (och som används av olika flygcertifierade inrättningar tillsammans med [numera datorstyrda] justeringsprotokoll i olika regioner för t.ex. den internationella lufttrafiken och associerade lokala markkontroller).

— I andra ord: Vi kan HELT bortse ifrån lokala ändringar i a-faktorn, och generalisera sambandsformerna med det internationella standardvärdet för a på Jordytan (~9,81 M/S²).

— f (h) [»funktionen för h»] får emellertid — och ska i slutänden — uppenbarligen också innefatta T-faktorn

[typ T=T₀ – hk med k som FallTakten i T]: T avtar med höjden (h) upp till troposfärens övre del (tropopausen, ca 10 KM), vilket också den bestämda integralformen ovan redan antytt.

— Det betyder i så fall att integralformen för funktionen till h — F[h] — eventuellt måste skrivas på flera variabler med (möjliga) interna integraler. Vi genomför inte den analysen här, utan söker istället en matchande slutgraf i som bara ska ha till uppgift att hålla jämna steg med (naturligt experimentellt observerbara jämförliga) tabelldata.

THTB, Tryckformens HöjdTemperaturBeroende

Det är tydligt att T-formen BÖR avta med stigande höjd, i varje fall upp till troposfärens övre del (grovt 10 KM, ref. PDAS).

— Olika webbkällor [Mar2014] redovisar olika LINJÄRA temperaturminskningar i Jordatmosfären med växande altitud (höjd över marken), typ

T[LS], LapseRate — FallTakten, LS min sv. förk. för »fallet», LapSe

T(LS) = 0,00 30 | 60 | 65 | 70 |°C/M ; Se även i Schlatter2009 s21ö:

T = (T₀ – hk) ;

k anger den s.k. [Temperatur-] FallTakten , eng. LapseRate, konv. ofta bet. Γ grek. Gamma;

Se även i ATFT.

Sätter vi in T-formens del först får vi med (a=9,81M/S²)(U=28,952127)/[R=8314,9148 (J/°K)/KG]=0,0341579 °K/M

–eEXP = h(0,0341579)/(T₀ – hk) ; EXP betyder exponenten till e:

= (0,0341579)/(T₀/h – k)

eEXP = –(0,0341579)/(T₀/h – k) ; T₀ = 288,15°K = 15°C Numera ofta alternativt använd standardtemperatur vid Jordytan [STP]

= (0,0341579)/(k – T₀/h) ; Vi testar en återderivering för att se hur originalet kan se ut:

Dn (k – T₀h^–1)^–1 = (–)(k – T₀h^–1)^–2(0 – [–]T₀h^–2)

= –(k – T₀h^–1)^–2(T₀h^–2)

= –T₀/h(k – T₀/h)²

Vi ser att variantformen i original tydligen blir (väl) komplicerad att försöka beskriva på reguljär matematisk-fysikalisk form. Vi lämnar den delen här, frånsett deriveringen ovan som antyder vartåt ursprungsformen lutar.

Med den T-justeringen finner vi direkt en nära passning med StandardAtmosphere höjddata, se graferna (GRAFp1) från TRYCKET med sambandet för GRAFp1.

T[LS]-variationen

Med ytterligare en justering för k-faktorn

k := T(LS)n^–h ; T(LS) från PDAS internationellt atmosfäriska tabelldata upp till 10 KM är 0,0065°C/M

Prövning för n-basen i PDAS-matchning visar n=1,000067:

ges

eEXP = (0,0341579)/(0,0065·1,000067^–h – T₀/h) ; T0 i °C:

Se dessa resultat i Slutgraferna med Jämförande PDAS-data: precisionen mot PDAS tabelldata ligger som sämst på 98% — så nära »fullträff» vi kan önska.

Jämförande grafer nedan visar först hur sambandet [‡] i den helt förenklade p-formen matchar etablerade variationsformer för atmosfäriska trycket (Wikipediaartikelns gröna graf nedan höger). Därefter visas hur precisionen ökar mot PDAS tabelldata med här härledda sambandsformer enligt ovan givna genomgångar.

Wikipedia, Atmosphere of Earth Mar2014

Graf [Unit60p]

(1/10000)(105357.35)è'–(x10000)/8314.9148

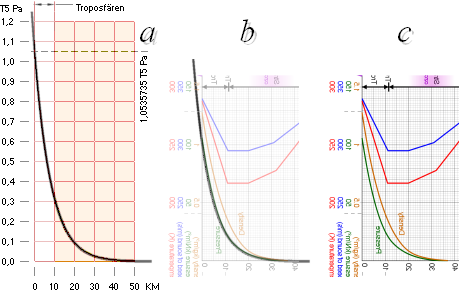
a: resultatgrafen ovan; b: inpassad till jämförelse med Wikipedias gröna atmosfäriska tryckgraf, länken nedan, separat i c [ingen redovisad sambandsform verkar finnas [2014-04-01]], roterad +90°, spegelvänd kring vertikalaxeln

http://upload.wikimedia.org/wikipedia/commons/9/9d/Comparison_US_standard_atmosphere_1962.svg

från Wikipedia Atmosphere of Earth, Physical properties

NOTERING 1: h-värdet är i praktiken begränsat till max grovt 10 KM, alltså upp till MAX troposfären inkluderat — på grund av Jordatmosfärens sammansatta dag-nattFysik: Jordrotationen tillsammans med Solvärmen åstadkommer skiktade atmosfäriska lager med växlande egenskaper. Se även översikt i Jordatmosfären.

Formen ovan för godtyckliga avstånd h från markytan beskrivs konventionellt bl.a. i Wikipedia

Wikipedia — Barometric formula DERIVATION [2014-03-26]

http://en.wikipedia.org/wiki/Barometric_formula

med formen

P =P₀e^–Mgz/R*T

M ”Molar mass of Earth's air (0.0289644 kg/mol)”; R* ”Universal gas constant for air: 8.31432 N·m/(mol·K)”

g som a=Gm/r²: z som h

och i

HYPERPHYSICS — The Barometric Formula [2014-03-26]

http://hyperphysics.phy-astr.gsu.edu/hbase/kinetic/barfor.html - c2

med formen

P_h =P₀e^–mgh/kT

; m ”mass of one molecule”; k ”Boltzmann’s constant”;

g som a=Gm/r²

Men var hittar man experimentella värden att kolla resultaten mot?

Det verkar (1Apr2014) helt hopplöst på webben att få tag på någon webbkälla som redovisar eller bara berättar om VERIFIERANDE EXPERIMENTELLA RESULTAT. Wikipedia är hopplöst fall. Vad man däremot hittar en uppsjö av är typen KidsExperiments och ÖlburksExperiment och ExpertTabellerUtanReferenser och ComputedModelData.

— Efter visst letande hittar vi så äntligen en på USATODAY

UsaTodayRef

STANDARD ATMOSPHERE TABLES 2005 [2Apr2014-04-01]

http://usatoday30.usatoday.com/weather/wstdatmo.htm

”The standard atmosphere is based on mathematical formulas that reduce temperature and pressure by certain amounts as altitude is gained. But, the results are close to averages of balloon and airplane measurements at various altitudes.”;

— Källan anger sin datakälla från Aerodynamics for Naval Aviators; ett omfattande PDF-dokument från 1965 för jaktplansflyg (stridspilotutbildning); På sidan 5 finns en höjdtabell, f.ö. den enda i dokumentet, ICAO STANDARD ATMOSPHERE.

— Webbsökning på ”standard altitude table” leder till en nyare källa (med samhörande värden) med (mera noggranna) tabellvärden upp till 30KM,

The Engineering Toolbox — INTERNATIONAL STANDARD ATMOSPHERE

http://www.engineeringtoolbox.com/international-standard-atmosphere-d_985.html

— Men källan redovisar varken källform eller datum (fortfarande vanligt i amerikanska sammanhang).

PDAS StandardAtmosphereData, se även Schlatter2009

— En (ännu) mera precis tabell, upp till 86 KM i 2KM-intervall, finns på

Public Domain Aeronautical Software (PDAS) — A SAMPLE ATMOSPHERE TABLE (SI UNITS)

http://www.pdas.com/atmosTable1SI.html

från U.S. Standard Atmosphere 1976.

— Information om olika institutionellt fastställda standarder för Jordatmosfären finns på

@INTERNET Wikipedia International Standard Atmosphere [2014-04-01]

http://en.wikipedia.org/wiki/International_Standard_Atmosphere

Med de mera experimentellt fastlagda uppgifterna kan nu ev. anslutande grafiska former prövas mera framgångsrikt. Se utvecklingen av de samband som här har använts från Tryckvarianten.

Tabellvärdena nedan från StandardAtmosphere med angivna grafer.

Med en ytterligare prövning för maximal passning ges ytterligare efterföljande samband med jämförande tabelldata och grafer:

TRYCKET:

EM

Experimentellt matchande:

Tabelldata från UsaToday

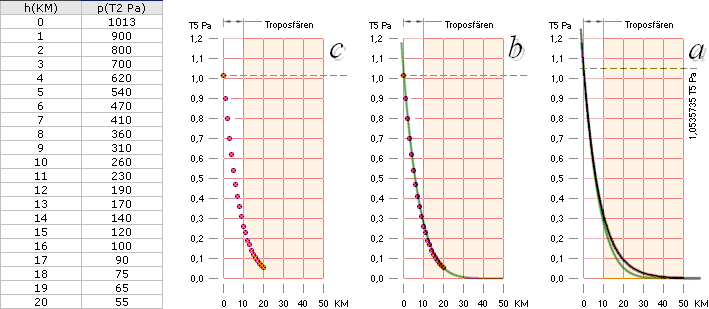
a: föregående resultatgraf [‡], svarta, tillsammans med den modifierade T-grafen, gröna GRAFp1 nedan;

b: tabelldatat, experimentellt matchande värden med inprickade grafiska punkter tillsammans med gröna grafen;

c: tabellvärdena från USATODAY-källan — som ska föreställa de mera tillförlitliga data för experimentell orientering.

— Beteckningen T2 Pa för 100-tal Pascal = 100-tal N/M².

GRAFp1 — mera exakt i Slutgraferna

Graf [Unit60p] — gröna grafen

(1/10000)(101300)è'(341.579)/(30–288.15/x) ; = (1/10000)(101300)è'(0.0341579)/(0.0030–288.15/x10000)

Se utvecklingen i e-exponenten från T(LS).

BILDORIGINAL Apr2014 — Varken InternetExplorer, GoogleChrome eller MozillaFirefox webbläsarna förmår återge originalet: alla förvanskar originalet och gör det mer eller mindre oläsligt. Endast typen TimesNewRoman storlek 9 verkar ge likvärdiga presentationer:

p = 101300e^{0,0341579/(0,003 – 288,15/h)}

Gröna grafens samband — nära överensstämmande med experimentella höjdvärden från ballonger och flygplan enligt USATODAY-webbkällan ovan, tabellvärdena.

— Nära praktiskt experimentellt samhörande atmosfäriska tryckvärden med växande avstånd från marken [tabellvärdena och grafvärden stämmer här hyfsat upp till i 20 KM].

NATURKUNSKAP: Det blir (naturligtvis mycket) mera intressant att arbeta med ämnet om man kan närma sig naturordningen. Med ovanstående [atmosfäriska tabelldata] VET vi att sambandet verkligen har i varje fall någon motsvarande naturlig förankring.

Efter ytterligare justering och normalisering — T₀=0°C=273,15°K och p₀=101325 Pa normaliserar för STP — visar det sig att grafvärdena med vissa smärre mellanliggande överhopp i den nedre delen 10-20 KM kan fås att överensstämma ända upp till UsaToday-tabelländen 35 KM:

BILDORIGINAL Apr2014 — Varken InternetExplorer, GoogleChrome eller MozillaFirefox webbläsarna förmår återge originalet: alla förvanskar originalet och gör det mer eller mindre oläsligt. Endast typen TimesNewRoman storlek 9 verkar ge likvärdiga presentationer:

p = 101325e^{0,0341579/(0,00123 – 273,15/h)}

NOTERING: För att inte få DIVISION MED NOLL för h=0 måste en decimalform läggas till i Kalkylen [i mitt Kalkylkort tillagt h+0,00000000001 PDASp Tabell6 Blixt2014.ods].

Graf [Unit60p] — gröna grafen

(1/10000)(101325)è'(341.579)/(30–273.15/x)

En mellanliggande som också plockar 10-20 KM-intervallet, men i gengäld missar slutdelen fram till 35 KM, fås med T-koefficienten 0,00123 ersatt av 0,002. Skillnaderna är alltså små.

(1/10000)(101325)è'(341.579)/(20–273.15/x)

TÄTHETEN:

Med samma databas som i UsaToday men i intervall om 2KM (och med mera noggranna värden) ges tabelldata för luftens täthet från PDAS (Public Domain Aeronautical Software) samstämmigt med sambanden nedan:

ρ = pU/RT ; T= T₀ – h(t°C/M)

= (U/RT)·101300e^{0,0341579/(0,003 – 288,15/h)}

= [(28,952127)/(8314,9148 (J/°K)/KG)(288,15°K – h0,0065°C/M)]·101300e^{0,0341579/(0,003 – 288,15/h)}

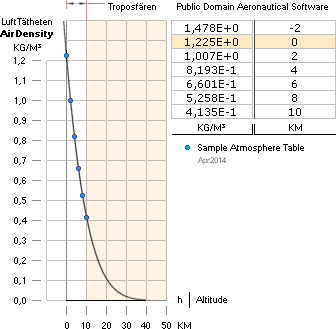
Graf Uni20p

10[28.952127/(8314.9148[288.15–0.0065(x10000)])](101300)è'(0.0341579)/(0.0030–288.15/x10000)

Kurvan stämmer med tabellkällan endast upp till max 10 KM med T(LapseRate)=0,0065°C/M. Med vissa smärre differenser får man bättre närmevärden för atmosfären även över 10KM-gränsen via lägre T(LR), typ 0,003°C/M (kurvfoten blir snävare med lägre täthetsvärden).

— Men i den skala som täthetsgrafen visas ovan är skillnaden mellan de olika värdena mot tabelldatat så snäv att den knappast alls är märkbar.

TEMPERATUREN:

Wikipedia (Atmosphere of Earth, Physical properties) visar en graf med ett linjärt temperaturfall på ca 0,007°C/M upp till ca 10 KM. Andra etablerade källor ger liknande värden; PDAS-källan ansluter för sin del till ett värde 0,0065°C/M (orangea linjen med datapunkter nedan) upp till 10 KM-nivån. Grafen nedan ger en orientering med PDAS-tabelldata inprickade till jämförelse med grafer för de bägge nämnda T(LapseRate)-värdena.

— Se även orienterande höjdskalor i Jordatmosfären.

PDAS, LapseRate 0,0065 °C/M — Se även Schlatter2009 s21ö

Standard Atmosphere

T = T₀ – h(t°C/M) ; h anger höjden över marken [Altituden]

t°C/M anger T[LapseRate]-värdet, sv. FallTakten

————————————————————————————————

Graf Unit20p

(1/15)[15–0.0065(x10000)]

PDAS-källans temperaturvärden i tabellutdraget ovan ger upp till 10KM en T[LS]-form 0,0065°C/M.

— Offsetvärdet på +15°C [heldragna svarta/orangea] anges [numera] ofta som standardvärde mot tidigare 0°C [svarta streckade] vid havsytan [STP].

— Falltaktsvärdet I TORR, IDEALT ICKE VATTENÅNGSHALTIG, luft är altitudHYDROTRYCKSisotermerna T/h=0,0098°C/M

—————————————————————————————————————————————

— Som tabellvärdena visar, finns ett (definitivt) temperaturreglerat GRAFISKT STOPP vid nivån 10 KM som omöjliggör varje vidare HOMOGEN temperaturfunktion — raden med tabellvärden som visar konstant (–56,55°C) från 12-20 KM.

— Ser vi emellertid till HUR typgrafen via samma databas för TRYCKET ser ut i passningen, är det JUST på kredit av T(LS)=0,003°C/M som den grafen visar god överensstämmelse — t.o.m. ända upp till 20 KM.

— Den, som ovan, fristående atmosfärdatagrafen visar tydligt avvikande T(LS)-värden (omkring dubbla) med referens till hur samma faktor fungerar tillsammans med de andra faktorer som ingår i den tabellmatchande beräkningen för tryck och täthet.

— Det är uppenbarligen en MODELLDETALJ som vi (tills vidare) får leva med OM vi vill ha någotsånär hyfsade överensstämmande värden med vad som anses gälla praktiskt (i globala årsmedelvärden) i atmosfären.

— För att RELATERA graferna för TRYCK och TÄTHET — bägge dessa i deras enklaste form använder en helt linjär T(LS)-form: trycket via en egen separat T(LS)-form [THTB], och sedan tätheten som tryckprodukt med en egen särskild T(LS)-form [‡] — blir det alltså tydligt att vi (tills vidare) får tillåta »en viss oordning» med olika T(LS)-former [0,0065 resp. 0,003] — eller att det möjligen finns ännu en (enkel sambandsform) som med lämpliga kombinationer ger ett bättre resultat med samma T(LS)-former. I vilket fall står det klart att avvikelserna är SMÅ upp till 10 KM-gränsen, området vi är mest intresserade av här.

Slutgraferna, alla Tpρ från JAGVH — Aktuella graferna

Vidare utveckling ger slutlig precision — se utvecklingarna från Tryckvarianten

Försök med alternativa grafpassningar via ovanstående »krångliga temperaturInfo» visar sig ge en enkel tillfredsställande Tpρ-lösning i mer eller mindre perfekt matchning mot PDAS-datat, se tabelljämförelse nedan — upp till max 10 KM i god passning (sämst 98%) med PDAS tabelldata upp till 10 KM:

Trycket: Från (GRAFp1)

BILDORIGINAL Apr2014 — Varken InternetExplorer, GoogleChrome eller MozillaFirefox webbläsarna förmår återge originalet: alla förvanskar originalet och gör det mer eller mindre oläsligt. Endast typen TimesNewRoman storlek 9 verkar ge likvärdiga presentationer:

p = 101300e^{0,0341579/(0,003 – 288,15/h)}

(1/10000)(101300)è'(0.0341579)/(0.0030–288.15/x10000)

till

BILDORIGINAL Apr2014 — Varken InternetExplorer, GoogleChrome eller MozillaFirefox webbläsarna förmår återge originalet: alla förvanskar originalet och gör det mer eller mindre oläsligt. Endast typen TimesNewRoman storlek 9 verkar ge likvärdiga presentationer:

p = 101300e^{0,0341579/(0,0065/1,000067^h – 288,15/h)}

10KM: Formerna nedan de som använts i grafprogrammet:

(1/10000)(101300)è'(0.0341579)/(0.0065[(1.000067'x10000)'–1]–288.15/x10000) ; OBS gäller bara till MAX h=10KM

1KM:

(1/10000)(101300)è'(0.0341579)/(0.0065[(1.000067'x1000)'–1]–288.15/x1000)

Ändring: Temperaturens falltakt T[LS] med växande höjd ändras svagt: vi börjar från marknivån med T[LS]=0,0065°C/M och slutar vid h=10KM på T[LS]=0,0033°C/M.

;

Tätheten: Från

ρ = pU/RT → pU/R(T₀°C – h0,0065°C/M +273,15°K) ; p/Tρ=p/T(pU/RT)=pRT/TpU=R/U=287,1953 J/KG°K;

till

= p(28,952127)/(8314,9148 (J/°K)/KG)(15°C – h0,0065°C/M + 273,15°K) = pU/RT;

ρ = 101300e^{0,0341579/(0,0065[1,000067^–h] – 288,15/h)}(28,952127)/(8314,9148)(15°C – h0,0065°C/M + 273,15°K)

10KM:

10[28.952127/(8314.9148[288.15–0.0065(x10000)])](101300)è'(0.0341579)/(0.0065[(1.000067'x10000)'–1]–288.15/x10000) ; OBS gäller bara till MAX h=10 KM

1KM:

10[28.952127/(8314.9148[288.15–0.0065(x1000)])](101300)è'(0.0341579)/(0.0065[(1.000067'x1000)'–1]–288.15/x1000)

;

Temperaturen: Samma:

T = T₀°C – h0,0065°C/M | + 273,15°K ; °C | °K ; Fristående temperaturens FallTakt ; OBS gäller bara till MAX h=10 KM

= 15°C – h0,0065°C/M | + 273,15°K ; °C | °K

Jämförande, PDAS — PDAStemp

Kalkylkortet Tabell6 PDAS

Ovan vänster tabellutdrag från PDAS Standard Atmosphere. Ovan höger (Tpρ)ref visar värdena från nedanstående grafers samband, se från Slutgraferna. %-värdena har beräknats (Tpρ)ref / (Tpρ)PDAS. Som vi ser är överensstämmelsen i det närmaste perfekt. Därmed kan sambanden användas för översiktliga beräkningar — men obs bara upp till troposfärens tak, max ca 10 KM.

AktuellaSlutgaferna — HYDROTRYCKET — Jämförande PDAS-data

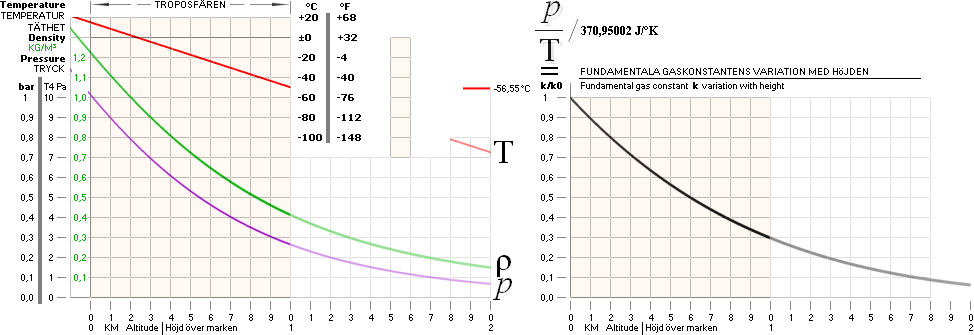
Slutgraferna enligt ovanstående samband [‡] i utvecklingar från Tryckvarianten. Notera att sambandsformerna med PDAS tabelldata ENDAST gäller [normaliserat — i praktiken förekommer stundtals stora variationer över olika regioner och säsonger, även dagtid] upp till max 10 KM — därefter gäller (från 12 KM) konstant temperatur –56,55°C, och därmed brutna samband för tryck och täthet. Föregående exempel (med andra etablerade jämförelser [Wikipedia] [UsaToday]) visar dock att tryck- och täthetsgraferna »ändå fortsätter att stämma hyfsat bra» upp till 20-30 KM. Men temperaturdelen gäller då inte längre.

— Högerkurvan för k/k0 har beräknats som [p/T]/[101325 Pa], se dessa samband från Slutgraferna.

k(h) = k(STP)·(k/k₀) = (370,95002 J/°K)·(k/k₀) ; Specific fundamental gas constant for actual altitude, idealized

Tpρ-precisionen i de nu anpassade sambanden upp till 10 KM visas till höger i jämförelsetablån mot PDAS tabelldata till vänster med slutgraferna ovan underst..

— Vi VET här INTE vilka beräkningsgrunder som ligger bakom PDAS-tabellens värden, bara ATT VISS matematik omnämns i samband med tabellvärdenas (»close-to») standardiserade normalisering (det är Priset vi får betala för att INTE tillhöra International Pilot Association — Gratis Access till LandningsFöreskrifterna — detaljerna finns nog säkert också att tillgå för allmänheten, men ännu bara via stadsbiblioteken; privata inköp av den typen av samlingsverk brukar bli dyra affärer);

”The standard atmosphere is based on mathematical formulas that reduce temperature and pressure by certain amounts as altitude is gained. But, the results are close to averages of balloon and airplane measurements at various altitudes.”;

UsaToday, STANDARD ATMOSPHERE TABLES 2005 [2Apr2014-04-01]

Det enda som intresserar oss här är blotta möjligheten att få fram någon (grovt) MED NATURLIGA OBSERVATIONER överensstämmande rent matematisk form för allmänna översiktliga atmosfäriska beräkningar — vilket förenklar överskådligheten i den vidare översikten: Det som är av intresse här är molnbildningen med vattenångtryck och vattendroppsbildning — TNED-teorin för molnladdningens uppkomst.

Kommentarer till PDAS-datat:

— Man SKULLE KANSKE TYCKA att temperaturfalltaktens LINJÄRA form [‡] (0,0065°C/M) i PDAS-tabellen MÖJLIGEN (kanske) är förenklad, eftersom den mera avancerade motsvarande T-formen i tryckdatats goda överensstämmelse (0,0065/1,000067^h) just är av mera avancerad form (som börjar på 0,0065 och slutar på 0,0033 vid h=10KM). Uppgift om den detaljen finns emellertid (veterligt) inte i tabellkällan.

— Tas konstant T(LS)=0,0065°C/M för p-formen, växer felet och blir vid h=10KM procentuellt 82,71%: en märkbar skillnad.

— Det finns också, möjligen, andra möjligheter med (marginella) variabler i p-formen:

Koefficienternas sammansättning — med möjliga utrymmen för variabler

Koefficienten 0,0341579 [(M/S²)/[(J/°K)/KG]=(M/S²)KG°K/J=°K/M] är sammansatt av faktorerna Ua/R; tyngdkraftaccelerationen a måste uppenbarligen förstås som en konstant med h-variabeln kopplad just till marknivån (h=0);

· a-faktorn ska alltså INTE kunna ändras (om inget annat gäller, se utvecklingen från Hydrostatiska trycket);

· Luftmolekylens medelmässiga atomvikt U — här med genomgående samma sammansättning överallt i hela troposfärintervallet 0-10 KM — antar möjligen en högst marginell variabel med växande altitud (höjd över marken) — vi ser här U=28,952127 som en konstant (separat webbkälla upplyser att sammansättning inte ändras under 100 KM altitud, se Schlatter2009);

· Allmänna gaskonstanten R (=kNu): k VET vi varierar med h enligt k=p(V=1M³)/T för varje särskilt höjdavsnitt; u är universell och ändras inte; Däremot ändras Loschmidts tal N med tätheten. Emellertid ger i slutänden kvoten R=kNu oförändrat värde: R är konstant och oberoende av h.

— Summa summarum: det finns tydligen inga andra variabler att konsultera än de redan verksamma: Temperaturen via altituden (h).

Det är bara tryckformen (p) som enbart använder den speciella FallTaktsVariabeln (0,0065/1,000067^h): Täthetsformen (ρ, grek. rho) och temperaturformen (T) använder bägge samma konstanta atmosfäriska höjdFallTakt 0,0065°C/M.

Vi vet (här, som sagt) inte närmare detaljerna bakom PDAS tabelldata, TYP huruvida den (här) grafmatchande T(LS)-konstantens smärre exponentiella altitudvariation i p-formen har någon motsvarande teoretisk täckning i PDAS — att den har praktisk dito är alldeles tydligt, se Jämförande PDAS — eller om det just bara är en grafisk detalj som tillfälligtvis visat sig passa in på troposfärens normaliserade globala genomsnitt.

I vilket fall utpekar den här genomgångna matematiken för Tpρ-sambandens PDAS-matchningar följande allmänna sammanhang:

— Tryckberoendet PÅ temperaturfalltakten — (0,0065°C/M)1,000067^–h — ändras löpande från marknivåns 0,0065°C/M till (troposfärens toppnivå) tropopausen runt 10 KM vid 0,0033°C/M; den ordningen berör INTE temperaturfalltakten som sådan 0,0065°C/M räknat från marknivån, men har viss inverkan på gastäthetens ändring genom p-beroendet via sambandet ρ=pU/RT. Det betyder att atmosfäriska tryckformen (p) med varierande höjd (h) uppvisar ett ensidigt beroende av fasonen med den variabla falltaktens konstant, medan täthetsformen (ρ) — som beror av både p och T — har en »dubbel» beroendefason: dels på den variabla falltaktens konstant via p och dels fristående från denna via den rena T-formens falltaktskonstant (0,0065°C/M).

Därmed har vi nått slutmålet: en konsistent sammanhängande matematisk översiktsbild av temperatur, tryck och täthet som (här) kan användas (förnämligt) TILLSAMMANS MED atmosfäriska standardiserade tabelldata [PDAS] — för grov översiktlig beskrivning av molnbildningen: vattenångtryckets sublima matematik i vidare koll på grunderna i blixturladdningens RELATERBARA fysik.

*

SchlatterAtmosphere2009

BRA ALLMÄNT ATMOSFÄRISKT ETABLERAT REFERENSVERK

(skrivet av erfaren meteorolog; utförlig, välskriven, bra referenser):

En allmän PDF-referens som beskriver atmosfärens gasinnehåll (upp till 1000 KM) i etablerad matematik (MED förklaringar) finns på

Earth System Research Laboratory — ATMOSPHERIC COMPOSITION AND VERTICAL STRUCTURE — Thomas W. Schlatter 2009

http://ruc.noaa.gov/AMB_Publications_bj/2009 Schlatter_Atmospheric Composition and Vertical Structure_eae319MS-1.pdf

Konstant U till 100 KM, s1:

”Turbulent mixing keeps the relative concentrations of gases nearly constant in the lowest 100 km. At higher altitudes, molecular diffusion controls the concentrations, with the lighter gases becoming relatively more abundant with increasing altitude.”, s1Abstract,

;

”This relationship of the partial pressures of two gases at different altitudes says that the relative abundance of the “lighter” gas increases with altitude. This property is not observed below about 100-km altitude because of turbulence, the bulk motion of large volumes of air that effectively mixes the component gases of air so that their relative concentrations do not vary from the surface to about 100 km.”, s6n,

;

”As noted earlier, the mean molecular weight remains constant until near 100-km altitude because of turbulent mixing.”, s9n,

Lapse Rate, s21ö:

”The decrease of temperature with height is called the lapse rate, expressed as (–dT/dz). The atmospheric lapse rate seldom exceeds 9.8°C cooling per kilometer of altitude. This is called the dry adiabatic lapse rate Γ_d .

Γ_d = g / c_p , (26)

where c_p is the specific heat of air at constant pressure (~1005 J kg^–1 K^–1 ). Note that

dT/dz = –Γ_d. The nomenclature arises because this is the rate at which a volume of cloud-free air, hypothetically isolated from its surroundings (no heat exchange), will cool if forced upward or warm if forced downward.”, s21ö,

;

”γ = 0.0065 K m^–1 is the tropospheric lapse rate in the ICAO standard atmosphere.”, s33ö.

Standard Atmospheres, s30m:

”Standard atmospheres are prescriptions of atmospheric properties, primarily as a function of altitude, useful for engineering applications. One very widely used standard atmosphere is the U.S. Standard Atmosphere, 1976, already referenced several times.”, s30m.

HydroTryckintegralen, s8n:

”The change in pressure with altitude is given by

∂p/∂z = – ρg , (8)

where g is the acceleration due to the Earth’s gravity. At the Earth’s surface, g is approximately 9.807 m s^–2 . With the help of the ideal gas law, one can rewrite Equation (8) as

(1/p)∂p/∂z = – g/RT .

This expression can be integrated from sea level (z = 0) to some higher altitude z, or equivalently from the pressure at sea level p₀ to the pressure p at altitude z. The result is

p = p₀ exp(– _0→z ∫ g/RT dz) . (9)

For a specific gas, R is constant with altitude, g decreases slowly with altitude, and T may increase or decrease. For determining pressure at various altitudes in a standard atmosphere (see section 5.5), Equation (9) may be integrated numerically. For now, it is useful to define a scale height H as

H = RT/g (10)

H has dimensions of meters, as it must. The physical significance of H is that, if it may be considered approximately constant, the pressure of a gas will decrease by the factor 1/e [förklaring i texten fattas till 1/e — men ska förmodligen åsyfta på faktorn e^– = 1/e = 1/EXP] as altitude increases by the scale height. Note that H depends upon the type of gas under consideration, in particular, upon its molecular mass (because R = k/m). The implications of this are discussed in section 3.”, s8n.

Global Electrical Circuit beskrivs (s41).

TroposfärenFM

TROPOSFÄREN — eller enklare och grovt »klimatsfären» — är avgörande i verkningssätt och sammansättning om vi vill få en någotsånär fördjupad inblick i naturgrunderna bakom blixturladdningens fysik: molnbildningens dynamik. Focus Materien 1975 ger en utmärkt sammanfattande beskrivning med vissa grunddata, här i citat:

”Värmestrålningen

Inom troposfären, som i genomsnitt sträcker sig till en höjd av 10 km på mellanbredderna och till 18 km i tropikerna, avtar temperaturen i allmänhet med höjden; temperaturavtagandet är i medeltal 6–7°C per km. I individuella fall kan dock temperaturändringen med höjden vara mycket växlande från skikt till skikt. På mellanbredderna är temperaturen i tropopausen –55°C à –60°C, i tropikerna ca –80°C.

Troposfären är vädrets och klimatets region och därmed den viktigaste för livet på jorden. Avgörande för väder och klimat är instrålningen från solen, strålningen från jordytan och atmosfären, samt den värmetransport som sker genom luftens cirkulation. Det är endast den del av solstrålningen som ligger inom våglängdsområdet 300–800 nm, som är av betydelse för troposfärens energiförhållanden. Inom meteorologin är det brukligt att kalla denna strålning för kortvågsstrålning. På sin väg genom troposfären påverkas den huvudsakligen på två sätt: genom diffus spridning mot luftens molekyler och stoftpartiklar, varigenom den sprids åt alla håll (diffust dagsljus gör att man ser även i skuggan) samt genom absorption i och reflexion mot molnen. Resten av strålningen når jordytan, där den dels reflekteras, dels absorberas och då värmer denna.

Jordytan i sin tur utsänder mot sin temperatur motsvarande strålning inom området 4–100µm med intensitetsmaximum i 10 µm, inom meteorologin vanligen kallad långvågsstrålning. Vissa våglängder av denna strålning absorberas av vattenångan och koldioxiden i luften, andra passerar ut mot rymden. Denna absorption i atmosfären av långvågsstrålning jämte det värme, som frigörs vid kondensation i atmosfären av det vatten som avdunstar från jordytan, åstadkommer den troposfäriska luftens uppvärmning. För förhållandena i troposfären har alltså jordytan och dess ytbeskaffenhet (barmark, vatten, snö, is) avgörande betydelse.”, [FMs498sp1m].

FlaskExperimentet

MOLNBILDNINGENS TEKNISKA FYSIK

ENKELT KÖKSEXPERIMENT KLARGÖR FYSIKGRUNDERNA

TEMPERATURENS INVERKAN PÅ LUFTENS VOLYM Sats: Uppvärmd luft med temperaturen T som omges av luft med lägre temperatur t genomgår under avsvalningen en volymminskning; Volymminskningen med temperatursänkningen överensstämmer med allmänna gaslagen (pV=kT) OM — och endast då — tryckfaktor (p) och gaskonstant (k) bevaras enligt p/k=konstant=T/V. Fundamentala gaskonstanten (k) är specifik för varje luftregion och alltid konstant via en bestämd fast referensvolym (1M³) enligt sambandsformen p/T=k/(V=1M³); temperaturvariationer (T) ger motsvarande tryckändringar (T→p). Experimentet ICA-butikerna har (2014) speciellt tunna läskedrycksflaskor i plast av den avbildade typen (PÄRONDRYCK) — ju tunnare desto snabbare och större märkbar effekt. — Håll den öppna tomma rumsvarma flaskan upp och ner över kokande vatten så att flaskans inre fylls upp med den uppvärmda fuktiga luften, och skruva sedan på kapsylen (hårt). Ställ sedan flaskan på disk bänken och kolla. — Vartefter den uppvärmda inre fuktiga flaskluften kyls ner till den omgivande rumstemperaturen ser vi en märkbar formförändring i flaskkroppen. — Inom 20 sekunder ser vi hur flaskan börjat dra ihop sig, och den formar med stor sannolikhet en triangel, vänstra bilden. — Skruvar vi av kapsylen hör vi hur rumsluft viner in i flaskan, och den återtar sin ursprungliga form, inre tryck och volym normaliseras, högra bilden.

EXPERIMENTET BEVISAR OCH BESKRIVER tydligen i ett specifikt atmosfäriskt skikt VOLYMMINSKNING MED TEMPERATURSÄNKNING

Samma försök, men längre tid för synbart resultat

Testa också försöket alternativt genom att hälla i en liten mängd hett vatten på bottnen i den rumsvarma flaskan; Vänta tills den varma luften fyller upp flaskans inre. Skruva sedan på korken och mät tiden tills någon ändring syns. Nu tar det betydligt längre tid, eftersom vattenmängden [grovt 10ggr större täthet än luft] på flaskbottnen tar längre tid på sig i avsvalningen och därför håller luften ovanför uppvärmd. Också flaskans plastmaterial uppvärms märkbart genom fördröjningen, och det tar betydligt längre tid att se något resultat. Ställer vi in flaskan i kylen eller frysen snabbas resultatvisningen upp.

— Test med en liten mängd hett (kokande) vatten i flaskans botten, hårt åtskruvad kapsyl, och flaskan som sedan får stå i rummet och svalna, visar tydliga resultat först efter ca 3 minuter. Jämför ovan med enbart varmångluften; resultat efter 20 sekunder.

— Vi kan mäta hur många procent av flaskcirkelns tvärsnittsyta som reduceras med volymminskningen:

— Diametern vid etiketten är ca Ø=2R=64mM, tvärsnittsytan A=πR²~3217 mM²; Volymminskningen sker via en inre mindre cirkel ca 2r=50mM som avgränsar en segmentyta av tre med upptagande sektorvinkeln ca a=75°;

Segmentytan är sektorytan (båglängden·R/2) A(SEK) = R·rad·R/2 = R²·rad/2 = R²·[a°π/180]/2)

minus inre triangelytan (basen·höjden/2) [PREFIXxSIN];

A(T)=[2Rcos(a/2)·Rsin(a/2)]/2=[R²cos(a/2)·sin(a/2)]=[R²cos(a)·1/2], se nr9 i Vinkelsummateoremet;

A(SEG)=R²·[a°π/180]/2)–[R²cos(a)·1/2] = (R²/2)[a°π/180 – cos a] = 175,6524 mM² ~ 176 mM²;

176/3217 = 0,0547093 ~ 5%; För alla 3 segmenten totalt drygt 15% tvärsnittsyta bortfaller alltså genom volymminskning.

— I en cylinder är volymen proportionell mot tvärsnittsytan (V=A·h) och procentdelen gäller därför också volymen.

— Bortser vi ifrån plastens isolerande inverkan och tänker oss MOTSVARANDE FRI LUFT som stiger uppåt är det tydligt att tiden för VÄRMELÄCKNINGEN, anpassningen till den omgivande luftens temperatur, bör reduceras betydligt.

— I JAVKbasic visas hur vi med relativt enkla medel kan grovmäta vad som gäller i den delen: 122°C/M/S.

Volymens avtagande beror på att luftens gasbollar tappar rörelseenergi i takt med T-läckningen till t-nivån. Plastflaskans material gör visst motstånd mot volymminskningen under avsvalningen (inuti flaskan bildas ett undertryck, ett lägre p-värde än utanför flaskan, vi HÖR det sedan när vi öppnar korken och rumsluft viner in i flaskan och återställer p) och kan därför inte riktigt tillämpas på allmänna gaslagen, som här skulle kräva ett oändligt elastiskt flaskmaterial om formen p/k=konstant=T/V skulle gälla. Frånser vi dock detaljen med flaskans begränsade elasticitet kan vi (således) förstå att volymminskningen i givet tryckrum entydigt KAN beskrivas av kvoten T/V=konstant.

Mera tydliga data

I JAVKbasic beskrivs ett enkelt köksexperiment på helt fri icke innesluten uppvärmd fuktig luft som vi, med relativt enkla medel, kan ta ut preliminära grovvärden ifrån. Mätning visar stighastighet 0,6 M/S och avsvalningshastighet 122°C/M/S. Med den upplysningen har vi fått ett bättre belägg för den ISOLERANDE inverkan som plastmaterialet påtvingar den innestängda fuktiga luften i Flaskexperimentet. Med andra ord: fri, icke innestängd luft, värmeläcker = tappar värmegrad oerhört snabbt över mindre avstånd; över hundratal meter, inom sekunder.

LUFTFUKTIGHETEN i sammanhanget kan vi (här) INTE beskriva i några direkt meningsfulla kvantiteter, eftersom vi alldeles tydligt kan se att vatten fälls ut (omgående) på flaskans innerväggar. Därmed ändras betingelserna. För att studera luftfuktighetsaspekten mera konkret krävs i egentlig mening INGEN INNESLUTNING ALLS: endast optiska experiment (som inte nämnvärt påverkar vattenångan i luften) blir meningsfulla här. Varje inneslutning nämligen kommer tveklöst att uppvisa egenartade vattentivolin med inneslutningens material.

— Däremot visar och klargör det ytterst enkla flaskexperimentet PRINCIPEN hur uppvärmd vattenångsmättad luft beter sig inuti en fast omgivnings temperatur: volymen avtar.

Ämnet — i referens (Apr2014) till etablerade beskrivningar @INTERNET — har visat sig innehålla närmast otroliga fallgropar i funktionssättet, och som förefaller helt omöjliga att komma till rätta med utan, som här, direkt klargörande ENKLA KÖKSexperiment.

— Se särskilt genomgångarna i VRF | EKoG | ATFT.

FlaskExpeditionen

MOTSVARANDE ATMOSFÄRISK FLASKEXPEDITION —

klargör svårigheterna kontra FlaskExperimentet:

FlaskExperimentet FÖREFALLER avgöra »HELA historien». Men redan pionjärerna i vetenskapen om Jordatmosfären upptäckte strax att det omgivande atmosfäriska TRYCKET har avgörande betydelse. Så, man skulle förmoda att den senare delen överväger?

— Genomgången [VRF | EKoG | ATFT] har visat sig innehålla aspekter som inte riktigt »utfaller så enkelt». Vi vet här (ännuApr2014) inte på vilket sätt, om alls, som en AVGRÄNSAD, typ nedan, innesluten gas ALLS kan liknas vid det som händer i atmosfären med FRIA icke-avgränsade (vertikala) varmluftspelare [‡] som sträcker sig in i olika höjdskikt. Satsen om Jordatmosfärens volymkonstans [MOTEF] [JAVK] medger heller inget (direkt) utrymme för »volymexpansioner» eller »volymkompressioner» i fria icke avgränsade luftpelare då hela den klimatprocessen via Solenergin kan förklaras och beskrivas på konvektionsströmma [Värmeläckningen].

— I vilket fall är det viktigt att känna till argumenten med basdetaljerna som framgår i nedanstående experimentresultat.

BILDKÄLLA [2014-04-09]: @INTERNET Wikipedia Atmospheric pressure http://en.wikipedia.org/wiki/Atmospheric_pressure

TRYCKETS INVERKAN PÅ LUFTENS VOLYM [Ŧŧ, t-streck] Sats: Innesluten luft med lägre tryck ŧ som införs till luft med högre tryck Ŧ genomgår en volymminskning; Innesluten luft med högre tryck Ŧ som införs till luft med lägre tryck ŧ genomgår en volymökning; Volymändringen som visar sig med tryckändringen överensstämmer med allmänna gaslagen (pV=kT) OM — och endast då — fundamentala gaskonstanten (k) och temperaturen (T) bevaras konstant under hela ändringsförloppet enligt pV=energikonstant=kT; — Fundamentala gaskonstanten (k) — liksom en specifik medelbaserad atmosfärisk medeltemperatur (T), se LapseRate [PDAS ger 0,0065°C/M upp till 10 KM] — är specifik för varje luftregion: bägge k och T avtar entydigt inom troposfären med växande avstånd (altitud h) från Jordytan, se Slutgraferna samt Tabell hkT nedan. — MEN: Nu visar det sig att produkten kT INTE är konstant med varierande altitud: kT avtar med växande höjd, vilket beror på att k avtar snabbare än T: kT-formen kan inte tillämpas — men har tydlig koppling: volymändring med tryckändring.

Bildsviten:

Luftfylld plastflaska som förseglats vid 4300 M höjd och sedan tagits med vid nedstigning och fotograferats vid delhöjderna 2700 M och 300 M. Det högre atmosfäriska trycket längre ner mot marken pressar ihop den tydligt trycklägre toppluften.

EXPERIMENTET BEVISAR OCH BESKRIVER i transporten mellan olika specifika atmosfäriskt skikt VOLYMÖKNING MED TRYCKMINSKNING;

EXPERIMENTET BEVISAR OCH BESKRIVER i transporten mellan olika specifika atmosfäriskt skikt VOLYMMINSKNING MED TRYCKÖKNING;

TabellhkT

Värdena för k och T och deras produkt kT — motsvarande bildsvitens höjdvärden och samstämmigt [PDAS] med PDAS atmosfäriska tabelldata — visas i Tabell hkT nedan [PDAS Tabell6 i Blixt2014.ods]:

Tabell hkT — jämförande kT-värden med varierande höjd över Jordytan

——————————————————————————————

h M	k J/°K	T °K	T °C	kT J	p Pa
4300	224,682	260,2	–12,95	58462	58462
2700	267,200	270,6	–2,55	72304	72304
300	341,501	286,2	13,05	97738	97738
0	351,553	288,15	15	101300	101300

Tabellvärdena ansluter till standardiserade/normaliserade atmosfäriska tabelldata upp till max h = 10 KM enligt PDAS.

NOTERA att k-värdet vid havsnivån h=0 [STP] får något olika värde beroende på valet av referenstemperatur:

— Med T=0°C och normaltrycket 101325 Pa ges k = p[V=1M³]/T = (101325 Pa)/(273,15°K) = 370,95002 J/°K;

— PDAS använder T=15°C och normaltrycket [nära] 101325 Pa: k = (101300 Pa)/(288,15°K) = 351,55301 J/°K;

— Flera olika standarder finns i omlopp med marginella skillnader vid Jordytan.

Jmfr, TabellhkT

Jämför även tabellvärdena ovan: Förhållandet mellan minsta/största T i °K är 260,2/288,15=0,9030019 medan motsvarande för k-faktorn är 224,682/351,553=0,6391127: k-ändringen är klart större.

— Separata värden för trycket (separat beräkning, se Slutsambanden) vid samma jämförande höjdvärden (4300 M, marknivån) visar 58462Pa/101300Pa=0,5771174: tryckändringen ligger klart över temperaturändringen.

Det är tydligt att allmänna gaslagen på formen pV=energikonstant=kT INTE RIKTIGT kan tillämpas i sådana sammanhang: produkten kT avviker tydligt märkbart från den idealt konstanta energifaktor som allmänna gaslagen på den angivna formen kräver för sin giltighets del med varierande altitud (h).

— Vi kan (möjligen) deltolka den detaljen (om inget annat) som följande:

uppvärmd markluft som avancerar uppåt, innehåller successivt MERA ENERGI kT relativt varje tangerad specifik altitud, eftersom det finns en specifik kT för varje nivå och kT avtar med höjden, och det bibringade markuppvärmda luftpaketet avger därför motsvarande [successivt MERA ANDEL] värme till varje successivt högre och svalare nivå

— Med andra ord: tillståndsändring med konstant temperatur — isotermisk tillståndsändring; tillståndsändring som är temperaturOberoende — gäller INTE mellan olika atmosfäriska skikt: kT=E varierar med altitud.

— Det betyder EMELLERTID inte att någon typ av ”adiabatisk konversion” gäller (DÅ): Räkneexempel [EKoGex2] på värdena ovan via det som konventionellt kallas ”adiabatiska gaslagen” visar heller ingen överensstämmelse.

— Genomgången [VRF | EKoG | ATFT] har visat att den moderna akademins välkända ”adiabatbegrepp” sett i den relaterbara fysikens ljus förefaller väl illa tilltygat, milt sagt, och inte alls uppvisar någon sammanhängande begriplig konsistens i termodynamikens elementa, medan däremot sambanden gör det — exakt samma formalia som i etablerad mening — i termer av relaterad fysik. Samma matematik, helt skilda beskrivningsgrunder.

AGG, Allmänna gaslagens grundsamband — Figurförklaring

DEN ENKLA MODELLEN till Allmänna gaslagen

— en enda kollektiv gasboll:

— ALLMÄNNA GASLAGEN betecknas ofta i etablerad litteratur som Ideala Gaslagen (eng. Ideal Gaslaw). Emellertid anges den också ibland på formen General Gas Law.

— Intressant GoogleSökning [25Apr2014-04-25] visar ”general gaslaw”=”general gas law” 158.000 sökträffar mot ”ideal gaslaw” 2.390 och ”ideal gas law” 756.000.

pVBasic, pV→T→pV

— Vi noterar RELATERAD FYSIK att materiefysiken inte innehåller ORSAKEN till T — materiefysikens pV kan inte generera T>0 med början från 0:

— Enda kandidaten i materiefysiken från T=0 är volymen (V), trycket står redan på noll via T=0 — figuren nedan vänster, a. Ökas volymen händer emellertid ingenting med den vilande gasbollen, eftersom ingen rörelseenergi REDAN existerar att »manipulera gasbollen» med via någon mekanisk anordning med volymändring, typ rörlig kolvtopp i en gascylinder i kontakt med en redan befintlig rörelse hos gasbollen [Se ExpaKomp].

— Däremot får tryckformen (p) i massfysiken en avgörande roll för T-bildning via gravitationens inverkan, och som blir den enda primära orsaken till T, enligt relaterad fysik: värmebildning genom massdestruktion. Se utförligt i relaterad fysik från stjärnfysiken [Strålningstryckets termonukleära ekvivalent] [Stjärnornas allmänna tryckekvation]. Vi förutsätter dessa här bekanta.

a: En ideal gas representerar vid absolut noll grader Kelvin, T=0°K, en idealt vilande rörelselös KRISTALL på Jordytan i en låda (blå) med löst lock (rött). Vi illustrerar den kristallen här med EN enda gasboll som representant för hela det ideala kristallkollektivet. Den ideala gasens kollektiva atomrepresentant, den blå gasbollen, besitter ingen rörelseenergi i detta läge: temperaturen är absolut noll och ingen materiell fysikalisk rörelse existerar.

b: Tillförs den ideala gasbollen PLANCKSTRÅLNING E=hf, samma som elementär värmestrålning [högerfiguren illustrerar hur gasbollen successivt kan förstås börja uppvisa en vibrerande gestalt i takt med att hf-energi genomtränger bollkroppens elektromekanik] — som medför att gasbollen påförs sådan vibrationsenergi att den börjar lösgöra sig från, vibrera mot, botten och lock — har kristallen övergått till en IDEAL GAS med T>0. Gasen uppvisar VOLYM (V) genom gasbollens rörelseenergi (E=mv²/2). Gasbollens stötar mot det upplyftade locket, här förenklat och exakt idealiserat endast i vertikalled, kan utöva ett (mot-) TRYCK (p=F/A=Fd/Ad=E/V=kT/V) i proportion till en pålagd lockvikt (m).

— Gaskonstanten k=pV/T sammanför alla möjliga kombinationer eller TILLSTÅND mellan tryck (p), volym (V) och temperatur (T) [MEKANISKA GASLAGEN].

— Är också temperaturen (T) konstant beskriver kT alla möjliga pV-kombinationer. Är istället trycket (p) konstant beskriver p/k alla möjliga T/V-kombinationer, och är volymen (V) konstant beskriver V/k alla möjliga T/p-kombinationer. Allmänna gaslagen beskrivs mera vidlyftigt i ALLMÄNNA GASLAGEN.

I efterföljande figurillustrationer utnyttjas ovannämnda maximala förenkling [‡] som relaterar beskrivningens detaljer i praktiska sammanhang. Den enkla bilden ger oss direkt tillgång till sambanden och deras absolut yttersta extremgränser.

— Alla gasbollar i en ideal gas — inga attraktionskrafter existerar mellan gaspartiklarna — är här sammanförda till EN enda kollektiv gasboll med en enahanda endimensionell (y) vertikal rörelseprofil. Den kollektiva Gasbollen befinner sig på Jordytan i en sluten behållare (blå) med rörligt lock (röd). På locket vilar en vikt (m) med motsvarande tyngdkraftsverkan; Gasbollens upprepade stötar mot locket och dess tyngd motsvarar ett visst tryck (p=F/A) inom den inneslutna volymen (V).

— Gasbollens rörelseenergi kan regleras genom en värmeplatta under den blå behållaren: rörelseenergin tillförs gasbollen genom värmestrålning eller generellt Planckstrålning (E=hf); strålningstillförseln skapar interna vibrationer i den kollektiva gasbollen och ger den därmed rörelseenergi Ekin=mv²/2 relativt den blå behållarens botten och röda lock.

— Så länge Ekin tillförs gasbollen, uppför den sig i inneslutningen som en fullständigt idealt elastisk boll helt utan förluster då den studsar upprepat mot botten och lock med oförändrad kraft, det vi kallar konstant temperatur (T).

— Gasbollens medelhastighet (v~500M/S vid 20°C luft) kan förstås som ett uttryck för värmegraden (T).

— Notera att allmänna gaslagen beskriver tillstånd. INTE det mellanliggande arbetet — accelerationen — som skiljer de olika tillstånden från varandra. För det senare fallet, se exempel i CpMinusCv.

AllmännaGaslagenKonstanter:

Konstant tryck | Konstant volym | Expansion | Kompression | Figurförklaring

AGKT, Konstant tryck: isobar

KONSTANT TRYCK — pV = kT = E : isobar — Illustrationen till vänster sammanfattar de olika tillstånden vid konstant TRYCK (p) då värmegraden är högre (höger) eller lägre (vänster). — Högre värmegrad betyder större rörelseenergi Ekin=mv^2/2 och därmed en LÄNGRE MEDELVÄG hos gasbollen per tidsenhet, analogt en uppehållande större volym: gasbollen hinner avverka allt längre väglängder på samma tid, och därmed förmåga att SPÄNNA UPP allt större inneslutning = volym på samma nedtryckande kraft (ma).

Konstant tryck | Konstant volym | Expansion | Kompression | Figurförklaring

AGKV, Konstant volym: isokor

KONSTANT VOLYM — pV = kT = E : isokor — Illustrationen till vänster sammanfattar de olika tillstånden vid konstant VOLYM (V) då värmegraden är högre (höger) eller lägre (vänster). — Högre värmegrad betyder större rörelseenergi Ekin=mv^2/2 och därmed en LÄNGRE MEDELVÄG hos gasbollen per tidsenhet. Den längre medelvägen skulle här också öka volymen med given lockvikt. För att behålla samma volym och därmed låsa locket i konstant position med högre temperatur, måste en motsvarande större vikt läggas på locket. Den större vikten motsvarar det högre trycket via den högre temperaturen.

Konstant tryck | Konstant volym | Expansion | Kompression | Figurförklaring

AGKE, EXPANSION — konstant temperatur: isoterm — icke konstant temperatur: icke-isoterm

expansion som INTE innefattar orsaksgrunder till primär värmebildning EXPANSION — ——————————————————— BEVARAD TEMPERATUR pV = kT = E : isoterm FULLSTÄNDIG AVKYLNING pV = kT = E : (konv. adiabat) — Illustrationen till vänster sammanfattar de MAXIMALT DIAMETRALT SKILDA tillståndssätten vid YTTRE FÖRORSAKAD expansion: — Gasens inneslutning påtvingas en volymär utvidgning som kan yttra sig i två olika ytterligheter: Konstant temperatur (vänster): locket dras upp med gasbollens medelhastighet (v) INNAN gasbollen når fram, och följer sedan gasbollens hastighet: temperaturen (T), rörelseenergin Ekin=mv^2/2 hos gasbollen, bevaras; ingen ändring i kT=Ekin inträffar. Fullständig avkylning (höger): locket inväntar den annalkande gasbollen, och hämtar upp denna mjukt genom motsvarande mjuka lockacceleration så att gasbollens normala studs REDUCERAS HELT med lockets motsvarande hastighetsökning: — Locket har nu absorberat HELA gasbollens rörelseenergi, och gasbollen följer med i lockrörelsen, vilande relativt detta, ända tills locket börjar avstanna; sker den avstanningen också mjukt på lämpligt sätt, finns ingenting kvar åt gasbollen att avancera på: absolut nolltemperatur har uppnåtts. Dvs, total absolut avkylning.

Konstant tryck | Konstant volym | Expansion | Kompression | Figurförklaring

AGKK, KOMPRESSION — konstant temperatur: isoterm — icke konstant temperatur: icke-isoterm

kompression som INTE innefattar orsaksgrunder till primär värmebildning KOMPRESSION — ——————————————————— BEVARAD TEMPERATUR pV = kT = E : isoterm FULLSTÄNDIG UPPVÄRMNING pV = kT = E : (konv. adiabat) — Illustrationen till vänster sammanfattar de MAXIMALT DIAMETRALT SKILDA tillståndssätten vid YTTRE FÖRORSAKAD kompression: — Gasens inneslutning påtvingas en volymär sammandragning som kan yttra sig i två olika ytterligheter: Konstant temperatur (vänster): locket trycks ner med gasbollens medelhastighet (v) EFTER att gasbollen studsat tillbaka från locket, och följer sedan gasbollens hastighet: temperaturen (T), rörelseenergin Ekin=mv^2/2 hos gasbollen, bevaras; ingen ändring i kT=Ekin inträffar. Fullständig uppvärmning (höger): locket inväntar den annalkande gasbollen, och accelererar upp mot denna med maximal sluthastighet precis då gasbollen touchar locket och börjar sin avstanningsprocess före återstudsen. Därmed pressas lockets maximala rörelseenergi in i gasbollens ansvarsrum, och den kan svara med en motsvarande kraftigare studsenergi, analogt högre, tillförd rörelseenergin Ekin=mv^2/2. — Gasbollen har nu absorberat HELA lockets rörelseenergi, och temperaturen kommer därmed HELT att bestämmas av kraften i lockanslaget. Fullständig uppvärmning har uppnåtts.

Konstant tryck | Konstant volym | Expansion | Kompression | Figurförklaring

SYFTE 1 med uppställningen ovan främst för Expansion och Kompression, är att klargöra och förtydliga en del uppenbart etablerade BEGREPPSMISSBRUK:

— Speciellt i Jordatmosfäriska sammanhang brukar etablerade källor UTESLUTANDE hänge sig åt följande generaliserade påståenden [CentralAdia] [AdiaRef]:

1. luft som stiger uppåt expanderar OCH AVKYLS DÄRFÖR (”adiabatiskt”);

1. luft som sjunker neråt komprimeras OCH UPPVÄRMS DÄRFÖR (”adiabatiskt”);

— Ytterlighetstillstånden i Expansion och Kompression visar att BÄGGE PÅSTÅENDENA ÄR eller kan/får förstås vara GODTYCKLIGA GENERALISERINGAR, samt för det fallet att volymändringen SKULLE MEDGES ske i figurbeskrivningens vänstra kolumn — praktiskt taget utan överförande arbete till gasen — tydligen direkt felaktiga.

— Ytterligheterna i volymändringsfallen ExpansionKompression beskriver alla grader av godtyckliga övergångar mellan isotermisk (utan temperaturändring) volymändring och icke-isotermisk

Jag skulle här inflika adiabatisk i modern akademisk mening, men sammanhanget är INTE så »enkelt»:

— Adiabatbegreppet i MAC har visat sig ha sin grund, upphov och stöd ENBART i den rent matematiska behandlingen av sambandsformerna genom ”Termodynamikens första huvudsats” och där uteslutande VIA ”DåQärNoll”.

— I relaterad fysik [VRF] finns ingenting sådant som ett ”DåQärNoll”.

— Därmed kan inte heller en RELATERAD beskrivning läggas fram som stödjer term och begreppsvalet ”adiabatisk” i någon ENTYDIG eller SAMMANHÄNGANDE form. Blotta tillskrivandet av någon tydlig eller klar innebörd av termen ”adiabatisk” kan därför inte genomföras här, varken med referens till den moderna akademins nomenklatur, eller någon möjlig beskrivande ordning i relaterad mening alls.

— Det finns dock en sammanställd ”etablerad gruppering” i citat från Wikipedia, se MACadiaRef, där (här) relaterbara referenser infogats för orienterande ledning.

(med temperaturändring) volymändring, och det är bara en PRECISERAD KONSTRUKTION som kan klargöra vilket som är vad. Den »konstruktionen» emellertid, i presentationen av etablerade beskrivningar i Jordatmosfäriska sammanhang, lyser (i det hittills upphittade, Apr2014) STÄNDIGT med sin frånvaro: man talar UTESLUTANDE om ADIABATISK volymändring, dvs.,

volymändrande arbete som leder till att gastemperaturen ändras [CitatAdiaRef],

i etablerad mening, utan någon som helst preciserad beskrivning, eller ens en notering som markerar att man uppfattat distinktionen.

— Vänsterkolumnens ytterlighetsfall i AGKE, och försåvitt den fysikbeskrivningen är tillämplig, och endast då, bevisar att den etablerade beskrivningen — favoriseringen av högerkolumnens alternativ — uppenbarligen är föremål för GODTYCKE.

SYFTE 2 med uppställningen ovan [AGKE] — främst för Expansion och Kompression — är (således) att klargöra och förtydliga — den annars och tydligt, sällsynt svårhanterliga — begreppsBILDEN i den etablerade termen ”adiabatisk”:

— Den etablerade termen ”adiabatisk”, som det ser ut,

1. är djupt obskyr — i princip omöjligt att förstå innebörden i ENLIGT GÄNGSE BESKRIVNINGSSÄTT [FMadia | CentralAdia | AdiabaticRef] kontra RELATERAD mening

[VRF | EKoG | ATFT | HeatBasic | ”DåQärNoll” | NollQno] — och

2. missbrukas (tydligen våldsamt) i etablerade kvarter, om vi förstått saken rätt:

— Ytterligheterna [AGKE] i expansion och kompression UPPVISAR VARANDRAS MOTSATSER, samma rörelseschema men i olika verkningssätt beroende på konstruktionens avancerade möjligheter;

Den ena ytterligheten [AGKEväkol] utpekar en isoterm [pV=kT],

en (tryck)-volymändring expansion-kompression UTAN temperaturändring,

den andra ytterligheten [AGKEhökol] utpekar en icke-isoterm [pV=kT],

en (tryck)-volymändring expansion-kompression MED temperaturändring, alltså, om vi i kompressionsfallet frånser lockets rörelseenergi = värmeöverföring till gasen, en motsvarande ”IDEALT KONVENTIONELL MODERN AKADEMISK adiabatisk process”: volymändring med temperaturändring, idealt fullständig nolltemperatur eller total upphettning.

— Mellan dessa ytterligheter [AGKE] finns tydligen alla grader BEROENDE PÅ KONSTRUKTIONEN:

— HUR verkan sker beror på VILKEN konstruktion som avses.

— Så: Vadan den moderna akademins förkärlek för alternativet [AGKEhökol]?

— Ingen etablerad källa verkar ens ha uppmärksammat ATT en distinktion finns mellan TVÅ ytterligheter. Man verkar genomgående utgå ifrån att bara EN av de beskrivna alternativen existerar — temperaturändring med volymändring — utan att referera till någon REDOVISNING.

WikiFriExp

Det förmodligen närmaste vi kan komma den nu synliga etablerade Webblitteraturen @INTERNET i ämnet MODERN AKADEMINS FÖRKÄRLEK FÖR [AGKEhökol]

— den obesvarade frågan om etablissemangets utelämnade alternativ [AGKEväkol] som inte verkar finnas med i den etablerade beskrivningen av temperaturens inverkan under volymändring

— är Wikipediaartikeln på FRI EXPANSION:

@INTERNET Wikipedia, Free expansion [2014-04-25]

http://en.wikipedia.org/wiki/Free_expansion

”Real gases experience a temperature change during free expansion. For an ideal gas, the temperature doesn't change”

Wikipediaförfattarna preciserar inte föremålet för ”free expansion”. Eller rättare sagt, Wikipediaförfattarna FÖREFALLER (Wikiartikelns illustration) besitta en viss ej närmare redovisad förkärlek för ”kubiska volymer”. Vi studerar det.

Om KOLVYTAN är STOR i Wikipediaförfattarnas motsvarande FreeExpansionExempel (figuren ovan ger en möjlig antydan), så att huvuddelen av gaspartiklarna i princip ligger utspridda över den ytan, och gasen därifrån tillåts expandera fritt, antingen genom att kolven dras ut (med gaspartiklarnas medelhastighet, samma som AGKEväkol), eller att partiklarna tillåts expandera fritt, är det tydligt att SÄTTET med den utbredda ordningen FÖRE expansionen ger OMEDELBART STÖRRE FRI MEDELVÄG för gasbollarna, än om de (som i Wikipediaartikelns illustrerade fall) måste trängas med varandra på en »maximalt kubisk volym (med minimal öppning)».

— Det är, med andra ord, SÄTTET det hänger på, hur mycket och i vilken grad gasbollarna SER en snabbt tillgänglig öppen FRI expansionsväg.

— Tas den aspekten med — konstruktionen — är det tydligt att (även i detta fall) två ytterligheter finns: den ena med maximalt trångbodda gasbollar som tävlas att komma ut och därmed hinner tappa betydlig rörelseenergi, analogt temperatursänkning, innan de når den vidare rymden, och den andra med »havsutsikt från början» där i stort sett samtliga gasbollar hittar en direkt friväg och med påföljden att i stort sett ingen temperaturändring alls inträffar under utflykten.

— Endast exceptionellt trånga utrymmen, således, kan förstås och relateras ansluta till påståendet ”gases experience a temperature change during free expansion”.

— Maximalt vida utrymmen — däremot , som DET AKTUELLA FALLET FÖREFALLER VARA: vårt aktuella fall i Jordatmosfärens troposfäriska luftcirkulation, konstant volym — omfattas (uppenbarligen) KNAPPAST av den satsbilden.

EXEMPEL på hur HÖGERKOLUMNEN [NoAdia] i ExpaKomp-komplexet favoriseras av floran etablerade författare visas f.ö. vidare genom citat, jämförande exempel och referenser i ADIABATBEGREPPET I MODERN AKADEMI.

CpMinusCv

Termerna Cp och Cv

Arbetet som åtgår för att lyfta den fasta tryckvikten (m vänster) till en högre nivå via den högre temperaturen (m höger), beskriver skillnaden mellan värmekapacitiviteten vid konstant tryck, och värmekapacitiviteten vid konstant volym: E = Cp — Cv.

VÄRMEKAPACITIVITETEN k/m — pV/Tm = k/m = (E/T)/m : — Illustrationen till vänster ansluter till TANKEEXPERIMENTET i Wikipediaartikeln om Heat capacity ratio, citerat nedan. Illustrationen här till vänster är densamma som i ALLMÄNNA GASLAGENS GRUNDSAMBAND Konstant tryck [AGKT]. CV : värmekapacitet och värmekapacitivitet för luft vid konstant volym: — Man innesluter en bestämd mängd luft i en cylinder med bestämd volym (V) vid en bestämd temperatur (T) med en bestämd vikt (m) på cylinderlocket. — Man låser locket för konstant volym och mäter sedan hur mycket värmeenergi (E) som åtgår för att höja den innestängda luftens temperatur med 1°C på det högre tryckets bekostnad. k-värdet man får i J/°C benämns värmekapaciteten för luft vid konstant volym (CV). CP : värmekapacitet och värmekapacitivitet för luft vid konstant tryck: — Frikopplas sedan det låsta cylinderlocket, fortfarande med samma tyngd på cylinderlocket och som garanterar bevarat tryckvärde, och cylindervolymen nu tillåts expandera fritt på det bevarade tryckets nivå tillsammans med föregående bevarad temperaturstegring (1°C), åtgår ett visst separat arbete (acceleration) för att komma upp till allmänna gaslagens motsvarande tillståndsekvivalent (pV=kT) via den högre temperaturen, den större volymen och det konstanta trycket. — Det extra separata arbetet motsvarar energiskillnaden lyftarbetet mellan de bägge olika figurnivåerna. — Det extra arbetet tillsammans med föregående uppmätta C(V)-energi motsvarar värmekapaciteten för luft vid konstant tryck (CP). Med tillägg av luftmassan (m) benämns energivärdena som specifikt värme eller värmekapacitivitet, J/KG°K; C = k/m=R/U. Det är den (del-) mängd energi (per KG) som krävs för att värma upp luften (ämnet generellt) 1°C [ref. Wikipedia Heat capacity]. — Figuren till vänster illustrerar ARBETET — nivån [C =k/m=R/U] — som skiljer de bägge tillstånden från varandra [konv. R i (Cv + R)/Cv = Cp/Cv = γ = (o + 2)/o, ref. Wikipedia Heat capacity ratio]. — Jordatmosfären med variationerna inom troposfären via PDAS tabelldata och Slutgraferna uppvisar den illustrerade nivåskillnaden [C =k/m=R/U=] CP – CV = 287,20 J/KG°K på varje specifik atmosfärisk nivå (upp till max 10 KM).

Notera att terminologin i MAC (ofta. ref. Wikipedia, Heat capacity ratio) använder versalsuffixen PV för värmekapacitivitet (J/KG°K) och gemensuffixen pv för värmekapacitet (J/°K).

Värmekapacitiva sambanden generellt:

Cp/Cv = (o+2)/o = γ = 1+2/o; Cp/Cv – 1 = 2/o; (Cp – Cv)/Cv = 2/o; o = 2Cv/(Cp – Cv) = 2Cv/R/U) .

— Se även i GammaEkvivalenterna.

Det har här uppmärksammats [AGG] att det existerar något som ser ut som en uppenbar vanföreställning inom den moderna akademins etablerade författarled i ämnet elementär termodynamik:

— se ExpansionKompression i Allmänna Gaslagens Grundsamband här till jämförande referens:

— Så snart en sluten (cylindrisk) inneslutning föreligger, tillsammans med en volymändring, verkar den moderna akademins författarämnen av här ej närmare känd anledning ha fått för sig att en automatiskt associerad TEMPERATURÄNDRING är för handen, en s.k. adiabatisk dito [CentralAdia].

— De allra enklaste och mest elementära ytterlighetsfallen i ExpansionKompression visar att det finns TVÅ alternativ att välja på. Vilket som gäller, och i vilken utsträckning beror på SÄTTET, konstruktionen, som volymändringen utförs på: Antingen 1. isotermiskt UTAN temperaturändring eller som 2. icke-isotermiskt absolut temperaturändrande (konv. ”adiabatiskt”), i mer eller mindre utsträckning.

— Alla grader mellan dessa ytterligheter är möjliga — och det finns tydligen ingen FÖREGIVEN ENTYDIG form för vilket alternativ som gäller i en viss applikation MED MER ÄN MAN SPECIFICERAR PREMISSERNA — vilket heller ingen synbar främsta webbuppsats i ämnet verkar ha uppmärksammat;

— Ingen ännu (Apr2014) upphittad etablerad källa verkar ha uppmärksammat den isotermiska ytterligheten i ExpansionKompression: volymändring UTAN temperaturändring. Webben verkar helt orepresenterad på ens en antydan till notering i ämnet DÄR istället en FAVÖR FÖR ADIABATISMEN PRESENTERAS, typ exemplet nedan (rödmarkerat): ingen referens ges, bara lösa, orelaterade påståenden.

— Citatet nedan innehåller ett exempel (rödmarkerat). Men många (många) andra finns.

WikiHeatCap

@INTERNET Wikipedia Heat capacity ratio [2014-04-15]

http://en.wikipedia.org/wiki/Heat_capacity_ratio

”To understand this relation, consider the following thought experiment. A closed pneumatic cylinder contains air. The piston is locked. The pressure inside is equal to the outside air pressure. This cylinder is heated to a certain target temperature. Since the piston cannot move, the volume is constant. The temperature and pressure will rise. When the target temperature is reached, the heating is stopped. The amount of energy added equals C_V. The piston is now freed and moves outwards, expanding without exchange of heat (adiabatic expansion). Doing this work it cools the air inside the cylinder to below the target temperature. To return to the target temperature (still with a free piston), the air must be heated. This extra heat amounts to about 40% more than the previous amount added. In this example, the amount of heat added with a locked piston is proportional to C_V, whereas the total amount of heat added is proportional to C_P. Therefore, the heat capacity ratio in this example is 1.4.”

Speciellt frekvent ser man i etablerade framställningar uppfattningen om ’adiabatisk temperaturändring’ i samband med luftcirkulationen i Jordatmosfären [CentralAdia]: varm markluft som stiger mot kallare områden påstås utan vidare avkylas på adiabatisk grund: luften expanderar först via det lägre trycket högre upp i atmosfären, vilket i princip är korrekt, men man säger sedan att luften DÄRFÖR avkyls (’adiabatiskt’). Se särskild beskrivning i ATFT.

Ytterligheten med isotermen i AGKE (Expansion) visar att expansionen LIKAVÄL kan förstås UTAN temperaturpåverkan (speciellt om expansionen sker långsamt) — men det beskrivningssättet verkar inte finnas representerat i MAC: temperatursänkningen med växande altitud utpekar — då, i så fall — ingen koppling till ”adiabatism”, utan istället en naturlig avsvalning [ATFT | ATFTrel | VLAFS] (atmosfärisk luftvärmekallning på värmekapacitiva konstanten Cp—Cv=287,20 J/KG°K).

— Ingen ANNAN referens verkar ges till den tydligt obskyra ”MAC-adiabatiska förkärleken”, utom via ”termodynamikens första huvudsats” (Q=W+U): man sätter ”Q=0” [FMadia] och utvecklar sedan ”adiabatiska gaslagen” K=PV^γ — som helt säkert gäller för SÅDANA inneslutna cylindriska konstruktioner där gasmassan SÄKERT bringas i MAXIMAL KONTAKT med den volymförändrande KOLVTOPPSYTAN (som t.ex. i dieselmotorn).

— Att Jordatmosfären skulle vara tillämplig på den typen av mekanisk anordning (cylinderinnesluten luft som tvingas expandera och komprimera via en rörlig kolv med maximal luftpartikelkontaktering) finns här inga upphittade referenser till, och heller inte någon direkt synbar logisk förankring i. Snarare ser vi att uppstigande varm markluft SVALNAR [VLAFS | JAVKbasic] naturligt, och återvänder konvektivt till marken igen på Solvärmens arbetande effekt med återuppvärmning ner mot markdelen och den konvektionsström varmt-upp-avsvalning-kallt-åter-uppvärmning som Solenergin ger upphov till i atmosfären [MOTEF].

— Det är (i andra ord) något som inte stämmer i den etablerade beskrivningen — ELLER att det här författarämnet har missat någon väsentlig detalj: den delen eftersöks här löpande, kontinuerligt genom prövningar, jämförelser, sammanställningar, exempel: Ämnet är omfattande, och (långt ifrån) allt som finns visas inte i gratisutbudet på webben @INTERNET.

— Det är, tydligen, inget fel på sambanden. Det är sättet och omständigheterna som sambanden påstås figurera i [ATFTsammanfattning], och som (verkligen) inte FÖREFALLER visa någon överväldigande Reson i MAC-presentationen.

Förklaringen ligger tydligen [ATFTsf] i »den till synes komplicerade matematiska algebran»: Modern akademi har INTE NÅGOT ÖVERVÄLDIGANDE ÖVERTYGANDE LOGISKT SÄTT ATT BESKRIVA TERMODYNAMIKENS DETALJER PÅ: beskrivningssättet i MAC är tydligt KRÅNGLIGT, SVÅRTILLGÄNGLIGT, SVÅRBEGRIPLIGT, SVÅRNAVIGERAT (till max).

— Se speciellt den jämförande genomgången i ATFT.

Jämför FÖRST: »isolerat system».

— Redan från ruta ett mer eller mindre kraschlandning. Alla fysikaliska kroppar värmeläcker [‡].

Exempelutvecklingarna som kopplar:

— För att få visshet i saken, måste vi först RELATERA ’adiabatiska gaslagen’ — få exakt vetskap om vad »saken» innebär.

— Se utförligt från VRF och EKoG, med särskild syntes i ATFT.

VLAFS, VLbasic, VärmeLäckningens ArbetsFrihetsSats i RELATERAD FYSIK

Satsen om den materiella

VÄRMELÄCKNINGENS ARBETSFRIHET — arbete kan inte anställas på värmeläckagets energi

· 1. Värmeläckning ΔQ förutsätter närvaro av en värmekälla;

· Värmeläckning kan bara förekomma där absoluta temperaturen är större än noll, analogt där NÅGON rörelseenergi (Ekin=mv²/2) finns tillgänglig;

· 2. Ett ämnes minsta värmeläckande enhet kan förstås vara varje enskild atom i ämnet;

· 3. Värmeläckningens minsta kvantitet Q1–Q2=ΔQ=Q/[n→∞] är varje minsta tillskott (Δ) i värme som håller eller definierar en kropps, ett ämnes eller en avgränsad forms konstanta temperatur, analogt värmeläckningens uppvägande kvantitet;

· 4. Värmeläckning är den (periodiska) energiförlust enheten undergår vid varje dess (periodiska) ÄNDRING — för atomer i fasta/flytande ämnen, gittersvängningarna omkring jämviktsläget och som vi vet genom enkla köksexperiment (metaller [Variabla fasta atomavstånd]) ökar i omfattning med ökad temperatur; för atomer i gaser, gasbollarnas (upprepade) kollisioner inom kontaktintervallet, och som vi också vet genom enkla köksexperiment [Flaskexperimentet] ändras med temperaturen [VLbasic];

· 5. Värmeläckningens belopp (·3) är samma som den omgivande värmekällans (Planck-) energipåfyllande tillståndsbild (E=hf) som innebär konstant temperatur med idealt noll förluster (fullständigt idealt elastiska gaspartikelkollisioner), motsvarande en konstant energipåfyllande tillståndsbild för den enskilda läckenheten;

· 6. Värmeläckning kan inte anställas för arbete: Eftersom [HeatBASIC] alla kroppar värmeläcker genom kropparnas atomers inbördes ömsesidiga växelverkan, finns ingen ordning, sätt, mekanism, konstruktion eller annan form av inrättning för att få ett värmeläckage att utföra arbete; värmeläckage är en egenskap som inte kan elimineras;

· 7. För att ett arbete ska kunna utföras mellan två skilda temperaturnivåer — differens i rörelseenergi och därmed en principiell POTENTIAL för arbete — krävs att energidifferensen eller temperaturdifferensen måste vara större än energin i värmeläckningen [VRF]: Q = W + L; arbetet (W) plus värmeläcket (L) definierar påenergins (Q) minsta möjliga kvantitet för att verkställa minsta möjliga arbete;

· 8. Är energidifferensen (Q1–Q2=L=Q) exakt lika med värmeläcket (L), analogt temperaturdifferensen
(T1°–T2°=T°=L°) lika med läckvärmegraden (L°), gäller uppenbarligen W=0 enligt
Q = 0 + L; Q=L; inget arbete kan anställas på värmeläckagets energi. Eller alternativt; inget arbete utförs för tillfället på given värmebas; »maskinen» står vilande eller avstängd för tillfället; jämför värmeplattan som står på (Q) men som inte används till något (L). Arbetsformen (W) är därmed generellt godtyckligt associativ — »det som passar».

AtmosAdiabatMAC; 12Apr2014 — RelateratAdia, TermoRelFys —

PascoCitat

PASCO PRODUCTS — Adiabatic Gas Law Apparatus [2014-04-15]

http://www.pasco.com/prodCatalog/TD/TD-8565_adiabatic-gas-law-apparatus/

”Adiabatic and isothermal processes are difficult for beginning physics students to understand.”

BKLadia

”Adiaba’tisk (grek. adiabato’s, ogenomtränglig, sluten), kallas förändringen av en gasmassas tryck, volym och temperatur utan tillförande av värme från l. till omgivningen. Komprimeras en gas hastigt, åtgår härtill ett mekaniskt arbete, som övergår till värme, åstadkommande en ökning av gasens värmeinnehåll varför gasens temperatur stiger. Om gasen i stället hastigt får expandera, uträttas vid expansionen ett mekaniskt arbete, som motsvarar en viss förlust av gasens värmeinnehåll varför gasens temperatur sjunker.”, [BKL.I.sp85n].

AdiabaticMAC

Med fortsättning från TILLÄMPNINGSEXEMPEL ”Adiabatiska gaslagen”

ADIABATBEGREPPET I MODERN AKADEMI

Se även i Förtydligande till allmänna gaslagen i Entropibegreppet [adiabattermen omnämns där i förbigående].

GoogleSökning [2014-04-25]: »what is ”adiabatic”?»; RESULTAT:

———————————————————————————

”adiabatic / ... / Physics

adjective adjective: adiabatic;

1. relating to or denoting a process or condition in which heat does not enter or leave the system concerned.

"the adiabatic expansion of a perfect gas"

• impassable to heat.

noun noun: adiabatic; plural noun: adiabatics

1. a curve or formula representing adiabatic phenomena.”

REDAN I ENTROPIBEGREPPET genomgicks detaljerna med den moderna akademins förstörelselusta i fysikgrunderna — TENDENSEN att uppfinna fysiken snarare än att härleda den — här (återigen) speciellt uppmärksammat angående ”Termodynamikens första huvudsats”, eng. First Law of Thermodynamics:

@INTERNET Wikipedia, First law of thermodynamics [2014-04-25]

http://en.wikipedia.org/wiki/First_law_of_thermodynamics

”The first law of thermodynamics is a version of the law of conservation of energy, adapted for thermodynamic systems. The law of conservation of energy states that the total energy of an isolated system is constant”.

Fysiken i relaterad mening innehåller inga slutna system — ALLA FYSIKENS KROPPAR VÄRMELÄCKER, ISOLERADE SYSTEMETS URSPRUNG, MACcitatTermodynI. Med den avgörande skillnaden i föreställningssätt, försvinner också grunden till en ömsesidigt relaterbar fysikbeskrivning. Se även här särskilt från VÄRMEGRUNDERNA I RELATERAD FYSIK, och ”adiabatiska gaslagen”. SPECIELLT Begreppet ”adiabatisk” har insmugit sig (successivt, exakta källverk saknas här) i vetenskapshistorien i samband med termodynamiken, dess ständiga flöde av nyformuleringar i ljuset av begreppet ”system” — och därmed breddat oklarheterna ytterligare; bevis: jämför det inledande citatet ovan: möjligheten att greppa innebörderna enbart i regi av den moderna akademins nomenklatur är erkänt begränsade. Exemplen nedan ansluter till den detaljen med jämförande citat i relaterade referenser.

*

— Är termen eller begreppet ADIABATISK i modern akademi en PSEUDOTERM — den grundas på (idel) missgrepp inom modern akademi, fraser, härmningar, och som i relaterade ljus FÖREFALLER uppdaga något som mest liknar elementär okunnighet om och i ämnet naturfysik — eller finns det någon begriplig (ännu Apr2014 inte upphittad) beskrivning som förklarar innebörden utan att skapa flera frågetecken än de som ska rätas ut?

— Det är inget fel på sambanden, märk väl. Se jämförande exempel i ”Adiabatiska gaslagen”.

Den här centralt uppmärksammade förbistringen — föremålet för hela saken:

— Uppfattningen att VOLYMÄNDRING har en OBETINGAD FYSISK KOPPLING till TEMPERATURÄNDRING, och som populärt benämns adiabatisk tillståndsändring.

[VRFsf]: DE RELATERBARA FUNKTIONERNA för icke isotermiska volymändringar och isotermiska volymändringar illustrerar, tydligen, adiabatbegreppets (också tydligt, ypperligt sammansatta) språkförbistring med den ständigs strömmen exempel från etablerade korridorer, speciellt i ämnet Jordatmosfärens luftcirkulation.

— Jag måste dock reservera mig: Termodynamiken är OERHÖRT OMFATTANDE, och långt ifrån »allt etablerat» finns tillgängligt på webben för den som intresserar sig för basbegreppen, deras historia och utveckling. Om (emellertid) ingen revolutionerande UTRÄTANDE etablerad förklaring dyker upp som kan lappa ihop den — här — uppenbart uppdagade avgrunden i språkförbistringen inom begreppet adiabatisk, har vi bara att konstatera faktum: beskrivningen av sambandens innebörd i etablerad litteratur är milt sagt bedrövlig.

CentralAdia, AtmosMACadia

CENTRALA SPRÅKBUTIKEN I MODERN ATMOSFÄRISK AKADEMI verkar vara den här:

:

— luftvolymens atmosfäriska expansion-kompression förorsakar luftens avkylning-uppvärmning och benämns adiabatisk process [‡]

Dictionary.com — SCIENCE DICTIONARY — American Heritage 2002 [27Apr2014-04-25]

http://dictionary.reference.com/browse/adiabatic

”The adiabatic cooling of air as it rises in the atmosphere is the main cause of cloud formation.”

Lösa påståenden utan i citatet angivna naturvetenskapliga referenser.

RELATERAD FYSIK:

:

— 1. icke isotermiska volymändringar och isotermiska volymändringar betecknar två motsatta ytterligheter med alla möjliga mellanliggande gradskillnader:

— Det finns ingen obetingad temperaturändring med volymändring [AGKE] [EKoGex]:

ena delen innefattar volymändring UTAN temperaturändring — entydigt isotermisk process — medan

andra delen innefattar volymändring MED temperaturändring — entydigt icke-isotermisk process,

men distinktionen verkar inte ens finnas uppmärksammad i någon begripligt relaterad framställning i etablerade korridorer: det man möter i etablerade meningar (Apr2014) är UTESLUTANDE en tydligt favoriserad — men utan närmare förklaring — framhållning av det icke-isotermiska alternativet. Det är det anmärkningsvärda: alla tycks använda det men INGEN ger någon närmare förklaring till varför. Det finns en formell förklaring [DåQärNoll] [TILLÄMPNINGSEXEMPEL ”Adiabatiska gaslagen”], men den formalian är — i relaterbara termer, se från VRF — så GÖMD i relationsbeskrivningen att den inte framgår med mer än, som det ser ut, RELATERAD FYSIK träder in på scenen och ställer fram en del jämförande påpekanden till påseende: en vanlig ordinär student har, tydligen, inte en chans att se sammanhangen, eftersom termen »sammanhang» HELT dikteras av den moderna akademins uppfunna naturfysikbegrepp, varav det närmast populära verkar vara, just ”då ΔQ=0”.

— 2. markluftvolymens ETABLERAT »atmosfäriska expansion» vid högre altituder sammanhänger med — enligt modern akademi — ”adiabatic cooling” men enligt här ej närmare bekräftad RELATERAD GRUNDFYSIK som inte medger något större utrymme för den påstådda expansionen — som i modern akademi anses leda till den påstådda temperaturminskningen — utan istället hänför temperaturminskningen som en markluftens naturliga avkylning med växande avstånd från Jordytan [ExempelFlaskExperimentet: Volymen avtar — snabbt — hos uppvärmd luft som får svalna i fast värdskikts fasta tryck].

Se utförligt RELATERAT i »LuftKonventionen»:

Luften KALLNAR vid uppstigning, lämnar ifrån sig sitt vattenånginnehåll för molnbildning, och ÅTERUPPVÄRMS vid nedströmningen — allt på Solenergins räkning — för ny vattenångtransport.

DET FÖREFALLER — här fortfarande (Apr2014) utan upphittad motsvarande etablerad beskrivning — med andra ord som att klimatprocessen med luftens cirkulation med varmt-upp-avsvalning-kallt-åter-uppvärmning inte har ett spår med någon VOLYMÄNDRANDE EFFEKT att göra, utan rätt och slätt är en EFFEKT av NATURLIG TERMISK AVSVALNING med upprepad SOLUPPVÄRMNING:

— uppåtstigande uppvärmd markluft svalnar inte av därför att den skulle vara föremål för den akademiskt populära inneslutna cylinderkonstruktionen med en rörlig kolv som beskrivs av ENTYDIG ICKE-ISOTERMISK VOLYMÄNDRING och som förorsakar motsvarande temperaturändringar EFTERSOM [noAdia] det inte finns någon synbar känd fysiknatur som beskriver obetingad temperaturändring med volymändring [AGKE] [EKoGex].

Sakkärnan som uppdagats upprepas här igen [TILLÄMPNINGSEXEMPEL ”Adiabatiska gaslagen”]:

— Det är inget fel på sambanden. Det är beskrivningen av deras innehåll saken gäller, vad sambanden betyder, vad de beskriver.

Den helt enkla relaterade fysikförklaringen till Jordklimatsfärens Solenergiunderhållande luftcirkulation skulle då vara:

— Markluftens inträde i ett högre hydrostatiskt atmosfäriskt skikt innebär att den gästande markluftens högre Tpρ-värden tvunget måste uttömma sig i och därmed anta värdskiktets lägre Tpρ-värden: Det sker genom VÄRMELÄCKNING (T avtar) och FRI EXPANSION (pρ avtar). Det finns ingenting sådant obetingat [noAdia] i fri naturligt icke avgränsad atmosfär, relaterad fysik, som att ”temperaturen avtar på grund av expansion”: Temperaturen avtar på grund av VÄRMELÄCKNING [FlaskExperimentet]: Planckstrålning; avsaknad av energipåfyllning för upprätthållande av aktuell rörelseenergi (E=kT). Fria expansionens tillståndsändring i värdskiktet kopplar en återvändande konvektionsström med markskiktet.

:

— Toppluftens inträde i ett lägre hydrostatiskt atmosfäriskt skikt innebär att den gästande toppluftens lägre Tpρ-värden tvunget måste berika sig i och därmed anta värdskiktets högre Tpρ-värden: Det sker genom VÄRMEABSORPTION (T ökar) och TVUNGEN KOMPRESSION (pρ ökar). Det finns ingenting sådant obetingat [noAdia] i relaterad fysik som att ”temperaturen ökar på grund av kompression”: Temperaturen ökar på grund av VÄRMEABSORPTION: Planckstrålning; tillgång på energipåfyllning för upprätthållande av aktuell rörelseenergi (E=kT). Kompressionskraften är konvektiv och kan bara ges från Solvärmen.

Vi kan bara fortsätta eftersökandet av — eventuellt — mera revolutionerande beskrivningar och som kan »rädda» det ANNARS tydligt uppenbart milt sagt obskyra begreppet adiabatisk i modern akademi.

— Vi studerar några exempel genom etablerade citat.

ADIABATISKA SÄTTET I MODERN AKADEMI —

genom citat

—————————————

HUR MAN RESONERAR ETABLERAT I BESKRIVNINGEN AV MOLNBILDNINGENS ALLMÄNNA FYSIK

Se även relaterad jämförande beskrivning från FlaskExperimentet

’No heat transfer cooling’

(min [satiriskt] ordlekande sammanställande rubrik — nivån 2014 på modern akademi i ämnet termodynamik):

WikiAdia

@INTERNET Wikipedia Adiabatic process [2014-04-09]

http://en.wikipedia.org/wiki/Adiabatic_process

”An adiabatic process (/ ... /; from the Greek privative "a" + "diavaton") is a process that occurs without the transfer of heat or matter between a system and its surroundings.[1][2]”.

WhatIs.com — DEFINITION adiabatic cooling [2014-04-09]

http://whatis.techtarget.com/definition/adiabatic-cooling

”Adiabatic cooling is the process of reducing heat through a change in air pressure caused by volume expansion.”

I relaterad termofysik [NollQno] [VRF] [ÄNDRINGSLAGARNA] existerar ingen ändring av tillstånd utan ett arbete, och därmed heller inte utan värmeomsättning [PLANCKSTRÅLNINGEN E=hf]: omsättning, överföring, transport, av värme föreligger ALLTID i samband med en tillståndsändring. Undantag existerar inte [NeutrinoBASIC].

— Antar vi ovanstående citerade SÄTT att beskriva, hamnar vi tveklöst strax i »dörren-är-handtaget»-filosofin, där inget längre är visst och allt strax blir föremål för godtycke. Jämför den möjliga vanvettsmeningen i ljuset av ovanstående citatmeningar: »arbete — tillståndsändring — sammanhänger INTE med värmetransport».

— Vi kan inte anlita den typen av källa för någon SERIÖS naturvetenskaplig uppgift.

— Vi kan, tydligen och följaktligen, INTE anlita en sådan källa för någon NATURVETENSKAPLIGT BETRODD uppgift: den krossar grundbeskrivningen, ger orden innebörder som strider mot varandra.

— Vi hittar flera liknande väl etablerade exempel med samma ordfällor:

FMadia

”En tillståndsändring kallas adiabatisk om värme varken tillförs eller bortförs, dvs. då ΔQ=0.”, [FMs322sp1mö].

I RELATERAD FYSIKALISK MENING [NollQno] [VRF] [ÄNDRINGSLAGARNA] finns som sagt ingenting sådant i fysiken: alla tillståndsändringar i fysiken omsätter värme: utan undantag.

— Därmed är språkförbistringen avtäckt: man kan inte använda ett lärosystem till något begripligt som uttrycker sig på ovan citerat sätt. Den som vill avancera på det lärosystemets villkor, får tydligen finna sig i att försöka härma favoriterna.

Den hittills (Apr2014) enda upphittade ursprungskällan bakom ATTITYDEN ”tillståndsändring utan värmetransit” är just den citerade typografin: ”då ΔQ=0”. Den formalian återkommer ständigt i den moderna akademins rent motsvarande matematiska behandlingen av ämnesfrågan (här i samtliga upphittade webbkällor). Som vi har sett [NollQno], har den delen ingen relaterad fysisk soliditet. Och, som det ser ut, vi behöver den heller inte för att utveckla de motsvarande termodynamiska sambanden [TILLÄMPNINGSEXEMPEL ”Adiabatiska gaslagen”].

— Verkligt intressant vore det (då) om vi kunde hitta något ENDA relaterat beskrivande etablerat exempel som visar att ”om man undvarar DET, går DET inte”.

— Eftersökningen fortsätter oförtrutet.

— ”ΔQ=0” försöker, tydligen, uttrycka det här:VÄRMELÄCKNING [VLA].

— Parametern VÄRMELÄCKNING ingår inte i MAC-sambanden [VRF] [ClausiusOriginal].

— MAC-formalian med ”ΔQ=0” har tydligen ingen annan RELATERBAR innebörd än värmeläckningsprocess: avsvalning; tillståndsändringar utan tillförande av energi.

Jämför det internationellt etablerade begreppet eller termen

Dry Adiabatic Lapse Rate, sv. torrluftsAdiabatiska falltakten:

Temperaturfalltakten i Jordatmosfären (inom troposfären) beskriver en medelform för de olika atmosfäriska skiktens inbördes NATURLIGA VÄRMELÄCKAGE, avtagande temperatur, med växande altitud (höjden h över marken). PDAS tabelldata använder värdet 0,0065°C/M (upp till max h=10 KM)

Men begripbarheten blir kass:

— Jämför kraschlandningen

’värmeläckning ΔQ=0 är att värme varken tillförs eller bortförs’.

TERMODYNAMIKENS FÖRSTA HUVUDSATS i modern akademi:

FMtermo1

”Termodynamikens första huvudsats

Termodynamikens första huvudsats innebär energins bevarande och uttrycks på olika sätt. Enklast kan sägas att om man har ett system och tillför det värme och uträttar arbete på det, så har systemets energi ökat med det tillförda värmet och det utövande arbetet. Detta kan också skrivas: den värmemängd Q som tillförts systemet och det arbete W som uträttats på systemet är lika med ökningen i energi U hos systemet: denna energi kallas ofta inre energi:

Förändringen i U = Q + W

”, [FMs318sp2m];

:

”Termodynamiska system

Med begreppet system menar man i termodynamiken en bestämd mängd materia begränsad av någon bestämd yta.” , [FMs318sp1ö].

— Varje form av arbete som utförs PÅ en kropp uppvisar ALLTID någon form av VÄRMEFÖRLUST till omgivningen [VLA] — och den omfattas tydligen inte i ovanstående beskrivningssätt.

”tillförd energi + ännu mera tillförd energi”.

TermoRelFys, AtmosAdiaMAC

OM vi istället söker en tillståndsändrande allmän fysikalisk FUNKTION — helt oberoende av »kropp» eller »system» — kommer vi till den relaterbara fysikens värmebeskrivande satsbilder. Se utförligt från VRF. Men den formalian ingår som sagt inte i MAC.

— Satsbilden för värmefysiken i relaterad fysik kan illustreras (förnämligt):

Q (PÅFYLLANDE ENERGI)	=	W (UTFÖRANDE ARBETE)	+	L (VÄRMELÄCK)
E = Q	=	30Maj2009 E1 Bild Maskros2_16 · Nikon D90	+
påenergi		utförande arbete		värmeläck

— ADIABATISK — tillståndsändring som inte inbegriper värmetransitering, varken in eller ut — har ingen relaterbar fysikalisk representation, EFTERSOM all fysikalisk ändring just bygger på eller förutsätter värmeläckning [VLA] [VRF]: en värmetransport (jämför Solvärmen).

AdiabaticRef, AtmosMAC

GoogleBooks

CLIMATE CHANGE SCIENCE:

A MODERN SYNTHESIS: VOLUME 1 - THE PHYSICAL CLIMATE, Farmer et al, 2013

”Adiabatic A process in which heat does not enter or leave a system. In the atmospheric sciences, adiabatic processes are often used to model internal energy changes in rising and descending parcels of air in the atmosphere. When a parcel of air rises it expands because of a reduction in pressure. If no other non-adiabatic process occur (like condensation, evaporation and radiation), expansion causes the parcel of air to cool at a set rate of 0.98°C per 100m. The opposite occurs when a parcel of air descends in the atmosphere. The air in a descending parcel becomes compressed. Compression causes the temperature within the parcel to increase at a rate of 0.98°C per 100m.”, s505.

— Webben (Apr2014) innehåller EN STOR MÄNGD LIKNANDE »METEOROLOGISKT LÄROMATERIAL» — typ barnbokslitteratur med stora fina illustrationer och snygga grafer och diagram med en flod av LÖSA ORELATERADE PÅSTÅENDEN från ”väderproffs”. Vi har inte en chans att varken studera eller granska KRITISKT den strida floran av de olika påståendena som serveras, typ ovan: vi kan i grunden inte bemöta den typen utom på någon rent retorisk väg: utan vetenskapliga referenser. Vi VET inte vilka referenser författarna HAR bakom kulisserna — vilket i princip gör den typen av ”läromedel”, hur meriterad den portalen än är, till värdelös smörja. Vi bör ha den detaljen i minnet med följande (således delvis helt ovetenskapliga) genomgång.

— Strävan med hjälp av @INTERNET att få fram verkliga referenser till (typ ovan i citat) »den etablerade meteorologins molnbildningsdiktat» verkar helt sakna gensvar. Barnbokslitteratur.

— VARJE AVGÖRANDE påstående som framställs SKALL vara återförbart på en redovisande, relaterbar, fysikgrund. Annars är påståendena värdelösa ur naturvetenskaplig synvinkel.

— Vem som helst kan sammanställa ”snygga illustrationer” och påstå än det ena, än det andra. Den etablerade Meteorologin verkar vara ett sådant centrum: Barnbokslitteratur; ”vuxen berättar för barn”.

Citatexemplet ovan är ett praktexemplar på CentralAdia — RelateratAdia: »temperaturen avtar på grund av volymminskning»:

”expansion causes the parcel of air to cool”;

”Compression causes the temperature within the parcel to increase”

— Se särskild citatbeskrivning för begreppet ”air parcel”, sv. luftpaket.

:

Det faktum att

Det inte finns någon obetingad temperaturändring med volymändring [AGKE] [EKoGex]

verkar inte vara någon uppmärksammad fysikordning för källförfattaren till ovanstående (och många, många liknande finns).

— Det är påståenden som alldeles tydligt men av här ej närmare känd anledning favoriserar den icke-isotermiska volymändringens alternativ (fullständig avkylning/uppvärmning) före det isotermiska, se dessa bägge nämnda i grundbeskrivningen i AGKE.

— Av allt att döma finns ingen annan grund till ovanstående tydligt — enligt AGKE — orelaterade påståenden, än just den allmänna moderna terminologin från ”då ΔQ=0”, och som, tydligen även i detta fall, obetingat och oreflekterat associeras med ”Adiabatiska gaslagen”: temperaturändring genom volymändring.

— Bokens påståenden

”expansion causes the parcel of air to cool”;

”Compression causes the temperature within the parcel to increase”

är — i ljuset av AGKE — uppenbarligen helt tagna ur luften, uppenbart favoriserade mot den icke-isotermiska volymändringens alternativ och utan någon som helst vägledande motivation för den favoriseringen, och därmed direkt felaktiga, uppenbart vilseledande påståenden. Ingen människan kan få ut något begripligt ur det, ursäkta, svamlet.

— Och som redan noterats: det är samma över hela det etablerade utbudet: samma fraser, samma ”då ΔQ=0”-sättning med hänvisning till ”Termodynamikens första huvudsats”. Inget annat. Jämför VRF.

— ”at a rate of 0.98°C per 100m” ansluter f.ö. till den s.k. falltakten (eng. lapse rate) som avser/kopplar DET FASTA HYDROSTATISKA SKIKTETS temperaturkaraktär för varje specifik atmosfärisk nivå (PDAS anger standard 0,0065°C/M upp till max 10 KM — den standarden avser MÖJLIGEN luft MED vattenånga, men det är svårt att få fram klara och tydliga referenser).

— Se hur det sambandet och det värdet härleds relaterat i ATFT.

VärmebildningenBASIC

För att erinra generellt i relaterad fysik:

WORK CAUSES HEAT.

Se även mera utförligt (uttömmande) i ALLA FYSIKENS KROPPAR VÄRMELÄCKER och speciellt, i koppling till Allmänna gaslagen, ORSAKEN TILL T INRYMS INTE I ALLMÄNNA GASLAGEN.

· Värmestrålningens uppbyggnad börjar från NOLL i Planckstrålningen med energibildningen från massdestruktion (m→γ) [NEUTRINOSTRÅLNINGENbasic];

· Strålfrekvenserna börjar från högsta [NEUTRINOspektrum] och avtar via naturlig värmeläckning mot NOLL på principen Comptonspridning [COMPTONEFFEKTEN] om ingen påfyllande förlustkompenserande energikälla (arbete) finns;

· Elektromagnetiska strålningens energireduktion E=hf=h(f₀–f₁) vid växelverkan [COMPTONEFFEKTEN] med materien garanterar att värmesvängningarna mellan gasatomer eller atomer generellt i ett ämne — temperaturen eller rörelseenergin mv²/2 — avtar spontant — avkylning — just genom att inget PÅFYLLANDE ARBETE utförs för att kompensera den obönhörliga naturliga energireduktionen, värmeläcket, samma som naturlig avsvalning;

· Fysiken har inget arbete att ställa fram som orsak till temperaturminskning [VLAFS].

ALLT ARBETE FÖRORSAKAR VÄRME.

Från Orsaken till T — i klargörande relaterade beskrivande exempel

Värme i relaterad mening är en masslös överföring av induktiv elektrisk effekt från en högfrekvent strålkälla som bygger på massdestruktion (m→γ) — massans omvandling till värme och ljus: Solen:

p→T; tryck bildar värmegrad; [GRUNDÄMNESBILDNINGEN] [STJÄRNFYSIKEN].

— Med den värmegrunden kan sedan temperaturen eller värmegraden T i sin tur i MATERIEFYSIKEN bilda pV (tryck p och volym V) enligt E=kT=pV:

T→p; värmegrad bildar tryck.

— Materiefysiken har inte massfysikens värmegrund, utan tvingas disponera sitt värmeinnehåll på kredit från den mera djupare liggande massdestruktiva processen:

— all värmebildning — tillgänglig energi — i materiefysiken grundas på massfysikens massdestruktioner:

grundämnesatomerna.

— Materiefysiken — fasta ämnen som bygger på redan färdigbildade atomer och deras kemiska bindningar som uppkommit i samband med djupare liggande processer som innefattar massdestruktioner, alltså kärnreaktioner — har med andra ord bara kapital att framställa värme genom kemisk-mekaniska verkningssätt:

— Materiefysiken kan styras för att ta ut värme, upplagrad energi, från kemiska föreningar eller överföra mekaniskt arbete (påföra ämnesatomer rörelseenergi) till värmestrålning (elektrisk effekt).

Materiefysiken således:

— För att bilda TRYCK (p) måste ovillkorligen energi — värme — FÖRST tillföras någon MATERIELL ANORDNING och vars delar sedan genom olika mekaniska lösningar kan ändra trycket i någon inneslutning. Och alltså kan AV PRINCIP tryck som sådant i materiefysiken INTE bilda — alstra, generera, vara primärform för — värme;

tryckändring i materiefysiken kräver istället en primär värmekälla, energi, som grund för ett arbete.

— För att bilda VOLYM (V) måste ovillkorligen energi FÖRST tillföras någon MATERIELL ANORDNING och vars delar sedan genom olika mekaniska lösningar kan ändra volymen i någon inneslutning. Och alltså kan AV PRINCIP volym som sådan i materiefysiken heller INTE bilda — alstra, generera, vara primärform för — värme;

volymändring i materiefysiken kräver istället en primär värmekälla, energi, som grund för ett arbete.

— SAMMANHANGET i dessa ordningar GARANTERAR och SÄKERSTÄLLER att

· arbete alltid är förknippat med värmebildning, vare sig massfysikaliskt eller materiefysikaliskt;

· värmebildning alltid är förknippat med arbete, vare sig massfysikaliskt eller materiefysikaliskt;

· avsaknad av värmebildning alltid betyder avsaknad av arbete;

· arbete aldrig kan skapa förutsättningar för avsaknad av värmebildning;

· avsaknad av värmebildning aldrig kan koppla arbete;

· varmt aldrig kan förorsaka kallt;

· kallt aldrig kan erhållas ur varmt;

· avkylning aldrig förorsakar uppvärmning;

· avkylning alltid betyder avsaknad av arbete;

· avkylning alltid betyder avsaknad av värme;

· uppvärmning aldrig förorsakar avkylning;

· allt arbete förorsakar värmebildning;

Konsekvent, utan undantag, utan kompromisser, utan luckor, utan avbrott, utan brister.

— Fysikbeskrivningen får INTE innehålla MOTSÄGELSER på något enda av dessa eller med dessa samhörande områden, då i annat fall vi hamnar i UPPENBARA MOTSÄGELSER, inkonsistenta meningsgöranden, obegripliga underförstådda privata hemmabioföreställningar som inte ens Maskinisten har någon koll på.

Jämför en MOTOR som utför EXPANSIONSARBETE [AGKE]:

— Erinra först att luftmolekylernas medelhastigheter i luft ligger runt 500 M/S vid 20°C och bara blygsamt mindre vid lägre temperaturer.

Kolven i cylindern som dras ut [AGKE] och verkställer ÖKAD VOLYM presenterar för gaspartiklarna en STÖRRE FRIVÄG: på den erbjudna större frivägen både kan [icke-isotermiska alternativet] och inte kan [isotermiska alternativet] gaspartiklarna reducera sina inbördes rörelseenergier, helt beroende på SÄTTET som volymändringen sker på:

det finns ingen obetingad, föregiven, fysik som säger att expansionen MÅSTE välja icke-isotermiska alternativet.

— Och sedan på samma sätt med kompressionsrörelsen:

det finns ingen obetingad, föregiven, fysik som säger att kompressionen MÅSTE ta icke-isotermiska alternativet.

I vilket fall:

— ARBETET som kolven utför alstrar värme i cylinderväggarna och allt material som kopplar kolvanordningens rörelsemässiga tillståndsändring, och därmed (i mer eller mindre ringa grad) ett visst (mindre) temperaturtillskott till gasmassan.

Expansionen som förtydligande exempel

— BARA OM Kolvutdraget TAR MED SIG en nedbringad gasbollshastighet — BARA de gasbollar som hinner träffa kolvtoppen under dess tillbakaryckning — DÅ KAN den rörelsen aktivt BIDRA till en DIREKT temperatursänkning hos gasen, analogt minskning i rörelseenergi hos de berörda gasbollarna: kolvdraget med volymexpansionen bidrar aktivt DIREKT till en avsvalning — i proportion till den berörda kolvtoppytan.

— Sker rörelsen däremot lika snabbt som gasbollarnas medelhastighet, isotermiska alternativet i AGKE, får kolvrörelsen ingen inverkan: volymökning utan temperaturändring.

— HUR verkan fungerar beror uppenbarligen på konstruktionen och SÄTTET kolvrörelsen sker på.

Se utförligt i AGKE.

Jämför f.ö. det omvända fallet — inte riktigt samma villkor gäller:

När kolven trycks in och volymen avtar, tvingas kolvens toppyta att TRÄFFA gaspartiklar på en MINDRE FRIVÄG — som att börja HAMRA MOT ett material: materialets atomära partiklar tar upp hamringsenergin som VÄRMETILLSKOTT:

— I motsvarande utdragande rörelse finns i varje fall en rent teknisk möjlighet för kolven att »springa ifrån» gasbollarnas medelhastighet, och inte låta någon enda gasboll hänga med (isotermiska alternativet). Det kontaktlösa sättet finns principiellt inte då kolven rör sig komprimerande: den MÅSTE träffa = överföra träffrörelsen på gaspartiklarna, speciellt om kolvrörelsen är snabb.

Det betyder uppenbarligen detsamma som att värme — kolvrörelsens rörelseenergi — överförs på gaspartiklarna, och därmed deras motsvarande högre rörelseenergi:

arbete förorsakar uppvärmning, aldrig avsvalning.

— Det finns ingen arbetande kraft i fysiken som genererar avkylning. Allt arbete i fysiken genererar VÄRME.

Allmänna gaslagens samband kan inte tillämpas på dynamiken MELLAN olika atmosfäriska skikt — DÄRFÖR ATT dessa bestäms hydrostatiskt [HYDROTRYCKET] av Jordgravitationen och formar tillsammans med Solvärmen och Jordrotationen den sammansatta skiktade Jordatmosfären. Allmänna gaslagen kan bara tillämpas INOM ett specifikt skikt med en specifik fundamental gaskonstant (k/[V=1M³]=p/T):

— Fundamentala gaskonstanten (k) avtar f.ö. inom troposfären entydigt med växande höjd, grafen nedan:

kk0

k(h) = k(STP)·(k/k₀)

= (370,95002 J/°K)·(k/k₀) ; Specific fundamental gas constant for actual altitude, idealized

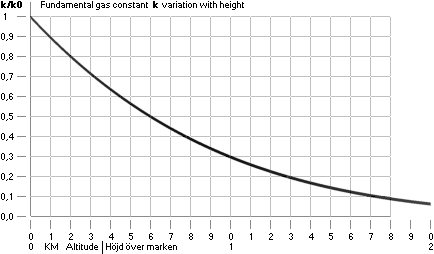
Graf Unit20p — [k/[V=1M³]=p/T]/[T]/k0

(10)([101300]è'0.0341579(0.003–288.15[1000x]'–1)'–1)[(273.15–[1000x]0.003)'–1][(370.95002)]'–1

k = p(V=1M³)/T ; pV = kT:

y = k/k₀

= k(h)/k₀ ;

k₀ = k(STP)

= 370,95002 J/°K :

y = [p/T]_h/k₀ ; k = k(h) ; k₀ = k(STP) :

k(h) = y · (370,95002 J/°K) ; Specific fundamental gas constant for actual altitude, idealized

k0 = 370,95002 J/°K är fundamentala gaskonstanten i marknivån vid STP. k beräknas separat genom minskningen i Jordatmosfärens hydrostatiska tryck p [Se GRAFp1] med växande höjd och avtagande temperatur (T) via en och samma fasta referensvolym [1M³].

— Se även samma graf som ovan i Slutgraferna, men med marginellt skilda koefficienter (skillnaden syns inte i denna skala).

Allmänna gaslagen kan alltså INTE användas för att beskriva händelseförlopp MELLAN olika höjdskikt. Bara INOM varje — på alldeles samma sätt som att vi här på markytan kan använda allmänna gaslagens samband (pV=kT).

WikipediaInternalEnergy

OCH vi ser här, återigen hur favoriseringen av icke-isotermiska alternativet [noAdia] ges företräde i beskrivningen av Jordtroposfärens luftcirkulation:

Wikipedia samma [‡]:

@INTERNET Wikipedia, Adiabatic process [2014-03-26]

http://en.wikipedia.org/wiki/Adiabatic_process

”When a parcel of air descends, the pressure on the parcel increases. Due to this increase in pressure, the parcel's volume decreases and its temperature increases, thus increasing the internal energy.”,

;

@INTERNET Wikipedia, Lapse rate, Dry adiabatic lapse rate [2014-04-15]

http://en.wikipedia.org/wiki/Lapse_rate

”Under these conditions when the air rises (for instance, by convection) it expands, because the pressure is lower at higher altitudes. As the air parcel expands, it pushes on the air around it, doing work (thermodynamics). Since the parcel does work but gains no heat, it loses internal energy so that its temperature decreases. The rate of temperature decrease is 9.8 °C/km (5.38 °F per 1,000 ft) (3.0°C/1,000 ft). The reverse occurs for a sinking parcel of air.[7]”.

— Kommentar till sista citatet:

— It expands because the higher hosting atmospheric site has lower density, lower pressure and hence offers a HIGHER DEGREE OF A FREE PATH for the upcoming air’s gas particles to move into — same condition as cooling: no work is done in cooling as Work is defined as the Cause, not loss, of Heat; No work is done in atmospheric ADOPTION from lower warmer air rising into higher cooler SITES; each atmospheric site occupies a hydrostatic domain in temperature (T), pressure (p) and density (ρ): Atmospheric sites all have decreasing Tpρ-values with increasing height. No work is done by cooling: work always causes warming. HeatBasic. Please.

— Men för all del: visa att jag har fel. Jag söker hela tiden efter ett sådant insteg.

LuftKonventionen

Så här fungerar det enligt vad som f.n. kan utläsas ur relaterad fysik:

— Svårigheten att anställa en beskrivning för fri, kallare luft som via konvektion återvänder till den varmare marken från högre svalare delar är uppenbar därmed att ingen tvingande inneslutning existerar som tvingar luften att följa med. Det är bara den naturliga Solenergibaserade atmosfäriska konvektionskraften som kan styra den rörelsen, och den kräver en markkoppling som uppvisar ett visst (konvekterande) undertryck (luftmassunderskott från föregående uppstigande uppvärmda markluft). I annat fall finns inget utrymme att inhysa den nedströmmande luften. Följdsatsen skulle bli: den luften pressas (komprimeras) inte in i markden, den DRAS (värmekonvekterar) in. Etablerade meningar som beskriver detaljen har eftersökts men ännu (Apr2014) inte upphittats.

— Soluppvärmd markluft stiger upp mot kallare nivåer, och AVKYLS där genom SUCCESSIVT UPPÅTSTIGANDE VÄRMELÄCKNING [LapseRate]; Luftmassunderskottet vid marknivån i tomrummet från den uppstigande markluften skapar ett motsvarande konvektivt MARKMASSAundertryck (luftmassdeficit), och motsvarande i det övre inträngande atmosfäriska skiktet ett konvektivt TOPPLUFTMASSAundertryck (luftmassexcess), ett massövertryck. Paret massöver- och undertryck har INTE den aktuella hydrostatiska trycknivån utrymme för, och vilka par harmonierande motställningar, således i Solvärmens kraft och energi, skapar en KONVEKTION, en sluten luftströmningsväg. Luftströmningsvägen tvingar den övre avkylda toppluften att återvända till marken igen, SUCCESSIVT UPPVÄRMD på nervägen på Solvärmens bekostnad och med allt kortare avstånd till den allt varmare marknivån — för ny upptransport av vattenånga för molnbildning, osv.

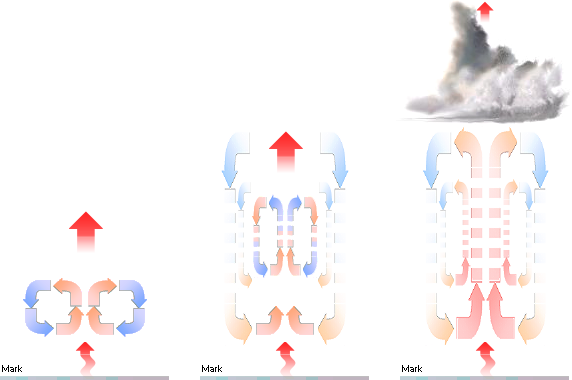
Hur luftcirkulationen med den Solenergiförsörjda konvektionen kan förstås relaterat [EV]: uppvärmd markluft som stiger, förlorar temperatur inte på grund av någon volymär expansion [noAdia] [JAVK] utan på grund av naturlig avsvalning [Flaskexperimentet | JAVKbasic | VLAFS] i takt med växande avstånd från den Soluppvärmda markytan. När den kallare luften återvänder till marken, gör den det genom motsvarande successiva uppvärmning på den allt högre markvärmen från Solmarkarbetet, och inte på grund av att den kallare luften komprimeras.

— Framställningssättet FÖREFALLER uppvisa att Jordatmosfären inte alls över huvudtaget visar någon som helst analogi med en gas i en innesluten cylinder med en kolv i en sådan speciell konstruktion som med kolvens utdrag och intryck på den vägen reglerar gastemperaturen. Men just detta sistnämnda förefaller vara enda alternativet i modern akademisk beskrivning i ämnet [”Adiabatiska gaslagen” | ATFT]. Se vidare med citat i CentralAdia och AdiabaticRef.

— Temperaturökningen i den svalare nedåtstigande luften skulle då kunna förklaras genom den nämnda Solenergiunderhållande konvektionskraften: Luften ERHÅLLER FÖRNYAD rörelseenergi FRÅN den lägre nivåns HÖGRE hydrostatiskt fasta temperatur, VIA Solvärmens markuppvärmande primärfunktion, och anpassas så DIT — inte får ökad temperatur för att tätheten och trycket vid marken är högre, utan JUST på grund av FÖRNYAD UPPVÄRMNING från Solens markvärme. Inget annat.

— Det finns här veterligt ingen DIREKT analogi mellan typ en sluten cylinder med en kolv som pressar ihop och drar ut luft kontra det som händer i atmosfären vid luftströmningar. Det förefaller uppenbart EFTERSOM 1. vardagsluften vi vistas i INTE har någon avgränsad inneslutning och 2. att HELA ENERGINOTAN med energin till luftströmningarna just står på Solens bord — INTE på typ någon FöretagarRepresentation som det står ”kompression” och ”expansion” på — och 3. att Jordatmosfäriska skikten är hydrostatiskt fixerade i temperatur, tryck och täthet och därför rimligtvis heller INTE är i stånd att utföra något motsvarande arbete liknande en kolv i en sluten gascylinder som dras ut och trycks in. Avsaknaden av säkra, klara och tydliga experimentella motsvarigheter som kan bekräfta eller dementera dessa synpunkter försvårar också förståelsen för molnbildningens precisa grunder.

NLA, NaturligaLuftAvsvalningen

Vad som inte omnämns (mest synligt, Apr2014) i etablerade beskrivningar är (dessutom) motsvarande fenomenresultat i det enkla FlaskExperimentet: Uppvärmd luft som svalnar INOM ett givet luftområdes tryckvärde, genomgår tveklöst en volymminskning. I det Jordatmosfäriska fallets olika skikt visar det sig emellertid att tryckändringarna (57%) inbördes mellan olika höjdskikt avtar snabbare med höjden än temperaturen (90%). Tryckminskningen överväger alltså, och därmed motsvarande volymökning (för inneslutna experimentvolymer: notera att volymskikten i Jordatmosfären är fixa och konstanta: volymen ändras aldrig där, se från JAVK). Emellertid är en stigande luftpelare ett komplicerat system med ett yttre och en inre kärna, och vi vet här strängt taget inte HUR den detaljen fungerar i praktiken. Med tillgång till gratisutbudet på webben verkar heller ingen direkt översvallande nyfikenhet finnas i det publika klargörandet av ämnets sammansatta natur. Heller verkar ingen bekräftande uppgift finnas synlig i ämnet som omnämner motsvarande resultat från det enkla köksexperimentet, komplementet till flaskexperimentet, och som visar den uppvärmda uppåtstigande fuktiga luftens avsvalningstakt 122°C/M/S, se JAVKbasic. Men, frånsett de aspekterna:

Expansions- och kompressionstendenserna måste finnas genom tryckets olika grader i Jordatmosfärens olika höjdskikt. Det är klart. Se särskilt resultatet från FlaskExpeditionen. Men då konvektionsbildningen kräver en sluten luftväg övre-nedre, FÖREFALLER expansions- och kompressionstendenserna inte kräva mera verksamhetskraft än att de just VERKSTÄLLER konvektionsdynamiken, och därmed knappast påverkar den lokala luftmassan med någon nämnvärd volymändringsförorsakande temperaturändring — och då förutsatt sämsta fallets fysikbeskrivning med giltighet av det icke-isotermiska alternativet i AGKE, se även i noAdia. Är den synpunkten felaktig, måste någon form av förtydligande bevis existera. Det eftersöks (Apr2014) men har ännu inte upphittats.

Luften KALLNAR vid uppstigning, lämnar ifrån sig sitt vattenånginnehåll för molnbildning, och ÅTERUPPVÄRMS vid nedströmningen för ny vattenångtransport.

Det finns här veterligt inget annat att härleda. Variationerna i tryck och täthet är fasta egenskaper i de atmosfäriska skikten, och dessa utför inget arbete på luftströmningen [VLAFS], endast KARAKTÄRISERAR aktuellt lufttillstånd: De atmosfäriska skikten utför inget arbete. Det är bara Solen (och Jordrotationen som blandare) som utför arbete; De atmosfäriska skikten med varierande temperatur, tryck och täthet [SLUTGRAFERNA] utgör fasta, fixa termogravitella tillståndsdomäner [HYDROTRYCKETslutgraferna].

— Solen utför arbetet: Det finns bara en knapp att välja på: uppvärmning. Resten »är» NATURLIG AVSVALNING [VLAFS]. Relaterad fysik. Är den synpunkten felaktig, måste någon form av förtydligande bevis existera. Det eftersöks (Apr2014) men har ännu inte upphittats.

Här ett exempel på en mera försiktig formulering och som tydligen undviker ovanstående behandlade felfällor:

CHANGES IN THERMO VARIABLES AS A PARCEL RISES, METEOROLOGIST JEFF HABY

http://www.theweatherprediction.com/habyhints2/502/

”A parcel of air expands and becomes less dense as it rises. This occurs because the air pressure lowers around the parcel as it increases in altitude. The volume of the parcel increases since it is expanding.

The temperature of a rising parcel always cools even though it is becoming less dense.”;

:

”The mass of the parcel remains constant since adiabatic theory assumes no exchange in mass between parcel and environmental air. The only exception to this is the consideration of rain leaving a saturated parcel once it is condensed out.”;

Följande exempel ansluter däremot (häftigt) till föregående felforum — samma typ, fast tydligare: pV = kT:

Oregon State University — ADIABATIC PROCESSES AND LAPSE RATES [2014-03-26]

http://blogs.oregonstate.edu/suitcase/files/2012/07/Humidity.pdf

”The drop in temperature is a result of the decrease in atmospheric pressure at higher

altitudes.”;

;

”It is very important to understand how adiabatic processes work, if you want to understand what happens to moisture in the atmosphere”;

Här ett etablerat exempel som omnämner betydelsen av att eliminera täthetsaspekten i väderatmosfären:

University College Dublin — THE HYDROSTATIC EQUATION [2014-03-26]

http://maths.ucd.ie/met/msc/fezzik/Phys-Met/Ch03-Slides-2.pdf

”In meteorological practice it is not convenient to deal with the density of a gas, ρ, the value of which is generally not measured. By making use of the hydrostatic equation and the gas law, we can eliminate ρ:

∂p/∂z = –pg/RT = – pg/R_dT_v

”.

— Tecknet ∂ — ”stiliserat d” [»STILd»] från Legendre 1786 och Jacobi 1841 — används konventionellt (ofta) för att särskilja ordinära differentialer (dx) från partikulära (∂x): partikulära differentialer förekommer (oftast) i flera versioner i en och samma integralform [jämför ∂(xyz)] och integreras en i taget med övriga som konstanter. Se även webbreferenser på partial derivative.

EtableradeGrovvärden

Allmänt etablerade grovvärden till jämförelse

FOCUS MATERIEN 1975 s496-497 visar illustrerat Jordatmosfärens olika detaljer;

— Upp till grovt tropopausen (troposfärens övre gräns, ca 10 KM) avtar luftens täthet från markens 1,2 KG/M³ till tropopausens 0,4 KG/M³:

ρ(h) = 1,2 KG/M³ – h(1,2–0,4=0,8 KG/M³)/10.000M ; h max = T4 M = 10 KM

= ρ₀ – h(8 t5 KG/M³)/M

Luftens täthet (Rho) ρ avtar med höjden h.

ρ₀ Luftens täthet 1,2916296 KG/M³ vid STP, eller annat utgångsvärde vid marknivån.

Det är också det huvudsakliga intervallet 0-10 KM för Jordytans atmosfäriska molnfysik [PDAS].

— Samma källa (vä.n.) samma uppslag anger ”Temperaturen avtar i regel uppåt med i genomsnitt 6°C per km.”.

— Det betyder en grovt linjär temperaturminskning med höjden (h)

T(h) = T₀ – h(0,006°C)/M ; h max = T4 M = 10 KM.

Temperaturen T avtar med höjden h.

T₀ aktuell lokal utetemperatur i °C.

— FOCUS MATERIEN 1975 s496-497 ger också ungefärliga (illustrerade) tryckminskningen med växande höjd

p(h) = p₀ – h(101300–26500)Pa/10.000M ; h max = T4 M = 10 KM.

= p₀ – h(7,48 Pa)/M

Atmosfäriska trycket p avtar med höjden h.

p₀ marktrycket vid STP 101325 Pa — eller annat utgångsvärde vid marknivån

Förhållandet (gaslagen, p/T=k/V) ger då efter de rena variationsfaktorerna

p/T = (7,48 Pa)/(0,006°C) ; Jämförelsen grovt upp till max 10 KM [hela troposfären].

~ 1247 Pa/°C ;

Atmosfäriska trycket avtar med växande höjd över marken enligt 1247 Pascal per grad Celsius.

— I termer av allmänna gaslagen skulle man tolka det som att ändringen

p/T = k/V = konstant 1247 Pa/°C.

De mera reguljära variationssambanden genomgås mera ingående i HYDROTRYCKET.

AirParcel

University of Alabama —

ESTIMATION OF THE LIFTING CONDENSATION LEVEL, CODY KIRKPATRICK (2006)

[2014-03-26]

http://talismanred.com/work/lclderivation.pdf

”The air parcel ascends adiabatically ..”

AIR PARCEL i MAC en luftballong av tunt superelastiskt gummi:

LAPSE RATES AND AIR PARCELS, Fovell 2004 [2014-03-26]

http://www.atmos.ucla.edu/~fovell/AS3downloads/lapse_rates.pdf

”The air parcel is an important and useful conceptual device in atmospheric sciences. We make a

parcel by gathering together a usually unspecified amount of air and pretend the air is surrounded

by an invisible boundary that insulates the parcel air from its surrounding environment. The parcel

boundary, however, is flexible, permitting the air inside to expand or contract as conditions dictate.”

@INTERNET Wiktionary air parcel [2014-03-26]

http://en.wiktionary.org/wiki/air_parcel

”(physics, meteorology) An imaginary body of air to which may be assigned any or all of the basic dynamic and thermodynamic properties of atmospheric air.”,

;

”It cannot be given precise numerical definition, but a cubic foot of air might fit well into most contexts where air parcels are discussed, particularly those related to static stability.”

ClausiusOriginal

2014IV21

Två inbördes olika sätt finns i modern akademi att uttrycka allmänna värmetillståndets fysik [Källa: Wikipedia, First law of thermodynamics, Description]. Bägge använder termen ”closed system” för värmeobjektet lika med kroppen eller anordningen (en gas):

1. Clausius original: ΔU = Q – W ; U inre energi, Q tillförd värmemängd, W arbetet

2. Plancks konvention: ΔU = Q + W ; U inre energi, Q tillförd värmemängd, W arbetet

I Clausius original är W arbete som utförs av ”systemet” (relaterat: av kroppen, anordningen, gasen); ändringen i gasens inre energi är lika med tillförd värmemängd – ev. arbete utfört AV gasen

I Plancks konvention är W arbete som utförs på ”systemet” (relaterat: på kroppen, anordningen, gasen); ändringen i gasens inre energi är lika med tillförd värmemängd + ev. utfört arbete PÅ gasen

IE, Inre Energin, eng. internal energy

Inre energin (U, eng. internal energy) motsvarar (relaterat)

ideala allmänna gaslagens rörelseenergier över absoluta nollpunkten

Alltså, motsvarande ett ämnes eller en gas’ inre molekylära eller atomära vibrationstillstånd [Figurförklaringen], analogt ÄMNETS MOMENTANA VÄRMEINNEHÅLL, eller enklare ämnets momentana tillstånd (med hänsyn till värmegradens magnitud, alltså absoluta temperaturens aktuella värde).

— Wikipedia (Internal energy) anger inre energin abstrakt som ”refers to energy contained within the system”, medan en del andra källor är mera konkreta (Hyperphysics, Internal energy) med ”Internal energy is defined as the energy associated with the random, disordered motion of molecules”.

— I relaterad mening blir inre energin samma som den energi, aktuella Planckstrålningen E=hf, som genomströmmar och skiljer ämnet från absoluta nollpunkten (T= 0°K = materiefysikens fullständiga rörelselöshet): inre (materiella) energin är noll om T=0, och endast då.

FOCUS MATERIEN 1975 använder Plancks konvention (internationellt IUPAC-konventionen) medan Wikipediaartikeln (i huvudsak, som många andra) använder Clausius originalform [mera lämpligt i konkret beskrivning av värmetekniska maskintillämpningar].

HÄR SLUTAR SEKTIONEN OM GRUNDBEGREPPEN TILL MOLNBILDNINGENS TEKNISKA FYSIK.

The END.

Bildkälla: Författarens arkiv · MONTAGE: 2Jun2014 E10 Bild 39 — 1Jun2014 E9 Bild 43 · Nikon D90

— Always a New Beginning.

Universums Historia — TGF2014a — Jordatmosfäriska molnbildningens grundbegreppp

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

TGF2014

ämnesrubriker

innehåll

MOLNBILDNINGENS GRUNDBEGREPP

PART 1: GRUNDBEGREPPEN I MOLNBILDNINGENS TEKNISKA FYSIK

MOTEF

Primärformen

Konvektionen

MOTEFexpBasic

Värmeläckningen

HydroTransiten

EtableradVerifiering

MACadiaRef

Bilmotorn

EKoG

AdiaTransformen

VTE

FG

iROT

EKoGh

GammaRef

CpCvRef

EKoGekv

WikiAdiaGasRef

EKoGT

EKoGex1

EKoGex2

GES

PMT

noAdia

noIsotermVol

FETF

MKonKonvek

Studieexempel, molnbildning under 5 minuter

JAVK

JAVKbasic

KOKOV förklaring

KOKOV

MACadia

AdiabaticCitatWikipedia — DEL 1

DEL 2

DEL 3

WhyNotAdia

VLbasic

ATFTrel

VRF

VLA

PE

TEadiaG

Då Q är Noll

VLAE

noF

NollQno

IsoThermalWiki

VRSsf

ATFT

ATFTh

ATFTex

ATFTnot

GammaEkviv

ATFTsf

DABL

ATFTekv

RdivUref

TAI

JAGVH

HydroTrycket

Tryckvarianten

aJY

UaRef

UaRef2

ENKLApFormen

aRef

aFaktornRef

THTB

LapseRate

TLSvar

WikiAtmPref

WikiTempGraf

WikipediaPref

UsaTodayRef

StandardAtmosphereData

TRYCKET

EM

GRAFp1

TÄTHETEN

TEMPERATUREN

PDAStemp

TLSref

Slutgraferna

pEND

kDIVm

rhoEND

Tend

SlutgrafernaPDAS

SlutgrafernaAkt

SchlatterAtmosphere2009

TroposfärenFM

FlaskExperimentet

Mera tydliga data

FlaskExpeditionen

Tabell hkT

TabellhkTjmf

AGG

Figurförklaring

pVbasic

AGK

AGKT

AGKV

AGKE

AGKK

WikiFriExp

CpMinusCv

WikiHeatCap

VLAFS

AtmosAdiabatMAC

RelateradAdia

PascoCitat

BKLadia

AdiabaticMAC

CentralAdia

WikiAdia

FMadia

FMtermo1

TermoRelFys

AdiabaticRef

HeatBASIC

kk0

WikipediaInternalEnergy

LuftKonventionen

NaturligaLuftAvsvalningen

STILd

EtableradeGrovvärden

AirParcel

InreEnergin

referenser

[BKL] BONNIERS KONVERSATIONS LEXIKON, 12 band A(1922)-Ö(1928) med SUPPLEMENT A-Ö(1929)

[BA] BONNIERS ASTRONOMI 1978 — Det internationella standardverket om universum sammanställt vid universitetet i Cambridge

[FM] FOCUS MATERIEN 1975, Focus uppslagsböcker Stockholm, Almqvist & Wiksell förlag AB Stockholm; tryckår 1979 Uppsala

[HOP] HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i UniversumsHistoria, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1,602 t19 C ...................... [ref. FOCUS MATERIEN 1975 s666]

ε₀ = 8,8543 t12 C/VM ............. [ref. FOCUS MATERIEN 1975 s666]

MKSA-systemet:

MeterKilogramSekundAmpere, det (en gång) internationellt standardiserade enhetssystem; det är alla enheter som krävs för fysikbeskrivningen.

— M, KG, S och A motsvarar också de enhetliga universella fysikaliska storheter distans (d). massa (m). tid (T|t), och elektrisk strömstyrka (I|i) som definierar fysikens samband.

— MKSA-enheterna används genomgående i UniversumsHistoria, om inget annat anges särskilt.

— Men notera också (den nära ofattbart, komiskt) STORA SVÅRIGHETEN att hitta webbreferenser (Mar2014):

— Sökning på ”MKSA-system” resulterar i träffar överst med rubriken MKS-system (Wikipedia MKS system of units): Ampere fattas för att fullständiga fysikbeskrivningen.

— INTERNATIONELL STANDARD (2014: SI, eng. Standard International, eg. International System of Units, http://en.wikipedia.org/wiki/International_System_of_Units) har INTE enhetliga normer för enheternas FORM; Väl finns MKS och A-enheterna i SI-systemet. Men de SKRIVS ofta godtyckligt (se Wikipediaartikelns tabell) i teckenformen och med kaotiska resultat [jämför PREFIXEN nedan]: Vi ser numera ofta i etablerade beskrivningar beteckningar som (vad vi mestadels kan förstå) avser typen meter (M) som massa (m), kilogram (KG) som någon konstant·gravitationskonstanten (kg), sekund (S) som spatium (s) — annan term för distans, d — och så vidare.

— Det är heller inte att förvänta annat i ett lärosystem (MAC generellt) där det förväntas av eleven och studenten att det viktigaste i undervisningen är att göra som den lokalt begåvade och akademiskt meriterade läraren säger, inte förstå innehållet — definitivt inte ifrågasätta det: Läroplanen har inte TID med det.

— Notering [31Mar2014] specifikt för Wikipedia @INTERNET: Skriver man in MKSA i Wikipedia sökbox med Enter, omdirigeras man till, just, artikeln om International System of Units.

PREFIXEN FÖR bråkdelar och potenser av FYSIKALISKA STORHETER

Här används genomgående och konsekvent beteckningarna

förkortning för förenklad potensbeteckning

d deci t1

c centi t2

m milli t3

µ mikro t6

n nano t9

p pico t12

f femto t15

Alla Enheter anges här i MKSA-systemet [Se International System of Units] (M meter, KG kilo[gram], S sekund, A ampere), alla med stor bokstav, liksom följande successiva tusenprefix:

K kilo T3

M mega T6

G giga T9

T tera T12

Exempel: Medan många skriver cm för centimeter skrivs här konsekvent cM (centiMeter).

— I förekommande fall (ytterst sällsynt här) då enheten gram används — för att undvika onödig sammanblandning med Giga-prefixet — används enhetsbenämningen gram; 1 gram = 1KG/1000.

tT t för 10^–, T för 10⁺, förenklade exponentbeteckningar

MAC ofta använd förkortning för modern akademi i Universums Historia (eng. Modern ACademy)

TNED — Related PHYSICS And MATHEMATICS

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också

RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

SHORT ENGLISH — TNED in general is not found @INTERNET except under this domain

(Universe[s]History, introduced @INTERNET 2008VII3).

TNED or Toroid Nuclear Electromechanical Dynamics is the dynamically equivalent resulting description following the deductions in THE PLANCK RING, analogous AtomNucleus’ Deduction. The description according to TNED is related, meaning: all, each, details claim to be fully logically explainable and understandable, or not at all. With TNED is (hence) also understood RELATED PHYSICS AND MATHEMATICS. See also the emergence of the term TNED in AtomNucleus’ Deduction.

Senast uppdaterade version: 2018-12-27

*END.

Stavningskontrollerat 2014-06-07.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

∫ ∫ √ τ π ħ ε UNICODE — ofta använda tecken i matematiska-tekniska-naturvetenskapliga beskrivningar

σ ρ ν ν π τ γ λ η ≠ √ ħ ω → ∞ ≡

Ω Φ Ψ Σ Π Ξ Λ Θ Δ Γ Ŧ ŧ

α β γ δ ε λ θ κ π ρ τ φ ϕ σ ω ϖ ∏ √ ∑ ∂ »stiliserat d» ∆ ∫ ≤ ≈ ≥ ˂ ˃ ˂ ˃ ← ↑ → ∞ ↓

ϑ ζ ξ

Pilsymboler, direkt via tangentbordet: Alt+24 ↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬

Alt+23 ↨ — även Alt+18 ↕; Alt+29 ↔

åter till portalsidan · portalsidan är www.UniversumsHistoria.se