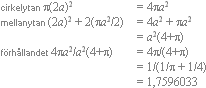2KÄRNRADIERNA DEL II 2008VII27 | 2008XI11 | a production · | Senast uppdaterade version: 2023-08-23 · Universums Historia

Kärnradierna | Inledande allmän beskrivning · Kärnradiedata på webben · Kärnmodellen · Deuteronens Hemlighet — Impulsmomentets 0,71r-kriterium · LaserEpokens nya Deuteronradie ·

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Kärnradiernas teori enligt TNED:

INSTABILA NUKLIDER · Betainstabila — Nuklidinstabila · Massdefektens inverkan på kärnradien · Elektronbesättningens inverkan på kärnradien · elektronmassans tyngdpunkt ·

Kärnradiebildningen genom Elektronbesättningen via np-strukturen · Kärnradierna för exceptionellt kortvariga-instabila nuklider (HALONUKLIDER) ·

Grafer:

Kärnradierna enligt TNED — resultatsammanställning · Allmänna kärndradiedata enligt TNED — resultatredovisning · kalkylkort · register till de kalkylkort somanvänds i denna artikel

Hofstadters kurvskara · Volymära Laddningstätheten i jämförande stapeldiagram · Se även kort inledande orientering i Inledning till Nuklidradierna Del II

Kärnradierna Del II 2008IX5 | generalgenomgång av atomkärnans storlek och utseende enligt relaterad fysik och matematik ·

Se även kort allmänt repeterande inledning i KÄRNFYSIKENS GRUNDBEGREPP ENLIGT TNED — Kort illustrerad repeterande inledning

UPPKOMSTEN AV KÄRNFYSIKALISKA SPÖKBEGREPP GENOM DEN AVANCERADE EXPERIMENTALFYSIKEN

Rent experimentellt, och i ljuset av massbaserade mätmetoder, är atomkärnan för alltid dömd att framstå som diffus, konturlös, utan varje spår av någon klart avgränsad figur.

Statistiska medelvärdesradien för protonen med grund i massbaserade spridningsexperiment anges 1-1,5 Fermi beroende på källverk — vilket betyder en osäkerhet på hela 67%.

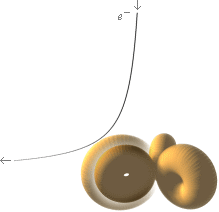
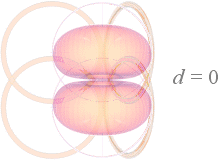
Även med en skarpt avgränsad kontur för atomkärnans radie, finns alltid ett växelverkande elektromagnetiskt fält mellan atomkärnan och varje yttre föremål. ”Bredden” på det fältet (antytt genom figurdelens ”halo”, figuren nedan, och som varierar med den avkännande partikelenergin) garanterar att formradien i vilket fall kommer att förvanskas och suddas ut genom den statistiska mängden avkännande kroppar: avböjningarna (spridningsvinkeln) sker på olika sätt och man får ett motsvarande diffust band i slutresultatet, hur man än räknar.

Statistiska diffusionen Atomkärnans växelverkan med omgivande masskroppar (elektroner eller andra atomkärnor, eller deras fragment) bygger liksom all övrig mekanik på att energiverkan sätts i relation till en tyngdpunkt — eller i atomkärnans fall i relation till en tyngdcirkel om vi räknar med ett kärnspinn. Men som vi redan vet från mekaniken, struntar tyngdpunkten (tyngdcirkeln) fullständigt i den FORM som den bär med sig: spridningsexperimenten arbetar i resultatdelen NETTO (när allt kommer till kritan) på tyngdpunkten/tyngdcirkeln, inte på den verkliga formkonturen. Denna detalj grusar definitivt varje möjlighet att få fram atomkärnans konturradie ur massbaserade experiment; Dessa kan som mest antyda tyngdcirkelns radie, inte den verkliga formkonturen — allra minst några strukturella detaljer.

En ljusbaserad mätmetod (E=hf) skulle vara idealisk OM man kunde mäta (det minimala) energiflödet i skuggbilden från en atomkärna — med en garanterad motsvarande mekanisk 3D-upplösning på minst 0,01 Fermi. Problemet är återigen detta, att det inte finns några (stabila) kroppar som kan ”hängas” (själva den fotografiska plåten) på sådana mått; Minsta atomkärnan ligger grovt runt 1,25±0,25 Fermi; Elektronen, som anses vara en ”punktpartikel” i dessa sammanhang kan heller inte användas eftersom elektronen i dessa sammanhang inte existerar fritt utan bara i resonanta svängningar inom sin moderatom och då betraktad som en oskiljbar enhet från denna; Atomens radie är i fasta ämnen (atomära medelavståndet) grovt sett 200 000 gånger större än atomkärnan. Inte heller en ljusbaserad mätmetod kan ge oss någon direkt bild av atomkärnan.

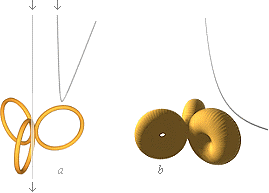
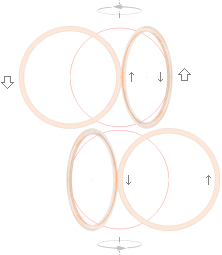
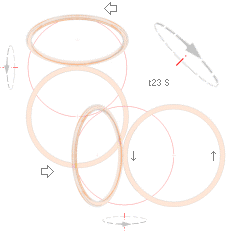
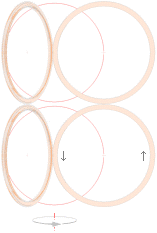
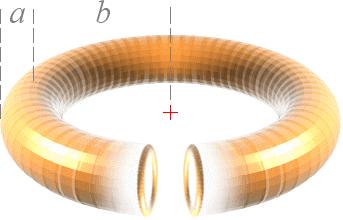
MED REFERENS TILL TNED möter till exempel elektronmassan som avkännande prob främst två skilda formkomplex (a och b), illustrationen till vänster — om energin är tillräcklig för att bryta igenom det yttre toppspinnet. (Elektronkomponenten med hastigheten v avböjs i vilket fall bort från atomkärnan av dess ytmagnetiska fält som sammanhänger med kärnspinnet). I alternativet (a) avkänns typiskt kärnans ytladdning på en trång volym vilket ger ett motsvarande statistiskt högt toppvärde på laddningstätheten: en del av strålpartiklarna går t.o.m. rakt igenom protonens yttre toppspinn utan att böja av alls. I de fall avböjningar sker, är de typiskt ”vassa”, dvs., med stora spridningsvinklar även inom små avvikelser från den centrala projektilstrålen, analogt stor växelverkan mellan målobjekt och strålobjekt. I alternativet (b) sprids däremot träffarna ut på större omslutande yta, analogt större volym och därmed betydligt lägre toppvärde på laddningstätheten. Vinkelavvikelserna blir långt ifrån så häftiga som i fallet (a).

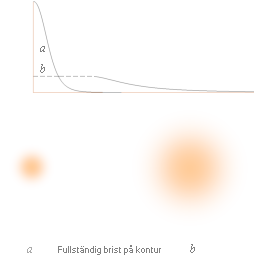
Motsvarande statistiska resultatgrafer (a och b) blir de typiska som visas i figuren nedan; vertikalskalan (typiskt) anger laddningstätheten och horisontalskalan anger avståndet från centrum.

För praktiskt exempel, se Hofstadters Kurvskara.

I jämförande stapeldiagram med TNED, se Laddningstätheten i jämförande stapeldiagram.

En ytterligare praktisk aspekt visas i CERN-kurvan.

Med en favoriserad allmän sfärisk idealism (funktioner av r) tolkas resultaten generellt i det senare fallet som [‡citat] ’bevis för att protonen innehåller små, hårda objekt’.

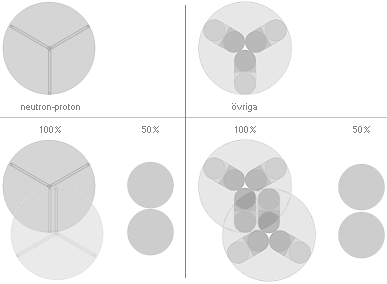
Den resulterande totalbilden, de diffusa punkterna under kurvorna ab här till vänster, uppvisar föga eller inget alls av den ursprungliga modellformen: det enda som framträder är en diffus punkt som tonar ut mjukt utan konturer eller några som helst detaljer. exempel med begreppet laddningsradie GENOM STATISTISKA MODELLER (av mycket komplicerad natur) — som alltså helt garanterat har suddat ut varje ursprung av originalet och förvandlat det till en diffus bild — kan man — så — MED GRUND I EN MYCKET EXAKT KÄRNFYSIKALISK GEOFYSIK (TNED — här till den prövande förebilden) framhäva olika statistiska medelvärden för olika växelverkande aktionsradier typ ”laddningsradien” — och som därmed också blir strängt bundna till en viss mätande METOD. En sådan medelvärdesform och som numera (speciellt från 1990-talet) används frekvent är just det kärnstatistiska begreppet ”laddningsradie”. Eller för den delen själva begreppet överhuvudtaget kärnradie baserat på experimentella resultat. Med ovanstående förutsättningar kopplar det begreppet INTE till byggnadens formfysik utan till byggnadens statistikiserade verkansfysik: En anpassad fysikbild gäller, då.

Eftersom medelvärdena HELT bygger på STATISTIK — som alltså enligt ovanstående resultat helt förvanskat ursprungets formfysik — finns inget annat kvar att välja på än det här: värdeformerna i det experimentella materialet avspeglar FYSIKALISKA SKUGGBEGREPP. De finns inte i fysiken — typ ”laddningsradie”, ”strukturradie”, ”kärnradie”, ”materieradie”, etc. — utan figurerar bara i den MATEMATISKA MODELL man använt för att sovra ut medelvärdena ur det rent experimentella råmaterialet.

Värdena kan återfinnas genom upprepade experiment ENDAST om man använder DEN metoden med just DESS villkor och matematiska förutsättningar.

Precisionen i mätvärdena som florerar i mängd på webben i olika tillgängliga pdf-dokument presenteras (från runt 2000) typisk med en ”laddningsradie” enligt r=N,nnnX Fermi med osäkerheten för X först i fjärde decimalen. Ett sådant utomordentligt gott kärnradievärde SKULLE gott och väl KUNNA ge skärpa och kontur åt atomkärnan. Men, som redan nyligen konstaterats ovan, med en allmän STATISTISKT UTSUDDANDE VERKAN som förlägger typ protonradien till i storleksordningen 1-1,5 Fermi beroende på METOD, analogt 67% oskärpa, blir precisionsvärdet värdelöst som konturbildare.

Figuren här till vänster, i fortsättning från ovan, ger ett (veterligt) utmärkt konkret exempel: Den enda bild som finns av atomkärnan från modern akademi och vetenskap, och som kan frammanas rent experimentellt, består av en diffus centralpunkt som tonar ut mjukt — utan några som helst konturer eller figurativa detaljer. I den bilden presenterar man motsvarande radievärde för den lättaste av alla atomkärnor (neutronen-protonen) enligt (typvärde i databaserna hos många webbkällor) 1,2 Fermi. I den verkliga bildens ljus — alla bidrag beaktade, grovt 1-1,5 Fermi — betyder det en bild av atomkärnan med runt ±25% oskärpa.

Man tycker att atomkärnan med sin enorma yttre volymtäthet även för den lättaste av alla atomkärnor — runt hundra miljoner miljarder eller i siffror

100 000 000 000 000 000 gånger vattnets täthet — skulle uppvisa en fasansfullt enormt skarp formkontur till skillnad mot allt övrigt. Problemet är — ALLTSÅ — att det inte finns några direkt fysiska verktyg som kan SE den bilden.

atomkärnans

allmänna Fermireferens

Av ovanstående två alternativ — massbaserat eller ljusbaserat — finns i princip bara ett enda som kan matcha TNED, det förstnämnda: massbaserade spridningsexperiment. Alltså enbart med hjälp av atomkärnor.

Varför är det klart? Därför att endast en vägande fysik kan inbegripa en direkt växelverkan mellan atomkärnornas tyngdcirklar, analogt tyngdpunkter, och därmed ge eller spegla en efter alla förhållanden optimal dynamisk preferens i relation till komponenternas aktuella formbyggnad. En ljusbaserad mätmetod saknar den vägande aspekten: ljuset är masslöst.

Elektronmassan (som enligt TNED består av mindre komponenter, se elektronmassans komponenter) lämpar sig mera för att inspektera atomkärnans täthet (laddningsfördelningen eller laddningstätheten, se HOFSTADTERS KURVSKARA) — och bör därmed ge de allra minsta motsvarande statistiska kärnradievärdena (grovt runt 1 Fermi). Används istället atomkärnor som projektilobjekt, finns en bättre chans att låta fysiken spela ut händelsernas gång genom atomkärnornas tyngdcirklar, vilket i så fall bör ge ett större statistiskt kärnradievärde (grovt 1,5 Fermi) jämfört med elektronmassan som projektil.

I källverket HANDBOOK OF PHYSICS McGraw-Hill 1967 (s 9|11- 9|12) redovisas fem olika oberoende massbaserade mätmetoder som alla ger någorlunda samstämmiga resultat. Den centrala metoden (nr3) baseras på s.k. spegelkärnor: man använder atomkärnor med samma masstal men omvända proportioner neutroner-protoner.

Genom en balanserad överläggning med enklast möjliga antaganden, redovisar källan en approximerad slutform för dessa experimentkärnor, alla av typen lättare, enligt R=r₀A^1/3 med r₀=1,37 Fermi.

Värdet 1,37 Fermi — motsvarande protonkärnans radie med A=1 — återfinns också i den omfattande HOP-källan på annat ställe i en tabell över fundamentala konstanter (HOP s7–27).

Värdet 1,37 Fermi är också precis (1,36621…) vad som framgår genom TNED från NEUTRONKVADRATEN — via Plancks konstant (h) med neutronradien

r_n = h/m_nc₀ där m_n är neutronmassan och c₀ ljushastigheten i vakuum.

RELATIONEN r_n/r₀ från neutronkvadraten kan också härledas med koppling till energicirkeln (R) i härledningen till Väteatomens Spektrum, samt då med koppling till den motsvarande tyngdpunkten för elektronmassan på avståndet r_e från atomkärnan och som enligt TNED definierar r₀ ur r_n genom elektronmassans utflyttning från neutronen via dess naturliga sönderfall till en Väteatom. Därmed kan ENLIGT TNED atom- och kärnfysikens enklaste grundparametrar (h c₀ r₀ r_n r_e R m_n m_e) sammanställas i en och samma grundekvation — med ett mönsterfel (0,000002 Fermi) som ENLIGT TNED är 10 ggr mindre än atomkärnytans strukturdjup (0,00002 Fermi).

Den precisionen motsvarar i makrofysiken med 1 Fermi motsvarande 1 mM en (till högglans) polerad stålyta (0,02 µM).

Zoomas den bilden ut tusen miljarder gånger (1/1000 000 000 000), är det den fysiska bilden av atomkärnan på plats.

Jämför kantskärpan:

MODERN AKADEMI:

Det finns inom modern akademisk litteratur — forskningsrapporter — en enorm uppsjö av mätningar på kärnradier. Men det finns ingen enhetligt presenterad precision som kan avtäcka någon enda konturerad form eller avgränsad struktur. Inte så mycket som en enda prick. Vi får aldrig SE något därifrån. Alla, samtliga författare och forskare, avhåller sig (noga) från varje sådant närmande. Mätvärdena man kommer fram till, är användbara just för den metodens vidkommande (vad man nu ska använda just den till, ivad den anses tjäna något ändamål). Allmängiltighet saknas helt. OM en sådan kunde frammanas, skulle man också få fram en kontur. Nu finns ingen sådan — i modern akademi. Med den mönsterform som TNED ställer fram genom NEUTRONKVADRATEN med grund i Atomkärnans härledning från Planckringen har vi alltså bara att se efter hur väl den stämmer — eller inte.

TNED (relaterad fysik):

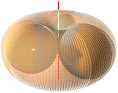
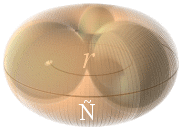
Planckekvivalentens protonTyngdcirkelradie 1,37 Fermi

Atomkärnan enligt TNED sedd med toppspinnet inkluderat.

SPECIELLT BILDEN AV ATOMKÄRNAN — ENLIGT TNED — behandlas vidare utförligt i detta avsnitt med tillhörande särskilda sektioner och avdelningar — till noggrann jämförelse med resultaten från modern akademi och vetenskap.

DEN MODERNA KVARKTEORINS GRUNDVAL

Textmarkeringen i citatet är min för nyckelbegrepp:

”Quarks

In 1980, Maurice Jacob (1933–) and Peter Lanshoff detected small, hard, objects inside the proton by firing high-energy electrons and protons at it. Most of the high-energy particles seemed to pass right through the proton. However, a few of these high-energy particles were reflected back, as if they had hit something. These and other experiments indicated that the proton contains three small, hard, solid objects. Thus protons are not elementary, but the objects inside them may be. These objects are now called quarks.”

[http://science.jrank.org/pages/6560/Subatomic-Particles.html],

Subatomic Particles

Copyright © 2008 Net Industries

Min översättning:

År 1980 påvisade Maurice Job (1933-) och Peter Lanshoff små, hårda, objekt inuti protonen genom att avfyra högenergetiska elektroner och protoner mot den. De flesta av de högenergetiska partiklarna verkade passera rakt igenom protonen. Emellertid, några få av dessa högenergipartiklar kastades tillbaka, som om de hade träffat någonting. Dessa och andra experiment indikerade att protonen innehåller tre små, hårda, solida objekt. Således är protoner inte elementära, men objekten inuti dem kan vara det. Dessa objekt kallas nu kvarkar.

Se även motsvarande experimentella resultat i Kollisioner mellan spinnpolariserade protoner (Experimentredovisningarna i SCIENTIFIC AMERICAN 1979/1987).

Speciellt för de ’tre små inre hårda objekten’, se 1/3-SpökFermiObjekten.

TYNGDCIRKELN

Begreppet TYNGDCIRKEL i modern akademi har varken en entydig eller allmängiltig innebörd inom kärnfysiken — därför att begreppet spinn för atomkärnan saknar enhetlighet i modern akademi.

Medan kärnfysiken enligt TNED helt bygger på ett grundläggande kärnspinn enligt impulsekvationen J₀+3J₁=0 från Planckringen, finns inom modern akademi ingen entydig innebörd för begreppet KÄRNSPINN. Se även utförligt i Spinnbegreppet i modern akademi. Atomkärnan som begrepp saknar helt allmängiltig ÅSKÅDNING i modern akademi (själva möjligheten till en sådan åskådning förnekas bestämt, oftast med allmän hänvisning till Heisenbergs osäkerhetsprincip, men också på grund av den begränsade våglängd som atomernas svängande elektronmassor kan förmedla i beskrivningen av fasta formsystem [typ molekyler och kristaller] och som gör att vi knappast någonsin kan få fram ens en skarp bild av en enskild atom, långt mindre en atomkärna), och kan bara av det skälet inte illustreras med något som helst åskådligt visuellt begrepp, allra minst ”spinn” — trots att spinnet är grundläggande för fysikens förklaring på nivån kärnfysik tillsammans med massa och laddning. Begreppet kärnmagnetiskt moment i modern akademi (se även Kärnmagnetisk moment i modern akademi) visar dessutom att det spinnbegrepp som LIKVÄL används av modern akademi och vetenskap för atomkärnan bara kan vara ett precesserande spinn (som ett snurrande mynt som just är på väg att lägga sig på bordet, alltså en krängrotation). Den moderna uppfattningen att atomkärnan består av inre partiklar, innebär dessutom ett införande av ytterligare detaljer som gör hela spinnbegreppet högst godtyckligt, irrationellt för den som inte är invigd och därmed helt omöjligt att förstå i någon som helst härledande relaterad mening, och som i slutänden bara innebär att inga direkta jämförelser kan göras med den bild av atomkärnan som framträder genom en motsvarande relaterad härledning. Se utförligt från PLANCKRINGEN.

För tyngdcirkelns begrepp enligt relaterad fysik (TNED), se vidare i Tyngdcirkelns betydelse för kärnradien.

kärnradierna från början

Med jämförande — traditionellt klassiskt — experimentella uppgifter

KÄRNRADIERNA FRÅN BÖRJAN

KÄRNFYSIKENS GRUNDBEGREPP ENLIGT TNED — Kort illustrerad repeterande inledning

Med atomkärnans härledning enligt TNED genom Planckringen och den därmed — enligt neutrinospektrum — härledda formen för Plancks strukturkonstant (h),

E = hf = (h/n_F)n_F f = h_F f_F

Se även atomkärnans härledning · ATOMKÄRNANS GEOMETRI · atomkärnans elektrogravitation

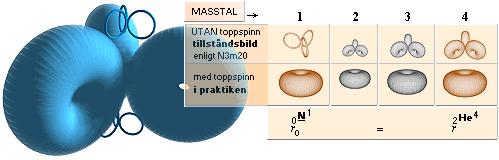
v v

l = å l _v ; f = å f_v ; c₀ = l f

v=1 v=1

framträder neutronkvadraten med de primära atomkärnornas ekvivalenta kärnradier och de därav följande (överlägsna) teoretiska atomvikterna enligt TNED — i jämförelse med modern akademisk teori (Weizäckerekvationen).

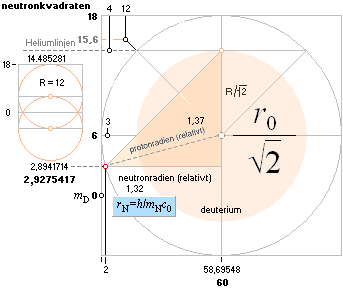
Med dessa basdata som grund, kan (nu 2008) en mera omfattande, allmänt jämförande presentation ges som visar hur väl TNED bekräftas av experimentalfysiken.

Grundreferensen på experimentalfysikens område för undersökning av atomkärnornas radier är (naturligtvis) de första banbrytande resultaten under 1950-talet — från pionjären Robert Hofstadter. Se från EPOKEN HOFSTADTER.

Närmast nedan följer en allmän genomgång av ämnet kärnradierna med vidare förgreningar till särskilda avsnitt och sektioner i ämnet.

kärnradierna

Med särskild inledning till — från Atomkärnans Storlek om ej redan bekant —

KÄRNRADIERNA

kärnradie · laddningsradie · strukturradie · materieradie · punktradie · massradie ·

Se även kort allmänt repeterande inledning i KÄRNFYSIKENS GRUNDBEGREPP ENLIGT TNED — Kort illustrerad repeterande inledning

distansbegreppen

2008IX8

Den statistiskt experimentella behandlingen av materiens allra minst observerbara detaljer har till synes speciellt under 1990-talet med vidare livgivit en flora av ytterst diffust orienterade ”distansbegrepp” i beskrivningen av atomkärnans utsträckning i 3D-rummet. Dessa distansbegrepp (m.fl.) är av typen

· laddningsradie (eng. charge radius)

· strukturradie

· medelradie

· materieradie

· punktradie

Alla dessa begrepp förekommer frekvent och omnämns i olika vetenskapliga rapporter som beskriver speciellt experimentella mätningar av atomkärnor i olika sammanhang.

EFTERSOM DET I MODERN AKADEMI inte finns någon fast mönsterform att återfalla på för atomkärnans beskrivande del, måste följdriktigt också alla — samtliga — experimentella och teoretiska parametervärden koppla strängt metodiskt (godtyckliga val), inte principiellt (fast föregivet):

Eftersom det inte finns några direkta kroppar med vars hjälp atomkärnorna kan direktstuderas, måste resultaten i de experimentella mätningarna man genomför tvunget bero på METODEN som används för ATT STUDERA OBJEKTET. Inte på objektet som sådant: Atomkärnan EXISTERAR INTE FIGURATIVT i den moderna akademins lärosystem — atomkärnan kan inte liknas vid en skruv som kan mätas med mikrometer. Därmed elimineras också automatiskt varje objektivt beskrivande av DET föremålet: Det finns inom modern akademisk litteratur — forskningsrapporter — en enorm uppsjö av mätningar på kärnradier. Men det finns ingen enhetligt presenterad precision som kan avtäcka någon enda konturerad form eller avgränsad struktur. Inte så mycket som en enda prick. Vi får aldrig SE något därifrån.

Vi kan studera många rapporter som uppehåller sig vid påstådda mätprecisioner i storleksordningen tiotusendelar eller hundratusendelar av en Fermi (1 Fermi = 1 femtoMeter = t15 M, grovt sett protonkärnans radie), dvs., typ R,rrrX Fermi med osäkerheten i X. En sådan precision skulle gott och väl räcka till för att beskriva konturer och detaljer i atomkärnans formbyggnad. Problemet är emellertid det att de olika experimentella metodernas naturliga fysik sprider ut de övergripande resultaten på ett intervall av våningar eller distanser som med exemplet protonen (Vätekärnan) ligger i storleksordningen 1-1,5 Fermi — analogt en oskärpa på runt 1/1,5=67%, och ingen avhandling existerar som kan råda bot på den spridningen.

Alla — samtliga författare och forskare — avhåller sig (noga) från varje sådant närmande.

Det är ungefär som att det ligger skruvar på olika lagerhyllor på olika höjd över verkstadsgolvet: precisionen finns visserligen, men man måste använda hela stegen i varje enskilt fall för att hämta just den skruven.

Mätvärdena man kommer fram till, är användbara just för den metodens vidkommande, men en allmänt giltig formbyggnad för atomkärnans presentation saknas helt i modern akademi och vetenskap.

Distansbegreppen typ ovan används i modern akademi och vetenskap ”inom det kvantmekaniska skruvsortimentet” med referens till olika metoder och modeller och matematiska program för att få fram resultat ur experimenthändelserna. Men sett till vår naturliga föregivenhet att också dessa begrepp skulle motsvara en BILD som sammanhänger med ”atomkärnan”, finns ingen koppling: De angivna begreppen är precis lika strukturlösa och intetsägande som precisionen i exemplet med protonradien 1/1,5=67% visar: en central punkt som tonar ut diffust utan konturer, utan detaljer, utan kontraster.

Vi ska (försöka) uppehålla oss vid dessa detaljer i den här presentationen — belysa och jämföra — samt studera ämnet från den enda härledningsbara fasta mönsterform som (här veterligt) finns — TNED — men som inte finns med i den moderna akademins lärosystem.

Kärnradiedata på Webben @INTERNET

Webbsökning på ämnet atomkärnornas radie är (Augusti 2008) en delvis högst deprimerande uppgift;

Rapport Oktober 2007 till nu (Augusti 2008)

— med upprepat sökande genom (minst) hundratals träffsidor med (säkerligen) tusentals dokument:

Det man hittar på webben kan indelas i tre kategorier (de två första även internt, per dokument):

· författare som refererar till experimentella mätdata men utan att ange eller referera konkreta värden som läsaren själv kan källkontrollera

· författare som dessutom presenterar alternativa grafiska samband — som därmed är värdelös information eftersom vi inte vet vad vi ska jämföra med och därmed heller inte kan avgöra graden av grafbildens relevans

· författare — ytterst få — som förbarmar sig med att basera framställningen på konkret läsbara värden som läsaren själv kan kontrollera

Praktiskt taget inga RELATERADE experimentella tabellredovisningar alls, inte någon enda i någon epok, finns tillgängliga. Verkligen. Men det finns en närmast enorm flod av författare som skriver OM sådana ”tabelldata” i vetenskapliga rapporter — i t.ex. pdf-filer. En del författare tycks omnämnda dessa ”grunddata”som om de vore allmänt kända, medan en del andra författare lämnar olika (mängder med) referenser till åter andra forskarfigurer och dokument, och som vi definitivt inte GRATIS kommer åt vidare enbart via webben. Saken kompliceras ytterligare av att vissa nya begreppsformer introduceras i stort med en ny epok, från omkring 1990 och vidare, med tillhörande nya mätmetoder — och värden som i jämförelse med ”den äldre skolan” verkar helt galna. Det tråkiga är, dessutom, att ingen författare som skriver om dessa verkar intresserad av att klargöra begreppen, inte på någon som helst nivå — dokumenten är som sagt ”modernt vetenskapliga rapporter” och inte direkt ägnade allmänheten. Den uppgiften — som ”utomstående betraktare” — får vi (tydligen) klara ut själva.

Endast i några få fall kan vi (min referens) hitta någon enstaka uppställning på mätdata (siffervärden) som ansluter till experimentalfysikens första epok (1950-1980). Sökning på GOOGLE-böcker KAN ge vissa resultat, men dessa är av typen ”begränsad granskning”, och många sidor (speciellt med figurer och tabelldata) är ofta utelämnande — eller ändras i granskningsstocken från dag till annan, eller annat, så att man inte säkert kan återfinna samma data i samma källa tidsoberoende. Detta bidrar ytterligare till en frustration i strävan att få fram grunddata från experimentella observationer — enbart med webben som hjälpmedel. För, vem vill (i takt med upptäckten av datorns bekväma cybervärld) anstränga sig med annat? Snabbaste vägen — webben — sparar mest tid, och tid kostar pengar i vår vardag.

två

skilda metoder

Uppgiften att sammanställa uppgifterna kompliceras dessutom (ytterligare) av att det (numera, som antyddes nyligen) finns två olika epoker med inbördes skilda preferenser:

· den klassiska experimentalfysiken med den massbaserade mätmetoden (utvecklades under 1950-talet)

· den nyare tidens ljusbaserade laserspektroskopi (utvecklades starkt under 1990-talet, samt vidare, se Laserhistoria)

Den senare epokens begreppsområde beskrivs i Laserspektroskopi. Mätdata på denna del är emellertid (ännu Augusti 2008) i princip obefintliga för de avgörande stabila nukliderna och som krävs för att kunna göra reguljära jämförelser med TNED. Forskningen på detta område pågår emellertid (intensivt), och man kommer säkert att finna på en metod som kan användas även för de stabila nuklidernas fall. Se även i RESULTATREDOVISNING AV KÄRNRADIERNA ENLIGT TNED, där finns i varje fall ett laservärde till jämförelse (Covello 2002, Herrmann 1997, m.fl.).

Närmast nedan beskrivs den massbaserade mätmetoden tillsammans med citat från etablerade verk — till jämförelse med TNED — naturligtvis i strävan att försöka hitta ansatser och uppslag som visar att TNED är fel modell. Jag har ännu inte lyckats knäcka den delen; För varje nytt försök, tycks ställningen hos TNED bara bli allt starkare. Se även en illustrerad kompletterande kort inledande beskrivning till den massbaserade mätmetoden i ATOMKÄRNORNAS RADIER GENOM EXPERIMENTELL MÄTNING.

Massbaserade Mätmetoder

ENLIGT TNED finns inget direkt sätt att mäta atomkärnans radie genom experimentella metoder [‡]: varje mätning inbegriper en fysikalisk växelverkan av en eller annan art, och inträngningen i atomkärnans toppspinn beror av strålpartikelns energi. Högre energier introducerar extramoment som därmed komplicerar — vränger — bilden ytterligare.

TNED särskiljer två olika metodtyper för mätning av atomkärnornas radie — med väsentligen olika karaktäristiska resultatvärden:

1. massbaserade metoder (elektronspridning)

2. ljusbaserade metoder (laserspektroskopi)

Olika mätmetoder ger olika resultat.

I det här blocket beskrivs den massbaserade mätmetoden — sett ur den synvinkel som kännetecknas av TNED. För den ljusbaserade metoden, se Laserspektroskopin.

DEN MASSBASERADE METODEN

Den massbaserade metoden använder främst elektroner som projektilobjekt;

I modern akademi och vetenskap känner man inga dimensioner för elektronmassans element. Man antar elektronen som ”punktpartikel”. Textmarkeringarna i citaten nedan är mina (stycken, nyckelord).

”2.1 Electron Scattering The first demonstration of obtaining nuclear size information using particle scattering experiments was Rutherford scattering in 1906. From α scattering on a target, Rutherford concluded the size of the nucleus is less than 10⁻¹⁴ m. Unlike α particles, electrons are structureless point-like objects that only interact electromagnetically. Therefore, electron scattering avoids the complexity of the strong interaction between the projectile and the target, and provides clean information about the charge distribution in the nucleus.”;

[Webbkällans URL-källreferens till den här PDF-filen (den sparades inte i den första genomgången, tyvärr) har i efterhand eftersökts (2008-08-05) men inte hittats],

DETERMINATION OF THE HELIUM-6 NUCLEAR CHARGE RADIUS USING HIGH-RESOLUSION LASER SPECTROSCOPY, s14

LI-BANG WANG, B.S., National Taiwan University, 1996

Min översättning:

Elektronspridning. Den första demonstrationen för att erhålla kärnradieinformation genom partikelspridning var Rutherfordspridningen 1906. Från alfaspridning på ett mål, konstaterade Rutherford att kärnans storlek är mindre än 10⁻¹⁴ meter. Till skillnad från alfapartiklar, är elektroner strukturlösa punktlika objekt som bara växelverkar elektromagnetiskt. Därför undgår elektronspridning komplexiteten hos den starka växelverkan mellan projektil och mål, och tillhandahåller därmed ren information om laddningsfördelningen i kärnan.

”The scattering of electrons from nuclei has given us the most precise information about nuclear size and charge distribution. The electron is a better nuclear probe than the alpha particles of Rutherford scattering because it is a point particle and can penetrate the nucleus.”,

[http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/elescat.html],

Electron Scattering from Nuclei, Department of Physics and Astronomy, GEORGIA STATE UNIVERSITY (2005)

En av de klart bästa källreferenserna till modern vetenskap: (ofta) noggrann, (förhållandevis) relaterad, förklarande.

Min översättning:

Elektronspridning från atomkärnor har gett oss den mest precisa informationen om kärnornas storlek och laddningsfördelning. Elektronen är en bättre kärnprob än alfapartikeln [Heliumkärnan] hos Rutherfordspridningen därför att det är en punktpartikel och kan penetrera kärnan.

Webbkällan ovan från GeorgiaUniversitetet ger en bra grundbeskrivning som kopplar till de första reguljära teoretiska kärnmodellerna under 1900-talets första hälft samt de banbrytande experimenten med elektronspridning som från 1950-talet genomfördes av amerikanen Robert Hofstadter med flera.

Därmed (menar man) har man ett idealiskt projektilobjekt med vars hjälp till exempel protonen och neutron kan undersökas i detalj — samt även övriga atomkärnor som målobjekt.

I TNED vet vi från härledningen till Planckringen att elektronmassans komponenter, verkligen, är så små att man kan approximera dem som ”punktpartiklar” i förhållande till, till exempel, vätekärnan.

Se vidare i illustration nedan.

Genom den spridning som elektronerna uppvisar efter växelverkan med målet, får man fram grunddata — som sedan slutbehandlas genom olika statistiska metoder och modeller.

Genom att växelverkan här är g-relaterad i försorg av de massbaserade elementen, alltså beroende på och i referens till de ingående kropparnas tyngdpunkter och — för de subatomära partiklarnas del, speciellt — tyngdcirklar, gäller enligt TNED följande:

resultatvärdena kommer INTE att avspegla atomkärnans ytterradie utan snarare, med alla variabler medtagna, just atomkärnans tyngdcirkel: medelvärdet i den växelverkande kraftformen.

Spridningsförsöken med massbaserade projektilobjekt

ATOMKÄRNANS TYNGDCIRKEL eller Planckringen som den kallas i TNED, verkar alltså också — verkligen — vara den genuina allmänna DYNAMISKA preferens som i ämnets inledning (se från Atomkärnans storlek) var önskemålet för en enkel, allmän referensfaktor för samtliga praktiska fysikaliska fall. Det finns också en (ytterligare) bekräftelse på den detaljen.

t-ringen och atomkärnan

t-ringen

protonkärnan

t-ringen i figuren ovan markerar skalenligt, relativt protonkärnan, sämsta fallets beräkning för t-ringens största diameter som elektronmassans komponent;

Motsvarande beräkningar i Spektrum ger antalet t-ringar per elektronmassa som (minst) 177062.

t-ringens egentjocklek däremot är så tunn att den inte på långa vägar framgår i denna skala. Se mera utförligt i Elektronmassans komponenter.

Med dessa små dimensioner blir elektronmassans komponenter idealiska som projektiler i olika spridningsförsök — till exempel för att studera protonkärnans formbyggnad. Förutsatt tillräcklig energi, kan t-ringarna penetrera även det inre av protonkroppens toppspinn.

Illustrationen nedan sammanfattar mera ingående energins olika aspekter i de olika typerna av massbaserad inträngning.

Se även inledande illustrerad separat artikel i ATOMKÄRNORNAS RADIER GENOM EXPERIMENTELL MÄTNING.

Elektronernas förmåga att penetrera atomkärnan

hög energi	mellanläge	låg energi

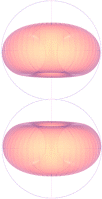
I illustrationen ovan finns tre olika sätt avbildade som motsvarar olika energier hos de inkommande elektronmassorna:

låg energi, mellanläge och hög energi.

Varje specifik energi motsvarar en slags fokuserande styrka hos elektronprojektilerna som ”ögon” för att se in i atomkärnans struktur.

Med liten energi, längst till höger, framstå atomkärnan i princip som en helt rund slät boll utan inre struktur. Kärnan kränger och spinner i vilket fall godtyckligt i sitt tillstånd och uppvisar därför utåt sett bara ”bollform”. Ökas energin, mellanläget, framstår strax en del oregelbundenheter i målformen. Oregelbundenheterna tillväxer drastiskt då projektilenergin ökas ännu mer, vänstra bilden.

Beroende på hur man ställer samman resultaten från spridningsförsöken — alltså vilken statistisk modell man använder — ges naturligtvis olika resultat: Det finns, verkligen, ingen enkel facitform som kan ställas upp för typ ”samtliga fall”. Beräkningsmodellerna är i vilket fall ytterst komplicerade.

Gemensamt för alla beräkningsmodeller (med referens till alla möjliga energier) är att resultatbilden uppvisar ”inre oscillationer”: värdena varierar i formen av toppar och dalar, motsvarande den inre kärnstrukturens växelverkan med elektronprojektilerna — vilket också krävs enligt TNED. Den bilden blir naturligtvis alltmer komplicerad med allt växande projektilenergi i och med att också den resulterande kraftväxelverkan ökar mellan kärna och projektil.

Vi kan emellertid direkt se EN allmän egenskap som man snabbt upptäcker med högre projektilenergier: då elektronprojektilerna tränger in innanför det yttre skalet, finns i fallet neutron-protonkärnan i grunden mestadels bara tomrum (beroende på projektilenergi också naturligtvis). Därmed får man på enklaste sätt en resultatbild som uppvisar en atomkärna som ”övergår mjukt i noll”; Man säger att ”atomkärnan har inget utpräglat hårt skal”.

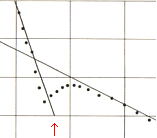
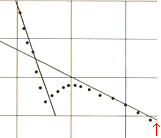
Illustrationen nedan från SCIENTIFIC AMERICAN 1979 ger av allt att döma en perfekt inledning till ämnet (se illustrationen nedan, samt efterföljande). Resultatkurvan nedan från CERN (centraleuropeiska högborgen för kärnforskning) visar på enklaste sättet de två mest utpräglade formaspekterna i atomkärnans geofysik enligt TNED. Begreppet tvärsnitt beskrivs i separat sektion, se Tvärsnitt om ej redan bekant. Vertikala skalan nedan anger tvärsnittet, horisontella skalan anger den motsvarande vinkelavvikelsen, eller med samma innebörd kollisionens häftighet (energiomsättningen).

CERN-kurvan

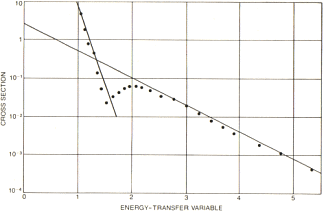
”ELASTIC SCATTERING CROSS SECTION was measured with unpolarized protons at the European Organization for Nuclear Research (CERN) near Geneva at an energy equivalent to 1,500 GeV. Because the spins of the colliding particles were not controlled the observed cross section is an average of all the pure-spin cross sections. The data are plotted as a function of an energy-transfer variable, which measures the violence of the scattering and is related to the scattering angle. The curve can clearly be resolved into two components with different slopes. The steep upper portion reflects glancing collisions that involve only a diffuse outer layer of the proton, whereas the more gradual decline of the lower segment suggests violent collisions between small, hard objects inside the proton. The objects seem to have a radius of about one-third fermi (one fermi being equal to 10^–13 centimeter). The trough between the two segments of the curve could represent interference between the two modes of scattering.”

The Spin of the Proton, Alan D. Krisch, SCIENTIFIC AMERICAN May 1979 s67

Min översättning:

ELASTISKA SPRIDNINGSTVÄRSNITT uppmättes med opolariserade protoner vid Europeiska Organisationen för Nukleär Forskning (CERN) nära Genève vid en energi ekvivalent med 1.500 GeV. Eftersom spinnen hos de kolliderande partiklarna inte var kontrollerade, är de observerade tvärsnitten ett medelvärde av alla spinnRena tvärsnitt. Data är utskrivna som en funktion av en energiöverföringsvariabel, vilken mäter våldsamheten hos spridningen och är relaterad till spridningsvinkeln. Kurvan kan tydligt upplösas i två komponenter med olika lutning. Den branta övre delen avspeglar snuddkollisioner som bara inbegriper ett diffust yttre skikt hos protonen, medan den mera lugna minskningen hos det lägre segmentet antyder våldsamma kollisioner mellan små, hårda objekt inuti protonen. Objekten verkar ha en radie på omkring en tredjedels Fermi (en Fermi är lika med t13 centimeter). Sänkan mellan de bägge segmenten hos kurvan kan representera övergången mellan de två spridningstyperna.

CERN-kurvans brantare del		CERN-kurvans flackare del

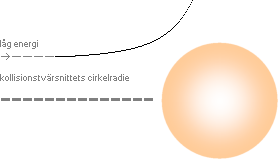
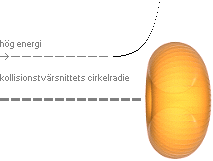
TNED-modellens förklaring till CERN-kurvan — det finns bara två typlägen att välja på, figurerna ovan. Med låg energi framstår atomkärnan enligt TNED som en rund boll utan inre struktur, vänstra delen ovan. Spridningsvinklarna/kollisionsenergierna, horisontella skalan, mellan strålpartikel och målpartikel ändras relativt litet med avtagande tvärsnitt, vertikala skalan. Ökas energin så att strålpartiklarna (här protoner med godtycklig orientering enligt CERN-experimentet) kan tränga in i målpartikeln — vilket i CERN-experimentet bara betyder att endera protonen vänder kortsidan till — ändras bilden (drastiskt), högra delen ovan: Ändringen i spridningsvinkeln med växande energi får ett annat, mera häftigt förlopp med markant växande vinklar/energier för minskande tvärsnitt. I mellanläget uppkommer statistiskt sett en medelvärdesbildad kurvform motsvarande CERN-kurvans mellandike. Med ytterligare växande energier bör vi få se ytterligare ”diken” enligt TNED.

SpökFermiObjekten

Med koppling till CERN-kurvan ovan: Eftersom det går alldeles precis 3 stycken likadana sfärer ovanpå varandra i den sfär som omskriver N3m20 toroidaggregatet och vilka två yttersta passar precis i den aktuella atomkärnans kärnbrunn, se figuren närmast ovan, kan dessa ”spöka” som »passande mått» för vetenskapen typ citatet ovan enligt ”Objekten verkar ha en radie på omkring en tredjedels Fermi” — analogt ungefär en tredjedel av kärnradien (protonradien approximeras i artikeln av Krisch med ca 1 Fermi). Se även separat artikel i Spökpartikeln 1/3 Fermi — senare bidrag, se [‡citat], visar att en del personer vidareutvecklat detaljerna med 1/3-Fermipartiklarna; Varje försök att förklara de experimentella resultaten från den utgångspunkten skapar endast nya parametrar — med ännu flera frågetecken.

Se även från ATOMKÄRNANS STORLEK.

Där ges en sammanhängande beskrivning till och härledning av KÄRNRADIERNA ENLIGT TNED.

Framställningen fortsätter nedan med beskrivningen av de experimentella — då banbrytande — resultaten som utvecklades under 1950-talet genom en av pionjärerna, R. Hofstadter.

EPOKEN HOFSTADTER

Experimentalfysikens allra första resultat, direkt från en av de framträdande banemannen på den traditionella klassiska kärnfysikens experimentella område, Robert Hofstadter, hans presentation från år 1961 enligt referensen @INTERNET, s570 Fig. 8;

ROBERT HOFSTADTER

The electron-scattering method and its application to the structure of nuclei and nucleons, Nobel Lecture, December 11, 1961

[http://nobelprize.org/nobel_prizes/physics/laureates/1961/hofstadter-lecture.pdf]

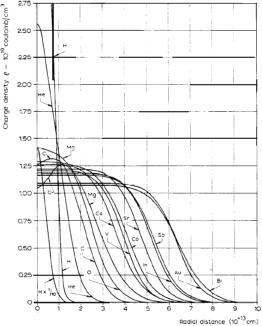
HOFSTADTER Nobel Lecture 1961

Robert Hofstadter (1915-1990), amerikansk fysiker född i New York 1915, Nobelpris i fysik 1961

Notera att grafen för Väte-1 försvinner upp långt över illustrationsrutan. I grafens nedre vänstra del finns en förminskad version markerad ’H × 1/10’.

Typkurvorna ovan, hur de beräknas, förklaras längre ner i artikeln PROTONENS LITTERÄRA REFERENSVÄRDE.

Som Hofstadter redan då (1961) påpekade, uppvisar Väte-1 och Helium-4 vissa likheter som skiljer dem från övriga atomkärnor, se citatet nedan (grafen längst ner t.v. i kurvskaran ovan markerad med ”H × 1/10” avser den branta H1-grafen förminskad 10ggr).

Originaliteterna hos Väte-1och Helium-4 är också precis i full enlighet med resultaten i TNED från Planckringens härledning (se den inledande figuren i Kärnradierna från början), masstalen 1 och 4 har i TNED samma kärnradie. Däremot finns inte Deuteriumnukliden (deut[e]ronen) med i Hofstadters kurvskara. I TNED uppvisar deuteriumkärnan en mindre ytterradie än Väte1-Helium4: Deuteronradien är 1/Ö2 gånger mindre än de ekvivalenta radierna för Väte1 och Helium4.

Deuteronens radie omnämns inte i Hofstadters skrift. Deuteronen representerar tydligen ett allmänt centralt problem inom den moderna akademins experimentalfysik, och Hofstadter berör också det ämnet genom beskrivningar som berör den allmänna teorin om deuteronen som sammansatt av två fristående partiklar, en neutron och en proton. Jämför,

”A neutron is in vigorous motion in the deuteron and this additional complication must be taken into account somehow. It is necessary at this point to introduce a relativistic theory of the deuteron to allow properly for the effects of the motion of the bound neutron.”

The electron-scattering method and its application to the structure of nuclei and nucleons, s575

ROBERT HOFSTADTER, Nobel Lecture, December 11, 1961

Min översättning:

En neutron befinner sig i energisk rörelse i deuteronen och denna extra komplikation måste på visst sätt tas i beaktande. Det är nödvändigt att introducera relativistisk teori för deuteronen på denna punkt för att på lämpligt sätt tillåta utrymme för effekterna av rörelsen hos den bundna neutronen.

TNED har ingen sådan problemställning — och vi kan därför inte vidare utnyttja Hofstadters beskrivning till någon jämförelse på den punkten.

Hofstadter skriver vidare:

”Note, however, the large disparity between the average central densities of the proton and all other nuclei. The alpha particle (⁴He) is also a unique case and exhibits a much larger central density than all heavier nuclei.”,

”Except for the extremely light nuclei of hydrogen and helium the constancy of the central nuclear density is clearly represented in the figure.”,

[http://nobelprize.org/nobel_prizes/physics/laureates/1961/hofstadter-lecture.pdf]:

The electron-scattering method and its application to the structure of nuclei and nucleons, s570 Fig. 8

ROBERT HOFSTADTER, Nobel Lecture, December 11, 1961

Min översättning:

Notera emellertid den stora olikheten mellan de genomsnittliga centrala tätheterna hos protonen och alla andra kärnor. Alfapartikeln (⁴He) är också ett unikt fall och uppvisar en mycket större central täthet än alla tyngre kärnor.

Utom för de extremt lätta kärnorna hos väte och helium, är den centrala kärntäthetens konstans tydligt representerad i figuren.

Notera att vertikalskalan i Hofstadters kurvskara ovan anger resultatvärden i laddningstäthet. Se även explicit i efterföljande citat.

Ovanstående referens markerar en av vetenskapshistoriens verkligt avancerade landmärken: Hofstadter och hans kollegers arbete förknippas med den första mera reguljära, mera fasta och ordinära uppfattningen om atomkärnorna genom en enhetlig metrisk (sfärisk) byggnad — med stöd av genuina experimentella observationer och den numera välkända ”kubgrafen” r=r₀A^1/3 och som kom att användas under en stor del av 1900-talet i olika kärnfysikaliska sammanhang.

TNED som den bakomliggande

generatrisen till resultatkurvorna från Hofstadter

Om vi räknar ut KÄRNLADDNINGEN (Z) fördelad över toroidaggregatets inre första underfraktala volym (samband i TOROIDYTAN)

— (Vol = 2pbpa² = 2p²ba²) — den volym som penetreras eller »stöts emot» av strålprojektilerna (elektronerna) i spridningsexperimentet då dessa tränger igenom toppspinnet

— ska vi, om allt stämmer enligt TNED, få ut motsvarande ”rakstaplar” till ovanstående Hofstadters kurvskara; Alltså rakt av ett toppvärde för volymladdningstätheten per en motsvarande kärnradie enligt Planckringens grundform från tyngdcirkeln (r₀=1,37 t15 M). Toppvärdet BÖR vara (väsenligt) större än Hofstadters toppvärde eftersom atomkärnan är generatris till dynamiken och elektronkomponenterna inte kan se exakt hela den inre effektiva volymen utan bara en diffus del (som minskar med ökande projektilenergi) och därmed ett typiskt lägre värde på volymladdningstätheten i Hofstadter-skaran.

Figuren nedan visar resultatet med referens till de nuklider/grundämnen som angetts av Hofstader, tabellen i figuren, samt angivet (r₀-prefixet) i samma täthetsskala som Hofstadters, T19 Coulomb per kubikcentimeter (T19 C/cM³);

VOLYMÄRA LADDNINGSTÄTHETEN — experimentell jämförelse med TNED

Kärnladdningen fördelad över volymen för atomkärnans första tre underringar enligt TNED-aggregatet N3m20, se grunddata i TOROIDYTAN.

Planckekvivalentens vertikala skala markerad r anger den råa volymära laddningstätheten i enheter T19 C/cM³ hos atomkärnan enligt TNED med hänsyn till den massinneslutning som ges av första fraktalnivån under toppspinnets nivå, de tre underringarna i aggregatet N3m20. Utvecklingarna till sambanden för värdena visas separat i Laddningstätheten. Se även separat tabell i JÄMFÖRANDE TABELL FÖR NUKLEÄRT VOLYMÄRA LADDNINGSTÄTHETEN.

Volymära Laddningstätheten r i T19 C/cM³

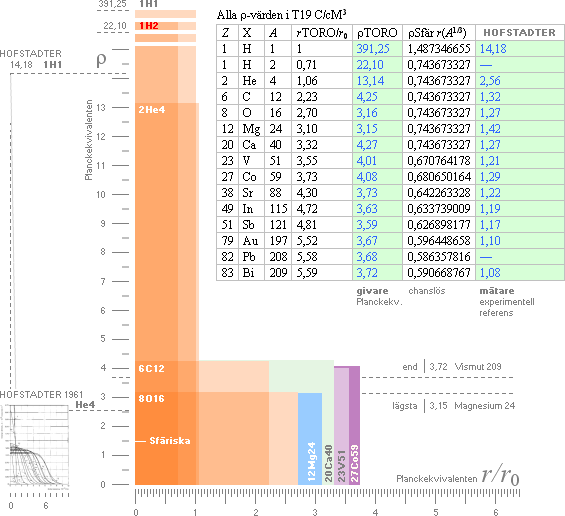
Tabellvärdena ovan anger r-värdet i samma skala som i Hofstadters grafer. Endast grafelementen fram till Kobolt (27Co59) i Hofstadters kurvskara har medtagits ovan till jämförelse då principen för resten är klar. Se mera utförligt i tabellen ovan, även separat i JÄMFÖRANDE TABELL FÖR NUKLEÄRT VOLYMÄRA LADDNINGSTÄTHETEN.

Om vi till matchning för Hofstadters kurvskara, här infälld till jämförelse ovan längst till vänster och med toppvärden i ovanstående tabell söker bland de tillgängliga modellaspiranterna toroidaggregatet N3m20 och Sfären, samt med hjälp av de radievärden som finns tillgängliga enligt teorierna, respektive kubgrafen r/r₀=A^1/3 och toroidgrafen, ser vi direkt från ovanstående resultattabell att den sfäriska modellen är helt chanslös från början: Väte-1-toppen (här endast knappt 1,5) måste vara minst Hofstadters uppmätta värde (14,18), annars går det inte. Det är tydligen bara N3m20-modellen (391,25) som kan fungera som GIVARE åt Hofstadters mätdata: alla kärnvärden ligger (grovt och generellt minst 3ggr) över de uppmätta.

OBSERVA att begreppet VOLYMÄR LADDNINGSTÄTHET i TNED är ett relativvärde i förhållande till antalet underfraktaler i aktuell ringnivå (se utförligt i ATOMKÄRNANS MASSTÄTHET), och därmed högeligen beroende av de energier man använder hos avkännande-inträngande partiklar. I beräkningarna för N3m20-aggregatet ovan har endast första underfraktalens ringar medtagits (se från TOROIDYTAN). Om än djupare nivåer tas med, blir värdena (betydligt) högre.

Se även efterföljande (mera förtydligade) stapeldiagram.

Resultatbeskrivning. Frånsett jämförelsen med deuteronen (1H2) som inte ingår i Hofstadters framställning, är det tydligt att principiellt samma relationsbas som i fallet Hofstadters kurvskaror också ställs fram av TNED;

Väte-1 med Helium-4 ligger skyhögt över övriga nukliders volymrelaterade laddningstäthet. Villkoret att atomkärnan enligt TNED också måste uppvisa typiskt högre råvärden än de experimentellt uppmätta, stämmer dessutom; För de tyngre nukliderna är Hofstadtertoppvärdena grovt sett 1/3 av TNED-värdena — se den infällda vertikalskalanpassade Hofstadtergrafbilden ovan till vänster. Den relationen blir naturligtvis större för de allra lättaste nukliderna eftersom skillnaden i volymär masstäthet är som störst där.

Vi ser också att nukliderna i stort med växande masstal enligt TNED — om det gäller att ge en grovt översiktlig bild — antar ett medelvärde i den volymära laddningstätheten som ligger mellan toppvärdena för Kol (4,25 | Hofstadter 1,32) och Syre (3,16 | Hofstadter 1,27). Denna (förgrovande) detalj ansluter utomordentligt till grundmodellen med vattendropparna (Kubgrafen) och som illustrerar atomkärnan som ett slags homogent ämne med i stort sett konstant volymär laddningstäthet — frånsett de allra lättaste nukliderna. Denna detalj syns tydligare om vi direkt tillämpar sfären på toroidradierna. Tabellen ovan visar att laddningstätheten i detta fall, och frånsett de första avvikande tre nukliderna, är tämligen jämn.

TNED-beräkningarna ovan har genomförts med de rådata och kalkylkort som redovisas i sektionen TOROIDYTAN.

I illustrationen nedan har ett motsvarande stapeldiagram gjorts för Hofstadters kurvskara, mitten, till mera tydlig jämförelse med toppvärdena för laddningstätheten (r) enligt TNED i vänstra delen, samt till jämförelse även motsvarande för den sfäriska modellen längst till höger. Radievärdena för Hofstadters kurvskara har här hängts på toroidskalans r/r₀-värden då Hofstadters radievärden i vilket fall endast är statistiska skuggbegrepp och i den nedanstående jämförelsen helt saknar specifik betydelse vid sidan av de aktuella toppvärdena för r.

Volymära Laddningstätheten r i T19 C/cM³

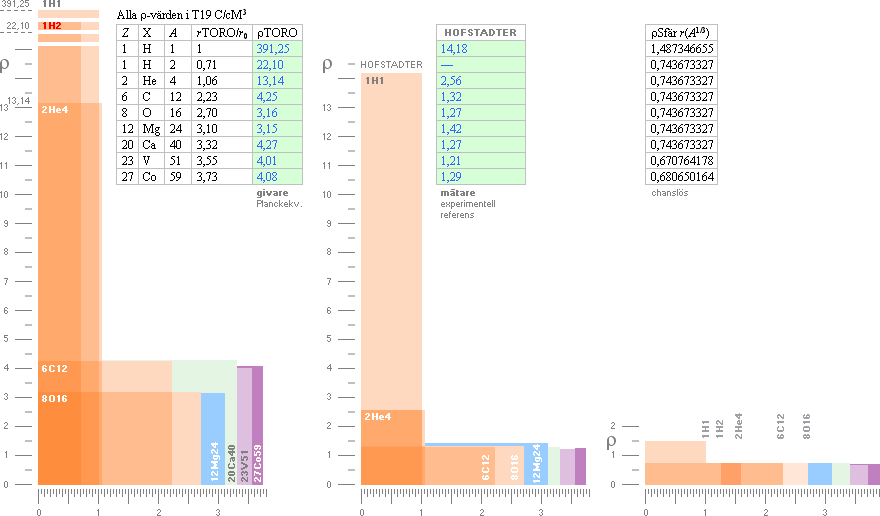
Planckekvivalenten r/r₀

Radieskalorna för toroidformen, vänster ovan, och Hofstadters kurvskara, mitten ovan, har satts på samma form för den bekväma jämförelsens skull, (r/r₀). Denna detalj är dock oviktig då vi endast studerar toppvärdena för r, analogt atomkärnans optimala (konturmässiga) laddningsbyggnad. Med TNED som preferens: hur mycket statistiska avancerade modeller man än uppbådar med utgångspunkt från Hofstadters mätdata och alla liknande, kan man aldrig räkna fram ”atomkärnans radie” på den vägen; Statistiken sönderbryter varje ordnad exakt byggnad, och begreppet ”kärnradie” från den utgångspunkten blir ett meningslöst begrepp. (Det är därför man i modern akademi hellre talar om begreppet ”laddningsradie” som mera ansluter till den statistiska medelvärdesbildningens teknik — som dock helt måste baseras på mättekniska metoder). Därmed har atomkärnan som begrepp också praktiskt taget utsuddats från området för skarpa distinkta presentationer.

Som vi ser till jämförelse är varje föreställning med sfären som modell för atomkärnan, högra delen ovan, helt chanslös. Toppvärdena hos den verkliga atomkärnan måste absolut vara naturligt större än varje mätvärde. Detta är också tydligen fallet enligt TNED med toroidmodellen från PLANCKRINGEN.

I modern akademi har man istället antagit just den sfäriskt omslutande formen som det huvudsakliga modellhuset — samt tolkat den branta skarpt kontrasterande Väte-1-delen i Hofstadters mätresultat som bevis för att det så sfäriska protonkärnhuset omsluter mindre (sfäriska) partiklar (som inte kan lösgöras individuellt). På den vägen har man sedan byggt upp ”kvarkteorin” (QCD) genom olika matematiska modeller i ljuset av den samlade kärnenergins möjliga fördelningar och därmed möjliga sätt att uppvisa ”deldroppar” vid splittring.

Jämför utvecklingen i TNED: här TILLÄMPAS de praktiska resultaten på EN REDAN FÄRDIGBILDAD TEORETISK KÄRNMODELL — som hela tiden UTVECKLAS OCH BARA VISAR MER AV SITT INNEHÅLL: den stämmer exakt, i alla lägen, och kan matcha, beskriva och förklara alla, samliga, experimentella resultat — eller så inte alls, och då måste hela modellen förkastas. I modern akademi däremot MODIFIERAS TEORIN STÄNDIGT, i princip för varje nytt experimentellt rön; Man har ingen modell att jämföra med, inte alls överhuvudtaget, utan anpassar hela tiden teorin efter mätningarna. Se även i ATOMVIKTERNA.

Hur ovanstående TNED-värden framkommit, beskrivs utförligt i Laddningstätheten enligt TNED.

Det EXPERIMENTELLT mest anmärkningsvärda med ovanstående »enkla» genomgång:

Spiken rakt upp för Väte-1 — samt även den stora skillnaden mellan Helium-4 och övriga på samma fason fast i mindre omfattning — är detsamma som en direkt bekräftelse på toroidmatematiken:

TNED och experimentalfysiken uppvisar samma kvalitativa preferenser.

Se även i Atomvikterna.

Det mest anmärkningsvärda med ovanstående enkla genomräkning och dess tydliga överensstämmelse i proportionerna med experimentellt uppmätta värden enligt Hofstadter, ligger tydligen helt och hållet i diagrammens vänstra del: den STORA kontrasten mellan främst Väte-1-delen (1H1) och alla övriga. Med TNED blir förklaringen till den detaljen enkel: Den KVALITATIVT MYCKET snävt hållna inre »spinkiga toroiden» BILDAR HELA GRUNDVALEN för den rent kvantitativa formmatematiken.

Allt bygger sedan vidare på de egenskaperna.

Därmed är TNED ytterligare bekräftad och verifierad som en kvalitativt korrekt naturgrundad matematisk fysikalisk beskrivning i kraft av resultaten från härledningarna i PLANCKRINGEN.

En reguljärt sfärisk (eller annan) modell skulle här vara helt chanslös på den detaljen — direkt från start, se högra delen i ovanstående illustration.

Därmed är i princip det önskade visat.

Resten av beskrivningen med referens till Hofstadter behandlar unika epokreferenser med allmänna samband (som ansluter till den konventionella, allmänna förenklade sfäriska kärnmodellen) och som används i olika beskrivande kärnfysikaliska sammanhang i litteraturen överlag. Vi behöver känna till dessa, också, för att förstå sammanhangen (vidare).

KÄRNFYSIKENS GRUNDBEGREPP

genom den moderna akademins etablerade referenser

Hofstadter sammanfattar på s569 sin tids kärnradieekvationer med referens till den sammanfattande sfäriska formen enligt sambanden nedan:

”The results of many of the above experiments covered a large range of nuclei and demonstrated that two simple rules can be used to summarize the scheme of construction of spherical nuclei, viz. :

c = (1.07 ± 0.02) · 10^–13 A^1/3 cm

t = (2.4 ± 0.3) · 10^–13cm = constant (6)

The first equation gives the principal parameter governing the size of a nucleus and describes the behavior with increasing A of a kind of « mean » nuclear radius. The second equation states that the nuclear skin thickness is constant. The second rule implies that there is some property of nuclear matter that causes the outer nuclear regions to develop an essentially constant surface thickness. The two rules together are responsible for the approximate constancy of the central charge density of nuclei.”

The electron-scattering method and its application to the structure of nuclei and nucleons, s569

ROBERT HOFSTADTER, Nobel Lecture, December 11, 1961

Min översättning:

Resultaten från många av experimenten ovan täckte ett stort område av kärnor och visade att två enkla regler kan användas för att summera schemat med konstruktion av sfäriska kärnor, viz. : (sambanden i 6 ovan).

Den första ekvationen ger den principiella parameter som bestämmer storleken hos en kärna och beskriver beteendet med växande A av typen « medel » kärnradie. Den andra ekvationen utsäger att kärnans yttjocklek [eg. »hud-tjocklek», med sv. hud motsv. eng. skin] är konstant. Den andra regeln underförstår att det finns någon egenskap av nukleär art som förorsakar de yttre kärnregionerna att utveckla en väsentligen konstant yttjocklek. De två reglerna tillsammans ansvarar för den approximativa konstansen hos den centrala laddningstätheten för atomkärnor.

Lägg märke till att det ingenstans i den moderna akademins historia tycks finnas någon som räknat med något ANNAT än att atomkärnans fundamentala geofysik skulle betingas av en PRIMITIV sfäriskt divergent funktionsform för radien r typ ”rundstrålande”. Enbart med den grunduppfattningen, och i ljuset av TNED, stängdes vägen effektivt till atomkärnans härledning i modern akademi.

konstanten r0

Generellt i litteratur som behandlar beskrivningen av atomkärnornas storlek möter vi också Hofstadters motsvarande approximerade samband för kärnradierna enligt typformen nedan, i TNED benämnd kubgrafen,

r = r₀A^1/3 ............................. kubgrafen approximerar kärnradierna

Se även särskild artikel i KUBGRAFEN där ovanstående samband härleds med referens till vattendroppens modell.

Det finns också källor på webben som refererar det allmänna experimentella området för konstanten r₀ (motsvarande proton-neutronradien) enligt t.ex.

”The value of r₀ consistent with the experimental data ranges from 1.18 × 10^–13 cm to 1.40 × 10^–13 cm for light nuclei.”,

@INTERNET GoogleBöcker med begränsad tillgänglighet

Nuclear Physics: An Introduction, S. B. Patel 1991

Min översättning:

Värdet på r₀ samstämmigt med experimentella data omspänner från 1,18 t15 M till 1,40 t15 M för lätta atomkärnor.

I den under 1900-talets senare epok allmänt (stadsbiblioteken) tillgängliga grundkällan HANDBOOK OF PHYSICS McGraw-Hill (1967) ges i tabell standardvärdet

r₀ = 1,37 t15 M

HOP-källan beskriver fem olika samstämmiga experimentella metoder för mätning av kärnradierna (varav metod nr4 med referensvärdet r₀ = 1,2 t15 M), bl.a. med referens till arbetena från Hofstadter (metod nr5).

En sammanfattande beskrivning av HOP-källans specifikationer med citat finns på artikeln HOP-källans r₀-värde.

Många källverk — speciellt på webben @INTERNET — använder emellertid (numera, i den allmänna beskrivningen) snarare referensvärdet

r₀ = 1,2 Fermi = 1,2 t15 M = 1,2 t13 cM .............................. (konventionellt skrivs Fermienheten 1 Fermi=1 t15 M ofta ”fm”, motsvarande femtoMeter)

Jämför t.ex. (de två f.n. bästa — mest förklarande, mest välskrivna — webbkällorna)

Microscopic World — 3 — The World of the Atomic Nucleus, Dr. Kenjiro Takada, 2006

[http://www2.kutl.kyushu-u.ac.jp/seminar/MicroWorld3_E/3Part2_E/3P22_E/nuclear_size_E.htm],

”R = 1.2 × A^1/3 fm (1 fm = 10^–15 m)”.

och

Department of Physics and Astronomy, GEORGIA STATE UNIVERSITY (2005)

[http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/nucuni.html],

”r = r₀A^1/3 where r₀ = 1.2×10^–15 m = 1.2 fm”.

WOODS-SAXON-FÖRDELNINGEN OCH

PROTONRADIENS LITTERÄRA REFERENSVÄRDE

Bägge ovannämnda källor relaterar värdet 1,2 Fermi (den senare källan redovisar sin del i avsnittet Nuclear Size and Density), men Takada (ovan) ger den mest utförliga beskrivningen.

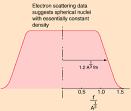
Grunden bakom 1,2-Fermivärdet benämns (typiskt) Wood-Saxon-fördelning (eng. Wood-Saxon distribution) och baseras på sambandsformen (se även efterföljande citat)

r₀

r(r) = —————— ....................... Wood-Saxon-fördelning; r = avståndet från en idealiserad sfärisk medelpunkt

1 + e^(r–R)/a

— med koppling till elektronspridningsförsök (sambandet ovan beskrivs mera utförligt nedan i efterföljande citat);

Wood-Saxonkurvan

WOOD-SAXON-KURVAN

Alla nedanstående konventionella exempelkällor

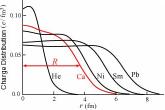
The World of the Atomic Nucleus, Kenjiro Takada 2006

[http://www2.kutl.kyushu-u.ac.jp/seminar/MicroWorld3_E/3Part2_E/3P22_E/nuclear_size_E.htm]

Hyperphysics — Nuclear Size and Density

GEORGIA STATE UNIVERSITY (2005)

[http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/nucuni.html]

The electron-scattering method and its application to the structure of nuclei and nucleons, ROBERT HOFSTADTER 1961 s569

[http://nobelprize.org/nobel_prizes/physics/laureates/1961/hofstadter-lecture.pdf]

(med flera liknande, se även Hofstadters kurvskara) använder på olika sätt och i olika sammanhang en generaliserad kurvform, den s.k. Wood-Saxxon-fördelningen (eng. Wood-Saxon distribution) i beskrivningen av begreppet kärnradie.

En av de bästa referenskällorna i ämnet (prisbelönt för tydlighet och koncis utformning) är (tveklöst) Hyperphysics, ovan mitten (GEORGIA STATE UNIVERSITY 2005). I anslutning till illustrationen (förminskad ovan) skriver källan:

”The most definitive information about nuclear sizes comes from electron scattering. The comparison of calculated and experimental radii for nuclei are very sensitive to the exact onset of the overlap between the probe particle and the nuclear matter. These comparisons have made it clear that there is a "tail" where the density of nuclear matter decreases toward zero. The nucleus is not a hard sphere.”

Hyperphysics — Nuclear Size and Density, GEORGIA STATE UNIVERSITY (2005)

[http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/nucuni.html]

Min översättning:

Den mest definitiva informationen om kärnstorlekar kommer från elektronspridning. Jämförelsen mellan beräknade och experimentella radier för kärnor är mycket känslig för det exakta inträdet hos överlappningen mellan den avkännande partikeln och kärnmaterialet. Dessa jämförelser har gjort det klart att det finns en ”svans” där tätheten hos kärnmaterialet avtar mot noll. Kärnan är inte en hård sfär.

Om vi återknyter till den inledande beskrivningen — DEN STATISTISKA DEFOKUSERINGEN — samt tar med den allmänt favoriserade sfäriska idealismen som bygger på en primitivt rundstrålande funktion för kärnradien, har vi i ovanstående webbkälla här ett direkt konventionellt citat som visar hur spridningsexperimenten favoriserar den sfäriska divergensmodellen vidare: den oskärpa som följer tvunget av den statistiska metoden frammanar uppfattningen om en oskarp, diffus övergång mellan inre och yttre: ”Kärnan har ingen skarpt avgränsad kontur”. Den statistiska metoden gynnar alltså enbart en vidare flora av spökbegrepp.

Jämför även nedanstående citatutdrag där denna detalj framgår än mera tydligt:

s8:

”

”,

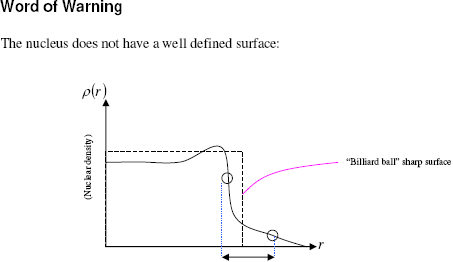
[http://porlhews.tripod.com/sitebuildercontent/sitebuilderfiles/nuclearphysics.pdf],

Nuclear Physics, Lecture notes taken from “Nuclear Physics” given in 2006 at Manchester University by David Cullen

Min översättning:

Varningsord

Atomkärnan har ingen väldefinierad yta: [illustrationen ovan].

Illustrationstexten beskriver den motsvarande jämförande streckade linjen som ”Biljardbollsskarp” yta .

Jämför korrekt påstående:

’The atomic nucleus does not have

a well defined SPHERICAL surface’

Atomkärnan har ingen väldefinierad SFÄRISK yta.

Atomkärnan har överhuvudtaget ingen EXPERIMENTELLT väldefinierbar kontur eller figur alls. Se vidare från Kärnradierna.

Mycket vore vunnet om författarna kunde klargöra sig på DEN punkten — själva.

Wood-Saxon-fördelningen har alltså redan från början avfärdat allt UTOM en diffus atomkärnebyggnad, och UTNYTTJAR den diffusheten för vidare.

Beträffande Wood-Saxon-fördelningskurvan klargör alltså de citerade exemplen:

FÖRDELNINGEN MÅSTE TVUNGET TOLKAS ENTYDIGT i favör för uppfattningen att atomkärnan INTE avslutas med någon typ ”hårt skal” — utan snarare en mer eller mindre diffus övergång till noll.

I funktionen r(r) tillväxer laddningstätheten (r) från r=0 — likt ljuset från en centralpunkt som sprids rundstrålande utåt — och som kan avta eller växa i olika partier, dock generellt med avtagande styrka då r växer obegränsat. Därmed har varje spår av atomkärnan (TNED) effektivt eliminerats. Enligt TNED finns ingen motsvarande funktion r(r) av den typ som figurerar i modern akademi. Det finns ingen annan direkt jämförelse med TNED än att modern akademi ingår som en (ytterst) primitiv aspekt.

DÄRMED ÄR HELA FRÅGAN OM ”ATOMKÄRNANS RADIE” PUNKTERAD — AVGJORD, enligt modern akademisk teori.

Den typen släpper nämligen inte in N3m20-aggregatet:

VARJE MEDELVÄRDESBILDANDE — statistiska — modellbegrepp inför — påtvingar — DIFFUSA OMRÅDEN till atomkärnans exakta form (TNED) och UTESLUTER därmed denna ur den statistiska resultatbilden: statistiken utesluter atomkärnans skarpa byggnad.

Jämför även CERN-kurvan.

ATOMKÄRNAN ENLIGT TNED — och som, tydligen, helt utklassar modern teori i ämnet ATOMVIKTERNA — kan inte tillämpas på någon typ ”Wood-Saxon-fördelning”; Det finns inget typ ”medelvärde” för typ ”laddningstätheten” i atomkärnan enligt TNED (se även i ATOMKÄRNANS MASSTÄTHET, samt vidare nedan). Det begreppet har ingen ABSOLUT kärnfysikalisk representation, utan är ett matematiskt (statistiskt, sfäriskt) modellbegrepp — som modern akademi och vetenskap söker påtvinga atomkärnan, eller rättare sagt: som modern akademi och vetenskap genom olika experiment och med full kraft försöker påvisa är en med naturen överensstämmande korrekt uppfattning.

Det går naturligtvis inte att MEDELVÄRDESBILDA atomkärnan enligt TNED utan att samtidigt demolera hela formbygganden: införa idéer om atomkärnan som inte existerar annat än som statistiska, matematiska kvantitativa modellbegrepp.

Det finns alltså — enligt TNED — ingen enda mätmetod som kan ange atomkärnornas radier med någon som helst ABSOLUT exakthet: värdena varierar beroende på metod och energi (grad av inträngning, jämför Kaplan-data). ”Exakta mätdata” blir därigenom endast relevanta som relativa MÄTDATA i den inbördes relationen eller STRUKTUREN för, säg, en uppsättning atomkärnor inom ett visst mätande energiintervall, och för en specifik metod. Vi kan alltså jämföra olika metodmätningar PER STRUKTUR — vilken riktning de antar — men inte per kvantitativa jämförande absolutvärden.

Wood-Saxonsambandet

Sambandsformen för Wood-Saxon-fördelningen anges konventionellt enligt

r₀

r(r) = —————— ....................... Wood-Saxon-fördelning; r = avståndet från en idealiserad sfärisk medelpunkt

1 + e^(r–R)/a

R-värdet drar ut grafen i x-led, mindre a-värde gör den fallande flanken brantare (mera vertikal).

med motsvarande grafiska form — »Wood-Saxonkurvan»

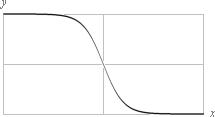
graf: y = (1+è'[x–1]/0.1)'–1

Funktion: y = [1+ e^(x–1)/0,1]^–1

Mittvärdet anges i bägge ovannämnda källor Takada och Hyperphysics som ”1,2 Fermi”, se även citat nedan.

Wood-Saxon-fördelningens sambandsform beskrivs konventionellt bl.a. av Takada i nedanstående citat; Takada visar en grafisk kurvskara — vars källgrund han dock inte närmare anger, men som i stort ansluter till samma typ som ovan i Hofstadters beskrivning — tillsammans med nedanstående textutdrag:

”Most nuclei are nearly spherical. Namely, many protons and neutrons collect to compose a spherical cluster, i.e. a nucleus. (Precisely speaking, some of them may not be exactly spherical but slightly deformed. We will later discuss the nuclear deformation.)

According to the experimental results shown above, the charge distribution in a nucleus, r(r), is well represented by a function

r₀

r(r) = —————— r = distance from center

1 + e^(r–R)/a

This is sometimes called the Woods-Saxon type function. In this function, the parameters r₀, R and a are adjusted to fit the numerical results to the experimental data.

Adjusting these parameters, we can well reproduce the experimental charge distribution. The value of the parameter R is the radius of the nucleus.

For example, the red-colored R shows the radius of the Ca nucleus.

In this way, precise investigations of nuclear radii have carried out for a wide range of nuclides. Not only electron scattering but also various methods have been used for this purpose and then it has been clarified that the nuclear radius is generally given by the following formula:

R = 1.2 × A^1/3 fm (1 fm = 10^–15 m)

where A = Z + N is the mass number of the nucleus.”

Microscopic World — 3 — The World of the Atomic Nucleus, Dr. Kenjiro Takada, 2006

[http://www2.kutl.kyushu-u.ac.jp/seminar/MicroWorld3_E/3Part2_E/3P22_E/nuclear_size_E.htm],

Min översättning;

De flesta atomkärnor är nära sfäriska. Många protoner och neutroner samlas, nämligen, för att bilda ett sfäriskt moln, egentligen en kärna. (Mera precist sagt, är en del av dem inte helt sfäriska utan lätt deformerade. Vi kommer senare att diskutera atomkärnans deformation).

Enligt experimentella resultat som visas ovan [Takadas figur], är laddningsfördelningen i en atomkärna, r(r), väl representerad av en funktion

[sambandet överst] r = avstånd från centrum

Detta kallas ibland för en (typisk) Woods-Saxon funktion. I denna funktion är parametrarna r₀, R och a justerade för att passa de numeriska resultaten av experimentella data.

Justerande dessa parametrar, kan vi väl återskapa den experimentella laddningsfördelningen. Värdet hos parametern R är kärnradien.

Till exempel visar den rödfärgade R [Takadas bifogade illustration, se nedan] radien hos Kalciumkärnan.

På detta sätt, har precisa undersökningar av kärnradier utförts för ett brett område av atomkärnor. Inte bara elektronspridning utan också varierande metoder har använts för detta ändamål, och det har då framkommit att kärnradien i allmänhet ges av den följande formeln:

[sambandet nederst]

där A = Z + N är masstalet hos atomkärnan.

För att kunna ge exakta referenser till den pågående beskrivningen i den här framställningen är det för den bekväma och omedelbara överskådlighetens skull nödvändigt att kunna visa de olika citatkällornas illustrativa koncept.

Figuren nedan är från Takadas textciterade framställning ovan. Till figuren hör en särskild text som angivits nedan.

Microscopic World — 3 — The World of the Atomic Nucleus, Dr. Kenjiro Takada, Kyushu University 2006

[http://www2.kutl.kyushu-u.ac.jp/seminar/MicroWorld3_E/3Part2_E/3P22_E/nuclear_size_E.htm]

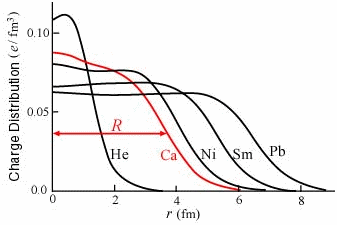
”[Experimental Data of Nuclear Charge Distributions]

The data obtained by the electron scattering. As an example, the red curve shows the proton distribution in Ca whose radius is shown by R.”.

Min översättning:

[Experimentella Data för Nukleär Laddningsfördelning]

Data som får från elektronspridning. Som ett exempel, visar den röda kurvan protonfördelningen i Kalcium [Ca] vilkens radie visas av R.

Takada ger dock ingen referens från vilka forskare eller under vilken epok ovanstående kurvdata framkommit:

Se dock s570 i Hofstadters originalverk från 1961,

[http://nobelprize.org/nobel_prizes/physics/laureates/1961/hofstadter-lecture.pdf].

Med referens till TNED framgår alltså framtiden för modern kärnfysikalisk teori: Eftersom den modelluppfattning man använder inte medger någon FAST föreställning om atomkärnan, tvingas man tuvhoppa, förr eller senare mellan olika ”spökbegrepp” som uppkommer ur det statistiska modellhavet: Man tvingas uppsöka (uppfinna) olika korrektionsattribut — se ytterligare t.ex. h=c — som tillsammans med nya begrepp typ ”laddningsradie” och metoder med förbättrad mätteknik som ansluter till den allmänna statistiska metoden försöker vattna på vad som kan räddas av det tydligt växande vetenskapliga ökendrivande kvarklandskapet.

I den efterföljande delen — se från Laddningsradien — ges en större mängd delcitat ur en mera allmänt hållen syntes vilken ges av nedanstående tre typexempel.

Angående Uppfattningen att kunna mäta typ kärnradie med grund i att man fastställt, noga, transientövergångar in till fjortonde decimalen …

2008VIII18:

INKONSISTENSER I DEN MODERNA VETENSKAPENS TOLKNINGSFÖRETRÄDEN INOM KÄRNFYSIKEN UPPMÄRKSAMMAT I LJUSET AV TNED

(Textmarkeringar i citaten är mina, alla citaten från pdf-dokument upphittade på webben):

9 Oct 2003

On the rms-radius of the proton, Ingo Sick,

s2:

”Introduction. The root-mean-square (rms) radius of the proton is a quantity of great interest for an understanding of the proton; it describes the most important integral property concerning its size. Accurate knowledge of the rms-radius of the charge distribution is needed for the interpretation of high-precision measurements of transitions in hydrogen atoms”.

Min översättning:

Introduktion. Rotmedelkvadrat (rms) radien för protonen är en kvantitet av stort intresse för en förståelse av protonen; den beskriver den mest viktiga integrala egenskapen beträffande sin storlek. Noggrann kunskap om rms-radien för laddningsfördelningen krävs för tolkningen av högprecisionsmätningar av övergångar i väteatomer.

Visst. LADDNINGSFÖRDELNINGSBEGREPPET I KÄRNFYSIKEN (TNED) har ingen bestämd mätteknisk preferens eftersom atomkärnans orientering varierar med mätmetod och energi, samt att atomkärnans laddning INTE bestäms i förhållande till volymen utan YTAN. Jämför t.ex. CERN-kurvan.

M.a.o.: det finns inget allmänt eller generellt eller entydigt ”noggrant värde för protonens laddningsfördelningsradie” — utöver formradien eller konturradien som sådan, men den tillhör TNED och ingår inte i den moderna akademins utbud.

11 DEC 1997 / 1 May 2006

What do we actually know on the proton radius?, Savely G. Karshenboim,

s3:

”2 The hydrogen Lamb shift for the proton radius

The nuclear dependent correction to the Lamb shift in the hydrogen atom as it is well known is of the form²

If the energy were [was] measured with high accuracy and all other contributions to energy were known one could extract the proton charge radius from hydrogen spectroscopic data.

________________________________

²We use a convention: h¹ = c = 1, = e². The nuclear charge Z is useful to classify the QED contributions and in the hydrogen atom indeed one has Z = 1. We always give expressions for E as for the energy, but the numerical values (in kHz) are given for the corresponding frequency value

f = E/h = E/2p.”,

h¹ anger bokens ”h-bar”, lika med h/2p.

Min översättning:

2 Vätets Lambskift för protonradien

Den nukleärt beroende korrektionen till Lambändringen i väteatomer, sådan den är välkänd, är av formen

[sambandet ovan]

Om energin mättes med hög noggrannhet och alla andra bidrag till energin var kända, kunde man extrahera protonens laddningsradie från vätespektroskopiska data.

_________________________________

²Vi använder en konvention h¹ = c = 1, = e². Kärnladdningen Z är användbar för att klassificera QED [Quantum Electron Dynamics] bidragen, och i väteatomen har man verkligen Z=1. Vi ger alltid samband för E som [giltigt för] energin, men de numeriska värdena (i KHz) är givna för det motsvarande frekvensvärdet

f = E/h = E/2p.

Min notering. Den här författaren har tydliga syntaxproblem med engelskan (singularis, pluralis, subjekt och predikat, pronomen [hänsyftande subjekt]). Jag har försökt dämpa ut det värsta i översättningen.

Återigen: ”extract the proton charge radius”, sv. extrahera protonens laddningsradie, har ingen fast eller bestämd koppling till kärnfysiken — ENLIGT TNED: resultaten beror på metod och energi.

Begreppet ”laddningsradie” existerar inte i TNED.

Notera också den moderna akademins och vetenskapens definition av ”charge radius”, som tidigare: man sätter h=c — samt vidare.

Man uppfinner alltså begrepp som normalt anses fullständigt felaktiga; h=c har ingen fysikalisk motsvarighet.

Det finns ingen jämförande referens; Jämförande referenser saknas.

19 Aug 2005

Proton radii and two-photon exchange, Peter G. Blunden, Ingo Sick

s1:

”I. INTRODUCTION

The recent progress in measurements of transition energies in the Hydrogen atom has been remarkable. The 2p-1s transition energy and the 1s hyperfine structure interval (HFS) are now known to 14 and 12 significant digits, respectively [1, 2]. The interpretation of these energies in terms of e.g. tests of QED now depends entirely on the accuracy with which the proton finite-size corrections are known.”.

Min översättning:

I. INTRODUKTION

De senaste framstegen i mätningar av övergångsenergier i Väteatomen har varit enastående. 2p-1-s övergångens energi och 1s hyperfinstrukturintervallet (HFS) är nu kända till 14 och 12 signifikanta siffror, respektive [1, 2]. Tolkningen av dessa energier i termer av (egentligen) tester av QED beror nu helt på noggrannheten med vilken protonens storleksändliga korrektioner är kända.

Kärnradien ändras med Planckenergin

ATOMKÄRNAN ENLIGT TNED HAR INGEN FAST, AV TRANSIENTÖVERGÅNGAR I ATOMENS ELEKTRONHÖLJE, OBEROENDE RADIE.

Spektrala övergångar (samma som atomens utsändande av ljus) sker DOCK oberoende av en viss nuklids radiella utsträckning PÅ EN FAST MÖNSTERFORM:

Energinivåernas struktur — svängningarna — i en nuklid bestäms av en fast g-baserad kärnstruktur, oberoende av hur kärnan är exciterad (E=hf): nivåerna ändras inte för att kärnan exciteras. MEN RADIEN KAN ÄNDRAS MED KÄRNANS OLIKA EXCITATIONSGRADER: J=mwr²=Ec^–2wr².

Eftersom atomkärnans tyngdcirkel ENLIGT TNED är g-baserad — inte ljusenergibaserad, men vilken distinktion saknas i modern akademi (se från neutrinospektrum) — måste rent kvantitativa icke kommutativt-kvalitativa energiekvivalenser ges i utbytet Er²; OM E ökar på grund av Planckenergi hf och som INTE innebär att kärnan får ökad g-massa, måste kärnan likväl som elektromekaniskt svängningsaggregat svara på den kvantitativa ekvivalensen E=(m®g)c² — och därmed via KONSTANT J anpassa r omvänt proportionellt:

J kan inte ändras utan en ändring av g-massan, analogt ett mekaniskt arbete, och som bara kan associeras med en process som utvecklar massförintelse (m®g) i atomkärnan, själva energin till J-ändringen: J=Ec^–2wr²; J(c/w)²=konstant, E och r² varierar omvänt proportionellt.

Atomkärnans radie bör alltså, verkligen, variera och fluktuera med hela atomens olika grader av excitation: hetare blir mindre, svalare blir större. Vi kan inte bortse ifrån energiekvivalenterna. EXEMPEL VIA J=mwr²=Ec^–2wr²: Om en atomkärna (proton) tar upp 1% av sin egenenergi (E) i Planckenergi (hf) kräver ekvivalensen med konstant J och konstant vinkelrotation (se nukleära spinnkriteriet) att r reduceras med runt 0,5%: (1,01E)(r/Ö1,01)²=Er².

Om energin i Väteatomen ändras med runt 10 eV, Väteatomens totala energi runt 940 MeV, ändras kärnradien närmast i åttonde decimalen, ovanstående förutsättningar.

Dessa aspekter finns emellertid inte med i modern akademi — eftersom man inte anser att massan har någon kvalitativ egenskap: atomkärnan enligt TNED, kraftstrukturen (se Atomkärnans gravitella härledning).

Det är märkligt detta att åse hur den moderna vetenskapens befolkning tycks förstå hela atomkärnan så utomordentligt detaljerat — utan att ha inblick i något alls.

Källtexten från citatkällan närmast ovan fortsätter:

”These finite-size corrections can be determined from elastic electron-proton scattering at low momentum transfer q.”.

Min översättning:

Dessa storleksändliga korrektioner kan bestämmas från elastisk elektron-proton spridning vid låg momentöverföring q.

Med referens till ”Fermikonstanten” i de olika spridningsmetodernas allmänna spridningsvärden 1,18-1,4 är det naturligtvis meningslöst med en ABSOLUT bestämning på säg 1,4nn med värden i tredje eller fjärde decimalen. En sådan precision i meningen ABSOLUT är fullständigt värdelös.

Som redan tidigare påpekats av andra författare, varierar ”Wood-Saxon-koefficienten” mellan ”1,18-1,4” beroende på metod — samt vidare beroende på energi (se t.ex. källreferensen till Kaplan-data). Vilket vill säga: det finns ingalunda någon mätteknisk EXAKT metod att avgöra kärnradierna på: olika metoder ger olika värden (massbaserad med olika projektiltyper, ljusbaserad); olika energier i en viss metod ger också olika värden: OLIKA INTRÄNGNINGAR. Det går inte att komma ifrån.

Söker man, då, ett ”medelvärde” för kärnradien, hamnar man likväl FEL, eftersom också LÄGET (se CERN-kurvan) hos atomkärnan är signifikant för en noggrann bestämning av kärnradien. Det läget — kärnans godtyckliga orientering i rummet — ingår alltid som ett statistiskt medelvärde ”för alla möjliga fall”. Skillnaden mellan extremlägena (TNED) är i sammanhanget MYCKET STOR (upp till 2/3) — se CERN-kurvan. Därmed blir varje ”exakt mätning” av kärnradien en fundamental omöjlighet — såvida man inte kommer på ett sätt att mäta kärnradierna med ”upprätt stående atomkärnor” typ spinnpolariserade experiment OCH där spinnriktningen inte ändras, alltså inte alls, under experimentet.

Exakta kärnradiemätningar kan bara vara signifikanta för just den exakta metoden, just den serien. Absolutvärdena är inte meningsfulla UTOM INOM den aktuella mätserien med just de förutsättningarna. En annan metod ger ett annat resultat — en annan nivå. Det går inte att mäta kärnradierna på någon som helst exakt fason.

Se även i inledningen från KÄRNRADIENS STATISTISKA UTSUDDNING.

Här är det alldeles tydligt att experimentnissarna redan har etablerat en SPECIELL STATISTISK EXPERIMENTELL METOD, dessutom av ytterst avancerad natur: laserspektroskopiska basinstrument, understödda av enorma datorberäknande program som ligger långt utanför varje normal människas räckvidd.

Det är, och förblir, precis som citatkällan i värdespridningen säger: alla mätdata varierar i kurvkoefficienter (zoomen) runt 1,18-1,4 Fermi (räknat grovt på massbaserade projektiler, och inom vissa rimliga energigränser).

Varje absolutjämförelse är utesluten.

laddningsradien

BEGREPPET LADDNINGSRADIE INFÖRS

Den moderna, klassiska kärnfysiken, tar (plötsligt) en ny riktning

Något inträffar (plötsligt) — nämligen — omkring 1990:

HOFSTADTER OMNÄMNER INGET BEGREPP TYP ’LADDNINGSRADIE’

2008IX1. Jo — men det blånekas av sökfunktionen:

s571n:

”It is an interesting fact that more recent determinations of the rms proton charge”,

s572ö:

”radius appear to converge on a value of (0.79 ± 0.08) × 10^–13 cm.”

[http://nobelprize.org/nobel_prizes/physics/laureates/1961/hofstadter-lecture.pdf]

The electron-scattering method and its application to the structure of nuclei and nucleons, Robert Hofstadter, Nobel Lecture, December 11, 1961

Min översättning:

Det är ett intressant faktum att nyare bestämningar av protonens rms laddningsradie verkar konvergera på ett värde (0,79 ± 0.08) × t13 cm.

PDF-SÖKMOTORN KLARAR INTE SIDÖVERLAPPNINGAR.

”charge radius” finns visst i Hofstadters skrift från 1961. Men sökmotorn klarar inte av att första ordet ligger sist på en sida och andra ordet överst på nästföljande sida. Sökningen på ”charge radius” ger noll resultat: ”Reader har sökt klart i dokumentet. Inga träffar”.

Här finns alltså ett FÄRSKT EXEMPEL på det ytterst äventyrliga i att försöka avgöra olika frågesporter @INTERNET genom att SÖKA: sökverktygen i de olika programpartierna ÄR UPPENBARLIGEN INTE FULLT UTVECKLADE FÖR ÄMNET.

Men historien brukar fungera så, att när ett begrepp väl ”dyker upp i litteraturen” kan det ha cirkulerat i vissa kvarter kanske under decennier eller mer. Här är säkra uppgifter på den punkten helt obefintliga.

Notering. Hofstadter omnämner inget om ”charge radius” eller ”0.8”… Fermi. Han omnämner heller inte ”proton radius”, och heller ingen siffra av typen ”1.2” eller ”1.37”. Däremot förekommer termen ”charge distribution” i Hofstadters beskrivning.

Det är här okänt huruvida termen ”charge radius”, laddningsradie, finns med i den mycket omfattande HOP-källan från 1967. Termen ”charge distribution”, laddningsfördelning, däremot finns med.

I referens med sökuppgift från @INTERNET (t.o.m. Augusti 2008) dyker termen

laddningsradie (eng. charge radius) tidigast upp enligt nedanstående källa från år 1989 (textmarkeringarna är mina);

Det här ligger (långt ner) i bakgrunden:

1975:

”It is shown that the proton rms radius should be determined from fitting a polynomial of second order to the low-q² form factors. The commonly used polynomial of first order yields radius values which are too small. The proton rms radius has been redetermined from an analysis of the electron scattering data measured at three laboratories. The best fit value is (r_E²)^1/2=0.87±0.02 fm.”

On the determination of the proton RMS-radius from electron scattering data, 14 Jul 1975, SpringerLink

F. Borkowski, G. G. Simon, V. H. Walther and R. D. Wendling, Institut für Kernphysik der Universität Mainz, Mainz, West-Germany

Min översättning:

Det visas att protonens rms-radie bör bestämmas från en polynomial inpassning av andra graden till de låg-q²-iga formfaktorerna. Den allmänt använda första gradens polynom ger radievärden som är för små. Protonens rms-radie har ombestämts från en analys av elektronspridningsdata uppmätta på tre laboratorium. Det bäst inpassade värdet är (r_E²)^1/2=0,87±0,02 Fermi.

Sedan poppar det här upp:

1989:

”An accurate value for the proton charge radius is of fundamental importance in nuclear physics, both in tests of the accuracy of quantum electrodynamic calculations and as a new standard for comparison in nuclear physics experiments. Discrepancies between previous determinations of the proton radius are so large as to preclude useful tests of theory. Hence, the objective of this work is to obtain a new determination of the proton charge radius.”

[http://adsabs.harvard.edu/abs/1989PhDT........66M],

Precision Measurement of the Charge Radius of the Proton, 00/1989

McCord, Miles Earl, Jr, THE CATHOLIC UNIVERSITY OF AMERICA

Min översättning:

Ett noggrant värde för protonens laddningsradie är av fundamental betydelse i kärnfysiken, både för att testa noggrannheten i kvantelektrodynamiska beräkningar och som en ny standard för jämförelse i kärnfysikaliska experiment. Avvikelser mellan tidigare bestämningar hos protonradien är så stora att de utesluter användbara tester av teorin. Således är föremålet för det här arbetet att uppnå en ny bestämning av protonens laddningsradie.

— Det finns inget sådant ”noggrant värde för protonens laddningsradie” i fysiken:

— Jo. Självklart, som en allmän medelvärdesform baserad på en stor mängd mätdata.

— Väl kan man i princip få fram mätdata på atomkärnan med en precision i hundratusendelar av en Fermi, men eftersom det inte finns någon fast mönsterbyggnad att hänföra atomkärnan till i modern akademi — ingen BILD av atomkärnans formbyggnad — finns heller ingen FAST NIVÅ att förlägga precisionsvärdet till eftersom metodmätningarna för protonradien varierar mycket — förgrovat mellan 1-1,5 Fermi. Den som menar annat: visa konturen.

— Det finns ingen ENHETLIG sådan, nämligen, kontur i termer av modern akademisk nomenklatur.

— Grundtermen är SFÄRSIK [Se Tilläggsartikeln i Wikipedia för Charge radius].

Andra källor dyker sedan (plötsligt — som en flod) upp med samma typ av meddelande (textmarkeringar är mina för att underlätta):

1993/7:

”In 1993 optical spectroscopic measurements of the hydrogen-deuterium isotope shift of the 1S-2S resonance [5] reached a precision sufficient to derive a new value for the deuteron structure radius [6] which deviates significantly from the electron scattering results.”

Hydrogen-Deuterium 1S-2S Isotope Shift and the Structure of the Deuteron (1997)

A. Huber, Th. Udem, B. Gross, J. Reichert, M. Kourogi, K. Pachucki, M. Weitz, and T. W. Hänsch, Max-Planck-Institut für Quantenoptik

Min översättning:

År 1993 nådde optisk spektroskopiska mätningar på väte-deuterium-isotop-skiftet hos 1S-2S-resonansen en precision tillräcklig för att erhålla ett nytt värde för deuteriums strukturradie, vilken avviker anmärkningsvärt från resultaten med elektronspridning.

1994:

”A new formula for the nuclear charge radius is proposed, dependent on the mass numberA and neutron excessN-Z in the nucleus. It is simple and it reproduces all the experimentally available mean square radii and their isotopic shifts of even-even nuclei much better than other frequently used relations.”

[http://www.springerlink.com/content/vg10027331536613/],

Simple formula for nuclear charge radius, 26 January 1994, Bozena Nerlo-Pomorska and Krzysztof Pomorski,

Theoretical Physics Department, The Maria Curie-Skodowska University

Min översättning:

En ny formel för kärnladdningsradien föreslås, oberoende av masstalet A och neutronöverskottet N–Z i kärnan. Den är enkel och reproducerar alla de experimentellt tillgängliga medelkvadratradierna och deras isotopskift för jämna-jämna nuklider mycket bättre än andra ofta använda samband.

Notering. Den här källan har dunkla referenser till de presenterade grafiska resultaten; Graferna som visas innehåller ospecificerade referensindex (parameterreferenser saknas eller är oklara), figurhänvisningarna i slutet av källtexten är oklara (källtexten anger figurbeteckningar som sedan inte återfinns i figurreferensen).

”New measurements of both deuteron and proton charge radii would be of great interest in both nuclear and atomic physics.”

DEUTERON RADIUS AND NUCLEAR FORCES IN FREE SPACE, 3 September 1994, Chun Wa WONG, Department of Physics, University of California

Min översättning:

Nya mätningar på både proton- och neutronradier skulle vara av stort intresse i både kärn- och atomfysiken.

1996:

”Although there has been a continuous interest in all deuteron observables, the observable root-mean-square (rms) charge radius r_ch and

the related but unobservable rms matter radius r_m have recently received special attention

[1, 4, 2, 3, 5, 6, 7, 8] [författarnas hänvisningar till verk under åren 1986-1992, min notering]. This is mainly due to unresolved discrepancies between experimental data and theoretical predictions.”

Meson and Quark Degrees of Freedom and the Radius of the Deuteron, 11 Oct 1996

A. J. Buchmann, H. Henning, and P. U. Sauer, Institute for Theoretical Physics, University of Hannover

Min översättning:

Fastän det har funnits fortlöpande intresse i alla deuteronens observerbarheter, har den observerbara laddningsradiens r_ch rot-kvadratmedelvärde (rms) och den relaterade men icke observerade rms materieradien r_m nyligen erhållit speciell uppmärksamhet. Detta beror i huvudsak på ej klarlagda oförenligheter mellan experimentella data och teoretiska förutsägelser.

2003:

”The cloudy history of experimental values for the proton radius has recently been clarified by a comprehensive analysis[4] of all the world’s electron-proton scattering data.”

Zemach Moments for Hydrogen andDeuterium, 14 Oct 2003,

J. L. Friar (Theoretical Division, Los Alamos National Laboratory), and

Ingo Sick (2Dept. fur Physik und Astronomie, Universität Basel)

Min översättning:

Den dimmiga historien av experimentella värden för protonradien har nyligen klarlagts genom en omfattande analys av världens alla elektron-proton-spridningsdata.

”We study the world data on elastic electron-proton scattering in order to determine the proton charge rms-radius. After accounting for the Coulomb distortion and using a parameterization that allows to deal properly with the higher moments we find a radius of 0.895 ± 0.018fm, which is significantly larger than the radii used in the past.”

”Past results. The initial electron scattering experiments on the proton were performed some 40 years ago by the Hofstadter group at Stanford [4, 5]. This data, mainly at medium q and not low q, was fitted using multi-pole form factors. From the parameters of the fit an rms-radius could be calculated. The resulting value of 0.81fm, which is still quoted in the literature, should have long been superseded by values coming from more precise data at lower q which are indeed sensitive to the rms-radius.”

On the rms-radius of the proton, 9 Oct 2003, Ingo Sick, Dept. fur Physik und Astronomie, Universität Basel

Min översättning:

Vi studerar världsdata på elastisk elektron-protonspridning för att bestämma protonens laddnings-rms-radie. Efter beaktande av Coulombdistorsion och användande en parameterisering som tillåter en ordentlig behandling med de högre momenten, finner vi en radie på 0,895 ± 0,018 Fermi, vilket är anmärkningsvärt större än den radie som användes tidigare.

Tidigare resultat. De första elektronspridningsexperimenten på protonen utfördes för omkring 40 år sedan av Hofstadter gruppen vid Stanford. Dessa data, i huvudsak med medium q till låga q, var ägnade att passa formfaktorer av typen multipol. Från inpassningsparametrarna, kunde en rms-radie beräknas. Det resulterande värdet på 0,81 Fermi, som ännu citeras i litteraturen, borde för länge sedan ha ersatts av värden som kommer från mera precisa data vid lägre q som, verkligen, är känsliga för rms-radien.

Och sedan — så — vidare.

Plötsligt verkar hela den sammanhängande historien — den som påbörjades av Hofstadter och hans kollegor (under 1950-talet) — bara sluta. Tvärt av. Bara End Punkt. Och lika plötsligt hoppar ett antal helt nya, andra, figurer in på scenen och till synes »börjar ”spexa” och ”veva med armarna”» — så väl hälften vore nog, citaten ovan.

Vad hände?

Det visar sig, längre fram i den här berättelsen, att begreppet ’laddningsradie’ är ett högeligen SKAPAT begrepp (medelvärdesbildning) och som innefattar ’parametrar’ som inte ansluter till någon som helst ANNAN logisk matematisk koppling alls än just experimentella medelvärden baserade på omfattande matematiska-teoretiska algoritmer: man sätter — uppfinner, för att exemplifiera — h=c, se vidare i separat avsnitt från NYA BEGREPP INTRODUCERAS RUNT 1990..

’dimmiga historien’?

Oo. Sedan när då — om man får fråga?

— Laddningsradie?

— Sedan när?

— Det verkar som att HELA den moderna akademiska kärnhistorien inte kan uppvisa ANNAT än idel dimbankar — som tycks driva omkring i den mänskliga vardagen, än hit och än dit, för att åsamka sina egna sensationer — från och till.

Det är märkligt att ingen av författarna ovan, eller andra, tycks reagera för att visa minsta vilja att ge någon koppling, beskrivning eller förklaring.

TYPDATA som vi presenteras inför och som, tydligen, uppvisar två inbördes olika epok- och begreppsreferenser är DELS av Hofstadter-typen

1,2 Fermi

och DELS av ”den nya tidens ännu odefinierade upphov” (men som tydligen redan förekom också på Hofstadters tid)

0,81 Fermi

— med nyare justeringar typ 0,86 Fermi eller 0,895 Fermi beroende på källverk (se exv. citatet närmast ovan).

Hur relateras dessa?

Den första — 1,2-Fermitypen — har vi redan klarlagt genom grunduppfattningarna med laddningsfördelningen, se från Wood-Saxon-funktionen, funktionen

r(r) = r₀[1 + e^(r–R)/a]^–1 ;

medelvärdesbildningarna utpekar värdet ca 1,2 Fermi som grundvärdet för r₀ i kubgrafen r=r₀A^1/3,

eller som det anges standardiserat i HOP-källan från 1967, r₀ = 1,37 Fermi = 1,37 t15 M

Denna typ hör ihop med de klassiskt kärnexperimentella resultat som sammanknippas med Hofstadters arbeten.

Svaret på den andra delen — 0,81 Fermi — verkade TILL EN BÖRJAN hart när omöjligt att hitta någon referens till på webben. Till slut hittades den dock — med hjälp av sökning på diskussionsforum där någon vänlig själ lämnat referens till GoogleBöcker — källan nedan;

s114:

”

Using the dipole form, the proton charge distribution becomes

r_ch(r) = r₀e^–q0^r

From this, we obtain the square of the charge radius of a proton,

ò r²r_ch(r)r² dr 12

<r²> = ——————— = ——— = (0.81 fm)²

ò r_ch(r)r² dr q₀²

”,

@INTERNET GOOGLE-böcker begränsad åtkomst

Introductory Nuclear Physics 1998, Samuel Shaw Ming Wong

Min översättning:

Med dipolformen, blir protonens laddningsfördelning

[övre sambandet]

Härifrån får vi kvadraten på laddningsradien hos en proton,

[undre sambandet]

NOTERING. Citatkällans q kopplar till en term av typen ”formfaktor” som sammanhänger med kärnmodellens preferenser.

Vi behöver inte känna till detaljerna i den delen här då det ämnet är reserverat för den moderna akademins experimentalstatistiska kärnmodeller.

Även om Samuel Wong (ovan) inte lyckas relatera kopplingen närmare, är det i vilket fall tydligt att termen laddningsradie har matematisk modellkoppling till grundformen med begreppet laddningsfördelning — och vilken senare del har direkt koppling till de olika (statistiska) modellerna i samband med utformningen av de (allra tidigaste) konkreta resultaten från elektronspridningsexperimenten — se från föregående PROTONRADIENS LITTERÄRA REFERENSVÄRDE.

Därmed är kopplingen till (det tydligen i allmän huvudsak omkring 1990 nyinförda) begreppet laddningsradie välrelaterad;

Protonens laddningsfördelning r_ch(r) är teoretiskt en funktion av avståndet (r) från ett föregivet centrum (vanligen en central tyngdpunkt); flera teoretiska-matematiska modeller finns. Sambandet (eller funktionen) ovan för r_ch(r) är samma som anges av Takada (eng. Wood-Saxon distribution, frånsett en extra adderande enhet i nämnaren);

Medan det är själva funktionen r_ch(r) som sådan som — verkligen — associeras med den metriska (största medelvärdesmässiga) utsträckningen hos protonen typ 1,2 Fermi, kallas integrala rotkvadratmedelvärdet av r_ch(r), se citatsambandet ovan, för protonens laddningsradie (eng. charge radius) och som tecknas inom en motsvarande knäckt parentes <r²>^1/2 där alltså r-formen blir föremål för en mera statistisk inventering.

Dvs., det är ”samma r” som i den laddningsfördelande funktionen r_ch(r), men taget genom en (integrerande) procedur.

Därmed är det klarlagt:

Begreppet laddningsradie är ett NYTT — annat — kärnmetriskt begrepp som (mera populärt på senare tid i samband med laserteknikens uppsving under 1990-talet) frammanats ur en teoretisk modell (som ingen tycks veta/förmå förklara grunderna för och som därför är föremål för djupare forskning) med olika föreställningar och uppfattningar om hur laddningsfördelningen är kopplad till någon geometrisk strukturbyggnad — för ändamålet att försöka komma underfund med uppmärksammande DISKREPANSER (i stort med början från 1990-talet) INOM KÄRNFYSIKENS METRIK men/och som man (ännu) inte förstår.

LADDNINGSRADIEN (0,86 Fermi för protonen) blir alltså en (ny) TYP verkansradie för kärnladdningen och som ÄNNU beror på modell då ingen riktigt vet hur man ska tackla ämnet (liknelsen med människor i ett mörkt rum som försöker beskriva föremålen genom att känna sig fram, känns påtaglig).

Därför finns det heller ännu ingen verklig ETABLERAD förklaring till vad som menas med ”laddningsradie” — verkligen — därför att ingen ännu förstår innehållet.

Se dock nydaningen i Wikipedia [efter 2008, detta dokuments författningsperiod]: den ursprungliga artikelformen Nuclear size numera [Jul2011] ersatt av Charge radius.

Se även från NYA BEGREPP INTRODUCERAS RUNT 1990.

TNED. I TNED är begreppet laddningsradie = formkropp perfekt och exakt definierat för atomkärnan — under DEN förutsättningen att inga störande moment finns med i bilden. Atomkärnan, dess ytform, ändrar (nämligen, vilket även möjligen alla inom modern akademi redan verkar ha förstått) sin laddningsbild mot gästande agenter med ökande grad av växelverkan då den avkänner »närgloende probtyper» — speciellt tydligt i fusionerna, men även i alla övriga kärnombyggnader där utbyte av eller växelverkan med energi-massa förekommer. Av den anledningen är det — som nyligen redan påpekades i PROTONRADIENS LITTERÄRA REFERENSVÄRDE — meningslöst att söka någon enhetlig ”formel” för ”atomkärnans laddningsradie”; vi VET redan att kärnladdningen är av typen eZ, idealt (perfekt) sfärisk, på stort avstånd från atomkärnan, men att denna detalj uppvisar ”upplösning” i 1818e-massivet ju närmare någon kropp kommer atomkärnan, analogt också beroende på den energi som detta besök är förknippat med: kärnan ändras dynamiskt, anpassar sig, vilket i TNED uttrycks bekvämt för samtliga fall genom atomens eller atomkärnans två grundekvationer

J_0K + 3J_1K = 0 ........................ impulsekvationen

F_BT + F_eZ = 0 ........................ kraftekvationen, komponenten F_eZ ger Spektrum och Kvanttalen

Därmed är (återigen) varje jämförande ansats med modern akademi dödsdömd redan från start: det går inte.

Därmed synes också ändamålet tydligt:

Modern akademi tycks eftersöka någon form av statisk atomkärna i fysiken.

Modern akademi BORDE veta det vid det här laget, genom floran av alla sina partikelexperiment: En sådan finns inte.

— Det finns dock ingenting som hindrar att man generaliserar alla möjliga experimentdata till en gemensam medelform. Men den får i så fall föga koppling till den aktuella formbild som TNED grundas på (Utförligt från Neutronkvadraten) och som (således) inte alls (längre) finns närvarande i modern akademi.

WIKIPEDIA som annars brukar vara främst på Google-tapeten om det gäller att beskriva en allmänt använd term, håller helt tyst på den här punkten.

Det gör också (ännu Juli 2008) samtliga övriga webbkällor @INTERNET. Det går inte att få fram ett enda ord i ämnet — frånsett bidraget ovan från Samuel Wong.

2011-07-06

Ny artikelrubrik Charge radius i Wikipedia (efter Jul2008)

Wikipedia har numera raderat all koppling till föregående artikelrubrik Nuclear size med ersättaren (Nuclear) Charge radius. Wikipedia-artikeln (ännu Jul2011 av kortare typ) ger en delvis kopplande beskrivning till nedanstående, men också en delvis fragmenterad dito (Lasergenombrottet omnämns inte, heller inte den dramatiska omvälvningen). Se vidare infogat tillägg i slutet av denna delartikel i Wikipedia Nuclear Size.

Det har nämligen (under 1990-talet) uppkommit ytterligare en ’flaskhals’:

Lasern.

Om vi (först) återknyter till Hofstadter och ”den klassiska partikelfysiken”, kan vi med hjälp av HOP-källan från 1967 få veta att SAMTLIGA FEM OBEROENDE MÄTMETODER — däribland (den femte) som Hofstadters högenergetiska elektrondiffraktionsexperiment — grundas på en massbaserad växelverkan: atomkärnans tyngdcirkel, i TNED impulsekvationen ovan. FÖLJAKTLIGEN uppvisade/uppvisar (fortfarande) också alla fem mätmetoderna inbördes konsistenta resultat.

Sambandsformerna som innefattar elektronmassans tyngdpunkt — helt utom modern akademi, se Härledningen till elektronmassans tyngdpunkt — understryker det resultatet ytterligare med central form i HOP-standardvärdet 1,37 Fermi.

Om vi sedan inför en ny typ av mätmetod

— klassisk spektroskopi uppklädd i laser, s.k. laserspektroskopi

— hamnar vi ENLIGT TNED i en helt ny situation:

Växelverkan är inte längre massbaserad, se Massbaserade mätmetoder, utan energibaserad, se Laserspektroskopi.

Se även utförligt från Neutrinospektrum för bekantskap med grundbegreppen, om ej redan bekant.

Atomkärnan i förhållande till laserproben — som helt enkelt är Planckenergins ljusfrekvenser hf — ses (idealt) precis som skuggan av själva föremålet i lampljuset: Laserenergin ser inte atomkärnans tyngdcirkel, känner ingenting av dess g-tyngd, bara atomkärnans totala energiinnehåll inramat av atomkärnan som en svängande kropp med fasta ytterkonturer (alltså, en elektromekanisk svängningsalstrare med strängt ändlig, begränsad utsträckning).

Den delen är omöjlig att få syn på med hjälp av (högenergetiska) bombarderande elektronmassor

— eftersom dessa tränger in i alla skrymslen och växelverkar med hela atomkärnans massa

— och därmed i ekvivalent impulsform på tyngdcirkeln som alltså lasern inte kan se.

Men — TNED — atomkärnans ytterkontur är ingalunda metriskt jämförbar med atomkärnans tyngdcirkel: Det skiljer på runt dubbla värdet (1/0,52 för A>1 och avrundat 1/0,5 för A=1).

Vad skulle vi — då — ha att förvänta OM vi tänker oss att kunna ”mäta kärnradien” med hjälp av en (ideal) masslös laserstråle?

Åh. Uppenbarligen: Vi skulle få svaret: ”runt dubbla tyngdcirkeln”.

Inte typ ”1 Fermi”

— utan istället typ ”2 Fermi”

— som typvärden för protonen-neutronen (och även deuteronen och Helium-4, enligt TNED).

Vad säger man då i den moderna akademins och vetenskapens kvarter

— i samband med ovan omtalade nydaningar och fram till nu

— i den saken?

Textmarkeringar i citattexten är mina;

1994:

”Experimental knowledge and theoretical understanding of the deuteron matter radius are reviewed. An experimental value of

rm(exp)=1.9502 (20) fm is found by using the 1962 Stanford data, the 1973 Monterey data and the 1981 Mainz data for the ratio of electron-deuteron to electron-proton elastic scattering cross-sections, plus the 1979 Erevan data and the 1990 Saclay data on electron-deuteron elastic cross-sections.”

DEUTERON RADIUS AND NUCLEAR FORCES IN FREE SPACE, 9 May 1994

Chun Wa WONG, Department of Physics, University of California, Los Angeles

Min översättning:

Experimentell kunskap och teoretisk insikt om deuteronens materieradie omvärderas. Ett experimentellt värde på rm(exp)=1,9502 (20) fm återfinns genom att använda Stanforddata från 1962, Monterey-data från 1973 och de 1981 (givna) Mainz-data som förhållandet för elektron-deuteron till elektron-protonelastiska spridningstvärsnittet, plus de (befintliga) Erevan-data från 1979 och Saclay-data från 1990 på elektron-deuteronens elastiska tvärsnitt.

1996:

”We study the world data on elastic electron-deuteron scattering in order to determine the deuteron charge rms-radius. After accounting for the Coulomb distortion we find a radius of

2.128±0.011 fm, which is in perfect agreement with the radii deduced from other sources. This removes a disturbing discrepancy first pointed out by Klarsfeld et al.”

On the rms-radius of the deuteron, ScienceDirect 1996

Physics Letters B, Volume 375, Issues 1-4, 16 May 1996, Pages 16-20, I. Sick and D. Trautmann

Min översättning:

Vi studerar världsdata på elastisk elektron-deuteron spridning för att bestämma deuteronladdningens rms-radie. Efter beaktande av Coulombdistorsionen finner vi en radie på 2,128±0.011 fm, vilket är i perfekt överensstämmelse med radierna erhållna från andra källor. Detta eliminerar en störande oförenlighet som först påpekades av Klarsfeld med medarbetare.

1997:

”This gives a deuteron radius of

(1.968 ± 0.006) fm and a charge radius of

(2.130 ± 0.010) fm.”

EDP Sciences 1997, The European Physical Journal, 2 December 1997

A consistent calculation of dispersion corrections in elastic electron-deuteron scattering

T. Herrmann (Fakultät f. Physik, Universität Kaiserslautern, D-67663 Kaiserslautern, Germany),

R. Rosenfelder (Paul Scherrer Institut, CH-5232 Villigen PSI, Switzerland)

Min översättning:

Detta ger en deuteronradie på

(1,968 ± 0.006) Fermi och en laddningsradie på

(2.130 ± 0.010) Fermi.

2004:

”Background: In October 2004, a group led by Argonne Physics Division's Zheng-tian Lu published a

measurement of the rms radius of the distribution of the two protons in the nucleus of 6He. The measurement was done at the division's ATLAS acclerator, which was used to make a beam of the radioactive 6He nuclei. Despite the fact that these nuclei have a half-life of only 0.8 sec., they could be collected in an atom trap and their charge radius measured to just better than 1%. The resulting rms radius for the distribution of protons in 6He was 1.912+- 0.018 fm -- considerably larger than the rms radius in 4He of only

1.455 fm. This very accurate measurement of such a short-lived nucleus generated considerable interest.”,

[http://www.alcf.anl.gov/collaborations/projects/comp_physics.php],

Argonne National Laboratory

Min översättning:

Bakgrund: I Oktober 2004 publicerade en grupp under ledning av Argonnes Fysiska Division, Zhen-tian Lu, en mätning av rms-radien för fördelningen hos de bägge protonerna i kärnan hos Helium-6. Mätningen genomfördes vid divisionens ATLAS-accelerator, vilken användes för att producera en stråle av de radioaktiva Helium-6-kärnorna. Trots att dessa atomkärnor bara har en halveringstid på bara 0,8 sekunder, kunde de samlas upp i en atomfälla och deras laddningsradie bestämmas till just bättre än 1%. Den resulterande rms-radien för fördelningen hos protonerna i Helium-6 var 1,912±0,018 Fermi — betydligt större än rms-radien för Helium-4 på bara 1,455 Fermi. Denna mycket noggranna mätning av en sådan kortlivad atomkärna föranledde ansenligt intresse.

Se även vidare på källsidan, figur med vidare finns. Notera att ”mätningarna” inbegriper DATABERÄKNINGAR som det tog 150 000 processtimmar att utföra.

Samstämmigt med ovan angivna He-4-värdet 1,455 Fermi är f.ö. även uppgiften från Suzuki från 2003, resp., 1,35 och 1,42 Fermi.

Kommentarer

Kommentarer:

FÖR DET FÖRSTA:

OM uppgifterna typ ”1,912” och ”1,968” Fermi för deuteronradien, analogt i r₀-enheter enligt TNED respektive 1,4 och 1,44 med r₀ som protonradien 1,37 t15 M har något fog för sig, är det tydligt att dessa radier är runt de dubbla från TNED-deuteronen: 2×0,71r₀ = 1,42r₀ (ej att beblanda med Suzuki-datat ovan för He-4).

Enligt TNED ska dessa mätdata i så fall vara laserbaserade, vilket också stämmer med ovanstående citatblock — förtydligat i citatblocket i Laserspektroskopin, samt även i nedanstående utdrag från webbkällan ATOMIC-PHYSICS-22.

Det är (nämligen) så — om saken är korrekt uppfattad — att författarsamlingen ovan INTE KLART OCH TYDLIGT UTSÄGER ATT MÄTRESULTATEN GRUNDAS PÅ LASERSPEKTROSKOPISK TEKNIK. Jämför siffervärdena ovan för ”charge radius” »2,128; 2,130» med motsvarande siffervärden i citatblocket i Laserspektroskopin: »2,130». Samma.

FÖR DET ANDRA:

TanihataEpoken

Hela saken — ”paradigmskiftet” — började 1985 när några forskare upptäckte att den utpräglat betaMinusAktiva ₃Li¹¹-nukliden — med en medellivslängd på ca 8,6 mS — ”uppvisade anmärkningsvärt större kärnradie än normalkärnans” — runt 2,5 gånger större [2‡] — och vilken experimentella mätning skedde på en massbaserad grund (genom kollisioner med Beryllium, Kol och Aluminiumkärnor PER 790 MeV/nukleon [1‡]) — extra moment. Se även i EXEMPEL.

1[‡] [http://prola.aps.org/abstract/PRL/v55/i24/p2676_1] 2008-08-11

2[‡] [http://www.tamu-commerce.edu/physics/carlos/papers/PLB314_1993_275.pdf] s275sp1n, 2008-08-27

1. ”In 1985 Tanihata and coworkers performed scattering experiments with light elements like helium, lithium and beryllium [1,2] and

found, completely unexpected, a huge matter radius for some of the isotopes close to the neutron drip line, e.g., 6,8He, 11Li, and 11Be.”,

2. ”Subsequent measurements of the magnetic dipole [3] and the electric quadrupole moments [4] excluded a large deformation of these nuclei and the picture of halo nuclei was established.”,

3. ”The determination of the nuclear charge radius of such nuclei with laser spectroscopy is of particular interest, because it is a model-independent benchmark for nuclear models.”,

4. ”The nuclear charge radius is extracted from the measurements of the isotope shift, which is the sum of the mass and the field shift.”,

”References

[1] I. Tanihata et. al., PRL 55, 2676 (1985)

[2] I. Tanihata et. al,. Phys.Lett. B 206, 592 (1988)

[3] E. Arnold et. al., Phys. Lett. B 197, 311 (1987)

[4] E. Arnold et. al., Phys. Lett. B 281, 16 (1992)”,

[http://www.gsi.de/informationen/wti/library/scientificreport2006/PAPERS/ATOMIC-PHYSICS-22.pdf], s266,

ATOMIC-PHYSICS-22, Ion trap design for a nuclear charge radius determination of ^7,9,10,11Be, D. Tiedemann et al, 2006

Min översättning:

1. 1985 utförde Tanihata och medarbetare spridningsexperiment med lätta grundämnen som helium, litium och beryllium [1,2] och fann, helt oväntat, en mycket stor materieradie hos några av isotoperna nära neutronens »drip line», alltså för ^6,8He, ¹¹Li och ¹¹Be.

2. Efterföljande mätningar av den magnetiska dipolen [3] och den elektriska kvadrupolens moment [4] uteslöt en stor deformation hos dessa nuklider, och bilden av halonuklider blev etablerad.

3. Bestämningen av den nukleära laddningsradien hos sådana nuklider med laserspektroskopi är av särskilt intresse, därför att den utgör ett modelloberoende bänkmärke för kärnmodeller.

4. Kärnans laddningsradie extraheras från mätning på isotopskiftet, som är summan av massa och fältskifte.

Strax efter denna händelse 1985 började forskare i allmänhet intressera sig för det nyupptäckta ämnet ”halonuklider”. Och nu (Augusti 2008) är webben (nära) proppad med olika vetenskapliga mätande avhandlingar med laserspektroskopiska rapporter på just olika exotiska s.k. halonuklider.

Hur hänger dessa uppgifter ihop — enligt TNED?

EXTRA MOMENT — masschokning eller mera egentligt kraftchokning — ENLIGT TNED föreligger i alla sammanhang där elektriska laddningar accelereras av en accelerationsspänning i ett slutet elektriskt system, se utförligt från PLANCKEKVIVALENTERNA. För elektronmassans komponenter är den delen mindre dramatisk (enligt TNED) eftersom komponenterna i vilket fall är ytterligt små relativt även den minsta atomkärna (vissa äventyr uppkommer emellertid även här om partikelenergierna är mycket höga — om det gäller noggrann formbestämning (se Neutronfragmenten): chokmassan lever ett eget, kortvarigt, liv när komponenten återgår till läge nollhastighet …). För ordinära atomkärnor ställer sig saken emellertid (enligt TNED) annorlunda eftersom atomkärnornas radie också inbegrips i massändringseffekterna.

Exakt HUR finns (ännu 2008) ingen beskrivning på i TNED (i min referens).

Generellt sett, med referens till impulsmomentet J=mvr=mwr² med konstant Jw, måste r avta med växande m. Om kollisionsenergierna är stora mellan olika växelverkande atomkärnor, och speciellt om dessa är av olika typ (väsentligen olika masstal), måste varje resultattolkning bli äventyrlig om det gäller att ”mäta kärnradien” genom sådana spridningsexperiment. Det är dessvärre precis vad experimenten från 1985 kring Tanihata-teamet uppvisar: MYCKET mera svulstiga (2,5 gånger [2‡]) radiedata än för normala nuklider (med data erhållna traditionellt genom elektronspridningsförsök). Vet man inte exakt vad man håller på med här, kan det sluta (väldigt) illa i slutänden med den typen av ”nya sensationella upptäckter”.

Tanihata med medarbetare beskjuter alltså år 1985 icke-stabila nuklider med andra atomkärnor [1‡]. Forskarna finner då, till stor uppståndelse, att kärnradierna verkar mycket större än normalt (2,5 gånger större [2‡]). Experimenten upprepas med samma entydiga resultat.

Upphetsningen borde inte vara SÅ välbesutten, eftersom objekten är av typen kortvariga, instabila nuklider och därför inte på något sätt har de stabila nuklidernas karaktär. Man borde snarare bli förvånad om dessa instabila typkärnor INTE skulle uppvisa abnorma data.

Se även vidare i Kärnradierna för instabila nuklider under bildning.

Forskarna tror sig då ha kommit på en hittills oupptäckt egenskap hos atomkärnorna. Det verkar som att 1. egenskapen för det första ansluter till den allmänt vedertagna teorin att atomkärnorna verkligen är sammansatta inuti av neutroner och protoner (jämför vattenkronan) och 2. att egenskapen också verkligen tycks visa på en mätmetod att räkna fram detaljer i den modellen.

Briljant.

Tanihatas resultat klassificeras (alltså) som sensationellt.

På bas av resultaten från forskarteamet kring Tanihata, utkristalliserades en ny, modifierad beräkningsteknik — som går ut på att justera gamla mätdata med korrektioner som ”ger” Tanihataresultat” på samtliga atomkärnor genom ofantliga datorstödda beräkningsprogram, typ ”laddningsradie med Coulombkorrektioner” — i allt för att stärka uppfattningen om atomkärnorna som en samlingsplats för enskilda neutroner och protoner. Citatet nedan ger en konkret fingervisning, textmarkeringen är min:

”Over the past decade, much progress has been made toward understanding nuclei as collections of neutrons and protons, taking into account all of the complications of their interactions. Precise characterizations of the those interactions together with vast increases in computer power now allow ab initio calculations of many nuclear energy levels.”,

[http://flux.aps.org/meetings/bapsfiles/all_DNP06.pdf] (sidan 2 överst),

9:00AM 1WA.00001 Scattering and reactions in ab initio nuclear theory, KENNETH NOLLETT, Argonne National Laboratory, October 2006

Min översättning:

Under det senaste decenniet har stora framsteg gjorts mot att förstå atomkärnorna som samlingar av neutroner och protoner, inbegripet alla komplikationer i deras växelverkan. Precisa karaktäriseringar hos dessa växelverkningar tillsammans med omfattande ökningar i datorkraft tillåter nu ab initio kalkyler för många nukleära energinivåer.

Med den senare utvecklingen av laserspektroskopin, som i sig enligt TNED generellt ger större kärnradievärden än den massbaserade metoden, bekräftas Tanihatas och hans medarbetares resultat — typ det ovan citerade på deuteronradien och Helium-4-radien, och som naturligtvis blandas ihop utan urskiljning. Med vidare.

I TNED finns ingen direkt sambandsform för atomkärnorna som visar deras momentana byggnad under till exempel den korta fusionsfasen, eller ett allmänt instabilt tillstånd under bråkdelar av en sekund — och som provoceras ytterligare genom att man bombarderar objektet med tunga atomkärnor [1‡], som i Tanihatas fall. Det skulle verkliga vara förvånande om atomkärnan under sådana förhållanden vore helt passiv. TNED lämnar emellertid inga direkta upplysningar på den punkten, så vi vet strängt taget ingenting i den frågan här. Se emellertid i KÄRNRADIERNA HOS NUKLIDER UNDER BILDNING. Däremot framgår analogierna tydligt mot de rent lasertekniska mätningarna, se Laserspektroskopin; Tanihatas experiment banade tydligen väg för lasertekniken som medel att presentera begreppet ”kärnradie” ur en ny, hittills orepresenterad synvinkel, och som därmed, just, puffat över fokus i frågan på metodbegreppet laser — tillsammans med dryga datorprogram.

I ljuset av TNED kan man alltså postulera följande strängt partiska slutsats (som ännu inte är avgjord):

Vad forskarna INTE känner till är TNED — förutsägelsen att ljusbaserad mätning, som inte växelverkar på någon gravitell grund med atomkärnan, tvunget också uppvisar en annan fason i resultatbilden än motsvarande massbaserade kollisionsexperiment: Man luras (speciellt i efterhand med laserteknikens utveckling under 1990-talet) att tro att man upptäckt någon ny egenskap hos atomkärnorna (eller rättare sagt, tror sig ha fått säkra belägg för kvarkteorin) då man i själva verket studerar effekterna av en ny mätteknik, laserspektroskopin — som händelsevis ansluter till svulstigheterna hos icke-stabila nuklider av typen b^– från kollisionsexperiment baserade på utpräglade kollisionsenergier — jämför PLANCKEKVIVALENTERNA som man heller inte känner till.

Det enda vi behöver invänta som helt kan AVGÖRA vad det här är fråga om, är oberoende lasermätningar på stabila nuklider — något som rent tekniskt ännu inte är möjligt. Men förhoppningsvis snart. Om TNED håller streck här, kommer man (nämligen) då att finna att resultaten bara i stort är en fördubbling av de äldre massbaserade experimentella värdena. Det är i varje fall vad TNED utsäger. Se mera utförligt från ATOMKÄRNANS STORLEK.

Eller sagt på annat sätt:

Forskarna använder nu två olika preferenser i uppfattningen om atomkärnornas fysik — i tron om att man studerar ett enhetligt resultat.

TNED utsäger att den ekvationen förr eller senare kommer att spricka — på rent experimentell bas. Den moderna vetenskapen närmar sig ett (slutligt) sammanbrott — eller att möjligen TNED är färdigt för soporna. I vilket fall kommer ett avgörande att bli uppenbart.

FÖR DET TREDJE:

I och med att ”data på neutronen och protonen” i dessa ovan typiska redovisade fall INTE (längre) avser något direkt fokus på den enskilda protonen och neutronen som fria existerande objekt, utan istället som element inuti tyngre atomkärnor, har fysiken som naturvetenskap (återigen i modern akademi) mistat ett av sina klassiska grundfästen: den konkreta fysiken. Ingen kan (längre) beskriva den — i ljuset av modern akademi.

Därmed, kan man säga, har begreppet ”kärnradie” definitivt tappat sin fysikaliska förankring;

Numera (2008) försöker man ”bestämma neutronradien” ur medelvärdesalgoritmer från tyngre atomkärnor genom nukleonvågmodellen (QCD-teorin) — med hjälp av laserspektroskopi och avancerade datorberäkningsprogram — som bara blir alltmer avancerade. Människan har för länge sedan försvunnit ur den bilden.

FÖR DET FJÄRDE:

Uppgiften ovan från Argonne National Laboratory,

”betydligt större än rms-radien för Helium-4 på bara 1,455 Fermi”

— som enligt TNED ger r(He-4)/r₀ = 1,455/1,37 = 1,0620437 — ansluter också till TNED. Verkligen. Kärnradierna för neutron-proton och Helium-4 är i TNED likvärdiga. Se från Impulsmomentets 0,71r-kriterium samt Härledningen till atomkärnan. Argonnekällan klargör (emellertid) inte varifrån värdet kommer.

Se även från början i KÄRNRADIERNA FRÅN BÖRJAN.

Med ovanstående genomgång har detaljerna i den massbaserade mätmetoden berörts, samt i någon mån relaterats i ljuset av nuvarande riktningar.

Genomgången fortsätter med den andra mätmetoden — laserspektroskopin. Den beskrivs närmast nedan i sektionen Laserspektroskopin.

Tillägg 2011-07-06 WikipediaNewArticle — tillägg från Begreppet Laddningsradie

http://en.wikipedia.org/wiki/Charge_radius

Wikipedia Nuclear Size

Föregående, ursprungliga, Wikipedia-artikel Nuclear Size finns inte längre. Den har (efter Jul2008) ersatts av (Nuclear) Charge Radius

Kärnradiebegreppet beskrevs tidigare (okänt ändringsdatum 2008-2011) på Wikipedia via rubriken Nuclear Size. Den är numera (Jul2011) ersatt av rubriken (Nuclear) Charge radius. Alla tidigare arkivdelar (TalkPage) har rensats bort och är i huvudartikeln (från en här ej närmare känd tidpunkt, någon gång efter Juli2008) ersatt av en beskrivning "rms charge radius". Se vidare utförligt med föregående citatdelar från Begreppet Laddningsradie.

Den generellt etablerat vedertagna helhetsbilden för begreppet kärnradie har med andra ord nu helt övergått till en medelvärdesbildad, sfäriserad, laddningsmodell;

Se särskilt en del av föregående nämnda citat [1975, 1996 och 2006] där olika matematiska algoritmbegrepp i ”den dimmiga historien” antyds för att ge substans åt begreppet laddningsradie,

SFÄRISK MODELL

Notera särskilt i Wikipediaartikeln användningen av ordet/begreppet SPHERE,

"the nucleus can be modelled as a sphere of positive charge",

samt vad som redan understrukits explicit för »den strängt ihåliga» neutron-protonformen [Se från Deuteronens Hemlighet], men som (ännu Jul2011 är obekant för det akademiska etablissemanget, se även i VOLYMÄRA LADDNINGSTÄTHETEN, jämförelserna med Hofstadters arbeten),

Medelvärdesbildningen

”because there is no definite boundary to the nucleus, the electrons "see" a range of cross-sections, for which a mean can be taken.”,

@INTERNET Wikipedia Charge radius 2011-07-06

http://en.wikipedia.org/wiki/Charge_radius

Notera, särskilt, att sambandsformen i Wikipedia-artikeln grundas på EXPERIMENTALFYSIK — alltså den PRAKTISKA medelvärdesbildningen, ”for the interpretation of electron scattering experiments”; Snarare än en fördjupad BILD av atomkärnan, är (således, fortfarande) »den nya tidens medelvärdesform» tydligen och således en helt totalt formbildsUtsuddad matematisk-fysikalisk ELEKTROMAGNETISK medelvärdesExperimentell mätSensorbild av HUR atomkärnan ses (i medeltal) av omgivande MätAgenter. Det finns, med andra ord, ingen ytterligare FORMGEOFYSIKALISK information/kunskap om atomkärnan att hämta i den moderna akademiska delen (Case Finally Closed).

Så framstår i ljuset av TNED också DEUTERONEN som betydligt mindre ihålig och med betydligt tätare laddningskropp än neutronen-protonen (flera hundra procent större spridningstvärsnitt eller »träffYtsForm, trots mindre ytterradie). Wikipediaartikeln specificerar (Jul2011) respektive laddningsradier

”

proton: Rp = 0.8768(69) fm

deuteron: Rd = 2.1402(28) fm

”

att jämföra med grunddata i TNED från Plancks konstant [se PLANCKRINGEN] och Neutronkvadratens tyngdcirkelradier [se Grundformen]

rP = 1,37 Fermi

rN = 1,32 Fermi

rD = 0,97 Fermi = rP/√2

Notera EMELLERTID, som redan påpekats: UNDERFÖRSTÅTT är i Wikipediauppgifterna (Jul2011) tydligen en underliggande experimentell LASERTEKNIK — den användes inte tidigare (före 1981, se Laserhistoria). Den är av allt att döma själva anledningen till »paradigmskiftet» [under 1990-talet; Se ovan från Kommentarer]. Wikipediaartikeln ger inget omnämnande (möjligen förklarligt därför att ämnets utomordentligt omfattande, beskrivande karaktär, dess svårigheter, går de flesta författare förbi — Wikipediaartikeln Charge radius kommer säkerligen att utvidgas betydligt framöver).

laserspektroskopi

ATOMKÄRNORNAS RADIER GENOM

LJUSBASERADE MÄTMETODER

Ljusbaserade metoder för mätning av atomkärnornas radier — Laserspektroskopi

Enbart med referens till Planckenergin E=hf och det maximalt upptagande tvärsnittet för atomkärnans energigenomströmning, atomkärnans toppspinnande tvärsnittscirkel, finns en principiell möjlighet att avkänna ett (mycket) noggrant värde för kärnans största radiella utsträckning. Figuren ovan (vänster) visar hur de optimala ”strålytorna” förhåller sig till varandra enligt TNED, analogt atomkärnan tagen med största vyn [hela cirkeln 4pa²] respektive sett från sidan [mellandelen a²(4+p)]. Figurdelen till höger ovan visar atomkärnans motsvarande tyngdcirkel (r) och kärnans yttre spinncirkel (Ñ, Alt+0209). Den senare är normalt sett inte detekterbar genom massbaserade spridningsexperiment, enligt föregående redovisning (se från Massbaserade spridningsexperiment).

I avsnittet om Atomkärnans dimensioner finns härledda samband för förhållandet mellan atomkärnans tyngdcirkel (r) och spinncirkel (Ñ) för respektive formaggregat med A=1 och A>1. I avrundade värden ges r=0,5Ñ för A=1 och r=0,52Ñ för A>1. Med referens till respektive Ñ=2r och Ñ=1,92r och den ovan härledda delytan 1/1,76 som minsta alternativet, analogt (avrundat) Ñ/1,76=0,57Ñ, kan den ljusbaserade mätmetodens resultatgränser för motsvarande atomkärnans radier anges som just mellan max 2r och min 2r/1,76=1,14r. Se vidare i Kärnradierna.

Laserhistoria. DEN LJUSBASERADE MÄTMETODEN utvecklades (starkt främst) under 1990-talet.

Laserspektroskopin utvecklas i stort från 1981 genom prisbelönta forskare (Bloembergen, Schawlow);

1997 prisbelönades Chu, Cohen-Tannoudji och Phillips ”for their developments of methods to cool and trap atoms with laser light” — sv, ’för deras utveckling av metoder för att kyla och infånga atomer med laserljus’, och som utgör grundvalen för möjligheten att bestämma t.ex. kärnradier (ÄNNU 2008 ENDAST via exciterade nuklidtyper, med reservation för de olika modelltolkningarnas företräden …) — samt vidare (laserminiatyriseringen) Alferov och Kroemer 2000.

Källa:

[http://nobelprize.org/educational_games/physics/laser/facts/history.html], Laser History.

Jämför

”Progress in atomic theory combined with novel laser spectroscopic techniques allowed now the first charge radius determination of very light, radioactive isotopes”,

[http://rnb7.pd.infn.it/abstracts/file14018.1.pdf] (2006),

Nuclear Charge Radius of the Halo Nucleus Lithium-11

Min översättning:

Framsteg i atomteorin kombinerad med banbrytande laserspektroskopiska tekniker tillät nu de första bestämningarna av laddningsradien hos mycket lätta, radioaktiva isotoper.

Sammanfattningsvis kallas mättekniken — med hjälp av laser för att ”mäta atomkärnorna” — för laserspektroskopi. Metoden bygger på att laserns ljusfrekvens kan ställas in mycket noga (s.k. ”dye-laser”) — för att till exempel matcha en resonansform som är associerad med en viss atomkärnas tillfälliga uppförande, som till exempel i fallet med betasönderfall. Genom olika sinnrika anordningar — och som naturligtvis ansluter till den hävdvunna modelluppfattningens matematiska apparat — bearbetas sedan mätdata från laserresonanserna i närmast ofantliga dataprogram med enorma räkneuppgifter — med olika ”kärnradier” i slutänden. Laserspektroskopins metod är med den beskrivningen alltså en högeligen indirekt mätmetod. Man använder bara i stort sett Planckenergins ekvivalent E=hf för att ”mäta vibrationerna” (f). Resten är rent räknearbete.

Det är — emellertid — här okänt i vilken utsträckning man kan avgöra ”skuggningen” hos hf-energin i den aktuella atomkärnans association, dvs., motsvarande skuggbilden av atomkärnans hf-projektion och som hela undersökningen tvunget måste bygga på. Oberoende av olika modeller och metoder kan man (emellertid) enligt TNED sluta sig till att gränsformerna i de bestämningarna bara kan vara de ovannämnda två ändlägena: I ena fallet framträder hela kärnradien, i andra fallet endast max ca 57% (1/1,76).

MINDRE (stabilt) metriska kärndata än så kan lasermetoden således inte detektera.

OM denna iakttagelse är korrekt, betyder det ENLIGT TNED att resultaten från laserspektroskopiska mätningar på atomkärnornas radie kommer att uppvisa (betydligt) större motsvarande ”matter radius”, alltså formradier, jämfört med resultaten från konventionella klassiska massbaserade spridningsexperiment — ända upp till max dubbla. Faktiskt.

Jämför (textmarkeringarna är mina, nyckelbegrepp)

2008-08-02 (1):

”isotope shifts determined by high-resolution laser spectroscopy”,

[http://www.triumf.ca/publications/pub/arch07/pp-07-45.pdf] s2,

Nuclear Charge Radius of Lithium-11, Rodolfo Sánchez (et. al.), Nov 2007;

Min översättning:

’isotopövergångar som bestäms genom högupplösande laserspektroskopi’.

”Remarkable are the results produced by our chiral potentials for the deuteron radius which agree accurately with the latest empirical value obtained by using the isotope-shift method.²⁵”, tabellen i boken på samma sida 125 anger 1,975 Fermi,

Challenges of Nuclear Structure, Aldo Covello, World Scientific, 2002.

Min översättning:

Anmärkningsvärt är resultaten producerade av våra chiralpotentialer för deuteronradien som överensstämmer noggrant med de senaste empiriska värdet erhållet genom användning av isotopövergångsmetoden.

”The analysis of the world data on electron-deuteron scattering yields 2.130 ± 0.010 fm for the deuteron charge rms radius. This value agrees with the one derived from optical isotope shifts [66] and from the low-energy properties of the deuteron as measured by N-N scattering (scattering length and asymptotic normalizations) [67]. The long standing discrepancy with the latter value had been removed when realizing that for scattering from Z=1 nuclei also Coulomb corrections are important [65].”,

@INTERNET GOOGLE-böcker begränsad åtkomst

Precision physics of simple atoms and molecules, Savely G. Karshenboim, Springer, 2007, s70.

Min översättning:

Analysen av världsdata på elektron-deuteron spridning visar 2,130±0,010 fM [femtoMeter = Fermi = t15 M] för deuteronens rms-laddningsradie. Detta värde stämmer med det som erhålls från optiska isotopövergångar och från de lågenergetiska egenskaperna hos deuteronen enligt mätning genom N-N spridning (spridningslängd och asymptotisk normalisering). Den långvariga avvikelsen mot det senare värdet hade tagits bort [författaren uppvisar här en väl sullig språklig syntax: hade?] (man blev tvungen att ta bort det) när man insåg att för spridning från Z=1-kärnor också Coulombkorrektioner är viktiga.

”This gives a deuteron radius of

(1.968 ± 0.006) fm and a charge radius of

(2.130 ± 0.010) fm.”,

EDP Sciences 1997, The European Physical Journal, 2 December 1997

A consistent calculation of dispersion corrections in elastic electron-deuteron scattering

T. Herrmann (Fakultät f. Physik, Universität Kaiserslautern, D-67663 Kaiserslautern, Germany),

R. Rosenfelder (Paul Scherrer Institut, CH-5232 Villigen PSI, Switzerland)

Min översättning:

Detta ger en deuteronradie på 1,968 ± 0,006 Fermi och en laddningsradie på 2,130 ± 0,010 Fermi.

Om vi söker ”gamla klassiska spridningsdata” på deuteronradien, kammar vi helt noll på webben: det finns inga sådana data (där, ännu). Genom andra källverk (HOP) framskymtar, emellertid, att deuteronradien möjligen kan ha förorsakat ”en inre långvarit vetenskaplig tvist” och som, tydligen, ingen vill tala om då den (möjligen) först visade att deuteronradien är MINDRE — betydligt — än neutron-protonradien, se vidare nedan i ’Deuteronens Hemlighet’. HOP-källan antyder det — men jag har i övrigt (ännu 2008) inte hittat någon annan referens. HOP-källan antyder att deuteronradien genom spridningsexperiment skulle ha uppvisat värdet ca 1,055 Fermi. Jämför även antydningarna i citatet nedan med ”dimmiga historien”, eng. ”cloudy history”,

”The cloudy history of experimental values for the proton radius has recently been clarified by a comprehensive analysis[4] of all the world’s electron-proton scattering data.”

Zemach Moments for Hydrogen andDeuterium, 14 Oct 2003,

J. L. Friar (Theoretical Division, Los Alamos National Laboratory), and

Ingo Sick (2Dept. fur Physik und Astronomie, Universität Basel)

Min översättning:

Den dimmiga historien av experimentella värden för protonradien har nyligen klarlagts genom en omfattande analys av världens alla elektron-proton-spridningsdata.

kärnmodellen

INOM DEN MODERNA AKADEMINS alla forskarkretsar i ämnet kärnfysik söker man (2008) (naturligtvis) genomgående utan undantag få fram mätdata på atomkärnan som kan inpassas i den allmänt vedertagna QCD-teorin (”kvarkteorin”) — och som bygger på föreställningen om atomkärnan som befolkad inuti (fritt rörliga neutroner-protoner — inuti atomkärnan).

© Adam-Hart Davis, Natural Science

[http://gallery.hd.org/_c/natural-science/_more2006/_more03/splash-crown-water-drop-on-blue-crazed-cracked-surface-frozen-2-AJHD.jpg.html] 2008.

På samma sätt som det inte finns någon klok människa som

— inför anblicken av vattendroppar som lösgör sig ur en vattenyta, eller vattendroppar som förenas och bildar en större vattendroppe

— menar att de mindre vattendropparna före separationen finns till som enskilda formobjekt i vattnet eller kan ses som sådana som rör sig som fristående enskilda objekt inuti den resulterande större droppen, så är det naturligtvis också med atomkärnan i naturboken — enligt relaterad fysik (TNED).

Atomkärnan ENLIGT TNED är en massans fundamentalform — helt utan inre beståndsdelar, precis som i vattendropparnas fall. Den moderna akademin däremot, som anser att atomkärnan just ÄR en samling mindre partiklar, kämpar (därmed) uppenbarligen med att beskriva en spökmodell.

Begreppet laddningsradie introduceras …

NYA BEGREPP INTRODUCERAS RUNT 1990

Detaljerna med den moderna föreställningen om partiklar i atomkärnan framgår — ymnigt — om man (t.ex.) läser de rapporter i PDF-format som finns i relativt stor mängd på webben i ämnet kärnfysik. Det är (här veterligt) ur den föreställningen, med tillhörande matematiska vidlyftigheter, som den egentliga betydelsen i begreppet laddningsradie kommer fram (eng. charge radius); Författarna bakom forskarrapporterna är (nämligen) inte lika angelägna att berätta bakgrunderna. Inte i något känt fall finns ännu (Augusti 2008) någon webbkälla som beskriver begreppen eller berättar deras historiska bakgrund (jag kan naturligtvis ha missat en del eftersom långt ifrån alla dokument är tillgängliga via webben). I TNED har begreppet ”laddningsradie” hur som helst ingen som helst konkret fysikalisk praktisk formmässig motsvarighet;

— begreppet »laddningsradie» kopplar inte till atomkärnans geofysik utan till dess växelverkande fysik — och som beror på valet av modell, omständighet och metod för att definiera en sådan växelverkan.

Se även i inledningen från STATISTIKENS FÖRDUNKLANDE AV KÄRNFYSIKEN.

Det nya begreppet Laddningsradie

Tillsammans med detta nya begrepp ”laddningsradie” (det omnämns mig veterligt inte i den äldre, klassiska experimentalfysiken under 1900-talet) kommer andra, liknade typ ”materieradie” (eng. matter radius), ”strukturradie” (eng. structural radius), och ”punktmaterieradie”, (eng. point matter radius), m.fl., och som numera (2008) florerar i samband med beskrivningar som berör atomkärnans dimensioner och metrik.

LASERSPEKTROSKOPISKA MÄTDATA är emellertid ännu (Augusti 2008) ytterst sparsamt representerade och på intet sätt (ännu) av den digniteten att något definitivt kan avgöras — även om vissa antydningar finns: jämför citaten närmast ovan. Det verkar, dessutom, hart när omöjligt att få fram GRATIS referensdata med webbens hjälp (@INTERNET) på experimentellt uppmätta kärnradier från tidigare epoker (eller för den delen, nuvarande) till jämförelse.

— Den här framställningen bygger helt på (sådana) GRATIS föreställningar. Se stjärnljusen, till exempel. Helt gratis. Bara att gå ut och titta och njuta. Den här framställningen är också ägnad att fortsätta på den vägen. Vi måste i vilket fall hjälpas åt — även i framtiden.

h=c — fullt allvar

h=mcr; h=c; 1/m = r

Om vi studerar begreppet laddningsradie på webben (2008) finner vi dessutom att det begreppet är förknippat med en synnerligen MYSKO MATEMATIK: man sätter h=c, fullt allvar. Vi studerar hur.

s21:

”The point-proton radius from the theory is converted to the charge radius using the formula (see Chapter 9):

<r_c²> = <r_pt²> + <R_p²> + N/Z<R_n²> + ¾(M_p)^–2,

<R_p²>^1/2 = 0.895(18) fm [Sick, 2003],

and

<R_n²> = –0.120(5) fm² [Kopecky, 1995, 1997].”,

DETERMINATION OF THE HELIUM-6 NUCLEAR CHARGE RADIUS USING HIGH-RESOLUSION LASER SPECTROSCOPY,

LI-BANG WANG, B.S., National Taiwan University, 1996

Min översättning:

Punktprotonradien från teorin konverteras till laddningsradien med formeln [sambanden ovan].

För de två övriga parametrarna, r_pt och M_p ger författaren först på sidan 96 (Chapter 9) en beskrivning enligt,

s96:

”In the nuclear theories using meson-exchange models, the distributions of protons and neutrons are calculated while treating both as point-like particles. By definition, the point-proton mean-square radius is the mean expectation value of the square of the position vector of the individual protons:

<r_pt²> = (1/Z) _i=1®Z å <0| r_i² |0> (9.1)

where r_i is the position of the ith proton measured from the center of mass, and |0> is the ground-state wave function of the nucleus.”;

Min översättning:

I kärnteorierna, med användande av mesonutbytesmodeller, beräknas fördelningen av protoner och neutroner i behandlingen av bägge som punktlika partiklar. Genom definition är punktprotonens medelkvadratradie det medelförväntade värdet hos kvadraten på positionsvektorn för de individuella protonerna [sambandet ovan]

där r_i är positionen för den ite protonen räknat från masscentrum, och |0> är grundtillståndets vågfunktion för kärnan.

På samma sida 96, via ett annat samband, framkommer att

”The additional term,

3

———

4M_p²

is the Darwin-Foldy correction of the proton radius (see section 9.5).”.

Min översättning:

Tilläggstermen [ovan] är Darwin-Foldy korrektionen för protonradien.

På sidan 100 klargör så författaren enligt nedan att med

h=mcr ges via h=c resultatet 1/m = r vilket författaren skriver ut enligt ledet

”

This is generally called the Darwin-Foldy correction of the proton radius.”;

DETERMINATION OF THE HELIUM-6 NUCLEAR CHARGE RADIUS USING HIGH-RESOLUSION LASER SPECTROSCOPY,

LI-BANG WANG, B.S., National Taiwan University, 1996, s100

Min översättning:

[ledet ovan] Detta kallas allmänt Darwin-Foldy-korrektionen för protonradien.

Det finns f.ö. en uppsjö av andra författare på webben (pdf-dokument) som använder samma typ, ovanstående är ingalunda någon unik förekomst.

Författaren sätter alltså, faktiskt, <r²> » 1/M_p². Vilket vill säga i klartext: i storleksordningen r² = 1/u² som ger

r = 1/u = 6 T26 (M) med u=1,66033 t27 KG, atomära massenheten. Fullt allvar. Jämför: ”Jag säger att 0,0025 ÄR en miljon”. Det är modern akademi i sitt esse; Ingen kan relatera en sådan ”matematik”. Ingen kan heller förstå den. Men det är, tydligen, den typ av ”överenskommelser” som måste göras i modern akademi för att alls, i slutänden, få ihop det med energiräkningen (Kommer man inte in på framsidan på vanliga öppettider, kan man alltid bryta sig in bakvägen). Jämför korrekt sätt,

r = 1,37 t15 M

1/u = 6,02289 T26 KG

Även källan

[http://www.jlab.org/div_dept/admin/publications/papers/01/THY01-06.pdf], s10, The deuteron: structure and form factors, M. Garçon and J.W. Van Orden, 21 Feb 2001,

använder en liknande faktor typ ”(0,75)(h/2p/m_p)” och som författaren refererar till som ”of relativistic origin [67]”, sv. ’av relativistiskt ursprung’ med ”[67] D.J. Beachey et al., J. Phys. G: Nucl. Part. Phys. 20 (1994) L143; and references therein.”, sv. ’…; och referenser däri’.

Något mer får man inte veta.

Verkligen.

Läsaren görs INTE ENS uppmärksam på typ ”OBSERVERA att den här presentationen innehåller ICKE HÄRLEDNINGSBAR MATEMATIK (referens…)”. Läsaren får, så att säga, upptäcka det själv när han ramlar över ända — och krossas mot klipporna FÖRST en bit längre ner;

Inte ens personer som försöker införa metafysiska resonemang i naturvetenskapen är hälften så företagsamma.

Varför klagar då undervisningsministerierna på den allmänna kunskapsnivån i matematik? Den är ju JÄTTEBRA. Det är ju bara att hitta på någon egen ekvivalent, typ a=MinVariablaKonstant som sedan kan insättas där man tycker det passar, när man inte förstår sammanhanget, och sedan postulera att det här rör sig om statligt underhållen naturvetenskaplig forskning.

GOOGLE-sökning Juli-Augusti 2008 — (allt utom IOP-kopplingar med liknande [det finns många sådana: man måste vara medlem eller betala för att få se innehållet]):

Alla tycks ANVÄNDA begreppet ”Darwin-Foldy correction” som vore det redan ett allmänt välkänt dito — Och ingen källa tycks finnas som förklarar termens bakgrund eller sammanhang — frånsett WANG-källan ovan (och som inte uppvisar någon egentlig förklaring, snarare en presentation).

Innehåll där ”Darwin-Foldy-termen” finns med figurerar f.ö. i samma avhandlingar som generellt behandlar KVARKTEORI. Se till exempel ”Darwin” i källan

[http://arxiv.org/PS_cache/hep-ph/pdf/9711/9711252v2.pdf] 9 Dec 1998,

Exchange current contributions to the charge radii of the nucleons, C. Helminen

En del författare anger ”Darwin-Foldy correction” enligt (fullständigt) 3(h/2p)²/4M_p²c², t.ex. (s6)

[http://www.triumf.ca/publications/pub/arch07/pp-07-45.pdf], Nov 2007

Nuclear Charge Radius of Lithium-11, Rodolfo Sánchez et al

Nej. Vi kan naturligtvis inte använda oss av en dylik matematisk formuleringskonst: den har ingen plats i RELATERAD matematik och fysik.

Om en naturvetenskaplig framställning inte är härledningsbar — om den inte kan relateras MED GRUND I DEN ELEMENTÄRA MATEMATIKEN — ska den inte finnas med — av den enkla anledningen att den DÅ saknar naturvetenskapligt värde. Om kunskapen INTE är härledningsbar är den HELT ointressant. Sten död.

Ämnet visar bara (återigen) att den moderna akademin ÄR urspårad — speciellt inom kärnfysiken.

Visa att jag har fel.

Om människor vill försöka förstå och sätta sig in i den naturvetenskapliga metoden och resultaten på området kärnfysik i modern akademi, kommer de snart att upptäcka att ämnet är nedlagt: Det finns ingen rationell — förklarande och beskrivande — uppsats i modern akademi inom ämnet kärnfysik. Referensen blir som ovan: Darwin-Foldy korrektion: h=c: Plancks konstant ersätts med ljushastigheten i vakuum för att få fram en ”korrektionsfaktor” r = 1/m med m som protonmassan. Ingen förklarar (på webben, ännu Juli 2008) vad det är, eller när det används. Det får du räkna ut själv.

Var därför speciellt uppmärksam på följande: Författare som ”meddelar ekvationer” utan att, noga, precisera parametrarna, och utan att relatera och exemplifiera innebörden, sprider i stort sett värdelös information. Kassera den typen. Bara rakt av. Hänvisa till korrespondensprincipen (subjekt och predikat gäller lika för alla), och naturvetenskapens allmänna syfte att vara upplysande, förklarande och beskrivande. Resten är preliminära sopor: ”charge radius”, ”laddningsradie”.

I DEN VIDARE RESULTATJÄMFÖRELSEN: var därför observant på ”charge radius”, sv. laddningsradie, i uppgifterna; Vi kan inte använda den typen här i någon som helst jämförelse med TNED för att kontrollera riktighet och rimlighet i data på kärnradier. Det finns ingenting sådant i TNED. Uppgifterna måste associera till atomkärnans avgränsande formbyggnad, en MASSBASERAD KANTLINJE eller motsvarande, självklart, inte till någon ”halo” eller ”kraftfältet i kring” eller ”min bästa kärnhistoria” eller liknande metafysiska noggrant experimentalstatistiskt datorunderstödda konturslott.

Här slutar huvudtexten. Efterföljande delar är bihang med beräkningsgrunder och redovisningar som (mera fördjupat) berör atomkärnans beskrivning enligt TNED.

END.

bihang

DEUTERIUMETS AVGÖRANDE BETYDELSE

— Se även i Deuteronens Hemlighet

finns väl dokumenterat i HOP (HANDBOOK OF PHYSICS 1967) — genom detaljerna i TNED:

Deuterium kräver en fusion av två grundaggregat (N3m20); Lösningen på den formmatematiken i ljuset av Planckringens härledning betyder en resulterande atomkärna med större kompakthet och därmed totalt sett en mindre största utsträckning; TNED kräver alltså att deuteronradien blir (betydligt) mindre än neutron-protonradien — i justerade värden ska deuteronradien vara r₀/Ö2 » 0,71r₀.

Se även i Deuteronens Hemlighet.

Det blev därför (i min historia, runt från 1993) angeläget att eftersöka någon antydan om en sådan förekomst i den tillgängliga (omfattande) HOP-källan. Följande händelse från utvecklingsarbetet finns dokumenterad (från DYNAMIKENS GRUNDER 1995X):

När källan i HOP (HANDBOOK OF PHYSICS) intensivgranskades (1995) återfanns på sidan (9–210) ett samband där deuteronradien, faktiskt, omnämndes. Emellertid och som vi — till en början — strax ska se, utan någon klar och avgörande entydig innebörd. Uttrycket som påträffades, vilket förenklats nedan med

r för r_º+, R för r_D och a för a´_+np, lyder

r = 2R(1–R/a) = 1,7 t15 M, a = 5,38 t15 M

där R=h¹/Ö 2µE_D (h¹= h/2p) anges som "den så kallade deuteronens radie". Termen E_D= 2,23 MeV anges som deuteronens bindningsenergi.

Nu förklarades inte termen µ närmare i HOP-källan, men genom systematisk sökning längre fram återfanns på sidan (9–197n, sp1)

"where µ is the reduced mass of the system".

Men värdet 2,23 MeV är just masskillnaden — (1,00866520+1,00782519–2,01410222)·932 = 2,23 MeV avrundat — så hur att tolka termen µ blev därmed en öppen fråga.

Emellertid syntes termen vid närmare eftertanke ha innebörden av själva deuteronmassan;

Med R=h/[2pÖ2m_DE_D]

— E_D i MeV, gånger T6 gånger 1,602 t19 Coulomb = E_D i Joule, m_D i atomära massenheter (2,01410222 u), gånger

1,66043 t27 KG = m_D i KG, h=6,625 t34 JouleSekunder

— får vi "r_D" = 2,16 t15 meter avrundat. Men detta värde satisfierar ingalunda ekvationen för r ovan;

värdet för r blir i Fermi eller t15 meterenheter lika med 2,58. Vilket, uppenbarligen, är något helt annat än det angivna

r = 1,7 Fermi

Vad står då r_D för i sambandet för r? Vi kan lösa denna fråga genom att utveckla leden enligt

r=2R(1-R/a), r/2=R–R²/a=(1/a)(Ra–R²), ra/2=Ra–R²; R²–Ra=–ra/2 = (R–a/2)²–(a/2)².

Vilket vill säga, man får en andragradsekvation; Lösningen ger

R = (a/2) ± Ö(a/2)² – ra/2

a = 5,38 t15 M

r = 1,7 t15 M

Lösningarna blir i Fermi

POSITIVA ROTEN

R = (a/2) ± Ö(a/2)² – ra/2

= (5,38/2) + Ö(5,38/2)² – (5,38)(1,7)/2

= 4,3219007

R = 4,32 ; Dividerat med protonradien r₀=1,37 ;

R = 3,15r₀ » 4,316 Fermi

NEGATIVA ROTEN

R = (a/2) ± Ö(a/2)² – ra/2

= (5,38/2) – Ö(5,38/2)² – (5,38)(1,7)/2

= 1,0580992

R = 1,058 ; Dividerat med protonradien r₀=1,37 ;

R = 0,77r₀ » 1,055 Fermi

Om formerna har någon relevans, är det tydligt att tredubbla protonradien för deuteronen (värdet 3,15) är osannolikt stort (kubformen med A=2 ger R=1,26 protonradier). Återstår alternativet med de 77 procenten.

TNED-justeringarna i Kärnradierna — tillsammans med mönstergrunden i Neutronkvadraten — krävde motsvarande reduktion 0,71 (exakt idealt 1/Ö2). Inte SÅ tokigt i jämförelse med 0,77 — om nu den uppgiften är/var relevant, vilket vi här ännu (2008) inte vet närmare.

Därmed hade HOP-källan (i vilket fall) givit en viss antydan i rätt riktning: Det såg ut som att TNED var på väg att överleva den första prövningen.

Det fanns alltså redan tidigt (långt innan TNED såg ljuset i min historia) tydliga linjer som visade analogierna.

Dock finns mig veterligt varken i HOP-källan eller på annat ställe någon uttalad observation som uppehåller sig vid möjligheten att deuteronens omfång skulle vara mindre än protonens. Det enda möjliga alternativet skulle i så fall vara i det faktum att man i modern akademi för deuteronens del talar om ”quadrupole moment”, sv. kvadrupelmoment, ett begrepp som innebär en kärndeformation [ellipsoidisk avsmalning utmed en motsvarande vertikal rotationsaxel (|)]. Men ingenting klart finns formulerat i den saken i de källor som hittills granskats.

Se även i Deuteronens Hemlighet.

UPPGIFTEN MED protonradien 1,37 Fermi från HOP-källan

DE FEM KLASSISKA massbaserade MÄTMETODERNA FÖR UNDERSÖKNING AV ATOMKÄRNORNAS RADIE

1. neutron scattering .................................................. | neutronspridning

2. a-decay, energy observations ............................... | alfasönderfall, energiobservationer

3. mirror-nuclei, energy observations ....................... | spegelkärnor, energiobservationer

4. mesic atoms, energy observations ......................... | mesoniska atomer, energiobservationer

5. high-energy electron scattering, diffraction ............ | högenergibaserad elektronspridning, diffraktion

Citatet nedan från sidan 9–11:

”

1. The Size of the Nuclei

A variety of methods can be used to explore nuclear radii and are found to provide consistent results. The nuclear size can be estimated (1) from the scattering cross sections of nuclei for fast neutrons (neutron wavelength l << nuclear radius), (2) from the energy-lifetime relationship i a decay (Sec. I, 3), (3) from the differences of the binding energies of ”mirror nuclei,” (4) the energy levels of mesic atoms, and (5) from high-energy electron-diffraction experiments.

”.

Min översättning:

Kärnornas storlek

En uppsättning metoder kan användas för att undersöka kärnradier och är befunna att ge konsistenta resultat. Atomkärnans storlek kan uppskattas (1) från spridningstvärsnitt hos kärnor för snabba neutroner (neutronvåglängden l är mycket mindre än kärnradien), (2) från energi-halveringstid förhållanden i alfasönderfall (Sektion I, 3), (3) från skillnader i bindningsenergi hos ”spegelkärnor”, (4) energinivåerna hos mesoniska atomer, och (5) från experiment med högenergibaserad elektrondiffraktion.

Källan genomgår sedan de fem metoderna mera utförligt. För metodbeskrivningen i (3) sammanfattar källan,

” The radii obtained in this way are closely approximated by

R = A^1/3r₀ r₀ = 1.37 × 10^–13 cm (3.3)

This gives for the root-mean-square distance of the nucleons from their center of mass

—

(r²)^1/2 = (3/5)^1/2R = 1.05 × 10^–13 A^1/3 cm

”.

Min översättning:

Radierna erhållna på detta sätt approximeras nära enligt [sambandet överst].

Detta ger för rotmedelkvadratens distans hos nukleonerna från deras masscentrum [sambandet underst].

För metod (4) sammanfattar källan

”

This method yields the values 1.2 × 10^–13 A^1/3 cm for the nuclear radius, if the nucleus is assumed to be spherical and to have a uniform charge distribution. The corresponding mean-square radius of the protons can be calculated to be

—

(r²)^1/2 = (3/5)[1.2 × 10^–13 A^1/3]² = 0.85 × 10^–26 A^2/3 cm²

This is considerably less than the value given by the preceding methods. It should be noted, however, that this method is accurate only for heavy nuclei (large Z).

”.

Min översättning:

Denna metod ger värden 1,2 × t13 A^1/3 cM² för kärnradien, om kärnan antas vara sfärisk och ha likformig laddningsfördelning. Den motsvarande medelkvadratradien hos protonerna kan beräknas vara [sambandet ovan].

Alla citaten ovan från

NUCLEAR PHYSICS s9–11

HANDBOOK OF PHYSICS, E. U. Condon, Second Edition 1967, McGRAW-HILL BOOK COMPANY

Lånad på Stadsbibliotek

Samma källa skriver på s7–27 i tabellen för fysikaliska konstanter (”Nuclear radius”, sv. kärnradie),

”

Nuclear radius R = r_nA^1/3 | r_n = 1.37 × 10^–13 cm

”,

TABLE 1.4. ADJUSTED VALUES OF CONSTANTS (1963)

QUANTUM MECHANICS AND ATOMIC STRUCTURE s7–27

HANDBOOK OF PHYSICS, E. U. Condon, Second Edition 1967, McGRAW-HILL BOOK COMPANY

Lånad på Stadsbibliotek

Atomkärnans storlek | 2008VIII3

ATOMKÄRNANS STORLEK — tyngdcirkeln

I all fysikalisk kraftväxelverkan återfaller komponenternas beteende och uppförande tvunget på typiskt motsvarande tyngdpunkter, tyngdlinjer, och tyngdcirklar (tyngdytor). Se GcQ-teoremet, om ej redan bekant.

Inom kärnfysiken explicit finns redan den grundformen formulerad och serverad som Plancks konstant (impulsmomentet eller rörelsemängdsmomentet) enligt

h = mcr = 6,62559 t34 JS med neutronmassan m=1,0086652u med u=1,66033 t27 KG, ljushastigheten i vakuum c=2,99792458 T8 M/S och neutronradien r=1,31966 t15 M.

I de (nu) klassiska spridningsexperiment som genomfördes i stort från efterkrigstiden (1945-) och framåt (mot 1970-talet) fanns alltså enbart de allra bästa förutsättningar för att få fram motsvarande protonens DYNAMISKT EKVIVALENTA kärnradie (1,37 t15 M) — atomkärnans beteende enligt dess tyngdcirkels radie — inte den reala materiella protonkroppens största utsträckning, märk väl.

Med atomkärnans härledning enligt PLANCKRINGEN och klarläggandet av atomkärnans dimensioner står det också klart att atomkärnans verkliga ytterradie — kärnan största utsträckning från tyngdpunkten — blir nära dubbelt så stor som tyngdcirkelns radie;

tyngdcirkeln ENLIGT TNED ligger ungefär på halva delen inåt, och räknar vi med formbyggnaden också blir alltså motsvarande reala kärnkropp längst ut max 2 gånger tyngdcirkelns radie.

HELA FRAMSTÄLLNINGEN I TNED bygger på den förutsättningen: alla samband utgår ifrån och grundas HELT på tyngdcirkelns metrik.

Generellt i fysiken kan man därför lika gärna säga så här: Det visuella är ALDRIG det dynamiska: den dynamiska formen är ALLTID mera kompakt än den visuella. Undantag existerar inte. Bevis: tyngdpunkten.

Alla fysikens beräkningar utgår UTAN UNDANTAG från att SE dynamiken via tyngdpunkter, tyngdcirklar, tyngdytor. KRING dessa finns den visuella kroppen (som alltså till största delen består av tomrum). Alla former kan därmed sägas bygga ytterst på atomkärnan och dess tyngdcirkel. Med andra ord på Planckringen.

I TNED har Bilden av Atomkärnan antagit Planckradien genomgående som ett beskrivande substitut för atomkärnan med innebörden av kärnans tyngdcirkel (r). Emellertid är atomkärnans ytterradie (kärnans största utsträckning, Ñ) INTE detsamma som kärnans tyngdcirkel.

Hur går dessa rent formtekniska detaljer ihop med härledningarna i TNED?

Med tanke på den enorma flod av möjligheter och variationer som atomkärnan kan uppvisa i växelverkan med andra atomkärnor, finns tydligen vissa villkor för den allmänna fysikbeskrivningen med grund i kärnfysiken speciellt:

VILLKOR:

För översiktens skull — samtliga problemställningar som berör kärnfysiken — behöver vi en enkel, allmän grundform, en enhetlig elementär tillståndsmodell och som i sig har den egenskapen att IDEALT KUNNA innefatta alla andra möjliga modeller — HELST VILL VI INTE ha en flora av olika tillståndsmodeller som var och en uppvisar sin specifika matematik; Varje sådan särskild tillståndsmodell måste under alla omständigheter, och i så fall, bli en senare fråga.

Allt annat är uteslutet för en solid översiktlig, allmän, enkel presentation av kärnfysiken.

Om naturen inte har reserverat en sådan modellform åt oss, är det kört. (Och, om vi letar); Det finns bara en grundform att välja på:

I kärnfysikens ljus måste vi kunna återföra atomkärnans dynamiskt verkande fysik på den veterligt enda existerande enkla preferens som alls finns:

tyngdcirkeln (r) i Planckringen h=mcr.

Ur den rent dynamiskt verkande synvinkeln, måste dessutom den tyngdcirkelns radie OCKSÅ PER MATEMATISK FYSIK — praktiskt, verkligen — beskriva VERKAN hos en motsvarande föreställande kärnradie. Självklart. Annars går det inte.

Det betyder att den beskrivningsgrunden tvunget måste ha direkta, experimentella, paralleller till den praktiska fysiken — annars kommer inte framställningen att bli översiktlig, inte begriplig, inte förklarande, varken matematiskt eller logiskt.

DESSA VILLKOR kräver tydligen en avancerad naturgrund som förklaring — OM det finns en sådan.

Det är bara resultaten i slutänden som kan avgöra hela saken — i ljuset av varje enskild människas förmåga att väga samman alla faktorer och ge ett slutligt omdöme.

· Genomgående i TNED — hela författningen Universums Historia — har Planckringens grundradie eller Planckradien (r=h/mc) använts som neutronradien (1,32 Fermi = 1,32 t15 M = 1,32 fM [femtoMeter]) med m som neutronmassan (1,0086652u, 1u=1,66033 t27 KG) och c ljushastigheten i vakuum (2,99792458 T8 M/S).

· Med referens till neutronkvadraten har sedan det mera (stabila) allmänna värdet för protonradien använts, 1,37 t15 M.

· Bilden av atomkärnan, inkluderat mönsterformen i NEUTRONKVADRATEN har (genom TNED) antagit Planckradien genomgående som ett beskrivande substitut för atomkärnan (neutronen) och sedan vidare därifrån genom fusionsfysiken till atomkärnor med större omfång.

Emellertid — och som vi i vilket fall måste komma tillbaka till i slutänden — är atomkärnans ytterradie (kärnan största utsträckning) INTE detsamma som kärnans tyngdcirkel.

Hur går DÅ DESSA RENT FORMTEKNISKA DETALJER ihop med härledningarna i TNED?

(Som det visar sig; Galant).

studier av atomkärnan

enligt TNED

Alla resultat — från atomkärnans härledning i Planckringen — bygger på att betrakta atomkärnans ytterdimension analogt med början från Planckradien (neutronradien r).

Men den praktiska, motsvarande atomkärnans ytterradie är enligt TNED i den härledda kärnmodellen N3m20, se Atomkärnans Dimensioner, runt dubbelt så stor eftersom tyngdcirkeln ligger ganska precis på halva tvärsnittscirkeln genom atomkärnan i spinnplanet.

fusionsgränsmassan
Planckekvivalenten	verkliga fallet	Planckekvivalenten	verkliga fallet

Illustrationen ovan vänster visar fallet i härledningen till fusionsgränsmassan enligt Planckekvivalentens Planckradie. Bilden närmast denna till höger visar den formtekniska detaljen i det ENLIGT TNED motsvarande verkliga fallet. Gränsfallet i härledningarna till nuklidseparationen (d=0) visas ovan i illustrationens högra hälft; Planckekvivalentens del till vänster och verkliga fallets atomkärna till höger — med toppspinnet inkluderat för att förtydliga ytterdimensionerna.

Eftersom kärnformerna i dessa härledningsfall PRIMÄRT berör endast neutron-protonformen, kan vi direkt se att ingen omedelbart uppenbar formvidrig orimlighet föreligger och som annars skulle ha gjort att vi kunde misstänka att hela beskrivningen urartar — på grund av dessa inbördes (tvungna) DUBBLA-HALVA storleksrelationer. Vi kan alltså direkt i de avgörande fallen se att härledningarna via Planckekvivalenten likväl är relevanta. Så långt OK alltså.

Spinnsynkroniseringen

Ytterligare en detalj understryker den saken — att Planckekvivalentens härledningar håller streck — enligt följande liknande jämförelse:

fusionsgränsmassan
Planckekvivalenten	verkliga fallet

I härledningen till fusionsgränsmassan, Planckekvivalenten ovan vänster, är det avgörande viktigt att närliggande atomkärnor som vidrör varandras omskrivna kärnsfärer via tyngdcirkeln i det verkliga fallet, närmast till höger om Planckekvivalenten i ovanstående illustration, också kan förverkliga en spinnsynkronisering som förberedelse för kommande fusioner. I figuren ovan längst till höger finns utritat motsvarande praktiska kärnfallets ordning enligt N3m20-aggregatet i primärformen med neutron-protonaggregaten — och som också därmed även ansluter till de härledda grundfusionerna i Solens energiproduktion, märk väl: blir det fel här, måste också resultaträkningen för Solens del vara helt galen.

I och med att de motvända kärnpolerna strävar att stöta ifrån varandra och därmed initieringen av en synkronisering, ser vi emellertid även här att en sådan (komplex) rotationsordning KAN förvekligas enligt nedanstående skisserade ordning (resultaten från Solfysiken är OK):

verkliga fallet	verkliga fallet	verkliga fallet	verkliga fallet

Ingenting hindrar protonaggregaten (N3m20) att

— under ett mycket kort ögonblick, i storleksordningen t23 sekunder med ideala beräkningar på tyngdcirkelns omkrets

t = 2pr/c = 2,8713 t23 S

— genomföra en justerande sammansatt rotationsmanöver för att harmoniera de motsatta spinnen. Med referens till N3m20-aggregatet, ser vi direkt med hjälp av den utritade tyngdcirkelns motsvarande sfäriska utsträckning, att protonaggregaten kan glida på denna idealsfäryta.

Därmed bekräftas villkoret som ställdes upp från början: modellen kan förklara även den motsvarande praktiska sidan av saken.

Täthetsbegreppet

Ytterligare en detalj berör den härledda formen för max neutrontäthet via omskrivna rätblocken kring Planckekvivalentens kärnform (1,82 T17 KG/M³) — och som är avgörande för hela härledningen till K-cellens kontraktion, detonation och expansion.

maximala neutrontätheten
Planckekvivalenten	verkliga fallet

I Planckekvivalentens fall, figuren ovan vänster, ligger kärnkropparna mot varandras kärnyta i spinnplanet. I verkliga fallets motsvarande kärnform, figuren ovan i mitten, måste toroidaggregaten delvis vara motsvarande inskjutna i varandra, bilden ovan till höger med d=0.

Här framträder också styrkan i den enklare Planckekvivalentens allmänna form (se utförligt från Atomkärnans härledning, om grundbegreppen med Planckringens fraktalsystem här är obekanta, resonemanget förutsätter den bekantskapen):

Vi kan från fall till fall med inskjutna atomkärnor i vilket fall aldrig avgöra någon ALLMÄNT exakt formanalog täthetsberäkning i atomkärnornas värld eftersom tätheten i atomkärnan ENLIGT TNED växer med fraktaldjupet, analogt att vi tar med allt djupare liggande ringnivåer; vi kan både se och inte se i ovanstående formillustration att täthetsvärdet både kan göras mindre och större beroende på formpreferensen; med de tre inre tunna ringarna ges en betydligt högre medeltäthet än via enbart toppspinnets ytform; mellan dessa ligger Planckekvivalenten — perfekt för vår del som en medelmässig allmänform ”för samtliga fall”.

Sammanhanget visar alltså — återigen — att Planckekvivalentens enkla begrepp (dvs., »atomkärnan som lika med tyngdcirkeln») grejar saken åt oss. No Problemo.

Resultaten i slutänden har också visat att Planckekvivalentens formbyggnad ger rimliga värden. Se utförligt från Nuklidbildningen, Grundämnesbildningen, Himlakropparnas bildning.

TOROIDYTAN

TOROIDYTAN inre (se även Guldins Regler):

2pa2pb = 4p²ab | A=1: ab = r₀² · 0,011294 | A>1: ab = r² · 0,0580127

TOROIDYTAN yttre:

Ar = 2pt2p(a+b) = 4p²t(a+b)

Uppställningarna nedan är primärt ägnade prövning för kontrollräkning av toroidytorna genom första fusionen (deuterium) med referens till den härledda toroidmodellen N3m20 enligt TNED. Grundreferensernas dimensioner beskrivs separat i Planckringens Dimensioner.

A=1: a = r0/42 b = r0(119 + 80Ö3)/84(3+2Ö3) r = r0/42(3+2Ö3) Ø = r(113+76Ö3) = r0(113+76Ö3)/42(3+2Ö3) b = a + Ø/2 = r0/42 + r0(113+76Ö3)/84(3+2Ö3) = (r0/42)(1 + (113+76Ö3)/2(3+2Ö3)) = (r0/42)(6 + 4Ö3 + 113 + 76Ö3)/2(3+2Ö3) = (r0/42)(119 + 80Ö3)/2(3+2Ö3) = r0[119 + 80Ö3]/84(3+2Ö3) TOROIDYTAN inre Ar = 4p^2ab: Ar = 4p^2ab = 4p^2(r0/42)r0(119 + 80Ö3)/84(3+2Ö3) = p^2(r0/21)r0(119 + 80Ö3)/42(3+2Ö3) = p^2r0^2(119 + 80Ö3)/882(3+2Ö3) TOROIDYTAN yttre Ar = 4p^2t(a+b). t = r0 · 0,5018416

A>1: a = r(–3/2+Ö3) b = r/4 r = r(7/2–2Ö3) b = a + r/2 = r(–3/2+Ö3) + r(7/2–2Ö3)/2 = r[–3/2 + Ö3 + 7/4 – Ö3] = r[–6/4 + 7/4] = r[1/4] TOROIDYTAN inre Ar = 4p^2ab: Ar = 4p^2ab = 4p^2r^2(–3/2+Ö3)/4 = p^2r^2(–3/2+Ö3) TOROIDYTAN yttre Ar = 4p^2t(a+b): t = r · 0,5179491 a+b = r(–3/2+Ö3) + r/4 = r(–5/4+Ö3); Ar = 4p^2tr(–5/4+Ö3) = p^2tr(–5 + 4Ö3)

r₀/koefficienten i t anger motsvarande visuella ytterradien. För A=1 blir den 1/0,5018416 = 1,9926606, för A>1 blir den 1/0,5179491 = 1,9306916.

t anger tyngdcirkelns radie. Utförlig härledning finns i ATOMKÄRNANS DIMENSIONER.

kalkylkort · toroidytorna · kontrollräkningar — flik1

alla kortflikar i den här presentationen öppnas i samma huvudkort

se även öppningsmanual om ej redan bekant

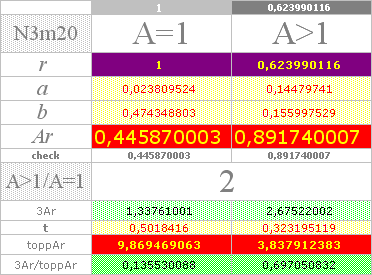
inmatningresultat ·

kontrollräkning, toroidytorna (kontrollkort, innehåller inre celluppställningar, ingår i ovanstående kortflik)

Observera att yträkningarna med summeringarna i individaggregat med summaytan lika med individytorna utgår ifrån grundtoroiden utan justeringar

(inte 1/Ö2 » 0,71 utan 0,6239901164 som ger den exakta ytsymmetrin via m=20 — som dock inte kan gälla i praktiken

— Se vidare från 0,71r-kriteriet).

kärnradierna

genom experimentell mätning

ATOMKÄRNORNAS RADIER GENOM EXPERIMENTELL MÄTNING — se även från Atomkärnans Storlek

Massbaserade spridningsexperiment

INGA DIREKTA METODER FINNS ATT MÄTA ATOMKÄRNORNAS RADIE — ENLIGT TNED

Se även i Tyngdcirkelns betydelse för kärnradierna i TNED

Figuren ovan vänster visar fallen med neutron-protonaggregaten enligt TNED, samt närmast till höger för övriga atomkärnor. I vilket fall ser vi genom en direkt enkel inspektion att formkropparna KAN intränga i varandra — i princip in till halva största ytterradien. Figuren ovan höger visar att detta fall även gäller med avseende på toppspinnet isolerat och det maximalt inträngande sättet som atomkärnorna kan sammanträffa på. Även här penetreras endera atomkärnans halva radie, analogt atomkärnans tyngdcirkel. Med hänsyn till kärnornas alla möjliga godtyckliga orienteringar finns alltså inget enda noggrant entydigt sätt att avgöra atomkärnans ytterradie genom massbaserade experiment — typ kollisioner mellan olika kärnor eller deras subatomära fragment (se Neutronfragmenten), elektronmassorna inkluderat.

Atomkärnan undandrar sig direkt experimentell observation — enligt TNED.

De betydligt mindre elektronmassornas komponenter (t-ringarna, se Elektronmassans komponenter) har den största penetrerande förmågan (med lämpligt pålagd energi) och uppvisar därför också de statistiskt minsta ”kärnradierna” (närmare 1 Fermi, se citat nedan). Med andra atomkärnor som avkännande element — typ protoner och neutroner — blir inträngningarna mera ”fyrkantiga” och därmed statistiskt sett också (betydligt) större (närmare 1,5 Fermi).

Jämför

”The value of r₀ consistent with the experimental data ranges from 1.18 × 10^–13 cm to 1.40 × 10^–13 cm for light nuclei.”,

@INTERNET GoogleBöcker med begränsad tillgänglighet

Nuclear Physics: An Introduction, S. B. Patel 1991

Min översättning:

Värdet på r₀ samstämmigt med experimentella data omspänner från 1,18 t15 M till 1,40 t15 M för lätta atomkärnor.

”Roughly speaking, we will take the nuclear radius to vary with the 1/3 power of the mass number R = r₀A^1/3, with r₀ ~ 1.2 – 1.4 × 10^–13 cm. The lower value comes from electron scattering which probes the charge distribution of the nucleus, while the higher value comes from nuclear scattering which probes the range of nuclear force.”,

[http://mightylib.mit.edu/Course%20Materials/22.101/Fall%202004/Notes/Part1.pdf],

22.101 Applied Nuclear Physics, 2004, Lecture 1 (9/8/04), Basic Nuclear Concepts, s4.

Min översättning:

Grovt sagt kommer vi att ta kärnradien att variera med potensen 1/3 för masstalet [A], R = r₀A^1/3, med r₀ ~ 1,2 – 1,4 × 10^–15 M. Det lägre värdet kommer från elektronspridning som avkänner laddningsfördelningen hos atomkärnan, medan det högre värdet kommer från kärnspridning som avkänner området för kärnkrafterna.

Se vidare i MASSBASERADE MÄTMETODER. Där ges bl.a. en citerad webbreferens till den banbrytande experimentalfysiken på området och som genomfördes under 1950-talet av forskarkretsen kring Robert Hofstadter.

Deuteronens Hemlighet | Impulsmomentets r/Ö2-kriterium | 2008VIII6

Se även inledande orientering i Atomkärnans Storlek

DEUTERONENS HEMLIGHET

atomkärnans radier enligt TNED

Impulsmomentets 0,71r-kriterium

Förenklingar i härledningarna till Kärnradierna

Deuteriumbildningen — se även till jämförelse Hofstadters kurvskara med volymära laddningstäthetens toppvärden — till jämförelse med TNED

	1H^1 + 1H^1 – (m®g) = 1H^2
r =1		r =1/Ö2

J = mwr² + mwr² = mwr² ; massökningen kompenseras av radieminskningen:

Deuteriumbildningens impulsmoment mvr enligt TNED, ovan-nedan. w från v = 2pr/T = (2p/T)r = wr; mvr = mwr².

; mw(r®r/Ö2)² + mw(r®r/Ö2)² = 2mw(r/Ö2)² = mwr²

På samma typsätt kan sedan impulsmoment mvr i bildningen av Helium-4 från två deuteriumkärnor återföras tillbaka på grundradien r för Väte-1 enligt

; 2mw(r/Ö2)² + 2mw(r/Ö2)² = 4mw(r/Ö2)² = 2mwr²

Väte-1 och Helium-4 får därmed samma kärnradie r=1 — men med olika inre formfaktorer — med den mindre mellanliggande deuteronradien 1/Ö2, så att vi får grundbilden:

ENLIGT TNED blir Deuteronradien mindre än neutron-protonradien — därför att formfaktorerna ändras (definieras) under fusionen. Föreningsytorna är lika stora — med konsekvenser. Se även beräkningsgrunder i Toroidytorna samt Deuteronradien i HOP.

MED ATOMKÄRNANS HÄRLEDNING FRÅN PLANCKRINGEN (J=mcr) framträder toroidaggregatet. Vi förutsätter här detta bekant från Planckringen. Toroidaggregatet (N[3]m[20]) (₁H¹) i sin första fusion till Deuteronen (tunga vätekärnan) måste deriveras (för derivering, se Derivata och Integral) i sina formfaktorer (toroidens formtyp: tunna smala inre ringar eller grova tjocka däck) för att vi ska finna de resulterande toroidala formfaktorerna (N och m) i grundaggregatet (N3m20) — eftersom i annat fall inget individvillkor alls kommer att existera för någon enda atomkärna: allmänt kaos, alla former och storlekar blir möjliga huller om buller.

Med villkoret att

· deriveringen, analogt fusionen, utnyttjar minsta möjliga energiförlust med mesta möjliga energihushållning, samt att

· vinkelrotationen (w=2p/T₀) inte ändras enligt grundvillkoret med nollsumma för atomens krafter och moment, analogt

· mesta möjliga kompakta slutprodukt eftersträvas,

ges tydligen för varje grundaggregat genom impulsmomentet

J = mvr = m(2pr/T₀)r = mwr²

summan

J = 2mw(r/Ö2)² = 2mwr²/2 = mwr² ; w=2p/T₀

Vi kan kalla detta samband för KärnImpulsmomentets 0,71r-kriterium enligt TNED.

Vilket vill säga: Slutprodukten ges samma impulsmoment (J) som komponenterna var för sig: massradiens kvadrat reduceras med samma faktor som totalmassans ökning.

Deuteronradien blir alltså r/Ö2 med r för grundaggregatet N3m20.

Men för att fastställa toroidformfaktorerna Nm i jämförelse med grundformen via Kubgrafen med den ideala vattendroppsmodellen som elementär referensbas, ges faktorvärdena N=3 och m=20 som den bästa matchande grundYtToroidKärnradieGrafen

— som uppvisar en reduktion i radie från r=1 till r=0,62. Inte från r=1 till 0,71.

Kärnradiernas grundgrafer

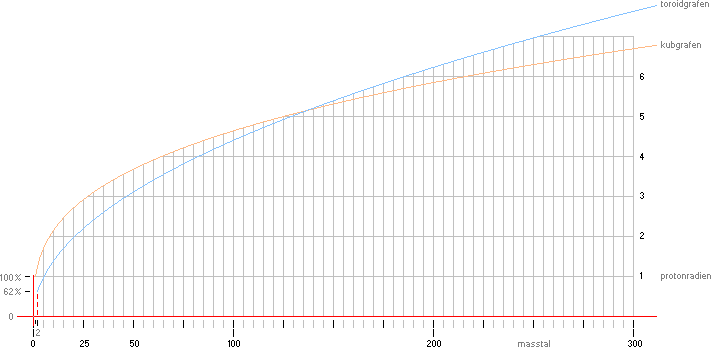
Kärnradiernas grundgrafer enligt TNED. Protonradien r₀=1,37 t15 M från Neutronkvadraten via Planckringen h=mcr.

Graferna ovan visar kubgrafen (orange r = r₀A^1/3) från vattendroppsmodellen och grundformen för toroidaggregatets ytgraf

[blått r = (0,4404609)r₀A^1/2]. Den senare framkommer i balans mot den förra genom ett ungefärligt (primärt) mittmasstalsmedelvärde (grovt 135-138) och som definierar formfaktorerna N=3 och m=20.

Grundaggregatet N3m20 fastställer med andra ord en radiereduktion på nära 38% enligt 1–0,62=0,38.

Med referens till den härledda ekvivalenten i impulsmomentets summering — som istället kräver runt 29% — blir därmed följande först och främst tydligt:

TOROIDGRAFENS JUSTERANDE KOMPONENTER ENLIGT TNED

massa-spinnkompensationen och massa-täthetskompensationen

Eftersom toroidaggregatets fraktala ringform är ihålig, växer analogt enligt TNED atomkärnans masstäthet (m/V) med växande fraktalnivå — se förklaring i atomkärnans masstäthet om ej redan bekant; Varje underliggande fraktalnivå bildar en mindre totalvolym jämfört med den närmast högre liggande ringnivån, samma totalmassa, i och med att det mesta av dess hålrum elimineras med den finare (också ihåliga) ringnivån. Totalt sett går därmed masstätheten mot oändligt med obegränsat växande fraktaldjup och vilken ordning grundlägger atomkärnans gravitella härledning enligt TNED. I försorg av den ordningen utkristalliseras två något olika kompensationsfaktorer i härledningen till kärnradierna.

· Den ena kompensationsfaktorn berör atomkärnans massa relativt atomkärnans centrala tyngdpunkt och därmed atomkärnans tyngdcirkel — massa-spinnkompensationen, se mera utförligt i massa-spinnkompensationen nedan.

· Den andra kompensationsfaktorn berör atomkärnans massa relativt den aktuella preferenstoroidyta som används vid härledningen av toroidaggregatets formfaktorer — massa-täthetskompensationen; se mera utförligt i massa-täthetskompensationen nedan.

Vi studerar dessa detaljer.

Dessa detaljer har tidigare berörts helt översiktligt i den inledande beskrivningen till Kärnradierna. Här följer en mera preciserad beskrivning.

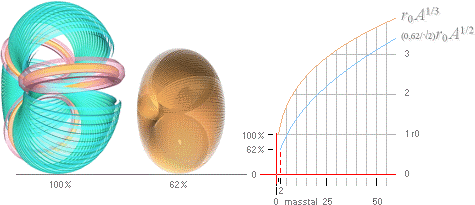
Formfaktorn från toroidhärledningen ger en koefficient 0,4404609 som för masstalet A=2 via toroidens ytfunktion A^1/2 ger faktorn 0,4404609Ö2 = 0,6229057 eller avrundat 62%.

KärnMassan i grundaggregatet (N3m20) (₁H¹) fördelad över dess första undre ringfraktala toroidyta, alltså de tre underringarna, skulle enligt Nm-bestämningarna matcha en radiereduktion på 0,62r. Impulsmomentets ekvivalens visar en större sådan på 0,71r. OM den senare gäller, är det tydligt att

· kärnmassan via 0,62r samlar massan längre in mot centrum än 0,71r och därmed en otillåtet stor förskjutning in mot centrum för massa-spinnförhållandet (mwr²=konstant med konstant w som ovan): för att utjämna den förskjutningen måste en motsvarande radieoffset (B) läggas till för att kompensera massa-spinnförhållandet så att atomkärnans tyngdcirkel förskjuts utåt i enlighet med impulsmomentets 0,71r-kriterium. Se vidare nedan från MASSA-SPINNKOMPENSATIONEN.

· 0,71r-kärnans inre första underfraktala ringyta blir (betydligt) STÖRRE jämfört med 0,62r-ytan; Men 0,71r-kärnan uppvisar en LÄGRE massYtTäthet relativt den mera masskompakta och mera högYtTäta 0,62r-kärnan OM vi IDEALT förlägger HELA kärnmassan till dess inre första underfraktala treringade toroidyta; för att kompensera för denna massa-täthetsreduktion — från 0,62r-GrundKärnan till 0,71r-ImpulsRealaKärnan — är det tydligt att ytterligare en radiell utvidgning måste ske för att atomkärnan inte ska balansera på en tyngdcirkel som hör till en kärnform med (betydligt) större massyttäthet. DEN DYNAMISKA ANSATSEN i den reduktionen ges tydligen via grundkärnan med 1–0,62=0,38 analogt 38% radiereduktion som en FUSIONSBASERAD ENERGITRANSIENT och som därmed tvunget omspänner samtliga möjliga fusionsprodukter — med massdefektsdynamiken inkluderad. För att försöka bena ut detaljerna i det komplexet måste vi ta hänsyn till kärnfysikens samtliga aktiva parametrar enligt TNED — speciellt fusionsdynamiken explicit. Se vidare nedan från MASSA-TÄTHETSKOMPENSATIONEN.

försök till förklarande illustrationer

linjära funktionskomplementets principbyggnad
	YtToroVärdet	±	EnLinjärÄndringsdelAvYtToroVärdet
=	T	±	T·LinjärFunktion
T(	1	±	ax)

r₀(B–x/N)=r₀LINE, x=A

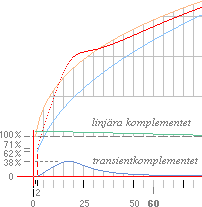
Resultatet av linjära och transienta komplementen bildar den resulterande röda grafen. Huvudtexten diskuterar hur de avgörande referenspunkterna till komplementens funktionsgrafer kan härledas enligt TNED.

transienta funktionskomplementets principbyggnad
	YtToroVärdet	±	EnTransientÄndringsdelAvYtToroVärdet
=	T	±	T·TransientFunktion
T(	1	±	ax[b+cx^n]^–m)

r₀[1+x(3+x⁵)^–0,7]=r₀TRAN, x=(A–2)/15;

Funktionerna LINE och TRAN tillsammans bildar resulterande funktionen (röd graf ovan) enligt

r = r₀basicTORO·LINE·TRAN

MASSA-SPINNKOMPENSATIONEN — eller Linjära Komplementet

Radieoffseten (B) ska maximera 0,71r från A=2 via en maximal koefficient (B=0,71/0,62) som sedan avtar mot en nollpunkt (@) i skärning med r₀-linjen via ett karaktäristiskt masstal; Ändringen kan på enklast sättet sättas som en helt linjär procentuell funktion av grundtoroidens värde för varje masstal A. Radietillskottets koefficient (B) blir störst vid A=2, noll vid en viss masstalsmedelpunkt som kan beräknas med ledning av övriga uppgifter i nuklidkartan enligt TNED (A=108), se vidare nedan, samt sedan avtagande linjärt mot nuklidspektrats ände (max A=300 enligt TNED). Vi studerar den detaljen nedan i nollpunkten (A=@).

Nollpunkten. I kärnytan för den positiva Z-laddningen (se laddningsdeplacementet) bidrar protonnuklidens kärnstruktur med en större utskjutning än neutronkomponenten, figuren ovan (notera att protonens teoretiska positiva deplacement motsvarar i storleksordningen en enhet på två tusen, neutronytan i sin tur ännu mindre, det är alltså fråga om ytterst sublima skillnader, se mera utförligt i Laddningsdeplacementet); Om alla atomkärnor kunde bildas av lika antal neutroner-protoner skulle också den resulterande kärnstrukturen ha samma typform för alla nuklider — och därmed i princip ett ständigt växande tillskott av massa-spinnkompensationen, analogt ett litet tillägg i tyngdcirkelns radie med växande masstal (A) för alla nuklider. Massa-spinnkompensationen skulle då INTE kunna vara linjär utan istället typ asymptotiskt avtagande mot nuklidkartans ände från max B-värdet (0,71/0,62). Emellertid växer andelen nuklidbildare med neutroner över andelen protoner märkbart från runt masstalet 15-20 (grovt sett från Neon) och vidare uppåt med en alltmer påtaglig neutronövervikt. Så har till exempel den enda stabila grundämnesnukliden för Guld (₇₉Au¹⁹⁷) andelen nuklidkvantabildare enligt fördelningen 79 protoner och 118 neutroner, en övervikt på 39 neutronkvanta. Det faktum att nuklidbildningarna INTE kan relateras strukturekvivalenta i kärnytorna med växande masstal, garanterar därmed att massa-spinnkompensationens funktion KAN ha en linjär typform. Vi studerar detta mera ingående.

Om vi utgår från att neutronstrukturen parkerar på, analogt ersätter protondeplacementets utskjutningar

— laddningsdeplacementet (se även den förenklade figuren ovan) i neutronkärnytan är mindre än det i protonkärnytan, vilket med samma ytterradie i bägge strukturerna blandade betyder att neutronytan ses jämnare än protonytan och därmed protonstrukturens fördjupningar längre in mot ringcentrum relativt kärnytan, och alltså kan man säga att neutronstrukturen parkerar sin mera ytutjämnande del på den mera gropiga protonstrukturens mest utskjutande plats

— och som därmed påtvingar tyngdcirkeln ett relativt den harmoniska strukturjämvikten större radievärde än tillbörligt

— bör en motsvarande reduktion, inåtdragning, ske av tyngdcirkelns radie från någon viss medelbaserad referenspunkt mellan lättare och tyngre nuklider.

Därmed är nollpunkten i linjekompensationens helt linjära funktion i princip motiverad.

Med hjälp av Nuklidkartans gränsvärde med maxA=300 kan vi — totalt för slutresultatet i kärnradiegrafen — rent grafiskt avläsa den ungefärliga nollpunkten (betecknad @ nedan, »at-sign», VID-tecknet från datorerans barndom och som användes för att markera adresser i dataflödet) genom att söka den kurvform (N-värdet i kalkylkortet nedan) vars toppvärde slutar på masstalet 300. Värdet vi finner (@=108) ligger nära mittpunkten mellan A=1-209; nollpunkten A=108 motsvarar precis mellanläget mellan de två enda stabila Silvernukliderna med masstalen respektive 107 och 109. A=209 — den enda stabila nukliden hos grundämnet Vismut — markerar f.ö. nuklidkartans definitivt översta gräns för alla stabila nuklider: Över den gränsen (atomnummer 83) finns inga stabila nuklider. Alla atomkärnor från atomnummer 83 och uppåt (masstal från runt 200 och uppåt) är tungt radioaktiva och sönderfaller förr eller senare via kärnklyvning. För denna del ges då analogt med den valda nollpunkten vid ”Silversnöret” (A=108) en allt större tyngdcirkelsreduktion med växande masstal upp mot gränsen vid 300.

kalkylkort · linjära komplementet — flik2

alla kortflikar i den här presentationen öppnas i samma huvudkort

se även öppningsmanual om ej redan bekant

inmatningresultat — för beskrivning, se närmast nedanstående härledningar

Med linjekompensationen (L) i skärning med 1-nivån i masstalspunkten eller »Silverpunkten» @=108 — vi får det värdet på rent grafisk grund genom att som nyligen påpekades söka den resultantgraf (transientdelen kan vi bortse ifrån i den prövningen, den är noll i nuklidkartans slutdel) vars toppvärde via ett givet N-tal uppnås vid nuklidkartans gränsvärde A=300, detta ger @-värdet enligt sambanden nedan (@=nN).

Med nollpunkten vid A=300 ges via Silverpunkten @=108 mera exakt värdet N=800. Utgångsvärdet 0,4404609 för k påverkas inte.

Små skillnader i k-värdet betyder att m-faktorn i N3m20-aggregatet inte blir exakt heltalig.

Parametrarna @BN med offsetvärdet (B), linjekoefficienten (N) och nollpunkten (@) kan alltså sammantaget bestämmas exakt om A=2-värdet ska ge exakt 1/Ö2 enligt 0,71r-kriteriet. Man får i sammanställning (från grundtoroidens härledning)

a = [0,4404609 · (r₀=1)(A=2)^1/2] = (0,4404609)Ö2 = kÖ2 ;

k = 0,4404609 från härledningen till toroidaggregatet N3m20

VILLKOR: vi söker b enligt

b · a = 1/Ö2 = bkÖ2 ;

b = 1/2k = 1,1351745 ;

b – 1 = n ;

n = 0,1351745 ;

n är den kortare kateten i triangeln med den längre kateten lika med det angivna masstalsvärdet @ vid L-skärningen med r=1-basen;

n = (@)tanL med tanL = 1/N från

b = (B–A/N) med

b = (OFFSET=B) – (A=2)/N som ger

B = b + 2/N = 1 + n + 2/N;

Därmed totalt

n = @/N med n=0,1351745 som ger

N = @/n ;

B = 1 + n + 2/N = 1 + @/N + 2/N

= 1 + (@+2)/N

Funktionen för Linjära Komplementet får formen (L) = r₀(B–A/N) med A som variabeln för masstalet. Kalkylkortet ovan ger basdata samt vidare.

För slutgrafen, se längre ner i KÄRNRADIERNA ENLIGT TNED.

MASSA-TÄTHETSKOMPENSATIONEN

Om vi först återknyter till en av grundillustrationerna (närmast nedan) i Nuklidbildningarna, den som illustrerar grundprincipen för en fusionsring, ser vi analogin enklare mot varje påbörjat fysikaliskt förlopp:

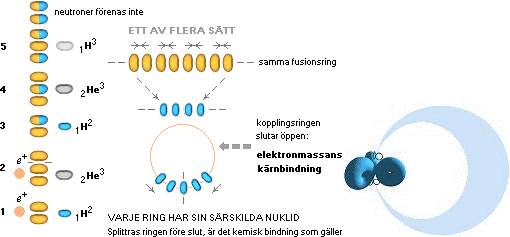
När väl fusionsringen är påbörjad kan den sedan svårligen brytas; den måste i princip fullföljas; Ringen sammanhålls och definieras av de närväxelverkande ytterst starka kärnkrafter (Coulombkrafterna som frigörs via de exponerande ±e-strukturerna i kärnytorna då dessa står i beredskap att förenas) som just definierar de ingående nukliderna i ringens bildning (se från Nuklidbildningarna) och som förutsätter att nuklidbarriärerna hos ringagenterna (idealt Planckringens omskrivna sfär) har passerats så att kärnorna ligger i laddningsläge för direkt fusion. OM — som i detta fall med en tillförd extra dynamisk faktor, fallet massa-täthetsfördelningsfunktionen — någon för hela ringens individer extra gemensam transientform föreligger, till exempel den som kopplar till massdefektsfunktionerna på en separat fördelningsform, som här är fallet, måste också alla ingående ringindivider gemensamt genomlöpa den transientbilden. Eftersom massfördelningsdynamiken i fusionsfasen högeligen inbegriper massdefekternas bildning och helt beror på dessa med fusionsringens ekvivalenta slutprodukt, blir det följaktligen också massdefektens allmänna preferensfysik som bestämmer referenspunkterna också i den här aktuellt observerade massa-täthetskompensationen som resultat av den kompenserande övergången från 0,62r-formen till 0,71r-formen — i allra största synnerhet klart om fusionsringen består av idel protonagenter. Vilket vill säga: toppvärdet i massa-täthetskompensationens funktionsgraf kan tydligen — på ett eller annat sätt — återföras relaterat på Järntoppens maximala massdefekt som ett motsvarande funktionsintervallets referensvärde.

Med ENBART protonaggregatet (N3m20) (₁H¹) som nuklidagent i den primära grundämnesbildningen — se utförligt från Nuklidbildningarna i GRUNDÄMNESBILDNINGEN med Udda-JämnaSerierna och noll neutronkvot — slutar den fusionsringen på individerna respektive (udda serien) ₂₉Cu⁵⁸ och (jämna serien) ₂₈Ni⁵⁶, analogt lätta nuklidgruppens bildning.
Tyngre nuklider kräver förekomster med neutronkvot större än noll, och därmed ett större transientintervall — ända upp till Amax=300.
OBSERVERA EMELLERTID: Även i fallet tunga nuklidgruppens bildning kvarstår naturligtvis toppreferensen (Järntoppen) för massa-täthetstransientens energipreferens med max massdefekt vid Järntoppens 18-gräns: Den gränsen kan inte ändras. Den är grundläggande såväl för den lätta nuklidgruppens bildning som för den tunga nuklidgruppens bildning då 18-gränsen i vilket fall inte kan överskridas som sådan.

Intervallet för massa-täthetskompensationen kommer därmed i vilket fall att betingas av ett huvudintervall som innefattar masstalen (avrundat) 1-60 med 18-gränsen (eg. 17,75) vid exakta A=56.

Med särskild referens till den lätta nuklidgruppens bildning kan energitransientens primära masstalsintervall för massa-täthetskompensationen därmed sättas tämligen noga enligt TNED till max 58 med speciell referens till primära uddaserien omnämnd ovan som slutar på ₂₉Cu⁵⁸. Hela reduktionskapitalet på runt 38% för massa-täthetskompensationen kan då fördelas på det intervallet via en motsvarande effektfunktion, analogt en transientfunktion av den kända typen

y = x(a+x²)^–2 ..................................... effekttransientens typfunktion, samma typfunktion som används i K-cellens värmefysik

och vars toppvärde uppnås vid

E_tP[max]/E_max = 1/4 vid P_max ............... samma typfunktion som används i K-cellens värmefysik

Även om nuklidbildningen utsträcks över masstalsintervallet 1-60, måste det toppvärdet, tydligen som ovan, bevaras i kraft av att det bygger på massdefektens intervall VID A=60 och varifrån de tyngre nukliderna sedan får en allt avtagande massdefekt ner mot Heliumnivån (14,5) som bildar generatrisen för nuklidkartans gränsvärde enligt TNED. Enda skillnaden i fallet med den tunga nuklidgruppens bildning blir att transientkurvan inte planar ut så snabbt från toppvärdet (runt masstal 15-20, se vidare nedan) i och med att intervalldelen utsträcks från avrundat A=60 till A=300: Tunga nukliderna uppvisar avtagande massdefekt med växande masstal från A=56 medan den lätta nuklidgruppen istället uppvisar växande massdefekt från A=1 upp till A=56.

Transienttoppen vid A=15-20 specifik för den lätta nuklidgruppen (se vidare nedan) bör alltså kvarstå.

Utgår vi ifrån att energiutvecklingen (E) från 0-100% är direkt proportionell mot masstalet [(1)-2]-58, och effekttoppen som ovan nås vid 0,25E(max), hamnar massa-täthetskompensationens toppvärde vid masstalet 58/4=14,5 eller avrundat A=15; DÄR förlägger vi analogt massa-täthetskompensationen eller Transientkomplementets maximala radieutvidgning på angivna 38%.

Studerar vi nukliderna i PERIODISKA SYSTEMET, ser vi att det också finns en speciell strukturtopp kring masstalen upp till 20: alla atomer upp till masstal 20 (Neon) har fyllda elektronskal från botten. Ungefär från masstal 20 och vidare uppåt blir inslaget av motsvarande kärnstruktur för neutronnuklidkvanta allt mer märkbart. Det betyder att protonkärnytans ekvivalenta laddningsdeplacement alltmer kommer att trängas undan av en mera jämn kärnytstruktur och som därigenom via deplacementets relativa tillbakagång påverkar atomkärnans tyngdcirkel. Vi kan därför räkna med att effekttoppen i massa-täthetskompensationen också — helt säkert — har sitt maximum i detta område, alltså runt masstal A=15-20.

HELA PROCESSEN med massa-täthetskompensationens bildning kan alltså i princip sammanfattas i en och samma fusionsring (se från Nuklidbildningarna) — och som begränsas till max masstal 58 (eller grovt runt 60) enligt härledningen av fusionsserierna från TNED i Nuklidbildningarna.

Övre grafen motsvarar den ordinära, obegränsat utsträckta effekttransienten y=2,55x(2+0,6x²)^–2. För att matcha den formen inom ett begränsat intervall måste inre exponenten ökas så att transientens fallande flank reduceras rimligt motsvarande nollvärde vid intervallets slut. Undre kurvan visar en sådan typ på formen y=x(3+x⁵)^–0,7.

y-funktionen ovan gäller med x-variabeln obegränsat utsträckt. För att få den funktionsformen på ett ändligt bestämt intervall måste funktionsformen komprimeras i x-led. Det sker genom att söka en motsvarande kompressionsfunktion som bygger på att öka den inre exponentkoefficienten så att funktionskurvan nollas rimligt inom det givna intervallet. En ungefärligt motsvarande transientpulsform i masstalsintervallet 1-60 ges då av funktionen överst i ledet nedan

y = x(3+x^5,5)^–0,7 ............................ lätta nuklidgruppens bildning, inre exponenten är 5,5

y = x(3+x^5,0)^–0,7 ............................ tunga nuklidgruppens bildning, inre exponenten är 5,0

med x = (A – 2)/15. Observera att denna funktionsform också måste bli ungefärlig, mer eller mindre.

Den övre transientkonturen ges med exponentvärdet 5 i ovanstående y-funktion.

Den undre transientkonturen ges med exponentvärdet 5,5.

Med inre potensen x⁵ ges transientens fallande del en mera flack avslutning mot A=300 (samt en liten dragning mot 20-hållet för transientens toppvärde), se från Tunga nuklidgruppens certifiering, särskilt i Maximalringens komponenter. Men denna del är också ungefärlig och kan — här veterligt — bara avgöras genom prövning mot kända mätdata. I vilket fall är skillnaden mellan de olika kurvorna marginell (3% vid A=32, runt Svavel, sedan betydligt mindre omkring).

Men i och med att den lätta nuklidgruppens individer (ju) på sätt och vis ingår i, eller bildar grunden för, den tunga nuklidgruppens bildning — ehuru på bas av olika neutronkvoter — kan det tyckas underligt att skilja ut kärnradier som speciella inom den lätta nuklidgruppens nuklider till skillnad från samma typnuklider såsom innefattade i den tunga nuklidgruppens bildning. Om vi frånser dessa (möjliga, mindre) skillnader, blir valet för en mera generellt användbar kärnradiefunktion att använda den lägre exponentformen (typiskt 5) och som därmed inkluderar hela nuklidkartan, från masstal 1 till masstal 300. I den sammanfattande kärnradiefunktionen, enligt TNED för samtliga masstal, blir det därför mera naturligt att använda detta senare alternativ.

Se även vidare i resultatframställningen KÄRNRADIERNA ENLIGT TNED.

Därmed är den allmänna formen klarlagd beträffande kärnradierna enligt TNED — och såvitt reellt också tillämplig på naturfysiken:

En atomkärnans ytterradie bestäms (marginellt) olika från fall till fall beroende på HUR atomkärnan bildas — alltså beroende på primär fusionsbildning med eller utan närvaro av aktiva neutroner, inkluderat alla möjliga kombinationer:

En och samma nuklid kan bildas ur fusionsringar med olika neutronkvot, och därmed olika kärnradie — enligt massa-täthetskompensationen. Det finns med andra ord, verkligen, ingen enkel, typ ”fast”, ekvation för atomkärnornas radie.

Utöver massa-täthetskompensationen tillkommer ytterligare radietillskott för massdefekterna (typiskt runt max 4% med exemplet från neutronen-protonen).

Dessa delar innebär emellertid speciella — ytterligare — komplikationer och har helt bortsetts ifrån i den allmänna grafiska sammanställningen, se KÄRNRADIERNA ENLIGT TNED nedan.

NOTERA OCKSÅ EXPERIMENTELLT:

Frånsett möjligheten att »mäta exakt» på enskilda atomkärnor;

Den hittills kända experimentalfysiken med mätning av t.ex. atomvikter kännetecknas av en statistisk medelvärdesbildning (genom s.k. masspektroskopi, som bygger på magnetisk separation) för ett stort antal kärnindivider. Med hänsyn till de ovan omnämnda möjliga olikheterna i samma typnuklider, samma masstal, men som bildats ur olika neutronkvoter, finns ingen som helst statistisk möjlighet att avgöra någon precision i den frågan: nuklider av samma typ uppträder naturligt i samma kollektiv (samma masstal).

Uppenbarligen inte med mer än man får fram en teknik att mäta direkt på enskilda atomkärnor (som bildats under kända fusionsförhållanden på kända neutronkvoter), kan »frågan om atomkärnornas exakta radier» avgöras.

Fortsättning i KÄRNRADIERNA ENLIGT TNED — allmänt sammanfattande resultatredovisning.

KÄRNRADIERNA ENLIGT TNED

— graferna utom kubgrafen A^1/3 gäller från masstal A=2, se även grundbeskrivning ovan med särskilda noteringar

KÄRNRADIERNA FÖR ATOMKÄRNORNAS TYNGDCIRKLAR ENLIGT TNED beskrivs enligt nedanstående röd graf. Graferna för Transientkomplementet och Linjära komplementet visas separat utbrutna — tillsammans med några inlagda experimentella mätdata (från Irving Kaplan, Nuclear Physics [1955 | 1962]).

Notera ENLIGT TNED att experimentell bestämning av kärnradier är (starkt) beroende på typ av mätmetod — ingen exakt sådan finns. Se utförligt från avsnittet KÄRNRADIERNA.

Notera även med referens till de utanförliggande öppna svarta datacirklarna i figuren nedan (Kaplan-data [1962]);

Största avvikelsen visar runt 12% mellan röda grafen och mitten på de öppna svarta Kaplancirklarna;

Avvikelser på upp till 14% anges i vissa källverk som skillnaden mellan olika resultatvärden från massbaserade spridningsexperiment beroende på om projektilkroppen är en elektronmassa eller atomkärna (1–1,2/1,4 » 14% se citat);

Kaplankällan — projektilelement: neutron — redovisar internt att radievärdet också påverkas av projektilenergin (för grafens vidkommande dock i försumbar omfattning, mindre än 1,5% enligt Kaplan, se källredovisningen);

Radiella avvikelser som funktion av massdefekter ingår INTE i nedanstående TNED-grafer; antas generellt en viss nuklid på konstant impulsmoment J=mwr² med konstant vinkelrotation w (se Nukleära spinnkriteriet från Kvanttalen), ändras radien med inverterade roten ur massändringen:

EXEMPEL: Med en atomär massdefekt på m_D=10e per ekvivalent bildningsneutron, blir massminskningen 10/1836=0,00544662 eller 0,5%; roten ur 1,005 ger radieökningen, avrundat lika med 0,25%; radien ökar med en faktor 1,0025; Observera dock att denna sambandsform endast är grovt orienterande med den slutna kärnan som preferens, alltså utan hänsyn till den faktiskt uttransporterade atomära elektronmassan och som ytterligare bidrar till en något större kärnradietyngdcirkel (radieskillnaden neutron-proton är nära 4% till jämförelse — från 1,32 Fermi till 1,37 Fermi); Slutgrafen kommer generellt sett att ligga något högre upp — inkluderat att vissa stabila nuklider med samma masstal A erhåller olika kärnradier på grund av olika massdefekter, se t.ex. de stabila nukliderna Kalium-40 och Kalcium-40, resp.

₁₉Kalium⁴⁰_17,2859409 och ₂₀Kalcium⁴⁰_17,3496843: Kalcium-40 har den högre atomära massdefekten och därmed en något större nominell kärnradie än Kalium-40 — ENLIGT TNED; Exemplet visar att det inte finns någon sammanhängande generellt kontinuerlig funktion för att beräkna kärnradierna för alla möjliga fall. Se även särskild beskrivning i Kärnradien som funktion av elektronmassans utflyttning.

Kärnradierna för instabila nuklider ingår INTE heller i nedanstående TNED-grafer; För att beräkna dessa enligt TNED krävs icke-kontinuerliga funktioner — alltså med värden per aktuell nuklid utan mellanliggande funktionsvärden — som baseras på de enligt TNED-grafen nedan (röd) fasta grundvärdena, samt vidare beroende på graden av energiinnehåll i aktuell nuklid; Den analysen innefattar bekantskap med Nuklidkartan AZ och som ansluter till den allmänna beskrivningen av de instabila nuklidernas sönderfall (se separat i Kärnradierna för instabila nuklider enligt TNED).

Med referens till neutron-protonradieändringen på max 4% är det rimligt att räkna med radiella avvikelser på grund av massdefekter (samt instabila nuklider särskilt) grovt i den storleksordning som förhållandet nedan visar i figuren mellan röd graf och omgivande cirklar.

Vi kommer förmodligen EXPERIMENTELLT SETT aldrig närmare exakta data på atomkärnornas tyngdcirklar än så: radierna fluktuerar ständigt ENBART beroende på atomkärnans energiinnehåll (impulsekvationens tyngdcirkelbalans, dock marginellt …), för att inte sedan tala om partikelacceleratorer i experimentalfysiken som påtvingarna kärnorna extremt högra extramoment — från stund till annan. Men också dessa områden är (ännu) svåra att beskriva. Vidare följer.

Kärnradierna genom atomkärnans tyngdcirkel

från Planckringen Enligt TNED

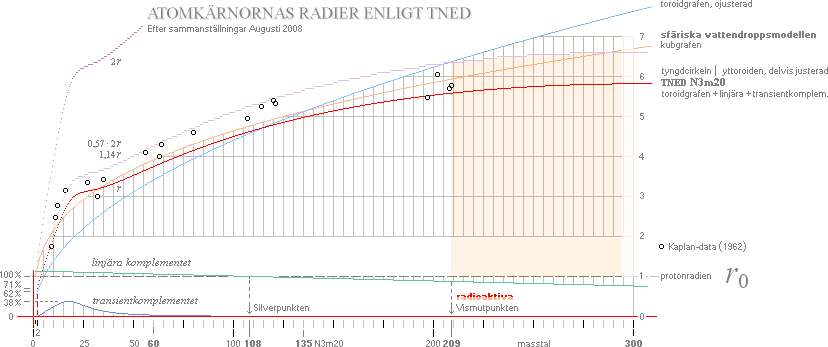
Särskilda förklaringar i separata sektioner · Silverpunkten · Vismutpunkten · linjära komplementet · transientkomplementet · gränserna 2r och 1,14r ·

HORISONTELLA SKALAN anger masstalet A. VERTIKALA SKALAN, enhet protonradien r₀ = 1,37 t15 M från HOP [Table 1.4 s7–27] samstämmig med Neutronkvadraten via Planckringen

h=mcr=6,62559 t34 JS, med neutronmassan m=1,0086652u med

atomära massenheten u = 1,66033 t27 KG och ljushastigheten c=2,99792458 T8 M/S, r blir avrundat 1,32 Fermi: med neutronsönderfallet ges 1,37 Fermi enligt TNED, se utförligt från NEUTRONKVADRATEN.

Kaplan-data (se särskild källbeskrivning), svarta ringar, anger mätdata på 19 nuklider från boken NUCLEAR PHYSICS (1962, [originalet från 1955]) av IRVING KAPLAN, s387 Table 16–5. Separata beräkningar från NEUTRONKVADRATEN visar enligt TNED att nuklidkartan planar ut (slutar) vid max A=300 (absolut max 317), vilket är samstämmigt med ovanstående röd graf.

Grafdelarna markerade med 2r och 1,14r ansluter — teoretiskt enligt TNED — till de ljusbaserade mätmetoderna från föregående beskrivning i ATOMKÄRNORNAS RADIER GENOM EXPERIMENTELL MÄTNING, se Kärnradierna genom lasern. Dessa ska enligt TNED endast avse mätdata från typ laserspektroskopiska mätningar. Uppgifter på sådana mätningar är emellertid ännu (Augusti 2008) i princip obefintliga (intensiv forskning pågår). Se vidare nedan i Resultatredovisning.

Kubgrafen : r = r₀A^1/3 ................................................... räknas från A=1

YtToroidgrafen : r = (0,4404609)r₀A^1/2 ............................... räknas från A=2

Linjära : r = r₀(1,1377–A/800) ............................... räknas från A=2, se massa-spinnkompensationen

Transient : r = r₀[1+x(3+x⁵)^–0.7] .................................. x = (A – 2)/15, räknas från A=2, se massa.täthetskompensationen

Slutgrafen : r = (1,1377–A/800) · [1+x(3+x⁵)^–0.7] · (0,4404609)r₀A^1/2 » r₀A^1/3, räknas från A=2, se Kalkylkortet LinjäraKomplementet

RESULTATREDOVISNING | GRUNDFORM: se från Deuteriumbildningen

Resultatredovisning genom uppsamlade allmänt tillgängliga data på webben @INTERNET Augusti 2008 — atomkärnornas radie

Möjligheten att få fram mätdata genom webbsökning @INTERNET är (ännu Augusti 2008) ytterst begränsade — trots en närmast enorm mängd dokument som behandlar ämnet. Se vidare (delvis) utförlig rapportbeskrivning i KÄRNRADIEDATA PÅ WEBBEN. Sammanställningen nedan visar webbens andel.

KAPLAN-DATA (urspr. i kopia från prof. Ingvar Otterlund, Lunds Universitet 1996) [-1962]:

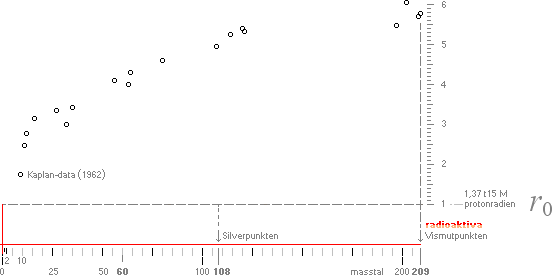
Kaplan-data (1962|1955), NUCLEAR PHYSICS av IRVING KAPLAN, s387 Table 16–5, Nuclear Radii From Neutron Cross Sections at High Energies.

Tabellvärdena omräknade av mig i r0-enheter som ovan: Kaplanvärdena dividerade med 1,37. Kaplans tabell omfattar 19 grundämnen betecknade _ZX^A nedan, men Kaplan anger bara ämnets kemiska beteckning utan annan specifikation, nukliderna nedan de i grundämnet mest representerade enligt atomviktstabellen i HOP,

₄Be⁹, ₅B¹¹, ₆C¹², ₈O¹⁶, ₁₃Al²⁷, ₁₆S³², ₁₇Cl³⁵, ₂₆Fe⁵⁶, ₂₉Cu⁶³, ₃₀Zn⁶⁴, ₃₄Se⁸⁰, ₄₇Ag¹⁰⁷, ₄₈Cd¹¹⁴, ₅₀Sn¹²⁰, ₅₁Sb¹²¹, ₇₉Au¹⁹⁷, ₈₀Hg²⁰², ₈₂Pb²⁰⁸, ₈₃Bi²⁰⁹.

Kaplan anger två olika energivärden, resp. 14 och 25 MeV, det senare markerat med orange ovan, ljusgrå textmarkering innefattar två separata uppgifter med bägge energivärdena, skillnaden ges marginellt (mindre än 1,5%) bara för de två sista med den något större kärnradien motsvarande det större energivärdet. För dessa fall har det lägre värdet använts i jämförelsen med TNED.

Notera att massbaserade spridningsförsök enligt TNED också innefattar en betydande masschokning med växande partikelenergier från partikelaccelerationen speciellt för kärnbaserade projektiler typ neutroner och protoner och tyngre. Effekten av sådana kollisioner med avseende på vrängningen i kärnradievärden relativt atomkärnor som inte utsätts för sådana kollisioner saknas ännu (Augusti 2008) i denna framställning. Ovanstående Kaplandata bör därför ses med en viss försiktighet i jämförelsen med TNED — de extra momenten KAN medföra (stora) radietillskott, samt att även projektilpartiklarnas storlek ger något större resultatvärden jämfört med elektronmassor som projektilagenter. Differenser på så mycket som runt 14% omnämns i den etablerade litteraturen

(1–1,2/1,4=0,1428571), se citat.

WEBBEN @INTERNET [-2008] (se rapport i Kärnradiedata på Webben):

Osawa (2001), [http://www.riken.go.jp/lab-www/library/publication/review/pdf/No_39/39_088.pdf] s89 Fig. 2; Källans angivna mätmetod:

spridningsexperiment på gruppen Kol, Kväve, Syre, Fluor med isotoper, ”The open circles represent radii obtained from reaction cross sections at intermediate energies.¹⁵⁾”, ”15) E. Liatard et al.: Europhys. Lett. 13, 401 (1990).”; Här har endast de stabila isotoperna medtagits — vilket utesluter källans mätdata på Fluor.

Källdata är givna i grafisk form, vilka uppmätts och omräknats som ovan med följande källpreferens:

”In the calculations, we assumed a Woods-Saxon shape for the potential, fixed the radius parameter to be parametrized as 1.22A^1/3”, s89sp1; För att få Osawa-värdena (rO = {C^12|13 2,48|2,41; N¹⁴ 2,6; O¹⁶ 2,64}) i TNED-grafens r/r₀-referens måste rO divideras med ovannämnda Woods-Saxonkoefficient 1,22 så att den rena kubgrafens motsvarande grundfunktion A^1/3 framstår (rO = {C^12|13 2,03|1,98; N¹⁴ 2,13; O¹⁶ 2,16}). Notera ”assumed” för zoomkoefficienten 1,22: nuklidgruppens placering i lodled beror i hög grad på detta ”assumed” och som också varierar i olika källverk (1,07-1,4).

Uppgifterna från Osawa är emellertid också delvis odefinierade (på ytterligare annat sätt) i TNED: Osawa anger på inledningssidan 88 att ”The reaction target was carbon and secondary beam energies at the middle of the target were approximately 950 A MeV”. Spridningsexperimenten här bygger alltså på kolliderande atomkärnor med tilläggsenergier på drygt en neutronmassa (940 MeV) per kärnnukleon. Enligt härledningen till PLANCKEKVIVALENTERNA ges motsvarande massändringseffekter under accelerationsprocessen, och med hänsyn till impulsmomentet (J=mvr=mwr²) också förändringar i kärnradierna. Exakt hur vet vi här inte, varför uppgifterna från Osawa måste tas med (ytterligare) viss försiktighet.

Tomaselli (2008), [http://www.gsi.de/informationen/wti/library/scientificreport2000/Nuc_St/54/Li2000.pdf] Table 1; Källans angivna mätmetod:

spridningsexperiment. Källan anger i Table 1 Be-9-nukliden ”⁹Be R exp. matter [5] 2.38(1) fm”, med källredovisningen enligt ”[5] I. Tanihata et al., Phys. Lett. B 206, 592 (1988)”.

Covello (2002), @INTERNET GOOGLE-böcker begränsad åtkomst; Challenges of Nuclear Structure, Aldo Covello, World Scientific 2002; Källans angivna mätmetod:

laserspektroskopi, men källan skriver inte ut det explicit utan det ligger inbäddat i expertbegreppet ’isotope shift method’, se nedan.

Tabell och text s125; ”Remarkable are the results produced by our chiral potentials for the deuteron radius which agree accurately with the latest empirical value obtained by using the isotope-shift method.²⁵”; se svensk översättning i citatblocket, tabellen i boken på samma sida 125 anger 1,975 Fermi; I separat sektion ges citat från olika källor som visar att termen isotope-shift method ansluter till laserspektroskopiska mätmetoder. Samma typdata ges i källan nedan (Herrmann) men man kommer inte åt hela den artikeln, och sammanfattningen klargör heller inte att det är fråga om laserspektroskopiskt grundat material.

Herrmann (1997), A consistent calculation of dispersion corrections in elastic electron-deuteron scattering, EDP Sciences 1997, The European Physical Journal, Eur. Phys. J A 2, 29-40, 2 December 1997, T. Herrmann et al; Källans angivna mätmetod:

laserspektroskopi, men källan skriver inte ut det explicit utan det ligger inbäddat i expertbegreppet ’isotope shift method’, se noteringarna ovan;

”This gives a deuteron radius of (1.968 ± 0.006) fm and a charge radius of (2.130 ± 0.010) fm.”. Beteckningen ”fm” anger femtoMeter, samma som Fermi eller t15 M. Värdet 1,968 Fermi är av samma typ som ovan i källan från Covello. Se även i citatblocket.

Suzuki (2003), @INTERNET GOOGLE-böcker begränsad åtkomst, Structure and Reactions of Light Exotic Nuclei, Yasuyuki Suzuki, Kazuhiro 2003; Källans angivna mätmetod:

spridningsexperiment, s400n:

”

Table 13.9: Theoretical radii (in fm) of the point matter, proton and neutron distributions calculated in model versions 2 (cf. Table 13.1) for ⁴He, ⁶He and ⁸He, compared with empirical values [10, 68].

r_m r_p r_n

Th Exp.[10][68] Th Exp.[10][68] Th Exp.[10][68]

⁴He(0⁺) 1.42 1.35 | 1.42 1.42 1.35 | 1.43 1.42 1.35 | 1.43

”,

Uppgifterna för ⁶He och ⁸He här utelämnade eftersom dessa nuklider inte är stabila (det finns f.n. ingen radiell analys på den delen enligt TNED i min referens).

Referenserna [10, 68] är låsta för åtkomst. s401 är inte tillgänglig. s402:

”As regards empirical radii, there is some discord between them as well as their relationship with the presented theoretical results.”

”Both sets of empirical data quoted in Table 13.9 have been deduced from interaction cross section measurements.”,

Min översättning:

Vad gäller empiriska radier, finns en del motsättningar mellan dem såväl som deras förhållande till de presenterade teoretiska resultaten.

Bägge uppsättningarna empiriska data citerade i Tabell 13.9 har erhållits från växelverkanTvärsnittsMätningar [vilket antyder massbaserade spridningsexperiment].

HOP-deuteronen (1967), Källans angivna mätmetod:

spridningsexperiment, från HANDBOOK OF PHYSICS McGraw-Hill 1967, se särskild artikel. Värdet motsvarar 77% av protonradien r0.

varav uppgifter obs endast för stabila nuklider grundade på laserspektroskopi:

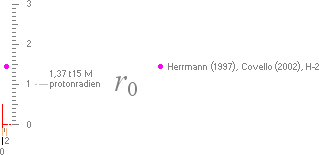
Se Covello och Hermann ovan.

Om det fortsätter så här (ungefär en hel BOK för att redovisa i princip EN kärnradie — eftersom källförfattarna tycks ha svårt med att klargöra begreppen) blir det här en lång historia.

ALLA OVANNÄMNDA TILLSAMMANS:

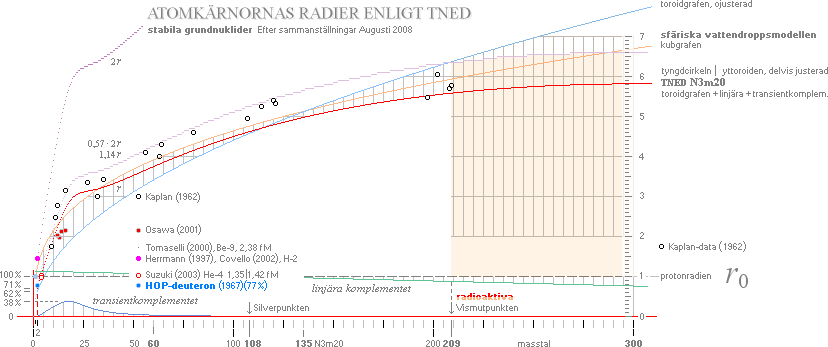
Särskilda förklaringar i separata sektioner · Silverpunkten · Vismutpunkten · linjära komplementet · transientkomplementet · gränserna 2r och 1,14r ·

Protonradien r0=1,37 t15 M anger vertikala skalans enhet. Horisontella skalan anger atomkärnans ekvivalenta bildningsantal av antalet neutroner och protoner, det s.k. masstalet (A). I TNED benämns andelen neutroner i A med begreppet neutronkvot. För grafens olika datadelar, se från Resultatredovisning. Se även ovanstående med avsnittslänkar i KÄRNRADIERNA ENLIGT TNED.

Speciellt är uppgiften från Suzuki (2003) samstämmig med teorin enligt TNED på Helium-4-radien. Även den laserspektroskopiska uppgiften på deuteriumradien från Covello (2002) stämmer också med TNED-teorin (se från Laserspektroskopiska mätningar). Vi ser emellertid också att nuklidvärdena från Osawa (2001) INTE ansluter väl till TNED-grafen (röd) för den massbaserade kärnradiebestämningen. Emellertid är dessa data fortfarande så ytterligt få (samt referenserna så osäkra) att frågan INTE får anses avgjord. Det behövs betydligt mera mätdata. För HOP-källans deuteronvärde, se särskild artikel i DEUTERIUMETS AVGÖRANDE BETYDELSE.

instabila

nuklidernas kärnradie

Under arbetets gång har flera uppslag framkommit som gjort en vidare och mera fördjupad beskrivning i TNED möjlig.

Här följer en av dem.

2008VIII13

KÄRNRADIERNA FÖR INSTABILA NUKLIDER

betainstabila kärnradierna

Kärnradierna för BETA-instabila nuklider enligt TNED

BETAINSTABILA NUKLIDERNA betasönderfall

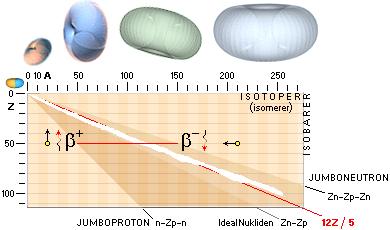
Med referens till en stabil nuklid _ZX^A refereras i TNED speciellt alla instabila nuklider _ZX^(A) med högre masstal (A) än denna med termen JUMBONEUTRON (b^–; _ZX^(A–)); Nuklider med lägre masstal kallas för JUMBOPROTONER (b^{+ ;} _ZX^(A+)). Deras sönderfallsmekanism visas illustrerat nedan med referens till den balanserande mittpunkten, motsvarande stabil nuklidform (se mera utförligt i NUKLIDKARTAN):

Jumboneutronen strävar mot stabilitet genom att avge en kärnelektron och vandrar därmed längre ner mot ett högre atomnummer (Z+1);

Jumboprotonen strävar på samma sätt mot sin stabilitet genom att ta upp en höljeselektron till kärnan och därmed avancera längre upp mot lägre atomnummer (Z–1). Bägge dessa nuklider klassificeras (även konventionellt) som betainstabila nuklider.

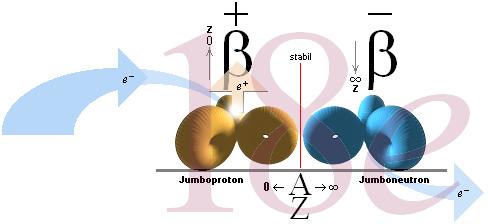
Genom att — med förebild från neutron-protonsönderfallet — jämföra nuklidpositionen för en viss instabil kandidat med känt masstal med en närmast känd stabil dito inom ett visst grundämne, kan ett allmänt samband ges enligt TNED för översiktlig — inte exakt — bestämning av den betainstabila nuklidens kärnradie. Vi studerar hur.

Med referens till en given stabil nuklid _ZX^A kallas i TNED varje dess isotop (nuklid med samma Z) med större masstal (A) en JumboNeutron. På samma sätt kallas varje dess isotop med mindre masstal för en JumboProton.

En Jumboneutron motsvarar i TNED alltså en nuklid som relativt sin stabila stamförälder har ett högre masstal (A). I princip betyder det att Jumboneutronen också initiellt sett bör ha en större kärnradie — eftersom kärnradiens grundform generellt enligt TNED växer med masstalet (A). ”Jumboneutronen” kan alltså i detta fall likställas med den stabila nuklid, samma masstal, som Jumboneutronen sönderfaller till — alltså också en nuklid med högre atomnummer (Z), med bibehållet masstal. I illustrationen nedan är denna del betecknad med instabila nuklidens motsvarande masstalsstabila radie. Läggs till denna stabila nuklid en extra elektron (som därmed ligger integrerad i strukturen via den kärnfusion som bildade den nukliden), bildas en Jumboneutron: Nukliden flyttas ner mot noll i nuklidkartan med ett mindre Z: Analogt säger vi att kärnstrukturen TAPPAR en enhet »protonstruktur»: kärnmassan ökar med den tillagda yttre elektronmassan.

Förutsätter vi för det givna masstalet även ett konstant impulsmoment (J=mwr²), tvingas därmed tyngdcirkelns radie avta — och därmed en förskjutning av tyngdcirkeln inåt centrum: kärnradien avtar för betaMinusAktiva instabila nuklider — räknat från normalradien för den nuklidens masstal.

Den extra elektronmassan som vi införde genom att gå baklänges i processen med att bilda en JumboNeutron ligger initiellt bara i kärnan från betaMinussönderfallets första stund. Denna elektronmassan förs sedan ut till atomhöljet (igen), vilket (eventuellt, om inte flera steg finns) resulterar i en stabil nuklid. Atomkärnan är alltså instabil under sönderfallsprocessen, och den återställer balansen genom att (successivt) föra ut elektronen, och därmed återställa tyngdcirkeln till läge större (igen) — på precis samma fason som i fallet neutron-proton. Om denna observation är korrekt grundad, betaändras Jumboneutronen till en stabil nuklid samtidigt med att kärnradien ÖKAR något (»tillbaka upp till den nominella kärnradien för den nuklidens masstal»).

DET RETORISKA DIAGRAMMET OVAN sammanfattar resonemanget och visar oss alltså hur vi kan räkna fram ett konkret medelbaserat nominellt värde för en viss betainstabil nuklid av typen Jumboneutron:

JUMBONEUTRONEN:

r(A2) – r_A1 r(A2) r_A1 r(A2) + r_A1

r_A1 + ———————— = r_A1 + —————— – ——— = ————— = r

2 2 2 2

(A2) är masstalet för den betainstabila nukliden och A1 är masstalet för den närmast liggande stabila nukliden i grundämnet med samma Z som (A2).

Detta värde är emellertid bara medvärdet mellan de möjliga ändlägena r(A2) och r_A1. Värdepunkten mellan dessa kan variera beroende på den aktuella betainstabila nuklidens energiinnehåll — som vi garanterat INTE har någon generellt exakt koll på i det enskilda nuklida fallet.

På samma sätt men åt andra hållet gäller för JumboProtonen:

Jumboprotonens masstal (A1) är alltid lägre än den stabila referensnuklidens A2 så att vi får motsvarande

JUMBOPROTONEN:

r_A2 – r(A1) r_A2 r(A1) r_A2 + r(A1)

r(A1) + ————— = r(A1) + —————— – ——— = ————— = r

2 2 2 2

Högre energiinnehåll innebär att atomkärnan uppvisar ett alltmer exciterat tillstånd (kärnan självsvänger kring tyngdcirkelns medellinje ända tills ett stabilt tillstånd inträder), och därmed i princip att nuklidradien också ökar. Men ingen framställning finns ännu (Augusti 2008, min referens) i TNED på den punkten (detaljerna måste också innefatta kärnstrukturen, och den är generellt sett mera knepig att lösa i de olika matematiska uppgifterna — som det har visat sig).

KALKYLKORT

MED RESULTATVÄRDEN FÖR ALLMÄN PRÖVNING

Kärnradiernas medelvärden enligt TNED för Betainstabila nuklider

kalkylkort · kärnradierna · A anger masstalet · lägsta masstal är 2 — flik3

alla kortflikar i den här presentationen öppnas i samma huvudkort

se även öppningsmanual om ej redan bekant

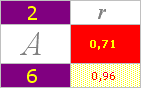
inmatningresultat · övre A-värdet anger stabila nuklidens masstal i givet grundämne (Z), undre A-värdet anger den betaINstabila nuklidens nominella masstal (kan anges godtyckligt).

Enheter i r/r₀, r₀=1,37 t15 M.

EXEMPEL MED KOLISOTOPERNA (från atomviktstabellen i HOP):

ZX^AmD	Z	X	A	r/r0	D	mDHOP
6C^1012,6216290	6	C	10	2,13	b+	12,6216290
6C^1113,7813878	6	C	11	2,18	b+	13,7813878
6C^1215,6594799	6	C	12	2,23	0	15,6594799
6C^1315,1931747	6	C	13	2,36	0	15,1931747
6C^1415,2409951	6	C	14	2,40	b–	15,2409951
6C^1514,3824741	6	C	15	2,44	b–	14,3824741
6C^1613,9991435	6	C	16	2,48	b–	13,9991435

För jämförelsen mellan TNED och HOP-tabellens data för atomvikterna, se ATOMVIKTERNA (TNED utklassar modern akademisk teori).

Fortsättning i Nuklidinstabila nuklidradierna.

nuklidinstabila kärnradierna

Kärnradierna för NUKLID-instabila nuklider enligt TNED

NUKLIDINSTABILA NUKLIDERNA nuklidsönderfall — Se även i Kärnradierna för BETA-instabila nuklider

I och med att de tungt radioaktiva nukliderna enligt TNED inte avger (någon märkbar) massa (elektronen) under sönderfallet, finns heller ingen egentlig särskild justering i kärnradierna för den nuklidgruppen (massavgivningen som föregår det aktuella utbrottet då kärnan delas är helt försumbar). Kärnradierna för den tunga radionuklidens grupp bör därmed följa samma mönster som de normalt stabila nukliderna (om inga ytterligare fördjupningar föreligger).

Laddningstätheten enligt TNED

Till kalkylkorten nedan.

Bilden ovan från diagramtexten i pdf-dokumentet till Hofstadters kurvskara,

”Charge density r — 10¹⁹ coulomb/cm³”, LaddningsTäthet r i T19 C/cM³

2008VIII30

Genomgående i denna presentation används (där inget annat anges) PREFIXEN I FYSIKALISKA ENHETER enligt MKSA-systemet (MeterKilogramSekundAmpere) med små bokstäver

för bråkdelarnas tusenmultipler (centi, milli, …) och stora bokstäver

för enheternas tusenmultipler (Kilo, Mega, …).

För termen laddningstäthet används här termen r (grek. rho, r i Symbol, r) generellt (också konventionellt) som termsymbol för täthet i olika sammanhang.

Med laddningstätheten som elektriska laddningen (Q) fördelad över volymen (V) enligt

r = Q/V_M .................. C/M³

ges enheten för r i Coulomb per kubikmeter.

I atom- och kärnfysiken används emellertid ofta laddningsenheten e=1,602 t19 C, lika med elementarladdningskvantumet eller elektronladdningen. Antalet enheter e betecknas i atomfysiken vanligtvis med bokstaven Z som associerar till det sk. atomnumret, samma som atomens negativa elektronhöljesladdning och lika med moderkärnans lika stora men positiva elektriska laddning.

Laddningstätheten kan då också skrivas mera upplysande enligt

r = Ze/V_M ................. C/M³

En bekväm, rent numerisk, enhetsform i kärnfysiken visar sig om vi också uttrycker volymdelen i r i enheter kubikcentimeter, cM³

— på grund av att atomkärnans storlek (protonradien) har visat sig ligga i storleksordningen Fermienheter, analogt

t15 M = t15 (100 cM) = t15 · T2 cM = t13 cM;

Volym kan alltid uttryckas med en volymfaktor (k) som ändras proportionellt mot en fast volymär grundenhet, säg r=1 Fermi eller 1 t13 cM.

Då kan laddningstätheten också skrivas mera generellt med grundenheten (r) i meter enligt

r = Ze/kr_M³ ................ C/M³

= Ze/2p²([n · r₀]³ · 0,0134618 ·3) ;

K = 2p²(n³ · 0,0134618 ·3) ; n anger funktionen för r-värdet i absoluta numeriska enheter (1) ;

r = Ze/Kr₀³

= Ze/Ka³(r_cM=1 t13 cM)³

k = Ka³ ;

= 2p²a³(n³ · 0,0134618 ·3) ;

r = Ze/kr_cM³

Med kuben på r = t13 cM ges då (t13 cM)³ = 1 t39 cM³ = 0,1 t38 cM³

— Och, som vi ser med e=1,602 t19 C, är exponenten t19 halva t38.

— Vi får då

r = Ze/k(0,1 t38) ................................ C/cM³

= Z/k · e/(0,1 t38) ............................ C/cM³

= Z/k · (1,602 t19)/(0,1 t38) ............ C/cM³

= Z/k · (1,602 t19)/(0,1 t19·t19) ..... C/cM³

= Z/k · (1,602)/(0,1 t19) ................... C/cM³

= Z/k · (1,602)/(0,1) · T19 ............... C/cM³

= Z/k · (16,02) ................................ T19 C/cM³

;

Enheten för laddningstätheten (r) blir alltså »automatiskt»

T19 Coulomb per cM³.

Det enda som återstår för att få värdet på r hos den aktuella formbyggnaden (atomkärnan) i T19e/cM³ blir att ersätta (16,02)/k med respektive numeriska resultatvärde (för givet Z). Notera (alltså) att det enhetliga MKSA-värdet för r fås genom att multiplicera r-värdet med T19 C/cM³.

I TNED gäller för toroidaggregatet N3m20 (se även basdimensionerna från TOROIDYTAN)

k = 2p²a³(n³ · 0,0134618 ·3)

a = 1,37 ..................................................................... från r₀=1,37 fM = 1,37 t15 M = a(1 t13 cM)

så att

k = 2p²(1,37)³(n³ · 0,0134618 ·3)

Den volymära laddningstätheten kan då skrivas enligt TNED mera exakt från masstalet A=2 enligt

r = Z/k · (16,02) ........................................................ T19 C/cM³

= Z[2p²a³(n³ · 0,0134618 ·3)]^–1 · (16,02)

= Z[n³ · 0,0134618 ·3]^–1 · (2p²a³)^–1 · (16,02)

= Z[n³ · 0,0134618 ·3]^–1 · (50,756473)^–1 · (16,02)

= Z[n³ · 0,0134618 ·3]^–1 · (0,01970191) · (16,02)

= Z[n³ · 0,0134618 ·3]^–1 · (0,1970191) · (1,602)

med n som den formfunktion som ger den aktuella volymen i rena relativa geometriska koefficienter.

I TNED är formfunktionen för n samma som grundformen för atomkärnornas radier utan hänsyn till inverkan från massdefekter eller elektronbesättningar (dessa ger i vilket fall bara marginella bidrag). n anges då i enheter enligt n=r/r₀ med r₀=1,37 fM.

För masstalet A=1 med Z=1 gäller specifikt med avseende på första underfraktalens toroidringar, djupare liggande fraktaler ger betydligt högre värden

r = Z[1³ · 0,000268904 ·3]^–1 · (0,1970191) · (1,602)

= 391,25 .................................................................. T19 C/cM³

Se även dimensionerna för A=1 och A>1 specifikt i TOROIDYTAN.

För den motsvarande IDEALT SFÄRISKA ATOMKÄRNAN ges med grundradien r₀=1,37 fM = a t13 cM sambandet

SFÄRISKA:

Q/V = Z[(n³)]^–1· 3(4pa³)^–1 · 16,02 ................................. T19 C/cM³

= Z[(n³)]^–1· 3(32,312574)^–1 · 16,02

= Z[(n³)]^–1· (0,09284311) · 16,02

= Zn^–3· (0,9284311) · 1,602

I efterföljande tabell kan vi studera två olika alternativ för sfären, dels med radien via den konventionella kubgrafen (n=r/r₀=A^1/3) och dels med samma n=r/r₀ som för toroidaggregaten.

Enhetsräkningarna nedan ger samma resultat som ovan.

(ENHETSRÄKNINGAR KAN tillhöra de mest krångliga matematiska övningar som existerar under stjärnhimlen garanterat

— Min rekommendation: utnyttja alla till buds stående exempel för att gå tillbaka och studera redan erkänt exakta lösningar [samla dem i en bok, vakta den med ditt liv: ju krångligare exempel, desto bättre övning]):

Q/V = Ze/2p²a²b

A>1:

= Ze/2p²(r³ · 0,0134618 ·3) .................................................. A>1

= Ze/2p²([n · r₀]³ · 0,0134618 ·3)

= Ze/2p²(n³r₀³ · 0,0134618 ·3) ............................................. C/M³ ; 1M = 100 cM ; 1cM = 0,01 M ;

= Ze/2p²(n³r₀³ · 0,0134618 ·3) ............................................. C/(100 cM)³

= Ze/2p²(n³r₀³ · 0,0134618 ·3) · 1/100³ ................................ C/cM³

Ovanstående insättning betyder att r₀-värdet fortfarande räknas i Meterenheter, men slutenheten blir som ovan, samt vidare nedan enligt

= Ze/2p²(n³r₀³ · 0,0134618 ·3) · t6 ......................................... C/cM³

= Z/2p²(n³r₀³ · 0,0134618 ·3) · t6 · e ...................................... C/cM³

Med

2p²r₀³ = 5,07564 t44 M ; 1/2p²r₀³ = 0,1970191 T43 1/M

ges

Q/V = Z/(n³ · 0,0134618 ·3) · (2p²r₀³)^–1 · t6 · e ............................ C/cM³

= Z/(n³ · 0,0134618 ·3) · (5,07564 t44)^–1 · t6 · (1,602 t19) .. C/cM³

= Z/(n³ · 0,0134618 ·3) · (5,07564)^–1 · T44 · t25 · (1,602) ... C/cM³

= Z/(n³ · 0,0134618 ·3) · (5,07564)^–1 · T19 · (1,602) ............ C/cM³

= Z/(n³ · 0,0134618 ·3) · (5,07564)^–1 · (1,602) ...................... T19 C/cM³

= Z/(n³ · 0,0134618 ·3) · (0,1970191) · (1,602) ..................... T19 C/cM³

= Z/(n³ · 0,0134618 ·3) · (0,01970191) · (16,02) ................... T19 C/cM³

Eller om vi fortsätter på ett alternativt (något mera krångligt sätt)

= Z/2p²(n³r₀³ · 0,0134618 ·3) · t6 · (1,602 t19 C) .................. C/cM³

= Z/2p²(n³r₀³ · 0,0134618 ·3) · t6 · (1,602 t19) ...................... C/cM³

= Z/2p²(n³r₀³ · 0,0134618 ·3) · t6 · (1,602 t19) · 1/T19 ......... T19 C/cM³

= Z/2p²(n³r₀³ · 0,0134618 ·3) · t6 · (1,602) · t38 .................... T19 C/cM³

= Z/2p²(n³r₀³ · 0,0134618 ·3) · t6 · t38 · (1,602) .................... T19 · C/cM³

= Z/2p²(n³r₀³ · 0,0134618 ·3) · t44 · (1,602) .......................... T19 · C/cM³

Med

2p²r₀³ = 5,07564 t44 M ; 1/2p²r₀³ = 0,1970191 T43 1/M

ges

Q/V = Z/(n³ · 0,0134618 ·3) · (2p²r₀³)^–1 · t44 · (1,602) ................. T19 · C/cM³

= Z/(n³ · 0,0134618 ·3) · (5,07564 t44)^–1 · t44 · (1,602) ....... T19 · C/cM³

= Z/(n³ · 0,0134618 ·3) · (5,07564)^–1 · (1,602) ...................... T19 · C/cM³

= Z/(n³ · 0,0134618 ·3) · 0,1970191 · (1,602) ....................... T19 · C/cM³

= a · 0,1970191 · (1,602) ....................... T19 · C/cM³

Eller (alternativt) mera utförligt:

= Z[2p²(n³r₀³ · 0,0134618 ·3 · ([0,01 M = 1cM]³)^–1 · T19)]^–1 · 1,602 t19 C ........ T19 C/cM³

= Z[2p²(n³r₀³ · 0,0134618 ·3)]^–1([0,01 M = 1cM]³) · t19 · t19 · 1,602 ................. T19 C/cM³

= Z[2p²(n³r₀³ · 0,0134618 ·3)]^–1· t6 · t38 · 1,602

= Z[2p²(n³r₀³ · 0,0134618 ·3)]^–1· t44 · 1,602

= Z[(n³ · 0,0134618 ·3)]^–1· (2p²r₀³)^–1 · t44 · 1,602

= Z[(n³ · 0,0134618 ·3)]^–1· (5,07564 t44)^–1 · t44 · 1,602

= Z[(n³ · 0,0134618 ·3)]^–1· (5,07564)^–1 · 1,602

= Z[(n³ · 0,0134618 ·3)]^–1· (0,1970191) · 1,602

= a · (0,1970191) · 1,602

SFÄRISKA:

Q/V = Z[(n³)]^–1· 3(4pr₀³)^–1 · t44 · 1,602 ....................... T19 C/cM³

= Z[(n³)]^–1· 3(3,23125 t44)^–1 · t44 · 1,602

= Z[(n³)]^–1· 3(3,23125)^–1 · 1,602

= Zn^–3· (0,928431) · 1,602

n anger funktionen för r-värdet i absoluta numeriska enheter (1).

kalkylkort · LADDNINGSvolymTÄTHETEN — flik4:

alla kortflikar i den här presentationen öppnas i samma huvudkort

se även öppningsmanual om ej redan bekant

2pbpa² = 2p²ba² | A=1: a²b = r₀³ · 2,68904 t4 | A>1: a²b = r³ · 0,0134618:

inmatningresultat · övre A-värdet anger stabila nuklidens masstal i givet grundämne (Z), undre A-värdet anger den betaINstabila nuklidens nominella masstal (kan anges godtyckligt).

r₀ = 1,37 t15 M Ñ = 2r₀

Som den inträngande komponenten ser atomkärnan dynamiskt (halva visuella) Som den icke dynamiskt växelverkande metriken definierar atomkärnans yttergränser enligt TNED (dubbla dynamiska)

OKÄNT InternetÖVERFÖRINGSFEL uppmärksammat först 4Apr2017:

— Ovanstående original — ursprungligen från Kalkylprogrammet i MsWORKS (användningen av MsWORKS förbjöds/vandaliserades oanmält av Microsoft i Windows Vista efter en VistaUppdatering — företaget vägrade ta bort den förorsakade uppdateringsfilen), senare anpassat efter OpenOffice, visade den här trevliga serveringen:

I övrigt inga uppmärksammade fel.

Volymära Laddningstätheten i T19 C/cM³

Alla r-värden i T19 C/cM³

Z	X	A	rTORO/r0	rTORO	rSfär rTORO	rSfär r(A^1/3)	HOFSTADTER	rTOROVisuella
1	H	1	1	391,25	1,487346655	1,487346655	14,18	55,01922551
1	H	2	0,71	22,10	4,206568589	0,743673327	—	3,11
2	He	4	1,06	13,14	2,501290014	0,743673327	2,56	1,85
6	C	12	2,23	4,25	0,808400212	0,743673327	1,32	0,60
8	O	16	2,70	3,16	0,602124234	0,743673327	1,27	0,44
12	Mg	24	3,10	3,15	0,59893344	0,743673327	1,42	0,44
20	Ca	40	3,32	4,27	0,812273802	0,743673327	1,27	0,60
23	V	51	3,55	4,01	0,763151588	0,670764178	1,21	0,56
27	Co	59	3,73	4,08	0,77561789	0,680650164	1,29	0,57
38	Sr	88	4,30	3,73	0,710733905	0,642263328	1,22	0,53
49	In	115	4,72	3,63	0,690889864	0,633739009	1,19	0,51
51	Sb	121	4,81	3,59	0,68316955	0,626898177	1,17	0,50
79	Au	197	5,52	3,67	0,698538697	0,596448658	1,10	0,52
82	Pb	208	5,58	3,68	0,70066097	0,586357816	—	0,52
83	Bi	209	5,59	3,72	0,70717516	0,590668767	1,08	0,52

Omräknat efter justering N=800 2008-08-26.

JÄMFÖRANDE TABELL FÖR NUKLEÄRT VOLYMÄRA LADDNINGSTÄTHETEN

2008VIII15

Grunddata på ämnesnukliderna i kurvskaran från Hofstadters presentation till jämförelse med resultaten i TNED.

Hofstadter anger inte nedanstående nuklidindivider till atomnummer och masstal, endast deras kemiska beteckning. Tabellen nedan har specificerat den delen (från atomviktstabellen i HOP) genom att ange den isotop som har störst representation i den nuklidgruppen.

r-värden markerade med vitt anger den del som medtagits i jämförelsen med Hofstadters kurvskara i VOLYMÄRA LADDNINGSTÄTHETEN.

Se även tabellförklaringen under tabellen. Visuella r=(PlanckEkv.r)1,923 från A=2 (förenklat värde 1/0,52=1,923 från 0,5179491).

Planckekvivalenten							Visuella
	ämne		a	radie	T19 C/cM^3		a	T19 C/cM^3
Z	X	A	Z/(n^3· 0,0403854)	r/r0	r	^ » HOF toppvärden		r
1	H	1	1239,60	1	391,25	14,18		55,02
1	H	2	70,03	0,71	22,10	—		3,11
2	He	4	41,64	1,06	13,14	2,56		1,85
6	C	12	13,46	2,23	4,25	1,32		0,60
8	O	16	10,02	2,70	3,16	1,27		0,44
12	Mg	24	9,97	3,10	3,15	1,42		0,44
20	Ca	40	13,52	3,32	4,27	1,27		0,60
23	V	51	12,70	3,55	4,01	1,21		0,56
27	Co	59	12,91	3,73	4,08	1,29		0,57
38	Sr	88	11,83	4,30	3,73	1,22		0,53
49	In	115	11,50	4,72	3,63	1,19		0,51
51	Sb	121	11,37	4,81	3,59	1,17		0,50
79	Au	197	11,63	5,52	3,67	1,10		0,52
82	Pb	208	11,66	5,58	3,68	—		0,52
83	Bi	209	11,77	5,59	3,72	1,08		0,52

a anger resultatvärdet för volymära laddningstätheten enligt TNED.

Enheten T19 C/cM³ är anpassad till Hofstadters kurvskara för direkt jämförelse.

»^HOF anger grafiskt uppmätta toppvärden från Hofstadters grafer i källskriften angiven i omedelbar anslutning till Hofstadters presentation.

r anger TNED-värdena till jämförelse med Hofstadters värden i T19 C/cM³.

Radievärdena för visuella delen fås approximativt som dubbla Planckekvivalentens tyngdcirkelradie (r) angiven i enheter r/r₀. För r-värdena, se KÄRNRADIERNA ENLIGT TNED, samt ovanstående kalkylkort för r-beräkningarna.

Planckekvivalenten: Som den inträngande komponenten ser atomkärnan dynamiskt (halva visuella, se från ATOMKÄRNANS STORLEK);

Visuella: Som den icke dynamiskt växelverkande metriken definierar atomkärnans yttergränser enligt TNED (nära dubbla dynamiska).

SKILLNADEN TNED(r)-HOFSTADTER(»^HOF):

Atomkärnans dynamik kan inte fullständigt penetreras av den inträngande masskomponenten (elektronmassa), denna kommer därför att avläsa en typiskt större volym — på grund av att projektilkropparna kastas ut från det inre av atomkärnan innan någon direkt kontakt sker med masskroppen. Observera dock att den avläsningsmagnituden högeligen också beror på projektilenergin — därmed fördelas tvunget den givna kärnladdningen på en experimentellt sett typiskt större volym och därmed lägre experimentvärde; Man får i spridningsexperimentets slutände en resultatform med lägre laddningstäthet (»^HOF) än den mera praktiskt giltiga råformen (r). Skillnaden mellan dessa avtar naturligtvis med att konturkroppen för den massinneslutande nuklidform tillväxer. Det är i varje fall den förklaring som är uppenbar enligt TNED.

HOFSTADTERS KURVSKARA: vertikalskalan 2,75/700p i pdf-dokumentet med visningsläge 234%.

Atomkärnans masstäthet | MPCompil | 2003III2

ATOMKÄRNANS MASSTÄTHET

Hela massan återförs på en och samma ringform (r) med växande masstäthet

Massfragmenteringen (MAFACE) i PASTOM (massan principstruktur)

[n®¥] · m/[n®¥] = m

utpekar i förening med energin som grundad på massa, laddning och spinn, ett fraktalsystem med ringar som består av ringar som består av ringar … i all oändlighet. Se utförligt från PLANCKRINGEN, om ej redan bekant. Ringarnas dynamik kopplar perfekt i analogi till de elektrofysikaliska principerna för en toroidspole (isolerad koppartråd som lindas på en toroidisk formkärna typ ringkroppen nedan). Ringarnas geometri kan därmed beskrivas utomordentligt genom toroidens formfysik.

Volymen för en toroid (se även Toroidytan) med cirkulär ringkropp är (Se tyngdpunktsmatematiken, alt. Guldins Regler; volymen är produkten av tvärsnittsytan pr_t² och rotationscirkeln med radien r genom tvärsnittsytans tyngdpunkt),

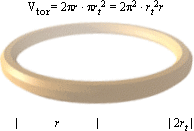
TNED lämnar ingen exakt upplysning om hur fraktalnivåerna ändras, frånsett första och andra nivån; Sätter vi förenklat n som aktuell fraktalnivå (toppnivån får n=1 [egentligen nollnivån i impulsanalogin]) och betraktar ringkroppens tvärsnitt (2r_t) som avtagande med motsvarande heltal för växande n så att 2:a ringnivån får (r_t)=r_t/2, 3:e ringnivån får (r_t)=r_t/3, osv., ges masstätheten (D) totalt enligt

D = m[V_tor=(2p²)r_t²n^–2r]^–1 ............................ D anger tätheten i KG/M³

= n²m[V_tor=(2p²)r_t²r]^–1

Se även i Atomkärnans Gravitella Härledning. Eftersom volymen hos varje ringfraktals egennivå beräknas med allt innanför ytan som kompaktvolym, men att den närmast mindre fraktalnivån i sin tur innehåller ihåliga ringkroppar, och så vidare i all oändlighet, bortfaller en stor del av den närmast övre moderringens volym på den aktuella fraktalnivåns mera kompakta volym. Totalvolymen kommer på så sätt att närma sig noll obegränsat med obegränsat växande antal fraktalnivåer (n). Masstätheten (D) går alltså tvunget mot oändligt då m fragmenterar — hur vi än räknar.

Denna detalj grundlägger f.ö. atomkärnans fullständiga okänslighet för gravitationens inverkan: atomkärnan kan inte krossas av gravitationen. Fraktalstrukturen som sådan i förening med elektriska kraftlagen F=k(Q/r)² visar därmed också att atomkärnan inte kan komprimeras: den står redan på noll enligt ovanstående fragmenteringsekvivalent Q/r = Q[n®¥]^–1/r[n®¥]^–1. Se även vidare i PASTOM (eng. Principal Structure of Mass, massans struktur), Atomkärnans inkompressibilitet, Atomkärnans härledning.

Tyngdcirkelns betydelse för kärnradierna | 2008VII

Se även från Atomkärnans Storlek

TYNGDCIRKELNS BETYDELSE FÖR BESTÄMNINGEN AV KÄRNRADIERNA ENLIGT TNED

genomträngningen

Genom att atomkärnan enligt TNED i sin kraftdynamik betingas av en central tyngdcirkel (r) i växelverkan med alla massbaserade energiutbyten, kommer också ”all påstötande verksamhet” att referera just tyngdcirkeln som typiskt ”atomkärnans radie” i alla massbaserade mätande experiment.

Se även från Atomkärnans Storlek.

Redan genom accelerationsspänningen 1 MV ges elektronen i vakuum hastigheten

u = c[1 – 1/[(UQ/m₀c²) + 1]²]^1/2 se sambandet för laddningshastigheten u genom accelerationsspänningen U i vakuum

lika med 0,94c. Om vi idealt förutsätter att kärnspinnet uppvisar c i kärnytans yttersta delar, avverkas vinkeln 120° eller 1/3 av hela omloppet hos protonkärnan med referensvärdet r=1,37 t15 M på tiden

T = d/c=2pr/3c = 9,57102 t24 S;

På samma tid hinner 0,94c-partikeln linjärt räknat

d = 0,94cT = 2,69716 t15 M

vilket är nära (1,96r) tvärs hela protonen! Rakt igenom bara.

I sådana experimentella sammanhang talar man emellertid snarare om flera hundra MeV än enstaka — men då räknar man också med avböjningar genom Coulombverkan vilket komplicerar bilden ytterligare.

SÅ:

Även för det som vi kan betrakta som ”relativt små energier” i elektronernas bombardemang av olika kärnkroppar — typ ’fjuttiga accelerationsenergier på 1 MeV’ — räcker dessa i princip gott och väl för att penetrera det inre av atomkärnan, innanför kärnans yttre toppspinn, och förutsatt att elektronen inte (av olika orsaker nämnvärt) böjer av från sitt spår; Atomkärnan är enligt TNED en öppen byggnad på flera olika sätt där olika yttre främmande partiklar mer eller mindre lätt kan slinka igenom utan större hinder — förutsatt tillräckligt höga hastigheter och insiktade på lämpliga partier.

Det är här HELT okänt vilken den MINSTA MÖJLIGA inträngningen är som en viss växelverkande partikel (t.ex. elektronmassa) kan åstadkomma på t.ex. en protonkärna. Men det ligger i sakens natur att det bör vara frågan om något betydelsefullt inträngningsvärde med referens till en absolut lägsta möjliga partikelenergi. Alltså: inte direkt noll.

Tvärsnittet

Därmed är saken klar:

Det går inte att avkänna atomkärnans ytterradie i dess egen form, inte i någon som helst absolut form med någon massbaserad instrumentering. Värdena man får blir alltid mindre än den sanna största radiella utsträckningen (med hänsyn till inträngningen genom atomkärnans toppspinn) med massbaserade hjälpmedel. Exakt hur, vet vi (här) ännu inte ehuru principen är klar; Man använder (nämligen) idealt en sfärisk laddningsmodell (som grundform) och anställer på den modellen en hypotetisk Coulombisk närväxelverkan enligt begreppet spridningstvärsnitt.

BEGREPPET TVÄRSNITT I DEN MASSBASERADE EXPERIMENTALFYSIKEN

Notera att begreppet ”tvärsnitt”, eng. ”cross section” i egentlig bemärkelse definieras som ”sannolikheten för växelverkan (mellan två partiklar)” (se exv. Wikipedia Cross section — physics) med typenheten ”yta”. Inte alla webbkällor klargör det explicit.

tvärsnittet	kollisionsparametern

Vänster: Om vi tänker oss att målkärnan ligger i krysset och strålpartikeln träffar målkärnan rakt på inåt inom dess projicerade skuggbild på avståndet i sidled r från krysspunkten, då kallas den cirkel som bildas av ytan pr² för spridningstvärsnittet med innebörden: För varje avstånd (r) från mittpunkten kommer strålpartikeln genom normal Coulombisk repulsion (eller attraktion) att påverka strålpartikeln genom t.ex. en avböjning (s°), figuren ovan höger. Det karaktäristiska r-värdet ger då en motsvarande avböjningsvinkel (s°); Mindre r ger kraftigare verkan och därmed större s. Analogt säger man att det s.k. tvärsnittet (eg. spridningstvärsnittet) avtar med växande spridningsvinkel, analogt ”kraftigare turbulens” vid sammanstötningen. Litet tvärsnitt, häftig växelverkan, stor spridning. Varje givet tvärsnitt innefattar sin specifika gränsvinkel (s°) med alla större s° inkluderade där — i formen av innefattade mindre cirkelytor, analogt mindre tvärsnitt.

En bra (den f.n. bästa) allmän källreferens till ovanstående begrepp finns (även) på webben @INTERNET i Hyperphysics — Georgia State University (2005), avsnittet SCATTERING CROSS SECTION. Se även den källans Alpha Scattering Geometry.

Men den verkliga atomkärnan ENLIGT TNED spelar bara en sådan ”perfekt sfär” på stora avstånd, inte på nära. Därför blir den sfäriska modellen heller inte särskilt användbar på TNED om det verkligen gäller att kolla närbilden (utom på stora avstånd förstås, men det räknas ju inte). Genom att atomkärnan hela tiden spinner och kränger, blir den sfäriska modellen — såsom den moderna vetenskapens experimentella substitut för atomkärnan enligt TNED — ytterst arbetsam i tolkningen av allmänna spridningsdata. Om målkärnorna är godtyckligt orienterade kan vi bara få ”medelvärden” — i princip, värdelös information. Den säger ingenting i sak.

I varje fall för partikelenergier som är tillräckliga för att bryta igenom atomkärnans yttre spinnskal, blir det allt tydligare att medelformen i den växelverkan bara kan ha atomkärnans tyngdcirkel som preferens. Vi får (som mest) veta tyngdcirkelns radie. Inget annat.

Se vidare från ATOMKÄRNORNAS RADIER GENOM EXPERIMENTELL MÄTNING.

kärnradierna

genom massdefekten

2008VIII22

KÄRNRADIEÄNDRINGEN ENLIGT TNED

SOM FUNKTION AV MASSDEFEKTEN

Massdefektens inverkan på Kärnradierna enligt TNED visar sig vara försumbar

LADDNINGSvolymTÄTHETEN — se grundbeteckningar och samband från TOROIDYTAN:

2pbpa² = 2p²ba² | A=1: a²b = r₀³ · 2,68904 t4 | A>1: ab = r³ · 0,0134618

Om vi utgår ifrån att MASSvolymTÄTHETEN är konstant,

m m · n

—— = ——— = konstant

V V · n

— oberoende av atomära massändringsfaktorn n = 1 – m_D/m_n — får vi generellt för toroidaggregatet volymreduktionen

nV = n · 2p²ba²

Om atomkärnans uppför sig med strävan att genomföra en så liten ändring som möjligt genom massdefektens fysik, analogt minsta möjliga kraft över minsta möjliga väg, kommer n-faktorn att relateras endast till det inre ringtvärsnittets ringradie a enligt

— se även resultatredovisningen nedan i kalkylkortet —

nV = 2p²b(aÖn)²

Den större ringradien b bibehålls då, analogt med minsta möjliga ändring i toppspinnets motsvarande omslutna volymyta. Vilket vill säga, atomkärnan reduceras enbart via den smala inre toroidringens radie aÖn. Som vi strax ska se, blir den ändringen mycket marginell sett till atomkärnan som helhet.

Atomkärnans tyngdcirkel beräknas från grunddimensionerna i N3m20-aggregatet enligt (r är radien i kärnbrunnens innersta lillcirkel som förenar de tre inre toppringarna, var och en med radien a+b)

r = r + a + b

Med tyngdcirkelns grundvärde lika med r_n=1 (neutronradien) är då

r = a(–1+2/Ö3)

a = r_n/42

b = r_n[119 + 80Ö3]/84(3+2Ö3)

= r_n · 0,4743488

Vi jämför tyngdcirklarna före (1) och efter (2) massdefekten (n) med ovannämnda villkor enligt

r₁ + a₁ + b a₁(–1+2/Ö3) + a₁ + b a₁(2/Ö3) + b a₁ + 3^1/2b/2 a₁ + 0,4107981 0,4107981 + 1/42

————— = ————————— = ————— = ————— = —————— = ————————

r₂ + a₂ + b a₂(–1+2/Ö3) + a₂ + b a₂(2/Ö3) + b a₂ + 3^1/2b/2 a₂ + 0,4107981 0,4107981 + n^1/2/42

kalkylkort · atomkärnans maximala radieminskning som funktion av atomära massdefekten — flik5

alla kortflikar i den här presentationen öppnas i samma huvudkort

se även öppningsmanual om ej redan bekant

inmatningresultat ·

Om formaggregatets proportioner bevaras exakt (kärnan zoomas ut), ges motsvarande

r_n/r = 1/n^1/3 ................................ kärnan bibehåller alla proportioner

Med a = r + a = konstant ges motsvarande för ändringen enbart på den större toroidcirkeln b enligt

r_n/r = (a+b₁)/(a+b₂)

med b₂ = nb₁ som ger

r_n/r = (a+b₁)/(a+nb₁) ................ kärnan ändras på den större inre toroidringens b-radie enbart

Kalkylkortet ovan visar resultaten: Med ändringsvariabeln enbart på inre toroidringens grovlek (2a) ges minsta formändringen, följt av ändringsvariabeln på hela formen (r) som betyder en ordinär förminskning, och sist på inre största toroidringens radie b som ger den största totaländringen via n-faktorn (ännu större förminskning sett till kärnans toppspinnande ytterform). Med villkoret för minsta möjliga ändring, analogt största möjliga energihushållning, väljer vi naturligt det första alternativet.

För neutron-proton-övergången med m_D=1,518 och r_n=1,32 Fermi, minskar r_n med runt 0,002%. Det är i den här framställningens ljus helt försumbart och kan bortses ifrån. Men ÄVEN om vi skulle räkna med ett sämsta fallet största skillnad (nb₁) blir minskningen ändå bara bråkdelar av procent, vilket heller inte spelar någon roll i den här framställningen; Med referens till neutronkvadratens mönstergeometri — med de fluktuationer som kan förekomma i det praktiska fallet, analogt med jämförelsen i atomvikter mellan TNED och HOP, i allmänhet A,aaaa eller bättre, i några fall A,aaa — kan vi knappast relatera en högre precision i antalet Fermidecimaler än max 3 för atomkärnornas tyngdcirklar, analogt r,nnn Fermi.

UPPFATTNINGEN ATT MASSDEFEKTEN SKULLE kunna VARA FÖRKNIPPAD MED EN BEVARAD TOPPSINNSRADIE är mindre relevant — analogt ett något litet växande b-värde med avtagande a-värde. Därmed (nämligen) demoleras tvunget den centrala och avgörande toroidens sammanhållning genom CENTRALKONTAKTERNA: reduceras a och samtidigt toppspinnets ytterradie bibehålls för atomkärnan totalt, tappar ringarna kontakten med varandra i centrum. Dessa kontaktpunkter måste under alla omständigheter bevaras då de bildar kärnans centrala dynamiska ”elcentral”. Därmed återstår bara de tre alternativen sammanställda i kalkylkortet ovan att välja på.

Impulsmomentets ställning klarlagd genom massdefekten

Med detta klarläggande är också frågan om impulsmomentets kvantitet (J=mwr²) avgjord i massdefektens ljus:

impulsmomentet måste minska analogt med massminskningen — alla faktorerna Jmr² avtar — ehuru minimalt om alternativet med a-reduktionen används (kalkylkortets r_n/r-resultat).

Formfaktorn i grundtoroiden (den som associeras med m20 i N3m20-aggregatet) ändras bara från 1/42 till 1/42,017. Även denna ändring är så liten att den inte spelar någon roll i den här framställningen.

För övriga atomkärnor tillväxer — då, tydligen — massdefekten successivt som funktion av fusioner med grundaggregatet N3m20 — och därmed återfaller alla ändringar för de tyngre nukliderna på grundaggregatets ackumulering på de tyngre nukliderna över masstalet (A). Vilket vill säga: Atomkärnans tyngdcirkel reduceras proportionellt mot endast massdefekten enligt föregående reduktionsfaktor n = 1 – m_D/m_n omsatt på minsta möjliga ändring av kärnans impulsmoment, analogt på toroidaggregatets a-faktor som ovan enligt aÖn. I omvänd mening kan grundaggregatets individer avdelas tillbaka med återbildningen inkluderad av deras egenskaper ur de tyngre atomkärnorna (vilket villkor [nuklidkriteriet] följer ur den grundläggande deriveringen av N3m20-aggregatet till det som gäller för masstalen från 2 och uppåt).

RESULTAT — kärnradiens ändring via massdefekten är försumbar:

Minskningen i radien hos atomkärnans tyngdcirkel — som funktion av att atomkärnan-atomen tappar massa under sin bildning till stabil nuklid — är uppenbarligen helt säkert försumbar i alla normala beräkningar enligt TNED.

Med minsta möjliga ändring i impulsmomentet under ombyggnaden, minskar aldrig kärnans grundtyngdcirkelradie mer än 0,027% och vilket gränsvärde gäller vid Järntoppen (m_Dmax=17,75). För neutron-protonsönderfallet blir motsvarande kärnradieminskning 0,0023%.

kärnradierna genom

elektronbesättningen

KÄRNRADIEÄNDRINGEN

enligt TNED

SOM FUNKTION AV ELEKTRONBESÄTTNINGEN

När neutronen sönderfaller till Väteatom frigörs samtidigt elektronmassa ur kärnlokalen och som bildar atomens elektronhölje — ekvivalent med en formteknisk deformation som påverkar totala tyngdcirkeln. Men den matematiken — elektronmassans struktur — ingår inte i materiefysiken.

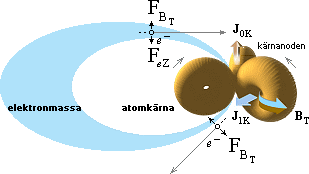
bakgrund

I TIDIGARE FRAMSTÄLLNINGAR — när ämnet ännu inte var så genomgånget som här — fanns uppfattningen (hos den här författaren) att massdefekterna skulle bidra till en ÖKNING i kärnradien. Eller rättare sagt, att neutronsönderfallet — med massdefekten inkluderad — skulle vara förknippat med en ökning i kärnradien. Massdefekten som sådan, som det nu visat sig (se KÄRNRADIEÄNDRINGEN SOM FUNKTION AV MASSDEFEKTEN), kan inte gå i god för en sådan ordning.

— Men elektronmassans utförsel från atomkärnan kan det. Vi ska studera den detaljen i den här avdelningen.

I TNED sammanhänger kärna och hölje i en och samma dynamiska byggnad enligt atomkärnas två kungsekvationer. Därmed ses elektronmassan utanför atomkärnan som en utvidgad del av atomkärnan, dock inte en stel sådan.

hävstångslagen

Eftersom elektronmassan, således, i vilket fall enligt TNED fungerar associerad med atomkärnan, kan vi också ställa upp ett motsvarande förenklat energi-momentresonemang (E=Fd) med grund i den välkända hävstångslagen

(Fd)₁ = (Fd)₂ ; (mad)₁ = (mad)₂ ; a₁=a₂ ;

(md)₁ = (md)₂ ................... HÄVSTÅNGSLAGEN INOM MEKANIKEN

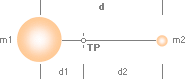
d = d₁ + d₂ ; d₁ = d/(1 + m₁/m₂) ; d₂ = d – d₁

Med kraftlagen F=ma — förutsatt samma a överallt i aktuell lokal, det Galileiska kraftrummet — ges från energin eller arbetet eller kraftvägen E=Fd den avgörande hävstångslagen m₁d₁ = m₂d₂.

Vi noterar att villkoret med Galileiskt kraftrum (samma accelerationskonstant överallt i mätlokalen) passar idealt även på detaljer av bestämda dimensioner inuti atomkärnan enligt TNED — eftersom gravitationen i atomkärnans kropp med avseende på sådana avgränsade detaljer är helt försumbar (se även i Atomkärnans Gravitella Härledning). För dessa förhållanden är det bara det yttre lokalt dominanta g-fältet som bestämmer preferenserna, analogt Jordytans lokala g-fält.

Hävstångslagen kan alltså tillämpas på atomen enligt motsvarande samband mr = m_e d med m som kärnmassan, m_e som elektronmassan, r som kärnradien och d som avståndet till elektronmassans tyngdpunkt.

Galileiskt rum, ett bekvämt begrepp för ett 3D-rum (xyz) där tyngdkraften överallt är idealiskt en och samma. Ett sådant typrum gäller på Jordytan inom vissa mindre områden, generellt inom en given s.k. ekvipotentialyta (idealt sfärisk geometri) — samma typ som bildade den ideala grunden för Galileo Galileis berömda banbrytande experiment med bronskulorna i den lutande rännan: kraftlagen F=ma.

samband

2008VIII23

PLANCKS KONSTANT h=6,62559 t34 JS (avr. 6,625, i viss litt. 6,626) sammanhänger med följande allmänna sambandsformer inom atom- och kärnfysiken ENLIGT TNED:

R = h(m_ec₀p)^–1 ........................... energicirkeln i härledningen till Väteatomens spektrum, se från Spektrum

= 7,72334 t13 M

r_n = h(m_nc₀)^–1

= 1,31974 t15 M .................. radien för neutronens tyngdcirkel

Tänker vi oss en enkel elementär balansvåg enligt hävstångslagen med balanspunkten d i m_nd = m_eR, ges

d = m_eR/m_n = m_eh(m_ec₀p)^–1/m_n = h(m_nc₀p)^–1 = r_n/p,

r_n/p = h(m_ec₀p)^–1

= 0,42009 t15 M .................. idealt nukleära jämviktsradien för neutronen och elektronen via atomära energicirkeln

= m_eR/m_n

ATOMÄRA ENERGICIRKELN FRÅN SPEKTRUM OCH KVANTTALEN fungerar emellertid INTE som någon reguljär tyngdpunktsreferens för elektronmassan enligt TNED, utan enbart som en medelbaserad impulsmomentscirkel kring vilken elektronmassan utför sina svängningar enligt villkoren i Kvanttalen (av de fem KVANTTALEN n q s_t µ_t F_t utgår de fyra sista från det s.k. huvudkvanttalet n, analogt med energicirkeln som definitionsbas). Tyngdpunktsanalogin ligger emellertid nära till hands — trots att den inte berör materiefysiken explicit. Och vi kan också finna en konsistent sådan mellan elektronmassan och Vätekärnan med hjälp av Neutronkvadraten — för att därmed klargöra atomkärnans beteende vid tillfället för själva besättandet av elektronmassa i den aktuella atomens hölje. Den händelse som kan relateras genom neutronsönderfallet är att kärnradien tvunget måste öka som funktion av att elektronmassan bildar en utdragen kärndeformation, och som därmed gör radien hos kärnans tyngdcirkel något större — generellt för nuklidkartan grovt sett runt 1% frånsett de allra lättaste atomkärnorna (nära 4% för övergången neutron-proton).

Grunden för den kopplingen är att ett ENLIGT NEUTRONKVADRATEN fast och rent mönsterförhållande kan utläsas mellan neutronradien r_n och protonradien r₀ (från kopplingen till deuteronbildningen, underförstått inkluderat via den möjliga protonindividen, se vidare den mera utförliga mönsterbeskrivningen i neutronkvadraten) enligt

r₀ = r_n (Ö8)/(1+Ö3)

= 1,3662137 t15 M

Kopplingen leder fram till en allmän syntes som sammanfattar kärn- och atomfysikens grundparametrar enligt TNED i ledet

r₀ = (m_er_nc₀/h)(r_e + pR[1–m_e/m_n]) · protonradien ur Plancks konstant, ljushastigheten, neutronmassan, elektronmassan

Termerna förklaras mera utförligt nedan i Resultatet i syntes efter Härledningen. Det visar sig att neutronmassan i detta samband INTE är kritiskt för r₀-värdet enligt

r₀ = 1,366216807 t15 M | m_e/m_n = 1/1838,624

= 1,366213663 t15 M | m_e/m_n = 1/1830,605 = (1,0043805)/(1838,624)

» 1,37 Fermi

Denna detalj har (på visst sätt) öppnat upp en del möjligheter för vidare tolkning (som innefattar dynamiken med delade elektronmassor mellan flera atomer och de olika överlappningsintervall som kan finnas). Men den delen kommer inte att föras längre i den här presentationen — utöver de resultat av mera allmän art som redovisas.

I den här framställningen räknas kärnradierna avrundat med två decimaler i Fermienheter, vilket ger

r_n = 1,32 Fermi

r₀ = 1,37 Fermi

Det betyder att proportionsfelet runt 1,366217/1,366213 = 1,0000029 — eller mönsterfelet, och i den mån skillnaden kan hänföras till ett sådant begrepp — helt saknar kvantitativ betydelse i den här presentationens ljus.

Denna detalj är också klar enligt följande.

LADDNINGSDEPLACEMENTET — se även delvis mera utförligt i Laddningsdeplacementet, och Kärnstrukturen — grundlägger kärnfysiken i TNED genom en laddningssumma noll genom ±e i atomkärnan med ett karaktäristiskt utskjutande positivt laddningsdeplacement som garanterar neutronens negativa kärnmagnetiska moment, och vilket ändras till ett positivt dito med neutronens sönderfall till en väteatom, se utförligt från NEUTRONENS SÖNDERFALL, illustrationen nedan.

protonens kärnyta

Med protonens kärnyta som exempel enligt TNED ges en direkt kvantitativ relationsbild för storleken hos laddningsdeplacementet (utskjutningen) med grund i förhållandet mellan kärnladdningen Z=1 och totalladdningen 1838,624 elektronmassor i protonaggregatet N3m20 utspritt på den inre ringkroppens grovlek r₀/20; Om i grovt orienterande termer kärnladdningens Z=1 står för ett deplacement på 1/1838 inom dimensionen r₀/20, ges totalt ett mönsterdjup på runt

r₀/20/1838 = r₀/36760

= (0,0000272034)r₀ ............. deplacementets strukturdjup i atomkärnans yta, r₀=1,37 t15 M

Värdet ger tydligen en djupform på i storleksordningen några hundratusendelar av kärnradien. Proportionsfelet ovan, som ligger en decimal längre ner, har därmed ingen som helst praktisk betydelse; Mönsterfelet göms effektivt av kärnstrukturen och dess naturligt fluktuerande variationer.

Det väsentliga i sammanhanget är resultatet att neutronradien tillväxer mot protonradien genom neutronens sönderfall — som funktion av elektronbesättningen. Nämligen — men vilken detalj inte ingår i den moderna akademins lärosystem — att elektronmassan avdelas från atomkärnan (neutronen) som en dennas förlängda utvidgning i den totala formen av en atom; Kärna och elektron bildar en enhet — I modern akademi och vetenskap däremot betraktas INTE elektronen som en enhet TILLSAMMANS med atomkärnan. Därmed relevansen i den motsvarande kärntyngdcirkelns utvidgning med motsvarande kärndeformation via elektronmassans utforsling. Sambanden ovan utgör, därmed tydligen, de mest elementära med hänsyn till vad som framgår genom Plancks konstant.

härledning

FÖR ATT FÅ MOMENTEKVATIONERNA F₁d₁=F₂d₂ TILL SAMBANDEN GENOM HÄVSTÅNGSLAGEN m₁d₁=m₂d₂ delar vi kärnmassan (m, neutronmassan) idealt i två lika delar med två motsvarande ideala lika masskroppar m/2. De bägge m/2-kropparna får BALANSERA — inte explicit rotera — kring sin gemensamma tyngdpunkt på avståndet r_n; r_n är den från Plancks konstant (h), neutronmassan (m_n) och ljushastigheten i vakuum (c₀) kända neutronens tyngdcirkelradie

r_n = h/(m_nc₀) ...................... neutronens tyngdcirkelradie, » 1,32 Fermi

Denna detalj visas som sekvens 1 enligt illustrationen nedan.

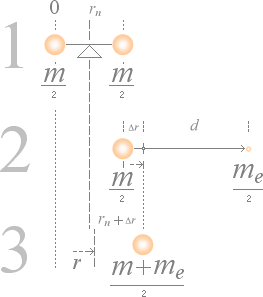
Vi tänker oss sedan att — sekvens 2 i illustrationen ovan — avdela motsvarande halva elektronmassa (m_e) från den masshalva (m/2) som vätter utåt atomrummet (åt höger i illustrationen ovan) — analogt med elektronmassans utförsel från kärnlokalen genom neutronsönderfallet som bildar Väteatomen. Sekvens 2 ger då genom hävstångslagen en ideal momentekvation

(m/2)Dr = (m_e/2)d

som efter förkortning av (1/2) ger det enklare

mDr = m_ed

Tillskottet Dr betyder, tydligen, att gemensamma tyngdpunkten för (m/2 + m_e/2) förskjuts utåt (höger) — med resultat i att r_n mellan de ursprungliga likformiga masshalvorna tvunget måste öka något till — sekvens 3 ovan — ett motsvarande något större r mellan de delvis nu marginellt men dock likväl deformerade masshalvorna som följd av elektronbesättningen.

Vi känner emellertid strängt taget inte den momentekvationen i någon bestämd form — eftersom vi inte känner det motsvarande (»slutgiltiga») avståndet mellan de bägge masshalvorna (m/2 och m/2+m_e/2); Momentekvationen skulle här ge mr=(m+m_e)a med d=r+a. Men då vi varken känner d, a, eller r finns ingen bestämd lösning.

I princip fås distansen a enligt

mr = (m+m_e)a ;

a = r · m/(m+m_e) ;

a = r(1+m_e/m)^–1 ;

a = r_n+ Dr ;

Om vi finner en approximativ lösning för r, kan vi sedan göra vidare jämförelser med en uppskattning av det relativa felet; I den här framställningen visar det sig att proportionsfelet (kalkylbladets referens, MsWORKS 4.0) i förhållandet mellan de olika kärnradierna i Fermienheter ligger i sjätte decimalen: a/(r_n+Dr) = 1,00000238; i presentationen används generellt inte mer än max tre Fermidecimaler.

Den närmast enkla approximationen för att reducera de okända faktorerna till endast en (r, frånsett Dr) blir att ersätta a med den (delvis) kända distansen r_n+Dr; Om skillnaden mellan r och r_n är liten, bör också felet i approximationen bli (mycket) litet. Vi kommer i vilket fall ändå i slutänden att få vissa felmarginaler beroende på att också atomkärnans m-kvantitet inte är enkel att bestämma exakt i den här balansanalogin: I sekvens 2, illustrationen ovan, är elektronmassan idealt delad i två hälfter varav den ena (vänstra) underförstått är associerad med »den vänstra fasta kärnmasshalvan» — för att därmed kunna räkna idealt på den högra balansdelen med elektronbesättandet utåt atomrummet; Då en sådan elektronmassahalvering med största sannolikhet INTE motsvarar något praktiskt fall, utan bara kan ses som en ideal förenkling, ligger redan en viss (mycket liten) osäkerhet i hela den här balansräkningen. Hela undersökningen går emellertid ut på att försöka finna en sambandsform där felformerna kan betraktas som försumbara, och därmed genom prövning en acceptabel kvantitativ härledning till den resulterande kärnradie som atomkärnan uppvisar efter neutronsönderfallet, analogt protonradien (r).

Sekvens 3 i illustrationen ger alltså slutmomentet

(m/2)r = (m/2 + m_e/2)(r_n + Dr)

som efter förkortning av (1/2) ger det enklare

mr = (m + m_e)(r_n + Dr) ;

r = (1 + m_e/m)(r_n + Dr) ; r/(1 + m_e/m) = r_n + Dr ; r/(1 + m_e/m) – r_n = Dr

I sammanfattning kan hela komplexet så långt förstås med beteckningar i nedanstående illustrationer.

d_e = D_r + d ; d = d_e – Dr ; (m/2)Dr = (m_e/2)d ;

mDr = m_ed

m/Dr = m_ed = m_e(d_e – Dr) ;

m/m_e = (d_e – Dr)/Dr = d_e/Dr – 1 ;

d_e/Dr = m/m_e + 1 ;

Dr = d_e/(m/m_e + 1) ; den resulterande momentarmen (m/2)r = (m/2 + m_e/2)(r_n + Dr) ;

mr = (m+m_e)(r_n+Dr)

r = (m+m_e)(r_n+Dr)/m = (r_n+Dr)(1+m_e/m) ;

Den atomfysikaliska konstant som vi säkert vet kopplar närmast till r_e är energicirkeln (den impulsmomentsgrundade referenscirkel i Spektrum kring vilken elektronmassan svänger i formen av stående vågmönster, se mera utförligt från Energicirkeln i Spektrum)

R = h(m_ec₀p)^–1

= 7,72334 t13 M

Jämviktscirkeln R med 2pR=l₀ för e definieras på nollzonens form (c_z=c₀/2, se potentialbarriären) i impulsmomentet för R från atomkärnans centralverkan enligt h=m_ec_zl₀.

Med hc_z fix kan ml₀ anta vilka som helst ömsesidigt inversa proportionaliteter varigenom jämviktscirkeln R kan definiera vilka som helst motsvarande slutna figurformer (R_x), dvs., olika svängningsformer. R avser alltså explicit INTE en reguljär tyngdcirkel för elektronmassan. Därmed kan R också, tydligen, gestalta en centralort för strukturekvivalenter till elektronmassans svängningsformer.

Se vidare utförlig beskrivning nedan från BEGREPPET TYNGDPUNKT FÖR ELEKTRONMASSAN.

Energicirkeln (också analog med innebörden av huvudkvanttalet n, enligt TNED) framkommer i samband med och är avgörande för härledningarna till Spektrum och Kvanttalen.

Med momentekvivalenterna, se ovanstående figurgenomgångar

d_e = r_e – 2r_n ;

D_r = d_e/(m/m_e + 1) ;

r = (r_n + D_r)(1 + m_e/m)

= (r_n + [d_e/(m/m_e + 1)])(1 + m_e/m)

= (r_n + [(r_e – 2r_n)/(m/m_e + 1)])(1 + m_e/m)

= r_n(1 + m_e/m) + (m_e/m)(r_e – 2r_n)

= r_n + r_nm_e/m + (m_e/m)(r_e – 2r_n)

= r_n + (m_e/m)[r_n + (r_e – 2r_n)]

= r_n + (m_e/m)[r_e – r_n]

= r_n + r_e(m_e/m) – r_n(m_e/m)

= r_e(m_e/m) + r_n – r_n(m_e/m)

= r_em_e/m + r_n(1 – m_e/m)

och en anpassning som utnyttjar koefficienter kända från neutronkvadraten (2Ö2=Ö8) samt p som redan figurerar i koppling till energicirkeln

r_e = R/pÖ8 ; 2pr_e = R/Ö2 ;

= h/p(m_ec₀p)Ö8

= h/m_ec₀p²Ö8

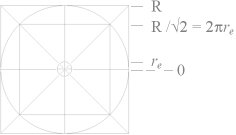
ges i fortsättning från r-leden ovan med insättning av r_e-ekvivalenten

r = (h/m_ec₀p²Ö8)m_e/m + r_n(1 – m_e/m)

= h/mc₀p²Ö8 + r_n (1 – m_e/m)

= h/mc₀p²Ö8 + (h/mc₀)(1 – m_e/m)

= (h/mc₀)(1/p²Ö8 + 1 – m_e/m)

= r_n · (1/p²Ö8 + 1 – m_e/m)

= r_n · (1+Ö3)^–1Ö8

RESULTAT:

Förutsatt att m_e/m_n = 1/1830,605 = (1,0043805)/(1838,624), ges då fullständig ekvivalens med mönsterformen från neutronkvadraten som visar

r/r_n = (1+Ö3)^–1Ö8 = Ö6 – Ö2

= (1 + 1/p²Ö8 – m_e/m) ;

r = 1,366213663 t15 M ;

Används för m_e/m_n istället det reguljära neutronmassavärdet i antal elektronmassor, m_n=1838,624 =(1,0086652u)/(0,000548598u), ges till jämförelse det obetydligt avvikande

r = 1,366216807 t15 M

= r₀

» 1,37 Fermi

Och som vi ser, är den proportionella avvikelsen (1,0000022) i dessa sammanhang HELT FÖRSUMBAR: m-kvantiteten är explicit INTE kritisk för att få t.o.m. ett mycket noggrant r-värde (in till miljondels Fermi). Se även i Laddningsdeplacementet som ytterligare understryker relevansen i det rent kvantitativa resultatet — sett till kärnstrukturens precision generellt enligt TNED.

KALKYLKORTET NEDAN med vidare beskrivning

visar resultaten i syntes.

R₀ = R/pÖ8 = 8,691815135 t14 M · R = h(m_ec₀p)^–1 = 7,72334 t13 M

kalkylkort · utvärdering för kärnradiens ändring som funktion av elektronbesättningen · beräkningarna ger protonradien 1,37 Fermi — flik6

alla kortflikar i den här presentationen öppnas i samma huvudkort

se även öppningsmanual om ej redan bekant

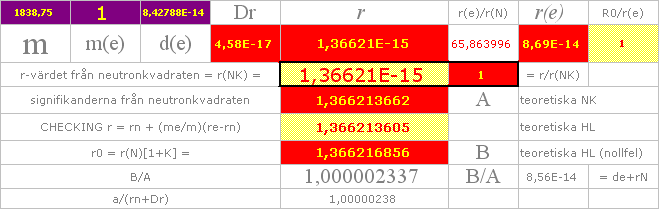
inmatningresultat ·

Nominella r₀-värdet från neutronkvadraten är r₀ = r_n 8^1/2/(1+Ö3) = 1,3662137 t15 M; K = 1/p²Ö8 – m_e/m

Neutronens tyngdcirkelradie är r_n = 1,319661061 t15 M = h(m_nc₀)^–1 | a = r₀(1+m_e/m)^–1

TEORETISKA RESULTATET VIA HÄVSTÅNGSLAGEN

r₀ = r_n(1 + 1/p²Ö8 – m_e/m) = r_n(1+K)

med de proportionella felgränserna genom olika alternativa testvärden på centralmassan m, m₀ anger protonmassan i antal e-massor

m i antal elektronmassor nedan:

m = 1836,0923 = m₀ 1838,624 = m_n 1838,75 1818 1830,605

R₀/r_e = 1,001426697 1,000052112 1,000000000 1,011225037 1,004377539 r_e = d_e+r_n+r_n

R₀/r_e = 1,016887932 1,015497892 1,026992691 1,019930733 r_e = d_e+r_n

d_e = 8,41550 t14 8,42743 t14 8,427882925 t14 8,33140 t14 8,39000 t14

(Fd)/NK = 1,000001577 1,000002301 1,000002337 0,999996342 1,000000000

r₀ = 1,366215817 1,366216807 1,366216856 1,366208664 1,366213663 protonradien t15 M

Kvoten R0/re fås exakt 1 med m=1838,75 och Dr=8,42788. 1838,75/1838,6235 = 1,0000688.

(Fd)/NK anger förhållandet mellan r beräknat dels från momentekvationerna (Fd) och dels från neutronkvadraten (NK).

Övergångsmassan som ger 1 ligger vid 1830,605

(Fd)/NK = r_n(1 + 1/p²Ö8 – m_e/m)/[r_n(Ö8)/(1+Ö3)], (Fd) refererar till hävstångsanalogin, NK till neutronkvadraten

(Fd)/NK = (1 + 1/p²Ö8 – m_e/m) · (1+Ö3)/Ö8

via hävstångslagen med energicirkeln · via neutronkvadraten

VÄTEKÄRNANS TYNGDCIRKELRADIE (r₀) kan alltså på visst sätt härledas ur VÄTEATOMENS ENERGICIRKEL R=h(m_ec₀p)^–1=7,72334 t13 M från Spektrum enligt

r₀ = (h/mc₀)(1 + 1/p²Ö8 – m_e/m) ; R = h/m_ec₀p = (m/pm_e)h/mc₀ ; h/mc₀ = R/(m/pm_e) = pRm_e/m ;

= R(pm_e/m)(1 + 1/p²Ö8 – m_e/m)

Eller, ekvivalent ur neutronkärnans tyngdcirkelradie (r_n = h/m_nc₀) enligt

= r_n (1 + 1/p²Ö8 – m_e/m)

= 1,366216312 ±0,000000495 t15 M

med elektronmassan m_e och kärnmassan m som VALFRITT

protonkärnans massa (Väteatomens massa minus elektronmassan), ger det lägre radievärdet 1,366216312 t15 M +4,95 t22 M = 1,366215817 t15 M

m₀ = 1,0078252u – 0,000548598u = 1,0072766u ........................ protonmassan i atomära massenheter u, 1u=1,66033 t27 KG

eller neutronkärnans massa, ger det högre radievärdet 1,366216312 t15 M –4,95 t22 M = 1,366216807 t15 M

m_n = 1,0086652u .......................................................................... neutronmassan i atomära massenheter u

TOLERANSEN LIGGER I VILKET FALL HELT UTANFÖR OMRÅDET FÖR DET HÄR FRAMSTÄLLNINGEN: Avrundade kärnradievärden används genomgående av typen två decimaler i området Fermi (t15 M) enligt

r_n = 1,32 Fermi ........................ neutronradien, tyngdcirkeln

r₀ = 1,37 Fermi ........................ protonradien, tyngdcirkeln

Øt = r₀/50 = 0,02r₀ ................... t-ringens diameter (sämsta fallets beräkningar, elektronmassans komponenter)

Kärnstrukturen med deplacementet innefattar i vilket fall kontinuerliga variationer och fluktuationer som gör precisionen i djupare mening meningslös.

Resultatet i syntes:

r_e elektronmassans momentrelaterade tyngdpunktsavstånd från Vätekärnan

för härledningen till protonradiens ekvivalent i neutronkvadraten

;

r₀ = r_n(1 + 1/p²Ö8 – m_e/m) ............................... (1 + 1/p²Ö8 – m_e/m) = (1+Ö3)^–1Ö8 ; MED m_e/m_n = 1/1830,605 = (1,0043805)/(1838,624)

= h(mc₀)^–1(1 + 1/p²Ö8 – m_e/m)

= R(pm_e/m)(1 + 1/p²Ö8 – m_e/m) ................... R = h(m_ec₀p)^–1, Väteatomens energicirkel i härledningarna till Spektrum och Kvanttalen

= (pm_e/m)(R + R/p²Ö8 – Rm_e/m) ................. r_e = R/pÖ8 ; 2pr_e = R/Ö2

= (m_e/m)(pR + r_e – pRm_e/m)

= (m_e/m)(r_e + pR[1–m_e/m]) .......................... r_n = h/(m_nc₀); 1/[m=m_n]=r_nc₀/h

= (m_er_nc₀/h)(r_e + pR[1–m_e/m_n]) ................... alla 8 basparametrar samlade: h r_n m_n m_e r_e R r₀ c₀

= 1,366216807 t15 M | m_e/m_n = 1/1838,624

= 1,366213663 t15 M | m_e/m_n = 1/1830,605 = (1,0043805)/(1838,624)

» 1,37 Fermi

r₀ = (m_er_nc₀/h)(r_e + pR[1–m_e/m_n]) · protonradien ur Plancks konstant, ljushastigheten, neutronmassan, elektronmassan

kalkylkort · grundläggande naturkonstanter — flik7

alla kortflikar i den här presentationen öppnas i samma huvudkort

se även öppningsmanual om ej redan bekant

inmatningresultat · Ö6 – Ö2 = (1 + Ö3)^–1Ö8 = 1,03527618 | 585 = 65 · 9 | 1 Fermi = 1 t15 M = 1 fM = 1 femtoMeter

NOTERA att olika källor använder delvis olika referensvärden till de olika konstanterna. Här har valts den uppsättning som ansluter till redovisningen under HOP för enhetlig referens.

BEGREPPET TYNGDPUNKT FÖR ELEKTRONMASSAN har vad vi vet i den praktiska bemärkelsen UR EXPERIMENTELL SYNVINKEL ingen bestämd definitionsgrund; Elektronmassans inre tillhör massfysiken, och den kan i vilket fall inte studeras på den bas som utmärker materiefysiken (generellt atomfysiken): Elektronmassan (atomskalets elektronmoln eller s.k. orbitaler) kan anta i princip alla möjliga typformer med inneslutna konturvolymer, och som dessutom kan ändras kontinuerligt med atomens energigenomströmningar, inkluderat kopplingar till andra atomer.

Man skulle i det läget vara benägen att säga: en elektronmassans tyngdpunkt — med avseende på minst två symmetriskt belägna punkter utanför atomens centrala tyngdpunkt — kan i princip ha vilket som helst värde eftersom elektronmassan med avseende på den punkten likväl kan anta olika formkonturer i en, vilken som helst, utsträckt rymdvolym — eller ha bara ett bestämt symmetriskt minst tvåpunkts- värde (för t.ex. Väteatomen) som fungerar som generell referens och som kan tillämpas ekvivalent för samtliga fall i allmänna energiräkningar.

Elektronmassans tyngdpunkt som sådan avgör i vilket fall absolut ingenting om elektronmassans utsträckning; Elektronmassans principiella (»orbitala») utsträckning fungerar oberoende av tyngdpunktens ort. Vi kan studera det genom ett motsvarande konkret formexempel;

Strukturekvivalenter till elektronmassans tyngdpunkter

ILLUSTRERAT MÖNSTEREXEMPEL

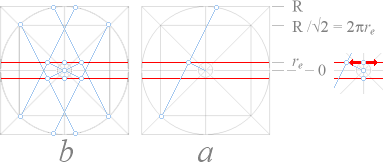
Figuren ovan (a) visar proportionerna i resultatet från kopplingarna till protonradien (r) via energicirkeln R och elektronmassans tyngdpunkt r_e, föregående beskrivning.

Om vi i högra figuren (a), den lilla delen ytterst till höger, utgår från de bägge kring kärncentrum symmetriskt belägna r_e-punkterna som den ideala orten för Väteatomens elektronmassa, se föregående genomgång från KÄRNRADIEÄNDRINGEN SOM FUNKTION AV ELEKTRONBESÄTTNINGEN, och därifrån via en normalvinkel (N) lika med noll grader i vertikaldelen (|) drar ut respektive elektronmassa i två lika symmetriska delar (¯|¯) som de röda pilarna antyder i den övre r_e-punkten, finns på enklaste sättet för varje sådan utdragning en normal (RätVinkel) till vinkellinjen för N som bildar korda (cirkelBågSkärandeLinje) med R i tvenne återigen likaledes symmetriska ändpunkter, figurexemplet i a.

Därmed kan elektronmassan via elektronmassans komponenter dras ut och fördelas lika via successiva symmetriska tyngdpunktsdelningar — med bibehållna respektive tyngdpunkter genom den beskrivna symmetriverkan — och därmed i netto ingen ändring relativt idealtyngdpunkten i r_e.

Figurexemplet i b visar vertikalsymmetrin fullständigt med referens till a-formen.

Som vi ALLTSÅ ser, kan R-cirkeln, verkligen, besättas med elektronmassans komponenter från r_e-punkterna — ehuru inte i någon exakt jämn symmetrisk fördelning över R-bågen — och det finns heller inget sådant fysikaliskt villkor, se föregående markerade stycke i Energicirkeln. Elektronen som kvantitet kan alltså, emellertid likväl rent positionsmässigt på visst sätt, befinna sig TILL EXEMPEL på R-bågen och samtidigt ha kvar tyngdpunkten idealt vid r_e-noderna. Därmed har det tydligen etablerats en strukturekvivalent till energicirkeln R med dess olika och möjliga svängningsformer, och som hela det här ämnet också handlar om: stående vågor, resonanser i elektronmassan (Se särskilt i Härledningen till Periodiska Systemet, om ej redan bekant).

Med en annan referensform än just R-cirkeln, kan samma PÅ-fördelning bildas, men med ändrade proportioner i den ojämna fördelningen relativt R-fallet. Därmed kan med utgångspunkt från r_e-punkterna i princip vilka som helst ytterkonturer (närmast »orbitaler») bildas av elektronmassans komponenter — och förutsatt dessa är av något större antal (se Elektronmassans komponenter, sämsta fallets beräkningar enligt TNED ger minsta antalet 177062 t-ringar för elektronmassan, vilken beräkning också grundas på R-cirkeln från Spektrum).

kalkylkort · vinkelfördelningen elektronmassans besättning · beräkningar för strukturekvivalent — flik8

alla kortflikar i den här presentationen öppnas i samma huvudkort

se även öppningsmanual om ej redan bekant

inmatningresultat ·

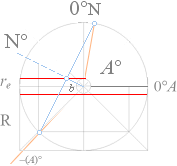
Allmänna samband med koppling till ovanstående figur

R = energicirkeln, alla samband i PREFIXxSIN:

r_e = R/pÖ8 = R(0,1125395) ;

b = origo till skärningspunkten med r_e-kordan; r_e/b = sinN; b = r_e/sinN ;

T = triangelvinkeln b.R ; b/R = sinT = r_e/RsinN;

A° = 90–(T–N) = 90–T+N = N + 90–T

= N + acos(r_e/RsinN);

–(A°) = A° – 360 ;

Nmax = asin(r_e/R) = asin(1/pÖ8) = 83,53827°

ALLMÄN RESULTATBESKRIVNING

A-vinkeln kan, verkligen, I PRINCIP fördela elektronelement från den övre r_e-punkten (vars symmetriska avdelningar glider på r_e-kordan åt vänster med växande N°) över hela den avgränsade övre r_e-sektorn, samt ytterligare nedanför r_e-kordan i bidrag till den undre delen

— in till en viss maxvinkel (här ca –(A°)= 129,2° med N° ca 70,4) och som sedan vänder tillbaka minskande igen då N går mot sitt maximum.

Därmed är det tydligt att elektronmassans idealt beräknande r_e-tyngdpunkt harmonierar fullständigt med den allmänna energicirkeln R i Spektrum och Kvanttalen.

Om det inte vore för neutronkvadratens mönsterkoppling för neutronradien till protonradien, skulle det heller inte finnas någon egentlig, fast, referens för en motsvarande r_e-tyngdpunkt — och som då, i princip, skulle hänga löst i fysiken.

NOTERING. Observera (Augusti 2008) att ovanstående begrepp är helt ny mark i fysiken: det finns (ännu) inga vetenskapliga avhandlingar som berör ”elektronmassans tyngdpunkt” eller någon typ ”elektronmassans strukturekvivalenter”. Det området är — tydligen — HELT reserverat för TNED. I modern akademisk teori finns heller ingen koppling till föreställningen att neutronradien skulle öka med sönderfallet till vätekärnan — med referens till de traditionella faktakällorna [ref. FOCUS MATERIEN 1975 s116sp1m ”… elektronen helt enkelt inte kunde rymmas i kärnan.”], anses det inte att elektronmassan kommer från atomkärnan: den möjligheten avfärdades redan tidigt med hänvisning till de Broglies vågekvation: elektronen skulle inte få plats i atomkärnan; i andra sammanhang, kvantteorin, anses dock elektronen vara en oändligt liten partikel (som dessutom tillåts besitta oändlig massa, se citat i Elektronen i modern akademi); det passar alltså på olika sätt i modern akademi, och du vet aldrig, och inte jag heller, vilket som gäller från stund till annan om du inte är insatt — eftersom den moderna akademins fysikbild är uppfunnen, inte härledd. Därmed förblir vägen stängd för modern akademi.

referens

Om mönsterkopplingen med r/r_n=(1+Ö3)^–1Ö8 till neutronkvadraten tas bort från r-sambandet nedan genom r=r_n,

r = r_n(1 + 1/p²Ö8 – m_e/m) ;

1 = 1 + 1/p²Ö8 – m_e/m ;

m_e/m = 1/p²Ö8 ;

finns heller inte längre något fast kriterium kvar för TYPEN ”elektronmassans tyngdpunkt”: Förhållandet urartar med m enligt

m = m_ep²Ö8 = ’27,915456 elektronmassor’

På den grunden är det tydligt att varje kopplande härledning helt saknas till något samband alls inom atomfysiken — vilketsom med en typ ”neutronmassan 1838,624e” som grundform. Sambanden har alltså därmed urartat och har ingen som helst begriplig innebörd.

Neutronkvadratens mönsterform med den utmärkta mönsterkopplingen

r/r_n=(1+Ö3)^–1Ö8 ger därmed alldeles tydligt en klar och koncis soliditet åt begreppet tyngdpunkt (r_e) för Väteatomens elektronmassa genom relationerna mot energicirkeln R.

Den solida byggnaden visar oss, tydligen, på ytterligare detaljer som av naturliga skäl inte kan härledas ur materiefysiken och som vi därför förut inte kunde veta något om, alls — motsvarande strukturekvivalenter, ovanstående exempel. Med deras hjälp kan vi nu verkligen se att atomfysikens övriga detaljer med t.ex. Spektrum också harmonierar: elektronmassan PÅ R-cirkeln FRÅN r_e-tyngdpunkten. Just med referens till denna senare del, atomens spektrum, att det (genom ovanstående beskrivning) verkligen tycks finnas en relevant koppling mellan materiefysikens spektrala grundbegrepp (R) och en djupare liggande massbaserad fast mönsterform (r_n och r i neutronkvadraten), bidrar alldeles tydligt till en djupare förståelse för atomfysikens allmänna begrepp såsom grundade på just fasta, tidlösa, naturgrundade och fullt härledningsbara mönsterformer — inga människoskapade uppfinningar.

Med ovanstående utvikningar står det därmed klart:

En »elektronmassans allmänna tyngdpunkt» kan omöjligen härledas ur materiefysiken, eftersom elektronmassan där representerar en odelbar kvantitet som grundlägger all fysikalisk mätning i formen av hela, odelbara, tal motsvarande hela antal våglängder som svänger i fasta resonanser kring den motsvarande energicirkelns (R) jämviktsform och som därmed grundlägger varje fysikalisk mätande anordning.

Av samma skäl kan heller inte »neutronradiens ändring till protonradien» härledas ur någon materiefysik, eftersom den härledningen också innefattar en process — de enskilda inre stegen och momenten, och därmed begreppet struktur — med elektronmassans komponenter som agenterna i utforslingen av massa från atomkärnan till atomhöljet. Det finns ingen sådan tillgänglig materiefysik i universums bok. Det området är alltså uppenbarligen reserverat för massfysiken. Vore det nu så illa att naturen INTE hade lämnat oss någon ”mönstersten” på vars chiffer vi kunde förstå funktionerna — nämligen och tydligen just neutronkvadraten — funnes heller ingen sambandsform typ ”mönsterkopplingen r/r_n=(1+Ö3)^–1Ö8” och därmed heller ingen motsvarande koppling till R-cirkeln i atomens spektrum.

Det enda som krävs för att sammanknyta materiefysiken med massfysiken till en härledningsbar enhet, blir med ovanstående utläggningar — således — en redan inneboende, naturligt föregiven mönsterform, fullkomligt härledningsbar ur naturlogiken, och som ensam kan ombesörja och sammanknyter alla detaljer till en begriplig harmonierande enhet — likt Pythagoras sats i matematiken. Eller med andra ord (alltså) neutronkvadraten. Neutronkvadratens koppling till atomvikterna i jämförelsen med modern akademisk teori (Weizäckerekvationen) har redan visat den suveräna överlägsenheten och träffsäkerheten hos TNED i det uppenbart harmoniska äktenskapet med experimentalfysikens resultat.

Värdet 1,37 Fermi

MÖNSTERKOPPLINGEN r/r_n=(1+Ö3)^–1Ö8 I NEUTRONKVADRATEN som visar r=1,37 Fermi kopplar direkt kvantitativt till HOP-källans tabellerade referensvärde för protonradien i kubanalogin. Det värdet kommer från en av Hopkällans fem beskrivna experimentalmetoder för massbaserad mätning av atomkärnornas radier (metod nr3, spegelkärnor, energiobservationer).

HOP-tabellvärdet r₀=1,37 Fermi för protonradien i kubgrafen r=r₀A^1/3 är ett epokvärde; det användes (som mest) under 1900-talets senare hälft (från 1963 och framåt), men har numera (från 1990-talet) knappast någon vidare innebörd i moderna vetenskapliga sammanhang. Den motsvarande ”klassiska r₀-kvantiteten” i kubgrafen tycks dessutom (numera) ha ersatts av värdet 1,2 Fermi — men ingalunda alla källor använder det värdet.

Att värdet r » 1,37 Fermi verkligen framgår ur neutronkvadratens mönsterkoppling

r/r_n=(1+Ö3)^–1Ö8 med r_n=h(m_nc₀)^–1 » 1,32 Fermi kan först möjligen synas som ett synnerligen sensationellt sammanträffande.

— Jag hade i varje fall aldrig brytt mig om att eftersöka någon sådan mönsterkoppling för min del i mitt uppdagande i ämnet om det inte hade varit just för HOP-värdet 1,37 Fermi. Det var på den vägen allt började i min historia.

Emellertid faller sig saken också naturligt ur den experimentella synvinkelns ljus: Metod nr3 av de fem redovisade i Hop-källan baseras på s.k. spegelkärnor — som dock bara är tillämplig på de lättare nukliderna; Man utnyttjar atomkärnor med samma masstal (A) som uppvisar olika proportioner motsvarande bildningsindivider protoner-neutroner — och kan på den vägen, via enklare antaganden, få fram resultat. Eftersom också, som tidigare antytts, atomkärnorna växelverkar med referens till just sina tyngdcirklar, kan metoden med spegelkärnorna vara just den helt idealiska för att få fram ett förhållandevis noggrant värde på just tyngdcirkeln. Att döma av sammanträffandet, är den förklaringen den mest troliga — OM det nu är så att det är TNED som gäller i fysiken.

Genom den tekniska utvecklingen på området LASER har (speciellt under 1990-talet) nya mätmetoder introducerats tillsammans med datorbehandling (enorma beräkningsprogram). Tillsammans med den allmänna uppfattningen att atomkärnan är en byggnad bestående av inre beståndsdelar, har samtidigt och därmed, också helt nya begrepp introducerats i samband som berör begreppet ”kärnradie”— t.ex. typ ”laddningsradie”, ”haloradie” m.fl. — och som är helt väsensfrämmande i termer av ”den klassiska experimentalfysiken” med sina massbaserade spridningsexperiment.

Därmed kan vi inte längre studera kärnfysiken på den gamla klassiska experimentalfysikens villkor — enbart. Laserspektroskopin har enligt TNED speciella företräden, och att beskriva dessa kräver därför särskild uppmärksamhet — speciellt som området (ännu) är ytterst snårigt och svårnavigerat: det finns knappast (ännu Augusti 2008) någon webbkälla alls som beskriver begreppen i något förklarande ljus — trots en närmast enorm flod av forskare/författare som använder begreppen i olika pdf-dokument och övriga rapportverk. Den allmänna strävan hos dessa författare är att försöka ”förklara” mätresultaten i termer av »den allmänna kvarkteorin»; Då vet vi att terminologin är därefter också: oerhört komplicerat, få hänger med.

kärnstrukturens inverkan

på kärnradierna genom elektronbesättningen

2008VIII26

KÄRNRADIEBILDNINGEN

genom elektronbesättandet (neutronsönderfallet)

SOM FUNKTION AV np-STRUKTUREN

eller Kärnradierna som funktion av AZ-strukturen

kalkylkort · kärnradierna genom elektronbesättningarna · enheter i 1,37 Fermi — flik9

alla kortflikar i den här presentationen öppnas i samma huvudkort

se även öppningsmanual om ej redan bekant

inmatningresultat · lägsta masstal A från 2.

turb avser sambanden i maximal ”turbulens”, analogt i kärnans bildningsögonblick då optimala omkastningar KAN föreligga enligt

r_A = r[1 + (A/Z)K]; Z/A är omkastade, samt divisionen med Ö2 utesluten — samt Planckekvivalentens stabila form multiplicerad med den visuella kärnans faktor 1/0,5179491 = 1,9306916 i fallen A>1. Jämför fallet Li¹¹ (8,6 mS) från Tanihata 1985.

Med från föregående härledningar

K = 1/p²Ö8 – m_e/m_n » 1/28

r₀ = r_n(1 + K)

;

OM ALLA ATOMKÄRNOR BYGGS med en A=Z=1-individ (neutronaggregatet), samt att alla atomkärnor också får samma kärnstruktur med A=Z, SKULLE vi på enklaste sättet kunna beskriva alla tyngre atomkärnors tyngdcirklar från A=2 och uppåt på motsvarande ändringsfaktor

r_A = r[1 + (Z/A)K] .................... A masstalet, Z atomnumret (motsv. antal ekvivalenta bildningsprotoner)

Grundradien r motsvarar funktionen för adderade grundindivider (r_n) typ vattendroppar enligt kubgrafen, modell r=r₀A^1/3.

Emellertid tillväxer motsvarande antalet ekvivalenta bildningsneutroner (A–Z=N) mera än antalet ekvivalenta bildningsprotoner (Z) med växande masstal (A): Nuklidkartan (AZ) ger en ungefärlig förekomstlinje med stabila nuklider approximerat omkring positionen A/Z=12/5.

Eftersom dessa överskottsneutroner tydligen INTE bidrar med något sönderfall r₀=r_n(1+K), ges heller inget tillskott för dessa fall i kärnradiens ökning. Därmed kan kärnradieutvidgningens dämpning återföras på faktorn (Z/A) tillsammans med den ordinarie K-faktorn.

Reduktionen med faktorn Ö2

Emellertid gäller kärnradiens utvidgning från r till r_n strängt taget endast för A=1. För övriga atomkärnor gäller som bekant enligt TNED att kärnradien UNDER FUSIONSFASEN reduceras med 1/Ö2 från masstal A=2.

Med denna ändring inkluderad kan den fullständiga kärnradieändringens samband genom elektronbesättningarna på enklaste sättet tecknas

r_A = r[1 + (Z/A)K/Ö2] ............................................................... A>1, Z>1

Med K/Ö2 = 0,0249457 = 1/40,087051 ges då approximerat med enkla koefficienter

r_A = r[1 + (Z/A)/40] .................................................................. A>1, Z>1

med r från tidigare utvecklingar enligt

r = r₀A^1/2(0,4404609)(1,1377 – A/800)[1 + x(3 + x⁵)^–0.7] ....... x = (A – 2)/15, se Kalkylkortet Linjära komplementet

;

r₀ = r_n[1 + K]

= 1,36621 t15 M

» 1,37 Fermi

r_n = h/m_nc₀

= 1,31974 t15 M

» 1,32 Fermi

K = 1/p²Ö8 – m_e/m_n

= 0,0352785

OBSERVERA DOCK att sambandsformerna ovan INTE gör anspråk på att vara fullständigt härledda.

Endast de faktorer har beaktas som synts relevanta för redan kända kärnegenskaper.

Skillnaden mellan nukliderna inbördes blir inte stor: i stort sett en radieökning med 1%, eller

r ·1,01 för samtliga nuklider — utom neutron-protonfallet som uppvisar den största ändringen med runt 4% (1,038).

kärnradierna hos nuklider under bildning

KÄRNRADIERNA HOS (INSTABILA)

NUKLIDER UNDER BILDNINGSFASEN

KÄRNRADIERNA HOS ATOMER SOM INTE UPPVISAR STABILITET — INOM MINUTER, TIMMAR, DAGAR, VECKOR, MÅNADER OCH ÅR

Med fortsättning från föregående Elektronmassans momentrelaterade tyngdpunktsavstånd från Vätekärnan

Se även i KÄRNRADIERNA FÖR BETAINSTABILA NUKLIDER.

När en viss särskild nuklid (atom med specifik atomkärna) bildas genom t.ex. fusion, finns i varje fall enligt TNED ingen explicit bestämd form för en motsvarande »atomkärnans radie». Komponenterna befinner sig, då, under häftig dynamisk ombyggnad som innefattar de möjliga fasväxlingar, fasvridningar och övriga fundamentala ändringar som tidigare omnämnts i samband med Nuklidbildningen där centralmassivet (1818e-stocken i varje ekvivalent bildningsneutron) undergår genomgripande förändringar.

Om vi enbart tar fasta på de parametrar som framkommit i ovanstående allmänna härledningar

r_A = r[1 + (Z/A)K/Ö2]

och som endast (enligt TNED) är tillämpliga på stabila nuklider, kan vi göra en motsvarande ”sämsta fallets omvändning” för att relatera en viss atomkärnas absolut optimalt motriktade kärnradie — som är maximalt regelvidrig för varje utifrån påträngande komponent — enligt

(r)_A = r[1 + (A/Z)K]· 1/0,5179491 .................... gäller från A=2

;

1. Divisionen med Ö2 har tagits bort — eftersom atomkärnan inte är färdigbildad än.

2. Kärnstrukturkoefficienten Z/A är omkastad — eftersom kärnkomponenterna INTE svarar på förhållanden som är normala UTANFÖR nuklidbarriären (utanför fusionskomponenternas omskrivna sfärer, analogt Coulombbarriären) och därmed KAN uppvisa diametralt dynamiska omkastningar — värre ju större motsvarande ekvivalenta neutronbildningstalet (A–Z) är.

3. Faktorn 1/t = 1,9306916 i fallen A>1 har lagts till — den stabila kärnans tyngdradiebegrepp är ODEFINIERAT (oscillerande) genom att fusionskomponenterna under fusionsfasen, eller allmänt inom det instabila tillståndet, BÖR uppvisa kärnytans maximala variationer UTÅT, analogt atomkärnans visuella ytterradie för yttre besökande element (vilket också i princip innebär att typ magnetiska moment och generellt laddningstätheten inte bör uppvisa några större olikheter mot normalfallet); t anger tyngdcirkelns radie relativt kärnans toppspinnande största ytterradie, se även i TOROIDYTAN och ATOMKÄRNANS STORLEK.

4. Är föreningsmomenten tillräckligt stora, resulterar fasväxlingarna i motsvarande (kortvariga) antinuklider, dvs., med laddningsstrukturen tillfälligt omkastad.

EXEMPEL:

Med den kortlivade (8,6 mS se källredovisning nedan) betainstabila individen ₃Li¹¹

ges i r₀=1,37 Fermieneheter

r r_A (r)_A

2,09 2,10 4,55

eller direkt i Fermienheter

r r_A (r)_A

2,86 2,88 6,23

r anger kärnradiernas grundform enbart genom masstalet (A), alltså utan hänsyn till massdefekt och elektronbesättning, och är därmed den »råa» kontinuerliga grundfunktionen för kärnradierna enligt TNED.

Vi hittar inga sådana exempel inom gruppen stabila nuklider. Det är heller inte ALLTID säkert att ovanstående instabila typer uppvisar den angivna karaktären, men det är alldeles tydligt att OM de uppvisar en sådan, den också bör ansluta till sambanden ovan; Vi känner inga andra villkor.

Jämför:

”In 1985 Tanihata and coworkers performed scattering experiments with light elements like helium, lithium and beryllium [1,2] and

found, completely unexpected, a huge matter radius for some of the isotopes close to the neutron drip line, e.g., 6,8He, 11Li, and 11Be.”,

”References

[1] I. Tanihata et. al., PRL 55, 2676 (1985)

[2] I. Tanihata et. al,. Phys.Lett. B 206, 592 (1988)”,

[http://www.gsi.de/informationen/wti/library/scientificreport2006/PAPERS/ATOMIC-PHYSICS-22.pdf], s266,

ATOMIC-PHYSICS-22, Ion trap design for a nuclear charge radius determination of ^7,9,10,11Be, D. Tiedemann et al, 2006

Min översättning:

År 1985 utförde Tanihata och medarbetare spridningsexperiment med lätta grundämnen som helium, litium och beryllium [1,2] och fann, helt oväntat, en mycket stor materieradie hos några av isotoperna nära neutronens »drip line», alltså för ^6,8He, ¹¹Li och ¹¹Be.

NOTERA ATT KÄLLTEXTEN INTE DIREKT KLARGÖR ATT DET ÄR FRÅGA OM KORTLIVADE INDIVIDER — inte alls stabila nuklider. Citatkällan ovan anger (här veterligt) inte heller skillnadens magnitud, se dock annan citatkälla nedan.

Se även citatet ovan i vidare mening i avsnittet från Tanihataepoken.

HUR stor? 2,5 gånger större.

Källa (2008-08-27):

s275sp1n:

”The ¹¹Li nucleus can be considered as a core of ⁹Li with a rms radius of approximately 2.4 fm surrounded by a halo consisting of two neutrons with a rms radius of approximately 6 fm [4,5].”,

s278:

”

[4] T. Kobayashi et al., Phys. Rev. Lett. 60 (1988) 2599; T. Kobayashi, I. Tanihata, Proc. Intern. Symp. on Structure and Reactions of Unstable Nuclei (June 1991, Niigata, Japan), ed. T. Suzuki (World Scientific, Singapore).

[5]N.A. Orr, N. Anantaraman, S.A. Austin, C.A. Bertulani, K. Hanold, J.H. Kelley, D.J. Morrisey, B.M. Sherrill, G.A. Souliotis, M. Thoennenssen, J.S. Winfield and J.A. Winger, Phys. Rev. Lett. 69 (1992) 2050.

”,

[http://www.tamu-commerce.edu/physics/carlos/papers/PLB314_1993_275.pdf],

Molecular bond effects in the fusion of halo nuclei, C.A. Bertulani, A.B. Balantekin, April 1992-July 1993

Physics Department University of Wisconsin USA

Min översättning:

Li¹¹-nukliden kan betraktas som en Li⁹-kärna med en rms radie på approximativt 2,4 Fermi omgiven av en halo som består av två neutroner med en rms radie på approximativt 6 Fermi.

OBSERVERA KVANTITETSREFERENSERNA. Olika webbkällor använder olika kärnradiebegrepp — som författarna bakom begreppen (ännu) är (erkänt) dåliga på att beskriva. Trots uppgifter i olika webbkällor om ”haloradier” verkar det hart när omöjligt att få fram just HALO-radiens kvantitet. Källan ovan är (förmodligen) ett unikt undantag.

Ämnet verkar i själva verket (ännu) så ”begreppsinfekterat” att jag själv INTE vill rekommendera någon läsare att ALLS anta något enda värde utan direkta referenser som anger värdekällan (typ citatet ovan). En artikel i New Scientist från 2 Oktober 1993 Nuclear trinity revealed in halo, Christine Sutton beskriver t.ex. Li¹¹-halonuklidens radie med värdet 3,16 Fermi — utan angiven referens. Källan @INTERNET Wikipedia Halo nucleus 2008-08-28 beskriver samma objekt Li¹¹ med ”tvärsnittet 3,16” Fermi och tillägger (till skillnad från New Scientistkällan) ”Its radius is close to that of ²⁰⁸Pb.”, sv. ’dess radie ligger nära den för Bly-208’, som med r=(1 Fermi)A^1/3 ger nära 6 Fermi med A=208.

Jag bara säger det: akta ”krönikörerna”. I stort sett ALLA åker på ändan i det här ämnet. Ta med ispiggarna (och kläd dig varmt också), ifall att.

UPPGIFTERNA STÄMMER ALLTSÅ MED TNED-VÄRDENA

(jag har upphört att förvåna mig längre för varje gång TNED »ryter i»: det stämmer alltid):

r_A-värdet för ₃Li¹¹ är enligt TNED max 1,82 × 1,37 = 2,49 Fermi; 6,23/2,49 = 2,502008, eller med ovanstående citats Fermivärden; 6/2,4 = 2,5.

Halveringstiden för Li¹¹ är f.ö. enligt uppgift ca 8,6 mS, Källa (2008-08-27), [http://www.lon-capa.org/~mmp/kap30/Nuclear/nuc.htm], interaktiv tabell.

KOMMENTAR — det är SÅ uppenbart:

När man inte ens känner DE STABILA NUKLIDERNAS EGENSKAPER — konventionella uppgifter från elektronspridningsförsöken anger t.ex. radievärden för Väte-1-kärnan i stort mellan 1 till 1,5 Fermi vilket är långt ifrån varje resonabel precision — hur mycket mindre ska man då med någon säkerhet alls kunna sluta sig till deras egenskaper genom att studera INSTABILA atomkärnor, och dessutom sådana som inte ens är varaktiga inom neutronens sönderfallsperiod 12-14 eller 15 minuter? Nej, nej och åter nej.

Jag vill mena att en sådan RESULTATPROKLAMERAD experimentalfysik tvunget måste bli MYCKET äventyrlig: Experimenten är alltid OK. Men resultaten — tolkningarna — har uppenbarligen ännu mycket att önska innan de kan ge något vidare perspektiv.

Så finns TILL EXEMPEL ännu (2008) inga som helst SÄKRA EXPERIMENTELLA RÅDATA på NEUTRONRADIEN OCH PROTONRADIEN.

”Neutronradietorkan” inom modern akademi och vetenskap är f.ö. i själva verket SÅ stor, att man numera (2008, att döma av floran forskningsdokument på webben) HELT övergått till att ”mäta på tunga nuklider” — för att därur försöka ”extrahera neutronradien” i kraft av QCD-teorin: uppfattningen att atomkärnan, verkligen, bl.a. innehåller ett antal fristående neutroner.

Enligt TNED finns ingenting sådant.

Atomkärnan enligt TNED är som den större vattendroppen som heller inte innehåller någon samling av mindre vattendroppar som snurrar omkring inuti. Därmed finns det heller ingenting sådant som ”stark växelverkan” i naturfysiken. Det är en modern akademisk uppfinning (från 1900-talets första hälft) för att få ihop det med uppfattningen/uppfinningen att de positivt laddade protonerna trängs omkring inuti atomkärnan. I TNED består fysiken bara av gravitation och elektricitet med atomkärnan som en helt partikelfri byggnad. Se även från atomkärnans härledning i PLANCKRINGEN.

Visa att jag har fel. Jag ska gladeligen överge det här skeppet om det kan påvisas vara ofarbart.

den nya deuteronradien

2008VIII29

DEUTERONRADIEN

I DEN NYA LASEREPOKEN

Ett — från TNED vinklat — exempel på hur nuvarande forskningsrapportering undanhåller väsentliga klargöranden — en situation författarna själva inte är medvetna om — som i slutänden enbart leder till förvirring

NEDANSTÅENDE CITERADE TEXTSAMMANHANG har här angivits på sin relativt utdragna längd — enbart för tillfället att belysa HUR textförfattarna använder och refererar de centrala mätvärdena i koppling till angivna parameterbegrepp. Nämligen inte alls i något som helst klargörande av vad hela saken handlar om: laserspektroskopiskt grundat material. Texten uppehåller sig istället vid ”elastic electron scattering”, sv. elastisk elektronspridning. Se vidare beskrivning efter citatblocket.

De textmarkerade delarna (röd-gult) i citatblocket närmast nedan är fokus i de partier som i vidare citerade delar längre ner klargör ämnets innehåll: att de centrala detaljerna helt hänger på och beror av laserspektroskopiska grundpreferenser, inte partikelexperiment.

Tabellen nedan samt citaten närmast från

Meson and Quark Degrees of Freedom and the Radius of the Deuteron

A. J. Buchmann, H. Henning, P. U. Sauer, 11 Oct 1996 — 17 June 2006

s3ö:

”

Table 1: Experimental structure radius r_d and charge radius r_ch of the deuteron.

The atomic physics experiment [14] gives the radius difference (r_ch² – r_p²)_exp = 3.795(19) fm²

”;

s13:

”[14] F. Schmidt-Kaler, D. Leibfried, M. Weitz and T. W. Hänsch, Phys. Rev. Lett. 70 (1993) 2261”;

s2ö:

”All calculations of deuteron charge properties require meson-exchange (MEC) corrections for the charge operator.”

s2n-s3:

”

Elastic electron scattering is often simultaneously performed on deuteron and proton

targets. The advantage of such a simultaneous measurement is that the corresponding ratio

of deuteron and proton charge form factors, F_ch(Q²)/G_Ep(Q²), can be extracted with a

smaller systematic error. Thus, the difference r_ch² – r_p², r_p² being the ms proton charge radius,

is experimentally determined with higher accuracy than the deuteron charge radius itself.

This is the reason why experimentalists prefer to analyze their data for the rms deuteron

structure radius r_d, defined by

r_d² = (r_ch² – r_p²) – r_n² – r_DF² (3)

The ms structure radius contains as dominant part the experimentally determined difference r_ch² – r_p²

From this one removes (i) the contribution of the neutron finite e.m. size, r_n²

being the neutron ms charge radius, and (ii) the relativistic Darwin-Foldy correction to the

nonrelativistic one-nucleon charge operator,

r_DF² = G_E^S(0)3/(4M_N²) = 3/(4M_N²) = 0.0331 fm²

where G_E^S(0)(Q²) is the isoscalar charge Sachs form factor of the nucleon and M_N the

isospin-averaged nucleon mass. In Eq. (3),

r_ch², r_p² and r_n² are observables and

r_DF² is a well-defined number.

The rms deuteron structure radius r_d can therefore be considered an

honest observable quantity of the same standing as the deuteron charge radius r_ch itself; in

many experiments it is determined with even higher accuracy.

The existing experimental values for r_d and r_ch are listed in Table 1.

”;

Min översättning (sista markerade delen endast):

Deuteronens struktur rms radie r_d kan därför anses en uppriktigt observerbar kvantitet av samma klass som deuteronens laddningsradie r_ch själv …

r_ch och r_d-data i citatkällans Table 1, resp. 2,13 och 1,96 är uppenbarligen samma data som i de mera preciserade typkällorna nedan (många liknande finns),

On the rms radius of the deuteron

Nuclear Physics A, Volume 637, Issue 4, 3 August 1998, Pages 559-575, Ingo Sick and Dirk Trautmann,

”We find a radius of 2.130 ± 0.003 ± 0.009 fm (±stat., ±syst.), which agrees with the information obtained from nucleon-nucleon scattering and from optical isotope shifts.”

Sv.; Vi finner en radie på 2,130±0,003±0,009 Fermi (±stat., ±syst.), vilket överensstämmer med informationen erhållen från nukleon-nukleon spridning och från optiska isotopskift.

GOOGLE-sökning på ”deuteron radius”:

”Deuteron Radius and Nuclear Forces in Free SpaceExperimental knowledge and theoretical understanding of the deuteron matter radius are reviewed. An experimental value of rm(exp)=1.9502 (20) fm is found by ...

adsabs.harvard.edu/abs/1994IJMPE...3..821W - Liknande sidor ”,

Sv.; DeuteronRadien och … Ett experimentellt värde på rm(exp)=1,9502 (20) Fermi är funnet genom …

”Extracting a value of the deuteron radius by reanalysis of the ...A new value, rD=1.9546+/-0.0021 fm, for the rms radius of the deuteron has been extracted by reanalyzing the experimental data for the ratio R(q2) of the ...

adsabs.harvard.edu/abs/1992PhRvC..45.2603M - Liknande sidor ”,

Sv.; Extrahering av ett värde för deuteronradien genom omanalys av … Ett nytt värde, rD=1,9546±0,0021 Fermi, för rms radien hos deuteronen har extraherats genom omanalys av experimentella data på förhållandet R(q2) hos …

Notera nyckelordet ”omanalys”ovan;

och med bakgrunden, tydligen (jämför referensen under citatkällans Table 1),

”In 1993 optical spectroscopic measurements of the hydrogen-deuterium isotope shift of the 1S-2S resonance [5] reached a precision sufficient to derive a new value for the deuteron structure radius [6] which deviates significantly from the electron scattering results.”;

”[5] F. Schmidt-Kaler et al., Phys. Rev. Lett. 70, 2261 (1993). The value for r_str in Fig. 4 was obtained by recalculating the theoretical isotope shift.”

Hydrogen-Deuterium 1S-2S Isotope Shift and the Structure of the Deuteron (1997)

A. Huber, Th. Udem, B. Gross, J. Reichert, M. Kourogi, K. Pachucki, M. Weitz, and T. W. Hänsch,

Max-Planck-Institut für Quantenoptik

Min översättning:

År 1993 nådde optisk spektroskopiska mätningar på väte-deuterium-isotop-skiftet hos 1S-2S-resonansen en precision tillräcklig för att erhålla ett nytt värde för deuteriums strukturradie, vilken avviker anmärkningsvärt från resultaten med elektronspridning.

[5] F. Schmidt-Kaler et al., Phys. Rev. Lett. 70, 2261 (1993). Värdet för r_str i Fig. 4 erhölls genom omräkning av den teoretiska isotopändringen.

ALLTSÅ LASERSPEKTROSKOPISKA DATA.

Se grundkopplingen från Två Skilda Mätmetoder

Hur tusan ska en godtycklig läsare kunna SE det i citatkällans referens?

Det omnämns inte. Ännu mindre klargörs det. Men det framgår, som ovan — med detektivarbete på referenserna:

optiska spektroskopiska mätningar på isotopskift grundas HELT på avancerad laserteknik;

”isotope shifts determined by high-resolution laser spectroscopy”,

[http://www.triumf.ca/publications/pub/arch07/pp-07-45.pdf] s2,

Nuclear Charge Radius of Lithium-11, Rodolfo Sánchez (et. al.), Nov 2007;

Min översättning:

’isotopövergångar som bestäms genom högupplösande laserspektroskopi’.

”Remarkable are the results produced by our chiral potentials for the deuteron radius which agree accurately with the lastest empirical value obtained by using the isotope-shift method.²⁵”, tabellen i boken på samma sida 125 anger 1,975 Fermi,

Challenges of Nuclear Structure, Aldo Covello, World Scientific, 2002.

Min översättning:

Anmärkningsvärt är resultaten producerade av våra chiralpotentialer för deuteronradien som överensstämmer noggrant med de senaste empiriska värdet erhållet genom användning av isotopövergångsmetoden.

”The analysis of the world data on electron-deuteron scattering yields 2.130 ± 0.010 fm for the deuteron charge rms radius. This value agrees with the one derived from optical isotope shifts [66] and from the low-energy properties of the deuteron as measured by N-N scattering (scattering length and asymptotic normalizations) [67]. The long standing discrepancy with the latter value had been removed when realizing that for scattering from Z=1 nuclei also Coulomb corrections are important [65].”,

@INTERNET GOOGLE-böcker begränsad åtkomst

Precision physics of simple atoms and molecules, Savely G. Karshenboim, Springer, 2007, s70.

Min översättning:

Analysen av världsdata på elektron-deuteron spridning visar 2,130±0,010 fM [femtoMeter = Fermi = t15 M] för deuteronens rms-laddningsradie. Detta värde stämmer med det som erhålls från optiska isotopövergångar och från de lågenergetiska egenskaperna hos deuteronen enligt mätning genom N-N spridning (spridningslängd och asymptotisk normalisering). Den långvariga avvikelsen mot det senare värdet hade tagits bort [författaren uppvisar här en väl sullig språklig syntax: hade?] (man blev tvungen att ta bort det) när man insåg att för spridning från Z=1-kärnor också Coulombkorrektioner är viktiga.

Samma citatdelar som ovan ingår också i sektionen om Laserspektroskopin.

NOTERA FÖRETAGSAMHETEN: 1. Ingen person i Modern Vetenskap och Akademi känner atomkärnan: alla famlar i mörkret, klart som Solen; 2. LIKVÄL tycks man inte darra det allra minsta på handen om det gäller att PLÖTSLIGT, när det visar sig INTE stämma, införa COULOMBKORREKTIONER — på detaljer som man alltså strängt taget inte har den blekaste aning om, och med syftet, naturligtvis, att KORRIGERA=anpassa MOT QCD-TEORIN, eftersom det är den alla anser gäller. Tala sedan om att försöka intvinga atomkärnan i modern akademi. Det går inte. No way. Men det är bara min uppfattning (än så länge).

Citatkällan Buchmann et al, föreger emellertid uppfattningen att tabellvärdena skulle komma från ett motsvarande ‘klassiskt’ massbaserat elektronspridningsexperiment;

”The atomic physics experiment [14]”, de flesta läsare vet inte DIREKT vad det innebär, och ”Elastic electron scattering”, sv. elastisk elektronspridning, och som anspelar på massbaserade spridningsexperiment, uppvisar alldeles tydligt en föregiven uppfattning att författarna talar om just massbaserade experiment — då de i själva verket talar om massbaserade experiment som i efterhand korrigerats (för anpassning till de nya laserresultaten, vilket inte utsägs men som framgår av sammanhanget här till beskrivning) med MATEMATISKA QCD-KORREKTIONER grundade på icke massbaserade, ljusbaserade (lasergrundade) experiment som uppvisar exceptionellt stora atomkärnor hos exceptionellt kortlivade instabila nuklider med grund i upptäckten 1985 av Tanihata et al, med vidare efterföljande utvecklingar.

Uppenbarligen är det INTE så: Korrektioner har infogats i efterhand (med typ ”after accounting for the Coulomb distortion”) för att matcha GAMLA SPRIDNINGSDATA mot NYA LASERSPEKTROSKOPISKA MÄTDATA — vilket ställer saken i ett helt annat ljus — och vilka avhandlingar (i mängd) poppar upp under 1990-talet — med grund i Tanihatas sensationella upptäckt (1985) av de s.k. HALO-nukliderna, med vidare.

Citatkällan nedan ger en utomordentlig beskrivning.

”11Li exhibits a large nuclear matter radius in comparison to other lithium isotopes. The discovery of this exciting phenomenon [1] [1] I. Tanihata et. al., PRL 55, 2676 (1985) started many investigations and soon the picture of two loosely bound neutrons orbiting a core of 9Li was established. The two neutrons form a long tail in the matter distribution, which these days is known as a ”halo”. Not only 11Li shows this intriguing behavior; many other short-lived and neutron rich isotopes, especially those close to the neutron drip line, form halo nuclei.

Important information about the interaction between the neutrons and the core protons can be obtained from the nuclear charge radius.”,

[http://www.gsi.de/informationen/wti/library/scientificreport2004/PAPERS/APHY-EXP-01.pdf] 2007-10-16/2004

The nuclear charge radii of the radioactive lithium isotopes, R. Sánches et al, (2004);

Min översättning:

11Li uppvisar en stor kärnmaterieradie i jämförelse med andra litiumisotoper. Upptäckten av detta spännande fenomen igångsatte många undersökningar och snart var bilden etablerad med två löst bundna neutroner kretsande kring en 9Li-kärna. De bägge neutronerna bildar en lång svans i materiefördelningen, vilket i dessa dagar är känt som en ”halo”. Inte bara 11Li visar detta förbryllande beteende; många andra kortlivade och neutronrika isotoper, speciellt de som ligger nära neutronens droppgräns, formar halonuklider.

Citatkällan Buchmann et al blir därmed att klassificera som ytterst obskyr och direkt vilseledande — sett på ytan;

I den tidigare historien

‘avviker elektronspridningsresultaten anmärkningsvärt’; i Buchmann-källan beskrivs samma objekt i ljuset av de senare korrektioner som gjorts genom laserspektroskopin, och som Buchmann-källan inte ens vidrör explicit, och som då, nu, plötsligt i Buchmann-källan, beskrivs som

‘experimentellt enhetliga’ — utan att författarna klargör DET sammanhanget.

Dessutom ser vi att citatkällan uppehåller sig vid ‘meson-exchange corrections’, med vidare; Den typen ingår överhuvudtaget inte alls i TNED eftersom atomkärnan enligt TNED inte innehåller några beståndsdelar — likt den större vattendroppen som bildas av de mindre heller inte innehåller några ‘mindre vattendroppar’.

Varför är klargörandet ovan viktigt?

Därför att det 1. beskriver ett experimentellt resultat, och det måste förklaras samstämmigt med den teori som gäller, 2. laserspektroskopiska mätningar (isotopskift) är icke-massbaserade och visar därför relativt massbaserade spridningsexperiment ENLIGT TNED INTE atomkärnans tyngdcirkel utan dess formkontur (energitvärsnittet i hf-energin): OM det är så, ges i så fall ett motsvarande samstämmigt mätvärde enligt TNED; visuella deuteronradien (r_d) är runt 2 Fermi. Mätvärdena är OK.

Innan vi säkert kan avgöra den delen, emellertid, krävs betydligt flera mätdata genom laserspektroskopiska experiment — på stabila nuklider med minimal yttre påverkan: atomen får inte störas märkbart eftersom även excitationsenergier (och i synnerhet masschokningar) påverkar resultatet enligt TNED.

Se även från KÄRNRADIER FÖR explicit INSTABILA NUKLIDER.

notering om atomära massdefekten

2008VIII22

NOTERING OM ATOMÄRA MASSDEFEKTEN FÖR UNDVIKANDE AV EV. MISSFÖRSTÅND

EXEMPEL:

Väteatomens massa i atomära massenheter (1u=1,66033 t27 KG) är

U(1H1) = 1,0078252

Neutronmassan är

U(0n1) = 1,0086652

Skillnaden är

U(0n1) – U(1H1) = 0,00084

Eller, räknat i elektronenheter

U(m_e) = 0,000548598

lika med

(8,4 t4)/(5,48598 t4) = 1,5311758

Atomära massenheten räknas emellertid relativt neutronmassan 1,0086652u som enhet.

Därmed ges atomära massdefektsvärdet något lägre i samtliga fall, här enligt

(1,5311758)/[U(0n1)] = 1,5180218 (eg. 1,5180399 med mera avancerad räknare).

Råvärdet i antal elektronmassor för den atomära massdefekten blir alltså alltid 1,0086652 gånger större än neutronreferensvärdet.

Kärnradierna 2008XI11

innehåll: SÖK äMNESORD på denna sida Ctrl+F ·

Kärnradierna

ämnesrubriker

innehåll

KÄRNRADIERNA DEL II — generalgenomgång 2008

Kalkylkort tabbflik — gäller internt för hela kortBlocket

kalkylkort · toroidytorna flik1

kalkylkort · linjära komplementet flik2

kalkylkort · kärnradierna flik3

kalkylkort · LADDNINGSvolymTÄTHETEN flik4

kalkylkort · atomkärnans maximala radieminskning flik5

kalkylkort · utvärdering för kärnradiens ändring flik6

kalkylkort · grundläggande naturkonstanter flik7

kalkylkort · vinkelfördelningen elektronmassans besättning flik8

kalkylkort · kärnradierna genom elektronbesättningarna flik9

Kärnradierna Del II

Uppkomsten av kärnfysikaliska spökbegrepp — genom den avancerade experimentalfysiken

Statistiska diffusionen

Fermireferensen

Den moderna kvarkteorins grundval

Tyngdcirkeln

Kärnradierna från början

Kärnradierna

Distansbegreppen

Kärnradiedata på Webben

Två skilda Mätmetoder

Massbaserade mätmetoder

t-ringen och atomkärnan, illustration

CERN-kurvan

SpökFermiObjekten

Epoken Hofstadter

Grunddata

Volymära laddningstätheten · experimentell jämförelse

Kärnfysikens grundbegrepp via Modern Akademi

Konstanten r0

Protonradiens litterära referensvärde

Wood-Saxon-kurvan

Wood-Saxon-sambandet

Laddningsradien införs i beskrivningarna

»Dimmiga Historien»

Tanihata-epoken

Ljusbaserade mätmetoder · laserspektroskopin

Laserhistoria

Citat om Deuteronen

Kärnmodellen

Nya (be)grepp introduceras från 1990

h = c

Deuteriumets avgörande betydelse

HOP-källan

HOP-källans 1,37 Fermi

De (klassiska) fem massbaserade experimentella metoderna för uppmätning av atomkärnornas radie

Atomkärnans storlek

Allmänna Villkoret för den allmänna fysikbeskrivning

Atomkärnan i grundstudie

Toroidytan

Kalkylkort toroidytorna

Kärnradierna via experimentell mätning

Massbaserade spridningsexperiment

Värdespridningen i citat

Deuteronens Hemlighet

Impulsmomentets 0,71r-kriterium

Fusionsvillkoren

Impulsmomentet

Kärnradiernas grundgrafer

Toroidgrafens justerande komponenter

Massa-spinn-kompensationen och massa-täthets-kompensationen

Massa-spinnkompensationen

Nollpunkten

Kalkylkort linjära komplementet

Massa-täthetskompensationen

Kärnradierna enligt TNED

Resultatredovisning

Kaplan-data

Kärnradierna instabila nuklider

Betainstabila kärnradierna

Kalkylkort kärnradierna, allmän prövning

Nuklidinstabila nuklidradierna

Laddningstätheten enligt TNED

Härledningar med kalkylkort

Atomkärnans masstäthet

Tyngdcirkelns betydelse för kärnradiernas bestämning

Genomträngningen

Begreppet tvärsnitt

Kärnradierna genom massdefekten

Kalkylkort

Kärnradierna via elektronbesättningen

hävstångslagen

Galileiskt rum

Laddningsdeplacementet

Härledning

Kalkylkort kärnradierna

Resultat i syntes

Kalkylkort naturkonstanter

e-massans tyngdpunkt

Kalkylkort vinkelfördelningen e-massans tyngdpunkt

Värdet 1,37 Fermi

Kärnradierna genom kärnstrukturen

Kalkylkort kärnradierna via AZ

Kärnradier hos nuklider under bildning

EXEMPEL Li11

Den nya deuteronradien · deuteronradien i laserepoken

Notering om atomära massdefekten

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

PREFIXEN FÖR bråkdelar och potenser av FYSIKALISKA STORHETER

Här används genomgående och konsekvent beteckningarna

förkortning för förenklad potensbeteckning

d deci t1

c centi t2

m milli t3

µ mikro t6

n nano t9

p pico t12

f femto t15

Alla Enheter anges här i MKSA-systemet (M meter, KG kilo[gram], S sekund, A ampere), alla med stor bokstav, liksom följande successiva tusenprefix:

K kilo T3

M mega T6

G giga T9

T tera T12

Exempel: Medan många skriver cm för centimeter skrivs här konsekvent cM (centiMeter).

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2023-08-23

*END.

Stavningskontrollerat 2008-09-18.

rester

*

PNG-justerad 2011-06-25

åter till portalsidan · portalsidan är www.UniversumsHistoria.se