Radioaktiva sönderfallets Fysik enligt TNED | halveringstiden · UNIVERSUMS HISTORIA | 2011X14 | a BellDHARMA production | Senast uppdaterade version YearMonthDayTime 2017-08-13

innehåll · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Nuklidkoefficienten | Slutformen | Speciella och Allmänna HalveringstidsSambandet | AlfaIsotoperna | Allmänna Koefficientsambandet

Alla Alfa-radionuklider

Alla radioaktiva nuklider

Allmän genomgång av radiofysikens matematik enligt relaterad fysik — allmänna aspekter på kärnfysiken som inte framkommer i den moderna akademins lärosystem

Inledande översikt

BILDKÄLLOR: Författarens arkiv · Kollage NikonD90 — VÅR:R17Maj2009Bild71

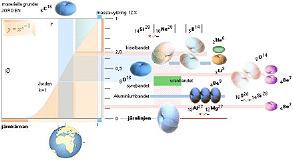
Gränserna ±25 [8pi] är enligt TNED absolutgränser [nuklidkoefficienten] som bestäms av ljushastighetens toppvärde [c0] via ytterst enkla tillämpningar från elektriska kraftlagen enligt härledningen till tH-sambandet. Dessa gränsdata ingår inte i den moderna teorin — men gränskurvans FORM gör det. Vidare i huvudtexten.

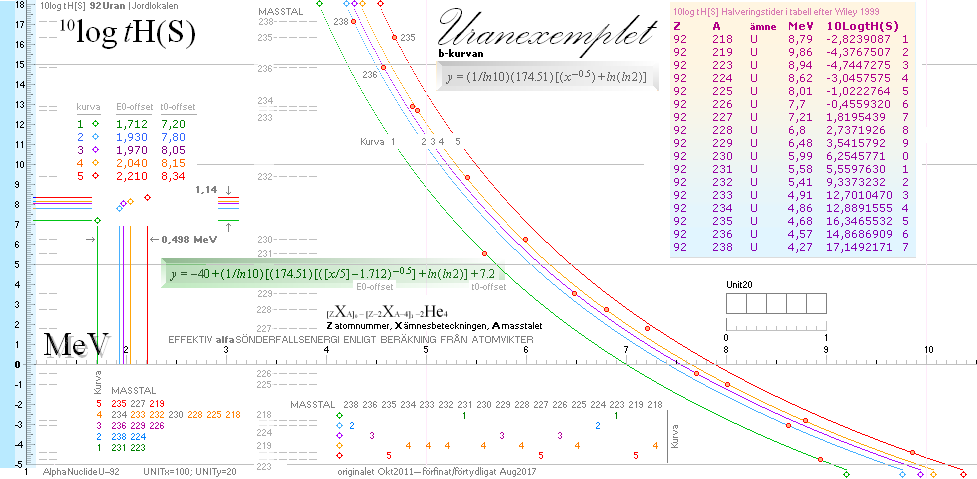
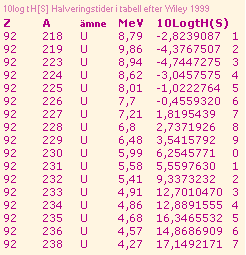
Alfanukliderna [ljusorangea] med data på alla [1999] kända alfakanaler med halveringstider från Wiley 1999 [[Tabell3KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]].

Betanukliderna [spridda punktfältet vänster] med basdata från Van Nostrand’s Scientific Encyclopaedia 1976 och McGraw-Hills Handbook of Physics 1967.

Kompletterande alfanukliddata från Alpha Sciences som belyser ämnets [utomordentliga] omfattning: många webbkällor som ger uppgifter på radionuklider återger bara en del av hela den fullständiga kartan [ovan ljusorangea] — plus en del exotiska nykomlingar. I vilket fall krävs, för den mera fullständiga bilden, att flera [minst 3] oberoende datakällor konsulteras för att få fram jämförande basdata. Bilden ovan ska föreställa en sådan — allmänt orienterande INLEDANDE översikt med grundliga, omfattande, referenser:

AlfaRadioNukliderna, Punktdiagram — Se även AlfaRadioIsotoperna, samma diagram som nedan men tillsammans med tH-universalen i TNED.

Nedan: Förminskad kopia för översikt över alla upptagna individer i Wileytabellen — en 2ggr förstoring visas i de bägge efterföljande stripsen. Varje xy-rektangel i skala 6 pixels per enhet [y-skala 10log tH, x-skala MeV] motsvarar en sträng nuklider i samlingen enligt skalbilden ovan [ljusorangea, alla tillsammans].

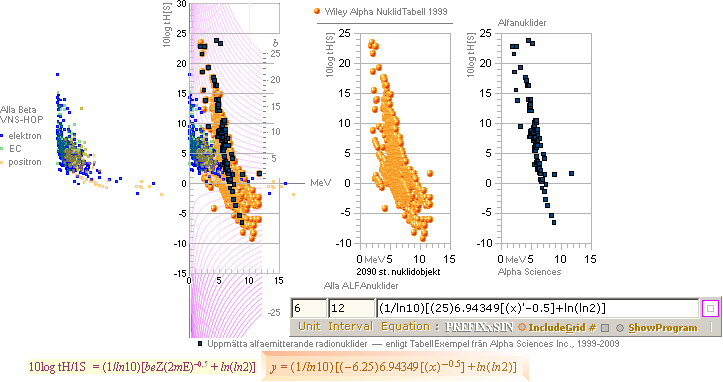
Alla [57st grundämnen inkl. artific.] alfaemitterande radionuklider enligt Wiley 1999 här åskådliggjorda i punktdiagram per atomnummer. y-skala 10log tH med tH som halveringstiden, x-skala MeV med MeV som alfaenergin i MegaElektronVolt. De färgade rektanglarna innefattar en överskjutande individ med lägsta MeV-värdet men som här utelämnats.

Nedan: För att visa upplösningen av databilderna ovan i en mera beskrivande vy, visas exemplifierat nedan den reguljära diagramformen [U-92 ovan] med utdragen x-skala för alla Uran-nuklider enligt Wileytabellen. Speciellt framgår de horisontella stråken med den relativt stora mängden nuklidindivider som uppvisar samma halveringstid på spridda alfaenergier.

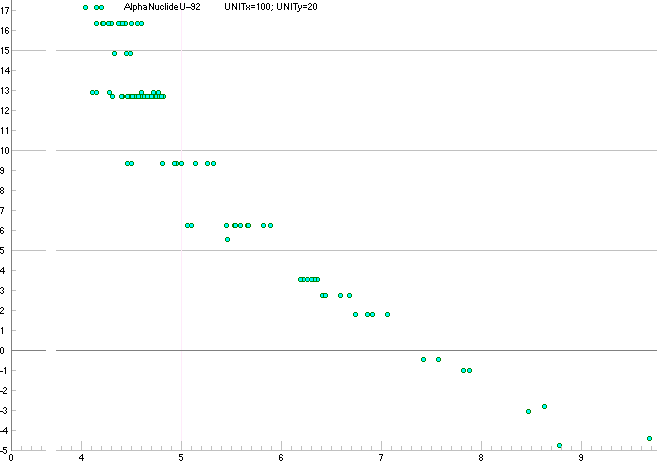
Ovan: Wileytabellens alla UranAlfanuklider. y-skala 10log tH[S], x-skala MeV.

— ANLEDNINGEN varför just ALFAkanalENERGIERNA [Wileytabellen] här används överhuvudtaget är följande:

— Webblitteraturen [Nov2011] »flödar över» av allehanda beskrivningar i koppling till Geiger-Nuttalls samband mellan halveringstid och sönderfallsenergi — i samtidig, exemplifierad, användning av just alfaKANALenergiernas rikt representerade spridda punktfält som ovan — se LabSpaceExemplet till jämförelse. Men DET punktfältets MeV-värden — alfaKANALenergiernas rikt representerade spridda punktfält som ovan — är INTE de som kopplar motsvarande halveringstid [tH]. Varför inte det då? Därför att Geiger-Nuttall-sambandets utgångspunkt, empiriskt och teoretiskt, är EN BESTÄMD ENERGI för en bestämd halveringstid [tH]. Inte flera;INTE alfaKANALenergiernas rikt representerade spridda punktfält som ovan, utan deras motsvarande nukliders entydigt bestämda sönderfallsenergi och som bara kan bestämmas via räkning med atomvikter.

— I exempelbelysningen av SAMMANHANGET behöver vi, således, använda typen ovan för att göra sammanhanget begripligt — samt försöka reda ut någon vettig allmänbild av HUR radiofysiken fungerar [egentligen].

Speciella och Allmänna tH-sambandet — se från Slutformen

2011XI27

Slutformen

Speciella och allmänna sambandet — halveringstiden tH

t_H = 1S(ln2)e^beZ/√2mE

Se särskild härledning i Härledningen till Radionuklidernas Halveringstid, enligt relaterad fysik.

10log tH/1S = (1/ln10)[beZ(2mE)^–0,5 + ln(ln2)]

10log tH/1S = (1/ln10)[b[6,94348949](E_MeV)^–0,5 + ln(ln2)]

Graf; y=(1/ln10)[(b)6.94349[(x)'–0.5]+ln(ln2)] ; bMAX=8pi=25,13274123;

–40+(1/ln10)[(25.133)6.94349[(x)'–0.5]+ln(ln2)]

–40+(1/ln10)[(174.51)[(x)'–0.5]+ln(ln2)]

Speciella tH-sambandet

Speciella sambandet — gäller varje enskild nuklid

Konstant Z — |tH|b|E(α)| varierar

Z, konstant för alla bE(α), anger atomnumret (kärnladdningen) för den avdelade partikeln i sönderfallet, generellt 2He4=alfapartikeln;

tH, halveringstiden varierar med sönderfallsenergi E(α) och nuklidkoefficient (b);

E(α), generellt sönderfallsenergin, beräknas enhetligt och entydigt via atomvikterna;

— Endast ett bestämt tH finns i den ideala nuklidformens unika förekomst som vore denna bildad i en och samma lokal med exakt samma betingelser utan variationer för en bestämd nuklidkoefficient (b) via en bestämd sönderfallsenergi E(α);

— tH kan INTE ha FLERA värden för ett och samma b på annat sätt än att också E(α) ändras med förbehållet att E(α)-värdet motsvarar den effektiva sönderfallsenergin;

— OM, enligt TNED, med dessa beskrivna förbehåll en och samma nuklid uppvisar SKILDA tH för SAMMA E(α) med E(α)-värdet som effektiva sönderfallsenergin, måste TVUNGET den nukliden innefatta multipla b:

— Den slutsatsen ligger (här) vid sidan av Wiletabellens data (som får förstås avse vad den tabellen rubricerar; alfakanalernas energier).

— Slutsatsen med multipla b-värden för samma nuklid klargör dock TNED-teorins väsentliga andemening — i varje jämförelse med teorin i MAC; halveringstiderna enligt TNED kan påverkas av en lokal neutrinoinfluens genom nuklidkoefficienten b som agent för att, via olika neutronkvoter för samma nuklidtyp, konservera nuklidernas möjligen marginellt skilda energigenomströmningar vid det kosmiskt primära bildningstillfället — speciellt i samband med nuklidernas primärt kosmiska bildning: neutrinoenergiernas speciellt påtagliga magnituder i det primärt lokala bildningsområdet. Jämför de exotermiska energivärdena som framkommer ur atomviktsberäkningarna i ljuset av den allmänna materietätheten vid primärbildningarna enligt Udda-Jämna-serierna i TNED.

— En och samma nuklidtyp kan via ursprung i olika neutronkvoter [också från andra sönderfall] sammansätta »en och samma nuklidtyp» [genom geologisk blandning i Jordkroppen] och som därmed, NATURLIGT, ger en motsvarande spridning i möjligheten med multipla b-värden för »en och samma nuklid». Den möjligheten synes inte föreligga i MAC, eftersom nuklidkoefficienten [b-termen nedan] inte ingår i MAC.

Den allmänna osäkerheten i mätningarna

— För Wileytabellens del är det bara uppmätta energier i de olika s.k. alfakanalerna som räknas. Med viss reservation [vidare nedan] kan vi därför, säkert, utesluta alfakanalerna som sådana, generellt — om det gäller att analysera effektiva sönderfallsenergier enbart, med hänsyn till samma halveringstidsvärden för samtliga ingående skilda kanalenergivärden — för samma alfanuklid.

— Ser vi så till en specifik alfanuklid, med alla specifika alfakanalenergier frånsett, och endast beaktar effektiva alfasönderfallsenergin, räknat i atomvikter

[ZXA]₀ – [(Z–2)X(A–4)]₁ – 2He4

återstår så en annan möjlighet — enligt TNED;

— Genom halveringstidssambandets 10log-form [Se från Slutformen]

10log tH/1S = (1/ln10)[beZ(2mE)^–0,5 + ln(ln2)]

med givet tH, E och Z, KAN nuklidkoefficienten [b ovan] teoretiskt i TNED anta olika värden för samma nuklidtyp OM den nuklidens olika möjliga primärbildning via olika neutronkvoter tas med i bilden; Med Jorden som bildningslokal för grundämnena enligt TNED, som exempel:

— Olika neutronkvoter bildar olika SKIKT i Jordkroppen; Samma nuklidtyp kan bildas på radiellt skilda ställen/avstånd i Jordkroppen, och därmed, garanterat i kraft av olika genomströmmande, främst, neutrinoenergier i bildningstillfället [Se utförligt i J-kropparnas expansion]. Därmed garanteras också, enligt TNED, olika betingelser för samma nuklidtyp just genom de olika energigenomströmningslokalerna i den primära grundämnesbildningen [för den specifika himlakroppen, eller den specifika rymdlokalen generellt, t.ex. mellan himlakropparna där bildningen blir speciell; se särskilt i TNED begreppet g-skuggning].

— Genom den påföljande konvektionen, med blandning och bakning av grundämnesmassorna, och som resulterar i de senare mineralkedjorna som bildar själva Jordkroppen så småningom, får varje grundämnesförekomst [i bergarterna] sin specifika sammansättning med en blandning av i princip alla förekommande neutronkvotsrepresentationer av det grundämnets olika nuklider; Med andra ord; Ingenting UTESLUTER att »en och samma nuklidtyp», på grund av primärbildningens olika möjliga neutronkvotslokaler, KAN inhysa »exakt samma nuklider» med exakt samma effektiva sönderfallsenergier, men skilda halveringstider — mer eller mindre. Dvs., b-koefficienten konserverar bildningslokalens specifika form och förklarar därmed de olika sätten.

— Genom att vi inte på förhand känner vilket b-värde som hör till vilken bildningslokal, eller ens någon form för hur b-värdet [eventuellt] varierar med bildningslokal, allt förutsatt grundämnesbildningen enligt TNED, kan vi heller inte förutsäga halveringstidernas variation på annat sätt än att »misstänka» en sådan variation.

— Därmed tillbaka till alfanuklidernas aktuellt uppmätta alfakanalenergier;

— Vi VET naturligtvis, då, heller inte SÄKERT huruvida ett eller annat alfakanalenergivärde i själva verket skulle avspegla en motsvarande »b-variabel nuklid» som ligger uppblandad med alla övriga, och i princip helt omöjlig att särskilja från övriga, speciellt om också »alla övriga» uppvisar samma »marginellt variabla» fason.

— DET är bilden som, spontant, frammanas ur TNED: Vi ser [förmodligen] en FRAGMENTERAD bild av ett ursprungligt, idealt »samma b-lokalvärde» för en given nuklidtyp, och som i själva verket bildats på olika lokaler, med efterföljande naturlig blandning i Jordkroppens inre, och med resultatet i den aktuella spridningen eller fragmentering i kartbilden kring den ideala kurvgrafen [Se AlfaIsotoperna].

— Därmed sagt i klartext: det är OMÖJLIGT att i NUTID och ur Jordkroppens mineralblandning få fram »en exakt ekvation» för de radioaktiva nuklidernas olika halveringstider; dessa är, och förblir just fragmenterade.

— Det helt ideala Begreppet om EN bestämd halveringstid för EN bestämd sönderfallsenergi har därmed, uppenbarligen, FRAGMENTERAT på möjligheten med olika neutron(bildnings)kvoter för en och samma nuklidtyp — och har därmed, i princip, mistat sin egentliga betydelse (och samtidigt inte: sambandsformens allmänna giltighet).

— Om vi därför, som här, i sammanställningen av olika mätdata, söker någon IDEALT ENHETLIG mönsterform för någon idealt prövande analys av ideala passningsformer med dito kurvor, måste vi alltså, tvunget, bortse ifrån den typen — multipla tH för samma E(α) — för att kunna ge en rättvis BILD av hur fysiken ser ut med en bestämd halveringstid för en bestämd sönderfallsenergi.

— Detta är här också helt oproblematiskt för Wileytabellens vidkommande, (OM, och) eftersom denna i vilket fall avser specifika alfakanalenergivärden, och vilka vi här måste förutsätta INTE interfererar med nyssnämnda motsvarande »multipla b-koefficienter».

— Det är, tydligen, avgörande viktigt att vi känner till dessa vassa hörn i radioanalysen — så att vi med fortsatt varsamhet, eventuellt, kan försöka få en fruktbar bild av helheten.

— Totalt 76 nuklidgrupper med totalt 158 individuella nuklider tillhör den nämnda typen enligt tabelldata från Wiley 1999; Alla dessa måste tvunget skalas bort ur bilden för att få en rättvis, enhetlig, utvärdering.

UTGALLRINGEN gjordes så som visas illustrerat i Resultatexempel:

— Wileytabellens original [grönblå punkter i Resultatexempel] innehåller generellt alfasönderfallens olika s.k. kanalenergier, det är tH-värden utspridda på samma horisontella värdelinje via olika MeV-värden — varje alfanuklid uppvisar generellt ett utspritt BAND av olika energier fördelade på olika återkommande intervall; alla dessa kanalenergier är mindre än effektiva alfasönderfallsenergin [frånsett möjligheten att moderkärnan också börjar från ett speciellt exciterat tillstånd].

— Genom att endast beakta den aktuella masstalsnuklidens tH-värde, lika för alla kanaler i den aktuella alfanuklidens s.k. alfaspektrum, och beräkna effektiva sönderfallsenergin, MeV-värdet via räkning på atomvikter, fås EN enhetlig, effektiv sönderfallsenergi för EN enhetlig halveringstid.

— De resulterande, så beräknade datapunkterna visas som röda punkter i Resultatexempel.

— Bägge redovisar hur de olika punktvärdegrupperna ser ut inbördes tillsammans; Rödpunkterna ligger längst fram till höger, största MeV-värdena, marginellt skilda från de största alfakanalenergivärdena.

Exempel 1

EXEMPEL: Uran-238;

b = [√2mE_α]ln[t_H/1S(ln2)]/eZ = 11,856;

E_α=4,267 MeV (RVA), (Wikipedia Uranium 4,270 MeV);

t(H)=4,51 T9 år [10log tH =17,1532805] (äldre uppgift [VNS]), (Wikipedia Uranium 4,468 T9 år)

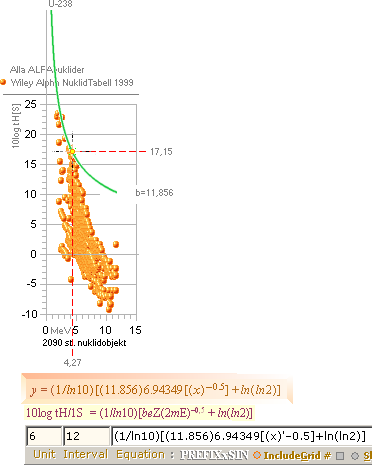
Ovan: Sönderfallspunkten för Uran-238 i tH-sambandet enligt TNED via halveringstiden 4,51 T9 år och effektiva sönderfallsenergin 4,267 MeV. Källdata i exempelhuvudet.

Allmänna tH-sambandet

Allmänna sambandet — gäller grupper av enskilda nuklider

Konstant bZ — |tH|E(α)| varierar med tilläggskoefficienter

Det finns bara EN, och endast en möjlig typkonstant för ett generellt »konstant b» att välja på i TNED för tH-sambandet: b = ±8π = b; den gränsformen bildar uppenbarligen enda möjliga användbara fasta och fixa preferensen för ett b som därmed — i varje fall i princip — kan tillämpas på alla |tH|E(α)|-fall;

;

— Alla möjliga halveringstider (tH) för varje specifikt avdelad kärnform (eZ, gen. alfapartikeln 2He4) och inget annat för alla möjliga sönderfallsenergier E(α).

— Anledningen varför bara den avdelade kärnformens kärnladdning [eZ] räknas i TNED är, enligt TNED, moderkärnans allmänna ±A909e som kan exponeras vid avdelningstillfället, och som bär ansvaret för den avdelande kraften; I förhållande till en potentiell Coulombladdning på minst A909e, A masstalet, blir VARJE specifik kärnladdning (Z, max runt 120) uppenbarligen helt ovidkommande. Se även mera utförligt i Härledningen.

— tH-sambandet med fast nuklidkoefficient (b) får då den allmänna

(generaliserade — se även begreppet universal för den mest allmängiltiga ekvationsformen generellt i TNED; en funktions godtyckliga placering i vertikalled)

formen som nedan från föregående speciella sambandsform — med enda skillnaden i tillägget med en variabeloffset (E0), samt en godtycklig kvadrantorientering [b-kurvan kan roteras i steg om 90°] av b-formens graf via ±;

tH-universalen

Speciella och Allmänna tH-sambandet

tH-universalen

t_H = ±1S(ln2)e^{beZ/√2m(E–E0)}

tH-universalen i kalkylkort [[Tabell2KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]].

Se särskild härledning i Härledningen till Radionuklidernas Halveringstid, enligt relaterad fysik.

10log tH/1S = ±(1/ln10)[beZ(2mE – X₀)^–0,5 + ln(ln2)] + 10log t₀

10log tH/1S = (1/ln10)[b[6,94348949](E_MeV – X₀)^–0,5 + ln(ln2)] + t₀ [t0-termen eg. negativ, tH-universalen flyttas neråt]

;

Graf; –40+(1/ln10)[(25.133)6.94349[(x–E)'–0.5]+ln(ln2)] – t

Graf; –40+(1/ln10)[(174.51)[(x–E)'–0.5]+ln(ln2)] – t

Den generaliserade kurvpassningen

NOTERA att KURVPASSNING också kan göras med ovanstående sambandsform alternativt typ [många olika KOMBINATIONER finns]

Graf; –40+(1/ln10)[1.897(Z=92)[(x–E)'–0.5]+ln(ln2)] – t

Den modifikationen ansluter alltså till olika inpassningsalternativ med referens till MODERKÄRNANS atomnummer — via alfapartikelns konserverade 2m-form i 1,897‑koefficienten;

— Genom att variera Z mellan radionukliderna [generellt för hela radionuklidkartan] 50-120 ges motsvarande kurvformer praktiskt taget som olika vertikalversioner och som kan flyttas efter lämpliga [experimentellt anpassade] positioner.

— Kurvsambandet kan med andra ord förstås innefatta olika möjliga kombinationer av olika möjliga sätt som nuklidkartans parametervärden kan beskrivas på.

— Därmed framstår STRUKTUREN tydligare:

— Vi har INTE att förvänta oss att det FINNS »exakta kurvsamband» som DEFINIERAR de olika halveringstiderna för de olika nukliderna från de givna sönderfallsenergierna — därför att sambandsformen alldeles tydligt just uppvisa en struktur av kombinationer som kan sammansättas godtyckligt: som att betrakta RESTERNA från en ursprunglig ren linje men som med tiden fragmenterat och expanderat i diversifierade strukturer; det finns inga exakta samband. Sedan kan vi [i alla fall] försöka anstränga oss för att bevisa motsatsen: något exakt matematisk bevis finns här inte.

— Dessa kurvekvationer är också den typ vi möter i olika etablerade fackverk som söker beskriva ämnet — utifrån den moderna akademins utgångspunkter.

y och yi²

y och yi²

Med halveringstidens (tH) allmänna avtagande med växande sönderfallsenergi (E) finns två grundsätt:

— Med växande sönderfallsenergi kan halveringstiden avta antingen avtagande — den normala tH-universalens y-kurva — eller avta växande — den normala tH-universalens y-kurva roterad 180°, motsvarande en formell funktionsoperation yi².

tH-universalen [den normala y-kurvan, blå ovan vänster] här normaliserad på en vertikaloffset [–40] för den mera visuella grundanalysen och som sedan kan anpassas med mera exakta offsetvärden. Exempel visas vidare i den efterföljande huvudtexten

— y-kurvans kvadrantrotation med i²=180° [övre högra, orange] fås grafiskt genom att sätta minus för y-kurvan, samt beakta dess vänstra symmetrihalva per en särskild variabeloffset som garanterar att gränslinjen inte överskrids [som dessutom kräver att det inre rotvärdet behandlas som ett absolutvärde, utförligt exempel visas i huvudtexten].

— Med y-kurvan kommer då att sammanhänga [generellt] ett lägsta gränsvärde, en motsvarande negativ offset, för sönderfallsenergin som garanterar att tH-universalen inte överskrider denna nedre offsetgräns i den allmänna inramningen;

— Med yi²-kurvan sammanhänger [generellt] ett största gränsvärde, också negativt, för sönderfallsenergin som garanterar att tH-universalen håller sig inom alfaradionuklidernas generaliserade gränser för sönderfallsenergierna.

E[0]: — Genom prövning på tabellverket, de upptagna alfaradionukliderna i Wileytabellen, ges sönderfallsenergins bägge undre och övre gränser enligt värdena respektive 1,91 MeV [gäller för den blå kurvan ovan] och 12,28 MeV [gäller för den orangea kurvan ovan]. Huvudtexten nedan ger exempel.

tH-universalens FORM kan placeras (kvadrantRoteras — multiplikationer med i, i²) godtyckligt i den ordinära kurvskaran (speciella sambandets skaror), således skärande de givna grundformernas variationer, och därmed (optimistiskt) SAMLA samhörande ordinära Z-nuklider efter deras EVENTUELLA samhörande växande — eller avtagande — masstal med varierande sönderfallsenergi.

EXEMPEL, tH-universalens placering

EXEMPEL

tH-universalens vertikalplacering

Med kännedom om

· E, effektiva sönderfallsenergin i MeV

· E[0], [teoretiskt] minsta möjliga offsetenergin i MeV

· tH, nuklidens halveringstid i 10-logaritmer

kan tH-kurvan [i allmänhet för huvuddelen av alla förekomster, jämför Allmänna RadioIsotopKartan] riktas in via direktberäkning för en hel Z-grupp via bestämning av tH-offseten från sambandet ovan [t0-termen här direkt negativ]

10log(tH/1S) = (1/ln10)[(8π)(6,94348949)(E_MeV – E₀)^–0,5 + ln(ln2)] – 10log(t₀)

enligt

10log(t₀) = (1/ln10)[(8π)(6,94348949)(E_MeV – E₀)^–0,5 + ln(ln2)] – 10log(tH/1S)

= (1/ln10)[(174,5089246)(E_MeV – E₀)^–0,5 + ln(ln2)] – 10log(tH/1S)

Hur den motsvarande, rent visuellt, placerade offsetbilden för tH-universalen ser ut enligt TNED redovisas i Allmänna Radioisotopbilden.

— E[0] = 2MeV [eg. 1,91 MeV] ger den översiktligt korrekta orienteringen för alla nuklider med atomnummer 112-85 via den ordinära tH-kurvans y-form;

— Från atomnummer 84 och neråt ges en märkbar ändring i bilden som kräver tH-kurvans kvadrantrotation [yi²-kurvan med generella E0-gränsen 12 MeV]; denna bibehålls sedan, tydligen, övervägande för alfaradioisotoperna fram till atomnummer 67 — en viss återgång sker i slutet av kartbilden för alfaradioisotoperna i atomnumren 55-52 [under den gränsen saknas här uppgifter].

— Notera att jämförelsen här via Allmänna Radioisotopbilden bygger på alfakanalernas energivärden från Wileytabellen. De reguljära effektiva sönderfallsenergiernas datapunkter är färre till antalet samt ligger i grafbildens framände [åt höger]. Skalan i kartbilden gör att dessa skillnader i denna översikt är marginella.

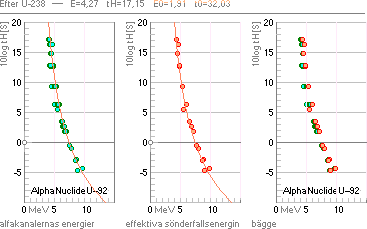
EXEMPEL 92UranAlfaRadioIsotoperna — tH-universalens allmänna precision — riktning efter 92U-238:

Ovan: Den orangea kurvan är tH-universalen som här offsetbestämts och placerats enligt sambandsformen ovan efter uppgifterna från Uran-238: 10log tH = 17,15 [4,51 T9 år], E = 4,27 MeV med E[0] = 2 MeV som avrundat ger 10 log [t(0)] = 33.

— Data för alfakanalenergierna från Wiley 1999; Effektiva sönderfallsenergierna från räkning via atomvikter enligt tabell LBL 2003.

— Se även en mera noggrann offsetbild via tH-universalen för Urangruppen i Uranisotoperna.

— SPRIDNINGEN mellan punktvärdena FÖRMODAS här [delvis] sammanhänga med en ursprunglig »ren ideal radionuklidlinje» men som FRAGMENTERAR i punktvärdena BEROENDE PÅ OLIKA RYMDKOSMISKT BELÄGNA BILDNINGSLOKALER — typ närmare eller längre ut från Vintergatans centrum; det är energigenomströmningen [neutrinoinfluensen] i bildningstillfället [»inbakningen»] som KAN spela roll enligt TNED; Jordlaboratoriska partikelacceleratorexperiment har knappast någon inverkan i de sammanhangen [kollisionsenergier förekommer inte i grundämnesbildningen enligt TNED]. Det finns emellertid ingen SÄKER bevisform [ännu] för denna detalj.

— Nedan, orangea kurvan, visas ett motsvarande exempel på yi²-passningen.

EXEMPEL 70YtterbiumAlfaRadioIsotoperna — tH-universalens allmänna precision — riktning efter 70Yb-158:

— Data för alfakanalenergierna från Wiley 1999; Effektiva sönderfallsenergierna från räkning via atomvikter enligt tabell LBL 2003.

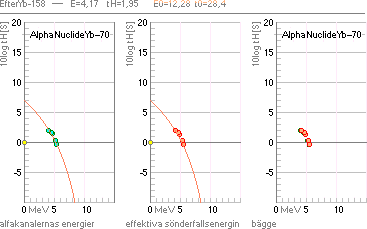
— Notera att rotvärdet måste bestämmas via absolutvärde i fallet med yi²-passningen som ovan [ingår automatiskt i DELPHI4Test2011-grafritningen som använts till denna presentation].

— Passningen med E[0]=12,28 MeV för yi²-kurvan gäller generellt [Se Allmänna Isotopkartan] för atomnumren 78-65; Atomnummer 64-61 uppvisar en tydlig övergång med olika offsetvärden och en blandning av y och yi²; Atomnumren 59-54 är orepresenterade i Wileytabellen; Z=55-52 uppvisar slutligen en y-form med noll E[0]-offset och konstant t0[MINUS40normalkurvan]=–2,33.

— Vissa Z-intervall [112-101; 100-85; 78-65; 55-52] verkar alltså tämligen homogena i den allmänna kurvpassning via tH‑universalen.

Denna detalj har också — som läsaren förmodligen redan observerat i BILDEN av AlfaRadioNuklidernas punktdiagram — direkt teoretisk-praktisk koppling:

— AlfaRadioSönderfall betyder kärndelning: produkterna går från en tyngre [högre Z] till flera lättare [lägre Z];

— Växande sönderfallsenergi E(α) betyder i allmänhet att halveringstiden avtar;

— Växande sönderfallsenergi E(α) betyder också (i allmänhet) en växande atomär massdefekt;

— Masstalet (A) avtar generellt i nuklidkartan — med växande atomär massdefekt då masstalet närmar sig Järntoppen (A=60) [Se även i Masstalets gränsvärde enligt TNED];

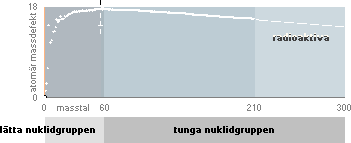
— Men också atomnumret (kärnladdningen Z) avtar generellt för nuklidgrupperna med avtagande masstal (inom vissa gruppkriterium); Vi skulle därför förvänta oss att den fasta b-formen

10log tH/1S = ±(1/ln10)[beZ(2mE – E₀)^–0,5 + ln(ln2)] + 10log t₀

mycket VÄL kan beskriva — omfatta, vidröra eller tangera MEN INTE EXAKT DEFINIERA per någon enskild kurvdel — tH-variationerna med referens till fasta Z-grupper.

Exempel 3 — UranIsotopExemplet

EXEMPEL: (92)Uran(218,219,223-236,238, Alla nuklider i WileyTabellen):

Nedan: TNED-kurvorna för alla alfaradionuklider [ listade i tabellen från Wiley 1999] i grundämnet Uran [Z=92] — med alfasönderfallsenergier i MeV för varje alfaradioisotop beräknade från atomvikter.

— Frånsett individen U-227 [nom. halveringstid 66 sekunder, kurvvärdet skulle här ge ca 89 sekunder] är det tydligt att KURVPASSNINGEN är tämligen god — för samtliga isotoper.

— Kurvformen — samma för alla punktvärden, enbart offsetförskjuten i xy-led enligt specifikt för alfasönderfallet

10log tH/1S = +(1/ln10)[beZ(2mE – E₀)^–0,5 + ln(ln2)] + 10log t₀

= –40+(1/ln10)[(174.51)[([x–E]/5)'–0.5]+ln(ln2)] – t

— visas nedan med respektive offsetvärden E[0] och t[0] infällda i diagrammet.Se även Grafritande Programmet för radionukliderna -- infört separat i efterhand Aug2017.

Allmänna koefficientsambandet: I MODERN AKADEMISK TEORI figurerar inte några motsvarande kurvpassningar, Exempel 3 ovan, trots principiellt samma ekvationsform; I MAC tillämpas istället den generaliserade b-formen från

10log(tH) = –40+(1/ln10)[1.897(Z=92)[(x–E)'–0.5]+ln(ln2)] – t

enligt
= A + B[CZ/√x + D] – E

Anledningarna är, här veterligt, flera:

1. den allmänna teoretiska grunden man åberopar för sönderfallets mekanik: alfapartikelns rörelseenergi [statistisk kvantfysik i den moderna akademins atomkärna]:

— I TNED existerar alfapartikeln aldrig som någon fristående form som försöker rymma ur atomkärnan FÖRE själva sönderfallstillfället [jämför vattendroppsanalogin]; I TNED räknas endast [mass]ENERGIN för avdelandet, den effektiva sönderfallsenergin — och som medför att alfapartikeln EFTER bildningen kan uppvisa i princip vilka energier som helst inom ett visst intervall; Medan TNED endast beaktar effektiva sönderfallsenergin, kurvbilden ovan i UranExemplet med den optimerade tH-universalen, bygger MAC-teorin uteslutande på en allmän BILD av SKILDA alfaenergier [Gamows teori]: alfakanalernas energier. Eftersom dessa INTE ger någon entydig värdebild för EN sönderfallsenergi, finns heller ingen ENTYDIG tH-koppling;

— Skippas emellertid alfakanalerna i MAC, försvinner samtidigt den teoretiska grund man åberopar för sönderfallets mekanik: den kvantmekaniska statistiken.

2. faktorn 2m i det förenklade ledet för tH-universalen:

— Sambandsformen ovan, enligt TNED och som TYDLIGEN i princip INNEFATTAR ALLA FÖREKOMMANDE numeriska värdeformer i MAC-SAMBANDen [Jämför Särskilda Exempelutdrag], BYGGER på att Z-faktorn får förstås som en GODTYCKLIG kurvpassningskoefficient med en entydigt bestämd underliggande alfapartikelmassa [√2m, se sambandsformen utvecklad i tH-universalen]; I den 2m-delen, eller i övrigt i sambandsformen, finns ingen koppling till någon moderkärna: ingen masstalskoppling för moderkärnan, ingen atomnummerkoppling för moderkärnan; TNED-härledningen baseras på centralmassivets ±A909e som garanterar att moderkärnans normala kärnladdning [Z] i vilket fall helt saknar betydelse vid själva sönderfallets korta tillfälle, se utförligt i Härledningen; centralmassivets matematik ingår överhuvudtaget inte i kärnfysiken i MAC. I motsvarande MAC-termer, blir TNED-allmänformen således, och därför, en GODTYCKLIG ALLMÄNFORM där i princip vilka som helst olika kurvpassningskoefficienter kan komma ifråga — och som därmed, i princip, kan formuleras på vilka som helst FIKTIVA [kärnfysikaliska] parametergrunder.

3. TNED-formens generaliserade tH-kurva avgränsas av ett bestämt maxvärde via 8pi: MAC har ingen motsvarande teori; nuklidkoefficienten ingår inte MAC.

4. MAC-teorins sambandsform grundas på en APPROXIMATION [algebraisk förenkling] från ett ursprungligt matematiskt-statistiskt resonemang med grund i den moderna kvantfysiken;

— Se exv., webbkällan [PDF]:

Citat

Quantum Mechanics of Alpha Decay

Dennis V. Perepelitsa, Brian J. Pepper, MIT Department of Physics, 2006

http://web.mit.edu/dvp/www/Work/8.13/dvp-quantum-paper.pdf

s1:

;

”Rewriting √b =(e√Z_α)(√Z_n/E_α), we have, as a good approximation to the decay constant:

(4)

(5)

This is known as the theoretical version of the Geiger-Nuttal Law, and its verification

is the primary aim of this experiment.”.

— Approximationen leder alltså [alldeles tydligt] till ovannämnda Koefficienta Allmänform: TNED-härledningens tH-samband — och som, tydligen, kan varieras med stora friheter.

— Att på MOTSVARANDE sätt försöka få kurvpassning för SAMTLIGA ALFAKANALENERGIER enligt experimentella uppmätningar blir här veterligt en OMÖJLIG uppgift — frånsett möjligheten att låta varje energiindivid få sin egen individuella kurva, en egen unik ekvation, och vilket i så fall gör att man har missat hela målet. Då kan man lika gärna använda det experimentellt uppmätta tH-värdet direkt ur tabell.

RÄKNEEXEMPEL — kurva 2, masstal 238 — som visar hur den teoretiska precisionen felar:

— Med ovanstående grafiska representation

10log tH/1S = –40 + (1/ln10)[beZ(2mE – E₀)^–0,5 + ln(ln2)] + 10log t₀

10log tH/1S = –40+(1/ln10)[b[6,94348949](E_MeV – 1,93)^–0,5 + ln(ln2)] + 7,80

och effektiva sönderfallsenergin för U-238 som

E(eff) = 4,2698248 MeV

som ger

10log tH/1S = 17,21726;

tH = 5,225839 T9 år

att jämföra med det uppmätta värdet [VNS, senare källor ger något lägre] för halveringstiden hos Uran-238

tH(U-238) = 4,51 T9 år

ser vi att precisionen är kass; Vi kan inte använda en sådan onoggrannhet för några mera exakta naturvetenskapliga ändamål — trots att kurvan ser ut att träffa »mitt i prick». Vi skulle behöva nuklidkartor stora som vardagsrumsväggar för att närma oss något användbart.

— För att få pixelupplösning på 100-delar i 10log.skalan, skulle bilden ovan behöva förstoras 5ggr (Unit100p); Med ett mera preciserat t(0)-värde på 7,73 hamnar vi likväl bara på slutvärdet 17,14726 som ger tH=4,4479104 T9 år — vilket är träff in till 98,6232911 %; bättre, men fortfarande klart otillfredsställande som precisionsdatabas.

— Exemplet bara understryker det redan tidigare påpekade i Den generaliserade kurvpassningen:

— b-formen är UNIK för varje nuklid och dess bildningslokal [den allmänna energigenomströmningen, speciellt för TNED med avseende på neutronoinfluenser, och vilket ämne fortfarande står under analys: vi vet det inte här säkert] och innefattar, för den allmänna beskrivningen av GRUPPER av alfaradionuklider uppenbarligen GODTYCKLIGA sätt att använda nuklidparametrarna på; atomnummer (Z), tilläggskoefficienter [E|t](0) för kurvpassning i xy-led och som kan utsträckas vidare till kopplingar med nuklidernas masstal, osv., eller ytterligare andra kombinationer (tilläggsfunktioner, av olika art);

— Ingen (känd) enkel funktion finns som genomskär en given radioisotopfamiljs ALLA individer;

— b-koefficienten [Se Nuklidkoefficienten] som variabel mellan ±8π är i sig föremål för SÅDANA generella variationer (ev. neutrinoinfluens) som GARANTERAR att INGEN FAST PREFERENS finns för bestämda tH-värden med »universellt bestämda b-värden» via bestämda E(α)-värden — på annat sätt än signifikant för den aktuella (neutrinoinfluerade) lokalen, typ hela himlakroppen eller dess närmaste omgivning.

Generaliserade kurvpassningens allmänna alfaradioisotopbild,

Se databasen från Alla radionuklider

För att understryka Den generaliserade kurvpassningens allmänna översiktsbild, just dess allmänna form, visas nedan hela isotopkartbilden över samtliga upptagna radionukliders alfakanalenergier [förminskat 50% från pixeloriginalet, samma databas som i AlfaRadioNuklidernas Punktdiagram] enligt Wileytabellen och via Allmänna tH-sambandets generaliserade enda kurva tH-universalen med xy-offset [X|t](0);

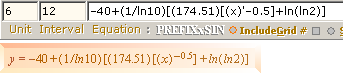
10log tH/1S = –40 + (1/ln10)[b[6,94348949](E_MeV – X₀)^–0,5 + ln(ln2)] + t₀

För kurvformerna y och yi², se utförligt i tH-universalen.

Nedan: Kurvpassningen för samtliga alfaradionukliders alfakanalenergier enligt Wiletabellen. Kurvformen som ovan med angivna offsetvärden enligt efterföljande tabelluppställning.

— Siffrorna överst anger atomnummer [Z]; Vertikalskalan 10log[tH/S]; Horisontalskalan i MeV.

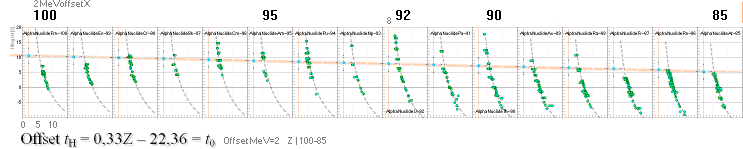
ENDA SKILLNADEN mot effektiva sönderfallsenergiernas värden är att dessa ligger i framkanten [åt höger] på kurvavsnitten, samt är betydligt färre till antalet. Se PoloniumExemplet.

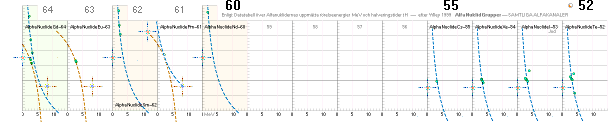
Kartbildens översiktliga syfte: Att DELS understryka godtyckligheten i alfaradionuklidernas spridning omkring en grundlinje — efter vilken individerna har fragmenterat till diversifierade positioner och som enligt TNED — möjligen — har sin grund i att OM samma mätningar görs TYP i någon lokal längre in mot Vintergatans centrum [högre energigenomströmning i bildningstillfället, generellt] en någon annorlunda [kanske mycket marginell] spridning visas; det finns inga exakt universellt fasta tillståndsvärden för halveringstider för en viss radionuklid. Det återstår emellertid att föra det påståendet till en mera exakt bevisning. Exempel på hur spridningen ser ut mera i detalj ges i UranExemplet. DELS understryks också att den allmänna kurvpassningsformen i kartbilden ovan kommer från härledningen till halveringstidssambandet enligt TNED.

Generaliserade alfaradionuklidkurvans offsetvärden — offsetdata till ovanstående kartbilder:

tH-offset (t0)	MeV-offset (E0)	Z-suc.	y | yi^2
–2,33	0	52-55	y
7,67	0	60,62,64,65,66	y
–2,00	8	61,63,64	yi^2
–10,67	11,33	65-74	yi^2
–9,00	11,33	75-78	yi^2
7,33	0,67	72	y
8,00	1,00	76,78	y
–12,33	13,67	79,82	yi^2
–7,33	13,00	83,84	yi^2
7,33	0	82	y
9,33	1,67	83	y
10,33	0,67	84	y
0,33Z – 22,36	2,00	85-100	y
11,33	2,00	101-112...	y

De grova offsetvärdena [E|t](0) till AlfaRadioIsotoperna i diagramkartan för [10log tH][MeV]

— enligt fasta b-formen

10log tH/1S = –40 + (1/ln10)[beZ(2mE – E₀)^–0,5 + ln(ln2)] + 10log t₀

Graf; y = –40 + (1/ln10)[(174.51)[(x)'–0.5] + ln(ln2)]

med referens till tabellen från Wiley 1999 för alfaradionuklidernas energier och halveringstider.

Offsetvärdena är angivna med referens till ovanstående graf.

;

— Med andra ord: MÖJLIGEN, men ännu inte med någon säkerhet, finns strängt taget inga fasta, exakta halveringstidsvärden, inte för någon radioaktiv nuklid.

— Det finns, emellertid här, inget som helst SÄKERT kriterium (än) för att avgöra vad som gäller.

— Det är dock på sin plats att omnämna sammanhanget för ev. vidare (speciellt som vissa observationer [Jenkins et al., 2006] gjort gällande en möjlig neutrinoinverkan från Solen på vissa radioaktiva nuklider samt generellt för TNED med referens till Månens recession — och därmed frågetecken för »den universella giltigheten» hos grunddata på vissa radionuklider).

Särskilda Exempelutdrag

Särskilda Exempelutdrag

EXEMPEL på webbkällor som specificerar explicita kurvformer för halveringstider och sönderfallsenergier för alfaradionuklider:

Kurvformerna nedan (1)[orange kurva]-(3) skiljer sig inbördes inte märkbart i Unit6pixels utom för (4)[grön kurva]; Källverket ger dock en synnerligen maximalt knapp upplysning om HUR sambanden kopplar beskrivningen: författarna talar inte om i den löpande beskrivningen vad de angivna sambanden representerar (man får läsa framställningen flera gånger och försöka luska ut vad som menas) — inte med ett endast ord, se citatdelen nedan;

Exempel Royer-Zhang

(1) log10[T_½] = –25.31 – 1.1629A^1/6√Z + 1.5864Z/√Q_α

(2) log10[T_½] = –26.65 – 1.0859A^1/6√Z + 1.5848Z/√Q_α

(3) log10[T_½] = –25.68 – 1.1423A^1/6√Z + 1.5920Z/√Q_α

(4) log10[T_½] = –29.48 – 1.1130A^1/6√Z + 1.6971Z/√Q_α

s1n:

”The α decay potential barrier is often described

using a finite square well for the one-body shapes plus an hyperbola for the

Coulomb repulsion between the α particle and its daughter. An arbitrary adjustment

of the parameters allows to reproduce roughly the experimental data. Here

the α decay potential barriers are determined in the cluster-like shape path within

a generalized liquid drop model² including the proximity effects between the α particle

and the daughter nucleus and adjusted to reproduce the experimental Qα.”,

; Många författare är (ypperligt) dåliga på att berätta, det enkla, vad termerna betyder (de vill INTE ha någon Extra Publik utöver Expertpanelerna): Termen ”Qα” används ofta i radionuklidsammanhang motsvarande effektiva sönderfallsenergin — alltsaå INTE specifika alfakanalenergier — med räkning via atomvikter. Men författarna i webbkällan verkar INTE avse sina sambandsformer EXPLICIT för effektiva sönderfallsenergier, utan istället för de experimentellt uppmätta alfakanalenergierna — vilket är det kaotiska syndromenet generellt i det konventionellt presenterade sakämnet (alfa)RadioNuklider; TEORIN i MAC KRÄVER »alfakanalbehandling» — den innestängda alfapartikeln som försöker komma ut ur atomkärnan enligt de kvantmekaniska statistiska sannolikhetskalkylerna, MAC-teorin — medan det enda entydigt existerande energivärdet som finns helt kör över alla »alfakanalenergier» och »specifika rymningsenergier» och går direkt på målet: mass(energi)differensen [Qα] med räkning via atomvikter.

s2:

”Analytical formulae for the α decay half-lives have been proposed². They lead

to rms deviations of respectively 0.285, 0.39, 0.36 and 0.35 for the even(Z)-even(N),

even-odd, odd-even and odd-odd nuclei².

(1)

(2)

(3)

(4)

”,

ALPHA DECAY POTENTIAL BARRIERS AND HALF-LIVES AND ANALYTICAL FORMULA PREDICTIONS FOR SUPERHEAVY NUCLEI, Guy Royer, Hongfei Zhang, June 2008/ Jan 2009,

http://hal.in2p3.fr/docs/00/35/60/24/PDF/royer-radioactivity.pdf

Redovisade kurvavsnitt

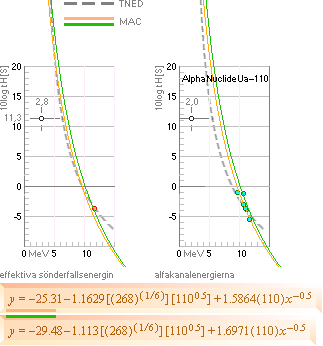
TNED-sambandet enhetligt detsamma som i hela alfaradionuklidkartan; Offsetjusterad, samma typkurva, för illustrerande översikt.

— Anledningen varför bara en datapunkt finns representerad i grafbilden för effektiva sönderfallsenergin [röda punkten] är att tabelluppgifterna [Wiley 1999] i denna presentation inte har något övrigt att bjuda på. Alfakanalenergierna [gröna punkterna] är desto mera rikt representerade.

Ovan visas kurvformerna från Royer-Zhang 2008 — här enhetligt med Z=110, A=268 för att få jämförande synbarhet på grafernas form — författarna [Table 2 s5] uppehåller sig huvudsakligen vid de allra tyngsta artificiella grundämnena [104-118] med masstal [A] grovt 250-300:

(1)y=–25.31–1.1629[(268)'(1/6)][110'0.5]+1.5864(110)x'–0.5

(2)y=–26.65–1.0859[(268)'(1/6)][110'0.5]+1.5848(110)x'–0.5

(3)y=–25.68–1.1423[(268)'(1/6)][110'0.5]+1.5920(110)x'–0.5

(4)y=–29.48–1.113[(268)'(1/6)][110'0.5]+1.6971(110)x'–0.5

— Med viss reservation för att inte författarnas alla villkorsvärden täcks av de illustrerade två huvudkurvorna, är det tydligt av kurvbilderna ovan att författarna avser en matchning mot experimentellt uppmätta alfakanalenergier EXPLICIT [gröna punkterna] — inte effektiva sönderfallsenergin [röda punkten] [Qα] för respektive nuklid, trots att författarna refererar [upprepat] till denna [Qα],

”... and adjusted to reproduce the experimental Qα”. Det är oklart vad författarna avser att analysen gäller — speciellt som kurvbilden av deras samband [gröna punkterna] ANTYDER att författarna mest intresserar sig för alfakanalernas energier snarare än effektiva sönderfallsenergier [röda exempelpunkten missas tydligt].

Nedan, citatkällans alla 4 kurvformer med samma Z=110, A=268:

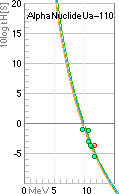
Citakällan missar målet ...

Källformen exemplifierar ämnesformens allmänna svårighet: Med ett minimum av KLARGÖRANDE VAD SOM MENAS lämnas definitivt heller inte mera än exakt NOLL bidrag i klargörande. [Meningen är att källförfattarna, inte vi här, ska KLARGÖRA vad som menas — genom TYDLIGA EXEMPEL].

— Speciellt framgår citatkällans 4st sambandsexempel — ett unikt värde för varje atomnummer [Z) och varje masstal [A] — enligt EN specifik kurva för varje alfaradionuklid; Analogt EN specifik tH-ekvation för varje specifik alfaradionuklid; Därmed tangeras I PRINCIP samma resultat som redan anställts i TNED;

— Varje nuklid har sitt särskilda b-värde [Nuklidkoefficienten] och som i vilket fall [för hela Jordlokalens experimentellt uppmätta nuklider, eller på andra orter] måste avstämmas teoretiskt mot experimentellt uppmätta värden, med motsvarande parametriska koefficientanpassningar. Jämför Allmänna Koefficientsambandet.

— Citatkällan medger emellertid ingen vidare analys — enligt följande [nedslående] uppmärksammande:

Citatkällan redovisar underliga data

”

Later on new α decay half-lives have been measured and they are compared with

the predictions of these formulae in the table 1 where Q and T are respectively in

MeV and s. The good agreement allows to provide in table 2 predictions of the

α decay half-lives of other possible superheavy elements4 with the help of the Qα

calculated from the 2003 atomic mass evaluation5.

”,

”

”,

ALPHA DECAY POTENTIAL BARRIERS AND HALF-LIVES AND ANALYTICAL FORMULA PREDICTIONS FOR SUPERHEAVY NUCLEI, Guy Royer, Hongfei Zhang, June 2008/ Jan 2009,

http://hal.in2p3.fr/docs/00/35/60/24/PDF/royer-radioactivity.pdf

;

Godtycklig kontroll:

;

RoyerZhang: 158Yb;4,172;4,3T6motsv.6,662757832

Wiley-LBL: 70;158;Yb;4,17;1,9513375

;

RoyerZhang: 160Hf;4,902;1,9T3motsv.0,285557309

Wiley-LBL: 72;160;Hf;4,9;1,1335389

;

— Medan sönderfallsenergierna verkar OK i jämförelsen RoyerZhang kontra Wiley-LBL, är halveringstiderna däremot uppenbart korrumperade; överensstämmelse saknas tydligt.

— Vad Royer/Zhang menar med ”new α decay half-lives have been measured” i någon källreferens är här okänt — medan det är uppenbart att författarna avstämmer ”compared with the predictions of these formulae” till de uppenbart icke överensstämmande tH-värdena (Wileytabellens tH-värden har här kontrollerats genom stickprov och visar samstämmiga värden med WolframAlpha och Wikipedia).

— Tyvärr kan, med ovanstående referens, ingen vidare meningsfull utsaga göras angående citatkällans mening. De redovisade kuravsnitten ger dock en viss orienterande översikt.

Exemplet Santoso 2000

Ytterligare ett exempel — här på Uranisotoperna, och som exemplifierar precisionen i detaljbeskrivningen (generellt från MAC);

s7:

”In the case of alpha decay for a number of uranium as parent nuclei, it

is found empirically , that the half life versus energy, fits relatively well the

observed data using an empirical plot given by

Log(τ / sec) = 148/√E/MeV – 55.0

The last term in this expression contains the values of Z’ and R

( the isotope number and radius of parent nucleus) experienced by the alpha

particle as an average values, which are not the same as the model considered.

”,

QUANTUM ESTIMATES OF ALPHA EMITTER LIFE TIME, Budi Santoso (2000)

http://aij.batan.go.id/fulltex/v32-n1-1-06/001.pdf

Denna citatkälla ger en hyfsat bra beskrivande teoretisk [utförlig] bakgrund — med tydliga sambandsformer.

Figuren nedan visar vad som menas med ”fits relatively well” enligt citatkällans föreslagna kurvform [orangea kurvlinjen nedan]. Jämför även TNED-normalkurvorna till Uranisotoperna.

— Exemplet understryker (återigen) huvudsaken: Det tycks inte finnas någon etablerad fattning på huruvida ANALYSEN ska avse — explicit — alfakanalernas energier, gröna punkterna, eller effektiva sönderfallenergierna hos respektive nuklid, röda punkterna. Resultatet TENDERAR att uppvisa ett virrvarr av »både-och», och vilket möjligen nedanstående exempelbidrag var ägnat att uppmärksamma, särskilt.

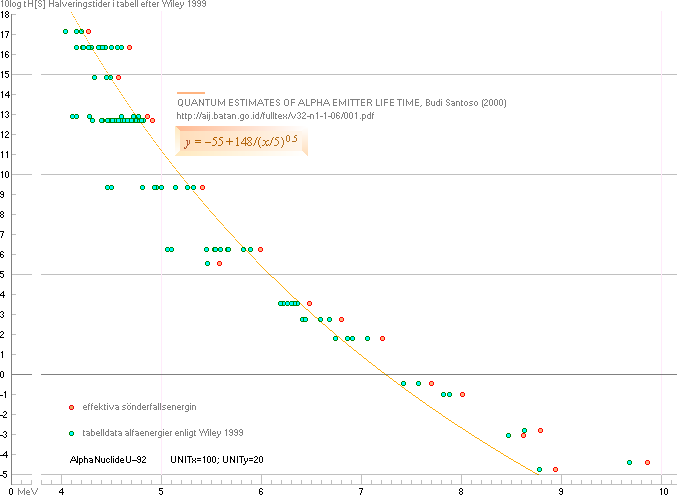
Den allmänna bristen på precision

Den allmänna bristen på precision

Beträffande den delvis ofullständigt

”The theory as presented above applies only to ground state decays between even-even nuclei, where α- particles have no internal angular momenta.”, se citatkällan nedan

beskrivande statistiska kvantfysikaliska sannolikhetsmatematiken man åberopar konventionellt för halveringstidsberäkningar kontra sönderfallsenergier, säger en av webbkällorna — sanningsenligt —

s19:

’”The agreement between the measured and the calculated α-decay half-lives is not exact, but the calculation is able to reproduce the trend of the half-lives within 1-2 orders of magnitude over a range of more than 20 orders of magnitude.”,

;

”Even though this oversimplified theory is not strictly correct, it gives us a good estimate of the decay half-lives.”,

ALPHA DECAY BRANCHING RATIOS AND ITS POSSIBLE IMPLICATIONS REGARDING NUCLEAR STRUCTURE, Ms. Gurvarinder, July 2010

http://dspace.thapar.edu:8080/dspace/bitstream/10266/1185/1/Gurvarinder_MSc.pdf

Det är förmodligen också det närmaste vi kan komma i varje etablerat närmande till varje försök att definiera halveringstider generellt för radionuklider från kända sönderfallsenergier. Citatkällan ovan innehåller heller inga exempel på kurvdiagram som visar de teoretiska värdena kontra de uppmätta.

Ogunbade-Rakityansky 2007

Webbkällan [[Tabell8KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]]

South African Journal of Science 103, March/April 2007 —

New theories of α-radioactivity — P.O.G. Ogunbade, S.A. Rakityansky

http://www.rakitsa.narod.ru/publ_02_09/47.pdf

ger en belysande beskrivning av det allmänna precisionsproblemet i MAC i ämnet TEORETISKA halveringstider (s1/155sp1):

”More than a century has passed since the discovery of radioactivity.

The first qualitative interpretation of α-decay was given

in the early 1920s in terms of tunnelling through a quantummechanical

potential barrier.^1,2 Numerous experimental facts

have been acquired since then, and many theoretical approaches

developed. Modern theories are able accurately to reproduce

the relative half-lives for a wide range of radioactive isotopes. It

is, however, far more difficult to account for their absolute

values. Nowadays, experimentalists continue to measure halflives

using constantly improving techniques, and theoreticians

pursue their quest for an adequate theory of α-decay.”.

Citatkällan ovan är (förmodligen, ännu Dec2011) den enda upphittade som i varje fall FÖRSÖKER beskriva ämnet utifrån den enda (möjligt logiska) vettiga utgångspunkt som finns: relativt effektiva sönderfallsenergin — utan att blanda in alfakanalernas diversifierade energispridningar för varje specifik nuklid. Källan skriver (s2/156sp2ö),

”The Qα term is the energy released in the decay process, the

so-called Q-value. It can be obtained either from the kinetic

energy of the α particle (corrected for the recoil) or from the

binding energies of the parent and daughter nuclei.”.

Källan genomgår sedan TRE olika matematisk-teoretiska metodformer

A The quasi-stationary decaying state approach

B The superasymmetric fission model

C The quasi-classical method

(alla variationer på samma kvantfysikaliska statistiska grundtema) som behandlar beräkning av halveringstiden för alfaradionuklider från givna nuklidparametrar och ovannämnda Qα-värde, här förstått samma som effektiva sönderfallsenergin. Citakällan redovisar värden (s157 Table 1) i en tabell tillsammans med jämförande resultatvärden från de tre metoderna på 16 utvalda nuklider.

— Författarna ger sambanden endast på abstrakt form [typ integralsamband], inga direkt beräkningsbara uttryck presenteras, endast resultaten redovisas i tabellform (se nedan).

— Författarna skriver i sin resultatredovisning (väsentligt för sammanhanget, s157sp2):

;

”

Results and discussion

To avoid unnecessary complications, we consider only nuclei

which decay to the daughter ground state with 100% probability

and for which the spins of both the initial and final states are

known.The masses of the nuclear ground states, needed for

determining the Q-values, are taken from the mass excess table

of ref. 32.

We did the calculations for a wide range of α-decaying nuclei,

using the three theoretical methods. The half-lives thus obtained

are presented in Table 1. For all the 16 nuclei we consider, the

calculations reproduce the experimental half-lives (taken from

ref. 16) to within a factor of 12 or better.The only exceptions are

the nuclei 208Po and 217Th, for which the effects of the proton and

neutron shell closure make it difficult to achieve good accuracy

with the simple potential.^6,7 Comparing the values of T1/2

presented in Table 1,we see that all three methods we tested give

similar results. Therefore, if one is satisfied with an order-of magnitude

estimate, the simplest, Method C, is an appropriate

tool. The half-lives obtained with Method A differ from those

from Method B not more than in 10%. Method C gives half-lives

that are practically identical to those obtained with Method B.

Method C slightly over-estimates the half-lives.The reason for

this is that it completely neglects the parent nucleus configuration

in which the α-particle is dissolved among other nucleons.

Despite this, the general trend of the half-lives calculated using

Method C is rather good. The more sophisticated Method B

takes into account the processes of the α-cluster dissociation. It is

not unexpected, therefore, that it gives a better agreement with

the experimental half-lives.”,

Ogunbade-Rakityansky 2007

Sammanställningen av författarnas tabellredovisning nedan i avvikelsediagrammet visar att vissa av påståendena i citatet INTE håller streck, medan andra gör det — 10log[tH]-skalan här samma som i Uranexemplet, för bästa överskådlighet (20pixels per enhet):

Avvikelsediagrammet efter citatkällans datavärden [[Tabell8KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]]

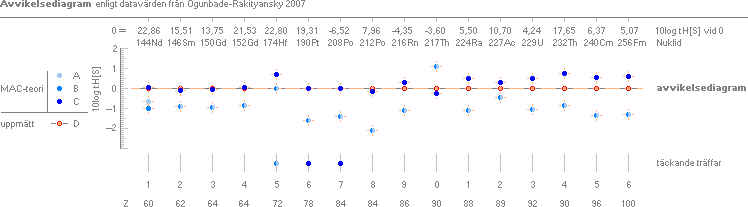
Blå punkter motsvarar citatkällans tre olika metodresultat ABC [citatkällans Table 1, sidan 157sp2n], beteckningarna ABC kopplas av citatkällan efter respektive metodstyckes genomgång, samt anges explicit i källans resultattabell. Orangea punkter motsvarar det experimentellt uppmätta tH-värdet [angivet T½exp i citatkällan]; Dessa har lagts på gemensam referenslinje, med varje nuklids 10log[tH]-referensvärde angivet överst i kolumnen, varefter citatkällans värdepunkter — här omräknade i 10-logaritmer — har avsatts vertikalt; Resultatbilden ovan visar hur de olika ABC-värdena ansluter till, eller avviker från referensvärdet, orangea medellinjen.

— Det mest framträdande är den generella bristen på precision — även med citatkällans mera avancerade tre metodexempel; endast tre heltäckande träffar av 16 möjliga, och då är ändå inte precisionen i dessa av typen direkt användbar för naturvetenskapliga syften. Som författarna själv uttrycker saken (föregående citatblock): ”It is, however, far more difficult to account for their absolute values”.

— Det framgår alldeles tydligt i 10log[tH]-värdena att AB-resultaten [ljusblå, mellanblå ringar] blir praktiskt identiska; de övertäcker varandra i 15 av de 16 fallen, och uppvisar den avgjort STÖRSTA avvikelsen.

— Emellertid påstår författarna att ”Method C gives half-lives that are practically identical to those obtained with Method B”; OM vi byter ut ”C” mot ”A” är påstående uppenbart välgrundat, enligt avvikelsediagrammet; Anomalin i källans påstående kan möjligen vara en felskrivning. Det är i vilket fall tydligt att metod C ger den bästa passningen, också enligt författarnas mening ”Despite this, the general trend of the half-lives calculated using Method C is rather good.” — men att även denna är uppenbart DIVERGENT i sin allmänna form: metodgrunden är uppenbarligen INTE analog med fenomengrunden.

Resultatbilden bara understryker det redan tidigare understrukna:

— Genom att känsligheten i sönderfallsenergin omfattar exponentiella numeriska värden som ligger långt utanför varje normalt beräknande kalkyl med bestämda flyttalsvärden, krävs en närmast oerhörd precision i varje tänkbar teori som vill försöka definiera halveringstider i alfabaserade radiosönderfall. Det finns här veterligt [Dec2011] ingen sådan precisionsbaserad, matematisk, teori som kan uppvisa motsvarande numerisk träffsäkerhet. TRENDLINJERNA framgår emellertid [Se Allmänna AlfaRadioIsotopbilden], ehuru fragmenterade på de olika nuklidernas utspridda värdepositioner [Jämför Urangruppens alfaradioisotoper].

— Det vore naturligtvis oerhört intressant OM, trots allt, en sådan teori fanns. En del människor har en sällsynt förmåga att utveckla den typen — efter att enträget ha intygat att något sådant inte kan existera.

För ev. vidare.

Korrumperade räkneexempel

2011XI27

Den »korrumperade» alfaEnergiLitteraturens räkneexempel

· Ett visst, entydigt experimentellt uppmätt bestämt Eα-värde, för en bestämd radionuklid, med en viss entydigt bestämd halveringstid (tH), finns inte.
Alfaspektroskopisk utrustning mäter olika serier av alfaenergier med olika intensitet och repeterbarhet via olika kemiskt renade [ytterst tunna] mätpreparat.

EXEMPEL:

Se exempeltabellen nedan.

· Varje alfanuklid uppvisar (eng. alpha spectroscopy, alpha channel energy) i allmänhet en uppsättning olika E(α)-värden för en och samma tH-nivå.

EXEMPEL:

Se exempeltabellen nedan.

· Föreställningen att kunna bestämma ett visst tH-värde för en viss radionuklid med en viss alfaenergi, har därmed ingen ENTYDIG fysikalisk motsvarighet, och därmed heller ingen ENTYDIG innebörd.

EXEMPEL:

WileyTabellen ger för U-233 31st olika alfakanalenergier [minsta 4MeV31; största 4MeV82] med en och samma halveringstid 10log[tH(S)] = 12,7 = 5,0118723 T12 S ~ 1,59 T5 år;

Atomnummer;Masstal;Ämne;EalfaMeV;10log tH[S]

92;233;U;4,69;12,70

92;233;U;4,41;12,70

92;233;U;4,62;12,70

92;233;U;4,31;12,70

92;233;U;4,54;12,70

92;233;U;4,68;12,70

92;233;U;4,59;12,70

92;233;U;4,63;12,70

92;233;U;4,47;12,70

92;233;U;4,48;12,70

92;233;U;4,46;12,70

92;233;U;4,66;12,70

92;233;U;4,57;12,70

92;233;U;4,50;12,70

92;233;U;4,61;12,70

92;233;U;4,64;12,70

92;233;U;4,76;12,70

92;233;U;4,63;12,70

92;233;U;4,51;12,70

92;233;U;4,80;12,70

92;233;U;4,82;12,70

92;233;U;4,66;12,70

92;233;U;4,75;12,70

92;233;U;4,51;12,70

92;233;U;4,73;12,70

92;233;U;4,75;12,70

92;233;U;4,57;12,70

92;233;U;4,70;12,70

92;233;U;4,40;12,70

92;233;U;4,78;12,70

92;233;U;4,80;12,70

;

Med b-värdet via minsta 4MeV31 fås

b-formen

b = [√2mE_α]ln[t_H/1S(ln2)]/eZ .... [Se härledning i KÄLLEXEMPEL]

= 8,853;

Bibehålls samma nuklidkoefficient b=8,853 med det alternativa sönderfallsenergivärdet 4MeV82 fås

tH = 3,17 T4 år — 5ggr kortare — som ger 12 = 10log(tH);

— En sådan spridning är värdelös som preciserad uppgift på halveringstid om det gäller mera omfattande tidskronologiska analyser — som i fallet med typ Jordens Urhistoria, och andra himlakroppars sammansättningar (baserat på radiometriska mätningar).

— För att tH-värdet (i exemplet) ska hålla sig på max en halvering av utgångsvärdet (1,59 T5 år) till 7,95 T4 år, får MeV-originalvärdet 4MeV3100 inte överstiga 4MeV5189 — vilket utesluter 22st av exempeltabellens 31st MeV-värden. Och då är, likväl, en sådan marginal en ren katastrof ur precisionssynpunkt för varje bestämt vetenskapligt ändamål: den typen kan inte användas.

— Om tH-värdets andra decimal inte får ändras mer än max 1 enhet (från 1,59 till 1,58), får MeV-värdet inte överstiga 4,311: 1/1000 max.

— Precisionen i MeV-värdena för soliditeten i tH-värdet, dess vetenskapliga användbarhet, utesluter med andra ord alla variabla alfakanalenergivärden av den presenterade typen.

EXEMPELBESKRIVNINGEN därmed endast hänför alfasönderfallets fysik till samma principiella domän som i fallet med betasönderfallen: elektronmassan uppvisar ett SPEKTRUM av skilda energier i samband med det observerade sönderfallet.

— Enda skillnaden mellan elektronsönderfallen och alfasönderfallen är att elektronsönderfallsenergierna är mera rikt representerade (konv. kontinuerligt spektrum) medan alfaenergierna uppvisar linjespridning (olika serier, sk. kanaler, med diskreta MeV-värden).

— Det motsvarande PROBLEMET I TEXTBÖCKERNA är följande:

— Flera (många, alla) författare exemplifierar med typ ETT BESTÄMT alfaenergivärde — när vi nu VET att den aktuella radioalfanukliden i själva verket och i de allra flesta fall uppvisar en SERIE OLIKA värden — men vilken ordning INTE omtalas, omnämns, beskrivs, eller på annat sätt klargörs:

Det finns inga allmänna kopplingar till enskilda alfaenergivärden

; Alltså de enskilda spridda värden som kan uppmätas från olika preparat via alfaspektroskopisk utrustning, för att klargöra exakt,

från bestämda halveringstider:

— DÄREMOT, för att klargöra exakt, finns det MÖJLIGEN allmänna kopplingar till entydigt bestämda sönderfallsenergivärden från bestämda halveringstider, med energivärdena entydigt beräknade efter entydigt bestämda atomvikter och som därmed UTESLUTER floran av SKILDA alfaenergivärden — nämligen i analogi med den empiriskt kända s.k. Geiger-Nuttalls sambandsform:

Exempel HyperPhysics

EXEMPEL:

HyperPhysics tar upp »beräkning av halveringstiden för Poloniumindividen Po-212»;

HYPERPHYSICS — Modeling Polonium-212 Alpha Half-life [2011-11-27]

http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/alptun2.html

”The illustration represents the barrier faced by an alpha particle in polonium-212, which emits an 8.78 MeV alpha particle with a half-life of 0.3 microseconds.”

Källan talar inte om att Po-212 uppvisar flera olika alfaenergier — även med inbördes olika halveringstider, se exempeltabellen nedan.

— HyperPhysicskällan behandlar tydligen sitt räkneexempel SOM OM det vore fråga om en BESTÄMD alfaenergi för en BESTÄMD halveringstid.

— Men källan ger ingen information: inget omnämnande, inget klargörande.

WileyTabellen ger 7st alfakanaler för Po-212 enligt

—————————————————————

Atomnummer;Masstal;Ämne;EalfaMeV;10log tH[S]

84;212;Po;11,65;1,65

84;212;Po;8,78;-6,52

84;212;Po;8,52;1,65

84;212;Po;5,11;1,65

84;212;Po;4,26;1,65

84;212;Po;3,98;1,65

84;212;Po;9,08;1,65

Värdet 10log(tH)=–6,52 motsvarar 0,302µS (3,02 t7 S) — det tH-värde av de 7 som HyperPhysicskällan plockar ut, men som källan lämnar utan vidare motivering eller omnämnande eller beskrivning (jämför i ljuset av tabellutdraget ovan).

— Effektiva sönderfalls(massa)energin för Po-212 är för övrigt (atomvikterna subtraheras 84Po212–82Pb208–2He4, beräkning från särskild tabell) 8,95 MeV att jämföra med HyperPhysicskällan utplockade 8,78 MeV.

(Alfaenergierna ska också alltid vara något lägre än effektiva sönderfallsmassan — finns avvikelser, beror dessa på att moderkärnan har överskottsenergi, se första och sista tabellindividerna ovan).

Räkningen via atomvikterna

Vilket tH-värde är det då som gäller för en viss AtomnummerMasstal (ZA) individ?

— Finns det överhuvudtaget någon sådan koppling?

ENLIGT TNED — relaterad fysik — skulle det finnas ett, endast ett, och ingenting annat än endast ett enda entydigt tH-värde för en bestämd ZA-individ som uppvisar en entydigt bestämd sönderfallsenergi, den här benämnda effektiva sönderfallsenergin;

Effektiva sönderfallsenergin: I RELATERAD MENING betyder, tydligen, en effektiv sönderfallsenergi samma som skillnaden i massenergi mellan den instabila atomens massenergi — den utlösande, ansvariga faktorn — och en närmast efterföljande stabil atoms massenergi. Dvs., samma som en verkställande sönderfallsenergi. Enda entydiga sättet att bestämma den massenergin är veterligt [vidare nedan] att räkna via atomvikterna före och efter.

— Om sönderfallet innefattar flera steg med mellanliggande instabila, men bestämda, atomvikter är sönderfallsenergin på de enskilda stegen tydligen uppdelad på dessa. Effektiva sönderfallsenergin gäller då, tydligen entydigt, mellan två närliggande, bestämbara, atomvikter tillhörande bestämda nuklider.

— Speciellt för typen alfasönderfall [se även utförligt nedan] blir den relaterbara innebörden av den verkställande sönderfallsenergin tydligen massenergidifferensen mellan den instabila moderkärnan och sönderfallsprodukterna [alfapartikeln plus resten], oavsett resterna är stabila eller inte [i kärnsönderfallen är ofta resten just också instabil, med ytterligare sönderfall].

— I betasönderfallen blir motsvarande — entydigt utläsbara — verkställande sönderfallsenergi tydligen massenergidifferensen mellan atomvikten hos den instabila moderkärnan och den närmast följande stabila atomens atomvikt; Vissa möjligheter framskymtar [således] med en uppdelning av massenergidifferenserna på olika STEG genom flera efterföljande sönderfall, och i så fall efter en algoritmisk ordning som här [Dec2011] INTE har någon beskrivning i TNED. Utgångspunkten är här, främst, entydiga massenergiskillnader i sönderfallen mellan två närliggande atomer utan mellanliggande steg.

— NOTERA att analysen i MAC blir motsvarande mera komplicerad relativt TNED eftersom neutrinostrålningen i TNED identifieras med partiklar i MAC och därmed aspekter på rörelseenergier som inte ingår i TNED. Det finns för närvarande ingen enhetligt [heltäckande] genomgång som beskriver helhetsbilden i ljuset av de radioaktiva atomernas fysik för jämförelserna TNED/MAC [men strävan är här att få fram en sådan bild].

— Enda entydiga sättet att få fram en sådan entydigt bestämd ZA-alfasönderfallsenergi är uppenbarligen att räkna via atomvikterna

[ZXA]₀ – [(Z–2)X(A–4)]₁ – 2He4

Men det värdet man DÅ får fram betyder att de uppmätta alfakanalernas energier blir »värdelöst skräp» som inte kan användas i bestämningen;

— Om vi tittar efter på t.ex. Wikipedia Uranium och tabellurvalet på Uranisotoperna (de som finns upptagna 2011-11-27)

ämne angiven alfaenergi MeV i Wikipedia Uranium

U-232 5,414

U-233 4,909

U-234 4,859

U-235 4,679

U-236 4,572

U-238 4,27

är det också, just, precis de MeV-värden vi finner med räkningen enligt atomvikterna. Till jämförande grund visar WileyTabellen resp 9;31;6;12;3;3 stycken alfakanalenergier för resp. masstalsindivid.

— Men: Det motsvarar, tydligen, INTE vad HyperPhysicsKällan försöker ge sken av: uppgiften gällde, tydligen, INTE att bestämma halveringstiden med utgångspunkt från effektiva sönderfallsenergin, utan utifrån ett av de uppmätta alfakanalernas MeV-värden [8,78 MeV] — och vilken syftesform dessutom inte klargörs i beskrivningen.

— Förtegenheten i urvalet verkar (således) kompakt;

— En webbkälla har eftersökts som beskriver dessa (de synnerligen oklara) detaljerna i klartext

— energier i samband med halveringstider för individuellt specificerade nuklider i koppling till Sönderfallets enhetliga preferensgrund för Geiger-Nuttalls sambandsform: EN bestämd halveringstid för EN bestämd nuklid med EN bestämd energi

— men har ännu (Nov2011) inte påträffats.

— Trots en närmast enorm mängd allmänt tillgänglig webblitteratur som beskriver ämnesområdet — alltifrån omfattande mätdatatabeller till apparatmanualer för alfaspektroskopisk utrustning — står de olika till synes inbördes delvis kaotiska uppgifterna om energier, individer, halveringstider och kriterierna för att särskilja/klargöra dessa, utan något uppmärksammat klarläggande eller ens ett omnämnande.

Se även i Q-begreppet.

Det ser alltså ut som att man, även (eller åtminstone) i vissa etablerade led, verkligen, beaktar värdet av ett enda bestämt alfaenergivärde för en bestämd radionuklid. Men, som sagt, att få fram det i KLARTEXT från någon etablerad PORT verkar hart när omöjligt.

Webbreferenser

Webben 28Nov2011-11-28

alpha energy calculation

poor — ringa representation

theoretical alpha energy

http://demonstrations.wolfram.com/GamowModelForAlphaDecayTheGeigerNuttallLaw/

http://labspace.open.ac.uk/mod/resource/view.php?id=431668

Alfaenergier, olika kanaler i mätdata

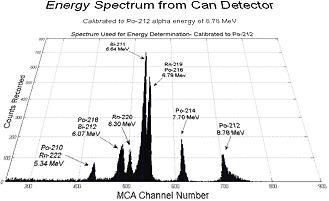
Quantum Mechanics of Alpha Decay

Lulu Liu, Pablo Solis, December 5, 2007

Quantum%20Mechanics%20of%20Alpha%20Decay[1].ppt

Finns även som PDF-dokument,

http://web.mit.edu/lululiu/Public/pixx/not-pixx/alpha.pdf

Främst: Källan visar en tydlig illustration med alfakanaler i en praktisk strålningsmätning — svårt få tag på liknande, tydliga, bidrag som VISAR praktiken bakom.

alpha spectroscopy

rich — stor mängd illustrerad beskrivning

alpha spectrum

rich — stor mängd illustrerad beskrivning

— VAD bestämmer URVALET av något VISST alfakanalvärde framför något annat i konventionella exempelberäkningar?

— Jämför:

PONERA att man HELT — i MAC — slopar föreställningen om »alfapartikelns kinetiska energi» som den katalyserande fysikfaktorn till Geiger-Nuttall-sambandet;

— I TNED betyder det: utmärkt teoretisk grund.

— I MAC däremot: hela »funktionsteorin» utraderas.

— Sett från MAC är effektiva alfasönderfallsenergin (konv. ofta [Q(α)]) omöjlig att förankra i MAC-härledningen till Geiger-Nuttall-sambandets form — därför att den härledande teorin (urspr. från George Gamow) bygger på föreställningen om »en oscillerande vattendroppe» i en vattenvolym (alfapartikeln i atomkärnan) som bumpar emot kärnväggen inifrån — tills droppen händelsevis lyckas rymma ur borgen och framträda som fristående kropp utanför kärnan: i allt statistisk sannolikhet. I TNED finns inte den typen; Den »vattendroppe» (delkärna) som lösgör sig ur huvudvolymen finns i TNED inte till i modervolymen före lösgörandet som någon fristående form. Vattendroppsanalogin är här helt exakt. I TNED är (därför) föreställningen om skilda alfaenergier ovidkommande, på samma sätt som elektronenergierna vid betasönderfall är det. Det avgörande är sönderfallsstyrkan — massenergin; en fast, bestämd dito för en bestämd radionuklids sönderfall, oavsett den radionukliden är si eller så exciterad (de olika alfaenergiernas kanaltoppar).

— I TNED kan vi därför (galant) HELT bortse ifrån »floran av olika alfaenergier», medan en sådan inställning betyder katastrof i MAC; MAC måste ha alfakanalerna för att få ihop det med »sannolikhetsteorin» — men som dock INTE förklarar det ofta enhetligt använda effektiva sönderfallsenergivärdet framför »alfakanalernas olika». Jämför HyperPhysicsExemplet.

— Vi vet ännu inte här vilka KRITERIER som används i MAC för att [TYP HyperPhysicsExemplet, eller LabSpaceExemplet] välja ut den ena eller andra alfakanalen i koppling till (den möjligen icke för dessa författare existerande) effektiva sönderfallsenergin kontra en fast halveringstid. Det är ytterst oklart vad som menas.

Exempel 2

EXEMPEL:

— Exempel: LabSpace

http://labspace.open.ac.uk/mod/resource/view.php?id=431668

(Figure 24, bild nedan) visar utvalda men icke alfakanalspecificerade nuklider (nedan efter effektiva sönderfallsenergin)

Atomnummer;Masstal;Ämne;EeffMeV;10log tH[S]

——————————————————

84;212;Po;8,95;-6,5243288

84;214;Po;7,83;-3,7843624

84;216;Po;6,91;-0,8386320

84;218;Po;6,11;2,2695129

94;236;Pu;5,87;7,9551662

94;238;Pu;5,59;9,4421036

94;240;Pu;5,26;11,3162064

94;242;Pu;4,98;13,0711620

88;222;Ra;6,68;1,5797836

88;224;Ra;5,79;5,4999948

88;226;Ra;4,87;10,7032239

92;228;U;6,8;2,7371926

92;232;U;5,41;9,3373232

92;234;U;4,86;12,8891555

92;238;U;4,27;17,1492171

(SeBildNedan)

för att illustrera Geiger-Nuttall-sambandets giltighet (kredibilitet per exempel) enligt följande:

LabSpace illustrationen

Jämförande exempel

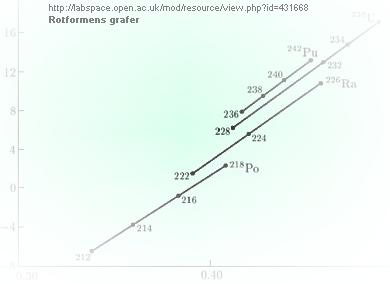
Ovan: Illustrationen I BELYSNING från LabSpace. Sambanden utritade på inverterade rotformen [y=(√E)/b] — en del webbkällor använder den typen, men många använder också den mera direkta y=b/√E som nedan. Vi studerar här endast den [nära] linjära samhörigheten mellan olika nuklidindivider.

— Till jämförelse visas Poloniumlinjen [Po] i bilden nedan med grund i en mera detaljerad tabelldatabas över aktuella alfaRadioNuklider; Vi studerar »principen» i HUR URVALET FUNGERAR i LabSpace illustrationen [många webbkällor visar samma fason som LabSpace, ännu Nov2011 har ingen påträffats som visar den bakomliggande kartbilden]:

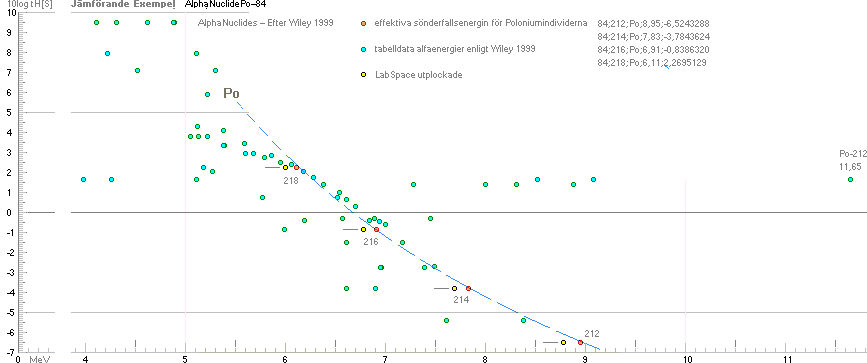
Ovan: Sammanställda tabelldata efter Wiley 1999 för Poloniums alla kända alfakanalers alfaenergier med halveringstider visas i grönblå ringar. LabSpace-källan säger ingenting om dessa värden — man har tydligen helt enkelt plockat ut de nuklidindivider — markerade gula ringar med svart kant — som PASSAR IN BÄST på den motsvarande framräknade teoretiska kurvan;

— Den blåstreckade kurvan med de röd-orangea ringarna är enligt TNED de effektiva sönderfallsenergier som motsvarar de angivna halveringstiderna för de enligt LabSpace specificerade 4 masstalsnukliderna [Po-212| 214| 216| 218]. Vidare i huvudtexten.

— Frågan gällde: Vilket är urvalskriteriet för LabSpace — och många andra liknande källor som vill illustrera ämnet, men som gör det utan att berätta om den tydligt apparenta bakomliggande STORA lösningsmängden; man har att välja och vraka på en stor mängd »passande värden» — att välja JUST de alfaenergier som passar in på den teoretiska kurvan, samt benämna dessa ”stämmer överens med DETALJERADE experimentellt uppmätta värden”?

— Uppenbarligen inget annat än en STOR mängd alternativa värdepunkter — som man inte ens berättar FINNS MED I BILDEN.

— Får man välja och vraka bland flera olika (totalt 66) alternativ (som man dessutom inte behöver redovisa för publiken utom de 4 utvalda) blir det förhållandevis enkelt (eller i varje fall enklare) att få ihop ett hyfsat slutresultat på givna kurvavsnitt. Källan i LabSpace omtalar ingenting om HUR urvalet för de 4 Poloniumnukliderna skett, endast bilden presenteras tillsammans med intygandet

”This agrees with the Geiger–Nuttall relation and a detailed comparison with experimental data is shown in Figure 24. ”,

LABSPACE — Scattering and tunnelling [2011-11-27]

http://labspace.open.ac.uk/mod/resource/view.php?id=431668

De 66 Po-värdena enligt Wiley 1999 är f.ö.

Atomnummer;Masstal;Ämne;EalfaMeV;10log tH[S]

84;190;Po;7,49;-2,70

84;192;Po;7,17;-1,48

84;192;Po;6,61;-1,48

84;193;Po;6,94;-0,44

84;193;Po;7,00;-0,59

84;194;Po;6,84;-0,41

84;194;Po;6,19;-0,41

84;195;Po;6,70;0,28

84;195;Po;6,61;0,67

84;196;Po;5,77;0,76

84;196;Po;6,52;0,76

84;197;Po;6,38;1,41

84;197;Po;6,28;1,73

84;198;Po;5,27;2,03

84;198;Po;6,18;2,03

84;199;Po;5,95;2,52

84;199;Po;6,06;2,39

84;200;Po;5,86;2,84

84;201;Po;5,60;2,96

84;201;Po;5,68;2,96

84;201;Po;5,79;2,73

84;202;Po;5,59;3,43

84;203;Po;5,39;3,34

84;203;Po;5,38;3,34

84;204;Po;5,38;4,10

84;205;Po;5,13;3,78

84;205;Po;5,22;3,78

84;205;Po;5,05;3,78

84;206;Po;5,22;5,88

84;207;Po;5,12;4,32

84;208;Po;5,11;7,96

84;208;Po;4,22;7,96

84;209;Po;4,31;9,51

84;209;Po;4,89;9,51

84;209;Po;4,88;9,51

84;209;Po;4,62;9,51

84;209;Po;4,11;9,51

84;210;Po;4,52;7,08

84;210;Po;5,30;7,08

84;211;Po;6,57;-0,29

84;211;Po;8,88;1,40

84;211;Po;7,45;-0,29

84;211;Po;6,89;-0,29

84;211;Po;7,28;1,40

84;211;Po;8,31;1,40

84;211;Po;8,00;1,40

84;212;Po;11,65;1,65

84;212;Po;8,78;-6,52

84;212;Po;8,52;1,65

84;212;Po;5,11;1,65

84;212;Po;4,26;1,65

84;212;Po;3,98;1,65

84;212;Po;9,08;1,65

84;213;Po;8,38;-5,38

84;213;Po;7,61;-5,38

84;214;Po;6,90;-3,78

84;214;Po;7,69;-3,78

84;214;Po;6,61;-3,78

84;215;Po;6,96;-2,75

84;215;Po;6,95;-2,75

84;215;Po;7,39;-2,75

84;216;Po;6,78;-0,84

84;216;Po;5,99;-0,84

84;217;Po;6,54;1,00

84;218;Po;5,18;2,27

84;218;Po;6,00;2,27

— Endast 4 av dessa finns som sagt representerade i LabSpace-illustrationen enligt ”a detailed comparison with experimental data”. Men källan säger ingenting om dessa — de återstående 62 individerna runt omkring.

(Wao).

— Men EXEMPELET är ingalunda signifikant för LabSpace; det ser likadant ut i varenda annan övrig etablerad »facklitteratur» i ämnet, åtminstone i de källor jag har skummat igenom (under ett antal veckor, ingen nämnd, ingen glömd).

— Försöken (upprepade, i flera perioder med dagar mellan) att hitta NÅGON etablerad källa som omtalar, beskriver och förklarar bakgrunden, har hittills inte givit resultat (Nov2011).

— Det är också, på visst sätt, förståeligt — svårigheten att hitta begripligt beskrivande etablerade källor i ämnet radionuklidernas matematiska fysik:

— Ämnet är närmast ofattbart, enormt, dels omfattande och dels så snårigt i begreppstermer [uppblandat med i stort sett normalt obegriplig matematisk fysik] att få [om ens några] är i stånd att ge någon vettig, ens behjälplig orientering i ämnet. Om den beskrivningen håller streck: Det betyder att ett SYNDROM utvecklats: man hänvisar till det som uppfattas som »pålitliga källor» — utan att någon riktigt vet vad dessa källor har för några premisser.

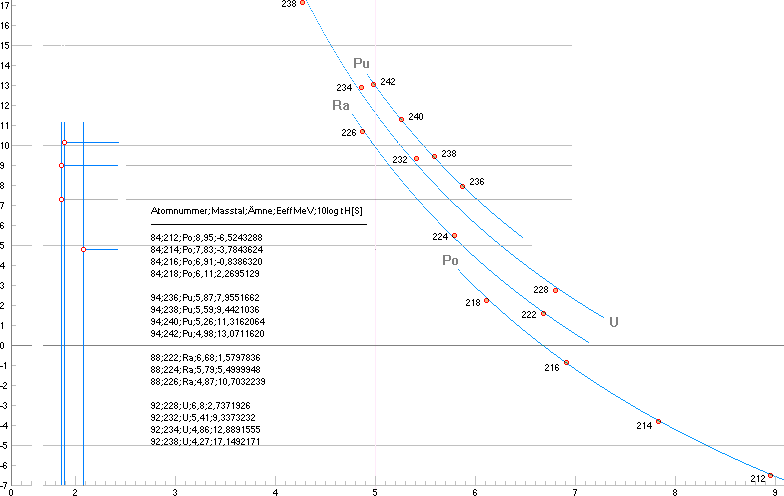
Den motsvarande TNED-kurvbilden för LabSpace-skaran skulle bli som nedan — efter effektiva sönderfallsenergierna med samma givna tH-värden (samma som LabSpace);

Nedan: Den fasta b-formen från Allmänna tH-sambandet,

10log tH/1S = +(1/ln10)[beZ(2mE – E₀)^–0,5 + ln(ln2)] + 10log t₀

Graf: y =–40+(1/ln10)[(174.51)[([x-E₀]/5)'–0.5]+ln(ln2)] + t₀, Unit20p

genomskär radionuklidfältets nedanstående fyra närmast matchande begränsade punkfält — till jämförelse med LabSpace-bilden.

— Men denna TYP av kurvmatchning är, enligt TNED, INTE den optimala för radionuklidernas del. Se här direkt till jämförelse punktbilden med TNED-kurvorna till Urangruppen. Det är en helt annan grundform — trots exakt samma matematiska skelett.

— Medan MAC-teorin använder variabla modernukliders atomnummer [Z] i sin kurvekvation, och som ger OLIKA kurvformer, har TNED en fast kurvform — efter nuklidkoefficientens maxvärde ±8pi — och som kan placeras godtyckligt i de olika kvadranterna för att undersöka ev. kurvmatchningar. Den delen kan inte nås av MAC-teorin.

— Exemplet nedan är — således — inget representativt för TNED-teorin, men visar å andra sidan att TNED-formerna ändå med viss finess kan hänga med — även i en modernt skruvad serv. Jämför TNED:s egen Urangrupp: samtliga kommer med.

— I TNED-teorin finns — å den andra sidan — ingen [här ännu känd] allmän matematisk form som kan placera den fasta b-formens kurva så att den träffar en viss nuklid; alla nuklidpositioner måste redan vara kända.

Se även Exempel 1 och Exempel 3.

Referenser

Referenser

[VNS]. Van Nostrand’s Scientific Encyclopaedia Fifth Edition 1976, Sönderfallstider enligt Table 3, s495-501.

[HOP]. Handbook of Physics, E.U. Condon, McGraw-Hill 1956-67, Atomvikter sidorna 9-65 – 9-86 Table 2.1.

[BA]. Bonniers Astronomi 1978, Det internationella standardverket om universum sammanställt vid universitetet i Cambridge

[EST]. Encyclopedia of Science & Technology, McGraw-Hill 1992

[FM]. FOCUS MATERIEN 1975

Observerade fel

EST-15s104 Table 1 Example (rad6). Felaktig beteckning 71La. Korrekt beteckning är 71Lu. La har atomnummer 57.

MAC

Här ofta använd bekväm förkortning för Modern Akademi (ofta i jämförelse med TNED).

Eα

Eα E_α ; även konv. samma som den allmänna energiparametern för alfapartikeln [alfapartikelns rörelseenergi] vid kärnsönderfall; Alfatecknet (α) indexerar alfapartikeln som Heliumatomen 2He4 [eller dess kärna].

Qalfa

Q-alfa och Q-value

”The Q value is the kinetic energy released in the decay of the particle at rest. For example, for neutron decay:^[2]

Q = (m_n – m_p – m_v – m_e)c²

where m_n is the mass of the neutron, m_p is the mass of the proton, m_v is the mass of the electron antineutrino and m_e is the mass of the electron.”.

@INTERNET Wikipedia Q value (nuclear science) [2011-12-08]

;

Jämförande exempel

JÄMFÖRANDE UTVÄRDERINGSEXEMPEL [8Dec2011] SOM BEVISAR OLIKA PREFERENSER:

TNED — atomvikternas mass-energidifferens = effektiva sönderfallsenergin [ref- HOP-tabellens värden från 1967]:

[uc²/eT6 = 931,4795168 MeV; u=1,66033 t27 KG; c=2,99792458 T8 M/S; e=1,602 t19 C];

E_α: 84Po207(206,9815580) – 82Pb(207–4=203)(202,9732290) – 2He4(4,0026031) = 0,0057259;

= 5,333558565 MeV

E_β+: 84Po207(206,9815580) – 83Bi207(206,9784380) = 0,00312;

= 2,906216092 MeV

:

Jämförande basVärden enligt WolframAlpha (konventionellt används något olika konstantvärden mot ovan):

[uc²/eT6 = 931,4940848 MeV; u=1,660539 t27 KG; c=2,99792458 T8 M/S; e=1,6021766 t19 C];

E_α: 84Po207(206,9815931) – 82Pb(207–4=203)(202,9733905) – 2He4(4,0026033) = 0,0055993;

= 5,215714829 MeV

E_β+: 84Po207(206,9815931) – 83Bi207(206,978471) = 0,0031221;

= 2,908217682 MeV

;

Jämför WolframAlfa-värdena:

E_α: Q–value

= 5,21581 MeV

E_β+: Q–value

= 1,88639 MeV

;

SLUTSATS — förutsatt att alla siffervärden grundas på felfria, relevanta räkningar:

— Medan E_α-värdet (bägge 5,215) är analogt i »Q-formen», är tydligen E_β+-värdet det inte (2,908 vs. 1,886).

— Det betyder att teorierna TNED/MAC via olika resultatvärdet INTE (på något enkelt sätt) kan anställas i någon generaliserad (enkel) jämförelse;

— PROBLEMET är att MAC-källorna (heller) INTE redovisar — tydligt — vad som gäller:

TROTS att WolframAlpha-data grundas generellt på den nyare tidens (delvis mera preciserade) värden för atomvikter (och konstanter, c frånsett —

ännu samma värde som gavs från mätningar under 1970-talet; 2,99792458 T8 M/S WolframAlpha anger inte de tre sista siffrorna)

är det tydligt att ÄVEN om man använder WolframAlpha-källans egna värden (med c=2,99792458 T8 M/S) en motsvarande massa-energi-analogi INTE finns i exempelfallet ovan med E_β+-värdet.

— Också andra etablerade webbkällor ansluter till samma »syndrom»:

Wikipedia citat

”As in the case of α-decay the difference between the mass of the parent nucleus, m_P and the

mass of the daughter, m_D plus the electron is the Q-value for the decay, Q_β
,

Q_β = (m_P – m_D – m_e)c² ,

42

and in this case the recoil of the daughter can be neglected because the electron is so much

lighter than the nuclei. We would expect this Q-value to be equal to the kinetic energy of the

emitted electron, but what is observed is a spectrum of electron energies up to a maximum

value which is equal to this Q-value.”, s42

BETA DECAY (källform och datumuppgift saknas)

http://www.hep.phys.soton.ac.uk/hepwww/staff/D.Ross/phys3002/beta.pdf

— I effektiva sönderfallsenergin (betasönderfallen, såväl som alfasönderfallen) finns ingenting sådant som det i citatet närmast ovan antydda »elektronMaxEnergin lika med sönderfallets massa-energiskillnad», enligt TNED, ”Q-value to be equal to the kinetic energy”.

— Effektiva sönderfallsenergin i TNED — relaterad fysik — räknas efter ATOMVIKTERNA. Inget annat.

— Men i TNED gäller också att NEUTRINOBEGREPPET inte ansluter till kinetiken: neutrino i TNED är em-strålning. Det finns ingen »kinetisk energi»-aspekt att lägga på varken betasönderfallet eller alfasönderfallet i TNED. Det enda som räknas är effektiva sönderfallsenergin, mass‑energi‑skillnaden mellan tillståndet före (modernuklidens mass-energi) och efter sönderfallet (summan av komponenternas massenergi). Inget annat. Se f.ö. Jämförande räkneexempel längre upp.

— Det är den ena sidan av saken, och som visar att begreppsgrunderna TNED/MAC definitivt inte är analoga i sönderfallspreferensernas energiräkning.

— Den andra sidan av saken är att man också, i MAC, stundtals talar om energibindningen per nukleon — vilket ytterligare förvärrar den jämförande förutsättningen TNED/MAC:

— Massdefekterna i relaterad fysik [se förklaringen med Inledande Jämförande Exempel] använder hela atomen som preferens, medan MAC använder endast kärndelarna; Det finns ingen enkel sambandsform mellan de olika sätten (energibindningsbegreppet generellt) i TNED och MAC, eftersom nuklidordningen mellan de olika sätten också via de olika preferenserna blir olika inbördes, vilket exemplet i länken ovan illustrerar.

— Med andra ord: här ser det maximalt kört ut; då bägge teorierna kan inte gälla samtidigt, måste endera förklaras primitiv i den andras ljus.

— Ytterligare en detalj som (möjligen) fördunklar »MAC-begreppet»:

— Wikipediacitatet längre upp påstår, tydligen generaliserande, att

”As in the case of α-decay ... plus the electron is the Q-value”

— Det är inte här känt vad som döljer sig bakom denna, högst, besynnerliga formulering: Den antyder att man generellt skulle räkna med EN elektron, oavsett komponenter. Det var något nytt.

[En liknande, analog, formulering som svar på direkt fråga finns på AnswersYahoo från Feb2010,

Q VALUE CALCULATION FOR BETA DECAY.?

http://answers.yahoo.com/question/index?qid=20100221072628AAEKx1G

].

— Andra webbkällor som försöker DEFINIERA Q-begreppet har här eftersökts, men ännu inte påträffats;

— En webbkälla har påträffats som ger samstämmiga exempelvärden, som ovan, med TNED:

”

Parent E(keV) Mode Jπ t½ Q(keV)

————————————————————

207Po 0 α 5/2- 5.80 h₂ 5215.9₁₀

0 EC 5/2- 5.80 h₂ 2909₆

”, s38

PARENT NUCLIDES FROM THE TABLE OF ISOTOPES

http://ie.lbl.gov/decay/parent.pdf

från

ERNEST ORLANDO LAWRENCE BERKELEY NATIONAL LABORATORY (LBL)

http://ie.lbl.gov/decay.html

med LBL:s portalsida

http://www.lbl.gov/

— Uppgiften 2909 KeV = 2,909 MeV för E_β+-värdet hos Poloniumnukliden 84Po207 stämmer betydligt bättre med TNED-resultatets 2,906216092 MeV än WolframAlpha:s 1,88639 MeV.

— Det finns alltså vissa tendenser på webben som ANSLUTER resultat och begreppsvis TILL samma preferenser som används i TNED — medan åter andra INTE gör det. Det är här inte känt vad som föranleder de uppmärksammade MAC-skillnaderna (utöver möjligheten och att också flera än författaren uppmärksammat den inte sällan I FYSIKDJUPET virriga nomenklaturen i MAC som omöjliggör en Logiskt Sammanhängande Beskrivning).

;

— Ofta [men inte alltid i klartext] används i konventionell facklitteratur beteckningssättet Q_α [Q(α), Q-alfa] för den (kinematiskt) effektiva sönderfallsenergin. Denna är dock INTE samma som massa-energi-differensen enligt räkning via atomvikter i TNED (se ovan från Q-alfa). Vad som gäller i MAC (Jämför Wikipediacitat längre upp med ”... plus the electron ...”) saknar här ännu [Dec2011] någon klar referent; Det är endast om respektive webbkälla ger en egen, klar, beskrivning av termformerna som någon vidare jämförelse kan göras.

tH

tH, t_H, förkortning för halveringstid i denna presentation. Konventionellt anges tH ofta T_½.

MeV

MegaElektronVolt, ofta använd förkortning inom atom- och kärnfysiken.

Samband:

—Elektriska energin anges generellt (efter utvecklingar från elektriska kraftlagen) E = UQ, fysikalisk enhet i Joule;

— Genom att dividera E(Joule) med elektronladdningen (Q[e]=1,602 t10 C), samt dividera ytterligare en gång med en miljon [1 T6] fås enheten i MeV enligt

E(Joule)/Q[e]T6 = E(MeV).

LBL Atomic masses 2003 — Lawrence Berkeley National Laboratory — Atomic Masses, Audi et al 2003:

[[Tabell1KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]]

A T O M I C M A S S A D J U S T M E N T

Atomvikter för masstalen 1 till 293 (t.o.m. atomnummer 118) — 3179 individuppgifter — Referenstabell för analys

KÄLLVÄG:

http://www.nndc.bnl.gov/masses/mass.mas03

från

http://www.nndc.bnl.gov/masses/

från

http://www.nndc.bnl.gov/amdc/

från

TABLE OF ISOTOPES ATOMIC MASS — DATA HOME PAGE

http://webcache.googleusercontent.com/search?q=cache:SKNTE7Dt43MJ:ie.lbl.gov/toimass.html+isotopic+masses&cd=21&hl=en&ct=clnk&gl=uk

— NOTERA att ovanstående gör det VÄLDIGT SVÅRT att få fram vilka KONSTANTER som har använts för vilka tabellreferenser i vilka avseenden;

— Atomviktsvärden anges, ja. Men vi vet inte vilken atomära massenhet som använts; Olika källverk ger något olika decimalvärden i slutet typ 1,66033..., 1,66043..., 1,66053.... Det vore BRA om tabellfolket kunder tala om vilken som används — i DIREKT anslutning till tabellen, INTE utspritt på TYP hundra länkområden runt omkring.

Wiley 1999

[[Tabell3KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]]

PDF-dokument — Wiley AlfaNuklidTabell 1999

WILEY INTERSCIENCE — 8th Edition of the Table of Isotopes: 1999 Update — Table 3. Alpha Particle Energies

http://www.wiley-vch.de/books/info/0-471-35633-6/toi99/toi.htm

Välj Table 3. Alpha Particle Energies,

leder till PDF-dokument med kopierbara tabellkolumner,

http://www.wiley-vch.de/books/info/0-471-35633-6/toi99/www/decay/table3.pdf

Noteringar — Wileytabellens användning i denna framställning

1. WILEY-Tabellen omfattar totalt 2090st nuklidobjekt med specificerade alfaenergier i MeV med halveringstider [tH];

— Tabellen innehåller 3 rader med utelämnad uppgift för tH-värde för individerna

163Os

230Pu

229Pu

— Dessa har tagits bort i upptagningen av datasamlingen för analysen till denna framställning.

2. I sammanställningen av de effektiva sönderfallsenergierna har alla individer AtomnummerNUKLIDMasstal i Wileytabellen med samma numeriska tH-värde [alla alfakanalenergier med samma uppgift på halveringstiden] eliminerats — utom den enda nuklidsignifikanta; För denna har sedan beräknats [via separat atomviktstabell, se LBNL 2003] effektiva sönderfallsenergin genom räkning via atomvikter.

— I 76 fall, individerna listade nedan, har SÅLEDES något olika tH-uppgifter medfört att [likväl] en och samma nuklid med en given effektiv sönderfallsenergi har fått [NÅGOT] olika tH-värden

Multipla tH-individer

Efter Wiley 1999

INDIVIDER MED SAMMA Effektiva sönderfallsenergi — men olika halveringstider:

Wileytabellens dataindivider har energibestämts (Eeff) i separat räkning genom massa-energiskillnaden mellan Wileyindividen (W) och dess alfasönderfallsprodukt (P) med hjälp av LBL-tabellens atomvikter, W–P=Eeff;

— Resultatindividerna har sedan kontrollerats via separat webbreferens i WolframAlpha med koll på, såvitt likartade (angivet med fetstil i resultattabellerna nedan), motsvarande halveringstider för att få jämförande/kontrollerande referens.

— Undersökningens syfte: att belysa en delvis uppmärksammad AVSAKNAD av begriplighet i allmänt framställda tabellverk.

— Jämför SÖNDERFALLETS ENHETLIGA PREFERENSGRUND i koppling till Geiger-Nuttalls samband: EN bestämd halveringstid för EN bestämd sönderfallsenergi för EN bestämd radionuklid.

— Resultatsammanfattning: det är tydligt att bristen på ordning är uppenbar. [Det är ALDRIG eleverna, seriöst, det är fel på — det är ALLTID lärosystemets fel om något inte fungerar].

Dataspecifikation: Atomnummer;Masstal;Ämne;EeffMeV;10logtH[S]; Eeff efter räkning via atomvikter [LBL 2003].

—————————————————————————————

Listade kolumnvis efter ämnen i bokstavsordning — Ac At Bh Bi Es Fm Fr Hf Hg Ho Hs Ir Lu Mt Pa Pb Po Ra Re Rn Sg Ta Tb Th Tl Tm Ua W — 28st

89;206;Ac;7,94;-1,4814861

89;206;Ac;7,94;-1,6575773

89;208;Ac;7,73;-1,6020600

89;208;Ac;7,73;-1,0222764

89;217;Ac;9,83;-6,1307683 89;217;Ac;9,83;-7,1611509	83;186;Bi;7,76;-1,8239087 83;186;Bi;7,76;-2,0087739	83;196;Bi;5,44;2,4885507 83;196;Bi;5,44;2,3802112	87;218;Fr;8,01;-3,0000000 87;218;Fr;8,01;-1,6575773	77;172;Ir;5,85;0,6434527 77;172;Ir;5,85;0,3010300
89;222;Ac;7,14;0,6989700 89;222;Ac;7,14;1,7993405	83;187;Bi;7,79;-3,0969100 83;187;Bi;7,79;-1,4559320	83;210;Bi;5,04;13,9819776 83;210;Bi;5,04;5,6366114	72;156;Hf;6,03;-1,6020600 72;156;Hf;6,03;-3,3526170	77;174;Ir;5,62;0,9542425 77;174;Ir;5,62;0,6901961
85;194;At;7,29;-1,3979400 85;194;At;7,29;-0,6020600	83;188;Bi;7,26;-0,6777807 83;188;Bi;7,26;-1,3565473	83;212;Bi;6,21;3,5602654 83;212;Bi;6,21;3,1760913	80;185;Hg;5,77;1,6910815 80;185;Hg;5,77;1,3344538	71;155;Lu;5,8;-2,5850267 71;155;Lu;5,8;-1,1674911 71;155;Lu;5,8;-0,8538720
85;197;At;7,1;-0,4559320 85;197;At;7,1;0,5682017	83;189;Bi;7,27;-0,1674911 83;189;Bi;7,27;-2,3010300	99;254;Es;6,62;7,3769505 99;254;Es;6,62;5,1506951	80;187;Hg;5,23;2,1583625 80;187;Hg;5,23;2,0569049	71;156;Lu;5,6;-0,7447275 71;156;Lu;5,6;-0,3010300
85;198;At;6,89;0,0000000 85;198;At;6,89;0,6232493	83;190;Bi;6,86;0,7993405 83;190;Bi;6,86;0,7923917	100;247;Fm;8,21;1,5440680 100;247;Fm;8,21;0,9637878	67;151;Ho;4,7;1,5465427 67;151;Ho;4,7;1,6739420	71;157;Lu;5,11;0,8325089 71;157;Lu;5,11;0,6803355
85;200;At;6,6;0,5440680 85;200;At;6,6;1,6720979 85;200;At;6,6;1,6334685	83;191;Bi;6,78;1,0791812 83;191;Bi;6,78;-0,8239087	87;200;Fr;7,62;-0,2441251 87;200;Fr;7,62;-1,7212464	67;152;Ho;4,51;1,6989700 67;152;Ho;4,51;2,2089785	109;266;Mt;11;-3,0969100 109;266;Mt;11;-2,4202164
85;202;At;6,35;-0,3372422 85;202;At;6,35;2,2600714 85;202;At;6,35;2,2648178	83;192;Bi;6,38;1,5976952 83;192;Bi;6,38;1,5682017	87;204;Fr;7,17;0,0000000 87;204;Fr;7,17;0,4149733 87;204;Fr;7,17;0,2304489	67;153;Ho;4,05;2,7466342 67;153;Ho;4,05;2,0791812	91;217;Pa;8,49;-2,7958800 91;217;Pa;8,49;-2,3098039
85;212;At;7,82;-0,9244530 85;212;At;7,82;-0,5030704	83;193;Bi;6,3;1,8260748 83;193;Bi;6,3;0,5051500	87;206;Fr;6,92;1,2013971 87;206;Fr;6,92;-0,1549020	67;154;Ho;4,04;2,2695129 67;154;Ho;4,04;2,8485586	82;187;Pb;6,4;1,1818436 82;187;Pb;6,4;1,2624511
85;214;At;8,99;-6,2533658 85;214;At;8,99;-6,1191864 85;214;At;8,99;-6,5767541	83;194;Bi;5,92;2,0606978 83;194;Bi;5,92;1,9777236	87;214;Fr;8,59;-2,4749552 87;214;Fr;8,59;-2,3010300	108;265;Hs;10,59;-3,0457575 108;265;Hs;10,59;-2,8096683	84;195;Po;6,75;0,2833012 84;195;Po;6,75;0,6665180
107;262;Bh;10,3;-0,9913998 107;262;Bh;10,3;-2,0969100	83;195;Bi;5,83;2,2624511 83;195;Bi;5,83;1,9395193	87;215;Fr;9,54;-7,0655015 87;215;Fr;9,54;-8,4559320	77;166;Ir;6,72;-1,9788107 77;166;Ir;6,72;-1,8210231	84;197;Po;6,41;1,4116197 84;197;Po;6,41;1,7291648

84;199;Po;6,07;2,5169318 84;199;Po;6,07;2,3941013	75;162;Re;6,24;-0,9706162 75;162;Re;6,24;-1,1249387	106;263;Sg;9,39;-0,5086383 106;263;Sg;9,39;-0,0969100	81;179;Tl;6,72;-0,7958800 81;179;Tl;6,72;-2,8538720	110;273;Ua;11,37;-0,9208188 110;273;Ua;11,37;-3,7447275
84;211;Po;7,59;-0,2873503 84;211;Po;7,59;1,4014005	86;197;Rn;7,41;-1,7212464 86;197;Rn;7,41;-1,1870866	73;157;Ta;6,35;-1,9956786 73;157;Ta;6,35;-2,3665315	81;187;Tl;5,32;1,1931246 81;187;Tl;5,32;1,7075702	74;158;W;6,61;-3,7958800 74;158;W;6,61;-3,0457575
84;212;Po;8,95;1,6541765 84;212;Po;8,95;-6,5243288	86;199;Rn;7,13;-0,2076083 86;199;Rn;7,13;-0,4948500	73;158;Ta;6,12;-1,4377071 73;158;Ta;6,12;-1,3098039	69;153;Tm;5,25;0,3979400 69;153;Tm;5,25;0,1702617
88;203;Ra;7,73;-1,4814861 88;203;Ra;7,73;-3,0000000	86;201;Rn;6,86;0,8450980 86;201;Rn;6,86;0,5797836	73;160;Ta;5,45;0,2304489 73;160;Ta;5,45;0,1903317	69;154;Tm;5,09;0,5185139 69;154;Tm;5,09;0,9084850
88;207;Ra;7,27;0,1139434 88;207;Ra;7,27;-1,2596373	86;203;Rn;6,63;1,4471580 86;203;Rn;6,63;1,6532125	65;149;Tb;4,08;2,3972446 65;149;Tb;4,08;4,1709888	69;155;Tm;4,57;1,6532125 69;155;Tm;4,57;1,3344538
88;213;Ra;6,86;-2,6777807 88;213;Ra;6,86;2,2159018	86;214;Rn;9,21;-8,1870866 86;214;Rn;9,21;-9,1611509 86;214;Rn;9,21;-6,5686362	90;216;Th;8,07;-1,5528420 90;216;Th;8,07;-3,7447275	110;271;Ua;10,87;-2,9586073 110;271;Ua;10,87;-1,2218487

Totalt 78×2+6 = 162 individer: 72 par, 6 tripletter.

TabellÄmnena efter atomnummer (Z):

65Tb 67Ho 69Tm 71Lu 72Hf 73Ta 74W 75Re 77Ir 80Hg 81Tl 82Pb 83Bi 84Po 85At 86Rn 87Fr 88Ra 89Ac 90Th 91Pa 99Es 100Fm 106Sg 107Bh 108Hs 109Mt 110Ua

;

Värden med fetstil, [OM det finns någon lika, eller i det allra närmaste lika (EX: WolframAlpha visar 31mS för Wileys 33 mS, Ra-203)] med motsvarande lika eller nära lika värde från WolframAlpha [Nov2011] — här endast för ORIENTERING i Wileytabellen HURUVIDA något av de angivna multipla tH-värdena HAR en motsvarande ENTYDIG make i någon ANNAN källreferens;

— Skriv in i sökboxen [Google] typ »ac-222 half-life» eller bättre »actinium-222 half-life» och tryck Enter; Google-sökningen visar ett [motsvarande anpassat] WolframAlpha-block överst; klick på det leder till WolframAlpha, och en uppställning data som visar resultatvärden.

— OMARKERAT GRUPPVÄRDE [ingen fetstil] betyder att Wolframvärdet avviker »mera markant» från Wileytabellens värde;

— I grafdiagrammen i denna presentation används i grundsättningen en max pixelenhet 20p för varje vertikal 10log tH[S]-enhet; Det betyder att max decimal upplösning i vertikalled är N,n5;

— Visar t.ex. Wiletabellen värdet 1,2558 och WolframAlpha värdet 1,34.. är avvikelsen runt 2 pixels — och då är det TVEKSAMT om uppgiften, alls, har någon MENING i ett PRECISIONSBASERAT kurvpassningssammanhang; den värdeformen markeras visserligen [med särskilda punktfärger] i denna framställning, men kommer inte att ingå i kurvpassningsanalysen.

— NOTERA att den ordningen också innefattar en viss äventyrlighet [osäkerhet]:

1. Mitt eget skummande godtycke i utvärderingen, utan redovisade WolframAlpha-siffror [vilket KAN innehålla FEL];

2. Ingenting exakt är känt, varken om Wileytabellens urgrunder, eller om WolframAlpha-data [WolframAlpha har ingen explicit redovisning av sina datavärden — annat än en allmänt världsambitiös »vi gör så gott vi kan, och du kan lita på oss»-policy; direkta källreferenser saknas];

3. Blotta jämförelsen ovan visar DELS att överensstämmelsen ibland är tämligen exakt [in till sista decimalen], och i vissa fall oacceptabel;

— Med den reservationen i bakhuvudet kan dataflödet i den här framställningen och dess tabellreferenser förstås bättre som ORIENTERANDE [med en viss anstrykning till »precist närmande»].

Inget annat.

— Vad BEROR avvikelserna i Wiletabellen[WolframAlpha-värdena] på? Hur kan en och samma alfaradionuklid uppvisa [ibland tydligt vitt] skilda värden?

— Det finns, tyvärr [ännu här känt] ingen etablerad beskrivning på den punkten.

;

— LITTERATURHÄNVISNINGAR [typ WIKIPEDIA] på associerade alfaenergier i uppgifter om olika radionukliders halveringstider, visar genom kontroll [källorna anger det inte själva, specifikt; sådana uppgifter har eftersökts men inte påträffats] att alfaenergivärdet är samma man får för effektiva sönderfallsenergin efter räkning via atomvikter. Dvs., EN ENTYDIGT BESTÄMD sönderfallsenergi för EN ENTYDIGT BESTÄMD halveringstid.

;

— Med referens till jämförande kontrollvärden på WolframAlpha-databasen [fetstilen i tabellblocket ovan]

http://www.wolframalpha.com/about.html

är det tydligt att Wileytabellens OLIKA tH-värden för samma alfaradionuklid INTE bottnar i någon analog fysikbeskrivning; de olika tH-värdena från Wiletabellen är uppenbarligen »bara avvikande mätvärden» — som dock reser den intressanta FRÅGAN hur. Tyvärr finns [här ingen känd] ingen källbeskrivning på den delen [från Wiley-domänen].

;

OM det [nämligen] verkligen SKULLE förhålla sig som tabellextraktet i Multipla tH-individer visar, multipla halveringstider för en och samma radionuklid, finns uppenbarligen inget BESTÄMT kriterium i fysiken för uppfattningen om EN bestämd halveringstid för EN bestämd radionuklid.

— En etablerad beskrivning, omnämnande, klargörande, eller kommentar har eftersökts på denna detalj, men [Nov2011] inte påträffats. [Nivån på beskrivningen generellt på webben 2011 innefattar, tydligen, inte det intellektuella djupet].

;

— OM förklaringen till de 72 paren plus de 6 tripletternas inbördes lika halveringstidsvärdena å andra sidan skulle vara den sensationella, att beroende på mätpreparatets explicita nuklidsammansättning kan OLIKA tH-värden insmyga sig och gömma sig bakom floran av alfakanalernas specifika energier — och som sedan svårligen kan upptäckas om man inte, som här, genomför en regelrätt räkning via atomvikter för varje alfaRadionuklids effektiva sönderfallsenergi, och, som här, genomför en grundlig kontroll — DÅ är det alternativet ÄNNU värre: för modern teori; halveringstiden påverkas märkbart av omgivningen.

;

— I många av fallen är skillnaden mellan de olika tH-värdena marginell [vilket avspeglar en naturligt marginell spridning i mätvärden], medan åter i en del andra fall skillnaden signalerar »direkt anmärkningsvärd»: flera tiopotenser.

— Den enda resoluta förklaringen skulle (därmed) vara att dessa olika värden avspeglar en bestämd OSÄKERHET i mätningarna [vilket i ljuset av fleraTiopotenserExemplen verkar mysko, se t.ex. 88;213;Ra; -2,677.. mot 2,12...; differensen runt 4 tiopotenser]; det finns m.a.o. inget SÄKERT bestämt värde för dessa fall — enligt tabellsigillets märkdatum.

— Det är här [Nov2011] ingenting VIDARE känt om dessa nuklider i ljuset av ovan omnämnda uppmärksammande.

I MAC undgår »multipelnukliderna» upptäckt, uppenbarligen, eftersom de gömmer sig bakom olika alfakanalenergivärden — och vilka man anser viktiga för det teoretiska sammanhanget.

Resultatexempel

Resultatexempel

Låt oss studera ett RESULTATEXEMPEL — med ovanstående införda justeringar, här från alfaradionukliden (84)Polonium — och som (förhoppningsvis) visar, belyser och exemplifierar VÄRDET i och av den här presentationen;

Nedan: Alla Wiletabellens angivna alfakanalenergivärden för Polonium;

GrönBlå

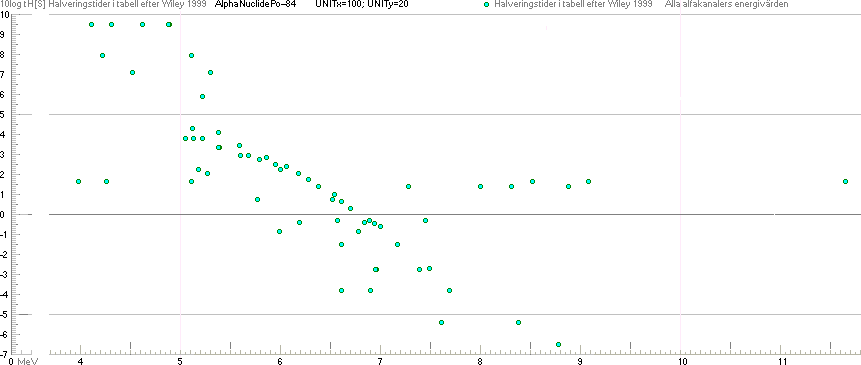
Att försöka »analysera» punktmängden ovan tillhör INTE de enklare uppgifterna — OM uppgiften ansluter till föremålet för radiofysikens ÖVERGRIPANDE matematik: att undersöka en sammanbindande kurvpassning mellan MÅNGA individer som var och en uppvisar EN bestämd halveringstid [tH] för EN bestämd sönderfallsenergi [men i diagrammet ovan representerade av flera MeV-värden på samma horisontlinje = tH-värde] — för en bestämd nuklid. En stor del av den punktmängden bortfaller med referens till den effektiva sönderfallsenergin som ger endast EN bestämd MeV-position för EN bestämd tH-nivå — men en del [många] webbkällor tycks »plocka friskt» i punkthavet för att illustrera »samhörigheten mellan teori och experimentellt uppmätta värden»; Se Exempel 2.

;

Nedan: Endast de ingående alfaradionukliderna med Effektiva sönderfallsenergin beräknad efter atomvikter [LBL 2003] för varje i WileyTabellen angiven alfaradionuklid — vilket utesluter alla multipla tH-värden för samma alfaradionuklid i föregående punktdiagram;

— För att avstämma OM NÅGOT av Wiletabellens angivna skilda tH-multipelvärden för en och samma nuklid har NÅGON ANNAN KÄLLREFERENS har Wileydata avstämts [manuell kontroll, per] via internetdomänen WolframAlpha och dess presenterade värden — via röda punktcirklar med gul fyllning; de återstående, »icke behöriga» i de multipla Wilegrupperna, har angivits med grå punktcirklar;

Röda

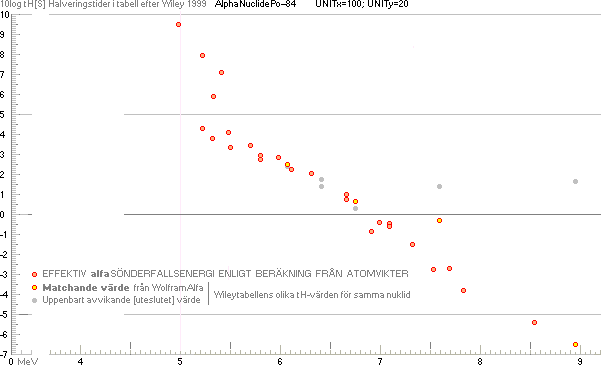
Ovanstående EXTRAKT från Wileytabellen motsvarar DEN EFFEKTIVA KURVPASSNINGSANALYSENs punktskara för alla rödmarkerade punktcirklar endast; endast ett entydigt bestämt halveringstidsvärde [tH] för endast en bestämd alfaradionuklid med endast en bestämd sönderfall[mass]energi [MeV]. Inget annat.

Hur diagramformen ovan har ritats ut:

— WileyTabellens datavärden har kopierats [från PDF, kolumnvis], bearbetats för numerisk anpassning i OpenOfficeKalkyl [tillsammans med atomviktstabellen från LBL 2003 för att få med alla nuklider upp till atomnummer 118], samt de SÅ extraherade datavärdena insatts i en textfil som kan läsas av en särskilt utformad programritningsrutin i DELPHI4; textfilen har sedan justerats efter WolframAlpha-data i [Se Multipla tH-värden] genom att Wileytabellens multipla förekomster har markerats [sist i textfilens komprimerade datakolumn] med bokstäverna AB; A för röd punktcirkel med gul fyllning och B för gråpunkterna; A sist, så att den ritas överst om förekomsterna ligger nära. Således; alla WileyTabellens data följer med, men markeras olika enligt ovan nämnda jämförande sifferexercis.

;

Nedan: Bägge föregående tillsammans;

Bägge

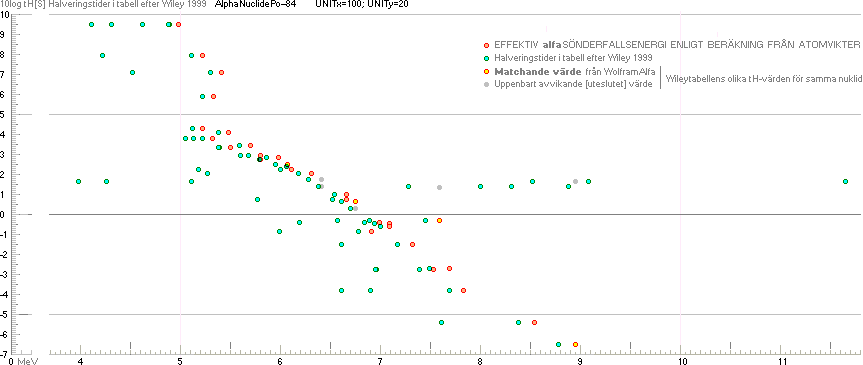
Här framgår speciellt att respektive alfaradionuklids effektiva sönderfallsenergi [alla rödmarkerade] ALLTID antar tH-gruppens [alfakanalernas] STÖRSTA värde; Som vi ser i Poloniumfallet ovan, den avvikande alfakanalpunkten längst till höger, finns ändå vissa fall där TYP moderkärnan är exciterad [annan förklaring saknas] och på den vägen kan påföra alfapartikeln extra energi.

— Punktdiagrammet ovan visar också DEN STORA SVÅRIGHETEN i den etablerade analysen av radiofysikens matematik;

— Om man URSKILLNINGSLÖST försöker att HITTA MATCHANDE SKÄRNINGSKURVOR [via statistisk kvantmekanik] för att INKLUDERA SAMTLIGA grönpunkter, är det givet — med den effektiva sönderfallsenergin i bakhuvudet — att uppgiften skapar ALLMÄNT KAOS; vissa punktvärden har helt enkelt ingen meningsfull innebörd för analysen med ETT tH-värde för ETT MeV-värde för en bestämd nuklid.

Summering

— GENERELLT, och märkligt som det kan tyckas, använder BESKRIVANDE webbkällor i allmänhet [Se Exempel 2] DET [rikt representerade alfakanalEnergibaserade] GRÖNA PUNKTHAVET som basfält för att illustrera Geiger-Nuttall-sambandets praktiska förankring — när det är tydligt att Geiger-Nuttalls samband — ett bestämt energivärde för en bestämd halveringstid — motsvarar det mindre rikt representerade RÖDA PUNKTFÄLTET. Men det punktfältet verkar inte tilldra sig någon översvallande uppmärksamhet från den etablerade författarskaran;

— Omnämnande i etablerad litteratur av det här gjorda uppmärksammandet angående multipla tH-individer via webbreferenser har eftersökts, men har inte påträffats [Dec2011].

Resultatbilden, med webbexempel, för betanukliderna är — snart sagt — ännu värre. Se särskilt i 29Cu64-exemplet.

GRAFRITANDE PROGRAMMET TILL RADIONUKLIDERNA efter tabelldata:

Här infört i efterhand efter sammanställningar 13Aug2017-08-13

GRAFRITANDE PROGRAMMET I DELPHI4-2011

— Programformen nedan från 2011 och dess detaljer blev oundgängliga för hanteringen av den stora datamängden — på enklast möjliga sätt (OpenOfficeGrafProgrammen i all ära: De är urusla på exakt diagramsättning, OpenOffice-programformen är en ren plåga om man vill vara REPETERANDE NOGA I PIXELSYSTEM Programmakarna förstår inte uppgiften).

Nukliddiagrammen efter programformen nedan — se t.ex. Exempel 3 — ritas upp via data från separata enkla textfiler efter enkla inslag av atomens kemiska namn, samt tabellområde och önskad xy-skala. Grafprogrammet ritar sedan upp detaljerna för vidare analys och hantering.

UNIVERSUMS HISTORIA — radioaktiva sönderfallets fysik enligt TNED

universumshistoria.se

RADIONUKLIDERNAS programbaserade DIAGRAMFRAMSTÄLLNING

i 2011-htm.dokumenten

zrefRF.htm

zrefRFbeta.htm

zrefRFkalkyl.htm

zrefRFmetOrigin.htm

zrefRFtH.htm

DELPHITest2011

Uni8 Test 2011

Med insättningarna ovan kopieras nedre vänstra datakartan till Urklipp, för vidare;

x(Unit)y((Interval)-värdenas ändras genom att skriva xy efterEff och ändra värdena i Unit/Interval-boxarna med Enter

— men ingen kopiering sker då om inte x=y=6.

— Standard xy-skala i pixelenheter från start är x=100 y=20.

Programformen nedan visar hur Alfa¦BetaDigrammen tillkom på bas av rena förpreparerade textfiler (med hjälp av WORD och OpenOffice) från inhämtat webbmaterial (Wiley-tabellerna 1999),

zzRAamEff¦zzRAamOrg¦zzRAbetaEff.txt.

Sedan Programfönstret maximerats tas aktuell radioatoms olika nuklidblock fram genom att ange atomens kemiska namn efter inslaget (alla ingående listas automatiskt vertikalt längst till höger på bildskärmen).

<AlfaDiagramEff>

<AlfaDiagramOrg>

<BetaDiagramEff>

— Kommandot verkställs sedan med Enter.

— Notera att programformen nedan är SAMMANSATT-INTEGRERAD med redan andra fungerande programformer som delar på en gemensam (GRAFRITNING) inmatningsbox, och därför inte direkt får förstår som ett helt eget fristående program. För ett sådant krävs en separat del som inte beskrivs här.

— Tabellreferenserna i kommentarerna nedan (Blått) är alla, eller ska vara, desamma som i htm-dokumentets referenser (med reservation för ev. namnändringar som gjordes där i efterhand).

{24Nov2011}

{Ha fönstret MAXIMERAT, annars skippas rutinen:}

{I Ekvationsboxen — tangent 0 — Skriv in (versalkänsligt):

AlfaDiagramEff<ÄMNESnamn> för alla effektiva sönderfallsenergier för radionukliderna;

endast En massenergi per nuklid:

Se RAam.ods Tabell5;

AlfaDiagramOrg<ÄMNESnamn> för alla uppmätta sönderfallsenergier;

alla förekommande AlfaKanaler enligt uppmätta data:

Se RFalfaW.ods Tabell5;

BetaDiagramEff<ÄMNESnamn> för alla effektiva sönderfallsenergier för betanukliderna;

}

{För INMATNINGEN, se Unit2 Edit4 EqScript: — se tillägget sist nedan}

Procedure PixelDiagram(U,D: string);

var

x,y,Ux,Uy: Integer;

H,W,nx,ny: Integer;

XS,YS,YB: Integer;

TS,US: TStringList;

A,B,E,F,M,N,P,Q: Integer;

C: Integer;

K: array [1..5] of string;

L: array [1..4] of Integer;

S,T,Z: string;

R,Rx,Ry: Real;

V: Word;

TC1,TC2,TC3,TC4: TColor;

Eff,Beta: Boolean;

Procedure DrawValue(x,y: Integer);

begin

with Form1.Image1.Canvas do

begin

{Det finns exempel — 29Cu64 — med alla ABC — inte alla täckande ...;}

{OM A|Beta- samma som B|EC — för dessa fall ritas halva B från mitten:}

if(Beta)and(Pixels[x,y] = TC3)then

begin

{Frame:}

Pixels[x-0,y-2]:=TC1;

Pixels[x+1,y-2]:=TC1;

Pixels[x+2,y-1]:=TC1;

Pixels[x+2,y-0]:=TC1;

Pixels[x+2,y+1]:=TC1;

Pixels[x-0,y+2]:=TC1;

Pixels[x+1,y+2]:=TC1;

{Center:}

Pixels[x-0,y-1]:=TC2;

Pixels[x-0,y-0]:=TC2;

Pixels[x-0,y+1]:=TC2;

Pixels[x+1,y-1]:=TC2;

Pixels[x+1,y-0]:=TC2;

Pixels[x+1,y+1]:=TC2;

exit;

end;

{Ofta är B|EC samma som C|BetaPlus — för dessa fall ritas halva C:}

if(Beta)and(Pixels[x,y] = TC4)then

begin

{Frame:}

Pixels[x+1,y-2]:=TC1;

Pixels[x+2,y-1]:=TC1;

Pixels[x+2,y-0]:=TC1;

Pixels[x+2,y+1]:=TC1;

Pixels[x+1,y+2]:=TC1;

{Center:}

Pixels[x+1,y-1]:=TC2;

Pixels[x+1,y-0]:=TC2;

Pixels[x+1,y+1]:=TC2;

exit;

end;

{Frame:}

Pixels[x-1,y-2]:=TC1;

Pixels[x-0,y-2]:=TC1;

Pixels[x+1,y-2]:=TC1;

Pixels[x-2,y-1]:=TC1;

Pixels[x+2,y-1]:=TC1;

Pixels[x-2,y-0]:=TC1;

Pixels[x+2,y-0]:=TC1;

Pixels[x-2,y+1]:=TC1;

Pixels[x+2,y+1]:=TC1;

Pixels[x-1,y+2]:=TC1;

Pixels[x-0,y+2]:=TC1;

Pixels[x+1,y+2]:=TC1;

{Center:}

Pixels[x-1,y-1]:=TC2;

Pixels[x-1,y-0]:=TC2;

Pixels[x-1,y+1]:=TC2;

Pixels[x-0,y-1]:=TC2;

Pixels[x-0,y-0]:=TC2;

Pixels[x-0,y+1]:=TC2;

Pixels[x+1,y-1]:=TC2;

Pixels[x+1,y-0]:=TC2;

Pixels[x+1,y+1]:=TC2;

end;

end;{endDrawValue}

label Over;

begin with Form1 do begin {PixelDiagram}

if WindowState<>wsMaximized then exit;

{°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.}

{UNITS:}

Ux:=100;

Uy:=20;

Z:='';

Eff:= False;

Beta:= False;

{BETA|MörkBlå — A|EC:}

TC3:= RGB(0,128,255);

{BETA|LjusBlå — B|EC:}

TC4:= RGB(164,200,240);

{Changing xyUnits — »if U+D=''» = ..xy Edit4:}

if U+D='' then

begin

if FlagUxy=True then FlagUxy:=False else FlagUxy:=True;

U:= pU;

D:= pD;

end;

if FlagUxy then

begin

Ux:= StrToInt(Edit2.Text);

Uy:= StrToInt(Edit3.Text);

end;

if U+D<>'' then

begin

pU:= U;

pD:= D;

end;

{pUD=LastUD.}

{°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.}

S:= ExtractFilePath(Application.ExeName);

{C:\Program Files\Borland\Delphi4\Projects\Proj2002Vista\.}

{BetaDiagramEffU:}

if D='Beta' then

begin

Beta:= True;

end else

if D='Eff' then

begin

Eff:= True;

TC1:= clRed;

TC2:= RGB(255,180,128);

end else

if D='Org' then

begin

TC1:= RGB(0,128,0);

TC2:= RGB(0,255,255);

end else exit;

if D='Eff' then D:='zzRAamEff.txt' else

if D='Org' then D:='zzRAamOrg.txt' else

if D='Beta' then D:='zzRAbetaEff.txt' else

exit;

if not FileExists(S+D) then exit;

{ClearAllImage:}

V:= VK_F2;

FormKeyDown(Form1,V,[]);

{Kör maximerat för RF-nukliderna:}

{T-range:}

{x: 0TILL10; y: -10TILL20}

H:= Image1.Height;

W:= Image1.Width;

ny:= H div Uy;

nx:= W div Ux;

XS:= 20;

YB:= H-20;

YS:= YB-10*Uy;

{xy-axes:}

with Image1.Canvas do

begin

Pen.Width:= 1;

Pen.Style:= psSolid;

Pen.Mode:= pmCopy;

{GRIDx = ... :}

Pen.Color:= clSilver;

for x:= 0 to ny div 5 do

begin

MoveTo(XS,YB-5*x*Uy);

LineTo(W-XS,YB-5*x*Uy);

end;

{FineLeft — PixelDiagram:}

Pen.Color:= clSilver;

for x:= 0 to ny {div 5} do

begin

MoveTo(XS,YB-{5*}x*Uy);

LineTo(XS+5,YB-{5*}x*Uy);

end;

{GRIDy | | | ... :}

Pen.Color:= RGB(255,235,250);

for y:= 1 to nx div 5 do

begin

MoveTo(XS+5*y*Ux,YB);

LineTo(XS+5*y*Ux,YB-(ny-1)*Uy-1);

end;

{FineBottom — PixelDiagram:}

Pen.Color:= clSilver;

C:= 5;

if Ux=100 then C:= 10;

for y:= 1 to nx {div 5} do

begin

MoveTo(XS+{5*}y*Ux,YB);

LineTo(XS+{5*}y*Ux,YB-C);

end;

{SpecialUx=100 — PixelDiagram:}

if Ux=100 then

begin

for y:= 1 to 10*nx do

begin

MoveTo(XS+10*y,YB);

LineTo(XS+10*y,YB-5);

end;

end;

{xyAXES:}

Pen.Color:= clGray;

{x:}

MoveTo(XS,YS);

LineTo(W,YS);

{y:}

MoveTo(XS,YB);

LineTo(XS,0);

{SKALOR:}

Font.Name:= 'Microsoft Sans Serif';

Font.Size:= 7;

Font.Color:= 0;

{SKALAx|Ux:}

for A:=0 to nx-1 do

begin

if Ux>=20 then

TextOut(XS-2+A*Ux,YB+1,IntToStr(A)) else if A mod 5 = 0 then

TextOut(XS-2+A*Ux,YB+1,IntToStr(A)) else Continue;

end;

{SKALAy|Uy:}

for A:=1 to ny-1 do

begin

if Uy>=20 then

TextOut(XS-11,YB-6-A*Uy,IntToStr(A-10)) else if A mod 5 = 0 then

TextOut(XS-11,YB-6-A*Uy,IntToStr(A-10)) else Continue;

end;

end;{endWithIm1 — PixelDiagram}

{DATA:}

{89;206;Ac;7,94;-1,4814861}

M:= 0;

P:= 0;

TS:= TStringList.Create;

US:= TStringList.Create;

try

TS.LoadFromFile(S+D);

N:= TS.Count;

if N=0 then exit;

{OK — LookForObjectNameU:}

for A:= 0 to N-1 do

if Pos(U+';',TS.Strings[A])>0 then

begin

P:= A;

S:= TS.Strings[P];

Break;

end;

if P<0 then exit;

{CountNumberU's:}

{P>0 — antal:}

for A:= P to N-1 do

if Pos(U+';',TS.Strings[A])>0 then

Inc(M) else Break;

{Gruppen räknas från P till M.}

{CheckValidNo»;»=4:}

Q:= 0;

for A:=1 to Length(S) do

if S[A]=';' then

begin

Inc(Q);

L[Q]:= A;

end;

if Q<>4 then exit;

{IfValid:}

{====}

Over:

{====}

{Lista alla Ämnen:}

for B:= 0 to N-1 do

begin

S:= TS.Strings[B];

Q:= 0;

for A:=1 to Length(S) do

if S[A]=';' then

begin

Inc(Q);

L[Q]:= A;

end;

DecimalSeparator:= '.';

{K[1]=Z; K[2]=A; K[3]=Ämne; K[4]=MeV; K[5]=10log tH:}

K[3]:= Copy(S,L[2]+1,L[3]-1 - L[2]);

US.Add(K[3]);

US.Sorted:= True;

end;

{SkrivUt:}

with Image1.Canvas do

begin

Font.Name:= 'Microsoft Sans Serif';

Font.Size:= 7;

Font.Color:= 0;

E:= -1;

F:= (H-50) div 13;

for B:= 0 to US.Count-1 do

begin

{TEST|BetaDiagramEffU:}

if B mod F = 0 then Inc(E);

TextOut(W-100 + E*50,10 + (B mod F)*13,IntToStr(B+1));

TextOut(W-85 + E*50,10 + (B mod F)*13,US.Strings[B]);

{TextOut(W-100,10+B*13,IntToStr(B+1));

TextOut(W-85,10+B*13,US.Strings[B]);

{Originalet.}

end;

{Units:PixelDiagram:}

TextOut(W-280,10,'UNITx='+IntToStr(Ux)+'; '+'UNITy='+IntToStr(Uy));

end;{endWithIm1}

{Listar alla Ämnen.}

{PixelDiagrammets Ämnesvärden — föregående inlästa PM-värden används:}

{Gruppen räknas från P till M.}

for B:= P to P+M-1 do

begin

S:= TS.Strings[B];

{Check&Count ; :}

Q:= 0;

for A:=1 to Length(S) do

if S[A]=';' then

begin

Inc(Q);

L[Q]:= A;

end;

if Q<>4 then exit;

{VALUES:}

{K[1]=Z; K[2]=A; K[3]=Ämne; K[4]=MeV; K[5]=10log tH: --- zzRAamEff¦zzRAamOrg¦zzRAbetaEff.txt:}

DecimalSeparator:= '.';

K[1]:= Copy(S,1,L[1]-1);

K[2]:= Copy(S,L[1]+1,L[2]-1 - L[1]);

K[3]:= Copy(S,L[2]+1,L[3]-1 - L[2]);

K[4]:= Copy(S,L[3]+1,L[4]-1 - L[3]);

if Z='' then

Z:= K[1];

{Adjust T|K[4,5]:}

T:= Copy(S,L[4]+1,Length(S));

if Pos(',',K[4])>0 then K[4][Pos(',',K[4])]:='.';

if Pos(',',T )>0 then T[Pos(',',T )]:='.';

if not (Char(T[1]) in ['0'..'9']) then T[1]:='-';

K[5]:= T;

if Eff then

begin

TC1:= clRed;

TC2:= RGB(255,180,128);

T:= K[5][Length(K[5])];

if Char(T[1]) in ['A','B'] then

begin

Delete(K[5],Length(K[5]),1);

case Char(T[1]) of

'A':

begin

TC2:= clYellow;

end;

'B':

begin

TC1:= clSilver;

TC2:= TC1;

end;

end;{endCase}

end;{endIfT}

end;{endIfEff — PixelDiagram}

{Tilläget ovan 29Nov2011 — Samma ämne, flera tH-värden, särskild analys.}

{TILLÄGG 5Dec2011 för BetaSönderfallen — zzRAbetaEff.txt:}

{Samma format som i Alfa.delen, men alla här med A|B|C i slutet:}

if Beta then

begin

{Tar upp bokstaven i slutet:}

T:= K[5][Length(K[5])];

{Raderar bokstaven i slutet:}

Delete(K[5],Length(K[5]),1);

case Char(T[1]) of

'A':

begin

TC1:= TC3;

end;

'B':

begin

TC1:= TC4;

end;

'C':

begin

TC1:= RGB(255,180,128);

end;

end;{endCase}

TC2:= TC1;

end;{endIfEff — PixelDiagram}

{DrawOut:}

Rx:= StrToFloat(K[4]);

Ry:= StrToFloat(K[5]);

x:= XS+round(Rx*Ux);

y:= YS-round(Ry*Uy);

DrawValue(x,y);

end;{endForB}

finally

TS.Free;

US.Free;

end;

{Aktuell Nuklid:}

Image1.Canvas.TextOut(W-380,10,'AlphaNuclide'+U+'—'+Z);

{°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.}

{CopyDiagramLeftBottom — if MultiGraphIcon(Ctrl+,) AND Ux=Uy=6:}

if(Ux=Uy)and(Ux=6)and(Label27.Caption='| | |')then

begin

Bmp1:= TBitMap.Create;

try

Bmp1.PixelFormat:= pf32bit;

dR:= Rect(0,0,91,211);

sR:= dR;

OffsetRect(sR,20,YB-180);

BitmapRect(dR,Bmp1);

with Bmp1.Canvas do

begin

CopyMode:= cmSrcCopy;

CopyRect(dR,Image1.Canvas,sR);

end;

ClipBoard.Assign(Bmp1);

finally

Bmp1.Free;

end;

end;

end;{endWithForm1}

end;{endPixelDiagram}

Unit2 Edit4:

Ex:

AlfaDiagramU, Enter

AlfaDiagramxy, Set Edit2¦4 as x¦y, enter — each second draws last original 100¦20 and new set xy for test; replace with Name to continue.

{°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.}

{PixelDiagram till RadioFysiken Unit8 24Nov2011:}

S:= Form1.Edit4.Text;

if (Pos('AlfaDiagramEff',S)=1)

or (Pos('AlfaDiagramOrg',S)=1)

or (Pos('BetaDiagramEff',S)=1)

then

begin

if Pos('xy',S)=15 then

begin

PixelDiagram('','');

exit;

end;

if Pos('Eff',S)=12 then

begin

if Pos('Alfa',S)=1 then

PixelDiagram(Copy(S,15,2),'Eff');

if Pos('Beta',S)=1 then

PixelDiagram(Copy(S,15,2),'Beta');

end;

if Pos('Org',S)=12 then

PixelDiagram(Copy(S,15,2),'Org');

exit;

end;

{°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.°ºo0·.}

END.

OVANSTÅENDE PROGRAMBLOCK från Nov2011 HÄR INFÖRT SEPARAT I EFTERHAND efter särskild kopiering från ursprungsprogrammet Test2011 i DELPHI4.

BellDharma Aug2017 — Universums Historia (@INTERNET först från 2008).

Multipla tH i TNED

Finns det förutsättningar i TNED för multipla halveringstider för en och samma sönderfallsenergi?

— Ja. Absolut:

Grundämnesbildningen enligt TNED i översikt — se även Månens Recession: en »direkt fullträff» i TNED-teorin för himlakroppsbildningen i Solsystemet

nuklidkartan AZ i TNED	neutronkvoterna	Diakvadraten med neutronkvoter och nuklidseparationer	grundämnesfördelningen
gränserna för stabila nuklider	samma nuklid på flera sätt	grundämnenas allmänna primära fördelning i och mellan himlakropparna	grundämnenas olika primära fördelning med Jorden som exempel

TNED: Från K-cellens expansion garanterar den sammanhållande gravitationen genom ljusets gravitella beroende [Se även i Översikt i jämförelse med Einstein] att huvuddelen av K-cellens centralkropp — neutronen eller Planckringen som massans-energins absoluta yttersta orsakspunkt, här benämnt neutronkallplasma, se från c0-kroppen där neutronbasen förklaras utförligt, hur den återbildas vid varje kontraktion i försorg av allmänna tillståndslagen, se särskilt i Hur K-cellen återvinns, och hur den påfylls till K-cellens centrala delar från den övergripande — eviga, obegränsade — c0-masskropp som energiräkningen kräver — är nedsläckt för normal elektromagnetisk aktivitet [c=0]. Det är bara den innersta centrala delen som är aktiv, alltid, garanterat av nollgravitationen i massmedelpunkten; Den alltid aktiva centraldelen garanterar av princip bevarandet av toppdivergensen [absolut största möjliga ljushastigheten c=2,99792458 T8 M/S, T för 10^+]. Se även mera utförligt teoretiskt om toppdivergensen i Absoluta Metriken.

— TÄNDZONEN [Se utförligt illustrerat i K-cellens allmänna expansion], idealt ett sfäriskt gränsskal, med gränsen mellan aktiv och icke-aktiv elektromagnetisk lokal, expanderar med c0 så snart K-cellen detonerat [Se K-cellens detonation]. Vartefter tändzonen sveper över K-cellens yttre delar, successivt med K-cellens egen avtagande expansion, aktiveras elektromagnetismen vilket i TNED benämns divergenständning. Det är första stadiet i himlakropparnas grundämnesbildning. K-cellens expansion medför explosiva utkastningar av delkroppar [J-kroppar] i olika system efter olika [här benämnda] resonansserier [Se även Solsystemets bildning]. Endast genom att de större J-moderkropparna besitter impulsmoment [marginellt små rotationer] kan uppkomsten av motsvarande fördelade impulsmoment [planeternas banrotationer] förstås i vårt Solsystem. Se särskilt noggrann genomgång av dessa avgjort viktiga detaljer i Galaxbildningen. Där detaljbehandlas Solsystemets roterande planetdetaljer enligt TNED, samt impulsmomentens yttersta orsaker generellt för himlakropparna [virvelbildningens uppkomst].

— Så snart divergenständningen är aktiverad för en J-kropp, kan neutronsönderfallet i kroppsmassan börja, och därmed förstadiet till grundämnesbildningen.

— J-kropparnas TYP — gaskroppar eller stenkroppar — beror på deras massa i förhållande till Optimala fusionsgränsmassan: kärnfysikaliska parametrar bestämmer alla, samtliga, gränsformer. Se utförligt från Jordens andra ekvation.

— Eftersom [den, på grund av den samlade gravitationen med i princip noll mellanrum mellan neutronerna, strängt sfäriskt formade] J-kroppen uppvisar största divergensen [största lokala c-värdet] i kroppssfärens centrum, enligt ljusets gravitella beroende, kommer också J-centrum att bli maximalt utarmat på neutroner från divergenständningen fram till slutet av perioden för neutronsönderfallet [normal 10-15 minuter]. Denna detalj garanterar, tillsammans med nuklidbildningen och dess principer via exotermiska kärnreaktionslagen en inre järnkärna. Nuklidbildningar med masstal högre än runt 60 [Se utförliga exempel i Grundämnesbildningens två basgrupper], omkring Järn-Kobolt-Nickel, kräver nämligen nuklidagenter med neutronkvoter större än noll [Se Nuklidbildningens fördjupning, och Den tunga nuklidgruppens certifiering], vilket på motsvarande sätt garanterar att det innersta av himlakroppen [speciellt av typen stenkroppar] i princip ALLTID blir RENT på allt utom nukliderna upp till Järntoppen.

— Eftersom gravitationen ökar med avståndet från centrum, och därmed avtagande c-värde utåt, bildas naturliga förutsättningar för en växande neutronkvot [lägre c betyder långsammare neutronsönderfall] och därmed en växande andel neutroner längre utåt kroppsranden i bildningen av nuklidringarna som föregår fusionsfasen. Det maximalt täta tillståndet i J-kroppen medger nämligen också maximala SÄTT för de sammanträngda neutronerna-Vätekärnorna att koppla ihop sig INOM varandras nuklidbarriärer under neutronsönderfallet — alltså UTAN att stöta bort varandra, eftersom de som sagt ligger innanför nuklidbarriärerna och därmed REDAN ligger LADDADE för fusion, och så snart neutronsönderfallets lokala dynamik medger det. Den detaljen är ofrånkomlig i TNED — och lika omöjlig att härleda i den moderna akademins lärosystem.

— Fusionsringarna ges alltså i princip GOD TID att »koppla upp sig» på de olika möjliga nukleära mönsterkopplingarna INNAN fusionsfasen inträder explicit. Den inträder definitivt då den elektromagnetiska aktiviteten från divergenständningen är fullt utbildad, och därmed de normalt repellerande Coulombkrafterna kan verka fullt ut. Se utförligt från Fusionsgränsmassan.

— Den häftiga fusionsfas som ovillkorligen följer på neutronsönderfallet, ger så himlakroppen dess primära grundämnessammansättning i exakt detalj — idealt inom bara en bråkdels sekund för hela J-kroppen, med motsvarande enorm energiutveckling. Färdigt. Resten handlar om J-kroppens avsvalning och mognad med inre konvektioner och mineralogisk blandning, beroende på TYP av J-kropp [Se utförligt från Jordens Andra Ekvation]. Särskilda formationer bildas för de mindre himlakropparna mellan de större. Se särskilt från G-skuggning.

— Speciellt MELLAN HIMLAKROPPARNA [vårt Asteroidbälte i Solsystemet, i vissa fall våra meteorider som blir meteoriter om de når Jorden] finns vissa förutsättningar [c=cMAX mellan himlakropparna] liknande det inre av himlakropparna själva och som direkt kan förstås betyda bildning av de kända järnhaltiga meteoriterna [upp till 90% järn, se G-skuggningen generellt] — med ytterligare avancerade typer [diamanthaltiga, med flera andra exotiska arter].

— Teorin för grundämnesbildningen i modern akademi är behäftad med så stora teoretiska svårigheter och komplicerade utläggningar med tillhörande mängder obesvarade detaljfrågor att ingen motsvarande jämförelse kan göras.

— I MAC anser man — som vi alla förmodligen redan känner väl från skolböckerna — att grundämnena i Jorden och planeterna ytterst sett kommer från gamla rester i stjärnor som exploderat. Dessa rester, menar man, har sedan dragits samman via lokal gravitation, samt via olika kollisionsscenarion bildat större kroppar [s.k. planetesimaler] som sedan i sin tur »format än större kroppar», och som i olika scenarion också »börjat glöda inuti». Beträffande uppkomsten av Solsystemets olika impulsmoment och deras fördelning, är problemen i MAC-teorin snart sagt ännu mera djupgående med mängder obesvarade detaljfrågor. Det finns ingen jämförande grund i MAC att ställa fram vid sidan av TNED.

Neutronkvotens avgörande inverkan

ang. multipla tH i TNED

— Som redan påpekats i Speciella tH-sambandet, samt i översikt redovisat ovan i Grundämnesbildningen enligt TNED i översikt:

— En och samma nuklidtyp kan via ursprung i olika neutronkvoter [också från andra sönderfall] sammansätta »en och samma nuklidtyp» [efter de primärt kosmiska nuklidbildningarna: genom geologisk blandning i typ Jordkroppen] och som därmed, NATURLIGT, ger en motsvarande spridning i möjligheten med multipla b-värden för »en och samma nuklid». Den möjligheten synes inte föreligga i MAC, eftersom nuklidkoefficienten [b-termen nedan] inte ingår i MAC.

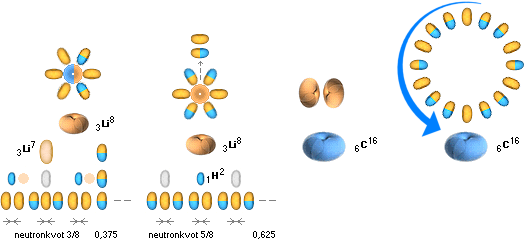
Neutronkvoten kan variera för en och samma slutnuklid, vilket garanterar att grundämnet får spridning inom J-kroppen redan från bildningstillfället. Neutronkvoten i J-kroppens centrum blir tvunget noll relativt J-kroppens rand med maximala neutronkvoten 1, enligt förutsättningen med max c i J-kroppens centrum [Se Ljusets gravitella beroende]. Mönsterkopplingarna för en fusionsring behöver (som här) nödvändigtvis inte vara plan utan kan lika gärna vindla sig i t.ex. en sfäriskt tätt sluten form, eller andra typer, beroende på. Kärnorna bestämmer själva allt eftersom de fysikaliska omständigheterna medger. Se även i Udda och Jämna Nuklidserierna som garanterar J-kroppens centrala järnkärna.

— Genom att neutronkvoten sammanhänger med varierande divergens (gravitellt bestämd lokal ljushastighet inom J-kroppen; centrum med max c betyder minsta möjliga neutronkvot, analogt snabbaste neutronsönderfallet föregående fusionsfasen [se även Frekvensens g-beroende], och därmed minsta möjliga neutronförekomst då fusionsfasen inträder, se utförligt från Grundämnesbildningen och J-kropparnas expansion), och denna definitivt sammanhänger kvalitativt med den härledande dynamiken till nuklidkoefficienten (b) i halveringstidssambandet enligt TNED, är det tydligt att b-formen kan förstås blir konserverad av sin specifika bildningslokal, oaktat lokala (neutrino)energigenomströmningar som, möjligen, ytterligare kan bidra till smärre variationer. Notera just »smärre»; endast en liten obetydlig variation i b-värdet kan resultera i en högst dramatisk ändring i halveringstiden. Jämför BeräkningsExemplet med Uran-238.

Se även mera utförligt i maximalringen.

— Det betyder EMELLERTID INTE i TNED — som däremot fallet otvivelaktigt av konsekvens blir i MAC — att hela radiofysiken, därmed, mister sin övergripande UPPGIFT och blotta grundval; Geiger-Nuttall-sambandets empiriska form; Den motsvarande Rutherfordska premissen (1900-talets början) [Se Citat] att tH-värdet är en konstant för en viss nuklid, och att den konstansen kopplar till styrkan i, av, och hos en visst bestämd sönderfallsenergi.

— I MAC, nämligen, finns ingen variabel nuklidkoefficient, b-termen nedan,

t_H = 1S(ln2)e^beZ/√2mE

i halveringstidssambandet (ovan från Slutformen i TNED);

— b-koefficienten i TNED däremot (se Nuklidkoefficienten) KAN ha koppling till de olika primära grundämnesbildningslokalernas olika, specifika, neutronkvoter [de olika sätt på vilka en viss nuklid kan bildas exotermiskt] och som, enligt TNED, kan konserveras specifikt genom dessa olika bildningslokalers olika neutrinogenomströmningsenergier i det kosmiskt primära bildningstillfället — och därmed en naturlig, marginell, spridning med resultat i en fragmentering på olika b-värden för samma nuklidtyp med samma effektiva sönderfallsenergi.

— b-koefficienten (Utförligt i Nuklidkoefficienten) grundas i TNED härledningsvis på potentialbarriärens energizon [c(z)], grundvalen till atomkärnans härledning i TNED; Eftersom denna parameter sammanhänger intimt med GRAVITATIONEN via ljusets g-beroende, bildas med särskild tydlighet direkta förutsättningar via speciellt de olika himlakropparnas g-former MED deras naturliga fördelning av neutronkvoter (noll från centrum, med växande utåt J-kroppens periferi, se särskild illustration), också en naturlig variationsbas för nuklidkoefficienten (b); Denna kan därmed, explicit, relateras variabel OBEROENDE av något begrepp om lokal energigenomströmning, enbart i kraft av en lokal gravitell variation från centrum (lägsta gravitationen) och utåt (största gravitationen).

— Det ligger emellertid också i den energigenomströmmande lokalens natur att också de närvarande atomkärnorna påverkas i sina speciellt energikonserverande INSTABILA bildningar, och dessa bildningars strävan att gå mot stabila tillstånd, speciellt genom små (marginella) avvikelser i kärnstrukturen — som KAN (här helt utan bevis) innefatta »långtidskonserveringar» av specifika neutrinoenergier: ytterst långsamma avgivningar med ytterst blygsamma belopp, enligt Plancks strukturkonstant i TNED.

— Sammansättningen av dessa bägge möjligheter — explicit skilda g-potentialer med tillhörande skilda neutronkvoter för bildning av samma nuklidtyper, tillsammans med motsvarande olika lokala neutrinoenergier i bildningslokalen via de radiellt olika belägna lokalerna — har alldeles tydligt förutsättningen för att forma den aktuella nukliden på olika b-värden. Därmed kan spridningen i tH-värden via ekvivalenta sönderfallsenergier förklaras (i varje fall kvalitativt, till att börja med) enhetligt i TNED — men inte på något motsvarande (kvalitativt) sätt i MAC: »atomkärnans härledning» ur Plancks konstant ingår inte i MAC.

— EMELLERTID finns ännu ingenting SÄKERT framställt i TNED som på något SÄKERT sätt stadfäster en eller annan praktisk grund för frågan om b-koefficientens variation. Det är ännu till viss del bara en trevande undersökning.

Editor2012II13

END.

Editor2011XII

Radioaktiva sönderfallets fysik i TNED | Alfaradionukliderna med tH-universalen

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Alfaradionukliderna i TNED

ämnesrubriker

innehåll

Alfaradionukliderna i TNED

Inledande översikt

AlfaRadioNuklider Punktdiagram

Uran92 Exempel skalupplösning

Halveringstiden tH — speciella och allmänna sambandet

Speciella tH-sambandet

Exempel 1 — b-kurvan för U-238

Allmänna tH-sambandet

tH-universalen

Den generaliserade kurvpassningen

y och yi²

EXEMPEL, tH-universalens vertikalplacering

Exempel 3 — UranIsotopExemplet

Generaliserade kurvpassningens allmänna alfaradioisotopbild

Särskilda Exempelutdrag

Exempel Royer-Zhang

Redovisade kurvavsnitt

Exemplet Santoso 2000

Den allmänna bristen på precision

Ogunbade-Rakityansky 2007

Korrumperade räkneexempel

b-formen

Exempel HyperPhysics — halveringstiden för Polonium-212

Räkningen via atomvikterna

Webbreferenser

Alfaenergier, olika kanaler i mätdata

Exempel 2 LabSpace

LabSpace illustrationen

Referenser

MAC

Ea

Q-alfa, Q-value

Jämförande exempel

Wikipedia citat

tH

MeV

LBL atomic Masses 2003

Wiley 1999

Multipla tH-individer

Resultatexempel

Poloniumkartan

Summering

GRAFRITANDE PROGRAMMET TILL RADIONUKLIDERNA

Multipla tH i TNED

Grundämnesbildningen enligt TNED i översikt

Neutronkvotens avgörande inverkan

referenser

Senast uppdaterade version: 2017-08-13

*END.

Stavningskontrollerat 2012-02-10.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

∫ √ τ πε ħ UNICODE — often used charcters in mathematical-technical-scientifical descriptions

σ ρ ν ν π τ γ λ η ≠ √ ħ ω →∞ ≡ ‖ ↔↕ ħ ƛ ℓ

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ ϕ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ˂ ˃ ˂ ˃ ← ↑ → ∞ ↓

ϑ ζ ξ

Arrow symbols, direct via Alt+NumPadKeyboard: Alt+24 ↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬

Alt+23 ↨ — also Alt+18 ↕; Alt+29 ↔

Alt+NumPad 0-25, 26-...

☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓

→←∟↔▲▼ !”#$%&’()*+,-./♦812...

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se