UNIVERSUMS HISTORIA ENLIGT RELATERAD FYSIK OCH MATEMATIK · GALAXBILDNINGARNA | 2009II7 2009IV25 | en BellDHARMA produktion | Senast uppdaterade version: 2021-12-09 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor ·

GALAXBILDNINGARNA — MERA UTVECKLAT Feb2019 I Solsystemen i Vintergatan inledning med Stjärnhopar och galaxbildningar DEL I galaxbildningarna — utförlig beskrivning · Allmän delningsklassificering · virvelbildningens elementära fysik · Den Inducerade Rotationens Uppkomst

materieöarnas form

I den följande beskrivningen kommer beteckningen J-kropp att användas i betydelsen av en kropp som avdelas från K-cellens maximalt täta centralkropp (se K-cellen), eller kroppar som avdelas sekundärt av moderkroppar av typen J.

Beteckningen ”J” har flera kopplingar; 1. bokstaven närmast före K i K-cellen; 2. impulsmomentets allmänna beteckning (se impulsmomentet) J=mvr i denna presentation.

Vinjettbild

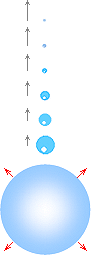
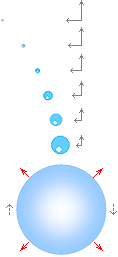
Tillägg övre höger nedan: Primära minidroppar — svåra att ta på grund av hög utgångshastighet och begränsad bildhöjd.

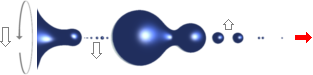
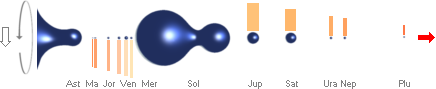
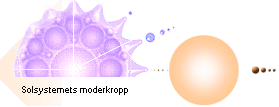
Rekylbilden från en vattendroppe som träffat en vattenyta, vänster (Nikon D90 Mars 2009) används i den här presentationen för att (förnämligt) illustrera detaljerna i K-cellens allmänna fysik enligt TNED — främst himlakroppsbildningen, Solsystemets kroppar här inlagda i vertikalremsa längst till vänster till jämförelse, dimensioner efter samma medeltäthet: — Droppbildningen uppvisar största dropparna i mitten, de minsta längst ut, och sedan även mindre i upprepade serier på givna (största) delkroppar, på principiellt samma sätt som planeterna och deras månar med Solen i mitten. — Vidstående fotografi från genomförda experiment med vatten kan ses representera vattenfysikens rent experimentella motsvarighet till K-cellens betydligt tätare primärkroppar och som I PRINCIP bör lyda samma kraftordning: primärkropparnas starka gravitation ersätter vattnets ytspänning och primärexpansionens detonationskraft ersätter rekylkraften. Se även från K-cellens brytning. Varje dropprekyl uppvisar en sekvens (resonansserie) vattendroppar som utgör rekylen från en enda fallande vattendroppe då denna träffar vattenytan (här) t.ex. i ett vanligt dricksglas. I experimentet fick enskilda vattendroppar träffa vattenytan periodiskt en gång ungefär varannan sekund (under den tiden hinner vattenytan på glaset stillas). Genom den fasta dropprytmen, blir det också (relativt) enkelt för fotografen att hitta rytmen med kameran. Se utförligt i Droppanordningen. Dropprytmen ordnades genom en enkel hydrostatisk koppling: från en tillbringare leds vatten i en PVC-slang (finns på välsorterade bensinstationer, typ Ø7mM) till ett utlopp i andra änden bestående av en tandpetare instucken i en bit hushållspapper som delvis skjutits in i slangöppningen (fungerar som »drällstrumpa»). Med lämpliga justeringar och slangöppningens placering (rakt ovanför vattenglaset), kan i princip hur noggranna droppfrekvenser (droppstorlekar och därmed droppkrafter) som helst ordnas med dessa ytterst enkla medel. Allt BellDHARMA originalmaterial i Universums Historia får användas fritt förutsatt källan anges — BellDHARMA Universums Historia (2009)

Webbexempel

BILDEN OVAN från

Natural Science Splash of stream of water drops multihue rainbow backdrop and ripples · Adam Hart-Davis (11 July 1999)

DHD Multimedia Gallery — FREE for your Website, PC and Projects

[http://mirror-uk-rb1.gallery.hd.org/index.jsp] 2009-02-12

användes i den tidigare versionen av detta htm-dokument som inledande illustration (Februari 2009).

För att förtydliga sammanhangen har följande delar lagts till (April 2009), med tillhörande ombearbetning från föregående htm-version (detaljer från föregående sättning har tagits bort och ersatts med nedanstående):

Fotografier och resultat från vattenrekyler i jämförande analys med himlakroppsbildningen enligt TNED

Hur rekylen bildas från den enda vattendroppen

Hur processen kan fotograferas

Hur rekylbilden stämmer med den primära himlakroppsbildningen enligt TNED

Hur väl vattnets fysik kan användas i sakbeskrivningen

Bildbevis för att rekylen innefattar virvelrörelser som kan ge vattendroppen spinn

Hur processen ansluter till teorin för uppkomsten av himlakropparnas primära rotation

Droppanordningen

Hur rekylen bildas från den enda vattendroppen

Hur processen kan fotograferas

För droppanordningen nedan vänster, se även separat kompletterande bilder

EXTRA UTRUSTNING

1. Tilläggslinser (»förstoringsglas») till Nikon-kameran (kostar ca 200 kr för ett set med tre). De är svåra att hantera i början på vattendropparna eftersom skärpedjupet blir ytterst smalt, men det ger sig med övning och tålamod.

1. Trådutlösare: En (nästan) ovärderlig hjälp vid fotograferingen är att ha en separat s.k. trådutlösare (kostar ca 500 kr); Man kan hålla avtryckaren bekvämt i handen och koncentrera sig på att fånga dropprytmen utan stressande kroppsställningar som kräver att man ska ha fingrar på kamerahuset. (Det finns också en billigare trådlös variant, men den klickar ibland om den inte är lämpligt riktad, och saknar dessutom trådutlösarens riktiga dubbelbrytande trycke).

2. En 500 W strålkastarlampa (finns på RUSTA [2009] för 49 kronor inklusive lampa, men utan kabel). Den ersätter alla (normalt sett hutlöst dyra) blixttillbehör förutsatt kamerans ISO-inställningar utnyttjas (antingen auto-iso eller manuellt) — (men köp till en trådlös nätströmställare [kostar under hundralappen för tre sådana på RUSTA] så att lampan [som snabbt blir rejält het] bekvämt kan kopplas på och av — det krävs också en stadig anordning [typ maskinskruvstycke] som lampbygeln kan fästas på). Man KAN också klara sig utan strålkastaren om man får dagsljus, helst solljus till hjälp.

ALLMÄN NOTERING — utmaningen att fotografera vattendroppningens detaljer

Ju kortare varaktighet, desto flera bilder måste man ta innan man (sannolikhetsvägen) träffar prick: det tar TID att knäppa sig fram genom verksamheten.

— Med kamerans angivna exponeringstid (1/4000 S ovan) visas motsvarande längdstreck för droppar som färdas någon väsentlig sträcka under den tiden. Mätning på fotografierna visar att de små primärdropparna som avdelas först (och som är svårast att upptäcka för amatören) har hastigheter på i storleksordningen upp emot 4M/S (1 mM per 1/4000 S). För att få en fotografisk precision på 0,1 mM för ett sådant objekt (vilket är ungefär de minsta dropparnas storlek) krävs alltså en exponeringstid på minst

1/T=d/v= 0,0001/4 = 2,5 t5 = 1/40 000 S. Nikon D90 klarar som mest 1/4 000 S.

— Det finns inga kameror i någon »normal prisklass» som klarar den uppgiften. Men även om man lyckas med det, krävs det MÅNGA foton innan man får fram bara några få bilder som visar de snabbaste delarna (läs: också de mest sällsynta i fotorutan).

— Till hit (April 2009), och med den begränsade (men avancerade) teknik som Nikon D90 uppvisar, har under ca en månads tid runt 10 000 foton tagits på vattendroppsbildningen: drygt 5 timmar effektiv fototid, sedan ett stort antal arbetstimmar för att gå igenom, rensa, sortera och klassificera, sammanställa och redigera — de flesta bilderna (60-90%) kasseras som skräp (den andelen minskar [stadigt] med växande erfarenhet och tekniskt kunnande), av resten återstår sedan i princip bara en handfull användbara bilder — eller möjligen bara en enda.

Rekylbilden

Hur rekylbilden stämmer med den primära himlakroppsbildningen enligt TNED

Hur väl vattnets fysik kan användas i sakbeskrivningen

RESULTAT: Vattendroppsbildningen vid rekylen från en vattendroppe mot vattenytan i ett dricksglas eller skål avbildar tydligen PRINCIPEN FÖR DEN PRIMÄRA HIMLAKROPPSBILDNINGEN ENLIGT TNED väl.

— Se till jämförelse från SOLSYSTEMETS BILDNING (bilden nedan, längst ut till höger).

Slutsatsen grundas på följande allmänna egenskaper enligt bilderna ovan samt illustrationen separat nedan:

1. resonansserien har en utpräglad mittdel med en största centralkropp som omges i bägge ändarna av mindre kroppar

2. resonansserien avdelar de minsta kropparna först, dessa ges de högsta hastigheterna, se PRIMÄRDROPPARNA nedan

3. resonansserien innefattar inre upprepningar (fraktaler), vilket motsvarar planeterna med deras månar

4. resonansseriens motsvarande förhållande mellan Solen och Jorden beräknat efter samma täthet kan i stort återfinnas också i vattendropparnas motsvarande proportioner, se illustrerad beskrivning i Storleksproportionerna.

PRIMÄRDROPPARNA

Hur man observerar de små primärdropparna högt uppe vid utsläppsnivån

Beviset för att de minsta dropparna har den högsta hastigheten (punkt 2 ovan)

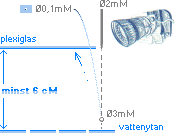
Med en separat handhållen bit plexiglas uppe vid utsläppsnivån (se Droppanordningen) alldeles vid sidan av dropputsläppet, ser man direkt om (små) droppar kommer upp dit underifrån: Små droppstänk framträder på glasets undersida.

Är utsläppshöjden över vattenytan mindre än ca 6-7 centimeter finns varken någon (nämnvärd) rekylverkan eller några observerade smådroppar uppe vid utsläppsnivån, enligt genomförda observationer (April 2009). Först från ca 7 cM ges resultat.

— Att droppar kan rekylera högre än utsläppsnivån bevisar direkt att dessa droppar har den största hastigheten av alla.

— Deras utgångshastighet (upp mot 4 M/S) och ringa storlek (omkring 1/10 mM) garanterar att de som mest framträder på bilderna som svaga streck även med kortaste exponeringstiden (Nikon D90) 1/4000 S.

— För beskrivning av droppanordningen, se särskild illustration i Hur rekylen bildas från den enda vattendroppen.

Storleksproportionerna

Storleksproportionerna

Hur väl vattendropparnas storlek avspeglar motsvarande Solsystemets proportioner med kropparna beräknade efter samma medeltäthet

Nikon D90 · VR 18-105mM · F/3.5-5.6G · 105mM · iso3200 · 1/4000 S - F/9 · OEV - Auto 0.0 · 2009 IV 19 · Tilläggslinser HOYA 1-3

Frånsett den fotograferande teknikens begränsning i upplösning och möjligheter att fokusera, se Hur processen kan fotograferas, och därmed fånga vattenrekylens alla detaljer, och därmed reservation för eventuellt befintliga mindre droppar än i ovanstående storleksrelation:

— I en viss mindre procent återkommande bilder visas i stort ovanstående fason: mellan två stora, eller bara nära en större, syns (diffust, ofta) en betydligt mindre droppe. Det är här okänt om ovanstående exempel möjligen uppvisar en gränsform i förhållandet största/minsta mellan närliggande droppar, eller om mindre finns:

— Vi vet att mindre droppar finns (se PRIMÄRDROPPARNA), men inte närmare OM sådana också finns (för närvarande osynliga med författarens nuvarande fotografiska utrustning) i någon utsträckning mellan närliggande större delkroppar.

— Typexemplet ovan klargör emellertid huvudsaken: i stort sett är det alldeles tydligt att vattendropparnas rekylfysik mycket väl förmår återge själva huvudprincipen beträffande den allmänna storleksordningen i den motsvarande primära resonansserie som utpekas av TNED i den primära himlakroppsbildningen, se från Jordens tredje ekvation (SOLSYSTEMETS BILDNING).

Vattenrekylens spinn

Bildbevis för att rekylen innefattar virvelrörelser som kan ge vattendroppen spinn

Hur processen ansluter till teorin för uppkomsten av himlakropparnas primära rotation

Nikon D90 · VR 18-105mM · F/3.5-5.6G · 48mM · iso3200 · 1/30 S - F/10 · OEV - Auto 0.0 · 2009 IV 22 · Tilläggslinser HOYA 1-3

Med hjälp av en fickspegel tillsammans med droppanordningen, kan man studera hur droppträffen bildar olika rörelser i vattnet — vilken som helst hård planyta duger naturligtvis, men just spegeln ger extra visuell effekt. När droppen träffar (här spegelytan) bildas samtidigt små luftbubblor. Med successivt inkommande droppar, bildar luftbubblorna »automatiska sensorer för rörelsedetektering» och som avslöjas på fotografier tagna med lämplig exponeringstid, som ovan 1/30 S. Fotot överst vänster visar hur en grupp luftbubblor spiralerar en kort stund direkt efter en droppträff.

På samma fason kan sedan motsvarande resultat utläsas ur fotografier tagna på den verkliga dropprekylens stavkropp, överst höger (notera att liknande typbilder inte alltid uppvisas i varje droppstav):

— Här ses tydliga horisontella rörelsestreck efter luftbubblor som befinner sig i den uppåtgående droppstaven. Rörelsestrecken bevisar att stavens radiella utsträckning avbildar/innefattar roterande moment.

— Därmed, såvitt korrekt uppfattat, kan vi vara säkra på att den uppåtgående kraftstaven AV PRINCIP KAN innefatta också rotationer som i så fall överförs naturligt på avdelade droppar och som följaktligen ger dessa spinn. Se vidare från Uppkomsten av rotationer.

inledning

Från enkla hemmaexperiment och vardagliga observationer (i köket) vet vi redan att vatten uppvisar speciellt intressanta effekter då det exponeras för olika krafter. Vinjettbilden ger ett utmärkt exempel på den karaktäristiska vattenfysik som framträder då en vattendroppe träffar en vattenyta. Med grundmaterialet i K-cellen från detonationstillfället som neutroner i närkontakt, här benämnt neutronkallplasma bildas liknande förutsättningar. Enda skillnaden är att neutronplasmats material är betydligt tätare än vatten, samt helt fritt från motsvarande inre elektriska eller magnetiska friktions- eller motståndskrafter, vilket betyder att neutronplasmat i motsvarande mening kan ses som en helt nollviskös vätska (noll flytmotstånd).

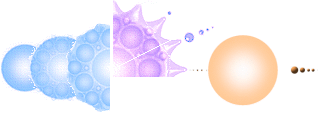
K-cellens detonation från max täthet 1,82 T17 KG/M³ följs av en expansion som påtvingar centralkroppen avtagande medeltäthet och därmed otvivelaktigt, på ett eller annat sätt, tvunget avbildar exakt samma typkraftsbild som i det enkla vattenfallet: en kraftvektor (från föregående droppfall) som skjuter upp (expansionskraften) genom en vattenyta och därmed åstadkommer en karaktäristisk avyttring med mindre delkroppar.

Webben innehåller numera (Februari 2009) en närmast enorm uppsjö av helt fantastiska fotografier av olika vattendroppsbildningar som sammanhänger med denna detalj, både med typen ytstudsar och resonanser (speciellt från kran- eller ventilöppningar), där vi i detalj kan studera motsvarande praktiska kraftbildningar till viss jämförelse. Tyvärr får bilderna i allmänhet inte visas utan särskilda tillstånd — och det finns en stor mängd att välja på.

Figuren närmast ovan antyder K-cellens expansion från detonationstillfället, med påföljande fas där den stora centralkroppen börjar avge mindre delkroppar. Se även vidare mera utförligt nedan i Hur K-cellens bryts. Då emellertid principen som ovan redan står klar, erbjuder Solsystemets himlakroppar en direkt prövande bas för en eventuell härledning av en eventuell motsvarande sträng av avdelade kroppar och som därmed bör följa, likt vattnets fall, vissa grundläggande resonansvillkor. Härledningen visas i JORDENS TREDJE EKVATION, och det är tydligt att formen avspeglar analogi med Solsystemets inre ordning. Det ger oss en (stark) indikering på att Solsystemet också har bildats på det beskrivande, principiella, sättet.

Härifrån kan nu, vidare, ytterligare prövande beskrivningar genomföras till jämförelse med de praktiska fallen.

Speciellt föreningen mellan expansionen som skjuter ut och gravitationen som drar ihop hjälper oss att genomföra uppställningar av enklast tänkbara vågfunktioner med vars hjälp vi kan navigera i de olika möjliga sätten som de olika avdelade kroppsbildningarna kan uppvisa. Därmed ges en efter enklast tänkbara förutsättningar maximalt överskådlig helhetsbild som kan anställas i jämförelse med kända observationer, och på den vägen ge oss en någorlunda säker uppfattning av teorins riktighet — eller haveri.

Innehåll:

SPIRALFORMENS KOSMISKA URSPRUNG

Virvelbildningens elementära fysik

Den Inducerade Rotationens Uppkomst

Illustrerad sammanfattning

Planetrotationernas upphov

PLANETERNAS PRIMÄRA ROTATIONER

centralaccelerationen

GALAXBILDNINGARNA — K-cellens brytning — materieöarnas uppkomst i universum

Stjärnhopar och galaxbildningar DEL I

Allmän delningsklassificering

Hur delkropparna avdelas — uppkomsten av roterande moment

Nolldivergenszonen indelar alla kroppar i två klasser

HUR K-CELLEN BRYTS

Plasmahoparnas Fördelning i K-Cellen

K-cellens innervägg

Massavyttringens allmänna enkla Vågfunktion för K-cellens brytning

Solsystemets ålder

Stjärnhopar och galaxbildningar DEL II

GEMENSAMMA EXPANSIONSRIKTNINGEN — Hur konstant medeltäthet bevaras

PLANETSYSTEMENS GRUNDFORMER

v-SPRIDNINGENS UPPKOMST

Galaxbildningarna — ALLMÄNNA MATEMATISKA SAMBAND

Spiralkurvans Ekvation

Kriteriet för strukturernas bevarande

Strukturexempel från BONNIERS ASTRONOMI

GASDISTRIBUTIONEN MELLAN DELKROPPARNA

ALLMÄN KLASSIFIKATION

REGELBUNDNA SLUTFORMER — De olika galaxklasserna

OREGELBUNDNA SLUTFORMER

STJÄRNFORMATIONERNAS INDELNING OCH KARAKTÄRISTIK ENLIGT ETABLERAD KOSMOLOGI — Referenser

SPIRALFORMENS KOSMISKA URSPRUNG

Ett centralflöde beskriver också en rotation

TNED, relaterad fysik:

Ända från atomkärnans impulsekvation

F_BT + F_eZ = 0

och dess allmänna led som beskriver föreningen mellan flera atomer (»kemiekvationen»)

(F_BT+F_eZ)₁+(F_BT+F_eZ)₂+(F_BT+F_eZ)₃+…+(F_BT+F_eZ)_n = 0

ligger impulsmomentets spinndel från atomkärnans härledning genom Planckringen (h=mcr) inneboende och som säkerställer en redan befintlig »virvelitet» som grund för varje aspekt på materiefysikens sammansättning av substanser och ämnen. Laddningsflödet mellan kärna-hölje i de atomer som bildar molekyl, ger vid föreningstillfället atom-atom en motsvarande tillståndsändring i det gemensamma spinnflödet och som därmed också avbildar en motsvarande ändring i (den kemiskt spinnkopplade) rotationen. Vilket vill säga: alla (fritt rörliga) molekylära föreningar (speciellt de organiska) måste — undantag existerar inte — tvunget uppvisa VIRVELSTRUKTUR (spiral).

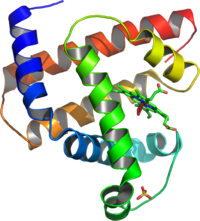
Myoglobin @INTERNET Wikipedia Protein 2009-02-14, 3D-modell. Bilden visar den motsvarande sammanhängande spiralstrukturen för proteinet myoglobin (syrebindande molekyl i muskelvävnad [köttets röda färg]) som är sammansatt av 153 aminosyror. Strukturen bestämdes genom röntgenkristallografi av Kendrew med medarbetare år 1957 (Nobelpriset i kemi 1962, Kendrew och Perutz).

Spiralstrukturen visar sig först i PROTEINERNA (flera hundra aminosyror) [även enzymer (”Enzymes are generally globular proteins”, sv. ’enzymer är generellt globulära proteiner’, ref. Wikipedia Enzyme 2009-02-14)], vars byggstenar är de molekylärt enklare aminosyrorna (tiotal H-N-C-O-atomer), typ exemplet ovan;

I cellernas inre formar proteiner ett inre kroppsnystan (histonen) kring vilket DNA-molekylen vindar sig ungefär som moln kring högt belägna bergsmassiv, ref. Wikipedia |Histone|DNA 2009-02-14; DNA-molekylen som sådan är också spiralformad; Via vissa vitala kvävebaser (GeACT; Guanin-Adenin-Cytosin-Tymin) bildas en central stam i den mera övergripande DNA-molekylens spiral; ”Kvävebasernas ordningsföljd i DNA-molekylen bestämmer uppbyggnaden av kroppens alla proteiner.”, ref. Wikipedia DNA 2009-02-14; DNA-spiralen vrider sig kring »GeACT»-stammen, och själva spiralremsorna eller längstrådarna (eng., strand) består av komplement av fosfat [Fosfor-Syre] och s.k. deoxyribose [Kol-Väte], »FosKov», så att en ”stege” bildas med »GeACT»-pinnar sammanbundna av motstående »FosKov»-sidor.

Denna principbyggnad visar dels att den mera avancerade DNA-strukturen (som kan reproducera proteiner) ”matas” av en inre mera primitiv proteinkropp (histonen), och dels den tydliga uppdelningen i två olika grundstrukturer som bägge krävs för att en cell ska kunna utvecklas: proteinbasen och DNA-strukturen. Medan den förra i princip kan utvecklas spontant ur grundämnena enligt MILLERS EXPERIMENT, är det tydligt att DNA-formen inte kan uppkomma lika spontant: den kräver, tydligen, en väl utbildad, mera primitiv, proteinbas — på samma sätt som proteinerna tydligen kräver de mera primitiva aminosyrorna, som i sin tur kräver de mera primitiva grundämnena.

Artikeln på @INTERNET Wikipedia DNA 2009-02-14 är fantastiskt väl illustrerad och refererad; Utbytet mellan den centrala/omgivande histonen och den kringvirade DNA-strukturen visas med ovanstående (talande) modellillustration.

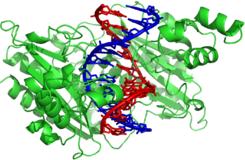
Bilden ovan visar symbiosen mellan (grönt) restriktionsenzymet EcoR5 och (rött-blått) DNA; den förra verkställer en ordnad uppdelning av den senare. Enbart bilden som sådan visar (tydligen) huvudsaken: vem det är som betjänar vem.

DNA-molekylens diamagnetism (Ref. [http://www.physto.se/~hansson/nordforsk0803/Talks/tapash_dna.pdf] (2005), Finding Physics in DNA, Dr. Tapash Chakraborty, University of Manitoba, Canada) — den stängs av och sätts på med hjälp av olika katalyserande enzymer för att verkställa olika faser i celldelningens mekanism — är f.ö. också ett slående exempel på den uppenbart välriktade välordning som grundlägger de spiralkopplande funktionerna — med vidare.

VIRVELBILDNINGENS ELEMENTÄRA FYSIK

2009-02-13

Ett centralflöde innefattar också en rotation — se även Inledningen ovan

Virvelbildningens Fysik beskrivs frekvent i olika webbkällor — men framställningarna är (generellt, veterligt, ännu Februari 2009) ypperligt svårbegripliga (speciellt i matematikdelen där man genomgående använder högskolematematikens vektoralgebra i försöken att beskriva ämnet).

I den här presentationen tar vi ett (mycket) enklare grepp och berör bara de absolut centralt praktiska aspekterna — garanterat helt utom högskolematematiken.

HASTIGHETEN på r från centrum i en roterande rörelse kan skrivas

v = d/t = 2pr/T₀ = (2p f )r = wr

w = konstant;

Konstant vinkelhastighet (w) betyder HJUL, samma som stel rotation på samma fasta kropp genomgående, oberoende av avståndet (r) från centrum;

periferihastigheten v växer då med växande r.

v = konstant;

Konstant periferihastighet betyder VIRVEL, samma som att (t.ex.) vinkelhastigheten (w) avtar inifrån och ut, analogt avtar med växande r;

Virveln kan vara olika stark beroende på om v är konstant som ovan

— eller om v är växande (rotationen går mot HJUL, allt svagare virvel) eller avtagande (allt starkare »virvelitet») med växande avstånd (r) från centrum.

Hur virvlar uppkommer framgår elegant i observationer av vatten. Vi studerar hur.

	UPPKOMST Oavsett sammanhang: i alla material där någon tillståndsförändring uppkommer, sker tillståndsändringen alltid (momentant) utmed NÅGON riktning (se Ändringslagarna). Vi ska här kalla den riktningen för advektionsriktning (»den primära materialändringsriktningen», termen advektion, eng. advection, används inom hydrodynamiken som motsvarande begrepp för transportmekanism i vätskor [även i luft inom meteorologin]). Med en mera stadigvarande sådan riktningsförändring, till exempel genom att ett material påtvingas flöde i viss riktning — t.ex. tömning av vattenkärl genom en bottenventil; handfat, diskho, badkar är utmärkta exempel — sker en motsvarande materialpåfyllning vinkelrätt mot »urtappningsriktningen» för att kompensera materialbortfallet i den riktningen. Bilderna här till vänster togs vid ett besök på Bullerforsens kraftstation i Borlänge (Augusti 1995). Genom det starka suget underifrån vattenturbinernas påfyllningsöppningar ges uppe vid ytan alldeles invid dammluckorna rikliga tillfällen att studera uppkomst, utveckling och spridning av vattenvirvlar.

Bildkälla ovan: Bullerforsen i Borlänge Augusti 1995. Föfattarens privata arkiv.

Bilderna visar hur vattenvirvlar uppkommer i serier och perioder i det starka draget från kraftverkets vattentappning långt ner under ytan.

DEN INDUCERADE ROTATIONENS UPPKOMST — virvelbildningen i detalj

Den Inducerade Rotationens Uppkomst

Från virvelbildningens elementära fysik — se även från Hur delkropparna avdelas

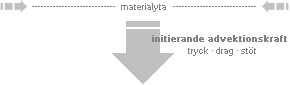
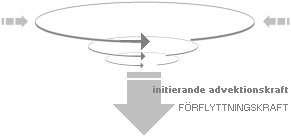
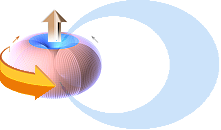
Illustration närmast ovan antyder hur advektionskraften först åstadkommer »en ytbula» i kraftriktningen (nedåt). Tillståndsändringen betyder en »grop» som det omgivande materialet faller ner i, analogt »attraheras runt om» motsvarande den vakans som advektionen (ytbulan) bildar. Denna detalj kan alltså även uppstå i luftströmmar (gaser) med typ plötsliga undertryck som driver ner material från högre till lägre höjder, principen är densamma för alla substanser.

Sammandragningen (sett ovanifrån) mot advektionspunkten i centrum bör med hänsyn till materiepartiklarnas ändliga utsträckning knappast någonsin, exakt, träffa prick på advektionsriktningens mittpunkt; På ett eller annat sätt, med grund i olika, redan befintliga molekylära (termiska) och substantiella rörelser, kommer materialströmningen in mot centrum att gå vid sidan av ideala (momentant geometriska) centralpunkten. Detta leder obönhörligt till vridande moment (Fd=E) kring centralpunkten och därmed, på ett eller annat sätt, i en eller annan mening, en uppkommen rotation som här benämns INDUCERAD ROTATION; Strömningsmaterial i allmänhet (som det visar sig) »rättar in sig» efter någon minsta (lokalt dominant) rörelseriktning, och det blir sedan den som, tillsammans med advektionen, bestämmer huvudriktningen och grundlägger trögheten i den vidare strömningshistorien.

Därmed, figuren ovan vänster, har en SPIRAL bildats, eller som vi säger, en VIRVEL: advektionen som i vattenvirvelns fall drar neråt och ytinströmningen över som fyller på; Rotationen är störst i mitten och avtar sedan ut mot noll — allt snabbare ju mera trögflytande (visköst) materialet är. Ju större draget är i advektionsriktningen, desto kraftigare blir virveln.

Bilden ovan samma som den översta i föregående bildsvit, här förstorad.

ILLUSTRERAD SAMMANFATTNING — DEN INDUCERADE ROTATIONENS UPPKOMST

GENOM K-CELLENS INITIELLA EXPANSION SOM ALLMÄN GRUND FÖR HIMLAKROPPARNAS PRIMÄRA ROTATION

Se även längre upp från huvudartikeln

a	b	c	d

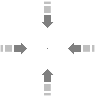
a: Ansatsen till någon flödesriktning (EXPANSIONSKRAFTEN i K-cellens fall) vinkelrätt mot materialytan innebär en relativ förflyttning av materialets element i ändringsriktningen. Det FRAMTVINGAR EN MOTSVARANDE PÅFYLLNING I ANSATSPUNKTEN; omgivande material strömmar mot ansatspunkten, vilket bildar den inducerade rotationens grundmoment.

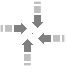
b: Med ändliga dimensioner för materialpartiklarna, som dessutom själva uppvisar impulsmoment (mvr), blir sannolikheten försvinnande liten för att motströmmande partiklar ska träffa varandra precis på den idealt geometriska mittpunkten; Genom att partiklarna har utsträckning och därmed kan utbilda vridande moment kring en (partikelns) tyngdpunkt, eller kring flera partiklars gemensamma tyngdpunkt, är det tydligt att också ett vridande moment (Fd) bör uppkomma i den centralt sammanflödande regionen som effekt av en uppkommen flödesriktning (expansionen) rätvinklig materialytan;

c: Den sammansatta rörelsen i övergången mellan ytströmning (a) och djupströmningen (expansionen) som är orsaken till processen, bildar därmed tvunget en spiral eller virvel utmed djupströmningens huvudaxel;

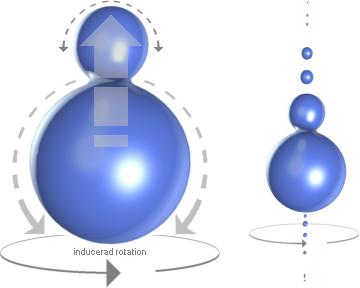
d: Beroende på materialets egenskaper och tiden för djupströmningens verkan, analogt styrkan i responsen från de påfyllande materialpartiklarna, bildas alltså därmed en mer eller mindre utpräglad centralrotation. Därmed har den inducerade rotationen etablerats. I K-cellens fall, där djupströmningsfaktorns hastighetskomponent under alla omständigheter dels är relativt stor och dels kan anses (ytterst) kortvarig, eftersom den omedelbart upphör med J-kropparnas avdelning, är det tydligt att den totalt resulterande rotationen på de avdelade kropparna också bör bli ytterst marginell — ehuru faktisk. Utan dess inverkan blir det (här veterligt) omöjligt att härleda himlakroppsrotationernas primära orsaksgrunder.

Rotationens primära upphov för samtliga universums avdelade kroppar , kan därmed ENLIGT TNED återföras på ovanstående redovisade rent kvalitativa orsaksgrund, den inducerade rotationen. Observera emellertid att dessa primära rotationer inte är identiska med de slutliga rotationerna för planeter och stjärnor då dessa ENLIGT TNED erhåller tilläggsrotationer under himlakroppsbildningens fusionsfaser; För planeternas del bara vid själva bildningstillfället (men desto mera häftigt), för stjärnornas del fortlöpande med den kontinuerliga energiomsättningen. Se även vidare i Rotationens inverkan på stjärnans fysik.

Planetrotationernas upphov:

Med tillämpning på den primära himlakroppsbildningen enligt TNED

HUR ROTATIONERNA FÖR SOLSYSTEMETS HIMLAKROPPAR FRAMGÅR UR DEN INDUCERADE ROTATIONEN

ORIGINALFÖRFATTNING Apr2009 — mera utvecklat Feb2019 i SOLSYSTEMEN I VINTERGATAN ¦ Planetaxlarna ¦ Planetkropparnas egenrotation

PLANETERNAS PRIMÄRA ROTATIONER

Tabelluppställningen nedan visar hur rotationsaxlarna är orienterade i samlingen Solsystemets himlakroppar.

7,25	2,11	177,3	23,44	25,19	3,13	26,73	97,77	28,32	119,59
Solen	Merkurius	Venus	Jorden	Mars	Jupiter	Saturnus	Uranus	Neptunus	Pluto

Axellutning i grader relativt ekliptikan, källuppgifter specifikt för varje planet från @INTERNET eng. Wikipedia 2009-02-16.

V

i tycker att den (synnerligen) enkla exempeluppställning som ges från K-cellens expansion med den inducerade rotationen som grund för virvelbildningen i allmänhet också (galant) borde kunna förklara, eller beskriva, den nu observerade ordningen i Solsystemet — då det i vilket fall är klart hur detta bildas i princip. Följande illustrerande genomgång tycks visa att så också är fallet.

Med Virvelbildningens grund genom expansionskraften garanteras av princip att varje avdelad J-kropp från K-cellen KAN erhålla en minsta möjliga primär rotation. Denna del säkerställer att sådana J-kroppar som typ galaxerna också (i allmänhet) kan uppvisa olika typrotationer, och därmed också deras egna inre avdelande J-kroppar typ Solsystemets moderkropp. Illustrationen i a här till höger antyder en given rotationsordning hos en sådan typkropp där de avdelade J-kropparna, tillsammans med expansionen, i sin tur erhåller motsvarande vridande moment (Fd=E), se även i figurerna b och c nedan. Vridmomentets egenskap är att ge alla avdelade J-kroppar en harmonisk rotation kring en deras gemensamma tyngdpunkt, i vårt fall Solen. Enligt kända observationer roterar också alla planeter åt samma håll kring Solen, moturs sett från ekliptikans norra del [ref. ENCARTA 99 Solar System]. Vi ser att detta fall stämmer utmärkt med K-cellens förutsättningar.

a

I J-kropparnas aktuella avyttring från sin moderkropp kan vi nu studera den inducerade rotationen:

Alla J-kroppar i samma resonanssträng genomlöps av en och samma gemensamma expansionsvektor (röd pil), den som triggar den inducerade rotationen. Men ingenting säger att den inducerade rotationsriktningen nödvändigtvis måste vara lika riktad i alla partier — men vi kommer dock här för enkelhetens skull att förutsätta en sådan, likformig, rotationsriktning enligt figurens vänstra del.

b

D

e orangea staplarna, figurdelen i c nedan markerade från centralmassorna neråt-uppåt, representerar en grov diagrammatisk bild av delkropparnas slutliga periferihastighet (v) relativt Solkroppen — v avtar med växande avstånd från Solen som gemensam tyngdpunkt. Också denna detalj stämmer utomordentligt med Solsystemets fall: planeternas omloppshastighet avtar med växande avstånd till Solen. Det är EMELLERTID INTE direkt uppenbart hur denna detalj kan återföras på J-kropparnas avyttring genom expansionsfasen. En särskild del i PLANETSYSTEMENS GRUNDFORMER beskriver denna detalj explicit (se särskilt i v-spridningens uppkomst). Vi förutsätter den här bekant för den vidare, följande beskrivningen där vi helt frånser omloppshastigheterna och bara koncentrerar oss på den principiella uppkomsten av planeternas primära kroppsrotationer.

J-serien eller »kroppssträngen» som antyds här i figurdelen i c (mörkblått) visar hur Solsystemets motsvarande kroppar bör ha avyttrats från sin större moderkropp (vänster). Från denna och utåt således Asteroiderna, Mars, Jorden, Venus, Merkurius, Solen, Jupiter, Saturnus, Uranus-Neptunus och Pluto, samt ytterligare inkluderat de nämndas eventuella månar.

c

Lås oss därmed analysera situationen från tillfället då den inducerade rotationen ses gemensam för hela J-strängens delkroppar, figurdelen d nedan.

M

ed AVRULLNINGEN av J-strängens kroppar från moderkroppen till Solsystemet, kan vi idealt se att J-strängens kroppar kommer att vrida sig kring tyngdpunkten (Solkroppen). I figurerna ovan (a-c) är denna systemrotation avbildad sett ovanifrån och moturs (snabbast närmast Solen, långsammare längre ut, se v-spridningerns uppkomst).

I delfiguren d här till höger betraktas situationen sett snett ovanifrån, den markerade rotationsriktningen för hela J-systemet under Solkroppen. Rätvinkligt den huvudrotationen visas de ikoniserade planeterna med deras inducerade gemensamma rotationsriktning. Då den inducerade rotationen bör yttra sig markant för små kroppar relativt större för given expansionskraft, kan vi med hänsyn till Solkroppens helt överlägsna storlek relativt J-systemets övriga kroppar helt frånse Solens inducerade rotation (den förutsätts således här helt försumbar) och enbart koncentrera beskrivningen till de långt mindre planetkropparna.

d

Den inducerade rotationens tvärriktade impulsmoment (J=mvr) relativt den ordinära J-strängens mera stabila rotation, påtvingas riktningsförändrande krafter genom huvudrotationens cirkulära genomgång: riktningen ändras hela tiden. Figurdelen i e till höger visar denna instabila situation för den primärt uppkomna inducerade planetrotationen omedelbart vid/efter kroppsavyttringen.

e

Då ingen underhållande energi finns för att bevara ett sådant tillstånd, tvingas den inducerade rotationsaxeln (idealt) att flippa (vrida upp sig) så att den intar samma axelriktning som huvudrotationen — eller (mera egentligt) ställa in sig i ett (krängande) mellanläge mellan huvudrotationens axel och den primärt givna inducerade rotationsaxeln.

f

Därmed har jämvikt uppnåtts. Planeternas rotationsaxlar kommer följaktligen, mer eller mindre, att rada upp sig i samma riktning som den primära omloppsriktningen. Delfiguren i g till höger visar den ideala situationen, och det är den vi borde återfinna i Solsystemets fall — OM bildningen sker efter J-strängarnas kroppsresonanser enligt virvelbildningens principer.

g

O

m vi jämför med föregående tabelluppställning (Planetaxlarnas lutning) som visar data på det praktiska fallet, ser vi att »ordningen gäller i stort sett». Alla planeters rotationsaxlar är samriktade med det primära omloppsplanets rotationsaxel utom Uranus och Pluto. De avvikelser som finns kan beskrivas på följande grund.

I

det praktiska fallet (vi frånser här fusionsfasen i himlakroppsbildningen), där också planeternas lägen påverkar varandra inbördes med olika krafter i olika banavsnitt, samt med hänsyn till omloppsbanans omfång (högre känslighet med mindre avstånd till den gemensamma tyngdpunkten) kan vi (utan vidare) sluta oss till att kropparna tvingas inta olika jämviktslägen som innefattar typen »svängande snurror» — som ett snurrande mynt som just lägger sig på ett plant underlag, en s.k. precessionsrotation: Planetens axel ställer inte in sig exakt rätvinkligt omloppsplanet, utan bildar en större eller mindre vinkel mot detta (speciellt Jorden, Mars, Saturnus, Neptunus). I fallet Pluto (120°) befinner vi oss långt utanför systemets gemensamma tyngdpunkt, och har bara av den anledningen en viss rätt att förvänta oss vissa avvikelser (Plutos omloppsbana är också den som avviker mest från de övriga).

I fallet Uranus (98°) finns även en annan aspekt (utöver att den kroppen redan ligger långt ut i periferin), nämligen dess redan kända symbios med grannen Neptunus.

I SOLSYSTEMETS UPPKOMST härleds en resonansserie som förutsätter att Uranus-Neptunus från början bildade en tvillingdroppe (som separerade relativt långsamt). Det är här inte närmare känt om också Uranus (bibehållna) tvärrotation kopplar till den detaljen, eller om rotationsaxelns nära bevarade ursprungliga läge (fortfarande enligt TNED) kan beskrivas på detaljer som eventuellt sammanhänger med dessa planeters månar.

Hur som helst, måste i vilket fall och för samtliga kroppar mera ingående beräkningskomplex sammanställas om det gäller mera noggranna undersökningar.

Beskrivningen till hit har emellertid, redan tillräckligt, fokuserat på den tydliga rent kvalitativa ordningsharmoni som, tydligen, sammanhänger med den allmänna beskrivningen i K-cellens expansion, och det råder därför knappast här (längre) något tvivel om rimligheten i resultaten.

Se även längre ner i PLANETSYSTEMENS GRUNDFORMER.

centralaccelerationen

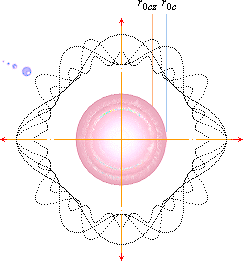
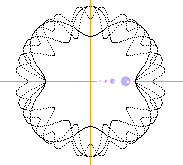
VI KAN PÅ ENKLASTE SÄTTET få en viss matematisk uppfattning om »virveliteten», alltså virvelstyrkan, i varje del av virveln om vi erinrar den enkla härledningen till centralaccelerationen, figuren nedan;

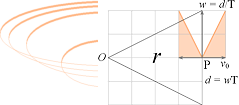
v₀/w = d/r = wT/r ; v₀/T = a = w²/r = a_w = å

ADVEKTIONEN (nedströmningen i vattnets fall) är som störst i centrum (»vertikala vattenströmningshastigheten v») och avtar sedan utåt. Vi kan därmed på visst sätt använda ett v-värde för varje r-värde i en motsvarande konvektionsanalogi så att v-värdet ÄVEN motsvarar ett YT-v-värde i advektionens motsvarande ytvända del. Därmed ges en motsvarande acceleration om vi sätter v=v₀ med illustrationens beteckningar så att vi får

å = v₀/T = a = w²/r

med w som periferihastigheten på r från centrum enligt

rå = w²

Med T = 1S ges

rv₀ = w² · S ;

w = Ö rv₀S^–1

EXEMPEL:

Med v₀=1M/S nära centrum i ett observerat fall skulle vi på avståndet 1 cM från virvelns centrum få en periferihastighet på 0,1 M/S.

Motsvarande praktiska fall finns f.n. ingen refererande mätuppgift på.

I K-cellens fall, faserna med J-kropparnas avdelning, måste vi i vilket fall räkna med mera kortvariga flödesändringstillfällen — precis just vid avdelningstillfället — och därmed också av allt att döma en mera snäv dynamik med mera begränsade kopplingar till den motsvarande hydrodynamikens principer.

Om den nuvarande praktiken ingår i ämnet, blir av allt att döma de motsvarande rotationerna i J-kroppars avdelning som följd av expansionen som den drivande motsvarande advektionskraften ytterst blygsamma. Det viktiga i sammanhanget för förklaringen till himlakropparnas nuvarande observerade rotationer är emellertid inte rotationens magnitud i själva J-kropparnas avdelning, utan det faktum ATT någon rotation ALLS bildas i det skedet. Den ordinära, egentliga rotationsbildningen för himlakropparna inträder av allt att döma (nämligen först) istället vid den häftiga fusionsfasen för planeternas del, och för stjärnornas del genom den fortlöpande energiproduktionen. Det viktiga är, just, att det finns en viss minsta befintlig rotation att bygga på.

Galaxbildningarna

Universums Historia ENLIGT RELATERAD FYSIK OCH MATEMATIK

GALAXBILDNINGARNA

eller

K-cellens brytning — materieöarnas uppkomst i universum

2009II11 från originaldokumentet (doc) UNIVERSUMS HISTORIA 2004X10

Vi noterar först den relaterade fysikens annorlunda utgångspunkt i jämförelse med modern akademi och vetenskap: Himlakroppsbildningen i relaterad fysik (TNED)

	RELATERAD FYSIK
från max värme	strukturkriterium finns — Solfysiken och galaxbildningen framträder galant

börjar från maximal täthet och expanderar sedan utåt.

I modern akademi däremot

	MODERN AKADEMI
från max kyla	strukturkriterium saknas — varken Solfysiken eller galaxbildningen förstås

börjar himlakroppsbildningen i stora utspridda gas- och stoftmoln som antas sammandras av gravitationen och som därifrån bildar himlakroppar.

— Varför kan den moderna akademins teoretiker inte börja direkt från det maximalt täta tillståndets fysik (efter Big-Bang), utan insisterar på att materiebildningen nödvändigtvis ska spridas ut på enorma stoftstråk för att först därifrån sammandras till motsvarande tätare materieöar?

— Därför att den moderna akademins uppfattning om ”begynnelsetillståndet”, alltså ”Big-Bang”, inte innefattar någon annan möjlig förklaring till händelseförloppet än typ exploderande vätgas; modern akademi har inget begrepp om fusionsringar i samband med divergenständning; från neutronens sönderfall i positiv divergens. Därför tvingas man, följdriktigt, också söka förklaringarna utifrån typen mest utspridda tillståndets fysik.

UNIVERSUMS HISTORIA ref. MPcKOSMOS_3.wps

Se även J-KROPPENS EXPANSION

K-cellens expansion

Stjärnhopar och galaxbildningar DEL I

Se även HIMLAKROPPARNAS ALLMÄNNA EXPANSIONSFYSIK — en jämförande översikt mot konventionell kosmologi

En allmän beskrivning av hur K-cellens plasmakropp bryts ges i K-CELLENS BRYTNING.

En vidare översikt av hur J-kropparna avdelas och formeras ges i artikeln Stjärnhopar och galaxbildningar DEL II.

; Allmän delningsklassificering

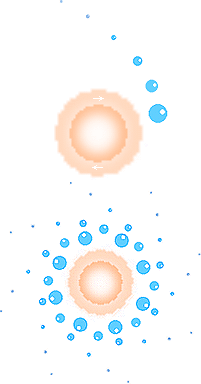
K-CELLENS SUCCESSIVA AVYTTRING AV DELKROPPAR (J) kan beskrivas genom ett principiellt fraktalt-logaritmiskt system av den typ som vidstående illustrationer skisserar. Exakt vilket detta system är, är emellertid en mera intrikat fråga. Eftersom delkropparna avyttras på delvis olika sätt — dels från K-cellens yta och utåt, och dels inåt mot centrum från K-cellens inre zonvägg — finns veterligt ingen direkt enkel och generell delningsform för hela komplexet; Delkroppar med given initialmassa som uppträder i en viss sekvens kan förekomma även i helt andra sekvenser varför en strikt behandling av hur delningen sker ifrån nu kända massor i de olika regionerna knappast låter sig beskrivas i någon enkel form.

Delningsalgoritmen för Solsystemet är dock känd i detalj och beskrivs i SOLSYSTEMETS UPPKOMST.

Följande beskrivningar är endast grovt orienterande — i någon koppling till vidstående skisserade delningsordningar.

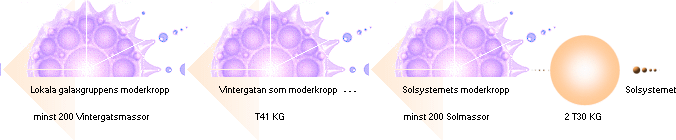
DELNINGSFORMERNA kan beskrivas på olika sätt beroende på graden av matematisk komplexitet. Ovanstående är enkla grundformer med Vintergatsmassan (grovt och runt T41 KG) som referens.

En mera massexakt orienterande delningsbild ges med beaktande av resultaten från K-CELLENS VÄRMEFYSIK.

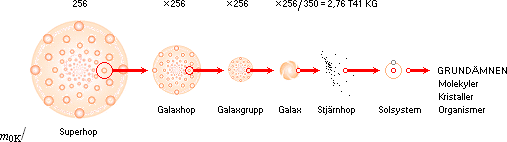
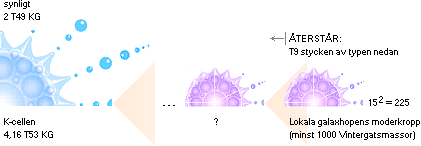
Med en avrundad delning på 1/350 mellan totalmassan bakom värmeeffektens utveckling och den synliga taget som ett medelvärde för hela K-cellen kan en delningsform med 16×16 kroppar i varje idealt likadan successivt mindre delkropp ner till galaxnivån beskriva hela K-cellens uppdelning med basen 256 enligt

4,16 T53 KG / (256 × 256 × 256 × 256) / 350 = 2,76735 T41 KG

Vintergatans synliga massa är ca 1,4 T11 Solmassor [BAs313 Tab.15.2] eller 2,7846 T41 KG vilket stämmer ungefärligt med ovanstående enklare delningsform. Man får då en grovt generaliserande bild som indelar K-cellens uppdelning i fyra fraktalgrupper: Superhopar med drygt 16 miljoner Vintergatsgalaxer i varje, Galaxhopar med drygt 65 000 Vintergatsgalaxer i varje, Galaxgrupper med ca 250 Vintergatsgalaxer i varje, och slutligen Vintergatsgalaxen som masspreferens.

Eftersom galaxbildningarna ingalunda är likartade varken till massa eller typ, och dessutom galaxerna i allmänhet utspridda över stora områden med mindre gruppbildningar från par till flera, blir denna indelning inte helt rättvis mot den verkliga fördelningen — men ger ändå en relativ orientering.

Det är också, ungefärligen, efter denna modell den konventionella kosmologin beskriver den allmänna kosmiska massfördelningen — inkluderat vissa inbördes meningsskiljaktigheter beträffande superhoparnas vara eller icke vara [EST-7s536sp2n Galaxy, Clustering].

; Allmän matematisk fysik

K-CELLENS UPPDELNING I MINDRE DELKROPPAR kan återföras på enkla vågekvationer i polära koordinater [Se särskild beskrivning i K-CELLENS BRYTNING] och som ansluter till enkla principer i hydrodynamiken.

Här följer en allmän beskrivning av principen.

Hur delkropparna avdelas — uppkomsten av roterande moment

Med inledning från Virvelbildningens elementära grunder och uppkomsten av inducerad rotation

Eftersom kallplasmat motsvarar en nollviskös supervätska kan dess allmänna beteende återföras på hydrodynamikens principer — vatten.

Expansionskraftens effekt i den nollviskösa ytdelen med avyttring av individuella J-sfärer kan liknas vid den rekylverkan som uppkommer då man släpper en vattendroppe mot en vattenyta. Vid uppstudsen trycks vatten via omvända kraftvektorn upp i en topp från vilken vätskeströmning sker ekvivalent neråt på utsidorna mot basen. Toppunkten beskriver då en ideal punkt från vilken utgår radiellt växande ytströmningshastigheter. Se även i Virvelbildningens elementära grunder. Ett sådant punktbegrepp beskriver ekvivalent samma element som finns i centralaccelerationen, analogt ett centrifugalkomplex med impulsvektorerna riktade utmed radius vektor. Med andra ord avbildas ekvivalent samma element som i fallet med en rotation. Principen för uppströmningen mot toppunkten med nedåtströmmande ytdelar visas i bilden nedan. Därmed uppkommer, på ett eller annat sätt av princip, i större eller mindre grad, en tvungen roterande rörelse, åt endera hållet;

Hastighetskomponenten (v₀) i upp/utströmningen är i det enklaste fallet proportionell mot rotationen, å=w²/r=v₀/T i centraldelen. Men då denna utsätts för friktion av den övriga kroppen med vidare utjämningar kan beräkningen inte enbart göras på en enkla grunden. I J-kropparnas fall finns dessutom v₀ bara till just under J-kroppens avyttring, vilket ytterligare begränsar rotationsbildningens magnitud, och i en eventuellt uppkommen rotation bör den därför bli högst marginell, ehuru av principiell typ. Dvs., en roterande ordning KAN uppkomma med J-kroppars avyttring från sin moderkropp, men den totalt resulterande vinkelrotationen bör av allt att döma bli (mycket) marginell.

I JÄMFÖRANDE EXEMPEL med uppgifter från Vintergatan — Solens hastighet runt Vintergatans centrum är grovt 200 KM/S eller v=2 t5 M/S på radien ca 30 000 lå eller R=2,84 T20 M — ges en omloppstid på T = 2pR/v = 8,9 T15 sekunder avrundat, eller 280 miljoner år. Det exemplet visar hur ypperligt svag den roterande faktorn kan vara i ett praktiskt fall som berör en så stor primärkropp som den associerad med Vintergatan. Det är alltså i vilket fall fråga om ytterst marginella rotationer.

Vid ett visst maximum snöps toppdelen av i formen av en huvudsfär som efterföljs av en sträng av mindre småsfärer (resonansverkan) beroende på kraftdynamiken. Figurerna nedan antyder verkningssättet.

Principiellt samma typiska proportioner återfinns i observationerna av rekylen hos vattenytan som studsar tillbaka uppåt då den träffas av en enskild vattendroppe.

Fotografierna i beskrivningen av droppanordningen ger några exempel.

— Analogin mellan K-cellens neutronkallplasma och vattenfysiken bevisas av återkommande exempel som visar hur ”mikrodroppar” uppträder tillsammans med de ordinarie vattendroppar som bildas i rekylen från en vattendroppe som träffar en vattenyta, se från vinjettbilden, samt i droppanordningen.

— Med vissa reservationer för den fotograferande teknikens begränsningar, samt den uppenbara skillnaden i täthet i de skilda fallen vatten/neutronkallplasma visar det sig att proportionerna i jämförelsen med Solsystemets himlakroppar (i primärfallet alla med samma täthet och därmed i analogi med vattnets fysik) är tämligen analog med de observerade resultaten från försöken med vattendroppsbildningen från rekylverkan.

Droppanordningen, särskilda detaljer

Droppanordningen visas nedan i särskilda detaljer. Se även droppanordningens huvudillustration.

Allt originalmaterial i Universums Historia får användas fritt förutsatt källan anges — BellDHARMA 2009II27, AF-S NIKKOR 18-105 Nikon D90.

Bilderna närmast ovan visar den enkla men exakta och effektiva droppanordningen: exakt period och styrka (droppstorlek och avstånd över vattenytan) kan justeras efter önskemål. Från tillbringaren leds vattnet via en PVC-slang till öppningen som består av en tandpetare invirad i hushållspapper. Genom att trycka in den helt lätt i slangen ges en minimal vätskeväg till tandpetaren från vilken enskilda droppar kan avdelas i noggranna återkommande perioder runt sekunden och uppåt och med ständigt återkommande samma vattendroppsstorlek. Förhållandena blir idealt desamma för varje droppe som träffar, förutsatt vattenytan hinner jämnas ut. Droppbildningen kan börja så snart slangöppningen i droppänden ligger lägre än tillbringarens vattenyta.

OM den underliggande moderkropp som ovanstående delkroppar (J) avyttras från i sig också besitter någon (minsta) rotation, tillkommer ytterligare vridande moment på de ovan motsvarande avbildade avyttrade delarna. Se vidare i Solsystemets bildning, där just sådana moment uppenbarligen måste finnas med för att kunna förklara systemets fysik.

I konsekvens av den beskrivna advektionen i samband med K-cellens allmänna expansion och de krafter som föranleder J-kropparnas successiva avyttringar, finns alltså vissa förutsättningar för de avdelade enskilda kropparna att uppvisa ett initiellt om än litet roterande moment (J-spinn).

Men det finns också andra faktorer som kan bidra till J-spinn: inbördes gravitation mellan de expanderande delhoparna, se nedan.

I den rent matematiskt beskrivande händelsen som förklarar HUR J-kropparna avdelas, har vi för närvarande bara en egentlig (exakt) grundmall. Nämligen Solsystemets bildning och den resonansserie som uppvisas tydligt i det fallet. Se utförligt i JORDENS TREDJE EKVATION. Enligt den ordningen följer de avdelade J-sfärerna ett bestämd mönster: (generellt) större sfärer inåt (med en svans av småsfärer) och mindre utåt, tillsammans med den eventuellt uppkomna rotation som diskuterats ovan, se från Virvelbildningens grunder.

KROPPAR MED STOR INITIALMASSA

har större förmåga att bilda samlade plasmahopar i ytdelarna då dessa expanderar än mindre J-kroppar.

Spridningsgradienten mellan närliggande neutroner är (nämligen) i det förra fallet liten vilket gynnar den inbördes sammanhållande gravitationen.

Då delkropparna divergenständer, expanderar de i sin tur på formen för små (mindre) J-kroppar.

Hur kroppsytorna bryts upp beskrivs nedan från K-cellens brytning.

kroppsklassificeringen

Nolldivergenszonen indelar alla kroppar i två klasser

KROPPARNAS ALLMÄNNA KLASSIFICERING GENOM NOLLDIVERGENSZONEN

Med hänsyn till huruvida den avdelade kroppen har eller inte har en egen nolldivergenszon, kan alla avdelade kroppar under K-cellens expansion där den maximala tätheten

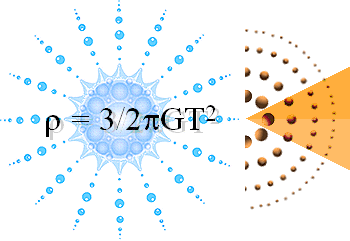
r_max=1,82 T17 KG/M³ bevaras indelas i två klasser. Kroppar som har en egen nolldivergenszon är kroppar med radier lika med eller större än

r_0c=c₀Ö(3/2pGr_max) = 5,94556 T4 M @ 60 KM [Se Nolldivergenszonens radie ur tätheten] med massor lika med eller större än

m_0c=r_maxV=r_max4pr³/3= (c₀/ÖG)³(6/pr_max)^1/2 [Se J80-massan] =1,60227 T32 KG @ 80 Solmassor (Solmassan är 1,989 T30 KG). Frånsett det exakta gränsfallet r_0c har alla sådana större J-kroppar möjlighet att i sin tur avdela mindre kroppar som initiellt sammanhålls internt av gravitationen på bibehållen maximal täthet.

Alla övriga, analogt mindre och lättare J-kroppar har en direkt möjlighet att bilda egna slutliga stationära himlakroppar. Dynamiken för bildningen av dessa fasta kroppar beskrivs per matematisk fysik galant i JORDENS FJÄRDE EKVATION. Det är nämligen så att det finns en speciell gränsmassa [Se JORDENS ANDRA EKVATION], en fysikalisk kosmisk referenskropp som noga kan beskrivas utifrån kärnfysikens parametrar i balansen mellan expansionstryck och g-tryck och på vars formbas alla övriga kroppar kan beskrivas, inkluderat grundämnessammansättning. Med Solsystemets himlakroppar som enda kända alternativ, är det Jorden som bildar den fysikalisk lokalen med primärmassan 6,8 T24 KG, vilket är nuvarande Jordmassan plus 12%. Venus ligger närmast under men är för liten (motsv. 28% avyttring), och närmast större är Uranus med 86,9 T24 KG vilket skjuter långt över gränsen. [Se även JORDENS FÖRSTA EKVATION].

‡[1] Se JORDENS FEM EKVATIONER i särskilt avsnitt.

Massor större än 80 Solmassor [Se J80-MASSAN] har vad vi vet ingen himlakroppsmässig representation — J80-kropparna är de allra största egenkroppar som kan finnas

EN DELVIS DIREKT BEKRÄFTELSE på r_0c-gränsmassans storlek 80 Solmassor ges genom den konventionella astronomins allmänna uppgifter.

Genom en allmän kartläggning av de synliga himlakropparna, alltså stjärnorna, har man fastställt vissa övre och undre gränser för deras massa.

BONNIERS ASTRONOMI 1978 ger på sidan 54 en tabellöversikt över ”observerade egenskaper hos normala stjärnor”. Med Solens som preferensen 1 anger man en högsta gräns för stjärnmassorna på 70, lägst 0,05 Solmassor. Referensen [BAs78sp1mö] ger dock en delvis annan (allmän) uppgift (”väsentligen 50 Solmassor”). Se vidare i J80-MASSAN.

Observationerna (från 1978 och tidigare) är alltså »någorlunda samstämmiga» med det absoluta teoretiska gränsvärdet på max 80 Solmassor. En del av J-kroppens yta försvinner också ur J-kroppens g-fält i samband med divergenständningen [Se JORDENS FEMTE EKVATION], vilket ger det praktiska värdet mindre än 80 Solmassor. Exakt hur mycket mindre är en sublim fråga som berör exakta parametrar i atomkärnans fysik. Hur primärmassorna beräknas beskrivs utförligt i JORDENS FEMTE EKVATION.

Beroende också på var moderkroppen befinner sig i förhållande till den kosmiska divergenszonens svepradie finns en uppsjö av olika sätt som sprängkraften i moderkroppens expansion kan realiseras på; Tändningen kan ske snabbt eller långsamt när kallplasmat förvandlas till normalt elektriskt aktiva atomkärnor.

En allmän översikt av hur J-kropparna avdelas och formeras ges i artikeln Stjärnhopar och galaxbildningar DEL II.

Hur K-cellen bryts upp i mindre delkroppar beskrivs mera inträngande i K-CELLENS BRYTNING.

Hur galaxernas spiralstruktur bildas beskrivs särskilt i GALAXBILDNINGARNA.

Hur galaxstrukturerna bevaras beskrivs särskilt i STRUKTURKRITERIET.

ref. MPcKOSMOS3.wps

UNIVERSUMS HISTORIA — K-CELLENS BRYTNING

[ref. MPcKOSMOS.wps · MPcKOSMOS_3.wps · TNED115C.BMP]

HUR K-CELLEN BRYTS

K-CELLENS BRYTNING 2004XI11

Vidare i GALAXBILDNINGARNA och Stjärnhopar och galaxbildningar DEL I

DEN ALLMÄNNA HIMLAKROPPSBILDNINGEN UNDER K-CELLENS EXPANSION

Se även i J-kropparnas Expansion

Plasmahoparnas Fördelning i K-Cellen

PLASMAHOPARNAS FÖRDELNING I K-CELLEN

En enkel kvalitativ analys visar att sättet för kallplasmat (se kallplasma) att samla sig i hopar (internt i K-cellen under expansionen) enklast sker 1. på gemensam minsta spridningsvinkel med lägsta expansionshastighet (minsta motståndets lag), vilket (med referens till en initiellt gynnsam tyngdpunktsansats) medför att neutronerna i kallplasmat samlas i begynnande smågrupper, som får en gemensam expansionsriktning med en gemensam tyngdpunkt, som sedan tillväxer 2. genom att den inbördes gravitationen mellan två närliggande lika stora hopar taget över hela K-cellen är starkare ju mindre avståndet är mellan de lika stora hoparna (ytmarkerade illustrationens vänstra del), och att därför processen fortskrider 3. genom att hoparna totalt sett samlas till större inåt och mindre utåt (illustrationens högra del) En enklare beskrivning med samma resultat: Betrakta mängden neutroner efter detonationsögonblicket som en samling kulor som drar iväg explosivt från ett sfäriskt centrum. Eftersom expansionshastigheten är som störst längst ut och därmed också den radiellt vinkelrätt riktade separationskraften mellan neutronerna som störst, bör också de avdelade kropparnas storlek bli som allra minst längst ut. Längre in, med allt avtagande expansionshastighet och därmed lägre separationskraft, kan allt större kroppar bildas. Därmed fås — i princip — typbilden ovan, högerdelen: många små ytterst, få stora innerst. Se även i Expansionsmatematiken. Vartefter nolldivergenszonen sedan sveper över de avdelade kropparna, uppför de sig som miniatyrer av K-cellen i detonationsfasen. Därmed kan hela systemet successivt fragmentera ner på elementarceller typ galaxer med inre undersystem typ Solsystemet.

Den enkla kvalitativa analysen, ovanstående tre punkter, utpekar att plasmahoparna blir som störst nära centrum men minst till antalet, mindre längst ut men desto flera.

Medeltätheten för hela K-cellen kan på detta sätt i stort sett förstås bevaras.

Om vi ser till den principiella brytningen, initiellt, i K-cellens yta där de allra första mindre, yttre delkropparna börjar avdelas, är vi, tydligen, hänvisade till rena analogier som bygger på de två enda existerande krafterna: expansionen som pressar ut och gravitationen som snöper åt:

Expansionen pressar ut — gravitationen drar in:

vattenrekylen ytspänningen

Nikon D90 · VR 18-105mM · F/3.5-5.6G · 48mM · iso3200 · 1/4000 S - F/9 · OEV - Auto 0.0 · 2009 IV 21 · Tilläggslinser HOYA 1-3

I de jämförande vattendropparnas fall kompenseras den avsnöpande g-kraften av ytspänningskrafter.

MED TYDLIGA ANALOGIER TILL VATTENFYSIKEN (hydrodynamiken, ytspänningen ersätter delvis gravitationen) — många fina fotografier av vattendroppar finns på webben [men ytterst få tillåter att bilderna visas]):

HUR VI ÄN RÄKNAR kan avdelningen av de första (och senare) kropparna från K-cellens huvudkropp ställas på enkla elementära polära vågekvationer (se Polära Koordinater): inåt centrum avtar frekvensen och ökar våglängden, analogt allt större masskroppar med allt lägre expansion.

Expansionen tvingar neutronkallplasmat att samlas i våghopar: expansionen skjuter på utåt och gravitationen drar ihop inåt.

Massvågorna avdelas från K-cellens kropp som separata sfäriska J-kroppar när den (inom hydrodynamiken) motsvarande ytspänningens gränsvärde uppnås i vågtoppen.

Växande våglängd medför större vågmassa:

Våglängden INÅT CENTRUM växer och avtar utåt periferin med K-cellens expansion;

Medelavstånden mellan neutronerna taget för hela K-cellen växer med växande expansion.

Därmed tvingas allt större massor ihop på allt längre massvåglängder, analogt längre in mot centrum.

Kortaste massvåglängden ges via neutronens diameter 2,64 t15 M, och dessa finns principiellt endast längst ut.

MED DE ENKLAST TÄNKBARA VÅGEKVATIONERNAS GILTIGHET — och med vissa analogier till den redan kända vattenfysikens praktik (tack vare många bidragsgivare på webben, och övriga, som visat intresse för att fotografera vattendroppens dynamik som därmed är ytterst väl representerad) — avdelas tydligen J-kropparna efter vissa resonansmönster. Se vidare i JORDENS TREDJE EKVATION (Solsystemets bildning).

Resonansvillkoren förekommer alltså, tydligen, vare sig vi betraktar K-cellens initiella expansion, före de senare divergenständningarna, eller om vi ser till det senare skedet, då de avdelade J-kropparna i sin tur expanderar efter detonationsfasen genom de aktuella divergenständningarna.

Webben innehåller många bilder på vattendroppsuppdelningar från typ vattenkronor och (speciellt) kranöppningar. Webbkällorna (de är många) är emellertid (generellt) ypperligt dåliga på att tala om vad som gäller i användningen/referensen till de ofta mycket fina bilderna — utom exemplet från Adam Hart-Davis som är ett föredöme. Någon direkt beskrivning av webbinnehållet kan därför, tyvärr, inte visas/refereras här. Principen är dock klar och man kan själv, till viss begränsad del, studera verkningssättet genom enkla hemmaexperiment i köket. (Den som vill försöka fotografera ämnet på egen hand får räkna med en första investering [nypris] på i varje fall runt 10-12 000 kr [Februari 2009]).

K-cellens innervägg

Eftersom K-cellens expansion initiellt sker med hög hastighet, se från K-cellens expansion, och därmed K-cellens innervägg redan omedelbart blir föremål för den triggande nollzonens divergenständning, har vi en viss rätt att förvänta oss att dessa områden kommer att utveckla en blandning mellan sammanförda hopar (inbäddade i) och frigjord vätgas. Exakta beräkningsmodeller saknas för närvarande, men som redan påpekats ovan, följer vissa enklare vågfunktioner av grundanalysen, vilket även kommer att behandlas vidare nedan.

Den mellanliggande massan mellan K-cellens yttre och inre massyta här ej utritad.

Den inre K-kärnan är i början av expansionen inte synlig i illustrationens K-cell-skala.

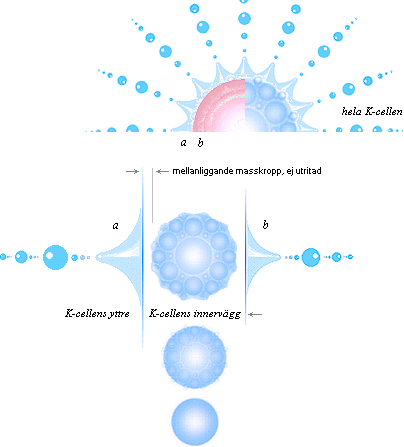
Illustrationen ovan sammanfattar principen. K-cellen avdelar sfäriska masskroppar både utåt och inåt vartefter expansionen fortskrider.

Olika gränsvärden bestämmer massornas storlek och antal i vågfunktionerna.

Intill en viss tid avdelas därför endast vätgas i det inre av K-cellen. Se vidare nedan.

Massavyttringens allmänna enkla Vågfunktion för K-cellens brytning

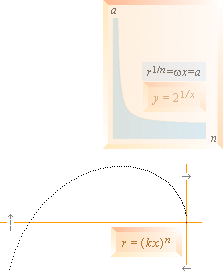
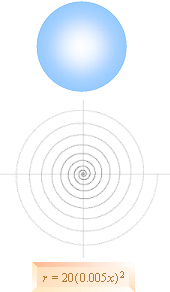
r = R + (a · sin f x)ⁿ

f anger frekvens — vågfunktionsformen ovan är den polärt enklaste

PRINCIPEN för vågbildningen beskrivs ovan. Se från K-CELLENS BRYTNING.

		STORA J-KROPPAR uppvisar samma principiella beteende som hela K-cellen, men med mindre dynamik. Alla kroppar som avdelas från K-cellen (alla J-kroppar) som har egen nolldivergenszon kan också själva avyttra mindre J-kroppar. Beroende på VAR moderkroppen (J) befinner sig — på väg ut från K-centrum, eller in till — samt hur stor dess massa är, sker divergenständningen på olika sätt.
Växande våglängd innesluter växande massa Kortaste våglängden är 2,64 t15 M	På samma sätt avdelas massor inåt.	Större avdelad kropp (J) från K-cellen.
		SCHEMATISKT
POLÄRA KOORDINATER	POLÄRA KOORDINATER

Analogt med fördelningsbilden i Plasmahoparnas fördelning:

Vartefter expansionen fortgår, avdelas J-kroppar (initiellt) med början från periferin via de kortaste våglängderna och sedan längre inåt via växande våglängd med allt större masskroppar.

OVANSTÅENDE DELAR kan sammanfattas med en mera inträngande illustration enligt nedan.

Angivna kvantiteter härrör från resultaten i K-cellens värmefysik.

ATT OBSERVERA SPECIELL för K-cellens expansion — i resultat från K-cellens värmefysik

Den synliga massan som universums materiehopar bildas på är endast 1/355 av den totala som värmebildningen använder. Enorma mängder vätgas bör frigöras initiellt från K-cellens innervägg under expansionen, samt vidare med växande plasmahopar successivt stora mängder stoft (Kiseldamm), sand, grus och mindre silikatblock, samt dito järnblock (Se utförligt från GRUNDÄMNESBILDNINGEN).

r_0c ................ radie 750 ljusår = 7,0955 T18 M · medeltäthet 1,3 t11 KG/KBM

K-cellens innervägg · K-cellens yta vid 209 300 ljusår ®| (20 meter utanför skärmen)

r_cz r_0c

efter 750 år positiv divergens kallplasma

Nollzonen innesluter 68 670 Vintergatsmassor efter 750 års expansion. Beräknat efter K-cellens medeltäthet.

Se även kalkylkortet för K-cellens värmefysik.

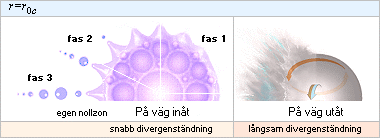
Beroende på J-kroppens massa, samt om den är på väg inåt K-centrum (vilket innebär snabb divergenständning) eller bort ifrån (långsam tändning) finns en stor mängd olika sätt som J-kroppen kan bilda sin slutform på.

ZONSKÄRNINGARNA för de olika delarna av K-cellen — utifrån givna inneslutna massor — och som styr divergenständningarna, är i tider

T_{INTERSECT r0c} = m_K(G/2c₀³) ................................. nollzonen passerar delmassans sfäryta

T_{INTERSECT r0cz} = (8/Ö27)T_{INTERSECT r0c} ................. barriärzonen passerar delmassans sfäryta

v = 2c₀ .............................................. momentana expansionshastigheten då delmassan skärs av nollzonen

Sambanden beskrivs och härleds utförligt i Zonskärningarna.

Vi kan genomföra en matematisk grovanalys utifrån en given medeltäthet för hela K-cellen, fördelat på en bestämd masshop (m_H), för att få en grov uppfattning om medelavståndet mellan masshoparnas tyngdpunkter — som ger en ungefärlig bild av hur långt K-cellen hunnit i ett visst skede i sin inre anhopning av större massor;

n = m_0K/m_H ........................................ antalet masshopar

V = 4pr³/3 ........................................... volymen via aktuell radie

= m_0K/r ........................................... volymen via aktuell medeltäthet

d = (V/n)^1/3 ......................................... kubiska medelavståndet mellan hoparna (H)

= (m_H/r)^1/3

Detta samband är emellertid ännu så länge bara en allmän prövningsform: vi vet strängt taget inget kriterium för vilket expansionstillstånd som innehåller vilken storlek på m_H.

Exempel:

Med m_H=neutronmassan 1,67 t27 KG och tätheten 1,3 t11 KG/KBM (expansionen efter 750 år) blir medelavståndet mellan neutronerna ca 5µM;

Sätter vi istället m_H=Vintergatsmassan_SYNLIGA 2 T41 KG blir värdet nära 1,7 miljoner gånger avståndet (1,495 T11 M) Jorden-Solen — men bara 0,0005 gånger Vintergatans nuvarande radie (ca 50 000 ljusår, 1 ljusår är avrundat 9,46 T15 M). Varje masshop representeras då av en kallplasmasfär med storleken 10 gånger Jorden [r=(3m/4pr)^1/3].

Används resultatet från K-cellens värmefysik (reala medelmassan gånger grovt 350) blir d-värdet 1,75 T18 M, eller ca 185 ljusår.

Sätter vi m_H=1000×Vintergatsmassan_REALA= 6 T44 KG, grovt massan_REALA hos en galaxhop, ges d@3,6 T18 M eller ca 380 ljusår.

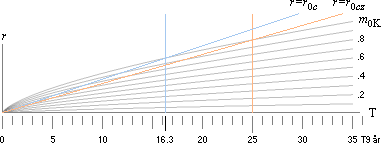
Solsystemets ålder — 20,805 T9 år enligt TNED
Tidpunkten för Solsystemets uppkomst — via galaxernas nuvarande medelavstånd
MELLAN 5-10 MILJONER ÅR TIDIGAST — efter K-cellens detonation

I Resultatredovisning i K-cellens värmefysik med utförliga härledningar i Härledningar visas hur Universums ålder enligt TNED framkommer på värdet 20,81578 T9 år

[20 815 780 000 år]. Med en minuend på max 10 miljoner år, beskrivningen nedan, blir [i vår nutid] Vintergatan och Solsystemet runt 20,805 T9 år gammalt [T för 10^+].

Beskrivning

Enligt gängse uppgifter [BAs324sp2n] är medelavståndet (d) mellan två medelstora galaxer relativt litet, bara runt 150 galaxdiametrar eller ca 3 Mpc (nära 10 miljoner ljusår, eller ca 9,5 T22 M). För att ge galaxbildningen denna marginal, från K-cellens innervägg och inåt mot K-centrum, måste innerväggen (r_0c) minst ha avancerat just till 3 Mpc (eller halva detta värde om vi tar med en sfärisk utsträckning åt bägge hållen). Genom kalkylkortet för K-cellen — eller direkt via t=d/v från v=d/t med d=3Mpc=9,5 T22 M och v=c₀=2,99792458 T8 M/S — finner vi att expansionstiden för r_0c=3Mpc motsvarar ca 10 miljoner år. [K-cellens Plancktemperatur från värmestrålningen är då 29,6 °K]. Först från denna tidpunkt (eller minimum halva) kan vi förlägga fasen för Solsystemets bildning, analogt Solsystemets J-moderkropp och dess högre generationer som kan återföras på en motsvarande Vintergatskropp.
Om den primära J-kropp som så småningom ska bilda Vintergatsmassan puttas inåt mot K-centrum från en större J-kropp precis på innerväggens hastighet, kommer den i stort att befinna sig vilande — samt mycket nära — relativt K-cellens centrum. Därmed garanteras ett optimalt stort värde på den lokala ljushastigheten i den omgivande rymden (i det närmaste lika med toppdivergensen c₀). Att den primärkropp som ska ge Solsystemets delkroppar just befinner sig i en optimal c₀-region är förutsättningen för att också den beräknade gränsmassan (6,80016 T24 KG, se JORDENS ANDRA EKVATION) ska vara giltig, samt det optimala termogravitella jämviktstrycket [se JORDENS FÖRSTA EKVATION] som definierar den termiska jämvikten för gränsmasskroppen. Dvs., toppdivergensen — med försumbar lokalt dominant gravitation från K-cellens totala massa — garanterar en optimal fysikalisk dynamik med avseende på de lokala elektriska och magnetiska krafternas verkan. Lägre divergens sänker dynamiken med kvoten c/c₀. Det var den detaljen som hela den här historien introducerades på. Se även från divergensen c₀. Se även Absoluta metriken.

UNIVERSUMS HISTORIA ref. MPcKOSMOS3.wps

Stjärnhopar och galaxbildningar DEL II

[Se Inledning i DEL I] · Se även separat artikel i GALAXBILDNINGARNA

Vartefter nolldivergenszonen sveper fram över K-cellen med topphastigheten c₀ tänds områdena upp och återinträder med normala elektriska och magnetiska funktioner.

Varje delkropp som på detta sätt divergenständer kommer i stort att uppföra sig som K-cellen vid detonationsögonblicket. Otaliga sätt, kombinationer och möjligheter finns som divergenständningen kan ske på. Ovanstående illustration till höger visar några möjliga skisserade alternativ i sekvens. Se även allmän beskrivning i K-CELLENS BRYTNING.

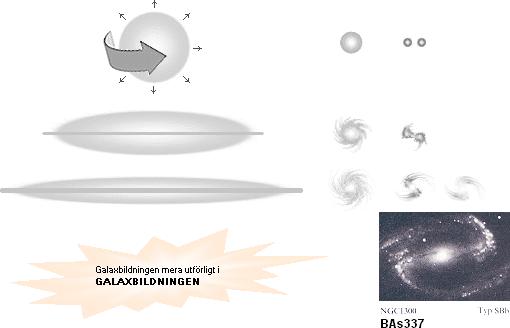
Råplasmakroppen till slutformen är i den senares skala knappast synlig.

Vintergatsmassan ca 2 T41 KG är i sin kallplasmaform ganska precis 10 ggr Jordens storlek.

Färdigbildad (nuvarande) omspänner den en skiva med ca 50 000 ljusårs radie.

I slutformens skala kommer alltså själva bildningen att se ut som en ur tomma intet uppväxande form.

EN MYCKET STOR J-KROPP som har ett utpräglat impulsmoment mvr och som expanderar från sitt maximalt täta materietillstånd, tvingas uppvisa en utpräglad rotationsellipsoid. Skivdisken bevarar alltid i sitt spinnplan en karaktäristisk motsvarighet i exakt matematisk fysik till ett snitt genom en motsvarande g-sfär.

Delkroppar som avges i spinnplanet följer principen för stora J-kroppar medan områdena längre upp mot noderna uppvisar en tendens mot gasexpansioner.

Dubbelkopplande J-kroppar av ovanstående illustrerade typ ger karaktäristiska ”stavgalaxer”, men många andra typer kan också härledas.

OBSERVERA att inte alla (typ) galaxkroppar har ett initierande J-moment mvr. Många har nästan ingen egenrotation alls och framstår därmed — slutligt — som ”klotgalaxer” eller stora stjärnhopar.

Det som bestämmer vilket som är vad kan återföras på följande enkla analogi i K-cellens initierande expansionsfas.

Minsta spridningsvinkelns princip — sammanlänkande delkroppar

GEMENSAMMA EXPANSIONSRIKTNINGEN

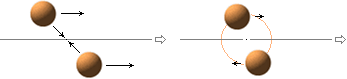
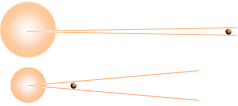
Partiklarna i de inbördes plasmahopar som bildas genom inbördes gravitation kan utbilda vridande moment som följd av hopens sammandragning.

Bilden ovan visar hur två något lägesskilda kroppar med något olika expansionshastigheter kan bilda en nettorotation då gravitationen sammandrar dem.

Vinkelrotationen blir resten av skillnaden mellan expansionshastigheterna.

Som följd av sammandragningarna, men beroende på hur hopen samlas, kan hopar i formen av samlade större individuella sfärer på detta sätt uppvisa större eller mindre (eller inget) axelspinn. Eftersom plasmakropparna tillsammans bildar en supervätska bör den partikulära sfärkroppen också uppvisa (långsamma) ytvirvlar som sammansätter sig med den allmänna rotation kroppen erhållit som följd av sin starka gravitella sammandragning. Endast kroppar som har utbildat ett eget axelspinn har förutsättningar för att bilda de karaktäristiska virvelstrukturerna med grund i rotationsellipsoider.

Se även i

PLASMAHOPARNAS FÖRDELNING I K-CELLEN

Hoparna samlas på gemensam spridningsvinkel (”samma lokal”) med minsta gemensamma expansionshastighet (samma ekvipotentialyta) vilket resulterar i mindre utåt och större inåt.

Därmed kan en i stora drag konstant medeltäthet bibehållas.

Planetsystemens grundformer:

ORIGINALFÖRFATTNING Apr2009 — mera utvecklat Feb2019 i SOLSYSTEMEN I VINTERGATAN

PLANETSYSTEMENS GRUNDFORMER

Initiellt får alla avyttringar från samma moderyta samma spinn

Galaxcellens orientering i K-cellens struktur är uppskattad.

Den undre sekvensen (J-kropparna i högra bilddelen, till vänster om den stora mittkroppen) är starkt komprimerad på en längre tidsmässig utveckling. Principen visar hur kropparna binds till den större centralkroppen och hur rörelseriktningarna fungerar.

Alla kroppar avyttras efter samma grundläggande (hydrodynamiska) princip, IMPULSMOMENTET J=mvr:

En expanderande kropp med J* — så länge den egna massan är stor relativt de avyttrade delmassorna — avdelar växande delar r genom att sänka deras delgivna v (perifera hastigheten) så att J bevaras konstant.

*Här förutsätter vi att ”den expanderande J-kroppen” idealt och initiellt utgörs av HELA Solsystemets samtliga primärkroppar i en deras gemensamma J-sträng, idealt sfärisk med J=mvr. Det är nämligen viktigt att säkerställa att kvantiteten ROTATION i Solkroppens fall INTE obetingat får associeras med själva Solklotet (och heller inte med någon annan av delkropparna) utan snarare en vridning av de omgivande kropparna kring Solkroppen som en slags kullagrad medelpunkt. Denna vridningsmekanism garanteras av moderkroppens rotation (v) där sedan Solsystemets J-sträng (i princip) avrullas på v med J-kropparnas (successiva) avyttring. Beskrivningen är alltså här (något) förenklad.

v-SPRIDNINGENS UPPKOMST I SOLSYSTEMETS OMLOPPSBANOR

J-avrullningen, med samtidig expansionskraft som separerar J-kropparna — och för sin del uppvisar den största expansionshastigheten för de kroppar som befinner sig längst ut, lägre längre in — medför således en SPRIDNING av expansionshastigheten på — sett med Solkroppens medelpunkt som referens — inbördes skilda riktningar. Figuren närmast ovan med de långa inbördes divergenta v-pilarna antyder denna spridning med referens till moderkroppen. Nettoresultatet, med referens till J-systemets tyngdpunkt (Solkroppen) blir att den renodlade v-formens omloppskomponent (t.ex. från motsvarande vektorpilen i mitten) avtar åt bägge hållen så att v-magnituden blir störst för delkropparna närmast Solen och sedan avtar med växande avstånd.

Så är det också i det aktuella fallet med planeterna i Solsystemet: omloppshastigheten är störst för Merkurius (47,9 KM/S), närmast Solen, och minst för Pluto (4,7 KM/S), längst ut.

Vartefter de avdelade J-kropparna expanderar ut från Solkroppen efter avyttringen från J-systemets moderkropp, infångas-bromsas delkropparnas expansion av Solens gravitation tills endast den renodlade v-formens omloppskomponent kvarstår. Därmed har det bildats en ideal förutsättning för en idealt cirkulär omloppsbana kring Solen på utgångshastigheten v rätvinkligt linjen Solen-Planeten. Denna del garanterar att samtliga omloppsbanor blir i det närmaste cirkulära. Med ellipsvinkeln som 90 grader för den helt cirkulära banan är ellipsvinklarna för planetbanorna i det praktiska fallet i tur och ordning [BAs161, excentricitetstalet omräknat till ellipsvinkeln]

Mer 78,1; Ven 89,6; Jor 89,0; Mar 84,6; Jup 87,2; Sat 86,8; Ura 87,3; Nep 89,5; Plu 75,5.

Jämförelsen visar alltså att samtliga planetbanor i det närmaste är eller ligger helt nära cirkulära banformer.

Det blir alltså, hur vi än räknar, expansionskraftens (radiellt) utskjutande vektor som

tillsammans med moderkroppens marginella rotation och de bromsande gravitationskrafterna och därmed en initiellt sammansatt spiralrörelse

bildar grundvalen för de avdelade J-kropparnas slutliga hastighetsvektorer i Solsystemets omloppsbanor.

Se även i SOLSYSTEMETS UPPKOMST med härledningen till den aktuella resonansserien.

Med flykthastigheten v=Ö 2GM/R som den allmänna gränsformen för varje J-systems kroppar, kan vi genomföra en grovräkning för att kontrollera rimligheten i ovanstående marginellt antydda vinkelspridning: den måste vara (ypperligt) liten eftersom expansionshastigheten i K-cellens divergenständningar initiellt genomgående ENLIGT TNED är exceptionellt hög — i Solens fall strax under halva ljushastigheten räknat från kallplasmats maxtäthet

r = 1,82 T17 KG/M³ = M/(4pR³/3) = 3M/4pR³:

R³ = 3M/4pr ;

v = [2GM/(3M/4pr)^1/3]^1/2

= [2GM(4pr/3M)^1/3]^1/2

= [2GM·4^1/3M^–1/3(pr/3)^1/3]^1/2

= [G·2^5/3M^2/3(pr/3)^1/3]^1/2

= [G·(32/3)^1/3M^2/3(pr)^1/3]^1/2

= G^1/2(32/3)^1/6M^1/3(pr)^1/6

= M^1/3G^1/2(32pr/3)^1/6 ; r = 1,82 T17 KG/M³;

= M^1/3(0,0110392 [KG]³M/S) ; Solmassan (M) är grovt 2 T30 KG;

v = 1,39085 T8 M/S

UPPENBARLIGEN ENDAST under den förutsättningen att vinkelspridningen mellan de avdelade J-kropparna är (ypperligt) liten, finns förutsättningar för det praktiska fallets observerade omloppshastigheter, som mest från Merkurius strax under 50 KM/S. Med en överslagsräkning (sinus eller cosinus vilketsom) ges i PREFIXxSIN

(cosa)/(cos 90–a) = (cosa)/(sina) = K = tana = vMER/vFLYKT = (5 T4 M/S)/(1,39085 T8 M/S) = 3,59492 t4 ;

a = atan K = 0,0205973°

Pildivergensen i ovanstående illustration till åskådlig jämförelse är tecknad på 1°. Den mera praktiska sidan av saken lutar alltså åt att vinkelseparationen i Solsystemets fall vid J-kropparnas avyttring är så liten (50 ggr mindre) att den inte ens kan observeras/illustreras direkt med blotta ögat. Detta understryker också det som tidigare vidrördes beträffande den (möjligt) inducerade rotationens magnitud för de primära moderkropparna, att den, i de fall den alls förekommer, bör vara mycket liten.

Resultaten understryker (således, återigen) att fysikbeskrivningen i ljuset av TNED (i stort sett) uppvisar ett redan dukat middagsbord:

— Istället för att störta samman i orimligheter och uppenbara motsägelser, radar allt bara upp sig i varje försök att upptäcka möjliga felkällor.

Det betyder att avgivna kroppar kring moderkärnan uppvisar en spiralstruktur

— med högre v närmare J-kärnan och lägre längre ut.

En mera komplicerad bild gäller generellt eftersom också m avdelas och till slut helt upplöses om J-kroppen initiellt är större än ca 80 Solmassor. I de allmänna fallen blir resultatet hur som helst en eller annan form av efterlämnad spiralstruktur om J-moderkroppen initiellt har någon egenrotation eftersom via denna massavyttringarna (mvr) tvunget ändras med J-kroppens expansion under avyttringsfasen. En separat beskrivning av galaxbildningen ges i GALAXBILDNINGEN.

När den roterande centralkroppen helt upplösts av divergenständningen återstår ett fragmenterat karaktäristiskt virvelmönster — som ett minneskort av hela bildningsprocessen. Centralkroppen finns inte längre, men »minnet» av hur den upplöstes finns kvar. Hur den samlade materien i området sedan beter sig beror på omständigheterna.

Har J periferihastigheten riktad °¯ får en avgiven kropp rotationsriktningen ¯° relativt J-ytan då den frigörs.

Rotationen växer med den avgivna kroppens storlek analogt med avrullningens längre omkrets mot moderkroppen (samma v-form).

Är moderkroppen mycket stor medföljer (i allmänhet) en sträng av mindre småkroppar omedelbart efter en större enligt den princip som återfinns inom hydrodynamiken

— principen kan studeras utomordentligt i uppstudsen från vattendroppen som får träffa vattenytan.

— Den droppe som träffar ytan ger genom rekylverkan en uppstuds som uppvisar den karaktäristiska flerdroppsbildningen.

Alla avyttrade kroppar får samma rotationsriktning

Alla moment J=mvr

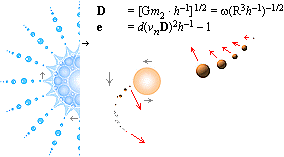
bildas vid avyttringen från moderkroppen (_mJ).

Den centralt tunga kroppen (J_s, stora orangea ovan) i serien av avyttrade delkroppar blir orten för centralkraftsverkan (Keplermomentet K=vd) med de omgivande mindre delkropparna i banformerna

x = (2d[1+e]y – y²[1–e²])^1/2................. CEPH-EKVATIONEN CirkelEllipsParabelHyperbel

Genom J=mvr avtar v med växande r för givet m, impulsmomentets bevarande.

Massan m innefattar då de avdelade J-kropparna (vi måste då se hela avyttringen via en sammanhängande sträng av ännu sinsemellan ej avdelade motsvarande droppar).

Denna del är emellertid relevant endast så länge den avyttrade massan är liten relativt moderkroppens m — som slutligen kommer att upplösas.

Med v som index i riktning vertikalt nedåt (¯) avdelas delkropparna J₁+J₂+J₃+…+J_n med högsta index först (längst ut) i avtagande v¯ med växande r. Se särskilt från v-spridningens uppkomst (Framställningen är delvis förenklad). Deras hastigheter relativt v kan då skrivas (typiskt) v–1, v–2, v–3, …, v–n.

OM J_s är en STOR delkropp relativt övriga n delkroppar, infångas dessa av J_s gravitation.

Banformerna relativt J_s, frånsett de mindre kropparnas inbördes växelverkan och asfäriciteter som följd av inre rotationer, elektriska och magnetiska fenomen, beskrivs genom centralverkan enligt

x = (2d[1+e]y – y²[1–e²])^1/2................. CEPH-EKVATIONEN CirkelEllipsParabelHyperbel

m₂ J_s-massan

h =1M/S²

D = [Gm₂ · h^–1]^1/2 = w(R³h^–1)^–1/2, 2R för slutna banformerna anger största banvidden, w anger vinkelrotationen

e = d(v_nD)²h^–1 – 1

v_n omloppskroppens tangentialhastighet vid d

d avståndet J_s-J_n då v_n är rätvinklig radius vektor

I typexemplet med Solsystemet är (idealt) J_s delkropp Nr 7 räknat från moderkroppen. J_n-kropparnas hastigheter relativt J_s blir då med riktningen v¯ efter växande hastigheter, från lägre till högre enligt

v₆:=v₆–v₇, v₅:=v₅–v₇, v₄:=v₄–v₇, v₃:=v₃–v₇, v₂:=v₂–v₇, v₁:=v₁–v₇, och på andra sidan samma

v_n:=v_n–v₇ som ger negativa hastigheter med riktningen relativt J_s. Delkropparnas rotation kring J_s blir alltså av typen ¯° med moderkroppens v¯ till vänster om J_s-systemet.

I den stela analogin bildar följaktligen J_s en centralkropp kring vilken de mindre delkropparna roterar, och vilket principiella system vi nu redan vet är analogt med Solsystemet.

UNIVERSUMS HISTORIA [ref. MPcKOSMOS_4.wps] GALAXBILDNINGARNA

Galaxbildningarna 2004XI13 — 17

Med vidare beskrivning från K-CELLENS BRYTNING — Se Inledning i Stjärnhopar och Galaxbildningar DEL I

Inledning

För att den följande presentationen ska bli meningsfull, måste det finnas en jämförande referens.

Den ges i särskild del som sammanfattar den konventionella kosmologins indelning av stjärnsamlingarnas olika grupper med deras karaktäristika. Se STJÄRNFORMATIONERNAS INDELNING OCH KARAKTÄRISTIK ENLIGT ETABLERAD KOSMOLOGI.

Relaterad fysik

GALAXBILDNINGARNA

ENLIGT RELATERAD FYSIK

SPIRALKURVANS EKVATION

INDIVID OCH STRUKTURKRITERIET

Vi förutsätter här förtrogenhet med grundbegreppen i DEL I (Stjärnhopar och Galaxbildningar).

ALLMÄNNA MATEMATISKA SAMBAND

Ett föremål som kastas ut med hastigheten v_L från en med marken fast förbunden roterande karusell med rotationen v_P beskriver en rätlinjig bana som definieras av resultanten till komponenterna v_L och v_P enligt v=v_P+iv_L, Fig:1a.

Fig:1

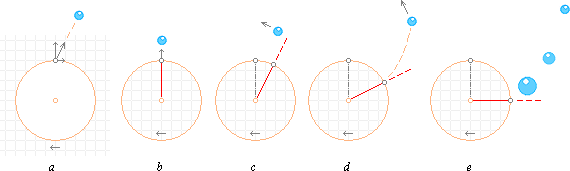
Karusellens gravitella inverkan på föremålet kan betraktas som helt försumbar.

I den g-styrda avyttringen av delkroppar (J) är däremot varje delkropp initiellt starkt g-bunden till moderkroppen via vertikallinjen (L) som J kastas ut på, Fig:1b. Men vartefter J expanderar från centralpunkten, tappar den allt mera av sin g-bindning till L och avviker därmed i växande grad från L, Fig:1c-d.

Expansionen upphör aldrig helt.

Av det allmänna sambandet för expansionshastigheterna följer att J-kropparna längst ut expanderar snabbast.

v = Ö 2Gm₂/r ........................ momentanvärdet v via sfären med radien r som innesluter massan m₂ ; samma som flykthastigheten

Med r=r₀+s, s den reala expansionen, innehar alltid den störst omslutande massan m den högsta expansionshastigheten. Dvs., v avtar med avtagande omslutande massfär förutsatt att expansionsenergin (g-energin) är ekvivalent med rörelseenergin, att medeltätheten bevaras, och vilka villkor just utgör det ideala fallet i expansionsmatematiken.

Resultatet totalt av den successiva avyttringen med mindre delkroppar längst ut och större längre in kan därmed generellt sammanfattas på en spiralkurva, antydd i Fig:1e, samt i Fig:1f nedan.

Fig:1f

w®0

Betrakta funktionen r^1/n=wx=a För ett givet bestämt avstånd (r) mellan moderkroppen (J0) med massan m=f(n) och den avyttrade delkroppen (J) utmed lodlinjen (L) finns en bestämd vinkel (a) vid en bestämd tidpunkt (t=x) om J0 har någon vinkelrotation (w=2p/T0) skild från noll. a/2p=t/T0=A/360 ; a=(2p/T0)t=wt ; t=x Då n®¥ går a mot ett gränsvärde större än 0 som bestäms av vinkelrotationen w vilken bestämmer magnituden för moderkroppens rotation. Endast om w är noll är också a noll. Funktionen för r blir då ekvivalent spiralfunktionen r=(wx)^n

Spiralkurvans Ekvation

SPIRALKURVANS EKVATION — r=(kx)ⁿ

Större modermassa med egen divergenszon innebär idealt kraftigare expansion och därmed högre expansionshastigheter, analogt större rörelseenergier.

Större vinkelrotation hos modermassan motsvarar växande vinkelkoefficient k i faktorn kx med x som rotationsvinkeln.

Eftersom utslagsvinkeln x mellan givet r och avyttringslodlinjen (L) för en givet avyttrad delkropp J (Fig:1c) blir allt mindre med växande expansionshastighet, analogt avtar med växande modermassa (n), kan alltså den större modermassan relateras till en större faktor n och därmed en allt mera utdragen spiralkurva enligt polärfunktionen r=(kx)ⁿ.

Rotationen och initialmassan är de enda två primära faktorer som styr formbildningen. Vi frånser då växelverkan mellan närliggande delkroppar.

I mera exakta beräkningar måste vi ta hänsyn till att moderkroppens vinkelrotation (w) avtar via impulsmomentets växande r-faktor under expansionen, mvr=mwr². Moderkroppens centralmassa m avtar naturligtvis också, vilket reducerar w-reduktionen. Det finns emellertid en stor mängd olika möjligheter för hur dessa kombinationer kan förlöpa. I grundformen kan vi på enklaste sättet betrakta moderkroppens massa som konstant tillsammans med en begränsad avdelad sträng av J-kroppar, där också vinkelrotationen (för tillfället) kan betraktas konstant. Om avyttringarna sker i perioder, både kan och inte kan modermassan få en lägre initiell vinkelrotation för varje ny utputtningssekvens, beroende på hur stora massor som avyttrades i föregående och aktuell vinkelrotation. Dvs., om till exempel mr² varierar exakt omvänt proportionellt (under någon period) konserveras w eftersom J=mvr är konstant. Det finns alltså inga generella formgrepp att ta här: många skilda former är möjliga.

Kriteriet för strukturernas bevarande

STRUKTURKRITERIET

Under de ideala förutsättningar som bevarar ekvivalensen mellan gravitationsenergin och rörelseenergin ENLIGT EXPANSIONSMATEMATIKEN med bibehållen medeltäthet, bildar spiralkurvorna enligt SPIRALKURVANS EKVATION motsvarigheten till de helt räta radiella expansionslinjerna som är aktuella för en expanderande moderkropp (J₀) som helt saknar egenrotation.

Med dessa ideala förutsättningar konserveras alltså de radiella expansionsriktningarna — såväl som de spiralkurverade — på sin moderkropps g-energi. Härav följer att

hela expansionsformens struktur bevaras på just expansionskurvorna — vare sig dessa är av det ena eller det andra slaget. Med andra ord:

Kriteriet för strukturernas bevarande

INDIVID OCH STRUKTURKRITERIET

det är ur energisynpunkt, och förutsatt ovanstående villkor beaktade, omöjligt att utplåna moderkroppens bildningsstruktur, vare sig denna gestaltar den ena eller den andra formen: alla bildningsformer garanteras en egen bevarad form och strukturidentitet under hela deras levnad — oberoende av komplexitet

Strukturkriteriet är alltså ren expansionsmatematik: obegränsad utvidgning — i garanti från ekvivalensen mellan kinetisk och gravitell energi som återfaller på tillståndsekvationen via (m®g) — grundad på evig kontraktion [Se TILLSTÅNDSEKVATIONEN]. Exempel på analogier: En boll studsar aldrig högre än kraften som inläggs i ihoppressningen. En kropp utvecklar aldrig större energi än den på vilken kroppen erhållit sin form. Helt självklara saker, tycker vi — när kunskapsdörren väl en gång öppnats. Jämför även från K-CELLENS DETONATION, Atomkärnans formbevarande kraft.

Strukturexempel från BONNIERS ASTRONOMI s332-333 Fig.16.10 · Hale Observatories USA · Spiralgalaxer ordnade efter växande armöppningar.

”Observera att den centrala ansvällningens storlek avtar från vänster till höger.”

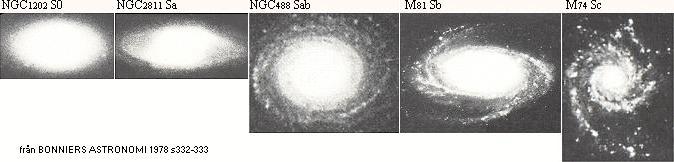
Beteckningen typ NGC1202 är namnbeteckning. Beteckningen typ S förklaras utförligt i

STJÄRNFORMATIONERNAS INDELNING OCH KARAKTÄRISTIK ENLIGT ETABLERAD KOSMOLOGI.

Vartefter expansionen fortskrider och de avyttrade delkropparna utvecklar sina interna divergenständningar, bevaras de ursprungliga moderkropparnas tyngdpunkter — analogt de successivt avdelade J-kropparnas ursprung enligt kriteriet för strukturernas bevarande — medan strukturen totalt sett sprids ut över allt större områden på allt fler delmassor. Struktur och form bevaras därmed med den ytterligare ingrediensen att gestalterna endast blir mäktigare och rikare på detaljer — samtidigt som varje central modermassa upplöses och hela systemet antar en mera komplex matematisk fysik. Alla spår av ”ursprungliga tyngdpunkter” blir effektivt igensopade (för alla som inte känner hela hemligheten). Endast strukturen, formen eller gestalten framträder.

Genom den vidare expansionen med den åtföljande GRUNDÄMNESBILDNINGEN förgrenar sig strukturkriteriet än djupare och vidare med slutpunkt i de olika materialen (kristallerna, molekylerna) och organismerna — vilkas formgestalt efter viss evolutionär tid TYDLIGEN omsluter tänkande och förnimmande varelser. Utvecklingen av samhällen, kulturer och civilisationer utgör — följaktligen, tydligtvis — en fortsättning.

Därmed bör vi inte (längre) fundera över frågan varför den traditionella kosmologin står handfallen inför gåtan om de kosmiska strukturernas bevarande — speciellt spiralstrukturerna har tilldragit sig särskilt intresse och meningsutrymme, se vidare citat i STJÄRNFORMATIONERNAS INDELNING OCH KARAKTÄRISTIK ENLIGT ETABLERAD KOSMOLOGI. Man har nämligen utgått ifrån fel föreställning: strukturernas bildande utifrån och inåt. Inte inifrån och utåt. Man känner inte till någon expansionsfaktor, den som hela historien hänger på — därför att man aldrig har brytt sig om att se saken från den utgångspunkten. Se även i HIMLAKROPPARNAS ALLMÄNNA EXPANSIONSFYSIK.

Fig:2

a	b

Olika kombinationer ger olika slutprodukter från den initiella expansionsfasen. Ytterligare förändringar tillkommer med undernivåernas expansioner.

Genom att många olika kombinationer (kn) är möjliga, finns knappast två identiska slutformer eftersom varje delform (galax) under expansionen också i exakt mening betingas av sin växelverkan med närliggande kroppar. Nedanstående illustration i två dimensioner visar ett ringa urval av möjliga svängningsformer som moderkroppen kan anta — föregående avyttringarna och beroende på omständigheter. Alla formerna beskrivs i grunden av polärfunktionen r=R+(A[sinax]+B[Csinnx])^2,5 som kan varieras på ett otal sätt.

Fig:3

För att kontrollera exakta slutformer måste omfattande beräkningar genomföras med hänsyn till samtliga ingående masspunkter. Knappast med andra medel kan man erhålla svaret på frågan hur en viss formstruktur utvecklas. Här ska endast grunddragen från den primära avyttringen genomgås då grundstrukturerna och deras parametrar redan står klara.

GASDISTRIBUTIONEN MELLAN DELKROPPARNA

Under alla förhållanden frigörs stora mängder vätgas ur kallplasmat från delkropparnas ytor under divergenständningen.

Formsystem (galaxer) som slutar på typen i Fig:2a (klotgalaxer) kan lättare ta upp mellanliggande gas än typen i Fig:2b (spiralgalaxer).

Fig:4

Stora sfäroida delkroppssystem med inbördes (cirkulära) likformiga rörelser kan lätt ta upp mellanliggande gas och förena denna med den egna (stjärn-) kroppen.

System med delkropparna utdragna i strängar eller spiralarmar saknar den möjligheten. Här är gasen anvisad att kvarstanna i strängen av dess sammanlänkande delkroppars g-krafter. På detta sätt växer strukturen, och gasmängden, med spiralarmarnas mera utsträckta form.

Den utdragna spiralarmen binder gasmassorna i den underliggande kroppssträngen, mera utpräglat ju mera utdragen armen är; Ju snävare spiralarmarna ligger desto mera exponeras gasen för en mera sfäriskt eller ellipsoidiskt homogen form av delkroppar vars rotationer i tidens längd lätt samlar upp den mellanliggande gasen.

Gasinnehållet bör alltså växa med växande spiralarmsöppningar.

Därmed framstår typen i Fig:2a (motsvarande ovan vänster) som en galax med ringa gasinnehåll, medan typen i Fig:2b (motsvarande ovan höger) blir en utpräglad gasiskt bestyckad galaxform.

OM spiralarmarnas grad av öppenhet förutom stor modermassa (stort n) också avspeglar hög initiell egenrotation [stora kn i r=(kx)ⁿ], följer härav också en motsvarande stark avplattning med skivbildning i slutformen.

Fig:5

Ju större avplattningen blir, desto mera förskjuts gravitationens maximum för hela formen till skivplanet, bort från galaxnoderna; under expansionsfasen kan moderkroppen släppa ifrån sig allt mera massa i rotationsaxelns riktning där gravitationskraften blir som lägst.

För att få fram den erforderliga separationskraft som kan bilda den utdragna spiralen bör alltså moderkropparna till avplattade slutformer vara särskilt stora.

Spiralgalaxer med ungefär samma avplattning (och ungefärligen lika spiralöppningar) bör följaktligen ha i stora drag ungefär likartad modermassa och därmed likartad slutmassa.

Moderkroppar med stor initiell rotation men mindre massa och därmed låg separationskraft, bör uppvisa utpräglade ellipsoidiska slutformer utan spiralstruktur, dvs., med ringa gasinnehåll.

Fig:6

Dessa initiellt högroterande kroppar bör under expansionen behålla (betydligt) mera massa än spiraltypen därmed att avyttringskraften i modermassan är initiellt mindre varigenom g-kraften får ett optimalt samlat centrum.

Massorna för klottypen bör alltså kunna variera i betydligt större omfattning än massorna för spiraltypen där förhållandet mellan rotation och initialmassa är mera känsligt för att få fram just spiralstrukturen (eller den karaktäristiska sinusformade avplattningen).

ALLMÄN KLASSIFIKATION

Genom ovanstående genomgång kan följande typformer särskiljas med hänsyn till initiell rotation och massa.

REGELBUNDNA SLUTFORMER

Fig:7

a	b	c	d
Liten J-rotation, stor J-massa Ringa gasinnehåll	Högre J-rotation, mindre J-massa Litet eller ringa gasinnehåll	Hög J-rotation, liten J-massa Litet eller inget gasinnehåll	Hög J-rotation, stor J-massa Stort gasinnehåll
Gasen samlas på mobila massor	Gasen samlas på mobila massor	Gasen samlas på mobila massor	Gasen kvarhålls av armarna
klotformig	elliptisk	linsformad	spiral

De regelbundna slutformerna blir naturligt de expansionssystem som i stort sett har fått utvecklas utan större inverkan från närliggande liknande initialmassor.

OBSERVERA ATT formen expanderar under hela sin utveckling — enligt J-kropparnas allmänna primära utvidgning från kallplasmatillståndet från K-cellens detonation och vidare via EXPANSIONSMATEMATIKEN. Först initiellt snabbt, sedan med avtagande magnitud.

I den matematiska grundformen frånser vi effektförlusterna (täthetsändringar med bildning av värme och ljus) som reducerar expansionen. Men då dessa delar i stort är marginella kan vi i den grova översikten idealisera formerna på den ideala ekvivalensen mellan kinetisk och gravitell energi (som i princip innebär att formerna kommer att expandera i evighet).

Expansionstiden följer därmed på vanligt sätt

T = 2Ö(3/8pGr) .................... = Ö(3/2pGr) ......................... expansionstiden ur medeltätheten

r = 3/(2pGT²) ........................................................................ medeltätheten ur expansionstiden

Dessa exakta samband inbegriper emellertid HELA den ursprungliga primära J-modermassan — inkluderat de delar av den som i tidens längd alltmer försvinner från den centrala alltmer samlade slutformen. Den uppskattade nuvarande formmassan för en viss galax kan alltså inte direkt användas i ovanstående samband — med mer än man känner yttergränserna för kroppens totala expansion. Volymen av den sfär som omskriver Vintergatan (R=50 000 ljusår cirka) ger med den synliga massan 2,78 T41 KG medeltätheten 6,27 t22 KG/KBM, vilket skulle ge en expansionstid på blott 0,1 miljarder år. Expansionsvärdets idealt reala medeltäthet bör alltså vara betydligt lägre.

Vi känner nu emellertid hela K-cellens allmänna matematiska fysik från K-CELLENS VÄRMEFYSIK och vet att delkropparnas lokala utveckling beror av den lokala divergensen c och därmed av avståndet från detonationscentrum c₀. Därmed kan vi också beräkna motsvarande reala expansioner (Vintergatans nuvarande reala expansionssfär blir runt sagt minst 20 gånger den skivdisken omskrivna). Sett från områden där toppdivergensen råder finner man alltså allt yngre system ju längre ut mot K-cellens rand man ser.

Då det emellertid krävs minst flera (många) miljarder år för det organiska livet att byggas upp på, har det redan hunnit gå långa tider innan människan av princip kan börja studera himmelsobjekten. Med hänsyn till dessa tidrymder bör skillnaden mellan olika system, alltså galaxer sedda på olika avstånd, vara mindre märkbar: De ser alla i stort sett likadana ut — oberoende av inbördes avstånd.

OREGELBUNDNA SLUTFORMER

De expansionssystem som utvecklas genom nämnvärd ömsesidig växelverkan bör i slutformen bli utpräglat oregelbundna.

Sådana formsystem bör analogt uppvisa en allt mindre ordnad rörelseform i proportion till graden av växande växelverkan.

BONNIERS ASTRONOMI 1978 s325 Fig.16.5 Yerkes Observatory USA · NGC4449

Där rörelsen är minimal och strukturen oregelbunden, har den mellanliggande gasen heller ingen större möjlighet att samlas upp av omgivande (stjärn-) kroppar.

De oregelbundna massystemen bör därmed över avsevärt längre tider bevara en stor andel av den initiellt bildade vätgasen från kroppsytorna i divergenständningarna.

Följande allmänna observationer till jämförande bekräftelser. Fetstilen är min markering.

De klotformiga materiehoparna eller klotgalaxerna benämns allmänt som elliptiska galaxer.

”Med tanke på att galaxernas ålder ligger kring ca 10¹⁰ år, borde man ju kunna förvänta sig att alla galaxer skulle innehålla stora mängder gas och stoft, men detta gäller i allmänhet inte för de elliptiska galaxerna.”

”Det är i regel bara i kärnorna hos en del elliptiska galaxer man finner spår av gas, och inte heller där står denna för mer än några tiondels procent av massan.”

BONNIERS ASTRONOMI 1978 s331sp2n

”Den stora skillnaden mellan spiralgalaxer och elliptiska galaxer finner vi när vi studerar objekt tillhörande population I (unga stjärnor, gas och stoft). I de elliptiska galaxerna saknas dessa utanför själva kärnan, men de framträder i form av en skiva med en del gas och stoft i Sa‑galaxerna och blir allt mer framträdande i galaxer av typ Sb och Sc, för att slutligen helt dominera Sd‑galaxerna. Den bråkdel av galaxens massa som utgörs av neutralt interstellärt väte ökar från ca 2 % i typ Sa till ca 15 % i de öppna Sd‑galaxerna (fig. 16.19). En annan olikhet är att spiralgalaxerna är mycket blåare än de elliptiska — medan de sistnämnda normalt har ett B–V‑färgindex kring 0,9, ligger värdet för typ Sc mellan 0,5 och 0,6. Denna färgskillnad beror på förekomsten av unga stjärnor med stor massa i spiralgalaxerna. Genomsnittsantalet sådana stjärnor med åtföljande H⁺‑regioner ökar med stigningsvinkeln; Sa‑galaxerna har bara några få H⁺‑regioner, medan galaxer av typ Sc och Sd är fyllda av dem. Detta leder till två viktiga slutsatser. För det första omvittnar det att där det finns mycket gas, där bildas det också många nya stjärnor. För det andra visar det att den relativa betydelsen av population I i spiralgalaxerna är direkt korrelerad med spiraltypen (fig. 16.10 och 16.11). Detta är ett ytterligt viktigt resultat, eftersom det visar att spiralmönstren inte är slumpbetingade, utan måste ha ett fundamentalt samband med övriga egenskaper hos spiralgalaxerna.”

BONNIERS ASTRONOMI 1978 s332sp2

FORM- OCH GAS-OBSERVATIONERNA är alltså i stort analoga med de allmänna resultat man kan sluta sig till ur J-kropparnas sekundära avyttringar.

BETRÄFFANDE DEN KONVENTIONELLA KOSMOLOGINS GALAXBILDNINGSTEORI är det värre med bidragande citat [BAs309sp1ö Vintergatans uppkomst, s343sp2ö Protogalaxernas uppkomst]. Se även i Diskussion nedan.

Om man enbart får utgå ifrån föreställningar om stoft och gas — med i stort sett ett totalt samlat impulsmoment noll — för att därur söka en — främst — spiralgalaxbildningsteori, är det klart att den uppgiften i ljuset av ovanstående är och förblir en ren omöjlighet. Det finns ingen som helst beröringspunkt med J-kropparnas allmänna massavyttringar. Det finns heller ingen förutsättning för att kunna förklara strukturernas bevarande över extremt långa tidrymder — det är bara en matematisk expansionsfysik som kan hantera den uppgiften.

Man föreställer sig att virveln bildas ur gas och stoft som dras ihop av gravitationen »från en magisk punkt» likt vattenvirveln som bildas i diskhon när proppen dras ur. En sådan virvelteori går alldeles utmärkt att realisera när det redan finns ett omgivande starkt tyngdkraftsfält — och en strömningsöppning — med bestämd riktning. I tomma rymdens moderna kosmologi däremot finns ingen sådan komponent. Källan ovan [BAs343sp1m] säger det också rakt ut: man vet inte svaret på den intrikata frågan om hur galaxerna bildades. Man kan bara observera resultatet.

Diskussion — olika källverk belyser olika svårigheter, TNED förklarar

— Vad det är som hindrar spiralbildningen hos de elliptiska och oregelbundna galaxerna? [FMs631sp2].

— Deras initialmassor och egenrotationer är för små.

De elliptiska galaxformerna har ingen förutsättning för att kunna putta iväg de avdelade delkropparna med tillräcklig kraft på grund av den mindre J-massan som betyder en svagare separeringskraft mellan de avdelade delkropparna. Endast stora J-massor har en sådan potential, förutsatt tillräcklig rotation. Är initialrotationen för liten, slutar kroppen som en elliptisk galax.

Oregelbundna galaxer kan bildas som resultat av delkroppar som avyttras mellan en eller flera större moderkroppar — eller generellt som följd av områden med långsamma divergenständningar (som fragmenterar ner moderkroppens impulsmoment på nivån frigjord vätgas). Totala impulsmomenten i sådana (kolliderande) mellanstråk blir idealt noll och därmed är förutsättningen för en samlad rotationsordning utraderad.

Elliptiska eller andra typer är alltså redan avgjort i och med J-kroppens initiella avdelning: massa och egenrotation.

Det är också därför man finner spiralgalaxerna företrädesvis i utkanterna på galaxhoparna, inte i centrum. Största delkropparna avges längst ut, se MASSAVYTTRINGENS ALLMÄNNA VÅGFUNKTION.

Spiralgalaxernas slutmassa ligger runt grovt T11 Solmassor. En stor del av deras initialmassa försvinner ut, upp över galaxpolerna vid divergenständningen och efterlämnar bara själva diskformen. Den lägre centrifugalkraften vid polerna gynnar avyttrade J-kroppar att bilda samlade hopar (klotformiga stjärnhopar) varav en del i slutänden kan kvarhållas av galaxens samlade g-kraft. Dessa klothopar »parkerar» i stort på godtyckliga ställen inom galaxens omskrivna sfär. (De inbördes avyttrade J-individerna i en sådan klothop får därmed en proportionsvis lägre möjlig primär egenrotation och ansluter därmed till motsvarande matematik som tidigare beskrivits för klotformiga eller elliptiska galaxtyper). Ellipsgalaxerna å andra sidan har mindre initialmassa och behåller i gengäld mera av den därmed att deras initiella separationskraft på de avyttrade delkropparna är lägre. Därmed kan också deras slutmassa variera inom betydligt större områden: dvärgarna på runt T5 Solmassor till överjättarna runt T13 Solmassor.

— Men vad säger dig att spiralstrukturen, sådan den här framkommer genom delkropparnas avyttring, är något som består och är den verkliga förklaringen till spiralformen?

— Studera STRUKTURKRITERIET.

— Ingenting annat än resultatet av utputtningen enligt det enkla sambandet i SPIRALKURVANS EKVATION — r=(kx)ⁿ; funktionen är expanderande med bevarad ekvivalens mellan rörelseenergin och gravitationsenergin. Det är inte bara spiralstrukturen som bevaras: alla kroppsstrukturer bevaras. J-kroppen slutar (idealt) aldrig riktigt att expandera om än takten sker allt långsammare. Betrakta för omväxlings skull omvändningen: Hur gör du för att utplåna den givna strukturen? Visa.

Expansionen som initieras av J-kroppen under divergenständningen, avstannar aldrig helt. Detta gäller även för kroppar som Jorden och Solen. De fortsätter att expandera, men i allt mindre omfattning. Denna expansionskomponent finns inte med i den traditionella kosmologin eftersom man där har en helt annan uppfattning om hur stjärnhopsbildningarna gått till. Nämligen utifrån och in — inte inifrån och ut. Se även i HIMLAKROPPARNAS ALLMÄNNA EXPANSIONSFYSIK.

— Varför visar galaxer av typen E (elliptiska) och S0 (linsformade) en större tendens än spiralgalaxer att samlas i hopar? [EST-7s536sp2mn].

— Därför att spiralgalaxernas J-massa är större än typen E och S0 och därmed — i referens till en moderkropp som kan inhysa alla galaxtyper tillsammans — kan relateras till moderkroppens yttre delar [Jämför MASSAVYTTRINGENS ALLMÄNNA VÅGFUNKTION]. Då dessa yttre delar också besitter en högre expansionshastighet än mera centralt liggande delar blir skillnaden mellan central (E och S0) och perifer anhopning (S) naturlig. Därmed, beroende på moderkroppens initiella J-massa, samlas naturligt typen E och S0 längre in, alltså i hopar, medan spiraltypen antingen fördelas på hela hopens periferi, eller drar iväg (i mindre grupper) långt utanför hopen, eller inte förekommer alls om modermassan är av typen mindre (massvåglängden räcker då inte till för att avdela S-typens delkroppar).

UNIVERSUMS HISTORIA [ref. MPcKOSMOS_4.wps] GALAXBILDNINGARNA

Galaxbildningen enligt konventionen

STJÄRNFORMATIONERNAS INDELNING OCH KARAKTÄRISTIK ENLIGT ETABLERAD KOSMOLOGI

Följande allmänna uppgifter är till jämförelse.

Uppgifterna är hämtade från BONNIERS ASTRONOMI 1978 Det internationella standardverket om universum sammanställt vid universitetet i Cambridge, synkoperat [BA] i denna skrift med sidangivelser.

Allmänna begrepp

Solmassan 1,989 T30 KG [BAs9]. Utom konventionen används här förenklingen T för 10⁺, t för 10^–.

Ljusår 9,46073 T15 M (3600S×24×365,25×2,99792458 T8 M/S), förkortas här lå.

Parsec förkortas pc, lika med 3,0856 T16 M [BAs9], lika med 3,2614819 ljusår.

Galax, stor (flera miljarder) ansamling av stjärnor [BAreg].

Kvasar, stjärnliknande objekt med hög rödförskjutning [BAreg].

Galaxerna indelas i olika typer: elliptiska (E), spiral (S), linsformade (SO [EST-7s535sp2], S0 [BAs335sp2mö]), samt oregelbundna galaxer (Irr).

De mest ljusstarka galaxerna är vanligen av typen elliptiska [EST-7s535sp2].

Generell spridning och förekomst: ”For reasons which are unknown, there is a tendency for E and SO galaxies to be concentrated in large clusters more strongly than spirals.”, [EST-7s536sp2mn].

Generella storlekar: 2 till 50 Kpc (6500 till 165 000 lå) [BAs324sp2ö].

Medelavstånd: ca 3 Mpc (150 galaxdiametrar) [BAs324sp2n].

Spiralgalaxernas rotationsriktning: anges inte explicit i källorna [BA][EST][ENCARTA 99-]. Det finns dock en ritning i [BAs310] med vidare i anslutning till beskrivningen av Vintergatan som antyder att rotationsriktningen är analog med den för en luft- eller vattenvirvel, alltså utifrån och in med armarna släpande. Källan FOCUS MATERIEN 1975 [FM] beskriver dock problemet på ett utomordentligt sammanfattande sätt som här ges i särskilt citat. Fetstilen är min markering.

”En intressant fråga är hur spiralstrukturen hos galaxerna uppstår, men den är mycket svårlöst eftersom de olika teorierna inte i någon större utsträckning kan kontrolleras med hjälp av observationsresultat. Att galaxernas rotation har en avgörande betydelse får anses stå över varje tvivel, men det finns många andra faktorer att ta med i beräkningen. Till dessa hör det mystiska kraftfält, som man fått uppmärksamheten på i samband med studiet av den interstellära polarisationen (se ovan). Man kan föreställa sig ett rätt stort antal rimliga kombinationer av olika kraft‑ och rörelsefält i en galax som är i stånd att framkalla spiralstruktur av samma typ som den observerade. Det betyder att man måste veta mycket mer om spiralerna än enbart hur de ser ut, innan man kan tala om hur de har uppstått. När det gäller t.ex. rotationsriktningen är det mest troliga att galaxerna roterar med armarna släpande efter. Kunde man alltså genom observation fastlägga att samtliga galaxer roterar i den ena eller den andra riktningen, kunde antalet tänkbara teorier reduceras.

Även när det gäller spiralarmarnas uppbyggnad finns det många obesvarade frågor. Är stjärntätheten t.ex. större i armarna än i mellanrummen mellan dem, eller är det bara det interstellära lysande vätet och de ljusstarka, nybildade stjärnorna som definierar dem? Är det kanske rentav så, att såväl gas som stjärntätheten är densamma över hela galaxen, medan det mörka stoftet ligger arrangerat i ett bestämt mönster som definierar mellanrummen mellan spiralerna så att armarna själva är enbart skenbildningar?

Dessa exempel kan illustrera svårigheterna att komma tillrätta med problemet om Vintergatans och de andra galaxernas rotation och spiralstruktur. Beträffande det senare har man även att kämpa med omvändningsproblemet, nämligen vad det är som hindrar spiralbildningen hos de elliptiska och oregelbundna galaxerna.”

FOCUS MATERIEN 1975 frn.s631sp1n

Grundämnen: halten av tyngre grundämnen växer in mot galaxernas centrum [BAs326sp1mn].

Beskrivning

— sammanställning av gängse allmänna kosmologiska data (grundbegrepp)

Elliptiska galaxer [BAs331]. Beteckning: En. Klassifikation: lillaxel a storaxel b. Samband: a/b=1–n/10, n=10(b–a)/b. Faktorn n anger ovaliteten eller sfäroidens observerade tillplattning. Största tillplattningen anges E7 (a/b=0,3). n=0 anger sfärisk form, E0.

Massa: T5 Solmassor (dvärgar) till T13 Solmassor (sällsynta jättegalaxer [BAs324sp2m]) [BA s331sp1n, s335sp2m], huvudparten runt T11 Solmassor [BAs331sp2ö].

Förekomst: företrädesvis i (centrum av) galaxhopar [EST-7s535sp2] [BAs351sp1m].

Storlek: ca 5 Kpc radie (16 000 lå) [BAs340sp1ö]. Tusental till flera hundra tusental ljusår [EST-7s535sp2].

Rotation: ”perfekt rotationssymmetri” [FMs630sp2mn]. Diagram på bildsida [BAs339] anger i stort en rotationssymmetri på 100 KM/S i utkanten (±45 bågsekunder) för ett uppmätt objekt (NGC4697).

Gasinnehåll: mycket liten gas eller stoftmassa [BAs340sp1ö] — men en förmodat stor mängd osynligt material [BA s331sp2m, s339sp1n].

Struktur: sfäroidisk lysande anhopning, i övrigt ingen [BAs332sp1ö].

Linsformade galaxer [BAs335sp2ö]. Beteckning: S0 [SO EST-7s535sp2]. Klassifikation: övergångsklass [EST-7s535sp2], ingen särskilt angiven.

Massa: ingen särskild uppgift (gränsfall mellan typen E och S).

Förekomst: ingen särskild uppgift (gränsfall mellan typen E och S).

Storlek: ”bland de allra plattaste stjärnsystem som man känner till finns många linsformade galaxer”, [BAs335sp2m], i övrigt ingen uppgift. Se vidare i struktur nedan.

Rotation: ”perfekt rotationssymmetri” [FMs630sp2mn].

Gasinnehåll: ringa eller inget (mindre än typen E) [BAs335sp2ö].

Struktur: ”has a disc superimposed on an otherwise elliptical type of light distribution”, [EST-7s535sp2n]. ”mycket lika Sa-typen”, [BAs335sp2mö].

Spiralgalaxer [BAs332]. Beteckning: S (spiral) eller SB (barred spirals, stavspiraler) [EST-7s535sp1n]. Klassifikation: Beteckningarna S(B) kompletteras med tilläggsbeteckningar a-d i stigningsvinklar — i steg om 5° för spiralarmarnas avtagande snävhet, analogt mera markant spiralform [BAs332sp1mn]. Tillägget ”a” anger en stigningsvinkel på ca 10°, ”b” ca 15°, ”c” ca 20° och ”d” ca 25°. Ännu mera öppna spiraler betecknas Sm. Vintergatan klassificeras som typen Sb.

Massa: nästan alla typiskt T10 till T11 Solmassor [BAs335sp2m].

Förekomst: (uteslutande) i periferin av galaxhopar [BAs356sp2m].

Storlek: Typiskt R=50 000 ljusår i radie [EST-7s535sp1n], skivans tjocklek ca 1000 ljusår, centrala ansvällningen har olika grader av täthet med växande in mot centrum och kan variera beroende på typ (Vintergatan ca R/7 ovan skivplanet [FMs632], men det beror på hur man betraktar täthetsaspekten). Spiralgalaxerna omger sig med en stor och vid s.k. halo (mer eller mindre sfäriskt format diffust område) av vad man kallar gamla stjärnor (den s.k. population II), halons omfattning i stort som hela galaxens utsträckning [BAs313sp1ö].

Rotation: typiskt 100 KM/S i kärnan (1Kpc, ca 3,25 T3 lå) [BAs340sp2mö] som uppvisar fast rotation. Hastighetens ökning med radien når maximum vid ca 3-8 Kpc (ca 10-25 T3 lå), därefter avtar hastigheten utåt. ENCARTA 99 (Galaxy, Rotation of Spiral Galaxies) menar — med vidare tung argumentering — att HELA spiralgalaxen roterar med växande hastighet utåt. Referensen [EST 1992] intar en mellanställning [EST-7s536sp1m]: ”Usually, the inner regions of a galaxy undergo solid body rotation (velocity proportional to radius), while the outer regions rotate differentially (velocity constant).”. Uppgifterna från de tre olika källorna är alltså inte särskilt samstämmiga — utom beträffande galaxens centrum. Om man gör vissa idealiseringar och frånser vissa smärre olikheter, kan de tre olika källorna jämkas ihop, men med en tämligen oprecis beskrivning som resultat.

Gasinnehåll: proportionellt mot växande spiralöppning [BAs332sp2n].

Struktur: växande med växande spiralöppning.

Oregelbundna galaxer [BAs335sp2n]. Beteckning: Irr [EST-7s535sp2n]. Klassifikation: ingen särskilt angiven.

Massa: typvärde ca T10 Solmassor [BAs335sp2n].

Förekomst: ingen särskild uppgift.

Storlek: ingen särskild uppgift (varierande). Se vidare massuppgiften ovan.

Rotation: ingen uppgift.

Gasinnehåll: det största av alla galaxer, upp till 25% av totalmassan [BAs327sp1m].

Struktur: ingen särskild (”mera sällan kärna” [BAs335sp2n]).

END.

Galaxbildningarna

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Galaxbildningarna

ämnesrubriker

innehåll

GALAXBILDNINGARNA

Vinjettbild

Fotografier och resultat från vattenrekyler i jämförande analys med himlakroppsbildningen enligt TNED

Droppanordningen

Rekylbilden

Storleksproportionerna

Vattenrekylens spinn

inledning

Innehåll

SPIRALFORMENS KOSMISKA URSPRUNG

Ett centralflöde beskriver också en rotation

Virvelbildningens elementära fysik

Den Inducerade Rotationens Uppkomst

Illustrerad sammanfattning

Planetrotationernas upphov

PLANETERNAS PRIMÄRA ROTATIONER

Centralaccelerationen

GALAXBILDNINGARNA — K-cellens brytning — materieöarnas uppkomst i universum

Stjärnhopar och galaxbildningar DEL I

Allmän delningsklassificering

Hur delkropparna avdelas — uppkomsten av roterande moment

Nolldivergenszonen indelar alla kroppar i två klasser

HUR K-CELLEN BRYTS

Plasmahoparnas Fördelning i K-Cellen

K-cellens innervägg

Massavyttringens allmänna enkla Vågfunktion för K-cellens brytning

Solsystemets ålder

Stjärnhopar och galaxbildningar DEL II

GEMENSAMMA EXPANSIONSRIKTNINGEN — Hur konstant medeltäthet bevaras

PLANETSYSTEMENS GRUNDFORMER

v-SPRIDNINGENS UPPKOMST

Galaxbildningarna — ALLMÄNNA MATEMATISKA SAMBAND

Spiralkurvans Ekvation

Kriteriet för strukturernas bevarande

Strukturexempel från BONNIERS ASTRONOMI

GASDISTRIBUTIONEN MELLAN DELKROPPARNA

ALLMÄN KLASSIFIKATION

REGELBUNDNA SLUTFORMER — De olika galaxklasserna

OREGELBUNDNA SLUTFORMER

STJÄRNFORMATIONERNAS INDELNING OCH KARAKTÄRISTIK ENLIGT ETABLERAD KOSMOLOGI — Referenser

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

[BA]. BONNIERS ASTRONOMI 1978, Det internationella standardverket om universum sammanställt vid universitetet i Cambridge

[EST]. Encyclopedia of Science & Technology · McGraw-Hill 1992

[FM]. FOCUS MATERIEN 1975

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

et al, allmän förkorting (i engelskan) som används för att ange typ X et al, X med medarbetare, eller X med kolleger

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2021-12-09

*END.

Stavningskontrollerat 2009-02-20 | 2009-04-25

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se