Radioaktiva
sönderfallets Fysik enligt TNED | UNIVERSUMS HISTORIA | 2011X14 | a BellDHARMA production | Senast uppdaterade version YearMonthDayTime 2020-04-07
innehåll ·
webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor
Nuklidkoefficienten i Kombinerade Sönderfallstyper | Nuklidfaktorn
i betasönderfallet |
Betasönderfallens
matematiska fysik i TNED

BILDKÄLLOR: Författarens arkiv
· Kollage NikonD90 — Excur2.1Jun2009Lingonklockor2Bild1·Ängsblommor5Jun2010.2Bild6·Excur4Granheden19Apr2010Bild1.04·SommarlanskapSverige5Jun2010.2Bild10
Beskrivningen i detta dokument kompletterar huvuddokumentet
i Radioaktivitetens
Fysik enligt TNED med BETASÖNDERFALLETS NUKLIDER i
motsvarande översikt till Alfanuklidernas
Allmänna Isotopkarta (Allmänna radioisotopbilden).
Halveringstidssambandet
för betasönderfallen
|
Från
B/p-utvecklingen i Kärnsönderfallet BILDKÄLLA: Författarens arkiv · Vattenrekyl |
Mot varje tillståndsändring [från Ändringslagarna] i atomen måste tvunget svara en
elektromagnetisk vågrörelse, av en eller annan form, som avspeglar den
verkställande tillståndsändringen; Atomkärnan (enligt TNED)
grundas på en sammansatt ±e-struktur med en utpräglad ytladdning (atomnummer
Z) och vars ändrade tillstånd följaktligen anställer en motsvarande ändring i
den elektromagnetiska vågstrukturens signatur: signal. hela
atomen ekvivalenter
i summa ————————————————————————— [n±e]0 = [n±e]1 + [n±e]2 + … ; avdelning
n±e kvarvarande
del ————————————————————————— [n±e]0 – (m→γ) – [n±e]1 = [n±e]2 – (m→γ) : — 1-delen kan inte avdelas från 0-delen på annat sätt än
genom att ett ARBETE (m→γ) utförs; arbetsenergin måste tas
någonstans ifrån; den tas ifrån 1-delen genom massdestruktion
(m→γ),
med motsvarande netto i underskott på den kvarvarande 2-delen. — Massdestruktionen ENLIGT TNED arbetar på energins bevarande genom
induktionen [COEI]; — ±spinnen i atomkärnans fraktalstruktur enligt TNED, med
motsvarande ±-laddningar, annihileras |
τ – + τ+ = 0 ................................................... laddning
sτ– + sτ+ = 0 ................................................... spinn (rörelse)
mτ– + mτ+ = 2mτ →
γ
...................................... massenergin,
arbetet som omsätts vid (ombyggnaden associerad med) sönderfallet
tillsammans med massans struktur, medan massenergin bevaras
genom induktionsverkan [med ett fast tidsintervall T i association med
massdestruktionen, ökar induktansen L=RT med avtagande laddning Q under
energins bevarande; E=UQ=RI(T/T)Q=RTQI/T=LQ²/T²; se även i K‑CELLENS VÄRMEFYSIK]; Därmed
överförs massenergin masslöst på omgivande elektriska laddningar.
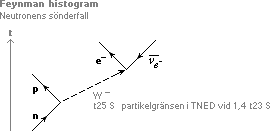
Betaemissionerna i TNED
2011XI5
Betaemissionerna
Se även ELEKTRONEMISSIONSEXPERIMENTET
FRÅN 1957 — tidiga experimentella bevis för HUR
elektronmassan avdelas från/ur atomkärnans lokal
— Frigörandet av varje e/n-element [Se ELEKTRONMASSANS KOMPONENTER]:
Atomkärnans inre ringspinn har bara (vad vi vet enligt TNED) EN grundpreferens att utgå ifrån; toppdivergensen (c0).
— Men för att elektronelementet (e/n) ska KUNNA komma ut från den matematiken, måste ringspinnets PREFERENShastighet vara mindre än toppdivergensens.
Sambandsformerna vi har att utgå ifrån i TNED är de följande:
u = c√ 1 – 1/[(UQ/m0c2) + 1]2
PLANCKENERGINS EKVIVALENTER — laddningshastigheten u från accelerationsspänningen U
u = c√ 1 – 1/[(E/m0c2) + 1]2 — Planckenergi-massekvivalentens
laddningshastighet u för elektronen från uppmätta elektronenergin E
m0/m = √ 1–(u/c)2
.............. Planckenergins
massekvivalent
Med exempel från Neutronsönderfallet ATOMVIKTER i u=1,66033 t27 KG
———————————————————————————————
Neutronen Väteatomen Energidifferens [neutrino, (m→γ)]
———————————————————————————————
1,008665200 1,007825200 0,0008400 u
939,5509731 938,7685303 0,7824428 MeV
———————————————————————————————
Nettodifferensen E(diff)=0,7824428 MeV innefattar HELA övergången neutron-Väteatom — inkluderat den rörelseenergi som den frigjorda elektronmassan besitter relativt sin moderatomkärna.
— Men den rörelseenergin kan uppenbarligen INTE vara densamma som utvecklades då elektronelementen avdelades, i TNED via det inre ringspinnet:
— Elektronelementen i Väteatomen »snurrar» ingalunda kring vätekärnan med hastigheter typ c. Vi studerar det.
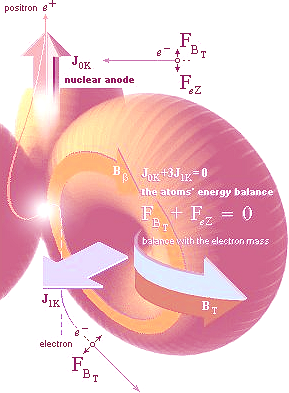
Kraftekvationen FBT+FeZ=0 som avser elektronelementet, och därmed hela elektronmassan, gäller med avseende på kopplingen element-HELA atomkärnan — utan närvaro av det inre ringspinnet [3J1K i J0K+3J1K=0].
— Men närvaro av det inre ringspinnet är just vad som, tvunget, föreligger vid tillfället för elementets avdelning.
HUR hanterar atomkärnan den situationen?
— Utför vi räkningen på E(diff)=0,7824428 MeV för E i u-formen får vi
u/c = √ 1 – 1/[(UQ/m0c2) + 1]2
= 0,9183278
Elektronelementets avdelningshastighet
Elektronelementets avdelningshastighet från de inre spinnringarna är ekvivalent ~0,92c. När elementet kommer ur kärnbrunnen och in i området för »den reguljära yttre atomkärnans form», ser elementet inte längre ringspinnen, utan endast hela atomkärnan där summan av ringspinnen är 0; = FBT+FeZ. Härifrån fungerar nu elementet som en ordinär del i elektronmassan; elementet får en viss (mindre) hastighet (v) relativt hela atomkärnan och som elementet behåller så länge kraftekvationen gäller.
— Därmed garanteras den kontinuerliga STRÖMNINGSBANAN mellan kärna och höljeselement som omnämndes i kraftekvationens härledning.
Vi SKULLE (till att börja med) kunna anta v-värdet för elementet utanför kärnan som v/c=1–u/c, så att
v/c + u/c = 1 = (v+u=c)/c
;
— Elementet ges (som preferens) samma hastighet relativt hela atomkärnan som relativt de inre ringar [se generellt utförligt i TNED från Plancks strukturkonstant om ej redan bekant] från vilka elementet avdelas [(1–0,92)c]. Toppdivergensen (c0) sätter i vilket fall en absolut högsta v-gräns (som aldrig kan bli exakt c0).
;
— Är v/c=1–u/c en maxform?
— Uppenbarligen, ja. Det går inte att komma över c-summan.
— Är den slutliga v-formen icke-linjär (vilket den är) kommer ytterligare en del rörelseenergi att tvingas återföras till atomkärnan.
— Vi kan här i TNED kalla den återföringsenergin till atomkärnan för »mass(CHOK)rekyl»;
— För att få ut elementet (som påtvingar det en kraft- eller masschokning) måste kärnan avdela en utkastningsenergi vars övergripande del kärnan sedan måste återta (masschokningsenergin återlämnas [nästan hela]) för att det avdelade elementet ska kunna anpassas till kärnan: en konstant ström enligt kraftekvationen (som grundlägger spektrum och kvanttalen).
MASSÖKNINGEN för u/c~0,92c blir [[Tabell1KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]]
m0/m = √ 1–(u/c)2
= 0,3958208 ;
m/m0 ~ 2,53
Men den delen måste återlämnas till atomkärnan för att elementet ska normaliseras på sin ordinarie v-form (0,08c).
— Enda möjligheten för att den energiräkningen [Q-systemets totala massa bevaras intakt] ska stämma är tydligen följande funktionella energiflödestyp:
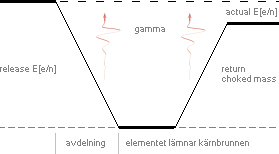
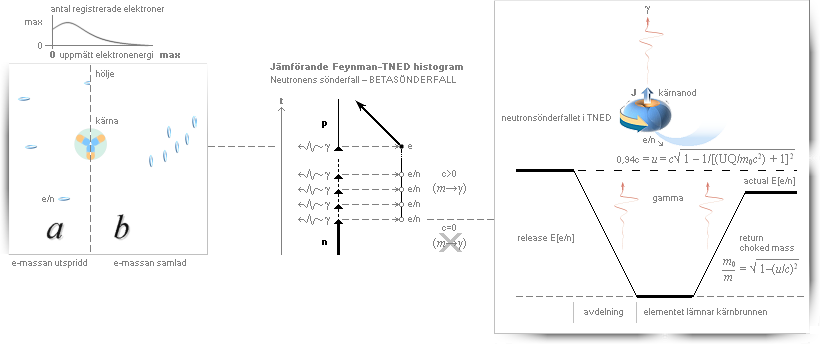
Varje ÄNDRING som
atomkärnan genomgår åtföljs ALLTID av NÅGON elektromagnetisk (em-) aktivitet
som avspeglar kärnstrukturens ±e-väv och hur den ändras genom det nya
tillståndet; Generellt betecknas alla sådana em-variationer från atomkärnan i TNED med GAMMA-symbolen
[γ]; Gamma-aktiviteten kan vara allt ifrån de allra kortast detekterbara
våglängder som konventionellt brukar förknippas med kärnsvängningar, till de
ENLIGT TNED mera djupliggande [i TNED reguljärt betecknade] NEUTRINOVÅGLÄNGDERNA [utförligt i NEUTRINOSPEKTRUM] och som kan [och bör]
variera mellan olika nuklider. Det finns här veterligt ingen enkel,
övergripande form för denna del som innefattar alla möjliga fall. Även den
individuella atomens aktuella energitillstånd spelar [naturligtvis] in;
— Vissa em-nivåer
[reguljär gammastrålning, typ annihilationsvåglängder] KAN vara makroskopiskt
synliga direkt via atomernas elektronhöljen, och vissa inte. I de senare fallen
kan de kortare neutrinovåglängderna fortfarande påverka en atoms atomkärna med
excitationsenergi och som, i vissa fall [på
redan känt sätt], kan framkalla atomära ljusemissioner för vidare
detektering.
— Även omvändningen bör gälla (elektroninfångning) med samma principiella matematiska fysik;
— Elementet (åter-) accelereras av kärnbrunnens specifika tillståndsfysik (här betainstabilitet), och elementets egenenergi summeras med atomkärnans (likt vattendroppen som återvänder till moderytan ur vilken den avdelades).
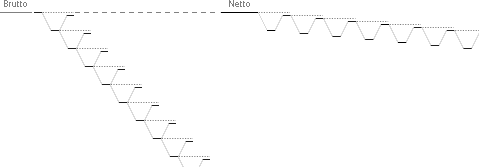
Så kan vi se hur TNED vill ha det i stort:
— Hela processen förlöper så, i enskilda steg (figuren ovan), ett element i taget och med tillhörande gammakomponenter, tills alla de n elementen (673026) är avdelade.
— Kortast möjliga avdelningstid blir med ideala spinnhastigheten (c0) som absolut fysikalisk preferens lika med ett varv hos atomkärnans tre inre underringar. För neutronens del minst (r0=1,32 Fermi med 1:a underfraktalernas ringar, ca halva det värdet) t=d/v=πr0/c=1,3832577 t23 S [t för 10^–].
— Atomen som helhet kan, på grund av sin allmänna koppling till (och grund i) Plancks konstant (h=mcr) inte arbeta på delar av elektronmassan och dess laddning i makrofysikalisk mening. Resonanserna som styr atomernas elektronhöljen och deras energinivåer, är kopplade till elektronmassan som en enastående, odelbar, kvantitet (e=1,602 t19 C), och (ev. makroskopiskt detekterbara gammakomponenter frånsett) ingenting kan ses av själva det avdelande förloppet.
— Ingenting händer förrän sista elektronelementet kommit på plats.
— I takt med att atomkärnan avdelar elektronelementen, tvingas också atomkärnan lagra upp alla »mass(CHOK)rekyler»; Dessa kan förklaras visas i form av extra deponerbar (induktions-) energi och som kommer att frigöras (som speciella »kärnvibrationer», alltså gammastrålning) då betasönderfallet »tänder» makroskopiskt.
— Det är den BILD som TNED, här alldeles tydligt, målar upp av de kända ingredienserna via energiräkningen totalt.
Men:
— Hur fungerar elektronelementen, under tiden, fram till »tändningen»?
— Uppenbarligen INTE I DIREKT (slutlig) koppling till kraftekvationens 0=FBT+FeZ-form, eftersom den delen strängt taget INTE är aktuell UTOM för den stabila atomen, då betasönderfallet redan fullbordats.
— Den enda (vettiga), rent matematiskt-fysikaliska energislutsats man kunde drav av den omständigheten skulle vara att INGEN PÅVERKAN ALLS, inte från någon atomkärna, finns för den del element som avdelats, och så länge hela elektronmassans avdelande inte fullbordats; atomen/atomkärnan »väntar» tills hela e-kvanta föreligger.
— OM så skulle vara fallet, måste ALLTSÅ elementets v-form inte bara reduceras från neutronsönderfallets exempel 0,08c utan även HELT i noll; elementen flyter tills »makroskopiskt kvantiserad tändning» inträffar.
— Scenario:
— Kärnan avdelar elementet på rörelseenergin E — som sedan återtas, alltsammans E minus gammakomponenter i anslutning till massdestruktioner (m→γ) — av kärnan; Sedan, längre fram, frigörs Den SÄRSKILT UPPLAGRADE energin i samband med att också kärnytan ändrar sin kärnladdning med en enhet; kärnan avger en gammapuls (som KAN ligga i neutrinoområdet enligt TNED, se NEUTRINOSPEKTRUM), och som signalerar »tändningen fullbordad».
— Den högre kärnladdningen är ägnad att infånga den avdelade elektronmassan — vid OBS ett enda unikt tillfälle;
— Då elementen attraheras till kärnan (via den plötsligt uppkomna högre kärnladdningen med +1e), genomgår de samtidigt DEN strukturella normalisering som slutar på att elementen inrättar sig i DET vissa karaktäristiska resonansmönster som kännetecknar just den atomen i dess bindning med andra atomer och som bygger på en kontinuerlig STRÖMVÄGSKOPPLING mellan kärna-element enligt just kraftekvationen.
— NOTERA de många möjligheterna som den nytillkomna
elektronmassan kan svara på: beroende på HUR elementen har spritts ut bland de
övriga, redan befintliga och i arbete, kan alla grader av
»elektronmassans rörelseenergi» uppvisas; Nära NOLL om elementen redan ligger
maximalt utspridda, eller integrerade; MAX (0,782 MeV) om elementen ligger
lämpligt i förhållande till NÅGON närliggande atoms (kombinerade) respons som
därmed KAN lämna ett »scintillationsspår» efter sig då elektronmassan inträder
någon atoms besättning (eller utträder någon annans).
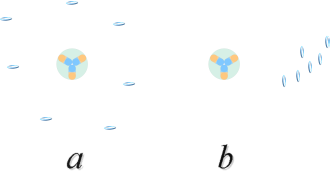
a: [Högre sannolikhet]: Elektronmassans element ligger maximalt
utspridda, integrerade med de redan etablerade resonanserna; knappast någon
märkbar reaktion alls sker mellan moderkärnan och elektronen då kärnan visar
upp sin +1e-laddning; Man registrerar en maximalt LÅG elektronenergi [i princip
noll].
b: [Lägre sannolikhet]: Elektronmassans komponenter ligger
maximalt samlade; när moderkärnan visar sin +1e-laddning, sker också en
maximalt Coulombiskt samlad attraktion; elektronmassan KAN uppvisa maximal
elektronenergi [max 0,782 MeV för neutronsönderfall, frånsett ev. tillskott som
avspeglar moderkärnans extra energier].
— I modern akademi
tolkar man SPECIELLT den normalt GÅTFULLA noll-energin hos elektronen som bevis
för att neutronsönderfallet också emitterar en ANNAN PARTIKEL [konv. neutrino]
men som inte är direkt synlig i makrofysiken. Dess uppgift blir då att »forsla
bort den överskottsenergi» som INTE elektronen uppvisar — speciellt om denna
visar noll.
— Se [en av de bästa webbkällorna] HYPERPHYSICS för vidare [TNED-jämförelse och] förklaring av det
konventionella synsättet.
— Det är I STORA DRAG vad man kan utläsa av sammanhangen enligt TNED.
— »Tändaccelerationen» av hela e-massan är av allt att döma själva den makroskopiskt mätbara effekten av hela händelseförloppet; man mäter (som mest [frånsett ev. ytterligare tillägg från moderkärnan beroende på tillstånd]) HELA energiskillnadsbeloppet (0,782 MeV) som »den uppkomna elektronens rörelseenergi».
— Men som vi redan har förstått av HUR elektronmassans komponenter kan fördela sig i närområdet, nämligen i samverkan med de redan etablerade strukturerna, finns många olika möjligheter; Allt ifrån att elektronelementen knappast alls reagerar på den Coulombiskt kärnassocierade tändpulsen — genom att de redan är maximalt integrerade med den redan befintliga elektronpopulationen — till max reaktion om elementen ligger så tillgängliga att de kan svara direkt på en plötsligt uppvisad Coulombattraktion. Det är också helt i enlighet med den ordning som de experimentella resultaten visar.
Det man mäter på i makrosammanhang, det man SER av den avdelade elektronen, skulle alltså med beskrivningen ovan vara en SEKUNDÄR FYSIKALISK DYNAMIK.
Nuklidfaktorn i betasönderfallet —
Halveringstidssambandet för
betasönderfallen
HalveringstidsSambandet för betasönderfallen i TNED
I Källexempel visades hur nuklidkoefficienten (b) kan beräknas [[Tabell1KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]] i fallen med kärninstabila nuklider (A=1S),
b = [√2mEα]ln[tH/(ln2)]/eZα ........................... nuklidkoefficienten
till kärnsönderfallen i TNED
Eα anger den uppmätta alfaenergin (Z=2) och tH den uppmätta halveringstiden.
— Som visats ovan i genomgången från Betaemissionerna i TNED, har begreppet »rörelseenergi för elektronen» ingen signifikant innebörd för själva sönderfallsprocessen. Den signifikanta faktor som bestämmer — eller rättare refererar — hela sönderfallets KRAFT (motsvarande alfapartikelns impuls i kärnsönderfallet) är enbart den överskjutande massa som betanukliden uppvisar från sin bildning till sönderfallets slut (i enskilda steg om flera än ett).
— För att få fram ett motsvarande Ee-värde i betasönderfallet, behöver vi alltså bara beräkna masskillnaden mellan primärnukliden och dess närmast lägre sönderfallsprodukt.
— Med elektronladdningen Z=1 kan därmed samma b-form
också användas för betasönderfallet generellt enligt modifikationen
b = [√2meEβ]ln[tH/(ln2)]/e .............................. nuklidkoefficienten
till betasönderfallen i TNED
b = [√2meEβ]ln[tH/(ln2)]/e
;
b(ALFA)/b(BETA) = ([√2mαEα]ln[tH/(ln2)]/eZα)/([√2meEβ]ln[tH/(ln2)]/e)
= [√ mαEα]/Zα[√ meEβ]
= [√(mαEα)/(meEβ)]/Zα
För Eα=Eβ gäller tydligen
bα/bβ = (√ mα/me)/Zα
=
42,7084842; för
alfa = 2He4 [Z=2]
;
Från slutformen för halveringstidssambandet tH ges då motsvarande explicita sambandsform för betasönderfallen enligt
tH = 1S(ln2)ebeZ/√2mE
Z = 1 ;
m = me ;
10log tH/1S =
10log[(ln2)ebe/√2mE]
10log tH/1S =
(1/ln10)ln[(ln2)ebe/√2mE]
10log tH/1S =
(1/ln10)ln[ebe/√2mE + ln(ln2)]
10log tH/1S =
(1/ln10)[be(2mE)–0,5 + ln(ln2)]
Räknas E i MeV — E(Joule)
= E(MeV)·e·T6 — fås förenklingen
be(2mEJ)–0,5
= be(2mEMeV·e·T6)–0,5
=
be(2me·T6)–0,5(EMeV)–0,5
=
b[e2/(2me·T6)]0,5(EMeV)–0,5
=
b[e/(2m·T6)]0,5(EMeV)–0,5
; m = 0,000548598(u=1,66033 t27 KG); e=1,602 t19 C;
=
b(296,5459113)(EMeV)–0,5 ;
10log tH/1S =
(1/ln10)[b(296,5459113)(EMeV)–0,5 + ln(ln2)]
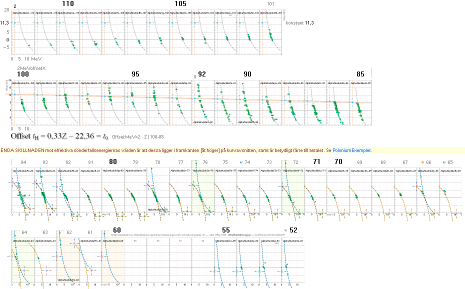
Graf; y=(1/ln10)[(b)296.5459113[(x)'–0.5]+ln(ln2)]
(1/ln10)[(25.133)296.5459113[(x/5)'–0.5]+ln(ln2)]
Se vidare från tH-universalens betaform.
TNED/MAC-sönderfallen — Jämförande beskrivningar i TNED
och MAC
RADIOAKTIVA SÖNDERFALLEN I JÄMFÖRANDE BESKRIVNINGAR
Vad utmärker TNED
framför MAC i sönderfallsfysiken?
1. Den allmänna kartbilden som visar det tunga radioaktiva sönderfallets alfanuklider generellt över hela fysikens nuklidkarta (Nedan från AlfaIsotoperna):
En motsvarande — allmän —
kurvpassning som ovan är inte möjlig att härleda i MAC;
— Den aktuella
kurvpassningen, ovan, baseras på det som garanterat inte finns i MAC:
nuklidkoefficienten [se b-faktorn i exponenten till tH-universalens betaform] som, enligt TNED, bestämmer halveringstiden [tH, konv. T½]
tillsamman med sönderfallsenergin, b-faktorn med maxvärdet ±8π — urspr.
från TNED-härledningarna i potentialbarriären med energizonen via ljusets gravitella beroende — hela grundteorin till ATOMKÄRNANS
HÄRLEDNING och som garanterat INTE återfinns i den moderna akademins
lärosystem. Se utförligt i Härledningen
till halveringstiden enligt TNED.
— En generellt
överskådlig kartbild av alfanukliderna, som ovan, skulle därmed vara OMÖJLIG i
MAC: Det finns ingenting sådant i MAC: ingen motsvarighet; ingen make.
2. Den allmänna koefficientformen till sambandet för halveringstiderna;
10log tH = A +
B[CZ/√x + D] –
E
Allmänna koefficientformen är av samma matematiska form som den sambandsform som brukar användas i MAC (Se särskilt i Citat) vid beskrivning av det radioaktiva sönderfallets kärndelar (främst alfasönderfallen), och som grundlägger aspekten i punkt 1 ovan;
— På samma sätt som tillfälligt vilande vattendroppar på vattenytan FÖREFALLER vara självständiga, isolerade, kroppar, skilda från ytan och dess sammandragande krafter (som normalt sett omöjliggör nedanstående fotograferade situationer), så är det också enligt TNED med de avdelade kropparna i de radioaktiva sönderfallens verkliga fysik: de avdelade kärnfragmenten finns aldrig till FÖRE avdelandet som några förmodade »fristående partiklar» INUTI moderkärnan (den övergripande vattenvolymen), eftersom atomkärnan enligt TNED är en massans fundamentalform.

BILDKÄLLA: Författarens arkiv — Tillfälligt vilande
vattendroppar på vattenytan efter dropprekyler — NikonD90 · Sammansatt
fotokollage av tre separata fotografier · 19Apr2009Bild650/693/651/Drop17isoAuto.
— I MAC däremot, är det just precis vad som hävdas: »partikeldroppen inuti modervolymen» försöker rymma sin fångenskap, och lyckas till slut (genom kvantmekanisk statistik), vars APPROXIMERADE matematiska form i MAC i slutänden (Se särskilt i Citat) ansluter till Allmänna Koefficientformen.
— Det förefaller med andra ord finnas enbart skäl som indikerar TNED som matematisk grund.
Nuklidkoefficienten i Kombinerade sönderfallstyper
BILDKÄLLOR: Illustrationer och fotografier [i olika montage] från
författarens arkiv för UNIVERSUMS HISTORIA Dec2011.
I TNED finns från J-KROPPARNAS
BILDNING och expansion alltid möjligheten vid GRUNDÄMNESBILDNINGEN att en och samma
typnuklid — samma atomnummer [Z] med samma masstal [A] — genom olika neutronkvoter — HUR
nuklidfördelningen ser ut i den aktuella grundämnesbildningslokalen, exempel
ges i Basnuklider med olika neutronkvot och Grundämnesbildningens två basgrupper — kan innefatta samma
nuklidtyp men bildad i skilda lokaler, och därmed med olika
energigenomströmningar vid bildningstillfället, här främst beträffande neutrinostrålningens ev. inverkan i den primära
grundämnesbildningen, och som [här, i TNED
endast] är föremål för närmare analys beträffande möjliga influenser i
det radioaktiva sönderfallets matematiska fysik. Denna möjlighet, tillsammans
med de allmänna instabila sönderfallen som också kan bilda en given nuklid som
slutprodukt [Jämför som ett exempel stabila
26Fe56 från instabila 24Cr56], ger flera möjliga förklaringar till
varför en och samma nuklidtyp, i många observerade fall, uppvisar en kombination
av olika sönderfallstyper — med olika genomsnittliga procentuella
fördelningar per typ.
Av de drygt 200 specificerade alfaemitterande radionukliderna i HOP-tabellen — från 1966 — är hälften associerade med andra sönderfallstyper (antalet inom parentes); pa(1); 2a(1); a,SF(16); B–,a(14); B–,a,SF(1); B+,a(3); B+,EC,a(1); EC,a(60); EC,B–,a(1); EC,a,SF(1); p,2a(1) — a alfa, SF SpontaneousFission, B– BetaMinus, B+ BetaPlus, EC Electron Capture, p proton.
— 97 st står angivna som »rena» alfaemitterare, a(97).
— Idag [Dec2011] är antalet tabellerade radionuklider av alfatyp betydligt större; Medan HOP-tabellen från 1966 tar upp 200 st alfaemitterare, innehåller tabellen från Wiley 1999 drygt 2000 stycken (2090) instabila nuklider av alfatyp (Se högra delen i översikten AlfaBeta).
— Wileytabellen (från 1999) innehåller även EN SYNBARLIG basinformation (i kolumnen Intensity) om andelen alfasönderfall per 100 modernuklidsönderfall; I den grova översikten är det övervägande antalet fall av typen icke-100%. Men som WileyExemplet (längre ner) visar, är dessa uppgifter tydligen — hela tabellen — som det får förstås, förbehållna andelen alfaKANALenergivärden — inte olika värden från någon ordinär multisönderfallsform.
— Men alla uppgifter om halveringstid — med grund i någon teorin för sönderfallet — måste avstämmas till dessa precisa grunddata:
— Det gör — sammantaget — TYPEN Wileytabellen VÄLDIGT äventyrlig [för att inte säga direkt: »värdelös»], om det gäller att försöka KONTROLLERA experimentella resultat mot teoretiska.
Nämligen så:
— Radiometriska data grundas på (omsorgsfullt kemiskt renade preparat med) omfattande kollektiva atomgrupper även i små preparat; ingen mätning kan (med dagens teknik) ske på enskilda atomer;
En viss orientering i vilka mättekniska svårigheter som finns
i fallet alfasönderfall ges i [Nov2011, källdatum saknas]
USA ENVIRONMENTAL PROTECTION AGENCY
Tutorial 4.4 — Alpha Spectrometry 1: Principals
http://www.epa.gov/safewater/radionuclides/training/transcripts/tutorial_4.4.pdf
”The resolution for alpha
particle energies with routine laboratory methods is between 40 and 100 keV, mainly dependent upon the
technique of the analyst. Since both of these radionuclides are chemically the same,
they cannot
be chemically separated. Since their alpha particle energies are so close, they cannot be
spectrometrically separated. This means that when the results for plutonium are reported for these two
isotopes, it is usually reported as the sum of the activity of the two
radionuclides.”
—För en viss radionuklid som uppvisar multisönderfallstyper med en viss aktivitet, fördelas sönderfallet med vissa procent på en viss sönderfallstyp, och halveringstiden blir tvunget en medelvärdesbaserad parameterform utslagen på alla ingående sönderfallstyper.
— Citatkällan nedan exemplifierar en etablerad koppling till multipla sönderfallstyper (Se även Wikipedias Branching fraction, där omnämns vidare det centrala begreppet partial decay constant och som annars verkar hart när omöjligt att hitta i det stora ämnesutbudet).
”Some radionuclides may have several different paths of decay. For example, approximately 36% of bismuth-212 decays, through alpha-emission, to thallium-208 while approximately 64% of bismuth-212 decays, through beta-emission, to polonium-212.”,
@INTERNET Wikipedia Radioactive decay Decay chains and multiple modes [2011-12-10]
På artikeln om
Bismuth-212 anger Wikipedia halveringstiden med DET ENDA värdet 60,55(6)
minuter.
— Med en och samma
modernuklid är det bara specifika nuklidparametrar och absoluta sönderfallsenergier
som kan bestämma gränserna för halveringstiden [moderkärnans struktur och
energi]: en och samma modernuklid kan INTE uppvisa samma halveringstider
för olika typsönderfall [med mer än
sönderfallsenergierna är samma]; alfasönderfallet för sin del går
från ett högre Z till ett lägre Z för sönderfallsprodukterna, medan betaMinussönderfallet
för sin del [aktuellt för Bi-212 ovan] går från ett lägre Z till ett högre;
halveringstiderna för dessa bägge skilda sönderfallstyper kan därför omöjligen
vara lika [om inte också samma
sönderfallsenergier gäller];
— Med en given
modernuklid, finns bara två variabler att välja på; kärnstruktur och
energiinnehåll. OM, som här, sönderfallstyperna förgrenas på två olika, bör
också sönderfallsenergierna rimligen göra det, och därmed skilda
halveringstider; Uppgiften om ETT halveringstidsvärde för en
multisönderfallstyp är, tydligen, en ofullständig uppgift — en medelvärdesform.
Den är i sig värdefull endast om de procentuella sönderfallsdelarna anges.
— De allmänt tillgängliga
sönderfallstabellerna har emellertid INTE den typen av omfattning. Vidare i
huvudtexten.
Se även generell listning av de olika individuella
sönderfallstyperna i
RADIOACTIVE DECAY MODES — Lawrence Berkeley Laboratory
http://ie.lbl.gov/education/decmode.html
Vad vi skulle behöva, är en UTFÖRLIG tabellredovisning av exakt vilka alfasönderfallsnuklider som är av typen RENA och vilka som inte är det, och i de sistnämnda fallen, en KLAR redovisning av de kombinerade sönderfallens olika procentuella andelar, för att därmed kunna pröva teoretiska halveringstider på VARJE radioaktiv nuklidtyp.
— Det finns, här veterligt, ingen allmänt tillgänglig sådan uppställning — för analys (kopierbara tabelldata som enkelt kan maskinkodas för transfereringar till kalkylceller och annan programbas).
Det finns dock flera olika interaktiva NUKLIDKARTOR på webben som bygger på manuell inmatning för att få fram enskilda fullständiga nukliddata på en viss nuklidtyp, se exv. Isotope Charts från
LAWRENCE BERKELEY NATIONAL LABORATORY
;
Webbkällan ovan innehåller en TILL SYNES omfattande databank
på alla radioaktiva nuklider;
— Dock har källan här veterligt inga tillgängliga tabeller
som specificerar den procentuella andelen sönderfall i KOMBINERADE SÖNDERFALL
och som [med referens till HOP-tabellen
från 1967, med här pågående utvärdering] tydligen utgör huvuddelen av
alla radioaktiva nuklider; endast medelbaserade uppgifter finns. Utan sådana
avgörande data, kommer vi ingenvart i teoretiska jämförelser med experimentella
mätdata.
Därmed faktum:
— Bilden av sambandet mellan halveringstid och sönderfallsenergi kan OMÖJLIGEN göras enhetlig, eller motsvarande exakt; Vidare citat nedan i Cu-exemplet endast understryker det, ”only the total decay constant is observable”.
— Det finns, tydligen, [ännu 2011] ingen särskiljande apparatur som kan avgöra vad den ena sönderfallstypen uppvisar i förhållande till den andra, om de är lika med si eller så hög grad av mätnoggrannhet, eller om det finns tydliga skillnader.
EXEMPEL Wileytabellen 1999 för U-238:
”8th Edition of the Table
of Isotopes: 1999 Update
Table 3. Alpha Particle Energies
An energy-ordered list of
alpha particle energies is given in Table 3. Their absolute intensities (alphas
per
100 parent decays) are
also indicated.”;
Energy
Intensity Parent
————————————————————————————————
4038
5 0.078 12 238U(4.468×109 y)
4151
5 20.9 27 238U(4.468×109
y)
4198
3 79.0 27 238U(4.468×109
y)
WileyTabellen ger ingen information om
1. vad tilläggs- och hänvisningssuffixen betyder;
2. att energivärdet gäller i KeV
3. att alfaenergierna INTE är reguljära sönderfallsenergier,
utan just alfa-KANAL-energier;
— Exemplet ovan (utdraget 92-Uran-238) från Wileytabellen klargör EXPLICIT att tabelluppgifterna på ”Intensity” är värdelösa — eftersom tabellen generellt anger alfaKANALenergier, inte effektiva sönderfallsenergier.
— Det betyder, att tabellen, strängt taget och helt visst, är äventyrlig att handskas med, eftersom det inte KLART framgår vad tabellvärdena
· går ut på
· avser
· har för innebörd
— Ytterligare en detalj försvårar: Den allmänna svårigheten att HITTA gratis allmänt tillgängliga WEBBREFERENSER som TYDLIGT och KLART beskriver det radioaktiva sönderfallets databaser så att man själv kan se och kolla upp.
— ”Table of radioactive decay” (och liknande) ger inga andra sökresultat på Google än KARTBILDER med manuella inmatningar för enskilda, utförliga, nukliduppgifter (som ändå inte innehåller vad vi söker). Utöver ovanstående träffkälla (LBL): I princip noll, inte ens i närheten;
— Svårigheten att, ens, få fram någon grundläggande information i etablerade led om ATT de kombinerade sönderfallens fysik ens existerar, är också uppenbar:
Den förlösande sökfrasen — som visar många förekomster i
sakämnet — men också många i icke allmänt åtkomliga dokument:
partial decay constant
http://en.wikipedia.org/wiki/Branching_fraction
;
WikipediaKällan ger i sin External links flera
PORTALEXEMPEL på webbkällor som ska föreställa AVANCERADE källor som
tillhandahåller OMFATTANDE NUKLIDDATA: Dessa är dock [ännu] av typen maximalt
KRÅNGLIGA referenser som garanterat INTE är enkla att använda UTOM FÖR EXPERTER.
Jämförande
webbexempel på avancerade kärndatabaser — som INTE fungerar
JÄMFÖR 29Cu-64-exemplets
datavärden [nedan] med en av Wikipediareferenserna ovan
[mycket avancerad, IAEA]

Relational ENSDF — Sept. 2011 snapshot of the ENSDF database
maintained by the International Nuclear Structure and Decay Data Network,
under the auspices of the IAEA.
NUCLEAR STRUCTURE AND DECAY DATA - IAEA FOR NUCLEAR DECAYS
http://www-nds.iaea.org/relnsd/NdsEnsdf/QueryForm.html
;
SnabbManual:
I INMATNINGSFÄLTEN för »Symbol Z»,

skriv in »Cu 29»; Kryssa sedan för
(överst som i den infällda bildkopian) checkBoxarna markerade Q(β) och
Half Life. Välj sedan Search (längre ner);
— Ett tabellresultat kommer (strax)
fram, med bland annat BetaSönderfallsdata på 29Cu64;
— Maximera fönstret (Alt+Space+X+Enter)
så att tabellens »G.S. Decays» blir synlig. Där visas de procentuella andelarna
av de specifikt skilda sönderfallstyperna:
![]()
Bildkopia av IAEA.databasen, textkopia nedan
”ec β+
61.5
β– 38.5
”.
— Hänvisningssiffrornas innebörd [”3”] verkar inte uppta
tabellmakarnas allra mest intensiva intresse att klargöra innebörden av.
Uppgift saknas.
— Vart tog uppgiften vägen om uppdelningen i resp 43%EC,
38%β–, 19%β+?
— Inte ett spår.
— Vi kan inte, per jämförande analys,
använda en sådan databas — där uppenbart väsentligen skilda uppgifter
föreligger i olika etablerade källverk och som alldeles tydligt här skulle ge
MÄRKBART STORA alternativa skillnader;
— Jämför illustrationsdiagrammen
till Cu-exemplet — tillsammans med (ytterligare) tydligt
oklara uppgifter vad som menas med
sammansättningen ”ec β+”;
— Uppgiften ”ec β+ 61,5%” skulle här
i den oberoende summeringen ge den parbaserade värdeformen 2×0,615=1,23 gånger
normalvärdet för tH, att jämföra (se exempelräkningen i TNED-tH-summeringen) med
sammanställningens tripelbaserade delvärden 1,29(43%) och 0,57(19%), som
»summerar» IAEA-databasens motsvarande 62%;
— Vi kan inte använda en sådan (milt
sagt turbulent, kaotisk) uppgift till något meningsfullt; Varje försök till
precisionsanalys självutesluts.
Wikipediareferensen
NUCLEONICA
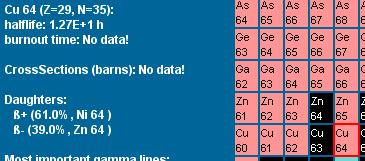
http://www.nucleonica.net/unc.aspx
visar för sin del ytterligare en ny speceributik av
alternativa värden i 29Cu64-exemplet,
här (som ovan i bild) 61%β+, 39%β–;
— Inget omnämnande av EC [electron capture]. [Ajaj].
— Inte heller den databasen är, således, användbar [men
REKLAMEN i Nucleonica utlovar TYP världens främsta och bästa databank för
forskare och studenter över hela världen i kärnfysikaliska sammanhang]. Det
kanske blir bättre framöver — OM och när väl begreppet SAMARBETE mellan de
olika dataportalerna blir av.
— OBSERVERA FÖR
NUCLEONICA [Dec2011]:
— Man skyltar med ”Free
Access” men det är RESTRICTED Access som gäller:
För att få tillgång till
Nucleonica får man INTE vara anonym; man måste DESSUTOM fylla i ett STRÄNGT
formulär med uppgifter om Organisation och JobbBefattning. Inga uteliggare här
inte.
— Man kan undra över
anledningen att INTE tillåta en allmän, obetingad, insyn i det som KALLAS
kunskap: Planeten är rund. Men det kanske beror på en allmänt deklarerad,
underlig, uppfattning om termen eller begreppet KUNSKAP:
”Nucleonica is an innovative
professional and technical resource for knowledge creation and competence building for the worldwide nuclear
science community.”.
— I RELATERAD FYSIK skapas inte kunskapen. Aldrig. Kunskap
DELAS. Alltid. Kunskapen är föregiven människan av NATUREN, och den HÄRLEDS ur
grundlagar som framkommer ur elementära grundstudier i ämnena matematik
och fysik
genom sanningsbegreppet
som grundval för hela verksamheten, eller så inte alls. Det kallas i relaterad mening för naturvetenskap — tillgänglig för
alla.
— Ingen enda individ utesluts. Ingen individklassificering
existerar. Alla är lika välkomna. Alla som vill, och har TID, får vara med [och
uppmuntras att vara aktiva, att utveckla, härleda, bidra, bygga och leva
TILLSAMMANS]. Kunskapens värsta fiende är [således] olika HINDER mellan
individerna: att INTE få, eller kunna, DELA MED SIG.
M.a.o.:
— TROTS en till synes (mycket) avancerad databas
[ovanstående IAEA-akronym
enbart], allmänt tillgänglig på webben, är den TYDLIGEN ändå så långt ifrån
preciserad att uppgifterna, tydligen, INTE kan användas för ANNAT än dekorationer till julgransbelysningen.
— Det kanske blir bättre med tiden.
— Efter många försök:
EN UPPHITTAD:
— Termen Branching
Decay är här, tydligt sett från TNED, helt olycklig;
MultiMODE-sönderfall eller MultiTYPE eller CombinedTYPE är det korrekta:
Kan inte textkopieras
”Several times in this chapter the possibility of competing modes of decay has been noted”;
;
”In such competition, termed branching deacay ... the parent nuclide may decay to two or more different daughter nuclides ... where for each branching decay a partial decay constant can be determined. These constants are related to the total observed decay constant for the parent nuclide as
λtot = λ1 + λ2 + … (4.51)
Each mode of decay in branching may be treated separately: the decay in an individual branch has a half-life based on the partial decay constant. Since only the total decay constant (the rate with which the mother nuclide ...) is observable directly, partial decay constants are obtained by multiplying the observed total decay constant by the fraction of parent decay corresponing to that branch.”;
;
”64Cu decays 43% by electron capture, 38% by negatron emission, and 19% by positron emission. The observed total decay constant is equal to 0.0541 h–1 based on the half-life of 12.8 h. The partial constants are:
λEC = 0.43 × 0.0541 = 0.0233 h–1
λβ– = 0.38 × 0.0541 = 0.0206 h–1
λβ+ = 0.19 × 0.0541 = 0.0103 h–1
These partial constants correspond to partial half-lives
of 29.7 h for electron capture decay, 33.6 h for β– decay, and
67.5 h for positron decay.”, s84; uppgift om författare och datum sdaknas
UNSTABLE NUCLEI AND RADIOACTIVE DECAY — RADIOCHEMISTRY AND NUCLEAR CHEMISTRY
http://jol.liljenzin.se/KAPITEL/CH04NY3.PDF
— Samma källverk
återfinns på GoogleBöcker som
Radiochemistry and nuclear chemistry By Gregory R. Choppin,
Jan-Olov Liljenzin, Jan Rydberg [2002]
Andra etablerade fackverk ansluter till ovanstående
[»partiella sönderfallskonstanten» är INTE experimentellt
observerbar, utan resultatet av en TEORETISK matematisk räkneoperation]:
s102;
”Note that each partial activity λiN in Eq. (6.7) decays at the rate determined by the total decay constant λ, rather than λi itself, since the stock of nuclei (N) available at time t for each type of disintegration is the same for all types, and its depletion is the result of their combined action.”,
GoogleBöcker — Observera att granskningen är
begränsad [inte säker att man kan få fram samma ställe upprepat]
Introduction to Radiological Physics and Radiation Dosimetry
By Frank Herbert Attix
[2008]
WEBBKÄLLOR man sedan hittar AV SAMMA TYP (utförlig beskrivning av termen branching decay):
Kan inte textkopieras — ”får inte visas på webben”, se författarens inledning To the Reader,
”... they are not allowed to pass it or a copy of it in any form to a third party. Neither can they display it on the web.”,
http://nasa.web.elte.hu/lne/Arabok_e_100129.pdf
;
— Man tillämpar tydligen generellt sambandsformen (radiokonstanten λ)
T½ = ln2/λ = ln2/(λEC + λβ)
≠ (T½)1 + (T½)2 + (T½)3 + …
= ln2/(λ1 + λ2 + λ3 + …)
= ln2/(ln2/tH1 + ln2/tH2 + ln2/tH3 + …)
= 1/(1/tH1 + 1/tH2 + 1/tH3 + …)
(som det kanske inte heller får berättas om ...). »PayPerView», kanske ... .
Andra summeringssätt
— Det finns dock inget direkt nukleärt som hindrar summeringssättet
tH = tH1 + tH2 + tH3 + …
under förutsättningen att
[d anger antalet multisönderfallande typer i samma
nuklid, abc respektive procenttyp;
— Varje typ sönderfaller på sitt sätt, i huvudsak oberoende
av andra individers sönderfallssätt;
— Summan av alla sönderfall i TID ges som en
medelvärdessumma för alla individuella halveringstider tagna med hänsyn till
antalet sönderfallande individtyper (d); BetaMinus, BetaEC, BetaPlus,
Alfa, Proton, Neutron, SpontanDelning ...]
tH = [atH + btH + ctH + … = dtH]/d
tH = tH[a + b + c + … = d ]/d
— Kan man, på något EXPERIMENTELLT sätt, avgöra om endera tH-summeringssättet — via inverterade aktivitetssumman 1/tH1 + 1/tH2 + 1/tH3 + …, eller via individuellt oberoende halveringstiderna atH + btH + ctH + … — är det sätt som den experimentellt uppmätta fenomenformen uppvisar (eller föredrar)?
Citatdelen i Cu-exemplet
säger i varje fall nej;
”only the total decay constant is observable”
— Det finns inget sådant experimentellt sätt. Det är dock
här okänt hur man resonerar i ämnet.
— Det verkar också vara ytterst tunnsått med
grundinformation på webben i saken [Dec2011].
— Se även Citat Prussin 2007.
Ingen allmänt tillgänglig mera utförlig beskrivning verkar finnas
HUR man mäter multipla sönderfall i ett givet radioaktivt preparat.
— INSTRUMENTERINGEN kunde man tro registrerar, i vilket fall, en viss mängd sönderfall av typen abc…med motsvarande procentuella andelar; Hela preparatets totala (halverande) sönderfall blir, i vilket fall, medelvärdet av de samverkande individuella sönderfallen, vare sig sönderfallen sker på det ena eller det andra sättet.
”partial decay constants are obtained by multiplying the observed total decay
constant by the fraction of parent decay corresponing to that branch”;
— Se citatet i Totala sönderfallskonstanten:
— I klartext från meningsdelen ovan; Man KAN, genom olika sinnrika experimentanordningar, skilja mellan typerna BetaEC och BetaPlus (moderkärnorna uppvisar olika fason) — och därmed säkerställa en viss entydig form för procentuell fördelning av respektive typ.
— Det är också vad citatmeningen utsäger: Genom att överföra den uppmätta procentuella andelen uppmätta tillfällen för den speciella sönderfallstypen, ges motsvarande aktivitetsprocent.
se webbcitatet från 29Cu64-exemplet
— I fallet inverterade aktivitetssumman
1/tH1 + 1/tH2 + 1/tH3 + …, samma som summerande frekvenser
(1/ln2)(λ1 + λ2 + λ3 + …,
befinner vi oss i samma (prekära) situation som i fallet med normal bildning av KÖ: frekvenserna överlappar INTE varandra; varje sönderfall väntar (snällt, som personer i en kö) frekvensmedelbaserat (vad man är tilldelad) tills den sönderfallande nukliden (i tur) är färdig med sin frekvensandel; först då genomförs den köande individens aktivitet.
— Den naturliga situationen för individuella aktiviteter (sönderfallen) är (naturligtvis, och i stället) att alla individer sönderfaller (utför sina sysslor) SPONTANT, efter sina förutsättningar, allt eftersom den egna INRE fysiken bestämmer, som om något begrepp om »kö» inte existerar.
— Men det sättet förekommer inte i moderna kvarter, se citatdelen om totala sönderfallskonstanten från Cu-exemplet.
— Halveringstiden (tH=ln2/λ) som sådan utsäger heller inget annat: om mängden radioaktiva atomer vid början av mätningen är N, utsäger värdet av halveringstiden tH (konv. ofta T½) att mängden efter tiden tH är N/2. Inget annat.
— Har man under den tiden (tH) registrerat (29Cu64-exemplet)
43%λEC
38%λβ–
19%λβ+
finns inget direkt inneboende i de sifferdata som berättar om HUR procentdelarna ligger fördelade i »frekvenser» eller »halveringstider»; 43% elektroninfångningssönderfall har registrerats, 38% BetaMinus-sönderfall, och 19% betaPlus-sönderfall.
— OM anledningen till svårigheten att inte direkt kunna observera vilket typsönderfall som föreligger i en och samma nuklidtyp [β–, EC, β+] är att de olika typsönderfallen inte enkelt låter sig objektiviseras i någon känd instrumentering, är det tydligt att enda sättet att avgöra fördelningen är genom kemisk analys av sönderfallsprodukterna. Tyvärr (vilket är det underliga) verkar det inte finnas någon allmänt tillgänglig webbkälla som berättar om dessa, avgjort viktiga, detaljer. Eller så finns det sådana källor, men de är svåra att hitta.
— Det mest intressanta i sammanhanget är: VAD, exakt, har föranlett det konventionella valet av den inverterade aktivitetssummeringen (nedan höger längst ut) framför andra alternativ? Ingenting sägs om det.
29Cu-64-exemplet — se även ytterligare alternativa källdata
i Webbexempel
|
Alla tillsammans |
tH
= tH1 + tH2 + tH3 + … |
tH
= (tH1 + tH2 + tH3 +
…)/(11+12+13+…) |
tH
= (1/tH1 + 1/tH2 + 1/tH3
+ …)–1 |
|
|
|
|
|
|
Normalformen |
Direkt procentuell SUMMERING |
Sant Procentuellt MEDELVÄRDE |
Direkt procentuellt INVERTERAD
SUMMERING |
— Nukliden 29Cu64 uppvisar [enligt nu kända experimentella
observationer] TRE olika sönderfallstyper: BetaMinus, BetaEC [eng. Electron Capture, sv.,
elektronInfångning], BetaPlus; halveringstiden totalt för nukliden 29Cu64 är angiven [VNS] som tH=12,82 timmar
[10log tH/S = 4,664190526].
— Beroende på tolkningssätt i
medelvärdesbildningen från de procentuellt uppmätta sönderfallstyperna
[38%BetaMinus, 43%BetaEC, 19%BetaPlus], ges motsvarande olika värdebilder,
de tre högra punktdiagrammen ovan.
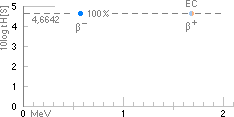
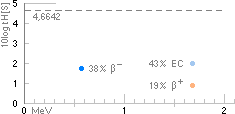
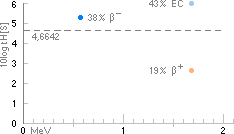
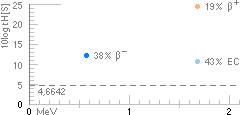
— 29Cu64-exemplet visar punktdiagrammen i
HALVERINGSTID[vertikala, 10log tH] och effektiva
SÖNDERFALLSENERGIN[horisontella, MeV] med de tre olika möjliga
medelvärdesbildningssätten från Normalformen som inte gör någon
åtskillnad mellan de olika sätten. Notera att effektiva sönderfallsenergierna
enligt TNED i typfallen BetaEC och
BetaPlus är identiska.
— Konventionellt används sättet längst till
höger. Motivering till det valet har eftersökts i det tillgängliga
webbutbudet [Dec2011], men inte påträffats. Alla tre sätten ger samma
tH-medelvärde.
— Beroende på VILKET av de tre sätten som
gäller i praktiken, ges [delvis våldsamt] OLIKA översiktsdiagram av
förhållandet halveringstid-sönderfallsenergi.
De Tre
MedelvärdesSummeringssätten
— Det finns — nämligen principiellt matematiskt främst — TRE olika sätt, alla med samma nettoresultat tH;
tH = tH[a + b + c + … = 1]/1 ; KÖ-sätt 1: nukliderna bildar tidsKÖ, väntar på sin tur
tH = tH[a + b +
c + … = d]/d
; Oberoende medelfördelning: varje nuklid sönderfaller
oberoende av andra
tH = 1/(1/tH1
+ 1/tH2 + 1/tH3 + …) ; KÖ-sätt 2: sättet som används i MAC: nukliderna bildar frekvensKÖ, väntar
på sin tur
= ln2/(λ1
+ λ2 + λ3 + …)
KöSätten 1&2: först den, sedan den, sedan den.
Oberoende: Närhelst du kan.
— Oberoendet i mellansättet — det finns inga vänt- eller köförlopp — bestäms av d-faktorn; Antalet typsönderfall (d) för just den nukliden (givna ZkärnladdningAmasstal), vilket skulle återfalla på SÄTTET eller fasonen som just den nukliden bildades på;
— Enligt TNED medför olika neutronkvoter detsamma som olika bildningslokaler i teorin för grundämnenas primärbildning, även inom samma himlakropp. Därmed en naturlig flora av olika möjliga kärnmässiga »inbakningsstrukturer» [främst beträffande neutrinoenergierna, lokalt] med avseende på bildningslokalens övergripande energigenomströmning — och som, enligt TNED, om en sådan fysik föreligger, skulle vara den enda aspiranten för att förklara de olika typförekomsterna i olika sönderfall för en och samma ZA-nuklid.
(Det är som grannar i samma villaområde; alla har gräsmattor, men »det växer olika saker i buskarna runt omkring»).
Allmänna Koefficientsambandet,
ref.
Allmänna koefficientsambandet
RADIOAKTIVA SÖNDERFALLETS FYSIK I TNED
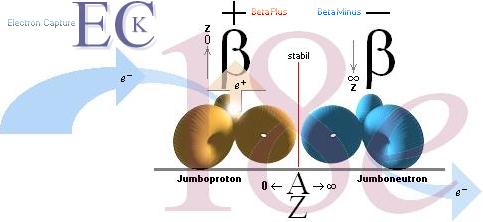
BetaEC [EC av eng. Electron
Capture, sv. elektroninfångning]:
— Atomen (eg. atomkärnan) är för lätt [har för liten massa,
»JumboProton»] för att passa sin aktuella Z-form;
— Finns det en atomtyp med lägre Z och med en massdifferens
som är MINST lika med bindningsenergin för någon av atomens [innerst]
tillgängliga elektronmassor, kan betasönderfallet ske genom elektroninfångning;
Kärnan tar upp en höljeselektron [EC] och avger motsvarande massenergiöverskott
[i form av generell gammastrålning] i
bildningen av den stabila atomen med det lägre Z-värdet [flera enskilda Z-steg kan behövas innan stabilt
tillstånd inträffar].
BetaPlus: Samma typ som EC ovan,
men atomen besitter en högre massexcess [massöverskott] lika med
MINST 2 elektronmassor [0,511×2=1,022 MeV]; Är massöverskottet till närmast
lägre Z-atom större än 2e kan moderatomen göra sig av med den massenergin genom
att, »enklare», avdela en positron; Positronen kommer sedan, i vilket fall att
annihileras tillsammans med en yttre höljeselektron
— i den aktuella moderatomen, eller i någon annan atom och
vilket i stort går på ett ut mellan atomerna som familj —
och vars totala annihilationsenergi därmed i slutänden i vilket
fall återförs i ekvivalens på den betainstabila atomens massexcess.
BetaMinus: Atomen är för tung [har
för stor massa, »JumboNeutron»] för att passa sin aktuella Z-form:
— Finns det någon atomtyp med högre Z-värde — i princip med aldrig
så litet MINDRE massa — kan moderatomen betasönderfalla dit genom att
avdela en elektronmassa på massa-energiskillnaden [gen., MINST arbetet för
ombygganden].
— I MAC gäller samma principiella funktionsbeskrivning — bara med
skillnaden att man anser att positronen resp. elektronen DELS är en PARTIKEL [i
TNED en mängd, en hop] och
DELS inte avdelas UR [eller återvänder TILL] moderkärnan [som vattendroppar UT
UR eller IN TILL vattenytan] utan SKAPAS resp. FÖRINTAS [strax utanför],
eftersom elektronen i den moderna akademins lärosystem inte ingår i
ekvivalensformerna för atomkärnans matematiska fysik. Se vidare i Atomkärnans härledning enligt TNED.
I MAC-teorin
för halveringssambandet (Se Geiger-Nuttalls
samband), här komprimerat som Allmänna Koefficientsambandet i TNED (x
sönderfallsenergin, C nuklidkoefficienten i TNED — den finns inte, explicit, i
MAC),
10log tH = A +
B[CZ/√x + D] –
E
finns ingen rent teoretisk koppling
mellan SKILDA halveringstider (tH,
konv. T½) för En bestämd nuklid med En bestämd sönderfallsenergi (x ovan) — begreppet
»sönderfallsenergi» i MAC är dessutom föremål för vissa oklarheter; dels
beträffande alfaradionukliderna och de olika alfa-kanal-energierna (det s.k.
»Q-värdet», se utförliga jämförande referensexempel i Jämförande
Exempel), och dels beträffande betanuklidernas konventionellt
benämnda förgreningssönderfall (eng. Branching Decay, partial
decay constants), typ betaEC, BetaPlus, BetaMinus för en och samma
atomnuklid (TNED‑dynamiken för dessa som i illustrationen ovan, se även
från NEUTRONEN
och Nuklidkartan
AZ ).
— Jämför 29Cu64-exemplet
i citat — nedan i tabellerad form för mera ingående jämförelse.
|
|
29Cu64
EC |
29Cu64
β+ |
29Cu64
β– |
elem. |
|
U |
63,9297590 |
63,9297590 |
63,9297590 |
u |
|
→ |
28Ni64 |
28Ni64 |
30Zn64 |
elem. |
|
U |
63,9279580 |
63,9279580 |
63,9291450 |
u |
|
Udiff |
0,0018010 |
0,0018010 |
0,0006140 |
u |
|
Ediff |
1,6775946 |
1,6775946 |
0,5719284 |
MeV |
Atomvikterna [U] här från
HOP-tabellen 1967. Används atomvikterna
från LBL 2003 ges till jämförelse motsvarande slutvärden i MeV
1,6750088
1,6750088 0,5793439
Dessa skillnader är
osynliga i den grafvisande upplösning som exemplifieras i UranIsotopExemplet [det exemplet används här generellt för att visa och exemplifiera
skillnaden i precision mellan olika teoretiska värden].
— Notera att jämförelsen
HOP[1967]/LBL[2003] inte är riktigt rättvis; de olika källverken har också
något marginellt olika konstanter för atomära massenheten som [här utan
redovisning] delvis jämnar ut skillnaderna. LBL-datat som sådant skiljer sig i
femte eller sjätte decimalen för atomviktsvärdet jämfört med HOP-källan. Dessa
smärre skillnader har här [veterligt] ingen djupare innebörd. Det är dock
viktigt att känna till någon referens som visar hur de olika källepokerna ser
ut tillsammans.
— Man intygar det också i modern
akademi — särskilt — att det är OMÖJLIGT att halveringstiden (tH), alls, kan ha
NÅGON fysikalisk variabel. Den meningen görs med hänvisning till att TEORIN för
tH-sambandet i MAC bygger på STATISTISK SANNOLIKHET, med stöd av »fundamentala
fysikaliska konstanter»:
THE DECAY CONSTANT in Hyperphysics,
http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/alptun2.html
- c2

”What could you do to change the polonium half-life? The
answer is that there is no way
to experimentally change that parameter because it ultimately depends upon the values of fundamental
physical constants.”.
— I TNED
finns inget sådant beroende.
— Medan MAC-teorin
utgår ifrån att »vattendropparna på vattenytan» (de avdelade kärnfragmenten)
också finns till INUTI vattenvolymen (atomkärnan)

BILDKÄLLA: Författarens arkiv — Tillfälligt vilande vattendroppe
på vattenytan efter dropprekyl — NikonD90 · 22Mar2009Bild139Drop16 —
Fenomengrund: [här veterligt] den avdelade droppens SPINN gynnar separationen.
— och de olika sönderfallen därför
»förklaras» av en statistisk sannolikhet [urspr. Gamows
teori från 1928] som bygger på att »den innestängda droppen»
försöker rymma modervolymen [eng. tunnelling effect] med hänsyn till »den
Coulombiska potentialbrunnen», och vilket företag fången till slut lyckas med, sambandsformen
generellt som ovan (formellt ingen skillnad mot TNED)
— finns ingenting sådant i TNED; de
avdelade kärnfragmenten existerar inte som fristående partiklar inuti kärnan
FÖRE avdelandet, utan blir vad de är just VID avdelandet: Atomkärnan
enligt TNED är massans fundamentalform; den innehåller inga
fristående beståndsdelar, men kan skrivas på sådana på samma sätt som enheten 3=1+1+1.
Se vidare från Härledningen
till sambandet för halveringstiden enligt TNED. Därmed utgår
begreppet sannolikhet HELT — i relaterad mening.
— I TNED figurerar istället en nuklidkoefficient
(C i Allmänna
Koefficientformen);
— Se även allmän beskrivning i Kombinerade Sönderfallstyper;
— Nuklidkoefficienten i TNED sammanhänger
(EVENTUELLT — vilken teori här
gäller till prövning; för att förklara »vissa fenomen» ...) med
»atomkärnans elektriska genomsläpplighet» med grund i teorin för NUKLIDENS
ENERGIGENOMSTRÖMNING (neutrinostrålning) vid DET PRIMÄRA
(kosmiska) BILDNINGSTILLFÄLLET: Samma nuklid kan bildas på flera (många) olika
sätt beroende på grundsammansättningen neutroner-protoner(Vätekärnor), i TNED
benämnt neutronkvot, och därmed i olika lokaler (inuti himlakroppar, mellan
himlakropparna), och därmed via principiellt olika neutrinobaserade
INBAKNINGSSTRUKTURER vid nuklidens bildningstillfälle;
— Grundämnesbildningen enligt TNED, med
hänsyn till den primära neutrinostrålningens komponenter, har bara betydelse i
det övergripande kosmiska sammanhanget — på grund av de höga
energiomsättningarna (jämför Udda-Jämna-serierna), och har knappast
någon betydelse i artificiella (partikelaccelererade) tillämpningar.
— Utöver den möjligheten, finns (här
veterligt) ingen annan faktor i TNED som kan påverka en och samma atomkärna i
det denna uppvisar en enhetlig sönderfallsenergi (typ BetaEC, BetaPlus) men med
SKILDA halveringstider. Det kan uppenbarligen bara vara en specifik KÄRNPARAMETER
(här C, nedan i Allmänna
Koefficientformen) som kan ombesörja en dylik fysik, och
förutsatt exakt samma sönderfallsenergier (x);
10log tH1 = A +
B[C1Z/√x + D] – E
10log tH2 = A +
B[C2Z/√x + D] – E
Alla övriga parametrar är identiska.
— Enda uppenbara skälet varför
MAC-teorin INTE kan innefatta den detaljen — en nuklidvariabel (C ovan) — är
att den statistiska sannolikhetsmodellen använder en matematisk fysik som går
ut på »bestämda fysikaliska konstanter» i sambandsformen ovan, se HyperPhysicsCitatet.
Möjliga förklaringen
till MAC-valet
FÖLJAKTLIGEN
— som enda »logiska förklaringen» till
MAC-framställningarna i ämnet (eftersom det verkar omöjligt att få fatt på
något i KLARTEXT från Expertpanelerna):
— Det modernt akademiskt antagna
SÄTTET med att tilldela halveringstidsbegrepp (olika tH-värden) för
multipla SÖNDERFALLSTYPER (konv., eng. Partial Decay Constants, Branching
Decay) beror på att man (av
teoretiska skäl, halveringstidssambandet) PRIORITERAR
sönderfallskonstanten (λ=ln2/tH) framför halveringstiden (tH=ln2/λ),
vilken senare sedan OMDEFINIERAS enligt (p, procentuella andelen i den multipla
sönderfallstypen)
λ = λ1 + λ2 +
λ3 + … ; 29Cu64Ex: 1,50422 t5 Hz
= λp1+λp2+λp3+ … ;
= λ(p1+p2+p3+ …) ; 29Cu64Ex: λ[0,43 + 0,38 + 0,19]
med motsvarande
tHn = ln2/λpn
;
— »Partiella Halveringstiderna» kan
INTE summeras meningsfullt till normalvärdet (tH) med denna metod,
tH = (ln2/λ)(1/p1
+ 1/p2 + 1/p3 + … ) ; 29Cu64Ex: 46080 S
= tH(1/p1 + 1/p2 + 1/p3 + … ) ;
eftersom inverterade procentsumman, i
så fall, blir större än 1 (här 10,22031824).
— Men: Det är ändå så man räknar — ger betydelse
åt »de partiella tH-värdena» — fackmässigt i MAC. Se exv. räkneexemplet
@INTERNET Wikipedia Branching fraction
[2011-12-15],
http://en.wikipedia.org/wiki/Branching_fraction
”For example, for spontaneous decays of
132Cs, 98.1% are ε or β+ decays,
and 1.9% are β−
decays. The partial decay
constants can be calculated from the branching fraction and the half-life of 132Cs (6.479 d),
they are: 0.10 d−1 (ε
+ β+) and .0020 d−1 (β−). The partial
half-lives are 6.60 d (ε + β+) and 341 d (β−). Here
the problem with the term
partial half-life is evident: after 346 days almost all the nuclei will
have decayed.”:
— Vi räknar från normalformen tH=6,479
d med λ=ln2/tH=0,106983667,
tH1: 6,479/0,981 = 6,604485219 d
tH2: 6,479/0,019 = 341,0000000 d
λ1: ln2/tH1 = 0,104950977 Hz
λ2: ln2/tH2 = 0,002032689 Hz
λ1+ λ2 = λ = 0,106983667
tH1+ tH2 = 53,65094694tH ≠
1tH
och vilka värden vi direkt ser
överensstämmer med Wikiartikelns.
— ENDA SÄTTET — genom någon
medelvärdessummerande form — att få tillbaka det ursprungliga normala tH-värdet
(exemplets tH=6,479 d) från »MAC-partierna» tH1&2 SKULLE bli, uppenbarligen
(ekvivalenten)
tH(6,479) = [tH1(p1=0,981) + tH2(p2=0,019)]/2
=
[6,479 + 6,479]/2 = 6,479
— Men den ordningar har ingen
representation i MAC (och inte heller i fysiken).
— I MAC-teorin låter man, tydligen, den
icke-summerande tH-bilden stå som den är: ingen tycks kommentera den, i varje
fall inte så det syns i de mest framträdande [Dec2011], allmänt tillgängliga,
webbkällorna i ämnet » partial half-life», »partial decay constant».
— ANLEDNINGEN varför begreppet för
halveringstiden (tH) i MAC får stå tillbaka för aktivitetsbegreppet (λ),
för att summera, skulle, då, enbart vara den att man INTE kan utgå, teoretiskt,
ifrån tH-formen som den bestämmande, eftersom, som nyligen påpekades (se från HyperPhysicsCitatet), teori saknas för
denna som VARIABEL i samma nuklid, och varför man istället (därmed, och
således) prioriterar sönderfallskonstanten (λ) genom att definiera
halveringstiden (tH) därifrån:
ln2
tH = —————— = T½ ....................... definitionsgrunden
i MAC för halveringstiden i multipla sönderfall
λ
— Som en del föregående citat visat (Se
från citatet i Totala
sönderfallskonstanten samt nedan från Prussin 2007), verkar den enda befintliga »direkt experimentella
grund» som alls existerar också vara densamma som mäter den procentuella förekomsten av en viss
sönderfallstyp i förhållande till alla ingående typer, alltså i förhållande
till totala sönderfallet (100%), och sedan överför den procentsatsen på
motsvarande »partial
decay constant».
se även citatdelen i Totala
sönderfallskonstanten
GoogleBooks,
NUCLEAR PHYSICS FOR APPLICATIONS — A Model Approach, Stanley G. Prussin, 2007
s52;
”The relative intensities of decay to any pair of levels is just given by the ratio of their partial decay constants. In the present case, the experimental intensities, given as the percentage of all β decays, represent the experimental measurements of the relative decay constants for β decay to each level. As in most cases, the decay probabilities vary over a very large range. In practice, the range is often limited by the sensitivity of the experimental arrangement used for the measurements.”
;
NOTERA att GRANSKNING AV citat från GoogleBöcker KAN
utestängas vid upprepad sökning eftersom [mestadels] endast en del av den
aktuella bokens avsnitt visas synliga.
M.a.o., KONVENTIONELLT räknar man (tydligen) bara med inverterade aktivitetssumman (mindre/större=p):
λ1/λ0 = a%
λ =
ln2/tH ;
radiokonstanten,
sönderfallskonstanten
”… the branching fraction … . It is equal to the ratio of the partial decay constant to the overall decay constant.”,
@INTERNET Wikipedia Branching fraction [2011-12-11]
— Se även [m.fl.]
UNIVERSITY OF WATERLOO — Radioactive Decay Energy and
Particles
http://www.science.uwaterloo.ca/~cchieh/cact/nuctek/assgn5a.html
”Note the relationship
between the overall decay constant and the partial decay constant:
Overall λ = Σ
λpartial or λpartial = fraction *
λoverall ”.
λPARTIAL = fraction
· λOVERALL
;
Wikipedia 2012, totala
sönderfallskonstanten
@INTERNET Wikipedia, Radioactive decay, Alternative decay
modes [2012-01-01]
http://en.wikipedia.org/wiki/Radioactive_decay
”When measuring the production of one nuclide, one can only observe the total decay
constant λA.”
;
λ = ln2/tH ; konstant för given nuklid och
sönderfallstyp — frekvensparameter; radiokonstanten
= ln2/N0î ;
λ1/λ0 = (1/tH)1/(1/tH)0
= (tH)0/(tH)1
= a% ;
(tH)1 = (tH)0/a% ;
(tH)1a% = (tH)0 ;
ORDNINGEN [inverterade aktivitetssumman] ÄR alltså OMVÄND — konventionella sättet:
λ = λ1 + λ2 + λ3 + λ4 + …
= ln2/tH1 + ln2/tH2 + ln2/tH3 + ln2/tH4 + …
= ln2(1/tH1 + 1/tH2 + 1/tH3 + 1/tH4 + … )
= ln2/tH ;
tH = (1/tH1 + 1/tH2 + 1/tH3 + 1/tH4 + … )–1
;
I den oberoende medelsummeringen — den relaterbara, sammanhängande logikens och fysikens mening, här helt orepresenterad i litteraturen, och här till vidare prövning för undersökande jämförande resultat — multipliceras normal-tH-värdet (alla typsönderfallen tillsammans) med den procentuella andelen (p) för det typsönderfallet tillsammans med antalet (d) typsönderfall som gäller för den nukliden. Det skulle ge motsvarande sönderfallskonstanter (λ=ln2/tH)
λ = ln2(1/tHp1d
+ 1/tHp2d + 1/tHp3d
+ 1/tHp4d + … ) ; stämmer INTE
= (ln2/tHd)(1/p1 + 1/p2 + 1/p3 + 1/p4 + … ) ; stämmer INTE
=
(ln2/tH)(p1 + p2 +
p3 + p4 + … ) ; stämmer OK
=
λ1 + λ2 + λ3 + λ4
+ … ; stämmer OK
ordningen måste stämma
EKVIVALENT på den direkt procentuella summeringen oberoende av d
och halveringstider
tH = (tHp1d
+ tHp2d + tHp3d
+ tHp4d + … )/d ; med
formell ekvivalent
= (tHd)(p1 + p2 + p3 + p4 + … )/d
ordningen måste stämma
EKVIVALENT på den direkt procentuella summeringen oberoende av d
TABELLDATA för att kontrollera ovanstående formalia, verkar emellertid INTE finns allmänt tillgängligt på webben (utom för enstaka atomers enstaka masstalsnuklider; interaktiva NUKLIDKARTOR, eng. Charts, finns på webben och som man måste knappa in särskilda nuklidparametrar, specifikt, för VARJE nuklid för att få fram enskilda data; att samla analysdata på det sättet för vidare jämförelse är uteslutet på grund av den stora mängden nuklider [tusentals] och därmed den tid det tar att genomgå varje enskild nuklid manuellt; det är bara en maskinell algoritm på en användbar, kopierbar, tabellform som kan klara den biten): Det som krävs är datatabeller över samtliga betanuklider — med VARJE betanuklid specificerad på aktuella (partiella) sönderfallsprocent. Tabellerna generellt som finns allmänt tillgängliga, ger bara det sammanräknade, totala, halveringstidsvärdet för alla de olika sönderfallstyperna tillsammans. Dessa data, som analysvärden, är därför »tämligen värdelösa». De kan på sin höjd ge en (ytterst) diffus bild av terrängen.
Varför Lambdasummeringen är OK
Varför λ = λ1 + λ2
+ λ3 + … är OK
Man kan också, eventuellt, klargöra saken så:
FORMEN för sönderfallskonstanten [konv. λ]
definitionsgrunden generellt för [allmänna] sönderfallskonstanten
[eng. decay constant]:
ln2
λ = —————— som medför tH = ln2/λ
tH
gäller med tH [konv. T½] för ALLA sönderfallets samtliga
sönderfallstyper tillsammans, alltså hela nuklidformens totala aktivitet.
— FÖLJAKTLIGEN gäller för den multipelsönderfallande
nuklidens SPECIFIKA radiokonstant [λ(n)] med p lika med procentfaktorn
definitionsgrunden generellt för SPECIFIKA sönderfallskonstanten
[eng. partial decay constant]:
ln2
λn =
—————— · pn = λ · pn
tH
— Men: Det finns ingen specifik — inneboende — koppling till
tH[n] i denna FORM, endast hela tH finns, specifikt, med i nämnaren.
— I MAC gör man, helt enkelt, en EGEN [tvungen] definition
på »partiella halveringstiden» tHn av formen
definitionsgrunden i MAC för SPECIFIKA sönderfallskonstanten [eng. partial
decay constant]:
ln2
ln2
tHn = —————— =
—————— = tH/pn
λn λ · pn
— Vilket vill säga: I modern akademi PÅTVINGAS
halveringstiden tH underordnande
av sönderfallskonstanten λ — TROTS att den senare definieras genom
den förra, nämligen generellt via sambandet för halveringstiden enligt [konv.] Geiger-Nuttalls samband:
energiberoendet, främst.
— RESULTATET, främst, blir OMÖJLIGHETEN att kunna summera
halveringstider på motsvarande procentsatser; Istället för att få procentsumman
1 för alla tH, så att tH-summeringen bildar samma dynamiska ROT som summeringen
av sönderfallskonstanterna, λ-summeringen, blir tH-procentsummeringen
ALLTID större än 1 med ovanstående MAC-metod.
— Därmed faller också hela konsistensen med föreställningen
om EN bestämd halveringstid för EN bestämd sönderfallsenergi för EN bestämd
nuklid; tH-relationerna urartar, tydligen.
— I TNED — relaterad
fysik — får man inte göra så.
— ÄR utgångspunkten den, att det är halveringstiden som
styr, bestämmer och definierar sönderfallskonstanten enligt
ln2
λ = —————— ....................... allmänna radiokonstantens definition från
halveringstiden tH
tH
med [Allmänna
Koefficientformen för halveringstidssambandet, gäller både
MAC och TNED, härlett från TNED]
10log tH = A + B[CZ/√x + D] – E
då gäller också den formen — och inget annat.
— I TNED summeras — således — halveringstiderna I PRIORITET
enligt
tH = (tHp1d
+ tHp2d + tHp3d
+ tHp4d + … )/d ; med
formell ekvivalent
= (tHd)(p1 + p2 + p3 + p4 + … )/d
ordningen måste stämma
EKVIVALENT på den direkt procentuella summeringen oberoende av d
inkluderat samma ordning som i MAC för
sönderfallskonstanterna
enligt
λ =
(ln2/tH)(p1 + p2 +
p3 + p4 + … ) ;
=
λ1 + λ2 + λ3 + λ4
+ … ;
ordningen måste stämma
EKVIVALENT på den direkt procentuella summeringen oberoende av d
— Som redan tidigare påpekats, kan MAC
inte anta den formen — eftersom teori saknas i MAC för variabla tH för samma
typnuklid [»tH kan inte påverkas»,
men vilket uppenbarligen motsägs av de multipla sönderfallens ekvivalenta
nuklider: olika tH för samma nuklid — exemplen generellt skulle här vara BetaEC
och BetaPlus], och vilken teoretiska detalj — tydligen, och uppenbarligen, i
varje fall i den här framställningens ljus — är förklaringen till varför MAC
prioriterar λ-summeringens formbild som definitionsbas ÖVER tH-formens.
Man får inte göra så i relaterad mening. Gör man det ändå, är det alldeles
tydligt ett integritetsbrott: ett Naturbrott.
— Resultatbilden i TNED
kommer, alltså, att ge helt andra översiktsbilder [Se 29Cu-64-exemplet] i diagrammen för
halveringstider-sönderfallsenergier. Medan MAC hävdar [till experimentell
prövning] typen 1/a + 1/b + 1/c + … i
de d stycken procentdelarna a+b+c+…=1 för halveringstiderna, hävdar TNED motsvarande
ad + bd + cd för respektive sönderfallstyp och med totalsumman [ad + bd + cd +
…]/d=1, samma som uppställningen ovan.
— Jämförelserna försvåras [ytterligare] av föreställningen
om KINETIK i MAC för olika detaljer [neutrinos] i sönderfallsenergierna, och
som i MAC föranleder ytterligare uppdelningar [som urskiljer flera komponenter
i effektiva sönderfallsenergierna — massa/energiskillnaden räknat efter
atomvikter mellan instabila och stabila — typ neutrinoenergier och
gammastrålning. I TNED behandlas dessa som EN komponent i sönderfallsenergi. Se
utförligt från Härledningen].
Totala radioaktiviteten (λ) står för given nuklid ALLTID i relation till totala sönderfallet oberoende av antalet sönderfallstyper — och ska därför också, regelmässigt, ställas i relation till den procentuella andelen av respektive sönderfallstyp, precis som ovan och som också tillämpas korrekt i konventionella termer (p, aktuell procentsats):
λ = (ln2/tH)(p1 + p2 + p3 + p4 + … ) = λ1 + λ2 + λ3 + λ4 + …
DÄREMOT FÅR INTE i relaterad mening — som man ändå gör konventionellt — halveringstiden räknas som funktion av partiella aktiviteten (radio- eller sönderfallskonstanten λn enligt λn=ln2/tHn). Därför nämligen att de partiella halveringstiderna måste avse individuella, oberoende nuklidsönderfall — INTE explicit beroende av relationen till den procentuella andelen av respektive sönderfallstyp — alltså inte beroende av sönderfallskonstanten explicit (λ=ln2/tH), utan beroende av (halverande) sönderfallstiden (tH=ln2/λ), som definierar sönderfallskonstanten (som sönderfallstidens invers), analogt frekvensen eller aktiviteten — utan även beroende av den procentuella andelen i relationen till antalet (d) ingående sönderfallstyper.
— Halveringstidernas partiella värden måste enligt det resonemanget alltså bestämmas enligt (tHn=tHpnd)
tH = (tHp1d + tHp2d + tHp3d + tHp4d + … )/d = (tHd)(p1 + p2 + p3 + p4 + … )/d = tH(1)d/d = tH
— Medan antalsdelen är egal för den partiella aktiviteten (det är bara procentsatserna som summeras rakt upp till 100%), är den avgörande för den partiella halveringstiden (antalet nuklidskilda halveringstider som summerar hela sönderfallets 100%). Därför måste, i relaterad mening, tH och λ bestämmas efter sina specifika kriterium, som ovan.
Skulle ovanstående antagna samband för de partiella halveringstiderna visa sig vara felaktig, har utläggningen i vilket fall tjänat syftet att framställa resultatbilden för en exemplifierad felform. Det enda som (nämligen, här veterligt) kan visa vad som gäller, är en sammanställning av sönderfallens mera omfattande data för att därigenom få fram eventuella STRUKTURER som kan visas sammanhänga med de olika matematiska sambandsformerna.
Medelvärdessumman i TNED
för halveringstiderna
Inbördes självständigt radioaktiva nuklider bör, som det möjligen får förstås, vara (mestadels) självständigt oberoende av varandras sönderfallsdynamik, så att varje TYP kan uppvisa sin egen individuella karaktär. Detta ansluter också till grundteorin (både i TNED och MAC) att det finns EN bestämd halveringstid för EN bestämd instabil nuklid med EN bestämd sönderfallsenergi; Se sambandet för halveringstiden (konv. Geiger-Nuttalls samband).
Men en regelrätt SUMMERING av den antydda typen T(½)0=T(½)1+T(½)2+… avspeglar ingen sådan oberoende fysik; förutsättningen för typen T(½)0=T(½)1+T(½)2+… är, tydligen, att en successiv KÖ »bildas», så att den ena nukliden väntar med sitt sönderfall tills den andra är färdig, och så, att inga överlappande sönderfall sker mellan de olika typgruppernas nuklider.
— Mera relevant för den självständiga, oberoende, typen är istället att sönderfallen sker spontant, oberoende av varandra, och därmed via en INRE medelvärdesbildning, i netto samma som T(½)0=T(½)1+T(½)2+… men på formen
T(½)0 = [T(½)1 + T(½)2 + T(½)2 + …]/d
T(½)0 = [aT(½)0 + bT(½)0 + cT(½)0 + …]/d
T(½)0 = T(½)0[a + b + c + … = d]/d
med d=antalet sönderfallstyper och a+b+c+…=d med abc… som procentuella andelarna, respektive, gånger d;
T(½)0 = T(½)0[ad + bd + cd + …]/d
T(½)0 = T(½)0[ad + bd + cd + …]d/d
T(½)0 = T(½)0[ad + bd + cd + 1 ]d/d
;
tH = tH(1/1)
= tH([a + b + c = 1]/1)
= tH([a + b + c = 1]/1)
= tH([a + b + c = d]/d)
= tH([ad + bd + cd = 1d]/d)
;
Jämför 29Cu64-exemplet:
;
tH = tH([0,43]3 + [0,38]3 + [0,19]3)/3 ; TNED-summeringen
= tH([1,29 + 1,14 + 0,57)/3
= tH([1,29 + 1,14 + 0,57)/3
;
=
tH/[0,43] ; tH/[0,38] ; tH/[0,19] ; MAC-summeringen
= tH(2,33) ; tH(2,63) ; tH(5,26) ;
Om INTE nukliderna »väntar på varandra» enligt de procentuella fördelningarna a + b + c = 1, utan istället antar en MEDELVÄRDESBILDNING utöver (genom) varandras sönderfallande domäner, fås medelvärdesbildningshalveringstiderna enligt
tHad + tHbd + tHcd + ...
med medelvärdesbildningen tH för hela nuklidgruppen (samma masstal, samma atomnummer)
tH = tH([ad + bd + cd]/d)
= (tHad + tHbd + tHcd)/d
d=multipliciteten i det kombinerade sönderfallet (antalet olika sönderfallstyper) och a+b+c+...=1 lika med den procentuella summan av de enskilda sönderfallens delbidrag.
tH-universalen för betanukliderna i TNED
Med fortsättning från Nuklidfaktorn
i betasönderfallet
— Betasönderfallens b-kurvor (Se Illustration AlfaBeta) uppvisar i stort sett 100 ggr lägre b-värden (för b-termen, se Nuklidkoefficienten) än motsvarande för alfasönderfallen (Se från Generaliserade kurvpassningens allmänna alfaradioisotopbild [allmänna radioisotopbilden]). Denna omständighet gör att ingen direkt motsvarande generaliserad betaform finns; övre kurvgränsen går vid b=8π. För att normalisera en motsvarande jämförande grafisk bild, kan vi därför »låna från alfakurvan» genom en relationskoefficient — och för att på den vägen eventuellt finna någon liknande allmän passning i de olika betavärdena. Beskrivningen närmast nedan visar hur anpassningen görs.
I halveringstidssambandets allmänna form (Se Slutformen; för b-koefficienten, se Nuklidkoefficienten)
tH = 1S(ln2)ebeZ/√2mE
skiljer sig sönderfallstyperna alfakärnsönderfall och betasönderfall endast med avseende på kärnladdningstalet (atomnumret Z) och den avdelade kärnmassan, respektive hela heliumatomen [m(α)=4,0026031u] och hela elektronmassan [m(β)=0,000548598u], massvärdena här från HOP-referensen.
— Med den allmänna formen för halveringstidens 10-logaritm,
10log tH/1S = (1/ln10)[beZ(2mE)–0,5 + ln(ln2)] ;
[beZ(2mE)–0,5 = (10log tH/1S)(ln10) – ln(ln2) ;
förhåller sig sönderfallstyperna alfa och beta till varandra genom de variabla sönderfallsenergierna enligt
bα/bβ = [Z/√2m]β/[Z/√2m]α
= [1/√2mβ]/[2/√2mα]
= [√ mα/mβ]/2
= [√ (4,0026031)/(0,000548598)]/2
= 42,70848422 ;
För att få ANALOGT [nuklidkoefficient-] JÄMFÖRANDE
grafformer alfa-beta ska, tydligen, alfaformens typgraf förminskas 42,7 ggr.
— Se vidare översiktsillustration i Betasönderfallande nuklider.
Graf; (1/ln10)[(174.51)[(1/42.7)(x)'–0.5]+ln(ln2)]
— Allmänna tabelldata från epoken 1900-talet [VNS/HOP] visar att alla kombinationer [alfa
med beta] finns exemplifierade [utom samtidiga BetaMinus BetaPlus].
— För dessa multipla sönderfallstyper anges dock endast en
enda specifik halveringstid.
— Det faktum att dessa äldre tabelldata — således — INTE är
strikt upplysande i värdeformerna, medför också att motsvarande utvärderingar i
analysen får stå tillbaka, tills ev. vidare uppgifter framkommer. Det är ännu
[Dec2011] inte klarlagt huruvida sådana, allmänt tillgängliga, tabelldata ens
finns. Webben innehåller förvisso många referenser på området, men är samtidigt
också svårtolkad, och delvis svårtillgänglig. Strävan är här att fortsätta
sökandet efter användbara tabelldata [tusentals uppgifter samlade på en
användbar form] som kan tjäna för en vidare jämförande översikt.
Med alfaformens tH-universal [[Tabell2KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]]
10log tH/1S = (1/ln10)[b[2e/(m·T6)]0,5(EMeV)–0,5 + ln(ln2)]
10log tH/1S = (1/ln10)[b[6,94348949](EMeV)–0,5 + ln(ln2)]
på absolut största b-värdet bMAX=8π
10log tH/1S = (1/ln10)[(8π)[6,94348949](EMeV)–0,5 + ln(ln2)]
10log tH/1S = (1/ln10)[(174,5089246)(EMeV)–0,5 + ln(ln2)]
skulle då ges för betakurvorna motsvarande »tHbetaUniversal»
10log tH/1S = (1/ln10)[(1/42,70848422)(174,5089246)(EMeV)–0,5 + ln(ln2)]
10log tH/1S = (1/ln10)[(4,086048189)(EMeV)–0,5 + ln(ln2)]
Graf; (1/ln10)[[(4.086)(x)'–0.5]+ln(ln2)]
I tH-universalen visas särskilt för alfasönderfallens del hur en generaliserad kurvform — från tH-formen ovan — kan användas för att, generellt och översiktligt, få en HYFSAD »landskapsbild» av HUR alfasönderfallens nuklider ligger fördelade i nuklidkartan generellt.
— Vi kan få samma översiktsbild för betasönderfallens förekomster genom att utnyttja ovanstående numeriska alfa/betarelation (~42,7); alfakurvans tH-universal dämpad 42,7 ggr.
— Översikten nedan i Betasönderfallande Nuklider visar hur den resulterande brantare tH-betagrafen framträder tillsammans med de (tydligt bristfälliga, se utförligt från Nuklidkoefficienten i Kombinerade sönderfallstyper) tabelldata som här använts från de äldre tabellkällorna i VNS(1976) och HOP(1967).
— Förhoppningen här (Dec2011) är att få fram mera exakt jämförande tabelldata som kan visa OM ev. också betavärdena följer någon generaliserad kurvtrend. Jämför AlfaIsotoperna.
Se även från Betasönderfallets
Matematik i TNED
Betasönderfallande nuklider
———————————————————————————————
TabellÖversikt — notera att betapunktvärdena ännu [Dec2011]
HÄR är specificerade endast på den allmänna halveringstiden [samma tH-värde för
alla sönderfallstyper, där flera sådana förekommer]; Se vidare förklaring från Kombinerade Sönderfallstyper.
Nedan: Översiktlig jämförelse mellan betasönderfall [Tabell VNS1976/HOP1967]
och alfasönderfall [Tabell Wiley 1999].
Punktdiagrammen redovisar VERTIKALT 10-logaritmern för halveringstiderna i
sekunder, HORISONTELLT den motsvarande sönderfallsenergin i MeV
[MegaElektronVolt] enligt massa-energidifferenserna med räkning via atomvikter. Datastocken i
punktdiagrammen nedan är speciellt för betanukliderna INTE optimalt omfattande
[många ytterligare är kända, men som inte finns med här], utan avspeglar endast
de förekomster som tagits upp av respektive tabellkälla.
— Tillgången på kopierbara tabellverk på webben för
jämförande analyser är [ännu Dec2011] relativt begränsad; Dels beroende på att
originalen, om man hittar några alls, ofta med tusentals poster, inte alltid är
enkla att automatisera på extraherade tabelldata — man är i stort hänvisad till
förekommande PDF-dokument; Dels beroende på synnerligen omständliga
sökkriterium som måste uppfyllas för att alls hitta NÅGOT; Och dels beroende på
att inte alla källor är allmänt tillgängliga.
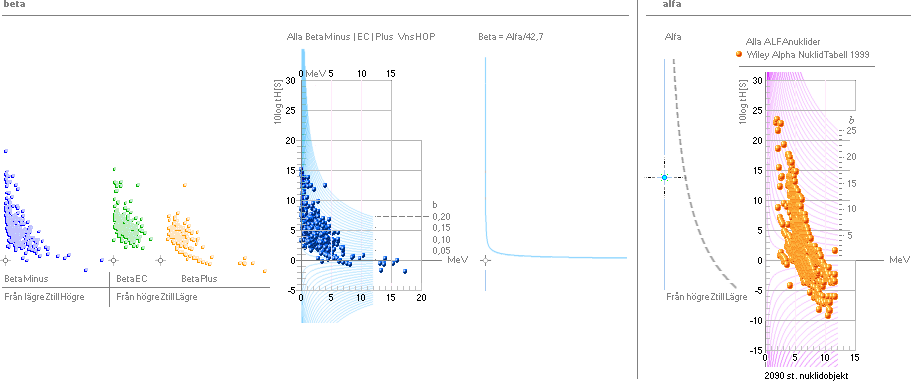
KOMPLIKATIONERNA I
BETASÖNDERFALLET — för att jämföra med kärnsönderfallet generellt — beror
delvis på att betasönderfallets tre olika SÄTT — BetaMinus, BetaEC [EC för eng. Electron Capture, sv., elektroninfångning],
BetaPlus — också uppvisar olika Z-riktningar i sönderfallen.
— Medan kärnsönderfallen
generellt [t.ex. alfasönderfallen, höger ovan] uppdelas på lägre Z-komponenter
från en given modernuklid, uppvisar BetaMinus omvändningen: från lägre Z till
ett högre; BetaEC och BetaPlus däremot Z-sönderfaller analogt med
kärnsönderfallen: från ett högre Z till ett lägre.
— Medan alfasönderfallen
uppvisar en generell kartbild [Se Allmänna
RadioIsotopbilden] som tämligen väl följer den generaliserade tH-formens kurvbild
[Se Allmänna
tH-sambandet], streckad ovan höger, finns ingen lika »enkel och tydlig» passning
i betafallen [med referens till ovanstående
givna datastock].
— NUKLIDKOEFFICIENTEN
I TNED för betasönderfallen [faktorn b, Se Nuklidfaktorn
i Betasönderfallet] är, punktdiagrammet [blått] ovan mitten, grovt 100ggr lägre
jämfört med alfasönderfallens b‑värden. Det ger en motsvarande
generaliserad tH-kurva för betasönderfallens nuklider [blå kurvan ovan] lika
med alfakurvan dividerad med 42,7 — grovt ett rektangelhörn.
— Med den formen
[kurvfotens praktiskt horisontella utsträckning] blir det praktiskt taget
uteslutet att kunna samla flera [än två] betaindivider i samma kurvavsnitt med
avseende på kollektiva Z-grupper.
— Vilket vill säga: Betasönderfallens
förekomster kan inte på samma sätt som alfasönderfallen beskrivas i någon
direkt uppenbar sammanhängande kartbild [med
referens till ovanstående givna datastock]:
— Bilden för
betasönderfallen är påtagligt fragmenterad.
— I MAC figurerar olika
teoretiska närmanden som PÅSTÅR möjligheten att beräkna sönderfallstider för
betanuklider från kända sönderfallsenergier. Dessa referenser är emellertid [ännu Dec2011] så komplicerade,
abstrakta [och i avsaknad av begripligt utläsbara resultat] att ytterligare
omnämnanden här helt lämnas för vidare: det finns, här veterligt, inga
jämförande resultatdata att studera [på något
för läsaren begripligt sätt].
— I fallet med
alfasönderfallens teoretiska precision: se till jämförelse Särskilda
Exempelutdrag [utbytet är (ännu 2011) magert, långt ifrån någon användbar
naturvetenskaplig precisionsmatematik].
Med hjälp av basdata från ovanstående källor [Tabell VNS1976/HOP1967] kan vi studera en del allmänna
ordningar som — möjligen — underlättar överblickbarheten i den övergripande
bilden av sönderfallen [och vetenskapen om deras natur], så som dessa får
förstås enligt TNED;
BetaMinus |
BetaEC |
BetaPlus |
Alfa
— För allmän orientering i konventionella termer, se främst
[Dec2011]
WIKIPEDIA Radioactive decay
http://en.wikipedia.org/wiki/Radioactive_decay
HYPERPHYSICS Radioactivity
http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/radact.html
Diagrammen nedan — med
tabelldata från VNS1976/HOP1967 — visar
— HUR de tabellspecifika
halveringstiderna [10log tH] varierar med sönderfallsenergierna [MeV] i de tre
olika betafallen — samt för jämförelsen också i alfafallen [från en särskild
webbkälla, se underst, med ett mindre antal redovisade alfaradionuklider];
MeV-värdena inte explicit angivna, tabellerna har ordnats efter stigande
MeV-värden i numrerat antal endast;
— HUR nuklidkoefficienten
[b-värdena, se b-koefficienten i exponenten till tH-universalens betaform] varierar efter motsvarande
växande MeV-värden i de aktuella förekomsterna;
— HUR halveringstider
[10log tH] och sönderfallsenergier [MeV] varierar med växande MeV-värden för
datastockens konstanta b-medelvärde;
— HUR halveringstider
[10log tH] varierar med avseende på växande nuklidkoefficient [b-värdet];
— Den karaktäristiska
sönderfallstypen enligt TNED, som nedan illustrerat ikoniskt i vänstra
figurdelen [Se även översiktsbeskrivning i Allmänna
Koefficientsambandet]:
— RÖD KURVA visar
sönderfallsenergin för vertikalskalan i MeV, BLÅ KURVA visar motsvarande
halveringstiderna i deras 10-logaritmer [10log-värdet samma som exponenten till
10 i sekunder, typ skalans 5 som 10^5 = 100 000 sekunder], ORANGE KURVA visar
motsvarande variationer i nuklidkoefficienten enligt TNED.

BetaMinus: samma som
elektronemission, anges vanligen β–. Atomen går från en lägre kärnladdning
[Z] till en högre, alltså mot typen tyngre nuklid, den avdelade elektronen
stannar kvar inom atomen;
— Sönderfallsenergin
kan [därför], i princip, vara hur liten som helst, det som gäller är att det
finns någon stabil produkt vars atomvikt är mindre än den betainstabilas.
— Se även Elektronexperimentet från
1957 som visade att atomen emitterar elektroner-positroner
’företrädesvis i spinnriktningen’.

BetaEC: [EC här från eng.
Electron Capture, sv., elektroninfångning]. Atomen går från högre till lägre
kärnladdning [Z];
— Sönderfallsenergin
minst lika med bindningsenergin för den elektron som atomkärnan fångar upp.
BetaEC figurerar ofta tillsammans med/som alternativ till BetaPlus, nedan.

BetaPlus: samma som positronemission,
anges vanligen β+, även samma nettoverkan som BetaEC, se närmast ovan,
fast tvunget med större sönderfallsenergi;
— Sönderfallsenergin minst
lika med den avdelade positronens massenergi plus en elektron [0,511×2=1,022
MeV], eftersom den avdelade positronen utanför atomkärnan i vilket fall kommer
att annihileras tillsammans med någon yttre elektron, och den energiräkningen
bara har den ansvariga betainstabila atomen att återfalla på.
— Se även Elektronexperimentet från
1957 som visade att atomen emitterar elektroner-positroner
’företrädesvis i spinnriktningen’.

Alfasönderfall: generellt [i TNED] samma som kärnsönderfall
av alla möjliga typer. Kärnsönderfallen i allmänhet uppvisar avdelning av
en Heliumkärna [2He4], vilken procedur gett Heliumkärnan namnet »alfapartikel»,
grek., lilla a, α ;
— Sönderfallsenergin
är naturligt [något] större än motsvarande betasönderfallsenergier, samt
nuklidkoefficienten [b-värdena] tydligt runt ca 100 ggr större för alfa än för
betafallen.
— NOTERA att b-koefficienten inte ingår i den moderna
akademins teori i ämnet.
Alla källdata till ovanstående elektronsönderfallsdiagram
från [Tabell VNS1976/HOP1967].
Alfasönderfallets källdata särskilt från separat webbkälla [Se även denna i Källexempel]:
ALPHA SCIENCES, Alpha Sciences Inc.,
1999-2009, se http://www.alphacounting.com/increasing_alpha_emitters.html
Teorin
för betaemissionen enligt TNED END.
2011XI5
ALLMÄNNA WEBBREFERENSER
Bromsstrålning, Feynmandiagram och Tidssymmetri
(»stoppstrålning», samma som
induktionseffekten från accelererande/retarderande
elektriska [elektroner] laddningar);
Notera att
FeynmanDiagrammen [se särskild termbeskrivning i
exv. Wikipedia, Feynman diagram] i figurerna nedan INTE
tar hänsyn till den aktuella naturliga attraktionen som finns mellan p+ och
e– i neutronsönderfallets komplex;
— Själva förklaringen till att e– accelereras i neutronsönderfallet,
enligt experimentella observationer (scintillationssensorer), ingår inte i
beskrivningen — det finns heller inga webbkällor som ger upplysning i saken
[Okt2011]:
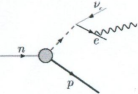 Electron Bremsstrahlung
Electron Bremsstrahlung
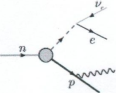 Proton
Bremsstrahlung
Proton
Bremsstrahlung
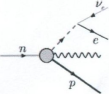 Direct Emission from Weak Vertex
Direct Emission from Weak Vertex
;
Källa:
RADIATIVE NEUTRON DECAY — Rare Decay Modes of The Neutron
J.Byrne, Department of Physics and Astronomy, University of Sussex, Brighton BN1 9QH, Sussex, U.K.
TPFNP Workshop, USC, Columbia SC, October 14, 2005
http://www.physics.sc.edu/TPFNP/Talks/JBYRNE.pdf
;
”
In addition to its normal three-body decay process
n → p + e– +ve
the neutron also decays weakly through tw processes:
1. Radiative Neutron Decay.
n → p + e– +ve + γ
2. Decay into an Antineutrino
and a Hydrogen Atom.
n → H + ve
”. (Pilsymbolen → i källan har dubbelstreck typ =>).
Tidssymmetriska detaljer
ingår i det etablerade sättet
NOTERA OCKSÅ de stundtals tidsomvända
partikelpilarna i FeynmanDiagrammen
(vissa, inte alla, källor), Jämför:
”Antimatter
Feynman suggested that a positron (or any other antiparticle) is like a particle travelling backwards in time. So, on a Feynman diagram, this is represented as a line with an arrow pointing downards.”,
SCIENCE & TECHNOLOGY datumuppgift
saknas — Feynman diagrams
http://resources.schoolscience.co.uk/STFC/16plus/partich6pg3.html
Se även (ingen direkt KLAR beskrivning …):
“Feynman avoids exposing the reader to the mathematics of complex numbers by using a simple but accurate representation of them as arrows on a piece of paper or screen.”,
”(These must not be confused with the arrows of Feynman diagrams which are actually simplified representations in two dimensions of a relationship between points in three dimensions of space and one of time.) ”,
“The amplitude-arrows are fundamental to the description of the world given by quantum theory. No satisfactory reason has been given for why they are needed. But pragmatically we have to accept that they are an essential part of our description of all quantum phenomena.”,
@INTERNET Wikipedia Quantum electrodynamics 2011-11-07
En annan källa uttrycker saken,
”One intriguing feature of Feynman diagrams is that antiparticles are represented as ordinary matter particles moving backward in time—that is, with the arrow head reversed on the lines that depict them.”,
ENCYCLOPAEDIA BRITANNICA — Feynman
diagram (från Google-sökning 2011-11-07) inget artikeldatum anges —
1632 kanske …
http://www.britannica.com/EBchecked/topic/205708/Feynman-diagram
Inte alla etablerade webbkällor använder den konventionen; Jämför HyperPhysics (Neutron Decay).
I TNED genomgås med särskild noggrannhet betingelserna för fysikens lagar som garanterat icke tidssymmetriska, se från Tidens pil med utförliga exempelgenomgångar i Åldrandets princip; samtliga fall genomgås.
— W-bosonen (W–) som figurerar i den moderna akademins neutronsönderfall sägs besitta en vilomassa ”almost 100 times as massive as the proton” [ref., samma källa som nedan]. Hur kommer en sådan Artikel in i bilden med en enda neutrons sönderfall?
”The W bosons have a positive and negative electric charge of 1 elementary charge respectively and are each other's antiparticle. The Z boson is electrically neutral and its own antiparticle. All three of these particles are very short-lived with a half-life of about 3×10−25 s.”,
@INTERNET Wikipdeia W and Z bosons 2011-11-07
Jämför utdrag från PhysicsForums:
”An isolated neutron, changes to a proton within 15 minutes by one of the down quarks becoming an up quark.
Why does the change need to include the intermediate step of the heavy W boson?
Where did all the W boson mass come from and where did it go?”,
;
“… you can assume that momentum is conserved, and say that the energy of the W is different from what is given by the formula above, i.e. that energy is briefly not conserved, but it's OK because of the short time involved in the decay, and the Heisenberg Uncertainty Principle.”
PHYSICS FORUMS — Neutron to Proton
http://www.physicsforums.com/showthread.php?t=241405
:
Anledningen bakom
ovanstående moderna utflykt:
— Plancks strukturkonstant ingår inte i den moderna
akademins föreställningssätt: atomkärnans härledning.
— Därmed finns i MAC bara EN osäkerhetsnivå
[Se Osäkerhetsprincipen]. Nämligen DEN som
bestäms uteslutande av makrofysikens elektriska elementarkvantum
[elektronmassan] — och som därmed FÖRBJUDER modern akademi att presentera
ÅSKÅDLIGA BILDER AV ATOMKÄRNAN.
— I TNED finns inte den
begränsningen; Atomkärnans
struktur av obegränsade fraktalnivåer med motsvarande Plancknivåer [h/n]
gör att den modernt akademiskt antagna föreställningen om en ABSOLUT osäkerhet
i nivån n=1 bortfaller;
— Enligt TNED [relaterad
fysik] finns ingen absolut osäkerhet i fysiken; alla osäkerheter är RELATIVA
till aktuell (kärn-) nivå: pennan ritar bara precis så fint som den är vässad.
— Därför är också
ovanstående citerade akademiska hållning i ämnet, sett från TNED, ren
vetenskaplig FIKTION — ett beskrivningssätt som måste KOMPENSERA sig med
UPPFUNNA former i ersättning för de naturliga SOM INTE ERKÄNNS.
M.a.o., och i modern akademi :
— LÄS: Du får fråga. Men du kommer aldrig någonsin att få ett svar.
— Modern akademi har för länge sedan (i stort med början från slutet av 1800-talet) frångått kausaltänkande AV PRINCIP genom flera olika historiska tillfällen.
— Uppfattningen att fysikens lagar är tidsreversibla, att massa kan skapas ur ljus, att elektronen får uppfattas som en punktpartikel med oändlig massa, med flera liknande, formar en helhetsbild i vars allmänna kapitala förmågor man just kan undra över vad INTE kan »beskrivas och förklaras». Exemplet med W-bosonen — runt hundra neutronmassor — i neutronsönderfallet ovan är ytterligare ett exempel.
Partikelbegreppets
gränsform i TNED
— Jämför f.ö. tidsuppgiften på W-bosonens existens: runt t25 S (t för 10–), Wikipediacitatet ovan:
— I TNED bestäms den absoluta fysikaliska gränsen för begreppet partikel av
den minsta atomkärnan
(neutronen från Plancks konstant eller PLANCKRINGEN h=mcr)
med absolut maximala periferispinnhastigheten som ljusets topphastighet (c0) med den TID (t) som den första underfraktalnivåns tre ekvivalenta formringar kräver för ETT fullbordat varv;
— Nämligen i definitionen av atomkärnans impulsekvation, J(0K)+3J(1K)=0; Tiden beräknas genom omkretsen 2πR med inre ringspinnets radie nära lika med halva neutronradien (2R=r=1,32 t15 M med neutronmassan 1,0086652u med u=1,66033 t27 KG, c0=2,99792458 T8 M/S och Plancks konstant h=6,62559 t34 JS)
t = πr/c0 = π(1,32 t15 M)/(2,99792458 T8 M/S)
=
1,3832577 t23 S ........................................... absolut minsta möjliga VARAKTIGHET för begreppet
partikel i relaterad fysik
Formationer kortare än den gränstiden saknar ENLIGT TNED varje möjlighet att framstå som något fysikaliskt entydigt partikulärt (nukleär massform).
— Partikelbegreppet är i relaterad fysik (TNED) alltså inte alls tillämpligt på tidsintervall MINDRE än avrundat 1,38 t23 S. Det är 46 gånger [ 1,38 t23 / 3 t25 = 46] den angivna Wikiartikelns W-bosons livstid. I TNED blir en sådan massform, tvunget, en utpräglad tillfällig kraftform (oftast via en enorm chokmassa [Se KRAFTCHOKNING i MAFEM, massa-kraftutbytesmekanismen som beskrivs via Planckekvivalenterna] som påtvingas ordinära kärnpartiklar genom lika enorma partikelacceleratorer); Ingen partikel [J(0K)+3J(1K)=0].
— Det ger ytterligare en anledning (att lägga till de övriga) varför modern akademisk teori och TNED inte kan anställas i någon inbördes (rättvis) jämförelse.
— I TNED är (och förblir) modern akademi en PRIMITIV inrättning. Exemplen ovan enbart understryker.
Den som försöker FÖRSTÅ KÄRNFYSIKEN från den moderna akademins utgångspunkt, måste (således) beflita sig om att ANTA REGELVERKET som bla. utsäger oändlig massa för elektronen som oändligt liten. Bara av den anledningen reduceras alla möjliga paralleller till TNED — till exakt noll.
— I TNED är varken elektronen en partikel eller har oändlig massa — elektronen i TNED är en hop, en mängd. Se utförligt från atomkärnans härledning och elektronmassans komponenter, om ej redan bekant.
Angående detektering av elektroner i betasönderfall
Citat från webbkällor
Impuls (eng. linear momentum) och rörelseenergi (kinetisk
energi) för elektronen i samband med betasönderfall
Momentum and kinetic energy spectra of electrons and
positrons
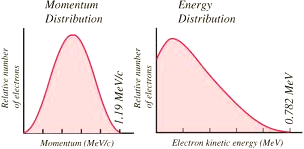
Decay of the Neutron
http://hyperphysics.phy-astr.gsu.edu/hbase/particles/proton.html
;
Se även från samma källa
Energy and Momentum Spectra for Beta Decay
http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/beta2.html
Fermiteorins allmänna kurvformer
för ändamålet — statistisk kvantmekanik
Samma TYP av p-E-grafer som i HyperPhysics, även i
http://socrates.berkeley.edu/~phylabs/adv/ReprintsPDF/BRA%20Reprints/03%20-%20Beta%20Decay.pdf
;
Se även
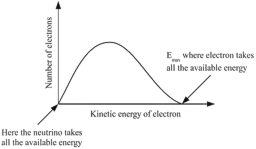
UNIVERSITY OF SYDNEY — Experiment 20. Beta Decay, s20-3
http://www.physics.usyd.edu.au/pdfs/current/sphys/3yr_lab/Expt_20.pdf
Bl.a. Bi-207 används som
betaemitterare, dokumentet beskriver hur elektronerna detekteras med moment och
energier.
Neutronsönderfallets detektering (källan använder dubbelstreckad pil samt strecket under v-tecknet över detta för »anti-»):
“The emission
of a weak continuous γ-ray spectrum
during the β-decay of the free neutron
n → p + e− + νe + γ (1)
provides an example of a general process described as
internal bremsstrahlung, which results from the dis-
placement
of electric charge which occurs whenever
charged particles are created or destroyed.”,
JOURNAL OF RESEARCH OF THE NATIONAL INSTITUTE OF STANDARDS AND TECHNOLOGY, Volume 110 Number 4 July-August 2005
Search for Radiative β
-Decay of the Free Neutron
Byrne et al., (Aug2004); Webbkälla genom
GoogleSearch
Search for Radiative
β-Decay of the Free Neutron — Quick View
http://docs.google.com/viewer?a=v&q=cache:K7b8gu-WdZAJ:nvl.nist.gov/pub/nistpubs/jres/110/4/j110-4byr2.pdf+neutron+decay+energy+distribution+filetype:pdf&hl=en&gl=uk&pid=bl&srcid=ADGEESiiLbm_vRARdGNdyEc49Y9YHzQjg4pmqefWKt8qXPtXuVxKbSXT488rcRMo3-aDMaDQKO3MARpRsTwaC4dbH2SDnqdcioZWXxR8yNM62rg2p_6Q2q2etP-INkt8MFhJLQ0WZymZ&sig=AHIEtbTEgkScRyGKvCeV9vUnBRexWNwYEQ
In general; electron
acceleration in beta decay
Electron acceleration in neutron decay?
Om vi tar det från MAC (Modern akademi):
neutron →
Väteatomkärna(e+) + accelererad elektron(e–)?
— Hur kan t.ex. en elektron detekteras som framträder ur ett neutronsönderfall och som alltså kommer att tillhöra en Väteatom med dess protonkärna?
— Borde inte den framträdande elektronen OMEDELBART associera sig med SIN moderkärna? Vad har en nybildad elektron att göra »ute i buskarna», och framför allt: Hur kommer den ut? Varifrån kommer PUTTEN?
— Atomkärnan är ju positiv, elektronen negativ, så hur fasen går det ihop?
— Elektronen borde, tycker man, STANNA KVAR (om den inte absorberas, helt).
— Man kan ju inte, direkt, hänföra »elektronens UTGÅENDE acceleration» till en reaktion mellan den extra +1e-laddning som påförs neutronkärnytan i formen av den nybildade protonkärnan och den negativt laddade elektronen, det är absurt. Så, varifrån kommer »accelerationskraften»?
— Electron acceleration in neutron decay?
— Hur kan elektronen
accelereras i neutronsönderfallet?
Det verkar inte finnas något svar på den frågan — i
etablerade kvarter.
— "beta decay electron acceleration", No results found. (7Okt2011).
— "electron acceleration in beta decay", No results found. (7Okt2011).
— "beta decay accelerated electron", No results found. (7Okt2011).
Jämför:
“Because the protons in the nucleus and the b particles have opposite charges, they attract each other, and the b– must therefore acquire sufficient kinetic energy to overcome this attraction in order to escape the nucleus. This has been likened to a particle having sufficient energy to crash through the walls of a well.2 In some b– emitters, the successful escape of a b‑particle into the continuum is a relatively infrequent occurrence—hence the inferred long half life (t½) of the nuclide.”,
Billion-Fold Acceleration of Radioactivity Demonstrated in Laboratory
John Woodmorappe, August 1, 2001
http://www.answersingenesis.org/articles/tj/v15/n2/acceleration
;
Underförstått i MAC:
— Elektronen accelereras inte
av någon elektrisk laddning, utan av någon form av stötande icke-elektriskt
kopplande kraft.
— I varje fall i TNED är atomkärnan en sammansatt
(ekvivalent) ±e-struktur som bara har just en elektromagnetisk mekanik att
uppvisa; intag och avdelning kan bara ske elektromekaniskt — vilket i
±e-strukturens ljus blir en helt enkel avhandling; atomkärnan justerar själv
balansräkningen i ±e-regionen för att utge, eller inta, någon komponent.
— Planckekvivalenterna har redan, noga,
genomlyst det kapitlet; massökningseffekter kan bara sammanhänga med elektriska
laddningar som accelereras av ett elektriskt fält i ett slutet elektriskt
system (typ atomkärna-elektron) där totala massan bevaras intakt.
— Den delen hänger (alltså)
inte riktigt med i MAC;
— Man räknar (tydligen) helt
kallt med »någon form av mekanism» — som saknar generell begriplighet.
;
Hur kan elektronen accelereras i
neutronsönderfallet?
TNED
— jämför enkelheten i TNED:
Neutronsönderfallet:
Elektronmassans komponenter frigörs successivt från kärnbrunnen
[via en komplex
±e-transaktion som kan både ta emot och avdela såväl +e som —e] under hela
betasönderfallets fas, enligt TNED.
— Men ingenting händer med elektronen förrän HELA
elektronmassan — elementarladdningskvantumet — har avdelats.
Det är uppenbarligen det grundläggande RESONANSKRITERIET
från Plancks
konstant [h=mK med K=vr från Keplermomentet] som bär ansvaret:
— Svängningsformer [fasta, bestämda mönster eller resonanser]
kräver ett fasat, bestämt individkriterium [endast en HEL enhet]; Det
satisfieras av Plancks konstant [h=mcr] dels i kärnfysiken via NEUTRONEN [nukleonenheten] och dels i
atomfysiken via ELEKTRONEN
med koppling till PERIODISKA
SYSTEMET [med Kärnmatrisiska
Algoritmen från Keplermomentet].
I TNED är det enkelt att se hur den bildade elektronen kan accelereras av den
kommande positivt laddade moderkärnan:
— Så länge sönderfallet
varar, skickas elektronmassans komponenter ut utanför atomkärnan av
sönderfallets verksamma krafter [utförligt i Centralkontakterna]; Elementen [tau-ringarna]
kan anta olika möjliga blandningar tillsammans med redan etablerade
elektronmassor.
— När sönderfallet är
fullbordat, ändras moderkärnans ytladdning [snabbt] till +e;
— På samma sätt som i
fallet med ELEKTRONENS BUBBELKAMMARSPÅR kan nu den nybildade
elektronen reagera på »den inkommande positiva laddningen» som en elektron gör
i bubbelkammarvätskan på en inrusande proton:
— PLUSLADDNINGEN
attraherar elektronen [mer eller mindre beroende
på hur elektronmassan ligger utspridd, eller samlad] som dras ut ur den
lokala atomgruppen och därmed följer det karakteristiska spårmönstret [om också
ett yttre magnetfält finns närvarande].
— Det är uppenbarligen
den typen av accelererad elektron som de olika makroskopiskt avkännande
mätsensorerna detekterar.
— Eftersom alla atomer i
ett ämne, i en viss bindning eller inom en viss lokal kan dela godtyckligt på
varandras elektronelement [Se Kemi-
och Kraftekvationen], kommer den nybildade elektronmassans komponenter i vilket
fall att fördelas jämnt över hela gruppens besättningar. Därmed [och först då]
har den aktuella, stabila och icke-exciterade, väteatomen bildats.
Väteatomen:
Fullbordat neutronsönderfall.
Feynman-diagrammen i MAC — jämförande referenser med TNED för betasönderfallets matematik
|
|
http://www.docstoc.com/docs/43321431/TAP-536—6-Feynman-diagram-student-activities |
Redan fullständigt genomlyst i TNED: masskapelse förekommer inte i fysiken — garanterat av massförintelsen i energilagen — som modern akademi INTE SÄLLAN MEDVETET, tvunget, gör våld på: massa kan förintas — därför att den inte kan skapas — relaterad
fysik |
|
a |
b |
c |
a: HYPERPHYSICS [http://hyperphysics.phy-astr.gsu.edu/hbase/particles/proton.html] visar exempel via
neutronens sönderfall.
b: Samma fenomen, annan
webbkälla — lägg märke till att den med elektronen associerade antineutrinon
här har en omvänd tidspil: olika källor tecknar olika flöden — därför att det
inte finns någon varken klar eller bestämd LOGIK som talar om varför, eller
HUR. Jämför Källa3: ”No satisfactory
reason …”.
c: Feynman-diagrammets
princip enligt etablerade referenser — här som ett rent HISTOGRAM för vidare
jämförelse med TNED [se nedan]; Med termen histogram förstås här ett speciellt bildkoncept
för händelseutveckling [vanligen utmed en angiven tidspil]. För ingående
beskrivning av Feynmandiagram, se exv. Wikipedia Feynman diagram,
http://en.wikipedia.org/wiki/Feynman_diagram
Jämför enligt relaterad fysik:
ab: Elektronmassans
möjliga fördelning i det lokala atomkollektivet efter betasönderfall [Se
utförligt från Betaemissionerna i TNED; Se även Konventionella
källor], relaterad fysik, utesluter varje matematisk koppling till den
moderna akademins föreställning om FYSIKEN i betasönderfallet. En
histografisk parallell till den moderna akademins Feynmandiagram visas i figuren ovan,
mitten. Som vi ser, med kännedom om det moderna alternativet [‡ref], är varje parallell eller
jämförelse på matematisk bas UTESLUTEN. Helt, och fullt.
— Det man mäter på i
detekteringen av elektronerna från betasönderfall är — enligt TNED — en sekundär effekt av
det primära
avdelandet av elektronmassa. Den delen syns inte makroskopiskt — förrän
HELA e-massan avdelats och därmed motsvarande kvantiserade verkan visar sig.
Men då har, så att säga, tåget redan gått.
— På den grunden blir
det, enligt relaterad fysik, möjligt att använda exakt samma sambandsform för
beräkning av halveringstiden också för betasönderfallen som i fallet med de
kärninstabila nukliderna.
— Enda skillnaden blir
att Z får värdet 1 och E-faktorn hänförs till massenergiskillnaden i
betasönderfallets steg: begreppet om »elektronens olika rörelseenergier»
i betasönderfallet som någon signifikant faktor, bortfaller därmed helt och
hållet i TNED.
I TNED finns ingen som helst matematiskt
jämförande analogi eller parallell till det (matematiskt) etablerade begreppet Feynmandiagram (vilket är ett ytterst
matematiskt komplicerat modernt akademiskt begrepp med exceptionellt dryga och
omfattande integraler):
— Tidsreversibilitet finns inte i TNED [Se Åldrandets princip i Tidens pil i Entropibegreppet i relaterad fysik].
— Det finns heller inget begrepp i TNED för skapelse av massa [Se Energilagen i POM]; massa i TNED, relaterad fysik, är struktur [Se Atomkärnans härledning som massans fundamentalform], och den kan inte skapas av masslös energi (ljus), lika litet som en femkrona kan skapas med hjälp av den masslösa strålningen från partikelacceleratorer. Det finns ingenting sådant i relaterad fysik; I relaterad fysik gäller (som bekant) att Planckenergins E=mc² är kvantitativt giltig med massenergiernas massekvivalenter enligt (m→γ)=(m←γ) men kvalitativt icke ekvivalenta enligt (m→γ)≠(m←γ) på grund av den kvalitativa (strukturbaserade) irreversibiliteten i massdestruktionen (m→γ) enligt energilagen i relaterad fysik. I modern akademi finns ingen kvalitativ aspekt på kärnfysiken — eller energilagen [‡1]. Därav skillnaderna — och den underförstådda, obetingade, matematiska sammanblandningen i Planckenergin E=hf=(m→γ)c².
— Det finns i TNED heller inget begrepp om en partikel för tidsintervall som understiger 1,4
t23 S (t
för 10^–)
[Se Patikelbegreppets
gränsform i TNED];
I fallet neutronsönderfall, talar man om en »W-boson» med varaktigheten ca 1
t25 S [Se Citat i Källa5].
— Speciellt strukturbegreppet i relaterad fysik med Plancks strukturkonstant, omöjliggör
varje både kvantitativ och kvalitativ parallell till den moderna akademins
begrepp. Speciellt medför det att själva åskådligheten som begrepp för
atomkärnans del är helt uteslutet i MAC.
— Dessa detaljer tillsammans [enbart energilagen i TNED räcker] bildar en
omöjligt eliminerbar differens mellan TNED och MAC som garanterar två helt
inbördes väsensskilda fysikbeskrivningar. Bägge kan inte vara giltiga.
—————————————
[‡1] Begreppet »energilag», dess motsvarande
engelska form »energy law», finns egentligen strängt taget inte i modern
akademisk litteratur, man använder formen »conservation of energy»; Focus
Materien 1975 s65sp2n använder begreppet »energiprincipen» med samma innebörd
som i energilagen i relaterad fysik: oförstörbar;
”... nämligen den sats som kallas energiprincipen och som
lyder: Energin i ett slutet system kan aldrig öka eller minska. Denna sats, som
också brukar kallas satsen om energins oförstörbarhet, kan inte bevisas men den
har ännu aldrig visat sig slå fel.”.
[VNS]. Van Nostrand’s Scientific Encyclopaedia Fifth Edition 1976, Sönderfallstider enligt Table 3, s495-501.
[HOP]. Handbook of Physics, E.U. Condon, McGraw-Hill 1956-67, Atomvikter sidorna 9-65 – 9-86 Table 2.1.
[EST]. Encyclopedia of Science & Technology, McGraw-Hill 1992
modern akademi (här ofta förk. MAC)
TNED — Related PHYSICS And MATHEMATICS
(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska
Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som
följer av härledningarna i Planckringen
h=mnc0rn, analogt Atomkärnans
Härledning. Beskrivningen enligt TNED är relaterad,
vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt
logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås
(således) också
RELATERAD FYSIK OCH MATEMATIK. Se även
uppkomsten av termen TNED
i ATOMKÄRNANS HÄRLEDNING.
END.
Editor2011X
Radioaktiva Betasönderfallets fysik i TNED
innehåll: SÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER
Radioaktiva
Betasönderfallets fysik i TNED
ämnesrubriker
innehåll
Källa 1 — RADIATIVE NEUTRON
DECAY — Rare Decay Modes of The Neutron
Källa 2 — SCIENCE &
TECHNOLOGY — Feynman diagrams
Källa 3 — @INTERNET
Wikipedia Quantum electrodynamics
Källa 4 — ENCYCLOPAEDIA
BRITANNICA — Feynman diagram
Källa 5 — @INTERNET
Wikipdeia W and Z bosons
Källa 6 — PHYSICS FORUMS
— Neutron to Proton
REFERENSER
referenser
Senast
uppdaterade version: 2020-04-07
*END.
Stavningskontrollerat 2012-02-10.
*
åter till portalsidan
· portalsidan är
www.UniversumsHistoria.se
∫ ∫ √ τ πε ħ UNICODE — often used charcters in mathematical-technical-scientifical
descriptions
σ
ρ ν ν π τ γ λ η ≠ √ ħ
ω → ∞ ≡ ‖ ↔↕ ħ ƛ
ℓ ∫
Ω
Φ Ψ Σ Π Ξ Λ Θ Δ
α
β γ δ ε λ θ κ π ρ τ φ
ϕ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫
≤ ≈ ≥ ˂ ˃ ˂ ˃ ← ↑ → ∞ ↓
ϑ
ζ ξ
Arrow symbols,
direct via Alt+NumPadKeyboard: Alt+24
↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬
Alt+23
↨ — also Alt+18 ↕; Alt+29 ↔
Alt+NumPad 0-25, 26-...
☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓
→←∟↔▲▼
!”#$%&’()*+,-./♦812...
*
åter till portalsidan
· portalsidan är
www.UniversumsHistoria.se