NEUTRONENS FRAGMENT | Komplement Del II | 2010VII5 | Senast uppdaterade version: 2014-02-08 | en BellDharma produktion |

innehåll · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Snabbguide till neutrinobegreppet · Neutronfragmenten i relaterad fysik · Oförklarade Massunderskott i Partikelfysiken INLEDNING · Massunderskotten · MIC · Partikelnomenklaturen ·

Från Exempelframställningen till Neutronfragmenten

Uppdagade, obemärkta, massunderskott i fysiken enligt TNED vid partikeldelning

Partiklarna: TNED säger delning. MAC säger skapelse. Mass-Energierna: TNED säger utbyte. MAC säger skapelse. Massfysiken står orepresenterad i MAC.

BILDKÄLLA: Författarens arkiv · Drop19iso3200Bild131 · Apr2009 · NikonD90 Fyra friliggande vattendroppar — efter rekyl från EN [1] droppe som träffade vattenytan. På samma sätt som en vattendroppe tillfälligt kan glida PÅ vattenytan utan att dras in så kan också ENLIGT TNED en atomkärna (vattenytan) avdela en del av sig själv ENDAST UNDER FÖRUTSÄTTNINGEN att den avdelade droppen får SPINN (J=mvr): den självständiga droppen kan bara bildas som en del av en utskjutande kraft som innefattar en roterande rörelse. Annars inte.

Utan spinnet dras droppen in direkt av vattenytan. Men spinn — massa — kan inte skapas utan en redan befintlig massform: spinn kan inte skapas av ljusenergi, endast ur en redan befintlig spinnande massform — enligt TNED. Mycket starkt argument. Argumentet leder oundvikligen till följande: ATOMKÄRNAN UPPVISAR MASSUNDERSKOTT VID DELNING — enligt TNED; men det kan inte upptäckas i modern akademi [‡] på grund av chokmassan från partikelaccelerationen. Utförligt från Spårbilden. TNED ansluter tydligen till samma principiella partikelfysik som gäller vid uppkomsten av vattendroppar ur vattenytan: TNED säger delning. MAC säger skapelse. Utförligt från Spårbilden. Här ges motsättningen i elementär matematik enligt TNED.

Neutronfragmenten.htm ......................... originalförfattningen från 2008 — bubbelkammarbilden från FOCUS MATERIEN 1975 med inledande exempelbeskrivning NeutronfgmKompl1.htm ......................... partikeldelningens principer i TNED med Exempel NeutronfgmKompl2.htm .................. Massunderskottet, MIC-ekvivalenterna — ovanstående mera ingående med samband SolNeutrino.htm .................................... neutrinostrålningen från Solen enligt TNED

För att fullständiga den påbörjade beskrivningen i NEUTRONFRAGMENTEN (2008) har närmast vidstående kompletterande htm-dokument utformats (våren-sommaren 2010).

Partikelbildning med masschokning — Exempelframställningen i analys · MIC-ekvivalenterna · Kalkylkortet ·

Neutronfragmenten i relaterad fysik — NEUTRONFRAGMENTEN Del II

2010VI16

Neutronfragmenten i relaterad fysik

»nybörjarens original», från 2008 — NEUTRONFRAGMENTEN Del I

Originalversionen av NEUTRONFRAGMENTEN 2008VI26 — delvis ofullständig beskrivning bevarat original, numera endast för exempelreferens

Utvidgad version av NEUTRONFRAGMENTEN 2010VI16 — fördjupad förklaring med fullständig beskrivning diskuterar ovanstående med exempel

»proffsversionen», från 2010 — NEUTRONFRAGMENTEN Del II detta htm-dokument

Med slutresultat att g-massa inte kan skapas ur masslös energi [‡] har flera detaljer uppmärksammats i efterhand från originalförfattningen i NEUTRONFRAGMENTEN 2008VI26. Därmed har den relaterade beskrivningen kunnat fullständigas i analogi med Focusoriginalets termbeteckningar som ovan.

Detaljer som ENLIGT TNED framkommit i efterhand och som föranlett det här tillägget är följande:

1. vid kollision med tillräcklig energi delas protonen som vattendropparna i en »splash» — protonen splittras inte

2. avdelningen kan beskrivas matematiskt genom en karaktäristisk kärndelningsvåglängd som tvunget måste vara kortare än kärnradien

3. droppdelningarna kräver ingen massdestruktionsstrålning (m→γ) i sig, kärnstrukturen bevaras vid delningen

4. de avdelade dropparna motsvarar instabila kärnfragment som enligt TNED tvunget måste uppvisa massdestruktionsstrålning (m→γ)

5. massdestruktion förekommer bara då den avdelade kärndroppen ändras (sönderfaller) i sin ursprungliga ekvivalenta ±e-struktur

FORMULERINGAR med avgörande klargöranden i dessa punkter fanns inte vid tiden för originalframställningens författning (2008VI26).

DETALJER I SÖNDERFALLSDYNAMIKEN (protonen kan inte splittras, men den kan delas) tillsammans med NEUTRINODYNAMIKEN GENERELLT (neutrinospektrum enligt TNED kontra den moderna akademins teori) har medfört att den ursprungliga framställningen om NEUTRONFRAGMENTEN har fått en vidare beskrivningsgrund med en (betydligt) mera detaljerad förklaringsgrund. För att bevara ursprungsbeskrivningen i NEUTRONFRAGMENTEN med dess delvis ofullständiga genomgång i ljuset av ovanstående punkter, har originalförfattningen bevarats tillsammans med en beskrivande EXEMPELFRAMSTÄLLNING (med anpassade smärre ändringar i förtydligande syfte). Den används som diskussionsgrund i HUVUDFÖRFATTNINGEN Neutronfragmenten i relaterad fysik för att (Med Focuskällan som exempel, nedan) relatera och belysa omfattningen av spårbildens allmänna fysik — i ljuset av en mera relaterad referens till delpartiklarnas experimentellt kända egenskaper. Enda skillnaden i sak mellan den nu äldre NEUTRONFRAGMENTEN och nuvarande huvudförfattningen (detta htm-dokument) är att den senare har utvecklats på den förras grund (Energilagen) — med de ovanstående punkternas fördjupning och med slutmål i samma beteckningsbestyckning som i Focuskällans originalteckning. Grundprincipen är densamma: massans kvalitet kan inte skapas ur massans kvantitet (Energilagen) — DÄRFÖR att massans kvalitet (strukturen) kan förstöras (massförintelsen som ger värmen och ljuset) men inte kvantiteten (energiekvivalenten). Se vidare, mera utförligt nedan från Massunderskotten.

Massunderskotten, rubrik

Inledning till Oförklarade massunderskott i partikelfysiken — grunderna i original beskrivs i Exempelframställning

MASSUNDERSKOTTEN — enligt TNED

Massunderskotten ·

Inledande beskrivning

Se större bild i originalförfattningen · Se även förstorad spårbild

Bubbelkammarfotografiet från FOCUS MATERIEN 1975 s139

Kärnmening:

Protonmassorna efter kollisionen kan omöjligen och med de bildade delpartiklarnas bevislighet vara samma som protonmassorna efter kollisionen: Summan av alla energier kan inte överstiga det elektriskt slutna accelerationssystemets totalenergi (protonmassan exemplifierad):

mp + mU – (m→γ) –[mU] = mp – (m→γ)

mp + mU – mx – (m→γ) –[mU] = mp – (m→γ) – mx

ingen energi skapas, ingen energi försvinner.

Kärnmeningens förankring:

Protonmassan (mp) masschokas i partikelaccelerationen med mU, pp-kollision bildar delpartiklar mx som delvis genomgår sönderfall med massdestruktion (m→γ); när restpartiklarna återgår till vila kräver det slutna elektriska accelerationssystemet tillbaka exakt samma mU som det lämnade ut under acceleration av mp enligt elektriska laddningens matematiska fysik Q=√(m/R)(A/dT): ingen massa skapas, ingen massa försvinner, Q bevaras intakt (utförligt från PLANCKEKVIVALENTERNA); Sedan ev. massdestruktioner frånräknats återstår i netto: mp – mx. Underskottet i p kan tydligen återföras på kollisionstillfället (pp);

Protonmassorna efter kollisionen kan SÅLEDES omöjligen och med de bildade delpartiklarnas bevislighet vara samma som protonmassorna efter kollisionen (mp ≠ mp–mx); mx ≠ mU.

NOTERA att eftersom protonmassorna behåller sina mU så länge de har impuls, uppträder de som ordinära masspumpade protoner: ingenting märks av någon förmodad massdeficit i partikelspåret som sådant.

Detaljen kan varken upptäckas praktiskt, och inte heller teoretiskt i den moderna akademins lärosystem eftersom man där endast beaktar massenergins kvantitativa ekvivalent, inte dess kvalitativa bas:

Energi-Massa ekvivalenten,

även mera utförligt längre ner

E = (m→γ)c² = (m←γ)c² ...................... kvantitativa energiekvivalensen från energilagen

Massans kvalitativa struktur kan upplösas fullständigt (±e, laddning och spinn tar ut varandra, bara massans kvantitet återstår via induktionen från ±e-förintelsen) DÄRFÖR att den INTE kan skapas:

E = (m→γ)c² ≠ (m←γ)c² ...................... kvalitativa energiekvivalensen (entropin kan inte omv.)

Med andra ord — och förutsatt korrekt uppfattat: pp-kollisioner kan tydligen förstås ske på samma sätt som en vattensplash: delning av redan befintlig g-massa.

Ingen massa skapas — men det ser så ut om man enbart beaktar massenergins kvantitativa sida.

Vi studerar hur.

Massunderskotten

2010-06-13

Oförklarade massunderskott i partikelfysiken

Snabbgenomgång av problemformuleringen för den som redan känner till GRUNDBEGREPPEN I RELATERAD FYSIK

Mera utförligt — illustrerad och refererad genomgång · se även ovanstående korta inledning.

Se även alternativ snabbgenomgång (kortare, mera komprimerat) i ovanstående INLEDNING.

Det förutsätts här att läsaren är förtrogen med grunderna i TNED enligt ATOMKÄRNANS HÄRLEDNING — atomkärnans ekvivalenta laddning-massa-spinnstruktur med ±e från neutronen via Plancks konstant, analogt PLANCKRINGEN

h=mcr=(neutronmassan)(ljushastigheten)(neutronradien)=6,626 t34 JS.

Snabbgenomgång

Snabbgenomgång av problemet

1. Elektronmassans massökning

2. Bubbelkammarfotografi med partikelbildning

3. Motsvarande balansräkning, kosmisk proton

1. Elektronmassans massökning med elektrisk acceleration

KREDIBILITETEN i det experimentella påvisandet av elektronens massökning genom elektrisk acceleration ges excellent genom skolfysikens demonstration av TRÅDSTRÅLERÖRET (r=mv/BQ). I Relaterad Fysik beskrivs fenomenet (lika excellent) från ELEKTRISKA LADDNINGENS HÄRLEDNING [Q=√(m/R)(A/dT)] genom PLANCKEKVIVALENTERNA, specifikt Planckenergins massekvivalent [m0c²=mccu=E=konstant som leder till den redan kända formen m/m0=√1–(u/c)²]: systemets massa bevaras intakt. Ingen massa skapas, ingen massa försvinner. Fenomenformen grundas HELT på proportionaliteten (m/R) i Q som garanterar att fenomenformen bara fungerar i elektriska accelerationer: R(Ω) finns inte i mekaniken. Accelerationsmassans ökning tas från en motsvarande massminskning i det stationära materialets massbesättning genom elektrisk induktiv omformning enligt E/(±Q)=U, dvs., energin är proportionell mot accelerationsspänningen. När accelerationselektronerna återgår till viloläget, återlämnas massökningsdelen till den fasta systemdelen så att energiräkningen går ut på konstant bevarad massa. Massan från massökningseffekten inom elektrofysiken benämns här chokmassa [egentligen kraftchokning enligt MAFEM; m=F/a]

För den som inte känner grunderna, särskilt: Chokmassan får g-vägande egenskap genom att den ordinära massans inre kraftverkan ökar med energin i accelerationsfältet (m=F/a; E=UQ=Fd=mad). Däremot finns i Relaterad Fysik (utförligt från ENERGILAGEN) ingen grund för en rent kvalitativ uppkomst av g-vägande massa ur ren masslös em-strålning. Det är viktigt att hålla den aspekten i minnet i den följande genomgången eftersom just den rent kvalitativa aspekten i massa-energiekvivalensen i modern akademi INTE beaktas. I Relaterad Fysik gäller därför med energilagens giltighet:

E = (m→γ)c² = (m←γ)c² ...................... kvantitativa energiekvivalensen från energilagen

Massans kvalitativa struktur kan upplösas fullständigt (±e, laddning och spinn tar ut varandra, bara massans kvantitet återstår) DÄRFÖR att den INTE kan skapas:

E = (m→γ)c² ≠ (m←γ)c² ...................... kvalitativa energiekvivalensen

2. Bubbelkammarfotografi med partikelbildning ur en proton-protonkollision från en partikelaccelerator

På samma sätt som i elektronfallet påförs chokmassa till protoner som accelereras i en partikelaccelerator. I fotografier från inmonterade kameror i en bubbelkammare kan man, i ett vårt exempelfall, studera hur en inkommande projektilproton kolliderar med en målproton och bildar en mindre spray av delpartiklar. Liknande partikelfragment (typ Pion och Myon) hade redan observerats från slutet av 1940-talet (Perkins 1947) genom s.k. fotografiska emulsioner där man kunnat bestämma partikelmassorna med hyfsad noggrannhet. Därmed sagt att KREDIBILITETEN för dessa partikelfragments angivna s.k. vilomassor (här veterligt) måste anses tämligen stabil. Men därmed uppkommer också ett dilemma — problemet i sak. Eftersom accelerationsprotonens chokmassa, delvis fördelad på kollisionskomponenterna, enligt elektronanalogin ovan tvunget går förlorad till det fasta systemet då partiklarna återgår till viloläget, samt i det faktum att partikelspåren visar hur delpartiklar uppkommer TILLSAMMANS MED angivna protoner, uppkommer i den summerande energiräkningens ljus ett massunderskott på protonernas räkning motsvarande de bildade partiklarnas vilomassor; Protonmassorna efter kollisionen kan omöjligen och med de bildade delpartiklarnas bevislighet vara samma som protonmassorna efter kollisionen. Notera att denna omständighet, massdeficiten, omöjligen kan observeras i partikelspåren, varken praktiskt eller teoretiskt enligt rådande föreställningar, eftersom de angivna protonerna då fortfarande besitter chokmassans status och därför uppträder som ordinära masspumpade protoner. Ingenting av anomalin syns i bubbelkammarfotografiet.

3. Motsvarande balansräkning för en kosmisk protonkollision

PLANCKEKVIVALENTERNA ingår inte i modern akademi ehuru sambandsformernas matematik gör det. Den detaljen har, motsvarande exemplet ovan, lett till en bevisbar kvantitativ MEN INTE KVALITATIV överensstämmelse i tolkningen av den kosmiska strålningen i mätningen av Myonernas halveringstid och påträffade mängd nere vid markytan (utförligt i BEVISET FÖR MULTIPLA c). Resultatet av den rent matematiska överensstämmelsen visar att med ekvivalent impuls (mv) kan Myonmätningarna förklaras kvantitativt ekvivalent på exakt samma matematik med en högre hastighet och konstant vilomassa istället för med lägre hastighet och konventionellt förmodad påförd extra chokmassa. I Relaterad Fysik finns inte den elektriska laddningens R-faktor med i Q=√(m/R)(A/dT) OM Q accelereras på rent MEKANISK väg. Med den prövande förutsättningen att den kosmiskt inkommande protonen fått sin hastighet (typiskt normalfallen runt impulsekvivalenta 10c) på rent mekanisk väg besitter den heller ingen chokmassafördelande egenskap. Partiklarna som bildas då projektilprotonen träffar på en stationär proton måste därför, tvunget, tas ifrån de bägge enda existerande protonmassorna. Slutresultatet blir därmed alldeles detsamma som i fallet ovan, med enda skillnaden att chokmassaenergin ersätts av en kinetisk impulsekvivalent men utan den g-vägande chokmassans egenskap. I vilket fall således: Protonmassorna efter kollisionen kan omöjligen och med de bildade delpartiklarnas bevislighet vara samma som protonmassorna efter kollisionen.

SAMMANFATTNING

MASSUNDERSKOTTET KAN INTE UPPTÄCKAS MED KONVENTIONELLA MEDEL

Enbart med tillgång till artificiella partikelacceleratorer och deras avgörande chokmassa, finns ingen möjlighet varken praktiskt eller teoretiskt i den moderna akademins lärosystem att upptäcka den ovan påtalade massdeficiten: protonmassornas massunderskott efter kollisionen. Så länge protonerna besitter impuls från projektilprotonens kollisionsfördelning, och därmed motsvarande fördelning av chokmassa, uppför sig partiklarna som ordinära masspumpade kopior vars banor och karaktärer kan utläsas (tämligen exakt) ur bubbelkammarfotografiets partikelspår och med kännedom om dimensioner och kammarens pålagda yttre magnetfält. Fenomenformen ligger helt dold. Enbart med den moderna akademins lärosystem är det med andra ord OMÖJLIGT att upptäcka det ovan påtalade massunderskottet, av princip.

Utförlig genomgång

Mera utförlig genomgång med illustrationer och referenser

1. Elektronmassans massökning med elektrisk acceleration

2. Bubbelkammarfotografi med partikelbildning ur en proton-protonkollision från en partikelaccelerator

3. Motsvarande balansräkning för en kosmisk protonkollision

1. Elektronmassans massökning med elektrisk acceleration

TRÅDSTRÅLERÖRET sammanfattar utomordentligt experimentalfysiken på skolnivå för demonstration av elektronmassans ökning genom elektrisk acceleration, r=mv/BQ

trådstråleröret

Trådstrålerör med Helmholtzspolar GYMNASIETS FYSIK åk2 s195 Liber 1979/80

Glaskulan i mitten har samma funktion som kärlet som innesluter bubbelkammarvätskan i en bubbelkammare. De bägge stora runda smala ringarna omkring är Helmholtzspolar som ger ett nära homogent magnetfält rakt genom centrumkulan som för trådstrålerörets del är fylld med vätgas av lågt tryck. I ena ändan av röret (höger) sitter en liten elektronkanon. Med pålagd spänning accelereras elektronerna och böjs av i en ring genom växelverkan med det yttre magnetfältet. Genom en graderad skala kan man avläsa hur ringen sväller och krymper med växande avtagande accelerationsspänning; Den större elektronmassan utverkar en större centrifugalkraft än den mindre elektronmassan och uppvisar därför en större ring.

PLANCKEKVIVALENTERNA I TNED beskriver elektronmassans massökning enligt Planckenergins massekvivalent

m₀/m = √1–(u/c)² ........................... PLANCKENERGINS MASSEKVIVALENT i ^Qm ändras med växande u

med den uppnådda hastigheten u från den elektriska accelerationen med spänningen U.

u = c√ 1 – 1/[(UQ/m₀c²) + 1]² .......... laddningshastigheten u för Q från accelerationsspänningen U

Planckekvivalenterna beskriver, härleder och förklarar ingående hur massändringen fungerar, hur hela det elektriskt slutna systemets massa bevaras och konserveras utan att någon extra massa skapas eller någon extra massa försvinner enligt

m₀c² = mcc_u = konstant = E ............. systemets egen inre energi

Dessa detaljer är (eller BÖR) redan vara väl experimentellt kända i den redan etablerade vetenskapen.

Se mera utförligt i PLANCKEKVIVALENTERNA om ej redan bekant.

Allmänna sambandsformer (Q kan inte härledas av MAC):

Q = √ (m/R)(A/dT) .................. R finns inte i mekaniken, bara i elektrofysiken

m och R varierar exakt med bevarande av den elektriska laddningen Q i det elektriska accelerationsfältets försorg. m/R-kvoten garanterar massändringens exakta proportionalitet mot accelerationsspänningen (E/Q=U), utförligt från PLANCKEKVIVALENTERNA och HÄRLEDNINGEN TILL ELEKTRISKA LADDNINGEN.

För den accelererade laddningen gäller

m(e^–) = m₀(e^–) + m(U) ................... masschokning, elektronmassans acceleration i elektriskt slutet system

När elektronmassan återgår till vila, lämnas chokstocken m(U) tillbaka till systemet: m återgår till m0 (vulgärt uttryckt: så att ingen ska inbilla sig att man får något extra, gratis, här i världen) — vilket sker induktivt via induktionsresistansen R i Q=√(m/R)(A/dT) på omgivande laddningsbesättningar, utförligt i MAFEM. Därmed bevaras systemet intakt: Ingen massa skapas. Ingen massa försvinner.

2. Bubbelkammarfotografi med partikelbildning

Motsvarande samband genom proton-proton-kollisionen (exemplifierat med Lambdaº, se bild nedan):

Λ⁰ = p⁺ + m(U) = [m(U)1 + (p⁺ – m)] + [m(U)2 + (m=π^–)] … ............. med masschokning, partikelaccelerator, bubbelkammarfoto

I konventionell partikelfysik beskrivs pp-kollisioner (pp för proton-proton, typiskt) som i nedanstående bild, här med proportionella massformer [m/M=(r/R)³] från TNED för illustrationens översikt

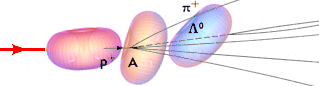
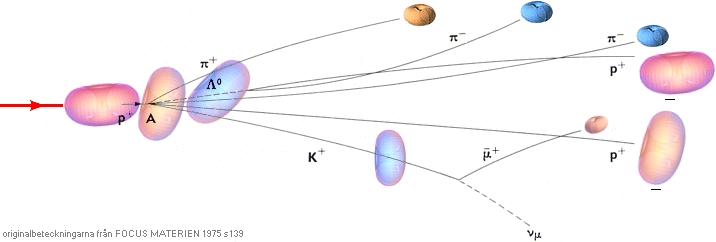
Bubbelkammarspåren i Focuskällan

Strålknippet i bilden nedan med beteckningar (men inte ikonerna)

från FOCUS MATERIEN 1975 s139, bubbelkammarfotografi i källan samma sida separat

ikon	part.	MeV
	π^+	139,6
	π^–	139,6
	π^–	139,6
	p^+	938,2
	Λ^0	1116
	p^+	938,2
	K^+	494
	µ^+	105,66
ikon	part.	vilom.

Från vänster kommer en källproton från en partikelaccelerator in i mellanrummet mellan ett par Helmholtzspolar i en bubbelkammare. Riktningen på magnetfältet i bubbelkammarfotografierna är konventionellt upp mot betraktaren (e– böjer av uppåt, e+ neråt, se Högerhandsregeln). Vid incidenspunkten (A) träffar källprotonen på en målproton. Kollisionen är våldsam, och resultatet syns i bubbelkammaren som ett antal karaktäristiska spår av olika partiklar med olika egenskaper och som fotograferas med speciellt inmonterade kameror för senare analys. Partikelikonerna i figuren har enligt TNED gjorts ungefär proportionella mot protonens masstäthet som enhet [m/M=(r/R)³]. Alla värden i MeV anger motsvarande konventionellt benämnda vilomassor.

Myonen (µ) sönderfaller längre fram till en positron, Pionerna (π) längre fram till Myoner [‡].

Övre sönderfallet motsvarar differensenergin 1116–(139,6+938,2)=38,2 MeV och undre sönderfallet 494–105,66=388,34 MeV.

π⁺ + π^– + π^– + K⁺ = 3×139,6 + 494 = 912,8 < 938,2; diff = 25,4

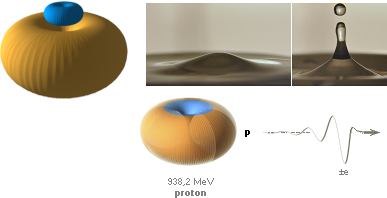
Principen är densamma som för en vattensplash: en spray av smådroppar kastas ut från den normalt helt släta vattenytan då en fallande droppe träffar. Se även särskild beskrivning i MIC-EKVIVALENTERNA.

»Vattensplash» (vattenplask) eller mera egentligt, vattenkrona

© Adam-Hart Davis, Natural Science 2008.

http://gallery.hd.org/_c/natural-science/_more2006/_more03/splash-crown-water-drop-on-blue-crazed-cracked-surface-frozen-2-AJHD.jpg.html

Summan generellt för alla möjliga typer av massdelpartiklar x1+x2+x3+...+xn som associeras med bildningar i eller omkring en given protonkollision via elektrisk partikelacceleration kan skrivas på samma sätt som i fallet med elektronens acceleration men här mera sammansatt enligt

Σx_n = [m(U) + m(p⁺–m)]₁ + [m(U) + m(p⁺–m)]₂ + [m(U) + m(p⁺–m)]₃ +… = p⁺ + m(U)

Summan av alla delpartiklar — associerade med EN proton — och deras energier inkluderat inre delningar och avgivningar är lika med utgångsmassan (p+) plus chokmassan från partikelacceleratorn m(U);

Varje delpartikels massenergiekvivalent kan (självklart, samma som reguljär speceriinventering) skrivas som en summa av delchokmassan m(U)n och en massavdelning från utgångsmassan m(p⁺–m)n,

x_n = [m(U) + m(p⁺–m)]_n

När ursprungspartiklarna återgår till vila efter kollisionen och chokmassan, som i fallet med elektronmassans acceleration, återgår till noll i det vilande slutna elektriska systemet återstår tydligen

(x_n) = [0 + m(p⁺–m)]_n

= [m(p⁺–m)]_n .................. restprotonen frånsett, i samtliga fall en slutlig elektron eller positron

Därmed för ursprungsprotonens del också likaledes en massdeficit proton enligt

m(p⁺) = [m(p⁺–m)]

RESULTAT:

(endera) Protonen som kommer ut från kollisionen kan med energiräkningens matematik omöjligen ha den vilande ursprungsprotonens vilomassa (938,2 MeV/c²); protonen före kollision och protonen efter kollision kan omöjligt vara samma.

Med ovanstående resultatgenomgång skulle SÅLEDES och snarare följande förtydligande gälla: samma koncept, men med (närmast — minst) ändrade protonmassor i slutdelen enligt

Orsaken

övre: 938,2 – 139,6 = 798,6 MeV ..................... källprotonen tappar 14,8%

Observera att så länge chokmassan ligger kvar i målprotonen från kollisionsögonblicket, syns naturligtvis ingenting av den slutliga massdeficiten i partikelspåret. Deficiten (underskottet) kommer fram först (successivt) med protonens återgång till vila.

unre: 938,2 – (2×139,6+494) = 165 MeV ......................... målprotonen tappar 82,4%

MED FÖRUTSÄTTNINGEN ATT DE ANGIVNA DELPARTIKLARNA AVGES MED EGNA SJÄLVSTÄNDIGA EGENMASSOR ENLIGT ANGIVNA VÄRDEN.

3. Motsvarande balansräkning för en kosmisk protonkollision — samma

ENLIGT TNED — men inte i modern akademi (MAC): konceptet är helt orepresenterat, se utförligt från PLANCKEKVIVALENTERNA — blir slutresultatet (men inte spårdynamiken) alldeles detsamma som i uppställningen närmast ovan om vi istället ersätter den artificiella partikelacceleratorns källproton med en inkommande kosmisk proton som, enligt TNED, accelererats på rent mekanisk väg (Se utförligt exempel i BEVISET FÖR MULTIPLA c);

Enda skillnaden är att chokmassan m(U) ersätts av rörelseenergin (2Ekin/v²)=m(E):

Q = √ (m/R)(A/dT) ................................................................................. R finns inte i mekaniken; Alltså gäller:

Motsvarande samband genom proton-proton-kollisionen (exemplifierat med Lambdaº i bilden ovan):

Λ⁰ = p⁺ + m(E) = [m(E)1 + (p⁺ – m)] + [m(E)2 + (m=π^–)] … ............. utan masschokning, kosmiska strålningen, TNED

Generellt kan bildningen av alla möjliga typer av massdelpartiklar x1+x2+x3+...+xn från en given kosmiskMekanisk proton (med exempel från BEVISET FÖR MULTIPLA c) skrivas enligt TNED

Σx_n = [m(E) + m(p⁺–m)]₁ + [m(E) + m(p⁺–m)]₂ + [m(E) + m(p⁺–m)]₃ +… = p⁺ + m(E)

Summan av alla delpartiklar och deras energier inkluderat inre delningar och avgivningar är lika med utgångsmassan (p+) plus massekvivalenta kinetiska energin från den inkommande protonens impuls (mv);

Varje delpartikels massenergiekvivalent kan skrivas som en summa av delenergin m(E)n och en massavdelning från utgångsmassan m(p⁺–m)n,

x_n = [m(E) + m(p⁺–m)]_n

När ursprungspartiklarna återgår till vila efter kollisionen återstår bara de normala vilomassorna

(x_n) = [0 + m(p⁺–m)]_n

= [m(p⁺–m)]_n .................. restprotonen frånsett, i samtliga fall en slutlig elektron eller positron

Därmed för ursprungsprotonens del också likaledes en massdeficit proton enligt

m(p⁺) = [m(p⁺–m)]

RESULTAT:

(endera) Protonen som kommer ut från kollisionen kan med energiräkningens matematik omöjligen ha den vilande ursprungsprotonens vilomassa (938,2 MeV/c²); protonen före kollision och efter kollision kan omöjligt vara samma.

Slutresultatet för massorna i bägge fallen är alltså samma.

I den kosmiska protonens fall tillkommer dessutom och tydligen en annan motsvarande bubbelkammarspårbild. Chokmassor m(U) ingår inte enligt TNED eftersom

1. de inkommande kosmiska partiklarna bara kan få sina hastigheter på mekanisk väg och därför också

2. partikelhastigheter över c inte lämnar elektriska spår och därför saknar jämförande grund med partikelacceleratorfallet samt

3. energierna är starkt olika i jämförelse mellan partikelacceleratorn och naturfallet även om ingångsimpulserna är helt ekvivalenta (se ENERGIERNA i MIC-sambanden).

OM man i ljuset av ovanstående resultat — som framhåller fysikbeskrivningen från TNED som adekvat — försöker beskriva den naturkosmiska strålningen på partikelacceleratorns fysik (vilket är precis vad som skett i MAC enligt TNED) måste naturbeskrivningen tvunget bli motsvarande begränsad. Det är därför angeläget (främst för den här författaren) att försöka hitta bevis som mera ingående kan bekräfta — eller dementera — soliditeten i TNED.

Varför massunderskottet inte kan upptäckas i MAC

— Varför har saken inte observerats i modern akademi?

OVANNÄMNDA PROBLEMKONCEPT (se Orsaken) har inte observerats i modern akademi (MAC) — alldeles tydligt på grund av att man i MAC enbart ser till den rent kvantitativa massa-energiekvivalenten (massans mängd)

E = (m→γ)c² = (m←γ)c² och inte har observerat

den rent kvalitativa aspekten (massans struktur)

E = (m→γ)c² ≠ (m←γ)c²

Se utförligt från ENERGILAGEN med primära massförstöraren (mc²) och ATOMKÄRNANS HÄRLEDNING.

— Har man bara en rent KVANTITATIV fysikuppfattning, behöver man inte bekymra sig om kvaliteterna.

Vad händer med restprotonen?

Se vidare i Restprotonens öde.

Här slutar artikeln om

Oförklarade massunderskott i partikelfysiken

Se även HUR DET FUNGERAR i den mera elementära grundbeskrivningen i NEUTRONFRAGMENTEN i relaterad fysik som framkom i samband med den mera kritiska granskningen som behandlas i EXEMPELBESKRIVNINGEN

(tillsammans med uppmärksammandet av neutrinofysikens betydelse överlag — se särskilt från Neutrinobegreppet i TNED om ej redan bekant).

Se även särskilt analysexempel (som belyser en del av ämnets svårigheter) med koppling till originalförfattningen i EXEMPELBESKRIVNINGEN;

Genomgång av argument och förklaringar tillsammans med den första framställningens mera ofullständiga beskrivning — lösningarnas argument.

KÄRNDELNINGEN

Kärndelningen

Hur neutronen-protonen kan delas — med analog utgivning av nya neutrinonycklar

© Adam-Hart Davis, Natural Science 2008.

http://gallery.hd.org/_c/natural-science/_more2006/_more03/splash-crown-water-drop-on-blue-crazed-cracked-surface-frozen-2-AJHD.jpg.html

Hur neutronen-protonen kan delas — med analog utgivning av nya neutrinonycklar

Bilden ovan (en »vanlig vattensplash») illustrerar PRINCIPEN för kärnpartikeldelning genom kollision i TNED enligt MIC (Mass Interactive Connection), konv. de Broglies vågekvation λ = h/mv.

Atomkärnan i TNED bygger på obegränsad fraktalstruktur — det är omöjligt att undvika att den massdestruktionsstrålning som kärnan uppvisar vid sin bildning (och delning) också sammanhänger med en viss motsvarande struktur: neutrinoNyckeln.

Bilden ovan visar motsvarande ikoniska kärndelning enligt TNED med motsvarande jämförande vattenanalogi.

Bilden nedan (bilden länkar till det större originalet) sammanfattar partikelbildningen enligt MIC tillsammans med härledda samband och uppgifter om den aktuella partikelns vilomassa.

MIC-ekvivalenterna

Om nuklidbyggnaden (spinnet) genombryts på en energilängd mindre än dess egen formfaktor (kärnradien närmast) kan spinnet (rent mekaniskt) brytas upp och därmed tvinga kärnan i spinndelning (kärnan avdelar sin redan bundna ±e-struktur i formen av miniatyratomkärnor likt vattendroppar från en splash). Beräkningarna enligt TNED genom neutronens-protonens härledda N3m20-aggregat ger de genombrytande impulsvåglängderna i direkt illustrerad jämförelse enligt MIC-ekvivalenterna.

Hyperoner och Mesoner

Då vi därför vänder oss till det enda återstående neutrinoalternativet som enligt TNED kan finnas i neutronens möjliga fragment finns tydligen ingenting annat att välja på än typen kärnassocierad neutrinostrålning;

Stabila underavdelningar till neutron-proton existerar inte. Det finns inga sådana observerade partiklar. I den mån en proton (eller neutron) förlorar kärnmassa (±e-struktur), eller sett från den avdelade kärnmassans motsvarande ±e-struktur, måste nukliden tydligen uppträda som en massdeficit nuklid, (nuklid med massunderskott) motsvarande (under)exciterad, och blir därför, i den mån den existerar som exciterad under någon begränsad tid, också tvunget instabil — ända ner till den enda möjliga slutprodukten. För protonens del kan slutprodukten bara vara den massdeficita nuklid (och som vi inte känner närmare) som strävar att återta sitt massunderskott i formen av den tidigare avdelade delkärnmassan. Delkärnmassans instabila tillstånd kan uppenbarligen bara leda till antingen 1. ett återställande genom någon form av återförening eller 2. kärnstrukturens totala upplösning, analogt massdestruktion (m→γ) och vilken stabila slutprodukt bara kan bli av betatyp: elektron (eller positron). Inga andra kända stabila partikeltyper finns att välja på.

Protonens (eller neutronens) möjliga delningsformer utgår ifrån den konventionellt benämnda kärninstabila gruppen HYPERONER, vidare nedan. Därifrån kan sedan den exciterade protonen UPPDELAS på sin excitationsenergi till den konventionellt benämnda gruppen MESONER.

Protonens (eller neutronens) kärninstabilitet kan tydligen initieras genom att utsätta nukliden för kollisionsenergi. I TNED kallas den typen för massinteraktiv impuls (MIC, λ = h/mv, konv. de Broglies vågekvation). Impulsvåglängden (λ) måste vara mindre än atomkärnans verkliga spinnformradie, vilket rent mekaniskt garanterar att nuklidbyggnaden genombryts på en energilängd mindre än dess egen formfaktor (spinnet bryts upp och delas tvunget). Därmed kan MIC-våglängden förstås vibrera = excitera endera eller bägge kollisionsprotonerna till kärndelning. För kärnradierna i TNED explicit, se ATOMKÄRNANS STORLEK i KÄRNRADIERNA DEL II. Där ges grunderna till den matematik som används här.

Delningstillståndet kan återföras på ett motsvarande identifierat tillstånd som konventionellt associeras med den kärninstabila gruppen HYPERONER:

Hyperoner (övergruppen)

— kärnformer som innefattar en ordinär nukleonindivid — hyperoner KAN sönderfalla till en proton eller neutron

(Lambda, Sigma, Xi, Omega). Se t.ex., @INTERNET Wikipedia Hyperon · List of hyperons 2010-06-08].

Etym. från Grek, hyper, över (stegring över det normala).

Därifrån kan sedan den exciterade protonen AVDELAS VIDARE på sin excitationsenergi — helt utan massdestruktion, på samma sätt som vattendroppsdelningar via inre svängningar som bryter formen — till den konventionellt benämnda gruppen MESONER [‡]:

Mesoner (mellangruppen)

— kärnformer som saknar en ordinär nukleonindivid — mesoner kan inte sönderfalla till en proton eller neutron

(Pion, Kaon, Myon, Tauon, Eta, Rhå, lillaOmega, lillaFi, D, J/Psi, B, Ypsilon).

Se t.ex.,

@INTERNET Hyperphysics Mesons 2010-06-08,

HYPERPHYSICS — Mesons (tabell)

http://hyperphysics.phy-astr.gsu.edu/hbase/particles/meson.html#c1

Etym. från Grek me’sos, i mitten (befintligt).

Se även NEUTRONFRAGMENTEN för illustrerat exempel.

Se även sammanställning i Partikelnomenklaturen.

Sönderfallet från mesongruppen ner mot stabila (separata) ±e sker sedan genom massdestruktioner på vanligt sätt enligt TNED — OM sönderfallet inbegriper någon strukturell ändring i kärnformen. Det ska här sägas med en gång att det inte finns någon ENTYDIG koppling i dessa delar mellan TNED och de nu kända experimentellt observerade partikelformerna på annat sätt än att (typ) delningsställena, eller sönderfallsställena, uppvisar motsvarande tomma rekylspår då (motsvarande) neutrinostrålningens rekyl (Se Neutrinorekylen) aktiveras; Se exemplet från Focuskällan, nedre spåret, med delningen från Kaonen (K+) till Myonen (µ+): MyonNeutrinon lämnar inget spår — men det finns här ingen garanti för att »tomspåret» INTE skulle kunna vara en neutral, mindre, partikel — men vi antar tills vidare att den inte är det.

Neutrinostrålningen frigör den ursprungliga strukturdelen (±e-bindningen) som erhölls från moderkärnan. Därmed kan den aktuella stabila slutliga sönderfallsprodukten eller betakomponenten (e– eller e+) blottläggas — direkt (Som i fallet ±Myon till ±e) eller efter flera liknande urkopplingar om sådana medges.

Myonen (upptäcktes 1936 [‡3.1]) och Tauonen (upptäcktes 1975 [1974-1977] [‡2.1])

I modern akademi finns i nutid (Jun2010) två kända mellanformer, Myonen (105,66 MeV) och Tauonen (1 777 MeV), som kopplar övergången i protonsönderfallet från Mesongruppen ner till elektron eller positron (±e) — men den klassificeringen är delvis »korrumperad» eftersom Tauonen också kan återbilda protonen (eller neutronen) vilket inte Myonen eller Elektronen kan [‡]; Tauonen kan (frånsett Hadronerna [Mesongruppen+(neutron-proton)+Hyperongruppen]) sönderfalla direkt till någon av ±e, eller till Myonen som själv bara kan sönderfalla till någon av ±e. Med denna egenskap hänförs Tauonen och Myonen till »den lätta» gruppen benämnd Leptoner [Etym. lepto’n av Grek. lept’os, tunn] tillsammans med ±e.

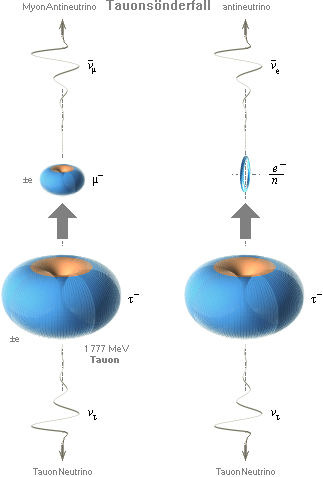
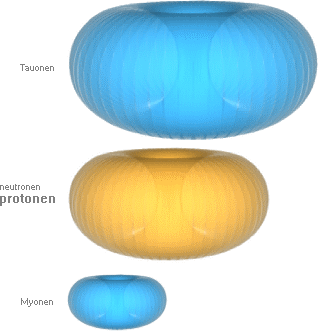
Illustrationen nedan visar motsvarande neutrinoassocierade rekyler med Myonen (µ–) och Tauonen (τ–) med ikonstorlekar motsvarande proportionerna till neutron-protonmassan [m/M=(r(R)³].

Neutrinorekylerna

Myonen och Tauonen

Notera att Tauonsönderfallen också inbegriper möjliga »återfall» till nukleoner (eg. till hadroner [‡], direkta uppgifter på möjligheten att återfalla till just en neutron eller en proton finns dock här veterligt inte på webben Jun2010) .

—————————————————

[‡] Artikeln i Wikipedia Tauon, Tauon decay påstår det men utan andra referenser än Tauonens egenmassa (1 777 MeV).

Den allmänna teckningen för Taureaktioner med atomkärnor (N) brukar skrivas

ντ + N → τ– + X

med ντ som TauonNeutrinon, N målkärnan, τ– Tauonen och X delningsprodukten

[Ref. The Decay of Tau Leptons Produced in Neutrino-Nucleon Scatterings — Mayumi Aoki et al., s1n, Aug2005].

Neutrinotermen i modern akademi i detta sammanhang associeras explicit (närmast) med Myonen som sönderfaller associerad med en specifik MyonNeutrinotyp (ovan höger underst, och mitten överst) och explicit med Tauonen (högre upp i »sönderfallsligan») som också sönderfaller associerad med en specifik TauonNeutrinotyp (ovan mitten underst) — precis som TNED vill ha det med specifika nuklidnycklar för varje specifik kärnmassdestruktion (m→γ).

Myonsönderfallet beskrivs konventionellt i @INTERNET Wikipedia Muon 2010-06-17 enligt

Bildkopia

Vänstra ledet ovan motsvarar illustrationens högra bilddel.

Tauonsönderfallet beskrivs konventionellt analogt på samma sätt i @INTERNET Wikipedia Tauon, Tauon decay 2010-06-06

Bildkopia

Webbkällan nedan (NEUTRINO PHYSICS) beskriver Tauonsönderfallet alternativt enligt

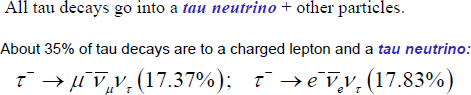
Bildkopia från

NEUTRINO PHYSICS —

http://lib.qserty.ru/static/lectures/62_pp05-L12.pdf

De bägge sätten i ovanstående teckning motsvarar de bägge mittre bilddelarna benämnda Tauonsönderfall i ovanstående illustration respektive.

Se även

Utförlig konventionell beskrivning av alla typerna neutrino-antineutrino i

NEUTRINO PHYSICS —

http://lib.qserty.ru/static/lectures/62_pp05-L12.pdf

Beskriver också inverterad betaomvandling.

Källan ovan beskriver också de experimentella grunderna för hur man redan tidigt (1962) säkert kunde veta att de olika neutrinotyperna MyonNeutrino och ElektronNeutrino inte var inbördes utbytbara mot varandra.

Låt emellertid iaktta en viss försiktighet i någon FÖRMODAD symbios mellan MAC och TNED, speciellt i dessa sammanhang: I modern akademi är neutrino en masspartikel (se jämförande tabell); I TNED är neutrino masslös em-strålning (Se från Neutrinobegreppet i TNED). Det är som att försöka blanda olja med vatten.

Se även

Man känner inte neutrinotyperna fullständigt:

(U.S. DEPARTMENT OF ENERGY) BERKELEY LAB — The Surprising Neutrino, 2009

http://www.lbl.gov/Publications/YOS/Mar/neutrinos-2.html

”The muon neutrino is a slightly heavier mixture of the three mass states, while the proportions in the tau-flavored neutrino are unknown – so uncertain we’re unsure whether the tau flavor is the heaviest or lightest. The missing piece of the puzzle is the “mixing angle” that controls how much of the tau flavor consists of the electron-neutrino mass state.”.

SAMMANFATTNING

MyonNeutrinostrålning och TauonNeutrinostrålning blir med ovanstående genomgång i TNED av samma principiella karaktär som de enligt TNED övriga ordinära nuklidneutrinostrålningskaraktärerna: varje nuklidformation uppvisar sin specifika uppsättning neutrinofrekvenser och neutrinovåglängder. De olika neutrinotyperna visar med andra ord unika NYCKLAR, profiler eller »språkröster» som inte kan utbytas mot varandra.

Neutrinotypernas neutrinonycklar

MYONNEUTRINOS OCH TAUONNEUTRINOS — de nu kända enda demonteringsnycklarna till NeutronKÄRNfragmentStrukturerna

Neutrinotypernas olika neutrinonycklar

Eftersom alla nuklider (specifika atomkärnor) som bildas av neutroner och deras sönderfall (väteatomer) delar samma gemensamma ekvivalenta elektron-positronmassor, delas också alla nuklider ENLIGT TNED med masstalen från 1 och uppåt på samma två uppsättning s.k. betaassocierade neutrinonycklar: Antineutrinonyckeln (v) som hör till elektronassocierade processer, och neutrinonyckeln [v] som hör till positronassocierade dito.

Genom föregående (och kommande) genomgång står det tydligen enligt TNED redan klart att alla övriga neutrinonycklar tvunget måste höra till typen »radionycklar»: neutrinostrålning [i TNED samma som massdestruktionsstrålning (m→γ)]. Det betyder en för varje kärntyp unik struktur av frekvenser och våglängder som inte kan utbytas mot varandra — likt neutrinostrålningen som sammanhänger med det tungt radioaktiva sönderfallet (Se Radiomath). Det är i TNED neutrinostrålning associerad med reguljära kärnsönderfall (fission) och reguljära kärnföreningar (fusioner).

Se större bild längre ner

Atomkärnans byggnad kan tydligen enligt TNED beskrivas så att den tvunget kommer i UPPBRYTANDE svängning då den påförs en impuls (kollisionsstöt, MIC) med en massinteraktiv våglängd mindre än kärnradien; För att återställa balansen söker kärnan göra sig av med överskottsenergin, vilket kärnan (här veterligt) gör på samma sätt som vattenytan i rekylkraften från den enda droppen som träffar: Genom att skjuta iväg (dela upp sig i) delformer. (Först Krona, sedan rekylPelare).

NOTERING (Jun2010). Vattenkronor är svåra att fotografera med skärpa eftersom droppbildningen sker med hög hastighet. Det krävs slutartider på (minst) 1/10 000 sekund, vilket betyder extremt dyra kameror — ingenting för oss vanliga amatörer. Rekylpelaren däremot är lagom lugn (OK med 1/4000 sekund) och kan fotograferas med (system)kameror i den mera rimliga (men fortfarande relativt dyra) prisklassen.

PARTIKELDELNINGENS MATEMATIK

— Hur VET vi att TNED-begreppet för NEUTRINO kan tillämpas på resultaten från MODERN AKADEMI med komponenterna TauonNeutrino och MyonNeutrino?

Det finns hur många neutrinonycklar som helst …

Partikeldelningens matematik

Med utgångspunkt från protonen (vätekärnan) som den stabila kärnfysikens grundindivid

— Partikeldelningen t.ex. från Focuskällans nedre Kaon+ till en Myon+ med angiven MyonNeutrino innefattar 388,34 MeV — »det är alldeles tydligt fråga om en SUMMA av massdestruktion (m→γ) OCH gammaexcess».

— Men hur tusan ska vi kunna veta något om VAD som är VAD i den kaksmeten?

— Vi VET det inte. TNED framställer sin egen kärnfysik självständigt med grund i härledningarna från PLANCKRINGEN och den ekvivalenta fraktala struktur som atomkärnans kraftväv bygger på, se speciell redovisad jämförelse i ATOMVIKTERNA. Endast om redan kända experimentellt observerade fenomenformer kan fås att passa in på dessa strukturbegrepp i TNED finns grund för en beskrivande framställning. Vad sedan motsvarande fenomengrund kalls för i modern akademi är en annan fråga.

— Med sambandsformen λ=h/mv (MIC) som kraftbas för att få en BRYTFORM på protonens spinnradie och därmed verkställa kärndelning

— OBS just kärndelning, INTE sönderfall, sådana nukleärfissioner är alltid förknippade med massdestruktion (m→γ), vilket INTE är det påtriggande fallet i MIC-sambandet ljus (vilket vi villkorslöst utgår ifrån); det som igångsätter verksamheten är en mekanisk stöt som genomtränger kollisionsobjekten med karaktäristiska våglängder under kollisionsögonblicket

— finns i princip enligt TNED via atomkärnans obegränsade fraktaldjup hur många sätt som helst att välja på beroende på energinivåer.

I dagens läge (Jun2010) finns dock bara endast TVÅ EXPERIMENTELLT KÄNDA olika sätt att välja på och som, tydligen, kan associeras med massdestruktionsstrålning (m→γ) i sina sönderfall enligt TNED:

1. med resultat i en kärnmassa större än protonens HÖGSTA ENERGIN kortaste våglängden (1 777 MeV), Tauon

2. med resultat i en kärnmassa mindre än protonens LÄGSTA ENERGIN längsta våglängden (105,66 MeV), Myon

BILDKÄLLA: Författarens arkiv · Vattenfysiken 2009 · Nikon D90 · Bild34Drop17iso3200 ·

Möjliga BildANALOGIER TILL KÄRNFYSIKENS KOLLISIONSDYNAMIK

Den substratmassa (±e, samma som i moderatomen) som avdelas för bildningen av typerna resp. Myon och Tauon innefattar i vilket fall samma typstruktur som i protonaggregatet (»vattenytan») — Analogt, detsamma som en ekvivalent ±e-struktur som summerar nollmoment, nollspinn och nolladdning (atomkärnans grundegenskap enligt TNED) tillsammans med bindningsstrukturer. Enda möjligheten för dessa bägge ytterlighetsfall att KOMMA NER (sönderfalla åter) till substratet, den stabila elektronen (eller positronen som förintas tillsammans med en elektron), är ATT bindningsstrukturen löser upp sig. Det kan den bara göra genom massdestruktion (m→γ), spelar ingen roll VAR den gör det, bara ATT möjligheten existerar. Det är i TNED detsamma som neutrinostrålning.

DÄRFÖR kan vi i TNED helt SÄKERT säga att kollisionshändelser mellan atomkärnor som leder till kärndelningar också (längre fram i processen, om den inte av olika anledningar avstannar och vänder tillbaka) kommer att utlösa massdestruktion (m→γ) , i TNED detsamma som neutrinostrålning.

Eftersom bägge (1)(2) ovan — för protonens del, vårt huvudexempel — TYDLIGEN INTE sammanhänger med massdestruktion från den förbrukningsbara 18e-delen i kärnstrukturen (se 1818-massivet) — Se även förklarande notering ‡ nedan om ej redan bekant — utan tydligen just måste komma från 1818-massivet, är TYPEN nuklidneutrino given

(TILL SKILLNAD FRÅN BETAneutrino, denna massdestruerar i BETASÖNDERFALLEN på 18e-delen, garanterat skild från nuklidtypen vars neutrinoassociation ligger på 1818e-massivet)

— SAMT att varje delkropp FÖLJRIKTIGT tvunget får sin specifika (NUKLIDASSOCIERADE) neutrinonyckel, på samma sätt som varje ordinär nuklidbildning har sin uppsättning neutrinofrekvenser och neutrinovåglängder.

Nuklidassocierad neutrinostrålning i TNED (radionuklider [tungt radioaktiva nuklider], fusioner och fissioner)[1818e-associerad] sammanhänger med kärndelningar, vilket inte betaassocierad (atomnummerändrande) neutrinostrålning gör [18e-associerad] (Se vidare från RadioMath);

OM terminologin är (naturligt) konsekvent, ska då också kollisionsassocierad neutrinostrålning (MIC) på samma sätt sammanhänga med typen nuklid eftersom det är fråga om kärnuppdelning. Därmed skulle, enligt TNED, typerna MyonNeutrino och TauonNeutrino (likväl) vara just nuklidassocierad neutrinostrålning: massdestruktionsstrålning som sammanhänger med kärndelningar. I modern akademi däremot (TNED-grunderna orepresenterade) framställs MyonNeutrino och TauonNeutrino tillsammans med elektronNeutrino i ett begreppssystem som saknar specifikt nuklidassocierad koppling (Konv. begreppet leptoner). Solens neutrinoproduktion till exempel framställs i MAC med föreställningen att den skulle vara av typen elektronNeutrino

[Ref., ”The Sun should emit only electron neutrinos as they are produced by H–He fusion.”, @INTERNET Wikipedia Solar neutrino problem 2010-06-15].

I TNED finns ingenting sådant: inte beträffande några fristående enskilda fusionssteg, inte beträffande fusionsfysiken överhuvudtaget. Omsatt i TNED (relaterad fysik) skulle den moderna ordningen (med andra ord) skapa terminologiskt kaos. Kärnassocierad neutrinostrålning är (tydligen) ett begrepp som inte finns i modern akademi.

För att frammana motsvarande neutrinodämpning (eller neutrinoändring) i TNED, måste MAC tydligen tillgripa ytterst komplicerade matematiska modeller (»neutrinooscillation») som tillskriver neutrinofenomenet en massa som i termer av relaterad fysik (TNED) inte existerar. Se mera utförligt från Solens neutrinoproduktion.

‡ OM neutrinostrålningen från MIC-kollisionerna skulle sammanhänga med 18e-delen i kärnstrukturen, är det tydligt att en ytterligare reduktion i 18e-delen för protonens vidkommande medför, i samma fysik som den ordinära betaemissionens dynamik, en (tillfälligt) motsvarande högre massdefekt …

— Men varför skulle inte det gå? Högre massdefekt betyder ju hårdare nuklidbindning — och därmed motsvarande större mängd elektronemission, vilket just precis blir resultatet av MIC-kollisionerna: atomkärnan avdelar kärnsubstrat som grund för kärndelarna. Det är väl klart.

— Ja. Men det aktuella fallet gäller inte en ensidig utgivning av elektroner (eller positroner) utan en TYDLIG kärnstrukturbunden ±e-utgivning i ljuset av MIC-kollisionens svängningsenergi och vilken ±e-struktur onekligen, tvunget, tillhör nuklidformens energiekvivalent; FORMEN kan bara tas från nuklidstocken 1818e.

— ENBART i kraft av den argumenteringen kan den efterföljande neutrinostrålningen, dvs., massdestruktionen vid det ytterligare sönderfallet som leder till elektron eller positron, (här, veterligt) förstås associerad med 1818e-massivet.

Därmed framstår klassificeringen av neutrinotypen i samband med MIC-kollisioner helt entydigt i TNED: nuklidbaserad. Inte betaassocierad.

Det skulle alltså finnas hur många andra huvudsakliga alternativ att välja på som helst, enligt atomkärnans fraktalstruktur i TNED: det finns utöver den vanliga betatypen hur många neutrinotyper som helst. Se även liknande tankegångar i referat längre ner från vissa etablerade forskarhåll.

OBSERVERA DOCK ATT DESSA PÅSTÅENDEN i följd av TNED här (ännu) står helt experimentellt obevisade.

Att sedan delkropparnas sönderfall OCKSÅ sammanhänger med gammaexcess är självskrivet i sig enbart via det givna MIC-sambandet (λ=h/mv): tillståndet är av övergående natur och en ren följd av kollisionen; atomkärnan söker återgå till sin ursprungliga jämvikt genom att göra sig av med allt den kan, och efter sin egen specifika balansräkning.

VAD SEDAN DEN MODERNA AKADEMIN INLÄGGER FÖR NÅGRA INNEBÖRDER OCH BETYDELSER I SIN NEUTRINOBIL har i grunden inte med saken att göra. Vilket som är vad kan i vilket fall bara avgöras genom en separat jämförande analys.

Forts. i Kärndelningarna via MIC.

MASSINTERAKTIVA SAMBANDET Mass Interactive Connection — konv. de Broglies vågekvation från 1924

MIC

Beskrivningen nedan visar hur sambandet i MIC kopplar massavdelningarna

HUR NUKLIDASSOCIERAD NEUTRINOSTRÅLNING KAN UPPVÄCKAS GENOM PARTIKELKOLLISIONER

MIC — λ = h/mv — beskriver hur kärndropparna avdelas

Se även särskild del i MIC.

MIC (Mass Interactive Connection i TNED, konv. de Broglies vågekvation) λ = h/mv beskriver omsättningen mellan elektrisk och mekanisk energi på kärnfysikens nivå (Se konv. särskilt i neutrondiffraktion).

FÖRENKLAT INLEDANDE RÄKNEEXEMPEL

En proton som uppvisar en rörelseenergi (Ekin) på (runt) sin egen massekvivalent,

Ekin = mv²/2 = (938,2 MeV)e = mc², m = (938,2 MeV)e/c²; v = √ 2(938,2 MeV)e/[(938,2 MeV)e/c²] = √2c² = c√2

med en motsvarande rörelsemängd eller impuls

mv = [(938,2 MeV)e/c²](c√2) = [(938,2 MeV)e/c](√2)

= 7,09009 t19 KG(M/S)

uppvisar en MIC-våglängd på

λ = h/mv = (6,626 t34 JS)/[7,09009 t19 KG(M/S)]

= 9,34542 t16 M.

λ-värdet är 0,682148 av r₀ = 1,37 t15 M = protonradien.

Det betyder att MIC-våglängden (0,682148)r₀ är kortare än kärnradien (1)r₀ — vilket bör påtvinga atomkärnan ett principiellt instabilt tillstånd. Med referens till fysikens allmänna jämviktsdynamik kan situationen förstås på följande sätt:

Atomkärnan försöker återställa (»parera») balansen, vilket resulterar i att kärnan tvingas göra sig av med massa: kärnan börjar avdela delar (m) av sin kärnstruktur (±e) som följd av MIC-svängningarna.

— Analogin till vattenfysiken

(hydrofysiken [läran om vätskornas fysik], eller här mera egentligt hydrodynamiken, läran om och studiet av vätskors rörelse)

är (eller bör vara) tämligen exakt;

BILDKÄLLA: Författarens arkiv · 2009

Bild4·Drop15iso3200

Den avdelade ±e-massan kan förstås bilda ett massubstrat för en moderkärna i likhet med dess spinnstruktur — som en liten miniatyrproton likt vattenmolekylerna som bildar substratet för den avdelade vattendroppen.

Den sammanbindande kärnstrukturen måste frikopplas (brännas av) innan elektronmassan kan visa sig separat.

ENBART av anledningen att varje avdelad kärndroppe HAR någon ±e-struktur har den också en sammanbindande struktur som hindrar elektronen eller positronen från sig att visa sig. Eftersom kärndroppen är instabil (den existerar normalt inte utom i kraft av häftiga partikelkollisioner, och då bara tillfälligt som vattendropparna i en vattensplash), måste den förr eller senare exponera just elektronen eller positronen som slutstation — enda återstående stabila partikelformen — i sönderfallet. Det betyder att strukturbildningen ±e måste brännas av. För det krävs extra arbete, och energin för det arbetet kan bara tas ifrån den strukturbindande massan (±e) i form av enligt TNED massdestruktionsstrålning eller neutrinostrålning, Därmed är elektronen (eller positronen) löst från kärnbindningen och den ursprungliga kärndroppens sönderfallsprocess har därmed upphört.

Kärndelningarna via MIC

Därmed kan kollisionsdelningarna från MIC (λ=h/mv) formuleras enhetligt enligt TNED:

Proton-proton-kollisionerna bildar kärnsvängningar via MIC (λ=h/mv). Likt vattendroppsrekyler DELAS protonerna på den kollisionssvängande mekaniska vågenergins räkning: originalprotonerna kommer i MASSDEFICIT (massunderskott) genom de avdelade substraten eller »kärndropparna». Kärndropparna delas på MIC-svängningarnas uttömmande (gammaexcess, alla våglängder i storleksordningen lika med bråkdelar av atomkärnans radie). Gammaexcessen avges TILLSAMMANS med massförstörande (m→γ) sönderfall av (Jun2010) ÄNNU KÄNDA endast TVÅ HUVUDTYPER (konv. TauonNeutrino [dropptypen större än protonen] och MyonNeutrino [dropptypen mindre än protonen]). Dessa massdestruktiva associerade sönderfall återfaller ytterst på individuellt inbördes stabila ±e (±e tillsammans i särskild massdestruktion, se Parannihilation).

Protonaccelerationsenergin (antal protonmassor) och den resulterade protonkärnsvängningsvåglängden (MIC λ/2r0) kan för varje känd partikel x bestämmas med insättning av grundsambanden i kalkylceller (nedan, från OpenOffice, exemplet med Tauonens ViloBildningsMassa m0=1777 MeV/c²);

Kalkylkortet

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN MIC.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/MIC.ods

Kalkylkortet med inmatad vilomassa för Tauonen 1 777 MeV/c². Se även särskild beskrivning i Kalkylkortet.

Kalkylkortets samband beskrivs i efterföljande Härledningar.

Kalkylkortet beräknar aktuell energi i antal protonmassor som krävs av en partikelaccelerator för att accelerera en proton som i kollision med en stationär proton kan bilda/framvisa/uppvisa/syntetisera en partikel med vilomassan x(MeV).

Kalkylkortet ger även motsvarande MIC-våglängd (MIC2) i protonaggregatets referens enligt TNED (N3m20-aggregatet).

Figuren nedan ger grunddata på MIC-våglängder i N3m20-aggregatet med hänsyn till de konventionellt benämnda partikelfragmentens etablerade grunddata. Se även i NUKLIDRADIERNA Del II.

Att kalkylkortets resultatvärden och samband överensstämmer med konventionellt (relativistiska) sambandsformer [Jämför PLANCKEKVIVALENTERNA] kan studeras till exemplifierad konventionell jämförelse bl.a. i webbkällan (med exempel s2n motsv. x=135 MeV)

UNIVERSITY OF EDINBURG — RELATIVISTIC SCATTERING — R.J. Cole, November 2008

http://www2.ph.ed.ac.uk/teaching/course-notes/documents/62/1127-dr18.pdf

Se även ytterligare webbkällor längre ner i Härledningar till sambanden.

MIC-ekvivalenterna

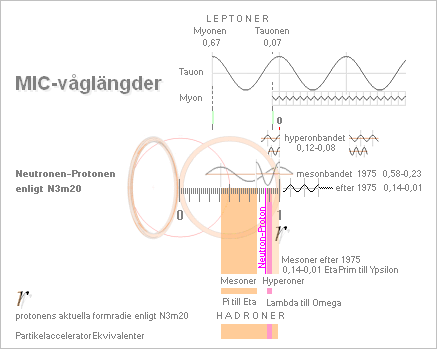
Bilden nedan sammanfattar i översikt ovanstående kalkylresultat med

TNED-ekvivalenter till MIC-våglängderna

för de subatomära partikelfragmenten från proton-protonkollisioner i artificiella partikelacceleratorer med grunddata (vilomassor) sammanställda från allmänt tillgängliga webbkällor (Jun2010)

Figurförklaringar:

LEPTONER ................ utöver elektronen, alla partikelformer som NÄRMAST kan sönderfalla till elektron-positron (Myon · Tauon) [‡]

MESONER ................ kollisionsformer som INTE innefattar protonindividen som sådan (mesoner kan inte sönderfalla till proton eller neutron) [‡]

HYPERONER ............. kollisionsformer SOM innefattar protonindividen som sådan (hyperoner sönderfaller till protoner-neutroner och mesoner) [‡]

HADRONER .............. mesoner PLUS hyperoner [FMs140sp2mn]

Etym.; lepton [liten], partikel med liten massa; meson [mellan], medelklassen; hyperon [över], överklassen; hadron [tjock, svulstig], tjockklassen.

Inre bildsnittet från N3m20-aggregatet i ATOMKÄRNANS HÄRLEDNING motsvarar neutronens-protonens inre spinntoroidform, se även PLANKRINGENS DIMENSIONER. NOTERING: Elektronmassans Element enligt TNED syns inte i denna skala.

Obs: MIC-våglängderna gäller genom ekvivalenta impulser enligt mekaniska m₀v = elektriska mu enligt anslutning till motsv. partikelbildningar i den kosmiska strålningen enligt TNED — se särskilt i BEVISET FÖR MULTIPLA c. Se vidare i HÄRLEDNINGAR.

Kärnikonernas storlek har anpassats efter neutron-protonkärnans masstäthet enligt m/M=(r/R)³. För vilomassorna till Myonen-Tauonen, se särskilda referenser i Myonen och Tauonen. Se även tabell i Partikelnomenklaturen.

Från MyonNeutrio till TauonNeutrino i TNED. Genom PLANCKS STRUKTURKONSTANT får, i TNED, varje nuklid sitt karaktäristiska neutrinospektrum, se från Neutrinosignaturen. Neutrinosignaturen fungerar som en specifik unik NYCKEL och som sammanhänger med just den nuklidens bildning (och sönderfall). I TNED grundas alla nuklidbildningar på att de lättaste grundämnena byggs upp från de högsta neutrinofrekvenserna så att de redan bildade lättare ämnena inte sönderbryts på de tyngre ämnenas bildningsenergier. Se specifikt från GRUNDÄMNESBILDNINGEN. Eftersom neutrinostrålningen i TNED är ren masslös em-strålning med frekvenser som (vida) understiger atomkärnans egna dimensioner, fungerar också neutrinonycklarna som ordinära ljuskvanta som ändrar frekvens vid genomgången av (speciellt tät) materia enligt COMPTONEFFEKTEN. Om ändringen gäller en dämpning, sker den från högre till lägre frekvenser, analogt från kortare till längre våglängder. Därmed finns också möjligheten att den med Myonbildningen (eller sönderfallet) associerade MyonNeutrinostrålningens specifika nyckel KAN »övergå» (frekvensdämpas) till TauonNeutrinostrålningens specifikt mera nuklidtunga nyckel.

I modern akademi finns inte den beskrivna teoretiska grunden (på grund av den moderna akademins neutrinobegrepp som en partikel med spinn, se Jämförande tabell). I modern akademi tvingas man istället — med referenserna enligt TNED — uppfinna att neutrinostrålningen har massa (består av vägbara partiklar). Därmed kan man beskriva övergången med hjälp av begreppet »neutrinooscillation» (som grundas på en masskvadratsfunktion i den redan omfattande teorin).

Ett nyligen (31Maj2010) utkommet pressmeddelande från CERN har meddelat att OPERA-projektet (startades 2006 enbart för tillfället att försöka påvisa en förekomst av TauonNeutrino från MyonNeutrio, max 5 tillfällen på 10,4 år) har detekterat en TauNeutrino in till 98% säkerhet — från CERNs MyonNeutrinoKälla belägen 73 mil genom Jordskorpan från OPERA-detektorn i Italien (Gran Sasso); Man har riggat ett omfattande blocksystem med tunna blyblad för att kunna fånga en ev. TauonNeutrino som bildas från MyonNeutrion på vägen genom Jordskorpan. TauonNeutrinon kan bilda (»låsa upp») en Tauon i växelverkan med någon av blyets atomkärnor och ger därmed ett speciellt signalspår som kan analyseras.

En presentationsfilm som beskriver OPERA-projektet konventionellt finns på YouTube,

http://www.youtube.com/watch?v=ufCyDHSAvLE&feature=youtu.be&a

En av vetenskapsmagasinens artiklar beskriver nyheten från 10 Maj 2010 i webbkällan

ETHlife — TAU NEUTRINO LIKELY OBSERVED IN OPERA DETECTOR — 1 Juni 2010

http://www.ethlife.ethz.ch/archive_articles/100601_Neutrino_oszillation_su/index_EN

Kompletterande beskrivningar på själva anordningarna i OPERA-projektet finns i

The OPERA long baseline neutrino oscillation experiment — G Wilquet (2008)

http://iopscience.iop.org/1742-6596/110/8/082022/pdf/jpconf8_110_082022.pdf

FÖREGÅENDE RESONEMANG ANTYDER ATT man med allt högre kollisionsenergier kommer att upptäcka — ännu längre in (i fraktalstrukturen enligt TNED) liggande NEUTRINONYCKLAR — inte bara typen MyonNeutrino och TaounNeutrino som det är I DAGENS LÄGE, utan också flera liknande via motsvarande partikelvåglängder kortare än Tauonens.

Med, således, allt högre kollisionsenergier i TNED-fraktalernas ekvivalenta oändlighetsrike skulle vi till slut hamna i den motsvarande ordinära NUKLIDNEUTRINObanken enligt TNED (se från PLANCKS STRUKTURKONSTANT) med OBEGRÄNSAD MÄNGD NEUTRINONIVÅER. Inte enbart TVÅ utöver den konventionellt benämnda s.k. vanliga betatypen.

— Nämligen; På samma sätt som en Tauon kan sönderfalla till en Myon, skulle (väl) i princip en »superTauon» kunna sönderfalla till en Tauon. Och sedan vidare i allt högre ordning (UltraSuperTauon, ÖverUltraSuper…). Hur kan den typen uteslutas? Fraktalsystemet är ju givet i TNED.

Mera Neutrinos

— Artikeln på Lepton i Wikipedia omnämner just det (Jun2010); En del redan etablerade forskare menar att det skulle finns en fjärde elektrongeneration med angiven gränsmassa (100,8 GeV = 100 800 000 Mev)/c²

”while its associated neutrino has a mass of at least 45.0 GeV/c².[14]”

— en betydande djupdykning i fraktalformerna.

— Det är just precis det rent kvalitativa som TNED utpekar i ljuset av föregående resonemang — med vidare. Det finns ingen slutlig gräns, eftersom Atomkärnans fraktala ytform enligt TNED går mot oändligt i masstäthet med växande fraktaldjup. Se f.ö. ATOMKÄRNANS HÄRLEDNING DEL II. TNED själv anvisar dock (här veterligt) ingen direkt manual till fraktalserierna — utom till första och andra nivåerna (N3m20, se PLANCKRINGENS DIMENSIONER).

— Jordens ändliga begränsade storlek och partikelexperimentens kostnadsprojekt sätter definitiva gränser för dylika försök: FÖRR ELLER SENARE behövs det partikelacceleratorer i storleksordningen Jordbanan runt. Förr eller senare måste experimentalvetenskapen släppa greppet om partikeldjupet.

HÄRLEDNINGAR

Härledningar

HÄRLEDNINGAR till sambanden i MIC-ekvivalenterna

För energiräkningen i det elektriska systemets referens gäller den lokala ljushastigheten (c) med referens till en lokalt fix fältpunkt i den lokalt dominanta gravitationen [GcQ-teoremet i TNED]. I vårt fall betyder det detsamma som det fasta rummets föremål via Jordskorpan och den underliggande Jordkroppen. I det elektriska fältets referens med energin E=mc² kallar vi den fixa g-punktens elektriska referens för ett så kallat (eng.) Center of Mass System (CMS, ofta bara CM), sv. »mittMassaSystem». De bägge protonerna som ska accelereras summerar via E=mc² en nollsumma av impulser och moment; Resultatet ska bli en AVDELAD kärndel här betecknad x med protonerna betecknade p.

Sambanden för CMS ger då (:= används som tilldelningslikhet för att slippa indexera beteckningarna, jämför a:=a+b som tilldelar en ny innebörd [:=] åt en redan använd)

Center of mass;

m(p+x) + m(p+x) := m(p) + m(p) + m(x)

ENERGIERNA;

2m(p+x)c² = 2m(p)c² + m(x)c²

c² FÖRKORTAS BORT;

2m(p+x) = 2m(p) + m(x)

RESULTAT;

m(p+x) = m(p) + m(x)/2

PLANCKENERGINS massekvivalent;

m(p)/m(p+x) = √ 1 – (u/c)²

PROTONHASTIGHETEN u;

u/c = √ 1 – [m(p)/m(p+x)]²

= √ 1 – [m(p)/(m(p) + m(x)/2)]²

LABORATORIESYSTEMETS REFERENS med en av protonerna vilande som målobjekt;

I CMS (mittmassystemet) förstås beloppet (u/c) för var och en av protonerna — inbördes på väg mot varandra enligt elektriska nollreferenspunkten för ideala totala massdestruktionen E=mc². För att kunna addera dessa hastigheter i det praktiska fallet med ena protonen vilande och den andra med hela impulsenergin från partikelacceleratorn — och på ett sätt som bevarar det slutna elektriska systemets begränsade ändliga topphastighet (c) — måste en speciell sambandsform användas. Vi studerar här direkt hur den kan härledas på det allra enklaste sättet — garanterat utan krångliga omskrivningar, bara ren grafisk (matematisk) geometri.

SAMMANSATTA HASTIGHER

i PARTIKELFYSIKENS ELEKTRISKA ACCELERATIONER — (Konv. relativistisk addition av hastigheter)

Det är från GRAFLÄRAN känt att funktionen i Fig:1 bildar en (den mest harmoniska) kurva som har gränsvärdet 1 för alla möjliga (dubbla) x-värden (x+x) mellan noll och 1. Eftersom vi är ute efter »en elementär summerare mot 1» (toppvärdet c) kan vi alltså helt enkelt ersätta respektive x-värde med ett alternativt värde — för exemplets del a=0,3 — mindre än 1 enligt typkurvan i Fig:2. I vilket fall bevaras därmed MAX SUMMA 1 och så länge alternativvärdet a<1 för alla x mellan 0 och 1. Sambandet kan då tecknas generellt i form av två olika värden (summerande hastigheter, bägge mindre än 1), här i formen av en fast koefficient (a) och en variabel (x) mellan 0 och 1 enligt sambandet i Fig:3.

Eftersom det elektriska systemets absoluta hastighetsgräns för acceleration av mobila laddningar inom systemet är en enhet lika med den lokalt gravitellt bestämda ljushastigheten c=1 [GcQ-teoremet i TNED] får vi direkt ur sambandet i Fig:3 motsvarande fysikform

uΣ = y = (a+x)/(1+ax/c²) ............................... M/S, sambandet för summerande hastigheter (a+x)<c inom c

med a och x som separata hastigheter, bägge begränsade av max a=x=c=1.

y = (x+x)/(1+xx) x	y = (0,3+x)/(1+0,3x) x	y = (a+x)/(1+ax)	samma som Fig:1 y = 2x/(1+x²) = 2/(x+1/x)
Fig:1	Fig:2	Fig:3	Fig:4

Sambandet (uΣ) är samma som används konventionellt med typbenämningen (eng.) Relativistic Addition of Velocities.

För konventionell beskrivning, se exv,

NUMERICANA.com · How do relativistic speeds add up? — 2005

http://www.numericana.com/answer/relativity.htm

Particle production threshold energies

http://galileo.phys.virginia.edu/classes/252/particle_creation.html

PDF:

http://galileo.phys.virginia.edu/classes/252/particle_creation.pdf

Modern Physics · TRANSFORMING ENERGY INTO MASS: Particle Creation — Michael Fowler, University of Virginia (1999)

@INTERNET Wikipedia Velocity-addition formula 2010-06-10

m.fl.

Varje sådan sammansatt hastighet kan sedan på samma sätt betraktas som endera av hastigheterna (a eller x) för matematisk konstruktion av ett godtyckligt antal summerande hastigheter inom det slutna elektriska systemets laddningsaccelerationer, typ

uΣ = z = (y+x)/(1+yx/c²) M/S osv.

med y som i föregående.

Speciellt om de bägge hastigheterna är ekvivalenta (a=x) fås den enklare sambandsformen i Fig:4 (samma som i Fig:1).

Vi måste använda den typformen i beräkningar av den s.k. VILOMASSAN (eg. ENERGIN) som krävs för att bilda en viss SUBSTRATPARTIKEL (Meson, Hyperon, Myon m.fl., de experimentellt uppmätta s.k. vilomassorna brukar anges typiskt i MeV i tabeller) — från (i de flesta fall) en projektilproton och en målproton. Känner man vilomassorna, kan energierna beräknas som krävs för att en typisk strålproton från en partikelaccelerator ska kunna producera det aktuella kärnsubstratet tillsammans med en stationär målproton. Substratet som sådant kan beskrivas enligt TNED på typformen (exempel som ansluter till originalförfattningen i NEUTRONFRAGMENTEN)

Λ⁰ = p⁺ + m(U) = [m(U)1 + (p⁺ – m)] + [m(U)2 + (m=π^–)] … ............. med masschokning, partikelaccelerator, samband enligt TNED

Den motsvarande konventionella teckningen (bildningsenergierna skrivs vanligen aldrig ut) skrivs ofta

Λ⁰ → p⁺ + π^–

Härledningen fortsätter med

HASTIGHETERNA SUMMERAS;

u/c := 2(u/c=a)/[1+(a)²] = k ............... Particle production threshold energies, ’relativistic addition of velocities formula’

:= 2/[1/a + a] = uΣ/c ;

uΣ/c = 2/[1/a + a] ; a = √ 1 – [m(p)/(m(p) + m(x)/2)]² ;

RESULTATET GER DEN SÖKTA KÄLLPROTONENS ENERGI [m(p+x)’] för bildning av partikeln x med massan m(x);

√ 1 – k² = m(p)/m(p+x)’ ;

m(p+x)’/m(p) = 1/√ 1 – k² ; anges i antal protonmassor i kalkylkortet

Här används värdet (938,2 MeV)/c²=(E=UQ)/c²=m för protonmassan.

MIC-kärnsvängningens våglängd beräknas som tidigare från

λ = h/m₀v .................... M, kärnsvängningens våglängd som garanterar att atomkärnan avdelar sina partikelsubstrat

= h/mu

Massan m är den accelererade källprotonens massa [m(p+x)’] och v är protonens motsvarande mekaniska hastighet genom protonens vilomassa m0. Hastighetsbeteckningen u anger protonens motsvarande uppnådda hastighet i partikelacceleratorn, alltid lägre än c. Likheterna bygger på given impuls [mu=m0v], samma som i BEVISET FÖR MULTIPLA c. För atomkärnans radie finns i KÄRNRADIERNA DEL II en ingående beskrivning enligt TNED som skiljer på atomkärnans tyngdcirkel (Planckekvivalenterna via r0=1,37 t15 M för protonradien) och atomkärnans yttre form (den MIC-relaterade verkansradien). Skillnaden mellan dessa är ganska precis en faktor 2 [1,9926606 se Planckringens dimensioner för A=1], och man får alltså MIC-våglängden relativt atomkärnans formradie enligt (kalkylkortets MIC2 λ/2r0)

λ/r = h/2m₀vr₀

= h[m₀·1/√(1/(2/[1/a + a])² – 1)]^–1/2r₀

= h[1/√(1/(2/[1/a + a])² – 1)]^–1/2m₀r₀

= h[√(1/(2/[1/a + a])² – 1)]/2m₀r₀

= h[1/(2/[1/a + a])² – 1]^½/2m₀r₀

= h[–1 + [a^–1 + a]²/4]^½/2m₀r₀

= h[–1+[a^–1 + a]²/4]^½/2m₀r₀

med

a = u/c

= √ 1 – [m(p)/(m(p) + m(x)/2)]²

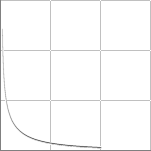
Då m(x) växer obegränsat går a=u/c mot 1; Kvoten λ/r går då obegränsat mot noll.

graf — testadOKmotKalkyl

y=[–1+0.25[a+a'–1]'2]'0.5

a=([1–(1+x)'–2]'0.5)

y=[–1+0.25[([1–(1+x)'–2]'0.5)+([1–(1+x)'–2]'–0.5)]'2]'0.5

x

Från BEVISET FÖR MULTIPLA c gäller förhållandet mellan partikelacceleratorns begränsade (u=vR)<c och det idealt mekaniska v sambandet

Hastighetsrelationen

TNED:

v/v_R = 1/√1 – (v_R/c)²

v_R = uΣ

Därmed kan v/c också beräknas enligt

v/c = 1/√ (c/v_R)²–1

Chokmassan

Chokmassan:

Chokmassans storlek (totalt med projektilprotonen innefattat) fås ur Planckenergins massekvivalent [Se utförligt från MAFEM i PLANCKEKVIVALENTERNA]

m₀/m = √1 – (uΣ/c)² = √1 – (2/[a+1/a])²

genom laddningshastigheten i vakuum

u = c√ 1 – 1/[(UQ/m₀c²) + 1]² .......... laddningshastigheten u för Q från accelerationsspänningen U

via accelerationsspänningen U för laddningen Q med vilomassan m0;

(u/c)² = 1 – 1/[(UQ/m₀c²) + 1]² ;

1 – (u/c)² = 1/[(UQ/m₀c²) + 1]² ;

√1 – (u/c)² = 1/[(UQ/m₀c²) + 1] ;

m/m₀ = (UQ/m₀c²) + 1 ;

Med E=UQ lika med accelerationsenergin och m0=E/c² i MeV kan kvoten (UQ/m₀c²) också skrivas explicit för protonvilomassan 938,2 MeV som partikelacceleratorns enda partikelprojektil

(UQ/m₀c²) = E(MeV)/[938,2 MeV]

= n(p)

Chokmassakvoten via accelerationsenergin i antal protonmassor därmed

m/m₀ = n(p) + 1

Dvs., endast om accelerationsenergin är noll [n(p)=0] är m=m0.

ChokmassaExcessen eller effektiva chokmassan — den aktuellt överskjutande massan Δm = m–m0 = m(U) — blir alltså

(m₀+Δm)/m₀ = n(p) + 1 = 1 + Δm/m₀ ;

Δm/m₀ = n(p) ;

Δm = m₀(UQ/m₀c²)

= (UQ/c²)

= m/m₀ – 1

E(MAC)

—————————————————————————————————————————

E(MAC):

——————————————————————————

ProtonImpulsen [betecknad m(uΣ/c) i kalkylkortet] gånger (uΣ/c)/2 ger rörelseenergin E(MAC):

p = mv ;

E(kin) = mv²/2 ;

Anges v i c0-enheter fås

E(kin)/c₀² = m(v/c₀)²/2 ;

vilket är samma uttryck som gäller för massan i energi-massaekvivalenten E=mc². Med ytterligare en division med protonmassan (m0) ges kinetiska energin E(kin) i antal protonmassor — som enkelt kan ersättas med protonmassans ekvivalenta MeV-värde

(E/e/T6)=mc²/e/T6 = (1,0072766u)c²/e/T6 = 938,25747 MeV

— i MIC-kalkylerna här ersatt av Focustabellkällans 938,2 MeV för enhetliga referenser.

;

E(kin)/m₀c₀² = m(v/c₀)²/2m₀ ;

= (m/m₀)(v/c₀)²/2

= E(MAC) ;

v = uΣ

E(TNED)

—————————————————————————————————————————

E(TNED):

——————————————————————————

ProtonImpulsen [betecknad m0(v/c) i kalkylkortet] gånger (v/c)/2 ger rörelseenergin E(MAC):

På samma sätt som ovan för E(MAC) fås här direkt med v=v och m=m0

E(kin)/m₀c₀² = m₀(v/c₀)²/2m₀ ;

= (v/c₀)²/2

= E(TNED) ;

Energierna

—————————————————————————————————————————

Energierna:

——————————————————————————

Jämförelsen mellan E(TNED)största och E(MAC)lägsta ger

(v/c₀)²/2

——————— = E(TNED) / E(MAC) =

(m/m₀)(uΣ/c₀)²/2

;

(v)²

——————— = (v/uΣ)²(m₀/m) =

(m/m₀)(uΣ)²

;

(v/uΣ)²(m₀/m) = [1 – (uΣ/c)²]^–1(m₀/m)

= [1 – (uΣ/c)²]^–1√1 – (uΣ/c)² ; a=(uΣ/c)² ;

= [1– a]^–1[1 – a]^1/2

= (√b)/b = 1/√b

= [1– a]^–1/2

= [1– (uΣ/c)²]^–1/2

= 1/√ 1– (uΣ/c)²

E(TNED)

= —————

E(MAC)

Vilket vill säga:

Då kvoten (uΣ/c) går mot 1, analogt då uΣ går mot c=c₀, går TNED/MAC mot oändligt (∞).

Emellertid är impulserna p(TNED)=p(MAC) ekvivalenta:

p(TNED) = p = m₀v ;

p(MAC) = p = muΣ ;

m₀v/muΣ = [m₀/m](v/uΣ)

= [√1 – (uΣ/c)²]/√1 – (uΣ/c)²

= 1

p(TNED)

= —————

p(MAC)

Med dessa förhållanden som giltiga, går det alltså inte att jämföra partikelspår från stationära partikelacceleratoranordningar med — enligt TNED — naturkosmiska strålfall [Se Naturfallet utesluter elektrisk acceleration]; I dessa finns inte R-komponenten med i Q=√(m/R)(A/dT) och därmed heller ingen förutsättning för chokmassan. Medan impulserna är desamma, p(TNED)/p(MAC)=1, är energierna det inte. Därmed utvecklas tvunget olika materiell växelverkan i de olika fallen:

Partikelspår från naturlig kosmisk strålning kan inte jämföras med artificiella partikelspår från partikelacceleratorer — enligt TNED. Men i MAC är det den enda metod man känner till som kan användas för att få fram jämförande spår- och energireferenser till (hur att tolka) det naturliga kosmiska fallet. Se särskilda citat.

ENDHärledningarKalkylkortetNeutronfragmenten.

Myonen, Tauonen

Då Tauonen bildas uppvisar den en (1) negativ elektrisk elementarladdning

(–1e = –1,602 t19 C).

Protonen med de enligt TNED substratbaserade delpartiklar — Tauonen och Myonen — som konventionellt tillsammans med elektronmassornas framträdande generellt associeras med neutrinostrålning. I TNED har varje nuklidtyp sin neutrinoprofil analogt med substratets kärnstruktur

—————————————————————————————

—————————————————————————————

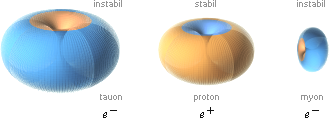
tauon 1 777 MeV [‡2], se fotnot nedan

proton 938 MeV Se tabell i Partikelnomenklaturen

myon 106 MeV Se tabell i Partikelnomenklaturen

—————————————————————————————

Proportionerna i illustrationen enligt TNED efter ideal masstäthet analog med neutronen-protonen enligt (r/R)=(m/M)^1/3

Om Tauonen bildas, sönderfaller den (frånsett möjligheten till Hadrongruppen) strax [‡1] till en Myon (µ) med bibehållen elektrisk laddning — alternativt direkt till en elektron [‡2] — som sedan i sin tur sönderfaller till en elektron (Medellivslängd 2,196 t6 S [‡3]). Dessa partiklar har sina egna antipartiklar.

I fallet med motsvarande antipartiklar (i TNED samma partikelstruktur men med omvänt kärndeplacement [Se Deplacementet], analogt omkastad ytladdning) slutar sönderfallet på motsvarande positron. Se även Exempelframställningen till NEUTRONFRAGMENTEN.

Massdestruktionerna (m→γ) som sammanhänger med sönderfallen för Tau&My får ALLTSÅ på samma sätt som i den vanliga neutronfysikens fall också respektive ett par unika neutrinostrålningsnycklar (aktuella[+]|antitypen[–]).

—————————————————————————

Fotnoter till huvudtexten närmast ovan:

—————————————————————————

[‡1]: Medellivstid (Lifetime) för Tauonen 5 t13 S. Ref. 2010-06-06 Tabell i

ETACUDE SCIENCE PARK — 2010

http://sciencepark.etacude.com/particle/classification2.php

;

[‡2]: @INTERNET Wikipedia Tauon, Tauon decay 2010-06-06

[‡2.1]: @INTERNET Wikipedia Tauon, History

[‡3]: @INTERNET Wikipedia Muon 2010-06-06

[‡3.1]: @INTERNET Wikipedia Muon, History

—————————————————————————

Neutronens sönderfall, referenser

”Equation (7.3) implies an instability of the free neutron. It decays [5] with a mean life of about 12 min”,

HOP 1967, s9–195.sp1n

;

”… neutronen sönderfaller som redan tidigare omtalats till proton + elektron (+ neutrino) med en medellivstid av omkring 13 minuter”,

FOCUS MATERIAN 1975 s138sp2n

;

”Neutronen är en neutral elementarpartikel, som är instabil och sönderfaller i en proton, en elektron och en antineutrino med en halveringstid på 12 minuter.”,

BONNIERS ASTRONOMI 1978, s478sp2n

;

”The neutron has a negative magnetic moment of -1.913141 nuclear magnetons or approximately a thousandth of a Bohr magneton. The currently accepted value of its half-life is 615 s +/- 1.4 s [10,25min]. The corresponding value of the mean life, which is now more commonly used, is 887 s +/- 2s [14,78min].”,

ENCARTA 99 Neutron

;

”While bound neutrons in stable nuclei are stable, free neutrons are unstable; they undergo beta decay with a mean lifetime of just under 15 minutes (885.7±0.8 s [14,7617min]).[2]”,

@INTERNET Wikipedia Neutron 2010-05-25

MAC säger skapelse

Etablerade referenser

———————————————————————

Etablerade referenser som explicit använder benämningen Skapelse (eng. Creation) i samband med partikeldelning och utbytet energi-massa inom kärn- och termofysiken

Det finns naturligtvis en stor mängd webbkällor som, explicit, använder typen ’skapelse’ i samband med energi-massaekvivalenten E=mc². För att ge NÅGOT exempel har de bägge nedanstående utvalts som representativa (i något olika epoker och landsändar).

GYMNASIETS FYSIK årskurs 3 Liber 1980,

”Detta betyder att vid kollisionen har 0,0012·1,66·10^–27 kg materia skapats.”.

TRANSFORMING ENERGY INTO MASS: Particle Creation — Michael Fowler, University of Virginia (1999)

Författaren använder ’create’ frekvent (på 7 ställen), ’creation’ på 2 ställen

Jämför:

Massa skapas på webben

GOOGLESÖKNING 10Jul2010

—————————————————————————————————————

sökfras exakt träffar eng. sv. motsv. sv. fras

———————————— ————— ——— ——————

”mass creation from energy” 5 — se nedan, massa från energi

”energy can create mass” 474 1 ”energi kan skapa massa”

”mass from energy” 3 140 0 ”massa från energi”

”mass is created” 14 400 147 ”massa skapas”

”energy creates mass” 1 500 0 ”energi skapar massa”

Kalkylkort

Kalkylkortet — MIC-ekvivalenterna

Beskrivning

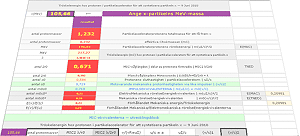
Kalkylkortet MIC.ods

Kalkylkortet till MIC-ekvivalenterna innehåller flera ’rutor’ som (har och) kan användas för analys och kontroll.

Överst finns Resultatblocket

— mata in MeV-värdet för partikeln (x) som ska frambringas ur pp-kollisionen, blocket under visar huvudresultaten.

;

Under resultatblocket finns det råa cellblocket som resultatdelen utvecklades på, med inre avgränsade resultatrutor. Dessa används för kompletterande dataresultat. Huvudblocket återges här i bild på länken till Kalkylkortet (från utvecklingarna).

;

Underst finns kontrollceller som använts vid kontroller till grafritningen (separat), samt längst ner blocket med använda konstanter.

Kalkylkortet ligger helt öppet och kan ändras och modifieras efter behov (efter öppning i OpenOffice, se Öppningsmanualen om ej redan bekant).

För härledningarna till kalkylkortets samband, se Härledningarna till MIC-ekvivalenterna.

SNABBGUIDE TILL NEUTRINOBEGREPPET

Snabbguide till Neutrinobegreppet

Neutrinobegreppet i relaterad fysik — Neutrinobegreppet i modern akademi

Neutrinobegreppet i relaterad fysik — masslös em-strålning med profilerade våglängder kortare än atomkärnan

Neutrinobegreppet

I relaterad fysik (TNED) kallas allt arbete (all värme och ljus) som används för ombyggnad av en atom eller dess atomkärna för neutrinostrålning med benämning och beteckning massdestruktion (m→γ) eller med samma innebörd massdestruktionsstrålning (’m till gamma’); Neutrinon i TNED är em-strålning. För att verkställa ombyggnaden måste atomen ta energin till arbetet från sin egen massa enligt energilagen som därmed omvandlas via den kvantitativa massenergiekvivalenten E=(m→γ)c².

Många av de naturliga grundämnesatomerna (X) har isotoper (samma atomnummer [Z] men olika masstal [A]) som uppvisar spontana s.k. betasönderfall (X avger en elektronmassa, e^–) där just (m→γ) ingår, inkluderat neutronen. Betasönderfallet skrivs då i relaterad fysik

_ZX^A → _Z+1X^A + e^– + (m→γ)_ve– med exemplet neutronens sönderfall

₀n¹ → ₁H¹ + e^– + (m→γ)_{0,782 MeV}

1,0086652u = 1,0072766u + 0,000548598u + 0,00084u

1,0086652u = 1,0078252u + 0,00084u

Atomen X ökar sitt atomnummer (Z) med en laddningsenhet (Z+1) i samband med emissionen av en elektronmassa (e^–) ur kärnstrukturens ±e-struktur av A(1818e+18e+k–mD). Arbetet (m→γ) är det som krävs för kärnombyggnaden under elektronemissionen och som upphör — arbetet slutfört, stabil byggnad — då elektronmassan förts ut till atomhöljet.

Atomkärnans struktur

I TNED byggs alla grundämnesatomer via GRUNDÄMNESBILDNINGEN upp från lättare till tyngre genom neutrinostrålning som börjar från de högsta frekvenserna med de kortaste våglängderna och slutar på de lägsta frekvenserna med de längsta våglängderna, vilket garanterar att de först bildade lättare ämnena inte sönderbryts på de tyngre ämnenas högre bildningsenergier (Plancks strukturkonstant).

Neutrinonycklarna

Det betyder i klartext: varje bestämd nuklid (varje atoms centrala kärnform, dess specifika byggnad) med bestämt masstal (A, antalet primära neutronindivider [med möjliga neutronsönderfall till protoner inkluderat] som atomen byggdes upp på) också är associerad med en specifik neutrinonyckel — precis som Du och Jag har olika nycklar till våra lägenheter och hem. Eftersom alla _ZX^A med samma A kan sönderfalla »mjukt» (isobariskt, bevarar A) till atomer med andra Z enbart med emission (eller absorption) av en (eller flera) elektronmassor (e^–), delar också alla sådana »mjuka sönderfall» (betasönderfallen) på en och samma neutrinostrålningstyp, enligt föregående resonemang (olika nycklar för bildning av olika A). I TNED kan den typen också kallas (som den gör konventionellt) elektronassocierad neutrino(strålning) [ve–, konv. antineutrino, se nedan]. Motsvarande för positronen benämns då positronassocierad neutrino(strålning)[ve+, konv. neutrino].

Eftersom neutrinostrålningen i relaterad fysik (TNED) i vilket fall bara är »vanlig em-strålning» men associerad med våglängder kortare än atomkärnan och som därför inte direkt kan avkännas av atomens vibrerande elektronmassakvantum, besitter den precis som i det vanliga em-fallet koppling till Comptoneffekten; precis som kolliderande biljardbollar kan »neutrinofotonerna» tillsammans med atomkärnorna omsätta energiändringar (både uppåt och neråt). De olika neutrinonycklarna kan därför »enkelt» ändras med neutrinostrålningens naturliga genomgång i materia — till exempel (som mest tydligt) i Solen med de mest högtäta delarna som prövningsexempel, eller direkt genom hårda berget med speciellt avkännande anordningar (KamLAND-projektet, OPERA-projektet).

Neutrinobegreppet i modern akademi — en spinnande punktpartikel — som kräver massa för att matcha de senaste experimentella rönen

Neutrinobegreppet

I konventionell mening har arbetet (m→γ) i samband med just betasönderfall (atomen ändrar kärnladdning [Z] med bevarat masstal [A])

· tilldelats benämningen neutrino (Fermi 1934, se Neutrino Historik), samt

· tilldelats egenskapen partikel med spinn i konsekvens av det regelsystem med spinn, impuls och laddning som antagits i modern akademi i samband med utvecklingen av atomfysiken under främst början av 1900-talet. Se t.ex. @INTERNET Wikipedia Beta decay, History 2010-07-11,
”A second problem was that the spin of the Nitrogen-14 atom was 1, in contradiction to the Rutherford prediction of ½.”.
Se även jämförelsen i spinnbegreppet mellan TNED/MAC i Jämförande Tabell.
Se även ”Since the number of spin-1/2 nucleons …” i
BETA DECAY — Douglas Ross, Southampton University (2009)
http://www.hep.phys.soton.ac.uk/hepwww/staff/D.Ross/phys3002/beta.pdf
, samt

· tilldelats beteckningen v (Grek. v, n) — med specifika benämningar (se även grundbeskrivningen ovan) antineutrino (v=ve–) för den elektronassocierade neutrinon och ordinär neutrino (v=e+) för den positronassocierade neutrinon.

Atomkärnans struktur

I modern akademi (MAC) finns ingen åskådlig byggnad för atomkärnan [‡] — den betraktas väsentligen som strukturlös, punktformad, omöjlig att illustrera, abstrakt — med samtidiga floder av den moderna akademins vektorer (pilfigurer) som störtar sig över den punktlika abstraktionen [konv. spridningsexperiment, eng. scattering experiment|process] i hopp om att upptäcka den hemliga ingången.

Det finns därför ingen jämförelse att göra med relaterad fysik (TNED) på den punkten.

Nettoresultatet blir (följaktligen) att man i moderna kvarter likväl försöker komma underfund med »atomkärnans struktur», inte minst beträffande olika partikelexperiment — samtidigt som man bestämt förnekar varje form av åskådlighet, som ovan [‡].

Neutrinonycklarna

I slutet av 1960-talet (Bahcall 1967 [‡]) genomfördes de första instrumentbyggena för att pröva den totala teoretiska kredibiliteten i den moderna akademins lärobyggnad för fysiken, främst genom neutrinofysikens teori — på Solen som neutrinokälla. Genom en enklare överslagsräkning (separat) kan man MED MODERN TEORIN sluta sig till att ca 3% av Solens totala energiproduktion bör visa sig i formen av den förväntade s.k. elektronneutrinostrålningen (ve–) från Solen.

Neutrinoproblemet

Man fann bara 1/3 [‡].

En mindre upprymd anda infann sig med andra ord med det (djupt) nedslående resultatet.

Så föddes Neutrinoproblemet eller som det numera också kallas, Solära neutrinoproblemet.

Först nu (efter ca 40 år av neutrinoångest) börjar man hinna ifatt (med rejäla experimentella belöningar, se OPERA-projektet, KamLAND-projektet, m.fl.). Se även @INTERNET Wikipedia List of neutrino experiments 2010-07-13.

Svårigheten rent experimentellt är uppenbar:

Neutrinofenomenet uppvisar ytterst svag växelverkan med materien; Vilka konstruktioner man än väljer för instrumenten, blir de 1. stora, 2. svulstiga, 3. kräver extremt avancerad (ren) materialteknik och blir därmed 4. (extremt) kostsamma projekt som bara kan genomföras med internationella samarbeten mellan många olika forskare och inrättningar.

Mot slutet av 1990-talet hade man påvisat det som numera populärt kallas ”neutrinooscillation”, numera främst bevisat av KamLAND och OPERA-projekten: Neutrino av en viss typ kan för det första ändras [eg. »försvinna ur sikte»] (Se bl.a. KamLAND-projektet) och för det andra (nu 2010) transpon(er)as till neutrino av en annan typ (Se OPERA-projektet);

Som kronan på verkat meddelades från OPERA-projektet nyligen (31Maj2010) en (in till 98% säkra) observation av en TauonNeutrino med ursprung i en MyonNeutrinokälla [‡].

Neutrinon har massa

Med den teori som antagits i modern akademi för neutrinofenomenets klassificering (som ovan, partikel med spinn) är enda möjligheten för en sådan neutrinotransposition att neutrinon som sådan måste associeras med begreppet massa (eg. en masskvadrat). Annars kan själva neutrinoändringsfenomenet inte beskrivas på den moderna akademins språk.

Därför säger man i moderna kretsar att ”neutrinon har massa”. Inte för att man på något som helst sätt (ännu) kunnat bevisa det genom direkt mätning att neutrinon verkligen besitter vägbar massa, utan för att teorin kräver det.

Vidare följer.

Särskilda webbkällor som beskriver ämnet och som innehåller sammanställda, vidare, referenser (med delvis utförliga beskrivningar):

@INTERNET Wikipedia Neutrino 2010-07-12

MEASURING THE 7BE NEUTRINO FLUX FROM THE SUN:

Calibration of the Borexino Solar Neutrino Detector — Steven E. Hardy, Mar2010

http://scholar.lib.vt.edu/theses/available/etd-04092010-132651/unrestricted/Hardy_SE_D_2010.pdf

finns på

http://scholar.lib.vt.edu/theses/available/etd-04092010-132651/

——————————————

[‡Bahcall 1967] Solving the Mystery of the Missing Neutrinos — John N. Bahcall, 28 April 2004

http://nobelprize.org/nobel_prizes/physics/articles/bahcall/

SUMMERING

I relaterad fysik (TNED) finns inte den moderna akademins vidlyftiga matematiska övningar: I TNED ändrar neutrinostrålningens olika profiler karaktär då strålningen på vanligt sätt, ehuru mera kortvågig och med grund i Plancks strukturkonstant, växelverkar med materien enligt Comptoneffekten. Se även efterföljande exempel i Partikelbildningen med projektilobjektet som neutrinostrålning.

Att neutrinostrålningen verkligen fungerar så som förespråkas av TNED visas i Neutrinobegreppet i Solfysiken: I analogi med Bahcalls databas från 1997 för neutrinotvärsnittets energifunktion, utförligt i Neutrinostrålningen från Solen ser TNED ut att kunna servera de värden som framträder genom vad som påstås gälla genom nu kända experimentella observationer.

Notera dock (som ovan): det finns (veterligt ännu 2010) ingen instrumentering som kan mäta neutrinostrålningens energier med godtycklig precision, inte ens huvuddelen av det som kommer från Solen [‡] — vilket betyder att inga som helst SÄKRA utsagor kan fastställas, än. Mätningarna måste därför tills vidare avgränsas till speciella områden, och först successivt därifrån utvidgas vidare med teknikens utveckling.

För vidare.

Hur (m→γ)-faktorn upptäcktes (Fermi, 1934)

Redan tidigt (Meitner, Hahn 1911)[@INTERNET Wikipedia Beta decay, History 2010-07-13] observerades hur naturliga grundämnen (X) uppvisade s.k. betasönderfall

X avger en elektronmassa (e^–) och ökar samtidigt sitt atomnummer (Z) med en laddningsenhet

_ZX – e^– → _Z+1X

Genom mätningar upptäckte man strax att elektronmassan vid emissionen från X hade ett s.k. kontinuerligt energispektrum: elektronmassan såg att kunna anta alla möjliga energier mellan ett minsta och ett högsta värde.

TNED förklarar:

När kärnan emitterar elektronmassa kan emissionen ske med olika belopp beroende på den överskottsenergi som atomen/kärnan för tillfället besitter. Vi kan likna det vid en vanlig ordinär rekylverkan: för att få loss elektronen krävs först ett visst minsta arbete (m→γ) lika med minsta möjliga massdestruktion för att få jobbet utfört (för neutronsönderfallets del lika med 0,782 MeV, se särskild resultaträkning). Med den minimienergin frigörs elektronmassan ur atomkärnans ±e-struktur enligt TNED på kärnspinnet — och behåller sedan den kontakten genom atomkärnans kraftekvation. Neutrinostrålningsenergin (m→γ)=0,782 MeV kan då sägas motsvara absoluta rekylbalansens minsta värde, i allt enligt TNED.

Säg nu att atomen-atomkärnan besitter någon extra energi som den passar på att göra sig av med i samband med elektronemissionen. Elektronen kan då emitteras med extra rörelseenergi, alternativ kan ytterligare läggas på massdestruktionen, eller en blandning av bägge, vilket som är vad bestäms i vilket fall av atomkärnan själv enligt dess egen lokala balansräkning.

Med en stor mängd observationer som innefattar olika förutsättningar, och därmed olika energisituationer, kommer en yttre observatör SOM INTE KÄNNER TILL MINIMIVÄRDET (m→γ)=0,782MeV att just för de fall då elektronens observerade emissionsenergi är lika med eller mindre än just 0,782 MeV konstatera: här fattas något; totala energin efter emission är mindre än före; för att det ska stämma måste det finnas någon utfyllande faktor som kan förklara underskottet (noll till minus 0,782 MeV).

Så upptäcktes (m→γ)-faktorn som fick namnet neutrino (Fermi, 1934).

Genom det partikelsystem som redan hade antagits, kom också neutrinon att införlivas med det moderna spinnets partikelnomenklatur.

Se även jämförande konventionell beskrivning i (t.ex.) @INTERNET Wikipedia Neutrino, History 2010-07-13.

Se även efterföljande EXEMPEL 2 — exempel på neutrinospridning i relaterad fysik genom det första experimentella uppdagandet Nov1970.

Neutrinospridning

2010VII12

MED GRUNDEXEMPEL I DEN FÖRSTA NEUTRINOSPRIDNINGSBILDEN ZGS November 1970

Partikelbildningen med projektilobjektet som neutrinostrålning (m→γ) enligt relaterad fysik

Konv. neutrinospridning, eng. neutrino scattering

Härledning:

— ENBART FRÅN ett visst minsta möjliga ±e-massubstrat som avdelas principiellt enligt TNED från en proton

m(p) = m(p) – m(x) = m([p]) + m(x)

med (exemplifierat, Λ representerar en godtycklig partikel)

m(x) + m(γ) = m(Λ)

finns i varje fall enligt TNED — med kvantitativa massa-energiekvivalenten E=(m→γ)c²=(m←γ)c² — principiell giltighet för VARJE partikelreaktion av typen

(m→γ) + m(p) = m([p]) + m(x)

som KAN uppvisa

m(x) > m(p)

Därför nämligen att differensen i sådana fall alltid kan utfyllas med en mass-energiekvivalent

(m→γ)_n = [m(γ)=(h/c²)f]

som alltid kan tas från en primär neutrinostrålare (m→γ), och vilken i princip kan vara hur stor som helst.

— Massorna som g-vägande aspekter kan vi inte ändra på, dessa måste enligt TNED alltid i vilket fall vara lika efter som före, och förutsatt att ingen massdestruktion (m→γ) sker genom delningen vid incidenspunkten.

Däremot kan, som ovan, energiekvivalenterna i princip fördelas godtyckligt bara råformen för energin finns genom neutrinokällan.

Därmed föreligger heller aldrig några egentliga invändningar, rent teoretiskt, mot att partikeldelningsprincipen enligt TNED också är fysiskt giltig för det fall att den normalt massiva partikelacceleratorprojektilen (vanligen protonen) kan ersättas an en konventionell em-strålning — särskilt i TNED i formen av massdestruktionsstrålning (m→γ), i TNED även benämnd neutrinostrålning. Se även Neutrinobegreppet i TNED mera utförligt.

EXEMPEL 1: från Fermilabs 4,5-meters (15-foot) bubbelkammare Experiment 45:

BILDKÄLLA: Fermilab nedan — övre bilden här något kontrast/skärpeförbättrad för tydligare framträdande

FERMILAB — History and Archives Project — FERMILAB SCANNERS UNCOVER SECRETS ON FILM

Source: The Village Crier Vol. 7 No. 11, March 13, 1975

http://history.fnal.gov/neutrino.html#neutrino

Källans bildtext, textmarkeringen min egen:

”An example of a rare neutrino event taken by Experiment 45 in the Fermilab 15-Foot Bubble Chamber. The neutrino (not visible) enters from the left and produces 5 charged prongs. In addition, the decay of a neutral lambda hyperon to a "V" is observed just above the interaction point.”.

Notera att artikelförfattarna inte preciserar magnetfältets riktning i spårbilden, eller andra djupdetaljer — Vi kan sluta oss till vad som är vad genom att räkna linjerna som laddningskvanta (±e): Frånsett den neutrala Λ0 som delas i en ±e, vilket vi kan frånse: tre upp, två ner, nettokärnladdningen bevarad ger en upp = målRestprotonen (e+, uppåt): magnetfältet (Högerhandsregeln) är riktat inåt, mot bildplanet.

Webbkällan säger det inte uttryckligen, men vi utgår här ifrån att incidenspunktens ”prongs” (eng. förk. prolongations, förlängningar) utgick ifrån träff på en proton i bubbelkammarvätskan (flytande väte, deuterium eller en mix av väte och neon, ”When operating, the chamber was filled with liquid hydrogen, deuterium, or a mixture of hydrogen and neon.”).

Reaktionen kan då skrivas enligt partikeldelningsprincipen i TNED med massans och energins bevarande före-efter enligt (här explicit förtydligat enbart för att belysa den tyngre LambdaNollpartikeln, texten berättar inte vilka de övriga antas vara)

(m→γ) + m(p) → m(p)–m(x) + (m→γ)_x+m(x) + ytterligare

(m→γ) + m(p) → m([p]) + Λ⁰ + ytterligare

E + 938,2 = PPP,pp + 1116 + X

Med m(p) = 938,2 MeV och Λ⁰ = 1116 MeV finns ett massunderskott på m(Λ)=1116–938,2=177,8 MeV. Med energimassaekvivalensen E=(m→γ)c² kan det massunderskottet ersättas energikvantitativt av neutrinostrålarens ingångsenergi (här utan uppgift). Den kvantitativa energiekvivalensen certifierar således enligt TNED att till synes ’tyngre partiklar’ än målpartikeln (p) kan framträda ur växelverkan mellan massa (p) och masslös em-strålning (m→γ).

Se även Focusexemplet — ytterligare ett LambdaNoll-exempel men med fast projektilobjekt.

EXEMPEL 2: från Argonne National Laboratorys 3,5-meters (12-foot) ZGS bubbelkammare Nov 1970:

Bilden nedan från Argonne-Wikipediaartikeln — här uppljusad med tydligt synbar spårbild

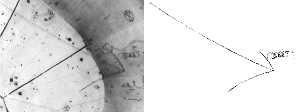
— samt spårförtydligad höger, se även förstoring längre ner

”The world's first neutrino observation in a hydrogen bubble chamber was found Nov. 13, 1970, on this historical photograph from the Zero Gradient Synchrotron's 12-foot bubble chamber. The invisible neutrino strikes a proton where three particle tracks originate (right). The neutrino turns into a muon, the long center track. The short track is the proton. The third track is a pi-meson created by the collision.”,

ARGONNE HISTORY — Understanding the Physical Universe, datumuppgift saknas (som så ofta i amerikansk vetenskapslitt.)

http://www.anl.gov/Science_and_Technology/History/Anniversary_Frontiers/physhist.html

Även

@INTERNET Wikipedia Neutrino 2010-07-12

Notera att artikelförfattarna inte heller här preciserar magnetfältets riktning i spårbilden — Även här kan vi sluta oss till vad som är vad genom att räkna linjerna som laddningskvanta (±e): en upp, två ner, nettokärnladdningen bevarad ger en ner = målRestprotonen (e+, böjer av neråt): magnetfältet (Högerhandsregeln) är riktat inåt, mot bildplanet. Notera även elektronen som dras ut av restprotonen. Se även liknande i ELEKTRONENS BUBBELKAMMARSPÅR.

den första neutrinoobservationen (Nov1970) se källan ovan;

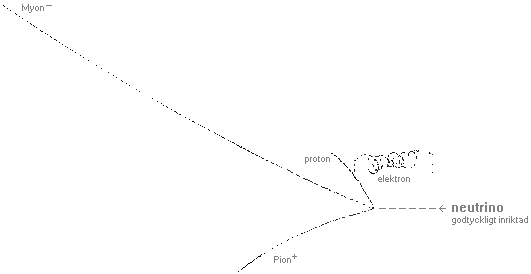
spårbilden och dess detaljer;

På samma sätt som i EXEMPEL 1 kan spårbilden tecknas, här mera preciserat

(m→γ) + m(p) → m(p)–m(x)₁–m(x)₂ + (m→γ)₁+m(x)₁ + (m→γ)₂+m(x)₂

(m→γ) + m(p) → m([p]) + π⁺ + µ^–

E + 938,2 = 692,94 + 139,6 + 105,66

Enligt TNED finns varken det ena eller det andra i källtextens påstådda ”turns into”, ”created by”. Den meningstypen — ofta förekommande i modern litteratur — är (sagt på annat sätt) bara en bekväm omskrivning med en underförstådd föreställning att den kvantitativa energimassaekvivalensen E=(m→γ)c² också skulle vara KVALITATIV. I TNED finns ingenting sådant. Neutrinon absorberas (idealt) av målprotonen, som då delas på samma sätt som vattendroppar som framträder ur vattenytan från en kraftvektor som avdelar dropparna på SPINN.

Kommentar till Exempel 2:

— I relaterad fysik (TNED) i EXEMPEL 2 finns ingenting sådant som ’neutrinon förvandlas till Myon’; Protonen avdelar tydligen en Myon och en Pion. Här skulle det alltså finnas ett enastående tillfälle för den som vill försöka att KULLKASTA TNED, helt och hållet — förutsatt att man kan få fram argument som kan visa att protonen i spårbilden ovan besitter full normal protonmassa. Visa. Enligt TNED är en sådan ekvation nämligen omöjlig: massorna före måste svara mot massorna efter, och förutsatt att ingen massdestruktion sker under själva delningstillfället; Neutrinon är i TNED ren masslös induktiv em-strålning och kan inte utveckla någon chokmassa som skulle kunna kompensera om neutrinon vore en motsvarande partikelaccelererad komponent, vilket den inte är enligt TNED.

— Enligt partikeldelningsprincipen i TNED ska restprotonen i EXEMPEL 2 dessutom försvinna in i bakgrunden då den saktar av och kan förena sig med sin restelektronmassa [Se Restprotonens öde]. Det tycks också precis vara vad bilden visar — i princip omöjligt att skilja från beteendet hos en ordinär protonmassa.

— Spårbilden i bägge exemplen visar enligt TNED alltså en delning. Ingen skapelse.

— Alla spårbilder med neutrinospridning från neutrinostrålare (m→γ) är f.ö. enligt TNED utomordentliga praktiska (sammansatta) exempel på Comptoneffekten:

energierna före = energierna efter (vi kan [möjligen] förutsätta att protonen absorberar hela neutrinoinfallet, vilket sedan fördelas på komponenterna — likt kraftvektorn som ansvarar för en vattensplash).

Förklaring

Partikeldelningsprincipen i TNED kräver (energivillkor, ytterst enkla) för kärnladdningens bevarande vid partikeldelningen att kollisionsobjektens (projektilmassans och målmassans) kärnladdningar före delningen är samma som efter.

Som redan påpekats i nämnda artikel betyder det i fallet med målprotonen som enda kollisionsobjekt att

alla övriga delmassor utom restprotonen tvunget blir kärnladdningsinstabila — och därför måste sönderfalla mot (inte nödvändigtvis direkt till) slutprodukternas internt stabila ±e (elektron e– eller positron e+) genom ytterligare sekundära delningar men nu som motsvarande reguljära kärnsönderfall med massdestruktion (m→γ) för att kunna frikoppla ±e-strukturen i separata respektive e+ och e– — i TNED analogt associerad neutrinostrålning (m→γ).

Principen för detta sönderfall följer alltså, i princip, den vanliga EXOTERMISKA KÄRNREAKTIONSLAGEN i TNED enligt

K1 + K2 – (m→γ) = K

Eller, analogt för delningen eller sönderfallet

(m→γ) + K = K1 + K2

OMVÄNDNINGEN (m→γ) + K betyder alltså att energin som krävs för (den associerade) ±e-strukturupplösningen inte behöver tas från någon primärmassa i något kärnobjekt, utan ges direkt som projektil (Compton-) energi, varför den associerade del- eller sönderfallsprodukten kan frigöras direkt.

I neutrinospridningsfallen kan vi alltså (idealiserat) se den inkommande neutrinostrålenergin (E=hf) som en (efter Einsteins analogi, se Fotoelektriska effekten) kvantiserad neutrinofoton med ekvivalenta energimassan m=(E=hf)/c²=(h/c²)f som tas upp av målobjektet, och åstadkommer delningen tillsammans med deras rörelsemängder, idealt med m(hf) som den mekaniska massan i den förorsakande impulsen (med referens till det lokalt dominanta g-fältets referenspunkter, se utförligt från ljusets g-beroende om ej redan bekant, och således helt idealt) — sett från den lokalt g-dominerande g-relaterade incidenspunkten.

Neutrinonycklarna: Observera att neutrinostrålaren (m→γ) enligt TNED kopplar till olika neutrinoprofiler (Se Neutrinosignaturen); ElektronNeutrino (ve–, konv. v, antineutrino resp. ve+, konv. v, neutrino) associeras i TNED med reguljära betasönderfall (sönderfall som inte påverkar kärnstrukturen = masstalet [A], endast kärnladdningen = atomnumret [Z]); massdestruktioner associerade med kärnombyggnader enligt TNED besitter egna individuellt skilda neutrinoprofiler, unika för varje nuklidbildning (Utförligt i Neutrinospektrum ocfh Grundämnesbildningen). Se även i kortare sammandrag i Snabbguide till Neutrinobegreppet.

I partikeldelningen finns (således enligt TNED) explicit för nuklidneutrinonycklarna motsvarande nu kända två olika neutrinoprofiler: MyonNeutrino (νµ±) och TauonNeutrino (ντ±). Eftersom — enligt relaterad fysik (TNED) — respektive nukleära neutrinostrålare (m→γ) sammanhänger med (främst) olika kärnmassor, kan de olika neutrinonycklarna heller inte utbytas godtyckligt mot varandra. Dvs., typ MyonNeutrinostrålare v=(m→γ) i neutrinospridningsexperiment på målobjekt (X) åstadkommer bara en associerad Myonkärndel (M) tillsammans med övriga delar (X/n) [TYP: att du får låna min lägenhetsnyckel, betyder inte att du också får automatisk access till Handelsbankens bankvalv],

v + X → M + (X/n)

Och sedan på samma sätt för alla övriga typer.

Exemplet med Inverterade betasönderfallet

I den praktiska fysiken finns ett speciellt (sammansatt) exempel på ovanstående som inbegriper elektronNeutrino (ve–), här i komprimerad teckning enligt

ν_{e– 1,804 MeV} + p → n + e⁺

Exemplet beskrivs utförligt som grund i TNED för att belysa ett bevis för att energi och massa är kvalitativt skilda, ehuru kvantitativt utbytbara, se Partikelbeviset för att energi inte kan skapa massa. Reaktionen ingår f.ö. i KamLAND-projektet som grund för påvisande av neutrinostrålarens ändring (dämpning) i materialgenomgång (led i det konventionella påvisandet av de olika neutrinonycklarnas inbördes ändringar i växelverkan med materien). [Den bildade »neutronprotonen» förenas med en närliggande ordinär proton till Deuterium som möjliggör säker detektering och därmed jämförelse med den kända ursprungsmängden elektronNeutrino (m→γ) (från en uppsättning kärnreaktorer); därmed kan värdena jämföras för vidare. Mera utförligt i KamLAND-beviset].

Se även mera utförligt från NEUTRINOBEGREPPET I RELATERAD FYSIK.

NEUTRONENS FRAGMENT | Komplement Del II · Universums Historia

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Universums NEUTRONENS FRAGMENT | Komplement Del II

ämnesrubriker

innehåll

NEUTRONFRAGMENTEN i relaterad fysik

Komplement Del II — Atomkärnans massunderskott vid delning

Uppdagade, obemärkta, massunderskott i fysiken enligt TNED vid partikeldelning

Neutronfragmenten i relaterad fysik — NEUTRONFRAGMENTEN Del II

Inledning

Massunderskotten

Inledande beskrivning

Kärnmening

Kärnmeningens förankring

Energi-Massa ekvivalenten

Massunderskotten

Snabbgenomgång

Utförlig genomgång

Elektronmassans massökning med elektrisk acceleration

Trådstråleröret

Bubbelkammarfotografi med partikelbildning

Bubbelkammarspåren i Focuskällan

Orsaken

Motsvarande balansräkning för en kosmisk protonkollision

Varför massunderskottet inte kan upptäckas i MAC

Kärndelningen

Hyperoner och Mesoner

Neutrinorekylerna

Neutrinotypernas olika neutrinonycklar

PARTIKELDELNINGENS MATEMATIK

Bildanalogi

MIC

HUR NUKLIDASSOCIERAD NEUTRINOSTRÅLNING KAN UPPVÄCKAS GENOM PARTIKELKOLLISIONER

Förenklat inledande Räkneexempel

Kärndelningarna via MIC

Kalkylkortet

MIC-ekvivalenterna

Mera Neutrinos

Härledningar

Sammansatta Hastigher

MIC-kärnsvängningens våglängd

Hastighetsrelationen

Chokmassan

E(MAC)

E(TNED)

Energierna

Myonen och Tauonen

Neutronens sönderfall, referenser

MAC säger skapelse

Kalkylkortet

Beskrivning

Snabbguide till Neutrinobegreppet

Neutrinobegreppet i relaterad fysik

Neutrinobegreppet i modern akademi

SUMMERING

Hur neutrinofaktorn upptäcktes

Neutrinospridning

Partikelbildning med projektilobjektet som neutrinostrålning

Härledning

EXEMPEL 1 — Fermilabs Experiment 45

EXEMPEL 2 — Första neutrinospridningen November 1970

Förklaring

Exemplet med Inverterade betasönderfallet

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1,602 t19 C ...................... [ref. FOCUS MATERIEN 1975 s666]

[BA]. BONNIERS ASTRONOMI 1978

SIGMA 1-6, MATEMATIKENS KULTURHISTORIA av James R. Newman, Forum 1965, efter originalet The world of mathematics 1956

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också

RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

MAC — I UNIVERSUMS HISTORIA ofta använd allmän förkortning för Modern ACademy, modern akademi.

em- — I UNIVERSUMS HISTORIA ofta använd allmän förkortning för elektromagnetisk

Etym. ETYMOLOGISKA REFERENSER, BKL — Bonniers Konversationslexikon Band I-XII + Supplement, 1923-1929

MeV — Mega elektron Volt. Från energin E=mc²=UQ används U=1Volt och Q=e=1,602 t19 Coulomb; E/Q=eV=elektronVolt = E/(1,602 t19 C);
eV/T6 = MeV = E(Joule)/(e·T6) = E(MeV);
E(MeV) = E(Joule)/(e·T6)
E(J) = E(MeV)(T6)/(e=1,602 t19 C).
EXEMPEL: Elektronmassan m(e)=0,000548598(u=1,66033 t27 KG) motsvarar energin
E = m(e)·c² = (0,000548598u)(2,99792458 T8 M/S) = 8,18634 t14 J. Utryckt i MeV:
E(MeV/)c² = m(e) = (8,18634 t14 J)/(e·T6) = 0,511077 ............... elektronmassan i MeV(1/c²)

γ Grek. gamma, g, är i TNED (ofta) en generaliserad beteckning för massdestruktionsstrålning som [via Plancks strålningslag] byggs upp från kortare till längre våglängder med representation först vid gammanivån i materiefysiken.
Skrivsättet (m→γ), »m till gamma», betyder här ’massa som omvandlas till ljus och värme i materiefysiken’, från lägst gammanivån vilket generaliserat inbegriper värmefysiken överförd på materiefysikens atomkärnor och elektronmassor. Se även utförligt från Energilagen. Mera allmänt betyder (m→γ) massdestruktionsstrålning från primära massförstöraren E=mc².

Senast uppdaterade version: 2014-02-08

*END.

Stavningskontrollerat 2010-07-15.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

Ofta använda naturvetenskapliga symboler i UNICODE

σ ρ ν ν π τ γ λ η ≠ √

Ω Φ Σ Π Ξ Λ Θ Δ α β γ δ ε λ θ κ π ρ τ φ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ← ↑ → ∞ ↓

UnicodeStandard: TYPOGRAFIN I DETTA HTM-DOKUMENT HAR I DE FLESTA (MÖJLIGA) FALL UTNYTTJAT DEN TILLGÄNGLIGA (men krångliga) TECKENSNITTSSTANDARDEN FÖR UNICODE — SOM FINNS KOMPLEMENTÄRT TILL SYMBOL-TECKENSNITTET FÖR DET KLASSISKA GREKISKA ALFABETET SOM NORMALT ANVÄNDS I NATURVETENSKAPLIG LITTERATUR I OLIKA MATEMATISKT-FYSIKALISKT BESKRIVANDE SAMMANHANG med typexempel Ω Φ Σ Π Ξ Λ Θ Δ α β γ δ ε λ θ κ π ρ τ φ σ ν ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ← ↑ → ↓ ∞ . VISSA AV DESSA TECKEN UPPVISAR (med den här presentationens allmänna teckensnitt och storlek Times New Roman 9) EN NÅGOT SÄMRE REPRESENTATION ( t.ex. ett mindre tydligt pilhuvud, ett mera otydligt rottecken, m.fl.) OCH SOM GÖR ATT UNICODE-ALTERNATIVET (här ännu) INTE UTNYTTJATS FULLT UT. DET ÄR FÖR ÖVRIGT BARA WEBBLÄSARNA INTERNET EXPLORER OCH GOOGLE CHROME SOM LÄSER SYMBOLTECKENSNITTET (MOZILLA VISAR t.ex. Ö för rottecknet, etc.).

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se