Radioaktivitetens Matematiska Fysik enligt TNED

Radioaktiva sönderfallets Fysik — enligt TNED | UNIVERSUMS HISTORIA | 2011X14 | a BellDHARMA production | Senast uppdaterade version YearMonthDayTime 2017-09-19

innehåll · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

BILDKÄLLOR: Författarens arkiv · Kollage NikonD90 — SOMMAR:ExCur3.16Jun2009BildVK1.3·BildÄng2.3·VÅRVINTER:ExCur4.19Apr2010Bild1.32

Nuklidklassificeringen 1818 — UPPLYSANDE mönsterdata på kärnfysiken aldrig tidigare sett | HalveringstidsSambandets Härledning — enligt relaterad fysik | Sönderfallets Fysik

Radiofysiken enligt TNED — se Allmänna termer

RADIOAKTIVA SÖNDERFALLETS matematiska FYSIK ENLIGT TNED --- individuella halveringstider kan inte bestämmas exakt trots exakta samband — INLEDNING

ALLMÄN GENOMGÅNG

Resultat i överblick

Jordens ålder

Sönderfallet

Dissonansenergin

4,468 (5) T9 år

Precisionen i tH-U-238 måste förbättras

för att kunna avgöra eventuellt neutrinoinflytande

— som KAN avgöra frågan

Jenkinseffekten

kärninstabila och betainstabila atomer

radioaktiva sönderfallen

Jordkroppens ålder

Delningstillfället

Dissonansenergin Ehf

— individuella halveringstider [tH] kan inte bestämmas exakt, endast uppmätas kollektivt ungefärligt [Se Fragmenteringsargumentet]

— alfaradionukliderna uppvisar en viss tydlig Z-struktur [Se Allmänna RadioIsotopkartan], men utan exakt bestämbara inre referenser

— betanukliderna uppvisar [ännu] ingen bestämbar Z-struktur [Se 29Cu64-exemplet], multipla sönderfallstyper saknar entydighet [Se Nuklidkoefficienten i Kombinerade sönderfallstyper]

Allmän genomgång av kärninstabila och betainstabila atomer med utförliga referenser, jämförelser och exempel från det allmänt tillgängliga materialet på webben [Okt2011-Jan2012].

sektioner

ATOMEN BEVARAS — låga b-värden

ATOMEN DELAS — höga b-värden

Gränser, Delningar och Stabila Nuklider

Centrala artiklar

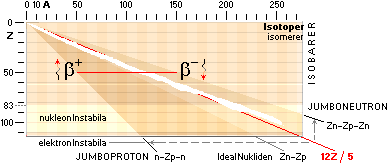
Nuklidgränskartan 1818 — zonerna för stabila och instabila nuklidområden

Elektronexperimentet 1957

Fragmenteringsargumentet

Nuklidklassificeringen 1818

Betainstabila

Kärninstabila

Nuklidstabilitetens gränser — Halveringstiden i relaterad fysik

Radiofysiken i TNED

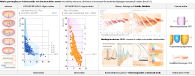
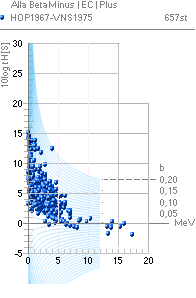
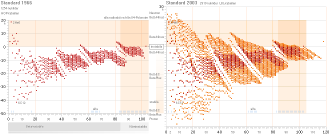
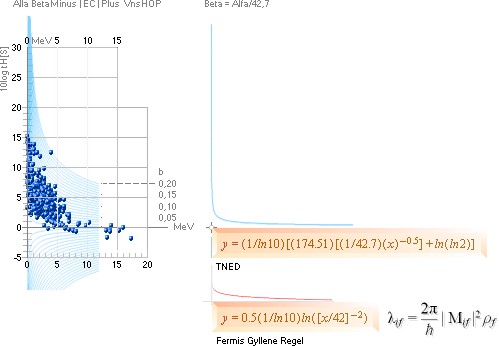
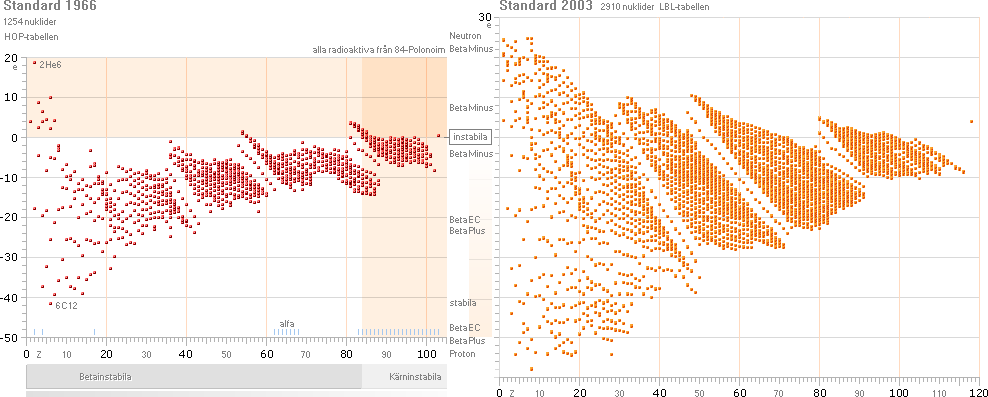
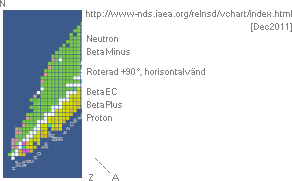
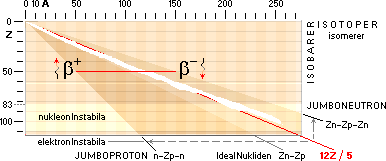
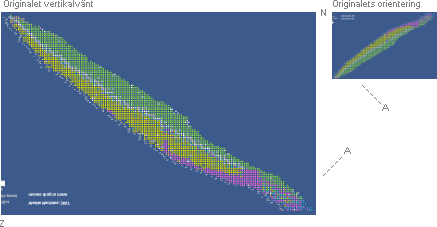
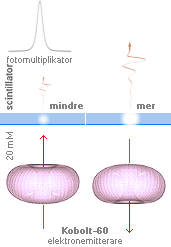
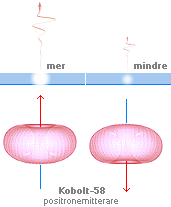
Grafsammanställningarna ovan visar hur respektive betainstabila och kärninstabila atomer uppvisar variationer i olika sönderfallstider [tH], vertikala skalan i 10log tH [värdesiffran anger exponenten till 10, enhet i sekunder], med avseende på den med sönderfallet entydigt associerade effektiva sönderfallsenergin, horisontella skalan i MeV.

— Nyare, allmänt tillgängliga, uppgifter på betainstabila nuklider i någon användbar tabelluppställning liknande den från VNS-HOP från epoken 1966/1976 har eftersökts på webben [Dec2011] men inte påträffats; Det finns, visst, olika tillgängliga tabellverk, men DELS är inte alla direkt användbara för maskinell avläsning av de numera tusentals olika individerna, och DELS finns olika uppgifter med diffus innebörd som försvårar sammanställningen [Se särskild genomgång i Kombinerade sönderfallstyper];

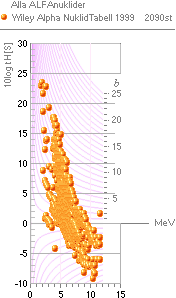
— Medan de kärninstabila nukliderna [ovan höger av alfatyp] uppvisar en viss strukturerad ordning, se Allmänna RadioIsotopkartan, råder i stort sett »allmänt kaos» i varje försök att få fram begripliga — enhetliga, användbara — data för betanukliderna. Vidare i huvudtexten.

Med kännedom om effektiva sönderfallsenergin (Eeff=Ê) och halveringstiden (tH) kan nuklidkoefficienten (b) bestämmas enligt [[Tabell1KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]]

b = [√2mÊ]ln[t_H/1S(ln2)]/eZ med

10log t_H/1S = (1/ln10)[beZ(2mÊ)^–0,5 + ln(ln2)] från

t_H = 1S(ln2)e^be^Z/√2mÊ

enligt Härledningen till halveringstiden i relaterad fysik. Sambandsformerna ovan redovisas sammanfattat i Slutformen med Källexempel. Hur tH-sambandet kopplar betanukliderna i relaterad fysik, beskrivs utförligt i Betasönderfallens matematiska fysik i TNED.

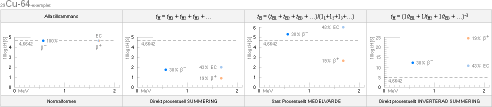
Speciellt uppmärksammat:

— Genom att det finns många nuklider av samma typ

— speciellt i betafallen (»Jumboprotoner») BetaPlus och BetaEC

— som sönderfaller till samma produkt, från högre till lägre Z, och därmed uppvisar exakt samma effektiva sönderfallsenergi (Ê), men olika procentuell fördelning i sönderfallsmängderna mellan de två typerna, och därmed tydligen olika, inre, halveringstider

— är det för dessa fall tydligt (från sambanden ovan) att endast nuklidkoefficienten (b) skiljer individerna åt; .

— OM sambandet mellan halveringstid (tH) och sönderfallsenergi (Ê) ska stämma överens med kriteriet i Sönderfallets enhetliga preferensgrund, analogt giltigheten av det konventionellt benämnda Geiger-Nuttalls samband, är det tydligt att enda möjliga sättet att särskilja en bestämd nuklid med bestämd sönderfallsenergi (Ê) från en annan i samma nuklidgrupp bara kan återfalla på någon intern differens i atomkärnans energibindningsstruktur eftersom, i relaterad mening, alla övriga kärntekniska parametrar är identiska för de bägge individerna. Dvs.: nuklidkoefficienten (b).

— I TNED återfaller, möjligen, den differensen på de olika individernas primära bildningssätt med avseende på olika neutronkvoter (olika bildningslokaler, specifikt olika neutrinogenomströmningsenergier). Därmed den rent kvalitativa förklaringen i relaterad mening till att olika atomindivider, idealt »exakt samma atomer» likväl internt, i samma atomgrupp uppvisar olika sönderfallstyper, (och även, möjligen, internt delvis skilda halveringstider — vi vet inte det här; mätning på enskilda atomer är, här veterligt, ännu så länge inte tekniskt möjligt).

— Med andra ord: halveringstiden (tH) för en viss radioaktiv atom kan omöjligen beräknas i någon som helst PRECISERAD mening; Alla atomer har för länge sedan FRAGMENTERAT på olika b-värden (via olika neutrinoenergibildningskriterium) och därmed en strängt upplöst kartbild (där man fortfarande kan spåra vissa linjer), och därmed i princip omöjligt att få reda på en viss nuklids b-värde på förhand. Det är endast totala (grova) medelvärden för hela gruppen som visas, och som därmed (effektivt) gömmer alla individuella skillnader.

— I varje fall med hänsyn till Wiletabellens förekomster av alfaradionuklider (ovan höger), är det tydligt att fragmenteringen i detta fall är mindre uttalad [Se från Alla Radionuklider], men ändå alldeles tydlig (se Uranexemplet).

— Däremot för betanukliderna finns, här ännu, ingen som helst känd ordning (utöver ovannämnda, allmänna). Se mera utförligt i Betasönderfallens matematiska fysik i TNED.

—————————— ‡

Effektiva sönderfallsenergin, massa-energiskillnaden från utgångsnuklidens hela atom till resterande atommassa efter fullbordat sönderfall.

Överblick AlfaBeta enligt TNED

2012I5

Överblick — radioaktiva sönderfallen Jan2012

Mycket svårt få KLAR allmän överblick — så som ämnet presenteras i facklitteraturen

Genom kartläggning (Se Alfaisotoperna) och utnyttjande av tH-universalen från nuklidkoefficienten med divergensgränserna ç=±c₀ i atomkärnan

— från Atomkärnans gravitella härledning med atomkärnan som en gravitationens- eller massans fundamentalform helt utan inre beståndsdelar via Planckringen och dess fraktalsystem av massekvivalenta m=m[n→∞]^–1[n→∞] impulsmomentsringar i respekt till Ljusets gravitella beroende genom Potentialbarriären och dess Energizon — dessa begrepp har framkommit genom TNED och ingår inte, och har heller ingen motsvarighet eller omnämnande, i den moderna akademins lärosystem —

finns — enligt TNED — en direkt orienterande överblick av en viss alfaradionuklids halveringstider (tH) med avseende på bestämda sönderfallsenergier [E(α)]. Diagrammen nedan exemplifierar sådana översikter — och understryker samtidigt deras tydligt oprecisa natur.

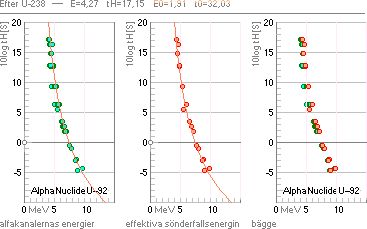
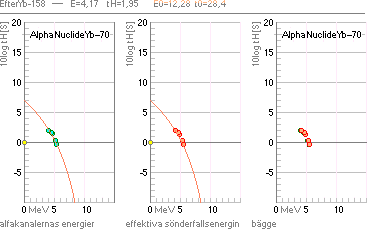
Figurerna ovan i utdrag från EXEMPEL där källupgifterna preciseras vidare. Diagrammen exemplifierar den övergripande precisionen i tH-universalens inprickning av ett visst alfaradioaktivt ämnes allmänna sönderfallstider [vertikala skalan] för givna sönderfallsenergier [horisontella skalan]. Gröna ringar motsvarar data för uppmätta alfakanaler, orangea ringar anger motsvarande effektiva sönderfallsenergier med räkning via atomvikter. tH-universalens normalorientering som y-kuvan ovan vänster, samt i kvadrantrotation yi² kurvan ovan höger anger anpassning efter respektive halveringstidens ASYMPTOTISKA avtagande med växande sönderfallsenergi [ovan vänster, 92Uran] och halveringstidens EXPONENTIELLA avtagande med växande sönderfallsenergi [ovan höger 70Ytterbium].

— Genom att tH-universalen i TNED bygger på energizonens divergensgränser ±c0 från atomkärnans gravitella härledning, och därmed en fast och fix gränskurva med olika xy-offset och kvadrantrotation, som ovan, på dessa begrepps grunder, och endast så, är det helt säkert garanterat att en motsvarande allmän överblicksbild i modern akademi INTE existerar. För motsvarande, allmänt tillgängliga, utbud på webben finns särskilt sammanställda exempel med jämförelser i listningen MAC‑precisionen allmänt. Se även, vidare, utförligt från tH-universalen.

Se utförligt EXEMPEL för tH-universalens placering.

— Närmare än så i precision tycks vi inte kunna komma: Nukliderna i ovanstående översikt — alla av typen alfanuklider — ligger utspridda, »fragmenterade», omkring en grundlinje (tH-universalen) som bara ungefärligt beskriver hela gruppens samlade variationer i halveringstider (vertikala) via sönderfallsenergier (horisontella).

En liknande översikt i fallen betanuklider har, här veterligt, ingen motsvarande ordnad struktur (men en sådan är föremål för eftersökande).

Komplikationerna i en motsvarande översikt i betafallen (Se även illustrerat i Betasönderfallande nuklider) är flera.

— Det enda vi med säkerhet VET i betafallens fall är de (via olika webbkällor) totalt uppmätta halveringstiderna (tH) tillsammans med procentuella andelar av de olika sönderfallsnuklidernas radioaktiviteter som observerats genom experimentella mätningar — Se särskilt Citat. Med den databasen som grund (Se Radiofysikens matematiska grund) ger MAC sin tolkning på det som kallas (eng.) partial decay constants medan TNED ger sin. Resultaten är INTE analoga — dessutom våldsamt skilda. Motställningen är dessutom och, här veterligt, omöjlig att avgöra via experiment (Citat) eftersom partiella halveringstiden inte [ännu med någon känd teknik] kan mätas experimentellt, endast de procentuella aktiviteterna (från kemiskt analyserade preparat, men den tillgängliga beskrivningen på webben är delvis svårtolkad på den punkten; inga direkt tydliga uppgifter finns [Jan2012]), och den grundformen är gemensam för både TNED och MAC. Se särskilt beskrivning i Halveringstidens Oberoende Summeringsalgoritm.

— Medan alfaradionukliderna alla uppvisar samma fason — sönderfall sker från högre kärnladdning (Z) till lägre Z — uppvisar betasönderfallen — inte sällan med blandade typer för samma nuklid, typ BetaEC och BetaPlus — olika Z-riktningar i sönderfallen (Se illustrerat enligt TNED i Sönderfallstyperna);

— BetaPlus (med BetaEC) sönderfaller som alfaradionukliderna, från högre Z till lägre Z, medan BetaMinus sönderfallet omvända vägen, från lägre Z till högre Z.

— Därmed grusas, effektivt, varje alfasönderfalls motsvarade ordnade struktur för ett visst grundämnes representation med olika »enkla översiktskurvor». Finns det sådana, är de, uppenbarligen, motvända i fallen BetaPlus kontra BetaMinus.

— Ytterligare en detalj i betasönderfallen försvårar varje (begriplig) kartbild av den sönderfallstypens överblickbarhet (i någon liknande tappning som i alfafallen): de multipla sönderfallstyperna som, typiskt, uppvisas av betanukliderna (Se särskilt från Nuklidkoefficienten i Kombinerade Sönderfallstyper); Den motsvarande benämningen i engelsk litteratur är branching decay, branching ratio, partial decay constants, etc.

— Det illustrerade exemplet i 29Cu64 visar, exakt, anledningen:

— Det finns, utöver halveringstidens normalform (totala medelvärdet av alla ingående bidrag, oavsett vilka dessa bidrag är och oavsett vilken teori man har om deras sammanhang, och här veterligt med grund i det allmänt tillgängliga materialet på webben -Jan2012), inga experimentellt tillförlitliga uppgifter om betanuklidernas specifika halveringstider. Se vidare, mera utförligt med jämförande exempel, från Nuklidkoefficienten i Kombinerade Sönderfallstyper. Se även den (nu enda här i TNED tillgängliga) översiktliga sammanställningen AlfaBeta i Betasönderfallande nuklider.

— Det finns, ännu slutligen, ytterligare (en sista) detalj som, möjligen, HELT sänker varje idé om att NÅGONSIN kunna få fram en »ordnad bild» av speciellt betanuklidernas halveringstider kontra sönderfallsenergier. Nämligen, det redan på olika sätt, framskymtade »musikstycket» att VARJE (beta-) nuklid i grunden har sin individuella halveringstid, om än marginellt skild från den aktuella betatypens allmänna medelvärde; Det finns lika många »betakanaler» som enskilda betanuklider. Det ansluter också (perfekt) till TNED-teorin för nuklidkoefficienten, se särskild beskrivning i Kopplingen till radiofysiken i Inledningen.

Jämför:

PRECISION HALF LIFE AND BRANCHING RATIO MEASUREMENTS FOR THE SUPERALLOWED ß EMITTER 62Ga,

Bronwyn Hyland 2005, Kan inte kopieras

http://www.physics.uoguelph.ca/Nucweb/theses/BronwynThesis.pdf

;

”In this experiment, twenty new γ rays and five new energy levels populated in the β decay of ⁶²Ga were observed.”, första sidan Abstract, onumrerad

;

”... the branching ratio changes when the beta threshold is raised, which had stumped everyone for months.”, sidan 2n, numrerad som i

— Ovanstående webbkälla är f.ö. ett (PDF-) exempel på den typ man, helst, INTE vill se: kan inte kopieras; det man hittar OM dokumentet på Google hittas INTE med sökverktyget INUTI dokumentet; radavståndet i PDF-dokumentet är av typen TRE rader mellan London-New York.

(Hitta en annan redaktör).

OM det är så, att man för varje ny TEKNISK innovation också upptäcker allt flera nivåer — betakanalerna ökar i antal med den tekniska utvecklingen — som källan ovan antyder, men ingalunda själv tycks vara förmögen att skriva ut i klartext, är det tydligt att enda underliggande drivande faktorn är antalet nuklider totalt.

Flera källverk behövs.

— NOTERA att (eng.) branching ratio (sv. förgreningsförhållandet) också används frekvent i webblitteratur som berör olika kärnreaktioner — konv. subatomära partikelfenomen som studeras särskilt i högborgarnas partikelacceleratorer. Den delen har explicit ingen koppling till ämnet radiofysikens matematik i den här presentationen — men den verkar vara klart överrepresenterad på webben om man söker på just branching ratio changes.

Alfaradionukliderna i den allmänna facklitteraturen

Mycket svårt att få en KLAR allmän överblick över ämnet — så som det presenteras av de mest synliga webbkällorna (Nov2011)

—————————————————————————————————

ALFAEMITTERARNA — den radioaktiva strålningens alfaemitterande nuklider

—————————————————————————————————

— Många av oss tror SÄKERT — med den här allmänna REPERTOAREN som referens (typisk)

— Betaspektrum är ett kontinuerligt spektrum, medan alfaspektrum

uppvisar diskreta energinivåer ...

att alfaemitterande nuklider uppvisar EN BESTÄMD ALFAENERGI för en bestämd nuklid (atomnummer, masstal).

— Det finns, veterligt, ingen källa som säger det explicit bokstavligt — men nära.

— Genom att (webb)källorna generellt [jämför nedan] delvis är SULLIGA i beskrivningen, samt att ämnet generellt också är KOMPLICERAT I DETALJER, verkligen, blir det kvarvarande minnesintrycket av ämnet LÄTT en favoriserad bild som refererar till »kontinuerligt» (vad som helst) för betasönderfallen och »diskret» (enahanda) för alfasönderfallen.

;

”ALFAPARTIKLARNAS ENERGI. Det har visat sig att de individuella alfapartiklarna från en och samma nuklid alla har praktiskt taget samma energi. Detta kan konstateras genom en enda blick på ett fotografi av alfapartikelspår i en s.k. dimkammare, eftersom alfapartiklarnas räckvidd i ett givet material är ett mått på deras energi (se s. 294).”,

;

”Att partiklarna har en bestämd energi är naturligtvis en konsekvens av att energitillstånden i kärnan är kvantiserade”,

FOCUS MATERIEN 1975 s133sp2m

HYPERPHYSICS — Electron and Antineutrino [2012-01-06]

http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/beta.html

;

”Early studies of beta decay revealed a continuous energy spectrum up to a maximum, unlike the predictable energy of alpha particles.”.

Det är inte så.

Tekniken att mäta de olika alfaenergierna faller under begreppet alfaspektroskopi (eng. alpha spectroscopy).

Några Webbkällor Jan2012 som beskriver alfaenergiernas spektrum:

A PRACTICAL GUIDE TO SUCCESSFUL ALPHA SPECTROSCOPY

http://www.canberra.com/literature/953.asp

Quantum Mechanics of Alpha Decay

Lulu Liu, Pablo Solis, December 5, 2007

http://web.mit.edu/lululiu/Public/pixx/not-pixx/alpha.pdf

En inledande, väl upplysande orientering i ämnet MULTIPLA ALFAENERGIER ges från webbkällan

USA ENVIRONMENTAL PROTECTION AGENCY — Tutorial 4.4 — Alpha Spectrometry 1: Principals

http://www.epa.gov/safewater/radionuclides/training/transcripts/tutorial_4.4.pdf

Se även vissa utdrag här i citat från källan närmast ovan i Multipla alfaenergier, för jämförande referenser;

— En och samma alfaemitterande nuklid uppvisar i allmänhet en SERIE spridda alfaenergier (konv. kanal)

Bilden ovan i detaljerat utdrag från U92Exemplet; Punktdiagrammets värden exemplifierar upplösningen horisontellt i MeV för alfakanalenergier, här med tabelldata från Wiley 1999, för de olika Uranisotoperna, vertikalskalan visar 10-logaritmern för halveringstiden i sekunder. Diagrammet tydliggör de multipla alfaenergivärdena för en viss masstalsnuklid och som [i varje fall i Wiletabellen] tillskrivs samma halveringstid. Vad vi INTE vet SÄKERT, är huruvida också de enskilda alfaradionuklidernas individer — varje atom — skiljer sig [ytterst marginellt] från sina grannar, så att det i grunden finns lika många skilda punktvärden som atomer i den gruppen.

— Alla de spridda MeV-alfavärdenukliderna uppvisar exakt samma halveringstid.

— Tabeller över alfaenergier uppvisar i många fall (flera) tiotal kanaler med spridda alfaenergier för en och samma radionuklid: det finns ingen ENDA, praktisk, »en» alfaenergi för en given halveringstid.

— Hur kan man då påstå, att de alfaemitterande radionuklidernas halveringstid »är proportionell mot alfaenergin»?

ALPHA DECAY OF ATOMIC NUCLEI

http://www.kutl.kyushu-u.ac.jp/seminar/MicroWorld2_E/2Part1_E/2P17_E/alpha_decay_E.htm

;

”Geiger and others measured the half lives of various alpha radioactive atoms and discovered a close relation between the energy of the emitted alpha particles and the half life. The relation was written

(Half-life of α-emitter) = C e^A^/√E, (1)

where E is the energy of the emitted alpha particles and A and C are the constants to be adjusted to agree with experiment.”,

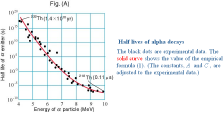
”It is clearly seen in Fig. (A) that the empirical formula (1) fits well to the experimental data.”.

NOT. Källan ovan anger överst i figuren (ovan kopierad och förminskad) ”232Th(1.4×10^10yr)”, underst ”218Th(0.11µS)”, utan andra specifikationer.

Jämför f.ö. bilden ovan med Alfaisotopkartan i TNED.

— Det är också det anmärkningsvärda i hela ämnet med radioaktivitetens matematiska fysik just beträffande den observerade »sulligheten» som framskymtar i grundbegreppens etablerade beskrivning:

— OM Geiger-Nuttalls samband (1) i citatet ovan ska gälla, måste också ett Sönderfallets enhetliga preferensgrund gälla som entydigt utpekar EN halveringstid för EN sönderfallsenergi via EN specifik atom- eller nuklidindivid, eller EN specifik grupp sådana individer, och vilket samtidigt utesluter gruppen multipla alfakanalenergier.

Alfakanalenergierna räknas inte:

— De multipla alfakanalenergierna har, i så fall, ingen som helst koppling till ovan nämnda Geiger-Nuttallsambandets halveringstidsekvation — som f.ö. är exakt samma formella typ som härleds här enligt TNED i som tH-sambandet, men via en helt annan teori. Se vidare särskilt i Allmänna koefficientsambandet där jämförelse görs mellan TNED-teorin och motsvarande i modern akademi. Se även jämförelsen i Källformerna till halveringstiden.

— Geiger-Nuttallsambandets enda enhetliga funktionsform kommer därför istället — OM det är Sönderfallets enhetliga preferensgrund som ska gälla — att avse de enda entydigt bestämbara sönderfallsenergier som bara kan bestämmas entydigt genom massa-energidifferenserna med räkning via atomvikter.

— Enligt den förutsättningen saknar följaktligen kanalenergierna betydelse för halveringstiden.

— Just den typen av formulering har också eftersökts på webben, för att klargöra ämnets natur och innehåll, men inte påträffats.

— Se även jämförande exempel i övrigt angående just alfaradionukliderna och deras halveringstider i exempellistan MAC-precisionen allmänt.

— Avsaknaden av klara besked från den etablerade facklitteraturen vad den menar med de, som ovan exemplifierats, tydligt oklara, icke specificerade, framställningssätten leder naturligtvis bara till en ytterligare förträngning av ämnets rent naturvetenskapliga sakinnehåll: finns det ett sådant, överhuvudtaget? Det verkar inte finnas något, allmänt tillgängligt, bestämt svar på den frågan, märkligt som det verkar.

Presentationen i detta dokument är till viss del ägnad att »städa upp i röran» och i varje fall försöka visa en del av ämnets rent naturvetenskapliga konturer — enligt TNED: det som finns experimentellt, och hur det ser ut i jämförelse med teorin.

Se särskilt, vidare, från Alla Alfa-radionuklider.

Relationen mellan sönderfallet och sönderfallets frekvens — sönderfallets matematiska grundform

Nn/N=λn/λ — sönderfallets individer N i sönderfallets frekvens λ lambda

Det antal nuklider i en viss nuklidgrupp Nn som sönderfaller [som utträder ur sönderfallets grupper] i hela ämnets totala nuklidgruppantal N, N som ordningstalet för en grupp eller enskild nuklid vilketsom, exempel nedan, förhåller sig som gruppens idealt fasta och fixa sönderfallskonstant [λn] till hela preparatets idealt fasta och fixa sönderfallskonstant [λ], och endast då;

N_n/N = λ_n/λ ........... grundform, både i TNED och MAC

N_n/λ_n = N/λ

λ_n = λN_n/N

λ = N·λ_n/N_n = N·(λN_n/N)/N_n = λ

Är speciellt Nn=1=varje enskild nuklids eget sönderfall [utträdet ur N-gruppen] gäller tydligen speciellt för hela sönderfallet att

λn = λ/N som betyder att varje enskild nuklids specifika sönderfall representerar sin egen sönderfallsfrekvens eller med samma innebörd sin egen sönderfallskonstant, varigenom sambandsformen bevisas explicit enligt λ=N·[λn=λ/N]/[Nn=1]=N[λ/N]/1=λ. Sedan på motsvarande sätt om Nn representerar en viss grupp av nuklider med samma λn med Nn som gruppens grupptal.

— Om, inom ett givet tidsintervall, av N=100 sönderfall en grupp Nn uppvisar Nn=20 sönderfall, och förutsatt att Nn-gruppens halveringstid [inverterade frekvensen] tas som en konstant för hela gruppens individer, kan också Nn-gruppens sönderfallsfrekvens eller sönderfallskonstant [λn] förstås förhålla sig till sönderfallsfrekvensen [λ] för alla de N sönderfallen som Nn till N, analogt Nn/N=λn/λ=20/100=0,2. Totala sönderfallet med alla sönderfallsgrupper summerar alltid enheten [här i förening med resten 0,8 som ger 0,2+0,8=1].

Webbreferenser

Webbreferenser till grundformen Nn/N=λn/λ

Referenserna på webben [Jan2012] som beskriver och framför allt klargör i tydliga och enkla termer den radioaktiva matematikens — också tydliga och i grunden — enkla elementära grund är ytterst knapphändiga, för att inte direkt säga obefintliga. Det enklaste är att säga att jag har FEL på den punkten.

Det enda klargörande i citatväg som hittills har upphittats ges från Prussin 2007, samt en delvis antydd, icke källrelaterad, mening från Wikipedia [WλJan2012].

— Relationsformen Nn/N=λn/λ är, här veterligt, den enda empiriskt relaterbara koppling som alls finns i association till de rent experimentellt observerbara ämneshalter som alls går att få fram vid radioaktiv mätning, och som just kopplar till olika nuklidgrupper med olika sönderfallstider, analogt multipla sönderfallstyper [Kombinerade sönderfallstyper]. Men inga allmänt etablerade tillgängliga källor verkar finnas som beskriver de observationerna i detalj, redovisar svårigheterna, och redogör för de olika möjliga tolkningssätten, eller ens omnämner deras observation [Andra summeringssätt].

— Avsaknaden av klara besked i ämnet står i anmärkningsvärd kontrast med den utomordentliga omfattningen (hela världen) av de praktiska intrumenttillämpningarna och deras beskrivningar och resultat [Webbreferenser — mer eller mindre urvattnat] och som webben verkar ha stor representation av, inte sällan utom direkt allmän insyn.

— Den kontrasten ger ytterligare skäl att ämnet som sådant, tydligen, är föremål för självsjunkning — långt under gränsen för någon acceptabel form som SKULLE kunna kallas naturvetenskap — till skillnad från naturSpekulation.

— Jämförelse mellan de olika, möjliga, tolkningssätten [29Cu64Exemplet] endast understryker helhetsbilden; ingen som helst allmänt etablerad ordning verkar finnas i ämnet.

Se även vidare nedan i Halveringstidens oberoende summeringsalgoritm — jämförande beskrivning som möjligen belyser en del av orsakerna till ovan uppmärksammade observationer.

Halveringstidens Oberoende Summeringsalgoritm — Se även grunden från Halveringssambandet

2012I1

INDIVIDSUMMERINGARNA i tH ENLIGT TNED

— som inte finns i MAC

TNED-teorin skiljer sig från MAC-teorin på flera avgörande punkter på grund av nuklidkoefficienten som inte finns i MAC-teorin;

— Främsta skillnaden: TNED-teorin baseras på härledbar fysikalisk dynamik, INTE på matematisk statistik. Se särskilt från Härledningen till halveringsTIDssambandet.

Genom att halveringstiden (tH) som begrepp redan från Härledningen OCKSÅ betyder/innefattar ett (1=ETT enda) individuellt sönderfallssteg — innefattat från 2 till 1=2/2 — kommer definitionen i TNED för ett helt radioaktivt ämnes sönderfall att innefatta också varje individs egen unika dynamik; summan av de individuella tH-värdena måste stämma med det uppmätta tH-värdet för hela ämnesgruppen. Nuklidkoefficienten [b=4πÑ] garanterar den individualiteten.

— Genom att radiokonstanten (λ=ln2/tH) avbildar hela det radioaktiva ämnets totala sönderfall genom procentuellt uppmätta andelar (då sådana ingår) för olika typnuklider gäller, tydligen både i TNED och MAC [‡], motsvarande procentuella uppdelningar (k=λn/λ) av respektive radiokonstanter (λn) på deras respektive nuklidgrupper (Nn/N=λn/λ) [‡] för hela ämnet enligt totala ämnessönderfallets aritmetiska enhetssumma

1 = λ₁/λ + λ₂/λ + λ₃/λ + …λ_N/λ ; .................... ämnets/preparatets totalt uppmätta radioaktivitet, grundform både i TNED och MAC

Respektive λn-värde kan inte observeras direkt, utan motsvaras av en experimentellt uppmätt delhalt av en viss sönderfallstyp i förhållande till hela mängdens sönderfall [‡]:

λ = λ₁ + λ₂ + λ₃ + …λ_N

Brytpunkten TNED-MAC:

— I MAC finns inte nuklidkoefficienten [b=4πÑ]; I TNED garanterar den att varje individuell nuklid kan ha principiellt unika egenvärden i det allmänna tH-sambandet. För att den individualiteten ska kunna bevaras i samtidig giltighet av hela preparatets totala halveringstid [tH], måste tydligen varje nuklids tH-bidrag också förhålla sig till hela ämnesgruppens alla ingående [N] radioaktiva nukliders bidrag i respekt till ovan nämnda radioaktiva deltermer.

— Det betyder att TNED antar ett summeringssätt som INTE kan förekomma i MAC-teorin, just på grund av nuklidkoefficientens garanterade tH-variationer och vilka variationer inte ingår i modern akademi. Jämför bl.a. HyperPhysicsCitatet.

— Summeringssättet i fråga enligt TNED är samma som att påstå — trivialt — att OM alla N radioaktiva nuklider har exakt samma tH-värde [1S=1S·N/N, mera utförligt nedan], har också hela preparatets totala halveringstid samma tH-värde som varje enskild nuklid genom att alla nuklider har samma radiokonstant λ[n]=λ/N med hela preparatets samlade λ=N[λ/N] via samma halveringstider enligt [vi återkommer upprepat till detta principled under beskrivningens gång för att klargöra sakinnehållet ur alla möjliga synvinklar]

t_H = (1S)(N[1/N]₁ + N[1/N]₂ + N[1/N]₃ + … + N[1/N]_N)/N = t_H = 1S ;

— Varje individs utträde ur gruppen (sönderfallet) bidrar följaktligen enligt TNED till hela ämnets sönderfall liknande TILLFÄLLET för individer (människor) i en sal att EFTER FRI VILJA gå ut ur lokalen utifrån egna förutsättningar, oberoende av direkta influenser från övriga — typ KÖER i väntan på pågående utträde för att själv kunna utträda. Dvs., varje individ bidrar genom ett »sant medelvärde för hela gruppen» eller »kö-oberoende summering» enligt typledet nedan: varje specifikt tH-värde [N=(1S)N] som tHn=N[λn/λ] (som ger λn=λ·tHn/N=λ·în)

tH-summeringen

t_H = t_H(N[λ₁/λ] + N[λ₂/λ] + N[λ₃/λ] + … + N[λ_N/λ])/N = t_H ................. aritmetiska medelvärdet med individernas gruppmedelvärden

= (t_H1 + t_H2 + t_H3 + … + t_HN)/N .......................................................... aritmetiska medelvärdet

Jämför MAC-teorin [ref. WIKIPEDIA Half-life, Decay by two or more processes, vidare nedan]: man använder — överprojicerar — giltigheten för hela preparatets alla nuklider λ=ln2/tH för att också »definiera» partiella radiokonstanterna enligt λn=ln2/tHn;

— Skulle den typen antas i TNED, leder den till den icke entydiga likheten λn = ln2/tHn = λ·tHn/N som ger λ = N(ln2)/(tHn)²; tHn är godtycklig och kan inte definiera en fast radiokonstant λ via en fast nuklid- eller nuklidgruppmängd N; likheten saknar mening, vidare nedan i huvudtexten.

— Resultatet i MAC blir att man istället för ovan tillämpar summeringstypen [citatkällor nedan] 1/tH = 1/tH1 + 1/tH2 + 1/tH3 + … + 1/tHn, vilket ger helt andra tH-värden jämfört med TNED.

— Summeringssättet [eng. harmonic mean] med inverterade summeringen tH = 1/[1/tH1 + 1/tH2 + 1/tH3 + … + 1/tHn] görs på TYP frekvenser som summeras i KÖ; FÖRST den, sedan den, sedan den … . Frekvenserna summeras efter KÖ, och ur deras summa antas sedan tH-värdet inverterat. I sönderfallsfysiken finns ingen sådan ordning OM individens sönderfallande, oberoende, frihet existerar, vilket är fallet i TNED; Det finns ingen köbildning i typen N[λn/λ], endast den bestämda andelen [λn/λ] av hela N-enheten.

— I TNED-fallet får varje nuklid istället sönderfalla närhelst den själv vill, inbegripet i typen N[λn/λ], enligt nuklidens allmänna bidrag till de N stycken grupperna eller nukliderna och utifrån en egen inre tH-konstant.

— Det betyder i TNED att radiokonstanten λ som partikulär värdeform λn saknar entydig koppling till en partikulär halveringstid: λn=ln2/tHn gäller inte. Det blir, tydligen, bara HELA preparatets radioaktivitet som kan tillämpas på HELA preparatets halveringstid: λ100%=ln2/tH100%; Partiella halveringstiderna [tHn] kräver med andra ord och tydligen, för bevarandet av tH-individualiteten som ovan, en särskild behandling.

— Därmed gäller inte samma matematiska ordning i TNED som i MAC — just på grund av den möjliga variationen mellan individernas tH-värden i allmänhet och de multipla sönderfallen [eng. multiple decays, decay modes, decay channels, decay routes, partial decay constants, m.fl.] i synnerhet.

— Eftersom, tydligen, saken inte kan avgöras experimentellt — Respektive λn-värde kan inte observeras direkt, utan motsvaras av en experimentellt uppmätt delhalt av en viss sönderfallstyp i förhållande till hela mängdens sönderfall [‡], se även i sönderfallets matematiska grundform — lämnas, tydligen, tolkningen öppen av de uppmätta värdena; Det behövs — uppenbarligen — någon [ännu ej i etablerade kretsar uppmärksammad] katalyserande faktor som kan skapa klarhet i frågan.

— Se speciellt namngivna artikelgrupper nedan [särskilt i WIKIPEDIA] som beskriver, speciellt, MAC-teorins tH-summeringsformer enligt

WIKIPEDIA Radioactive decay, Time constant and mean-life;

WIKIPEDIA Half-life, Decay by two or more processes;

WIKIPEDIA Exponential decay, Decay by two or more processes;

;

WIKIPEDIA Radioactive decay, Time constant and mean-life [2012-01-01]:

”Each atom ”lives” for a finite amount of time before it decays, and it may be shown that this mean lifetime is the arithmetic mean of all the atoms’ lifetimes, and that it is τ, which again is related to the decay constant as follows: τ = 1/λ”.

— Enligt TNED, som ovan, finns ingen praktisk innebörd i en sådan ALLMÄN form, eftersom varje enskild nuklid, enligt TNED, har sin individuella karaktär med ett specifikt tH-värde som inte är exakt lika som de övriga individernas [garanterat av den primära nuklidbildningen med de olika lokalernas neutronkvoter och därmed nuklidkoefficientens allmänna variation, enligt TNED], och därmed ett specifikt motsvarande τn-värde, tHn/ln2.

— MAC-formalian ovan med τ = 1/λ har alltså i TNED bara betydelse som ett allmänt matematiskt/numeriskt medelvärde för HELA det radioaktiva preparatets alla ingående nuklider tagna utan hänsyn till individuella variationer.

— Det betyder också, enligt TNED, att wikipediacitatets del ”may be shown” saknar fysikalisk representation: det finns ingen sådan fysik. Men visa gärna vad som menas, i detalj, så att ytterligare tillfälle ges att få understryka naturvetenskapen.

Speciellt i WIKIPEDIA Half-life, Decay by two or more processes, påstås

”For a proof of these formulas, see Decay by two or more processes” och som leder till

WIKIPEDIA Exponential decay, Decay by two or more processes, där ”proof”:et beskrivs

”Since τ = 1/λ, a combined τC can be given in terms of λs 1/ τC = λC = λ1 + λ2 = 1/τ1 + 1/τ2” — och så var det inte mera med det ”proof”:et.

— Dvs., wikipediaartikeln ger bara ett rent påstående, utan vidare beskrivning, grund, innehåll, förankring eller förklaring — därför att den förklarande grunden inte finns i MAC.

— Inget annat SÄTT finns, nämligen, i MAC än just DET sättet, eftersom tH-variabler inbördes mellan nukliderna inte ingår i MAC-teorin; MAC-sättet ovan utesluter dem också, konsekvent. Det är vad som kan utläsas direkt via TNED.

;

TNED MAC

———————————————————————————

t_H = (ln2)/λ ............................................ OK ; MACok

= (ln2)/(λ₁ + λ₂ + λ₃ + …λ_N) ............ OK ; MACok

λ_n = (ln2)/t_Hn .......................................... notOK ; MACok

λ_100% = (ln2)/t_H100% ..................................... OK ; MACok

λ_n = λt_Hn/N ............................................. OK ; inte i MAC

t_Hn = (ln2)/λ_n .......................................... notOK ; MACok

t_H100% = (ln2)/λ_100% ..................................... OK ; MACok

t_Hn = Nλ_n/λ ............................................. OK ; inte i MAC

RELATERAD FYSIK SOM OVAN: t_Hn bildar GRUNDFORMEN från sönderfallets matematiska grundform som tH-summeringens enda entydiga relationsfaktor, med villkoret inkluderat för variabla tH genom nuklidkoefficienten [b=4πÑ], men finns inte i MAC. Därav de i uppställningen ovan särskilt gjorda anmärkningarna »MACok» resp. »inte i MAC» för översiktens del. Se utförligt från Halveringstidens Oberoende Summeringsalgoritm.

t_Hn representerar därmed i TNED definitionen på partiella halveringstiden i partiella radioaktiviteten [λn] genom andelen uppmätta sönderfallsprodukter via N distinkt skilda sönderfallstyper [alternativt enskilda nuklidsönderfall] för hela ämnets radioaktivitet [λ]. Se särskilt sönderfallets matematiska grundform.

; Procentuella andelen av varje nuklids eget bidrag, men här explicit utan aspekter på sönderfallets tillfälle, beror av hela nuklidmängden N i hela ämnet (preparatet) — så att, i princip, varje enskild radioaktiv nuklid kan ha sitt särskilda, specifika, halveringstidsvärde (tH), och därmed individens specifika radiokonstant (λn≠ln2/tHn; λ100%=ln2/tH100%) enligt ovanstående summeringsalgoritm.

Jämförande likheter

— Notera (således, noga) det oberoende summeringsvillkoret:

— Genom oberoende tH-summeringen definieras entydigt bestämt [(1S)N=N]

tHn = N[λn/λ] som ger λn = λ·tHn/N = λ·în; partiella radiokonstanten (λn) avspeglar partiella medellivet;

— Och därmed λn≠ln2/tHn; Däremot gäller på vanligt sätt för hela ämnet λ100%=ln2/tH100%.

— Skulle, nämligen, sambandet λn=ln2/tHn gälla, skulle det, tydligen, också gälla att

λn = ln2/tHn = λ·tHn/N ;

λ = N(ln2)/(tHn)² ;

Det är inte rimligt att radiokonstanten (λ) för hela det radioaktiva ämnet återfaller på någon nuklids godtyckligt valda halveringstid (tHn): likheten är inte entydig. Därmed finns heller ingen relevans i den partiella sambandsformen λn=ln2/tHn. Dvs.;

— Radiokonstanten som partikulär värdeform (λn) har tydligen ingen entydig koppling till en motsvarande partikulär halveringstid (tHn) OM också halveringstidens oberoende summering (HOS) gäller: Radiokonstantens tH-delar gäller bara hela ämnet λ100%=ln2/tH100%. Inte delar.

Eller rättare sagt: Radiokonstanten som partikulär värdeform (λn) är inte självständigt oberoende av nuklidgruppernas antal (N) och totala sönderfallsfrekvensen (λ):

— Titta på sambandsformen för halveringstiden [tH] för HELA det radioaktiva sönderfallet och som gäller generellt i både TNED och MAC:

(1) t_H = ln2/λ

Sambandsformen beror bara av en enda enhet (1) för HELA det totala sönderfallet. Det finns inga delar att relatera.

— Titta sedan på »motsvarande» för en förmodad DEL av den radioaktiva besättningen:

(2) t_Hn = ln2/λ_n

— VAR finns relationen som bestämmer den aktuella n-delen? Jag ser ingen. NÅGON YTTERLIGARE faktor måste finnas med. Vi finner också en sådan — om vi ser till den alternativa skrivningen för DELen — från tH-summeringen och sönderfallets matematiska grundform Nn/N=λn/λ —

(3) t_Hn = N[λ_n/λ] ; N_fetstil=(1S)N

(4) λ_n = λt_Hn/N ;

DELen beror av den mängdfaktor [N] som särskiljer den obetingade enheten [1] från dess uppdelning i N olika, distinkt skilda sönderfallsgrupper. Och det är klart att en sådan indelning är osynlig för en obetingad ekvivalent av typen i (2) ovan; En relationsfaktor MÅSTE existera, och den definieras av förhållandet mellan den uppmätta delens andel [Nn] i förhållande till hela sönderfallet [N] via typformen Nn/N=λn/λ, vilket därmed ger en bestämd identitet också för de motsvarande halveringstiderna. Med andra ord:

— Sambandet i (2) kan bara gälla entydigt för HELA sönderfallet i formen av sambandet i (1), N=1, medan sambandet i (3) är det entydiga sambandet för sönderfallets delar, N>1.

— Jämför ENHETSFALLET med alla N nuklider på exakt samma tH=1S=N[λn/λ] med varje motsvarande individuellt associerad sönderfallskonstant λn lika med λn/λ=1/N och som summerar exakt samma tH=1S för summan av alla enskilda nukliders bidrag enligt

t_H = (1S)(N[1/N]₁ + N[1/N]₂ + N[1/N]₃ + … + N[1/N]_N)/N = t_H = 1S ;

— Med samma utgångspunkter men i MAC-teorins anda av inverterade summeringen

t_H = 1/[1/tH1 + 1/tH2 + 1/tH3 + … + 1/tHn]

ges tydligen felaktigt

= 1/[1/1S + 1/1S + 1/1S + … + 1/1S]

= 1/[1 + 1 + 1 + … + 1]Hz

= t_H → 0 S med växande N

— Exemplet visar, särskilt, att MAC-teorins summeringsalgoritm, [aritmetiskt] inverterade summeringen ovan [eng. harmonic mean] inte kan användas för att beskriva grundfallet med alla enskilda nukliders individuella bidrag till enheten [1]. I vidare mening, och således, inte heller då den enskilda nukliden, verkligen, skiljer sig i tH-värde från varje annan, marginellt eller radikalt.

— Vad innebär det ovan påstådda, enligt TNED, för det vi kan läsa i ämnet på webben från etablerade källor?

— För experimentellt uppmätta detaljer — som vanligt — ingenting utöver det som redan är känt.

— Det är, och förblir så, att TNED och experimentalfysiken [se särskilt i Atomvikterna] ska vara samma, eller i det närmaste samma, så nära man alls kan komma. Annars är hela framställningen i UNIVERSUMS HISTORIA, den här framställningen och alla andra i den domänen, komplett värdelöst skräp.

— Däremot för uppgifter om specifika halveringstider som kommer från MAC-teorins inverterade summeringsalgoritmer [‡] — MAC-tH-värden i samband med multipla sönderfall — råder milt sagt stränga olikheter mellan TNED och MAC. Se särskilt sammanställt illustrerat punktvärdediagramexempel i 29Cu-64-exemplet.

— De tydligt exponerade [våldsamt stora] skillnaderna verkar helt sakna experimentella förutsättningar för avgörande, eftersom de enskilda sönderfallskonstanterna bara kan bestämmas ur de enskilt observerade, procentuellt uppmätta ämneshalternas andelar av hela preparatets sönderfall. Se särskilt i Citat. Webbkällor — allmänt tillgängliga — som har uppmärksammat, och kan klargöra, problemet har eftersökts men inte påträffats. Det verkar vanvettigt, men är de facto det enda som framkommit in till skrivande stund [2Jan2012].

— Sönderfallet kommer alltså att bero av summan av de enskilda individernas aktiviteter. Aktivitetsbegreppet [ξ_N=N(ln2/t_H)] betyder den aktuella sönderfallsfrekvensen för antalet (N) radioaktiva nuklider; sönderfallet sker genom radio- eller sönderfallskonstanten (λ=ln2/tH) — aktiviteten (ξ, xsi) dividerat med aktuella antalet radioaktiva nuklider N.

Komprimerat

NUKLIDKOEFFICIENTEN [b=4πÑ] garanterar: Halveringstiden (tH) i TNED gäller för hela den radioaktiva nuklidgruppen (N) med avseende på varje enskild nuklidindivids (i huvudsak) enskilda halveringstid (tH[Nλ/λ_n]), oberoende av de övriga individernas sönderfallstillfällen i gruppen, enligt (enkla jämförande exempel längre ner)

t_H = t_H(_n=1_→N∑ [Nλ/λ_n])/N

= t_H( Nλ/λ₁ + Nλ/λ₂ + Nλ/λ₃ + … + Nλ/λ_N)/N

= t_H( λ/λ₁ + λ/λ₂ + λ/λ₃ + … + λ/λ_N)

= t_H( 1)

med sönderfallsfördelningen (λ/λ_n) — den procentuellt uppmätta sönderfallsmängden för en viss nuklid, om alls någon särskild — för varje nuklid i totala sönderfallet (λ=ln2/t_H) enligt sönderfallskonstanten (eng. decay constant)

λ = λ₁ + λ₁ + λ₁ + …λ_N

— Det betyder att varje enskild nuklid INTE behöver vänta på, eller på annat sätt ta hänsyn till tillfället då någon annan individ i gruppen sönderfaller, utan alla agerar utifrån sina individuella förutsättningar.

— I modern akademi tillämpar man också LambdaSummaformen närmast ovan — men INTE den individuellt oberoende medelvärdessummeringen för halveringstiderna (tH).

I MAC används istället en inverterad summering via Lambdafaktorn (λ, konv. sönderfallskonstanten) enligt (29Cu64-exemplet)

t_H = ln2/λ

= ln2/(λ₁ + λ₂ + λ₃ + … + λ_n)

= ln2/(ln2/t_H1 + ln2/t_H2 + ln2/t_H3 + … + ln2/t_Hn)

= 1/(1/t_H1 + 1/t_H2 + 1/t_H3 + … + 1/t_Hn)

EXEMPEL MAC — tH = 1; λ = 1 = 0,1 + 0,2 + 0,7 = λ₁ + λ₂ + λ₃:

tH = ln2 ;

tH = ln2/(λ₁ + λ₂ + λ₃)

= ln2(ln2/0,1 + ln2/0,2 + ln2/0,7)^–1

= ln2(1/0,14 + 1/0,29 + 1/1,01)^–1;

= ln2(6,93 + 3,47 + 0,99)^–1

= (1/0,1 + 1/0,2 + 1/0,7)^–1

= 0,0608695

≠ ln2

— Den inverterade summeringen betyder samma som att sönderfallen, de enskilda individuella frekvenserna (1/tH), väntar på varandra i KÖ: individuellt oberoende saknas. Därmed summerar heller inte de partiella halveringstiderna (tH_n=ln2/λ_n) den totala halveringstiden (tH=ln2/λ); sammanhanget framstår helt ologiskt. Ovanstående typ tillämpas i MAC. Se från 29Cu64-exemplet.

;

EXEMPEL TNED — tH = 1; λ = 1 = 0,1 + 0,2 + 0,7 = λ₁ + λ₂ + λ₃: N = 3;

tH = ln2

= tH(0,1N + 0,2N + 0,7N)/N

= tH(0,3 + 0,6 + 2,1)/N

= tH(0,1 + 0,2 + 0,7)

= tH

— Den oberoende medelsummeringen respekterar de enskilda individernas egna sönderfallstakter med hela sönderfallet som medelvärdessumman av alla individers enskilda bidrag; sammanhanget framstår helt logiskt — men tillämpas INTE i modern akademi.

Det är klart att bägge de exemplifierade sambandstyperna inte kan gälla samtidigt: någon av dem ger, tvunget, direkt felaktiga resultat.

— Det förefaller uppenbart att det bara är den oberoende summeringen — sanna medelvärdet av individernas bidrag — som är den naturliga, det rätta sättet.

— Varför inte den individoberoende summeringen i MAC?

Anledningen — som det får förstås — varför MAC-teorin inte KAN använda den individuellt oberoende medelvärdessummeringen:

— Nuklidkoefficienten [b=4πÑ] i TNED: Kriteriet på individuell variation.

— MAC-teorin har ingen sådan teori, ingen sådan komponent:

individuella variationer i halveringstider (tH) ingår inte i den moderna akademins teorier om radioaktiva sönderfallets fysik [‡].

— Därför — såvitt korrekt uppfattat — måste MAC-teorin använda en summeringsalgoritm som är ensidigt bunden till sönderfallskonstanten och dess fördelningsintervall, som ovan med

λ_n = ln2/t_Hn

enligt

t_H = ln2/(λ₁ + λ₂ + λ₃ + … + λ_n).

= ln2/(ln2/t_H1 + ln2/t_H2 + ln2/t_H3 + … + ln2/t_Hn)

= 1/(1/t_H1 + 1/t_H2 + 1/t_H3 + … + 1/t_Hn)

— Saken kan inte, heller, avgöras experimentellt eftersom det enda som syns, då olika nuklidgrupper framträder, är just de olika procentuella delarna av totala sönderfallet (λ).

— Se särskilt citat i Totala sönderfallskonstanten.

MAC-teorin måste alltså, likväl på ett annat sätt (multipla sönderfallstyper typ BetaEC och BetaPlus m.fl.), erkänna »variationer i halveringstid». Men då dessa (enligt MAC-teorin) bara berör explicit olika sönderfallstyper behöver man heller inte bry sig om de rena, inre, individfallen (nuklider av »exakt samma typ») men som framkommer naturligt i TNED-härledningen till tH-sambandet [‡], just via nuklidkoefficienten, och därmed individvariationerna av princip.

Jämför ett ENHETSEXEMPEL:

— Av 100 individuella radioaktiva nuklider av bestämd typ (masstal A, kärnladdning Z), varje nuklid med idealt exakt samma halveringstidsvärde (tH(1/N)N), och sönderfallskonstanten (λ) fördelad exakt lika med λ/100 på alla N=100 individer,

ges ekvivalent korrekt resultat

t_H = t_H(_n=1_→100∑ [100λ/λ_n])/100

= t_H( 100λ/λ₁ + 100λ/λ₂ + 100λ/λ₃ + … + 100λ/λ_N)/N

= t_H( λ/λ₁ + λ/λ₂ + λ/λ₃ + … + λ/λ_N)

= t_H( 1)

I motsvarande MAC-fall skulle resultatet tydligen bli

t_H = ln2(ln2/0,01 + ln2/0,01 + ln2/0,01 + …)^–1

= (1/0,01 + 1/0,01 + 1/0,01 + …)^–1

= (100 + 100 + 100 + …)^–1

= 1/(100·100 = 10 000)

= 0,0001

Detta sistnämnda resultat går inte att förankra i någon begriplig, sammanhängande, logik.

MAC approximerar TNED

Hur MAC-teorins detaljer kopplar till TNED generellt

Om Fermis gyllene regel och halveringstiderna generellt

FERMIS GYLLENE REGEL — kvantmekanisk statistik i modern akademi

λ_if = (2π/ħ)| M_if |² ρ_f

Se utförligt i HYPERPHYSICS Fermi’s Golden Rule, Fermi Theory of Beta Decay [2012-01-03]

http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/fermi2.html

;

”The transition probability λ is also called the decay probability and is related to the mean lifetime τ of the state by λ = 1/τ. The general form of Fermi's golden rule can apply to atomic transitions, nuclear decay, scattering ... a large variety of physical transitions.”.

Notera att FERMIS GYLLENE REGEL innefattar matematisk statistik vilket område är helt orepresenterat i UNIVERSUMS HISTORIA och därmed i tillhörande presentation av TNED: Den relaterade fysikens härledningar till kärnfysikens detaljer, samt det som följer av dessa, använder inga statistiska begrepp.

Sönderfallskonstanten (eng. decay constant, konv. λ=ln2/t_H) har samma innebörd som ovan för lambda (λ) i den s.k. Fermis gyllene regel (FGR, från 1934).

— Vi kan (från HyperPhysicskällan och den redan välkända halveringstiden t_H=ln2/λ) se HUR FGR kopplar till TNED speciellt via betasönderfallens halveringstider genom att studera den ovan angivna generella sambandsformen för FGR i jämförelse med den strukturform som ges via TNED-teorin, figuren nedan.

Grafdelarna ovan från jämförelsen mellan Alfa och Beta i TNED-beskrivningen av Betasönderfallande nuklider. Övre blå kurvan, tH-universalens betaekvivalent i TNED. Undre röda kurvan, MAC-teorins motsvarande, här generaliserade, funktion benämnd Fermis gyllene regel.

— Som redan påpekats i Allmänna Koefficientsambandet, leder MAC-teorins kvantmekaniska statistik för alfasönderfallens del till TNED-sambandet för halveringstiden tH (‡) via APPROXIMATIONER (Se särskilt Citat).

— Eftersom TNED-teorins tH-samband också gäller för betasönderfallen (och alla andra atomkärnrelaterade sönderfall), se utförligt från Nuklidfaktorn i betasönderfallet, finns på motsvarande sätt också en koppling (via approximationer) till MAC-teorins motsvarande FGR-metod. Vi kan se den kopplingen, tydligt, i de bägge ovan högra avbildade jämförande funktionsgraferna; TNED(blå, överst) och FGR(röd, underst) med den sistnämndas grundform (1/x²) justerad på 10log-funktionens form för jämförelse, samt halverad för närmast direkt matchning.

— Som vi ser, ligger funktionsformerna helt nära varandra.

— TEORIERNA är dock så väsensskilda som man alls kan tänka sig: det finns ingen som helst gemensam beröringspunkt (utöver 0123456789). Helt rent.

— Medan FGR-metodens teori är så abstrakt som det alls överhuvudtaget går,

garanterat förbehållet en så snäv grupp individer — tydligen också helt oförmögna att dela med sig av den förmodade insikten till resten av mänskligheten på något begripligt språk —

att begreppet naturvetenskap för den delen förefaller tveksamt,

ger TNED-teorin en SYNBARLIGT detaljerad, exakt och precis genomgång av kärnfysikens alla väsentliga funktioner på rent praktiskt dynamisk, logisk och vardagligt begriplig grund. Se utförligt från Atomkärnans härledning, om ej redan bekant.

TNED, relaterad fysik och matematik, innehåller ingen abstraktion, eller ska i varje fall inte göra det. Varje detalj ska framgå ur och vara helt återförbar på grundläggande, enkla och elementära naturliga funktioner som kan ses, studeras och begrundas av varje tänkande individ, utan särskilda meriter: Inga institutionella överbyggnader får förekomma.

— I Klartext: REDAN genom att vara född, ÄR du redan registrerad och därmed behörig att ta del av allt som rör naturvetenskapen. Du ska INTE behöva fylla i särskilda formulär för det, INTE behöva uppge NAMN, STATUS, STÄLLNING, BEFATTNING, ADRESS eller annat sådant förnedrande utlämnande i privatlivet — webben innehåller i en del fall rena skräckexempel. Möter du sådana Portaler: avstå. Jag gör det. De är UPPENBARLIGEN INTE seriösa i ämnet KUNSKAP. Men det är bara min mening.

Inledning med kort sammanfattning av Universums Historia enligt TNED

— Se särskilt Universums kritiska täthet som klargör K-cellens fysik i TNED genom PLANCKEKVIVALENTERNA som raderar relativitetsteorins (ända från 1905 uppenbart) felaktiga påståenden i fysiken och förklarar — i relaterbara, fullt begripliga termer med r-teorin innefattad som en PRIMITIV anordning — hela komplexets matematisk-fysikaliska formelapparat i detalj. Se särskilt jämförande exempel i EXPERIMENTELLA BEKRÄFTELSER. Speciellt Atomkärnans härledning med Atomvikterna genom (upptäckten av) Neutronkvadraten (TNED) bildar sedan hela den rent praktiskt konkret påvisbara grundvalen för Universums Historia — enligt TNED.

TNED:

Radiofysikens grunder

K-cellens kontraktion, efter expansionens avstannande och återvändande [Se Universums kritiska täthet], medför i gravitationens försorg [Se Ljusets gravitella beroende] att huvuddelen av K-cellens materiekropp kommer att befinna sig i elektromagnetiskt (förk. em) nedsläckt tillstånd: ingen em-aktivitet. Kärnreaktionslagen visar, genom omvändning [Se Hur K-cellen återvinns], att ett sådant tillstånd också kan förstås som en omvändning av fusionsbildningar: atomerna förlorar sina bindningar, och sönderdelas [via elektroninfångning] ner till grundkomponenten NEUTRONEN, i TNED samma som Planckringen. K-cellen i det läget kallas i TNED (naturligt) ett neutronkallplasma.

Genom att atomkärnan heller inte kan komprimeras [Se Atomkärnans inkompressibilitet], slutar K-cellens gravitella kontraktion med att huvudmassan i formen av de återvunna neutronerna klonkar ihop på hela den sammanlagda gravitella kontraktionsfasens rörelsemängd. Som visas i K-cellens detonation, blir resultatet oundvikligt: K-cellen detonerar — återstudsar — med exakt samma kraft som i stoppögonblicket. Därmed inleds, återigen, en ny expansionsfas [Se från Stjärnhopar och Galaxbildningar Del 1].

Energilagen, med sambandet mellan massa och energi, grundlägger hela verkningssättet genom grunden att energi varken kan skapas eller förintas utan måste förutsättas. Därmed massans yttersta ursprung: då energin varken saknar upphov eller slut, gör inte massan det heller.

Allmänna tillståndslagen visar energiräkningen för hela verkningssättet, med den, enligt energilagen nödvändiga c0-kroppen med NEUTRONEN — Plancks konstant h=m[neutronmassan]c[toppdivergensen]r[tyngdcirkelradien] — som energins/massans eviga, oskapade, upphovslösa masselement. Verkningssättet mellan K-cellen och c0-kroppen är att c0-kroppen förser [kontraherar, ytterst långsamt] K-cellen med neutronelement för att kompensera exakt den mängd som K-cellen förbränner via ljus och värme [Solar, Stjärnor] under varje expansionfas. Gravitationen säkerställer att endast ett inre centrum av c0-kroppen alltid är (pulserande) aktivt: K-cellens innersta kärna.

Strängen av kroppar som avdelas i sin tur från K-cellens större J-kroppar är alla av neutronkallplasmats maximala täthet [Se Maximala neutrontätheten 1,82 T17 KG/M³]. När kropparna avdelas — växande avstånd mellan kropparna betyder lokalt avtagande gravitation — ändras samtidigt det gravitella förhållandet; K-cellens allmänna Nolldivergenszon [gravitella gränsen för c=0] flyttas utåt med expansionen (med konstant hastighet v=c0 under hela K-cellens expansion). Då nollzonen passerar de expanderande kropparna, genomgår dessa divergenständning: c>0. Då den lokala divergensen (ljushastighetens gravitellt punktlokala värde, se även i DEEP) överstiger noll, kan neutronsönderfallet börja (pågår normalt 10-14 minuter). Därmed inleds (början till) fusionsfasen med bildningen av fusionsringar mellan de maximalt tätt liggande neutronkärnorna. Neutroner förenas inte. Himlakroppens innersta del kommer att sönderdelas (från neutroner till vätekärnor) först eftersom divergensen (c) i den lokala g-kroppens centrum alltid är som störst i mitten, där tar g-krafterna ut varandra: Maximal elektro/magnetisk/mekanisk kraftverkan.

(Sönderfallet i centrum sker från neutroner till Väteatomer; Väteatomernas elektronmassor kan förstås fungera på samma sätt som i fallet med Solfysiken i TNED, de drivs utåt av ett kärninduktivt neutrinostrålningstryck, och kvarlämnar rena protonkärnor i centrum).

Neutronkvoterna

I TNED indelas J-kroppen i motsvarande olika regioner efter motsvarande s.k. neutronkvot — sättet som en viss nuklidbildning kan genomföras på med hänsyn till antalet ingående neutroner i en viss fusionsring. En och samma nuklid kan (nämligen) bildas via olika neutronkvoter, och därmed på olika avstånd från centrum i himlakroppen. Se utförligt från Grundämnesbildningen. Från det att den innersta delen neutronsönderfallit »färdigt», och därmed fusionsfasen inleds — de tätt liggande frilagda protonkärnorna (med ev. kvarvarande neutroner) börjar förenas spontant eftersom de redan ligger innanför varandras nuklidbarriärer redan från ruta ett, se från Nuklidbarriären — och som i allmänhet betyder noll neutronförekomst i centrum, kommer den J-kroppen helt naturligt (efter vissa mellanspel) att detonera med stor kraft. Detonationen generellt för J-kropparna kan alltså förstås ske på liknande sätt som för hela K-cellen, fast i mindre skala — men fortfarande med närmast enorma, kortvariga, energiutvecklingar i samband med fusionsbildningarna [Se Grundämnesbildningens två basgrupper]. Grundämnesfördelningen PRIMÄRT blir därmed given för den himlakroppen med hänsyn till just neutronkvoten — samt en faktor nuklidseparation. Nuklidseparationen sammanhänger med en balans mellan inåttryckande g-kraft och uttåtdrivande Coulombkraft och som naturligt sammanhänger med kroppens primära massa. I TNED indelas alla himlakroppar efter den fysiska kropp med massan 6,80016 T24 KG som uppvisar exakt balans mellan krafterna inåt-utåt och som här kallas fusionsgränsmassan (Se Jordens andra ekvation). Det är den typkropp som kommer att uppvisa maximal rikedom på alla möjliga grundämnen då alla andra uppvisar antingen utpräglade gaskroppar eller stenkroppar (neutronkvoternas olika förskjutning mot olika extremlägen), med respektive motsvarande stjärnkroppar eller planetkroppar. Se Grundämnesfördelningen.

Kopplingen till radiofysiken

Ur ovanstående primära grundämnesbildning framgår också grundvalen för nuklidkoefficienten (b=4πÑ) i TNED-härledningen till halveringstidssambandet [‡] som antas gälla för alla radioaktiva atomer.

— Eftersom elektriska kraftlagen [Se från Härledningen] innefattar divergensen (c) i elektriska konstanten,

ε₀ = 1/R₀c₀ = 1/Rc = 1/2Rc_z

och därmed via potentialbarriärens energizon [c(z)] — stället där den elektriska laddningen av princip TAS av yttre elektriska fält, i försorg av ljusets g-beroende, och vars praktiska tillämpning exemplifieras i Härledningen, se Exempelreferens Spektrum — finns ingen möjlighet att undkomma också gravitationens inverkan på just b‑koefficienten I NUKLIDENS BILDNINGSTILLFÄLLE, speciellt den radioaktiva nukliden i denna presentation:

— En och samma nuklid har, tydligen enligt TNED, viss förutsättning för att KUNNA uppvisa en viss intern variation — som MÖJLIGEN kan koppla till nuklidkoefficienten (b=4πÑ). Variationen i b-värde skulle därmed visa sig (enbart vid tillfället för det radioaktiva sönderfallets avdelande av nuklidmassa, partiklar, från moderkärnan) mellan den nuklidtypens olika atomindivider och som därmed, via helt marginella differenser, SKULLE kunna uppvisa motsvarande marginella skillnader i halveringstider, se tH-sambandet. Variationerna skulle därmed förstås gälla mellan gruppens individer (och som i princip därför bara kan kontrolleras genom att mäta på enskilda atomer, vilket f.n. inte är tekniskt möjligt).

PROBLEM: Jordens ålder

— Därmed finns, enligt TNED, en viss, helt säker, teoretisk grund för den praktiska möjligheten att halveringstiderna (tH) är primärt lokalt beroende av sina primära bildningsregioner via b-faktorn; Uranbildning i Jordlokalens referens skulle därmed INTE vara densamma i b-koefficientens ljus som MELLAN himlakropparna, t.ex. i asteroidbältet [‡] mellan Mars-Jupiter, (det allmänt antagna) ursprunget till många av meteoriterna vars ämnessammansättning f.ö. används för »bestämning av Jordens ålder».

— Meteoriternas andel radioaktiva ämnen [Se Allmänt om åldersbestämning via meteoriter] bör, enligt genomgången ovan och såvitt korrekt naturgrundad, också uppvisa delvis andra sönderfallstider relativt de som gäller för Jordkroppens besättningar.

— Notera dock (noga) att inga som helst avgörande argument ännu finns för att avgöra någonting i frågan om speciellt meteoriterna och deras ursprung: ämnet i det avseendet uppvisar (ännu) föga mer än ren (kaotisk) spekulation, trevande utkast, och på sin höjd spännande teorier. Se även nedan i Meteoritfrågan.

— Notera att differenserna som krävs är (ytterst) marginella för att i slutänden uppvisa mer eller mindre dramatiska skillnader i halveringstider. Se Beräkningsexemplet för Uran-238.

— ENDA ANLEDNINGEN till intresset i denna presentation för dessa b-koefficientens möjligheter är det (mycket) starka argumentet i ämnet Jordens ålder som ges av Månens recession: den enda mekaniska urklocka vi känner. Räknas den baklänges, stämmer den så nära perfekt man alls kan önska med TNED-teorin för Solsystemets bildning. Med den nutida forskningens TEORETISKA FÖRUTSÄTTNINGAR i användning av Meteoriterna för dateringen [Meteoriternas ursprung], ges dock bara (grovt räknat) utrymme för Månen att stanna på halva nuvarande avståndet Jorden-Månen i baklängesräkningen.

— Notera också: Det finns ingen som helst anledning att betvivla de många samstämmiga, etablerade mätningar som gjorts [fram tills nu Dec2011] för räkningen på Jordens ålder och på bas av materialkännedomen med Jordkroppen som grund, allmänt ca 4,5 T9 [miljarder] år [Jordens ålder enligt MAC].

— Den uppgiften gäller speciellt med referens till användningen av olika meteoritmaterial.

— Det intressanta med dessa mätningar ÄR just deras (överväldigande) samstämmighet. Kan man inte påvisa ATT radioaktiviteten i ämnena SKILJER sig mellan olika rymdavsnitt, eller mellan olika uppehållsorter, vilket är vad TNED-teorin antyder som ovan i himlakroppar och mellan dessa — har NÄMLIGEN också TNED-teorin spelat ut sin roll, helt, och har ingen som helst substans. Inte här. Inte någonstans.

Meteoritfrågan

— Frågan om Jordens ålder med hjälp av data från meteoriterna kan därmed, enligt TNED, helt och hållet återföras på (den ännu generellt obesvarade) frågan om giltigheten för halveringstidssambandet med avseende på nuklider från olika bildningslokaler (Jenkinsgruppen Jun2011).

— Eftersom meteoritdateringen i vilket fall enbart tycks baseras på en allmän uppgift om en viss radioaktiv nuklids halveringstid

[Se Allmänt om åldersbestämning via meteoriter på webben] med referens till Jordlokalens nuklidbanker (man tycks inte mäta radioaktiviteten explicit hos meteoriter i samband med meteoritens åldersbestämning, uppgifter på den detaljen har eftersökts men inte påträffats),

kan hela sakfrågan heller (här veterligt) inte avgöras på någon annan detalj än just halveringstiden. Se Beräkningsexemplet för Uran-238, vilket ger en viss bild av de svårigheter man har att brottas med om uppgiften gäller att genomföra en mera precisionsbaserad mätning speciellt på Uran 238 — för att därmed kunna avgöra frågan.

Halveringstidssambandet

Impulsbegreppet (p=mv)

— generellt i TNED med avseende på atomkärnans tyngdcirkelradie [r i Planckringen h=mcr] — tillsammans med en allmän sönderfallskraft (F=ma) och ett allmänt begrepp halveringstid av mera elementär natur —

leder i Härledningen till den relaterade fysikens samband för halveringstiden [Se Slutformen]

(ln2)/t_H = Ae^–B/p halveringsTIDssambandet

med enhetskoefficienten A=1/1S. Med rörelsemängdens ekvivalent p²=m²v²=2mE via rörelseenergin Ekin=mv²/2 ges det likvärdiga sambandet för halveringstiden i TNED enligt

t_H = 1S(ln2)e^be^Z/√2mE halveringsTIDssambandet

med b-termen som den avgörande nuklidkoefficienten [b=4πÑ], nyligen omnämnd ovan (Kopplingen till radiofysiken).

— Sambandsformen är (exakt) densamma som anges i etablerad litteratur i formen Geiger-Nuttalls samband — den ursprungligen empiriska sambandsform (från 1911) som kunde förklara de experimentella resultaten, här explicit förtydligat på förekommande citerad form

λ = Ae^–B/√E, enligt Citat, med lambda λ (eng. decay constant, sv. sönderfallskonstanten) lika med ln2/tH.

— Men det som påstås i etablerad litteratur vara ”The Theoretical version of the Geiger-Nuttall law” visar sig i själva verket vara resultatet av en APPROXIMATION, ”as a good approximation”, [Se citatdelar i Allmänna Koefficientformen] vars rent matematiska grund härrör från en ”rewriting”, ”Rewriting √b = ...”, av ett kvantmekaniskt — statistiskt — resonemang [från George Gamow 1928] — således helt utan varje form av beröring med TNED, sambandet ovan.

;

— Utan att (nu) säga mera i den saken:

DET påminner om exemplet med de experimentella mätningarna av Ljushastigheten i strömmande vatten (Fizeaus experiment): experimentellt (Fresnels ekvation, 1818) samma resultat som enligt härledningen baserad på relaterad fysik — och »samma som Einsteins matematik» OM denna APPROXIMERAS (man utelämnar vissa detaljer för att åstadkomma vissa förenklingar). Utdraget nedan från slutet i TNED-beskrivningen av Fizeaus experiment:

Den relativistiska delen i saken visar således snarare, eller möjligen »mera», ett laborativt (algebraiskt uteslutande) sammanträffande på föregivna uttryck: relativitetsteorin har, egentligen, inte mycket att göra med experimentet av Fizeau.

— TNED har ingen som helst samhörighet med kärnfysikbaserad statistisk kvantmekanik.

— I TNED finns inte den avdelade kärnformen till FÖRE avdelandet, på precis alldeles samma sätt som att den avdelade vattendroppen ur modervolymen heller inte existerar som en fristående form inuti modervolymen, och som, enligt MAC-teorins kärnfysikgrundade statistiska kvantmekanik, söker rymma ur modervolymen. Det finns ingenting sådant i TNED. Skippar man approximationerna och håller sig till den relaterbara fysiken, är det alltså, tydligen, TNED som gäller.

— Atomkärnan är enligt TNED en massans fundamentalform [Se även i PASTOM], helt utan beståndsdelar, och som likt enheten (3) kan uttryckas ekvivalent på delsummorna 3=1+1+1, med vidare.

— TNED-teorin för halveringssambandet innehåller inga approximationer, och heller ingen sannolikhet, och heller ingen statistisk matematik överhuvudtaget.

— Se även till jämförelse särskilda citatdelar i Allmänna Koefficientformen där direkt jämförelse görs mellan MAC och TNED i anledning av sambandet för halveringstiden (tH) och frågan om det sambandets rent matematiskt härledande grunder.

Resultat i Jämförelse TeoriPraktik TNED/MAC

Ytterst nedslående för MAC.

— Strävan att — på bas av allmänt tillgänga webbkällor, och endast sådana så att läsaren själv ges en chans att avgöra — få fram precisa jämförande resultat med referens till MAC-teorin för radiofysikens matematik, har här uppvisat ett »virrvarr av uppgifter» (icke preciserade referenser) och data med en gemensam nämnare: avsaknad av precision [‡]. Precisionen i de MAC-presenterade exempel som här framkommit ligger (fortfarande) så långt ifrån de praktiskt, experimentellt uppmätta halveringstiderna, att varje precis användning av teorins värden självutesluts.

— I TNED bestämmer, som omnämndes ovan, neutronkvoten en »modul» för den radioaktiva individens halveringstid. Genom att varje nuklid kan bildas på flera olika sätt via olika netronkvoter, finns därmed (möjligen, vilket vi inte riktigt vet här än) också något olika betingelser för nuklidens halveringstid (också tillsammans med bildningslokalens primära neutrinoenergigenomströmning).

— I TNED betyder det i slutänden en FRAGMENTERING (Se Fragmenteringsargumentet); nukliderna blandas under förhistorien, mellan och inuti i himlakropparna med ådersystem av särskilda mineralstrukturer, och sedan vet ingen varifrån en viss atomindivid, i den nuklidtypen, kom ifrån. Med andra ord: Det blir enligt TNED också omöjligt att EXAKT bestämma någon halveringstid, eftersom nuklidkoefficienten (b i halveringstidssambandet) är praktiskt omöjlig att spåra och därför bara kan ge ett medelvärde — en grov orientering — för den aktuella nuklidgruppen NU.

— I andra ord: Enligt TNED existerar ingen exakt bestämbar halveringstid för någon enda radioaktiv nuklid; Värdena är fragmenterade på PRIMÄRA ursprungslokaler, som sedan länge gått förlorade och som, nu, bara syns som fragmenterade stråk. Jämför AlfaRadioIsotopKartan;

Del av Alfaradioisotopkartan i TNED.

tH-universalen är den allmänna »trendkurvan» i TNED som möjliggör ovanstående kurvsamlingstyper. tH-universalen bygger på nuklidkoefficientens optimala maxvärde, som i sig bygger på TNED-teorins förankring i POTENTIALBARRÄREN med ENERGIZONEN från LJUSETS G-BEROENDE och som grundlägger ATOMKÄRNANS HÄRLEDNING. Se särskild beskrivning i Vad utmärker TNED framför MAC i sönderfallsfysiken?, samt Kopplingen till radiofysiken ovan.

— Dessa kurvbilder är alltså omöjliga i modern akademisk litteratur, teori och beskrivning: tH-universalen är garanterat UNIK för TNED.

Den enda precisa uppgift som finns att få, måste därför enligt TNED baseras helt på experimentell uppmätning.

Betanuklidernas kaos i MAC

— Men också halveringstidsvärdena själva [tH] är — speciellt i betanuklidernas fall — föremål för »vissa bryderier», se särskilt från Nuklidkoefficienten i kombinerade sönderfallstyper. Ett sammanställt punktvärdeexempel på 29Cu64 finns illustrerat som översiktlig referens till vad (det sorgefulla) ämnet handlar om:

— Uppgifterna från modern akademi, i samtidig koll på grunderna, är här så kaotiska, ospecificerade och ofullständigt beskrivna, att (ännu Dec2011) ingen direkt praktiskt jämförande referens finns. Inte alls överhuvudtaget.

— Halveringstidsbegreppet i modern akademi för de kombinerade betasönderfallsnukliderna verkar i stort vara ett enda omfattande kaos av institutionella godtycken, utan någon som helst refererande, klargörande litteratur.

— I De Tre MedelvärdesSummeringssätten visas grunden till uppmärksammandet:

— Många betanuklider uppvisar sammansatta sönderfallstyper: ofta förekommer t.ex. BetaEC OCH BetaPlus. Men man kan inte, direkt, mäta fördelningen i (ev.) skilda halveringstider mellan dessa på annat sätt än att mäta de sönderfallande nuklidernas procentuella andelar (med olika metoder). Följaktligen kommer »partiella halveringstiderna» att bli resultat av motsvarande teoretiska beräkningar.

Motsättningen i tH för Betafallen

Relaterad fysik (TNED) kräver att varje radioaktiv atom sönderfaller, i huvudsak, efter SIN EGEN förutsättning i enlighet med Sönderfallets enhetliga preferensgrund — EN bestämd halveringstid (tH) för EN bestämd sönderfallsenergi (E) för EN bestämd radioaktiv nuklid (b) — I HUVUDSAK oberoende av hur de andra individerna sönderfaller. Det betyder i motsvarande summerande (partiella) halveringstider också en OBEROENDE summering via tH.

— I MAC däremot — eftersom ingen nuklidkoefficient (b) [som i TNED baseras på neutronkvoter från primärbildningen och därmed möjlig variabel för halveringstiderna] finns med i tH-sambandet, utan att detta istället bygger på en statistisk matematik — kan man inte anta den oberoende summeringsalgoritmen (oberoende tH via beroende b) då man i så fall förlorar grundteorin (b=4πÑ finns inte i MAC). Man använder i MAC istället en typ INVERTERAD summering. Nämligen [Se Möjliga förklaringar till MAC-valet] genom viktigheten att definiera halveringstiden (tH) på sönderfallskonstanten (λ) enligt tH=ln2/λ, och inte tvärtom som i TNED, λ=ln2/tH: utgångsfaktorn i TNED är tH [Se Härledningen, –dp/dF=t_H] — inte λ. Beroende på den prioriteten kan man också prioritera olika INRE medelsummeringssätt. Se utförligt från De Tre MedelvärdesSummeringssätten, eller mera detaljerat i detta htm-dokument från Halveringstidens Oberoende Summeringsalgoritm.

— De olika sätten ger olika INRE (partiella) summeringsresultat.

— Medan inre ResultatHalveringstiderna enligt MAC drar iväg våldsamt från preparatets uppmätta medelvärde [Se jämförande punktvärdesdiagram i 29Cu64-exemplet illustrerat], håller de sig mera samlade enligt TNED-teorin. Eftersom, heller, ingen direkt experimentell metod verkar finnas som kan avgöra vad som gäller i praktiken, se Citat, är det (här, Dec2011) omöjligt att komma vidare i beskrivningen:

— Betasönderfallens mera precisa halveringstider saknar f.n. tillförlitligt beskrivbara grunder.

Se mera ingående från HyperPhysicsCitatet, Möjliga förklaringen till MAC-valet, Varför Lambdasummeringen är OK, TNED-tH-summeringen, Halveringstidens Oberoende Summeringsalgoritm, Fragmenteringsargumentet.

MAC-precisionen, allmänt

——————————‡

Exemplet Santoso 2000

— Källan anger en kurvform som genomskär ett väl utspritt punktfält med Uranisotopernas alfaenergier som ”fits relatively well”;

— Exakt VAD källan menar med ”fits relatively well” i ljuset av den relativt stora punktmängden — här illustrerad — framgår inte;

— Som läsaren själv kan se, finns tydligen stort utrymme för GODTYCKLIGA KURVPASSNINGAR i det väl utspridda punktfältet.

;

Ogunbade-Rakityansky 2007

— Författarna exemplifierar tre olika MAC-metoder för teoretisk bestämning av halveringstiden;

— Det mest framträdande är den generella bristen på precision — även med citatkällans mera avancerade tre metodexempel; endast tre träffar heltäckande av 16 möjliga [Se Avvikelsediagram], och då är ändå inte precisionen i dessa av typen direkt användbar för naturvetenskapliga syften.

;

LabSpace-exemplet

— Källan exemplifierar: Konsten att välja ut 4 av 66, inte berätta varken OM det för läsaren eller HUR urvalet skedde, samt benämna resultatet ”a detailed comparison with experimental data”.

;

Se även ytterligare webbexempel till jämförelse i Särskilda Exempelutdrag.

——————————‡

Allmänna sammanhang

FÖLJANDE ALLMÄNNA SAMMANHANG FRAMGÅR MED REFERENS TILL

och är vad som kan utläsas genom

TNED

Inledning

1. Begreppet HALVERINGSTID i radioaktiva sönderfall uppfattas traditionellt under 1900-talet som en oföränderlig KONSTANT, se CITATBLOCKET — samt den kort sammanfattande vetenskapshistorien av hela sakämnet i PDF-dokumentet [i Introduction] Jenkinsgruppen Jun2011, här inte direkt citerat ”The widely held view ...”.

2. »INVEKTIVEN» från TNED kräver att neutrinoinfluenserna spelar en avgörande roll för radionuklidernas sönderfall, se från Sönderfallet uppvisar influens och Kriterium för instabilitet; Jordens ålder med Månens Recession ställer också upp visst ifrågasättande av halveringstiderna [men som ingalunda är någon enkel sak att avgöra; inget avgörande klarläggande finns ännu Dec2011].

3. INCITAMENT för invektiven verifieras delvis från Jenkinsgruppen — utan att fördenskull frågan [ännu] är avgjord.

4. DÄRMED framställningen i dess helhet: allmän genomgång av radiofysikens matematik och teori.

5. En ytterst noggrann PREFERENSGRUND för begreppet massa måste ges/finnas — speciellt enligt TNED — eftersom massbegreppet i atom- och kärnfysiken också inbegriper en kvantitativ ekvivalens mellan massa-energi: atomens massENERGI och atomens ekvivalenta divergensenergi har INTE samma gravitella preferenser i TNED. Denna detalj blir avgörande viktig för hela framställningens kredibilitet [SEKTION 2].

6. ANLEDNINGEN till den moderna akademins hållning enligt ”is a constant under all conditions” är FÖRMODLIGEN uppmätningen enligt ALFAENERGIERNA — i förening med den — enligt TNED — moderna akademins YTLIGA FYSIKUPPFATTNING GENERELLT — speciellt på nivån KÄRNFYSIK [Atomkärnans härledning] [Planckringen] [Planckekvivalenterna]:

— STYRKAN i alfapartikelns [Heliumkärnans] utkastning från radionukliden är ALLTID direkt proportionell mot nuklidens sönderfallstid [halveringstiden]. Det är så också i TNED, med tillhörande relaterad beskrivning. Men till skillnad från atomkärnan i modern akademi, är atomkärnan i TNED en STRUKTURKOMPONENT med grund i NEUTRINOSPEKTRUM [också utan representation i modern akademi]:

— TILLFÄLLET när nukliden sönderfaller beror NÄMLIGEN och SÅLEDES TVUNGET [i hög grad] på närvaro av neutrinoagenter. TNED-sambanden utnyttjar den detaljen för att kunna ställa upp en matematisk form för sönderfallet [Se särskilt i SEKTION 5].

— HELA den radioaktiva analogin kan [således] återföras på olika lokaler med TYP människor [i bibliotek, samlingssalar o dyl] som befolkas eller töms enligt olika kriterier och via »ömsesidig neutrinoinfluens». Tydligt. Se speciellt från Influensen.

— Högre influens [stor folksamling] innebär snabbare sönderfall och kortare nuklidlivstid, lägre influens [glesbygd] innebär längre livstid.

— Men omvändningen kan också gälla via motsvarande hämfaktor [Sönderfallstillfället] [Allmän reglering av sönderfallet]:

— Högre influens [stor folksamling] innebär ett saktare sönderfall och längre nuklidlivstid, lägre influens [glesbygd] innebär kortare livstid.

— Exakt inblick i hur det fungerar finns inte här. Framställningen ska förhoppningsvis bidra till en viss uppstädning, för vidare.

· Uppfattningen (från runt 1913) att det radioaktiva sönderfallet inte påverkas av något

”The rate of transformation of an element has been found to be a constant under all conditions”,

Ernest Rutherford RADIOACTIVE SUBSTANCES AND THEIR RADIATIONS — Cambridge/New York 1913, Från [2011-10-13]

Book digitized by Google from the library of the University of Michigan and uploaded to the Internet Archive by user tpb.

http://books.google.com/books?id=UeEdAAAAMAAJ&oe=UTF-8

gäller bevisligen korrekt endast med avseende på dåvarande, och nuvarande, begränsade Jordlokal;

· Neutrinobegreppet som ett fenomen av högfrekvent em(elektromagnetisk)-strålning (m→γ) utanför elektronmassornas resonansområden ingår inte i modern akademi och sönderfallets mekanik kan därför heller inte ses eller förstås betingas av, och ändras med, just neutrinoaktivitet; Det finns ingen teori — ingen förutsättning, inte alls överhuvudtaget — för något sådant i modern akademi;

· Tydliga indikationer på just det (Jenkins et al., 2006), att sönderfallshastigheten ÄNDRAS (marginellt, grovt max 0,1%) med neutrinoirradiansen från Solen, endast styrker neutrinofenomenets beskrivning och härledning enligt TNED: Neutrinos är i TNED em-strålning (m→γ) från massförintelse i atomkärnan i samband med olika övergångar som innefattar kärnombyggnad (Se särskilt från NEUTRONSÖNDERFALLET), ingen massform. Se särskilt TNED-teorin på denna punkt i Neutrinostrålningen från Solen; Det finns (således, och enligt nuvarande författning) ingenting DIREKT som utesluter TNED i kraft av redovisade observationer och data;

· En djupdykning i »sönderfallets konstans» avslöjar (emellertid) »vissa mekanismer» som i sig visar, eller snarare starkt ANTYDER, att sönderfallets matematik bara, och just, KAN avse en specifik lokal med en specifik neutrinobank (i vårt fall hela Jordklotet med främst förekomsten av Uran-238 och Thorium-232 — övriga är så ringa representerade att deras ömsesidiga inverkan [här] kan bortses ifrån) — se kort sammanfattning i Neutronkvotens avgörande inverkan;

· Med föreställningen att sönderfallsstyrkan (alfapartiklarnas energier) i den enskilda radionukliden är oberoende, men tillfället för nuklidens kärndelning beroende av neutrinoinfluensen från omgivande radiobank, frammanas uppfattningen att de fastställda värden på radionuklidernas halveringstider som erhålls från Jordytsmätningar INTE gäller kosmologiskt absolut utan ENDAST lokalt. Se även i Beräkningsexemplet Uran-238.

——————————‡

ALL ABOUT METEORITES — Origins of Meteorites, 1998-2011

http://www.meteorite.fr/en/basics/origins.htm

——————————‡

WIKIPEDIA — Age of the Earth [2011-12-27]

http://en.wikipedia.org/wiki/Age_of_the_Earth

”The age of the Earth is 4.54 billion years (4.54 × 10⁹ years ± 1%).[1][2][3] This age is based on evidence from radiometric age dating of meteorite material and is consistent with the ages of the oldest-known terrestrial and lunar samples.”.

——————————‡

Generellt om åldersbestämning via meteoriter på Webben:

»Meteorite Dating», »Methods in Meteorite Dating» [2011-12-26]:

— Inte i något beskrivet fall av de påträffade webbkällorna, inte ens en antydan, tycks man mäta radioaktiviteten från meteoriter:

— Som de följande citaten påpekar: Man mäter endast ämneshalter och beräknar sedan TIDEN via Jordbaserade uppmätta halveringstider (tH) för de aktuella ämnena enligt den helt enkla formen t = tH(mätdata).

— En metod att ta reda på vilka ämnen en meteorit innehåller är spektrografisk:

— Man tar ut en liten del av meteoritmaterialet, utsätter det för stark upphettning (förångning, jonisation) och låter sedan de så joniserade atomerna passera en masspektrometer (atomerna accelereras, passerar magnetfält, böjs av olika för olika atommassor, räknas via datoriserad sensor) för bestämning av de olika halterna.

;

TERRESTRIAL AGES OF METEORITES [2005]

http://www.lpi.usra.edu/books/MESSII/9011.pdf

”In accelerator mass spectrometry (AMS), the atoms of

the radionuclide of interest are counted directly using mass

spectrometry combined with nuclear accelerator techniques”, s892sp2m

;

METHODS OF DATING THE AGE OF METEORITES, Sep1998

http://www.meteoritestudies.com/protected_dating.htm

;

”The term in parenthesis, the amount of ⁸⁷Rb that decayed into ⁸⁷Sr can be related by the radioactive decay law:

⁸⁷Rb_original = ⁸⁷Rb_now * (e^lt)

where, e is the base of the natural logarithm, l is the rate of radioactive decay, and t is the elapsed time.”,

;

”Two of these quantities can be measured: ⁸⁷Sr_now/⁸⁶Sr and ⁸⁷Rb_now/⁸⁶Sr. By taking samples from various parts of a meteorite and plotting these results, the data will fall on a straight line whose slope characterizes the age of the meteorite.”,

;

”How are these Measured?

Scientists use a mass spectrometer to obtain these ratios. A small portion of a meteorite is vaporized in the device forming ions. These ions are accelerated in an electric field through collimating slits and subject to a magnetic field which causes the ions to follow a curved path. The ions are deflected accoreding to their mass. By adjustment of the strength of the magnetic field and suitable placemnet of an ion collector, the different isotopes can be measured with precision.”,

Webbkällan kan inte direktkopieras, ovanstående i manuell avskrift [2011-12-30]

;

RADIOMETRIC DATING, 1994/2002

http://weber.ucsd.edu/~jmoore/courses/anth42web/WiensDatingMeth02.pdf

;

”First one needs to measure the number of daughter

atoms and the number of remaining parent atoms and calculate the ratio between them. Then the half-life

is used to calculate the time it took to produce that ratio of parent atoms to daughter atoms.”, s4mn,

;

”t = h x ln[1 + (argon-40)/(0.112 x (potassium-40))]/ln(2)”, s4n

; t = tH(mätdata) ;

”When scientists began systematically dating meteorites

they learned a very interesting thing: nearly all of the

meteorites had practically identical ages, at 4.56 billion

years.”, s10sp1m,

;

”Evidence from the uranium, thorium, and lead

isotopes links the Earth's age with that of the meteorites.

This would make the Earth 4.5-4.6 billion years old.”, s10sp1n

;

OSPECIFICERAD WEBBKÄLLA

http://ull.chemistry.uakron.edu/radioanalytical/12_Nuclear_Dating.pdf

;

”All dating methods rely on: N₁ = N₀ e^–λ(t0^{– t}1⁾”, första bildsidan

tHmacTNED — källformerna till halveringstiden — HALVERINGSTIDEN, källformerna

Källformerna med λ = [ln 2]/tH, tH halveringstiden och E(α) alfapartikelns energi — allmänna halveringstidssambandet via kärnsönderfallets alfaenergier

Sambanden i MAC visade sig vid en översiktlig genomgång vara [sedvanligt] »flummigt» presenterade: Sambandsformens exponent lämnar en del övrigt att önska i den allmänna presentationen — OM önskemålet är att kunna uppvisa numerisk enhetsform. Genom denna observation, med vidare analys, visade sig en möjlig härledning enligt TNED — med vidare uppmärksammade, jämförande, korsreferenser.

Ursprung: Geiger-Nuttalls empiriska formel från ca 1911:

Med alfaradiosönderfallen som exempelreferens: B-faktorn i MAC innefattar, nedan vänster, ett Z-beroende [atomnummer] som hänförs till den sönderfallande radionukliden. I TNED är den Z-beroende faktorn relaterad till alfapartikeln [partikeln generellt som avdelas]; sönderfallsnuklidens Z är i TNED egal [beroende på den avdelande kraftens ±A909e som i vilket fall gör modernuklidens verkliga kärnladdning Z helt försumbar, se utförligt från Härledningen]. Således stora teoretiska skillnader;

Modern akademi (MAC) — radioaktiva sönderfallets matematik:

Relaterad fysik (TNED) — radioaktiva sönderfallets matematik:

λ = Ae^x

x =–B/√E_α

λ = Ae^x

x =–bQ_α/p_α

p_α = √2m_αE_α

”A is a constant that characterises the particular family of nuclei, and
B depends on the charge of the individual nucleus”, [ref.‡]

A = 1/1S, B = bQ = beZ = 4πÑeZ

TNED: Ingen aspekt för A-koefficienten läggs här på »olika nuklidfamiljer». Analysen i denna presentation är helt tillägnad den centrala sambandsformen med A som frekvensenhet [1/1S].

— Optimalt betyder A-faktorn en högre eller lägre amplitud hos tH-värdet, samt om en tilläggsterm [B] finns [λ=Ae+B] värdena ligger förskjutna i vertikalled.

— I TNED ges λ-FORMEN (λ, grek. lambda) för samtliga kärnrelaterade sönderfall enligt inverterade halveringstidssambandet (λ=ln2/tH): Men halveringstiden (tH, konv. ofta T½) kan, enligt TNED, inte bestämmas ur λ‑sambandet; tH i någon naturvetenskapligt användbar mening kan, enligt TNED, bara uppmätas experimentellt, och då istället användas i λ-sambandet för att bestämma den nuklidkoefficient (Ñ) som ingår i b-faktorn;

— TNED-teorin som helhet går ut på att det inte går att bestämma några exakta tH-värden alls, inte alls överhuvudtaget, just på grund av b-faktorn; b-faktorn sammanhänger enligt TNED med de radioaktiva nukliderna i deras primära grundämnesbildning med hänsyn till olika bildningslokaler, och därmed olika energigenomströmningsfaktorer som bakades in i nukliderna vid bildningstillfället — se utförlig beskrivning i INLEDNINGEN med Radiofysikens grunder, om ej redan bekant — och som genom (den förhistorisk) blandningen av nukliderna, i och mellan himlakropparna, medfört b-FRAGMENTERING; Vi kan se SPÅREN efter möjliga »exakta värden» — jämför AlfaRadioIsotopkartan — men de ligger kringspridda och ojämnt fördelade via b-värden som är praktiskt omöjliga att spåra i någon exakt mening; Ingen exakt tH-bestämning kan göras, därför att i princip varje nuklid har ett eget b-värde, om än marginellt skilt från sin egen nuklidgrupps medelvärde. Presentationen i detta dokument är tillägnad att beskriva, och förhoppningsvis i varje fall FÖRSÖKA förklara, den dramatiken.

— I MAC anses däremot λ-FORMEN också vara en direkt beräkningsbar sambandsform för halveringstiden (tH) — men då 1. med vissa tillägg och svårigheter som skiljer mellan olika sönderfallsklasser [olika matematik för Alfa och Beta], samt 2. uppenbara problem att få ihop det med PRECISIONEN i bägge [Se Resultat i Jämförelse TeoriPraktik TNED/MAC]; Ingen »nuklidfaktor» (Ñ) är känd i MAC..

— I moderna akademi (här förk. MAC) menar man att (lambda) λ-formen — samma som (det inverterade) sambandet för det radioaktiva sönderfallets halveringstid (här tH) också konventionellt benämnt som Geiger-Nuttalls samband — är direkt teoretiskt beräkningsbar med (enbart) kännedom om kärnfysikaliska parametrar.

s1662, INORGANIC CHEMISTRY, Wiberg et al., 2001 — GoogleBooks

Några exempel, för mera noggrann jämförelse, som kan hittas på webben studeras mera ingående och detaljerat i Mac-precisionen allmänt.

— I relaterad fysik (TNED) vet vi, strängt taget, inte det — än. Se Vissa observationer nedan.

— För att pröva ståndpunkten i TNED måste b-koefficienten beräknas ur experimentella uppgifter från känd energi (E) och halveringstid (tH) — som möjligen (och troligen enligt TNED) har en variabel naturbas beroende på i vilken lokal mätningarna görs (preferensen i TNED är stora områden, typ himlakroppar och mellan dessa, och därmed i koppling till energimiljön i större skala där nukliderna en gång bildades; För Jordlaboratoriska experiment [artificiella radionuklider] blir analysen i motsvarande grad mera besvärlig. Se en utförlig allmän genomgång i Inledningen).

Vissa observationer från 2006 [Jenkins et al.] indikerar en periodiskt återkommande årlig variation (”by the order of 0,1%”) i halveringstider för vissa radioaktiva nuklider [Kisel-32, betaaktiv] — vilket i TNED bara kan förklaras av neutrinopåverkan från Solen (Se Solirradiansens årliga variation); den årliga maximala differensen på Jordsnittskivan i Solirradians är ca 0,06%.

Månens recession

Framställningen nedan kopplar inte Månens recession fullständigt, men ger en kompletterande bakgrund. Det som fattas är senare upphittade — avgörande — uppgifter som fullständigar helhetsbilden.

— Se fullständigt beskrivning i MÅNENS RECESSION (Jul2017).

— Ytterligare en indikation finns, som MÖJLIGEN också understryker att uppmätta halveringstider på Jorden just också ÄR uppmätta halveringstider med Jordlokalens nuklidstam som bas — och inget annat. Nämligen:

Månens recession (Okt2011):

Se även originalbeskrivningen Mar2009 Månens recession

”Lunar laser ranging establishes the current rate of retreat of the moon from Earth at 3.82±0.07 cm/year (Dickey et al., 1994).”,

THE RECESSION OF THE MOON AND THE AGE OF THE EARTH-MOON SYSTEM, Tim Thompson, 2000

http://www.talkorigins.org/faqs/moonrec.html

Enligt TNED bildas Solsystemet via divergenständning [miniatyrer av K-cellens primära detonation] med koppling till masskroppar som avdelas från en större moderkropp — på alldeles samma sätt som vattendroppar bildas i rekylverkan från en enda droppe som träffar en lugn vattenyta. Sambanden kan beskrivas genom resonansserier, och det visar sig att den traditionellt benämnda s.k. Titius talserie är en sådan.

— Men det betyder också att — TYP — Månen från början [om inte direkt, så mycket nära] hade kontakt med Jordkroppen:

— OM det är korrekt [Från start följer Månen, belägen strax utanför Jordytan, med i Jordrotationen kring Solen] BORDE Månens banhastighet, om vi räknar baklänges från nuvarande konstant impulsmoment

J[Månen]=mvr=[7,35E T22 KG][2(pi)·(r=3,84E T8 M)]·r/[27,3216608796·86400 S] = 2,89E T34 JS, hamna på i stort sett nuvarande Jordkroppens banhastighet kring Solen [ca 30 KM/S].

— Det gör den också. På ca 2 Jordradiers avstånd blir Månens banhastighet runt Jorden v=30,84 KM/S.

— Bara den värdeformen är en mycket — läs MYCKET (extremt) — stark indikation som stödjer hela planetbildningsteorin enligt TNED [Jordens Tredje Ekvation] [PLANETROTATIONERNAS UPPHOV]. Ytterligare en detalj understryker den delen:

— Månens recession [nu 3,82 cM per år]. Vi studerar hur.

[Principen bakom Månrecessionen beskrivs i särskild artikel i Månens Recession. Vi förutsätter här full bekantskap].

[[Tabell6KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]]

Månens recession från början i TNED: Det är rimligt att utgå ifrån att Månkroppens allra första omloppshastighet kring Jordkroppen är av samma storleksordning [30 KM/S] som nuvarande Jordkroppens banhastighet kring Solen — eftersom i vilket fall resonansserien av bildade J-kroppar kommer att ha sina banvridande moment kringSolkroppens tyngdpunkt [Se utförligt i SOLSYSTEMETS BILDNING och Planetrotationernas upphov]; Antas den utgångspunkten, börjar Månkroppens rotation kring Jordkroppen — i samband med hela den primära strängen av planetkroppar som avdelas tillsammans med Solkroppen i den aktuella resonansserien — vid ca 2 Jordradiers avstånd från Jordcentrum, och med ideala banhastigheten 30,84 KM/S. I det skedet är kropparna helt säkert plastiska, och vidare [inom den närmaste tiden i samband med primärfusionsfasen] också flytande [glödande], vilket kan initiera en snabb introducerande recessionsfas Jorden-Månen tills kropparna antar en mera stel konsistens [inom säg 100 miljoner år]. I den mera stelnade situationen är recessionsfenomenet noll [Månen då på säg 5-10 Jordradiers avstånd, 6 KM/S, se illustrationen ovan]; Vartefter Jordkroppen svalnar och börjar släppa ifrån sig sin mineralt syrebundna del till den omgivande väteatmosfären [som blir allt tunnare med tiden som Jordkroppen sväller ut alltmera, se J-kropparnas expansion, och ytgravitationen inte orkar hålla den lättare vätgasen kvar], bildas ytvatten på Jordytan. Därmed börjar Månrecessionen igen, men nu i mycket långsam takt på grund av den ringa mängden Jordytvatten till att börja med; Vartefter Jordytvattnet tilltar, ökar också Månrecessionen, som sedan blir fullt utvecklad med [de nuvarande] oceanernas utbredning. Med TNED-teorin, som förlägger Jorden-Månen-Solsystemet 20,8 miljarder år bakåt enligt TNED, se Solsystemets ålder, kan Månen, kanske från ca 10 miljarder år bakåt, utföra sin recession tidsenligt, enligt skalorna ovan; Det krävs ca 10 miljarder år för Månen att nå sin nuvarande position om recessionen är konstant [vilket den garanterat inte är]. I praktiken torde recessionen [kanske] ha pågått under ca 15-18 miljarder år: ytterst långsamt i början och sedan successivt snabbare med ökad mängd Jordytvatten.

— Den senaste bergscykelns ålder ligger runt 3-4 miljarder år [kanske ända upp till 5 T9 år]: före den tiden finns inga säkra spår på Jorden idag som kan upplysa om EVENTUELLT föregående bergcyklers tillstånd och sammansättningar. Alla dessa spår är effektivt igensopade genom inre blandning och konvektion i Jordens [räknat bakåt i tiden allt hetare] inre.

— Konventionellt utgår man emellertid ifrån att Jorden bara haft EN bergartscykel — men TNED kräver flera sådana cykler [kanske ända upp till 5 st; 3×5=15 miljarder år — för att bygga upp bergryggarna till kontinentalplatåerna under den primära avsvalningsprocessen].

— Värdena till illustrationen har beräknats efter nuvarande impulsmoment J=mvr för Månen som konstant under hela perioden.

BeräkningsEXEMPEL — Uran238

Se även exempelräkningen i Dramatisk känslighet:

— b-koefficienten för Uran-238 med halveringstiden 4,51 T9 år [äldre uppgift från VNS 1976, eller som nedan, vilket spelar mindre roll i detta sammanhang] och alfaenergin 4,267 MeV [ref. Wikipedia Uranium-238, Alpha decay] är b=11,8592681 [Se b från Slutformen i Källexempel]

b = [√2mE_α]ln[t_H/1S(ln2)]/eZ ; u=1,66033 t27 KG; e=1,602 t19 C

= [√2(4,0026031u)(4,267·e·T6)]ln[(4,51 T9 · 3600·24·365,25 S)/1S(ln2)]/e(2)

= 11,8592681

För att påverka halveringstiden med 0,1% [0,001], samma storleksordning som Solirradiansens årliga variation på Jordklotets tvärsnittscirkelyta, krävs b=11,8595655 som ökar halveringstiden till 4,51451 T9 år;

4,51451/4,51 = 1,001.

— För att — på motsvarande sätt — fördubbla halveringstiden för Uran-238 till 9 T9 år krävs blygsamma endast b=12,0654776, en ökning med blott 0,206209 eller 1,7388%.

— Variationerna i b-värdena generellt följer variationerna i tH-värdena för alfaradionukliderna. Enligt Wileytabellen 1999 [sönderfallsenergierna beräknade separat efter atomvikternas massa-energidifferenser] ligger dessa mellan -9,65 och 12,64.

Jämför Chisté-referenskällan nedan som (på första sidan) visar tabell med osäkerheter i uppmätningen av halveringstiden för Uran-238, här anges endast tabellens rekommenderade värde [från 2004]:

4,468 (5) T9 år

[T för 10^+] — Osäkerheten i tredje decimalen

Siffran inom parentesen refererar till ±-osäkerheten för sist angivna siffra/siffror i det angivna värdet. Se Use of consice notation

NIST REFERENCE ON CONSTANTS, UNITS AND UNCERTAINTY — Fundamental Physical Constants [2011-12-26]

http://physics.nist.gov/cgi-bin/cuu/Info/Constants/definitions.html

238U-COMMENTS ON EVALUATION OF DECAY DATA, V. Chisté, M.M. Bé, Jan2006

http://www.nucleide.org/DDEP_WG/Nuclides/U-238_com.pdf

— Osäkerheten ±([4,468+0,005]/4,468 =1,001119) TÄCKER, tydligen gott och väl, beräkningsexemplet för Solvariationen [MAX 0,1%].

— OM den räkningen håller streck betyder det att det krävs mera avancerad teknik för att få fram mera exakta halveringstidsvärden för Uran-238 — för att i ämnet U-238 SÄKERT kunna UTESLUTA inverkan från Solens neutrinostrålning [MAX ±0,06%, Se Variationer i Solirradiansen].

— INTE förrän ett sådan resultat framkommer

— halveringstiden för Uran-238 med en garanterad osäkerhet inte större än ±0,06% [eg. ±0,03%], eller ca 4,468 [3], SÅ att man SÄKERT kan testa på Solvariationerna och se att dessa, säkert, INTE influerar Jordbankens U-238 —

kan vi, tydligen, inte heller UTESLUTA en längre halveringstid för Uran238 med referens till andra bildningslokaler — eller aktuella lokaler generellt — än Jorden. Se generell beskrivning från Inledningen [med TNED från GRUNDÄMNESBILDNINGEN].

— Den enda indikering som MÖJLIGEN — idag [Dec2011] ännu långt ifrån en säker sådan — ligger i NÅGON linje med TNED-teorin för halveringssambandets matematiska fysik, är observationerna från Jenkinsgruppen [2006-]: Variationer i Solens [neutrino-] strålning till Jorden följer samma periodiska variationer i halveringstider för vissa betainstabila nuklider som avståndet Jorden-Solen, samt också en period som sammanhänger med Solens egen rotation [32-dygnsrotationerna]. Variationerna är fastställda [Jenkinsgruppen Jun2011] — men SÄKERHETEN i de observerade variationerna berör ännu så länge endast [vissa] betainstabila nuklider.

— HALVERINGSTIDSSAMBANDETS TEORI för TNED:s del är dock helt klar. Se från Härledningen, samt Radiosönderfallets dynamik i TNED.

— Den enda oberoende källa som också ansluter till TNED är, som ovan Månen.

— Tas Månens recession baklänges (3,82 cM per år), når Månen fram till Jorden bara halvvägs om tidsgränsen är ca 4,5 miljarder år; 4,5 miljarder år är den ofta etablerat omnämnda Jordåldern (enligt TNED grovt samma som senaste bergartscykelns ålder);

— För att MED DEN RÄKNINGEN nå ända fram måste MINST 9 miljarder år finnas i bankens kassavalv, eller om recessionen går mycket långsamt i början på grund av litet ytvatten på Jordkroppen, med stor sannolikhet kanske minst runt det dubbla (upp mot 20 miljarder år förefaller INTE helt orimligt, men kan här explicit inte bevisas) — vilket stämmer nära perfekt i teorin med TNED (ytterst långsamt i början med litet ytvatten, sedan allt mera, successivt);

— Solsystemet bildades enligt TNED för 20,8 miljarder år sedan (beräknat från K-cellens värmefysik och expansionstakten från Detonationen, med referens till nuvarande medelavståndet mellan de närbelägna galaxerna); Jorden behövde möjligen MINST halva den tiden för utvecklingen med bergryggar och kontinentalplatåer med avsvalning (Se J-kropparnas värmefysik) för att så småningom tillåta fast ytvatten — början till fenomenet med Månens recession (Månkroppen skulle från början alltså ha roterat väldigt nära Jordkroppen — efter primärbildningen).

— Så långt stämmer indikatorerna (ungefärligt och grovt sett).

Men i så fall kan inte den Jordiskt uppmätta halveringstiden för U-238 vara någon universell konstant för samtliga nuklider U238 sett till hela universum. Nämligen INTE de som finns i (samband med) meteoriterna (vilkas olika ämnesförekomster man använt för Jordkroppens åldersbestämning med uppgiften 4,5 miljarder år);

För att mäta tiden via meteoriterna, blir man beroende av klockor vars tidskonstanter uppmätts efter Jordkroppens betingelser — de enda man känner — och därmed en uppenbar RISK. Den risken kan bara elimineras genom exakt inblick (Jenkinsgruppen Jun2011).

— TNED ställer upp, till prövning för HELA radiosönderfallets matematiska fysik, en specifik nuklidkoefficient (Ñ, max ±2) som kan härledas, se Nuklidkoefficienten, men som måste beräknas i understruken preferens till en LOKAL kännedom (med Jordkroppen som preferens) om uppmätt sönderfallsenergi (E) och uppmätt halveringstid (tH) — därför nämligen att vi vet strängt taget inte vad som gäller, än, beträffande »den av Rutherford från år 1913 förmodade halveringstidens universella konstans».

— tH blir alltså inte direkt teoretiskt beräkningsbar i TNED med mer än vi känner energiflödet i samtliga nuklidbildningslokaler; Det ämnet berör teorin för GRUNDÄMNESBILDNINGEN i TNED och som innefattar en MÖJLIG, integrerad (neutrinostyrd), energipåverkan; OM det finns en sådan påverkan, måste man, tydligen, känna energimiljön i den naturliga lokal som nukliden bildades i (typ i himlakropparna och mellan dessa) — vilket utesluter en specifikt Jordbaserad laboratorieuppmätt allmän halveringstidsform för en viss radioaktiv nuklid: begreppet halveringstid är INTE oberoende. Jämför Rutherfords mening från 1913.

— I klartext: Halveringstiden för radioaktiva nuklider av en viss typ KAN MÖJLIGEN vara en variabel — med grund i en avancerad neutrinoinfluens. Ämnet är (i så fall speciellt) tillägnat denna presentation.

— Innehållet i denna presentation färgas HELT av ovanstående: att söka bibringa en KLAR bild av radioaktivitetens elementa, sett från TNED — med möjliga paralleller till etablerade begrepp — för att MÖJLIGEN kunna avgöra frågan »om Månen har rätt eller fel» (Månens recession) — eller vad det ska föreställa.

——————‡ [2011-12-26]

Jenkinsgruppen Jun2011 sek.2; de bägge första nedan omnämns i inledande observationer från föregående forskning:

14Si32BetaMinus700y[VNS];

86Ra226Alfa1601y7,871MeV[W.Radium]multi;

MAIN Jenkinsgruppens observationsobjekt:

25Mn54BetaEC312,3d1,377MeV[W.Manganese]+Gamma0,834MeV

Allmän klassifikation

Betainstabila och nuklidinstabila atomer

TERMERNA BETAINSTABILA OCH NUKLIDINSTABILA ATOMER I DENNA PRESENTATION

Följande beteckningar används i denna presentation

K ............................ stabil

(K) ........................... betainstabil (b)

[K] ........................... nuklidinstabil (T)

Följande formella samband [deras STRUKTUR] framgår i relaterad fysik ur KÄRNREAKTIONSLAGEN (i sin tur ytterst från Allmänna tillståndslagen) och beskrivs mera utförligt till grund och sammansättning i efterföljande stycken.

Om atomen efter sin bildning är instabil och massdestruktionen (m→γ) fortlöper enligt

(K) – E_hf₁₈ = K = (K1+K2 – (m→γ) + _β0_γm) – E_hf18 ........................ betainstabil atom

är den instabila atomen betainstabil.

E_hf18 varierar från runt 3,5-0,5 MeV.

Om atomen efter sin bildning är instabil och massdestruktionen fortlöper enligt

[K] – E_hf₁₈₁₈ = K = [K1+K2 – (m→γ) + _T 0_γm] – E_hf1818 ...................... nuklidinstabil atom

är den instabila atomen nuklidinstabil.

E_hf1818 varierar obetydligt ENLIGT TNED, kvantitetsvärdet är helt försumbart [minsta möjliga energimängd som åstadkommer en nuklidändring, den går alltså mot noll].

Förekommer en kombination av bägge betecknas nukliden [(K)].

— Nedan följer en mera fördjupad beskrivning av begreppen.

Radioaktiva sönderfallet i relaterad fysik

— För ämnesorientering enligt konventionella begrepp, se t.ex. @INTERNET Wikipedia Radioactive decay.

— Den följande beskrivningen visar hur det radioaktiva sönderfallets matematiska fysik framgår enligt relaterad fysik.

— Referenser med jämförande citat och utdrag från konventionella källor ingår i framställningen.

Notera direkt från början skillnaden mellan begreppen i relaterad fysik (TNED) och modern akademi (här ofta förk. MAC), här i ämnet instabila atomer:

— TNED: Neutronens sönderfall [*1] [₀n¹–(m→γ)=₁H¹=p+e^–] inom ca 12-14 minuter bildar urtypen för betasönderfall — betasönderfall betyder att endast atomens elektronbild påverkas, atomkärnan bevaras intakt;

Massdestruktionen (m→γ)=E/c²=[hf=(h/n)fn]/c²=[E(hf)]/c² som krävs för arbetet att föra ut (från atomkärnan, eller till denna återinsätta) elektronmassan ansluter i TNED till neutrinobegreppet; begreppet neutrino i TNED står för högfrekvent em-strålning från massdestruktioner i atomkärnan, utom direkt detekterbar räckvidd för makrofysiken (våglängden understiger elektronmassans resonansfysik), enligt atomkärnans ekvivalenta Planckenergier E=hf=(h/n)fn, se utförligt från Atomkärnans härledning, Plancks strukturkonstant och Neutrinospektrum om ej redan bekant;

— Betasönderfallet sker genom att elektronmassans komponenter avdelas ur atomkärnan genom en konstant ström som ansluter till atomens kraftekvation [F(BT)+F(eZ)=0]; Kraftekvationen garanterar att strömmen fortsätter med kopplingen kärna-elektronhölje sedan hela elektronmassan avdelats och vilken koppling yttrar sig i formen av elektronmassans kärnenergibundna svängningar kring atomkärnan, just genom kraftbilden i F(eZ); Kraftbilden i F(eZ) definierar atomens Spektrum och därmed Grundämnenas periodiska system;

— Elektronmassans avdelningsprocess syns aldrig i makrofysiken, som tydligen TNED får förstås, endast tillfället då hela utgivningen kopplar resonans med elektriska elementarkvantat (e=1,602 t19 C) [som kopplar protonen (p) till processer som kan studeras makrofysikaliskt]; Fullständigandet i makrofysisk mening med produkten (Väteatomen p+e^–) kan registreras som en transientpuls [*2]. I modern akademi tolkas pulsen som en aktuell händelse i förening med emission av en massbaserad neutrinopartikel (s.k. antineutrino).

I fallet kärnsönderfall via kärnistabila atomer — atomkärnan delas vid sönderfallet i två eller flera komponenter — underhålls det kärninstabila tillståndet också av en motsvarande neutrinobaserad massdestruktion (m→γ)=E/c²=[hf=(h/n)fn]/c²=[E(hf)]/c² och som, enligt TNED (Se utförligt från Sönderfallet), pågår ända fram tills ett utbrott plötsligt inträffar, just då kärnan sönderfaller;

— Är delprodukten fortfarande kärninstabil fortsätter dissonansenergin E(hf) i massdestruktionen (m→γ)=[E(hf)]/c² tills ett nytt, plötsligt, utbrott med sönderfall inträffar, osv., och vilken process fortlöper ända tills ett stabilt tillstånd uppnås; Inte heller den neutrinostrålningen är direkt detekterbar (Se Dissonansenergin).

Sönderfallsmatematiken för de bägge instabila sätten beskrivs i TNED enligt leden nedan; varje nuklid K förutsätts naturligt exotermiskt bildad via fusion [Se GRUNDÄMNESBILDNINGEN enligt TNED] enligt KÄRNREAKTIONSLAGEN K=K1+K2–(m→γ) och som i fallen instabila atomer ger de bägge möjliga instabila typerna

(K) – E_hf₁₈ = K = (K1+K2 – (m→γ) + _β0_γm) – E_hf18 ................. betainstabila atomer, kärnan bevaras — betanuklider (konv. betasönderfall)

[K] – E_hf₁₈₁₈ = K = [K1+K2 – (m→γ) + _T 0_γm] – E_hf1818 .............. nuklidinstabila atomer, kärnan delas — radionuklider (konv. alfasönderfall)

18: Betanuklidernas massdestruktion (m→γ) under sönderfallet arbetar på den del som i TNED tillhör atomära massdefekten, max 18e.

1818: Radionuklidernas dito arbetar på atomkärnans centralmassiv, 1818e.

Sönderfallet uppvisar influenser,

se även fördjupat i Neutrinoinfluensen

Leden ovan

beskrivs mera utförligt från Atomens bildning.

— Dissonansenergin E_hf enligt TNED förklarar (galant) HUR det annars så gåtfulla radioaktiva halveringskomplexet fungerar enligt sambandsformen

t_H = N₀î ;

î = t_H/N₀ ;

medellivet î varierar direkt omvänt proportionellt med mängden N0 radionuklider med given fast halveringstid tH.

Se utförligt från Parameterbegrepp.

Ju flera individer (radionuklider) i samma rum, desto kortare blir medellivslängden för varje radionuklid; Sönderfallets tillfälle bildar tydligen en faktor som fördelas, sprids ut, JÄMNT mellan alla ingående individer, så, att aktiviteten varierar direkt proportionellt mot antalet; Individerna kommunicerar tydligen en fördelning; I TNED finns bara en agent för den uppgiften: neutrinostrålningen i den underhållande radionuklidens existens, den här benämnda dissonsenergin E_hf.

— I MAC finns inget motsvarande begrepp; man menar konventionellt att sönderfallet sker »spontant» i den aktuella partikeluppdelningen och utan föregående aktivitet [*3].

— Genom neutrinoinfluensen, dissonansenergin E_hf ovan, finns en naturlig kvalitativ fysikalisk förklaring till varför och hur individpåverkan från mängden ökar med växande individantal i rummet;

Aktivitetens naturliga avtagande med tiden

— Den totalt högre influensen från mängden NE(hf) påskyndar medeltillfället (î) för sönderfallets inträffande;

— I takt med att individerna lämnar rummet och mängden avtar, avtar också neutrinoinfluensen NE(hf) från alla kvarvarande N individer på den enskilda, vilket medför att aktiviteten också avtar.

— Det är också precis så det radioaktiva sönderfallets praktiska fysik fungerar, enligt framställda etablerade beskrivningar (se även Geiger-Nuttalls samband);

Citat FM 1975: ”Det radioaktiva sönderfallet är så vitt vi i dag vet en helt slumpmässig process. Det går alltså inte att förutsäga när en individuell kärna skall sönderfalla, och av två alldeles lika kärnor kan den ena sönderfalla nästa ögonblick och den andra först om tusentals år. Genom att även det allra minsta laboratorieprov innehåller ofantligt många kärnor är det emellertid möjligt att för varje nuklid bestämma en statistiskt definierad sönderfallshastighet. Denna brukar vanligen anges med hjälp av den tid som åtgår för att halva antalet kärnor i ett prov skall sönderfalla. Denna tid visar sig nämligen vara oberoende av det ursprungliga antalet kärnor i provet. Den kallas nuklidens halveringstid.”,

FOCUS MATERIEN 1975 s133sp1mn

— Med konstant halveringstid t(H) för en viss radionuklid, avtar radioaktiviteten enligt (det elementära) halveringssambandet N=N₀/2^T(ln2)/tH med växande tid (T), i enlighet med kvarvarande mängd N från utgångsmängden N(0).

— En motsvarande dynamiskt förklarande fysikbild till E_hf-influensen i MAC har eftersökts men inte påträffats: inget motsvarande omnämnande verkar ens finnas. Men: Det kan heller inte finnas någon sådan motsvarighet [*3] eftersom det i modern akademi inte finns någon uppfattning om en pågående aktivitet före själva det utbrytande kärnsönderfallet.

— Det rent KVALITATIVA »fenomenet» med individpåverkan via växande-avtagande radiomängder, î-sambandet ovan [‡], finns här veterligt (således, följdriktigt heller) inte ens omnämnt i MAC — i varje fall inte så det syns i de mest framstående etablerade källor som visas på Webben (Okt2011).

— När det sedan — dessutom — kommer till faktorn t(H), halveringstiden, det centrala begreppet — skiljer sig TNED från MAC ytterligare — Jämför det inledande citatet;

— I MAC återförs halveringstiden t(H) tydligen på ett statistiskt begrepp för en mängd radionuklider.

— I TNED återförs halveringstiden t(H) tydligen på den egenskap hos en viss typ av radionuklider som utpekas av nuklidkoefficienten [b=4πÑ]: den existerar inte i MAC (Se Brytpunkten TNED-MAC);

— Halveringstiden t(H) i TNED kan återföras på en nukleär egenskap som sammanhänger med nuklidbildningen (Utförligt i Neutronkvoterna från Radiofysikens grunder). Sambanden i slutänden ser likadana ut — men innefattar strängt olika (väsensskilda) innebörder:

MAC: (ln2)/t_H = Ae^–B/√Eα .................. Se Geiger-Nuttalls samband

TNED: (ln2)/t_H = Ae^{–beZ/√2mEα} ............ Se Slutformen från Härledningen

Se även jämförande beskrivning från Sambanden i MAC, samt Härledningen till Radionuklidernas Halveringstid enligt relaterad fysik.

— Se även i KÄLLEXEMPEL hur TNED-formen (nuklidkoefficienten b) framträder via en (mindre) serie experimentellt uppmätta radionuklider.

Kan halveringstiden (tH) påverkas enligt TNED?

Se även Multipla tH i TNED

— Med giltigheten av neutrinoinfluensens princip i TNED ligger det nära till hands att också förmoda att halveringstiden t(H) för primärt färdigbildade radionuklider av en viss typ i t.ex. Jordkroppen skulle kunna påverkas (sekundärt) och inbördes av mängden närvarande radionuklider.

TNED-teorin för den aktuella nuklidkoefficienten [Se från Härledningen] bygger emellertid på en viss energigenomströmning i radionuklidernas primärbildning — och vilken energibild tvunget konserveras med radionuklidens färdigbildning (kärnstrukturen generellt enligt TNED). Därmed underförstått en typ av försegling (som i sig skulle kunna innebära att en och samma radionuklidtyp t.ex. Uran-238 får något olika tH-värden beroende på energilokal; Det är dock här ännu inte känt om det finns verkliga praktiska belägg för det);

— Nuklidkoefficienten kan sedan inte ändras (neutrinopåverkan kan bara excitera atomkärnan på energi, analogt påskynda tillfället för ett sönderfall som i fallet med många radioindivider med motsvarande kort medelliv för den aktuellt sönderfallande individen, î=t_H/N₀, inte åstadkomma strukturomvanlingar i atomkärnan efter dess primärbildning och som ändrar sönderfallets styrka);

— Nuklidkoefficienten bildar istället formen för den ovan antydda allmänna neutrinoinfluensfysiken; den, som via t(H)-formen garanterar den nämnda inbördes î-fördelningen (medellivet). Med andra ord: Utan en fast t(H)-preferens finns strängt taget heller ingen fast î-fördelning. Utan en sådan kollapsar hela komplexet (halveringssambandet gäller inte).

— Däremot kan, som redan påpekats, redan primärt färdigbildade radionuklider påverka tillfället för sönderfallet internt, inbördes på ovan beskrivet sätt (neutrinoinfluensens princip), utan att sönderfallsstyrkan påverkas (i princip samma som tH-värdet), och så att flera nuklider i samma rum åstadkommer en kortare medellivslängd (högre aktivitet) för de radionuklider som faktiskt sönderfaller, och vilken medellivslängd därmed ökar med avtagande mängd radioindivider (lägre aktivitet).

— Ja:

— OM alltså en (lämpligt avstämd) intensiv neutrinokälla riktas mot Jordkroppen (från t.ex. Solen) finns möjligheten att aktiviteten (hos någon motsvarande radionuklidfamilj) kan variera med avståndet till Solen (Solirradiansen på Jordcirkelskivan skiljer sig med 0,06%~max0,1% mellan sommar-vinter) — SOM OM det vore frågan om ett närvarande växande eller avtagande antal radionuklider som bidrar med E(hf)‑komponenter.

— Men, här veterligt: En sådan TEORI kan inte utvecklas kvalitativt i MAC — därför att [*3] modern akademi saknar uppfattning om en pågående aktivitet före själva det utbrytande kärnsönderfallet; Neutrinoinfluensens princip är, av — genom — samma princip, och i ljuset av den moderna akademins allmänna neutrinouppfattning — se neutrinobegreppet — utesluten av modern akademi.

Det är, förmodligen, också samma orsaksgrund som (tydligen) upprört [många] forskare i blotta möjligheten med en variabel sönderfallskonstant [se citatdelarna med början från Jenkins et al., 2006];

— VARJE sådan — teoretisk — möjlighet trotsar just den teoretiska grundvalen för den moderna akademins härledning [George Gamow 1928] till halveringssambandet [Se Geiger-Nuttalls samband]; den statistiska kvantmekanikens sannolikhetskalkyl. Jämför det kategoriska särskilda Citatet från Hyperphysics och samma källa mera allmänt i Half-Life-IndepencencyCitatet.

— I TNED finns inte den problematiken — men exakt samma kvalitativa (och kvantitativa) formella sambandsform. Se särskilt aspekterna på halveringstidssambandets formalia i jämförelsen MAC/TNED i Allmänna Koefficientsambandet. Härledningen till halveringstidssambandet i TNED — samma sambandsform som det konventionellt benämnda Geiger-Nuttalls samband — har inga spår av den moderna akademins statistiska inslag.

— Som citatvis visas i Allmänna Koefficientsambandet, finns i grunden ingen DIREKT koppling från MAC-teorin till halveringstidssambandets FORM; den kopplingen bygger på en APPROXIMATION — från den kvantmekaniska sannolikhetsteorin, en algebraisk förenkling — som leder direkt på TNED-formen: garanterat utan både approximationer och sannolikheter.

— I den rent TEORETISKA andan av den uppmärksammade variationen i radioaktiva sönderfall med (enda kandidaten) neutrinovariationerna från Solen (se sammanfattning i Jenkinsgruppen Jun2011), är det därmed alldeles tydligt — i varje fall sett kvalitativt från TNED — att den moderna teorins rent kvantmekaniska sannolikhet är utagerad: en primitiv fiktion som fick sin största spridning under 1900-talet. Åtminstone är det historieskrivningen enligt TNED på den punkten.

———————————————————————————————————————————

*¹

Länken till NIST-domänen finns inte längre. Den återfinns nu [Okt2011] på URL-adressen

http://www.nist.gov/pml/div682/grp03/trapped-neutron.cfm

*²

Direkt experimentell registrering av en transientpuls vid betasönderfall

”The emission of gamma rays is a compensation by the atomic nucleus for the unstable state that follows alpha and beta processes in the nucleus.”,

”The primary alpha or beta particle and its consequent gamma ray are emitted almost simultaneously.”,

”A few cases are known of pure alpha and beta emission, however, that is, alpha and beta processes unaccompanied by gamma rays”,

Microsoft ENCARTA 99 Radioactivity

som visar makroövergången från neutron till proton finns här veterligt inte.

”Beta decay of the neutron into a proton, electron, and electron antineutrino is occasionally accompanied by the emission of a photon. Despite decades of detailed experimental studies of neutron beta-decay, this rare branch of a fundamental weak decay has never been observed.”,

Journal of Research of the National Institute of Standards and Technology, Volume 110, Number 4, July-August 2005

Detecting the Radiative Decay Mode of the Neutron, Fisher et al., 2004

http://nvl.nist.gov/pub/nistpubs/jres/110/4/j110-4fis.pdf

— URL-länken ovan går INTE direkt till PDF-dokumentet [en domänspärr uppkommer];

— Använd istället Fetstilsrubriken ovan som sökterm, den leder till det aktuella dokumentet.

— Detektering av elektroner från neutronsönderfall kan ske med hjälp av ett elektriskt fält (konv. jonisationskammare, eng. ionization chamber, se exv. @INTERNET Wikipedia Ionization chamber 2011-10-27) som attraherar elektronerna (till någon mätsensor, eller styr dem för vidare); Atomer som joniserats via elektronbildningen formar en mätbar elektrisk (joniations-) ström, och därmed en detektering av en fullbordad elektronemission (från neutronsönderfall).

— Andra tekniker som (tillsammans med elektrondetektering) kan visa elektronemissionens fullbordan från neutronsönderfall bygger på detektering av den bildade protonen. En sådan teknik beskrivs bl.a. i PDF-källorna

JOURNAL OF APPLIED PHYSICS 99, 084904 2006

An electron transparent proton detector for neutron decay studies, Hoedi et al., 2006

http://digital.csic.es/bitstream/10261/21404/1/GetPDFServlet.pdf

Journal of Research of the National Institute of Standards and Technology, Volume 110, Number 4, July-August 2005

Simulation of Charged Particle Trajectories in the Neutron Decay Correlation Experiment abBA, Desai et al., 2004

http://nvl.nist.gov/pub/nistpubs/jres/110/4/j110-4des.pdf

— Neutronsönderfallet skrivs konventionellt i modern akademi (ν_e, elektronassocierad antineutrino)

n → p + e^– + ν_e + γ

medan TNED beskriver neutronsönderfallet genom att sammanföra gammadelen (γ) med neutrinobegreppet generellt i en enda form som massdestruktionsstrålning (m→γ)

₀n¹ → (₁H¹= p+e^–) + (m→γ)

Gammabeteckningen (γ) i (m→γ) generaliserar i TNED för samtliga fall som innefattar E=hf-kvanta.

— Generellt för betasönderfall (som inte sammanhänger med neutronsönderfall; Se även citatdelen ovan från Encarta) förekommer ofta direkt detekterbar gammastrålning [i TNED som del av totalenergin i E=(m→γ)c²]. Gammastrålningen i sådana fall yttrar sig som en »extrapuls» som atomkärnan emitterar vid fullbordat sönderfall — i händelse av överskottsenergi (som ofta, men inte alltid, är fallet).

— Däremot finns en motsvarande (indirekt) experimentellt känd reaktionsbild i det s.k. inverterade betasönderfallet (ν_e+p→e⁺+n), se Bevisen för neutrinooscillationer; Protonen (i lämpligt tillrett preparat) exciteras av ett neutrinokvanta och bildar en exciterad neutron under emission av en positron (e+), denna annihileras (under kort tid) med en omgivande elektron (e^–) och därmed en transientsignal; Ytterligare en signal bildas genom att neutronen i sig strax (efter ca 200mS) förenas med en omgivande proton och bildar en deuteron som yttrar sig i en direkt makrofysiskt detekterbar stöttransient.

———————————

*³

Sönderfallet sker utan inverkan från någon yttre källa

”Radioactive decay is the process by which an atomic nucleus of an unstable atom loses energy by emitting ionizing particles (ionizing radiation).”;

”The emission is spontaneous, in that the atom decays without any physical interaction with another particle from outside the atom.”,

;

”Radioactive decay is a stochastic (i.e., random) process at the level of single atoms, in that, according to quantum theory, it is impossible to predict when a given atom will decay.[1]”,

Wikipediaartikelns Referens [1]:

”Is it possible to predict when a given radioactive atom will decay?

No, its not. The decay of an individual atom is a random event. However, it is possible to predict when decay will occur based on probability, particularly when there are a lot of radioactive atoms around.”,

http://www.iem-inc.com/prhlfr.html

Källan anger ingen verifierbar referens — endast påståendet ges, utan vidare.

;

” The decay, or loss of energy, results when an atom with one type of nucleus, called the parent radionuclide, transforms to an atom with a nucleus in a different state, or a different nucleus”,

@INTERNET Wikipedia Radioactive decay 2011-10-25

http://en.wikipedia.org/wiki/Radioactive_decay

;

Se dock även en något friare hållning [med inre diskussion] — som kanske avspeglar ett mera ingående intresse — i Yahoo-Answers-artikeln från Sep2009,

IS RADIOACTIVE DECAY AN EFFECT WITHOUT A CAUSE?

http://answers.yahoo.com/question/index?qid=20090918061009AA4E8ZF

— LOGIKEN KRÄVER [underförstått] NÅGON katalyserande aspekt, frågeartikeln ovan med svaren belyser den detaljen.

Jämför Frekvensfunktionen.

Allmänt — Allmän inledning med termer och begrepp till Radiofysiken i TNED · För UNIVERSUMS HISTORIA Dec2011

BILDKÄLLOR: Författarens arkiv · Kollage NikonD90 · VÅRVINTER:R13Apr2010Bild169·VÅR:RF24Maj2010Bild1/3

ALLMÄNNA TERMER — radiofysiken TNED

Se även i RadioTermer, Halveringssambandet och Halveringstidssambandet

RADIOAKTIVT MATERIAL beskrivs generellt från upptäckten i slutet på 1800-talet som all materia som består av eller innehåller INSTABILA ATOMER; atomer som utsänder elektromagnetisk- och partikelstrålning. Konventionellt under 1900-talet klassificeras strålningstyperna i ordning från mindre till mera genomträngande enligt typerna alfa [Heliumkärnor, stoppas av ett papper], beta [elektronmassor, stoppas av en aluminiumfolie] och gamma [elektromagnetisk, stoppas av en blyskiva].

nuklidfamiljerna	nuklidgränserna	sönderfallstyper	AlfaIsotopKartorna	AlfaKartan	BetaKartan

familj	gränser — unika i TNED	typ	Kartor — unika i TNED	AlfaKartan	BetaKartan

— Radioaktiviteten som upptäckt fysikaliskt fenomen tillskrivs Henry Becquerel [1896] i samband med undersökning av fosforescerande material [ref. Wikipedia Radioactive decay, Discovery, 2011-12-24]. Tidigt upptäcktes ett empiriskt samband, Geiger-Nuttalls samband [1911] mellan det radioaktiva preparatets s.k. halveringstid och en karaktäristisk energi i det sönderfallande ämnets emitterade Heliumkärnor [konv. alfapartiklar]. I modern akademi härleddes sambandet [1928] av George Gamow [ref. Wikipedia Geiger-Nuttall law, Derivation, 2011-12-24] på bas av kvantmekanikens statistiska grunder — som utvecklades just under denna tid [mitten av 1920-talet].

— Samma sambandsform, men med grund i en helt annan teori, ges från TNED utförligt från Härledningen till halveringstidssambandet.

— Jämförelser, citat och exempel visar hur sambandet återspeglar de olika teorierna MAC och TNED; Se särskilt från tH i MAC/TNED.

— Speciellt — explicit — ingår inte i MAC den avgörande nuklidkoefficienten [b] som i TNED beskriver/förklarar det radioaktiva sönderfallets dynamik på sätt som medger viss [neutrino]influens på halveringstiderna. Denna detalj diskuteras specifikt från Dissonansenergin, men det finns ingen motsvarande teoretisk grund till jämförelse i MAC. Helhetsbilden i TNED blir därför också en annan.

— Se särskilt sammanfattande genomgång med vidare referenser från Sönderfallets enhetliga preferensgrund.

— Observationerna [från 2006] av Jenkinsgruppen — variationer i [neutrino]strålningen Solen-Jorden ger motsvarande variationer hos vissa betainstabila atomämnen — ger TNED-teorin visst kvalitativt stöd. Notera dock att inget [ännu Dec2011] är avgjort i ämnet.

— Tungt radioaktivt sönderfall betyder i den här framställningen samma som direkt kärndelning; moderatomen delas i två eller flera delprodukter. Dessa atom/kärnsönderfall kan i princip omfatta vilka som helst summerande delkärnor (K=K1+K2+...). De vanligaste (beskrivna) sönderfallen inbegriper Heliumkärnor (konv. alfapartiklar), neutroner och protoner, dessa (ibland även) tillsammans med tyngre delkärnor.

— Lätt sönderfall — betasönderfall hos betanuklider — betyder här motsvarande elektronändringar i atomen; kärnan bevaras intakt.

— Tungt sönderfall kallas här också förenklat radiosönderfall och nukliderna (något favoriserat oegentligt) radionuklider.

— Uppdelningen visas naturligt i TNED genom att betasönderfallen arbetar på massdefektskapitalet 18e och radiosönderfallen på centralmassivets 1818e.

Kriterium för instabilitet

Stabila tillståndets VerkningsGRUND i relaterad fysik: atomen som en [idealt] STABIL enhet behöver ingen påfyllning av energi för att fungera: summan av alla krafter och moment i atomen och atomkärnan är noll, se atomfysikens två kungsekvationer i TNED — J[0K]+3[J1K]=0 och F[BT]+F[eZ]=0; ingen energi omsätts för atomens blotta verkningsgrad; INSTABILT TILLSTÅND följer därmed den enkla principen [Se även Fysikens andra princip: all verkan baseras på jämvikt]:

kontinuerligt tillförande av ARBETE=ENERGI krävs för att underhålla ett icke stabilt tillstånd

— Varje instabil enhet [atom] kännetecknas av att den utför ett ARBETE; eftersom all verkan baseras på jämvikt, blir arbetets strävan mot STABILITET — arbetets upphörande, stabila tillståndets fysik: jämviktens princip.

Instabila atomerna i TNED

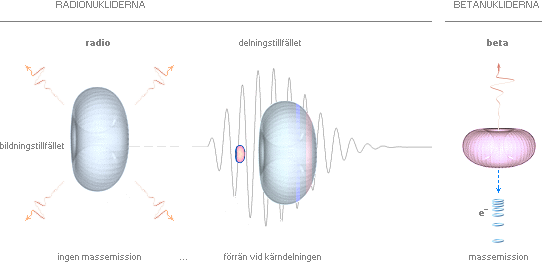
Radiosönderfallets kontinuerligt instabila tillstånd underhålls enligt TNED av en kontinuerligt pågående, minimal, massupplösning som krävs för ARBETET som underhåller det icke-stabila tillståndets inre självsvängningar i atomkärnan;

— instabila tillståndets fysik kräver obönhörligen ENERGI för att fortlöpa.

— Den minimala »radioemission» som krävs för att underhålla tillståndet och dess energiräkning, helt utan partikulära emissioner, sammanhänger i TNED med Plancks strukturkonstant; minsta möjliga energiomsättning på högsta möjliga frekvens — i TNED atomkärnans djupast liggande strukturer. Radioemissionerna tillhör enligt TNED neutrinostrålningen som inte direkt kan detekteras av makrofysikens elektronsvängningsfysik.

Betasönderfallets motsvarande tillstånd kräver också underhållande sönderfallsenergi, men i detta fall, enligt TNED, sker också samtidigt en kontinuerlig emission av elektronmassans komponenter, utspritt över HELA betasönderfallets period, ända ifrån betanuklidens bildningstillfälle. Se mera utförlig beskrivning i Betasönderfallens matematiska fysik i TNED. Se även i Elektronmassans emission i kärnans spinnriktning.

— Klassifikationen betanuklider och radionuklider beskrivs mera utförligt i denna presentation från Allmän Klassifikation.

Termfavoriseringen med »radio-» i TNED kommer här ifrån detaljen som utmärker kärnsönderfallen framför icke-kärnsönderfallen: den kontinuerligt pågående massdestruktionen [i TNED neutrinostrålning enligt Plancks strukturkonstant E=(h/n)nf ] som med den motsvarande kontinuerliga högfrekventa underhållande instabilitetens E=[h/n]nf-komponenter driver nukliden mot tillfället för plötslig kärndelning; radionukliden »sänder kontinuerligt», utan massemission. Radioemissionerna sker dock på neutrinovåglängdernas nivåer enligt TNED och som inte direkt kan detekteras. Se vidare från RADIONUKLIDENS BILDNING.

— Emellertid föreligger, på visst sätt fast i annan fason, också motsvarande i betasönderfallet via elektronmassans avdelning/upptagning; Men medan betasönderfallen, via elektronmassorna, delar på samma kärnfragmentbas — elektronmassans komponenter — och därmed är lika för alla betaaktiva nuklider, gäller olika byggformer inbördes mellan de kärninstabila [»radiobaserade»] nukliderna.

HALVERINGSSAMBANDETS ALLMÄNNA BETYDELSE FÖR DET RADIOAKTIVA SÖNDERFALLETS FYSIK

I halveringssambandet (Se särskild härledning i Halveringssambandet, om ej redan bekant)

N = N₀/2^T/tH

= N₀/e^T^(ln2)/tH ............ halveringssambandet, antal återstående radionuklider efter T

e^T(ln2)/t_H = N₀/N ; T(ln2)/t_H = ln(N₀/N) = ²log(N₀/N)·ln2 ; T/t_H = N₀/N

N kvarvarande radionuklider efter tiden T, N₀ utgångsmängden radionuklider, t_H halveringstiden (från N₀ till N₀/2)

är faktorn [radiokonstanten] (ln2)/t_H ENERGIBEROENDE enligt Geiger-Nuttalls (från 1911) samband

(ln2)/t_H = Ae^–B/√Eα

A[B=b(Z–2)] är nuklidspecifika koefficienter och E_α anges som den aktuella (bindningsenergin) eller alfaenergin;

— När radionukliden sönderfaller, emitteras (ofta) en ₂Helium⁴-kärna (alfapartikel, kärnstabil), ibland också tillsammans med (flera) tyngre (instabila) delningsprodukter (som också kan variera inom relativt vida områden).

— Genom de första mätningarna som genomfördes (i början på 1900-talet) visade det sig att radionuklider i samma nuklidfamilj uppvisade likartade E_α-värden. Vi studerar den detaljen — i relaterad mening — i Härledningen till Radionuklidernas Halveringstid, enligt relaterad fysik.

Parameterbegrepp

Se även i Radiotermer

Parameterbegreppen till radioaktiva sönderfallets matematiska fysik enligt TNED

— MedelsönderfallsINTERVALLET per 2 sönderfallsindivider i ett givet preparat med utgångsmängden N₀ stycken radionuklider

[N₀=m_MASSAN/u_1,66033
t27U_ATOMVIKTEN] motsvarar ett »medelliv» (î, här tecknet Alt+0238 för att särskilja, enhet i sekunder) för varje radionuklid i det aktuella preparatet.

Medellivet

î medellivet för en radionuklid med hänsyn till mängden individer i samma klass
[samma preparat, samma typ], î som i-flex, Alt+0238, enhet: Sekunder

— Medellivet (î) blir den (medel-) tid som förflyter mellan (idealt) två på varandra efterföljande sönderfall (generellt alfaemissioner, sönderfallets absoluta kriterium genom experimentell observation), var som helst i preparatet.

— Frekvensen (f), samma som antalet (n) sönderfall per sekund (S) kan då skrivas ekvivalent

N₀/t_H = 1/î = n/S = f ........... sönderfallsfrekvensen [»basradioaktiviteten»], enhet i Hz,
samma som antal per sekund [Hz], eller Becquerel[Bq]/[ln2]; [ln2×]Hz=Bq, vidare nedan

t_H motsvarar begreppet halveringstid — med följande GRUNDFÖRKLARING:

Halveringstiden

— Relationen N₀/t_H framgår direkt i ekvivalens med de övriga i ledet närmast ovan genom villkoret med de bägge sönderfallsindividerna (N₀=2);

— 2 radionuklider övergår i 1 återstående radionuklid efter medellivet (î=t_H). Då gäller halveringstiden

t_H = N₀î ...................... halveringstiden [elementärt: från 2 till 1 med startvärdet N₀=2]

Radioaktiviteten

— Med faktorn ln2 [logaritmiska halveringskoefficienten från motsvarande e-sambandet, se även blåstripen nedan] gäller då

radioaktiviteten här betecknad (xsi) ξ enligt

f·(ln2) = N₀(ln2)/t_H

= (ln2)/î

= ξ_N .......................... [ξ xsi] radioaktiviteten [i Bq], grundparameter, uppmäts med instrument

Halveringssambandet N=N₀/2^T/tH=N₀/e^T(ln2)/tH via N₀/N=e^T(ln2)/tH visar ln(N₀/N)=T(ln2)/t_H med (ln2)/t_H som radiokonstanten

KONVENTIONELLT används motsvarande begrepp (radioaktiv) sönderfallskonstant (eng. decay constant) med beteckningen Lambda (λ) enligt

λ = (ln2)/t_H ................. konventionella sönderfallskonstanten

= ξ_N/N₀

Därmed halveringstiden

t_H = (N₀/ξ_N)ln2 = N₀î med

N₀ = m_MASSAN/u_1,66033
t27U_ATOMVIKTEN

TNED Motsvarande konventionella beteckningar [Jämför @INTERNET Wikipedia Radioactive decay 2011-10-27]

t_H t_½ eng. half-life, halveringstid, sekunder S

(ln2)/t_H λ eng. decay constant, sönderfallskonstant, 1/S

t_H/(ln2) τ eng. mean lifetime, medellivstid, S

î orepresenterad, medellivet som varierar dynamiskt med sönderfallet t_H/N₀, S

Villkor för sönderfall, halveringssambandet

OM halveringstiden t_H är en fast tidskonstant för en viss typ av radionuklid i en bestämd radiofamilj, gäller tydligen från

N₀î = t_H

att medellivet

î = t_H/N₀

hos varje ingående radionuklid i den familjen (det aktuella preparatet) avtar med växande individmängd N₀ — och omvänt, anpassar sig växande med avtagande individmängd N₀.

— Det finns då ALLTID en sista radionuklid som ALLTID får en maximal livslängd, samma som halveringstiden. Och på samma sätt åt andra hållet; det finns alltid en först sönderfallande nuklid med en minsta livslängd.

T_N0 = –t_H(ln[1–1/N₀])/(ln2) ....... livslängden för den radionuklid som sönderfaller först av alla

T₁ = t_H(lnN₀)/(ln2) ................... livslängden för den radionuklid som sönderfaller sist av alla

— Varje preparat, med en större eller mindre utgångsmängd radionuklider N₀, anpassar sig tydligen automatiskt med en intern, »Demokratisk Fördelning» av medellivslängder enligt sambandsformen för î ovan.

— Vartefter preparatets radionuklider sönderfaller, uppför sig med andra ord preparatets allt mindre kvarvarande antal radioaktiva nuklider som ett nytt N₀ med samma t_H;

— EXEMPEL 1: t_H=16S, N₀=16 som från N₀ ger

î =t_H/N₀=(16S)/(16) = 1S; efter t_H=16S återstår 8 individer;

î =t_H/N₀=(16S)/(8) = 2S; efter t_H=16S återstår 4 individer;

î =t_H/N₀=(16S)/(4) = 4S; efter t_H=16S återstår 2 individer;

î =t_H/N₀=(16S)/(2) = 8S; efter t_H=16S återstår 1 individ;

î =t_H/N₀=(16S)/(1) =16S; efter t_H=16S återstår 0 individer;

Medellivet (î) för alla kvarvarande radioindivider ökar med sönderfallets fortlöpande.

— OM halveringstiden t_H är en fast tidskonstant för en viss typ av radionuklid, och endast då, gäller alltså:

OM radionuklidens medelliv î ändras med individmängden N₀ via en nuklidkonstant t_H

î = t_H/N₀ ....... medellivet î, halveringstiden tH, utgångsmängden N0

Sönderfallstillfället î för medelnukliden — radioaktiviteten — regleras av den närvarande mängden

finns uppenbarligen någon form av dynamiskt verkande influens som styr fördelningen.

I TNED härleds influensfysiken i den kärninstabila atomen på en försvinnande liten dissonansenergi Ehf1818 som underhåller kärninstabiliteten tills dess sönderfallsutbrottet inträffar Sambandet för kärninstabila nuklider i TNED grundas på EXOTERMISKA KÄRNREAKTIONSLAGEN K=K1+K2–(m→γ) enligt

[K] – Ehf1818 = K = [K1+K2 – (m→γ) + _T 0_γm] – Ehf1818

Elimineras dissonansenergin ur ledet, gäller stabil nuklid. Se vidare utförligt från Samband.

— OM INTE någon inre dynamisk fördelning skulle finnas, finns heller ingenting som säger att ALLA nuklider med ett visst î INTE skulle sönderfalla på en och samma gång, eller nära. Exempeltabellen ovan skulle då kollapsa och sakna mening. Den dynamiska fördelningen certifierar med andra ord att en motsvarande influensfysik, en kommunikation av någon form, existerar inbördes mellan individerna — som om de alla vore inneslutna i en och samma enda t_H-radionuklid.

Mönsterexempel

— EXEMPEL 2:

Uppdelning av N0 radionuklider på olika preparat bevarar sönderfallets enhetliga numeriska status — förutsatt [LJUS-]avstånden mellan nukliderna ligger inom tH.

Figuren ovan föreställer två laboratorieprov ab med vardera 16 radionuklider av samma t_H=16S-typ.

— I fallet a finns alla 16 nukliderna i ett och samma preparat; î=t_H/N₀=16S/16=1S.

— I fallet b är de 16 radionukliderna i b uppdelade på 4 likadana preparat; î=t_H/N₀=16S/4=4S per.

Följer vi utvecklingen i de bägge fallen efter medellivssambandet î=t_H/N₀, ser vi att samma individantal LIKVÄL totalt sett återstår efter varje t_H=16S.

— Exempelräkningen i b-fallet efter 2:a t_H=16S-intervallet SKULLE egentligen stanna där EFTERSOM varje preparat bara har EN individ kvar: det finns inget ytterligare att dela på (de 4 preparaten gäller bara till och med sönderfall nummer två).

— Med INFLUENSDYNAMIKENS CERTIFIERING — och förutsatt att de 4 skilda preparaten inte ser varandra på större avstånd än vad ljushastigheten hinner koppla via t_H-konstanten — kan LIKVÄL de singulärt bestyckade preparaten i radkolumn b2 samverka som om de vore del i samma masskropp (a2).

SOM VI FÖRSTÅR — eftersom atomkärnornas sönderfall inte påverkas av makrofysikens elektromagnetism (inte i praktiken, inte i teorin, varken i TNED eller MAC) — finns bara en influensagent att utpeka i anställningen av influensens orsak: neutrinostrålningen ENLIGT TNED [Ehf1818].

— Ju fler individer i samma lokal, desto större påverkan med följd i att medelsönderfallstillfället för den enskilda radionukliden påskyndas;

— Vartefter lokalen töms på individer, avtar den influensen, så att medelsönderfallstillfället blir allt längre.

— Den (galant) förklarande funktionsteorin finns inte i MAC — neutrinobegreppet har inte den statusen där.

I Härledningen till Radionuklidernas Halveringstid, enligt relaterad fysik beskrivs HUR halveringstiden t_H kan härledas relaterat ur styrkan eller kraften (F) med vilken en viss partikel frigörs i sönderfallet (generellt Helium-4-kärna eller alfapartikeln) ur en viss kärninstabil modernuklid.

— Härledningen ger samma typsamband som det konventionellt benämnda Geiger-Nuttalls samband, men efter ovan angivna förutsättningar — och som alltså ENBART och således återfaller på fysiken för EN — 1 — atomkärna, den aktuella radionukliden. Statistiska begrepp existerar inte.

Fortsättning i Härledningen till Radionuklidernas Halveringstid, enligt relaterad fysik.

Härledningen enligt TNED, alfasönderfallet — Radionuklidernas halveringstid, sambandet för halveringstiden tH

2011X19

Inledande Beskrivning

— IDEALT kommer TNED-härledningen för alfapartikelns avdelning från moderkärnan att göras SOM OM HELA sönderfallsenergin läggs på alfapartikeln i form av rörelseenergi (ideal, klassisk mekanik);

— Detta är [emellertid, och NÄMLIGEN] ALDRIG det praktiska fallet: Det finns alltid en viss rekylverkan mellan modernuklid och avdelad kärnpartikel, samt att modernukliden kan besitta olika excitationsenergier som ger ytterligare grund för en experimentellt uppmätt flora av [mindre] olika diskreta alfaenergier.

— Det visar sig [nämligen] att OM föreställningen om en FAST halveringstid för en FAST sönderfallsenergi ska ha någon ENTYDIG fysikalisk mening [Geiger-Nuttalls empiriska samband med Sönderfallets enhetliga preferensgrund] finns bara en och endast en enda möjlighet: Att sönderfallsenergin i alfafallet räknas på atomvikterna via effektiva massa‑energidifferenser.

— Genom att använda alfapartikelns rörelsemängd som IDEAL grund förenklas därmed härledningen väsentligt då slutformen sedan, enkelt, kan — och kommer att — återföras på sönderfallsenergin av princip. Hur sambanden ser ut i slutänden kommer att framgå, detaljerat, av den följande beskrivningen.

Se även motsvarande TNED-teori för betasönderfallets mekanik i Betasönderfallens matematiska fysik i TNED och Nuklidfaktorn i betasönderfallet — Halveringstidssambandet för betasönderfallen; i TNED kan samma grundform tillämpas generellt för samtliga fall. Notera dock de övergripande svårigheterna i översiktsbilden generellt för hela gruppen instabila atomer; Se särskild beskrivning — i översikt — från Fragmenteringsargumentet.

Rekylverkans impulssumma –m1v1=m2v2 [tyngdpunktens rörelsemängd bevaras] som ger –v1=(m2/m1)v2 och därmed

vLAB=v2–v1=v2(1–m2/m1) innebär bara en marginell reduktion [m1&m2 nedan resp. Helium och Uran]

[1–4/238=1–0,0168067=0,9831932] — i allmänhet med m1=Moderpartikeln [typ Uran-238] och m2=Helium-4-kärnan.

— Heliumkärnan frigörs med en kraft som [kan förstås] utbildas från Moderkärnan. Därmed utges Heliumkärnan också relativt Moderkärnan.

— I LABORATORIETS REFERENS syns emellertid bara Heliumkärnans rörelseenergi [vLAB], som alltså framstår något mindre än den som kärnans kastades ut på från Moderkärnan [v2].

— För OBSERVATIONSÄNDAMÅL ska alla experimentellt angivna data anges i LABORATORIETS REFERENS [om inte annat anges], analogt som en observatör eller en fast mätsensor ser det — om inte uppgifterna generellt ska urarta i referenskaos.

— Jämför artikeln om Decay energy på Wikipedia [2011-10-20]: inte ett enda ord sägs om FRAME [lab, laboratory eller annat]. Vi måste dock utgå ifrån att ALLA observationsdata är LAB-data, som ett fast mätinstrument ser det, om inget annat anges.

— I TNED figurerar inte Coulombkraftens normalt ömsesidiga yttre kärnrepulsion vid fission (figuren ovan ger viss orientering):

— Med spinnets bevarande avdelas alla kärndelar (analogt med hydrodynamikens vattendroppsexempel) i spinnaxelns riktning och väsentligen via en utkastande kraft F=p/t=ma=mv/t.

— Den enda elektriska parameter som TNED använder för moderkärnans del är en möjlig variation i atomkärnans kraftstruktur via ett det (motsvarande nukleära) kapacitivitetstalet (ε). Moderkärnans ytelektriska laddning (Z) figurerar inte i TNED vid fission — eftersom det i vilket fall är centralmassivets laddningsstruktur (±A909e) som ombesörjer och verkställer funktionen: Ze är helt försumbart vid sidan av moderkärnans verkställande kraftdel ±A909e. Det enda vi behöver veta i moderkärnans fall är (således) moderkärnans massa (för beräkningen av rekylverkan via vLAB) — samt dess avgörande (relativa) »radioaktiva kärnstyvhet» som nuklidkoefficienten Ñ (Ñ, »N-variabeln», varierar i stort [för huvuddelen av radionukliderna] mellan 0,25-1,25, men kan i princip, med alla universums lokaler innefattade enligt TNED, innefatta allt möjligt mellan ±2). Ñ är den avgörande nuklidfaktor som enligt TNED tydligen får förstås finbestämma kraftmagnituden och därmed den slutliga rörelseenergin i alfapartikelns avdelning från moderkärnan. Höga Ñ är, som det visar sig, i allmänhet förknippade med långa halveringstider (och låga sönderfallsenergier), låga Ñ med korta halveringstider (och något större sönderfallsenergier).

— Något direkt samband som utpekar ett visst Ñ-värde för en viss nuklid finns här veterligt inte; Ñ-koefficienten kopplar helt säkert till neutronkvoterna i TNED-teorin för den primära grundämnesbildningen (Utförlig genomgång i Inledningen), typ det primära ursprunget för Uran-238. Men eftersom Ñ-faktorn bara är aktuell VID sönderfallet (då atomkärnan avdelar motsvarande sönderfallselement), finns heller ingen normalt tillgänglig referensbild med vars hjälp ytterligare upplysningar om Ñ-faktorn kommer i dagen.

— PROBLEMET är alltså det, att »kärnstyvheten» Ñ är en specialparameter som (veterligt, enligt TNED) bara sammanhänger med (vad atomkärnan visar upp vid) radioaktiva sönderfall (fissionen), och primärt vad atomkärnan genomgår vid den aktuella nuklidens primära bildning (fusionen). Innefattas neutrinostrålningens möjligheter i denna bild generellt, blir Ñ-faktorn även beroende av parametrar som, explicit efter nuklidens bildning, också ligger utanför Jordlokalens domäner, t.ex. en möjlig influens från Solen; Ñ kan inte bestämmas ensidigt »universell» med (enbart) Jordlokalen som mätpreferens — därför att olika lokaler i grundämnets bildning [‡] sammanhänger dels med olika energigenomströmningar, dels med de olika primära bildningslokalernas nuklidkvoter [Se Neutronkvotens avgörande inverkan], och därmed möjliga sätt att påverka Ñ.

— Genom att — eller möjligen OM — varje radionuklidfamilj enligt TNED har sitt specifika neutrinospektrum, fördjupas problemet ytterligare genom att olika radionukliders specifika Ñ kan konserveras (»bakas») i nuklidbildningen: Bildningslokalen bildar en (konserverad) preferens; Olika radionuklider påverkas olika av (och genom) varandra.

— Eftersom vi (således, enligt TNED) inte känner basdata, måste — tvunget — kärnparametern Ñ beräknas via mätdata utifrån uppmätt halveringstid (tH) och radioaktivitet ξ (här grek. xsi; se även särskild termbeskrivning i Radiotermer om ej redan bekant). Först med Ñ så bestämd kan ytterligare detaljer avgöras (enligt TNED), och då bara säkert med Jordkroppens aktuella radionuklid (Ñ) som känd preferens.

— Kärnstrukturens förmåga att växla, ändra och utnyttja ±e-strukturen (±A909e) borgar i vilket fall för en effektiv avdelning av en delkärna i själva det avdelande ögonblicket (samt i motsvarande omvända fall, fusion). Kärndelarna som Coulombiska element i bilden av vad atomkärnorna ser genom varandras gemensamt riktade kärnspinn på närhåll där fusioner-fissioner figurerar enligt TNED skymmer, också i vilket fall, det mesta av kärnornas normalt — över de större avstånden — verksamma Coulombiska krafter. På stora avstånd är kärnornas inbördes spinnsynkronisering (som bara realiseras då kärnorna vidrör och inträder varandras nuklidbarriärer, analogt vid fusion-fission) helt bortkopplad och därmed den »fullt normala» Coulombiska kraft som därmed aldrig aktualiseras i TNED i härledningen av det radioaktiva sönderfallets grundmatematik. Den Coulombbilden används alltså inte här utom för att specificera den avdelade partikelns kärnladdning (eZ, vanligen 2Helium4-kärnan eller den s.k. alfapartikeln) via elektriska kraftlagen generellt. Den avdelande Moderkärnans kärnladdning bortses således helt ifrån. (Kärnladdningen Z ligger i vilket fall från Vismuts Z=83 och naturligt upp till Uranets Z=92 [upp till numera (2011) 118 för de artificiellt producerade radionukliderna], samt i några enstaka fall lägre för en del lättare grundämnen [2Helium, 3Litium, 4Beryllium, 5Bor, 17Klor, 62Samarium, 63Europium, 64Gadolinium, 65Terbium, 66Dysprosium, 67Holmium, 68Erbium]).

— Däremot är moderkärnans elektriska töjbarhet eller den motsvarande mekaniska styvheten avgörande (som bestämmer den avdelande kraftens styrka [motsv. vattnets eller vätskans viskositet, flytbarheten]).

— Kärnstyvheten kan som nyligen vidrörts i TNED relateras till kapacitivitetstalet (ε0) på ett speciellt sätt (Ñε0, maxÑ=±2) [Se från Nuklidkoefficienten] — men (ännu i TNED) utan direkt identifikation med någon specifik modernuklid; Villkoren ställer upp olika lokaler med inbördes beroenden som i stort sett gör hela den analysen »omöjlig». Utförligt i Inledningen.

— Det är (ännu i TNED) bara delvis (teoretiskt) genomlyst hur en viss (radioaktiv) nuklid kopplar ämnet, se särskilt från Neutronkvotens avgörande inverkan. Det finns dock vissa experimentella paralleller (typ observerad påverkan av Solneutrinoirradiansen på Jordkroppen, Jenkins et al., från 2006).

— Den analysen står (följaktligen) till vissa delar under författning i denna presentation.

Halveringstiden (tH) kan beräknas ur mätvärden om man från ett känt preparat kan mäta radioaktiviteten (ξ [här grek. xsi] i Bq, Becquerel, antal sönderfall per sekund [gånger ln2]) enligt

t_H = (ln2)N₀/ξ_N

[N₀ =m_MASSAN/u_1,66033
t27U_ATOMVIKTEN]

Genom att också — idealt — mäta radionuklidernas medelmässiga alfaenergier (E_α) kan man beräkna moderkärnans motsvarande medelmässiga b-Ñ-värde ur sambandet för halveringstiden (TNED-versionen av Geiger-Nuttalls samband)

t_H = [(ln2)/A]e^be^Z/√2mE

enligt (mZE anger alfapartikeln, A=1Hz=1/1S)

b = [√2mE]ln[t_HA/(ln2)]/eZ

= [mv]ln[t_HA/(ln2)]/eZ

— Frågan om alfaenergiernas uppmätning är emellertid också komplicerad:

— Ingen entydigt bestämd värdeform finns i praktiken;

— Alfaenergierna [Se Alfaenergier, olika kanaler i mätdata] uppvisar i praktiken grupper med olika värden (s.k. kanaler från eng. channels). Det betyder, i TNED, att vissa komplikationer kommer in i bilden beträffande den enhetliga tolkningsbilden av halveringstider och sönderfallsenergier. En utförligt genomgång av detaljerna beskrivs här från Fragmenteringsargumentet, med vidare jämförande exempel i den sammanställda AlfaRadioIsotopkartan.

Vi kan i vilket fall, här enligt TNED på grund av den obestämbara nuklidfaktorn och som omnämndes längre upp i Problemet, inte bestämma »en absolut halveringstid tH» för ett visst radioämne UTAN att också känna alla omkringliggande — kosmiska, Solära — parametervärden tillsammans med den aktuella atomkärnans elektromekanik — vilket veterligt tecknar en omöjlig ekvation;

— Det vi kan göra är att utnyttja situationen för att försöka bestämma [eller pröva] radionuklidens kärnstatus [b=4πÑ] från experimentella mätningar [tH och ξ] och sedan därifrån försöka med gåtan om ev. inverkan från övriga lokaler, t.ex. inverkan från den varierande neutrinoinstrålningen från Solen — om det är den som gäller.

Grunden för Ñ — NUKLIDKOEFFICIENTEN

Nukleära kapacitiviteten

Grundteorin för energimiljöns inverkan på radionukliderna i bildningstillfället — enligt relaterad fysik

grundteorin för energimiljöns inverkan på radionukliderna i bildningstillfället

Från Slutformen till tH-sambandet:

— Det säger dock INGENTING OM ORSAKEN till den aktuella p=mv. Alltså i princip kan det vara ... /[p+INITIERING från nuklidbildningen].

— RIBBAN placeras olika högt för olika nuklidmassor [materialblock] av samma typ beroende på energitätheten där de bildades.

— SAMT ÄVEN att TYP Solen, genom neutrinoinfluens OCKSÅ kan påverka p-summan, så att medellivet — radioaktiviteten — SES variera.

— Har atomkärnan ett högre energiinnerhåll än normalt [eller lägre], är det klart att också varje utträngande rörelsemängd får ta del av den aktiviteten.

— EFTERSOM p bildas först ur atomkärnan vid sönderfallet — inte att p finns FÖRE — INGÅR »kärnnivån» automatiskt.

RADIONUKLIDENS EGENSKAP är just att uppvisa instabilitet = inre självsvängning, ett pågående arbete som underhåller instabiliteten tills jämvikt (sönderfall) uppnås. I det tunga (kärnsönderfallande) radiofallet uppnås stabilitet efter första eller flera efterföljande kärnsönderfall, eller en kombination av sådana och det lättare betasönderfallet.

— Teorin i TNED för radionuklidens bildning blir därmed »enkel»:

— Med minsta möjliga lokala energigenomströmning (neutrinostrålning , endast den kan påverka kärnstrukturen enligt TNED) bildas också motsvarande kärninstabila nuklider (radionuklider) med största möjliga »kärnseghet» och därmed maximalt långa sönderfallstider. Se vidare kraftledet (F) nedan.

— Med allt högre neutrinobaserad energigenomströmning (E) i bildningslokalen kan E (till viss del, vilket vi måste förutsätta) tillfälligt för sönderfallets fysik KONSERVERAS av kärnstrukturen TILLSAMMANS med den ordinarie radioinstabila kärnstrukturens nuklidindividuella karaktär. Den extra neutrinoinfluensen SKULLE därmed medföra samtidigt, följaktligen i konsekvens av kärnseghetens princip om det här resonemanget håller streck, att kärnsönderfallet snabbas upp — marginellt eller påtagligt med växande energitillskott; större energi, snabbare process.

— När nuklidbildningarna — generellt naturligt enligt TNED — väl har genomförts, finns inte längre samma förutsättningar för yttre (neutrinoinfluerad) påverkan [jämför de olika bildningslokalerna enligt TNED];

Från Jordens Tredje Ekvation; Solsystemets kroppar efter samma täthet.

— RELATERAD FYSIK: Varje himlakropp och område [meteorider] mellan himlakropparna [Se G-skuggning] har sin egen specifika grundämnesbildningslokal med specifika förutsättningar [Se GRUNDÄMNESBILDNINGEN]. MÖJLIGEN spelar den övergripande energimiljön vid nuklidbildningen enligt TNED [typ hela Jordkroppen, knappast enskilda partikelexperiment i CERN] en roll för de olika radioaktiva nuklidernas EVENTUELLT OLIKA fason i olika bildningslokaler;

— Men vi vet inte det här [ÄN, säkert].

— Vissa observationer [Jenkins et al., 2008] av radioaktiva sönderfall som varierar med avståndet till Solen [årliga periodiskt återkommande variationer i storleksordningen 0,1%] har tillkännagivits, vilket skulle vara en [säker] indikering. Det finns dock ännu [Nov2011] ingenting säkert framställt i ämnet — man har ingen teori för ett sådant fenomen i modern akademi. Här undersöks ev. förutsättningar enligt TNED, enbart: Vi eftersöker en enhetlig — uttolkningsbar — matematik, om alls.

— Neutrinoenergierna är tvunget (våldsamt) höga i bildningstillfället (Jämför Udda och Jämna nuklidserierna), för att sedan i stort sett bara återfinnas från de resulterande himlakropparnas radionuklider, samt från centraldelarna i stjärnornas energiomsättning (Väte till Helium). En viss neutrinoinfluerad påverkan måste alltså av princip fortfarande finnas, men då i betydligt mindre omfattning än vid nuklidbildningarna enligt TNED (Se från GRUNDÄMNESBILDNINGEN). Det mesta vi kan få bevittna i det avseendet bör alltså i vårt fall vara inverkan från Solen — frånsett vår egen radionuklidbaserade Jordbank av (största andelen) främst Thorium och Uran, men som för vår del (i enstaka människoåldrar sett) framstår som tämligen konstant.

— Klart. Det är hela teorin.

— Ju mera energi som kärnan kan ta upp vid sin bildning, ju högre blir potentialen att också göra sig av med tillskottet.

— Det ansluter perfekt till den allmänna FLÖDESFYSIK vi ständigt ser i de naturliga sammanhangen: ju mera vatten i röret, desto högre tryck och desto större benägenhet att utjämna. Ju högre spänning, desto kraftigare urladdning. I radionuklidernas fall betyder den extra kraften speciellt kort medelliv (î). Liten kraft, långt medelliv. Påverkas individen kraftmässigt i någon nämnvärd utsträckning, förkortas också (i allmänhet) medellivet.

Kraftledet

— I elektriska kraftlagen F = (1/4πε₀Ñ)(Q/r)² [Ñ förklaras nedan] tillväxer kraften (F) om laddningens (eller materialets i makrofysiken) elektriska ledningsförmåga (1/Ñε₀) ökar — analogt då Ñε₀→0.

— I makrofysiken kan emellertid Ñε₀ bara öka (med Ñ från lägst 1), vilket motsvarar en allt större elektrisk isolation; Högre Ñ-värde, större isolation. Atomkärnan — som ett HÄR TILL PRÖVNING motsvarande elektriskt hårt (höga Ñ) eller mjukt (låga Ñ) material — behöver inte bry sig om den omständigheten. Anledningen är sambanden i POTENTIALBARRIÄREN med energizonen, som ställer upp (delvis) andra möjligheter i kärnfallet:

— Med en särskilt avgränsad specifik nuklidorienterad principiell form för Ñ-koefficienten enligt Ñ=ç/c_z — med c_z från potentialbarriären (energizonen) och vilken form här kommer att användas för vidare — inte bara kan Ñ förstås bli mindre än 1 av princip, utan uppvisar också ett motsvarande praktiskt exempelfall om vi får låna specifika värden från redan härledda komplex (Ñ=0,0145936, se Ñ-sambanden, ç/c_z=Ñ). Nämligen i fallet med elektronmassans komponenter enligt härledningarna i Spektrum [Se divergensvärdet v=2,18..T6 M/S i Väteatomens grundradie]; Se beskrivning i Exempelreferens. Det väsentliga i exemplet är vätespektrumets c_z-värde (v); Det faktum att det alls kan ha någon värdeform mindre än c_z=c₀/2 är det enda bevis som behövs (här) för att (också till vidare prövning) kunna bygga en praktiskt förankrad nuklidkoefficientform just av typen Ñ=ç/c_z; Utan ett praktiskt värdeexempel, skulle heller ingen vidare framställning kunna göras (med någon praktisk förankring). Det, och inget annat, bildar förutsättningen för den vidare framställningen.

— Med stöd av resultatet i härledningen till Vätets spektrum finns (således) visst skäl för en prövande härledning; Syftet är (också) att uttnyttja tillfället för att försöka härleda (påvisa) en »exakt samma princip» för atomkärnans egen inre kärnstruktur, där elektronmassans komponenter ingår som ekvivalenta fraktalnivåer.

För grundbegrepp, se utförligt från Atomkärnans härledning, samt även i ELEKTRONMASSANS KOMPONENTER om ej redan bekant.

D=Q/A=ε₀ΞÑ

SAMMANFATTNING — hur atomkärnans elektriska fysik kan förstås variera med radionuklidernas sönderfallstider

— Energigenomströmningen vid radionuklidens bildning KONSERVERAS av radionuklidens instabilitet, självsvängningen, samt avtar [möjligen] med tiden i ämnets sönderfall.

— Sönderfallskraften [F=K/Ñ] ökar med det lägre Ñ i sönderfallstillfället. Ñ<1 kan inte visa sig makrofysiskt på annat sätt.

— Resonemanget stämmer också med impulsmomentets bevarande, h=mcr, med bildningsenergin innefattad:

— För att bevara h=konstant med konstant divergens c, nuklidmassan m och tyngdcirkelradien r, måste med ett energitillskott till m [massenergi] nuklidens tyngdcirkelradie avta. Men energitillskottet i radionuklidernas fall sammanhänger med NUKLIDINSTABILITET. Vilket betyder att nukliden TVUNGET självsvänger omkring [den reducerade] tyngdcirkeln; Svängningen innebär att en och samma tyngdcirkel kan uppvisa många olika YTFASONER beroende på svängningens form.

— Därmed blir laddningstätheten D=Q/A med givet Q också lägre i den svängande radionukliden i proportion till det [möjliga] lokala energitillskottet vid radionuklidens bildning.

— MEN: Det skulle betyda att en motsvarande MINDRE YTA med högre laddningstäthet D=Q/A, och därmed ett större Ñ-värde än 1, vore omöjlig enbart i kraft av den mindre kärntyngdcirkelns koppling till den högre energins större svängande kärnyta [generellt kan atomkärnan inte komprimeras i TNED, se Atomkärnans inkompressibilitet].

— Det finns en utväg ur detta till synes nedslående argument.

— Atomkärnans svängning omkring tyngdcirkeln på grund av kärnans instabilitet, samt tyngdcirkelns extra indragning [för impulsmomentets bevarande] på grund av extra tillförd energi [som ökar självsvängningen] är för Ñ-faktorns del betydelsefull endast vid själva kärnsönderfallet. Ñ-faktorn har ingen annan funktion att fylla i den matematiskt beskrivande uppsatsen enligt TNED, än just att FÖRKLARA den avdelade alfapartikeln, dess laddning Q och impuls p. Inget annat.

— Vi VET redan — i termer av TNED via POTENTIALBARRIÄREN och nuklidbildningarnas fysik — att STORA [kortvariga] självsvängningsförlopp inträder VID fusion (förening), och fission (delning), SAMT att atomkärnan vid dessa tillfällen TVUNGET måste exponera centralmassivets ±A909e, A här masstalet, allt eftersom kärnans balansräkning kräver det.

— Problemet avgörs alltså på termen Q; Laddningstäthetens TILLVÄXT D=Q/A=ε₀ΞÑ i sönderfallsögonblicket, då också Ñ visar sig, nämligen för tillfället att avdela alfaQ med alfap, kan tydligen ekvivalent återföras på just kärnans uppvisning av den inre, normalt gömda Q-bankens förkrossande normalt sett gömda potential [±A909e]. Med andra ord; Vi behöver, tydligen inte alls, koncentrera HÄRLEDNINGEN av varierande D, analogt Ñ, på kärnytan, utan kan istället LUGNT se händelseutvecklingen i försorg av det tillfälla Q-kapitalets inre föreställningar: Q kan tillfälligt ÖKA [eller minska] för att definiera visningen av det högre [eller lägre] Ñ-värdet vid alfapartikelns avdelning. Och sedan åter till normala Ñ=1.

— Det lägre eller högre Ñ i radionuklidens självsvängning SKULLE ALLTSÅ visa sig, således, endast då radionukliden sönderfaller.

— Därmed kan ändringen i D=Q/A=ε₀ΞÑ vid sönderfallet helt återföras på kärnans inre Q-dynamik via centralmassivets ±A909e, A här masstalet.

— Vi behöver aldrig, explicit, BLANDA IN den stadigvarande kärnytan [A i D=Q/A] i komplexet, den delen gäller i vilket fall INTE vid själva sönderfallet.

— Radionuklidens radioaktivitet skulle därför, också i summa sagt, MÖJLIGEN HELT kunna återföras på nuklider som skiljer sig från Ñ=1.

— I så fall ska vi INTE hitta någon enda radionuklid med b-värdet Ñ4π=12,56637. I tabellen till KÄLLEXEMPLET ingår en individ med närmaste b-värdet b=12,038343 från Hafnium [Hf]-174 med halveringstiden tH=2 T15 år och alfaenergin Eα=2,5 MeV. Närmast övriga ligger på 11 och 16.

— Nuklidsjälvsvängningens underhållande drivkraft tvingar [möjligen] den upplagrade tillskottsbildningsenergin att avges successivt [i hur små portioner som helst enligt Plancks Strukturkonstant], och därmed i konsekvens [möjligen] en inre normalisering i tidens längd mot Ñ=1. Genom att [emellertid] energi alltid avges i sönderfallen ligger det närmare till hands att också ev. upplagrad extraenergin omsätts vid dessa tillfällen. Därmed kan en normalisering till Ñ=1 förstås ske automatiskt för alla nuklider vars sönderfall resulterar i ett stabilt tillstånd. [Ingen extra normaliseringsteori behövs].

Nukleära kapacitiviteten — grunden

2011X22

Nukleära kapacitiviteten — Ñ Läs som N-variabel [Alt+0209]

VAD VI VET enligt TNED (i min referens) är att atomkärnans fasta egenskaper bara kan påverkas rudimentärt då nukliden bildas, alltså vid fusion (förening) eller fission (delning). Se från GRUNDÄMNESBILDNINGEN enligt relaterad fysik, om ej redan bekant. Bildningslokalens energigenomströmning bör, om den är märkbar, spela viss roll [exakt hur finns ingen framställning på — utöver det som omnämnts i föregående block];

— Utöver dessa tillfällen finns bara en RENT TEKNISK möjlighet. Nämligen via neutrinopåverkan. Neutrinostrålning en i TNED [Se utförligt från NEUTRINOSPEKTRUM] kan påverka en atomkärna om Plancknivån [E=hf=(h/n)fn] är anpassad för en sådan påverkan. Vilket som gäller bestäms av den aktuella atomkärnans egen fraktalstruktur.

— Det finns dock här ingen (enligt TNED) känd generell matematik som beskriver de olika fallen utöver den allmänna matematiska fysik som beskrivs nedan i Nukleära kapacitivitetens matematiska fysik med grund i elektriska kraftlagen.

Härledningen till halveringstidssambandet fortsätter — efter mellanstycket nedan — från Grunden.

Nukleära kapacitiviteten — matematiken

Se Grunden från NUKLIDKOEFFICIENTEN

2011X21

Nukleära kapacitivitetens matematiska fysik — matematiken för Ñ Läs som N-variabel

— Om det gäller atomkärnan enligt TNED [se Potentialbarriären] finns ett allmängiltigt sätt att relatera varierande laddningstäthet D, både uppåt och neråt, som funktion av kärnsvängningar i princip.

ε₀ = 1/R₀c₀ = 1/Rc = 1/2Rc_z ;

— Erinra först makrofysikens begrepp [Se termerna nedan mera utförligt i Elektrisk och Magnetisk Polarisation]:

D = Q/A = ε₀Ξ + nε₀Ξ = ε₀Ξ(1 + n) = ε₀Ξε_r dielektricitetstalet ε_r ALLTID större än 1, D ökar (A minskar)

Exempelreferens Spektrum

Nukleära kapacitivitetsfaktorn Ñ

Praktisk, säker exempelreferens från Vätets Spektrum:

— I Spektrum fick vi till jämförelse [Se Väteatomens grundradie] den motsvarande DIVERGENSEN v=ξ/n [ξ, xsi] enligt 2,1875325 T6 M/S eller v/c(0)=0,00729682, eller avrundat 7/1000 av c(0).

— Den praktiken visar att en teori för en »nukleär kapacitivitet» [Ñ] kan antas — för vidare prövning — här, endast, med stöd i ovannämnda tillämpbarhet på elektronmassans komponenter, och därigenom via neutronsönderfallet en motsvarande PRINCIPIELL förankring i atomkärnan, och endast så;

— Kärnomvandlingar enligt TNED innefattar i vilket fall POTENTIALBARRIÄREN med ALLA inre möjliga omsättningar av atomkärnans centralmassiv ±A909e; Kärnan avgör själv, från fall till fall, vad som gäller, och det är (således) här en helt meningslös uppgift att försöka reda ut »alla möjliga fall» genom »en enhetlig ekvation». Vi behöver [därför] endast koncentrera oss på de enklaste grundsambanden;

Beskrivning, divergensgränserna ç=±c0

— I normala fall ligger energizonen — där elektriska laddningens massa TAS enligt relaterad fysik — vid c(0)/2=c(z).

— OM — på samma sätt som i härledningarna i SPEKTRUM men här omsatt på motsvarande fall i atomkärnans fraktalstruktur — svängningar omkring nuklidens tyngdcirkel sätts i samband med varierande eller fluktuerande kopplingar till c(z), och ALLA MÖJLIGA FALL beaktas — även inkluderat omkastningar av flödesriktningarna i kärnmassivets ±A909e, och som därmed även innefattar alla antipartikelfall — är det tydligt att variationer i c(z) som ç (c-komma) som mest kan omspänna ç=±c(0). Det bildar den praktiska och teoretiska absolutgränsen för kärnans dynamik, samtliga möjliga fall medtagna. Vi kan därmed sätta »nukleära kapacitivitetskoefficienten»

Ñ=ç/c_z som kopplar till elektriska kraftlagen F = (1/4πε₀Ñ)(Q/r)² = (Q/4πε₀Ñ)Q/r² = (Q/4πε₀Ñ)Q/r² [sfäriskt via 4π] enligt följande:

— En generell »nuklidkapacitivitet» SOM obs BARA KAN FÖRSTÅS GÄLLA VID DET AKTUELLA KÄRNSÖNDERFALLETS TILLFÄLLE, inget annat, gäller enligt

Ñε₀ = 1/Rç = ε₀ ± ñε₀ = ε₀(1±ñ);

— Sammansättningen för laddningstätheten [D, se Elektrisk och Magnetisk Polarisation] totalt i atomkärnan under fission [och fusion] kan då skrivas

D = Q/A = ε₀Ξ ± nε₀(Ξ) = ε₀Ξ(1 ± ñ) = ε₀ΞÑ med nukleära dielektricitetstalet Ñ; D minskar (A ökar), eller D ökar (A minskar), med Ñ.

— Atomkärnans relaterade dielektricitetsfaktor — här specifikt relaterad för radioaktiva nuklider — påverkar inte makrofysikens elektrodynamik.

Ñ-sambanden

— Kärnytans [A] variation omkring kärnspinntyngdcirkeln som specifik följd av den radioaktiva nuklidens självsvängning SPECIELLT VID DET AKTUELLA KÄRNSÖNDERFALLETS TILLFÄLLE, relativt det fasta Q, kan DÅ tolkas som en funktion av motsvarande indragningar eller utvidgningar:

— indragning: ÑDç avtar [b→0, tH→0, »kärnan mjuknar»], ytan A ökar; utvidgning: ÑDç ökar, ytan A avtar [b→∞, tH→∞, »kärnan hårdnar»].

— Ñ måste TVUNGET kunna bli NEGATIVT; Ñ=x/4π; ç/c_z = Ñ = max±2, ç (max ±c₀) kan bli negativt (omvänt flöde, samma som antipartikelform) ...

— ±x_max blir b=(Ñ=±2)×4π=±25,132741 (om inga andra koefficienter spelar in).

— indragning: ÑDç avtar [b→0, tH→0, »kärnan mjuknar»], ytan A ökar; utvidgning: ÑDç ökar, ytan A avtar [b→∞, tH→∞, »kärnan hårdnar»].

— RESULTATET av varierande Ñ [normalt=1 för stabila nuklider] för atomkärnans del skulle därmed bara bli att kärnan I ALLMÄNHET agerar mer

[kortare halveringstid] eller mindre

[längre halveringstid] styv, töjbar och därmed AVDELNINGSBAR [»delningspermeabel»] [permeabel, genomsläpplig] —

samt att dessa egenskaper SPECIFIKT endast kopplar till tungt [kärnsönderfallande] radioaktiva nuklider, och då, VID det aktuella kärnsönderfallet.

Inget annat. INGET ANNAT. Noga.

— M.a.o.:

— ENDAST tillfället för den kärnavdelande proceduren.

PraktikKollen

— GRUNDMATEMATIKEN ovan stämmer [tämligen hyfsat] med tillgängliga data på halveringstider och alfaenergier. Högre b-värden = längre halveringstider. Korta halveringstider = låga b-värden; Hittills, enligt etablerade tabellverk [Se KÄLLEXEMPEL]; Största b=17,62 och lägsta b=–6,25 [[Tabell1KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]]. Vi känner dock [här, ännu] ingen matematisk fysik som FULLSTÄNDIGT förklarar hur Ñ-faktorn kopplar till olika nuklidfamiljer — utöver grundteorin för energimiljöns inverkan på radionukliderna i bildningstillfället.

— Men den delen är emellertid, uppenbarligen, ändå INTE tillräcklig i sig för att förklara floran av olika b-nuklidvärden eftersom känsligheten tydligen är SÅ stor [Se Dramatisk känslighet från KÄLLEXEMPEL] att möjligen [vilket här ännu inte är klarlagt] inverkan från Solen KAN spela viss roll — eller generellt jämförelser mellan olika lokaler med Jordkroppens nuklider som FÖRMODAD UNIVERSELL preferens. Det är vad som måste undersökas vidare.

Insättning i sönderfallets grundsamband e^b^Q/p

Med som ovan härletts — enligt TNED — nukleära kapacitivitetsfaktorn (Ñ, Alt+0209)

D = Q/A = ε₀Ξ ± nε₀(Ξ) = ε₀Ξ(1 ± ñ) = ε₀ΞÑ nukleära dielektricitetstalet Ñ, D minskar (A ökar) eller ökar (A minskar) med Ñ;

därmed

;

U=Fr/Q=Rc(Q/r)=(p/t)r/Q=pv/Q=E/Q, som ger U/v=p/Q

;

F = (1/4πε₀Ñ)(Q/r)² = (Q/4πε₀Ñ)Q/r² = (Q/4πε₀Ñ)Q/r² ; sfäriska

Fr = (Q/4πÑ)Q/rε₀ ;

b-koefficienten

Nukleära Kapacitiviteten

Q = (Q/4πÑ) ; b = 4πÑ ; alfapartikeln som avdelas vid avdelningstillfället: Ñ tillhör explicit den radioaktiva moderpartikeln

Q = (Q/b) ; Q avdelas ur moderkärnans Q/b

Fr/Q = Q/rε₀ = U ;

F = ma = mv/t = p/t ;

Fr/Q = U = (p/t)r/Q = pr/tQ = pv/Q ;

U/v = p/Q = p/(Q/b) = bp/Q ;

Q/p = (Q/b)/p ;

bQ/p = Q/p ; För att enhetsbilda storheten i v/U=Q/p med enheten M/VS måste b associeras med en enhet VS/M

bQ/p = 4πÑQ/p

= 4πeZÑ/p

;

Ñ i atomkärnan [med utvidgat område] ersätter makrofysikens ε_r.

makrofysikens begrepp till jämförelse:

D = Q/A = ε₀Ξ + nε₀Ξ = ε₀Ξ(1 + n) = ε₀Ξε_r dielektricitetstalet ε_r ALLTID större än (eller=) 1, D ökar (A minskar).

Se vidare i beskrivningen från HÄRLEDNINGEN.

B/p — från Slutformen i härledningen till sambandet för halveringstiden, exponenten till e-formen

BILDKÄLLA: Författarens arkiv · 2009IV20 · NikonD90

B/p

Hydrodynamiken hjälper till med tolkningen av faktorkoefficienten B i förening med impulsen p=mv.

— I TNED finns inga snurrande alfapartiklar i atomkärnan. Alfapartikeln avdelas istället enligt TNED på samma sätt som i fallet med vattendroppar. Avdelningstillfället avbildar en spänningstöjning (både mekanisk och elektrisk) som hjälper oss till »korrekt sambandsform direkt».

För ändamålet kan användas en term med begrepp »(nukleär-) elektrisk töjning» [Ξt=U/v=p/Q, VS/M];

— När moderkärnan avdelar en (eller flera) partikel uppvisas naturligt en motsvarande spänningsbildning mellan de olika delar som ansvarar för kärnans deformation, just i avdelningstillfället, och som leder till själva avdelningen. Grundformen, TNED, fås ur elektriska kraftlagen

F=Rc(Q/r)² enligt U=Fr/Q=Rc(Q/r)=(p/t)r/Q=pv/Q=E/Q, som ger U/v=p/Q.

— Inför vi nämligen B=bQ med b-koefficienten b=U/v en nuklidens elektriska töjningskoefficient (b, VS/M) [»kärnstyvheten»]

ges korrekta fysikaliska storheter med numerisk enhetsform

b(VS/M)(Q/p)(M/VS) = b(Q/p)

ALLMÄNNA sambandet från föregående utvecklingar för det radioaktiva sönderfallets halveringstid (t_H) enligt TNED får då formen

N₀î = _K=[S(ln2)]e^B/p = t_H = Ke^B/p

= Ke^b^Q/p

= Ke^be^Z/mv

= Ke^be^Z/√2mE

— För sammansättningen av töjningskoefficienten b, se Nukleära kapacitiviteten enligt TNED.

— Med radioexemplet U-238 på Heliumkärnans (U=4, Z=2) alfaenergi E=4,267 MeV för t_H=4,51 T9 år och med A=1, inga andra termer, blir b=11,8555 VS/M. Ökas »kärnstyvheten» b med bara 1,74% till b=12,06 fördubblas t_H till 9,02 T9 år. Det är alltså väldigt känsligt.

Grund, Inledning

Härledningen till sambandet för halveringstiden enligt TNED

Se även konv. Geiger-Nuttalls samband.

— INLEDNINGEN ger en mera beskrivande förklaring till bakgrunden för följande rent matematiska utläggning:

Termerna nedan beskrivs utförligt i Parameterbegrepp — t_H halveringstid (konv. ofta T½), î medelliv, N₀ utgångsmängd radionuklider;

— Från t_H=N₀î=[p=mv]/[F=ma]=v/a=v/(v/t)=t=p/F ges varianten (dy/dx)

(1) N₀î = t_H = –dp/dF = âî

För att medge optimala koefficienter för senare enhetsanpassning av fysikaliska storheter används här a-flex [Alt+0226], â=koefficienter·N₀ som ger det enklare

âî = –dp/dF = t_H = koefficienter·N₀î

Minustecknet [negativ tangensform \] anger att funktionskurvan för medellivet (î) måste avta (ändras omvänt \) med växande rörelsemängd (impulsen p=mv) med avseende på den verksamma sönderfallskraften F=ma.

Motivation

— Det avtagande î för växande F (för en viss kärnpartikel med given tyngdcirkelradie r) motiveras generellt av Planckenergin E=hf=h/T=Fd; ET=h=mcr=konstant; Ökar Energin måste Tiden avta för att bevara nuklidens massa (och energi), toppdivergensen (c0) och kärnradiens ekvivalenta tyngdcirkelradie (r).

Differentialekvation

— Därmed differentialekvationen

(2) dF = –(âî)^–1p dp = d[dp/dt] ; a-flex [Alt+0226] â = [A/B(ln2)]koefficienter · N₀

med lösningen

∫ dF = –(âî)^–1 ∫ p dp = ∫ d[dp/dt]

(3) F = –(âî)^–1(1/2)p² = dp/dt

Kraftvarianten (impulsderivatan) F=p/t=dp/dt ger ytterligare en (möjlig) variant

(4) dp/dt = –(âî)^–1(1/2)p²

med differentialekvationen

(5) 2p^–2dp = –dt(âî)^–1 ; 2p^–2dp = –dt([A/B(ln2)]N₀î)^–1

med lösningen

∫ 2p^–2dp = – ∫ dt(âî)^–1

— Erinra från FORMLAGARNA att

∫ dx/(Ax) = ln(Ax), = ∫ dx/(x) = lnx ; [ln(P)]’=(P)’/(P), se Logaritmderivatan; (Dn Ax)/Ax = A/Ax = 1/x ;

Funktionskurvan för ln[Ax] har konstant derivata [kurvformen ändras inte] för alla A utom 0; Olika A endast placerar kurvan i olika vertikalled [via 1/A som x-interceptet, skärningen med x-axeln].

(6) 2p^–1(–1) = –ln(âî) ; 2Bp^–1 = ln([A/(ln2)]N₀î)

(7) 2p^–1 = ln(âî) ; 2Bp^–1 = ln([A/(ln2)]N₀î)

Eftersom rörelsemängden eller impulsen p=mv alltid sammanhänger med ett aktivt sönderfall, existerar inget p=noll. Men även OM p är obetydligt större än noll, räcker det ändå inte; Moderkärnan har (minst) en normal rumstempererad rörelseenergi som dessutom aldrig kan bli helt noll (absoluta termiska nollpunkten existerar inte i det ljusaktiva universumet). För att en alfapartikel ska bli mättekniskt synlig, måste den alltså, från moderkärnan, ges MINST den lokala kroppens (atomära) värmerörelseimpuls (p₀=pTH); Motsvarande medelliv skulle då bli î=(1/â)e^2/pTH och därmed den bestämda integralen från (7) som

(8) ln(âî) = 2(p+p₀)^–1 ;

Är variabeln p=0 gäller ln[âî]=2/p0. p0 beror på lokalens termiska tillstånd, analogt ämnets kemiska sammansättning [de flesta radiotyper är metaller].

Vi frånser dock denna utvidgning i detta skede för att förenkla termhanteringen. En vidare beskrivning av integrationsgränserna för den bestämda integralen till (7) beskrivs i Integrationsgränserna.

— Med e^a=P som ger a=lnP har vi därmed från nr7 (den integralt obestämda) principlösningen

(9) e^2/p = âî ;

— Faktorn â innefattar nuklidkoefficienter [â=AN₀(Bln2)^–1] tillsammans med utgångsmängden N₀:

— Eftersom, enligt lösningarna i (6) och (7), koefficienter till logaritmintegralens variabel (î) kan användas godtyckligt inom och utom association med variabeln, kan vi tydligen matematiskt-fysikaliskt godtyckligt (alltid till prövning) utnyttja situationen i (5) för att avdela den för utjämningen av den fysikaliska storheten för impulsens invers i exponentens numeriska enhetsform nödvändiga faktorkoefficienten (B) till vänsterledet enligt

(5.1) 2Bp^–2dp = –dt(âî)^–1

som ger motsvarande slutlösning i (9) enligt [â=KBN₀ i (5)]

(9.1) e^B/p = KN₀î

För att matcha transformationen mellan e-logaritmen och 2-logaritmen (se även blåstripen nedan) måste K (främst) avdela en faktor 1/ln2 så att vi i grundformen t_H=(N₀/ξ_N)ln2=N₀î kan få tillbaka t_H med koppling till allmänna radiokonstanten via K=A(ln2)^–1 — och därmed mera fullständigt

(9.2) e^B/p = AN₀î(ln2)^–1

= A(ln2)^–1t_H som ger

Slutformen, Grund

(ln2)/t_H = Ae^–B/p halveringsTIDssambandet

Halveringssambandet N=N₀/2^T/tH=N₀/e^T(ln2)/tH via N₀/N=e^T(ln2)/tH visar ln(N₀/N)=T(ln2)/t_H med (ln2)/t_H som radiokonstanten

A-koefficienten får i ekvivalens mellan leden enheten 1/S=Hz:

Eller ekvivalent

N₀î = 1S(ln2)e^B/p = t_H

(9.3) Se vidare i Utvecklingen av B/p samt i b-koefficienten

t_H = 1S(ln2)e^B/p

t_H = 1S(ln2)e^b^Q/p

t_H = 1S(ln2)e^be^Z/mv

t_H = 1S(ln2)e^be^Z/√2mE

10log tH/1S = 10log[(ln2)e^be^Z/√2mE]

10log tH/1S = (1/ln10)ln[(ln2)e^be^Z/√2mE]

10log tH/1S = (1/ln10)ln[e^be^{Z /√2mE + ln(ln2)}]

10log tH/1S = (1/ln10)[beZ(2mE)^–0,5 + ln(ln2)]

Räknas E i MeV — E(Joule) = E(MeV)·e·T6 — fås förenklingen

beZ(2mE_J)^–0,5 = beZ(2mE_MeV·e·T6)^–0,5

= be(Z=2)(2me·T6)^–0,5(E_MeV)^–0,5

= b[(2e)²/(2me·T6)]^0,5(E_MeV)^–0,5

= b[2e/(m·T6)]^0,5(E_MeV)^–0,5 ; m = 4,0026031(u=1,66033 t27 KG);

= b[6,94348949](E_MeV)^–0,5 ;

10log tH/1S = (1/ln10)[b[6,94348949](E_MeV)^–0,5 + ln(ln2)]

Graf; y=(1/ln10)[(–6)6.94349[(x)'–0.5]+ln(ln2)]

–40+(1/ln10)[(25.133)6.94349[(x/5)'–0.5]+ln(ln2)]

t_H = 1S(ln2)e^{4πÑeZ/√2mE}

;

î_medellivet = 1S(ln2)N₀^–1·e^B/p = t_H/N₀

IMPULSEN p=mv för masspartikel m [Heliumkärnan] som emitteras ur radionukliden B ökar med avtagande medellivslängd î för B i preparatet N0.

— Den utträngande rörelsemängden [ p ] i massformen [BN₀] avspeglar ett motsvarande medelliv [ î ] för B.

Med den slutliga utvecklingen av B/p i Exponenten till e-formen ges sambandet för halveringstiden t_H i TNED enligt

t_H = Ke^b^Q/p = Ke^be^Z/mv = Ke^be^Z/√2mE

K = 1S(ln2)=A(ln2)

vilket är samma sambandsform (men med olika inre betydelser) som det konventionellt tecknade i Källa 1,

(ln2)/t_H = Ae^–B/√Eα

KÄLLEXEMPEL

b-formen

I Exponenten till e-formen visas hur slutformens exponentkoefficient B i B/p kan tolkas, tillsammans med alfaimpulsen p, för att enligt TNED nå fram till den slutgiltiga sambandsformen för halveringstiden t(H); B innefattar en avgörande nuklidkoefficient av formen b=Ñ4π med Ñ=max±2.

— b kan då beräknas (diagrammet nedan ger ett exempel) enligt

b = [√2mE_α]ln[t_H/1S(ln2)]/eZ = [p=mv]ln[t_H/1S(ln2)]/eZ

— Diagrambilden nedan visar data på halveringstider t_H, alfapartikelenergier (i laboratoriets referens) E_α och nukleära kapacitivitetskoefficienter b=4πÑ beräknade som ovan ur tabelldata från ALPHA SCIENCES.

— Vi observerar särskilt att b (med nedanstående källreferens, bMAX17,62 och bMIN–6,25) håller sig inom tillåtna max

b=(Ñ=±2)×4π=±25,132741. OM b-värdet skulle överträda den gränsen, innebure det att också TNED-teorins ±c₀-gräns skulle överträdas — och därmed kass teori: TNED gäller inte.

KÄLLEXEMPEL [[Tabell1KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]]

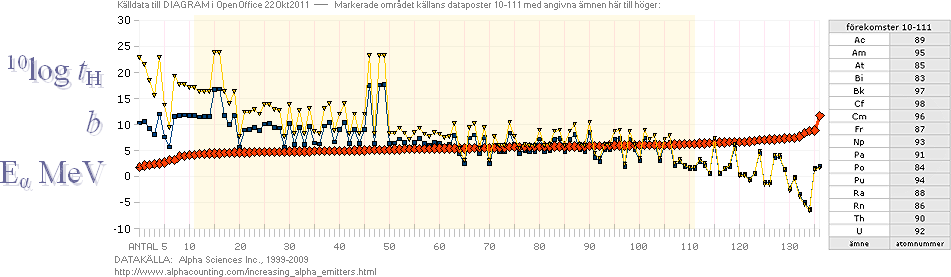
Källexemplet ovan visar en mindre dataserie med horisontalskalans 136st radioaktiva atomnuklider med uppgifter på sönderfallsenergier, röda punktvärdenas vertikala värden i MeV för alfapartiklar som avdelas från den radioaktiva atomens atomkärna med tillhörande halveringstid, vertikala skalan med den gulmarkerade diagramkurvans 10-logaritmvärde för halveringstiden i sekunder. Vertikalskalans b-värden i diagrammets mörkblåmarkerade del är beräknade från TNED-teorins nuklidkoefficient b=4πÑ. Av diagrammet framgår speciellt tydligt hur b och tH följs åt och varierar, samt hur dessa avtar generellt med växande E, samt också att »bandbredden» i [b och] tH är mycket stor omkring E-värdena 5 MeV: som mest grovt 10-15 tiopotenser.

Halveringstiden tH i Sekunder; bMAX = 17,62 för Pu-239 med tH = 5,5 T15 år och Eα = 5,16 MeV; bMIN = –6,25 för Po-212 med tH = 0,3µS och Eα = 8,79 MeV

För datakällan ALPHA SCIENCES, Alpha Sciences Inc., 1999-2009, se http://www.alphacounting.com/increasing_alpha_emitters.html

Dramatisk känslighet

— NOTERA den nära följsamheten och överensstämmelsen mellan ¹⁰log(t_H) och b; Varje ytterst MINSTA lilla ändring i b-värdet resulterar i en dramatisk ändring i halveringstiden (t_H) — med i stort sett oförändrad alfaenergi (E_α).

— Med Uran-238 som referens: b-koefficienten för U-238 — beräknas från (t_H) och (E_α) — är

b₀=11,8592681 med E_α=4,267 MeV och t_H=4,51 T9 år (tH-värdet äldre data från VNS-5);

— För att öka eller påverka halveringstiden med 0,1% (Solens ändring i neutrinoirradians på Jordkroppens tvärsnittsyta mellan sommar-vinter, till jämförande räkneexempel, se Solirradiansens variation) till t_H=4,51451 T9 år med bibehållen alfaenergi, behövs blott

b₁=11,8595655; b₀/b₁=0,9999749 eller en ökning i b-värde med 0,0025044% ~ 0,003%.

— För att fördubbla halveringstiden till t_H=9,02 T9 år krävs (samma E_α) b=12,0654776; en ökning med 0,206209 eller 1,7388%.

— Det är alltså (i vilket fall) fråga om SMÅ variationer med STORA konsekvenser.

— Om det skulle vara så att energigenomströmningen vid radionuklidens bildning är avgörande för b-värdet via olika bildningslokaler, är storleksordningen 1,7% i skillnad mellan olika lokaler högst rimlig i ljuset av grundämnesbildningen enligt TNED; halveringstiden för ett givet ämne skulle därmed ingalunda vara någon universell konstant med Jordlokalen som mätpreferens.

— Det finns emellertid här (Nov2011) ingen som helst säker beskrivning på vad det är som gäller — än.

Se även ovanstående mera utförligt i BeräkningsEXEMPEL som ger ett understrykande exempel på känsligheten för Uran-238.

Integrationsgränserna

INTEGRATIONSGRÄNSERNA 2011-10-20

t_Hmin

Med (9.3) enligt

t_H = [(ln2)/A]e^B/p

ges lägst

t_Hmin = [(ln2)/A]e^B/pMAX

Moderkärnan har ett begränsat energiuttag för att avdela en komponent. Som ett absolut gränsfall kan vi betrakta

E_max = (m₁–m₂)c² = m₂v²/2 = mc²

Moderkärnan (m₁) minus alfapartikeln (m₂) ger maxenergin som alfapartikeln kan avdelas på. Då gäller tydligen

2(m₁/m₂ –1) = (v/c)²

Med absolutgränsen v=c gäller då också

m₁/m₂ = 3/2 ; m₂ = m₁(2/3) ;

Alfapartikeln måste vara minst 2/3 av moderkärnan vid max v=c om hela resterande moderkärnans massenergi ska användas för att avdela alfapartikeln.

— Som ett gränsfall kan vi beakta max masstal enligt TNED från NEUTRONKVADRATEN som A=311u. 2/3 av den massan blir avrundat A=207, som med v=c ger maximala rörelseenergin för A=207 som alfapartikel enligt (u=1,66033 t27 KG, c=2,99 792 458 T8 M/S)

E_MAX = 207uc²/2 = 1,54445 t8 J

p_MAX = 207uc = 1,03035 t16 NS

Maximala impulsen (p=mv) för att få minsta halveringstiden (t_H) måste emellertid förutsätta också minsta alfapartikelns agent. Nämligen för att exponenten i sambandet totalt också innefattar alfapartikelns kärnladdning (Z). Med A i storleksordningen 207 hamnar vi omkring Z=82-84 (Bly,Vismut, Polonium).

— Max rörelseenergi på idealt mekanisk väg för Helium-4, den ordinära alfapartikeln, är

E_MAX = 4uc²/2 = 5,96892 t10 J

p_MAX = 4uc = 1,99101 t18 NS

Med nominella exponentkoefficienten B=2_Ze4π (och A-koefficienten=1) ges

t_Hmin = [(ln2)/A_=1Hz]e^B/pMAX

= 5,2367943 S

Utnyttjar vi den ideala gränsformen för obegränsat växande p som ger

t_Hmin = (ln2)S·1

för att få alla möjliga värden mot noll, ges generellt

t_H = [(ln2)S]e^B/p – (ln2)S

= [(ln2)S](–1+e^B/p)

— SVÅRIGHETEN att bestämma något mera exakt minsta t_H-värde avgörs (således) av B-faktorns Ñ-komponent, nominellt 4π.

— Med närmast ovanstående led ges idealt optimal möjlighet för t_H-värdet att närma sig noll obegränsat.

;

t_Hmax

Vidare från (9.3); Via en minsta impuls p(THERMAL)=mv(THERMAL), ges ett största t_H enligt p=p[TH]

t_Hmax = [(ln2)/A]e^B/(p[TH])

Alfapartikeln måste, i laboratoriets referens, kunna uppvisa minst p[TH], vilket med moderkärnans kraftbas och dess avdelningsrekyl som referens betyder ett marginellt högre p-värde. I rumstemperatur (20°C) är luftmolekylernas medelhastighet i laboratorierummets referens grovt och runt 500 M/S. Det ger för Helium-4-kärnan en minsta rörelseenergi vid

E_MIN = 4u(500 M/S)²/2 = 8,30165 t22 J

p_MIN = 4u(500 M/S) = 3,32066 t24 J

= p[THermal]

Med nominella exponentkoefficienten B=2_Ze4π ges då för Helium-4-kärnans avdelning från en moderkärna dess maximala halveringstid

t_Hmax = [(ln2)/A_=1Hz]e^B/(p[MIN])

= [(ln2)S]e^{1,2124894 T6}

= [(ln2)S]10^{(10loge)(1,2124894 T6)}

= [(ln2)S]10^526577,46

Därmed kan sambandet skrivas mera egentligt, inkluderat föregående resultatbild från tHmin

t_H = [(ln2)S]e^{B/(p
+ p[TH])} – [(ln2)S]

= [(ln2)S](–1+e^{B/(p
+ p[TH])})

med alfapartikelns (effektiva, verkställande) p=mv från allt större än noll.

Sambanden i modern akademi

Grund

MAC

Källa 1 anger Geiger-Nuttalls relation, den empiriskt utarbetade sambandsformen, enligt (9.2) ovan på formen

(ln2)/t_H = Ae^–B/√Eα

med E_α som alfapartikelns energi — men ger ingen sammanhängande klarhet i hur detaljerna hänger ihop.

— Det är, alltså, samma form som den ovan härledda i (9) [Se Slutformen] — OM partikelmassan (m) multipliceras med partikelenergin (E) enligt mE=mmv²/2=(mv)²/2=p²/2 med √mE=√p²/2=p/√2. Enhetsändringens justering kan återföras på B-koefficienten.

— Dvs.; mE=p²/2; p=√2mE; √E=p/√2m.

— OM massan (m) associeras med den avdelade Heliumkärnan (eller någon annan avdelning), och den betraktas som konstant, ges √2m också som en konstant, och därmed B-koefficientens motsvarande anpassning.

— Det går, i så fall, på ett ut om man använder alfapartikelns (rörelse-) energi (E) eller dess impuls (p).

— SÄG (sedan) inte den ENORMA omständlighet som ovanstående sambandsform RENDERAR i modern akademisk facklitteratur. Det är sannolikhet, kvantfysikaliska specialbegrepp och snurrande och studsande partiklar i atomkärnan som poppar upp och, garanterat, gör rent hus med publiken. Noll applåder. Det finns inte en själ, ens på ståplats. Man blir så fängslad att man (snart sagt) får betala för att gå UT.

— p-termen återfinns i den etablerade ämnesbeskrivningen typ Källa 1 nedan enligt m[V(r)–E_α]=mV(r)–mE_α med mE=p/√2m som ovan;

T ≈ exp[ –2 _r_1→r0 ∫ (2m[V(r) – E_α])^0,5ħ^–1dr], [Källa 1 ekv. 7.56];

T ≈ exp[ –(√2µ)ħ^–1 _Ra_→R ∫ [V(r) – E_α]^0,5dr], [Källa 2 DETAILS] med [µ förklaras inte]

V(r) = 2Ze²/4πε₀r, E_α= 2Ze²/4πε₀R_α som ger

V(r) – E_α = 2Ze²/4πε₀r – 2Ze²/4πε₀R_α = (2Ze²/4πε₀)(1/r – 1/R_α), källan förklarar inte termen µ, inte heller ħ=h/2π;

”where V(r)... is the repulsive Coulomb potential energy between the α-particle (charge +2e) and the daughter nucleus (charge +Ze)”,

”The energy of the emitted α-particle is given by E_α..., where R_α is the distance from the center of the nucleus at which the α becomes a free particle, while R is the approximate radius of the nuclear potential well in which the α is originally bound.”,

”The transition probability per unit time approximates the reciprocal of the half-life for α-decay, thus t_½≈1/|T|².”.

Källan2 beskriver hur integrala lösningen till (1/r – 1/Rα) kan APPROXIMERAS [med följd i ytterligare en angiven ledform som inte preciseras närmare i någon direkt anknytning till slutformen — man får skriva-räkna ut den delen själv — och som tydligen får förstås koppla dit].

— Det finns i TNED ingen SÅDAN specifik r-koppling som antyds av utvecklingsformerna ovan (Källa 1 och Källa 2). Atomkärnan i TNED innehåller inga andra inre partikulära detaljer än kärnstrukturens EKVIVALENT fraktala form (m/[n→∞])[n→∞]=m och som inte tillåter någon annan definition på massans fundamentala form än just atomkärnan. Det finns i TNED inga separata partiklar inuti atomkärnan, typ alfapartikelns ovan föreslagna inneslutning i kärnans potentialbrunn — och därmed ingen SANNOLIKHET för någon FORM att KOMMA UR något omslutande.

— Det finns alltså här, främst, olika sätt att tolka AB-koefficienterna.

Gamow ref.

En fullständig härledning till Geiger-Nuttalls samband enligt den moderna akademins kärnteori [från George Gamow 1928] visas

[med uppslag från

http://answers.yahoo.com/question/index?qid=20090421083841AAAMnGd

] i Gamow theory of alpha decay Nov1996

http://www.phy.uct.ac.za/courses/phy300w/np/ch1/node38.html

;

— Man utgår ifrån sin kärnpartikelvågmodell med potentialbarriärer och transmissionskoefficienter ”obtained from 2nd year quantum mechanics” med ”barrier shape in the form of the WKB approximation” som via [”quantum tunneling”] beskriver ”classical turning points of the motion inside and outside the barrier”. Omsättningen på elektriska kraftlagen [F=kQ1Q2/r²] leder sedan tillsammans med grundparametrarna till en slutform med motsvarande vidlyftiga innebörder. Det vi ser typ Wikipedias artikel på Geiger-Nuttall law av den delen är bara [Okt2011] en förenklad termform. Källan närmast ovan visar den fullständigt härledda slutformen

ln λ = ln λ₀ + ħ^–1(32Z_αZ_Dm_αRe²/4πε₀)^1/2 – 2π(ħc4πε₀)^–1(m_αc²/2Q_α)^1/2

= a’ – b’/√Q_α

— NOTERING: 2π(ħc4πε₀)^–1(m_αc²/2)^1/2 = 9,25434 T39. Med inversen till energiroten ökas det värdet på ytterligare. Det är [alltså] inte direkt uppenbart hur den sambandsformen kopplar till den praktiska resultatdelen —som för U-238 ligger i storleksordningen tH=1,42 T17 S = (ln2)/λ;

— lnλ = ln[(ln2)/tH] = –39,86 avrundat. Däremot stämmer mellanräkningen betydligt bättre med 10log[9,25434 T39] = 39,966345. Men det anges inte i källan — med faktum att √Qα inte finns med i exempelräkningen. [Kaos råder].

— TYVÄRR är det så med [de flesta] källverken: Man stoppar skeden i sopptallriken, men finner det sedan för mödosamt att föra skeden till munnen: GE FULLSTÄNDIGA UTVECKLINGSEXEMPEL så att läsaren kan läsa = kontrollera sammanhanget. Källan ovan är ofullständig.

— Ser vi till Källa 1 och dess motsvarande uttryck [ekv. 7.58],

ln λ ~ –b(Z–2)/√E_α

Wikipedia Geiger-Nuttall law anger [2011-10-16] motsvarande liknande [notera Minustecknens Tivoli ...]

ln λ = –a₁Z/√E – a₂

ser vi i jämförelse ovan mellan föregående källas b’ och b(Z–2) att icke mycket detaljer stämmer överens eller kan utläsas mellan de bägge källverken. Är TYPEN (Z–2) en separat utveckling från någon speciell gren, eller kanske empiriskt grundad? Källan ger inga svar. Vad är b?

— Genom att det [HELLER] inte finns någon motsvarande STATISTISK analogi i TNED

— alla »uträkningar» som berör »NUKLIDINNEHÅLL» och det som i MAC förmodas ske där, analogt »kärnpartikelradier inuti kärnpartikelradier», har ingen förankring i relaterad fysik, TNED —

bortfaller också dessa delar som helt fiktiva i TNED.

Rutherfords formulering,

se även Rutherfordcitatet i webbform

Rutherfords formulering

Rutherfords (numera sedan Jenkins et al., 2008 omdiskuterade) formulering från 1913

”The rate of transformation of an element has been found to be a constant under all conditions”,

Ernest Rutherford RADIOACTIVE SUBSTANCES AND THEIR RADIATIONS — Cambridge/New York 1913, Från [2011-10-13]

Book digitized by Google from the library of the University of Michigan and uploaded to the Internet Archive by user tpb.

http://books.google.com/books?id=UeEdAAAAMAAJ&oe=UTF-8

är nog helt korrekt — om vi håller oss till Jorden (Jordkroppen) som laboratorium. Man har heller ingen rätt att förvänta sig ett annat resultat i formuleringar som är daterade år 1913. I dagens läge (2011) finns (just) experimentella uppgifter som visar (eller påstår sig visa) att vissa atomers radioaktiva sönderfall varierar med avståndet till Solen, analog varierar med (i termer av relaterad fysik) neutrinoinfluensen från Solen. Experimenten [de första från Brookhaven National Laboratory (BNL) 1982-1986] och deras resultat omges av stora (fundamentala) svårigheter i modern akademi, och har delvis därför kommit i skymundan, se Citatblocket. I TNED ställer sig dock saken annorlunda.

— Först nu (2011), genom Jenkinsgruppens resultat (2008), har äldre resultat (som efter nu 25 år nära nog glömts bort, citatet nedan) kommit i mera publik dager. Det som inte visas, observeras heller inte:

”No other lab tried to repeat the experiment, and the anomaly remained unexplained. “People just sort of forgot about it, I guess,” says Alburger, who retired shortly after the results came out.”,

22Nov2008 — PALEO GROUP — RADIOACTIVE DECAY RATES CAN CHANGE

http://www.dinosaurc14ages.com/changedecay.htm

Sönderfallsstyrkan MAC/TNED

MAC

sönderfallsstyrkan i den enskilda radionukliden beror endast av den aktuella nukliden och är alltså oberoende av yttre faktorer;

tillfället för nuklidens kärndelning är enligt experiment [Rutherford et al. (1913)] oberoende av influenser från (den lokalt Jordbaserade) omgivningen;

TNED

sönderfallsstyrkan i den enskilda radionukliden beror endast av den aktuella nukliden och är alltså oberoende av yttre faktorer;

tillfället för nuklidens kärndelning är enligt sönderfallsdynamiken beroende av neutrinoinfluenser från omgivningen;

Jordkroppen har sin egen specifika lokala preferens med majoriteten radionuklider U-238 och Th-232; Andra regioner med andra sammansättningar uppvisar andra flöden

Formuleringen av halveringssambandet (tillfället) i MAC är alltså enligt relaterad fysik Jordlokalt betingad; Alla uppmätta resultat gäller explicit för Jordytan (Jordkroppen) — samt för radioagenter med speciellt ringa förekomst, generellt för hela universum (med ett fel som växer med den lokala ansamlingen).

Samband

RADIOAKTIVA SÖNDERFALLETS ALLMÄNNA SAMBANDSFORMER

SÖNDERFALLETS ALLMÄNNA SAMBANDSFORMER enligt relaterad fysik

Enligt TNED finns två allmänna sambandsled inom den elementära kärnfysiken som ansluter till de processer som kallas radioaktiva. De förekommer i samband med alla instabila atomkärnors ändring mot ett stabilt tillstånd och ges via de två typleden

(K) – E_hf₁₈ = K = (K1+K2 – (m→γ) + _β0_γm) – E_hf18 ................ betainstabila atomer, kärnan bevaras — betanuklider

[K] – E_hf₁₈₁₈ = K = [K1+K2 – (m→γ) + _T 0_γm] – E_hf1818 ............. nuklidinstabila atomer, kärnan delas — radionuklider (TNED-beteckning)

Leden beskrivs ingående i följande presentation.

Atomens bildning

K=K₁+K₂–(m→γ)

MASSDESTRUKTIONEN (m→γ) i den divgergensenergi E=mc² som krävs för ombyggnadsarbetet via KÄRNREAKTIONSLAGEN K=K1+K2–(m→γ) bär ansvaret för NEUTRINOBEGREPPET i TNED: neutrinostrålning är (högfrekvent, nukleär) em-strålning, inte massa, inte partikulärt g-vägande objekt. Se särskilt i Neutrinostrålningen från Solen, om ej redan bekant. Omständigheterna, här i RELATERAD FYSIK, grundas på Atomkärnans härledning från Plancks konstant (h=mcr) som visar att h är en strukturkonstant och därmed Neutrinospektrum. Det är avgörande viktigt att läsaren, för den fortsatta begripligheten, känner till dessa nämnda grunder.

Följande kan utläsas obehindrat DIREKT ur TNED (se från Atomkärnans härledning):

0_γm; Se även i Sektion 2

Eftersom massenergin E_m och (neutrino)gamma(γ)energin E_γ är kvantitativt utbytbara mot varandra enligt E_m=E_γ=mc²=hf, analogt (m→γ)=(m←γ) gäller också att

K=K+0_γm=K+E_γ–E_m;

0_γm= E_γ–E_m

— Om, nämligen, K bildas i en lokal med E_GAMMA, måste K tvunget — om det också är dynamiskt möjligt — avyttra extramassa E_m [=(m→γ)c²] utöver (m→γ) för att energiekvivalensen ska bevaras;

[Avyttring i sig av E_m kan ske direkt genom partikulär avgivning, eller explicit genom separat massdestruktion (m→γ); vad som gäller avgörs av den aktuella atomnukliden själv beroende på aktuell intern balansräkning].

Stabil

Om atomen (K) efter sin bildning (se GRUNDÄMNESBILDNINGEN) K=K1+K2–(m→γ) är stabil, är massdestruktionen (m→γ) eller neutrinostrålningen i samband med nuklidbildningen också den uteslutande enda energimässiga avyttringsfaktor som förekommer i samband med den atomens bildning. Ingen ytterligare aktivitet förekommer.

— Förekomsten av icke stabila nuklider kräver en motsvarande energiräkning med en motsvarande underhållande drivkraft [(m→γ)], se dissonansenergin [E(hf)]. Den delen härleds i RADIONUKLIDENS BILDNING, sambandsformen

K = K₁ + K₂ – (m→γ) – E_hf .................

kärnreaktionslagen med radioaktiva sönderfallets underhållande drivkraft [E_hf] enligt TNED

som grundlägger sönderfallets relaterbara fysik enligt följande allmänna uttryck.

Instabil

Betainstabila (_β0_γm)

Om atomen (K) efter sin bildning K=K1+K2–(m→γ) är instabil och massdestruktionen (m→γ) generellt fortlöper enligt tillägget E_hf₁₈

(K) – E_hf18 = K = (K1 + K2 – (m→γ) + _β0_γm) – E_hf18 ........................ betainstabil atom

E_hf18 varierar från runt 3,5-0,5 MeV för hela nuklidspektrat.

Elektronmassa avyttras MED KONSTANT STRÖM under hela det instabila tillståndet enligt kraftekvationen — flödet fortsätter sedan i formen av kopplingen kärna-elektronmassa

är den instabila atomen betainstabil. Faktorn E_hf18 kopplar till den motsvarande neutrinostrålningsenergi [med ett motsvarande, separat eller förlängt (m→γ)] som atomnukliden sänder ut så länge betasönderfallet (kärnombyggnaden) pågår. Prefixet 18 ansluter till massdefektskapitalet i NEUTRONKVADRATEN, max 18 elektronmassor (vid »Järntoppen» 17,75e för Järn).

Nuklidinstabila (_T0_γm)

Om atomen [K] efter sin bildning K=K1+K2–(m→γ) är instabil och massdestruktionen (m→γ) fortlöper enligt tillägget E_hf₁₈₁₈

[K] – E_hf1818 = K = [K1 + K2 – (m→γ) + _T 0_γm] – E_hf1818 ...................... nuklidinstabil atom

E_hf1818 varierar obetydligt, kvantitetsvärdet är helt försumbart (minsta möjliga energimängd som åstadkommer en nuklidändring).

Ingen massa avyttras, endast den minimala neutrinostrålningen E[hf1818] visas, fram till GENOMBROTTET då kärnan plötsligt genomgår delning.

är den instabila atomen nuklidinstabil. Faktorn E_hf1818 kopplar till den motsvarande neutrinostrålningsenergi [med ett motsvarande, separat eller förlängt (m→γ)] som atomnukliden sänder ut så länge nuklidsönderfallet (kärnombyggnaden) pågår. E_hf1818 kallas också här speciellt för dissonansenergin. Prefixet 1818 ansluter till atomkärnans centralmassiv, varifrån energin till ombyggnaden tas. Villkoret (i TNED) för storleken hos sönderfallsenergifaktorn E_hf1818 är att den, med hänsyn till kärnans fraktalbyggnad, måste associera till de allra finaste delarna med de allra lägsta energierna och därmed de allra högsta frekvenserna. Vilket betyder: absolut minsta möjliga neutrinoenergi. Det är, enligt TNED, genom en ackumulerad (tidsbestämd) process som den verksamheten sedan plötsligt, och med stor kraft, åstadkommer den aktuella kärndelningen.

Radioaktiva sönderfallets dynamik

Radioaktiva sönderfallets dynamik

Radioaktiva sönderfall — med kärndelning

HÅRDA SÖNDERFALL

EFTERSOM JÄMVIKTEN BESTÄMS GLOBALT genom alla individers samverkan och bidrag

bestäms också energifördelningen kring nominella atomvikten av mängden radioaktiva nuklider: deras tillstånd och skede i sönderfallen och de med dem tillhörande relativa eller absoluta energinivåerna.

Så länge obalans råder, och därmed självsvängningen regerar, svarar varje nuklid med en motsvarande massdestruktion (m→γ) som underhåller drivkraften i den energi som krävs för att putta nukliden mot läge jämvikt — via olika sönderfallsprocesser som kärnan själv bestämmer från fall till fall.

Kärnreaktionslagen beskriver hur jämvikten fungerar i den kvantitativa ekvivalensen mellan γ-energi och m-energi.

[Se SEKTION 2].

Följaktligen existerar det för varje radioaktiv nuklid ett största (γ-energin) och ett minsta (m-energin) energivärde med exakt balans kring nominella atomvikten (massa-energi-ekvivalenten) som motsvarar den ideala nuklid som skulle finnas om självsvängningens komponent inte existerade.

BANDBREDDEN γm avtar i amplitud vartefter individerna i gruppen sönderfaller till andra länkar. Sönderfallet kan i princip ske var som helst inom bandet. Övervikter åt det ena eller åt det andra hållet relativt medelvärdet justeras automatiskt genom kärnreaktionslagens enkla samband.

Radionuklidens bildning — neutrinoinfluensens allmänna koppling till radioaktivitetens relaterbara fysik enligt TNED

Radionuklidens bildning enligt relaterad fysik

TYNGDCIRKELN

Se även mera utförligt från ATOMKÄRNANS TYNGDCIRKEL om ej redan bekant

Radioaktiva sönderfallets grundform enligt relaterad fysik — från KÄRNREAKTIONSLAGEN K=K1+K2–(m→γ) — härleds nedan

K = K1 + K2 – (m→γ) – E_hf

E[hf] markerar den nödvändiga neutrinoinfluensen enligt relaterad fysik som STYR SÖNDERFALLSTILLFÄLLET utan att inverka på halveringstiden.

I allmänhet används här de särskiljande termerna betanuklid med betasönderfall och radionuklid med radiosönderfall för de olika fallen betasönderfall och kärnsönderfall.

I modern akademi används [i allmänhet] motsvarande begrepp betasönderfall och alfasönderfall.

RADIONUKLIDENS BILDNING

Radionuklidens sönderfallsdynamik kan inte igångsättas utan neutronsönderfall [₀n¹–(m→γ)=₁H¹=p+e^–]

Det är uteslutet — i referens till en nominell atomvikt. (Se bakgrunden till 0γm — halveringssambandets fullständiga form).

Tyngdcirkeln

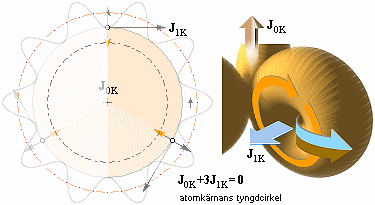
Radionuklidens sönderfallsfysik kan förklaras på tyngdcirkelns ekvivalenta självsvängning.

Självsvängningarna genererar kontakteringar av alldeles samma fason som i det vanliga ordinära betasönderfallets mekanism [Se Centralkontakterna], vilket leder till massdestruktion (m→γ).

Dissonansenergin E_hf

Radionuklidens bildning

Se även särskilt i Dissonansenergin i sönderfallet

Energin som underhåller svängningen ges (tvunget via energiräkningen) från en viss minsta kontinuerlig massdestruktion (m→γ) [från en särskild Planckenergi E_hf=(m→γ)c²=hf=(h/n)nf; genom att f i E=hf går mot noll, och samtidigt de djupast liggande fraktalnivåerna i atomkärnan penetreras enligt Plancks strukturkonstant h/n, se från Atomkärnans härledning, kan en ytterst liten makrofrekvens och därmed en ytterst liten Planckenergi ansvara för en i princip obegränsat hög bottenfrekvens om n tillåts växa obegränsat, och vilket är fallet i TNED] som — tydligen för det instabila fallet — initieras vid radionuklidens exotermiska bildning K=K1+K2–(m→γ)–E_hf;

Neutrinoinfluensen

— E_hf blir därmed den dissonansenergi som ansvarar för underhållet av det instabila tillståndet — och som därmed ansvarar för den allmänna neutrinoinfluensen på alla omgivande nuklider. Självsvängningens grund kan (således) återföras på en obalans i kärnans ringväv; Jämvikten [Se Atomkärnans impulsekvation] J_0K+3J_1K=0 garanterar en stabil nuklid, men den motverkas av dissonansenergin från (m→γ) som underhåller obalansen.

— Obalansen kan yttras på TVÅ sätt: dels avseende hela atomens kapital för MASSDEFEKTEN (E_hf₁₈-delen) där kärnan bevaras intakt och endast atomens elektronhölje påverkas (betasönderfall, lätta sönderfallet), eller avgränsat till centralmassivet (E_hf₁₈₁₈-delen) som framtvingar en kärndelning (nuklidsönderfall, tunga sönderfallet).

Stabilitetsgränserna

Med undantag för några alfasönderfallande isotoper i den lätta nuklidgruppen enligt HOP-tabellen

— 2He5, 4Be8 och 17Cl32 samt i den tunga gruppen nukliderna i intervallet Z=62(Samarium)-68(Erbium), alla med en eller flera alfasönderfallande isotoper

— är KÄRNSÖNDERFALL via självsvängning i atomkärnan enligt TNED ett faktum för alla atomkärnor då centralmassivets 1818e-stock överskrids.

Självsvängningarna i atomkärnan inträder definitivt och generellt för alla atomkärnor — med ovannämnda alfaundantag i de lägre atomnumren — från den alfasönderfallande Vismut-nukliden 83Bi211 då centralmassivets 1818e-stock överskrids enligt den 1818-baserade räkningen via atomviktsdifferensen [U(D)]

U_D [=U_A–U_A–2–U(₀n¹)] > 1818e;

—Med Vismut ₈₃Bi²¹¹ ges UDiff = 1819,621654e enligt HOP-tabellens värden

(210,9873 – 208,980394 – 1,0086652 = 0,9982408)u = 1819,621654e, e=(5,48598 t4)u

Vismut-209 blir den sista stabila nukliden i hela atomkartan: Alla efterföljande atomers Z-grupper och deras isotoper, från Polonium (84Po) och vidare, är kärninstabila.

Beskrivning, UDiff-värdet

Ett sätt att få en relativt sammanhängande BILD speciellt för översikten av STABILITETSFORMERNA i kärnfysiken — som det har visat sig, för ändamålet att avbilda/klargöra TNED med Neutronkvadratens referensbild av centralmassivets 1818e och atomära massdefektens 18e-intervall på praktiskt uppmätta referenser — är att räkna igenom alla atomvikter (U) för alla isotoper »mellan två närliggande» enligt »1818-algoritmen»

[U_A+2 – U_A – U(₀n¹)]

————————— – 1818 = U_DIFF₁₈₁₈

U(m_e)

METOD: Man börjar med nummer två [A+2] i den stigande masstalsordningen för ämnestabellens första nuklidförekomst, subtraherar första nuklidens atomvikt från [A+2]-atomvikten, drar bort en neutronmassa U[n], dividerar med elektronmassan U[me] och slutligen subtraherar 1818 elektronmassor. Resterande elektronantal visar ±-överskottet från 1818-linjen.

— Värden nära omkring ±0 visar sig motsvara MAXIMALT INSTABILT tillstånd; Kol-12, fysikens i särklass mest exceptionellt stabila atom, visar drygt –41 och i vilket negativa område också de övriga stabila nukliderna återfinns. Se särskild graf i Stabila Överst.

— Positiva UDiff-värden visar sig motsvara främst BetaMinusnuklider, med vidare. Se mera utförligt i efterföljande punktdiagram.

— Genom att A-nukliden, sambandet ovan, summeras subtraherande — U[A] + U[n] — med neutronmassan, får sambandsformen på viss sätt karaktären av att »analysera» [CENTRALMASSIVETS ÖVER- ELLER UNDERSKOTTSBAS i] neutronmasskillnaden mellan två närliggande masstal i tabellserien, typ idealt U[A+2] – U[A+1].

Punktdiagrammet nedan vänster visar resultatet för UDiff-förekomsterna i HOP-tabellen från 1966/67. Punktdiagrammet höger ger motsvarande via tabelldata från LBL-källan 2003.

Nuklidklassificering enligt TNED efter centralmassivets preferens 1818e -- Alla förekomster enligt UDiff = (U[A+2] -- U[A] -- U[n])/U[e] -- 1818.

— PUNKTDIAGRAMMEN NEDAN har ritats i OpenOfficeKalkyl med hjälp av alla källupptagna nuklider som räkningen kan göras på [alla utom de bägge första i varje Z-grupp]. Diagrammen har sedan precisionsjusterats, och modifierats på annat sätt, för exakt pixelpassning [OpenOfficeKalkyl, och övriga OO-verktyg, saknar fortfarande funktionella rutiner: — OM den programmiljön rensades upp, och städades, skulle den bli glänsande].

Horisontalskalan: Atomnummer [Z], samma som kärnladdning. Tabellnukliderna för varje Z-värde är sedan ordnad i tabellkällan med stigande masstal [A]. I punktdiagrammet är den masstalsordningen INTE sträng, men följer »i stort sett» nerifrån och uppåt om vi börjar, typ, längst ner [från 6C12, diagrammet nedan vänster nederst].

Vertikalskalan: UDiff-värdet i antal elektronmassor [e] — samma som i Atomära Massdefekten i TNED, fast här utvidgat över 18-gränsen [Se utförligt från NEUTRONKVADRATEN, om ej redan bekant].

BetaEC, EC från eng. Electron Capture, sv. elektroninfångning. För de tillkomna sönderfallstyperna högra diagrammet [Neutron, BetaEC, Proton] se Webbens Interaktiva Nuklidkartor.

HOP-tabellens data: Se HOP-konstanterna.

LBL-tabellens data: Endast data på atomvikter. INGEN SPECIFIK TABELLINFORMATION verkar finnas i själva tabelldokumentet; LBL-källan har tydligen ingen TYDLIG information om VAD, exakt, källan använder som definierande PREFERENS i begreppet atomära massenheten — eller ENS ett angivet förhållande neutronmassan/elektronmassan [1838,62 i HOP];

— UDiff-värdet har — därför, här — LBL-formerats genom CODATA-uppgifterna på förhållandet m[n]/m[e] [»neutron electron mass ratio»],

CODATA m[n]/m[e] = 1838,6836605

— Den uppgiften har sedan använts för att beräkna motsvarande m[e] ur LBL-tabellens U[n]=1,0086649-uppgift.

— En KLART UTTYDBAR uppgift från LBL-källan vilken den atomära massenhetsprecision är som använts har f.ö. eftersökts men inte påträffats. Se f.ö. exempel på hur olika källor ger olika u-värden i HOP-konstanterna.

— Värdeformerna är här inte kritiska [i skalan ovan: de täcker över varandra, utan synbar skillnad].

———————————

‡ CODATA-data [Internationellt rekommenderade värden för konstanter] nås företrädesvis på webben [Dec2011] genom URL:en http://physics.nist.gov/cuu/Constants/F.

Bilden nedan visar samma som ovan — men med datat från 1966 lagt på datat [logiskt AND] från 2003, till jämförelse. Diagrammens skaldelar beskrivs i Nuklidklassificeringen enligt TNED.

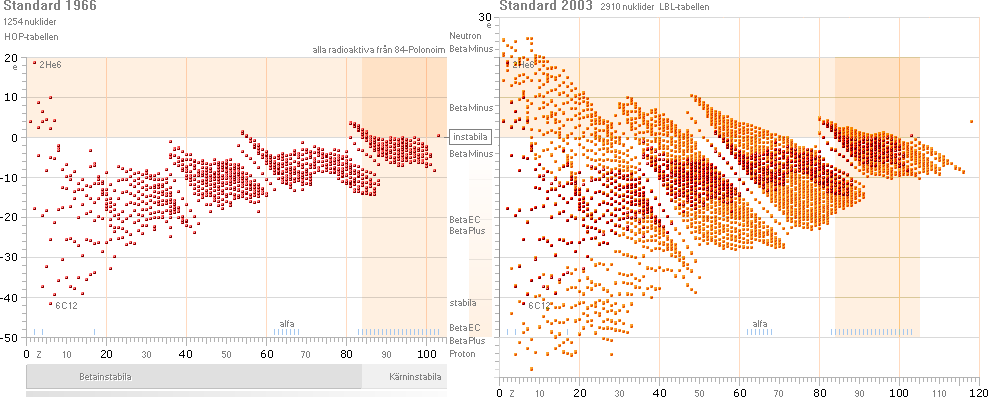
Webbens Interaktiva Nuklidkartor, exempel

LBL-tabellens Udiff-LOKALER — inte specifikt värdena — i punktdiagrammet Nuklidklassificeringen 1818e återfinns analogt — men inte identiskt — i den interaktiva webbkällan för data på atomfysikens atomkärnor och deras isotoper,

— Notera [Dec2011] hur webbkällan ovan visar nuklidkartan [omtalas, som vanligt, INTE i läsarens vy]:

— Ovan: Vertikalskalan antal neutroner [N], horisontalskalan kärnladdningen [Z], diagonalt masstalet [A].

— Speciellt för nybörjaren är den typen INTE rolig. Tyvärr, är det mera av regel än undantag i »etablerade facksammanhang» att läsaren undanhålls avgörande viktig grundinformation, i exempel som ovan, som dessutom är ENKEL att tillfoga av författaren.

— Genom att kartans axlar för Z och A inte är rätvinkliga, kan heller ingen direkt jämförelse göras med AZ-kartan i TNED. Tyvärr.

Kartan ovan från

THE — IAEA — LIVE CHART OF NUCLIDES

http://www-nds.iaea.org/relnsd/vchart/index.html

— Använd [också, med fördel] Wikipediareferenserna i External links på Radioactive decay [2011-12-23]

http://en.wikipedia.org/wiki/Radioactive_decay

för att testa olika webbexempel som ger allmän åtkomst för nukliddata.

— Hur kartan ovan används: Förstora med +-knappen [tillbaka med –knappen], det blir enklare att hovra med musen över objekten då.

— IAEA-Datakartan roterad +90° och horisontalvänd som ovan, motsvarar [men är inte identiska med] punktdiagrammets XY-skalor med respektive XY som punktdiagrammets ZA.

— Det är från den analoga positionsbilden som ovanstående LBL-punktdiagram, här, kompletterats med uppgifterna [överst] Neutron-BetaMinus och [underst] BetaEC-BetaPlus-Proton. EC från engelskans Electron Capture, sv., elektroninfångning.

Stabila överst: Till jämförelse med de rena UDiff-värdena i Nuklidklassificeringen 1818e visas nedan överlagt i grönaktiga datapunkter alla motsvarande stabila nuklider [268st] som är beräkningsbara i samma UDfiff-samband. Som vi ser, ligger samtliga stabila under 0-gränsen. DEN ORGANISKA BYGGNADENS mest stabila, och rikt kombinerbara, nuklid — Kol-12 — visar sig [tydligen] här i sitt alldeles rätta element: allra längst ner. Se även 6C12 och atomära massenheten.

— Diagrammens skaldelar beskrivs i Nuklidklassificeringen enligt TNED.

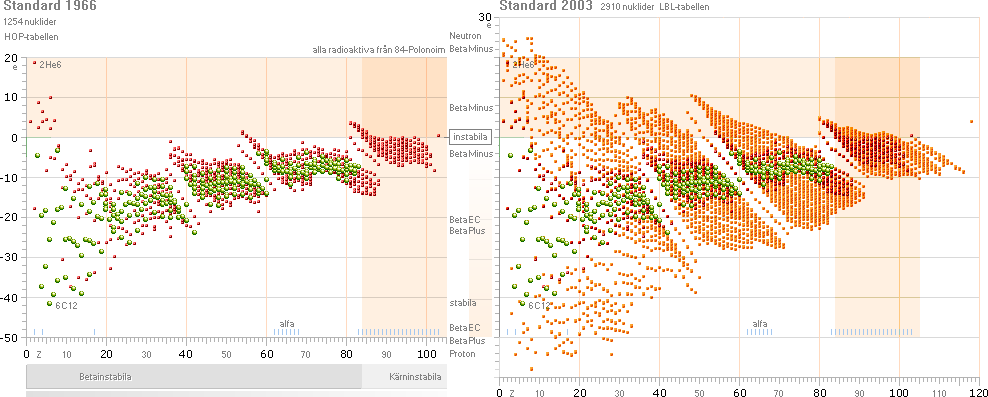
[RÖD] vänster: Alla atomvikter HOP-tabellen 1966/67 [ORANGE] höger: Alla atomvikter LBL-tabellen 2003 [OLIV] bägge: Alla stabila nuklider enligt HOP-tabellen

Varifrån kommer alla NYA isotoper?

— Webbkällor [som visar data och tabeller från atomfysiken] är GENERELLT URDÅLIGA på att REDOVISA DATAGRUNDER FÖR TERMER, KONSTANTER OCH BETECKNINGAR [Ytterst omständligt att få reda på NÅGOT] tydligt: Flera webbkällor finns [Dec2011] som stoltserar med InterAktivaNuklidKartor med JätteMycket DATA — som vilken som helst ExperimentNisse kan sitta hemma och snickra ihop med tidens gång.

— VET man inte varifrån uppgifterna kommer, är uppgifterna VÄRDELÖSA. Sopor.

GRUNDInformation om ARTIFICIELLA ISOTOPER finns bl.a. på [det är så dåligt i ÖVRIGT att det inte är SANT]

CROATIAN-ENGLISH CHEMISTRY DICTIONARY & GLOSSARY

http://glossary.periodni.com/glossary.php?en=artificial+radioactive+isotope

Se dock även [mera fördjupat] i

NUCLEAR MEDICINE, RADIO-ISOTOPES AND NUCLEAR REACTORS

http://www.ccnr.org/isotopes.html

Artificiella radioisotopkällorna

— Kärnreaktorer och, framför allt, partikelacceleratorer har utvecklats (explosionsartat) under 1900-talet. Genom dessa har (enorma) mängder med »nya ämnen» bildats — för längre eller kortare varaktighet — och som just bildar GRUNDEN för den numera [2011] stora mängden tabellerade nuklider, den allmänna nuklidbilden som ovan från 2003 — som det får förstås.

— Knappast med stöd av webbkällorna får man veta exakt VILKA dessa nytillkomna är. Det är bara med tillgång till en äldre referenstabell och jämförelser som den uppgiften kommer fram — direkt. Se ovan från Nuklidklassificeringen 1818e.

Redan med HOP-tabellen från 1966 introduceras läsaren för en del »artificiellt bildade» isotoper.

— En del av dessa förekommer »naturligt» i forskningen som bi- eller restprodukter i samband med särskilda kärnreaktioner [baserade på partikelacceleratorexperiment]. HOP-tabellens förekomster av artificiella isotoper får [därmed] karaktären av att ha OBSERVERATS i samband med experiment med andra huvudsyften än att producera artificiella isotoper. HOP-tabellen ger dock inga specifikationer på den punkten [liksom heller inte dagens tabellverk runt 2010 gör det].

— Den senare tidens utveckling [upp mot 2000] har i större utsträckning fokuserat på just PRODUKTION av nya isotoper. Dels för att undersöka kärnfysikaliska parametergrunder [MAC-teorierna i kärnfysiken], och dels [i vissa fall] som verktyg och instrument för att genomföra åter andra experiment och allmän datainsamling inom naturvetenskapen [ofta avancerat inom medicinen] .

Jämför även

HOWSTUFFWORKS — RADIOACTIVITY 1998-2011

http://science.howstuffworks.com/radioactivity-info3.htm

”Scientists produce more than 900 different kinds of artificial radioisotopes for use in science, medicine, agriculture, and industry.”.

— Ingen källa anges dock.

Se även industriföretag som producerar isotoper i

NRG — NUCLEAR SERVICES FOR ENERGY, ENVIRONMENT & HEALTH

http://www.nrg.eu/irradiation-development/medical-isotopes/

— Webbsidan ger några exempel i lista [i huvudsak för medicinska ändamål].

En LISTA med specificerade nuklider [ordnade kronologiskt efter upptäckt eller artificiell produktion] har eftersökts men ännu [Dec2011] inte påträffats.

Speciellt utpekas i Nuklidklassificeringen 1818e den exceptionella stabiliteten hos 6C12 — den nuklid med negativt UDiff som uppvisar allra lägsta UDiff-värdet (-41,609) av alla stabila nuklider — samt (via agenten 2He6) den stabila »vanliga 2He4» som den s.k. alfapartikeln som figurerar i samband med de flesta kärnsönderfall: UDiff-värdet (18,726 via U[A+2] som 2He6) kopplar närmast till Helium-4-nukliden som den, därmed, mest stabila UDiff-nukliden med positiv differens.

— I LBL-tabellens UDiff-värden Nuklidklassificeringen 1818e från 2003 göms dessa bägge i hopen av (andra) omkringliggande artificiellt producerade instabila nuklider — vilket på sitt sätt ytterligare understryker det speciella värdet av att se tabeller från olika epoker; 2He4 och 6C12 har inte minskat i anseende sedan 1966, trots omgivna av betydligt flera grannar.

— Sagt på annat sätt — se sammanställningen i Nuklidklassificeringen 1818e:

— Alla stabila nuklider kännetecknas ENLIGT TNED av

U_A+2–U_A–U(₀n¹) < 1818e

Tillägg — FÖRTYDLIGANDE konstanten E_hf — 2011X29

Dissonansenergins konstans

Tillägg — FÖRTYDLIGANDE konstanten E_hf — 2011X29

— Den enda PLAUSIBLA utgångspunkten [för vidare prövning enligt TNED] i kärnsönderfallens fall beträffande E(hf), dissonansenergins magnitud — från radionuklidens bildning, under medellivet, och fram till kärndelningen

— kan bara koppla till nuklidbildningens enskilda nukleonindivid: neutronen. Alla nuklider bygger i vilket fall på den delen, i fusioner och i fissioner.

— Om dissonansenergin E(hf) i kärnstrukturen har, och vilket vi förutsätter här, en enhetlig energikoppling till alla möjliga radiosönderfall, bör också den ENLIGT TNED försvinnande lilla massdestruktion E(hf) som underhåller det instabila tillståndet fram till kärndelningen innefatta, eller kunna återföras på, just NEUTRONEN och dess strukturbidrag — oberoende av typ av radionuklid.

— Fraktalbilden med massformens ekvivalent

m=(m/[n→∞])[n→∞]

i varje atomkärna i TNED bildar i vilket strukturfall en obegränsat liten MINSTA MÖJLIGA DEL med en motsvarande Planckenergifraktal E=[h/n]nf som därmed tecknar en minsta möjliga dissonansenergi E(hf) — vare sig vi talar om en neutron, eller en urankärna. Principen är i bägge fallen densamma.

— Alltså kan, speciellt i radiosönderfallet, dissonansenergin E(hf) — som radioaktiviteten underhålls på ENLIGT TNED fram till sönderfallet — också förstås som, i princip, en konstant.

AZ-kartan i TNED


AZ-nuklidkartan enligt TNED. A masstalet, Z atomnumret. Utförligt i Nuklidstrukturen.	Ovan till närmast jämförelse i MAC: »NAZ-kartan» på webben

Notera MAC-kartan, ovan höger, dess nuklidskalor: OVAN HÖGER: Vertikalskalan kärnladdningen [Z], horisontalskalan antal neutroner [N], diagonalt masstalet [A].

— I TNED-AZ-kartan, ovan vänster [vita mittstråket alla stabila nuklider], ligger neutronantalet [N] integrerat enligt N = A -- Z.

— Genom att MAC-kartan, ovan höger, har skalorna AZ orienterade 45° relativt varandra, att jämföra rätvinkligt [90°] med TNED, finns ingen direkt jämförelse. RIKTNINGARNA är dock analoga i bägge fallen; BetaMinus [gröna] åt höger, BetaEC och BetaPlus [gula] åt vänster relativt den stabila mittlinjen. Området med violett, höger ovan, anger alfasönderfall.

— Genom att baka in A-skalan i 45°, ovan höger, missar man, tydligen, den [för nybörjaren så viktiga] mera övergripande enhetliga MAXIMALT ENKLA översiktsbilden med termbegreppen, ovan vänster.

Isotoper, alla nuklider [specifik atoms atomkärna] med samma kärnladdning [Z]; konv. samma protonantal.

Isobarer, alla nuklider med samma masstal [A] men olika kärnladdning [Z]; konv. samma masstal.

Isomerer, [eg. nukleära isomerer] nuklider med samma AZ som skiljer sig internt via något [exciterade] olika energiinnehåll; konv. olika energitillstånd. [Ref. Wikipedia Nuclide, 2011-12-25].

Tillägg 2011X14

Med villkoret att kärnstrukturen i det pågående radioaktiva kärnsönderfallet (föregående det slutliga utbrottet då hela kärnan delas) ska ändras (byggas om) — från de allra lägst liggande fraktalnivåerna och därmed i motsvarande mening den praktiska strukturens allra djupast liggande del, och därmed enligt TNED — med minsta möjliga energi (E) på högsta möjliga Planckfraktala frekvens [E=(h/n)fn]→0 med n→∞, ligger det naturligt i sakens natur att dissonansenergin (E_hf) ALLTID kommer att framstå som en konstant för en given nuklid (given kärnstruktur).

— Med nuklidformen [Se RADIONUKLIDENS BILDNING]

[K₁ + K₂ – (m→γ) + (E_γ–E_m=0_γ_m)] – E_hf = K

betyder det tydligen totalt — via den primära bildningsformen K1+K2–(m→γ) — att den aktuella nuklidens atomvikt (U) kommer att självregleras via 0_γ_m i förening med dissonansenergin E_hf. Se även i Atomviktens medelvärde hur jämvikten i 0_γ_m kan förstås fördelad i »självregleringen» från »BigBang» och vidare (genom Grundämnesbildningen) för en given nuklidfamilj.

— Dissonansenergin E_hf kan alltså förstås som konstant, lika för samtliga radionuklider av samma typ, också med bibehållen atomvikt (U), trots att radionuklidens g-massa är i kontinuerligt avtagande.

— Enligt gängse tabellreferenser [VNS][HOP][ENCARTA-99 Radioactivity (Artificial Radioactivity)] har ingen atom från atomnummer 83 och uppåt stabila nuklider. Nuklidinstabiliteter förekommer emellertid redan för vissa isotoper i grupperna med atomnumren 2-5, (17) och 62-68, vilket indikerar att obalansen inte nödvändigtvis beror på en viss övre gränsvikt, utan snarare på mönsterstörningar i kärnans allmänna strukturkombinatorik.

Obalansen i resonansmönstren för J_0K+3J_1K=0 kan alltså som ovan förstås initieras, tvunget, från radionuklidens bildning där E_hf-energin från massdestruktionen (m→γ) inte avstannar, som i fallet med en stabil nuklidform, utan fortsätter och yttrar sig i arbetet för underhållet av kärnans instabilitet eller självsvängning fram till kärndelning.

Massdestruktionen fortlöper kontinuerligt utan avbrott tills mönsterresonans enligt J_0K+3J_1K=0 uppnås. Därmed är nukliden stabil och i resonans.

— Radionuklidens sönderfall bildar alltså genomgående en exotermisk process med fortlöpande utgivande av värme och ljus från (m→γ) enligt

τ – + τ+ = 0 ................................................... laddning

s_τ– + s_τ+ = 0 ................................................... spinn (rörelse)

m_τ– + m_τ+ = 2m_τ → γ ...................................... massenergin, arbetet som omsätts vid (ombyggnaden associerad med) sönderfallet

Massförintelsen (m→γ) är i relaterad fysik enligt energilagen tvunget en kvalitativt irreversibel process [Jämför Solen]. Motsatta laddningar tar ut varandra; motsatta spinn upphäver varandra; massenergin bevaras genom induktionen enligt U_ind=E=^UQ/Q_s=L(di/dt)k=Λk [Se COEI]; Induktionen överför massenergin — utan hjälp av någon transporterande massa — induktivt på andra massor som därmed bildar de lokala materiella energikällorna för värme och ljus.

Eftersom massdestruktionen i det tunga radiosönderfallet inte arbetar på betasönderfallets nivå, och därför heller inte tar massa ur 18e-stocken, måste massdestruktionen ske på centralmassivets nukleonstock 1818e. Därför är det otvivelaktigt så att radionuklidens sönderfall — tveklöst, helt säkert — initieras på ett inre neutronsönderfall;

radionukliden strävar att sönderfalla isotopiskt.

(Därmed identifieras det konventionella begreppet isomer nuklid).

Kärndelningen

KÄRNDELNINGEN

Radiosönderfallet

RADIOSÖNDERFALLETS FYSIK I TNED

Reviderad genomgång från RadioNUDE_1&2.doc med stöd av vidare utvecklingar i K-ekvationen.wps

Det Radioaktiva Kärnsönderfallet

Reviderad genomgång från RadioNUDE_1&2.doc med stöd av vidare utvecklingar i K-ekvationen.wps

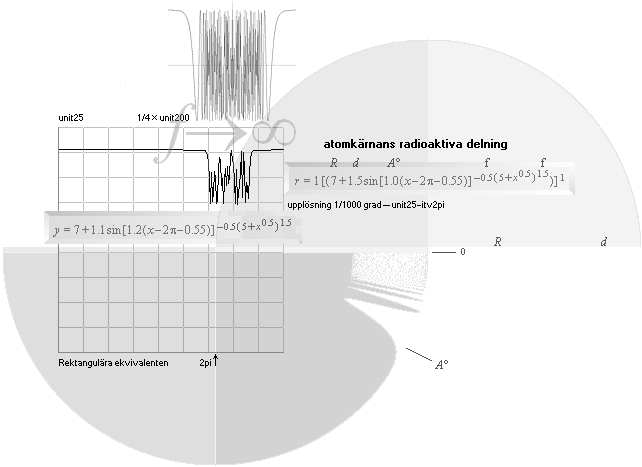
KärnInstabila atomer genomgår i allmänhet kärndelning inom ett mycket snävt tidsintervall [grovt inom t20 S, t för 10^–] i förhållande till den kärninstabila atomens instabila period [grovt t6 S till T20 S].

— Polärgrafen ovan, Cirkeln med den brutna bågen i slutet vid A° och därmed i stort sett oförändrad situation — jämn cirkel, ända fram tills kärnan plötsligt och med kort varsel genomgår delning genom en plötsligt starkt uppkommen självsvängning — illustrerar den bakomliggande, principiella funktionsmatematiken för delningsprincipen enligt TNED;

— Motsvarande vanliga rektangulära grafiska funktion visas illustrativt längst upp.

— Fenomenformen ansluter till TNED via atomkärnans obegränsade fraktala väv av understrukturer. Se utförligt från PLANCKRINGEN om ej redan bekant.

— Genom att, just, atomkärnan enligt TNED motsvarar en obegränsat sammansatt väv av frekvenser enligt Plancks strukturkonstant, finns de allra mest ideala förutsättningarna för att också härleda motsvarande maximalt sammansatta MATEMATISKA förlopp.

— Sambandsformerna studeras mera ingående i följande allmänna genomgång.

Jämviktens frekvensform

JÄMVIKTEN eller resonansen I TYNGDCIRKELN kan definieras med utgångspunkt från vilken som helst givna linjära frekvensform i polära koordinater i PREFIXxSIN enligt

r = r_T + A(sin axⁿ – sin axⁿ)^m = r_T

DISSONANS — brytningen av tyngdcirkelns cirkulära form — UPPKOMMER genom

r = r_T + A(sin axn – sin [a+(n→∞)^–1]xn)m ≠ r_T

där (n→∞)^–1 betyder varje minsta värde större än 0.

Beskrivning

I atomkärnans ringsystem enligt TNED förlöper varje ringspinn konstant, oupphörligt, utan slut med konstant bevarande av ett impulsmoment J=mvr. Se utförligt från PLANCKRINGEN. Ett sådant system liknar den ideala mekanikens exempel med ett mynt som man snurrar upp i tomma rymden. Om ingenting kommer i vägen, fortsätter myntet att snurra med samma konstanta periferihastighet v i all evighet utan att någonsin förtröttas. Ett sådant idealt mekaniskt system motsvarar ett passivt perpetuum mobile och kan återföras på en tyngdcirkel med radien r och massan m med periferihastigheten v och impulsmomentet mvr. Den periodiska rörelsen för en punkt i snurren kan uttryckas matematiskt på formen y=rsinω₀T där T är omloppstiden, ω₀ vinkelfrekvensen 2πf och r radien. I atomkärnan [utförligt från Planckringen enligt TNED] består den motsvarande ringen av elektriskt laddad massa ±Q=√(m/R)(A/dT) som genom sitt konstanta oupphörliga spinn åstadkommer elektromagnetiska vågrörelser på den beskrivna y-formen. Den stabila atomkärnans totala konstanta energi kan därför, om man så vill, återföras på en konstant energi- och strålningsekvivalent E=mc₀²=hf där h är impulsmomentets universella konstant 6,626 t34 JS och c₀ är ljusets topphastighet 2,99792458 T8 M/S med referens till Jordytans lokala gravitella dominans.

Sönderfallet

OM det i systemet av spinnande ringar uppstår en aldrig så liten skillnad, av just den ovannämnda principiella matematiska formen, finns också förutsättningen för bildningen av en (maximalt liten) störning genom samverkan mellan de olika vågrörelserna. Störningen innebär ett hinder för impulsmomentet som därmed motverkas, och för att den störningen ska kunna fortsätta måste det finnas en DRIVKRAFT.

— Det är ENLIGT TNED energin bakom denna drivkraft som tvunget bildar den centrala motoriken speciellt i det tunga radioaktiva sönderfallet, en kontinuerlig minsta möjliga minimala massförbränning (m→γ). När nämligen störningen [har ackumulerat effekter under tillräcklig tid och därmed] blir tillräckligt stor, och då behöver den bara verka under ett litet ögonblick, genombryts hela kärnstrukturen (liknande en uppdämd lavineffekt, eller elektrisk urladdning) och den instabila atomkärnan sönderfaller snabbt till en lättare länk.

Sönderfallsteorin i TNED

En beskrivning i fem sektioner

TEORIN FÖR DET RADIOAKTIVA SÖNDERFALLET

teorin för det radioaktiva sönderfallets fysik och dynamik enligt TNED

Allmän nuklidKlassifikation

Allmänna specifikationer

Sönderfallets allmänna fysik

Nuklidinstabila atomer

Allmänna samband

Sektion 1

Allmän nuklidKlassifikation enligt TNED

allmän klassifikation

SEKTION 1

allmän klassifikation

BILDKÄLLOR: Författarens arkiv · TNED-Kollage NikonD90 · VÅRVINTER:R16Apr2010VikBild201

Bildningen av alla atomer kan härledas exotermiskt ur exotermiska fusionslagen från KÄRNREAKTIONSLAGEN K1 + K2 – (m→γ) = K

Bildningen börjar från neutronen som föregivet atomelement. Den kvalitativt irreversibla massdestruktionen (m→γ) bildar den exotermiska energi som krävs för atomens ombyggnad.

Atomvikten. Eftersom massa och energi är kvantitativt utbytbara enligt (m→γ)=(m←γ), från massenergiekvivalenten E=mc²=hf, måste begreppet atomvikt (U) generellt grundas på en gamma(γ)-ekvivalent. [Se även i SEKTION 2].

ASPEKTER på huruvida denna detalj också ansluter till experimentella metoder för uppmätning av atomvikter ges i följande stycke:

Experimentell masspektroskopisk uppmätning av s.k. relativ atomvikt beskrivs utförligt i HOP [HOP s7-139–7-151][HOP s9-64sp1n]. [Se även i GFåk3s225].

Relativa atomvikter bestäms (traditionellt under 1900-talet) genom masspektroskopi. Metoden bygger på att mätobjektet (joniserat preparat i stråle) passerar sektoriellt avgränsade elektriska och magnetiska fält som åstadkommer avböjningar (r) i proportion till den joniserade atomens massa (r=m · v · 1/BQ). Man erhåller då ett så kallat masspektrum ur vilket de relativa atomvikterna (eller möjligen massenergierna) kan utläsas med olika metoder. Mätvärdena underkastas sedan olika jämförande analyser, samt en slutlig omfattande datorbehandling [HOP s9-87sp1n] där den slutliga atomvikten fastställs som ett medelvärde för varje uppmätt nuklidgrupp. Noggrannheten i HOP-källans referens [1967] är högt driven mätt med den praktiska fysikens mått och ligger för atomvikterna i den lättare nuklidgruppen (upp till masstal ca 60) i sjätte decimalen (eller bättre).

Värdena som erhålls direkt matematiskt ur Neutronkvadraten i TNED framgår till jämförelse som excellent överensstämmande med HOP-värdena [HOP Table 2.1 s9-65—9-86].

Se utförligt i ATOMVIKTERNA.

Distinktionen mellan γ-energi och reguljär g-massa finner enligt TNED sin djupare innebörd i den fulla beskrivningen och förklaringen av atomens olika tillstånd från jämviktsgrunderna i de allmänna impuls och kraftekvationerna J_0K+3J_1K=0 och F_BT+F_e_Z=0. Dessa ingår inte i den konventionella behandlingen av atomfysiken eftersom man där inte gör någon åtskillnad mellan massans kvalitativa grunder (m→γ) och dess kvantitativa ekvivalenter (m→γ)=(m←γ) utan behandlar alltsammans som kvantiteter utan urskiljning.

— Presentationen här utgår ifrån en beskrivning med tonvikt på den tunga radioaktivitetens fysik och dynamik; Betasönderfallets mekanik finns redan principiellt beskriven i TNED i detalj genom Centralkontakterna och Neutronens Sönderfall. Det finns dock vissa, vidare, aspekter på betasönderfallets mekanik som i efterhand, med denna presentations mera detaljerade författning också renderat en djupare betydelse för viss vidare genomgång. Se särskilt i Betasönderfallens fysik i TNED, samt med löpande hänvisningar i beskrivningen.

Om massdestruktionen (m→γ) är avslutad med bildningen av nukliden K är atomen stabil och endast då.

Om massdestruktionen (m→γ) inte är avslutad med bildningen av K är atomen instabil.

Om atomen är instabil, fortlöper (kontinuerligt och linjärt) massdestruktionen (m→γ) tills ett stabilt tillstånd uppnås.

Sektion 2

g-massa och gamma-massa, excitationskriteriet

Allmänna specifikationer

SEKTION 2 0_γm

Allmänna specifikationer

BILDKÄLLOR: Författarens arkiv · TNED-Kollage NikonD90 · MOLN:ExCur17.21Sep2011Moln20

Alla atomer _ZX^A , Z atomnummer A masstal, som bildas exotermiskt från kärnreaktionslagen K1+K2–(m→γ)=K har en fast, bestämd atomvikt U. Den är identiskt densamma för alla individer med bestämt ZA och den bestäms absolut av kärnreaktionslagen. Eftersom massenergin E_m och gamma(γ)energin E_γ är kvantitativt utbytbara mot varandra enligt

E_m=E_γ=mc²=hf, analogt (m→γ)=(m←γ)

gäller

K = K+ 0_γm = K + E_γ–E_m

Dvs.,

0_γm = E_γ–E_m

Om K bildas i en lokal med E_GAMMA, måste K tvunget — om det också är dynamiskt möjligt — avyttra extramassa E_m utöver (m→γ) för att energiekvivalensen ska bevaras.

Begreppet atomvikt

Begreppet atomvikt (U)

i praktisk fysik grundas därför tvunget på en γ-ekvivalent snarare än en vägbar g-massa. [Se även i SEKTION 1].

Atomvikten i fallet stabila nuklider är emellertid och tvunget en exakt vägande g-ekvivalent eftersom ingen massdestruktion existerar för dessa fall. Dock kan vissa utbyten ske inom vissa energiintervall. Kriteriet för jämvikt i detta fall beskrivs vidare nedan.

Eftersom atomkärnans tyngdcirkel enligt TNED är g-känslig på m i J=mvr och som inte har någon kvalitativ gammaekvivalent, är atomens tillstånd tvunget exciterat

om E_GAMMA>0 och därmed också E_m>0. Trots att en rent kvantitativ jämvikt råder i energihänseende i fallet E_GAMMA>0, fattas alltså aktiv g-massa för att atomen ska uppvisa resonans i bevarandet av atomens allmänna impulsekvation J_0K+3J_1K=0. Skillnaden mellan E-jämvikt och g-jämvikt kan därför endast vara den att E-jämvikten motsvarar en svängning omkring ideala jämviktstillståndet, ett exciterat tillstånd som bildas momentant eller som underhålls kontinuerligt av en yttre energikälla, medan g-jämvikten betyder en perfekt balanserad atom utan yttre påverkan. Gravitell jämvikt kan alltså bara komma ifråga för stabila nuklider. Atomens allmänna impulsekvation J_0K+3J_1K=0 är med andra ord en g-form och kan inte efterhärmas genom att ersätta m med svängningsenergi. Därför innebär E_GAMMA>0 tvunget detsamma som ett exciterad tillstånd. Om gammaenergin överstiger vissa tröskelvärden, kan kärnan avge motsvarande g-massa i utbyte för att bevara den allmänna energijämvikten, men kärnan befinner sig då i gengäld i ett exciterat tillstånd.

· atomvikten för stabila nuklider avser exakt g-massa

· atomvikten för betainstabila nuklider avser exakt g-massa vid tillfället för den betainstabila nuklidens exotermiska bildning

· atomvikten för radionukliderna avser en gammaekvivalent; nukliden tappar kontinuerligt g-massa genom den internt frigjorda dissonansenergi (m→γ) som krävs för att driva den instabila nukliden mot stabilitet, analogt ett delningstillfälle och därmed närmare en resonans

Tillägg 2011X27

NOTERA i fallet betasönderfall; ATOMENS g-massa genomgår ingen förändring på grund av elektronemissionen som sådan (t.ex. neutronsönderfallet som resulterar i Väteatomen); den massdel, elektronmassan, som atomkärnan avdelar stannar kvar inom atomen; atomvikten bevaras intakt.

— Betanuklidens massändring (vid elektronemission, BetaMinus) återfaller därmed på den massdestruktion (m→γ) som krävs för ombyggnaden, samma typ av dissonansenergi (m→γ) som i fallet med radionukliderna, men här associerad med elektronemission.

Betasönderfallens nuklider indelas i huvudsak i tre typer — se även illustrerat i Sönderfallstyperna:

—————————————————————————————————

BetaEC [EC här från eng. Electron Capture, sv., elektroninfångning], atomen går från högre till lägre kärnladdning; sönderfallsenergin minst lika med bindningsenergin för den elektron som atomkärnan fångar upp;

BetaPlus, samma princip som BetaEC fast tvunget större sönderfallsenergi; sönderfallsenergin minst lika med den avdelade positronens massenergi plus en elektron [0,511×2=1,022 MeV], eftersom den avdelade positronen utanför atomkärnan i vilket fall kommer att annihileras tillsammans med någon yttre elektron, och den energiräkningen bara har den ansvariga betainstabila atomen att återfalla på;

BetaMinus; Atomen går från en lägre kärnladdning [Z] till en högre, alltså mot typen tyngre nuklid, där den avdelade elektronen stannar kvar inom atomen; sönderfallsenergin kan därför, i princip, vara hur liten som helst, det som gäller är att det finns någon stabil produkt vars atomvikt är mindre än den betainstabilas.

— Det finns, på visst sätt, en intrikat frågeställning i detta betasönderfallande sammanhang, och som ansluter till sättet (traditionellt konv. masspektrograf) att mäta atomvikter.

— Eftersom makrofysiken INTE reagerar på delar av elektronladdningen — och därmed i princip måste visa samma »korruption» för motsvarande massdelar — ligger det i den instrumentellt, konsekvent, makroskopiskt mätande apparatens natur att heller INTE kunna skilja mellan delar av e=1,602 t19 C och motsvarande delar av m(e) 9,11 t31 KG.

— En betainstabil nuklid ZXA under elektronmassaemission med Z under pågående ändring enligt TNED ska alltså rent mättekniskt INTE uppvisa någon annan fason i motsvarande massa än exakt ZXA — oaktat att det verkliga Z är föremål för en pågående sönderdelning eller uppdelning som kommer att medföra en slutatom av typ Z’X’A. Först sedan elektronemissionen är fullbordad kan produkten visa sig som just en Z’X’A-atom.

— Vid den betainstabila atomens ZXA bildning

(K) – E_hf₁₈ = K = (K1+K2 – (m→γ) + _β0_γm) – E_hf18 ................. betainstabila atomer, kärnan bevaras — betanuklider (konv. betasönderfall)

finns det (alltså) bara EN möjlighet för en associerad massdestruktion (m→γ) att åtfölja det förestående betasönderfallet:

— Att ZXA-atomen vid sin bildning uppvisar ett energiöverskott på (minst) (m→γ)=(m←γ).

— Fattas (nämligen) energi efter sönderfallets fullbordan, trots avgivet (m→γ), att atomen alltså skulle (börja sönderfallet från ingen överskottsenergi och därmed) uppvisa ett energiunderskott (m→γ) efter fullbordat sönderfall, är atomen uppenbarligen fortfarande instabil (»exciterad»), och processen med (m→γ) kommer då att fortsätta tills ett stabilt tillstånd uppnås.

ENERGILAGEN gör det OMÖJLIGT att åstadkomma ÄNDRING utan tillförande av arbete=energi [*1]:

Alla instabila tillstånd som går mot stabila tillstånd karaktäriseras av ett ensidigt avgivande av energi:

— Det är i princip samma som att säga: Alla instabila tillstånd bygger på att energi tillförs från ett motsvarande stabilt tillstånd; Inget instabilt tillstånd kan förekomma utan att energi tillförs; Alla instabila tillstånd [rörelser, impulser p=mv] är exotermiska — avger energi.

— Den avgivna energin kan tolkas som arbetet som krävs för att åstadkomma ett stabilt tillstånd.

För att få fram ett tillstånd i fysiken som SKILJER SIG från ett STABILT tillstånd — det må vara på grund av radioaktivitet eller annat allmänt EXCITERAT TILLSTÅND — krävs enligt energilagen ett ARBETE, en TILLÄGGSENERGI, en motsvarande excitationsenergi. OM preferensen är ett stabilt tillstånd — en stabil atom — finns ingen annan fysikalisk möjlighet för att bilda en instabil situation från den givna stabila, än just att TILLFÖRA ENERGI — även för ändamålet att avlägsna energi [massdelar].

— I fallet betainstabila och nuklidinstabila atomer är det därför utom allt tvivel givet att den aktuella nukliden VID sin bildning — tvunget måste — ges MINST det extra energitillskott som sedan avdelas vid — alltsammans med en gång, eller litet i sänder fram till — tidpunkten då stabilitet uppnås.

— För betasönderfallets del betyder det MINST arbetet som krävs för ombyggnaden [fler eller färre elektroner i atomhöljet med motsvarande fler eller färre positiva elementarladdningar i kärnytan], samt [innefattat enligt TNED] arbetet som krävs för att separera elektronmassans komponenter ur atomkärnans fraktalkropp — på alldeles samma sätt som då större eller mindre rekylvattendroppar bildas ur den underliggande släta vattenytan [Se Illustration].

— För kärnsönderfallets del betyder det MINST arbetet som krävs för att [förbereda ombyggnaden för att kunna] separera de resulterande kärnprodukterna vid själva sönderfallet; Genom FUSIONSRINGARNA visas enligt TNED att atomernas elektronbesättningar i vilket fall medföljer AUTOMATISKT i de olika och möjliga kärnomvandlingarna, varför denna del också kan förstås ingå automatiskt integrerat i kärnsönderfallets dynamik.

— INFLUENSEN: Ju flera betanuklider med samma halveringstid (tH) som förenas i samma rum, desto mera fördelas deras gemensamma influens på tH-fysiken

(som bör vara av samma principiella kinematiska typ som i radionuklidfallet, men med delvis andra, mera komplicerade parameterkomplex och som här inte är närmare kända)

från den gemensamma (m→γ)-utstrålningen; Därmed kortare medelliv med växande utgångsmängd för de sönderfallande betanukliderna, längre med mindre, enligt samma princip som för radionukliderna, î=tH/N0 (Se från Sönderfallet uppvisar influenser);

— tH-formen, såvitt alls tillämplig på halveringssambandet, måste i vilket fall (med eller utan teoretisk förklaring) tvunget innefatta en autonomi, en självreglerande fördelningsdynamik som medför att sönderfallstillfällena sprids ut på mängden och inte hopas (klumpas) vid samma tillfällen med växande individmängd. Och på samma fason vid minskande individmängd som medför successivt ökad medellivslängd för alla kvarvarande; Sista individen får alltid längsta medellivet î=tH/1=tH (med en multipel för alla föregående halveringar).

Funktionssätt

Sönderfallsinfluensens funktionssätt för radionukliderna är i TNED formulerad på följande sätt:

— Det är som att koka ägg med många fickspeglar en solig förmiddag. Fler speglar ger snabbare temperaturökning, färre långsammare. Aktiviteten varierar i proportion till mängden.

— Summan av bidragen från alla nukliders dissonansenergier E(hf) på varje individ medför ett naturligt större bidrag [»tryck»] på den enskilda radionukliden. Därmed, enligt det större antalet N(0), ges för medellivet î=tH/N(0), tH konstant, ett mindre î-värde som [utjämnar det extra trycket och] motsvarar den högre radioaktivitetens högre frekvens 1/ î i sönderfallen. Och motsvarande, med minskande radiomängd: färre kvarvarande radionuklider ger en mindre totalsumma E(hf)-influens på den enskilda individen, och därmed en lägre aktivitet, analogt mindre kraft för att påskynda sönderfallets tillfälle i den givna mängden.

— Samma resonemang kan tillämpas på betanukliderna och deras inbördes dissonansenergier E(hf).

— För MEKANISMEN bakom sönderfallets tillfälle enligt TNED, se från Kärndelningen.

(m→γ) bestämmer preferenserna

DE SKILDA PREFERENSERNA — stabila, betainstabila och nuklidinstabila — har sin grund i den tvungna interna massdestruktion (m→γ) som otvivelaktigt är förknippad med atomer som befinner sig i sönderfall. Trots en utförlig beskrivning av masspektroskopins allmänna grunder i HOP-källan [HOP s7-139–7-151] finns inga direkta omnämnanden av frågan som berör den g-vägande aspekten i begreppet atomvikt. Det är heller inte att vänta i en allmän teori om fysiken som helt och hållet grundas på föreställningen om en obetingad ekvivalens mellan massa och energi. Beträffande frågan HUR man burit sig åt att mäta på betainstabila nuklider finns heller inga direkta omnämnanden. Med grund i HOP-tabellen för atomvikterna finner man att massdestruktionen vid betasönderfall varierar mellan 3,5e (0,00192u) för de lättaste till runt 0,5e (0,000275u) för de tyngsta atomerna. Speciellt med de lättare nuklidernas allmänna precision i mätvärdena, omkring sjätte decimalen eller bättre enligt HOP-källan, är det tydligt att en så stor differens som 0,002u är utesluten. Enda möjliga tolkningen i fallet betainstabila nuklider kräver därmed att man vid mätningarna utgått ifrån helt »färska» nuklider. Det finns dock vissa frågetecken på den punkten, speciellt beträffande de mera långlivade typerna, och HOP-källan ger heller ingen ledning i den frågan.

HOP-källan skriver på sidan 9-63 i samband med presentationen av den omfattande atomviktstabellen

Citat HOP

”Nuclear transformation energies can be employed through the equivalence of mass and energy (E = Mc²) to verify directly measured atomic masses, to calculate radioactive atomic masses, and to obtain a number of stable atomic masses that have not been directly determined.”

[HOP s9-63sp1n]

Källan använder på flera ställen i beskrivningen frasen ”the energy equivalent of the atomic-mass”. På samma sida (spalt 2) antyder källan, vidare, att mätningar på radioaktiva nuklider skulle tillhöra sällsynta företeelser

”Thus β^– energies can be employed to determine atomic‑mass differences, and, in the few cases where mass measurements of radioactive nuclei have been made, directly determined mass differences can be compared with β^–-decay energies.”

[HOP s9-63sp2m]

MÖJLIGEN ligger det mera räknearbete än experimentalfysik bakom HOP-tabellen. Källan antyder att man använder vissa noga bestämda nuklider som referenser för att bestämma andra, och tanken ligger nära till hands att man också har använt (och fortfarande använder) olika indirekta metoder vid ”mätningen” av atomvikterna för betainstabila och direkt tungt radioaktiva nuklider. Exakt hur vet vi inte, men HOP-källan berättar på sidan 9-87 (sp1m) om en del olika grepp som har utvecklats för att av givna kända kunna beräkna en ”accurate mass difference” för medtagna okända

(Inblicken i hur man gått tillväga är mest intressant som uppslag för att hitta eventuella felkällor — främst i den här presentationen).

——————————————

*¹ Ingen ändring av ett givet tillstånd som innefattar graviterande massa (m) är möjlig utom genom en acceleration a=v/t: föremålet måste kunna uppvisa en positionsändring, denna kräver tid (t), och på den tiden utbildas en hastighet (v); Accelerationen av massan (m) betyder samma som kraften F=ma; Distansen (d) som kraften verkar igenom, för att få till stånd ändringen, blir arbetets väg; Produkten av vägen och kraften är arbetet eller energin E=Fd=mad.

— Så kan ingen ändring komma till stånd — utom genom ett arbete.

Sektion 3

sönderfallets allmänna fysik

Sönderfallets allmänna fysik

SEKTION 3

Sönderfallets allmänna fysik

BILDKÄLLOR: Författarens arkiv · Kollage NikonD90 · FÖRSOMMAR:RF24Maj2010VikBild133·VÅRVINTER:R16Apr2010VikBild201

Följande beteckningar används i denna presentation

K ............................ stabil

(K) ........................... betainstabil (β)

[K] ........................... nuklidinstabil (T)

TYPFORMEN för följande samband förklaras utförligt från Radionuklidens bildning och RADIOAKTIVA SÖNDERFALLETS ALLMÄNNA SAMBANDSFORMER.

Om atomen efter sin bildning är instabil och massdestruktionen fortlöper enligt

(K) – E_hf₁₈ = K = (K1+K2 – (m→γ) + _β0_γm) – E_hf18

E_hf18 varierar från runt 3,5-0,5 MeV — enligt genomförd grovkoll på tabelldata från HOP-källan.

är den instabila atomen betainstabil.

Om atomen efter sin bildning är instabil och massdestruktionen fortlöper enligt

[K] – E_hf₁₈₁₈ = K = [K1+K2 – (m→γ) + _T 0_γm] – E_hf1818

E_hf1818 varierar obetydligt, kvantitetsvärdet är helt försumbart (minsta möjliga energimängd som åstadkommer en nuklidändring, den går alltså mot noll).

är den instabila atomen nuklidinstabil.

Förekommer en kombination av bägge betecknas nukliden i denna presentation [(K)].

E_hf1818-ledet har ingen konventionell motsvarighet; ingen elektromekanisk (hjälp-) modell av atomkärnan finns i modern akademi.

E_hf18-ledet har heller ingen konventionell motsvarighet eftersom man inte behandlar massdefekten från hela atomens impuls och kraftekvationer J_0K+3J_1K=0 och F_BT+F_e_Z=0 utan istället relaterar massdefekten till atomkärnan. Se vidare enligt TNED från NEUTRONKVADRATEN med särskilt jämförande exempel i MASSDEFEKTEN I MODERN AKADEMI.

— Massdestruktionens arbetssätt för det radioaktiva sönderfallet beskrivs i TNED enligt nedanstående sammanfattningar;

Massdestruktionen i E_hf18 är av samma typ för alla atomer. Den kan direkt återföras på ekvivalenten (eg. elektronekvivalenten) E=hf.

Massdestruktionen E_hf18=(m→γ) arbetar i massdefektens kapitalstock 18e och påverkar inte neutronnukleonens centralmassiv 1818e.

Massdestruktionen i E_hf18 tvingar därför atomen att ändras (sönderfalla) isobariskt genom en analog ändring i elektronhöljet.

Massdestruktionen i E_hf1818 däremot, är unik för varje särskild nuklidtyp _ZX^A. Den kan inte återföras på en elektrongenererad ekvivalent E=hf.

Massdestruktionen i E_hf1818 tvingar atomen att sönderfalla primärt isotopiskt genom en analog nukliddelning genom dissonansbildning från E_hf1818.

Dissonansenergin i E_hf1818 påverkar neutronnukleonens centralmassiv 1818e med ett unikt neutrinofrekvensspektrum [Se Plancks strukturkonstant] för varje särskild nuklid.

I betasönderfallet frigörs elektronmassa från atomkärnan samtidigt med massdestruktionen i E_hf₁₈. Något sådant samtidigt frigörande av separata massdelar från kärnan förekommer enligt TNED inte i radiosönderfallet via E_hf1818. Där omsätts istället massdestruktionen fullständigt på em-svängningar (»kontinuerlig radio») som fortlöper med kontinuerligt avtagande g-massa för nukliden tills kärnan uppnår stabilitet. I betafallet (med neutronsönderfallet som förebild) bildar den frigjorda elektronmassan en primär KONSTANT elektronström som kan betraktas som att atomkärnan utvidgas genom att avdela en del av sig själv. Den elektronmassaström som den frigjorda elektronmassan bildar upphör inte med själva e-massans frisläppande från kärnan utan fortsätter enligt TNED kontinuerligt. Elektronströmmen bildar en kommunicerande, strömstyrd, jämvikt med atomkärnan enligt kraftvektorledet F_BT+F_e_Z=0 där faktorn F_e_Z explicit leder till härledningarna i Spektrum och som grundlägger atomens förmåga att förena sig med andra atomer.

Se även i NeutronSönderfalletNOT2 som ger en del etablerade referenser i samband med (den allmänna svårigheten i experimentell) detektering av tillfället då en elektron framträder i makrofysiken från en betaprocess.

ör att atomkärnan ska erhålla optimal homogenitet i sin strukturform under massavbränningen, är det givet att massdestruktionen måste ligga i de djupaste nivåerna med de högsta frekvenserna [Se Plancks strukturkonstant] och de lägsta amplituderna enligt (Se även Radionuklidens bildning)

τ – + τ+ = 0 ................................................... laddning

s_τ– + s_τ+ = 0 ................................................... spinn (rörelse)

m_τ– + m_τ+ = 2m_τ → γ ...................................... massenergin, arbetet som omsätts vid (ombyggnaden associerad med) sönderfallet

Massförintelsen (m→γ) är i relaterad fysik enligt energilagen tvunget en kvalitativt irreversibel process. Motsatta laddningar tar ut varandra; motsatta spinn upphäver varandra; massenergin bevaras genom induktionen enligt U_ind=E=^UQ/Q_s=L(di/dt)k=Λk [Se COEI] [Utförligt i ENERGILAGEN och Massdestruktionens fullständiga matematiska fysik]; Induktionen överför massenergin — utan hjälp av någon transporterande massa — induktivt på andra massor som därmed bildar de lokala materiella energikällorna för värme och ljus. Se även i INDUKTIONEN och MAGNETISMEN för grundbegreppen enligt relaterad fysik, om ej redan bekant.

Sektion 4

Nuklidinstabila atomer — sönderfallets allmänna dynamik

nuklidinstabila atomer

SEKTION 4

nuklidinstabila atomer

BILDKÄLLOR: Författarens arkiv · Kollage NikonD90 · ÄNGEN:ExCur3.16Jun2009Bild3·VATTNET:ExCur16.13Aug2011Bild22·TALL-BJÖRK:ExCur9.2Okt2010Bild13-5

[K1+K2 – (m→γ) + _T 0_γm] – E_hf₁₈₁₈ = K

Se Samband

Nukliden i en nuklidinstabil atom, samma som kärninstabil atom, benämns här särskilt radionuklid (med radioaktivitet, radiokonstant, etc).

Massenergiekvivalensen

Genom nuklidsönderfallet (m→γ)=E_hf1818 [Se från Radionuklidens bildning] i en lokal med N₀ givna radionuklider av typen _ZX^A lämnas ett naturligt gammabidrag från varje enskild radioindivid till alla övriga N₀–1 individer. Energitillskottet innebär att E_γ>0 och därmed ett motsvarande E_m>0 varigenom atomviktens energiekvivalent för nukliden bevaras.

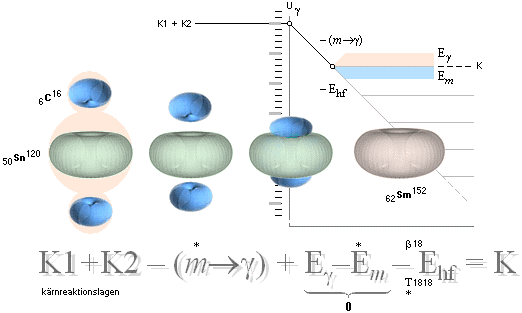
Massdestruktionen (m→γ)=E_hf1818 måste förstås integrerat med, och initierad med början från, nuklidbildningstillfället där kärnstrukturen omedelbart och absolut bestämmer formen för vilken kärntyp som den primära fusionen avser. Med den förutsättningen integreras följaktligen därmed också den ömsesidiga influensen av befintligt avgiven [(m→γ)=E_hf1818]-energi under fusionsbildningen; Alltså föreligger redan under fusionsbildningen ett principiellt tillskott i E_γ; Därmed kan en automatiskt spridning eller fördelning av atomvikten förstås genom två gränslinjer med mellanliggande nominell exakt atomvikt U.

Massenergiekvivalentens sönderfallskurva

Funktionsformen avbildad ovan beskrivs i Frekvensfunktionen samt mera ingående i Allmänna sönderfallsformen med grunder i utförlig beskrivning från Radionuklidernas EGAMMA-Emassa-dynamik och Atomviktens medelvärde.

— Övre gränslinjen bestäms av E_γ, undre gränslinjen bestäms av E_m. Summan av dessa är noll, och därmed konserveras atomviktens energiekvivalent U_γ.

— Men den nuklidinstabila atomen är, betraktad som stabil, inte färdigbildad i och med fusionsfasen, utan massdestruktionen fortsätter på nuklidsönderfallet eller dissonansenergin (m→γ)=E_hf1818. Därmed påverkas också nuklidens energibalans, efter själva fusionstillfället, relativt den bestämda atomvikten U i den ofullbordade nukliden

[K1 + K2 – (m→γ) + E_γ – E_m] = K

vars sönderfallsdynamik fortlöper tills ett stabilt tillstånd uppnås [Se SEKTION 1]. Komponenten E_γ kommer från omgivande radionukliders bidrag via deras (m→γ)=E_hf1818. Den egna nuklidens (m→γ)=E_hf1818 förutsätts mindre än summan av den omgivande mängdens bidrag (vilket förefaller självklart).

BANDBREDDEN, avståndet mellan gränslinjerna E_γ och E_m, bestäms av mängden givna radionuklider N. Större N betyder en större mängd påförd energi på varje individ.

Genom balansen

E_γ – E_m= 0

tvingas nukliden avyttra motsvarande g-massa, större ju större N. Därmed drivs radionukliden (stegvis) till ökad instabilitet (eg. ofrånkomligt närmare kärnsönderfallets ögonblick). Radionukliden sönderfaller i exakt frekvensmässig proportion till den lokala mängden radionuklider av given typ. Stort N betyder hög frekvens, litet N betyder låg frekvens.

Sönderfallsstyrkan

sönderfallsstyrkan

STYRKAN

sönderfallsstyrkan

STYRKAN med vilken det enskilda radiosönderfallet sker (idealt isolerad nuklid) har bara den aktuella nuklidens struktur att återfalla på och kan därför kopplas unikt till E_hf1818.

DEN AVGÖRANDE VIKTIGA FRÅGAN HURUVIDA sönderfallsstyrkan för den enskilda radionukliden också BÖR vara konstant, oberoende av neutrinoinfluensen från mängden omgivande radionuklider (vi vet det strängt taget inte) kan till viss del avgöras på följande argumentbas.

(Sönderfallsstyrkan i den enskilda nukliden exponeras experimentellt genom observationer av heliumenergierna för alfaaktiva radionuklider, eller genom inducerade sönderfall som åstadkommer heliumavyttringar).

Det enda som krävs för att avgöra frågan i princip sett från TNED, är huruvida olika resonansmönster kan sönderbryta en kropp med oändligt frekvensspektrum (atomkärnan) så att den uppdelas i olika reaktionsenergier, inte blott en och samma. Om triggtillfället — som leder till uppdelningen — 1. börjar från de allra högsta frekvenserna med de allra lägsta energierna (Plancks strukturkonstant) och 2. sprids accelererat genom energier som frigörs från massdestruktionerna i brytningskontakterna (lavineffekt), och 3. kombinationen av triggmönster i princip är oändlig samt 4. ackumulerande med växande bidrag från omgivningen, är svaret på frågan redan ett givet och entydigt ja. Sönderfallsstyrkan är konstant.

Förtydligande förklaring:

— I och med att resonansmönstren, analogt alla möjliga dissonansenergier, KAN sönderbryta eller dela kärnan i godtyckliga komponenter, återfaller själva delningsformen endast på den aktuella kärnans inre interna sammansättning, inte på vilka mönster som sönderbryter den och åstadkommer delningen, om delningstillfället inträffar tidigare eller senare. Styrkan i delningstillfället, avseende komponenternas beteende, blir därmed oberoende av den katalyserande dissonansformen (då denna i vilket fall kan sönderbryta alla möjliga radionuklider), men beroende av den aktuella nuklidens struktur. Därmed är saken klar beträffande frågan om sönderfallsstyrkan.

— Med andra ord: sönderfallsstyrkan är en konstant försåvitt den aktuella nuklidens kärnstruktur är det.

Sönderfallstillfället

sönderfallstillfället

TILLFÄLLET

sönderfallstillfället

TILLFÄLLET när sönderfallet sker, beror däremot TVUNGET ENLIGT TNED på neutrinoinfluensen från den totala radiomassan.

— Tillfället är, som det får förstås, ett resonansvillkor som bestäms av summan av alla samverkande bidrag.

Högre (GYNNANDE) influens innebär snabbare sönderfall och kortare nuklidlivstid, lägre influens innebär längre livstid.

— Se även mera utförlig beskrivning i Sönderfallsinfluensens funktionssätt för radionukliderna.

Konstanten E_hf — minsta möjliga DISSONANSENERGIN till kärnsönderfallet

Radionuklidens atomvikt KAN ALLTSÅ FÖRSTÅS SOM ATT DEN balanseras kollektivt via E_γ=NE_hf via den kollektiva dissonansenergin (E_D)

E_D = E_γ – E_hf

= NE_hf – E_hf

= (N–1)E_hf

på individen via föregående beskrivna 0_γ_m=E_γ–E_m enligt

0–E_hf = E_γ–E_m–E_hf ;

0–E_hf = E_γ–E_hf–E_m ;

0–E_hf = E_γ–E_D–E_m ;

0 = [ED+E_hf] – E_m ;

ED = (N–1)E_hf ;

0 = [(N–1)E_hf + E_hf] – E_m

0 = [NE_hf – E_hf + E_hf] – E_m

= NE_hff – E_m ;

NE_hf = E_m

= E_γ

Vi observerar möjligheten då radionukliden omges »exakt» av bidraget E_hf från omgivande typagenter enligt

[K] – E_hf + E_hf = K + E_hf = [K]

I detta fall är (tydligen) sönderfallet tillfälligt hämmat i försorg av omgivningens bidrag. Högre inströmning påverkar E_γ och därmed E_m.

DISSONANSENERGIN i massdestruktionen E_hf1818 underhåller självsvängningar i atomkärnan som förr eller senare leder till att kärnan delas.

I den allmänna kvantitativa beskrivningen av radiosönderfallet — som det kan utläsas enligt TNED — betraktas energivärdet för E_hf1818 som helt försumbart i förhållande till atomens g-massa.

— Dissonansenergin i E_hf1818 blir i TNED (således) tvunget en ytterst högfrekvent E=(h/[n→∞])[n→∞]f och lågenergetisk [E=(h/n)fn]→0 svängningsenergi som inte kan elektrondetekteras eftersom dess våglängdsområde tillhör kärnfraktalernas allra djupast liggande nivåer [Se NEUTRINOSPEKTRUM]; Det finns ingen direkt möjlighet att mäta E_hf1818, vi ser bara effekterna av dess verkan.

Tar vi bort E_hf1818 ur kärnreaktionslagen, erhåller vi endast uttrycket för en stabil nuklid, vilket inte är radiofallet.

EFTERSOM massdestruktionen i betafallet E_hf18 INTE arbetar på centralmassivets 1818e finns till jämförelse i fallen betainstabila atomer heller ingen ömsesidig koppling mellan tilläggsdestruktionen E_m och 1818e. Det innebär, tydligen enligt TNED, att betasönderfallen och deras associerade neutrinobetaekvivalenter (m→γ) inte åstadkommer någon nuklidförändring.

— Inverkan på en enskild betainstabil nuklid via E_hf18 från övriga betainstabila nuklider kan endast påverka E_GAMMA och därmed endast hämma betasönderfallet genom att addera sig med den reguljära neutrinobetadestruktionen (m→γ).

— I fallet radionuklider är effekten den rakt motsatta: E_hf från omgivande radioagenter påskyndar sönderfallet (då bidraget skiljer sig från E_hf).

— EFTERSOM emellertid också massdestruktionerna (m→γ) för samliga fall i exotermiska fusionsbildningar omspänner hela nuklidstrukturen och därmed även innefattar neutrinonivåerna i E_hf18 kan den exotermiskt avgivna »E_hf1818-energin» i nuklidbildningens (m→γ) också agera hämmande på normalt betasönderfallande »E_hf18-nuklider».

— Denna detalj är avgörande viktig i den primära grundämnesbildningen enligt TNED, där bildningen av den tunga nuklidgruppens atomer kräver närvaro av vissa tillfälligt hämmade eller avstängda normalt betainstabila nuklider som kan agera fusionsagenter. Se utförligt från Den tunga nuklidgruppens Certifiering.

— Men kan ökad neutrinoinfluens också bidra till att betasönderfall påskyndas?

— Enligt betasönderfallets allmänna nuklidform

(K) – E_hf18 = K = (K1+K2 – (m→γ) + _β0_γm) – E_hf18 ........................ betainstabil atom

i princip JA — enligt E_GAMMA-faktorn i

= K = (K1+K2 – (m→γ) + E_γ–E_m) – E_hf18 ;

— OM (händelsevis) ett yttre neutrinoenergitillskott i E_γ motsvarar en avsättning i E_hf18, och förutsatt atomen/atomkärnan medger den typen (vilket vi inte känner något allmänt verifierbart kriterium för här) är det tydligt att tillskottet kan påskynda sönderfallet. Det finns dock här (veterligt) inget direkt praktiskt exempel att peka på. Se även Allmän reglering av sönderfallet nedan.

Atomvikten betainstabila

Atomvikten för betainstabila nuklider. Den betainstabila nukliden kan inte som radionukliden kompensera massdestruktionen successivt via E_m i koppling till faktorn E_γ.

För att den betainstabila nuklidens atomvikt (K) ska stämma med kärnreaktionslagens energiekvivalenter, måste därför (K) gälla vid dess bildningstillfälle, initiellt då betasönderfallet precis befinner sig på startpunkten, enligt K1+K2–(m→γ)=(K). Den stabila nuklid som, i slutänden, följer efter detta tillstånd blir (K)–E_hf18=K.

Allmän reglering av sönderfallet

Allmän reglering av sönderfallet. Om den instabila nukliden Ξ (Xsi) i Ξ–E_hf=K tar emot exakt en neutrinobetaekvivalent E_hf från omgivningen så att Ξ–E_hf+E_hf=K+E_hf=Ξ gäller, är sönderfallet ekvivalensmässigt tydligen tillfälligt och energimässigt fullständigt hämmat. En ökning utöver E_hf gör atomen i betafallet exciterad (upp till en viss nivå där elektronmassor kan avyttras i utbyte; under denna nivå avges eller bara reflekteras överskottet som återförd em-strålning). I radiofallet kopplas tillskottet direkt till E_γ och därmed till ett motsvarande E_m.

— EXPLICIT FÖR BETASÖNDERFALLEN gäller alltså tydligen att kontinuiteten mellan E_m och E_hf18 är bruten: E_m har kontinuerlig koppling till centralmassivets 1818e, E_hf18 har det inte. Speciella fall inträder om en yttre påförd energin (E_hf) överstiger elektronbindningsenergin (i atomen i allmänhet, eller i nukliden i synnerhet) varvid utbyte massa-energi kan ske.

SÖNDERFALLETS REGLERING — Hämfaktorn

I en given radiomassa finns alltid två individer AB som är de sista i sin radiogrupp. Men deras livslängd ändras med initialmängden (Se vidare från Halveringssambandet). En större initialmängd N₀ betyder längre livslängd för AB, mindre initialmängd betyder kortare livslängd för AB. Om vi ser saken från AB är det tydligt att växande antal hämmar AB-sönderfallet, ett litet antal gynnar det.

Men hämfaktorn finns tydligen inte där sönderfallen sker. Där råder istället omvända fallet: Ju större initialmängden är, desto snabbare sönderfaller två radioindivider; En mindre initialmängd ger ett större tidsavstånd mellan två individer som konsekutivt lämnar gruppen. Och alltså gynnas aktiviteten i det sönderfallande området med växande initialmängd, medan den hämmar icke sönderfallande områden. Följaktligen framstår slutsatsen som självklar att aktiviteten har ett principiellt centrum och en principiell periferi.

KÄRNREAKTIONSLAGEN FÖR RADIONUKLIDERNA

[K1 + K2 – (m→γ) + _T 0_γm] – E_hf1818 = K

innefattar av princip en sådan centrum-periferifaktor via neutrinobasen E_hf1818. Men vi får då inte tänka oss periferin på vanligt sätt, utan istället som ett idealt band inuti en idealt homogent fördelad radiomassa.

Omgivande radionukliders bidrag via E_hf1818 medför, tydligen, in till en viss gräns att den enskilda nuklidens massdestruktion E_hf1818 hämmas [Se även föregående Konstanten E_hf och Allmän reglering av sönderfallet]. Därmed stryps tillfälligt sönderfallsbenägenheten. På bägge sidor om E_hf1818-gränsen ökar aktiviteten, dels inåt mot ett tänkt idealt sfäriskt centrum och dels utåt mot en tänkt ideal sfärisk periferi. I praktiken finns emellertid inga sådana ideala radiofördelningar, utan hämfaktorn kan fritt kombinera sig genom olika mönster och fluktuationer som ständigt varierar. Tendensen bör vara en högre aktivitet in mot ett preparats centrum om radionukliderna ligger jämnt fördelade, men det finns ingenting som explicit säger att så måste vara fallet eftersom totaleffekten bestäms av summan av alla samverkande vågrörelser och därmed resonansvillkor.

Eftersom kvantiteten E_hf1818 dessutom dels är försvinnande liten och dels ligger i neutrinospektrat som inte är direkt tillgängligt för elektrondetektering och därför heller inte direkt kan påvisas, kan vi knappast räkna med att få fram några direkta experimentella mätvärden på mönsterformerna, även om vi kan sluta oss till deras existens via ovanstående grundsamband.

Se även (vidare) i BEGREPPEN CENTRUM OCH PERIFERI.

Sektion 5

Allmänna samband för radionuklidernas sönderfall

allmänna samband

SEKTION 5

allmänna samband

BILDKÄLLOR: Författarens arkiv · Kollage NikonD90 · VÅRVINTER:R16Apr2010VikBild201-207·ÄNGSLILJOR:ExCur5.14Jul2010Bild35· TNED från Fysikens 7 Principer

Det radioaktiva sönderfallets dynamik

Atomkärnans bildning grundas på neutronnukleonens fasta centralmassiv 1818e+k plus en förbrukningsmassa på 18e som sammanhänger med massdefekten. k är en tilläggsmassa med viss osäkerhetsmarginal (max 2,7e) som varierar beroende på kommersiella tabellverk och parametrar.

Radionuklidens bildningsform med atomkärnans tyngdcirkel beskrivs i separat del i Radionuklidens Bildning.

Gemensamt för alla sönderfallsprocesser är en viss massdestruktion (m→γ) som ger energin till kärnans ombyggnad.

Denna energi avges kontinuerligt under hela sönderfallscykeln och avstannar först när kärnan uppnår ett stabilt tillstånd.

Alla grundämnen har instabila isotoper som uppvisar betasönderfall.

På empirisk grund [HOP 1967] innefattas de hårt radioaktiva nukliderna av atomnumren i grupperna 2-5, 62-68, samt från 83 och uppåt.

Sönderfallet

Delningstillfället ·

SÖNDERFALLET

Vågfunktionen rT+Fa — Frekvensekvivalenten

Atomkärnan med tyngdcirkeln r_T innehåller alla frekvenser, från c/2r_T och uppåt obegränsat, genom en ekvivalent funktion r_T+F_a. F_a kan vara godtycklig, bara den beskriver frekvensstrukturen. Stabil nuklid, analogt idealt stabilt tillstånd, råder när F_a återkopplas av en likadan funktion F_b så att

r_T+k(F_a–F_b) = r_T+k(0)

vilket definierar den rena ostörda tyngdcirkeln. Faktorn k kan i princip vara vilken som helst multiplikator eller funktion. Minsta ändring i F_b förorsakar svävningar i hela strukturen som vid en viss frekvenslokal antar maximala amplituder, motsvarande formen för ett utbrott. Utbrottet motsvarar eller bidrar till kärnans delning. Om ändringen (ΔF_b) i F_b tidsrelateras med början från nollpunkten, kan utbrottets tidslokal ställas i relation till ΔF_b på sådant sätt att ett allt lägre ΔF_b driver utbrottets punkt allt längre in i strukturen och därmed allt längre bort i tiden.

Dissonansenergin

dissonansenergin

Med ett allt mindre ΔF_b kan därmed associeras en allt lägre dissociationsenergi eller DISSONANSENERGI som kopplar till E_hf1818 via (m→γ) i radionuklidens sönderfallsform [se SEKTION 2 och SEKTION 3]: utbrottet förläggs allt längre bort från nollpunkten ju lägre dissociationsenergin är. En stabil atomkärna definieras då av exakt noll dissociationsenergi (E_D), analogt

r = r_T + k(F_a–F_b) = r_T + k(0) = r_T

För en sådan, stabil, nuklidstruktur gäller att hur många som helst individuella nuklider kan förekomma, alla med exakt samma fysikaliska egenskaper. Mängden har inget som helst inflytande på den enskilda individen. För radionukliderna är alltså situationen en annan.

Allmänna sönderfallsformen

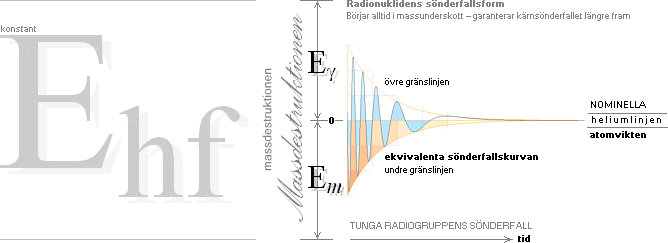
Allmänna sönderfallsformen för de kärninstabilt radioaktiva nukliderna enligt TNED. Den kärninstabilt radioaktiva nukliden börjar ALLTID — från sin bildning — från ett läge med massunderskott, vilket uppvägs av en motsvarande ekvivalent kvantitativ excitationsenergi, så att energibalansen bevaras genom hela sönderfallet, och som garanterar att kärnan också sedan sönderfaller — INTE slutar stabil — VID själva kärndelningen längre fram i historien. Funktionsformens detaljer beskrivs vidare nedan i huvudtexten, samt mera ingående i Frekvensfunktionen med grunder i utförlig beskrivning från Radionuklidernas EGAMMA-Emassa-dynamik och Atomviktens medelvärde.

Varje enskild radionuklid i nuklidgruppen X bidrar med sin dissonansenergi Ehf. Hela X-gruppens totala dissonansenergi E_D=NE_hf bildas på summan av alla N enskilda bidrag så att E_D/N=E_hf=nE_D/nN råder i varje tidpunkt oberoende av gruppens ålder.

Dissonansenergi och nuklidenergi bör alltså vara proportionella enligt E_hf/U=konstant=nE_hf/nU.

Proportionaliteten garanterar att ingen radionuklid i X någonsin upphör med sin massdestruktion (m→γ) så länge nukliden har någon g-massa kvar att förbränna. Dvs., en radionuklid kommer alltid att vara en radionuklid om det så gäller att den bränner av sig själv in till sista prick.

Om dissonansenergin E_hf också associerar ett medelvärde (samma beteckning) som gäller i varje tidpunkt, gäller också proportionaliteten mellan E_hf och antalet kvarvarande radionuklider (N) enligt E_hf/N=konstant=nE_hf/nN.

Allmänna sönderfallsformens förklaring, graf

FÖRKLARINGEN till det radioaktiva sönderfallets dynamik, enligt TNED, kräver alltså en naturligt exakt medelvärdesbildning omkring nominella, standardiserade tabellmässiga experimentellt uppmätta atomviktsvärdet, figuren ovan. Vågfunktionen i illustrationen ovan ansluter till Frekvensfunktionen som beskriver sönderfallets kvantiteter i detalj.

Se även i Radioaktiva sönderfallets dynamik.

Instabiliteten bygger på en viss minsta kontinuerlig massdestruktion (m→γ) vilket innebär att ingen individ i gruppen har konstant g-vägande massa. Eftersom dissonansenergin Ehf också påverkar olika nuklider på olika sätt beroende på aktuell position, finns heller inte två nuklider i gruppen med samma massa. Varje radionuklid är unik.

Blotta existensen av en instabil nuklidform X innebär i konsekvens att mängden individuella nuklider i X alla och tvunget måste uppvisa en viss spridning i fysikaliska egenskaper. I annat fall funnes ingen förutsättning för ett begrepp om instabilitet: Inte alla individer i X kan ha samma vikt, men energimedelvärdet av alla måste tvunget ansluta till den ideala tyngdcirkel för X som skulle finnas om inte instabiliteten existerade. Instabila nuklider i familjen X kan alltså återföras momentant i varje skede av tiden på en generell logotypisk primär nuklidtyngdcirkel som svänger mellan två ytterlighetscirklar. Varje enskild nuklid bidrar med sin del i utformningen av primärsvängningens amplitud för hela X-gruppen.

Därmed är resonemanget återfört på den föregående beskrivna allmänna vågfunktionen r_T+F_a.

Delningstillfället

Delningstillfället sker snabbt.

I generell experimentalfysikalisk mening beskrivs alla energiyttringar som sammanhänger med tungt radioaktivt sönderfall i samband med atomkärnans själva delningstillfälle. Fram till denna punkt ser man inga direkta spår av någon radioaktivitet.

Jämför konventionellt i modern akademi:

”Radioactive decay is the process by which an atomic nucleus of an unstable atom loses energy by emitting ionizing particles (ionizing radiation). The emission is spontaneous, in that the atom decays without any physical interaction with another particle from outside the atom.”,

http://en.wikipedia.org/wiki/Radioactive_decay

@INTERNET Wikipedia Radioactive decay [2011-12-17]

MIC

Liksom vanliga stabila kärnor, lyder emellertid också radionukliderna under MIC (i TNED Mass Interactive Connection, J=m[c=λf]r=E/f=mc²T=mvc/f =mvλ, samma som konv. De Broglies vågekvation, λ=h/mv) som innebär att en kärna både kan ta upp och avge em-strålning inom ett visst excitationsområde. För radionuklidernas del innebär denna möjlighet explicit att komponenterna efter delningstillfället kan innehålla viss överskottsenergi som under ett kort ögonblick omedelbart efter delningen yttrar sig i den detekterbara gammastrålningens frekvensområde.

Denna typ av strålningsemission MIC-transfereringarna, är emellertid inte förknippad med någon samtidig massdestruktion (m→γ), och ingår därför strängt taget inte i det radioaktiva sönderfallets dynamik. I den konventionella beskrivningen av radionukliderna, innefattas den dock och anges i förekommande tabeller med beteckningen γ (grek. lilla gamma).

MIC-energin blir en naturlig komponent i samband med radionuklidens delning. De frånskjutande moment som komponenterna delas på innefattar svängningar med rekyleffekter och därmed alltid ett eftersvall som kan yttra sig i γ-strålning på kärndiameterns nivå och därmed direkt detekterbar.

Några exakta uppgifter på tidrymden för delningstillfället finns här inte. I HOPs9-261sp1ö anges generellt tiden t14 S för (inducerade) fissioner, men spridningen är möjligen stor mellan bildningen av tunga och lätta delkärnor. Experimentella data på det naturliga delningstillfället är (naturligtvis) obefintligt — det kan 1. inte förutsägas och 2. om än så vore fallet kan man (vad vi vet, ännu) inte mäta på en enskild atomkärna. Då emellertid separationsdynamiken enligt TNED är densamma som för fusionerna bör delningstillfället (för de lättaste delkomponenterna) ligga någonstans mellan (lägst) t22 S [ekvivalenta kortaste tiden för nukleär koppling 0-360° via ljushastigheten med hänsyn till toppspinnet, se Fusionstidens beräkning] och (högst) t20 S, men dessa värden är högst grova och endast orienterande.

Kärndelningen i modernukliden

Kärndelningen i modernukliden börjar enligt TNED (minsta motståndets verkan) på lägsta momentets punkter, vilket är i kärnbrunnens centrum. Genom den lavineffekt som uppkommer via dissonanseffekten vid delningstillfället (allmänna vågfunktionen r_T+F_a), bildas — som TNED får förstås — på mycket kort tid ett kärnembryo i kärnbrunnen. Embryot växer med hög hastighet till den avyttrade delens kärnform. Under processen bevaras summan av alla moment konstant. Utöver kärnenergierna, avdelas alltid en särskild energimängd eller en »svängningspott» som åtgår för att separera komponenterna och som sammanhänger med de olika motvända kärnstrukturerna vid delningstillfället. Se även mera ingående från Nuklidbarriären i Nuklidbildningarna.

Fragmenteringsargumentet

Eftersom energikomponenten i de motvända kärnstrukturerna vid delningstillfället tillhör en specifik nuklidstruktur och därför bör vara exakt densamma för samma radionuklidtyp, bör också rörelseenergin för den utkastade delkärnan vara en exakt värdemätare på en viss radionuklids (kosmologiskt) lokala sönderfallsstyrka: Högre energi indikerar ett snabbare generellt sönderfall.

I praktiken är det mera komplicerat:

— Varje atom har sin lokala energigenomströmning, och två exakt energiidentiska atomer existerar inte vad vi vet. Det finns alltid smärre skillnader, och dessa omsätts också i de olika individuella fallen med, exemplifierat, typiska alfasönderfall. Istället för att uppmäta en och samma alfasönderfallsenergier för alla ingående radionuklider i ett preparat, uppmäter man [Se eng. Alpha Spectroscopy] s.k. olika KANALER [eng. alpha channels] med inbördes dels spridda energivärden och dels utspridda på olika tidpunkter, mera sällan eller mera ofta. Se illustrerat webbutdrag i Alfaenergier.

Genom att (helt enkelt, i termer av vad som framställs i moderna kvarter) mäta den utkastade delkärnans rörelseenergi (ofta alfapartikeln, samma som Helium-4-kärnan) får man ett relativt mått på radionuklidens livslängd.

I modern akademi sammanhänger denna ”klassiska fenomenform” från Rutherford (1913) med sambandet mellan alfaenergi och halveringstid, i konventionen känt som Geiger-Nuttalls samband;

Enda generella, entydiga sättet FÖR DEN JÄMFÖRANDE ANALYSEN att få fram, och använda, EN bestämd sönderfallsenergi för EN bestämd radionuklid, är uppenbarligen och tydligen att använda en räkning via atomvikter [här benämnt effektiva sönderfallsenergin]: skillnaden i mass-energi före och efter.

Sönderfallets enhetliga preferensgrund

— Detta SÄTT är, emellertid, ingenting som direkt framskymtar i den allmänna, etablerade beskrivningen, utan snarare här den enda kända preferens som kan användas alls, om någon, för att få fram entydigt användbara resultatvärden till jämförande analys i koppling till just Geiger-Nuttalls [från början empiriskt upptäckta] sambandsform:

EN bestämd halveringstid för EN bestämd sönderfallsenergi för EN bestämd alfaradionuklid.

Därmed bortfaller — helt — betydelsen av uppmätningen av de olika alfakanalerna, de olika alfaenergierna. Dessa har, tydligen, ingen betydelse i ljuset av en entydig sambandsform av ovan preciserade typ — och tillsammans med olika jämförande teoretiska beräkningar från bestämda energipremisser, vilket är fallet här enligt TNED.

— I TNED finns, nämligen, också en annan aspekt som ökar svårighetsgraden än mer i denna redan uppenbart snåriga »radiodjungel»:

— Som visas översiktligt i Multipla halveringstider i TNED finns, genom nuklidbildningens sätt enligt TNED via nuklidkoefficienten och i ljuset av TNED-härledningen till motsvarande Geiger-Nuttallsambandet, se Härledningen, absolut uppenbara möjligheter för en och samma typnuklid — givet masstal, given kärnladdning, given kärnenergi, men likväl via en differens i SÄTTET att »baka in kärnstrukturerna» vid de primära grundämnenas fusionsbildningar — att uppvisa olika halveringstider;

— T.ex., en viss alfaradionuklid med bestämt masstal; Den bestämda alfaradionukliden KAN enligt TNED, teoretiskt, bilda olika b-koefficienter [TNED-faktorn i tH-sambandet, se Slutformen, som kopplar den aktuella sönderfallskärnan] beroende på den neutronkvot som gällde vid alfaradionuklidens primära bildning; Samma nuklidtyp, samma effektiva sönderfallsenergi, men olika halveringstider beroende på hur neutronkvoterna, samma som bildning i olika [neutrino]energigenomströmningslokaler, bildar sina karaktäristiska atomkärnor. Se mera utförligt från avsnittet om Multipla halveringstider i TNED.

FRAGMENTERINGSARGUMENTETS sak

— Med tillkomsten av synpunkten på b-koefficientens koppling till neutronkvoten, finns det inte längre någon MÄTTEKNISKT HELT SÄKER preferens för att avgöra vad som är vad, då uppenbarligen SAMTLIGA lokala atomer och nuklider [Främst via Jordmineralerna för vår del] genom ömsesidiga influenser, sönderfall och blandningar i tidens längd, tydligen, har fragmenterat — för länge sedan.

— Det vi kan se, enligt TNED, blir bara »vissa spår» av en från början »idealt sammanhängande grafisk funktionsform», och vars fragmentering just de olika bildningslokalerna bär ansvaret för. Det blir omöjligt att undkomma den konsekvensen, enligt TNED.

— Till jämförelse, och för att klargöra mera exakt vad som menas i ljuset av ovanstående utläggningar, finns enligt TNED Allmänna RadioIsotopKartan som, tydligen, visar SPÅREN och FRAGMENTERINGEN i fallet alfaradionukliderna.

— En motsvarande »kurvpassningskarta» för alfaradionukliderna i den moderna akademins lärosystem KAN INTE HÄRLEDAS — därför att kurvpassningsformen bygger just på nuklidkoefficienten [b-formen] via EN »masterkurva» [Se från Allmänna tH-sambandet och tH-universalen] och vars matematiska fysik i TNED ytterst grundas på potentialbarriärens energizon med ljusets gravitella beroende ENLIGT RELATERAD FYSIK — och därmed direkt PLING på Atomkärnan Härledning: definitivt INTE möjlig i MAC. Motsvarande kurvpassningar i MAC ges [som kanske redan bekant] via en mängd olika kurvformer [Exempel ges via LabSpace-illustrationen] som alla ansluter till MAC-teorin för motsvarande Allmänna Koefficientsambandet [Geiger-Nuttallformen »i syntes», enligt TNED].

— Den enhetliga, översiktliga kartbild i radiofysikens allmänna beskrivning som ges via TNED finns inte i den moderna akademins lärosystem — och kommer heller aldrig att finnas där.

— Med dessa detaljer klarlagda, och endast då, kan vi ALLTSÅ och LIKVÄL nu [äntligen] koncentrera oss på den egentliga — ideala — radiofysikens grundbegrepp då vi, som ovan, känner de underliggande begränsningarna — enligt TNED.

Eftersom en viss typ av radionuklid alltid utgår ifrån ett bestämt svängningstillstånd genom deformationen i atomkärnans motsvarande tyngdcirkel, och därför också bör påföra en och samma typ av avyttringsnuklid samma grundläggande svängningsenergier (idealt innefattat rekylverkan, samt arbetet för alla ombyggnader), är det tydligt att den avyttrade delnuklidens utgångshastighet bör vara ett mått på sönderfallsstyrkan i radionuklidens dynamik (eller, med viss försiktighet, dess livslängd). Högre hastighet betyder en större andel överförd radiosvängning vid (som ofta är fallet) Heliumkärnans bildning i modernukliden, därmed en högre magnitud i strävan mot stabilt tillstånd, och därmed en kortare livslängd för radionukliden.

Från denna »enkla» analogi finns, i TNED, ett sätt att härleda en allmän ekvation för radioaktivitetens varaktighet — halveringstiden för en viss radionuklid (Se utförligt från Härledningen till halveringstidssambandet i TNED, samma typform som Geiger-Nuttalls empiriska samband men med annan grundteori), här med förebild och exempel i alfaradiosönderfallet.

Komplikationerna i betasönderfallen relativt alfaradiofallen

I TNED, men inte i MAC, visar det sig att samma matematiska form (tH-sambandet) också kan tillämpas generellt för samtliga fall — även betasönderfallen; Se utförligt från Betasönderfallens matematiska fysik i TNED. Dock inte utan en observerad (stor) dramatik;

Nuklidkartan ovan i översikt visar grundämnesnuklidernas indelning efter masstal [horisontella axeln] i de bägge huvudgrupperna lätta och tunga nukliderna. De kärninstabila nukliderna återfinns i stort sett uteslutande i den tunga gruppen [från masstal runt 210], den streckade slutdelen ovan höger. Speciellt alfaradionukliderna utmärker sig här med de ovan [i sig dramatiskt, se från Fragmenteringsargumentet] beskriva egenheter och som — som det tydligen får uttolkas i TNED — avbildar en FRAGMENTERAD FUNKTIONSBILD av hela alfaradiofysiken på en bestämd sambandsform, se AlfaRadioIsotoperna särskilt.

— Någon direkt liknande eller motsvarande uttydbar ordning finns enligt TNED inte i fallet betainstabila nuklider;

Nuklidkartan i översikt

Nuklidkartan AZ ovan, A masstal Z atomnummer = kärnladdning, visar enligt TNED översiktligt hur de betainstabila nukliderna [β±] ligger spridda på bägge sidor ideala nuklidstatiska medelvärdeslinjen [röda, 12Z/5] — det vita stråket där de stabila nukliderna ligger samlade.

— KOMPLIKATIONERNA jämfört med »den enkla alfaradiokartan» [se utförligt från Fragmenteringsargumentet ovan] består för betasönderfallens del i att det finns TRE olika sönderfallstyper i TVÅ grupper — β+ vänster ovan som, ofta i förening med ElektronInfångning [eng. Electron Capture] sönderfaller från högre Z till lägre, precis som alfaradionukliderna gör, och β– som sönderfaller åt andra hållet;

— Med den diametrala ordningen blir varje motsvarande ENHETLIG kartbild för betasönderfallens del, och som SKULLE motsvara alfaradionuklidernas relativa välordning — OM ordningen vore ideal — UTESLUTEN.

— Kort sagt: Betasönderfallens eventuella STRUKTURBILDER i [eventuellt befintliga] funktionsformer blir, enligt TNED, FRÄMST på grund av de motsatt diagonalt isobariska [se termerna i figuren ovan] sönderfallsriktningarna omöjliga att sammanfatta på någon alfaradionuklidernas motsvarande enhetliga ordning. Det är uteslutet. Det man MÖJLIGEN skulle kunna finna är funktionsanalogier mellan betasönderfallens EC, β+ och alfaradiosönderfallen då dessa har samma isobariska sönderfallsriktning. Men även detta uppslag visar sig innehålla inre [starkt funktions-] fragmenterande detaljer;

— I de speciellt separata artiklar som framkommit under denna presentations författning,

Vad utmärker TNED framför MAC i sönderfallsfysiken?

Nuklidkoefficienten i Kombinerade sönderfallstyper

framkommer en högst nedslående totalbild av den etablerade framställningens detaljer i ämnet — främst den här:

Se 29Cu64-exemplet. Tabellen ovan sammanfattar, i redovisade datapunkter, beskrivningen nedan.

1. DELS förekommer — med referens till olika tabellkällverk på webben [Dec2011]; Se Jämförande Webbexempel — uppgifter med uppenbart inbördes olikheter så stora att de INTE kan användas för någon PRECISERAD jämförelse i resultatredovisningar för matematiskt framräknade samband i de olika teorierna i TNED kontra MAC.

2. DELS förekommer en ALGORITMISERAD SUMMERANDE INDELNING i MAC — beträffande de s.k. [eng.] partial decay constants — och som helt kolliderar med ordningen i Sönderfallets enhetliga preferensgrund, den ordning som krävs för att kunna genomföra någon BEGRIPLIG jämförelse från en FAST matematisk grund — enligt TNED.

— Medan MAC-teorin anser att de s.k. partiella halveringstiderna — som inte kan observeras direkt experimentellt, endast slutas till genom uppmätta procentuella andelar, se särskilt Citat — summeras genom inverterad aktivitetssummering, [den ger våldsamt avvikande s.k. partiella halveringstider]

1/t_H1 + 1/t_H2 + 1/t_H3 + …

används konsekvent i TNED — enligt ordningen i Sönderfallets enhetliga preferensgrund — snarare den mera enhetliga individuellt oberoende medelvärdesbild som också beror av antalet multipla sönderfallstyper [d] enligt [abc … resp. procentuellt uppmätta andelar i d-gruppen; jämför 0,43·3+0,38·3+0,19·3=3·1]

[Se utförligt i De Tre MedelvärdesSummeringssätten]

t_H[a + b + c + … = d]/d

— Det finns, här veterligt, ingenting EXPLICIT EXPERIMENTELLT som kan avgöra vilken medelvärdessummeringsform som är den korrekta av de bägge ovan angivna [Se särskilt Citat]: dessa bägge, plus en ytterligare, ger i vilket fall samma slutresultat, se utförligt i De Tre MedelvärdesSummeringssätten.

— I TNED är det bara det övergripande Sönderfallets enhetliga preferensgrund som talar om vilket som är vad, och hur man ska välja vilket som ska gälla.

— Därmed, och i summa sagt, har varje möjlig jämförande resultatbild med MAC-beskrivningar i ämnet betasönderfallens matematiska radiofysik utraderats. Helt, komplett, fullständigt. Det är med andra ord helt meningslöst att ens leta efter resultatdata i MAC med de ovan beskrivna förutsättningarna;

— Hänvisa till Tabellexemplet 29Cu64 som exemplifierar de olika datakällorna och deras resulterande datapunkter, och som visar det MENINGSLÖSA i begreppet jämförande precision i MAC i ämnet betasönderfallens matematiska fysik.

Matematisk beskrivning

Matematisk beskrivning av kärndelningen enligt TNED — alla frekvenser 0 till f →∞

ATOMKÄRNANS TOTALA FREKVENSSPEKTRUM, motsvarande den föregående spiralformen [‡], kan komprimeras på formen y=A(sin x^–1)=A(sin f). Funktionen beskriver alla frekvenser från [f→∞] till 0. I polära koordinater fås samma form genom att lägga y på en grundcirkel r_T som ger r=r_T+A(sin x^–1). Atomkärnans stabila återkoppling kan därmed beskrivas på tyngdcirkeln r_T enligt r=r_T+A[(sin [x]^–1) – (sin [x+a]^–1)] med a=0 som ger r=r_T. Kurvbilderna nedan illustrerar motsvarande grafdelar.

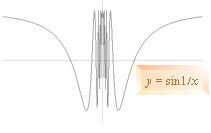
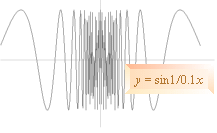
MINSTA MÖJLIGA TILLSKOTT I TIDEN (Δx) i a-delen bildar en störning med obegränsat smal bandbredd. För att effekten ska bli synlig på r_T i den illustrerade funktionens skala måste a vara i storleksordningen minst 0,000001. Lägre värden ger ingen synbar skillnad mot r=r_T. I det motsvarande praktiska fallet går a-värdet initiellt mot noll obegränsat, vilket betyder att ändringen via (m→γ) i kärnstrukturen börjar från de allra djupast liggande nivåerna med de allra högsta frekvenserna. Hur den typen av frekvensbyggnad kopplar generellt till atomkärnan enligt TNED beskrivs utförligt i Plancks strukturkonstant.

sinusekvivalenten — från Delningstillfället

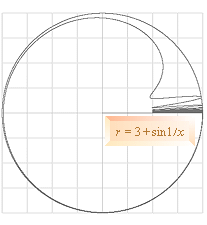
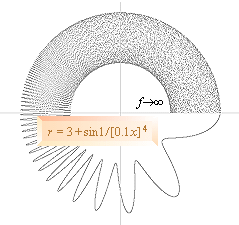
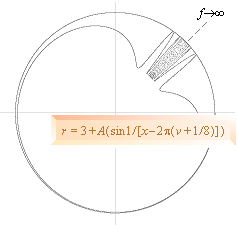
För att relatera ändringsbilden över hela kärnstrukturen på ett korrekt och rättvist sätt, måste varje ändring i de djupast liggande nivåerna ges TID att omspänna hela kärnstrukturens frekvensspektrum, analogt kärnans totala byggnad av motsvarande fraktala ringformer. En sådan tidsfunktion kan beskrivas cykliskt med ett helt varv i polärfunktionen

r_T+A(sin x^–1). För varje sådant varv sker en viss ändring i kärnstrukturen, dels primärt via den egna, enligt TNED nära obetydliga neutrinobaserade, massdestruktionen (m→γ) som underhåller sönderfallets status och dels sekundärt genom influensen från omgivande radionukliders (m→γ)-emissioner. Ändringen byggs upp eller ackumuleras successivt med växande tid ju längre den kollektiva (m→γ)-emissionen pågår. Vid en viss tidpunkt är ändringspotentialen mättad för en viss radioindivid. Varje ytterligare (m→γ)-emission från denna punkt, från den egna kärnan eller från kollektivet, medför att kärnan svarar med ett utbrott som resulterar i omedelbar (oåterkallelig) kärndelning. Kärndelningen inträffar på frekvensmaximum, analogt från kärnstrukturens allra djupaste delar, enligt Plancks strukturkonstant.

UTBROTTET

Två olika sätt (betecknade r₁ och r₂) finns att beskriva kärndelningstillfället matematiskt via sinusfunktionen r=r_T+A[(sin [x]^–1) – (sin [x+a]^–1)], A en godtycklig amplitudkoefficient. Det finns också andra sätt, men då kommer vi (förmodligen, helt) att förlora oss i matematiken vilket inte är av nöden i detta skede. Det ena sättet (r₁) förlägger nuklidens startpunkt bakåt i tiden på dess livstidsavstånd [t =T(A)] från delningstillfället (T) och låter sedan kärnan avverka sina frekvenskopplande cykler (nT₀) tills livslängden har uppnåtts. Denna punkt nås bara vid ett enda tillfälle och motsvarar sinusfunktionens frekvensmaximum där också maximal (i princip oändlig) tyngdcirkelbrytande amplitud uppnås. Det andra sättet (r₂) består i att frekvensmaximum passeras cykliskt, upprepat antalet n=t/T₀ gånger med en motsvarande absolut amplituddämpning (som annars spräcker kärnan redan inom första varvets första bågsekund) intill dess kärndelningen plötsligt inträffar vid T=t. (Bägge sätten ger naturligtvis samma slutresultat).

(r₁). Funktionens frekvensmaximum (f→∞) kan vridas moturs n varv och ställas på vinkelpositionen d_0-1 av cirkelintervallet i (n+1)-varvet enligt r=r_T+A(sin [x–2p(n+d)]^–1). För att komma fram till frekvensmaximum måste x avverka n varv. Ett varv avverkas på tiden T₀ med motsvarande frekvens 1/T₀=f₀. T₀ motsvarar atomkärnans återkoppling genom hela sitt frekvensspektrum. Idealt via ljusets passage genom kärndiametern via ljushastigheten c₀ i Jordlokalens referens (c_0J=299 792 458 M/S) är T₀=r_NUKLIDRADIEN/c₀ (ca 5 t24 S för protonaggregatet med r₀=1,37 t15 M, analogt f₀=2 T23 Hz, övriga följer approximativt r=r₀A1/3). Med omkretsen som preferens ges en längre tid approximativt enligt

T₀=πr_NUKLIDRADIEN/c₀. För de tyngsta nukliderna ges ett övre värde på ca t22 S.

Sambanden för xn:

x/2π=T/T₀ ; x=T2π/T₀=ω₀T=T2πf₀ ; n=t/T₀=tf₀ ; x–n2π=2πf₀T – 2πf₀t=2πf₀(T – t) ;

x–n2π=2πf₀(T – t). t anger nuklidens livslängd. (T–t) räknat negativt från –t upp till 0 ;

r=r_T+A[(sin [2πf₀(T–t)]^–1) – (sin [2πf₀(T–t) + (a→0)]^–1)], A här en godtycklig amplitudkoefficient som ovan.

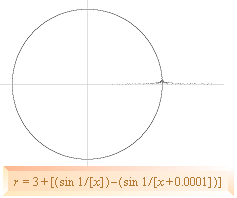
(r₂). För att den matematiska beskrivningen av radiodelningens abrupta delningstillfälle ska bli meningsfull i

r=r_T+A[(sin [x]^–1) – (sin [x+a]^–1)], se grundformen från Vågfunktionen, är det tydligt att A-faktorns cykliskt ackumulerande form måste vara högeligen exponentiellt betingad av tillväxt från ett absolut minsta värde, upp till den punkt där kärndelningen sker.

Faktorn a som obegränsat närliggande noll, med tillhörande minsta möjliga ändring, ger med givet A=1 en obegränsat stor amplitud i ändringen. Normalt sett, är det denna höga amplitud vi skulle associera med själva delningstillfället, den punkt som bryter kärnans tyngdcirkel i en definitiv formändring. För att undertrycka denna, och ge den ett mera relevant litet värde i radionuklidens början, måste alltså A-faktorn åstadkomma en motsvarande dämpning.

A-faktorn ska därmed i princip visa 0 ända fram till delningstillfället då den plötsligt ger 1.

En sådan, ideal, funktion beskrivs av ett rektangelhörn enligt formen

y = (1 + [x + (m→0)]^–[n^→∞])^–1

Grafen ovan visar funktionen exemplifierat.

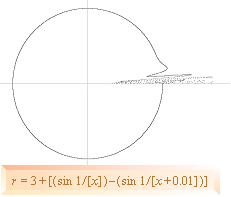
Faktorn (m→0) krävs för att amplituden vid T=0 också ska bli 0.

Med T som tiden och t som delningstillfället ges x_t=T/t. Funktionen uttrycker analogt att utbrottet sker på frekvensen 1/x=1, vilket motsvarar våglängden för den aktuella nuklidens kärndiameter. Funktionen således totalt i PREFIXxSIN enligt

r = r_T+(1 + [T/t + (m→0)]^–[ⁿ^→∞])^–1[(sin [ω₀T]^–1) – (sin ω₀[T + (a→0)]^–1)]

SOM VI SER blir funktionsbeskrivningen fullständigt trivial. Vi får i princip ett hörn av en rektangel med hela funktionen upphängd på den simpla tidsfaktorn t. Med den ömsesidiga influensen mellan radionukliderna är det dock tydligt att t-faktorn måste bli ypperligt komplicerad. Det finns emellertid en generaliserande väg som (exakt) beskriver denna sublima faktor. Den bestäms av radiokollektivet med referens till en bestämd radiolokal och relateras till (den statistiska) tidpunkten för radionukliden N_n då den lämnar gruppen genom sitt sönderfall. Sambandet är

t = t_H (ln2)^–1ln(N₀/[1+N₀–N_n])

och behandlas i det följande [Se explicit i FREKVENSFUNKTIONEN].

Illustrationerna ovan

Utbrott sker när tyngdcirkelns deformation överstiger atomkärnans sammanhållande elasticitet. (Fluktuationerna som bestämmer dessa töjningar är med kärnans enorma YT-täthet (se Atomkärnans gravitella härledning) utomordentligt små — alla illustrationer blir tvunget grymt överdrivna). För det synbarliga illustrativa ändamålet måste a-faktorn sättas minst 0,000001. I det praktiska fallet ligger den obegränsat nära 0 med en obegränsat stor dämpning (A=0) eftersom utslaget i annat fall skulle bli obegränsat stort.

SektionerEND.

Slutförd genomgång 18Dec2011 efter föregående arbeten 10Okt2004.

Frekvensfunktionen

Det radioaktiva sönderfallets allmänna frekvensfunktion i PREFIXxSIN enligt TNED — exemplifierad

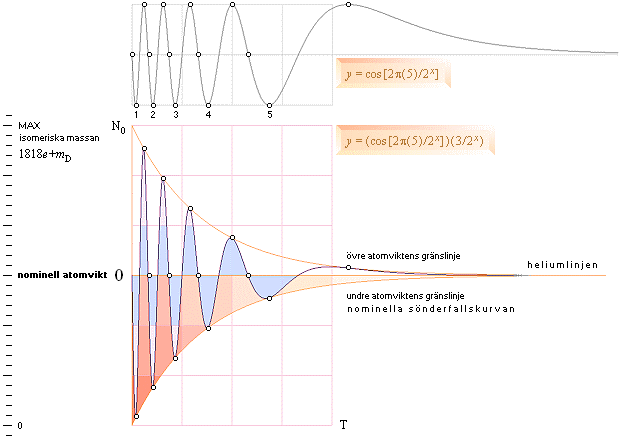
Graf; y = (3/2'x)cos2þ5/2'x

Allmänna samband:

T = t_H(ln2)^–1ln(N₀/N) ..................... tidpunkten för N kvarvarande radionuklider

tidpunkten ligger på mittlinjen (Heliumlinjen) på fallande flank

ξ_N = kN .......................................... radioaktiviteten

k = (ln2)/t_H ..................................... radiokonstanten, konv. ofta λ=ln2/T_½

GENERELLT FÖR SAMTLIGA PERIODISKA SINUSFUNKTIONER i PREFIXxSIN y=sin(2πf)x gäller lutningen 2πf=tanA på stigande flank (här utan bevis — beviset, ingående, ges via sinusvågens härledning genom cirkelns förflyttning utmed x-axeln via konstant cirkelrotation och den fasta cirkelbågpunktens skuggprojektion på y-axeln). Eftersom

ξ_N=kN=(ln2/t_H)N uttrycker en frekvens S^–1 får man funktionsekvivalenterna (principuppställningen nedan, första blocket, förklaras i det efterföljande derivatablocket)

; F’ = –[ N ](1/t_H)ln2 · 1 = –f = –ξ_N

; = –[2πN ](1/t_H)ln2 · 1 = –2πf = –tanA

; = –[2πN ](1/t_H)ln2 sin [2πN ]

;

TANGENSFORMEN eller derivatan till funktionen F=cos n(P), med (P) som en godtyckligt sammansatt funktion i x, är [Se FORMLAGARNA] i PREFIXxSIN

Dn cos n(P) = n Dn(P) sin n(P).

Med (P)=2^–T/t^H och n=2πN₀ ges då via 2πN₀/2^T/t^H sambandet

Dn cos [2πN₀/2^T/t^H]

= [2πN₀] Dn 2^–T/t^H sin [2πN₀/2^T/t^H]

= –[2πN₀/2^T/t^H](1/t_H)ln2 sin [2πN₀/2^T/t^H]

; = –[2πN ](1/t_H)ln2 sin [2πN ]

och vilket vi ser är samma som i utvecklingen direkt från frekvensen ξ_N ovan. Med andra ord [Se även från begreppen derivata och integral om ej redan bekant]: Varianten y’=2πξ_Nsin2πN beskriver sönderfallet integralt enligt

∫ y’dt = y = Ncos2πN.

DET KÄRNDELANDE RADIOAKTIVA SÖNDERFALLET med antalet N kvarvarande radionuklider efter tiden T från ett givet antal N₀ med halveringsperioden t_H enligt

N = N₀/2^T/t^H

beskrivs alltså per individuellt nukleärt sönderfall idealt in till sista nuklid genom den harmoniska funktionen

y = cos2πN (exemplifierat i illustrationen med N₀=7) enligt

y = cos[ω₀ · f (T)] = cos2πN .......................... frekvensfunktionen, grundform

N = N₀/2^T/t^H ......................... sönderfallsfunktionen

y = Ncos2πN ....................... fullständiga sönderfallets funktion

y’ = 2πkNsin2πN .................. frekvensfunktionens variation, =2πξ_Nsin2πN

i PREFIXxSIN.

Nollställena i toppen (varje n+1/4 varv 0,25; 1,25; 2,25; 3,25; …) ges av x=ln[7/(1/4+[N₀–N_n])]/ln2 med N₀=7.

Nollställena i botten (varje n+3/4 varv 0,75; 1,75; 2,75; 3,75; …) ges av x=ln[7/(3/4+[N₀–N_n])]/ln2 med N₀=7.

Nollställena i mitten (varje helt varv n= 0; 1; 2; 3; 4; 5; 6; 7; …) ges av x=ln[7/( 1 +[N₀–N_n])]/ln2 med N₀=7.

Topparna vrids analogt med logaritmfunktionen så att ovanstående värden också utgör x-skärningen mellan de bägge funktionerna.

Sönderfallande nuklid utgår ur mängden (primärt, minsta massan, se Alltid lägsta massnukliden) i botten av frekvensformen via

T_n=t_H(ln2)^–1ln[N₀/(3/4 + N₀–N_n)]. Men sönderfallen kan ske var som helst inom intervallet.

En sammanställd mera utförlig beskrivning ges i Radioaktiva Sönderfallets Dynamik.

För att förklara det tungt radioaktiva sönderfallets motorik, måste radionukliden kontinuerligt under hela sin livstid förbruka en viss minsta massa (m→γ) som underhåller energin i sönderfallets dynamik (dissonansbildningen som senare åstadkommer själva delningstillfället).

Nuklidens atomvikt (U, se Begreppet Atomvikt i radiosönderfallet) bevaras genom en medelvärdesform som beskrivs av kärnreaktionslagen på annan plats;

— Se

G-massa och Gamma-massa,

Sönderfallets allmänna dynamik,

Allmänna samband för radionuklidernas sönderfall,

Atomviktens medelvärde, Radionuklidernas E_GAMMA-E_massa-dynamik, .

Ovanstående kurvform beskriver denna medelvärdesform, enligt TNED.

Radionuklidernas EGAMMA-Emassa-dynamik

Radionuklidernas E_GAMMA-E_massa-dynamik

Vartefter sönderfallet fortlöper, minskar aktiviteten (eller gradienten) i den totala massdestruktionen (m→γ) eller neutrinoinfluensen som den enskilda radionukliden nås av från alla övriga via deras dissonansenergier E(hf). Från ett maxvärde (nuklidbildningen) vid N₀ går den totala inverkan av den aktuella dissonansenergins massdestruktion (m→γ)’ på hela gruppen mot noll analogt med att individantalet N också går mot noll i takt med radiosönderfallet. [Se även i Funktionssättet].

— Man kan därför i en ekvivalent uppställa grundvillkoret att de radionuklider som sönderfaller från start också sönderfaller på motsvarande maxvärdet (m→γ) för den aktuella nukliden, dvs. nukliderna i botten av medelvärdesformen nedan, och sedan allt mindre (dvs. mot atomviktens medelvärde).

Allmänna sönderfallets funktion

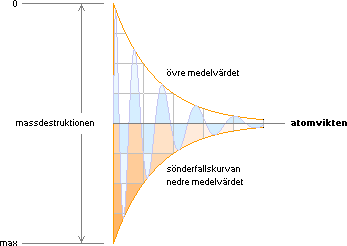
Vid radionuklidbildningen måste MINST sönderfallsenergins magnitud påföras atomen i extraenergi för att den efter sönderfallet INTE ska missa läget stabil nuklid; Se den övre delen av ovanstående grafdel. Men det innebär samtidigt ett POTENTIELLT SVAR från den nybildade atomen; Atomen svarar med att UTGE MOTSVARANDE MASS-ENERGI för att bevara ATOMVIKTEN [U] för den nukliden konstant; Se den undre delen av ovanstående grafdel.

— Vartefter tiden går och sönderfall sker från de radionuklider som är mest exciterade och därmed i störst behov av att finna stabilitet, vilket betyder att kurvans brantaste delar försvinner successivt, sker en utjämning mot ideala atomviktens mittlinje i takt med gruppens [universums] åldring.

— ÄVEN om möjligheten SKULLE finnas för den nybildade radionukliden att ENBART uppvisa den exciterade överdelens energitillskott, alltså utan någon motsvarande massutgivning för att kompensera, måste LIKVÄL i kraft av ARBETET som åtgår för att behålla radionukliden i dess självsvängande instabilitet en viss massavverkning tas från atomkärnan för att ge arbetskraften till instabilitetens underhåll och därmed i vilket fall en viss massreduktion.

— Sagt på annat sätt: ingen instabil atom existerar som kan bevara sin instabilitet i evighet — därför att det instabila tillståndets bevarande kräver/visar energi.

— I den allmänna beskrivningen av radionuklidernas sönderfall kan vi därför [till prövning] anta ovanstående allmänna fördelningsbild i bevarande av ursprungsindividens atomvikt — på kvantitativ massa-energibas.

När den N:te individen sönderfaller vid tillfället då N individer finns kvar, bildar de kvarvarande ett högre massmedelvärde för atomvikten. Aktiviteten i massdestruktionen ligger då huvudsakligen på de nuklider som har den största massan; Dissonansenergin riktas med fokus på den individ i undergruppen som har den lägsta massan, analogt den nuklid med största receptibiliteten, analogt största relativa underskottet, det är den individ som uppvisar de mest angelägna förutsättningarna för att, naturligt, ta emot den största energimängden från alla övriga i dissonansfrekvenserna.

— Samtidigt, vartefter överdelen E_GAMMA fortsätter bränna av sin massdel genom de enskilda nuklidernas dissonansenergier [E(hf)], sjunker hela gruppens massmedelvärde.

— Då bottennukliden sönderfaller, på grund av den nyligen omnämnda högre influensen och därmed lämnar gruppen, antar denna ett något högre medelvärde, och därmed hela kurvformen i avtagande mot noll i takt med att universum (de kvarvarande radionukliderna) åldras.

— På det sättet är det möjligt att förstå den reducerade skillnaden mellan de nuklider som har den största massan och de som har den lägsta; den sönderfallande nukliden blir alltid den i gruppen med den lägsta massan, den som uppvisar den största potentialen i massunderskott och som därmed uppvisar den starkaste strävan att uppnå jämvikt (via sönderfall).

Eftersom sönderfallen kan återföras på vågformer som följer ljushastigheten och därmed är fördröjda i föreställningen om »exakt» tidpunkt för ett visst sönderfall, kan hela processen — totalt — också återföras på en dämpad, (högfrekvent) svängning vars frekvens dock avtar med det minskande antalet kvarvarande individer. Frekvensen vid givet N motsvarar aktiviteten eller antalet sönderfall per sekund, ξ_N=kN=(1–2^–1/tH)N=(1–1/2^1/tH)N₀/2^T/tH. Se utförligt från Frekvensfunktionen.

Sönderfallets utveckling

Hur det radioaktiva sönderfallet utvecklas enligt TNED

Följande framgår teoretiskt enligt TNED i den allmänna förklaringen till det radioaktiva sönderfallets fysik:

Följande analys kan inte genomföras i den moderna akademins lärosystem — Plancks strukturkonstant h/n med obegränsat växande n enligt ATOMKÄRNANS HÄRLEDNING från Planckringen [NEUTRONEN] h=mcr i TNED via massans principiella struktur [PASTOM] från massekvivalenten m=[m/n]nm finns inte i modern akademi; heller ingen motsvarande Planckenergiekvivalent E=hf=[h/n]nf, och därmed ingen minsta möjliga energi Emin=hfmin på högsta möjliga frekvens Emin=hfmin=[h/n]nfmin=[h/n]fmax och som hela TNED-teorin för radiosönderfallets fysik bygger på.

Betasönderfallet: [Figuren höger];

Sönderfallet får inte sluta på massunderskott: inte för den stabila individen, inte för någon mellanliggande heller; Vid sönderfallets slut måste den stabila atomen ha garanterad fast atomvikt [U2]. Därmed finns bara ett sätt för den betainstabila atomen att bildas [U1]: i excess, överskott, av massenergi, utan DIREKT avgivande av motsvarande g-massa [E(m)]; denna avges blott så småningom genom sönderfallets process fram till betasönderfallets fullbordan.

Kärnsönderfallet: [Figuren mitten];

Sönderfallet får inte sluta på massunderskott för den stabila individen [U2] — men måste göra det för primärnukliden [U1], i annat fall är denna stabil.

;

— Radionukliden måste — tvunget — bildas på MINST en extra överskottsenergi [U1+Egamma] som motsvarar ARBETET FÖR UNDERHÅLLET AV DET STABILA TILLSTÅNDET ända fram till KÄRNDELNINGEN.

;

— Om överskottsenergin E, som i figurdelen a, bara exciterar U1-atomen utan att någon massenergi utbyts, kvarlämnas en stabil U1-atom sedan energiöverskottet avklingat, och vilket inte är vårt fall; För att vara tillämpligt på en radionuklid måste med andra ord överskottsenergin [Egamma] motsvaras av ett aktivt massenergiutbyte [Em], mittfiguren, så att avklingandet av Egamma, via ett motsvarande kvarlämnat massunderskott [Em] leder fram till en brytpunkt där det instabila tillståndet leder till kärndelning av primärnukliden, alltid i massunderskott, och därmed möjlighet att återställa balansen genom kompenserande energi-massa-emissioner genom de avdelade, nya, atomkärnorna. Det är den enligt TNED, här veterligt, enda logiska förklaringen till instabiliteten i fallet radionuklider.

;

— Skulle överskottsenergin från start [Egamma] vara lika stor som U1–U2, figurdelen i b, är vi i princip tillbaka i a-fallet med stabil nuklid vid U2 och därmed bara en avklingande excitationsprocess utan kärndelning, vilket inte är radiofallet. Det betyder att även fallet i figurdelen i b bortfaller av princip — särskilt genom att massa-energiekvivalsensen i det fallet inte bevarar konstant atomvikt för U1;

Som vi vet ligger alla [på och i Jorden naturligt förekommande] atomvikter [U] för alla nuklider mycket litet vid sidan av enhetstalen;

— Det finns I DEN NATURLIGA FÖREKOMSTEN PÅ JORDEN inga atomvikter typ U,5nn..., och som möjligen skulle bli fallet i b-alternativet;

— Atomvikterna — med referens till HOP-tabellen [1967] — är alla av typen U,9nn... och U,0nn...; HOP-tabellen från 1967 slutar på som mest 103Lw257 med 257,098.. .

— Jämför med »Dagens Tabeller» [2011]: De omfattar en stor (växande) mängd artificiellt framställda radionuklider, långt utöver det naturliga beståndet [max92Uran]; För individen 118[Ui]293 slutar atomviktsvärdet [LBL 2003] på 293,21467.. , samt vidare med utvidgade masstal från lägre atomnummer, typ 100Fermi259, som visar U,100.., med vidare. Eftersom dessa, i vilket fall [vad man vet], inte finns till mineralogiskt [naturligt i Jordmaterialet, eller i material som når Jorden utifrån rymden], finns heller inga direkt Jordnära praktiska jämförelser att åberopa. Vi håller oss till just typen Jordnära [tills vidare].

;

— När radionukliden bildas [U1, figuren i mitten] och den påförs extra energi [Egamma] — garanterat utan den moderna akademins artificiellt påtvingade extramoment i formen av kolliderande atomkärnor och vilket i TNED garanteras av miljön i den primära GRUNDÄMNESBILDNINGEN, se exempel i MAXIMALRINGENS KOMPONENTER — och den samtidigt gör sig av med motsvarande massenergiekvivalent [E(m)] för att få energijämvikt, kan ARBETET MED ATT UNDERHÅLLA INSTABILITETEN den fortsatta tiden fram till dess kärndelning sker, ÅTERFÖRAS PÅ att radionukliden, avdelar en liten OBETYDLIG extra arbetsenergi [fallet a, som adderas till den primära, redan befintliga Em-delen från nuklidbildningen; en naturlig spridning finns mellan nuklider med ett största Egamma och ett minsta, och därmed ett största Em och ett minsta] från en motsvarande liten massdestruktion, en dissonansenergi [E(hf)]; SUMMAN AV ALLA radioindividers E(hf) på den individ N som har lägsta massan, kan också förstås utöva den största INFLUENSEN [som kan påskynda tillfället för, men inte styrkan i, sönderfallet] på N jämfört med övriga; Då N sönderfaller, alltid lägsta massnukliden, och lämnar radiogruppen, ökar massmedelvikten i gruppen; Vartefter nukliderna med den lägsta massmedelvikten SÅ lämnar gruppen, går hela gruppens medelatomvikt mot ideala massatomvikten [U1], och i takt med gruppens [universums] åldring. Vartefter gruppen åldras och sönderfaller, avtar skillnaden eller BANDBREDDEN mellan Egamma och Em för de kvarvarande.

;

— Att radionukliden N med atomvikten U1 med sitt relativa massunderskott [E(m)] avdelar en delkärna och själv övergår i en stabil nuklid med atomvikten U2, innebär ALLTID en samtidig möjlighet att, för det egna vidkommandet, UTJÄMNA MASSUNDERSKOTTET — MAX ½ neutron från nuklidbildningen räknat — och förutsatt utrymme finns för det. Därmed framstår INTE det relativa massunderskottet i sig som någon hämmande detalj i fallet radionuklider.

— Sammanhanget bygger dock på att motsvarande experimentellt uppmätta atomvikter OCKSÅ naturligtvis beaktar massenergins kvantitativa ekvivalens.

— Så verkar också vara fallet, se särskilt i Citat.

— Med INFLUENSASPEKTEN medräknad, är det därför mest logiskt att förstå radiosönderfallet på den beskrivna mittre figurens Egamma-E(m)-form med alternativet i figurdelen a integrerat.

— Det är i varje fall den del som här närmast framkommit ur och föreligger i TNED till prövning för radiosönderfallets fysik generellt.

Alltid lägsta massnukliden — Allmänna sönderfallets grafiska form

Varför »dissonansenergierna ’riktas’ mera» mot radionukliden med det största massunderskottet

än övriga — varför nukliden med största massunderskottet sönderfaller först

Det större massunderskottet E(m) med den motsvarande högre gammaekvivalenten E(gamma) medför i summan av E(hf)-bidragen (dissonansenergin) från hela gruppens individer en motsvarande totalt större gammaaktivitet på individen med lägsta E(m), analogt största massunderskottet. Därmed kan förstås en motsvarande snabbare avverkning: Högre grad av aktivitet proportionellt mot energiinnehållet — E=hf=h/t; t=h/E; växande energi (E) med konstant kärntyngdcirkel (h=mcr) [kärntyngdcirkeln är bara känslig på g-massa] — medför avtagande tidsintervall (t) under vilket energitillståndet [i Planckringen h] verkar;

— Avverkningen kan alltså förstås snabbas upp i tid mot sönderfallstillfället — för den nuklid som uppvisar största massunderskottet; det blir alltid radionukliden med det största massunderskottet som ges automatisk prioritet i sönderfallskön genom att dess gammaenergi också är den största och blir ännu större genom de totalt summerande gammaenergierna [i TNED samlingsnamn för det mera egentliga begreppet neutrinoenergier från massdestruktionerna (m→γ)] från alla i gruppen; Efter sönderfallet har alltså medelvärdet för gruppens massunderskott avtagit. Genom fortsatt sönderfall går följaktligen gruppens massmedelvärde mot den nivå som representeras av det allra minsta massunderskottet, analogt ideala atomvikten för den instabila nuklidtypen.

— Den teorin är omöjlig i modern akademi; TNED-teorin bygger på Planckfraktalerna med NEUTRINOSPEKTRUM i atomkärnan, och det sammanhanget kan inte nås av modern akademi. Jämför även i Osäkerhetsprincipen.

Betasönderfallets mekanik enligt TNED

Se även i Radionuklidernas EGAMMA-Emassa-dynamik, samt även delvis mera utförligt och i detalj i Betasönderfallens matematiska fysik i TNED.

Varför betasönderfallet sker med kontinuerlig emission

av elektronmassans komponenter ända fram till stabil atom — ända ifrån betanuklidens bildningstillfälle

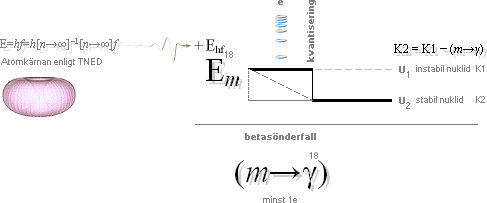
— På samma sätt som i fallet med vattendroppens lösgörande ur den större vattenvolymen [Se även i B/p], att den fysiken obönhörligt sammanhänger med en motsvarande kraft för varje droppform, så att successionen av droppar som avdelas sammanhänger med successionen av avdelande krafter,

BILDKÄLLA: Författarens arkiv — Bild18DropDISK 21Apr2009 · NikonD90

så måste också elektronmassans framträdande förklaras och beskrivas i relaterad fysik som följd av elektronmassans definition i formen av en summa beståndsdelar. Se utförligt från ELEKTRONMASSANS KOMPONENTER (tau[τ]-ringarna), om ej redan bekant.

— Framträdandet av varje tau-ring i elektronmassan kräver ett motsvarande ARBETE för det motsvarande avdelandet;

— Eftersom den betainstabila nuklidens bildning, tvunget, måste börja från en nivå med massöverskott, vilket garanterar en stabil atom vid sönderfallets slut, utan massunderskott, och därmed i kraft av det instabila tillståndets natur, en kontinuerlig massdestruktion (m→γ) från den betainstabila atomens bildning, ända fram till tillfället då stabil atom gäller, kan massdestruktionen förstås ske ekvivalent med en motsvarande kontinuerlig ström av avdelade/framträdande τ-ringar i elektronmassan. Se mera utförligt och detaljerat i Betasönderfallens matematiska fysik i TNED.

— En motsvarande kontinuerligt successiv avdelning av elektronmassakomponenter kan därmed förstås verkställas i takt med massdestruktionen (m→γ).

Det FÖREFALLER med andra ord uteslutet att elektronmassan skulle kunna avges på något annat sätt än UTSPRITT ÖVER HELA INSTABILITETSPERIODEN: inte komprimerat vid den periodens slut.

— Vi studerar den svårigheten, särskilt.

— Men vad säger att tidsintervallet för avdelningen av τ-ringar ska vara utspritt över HELA perioden från den betainstabila nuklidens bildning fram till sönderfallets slut? Varför inte avgränsat till ett kort intervall just vid slutet av den perioden, typ en mikrosekund eller så?

— Ingenting annat än att INGEN ANNAN MASSDESTRUKTION föreligger än den associerad med τ-ringarnas avdelande.

Det finns, vad vi vet, bara två atominstabila typer att välja på: beta[elektron‑]instabila och kärninstabila. Eftersom kärninstabila atomer slutar på kärnsönderfall, analogt delningar som i TNED innefattar nuklidenhetens (neutronens) centralmassiv 1818e, och som inte påverkar nuklidenhetens atomära massdefektsdel på 18e, och vilken senare del är reserverad för betasönderfallen, finns här veterligt heller inga övriga massdestruktionsalternativ än de som arbetar associerat med respektive e-stock.

Betanuklider kärndelas inte, och ska därför heller ingen annan associerad massdestruktion ha, enligt ovan, än den som sammanhänger med elektronmassans frigörande (eller upptagande).

— OM betasönderfallet också (likt kärnsönderfallet) trots allt SKULLE besitta någon intern, extra massdestruktion, som FÖRBEREDER atomen för en slutlig övergång, inom ett maximalt kort tidsintervall, SKULLE också betasönderfallet KUNNA förstås ske bokstavligt i samma ögonblick som själva det slutliga utbrottet sker.

— Vi skulle då behöva veta på vilken massgrund en separat förmodad massdestruktion skulle bildas; Då ingen sådan separat grund är känd (i TNED) kan vi heller inte räkna med att en förmodad separat massdestruktion har någon funktion att fylla: beskrivbarhet saknas. Den möjligheten utesluts därför här som kandidat i beskrivningen av det radioaktiva sönderfallets fysik i TNED.

Bevis:

Generellt kan inte en kärninstabil nuklid TRIGGA fram en betainstabil atom genom intern massdestruktion — därför att den betainstabila atomen TVUNGET måste börja på en större g-massa än den som gäller vid betasönderfallet — excessen åtgår som arbete, massdestruktion, för att bygga om atomen och låta elektronen framträda — medan den kärninstabila atomens atomkärna TVUNGET måste börja på ett massunderskott, så att den primärt kärninstabila nukliden vid sönderfallets slut, vid själva kärndelningen, kan garanteras INTE bli stabil, utan just tvingas sönderfalla i minst två skilda atomkärnor, vilket INTE är betasönderfallets fall.

— Detaljerna bara understryker hur TNED tycks förklara det radioaktiva sönderfallets fysik — helt enligt logiken, utan att resa frågetecken:

;

Betainstabilitet betyder i TNED ett speciellt instabilt tillstånd i atomkärnan som beskrivs i sektionen om CENTRALKONTAKTERNA;

— De tre inre atomkärnans ekvivalenta, första underfraktalens kärnringar uppvisar inbördes dissonans för alla betainstabila fall. Dissonansen medger samtidig möjlighet för massdestruktionen (m→γ) att realisera ett frigörande, eller upptagande, av elektronmassa, och endast då.

I läget för betastabil jämvikt finns ingen motsvarande möjlighet för betaassocierad massdestruktion; Massdestruktion för betasönderfall är i läge OFF för en betastabil atom.

— För en rent kärninstabil atom, utan betainstabilitet, kan en massdestruktion ske på ett annat sätt (MÖJLIGEN från atomkärnan som helhet, genom hela kärnstrukturen, alla delar, inte enbart från kärnbrunnens centralområde) [Ingen särskild framställning finns dock ännu Nov2011 på denna detalj]; Massdestruktionen skulle då verkställas genom att hela kärnstrukturen befinner sig i självsvängning, och därmed med en massdestruktion som ansluter till atomkärnans allra lägsta (djupast liggande) kärnstrukturenergi

Emin=hfmin=[h/n]nfmin=[h/n]fmax

med motsvarande högsta frekvenser — utan att påverka betadissonansernas energiområde. Sambandsformen ovan samma som i Plancks strukturkonstant.

— Det är därför HELT UTESLUTET att betasönderfallets process SKULLE kunna innefatta en motsvarande försvinnande liten massdestruktionshistoria, liknande den som figurerar i kärnsönderfallens fall, för tillfället att INITIERA, eller förbereda, för en slutligt SNABB elektronemission, i omedelbar anslutning till betasönderfallets slut. Det är alltså UTESLUTET i TNED.

— Framställningen i TNED har tidigare inte gjort anspråk på att beskriva radiosönderfallet explicit i någon som helst detalj, och har därför endast räknat med den möjligheten att sönderfallet i fallet betainstabila atomer (speciellt för neutronen, se utförligt från Neutronens Sönderfall) sker under det samma tidsintervall som motsvarande massdestruktion för frigörelsearbetet verkställer, i vilket fall under just ett INTERVALL.

Diskussion, betamekaniken

— Men det finns (ytterligare) ett annat argument som, möjligen, ser ut att kunna avgöra detaljfrågan om betasönderfallets tillfällen, fullständigt sammanfattande, på samtliga punkter;

— RENT EXPERIMENTELLT, nämligen, uppvisas vid betasönderfall »betydande rörelsemängder» hos »den nybildade elektronen». Hur kan det förklaras i ljuset av föregående beskrivna allmänbild?

— Om elektronen sprids ut på sina komponenter över en längre tid, och sedan PLÖTSLIGT ska visa sig i form av en kollektivt uppvisad elektronmassarörelsemängd, förefaller (min uppfattning) en rationell förklaring i den typen av beteende mindre sannolik.

— Det förefaller snarare så, att elektronmassan ur betasönderfallet uppträder med kort varsel, med en gång, och då med sin fulla samlade totala, observerade, rörelsemängd.

— Jo. Du kan det, på följande sätt;:

— Elektronmassans koppling till makrofysiken går via enskilda elektronladdningskvanta; halva eller 1/100000 duger inte, eller någon annan del. Det måste vara hela.

— OM modernukliden avdelar enskilda e/n, utspridda över hela sönderfallets period, från nuklidbildningen tills stabil atom uppnås, kopplas likväl INTE den emissionen till ett e-kvanta förrän HELA avdelandet är fullbordat: in till sista e/n.

— Hur reagerar moderkärnans kärytladdningsstruktur på det tillfället?

— Naturligt: Den bibehåller sin ursprungliga BILD — ända från betanuklidens bildningsögonblick — fram till »kopplingen», om den perioden så skulle omspänna miljarders miljarders miljarder år, spelar ingen roll:

— Jag skulle säga; Ytterst sofistikerat att vänta med hela urladdningsförfarandet, och göra detta så homogeniserat som möjligt genom att avvakta tills alla kommit på plats, och sedan utlösa hela effekten genom minsta möjliga kraft: den slutliga e/n;

— Förklaringen skulle då, i så fall, vara: Plötsligt ändras kärnytladdningen med 1 enhet; atomkärnan uppträder under en kort stund som joniserad [eftersom den i vilket fall inte samlat på sig de utgivnas attraktion under utgivningens intervall, vidare i argument nedan], och kan därför ACCELERERA — återta, samla till sig — i ett enda moment alla de utgivna elementen e/n till den stabila atombindningen.

— Är energin i den accelererade elektronen tillräcklig, kan den påverka närliggande elektronhöljen (som vi redan studerat i en del bubbelkammarfotografier [Se Sekundära Elektronemissioner i ELEKTRONENS BUBBELKAMMARSPÅR]) och åstadkomma sekundära jonisationsspår.

— På samma sätt vid s.k. elektroninfångning (eng. electron capture, ofta förk. EC):

— Via KÄRNBRUNNEN [atomkärnans axiella spinncentrum i TNED, se utförligt från Atomkärnans Härledning] återtar kärnan varje e/n successivt från atomhöljet med den naturliga strömningspassagen av elektronmassans komponenter genom kärnbrunnen via KRAFTEKVATIONEN. Inte förrän intaget är fullbordat på sista e/n kommer kärnytan att uppvisa någon ändring.

— Men vad säger att atomkärnan skulle VÄNTA med att anpassa sin YTLADDNING tills sista e/n avdelats, till exempel från ett visst Z till Z+1?

— Borde inte atomkärnan istället anpassa sig allt eftersom, och därmed också infånga VARJE avdelad e/n [nTNED=673026], allt eftersom, även om det inte syns i makrofysikens e-kvantumvärld?

— De observerade elektronernas rörelseenergier vid betasönderfall, grovt mellan 0,1-10 MeV;

— VORE rörelseenergierna (0,1-10 MeV) utspridda på alla e/n, blir det svårt för oss (i efterhand) att förklara NÅGOT enhetligt UPPMÄTT MeV-värde alls större än MAX 10/673000=0,0000148588 MeV = 14,85 eV ÅT GÅNGEN. Blotta faktum med en uppmätt MeV-form vid NÅGOT tillfälle är en tydlig indikering på att HELA elektronmassans rörelseform finns med — via någon motsvarande maximalt KORT reaktions- och händelsetid.

Jämför (även) den fraktala kärnstrukturen i TNED:

— Med sista e/n avdelat, inträder (underförstått, i ljuset av ovan skisserade »maskinfunktion») en STRUKTURKOPPLING [vi vet inte exakt HUR, bara ATT den verkställs] som yttrar sig i att en STRUKTURVÄXEL reglerar fram en kärnytladdning [under ett minsta möjliga tidsintervall med hänsyn till kärnspinnets närmaste underfraktal, i storleksordningen runt t20 S, se Fusionstiden], under det att kärnspinnet avancerar ETT varv. Den förklaringen är fullt möjlig med hänsyn till en kopplande växel i kärnbrunnen som får omspänna hela atomkärnan via kärnspinnet, alltså successivt, men ändå på kortast möjliga tid [i stort analogt med tiden för kärndelning eller kärnförening generellt].

— Det kan liknas vid en ytterst känslig balansvåg; inte förrän det allra sista milligrambladet faller ner i vågskålen, tippar armen över i exakt jämvikt. Inte förr. Aldrig. Undantag existerar inte.

Atomviktens medelvärde

UNIVERSUMS ÅLDRING

Atomviktens medelvärde och 0γm — enligt TNED

Från 0γm; GRUNDÄMNESBILDNINGEN innefattar, tydligen, bildning av radionuklider vars energiräkning, direkt från start, kräver just GAMMAm-faktorn (0γm). Giltigheten av GAMMAm-faktorn [0_γm=E_γ–E_m] kräver med andra ord en motsvarande BILD av sönderfallets dynamik med ett högsta Egamma och ett lägsta Emassa som med fysikens nödvändighet i energiräkningarna måste följas åt genom sönderfallets (hela universums) historia. Följande kan utläsas vidare av den detaljen med referens till att just NEUTRONEN — Plancks konstant = neutronmassan gången absoluta toppljushastigheten gånger neutronens tyngdcirkelradie — är den nuklidindivid som (enligt relaterad fysik) bestämmer alla övriga nukliders dynamik; energiräkningen återförs på grundindividen.

ATOMVIKTENS MEDELVÄRDE

VARTEFTER UNIVERSUM ÅLDRAS och aktiviteten avtar i de olika radiolokalerna, avtar också bandbredden (extremgränserna) i radionuklidernas γm-fält [0_γm=E_γ–E_m] och går mot nominella atomviktsvärdet [U].

;

MAXIMALA SPRIDNINGEN I γm-FÄLTET per nuklid vid vilken alla radionuklider från början med neutronen som preferens flyter ihop är ±1/2 neutronmassa, totalt max 940 MeV = neutronenergin. En radionuklid kan därmed som mest under hela sin levnad avyttra en teoretisk massdestruktion (m→γ) i formen av dissonansenergi [E_hf] på just en halv neutronmassa med referens till nuklidens nominella atomvikt.

Eftersom dissonanserna förhåller sig som delningarna på halveringstiden t_H gäller

E_DN = E_Dmax2^–T/tH

±U_max = U_nom ± E_DN/c₀²/u_{1,66033
t27 KG}

Det finns emellertid ingen direkt (uppenbar) koppling som omtalar vid vilken nivå en viss radionuklid börjar sin bana med referens till den naturliga grundämnesbildningens ursprung.

Exempel

Om nuvarande mängd Uran 238 med (preferens Jorden) halveringstiden 4,51 T9 år bildades för 20,8 miljarder år sedan, är ursprungsmängden nu och därmed aktiviteten reducerad med 2-exponenten 20,8/4,51=4,6 gånger. Det ger en mängdreduktion på 2^4,6=24,25. Om Uranet från början hade ett U_γmax på ±(1/2)(1,0086652u=940 MeV) skulle nuvarande extremgränserna gå vid ±(1/2)(940/24,25=38,76)=±19,38 MeV eller ca ±38e-massor, eller ca ±0,02u. För att kunna uppmäta/kontrollera en så liten skillnad i γm-atomvikt mellan olika radioindivider i samma ämne måste man ovillkorligen mäta på enskilda atomindivider. Inga sådana data är här kända (Okt2011).

Radioenheten

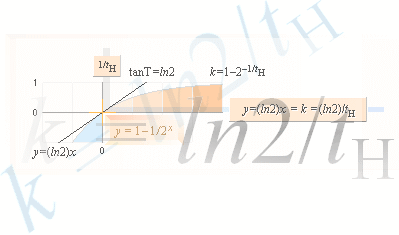
Radioenheten

Vissa aspekter på fysiken tycks ha särskilt förnämliga matematiska hemvister.

Normalt sett, skulle vi ha formidabla NUMERISKA problem med tidsskalorna för radionuklider med stor spridning på halveringstiden t_H.

Radiokonstanten k=1–2^–1/tH ställer till exempel upp definitiva numeriska datortekniska problem när t_H blir större än T15 sekunder (T för 10^+). Det finns normalt sett inga (praktiskt visande) datamaskiner eller kalkylatorer eller räknedosor som kan hantera flyttal av formen

1–0,999999999999999…n… . Resultatet ger 0; Formen 0,999…n ger alltid 1. Det hänger alltså på antalet signifikander som tvunget begränsar varje datorsystem.

Funktionen y=1–2^–x löser problemet automatiskt; Små x-värden ansluter praktiskt till lutningen i origo, tanA=ln2. Då är y-värdet y=ln2 · x — med utomordentlig numerisk precision — analogt k=ln2/t_H.

Men hur blir det för nuklider med korta t_H?

Problemet är principiellt detsamma där. Om t_H blir omkring 0,032 S (kalkylator med 9-13 signifikander) och mindre ger k-värdet reguljärt 1–0,000000000000000…n…=1. Även i detta fall finns en punkt där varje flyttalssystem hänger sig. Grundfelet i denna del är emellertid radioenhetens inre tidsenhet: 1 sekund. Det är inte logiskt att relatera men väl att ange antalet sönderfall per sekund för en nuklidgrupp X vars halveringstid ligger omkring eller under 1 S. Sönderfallsfrekvensen bör i så fall relationsmätas eller beskrivas på en betydligt kortare tidsenhet.

Galant löser sig detta problem på samma sätt. Idealet vore om alla radionuklider kunde behandlas på ett sådant sätt, att förhållandet mellan halveringstid och tidsenheten för relaterat sönderfall vore exakt likadan oberoende av t_H. Med förebild från sådana radionuklider som Uran 238 med t_H=4,51 T9 år [VNS1976] = 1,423 T17 S ligger förhållandet mycket högt enligt

(1,423 T17 S)/1S, där k beräknas k=ln2/t_H. Om vi bibehåller samma relation även för alla övriga radionuklider, påtvingas alla med korta t_H automatiskt en motsvarande kort sönderfallsmätande tidrymd, vilket är precis vad idealet säger. För samtliga praktiskt numeriska fall kan alltså radiokonstanten (konv. ofta λ med, här, tH som T½) tillämpas enligt

k = ln2/t_H ............................................ radiokonstanten, urspr. från 1–2^{–TIMEUNIT/tH}

Med denna modifikation erhåller k automatiskt en standardiserad universell frekvensenhet S^–1. Därmed kan radioaktiviteten skrivas direkt och enklare

ξ_N = kN ................................................ radioaktiviteten via mängden N

Se även i RadioTermer.

Begreppen centrum-periferi

Aktiviteten har ett principiellt centrum och en principiell periferi:

Dynamiken i hela processen bygger dels på

· ett aktivt kvantitativt centrum där utfallsstyrkan växer med växande N₀ (utgångsmängden), och dels

· en kvantitativ periferi där utfallsstyrkan hämmas, analogt livslängden för de sista individerna växer med växande N₀.

Begreppen centrum-periferi behöver inte vara geometriska.

Med viss fortsättning från Halveringssambandets fullständiga härledning

ktivitetsaspekten i det radioaktiva sönderfallet fysik — som det visar sig — kan mycket förtydligas i klarläggandet av processens dynamiska kärna genom att anställa liknelsen med ett stort rum som fylls av människor. Ju större mängd individer som finns samlade, desto större möjlighet bereds för att flera personer uppvisar en viss benägenhet att utföra en viss handling; Vi vet (här) inte vilken, vi bara antar någon (anständig). För att konkretisera »mängdbeteendet som beror av mängden» kan vi använda en viss benägenhet att utträda ur den lokala gruppens individer. Vi kan då fråga oss vad som styr individens handlande, vad det är som påverkar eller influerar individen. Svaret ligger tydligen i mängdens kvantitet. Om varje individ bidrar med en viss faktor som sprids eller »strålar ut på alla övriga», blir summan på den enskilda individen allt större ju flera individer som finns i lokalen. Därmed är centrumdelen principiellt förklarad.

Om individen befinner sig i en sådan position i lokalen att hela omgivningens bidrag precis uppväger individens och alla grader emellan (alltså »i strålperiferin»), har vi också i princip identifierat den kvantitativa periferidelen i dynamiken. Från den punkt där individen känner sig påverkad, motverkas eller hämmas den egna interna aktiviteten (dock utan att dess motoriska grund upphör, jämför vidare superpositionsprincipen) och går mot ett nollvärde då det egna bidraget uppvägs av hela mängdens influens. Över denna nollpunkt, åt andra hållet där mängdens influens blir större, befinner sig individen allt mer i det kvantitativa centrum och därmed i större påverkan.

Mängdanalogin får på detta sätt ett naturligt centrum och en naturlig periferi där aktiviteten är som störst i centrum (som inte behöver vara geometriskt).

Halveras hela gruppens individer, halveras också influensen på varje individ, och om förhållandet mellan varje individs eget bidrag och mängdens är försumbart med avseende på hur antalet individer ändras (i exakt mening är så aldrig fallet), kan man säga att dynamiken i stort bevaras med gruppens halvering. Beteendet följer därmed (i stort) också halveringssambandet.

På samma sätt kan vi relatera fallet där endast den hämmande faktorn förekommer.

Om varje individ har en viss konstant benägenhet att utträda ur den lokala gruppens individer, och den benägenheten hämmas ju flera individer lokalen innehåller, gäller likväl och på vanligt sätt att gruppen halverats efter tiden t_H. Därmed har också hämfaktorn halverats så att principiellt samma dynamik råder som vid början av den första perioden. Efter ytterligare t_H har så gruppen på nytt halverats med en ny åtföljande total halvering av hämfaktorn, och så vidare. Även denna process kan alltså återföras på halveringssambandet.

rån denna enkla genomgång är det uppenbart att den fysikaliska dynamiken bakom sönderfallsprocesserna tvunget inbegriper ömsesidig influens.

Enligt TNED finns två allmänna sambandsled som ansluter till de beskrivna processerna. De förekommer i samband med alla instabila atomkärnors ändring mot ett stabilt tillstånd och ges via de två typleden [Se från RADIONUKLIDENS BILDNING] beskrivna i Samband för betainstabila och nuklidinstabila atomer, respektive

(K) – E_hf₁₈ = K = (K1+K2 – (m→γ) + _β0_γm) – E_hf18 .................. betainstabil atom

[K] – E_hf₁₈₁₈ = K = [K1+K2 – (m→γ) + _T 0_γm] – E_hf1818 ............... nuklidinstabil atom

Massdestruktionen (m→γ) som underhåller sönderfallets tillstånd är, enligt TNED, tydligen den enda fysikaliskt tänkbara faktor som kan åstadkomma någon relaterbar PRAKTISK ÖMSESIDIG INFLUENS av ovan beskrivna publika kaliber.

— Med neutrinobegreppet i TNED som massdestruktionens verkställande agent blir det med andra ord också tydligt att den enkla sambandsformen för medellivet î=tH/N0 — influensens variation med följ i medellivets ändring med antalet sönderfallsagenter (N0), från en fast halveringstid (tH) för en viss nuklidtyp — också är tillämplig på såväl betasönderfallen som kärnsönderfallen.

— Se även den inledande beskrivningen generellt om neutrinoinfluensen.

Radioaktivitetens matematiska fysik beskrivs relaterat (enligt TNED) från RADIONUKLIDENS BILDNING.

Halveringssambandet, fullständig form

Halveringssambandet — förklaringen till halveringstiden t_H

BEGREPPENS ELEMENTÄRA BESKRIVNING ENLIGT TNED

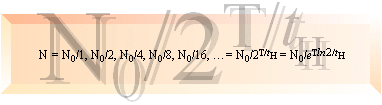
Eftersom dissonansdynamiken bestäms av summan av alla samverkande vågrörelser från alla enskilda bidrag (Se utförligt från Plancks strukturkonstant) E_hf=h_nf_n=hn^–1nf är det givet att också OMGIVNINGEN i vilken en viss radionuklid finns till spelar en helt avgörande roll.

Från början är det totala antalet radionuklider av halveringstypen t_HHHHH lika med N₀. Efter tiden t_H är antalet halverat. Därmed är också totala dissonansenergin Σhf på den enskilda nukliden halverad. Influensen från omgivningen har alltså minskat, och därmed avtar också sönderfallstakten för alla kvarvarande nuklider. Kvarvarande nuklider som ännu inte sönderfallit får en allt växande medellivslängd i takt med att grundämnet sönderfaller och kvarlämnar allt färre individer under allt längre tider.

Proportionaliteten mellan dissonansenergin (E_hf) och antalet kvarvarande radionuklider (N) är alltså konstant enligt NE_hf/N=konstant=E_hf. Om N₀ delas i B delar, bildar varje delmängd N/B en ny grundstock som i tid har samma egenskap som N₀; delningen av (N/B) i B delar tar lika lång tid som delningen av N₀ i B delar eftersom NE_hf/N=konstant.

Halveringssambandets allmänna giltighet i fysiken

HALVERINGSVILLKORET

Halveringstiden t_H kan idealt betraktas som en fast preferens — ”to be a constant under all conditions” — OM procesessen utvecklas som ovan beskrivet:

— OM kvarvarande individer med hela gruppen uppvisar exakt samma fysikaliska egenskaper och dynamik som gäller från T₀ till t_H, och endast då, kommer individantalet åter att ha halverats efter t_H, och endast då.

— OM också fortsättningsvis samma fysikaliska betingelser bibehålls för gruppen kvarvarande individer då T→∞, följer gruppens totala uttunning eller sönderfall det s.k. halveringssambandet

N=N₀/2^T/tH=N0/e^Tln2/tH med N kvarvarande individer efter tiden T.

Halveringssambandet

HÄRLEDNINGEN

— T är totala sönderfallets tidrymd som räknas från 0 då antalet är N₀. Antalet kvarvarande individer efter tiden T i successiva t_H-enheter 0 1 2 3 4 … blir då det s.k. halveringssambandet

N = N₀/1, N₀/2, N₀/4, N₀/8, N₀/16, …

= N₀/2^T/tH

= N₀/e^T(ln2)/t^H ................................... halveringssambandet, antal återstående efter T

e^T(ln2)/t_H = N₀/N ; T(ln2)/t_H = ln(N₀/N) = ²log(N₀/N)·ln2 ; T/t_H = N₀/N

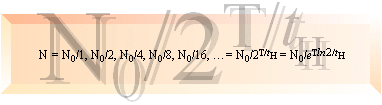
Antalet kvarvarande radionuklider vid tiden T med halveringstiden t_H.

För varje halvering av befintlig grundämnesmassa har dissonansenergin också halverats, eftersom varje radionuklid bidrar med en bestämd dissociativ grundkvantitet (Se E_hf i Radionuklidens bildning). Därmed har kvarvarande nuklider erhållit en totalt högre livslängd än sina föregående kompanjoner.

RadioTermer, Samband

N = N₀/2^T/tH .......................... halveringssambandet,

antalet kvarvarande individer efter tiden T=t_H[²log(N₀/N)]

k = t_H^–1ln2 ............................. radiokonstanten samma som sönderfallskonstanten

— antas konstant med referens till ett givet preparat (konv. beteckning ofta λ)

ξ_N = kN ................................... radioaktiviteten

— mäts i Bq, Becquerel, (ln2 ×) antal per sekund, =Hz(ln2), basparameter

= N(ln2/t_H) ;

N = m_MASSAN/u_1,66033
t27U_ATOMVIKTEN

t_H ..................................................... halveringstiden, enligt t_H = N₀ξ_N^–1ln2

N₀ .................................................... utgångsmängden, basparameter

T ...................................................... tiden

T_N0 = t_H(²log[1–1/N₀]^–1) .......... livslängden för den först sönderfallande radionukliden;

sätt N=N₀–1 i T ovan ;

= –t_H(^elog[1–1/N₀])/(^elog2) se Logaritmlagarna

= –t_H(ln[1–1/N₀])/(ln2) ....... livslängden för den radionuklid som sönderfaller först av alla

T₁ = t_H(²logN₀) ....................... livslängden för den sist sönderfallande radionukliden;

sätt N=1 i T ovan ;

= t_H(^elogN₀)/(^elog2)

= t_H(lnN₀)/(ln2) ................... livslängden för den sista växer med utgångsantalet

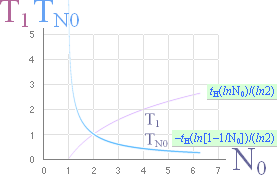
GrafT1Sista y=(1/ln2)lnx; Unit25 • GrafTN0Första y=–(1/ln2)ln(1–1/x); tH=1=konstant

SOM VI SER: tillfället då individen agerar utträder ur gruppen påverkas av mängden närvarande:

— Det ligger i det ENKLA HALVERINGSSAMBANDETS NATUR — inte »ENBART via TNED» — att »radionukliderna uppvisar INFLUENSBEROENDE EGENSKAPER», trots att några sådana inte alls kan påvisas experimentellt på Jordytan och med referenserna från Ernest Rutherford från år 1913

— Ju FLER utgångsindivider N0, grafen ovan, desto längre blir livslängden för T1 [den som lämnar sist] och kortare för TN0 [den som lämnar först]. Det som visar det mest, slående, signifikanta i den »enkla» matematiken, ljusblå grafen ovan, är [således, för tydlighetens skull] den som lämnar först; influensen på den som lämnar först ökar med antalet närvarande individer av samma sort — även om vi inte kan säga direkt VILKEN det blir. Ju fler individer i samma grupp, desto snabbare lämnar den första. Det om något visar, eller UNDERFÖRSTÅR, tydligt en [enligt TNED verksam neutrino-] INFLUENS.

De bägge (matematiska) följdsatser för T₁ och T_N0 som följer direkt ur halveringssambandet beskriver tydligen en influensmekanik: sönderfallet besitter

en variabel influensfaktor. Den varken omnämns eller omskrivs dock (här veterligt) i etablerade källor.

I den matematiska analysen har man den avtagande [minus] variationen dN/dT=–kN med differentialekvationen dN/N=–kdT som ger integralledet

∫ dN/N=–k ∫ dT. Integrala lösningen är lnN=–kT och universalen blir lnN=–kT+C som ger Ce^–kT=N. Vid T=0 är N=N₀ och därmed C=N₀ som ger N=N₀e^–kT. Vid T=t_H återstår hälften vilket ger N₀/2=N₀e^–ktH varav 2=e^ktH och därmed ln2/t_H=k=sönderfallskonstanten eller radiokonstanten.

Aktiviteten eller antalet sönderfall per sekund vid T fås ur

(N–N₁)/(T–T₁=1Sekund) = (N₀2^–T/tH – N₀2^–T1^/tH)S^–1

= N₀(2^–T/tH – 2^–(T+1)/tH)S^–1 = N₀(2^–T/tH – 2^–T/tH 2^–1/tH)S^–1

= N₀2^–T/tH(1 – 2^–1/tH)S^–1 = N₀2^–T/tH · (k_a · S^–1) = (k_aS^–1)N =kN=ξ_N=radioaktiviteten vid T.

Termen k_a=1–2^–1/tH kräver för sin förklarande koppling till radiokonstanten k en särskild artikel som sammanhänger med den numeriska analysen, vilken här förutsätts bekant

[Se Radioenheten].

Därmed gäller också formellt ξ_N=ξ_N0/2^T/tH från kN=ξ_N=k·N₀/2^T/tH via ξ_N0/2^T/tH=k·N₀/2^T/tH.

Beskrivningen ovan som uppmärksammar begreppet »neutrinoinfluens» finns (här veterligt) inte upptagen eller omnämnd i någon motsvarande tappning i den allmänna etablerade facklitteraturen — dess allmänt tillgängliga s beskrivning i ämnet radiosönderfall. Medan grundsambanden, här, också är samma som i den redan etablerade litteraturen, skiljer sig TNED-formerna på flera avgörande sätt från den etablerade uppfattningens grunder. I Sektion 5 [Allmänna samband för radionuklidernas sönderfall] ges en vidare generalgenomgång med fokus på vilka de olika brytpunkterna är, och hur dessa ter sig genom de möjliga jämförelser som framkommit genom denna presentation.

— För vidare konventionella referenser — motsvarande ovanstående till jämförelse — se här närmast Wikipediaartikeln på Radioactive decay, [2011-12-19]

http://en.wikipedia.org/wiki/Radioactive_decay

Speciellt sektionen Changing decay rates är central, där en del aspekter ges på den senaste tidens [föranlett av Jenkins 2006] uppmärksammade ev. influenser i halveringstidens vara och icke vara (Se Solirradiansens Årliga Variation). Emellertid omnämns i den wikipediabeskrivningen ingenting som berör det ovan allmänt omnämnda influensfenomen som INOM halveringstidens (absoluta) konstans, tydligen, kan förstås styra det radioaktiva sönderfallets fysik.

Livslängden för den n:te individen — tidpunkten då individen N_n utgår ur gruppen — är t = t_H(ln2)^–1ln(N₀/[1+N₀–N_n] [Separat framställning i Frekvensfunktionen].

Se även grundbeskrivningen med exempel i Parameterbegreppen.

Med

ξ_N = ln2/î

får man alltså generellt

N₀/ξ_N = t_H/ln2 ; t_H = (ln2)N₀/ξ_N = N₀î

t_H = N₀ξ_N^–1ln2

= N₀f^–1

= N₀î

EXEMPEL

I 1 gram rent U-238 finns

N₀ = (0,001)/u_{1,66033 t27}U₂₃₈

= 2,53062 T21 stycken uranatomer.

OM aktiviteten hos 1 gram rent U-238 är uppmätt till

ξ_N = 12 324,572 Bq

som innebär att varje Uranatom genomgår medellivet

î = ln2/ξ_N

= (0,6931471)/(12 324,572 Bq)

= 5,6241 t5 S

= 56,241075 µS

med aktiviteten

ξ_N = ln2/î

på Jordytan får man halveringstiden för just 1 gram U-238, och ingenting annat än just 1 gram U-238 direkt ur halveringssambandets konstanter och koefficienter SOM OVAN enligt

t_H = N₀ξ_N^–1ln2

= [(0,001)/u_{1,66033 t27}U₂₃₈]ξ_N^–1ln2

= 1,42324 T17 S

= 4,51001 T9 år.

Värdet är samma som det gängse angivna i faktalitteraturen [här från VNS1976, senare justeringar ger ett något lägre värde];

Notera att aktiviteten för 2 gram också blir dubbla mot aktiviteten för 1 gram.

Halveringstiden gäller oberoende av antalet.

Halveringsparametern t_H gäller alltså ämnet — inte ämnesmassan.

— Se även vidare i BEGREPPEN CENTRUM OCH PERIFERI.

Citatblock — Halveringssambandet med halveringstiden från början — RADIONUKLIDERNA PÅ WEBBEN

Citatblock — Halveringssambandet från Dok1.doc 2009-02-28

2011X-XII

RADIONUKLIDERNA — halveringsbegreppen på Webben

Halveringstid (tH konv. T½) och Halvering sammanhänger, på visst sätt matematisk oberoende, genom halveringssambandets (relativt) enkla härledningsform:

N = N₀/1, N₀/2, N₀/4, N₀/8, N₀/16, … = N₀/2⁰, N₀/2¹, N₀/2², N₀/2³, N₀/2⁴, … = N₀/2ⁿ = N₀/2^T/tH

Varje given bestämd utgångsmängd (N0) som delas i hälften, upprepat n gånger, ger den återstående mängden N som N=N0/2ⁿ. Jämför N0=64; upprepad halvering efter 4ggr ger kvarvarande N=64/21/22/23/24=(32;16;8;4)=64/2⁴=64/16=4.

— OM varje halvering sker på exakt samma tid, halveringstiden (tH), kan hela tidsintervallet (T) från start (T=0) till T omsättas ekvivalent på antalet halveringar enligt n=T/tH, vilket ger halveringssambandet

N = N₀/2^T/tH = N₀/e^Tln2/tH .................................. se halveringssambandet i denna presentation

N₀/N = 2^T/tH ; T/t_H = ²log(N₀/N) = ^elog(N₀/N)/^elog(2) [Se Logaritmlagarna]; ^elog = ln ; T(ln2)/t_H = ln(N₀/N); N = N₀/e^Tln2/tH

— Det är också den grundläggande sambandsform som används konventionellt i beskrivningen av det radioaktiva sönderfallet — ofta på formen N(t)=N₀e^–λt. Se särskilt i

@INTERNET Wikipedia Radioactive decay [2011-12-20]

http://en.wikipedia.org/wiki/Radioactive_decay - Mathematics_of_radioactive_decay

Halveringstiden som konstant stadfästs

Omkring sekelskiftet genomförde Ernest Rutherford och andra pionjärer omfattande mätningar på olika radioaktivt sönderfallande ämnen och fann, som Rutherford själv uttrycker saken [‡],

”The rate of transformation of an element has been found to be a constant under all conditions”.

Därmed blev begreppet halveringstid stadfäst inom den moderna akademins lärosystem som den för varje radioaktiv nuklids karaktäristiska, universellt förmodade, sönderfallskonstanten (λ=ln2/tH).

— Den har också antagits så, ända fram till våra dagar [Jenkins et al., 2006, Fischbach et al. 2011];

— Observerade variationer i [som det får förstås] Solens neutrinoemissioner, dels beroende på Jordens årliga avståndsvariation till Solen och dels beroende på en specifik rotationsperiod i Solens inre, visar att vissa betainstabila nuklider uppvisar motsvarande variationer i halveringstid, se sammanfattningen Jun2011 från Jenkinsgruppen som ovan.

— Citaten nedan avspeglar uppfattningar (och strömningar) i grundbegreppen [före Jenkinsgruppen 2006/8].

Förekommande fetstil (och annan markering) inuti citaten är min markering (om ej redan i originalet):

Det är (delvis) löjligt att de etablerade fackkällorna nedan inte kan tala om ANLEDNINGEN — (de senare under 1900-talet) uppmätningen av alfaenergierna — till VARFÖR det påstådda icke ändringsbara förhållandet ANSES gäller;

Rutherfords desintegrationsteori 1902

”Detta och liknandefenomen förklaras av Rutherfords desintegrationsteori (1902), som innebär, att de radioaktiva ämnenas atomer spontant sönderfalla, varvid en del av atomen utkastas i form av α- l. β-strålar, de senare vanl. åtföljda av γ-strålar, och det ursprungliga ämnets atomer övergå till atomer av annat slag.”,

”Den tid, som åtgår för att hälften av ett ämne skall transformeras, kallas halveringstid (någon gång period) och utgör en för varje radioaktivt ämne karaktäristisk konstant, som ändras av intet men som är mycket olika för olika ämnen.”,

BONNIERS KONVERSATIONS LEXIKON IX 1926 sp806mö

Rutherfords teori från 1902 finns vidare väl omskriven i Nobelpristalet från 1908 [Kemipriset], se

Award Ceremony Speech — Royal Academy of Sciences, December 10, 1908

http://www.nobelprize.org/nobel_prizes/chemistry/laureates/1908/press.html

http://www.shvoong.com/exact-sciences/374478-radioactivity-decay-constant-half-lives/

2009-02-28, källverket saknar datumreferens

SHVOONG — Summaries and Short Reviews — world-wide center for abstracts

”All radioactive material undergoes radioactive decay at a certain rate regardless of external influences, such as pressure or temperature”;

”Radioactivity, Decay Constant and Half-Lives by Gay Ann Birkman”, källans bibliografiska (källförteckningsmässiga) referens.

Min översättning:

Allt radioaktivt material genomgår radioaktivt sönderfall med en viss hastighet oberoende av yttre inverkan, såsom tryck eller temperatur.

Källan tycks inte omnämna någon av de ”mysterier” som halveringssambandet tydligen förutsätter.

Se även samma typ i

http://www.rocw.raifoundation.org/biotechnology/BTechbiotech/baicchemistry/lecture-notes/lecture-06.pdf

2009-02-28, källverket saknar datumreferens

LESSON 6, DISINTEGRATION THEORY OF RADIOACTIVITY, Copyright Rai University;

”The disintegration is independent of all physical and chemical conditions like temperature, pressure, chemical combination etc.”

Min översättning:

Sönderfallet är oberoende av alla fysikaliska och kemiska förhållanden som temperatur, tryck, kemisk kombination etc.

Källan tycks inte omnämna någon av de ”mysterier” som halveringssambandet med dess inneboende halveringstidskonstant tydligen förutsätter. Se särskild beskrivning i Sönderfallet uppvisar Influenser.

Samt även i

Hyperphysics — Georgia State University, Department of Physics and Astronomy

http://hyperphysics.phy-astr.gsu.edu/Hbase/Nuclear/halfli2.html

2009-03-01,

”The half-life is independent of the physical state (solid, liquid, gas), temperature, pressure, the chemical compound in which the nucleus finds itself, and essentially any other outside influence. It is independent of the chemistry of the atomic surface, and independent of the ordinary physical factors of the outside world. The only thing which can alter the half-life is direct nuclear interaction with a particle from outside, e.g., a high energy collision in an accelerator.”;

Min översättning:

Halveringstiden är oberoende av det fysikaliska tillstånd (fast, flytande, gas), temperatur, tryck, den kemiska sammansättning i vilken atomkärnan finns, och väsentligen varje annan yttre inverkan. Den är oberoende av kemin hos den atomära ytan, och oberoende av de ordinära fysikaliska faktorerna hos den yttre världen. Det enda som kan påverka halveringstiden är direkt nukleär växelverkan med en partikel utifrån, dvs., en högenergikollision i en accelerator.

— Jämför även motsvarande grundbegrepp i MAC via @INTERNET Wikipedia Radioactivity 2009-03-03:

”Therefore, given a sample of a particular radioisotope, the number of decay events −dN expected to occur in a small interval of time dt is proportional to the number of atoms present.”,

@INTERNET Wikipedia Radioactivity, Decay timing 2009-03-03

Citaten bara bekräftar det redan sagda:

I modern akademi har man ingen annan preferens för den radioaktiva mätningen än laboratorieprovet, analogt uppmätningen av alfapartiklarnas energier och som grundlägger de olika radionukliderna sönderfallskonstanter — »oberoende av yttre omständigheter».

— Begreppet »neutrinospektrum» finns inte i modern akademi.

Se dock (t.ex.) i

http://www.sciencemag.org/cgi/content/abstract/181/4105/1164?ck=nck

2009-02-28;

Science AAAS, Pressure Dependence of the Radioactive Decay Constant of Beryllium-7

där marginella effekter antyds i sönderfallskonstanten beroende på (mycket höga) tryck.

Rutherfords desintegrationsteori från 1902 bildar det naturliga upphovet till begreppet halveringstid (Se Rutherfords mening i citat) — och därmed den runt sekelskiftet 1900 först empiriskt upptäcka sambandsformen för halveringstiden (tH), analogt sönderfallskonstanten (k=ln2/tH) som kallas Geiger-Nuttalls samband. Se ovan i Citatblocket halveringsbegreppen på Webben, som avspeglar grunduppfattningen i olika citat med föreställningen om konstant halveringstid, analogt en specifik sönderfallskonstant för varje specifik radioaktiv nuklid.

— Men halveringssambandets integrerade halveringstidskonstant, dess matematiska-fysikaliska grund i sekelskiftets fysikuppfattning, är strängt just kemisk (atombaserad: materiefysik, inte massfysik). Den tilldelas också just det kemiska intresset i källbeskrivningen nedan;

(runt 1900 fanns ingen etablerad modell för atomkärnan, kärnan som sådan avtäcktes först runt 1911 genom Rutherfords berömda spridningsexperiment)

http://nobelprize.org/nobel_prizes/chemistry/laureates/1908/press.html

2009-02-28,

The Nobel Prize in Chemistry 1908, December 10, 1908;

”The above-mentioned disintegration theory and the experimental results upon which it is based, are synonymous with a new departure in chemistry, involving a fresh and decidedly extended comprehension of the very basis of that science.”.

Min översättning:

Den ovannämnda desintegrationsteorin och de experimentella resultat på vilka den är baserad, är synonyma med en ny utgångspunkt inom kemin, involverande en frisk (fräsch) och bestämt extensiv omfattning av den blotta grunden i den vetenskapen.

;

Längre än så kommer vi inte i grunderna: Halveringssambandets teoretiska grunder med den integrerade halveringstiden (tH) — sönderfallskonstanten (k=ln2/tH) — utgår tydligen varken ifrån kännedom om eller hänsyn till egenskaper i atomkärnan. Det är, från den rent moderna akademins vetenskapligt historiska grund, alldeles tydligt ett rent matematiskt formelverktyg — och som, enligt vad som påstås (under hela 1900-talet) visat sig stämma väl med praktiska ordningar inom våra givna lokaler — typ Jordytan och dess (radioaktivt) mineralogiska sammansättningar.

— Här, med ännu [Dec2011] ensidig referens till Jenkinsgruppen (Jun2011) — och därmed ännu med referens till enbart betainstabila nuklider — har tydligen den ovannämnda ”klassiskt modernt akademiska uppfattningen” med sönderfallskonstanten (k=ln2/tH) visat sig innehålla rämnor; Vissa betainstabila nukliders halveringstider, deras sönderfallskonstant (k=ln2/tH), visar sig variera (ca 0,1%) med Jordens årliga avståndsvariationer till Solen (det är alltså neutrinoinfluenser som det gäller, då inga andra kandidater finns), samt även beroende på en inre Solperiod (32 dygn).

— Det är också i full kvalitativ enlighet med förutsättningarna i TNED:

— Utan en inre grund som baseras på neutrinoinfluenser (Se här utförligt från Dissonansenergin), blir det, enligt TNED, omöjligt att härleda en begriplig, sammanhängande matematik för fysiken bakom radioaktiviteten: hur den fysiken fungerar SPECIELLT för delningstillfället i fallet radionuklider (Se Sönderfallet i SEKTION 5), samt hur fysiken beskrivs enligt TNED för betasönderfallen (Se Betasönderfallets mekanik enligt TNED samt särskilt i Betasönderfallets matematiska fysik i TNED).

— Fenomengrunden i TNED får inte enbart ha någon ensidig matematisk grund som preferens utan måste naturligtvis OCKSÅ ha någon motsvarande fysikaliskt grundad ordning som DYNAMIKEN kan återfalla på. Det är neutrinoinfluenser. Utan dessa kollapsar hela TNED-teorin. Se utförligt i denna presentation från Sönderfallsteorin i TNED.

Geiger-Nuttalls samband — alfaenergierna — Källformerna

Se även i Sambanden i MAC

KÄLLFORMERNA — halveringstidssambandet (t_H konv. T_½)

KÄLLFORMEN FÖR ALFAENERGIERNA TILL DE RADIOAKTIVA HALVERINGSTIDERNA

— Utöver vad som redan framkommit i HOP-källan (från s9-6) finns en del (kompletterande) upplysande referenser på webben:

http://openlearn.open.ac.uk/mod/resource/view.php?id=292823

— föregående, numera [Okt2011] borta, finns inte [se vidare referens längre ner]

2009-03-01,

Learning Space — The Open University — Scattering and tunneling;

”

Alpha decay was discovered and named by Rutherford in 1898. It was soon established that each type of alpha-decaying nucleus emits an alpha particle with a characteristic energy, E_α. While these alpha emission energies cover a fairly narrow range of values (from about 2 MeV to 8 MeV), the half-lives of the corresponding nuclei cover an enormous range (from 10⁻¹² s to 10¹⁷ s). Experiments showed that, within certain families of alpha-emitting nuclei, the half-lives and alpha emission energies were related to one another. Written in terms of the decay constant,

λ = (ln 2)/T_1/2, this relationship can be expressed in the form

λ = Ae^–B/√E^α , (7.54)

where A is a constant that characterises the particular family of nuclei, and B depends on the charge of the individual nucleus. We shall refer to this empirical law as the Geiger-Nuttall relation.

”;

ROTTECKNET i citatoriginalet med »upphöjt till 1/2».

”Despite all this information, by the early 1920s alpha decay had become a major puzzle to physicists. The cause of the observed Geiger-Nuttall relation was not understood. Attempts to explain it on the basis of classical physics, with the alpha particle initially confined within the nucleus by an energy barrier that it eventually manages to surmount, did not work. In some cases the observed emission energies were too low to be consistent with surmounting the energy barrier at all. So, how could the alpha particles escape, why did their emission lead to such a staggering range of half-lives, and what was the origin of the Geiger-Nuttall relation?

”;

Källtexten ovan återfunnen på OpenLearn LabSpace [Okt2011], Scattering and tunneling

http://labspace.open.ac.uk/mod/resource/view.php?id=431626

Se vidare i webbkällans artikel — jämförelse med experimentellt uppmätta värden, se LabSpaceExemplet.

Se även ovanstående källas samband beskrivet (delvis mera utförligt) i PDF-dokumentet [första sidan direkt]

The Quantum Mechanics of Alpha Decay, Lulu Liu, Pablo Solis Dec2007

http://web.mit.edu/lululiu/Public/pixx/not-pixx/alpha.pdf

;

”Alpha decay has been a source of confusion for clas-

sical physicists for quite some time.”

Samt även (mera förtydligat) i [MEN AKTA: tar flera sekunder (runt 10-20, interaktiva detaljer) att öppna]

http://demonstrations.wolfram.com/GamowModelForAlphaDecayTheGeigerNuttallLaw/

I övrigt (Okt2011) verkar det tunnsått med utvecklingsreferenser.

Jämför [källan diskuterar en ekv. (1) av formen: logT_½ = aQ_α^–1/2 + b]:

”However, the Geiger-Nuttall law in the form of Eq. (1) has limited prediction power since the coeffcients a and b change for the decays of each isotopic series [2, 3]. Intensive works have been done trying to generalize the Geiger-Nuttall law for a universal description of all detected α-decay events [4, 5].”,

IOPscience — URL-adressen fungerar inte återkopplande (sök på nedanstående artikelrubrik istället)

NUCLEAR CLUSTERING AND GENERALIZATION OF THE GEIGER-NUTTALL LAW 100 YEARS AFTER ITS FORMULATION, Qi et al.;

Tydlig datumuppgift saknas. Jag undviker den här webbkällan — i väntan på bättre ordning i butiken.

De allra SÄMSTA KÄLLORNA är de man måste LETA i — länge — för att EVENTUELLT hitta exakt kronologiskt källdatum. IOPscience är NOGA med att ange, på särskild rad, en helt fullständigt totalt meningslös källreferens. Nämligen: när du laddade ner kopian. Vilka andra användardetaljer Spionerar Företaget på? Du kan vara säker. Obehagligt ställe.

Ytterligare en upphittad källa — som beskriver radioaktiviteten mera utförligt [2011-10-25],

accessscience — 10th edition of McGraw-Hill's Encyclopedia of Science & Technology

Radioactivity, McGraw-Hill Companies, 2008

http://accessscience.com/content/Radioactivity/569000

Men det går inte att återkomma dit på den URL-adressen — en WebbEncyklopedi som kräver BETALNING med Pay Per View [30 dollar per dygn, det är ofattbart vilket ocker] — OM man händelsevis, som här, INTE får upp em sökträff på Google — och som sedan, kanske, INTE går att återkomma till MED MER ÄN MAN BETALAR. Vila i frid.

McGraw-Hill-källan ovan beskriver — illustrerat, med samband

(i Wikipediastil, men delvis bättre; med tydligt läsbara matematiksuffix, med mera; och delvis sämre: praktiskt taget inga REFERENSER ges till floran av olika PÅSTÅENDEN: inte minsta chans finns, då, att kontrollera verifierbarheten och då är källan i princip helt totalt komplett värdelös) —

Geiger-Nuttalls samband (”Geiger-Nuttall rule”), i huvudsak av samma form som i Källa 1 [dess ekv. 7.55; V(r)=2(Z–2)e²/4πε₀r, se jämförelserna i Sambanden i MAC] samt radioaktiviteten generellt tillsammans med betasönderfallen. Även här är det (således) det statistiska inslaget som dominerar framställningssättet. (Med notiserna ovan är det mera lyckligt än olyckligt [ingen större sorg] att källverket INTE har allmän gratis åtkomst).

Citatblock — observerad påverkan från Solen på vissa radioaktiva nukliders halveringstid

RadioNuklidDynamiken 2009III8 — Från originalförfattning i RadioNUDE.doc 2004X10

Med vidare bearbetning och färdigställande Okt/Dec2011

Citatblock — halveringstidens eventuella påverkan

radioaktiva sönderfallets fysik

Variationer i radioaktiva sönderfallets halveringstid (tH) — ännu så länge observerat endast för vissa betainstabila nuklider [från Jenkins et al., 2006] — inte bara har observerats med Jordens årliga avståndsvariationer till Solen [‡], utan innehåller även en varierande finstruktur på ca 32 dygn [‡] som avslöjar vissa rotationsdifferenser i Solens inre. Enda (logiskt) möjliga kandidaten för variationerna — (både i MAC och TNED) — är neutrinostrålningen från Solen.

Jenkins et al 2008 [observationer av smärre variationer i halveringstid hos betainstabila nuklider]

UPPHITTAT 2009-03-14

Oct 2, 2008;

PhysicsWorld — The mystery of the varying nuclear decay (Jenkins et al) Oct2008

http://physicsworld.com/cws/article/news/36108

;

”It is well-known that a radioactive substance follows a fixed exponential decay, no matter what you do to it. The fact has been set in stone since 1930 when the “father” of nuclear physics Ernest Rutherford, together with James Chadwick and Charles Ellis, concluded in their definitive Radiations from Radioactive Substances that “the rate of transformation…is a constant under all conditions.” ”,

;

”But this is no longer the view of a pair of physicists in the US. Ephraim Fischbach and Jere Jenkins of Purdue University in Indiana are claiming that, far from being fixed, certain decay “constants” are influenced by the Sun.”.

Se vidare från Jenkinsgruppen Jun2011 — observationerna inte bara håller, utan fördjupas — med vidare;

”There is by now overwhelming evidence of anomalous and unexpected time-dependent features present in the count rates of various nuclei.”

— Ovanstående ledde — tydligen, från uppmärksammandet 2006, se vidare citat nedan — till en mindre »jordbävning» i (vissa) forskarkretsar; En efterföljande butik av »papers and reports» (inkluderat Wikipedia, se särskilt Wikipediacitat Dec2011) ville avfärda Jenkinsgruppens observationer på olika suspekta grunder. Nu [Dec2011] finns ytterligare genomgångar som stärker, och fördjupar, Jenkinsgruppens resultat och som, som det får förstås, innebär ett slutligt, ofrånkomligt ställningstagande för fenomenets accepterande — om inget annat oförutsett inträffar. Se särskilt i rapporten Jenkinsgruppen Jun2011.

— Se även i Beräkningsexempel Uran238: villkoren för att avgöra saken för uranets del.

— Nedan följer en del av (de mest framträdande) webbkällornas olika rapportering (och mening) i ämnet — från Jenkinsgruppens ursprungliga rapport 2006, fram till nuvarande [Dec2011].

Rutherford 1913

— Aktiviteten INDIKERAS variera med neutrinoinfluenserna — här främst från Solen — men ingen förstår verkningssättet i MAC;

— Jämför INLEDNINGSVIS (för att understryka dramatiken) »den klassiska meningen» från Ernest Rutherford i boken

RADIOACTIVE SUBSTANCES AND THEIR RADIATIONS 1913, s167:

;

Ernest Rutherford RADIOACTIVE SUBSTANCES AND THEIR RADIATIONS — Cambridge/New York 1913, s167; Från [2011-10-13]

Book digitized by Google from the library of the University of Michigan and uploaded to the Internet Archive by user tpb.

http://books.google.com/books?id=UeEdAAAAMAAJ&oe=UTF-8

Ändringen på 0,1%

”Fischbach and Jenkins first began looking for fluctuations in nuclear decays in 2006 after they came across the report of an experiment performed at Brookhaven National Laboratory (BNL), New York, between 1982 and 1986. The BNL team found that over that period the decay constant of silicon–32 — relative to a long-lived standard — modulated around its usual value of about 172 years by the order of 0.1%.”,

PhysicsWorld — The mystery of the varying nuclear decay (Jenkins et al) Oct2008

http://physicsworld.com/cws/article/news/36108

Jämför motsvarande, rent teknisk-matematiska irradiansförhållande Jorden-Solen genom Jordens årliga avståndsvariation till Solen:

Solirradiansens årliga variation — angående observationerna från Jenkinsgruppen [från 2006]

Solirradiansens årliga variation

[[Tabell3KALKYLKORTdirekt]•[KalkylkortBESKRIVNING]]

Jordens snittcirkelyta A=πR², sådan den ses från Solcentrum (perspektivbilden), varierar (figuren ovan) med avstånden ab sommar-vinter som följd av Jordbanans marginellt elliptiska form [Wikipedia, Earth’s orbit].

— Jordsfärens snittcirkelyta som ses av Solcentrum i de bägge fallen, kan beskrivas genom förhållandet mellan R (som Solen — eg., Solens absoluta ideala centrum — ser som minsta) och c (som Solen ser som största) genom motsvarande förhållanden mellan avstånden ab; R/a=c/b som ger R/c=a/b. Förhållandet mellan cirkelytorna ger

A(R)/A(c)=πR²/πc²=(R/c)²=(a/b)². Förhållandet mellan tillökningen (R–c) och R blir motsvarande

(R–c)/R=1–c/R=1–b/a. Förhållandet mellan motsvarande cirkelytor blir

C = (R–c)²/R²=[(R–c)/R]²=[1–c/R]²=[1–b/a]² = (R²–2Rc+c²)/R² = R²/R² – 2Rc/R² + c²/R² = 1 – 2c/R + (c/R)² = 1 – 2b/a + (b/a² = (1–b/a)²;

I Jordens fall gäller [Wikipedia, Earth’s orbit] b=0,98329134AU och a=1,01671388AU som ger C=1,00108063. Eller via en ±-halvering (sämsta fallet):

1–b/a=±0,017, som ger C=(1–b/a)² = 0,000289, eller ±0,03% avrundat.

b/a=0,983/1,017~0,967; 1–0,967=0,033, /2~0,017, ref. Wikipedia Earth’s orbit 2012-02-09, b=Perihelium, a=Apohelium.

— Grovt sett totalt skulle Jordens årligt varierande avstånd till Solen, via Jordcirkelskivan som en grov preferens, kunna bidra i IRRADIANS (neutrinobestrålning) med max 2×0,03%=0,06% [eg. 0,000578 ~ 0,001] eller grovt avrundat uppåt till absolut MAX 0,1%.

Jämför citatet nedan:

”The re- analysis of these data by the Fischbach group indicated that in both experiments there were similar time-dependent variations in the measured counting rates at the level of about 0.1 %. Moreover, during a period of about 3 years in which both experiments were collecting data at the same time, the observed time variations showed a remarkable correspondence.”,

Radioactive Decay and the Earth-Sun Distance, John G. Cramer, Published in the May-2009 issue of Analog Science Fiction & Fact Magazine

http://www.npl.washington.edu/av/altvw147.html

Dementi ...

”Taking data from NASA’s Cassini probe, Cooper noted that the decay of the plutonium–238 thermoelectric generators on board scarcely veered from the usual exponential law as the spacecraft went as close to the Sun as Venus and as far as Saturn.”,

The mystery of the varying nuclear decay 2 Oct 2008

http://physicsworld.com/cws/article/news/36108

Och dramatiken fortsätter:

’the decay constant is not really a constant’

MAC-aspekter på neutrinologiken

”What is more, the modulation appeared to be almost in phase with the varying distance of the Earth to the Sun: in January, when the Earth is closest, the decay rate was faster; in July, when the Earth is farthest, it was slower.”,

;

”The trouble with this interpretation is that neutrinos are only susceptible to the weak interaction, which governs beta decay. Although the silicon in the BNL experiment beta decays, the radium in the PTB experiment alpha decays — a process that is governed by the strong interaction. Nonetheless, Fischbach and Jenkins think radium exhibits the modulation because many of its decay products — such as lead–214 and bismuth–214 — do in fact beta-decay.”,

;

”“To summarize, what we are showing is that the decay constant is not really a constant.””,

Okt2008, PhysicsWorld — The mystery of the varying nuclear decay

http://physicsworld.com/cws/article/news/36108

Se även (illustrerat diagram) i

AstroEngine, Publication: Jenkins et al. 2008

http://www.astroengine.com/?p=1189

;

A Strange Connection: Could Nuclear Decay Rates be Influenced by Distance From the Sun? 2Sep2008

”Generally speaking, the decay rates of radioisotopes should remain pretty constant regardless of external forces or drivers. However, in the 1980′s, scientists in Brookhaven National Labs in the US and at the Physikalisch-Technische Bundesandstalt in Germany found some strange and unexpected variations in the decay rates of silicon-32 and radium-226. No cause was found and a pattern didn’t appear to exist. That was until Jere Jenkins and colleagues from Purdue University, Indiana, made a stunning discovery.”.

Se emellertid (dementi genom andra ämnesexperiment) i (klicka på Download PDF för att läsa den kopierbara versionen)

Evidence Against Correlations Between Nuclear Decay Rates and Earth-Sun Distance

Norman et al., Feb2009

http://escholarship.org/uc/item/6sz921hn.pdf

”In conclusion, we find no evidence for correlations between the rates for the decays of ²²Na, ⁴⁴Ti, ¹⁰⁸Agm, ¹²¹Snm, ¹³³Ba, and ²⁴¹Am and the Earth-Sun distance. We set limits on the possible amplitudes of such correlations (2.5 – 37) times smaller than those observed in previous experiments1,2,3. Our results strongly disfavor the suggestions by Jenkins et al.⁴ of an annual variation based on a previously unobserved field produced by the Sun or the annual variation in the flux of solar neutrinos reaching the Earth.”,

Se dock, återigen (07/2009), experimentella stöd för den första observationen i

http://adsabs.harvard.edu/abs/2008arXiv0808.3156J

Perturbation of Nuclear Decay Rates During the Solar Flare of 13 December 2006

”Abstract

Recently, Jenkins, et al. have reported the detection of correlations between fluctuations in nuclear decay rates and Earth-Sun distance, which suggest that nuclear decay rates can be affected by solar activity. In this paper, we report the detection of a significant decrease in the decay of 54Mn during the solar flare of 13 December 2006, whose x-rays were first recorded at 02:37 UT (21:37 EST on 12 December). Our detector was a 1 uCi sample of 54Mn, whose decay rate exhibited a dip coincident in time with spikes in both the x-ray and proton fluxes recorded by the GOES-10 and 11 satellites. A secondary peak in the x-ray and proton fluxes on 17 December at 12:40 EST was also accompanied by a coincident dip in the 54Mn decay rate. These observations support the claim by Jenkins, et al. that nuclear decay rates vary with Earth-Sun distance.”.

Det har nu (Okt2011) gått ett tag sedan ovanstående (turbulenta) innehåll såg dagens ljus.

— Vad säger man idag om Jenkinsgruppens uppseendeväckande upptäckt (2008)?

(Debatterna pågår — ingen vet — avvikelserna är små, men faktiska; Det ser ut som att den delen är mer eller mindre allmänt erkänd, dock ännu »utan direkt offentlig mening»]).

»radioctive decay, jenkins»:

”It's a mystery that presented itself unexpectedly: The radioactive decay of some elements sitting quietly in laboratories on Earth seemed to be influenced by activities inside the sun, 93 million miles away.

Is this possible?

Researchers from Stanford and Purdue University believe it is. But their explanation of how it happens opens the door to yet another mystery.”,

;

”Purdue nuclear engineer Jere Jenkins, while measuring the decay rate of manganese-54, a short-lived isotope used in medical diagnostics, noticed that the rate dropped slightly during the flare, a decrease that started about a day and a half before the flare.”, (13Dec2006)

;

”"It's an effect that no one yet understands," agreed Sturrock. "Theorists are starting to say, 'What's going on?' But that's what the evidence points to. It's a challenge for the physicists and a challenge for the solar people too."”,

STANFORD UNIVERSITY News, Stanford Report, August 23, 2010, DAN STOBER

http://news.stanford.edu/news/2010/august/sun-082310.html

”the rate dropped slightly during the flare”:

”Or the sun may emit fewer neutrinos during a solar flare, which would explain the December 2006 event.”,

;

”But some physicists take the results seriously and are searching old data for previously unnoticed effects. If the variations turn out to be genuine, theories may need revision, or new theories may be needed. “There’s no known theory that will predict something like this,” says theoretical physicist Rabindra Mohapatra of the University of Maryland in College Park.”,

22Nov2008 — PALEO GROUP — RADIOACTIVE DECAY RATES CAN CHANGE

http://www.dinosaurc14ages.com/changedecay.htm

Ytterligare artiklar som (mera utförligt) omnämner aspekten med neutrinostrålning från Solen som orsaksgrund, enligt Jenkins, ges citatvis i webbkällan nedan,

TECH POWER FORUMS — Radioactive decay is not a constant, Jul2011

http://www.techpowerup.com/forums/showthread.php?t=149245

” "Everyone thought it must be due to experimental mistakes, because we're all brought up to believe that decay rates are constant," Sturrock said. ”,

;

”Jenkins and Fischbach guessed that the culprits in this bit of decay-rate mischief were probably solar neutrinos”,

;

”Their findings strengthened the argument that the strange swings in decay rates were caused by neutrinos from the sun.”,

;

” But there's one rather large question left unanswered. No one knows how neutrinos could interact with radioactive materials to change their rate of decay.

"It doesn't make sense according to conventional ideas," Fischbach said. Jenkins whimsically added, "What we're suggesting is that something that doesn't really interact with anything is changing something that can't be changed."

"It's an effect that no one yet understands," agreed Sturrock. "Theorists are starting to say, 'What's going on?' But that's what the evidence points to. It's a challenge for the physicists and a challenge for the solar people too."

”.

Det finns också ett aviserat »paper» på iopScience [inte gratis tillgängligt för allmänheten utom en kort sammanfattning] från Aug2011,

CONCERNING THE PHASES OF THE ANNUAL VARIATIONS OF NUCLEAR DECAY RATES , Sturrock et al., Aug2011

http://iopscience.iop.org/0004-637X/737/2/65

”Recent analyses of data sets acquired at the Brookhaven National Laboratory and at the Physikalisch-Technische Bundesanstalt both show evidence of pronounced annual variations, suggestive of a solar influence.”.

Wikipedia dementerar

Jämför motsvarande »dementisida» — som åberopar ”a subsequent paper” från 2009:

@INTERNET Wikipedia Radioactive decay, Changing decay rates [2011-12-20]

http://en.wikipedia.org/wiki/Radioactive_decay - Changing_decay_rates

”However, such measurements are highly susceptible to systematic errors, and a subsequent paper[12 Norman, E. B.; et al. (2009). "Evidence against correlations between nuclear decay rates and Earth–Sun distance". ] has found no evidence for such correlations in six other isotopes, and sets upper limits on the size of any such effects.”.

Det behöver inte finnas någon motsättning mellan Norman-gruppens förutsättningar och resultat [2009], Wikipediacitatet ovan, och Jenkins-gruppens [2008]: fenomenet KAN omfatta bägge [på, som vanligt, oväntat sätt], med en inneboende sammansatthet som ännu inte uppdagats.

— Det väsentliga är att man kunnat påvisa NÅGON variation — i jämförelse med uppfattningen att INGEN sådan kan förekomma, och försåvitt nu observationerna verkligen håller streck.

— En webbkälla finns nedan som fiskat upp en färskt exempel i den andan, och som direkt ansluter till (och förklarar den efterföljande bakgrunden i) Wikipediacitat ovan:

”Javorsek et al. write:

The inference from our analysis that different nuclei may be affected differently by an external source could help to explain recent papers by Norman et al. and Cooper who have set limits on possible variations in the decay rates of several nuclides. […]it is reasonable to suppose that the same complex details of nuclear structure (e.g. nuclear wavefunctions, angular momentum selection rules, etc.), which are responsible for the fact that half lives vary from fractions of a second to tens of billions of years, could also affect the response of different nuclei to some external influence.¹⁶[Javorsek II D, Sturrock P, Lasenby RN, Lasenby AN, Buncher J, Fischbach E, Gruenwald T, Hoft A, et al. (2010) Power spectrum analyses of nuclear decay rates. Astropart. Phys. 34(3):173–178 ]”,

TASC · Triangle Association for the Scienceof Creation — Radioactive Decay Rates May Change — Dec2011

http://tasc-creationscience.org/content/radioactive-decay-rates-may-change

Jenkinsgruppen Jun2011

Dramatiken avgjord — variationerna gäller även en observerad inre Solrotation på 32 dygn

Jenkinseffekten: Observerade ändringar i radioaktivt betasönderfall med variationer i avståndet till Solen [från Jenkins et al., 2006]

Ett nyligen framställt kortare PDF-dokument från Jenkinsgruppen (Fischback, Jenkins, Sturrock, Jun2011) finns nu på webben [här uppmärksammat Dec2011] i nedanstående länk; Författarna darrar uppenbart inte på manchetten i det man konstaterar (sek.4) att ”överväldigande bevis” nu finns för att HASTIGHETEN i radioaktiva sönderfall påverkas av variationer i avståndet Jorden-Solen, samt speciellt också ändras via variationer i det inre av Solens rotationer.

”There is by now overwhelming evidence of anomalous and unexpected time-dependent features present in the count rates of various nuclei.”;

EVIDENCE FOR TIME-VARYING NUCLEAR DECAY DATES:

EXPERIMENTAL RESULTS AND THEIR IMPLICATIONS FOR NEW PHYSICS, Fischbach et al., Jun2011

http://arxiv.org/PS_cache/arxiv/pdf/1106/1106.1470v1.pdf

”Unexplained annual variations in nuclear decay rates have been reported in recent years by

a number of groups. We show that data from these experiments exhibit not only variations

in time related to Earth-Sun distance, but also periodicities attributable to solar rotation.”, sek.1,

Periodiciteten på 32 dygn

”Further analysis of the BNL, PTB, and Parkhomov data sets has indeed revealed evidence of a ~32 d periodicity”, sek.2n,

;

”Although the preceding discussion, along with the analysis in Section 2, suggests that the

decay process is being influenced in some way by the Sun, there is at yet no detailed mechanism

to explain how this influence comes about. Our discussion of neutrinos and neutrellos is an

attempt to frame a future theory by outlining some of the specific characteristics that it should

possess, given the limited experimental data currently available.”, sek.4ö.

Se även i vidare fortsättning för UNIVERSUMS HISTORIA i Jenkinseffekten i relaterad fysik i htm-dokumentet Meteoriternas ursprung — hur meteoriternas mineral och deras orbitala ursprung kan förklaras i relaterad fysik.

Se även i Jordens ålder.

Wu 1957

The Cobalt-60 experiment from 1957

ElektronEmissionsExperimentet från 1957

— från Wu, Ambler, Hayward, Hoppes och Hudson, här illustrerat enligt TNED

The experiment of Wu, Ambler, Hayward, Hoppes and Hudson

— Det banbrytande experimentet från 1957 som visade att elektronemissionerna ges företrädesvis i atomkärnornas spinnriktningar — vilket stämmer kvalitativt utomordentligt med TNED.

Illustrativ modell	Nedkylning, spinnsynkronisering	Polarisering	Mätning: diametrala spinnriktningar Co60	Mätning: diametrala spinnriktningar Co58	Anordningen 1957

a	b	c	d	e	apparatbeskrivning

a: Atomkärnans signifikanta detaljer enligt TNED. b: den primära kärnspinnpolariseringen i experimenten från 1957. c: anordningen för att rikta kärnspinnen mot den avkännande scintillationsdetektorn. d: experimentella resultaten från Kobolt-60-kärnorna och deras elektronemissioner. e: motsvarande experimentella resultaten från Kobolt-58-kärnorna och deras positronemissioner.

Apparatbeskrivningen:

The Reversal of Parity Law in Nuclear Physics

http://physics.nist.gov/GenInt/Parity/expt.html

c: spolen för vertikala spinnriktningen

”Next, a vertical solenoid was raised around the lower end of the outer dewar to provide a magnetic field for polarization of the ⁶⁰Co nuclei. After the beta emission had been measured for this condition, the direction of the magnetic field was reversed and the beta emission again measured for the nuclei now polarized in the opposite direction.”, 112sp2mn,

Reversal of the Parity Conservation Law in Nuclear Physics

http://nvl.nist.gov/pub/nistpubs/sp958-lide/111-115.pdf

Se även citatet från HOP om experimentet ovan i BT-fältet.

— I omnämnandet av experimenten från 1957 [Wu et al.] som visade att elektroner (från betaaktiva Koboltatomer) emitteras företrädesvis i atomkärnornas [polariserade av yttre starka magnetiska fält] spinnriktningar (och som därmed ansluter till spinnbegreppet för atomkärnan enligt TNED), fanns underförstått (samt i framställningarna [Se Parbildning] i ELEKTRONENS BUBBELKAMMARSPÅR, riktningarna för ±e) att emissionsfenomenet skulle vara ANALOGT med detektionsfenomenet.

— Ingen explicit framställning har tidigare gjorts på den punkten i Universums Historia.

— Genom detaljer som först nu framkommit i samband med det radioaktiva sönderfallets fysik, har den detaljfrågan hamnat i starkt fokus.

Ovanstående sammanställda illustrationer med tillhörande källreferenser ger en mera detaljerad översikt.

Editor2011XII20

Om Wu-experimentet generellt på Webben 2011

ERINRA att Wu-experimenten (från 1956) var ägnade att studera (motbevisa) PARITETSPRINCIPEN — bilden (som ofta visas illustrerat i fackböcker) med en spinnriktad atomkärna i en SPEGEL uppvisar motsvarande symmetri

— trots att en BILD av atomkärnan är FÖRBJUDEN i modern akademi; se exv. i PDF-dokumentet s256

(även vidare här längre ner)

http://www.actaphys.uj.edu.pl/vol39/pdf/v39p0251.pdf

s256, BILD av atomkärnan i spegling

;

Wu-experimentet kan sägas avbilda den »spegelbildsprincipen»; OM paritetsprincipen skulle vara giltig, skulle det heller inte spela någon roll hur kärnspinnen vore orienterade relativt spegeln (scintillatorn som räknar elektronerna, rätvinkligt spinnaxlarna). Wu-experimenten visade att paritetsprincipen INTE gäller: resultaten är olika beroende på spinnaxelns riktning ±180°. Inget mer. Inget mindre.

En mera REGULJÄR experimentellt belagd observation som ligger i linje med TNED är den betaassocierade gammastrålningen, till exempel i Wu-experimenten. Källan nedan skriver,

”The cobalt-60 nucleus emits both β and λ rays. The degree of polarization can be measured by the anisotropy of the gamma radiation, which is emitted more in the polar direction than in the equatorial plane.”,

THE DOWNFALL OF PARITY — THE REVOLUTION THAT HAPPENED FIFTY YEARS AGO

Andrzej K. Wróblewski, Physics Department, Warsaw University, Jan2008

http://www.actaphys.uj.edu.pl/vol39/pdf/v39p0251.pdf

I TNED emitteras elektroner ut från kärnkatoden (neråt, under kärnan i figuren vänster); positroner i kärnanodens riktning, samma som magnetiska kärnspinnriktningen, där även den åtföljande gammastrålningen (m→γ) visar sig (tillsammans med elektronemission, och på det komplicerade sätt som denna presentation är föremål för att försöka utreda, helt). Se även i Neutrinorekylerna hur de olika partikelemissionerna yttrar sig enligt TNED.

— Citatdelen ovan är alltså en TNED-analog beskrivning — vilket fördenskull INTE bevisar något i favör för TNED, explicit. [Betydligt mera detaljerade experimentella beskrivningar behövs innan vi (ev.) når dit].

— Citatkällan ovan (Wróblewski, s260) envisas emellertid med att, från Wu-experimentet, ansluta sig till TNED-analogin ytterligare enligt följande illustrativa, klargörande bidrag:

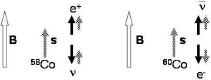
”Fig. 2. Comparison of beta decays of ⁶⁰Co and ⁵⁸Co. The electrons from the ⁶⁰Co decay are emitted preferentially into the hemisphere opposite to the nuclear spin s, whereas the positrons from the ⁵⁸Co are emitted preferentially along the spin of

the nucleus.”,

Andrzej K. Wróblewski, Physics Department, Warsaw University, Jan2008

http://www.actaphys.uj.edu.pl/vol39/pdf/v39p0251.pdf

— Det är, uppenbarligen, samma som emissions- och riktningsordningarna enligt TNED — men det är, som sagt, här inte känt hur man når den riktningsordningen i modern akademi, trots mängder med (PDF-) dokument som beskriver ämnet; det fattas (här, ännu Nov2011) detaljer i beskrivningssättet från det etablerade fackhållet som förklarar kopplingen till spinnriktningarna.

— Föreställningen om en BILD (vektor) överhuvudtaget för atomkärnan i MAC, se särskilt citat, gör ämnet ännu mera besvärligt att reda ut — från det moderna hållet; man erkänner GENERELLT ingen SYNBARHET (åskådlighet) för dimensioner i atomkärnornas storlek.

(KONSEKVENT ska man då heller inte tala om »vektorer» och annat ASSOCIERAT. Vi VET dock redan, och emellertid, som redan bekant, att människan INTE fungerar så enkelspårigt).

Se även komplement i klargörande till ovan i Webbkällan (s120-121) — tar extra lång tid att ladda upp

OBSERVATION OF PARITY NON-CONSERVATION

http://neutrino.physics.wisc.edu/teaching/PHYS741/PHYS741_lecture_7.pdf

”Result: more electrons emitted preferentially in one direction.”.

Ytterligare en Webbkälla av samma illustrativa typ som ovan (s10),

DOES QUANTUM ELECTRODYNAMICS HAVE AN ARROW OF TIME?

http://philsci-archive.pitt.edu/2571/1/radiation4.pdf

Varifrån författarna fått dessa flödesbilder, varken framgår eller beskrivs. Jämför även generellt universitetsinstitutionernas labbpreferenser (Lund 1996).

Lund 1996

Om atomkärnans åskådbarhet generellt

Notera att blotta föreställningen om någon åskådlig BILD av atomkärnan överhuvudtaget inte anses möjlig i den moderna akademins lärosystem (Lunds universitet, citat nedan).

”Vi anser, att vi känner den vanliga materiens struktur väl. Emellertid är det alltid vanskligt att åskådliggöra hur materien ”ser ut” med bilder från vår vanliga föreställningsvärld. I vår vardag rör vi oss med dimensioner ner till storleksordningen millimeter, och det är sällan möjligt att överföra våra föreställningar till en värld som är mer än femton tiopotenser mindre än den som vi har erfarenhet av. Även om bilderna kan illustrera ett fenomen, blir de ofta dåliga i andra avseenden.”,

LUNDS UNIVERSITET, Fysiska institutionen, 1996-09-10

— Elektronmassans svängningar är beroende av atomkärnan som »maskinbas» (Se Kärnmatrisiska Algoritmen), och kan därför inte explicit penetrera atomkärnans detaljer — och knappt ens atomens olika regioner. Med uppfattningen att makrofysikens ljusvåglängder också bestämmer åskådningens gränser, vilken föreställning är allmänt förhärskande i modern akademi (speciellt bland ledet läkare när de olika åskådningsfrågorna är aktuella), se citatet från den etablerade lärostolen ovan, »förbjuds» därmed också varje åskådlig föreställning om atomkärnan. Se även vidare i Osäkerhetsprincipen, som ytterligare understryker den moderna akademins begränsade åskådning av och i fysikens djupare domäner.

Referenser

Referenser

[VNS]. Van Nostrand’s Scientific Encyclopaedia Fifth Edition 1976

Alla angivna sönderfallstider i denna skrift refererar till ovanstående enligt Table 3, s495-501 om inget annat anges.

[HOP]. Handbook of Physics, E.U. Condon, McGraw-Hill 1956-67

Se de särskilt angivna, och här använda, konstanterna generellt från HOP-källan i HOP-konstanterna.

Alla angivna atomvikter i denna skrift grundas på tabellverket i HOP-källan, 9-65 – 9-86 Table 2.1., Nuclear Masses

Fördelen med HOP-tabellen: Alla NATURLIGT FÖREKOMMANDE ISOTOPER finns angivna [alla kända upp till år 1966] med data för respektive mineralogiska förekomster, samt angivna kända sönderfallstyper, dock utan data på halveringstider;

— VNS-tabellen [från 1975/76] kompletterar [nära heltäckande] HOP-tabellen med specificerade halveringstider, dock endast totala halveringstider för varje nuklidgrupp.

— De senare utvidgade nuklidtabellerna [upp mot år 2000] innefattar en nära enorm mängd artificiellt producerade instabila nuklider som i vissa fall går långt utöver området för HOP-VNS-tabellerna.

[BA]. Bonniers Astronomi 1978, Det internationella standardverket om universum sammanställt vid universitetet i Cambridge

[EST]. Encyclopedia of Science & Technology, McGraw-Hill 1992

[FM]. FOCUS MATERIEN 1975

[GF]. Gymnasiets Fysik 1977-1980, åk 1-3, Liber Läromedel

[BKL]. Bonniers Konversations Lexikon 1922-1929, Band I-XII med Supplement

Observerade fel

EST-15s104 Table 1 Example (rad6). Felaktig beteckning 71La. Korrekt beteckning är 71Lu. La har atomnummer 57.

tH, t_H, förkortning för halveringstid i denna presentation. Konventionellt anges tH ofta T_½.

Multipla alfaenergier

En inledande, väl upplysande orientering i ämnet MULTIPLA ALFAENERGIER ges från webbkällan [Nov2011]

USA ENVIRONMENTAL PROTECTION AGENCY — Tutorial 4.4 — Alpha Spectrometry 1: Principals

http://www.epa.gov/safewater/radionuclides/training/transcripts/tutorial_4.4.pdf

Webben innehåller sparsamt med basinformation om detaljerade grunder i ämnet multipla alfaenergier.

— Källan ovan utgör, tydligen, ett undantag.

NEDAN GES NÅGRA Centralt belysande beskrivningar i citat från källan ovan (källtexten refererar dock till illustrerat material som inte ingår i dokumentet):

Hur alfaemissionerna görs

"Alpha particles emitted by the nucleus have a characteristic energy. For most alpha emitters this energy is between 3 and 10 MeV. Alpha emission by the nucleus can result in alpha particles of different energies. Only one alpha particle is emitted per decay of the nucleus, but each decay can result in an alpha particle of a different energy. This is because any group of 2 protons and 2 neutrons within the nucleus can form the alpha particle that is ejected.",

;

Specifika alfaenergier

"The plot on this slide shows an energy spectrum for a sample containing 242Pu. The y-axis represents the total number of decays that occur (or what we refer to as counts) at a specified energy. This radionuclide has two alpha particles that are emitted one of 4901 keV and one at

4856 keV. The alpha particle energy which is more frequently observed is the one with energy of 4901 keV. This energy is determined by finding the maximum in the curve shown. Note that just to the left of the maximum there is a small shoulder on the curve. This is the contribution from the 4856 keV alpha particle. Although we cannot determine from this plot the exact percentage of the time we observe each energy, the approximate ratio is 3:1. This means that if we had 100 atoms of 242Pu decaying that 75 would yield an alpha peak at 4901 keV and 25 would yield an alpha peak at

4856 keV.",

;

Observationernas begränsningar

"Plutonium has several long-lived radionuclides that are alpha emitters. Pu-239 has four alpha particle energies as noted on the slide and 240Pu has 2 alpha particle energies. Note that the energies of the six different alpha particles only differ by 64 keV. Resolution is the ability of the spectrometry system to differentiate between two different alpha particles. The resolution for alpha particle energies with routine laboratory methods is between 40 and 100 keV, mainly dependent upon the technique of the analyst. Since both of these radionuclides are chemically the same, they cannot be

chemically separated. Since their alpha particle energies are so close, they cannot be spectrometrically separated. This means that when the results for plutonium are reported for these two isotopes, it is usually reported as the sum of the activity of the two radionuclides.",

;

Historiskt om alfaspektroskopin

"Historically, the technique used to determine the alpha particle energies used an instrument that had very good resolution. However the instrument was not very rugged, and the energy of emission of the alpha particles was measured as a function of increasing voltage across the detector. The voltage was controlled in increasing increments by setting an upper and a lower level discriminator and measuring the instrument response. The lower level discriminator was then moved to the upper level discriminator setting and the upper level discriminator was moved up by the voltage

difference between the two discriminators. That span between the two discriminators was referred to as a “channel.” The midpoint energy of the channel is considered the energy of emission being measured. The electronics of the instrument were configured so that only a response within the energy range measured was recorded and not energies that were higher or lower. This configuration of counting was known as a single channel analyzer or SCA.",

;

Dagens instrument, kanaltermen

"The sophistication of instruments has increased significantly over the last 70 years. We no longer use SCAs to measure the alpha particle emission from a sample. The electronic circuitry in instruments can measure the energy of the incident alpha particle and distinguish between different responses from alpha particles of different energies. It then can save and accumulate each of these responses separately in storage location for each energy. We continue to use the

term “Channel” to identify these storage locations. Current alpha spectrometric detectors can be calibrated so that each channel corresponds to ~8–10 keV of energy. The spectrum shown on the slide is a histogram showing the number of counts recorded in each channel. Note that even though alpha particle energies based on the nuclear decay should be “monoergic,” that is, one energy, the alpha spectrum is spread out over several

channels or energies. This spread of energy is due to the way alpha particles interact with mater. The multichannel analyzer also has a visual display so that the analyst can observe the actual energy spectrum. Some of the responsibilities of the analyst are to assess the shape, energy correctness and resolution of all alpha peaks in the spectrum.",

USA ENVIRONMENTAL PROTECTION AGENCY — Tutorial 4.4 — Alpha Spectrometry 1: Principals

http://www.epa.gov/safewater/radionuclides/training/transcripts/tutorial_4.4.pdf

Jordens ålder

Frågan om JORDENS ÅLDER har tidigare i UNIVERSUMS HISTORIA berörts i avsnittet om Den Urgamla Jorden, och då med särskild tonvikt på J-KROPPARNAS VÄRMEFYSIK.

— Det finns ännu (Feb2012), och frånsett den enda kända exakta mekaniska klocka som finns, Månens recession, inget känt säkert sätt — genom klara, tydliga och väl relaterbara argument — som kan undanröja alla tvivel beträffande uppgiften om Jordkroppens ålder (20,82 miljarder år enligt TNED; 4,5 miljarder år enligt MAC) — ehuru otvetydiga uppgifter finns beträffande de nu äldst kända bergmineralen, runt 4-5 miljarder år.

Komplikationer har uppkommit (för MAC) genom Jenkinsgruppens observationer (Jenkins 2006). Observationerna stadfäster (Jenkinsgruppen Jun2011) det radioaktiva sönderfallets principiella variabilitet (endast direkt uttalat för betainstabila nuklider och då ännu i försiktiga ordalag, då mera mätdata krävs för att få bättre underlag för vad som gäller) i inverkan från Solen: ingen tvekan råder längre om att det radioaktiva sönderfallets fysik påverkas av de årliga avståndsvariationerna Jorden-Solen, samt även internt via inre Solvariationer (Jenkinsgruppens observation av 32-dygnsperioden).

Komplikationerna medför att all beskrivning, tolkning och behandling av de radioaktiva isotopernas sönderfall i samband med olika radiometriska dateringskomplex som behandlar objekt UTANFÖR Jordlokalen INTE kan anses tillförlitliga förrän man får säker klarhet i på vilket sätt, om alls, de radioaktiva isotoperna generellt berörs av Jenkinseffekten. Därmed utesluts (här) tills vidare alla värdemässiga aspekter på ämnesområden som berör Jordkroppens ålder, Solsystemets ålder och Universums ålder och som innefattar radiometrisk teknik.

Se även särskilda beskrivningar som ansluter till svårigheterna i

· Jenkinseffekten i relaterad fysik

· Jenkinseffektens AlfaBetaKomplikation

· Jenkinseffektens omedelbara konsekvenser

I Beräkningsexempel visas hur nuvarande värdeprecision på halveringstiden för U238 måste skärpas med minst en decimal för att man, via direkta mätningar på Uranet i Solens inverkan, SÄKERT ska kunna avgöra frågan för Uranets del.

— Innan dess, är varje (här) anförd mening i frågan om Jordkroppens ålder och Solsystemets ålder och Universums ålder — EXPLICIT via metoder och teorier som baseras på radiometrisk teknik med hjälp av Uran-Blymetoden med hjälp av objekt UTANFÖR Jordlokalen (meteoriter) — helt utan upplösande, förklarande och klargörande meningsfull innebörd.

Editor2012II9