LJUSETS POLARISATION | 2005 | 2008VII1 | Senast uppdaterade version: 2011-10-10 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

LJUSETS POLARISATION

Det är sedvanligt att beteckna ljus från allmänna ljuskällor som Solen och lampor med typen opolariserat. Den polariserande aspekten kommer in i bilden när sådant opolariserat ljus genomgår någon form av »linjärisering» — som till exempel när Solljus reflekteras och bryts av vatten, i allmänhet av en transparent (genomskinlig, brytande eller refraktiv) materialyta. Undersökning av sådant ljus visar en påtaglig skillnad i beteende mellan det inkommande (ursprungliga) och det reflekterade (resulterande) ljuset. Ett enkelt köksexperiment visar vägen.

köksexperimentet

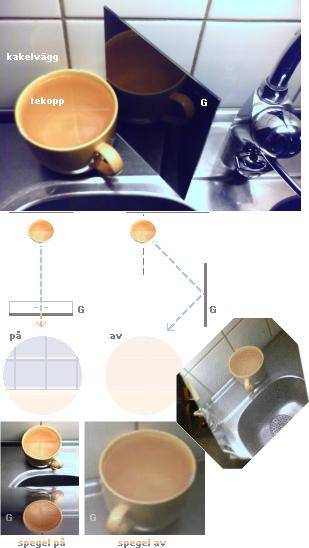
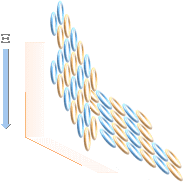
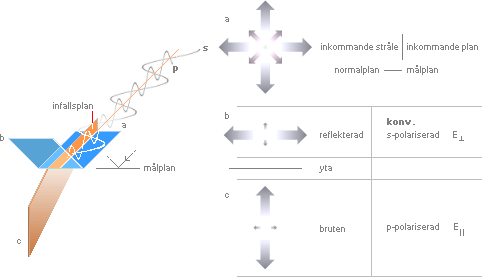
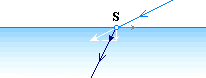
Ljusets polarisation ETT ENKELT KÖKSEXPERIMENT VISAR MED EN TEKOPP, VATTEN OCH EN HANDHÅLLEN GLASPLATTA En vattenfylld tekopp placeras framför den belysta diskbänkens kakelvägg (eller annan tydligt mönstrad yta som är lätt urskiljbar). Kaklets spegelbild (S) i tekoppens vattenyta ska inspekteras genom frontsidan på en mindre handhållen glasplatta (G). På dess baksida har en svart klippkartong monterats med dubbelhäftande tejp för att framhäva endast framsidans spegelbild. I nedre vänstra delen av illustrationen ses S i G ovanifrån. Om G vrids upp (åt höger) i höjd med huvudet, ses S gradvis försvinna. Vid en specifik vinkel är S utsläckt, helt och hållet. Denna reflexionsutsläckning relateras såsom förorsakad av en (tvåvägs) polarisation hos ljuset. Vi ska studera det fenomenet ur flera olika synvinklar (och material) i den här framställningen, samt visa hur TNED (galant) förklarar funktionssättet — genom elektronmassans komponenter.

Ljusets polarisation är en av de tre egenskaperna reflexion, refraktion (brytning) och polarisation i ljusets materiella eller optiska natur. Medan den reflektiva och refraktiva egenskapen är välbekant genom direkt daglig observation — genom vattnet i teet eller kaffet vi dricker — är den polariserande effekten mindre bekant. Experimentet som beskrivs ovan visar rent praktiskt hur den polariserande fenomenformen kan studeras excellent i detalj med ytterst enkla medel. Men vilken är förklaringen?

Du hittar den garanterat inte i modern akademi, inte i någon bok, inte i någon skrift, inte på webben — utom i den begränsade mening som garanterat INTE innefattar ovanstående köksexperiment. Anledningen till det kommer också att beskrivas ingående i den här framställningen (se särskilt i Ljusets polarisation i modern litteratur).

ljusmodellernas matematiska grunder

Ljusmodellens matematiska grunder

LJUSMODELLERNA

IMPULSMOMENTET

h=mcr=mccT=mc²/f = E/f

definierar energin genom begreppet frekvens (f) enligt Planckenergin

E = hf

Det är samma principiella periodiska genomgång som håller atomkärnan levande och verksam: massa (laddning) och spinn (periodisk rotation).

Med en liknande periodisk svängning för atomernas slutna elektronsystem, vidareförmedlas också energin till all elektromagnetisk strålande verksamhet med grund i den elektriska laddningen från en ljuskälla (S) till all övrig materia.

Varje ljusbärande riktning (r) eller som vi säger ljusstråle (L) från S innehåller då en bild av alla möjliga f i E hos S så att vi för varje färg (f) i varje ljusstråle får en definition av dess energi enligt Planckenergin E=hf.

Ett material (M) som träffas av en ljusstråle L utvecklar då för en given frekvens eller färg f en motsvarande Planckenergi hf genom elektrisk och magnetisk påverkan på materialets atomära laddningar. Vilket vill säga: Energin visar sig först i M, den har ingen representation i tomrummet mellan S och M — även om vi rent matematiskt i kvantiteter kan använda en sådan (förenklad) modellform SOM OM det fanns ett M på varje punkt i L mellan S och M.

MODELLFORMEN vi då använder kommer, på samma sätt, att ”innehålla” de i M motsvarande uppmätbara elektriska och magnetiska svängningsriktningarna som följd av f-matningen.

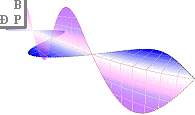
Därmed kan vi också, med L som den ljusbärande huvudriktningen (z) forma matematiska plan (xy) som illustrerar de olika elektriska och magnetiska fältplanen i det centrala tvärsnittet genom L, typ bilden ovan, hos den så uppbyggda matematiska modellen för ljusets utbredning.

Därmed kan vi också på motsvarande sätt relatera de olika s.k. ljusplanen till olika förutsättningar med olika materiella egenskaper i ljusets växelverkan med materien, typ plana materialytor motsvarande ”inkommande reflekterande” och ”inkommande brytande”, typ bilden ovan.

Observera därmed hur ”fenomenfysiken” (plötsligt genom matematiken) blivit så abstrakt att vi enbart på matematikens grund svårligen kan känna någon praktisk gemenskap med den uppbyggda modellen: Ljuset ser inte ut så.

Se mera utförligt i LJUSETS OPTISKA NATUR.

ljusets grundform

GENERELLT OM

LJUSETS POLARISATION SOM ALLMÄNT BEGREPP

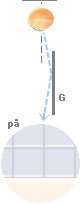
Med ovanstående förenklade ikon som illustration för ljusets grundform:

På grund av att LJUS kan förstås som en masslös utbredning med ändlig hastighet (c) av elektriska potentialändringar (accelerationer i alla möjliga riktningar) med alla möjliga frekvenser — relativt referenspunkter i ett omgivande dominant gravitationsfält som till exempel Jordytans mineralkropp (och dess olika människoskapade byggnader) — kan varje ljusstråle (ideal geometrisk linje) som går genom tomrummet liknas vid en centralaxel eller »ljuslinje» kring vars tvärsnitt homogent expanderande vektorer (pilar) utgår motsvarande svängningarnas periodiskt växlande elektriska och magnetiska fältstyrkor genom en idealt given mätpunkt. Det innebär att en

polarisation är varje strukturell ändring av det centralsystemets inre homogena (opolariserade) ordning (och vilken ändring sker företrädesvis i kontakt med plana materieytor eller motsvarande kristallplan). Det innebär att ljuset obönhörligen kommer att uppvisa sådana ändringar då det träffar på ett material — men på olika sätt beroende på de olika materialens strukturella egenskaper.

enkel observation

Speciellt från den punkt ett sådant opåverkat eller med ett viktat begrepp opolariserat ljus möter en plan genomskinlig yta som till exempel vatten, kan polarisationens resultat studeras i detalj med direkt observerbara effekter som ovan i det enkla köksexperimentet.

naturliga kristaller

Naturen har också utvecklat speciella kristaller, så kallade dubbelbrytande kristaller (eng. birefringent crystals). Den mest prominenta av dessa — som dessutom kan bli rejält biffig — är Kalcit, CaCO3, en av de mest vanligt förekommande mineralerna på Jordytan dessutom — i en del fall med närmast enorma kristallstorlekar, se @INTERNET Wikipedia Calcite för bild. I en sådan dubbelbrytande kristall bryts ljuset utmed två stråk istället för normalt utmed bara ett enda.

Med hjälp av sådana (små) typkristaller, numera tillgängliga i formen av (inpressade) ytskikt i solglasögon av typen polaroid, kan man utföra enkla experiment för att undersöka ljusets polariserande egenskaper via polaroidkristallens givna riktningsfysik.

Om ljuset från en speglande vattenyta betraktas genom ett polariodglas kan man med glasets vridning 0-±90grader se hur spegelbilden ömsom släcks ut och ömsom förstärks beroende på vridningsvinkeln.

LJUSET FRÅN

BILDSKÄRMEN ÄR POLARISERAT

Speciell Notering.

Även ljuset från en LCD-bildskärm är polariserat. Använd ett av glasen från ett par polaroidsolglasögon för att kolla själv: vridning av solglaset släcker skärmljuset.

allmänna förutsättningar

DJUPT ROTADE VANFÖRESTÄLLNINGAR OM LJUSETS NATUR I MODERN AKADEMI | 2008VII6

Alla elektronmassor är atombundna genom resonanser, det är svängningar i formen av s.k. stående vågor (motsv. akust. toner) eller fasta mönster; För att frigöra en elektron ur ett sådant resonansmönster krävs en motsvarande svängningsenergi (E=hf):

»atomerna kan emittera och absorbera strålning endast i bestämda kvantiteter».

Elektronresonansernas atomära bindningar härleds ekvivalent ENLIG TNED genom kraftkomponenten F_eZ i atomens kraft- eller kemiekvation F_BT+F_eZ=0 genom Keplerresonanserna i formen av GRUNDÄMNENAS PERIODISKA SYSTEM. Resonansmönstren innebär att bindningsenergin för en elektron till sin förälderatom växer med svängningens frekvens (f) enligt Planckenergin E=hf — den härleds från impulsmomentet eller PLANCKRINGEN J=mcd med J/d=mc via divergensenergin E=mcc=cJ/d och c=d/T=d·f som ger E=cJ/d=(d·f)J/d=Jf med J som Plancks konstant h=6,626 t34 JS. Därmed har begreppet foton ingen innebörd i TNED. Se även utförligt i PEFECT.

I modern akademi känner man inte periodiska systemets (synnerligen »enkla») härledning genom Keplerresonanserna — och heller inte atomkärnans härledning genom Planckringen. Då man (således) under 1800-talet (år 1887, 13 år före upptäckten av ”det universella verkanskvantumet” eller Plancks konstant) upptäckte den fotoelektriska effekten — ljus med en viss minsta frekvens kan ”slita loss elektroner” från en metallyta, och man finner vid mätningar att de frigjorda elektronernas energi beror på den använda ljusagentens frekvens — associerade man INTE fenomenet med egenskaper hos materien — nämligen elektronens resonansberoende atomära bindning — utan med egenskaper hos ljuset! Man når — nämligen — exakt samma kvantitativa resultat om man postulerar en matematisk modell av ljuset i formen av ”virtuellt åkande partiklar med energin hf” kallade fotoner, men till priset av att den rent kvalitativa förklaringen till både ljusets och massans fysik förloras (som modern akademi nu i vilket fall missade).

Det var — strax efter Max Plancks banbrytande arbeten precis i början av 1900-talet — Albert Einstein som föreslog fotonen som förklaring till den fotoelektriska effekten. Planck själv menade (precis som vi gör här, ref. TRETTIO ÅR SOM SKAKADE FYSIKEN George Gamow, Prisma 1968, s33) att kvanteffekten snarare var en egenskap hos atomerna: ”atomerna kan emittera och absorbera strålning endast i bestämda kvantiteter”.

I TNED finns inga ”fotoner”; Men då den moderna akademins uppfattning av begreppet ”spinn” också har ”fotonen” som en fundamental beståndsdel i den teoretiska byggnaden, innebär det att spinnet som begrepp i koppling till de atomära sammanhangen får en helt annan innebörd i TNED jämfört med den modern akademins uppfattning. Se utförligt i Spinnbegreppet i modern akademi, där ges jämförande korsreferenser.

Fotonen som begrepp är ett kvantitativt, matematiskt, användbart verktyg för att beskriva ljusfysikens olika händelsedelar. Men om man tar fotonen bokstavligt, missar man fysikens kvalitativa förklaring: Ljusets utbredning är masslös, energilös; Ljuset uppvisar ingen transportform, bara olika tillstånd med elektriska potentialer som ändras relativt fixt givna gravitella fältpunkter genom den g-beroende ändliga divergensen (ljushastigheten c). Energin som ljuset utvecklar transporteras inte över avstånd utan utvecklas som en lokal källenergi där ljusstrålen träffar på materia, inte målenergi som uppkommer då materialet ”träffas” av den ”utsprutande ljuskällans fotonpaket”.

Se även i COEI (Energins bevarande genom induktionen).

LJUSETS POLARISATION | 2008VII1

huvudvyn

GRUNDBEGREPP

ELEKTRONMASSAN

t-ringen atomkärnan

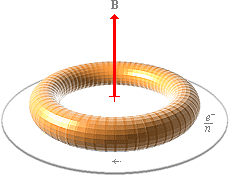
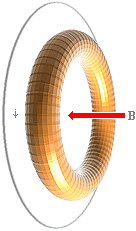
Bilden till vänster visar atomkärnans övergripande toroidform enligt TNED sådan den framkommer i härledningen till atomkärnan genom PLANCKRINGEN. Den lilla ringen över kärnbrunnen visar dimensionen för sämsta fallets skalenliga beräkning av elektronmassans komponent (t-ringen, tau-ringen) som max 1/50 av protonradien 1,37 t15 M. Det är dessa ringkomponenter som ENLIGT TNED bildar elektronmassans element. Elektronelementet eller t-ringen lyckas med vad både kvantfysiken och vågmekaniken garanterat misslyckas med: En enhetlig förklaring och beskrivning av ljusets brytning (refraktion), reflexion och polarisation. Det är vad den här framställningen kommer att handla om.

t-ringens egenskaper

t-ringens egenskaper

Av ålder är det bekant att all materia består av små delar åtskilda av tomrum. Smådelarna kallas atomer. Enligt TNED består varje atom av en atomkärna som kan härledas ur PLANCKRINGEN omgiven av elektronmassor som frigörs ur atomkärnan med början från NEUTRONEN. Varje elektronmassa (me ) består av minst 177062 enskilda t-ringar (se Elektronmassans komponenter). t-ringarna är sammanknutna med sin förälderkärna via atomens två impuls och kraftekvationer i formen av mönster (stående vågor eller resonanser) kring atomkärnan. De olika mönsterformerna växelverkar inbördes och bildar GRUNDÄMNENAS PERIODISKA SYSTEM som grundlägger atomernas möjlighet att förenas och bilda större kroppar; det vi kallar för molekyler (förenade atomer) och kristaller. Därmed kommer varje kropp att uppvisa sin yta utåt tomrummet genom kroppsytans elektronmassor eller t-ringarna. Eftersom t-ringarna uppvisar karaktäristiska elektriska och magnetiska egenskaper enligt speciella beskrivningar i Spektrum och Kvanttalen, blir det också dessa som bär ansvaret för fenomengrunderna i ljusets tre egenskaper med reflexion, refraktion och polarisation. Emellertid ingår inte t-ringarna (sedan 1927) i den moderna akademins lärosystem, varför man heller inte känner till beskrivningen av ljusets fysik genom dem.

t-ringens elektriska fält är som störst i dess ringplan.

Genom t-ringens inre fraktala strömstruktur (se utförligt från PLANCKRINGEN) får t-ringen också en utpräglat central magnetpol (B). Genom att olika material förenar olika atomer genom olika mönster eller resonanser, kommer t-ringarnas magnetiska och elektriska delar att samverka i motsvarande strukturer som bildar de två huvudgrupperna absorbatorer och reflektorer.

elementära materialgrunder enligt TNED

ABSORBATORER OCH REFLEKTORER

MATERIENS TVÅ HUVUDGRUPPER

All fast materia kan indelas i två skilda materiegrupper — med hänsyn till en högst enkel klassifikation baserad på elektronmassans komponenter (t-ringarna) och hur de är materiellt bundna till sina förälderatomkärnor, och som kommer att beskrivas mera ingående i den löpande texten. Den ena gruppen kan sägas bestå av absorbatorer och den andra av reflektorer. Individen i gruppen absorbatorer kallas absorbator. Individen i gruppen reflektorer kallas reflektor. Respektive individs egenskap kallas absorberande och reflekterande med respektive förmåga att uppvisa absorption och reflexion. I viss litteratur används i stället för ordformen reflexion alternativet reflektion. I denna presentation används typen som associerar till reflex, alltså motsvarande det vi associerar med återkastning (återledning eller återkoppling).

Respektive grupp beskrivs mera ingående i respektive avsnitt om Absorbatorer och Reflektorer. Här följer först en allmän genomgång för att komma fram till ljusfysikens allmänt utbredande egenskap i och genom materien.

huvudgrupper

Alla material exponerar sin yta genom atomära elektronmassor (m_e ).

Elektronmassorna bildar (konventionellt) s.k. orbitaler kring förälderatomkärnan, vilket betyder olika mönsterformer som är låsta i resonans typ interfererande vattenvågsmönster. Se särskilt resonanserna i PERIODISKA SYSTEMET. Beståndsdelarna i de mönsternäten, själva vibratorerna eller enligt TNED t-ringarna, användes förvisso också från början i modern akademi för att förklara atomens spektrum genom banemännen Werner Heisenberg och Erwin Schrödinger och deras berömda matris och vågekvationer från omkring 1925. Men dessa element förkastades redan från år 1927: de ansågs inte förenliga med relativitetsteorin. I TNED däremot är detta inget problem. Se utförligt från PLANCKEKVIVALENTERNA om ej redan bekant.

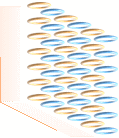
ABSORBATORER visar den elektriska sidan hos ^em mot betraktaren (t-ringarna står på högkant utåt betraktaren).

REFLEKTORER visar den magnetiska sidan hos ^em mot betraktaren (t-ringarna ligger som mynt utåt betraktaren).

absorbator	reflektor

Absorbatormaterialet sett stiliserat ovanifrån materialytan; elektronmassans starkaste elektriska sida vänds mot betraktaren. Närliggande ringar (uppåt-nedåt, blått-gult i illustrationen) formar djupgående plan där ringarna hålls ihop enligt deras ömsesidiga samverkande magnetiska fält från ringströmmarna (se Elektronens spinn); Varannan ring ligger flippad 180° vilket formar den harmoniska kopplingen. Närliggande plan strävar att attraheras beroende på den magnetiska kraftens plansymmetri.

Hela systemet bygger på atomer som har litet eller inget utrymme för att dela på elektronmassor över större rymdavstånd; elektronbilden är mer eller mindre hårt bunden med få eller inga fria ledningselektroner och materialet kännetecknas därför i allmänhet av att inte gärna släppa igenom elektrisk ström.

Reflektormaterialet sett stiliserat ovanifrån materialytan; elektronmassans magnetiska sida vänds mot betraktaren. Ringarna hålls samman beroende på deras ömsesidiga samverkande magnetiska fält från ringströmmarna (se högerhandsregeln): varannan ring ligger flippad 180° vilket bildar den sammanhängande kopplande harmonin.

Systemet bygger på atomer som har stort utrymme för gemensam delning av elektronmassor över stora områden. Genom denna mindre uttalade elektriska bindning till respektive atomkärna binds t-ringarna istället ihop planmässigt sida vid sida för att bilda ett ”sammanhållande skal” kring materialet och som därmed enkelt kan flyta omkring som »allmänt transportmedel» för elektriska och termiska ändamål.

Ringströmmarna är egenskaper med grund i energins oförstörbarhet (atomen och dess element summerar nollkraft och nollmoment och behöver ingen påfyllning för att fungera).

Notera för illustrationerna allmänt med t-ringarna att:

I den verkliga fysiken är t-ringarna separerade av stora mellanrum i förhållande till ringarnas storlek. Jämför den inledande huvudvyn med den skalenliga proportionen mellan protonkärnan och t-ringens absolut teoretiskt största diameter (1/50 av protonradien).

KOMBINATIONEN AV MATERIALTYPERNA

bildar (naturligtvis) i sin tur speciellt typiska material som uppvisar sina särskilda strukturer och egenskaper.

Det är emellertid även uppenbart genom t-ringarnas utpräglade elektriska-magnetiska egenskaper att märkbara effekter hos olika material med olika förutsättningar bör kunna observeras med hjälp av pålagda yttre elektriska och magnetiska fält.

Nedanstående illustration ger en orienterande sammanfattning.

Faraday och Kerreffekterna

a	b	c

c: t-ringens elektromagnetiska egenskaper uppvisar direkt känslighet för yttre magnetiska och elektriska fält.

a: Ett transparent (genomskinligt) material som glas bör ha den illustrerade materialytans typiska t-ringstruktur beroende på den allmänna atombindningen med få eller inga fria elektroner i atomskalens yttersta s.k. valensband (se Absorbatorer).

b: Med ett pålagt (starkt) yttre magnetiskt fält (B) genom materialytan, eller ett (starkt) elektriskt fält (X), bör materialytans t-ringar tiltas (tippa) — olika beroende på materialtyp, analogt t-ringarnas lokalt atomära bindning. Ljusets utbredning genom materialet borde därmed i motsvarande mening uppvisa (polariserande och brytande) effekter beroende på riktningsändringen i den induktiva responsen från de tiltade t-ringarna.

Sådana effekter påvisades också tidigt experimentellt och kallas efter sina upptäckare Faradayeffekten i det magnetiska fallet och Kerreffekten i det elektriska fallet — men utan teori för motsvarande t-ringar. Se dessa avsnitt särskilt för utförlig beskrivning.

HISTORIA

År 1845 upptäckte Michael Faraday den magnetiska effekt i ljusets materialfysik som senare fick namnet Faradayeffekten. Trettio år senare, 1875, påvisade John Kerr den motsvarande elektriska effekten senare benämnd Kerreffekten, eller mera specifikt den elektro-optiska Kerreffekten, och som strax år 1877 efterföljdes av Faradays magneto-reflektiva del, påvisat direkt på en magnetpol, benämnd den magneto-optiska Kerreffekten.

Praktiskt INGENTING finns skrivet i det allmänna svenska fysikmaterialet FOCUS MATERIEN 1975 om Faradayeffekten. Kerreffekten finns omnämnd, samt illustrerad, men ingen djupare beskrivning finns i ämnet. Det äldre svenska 12-bandiga uppslagsverket från 1920-talet [BONNIERS KONVERSATIONSLEXIKON] har heller ingen beskrivning av Faradayeffekten, trots att den omnämns. Detta associerar (naturligtvis) en referens till ämnet av typen »något svårt»; Man undviker att ta upp ämnet då det (egentligen) saknar rationella, begripliga begrepp i beskrivningen. Med TNED däremot kommer de annars ”obegripliga” Faraday och Kerreffekterna in i ett helt annat ljus. Men vi behöver först förstå ljusets polarisation innan dessa fenomendetaljer kan förstås eftersom de bygger på polarisationens sammansatta fysik.

Se vidare utförligt i Faradayeffekten och Kerreffekten.

MATERIEN SOM LJUSKÄLLA

hur ett material kan bilda det vi associerar till ”ljusstrålar” och som vi måste använda för att beskriva huvudsaken — ljusets polarisation.

När ett material upphettas, blir samtidigt materialets struktur mera diffus och skillnaden mellan de olika materiegrupperna blir mera flytande. t-ringarna antar alltmera slumpartade riktningar; När materialet är så upphettat att det börjar sända ut synligt ljus har riktningsbegreppet för den enskilda t-ringen helt förlorat sin innebörd. Ju mera upphettningen fortskrider, desto mera antar t-ringen (inom en allt kortare tidrymd) allt snabbare alla möjliga lägen relativt sin tyngdpunkt. Därmed närmar den sig (inom allt kortare tidrymd) formen för en ideal elektriskt laddad sfär.

MED VÄXANDE TEMPERATUR

SKULLE alltså varje t-ring KUNNA betraktas utåt sett som en ideal elektriskt laddad sfär med sin inre roterande, vaggande och vridande eller som vi också säger oscillerande basring, allt mera ju mera oordnad ringens association är till närliggande ringar, och vilken oordning motsvarar allt högre temperatur — och därmed associerade utstrålning av ljus.

Vi kan emellertid använda samma slutresultat med »t-sfären» för alla möjliga vågrörelser som emitteras (och absoberas) av ett material — med hänsyn till en specifik riktning , analogt en s.k. ”ljusstråle”. Nämligen med referens till mängden t-ringar som deltar i eller bidrar till ljusets energiutstrålning i just den riktningen. Nämligen (med en ännu högre växel) genom den allmänna Planckenergin (E=hf); I varje riktning eller ljusstråle finns representerat alla möjliga frekvenser (f, se även Plancks strålningslag) motsvarande alla möjliga bidrag från alla möjliga t-ringar i deras lägesändring inom en viss rymddomän eller område och som för materiefysikens del inte väsentligen får betraktas som obegränsat litet; med hänsyn till t-ringarnas ändliga dimensioner måste rymdområdet ha en viss utsträckning motsvarande atomens volym eller delar av den.

ljusets optiska natur

	LJUSETS OPTISKA (MATERIELLA) NATUR Ð0-strålen. Laddningarnas alla möjliga oscillationer eller frekvenser (f) i atomerna bildar en allmän ”ljusstråle” (Ð0) i varje given riktning; Varje frekvens motsvarar en viss färg eller ton med en viss energi (E=hf). Ljusstrålen som begrepp blir lika med kortaste kraftvägen i den allmänna induktionsverkan för ljusets masslösa utbredning (divergensen, c) genom tomrummet och utmed vilken linje en motsvarande påverkan kan ske på andra materiesystems laddningar.
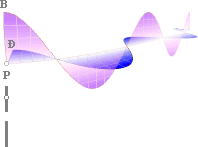
Ljusvågen är en matematisk modell — ingen fysikalisk realitet	VÅGPLANETS »KLASSISKA» MODELL Med alla möjliga frekvenser (f) givna för ljusstrålens definition enligt Planckenergin (E=hf) i varje dess gravitellt relaterade fasta rymdpunkt (P) i ljusstrålens utbredningsrikting eller »pumpriktningen» (z) — potentialändringens största induktiva magnitud (Ð0) som ljusstrålens elektriska huvudvektor — kan vilken som helst speciella svängningsriktning för en motsvarande ideal laddningskropp som fältgeneratris anges genom att specificera respektive xy-komponenter elektriska (X [Grek. xsi, X] eller Ð [Alt+0208]) och magnetiska (B) med tillhörande fältstyrkor. Mera löst sagt, kan ETT LJUSPLAN med godtycklig orientering eller vridning (xy) kring z-riktningen specificeras som DEN MATEMATISKA CYBERRYMDENS MODELL av ljusets utbredning — i varje tidpunkt, i varje reellt fysikalisk given positionspunkt i den relaterade gravitellt givna rymden.
Varje par mot varandra rätvinkliga svängningsplan illustrerar var för sig laddningsändringens optimala elektriska och magnetiska fältvariationer	Men MEDAN de uppmätta B och Ð magnituderna i P således kan monteras MATEMATISKT med två varandra vinkelrätt skärande vågplan, ett med B och ett med Ð som antyds i figuren, finns (således) ingen motsvarande “vågutbredning i den fysiska rymden”. Den instrumentellt uppmätta vågamplituden i P beskriver (således) inte någon fysikalisk rörelse av något slag, bara en instrumentellt varierande kvantitet amplitud (B och ÐÛU via f på Q i E=UQ=hf) som ändras med tiden i en fast given mätpunkt (P), analogt den mätande anordningens gravitellt relaterade referenspunkt. Det finns följaktligen ingen verklig vågutbredning för ljuset (B och Ð i P), bara olika tillstånd i givna rymdpunkter — med variationer i närliggande rymdpunkter som ändras analogt med avståndet från primärkällan och med den ändliga ljushastigheten c. Ljusvågen som populärt fysikaliskt begrepp är en bekväm — och synnerligen kraftfull — matematisk modell. Men ingen fysisk realitet. Med hjälp av parplanen (ÐB) får man en formell matematiskt beskrivande grund för hur ljuset uppför sig då det träffar en materialyta genom ljusets bägge mest uppenbara egenskaper, att brytas och reflekteras.
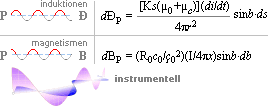
Ljuset själv uppvisar ingen vågutbredning	Eftersom · den magnetiska verkan (B) beror av laddningshastighet (v) relativt ett omgivande dominant g-fält, · att derivatan (tangensformen) för v är accelerationen [v=2d/T, v’=dv/dT=–2d/T2=–a], · att accelerationen (a) associeras med induktionen (Ð), kan den induktiva funktionsgrafen härledas från magnetismen som den senares derivata (Exemplet nedan i PREFIXxSIN).
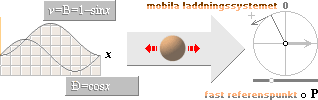
Exempel (se figuren till höger): Med den rent funktionella förenklingen v=B=f (x) som laddningsändringens signifikanta variationsform, får man direkt den induktiva variationsformen enligt Ð=v’=Dn v. I exempel med v=1–sinx i PREFIXxSIN ges v’=(sin x)’=cos x=Ð. På liknande sätt undersöks övriga variationsformer.
Sambandsformerna ovan för induktionen och magnetismen ges enligt TNED. Se utförligt från induktionen och magnetismen.	Det ger oss en direkt matematisk bekräftelse på att källskapade faser för induktion och magnetism inte är samma, analogt sin ¹ cos; största v ger största B, men noll Ð. ENERGIN som krävs för att underhålla ljusets svängningar på omgivande materiella system kan med hänsyn till elektriska fältstyrkans grundelement, den elektriska potentialen (U), skrivas formellt U = Fr/Q = E/Q med rörelseenergin E=mv^2/2. Det ger oss elektriska fältstyrkan X = F/Q = U/s; Elektriska fältstyrkans toppvärde (X) kan med given distansparameter (s) och laddning (Q) därmed återföras på ett motsvarande toppvärde (v) för laddningens hastighet och som bildar e-fältets potentialform. Därmed kan ENLIGT TNED också den uppmätta elektriska fältstyrkans toppvärde, baserad på den mätande energins bas, associeras med den magnetiska fältstyrkans toppvärde — analogt den energi som matar ljuset; v-formens energibas bestämmer fasen. Se vidare från Ljusets polarisation. Där visas illustrerat mera ingående hur det fungerar enligt TNED. Illustrationen nedan, högerdelen, visar den konventionella föreställningen om magnetism (B) och induktion (Ð) i ljusets utbredning — där också B och Ð ligger i fas (enligt experimentella observationer).
fysiska	instrumentella
i-riktningen definierar begreppet ljusstråle som den resulterande sammanfattningen av riktningen för STARKASTE ÄNDRINGEN i POTENTIAL i alla möjliga svängningsriktningar hos ljuskällans laddningar i den riktningen. Ljusets huvudvektor (Ð0) ligger alltid rakt fram i i-riktningen, förorsakande motsvarande svängningar hos en laddning (på stort avstånd) från ljuskällan.	Litterära [Klassiska] Exempel som ansluter till denna typ torde vara överrepresenterade — finns till exempel i FOCUS MATERIEN 1975 s261, GYMNASIETS FYSIK åk3 Liber 1980 s101, @INTERNET Wikipedia Electromagnetic radiation 2008-07-03 [m.fl.].

Situationen med t-ringen i formen av en ideal elektriskt laddad (roterande) sfär bildar också utgångspunkten i den relaterade fysikens beskrivning (TNED) av ljusets materiella utbredning;

Eftersom den elektriska potentialen är som störst framåt-bakåt i t-sfärens rörelseriktning (idealt i ringplanet), kommer med samma mening framåt-bakåt-kortaste-vägen-varje s.k. ljusstråle

— analog med en bestämd ideal geometrisk riktning mellan den upphettade materialytan och en (avlägsen) betraktare att

— enligt Newtons tredje lag

— innehålla den allra största och starkaste elektriska trögheten eller induktionen. Vilket vill säga; Materialets inre svängningar uppvisar den allra starkaste verkan på omgivande materials t-ringar i samma riktning som huvudvektorn eller ljusstrålen (Ð₀) — genom att i den riktningen, och endast så, förorsaka motsvarande, motvända, MAXIMALA rörelseändringar hos det materialets t-ringar.

På så sätt fortplantas ljuskällans t-oscillationer, först genom tomrummet via divergensen (c) till omgivande material, och sedan därifrån vidare (i huvudsak) genom materialets egna t-svängningarna internt — samt sedan ytterligare vidare utåt och med materialets t-svängningar som en ny svängningskälla med sina specifika egenskaper.

vågplanModellens ursprung

VÅGPLANsMODELLENS URSPRUNG — se även i Vågplanmodellens begränsning

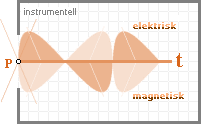
Inverkan av det masslösa ljuset genom tomrummet via hastigheten c mäts i vilken som helst gravitellt dominant rymdpunkt P genom någon anordning som kan avkänna styrkan i elektriska (X eller Ð) och magnetiska (B) fält. Den avkännande instrumentella resultatbilden, illustrationen nedan längst till vänster, ger en motsvarande vågform i rymdpunkten P betecknad som ett tidsmässigt (t) utsträckt tvåvägs plan med inbördes rätvinkliga elektriska och magnetiska amplituder. Denna modell är också ansvarig för den konventionella uppfattningen av ljus som en ljushastigheten c (®) rätvinklig (|) planvågsutbredning av elektrisk och magnetisk fältstyrka.

Konventionella beteckningssätt Figuren närmast till vänster visar beteckningssätt i sammanhang som berör LJUSETS POLARISATION och som man (vanligen) finner i konventionell litteratur. Beteckningarna sp står för s ....... s-polariserad p ....... p-polariserad @INTERNET har många källreferenser i ämnet — på engelska. Sök på Polarization. Den konventionellt svenska representationen är däremot (ännu 2008 ytterst) sparsam.

Med denna excellenta kvantitativa modell — tillsammans med den kvantitativa matematiska modellen av fotonen (se FOTOELEKTRISKA EFFEKTEN) som den ljustransporterande lastbilen — förklaras fysiken emellertid från »en instrumentell cyberrymd» snarare än från den verkliga 3D-rymden: ljus i verkligheten transporterar ingen massa — uppvisar inga åkande partiklar (»fotoner»), interfererar inte med kinetiken (c och v adderas inte), utvecklar följaktligen heller ingen centrifugalkraft, och uppvisar därför inga planbärande vågor heller. Dessa nämnda instrumentella verktyg är utmärkta för att beskriva det rent kvantitativa uppförandet hos ljuset, men ger ingen förklaring till den verkställande mekanismen.

Till exempel i beskrivningen av ljusets polarisation (figuren ovan högra), är planvågens grundverktyg avgörande och oundgängligt och kan inte undvaras. Men för att ge åtminstone någon ledtråd till ”varför” och ”hur” de verkställande detaljerna blir verkställande, måste ytterligare »cyberspaceprylar» uppfinnas (efterhand) men som inte har någon motsvarande verklig 3D fysisk representation (typ “oscillating dipoles”, ”oscillerande dipoler”). Utöver den mest uppenbara ljusfenomenformen av dem alla, reflexion, ges ett annat grundexempel i Ljusets brytning i vatten. Vilket vill säga: Ljusplanet är oundgängligt för härledningen, men planet som sådant har ingen 3D-representation.

Den kvantitativa instrumentella punktmodellen med sina ”Planvågor i CyberRymden” kan inte undvaras för en exakt matematisk beskrivning av ljusets natur — dess perceptiva och observerbara verkan tagen över större eller mindre domäner.

Men HUR fungerar det då — UTAN dessa hjälpplan? Svaret på den frågan ges enligt TNED i den följande sektionen om Ljusets polarisation.

Den starka potentialen i ljusstrålens framriktning ger också verkan åt magnetismen med en motsvarande magnetisk effekt; Omkring huvudvektorn (Ð₀) med sin induktiva verkan längs strålens utbredningsriktning, sprids ljusstrålens maximalt verkande magnetiska fält — liksom ringarna på vattnet sprids omkring träffpunkten. Därmed uppvisar varje ljusstråle både en induktiv verkan (Ð) i strålriktningen och en magnetisk verkan (B) rätvinklig strålriktningen, runt om. Se även explicit i Den klassiska modellens begränsning.

Därmed har vi nått fram till målet och kan nu beskriva det verkliga händelseförloppet då ljus träffar en materialyta, illustrationen nedan.

LJUSETS POLARISATION | Ljusets polarisation | 2008VII1

grundformen för

ljusets polarisation

I fortsättning från föregående inledande allmänna materialbeskrivning

Ljusets polarisation ENLIGT TNED

Inledande beskrivning

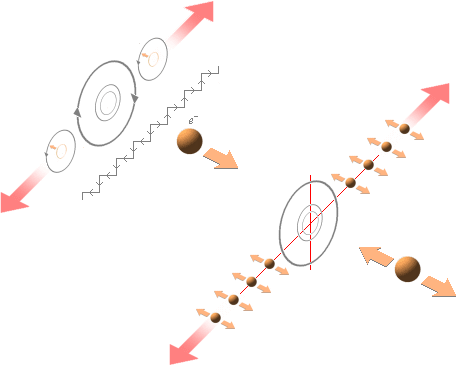
När ljus träffar en materialyta, sätter det ytmaterialets elektriska laddningar i en motsvarande rörelse relativt ljusets primära källa och dess föredragna referens för riktningsbegreppet — alltså ljusstrålens riktning enligt Planckenergin hf.

Med referens till det magnetiska fältet som bildas rakt fram från den primära ljusstrålen

— den stora cirkeln i centrum i ovanstående illustrationsdelar med ljusstrålen i dubbelpilarnas riktning

— utvecklar de omgivande laddningarna — alltså t-ringarna i materialets atombundna elektronmassor

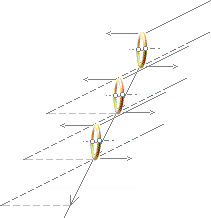
— motriktade, egna, magnetiska fält (B) då de måste svara på den induktiva inverkan från primärkällan: den elektromagnetiska kopplingen hamnar ”i baktakt” som följd av Newtons tredje lag där orsaken till varje ändring strävar att motverkas. Detta sekundära B-fält blir alltså motriktat ljuskällans primära B-fält, vilket leder till att det mottagande materialets ytladdningar tenderar att vandra iväg utåt bort från ljusstrålens centralaxel. Med den fram och återgående induktiva pumpningen i ljusstrålens huvudsakliga längsriktning, illustrationen överst, är det tydligt att den expansionsströmmen uppvisar en kring ljusstrålens centralpunkt symmetriskt expanderande rörelse i sicksack enligt illustrationens antydan.

iP-strömmen

Den stadigt utåtflytande sicksackvägen betyder en konstant ström (i_P). Energin till i_P-strömmen underhålls av Planckenergin (hf) i ljuskällan. Det är denna konstanta INRE ELEKTRONSTRÖM i_P som ENLIGT TNED bär ansvaret för det fenomen vi kan studera i det enkla köksexperimentet och som vi ska kalla för ljusets polarisation — vi ska längre fram studera den funktionen mera i detalj och i jämförande korsreferens med den moderna akademins föreställningar på området. Nämligen, som vi senare ska se, genom någon ändring i den strömmen — med motsvarande klart iakttagbara naturfenomen som följd.

Konstantströmmen i_P beror (naturligtvis) högeligen på materialets struktur, alltså t-ringarnas inbördes kopplingar och låsningar, och existerar endast inom elektronmassan genom dess t-ringar. Därmed vet vi redan nu svaret på varför ämnet garanterat INTE finns med i den moderna akademins vetenskapliga litteratur: man erkänner inte formegenskaper eller beståndsdelar för elektronmassan (från 1927).

Konstantströmmen i_P försöker alltid att bygga en ström med laddningar som flyter iväg bort från den ideala ljusstrålens geometriska linje och vars grundform vi kallar för opolariserat ljus. Vilket vill säga; Opolariserat ljus är ljus med en centralt expanderande idealt homogen konstantström i_P som inte uppvisar någon dislokation, ändring eller annan flödesväg.

Om den centralt expanderande strömmen i_P ändras i favör för någon särskild riktning, eller bereder plats för en sådan, bildas en motsvarande komplex flödesstruktur i t-strömmarna i formen av en specifik polarisation. Den enklaste formen har vi redan studerat praktiskt ovan i föregående beskrivna köksexperiment, det vi kallar för en planpolarisation eller en linjär polarisation. Det är samma typ som bildas när ljuset träffar en materialyta som i sig har egenskapen att både kunna reflektera och bryta.

Ljusets reflexion och brytning

Allmän inledande beskrivning

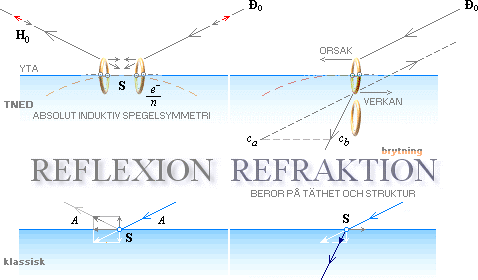
Principformen för ljusets reflexion och ljusets refraktion (ljusets brytning) blir därmed också klar ENLIGT TNED — med grund i elektronmassans t-ringar, illustrationen ovan. Funktionssättet beskrivs detaljerat i respektive artiklar Reflexion och Refraktion. Vi kan emellertid redan här, av illustrationens syntetiserande form, direkt se varför och hur alla s.k. klassiska försök måste misslyckas i strävan att förklara ljusets fysik utifrån andra aspekter än t-ringens:

— vågmekaniska modeller är uteslutna i t-ringens fysik

— impulsmekaniska modeller typ kulmodeller är uteslutna på grund av den favoriserade idealismen med kulans geometri: sfärisk går inte

— konventionella kvantmekaniska modeller är också uteslutna med t-ringen som en komponent i e

— samtidigt som vi ser hur var och en av dessa grenar (lätt) ERHÅLLER sin specifika del genom dynamiken från t-ringarna;

— Det är bara t-ringen ensam som kan förklara och beskriva alla funktionssätten — enhetligt. TNED.

Låt oss därmed — med ovanstående klargöranden — studera ljusets polarisation som fysikaliskt fenomen mera ingående.

LJUSETS POLARISATION | Ljusets polarisation | 2008VII1

I fortsättning från inledningen

LJUSETS POLARISATION

i_P-strömmen stämmer också väl med observationerna från det enkla köksexperimentet; Den reflekterade bilden från vattenytan blockeras speciellt av gränsvinklarna enligt nedanstående illustration.

När ljus utmed riktningen i H försöker reflektera ljusets utmed sicksacklinjen, blockeras den riktningen av polarisationsströmmens riktning — som ger en motsvarande diodfunktion: ljuset kommer inte fram. Därmed finns ingen induktivt reflekterande väg tillgänglig. Speglingen kommer i läge OFF.

Notera att den detaljen inte kan förklaras av vågmodellen. Se vidare nedan.

Notera också att nedanstående experimentredovisning verkar vara unik i sitt slag — Webben (2008) innehåller många (engelska) beskrivningar av polarisationens fenomen, men de beskrivs genom förhållandevis krångliga och tekniskt komplicerade anordningar som är svårt att omsätta för en person med normalt intresse för kökets enkla utrustning. Se utförligt i Köksexperimentet.

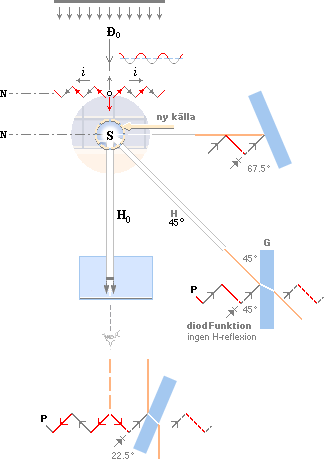
Med viss reservation för värdenas noggrannhet i ljuset av det mycket enkla experimentet, visar de tre ovan illustrerade positionerna den maximalt blockerande observationsvinkeln som släcker ut spegelbilden från tekoppens vattenyta.

Polarisationsströmmen (i_P) är alltid vinkelrät mot den huvudsakliga ljusstrålens riktning (Ð₀). I detta fall bestäms Ð₀ av det reflekterade ljuset från kakelväggen vilket bestämmer Ð₀-riktningen.

Med H₀ som den resulterande reflekterade huvudriktningen från vattenytan S som en ny lokal induktiv källa

— med H som varje induktiv riktning från S med vinkeln H°

— och G° som den separata glasvinkeln mot riktningen Ð₀H₀, vidare P° som polarisationens medelmässiga vinkel i sicksackspåret, här antagen som P°=45° från riktningen Ð₀H₀, blockeras det reflekterade ljuset från H vid positionerna

2G° + H° = P° = konstant

I figuren ovan är tre av positionerna markerade enligt skaran

H° = {0; 45; 90}

G° = {22,5; 0; –22,5}

Brewsters vinkel

Optimala observationsvinkeln (konv. Brewsters vinkel)

När brutna och reflekterade riktningarna bildar en rät vinkel 90°, kan ett maximalt antal interferensfria komponenter, det är vektordelar som är helt fria från inbördes interferens, fortplantas utmed de två riktningarna utan att blandas. Det betyder också att den motsvarande (i)P-strömmen får den minst interfererande komponenten från andra delar, och kommer därför att uppvisa dess mest skarpa och fokuserade effekt i blockeringen av den induktiva vägen för den reflekterande H-strålen. Den reflekterande vinkeln över vattenytan i denna situation är 37° enligt beräkningen från vattnets brytningsindex n=4/3

sinA/sinW = n; sinW₀/cosW₀=n=cotW₀;

acot(n=4/3) = W₀

= 36,869898°

Beräkningen av den konventionellt benämnda Brewstervinkeln W₀, ovanför vattenytan.

Trigonometriska relationer enligt PREFIXxSIN

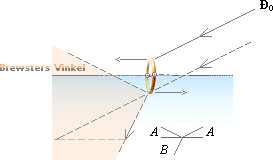
P-strömmen har minst interfererande komponenter när djupdelen och ytreflektionen bildar exakt 90 grader. Den reflekterande vinkeln för vattenytan blir i det fallet 37°, konventionellt benämnd Brewstervinkeln.

Brewstervinkeln är den ”huvudvinkel” vi tangerar i köksexperimentet då vi ser spegelbilden från tekoppens vattenyta helt utsläckt.

Med detta klargörande kan den fullständiga experimentella observationen i polarisationsfenomenet studeras i detalj.

LJUSETS POLARISATION | 2008VII1

Polarisationseffekten via Nicolprismat

I en dubbelbrytande kristall, som den typ som används i solglasögon (Nicolprisma), uppnås samma effekt som i köksexperimentet med enbart H₀-ljuset rakt framifrån från S.

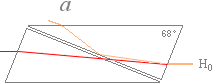
Nicolprismat vid a. Den reflekterade vattenbilden H₀ inträder Nicolprismat, följer den orangea vägen, och reflekteras ut vid a, bort från kristallen. Den återstående röda delen är bottendelen av ljuset från tekoppen (den svarta delen i figuren nedan) motsvarande »det opolariserade ljuset», och som passerar nästan rakt igenom kristallen. Om prismat vrids 90°, syns även H₀-ljuset.

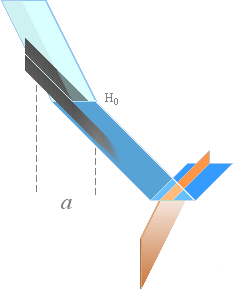
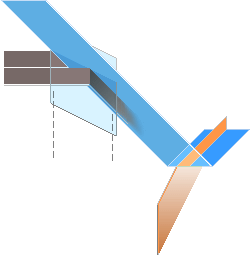
Förenklad ljusväg med illustrerade vågplan för det H₀-polariserade ljuset från tekoppens vattenyta.

Eftersom ljuset i vilket fall ändras (polariseras) då det möter en reflekterande-brytande materialyta, kan varje ljusstråle som träffar en materialyta beskrivas förenklad som ovan via två mot varandra vinkelräta ”ljusvågsplan”: Ena planet motsvarar ljusvektorerna i materialytans plan analogt med reflektionen, det andra planet motsvarar den del som bryts ner in i materialet.

För varje ändring i ljusvägen, som resultat av att ljusstrålen träffar på något objekt, ändras proportionerna mellan det kvarvarande ljusets brytande-reflekterande delar. Ljusvägen kan på så sätt illustreras med olika planuppdelningar och undertryckningar i olika brytningar, typ illustrationen ovan, för att därmed belysa varje effekt och verkan som sammanhänger med ljusets rent divergenstekniska växelverkan med materien.

Illustrationen ovan vid brytpunkten markerad med H₀ anger motsvarande brytning i det handhållna glaset (G) då spegelbilden från tekoppen betraktas rakt ovanifrån.

I gängse teori används också utbredningen med de bekväma ljusvågsplanen (i mera renodlad matematisk mening) för att beskriva polarisationseffekter i typ ovannämnda Nicolprisma. Emellertid kan inte en motsvarande kvalitativ beskrivning göras med planteorins hjälp.

Vi studerar hur.

Vågplanmodellens begränsning

Enligt gängse vågplanmodell tillämpad på köksexperimentet (se även tydligare i Ljusets polarisation i modern litteratur)

— figurens högra del nedan där den handhållna glasskivan (G) i den vertikala positionen ersätter den föregående omnämnda Nicolkristallen, samma resultat

— skulle elimineringen av spegelbilden

— som kommer från tekoppens vattenyta i det långa blå reflekterade planet i högerfiguren nedan

— förklaras så att bottenljuset från koppen (det mörka vertikalplanet) reflekteras maximalt av den handhållna glasplattan (G), medan vattenytans spegel, det blå planet, inte kan uppvisa en sådan reflekterande förmåga utan istället passerar genom G.

Ju mera parallellt till det blå planet som skärningen G-BlåPlanet blir, desto starkare skulle koppens bottenbild framträda och desto svagare vattenytans reflexion.

Men detta vågplanteoretiska resultat motsäger den enkla observationen i köksexperimentet, vänstra delen i ovanstående illustration:

Med den minsta möjliga skärande vinkeln mellan G och ljuset från vattenytans spegelbild M i G, framträder M starkare. Inte svagare:

Speglingen kommer i läge PÅ. Inte av.

Det allmänna resultatet är alltså:

· Den förhärskande vågmodellen är oförmögen att inkludera resultaten från det enkla köksexperimentet;

· Den fullständiga polarisationens fenomen ligger utanför området för vågplanmodellen.

Låt oss studera hur TNED (då) kan förklara funktionen i Nicolkristallen.

LJUSETS POLARISATION | Nicolprismats polariserande egenskap enligt TNED | 2008VII1

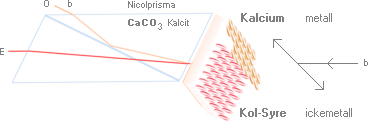
TNED FÖRKLARAR

NICOLPRISMATS POLARISERANDE EGENSKAP

För att förklara avstängningen av vattenytans reflekterade ljus från det enkla köksexperimentet genom en motsvarande Nicolkristall, måste vi förutsätta ett anisotropiskt material: ett material som uppvisar olika inbördes strukturer.

Se även från Refraktionens grundläggande förklaring.

Vi studerar detta.

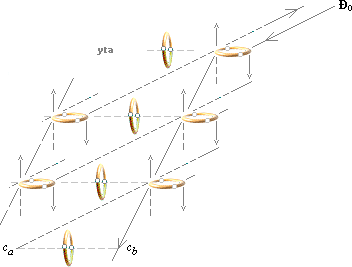
Den ovan illustrerade antydda ytstrukturen är en mix av de föregående beskrivna ideala materialen för absorbatorer och reflektorer.

vertikala systemet	isolator	elektrisk
horisontella systemet	konduktor	magnetisk

Termen konduktor (från eng. conductor) används här liktydigt med betydelsen (elektrisk) ledare enbart för den lingvistiska syntaxens harmoni

Bara om det antas en elektrisk-magnetisk separerande ordning i ytstrukturen hos elektronmassans t-ringar, där en del ringar är hårdare bundna till atomerna (vertikala systemet) än andra (horisontella systemet), existerar ett kriterium för att separera ljusets oscillationer. Låt nämligen det reflekterade ljuset (H₀) från vattenytan vara den inkommande betecknade riktningen Ð₀ ovan. Om det horisontella t-ringsystemet är flytande, är det också ett idealt djupöverförande medium för den induktiva polarisationsströmmen som kommer från H₀. Om denna djuppenetration också motsvarar den dubbelbrytande så kallade ordinära ljusstrålen, kommer den att reflekteras ut och bort från ljusets huvudutgång — den så kallade extraordinära ljusstrålen, där praktiskt taget all H₀-polariserande drift är eliminerad. Därmed stängs spegelbilden av.

En vridning av kristallen 90° innebär att den polariserande strömmen inte så enkelt kommer att hitta en resonant struktur att gå igenom eftersom den i så fall måste penetrera de vertikala mera hårt bundna t-ringarnas struktur. Då blir inte heller H₀-ljuset samlat på något enkelt sätt av det horisontella systemets t-ringar, utan blandas istället med hela kristallstrukturen och kommer därmed också att löpa den extraordinära strålens väg. Därmed framträder spegelbilden.

SOM VI SER kan funktionssättet förklaras kvalitativt utomordentligt (med yttersta enkelhet) — blott grundfunktionen är fattad i fenomenformerna med reflexion och refraktion ENLIGT TNED.

Nedan visas hur polarisationen presenteras (klassiskt) i konventionell litteratur — och varför man missade den fullständiga beskrivningen.

LJUSETS POLARISATION | Ljusets polarisation i modern litteratur | 2008VII1

LJUSETS POLARISATION

I MODERN KLASSISK LITTERATUR

Som nyligen observerades: Den konventionella vågplanmodellen duger inte för förklaringen till det enkla köksexperimentet. Heller finns inte (här veterligt) det enkla experimentet rapporterat i den tillgängliga litteraturen.

Från den stund polarisationsfenomenet inspekterades mera i vetenskaplig detalj under 1800-talet

— Bartholinus 1669, Huygens-Newton 1672, Young 1801, Malus 1808, Arago-Biot 1811, Brewster 1812, Fresnel 1821

källa @INTERNET

Polarized Light in Nature and Technology History, [http://polarization.com/] 2007-09-10,

— gjordes anordningarna med sikte på att studera enskilda optiskt koncentrerade ljusstrålar

— nämligen för bekvämligheten att kunna genomföra noggranna mätningar i (vinkel och) intensitet.

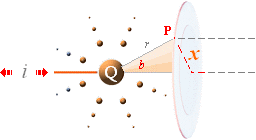
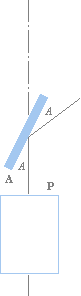
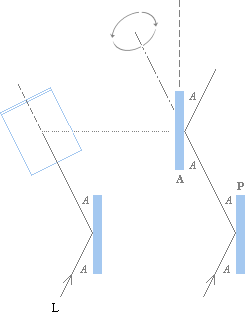
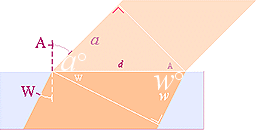
Med referens till en äldre källa [BKL IX 1926 sp362], beskrivs ljusets polarisation liknande ovanstående figurer. En inkommande ljusstråle (L) reflekteras en vinkel A av ytan hos glaset P, reflekteras sedan till en annan parallell glasskiva A, och därifrån vidare. Om glasskivan A (den kallas i källan analysatorn) är fast förbunden med och vridbar kring den reflekterade strålen A från glaset P (polarisatorn), ses det slutreflekterade ljuset från glas A som tydligast då PA är parallella, så som det visas i den högra illustrationsdelen ovan — och som svagast när PA är ömsesidigt vinkelräta (illustrationsdelen i mitten). Vid den senare positionen, med glas A sett ovanifrån-underifrån glas P, den vänstra illustrationsdelen, uppvisar A samma fixa vinkel A mot vridaxeln som i det parallella PA fallet, den högra illustrationsdelen. Vilket vill säga; för en synlinje nära utmed P-glasets yta, vilket betyder ett litet A, bör den svagaste spegelbilden också vara nära parallell med synlinjen. (Om A tillsammans med den brutna delen genom glaset bildar rät vinkel, hävdar källan att den så bildade A=A₀, den så kallade polarisationsvinkeln, ger den svagaste bilden med rätvinkliga PA).

I det enkla köksexperimentet är det klassiska vetenskapliga arrangemanget ovan representerat av endast en riktning: rakt ut från kakelväggen, 0-90 grader mellan diskbänk och kökstak.

Synfältet i sidled med vinkeln H° finns inte med.

Om vi återvänder till köksexperimentet och tittar mot tekoppen genom att nudda med synlinjen över koppens öppningskant med minsta möjliga synvinkel A, då kan vi helt klart fortfarande se spegelbilden M i G med full skärpa. Vridning av den handhållna glasplattan G därifrån, resulterar att M återigen börjar blekna och försvinna och gör så till synes helt vid en vinkel approximativt en fjärdedel av en rät (använd en uppslitsad tom hushållspappersrulle eller liknande med lämpligt stöd som glasskivan G kan skjutas in i för att få en enkelt vridbar anordning och som ger en mera noggrann grund för vinkelmätning). Men denna typ finns inte med i det ovanstående singulära strålarrangemanget.

I själva verket verkar inte det enkla köksexperimentet alls finnas observerat i gängse litteratur.

Den föreställning man har allmänt i fysiken inom modern akademi på den här nivån medger heller ingen sådan association.

LJUSETS POLARISATION | reflexion | 2008VII1

REFLEXION

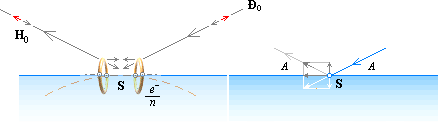
Reflexion i praktiken, enligt TNED. Reflexion i klassisk teori.

Reflexion. Den induktiva verkan i den inkommande strålriktningen Ð₀ (De-e, Alt+0208) åstadkommer i den reflekterande spegelpunkten (S) en fram och återgående vippning av t-ringen. I denna presentation är det absorberande materialet vatten sett genom en (del av en) helt lugn yta. S formar en ny induktiv källa (Q_s) enligt dess egen lokalt etablerade elektriska potentialbild med respekt till den omgivande gravitellt dominanta rymden. Källringens tillståndsändring överförs induktivt (kortaste ljusvägen) till en närliggande t-ring (i riktning Ð) utmed vattenytan.

Ökningen i intensitet med avtagande vinkel (A, här tagen med 0° vid vattenytan). Vid vertikala 90° är effekten praktiskt taget noll. Den induktiva effekten för lika laddningar ger ömsesidigt motsatta rörelseändringar (ringarnas inre elektromagnetiska väg är kortare-snabbare än em-vägen från den primära ljuskällan): ytgrannen tvingas vagga direkt motsatt källringen. Ringparet formar då idealt en absolut induktiv spegelsymmetri, överförande tillståndsändringarna i huvudstrålen Ð₀ på en ny, reflekterad (källförankrad) huvudvektor H₀.

Symmetrin hos paret garanterar att reflexionsvinkeln blir exakt lika den inkommande förorsakande vinkeln (A).

Exakt samma sak uttrycks av impulslagen, eller spegellagen eller reflexionslagen: Ytpunkten (S) ses som »hård» av det infallande ljuset, och tar därför inte emot den djupverkande komponenten i riktformen i S-punkten; därmed kastas djupkomponenten tillbaka uppåt med samma belopp, se figuren ovan till höger.

Denna detalj är också, enligt relaterad fysik (TNED), helt i enlighet med ljusets masslösa utbredning c som inte kan växelverka kinetiskt med materien. Ytpunkten (S) lämnas intakt.

Notera att en laddning (Q_s) med en idealt sfärisk laddningsgeometri svårligen skulle kunna ombesörja en reflekterande ordning, alls överhuvudtaget. Ringformen (J=mvr) garanterar dynamiken.

LJUSETS POLARISATION | refraktion | 2008VII1

LJUSETS BRYTNING

REFRAKTION

Refraktion. DJUPVERKAN av ytringarnas induktiva vaggningar (se Reflexion) kommunicerar ett vridande moment (eng. torque) riktat motsatt riktningsändringen hos ringarnas toppdel. Vridmomentet genom en källrings bottenpunkt motsvarar en motsatt induktiv verkan i (materialets) ljushuvudvektor (Ð). Resultanten ger en fördröjd djupinduktans på ringens tröghet och som motsvarar en reducerad utbredningshastighet i riktningen för den brutna (b) strålen (b₀). Förklaringen är emellertid avancerad, som man kunde förvänta.

Ljusbrytningen enligt TNED	Ljusbrytningen enligt den klassiska mekaniken

RINGAR I DJUPLED som idealt står rakt ovanför varandra släpper inte igenom c i den leden (vi minns från g-härledningen till atomkärnan att ringytan i atomkärnans massform definierar massa som c=0: inget ljus passerar där). Om ringarnas vickaxlar har samma orientering (parallellt med ytans utvidgning), ges heller ingen ömsesidig induktiv verkan mellan ringarna. Induktionsriktningen måste ha någon komponent skärande ringplanet för att ringen ska kunna vickas, därmed källande induktionen vidare neråt.

Med en sålunda relaterad djupledsgående ideal ömsesidig täckning, och därmed nedsläckning av varje djup reguljär genomgång c (med liten verkan dock i en gas), är det hur som helst uppenbart att det är positionsändringen i t-ringen — inte ljusets hastighet — som bär ansvaret för den vidare färgutbredningen (f , frekvensens utbredning genom materialet) i formen av en ny, lokal induktionskälla.

Den klassiskt härledda, abrupta intervallösa direkta övergången i ljusbrytningspunkten (ljusets absoluta acceleration) mellan t.ex. luft och vatten blir därmed väl förankrad: den skarpa intervallösa brytningen återfaller på egenskaper i två skilda materierum med inbördes skilda strukturer och därmed i princip ideala, intervallösa, övergångar från det ena till det andra — i kraft av mängden t-ringar som ombesörjer transiteringen t.ex. från vakuum till glas. Det är så tydligt det kan bli.

För att etablera en ringkoppling på en frekvens f i och genom materialet, måste orsaksvektorn, verkansvektorn, och resultanten från ytdelen, upprepas allt igenom hela materialet — från ring till ring. Illustrationen ovan visar hur ringkopplingen kan tänkas i princip enligt den diskuterade verkan. Resultantens riktning, ljushastigheten (c_b) i materialet, bestäms av hur ringarna är atombundna (energiresonanser enligt Planckenergin hf), den relativa ringtätheten (antalet ringar per volymenhet) — och därmed i princip materialtätheten. Vektorkomponenterna pekar på en ideal sågtandsformad ekvivalent flödesväg som den tomma rymdens ljusutbredning c måste ta för att trigga och koppla t-ringarna i deras djupgående induktiva verkan.

För att koppla f via ringar på den kortare djupvägen, uppkommer således en fördröjning relativt tomrummets c i utbredningen av f genom materialet. Analogt med den längre vägen och den motsvarande längre tiden som tomrummets c uppehåller sig i materialet, uppkommer motsvarande uppvärmning (energiförluster).

Förhållandet mellan den extra ljusvägen, som är samma som våglängden i ytdelens ljushastighet c_a , och den resulterande effektiva ljusvägens våglängd med ljushastigheten c_b i materialet, matchar därmed förhållandet mellan de skilda hastigheterna; Våglängden (l) i materialet reduceras analogt och direkt proportionellt med reduktionen från c_a till c_b med bevarad frekvens f. Det är viktigt att lägga märke till.

FÄRGEN f=c/l bestämmer således en konstant relation

c_a/l_a = c_b/l_b = f

Denna ekvivalens ger brytningslagen — här i PREFIXxSIN med vinklarna a°=90–A och w°=90–W räknande från materialytan motsvarande 0° (konventionellt räknas vinklarna 90 grader rakt upp från materialytan via A och W) enligt

c_a/c_b = l_a/l_b = (a/d)/(w/d) = a/w

= n

= (cosA)/(cosW)

= (sina)/(sinw) ................. brytningslagen, gäller för en specifik frekvens

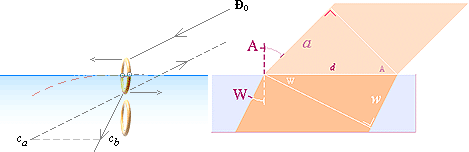
Vi ser att detta resultat (illustrationens vänstra del) är samma som resultatet från den mera klassiska geometriska härledningen i

Ljusbrytningen i vatten, som också motsvarar vågplanets ljusmatematik i PREFIXxSIN

a/w = lA/lW =cA/cW =(a/d)/(w/d) = cosA/cosW = sin(90–A)/sin(90–W) = sina/sinb = n

Vi noterar (återigen) att en motsvarande beskrivning-förklaring med hjälp av en idealt sfäriskt formad ytladdningsgeometri för laddningens grundform vore omöjlig för fenomenets fysik: Det är tydligen bara t-ringen som klarar naturfysiken.

Brytningslagen och dess praktiskt härledande grunder visas mera matematiskt sammanfattande i LJUSBYTNINGEN I VATTEN.

LJUSETS POLARISATION | Absorbatorer | IaM_TNED2 | 2008VII1

absorbatorer

Alla material exponerar sin yta genom atomära elektronmassor (m_e ).

ABSORBATORER visar den elektriska sidan hos m_e mot betraktaren (t-ringarna står på högkant utåt betraktaren).

REFLEKTORER visar den magnetiska sidan hos m_e mot betraktaren (t-ringarna ligger som mynt utåt betraktaren).

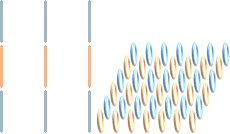
Absorbatormaterial sett stiliserat ovanifrån materialytan; Vyn visar den elektriska huvudsidan av elektronmassans ringelement mot betraktaren. Närliggande ringar (uppåt-nedåt, blått-gult i illustrationen) formar djupgående plan där ringarna hålls ihop enligt deras ömsesidiga samverkande magnetiska fält från ringströmmarna (se Elektronens spinn) med varannan ring flippad 180° för att forma den harmoniska kopplingen. På samma sätt strävar närliggande sådana plan att attraheras beroende på den magnetiska kraftens plansymmetri. Hela systemet bygger på atomer som har litet eller inget utrymme för att dela på elektronmassor över större rymdavstånd; elektronbilden är mer eller mindre hårt bunden med få eller inga fria ledningselektroner och materialet kännetecknas därför i allmänhet av att inte gärna släppa igenom elektrisk ström.

Därför att absorbatorer har ringa partiellt fria valenselektroner

— det är elektroner som normalt förknippas med atomernas kemiska föreningar och som ligger ytterst i atomskalen

— uppvisar också deras t-ringar en tätare atomär bindning: Varje t-ring (med små fluktuationer) »tittar» på sin förälderatomkärna i den riktning där t-laddningen är som starkast, vilket är i dess ringplan. Därmed uppvisar t-ringen också ett (bekvämt) handtag vid ytan.

Den magnetiska kraften från ringspinnet (s_t=±1/2 se utförligt i Kvanttalen) drar ringarna mot varandra om varannan t är flippad 180°, se ovanstående illustration. Därmed strävar de kollektivt atombundna t-ringarna att forma ett djuppenetrerande materialplannät.

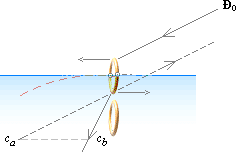
LJUSETS BRYTNING (refraktion, se Refraktion) är ideal för en absorbator. t-ringarnas tvärställda riktning ger den helt ideala, optimala förutsättningen för en (avancerad) utbredning i materialets djupled. Se utförligt i REFRAKTION.

Reflexion

Både absorbatorer och reflektorer har (nära) samma principiellt (goda) förmåga att återkasta (reflektera) inkommande ljus. Det som skiljer är emellertid att en reflektor kännetecknas av att t-ringarna i materialytan inte är tvärställda denna som i fallet ovan utan istället mera ytparallella, se utförligt i Reflexion. Därmed, kan man säga, blir ett reflektormaterial en bättre, mera effektiv, reflektor än en absorbator som därmed uppvisar en relativt sett mindre reflexionsförmåga. Jämför t.ex. vattenytan på en sjö: Den uppvisar under speciellt lugna och klara förhållanden en nog så tydlig spegelbild. Tydligheten ökar (dessutom) med en allt lägre blickpunkt (därför att andelen ljus som kommer från vattnets djupdel minskar med synvinkeln över vattenytan): med blicken strykande över en vattenyta ges starka (högintensiva) spegelbilder.

LJUSETS POLARISATION | Reflektorer | IaM_TNED2 | 2008VII1

reflektorer

Alla material exponerar sin yta genom atomära elektronmassor (m_e ).

ABSORBATORER visar den elektriska sidan hos m_e mot betraktaren (t-ringarna står på högkant utåt betraktaren).

REFLEKTORER visar den magnetiska sidan hos m_e mot betraktaren (t-ringarna ligger som mynt utåt betraktaren).

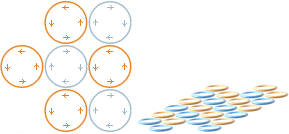
Reflektormaterialet sett stiliserat ovanifrån materialytan; elektronmassans magnetiska sida vänds mot betraktaren. Ringarna hålls samman beroende på deras ömsesidiga samverkande magnetiska fält från ringströmmarna (se högerhandsregeln): varannan ring ligger flippad 180° vilket bildar den sammanhängande kopplande harmonin.

Systemet bygger på atomer som har stort utrymme för gemensam delning av elektronmassor över stora områden. Genom denna mindre uttalade elektriska bindning till respektive atomkärna binds t-ringarna istället ihop planmässigt sida vid sida för att bilda ett ”sammanhållande skal” kring materialet och som därmed enkelt kan flyta omkring som »allmänt transportmedel» för elektriska och termiska ändamål.

Ringströmmarna är egenskaper med grund i energins oförstörbarhet (atomen och dess element summerar nollkraft och nollmoment och behöver ingen påfyllning för att fungera).

Därför att reflektorer uppvisar partiellt fria valsenselektroner, kollektivt mobila i materialet, har t-ringarna som elektronmassans komponenter ingen uttalad speciell atombindning, utan kan organisera sig lokalt för bästa utförande: den magnetiska kraften från ringspinnet (s_t=±1/2, se Kvanttalen) drar ringarna tillsammans om varannan ring är flippad (omvänd) 180°, se illustrationen ovan. Resultat: de kollektivt atombundna t-ringarna eftersträvar att bilda ett sammanhängande skal kring materievolymen.

Notera för illustrationerna allmänt med t-ringarna att:

I den verkliga fysiken är t-ringarna separerade av stora mellanrum i förhållande till ringarnas storlek. Jämför den inledande huvudvyn med den skalenliga proportionen mellan protonkärnan och t-ringens absolut teoretiskt största diameter (1/50 av protonradien).

TNED ger ingen upplysning om t-ringarnas mera exakta dimensioner än vad som kan utläsas ur ett sämsta fallets absoluta maxvärden: Ett minsta värde för antalet t-ringar i m_e är 177062 enligt sämsta fallets beräkningar i Spektrum från resultaten i PLANCKRINGEN. Varje försök att (med enkla medel) få fram mera precisa uppgifter från TNED på denna punkt stöter på kompakta (fraktala) motstånd — som veterligt inte har några direkt enkla lösningar (men det kan kanske bero på den här författarens begränsning).

Det finns dock en rent statistik möjlighet att eftersöka (vissa) kopplingar, men den delen kräver samtidigt en vidare, rent statistisk, bas med tillhörande programuppgifter, och den avdelningen ligger helt utanför den här presentationens ramar.

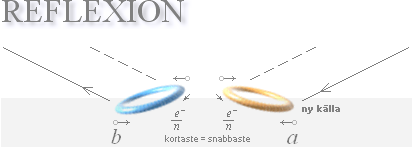
Inkommande ljus vid a förorsakar en tillståndsändring i målringen (T). Som ändringen är accelererad, utbreds en induktiv verkan i ändringens riktning med lokal hastighet c för att rapportera potentialändringen i respekt till T. När denna rapport når den närmaste grannen, svarar denne med en motsatt ändring för att motverka orsaken (Newtons tredje lag). Varje inkommande ändring på en första t-ring (T) blir så en ny induktiv källa och vilken ändring utbreder sig genom hela ytelektronmassan, eller den aktuellt berörda delen. Därigenom kan två angränsande t-ringar alltid återföras av princip på en absolut ideal induktiv spegel, i perfekt analogi med den elementära impulslagen från mekaniken, eller spegellagen från optiken och som beskriver den klassiska härledningen till ljusets brytning.

Det är hur ytljuset reflekteras från ett reflektivt material (vanligtvis en metall). Se även mera utförligt i Reflexion.

Refraktionen hos en reflektor är minimal.

Som ljuset (Jordbaserade laboratorium) produceras från elektroner i atomer i en primär ljuskälla (PS), finns det också ett bestämt energitvärsnitt av induktiv utbredning i respekt till en volyms masstäthet eller ytmasstäthet hos PS — jämförbart med normala Jordbaserade material. Det tvärsnittet berör en medelmässig fördelning av ”antalet täckande t-ringar” relativt ett materials atomtäthet. Ur denna grundprincip kan man utan vidare beräkningsgrunder sluta sig till följande allmänna riktlinjer.

Refraktion — brytning

Som ”toppytan” (tA) hos upprätt stående ytringar (|^¬) vid ett materials yta (—) uppvisar en försvinnande liten del av ytarean (A) som sådan, har t-ringar som ligger mera platt (–) på samma yta A proportionellt (enormt) mycket större tA-täckning. Så, uppskattningsvis med bara några få ytskikt med t-ringar i A bör den induktiva energin från primärkällan PS ha absorberats av de flatliggande ömsesidigt djuptäckande tA-ringarna och deras symmetriska induktiva reflektiva samverkan; Desamma primära skikt är de enda element som kan ha ansvaret för den lokala primära induktiva egenkällan i materialet, och därmed hela basen i resonemanget. Då blir den brytande delen försumbar: Inverkan från primärkällan får aldrig någon uttalad djupkomponent i ett reflekterande material — därför att nära hela den inkommande energin kastas tillbaka ut induktivt av de (delvis) varandra djuptäckande ”flatringarna”.

LJUSETS POLARISATION | Faradayeffekten | 2008VII1 | För konventionell källreferense, se Källreferenser

FARADAYEFFEKTEN

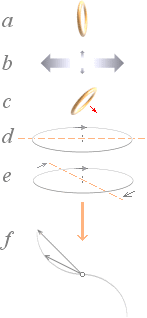
Faradayeffekten a: Så som antaget för ett absorberande material, är dess (yt-) elektronmass-t-ringar i allmänhet orienterade upprätt i respekt till deras elektriskt hårda atomiska bindning. c: Om ett yttre magnetiskt fält (B) läggs med B-riktningen in genom materialytan, tenderar t-ringarna att tiltas ned mot materialytan i samriktning med B. Se t-ringens egenskaper. d, e : De nedvikta t-ringarna tvingas uppvisa precesserande rotation (som ett snurrande mynt som just lägger sig) på grund av B och den normala atombindningens karaktär (se även t-ringens motsvarande uppförande i Kvanttalen), allt starkare med växande B-styrka. b, f: Med ett företrädesvis redan polariserat ljus (b) riktat mot t-ringarnas ytmaterial, kommer den expanderande polarisationsströmmen (¬ ®) att koppla direkt till de precesserande t-ringarna (f); Resultatet kan återföras på en resulterande (precessionsvriden medel-) rotationsvinkel (A) som leder till att polarisationsströmmens riktning ändras. Rotationsvinkeln A kommer (således) att bero delvis på styrkan hos det yttre B-fältet, liknande kopplingspedalen i en bil som genom olika tryck vidhäftar mer eller mindre mot den spinnande motorns transmissionshjul, och delvis på ljusets våglängd (l, kopplingstiden eller trögheten) i den polariserande strömmen: ju längre våglängd, desto större vinkel. Vilket vill säga; rotationsvinkeln (A) kommer att bero på B och l för varje specifikt atomplan i materialdjupet utmed linjen för det inkommande ljusets utbredning. Följaktligen beror rotationsvinkeln A på den totala längden hos ljusvägen l som funktionen (f) för skaran lBl enligt a = f (l,B,l) med A i radianer. För en given våglängd således A=kBl med k som en proportionalitetskonstant som inbegriper specifika materialparametrar enligt specifika atombindningar. Rotationen A via ett yttre pålagt magnetfält kallas Faradayeffekt.

LJUSETS POLARISATION | Kerreffekten | 2008VII1 | För konventionell källreferense, se Källreferenser

KERREFFEKTEN

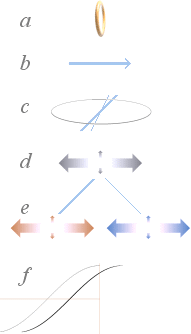
Kerreffekten a: Samma förutsättningar som ovan i Faradayeffekten. b, c: Ett elektriskt fält som läggs över materialet med e-fältets riktning parallellt med materialytan och därmed i motverkan mot t-ringarnas ordinära atombindningar, kommer att superponera en fast men delad t-ringstruktur med en motsvarande tvådelad brytningsform (refraktionsdelning) i ljusets utbredning genom materialet. d, e: En inkommande stråle polariserat ljus kommer då att delas i två principiellt olika strålar, var och en med sin särskilda utbredning genom materialet, en så kallad dubbelbrytning (bi-refraktion). Som i normal ljusbrytning, beror den brytande magnituden (n) på våglängden (l). I detta fall kommer n också att bero på kvadratstyrkan i det pålagda elektriska fältet (X^2). f: Som strålen fortplantas genom materialet, utför de motsvarande hastigheterna en fasförskjutning (Dd). Dd kommer alltså att utvidgas med utbredningsdistansen l i materialet. Fasförskjutningen för en given våglängd kan då uttryckas generellt enligt Dd = kX^2l med k som en proportionalitetskonstant som inbegriper specifika materialparametrar enligt specifika atombindningar. Uppkomsten av en tvådelad ljusväg genom det yttre pålagda elektriska fältet kallas Kerreffekt — explicit elektro-optiska Kerreffekten. Den motsvarande magneto-optiska Kerreffekten är den rotation i polarisationsströmmen som ljusstrålen genomgår i den ovan beskrivna Faradayeffekten efter reflexion direkt från en magnetpolyta. Som förskjutningen (Dd) utför en fullständig ljusblockering när de bägge skilda vågformerna tar ut varandra, kan också Dd-formen relateras till typ polarisationsvinkelrotation liknande fallet i Faradayeffekten.

KONVENTIONELLA REFERENSER TILL FARADAYEFFEKTEN OCH KERREFFEKTEN | Källreferenser

KÄLLREFERENSER

FARADAYEFFEKTEN

Experimentanordning finns (2007-10-12) TYDLIGT BESKRIVEN bl.a. på

[http://www.teachspin.com/instruments/faraday/index.shtml][TEACHSPIN Instruments Designed for Teaching],

samt även, annan typ

(den som Faraday själv använde) på

[http://www-ph.postech.ac.kr/Edulab/phy-esp2/web/pdf/2_6_01.pdf]

[PHYWE series of publications • Laboratory Experiments • Physics • PHYWE SYSTEME GMBH • 37070 Göttingen, Germany]

Webbkällor som refererar Faradayeffektens matematiska samband (typ A=kBl) finns bl.a. på

Physics 121, Advanced Laboratory, THE FARADAY EFFECT

[http://www.physics.uci.edu/~advanlab/faraday.pdf]

The Faraday Effect, Jason D. Darfus, Physics Department, The College of Wooster, Wooster, Ohio 44691, [May 1, 1997]

[http://www.wooster.edu/physics/jrIS/Files/Darfus-TheFaradayEffect.pdf]

Källan ovan specificerar inte vinkelenheten, men källorna nedan antyder bägge att vinkeln ska räknas i radianer.

[http://www-ph.postech.ac.kr/Edulab/phy-esp2/web/pdf/2_6_01.pdf]

[http://www.physics.uci.edu/~advanlab/faraday.pdf],

”V = –K(e/2mc²)l (dn/dl) (This formula is valid in cgs units for which the Verdet constant has units of radians per Gauss-cm.)”.

KÄLLREFERENSER

KERREFFEKTEN

Experimentanordning finns (2007-10-12) på

[http://www.nikhef.nl/~h73/kn1c/praktikum/phywe/LEP/Experim/2_6_02.pdf]

MEN FÖRFATTARNA HAR TROTS TYDLIGA SNITTILLUSTRATIONER HELT MISSAT ATT BESKRIVA ELEKTRISKA FÄLTETS ORIENTERING. Man får typ ”GISSA LÖSNING”.

En (betydligt) mera klar referenskälla är

An Investigation Into the Kerr Electro-Optic Effect, Matthew B. Stone

The Johns Hopkins University, Department of Physics and Astronomy, First Year Graduate Student Seminar, Spring 1997

[http://www.pha.jhu.edu/~mstone/Kerr/kerrpaperentire.html]

Där anges också Kerreffektens typsamband (Dd = kX²l) enligt ”Dn = KlE²”.

LJUSETS POLARISATION | Ljusbrytningen i vatten | 2008VII1

DEN KLASSISKA HÄRLEDNINGEN — se även motsvarande med t-ringarna i Refraktion

LJUSBRYTNINGEN I VATTEN

	n » 4/3
a	b	c	d	e

Ljusets brytning (refraktion) i vatten

Ett grässtrå genom vattenytan visar grunderna (eller en blompinne i tekoppen). Om vi tittar i stråets riktning (a) ser vi bilden i (b). Den brutna delen under ytan ses längst upp. Sänker vi blickpunkten tills den brutna delen framträder som en punkt, då tittar vi i samma riktning som den i vilken ljuset från luftsidan lämnar (eller inträder) vattenytan i brytpunkten. Denna synlinje är markerad röd i (c). Komponerar vi ihop dessa vyer till en gemensam matematiskt beskrivande ljusvy, får vi den analytiska bilden i (d). Den är förstorad och bestyckad i (e) och visar hur ljusstrålen fungerar från luft till vatten (eller omvända vägen).

Förhållandet mellan sträckorna a(luftdelen) och w(vattendelen) är samma som brytningsindex (n), eller refraktionsindex.

Brytningen beror av ljusets våglängd (tidsperioden i d-baslinjen, E=hf). Blått har kortare period (större f-värde) med högre energi och bryts därför något kraftigare (n=1,34) än rött som har något längre period med något mindre energi (n=1,31).

För vatten blir medelvärdet av bägge ca 1,33 eller 4/3. Plexiglas visar ca 1,45. Vanligt industriglas anges ca 1,5.

I trigonometriska ekvivalenter (se även i Trigonometrin om ej redan bekant) definieras brytningsindex (n) enligt relationerna från räta vinklar i PREFIXxSIN

a/d = cosA = sin(90–A=a°) = sina; ......................... vinkeln a räknas från vattenytan och uppå (luftvinkeln)

w/d = cosW = sin(90–W=w°) = sinw; ..................... vinkeln w räknas från vattenytan och neråt (vattenvinkeln)

cosA/cosW = (a/d)/(w/d) = a/w = sina/sinw = n ..... större sidan dividerat med mindre sidan

I ovanstående förenklingar skiljer vi mellan sidorna aw och vinklarna aw om inga missförstånd uppkommer.

Ljusbrytningens fysik beskrivs mera ingående i REFRAKTION.

BRYTNINGSLAGEN

Eftersom ljushastigheten (c) över bestämda intervall bestäms (i ideal gravitellt homogen rymd) efter tillryggalagd väg (s) per tid (T₀) enligt

c = s/T₀

blir för ljus med bestämd frekvens (T₀=1/f) förhållandet mellan de olika väglängderna (aw) genom den gemensamma perioden (T₀) i föreningsytan (d-längden)

— med

c_a = a/T₀ ................... som gäller luftvägen

c_w = w/T₀ ................... som gäller vattenvägen

— lika med förhållandet mellan ljushastigheterna i de skilda genomgångsrummen enligt

c_a/c_w = (a/T₀)/(w/T₀) = a/w ;

c_a/c_w = n = sina/sinw ............... brytningslagen

Ljushastigheten i de olika rummen förhåller sig som de avverkade distanserna med given tidrymd

LJUSETS POLARISATION | Den Klassiska Vågmodellen i Ljusets Utbredning | 2008VII1|5

Se med vidare koppling från Ljusets optiska natur

VÅGPLANETS »KLASSISKA» MODELL

FOCUS MATERIEN 1975 är ett ypperligt allmänt samlande referensverk (på svenska) i allmän fysik för perioden under 1900-talets senare hälft. Det verket kan (med fördel) användas för en vidare referens i beskrivningen av fysiken generellt.

Att bildningen av periodiskt variabla elektriska och magnetiska fält i samband med beskrivningen av ljuset som ”en elektromagnetisk vågrörelse” skulle vara förknippat med någon form av oscillerande elektrisk laddning framskymtar INTE i FOCUS MATERIEN 1975, varken i text eller bild. Uppkomsten av den elektromagnetiska vågbildningens natur beskrivs genomgående i termer av vågrörelser med amplituder och svängningar. Fetstilen min markering:

”Från en radiosändare, en ljuskälla eller ett g-strålande radioaktivt preparat utsänds elektromagnetisk vågrörelse. De fysikaliska storheter som deltar i svängningen är i detta fall ett elektriskt och ett magnetiskt fält. Någon materia för svängningens fortplantning krävs inte: vågrörelsen går således obehindrat fram i vakuum. Den elektriska och den magnetiska fältstyrkan är alltid riktade vinkelrätt mot varandra och vinkelrätt mot fortplantningsriktningen.”

FOCUS MATERIEN 1975 ill.s261ö

”Ljus betraktat som elektromagnetisk svängningsrörelse har en elektrisk och en magnetisk vektor (svängande fältvektor) i rät vinkel mot varandra och i ljusets fortplantningsriktning. I ljus från vanliga ljuskällor är den genomsnittliga svängningsamplituden för den elektriska vektorn, vilken betraktas som den egentliga ljusvektorn, samma i alla riktningar. Sådant ljus sägs vara opolariserat.”

FOCUS MATERIEN 1975 ill.s278ö

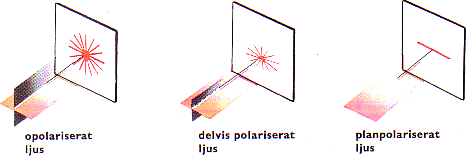
Ovan, källans illustration s278ö

FOCUS MATERIEN 1975 omnämner ”atomer och molekyler” i samband med ”ljusets uppkomst och detektering” (s280sp1mö). Men texten innehåller ingen beskrivning av något sådant som typ ”oscillerande elektrisk laddning”. Terminologin tycks helt vara tillägnad termer som frekvens, våglängd och spektrallinje i koppling till (s281sp1mn) ”den teoretiska modellen för mekanismen vid ljusets emission från en atom eller en molekyl”. Vi får inte veta mycket mer än så. Att det är laddningarnas lägesändring som bildar ljusfenomenets grund, finns alltså därmed inget specifikt citerande avsnitt att referera till. Det framskymtar underförstått, men står inte uttryckligt.

I GYMNASIETS FYSIK åk3 Liber 1980 däremot beskrivs (s95) uppkomsten av elektromagnetisk strålning tydligt och klart med hjälp av ”en elektriskt laddad kula”:

”Låt oss betrakta en elektriskt laddad kula som, upphängd i en spiralfjäder, svänger upp och ned. Denna rörliga laddning kan uppfattas som en varierande elektrisk ström. Genom kulans rörelse skapas ett varierande elektriskt fält i dess omgivning.

En varierande elektrisk ström ger som bekant upphov till ett varierande magnetisk fält. Enligt Maxwell alstrar ett varierande elektriskt fält också ett varierande magnetiskt fält. Detta skapar i sin tur ett varierande elektriskt fält etc.

Man får således en successiv koppling mellan elektriska och magnetiska fältändringar i omgivningen av en oscillerande laddning. Fältvariationerna breder ut sig åt alla håll. Detta innebär att kulan utstrålar energi i form av en elektromagnetisk vågrörelse.”

GYMNASIETS FYSIK åk3 Liber 1980 s95n

Boken beskriver sedan (s101) hur de elektriska och magnetiska fälten på stort avstånd från en antenn som matas med oscillerande laddningar ligger i fas: både maxvärde och nollvärde för både elektriska och magnetiska fältstyrkor uppnås tidsmässigt samtidigt.

Det är denna referens som här kallas »klassisk»: den oscillerande elektriska laddningens lägesändring tillämpad underförstått på atomära ljusbildande elektronsystem, och som bildar ”den elektromagnetiska vågutbredningen”. Vilket vill säga: underförstått alla möjliga svängningsriktningar sammanförda till en vågplansmässig syntes — och som i kraft av svårigheterna att formulera grunderna teoretiskt inte har någon exakt motsvarande beskrivande ordning i modern teori — typ FOCUS MATERIEN ovan.

Om vi eftersöker en motsvarande matematisk bild för HUR en motsvarande uppfattning av ”de mot varandra vinkelräta elektriska och magnetiska fältens utbredning i fas” fungerar, leds vi (enligt relaterad fysik) till följande »ekvivalent»:

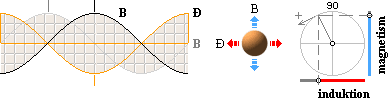
I en mätpunkt (P) på ett (stort) avstånd (x, horisontella axeln) från källan (S) kan man uppmäta elektriska och magnetiska fältvariationer (xy) periodiskt och i fas om, och endast då, källan består av en singulär laddning som svänger motsvarande periodiskt i xy-planet där elektriska amplituden räknas i x-led och magnetiska amplituden räknas i y-led, figuren ovan. Vilket vill säga: resultatet motsvarar en laddning som roterar i en (liten) cirkel i xy-planet: huvuddelen i styrkan hos den variabla elektriska fältstyrkan kan återföras på en elektrisk laddning som uppvisar periodisk ändring utmed x-axeln, huvuddelen i styrkan hos den variabla magnetiska fältstyrkan kan återföras på en elektrisk laddning som uppvisar periodisk ändring utmed y-axeln. Att B-styrkan från en kort rakledare s på stort avstånd från denna skulle vara störst just rätvinklit strömleden i s är dock endast en förmodan, ingen väl underbyggd matematisk nödvändighet. Se vidare i B-vinkeln i APPENDIX.

SOM VI EMELLERTID SER, blir denna ”illustration” hur som helst »till synes kaotisk» — i någon förment ”förklarande mening” för typ ”alla möjliga riktningsändringar” för alla möjliga laddningsändringars bidrag i ett materials atomer och deras elektronmassor som bildar en ljuskälla: Ovanstående illustration har i den praktikens ljus uppenbarligen ingen direkt upplysande kraft. Vilket vill säga: illustrationen förklarar i grunden ingenting — trots dess elektriska-magnetiska fasanalogi till gängse presentationssätt.

Eller med andra ord: Det finns — uppenbarligen — inget enda specifikt sätt att medelvärdesbilda en elektromagnetisk fasbild (typ ovanstående illustration) av en ljuskällas ”alla möjliga laddningsändringar” för att återföra em-bildningen på laddningsändringarna som ljusets upphov. Uppgiften är omöjlig. Ljusets utbredning kan inte beskrivas, eller ens förklaras, på det sättet. Därför (nämligen) att hur vi än ”illustrerar och har oss” med den saken kommer varje sådan illustration att bli specifik endast för varje motsvarande elektrisk svängande anordning — typ ovanstående i sig uppenbart begränsande illustrerade funktion OM den var tänkt att beskriva ljusutbredningens allmänna vågfysik.

Ett annat sammanfattande sätt att beskriva kärnpunkten i hela saken är det följande:

OM vi tar med alla möjliga svängningsriktningar i ett oscillerande laddningssystem typ atomernas elektronmassor i en ljusskälla — och vi utnyttjar motsatta alternativ i par — är det tydligt att vi hamnar på netto noll. Riktningarna tar ut varandra. Ingen särskild riktning gynnas. Naturligtvis inte.

Men hur förklaras då den faktiska ljusstrålens utbredning, det faktum ATT den påverkar avlägsna laddningar?

Förklaringen ENLIGT TNED (relaterad fysik) är att varje ljusstråle i den ljusmatande energin (E=hf) utpekar sin egen kraftväg (som de utgående strålarna från ett lysande klot); Kraftvägen (E=Fd) samlar den ljusdrivande energin bakom källans laddningsändringar i ljusstrålens enda riktning framåt-bakåt genom potentialändringar (elektriska fältstyrkan X=dU/ds) i ljusstrålens riktning; Därmed, på varje möjligt avstånd, i vilken som helst punkt på strållinjen, bildar X DÄR en induktiv verkan (Ð) i pumpriktningen (ds) och en magnetisk verkan (B) rätvinkligt denna (och som enligt TNED bär ansvaret för den avgörande polarisationsströmmen) och vilka bägge induktiva-magnetiska verkningar ingriper i elektronmassornas komponenter och via ljusenergins underhållande kinetiska hastighetskomponent (E=mv²/2=UQ=XsQ) garanterar att varje mätande anordning (på stort avstånd från källan) SER exakt energifas i maximum och minimum amplituder i bägge de elektriska och magnetiska fälten.

MEN denna (helt glänsande) beskrivning är omöjlig utan hjälp av just elektronmassornas komponenter.

Ljusstrålens praktiska verkan enligt denna beskrivna form — alltså enligt TNED märk väl, den finns inte i modern akademi — illustreras f.ö. utförligt i Ljusets polarisation.

DEN FÖREGÅENDE OVAN ILLUSTRERADE MODELLEN — explicit för magnetfältets del — är alltså riktningsmässigt felaktig relativt den praktiska funktionen: B-fältets riktning på avståndet x från ljuskällan (S) i en rymdpunkt (P) finns inte med i den praktiska ljusstrålens utbredning. Inte alls överhuvudtaget. Vi studerar detta.

det yttre B-fältet —

den klassiska

modellens begränsning

Enligt TNED — se Ljusets polarisation — kan ljusets elektromagnetiska utbredning INTE LOGISKT (och inte fysiskt) förklaras med hjälp av VÅGPLANETS »KLASSISKA» MODELL:

vågplanen som resultat av ”elektriska och magnetiska fältstyrkor som fortplantas genom rymden med ljushastigheten (laddningarnas alla möjliga svängningsriktningar)” från ljuskällan. Den uppfattningen finns representerad enligt ovanstående genomgång.

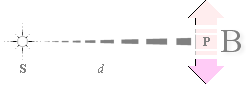
HUR ska man nämligen i sådant fall — illustrationen ovan — kunna förstå den fysiska närvaron av t.ex. den magnetiska fältstyrkan B i en punkt P på avståndet d från en långt avlägsen ljuskälla S?

Är B ibland ”riktat uppåt” och ibland ”riktat nedåt” — på samma sätt som man i ett laboratorieexperiment lägger på ett yttre B-fält över ett rymdområde P? Eller är det alla möjliga riktningar som gäller?

Enligt TNED fungerar inte ljusfysiken så.

Det finns inget typ ”växlande B-fält” i rymdpunkten P på d från S, och som typ ”färdas genom tomrummet med ljushastigheten c”.

Det är istället den reduktionsfria ofördröjda induktionsverkan i ljusstrålens utbredningsriktning som PUMPAR FRAM LOKALA potentialändringar i det omgivande dominanta gravitationsfältets fasta referenspunkter, fram och åter (med alla möjliga frekvenser enligt superpositionsprincipen) över d med hastigheten c — och med likaledes verkan och effekt i P: att det DELS bildas en motsvarande induktiv respons på ev. befintliga målladdningar i P som följd av den induktiva dipolfältstyrkan (Ð) i P från S via d, och DELS en magnetisk ringexpansion — likt ringarna på vattenytan som bildas av den fallande vattendroppen — på vanligt sätt men här explicit kring ljusstrålen — inte utifrån 3D-rymden, tvärs genom — med början från P-centrum också som följd av potentialändringarna i P via d från S. Se även i Magnetismen.

Därmed finns inget ”lokalt yttre B-fält” i P från ljusverkan — bara en lokalt uppkommen elektrisk-magnetisk respons i P via d från S;

Det finns därmed heller inga ”elektriska och magnetiska fältvågor som utbreder sig genom tomrummet” för ljusets fortplantning. Den uppfattningen är »bara» en (populariserad, vulgär) matematisk modell.

Men varifrån kommer då uppfattningen att bägge maximum för e-fältet och B-fältet är i fas om man mäter dessa i P?

Svaret på den frågan är enklare än man kan tro, och som redan till viss del vidrörts ovan;

ENERGIN som krävs för att underhålla ljusets svängningar på omgivande materiella system kan med hänsyn till elektriska fältstyrkans grundelement, den elektriska potentialen (U), skrivas formellt

U = Fr/Q = E/Q med rörelseenergin E=mv²/2. Det ger oss elektriska fältstyrkan X = F/Q = U/s; Elektriska fältstyrkans toppvärde (X) kan med given distansparameter (s) då återföras på ett motsvarande toppvärde (v) för laddningens hastighet och som bildar e-fältets potentialform. Med grund i materialförklaringen enligt TNED som grundas på elektronmassans t-ringar och som matas av v-formen i den enkla exemplifierade källgrundade deriveringen, kan därmed också den uppmätta elektriska fältstyrkans toppvärde — baserad på den mätande energins bas — associeras med den magnetiska fältstyrkans toppvärde — analogt den energi som matar ljuset; v-formens energibas bestämmer fasen.

Varje (noga) mätande anordning kommer (således) — hur som helst — att »konstatera» absolut exakt fasstyrka mellan e-fält och B-fält med hänsyn till den energi som matar ljuset; e-fält och B-fält från (utpräglade) ljusstrålar uppvisar inom atomens elektronmassor maximum och minimum samtidigt — trots att källformen uppvisar en fasförskjutning med induktionens maximum som kommer före magnetismens, och som inte kan mätas direkt ehuru grunden för den materiella energimätningen. Se vidare från Ljusets polarisation. Där visas illustrerat mera ingående hur ljusstrålen fungerar då den träffar på materien.

Föreställningen om ”alla möjliga riktningar” från ljuskällans oscillerande laddningar tar i realiteten ut varandra i nolleffekt och har därför ingen representation i ljusstrålens utbredning: Atomen summerar nollmoment och nollkraft, överallt. Det som däremot har representation är den energi som driver svängningarna i ljuset— alla möjliga frekvenser eller som vi säger färger eller toner — och den energin omsätts alltid över kortaste-snabbaste kraftvägen som är största potentialändringarna som är lika med ljusvägen eller ljusstrålen mellan källa-mål. Det finns med andra ord ENLIGT TNED bara en (primär, förorsakande, energikopplad) svängningsriktning i en ljusstråle: rakt framåt-bakåt.

Den konventionella beskrivningen undgår dessa fördjupningar.

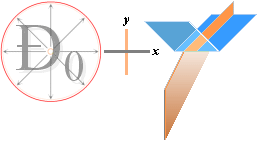
Genom potentialändringarna i rymdpunkten P i ljusstrålens väg — omsatta på ett instrumentsystem och därmed matematiska funktionskurvor i P — kan man alltså i en motsvarande »cyberrymd» konstruera MOTSVARANDE MATEMATISKA RYMDPLAN som jämte P-linjens förlängning som ljusstråle (Ð₀-strålen) uppvisar de karaktäristiska elektriska och magnetiska fältvariationerna. Speciellt, eftersom ljusstrålen i kontakt med ett material genomgår polarisation, alltså ändring, kan de olika svängningsplanen också modelleras (företrädesvis med referens till något materials planyta) på två primärt skilda, mot varandra vinkelräta plan motsvarande den brytande och den reflekterande vågfunktionens delar, typ illustrationen ovan höger.

En mera, direkt handfast, illustration till ljusutbredningens (matematiska) fysik blir med ljuskällan i form av en ideal rundstrålande sfär: energin ges i varje riktning i form av just den ljusstrålen. Men det visste vi ju redan!

LJUSETS POLARISATION | APPENDIX | 2008VII1

APPENDIX

Bvinkeln

ANALYS 2008-07-04

B-styrkans maximala vinkelriktning

Vi undersöker först hur magnetiska fälstyrkan förhåller sig till riktningarna respektive i ledarens längsriktning (—) och vinkelrätt denna (|) med given (kort) ledarlängd (s).

Från Rakledarens fullständiga samband i avsnittet om Magnetismens specifika ekvationer hade vi i PREFIXxSIN

B_Ps = µ₀(I/4px)(sinb_L+ sinb_R) ................. rak ledare,alla vinklar, 1Tesla=1VS/M²

Vi utnyttjar endast vänsterdelens rätvinkliga bidrag,

b_R = 90;

vilket med sin90=1 ger oss

B_Ps = µ₀(I/4px) sinb_L

Vi vill nu undersöka bara en del av rätvinkelns bas i formen av en elektrisk ledare, motsvarande en kort strömled i analogi till rörelseleden hos en oscillerande elektrisk laddning och dess generering av motsvarande magnetiska fält. Vi får då principbilden enligt

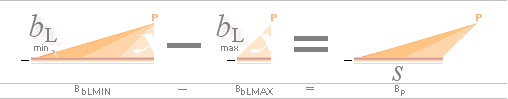
med

B_Ps(max) = µ₀(I/4px) sinb_L(min)

B_Ps(min) = µ₀(I/4px) sinb_L(max)

;

B(—). Magnetiska fältstyrkan i ledarens längsriktning beräknas då med ett motsvarande x som avviker obetydligt från ledartrådens cirkulära radie, enligt sambanden

B(—) = B_Ps(max) – B_Ps(min)

B(—) = µ₀(I/4px)(sinb_L(min) – sinb_L(max))

Respektive vinkeldelar har explicit relationerna

x/(s+d) = tan b_LMIN

x/d = tan b_LMAX

Med sin = (1+tan²)^–1/2 från trigonometrin har vi också för B(—)-formen

sinb = (1+[x/d]²)^–1/2

som i B(|)-formen rätvinkligt B(—) måste formuleras motsvarande

sinb = (1+[d/s]²)^–1/2

med d som den aktiva variabeln.

B(|). Med det ordinära sambandet för B med x mitt på ledarlängden s ges direkt

B(|) = µ₀(I/4px) 2sinb_L

Här motsvaras f.ö. x(|) av B(—)-delens d-värde (med litet s-värde).

Funktionens aktiva parametrar. För att undersöka värdeformernas maxima och minima behöver vi endast undersöka variationerna genom x(|);

Vi sätter fysikdelens

µ₀(I/4p) = K = 1

med K som en konstant koefficient så att vi får den rena grafiska funktionsformens aktiva del

B(—) = x^–1(sinb_L(min) – sinb_L(max))K

= x^–1([1+(x/[s+d])²]^–1/2 – [1+(x/d)²]^–1/2)K

B(|) = d^–12sinb_LK

= d^–12(1+[d/s]²)^–1/2K

Med hjälp av (här) MsWORKS (4.0) kalkylbladsprogram kan ett kalkylkort (fungerar inte aktivt i webbläsare) sättas upp för kontroll och analys enligt nedanstående.

kalkylkort 1 · endast bild · vinkelmetoden

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik4 Kalkylkort 1 — Vinkelmetoden — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

kalkylkort 2 · endast bild · distansmetoden

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik4 Kalkylkort 2 — Distansmetoden — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

Beroende på den numeriska begränsningen i kalkylprogrammet med så små vinkelvärden som möjligt, får vi något olika värden beroende på vinkelmetod eller distansmetod i inmatningen av basparametrarna.

Det nödvändiga framgår emellertid:

NUMERISK jämförelse mellan B-värdet i ledarens längsriktning (—) och B-värdet rätvinkligt detta (|) visar att B(|) är större än B(—) med (minst) en tiopotens.

Slutsats:

Magnetiska fältstyrkan på avståndet r från en rakledare med längden s<<r är mindre i framrikningen än rätvinkligt denna.

Vi observerar att hela analysen bygger på en ideal sfärisk laddningsgeomnetri.

Undersöker vi om också B-styrkan rätvinkligt s är den totalt sett största med hänsyn till alla vinklar omkring s, analogt alla B-värden på r från s, finner vi att så INTE är fallet:

Optimala B-värdet då s®0 för givet r är atan(1/Ö2)=35,26439°.

Vi kan dels pröva detta numeriskt genom ett kalkylkort (vi prövar olika värden och ser att förhållandet x/d = 0,7071067 = 1/Ö2 är det optimala),

kalkylkort 3 · endast bild · distansmetoden · separat analys

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik4 Kalkylkort 3 — Vinkelmetoden · separat analys — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

Eller nå samma resultat genom en separat derivering — här med en tillhörande klargörande grafisk formanalys:

Aktiva funktionsgrafen skrivs som ovan för B(—) enligt

y = –(1/x)([1+(x/[s+d])²]^–1/2 – [1+(x/d)²]^–1/2)

Grafen

5[x'–1]([(1+[x/1.1]'2)'–0.5]–[(1+[x/1]'2)'–0.5])

ger en positiv topp vid ±xMAX den är 0,7071067 med minsta tillskottet (s®0) och ca 1,2725 med största (s®¥)

Vi kan se den genom att förstora grafen med litet s enligt grafexemplet

y = 5000[x'–1]([(1+[x/1.001]'2)'–0.5]–[(1+[x/1]'2)'–0.5])

DERIVERING:

Betrakta magnetfältstyrkans aktiva funktion f (B) enligt

y = –(1/x)([1+(x/[s+d])²]^–1/2 – [1+(x/d)²]^–1/2);

En »förenklad» derivering av y-formens nollderivata kan göras direkt på komponenten (1+(x/[s+d])²]^–1/2) — eftersom vi i vilket fall söker den aktiva parameterderivatans form med avseende på variabeln x för hela distansen s+d=a. Detta ger oss

y’ = Dn –(1/x)([1+(x/a)²]^–1/2)

= Dn –[x²+(x⁴/a²]^–1/2

= (–1/2)[x²+x⁴/a²]^–3/2[2x+4x³/a²] = 0;

Vi utnyttjar bara den aktiva parameterdeln (0=x²+x⁴/a² ger bara x=a frånsett minustecknet och är inte den parameterdel vi söker)

0 = 2x+4x³/a² ;

2x = –4x³/a² ;

1 = –2x²/a² ; frånsett minustecknet (kvantitativa absolutderivatan);

1/2 = (x/a)² ;

1/Ö2 = x/a ;

A = atan 1/Ö2 = 35,26436° ;

Vilket skulle visas.

Slutsats:

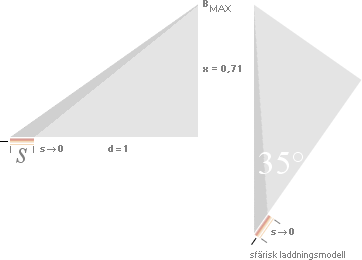
För en obegränsat kort elektrisk rakledare med längden s som bildar magnetisk fältstyrka (B) genom strömfaktorn K=µ₀(I/4p)

gäller att största B-värdet bildar vinkeln ca 35° eller atan(1/Ö2)=35,26436° mot s-riktningen.

TOTALT RESULTAT:

Största B-verkan ligger inte rätvinkligt s utan med vinkeln (avrundat) 35° mot s.

Observera dock att förutsättningen är att B-punkten ligger i framriktningen utanför s på avståndet d från s med s<<d.

LJUSETS POLARISATION | APPENDIX | 2008VII1

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Ljusets polarisation

ämnesrubriker

innehåll

LJUSETS POLARISATION

köksexperimentet

ljusmodellernas matematiska grunder

ljusets grundform

allmänna förutsättningar

Grundbegrepp

elektronmassan

t-ringens egenskaper

Elementära materialgrunder

materiens två huvudgrupper

absorbatorer och reflektorer

Faraday och Kerreffekterna

historia

Materien som ljuskälla

ljusets optiska natur

vågplanmodellens ursprung · VÅGPLANsMODELLENS URSPRUNG

Ljusets polarisation

expansionsströmmen

iP-strömmen

ljusets reflexion och brytning

ljusets polarisation

Brewsters vinkel

polarisationseffekten via Nicolprismat

vågplanmodellens begränsning

Nicolprismats polariserande egenskap

Ljusets polarisation i modern klassisk litteratur

Reflexion

reflexion i praktiken enligt TNED · reflexion i klassisk teori

Refraktion

ljusets brytning i praktiken enligt TNED · ljusbrytningen enligt klassisk teori

FÄRGEN

Absorbatorer

absorberande material

Reflektorer

reflekterande material

Faradayeffekten

ljusändring genom yttre magnetisk påverkan

Kerreffekten

ljusändring genom yttre elektrisk påverkan

Ljusbytningen i vatten

brytningslagen

Vågplanets klassiska modell

Den klassiska vågmodellen

APPENDIX

B-vinkeln

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

[FM]. FOCUS MATERIEN 1975 — Almqvist & Wiksell Förlag AB Stockholm 1965 — Andra reviderade upplagan 1975:

Det senare 1900-talets i särklass bäst sammanfattande allmänorienterande (svenska) verket i allmän fysik.

[BKL]. BONNIERS KONVERSATIONS LEXIKON 1922-1929 Albert Bonniers Förlag Stockholm

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2011-10-10

*END.

Stavningskontrollerat 2008-07-03|06

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se