SOLFYSIKEN · FUSIONERNA · SOLENS ENERGIPRODUKTION 2008II10 a BellDHARMA production · Stjärnfysikens fundamentala grunder enligt TNED | Senast uppdaterade version: 2018-10-21 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Solfysiken · Fusionerna · Solens energiproduktion | 2008II6

Innehåll Energiproduktionen i sammanfattning

Detaljerad beskrivning

Med fortsättning Från Solfysiken

SOLENS ENERGIPRODUKTION

Det innersta av hela Solkärnan garanteras ENLIGT TNED neutronfrihet initiellt när Solen bildas som J-kropp i K-cellens expansion efter divergenständning. Det är klart därför att nuklidbildningens dynamik [utförligt från GRUNDÄMNESBILDNINGEN] uppvisar de kortaste tidrymderna där divergensen är som störst (c₀), och den är så alltid med referens till J-kroppens tyngdpunkt. Vi frånser då, i viss mån, det som tidigare kallats g-skuggning och som kan åstadkomma att c₀-punkten förskjuts.

Deuteriumfrågan

I atomkärnans oändliga fraktala struktur av J-ringar och deras möjliga ±-kombinationer, se utförligt från Planckringen för atomkärnans härledning, är det uteslutet att det finns en ordnad synkronisering mellan två närliggande atomkärnor före divergenständning av J-kroppen. Varje ordnad synkronisering mellan två närliggande atomkärnor förutsätter nämligen, och bygger helt på, att de kan känna av varandras ytstruktur och därmed anpassa sig till varandra dynamiskt; Enda sättet för en sådan ordning är uppenbarligen i positiv divergens. Vilket vill säga: Närliggande atomkärnor i neutronkallplasmat som befinner sig innanför varandras nuklidbarriärer, alltså i negativ divergens, och vilket normalt sett i positiv divergens skulle medföra fusion, uppvisar från divergenständningen analogt begynnande positiv divergens, en inbördes fullständigt oordnad synkronisering mellan varandras J-ringar. De kommer därför obönhörligen att stöta ifrån varandra. Anledningen till detta uppmärksammande är (naturligtvis) förmodan att eftersom statistiskt sett 50% av atomkärnorna bör vara spinnsynkroniserade i kallplasmats tätt liggande atomkärnor, det omedelbart bildas deuterium i centraldelen vid den J-kroppens divergenständning. Så är alltså inte fallet.

Därmed utgår vi ifrån för Solens del och alla övriga stjärnor den typbild i Solens centrum som ges av nedanstående illustration ENLIGT TNED. Förekomsten av fritt deuterium generellt i universum (ca 1 del på 100 000 enligt konventionella källor) bör alltså bli mycket liten: Det deuterium som bildas centralt i stjärnorna utgör endast ett led i de fusionsringar som leder till tyngre atomkärnor, och bör alltså i stort sett vara helt orepresenterat i den universellt observerbara sammansättningen.

Strålningstrycket garanterar att det inre av Solklotet förblir intrinsiskt rent på elektronmassa (utförligt i SOLKLOTETS ELEKTRONFRIHET). Elektronmassan parkeras i Solytan och lämnar därmed en inre ren, fullständigt joniserad eller s.k plasmatisk Solkropp. Vi studerar detta.

Solens energiproduktion — se även från Stjärnornas Allmänna Tryckekvation

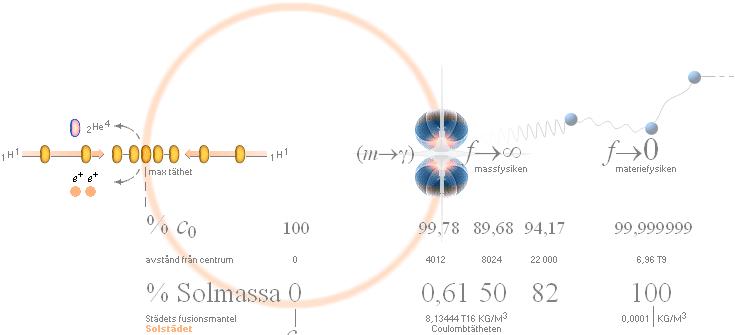
Solstädets basparametrar (ref. Kalkylkort stjärnmassans radiella variation · Stjärnfysiken2005 )

För ljushastighetens fysik speciellt i gravitationsfysiken: se GcQ-teoremet, ljusets g-beroende och (speciellt) GPS-exemplet (med flera) för inledande kännedom, om ej redan bekant.

Solmassans gravitella övertryck pressar atomkärnorna över varandras nuklidbarriärrer — en gång vart elfte år i den inre högtäta Solkärnan, se Fusionsperioden. Solstädet producerar, utöver en stor mängd strålenergi, också Helium-4 och positronmassa (e⁺): 2 stycken e⁺ frigörs ur råstocken på fyra Väte-1, per producerad Helium-4-atom, och som transporteras upp till Solytan i kraft av strålningstrycket. Illustrationen ovan ger en översikt. Se även i Solens Energiräkning.

LJUSETS GRAVITELLA BEROENDE garanterar att Solens tyngdpunkt håller maximalt lokal divergens c=c₀; Därifrån avtar c till 90%c₀ vid städmantelns maximala täthet [Se STJÄRNSTÄDET] — och växer sedan återigen mot 100%c₀ då avståndet växer obegränsat. Divergensens 10%-iga reduktion, med tillhörande reduktion i kraftrepulsionerna vid städytan, garanterar att

spridningen med max c i centrum tvingar stjärnans egentliga fusionsområde med maximal täthet att bara finnas till just i det centralt täta klotskalet — inte i centrum

Strålningstrycket, som utgår från städytan ur fusionsenergin, garanterar genom sin större effekt på större laddningar att det Helium-4 som bildas, samt varje annan tyngre nuklid, drivs utåt mot det yttre av stjärnklotet tillsammans med positronmassan som frigörs vid deuteriumbildningarna. Samtidigt ersätts vakanserna av motsvarande inströmmande väte, dels både utifrån och inifrån stjärnklotet, och som alltså bereds motsvarande tillträde till städytan då Heliumbesättningarna försvinner därifrån. Vilket vill säga: så länge det finns en sådan tillgång på Väte-1 i städmantelns omgivning som motsvarar städmantelns fusionsvåg vid gravitella övertrycket p–p_e=^gp, kommer stjärnan att producera exakt motsvarande strålningstryck — och därmed underhålla fortsatt Väte-1-inströmning i princip »intill sista droppen»: stjärnstädet underhåller en konstantström [Se även i SOLENS KAPACITANS]. Det är, tydligen, Solkärnans oerhört effektiva och avancerade energimaskin: den brinner i princip från första till sista stund på en och samma »påstämplade lampeffekt». Konstant. Stadigt. Helt säkert. [Se även beräkningsexempel för Solens livslängd i TIDSEKVATIONEN].

Periodisk pulsning

MED DEUTERIUMBILDNINGEN SOM SOLENERGINS BASFUSION — 1H1 + 1H1 – (m®g) = 1H2 + e⁺

MASSKLOTET (R) PÅTVINGAS PERIODISK PULSNING

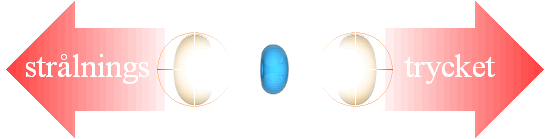
1. SÅ LÄNGE ENERGIFASEN I STRÅLNINGSTRYCKET (^gp) är i växande, avtar analogt (potentialen i) det fusionstriggande g-övertrycket (p – p_e), vilket innebär att »fusionstrycket» avtar. När ^gp når sitt maximum råder exakt balans enligt allmänna tryckekvationen (p–p_e – ^gp = 0) och ingen fusion kan ske.

2. VARTEFTER strålningstrycket ^gp avtar, tillväxer g-trycket återigen, vilket betyder att städet »laddar om» för en ny fusionsvåg.

;

Massklotet (R [STJÄRNSTÄDET]) påtvingas en periodisk pulsning.

fusionspulsen

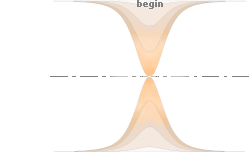
Eftersom fusionsfasen inleds då g-trycket är som störst och arbetar på ett (extremt tunt) mantelskikt i städklotets massa — och därmed också bör utsträckas så långt i tiden som krävs för att genomföra fusionerna (max t20 S, se fusionslängden i Nuklidbildningarna) — bör också fusionsfasen i sig vara mycket kortare än den efterföljande strålfasen då den frigjorda strålenergin (g) omsätts. Längden i tid för den senare (g) beror på hur det täta städskiktet fungerar som isolator — och därmed hur lång tid den stråltryckande verkan agerar. För ändamålet kan vi alltså illustrera det periodiska fusionsförloppet med en cyklisk funktion av nedanstående typ; Den egentliga fusionsfasen, mycket kort, är aktuell endast i toppen av varje period. Vi kan kalla den en fusionspuls.

fusionens cykel

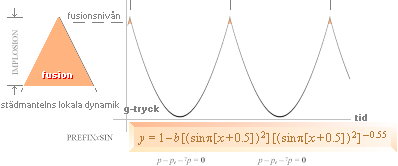
Fusionsperiodens principiella cykliska förlopp. Endast en liten del av kurvytan innefattar själva fusionsfasen eller fusionspulsen.

Fusionscykelns allmänna verkan:

Eftersom stjärnan strängt taget också tappar en ytterst liten del av sin massa genom varje ny fusionsfas, kan den inte (riktigt) hitta en exakt återkommande period (t_P). I tidens längd bör perioden som sådan bli (marginellt) kortare — också med tanke på att Solkroppen kontinuerligt genomgår ämnesändring (central täthetsökning) tillsammans med den marginella massförlusten, och därmed täthetsändring: mindre massa, kortare period.

Vi kommer dock här (i allmänhet där inget annat anges) att räkna med en exakt period (t_P) motsvarande vad som gäller vid stjärnans primära födelse då massbortfallet i vilket fall i sammanhanget är försumbart (totalt ca 0,7% för Solens del).

Längre fram i den här beskrivningen ges en allmän härledning till fusionsperiodens längd t_P (se fusionsperiodens beräkning). I denna ingår elektronskiktets tjocklek som en avgörande parameter och som kommer från härledningen till Solens elektrogravitella radie; Om elektronskiktets tjocklek i en godtycklig primärstjärnas stjärnyta varierar som effekten mellan olika stjärnor, alltså enligt koefficienten (mSTAR/mSUN)³ [Se STJÄRNORNAS EFFEKT], ges t_P ett initiellt högre värde för en allt mindre stjärnas egenmassa (minimum mSOL/165). Mindre stjärnmassa ger alltså LÄNGRE period; Tunga stjärnor får korta perioder, motsvarande en häftigare förbränning (se även Massa-Luminositetsrelationen). Denna aspekt berör bara själva stjärnans egenmassa, inte vad som händer under stjärnans brinntid;

OM, under stjärnans aktuella brinntid, städradien (och elektronskiktet, vilket här frånses) minskar blott med mycket små värden (runt 50 meter från start för att få den nu beräknade medelperioden på 11,1 år, se från fusionsperioden), förkortas perioden (t_P) med stjärnans brinntid. Det ger linjärt ENLIGT TNED (se utförligt i fusionsperioden) att städradien minskar med 50(121/21)=288 meter under Solens hela livslängd (121 miljarder år med ideal förbränning 100% Väte-1 till 100% Helium-4). Eller (50/21) runt 2,4 meter per miljard år; 2,64 t8 meter (26 nM) per varje 11,1-årspuls. Här bör dock också omnämnas att det (verkligen) finns flera svårigheter i de ingående parametrarnas (exakta) beräkning och som gör att vi (likväl) måste iaktta en viss försiktighet i alltför förhastade slutsatser; Solfysiken ökar i svårighetsgrad ju mer exakt vi försöker härleda den (parametrarna blir flera, som t.ex. här med införande av antydda parametrar som beskriver hur en stjärna ändras i sin ämnessammansättning under brinntiden).

implosion

Under den korta fusionsfasen bildas också en (betydande) implosion (komprimerande explosion) eftersom antalet atomkärnor per bildad Helium-4-kärna minskar med tre kärnor: från fyra Väte-1 till en Helium-4. Implosionen betyder samma som att det fusionsbärande mantelskiktet kollapsar (störtar in) när fusionsvågen går.

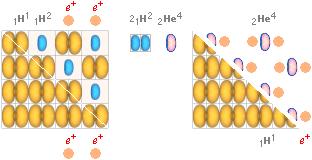
Utrymmet ökar genom fusionsfasen från fyra toroider Väte-1 till en Helium-4. Positronmassornas utrymme (e⁺) betraktas här i vilket fall försumbart.

För atomkärnans geometri, se atomkärnans härledning från Planckringen. Se även i Planckringens Dimensioner.

Implosionens allmänna verkan

Implosionsvågen drar (naturligtvis) med sig skikten ovanför och sprids därmed ända upp till Solytan, där den reflekteras av Solens g-sfär (mekaniska vågenergin stannar inom Solklotet, se vidare i VÅGENERGIN och Reflexionsgränsen) och kastas tillbaka som rekyl mot städmanteln (se Rekylvågen) — där den följaktligen adderas med g-trycket. Därmed måste vi också (optimalt) räkna med att fusionsperioden uppvisar (minst två) OLIKA triggpunkter: En som ger en något kraftigare tryckverkan (när rekylvågen sätts ihop med den normala g-verkan) och en som ger den normala. Enligt TNED är det (tydligen) denna rekylvågseffekt som ligger till grund för Solmagnetismens periodiska ändring (se utförligt från Solens allmänna magnetfält, där ges också en kvantitativ härledning).

Om det tar tiden t_P för strålenergin=vågenergin att gå mellan Solcentrum och Solytan och för strålenergins del precis börja stråla ut från Solytan efter t_P, och det tar lika lång tid t_P för den mekaniskt reflekterade rekylvågen att komma åter till Solcentrum, idealt baklänges till exakt samma ställe vid nodkällan, är det tydligt att g-trycket får extra hjälp. Därmed får påföljande fusionsfas ett motsvarande något större masstryck än normalt. Men eftersom den mekaniska vågenergin måste stanna inom Solklotet och den är lika med strålenergin [Se STRÅLENERGIN=VÅGENERGIN], framtvingas en fördelning i nästföljande fusionsfas med ett motsvarande mindre masstryck så att summan för de två något olika delperioderna går på ett ut. Solkroppen MÅSTE i vilket fall självjustera sin inre vågfysik så att korrekt energiräkning ges i slutänden. [Sedan kan vi alltid bry våra huvuden med frågan om exakt hur justeringen går till; Den frågan är för tillfället (här) inte den överhängande].

Framställningen fortsätter nedan i Fusionsfasens omfattning.

Innehåll i sammanfattning · Solens energiproduktion

Solperioden

Flera orsaker finns varför modern teori garanterat inte kan härleda Solens elementära basfysik — den är enkel, inte komplicerad:

t_P = A_Rm_0TRANSIT^–1h_r(r_Cr_r)^1/2 · 1S = 3,610545534 T8 S = 11,44112839 år

gäller från Solens första dag (medelvärdet nu är ca 11,1 år: Solkroppen genomgår kontinuerlig täthetsändring som påverkar perioden med ytterst små värden)

A_R=(4pR²), R=Ekvivalenta Städradien=4012 M för Solen, r_C=8,13444 T16 KG/M³ Ekvivalenta Städkärnans maximala Coulombtäthet, (atomkärnorna vidrör varandras omskrivna sfärer)

h_r=Ekvivalenta isolerade elektronskiktets tjocklek i Solytan = 340 KM beräknas från Solens elektrogravitella radie r_G=6,97 T8 M …,

r_r=8,9277145 t5 KG/M³ Ekvivalenta yttätheten, m_0TRANSIT=5,15021 T11 KG via Solära Råeffekten P_R=3,3 T26 W;

med Solens fotometriska effekt P=3,84 T26 W ges m_0TRANSIT ca 6 T11 KG och t_P endast 9,82 år: inte så träffsäkert.

Solmagnetismen

Variationerna i Solens polära magnetiska fält på observerade ±50 G (1G=0,0001 T) med maximala variationer ute vid Jordbanan på ±50 nT, förklaras genom helt ideala parametrar i Solenergiräkningen:

SOLENS RÅEFFEKT P = A²r_r²Gc₀/18 = A²e₀ (1VM^–1C^–1S^–3KG) = 3,3 T26 W producerar per sekund totalt 15,4 T37 positronmassor med fusionerna från fyra Väte-1 till en Helium-4 och som måste brännas av i samma takt per sekund:

MOTSVARANDE ELEKTRONbrännmassan förlagd IDEALT till Solytan (ideal polarisation) tagen på Solekvatoriella SIDERISKA omloppstiden 25 dygn ger GRUNDSTRÖMSTYRKAN

I(e^–)₀ = (15,4 T37 × 1,602 t19 C = 2,46708 T19 C)/(86400S×25dygn) = 1,14216 T13 A

som på runt 11 år (160,71 stycken 25-varvsintervall) ackumuleras till

I(e^–)_tP » 1,84 T15 A konstanta ytsolära elektronströmmens ekvivalent

För att den strömmen tillsammans med en inre motriktad positiv jonström ska åstadkomma observerade ±50 Gauss vid Solpolerna,

krävs motsvarande inre Ekvivalenta Solära effektiva kärnströmmen på Ekvivalenta Solstädets radie (R) enligt värdena nedan,

polära I(Q⁺) Ampere I(e^–) Ampere BP(Q⁺) Gauss BP(e^–) Gauss BP Gauss

3,17587 T24 1,84 T15 +5918,46 –5868,47 +50,00

3,12221 T24 1,84 T15 +5818,46 –5868,47 –50,00 relation 1,0171865 differens 5,366 T22

DEN idealt joniserade motsvarande inre Solkärnan med maximal Coulombtäthet (atomkärnorna ligger helt nära varandra) åstadkommer en IDEAL AVSKÄRMNINGSEFFEKT som tillsammans med en förmodad högre inre ekvivalent rotation i Solkärnan resulterar i en viss relation mellan inre kärnström och yttre ekvatorialström; Ekvatorialströmmen motsvarande värden ute vid Jordbanan blir med ringens förenklade modellform (se separat modellredovisning)

ekvatoriella I(A) A I(A0) A B(JORD) nT

4,61451 T18 1,84 T15 –50,0000

1,38434 T17 1,84 T15 +50,0000 relation 0,03 differens 4,47607 T18

Solmagnetfältets periodiska växling ±50 G

Solmagnetfältets periodiska växling ±50 G bygger på ekvivalens mellan strålenergi och mekanisk vågenergi; Vågenergin stannar kvar inom Solkroppen medan strålenergin kontinuerligt passerar ut från Solen;

NOTERA ATT DEN IDEALA SOLFYSIKENS MODELL INTE KAN HÄRLEDAS AV DEN MODERNA TEORINS FÖRUTSÄTTNINGAR. Se utförligt från den Moderna Akademins Solteori;

Vågenergin i samband med DEN IDEALA FUSIONSMEKANIKEN I SOLKÄRNAN bildar en rekylvåg som efter första fusionsvågen återkommer till Solkärnan efter 2t_P: Det tar tiden t_P upp till Solytan, och sedan tiden t_P tillbaka ner; rekylvågen adderas till reguljära gravitella tryckvågen, en extraeffekt bildas och som sedan av ekvivalensen mellan vågenergi och strålenergi garanterar att endast 3:e, 5:e, 7:e, 9:e osv. fusionsvågorna tillåts summera med rekylvågor; därmed kan den något högre udda strömstyrkan på 3,17587 T24 A styras ut via rekylvågen; Solen tvingas av sin egen energiräkning självreglera jämna fusionsvågor på den något lägre strömstyrkan 3,12221 T24 A. Därmed återkommer Solmagnetiska polfältet med samma magnetiska pol en gång per dubbla Solperioden (i medeltal runt drygt 22 år).

Solfläckarnas uppkomst

Solfläckarnas uppkomst relateras till de ur Deuteriumfusionerna producerade EKVIVALENTA POSITRONMASSORNAS UPPSTIGANDE FRÅN SOLSTÄDET TILL OCH FÖRBRÄNNING I SOLYTANS ELEKTRONSKIKT.

Inget mer. Inget mindre.

Strömvärdena stämmer, såväl som det medelmässiga solfläcksantalet relaterat till Solens medelenergi, såväl som solfläckarnas polariteter med fenomenen typ flares och dess detaljer.

Fusionsfasens omfattning

FUSIONSFASENS OMFATTNING

6 T11 KG transitmassa per sekund — baserat på Solens fotometriska effekt (3,84 T26 W) avrundad som 4 T26 W. Se vidare från Energireferensen.

Fusionsvågen börjar vid polerna

se även från FUSIONSVÅGORNA I SOLEN i FUSIONSVÅGENS PERIOD

IDEALT för en helt oroterad stjärnkropp verkar det fusionstriggande g-övertrycket HOMOGENT över hela städytan.

Det betyder att fusionerna börjar samtidigt, överallt, i ett givet ytskal i städklotet och med den fusionskraft som anvisas av g-övertrycket — specifikt för varje given stjärnmassa — enligt allmänna tryckekvationen (^gp=p–p_e).

Uppvisar städklotet rotation

vilket bör vara fallet för samtliga stjärnor, initiellt genom primärbildningarna i K-cellens expansion — om än rotationen normalt sett anses försvinnande liten

motverkas g-trycket av centrifugalkraften och därmed en reduktion i nukleära barriärtrycket [Se NUKLIDBARRIÄREN] — vilket innebär att ett lokalt största punkttryck uppstår vid rotationsnoden — städmantelns tunnaste område.

Det BÖR alltså bli från rotationspolerna

som vi har en viss rätt att förvänta oss att den periodiska fusionsvågen tvunget utgår —

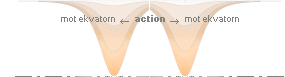
och avtar i styrka mot ekvatorn.

fusionsvågen

Fusionsvågen

Vågen som börjar vid rotationspolen (eller där g-trycket är som störst) och drar sig mot ekvatorn kallas här en fusionsvåg.

Fusionsvågens period

FUSIONSVÅGENS PERIOD

PER SEKUND omsätts avrundat (se beräkningsblocket nedan) ca 6 T11 KG material vid Solens centrala städ med konventionella fotometriska Soleffekten avrundat 4 T26 W, vilket skulle motsvara en fusionsperiod på 1 Hz.

energireferens

4([14,5–1,5=13] m_{e 9,11521 t31})c_3T8²=4,26591 t12 J ............. energin från fyra väteatomer till en helium-4-atom

3,3011376 T26 W ..................................................................... Energiutgivningen per sekund enligt TNED, se Solära Råeffekten

Se även mera utförligt i Solens Råeffekt, Solens Fotometriska Effekt

Antal H-He-fusioner per S: (3,3 T26 W)/(4,3 t12 WS) @ 7,7 T37

sekundTransitMassan

He-4-massa: 4×1,66033 t27 KG × 7,7 T37 = 5,11381 T11 KG @ 5 T11 KG per S = m_0TRANSIT1

mera noggrant

m_0TRANSIT1 = 4uP·1S/4 · 13m_euc₀² = P/(m_DHe4–m_DH1)c₀²·1S

= (3,3011376 T26 W)·1S/13(0,000548598)(2,99792458 T8 M/S)²

= 5,15021 T11 KG

Med konventionella avrundade effektvärdet P = 4 T26 W ges

He-4-massa: 4×1,66033 t27 KG × 9,3 T37 = 6,17642 T11 KG @ 6 T11 KG per S = m_0TRANSIT2

Mantelskiktet kring städkärnan för det fallet skulle emellertid bli endast en handfull atomkärnor;

(13 st; Kvadratiska kärnytan [Se PLANCKRINGENS DIMENSIONER] [2×1,37 t15 M]² fyller på städytan 4p[4012 M]² antalet 2,6942 T37 sådana; 6 T11 KG Väte-1-kärnor [största tätheten] innehåller

6 T 11 KG/[1,0078252×1,66033 t27 KG]=3,58568 T38 sådana; med (3,58568 T38)/(2,6942 T37) ges 13,308865 stycken tätt närliggande skikt av angränsande atomkärnor).

Problemet att finna extremgränserna för fusionsperioden (mera exakt) inger oss (här) en viss nedstämd förhoppning av typen komplicerad — eftersom vi inte vet städkroppens termiska (neutrino-) isolation. Det finns emellertid en helt säker genväg och som ansluter till effektberäkningarna genom Stefan-Boltzmanns strålningslag. Vi studerar hur.

TERSAFE

Termiska sämsta fallets avkylningssamband

E

N KROPP MED YTAN A som utstrålar energin E per sekund lika med effekten P=E/t återfaller för sämsta fallets fysik på den atomära kärnyta som kroppsmassans atomer bildar tillsammans; Nämligen i Planckstrålningens ljus med alla möjliga våglängder representerade i atomkärnans genomströmning som absolut sämsta fallets generatris till värmeflödet. TIDEN i sämsta fallet, lika med en garanterad absolut minsta tid (t_P) som värmeflödet fortsätter utan ändring sedan P nollas, upphör, stängs av, blir då (helt enkelt) kärnytan dividerad med kroppsytan

t_P = A_K/A · 1S

Kvoten A_K/A anger antalet energigenomströmningssekunder med E/1S=P. Därmed kan vi — helt säkert — beräkna Soleffektens absolut minsta kontinuerliga effekttidrymd — OM fusionsenergin ges intermittent, alltså stötvis.

ANALOGT EXEMPEL:

Minsta spisplattan i köket (normal standard Järn56) är ca 15 cM tvärs; ytan är 0,0176714 M². Med utstrålning på baksidan ges minst ytan runt 0,03 M². Om plattan håller 1 KG Fe56 består den av runt 1/(56u_{1,66033 t27 KG})=1 T25 atomer; Varje järnatom i TNED har approximativt topptoroidytan (se bihangsblocket nedan)

[2p · (r₀56^1/3)/2]²@2,7 t28 M², vilket totalt för plattans 1 KG järnatomer ger kärnytan

(1 T25)(1 t27)@0,003 M² ;

Sluträkningen t_P=0,003/0,03 ger då att plattan kommer att utstråla den värmeeffekt den hade då den stängdes av under MINST

t_P=0,003/0,03 = 0,1 sekunder — efter avstängningen. Helt säkert.

N

u kan vi räkna på Solen på precis samma sätt.

Med E=Pt genom en (1) Solyta (A) per sekund ges t_P stycken Solytor i totala kärnytan

A_K:

(A_K/[A/1S]) = t_P;

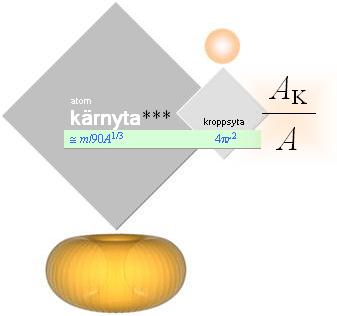
*** samband: toroidala toppkärnytan TNED [Se även allmänt i PLANCKRINGENS DIMENSIONER]:

A_K = (m/Uu)(pr)² ; topptoroidytan approximerad (pr)²

r @ r₀A^1/3 ; (gäller ej för A från 2 till 4; r_A=2=0,71r₀; r_A=3=0,95r₀; r_A=4=r₀)

U @ A = masstal ;

r₀ = 1,37 t15 M ;

A_K @ (m/Au)(pr₀A^1/3)² = mA^–1/3(pr₀)²/u = mA^–1/3(pr₀)²/u = mA^–1/3(0,0111569) ;

A_K @ m/90A^1/3 ; (uppskattat max 5% fel)

Toroidytan för protonen med r₀=1,37 t15 M fås approximativt genom rotationen av omkretsen

2p(r₀/2) [se även GULDINS REGLER] hos toroidringen via toppspinnets rotationscirkel med approximativt samma mått, alltså totalt A=(pr₀)².

Kärnradien (r) för övriga kärnor ges approximativt r=r₀A^1/3 med A som kärnans masstal.

Vi beräknar t_P (samt en del andra) enligt följande;

fusionsvågens

svephastighet

t_e

FUSIONSVÅGENS SVEPHASTIGHET genom städytan kan bestämmas (sämsta fallet) med hjälp av atomkärnans (förenklade) barriärparametrar (Väte-1-bas) via elektriska kraften F=123 N som ger deformationshastigheten i vågen v=aT=Ö 2Fr/m=1,4191817 T7 M/S (@ 0,05c). Från nodpunkten till städekvatorn med radien R=4012 M i Solens fall, ges tiden

t_e = (2pR/4)/v = 4,44061 t4 S

@ 0,4 mS

Vi får dock inte utesluta att den verkliga löptiden blir (betydligt) längre — vi känner ännu inte den fysiken exakt.

elektriska barriärkraften

Minsta barriärkraften med Väte-1 är F=k_{9 T9 VM/C}(Q_{1,602 t19 C}/r_{1,37 t15 M})²@123 N vid kärngränsens omskrivna sfär och därmed densamma minsta kraft, sämsta fallet, med vilken fusionerande nuklider attraheras innanför barriärzonen. Den attraherande accelerationen över r, sämsta fallet med Väte-1, blir då

a=F/m=7,35064 T28 M/S² på tiden T=Ö(2r/a)=1,93068 t22 S, vilket ger hastigheten över Coulombbarriären

v=aT=Ö 2Fr/m=1,4191817 T7 M/S (@ 0,05c).

Absoluta periodgränserna

Från TERSAFE — Se beskrivningen från Fusionsvågens period

ABSOLUTA PERIODGRÄNSERNA

FÖRUTSATT ABSOLUT JÄMN EFFEKTUTSTRÅLNING UTAN MELLANLIGGANDE AVBROTT

kortaste fusionsperioden

t_Pmin 33 sekunder

TRANSITMASSAN (Väte-1-bas) på m=6 T11 KG per sekund (4 Väte-1 till 1 Helium-4 med effekten 4 T26 W) anställer en lägsta atommassa vars effektiva strålningsflöde minst per fusionsvåg genomtränger en energiyta motsvarande städytan (R=4012 M se Städradien) och som ger absolut kortaste fusionsvågens period på

33 sekunder — absolut inte under några som helst omständigheter mindre enligt ovanstående kärn-effekt-tekniska förutsättningar — enligt följande:

t_P = A_K/A · 1S = ([6 T11 KG]/90)/(4p· [4012 M]²) @ 33 S

För att upprätthålla effekten jämnt utan avbrott blir transitmassan motsvarande större med t_P-värdet;

Tjockleken på fusionsskalet i städet (eftersom det i vilket fall är mycket tunt kan beräkningen förenklas enligt r_C=m/A_Rh) kan då beräknas, sämsta fallet:

h = m_TRANSIT/A_Rr_C. Med t_P=33 S ges absolut minsta städmantelns tjocklek

h = (33×6 T11 KG)/(2 T8 M²)(8,13444 T16 KG/M³)

= 1,2 t12 M = 1,2 pM.

längsta fusionsperioden

t_Pmax 115 år

HELA SOLMASSAN m=1,989 T30 KG innesluten av hela det synliga Solklotets g-radie med ytan A=4p(6,97 T8 M)² anställer på samma sätt en största atommassa vars effektiva strålningsflöde minst per fusionsvåg genomtränger Solens g-yta och som ger absolut längsta fusionsvågens period på

115 år:

t_P = A_K/A · 1S = ([1,989 T30 KG]/90)/(4p· [6,97 T8 M]²) = 3,62006 T9 S

För att upprätthålla effekten jämnt utan avbrott blir transitmassan motsvarande större med t_P-värdet;

Tjockleken på fusionsskalet i städet kan då beräknas, sämsta fallet:

h = m_TRANSIT/A_Rr_C. Med t_P=3,63047 T9 S ges absolut minsta städmantelns tjocklek

h = (3,62006 T9×6 T11 KG)/(2 T8 M²)(8,13444 T16 KG/M³) = 1,33508 t4 M.

RESULTAT

(ref. P_SOL=4 T26 W):

Solstädets fusionsmantel är ENLIGT TNED

inte mindre än 1,2 pM (= 0,000 000 000 001 2 M = 1,2 t12 M), och

inte större än 0,134 mM (= 0,000 134 M = 1,34 t4 M)

Fusionsperiodens detaljer

Om vi strängt håller oss till en energibeskrivning som går ut på villkoret att hålla effektflödet konstant så att inga (medelmässiga) luckor visar sig, utkristalliseras den periodiska ordningen (tP) naturligt — enligt nedanstående illustrerade beskrivning i översikt.

fusionsperiodens detaljer

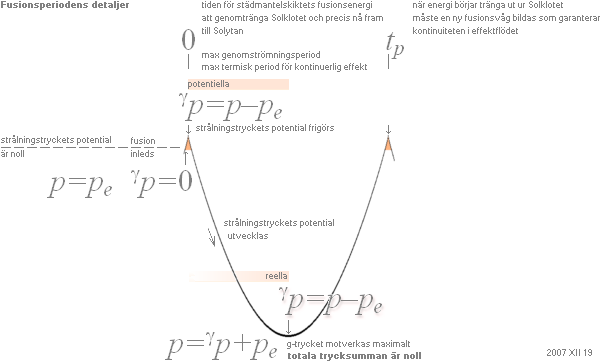
beskrivning

Max termisk period för kontinuerlig effekt. Med tiden (t_P) för energin från föregående fusionsfas att helt fylla upp Solklotet, från städytan till Solens g-radie och därmed precis nå fram till Solytan — för att därifrån sedan börja stråla ut — är det tydligt att den utfyllnadsdelen också samtidigt börjar avta med utstrålningen från Solytan.

För att Soleffekten inte ska uppvisa luckor eller avbrott

— och förutsatt kontinuerligt effektflöde från Solytan,

som därmed också kommer att innefatta definitionen på största möjliga tidsperioden för fusionsvågens nybildning,

analogt max termisk period för kontinuerlig effekt

— ska därmed en ny fusionsfas inledas (exakt) då stråleffekten från föregående fusionsfas börjar uttränga ur Solytan. Perioden t_P,

Strålningstrycket (^gp) som frigörs (potentiellt) under den korta fusionsfasen (t_F, se den orangefärgade toppen på ovanstående kurvform), kräver i strålutbredningens och den termiska isolationens försorg en viss tid för att breda ut sig och motverka g-trycket maximalt. Under den korta tidsperioden (t_F) råder alltså (idealt) jämvikt mellan g-trycket och strålningstrycket tillsammans med Coulombtrycket (p_e), p=^gp+p_e. Därifrån avtar sedan strålningstryckets inverkan och går mot noll vid gränsen (kurvans bottenpunkt) där g-trycket genom sin ekvivalens med Coulombtrycket (p_e) återigen precis är på väg att förbereda nästa fusionsfas (^gp=0). Är stjärnmassan då (fortfarande) större än m_0SLIM trycks atomkärnorna in över varandras nuklidbarriärrer och en fusionsfas inleds (återigen) med frigörande av strålningstryckets potential enligt (m®g).

I följd av de ovan beskrivna detaljerna för fusionsperioden (t_P) är det alltså tydligt att man kan formulera saken så att en ny fusionsfas inleds (idealt) precis då materialet, implosionsvågen och stråleffekten från föregående fusionsfas når upp till Solytan. Eller sagt på annat sätt: Varje fusionsfas bildar material och effekt som tar tiden t_P sekunder att nå upp till Solytan — och sedan (sämsta fallet) lika lång tid att uttömma sig ur Solklotet. Med andra ord 2t_P. Illustrationen nedan visar synkroniseringens konsekvenser.

fusionsperiodens

synkronisering

För att säkra överlappningen med början från uttömningen ur Solklotet måste alltså en andra fusionsvåg fungera synkroniserat med den första så att när stråleffekten från den första vågen precis lämnat Solkroppen, stråleffekten från den andra också, just, precis har nått fram till Solytan och därmed kan fortsätta där den föregående slutade, samma konstanta effekt.

Det är i summering den exakta ordning som ENLIGT TNED ställs upp av fusionsfysiken enbart med villkoret att Soleffekten ska synas kontinuerlig: utan avbrott.

EXPERIMENTELL BEKRÄFTELSE PÅ KONTINUERLIGA EFFEKTVILLKORET

Jämför citat:

”Fossila fynd på jorden ger vi handen att solen har strålat ut energi i ungefär samma takt som nu i ca 4 × 10⁹ år.”

BONNIERS ASTRONOMI 1978 s50sp2ö

”Vi har som ovan nämnts säkra geologiska indicier för att den mängd solstrålning som jorden per tidsenhet tagit emot förändrats mycket litet på de 4,5 × 10⁹ år som jorden existerat.”

BONNIERS ASTRONOMI 1978 s55sp1ö

Med ovanstående, i citat redovisade experimentellt observerade grund antagen som definitiv, är det tydligt att Solen också i praktiken utstrålar sin effekt praktiskt taget kontinuerligt, utan avbrott. Därmed är (så långt) det teoretiska effektvillkoret certifierat-garanterat som praktiskt relevant.

Positronmassans uttömning i Solytan

Sammansättningen av fusionsvågorna 1 och 2 från Fusionsperiodens synkronisering bildar i Solytan en uttömmande funktion som kan återföras på den bildade positronmassan från de nyligen beskrivna fusionsvågorna 1 och 2. Funktionsformen för positronmassans avbränning i Solytan får då utseendet enligt nedanstående typgrafer.

Positronmassans

uttömning i Solytan

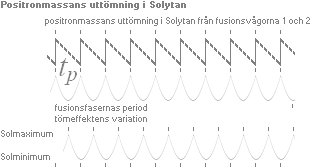
Avbränningen med positron-elektronmassornas procentuella andel av den utstrålande Solenergin uppgår till endast ca 7,5% (se redovisning nedan).

SOLFUSIONSENERGIN — resultaträkning med 4Väteatomer till 1Heliumatom

Den avgjort största andelen energi 92,5% som Solen producerar består av icke parannihilerad strålning. Den parannihilerade strålningen upptar bara 7,5%.

[Parannihilation kallas den ömsesidiga massförintelsen av en elektron och en positron].

Nettoenergin från fyra Väte-1-atomer till en Helium-4-atom, ±e inkluderat, frigör (u=1,66033 t27 KG)

(K1+K2) – K = (m®g)

4(1,007825u) – (4,002603u) = 26,73126384 MeV

Av denna energi utgörs endast 2MeV av parannihilationer (2 par ±e med 1MeV per par); 1 par ±e ger

E = (2m_e)c² = (2×0,000548598u)(2,99792458 T8 M)²

= 1,63726 t13 J; E/(Q_e=1,602 t19 C)/T6 = 1,0220155 MeV; 2 par ger

2×2m_e(MeV) = 2,044031

(2,044031)/(26,73126384) = 0,0764659 » 7,5% grovt avrundat

När positronmassorna först dyker upp i den elektronrika Solytan börjar uttömningen från noll, växer till ett maximum och avtar sedan åter mot noll innan nästa positronskeppning anländer. Därmed kan positronavbränningen i Solytan ställas på samma typgrafiska funktion som fusionsgrafen [Se Fusionsperiodens detaljer], men med en offset på t_P/2 relativt t_P, se den undre grafen ovan benämnd tömeffektens variation. Vi kan också kalla den speciellt för Solmaximums vågfunktion. Denna del beskriver ett motsvarande Solmaximum då aktiviteten totalt från de uppvällande positronmassorna når maximum, vilket blir ungefär i mitten av tömgrafens fallande flank. Vid positronavbränningscykelns slut, och därmed början på nästa avbränningsfas, råder ett motsvarande Solminimum.

Eftersom e⁺-massan dels bildas genom en fusionsvåg som går från städpol till städekvator och dels drivs ut från Solstädet av strålningstrycket (och i viss mån av attraktionen mot Solytans utpräglade elektronbesättningar), men tvingas rotera kring det lokala magnetfält som för tillfället är det förhärskande (och som idealt genomtränger Solstädet), samt att lika laddningar i samma strömriktning strävar att rätta in sig på gemensam färdlinje i den inbördes ömsesidiga magnetiska inverkan, är det tydligt att

e⁺-materialet från fusionsfasen tvunget måste dyka upp i annihilerande förening med elektronmassan i Solytan medelmässigt periodiskt vid en viss högsta latitud — aldrig direkt från rotationspolerna.

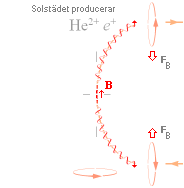
FUNKTIONSSÄTTET ENLIGT TNED. Positronmassan tillsammans med det bildade Heliet drivs mot Solytan av strålningstrycket och tvingas därmed gå i spiral uppåt kring det lokala magnetfältet vare sig detta är av den ena eller den andra polariteten. Laddningen kan inte undfly denna spiralbana, som därmed påtvingar laddningen en lång färdtid upp till ytan. Genom ömsesidig magnetisk fältverkan dras samtidigt de positiva laddningarna mot varandra (F_B) enligt kända elementära verkningssätt för magnetismen.

Positronmassans

latitudella variation

Motsvarande verkningssätt för positronmassans latitudella uppdykande och utebbande i Solytan får därmed samma grafiska typform som den ovan visade för positronmassan uttömning. Graferna nedan visar den respektive ordningen med hänsyn till de bägge rotations-, analogt ovannämnda, fusionsnoderna.

Positronmassans latitudella variation eller latitudgränsernas vågfunktion (övre delen ovan) kan beskrivas matematiskt i PREFIXxSIN på formen

y = –a(b[cos px][sin px])([sin px]²)^–0.55 .................... latitudgränsernas vågfunktion

Denna funktionsform (inte en helt rät linje) utgör (nämligen) dynamiska komplementet till den föregående beskrivna CYKLISKT BASERADE fusionsperiodens vågfunktion,

y = a–[(sin px)²][(sin px)²]^–0.55 ................................ fusionsperiodens vågfunktion

Dessa bägge ekvationer beskriver (nämligen) tillsammans den fullständiga (elementära) ordningen för en roterande kropp (ring) som expanderar och kontraherar periodiskt (pulsning med rotation). Sambanden är exakt desamma som används i den elementära beskrivningen av Pulsarerna enligt TNED.

jämförande grunddata

Jämför grunddata genom observationer:

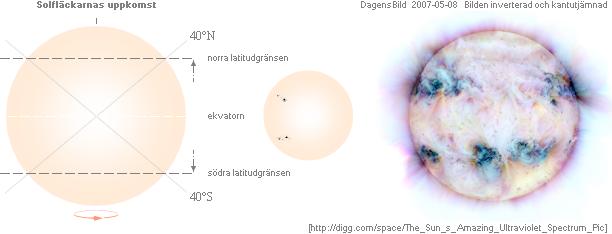
Höger: Bild av Solen i uv-ljus där Solfläcksbandets strålande aktiviteter framgår tydligt i analogi med (efterklangen från) effekterna av polfusionerna enligt TNED. Bilden kopierad (inverterad och kantutjämnad) från @INTERNETkällan

http://digg.com/space/The_Sun_s_Amazing_Ultraviolet_Spectrum_Pic

; (Dagens Bild 2007-05-08):

Sun_uvsun_trace_big.jpg

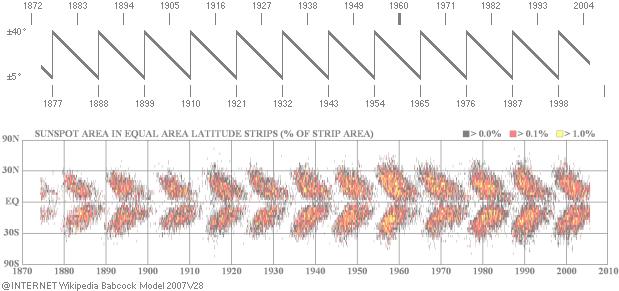
· Solfläckarnas livslängd: dagar till månader.

· Solfläckarna dras successivt mot ekvatorn, nya uppträder från allt lägre, sekundära latitudgränser.

· Efter en medelperiod på 11år (lägst 7, högst 17 [BAs140sp2n]) dyker nya fläckar upp igen vid primära latitudgränserna (vid max ±40°; olika källor anger olika värden).

· Solfläckarnas antal är litet i cykelns början [@INTERNET Wikipedia Sun 2007-05-27], och växer sedan till ett maximum (efter 5-6 år).

· Solfläckarna försvinner slutligen vid ca ±5° [BAs141sp1ö] varvid nya dyker upp igen vid de övre gränserna.

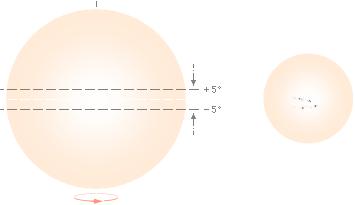
Nedanstående diagram visar det karaktäristiska s.k. fjärilsdiagrammet för Solfläckarna i förekomst och spridning under varje period.

Sett i stort är det tydligt att diagrammets allmänna form avspeglar den ovan beskrivna tömgrafens form (positronmassans latitudella variation).

fjärilsdiagrammet

praktiska Solvärdet t_P

SOLENS t_P ENLIGT TNED BÖRJAR FRÅN 11,44 ÅR

Av ovanstående genomgång (se från Fusionsvågens period) är det tydligt att fusionsvågens period bör vara identisk med den observerade s.k. Solcykelns period på (i medeltal avrundat) 11 år [perioderna varierar mellan lägst 7 år och högst 17 år, ref. BAs140sp2n]. TNED ger värdet 11,44 år från Solens första dag. Se vidare i Solens Fusionsperiod.

Framställningen fortsätter med beskrivningen av VÅGENERGIN nedan.

Vågenergin | 2008I3 | SunFusion.doc

VÅGENERGIN

VÅGENERGIN

VÅGENERGINS BILDNING FRÅN SOLENS CENTRALA STÄDKÄRNA

Vågen bildas …

VÅGENERGINS GENERATRIS är Coulombrepulsionens KOLLAPS — då g-trycket precis pressar atomkärnorna över nuklidbarriärerna och kärnorna börjar förenas. [Se utförligt från STJÄRNORNAS ALLMÄNNA TRYCKEKVATION]. VID den tidpunkten utvecklas ÄNNU ingen fusionsenergi: Den instörtande KRAFTEN vid Coulombkollapsen bildar alltså

lika stor vågenergi som den kommande fusionskraften-strålningstrycket måste utveckla för att trycka tillbaka materialet i motsvarande jämvikt — så att g-kraften kan bilda en ny, liknande fusionsvåg med (i det närmaste) samma utvecklande effekt.

vågenergin = strålenergin

Med andra ord:

mekaniska vågenergin genom Coulombkollapsen som föregår fusionsfasen blir TVUNGET lika med strålenergin.

Vågenergin som utvecklas — föregående fusionsfasen — måste alltså vara lika stor som den energi som Solen utvecklar ur de aktuella fusionerna — per sekund. Energin från massdestruktionerna (m®g) runt 4 T26 J i fusionerna genomlöper med andra ord Solytan per sekund med samma värde som vågenergin från tryckrekylen som sammanhänger med fusionsbildningen.

;

DEN MEKANISKA VÅGENERGIN FRÅN FUSIONSFASEN är ENA HALVAN, med samma energibelopp, som andra halvan som är fusionsenergin och som »lyfter tillbaka» Coulombkollapsen så att en ny fusionsvåg återigen kan bildas genom g-trycket. Solen »pumpar», tydligen, på det sättet en och samma energi (4 T26 J) multiplexat i två faser; dels som (Coulombkollapsande) vågenergi, dels som (rekylerande) strålningsenergi.

vågenergin = strålenergin

Kraften som frigörs vid Coulombkollapsen (Coulombrepulsionen p_e kollapsar: E=Fd_DOWN) — vilket sker då gravitella övertrycket (p) pressar atomkärnorna över varandras nuklidbarriärer och fusionsfasen inleds — är lika stor som den kraft (: E=Fd_UP) som frigörs ur fusionsprocessen, som återställer balansen och som upprätthåller periodiciteten genom det motriktade strålningstrycket (^gp). Det finns, veterligt, ingen annan vågräkning att välja på.

Jämvikt råder då strålningstrycket precis uppväger den deformation som bildades av g-övertrycket (p–p_e) i TNED enligt stjärnornas allmänna tryckekvation,

p–p_e–^gp=0. Från denna punkt, då inget annat alternativ finns, bestäms perioden fram till nästa fusionstriggande genombrott av neutrinoisolationen eller värmetrögheten i den strålningsenergi som frigjordes ur fusionerna och som under viss tid konserveras av det täta materialet i städytan under Planckstrålningens uppbyggnad (Solens allmänna värmespektrum) och därmed åstadkommer en fördröjning tills dess g-övertrycket åter tar över.

Vågenergin E — den periodiska processen — i deformationen Fd_DOWN blir alltså ekvivalent med hela den energi Fd_UP som per sekund frigörs ur fusionerna — i Solens fall grovt 4 T26 W/S — och som tvunget fortplantas ut till Solytan och där åstadkommer ett mönster av »ringningar»; Den vågenergin stannar inom Solklotet, den slipper aldrig ut (vilket i så fall skulle krossa energiräkningen) och blir alltså integrerat ekvivalent med hela Solenergin, faktiskt, enligt ovanstående resonemang; Vågenergi och strålenergi får samma kvantitativa värde och upprätthålls i två faser:

en passiv icke fusionsbaserad gravitell konvergens och

en aktiv fusionsbaserad stråldivergens.

Vilket vill säga: Med hela Solens strålenergi E som lämnar, utgår ur, Solen, blir vågenergin från Fd_DOWN också lika med E, men vilken energi aldrig lämnar Solkroppen utan stannar kvar inom g-klotet och underhåller dess mekaniska svängningar eftersom dessa är en ren nödvändig konsekvens av bildningsmekanismen i fusionsbildningen. Det är uppenbarligen så avancerat det kan bli ur effektiviseringens synvinkel.

Vågenergins transport till Solytan · Frekvensrelationen

Fortsättning från Vågenergin

VÅGENERGINS TRANSPORT TILL SOLYTAN

FREKVENSRELATIONEN

f = c/l

NORMALT SETT: Om vi TILL EXEMPEL betraktar ett avsnitt av Stilla Havet inom 50 mil (500 KM) som plötsligt, inom en sekund, sjunker ner två decimeter på grund av en djuphavsförkastning som uppkommer som följd av kontinentalsocklarnas naturliga drift, betraktar vi teoretiskt en vattenvåg med amplituden 0,2M som tvingas dra över havet med hastigheten 500 KM/S. Om vi räknar helt förenklat rektangulärt med höjden 0,2M och bredden 500 000 M ges »vågytan» A=100 000 M².

När vågen kommer in mot land, där havet är betydligt grundare, pressas vågdjupet upp i amplitud. Följd: Våglängden minskar, samma nettoyta intakt (energiytan). Är våglängden säg d=1 KM blir våghöjden i princip h=A/d=100 M. Den vågen dränker effektivt allt i dess väg. [Samma havsvågrelaterade fenomen på Jordytan kallas Tsunami].

Illustrationen ovan visar principen för en sådan oceanisk jordbävningsvåg: våglängden avtar med avtagande vattendjup; frekvensen hålls konstant genom att hastigheten avtar i samma grad; f=c/d=konstant.

Vågenergins täthetsoberoende

Fortsättning från Vågenergin, Frekvensrelationen

VÅGENERGINS TÄTHETSOBEROENDE

VÅGENERGINS TÄTHETSOBEROENDE

I g-homogena material — som i exemplet ovan — förutsätter man att massan per meter är konstant i alla partier rR; m_r/d_r = m_R/d_R. Då gäller också en homogen integral metrik för energin som ytan av effektens funktion [f (P)] med avseende på tiden (dE=Pdt). För icke g-homogena material kan man substituera [alla substitutioner är giltiga genom a/a=1] tätheten (r, grek. rhå) enligt

(m_r/h_r²d_r)h_r² = (m_R/h_R²d_R)h_R² ; r_rh_r² = r_Rh_R² som ger

(h_r/h_R)² = r_R/r_r ;

h_r/h_R = Ö r_R/r_r ;

Solära ytenergikoefficienten

I Solens fall (Väte-1-bas) är ENLIGT TNED centraltätheten r_R=(8,13444 T16 KG/M³=r_C) och yttätheten vid Solens synliga rand r=6,96 T8 M lika med

r_r=(8,98 t5 KG/M³) vilket ganska precis ger Solära ytenergikoefficienten

h_r/h_R = 3,0 T10.

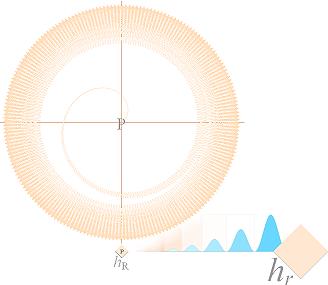
Energiytan som transporteras från Solens inre (h_R)² till Solens yttre (h_r)² är med hänsyn taget till de olika tätheterna en och samma enligt vågenergins täthetsoberoende: från fusionsmanteln i städytan till Solranden; h_r = h_RÖ r_R/r_r. Illustrationen ovan — spiralbildningen från Solens inre till dess yttre gränsradie — visar principen för vågfunktionens matematiska form

r = [A + a(x^3,5)cos nx^w]^{–1/(x+0,01)} i PREFIXxSIN, w=1

med utgångspunkt från det centrala Solstädet. Vågenergin stannar inom Solklotets g-radie medan strålenergin läcker ut.

Se mera utförligt nedan i Solens Allmänna Vågfunktion.

Solens fusionsperiod | 2008I5

Solens fusionsperiod

Fortsättning från Vågenergin, Frekvensrelationen, Vågenergins Täthetsoberoende

SOLENS FUSIONSPERIOD

SOLENS FUSIONSPERIOD —

11,44 år från start Enligt TNED

Från vågenergins täthetsoberoende

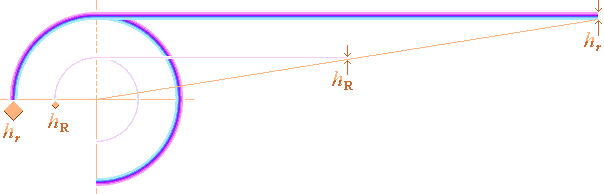
Illustrationen visar det förenklade sambandet från FUSIONSSKALETS TJOCKLEK tillsammans med principen som redovisas i VÅGENERGINS TÄTHETSOBEROENDE och som kopplar energitransiteringen mellan Solkärnan och Solytan. Genom denna enkla form visar det sig (nämligen) att fusionsperioden (t_P) kan beräknas analogt med den redan kända Solcykeln på runt 11 år; Se vidare nedan från Beskrivning. Sambandet för

FUSIONSSKALETS TJOCKLEK h=t_Pm_0TRANSIT/A_Rr_CS^–1 (transitmassans multipel blir t_P) är en praktisk förenkling från r_C=m/A_Rh då h-skiktet relativt r i vilket fall är mycket litet; I h_R-fallet gäller minsta 1,2 pM och största 0,134 mM från ABSOLUTA PERIODGRÄNSERNA genom TERSAFE (sämsta fallets säkra värden). Därmed är också beräkningsgrunden etablerad för fusionsperioden.

beskrivning

Motsvarande energiskikt i den lilla täta Solkärnan som bär ansvaret för att elektronmassan förs ut till Solytan i strålningstryckets försorg, är fusionsskalets tjocklek (h_R) i städklotets yta — 1,2 picometer för minsta manteltjockleken OM fusionsperioden är minsta värdet 33 sekunder och 0,134 millimeter för största manteltjockleken OM fusionsperioden är största värdet 115 år, se beräkningarna för t_P i Absoluta periodgränserna i Fusionsvågens period.

VÅGENERGINS TÄTHETSOBEROENDE h_r/h_R = Ö r_R/r_r

Elektronskiktets tjocklek i Solytan (h_r) kan då återföras på fusionsskalets tjocklek (h_R) genom vågenergins täthetsoberoende h_r/h_R=(r_R/r_r)^1/2 eftersom aktiviteten i h_R bär ansvaret för bildningen i h_r. Vilket vill säga: Hela Solmassans elektronbesättning etableras på Solytans yttersta skikt med höjden h_r genom fusionsenergins strålningstryck (^gp) från Solstädets tunna ytmantel h_R; Vågenergierna i de olika skikten h_rh_R är med hänsyn till de skilda tätheterna ekvivalenta.

DÅ, och endast då, kan också fusionsperioden (t_P) beräknas exakt initiellt för alla stjärnor med känd ämnesbas enligt sambandet för fusionsskalets tjocklek

h = t_Pm_0TRANSIT/A_Rr_C S^–1 (transitmassans multipel blir t_P)

via

t_P = hA_Rr_C/m_0TRANSIT S

med

h = h_R = h_rÖ r_r/r_R ; r_R = r_C ; r_Ch_R = r_Ch_rÖ r_r/r_R = h_rÖ r_Cr_r

från vågenergins täthetsoberoende

fusionsperioden

som ger PRIMÄRSTJÄRNANS FUSIONSPERIOD

t_P = A_Rm_0TRANSIT^–1h_r(r_Cr_r)^1/2 · 1S

rC ändras under primärstjärnans livstid maximalt från Väte-1 till Helium-4 med en faktor 4 (nuklidtätheten baseras på samma kärnradie med olika kärnmassa, se GrundNukliderna); Städradien R med given massa ändras med tätheten enligt (rCVäte/rCHelium)^1/3 = 0,25^1/3, Städytans ändring ger kvadraten 0,25^2/3; Totala koefficientändringen med städytan och tätheten ger en total reduktion för tP på 0,25^2/3 · 4^1/2 = 0,7937005 vid tiden för stjärnans Vätedöd; Värdena för yttätheten rr, elektronskalets tjocklek hr och transitmassan m0Transit betraktade som konstanta. Motsvarande reduktionsvärde från Solperiodens nuvarande observerade medelvärde 11,1 år mot det beräknade tp=11,44 år enligt nedan och som visar att Solen slutar på tp=9,4 år, blir 9,4/11,44=0,8216783;

Felet ligger på ca 3%(som kan tillskrivas fluktuationer i de angivna konstanterna).

tP för en godtycklig primärstjärna är längre för små stjärnor; Om elektronskiktets tjocklek i Solytan varierar som effekten mellan olika stjärnor, alltså enligt koefficienten (mSTAR/mSUN)³, antar t_P större värden då stjärnans egenmassa är allt lägre (minimum mSOL/165). Mindre stjärnmassa ger alltså LÄNGRE period. Denna aspekt berör bara själva stjärnans egenmassa, inte vad som händer under stjärnans brinntid; Med förutsättningarna beskrivna ovan förkortas tP under stjärnans brinntid på grund av att stjärnans inre täthet ökar (städradien avtar).

Faktorerna A_Rm_0TRANSIT(r_Cr_r)^1/2 är kända. A_R-värdet är stjärnstädets yta (4pR²) med städradien R=4012 M för Solen. r_C är (initiella) centraltätheten (med elektronmassan inberäknad) 8,13444 T16 KG/M³ och r_r är yttätheten 8,9277145 t5 KG/M³.

Elektronskiktets tjocklek h_r i Solytan kan beräknas genom sambandet för SOLENS ELEKTROGRAVITELLA RADIE (r_G=6,97 T8 M, fotometriska=synliga radien är mindre med ca 1000 KM). Det sker genom att i atomvikten (m_A) för stjärnans ämnesbas dels ta med elektronmassan som då ger den minsta Sol-g-radien, och dels utelämna elektronmassan i m_A — och som ENLIGT TNED är det praktiska fallet i hela Solklotet utom ytan — som då ger den största Sol-g-radien. Differensen mellan dessa ger h_r och man finner värdet (avrundat)

h_r = 340 KM

Med de mera noggrant valda parametervärdena (grundvärden utan avrundningar) ges då (medel-) värdet för Solens fusionsperiod från Solens första dag enligt

t_P = 11,44112839 år

från

t_P = h_RA_Rr_C/m_0TRANSIT S = (1,13015 t5 M)(2,02270111 T8 M²)(8,13444 T16 KG/M³)/(5,15021 T11 KG) · 1S

= 3,610545534 T8 S [se kalkylkort Solradien]

= 11,44112839 år ........................... Solens fusionsperiod från start

Faktiskt.

Enligt BONNIERS ASTRONOMI 1978 [BAs140sp2n] varierar Solcykelns medelvärde kring 11 år med som lägst 7 år och som mest 17 år.

Den nu (runt 2000) uppmätta Solcykelns medelperiod [ref. @INTERNET Wikipedia Solar cycle 2008-01-04] anges som

t_P = 11,1 år ........................................ det nu (efter runt 20 miljarder år) uppmätta medelvärdet

En annan källa (som inte redovisar sin preferens utom i rubriken nedan) anger

”Sun Spot Cycle 11.4 yr”

@INTERNET NASA 1 September 2004

nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html

2008-01-17

Denna sistnämnda uppgift behöver inte vara fel (men det är i detta skede ingen enkel uppgift att reda ut vad som menas genom att försöka gissa sig till vad citatförfattarna har tänkt på, det bästa är att fråga dem själva). Se vidare i Solfläckens uppkomst.

kalkylkort Solradien · se utförlig härledning i Solradien

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik1 Kalkylkort 2 — Solens gravitella radie — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

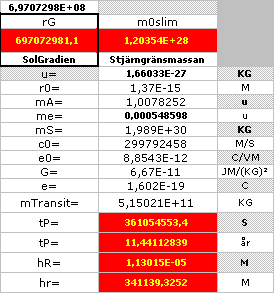
Kalkylkortet här endast i bild (kakylfunktionerna [från MsWorks 4.0] fungerar inte DIREKT i webbläsare).

TEORETISKT OCH PRAKTISKT t_P-VÄRDE

För att få 11,1-årsvärdet från t_P-formen ovan räcker det om Solens städradie R=4012 meter görs mindre med 52 meter — en minskning som KAN sammanhänga naturligt med Solens successiva ämnesändring till Helium-4 (runt 26 nM minskning per varje 11,1-årspuls), men som det ännu (2008-01-07) här inte finns någon analys på. (Att testa sådana beräkningsformer betyder att svårighetsgraden ökar betydligt eftersom allt flera parametervärden måste avstämmas allt mera noggrant, vilket kräver en allt mera ingående kännedom om detaljerna …).

Referens:

Flera källverk på @INTERNET redovisar Solperiodernas räkning (via solfläckarna) från (i varje fall) år 1700

(hela kataloger finns över solfläcksräkningar ända från 1700-talet

ftp://ftp.ngdc.noaa.gov/STP/SOLAR_DATA/

). Om vi gör en periodisk analys (med hjälp av FS-grafernas form) finner vi att vågtåget visserligen ingalunda helt perfekt täcker för de observerade topparna via motsvarande graftoppar, men att medelperioden på runt 11år (eller möjligen ett uns mindre) ändå i stort matchar hela observationsperioden.

Det är tydligt att det finns (flera mindre periodiska) inre fluktuationer, typ frekvensmodulationer, men ingenting är här (ännu 2008-02-08) känt om deras matematiska form i någon mening som skulle kunna beskriva variationernas ordning närmare.

Över kortare perioder av hela observationsintervallet (1700-NU2008) kan man f.ö. se nära överensstämmande intervall på lägst 10,8 och högst 11,1 år.

Förklaringen ENLIGT TNED till det nu lägre medelvärdet på 11,1 år relativt det teoretiskt beräknade utgångsvärdet på 11,44 år (3% skillnad) kan vara den följande.

Vartefter Solen producerar det tyngre Heliet från det lättare Vätet, genomgår det inre av Solen motsvarande täthetsändringar. Vi kan därför förmoda att startvärdet på runt 11,44 år — om nu det är det rätta — långsamt avtar mot kortare genom att städytan minskar något (m_0TRANSIT ändras endast försumbart marginellt); effektvärdets ändring har knappast någon märkbar inverkan eftersom massförlusten totalt för Solens hela livstid i det avseendet endast uppgår till runt 0,7%. Minskningen totalt måste alltså ligga på typformen

h_R(minskande)A_R(minskande)r_C(ökande).

rC ändras under primärstjärnans livstid maximalt från Väte-1 till Helium-4 med en faktor 4 (nuklidtätheten baseras på samma kärnradie med olika kärnmassa, se GrundNukliderna från Nuklidradierna); Städradien R med given massa ändras med tätheten enligt (rCVäte/rCHelium)^1/3 = 0,25^1/3, Städytans ändring ger kvadraten 0,25^2/3; Totala koefficientändringen med städytan och tätheten ger en total reduktion för tP på 0,25^2/3 · 4^1/2 = 0,7937005 vid tiden för stjärnans Vätedöd; Värdena för yttätheten rr, elektronskalets tjocklek hr och transitmassan m0Transit betraktade som konstanta. Motsvarande reduktionsvärde från Solperiodens nuvarande observerade medelvärde 11,1 år mot det beräknade tp=11,44 år enligt nedan och som visar att Solen slutar på tp=9,4 år, blir 9,4/11,44=0,8216783;

Felet ligger på ca 3%(som kan tillskrivas fluktuationer i de angivna konstanterna).

Därmed skulle fusionsperioden ha tappat ca 11,44-11,1=0,34 år på Solens nuvarande brinntid, runt 20 miljarder år enligt TNED.

Solsystemets bildning är enligt TNED beräknad till 5-10 miljoner år efter K-cellens detonation, vilket med K-cellens expansionsmatematik enligt TNED grundas på det nu uppmätta medelavståndet mellan galaxerna i den lokala galaxgruppen, ca 3 Mpc [BAs324sp2n], se vidare i K-cellens Värmefysik).

Med Solens ideala livstid på runt 120 miljarder år

(observera att tidsberäkningarna ger andra resultat i modern teori där man utgår från andra förutsättningar; idealvärdena blir samma, men Solens ålders blir bara runt 1/10 av idealets drygt 100 miljarder år med den moderna akademins preferenser)

— från 100% Väte-1 till 100% Helium-4, baserat på Solära Råeffekten 3,3 T26 W med en massförlust på endast 0,7% från energiproduktionen

— tappar Solen linjärt räknat (0,34)(120/20)=(0,34)·6=2,04 år av Solcykelperioden totalt vid slutet av sin energicykel.

Solcykeln (t_P) slutar alltså på runt 9,4 år med ovannämnda förutsättningar — om grovt 100 miljarder år ENLIGT TNED — med praktiskt taget konstant effekt, hela tiden.

Beskrivningen av Solens Energiproduktion enligt TNED fortsätter nedan i artikeln Frekvensens täthetsvariation.

Frekvensens Täthetsvariation

Från vågenergins täthetsoberoende

FREKVENSENS TÄTHETSVARIATION

FREKVENSENS TÄTHETSVARIATION

Finns inte i g-homogena material

Våglängden ökar, frekvensen avtar; amplituden går mot noll från ett visst gränsvärde . . .

För att energiytan (A) ska bibehållas i vågen som bildas i den högre tätheten, in i den lägre tätheten, måste alltså A enligt vågenergins täthetsoberoende tillväxa med avtagande täthet. Frekvensrelationen f=c/d, som i normalt g-homogena material ger att c och d ändras proportionellt, gäller då inte längre eftersom våglängden d måste tillväxa enligt tillväxtvillkoret för A. Härav följer att våglängden måste öka med lägre täthet, vilket ger att f=c/d också tvingas avta:

f avtar i Solens fall med avtagande täthet i vågenergins bevarande;

Vågorna packas utåt.

Med bevarad vågyta för energin mellan inre och yttre samt avtagande frekvens med växande våglängd, packas vågorna tydligen upp mot Solytan med en obegränsat avtagande amplitud som närmar sig Sol-g-radien obegränsat utan att någonsin tangera den. OM Solens synrand också vore g-randen, skulle (således enligt TNED) ingen vågaktivitet alls kunna iakttas där, eftersom amplituden i g-ytan har det tvungna gränsvärdet noll. I praktiken är området närmast under g-ytan i själva verket osynligt på grund av den starka rekombinationen mellan atomkärnor och elektronmassor (se Solranden). Det vi ser är istället en bit längre ner, in mot Solkroppen, där tydliga vågändringar med relativt liten amplitud har observerats (i storleksordningen någon KM men dessa mätningar är svåra att genomföra). Det är i varje fall den förklaring som kan utläsas enligt TNED.

Framställningen i Solens Energiproduktion fortsätter nedan med artikeln om Solens allmänna vågfunktion.

Solens allmänna vågfunktion · | 2007IV25

Solens vågfunktion

Solmatematikens typiska formart i exempel enligt TNED

SOLENS VÅGFUNKTION

SOLENS VÅGFUNKTION

SOLENS POLÄRA VÅGFUNKTION ENLIGT TNED I PREFIXxSIN

r = [A + a(x^3,5)cos nx^w]^{–1/(x+0,01)}

r = [A + a(x^3,5)cos nx^w]^{–1/(x+0,01)}

Vi ska här följa exakt hur Solens Vågfunktion kan sättas på en RELATIVT enkel matematisk form, samt hur denna sedan visar upp tämligen tillfredsställande kvantitativa rådata som vi kan kontrollera mot redan kända allmänna observationsdata. Speciellt viktig är härledningen till Solens vågmekaniska reflexionsrand; utan den går TNED helt bet på härledningen till Solmagnetismens observerade 22-åriga periodiska ändring.

kort teknisk notering

DATORERNAS STANDARDPROGRAM (nu runt 2008) BORDE innehålla ENKLA grafritande verktyg — utan obegripliga finesser som ingen vanlig dödlig begriper. Men det är en ytterst känslig fråga att dryfta i dessa tider: nog finns det grafritande program att hämta på INTERNET. Jodå. Men kolla påtet! Jag skulle inte stå ut en sekund med dylika anordningar. Hua. Jag gjorde (alltså) mitt eget program, personligt för min egen hemmadator (i Delphi för många år sedan) och har använt det (med ständig glädje) för att illustrera och utveckla detaljerna i den här presentationen. (Bara så att du vet, ifall du undrar).

beskrivning

Vi studerar hur vågfunktionen framväxer ur de allra enklaste sambanden

VÅGFUNKTIONEN I SOLEN I POLÄRA KOORDINATER enligt TNED

Centrala vågfunktioner inom en sfärisk kropp — Solens fall ENLIGT TNED — kan återföras (illustrativt) på funktioner i polära koordinater radien (r) som en växande (moturs) roterande funktion av vinkeln (v), r=f (v). Exemplen nedan använder v=x med PREFIXxSIN.

exempel: r = x

1t

En konstant (A) lägger till en startoffset och en exponent (n) ändrar funktionens tillväxthastighet eller form.

exempel: r = 1+[x^0,5]

1+(x'0.5)

1t

Är v sammansatt av olika variabla parametrar

v₁, v₂, v₃, … — Solens fall — kan funktionen skrivas mera komprimerat

r = f (v₁, v₂, v₃, …) motsvarande

r = f (x1)f (x2)f (x3) …

exempel: r = 3+[x^0,5]0,2cos20x

3+(x'0.5)0.2cos20x

1t

Vågfunktionen cos nx avbildar den egentliga vågformens utbredning. I exemplet är n=20.

Större x-exponent (i exemplet m=0,5) gör att amplituden i cosinusvågen växer kraftigare med växande avstånd från centrum. Med m=0 är tillväxten också noll och funktionen övergår i den konstanta cirkelformen r = 3+0,2cos20x.

1t

Om vi fortsätter på exponentialfunktionen med m=0,5 med ytterligare ritade varv, är det just exponenten (i exemplet m=0,5) som garanterar att vågformen ritas ständigt växande; Efter 20 varv ser bilden ut så här:

exempel: r = 3+[x^0,5]0,2cos20x

3+(x'0.5)0.2cos20x

20t

Amplituden eller dämpningen justeras genom att ändra koefficienten i exemplet angiven som 0,2. Sätts den 0, ritas bara en cirkel med radien 3 enheter.

Genom att x kan växa obegränsat, tillväxer också hela formen obegränsat med allt flera ritade varv.

Vi vill emellertid ha en begränsad, bestämd Solradie som vågfunktionen inte kan rymma ur;

Exponentialisering av hela funktionsformen för r förverkligar saken enligt [f (x)]^{–1/(x+OFFSET)}. I exempel,

exempel: r = [3+(x^0,5)0,2cos20x]^{–1/(x+0,01)}

[3+(x'0.5)0.2cos20x]'–1/(x+0,1)

10t

Hela vågfunktionen finns nu inom en begränsad radie som bestäms av funktionsenheten (Solen som fysisk kropp): då x går mot oändligt, går r mot enhetsradien. Därmed kan Solens interna vågfunktioner avbildas enligt TNED.

Den ursprungliga offsetkonstanten, i exemplet A=3, får genom den införda offsetfaktorn i exponentialiseringen (a=0,01 i exemplet) en ändrad innebörd;

exempel: r = [(10⁵)+(x^0,5)0,2cos20x]^{–1/(x+0,01)}

[3(10'5)+(x'0.5)0.2cos20x]'–1/(x+0,1)

10t

Genom att ändra konstanten (A, lägst 1) mot allt högre värde blir vågfunktionens växande hastighet från centrum allt mera homogeniserad; Det betyder att ett högre A-värde gör skillnaderna mindre i vågens allmänna radiella utbredning inom Solklotets olika partier. Ett mycket högt A-värde skulle då betyda att vågutbredningen sker med praktiskt taget konstant hastighet, medan ett lågt A-värde indikerar att skillnaden i vågutbredningshastighet mellan inre och yttre är utpräglad.

Vi kan studera, med en given vågfunktion i exemplet y=cos5x, hur y-formen modifieras, utan att egentligen ändras, då den påförs andra funktioner av olika kurvatur. Exemplet nedan i rektangulära koordinater:

exempel: y = (x²); y = (x²)0,2cos5x; y = (x²) + 0,2cos5x

Om vi låter cos5x-funktionen ligga överlagrad på parabelfunktionen y=x², vilket ger totala funktionen y = x²+cos5x, ser vi, illustrationens övre del, att cos5x-vågen får x²-bågen som grundlinje — och följer denna utan att ändras:

Vågen når hög höjd enbart med litet x om exponenten är hög; Vågens väghöjd förkortas alltså (stiger allt brantare) — och skulle då, normalt sett, avspegla högre utbredningshastighet med exponenten (m) allt större än 1. Med exponentieringens fasta gränsradie bildas emellertid en rakt motsatt effekt: Ju högre exponent m i polärfunktionen r=[A+x^m]^{–1/(x+0,01)} desto trängre blir spiralen som utvidgas från centrum för varje givet x: proportionellt sett avtar utvidgningen med högre m-värde. Exponenten m>0 i funktionstermen x^m motsvarar följaktligen en avsaktning eller dämpning i vågformens utbredningshastighet — och därmed en viss äventyrlighet i vågformens allmänna figur tillsammans med vågfunktionens grundform (cos nx). Vi ska därför, här, helt och hållet undvika ovannämnda alternativ och därmed inte sammanställa vågfunktionen totalt på flera variabelbestyckade funktionstermer än en.

Införlivar vi å andra sidan cos5x-vågen med x²-bågen, illustrationens nedre del, vilket ger totala funktionen

y = x²cos5x, kommer cos5x-vågens amplitud istället att förstoras på x²-bågens kontur — med x-baslinjen som bibehållen grundreferens. [Om vi vill att cos5x-vågen bara ska svänga med amplituder över x-baslinjen skriver vi samma funktion y = x²(1+cos5x)].

Om vi alltså bara vill ändra amplituden för vågfunktionen (cos5x) med växande avstånd från nollpunkten, ska vi söka funktioner av typen r = f (x₁)f (x₂) med endera variabelfaktorn på exponentialformen x^m, totalt typ r= x^m(1+cos nx).

För Solens del finns enligt TNED tre parameterformer i vågbildningen:

1. våghastighetens och våglängdens avtagande med temperaturens avtagande mot Solytan med konstant frekvens i referens till Jordfysikens normala g-homogena objekt och därmed amplitudens växande mot Solytan,

2. vågytans ändring med tätheten i stjärnfysikens icke g-homogena material för bevarandet av energiytans konstans och därmed ytterligare en amplitudförstärkning tillsammans med en våglängdsökning i netto mot Solytan,

3. frekvensminskning mot Solytan som följd av inverkan från 2 på 1 ovan.

(Totalt i netto: våglängd och amplitud växer mot Solytan in till ett gränsvärde, frekvensen avtar. Vidare nedan i Reflexionsgränsen).

I Solen avtar temperaturen enligt TNED (inverterat) i rektangulära koordinater som funktion av r^1,5 [Se SOLENS FÖRSTA EKVATION]. Temperaturens avtagande innebär, med referens till den normala Jordfysikens materierum, att både våghastighet och våglängd avtar med bibehållen konstant frekvens. Med vågenergins bevarande innebär det att amplituden växer på bekostnad av den kortare våglängden — på samma sätt som långa vattenvågor på djupt vatten med hög hastighet saktar ner och blir kortare men högre då de kommer in mot grunda stränder. Omsatt i polära koordinater blir då amplitudförstärkningen för växande radie som funktion av temperaturminskningen av formen r=x^1,5.

Ytterligare en amplitudförstärkande parameter finns i Solens fall. I TNED är Solen och alla stjärnor icke g-homogena material — vilket betyder att de INTE finns med i den vanliga Jordfysikens typmaterial och därför undandrar sig direkta experimentella observationer. VÅGENERGINS TÄTHETSOBEROENDE, h_r/h_R=Ö(r_R/r_r), måste därför anställas på den substituerade variabla täthetens form för att få en bevarad ekvivalens med integrala energiytan. Denna omständighet i Solfysiken leder enligt TNED till att amplituden (h) ändras enligt h = r²· h_R/R²; täthetens variation enligt TNED i Solen lyder r=r^–4r_RR⁴; vi tillämpar h/h_R=Ö(r_R/r) från ovan — som med insättning av

r=r^–4r_RR⁴ ger angivna h = r²· h_R/R². I polära koordinater med växande r blir motsvarande amplitudfunktion r=x².

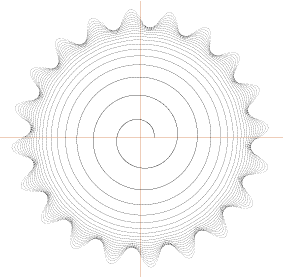
Totalt för bägge amplitudändringarna (x^1,5x²) ges alltså magnituden r=x^3,5. Vågfunktionen i polära koordinater för Solens del enligt TNED kan då skrivas totalt

r = [A + a(x^3,5) · cos nx]^{–1/(x+0,01)}

Frekvensdämpningen innebär i vilket fall att vågorna som bildas från det centrala stjärnstädet (R=4012 M i Solens fall) packas mot Solytan. Hela den exponentierade funktionsformen bygger redan på den förutsättningen, och konstanten A kan användas för att modulera frekvensdämpningens magnitud; Stort A dämpar häftigheten i reduktionen av frekvens från centrum till periferi (linjär ytpackning); litet A (minimum 1) visar maximalt stor skillnad i frekvens mellan centrum och periferi (exponentiell ytpackning).

Ökningen i våglängd mot Solytan

VÄXANDE VÅGLÄNGD

exempel: cos10x^0,3

enda funktionsformen som kan göra våglängden växande med växande avstånd från nollpunkten

Exemplet ovan visar hur funktionen måste modifieras för att möta villkoret med netto växande våglängd mot gränscirkeln; Vinkelvariabeln exponentieras med koefficienten w, vilket med w=1 ger oförändrad våglängd och med w®0 obegränsat stor våglängdsökning. Vågfunktionen i polära koordinater totalt därmed i PREFIXxSIN

r = [A + a(x^3,5)cos nx^w]^{–1/(x+0,01)}

exempel: r = [1+(10⁵) + (x^3,5)(1 + cos50x)]^{–1/(x+0,01)}

[1+(10'5)+1(x'3.5)(1+cos50x'1)]'–1/(x+0.01)

unit500 20t MethodPoint · w=1

2007IV26

FRÅN SOLRANDEN tar strålningsenergin över.

Eftersom ena delen av vågenergin (se Vågenergin) genereras av det passiva g-trycket, har den delen ingenting att göra utanför Solranden. Det stämmer också med energiräkningen totalt, eftersom energin förknippad med Solen är och förblir ren strålningsenergi: det som uttränger ur Solytan. Parameterformerna ovan ansluter också till den ordningen, ty som vågorna närmar sig Solranden, växer våglängden (exponenten w i cos nx^w); vågens energiyta kan bevaras genom att amplituden (tvunget) fördelas avtagande med obegränsat växande våglängd — och vilken process i princip kan fortgå hur länge som helst utan att vågorna ändå riktigt når fram till gränsradien.

Emellertid som vi nyligen konstaterade med den stränga amplitudfunktionen r=x² — i förening med hela vågfunktionens gränscirkel som Solens g-radie — bildas en brytpunkt (strax under g-ytan) där amplituden tvingas gå mot noll. Denna gräns bildar tydligen Solkroppens motsvarande materiella vågmekaniska reflexionsyta (r_R). Den ger tydligen den vågmekaniska förutsättningen för en tvär och skarp brytgräns — i storleksordningen inom grovt 1-5 KM strax under g-ytan, se nedan i Solära Vågfunktionens Mekaniska Reflexionsyta; En del av vågenergin bryts in mot g-randen, en del reflekteras tillbaka inåt Solcentrum.

Fortsättning nedan i VÅGFUNKTIONENS REFLEXIONSYTA.

Mekaniska Reflexionsytan

Solära Vågfunktionens Mekaniska Reflexionsyta

SOLÄRA VÅGFUNKTIONENS MEKANISKA REFLEXIONSYTA

SOLÄRA VÅGFUNKTIONENS

MEKANISKA REFLEXIONSYTA

Solens Helioseismologiska grunder enligt TNED

inledning

Den unika stjärnfysiken

FUSIONSVÅGENS AVKLINGANDE

2007V1

Utanför Solens g-yta finns inte längre någon förutsättning för VÅGMATNING [Se från VÅGENERGIN].

På samma sätt som en snabb långvågig lågamplitudig Stillahavsvåg som bildas av oceaniska bottenförkastningar växer till hög höjd med kort våglängd och låg hastighet och slutligen kollapsar genom att falla ihop på sin egen tyngdhöjd då den kommer in mot stränder som blir allt grundare för att till slut helt sakna vattendjup, så måste också den mekaniska rekylformen (motsv. havsvågen) från fusionsvågen (motsv. havsbottnens snabba korta rörelse) som bildas i Solstädet uttömma sig över Solytans rand genom en amplitudkollaps.

Den enda energi (strålenergin) som lämnar Solen (Solvindens utflödande material bortses ifrån på grund av dess ringa del) garanterar att den energiräkningen också är förbehållen just strålningsenergin (konv. grovt 4 T26 WS) — vilket därmed tvingar den passiva g-vågsbildningen som sammanhänger med fusionsvågens fortplantning från det inre till Solytan att också stanna inom Solkroppen.

Det går alltså inte att härleda någon separat energiräkning för den mekaniska fusionsvågen

Det går alltså inte att härleda någon egentlig energiräkning för den mekaniska fusionsvågen: Den är och förblir en svängande del av Solkroppen — som matas av energin i den rekylerande fusionsverkan som följer på g-övertrycket. Vilket vill säga: vågenergin är lika med strålenergin. Det finns (utöver ljudvågorna) ingen liknelse för det i den kroppsfysik vi normalt känner till.

Men STÄLLET där fusionsvågorna uttömmer sig — kollapsar över Solytan, som nyligen omnämndes — är uppenbarligen INTE ställena där vågorna kan observeras; Solens g-rand är som tidigare beskrivits i Solranden och Solklotets Elektronfrihet ett utpräglat rekombinationsområde och har teoretiskt noll synbarhet; synbarhetsranden ligger tvunget en bit under g-randen dvs., i Solens synliga yta.

Vi betraktar här ALLTSÅ AV PRINCIP ett FÖNSTER mellan synliga Solytan och den Solens kroppsradie över vilken fusionsvågorna slutligen uttömmer sig eller kollapsar — likt vågorna som sköljs in över en strand. Som den Solranden uppenbarligen ÄR den beräkningsbara g-radien 6,97 T8 M, till skillnad från den synliga fotometriska Solranden 6,96 T8 M [Se utförligt från SOLENS GRAVITELLA RADIE], är det tydligt att fönstret ifråga inte kan vara annat än, ÄR eller ligger inom, differensen ca 1000 KM.

Hur kan vi få klarhet i den saken genom Solens allmänna vågfunktion?

— Genom att insätta varvintervall x:=[x+2pn] i polärfunktionen

r = [1+(10^e)+([x+2p0]^3.5)(1+cos200[x+2p0]¹)]^[–1/([x+2p0]+0.01)]

— samt tilldela bara ett enda varv för ritningen så att vi via n kan rita upp ett varv på godtyckligt ställe i hela funktionen;

— Vilket vill säga; Vi kan med den metoden, genom prövningar, direkt se var amplituden börjar avta och på den vägen söka svaret på en eventuell rimlighet i funktionen.

— Det visar sig emellertid bli en rätt klumpig analys då vi för höga konstantvärden (A) i vågfunktionen

r = [A + a(x^3,5)cos nx^w]^{–1/(x+0,01)}

måste förstora vågen för att den ska synas över huvud taget, och därmed eventuellt våld på funktionen som helhet.

— Ett bättre sätt är (alltså) att utföra direkta aritmetiska operationer (som dock måste bli av typen mera krävande). Vi studerar detta — lösningen är enklare än man kunde tro.

lösning PREFIXxSIN:

I den polära funktionen

r = [A + a(x^3,5)cos bx^w]^{–1/(x+0,01)}

tilldelar vi en metodidentifierare för x

x:=[x+2pn] såsom varvspecificerare via heltaliga värden på n, för att med givet n beräkna en fasändring (cosinus minus sinus) motsvarande differensen

d = [A + a(x^3,5)cos bx^w]^{–1/(x+0,01)} – [A + a(x^3,5)sin bx^w]^{–1/(x+0,01)}

Genom att sedan, via prövning, jämföra närliggande d från konsekutiva n kan vi avgöra VAR amplituden (d) är i avtagande mot gränscirkeln från att tidigare ha varit i växande från centrum.

cos–sin i PREFIXxSIN ger halva motsv. sanna amplituden

Solkroppens vågmekaniskt reflektiva gränsyta (övre delen) går vid r_G(1–cosinus)=h under r_G.

Där antar amplituden (d) sitt största värde. Därifrån går d mot noll in till r_G.

Efter analys ser vi strax att d kan förenklas genom att i metodidentifieraren för x sätta x=0 så att vi får x:=2pn och som direkt ger oss

sin 2pn = 1 och cos 2pn = 0 i PREFIXxSIN; Vi får då det enklare

d = [A + 0]^{–1/(x+0,01)} – [A + a(x^3,5)1]^{–1/(x+0,01)} ;

d = [A]^{–1/(x+0,01)} – [A + a(x^3,5)]^{–1/(x+0,01)}

= cosinus – sinus

kalkylkort Reflexionsgränsen | 2008I9 | gränsvärdet (d) för mekaniska vågornas största amplitud i Solytan före utgången till g-ytan · resultat · se från Vågfunktionen

BuggPåWebben? Vad händer egentligen på webben? Förslaget ovan presenterades Juni2008 från Webben efter ett antal uppladdningar. Korrekt objekt är enligt nedan (såvitt inte förvanskat också det).

Hur uppstår dylika överföringsfel? Vet inte.

— En observerad möjlighet (Apr2010): FLASHMINNEN upphör, tydligen, att fungera tillförlitligt efter viss tid, här ett KINGSTON DataTraveller (1GB): efter många upprepade överföringar i samma USB-katalog mellan olika datorer (överföring, radering, överföring, osv) visade sig allt oftare överföringsfel typ svarta bildrutor, underliga (kryptiska) htm-avsnitt etc. [Byte till annan lagringsdress har hittills inte visat några direkta fel …].

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik1 Kalkylkort 3 — Reflexionsgränsen — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

Kalkylkortet (här endast i bild) innehåller inre uppställningar som inte visas utfällda här. Endast resultatredovisning.

beskrivning

Beräkningen av d-toppvärdet är krävande — den görs (här) i tre steg:

INITIERING: varvtalet (n i x=2pn) ökas i tiopotenser tills d-värdet d_mainUT hamnar på UTsidan;

Vad som är insida och UTsida avgörs genom att lägga till p (ett halvt varv) och se efter om d-värdet blir större (d ligger på insidan av d-toppvärdet) eller mindre (d ligger på utsidan av d-toppvärdet).

HALVERING: d_mainUT halveras successivt (max 5 ggr) tills d-värdet d_mainIN hamnar på insidan;

ITERATION GENOM MEDELVÄRDESBILDNING: d-värdets toppvärde söks från d_mainIN genom speciella villkor (så att man slipper integrera koden med ovanstående två utrymmeskrävande initieringar) — som hela tiden ”puttar” det resulterande d-värdet mot dess naturliga toppvärde.

NOTERING: Iterationen KAN bli besvärlig ändå (om dämpfaktorn är mycket liten). Man får då införa en särskild subtrahend (t.ex. 1000 varv) i varvfaktorn som iterationen sedan justerar automatiskt.

Man får alltså, i vilket fall, pröva sig fram till bästa värdet. Kalkylkortet ovan medger kontroll genom manuella värden [n(varv)].

reflexionsgränsen

RESULTAT

Det visar sig att DÄMPNINGEN (a) i vågformen har avgörande stor betydelse för drivningen av amplitudändringsgränsen mot gränscirkeln.

Exempel: Med endast en spiralfaktor (A) på 10 men med en vågdämpning på t6 (0,000001) visar sig amplitudändringsgränsen mot gränscirkeln vid ca 99,52%, n=80. Alla vågor innanför-utanför den gränsen är i avtagande.

resultatvärden

TRIGONOMETRISKA AMPLITUDVÄRDET med enheten 1 i vågfunktionen motsvarar gränsradieenheten 1 lika med Solens g-radie.

Med fusionsvågens amplitudvärde i storleksordningen 10µM måste alltså dämpfaktorn (a) initiellt ha värdet (t5 M)/r_G=1,4 t14 avrundat.

Med den förutsättningen ges ideala toppamplituden

d/2 = 2,35 t4 r_G

= 163,6 KM vid n=4585 och A=1.

Amplitudändringsgränsen (d-toppen) mot gränsklotet (r_G) blir då

r_dMAX = 0,99997594r_G —

som betyder avståndet (våggränsens toppvärde)

r_G(1–cosinus) = h = 16,8 kilometer innanför r_G-randen.

DÄRMED ÄR

SOLÄRA VÅGFUNKTIONENS

MEKANISKA REFLEXIONSYTA

DEFINIERAD SOM h

Alla vågrörelser innanför denna toppunkt uppvisar amplituder som uttömmer sig i noll mot g-randen samtidigt som våglängden fortsätter att växa (mot obegränsat).

Amplitudändringsgränsen (h), från växande inifrån till avtagande utåt mot g-ytan, betyder samma som en (relativt) SKARP kroppsgräns som KAN uppfattas som en definition av brytgränsen (som kan sträcka sig till g-randen) mellan Solklotets interna vågmekanik och den omgivande rymdens materierum — så att Solen inte övergår omärkligt, kontinuerligt i rymden, utan att ha någon vågmekaniskt reflektiv kroppsyta alls.

Solens 22-årsperiod

TNED VORE REJÄLT ILLA UTE om h-värdet från a-värdet i vågfunktionen skulle skilja sig mycket från g-randen. Här ligger h-värdet som vi ser tämligen nära typ »plåster» sett med Solens mått. VI NOTERAR att maxamplituden (dubbla d) på runt 327 KM f.ö. stämmer nära överens med ideala elektronskiktets tjocklek (runt 340 KM) och som grundlägger härledningen till Solperioden på 11 år. Se från föregående Fusionsperioden.

Solens 22-årsperiod

ORDNINGEN FÖR FUSIONSPERIODEN kommer med definitionen för reflekterande vågmekaniska skiktet vid h som ovan följaktligen att resultera i en motsvarande extra g-kraft, först och främst vid den tredje t_P-perioden; implosionsvågen från t=0 i första fusionsvågen tar tiden t_P för att nå upp till h där den reflekteras och kommer åter efter t_P, lagom till fusionsvåg 3 där den följaktligen adderas med g-trycket; Med större tryckkraft bör det uppstå en motsvarande kraftigare (djupare) fusionsreaktion. Därmed bör fusionsvågen nr 3 alltså få ett motsvarande större masstryck än normalt — och sedan den femte, sjunde, nionde, osv.;

Eftersom den mekaniska vågenergin — och den är lika med strålenergin (se utförligt från vågenergin) — måste stanna inom Solklotet, framtvingas (tydligen) en fördelning i närmast nästföljande fusionsfas (fjärde, sjätte, åttonde, osv.) med ett motsvarande mindre masstryck så att summan för de två något olika delperioderna går på ett ut. Om detta är korrekt mot den verkliga Solfysiken, har vi därmed fått på bordet två något olika t_P-perioder i kraft av det reflekterande ytskiktets mekanik (h), och därmed en summerande period på avrundat 22 år — eller mera noga räknat 22,88 år från Solens första dag enligt Solens Fusionsperiod. 22-årsperiodens växling med de olika intryckens praktiska verkningar beskrivs mera utförligt från Solens allmänna magnetfält.

Härledningen till Solfysikens detaljer fortsätter i det efterföljande avsnittet om SOLFLÄCKENS UPPKOMST.

Modern Solteori

Från Solens Vågfunktion

MODERN VETENSKAPLIG SOLTEORI

DEN MODERNA VETENSKAPENS TEORI OM VÅGRESONANSERNA I SOLYTAN

I den moderna vetenskapens traditionella Solmodell är rörelseenergin (värmet) hos atomkärnorna, som grundlägger fusionerna, INTE en passiv mottagande dynamisk faktor utan en aktiv, givande sådan: värmet (strålenergin) bildas ur och upprätthålls av fusionsenergin, men man framställer saken så att det är temperaturen som bildar strålningstrycket (T®p) — inte temperaturen som bildas av p, därför att ”p” i modern teori inte har någon kärnfysikaliskt relaterad grund (det är neutrinospöket som agerar här, se från PLANCKS STRUKTURKONSTANT och NEUTRINOSPEKTRUM).

För att härleda vågenergin till Solytans vågresonanser tvingas man därmed TA av det energikapitalet för att kunna bilda fenomengrunden i Solytan, vilket därmed reducerar den aktuella stråleffekten och intvingar energin i ett vågresonanskonserverande tillstånd — som inte tillåter någon utstrålning alls med referens till energiräkningen enligt TNED:

vågenergin = strålenergin.

Ingenting alls omnämns (ännu veterligt 2007-04-21|2008-02) i tillgängliga källor (på @INTERNET) om några effekt- eller energivärden i association till Solytans vågfenomen. Det förutsätts (tydligen) att dessa energier är så små att de är försumbara vid sidan av huvudenergin.

beskrivning

I modern akademi (MAC) finns ingen aktiv g-komponent; gravitationen har ingen signifikant fusionstriggande verkan i den konventionella Solmodellen; MAC härleder Solfusionerna på typ partikelaccelerator med slumpvis kolliderade atomkärnor, inte på lugna säkra höga g-tryck. Vågenergin = Solenergin kan alltså inte härledas i MAC; Modern akademi har ingen uppfattning om en maximalt tät inre liten kompakt Solkärna. Hur härleder man den då, vågenergin?

Specificerade uppgifter från MAC på vågresonanserna i Solytan verkar (runt 2007-04) vara en hart när omöjlig uppgift att få fram: OM värden anges på (t.ex.) ”ljudhastigheten i Solen” eller ”våghastigheten i Solen” är dessa av typen allt från 0,01 M/S till 190 KM/S, inte sällan i en kaotisk röra av andra ”uppgifter” av så obskyr grund att man nära nog blir knäckt (det krävs här minst en hel sida för att redovisa exempel). Beträffande uppgifter om VÅGENERGI för Solytans vågresonanser, finns mig veterligt (2007-04-21) ingen specificerad uppgift alls — men väl en synbarlig omfattande volym som beskriver ämnets teoretiska grunder [@INTERNET Local Helioseismology] — Dock på den sedvanliga högskolematematikens nivå som endast är förunnat ett fåtal människor att förstå; En vanlig praktiskt levande människa kan, tyvärr, inte läsa sig till någon vettig beskrivning av ämnet. Tyvärr. Men vi behöver å andra sidan heller inte konsultera de förnämligheterna för att få reda på huvudsaken.

Så härleds vågenergin i Solytan av MAC — enligt TNED

Med enklare citat av mera allmän natur, se sammanställningen nedan, samt uppsättningen föregående omnämnda grunddata enligt TNED, kan man sluta sig till grundpartierna i MAC-teorin för vågresonanserna i Solytan enligt följande:

YTDATA 2007IV SOLEN

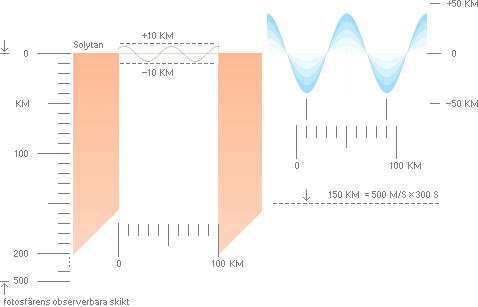
h = 10-tal till 100-tal kilometer, v = 100-tal M/S, t = 300 S = 5 min.

Period:

”a period of about five minutes”

@INTERNET

http://ase.tufts.edu/cosmos/print_chapter.asp?id=25

2007-04-17.

”in a period of 296 seconds”,

@INTERNET

http://physics.usc.edu/solar/history.html

2007-04-17.

Hastighet:

”a few hundred meters per second”,

@INTERNET

http://ase.tufts.edu/cosmos/print_chapter.asp?id=25

2007-04-17.

”at a speed of 500m/s”,

@INTERNET

http://physics.usc.edu/solar/history.html

2007-04-17.

[150 KM = 500 M/S × 300 S; 60 KM = 200 M/S × 300 S];

Amplitud:

”tens of thousands of meters”,

@INTERNET

http://ase.tufts.edu/cosmos/print_chapter.asp?id=25

2007-04-17.

”amplitudes of hundreds of kilometers”,

@INTERNET Wikipedia Helioseismology 2007-04-17.

”Solar pressure waves are generated by the turbulence in the convection zone, near the surface of the sun, and certain frequencies are amplified by constructive interference. In other words, the turbulence ”rings” the sun like a bell.”

@INTERNET Wikipedia Helioseismology 2007-04-20

Min översättning:

Solära tryckvågor bildas av turbulens i konvektionszonen, nära solytan, och vissa frekvenser förstärks genom konstruktiv interferens. Med andra ord, ”ringer” turbulensen Solen som en ringklocka.

MAC-teorin

I föregående räkneexempel visades att totala vågenergin per fusionsvåg som ges en gång vart elfte år blir grovt 3 T8 gånger sekundenergin (konv. 4 T26 W): Om man bara tar ett ytskikt av dessa 300 000 000 idealt koncentriska vågskal, säg 1000-10000 eller något åt det hållet, samt försöker bygga en teori om att orsaken till vågbildningen i detta tunna ytskikt skulle vara ”turbulens i den underliggande konvektionszonen” — med den moderna akademins ytterst avancerade och sofistikerade matematiska resonansteorier som garanterat ingen normal person förstår ens en inledning till — blir det ENKELT att GÖMMA den försumbara vågenergin eftersom den bara utgör en bråkdel (säg 1/10000) av hela Solenergin och som i vilket fall är omöjligt att mäta exakt, på grund av fluktuationer i Solen generellt.

Modern vetenskap kan för sin del inte beskriva Solen enligt TNED, inte alls överhuvudtaget, därför att, som nyligen påpekades, den passiva g-komponenten som fusionstriggare inte ingår i MAC: Fusionerna i Solen triggas enligt MAC av hastighet. I TNED finns inte den komponenten med (den är i princip exakt noll), utan det är tryck som gäller.

EXEMPEL PÅ HUR MODERN NATURVETENSKAPLIG UTTOLKNING INTYGAR ATT DEN INTE GÖR NÅGOT FEL I FYSIKEN

inledning

Temperatur OCH tryck hör (alldeles helt säkert) ihop med en och samma atommodell:

Genom att ensidigt försöka påvisa sammanhang som berör t.ex. temperaturen — vilket obönhörligt kräver en konsultation av atommodellens tryckfysik — för att därmed tro sig bevisa att atommodellens teori är riktigt, bedrar man sig; Bägge delarna samverkar till och avhandlar samma modellform.

På samma sätt;

Att ensidigt försöka påvisa sammanhang som berör TRYCK — vilket kräver en konsultation av atommodellens temperaturfysik — för att därmed tro sig bevisa att atommodellens teori är riktigt, är OCKSÅ att bedra sig; Både tryck och temperatur samverkar och avhandlar samma modellform.

Korrekt [IDEALT] sätt är att jämföra två OBEROENDE atommodeller med inbördes SKILDA temperatur-tryckfysik. Endast den av de två modellerna som kan INBEGRIPA den andra som PRIMITIV kan med rätta betraktas som korrekt fysikaliskt beskrivande. OBSERVERA (därmed) att medan SOLYTANS VÄRDEN (som t.ex. täthet och temperatur) delas lika av bägge de annars helt motsatta teorierna i MAC och TNED, finns ingen som helst beröringspunkt mellan de skilda teorierna under Solytan. Vilket vill säga: Soldata från SOLYTAN kan (i sig) inte avgöra något i sammanhanget.

EXEMPEL

textmarkeringarna i citaten är mina

”Helioseismology was able to rule out the possibility that the solar neutrino problem was due to incorrect models of the interior of the Sun.”

@INTERNET Wikipedia Helioseismology 2007-03-30

Min översättning:

Helioseismologin kunde utesluta möjligheten att det solära neutrinoproblemet skulle bero på inkorrekta modeller av Solens inre.

”New evidence also showed that the solar model predictions were reliable. In 1997, precise measurements were made of the sound speed throughout the solar interior using periodic fluctuations observed in ordinary light from the surface of the Sun. The measured sound speeds agreed to a precision of 0.1% with the sound speed calculated for our theoretical model of the Sun. These measurements suggested to astronomers

that the theoretical model of the Sun was so accurate that the model must also predict correctly the number of solar neutrinos.”

@INTERNET http://nobelprize.org/physics/articles/bahcall/ 2006-05-04

Min översättning:

Nya bevis visade också att solmodellens förutsägelser var tillförlitliga. År 1997 gjordes precisa mätningar av ljudhastigheten genom solens inre genom periodiska fluktuationer som observerades i vanligt ljus från Solytan. Den uppmätta ljudhastigheten överensstämde med en noggrannhet på 0,1% med ljudhastigheten beräknad för vår teoretiska Solmodell. Dessa mätningar antydde för astronomerna att den teoretiska Solmodellen var så noggrann att modellen också måste förutsäga korrekt antalet solära neutriner.

Dessa påståenden — att solära tryckobservationer skulle bevisa att den moderna vetenskapens stellära uppfattning är korrekt — är uppenbarligen inte helt korrekt. Vi studerar hur.

EN modell man har av fysiken och som bygger på grundläggande förutsättningar med temperatur OCH tryck — motsvarande EN generell atomteori — kan uppenbarligen INTE bevisas vara korrekt genom att ensidigt utgå ifrån TRYCKMÄTNINGAR GRUNDADE PÅ ATOMTEORIN eftersom dessa tvunget måste grundas på temperaturanalogier ENLIGT atommodellen, eller genom att ensidigt utgå ifrån TEMPERATURMÄTNINGAR GRUNDADE PÅ ATOMTEORIN eftersom också dessa tvunget måste grundas på föregivna tryckanalogier ENLIGT atommodellen. Ingen av dessa aspekter kan ALLTSÅ bevisa den andra absolut.

Det är en villfarelse.

För att verkligen kunna bevisa att bägge premisserna tryck-temperatur är förenliga med naturfysiken, måste det finnas, tydligen, en helt oberoende atommodell, med oberoende temperatur- och tryckanalogier och vars resultat kan jämföras med den alternativa modellen. Endast den modell som innefattar den andra modellen som »primitiv fysikbeskrivning» [VARFÖR den andra inte kan ge den innefattningen — uttömmande, utan att lämna obesvarade frågetecken] kan I RELATERAD MENING och helt korrekt uppfattas som fysikaliskt godtagbar — på en säker solid fysikalisk grund.

Jämför, verifierat:

”The sound speeds within the Sun are calculated from the Sun’s temperature profile in the standard solar model, estimated from knowledge of stellar physics and measurements of the Sun’s surface.”

@INTERNET [http://staff.washington.edu/aganse/helioseis/helioseis_rtapplet.html] 2007-04-06

Min översättning:

Ljudhastigheterna inom Solen beräknas från Solens temperaturprofil i den solära standardmodellen, uppskattad från kunskap om stjärnfysiken och mätningar av Solytan.

DET FINNS (glädjande nog) FÖRFATTARE som är tillräckligt vakna och observanta på ordningen för att, typ ovan citat, sprida upplysningen vidare. Dessvärre tycks (ännu) många populärförfattare bedra sig — typ de föregående citaten närmast under EXEMPEL.

BETRÄFFANDE SOLYTAN föreligger inga större skillnader mellan de ELJEST VITT skilda teorierna MAC/TNED: Samma yttemperatur, samma yttäthet, samma ljudhastighet, samma tryckresonanser. Det finns m.a.o. inget att hämta i PRECISIONEN. Jämför korrekt formulering (textmarkeringarna är mina):

originalet

…

that the theoretical model of the Sun

…

korrektion

…

that the theoretical model of the SURFACE OF THE SUN Sun

…

Och så här är det:

”For the Sun, no one source generates solar ”seismic” waves. The sources of agitation causing the solar waves that we observe are processes in the larger convective region. Because there is no one source, we can treat the source as a continuum, so the ringing Sun is like a bell struck continually with many tiny sand grains.”

@INTERNET http://soi.stanford.edu/results/heliowhat.html 2007-03-30

Min översättning:

För Solen, finns ingen enskild källa som alstrar de ”seismiska” vågorna. Ansatskällorna som förorsakar de solära vågorna vi observerar är processer i den större konvektiva regionen. Eftersom det finns ingen enda källa, kan vi behandla källan som ett kontinuum, så att den vibrerande Solen liknar en ringklocka som slås an kontinuerligt med många små sandkorn.

Det är — i ovanstående citats ljus — tydligt att den moderna akademin är välbefolkad av personer som har en speciellt djupgående förankring i kunskaperna om Solfysiken: ”there is no one source”.

Den ovanstående berörda moderna akademins stjärnteori, som vi har sett från fusionsperioden, har ingen som helst koppling till stjärnfysiken enligt TNED.

De grundläggande olikheterna mellan MAC och TNED beskrivs f.ö. mera ingående och utförligt enligt TNED från början i

Solfysiken.

Se även mera utförligt från Vad gör modern akademi för fel?.

SOLENERGINS TID I MODERN AKADEMI

Den moderna akademins allmänna uppfattning om TIDEN för energin mellan Solcentrum och Solytan har naturligtvis också en helt annan grund än den i TNED.

I den konventionella Solfysikens matematik, säger man [BAs60sp2m] (fetstilen min markering)

”Den termiska tidsskalan (eller Kelvin-Helmholtz’ tidsskala) kan sägas vara den tid det tar innan följderna av en plötslig ändring av energiproduktionen i en stjärnas inre blir märkbara i hela stjärnan. Detta är lika med den tid det tar för energin att färdas från centrum till ytan, och motsvarar också den tid stjärnan behöver för att stråla ut en signifikant mängd av sin upplagrade värmeenergi. Vi skriver:

½ GM ²

t (termisk) ~ ———— ( ~ 10⁷ år för solen )

RL

där M, R och L betecknar stjärnans massa, radie och luminositet.”

BONNIERS ASTRONOMI 1978 s60sp2m

Också ovanstående matematiska stjärnteori har, som vi har sett från fusionsperioden, ingen som helst koppling till stjärnfysiken enligt TNED.

De grundläggande olikheterna mellan MAC och TNED beskrivs f.ö. mera ingående och utförligt enligt TNED från början i

Solfysiken.

Framställningen fortsätter separat i SOLFLÄCKARNAS UPPKOMST;

Avsnitten har (för snabbare uppladdning) måst uppdelas i efterhand från ett större originaldokument med hänsyn till Webbläsningsteknikens begränsade uppladdningshastighet.

I den beskrivande ordningen följer nedan (efter det avdelade avsnittet ovan) SOLENS ALLMÄNNA MAGNETFÄLT.

Solens allmänna magnetfält

Solens allmänna magnetfält

BFLS-graferna (BÄFFÄLS baffles) BFLS

SOLENS ALLMÄNNA MAGNETFÄLT

2008I29

GENOM FÖREGÅENDE BESKRIVNINGAR (Solens energiproduktion med förklaringen till uppkomsten av solfläckarna och deras matematiska fysik) har (nu) samtliga Solfysikens grundparametrar genomgåtts — tillsammans med de allmänna referenserna till Soldynamiken sådan den framgår och kan härledas ur TNED — utom en, den sista i den övergripande beskrivningen av Solens allmänna fysik:

Solens allmänna magnetfält.

Solmagnetfältets fysik är ännu (2008) ett erkänt obeträtt område i den allmänna litteraturen — och föremål för ett stort och intensivt intresse ur många olika perspektiv: Ingen vet (ännu) med någon bestämdhet hur det fungerar, men det finns en (enorm) uppsjö av (pågående) teorier, animerade lösningsexempel på @INTERNET — och ännu mer beskrivande utläggningar. TNED har emellertid andra förutsättningar än de gängse. Vi studerar detta.

Solens allmänna magnetfält uppvisar enligt redan väl kända observationer

grunddata

· en periodisk polmagnetisk växling (NtillN) på ca 22 år,

· värdet (max) ±50 nT ute vid Jordbanan; UPPMÄTT magnetiskt fältstyrkevärde ute vid Jordbanan på (max) ±50 nT
[ref. @INTERNET Explanation of Solar Wind Dials, http://www.swpc.noaa.gov/SWN/sw_dials.html, där anges dagliga värden här ute vid Jordbanan i xyz-form tillsammans med andra parametrar]
med typiska medelvärden kring nT, och

· värdet (max) ±10-50 Gauss vid Solpolerna; en lokal solär ytmagnetisk polstyrka på ±10-50 Gauss (0,001-0,005 Tesla), värdena något olika beroende på referenskälla;
ref. ±10G [NASA/MSFC/NSSTC/Hathaway 2007/05], ±40G [http://www.astronomycafe.net/qadir/q1659.html], 50G [http://science.nasa.gov/headlines/y2001/ast15feb_1.htm].

AVGÖRANDE TNED-TEST FÖR SOLFYSIKEN

Kan TNED förklara den Solfysiken?

Uppfattningen att magnetiska fält alls finns på Solytan grundas på spektroskopiska observationer genom den s.k. Zeemaneffekten (1896, Nobelpris 1902 ref @INTERNET Wikipedia Pieter Zeeman).

Zeemaneffekten: De spektrala linjer som normalt emitteras av exciterade (upphettade) atomer (spektrallinjerna mäts med spektroskop; jämför en CD-skiva i reflekterat lampljus), genomgår en linjeuppdelning (finstruktur) om atomerna exponeras för ett yttre (starkt) B-fält. Genom att mäta linjebreddningen får man ett mått på B-fältets styrka. På delvis grundval av sådana typmätningar (Solfläckarna) har Solytans struktur kartlagts. I modern mening har man emellertid ännu (2007V24) inte lyckats uppdaga en djupförklarande teori för de observerade ytfenomenen — Generellt menar man att förklaringen till sådana fenomen som Solfläckar och Solprotuberanser är Solens ytmagnetiska fält genom Solytans differentiella rotation (ref @INTERNET Wikipedia Sun 2007-05-24).

avgörande TNED-test

Vi kan avgöra ställningen för TNED — i hela stjärnfysiken, och därmed fysiken överlag — genom att kontrollera TNED-teorins resultat mot de ovannämnda praktiska Solobservationerna. Framställningen nedan beskriver de väsentliga detaljer som sammanhänger med den förenklade Solmodell vi måste använda i prövningen.

bakgrund

BAKGRUND MED FÖRUTSÄTTNINGAR

För kvantitativa resultatvärden, se från PRÖVNINGSMODELLEN

Solens allmänna polarisation med en central positiv laddning Q och en lika stor yttre perifer negativ laddning Q uppvisar genom Solrotationen olika laddningar som (vi förmodar därmed) roterar åt samma håll.

Om radierna för laddningarnas strömvägar också vore (nära) lika, skulle knappast någon magnetisk effekt alls kunna påvisas. Den enligt TNED påtagliga skillnaden i radie mellan inre positiva Q och yttre negativa Q garanterar emellertid en betydande skillnad i magnetisk verkan mellan inre positiva och yttre negativa strömmar.

Effekten av den radieskillnaden kan dock i motsvarande grad reduceras genom att den inre Q-delen roterar snabbare än den yttre; En inre, högre strömstyrka bildas — och därmed ett inre starkare B-fält som teoretiskt, likväl, kan matcha B-fältet från Solytans negativa Q-del, och därmed likväl ge ett teoretiskt nollvärde. Emellertid får detta konsekvensen att B-fältet på stort avstånd från Solen bör ligga i favör för den yttre negativa Q-delens magnetism, alltså ett magnetiskt N-fält (+), sett med ekliptikan som visuell referens (och vilket vi vet INTE är det allenarådande fallet).

Solmagnetismen är emellertid INTE (ens) så enkel; En betydande elektromagnetisk skärmeffekt finns i Solkärnan enligt TNED — på grund av Solkärnans höga täthet och som vi måste räkna med. Detta gör den prövande bilden mera komplicerad — och samtidigt enklare. Men den är helt utesluten i gängse uppfattningar där Solfysikens elementära grunder istället är ställda på helt andra förutsättningar — se vidare i Modern Solteori.

SOLENS POLARISATION bygger enligt TNED på Solkroppens fullständiga inre joniserade Q⁺-kärna med det resulterande yttre tunna elektronskalet som garanterar Solens avgränsade synbarhet genom opaciteten;

Elektronskiktekts tjocklek beräknas enligt TNED ur Solens elektrogravitella radie (r_G=6,97 T8 M, ca 1000 KM större än fotometriska radien 6,96 T8 M) genom en enkel parameterändring mellan atombasens atommassa med respektive utan elektronmassa, värdet blir drygt 340 KM (h);

Elektronskiktekts tjocklek tillsammans med vågenergins täthetsoberoende ligger sedan till grund för beräkningen av Solens primära initiella fusionsperiod (t_P);

Periodvärdet ger 11,44 år (lägst 33 sekunder, högst 115 år, absolut sämsta fallets gränsvärden) och som gäller idealt från Solens första dag.

Solcykelns period anges konventionellt till 11 år (NASA anger ett värde 11,4 år för vad man kallar ”Sun Spot Cycle”) — med något olika specifika värden beroende på beräkningsgrunder, medelvärdet anges generellt avrundat till 11 år.

MED DEN BAKGRUNDEN ENLIGT TNED tillsammans med stjärnornas allmänna tryckekvation som garanterar Solens polarisation genom stjärnstädet finns inte mycket utrymme att välja på enligt TNED i en motsvarande allmän magnetisk Solmodell:

Solens magnetiska kropp enligt TNED består av en liten tät (relativt snabbroterande) inre positiv kärna (Solstädet) med ett yttre motsvarande elektriskt laddat negativt skal. Genom Solens rotation och därmed centrifugalkraftens inverkan, kan elektrondelen förenklas genom den antydda avgränsade skalformen (blått, som vi kommer att förenkla ytterligare på en enskild ekvatoriell strömring). Den inre täta positiva kärnan besitter extraordinära skärmande egenskaper på grund av den höga tätheten som dels reducerar inverkan av den aktuella laddningsströmmen beroende på riktning och dels reglerar denna genom att kärnsfären sväller och krymper i fusionsperioden. Genom ytterligare förenkling kan hela Solkroppen för en första prövning ställas på en ringformig (variabel) systembyggnad med avgränsade sektorer. Vidare i huvudtexten.

Modellen som används för den matematiska prövningen av Solmagnetismens beräkning beskrivs utförligt från Den förenklade prövningsmodellen.

Nedan beskrivs först den helt avgörande speciella detalj som sammanhänger med Solmagnetismens grunder enligt TNED: skärmeffekten.

skärmeffekten

SKÄRMEFFEKTEN —

OCH SOLMAGNETISMENS PERIOD

Genom städkärnans maximala täthet finns det enligt TNED ingen möjlighet att undkomma konsekvensen med en effektiv elektromagnetisk skärmning mellan motstående sfärhalvor i Solstädet. Vi studerar hur.

Vid fusionsfasens början är Solstädet maximalt komprimerat.

Genom att de tätt liggande atomkärnorna i Solstädet skymmer strålvägen för de underliggande kärnornas ytladdningar (erinra atomkärnans speciella egenskaper med härledningarna från Planckringen), garanterar Solstädets mantelyta en effektiv elektromagnetisk skärm som bara kommer att uppvisa städytans jonladdning. Hela den övriga laddningsstocken avskärmas. Faktiskt.

Mantelskärmen ger speciella konsekvenser då städmanteln öppnas upp, mer eller mindre, genom fusionsfasen; Den närmast enorma mängd Q⁺ som ligger under det avskärmande mantelskalet kommer naturligtvis att uppvisa en exceptionell känslighet i effekt mot den elektromagnetiska rymden utanför städmanteln — beroende på hur mycket mantelskalet utvidgas. Med bara en ytterst liten skillnad mellan två på varandra följande fusionsvågor som uppvisar sinsemellan bara en ytterst liten marginell skillnad — hur mycket städmanteln utvidgas och därmed mängden exponerade kärnladdningar (Q⁺) från avskärmningen — ges en motsvarande ytterst dramatisk MAGNETISK verkan. Vi studerar detta närmare.

FRÅN FUSIONSFASEN (se fusionens cykel), med strålningstryckets frigörande, börjar Solstädets fusionsmantelyta utvidgas på det utbildade strålningstryckets kraft.

rekylvågen

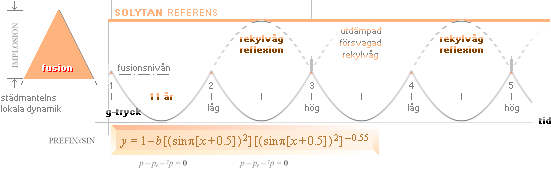
SOLENS VÅGMEKANISKA REFLEXIONSYTA garanterar att den mekaniska vågformen från fusionsfas nummer 1 i Solstädets mantelyta reflekteras åter till städkärnans rotpunkt från Solytan. Vi kallar den reflekterade delen här för rekylvågen; Då den så reflekterade rekylvågen når tillbaka till Solkärnan efter 2×t_P (se fusionsperioden) avrundat ca 22 år, adderas tydligen tryckkraften i rekylvågen med den ordinarie fusionspulsen nummer 3 så att denna åstadkommer ett djupare intryck — och därmed en något högre effekt: Solstädets mantel öppnar (skärmeffekten) upp en större mängd kärnladdningar Q⁺ jämfört med den ordinära fusionsvågens intryckande kraft och som därmed initierar en större magnetisk fältstyrka jämfört med föregående period.

Att inte också en motsvarande, likadan, rekylvåg genereras från den närmast föregående perioden och som skulle resultera i att varje fusionsfas skulle mötas av en motsvarande reflekterad rekyl från närmast föregående period, garanteras som redan klarlagts i VÅGENERGIN: Solens mekaniska vågenergi är densamma som Solens utstrålande energi: strålenergin är lika med vågenergin. Medan den förra fylls på och försvinner kontinuerligt ur Solkroppen, stannar mekaniska vågenergin INOM Solkroppen; OM en period innefattar en högre vågmekanisk energi, typ ordinärt g-intryck plus rekyl, tvingas Solen självreglera ordningen på nästföljande period så att INTE också denna uppvisar samma övertryckande fason. Vilket vill säga: Solen måste själv se till att energiräkningen stämmer; ytterligare rekylvågor tvingas, tydligen, av energiräkningen att dämpas ut. Det finns bara plats för en typrekyl, och den bildas följaktligen från 3:e, 5:te, 7:e, 9:e osv. fusionsvågorna, se även illustrationen ovan.

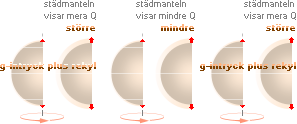
Solstädet pulsar alltså varannan period på en större exponerad kärnladdning Q⁺.

Motsvarande magnetiska effekt lämnar under 11-årsperioden ett avklingande »eko»:

Magnetismen från föregående aktiveringsperiod i den omfattande Solkroppen kvarstannar till viss del, och påverkas aktivt, ökande eller minskande, först med nästa aktiva period:

magnetiska vågfunktionen

graf 0.5([0.85(sinþ[x–0.5])'3]+cosþ[x–0.5])

Varje fusionspuls initierar en brytande B-flank. Eftersom fusionspulserna, med början från 3:e pulsen, adderar en ytrekyl på Solytans vågreflexionsradie, se Reflexionsgränsen, bildas sedan för varje 5:te, 7:e, 9:e, osv fusionspuls en högre tryckpuls, analogt en djupare inträngning som åstadkommer en motsvarande längre utkastning, och därmed en större Q+-exponering i avskärmningen, se från Skärmeffekten. Alltså kan den starkare pulsen bidra typiskt med en högre exponerad strömstyrka via Q+ än fusionspulser med jämna periodtal. Att pulserna håller takt mellan större-mindre garanteras av att Solens energiräkning håller vågenergin INOM Solklotet medan strålenergin har flöde genom, analogt försvinner kontinuerligt ur, Solytan — allt i kraft av rekylvågen. Därmed blir, tvunget, summan av en jämn (mindre) och en udda (större) likväl Solenergins medelvärde i netto: Solens strålande energi omsätter exakt Solens våg (ljud-) energi, se från Vågenergin. Det större intrycket ger en 11-årsperiod (se Fusionsperioden) med övervägande magnetisk nordpol (+) på Solens geografiska nordpol (norra ekliptikan) från Solkärnans exponerade kärnladdningar (Q⁺) som huvudgeneratris, det mindre intrycket ger en 11-årsperiod med övervägande magnetisk sydpol (–) på Solens geografiska nordpol från Solytans elektronskikt (e^–) som huvudgeneratris.

För kvantitativa resultatvärden, se från PRÖVNINGSMODELLEN

Den orangea pilmarkören underst till vänster i illustrationen ovan markerar fusionsfasens början i en udda period:

AKTIVA PERIODEN ges från fusionsvågens bildning och fram till halva t_P-perioden (5,5 år): Då Städmanteln öppnas ges en lokal magnetisk flödesanpassning till den lokalt öppnade mängden kärnladdningar Q⁺ via städmantels expansion:

Om föregående tillstånd kännetecknades av en magnetisk period av högt Q⁺-flöde, reduceras denna på en ny, lägre Q⁺-mängd. Och på samma sätt omvänt:

Om föregående tillstånd kännetecknades av en magnetisk period av litet Q⁺-flöde, tillväxer denna på en ny, högre Q⁺-mängd.

I vilket fall blir det (därmed) relativt enkelt att härleda den resulterande magnetiska periodens vågform: Den börjar med en fotpunkt som initieras av fusionsfasen vid t_P. Under halva denna period (5,5 år), upp till strålningstryckets maximum, får vi en stigande eller fallande flank som motsvarar den aktiva lokala Q⁺-justeringen. Däremellan stabiliseras den magnetiska fältstyrkan, mer eller mindre beroende på lokala strömningar. Om vi använder den vågform som närmast ansluter till föregående genomgångna vågformer från fusionens cykel, ges funktionen (på enklaste sättet) som ovan i PREFIXxSIN enligt

y = a([b(sin p[x+c])³] + cos p[x+c]) ............... magnetiska periodens vågfunktion

periodfunktionerna

SAMMANSTÄLLNING BFLS-graferna

SOLENS FYRA PERIODISKA FUNKTIONER

Med ovanstående framställning klarlagd, bildar Solfysiken ett system av fyra elementära vågfunktioner [BFLS, bäffäls, eng. baffles, vilket är ungefär vad det handlar om: engelskans ”baffle” betyder ungefär något som jävlas och är (eller har varit) särskilt mycket besvärligt] som alla kan uttryckas på relativt enkla elementära grunder med utgångspunkt från den centrala cykliska funktionen (F):

y = a([b(sin px)³] + cos px) ............................. B, magnetiska periodens vågfunktion

y = a–[(sin px)²][(sin px)²]^–0.55 ........................ F, fusionsperiodens vågfunktion

y = –a(b[cos px][sin px])([sin px]²)^–0.55 ........... L, latitudgränsernas vågfunktion

y = a–[(sin p[x+0.5])²][(sin p[x+0.5])²]^–0.55 ... S, Solmaximums vågfunktion, F-funktionen fasförskjuten 90°

B, Solmagnetismens allmänna vågfunktion, se från Solens allmänna magnetfält, skärmeffekten

F, Fusionsperiodernas vågfunktionen, se från fusionscykeln, fusionsperiodens detaljer

L, Latitudgränsernas vågfunktionen, se från fusionsperiodens synkronisering, positronmassans uttömning i Solytan, positronmassans latitudella variation

S, Solmaximums vågfunktion, se från positronmassans uttömning i Solytan

GRAFERNA I FASORDNING

Enkla samband BFLS-graferna Mera avancerade samband (frekvensmodulering i olika nivåer, OBS endast för prövning)

B, 0.5([0.85(sinþx)'3]+cosþx) OK 0.5([0.85(sinþ[x+cosþx/25])'3]+cosþ[x+cosþx/25])

F, 0.5–[(sinþx)'2][(sinþx)'2]'–0.55 OK 0.5–[(sinþ[x+cosþx/25])'2][(sinþ[x+cosþx/25])'2]'–0.55

L, –0.5((0.5[cosþx][sinþx])[[sinþx]'2]'–0.55) OK 0.5((0.5[cosþ(x+cosþx/25)][sinþ(x+cosþx/25)])[[sinþ(x+cosþx/25)]'2]'–0.55)

S, 0.5–[(sinþ[x+0.5])'2][(sinþ[x+0.5])'2]'–0.55 OK 0.5–[(sinþ[0.5+x+cosþx/25])'2][(sinþ[0.5+x+cosþx/25])'2]'–0.55

DE FYRA PERIODFUNKTIONERNA (BFLS) med perioden exakt 11 år har inlagts till jämförelse i nedanstående källldatareferens (Fjärilsdiagrammet överst och Solfläcksfrekvensen underst).

För B-grafens kvantitativa värden se Resultatredovisning från Skärmeffekten genom Prövningsmodellen.

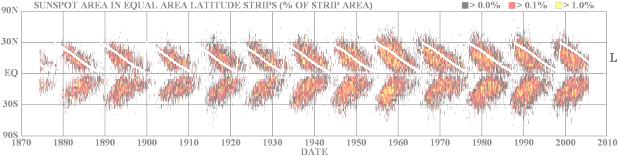
olika

De vita snedstrecken i det övre diagrammet motsvarar den inlagda L-formens funktion. Motsvarande inlagda vita del i den undre grafen visar S-funktionen. Mellan diagrammen är inlagt FB-funktionernas grafer.

I tidigare beskrivning har noterats att perioden på 11,1 år inte stämmer helt exakt överallt; Här är det tydligt att en (klar) förskjutning finns i den teoretiska fusionstoppen markerad vid 2009; den har i själva verket redan gått av stapeln (första observerade omvända solfläckarna som hör till den nya perioden januari 2008).

För kvantitativa resultatvärden, se från PRÖVNINGSMODELLEN

Bildkälla: FJÄRILSDIAGRAMMET (övre, Solfläckarnas latitudella fördelning) och SOLFLÄCKSFREKVENSEN (undre, Solfläcksytan i % av den synliga Solhemisfären) kommer från

@INTERNET NASA/Marshall Solar Physics

http://www.solarscience.msfs.nasa.gov/SunspotCycle.shtml

bildkällan används även av Wikipedia Babcock model 2007-05-28 m.fl.;

uppdateras månatligen med början från Maj 1874.

PERIODMATCHNINGEN

SOLFLÄCKSFREKVENSEN undre diagramdelen tillsammans med Solmaximumfunktionen (S) VISAR SPECIELLT TYDLIGT för det första att analogin i den enkla funktionsformen tycks vara av korrekt typ — samt (om trenden håller i sig) att den konstanta perioden på 11 år tenderar att dra iväg på en längre tidsskala än den som visar de uppmätta maxområdena; 11-årsintervallet i mitt bildoriginal ligger på 46 pixels, men ett intervall på 45 pixels tycks ge en bättre matchning (45/46 × 11 = 10,760869 år). Men det kan finnas flera faktorer som påverkar ordningen;

En mera ingående grafisk analys (som innefattar data ända från 1700) visar att periodformen tycks vara sammansatt av de två något olika perioderna på 11,1 år och 10,8 år — tillsammans med möjliga frekvensmodulationer av typen (FS-funktionen)

y = a–[(sin p[x+A])²][(sin p[x+A])²]^–0.55

med

A = (sin [cos p (x/n)])^t

Koefficienterna n och t anger frekvensmodulationen. Många olika sätt finns, ingen direkt enkel motsvarighet synes direkt uppenbar, även om tydliga sekvensen kan urskiljas. Det är i vilket fall tydligt att periodformen är sammansatt, men att den kan uttryckas med medelperioden på runt 11,1 år (med samtliga data medtagna under perioden 1700 till nu [2008]).

De två något olika perioderna framgår naturligt ur ovanstående beskrivna två olika fusionsintervall. Men det finns (ännu) här ingen direkt matematisk beskrivning av periodernas skillnad — annat än via relativtalet (från resultatredovisningen längre ner) 1,03 som ges från ekvatoriella strömstyrkorna och som (tydligen, eller möjligen) matchar/kopplar förhållandet (11,1)/(10,8) och som sammanhänger med den magnetiska periodväxlingen. Vi har under alla omständigheter att eftersöka en vidare undersökning för Solperiodens ordning, men den kommer inte att genomföras i denna presentation. Därmed avslutas härledningarna i Solfysiken enligt TNED på denna punkt.

Editor2008II5.

strålningstrycket OBSERVERA FÖR NYBÖRJAREN

Termonukleära strålningstrycket (^gp®T) är ENLIGT TNED till skillnad från det gängse materiebaserade elektrokinetiska strålningstrycket (T®^ep) en massbaserad värmegivande generatris som måste härledas separat på stjärnornas allmänna tryckekvation p–p_e=^gp genom gravitationstrycket (p) och Coulombtrycket (p_e). ^ep saknar helt betydelse för stjärnfysiken i TNED — men är det enda strålningstryck man känner till genom den moderna akademins lärosystem (se Jämförande Räkneexempel). Härledningen till ^gp kräver atomkärnans härledning, men den finns inte ens omnämnd i modern akademi. Se från Planckringen om ej redan bekant. Se även från beräkningsexempel i Koronafysiken.

sammandrag

Solfysikens två olika magnetiska perioder, uppkomst

För kvantitativa resultatvärden, se från PRÖVNINGSMODELLEN

SKÄRMEFFEKTEN. Då Solstädets mantel börjar utvidgas på det utbildade strålningstrycket avtar städmantelytans maximala täthet; städmanteln bildar normalt en elektromagnetisk skärm mot den underliggande laddningsmängden, den släpps INTE igenom; Men då städet utvidgas, exponeras en allt större del av dess inneslutna laddningsmängd (Q⁺). Vilket vill säga: den exponerade positiva kärnladdningsmängden ökar.

MAGNETFÄLTETS VÄXLING. Genom att fusionspulsen triggas på två något olika intryck, ett lägre (ordinära) och ett högre (extraordinära) på grund av rekylverkan från första fusionsvågen, exponeras en motsvarande mindre, eller större, del av kärnladdningarna i genom skärmeffekten. Detta ger två något olika strömtryck från Solstädet; De olika strömintervallen grundlägger två olika magnetiska perioder; En motsvarande större eller mindre B-styrka utbildas — eftersom olika mängd laddning via skärmeffekten kommer fram i respektive period.

När strålningstrycket efter ca 5-6 år utverkat sin del och städskalet återigen komprimeras före nästa fusionsfas, minskar B-fältet lokalt från städkärnan genom att städskalet återigen skärmar av alla Q⁺ innanför — men denna del påverkar inte omedelbart hela Solklotet. Vi får här (tydligen) tänka oss en viss efterklang (eko) av effekten från strålningstryckets aktiva fas (de ca 5-6 åren) och som s.a.s. hänger kvar till nästa period.

Med ovanstående klarläggande kan den observerade Solmagnetismens grundvärden testas mera ingående enligt förutsättningarna i TNED.

Prövningsmodellen beskrivs i detalj nedan, tillsammans med efterföljande resultatredovisning.

Skärmeffekten och Solmagnetismens period

prövningsmodellen

Se även särskilt i efterföljande elektriska grunddata · resultatredovisning ·

FÖLJANDE FÖRENKLADE RINGMODELL FÖR STRÖMMARNA I SOLKLOTET ENLIGT TNED (som kommer att reduceras på en inre och en yttre ekvatoriell ring)

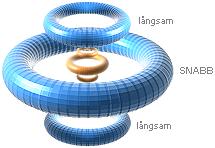
anställs i undersökningen av om TNED rent KVANTITATIVT kan satisfiera de observerade B-fältsvärdena på den givna Solmodellens form:

±50 Gauss (1G=t4 T) maxvärden vid Solpolerna,

med motsvarande maxvärden ute vid Jordbanan (magnetiska z-komponenten, alltså den som skär ekliptikan endast),

±50 nanoTesla (nT).

RINGMODELLEN är enkel och tydlig därmed att den bara använder de allra enklaste av den magnetiska fysikens samband — och därför kan kontrolleras och studeras av den som känner till den elementära experimentalfysikens matematik [Se utförligt från MAGNETISMEN]. Sambanden kommer här i vilket fall att beskrivas löpande.

DEN FÖRENKLADE

PRÖVNINGSMODELLEN

Sektorerna ab i illustrationen ovan med Solkroppen sedd ovanifrån norra ekliptikan (se xyz-referenser i Källuppgifter) markerar delar som tar ut varandra magnetiskt i Solekvatoriella planet relativt en mätpunkt typ Jorden (längre ut).

Tilläggsringen med den periodiskt producerade positronmassan (e⁺) kommer inte att användas explicit i de inledande beräkningarna men anges här för fullständighetens skull (e⁺-delen associeras initiellt i vilket fall med Q⁺-delen).

Figuren nedan visar hur idealiseringen med sektorerna är genomförd på enkla delar av rakledare.

Grunddata

R(Q⁺)_MEDELVÄRDE=10 000 M; R(e^–)=6,95 T8 M; x_SOL=r_G=6,97 T8 M; x_JOR=1 AU=1,496 T11 M

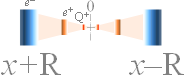
Illustrationen ovan (med närmast föregående) visar detaljerna enligt TNED: Solen som strömkomponent består av en inre (förmodligen snabbt) roterande helt joniserad städkärna, idealiserat som den inre mindre orangea strömringen. I Solskalet ligger idealt hela motpolen i form av totala elektronmassan och som roterar (idealt) med Solekvatorns hastighet (27 dygn relativt linjen Jorden-Solen), den yttre större blå ringen. Bägge ringarna roterar åt samma håll (moturs sett från ekliptikan) men med olika hastighet. Eftersom vi känner den B-matematiken väl, kan vi göra en grov (men säker) idealiserande beräkning genom att förenkla varje ring i formen av två (något) förkortade rakledare (d=R/2), mätpunkten utmed linjen för deras plannormal: Sektorerna ab lämnar inbördes lika stora motriktade bidrag och tar därför ut varandra: återstående effektiva del motsvarar ungefär 2r/Ö2, men inte hela denna del ger fullständigt bidrag; vi använder här förenklat och uppskattat totalt halva cirkeldiametern som ekvivalenten till den raka ledarens bidrag (r/2). Strömmarna i varje par rakledare är inbördes motriktade och deras B-fält motverkar varandra på ledarnas utsida.

MODELLENS METOD

Figuren närmast ovan visar den (här delvis uppskattade) effektiva återstående magnetiskt verkande rakledaren tagen med ±R/4=R/2. Modellen används vid utvärderingen i en första översiktlig grovberäkning av Solfältets magnetiska verkan på en godtycklig punkt på avståndet x från centrum (0) i Solekvatorsplanet.

Basdata för fältstyrkorna innefattar primärt endast inverkan från varje rakdel för sig så att en säker översiktlig uppfattning ges om den delens magnetiska bidrag. För mera precisa beräkningar tillkommer ytterligare, men vi återkommer till dessa längre fram.

Vi noterar redan här att den mera exakta magnetmatematik som ansluter till ringformade strömmar i praktiken är (ypperligt) komplicerad; Speciellt i Solfallet blir komplikationerna ännu mera komplicerade på grund av Solkroppens storlek där fördröjningarna mellan Solkroppens olika delar i allmänhet INTE kan bortses ifrån (minst 4,6 sekunder tvärs över Solklotet sett i vakuum). Vi kommer här, likväl i denna enkla grundform, att frånse alla fördröjningsaspekter för att på den vägen få fram helt elementära enkla skolexempel, till allmän prövning — utan komplicerade finesser som ändå ingen begriper.

GRUNDDATA för B-styrkorna är givna som ovan i det inledande punktstycket. Men vi återkommer till dessa nedan.

BERÄKNINGSGRUNDER

SPECIELLA FÖRUTSÄTTNINGAR

Förberedande inledning

Generellt för Solfysiken enligt TNED utgår vi idealt från att Solkärnan består av joniserade Väte-1-atomer med laddningen (Q⁺), alltså protoner — med en lika stor mängd negativ laddning i Solytan (e^–). Solkärnans omvandling av Väte-1 till Helium-4 [Se SOLENS ENERGIRÄKNING och SOLENS ENERGIPRODUKTION] medför en samtidig produktion (eg. frigörande) av två positronmassor (e⁺) per producerad Heliumatom [positronmassorna krävs explicit för energiräkningens del, och experimentalfysiken har bekräftat att det också fungerar så i praktiken]; Positronmassorna förs (i detta fall) upp till Solytan av strålningstrycket som medför att den polariserande laddningen mellan inre (Q⁺) och yttre (e^–) vid slutet av Solens brinntid har halverats. Se även i Solens Energiräkning.

SOM EMELLERTID REDAN VIDRÖRTS finns flera olika faktorer som gör att varje DIREKT ENKEL jämförelse Q⁺e^– (helt) mister begreppet analogi. Vi utgår därför istället ifrån vad som faktiskt framkommit, vad som utgör redan välkända grunddata på Solen, så att vi kan genomföra en så efter alla upptänkliga förutsättningar säker prövning som möjligt:

Skärmeffekten och Solmagnetismens period

BERÄKNINGSGRUNDEN FÖR FÄLTSTYRKAN I RINGPLANEN

BERÄKNINGSGRUNDEN med den givna korta rakledarens förenkling (bL=bR) ges här genom den konventionellt benämnda Biot-Savarts lag här i PREFIXxSIN enligt

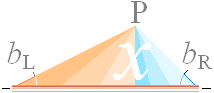
s

B_Ps = –µ₀I(sinb_L+ sinb_R)/4px ............................. 1Tesla=1VS/M², µ₀ = 1,25662 t6 VS/AM

B_Ps = –µ₀I · 2 sin atan[(x±R)/(R/4)]/4p(x±R) se föregående illustrations beteckningar

Huvuddelen av Solklotet är enligt TNED av typen låg täthet [Se Grunddata Solen] varför µ₀ kan tillämpas genomgående i översiktliga beräkningar.

ANMÄRKNINGAR

INRE Q⁺-RINGENS AVSKÄRMNING se Skärmeffekten medför att vi måste räkna bort magnetiska fältbidraget från Q⁺-ringens ena halva i beräkningarna utmed motsatta sidans ekvatoriella ringplan. Det finns, enligt TNED, ingen möjlighet att undkomma denna detalj: den är entydigt klar och koncis.

FÄLTSTYRKAN STRAX UTANFÖR SOLYTAN är enligt TNED i det praktiska fallet uppdelad (blå delen i figuren ovan) på många delsummerande parallellgående motsvarande strömringar mellan polerna. Det innebär att den förenklade enda ringformen (markerad vit ekvatoriell remsa ovan) kommer att uppvisa (våldsamma) fel i B-värdet nära Solytan. Exakt HUR stort felet blir, finns emellertid här ingen direkt möjlighet att kontrollera på annat sätt än att 1. utvidga modellen på allt flera (miljontals) latitudringar mellan polerna, en analys som dock inte kommer att genomföras här på grund av dess omfattning och 2. dividera B-värdet med ett uppskattat antal parallellinjer (miljontals) motsvarande delströmmar mellan polerna (samt addera en mindre uppskattad summerande del som funktion av vinkelavståndet). Vi nöjer oss här för dessa fall endast med att konstatera att OM vi från den förenklade enda ekvatoriella ringformen finner exceptionellt höga typvärden, vi i realiteten bör räkna med att de praktiska värdena reduceras betydligt genom den stora mängden parallellstråk (blå ytdelarna i illustrationen som i realiteten bör sträcka sig ända upp till polerna) både över och under ekvatorialringen. DESSUTOM TILLKOMMER för DEN specifika delen periodiska, från Solkärnan uppträngande positronströmmar innanför elektronskiktet, och vilkas motsatta B-fält ytterligare sänker det positiva ytvärdet utanför elektronskiktet. Dessa senare är emellertid, som vi har sett enligt TNED, just periodiska vilket ger utrymme för många olika variationer sett till Solcykeln som helhet. Därmed sagt i summa;

Magnetiska fältstyrkan i Solytans ekvatorialplan kan KNAPPAST förstås på annat sätt än, hur man än räknar, GENERELLT LIKA MED ±NOLL med mindre fluktuationer.

Det är precis också vad som visas i magnetogrammen (nedan) från Solytan: mellangrått anger ±0; Det är endast solfläckarna och de utpräglade polområdena som avviker märkbart;

Magnetiska fältstyrkan i Solytan är i det närmaste noll med små fluktuationer

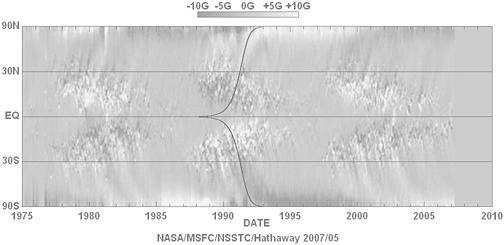
Källa: Solar Magnetic Field Map · Produced by: MSFC NASA, David H. Hathaway

http://www.solarviews.com/cap/sun/sunmag.htm

Views of the Solar System Copyright © 1995-2007 by Calvin J. Hamilton

Illustrationen ovan är ett gråskaleexemplar (som ger tydligare överblick) av originalet: ljusare partier än mellangrått är i originalet gula, mörkare partier än mellangrått är blå. Skalan ±10G anger magnetiska fältstyrkan (B) i enheten Gauss

(1G = 0,0001 [Tesla = VS/M²]). Notera att olika källor för samma diagram kan ha något olika skalor. Källan 2007-06-02

http://www.astronomycafe.net/qadir/q1659.html

för att exemplifiera, använder gränserna ±40G, samma diagram som ovan.

Skärmeffekten och Solmagnetismens period

BERÄKNINGSGRUNDEN FÖR FÄLTSTYRKAN GENOM SOLPOLERNA

BERÄKNINGSGRUNDEN för magnetiska polstyrkan ges från ringformen direkt enligt den redan (välkända) elementära magnetlagens koniska form (visas nedan i integral härledning från grundformen, se från Magnetismen om ej redan bekant, se även härledningen mera utförligt i Ciurkulära Konen)

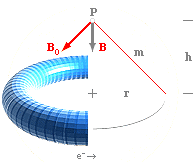
_0®2p ò dB_P = µ₀(r²)(I/4p m³) _0®2p ò d(2p) = µ₀Ir²/2m³ = B_P ;

B_P = µ₀Ir²/2m³

ANMÄRKNING

VI SER DIREKT att polstyrkans beräkning inte är kritisk på samma sätt för skärmningseffekten som i fallet det förenklade ringplanet. Eftersom Solkärnan (R=10 KM grovt i kalkylexemplen) är försvinnande liten relativt Solradien (r_G=6,97 T8 M), kommer i princip hela Solstädets elektriskt laddade ytmantel att bidra till polmagnetismen.

Strömbidraget från Q⁺-kärnan ska alltså enligt TNED bli (väsentligen) större för polstyrkan än för den ekvatoriella anslutningen. Den skärmningseffekt som gäller i polfallet kommer att inskränka sig till (maximalt, idealt) en halvering av hela Q⁺-kapitalet genom den kompletterande (motstående) sfärdelen som faller bort genom den motsatta sfärhalvans skärmeffekt.

Skärmeffekten och Solmagnetismens period

Elektriska grunddata

BERÄKNINGSGRUNDEN FÖR SolSTRÖMMARNA ENLIGT TNED

SOLENS sideriskt KONSTANTA roterande ELEKTRONSTRÖM framgår direkt ur Solens allmänna energiräkning och den kända Solrotationen enligt

förhållandena i SOLYTAN med elektronskiktets laddningsmängd (e^–):

I(e^–)₀ = (15,4 T37 × 1,602 t19 C = 2,46708 T19 C)/(86400S×25dygn) = 1,14216 T13 A

» 1,14 T13 A ..................... Solens konstanta elektronström

beskrivning

Genom Solens polarisation drivs initiellt från Solens första dag Solatomernas totala elektronmassa ut till Solytan. Från denna totalpott subtraheras sedan en konstant elektronmassa genom den motsvarande annihilerande positronmassa som produceras (genom Deuteriumbildningens mellanled i fusionsfasen) från Solstädet och drivs upp till ytan av strålningstrycket, och som medför att elektronstocken i Solytan vid tidpunkten för Solens död har halverats. Genom Energiräkningen produceras i medeltal från Solens råeffekt (3,3 T26 W) antalet 15,4 T37 positroner per sekund. Med konstant energiproduktion konsumeras lika stor mängd elektronmassa genom annihilationerna positron-elektron uppe vid Solytan och vilken energi f.ö. står för ca 7,5% av totala Solenergin. Så finns med andra ord alltid en absolut minsta aktivt elektronladdning

Q(e^–) = 15,4 T37 × 1,602 t19 C = 2,46708 T19 C

som deltar i Solrotationen och som garanterar en absolut lägsta motsvarande magnetisk aktivitet från elektronmassan.

Vi kan alltså anställa den negativa laddningsmängden Q(e^–)=2,46708 T19 C fördelad över hela Solkroppens rotationssfär; Strömstyrkan med avseende på Solrotationen blir då

I(e^–) = Q(e^–)/t

Solrotationen vid Solekvatorn är ca 27 dygn relativt linjen Jorden-Solen; På den tiden har tidslinjen på grund av Jordens årliga omlopp följt med 27/365,25 av Solvarvet; sideriska (absoluta, »sanna magnetiska») rotationen blir då 27–(27[27/365,25])=25,004106 eller avrundat 25 dygn (1 dygn = 86 400 S).

Elektronmassan Q(e^–) genom sideriska (absoluta) Solrotationen på 25 dygn ger då

Solens konstanta elektronström

I(e^–)₀ » 1,14 T13 A ..................... Solens konstanta elektronström

Vi kan insätta detta värde direkt i Polberäkningarna och se att vi får ett relevant Solvärde direkt (–36 Gauss); Det räcker emellertid inte för att styra ut dynamiken helt. Vi måste istället utgå ifrån ett betydligt högre värde enligt följande.

teoretiska strömvärdet

Om den (absolut lägsta) strömstyrkan I(e^–)₀ » 1,14 T13 A ackumuleras på 11 år genom 25-dygnsmultipler (11×365,25/25=160,71) ges ett högsta strömstyrkans referensvärde; Detta referensvärde motsvarar den positronmassa som frigörs i varje fusionsvåg: 160,71×(1,14216 T13 A)=1,83556 T15 A

I(e^–)_tP » 1,84 T15 A

Detta är vårt teoretiska utgångsvärde för den konstanta elektronström i Solytan som bildar Solmagnetismens ena komponent.

Den andra komponenten är variabel (och komplicerad, men inte helt omöjlig) och ges från den inre Q⁺-delen enligt nedan.

SOLKÄRNAN Q⁺:

Med Solekvatoriella medelströmmen I(e^–)₀=1,14 T13 A (från RåSoleffekten 3,3 T26W grundad på Väte-1 till Helium-4), grundad på positronbildningen i medeltal per sekund (N_e+=15,4 T37), ges motsvarande kärnjoniserade (ekvatoriella) strömstyrka via multipeln av positronladdningar ackumulerande under 11 år enligt Solekvatoriella referensrotationen (vi har inget annat att jämföra med)

I(Q⁺)₀ = (15,4 T37×1,602 t19 C×86400S×365,25dygn×11år)/(86400S×25dygn)

= 3,96484 T21 A;

Vi måste räkna med denna 11-årspott (minimum — också den bildade HeliumJonen tillkommer men som reduceras via motsvarande inströmning från ytan av joniserat Väte; Vi frånser dock tills vidare dessa detaljer — ) eftersom dess totala mängd frigörs direkt genom varje fusionsfas från Solkärnan, och därefter drar iväg uppåt Solytan.

INBERÄKNAT EN HÄR ÄNNU OKÄND INRE ROTATIONSHASTIGHET för Solkärnan (på grund av Solenergins vridande tillskott under årmiljardernas gång) som bör vara (betydligt) kortare än den yttre (ekvatoriella) på 27 dygn, ges en typiskt högre initiell strömstyrka

I(Q⁺)_tP = n(3,96484 T21 A);

I(Q⁺)_tP kan bestämmas via den förenklade ringmodellen genom de observerade Solpolsvärdena (±40 G) från den givna elektronkomponenten I(e^–)_tP=1,84 T15 A.

De ovan angivna grundvärdena, om de är korrekt uppfattade samt efter resultaten från den enkla testmodellen, ska beskriva gränserna för såväl Solpolernas ±B-ändring (max ±50 G) vart 11:e år som Jordvärdets dito (max ±50 nT, medelvärdet kring ental nT), bägge med korrekt tecken och kvantitet — i god (perfekt) matchning mot redan observerade värden. Inget annat accepteras.

Skärmeffekten och Solmagnetismens period

resultatredovisning

Summering av föregående utläggningar med SolMagnetfältets ModellGrunder i det konkreta resultatet:

BERÄKNINGARNA

METRISKA GRUNDDATA med ELEKTRISKA GRUNDDATA INSATT I DEN ENKLA MODELLFORMEN ger

polära I(Q⁺) Ampere I(e^–) Ampere BP(Q⁺) Gauss BP(e^–) Gauss BP Gauss

3,17587 T24 1,84 T15 +5918,46 –5868,47 +50,00

3,12221 T24 1,84 T15 +5818,46 –5868,47 –50,00 relation 1,0171865 differens 5,366 T22 ±a_(0–1)[0,5] + 0,5

ekvatoriella I(A) A I(A0) A B(JORD) nT SOLYTAN T enkelledare, se Fältstyrkan utanför Solytan

4,61451 T18 1,84 T15 –50,0000 +151,5622996

1,38434 T17 1,84 T15 +50,0000 +151,5655173 relation 0,03 differens 4,47607 T18

Solens magnetfält, dess periodiska växling och styrka, beskrivs tydligen utomordentligt av TNED.

Observera dock att resultaten ovan innefattar en mycket förenklad modell som bara uppvisar de allra enklaste grovdetaljerna (Solpolstyrkan och Jordvärdet).

FÖR SOLYTVÄRDET EXPLICIT

Om det höga Solytvärdet från den enda rakledaren divideras med ±500 000 delledare (mellan Solpolerna) reduceras närmaste ytvärdet till 0,0001515622996 Tesla; Från närmaste delledaren med medelavståndet runt drygt 2 KM till närmaste maken. Hur den lokala summeringen ser ut i det praktiska fallet är här inte känt. Gängse referenser anger magnetfältets styrka i Solytan till just ca 1 Gauss. Men det finns (ännu 2008-02-02, veterligt) ingen som kan specificera den uppgiften till polaritet. Se även i FÄLTSTYRKAN STRAX UTANFÖR SOLYTAN.

Vilket vill säga: Vi kan knappast få en enklare och mera galant beskrivning i syntes av Solfysiken.

ALLMÄNNA SAMBAND

±a_(0–1)[0,5] + 0,5; differensdelen som ska läggas till lägsta värdet

MED KÄNNEDOM OM VÅGFUNKTIONEN FÖR DEN MAGNETISKA FÄLTSTYRKANS VARIATION kan Solens magnetfält med dess förorsakande inre Solströmmar beräknas i detalj — med utgångspunkt från (OBS) den förenklade modellen och med de givna grunddata som angivits från instrumentella mätningar, gränserna som ovan ±50 Gauss (0,005 T) för Solpolerna och ±50 nT ute vid Jordbanan.

Samband: I(Q⁺)₀ + D(±a_(0–1)[0,5] + 0,5) = I(Q⁺)₀ + D(0,5)(±a_(0–1)+1);

I(e^–)_tP = 1,84 T15 konstant Solär Ytelektronströmstyrka för

polära:

I_POL(Q⁺)₀ = 3,12221 T24 A lägsta;

I_POL(Q⁺) = 3,17587 T24 A högsta;

differens:

D_POL = 5,366 T22 A;

ekvatoriella:

I_EKV(Q⁺)₀ = 1,38434 T17 A lägsta;

I_EKV(Q⁺) = 4,61451 T18 A högsta;

differens:

D_EKV = 4,47607 T18 A;

;

SOLENS Polrelaterade MAGNETISKA FÄLTSTYRKA (50G · ±a_(0–1))

I_POL(Q⁺) = I_POL(Q⁺)₀ + D_POL(0,5)(±a_(0–1)+1)

tillsammans med

SOLENS Jordrelaterade EKVATORIELLA MAGNETISKA FÄLTSTYRKA (50nT · ±a_(0–1))

I_EKV(Q⁺) = I_EKV(Q⁺)₀ + D_EKV(0,5)(±a_(0–1)+1)

beräknas alltså genom samma form med analoga (men bevisligen inte helt exakta) skalor mellan ändlägena polära ±50 Gauss och Jordrelaterade ±50 nanoTesla. Vi behöver alltså endast beräkna-ändra endera av strömstyrkans värden, bägge fungerar på samma skala (decimalvärdena kan variera något typ 4,99 relativt 5,00). Vi noterar att Magnetiska Positiva (N) polvärden vid Solens geografiska Nordpol ute vid Jordbanan ger ett motsatt riktat flöde enligt Magnetiska Negativa (S). Dvs., positiva Solpolsvärden ger negativa Jordpositionsvärden, och omvänt.

NOTERA OCKSÅ att ÄNDRADE metriska grunddata, här givna som ovan enligt

R(Q+)_MEDELVÄRDE=10 000 M; R(e–)=6,95 T8 M; x_SOL=r_G=6,97 T8 M; x_JOR=1 AU=1,496 T11 M,

också kommer att ändra referensvärdena för I(Q⁺)POL|EKV.

sammanfattning

UNDERSÖKNINGEN FÖR SOLENS DEL SKULLE GÅ UT PÅ att pröva om det ENLIGT TNED finns en (enkel) magnetisk modellform som kan ge de övergripande observerade Soldvärdena i teoretisk-matematisk form — runt max ±50 G vid Solpolerna, runt max ±50nT ute vid Jordbanan — samt konsistenta med det observerade sätt på vilket Solmagnetiska fältet ändrar sig periodiskt: med växlingar vart 11:e år, på en väl härledningsbar dynamiskt funktionell grund.

RESULTATET redovisas i nedanstående kalkylkort med föregående tabelluppställning.

Resultatet utpekar entydigt att

· Solmagnetismens polstyrka (±50G) med maximala ändringen ute vid Jordbanan (±50 nT), växling och 22-åriga period, KAN förklaras enligt TNED av en konstant elektronytström 1,84 T15 A med en inre variabel kärnjonström (max 3,17587 T24 A; min 1,38434 T17 A), varav konstantströmmen framgår direkt ur Solens energiräkning;

· prövningen har verifierat den enkla prövningsmodellen;

· de unika förutsättningarna, speciellt skärmningseffekten bortom allt tvivel garanterar en helt unik ställning — med TNED för Solfysikens härledning; sambanden kan INTE härledas av modern akademi.
Jämför även strålningstrycket.

källuppgifter, grunddata

UPPGIFTEN MAX ±50nT vid Jordbanan kommer från en @INTERNET-källa

[http://www.sec.noaa.gov/SWN/sw_dials.html];

Där anges (löpande, kontinuerligt var 15:e minut) magnetiska och andra satellitdata i xyz-värden på Solvindens sammansättning med magnetiska komponenter B(xyz). Figuren ovan orienterar komponenternas definition. Den för oss (här) mest betydelsefulla komponenten är B(z)-komponenten: Det är (här veterligt) bara Solens B-fält som kan bilda denna ekliptikala tvärkomponent (inverkan från Jordkroppen frånsett); Den maximeras något olika i olika källverk, men källan ovan anger det (hittills 2008-02-02) högsta maxvärdet ±50 nT (som inträffar ytterst sällan). Medelvärdet vid Jordbanan — anges generellt runt ental nano (miljarddels) Tesla (nT eller t9 T) — varierar också mellan olika källreferenser (och epoker med olika mätinstrument).

UPPGIFTEN MAX ±50 Gauss vid Solpolerna kommer från @INTERNET-källan (NASA) tidigare angiven i samband med beskrivningen av Solens allmänna ytmagnetiska fält genom magnetogrammet.

Beroende på källa varierar uppgifterna också här i de observerade Solpolsvärdena mellan 10-50 G:

±10 G [NASA/MSFC/NSSTC/Hathaway 2007/05]

±40 G [http://www.astronomycafe.net/qadir/q1659.html]

50 G [http://science.nasa.gov/headlines/y2001/ast15feb_1.htm].

Se även i Allmänna uppgifter.

kalkylkortet Solmagnetismen

Modellformen beskrivs utförligt från Den förenklade modellen

KALKYLKORTET TILL SOLMAGNETISMEN

1Gauss = 0,0001 Tesla; 10 000 G = 1T

kalkylkort Solmagnetismen · ±-värden sett från norra ekliptikan = idealt relativt Solekvatorn: Norra upp, Södra ner. 2008-02-02 | 2010-04-30:

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN c0kroppen.ods Flik1 Kalkylkort 4 — Solmagnetismen — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare Obs ALLA UTOM Internet Explorer — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn

http://www.universumshistoria.se/AaKort/c0kroppen.ods

Kalkylkortet här endast i bild (kalkylfunktionen fungerar inte direkt i webbläsare).

NOTERA

· att beräkningarna i ovanstående kalkylkort är TIDSABSOLUTA; vi endast undersöker de magnetiska fältstyrkornas värden SOM OM de gäller för en Jordfysisk modell i normal laboratoriemiljö;

· att RESULTATEN FÖREFALLER TRIVIALA på grund av den nära överensstämmelsen mellan TNED-modellen och de praktiska värdena; kalkylkortet ovan tjänar endast att verifiera de observerade värdenas allmänna inneboende samband, se föregående härledningar;
Vi får alltså (typiskt, men inte exakt) a Gauss Solpolär magnetisk fältstyrka vid Solära Nordpolen med gränsen ±50 G för –a nanoTesla Solgrundad JordbaneMagnetiska fältstyrka genom ekliptikan med gränsen ±50 nT;

· att polära bidragen från Solstädet och Solytan (0,59 T) i den enkla modellen enligt TNED bara ligger en liten bit över vad som allmänt anges för de (större) solfläckarnas magnetiska fältstyrka (0,3-0,4 Tesla).

Kommentar till skillnaden mellan polära och ekvatoriella I(Q⁺)

Som redan tidigare påpekades, måste Q⁺-bidraget för ekvatoriella beräkningen bli avsevärt mycket mindre än Q⁺-bidraget för polstyrkans beräkning, just på grund av skärmningseffekten. Vi har sedan att utrannsaka den mera fördjupade förklaringen till de fördelningar som bildar den skillnaden — men då är vi redan väl inne i Solfysiken enligt TNED. Uppgiften är (var) här främst att undersöka om TNED överhuvudtaget har någon ställning alls. Se vidare från resultatredovisningen.

allmänna uppgifter

ALLMÄNNA UPPGIFTER:

Enligt uppgift [NASA/MSFC/NSSTC/Hathaway 2007/05] växlar Solfältet B-styrka mellan MAX ±0,001 T (eller ±10 Gauss) vid OBS Solpolerna. ”Det allmänna Solmagnetiska fältet” sägs ligga runt 1 G eller 0,0001 T [BAs138sp2m; @INTERNET Wikipedia Sun, Magnetic field 2007-05-31], och fältstyrkan ute vid Jordbana (medelvärde) ca t9 T.

”If space were [was] a vacuum, then the Sun’s 10^–4 tesla magnetic dipole field would reduce with the cube of the distance to about 10^–11 tesla. But satellite observations show that it is about 100 times greater at around 10^–9tesla.”

@INTERNET Wikipedia Sun, Magnetic field 2007-05-31

Min översättning:

Om rymden vore vakuum, då skulle Solens t4 tesla magnetiska dipolfält reduceras med kuben på avståndet till ungefär omkring t11 tesla. Men satellitobservationer visar att det är omkring 100 gånger större vid omkring t9 tesla.

END.

Editor2008II11 | 2010IV16

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Solens energiproduktion

ämnesrubriker

innehåll

SOLENS ENERGIPRODUKTION

Solens energiproduktion

deuteriumfrågan

periodisk pulsning

fusionspulsen

fusionens cykel

innehåll i sammanfattning

Fusionsfasens omfattning

fusionsvågen börjar vid polerna

fusionsvågen

Fusionsvågens period

energireferens

sekundTransitMassan

TERSAFE · termiska sämsta fallets avkylningssamband

toroidytan, referens

fusionsvågens svephastighet

elektriska barriärkraften

absoluta periodgränserna

kortaste fusionsperioden

längsta fusionsperioden

fusionsperiodens detaljer

positronmassans uttömning i Solytan

positronmassans latitudella variation

jämförande grunddata genom observationer

fjärilsdiagrammen

praktiska Solvärdet

Vågenergin

vågen bildas

vågenergin = strålenergin

Vågenergins transport till Solytan

frekvensrelationen

vågenergins täthetsoberoende

Solära ytenergikoefficienten

Solens fusionsperiod

fusionsperioden

kalkylkort Solradien

teoretiskt och praktiskt tP-värde

frekvensens täthetsvariation

Solens allmänna vågfunktion

Solens polära vågfunktion enligt TNED

mekaniska reflexionsytan

kalkylkort reflexionsgränsen

reflexionsgränsen

Solens 22-årsperiod

Modern solteori

ytdata

hur modern naturvetenskaplig uttolkning intygar att den inte gör något fel i fysiken

Solens allmänna magnetfält

BFLS-graferna

grunddata

avgörande TNED-test

bakgrund med förutsättningar

skärmeffekten

rekylvågen

magnetiska vågfunktionen

periodfunktionerna

BFLS-graferna

sammandrag

Prövningsmodellen

grunddata

elektriska grunddata

teoretiska strömvärdet

resultatredovisning

Källuppgifter, grunddata

kalkylkort Solmagnetismen

allmänna uppgifter NASA

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

[BA]. BONNIERS ASTRONOMI 1978

t för 10^–, T för 10⁺, förenklade exponentbeteckningar: EX; t12 = 10¹²

PREFIXEN FÖR bråkdelar och potenser av FYSIKALISKA STORHETER

Här används genomgående och konsekvent beteckningarna

förkortning för förenklad 10-potensbeteckning, t för 10^–, T för 10⁺

m milli t3

µ mikro t6

n nano t9

p pico t12

f femto t15

Alla Enheter anges här i MKSA-systemet (M meter, KG kilo[gram], S sekund, A ampere), alla med stor bokstav, liksom följande successiva tusenprefix:

K kilo T3

M mega T6

G giga T9

T tera T12

Exempel: Medan många skriver cm för centimeter skrivs här konsekvent cM.

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2018-10-21

*END.

Stavningskontrollerat 2008-02-09 | 2010-04-16.

rester

BuggPåWebben?

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se