APPENDIX2 till
Induktionen och Magnetismen i Relaterad Fysik för UNIVERSUMS HISTORIA | 2011X7 | a ![]() production |
Senast uppdaterade version YearMonthDayTime 2024-07-02
production |
Senast uppdaterade version YearMonthDayTime 2024-07-02
innehåll | IndMagAppendix2.htm | · webbSÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla
webbsidor
Magnetismens detaljer i Relaterad Fysik MED Maxwells Analogier
Riktningsbegreppens
upphov för magnetismen — magnetismens detaljer i relaterad fysik MED
Varför
Maxwells matematiska/magnetiska mekanik inte kan harmoniera med magnetismens fenomen i relaterad fysik — generalgenomgång av Maxwells arbeten
1855-1861
Se även:
 BILDKÄLLA: Författarens
arkiv · Viken13Apr2010Bild201 · NikonD90 · Detalj
BILDKÄLLA: Författarens
arkiv · Viken13Apr2010Bild201 · NikonD90 · Detalj
Riktningsbegreppens upphov, magnetismen
2011IX14
Med vidare klargörande från [2007]
originalförfattningens ATT FÖRSTÅ B-VEKTORN i Hur B-vektorn förstås.
Angående nödvändigheten med M-vektorerna — om
ej redan bekant
Riktningsbegreppens
upphov för magnetismen
— magnetismens
detaljer i relaterad fysik
Magnetiska
fältriktningens orsaksgrunder i detalj
Magnetismens uppkomst komprimerat
|
statiska
fältflödena inom elektriska laddningen |
g-rymdens
referenspunkter |
magnetismens
uppkomst genom projektionen av a på b via hastigheten u relativt b |
||
|
|
|
|
||
|
a |
b |
c |
||
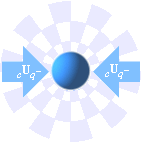
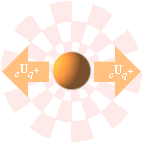
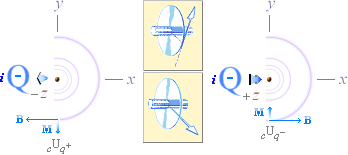
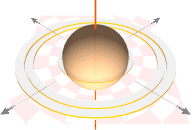
Med (a) elektriska laddningens potentialprojektioner
— samma som statiska elektriska laddningsfältets (c)U(q±) på det (b) omgivande lokalt dominanta g-fältets
fixa rymdpunkter (P) i följd av laddningens lägesändring (u)
— följer (c)
— i respekt till ljusets friställning från kinetiken som grundat på ljusets gravitella beroende
— en komplex överföring (se Kausalsambandet)
av (a) på (b) via ett normalplan till u, det här
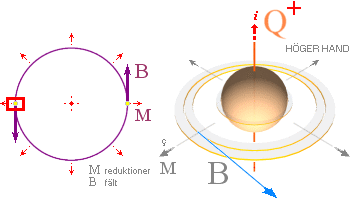
benämnda magnetiska ring-, fält- eller vågplanet (figurdelen nedan,
storcirkeln).
|
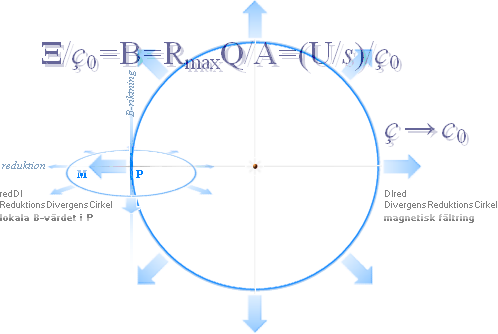
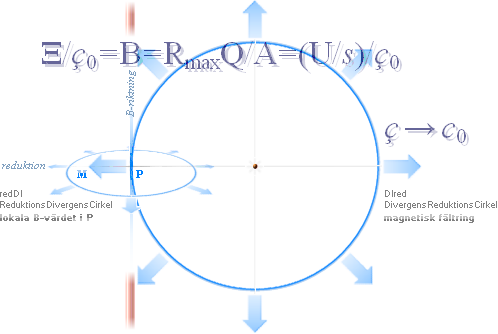
— ReduktionsDivergensCirkel ————————————————— magnetiska
punktfältstyrkan fältstyrkans [g-divergensrelaterade]
expansionsekvivalent från planvektorsummans
identitetskriterium [ekvivalensen mellan expansioner och
tangenter] B, magnetisk
fältstyrka, se NOMENKLATUR. DIred —
DivergensReduktionsCirkel ————————————————— magnetiska
fältringen Dess geofysiska
motsvarighet får förstås strängt differentiellt — se begreppet differential i
relaterad mening om ej redan bekant |
Ljusets friställning från kinetiken — elektrostatiska fältflödets
interna potentialåterkopplingar är inte additiva med
laddningens lägesändring [u] relativt ett yttre dominant gravitationsfälts
rymdreferenspunkter — medför att elektriska
laddningens potentialbild projiceras på lägesändringens g-punkter i form av
en lokalt differentiell rymdförtätning [Rmax] för bevarandet av elektriska
konstanten [Rc] i u-riktningen. — Därmed bildas en
magnetisk fältring med en lokalt lägre — reducerad — divergens [ç] för elektriska
konstantens bevarande och som strävar att uttömma sig i det tunnare rummets
fria toppdivergens [c]: reduktionerna bildar magnetismen. — De närliggande
reduktionernas lika kvantiteter i ringens bågform formar en naturlig
motsvarande tangentiellt [o| ] utsträckt fältkraftsriktning [magnetisk fältstyrka] vars magnitud avtar
med växande avstånd till ringens centralpunkt. — Beskrivningssättet generellt har eftersökts i den moderna
akademins lärosystem men inte påträffats. Jämför Maxwells
magnetiska mekanik. — För den illustrerade
sambandsformen till magnetismens bildning, se utförligt i Kausalsambandet. — För ReduktionsDivergensCirkeln, se även redDI. — Rätvinkliga
kopplingen mellan B-riktningen [DIred-cirkeln] och M-riktningen
[redDI-cirkeln] följer också enligt Planvektorsummans Identitetskriterium. Grunden till den
detaljen beskrivs nedan. |
— PROJEKTIONEN via u
åstadkommer tydligen en motsvarande resistiv förtätning
som i bevarande av elektriska konstanten (Rc)
tvunget reducerar g-divergensen (c) lokalt för planvågens differentiella del.
— Därmed garanteras planvågens expanderande utsträckning
från det tätare rummets reducerade divergens (ç) till den fria rymdens toppvärde (c).
— Eftersom ljushastigheten, den lokala divergensen, inte
är additiv med lägesändringen (u), garanteras att planvågens tjocklek bevaras
differentiell, helt utan dimensionell divergens. Det blir bara den reducerade
(förtätningen, den s.k. magnetismen) som expanderar rätvinkligt u.

Genom INVERKAN AV elektriska fältets potentialer [U=k(Q/r)]
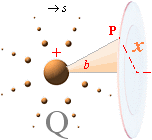
som inbördes SUMMERANDE [U=U1+U2], och endast då — vi kan som i bilden ovan
lägga två lika laddningars potentialbilder över varandras (grön vänster) och
därmed erhålla dubbla enskilda värdet — erhålls motsvarande variabla summan av
två lika Q-potentialer;
— Summeringen görs elementärt i en och samma gemensamma
planprojektion (här bildytan) genom en avståndsseparation (x,
horisontellt ovan i bildsekvensen) tillsammans med (här via PREFIXxSIN)
en motsvarande sinusprojektion (sinA=r1/r2)
av radiella potentialvärdet enligt
U = (U1 + U2) = k(Q/r1)
+ k(Q/r2)sinA = kQ[1/r1 + sinA/r2)]
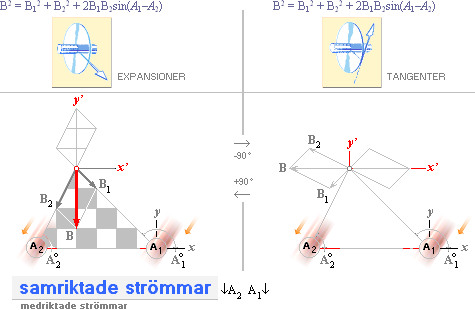
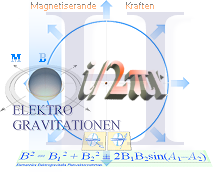
Denna sambandsform grundlägger Elementära Planvektorsumman
Elementära
Elektrogravitella Planvektorsumman
B2 = B12 + B22
± 2B1B2sin(A1–A2).
Den beskriver i relaterad fysik Ekvivalensen
för Expansionsvektorer och Tangentialvektorer interferensrymden mellan två kroppar med magnetiska,
elektriska och gravitella fält, vidare nedan.
— Ämnesformen tycks överhuvudtaget
inte (ens) ha uppmärksammats i den moderna akademins lärosystem.
Även fälten för elektriska och gravitella resultanterna mellan två
laddningar/massor innefattas av ovanstående sambandsform. De olika
planfältformerna beskrivs mera ingående i sektionen om Fältformerna:
De olika planfältformerna
beskrivs mera ingående i sektionen om Fältformerna som bilden ovan (förminskad) är hämtad från.
— Även fälten för elektriska och gravitella resultanterna mellan två
laddningar/massor innefattas av ovanstående fältbildsmatematik. Det tillhör
(nog) fysikens elementa att känna till dessa detaljer — men vissa
begreppsförvecklingar finns i jämförelsen med motsvarande ordning i den moderna
akademins lärosystem — se särskilt ELEKTRISKA FÄLTSTYRKANS FRIHETSSATS: skillnaden mellan
1/r-fält och 1/r²-fält.
— Planvektorsummasambandet visar explicit ekvivalens mellan expansioner och tangenter UTAN NÅGON DERAS
INBÖRDES INTERFERENS;
Planvektorsummans Identitetskriterium
Planvektorsummans
Identitetskriterium:
— Vektorformernas kvantiteter ger exakt samma
resultatvärden i de bägge fallen, men riktade
rätvinkligt varandra — och därmed i
garanti av att sakna projektion av varandras komponenter därför inte kan
summeras inbördes (trigonometriskt garanterad individuell immunitet):
Exakt samma matematiska
samband, här i PREFIXxSIN. Bägge riktningskomplexen — vänster,
expansionsvektorer [här inåtriktade] och höger, tangentialvektorer — får exakt
samma matematiska-trigonometriska form för strömflöden som har samma
längsriktning [medströmmar↓A1A2↓], sambandet nedan. VektorBeteckningen
B har
här valts enhetligt för bägge typerna.
Elementära
Elektrogravitella Planvektorsumman
De antydda diametrala
vektorparallellogrammerna motsvarar resultatbilden med medströmmarna tagna i
omvänd riktning [↑A1A2↑], se vidare riktningsprincipernas
förklaring och riktningsgrunderna längre ner i
huvudtexten.
— Övergången mellan
expansioner-tangenter ges — som vi ser — med vektorkroppens planrotation i
respektive medurs 90° från expansioner till tangenter och omvänt moturs 90°
från tangenter till expansioner. Det är alldeles tydligt att den ordningen
harmonierar PERFEKT med magnetismens kvalitativa fenomenbild ENLIGT RELATERAD
FYSIK. Vidare nedan i huvudtexten.
För motströmmar [↓A1A2↑] gäller
minustecken i sambandet ovan.
Sambandens härledning visas utförligt illustrerat i originalförfattningens EKVIVALENSEN MELLAN EXPANSIONER OCH TANGENTER.
Exakt Samma Samband sammanfattar också de
planfältbilder som ingår i elektriska dipol- och antidipolfälten, samt
gravitella fältet mellan två växelverkande kroppar, se Fältgeometrin. Sambandsformens övergripande betydelse kan
därför också i relaterad mening kallas Elementära
Elektrogravitella Planvektorsumman [ELEP].
— Elementära
Elektrogravitella Planvektorsumman bildar — därmed tydligen — summan av hela
den relaterbara fysikens totala vektorfundament för samtliga grundfysikaliska
fenomenbegrepp.
— Begreppsbilden som ovan finns här veterligt inte representerad i
den moderna akademins lärosystem. Där används istället den moderna akademins
vektorkalkyl — med speciellt uppfunna regelverk från 1800-talet — som garanterat
missar målet.
redDI — motsvarande detaljer i magnetismens
fysik har eftersöks i den moderna akademins lärosystem men inte påträffats
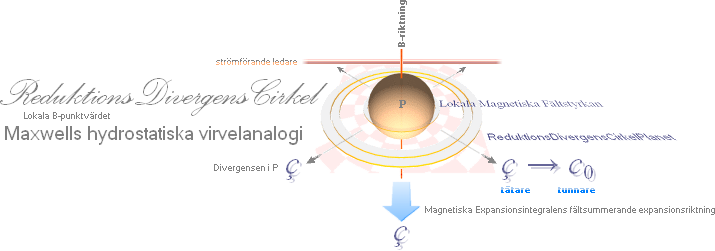
ReduktionsDivergensCirkeln
2011IX12— Med vidare förtydligande från originalförfattningen i B-vektorn — för detaljerade jämförelser med Maxwells
hydrostatiska virvelanalogi
Reduktions
Divergens Cirkeln
Trigonometriska
sambandet för den tvådimensionella vektorsummeringen med ekvivalenta resultat för
expansionsvektorer och tangentialvektorer, se Planvektorsummans Identitetskriterium
— nedan i illustration specifikt med
avbildning för expansionsvektorerna (tangentialvektorerna ges av den
resulterande vektorbilden genom multiplikation med –i, dvs., medurs rotation
90°),
Elementära Elektrogravitella
Planvektorsumman
definierar i relaterad fysik alla
elektriska strömvägars likvärdiga och likaberättigade magnetiska bidrag (B) i
en fix g-relaterad rymdpunkt (P) i formen av en (redDI) ReduktionsDivergensCirkel:
ReduktionsDivergensCirkeln [redDI-cirkeln] beskriver I RELATERAD
FYSIK magnetiska
fältringens [DivergensReduktionsCirkelns, DIred-cirkelns] lokala magnetiska divergensvärde [ç].
— RedDI-cirkeln relateras
till planet som skär genom strömlinjens längsutsträckning, med unik referens
till magnetiska fältstyrkans cirkulärpolarisation [motsvarande fältstyrkan
i mitten av en strömring] ,se artikeln nedan.
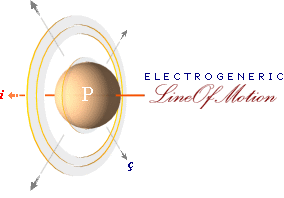
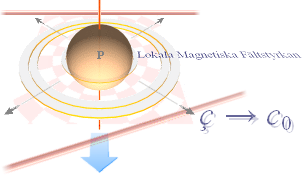
— Genom att g-divergensen är punktlokal
— illustrerat
av den slutna sfären, motsvarande punktens differentiella domän och därmed
praktiskt avgränsad till en motsvarande illustrativt obegränsat liten sfärisk
domän med idealt lokal homogen rymd
— kan den också
illustreras som en helt idealt homogen [differentiellt] vektoriell utsträckning
från en centralpunkt i sfärens mitt.
— Cirkulära snittet av
den idealformen formar ovanstående illustrerade magnetiska centralbegrepp.
Punktfältstyrkans cirkulärpolarisation
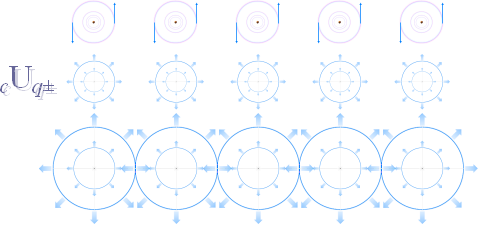
— Om strömstyrkan från
den givna strömledaren ökar, eller om strömledaren dupliceras och maken roteras
godtyckligt i det givna redDI-planet med gemensamt
bibehållen redDI-cirkel, är det tydligt att redDI i vilket fall summerar de
enskilda bidragen på ett och samma lokala punktvärde:
— RedDI skiljer inte på
ORTEN för magnetiska fältbidraget i P, eftersom redDI
avbildar en cirkulär vektordivergens: alla riktningar i samma cirkulära plan är
likaberättigade.
— Denna satsbild uttrycker
tydligen samma sak som att punktfältstyrkan är »cirkulärpolartiserad». Dvs., »magnetiska fältvektorn är RUND»,
inte flat — fast i illustrationerna används oftast en flat substitution.
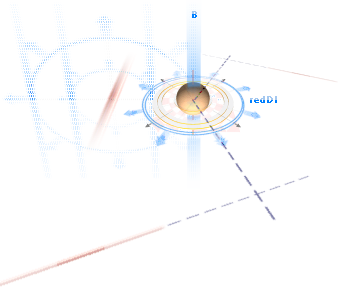
— Det
är samma som den tidigare (men mera kortfattat) beskrivna PRINCIPEN FÖR DEN CIRKULÄRPOLARISERADE B-VEKTORN:
Genom divergensreduktionerna som den egentliga magnetiska
fältdefinitionskraften, definieras den magnetiska fältstyrkans verkställande
vektor som ett likaberättigat summeringsobjekt — oberoende av de tillhörande
strömledernas orientering i ett deras skärande gemensamma plan. Dvs.:
fältstyrkans vektor kan i grunden förstås vara en 2D-vektor.
— Det är alltså samma princip som för magnetiska (M)
fältstyrkans summering i centrum av en strömförande ring: alla bidrag delar på
en och samma redDI, den i strömringens mitt; varje minsta strömledardel i
ringen bidrar lika med sin fältrings redDI, analogt (med idealt homogen
g-rymd) samma M-vektorbidrag (eftersom M-vektorn i grunden är en lokal g-divergens).
— Generellt: magnetiska fältvektorn är »rundpolariserad»; Det spelar ingen roll hur olika inbördes strömkällors
ledarutsträckningar är orienterade relativt varandra i ett deras gemensamt
skärande plan; alla ges samma status genom deras gemensamma summerande redDI.
Riktningsgrunderna
— Genom elektriska laddningens entydigt givna två enda
flödesriktningar (c)U(q±) via g-divergensens två enda möjliga laddningsåterkopplingsbilder eller
flödesriktningar som antingen relaterat 0-c eller c-0 (vi
associerar här till ljusets absolutacceleration) — positiva laddningar relateras med »utåtriktat
divergensflöde» 0-c som (c)U(q+), negativa laddningar med
»inåtriktat divergensflöde» c-0 som (c)U(q–) — framträder
helt naturligt ur ovan »enkla elementära genomgång» den inneboende ordningen
för hur vektorsummeringarna ska göras, tolkas och verkställas i den matematiska
planvektorsummeringens ljus.
NOTERA att begreppet potential U=k(Q/r)
i konventionell mening (i elektrostatiska fältet) INTE betraktas som en vektor
utan som en skalär (icke riktningsbetingad storhet). Jämför
”In classical electromagnetism, the electric
potential (a scalar
quantity denoted …”,
@INTERNET Wikipedia Electric potential
[2011-09-15]
I relaterad fysik däremot härleds emellertid
Q-fältets potentialbild (utförligt i Elektriska Fältet) entydigt via begreppet (divergens)IMPULS från g-divergensens
differentiella inverkan på avståndet r från Q-origo. Här utnyttjas den
fysiska verkan för Q-fältets egen inre elektrogravitella polaritetsutsräckning
(±) — vilket betyder en väl relaterbar riktningsform som definierar
Q-fältets fysiska utsträckning, och därmed en speciellt bestämt
relaterad vektorform.
— Den avgörande Differentialdetaljen (dT)
i Q=√(m/R)(A/dT) i Elektriska Laddningens Härledning och som i relaterad fysik kommer från ljusets absolutacceleration, är bägge detaljer som väl, i denna författnings ljus,
har eftersökts i den moderna akademins lärosystem men inte påträffats. En
elementär härledning till Q tycks
inte finnas överhuvudtaget i etablerade fackverk.
Är bidragen (1&2) inbördes motriktade (x=0,
illustrationens två sammanförda expansioner [gröna vänster] drar åt diametralt olika håll), analogt motsatta strömflöden, tar potentialerna ut
varandra med nollverkan,
U = (U1 + –U2) = 0
— Man kan alltså enbart på den enkla grunden ställa upp
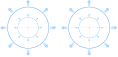
absolut entydigt fysikaliskt beskrivande typflödesbegrepp i magnetismen RENT
IKONISKT som nedan (positiva) enligt magnetiska EXPANSIONSVEKTORFORMERNA
(M) och (de resulterande) TANGENTIALVEKTORFORMERNA (B) — se även ExpansionsTangentEkvivalenterna i originalförfattningen, beskrivningen här är det mera
detaljerade komplementet. Beskrivningen nedan redovisar ordningen detaljerat —
och som sammanfattas, och kan förstås naturligt genom högerhandsregeln. (Studera, jämför, kontrollera — stämmer perfekt).
Riktningsprincipernas förklaring
Riktningsprincipernas
förklaring
|
|
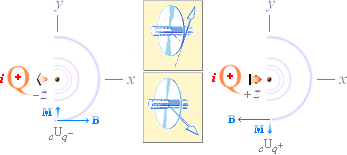
positiva
laddningens ikoniska riktningsform, summerande fältstyrkor |
negativa
laddningens ikoniska riktningsform, summerande fältstyrkor |
|
Villkoret
i summerande vektorer med två varandra motriktade lika strömflöden är att summan
måste bli noll. — Vidstående
riktningsformer [referens positiva] uppfyller det villkoret: — M-summan såväl som
B-summan nollas ut med varandra summerande motriktade i-strömmar. — Riktningsflödena för cUq± måste koppla konsekvent till
motsvarande diametralt orienterade M-expansionsvektorer för att en motsvarande
verkansmässig ekvivalent laddningspolaritet ska komma ifråga för den
summerande vektormatematiken. Vi studerar det
särskilt. De
diametrala M-riktningarna — positiva laddningen: — c-suffixet i cUq
associerar till det egna inre statiska Q-fältets egen flödesriktning och med
suffixet q± som specifik identifierare för positiv [q+] eller negativ [q–]
elektrisk laddning. För den summerande ekvivalensens giltighet måste alltså M-vektorn som vektorform avstämmas analogt med
den associerade inre, statiska, Q-flödesriktningen. |
Denna avstämning kan
likväl INTE förstås hämma eller inverka menligt på den entydiga innebörden av M som just en expansionsvektor — vare sig SÅ riktad
inåt eller utåt. M-vektorn blir i vilket fall den lokalt reducerade divergensen
[ç] som driver fältringen utåt, från det tätare [ç] till det tunnare [c], och
som därför, oavsett associerad med endera inre projicerade
Q-flödesriktningen, är agenten för själva den expanderande fenomenformens
kvantitativa fysik [den egentliga, verkställande, magnetiska fältvektorn].
Det föreligger därför ingen motsägelse mellan de diametrala M-riktningarna,
och förutsatt de här beskrivna divergensaspekterna beaktas: absolutformen för M återfinns som en »divergenscirkel», ett lokalt punkt-g-divergensvärde. |
Dvs., man kan i den
allmänna meningen välja godtycklig diametralpreferens för M-riktningen
analogt med »ç-expansionen» för summering av två eller flera bidrag,
ovanstående positiva/negativa är bara ett av de bägge sätten. — Denna detalj
harmonierar också fullständigt med de inbördes ordningarna i de expanderande
divergensringarna, vidare nedan. — Ordningarna stämmer
också helt överens med HÖGERHANDSREGELN. — Valet för z-axelns
polaritet är här analog med det naturliga PILOTSYSTEMETS xyz-referenser. — Motsvarande negativa laddningens ikoniska riktningsform för tangential- och
expansionsvektorerna blir i termer av strömflödesriktningar som visas ovan. |
|
|
positiva |
negativa |
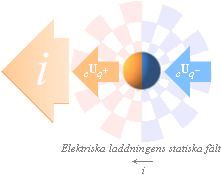
Motsatta expansioner (M) från
divergensprojektionerna av lika laddningar tar ut varandra (figurdelen i a
nedan).
|
|
|
|
|
a |
b |
c |
För en motsvarande tangentiellt
(B) bestämt referensriktning — vilken den än är — bildas motsvarande villkor
med en konsekvent motriktad vektorform i diametral riktning, (b),
och därmed magnetfältsringen som
en »avbildad
rotation» (c) för att få
nolleffekt med lika men motriktade strömflöden.
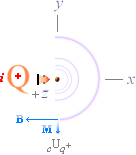
Preferensbeteckningarna
för en positiv elektrisk laddning med strömriktningen i pilosystemets
z-riktning.
— M för expansioner, B
för tangenter. Se även Ekvivalensen
mellan Expansioner och Tangenter i Planvektorsumman.
Allmänna magnetiska fältväxelverkan
2011IX18
Efter föregående
genomgångar
Allmänna
magnetiska fältväxelverkan mellan två strömleder
Verkan[B(Bled)PÅB(Aled)] = B(Bled)·sinA — krånglig formulering,
grymt enkel praktik: — |
|
Om
en elektrisk laddning (Q) förflyttas (u) i ett yttre B-fält av samma
beskaffenhet som den elektriska laddningens ideala (sfäriska) tvärsnitt, det
är u i samma riktning som B, flyttas Q endast idealt inom sin egen elektriska
längsprojektion [F/Qc=B] och ingen växelverkan med B kan därför ske.
För
att en växelverkan ska kunna ske, måste u ha någon komponent riktad
rätvinkligt B. — Eftersom verkan
således endast beror av u rätvinkligt B gäller följaktligen formellt för
kraftverkan mellan Q och B [magnetiska kraftlagen] F=BQu. |
— Om i ovanstående föregående illustration för de bägge
centrala riktningsbegreppen redDI och DIred införs en andra (sekundär) strömled (en B-ledare)
parallell med den givnas (A-ledarens) B-riktning — den vertikalt antydda
kopparledaren i figuren ovan till vänster parallellt med B-riktningen —
får vi en maximalt förenklad och samtidigt maximalt (»enkel») komprimerad illustration
som (på visst elegant sätt) anknyter till föregående beskrivna Planvektorsummans
Identitetskriterium:
— De bägge varandra korsande ledarnas redDI och
DIred antar parallellitet med varandras respektive DIred och redDI-cirklar;
A-ledarens redDI-cirkel motsvarar B-ledarens DIred-cirkeln (magnetiska
fältringen), och vice versa;
— Ingen vektorsummering kan ske i detta läge,
eftersom varken redDI- eller DIred-cirklarna uppvisar några andra projektioner i varandras
plan är räta linjer: det finns ingen bestämbar riktningspreferens att summera.
— Fältverkan från B-ledaren till A-ledaren är alltså avstängd.
Magnetiska fälten från respektive ledare växelverkar inte.
— Situationen är densamma som uppvisas då elektriska
laddningar färdas i samma riktning som riktningen hos ett yttre B-fält: ingen
kraftverkan existerar mellan det yttre B-fältet och det B-fält laddningarna ger
upphov till genom sin rörelse. Se även utförligt i Magnetiska kraftlagen.
— Konventionellt beskrivs situationen av den s.k. Lorentz Force (ref. @INTERNET Wikipedia Lorentz
force 2011-09-18), här magnetiska kraftlagen F=BQv med rät vinkel mellan riktningarna (vB)°=90.
Med (vB)°=0 är också F=0, så att vi med PREFIXxSIN kan skriva F=Qv·cos(vB)°·B.
— TILTAS ENDERA redDi- eller DIred-planen så att
ömsesidiga projektioner uppkommer, tillväxer således analogt och i kraft av Planvektorsummans
Identitetskriterium
(Det räcker med att endera redDi eller DIred uppvisar summerande
komponenter med motstående strömled eftersom redDi och DIred i vilket fall inte
summeras inbördes).
HELA B-växelverkan från noll och antar max då ledarna
ligger i ett gemensamt plan.
(Det sker alltså ingen VEKTORKOMPONENTUPPDELNING på grund av att endera
redDI eller DIred antar specifika komponentprojektioner i motstående ledares
motsvarande plan).
För att avgöra MAGNITUDEN I VÄXELVERKAN (V) mellan två godtyckligt
xyz-orienterade strömleder är det alltså tillräckligt att utvälja ena
(A-ledaren) som preferens med preferensplanet (Y, golvplanet i figuren nedan)
via A-ledarens utsträckning och normalen (x) till denna i förbindelse
med en fältpunkt (P) som verkan ska
summeras i;
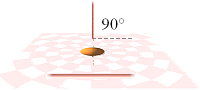
B-ledarens lutning (i PREFIXxSIN, sin0=1) vinkeln A mot Y-planet avgör då
B-ledarens verkansmagnitud på A-ledarens bidrag i P
enligt
Verkan[B(Bled)PÅB(Aled)]
= B(Bled)·sinA
A=0° (bägge
ledarna i samma plan) ger full verkan, A=90° (rätvinkliga ledare, inte i
samma plan) ger nollverkan, därifrån mot 180° motsvarande omvänd strömriktning
med åter full verkan vid exakta A=180°.
— B-ledarens orientering i Y-planet (sett ovanifrån) är
egal och inverkar inte. Det är endast graden av »3Dledarkorsning» som
gäller. (Med given A-vinkel kan B-ledaren »wobblas» eller precesseras
godtyckligt 0-360°).
Modern akademi
Den etablerade beskrivningen
av magnetismens inre växelverkande detaljer är, som redan tidigare påpekats,
(fortfarande) föremål för olika inre dispyter.
— Medan den s.k. Lorentz Force [konv. F=Qv×B] ger en utomordentligt
god kvantitativ beskrivning av funktionen tillsammans med riktningsbegreppen,
saknas fortfarande den djupbeskrivande detaljrikedomen i den moderna akademins
lärosystem beträffande magnetismens natur: hur.
Erinra även den påtagliga förbistringen —
och tydligheten — i NOMENKLATUR.
Jämför även citatblocket om magnetismen i modern akademi.
Se även de samlade artiklarna i Konsekvenser.
Allmänt
beträffande magnetismen i relaterad fysik
Magnetismens dockskåpsmatematik generellt
RELATERAD FYSIK
— Först och främst
beträffande magnetismen:
— Erinra sammanhangen för
den konventionellt benämnda magnetiska konstanten (µ0): µ0 bokstavligt
talat betyder noll magnetism. Sambanden gäller med hög noggrannhet endast om
elektriska laddningens lägesändrande hastighet är försumbar i jämförelse med
ljushastigheten. Detta är också det allmänna fallet i alla normala
(kommersiella) tillämpningar.
— En mera exakt matematik
blir (snabbt) motsvarande mera krävande;
— För den enskilda
laddningen som sådan (och i viss mån magnetismen generellt) finns en viss
(enklare) korrektion i termer av den här presentationens relaterade fysik, se Mekanisk-Elektriska sambandet.
Två sätt bilda magnetfält i moderna akademi
— I moderna kvarter möter
man (stundtals) meningen:
»Magnetfält kan bildas
antingen genom elektriska laddningar i rörelse, eller varierande elektriska
fält». Se exv.,
“Because there are two
things
that can create a magnetic field: an electric current and a variable
electric field (see Maxwell's equations).”, @INTERNET Yahoo Answers
2011-07-24,
http://in.answers.yahoo.com/question/index?qid=20110724091841AAQUxim
— I relaterad fysik är
dessa ett och samma:
— Magnetfält bildas
uteslutande med referens till ett lokalt dominant gravitationsfälts fasta och
fixa rymdpunkter i följd av elektriska laddningsrörelser relativt dessa fixa
rymdpunkter (momentana elektriska potentialreferenser via c).
— Fältbildningen ges via
ändringar i elektrisk potential från omgivande elektriska laddningars statiska
laddningsfält då dessa förflyttas relativt g-fältets fixa rymdreferenspunkter.
Det gäller oavsett ändringens form, om den sker med konstant hastighet eller
accelererat. Se utförligt från MAGNETISMEN.
— Jämför magnetfältet i
utrymmet mellan plattorna i en plattkondensator, eller magnetfältet utanför
änden på en krökt ledare: magnetfält bildas även där inga elektriska laddningar
finns som ansvarar för magnetfältets bildning: det är bara potentialändringen
(med fördröjning via ljushastighetens återkoppling, vilken vi vanligtvis
frånser) som räknas [i Noteringen nedan ges en referens].
Magnetfältet i
kondensatorfallet gäller oberoende av om uppladdningsströmmen är konstant eller
variabel — men (tydligen) många missar den aspekten på grund av den moderna
akademins synsätt i ämnet.
— I modern akademi
distribueras (mestadels) uppfattningen att magnetfält (istället, nödvändigtvis)
bildas med utgångspunkt från den elektriska laddningens yta då denna
förflyttas; Där det inte finns laddningar för tillfället, finns menar man då,
heller inga magnetiska fält [Noteringen nedan anvisar en experimentell referens —
motsvarande har eftersökts på webben men ännu (2011) inte påträffats].
— Men därmed missar man
också magnetismens allmänna fenomengrund: magnetfält bildas även både framför
och bakom en elektrisk laddning, direkt från tomrummets g-referenser, enbart i
följd av de, där, med ljushastigheten återkopplande, förändrade elektriska
potentialbildernas projektioner i de statiska laddningsfälten från respektive
moderladdningar.
Se mera utförligt i avsnittet om Amperes Kretslag.
I Parallellexperimenten från 1994 utfördes särskilda
mätningar på magnetiska fältstyrkan utanför ledarändarna i deras respektive
strömledsförlängningar och som endast bekräftade sambandsformen i den
motsvarande konventionellt benämnda Biot-Savarts lag.
Se även mera utförligt i RIKTNINGSBEGREPPENS
UPPHOV I MAGNETISMEN
Elektriska
fältflödets potentialdelar
EKVIVALENSEN MELLAN EXPANSIONSVEKTORER OCH
TANGENTIALVEKTORER för magnetismen
— se Planvektorsummans Identitetskriterium — om ej redan bekant
— med dessa vektorformers inbördes ömsesidiga
trigonometriska identiteter via sambandsformen i PREFIXxSIN
innefattar den relaterade fysikens alla flödesbegrepp och
allmänna fysik för den elektriska laddningens grundform. Dessa elementära,
internt statiska flödesbegrepp,
(som helt idealt stelt medföljer laddningen i dess
rörelse och inte ändras med mer än laddningen gör det)
kan i relaterad mening sammanfattas ikoniskt enligt
typfiguren nedan.

— Observera att begreppet elektrisk
fältstyrka INTE kan användas inom det statiska Q-fältet i någon relaterad
makrokosmisk mening: elektrisk fältstyrka (Ξ=U/d) kräver minst
två skilda laddningar. Se Elektriska fältstyrkans frihetssats, om ej redan bekant.
Se även i Elektriska fältets elementära divergens och Elektriska fältets gravitella koppling.
Maxwells analogier
I denna genomgång:
|
Rikt |
redDi och DIred |
Vektor |
Reduktions |
Riktnings |
Flödes |
Maxwells |
Maxwells |
MAC |
Vektorprodukten |
Kausal |
|
Begreppen |
Relaterad fysik |
Summeringen |
Divergens Cirkeln |
Principerna |
Formerna |
Virvelanalogi |
Magnetmekanik |
TNED |
i MAC |
Sambandet |
Maxwells
virvelanalogi från 1861
Maxwells virvelanalogi (från 1861)
Maxwells analogier
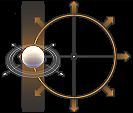
— Sinnebilden med
Q-cirkelprojektionen av Q-flödesdivergenserna i F=BQc, avbildar i princip EXAKT samma princip som Maxwells
grundmekaniska beskrivning (från 1861): föreställningen om de magnetiska
fältlinjerna som ”rotating vortices”, »roterande virvelstavar» eller
virvellinjer.
Jämför citatet nedan (källan talar om
Maxwell),
”In his
treatise on
"Electricity and Magnetism," Vol. II. p. 416, (2nd edition 427) after
quoting from
Sir W. Thomson on the
explanation of the magnetic rotation of the plane of the polarisation
of light, he goes on to
say of the present paper,
PREFACE. XXI
"A theory of
molecular vortices which I worked out at considerable length was
published in the Phil.
Mag. for March, April and May, 1861, Jan. and Feb. 1862."
- " I think we have good evidence for the opinion
that some phenomenon of rotation
is
going on in the magnetic field, that this rotation is
performed by a great number
of very small portions of
matter, each rotating on its own axis, that axis being parallel
to the direction of the
magnetic force, and that the rotations of these various vortices
are made to depend on one
another by means of some mechanism between them."”,
Från PREEFACE sidan xxi.n — The
scientific papers of James Clerk Maxwell (1890)
samt från samma källa
särskilt Maxwells teori s455 från 1861:
Maxwell introducerar VORTEX — virvelbegreppet — i magnetismens
beskrivning
s455m:
” Let us now suppose that the
phenomena of magnetism
depend on the
existence of a tension in the direction of the lines of force, combined
with a
hydrostatic
pressure; or in other words, a pressure greater in the equatorial
than in the axial
direction : the next question is, what mechanical explanation
can we give of this
inequality of pressures in a fluid or mobile medium ? The
explanation which most
readily occurs to the mind is that the excess of pressure
in the
equatorial direction arises from the
centrifugal force of vortices or
eddies in the medium having
their axes in directions parallel to the lines of force.
This explanation of the cause of the
inequality of pressures at once suggests
the means of representing
the dipolar character of the line of force. Every
vortex
is essentially dipolar, the two extremities of its axis being distinguished
by the direction of its
revolution as observed from those points.”.
Analogin med
expansionsvektorer (F/Qc=B) och centrifugalvektorer bildar samma grundfysiska
beskrivning som ansluter till hydrodynamikens virvelrörelser (Maxwells
huvudarbete, »magnetismens mekanik» från 1861).
Men där stannar också
kopplingen till Maxwell. Medan Maxwells arbeten beskriver en DIREKT mekanik,
blir motsvarande i relaterad fysik, på grund av ljusets friställning från kinetiken, en REN analogi.
Varken Maxwell själv,
hans samtida, eller nutida populationer i den moderna akademins korridorer har
någonsin haft en HÄRLEDANDE uppfattning om den elektriska laddningen som
grundad på DIVERGENSPRINCIPEN (se härledningen till Q). Man har därmed heller aldrig kunnat UTVECKLA de enkla
storheterna ur grundformen, typ ovan med B. I stället har den moderna akademins
vetenskapshistoria präglats av en ständigt utvidgad uppfinningsrikedom i
strävan att förklara fysikens grunder genom en akademisk intelligens
snarare än en påtaglig vilja, önskan och strävan att HÄRLEDA grunderna efter en
naturlig ordning. Begreppet »naturlig» är särskilt känsligt i moderna
korridorer. Därmed har också hela frågan om elektrofysikens detaljer kommit i
skymundan.
Notera särskilt
beträffande Maxwells analogier och deras motsvarande koppling till relaterad
fysik:
Magnetiserande
kraften
— Maxwell talar på sidan 184n [ON FARADAYS LINES OF
FORCE]
om MAGNETIZING FORCE [H=i/ℓ] — med vidare
samband från s194 [som i sig ansluter till samma typ som beskrivs i Amperes Kretslag]:
— I relaterad fysik relateras HELA strömmen
[i] — Q-projektionen på ledarens
tvärsnittsyta, och därmed omslutningen via den s.k. strömmens omslutande
linjeintegral — till den magnetiserande kraften [H] som åstadkommer
magnetiska kraftfält i hela Q-rummet, inte enbart i den
omslutande i-cirkelns planskiva.
— Denna detalj är genomgående ytterst oklar i
modern facklitteratur generellt (speciellt på webben), där det inte ALLS klart
framgår HUR man tänker sig att magnetismen bildas med referens till en laddad
partikels rörelse.
— Generellt — men felaktigt — TYCKS [därför att exakta klargörande meningar saknas]
man mena att magnetfält bildas som koncentriska ringar från laddningsytan ENBART. Det finns i modern akademi ingen
beskrivande del [eftersökt, men ännu inte
påträffad] som tydligt och klart beskriver HUR magnetfältet bildas. Nämligen
[enligt relaterad fysik] FRÅN DET LOKALT DOMINANTA GRAVITATIONSFÄLTETS
OMGIVANDE FASTA OCH FIXA RYMDPUNKTER [elektrogravitella
referenserna], med hänsyn till hur dessa SER potentialbilden i ÄNDRING från
laddningar i rörelse i rummet: magnetfält bildas överallt
i hela rummet [med ljushastighetens fördröjning] från en elektrisk
laddning i rörelse.
— Avgränsningen med MAGNETISERANDE KRAFTEN
blir därför [ytterst] äventyrligt i modern akademi [även i ljuset av Maxwells tidiga beskrivning], då man [tydligen]
blandar ihop de skilda fenomendomänerna mekanik och elektrogravitation [som
Maxwell garanterat inte kände till].
Maxwells beskrivningar lider av samma
grundläggande felsyndrom som alla övriga bidragares: expansionsintegralen finns inte med
i framställningssättet — elektrogravitationens distinktion från mekaniken — och
därmed i princip ett hejdlöst kaos i den motsvarande xyz-differentierade
matematiken;
— Den enda, och uteslutande enda,
praktiskt mätbara tillämpningen som mig veterligt existerar på
att få ut strömstyrka via uppmätt magnetisk fältstyrka (för ett godtyckligt rakt ledaravsnitt) är just via den
motsvarande Biot-Savarts lag (samma som expansionsintegralens lösning, och som
man utgår ifrån i magnetteorin i modern akademi).Genom att mäta B inom ett
snävt område och man känner ledarlängden (s) och avståndsgeometrin till
mätpunkten, kan strömledens strömstyrka beräknas. Men det är här inte vidare
känt hur man menar i den saken sett i den moderna akademins referenser: det
verkar ytterst svårt att få fram klara besked.
Se vidare aspekter i Amperes Kretslag.
ANGÅENDE MAXWELLS EMI [ElektroMagnetiskaInduktionen], s186mö
[motsv. Faradays lag],
:
”That this is the true expression for the law
of induced currents is shewn
from the fact that, in
whatever way the number of lines of magnetic induction
passing through the circuit be increased, the
electro-motive effect is the same,
whether the increase take
place by the motion of the conductor itself, or of other
conductors, or of magnets, or by the
change of intensity of other currents, or
by the magnetization or demagnetization of
neighbouring magnetic bodies, or
lastly by the change of intensity of the
current itself.
In all these cases the electro-motive force depends
on the change in the
number of lines of inductive magnetic
action which pass through the circuit*.”,
s186m, ON FARADAY'S LINES OF FORCE.
Också denna detalj
ansluter till närmast föregående påpekande:
— Man [tydligen ALLA FRÅN BÖRJAN] blandar ihop
de skilda fenomendomänerna mekanik och elektrogravitation:
— Det här är vad ALLA tror — är övertygade om
— gäller från början:
— LIKVÄRDIGT med att en ledare lägesändrar i
FIXT magnetfält, med påföljden att en spänning induceras, är att en FIX ledare
påförs ett VARIERANDE magnetfält.
— MEN DEN FYSIKALISKT FÖRMODADE FENOMENANALOGIN
GÄLLER INTE — särskilt visat genom Parallellexperimenten 1994: en spänning induceras i
en mätlinje via en varierande ström där ingen magnetisk fältstyrka existerar
— just på grund av de skilda fenomendomänerna mekanik och elektrogravitation: magnetism och induktion växelverkar inte i fysiken.
Se utförligt i Förtydligandet, samt Tre Jämförande Exempel där sammansattheterna
beskrivs mera konkret.
Magnetiska kraftlagen i modern akademi —
historiskt ursprung
[ref. @INTERNET Wikipedia
Lorentz force 2011-09-23]
http://en.wikipedia.org/wiki/Lorentz_force
Magnetiska kraftlagen F=BQu kallas ofta i nutida etablerad litteratur (eng.) Lorentz
Force med skrivsättet (källan ovan, den moderna akademins vektoranalytiska
notation)
F = q[E + (v×B)].
— Artikelkällan ovan
beskriver upphovet:
”From a modern
perspective it is possible to identify in
Maxwell's 1865 formulation of his field equations a form of the Lorentz force equation in relation to electric currents,[9] however, in the time of Maxwell it was not
evident how his equations related to the forces on moving charged objects. J. J. Thomson was the first
to attempt to derive from Maxwell's field equations the electromagnetic forces
on a moving charged object in terms of the object's properties and external
fields. Interested in determining the electromagnetic behavior of the charged
particles in cathode rays, Thomson
published a paper in 1881 wherein he gave the force on the particles due to an
external magnetic field as ½qv×B. Thomson was able to
arrive at the correct basic form of the formula, but, because of some
miscalculations and an incomplete description of the displacement current,
included an incorrect scale-factor of a half in front of the formula. It was Oliver Heaviside, who had invented the modern vector notation and applied them
to Maxwell's field equations, that in 1885
and 1889 fixed the mistakes of Thomson's derivation and arrived at the correct form of the magnetic force on a
moving charged object.[10] Finally, in 1892, Hendrik Lorentz derived the modern
day form of the formula for the electromagnetic force which includes the
contributions to the total force from both the electric and the magnetic
fields. Lorentz began by abandoning the Maxwellian descriptions of the ether
and conduction.”.
Maxwell själv skriver
(betydligt enklare uttryckt) i publikationen från år 1865 i A DYNAMICAL THEORY
OF THE ELECTROMAGNETIC FIELD från sidan 565,
”
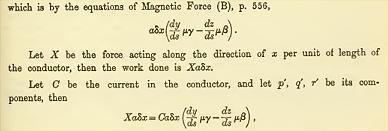
”,
A DYNAMICAL THEORY OF THE
ELECTROMAGNETIC FIELD publ. 1865 från sidan 565 i
INTERNET ARCHIVE — The
scientific papers of James Clerk Maxwell (1890)
http://www.archive.org/details/scientificpapers01maxw
med specifikationen på
s556 ”Coefficient of Magnetic
Induction (µ)” och som Maxwell sammanställer, samma sida
556 tillsammans med ”Magnetic force (a)” i en grupp (µa) med beteckningen B — och som leder till en
(här möjligen) något obskyr uttydning (Möjligen ska Maxwell tolkas motsv. Ba för korrekt
korresponderande fysikaliska storheter). Förkortar vi bort δx-termerna ges
(då) formellt, direkt korrekt:
Xa = Ca·Ba = arbetet; med c=i och
X=F och a=ℓ:
Fℓ = iℓ·Bℓ ;
F = iℓ·B
Det är, tydligen, exakt
Maxwells »enkla formulering» av magnetiska kraftlagen för en elektrisk laddning
F=BQv med Q=it och v=ℓ/t som ger motsvarande för en elektrisk strömled
F=B(it)(ℓ/t)=Biℓ.
— Det
vetenskapshistoriska uppslaget till magnetiska kraftlagen gavs tydligen (eller
kanske, formulerades nära direkt ) av Maxwell (1865).
Q-analogierna och Maxwells original
— Eftersom Maxwells
hydrodynamiska virvelanalogier
(Maxwells »magnetiska mekanik» i ON PHYSICAL LINES OF FORCE från
1861 med Maxwells analogier för fluidum — centrifugalkrafter och roterande
rörelser med mekaniska tryck och spänningar)
skiljer sig från den
relaterade fysikens gravitellt förankrade divergenshärledda kausallogik (se Kausalsambandet)
endast i klargörande av Ljusfysikens friställning från kinetiken
(som varken Maxwell eller hans samtida kände till, f.ö. hela
vetenskapshistoriens avgörande akilleshäl i sammanhanget),
kan man säga att Maxwell
redan i stort, och i allt, har formulerat »mekaniken» för hela
elektrodynamikens (och elektrogravitationens) väsentliga partier genom sin
omfattande matematiska genomgång.
— Vi återfinner i vilket
fall samma principiella mekaniska analogier i Maxwells framställning som här, i
den relaterade fysikens logik.
— Enda skillnaden är att
Maxwells magnetiskt STATISKA fältlinjer i relaterad fysik är mobila dito via reduktionerna
(ç=c-v) som ansvarar för fältlinjernas expansion mot toppvärdet för den
fria rymdens ljushastighet (ç→c0). Samt, att fältlinjerna som sådana i
den mekaniska analogin tillhör den lokalt bestämda gravitationens bestämmande divergens
(ljushastighet) i strängt differentiella domäner.
— Dvs., de mekaniska
analogierna är också just analogier och finns inte till som några
ändliga fenomendomäner i fysiken.
— Värre blir det med alla
de »Maxwellska intolkningar» som EFTER Maxwell (genom hela 1900-talet) inlagts
i hans matematik från den moderna akademins olika laboratorier. Jämför Vektorkalkylens sammanbrott inom magnetismen i modern
akademi. Se även närmast nedan i
Maxwells
magnetiska fältmekanik.
————————————————————————————————
En TOLK som visar Maxwells ursprungliga
ekvationer från 1865 och hur dessa skrivs i nutida modern notation finns i
PDF-dokumentet
On the Notation of MAXWELL’s Field Equations,
André Waser (2000)
http://www.zpenergy.com/downloads/Orig_maxwell_equations.pdf
Maxwells
arbete generellt i magnetismen
Maxwells avgjort största
svårighet är just föremålet för hans framställning (frn.s155, On Faraday's Lines of
Force): masslöst, tröghetslöst fluidum;
— Den av Maxwell benämnda
inkompressibla, tröghetslösa, masslösa VÄTSKAN som han bygger hela sin
beskrivning på.
— Det blir en strängt
ODRÄGLIG föreställning, eftersom hela den relaterbara fysiken utgår ifrån ÄNDRINGSLAGARNA:
får man inte RELATERA varje skeende i namn av en NATURLIG aktion och
reaktion (som alltså utesluts av Maxwells supervätska), finns naturligtvis
heller ingen NATURLIG grund för att förstå framställningens innehåll.
— Hela saken kommer då,
istället, att bero på författarens fantasi, uppfinningsrikedom, och förmåga att
(fängsla läsaren med att) beskriva detaljer.
— Det blir, följdriktigt,
också hela komplexets absoluta orsaksgrund;
— Var och en som frågar
efter HUR och PÅ VILKET SÄTT leds obönhörligt åter till Maxwells uppfunna,
fiktiva, och intygade »filosofiskt oberoende» supervätska.
— Det finns ingenting
sådant i fysiken.
Hur ska man då förklara
Maxwells resultat med avseende på den praktiska fysiken?
— Maxwells
virvelanalogier (hydrodynamikens centrifugalfenomen i samband med olika
flödesbegrepp) har en EXAKT fysiskt relaterbar, matematisk formell, koppling
till elektriska laddningens motsvarande (strömriktningsprojicerade) c(U)q±-divergensflöde.
— Den visuella ANALOGIN —
men inte mekaniken — i den flödesformen kopplar också i motsvarande del till
det föreställbara perceptet för divergensen
(den punktgravitellt bestämda lokala ljushastigheten) som sådan: den naturligt analoga, men icke mekaniskt
motsvarande, expansionsriktningen (Maxwells magnetiska fältlinjetvärsnitts
roterande vätska) som gestaltar ljusets motsvarande (homogent och idealt
sfäriska) utbredning över (minsta möjliga) intervall.
— Det är de exakt
kopplande analogierna, och som förklarar hur och varför överensstämmelser alls
finns, och utöver dem, intet.
— Som konkret jämförande
översikt i DEN SLUTLIGT ÖVERGRIPANDE RESULTERANDE skillnaden mellan modern och
relaterad mening: Se de Tre Jämförande Exemplen.
— Se även mera
övergripande
(som avskräckande exempel, som visar hur långt från
fenomenfysiken modern akademi befinner sig i termer av exakt relaterbar fysik,
och hur det sedan ser ut i reda kvantiteter)
i Magnetiska Expansionsintegralen.
— Maxwells samband (»Maxwells ekvationer») beskriver den tekniskt-praktiskt användbara (kommersiella)
magnetismens matematik i detalj — på formen för den förenklade magnetiska konstanten (µ0) men vars reella form, och i termer av relaterad fysik,
helt utesluter varje verklig förekomst av magnetism. Se utförligt i µ0. Jämför även Maxwells
”µ is the coefficient of magnetic induction,
which is unity in empty space
or in air.”,
s512mn ON PHYSICAL LINES OF FORCE
— Det rent tekniska
sammanhanget blir därmed just också den allmänt talande, summerande bilden av
portalfiguren, James Clerk Maxwell, som grundaren av hela den moderna tekniska
kulturens matematik i ämnet elektrofysik.
—————————————————————————————
ε0 = elektriska konstanten ; 8,8543 t12 (VM/AS=VM/C)
[FOCUS
MATERIEN 1975 s666]
R0c0
= 1/ε0 ; 1,12939 T11 C/VM
R0/c0
= µ0 ; 1,25662 t6 VS/AM
R0
= 1/c0ε0
= c0µ0 ;
376,72554 (V/A=Ω) rymdresistansen
c02 = 1/µ0ε0
; 8,98755 T16
(M/S)²
c0 = 1/√µ0ε0
; 2,99792458 T8 M/S
[ENCARTA
99 Light, Velocity]
—————————————————————————————
s192 [Maxwell beskriver Faradays konklusioner],
”the quantity of magnetic induction across any
section of the tube is constant”
Man kan utläsa magnetiska kraftlagen ur Maxwells skrifter (se BQu i MAC), men då inte i formen
som berör den elektriska laddningen, F=BQu, utan den elektriska
ledaren, F=Biℓ.
magnetic induction
Maxwell använder
genomgående termen magnetic induction för den relaterade fysikens
B=F/Qc=µH, B magnetiska fältstyrka, H magnetiserande kraften. Men inte på något
ställe i Maxwells samlade vetenskapliga skrifter ges någon direkt definition av
vad som menas med »magnetic induction». Termen B — magnetiska fältstyrkan —
definieras aldrig av Maxwell.
— Termen »magnetic
induction» omnämns först i bokens preface sidan xxii, och då i formen av ett redan omskrivet, etablerat
begrepp: ingen förklarande grund ges,
”...of the product of the
specific inductive capacity by the coefficient of magnetic induction, which last factor is...”. Sedan på samma stil via Maxwell,
hela boken igenom.
Maxwell ger s212 en hänvisning till ”See Prof. Thomson, on the Theory of Magnetic
Induction, PhiL Mag. March, 1851.”, men någon motsvarande
krönika går inte [Sep2011] att hitta på webben. Artikeln i Wikipedia om History of electromagnetic theory tycks även
den UTGÅ IFRÅN begreppet [electro-]»magnetic induction» utan att ge någon
specifik referens till hur eller varifrån begreppet uppkommit annat än typ
»Faradays observationer av elektromagnetisk
induktion» [1831].
Termen och begreppet
»magnetic induction» används, och beskrivs, således genomgående i modern
akademisk litteratur och tydligtvis som ett observationsfenomen: något
som uppstår — och försvinner — med strömmen. Det finns — tydligen — ingen
fenomenhärledning (inte ens ett försök). Se även i Nomenklatur
(begreppet »magnetisk induktion» i
relaterad fysik saknar relaterbar grund).
— Notera även coefficient
of magnetic induction (µ0=R/c) [s512mn ON PHYSICAL LINES OF FORCE]. Den används ännu i dag på samma form som Maxwell använde den
på sin tid: Alltså, med ensidig referens till den fria rymdens toppvärde för ljushastigheten (c0=2,99792458 T8 M/S). I relaterad fysik bildas magnetismen
som fysikaliskt fenomen enligt Kausalsambandet FÖRST med en reduktion rätvinkligt laddningens rörelseriktning
ç=c–u och som sedan garanterar den magnetiska fältringens utbredning med (nära)
ljushastigheten då ringens tätare ç går mot den fria rymdens tunnare c0. Därmed
finns ingen magnetism alls med användning av µ0=R0/c0. Den detaljen bara
understryker den YTLIGHET som tvunget framträder, samt omöjligheten i att
förstå fenomenet som sådant, om man enbart är hänvisad till den modern
akademins begrepp i magnetismen som fysiskt fenomen. Se även i Magnetiska Konstanten µ0.
— I termer av relaterad
fysik är B (magnetiska fältstyrkan) definierad dels (explicit för laddningen
självt) via elektriska laddningen (Q) från elektriska kraftlagen F=Rc(Q/r)² som en egenskap i den elektriska laddningens egen
flödesform, F/Qc=B, och dels via kausalsambandet i elektrogravitationen (ljusets friställning från kinetiken, ljusets gravitella beroende) genom uppkomsten av magnetismen [förenklat B=RmaxQ/A] utanför
Q på grund av dess rörelse (potentialbildens ändring med Q-fältets rörelse) —
relativt ett yttre lokalt dominant gravitationsfälts fixa och fasta
rymdreferenspunkter (se här närmast kortformen i Magnetiska expansionsintegralen). Se mera utförligt från Expansionsintegralen i MAGNETISMEN.
Om någon beskrivande
summering (alls) kan göras i ljuset av ovanstående genomgång, blir det denna:
— De referenser som figurerar
i jämförelsen mellan modern akademi och relaterad fysik, här inom magnetismen
specifikt, endast understryker ordningen:
— Medan det redan
etablerade sättet lämpar sig utmärkt för en kommersiell industri, är det
praktiskt taget värdelöst i fenomenbeskrivningen. Jämför (återigen) Citatblocket.
Aspekterna tjänar att belysa ämnet.
Med vidare fortsättning i
Maxwells
magnetiska fältmekanik — jämförande
fenomenbeskrivning i relaterad fysik.
Maxwells
analogier och Relaterad fysik — 7Okt2011
I denna genomgång:
|
Rikt |
redDi och DIred |
Vektor |
Reduktions |
Riktnings |
Flödes |
Maxwells |
Maxwells |
MAC |
Vektorprodukten |
Kausal |
|
Begreppen |
Relaterad fysik |
Summeringen |
Divergens Cirkeln |
Principerna |
Formerna |
Virvelanalogi |
Magnetmekanik |
TNED |
i MAC |
Sambandet |
Maxwells
magnetiska fältmekanik — jämförande fenomenbeskrivning i relaterad fysik
2011IX09
Varför Maxwells matematiska mekanik inte kan harmoniera
med magnetismens fenomenfysik
Varför
Maxwells matematiska mekanik inte kan harmoniera med magnetismens fenomen i
relaterad fysik
Maxwells magnetmekanik från 1861 i ON PHYSICAL LINES OF FORCE
Utdragen ovan från JAMES CLERK MAXWELL — ON PHYSICAL LINES OF
FORCE 1861 — till bildillustrationen nedan vänster, samt vidare i huvudtexten:
|
Maxwell 1855 | 1861 |
Relaterad fysik 1994 | 2011 |
|
|
|
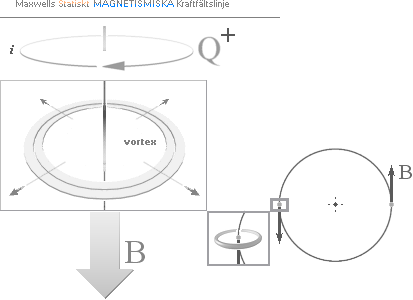
Maxwell beskriver PÅ SÄTT
OCH VIS g-divergensen i sin vortex-modell.
Men modellen urartar genom den bokstavliga analogi den tillskrivs i termer av
hydrodynamikens mekaniska begrepp.
— Notera att Maxwell själv tydliggjorde att hans beskrivningar
endast är, och ska uppfattas som, en matematisk modell, en hjälpbyggnad, till
[en första matematisk] beskrivning av magnetismens fenomenfysik. Men historien
tycks också ha stannat vid det; Maxwells matematiska modell via hydrodynamikens
mekaniska hjälpbegrepp används fortfarande [2011] i beskrivningen av
magnetismen — och kan olyckligtvis sägas ha ERSATT en verklig strävan att finna
en djupare fenomenbeskrivning. Se även i Citatblocket där magnetismens gåtfulla
natur intygas. Exakt HUR förytligad »Maxwells fenomenbeskrivning av
magnetismen» är, visas exemplifierat i Vektorkalkylens sammanbrott i MAC.
— Det är också ALLTID
modellens akilleshäl: Modellen återfaller på
modellen. DÄRFÖR är relaterad fysik Relaterad Fysik. Exakt Natur. No Problemo.
RELATERAD FYSIK: Magnetfältsmekaniken [utförligt från MAGNETISMEN] tillhör divergensen — ljusfysiken — inte kinetiken. Det är i princip det ENDA som skiljer
Maxwell från relaterad fysik, men som Maxwell och hans samtida ingalunda hade
någon klar bild över — och vilken situation väsentligen fortfarande kvarstår i
vår tid [2011], f.ö. ämnet för hela framställningen.
JAMES CLERK MAXWELL [1831-1879] var tydligen den förste
James Clerk Maxwell,ON PHYSICAL LINES OF
FORCE publ.1861 m.fl.
THE SCIENTIFIC PAPERS OF
JAMES CLERK MAXWELL, DOVER PUBLICATIONS, INC., NEW YORK [1890]
Finns som gratis PDF-dokument på Internet Archive,
http://www.archive.org/details/scientificpapers01maxw
som utförde ansatsen att [i varje fall försöka] beskriva den
magnetiska fältlinjens mekanik utifrån dåvarande möjliga beskrivningsgrunder.
Maxwells bidrag var att försöka beskriva B-fältlinjen genom begreppen mekanisk
spänning och tryck [eng., tension, stress, strain], samt i viss analogi till
hydrodynamiken via centrifugalkrafternas virvelrörelser [eng. vortex eller
eddies]. Maxwell från s452, källan som ovan:
s452:
”We are dissatisfied
with the explanation
founded on the hypothesis of attractive and repellent
forces directed towards
the magnetic poles, even though we may have satisfied
ourselves that the
phenomenon is in strict accordance with that hypothesis, and
we cannot help thinking
that in every place where we find these lines of force,
some
physical state or action must exist in sufficient energy to produce the
actual
phenomena.
My object in this paper is to clear the way
for speculation in this direction,
by investigating the mechanical
results of certain states of tension and motion
in a medium, and
comparing these with the observed phenomena of magnetism
and electricity. By
pointing out the mechanical consequences of such hypotheses,
I hope
to be of some use to those who consider the phenomena as due to the
action
of a medium, but are in doubt as to the relation of this hypothesis to
the experimental laws
already established, which have generally been expressed
in the language of other
hypotheses.”,
JAMES CLERK MAXWELL — ON PHYSICAL LINES OF
FORCE, s452ö
Från Maxwells samlade
vetenskapliga publikationer, 1890
Citaten nedan visar hur Maxwell tänkte sig den centrala
magnetismens mekanik, och hur VIRVELBEGREPPET introducerades i
beskrivningssättet.
[Varför
fick vi aldrig läsa dessa hyperintressanta historiska passager från pionjärerna
i den elementära fysikundervisningen? Det man inte görs uppmärksam på, kommer
heller ingen ihåg. Men vi (jag) vet redan anledningen: »— Vi har inte TID; det
finns inte plats för det i KURSPLANEN». Det kanske finns TID nu då...]:
— Maxwells beskrivning innehåller i termer av relaterad fysik
tydligen alla, samtliga, grundbegrepp — utom ljusfysikens centrala divergensbegrepp, se utförligt i
relaterad fysik i DEEP från GRIP om ej redan bekant.
s453ö:
”We come now to consider the
magnetic influence as existing in the form of
some
kind of pressure or tension, or, more generally, of stress in the medium.”,
;
”The general type of a
stress is not suitable as a representation of a
magnetic force, because a line
of magnetic force has direction and intensity, but
has no
third quality indicating any difference between the sides of the line,
which would be analogous
to that observed in the case of polarized light*.
We must therefore represent the magnetic
force at a point by a stress
having a single axis of
greatest or least pressure, and all the pressures at right
angles to this axis
equal.”,
;
s453N.
”The author of this
method of representation does
not
attempt to explain the origin of the observed forces by the effects due to
these strains in the
elastic solid, but makes use of the mathematical analogies
of the two problems to assist
the imagination in the study of both.”,
;
s455ö:
”It appears therefore
that the stress in the axis of a line of magnetic force
is a
tension, like that of a rope.”,
JAMES CLERK MAXWELL — ON PHYSICAL LINES OF
FORCE
Maxwell introducerar VORTEX — virvelbegreppet — i magnetismens
beskrivning
s455m:
” Let us now suppose that the
phenomena of magnetism
depend on the
existence of a tension in the direction of the lines of force, combined
with a
hydrostatic
pressure; or in other words, a pressure greater in the equatorial
than in the axial
direction : the next question is, what mechanical explanation
can we give of this
inequality of pressures in a fluid or mobile medium ? The
explanation which most
readily occurs to the mind is that the excess of pressure
in the
equatorial direction arises from the
centrifugal force of vortices or
eddies in the medium having
their axes in directions parallel to the lines of force.
This explanation of the cause of the
inequality of pressures at once suggests
the means of representing
the dipolar character of the line of force. Every
vortex
is essentially dipolar, the two extremities of its axis being distinguished
by the direction of its
revolution as observed from those points.”.
JAMES CLERK MAXWELL — ON PHYSICAL LINES OF
FORCE
MAXWELL KÄNDE INTE TILL LJUSETS GRAVITELLA BEROENDE [men BORDE har gjort det tillsamman med sina kolleger efter
James Bradleys upptäckt 1725 av aberrationen]
— det faktum, enligt här relaterad fysik, att den magnetiska fältinjens
centrala Maxwellska virvelmekanik TVUNGET innefattar just det som Maxwell [på grund av ljusfysikens gravitellt mycket
sammansatta natur och som Maxwell inte kände till]
INTE kunde se [här från citatblocket ovan s453ö]:
”but has no
third quality indicating any difference between the sides of the line”
— JUST en sådan, principiellt kvalitativ, skillnad måste tvunget
finnas: DIVERGENSFLÖDET [c] i reduktionerna [ç=c–v, se Kausalsambandet]
som ansvarar för fältvågens utbredning. Dock finns ingen kinetisk (mekaniskt kraftverkande) motsvarighet.
— Det är just precis vad som motsvarar det makrokosmiskt
föreställbara mekaniska fallet:
— Den magnetiska fältlinjens fysik
— såsom en expanderande fältring från strömkällans elektriska potentialändringar relativt det yttre omgivande rummets lokalt dominanta
gravitationspunkter
— måste TVUNGET ha kvalitativa egenskaper som just SKILJER
inre-yttre
— och som GARANTERAT inte kopplar till kinetiken: ljusets
fysik såsom grundad på GRAVITATIONEN.
Se DEEP från GRIP.
— Eftersom emellertid den analysen således innefattar DIVERGENSBEGREPPET SOM SAMTIDIGT DIFFERENTIALBEGREPP
— och det vet vi, just, hur modern akademi har utvecklat sig på
den fronten, se utförligt ENLIGT RELATERAD FYSIK OCH MATEMATIK från differentialbegreppet
— var det givet att Maxwell, trots de bästa föresatser och här
med den relaterbara fysikens begrepp, INTE kunde omfatta magnetismens fullständiga
beskrivning.
— Istället för »Maxwells statiska
virvelDivergens» blir i relaterad fysik
den magnetiska fältlinjen en LjusDynamiskt Gravitellt
betingad Fältvariabel med egenskaper som — på
grund av ljusets karaktär att inte vara additiv med kinetiken (Ljusfrihetssatsen) — helt saknar kinetikens beröringspunkter. Se utförligt från Kausalsambandet
för magnetismens och induktionens del.
— Däri ligger tveklöst hela den historiska Knuten med den [ännu
2011] etablerade moderna akademiska föreställningen om elektricitet och
magnetism, anledningen till att ämnet inte kan förklaras eller beskrivas i
detalj — med de tillgängliga begreppen i den moderna akademins lärosystem.
— Vi kan alltså rättvist inte säga att Maxwell hade FEL. Men vi
kan rättvist säga att Maxwells TID inte kände tillräcklig grund för en mera
vidlyftig formulering.
Fortsättning i Maxwells
magnetiska mekanik.
![]()
Trigonometriska
sambandet för den tvådimensionella vektorsummeringen med ekvivalenta resultat för
expansionsvektorer och tangentialvektorer, se Planvektorsummans Identitetskriterium
— nedan i illustration specifikt med
avbildning för expansionsvektorerna (tangentialvektorerna ges av den
resulterande vektorbilden genom multiplikation med –i, dvs., medurs rotation
90°),
Elementära
Elektrogravitella Planvektorsumman
definierar i relaterad fysik alla
elektriska strömvägars likvärdiga och likaberättigade magnetiska bidrag (B) i
en fix g-relaterad rymdpunkt (P) i formen av en (redDI) ReduktionsDivergensCirkel. Dess principiella (men inte aktuella) fysik ansluter
till Maxwells magnetiska mekanik på sätt som följer.
Maxwells magnetiska
mekanik
REDUKTIONSDIVERGENSCIRKELNs centrala form är
(tydligen) väsentligen av samma »mekaniska typ» som vi finner i detaljerna till
den »magnetmekanik» som beskrevs av James Clerk Maxwell [1861 i ON PHYSICAL LINES OF FORCE] — men utan kinetikens
inverkan. Det är, tydligen, också anledningen varför ämnet (ännu i denna dag
[2011]) står utan direkt begripbar beskrivning i modern akademi:
— Ljusfysiken kopplar
inte kinetiken (Ljusfrihetssatsen). Se speciellt från vic-felet.
— MEKANISKA BEGREPP i
elektrofysiken (tillsammans med ljusets fysik) urartar garanterat om man inte
vet EXAKT, in i minsta minutiös detalj, vad man sysslar med: inga frågetecken
eller ouppklarade fysiska djupfrågor får förekomma. Varje fenomengrundat
sakargument måste kunna mötas med EXAKT precision. Tvivel får inte förekomma.
Finns det, blir det FEL. Garanterat.
— Men Maxwell och hans
samtida (omkring 1860) kände inte till dessa begrepp: ingenting var varken
klarlagt eller närmare känt i ämnet (som det är ännu idag i moderna kvarter, vidare
nedan, jämför även citaten generellt som beskriver Magnetismen i modern akademi).
— Maxwells magnetiska
mekanik innehåller ingen dynamik för fältlinjens mobilitet: den finns — STÅR —
bara där som en »statisk virvelsträng», garanterat av Maxwells villkor
(uppfattning) att
”because a line of magnetic force has
direction and intensity, but
has no
third quality indicating any difference between the sides of the line”,
Maxwell s453ö
— Ingenting i Maxwells
beskrivning (eller den senare nomenklaturens etablerade fackverk, jämför Biot-Savarts lag) förklarar eller upplyser hur fältlinjen
kommer DIT den är (underförstått med dynamisk, mobil, koppling till den
aktuella elektriska strömled som utgör källan
— Se även VARFÖR modern akademi inte kan nå den djupförklaringen i Vektorkalkylens sammanbrott i MAC
[3 vektorled beskriver magnetismen i
relaterad fysik, modern akademi utelämnar de första två, och man börjar först
på den tredje: Biot-Savarts lag; sedan kan heller ingen begripa HUR det,
vektorfenomenet, hänger ihop]):
— G-divergensernas reduktioner som uttömmer sig från
det tätare magnetiska rummets fältringar (ç) till den tunnare fria rymden (c0)
ingår varken i Maxwells beskrivningar eller i den senare akademins teori. Man
använder generellt »ljusets topphastighet» (c0) underförstått i alla
beskrivningar. Se även i Magnetiska konstanten (µ0=R0/c0) hur begreppen
används — samt i NOMENKLATUR angående den allmänna begreppsförvirringen.
Det enda Maxwell omnämner
är antydan att försöka klargöra ämnet utifrån just den magnetiska fältlinjen
som en STATISK fenomenform, något som UPPKOMMER PÅ STÄLLET:
”... and
we cannot help thinking
that in every place where we find these lines of force,
some
physical state or action must exist in sufficient energy to produce the
actual
phenomena.”,
Maxwell s452
Magnetiska expansionsintegralen
Det verkar vara — då som
nu — att man HELT förbiser kausallogikens MAGNETISKA EXPANSIONSINTEGRAL, differentialekvationen i relaterad fysik i PREFIXxSIN enligt
dBPx = d(dBPs/dbs) = Rmaxç0–1(I/4πx)sinb db
med lösningen
dBPs = µ0(I/4πx)cosb
dbs
...................................... expansionsintegralens lösning
med likvärda formen via radien (r)
[ds/db=–x/cos²b=–x(r²/x²)=–r²/x; db=–x/r²,
minustecknet här frånsett, se även utvecklingarna i Fjärrverkan]
= µ0(I/4πr2)cosb
ds
och som dyker
upp först i moderna kvarter som den kända Biot-Savarts lag, här i konventionella PREFIXxCOS
dB = µ0(I/4πr2)sinb ds
och som ofta skrivs via begreppet vektorprodukt (vidare nedan)
dB = (I · ds×r/r3)(µ0/4π) ................................... TEKNISK ELEKTRICITETSLÄRA, E. Danielson Gleerups 1965 s45m
dB = (I · dl×r/r2)(µ0/4π) ................................... @INTERNET Wikipedia Biot-Savart law, r=r/r [2007-06-13]
Ref., @INTERNET Wikipedia Biot-Savart law
[2011-09-13], anger bägge ovan [skrivna på integralform].
Samt att man »hoppar in i
föreställningen» FÖRST från expansionsintegralens lösning, den s.k. Biot-Savarts lag.
— Vilket med exemplets
analogi vill säga:
Fullständiga magnetiska 3D-vektorkroppen
— Medan relaterad fysik
utgår ifrån helheten hos den följande illustrerade fullständiga magnetismens
3D-vektorkropp (se kompletterande beskrivning i Expansionsintegralen och Vektorkalkylens sammanbrott inom magnetismen i MAC),
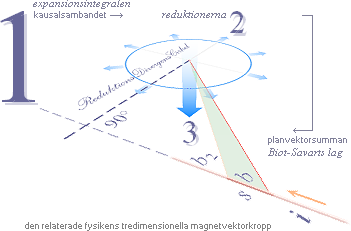
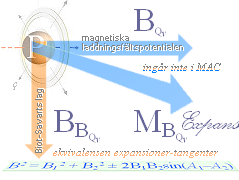
1: magnetiska
laddningsfältspotentialen från elektriska kraftlagen [B=F/Rc=RQ/A]
grundlägger expansionsintegralens differentialekvation,
2: lösningen till 1 ges
som reduktioner [ç=c–v] i g-divergens för bevarandet av
elektriska konstanten [Rc] via kausalsambandet från ljusets friställning från kinetiken med grund i ljusets gravitella beroende,
3: integrala lösningen
till 1 via 2, samma som Biot-Savarts lag, anger den magnetiska fältstyrkans
kraftvektorriktning — enligt experimentella observationer. 3 framgår också,
faktiskt, ur 2 direkt från Planvektorsummans ekvivalens [likaberättigande] för
expansioner [reduktionerna M] och tangenter [fältstyrkorna B] och som också
gäller för alla fysikens elementära fältbilder [elektricitet, magnetism,
gravitation], se Fältformerna.
börjar modern akademi
(allt sedan Maxwells magnetiska mekanik, 1861, tidigast från
Ørstedts upptäckt och Biot-Savarts experiment år 1820) härifrån:
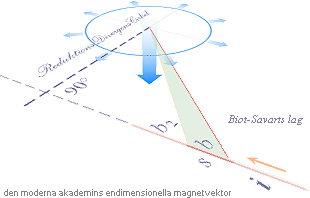
— Strunta i 1:an och 2:an
— strunta i Kausalsambandet och Planvektorsumman — och börja från 3:an MED ETT
allmänt UPPFUNNET VEKTORBEGREPP.
»— VI har inte TID,
kursplanen räcker inte till, för att GÅ IGENOM DETALJERNA: du SKRIVER det här,
eller så blir’e inga MERITER». Modern akademi.
Strömleden [s] bidrar i magnetiska
fältpunkten [P] på normalavståndet x från [förlängda] s med magnetiska
fältstyrkan [B].
— Men ingen i modern akademi kan förklara närmare HUR det
fungerar — regelverkets (vektorproduktens) »överensstämmelse» med eller
»definition» av fenomenformen är [som den fullständiga 3D-vektorkroppen visar] bara partiell :
— Genom ett [för
magnetismens del fenomenmässigt
ofullständigt, vidare nedan] under 1800-talet [från
1878 genom William Kingdon Clifford, se Wikipedia Cross product, History] uppfunnet begrepp VEKTORPRODUKT, och som idag [2011] i kraft av i stort sett
alla fackmässiga beskrivningar framstår närmast som en slags självständig
fysisk fenomengrund speciellt i
magnetismens belysande ljus [här i PREFIXxSIN], har tydligtvis och samtidigt all ANNAN
fenomenanalys ställts på undantag:
Klicka
på bilden för mera utförlig grundbeskrivning, om ej redan bekant.
UPPFINNINGEN består i att
införa — uppfinna — en tredje dimensionens riktform [z] FRÅN en given tvådimensionell planyta [ab].
— JÄMFÖR Planvektorsummans
Identitetskriterium — elementär 2D-trigonometri, ekvivalens mellan expansioner
och tangenter [relaterade fysikens 3D-magnetvektorkroppens 2:a
och 3:e vektorriktningar, se utförligt illustrerat i Vektorkalkylens sammanbrott i MAC] och
som, tydligen, klassificerar uppfinningsprincipen ovan såsom EN PRIMITIV
FÖRESTÄLLNING; Den visar med en gång den direkta begränsningen i
uppfinningen: uppfinningen kommer INTE att kunna omfatta magnetismens fenomenmässiga natur, bara kunna beskriva den
begränsat.
— I klartext: Begreppet
Vektorprodukt är för fenomenbeskrivningens vidkommande ett PRIMITIVT begrepp, men är tydligen det
enda man känner till i den moderna akademins lärosystem.
— NOTERA OCKSÅ BEGREPPETS
DELVIS REDAN ETABLERADE GRUND REDAN ÅR 1861; Se Maxwell s566, ”The force is
perpendicular to the current and to the lines of force, and is
measured by the area of the parallelogram ...”.
— Samt, tydligen redan tillämpat
tidigare av Ampere enligt Maxwells
”Ampere has shewn that
when currents are combined according to the law
of the
parallelogram of forces, ...”, s184ö, ON FARADAY'S LINES OF FORCE.
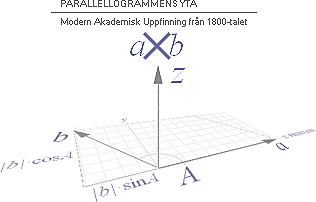
Modern akademi (1878):
vektorprodukten eller parallellogrammens
yta a × b = | a| | b| · cosA [här i PREFIXxSIN] ska tolkas FRÅN a TILL b med resultat i att
den resulterande värdemängden bildar en tredje vektor [z] i rät vinkel mot de bägge 2D-vektorerna och med sådan riktning
[här uppåt] en högergängad skruvs stigning har då den vrids just från a till b, alltså i princip samma
som högerhandsregeln:
— Handen framför oss på
bordet, kanten neråt, fingrarna slutna i riktning a till b, resulterande vektorn [z] i tummens riktning.
— Jämför hur olika
fackverk beskriver Biot-Savarts lag med hjälp av ovanstående begrepp.
För att illustrera (en
aspekt i) Praktiken —
— Den motsvarande
»magnetiska vektorproduktens vy» skulle därmed bli med B-vektorn i ändpunkten
av a-linjen ovan, inte i vinkelorigot,
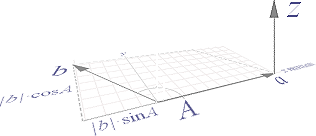
Med beteckningar enligt PREFIXxSIN.
[Vektorproduktens
regelverk är alltså en AKADEMISK uppfinning, ingen fysisk fenomengrund].
så att man får
motsvarande magnetiska vektorbild — enligt konventionella fackverk.
Jämför Biot-Savarts lag —
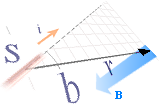
enligt dB = (I
· ds×r/r3)(µ0/4π).
— Men ingenstans i modern
akademi finns någon beskrivning som talar om HUR B-vektorn kommer UT till sin
position med utgångspunkt från agenterna som bär ansvaret för fenomenet: de
elektriska laddningarna i strömleden s.
— Färdas B-vektorn utmed
r? Om den gör det, hur så? Och om inte, hur är det då? Frågeställningen ingår
inte, inte alls överhuvudtaget, i modern akademi. Det gör heller inte expansionsintegralen som förklarar fenomenet.
— Maxwells virvelanalogi [s455m] beskriver också den magnetiska fältlinjen som en STATISK
fenomenform: stilla på stället, helt utan egenskaper som medger någon dynamik i
förflyttande led.
— I RELATERAD FYSIK kan »linjens stillastående» förstås bero på
att den kopplar till det underliggande materialet som framvisar magnetismens
kraftlinjer för experimentalfysikern. Fältlinjerna fysiska form kopplat alltså
tvunget till något material, medan fältringarna som sådana (reducerade g-divergenser) expanderar
kontinuerligt via ljushastigheten utåt från bildningspunkterna. Det syns aldrig
— det finns ingen motsvarande »mekanisk rörelse» — lika litet som ljusets
krökta väg kring Solen utvecklar centrifugalkrafter (se Solrandsavböjningarna från 1919).
För divergensen (ljushastigheten)
generellt i praktiken i relaterad fysik, se GPS-exemplet
och Absoluta metriken.
— Med andra ord: ovanstående process (z-vektorns placering är godtycklig i vektorproduktens
definition) avbildar ingen fysikaliskt kopplade fenomengrund,
utan BLIR en anpassning som görs allteftersom till ett uppfunnet matematiskt
regelverk med utgångspunkt från en observerad praktik, och i den mån någon
parallell alls existerar.
Det har,
uppenbarligen, ingenting med magnetismen som fenomen att göra. Någon förklaring
till HUR och VARFÖR beträffande fenomenformen finns (följaktligen
heller) inte. Jämför Citatblocket.
— Eller sagt, rent ut: vektorproduktbegreppet i modern akademi och för fenomenbeskrivningens del
tydligen mera förvillar, fördunklar och försvårar än hjälper, beskriver och
förklarar.
— För fenomenformen som sådan, finns absolut ingenting att
hämta, även om vektorprodukten som kvantitativ metod för beskrivning av storlek
och riktning förefaller utomordentlig.
— Vektorformen i vektorproduktens begrepp har uppenbarligen
ingen entydig definition: den måste, som vi ser, flyttas i princip godtyckligt,
helt ologiskt i relation till fenomengrunden, och efter regler som tydligen leder långt utanför den
fysikaliska praktiken.
— Det går följaktligen inte att använda begreppet vektorprodukt i magnetismens
fenomenbeskrivning — den formalian är uppenbarligen MENINGSLÖS.
— Det är den ena aspekten.
— Den andra aspekten endast understryker den första:
— OM man försöker beskriva magnetismen från modern akademis sida
måste Hela orsaksgrunden till magnetismens uppkomst — i relaterad fysik enligt Kausalsambandet —
tvunget HELT hoppas över eftersom begreppen skalär/vektor (i den praktiserade vektorprodukten för
magnetismen) inte passar ihop med den orsaksgrunden (begreppen skalär/vektor urartar och antar
varandras innebörd). Ett mera utförligt försök att beskriva den konfliktens
kärna finns från Regelbrott i Vektorkalkylen från Magnetiska Expansionsintegralen.
Expansionsintegralen för magnetismen ingår
inte i den moderna akademins lärosystem.
Här slutar artikeln om Maxwells
magnetiska fältmekanik.
Expansionsintegralens
grund beskrivs här komprimerat i sammanfattning nedan i artikeln Kausalsambandet komprimerat. Se även (enklare)
originalartikeln i Kausalsambandet, om ej redan bekant.
Kausalsambandet —
komprimerat — för originalartikelns beskrivning se Kausalsambandet
— I RELATERAD FYSIK är
Expansionsintegralens vektoriella representation inget mer och inget mindre än
(forts.)
↔Rc = ↕R’(c–u) = 1/ε = ↕Rmaxç0
Magnetismens fältfysik
enlig kausallogikens begrepp — saknar
uttryckbarhet i modern akademi
— Inverkan av elektriska laddningens [Q] hastighet [u] — den
ändrade potentialbilden från Q i den fixt g-relaterade rymdpunkten P
— överförs [komplext till –iu] rätvinkligt u, alltså i normal till
strömriktningen, och därmed via en divergensreducerad [ç=c–u] eller »rymdförtätad» planvåg som helt
utan tjocklek i bevarandet av elektriska konstanten [Rc] expanderar idealt
rätvinkligt u, och endast så. I princip EXAKT så som visas i vinjettbilden
nedan [ringar på vattenyta efter fallande droppe]:
Base • Fysikens
7 Principer | DIVERGENSEN
| Ljusbrytningen | Ljusfrihetssatsen
| Ljusets
Gravitella Beroende | Elektriska
Kraftlagen | Elektriska
Laddningen | Elektriska
Fältet |
Main • Kausalsambandet | MAGNETISMEN | Närverkan och Fjärrverkan | Magnetiska Kraftlagen | Expansionsintegralen | Magnetiska Konstanten | Planvektorsumman | Fältformerna | H | B i Q |
BILDKÄLLA: Författarens arkiv · TonMontage i
DELPHI4Test2011 · 21Apr2009VattenDropDiskBild3 • 23Apr2011BildR1Excur11 ·
NikonD90 · Detalj
Magnetismens specifika ekvationer · Rakledaren · Toroiden
· Spolen · Ringen · Konen | Elektromekaniska induktionen | Magnetisk och Elektrisk Polarisation | Järnkärnetransformatorn |
— Planvågen utgår idealt
från P som en helt cirkulär ringvåg som drivs från det tätare rummets ç till
fria rymdens c0 i kraft av en helt idealt g-homogen rymd [Ljusets Gravitella Beroende]. Slutvärdet [i någon
bestämd rymdpunkt] blir integrala summan av alla enskilda bidrag utmed expansionslinjen [mera utförligt i MAGNETISMEN].
— Reduktionernas
sammanhängande utsträckning över ändliga intervall sammanlänkar begreppet om
den magnetiska fältlinjens kraftmässiga utsträckning, samma som fältringens
tangenter.
— Elementära Elektrogravitella Planvektorsumman beskriver den ömsesidiga
ekvivalensen mellan expansionsvektorer och tangentialvektorer.
— Den fysikbeskrivningen
står tydligen helt — fullständigt — orepresenterad i modern akademi.
— Sambandsformerna leder
vidare till B = µs·I/A = µH ; dB = µ·I/A · ds enligt:
— Elektriska fältstyrkan [här»E-F»
Ξ=U/d=F/Q=RmaxçQ/A från elektriska kraftlagen] tagen över reduktionen [ç=c–u] uttrycker
magnetiska fältstyrkan [B],
B = Ξ/ç = F/Qç =
RmaxQ/A = Rmax[1/T]I/A = [ç/ç]Rmax[1/T]I/A = [Rmax/ç][s/T][1/T]I/A = [µ][s]I/A;
— Med införande av
vinkeln [b från noll till 90°, sin 0 = 1 i PREFIXxSIN] ges
dB = [µ/4π]·I/r² ·
sinb · ds som efter differentialtransformation ger likvärdiga
dB = [µ/4π]·I/x ·
sinb · db. Härledningen visar mera utförligt i Fjärrverkan och Kausalsambandet.
Se även utförligt i MAGNETISKA KRAFTLAGEN.
Därmed expansionsintegralens differentialekvation. Se utförligt i Fjärrverkan.
Men
den ingår inte i — omfattas inte av — den moderna akademins lärosystem.
Se Expansionsintegralen särskilt om ej redan
bekant.
Ovanstående enkla
logocept ingår heller inte i modern akademi: ljusets gravitella beroende, den
elektrofysikbeskrivning som följer därav, hur och i förhållande till vad
magnetism och induktion bildas och uppkommer.
Se även mera utförligt i KAUSALSAMBANDET, om ej redan bekant.
expansionsintegralens
differentialekvation, och som grundlägger den allmänna sambandsformen för Elementära Elektrogravitella Planvektorsumman [ELEP].
— ELEP definierar
explicit för magnetismen den avgörande »RÄTVINKELDUALA» ReduktionsDivergensCirkeln, [redDi] eller »skalären som likaberättigad vektor»:
— Se särskilt Planvektorsummans
Identitetskriterium [likaberättigandet mellan expansioner och tangenter].
— Den
fenomenbeskrivningen BLIR helt omöjlig i den moderna akademins begrepp vektorprodukt:
— RedDI-Cirkeln, magnetiska fältstyrkans lokalt g-relaterade punktväde, innefattar inbördes
rätvinkliga vektorfundament — expansioner och tangenter — som kompletterar
varandra i magnetiska fältlinjens beskrivning och förklaring.
Urgrunden till begreppet vektorprodukt har moderniserats (i olika steg) genom den
moderna akademins matematiska utvecklingshistoria (från epoken med
kvaternionerna under 1800-talet som föregick nuvarande vektoranalytiska begrepp
[ref.
@INTERNET Wikipedia Cross product, History 2011-09-18]).
Begreppet vektorprodukt framstår idag som det
enda »förklarande» alternativ som finns, alls, till magnetismen inom den
moderna akademins lärosystem.
— Jämför De inledande citaten från olika etablerade
källor angående kunskaperna/insikterna generellt i ämnet magnetism.
— Begreppet vektorprodukt
fanns inte på Maxwells tid (1860). Maxwells ekvationer sådana vi ser dem i
t.ex. Wikipedia är moderna omskrivningar av originalversionerna (Originalen
beskriver ämnet utifrån en sofistikerad 1800-talsbaserad xyz-matematik; Maxwell
använder själv nablasymbolen [omvända Δ-tecknet, här Ñ i symbol (finns
inte i Unicodetabellen)] i sin A Dynamical Theory of the Electromagnetic Field från 1864, PART VI,
ELECTROMAGNETIC THEORY OF LIGHT, s578, men förklarar inte dess innebörd på
annat sätt än via ett led av formen
d²/dx² + d²/dy² + d²/dz²
= Ѳ).
— Som vi redan studerat
alternativt i olika jämförelser med modern akademi från NOLLFORMSALGEBRAN, är det tydligt att
nomenklaturen i modern matematisk akademi är den mest olyckligt valda som
mänskligheten någonsin sett. Att försöka förstå FYSIKEN med en sådan
förutsättning, skrämmer (alldeles tydligt) bort flera än det lockar.
— Det är naturligtvis inte FEL att använda en matematisk METOD (vektorprodukt)
i beskrivningen av fysikens kvantiteter.
— FELET i sammanhanget är att associera metoden med FENOMENET,
eller göra anspråk på att vektorproduktens begrepp i fenomenbeskrivningen har
någon som helst fysikalisk signifikans. Som det också har visat sig i denna
genomgång, finns heller ingen koppling.
— Många använder den moderna akademins högskolebegrepp
(vektorprodukt) för att bl.a. beskriva magnetismens olika funktionssätt. Men
ingen har ännu visat sig i stånd att presentera en uttömmande beskrivning av —
ens — magnetismens elementära fenomenfysik med de begrepp som den moderna
akademins lärosystem tillhandahåller, begreppet vektorprodukt inbegripet.
— Jämför även i Vektorkalkylens sammanbrott i magnetismen i MAC.
g-divergens ljushastighetens lokala värde med referens till den lokalt
dominanta gravitationens inverkan, från Ljusets gravitella beroende.
— Divergensen är i relaterad fysik alltså det gravitellt punktlokala värdet på
ljushastigheten och som INTE bildas över intervall, se utförligt från DEEP.
Ljushastigheten i normal mening däremot
bildas över intervall som medelvärdet av ljusvägens g-divergenser.
reduktion divergensens lägre värde i den magnetiska
fältbildningen för bevarandet av elektriska konstanten, se utförligt i Kausalsambandet om ej redan bekant.
END.
Editor2011X7
Induktionen och Magnetismen APPENDIX2
innehåll: SÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER
Induktionen och Magnetismen APPENDIX2
ämnesrubriker
innehåll
APPENDIX2 —
Induktionen och Magnetismen i Relaterad Fysik
referenser
;
I denna genomgång:
|
Rikt |
redDi och DIred |
Vektor |
Reduktions |
Riktnings |
Flödes |
Maxwells |
Maxwells |
MAC |
Vektorprodukten |
Kausal |
|
Begreppen |
Relaterad fysik |
Summeringen |
Divergens Cirkeln |
Principerna |
Formerna |
Virvelanalogi |
Magnetmekanik |
TNED |
i MAC |
Sambandet |
Se även ALLMÄNNA STYCKEN SOM
BESKRIVER KONFLIKTEN mellan Modern Akademi och Relaterad Fysik speciellt
angående magnetismen: Ampere, Maxwell och B i MAC.
BILDKÄLLA: Författarens
arkiv · Viken13Apr2010Bild201 · NikonD90 · Detalj
Se även
|
|
|
|
StripesKontexter för
Induktionen och Magnetismen
Induktionen och Magnetismen kan [nära exakt] liknas vid
mekanikens hydrodynamik: En vattendroppe som efter träffen mot vattenytan
bildar expanderande ringar, magnetism, och fria droppserier via kraftrekylen,
induktion. Av ej närmare känd anledning [naturföraktet frånsett] varken
omskrivs eller används den analogin i den moderna akademins lärosystem.
Base • Fysikens 7 Principer | DIVERGENSEN | Ljusbrytningen | Ljusfrihetssatsen
| Ljusets Gravitella
Beroende | Elektriska Kraftlagen
| Elektriska
Laddningen | Elektriska Fältet | Fältfrihetssatsen |
Main • Induktionsdipolens
uppkomst | INDUKTIONEN | Närverkan
och Fjärrverkan | Induktionslagen | Induktansbegreppet
från elektriska konstanten |
Induktionens
specifika ekvationer · Ringen · Rakledaren · Transformatorlagen | Parallellexperimenten | Induktionsbegreppet
genom Parallellexperimenten | Allmänna
Materieinduktansen |
BILDKÄLLA: Författarens arkiv · Ovan: 21Mar2009VattenDrop10ABild46 · NikonD90 ·
TonMontage med DELPHI4Test2011, originalbilden förminskad tillsammans med
centraldetaljen i fokus · Nedan:
17Maj2009StrandBild130 · Detalj
Base • Fysikens 7 Principer | DIVERGENSEN | Ljusbrytningen | Ljusfrihetssatsen
| Ljusets Gravitella
Beroende | Elektriska Kraftlagen
| Elektriska
Laddningen | Elektriska Fältet | Fältfrihetssatsen |
Main • Kausalsambandet | MAGNETISMEN | Närverkan
och Fjärrverkan | Magnetiska
Kraftlagen | Expansionsintegralen | Magnetiska
Konstanten | Planvektorsumman | Fältformerna | H | B i Q |
Magnetismens
specifika ekvationer · Rakledaren · Toroiden · Spolen · Ringen · Konen | Elektromekaniska
induktionen | Magnetisk och Elektrisk Polarisation | Järnkärnetransformatorn |
BILDKÄLLA: Författarens arkiv · Ovan: 21Apr2009VattenDropDiskBild3 · NikonD90 ·
Detalj
Vektorkalkylens sammanbrott i magnetismen i modern
akademi — orienterande referens om ej redan bekant; Klicka
på bilden nedan för att komma vidare till huvudartikeln.
Magnetiska
Expansionsintegralen
Om
ej redan bekant: NOTERA för 3D-vektorkroppen B[Qv], M[B(Qv)] och B
[B(Qv)], här exemplifierat via Q+ för högerhanden med v i tummens riktning åt
höger: Den gäller SÅVÄL med referens till PUNKTVÄRDET
FÖR MAGNETISKA FÄLTSTYRKAN, alltså som »ett
ordinärt 3D-koordinathörn xyz» som med referens till HÄNDELSEVEKTORERNA:
Från elektriska laddningen Till VARJE rymdpunkt utmed linjen genom laddningens
centralpunkt i framriktningen [med ljushastighetens fördröjning] i v-riktningen
[vektorn här benämnd magnetiska laddningsfältspotentialen], sedan därifrån
[Kausalsambandet] Ut vinkelrätt TILL aktuell mätpunkt för B
[Expansionsintegralen, M-vektorn], och sist [Planvektorsummans ekvivalens för
expansioner och tangenter] vinkelrätt i fingrarnas nedvikta riktning den
aktuella fältkraftens fysiskt observerbara riktning [B(»Biot-Savart)-vektorn»].
Det finns alltså ingen »enkel matematiskt heltäckande form» för dessa bägge
Kompletterande SÄTT. De måste, tydligen, förstås utifrån DEN NATURLIGA
FENOMENFORMEN SOM SÅDAN — dels ett händelsevärde [xyz-följd], dels ett punktvärde [xyz-hörn]. Mera utförligt i Vektorkalkylens sammanbrott i MAC och EXPANSIONSINTEGRALEN.
— I modern akademi bortser man ifrån de bägge
två första vektorerna OCH DE CENTRALA KOMPLEX SOM FÖRKLARAR OCH BESKRIVER DEM: kausalsambandet och planvektorsumman.
— Se även artikelförteckningen i KONSEKVENSER. Den allmänna attityd man möter — i dessa
angelägenheter, från den moderna akademins sida — har redan tidigare belysts i
olika avsnitt och sektioner. Se främst Inledande Citat i ENTROPIBEGREPPET [ingen annan ordning än den som dikteras från
modern akademi får förekomma], samt GeneralCitatet beträffande förståndets föredömen i moderna
kvarter, samt generellt AGW [konsekvensexempel; AGW är historiens tveklöst alldeles främsta moderna
akademiska intelligensexempel på allmän avsaknad av förstånd i anledning
av föredömena — konflikten mellan Naturen och Modern Akademi]. Det är i ljuset av
dessa exempel alldeles tydligt att mänskligheten är fångad i en särskilt
avancerad historisk mörkergrop vars främsta konserverande företrädare utgörs av
den moderna akademins MATEMATISKA — självutnämnda — elit. Jämför [återigen] HerrefolksCitatet. Vi kan, tydligen, inte
komma närmare ett konkret exempel. [Exemplen visar tydligen: En samling extremt
storkäftade nollelement — modern akademis främsta matematiska elit, som poppar
upp FÖRST under 1800-talet med vidare — som sinsemellan intygar varandras
överlägsenhet mot resten av mänskligheten och i den andan sinsemellan OCKSÅ
utbyter betygande meriter i kraft av att uppfinna eget, förkasta
naturintelligensen och medverka till att mörklägga dess inneboende ordning,
allt medan Jorden segnar ner; Visst önskemål föreligger, således, att sopa
golvet RENT från den förekomsten. Det finns bara ett sätt: kunskap. Se exempel i Alla Tal].
Induktionen&Magnetismen
beskrivs [-8Okt2011] i Universums Historia enligt RELATERAD FYSIK i
htm-dokumenten
InduktionenOchMagnetismen.htm:
Allmänt illustrerad presentation och beskrivning;
Kausalsambandet, Nomenklatur, m.fl.
IndMag_Induktionen.htm:
Induktionens härledning med samband och
referenser
IndMag_Magnetismen.htm:
Magnetismens härledning med samband och
referenser
IndMagAppendix.htm:
Planvektorsumman, fältformerna,
elektriska fältet, potentialbegreppet, parallellexperimenten, matematisk syntes av Ind&Mag, Tre
Jämförande Exempel
IndMagAppendix2.htm (Tillägg Okt2011):
Riktningsbegreppen
i magnetismen, Maxwells analogier
JÄMFÖRELSER TNED/MAC
— Särskilt belysta
aspekter i jämförelsen mellan relaterad fysik (TNED) och modern akademi
(MAC) inom induktionen och magnetismen:
Htm-originalen IndMag
(2007-2008):
Förtydligandet av Faradays EMI, Magnetiska Expansionsintegralen med Biot-Savarts lag —
Magnetismen i MAC, Magnetiska konstanten µ0, Regelbrott i Vektorkalkylen, Tre Jämförande Exempel,
IndMagAPPENDIX(Tillägg Aug-Sep2011):
Maxwells
magnetiska mekanik, Amperes Kretslag — Magnetismen i Modern Akademi.
Senast uppdaterade version: 2024-07-02
*END.
Stavningskontrollerat 2011-10-08.
rester
*
åter till portalsidan
· portalsidan är
www.UniversumsHistoria.se
∫
√ τ π ħ ε UNICODE — often used charcters in
mathematical-technical-scientifical descriptions
σ
ρ ν ν π τ γ λ η ≠ √ ħ
ω → ∞ ≡ ↔↕ ħ ℓ
Ω
Φ Ψ Σ Π Ξ Λ Θ Δ
α
β γ δ ε λ θ κ π ρ τ φ
σ ω ϖ ∏ √ ∑ ∂ ∆ ∫ ≤
≈ ≥ ← ↑ →
∞ ↓
ζ
ξ
Arrow symbols, direct via Alt+NumPadKeyboard: Alt+24↑; 25↓; 26→; 27←; 22▬
23↨
— also 18↕; 29↔
Alt+NumPad 0-25, 26-...
☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓
→←∟↔▲▼
!”#$%&’()*+,-./♦812...
*
åter till portalsidan
· portalsidan är
www.UniversumsHistoria.se