Induktionsfysik och Supraledning i Relaterad Fysik för UNIVERSUMS HISTORIA | 2011VIII20 | a production | LatestUpdate YMDTime 2024-10-25 ♦ HumanRight is a knowledge domain

innehåll · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Allmänna Materieinduktansens Induktionsfysik och Supraledningens teori i TNED — 20Aug2011

BILDKÄLLA: Författarens arkiv · TonKollage med DELPHI4Test2011 · 13Aug2011[Sjöstrand1_22/27]Excur16•23Sep2011Landskap_01Excur17 · NikonD90 · Detaljer

För magnetismen speciellt, se NOMENKLATUR — en viss språkförbistring, även INOM modern akademi, är ett faktum.

Vilken är skillnaden mellan konventionella och relaterade?

— Maxwells ekvationer.

Vad är induktans och induktion?	Induktionsbegreppet i relaterad fysik	Induktionsmatematiken	Tilledarnas B-fält	Supraledning
Konventionella induktansmatematikens grund Konventionella induktansmatematikens grund
Kausallogiken förklarar begreppen	Magnetism och induktion i praktik och teori	integrationsgränser	planalternativet	Teori

Förord | Förtydligandet Faradays EMI | Härledningen till rakledarinduktansen I RELATERAD FYSIK | Induktionsdipolens uppkomst | Elektronmobilitet | Laddningsmobilitet | Drifthastighet |

Supraledningens absolut teoretiska grunder i relaterad fysik

Induktionsbegreppet

Allmänna sambandet för rakledarens induktans — i sammanställning från författningen KRAFTLAGEN 1999XII

Induktionsbegreppet i relaterad fysik

Kort Illustrerad Sammanfattning

Den uppmätta induktionsspänningen i C-linjen (figuren nedan) har ingen koppling till begreppet MAGNETISM:

— En magnetisk fältstyrka (B) från primärledarna (AB) i C-linjen finns — existerar — inte om AB-strömmarna är lika stora och samriktade (se även Tilledarnas B-fält): B från AB-ledarna är i sådana fall inte påvisbar, inte relaterbar överhuvudtaget. I modern akademi påstås, som vi vet (se från Kausallogikens samband), induktionen ha en bestämd och entydig koppling till magnetismen (Faradays lag) genom begreppet elektromagnetisk induktion; induktion förorsakas av varierande magnetiska fält. Se även IoM-implikationen. I relaterad fysik finns ingenting sådant: induktionen förorsakas av accelererande elektriska laddningar relativt referenspunkter i omgivande dominanta gravitationsfält. Se utförligt från Induktionsdipolens uppkomst. Feluppfattningarna beskrivs — och jämförs — särskilt i Magnetiska Fältintegralen och Magnetiska Konstanten. Samt här, speciellt för induktionen via experimentella observationer, vidare nedan.

— Magnetism och induktion är i relaterad fysik helt skilda fenomen. Se utförligt från Växelverkansfrihetssatsen. Se även utförligt från Uppkomsten av Induktion och Magnetism om ej redan bekant. Enbart likheterna som sådana i Kausallogikens sambandsexempel (närmast nedan) förklarar (en del) av varför, och hur, begreppen sammanblandas i den modern akademins lärosystem där en teori för Induktionsdipolen inte ens finns med (närmast nedanstående samband i utdrag från Jämförande uppställning):

(Λ/4πx)(1–0) = Λ (4πx)^–1 = Ð .................................................. induktion, V/M

= L(di/dt)(4πx)^–1 = µs(di/dt)(4πx)^–1

µ₀(I/4πx)1 = µ₀I (4πx)^–1 = B .................................................. magnetism, VS/M²

— Nedan följer en kortare genomgång av resultaten i Parallellexperimenten 1994.

Se en senare mera utvidgad version i PEX2024Intro ¦ PEX1994OriginalDetails — induktionsfenomenet framgår mera i detalj

— Webben (ännu idag 31Aug2011) tycks inte ha en enda artikel FRÅN DEN MODERNA AKADEMINS ETABLISSEMANG i ämnet experimentell induktionsmätning på raka ledare. Spolfysiken är desto mera välrepresenterad.

— Se även den inledande beskrivningen (Kausallogikens samband) som visar hur motsvarande etablerade sambandsform framgår ur den relaterade fysikens begrepp — för mera noggrann jämförelse.

Max kontinuerlig strömstyrka för fritt lagda kopparledare brukar anges konventionellt ca S=[6-10]A/mM² [ref. ELFAKATLOGEN 50-2002 s581sp1mn]. För en fritt liggande Ø0,5mM koppartråd skulle max kontinuerlig ström bli 10A×0,2mM²=2A. Anledningen till begränsningen är att ledaren utvecklar värme genom sin inneboende resistans. Experimentet nedan är därför helt omöjligt att genomföra med konstanta strömmar — tilledarna skulle börja glöda efter någon sekund och sedan brännas av. Med experimentkopplingens pulsviddsförhållande på 1mS [strömpulsens varaktighet] som repeteras med frekvensen 8Hz ges en effektiv strömledningstid på endast 1/125: ingen nämnvärd värmeutveckling hinner byggas upp. Det betyder att alla ingående komponenter kan användas helt utan kylande material, och det var med den förutsättningen som experimenten genomfördes.

— För vidare [Aug2011] behövs emellertid en mera avancerat utformad anordning [som eliminerar vissa onödiga tilläggsberäkningar i Experimentanordningen från 1994].

I[‖] = 2I[|]: Värdeformerna för strömderivatan di/dt i experimentet ger lika uppmätta värden på den givna mittledaren C med bägge AB och given toppström I som en av ledarna men med 2I .

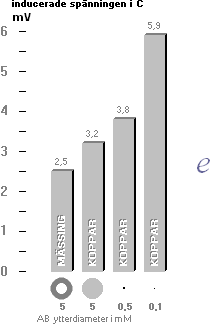
KOPPARLEDARNA e: Färre antal laddningsbärare med samma strömtryck di/dt kräver att varje enskild laddning tvingas bära en större andel av accelerationen dv/dt. Därmed motsvarande högre ledarinduktans, analogt större induktionsspänning i C-linjen.

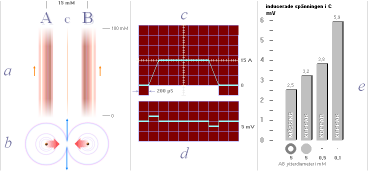
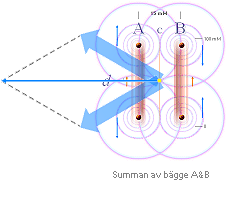
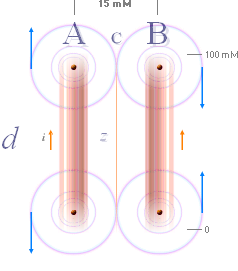
På mittlinjen (C) mellan två raka (a) och parallella (AB) strömförande ledare med lika stora strömmar (I) är magnetiska fältstyrkan (B) noll om strömmarna är samriktade (b). Detta gäller oberoende av om strömmarna är konstanta, om de är i växande eller i avtagande (c). Magnetiska fältstyrkan (B) på mittlinjen (C) är i vilket fall noll: Ingen magnetism kan påvisas där. Ledarnas material och dimensioner påverkar för övrigt inte magnetiska fältstyrkan, endast strömmen räknas.

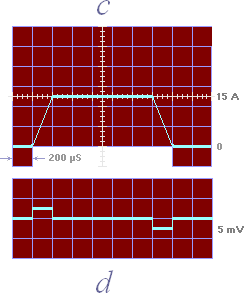
— Är strömmarna i växande eller avtagande (c) och man spänner upp en (tunn) mättråd på mittlinjen (C), induceras emellertid (d) — trots noll magnetisk fältstyrka i C — en påvisbar och mätbar elektrisk spänning (û) i C. Materialet i C visar sig vara egalt: Försök med olika material för C-tråden visar ingen ändring i den inducerade spänningen. Däremot (e), given strömderivata (c), ändras û i C dels med primärledarnas (AB) tvärsnitt och dels med deras material.

— Vänds strömriktningen i endera ledaren AB, uppmäts full B-styrka på mittlinjen C (enligt konv. Biot-Savarts lag, se även i Jämförande Uppställning), men ingen inducerad spänning kan då observeras i mittlinjen C.

— Experimenten genomfördes 1994 med max I = 30 A under 200µS (di/dt = 150 000 A/S) enligt redovisningen i PARALLELLEXPERIMENTEN.

En senare mera utvidgad version finns i PEX2024Intro ¦ PEX1994OriginalDetails — induktionen och magnetismen mera i detalj

— Magnetism och induktion existerar således skilda från varandra i den relaterade fysiken. Omnämnande av en motsvarande experimentform som ovan, eller dess motsvarande teori, har eftersökts i etablerade referenser men inte påträffats.

MÄTUNDERLAGET I OVANSTÅENDE är alldeles för litet för att berättiga till en övergripande funktionsgrafik med någon större tvärsäker innebörd. Mätningarna är emellertid, och tydligen, tillräckliga för att understryka fenomenaliteten som sådan i komplexet magnetism-induktion, den underliggande förklarande och beskrivande teorin. Samt, också tillräckliga för att utgöra ett visst underlag för en vidare matematisk prövning av en möjlig sambandsform som kan förklara de uppmätta kvantiteterna genom kausallogikens (den relaterade fysikens) försorg. Följande redovisar en sådan prövning.

— För begreppet »kausallogik» i detta sammanhang avses speciellt beskrivningar och härledningar ENLIGT RELATERAD FYSIK, se f.ö. utförligt ang. magnetismens och induktionens logiskt relaterbara grunder i Kausalsambandet och Uppkomsten av induktion och magnetism.

Den konventionella facklitteraturens beskrivning kopplar inte parallellexperimentets fenomenform

Jämför den konventionella facklitteraturen i Citatblocket — det finns ingen motsvarighet.

SÅLEDES MED REFERENS TILL PARALLELLEXPERIMENTET:

Induktion utan närvaro av B-fält inte bara finns. Induktionen varierar dessutom mätbart med strömkällans material och dimension, given strömderivata di/dt. B-fältet däremot, enligt PARALLELLEXPERIMENTET, påverkas inte det allra minsta av material eller dimensioner; för B-fältets del är det endast strömmens styrka som räknas.

— Vänds endera ledarens strömriktning, ges full B-styrka i C, men ingen som helst induktion kan då påvisas:

Ingen induktion trots full B-styrka. I vilket fall visar parallellexperimentet med andra ord och i klartext att magnetism och induktion existerar som väsensskilda fenomenformer i fysiken. Se även explicit från Kausalsambandet.

Se även delvis mera utförligt från MAGNETISKA EXPANSIONSINTEGRALEN — en del av förklaringen till varför och hur det har blivit så här tokigt i modern akademi: begreppet »elektromagnetisk induktion» saknar fysikalisk fenomenmässig förankring — men har blivit ett bekvämt sätt i modern akademi att FÖRENKLA induktionsfysiken genom att sammanföra den med MAGNETISMEN via MAXWELLS EKVATIONER: den moderna akademins antagna — uppfunna — vektorkalkyl.

Se även DE TRE JÄMFÖRANDE EXEMPLEN, där ges exakta kvantitativa jämförelser i sambandsformerna via redan etablerade fackverk. Se även särskilt MAGNETISKA KONSTANTEN µ0.

— Däremot gäller begreppet elektromekanisk induktion analogt med Faradays lag. Jämför exemplet med den vibrerande gitarrsträngen (också del i Parallellexperimentet från 1994, den delen finns omnämnd [mekanik, anordning] men inte redovisad i det aktuella webbdokumentet på grund av dess redan allmänt välkända fenomenform). Se även (inledningsvis) i Förtydligandet till Faradays EMI.

Jämförande induktanser

Facklitteraturens induktanssamband L_k (blå grafer nedan) stämmer inte så bra

DEN RELATERADE FYSIKENS HÄRLEDDA L0-SAMBAND visar nära exakt överensstämmelse med de uppmätta induktansvärdena i PARALLELLEXPERIMENTET. Däremot stämmer det konventionellt givna sambandet mindre bra med mätvärdena.

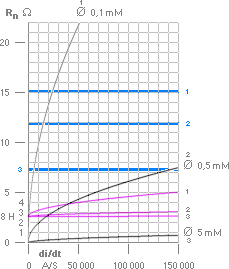
Kausallogikens härledda samband, graferna Grå-Violett nedan för en s=0,1M kompakt Kopparledare [ξ=2,6] med olika angiven diameter [Ø]:

Mörkgrå grafer: Rakledarlängdens induktansresistans Rn=R’ [per meter] växer med strömderivatan di/dt och mindre tråddiameter. R’ ingår inte i den konventionella rakledarens induktansform.

Violetta grafer: Rakledarens [rymdöverlagrade] induktans L0 för samma ledare, rakledarnas längd 0,1 M [ ξKOPPAR=2,6 ]:

Primärinduktansen hos en rakledare växer med växande strömderivata och tunnare tråd.

Blå grafer: Modern akademi. Inget beroende av material finns med [variabel induktansresistans R’ ingår inte]: Inget beroende av strömderivatan di/dt finns med.

Se värden i Tabell 1.

I termer av relaterad (kausallogiskt förankrad) fysik (se Kausalsambandet): I modern akademi återförs Lk-formen (tabellen nedan) på den sekundära induktionens ledargeometri (se Sekundärinduktionen om ej redan bekant, se även kortbeskrivningen i MAC-sambandet); Modern akademi har inget utvecklat föreställningssätt för begreppet primärinduktion och det elektriska fältets induktionsdipoler (dipolbegreppet beskrivs utförligt i Induktionsmatematiken) med referens till det lokalt dominanta gravitationsfältet (i modern akademi finns ingen motsvarande teori). Istället återförs induktionsfysikens begrepp på »magnetismens matematiska begrepp» via Maxwells ekvationer (eg. vektorkalkylen), och som sedan (på kaotiska sätt som, tydligen, ingen kan beskriva) begreppiseras som »induktion» med allmänformen »elektromagnetisk induktion»; I denna ingår inte den magnetiska fältintegralens differentialekvation (därför att den inte kan fås att stämma med — den kör över — Maxwells fältvektoralgebra) men väl dess resultat (konv. Biot-Savarts lag). Med Den (mycket) förenklade fysikbilden beskrivs sedan den s.k. elektromagnetismen i modern akademi genom samlingsbegreppet »elektromagnetisk induktion». Jämför Förtydligandet till Faradays EMI. Ingen varken förstår eller kan förklara det moderna akademiska detaljinnehållet utan att uppväcka djupgående frågekomplex som trotsar varje enhetlig beskrivningsform. I relaterad fysik finns ingen motsvarande komplexitet, detaljerna genomgås speciellt noga med jämförande referenser (se särskilt Tre Jämförande Exempel).

— Men kolla också den mycket speciellt utformade experimentanordningens förutsättningar: typ 30 Ampere genom 0,5mM trådar. Det finns inga normala sådana praktiska tillämpningsexempel (max kontinuerlig ström för en friliggande Ø0mM5 koppartråd är ca 2A); De (således) betydligt lägre strömmarna i normala tillämpningar döljer alla olikheter och får dem att framstå som kvantitativt obetydliga. I den fenomenmässiga fysikens förklaring däremot framgår sammanhangen tydligare (se särskilt Tre Jämförande Exempel).

	kausallogiken	modern akademi
rakledarens induktans	L0 = (µ0/2π + ηR’/c0)s(ξ)	Lk = (µ0/2π)s[ln(4s/d) – 3/4]
	ingen sekundärgeometri	sekundärgeometri
	induktansresistans R’	ingen induktansresistans

Observera att rakledarens primärinduktans alltid måste sluta på, eller utgå ifrån, motsvarande rymdens fria längdinduktans [µ₀/2π]s via den — här enligt kausallogiken — specifika primärledarens materialkoefficient (ξ), i detta exempel (ξ=2,6)[µ₀/2π][s=0,1].

Primärinduktansen i relaterad fysik är för normala ledare oberoende av ledarens kurvatur men beroende av materialet [R’] och dess strömderivata.

Se vidare i Härledningen.

R’ = R_n = r^–1[√[(di/dt)/πne](1M/S²)] ; r anger ledartrådens cirkulära radie, i grafen ovan resp., 2r=Ø{0,1; 0,5; 5}mM enligt experimenten.

Graf = [1/0.25](x/[4.26])'0.5: r i mM, x i T4 A/S

Graf = (10'8)0.261[30+0.75[1/0.25](x/[4.26])'0.5]/(3·10'8): L0 i t8 H

Graf = 0.261[30+0.75[1/0.25](x/[4.26])'0.5]/3: L0 i t8 H

Tabell 1 nedan redovisar hur facklitteraturens teoretiska samband [d] kopplar till de här (från Parallellexperimenten 1994) experimentellt uppmätta värdena [c(direkt),g(med hänsyn till mätlinjens speciella geometri κ=0,817)] — det är tydligt att den konventionella sambandsformen inte anställer någon mera precis överensstämmelse.

En senare mera utvidgad beskrivning finns i PEX2024Intro ¦ PEX1994OriginalDetails — induktionen och magnetismen mera i detalj

En delvis mera instrumentellt preciserad genomgång av de nedanstående tidigare (1994) mätresultaten med analyser och resultat.

Tabell 1 — mätdata för kopparledarna med konventionell jämförelse — di/dt = 150 000 A/S enkelledare, C-avstånd 15 mM. κ grek. Kappa.

		uppmätta	konventionellt beräknade	t8 H		TNED-κ-beräknade	TNED-L0-beräknade	TNED-beräknade
ØmM	uMÄTmV	Lκ=uMÄT/(di/dt)	Lk=(µ0/2π)s[ln(4s/d)–3/4]	d/2,78	e/g	L=uMÄT/(di/dt)κ	L0	h / g
5	3,2	2,133 t8 H	7,264 t8 H	2,61	1,00	2,611 t8 H	2,651 t8 H	1,02
0,52	3,8	2,533 t8 H	11,869 t8 H	4,27	1,38	3,101 t8 H	3,090 t8 H	0,997
0,11	5,9	3,933 t8 H	15,088 t8 H	5,43	1,13	4,814 t8 H	5,043 t8 H	1,05
a	b	c	d	e	f	g	h	i

Sambandet för L_k — se fackreferenser. t8H anger 10^–8 Henry.

KOLUMNERNA e-f med optimalt antagen delningskoefficient 2,78 har här insatts FIKTIVT enbart för att belysa den möjliga jämförande resultatredovisningen: konventionella sambandet +38% kolumn f kan i vilket fall tydligen inte mäta sig med det här kausalt relaterade +5% –0,3% kolumn i.

NOT 2: förtennad 0,5mM koppartråd.

NOT 1: isolerad 0,1mM koppartransformatortråd. Mätavstånd x=17mM, di/dt=25A/200µS. Mätvärdet (4,3 mV) anpassades ”linjärt” till 30A/200µS enligt

(30/25=1,2)(4,3)=5,16 @ 5,2mV.

Mätvärdet justerades sedan från mätresultatet vid x=17mM till x=15mM för enhetlig tabell enligt

(17/15)U=5,9; U=5,2mV | Denna delvis osäkra hoftning KAN möjligen vara fel på 5% [slutvärde 6mV2]:

Motsvarande beräknade uMÄT-värden är [u-flex] û=L[0]κ[di/dt] i mV: 3,2462 | 3,7846 | 6,1779 med ξ=2,6 och η=0,75.

L₀ = s(ξ)(R + ηR’)/c₀

= s(ξ)(R + (η)[√[(di/dt)/neA](1M/S²)](VS/AM)S)/c₀

R’ = R_n = [√[(di/dt)/neA](1M/S²)](VS/AM)S

ξ = U[R(s/c₀)(di/dt)κ]^–1

η = [U/[s(ξ)/c₀](di/dt)κ – R]/R’

κ-värdet i Tabell 1 baseras på härledningen till induktionen för rakledaren [Se även anordningen i PARALLELLEXPERIMENTEN]:

κ = (1/2p)[ln[tan(B/2)/tan(B₂/2)] + 1/tanB₁] = 5,1334708(1/2p) = 0,81 701 72

Verkan från primären på sekundären med bägge ledarna lika långa och placerade parallellt :

U = (Λ/2π)[ln tan[B₁/2] + 1/tanB₁] ; rakparentesen = 4,0708213 Λ=L(di/dt)

Se illustrerat, här i kortare form, från Induktionsspänningen i raka sekundärledare

;

Verkan från primären på överskjutande sekundärdelen (dubbla summan via ändsymmetrin) :

U = (Λ/2π) · ln[tan(B/2)/[tan(B₁/2)tan(B₂/2)]] ; ln[rakparentesen]= 1,0626495 Λ=L(di/dt)

Se illustrerat, här i kortare form, från Induktionsspänningen i raka sekundärledare

Summan av dessa dividerat med induktansfaktorn L=L(di/dt) ger κ ovan :

summa, U/(Λ/2p) = 5,1334708 = 4,0708213 + 1,0626495 Λ=L(di/dt)

tanB	tanB1	tanB2	← B&B2 till figurdelen i b
x/d	x/s	x/y
15/125	15/100	15/25

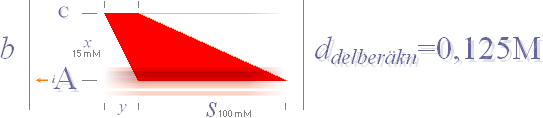
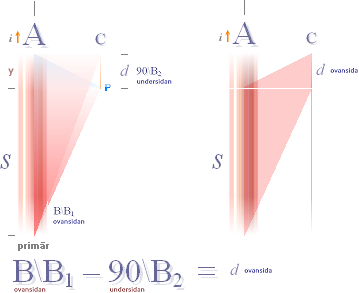
I figurdelen b görs delberäkningen via d=s+y=125mM på ena änddelen [y], resultatet multipliceras med två.

Utelämnas bidragen från ändarna (uppskattat till 25mM per) blir summan 4,0708213. För de aktuella mätningarna är denna ideala induktion inte realistisk. Variationerna mellan de olika alternativen är som synes ca 20%, idealdelen är därför värdelös som referens för explicit kvantitativa jämförelser (vilket dock inte bekommer relationsanalysen). Högerdelen av figuren nedan visar beteckningsformerna med de ingående vinklarna till ovanstående samband, här presenterade i syntes och sammandrag från mera utförliga härledningar [Förf.ref., Win95 DOKs97\Fysiken\Elmain Indukt99.wps].

— För vidare [Aug2011]: En bättre lämpad experimentanordning bör utformas som eliminerar [den osäkra] tilläggsdelen på 25mM, samt som är mera direkt lämpad för att mäta på olika material och dimensioner — utan krångliga anordningar.

NOTERING — för exakt kännedom angående de experimentella-observationella förutsättningarna i Parallellexperimenten från 1994:

I[‖] = 2I[|]

KRYPTIKEN ovan betyder: med dubbla ledare och 15mM centrumavstånd och given toppström I =15 A för strömderivatan A/S induceras i mittlinjen C på avståndet 7,5mM från endera primärledaren lika stor spänning med bara en ledare som för dubbel toppström 2I. MED NÄRA [men inte exakt] SAMMA RESULTAT kan C-linjen approximativt ersätta ena primärledarens plats, avståndet nu 15mM primär-sekundär, och halva den inducerade spänningen från föregående om toppströmmen är 2I.

— Det är med de förutsättningarna som kretsdata ovan har härletts, samt mätvärdena i Tabell 1 observerats.

— För den tunna 0,1mM Cu-tråden tillkom dessutom en mindre slutjustering då dess resistans gjorde att strömmen inte nådde ända upp till 2I. Se särskild notering.

Änddelarna

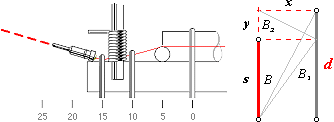
κ, grek. Kappa

κ-värdet

med beräkningarna enligt sambandet för sekundärinduktionen

I de mätningar som gjordes 1994 var ändarna till sekundärlinjen inspända enligt ovanstående konstruktionsdetalj (Förf.ref. DYNAMIKENS GRUNDER Del III 1995X, sidan8). Den markerade nollan i millimeterskalan under detaljerna markerar ströminloppet till primärledarna. Självklart induceras också spänning i sekundärlinjens ändar. Om vi tar med dessa i beräkningarna, ungefärligt (också andra detaljer med de mätande tilledningarna kan ha spelat roll, någon exakt redovisning på detta finns dock inte), med ett tillägg på 25mM för vardera änden tillkommer en faktor 1,0626495 för bägge ändarna till huvudlinjens

[ln tan(b/2) + 1/tanb]. Med endast 20mM tillägg blir faktorn 0,9179852 för de bägge 20mM ändarna. Värdet på tanb i experimenten var 0,075 med sekundären i mitten och 0,15 med sekundären på en av primärernas plats (det senare skedet av mätningarna).

Härledningar till koefficienterna

ξ, xsi (K i PRIMÄRINDUKTANSEN I SAMMANFATTNING) — mätvärdet 2,6 för Cu

Vi härleder allmänna sambandet för rakledarens primärinduktans [L0] med stöd av experimentellt uppmätta mätvärden för analys, prövning och kontroll av resultatet till jämförelse med konventionella samband.

L₀ = s(ξ)(R + ηR_n)/c₀

= s(ξ)(R + η[√[(di/dt)/neA](1M/S²)](VS/AM)S)/c₀

Vi härleder allmänna sambandet för rakledarens primärinduktans [L0] med stöd av experimentellt uppmätta mätvärden för analys, prövning och kontroll av resultatet till jämförelse med konventionella samband.

Vi väljer KOPPARLEDAREN med största ledardimensionen (Ø5mM Cu) för maximala gränsvärden:

— Om vi sammanställer induktionsspänningen (U) enligt den härledda kausallogikens samband (Se utförligt från Induktionen om ej redan bekant) tillsammans med tilläggskoefficienten (κ) för änddelarna i den aktuella experimentanordningen

κ = (1/2π)[ln[tan(B/2)/tan(B₂/2)] + 1/tanB₁] = 5,1334708(1/2π) = 0,81 701 72

har vi

U = (Λ/2π) · ln[tan(B/2)/[tan(B₁/2)tan(B₂/2)]] ; ln[rakparentesen]= 1,0626495 Λ=L(di/dt)

med totalsumman för κ-bidraget

U/(Λ/2π) = 5,1334708

= 4,0708213 + 1,0626495 ;

U = (Λ)(5,1334708)/2π

= L(di/dt) · (5,1334708)/2π

= [s(ξ)R/c₀](di/dt)(5,1334708)/2π

= [s(ξ)(R + ηR’)/c₀](di/dt)(5,1334708)/2π

= [(ξ)(R + ηR’)](s/c₀)(di/dt)(5,1334708)/2π

= [(ξ)(R + ηR’)]([0,1 M]/[2099792458 T8 M/S])(150000 A/S)(5,1334708)/2π

= [(ξ)(R + ηR’)][4,08791 t5 A]

= [(ξ)(R + ηR’)](s/c₀)(di/dt)κ

Vi har vissa skäl att anta att Eta-faktorn (η, accelerationskoefficienten, materialkonstant) är nära 1, samt att tilläggsinduktiva resistansen R’ i detta fall är försumbart liten (mindre än 1 Ω) relativt rymdresistansen R=ca 30 Ω. Det ger oss approximativt (med vissa äventyr)

~ [(ξ)(R + 0)](s/c₀)(di/dt)κ

= [(ξ)(R=29,98 Ω)][4,08791 t5 A]

= (ξ)(0,0012255 V) ;

Umät(5mM) ~ 0,0032 V ;

XSI--värdet 2,6 för Koppar — Xsi

ξ = (0,0032 V)(0,0012255 V)^–1

= U[R(s/c₀)(di/dt)κ]^–1 ;

ξ = 2,61 .................................. gäller för ren Koppar (typ elektrolyt)

xsi-faktorn [samma som K i Primärinduktansens Sammanfattning] framstår som konstant för given INDUKTIONSGEOMETRI κ OCH primärledarlängd s och strömderivata di/dt, men beroende av sekundärinduktionen U för olika primärledarmaterial. — Man kunde ev. inte önska en enklare uppgift?

— OM för en given sekundärmätarlinje (κ) med given primär strömderivata (di/dt), primärledarlängd (s) [oberoende av primärledardiameter (Ø)] olika primärmaterial anställs till mätande prövning, och som i fallet ovan med grövsta möjliga dimensionen Ø för minsta möjliga fel mot eta-faktorns R-komponent, är det tydligt att sambandsformen ovan kan användas för att få ett grovvärde på xsi-faktorn för samtliga material enbart genom att läsa av induktionsspänningen.

— Vilket vill säga: Faktorn ξ får bara specifik koppling till sekundärlinjens matematik (κ) genom en grövsta primärledare (typ ca Ø4-5mM).

— ξ är bara en explicit primärledarparameter under den förutsättningen.

— ξ kopplar därmed explicit endast till κ — via det grövsta primärmaterialets specifika U-värde på sekundärlinjens κ-form.

Xsi-faktorns allmänna innebörd — Koefficienterna

Se även sammanställningen i PRIMÄRINDUKTANSEN I SAMMANFATTNING,

µ_L = K(µ₀+µ_c) ..................... totala primära ledningsinduktansen per meter, K=ξ

Xsi-FAKTORNS ALLMÄNNA INNEBÖRD enligt relaterad fysik

I härledningen till rakledarens induktans visas hur den fria rymdens längdinduktans (µ0) skiljer sig från materierymdens längdinduktans endast genom en materiell koefficient (K, här samma som xsi ovan, ξ) tillsammans med det nödvändiga villkoret av en specifik massgrundad energizonsdivergens c(z) — stället där ett elektriskt fält TAR TAG I en materiell elektrisk laddning, se från Potentialbarriären (som inte ingår i modern akademi) om ej redan bekant.

— K-faktorn i sig fyller tydligen funktionen av en allmän (inre sammansatt) materiekoeffientsfaktor; K bör ha inre sammansättningar (inkluderat temperaturberoende) och som kopplar till en mera preciserad bild av den aktuella materiestrukturen. Vi frånser dock den ev. variationen i detta grundfall och ser K-faktorn som konstant.

— I PRIMÄRINDUKTANSEN I SAMMANFATTNING beskrivs K-faktorn

massändringsfaktor för den resistiva delen i ledarens genomsnittsladdning, beror på laddningarna i ledaren och deras relativa bindning till materiestrukturen (induktansens intensitet), lägst 1 (gäller för fri rymd), ingen högsta gräns (uppskattat 2,6 för koppar vid 20°C)

— Vad menas med det?

Materierummets allmänna längdinduktans från härledningen till rakledarens induktans,

µ_L = K(R/c_z)

innefattar materiens massrelaterade energizoner (för c_z se Potentialbarriären om ej redan bekant). Eftersom elektriska laddningen (Q) i relaterad fysik gäller och härleds som

Q = √ (m/R)(A/dT)

finns ALLTID ett variabelt inre massändringsberoende (m=RIq_c) där elektriska laddningar accelereras av givna elektriska fält i slutna elektriska system — som innebär med energins konstans att också systemets totala massa bevaras konstant. Se kausallogikens förklaring utförligt från Massökningseffekten inom elektrofysiken i Planckekvivalenterna, samt i MAFEM.

— Observera att dessa eller liknande detaljer inte ingår i den moderna akademins lärosystem: Q kan inte härledas i modern akademi — därför att divergensen, »ljushastighetens absoluta acceleration» a=c/dT, inte ingår i den moderna akademins föreställningssätt. Se den kausallogiska förklaringen utförligt från Ljusets fysik.

— Materiefysikens massgrunder, enligt kausallogiken, med energizonerna (där laddningarna tas) betyder därför tvunget att sambandsformen ovan för materiens längdinduktans, och utöver själva den materiella delen av R-faktorn, också tvunget måste betingas av (korrektionskoefficienter för) materialspecifika massa-resistansändringar i materien, nämligen via en allmän materialkoefficient (K). Därmed finns i varje fall rent praktiskt-tekniskt en förutsättning för att faktorerna KR tillsammans kan återspegla dynamiken i massa-resistansbyggnaden för ett visst material och för att kunna garantera att elektriska laddningens kvantitet och kvalitet bevaras, sambandet för Q ovan. Enbart R i µL-sambandet ovan går alltså inte.

— Det betyder bara att olika material, grundämnen och deras sammansättningar utöver deras specifika inre induktansresistanser och deras parametrar, se R(n), måste uppvisa en del ytterligare olika interna mönstertyper (laddningarnas strukturella bindningar, resonanser och gitterbyggnader) med olika grader av inbördes kopplingar och icke-kopplingar.

— Värdet på K kan inte understiga 1, och vilket fall inträffar då ingen strömändring föreligger, eller att betraktelsen avser den materiefria rymden, analogt då µL övergår i µ0, se Härledningen. K-värdet alltså allt möjligt större än 1 för materierummen och variabla strömmar.

Editor2011VIII24

η, eta

Vi härleder allmänna sambandet för rakledarens primärinduktans [L0] med stöd av experimentellt uppmätta mätvärden för analys, prövning och kontroll av resultatet till jämförelse med konventionella samband.

L₀ = s(ξ)(R + ηR_n)/c₀

= s(ξ)(R + η[√[(di/dt)/neA](1M/S²)](VS/AM)S)/c₀

Vi härleder allmänna sambandet för rakledarens primärinduktans [L0] med stöd av experimentellt uppmätta mätvärden för analys, prövning och kontroll av resultatet till jämförelse med konventionella samband.

Med mindre ledartvärsnitt framträder en större känslighet på faktorerna ηR’.

Eftersom induktionsresistansen

R’ = [√[(di/dt)/neA](1M/S²)] med A=πr²

och därmed

= r^–1[√[(di/dt)/πne](1M/S²)]

som för Koppar via di/dt=150 000 A/S ger

= (2/Ø)[√[(di/dt)/πne](1M/S²)]

= (2/Ø)(1,87644 t3 M)Ω

= Ø^–1(3,75288 t3 M)Ω ;

U = [s(ξ)R/c₀](di/dt)(5,1334708)/2π

= [(ξ)R](s/c₀)(di/dt)(5,1334708)/2π

= [(2,61)R][4,08791 t5 A]

= R[1,06742 t4 A]

= (R + ηR’)[1,06742 t4 A] ;

får vi

;

U/(1,06742 t4 A) = R + ηR’ ;

U/(1,06742 t4 A) – R = ηR’ ;

[U/(1,06742 t4 A) – R]/R’ = η ;

η = [U/(1,06742 t4 A) – R]/R’

= [U/(1,06742 t4 A) – R]/[Ø^–1(3,75288 t3 M)Ω]

= [U/(1,06742 t4 A) – R]Ø/[(3,75288 t3 M)Ω]

Om vi väljer ledaren Ø0,5mM med Umät=0,0038 V ges

= [(0,0038 V)/(1,06742 t4 A) – R]Ø/[(3,75288 t3 M)Ω]

η = 0,7488968

Eta-faktorn utpekar aktuella elektronmobilitetens medelvärde.

~ 0,75

= 3/4

;

U = [s(ξ)R/c₀](di/dt)(5,1334708)/2π

= [s(ξ)R/c₀](di/dt)κ ;

R = U/[s(ξ)/c₀](di/dt)κ

= (R + ηR’) ;

η = (R – R)/R’ ;

ηR’ = U/[s(ξ)/c₀](di/dt)κ – R ;

η = [U/[s(ξ)/c₀](di/dt)κ – R]/R’

; OM N=1:

R’ = [√[(di/dt)/neA](1M/S²)] med A=πr²

= r^–1[√[(di/dt)/neπ](1M/S²)]

;

Exakt lösning går inte eftersom U beräknas approximativt via R´=0 via xsi-faktorn.

— Man får i så fall välja [»simulera»] ett något avvikande U-värde för att få ut sämsta fallets gränsvärden [säg, sista värdesiffrans halva numeriska precision typ +0,5].

Eta-faktorns allmänna innebörd — ETA

Se även sammanställningen i PRIMÄRINDUKTANSEN I SAMMANFATTNING,

µ_L = K(µ₀+µ_c) ..................... totala primära ledningsinduktansen per meter

Eta-FAKTORNS ALLMÄNNA INNEBÖRD enligt relaterad fysik

Eta-faktorn [η] blir bara en korrektionsfaktor för elektronmobiliteten ne

Induktansresistansen R’= ηR_n som ingår i allmänna resistansfaktorn (R) i härledningen till rakledarens induktans, bildar tillsammans med toppdivergensen (c₀) den aktuella ledarens primärinduktans per meter enligt

µ_c = R’/c₀ = L₀/s = (ηR_n)/c₀

µ_c (mikro-c) anger ledarens primärinduktans (L₀) per meter (s), VS/AM;

µ_c beror på material, tvärsnitt och uppförande (sätt) från den relativa laddningsmobiliteten i ledaren och laddningarnas relativa bindning till materialets struktur.

— Den bindningen framtvingar ett di/dt-beroende av sammansatt typ.

— För fri rymd blir R(n)-faktorn noll då den fria rymden inte innehåller någon laddning och därmed heller ingen ström i strömderivatan, denna är noll — också analogt med fallet då ingen strömändring föreligger.

Materiella induktansresistansen (R_n) kan skrivas

R_n = [√ [(di/dt)/neA](1M/S²)](VS/AM)S

= r^–1[√ [(di/dt)/neπ](1M/S²)](VS/AM)S

R_n-parametrarna [(di/dt)/neA] är allmängiltiga för alla material, men alla material uppvisar ändå inte samma elektriska och termiska egenskaper med dessa parametrar givna [praktiska exempel på det är bl.a. föremålet för den här framställningen med parallellexperimentets mätvärden till jämförelse].

— För samtliga materialfall behövs alltså en elementär materialkoefficient (eta, η), karaktäristisk för just ett visst grundämne eller en viss materialsammansättning (under vissa bestämda villkor).

— Eta-koefficienten kan då förstås sammanfatta primärinduktansen per meter rakledare elementärt för alla materialfall som ovan enligt

µ_c = (ηR_n)/c₀ ;

µ_c/c₀ = [√ [(di/dt)/η^–2neA](1M/S²)](VS/AM)S

= r^–1[√ [(di/dt)/η^–2πne](1M/S²)](VS/AM)S

ETA-värdet kan i princip ha vilka som helst magnituder mellan, men inte lika med, 0-∞.

Det praktiska ne-talets multiplicitet

— Genom att eta-faktorn är direkt associerad med rotfaktorn, och där bara kan ha en, och endast en, variabel med given strömderivata och ledardimension, nämligen elektronmobiliteten ne, kommer eta-faktorn i slutänden också att koppla just till det motsvarande praktiska ne-talets multiplicitet.

— Om vi ALLTID utgår ifrån att ne-talet ska avse EN elektron per atom i ett material, kommer eta-faktorn, och i den mån den kan bestämmas, automatsikt att uppvisa en korrektion för antalet (N) medelfria elektronbärare i materialet enligt

(N) = η^–2

N-värdet kan vara både större och mindre än 1.

Härledningen till Allmänna Materieinduktansen

BILDKÄLLA: Författarens arkiv · 2Okt2010Höstbild47Excur9 · NikonD90 · Detalj

Teorin — allmänna materieinduktansen

Teorin som krävs för att förklara de experimentellt observerade mätvärdena i Tabell 1

Vi härleder allmänna sambandet för rakledarens primärinduktans [L0] med stöd av experimentellt uppmätta mätvärden för analys, prövning och kontroll av resultatet till jämförelse med konventionella samband.

L₀ = s(ξ)(R + ηR_n)/c₀

= s(ξ)(R + η[√[(di/dt)/neA](1M/S²)](VS/AM)S)/c₀

Vi härleder allmänna sambandet för rakledarens primärinduktans [L0] med stöd av experimentellt uppmätta mätvärden för analys, prövning och kontroll av resultatet till jämförelse med konventionella samband.

Teorin är i grunden enkel.

— Teorin utgår ifrån, och sammanknyter, grundaspekterna med Potentialbarriären (elektrogravitationens grundbegrepp) som utgör fundamentet till Atomkärnans Härledning. Det är den relaterade fysikens allmänna kausalordning (Se även Kausalsambandet och Ändringslagarna) som spelar ut sin egen föreställning mot den etablerade moderna akademins föreställningssätt, som det tydligen får förstås.

Dessa detaljer har, trots väl relaterbar förankring i den praktiska vardagen, tydligen aldrig funnit någon intressesfär i den moderna akademins kvarter.

Från den materiefria rymdens elektriska konstant R₀c₀=1/4πε₀=(8,8543 t12)^–1 VM/C = VM/AS

faktorn 4π kommer från elektriska kraftlagen F = Rc[Q/d]² = RcQ²/A = [1/ε]Q²/A med sfärytan A=4πr² som ideala divergensen för elektriska laddningens rymdgeometri

med kapacitivitetstalet ε₀=8,98743 T9 C/VM, ofta förkortat 9 T9 C/VM, framträder den materiefria rymdresistansen R₀=1/4πε₀c₀=(8,8542 t12)^–1c₀^–1 V/A = 376,72555 Ω. Den motsvarande materiefria FyraPi-rymdresistansen blir R=1/ε₀c₀=29,978866 Ω. Den motsvarande materiefria elektriska rymdkompaktheten eller längdinduktansen (L/s=RT/s=R/v=µ) beror på den materiefria rymdens divergens (toppvärdet för ljushastigheten c₀=2,99792458 T8 M/S) och definieras (mikro-) µ₀=R₀/c₀=1/4πε₀c₀²=1,25662 t6 VS/AM med motsvarande fyra-piform

µ=R/c₀=9,99987 t8 VS/AM, ofta förkortad 1 t7 VS/AM, också ofta konventionellt benämnd magnetiska konstanten. Se även grundgenomgången i elektriska konstanten.

Den fria rymdens längdinduktans (L/s=RT/s=R/v=µ)

µ₀ = R₀/c₀

har I KAUSALLOGIKEN — relaterad fysik — sin materiella motsvarighet via Potentialbarriärens energizon (c_z=c₀/2; c_z är stället där laddningskroppens g-massa TAS tag i) enligt materierummets allmänna längdinduktans

µ_L = K(R/c_z)

µ_L kan förstås övergå i den fria rymdens µ₀ med den materiespecifika allmänna materialkoefficienten K=1 via c_z=c₀/2 enligt

(R/c_z) = 2[R]/c₀

= (R + R’)/c₀

Övergången med K=1 gäller då den induktansstyrda specifika materieresistansen R’ övergår i noll, analogt konstant idealt ändringsfri ström eller nollinduktans.

— R’ får då tydligen förstås betingad av en specifikt materiebaserad strömderivata (di/dt) så att man sammantaget får skriva den allmänna materieinduktansen på den generella formen

µ_L = K(R/c_z)

= K(R + R’)/c₀

= K(R + ηR_n)/c₀

Den specifikt materieberoende strömderivatan (di/dt) för R_n i R’=ηR_n kopplar till materialets specifika atomstruktur: mängden tillgängliga elektriska laddningar (antalet elektronladdningskvanta e=1,602 t19 C) för strömtransporten (n) per M³, ledarens (idealt cirkulära) tvärsnittsyta [strömtätheten] A=πr².

— Dessa parametrar innefattar materialets täthet (medelatomvikt), och egentligen också en temperaturkoefficient som vi här, emellertid och (tills vidare), helt ska bortse ifrån. Temperaturen i normal vardaglig elektrisk apparatur är i vilket fall en parameter vi alltid försöker hålla så litet avvikande som möjligt från normal rumstemperatur — de aktuella experimentkopplingarna till att börja med.

Accelerationen av laddningarna i materialet

Vi förutsätter här förtrogenhet med grundbegreppen från induktionens härledningar:

induktionen som fenomenform svarar direkt proportionellt mot hur en elektrisk laddning accelereras. Se utförligt från Induktionen om ej redan bekant.

— Eftersom vi måste utgå ifrån att nollinduktion (û=0) sammanhänger med nollacceleration av materialets strömbärande elektriska laddningsmassor (a=0=dv/dt), samt faktum att materialets laddningsmassor ALDRIG RIKTIGT befinner sig i vila (v är aldrig noll) måste vi söka en grundform som bevarar en (primär) form för laddningarnas hastighet större än v och samtidigt med nollacceleration via nollinduktans.

— Vi finner en sådan via GEOMETRISKA MEDELVÄRDET

a = √ a₁a₂

= √ (dv/dt)₁(dv/dt)₂

= (dv/dt)

Den enda kända normaliserande grundform vi kan utgå ifrån för typ den andra rotfaktorns (dv/dt) är tydligen

(dv/dt)₂ = 1M/S² ;

(dv/dt) = √ (dv/dt)₁(1M/S²) ;

— Därmed kommer materialets induktiva beteende att styras av hur laddningarna accelereras via rothastighetsderivatan (dv/dt): från noll och uppåt, alltid med en konstant aktiv (primär) grundform på (1M/S²) och som därmed lägger hela dynamiken på just rotderivatan enbart.

Från Drifthastigheten v=I/neA för ledarens elektriska laddningar insätter vi nu I:=i med

(dv/dt)₁ = (di/dt)/neA

och därmed

a = √ (dv/dt)₁(1M/S²)

= √ [(di/dt)/neA](1M/S²)

Med direkt proportionalitet mellan den materierelaterade induktansresistansen R_n och laddningsaccelerationen a ges då

R_n = a · (VS/AM)S

= [√ [(di/dt)/neA](1M/S²)](VS/AM)S

= r^–1[√[(di/dt)/πne](1M/S²)] ; r anger ledartrådens cirkulära radie

y = [1000/0.25](x[10000]/[þ1.35603·10'10])'0.5: kopparledare, þ för pi

Graf = [1/0.25](x/[4.26])'0.5: r i mM, x i T4 A/S

Allmänna materieinduktansen

Därmed slutformen för allmänna materieinduktansen enligt den relaterade fysikens kausallogik som ovan med R(n)=R’

µ_L = K(R + ηR_n)/c₀

= K(R + η[√ [(di/dt)/neA](1M/S²)](VS/AM)S)/c₀

= L₀/s

Med den raka primärledarens avmätta induktionslängd (s) given har vi alltså rakledarens allmänna primärinduktans enligt

L₀ = sK(R + η[√ [(di/dt)/neA](1M/S²)](VS/AM)S)/c₀

= sξ(R + η[√ [(di/dt)/neA](1M/S²)](VS/AM)S)/c₀

Graf = (10'8)0.261[30+0.75[1/0.25](x/[4.26])'0.5]/(3·10'8): L0 i t8 H, se ovan från Rn

Graf = 0.261[30+0.75[1/0.25](x/[4.26])'0.5]/3: L0 i t8 H

Grafsambanden ovan samma som i Jämförande induktanser.

Via universella induktionslagen

û = L₀(di/dt)κ = Λκ

— kappa-faktorn (κ) beskriver den sekundärt inducerade spänningslinjens matematik

här speciellt omsatt på den primära rakledaren med L(0)=sξRc₀ —

= sξRc₀(di/dt)

blir den inducerade spänningen (û) i en sekundär rakledare parallell med den primära rakledaren lika med

û = sξRc₀(di/dt)κ

κ-faktorn (grek. kappa), generellt κ = K/2π, sammanhänger med sekundärledarens geometri, se särskilt via kausallogiken i rakledarens induktion.

Se Tabell 1 för jämförande resulatredovisning mot experimentellt uppmätta värden.

För koefficienternas Kη-värden för Koppar, se Xsi och Eta.

Kalkylkortet Tabell1 redovisar sambanden sammanställda med resultatvärden.

Här avslutas härledningsblocket till induktionsdelen.

Se även hur induktionsspänningen beräknas i de olika fallen för rakledare i Induktionsspänningen i raka sekundärledare.

Laddningsmobilitet, elektronmobilitet

BILDKÄLLA: Författarens arkiv · 21Jul2010VattensköljetBild23Excur6 · NikonD90 · Detalj

Elektronmobilitet, laddningsmobilitet

Enkel grundteori

På samma sätt som en vattenledning strömmar ut i eller genom ytan via en vattenfylld behållare, bör också ett materials atomers elektronmassor uppföra sig med avseende på kraftkopplingsdjupet från atomens yta till dess inre kärna: Strömflödet längst ut, längst upp, är relativt stort medan det längre in, längre ner, åtminstone i princip bör vara knappt märkbart.

— Jonisationsfenomen förekommer inte inom (normal) elektrisk strömledning.

— Det är klart därför att atomerna aldrig förlorar elektroner i ett kontinuerlig strömflöde. Elektronmassor som lämnar något område inom materialets lokaler fylls hela tiden på utan att någon elektron lämnar materialets övergripande rum.

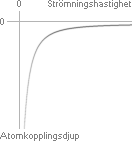
— Strömningshastighet och atomkopplingsdjup varierar beroende på hur materialet belastas. Variationsformen ovan enligt y=—1/x².

I varje fall i den följande beskrivningen kommer vissa samband att framgå.

KONVENTIONELLT används numera den allmänna termen elektrisk mobilitet [eng. Electrical mobility] till skillnad från elektronmobilitet som då konventionellt [Wikipedia] explicit avser elektron-hål-bildning i halvledare, se Wikipedia Electron mobility [2011-08-25]. I denna framställning används begreppet elektron- konsekvent för elektronsammanhang. I andra fall anges motsvarande termbegrepp förtydligat typ elektron-hål-mobilitet, för att särskilja beskrivningssätten direkt från den beskrivande lokalen.

ELEKTRONMOBILITETEN [enligt Wikipedia som ovan, Electrical mobility] definieras som drifthastigheten över elektriska fältstyrkan [µ=v/Ξ].

— Men drifthastigheten [här v=I/neA] beror just av elektronmobiliteten [här ne].

— Därmed förloras begreppets begripliga innebörd.

— Wikipediaartikeln ger heller ingen [Aug2011] vidare upplysning om vilka ev. typvärden som gäller för olika ämnen.

— Däremot ger Wikipediaartikeln på Electron mobility [25Aug2011] en viss vidare beskrivning

”Mobility is usually a strong function of material impurities and temperature, and is determined empirically, mobility values are typically presented in table or chart form. Mobility is also different for electrons and holes in a given semiconductor.”

— men fortfarande utan någon bestämd eller begriplig kvantitativ koppling till, till exempel, kopparledare [i normala tillämpningar].

— HYPERPHYSICS däremot ger en bättre orientering [som också ansluter till presentationen i det här htm-dokumentet], se Microscopic View of Ohm's Law, Microscopic View of Copper Wire.

Normal elektrisk ledning, relaterad fysik:

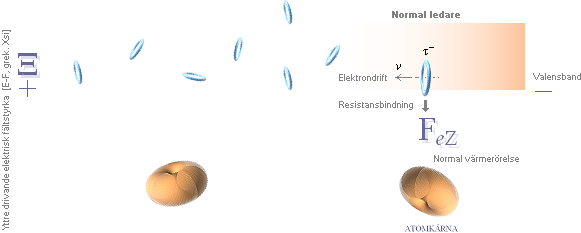
I en normal elektrisk ledning ligger elektronmassans komponenter maximalt glest utspridda enligt RESONANSVILLKOREN som grundlägger GRUNDÄMNENAS PERIODISKA SYSTEM. Varje elektronkomponent [tau-ringen, τ] har en bestämd kraftkoppling F[eZ] till sin moderkärna och som garanterar en aktiv resistans i makroströmvägen genom materialet.

Normal ledning

— I en sluten strömkrets förloras ingen elektronmassa. Begreppet jonisation och jonisationsenergi (atomens energiutbyte utåt sett för att släppa ifrån sig en eller flera elektronmassor) har följaktligen ingen direkt primär praktisk, relaterbar koppling till en normal strömgång i en elektrisk ledare.

— Elektronernas komponenter, τ-ringarna, kan ses som ett slags kraftdjupkopplat vatten till materialets atomkärnor: Strömningen är (naturligt) störst längst uppe vid ytan, analogt i det centrala strömloppet, och avtar sedan (exponentiellt) med kraftdjupet in till atomkärnan där τ-ringarna är som starkast bundna, och därmed minst strömkopplad rörelse.

— Vi behöver alltså aldrig bekymra oss om någon specifik »ledningsbandsmatematik» för att få reda på den rent kvantitativa laddningstransport som ett visst material uppvisar.

— Vi kan utan vidare utgå ifrån att varje atom i ledningsmaterialet ställer en (1) ledningselektron till makroströmmens förfogande. Den utgångspunkten kan sedan justeras genom att mäta eller beräkna motsvarande ledningsdkoefficient.

— Resultatet av den beräkningen eller mätningen kommer då att anvisa materialets praktiska strömdrag i antalet laddningsbärare.

— Utgångspunkten HÄR är nämligen den att laddningsmobiliteten vid VARIERANDE strömdrag BÖR variera på samma sätt som olika mängd djupvatten deltar i ytströmningsflödet beroende på strömningens storlek (och typ). Dvs., antalet laddningsbärare som deltar i strömmen — och därmed ledarens primära induktans, motstånd mot strömändring — bör variera, varför det blir meningslöst att försöka beräkna någon slags medelmässig »elektronmobilitet från start»; Varje material anpassar sig — i vilket fall — allt eftersom.

N, antalet deltagande elektroner i ledningsbandet — finns inga direkt säkra (allmänt tillgängliga) källor utom ämnets elektronkonfiguration

elektronmobilitet, laddningsmobilitet, ne

Vi använder HÄR generellt för varje ämne och varje material en grundform med ENDAST N=1 — en — LEDNINGSELEKTRON PER ATOM

ne = N(m/Uu=ρ[V=1M³]/Uu)(e=1,602 t19 C), C/M³

= N(ρ/Uu)e

En ledningselektron per Kopparatom är (också) den uppgift som (ofta) anges i konventionella fackreferenser, se t.ex. @INTERNET HyperPhysicsKällan.

Det finns heller inga »generella uppgifter» om elektronmobilitet i konventionella fackverk; Man använder också där olika mättekniker för att få fram ett aktuellt medelvärde i någon aktuell tillämpning.

;

U(Cu)=63,54(u=1,66033 t27 KG), ρ(Cu)=8930KG/M³ ger n=8,46466 T28,

ne(Cu)= 1,35603 T10 C/M³, elektrolytkoppar

Vissa prövningsräkningar har här gjorts för MÄSSING i Kalkylkortet Tabell1 — [en mera avancerad anordning måste utformas för mera omfattande mätningar], nedanstående N-form är i ovanstående presentations ljus OEGENTLIG då den baseras på den fasta, fixa yttersta valenselektronbilden från grundämnenas periodiska system. Beräkningarna kan dock tjäna till viss jämförelse — för vidare.

ne(mässing·SIS5165)= ne(Cu)×1,33

handelsmässing, typ rör:

MÄSSING SIS 51 65 :

Sammansättning : 61%Cu 1%Pb 38%Zn. Specifik vikt 8400 KG/M³.

Valensstruktur : (1e)×61%Cu + (4e)×1%Pb + (2e)×38%Zn; summa N=1,41(e)

(mera komplicerad sammanräkning):

61%63,54u + 1%204,19u + 38%65,37u = 65,642u ger n=7,70731 T28,

ne(MÄSSING SIS 51 65)N= 1,74094 T10 C/M³ = 1,2838532(Cu) [föreg. 1,33(Cu)]

Drifthastigheten

Begreppet Drifthastighet

Drifthastigheten

Laddningarnas strömhastighet genom den elektriska ledaren

STRÖMSTYRKAN .............. I = nevA

DRIFTHASTIGHETEN ....... v = I/neA

Se även ref. GYMNASIETS FYSIK åk2 Liber 1978/80 s50, samma samband används tillsammans med räkneexempel.

Sambandet för v i en elektrisk ledare härleds på följande sätt.

Med hastigheten v tillryggalägger elektronen (e) på tiden t en del s av ledaren enligt

v=s/t, s=vt

Om A är ledarens tvärsnittsyta (A=πr²) ges delvolymen via s enligt

sA=V_e=Avt

Med n elektroner per kubikmeter (Se även Laddningsmobiliteten) blir totala volymen

V=nV_e=nAvt

Enheten blir här dimensionslös, n = (n/M³)M³. Inför vi laddningen e för elektronen blir totala laddningen

Q = ne = neAvt = I/t

Och vi har således genom de två sista leden

I = vneA

I är strömstyrkan i Ampere; v drifthastigheten i M/S; n antalet elektroner per kubikmeter; e, elektronladdningen 1,602 t19 Coulomb; A, ledarens tvärsnittsyta, lika med pr² för cirkulära ledare.

EXEMPEL — strömhastigheten är bara bråkdelar av millimeter per sekund i vanliga kopparledare:

För en ström på 1 Ampere i en kopparledare med radien 0,56 mM (1 mM²) blir drifthastigheten 0,074 millimeter per sekund — OM N=1 ledningselektron per Kopparatom;

v = I(neA)^–1 = (1 A)(1,35603 T10 C/M³elektrolytkoppar·[0,001 M]²)^–1

= 7,37446 t5 M/S

~ 0,074 mM/S

Maxwells ekvationer — allmän översiktlig KVALITATIV orientering i relaterad fysik

Maxwells ekvationer — se även @INTERNET Wikipedia Maxwell’s equations http://en.wikipedia.org/wiki/Maxwell's_equations

En TOLK som visar Maxwells ursprungliga ekvationer från 1865 och hur dessa skrivs i nutida modern notation finns i PDF-dokumentet

On the Notation of MAXWELL’s Field Equations, André Waser (2000)

http://www.zpenergy.com/downloads/Orig_maxwell_equations.pdf

Vilken är skillnaden mellan konventionella och relaterade?

Maxwells ekvationer: Den moderna akademins vektorkalkyl som antogs (urspr. från kvaternionteorin) under 1800-talet, och som utesluter magnetiska expansionsintegralen — och som i termer av relaterad fysik innebär att magnetismen blir ett stympat induktionsfenomen och induktionen blir en stympad magnetism; I allt en förenklad (»dockiserad») fysikbild utan naturfysikaliskt DJUP; förenklingen fungerar generellt eftersom magnetismen i vilket fall ALLTID sammanhänger med STRÖM. Se särskilt illustrerad djupbeskrivning i Vektorkalkylens sammanbrott inom magnetismen i modern akademi.

— Betyder det att hela komplexet med Maxwells ekvationer är FEL?

— Studera DE TRE JÄMFÖRANDE EXEMPLEN, kvantitativa exempel med sambandsformer i direkt jämförande korsreferens konventionella/relaterade. Exemplen är framställda just i syftet att belysa, exakt, vari skillnaderna består;

— Konventionella sambandsformerna duger JÄTTEBRA för industriella precisionsbaserade tillämpningar inom elektrofysiken (Maxwells ekvationer), just på grund av att avvikelserna i normala Jordiska tillämpningar är obetydliga — se särskilt magnetiska konstanten µ0. Allvarliga, djupgående, oklarheter uppkommer emellertid när de fysikaliska fenomenformerna kommer på tal.

Vissa ifrågasättanden även från etablerat håll

— Ett visst ifrågasättande av Maxwells ekvationer synes ha framträtt även från etablerat modernt vetenskpligt håll omkring sekelskiftet 1900. Ewald Rasch (ELECTRIC ARC PHENOMENA 1913, Boken finns gratis i PDF-format på Internet Archive) beskriver saken på introduktionssidan (ix)n,

”Maxwell's curl equations may be true, indeed, in regard to the phenomena of propagation of electromagnetic waves of great length; but they are inapplicable and apparently fundamentally so in case of shorter wave lengths and higher frequencies, i.e., in case of phenomena pertaining to light proper. They give not the least hint as to the ultimate physical cause of light, which is of such importance for the technical problems of light production.”,

Ewald Rasch 1913, ELECTRIC ARC PHENOMENA s(ix)n, se även citatblocket Maxwells teori föråldrad i citatsamlingen till ELECTRIC ARC PHENOMENA i Blixturladdningens Fysiik 2011.

— Både ja och nej.

Se utläggningen närmast ovan.

— JA — definitivt, om det gäller beskrivningen av de fysikaliska fenomenformerna och möjligheten att göra dessa begripliga. De flesta människor har nog redan förstått det med exempel från modern akademi.

— NEJ — också definitivt, om det gäller att hitta rent tekniska brister i den industriella produktionen av precisionsbaserad elektroteknisk instrumentutrustning som baseras just på Maxwells ekvationer.

Se till exakt jämförelse De Tre Jämförande Exemplen. De visar och exemplifierar hur, och varför, det fungerar i praktiken (Se mera utförligt och kortfattat direkt i magnetiska konstanten µ0). Se även från Kausalsambandet som beskriver den relaterade fysikens magnetism och induktion från grunden.

— Ett annat sätt att säga hela saken på, mycket enklare (och som många s.k. vanliga människor redan har förstått med Exempel från Praktiken): Den moderna akademin representerar en primitiv intelligens under stjärnorna, samt anser denna vara överordnad. (Man möter, ofta, en extrem kaxighet, inte sällan över gränsen till ren elakhet, med auktoritär förkärlek, i framtoningen av just den primitiva sidan. Många av oss känner redan den attityden, väl. Utrymme för dialog, kommunikation, ges exakt lika med noll. Ingen kritik tillåts).

Induktans och induktion — kompletterande beskrivning till originalförfattningarna med Induktionsdipolens Uppkomst

Med Inledning till INDUKTIONSDIPOLENS UPPKOMST

Vad är induktans och induktion?

— I RELATERAD FYSIK:

— Induktans är elektrofysikens motsvarighet till massans motstånd mot rörelseändring i mekaniken;

— Induktion är den motsvarande inducerade elektriska spänning [och process] som utbildas då man försöker ändra en given fast strömstyrka. Se även direkt jämförande matematik i Integrala Analogierna.

— För begreppen i modern akademi, se från Kausallogikens samband nedan.

En elektrisk laddning (Q) som ÄNDRAR — accelererar (ökar) eller retarderar (minskar) — sin hastighet relativt referenspunkterna [R(eg)] i den omgivande rymdens lokalt gravitella dominans — Jordytan och dess fasta föremål för vår del — framtvingar en motsvarande LADDNINGSFÄLTSÄNDRINGSprojektion på alla R(eg) i ändringens riktning. Se även mera utförligt från Induktionen. VERKAN av denna projektion, i minskade eller ökande, bildar en motsvarande fältändringen MOTRIKTAD ELEKTRISK SPÄNNING, det vi (i relaterad fysik) kallar för en induktionsspänning (û). Induktionsspänningen är ALLTID proportionell mot Q-accelerationen (dv/dt). En elektrisk ledares karaktäristiska SÄTT att motsätta sig interna ändringar i laddningarnas strömflöde (olika material har olika sätt och under olika betingelser, vidare nedan) kallas induktans. Induktansens påverkan på allt elektriskt omgivande kallas induktion (i en del äldre litteratur även självinduktion).

— I relaterad fysik är magnetismen som sådan fullständigt oförmögen att åstadkomma lägesändringar hos elektriska laddningar om de inte redan befinner sig i rörelse relativt ett omgivande dominant g-fält.

— Ovanstående förklaringsbild ingår inte i modern akademi.

— I modern akademi används istället en (tydligen exceptionellt) obskyr uppfattning som utsäger att »induktion bildas av magnetism», se mera utförligt nedan från Kausallogikens samband. Anledningen är grundformen med elektromekanisk induktion: en vibrerande sträng i ett fast magnetfält uppvisar en inducerad spänning. I modern akademi har man antagit — uppfunnit — att också omvändningen gäller: hålls samma sträng fix och magnetfältet ändras, induceras återigen en ström i strängen i försorg av det varierande magnetfältet. Därav benämningen »elektromagnetisk induktion». Se även i Förtydligandet till Faradys EMI.

— I det sistnämnda fallet — vilande sträng i variabelt magnetfält — är det ENLIGT RELATERAD FYSIK inte magnetismen som förorsakar induktionen i den vilande strängen, utan de elektriska laddningarnas acceleration eller retardation i den materialkropp som magnetfältet utgår ifrån.

— För att visa att så är fallet, entydigt och utan möjlighet till misstag eller missförstånd, anställdes PARALLELLEXPERIMENTEN (1994).

En senare mera utvidgad beskrivning finns i PEX2024Intro ¦ PEX1994OriginalDetails — induktionen och magnetismen mera i detalj

Se särskilt det mera utförliga avsnittet i DIPOLBEGREPPET med TheQmove.

Vi ska i det följande återknyta till dessa (se nedan från Kausallogikens samband och den praktiska Elektrofysikens inledande grunder) och beskriva hur, på vilket sätt och varför magnetism och induktion uppträder helt fristående från varandra i fysiken, samt hur och på vilket sätt den moderna akademins utläggningar fungerar (och inte fungerar) i ämnet — samt även, och möjligen, hur denna vetenskap kopplar till supraledning (en delvis ännu 2011 erkänt gåtfull fenomenfysik).

Induktionen mellan parallella motströmmande rakledare är noll

Parallella ledare som för motriktade lika stora strömmar (figuren ovan) uppvisar i mittlinjen (C) en optimal magnetisk fältstyrka (B). B kan bestämmas från Magnetiska expansionsintegralen (konv. Biot-Savarts lag). Kalkylkortet Tabell2 Planalternativet innehåller cellblock där B-styrkan så kan beräknas (reglera –d i utrymmet mellan ledarna, x = deras centrumavstånd). Se även räkneexempel i MAGNETISMENS SPECIFIKA EKVATIONER.

— Är strömmarna växande/avtagande (di/dt) induceras emellertid i mittlinjen, trots full magnetisk närvaro, ingenting.

— Anledningen är med kausallogikens enkla begrepp, som vi ser, att de bägge lika men motriktade induktionsdipolerna tar ut varandra. Nettoresultatet blir noll, och ingenting induceras.

— Den närvarande magnetiska fältstyrkans motsvarande (di/dt)-ändring har ingen som helst betydelse för resultatet: ingenting induceras på mittlinjen.

— Induktionsdipolernas bildning i det avgörande omgivande dominanta gravitationsfältets rymdreferenspunkter [R(eg)], hur de uppkommer, hur de adderas och växelverkar, beskrivs INLEDNINGSVIS i försorg av ÄNDRINGSLAGARNA (urspr. Newtons tredje lag).

Induktionsdipolens uppkomst

— En mera ILLUSTRERAD motsvarande BILD som ansluter till den helt utförliga kausallogikens beskrivningsgrund är den nedanstående.

— Illustrationen och beskrivningen nedan användes ursprungligen i originalmanuskriptet [KRAFTLAGEN 1999XII], men togs explicit inte med i [de inledande] htm-versionerna:

Induktionsdipolens uppkomst

— En motsvarande kvalitativ beskrivningsform i den konventionella litteraturen har eftersökts men inte påträffats.

— Nedanstående förutsätter idealt sfäriska divergensbegrepp med grund från ELEKTRISKA LADDNINGEN och ELEKTRISKA FÄLTET.

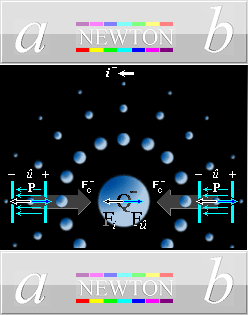
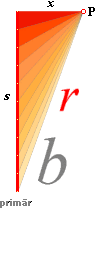
— Figurformen med den centrala idealt sfäriska laddningen [här –Q] illustrerar [via de omgivande mindre sfärerna] den fasta fältgeometrin för laddningens avtagande fältpotentialer med växande avstånd från centralkroppen. Elektriska laddningens [sfäriska] fältgeometri som sådan framgår direkt ur DEEP från GRIP [Fysikens 7 Principer — dessa finns inte kända som sådana i modern akademi, ehuru sanningsbegreppet inte gör det: allt utgår därifrån] via divergensens [ljusets] gravitella beroende [se DGD]. Se även Superpositionsprincipen [elektrostatiska-gravitella fältets bevarande oberoende av interferenser].

— Fi-delen är den strömdrivande kraften som sammanhänger med rörelseformens acceleration.

— Fû-delen bildar den motsvarande Fi-motverkan enligt NewtonIII.

— Fc-delen motsvarar den inneboende divergenskraftens polaritet [flödesriktningen för den fältåterkopplande divergensen eller ljushastigheten i elektriska Q-fältet] för negativ laddning [den relateras omvänd för positiv laddning].

— P betecknar de fasta referenspunkterna i det omgivande lokalt dominanta g-fältet [Jordytan och dess föremål för vår del].

— Originaltexten nedan från originalmanus 1999XII i FysINT.wps Fig:4 [s18] — Uppkomsten av den induktiva fältdipolen.

Figurbeskrivning

Newtons tredje lag

Motverkan till den lägesändrande kraften alstrar ett lika stort men omvänt fält relativt det som ändringen eftersträvar

a : F_i eftersträvar ett extrafält i F_c^–- fältets riktning, motkraften ger fältdipolen i P som en omvänd fältriktning.

b : F_i eftersträvar ett reducerat F_c^–-fält, dvs ett fält i riktningen (+) → (–) analogt med F_c^–-reduktionen, motfältet således (–) ← (+), och alltsåsamma fältdipol som för verkan på motsatta Q^–-sidan.

Från tyngdpunkten på Q^– anbringas den lägesändrande kraften ^→F_i. Ansatsen att ändra läget för Q innebär detsamma som en ansats att ändra den i P och från Q-systemet individuellt avbildade divergensen c analogt fältkraften F_c^–=k(dQ/dr)², vilket inte går. Följande inträffar på ömse sidor om laddningen.

a: Lägesändringen genom Kraften ^→F_i motverkar genom fältåterkoppling fältkraften ^←F_c^– som finns avbildad i rymdpunkten P. NewtonIII medför att motverkandet motverkas med en ^→F_i motriktad kraft. Lägesändringen innebär att Q-systemet projiceras resistivt på P med början från laddningens yta och sedan vidare utåt via fältåterkopplingen. I P genereras därmed ett mot lägesändringen och fältkraftens motverkan proportionellt växande motstånd analogt ett dipolfält û (u-flex) [– ← +]*** med en tillhörande ^→F_i motriktad kraft ^←F_û som genom fältåterkopplingen motverkar ^→F_i. Inverkan av ^←F_û på Q-kroppen sker alltså direkt med början från Q-ytan analogt med ansatsen för ^→F_i (primära induktionen). Innebörden av û har sedan ingen betydelse för Q utan bildar i stället grunden för en påverkan på omgivande Q-system (sekundära induktionen).

b: Lägesändringen genom Kraften ^→F_i gynnar genom fältåterkoppling fältkraften ^→F_c^–. NewtonIII medför att gynnandet motverkas med en ^→F_i motriktad kraft. Lägesändringen ger vidare alltså samma faser och förlopp som i a (forts. frn. ”Lägesändringen innebär …”).

F_i lägesändrande kraften, verkar på Q-origo

F_c^– fältåterkopplande kraften i Q.systemet

F_û induktionskraften, motverkar F_i

û motinducerade spänningen

*** under förutsättning att lägesändringen är accelererad (se komprimerat från Induktionen); Detta dipolfält (analogt F_û) ges i annat fall endast differentiellt. Att F_û är differentiell vid konstant hastighet framgår av att det inte finns någon acceleration för Q om lägesändringen sker likformigt, dvs. med konstant hastighet: Föreligger ingen acceleration, föreligger heller ingen kraft (F=ma, NewtonII), och alltså heller ingen motkraft.

Med kraftkomponenterna i endast lägesändringens riktning som de aktiva vektorerna, dvs. med giltighet för fältbilden i alla möjliga rymdpunkter P, ges verkan på samma sätt som i de bägge ovan beskrivna diametrala fallen a och b med enda skillnaden att vektorerna får trigonometrisk form (Gränsytan mellan halvsfärerna i a och b lämnar inga bidrag eftersom komponenterna i denna gränsyta mot riktningen i är noll).

INDUKTIONEN i elektrofysiken generellt har samma betydelse som MASSTRÖGHETEN i mekaniken: Varje försök att genomdriva någon ändring möter alltid ett proportionellt lika stort motstånd: Motståndet strävar alltid att bevara tillståndet. Se utförligt i Ändringslagarna. I elektrofysiken betyder motståndet mot strömändringen i en elektrisk ledare att en elektrisk motspänning bildas (samma som en motriktning till laddningens eget statiska flödesfält), en induktionsspänning, som försöker motverka ändringens orsak. Motståndet kallas induktans och motspänningen kallas induktion, inducerad spänning eller [äldre] även självinduktion.

Beskrivning,

induktionen

— En primärt strömförande [elektrisk] ledare [A]

vars strömflöde — de elektriska laddningarnas elektriska fältändringar — ÄNDRAS något, påverkar förutom sina egna inre PRIMÄRA strömleder också sekundärt varje ändringens parallellt liggande rymdlinje [C] UTANFÖR primärledaren med en motsvarande SEKUNDÄRT MOTINDUCERAD SPÄNNING [û]. Se även grundformerna separat i induktionen, om ej redan bekant. Referenspunkterna utgörs av referenspunkterna i det lokala dominanta gravitationsfältet [Jordytans fasta material]. Se även mera utförligt från Induktionen och Magnetismen.

— Har primärledaren [A] en stor mängd laddningsbärare [fria ledningselektroner] kan den primära strömändringen — ACCELERATIONEN eller RETARDATIONEN — fördelas så att varje laddning får bära en liten acceleration. Motståndet — induktansen — INTERNT i primärledaren mot dess egen strömändring blir då också motsvarande litet.

— I den yttre rymdlinjen [C] induceras då en motsvarande LITEN spänning [û]. Är istället den primära laddningsmassan [A] liten, måste varje laddning uppbära en större del av accelerationen. Primärledarens induktans [L] blir då i motsvarande grad större med en motsvarande högre induktionsspänning û i C.

— Den inducerade rymdspänningen û i C beror endast av den fria rymdens egenskaper, medan primärkällan [A] till û i C, frånsett den primära strömändringen [di/dt] som sådan, beror av primärledarens beskaffenhet: material [laddningsmobilitet], dimension [strömtäthet], längd.

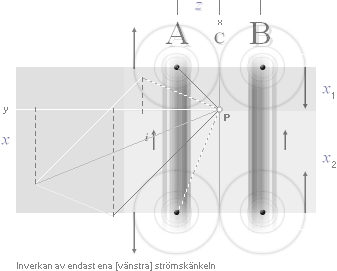
— Det rödmarkerade fältet i figuren ovan indikerar hur man på olika sätt kan bestämma den inducerade spänningens omfattning genom att ta hänsyn till olika induktionsvinklar och dito längder. I det elementära fallet räknar vi enbart på RAKA och PARALLELLA ledare av primär och sekundär typ.

— Kalkylkortet Tabellerna 1 och 2 innehåller sammanställda cellblock för grundberäkningar.

Kausallogikens samband

— Notera i modern akademi att induktionsspänningen anses härröra från magnetismen.

”If the current is increasing then a voltage opposing that change is created by the magnetic field of the coil”.

Inductors — HYPERPHYSICS [2011-08-28]

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/induct.html

;

”Electromagnetic induction is the production of voltage across a conductor moving through a magnetic field.”.

”This applies whether the field itself changes in strength or the conductor is moved through it.”,

@INTERNET Wikipedia Electromagnetic induction [2011-09-02]

http://en.wikipedia.org/wiki/Electromagnetic_induction

I kausallogiken [se Kausalsambandet] har magnetismen ingen koppling till induktionen: magnetism och induktion existerar helt skilda från varandra.

Se vidare utförligt jämförande referenser i µ0 samt Magnetiska Fältintegralen. Kausallogiken är orepresenterad i modern akademi. Se även i Tre Jämförande Precisa Exempel.

— Från kausallogikens härledning till RAKLEDARENS INDUKTION gäller

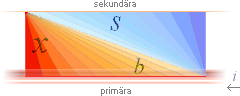
û = Λ [ln tan(b/2) + 1/tanb]/2π ............................. V

= Λκ = Λ[K]/2π) = L_c(di/dt)κ

tanb = x/s, s = x·cotb, û = u-flex

Λ = L_c(di/dt)

— L[c] är primärledarens egen inre interna primärinduktans, [di/dt] är strömderivatan eller strömändringen [här konstant].

— Genom att mäta û i en yttre parallellt med primärledaren belägen sekundärlinje [C] kan primärledarens primärinduktans [L] bestämmas enligt

L_c = û/[di/dt]κ

Se även universella induktionslagen.

Primärinduktansen [L(c), även L(0) i denna framställning] är en veritabel utmaning — den kräver först och främst speciella anordningar (höga strömstyrkor = speciellt avancerad elektronik) för att kunna mätas framgångsrikt. Vi ska försöka närma oss den detaljen i denna presentation.

MAC-sambandet

— Som redan noterats i Jämförande moderna resultat får man med en förenkling av ovanstående K-form (Kausallogikens samband) för rakledaren en motsvarande form för en s.k. självinduktion på primärrakledarens yta enligt

U = (Λ/2π)[ln(4s/d) – 2s/d] .................. V

Med Λ=L[di/dt] och induktansen L(c) = µ(L)s =U/[di/dt] ges motsvarande

U/[di/dt] = (µ_L/2π)s[ln(4s/d) – 2s/d]

och vilken motsvarande form vi återfinner i en del konventionell modern akademisk facklitteratur enligt

L = (µ₀/2π)s[ln(4s/d) – 3/4]

som den motsvarande s.k. självinduktionsformen generellt för raka ledare, s längden och d diametern:

;

Fackreferenser till Lk

Källan Elektronikens Grunder Del 1, John Schröder 1971, s124 specificerar (här t för 10–)

L= 2t7·l[ln(4l/d) – 3/4]

där 2t7 @ µ₀/2π = (1,25662 t6 VS/AM)/2π = 1,99997 t7 VS/AM.

Samma specifikation finns i Electronics Equations Handbook, Stephen J. Erst 1989 s7.

ELFA-katalogen (1998-99 [och senare], s624) specificerar

L= 0,002·l[ln(4l/d) – x]

med x som frekvensberoende [x=3/4 för låg frekvens] och L i µH med l och d i cM.

Frånsett x, således samma som föregående ovan.

Notera att den konventionella facklitteraturen varken specificerar ämnesform (ledarens material) eller strömändringens storlek (di/dt):

— Det underförstås att sambandet gäller oberoende av material och laddningsacceleration (vilket också är det praktiska fallet för små ändringar).

— Frånsett övriga aspekter:

— DEN NÄRA (principiellt exakta) ÖVERENSSTÄMMELSEN MELLAN SAMBANDEN ÄR ANMÄRKNINGSVÄRD

— eftersom induktionen och magnetismen är strängt åtskilda enligt relaterad fysik men intimt förenade enligt modern akademi.

NOT.: µ₀/2π=(R₀/c₀)/2π=1,99997 t7 VS/AM ~ 2t7

Med vidare fortsättning från

Induktionsbegreppet i relaterad fysik.

Citablock elektromagnetisk induktion

Citatblock EMI

”Sambandet mellan elektriska och magnetiska företeelser kan formuleras:

A. Elektricitet i rörelse (= elektrisk ström) ger ett magnetiskt fält.

B. Ett varierande magnetiskt fält ger i ledare, som befinner sig i fältet, en inducerad spänning.”.

TEKNISK ELEKTRICITETSLÄRA · E. Danielsson 1965 · s85

”Det är inte nödvändigt att ledaren förflyttas så att den skär över magnetiska fältlinjer. Det väsentliga är att en ändring av det magnetiska flödet inträffar. Det intima sambandet mellan elektriska och magnetiska yttringar innebär att varje ändring av ett magnetiskt fält ger upphov till ett elektriskt fält och vice versa.”.

FOCUS MATERIEN · 1975 · s226sp2mn

”Elektroner i rörelse alstrar alltid ett magnetiskt kraftfält, vilket utbreder sig vinkelrätt mot strömriktningen. Omvänt ger ett magnetiskt fält i rörelse kring en ledare alltid upphov till en elektrisk ström. I båda fallen talar man om elektromagnetisk induktion.”.

FOCUS TEKNIKEN · 1975 · s132n

”Om en elektrisk ledare i form av en sluten strömkrets befinner sig i ett magnetiskt fält och antalet magnetiska kraftlinjer som skär den av ledaren omslutna ytan förändras, uppstår (induceras) i strömkretsen en elektrisk spänning proportionell mot förändringen per sekund av antalet omslutna kraftlinjer.”.

BONNIERS KONVERSATIONSLEXIKON V · 1924 · sp1352

”induktion; företeelsen att ett varierande magnetiskt fält framkallar (inducerar) en elektrisk spänning i en ledande kropp som befinner sig i fältet.”.

BONNIERS LILLA UPPSLAGSBOK · 1973/1995

”The Faraday law in (1.81) [motsvarande induktionslagen U = –BA/T] applies whether the changing flux is the result of motion of the circuit in a field or whether the circuit is fixed in position and the magnetic field is changing.”.

HANDBOOK OF PHYSICS · McGraw-Hill 1964 · 4-15

Induktionsspänningen i raka sekundärledare

Induktionsspänningen i raka sekundärledare

Induktionsspänningen i raka sekundärledare

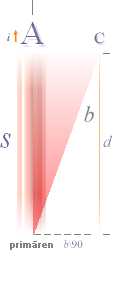
INTEGRATIONEN UTMED d

s=d: PUNKTINTEGRALEN till s tas över hela b-längden d=s, lika med över hela b-vinkeln:

från bTILL90° b\90 för alla bidrag från ideala sfäriska elektriska laddningsfältets övre del, och

från 90°TILLb 90\b för alla bidrag från ideala sfäriska elektriska laddningsfältets nedre del

a	b	c	d	e	f

Punktintegralen (figur a) i PREFIXxSIN

Ð_P = (L/4px)(1–cosb) ............................. V/M

är dipolfältstyrkan (Ð) i rymdpunkten (P) från hela den raka primärlängden (s);

— För att få den inducerade spänningen (û) i en sekundärlinje (C, figur b) parallell med och lika lång (d) som s, räknas alla fältbidrag i elektriska laddningens ideala sfäriska statiska fält (figur e) dels på ovansidan — integrationen på vinkeln bTILL90° b\90 — och dels på nedansidan — integrationen på vinkeln 90°TILLb 90\b, figurerna cdef. Detta »integrationssvep» täcker alla bidrag.

— Den inducerade spänningen i d-linjen, lika lång som och parallell med primärströmlinjen s, blir (se utförligt från Punktintegralen om ej redan bekant)

û = Λ [ln tan(b/2) + 1/tanb]/2π ............................. V

= Λκ = Λ[K]/2π) = L_c(di/dt)κ

tanb = x/s, s = x·cotb, û = u-flex

Λ = L_c(di/dt)

— L[c] är primärledarens egen inre interna primärinduktans, [di/dt] är strömderivatan eller strömändringen [här konstant].

— För att kunna beräkna hur avgränsade primära delavsnitt inducerar spänning i sekundära delavsnitt, typ nedanstående,

måste vi relatera till punktintegralens basform — samma som ovan b\90 med grundformen via 4pi, analogt med endast halva û-värdet för s=d,

û = Λ [ln tan(b/2) + 1/tanb]/4π ............................. V

och enligt följande.

Integrationsgränserna för variabla induktionssymmetrier

— Vi använder här exemplet från anordningen i Parallellexperimenten från 1994 där det gällde att bestämma de utskjutande sekundärändarnas bidrag (d-delen i figuren nedan).

Avståndet mellan primär-sekundär = x

— Förutsättningen här är att primärändens (s) ovansida avstämmer sekundärens (d) bottenpunkt (sTOP):

— Primärströmmen lämnar primärlinjen där (vid sTOP, vinkelrätt, rakt neråt), men primärströmmens riktning parallellt med d-tillskottet ger ändå bidrag till d-linjens fortsättning (i princip mot oändligt).

— Genom att utnyttja indexeringsgränserna direkt i (den ursprungliga differentialversion till) û-sambandet ovan, och som utgår ifrån och bygger på integrationsintervallet b\90 (bTILL90°), samt i beaktande av det bidragande laddningsfältets ovan- och undersida, kan uppgiften lösas på följande sätt, figuren ovan.

— Om punktintegralen sveper (vänstra figurdelen) mellan vinklarna B1(största) till B(minsta) motsvarar det laddningshalvornas ovandel sett mot den mottagande sekundärens d-del. Emellertid ingår i detta vinkelsvep B\B1 en y-del utmed s-primären som inte ska finnas med. Eftersom den delen (y) i laddningshalvornas ovandel har en motsvarande symmetrisk nederdel, kan den aktuella subtrahenden anges via integrationsintervallet 90\B2.

— Med intervalloperationen B\B1 – 90\B2 återstår så endast bidraget från laddningshalvornas överdel på den aktuella d-delen (högra figurdelen), vilket är lösningen:

û/(Λ/4π) = [ln[tan(B/2)] + 1/tanB] ;

;

_{(B\ B1)} [ln(tan[B/2]/tan[B1/2]) + y/x]

= ln[tan(B/2)] – ln[tan(B₁/2)] + 1/tanB – 1/tanB1

= ln[tan(B/2)] – ln[tan(B₁/2)] + (s+y)/x – (s)/x

= ln[tan(B/2)] – ln[tan(B₁/2)] + y/x

= lnA – lnB + y/x = ln(A/B) + y/x

= ln(tan[B/2]/tan[B1/2]) + y/x

;

_{–(B2\ 90)} –[ln(tan[B₂/2]]) + y/x]

= –[ln[tan(B₂/2)] + 1/tanB₂]

= – ln[tan(B₂/2)] – y/x

; summering ger

= ln(tan[B/2]/tan[B1/2]) + y/x – ln[tan(B₂/2)] – y/x

= ln(tan[B/2]/tan[B1/2]) – ln[tan(B₂/2)]

= ln[tan(B/2)/[tan(B₁/2)tan(B₂/2)]]

Resonemanget kan göras (mera grundligt) med samma resultat från punktintegralens differentialekvation, med motsvarande intervallblock — Se Intervallblockets förtydligande nedan.

— Genom att bägge ändarna räknas symmetriskt på C-linjen ges i slutänden dubbla sambandsformen ovan för d-tillägget (d=25mM enligt värdeformerna, se beräkningar i Kalkylkortet Tabell1), alltså via 2û/(Λ/4π)=û/(Λ/2π) enligt

Verkan från primären på överskjutande sekundärdelen (dubbla summan via ändsymmetrin) :

û = (Λ/2π) · ln[tan(B/2)/[tan(B₁/2)tan(B₂/2)]] ; ln[rakparentesen]= 1,0626495 Λ=L(di/dt)

Graf = ln([tan0.5atan15/(100+x)](tan[0.5atan15/100]tan0.5atan(15/x))'–1)

x:= 10x för horisontalskalan i grafen nedan.

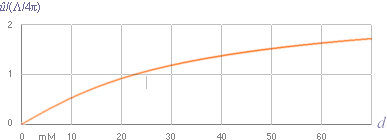
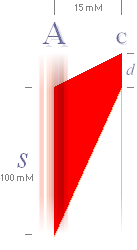
— Notera att induktionssambandet i sin grundform avser varje strömlinje som en ideal geometrisk mittlinje genom varje praktisk cirkulär ledare.

— Speciellt för små separationsavstånd, A-C i figuren ovan, kommer (därför) inte grundsambanden att visa korrekta resultat. Jämför den typiskt grova primärledaren ovan (A) med dess laddningar i huvudsak vid materialytan: grundformen urartar och kan inte användas för ett sådant fall. Med en sekundärinduktion på en C-ledare som befinner sig innanför primärledarens tvärsnittprojektion, måste grundformen vidareutvecklas för att ge relevanta resultat. Den delen omnämns här endast utan vidare.

Graferna nedan visar hur induktionsfaktorvärdet (vertikalskalan vänster) ändras (inom tilläggsintervallet d=0-11mM i ledarens parallellt förlängda linje C) för en s=0,1M lång rak idealt obegränsat tunn primärledare (A) för olika fasta separationsavstånd A-C (vertikalskalan höger) i mM.

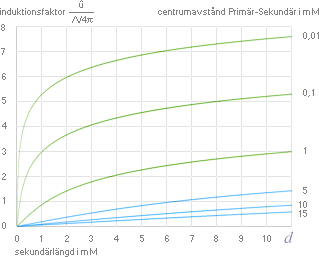
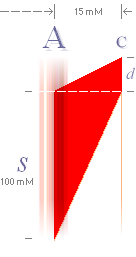
Graf = ln([tan0.5atan15/(100+x)](tan[0.5atan15/100]tan0.5atan(15/x))'–1)

Samma som föregående ovan, men med x i samma enhet som y.

Intervallblockets förtydligande

Om vi återknyter till avsnittet om Punktintegralen i Sekundära Induktionen, alla utvecklingar i PREFIXxSIN, sektionen

∫ dU = (Λ/2π) [ _0→90∫ cosecb db – _0→90∫ cosec2b db]

U = (Λ/2π) _0→90[ln tan(b/2) – – 1/tanb]

= (Λ/2π) [ln tan(b/2) – ln tan45° + 1/tanb – 1/tan90°]

Från trigonometrin minns vi att 1/tan90° är orepresenterat eftersom 1/(n→∞) aldrig uppnår 0. För exakta 90° blir alltså den värdemässiga representationen exakt noll. Detta ger oss

= (Λ/2π) [ln tan(b/2) – ln 1 + 1/tanb – 0]

och tar om samma härledningsform, men nu via det mera reguljära ursprungliga enkelsidiga (Λ/4π) samt istället för 0→90 utnyttjar integrationsgränsen B1→B2 får vi direkt

∫ dU = (Λ/4π) [ _B1→B2∫ cosecb db – _B1→B2∫ cosec2b db]

U = (Λ/4π) _B1→B2[ln tan(b/2) – – 1/tanb]

= (Λ/4π) _B1→B2[ln tan(b/2) + 1/tanb]

= (Λ/4π) [ln tan(B₁/2) – ln tan(B₂/2) + 1/tanB₁ – 1/tanB₂]

Den sambandsformen ansluter som vi ser till samma typform som den använda i föregående utnyttjande av integrationsgränserna direkt i Integrationsgränserna för variabla induktionssymmetrier.

Tilledarnas B-fält

Tilledarnas magnetiska fält

Tilledarnas magnetiska fält

NOTERA ATT LEDARNAS TVÄRSNITTSYTA FÖRUTSÄTTS IDEALT OBEGRÄNSAT LITEN I ALLA FÖLJANDE MATEMATISKA SAMBAND för att medge maximalt utrymme för samtliga möjliga fall.

— I det praktiska fallet får man beakta de särskilda begränsningar som gäller för en viss ledardimension och i det speciella fallet med magnetiska fältstyrkor [B] i närheten av ledarytan — eller i [den idealt tunna] ledarens längsriktning, t.ex. utanför förlängningen av en böj. B-styrkan i, inuti, en solid cirkulär ledare avtar i praktiken mot centrum och är där noll, vilket sätter begränsningen. Se särskild härledning med samband i B-fältet inuti Q.

Fig:1

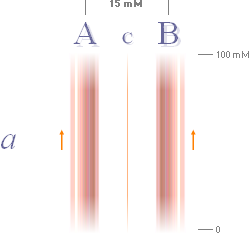
Sett ovanifrån, figurbilden ovan.

Sett framifrån, figurbilden nedan.

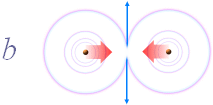
Figurdelen i (b), se även Högerhandsregeln, illustrerar hur den magnetiska fältstyrkan från de bägge parallella primärledarna (AB) helt tar ut varandra om strömmarna är lika stora och samriktade.

Planalternativet

Alla magnetiska fältbidrag kan elimineras ur C-linjen

Om tilledarna placeras i samma medelsnittplan som primärerna (A&B), figurdelen i (c) nedan, och förutsatt en omsorgsfullt genomförd konstruktionssymmetri — symmetriskt lika långa, symmetriskt lika dimensionerade ledare i samma homogena material — kan hela kretsbildens totala magnetiska fältbidrag elimineras (idealt fullständigt) ur den centrala och symmetriskt belägna mätmittlinjen (C). Alla primärdelens ledare kommer att ge symmetriska men motriktade fältbidrag som tar ut varandra i den symmetriska C-linjen.

PARALLELLEXPERIMENTEN från 1994 utnyttjade INTE nedanstående option. Den aktuella anordningens tilledningsalternativ visas i figurdelen [d] längre ner.

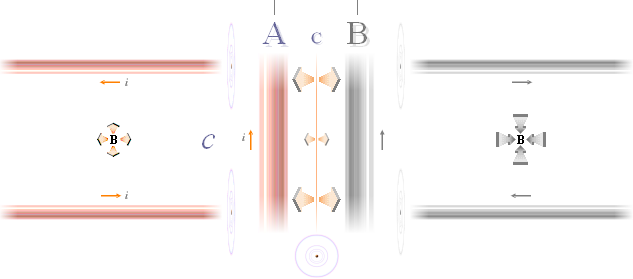
Om bara den ena [vänstra] strömskänkelns ledardel är elektriskt aktiv, och med de strömriktningar som figuren ovan anvisar, ges magnetiska fältbidragen från de parallella tilledarna med en resulterande B-styrka riktad rakt uppåt mot betraktaren i C-linjen. Pilarnas olika storlek i C-linjen motsvarar ikoniserat de olika fältstyrkorna.

— Nedan visas mera ingående den grafiska funktionen för hur den B-styrkan varierar utmed C-linjen. Exemplets strömstyrka är 30 Ampere och parallellavståndet 100 mM med C-linjen placerad 7,5 mM från vertikalledaren [A] som förbinder de parallella tilledarna. Vertikalskalan nedan i milliTesla. Beräkningarna finns samlade i Tabell2 i Kalkylkortet.

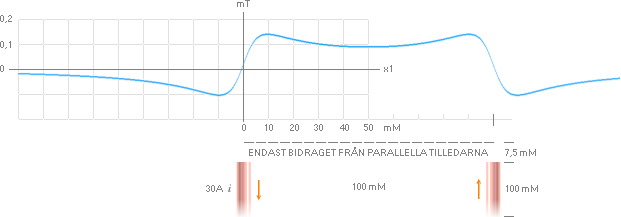
Sambandets grafiska ekvation finns [delvis illustrerat] redovisad i Kalkylkortet Tabell2 överst, den är uppdelad i en övre [vänstra] och en undre [högra] bidragsdel enligt respektive

yGRAFövre = (10'2)[3][(107.5)[([(107.5)'2]+[10x]'2)'–0.5]–(7.5)[([(7.5)'2]+[10x]'2)'–0.5]]/([10x])

yGRAFunre = (10'2)[3][(107.5)[([(107.5)'2]+[(100–10x)]'2)'–0.5]–(7.5)[([(7.5)'2]+[(100–10x)]'2)'–0.5]]/([(100–10x)])

med totala grafiska sambandet

yGRAF = 30([[(107.5)[([(107.5)'2]+[10x]'2)'–0.5]–(7.5)[([(7.5)'2]+[10x]'2)'–0.5]]/[10x]]+[(107.5)[([(107.5)'2]+[(100–10x)]'2)'–0.5]–(7.5)[([(7.5)'2]+[(100–10x)]'2)'–0.5]]/([(100–10x)]))

Alla sambandsformer utgår här ifrån den konventionellt benämnda Biot-Savarts lag. För B-styrkan utanför rakledaren skrivs den i PREFIXxSIN

B = µ₀(I/4px²)sinb .............................. grundformen för sambanden ovan

Se utförlig beskrivning och härledning i Magnetiska Expansionsintegralen, om ej redan bekant.

Blockalternativet

Figurdelen (d) nedan visar den aktuella konstruktionen (BLOCKALTERNATIVET) som användes i PARALLELLEXPERIMENTEN 1994. Tilledarnas längsutsträckningar ligger rakt under AB-ledarnas ändar. Sambanden för detta fall finns också redovisade illustrerat i Kalkylkortet Tabell2, andra blocket.

— En motsvarande grafisk redovisning för detta fall blir mera komplicerad med endast ena strömsidan representerad eftersom den delen uppvisar olika B-riktningar, sambandsgeometrin i figuren nedan till höger. Tas bägge strömsidorna med [delvis enklare härledning på grund av symmetrierna] får B-riktningen genomgående en och samma riktning — med strömmarna enligt exemplet så som visas i figurdelen nedan till vänster.

Grafbilden med bägge AB-delarna får samma typutseende som i föregående grafbild, men med högre värden [0,45 mT topp, mitten 0,21 mT], se Diagram-GrafExempel i Kalkylkortet Tabell3.

— Notera dock att B-riktningen i detta fall [B90] helt saknar komponenter som kan vektoradderas med B-komponenter från AB-ledarna i C-linjen. Dessa bägge olika B-riktningar är inbördes rätvinkliga, de adderas inte; laddningarnas rörelseriktningar i AB-ledarna är samma som B90-riktningen, ingen magnetisk växelverkan kan utbildas för detta fall. Se även i Magnetiska Kraftlagen.

— Ett Hallelement som mäter B-styrkan mellan AB-ledarna i C-linjen märker ingenting av B90-vektorerna [och vice versa].

— Parallellexperimenten från 1994 visade också att dessa delar inte har någon inverkan.

— En mera REGULJÄR experimentredovisning för induktionsmätning måste dock beakta dessa detaljer, och välja anordningen efter föregående PLANALTERNATIVA tilledningsdragning, för att säkert eliminera alla B-förekomster från den avgörande C-linjen.

Med grund i den allmänt förhärskande uppfattningen att magnetiska fält (B) bildas av elektriska laddningar i rörelse [enligt relaterad fysik i förhållande till referenspunkterna R(eg) i ett yttre dominant g-fält], visar den enkla fenomenverkan att en elektrisk laddning (Q+) i rörelse relativt R(eg) som bildar B-fältet [B(Q+)] växelverkar med ett (från en annan Q+-källa) yttre magnetisk fält (B), så, att (Q+) attraheras mot det område där B-fältens riktningar tar ut varandra maximalt (förtunningar), analogt repelleras från områden där B-fälten samverkar maximalt (förtätningar).

Elektriska laddningens växelverkan med B-fält

— Figuren nedan (abcd) sammanfattar det enkla grundregelverket för en positivt laddad elektrisk laddning Q+ som lägesändrar uppåt från bildytan mot betraktaren (idealt den associerade strömriktningen från induktionsspänningen i C-linjen i Fig:1a sett framifrån [bottenpunkten]). B betecknar magnetiska fältstyrkan i ett fast yttre magnetfält, F betecknar magnetiskt resulterande kraftverkan på Q+.

Fig:2

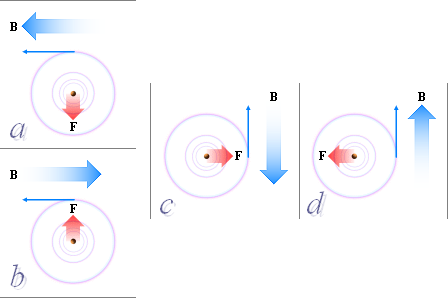
Verkan efter »minsta motståndets lag»:

Alla naturliga processer utvecklas alltid mot den punkt där motståndet är som lägst.

Se även en mera utförlig genomgång av riktningsbegreppen i Riktningsgrundernas upphov för magnetismen.

Blockalternativet, samband

Blockalternativet

Samband

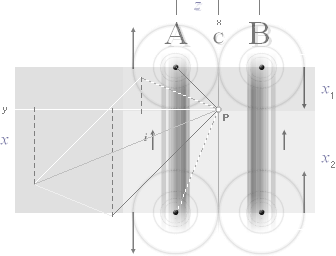
Sambanden nedan för beräkning av resulterande magnetiska fältstyrkan till storlek och riktning enligt figurbilden ovan — sambanden nedan avser endast den vänstra (ena) strömskänkeln som elektriskt aktiv; [vänstra ström-] skänkelns övre-nedre del gömmer tilledningarna med vardera längden s. Notera beteckningssätten [här på grund av olika typreferenser]: B-värdena relateras till den markerade xy-riktningen [det vanliga xy-systemet roterat +90°].

övre:

r = √ x₁² + z²

R = √ r² + s²

B = µ₀(I/4πr)(s/R) ................... se Specifika B-ekvationer (se även konv. Biot-Savarts lag)

By/B = x₁/r

Bx/B = –z/r

unre:

r = √ x₂² + z²

R = √ r² + s²

B = µ₀(I/4πr)(s/R) ................... se Specifika B-ekvationer (se även konv. Biot-Savarts lag)

By/B = x₂/r

Bx/B = +z/r

xy-komponenterna summeras var för sig, totala B-summan bli resultanten av dessa. B-vinkeln beräknas med KVADRANTVILLKOREN [speciell omvandlingsfunktion i kalkylprogram finns, här OpenOffice, ARCTAN2(x;y) som ger B-vinkeln i ± pi radianer — multiplikation med180/pi ger gradtalet]. Se Kalkylkortet Tabell2.

— Ovanstående [ i kalkylkortet ] kan användas med godtycklig utsträckning för x1 — positivt som ovan, negativt över toppdelen.

Här slutar framställningen om induktionsbegreppet i relaterad fysik med magnetismen i ljuset av parallellexperimenten med den tillhörande allmänna materieinduktansen.

Supraledning — inledning, se även i Förord

BILDKÄLLA: Föffattarens arkiv · 6Jun2010BlommorBild54RF2010/2 · NikonD90 · Detalj

Supraledning

Kort introduktion till Supraledning ENLIGT RELATERAD FYSIK — Resonanserna [Harmoniska Svängningar] styr hela fysiken. Se även Historisk Uppkomst med Konventionell Beskrivning

SUPRALEDNINGENS BESKRIVNING i detta htm-dokument ska (om allt stämmer), genom elektronmassans komponenter (τ-ringarna), ge en kvalitativt helt UTTÖMMANDE kvalitativ förklaring (genomgång) av samtliga fysikaliskt möjliga orsaker till fenomenet sett från den relaterbara fysikens synvinkel (TNED) — men ger (här) ingen övergripande matematisk beskrivning av alla möjliga fall.

— Eftersom τ-ringarna i TNED grundlägger atomens resonanser (se från PERIODISKA SYSTEMET) finns flera (många) olika möjliga sätt för supraledningen att gestalta sin specifika fysik, och därmed, tvunget, alla lika omfattande (som atomernas spektrum) om det gäller en rent matematisk beskrivning. De olika sätten som innefattar fenomenbeskrivning i ämnet supraledning ska alltså, enligt TNED, vara återförbara, bero, på mönsterresonanser inom elektronmassorna, men vilka resonansers mera precisa matematiska fysik den här framställningen INTE är tillägnad.

— Här berörs (inledningsvis) endast de allra enklaste grunderna (se från Sambandsformen enligt TNED).

— Hela bakgrunden till ämnet är (nämligen) endast den (här, helt enkla) uppmärksammade matematisk-fysikaliska kopplingen [från magnetismen via DIVERGENSEN (c) i Kausalsambandet] enligt

↨R_max/ç₀ = R₀c₀/ç₀²

och som via τ-ringarna med samma enkelhet leder till samma kvantitativa allmänna SUPRALEDAR-uttryck som används konventionellt i beskrivningen (se Meissnereffekten i citat)

B_z(x) = B₀e^–x/λ

Den följande presentationen härleder sammanhanget, samt i någon mån relaterar ordningen för funktionssättet i den mest uppenbara praktiken — sådant det kan utläsas enligt relaterad fysik.

Om ej redan bekant:

Resonansmönster

QTEK WindowsMobile 1,3 MegaPixel. Författarens Fotografier 2007IV17

ALLA INNESLUTNINGAR [»atomer»] som matas med eller innefattar en bestämd energi uppvisar MÖNSTER, stående vågformer, eller resonanser.

— RESONANSMÖNSTER generellt som fattningsgrund för fysiken i allmänhet:

— Resonanserna grundlägger hela materiefysiken genom GRUNDÄMNENAS PERIODISKA SYSTEM. Resonansmönstren (kända från alla naturpromenader om inte annat) genomtränger hela naturboken. Vi finner dem i alla naturliga strukturer.

BILDKÄLLA: Författarens arkiv · TonKollage med DELPHI4Test2011 · 26Jun2011Ängen2_24Excur14•2Jun2009Tall13Excur2 · NikonD90 · Detaljer

— Resonanserna kan studeras elementärt genom enkla köksexperiment: Hur fasta, stående vågmönster, bildas med hjälp av en vanlig disbalja i plast (bilden överst). Bumpa jämnt rytmiskt med ena handen på baljkanten för att mata vågenergin. Testa olika rytmer och styrka, olika (hexagonala) typmönster framträder. På samma sätt, som det får förstås, bildas olika mönster (konv. orbitaler) i och mellan atomerna via elektronmassorna. Härledningen till Periodiska Systemet bildar en grundform (Se även delvis vidare utförligt från Spektrum). Det är fysikgrunden vi bör känna till, elementärt.

Supraledning — fenomenformen enligt relaterad fysik

Att NOTERA:

— Supraledningens fenomenform ENLIGT TNED — relaterad fysik — saknar HELT paralleller i modern akademi, främst på grund av DIVERGENSEN, men också (än mer) på grund av ELEKTRONMASSANS KOMPONENTER: De (»vibratorerna») ingår inte i den moderna akademins atomteori;

— Modern akademi anser bl.a. att »elektronen är en punktpartikel med noll utsträckning och oändlig massa». Därmed effektivt punkt för varje vettig fenomenbeskrivning.

— Fenomenformen (enligt relaterad fysik) undgår — därmed likaledes — HELT varje form av logisk beskrivbarhet i termer av modern akademi. Ingen förstår eller kan förklara ämnet i den moderna akademins ljus — utom genom en mer eller mindre abstrakt matematik (successivt framväxt på experimentell grund).

— I TNED är elektronen ingen partikel, utan ett massa-laddningskvantum, en hop, en mängd. Se särskilt från Spektrum och Kvanttalen, om ej redan bekant.

— Följande framställning försöker ge en bild av HUR man ändå konventionellt har kunnat komma fram till en beskrivande grundmatematik i ämnet supraledning, sett från den relaterbara fysikens synvinkel (i kraft av författarens observationer).

Fenomenform Enligt Relaterad Fysik — Se även Historisk Uppkomst med Konventionell Beskrivning

SUPRALEDNING

För grundbegreppen ENLIGT RELATERAD FYSIK, se

MAGNETISMEN och speciellt HÖGERHANDSREGELN, samt Atomkärnans härledning med ELEKTRONMASSANS KOMPONENTER, om ej redan bekant.

För praktiska exempel på elektronmassans komponenter, se särskilt Spektrum och Kvanttalen, LJUSETS POLARISATION, Elektronens Bubbelkammarspår, CASIMIREFFEKTEN och Lambväxlingen, samt även GRUNDÄMNENAS BROTTHÅLLFASTHET, om ej redan bekant.

Normal elektrisk ledning:

I en normal elektrisk ledning ligger elektronmassans komponenter maximalt glest utspridda enligt RESONANSVILLKOREN som grundlägger GRUNDÄMNENAS PERIODISKA SYSTEM. Varje elektronkomponent [tau-ringen, τ] har en bestämd kraftkoppling F[eZ] till sin moderkärna och som hindrar en resistanslös makroströmväg genom materialet. Genom att τ-ringen är liten i förhållande till medelavståndet mellan ringarna, kan alla yttre, och inre, magnetfält passera obehindrat genom materialet utan någon nämnvärd störning.

Supraledning:

Elektronmassans förtätning skapar begränsning i magnetfältens genomträngning

kvantiserad ström via h/2e

F[eZ]-komponenten kan i egentlig mening inte elimineras från en elektronmassa, endast omfördelas mellan elektronmassans komponenter [beroende på skymningseffekter, analogt RESONANSVILLKOR]. Totala summan av attraktionen Atomkärna-Elektron förblir konstant. Genom den resonansbetingade effekten, kan vissa elektronstråk bildas med i princip NOLL atomkärneattraktion på bekostnad av att attraktion tillväxer i andra stråk [närmare atomkärnan]. Det är i varje fall den närmast liggande förklaringen enligt TNED.

↨R_max/ç₀ = R₀c₀/ç₀² normalfallets förenkling i »fri rymd» c₀ ~ ç₀ ↔ R₀c₀/c₀² = R₀/c₀ = µ₀

DET som helt undgår Modern Akademi — se mera utförligt i µ0. För reduktionen ç, ledet ovan, se speciellt från Kausalsambandet, om ej redan bekant.

Genom att τ-ringarna komprimeras eller »kondenserar» — ansvaret för det ligger helt på den sammandragande magnetismen inbördes mellan ringarna då de färdas åt samma håll, se Summerande B-fält i MAGNETISMEN om ej redan bekant — uppkommer delvis andra betingelser för magnetfält att passera materialet. Genom ansamlingen av ringar [Se Elektronmassans komponenter], analogt komprimerad elektronmassa, som betyder c=0 enligt DEEP från GRIP, tvingas genomlöpande magnetfält möta lägre, inte högre, lokal divergens. Magnetfältets utbredning i material tvingas följaktligen gå ikring, omsluta, det aktuella området. Det får tydligen förstås som att det massförtätade området INNESLUTS som i en väska eller låda av det genomträngande magnetfältet.

Kroppen som bildar det genomträngande fältet kommer följaktligen att kunna BÄRA MED SIG supraledarens elektron-atombesättning som om den vore en atom [atomkärna] i den egna fältkroppen. Styrkan i effekten är lika med styrkan i uteslutningarna. Det är i varje fall den mest uppenbara förklaringen enligt TNED.

↨R_max/ç₀ = R₀c₀/ç₀²

↔ normalfallets förenkling i »fri rymd» c₀ ~ ç₀

R₀c₀/c₀² = R₀/c₀ = µ₀

Se vidare beskrivning nedan i Supraledningens Uppkomst och Sambandsformen enligt TNED.

Kvantiserad ström via h/2e

Det mesta naturlige betraktelsesättet enligt TNED:

— När elektronmassorna — i vissa stråk — friläggs sin Coulombiska attraktion mot sina moderatomkärnor på bekostnad av att andra delar förstärker sina, allt i anledning av att temperaturen avtar och materialet inträder domänen för s.k. supraledning, och förutsatt att materialet också ingår i en sluten elektrisk krets, är det med hänsyn till strömmen som sådan naturligt att elektronmassornas komponenter sammandras magnetiskt på samma sätt som gäller i fallet med elektroner som dras ut av en förbipasserande protonkärna (attraherande elektriskt fält) i en bubbelkammare. Se Elektroncylindern i ELEKTRONENS BUBBELKAMMARSPÅR för praktisk jämförelse enligt TNED.

Elektriska laddningar som färdas likriktat [Se MAGNETISKA KRAFTEN], sammandras [och spinnsynkroniseras inbördes] på känt sätt av sina inbördes bildade magnetiska fältkrafter, och tenderar så att inrättas på gemensam strömlinje. På samma sätt som de enskilda lindningsvarven i en elektrisk spole av samma skäl utbildar inbördes attraherande krafter mellan de tätt liggande strömringarna, sker en inbördes magnetisk attraktion också mellan närliggande komponentringar i elektronmassan. Den attraktionen dämpas sedan av Coulombrepulsion endast då ringarna kommer helt nära varandra.

— Föreställningen om elektronmassans komponenter fanns från början (1925) med i modern akademi, men förkastades år 1927 med hänvisning till relativitetsteorin (se Vibratorerna). BILDEN I STORT, här beskriven, ingår därför inte i den moderna akademins lärosystem, liksom heller inte atomkärnans härledning gör det.

— Eftersom atomen som komponent i vilket fall bygger på KEPLERRESONANSER — se utförligt i GRUNDÄMNENAS PERIODISKA SYSTEM om ej redan bekant — och därmed grundas på de enskilda elektronmassornas resonanser (se även i SPEKTRUM OCH KVANTTALEN ), och därmed fundamentala kopplingar till Plancks konstant (h=mcℓ) genom motsvarande impulsmoment för elektronmassorna, är det också naturligt om de friställa-starkare kopplade elektronmassornas domäner resonansmässigt delas upp (först) i PAR — när materialet undergår strömdrag: Den detaljen är viktigt att ha i bakhuvudet för den relaterade fysikens beskrivning: Utan inre magnetisk fältväxelverkan går det inte.

— I normalfallet med vanlig rumstempererad elektrisk ledning gäller ett motsvarande spänningsberoende i elektronmassan uttryckt formellt i fysikaliska storheter enligt

E = hf = mcℓf = Ue;

h/e = E/fe = U/f = (m/e)cℓ

Om elektronmassorna omfördelas i svagare-starkare grupperingar, ger resonansvillkoret med impulsmomenten (h=mcℓ) enbart via enskilda elektronmassor ett motsvarande spänningsberoende

h/ne = E/fne = U(n)/f = (m/ne)cℓ

Därmed får tydligen förstås att supraledningens egenskap främst söker sig till en strömledning (via U) i formen av att öka den normala elektronkoefficienten (n) från n=1 till närmaste elektronparbildning, n=2.

Uppkomst — Supraledning

Uppkomst — Upptäck från 1911

SUPRALEDNING

För grundbegreppen ENLIGT RELATERAD FYSIK, se MAGNETISMEN och speciellt HÖGERHANDSREGELN

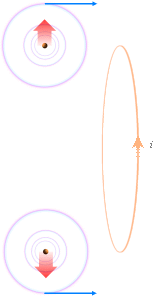
Spolen [vänster ovan] förs mot den vilande ringen: Den vilande ringen ser ett växande B-fält, analogt en primärström som är i växande: Det blir då de elektriska laddningarna i primärstömmens växande riktning som bestämmer den inducerade strömriktningen i den vilande ringen: ringströmmen ges motsatt spolströmmen. Ringströmmen bildar ett magnetfält som motverkar spolens magnetfält [konv. Lentz lag]. Bilden ovan illustrerar detta fall.

Spolen [vänster ovan] förs från den vilande ringen: Den vilande ringen ser ett avtagande B-fält, analogt en primärström som är i avtagande: Det blir då de elektriska laddningarna i primärstömmens avtagande riktning som bestämmer den inducerade strömriktningen i den vilande ringen: ringströmmen ges samriktad med spolströmmen. Ringströmmen bildar även i detta fall ett magnetfält som motverkar spolens magnetfält [konv. Lentz lag].

— Riktningsanalogin kan enklast memoreras via EN KONSTANT PRIMÄRSTRÖM på yttre sekundärledare: Ökas primärströmmen, induceras sekundärströmmar motriktade primärströmmens riktning; Minskas primärströmmen, induceras sekundärströmmar medriktade primärströmmens riktning [i äldre litteratur även konv. Maxwells regel]. I vilket fall är nettoeffekten av ändringarna ALLTID enligt TILLSTÅNDETS PRINCIP att SÖKA MOTVERKA ÄNDRINGENS ORSAK. Se även i ÄNDRINGSLAGARNA.

Nollresistansen i supraledare

En magnetstav eller (bilden ovan vänster) en strömgenomfluten elektrisk spole som förs mot en vilande elektriskt ledande ring (bilden ovan höger) inducerar i ringen en ström (i) motsatt riktad spolströmmen (konv. Lentz:s lag). Inducerade strömmen är alltid riktad så att nettoeffekten i slutänden söker motverka ändringens orsak (Se även Ändringslagarna).

I en vanlig normal elektrisk ledare kan induktionsströmmen bara påvisas så länge B-spolens rörelseriktning ändras. Så snart denna avstannar, avstannar också den inducerade ringströmmen. Anledningen är naturligtvis att den vanliga ringledaren uppvisar en inre RESISTANS: den inducerade elektronströmmen avstannar.

I en supraledare induceras också samma typström, men den inducerade strömmen avstannar inte. Man upptäckte genom experiment (först 1911 för Kvicksilver Hg som hade kylts ner till en kritisk temperatur), att den motsvarande inducerade ringströmmen fortsätter oavbrutet, som om supraledaren inte hade någon elektrisk resistans alls.

Magnetfältens uteslutning (eng. expulsion) ur supraledarens inre materialkropp

Men resistansfenomenet visade sig bara vara en del av fenomenverkan i supraledningen. Mätningar visade också att magnetfältet inuti supraledaren väsentligen försvagades (konv. Meissnereffekten).

Fenomenformen med magnetiska fältets uteslutning skiljer på två typer:

· Magnetfältens fullständiga uteslutning ur supraledaren, s.k. typ I (Aluminium, Zink, Kvicksilver, Bly, m.fl.)

· Magnetfältens delvisa uteslutning ur supraledaren, s.k. typ II (Niob, Vanadium — i allmänhet också speciella legeringar)

Ref., se Conventional superconductor

http://en.wikipedia.org/wiki/Conventional_superconductor

Speciellt typ II används i praktiska demonstrationer för att visa hur en magnet kan fås att sväva (levitera, eng. levitate) över en supraledare. Se speciellt nedanstående länk till en videosekvens [1min24sek in i videon; tag kring magneten med lyftning av denna tar den underliggande supraledaren med sig som i en omslutande väska]

SUPERCONDUCTORS AND MAGNETIC LEVITATION

http://www.supertightstuff.com/04/10/featured/superconductors-and-magnetic-levitation/

Om den överliggande magneten (videosekvensen ovan) liknas vid den övre ringströmmen (figuren nedan överst) och den underliggande supraledaren (typ II) liknas vid den undre ringströmmen — alltså en motinducerad strömriktning som fortsätter — är följande principresultat tydligt från den magnetiska grundfysiken:

— Nettoverkan mellan supraledarens magnetfält på dennas utsida (blå pilar nedan) och den överliggande magnetens magnetfält tar ut varandra.

— Det betyder tydligen att vi kan säga att supraledarens inducerade magnetism från den överliggande magnetens föregående rörelse exkluderar alla interna B-fält i supraledarens egen materiekropp. Konventionellt beskrivs detta (ofta) som att supraledaren uppvisar diamagnetism (omvänd para- och ferromagnetism, citat nedan).

— Magnetfältens motverkan i mellanrummet mellan kropparna visar samtidigt också att magneten utsätts för en repellerande kraft.

— Vi kan förstå att det är denna repellerande kraft som får magneten att sväva över supraledaren. Den typbeskrivningen är också den allmänna man brukar möta i ämnet:

”Superconductors are strongly diamagnetic. That is to say that they will repel a magnet.”,

THE MEISSNER EFFECT

http://www.users.qwest.net/~csconductor/Experiment_Guide/Meissner Effect.htm

;

”This means that diamagnetic materials are repelled by magnetic fields.”,

DIAMAGNETISM

http://en.wikipedia.org/wiki/Diamagnetism

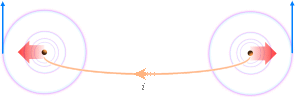
Repulsion mellan två strömringar illustrerad via motriktade ringströmmar.

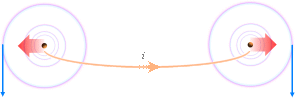
Men som också videosekvensen visar, är detta uppenbarligen inte hela sanningen.

Videosekvensen 1min:24sek; Experimentatorn lyfter magneten — och det underliggande supraledande materialblocket följer med upp.

— När den svävande magneten lyfts upp följer den underliggande supraledarens materialkropp med — som om den vore innesluten i en väska eller låda i den överliggande magnetens magnetfält.

— Magneten uppenbarligen både repelleras (på ena sidan) OCH attraheras (på andra sidan). Eller rättare sagt:

— Den supraledande kroppen både stöter ifrån och attraheras av magnetens magnetfält.

Den fenomenformen gestaltar uppenbarligen ingen vanlig teknisk fysik.

— Vad vi vet finns ingen motsvarande makrofysisk magnetdemonstration.

— Man kan få olika föremål att sväva fritt över (starka) magnetfält. Men att också få föremålet att följa med i en lyftrörelse som om föremålet fanns inneslutet i en väska, väskans material ett omgivande vanligt magnetfält, är här veterligt helt förbehållet supraledarens fenomenvärld.

— Jo. Det finns ett sätt — men bara delvis. Om den underliggande av två attraherande magneter är precis så tung att tyngdkraften uppväger attraktionskraften, finns i varje fall i princip möjligheten att den undre (magnet)kroppen följer med, svävande eller hängande. Men det är ett utpräglad attraktionsfenomen.

— Samma typ kan också i princip bildas (momentant) av gravitationen. Men också det är ett utpräglad attraktionsfenomen.

— Supraledaren uppvisar, tydligen och helt unikt, ett komplementärt motsvarande magnetiskt repulsionsfenomen.

Videosekvensen visar motsvarande: När den kritiska temperaturen nås, när den nedkylda supraledaren kommer över den gränsen [T(critical)], upplöser sig fenomenformen:

— Den föregående supraledarens materialkropp »ramlar ur magnetlådan».

Vad förorsakar »magnetlådan»?

— Det är den underliggande fenomenform som den moderna akademins vetenskapare arbetar med att försöka beskriva kvalitativt. Inget vet ännu (Aug2011).

— Man har en delvis förklaring, men då i (den sedvanliga moderna akademiska) formen av (för de flesta obegripliga) matematiska samband som ansluter till den moderna akademins vektorkalkyl (Maxwells ekvationer, med vidare). Detaljerna är (alltså, emellertid) i stort sett kryptiska och i princip omöjliga att förstå genom någon direkt logisk beskrivning. Jämför,

”The question of how superconductivity arises in high-temperature superconductors is one of the major unsolved problems of theoretical condensed matter physics . The mechanism that causes the electrons in these crystals to form pairs is not known.[7] Despite intensive research and many promising leads, an explanation has so far eluded scientists.”,

ONGOING RESEARCH, [2011-08-20]

http://en.wikipedia.org/wiki/High-temperature_superconductivity

— Det finns dock vissa klargörande stycken som belyser svårigheterna, och till viss del även förklarar vari själva svårigheterna består. Se t.ex.

ONGOING RESEARCH,

QUALITATIVE EXPLANATION OF THE SPIN-FLUCTUATION MECHANISM,

http://en.wikipedia.org/wiki/High-temperature_superconductivity

I korthet:

Man jämför den normalt lågtempererade supraledningens Cooper-elektronparbildning med den mera svårförklarliga högtempererade (över 30°K) s.k. elektronspinn-täthetens vågbildning:

— I det normalt supraledande fallet kan man se atomgittersvängningarna (eng. phonons) som den katalyserande orsaken till Cooper-elektronpar.

— I högtempererade supraledare figurerar istället det konventionellt benämnda ELEKTRONSPINNET (som ett förstadium till phonon-effekten). Istället för att temperatursänkningen leder till elektronparbildning genom effekter från direkta ändringar i atomgittersvängningar, är det i högtemperaturfallen elektronmassornas spinnfaktorer som spelar in och som förorsakar elektronparbildningen, och då också på annorlunda sätt, analogt i andra mönster (mera utpräglad Coulombisk repulsionsverkan inbördes mellan elektroner).

;

OVERVIEW,

MORE DETAILS,

http://en.wikipedia.org/wiki/BCS_theory

I korthet:

Detaljerna berör den teoretiska förklaringen till HUR elektroner kan forma s.k. Cooper-par, supraledningens absoluta fenomengrund (nollresistansfenomenet).

— Utläggningarna i etablerade termer är här milt sagt »flummiga»: man ANTAR att ”viss attraktion finns mellan elektroner” men utan att specificera orsaken — vilket som vi vet från TNED ställer sig helt annorlunda i ljuset av ELEKTRONMASSANS KOMPONENTER. Det är just fenomenet med ”attractive interaction” som bildar centralproblemet i den modern akademin supraledande ljus — och vars paralleller framgår lika tydligt genom TNED, förutsatt bekant, men som övergår i rena gåtfullheter i termer av den modern akademins lärosystem.

BCS-teorin

SUPRALEDARENS SUPRALEDNING — BCS-teorin via Cooper-par

BCS från Bardeen, Cooper, Schreiffer [1957]

Konventionellt, se t.ex.

BCS THEORY, [2011-08-20]

http://en.wikipedia.org/wiki/BCS_theory

beskrivs/förklaras supraledningen (nollresistansen) av att materialet bildar s.k. Cooper-elektronpar. Det sker genom att materialets inre atomgittersvängningar (konv., eng. phonons) avtar med avtagande temperatur, och därmed möjligheten för speciella inre gitter(elektron)resonanser att bildas. En av dessa skulle vara att atomgittrets elektroner kan bilda motsvarande förtätningar (genomgående, typ I, eller delvis typ II) som är omöjliga i vanlig temperatur. För dessa elektroner skulle då gälla att deras normala atombindning i princip helt och hållet upphör — och därmed noll förlustenergi i varje övergripande elektronflöde (ström). Dvs., noll motstånd. Hela BCS-teorin behandlar detaljerna (modern kvantmekanik) och ger de grundläggande sambanden (men teorin är inte heltäckande).

Meissnereffekten

SUPRALEDARENS magnetEXKLUSION — Meissnereffekten (1933)

”The Meissner effect is the expulsion of a magnetic field from a superconductor during its transition to the superconducting state. The German physicists Walther Meissner and Robert Ochsenfeld discovered the phenomenon in 1933 by measuring the magnetic field distribution outside superconducting tin and lead samples.”,

MEISSNER EFFECT

http://en.wikipedia.org/wiki/Meissner_effect

Nollresistansen självt kan PÅ VISST SÄTT förklara hur supraledaren utesluter magnetfälten ur den egna materialkroppen. Nämligen genom de nämnda inducerade ytmotströmmarna som supraledaren uppvisar då en yttre magnet förs mot (eller bort ifrån) supraledaren. Man säger att supraledarens egeninduktion tar ut magnetfältet från magneten. Analogt, magnetfältet »försvinner» ur supraledarens materialkropp.

— Men som vi nyligen konstaterade i exemplet med Videosekvensen, är supraledarens eget inducerade strömflöde uppenbarligen inte hela sanningen. Supraledaren beskriver både en repellerande och attraherande fenomenverkan på magneten.

— Medan supraledarens motverkande magnetfält kan förklaras av den nollresistiva inducerade strömmen, och därmed till viss del fenomenformen med de egenkroppsliga uteslutna magnetfälten, är det tydligt att någon annan fältförklaring ligger till grund för det faktum att supraledaren tydligen innefattas som ett omslutet föremål i en väska eller låda i den utanförvarande magnetens magnetfält — precis som supraledaren skulle vara en atom i magnetkroppens materierum: den följer med magneten i dess rörelse. När supraledningen upphör, ramlar den ur.

Den konventionellt främsta aspekten som (också) anförs till förmån för att utesluta att nollresistanseffekten (BCS-teorin) ensamt bär ansvaret för magnetfältsuteslutningarna, är följande:

”But if the material already had a steady magnetic field through it when it was cooled through the superconducting transition, the magnetic field would be expected to remain.”,

THE MEISSNER EFFECT [2011-08-20]

http://hyperphysics.phy-astr.gsu.edu/hbase/solids/meis.html

Min översättning:

Men om materialet redan hade ett fast magnetfält genom sig när det avkyldes genom den supraledande övergången, skulle magnetfältet förväntas bevaras.

Eftersom emellertid, Meissnereffekten, det redan från början befintliga magnetfältet i sammanhanget inte alls bevarades utan istället kunde konstateras försvinna (nästan helt), måste man utesluta att enbart nollresistansfenomenaliteten i sig skulle vara hela orsaken. Eller som HyperPhysicskällan ovan säger saken:

”Hence the active exclusion of magnetic field must be considered to be an effect distinct from just zero resistance.”,

THE MEISSNER EFFECT [2011-08-20]

http://hyperphysics.phy-astr.gsu.edu/hbase/solids/meis.html

Min översättning:

Alltså måste den aktiva uteslutningen av magnetfält förstås vara en effekt skild från just nollresistans.

Nollresistansen i sig förklarar inte den magnetiska uteslutningen — eller (som det visat sig här mest bekvämt att benämna saken) Den Magnetiska Lådan, eller (magnetiska) fältinbyggnaden kan inte förklaras enbart av nollresistans.

— Det ovanstående HyperPhysics-argumentet (omnämns f.ö. av många andra webbkällor) är naturligtvis det starkaste i ledningen för att försöka hitta en alternativ förklaring.

Vad beror fältuteslutningen-fältinbyggnaden på?

Inga direkta svar finns ännu (Aug-Sep2011) i etablerade kretsar på vad som förorsakar supraledningens fenomenform. Nedan ges ett centralt citat som belyser den (allmänt beskrivande) matematiska sidan av saken. Därefter ges en motsvarande bild sett från den relaterade fysikens sida, där den kvalitativa bilden framstår desto mera välrepresenterad.

Citat Meissnereffekten

”The discovery of the Meissner effect led to the phenomenological theory of superconductivity by Fritz and Heinz London in 1935. This theory explained resistanceless transport and the Meissner effect, and allowed the first theoretical predictions for superconductivity to be made. However, this theory only explained experimental observations—it did not allow the microscopic origins of the superconducting properties to be identified.”,

CONSEQUENCES [2011-08-20],

http://en.wikipedia.org/wiki/Meissner_effect

;

”A simple example geometry is a flat boundary between a superconductor [and .. what?] within free space where the magnetic field outside the superconductor is a constant value pointed parallel to the superconducting boundary plane in the z direction. If x leads perpendicular to the boundary then the solution inside the superconductor may be shown to be

B_z(x) = B₀e^–x/λ

From here the physical meaning of the London penetration depth can perhaps most easily be discerned.”,

LONDON PENETRATION DEPTH [2011-08-20],

http://en.wikipedia.org/wiki/London_equations

Källan anger ett samband för det s.k. Londondjupet λ [lambda] enligt [:=, konv., eng. defined to be]

λ := √mc²/4πn_se²

med elektronmassan m, ljushastigheten c, n[s] antalet supraledande laddningsbärare, e elektronladdningen

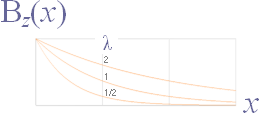
— Vi ser att funktionen ger ett allt snabbare avtagande B-värde med växande x-penetration ju mindre Londondjupet (λ) är.

— Jämför den vanliga ledarens B-värde innanför materialytan (Se B-fältet inuti Q)

Sambandsformen enligt TNED

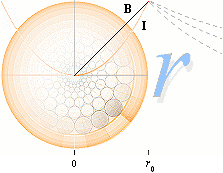
Sambandsformen enligt TNED

Genom att (Se Magnetiserande kraften)

B = µ₀H

= µ₀(I/2πr)

samt att (Se µ0)

ôR_max/ç₀ = R₀c₀/ç₀² Û R₀c₀/c₀² = R₀/c₀ = µ₀

gäller tydligen att

B = (R₀c₀/ç₀²)H

REDUKTIONEN (ç) som sådan som sammanhänger med den magnetiska fältvågens bildning (se Kausalsambandet) kopplar inga egenskaper i materialrum och bevaras därför intakt. Inte heller den fria rymdresistansen [R(0)] påverkas.

— Däremot kan divergensen (Se urspr. från Fysikens sjätte princip) påverkas OM B-flödet tvingas genomlöpa rymdområden som strängt taget avviker från ideala ordningen ç → c. Dvs.:

— Normalt avancerar den magnetiska fältringen enligt TNED genom att uttömma sin tätare fältform via den lägre divergensen (ç) mot den högre (c),

— Men säg att fältvågen istället möter en lägre divergens, nämligen massa (c=0, se från Fysikens sjätte princip):

— Reduktionerna kan då inte fortlöpa på vanligt sätt, utan tvingas »vänta» i försorg av den massuteslutande (c=0) fältövergången: Fältvågen får därmed tydligen förstås så att den går runt, eller bygger in, föremålet för uteslutningen.

— Genom att fria rymddivergensen enligt TNED [c(0)] i sådana fall tvingas anta massformens rumsockupation, finns inget annat att välja på än ett motsvarande avtagande (noll) lokalt B-värde. Den avtagande funktionsformens enklaste aspekt (homogen elektronmassafördelning) måste (således) tvunget skilja sig (betydligt) från den vanliga ledarens linjärt avtagande B-styrka in mot centrum, och därmed uppvisa ett exponentiellt avtagande — enligt någon fältfunktion (x) för [c(0)], typ (Wikipediaexemplet)

B_z(x) = B₀e^–x/λ

= (R₀/ç₀²)H₀[f(c₀)]

= (R₀/ç₀²)H₀[c₀e^–x/λ]

= (R₀c₀/ç₀²)H₀[e^–x/λ]

~ (µ₀)H₀[e^–x/λ]

= B₀[e^–x/λ]

vilket skulle vara den relaterade fysikens förklaring (samstämmigt med bröderna Londons matematik).

— Det supraledande tillståndet ENLIGT RELATERAD FYSIK åstadkommer tydligen att elektronmassorna delvis »kondenserar» i strömflöde på liknande sätt som i fallet med ELEKTRONENS BUBBELKAMMARSPÅR:

— Normalt sett ligger ELEKTRONKOMPONENTERNA utspridda i atomgittren. Några direkta cylinderkopplingar finns inte. Elektronkomponenterna är resonanskopplade till sina moderatomer och uppvisar ingen mera förtätad elektronmassa typ den vi möter när en laddad partikel (typ proton) drar förbi och drar ut en elektron från någon atombindning.

— När temperaturen, emellertid, sjunker, sjunker samtidigt energibindningen mellan elektronelementet och atomen (tau-ringens gitterbindningsenergi). Inte alla grundämnen uppvisar den aktuella effekten (t.ex. inte koppar, silver och guld), men vissa gör det (Niob, Vanadium): Vid en viss kritisk temperatur [T(critical)], och förutsatt ett visst makroströmflöde finns initierat, blir gitterbindningen så ringa att strömdraget, liknande då den förbipasserande protonen drar ut en elektron, överväger och medger en magnetisk attraktion mellan elektronmassans tau-ringar (figuren ovan från Elektroncylindern).

— I det läget skulle alltså enligt relaterads fysik magnetfältgenomströmningen inte längre vara betingad av de (mycket) utglesade tau-ringarnas spridda förekomster.

— Nu möts fältutbredningarna istället av en påtaglig masskoncentration över större rymdavsnitt.

— OM den massförtätningen bidrar signifikant till den lokala divergensformens reduktion, som i sambandet för Londonekvivalenten ovan, är det tydligt att det finns en rent kvalitativ förklarande koppling.

— Som emellertid elektronmassans komponenter förkastades redan från 1927 av modern akademi (se Vibratorerna), figurerar de inte nu heller (2011) som någon kvalitativ grund för fysikens förklaring. Därmed bortfaller också beskrivningen kvalitativa grunder HELT: ingen förstår fenomengrundens kvaliteter. Det är i varje så det framstår enligt TNED.

Elektronmassans komponenter bildar en kvalitativ förklaringsgrund (även till fenomenet med supraledning), som tydligen kan förstås koppla till den magnetiska fältteorin generellt i TNED: divergensen.

Kalkylkortet

Kalkylkortet

Kalkylkortet DIREKT FRÅN DEN HÄR WEBBLÄSAREN IndMag.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/IndMag.ods

Kalkylkortet

Tabell1 — induktionen, cellblock med beräkningar för parallella ledare

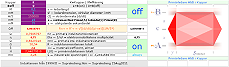
Tabell2 — magnetismen, cellblock med beräkningar för parallella ledare

PLANALTERNATIVET:

BLOCKALTERNATIVET:

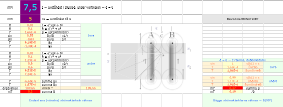
Tabell3 — diagram/grafexempel

g-divergens ljushastighetens lokala värde med referens till den lokalt dominanta gravitationens inverkan, från Ljusets gravitella beroende.
— Divergensen är i relaterad fysik alltså det gravitellt punktlokala värdet på ljushastigheten och som INTE bildas över intervall, se utförligt från DEEP.
Ljushastigheten i normal mening däremot bildas över intervall som medelvärdet av ljusvägens g-divergenser.

reduktion divergensens lägre värde i den magnetiska fältbildningen för bevarandet av elektriska konstanten, se utförligt i Kausalsambandet om ej redan bekant.

Förtydligandet Faradays EMI — förtydligande från originalets Notera den exakta innebörden av den elektroMEKANISKA induktionen

Förtydligandet till Faradays EMI

2011VIII20

Förtydligandet

till den relaterade fysikens observation

att Faradays Lag INTE innefattar »variabelt B genom fix ledare» ;

— det är en DEN bekväma tankekonstruktion som alla har låtit lura sig av:

— det finns ingen »elektromagnetisk induktion», bara en elektromekanisk:

— Också i en del (äldre) litteratur benämnd elektro-motorisk induktion.

Referenser som nedan — samt i härvarande ovanstående htm-block Induktionsbegreppet i relaterad fysik.

Faradays lag, begreppet elektromagnetisk induktion i modern akademi:

:

Sambandsformen U=dΦ/dT förklarar sig själv — i ljuset av gravitationen som den relaterbara fysikens referens för elektrofysikens fenomen

— (Sep2024): Men i och med att kopplingen mellan ljusfysik och gravitationsfysik är väl illa relaterad i moderna kvarter (Bevis: komplexet hänförs till Speciella-Allmänna Relativitetsteorin — och det vet ju alla att särskilt förskolebarnen är jätteförtjusta i den Undervisningen, Fig.1) har påpekandena här garanterat ingen som helst ingång i moderna korridorer (heller). Så den församlingen kan med gott samvete sussa vidare (Efterblivna, lågutbildade, intellektuellt avskärmade .. ursäkta .. Intelligensen är OK. Men intresset för innehållet är på väg ut .. tydligt föranlett av kärleken till att uppfinna nytt snarare än att härleda gammalt).

Elektromekaniska induktionen, Faradays lag:

BA=Φ=Bsd; BA/T=Φ/T=Bsd/T=U=Bsv (föreg. U=Bvl)

— Den inducerade spänningen är tidsändringen OCH INGET ANNAT för den fixa ledarens kurvatur (s) skärande det fixa B-fältet;

A/T = s · d/T

dU = Bs · d(d)/dT = B(dΦ/dT)

— B och s (eller B och d) måste vara fixa i enlighet med den fysiska referensen:

som följaktligen OCKSÅ modern akademi våldför sig på:

— Se FUNTOP Fundamental Theorem of Physics, fysikens 2:a princip som modern akademi, tydligen genomgående, våldför sig på:

en ändring kan inte betjäna en mätning utom från ett tillstånd av jämvikt eller likformighet

— Se FUNTOP: Fysikens lagar gäller FÖR system. Inte i system. »Inertialsystem» existerar inte i fysiken ENLIGT RELATERAD FYSIK.

Genom att kontinuerligt ändra B, ändras också hela referensen kontinuerligt:

— Det SKULLE överflytta referensen till ”B” istället för den lokala g-dominansens laboratorierum: Q-ändringen.

— Men en sådan överflyttning finns ingen RELATERAD fysikalisk grund för: magnetismen gäller med referens till det omgivande lokalt dominanta gravitationsfältets referenspunkter;

— ”B-fältet som sådant” har I TERMER AV RELATERAD FYSIK ingen självständig, fristående s.k. »relativ» existens.

— Därför kan inte B-fältet användas — inte förklaras, inte förstås, inte beskrivas, inte härledas i logisk mening — som referens.

— Och just därför gäller heller inte den förmodade ömsesidiga omvändningen — begreppet »elektromagnetisk induktion» — med »rörlig ledare i fixt B-fält» kontra »fix ledare i variabelt B-fält».

— Begreppet »elektromagnetisk induktion» är alldeles tydligt och, som här i exempel, djupt relaterbart en fundamental feluppfattning av fysikens fenomengrunder.

— Den inducerade spänningen i g-lokalen kommer följaktligen INTE att bero av B om B ändras — utan istället av en helt annan fenomenmässig karaktär, ehuru associerad med dess B-fält. Nämligen variationerna i de elektriska laddningarnas positioner som också (naturligtvis) ansvarar för bildandet av det varierande B-fältet (men som i moderna kvarter missförstås för att vara induktionskällan) och vilka variationer sker RÄTVINKLIGT B-fältets utsträckning: Alltså rakt framåt-bakåt i strömändringens riktning till skillnad från magnetismen som utbreds rätvinkligt induktionsdipolerna. Dessa variationer i de elektriska laddningarnas positioner relativt den omgivande rymdens fasta lokala g-dominans är den förorsakande grunden i det som i termer av relaterad fysik beskrivs som en ren elektrisk sekundär induktion, helt säkert skild från begreppet magnetism.

— Sekundärinduktionens fasta referens — nämligen i kraft av den fasta fysikreferensen som relaterar KÄLLAN bakom det varierande B-fältet — ÄR DET OMGIVANDE RUMMETS FIXA G-RELATERADE RYMDPUNKTER, inte »B-fältet som sådant»:

Induktionen ges från de — från en primärkropp — rörliga elektriska laddningarnas statiska potentialfält som ändras relativt det omgivande rummets fasta och fixa gravitella dominans. Därför existerar inte den förmodade »elektromekaniska induktionen», ehuru bekväm för tanken. Induktion uppkommer ur strömändringar. Inte ur magnetfält.

— Det resonemanget fördes, uppenbarligen, aldrig i modern akademi.

— Med vidare grund i härledningarna till induktionen och magnetismen (se särskilt från Kausalsambandet): Således:

I BA=Φ har (den sekundära) induktionen ingen koppling eftersom

praktik: se parallellexperimenten.

i teorin: se divergensen i tredje ändringslagen.

Jämförelse mellan MODERN AKADEMI och RELATERAD FYSIK: se tre jämförande exempel.

induktion och magnetism inte växelverkar: BA=Φ avser elektromekaniken. Inte induktionen.

— Se särskilt Induktionsdipolens uppkomst enligt relaterad fysik, om ej redan bekant.

— Se även uppkomsten av induktion och magnetism mera utförligt från Kausalsambandet.

— Se även Tre jämförande exempel för en konkret kvantitativ-kvalitativ jämförelse mellan modern akademi och relaterad fysik.

— DÄRFÖR gäller enligt relaterad fysik Faradays Lag (U = dF/dT) enbart elektromekanisk induktion: mobil ledare som rör sig i fixt B-fält (typ strängarna på en elgitarr).

— Observera (således) också följande:

— Genom de (mycket) närliggande matematiska analogierna, samt i de flesta normalt praktiska fall även de rent kvantitativt obetydliga skillnaderna, KAN MAN AVSEVÄRT »dockisera» induktionen — kvantitativt — genom att återföra dess kvalitet på primärladdningsändringarnas alstrade magnetiska fält — helt fel, men precis så som hände i modern akademi. En ändring i en ström alstrar ju i vilket fall en motsvarande magnetisk effekt.

— Dock sker den förenklingen (som vi har sett från Exemplen) med den avgörande nackdelen (OM man nu händelsevis tror att förenklingen är verklig naturvetenskap) att fenomengrunden mörkläggs, helt. Ingen förstår den. Ingen kan förklara den. Ingen kan beskriva den, utan att hamna i djupa bryderier om det gäller detaljer. På »dockskåpsytan» (marknaden) går det (i allmänhet dock alldeles) utmärkt. Jorden är en skyddad plats (som i de allra värsta fallen också upplåter nästen för allehanda rövargäng).

Förord till Induktionsfysik och Supraledning

Förord till Induktionsfysik och Supraledning

2011-09-30

Förord till Induktionsfysik och Supraledning

BILDKÄLLA: Föffattarens arkiv · 14Aug2011Skog1_03ExCur16 · NikonD90 · Detalj

DEN RELATERADE FYSIKENS ENKLA magnetiska KOPPLING till den redan kända — fenomenets centralt karaktäristiska — SUPRALEDNINGENS MATEMATISKA FYSIK [Bz(x)=B0/e^x/λ, magnetiska fältets exponentiella avtagande i supraledande elektriska ledare], innebär samtidigt ett fördjupat krav på absolut skärpa i den relaterbara fenomenbeskrivningens detaljer; Ämnet berör elektronmassans komponenter. Det blir — speciellt tillägnat ämnet supraledning — med andra ord (ytterst) viktigt att understryka en detaljerad fattning (väl relaterbar beskrivning) på, och konsistens i, alla elektrofysikens detaljer för att få en begriplig, relaterbar bild av funktionssättet. Supraledningen som ämne har tidigare inte behandlats i Universums Historia.

— För att betjäna den nämnda »klarhetens villkor», har en vidare (förtydligande) genomgång gjorts i de viktiga detaljer som berör induktionen och magnetismen;

— Inledningsvis från Induktionsfysik och Supraledning understryks Förtydligandet att Faradays Lag INTE innefattar »variabelt B genom fix ledare». Experimentella observationer enligt PARALLELLEXPERIMENTEN (1994) beskrivs här uttömmande med Rakledarinduktansens Härledning tillsammans med jämförande data från etablerad facklitteratur och tillhörande Kalkylkort i utförlig sammanställning av de ursprungliga beräkningsgrunderna (1994).

En senare mera utvidgad beskrivning finns i PEX2024Intro ¦ PEX1994OriginalDetails — induktionen och magnetismen mera i detalj

Se särskilt från det mera utförliga avsnittet i DIPOLBEGREPPET med TheQmove.

— RESULTATBILDEN beskrivs detaljerat i Induktionsbegreppet i relaterad fysik, tillsammans med utförligt relaterade härledningar till de ingående sambandsformerna.

— Speciellt central är Teorin för allmänna materieinduktansen.

— Med tillkomsten av Internet Archive, och de numera (2011) allmänt och gratis tillgängliga ursprungliga originalförfattningarna i PDF-format av bl.a. James Clerk Maxwell — den moderna akademins teoretiska grunder i speciellt magnetismen — har i den relaterade fysikbilden mera detaljerat sammanfattande beskrivningar utformats, främst från den centrala MAGNETISKA KRAFTLAGEN, för att betjäna alla detaljerade jämförelser. Dessa detaljer fullständigar (eller är i varje fall tänkta att göra det) helhetsbilden med en jämförande analys och genomgång av (de ofta påpekade svårfattliga, och svårbegripliga) grundbegreppen från Maxwell (Maxwells hydrostatiska virvelanalogier, Maxwells magnetiska mekanik, Magnetiska kraftlagen från Maxwell). Citat (med kommentarer, jämförelser och analyser) från etablerade källor ingår där så befunnits påkallat.

END.

Editor2011X9

Induktionsfysik och Supraledning

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Induktionsfysik och Supraledning

innehåll

Induktionsfysik och Supraledning

Förord

Induktionsbegreppet i relaterad fysik — Supraledningens absolut teoretiska grunder i relaterad fysik

Induktionsbegreppet — inledning

Max ström

Kausallogik — referens

Jämförande induktanser

Tabell 1 — mätdata för kopparledarna med konventionell jämförelse

Änddelarna

L0ref

KvärdetRef

Härledningar till koefficienterna

ξ, xsi (K i PRIMÄRINDUKTANSEN I SAMMANFATTNING)

Xsi-FAKTORNS ALLMÄNNA INNEBÖRD

η, eta

Eta-FAKTORNS ALLMÄNNA INNEBÖRD

Härledningen till Allmänna Materieinduktansen

Mikro0ref

MikroLref

Accelerationen av laddningarna i materialet

Allmänna materieinduktansen

Laddningsmobilitet, elektronmobilitet

HYPERPHYSICSref

KopparRef

Drifthastigheten

Maxwells ekvationer — allmän översiktlig KVALITATIV orientering i relaterad fysik

Induktans och induktion — kompletterande beskrivning till originalförfattningarna med Induktionsdipolens Uppkomst

Induktionsdipolens uppkomst

Figurbeskrivning

Illustrerad beskrivning

Kausallogikens samband

MAC-sambandet — hur konventionella sambandet framgår ur relaterade

Fackreferenser till Lk — induktanssambandet i MAC

Citablock elektromagnetisk induktion

Induktionsspänningen i raka sekundärledare

Integrationen utmed d

Integrationsgränserna för variabla induktionssymmetrier

Intervallblockets förtydligande

Tilledarnas B-fält

Planalternativet

Blockalternativet

Elektriska laddningens växelverkan med B-fält

Blockalternativet, samband

Supraledning

Inledning

Resonansmönster

Supraledning — fenomenformen enligt relaterad fysik

Kvantiserad ström via h/2e

Uppkomst — historiskt med fenomenbeskrivning

SUPERCONDUCTORSvideosekv

BCS-teorin

Meissnereffekten

Citat Meissnereffekten

Sambandsformen enligt TNED

Kalkylkortet

gDivergens

Reduktion

Förtydligandet till Faradays EMI

Förord till Induktionsfysik och Supraledning

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 MASS TABLE ¦ s9–65—9–86

m_n = 1.0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0.000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1.66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1.66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1.66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1.66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1.6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1.660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2.99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6.62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1.602 · t19 C .................... FOCUS MATERIEN 1975s666

[BA]. BONNIERS ASTRONOMI 1978

[BKL]. BONNIERS KONVERSATIONS LEXIKON Band I-XII med SUPPLEMENT, Alb. Bonniers Boktryckeri, Stockholm 1922-1929

[FM]. FOCUS MATERIEN 1975 — Fysikens, kemins och astronomins historia. Allt från atomen till universum — fysik, kemi, jordvetenskap och astronomi

SIGMA 1-6, MATEMATIKENS KULTURHISTORIA av James R. Newman, Forum 1965, efter originalet The world of mathematics 1956

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

MAC, i Universums Historia ofta använd förkortning för Modern Akademi (eng. Modern ACademy)

TNED — Related PHYSICS And MATHEMATICS — Se särskild djupbeskrivning av innebörden i begreppet relaterad framställning.

TNED — from The Beginning

———————————————

The Atomic Nucleus -- 1 - 4 ¦ TAN 1 ¦ TAN 2 ¦ TAN 3 ¦ TAN 4 ¦ AllKeplerMath ¦ AllKeplerMath+

FOR THE UNINITIATED READER (Sep2024):

We have two Resolution 217 in our known history — detailed to the last universal atom;

IN ORDER OF DISCOVERY-RECOGNITION — Resolution 217Short:

• Resolution 217(A) UDHR10Dec1948 — Universal Declaration of Human Rights: 8 introducing paragraphs P1-8,

30 following articles A1-30 — study them and try to learn them from within — test, question, analyze 24/7

— here in UH referred to as Humanright, the only (reminded) known universal Humanright knowledge domain:

gravitation, electricity: light, heat, magnetism — LIFE: The Periodic System of The Elements (KeplerResonances).

— The Atomic Spontaneous assembly — no decision, no voting — to you and me (and all the other fuckups).

P1: ” Whereas recognition of the inherent dignity and ..”. Guaranteed Eternal Protection. 24/7. No breaks.

• Resolution 217 (10Jan2024) — the TNED deduced rJCIRCLE-CheopsPyramidEnvelopingSphereRadius (rJ) number

defining the actual Flinders Petrie 1883 measured Cheops Pyramid (half) base (b) — in to a precision of

99.9999832% — verifying the (ContractedConstruct) TNED/Petrie investigated Cheops Building Plan: all Petrie’s measured values verified (BpointDetermination). It connects to The Origin of Script (See TheCLAIM — questioning the already long ago 2000y questioned idea of a Geographic Israel: the splitting of humanity — and the quest of its reunion).

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också

RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

SHORT ENGLISH — TNED in general is not found @INTERNET except under this domain

(Universe[s]History, introduced @INTERNET 2008VII3).

TNED or Toroid Nuclear Electromechanical Dynamics is the dynamically equivalent resulting description following the deductions in THE PLANCK RING, analogous AtomNucleus’ Deduction. The description according to TNED is related, meaning: all, each, details claim to be fully logically explainable and understandable, or not at all. With TNED is (hence) also understood RELATED PHYSICS AND MATHEMATICS. See also the emergence of the term TNED in AtomNucleus’ Deduction.

Senast uppdaterade version: 2024-10-25

*END.

Stavningskontrollerat 2011-10-09.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

∫ √ τ π ħ ε UNICODE — often used charcters in mathematical-technical-scientifical descriptions

σ ρ ν ν π τ γ λ η ≠ √ ħ ω → ∞ ≡ ↔↕ ħ ℓ

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ σ ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ← ↑ → ∞ ↓

ζ ξ

Arrow symbols, direct via Alt+NumPadKeyboard: Alt+24 ↑; 25 ↓; 26 →; 27 ←; 22 ▬

23 ↨ — also 18 ↕; 29 ↔

Alt+NumPad 0-25, 26-...

☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓

→←∟↔▲▼ !”#$%&’()*+,-./♦812...

*

PNG-utdataformerad

åter till portalsidan · portalsidan är www.UniversumsHistoria.se