TGF2014b — Universums Historia

UNIVERSUMS HISTORIA ENLIGT RELATERAD FYSIK OCH MATEMATIK | TGF2014b | 2014II18 | a BellDHARMA production | Senast uppdaterade version: 2021-06-11 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor ·

BlixtTGF2014a ........ Part 1 GRUNDBEGREPPEN I MOLNBILDNINGENS TEKNISKA FYSIK — basbegreppen till

BlixtTGF2014b ........ Part 2 BLIXTURLADDNINGENS FYSIK — Jordströmmar och Molnbildning

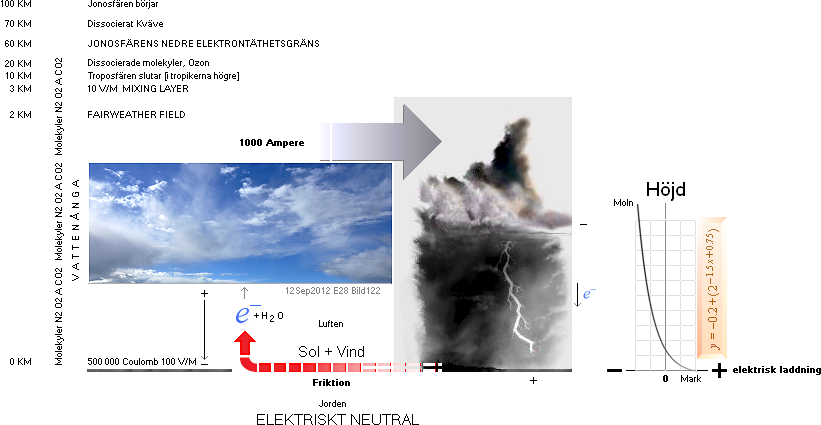
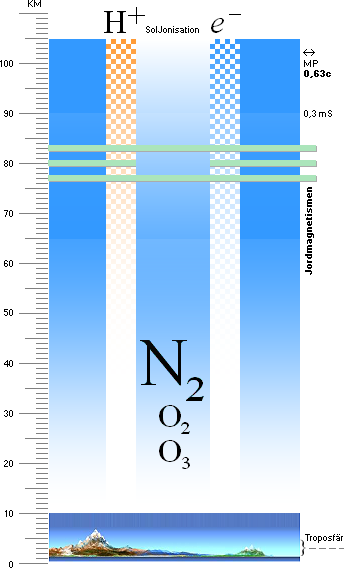
BLIXTURLADDNINGENS FYSIK 2014 — Solenergin på Jordytan verkställer ständigt olika former av massvariationer inom fasta volymer:

Solen arbetar på Jorden — VIA EN KONSTANT VOLYM

Planetströmmen

Parförening

H2Odata

KelvinEkvationens begränsningar

Naturblixt

InduktionInfluens

Jordfältet

Förutsättningarna

H2Opar

Jordströmmen

INTE KONDENSATION

Droppbildningen

KOF

TrädBlixtar

GRUNDBEGREPPEN: Från BlixtTGF2014a — 2014III27 — Blixturladdningens fysik 2014

OMFATTNINGEN är det första som slår en i vattenfysiken:

— Den ena detaljen leder till den andra, som kräver genomgångar av den och den gruppen deldetaljer, och som i sin tur nödvändiggör inblick i just de detaljerna, och som ... . Och så vidare. Knappast något ämne verkar ha så vida förgreningar i fysiken som just vatten: egenskaper, sättet att verka, allmänna tillämpningar, här speciellt för blixturladdningens fysik och allt som sammanhänger med den. Jämför innehållsförteckningen — den absolut mest omfattande i ett enskilt UniversumsHistoriaDokument. Och det är bara grundmatematik. Det har tagit (ett) år att sammanställa.

Bildkälla: Författarens arkiv · MONTAGE: 11Jun2013 E12 Bild 105 — 4Jul2012 E13 Bild17 · Nikon D90

Vissa svårigheter i möjligheten att FÖRSTÅ SAMMANHANGET i väderleken har visat sig via den etablerade litteraturen:

— Beskrivningen I ETABLERAD MENING av hur den cirkulerande vardagsluften uppför sig på varierande avstånd från marken (altitud) beträffande grundbegreppen temperatur, tryck, och volym — generellt bastermerna i allmänna gaslagen — har visat sig YTTERST svårtillgänglig — om uppgiften gäller detaljerad inblick enbart på kredit av etablerad nomenklatur [PascoCitat].

— Genomgången i avsnitten

VRF | EKoG | ATFT

visar en del av sammansattheterna. Inblicken i dessa förutsätts här bekant.

— För särskilt sammanfattad beskrivning med länkar, se från Jordfältet.

Kort sammanfattning:

Relaterad fysik:

Om ingen saklig argumentation existerar som vill dementera saken kan situationen tydligen förstås så:

— Trycket (p) avtar inte med höjden (h) på grund av att volymen (V) expanderar [pV=kT] (HjälpSambandet [HydroTransiten]) [JAVK], utan på grund av att massbundenheten (m) avtar med växande avstånd (h) från Jordytan via Jordgravitationens tyngdkraft,

Ytgravitella skaltrycket:

p = F/A = G(m/R)²/4πR² = Gm²/4πR⁴

= Gm²/4π(R+h)⁴ ; m = 5,975 T24 KG, G = 6,67 t11 JM/(KG)², R[ekv]=6,378 T6 M:

Jordatmosfärens massa är obetydliga bråkdelar av Jordmassan och m kan därför ses konstant i den jämförande grovräkningen:

Ekvivalenta Jordmassyttrycket:

p = m/A = m/4πR²

= m/4π(R+h)² ;

Bägge dessa visar entydigt ATT och HUR trycket p entydigt avtar med avståndet h från Jordytan.

och därmed avtagande täthet (ρ) på FAST volym — Jordatmosfärens volym är konstant [JAVK];

— Att expandera volymen i en cylinder genom att dra ut kolven

pV=kT=konstant: trycket p avtar, volymen V ökar [AGKEisoterm]

är alldeles detsamma i netto som att i EN BESTÄMD (komprimerad) FAST utgångsvolym V

med bestämt tryck p — atmosfäriska skiktets specifika hydrofysik till jämförelse

behålla volymen V (och trycket p) och minska tätheten ρ [grek. rho], och därmed minska massan m, enligt

pV=p[m/ρ]=kT=(ρV/U)R·T=konstant.

— Alltså: att tillåta att en viss gasmängd läcker ut ur [konvekterar åter till marken i Jordtroposfärens fall] den bestämda volymen V. Det beskrivningssättet verkar inte finnas synligt i den etablerade litteraturen i ämnet vattenbildning i moln. Man ser där istället (ensidigt) typbegrepp som ”adiabatisk expansion”. Se utförlig förklaring från MOTEF och AdiabaticMAC. Det är viktigt att vi har koll på dessa grunder.

— Jordgravitationen (F=ma=G[m/r]²) tvingar Jordatmosfären att tunnas ut från Jordytan och uppåt.

Jordtroposfäriska tryckets variation med höjden (h) över marken beskrivs av sambandet, se AktuellaSlutgraferna,

p = 101300e^{0,0341579/(0,0065/1,000067^h
– 288,15/h)} ; Tryckvariationerna inom Jordtroposfären i överensstämmelse med PDAS

OBS gäller endast upp till max 10KM.

Det är också precis så vi SER Jordatmosfärens olika hydrostatiskt BESTÄMDA skikt [JAGVH]:

— Inom en BESTÄMD volym (1M³) — ett bestämt RUM som vi kan flytta godtyckligt uppåt/nedåt och undersöka egenskaperna i — varierar temperatur (T), tryck (p), täthet (ρ) och gaskonstant (k) med varierande höjd, konstant volym. Se sammanställda grafer med samband och jämförande internationella tabelldata i Slutgraferna.

I syntes — Uppvärmning, transport, avsvalning:

Uppvärmning verkställs från Solen med transport och naturlig avsvalning av vattenånga för molnbildning inom ett fast Jordtroposfäriskt hydrostatiskt system där temperatur, tryck och täthet avtar entydigt (inom klimatsfären = troposfären) med växande höjd (upp till grovt 10 KM).

Speciellt det etablerade begreppet ”adiabatisk” förefaller ansvara för en speciellt stor del av språk- och begreppsförbistringen i ämnet molnbildningens elementära fysik. Se särskilt utförlig, jämförande och relaterad, exemplifierat belysande genomgång i ATFT:

— Det nämnda begreppet, eller termen över huvudtaget i relaterad mening som det har visat sig, har uppenbarligen, tydligen och väl relaterbarligen inte inom termodynamiken att göra.

Se även vidare i AGLV (ALLMÄNNA GRUNDBEGREPP FÖR LUFT OCH VATTENÅNGA), om ej redan bekant.

— Nedan följer allmänna referensartiklar för genomgång av de grundbegrepp med relaterad matematisk fysik vi tvivelslöst måste ha genomlyst för att kunna beskriva vattenbildningens molnfysik — även i ENKLA termer. Eftersom hela den framställningen (här) tillkommit i ljuset av motsvarande observerade oklarheter i etablerad litteratur, eller där ev. förklaringar framgår, ges motsvarande jämförande beskrivningar med citat och referenser där så är möjligt.

GVK, GasVärmeKapacitivitetsKonstanten

Relativa gastätheten via T

Ř, R-ca(ron) — Se grundsambandet med härledning i LuftBasic:

— RELATIVA tätheten för en viss gas (luft, vattenånga, eller annat) tillsammans med luft i H2O-fallet beräknas (isobariskt: för variabel volym, pV=kT) genom att först fastställa en relativ tryckvärmetäthetskonstant (gasvärmekapacitivitetskonstant, J/KG°K) eller en Relativ värmekapacitivitetskonstant (här Ř »R-ca[ron]») via STP för rena gastäthetsvärdet (i vattenångfallet ρ_H2O), och sedan tillämpa konstanten på variabla temperatur/tryckförhållanden:

Från allmänna gaslagen:

pV = kT ; pV/m = Tk/m = TŘ = p/ρ ; ρ = p/TŘ ; p = ρTŘ ; Ř i J/KG°K:

Ř = (p/T)ρ^–1 ; tryckvärmetäthetskonstant vid STP [Ř][GVK] J/KG°K

ρ = (p/T)Ř^–1 ;

För vattenånga — p/T = k/[V=1M³} = 101325 Pa / 273,15 °K = 370,95002 J/°K vid STP — blir Ř lika med

Ř_H2O = (101 325 N/M²)/(0,803919 KG/M³)(273,15 °K) ; M³N/M²KG°K=NM/KG°K=J/KG°K:

M³N/M²KG°K = (N/M²°K)/(KG/M³): tryck-temperatur-täthets-konstant, pTρ-konstant:

= 461,42711 J/KG°K ; Vattenångans Relativa pT-täthetskonstant vid STP, »ÅNGtryckvärmetätheten»

För luft vid STP blir Ř lika med

Ř_L = (101 325 N/M²)/(1,2916296 KG/M³)(273,15 °K) ; »RcaLuft»;

= 287,19535 J/KG°K ; Luftens Relativa pT-täthetskonstant vid STP, »LUFTtryckvärmetätheten»

Med T=273,15=T0 i p/T fås LUFTENS/vattenångans alternativa temperaturer 0 till 100°C enligt

pT₀/T = p(273,15°K)/(n°C + 273,15°K) ; Då enbart temperaturen ändras

= p/(1 + n°C/273,15°K) ; TemperaturAktuella LUFT/H2O-tätheten beräknas då

ρ = (p/T)Ř^–1 ; Relativa gastätheten [GVK]

= p[n°C + 273,15°K]^–1Ř^–1 ;

Vid n=100°C och bibehållet STP-tryck 101325 Pa [volymen V i pV=kT tillåts utvidgas] är vattenångans täthet tydligen

ρ_100°C = 0,588478 KG/M³

Hålls temperaturen konstant 100°C och trycket p ökar härifrån — pV=kT — måste volymen V i motsvarande mening avta om allmänna gaslagen gäller:

— Enda slutsatsen blir en fasövergång: vattenångan övergår till FLYTANDE VATTEN med BETYDLIGT lägre volym:

— Idealt i normal rumstemperatur är vatten ca 1250 ggr tätare än vattenånga.

— För att få vattnets täthet 1000 KG/M³ från 0,59 KG/M³ måste trycket IDEALT alltså öka 1000/0,59=1695ggr.

— Hålls istället volymen konstant och trycket varierar med T [pV=kT], sker ingen förändring i vattenångans täthet: p/T=kostant.

Täthetsformen ovan kan användas för att bestämma gasens egentäthet — det är gastätheten utan hänsyn till gasens samverkan (blandning) med andra gaser, typ vattenånga för sig och torr luft för sig.

— För gasernas blandform generellt, se GVK. För slutsambandet som använder alla ovan, se TMekv.

LpVar, Lufttryckets variation med höjden

Jordtroposfäriska tryckets variation med höjden (h) över marken beskrivs av sambandet, se AktuellaSlutgraferna,

p = 101300e^{0,0341579/(0,0065/1,000067^h
– 288,15/h)} ; Tryckvariationerna inom Jordtroposfären i överensstämmelse med PDAS

OBS gäller endast upp till max 10KM.

Jordatmosfärisk översikt:

Allmänna gaslagen får tydligen förstås direkt tillämplig på ett givet Jordtroposfärsikt skikt (0-10KM) på samma sätt som vårt markområde är det. Vi kan alltså obehindrat utföra beräkningar INOM ett visst hydrostatiskt bestämt troposfäriskt skikt med allmänna gaslagens hjälp. Vi måste bara se till att beräkningarna just innefattar det aktuella skiktets hydrostatiska profil (Hydrotrycket), och inget annat. Sambandsformerna för alla Tpρk finns sammanställda i AktuellaSlutgraferna.

— Mera grovt förenklade rent linjära motsvarigheter finns i EtableradeGrovvärden.

— Utgår vi generellt från konstant [primär] volym [GRUNDBEGREPPEN] — inom en hydrostatiskt bestämd domän [bestämd höjd över Jordytan] —

ingen exakt max avgränsad vertikaldistans finns: håller vi oss till max 100 meter i differens ger aktuellt beräknade tryckvärden (p) överensstämmelser i procent

0M/100M: 101,19 % i markplanet

10000M/10100M: 101,41 % 10KM upp, se PDAS Tabell6 i Blixt2014.ods AktuellaSlutgraferna —

skulle vi med ovanstående grovräkning räkna med [p/T=k/V=konstant] att INGEN nämnvärd TÄTHETSÄNDRING [ρ=p/TŘ] sker inbördes mellan gaserna luft och vattenånga då temperaturen varierar (och förutsatt att inget vatten utfälls ur vattenångan).

— Relationsbilden i slutänden via sambanden från TillämpningM [RhoVmålet] [Mex] [RHbasic] TillämpningM Tabell5A i Blixt2014.ods

— med kubiska medelavstånden för respektive vattenångmolekyler och luftmolekyler

— visar emellertid en mera nyanserad bild:

— De inbördes variationerna luft/vattenånga blir betydande när alla möjliga kombinationer mellan parametrarna RH | h | T beaktas, se slutformen i TMekv med kalkylcellerna i ovannämnda kalkyltabell. Den resultatbilden blir därmed den slutligt helt avgörande för ändamålet i det uppdraget att försöka beräkna vattendroppsbildningen (MultiH2O). Uppgiften är här att försöka avgöra och se om och hur blixturladdningens fysik kan avancera vidare på den detaljen..

MLT, MinLokalaTekopp, Exempel

— Hur är det [JAVKbasic]?

— I kökets rumstemperatur står en varm kopp te (Jordmarken) och ångar fuktig luft uppåt (kandidater till molnbildning över Jordmarken). Normala lufttrycket i rummet (pL) BÖR inte påverkas av den lilla tekoppens ångbad. Så: Hur fördelas trycken mellan den idealt ångfria rumsluften (pL) och den del där vattenångan (pV) är märkbar?

— Grundbegreppen i AGLV visar att det i själva den smala ångpelaren måste gälla p=pV+pL; Utan tekoppen skulle det bli p=0+pL. Enligt vår överläggning skulle emellertid pL inte ändras: tekoppens smala ångpelare (Jordmarkens partiellt uppvärmda markångslingor) påverkar knappast det omgivande rummets lufttryck. Och alltså skulle tillkomsten av den smala ångpelaren från tekoppen visa att ångpelarens totala lufttryck (den uppåtstigande fuktiga Jordmarksuppvärmda luftpelaren) är större än det omgivande lufttrycket med ångtryckets belopp (pV): p=pV+pL > pL=0+pL.

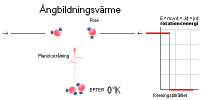
Ökas trycket (p) inom en konstant volym (V) med en associerad temperatur (T), och förutsatt bevarad fundamental gaskonstant k=pV/T, utsäger allmänna gaslagen (pV=kT) en ekvivalent tryckenergi (pV=E) som utpekar en motsvarande högre temperaturenergi (kT=E): tryckökningen motsvarar en högre rörelseenergi (temperatur) hos gasbollarna: gasen försöker breda ut sig i varje omgivande rums LÄGRE temperatur-tryckprofil.

— Så: varför visas ingen nämnvärd breddexpansion hos tekoppens ångpelare? Vad jag kan se, stiger (0,6M/S) ångslingorna från tekoppen lugnt och fint rakt uppåt. Ingen synbar bredexpansion.

— Det enkla JAVKbasic-köksexperimentet visade just, vad vi kan förmoda, orsaken: avsvalningstakten 122°C/M/S. Den uppvärmda mera voluminösa fuktiga ångluften krymper snabbt ihop [Flaskexperimentet] i takt med värmeläckningen till det omgivande rummet [VLASF], och som, som vi tror här, garanterar att den smala fina ångslingan bevaras, utan synbar bredexpansion.

— Det finns, här veterligt, ingen anledning att förstå molnbildningstekniken på någon annan fason (men upplysningen att den ståndpunkten skulle vara felaktig eftersöks regelbundet, med aldrig sinande stort intresse, och mottages tacksamt om den visar sig). Min slutsats: Den enkla tekoppens ångslinga utpekar, fast i mindre omfattning, molnbildningens tekniska fysik (i en perfekt naturmodell: utan fysiskt begränsande inneslutningar).

Saken kan alltså möjligen förstås så:

Genom tillkomsten av vattenånga [i konstant visuell referens volym [VizEx]] i luften ökas totala lokala trycket från idealt torra primära luften (pL) som summan [AGLV] av komponenternas enskilda idealt fria tryck, p=pV+pL — konstant referensvolym förutsatt [VizEx];

ISNAP

Ref. ISNAP., 2014-03-19 Instiutute for Structure and Nuclear Astrophysics

http://isnap.nd.edu/Lectures/phys20054/Lecture_7_Clouds_and_Aerosols-2.pdf

bildsida2:

”The total pressure of moist air is P = P_dry+ P_H2O with P_H2O being the partial

vapor pressure exerted by the water molecules in moist air.”,

”

SVP = A · e^βT

A = 6.11 mbar

β = 0.067 °C^–1

Alternative empirical formulas exist in abundance in literature and on the web!”,

— ISNAP-Webbkällan ger en genomgång med alla aktuella samband.

Aktuella sambandets numeriska form i referenssidan ovan verkar dock (som författaren möjligen också uppmärksammat) bara stämma delvis.

— De numeriska värden [likvärdigt samhörande till jämförelse med DewPoint-grafen i Wikipedia, Calculating the Dew point 2014-03-19] som verkar mera samstämmiga med andra liknande referenskällor finns sammanställda i Empiriska samband för vattenånga, samma som referenserna i SVP som använts i samtliga beräkningar i detta dokument.

Jämför nedan med citatets ovan:

Webbläsarna förstör presentationsformatet: ovan originalet i bild. Nedan TEXT Size 9pt — som verkar lämnas i fred:

SVP = C · e^a^/(1+b/T) ; Temperaturen T i °C: maximala luftfuktighetens ångtryck

SVP vattenångans mättnadstryck i Pascal = N/M²

C 610,78 Pa

a 17,2694

b 238,3 °C

T Temperaturen i °C: Obs: för T=0°C blir e-exponenten motsvarande 0: SVP [0°C] = C = 610,78 Pa.

Sambandsformen i ISNAP-källan innehåller inte tillräckligt antal parametrar.

Ytterligare för konstant Jordatmosfärisk volym

— högtryck och lågtryck i väderleken

Betrakta atmosfärens masstryck generellt: När Solen kommer fram och värmer upp en marklokal, tillförs rörelseenergi = värme likaledes lokalt (värmeexpansion).

— KNAPPAST ändras (ökas) Volymen vid Jordytan då [MOTEF], utan snarare bibehålls via Jorgravitationens fasta inneslutning med olika interna värmegrader — typ Min Lokala Tekopp [MLT]: Lokala lufttrycket (i lokalt atmosfäriskt skikt) kommer att variera (direkt proportionellt) med temperaturen (pV=kT): varmt och soligt betyder i allmänhet högtryck (värmeexpansionsvolym); kallt och mulet betyder i allmänhet lågtryck (värmekontraktionsvolym). Volymen på Jordytan som innesluter typ troposfären ändras, vad vi vet, inte med de variationerna.

AGLV, ALLMÄNNA GRUNDBEGREPP FÖR LUFT (L) OCH VATTENÅNGA (V) — relaterad matematisk fysik

ALLMÄNNA GRUNDBEGREPP FÖR LUFT (L) OCH VATTENÅNGA (V)

Inom en och samma bestämda volym (V):

— Tätheterna (ρ) förhåller sig som massorna (m):

ρ = m/V

= (m₁ + m₂ + m₃ + ... + m_n)/V ;

ρ_V/ρ_L = (m/V)_V/(m/V)_L ;

ρ_V/ρ_L = m_V/m_L ; Tätheterna förhåller sig som massorna

m = ρV

= (ρ₁ + ρ₂ + ρ₃ + ... + ρ_n)V ;

m_V/m_L = (ρV)_V/(ρV)_L ;

m_V/m_L = ρ_V/ρ_L ; Massorna förhåller sig som tätheterna

FN. fuktighetsnivån eller VÅM, VattenÅNGAmassAndelen, AGLV

m_V/m_L = M ; Fuktighetsnivån

VattenÅNGAmassandelen — eng. Mass MIXING ratio [ofta x_m] eller humidity level.

m_V

———— = 1/(1 + m_L/m_V) ; eng. specific humidity, specifika luftfuktigheten:

m_V + m_L

= q ;

1/(1 + m_L/m_V) = 1/(1 + ρ_L/ρ_V) ; Specifika luftfuktigheten.

JämförandeTabell

Jämförande tabell DIFFERENSEN AKTUELL VIKTSANDEL VATTENÅNGA M OCH SPECIFIK LUFTFUKTIGHET q inom Jordtroposfären [RH=100%] enligt grundsambanden i Slutgraferna

[i överensstämmelse med PDAS internationella tabelldata]:

——————————————————————————————————

h M	M %	q %	M/q %	T °C	T °K
10000	0,01	0,01	99,99	-50	223,15
8000	0,05	0,05	99,95	-37	236,15
6000	0,12	0,12	99,88	-24	249,15
4000	0,27	0,27	99,73	-11	262,15
2000	0,55	0,55	99,45	2	275,15
0	1,04	1,03	98,97	15	288,15

Från Kalkylkortet PDAS Tabell6 i Blixt2014.ods

Tabellvärdena ovan exemplifierar vårt arbetsbord i molnbildningens fysik inom troposfären:

— Differenserna mellan M (aktuella viktsandelen vattenånga i luften) och q (specifika luftfuktigheten) ligger som mest i andra decimalen (maxFEL 1,03% vid Jordytan). Den differensen är helt försumbar då komplexet i vilket fall innehåller betydligt vidare differenser sett enbart till (medelvärdena globalt) mellan tropikerna (troposfären upp till grovt 17 KM) och våra nordligare breddgrader (troposfären upp till grovt 10 KM) [59%].

— I den här framställningen FÅR vi därför MED praktiskt taget SAMMA KVANTITATIVA INNEBÖRD använda termen eller begreppet specifika luftfuktigheten analogt (»ekvivalent») med M=m_V/m_L = aktuella vattenångans massandel i luften (eng. mass mixing ratio).

— Se även jämförande grafer mellan de två nära lika sätten i SVPgrafen.

RHbegin, relativa luftfuktigheten

BEGREPPET RELATIV LUFTFUKTIGHET (RH eng. Relative Humidity) är M/M_RH100% = m_V/m_Vmax

Relativ luftfuktighet (RH) betyder samma som förhållandet mellan aktuell viktsmängd vattenånga (m_V) och den maximala (m_Vmax):

— Wikipedia, till exempel, har inte den befriande verifikationen: Wikipediaartikeln (Maj2014) på Humidity diskuterar ”Relative humidity” i termer av ”ratio of partial pressure”. Det är OK, men komplicerar ämnesfattningen för den som inte REDAN är expert.

— Däremot har (bl.a.) ArizonaUniversity den befriande beskrivningen:

AURH

THE UNIVERSITY OF ARIZONA — Atmospheric Sciences —

THE ATMOSPHERE AND THE WEATHER [2014-05-06]

http://www.atmo.arizona.edu/students/courselinks/fall12/atmo336/lectures/sec1/humidity.html

”The Relative Humidity (RH) is simply the mixing ratio divided by the saturation mixing ratio.

actual (measured) water vapor content U U

Relative Humidity ≡ RH = ——————————————————— = ——

maximum possible water vapor amount (saturation) U_s

”.

Den ordningen FÖRENKLAR HÖGELIGEN begripbarheten i hela komplexet:

RH = (m_V/m_L)/(m_V/m_L)_RH100%

= m_V/m_VRH100%

= (ρ_V/ρ_L)/(ρ_V/ρ_L)_RH100%

= ρ_V/ρ_VRH100%

RH = M/M_RH100%

= m_V/m_{V RH100%}

= ρ_V/ρ_{V RH100%}

Relativa Luftfuktigheten är — inom en och samma omgivande massbaserade luftdomän [m_L] — lika med massförhållandet mellan AKTUELL vattenånga och MAX vattenånga.

m_V/m_L = ρ_V/ρ_L ; Massorna förhåller sig som tätheterna

Se vidare i grundbegreppen från TillämpningM.

RHbasic, RH, se även i RHkomplementet — praktik i H2O i luft

PROBLEMET är inte att sambanden är komplicerade. Problemet är att »det spöregnar konstant» med MÄNGDEN sammansättningar i sambandsfloran. Att hålla reda på »vilka som säger vad» har vid genomgången

så länge den RELATERBARA framställningen ännu innehåller luckor — jämför sambandsformerna nedan med vad som visas i etablerad litteratur: finns inte i den synliga webbdelen

visat sig bli (exceptionellt) frustrerande. Ända fram till vändpunkten då den klara och koncisa befrielsen inträder — på några ytterst få rader — JÄVLAS ÄMNET KONSTANT. Bara först efter ändlösa återbesök med omsorgsfull koll på INNEBÖRDEN i termerna, upprepade kontrollräkningar på exempel som visar meterstora taggar utåt KONSTANT — för att man missar olika detaljer — med ständiga avbrott på grund av att det fattas avgörande VÄGMÄRKEN i ämnet, kommer befrielsen. Precis som det ska vara. Och är det inte så, står vi inte ut då heller, eftersom motståndet blir för LITET.

— Vi ska här försöka hänga med i naturströmmen genom att försöka precisera detaljerna.

VATTENÅNGANS AKTUELLA TÄTHET

för orienterande grovräkningar i samband med molnbildningen och därmed blixturladdningens fysik

Vattenångans aktuella täthet (ρ_V) inom Jordtroposfären framgår teoretiskt via ett speciellt samband (som framkommit genom denna presentations genomgångar — alla värden i anslutning till PDAS internationella tabellvärden) med kännedom om

· relativa luftfuktigheten (RH mellan 0-1 motsvarande 0-100%),

· höjden över Jordytan (h MAX10KM för Jordtroposfären) och

· lokala luftområdets aktuella temperatur (T i °C) enligt [TillämpningM]

ρ_V = RH · ρ_{V RH100%} ; Vattenångans aktuella täthet

ρ_V = RH · [(15°C – h·0,0065°C/M + 273,15°K)]^–1 · (1,323359 KG°K/M³) · e^{17,2694/(1+238,3/T°C)} ;

h-värdet i meter — OBS max 10KM, se översikt i Jordtroposfären — ger den aktuella troposfäriska hydrostatiskt bestämda lokalens temperatur [Se även motsvarande basformen till typen 0,0065°C/M i ATFT].

— T-värdet i °C i e-exponenten avser den aktuella lufttemperaturen i vilken vattenångan finns. Speciellt uppvärmd markluft som stiger uppåt genom de olika h-skikten kan i början — sett för varje specifikt h-skikt [PDAS T-värden] — förstås besitta ett något högre T-värde (i luftpelarens inre) än det aktuella h-skiktets fasta hydrostatiska T-värde. Jämför vårt eget markskikt, typ rumstemperaturen (med ett litet område med lokalt uppåtstigande ångande varmvatten): vi kan utföra experiment i den T-miljön, typ FlaskExperimentet med olika lokala T-värden, både högre och lägre.

— RELATIVA LUFTFUKTIGHETSTALET (RH = 0-100%) STYR andelen vattenånga (M) i luften inom en viss visuellt avgränsad volym:

— RH-talet reglerar eller styr M-talet (eng. MassMixingRatio, eller här andelen vattenÅNGmassa M=m_V/m_L=ρ_V/ρ_L) [AGLV].

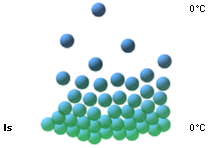
— FLASKEXPERIMENTET visar hur uppvärmd fuktig luft åstadkommer volymminskning då den fuktiga luften kallnar. Vi kan se den processen genom en fast visuell luftvolym där vattenångan samlas allt tätare med sjunkande temperatur (RH går mot max), och allt glesare med stigande temperatur (RH går mot noll).

— Med utgångspunkt i en given h-lokal (som ger p[h]T[h]) från ett givet M=ρ_V/ρ_L=m_V/m_L kan vi också se hur vattenångans massandel varierar med variationer i RH (0-1 motsv. 0-100%). Till exempel, som följd av lokala temperaturökningar (Solen kommer fram: vattenmolekylerna glesas ut) eller lokala temperaturminskningar (Solen går i moln: vattenmolekylerna tappar rörelseenergi och samlas).

— Jämför även RH-inverkan i räkneexemplet Mex:

p_V/p_L = (1,6070767)m_V/m_L = (1,6070767)M

M_RH100% = [(101325 Pa)/p(h)](3,75086 t3) · e^{17,2694/(1+238,3/T°C)}

= [p(h)]^–1(380,05588 Pa) · e^{17,2694/(1+238,3/T°C)}

M = (RH%/100)M_RH100%

Sambandsformerna understryker att andelen vattenÅNGmassa ÄNDRAS med variationer i RH-värdet: temperaturfluktuationer. Jämför DaggpunktenGrafVänster: för givet ångtryck (given daggpunkt) varierar RH omvänt omgivningstemperaturen.

FörtydligatExemplifierat:

— Säg att RH=0%: ingen vattenånga finns närvarande: M=0=0/m_L. Det är uppenbarligen korrekt.

— Säg att RH=100%: viss vattenånga finns närvarande: M=m_V/m_L. Det är uppenbarligen korrekt.

— Så MÅSTE alltså RH-värdet STYRA M-basen enligt

M = RH%·M_RH100%

Se härledningar från AGLV [ALLMÄNNA GRUNDBEGREPP FÖR LUFT (L) OCH VATTENÅNGA (V)] och TillämpningM.

M_RH100% betyder alltså maximala massandelen vattenånga i luft vid en viss lufttemperatur (T), motsvarande RH-värdet 100%, vid ett visst tropo-hydrostatiskt tryck p(h) på höjden h över Jordytan (gäller upp till max h=10KM [PDAS internationella Tabelldata]).

— Notera (som i räkneexemplet Mex) att M-formen KAN användas för att »relativisera maxandelen vattenånga» till RH-andelens del: Som räkneexemplet visade [MrelRef]: man utför bara »M=RH%·M_RH100%».

— Huvudrollsinnehavaren är alltså M. Inte RH. Men eftersom även variationerna i RH (DaggpunktenGraferExVä) tydligen styr M-formen, har RH-variationerna avgörande betydelse DÄRMED att RH=0 också medför att M=0:

— »M har huvudrollen» — men RH (temperaturen, hydrotrycket) »bestämmer scenariot».

VizEx

— Men HUR fungerar det i en FIX lokals volym (typ »daggbildning i dalsänkan»): Säg 70%RH vid 15°C, med sjunkande temperatur (T): luftens temperatur går mot den lägre daggpunkten (t), analogt RH-värdet går mot 100%.

— Ingen vattenångmängd tillkommer. HUR kan M tillväxa med RH?

— Sammandragning (i dalsänkan).

— REFERENSVOLYMEN (1M³) är ÖPPEN: vi ser bara till tillståndet inom det geometriskt avgränsade rummet, som en genomskinlig rent visuell KUB inom vars motsvarande fysiska verkliga rum vi studerar MOMENTANA (under dt) tillstånd:

— Vattenångtätheten ökar — M=m_V/m_L=ρ_V/ρ_L — inom den fast givna referensvolymen om T sjunker i fast omgivande p.

— Jämför Flaskexperimentet: gaserna strömmar inåt referensvolymen — och därmed högre täthet, som tydligen medför högre massinnehåll i den aktuellt visuella referensvolymen:

— SAMBANDSFORMERNA VISAR TYDLIGEN att man kan se det som att den omgivande markluftens täthet (ρL) inte förändras, och inte heller dess luftmassa (mL) inom den visuellt begränsade fasta referensvolymen: det är bara vattenångan som varierar signifikant: tätheten ökar, ångmassandelen ökar.

Volymkropparna illustrerar det vi tydligen måste använda i fattningen på variationerna:

— rent visuella referensvolymer.

— Men: Var finns den ETABLERADE motsvarigheten i den naturbeskrivningen?

— Den finns (i varje fall) innefattad i citatdelen från Arizona University [‡] i definitionen av relativa luftfuktigheten:

RH = (m_V/m_L)/(m_V/m_L)_RH100%

= m_V/m_VRH100%

— Det är, ju, Flaskexperimentet det, på pricken: Temperaturen avtar, den yttre materiellt avgränsade plastflask- volymen minskar; i det inre av flaskans fuktiga luft tillväxer vattenångtätheten inom en fast visuell volym med motsvarande högre massandel vattenånga.

— Jag vill mena det (men jag hittar ingen direkt etablerad bekräftande mening som säger det klart) att DET också är PRECIS vad som händer inuti markuppvärmd uppstigande luft som avkyls naturligt genom värmeläckningen: vattenångan i det inre av luftpelaren ökar i täthet med avtagande temperatur: den avtagande tätheten gynnar vattendroppsbildning (då daggpunkten nås) därmed att MEDELFRIVÄGEN, medelavstånden mellan vattenmolekylerna, just är i avtagande via värmeläcket. Det finns aldrig någon volymär expansion att tala om i samband med vattendroppsbildning i molnbaserna. Men, som sagt, den meningen behöver verifieras, eller dementeras.

— Se även Studieexempel, molnbildning under 5 minuter: ingen synbar bredexpansion.

Se vidare genomgång i SVP.

SVP — Integralformen — H2O i luft — Saturation Vapor Pressure, mättnadsångtryck

se särskilt SVP-grafen och pSVPgrafen

Vattenångans utövande EGENTRYCK

En etablerad sambandsform (utvecklades under 1800-talet av Clausius och Clapeyron, se Integralformen nedan)

för vattenångans absolut maximalt utövande EGENTRYCK vid olika temperaturer är

SVP = C · e^a^/(1+b/T) ; Temperaturen T i °C: maximala luftfuktighetens ångtryck

Temperaturen T i °C; SVP eng. förk. Saturation Vapor Pressure, sv. mättnadsångtryck: gäller vid max luftfuktiighet RH=100%

Ref. Empiriska samband för vattenånga;

Ett samlingsdokument finns på webben @INTERNET som sammanfattar de olika likartade SVP-sambandsformerna,

University of Colorado — SATURATION VAPOR PRESSURE FORMULATIONS, Holger Vömel, 2011

http://cires.colorado.edu/~voemel/vp.html

SVP vattenångans mättnadstryck i Pascal = N/M²

C 610,78 Pa Specifik vattenångkonstant [Källverken ger ingen närmare specificering]:

a 17,2694 Specifik vattenångkonstant

b 238,3 °C Specifik vattenångkonstant

T Temperaturen i °C: Obs: för T=0°C blir e-exponenten motsvarande 0: SVP [0°C] = C = 610,78 Pa.

Nedre temperaturgränsen går via SVP=1 som ger T = –64,542431 °C.

— Notera att OLIKA KÄLLVERK HAR NÅGOT OLIKA KOEFFICIENTFORMER i e-exponenten. Se exv.

ISNAP 2014-03-19 Instiutute for Structure and Nuclear Astrophysics http://isnap.nd.edu/Lectures/phys20054/Lecture_7_Clouds_and_Aerosols-2.pdf bildsida2;

— Deras samband [vid grov prövning] stämmer bara delvis med ovanstående.

— För T=100°C ges SVP[100°C] = 100659,2 Pa, vilket ligger NÄRA luftens normaltryck vid STP.

SVP = 610,78 · e^{17,2694/(1+238,3/T°C)} ; Vattenångans mättnadstryck via T°C

ln[SVP/(610,78)] = (17,2694)/[1 + (238,3)/T] ; integralform: ln(p/P) = a(1+b/T)^–1

(17,2694)/ln[SVP/(610,78)] = 1 + (238,3)/T ;

(17,2694)/ln[SVP/(610,78)] – 1 = (238,3)/T ;

T°C = (238,3)[(17,2694)/ln[(RH%/100)SVP/(610,78)] – 1]^–1

— Se IntegralformenSVP som orienterar i SVP-sambandets härledning.

— Är temperaturen

0°C (vid normaltrycket 1 atm = 101325 Pa=N/M²) och ingen vattenånga finns närvarande, ligger hela tryckbilden på luften — minimalt, praktiskt taget noll vattenånga finns då;

— Är temperaturen

100°C (vid normaltrycket 1 atm = 101325 Pa=N/M²) och dessutom RH=100% och alltså MAXIMAL vattenånga finns närvarande, ligger (litet mer än)

m_V/m_L = ρ_V/ρ_L ; Massorna förhåller sig som tätheterna [‡]

Separata resultatvärden framgår i Kalkylkortet TillämpningM Tabell 5A

halva tryckbilden istället på vattenångan — minimalt, praktiskt nära runt hälften luft finns då.

— EFTERSOM således luft och vattenånga DELAR PÅ TOTALA ATMOSFÄRISKA TRYCKET (p = pLUFT + pH2O) och vattenångan garanterat INTE kan vara maximal MELLAN 0 och 100°C, BÖR aktuella vattenångsmängden i luften (atmosfären) för alla möjliga utetemperaturer 0 till (i varje fall runt max öken) 50°C kunna bestämmas VIA kännedom om ett specifikt vattenångtryck med hänsyn till olika temperaturer och lokala atmosfäriska totaltryck.

— Det vattenångtryckets samband är JUST ovanstående SVP-formalia — gånger aktuella procenten (RH-värdet) luftfuktighet: RH=100% ger SVP som ovan, och sedan motsvarande LINJÄRT mindre för motsvarande RH-värden 100-0%, analogt koefficienter 1 till 0.

— Uttrycker förhållandet mellan partiella trycken (pH2Oactual)/(pLUFTactual) också aktuell vattenånghalt i luften?

— Ja

— om pH2Oactual också innefattar luftens aktuella relativa luftfuktighetstal (RH i %)

— enligt

(RH%/100)SVP = pH2Oactual ;

(RH%/100) = pH2Oactual / SVP

OCH vi dessutom lägger till en proportionalitetskonstant lika med förhållandet mellan gaselementens atomvikter,

(m_V/m_L) = (18,0154u)/(28,952127u)

= 0,6222478

= R

som ger (V, vattenångan; L luften)

R = (m_V/m_L =ρ_V/ρ_L)/(p_V/p_L)

Se utförligt nedan i Förhållandet mellan gaselementens atomvikter.

— Specifika luftfuktigheten anges [ISNAP] konventionellt som förhållandet mellan vattenångans täthet i luften (ρH2O=ρ_V) och luftens vattenfria täthet (ρLUFT=ρ_L), lika med förhållandet mellan viktsmängderna (m) inom samma volym:

q = (ρ_V)/(ρ_V + ρ_L) ; ρ_L utan vattenånga

= 1/(1 + ρ_L/ρ_V) ; Specifika luftfuktigheten

Wikipedia [2014-03-19 Humidity] definierar omvända kvoten ρH2O/ρLuft — via samma volym massförhållandet — som

”Specific humidity (or moisture content) is the ratio of water vapor, m_v, to unit mass of dry air m_a in any given volume of the mixture, and is sometimes referred to as the humidity ratio.[7] Specific humidity is approximately equal to the "mixing ratio", which is defined as the ratio of the mass of water vapor in an air parcel to the mass of dry air for the same parcel.[7]”.

Wikipediaartikeln samma sambandsform som ovan men med massan m istf. tätheten.

VLM

Luftfuktighetsnivån (eng. humidity level) anges [ISNAP] konventionellt som mass mixing ratio (massblandningsförhållandet)

— här hellre [VLM] VattenångaLuftMASSandelsFÖRHÅLLANDET — inom samma volym

x_m = ρ_V/ρ_L

= m_V/m_L

= (0,622478)p_V/p_L ;

Deltrycken förhåller sig genom en konstant som delmassorna

— Förhållandet mellan partiella trycken p_V=(pH2Oactual)/p_L=(pLUFTactual) uttrycker också aktuella vattenånghalten i luften.

— Den halten är alltså en MIX av totala mättnadshalten gånger relativa luftfuktighetstalet (RH%): (RH%/100)·MAX.

— Hur får man aktuella vattenångskomponenterna ur det?

— Partiella vattenångtryckets MAXIMALA del bestäms för varje given temperatur av SVP-sambandet. Det motsvarar ett RH%-värde lika med 100.

— Aktuella vattenångtrycket för aktuell luftfuktighet vid bestämd temperatur bestäms då som sambanden nedan (RH) anger: pH2Oactual=(RH%/100)SVP; (RH%)=pH2Oactual/SVP.

GasUrel, Förhållandet mellan gaselementens atomvikter

— Konventionellt [ref. ISNAP] benämns sambandsformen [här tecknad komprimerat, tryckrelationen]

p_V=pH2Oactual / p_L=pLUFTactual som ett massblandningsförhållande (eng.) Mass Mixing Ratio även benämnt humidity level:

ρ = m/V ; pV = kT; V = kT/p ; ρ = mp/kT ; p = kTρ/m ;

ρ = mp/kT ; kT=konstant ;

ρ_V/ρ_L = (m_Vp_V/kT)/(m_Lp_L/kT)

= (m_Vp_V)/(m_Lp_L)

= (m_V/m_L)(p_V/p_L)

= ([18,0154u]/[28,952127u])(p_V/p_L)

= (0,6222478)p_V/p_L; MassMixing Ratio

= (m_V/V=1M³)/(m_L/V=1M³)

= m_V/m_L ;

m_V/m_L = ρ_V/ρ_L ;

p_V/p_L = (1,6070767)m_V/m_L ;

Förhållandet mellan andelen vattenångsmassa (m_V) och luftmassa (m_L) gånger ~1,6=1/0,622 är samma som förhållandet mellan motsvarande partialtryck för vattenångan (p_V) och luften (p_L).

— Det förhållandet uttrycker emellertid INTE RH-värdet (RH-värdet anger bara andelen vattenånga av maximalt möjliga).

RH, se även i RHkomplementet och RHbasic

— RH-värdet anger procentuella andelen luftfuktighet av ett visst maximivärde;

— MassMixingRatio (M nedan) anger procentuella andelen vattenånga av luftmängden;

— För att få fram RH-värdet ur ovanstående måste OCKSÅ maxmängdens vattenångtryck (vid aktuell temperatur och tryck) vara känd.

— Eftersom SVP (Saturation Vapor Pressure) bestämmer vattenångtrycket för så mycket vattenånga som aktuell lufttemperatur tål, givet tryck, är också SVP-värdet samma som maximala vattenångtrycket pH2Omax=SVP med luftfuktigheten RH=100%.

— Aktuella luftfuktigheten — aktuella RH-värdet i % — ges då från

p = pLUFT + pH2O ; pH2Omax = SVP med RH=100% ;

p_H2Oactual = (RH/100)SVP ; Vattenångans aktuella atmosfäriska deltryck

som

— Vi vet VANLIGTVIS inte värdet på den aktuella atmosfärens vattenångtryck: sambandet ovan är rent formellt. Mera vanligt är att vi vet relativa luftfuktighetsvärdet [RH%], och på den vägen kan räkna fram ett motsvarande pH2Oactual via känd temperatur i SVP.

RH% = 100p_H2Oactual/SVP ; Aktuella Luftfuktigheten i %

VattenÅNGAviktsmängden, max H2O i luft — RH

AKTUELLA VATTENÅNGTYRYCKET är relativa luftfuktigheten (RH-värdet) gånger SVP.

— Procentuella vattenÅNGAviktsmängden (M=m_V/m_L) av luftviktsmängden kan vi lösa ut på följande former:

p_V/p_L = (1,6070767)m_V/m_L ; m_V/m_L Anger vattenångans viktsmängd i förhållande till den torra luftens viktsmängd [MassMixRatio]

= m · m_V/m_L ; Vi sätter m_V/m_L som MassMixingRatio = M — »procentuella andelen vattenånga»

= m · M ;

M = m^–1p_V/p_L ; p_L Torrlufttrycket:

p_V = p_Lm·M ; RH=100% ; m·M = (1,6070767)·m_V/m_L ;

p_VRH = p_H2Oactual ; Inkluderat RH-värdet:

= (RH%/100)SVP

= (RH%/100)p_Lm·M ;

RH% = 100p_H2Oactual/p_Lm·M

SVP = p_LmM ;

p_L = SVP/mM ;

RH% = 100p_H2Oactual/SVP

= 100p_H2Oactual/p_Lm·M ;

TillämpningM, H2OmaxLuft

Tillämpning M — TillämpningM | H2O Tabell5A i Blixt2014.ods

Vi beräknar (Saturation Vapor Pressure) maximala SVP-värden (RH=100%) för givna temperaturvärden (T°C) — 0-max100°C — och utnyttjar havsnivåns standardtryck STP enligt p=101325 Pa som grov allmänt jämförande preferens för att få motsvarande procentuella MassMixingRatio=M-värde vid STP enligt

M = m^–1p_V/p_L ; Ungefärliga viktsandelen vattenånga i luften

= p_V/(1,6070767)(101325 Pa) ; U_L/U_V = 1,6070767 ;

= p_V/(162 837,04 Pa)

= SVP/(162 837,04 Pa)

= 610,78 · e^{17,2694/(1+238,3/T)}/(162 837,04 Pa)

= 0,00375086· e^{17,2694/(1+238,3/T)} ;

M_RH100% = (3,75086 t3) · e^{17,2694/(1+238,3/T°C)} ; Vattenångans mättnadstryck via T°C

= m_V/m_L ; Procentuella viktsandelen absolut maximalt mättad vattenånga i luft vid STP:

= ρ_V/ρ_L ;

ρ_{V RH100%} = ρ_L · M_RH100% = ρ_L · (3,75086 t3) · e^{17,2694/(1+238,3/T°C)} ; STP-formen:

förtydligat

M_RH100% = m_V
RH100%/m_L

= (3,75086 t3) · e^{17,2694/(1+238,3/T°C)}

För att få motsvarande M(RH100%)-profil vid andra specifika tropo-hydrostatiska områden p(h) än p(STP) gäller tydligen

M(h)_RH100% = [(101325 Pa)/p(h)] · (3,75086 t3) · e^{17,2694/(1+238,3/T°C)}

= [(101325 Pa)/p(h)] · M(STP) ;

M(h)_RH100% = [p(h)]^–1(380,05588 Pa) · e^{17,2694/(1+238,3/T°C)} ; VattenÅNGmassandelen på h över Jordytan [max10KM] vid T°C

Procentuella viktsandelen absolut maximalt mättad vattenånga i luft vid aktuell altitud h — hMAX=10KM [Troposfären]

= m_V
RH100%/m_L

= ρ_{V RH100%}/ρ_L ;

ρ_{V RH100%} = ρ_L · M(h)_RH100%

= ρ_L · [p(h)]^–1(380,05588 Pa) · e^{17,2694/(1+238,3/T°C)} ;

= p(h)·U_L/RT · [p(h)]^–1(380,05588 Pa) · e^{17,2694/(1+238,3/T°C)}

= U_L/RT · (380,05588 Pa) · e^{17,2694/(1+238,3/T°C)} ; ×U_L eliminerar UL ur e-koefficienten [endast UV återstår]:

= 1/RT · (11003,426 Pa) · e^{17,2694/(1+238,3/T°C)} ; AllCheckedOK[8Maj2014]:

TMekv

= 1/T · (1,323359 KG°K/M³) · e^{17,2694/(1+238,3/T°C)} ; Ekvationsformen som används i Kalkylkortet Tabell 5A:

= 1°K/T · (1,323359 KG/M³) · e^{17,2694/(1+238,3/}^T^°C)

ρ_{V RH100%} = [(15°C – h·0,0065°C/M + 273,15°K)]^–1 · (1,323359 KG°K/M³) · e^{17,2694/(1+238,3/T°C)} ;

Temperaturformen [‡] T i °K i 1/T ansluter till altitudtemperaturen från marknivåns 15°C i PDAS internationella tabelldata för värden INOM Jordtroposfären med hMAX=10KM: NOMINELLA [»internationellt standardiserade»] altitudtemperaturen från marknivåns 15°C. Det T-värdet ges alltså som direkt HYDROSTATISK funktion av altituden h [LapseRate-formen] och kan därför INTE bestämmas separat.

— Temperaturformen T i °C i e-exponenten däremot tillhör SVP-formen och avser explicit vattenångtryckets aktuella temperatur, samma som aktuella lokala luftfuktighetstemperaturen. Därmed kan i varje fall rent teoretiskt variabla temperaturer användas på en fast hydrostatiskt bestämd altitud.

ρ_V = RH · ρ_{V RH100%} ; Vattenångans aktuella täthet

p_V/p_L = mM = m·m_V/m_L ;

RH·mM = p_V/p_L = m·m_V/m_L ;

p_V = RH · SVP

p_V/p_L = mM

RH = p_V/SVP

= p_V/p_LmM

= m_V/m_LM ;

RHM = m_V/m_L = p_V/p_Lm = ρ_V/ρ_L

SVP-grafen, SVP förk. Saturation Vapor Pressure —

Se även pSVPgrafen

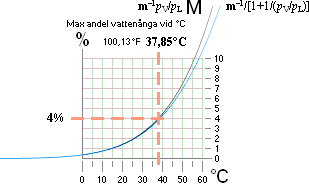
GRAFEXEMPLET NEDAN visar grovsvaret på frågan HUR mycket % vattenånga MAX (M) det kan finnas i luften — vid olika temperaturer T°C.

Procentuella VattenÅngMättnaden, RH

Grafen visar maximala (RH%=100) luftfuktigheten i motsvarande % viktsandel vattenånga av luftens viktsdel. Svarta grafen: M = m_V/m_L. Blå grafen visar till jämförelse motsvarande %-värde i förhållandet mellan vattenångtrycket och summan av torrlufttrycket och vattenångtrycket. Se även vidare i Daggpunkten.

Svarta — %= m^–1p_V/p_L:

100/[(0.00375)[è'17.2694/(1+[238.3/5x])]]

Blå — %= m^–1/[1+1/(p_V/p_L)]:

100/[1+1/(0.00375)[è'17.2694/(1+[238.3/5x])]]

— 4%-gränsen ligger runt T=37°C (37,85°C = 100,13°F). I etablerade korridorer [WebbRef] anges grovt sett det värdet som ett Jordglobalt maxmedelvärde för hur mycket vattenånga luften omkring Jordytan innehåller. Med maximala Jordytstemperaturen runt 60°C (sedan blir vi nog mer eller mindre stekta) blir motsvarande maxvärde 12,09% viktsandel vattenånga.

Väljer vi allt lägre tryckpreferensvärden

mindre preferenstryck än exemplets 101325 Pa — motsvarande allt högre h upp ovan mark — kan grovberäknas upp till max 2KM

pL = (101325 Pa – h ·11,6625 Pa/M)

flyttas kurvformen alltmer åt höger, analogt allt lägre %-värden för en given temperatur (T°C).

— Resultatformen visar översiktligt, verkligen, att andelen vattenånga i vår vardagliga luft är ytterst ringa. Men PÅ den delen hänger, tydligen HELA Jordens blixturladdningsfysik.

Integralformen — SVP-sambandet — Se även SVP-grafen med vattenandelen i %

SVP-sambandets integralform — relaterad sammansättning

—————————————————————————————————————————————————————————————————

HUR SVP-SAMBANDET HÄNGER IHOP RENT INTEGRALT FRÅN ENKLA ENERGIEKVIVALENTER

— enligt relaterad matematik

pSVPgrafen

Vattenångans mättnadstryck vid STP — Vattnets kokpunkt 100°C vid normaltrycket 101325 Pa

— TRYCKVÄRDET i Pascal [N/M²] avtar proportionellt mot graden av den s.k. RELATIVA LUFTFUKTIGHETEN [RH], denna är i grafen nedan lika med 100%; se från RHkomplementet.

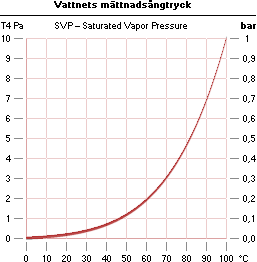
Graf Unit20p

(1/10000)([610.78]è'17.2694(1+238.3/[10x])'–1)

— Diagrammets T4 Pa betyder 10.000 Pa per enhet. 1 bar = T5 [Pa = N/M²].

— Vattnets kokpunkt — 100°C ovan — definieras etablerat som situationen då SVP-värdet tangerar lokala p-värdet: vattenångtrycket = lokala atmosfäriska trycket.

— För övriga fall [konv. Daltons lag] fördelas aktuella atmosfäriska trycket på summan av vattenångtrycket [beroende på luftfuktighet] + aktuella [torra, eng. dry] lufttrycket.

— EXEMPEL, grafvärden ovan: Vattnets kokpunkt vid ca 60°C gäller vid atmosfäriska trycket ca 20.000 Pascal [grovt ca 2KM ovanför troposfären, eller ca 12KM upp].

— NOTERA FÖR PREFERENSERNA att termen TRYCK för gaspartiklar [i Jordatmosfären] alltid betyder en VISS rörelseenergi [E], erhållen från någon värmekälla [Solen].

— Se även mera utförligt i grundteorin från Allmänna Gaslagen, om ej redan bekant.

Vi utgår från de enkla energiekvivalenterna i relaterad fysik;

— Uppgiften gäller att sammanställa en allmän integralform för tryck (p) som funktion av temperatur (T) för vattnets värmekapacitet E[H2O]/T = 4181,3 J/°K [ref., Wikipedia, SPECIFIC Heat capacity] — vilket leder till en allmän matematisk-fysikalisk formulering av vattenångans mättnadstryck (eng. Saturation Vapor Pressure).

UNIVERSELLT:

— Energibasen E[H2O]/T innebär att sambandsformen INTE är hydrostatiskt beroende — sambandsformen är alltså inte beroende av specifika atmosfäriska tryck: alltså tryck som ändras med tyngdkraftsaccelerationen: sambandsformen gäller oberoende av omgivande rums tillstånd, ENBART för vattnets energikapacitet: värmebildningen för vatten — fasen med ångbildning, resultatdiagrammet ovan — beror ENBART på rörelseenergin = temperaturen. Det betyder att sambandsformen KAN tillämpas på och insättas i samband med alla möjliga atmosfäriska tillstånd. Se även exempelbeskrivningen ovan under grafbilden, om ej redan bekant.

— Eller enklare uttryckt: vattnets ångbildning anpassar sig ALLTID till rådande lokala atmosfäriska förhållanden enligt ovanstående resulterande grafbild, se härledningen nedan.

— Se även vidare noteringar i slutet med sambandens koefficienter. Följande visar de rent formella greppen i relaterade termer.

RELATERAD MATEMATIK:

pV = kT = E ; V = kT/p ; E/k = T : Från Allmänna gaslagens sambandsgrupper:

pV/T = k = E/T ; E/T = värmekapaciteten J/°K

p/T = k/V = (E/T)/V ; Vi undersöker för H2O med suffixet V [vatten] och varianten [variationsekvationen, derivatan]:

dp/dT = k_V/V

= (E_V/T)/V

= (E_V/T)/k_VT/p

= pE_V/k_VT² ; Varianten dy/dx = y’ = f (x)(y) är en FOIVEVK

[en FörstaOrdningensInhomogenaVariant med EnVariabelKoefficient]

y’ + f (x)(y – A) = 0 ; FOIVEVK-varianten, allmän form: dy/dx = y’ = f (x)(A – y)

med differentialekvationen

dy/(y – A) = – f (x) · dx

med lösningen

ln (y – A) = – F(x)

och exponentformen

y = A + C e^–F(x)

med A=0, y=p och x=T och f(T) = K·T^–2 :

p = C e^–F(x) ; Koefficienten C får enheten Pascal och därmed en tryckkoefficient p0:

= p₀e^–F(x) ;

–F(x) = –(E_V/k_V) ∫ dT/T² ; För att 1/T²-integralen ska fungera som bestämd integral måste T-formen ha fasonen (1+T/b)² enligt

T := [1 + (T – 273,15°K)/a] = [1/a][a + (T – 273,15°K)] = [1/a][a + t] = 1 + t/a:

— I annat fall urartar funktionen med e^obegränsat;

Jämför rena integralen för 1/T²: F[T^–2] = T^–1/(–1):

–F(x) = (E_V/k_V)/T ; Integralens fullständiga lösning:

p/p₀ = e^ (E_V/k_V)/(T) ; T i e-nämnarens exponent betyder en obestämd integral; den blir bestämd om funktionen flyttas i x-led enligt

= e^ (E_V/k_V)/(c±T) ; Vi genomför istället motsvarande direkt bestämda integral från grundformen, som nyligen enligt ovan

[Vi ska komma fram till det redan kända SVP-sambandet; härledningen anpassas för det]:

e-exponentens integralform:

— Är absoluta temperaturen (t) noll gäller då e-exponentens integralkoefficient som (E_V/k_V)(1/a): Eller uttryckt direkt mera bekvämt med T-variabeln i °C:

T := [1 + T/b] = [1/b][b + (T°C)] = [1/b][b + T] = 1 + T/b:

— Är absoluta temperaturen (t) noll gäller då e-exponentens integralkoefficient som (E_V/k_V)(1/b):

Vi har då en differentell utgångsform till e-exponentintegralen som

dT/(1+T/b)² ; T°C = T°K – 273,15°K

Vi har nämligen i enlighet med FORMLAGARNA i EXP7 med direkt anpassning till vår aktuella nämnarform att

1/(1+T/b)² = 1/T²(1/T + 1/b)²

= T^–2(T^–1 + 1/b)^–2

= (P)ⁿDn(P) ; Därmed:

(P) = (1/T + 1/b) ;

Dn(P) = (1/T + 1/b)’ = (–1/T² + 0) = –T^–2 ;

∫ –(P)ⁿDn(P) = –(P)ⁿ⁺¹/(n+1) ; EXP7:

dT/(1+T/b)² = dT/T^–2(T^–1 + 1/b)^–2 ;

∫ dT/T^–2(T^–1 + 1/b)^–2 = ∫ dT/(1+T/b)² ; Vilket vill säga:

∫ dT/(1+T/b)² = 1/(1+b/T) : enligt

∫ dT/T^–2(T^–1 + 1/b)^–2 = ∫ dT/(1+T/b)² ; T°C = T – 273,15°K

= –(T^–1 + 1/b)^–1/(–1)

= (T^–1 + 1/b)^–1

= 1/(1/T + 1/b)

= b/(b/T + 1)

= b/(1 + b/T) ; Vi prövar återderiveringen:

Dn b(1 + bT^–1)^–1 = (–1)b(1 + bT^–1)^–2 · (0 + [–1]bT^–2)

= b(1 + bT^–1)^–2 · bT^–2

= b²(1 + bT^–1)^–2 · T^–2

= b²/T²(1 + bT^–1)²

= b²/(T + b)² ; T = 0°C garanterar att e-potensen bevaras på exponentens koefficient:

= 1/(T/b + 1)²

= 1/(1 + T/b)² ; Således integranden åter.

1/(b+T)² = 1/b²(1 + T/b)² ;

e-exponentens fullständiga form:

∫ dT/(b+T)² = (1/b²) ∫ dT/(1+T/b)² ; e-exponentens fullständiga integrala lösning således

(E_V/k_V) ∫ dT/(b+T)² = (E_V/k_V)(1/b²) ∫ dT/(1+T/b)²

= (E_V/k_Vb²) · b/(1 + b/T)

= (E_V/k_Vb)/(1 + b/T) ; (E_V/k_V = t) → °K ; b → °K ; Och därmed

p/p₀ = e^ (E_V/k_Vb)/(1 + b/T) ;

p = p₀e ^{(EV/kVb)/(1 + b/}^T⁾ ;

Jämför källformens samband

pSVP = 610,78 · e^{17,2694/(1+238,3/T°C)} ; Vattenångans mättnadstryck via T°C

Koefficienterna:

Med b = 238,3°K och koefficienten a = 17,2694 = E_V/k_Vb blir E_V/k_V lika med 238,3·17,2694 = 4115,298 vilket stämmer ungefärligt med uppgiften [Wikipedia, SPECIFIC Heat capacity] för vatten, 4,1813 J/gram/°K = 4181,3 J/KG°K; värmekapaciteten samma värde men i J/°K.

— Koefficienterna är resultat av utveckling och forskning seklerna 1800-1900.

Utgångsformen (1+T/b)² måste alltså börja på typen (absoluta temperaturvärden, vi bryter ut b-termen)

b²(b+T)² = [b(b+T)]² = [bT₀]²;

— Notera värmeformen (E/T): Det är bara materialets (här vattnets) värmekapacitet (J/°K) och temperaturen (T) — och en absolut lägsta tryckfaktor (610,78 Pa) — som styr sambandsformen: det finns inga explicita »beror-på-lufttrycket»-parametrar med i bilden.

RHkompl, SVP-sambandets integralform

KOMPLETTERAS pSVP-sambandet med en faktor RH% — relativa luftfuktigheten i % — ges motsvarande AKTUELLA VATTENÅNGTRYCKET [ref. Empiriska samband]

AKTUELLA VATTENÅNGTRYCKET MED HÄNSYN TILL RELATIVA LUFTFUKTIGHETEN:

För given luftfuktighet RH% avtar aktuella vattenångtrycket med avtagande lufttemperatur T.

p_H2Oactual = (RH%/100)(610,78)e^{17,2694/(1+238,3/T°C)} ;

— RESONEMANGET till den härledande formen för SVP-sambandet i moderna kvarter (Apr2014) är (betydligt) mera omständligt i etablerade referenser (som kräver särskilda insikter):

ETABLERAD JÄMFÖRELSE:

Jämför en etablerad beskrivning — hur SVP-sambandets sammansättning beskrivs etablerat

integralformen ln(p/P) = a(1+b/T)^–1 har tydligen upplösningen [vi deriverar tillbaka] [Formlagarna], [EXP7]:

Dn a(1+bT^–1)^–1 = (–1)a(1+bT^–1)^–2· (–1)bT^–2

= ab(1+bT^–1)^–2·T^–2

= ab[T(1+bT^–1)]^–2

= ab[(T+b)]^–2

= ab/(b+T)²

= a/(1+T/b)² ; Differentialkvoten [derivatan] blir:

dy/dx = [(p/P)]a/(1+T/b)² ; = dp/dT

= pa/P(1+T/b)² ;

dy/[(p/P)] = a/(1+T/b)² · dx ; Resulterande differentialekvationen.

Grundformen baseras tydligen på tryckändring med temperaturändringens kvadrat;

— I korthet — en mera ingående beskrivning finns på

MIT — 8.4 THE CLAUSIUS-CLAPEYRON EQUATION

(APPLICATION OF 1ST AND 2ND LAWS OF THERMODYNAMICS) [2014-03-25]

http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node64.html

Konventionella etablerade grundformen, MIT-källan ovan, för omvandling från värme till mekaniskt arbete [eng. Carnot cycle] ger grundformen i differentialer

dp/dT = h(f [g]) · [T(V[g] – V[f ])]^–1

p anger tryck

T anger temperatur

h anger värmemängd

f,g anger suffix

V anger volym

Idealiseringar med förenklingar som går ut på att

V[f ] är försumbart

V[g] ~ RT/p med R som [gas]konstant

leder så till den förenklade varianten [differentialkvoten]

dp/dT = h(f [g]) · [T(RT/p – 0)]^–1

= h(f [g])p/RT²

Med [TYP] R=P och h(f[g])=ab och T=[273,15°K + T°C]=[b + T°C] fås så

dp/dT = [(p/P)]a/(1+T/b)² ; = dy/dx

Därmed differentialekvationen

dp/[(p/P)] = a/(1+T/b)² · dT

som ger SVP-formen.

FOIVEVK-varianten allmänt:

Jämför även ett tidigare separat utvecklingsexempel med Strålintegralen — den kan också tillämpas direkt på FOIVEVK:

y’ + f (x)(y – A) = 0 ; FOIVEVK-varianten, allmän form: dy/dx = y’ = f (x)(A – y)

med differentialekvationen

dy/(y – A) = – f (x) · dx

med lösningen

ln (y – A) = – F(x)

och exponentformen

y = A + C e^–F(x)

— Tillämpningsexemplet med »STRÅLINTEGRALEN» — ljusets avmattning i intensitet (I) med distansen (x) i materialgenomgång (µ) — kan också användas direkt på FOIVEVK-varianten med A=0 enligt

dy/dx = µI = y’ = f (x)(A – y) ;

Med A=0 och f (x)=µI ges variantformen dy/dx = y’ = f (x)(A – y) → dy/dx = µI(–y) som direkt FOIVEVK-teckenkorrekt ger

differentialekvationen

dI/I = – µ · dx

med lösningen

ln I = – F(x)

och exponentformen

I = C e^–F(x) = I₀e^–µx

— C-koefficienten får automatiskt startvärdets intensitetsmaximum I₀ vid x=0, samt att hela funktionen direkt framträder avtagande med växande x. I utvecklingsexemplet för strålintegralen måste MINUSµ formuleras manuellt separat från början i varianten dI/dx. Här kommer minusdelen in automatiskt.

DAGGPUNKTEN — i givet atmosfäriskt skikt

forts. frn. SVP-grafen

Beskrivning — Daggpunkten

Daggpunkten — vattendroppbildningsgränsen — termerna t T RH

— DAGGPUNKTEN (eng. Dew Point) är den lägre värmegrad (t) ett moln med bestämd högre temperatur (T) och bibehållen relativ luftfuktighet (RH% eng. Relative Humidity) ska anta utan tryckändringar (isobariskt) (p) för att vattenångan i molnet ska kunna bilda vattendroppar.

— Allmänna gaslagen pV=kT HARMONIERAR MED en sådan ordning OM tryckfaktor p och gaskonstant k bevaras enligt p/k=T/V=konstant:

— T kan avta från T mot det lägre t om, OCH ENDAST DÅ, den aktuella luftvolymen V vid T antar en motsvarande trängre volym.

— Naturliga förutsättningar för den typen finns överallt där lokala temperaturminskningar förekommer: i moln som inträder kallare områden från varmare (speciellt uppströmningar från markuppvärmd luft mot kallare områden), moln som faller i tillfällig skugga, och generellt (tillkomsten av) centrala molndelar som solljuset inte direkt når in till; växande ångtäthet med ökad luftvattenånga bidrar till solljusspridningen och därmed temperatursänkning inåt molnmassan.

Förklaring — Daggpunkten

— Bråkdelen av största är lika med hela minsta:

Maximala vattenångtrycket [SVP=p(MaxH2Oair | t)] via en aktuell atmosfärisk lokala temperatur (t) kan uttryckas på samma ekvivalenta maximala vattenångtrycksvärdes (p) bråkdel (RH%/100) via ett motsvarande matchande högre temperaturvärde [SVP=p(H2Oair | T)] — [SVP(t)=(RH%/100)SVP(T)] — och som då definierar maximala vattenångtrycket vid RH%=100 enligt [SVP(t)=SVP(T)]: Det lägre temperaturvärdet t i den tryckekvivalensen (isobar[ism]en) kallas daggpunkt (eng. dew point).

— Det är samma situation som då ingen mer vattenånga ryms i luft med relativa luftfuktigheten RH% (eng. Relative Humidity), och vattenångan därför (för varje minsta ytterligare isobariska — med bibehållet tryck — temperatursänkning [övermättning]) kommer att fälla ut synligt vatten (H2Odata | NoDrop).

— Dessa sammanhangsbegrepp visar sig (ytterst) svårformulerade (och svårfattliga, även i etablerade led) så länge sambandsformerna och deras villkor inte är tydligt beskrivna. Se viss relaterad orientering i VattenWebben.

Samband — Daggpunkten

Sambanden för daggpunktens matematik finns i syntes i SVP-sambandet (eng. Saturation Vapor Pressure):

SVP = (610,78)e^{17,2694/(1+238,3/}^t⁾

= p(MaxH2Oair | t) ;

Maximala vattenångtrycket SVP via t kan då skrivas ekvivalent via en bråkdel (RH%/100) av ett högre maxvattenångtryck från ett högre T-värde enligt

p(H2Oair | T) = p(MaxH2Oair | t)

= (610,78)e^{17,2694/(1+238,3/}^t⁾

= (RH%/100)(610,78)e^{17,2694/(1+238,3/}^T⁾ ;

(RH%/100) = p(H2Oair | T)/(610,78)e^{17,2694/(1+238,3/}^T⁾ ; Relativa luftfuktigheten [eng. Relative Humidity]

med ekvivalenterna

Hela Minsta = Bråkdelen av Största ;

p(MaxH2Oair | t) = p(H2Oair | T)

(610,78)e^(17,2694)(1 + 238,3/t) = (RH/100)(610,78)[e^17,2694(1 + 238,3/T)] ;

e^(17,2694)(1 + 238,3/t) = (RH/100)[e^17,2694(1 + 238,3/T)] ;

(17,2694)(1 + 238,3/t) = ln((RH/100)[e^17,2694(1 + 238,3/T)]) ;

1 + 238,3/t = 17,2694[ln((RH/100)[e^17,2694(1 + 238,3/T)])]^–1 ;

238,3/t = –1 + 17,2694[ln((RH/100)[e^17,2694(1 + 238,3/T)])]^–1 ;

t = 238,3(–1 + 17,2694[ln((RH/100)[e^17,2694(1 + 238,3/T)])]^–1)^–1 ;

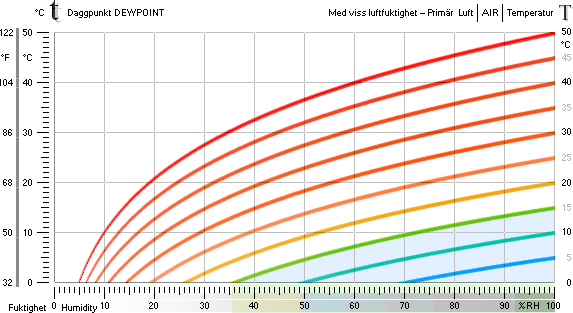
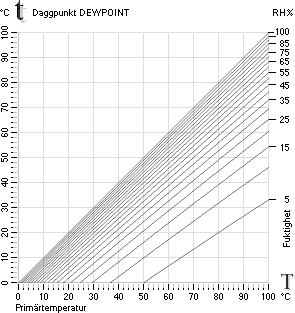
Grafer — Daggpunkten t med Relativa luftfuktigheten RH från primära lufttemperaturen T från SVP-sambanden


Daggpunkten t via relativa luftfuktigheten RH% för olika primära lufttemperaturer T	Daggpunkten t via primära T för olika RH%

Exempel — högra grafen — se även jämförande liknande graf i Wikipedia Dew point:

Daggpunkten — som ALLTID avser MAX relativ luftfuktighet RH%=100 — t = 12°C motsvaras entydigt av en bestämd primär lufttemperatur T = 20°C med RH = 60%: för att utan att vattenångtrycket ändras komma till DAGGPUNKTEN t=12°C — som alltid har max RH%=100 — måste luften börja från T=20°C med RH = 60%.

— Allmänna gaslagen pV=kT HARMONIERAR MED en sådan ordning OM tryckfaktor p och gaskonstant k bevaras enligt p/k=T/V=konstant: T kan avta från T mot det lägre t om, OCH ENDAST DÅ, den aktuella luftvolymen V vid T antar en motsvarande trängre volym.

Exempel — vänstra grafen:

Sommarluft med temperaturen T = 20°C [GuldGrafen] och luftfuktigheten RH = 60% kommer — om det luftpaketet genomgår en temperatursänkning utan att vattenångtrycket ändras — att fälla ut synligt vatten från ca t = 12°C och lägre. Följande karaktäristika sammanhänger med sambandsformerna till vänstergrafen ovan:

· För en given luftfuktighet RH%: vattenångtrycket avtar med avtagande temperatur T[färg] — Se särskilt pSVPgrafen: Från SVP-sambandet med som grundlägger ovanstående;

· Vattenångtrycket vid T[färg] med relativa luftfuktigheten RH% är lika med vattenångtrycket vid t med RH%=100;

t-horisontella linjen med fast vattenångtryck utpekar också ekvivalenter mellan olika T med olika RH:

· Vattenångtrycket via horisontella t-linjen som skär alla T[färg], utpekar för varje T[färg] en motsvarande luftfuktighet, vertikalt RH%:

För givet vattenångtryck [givet t-värde, horisontella]:

· relativa luftfuktigheten RH% ökar med avtagande lufttemperatur T[färg];

· relativa luftfuktigheten RH% avtar med tilltagande lufttemperatur T[färg].

GRAF y(RH):

0.1(238.3)(–1+17.2694[ln(x0.1[è'17.2694(1+238.3·50'–1)'–1])]'–1)'–1

Daggpunkten — se även ovan höger jämförande diagram i Wikipedia Dew point — analoga grafiska former:

GRAF y(T):

0.1(238.3)(–1+17.2694[ln(0.60[è'17.2694(1+238.3·[10x]'–1)'–1])]'–1)'–1

RH, relativa luftfuktighetstalet 0TILL1 motsv. 0-100%; x=T i °C — Se även Kalylkort för Daggpunkten i Tabell5 | 5A Blixt2014.ods.

Sambanden från webbreferensen i AGW visar sig överensstämma med Wikipediadiagrammet.

DP(tEllerRH) = 238,3(–1 + 17,2694[ln((RH/100)[e^17,2694(1 + 238,3·t^–1)])]^–1)^–1

RH i % (eng. Relative Humidity — relativa luftfuktigheten); t i °C

Med variabeln x=t ges motsvarande Wikipediadiagrammets grafer:

Med variabeln x=RH ges en tydligare bild av daggpunktens funktion av växande luftfuktighet för en bestämd (moln-) temperatur:

Form — Daggpunkten

DAGGPUNKTEN (t) är den lägre värmegrad ett moln med bestämd högre temperatur (T) och bibehållen luftfuktighet (RH%) ska anta utan vattenångtryckändringar för att vattenångan i molnet ska kunna bilda vattendroppar.

StudieEx, Daggpunkten

studieEXEMPEL daggpunktsbestämning MED VARIERANDE HÖJD ÖVER MARKEN

—————————————————————————

som antyder att vänstergrafen ovan är »Atmosfäriskt Absolut»:

—————————————————————————

p(STP) = 101325 Pa ;

T = 15°C = 59°F ; °F = °C·1,8 + 32:

RH = 50% ; Relativa luftfuktigheten i %, antaget vanligt värde:

p(SVP) = 1698,33 Pa ; Beräknat från SVP-sambandet med givet T:

p(SVP[RH]) = 849,17 Pa ; Beräknat från p(SVP)·RH%/100 = 0,5 p(SVP):

t = 4,63°C = 40,3°F ; Beräknat via SambandDaggpunkten

—————————————————————————

Vi avancerar nu uppåt till höjden 609,6 Meter = 2000 feet [1ft = 0,3048 M]:

h = 609,6 M = 2000 ft ;

p(h) = 94194 Pa ; Beräknat från p=101300EXP[0,034157941/(0,003 — 288,15/h)]:

NOTERA här att koefficientformerna i allmänhet INTE är överensstämmande mellan olika webbkällors interna referenser; LapseRate:en 0,003°C/M i sambandet ovan används INTE av den här jämförande referenskällan nedan för bestämning av T(h) utan istället snarare 0,0065°C/M:

T(h) = 15°C – h(0,0065°C/M) Se PDAS standard:

= 11,04°C = 51,9°F ; Med bevarad vattenmängd i den tunnare luften:

p(h)/p(STP) = (94194 Pa)/(101325 Pa)

= k(p) ; = 101300e^{0,0341579/(0,003
– 288,15/h)}/101300: »höjdvattenångtryckskonst.»

= 0,9296225 ; = e^{0,0341579/(0,003
– 288,15/h)}

~ 0,93 ; Relativa vattenångtryckets RH-värde p(SVP[RH]) = 850 Pa vid h blir:

0,93·849,17 Pa = k(p)·p(SVP[RH])

= 789,7281 Pa

= p(SVP[RH])_T(h) ;

~ 790 Pa ;

Vi beräknar sedan SVP-värdet vid motsvarande T(h)-värde 11,04°C:

p(SVP)_T(h) = 1312,08 Pa ; Beräknat från SVP-sambandet med givet T:

Vi kan nu beräkna motsvarande RH-värde:

RH(h) = k(p)·p(SVP[RH])/p(SVP)_T(h)

= p(SVP[RH])_T(h)/p(SVP)_T(h)

= (790 Pa)/(1312,08 Pa)

= 0,6020974

~ 60% ;

SambandDaggpunkten bestämmer sedan slutligt t via RH(h)=60% och T(h)=11,04°C:

t(h) = 3,55°C = 38,4°F ;

—————————————————————————

Se jämförande webbkällreferens med samma exempelvärden [det skiljer något i decimalerna]:

RELATIVE HUMIDITY AND DEW POINT AS A FUNCTION OF ALTITUDE -- A WAY TO ESTIMATE CLOUD CEILINGS

http://davidburchnavigation.blogspot.se/2012/09/relative-humidity-and-dew-point-as.html

— Med växande höjd över marken ökar RH och minskar t, bevarad ursprunglig mängd vattenånga förutsatt.

För att få ut vilket h-värde som svarar mot RH(h)=100%=TeoretiskMolnbildning är vi beroende av att Först beräkna ett separat T(h)-värde via T(LapseRate, sv. T-FallTakten) — och som varierar beroende på MODELL: Naturen varierar (delvis kraftigt) i olika områden, och teoretiska beräkningar måste använda en eller annan idealisering:

— Med det erhållna/antagna T(h)-värdet bestäms SEDAN ett p(SVP)_T(h)-värde, och därmed en koppling till RH(h):

RH(h) = k(p) · p(SVP[RH])/p(SVP)_T(h) = 1 =

= e^{0,0341579/(0,003 – 288,15/h)} · p(SVP)[RH])/p(SVP)_T(h)

= e^{0,0341579/(0,003 – 288,15/h)} · (RH) · p(SVP)_T/p(SVP)_T(h) ;

— Det betyder att vi, i vilket fall för att hitta h(VattenImoln) måste ITERERA fram RH(h)=100% genom att pröva olika h-värden — Från givna markLuftvärden T|RH;

p(SVP) = 610,78 · e^{17,2694/(1+238,3/T°C)} ; Från SVP-sambandet:

p(SVP)_T/p(SVP)_T(h) = e^{17,2694/(1+238,3/T°C)}/e^{17,2694/(1+238,3/T(h)°C)} ; Exponenten:

17,2694/(1+238,3/T°C) – 17,2694/(1+238,3/T(h)°C) = 17,2694[1/(1+238,3/T°C) – 1/(1+238,3/T(h)°C)] ;

— Och längre kommer vi inte på grund av formen för T(h)-värdet.

T(h) = 15°C – h(0,0065°C/M)

ln(p/p₀) = 0,0341579/(0,003°C/M – 288,15/h) ; Från GRAFp1

288,15/h = 0,003°C/M – 0,0341579/ln(p/p₀) ;

h = 288,15[0,003°C/M – 0,0341579/ln(p/p₀)]^–1 ; p/p0 i GRAFp1

Villkoret för h är att slutformen med RH% ska ge 100: INVERTERADE h-ledet ovan ska vara lika med T(h)-ledet längre upp × markens RH: Vi kan lösa ut h-faktorn, men då den i vilket fall beror ekvivalent av T(h)-värdet, som just använder h-värdet, finns ingen direkt enkel ekvationslösning.

— Insättning av sambanden i ett kalkylblad ger enklaste möjligheten att iterera h genom prövning för RH(h)=100%. Se DAGGPUNKTEN Tabell5|5A i Blixt2014.ods.

ITERATIONSEXEMPEL — Se DAGGPUNKTEN Tabell5|5A i Blixt2014.ods

med T(LapseRate)=0,0065°C/M:

För T=15°C vid STP och RH=50% får man med ovanstående referenser och samband h(VattenImoln)=2.160 M, RH(h)=100% och t(h)=0,93°C;

— Vattenångans viktsandel [GasUrel] i luften räknat från markförhållandena är då 0,79%.

— Ökas marknivåns RH till 80%, minskar h(VattenImoln) till 730 M med t(h)=10,23°C;

— Vattenångans viktsandel [eng. Specific Humidity] i luften räknat från markförhållandena är då 1,26%;

Viktsandelen vattenånga i förhållande till luftdelen är alltså i vilket fall (förvånansvärt) liten — samt att variationerna för VattenImolnHöjd är milt sagt märkbara.

— Test med variabla T(LapseRate)-värden visar att resultaten påverkas starkt av små variationer; lägre T(LapseRate)-värden kräver högre VattenImolnbildningshöjder.

— Webblitteraturen är (ännu Mar2014) relativt svår att konsultera i detaljuppgifter inom meteorologin (ytterst omfattande naturvetenskapsgren). Antydningen är att »T-Fallet» (ofta inom troposfären) varierar [0,65°C/KM (fuktig luft) till max 9,8°C/KM (torr luft), ref. Schlatter2009]. Ingen direkt allmän (säker) referensform finns (över längre tidsperioder) utöver generella globala årsmedelvärden på idealiserade atmosfäriska skiktmodeller, typ PDAS (och ICAO international standard) referensvärde 0,0065°C/M [ATFTekv].

— Exempelgenomgången ger oss — därmed, ganska — klara besked vad som gäller I STORT vid molnbildning, just beträffande vad vi kan förvänta gäller NATURLIGT för andelen vattenånga i »luft som är på väg att bilda moln». Vidare i H2Odata och Regndroppen.

— Daggpunkten kan uppträda naturligt

· genom primär molnbildning: vattenånga dunstar från marken och avkyls med växande höjd tills vattenångan (konv. kondenserar på aerosoler, RoWest2008) övergår i minimala vattendroppar (typ s.k. »vackert-vädermoln»), eller iskristaller (slöjor, finmönster, högt ovan mark);

· i redan existerande moln eller luft som skuggas (nattmoln genom nattväkter [avkylning] generellt);

· med fortsatt växande vattenavdunstning från marken i allt högre grad i redan existerande moln där solljuset alltmer utestängs och därmed temperaturen avtar ytterligare

Molnbildning — översiktlig allmän beskrivning enligt allmänna gaslagen — se även BildserieExempel på molnbildning under loppet av 5 minuter

PRINCIPEN FÖR MOLNBILDNING har diagrammet i DaggpunktenGrafer vänstra grafknippet som central:

— SOMMARTID, speciellt våra regioner Sverige-Norden-breddgrader: Från markområdet avdunstar vatten via en primärt soluppvärmd markluft med temperaturen T och en viss luftfuktighet [RH%] — och därmed en viss mängd luftbunden vattenånga redan från fasta marknivån. Sambandet i DaggpunktenGraferVänstra visar kurvor för T som genomskär vertikala luftfuktighetsvärden [RH%]: Horisontella skärningenVänster mellan dessa utpekar en DAGGPUNKT [t].

— OM T-värdet för den givna RH%-luften inom samma hydrostatiska region — konstant omgivande atmosfäriskt tryck — sjunker till t-värdet — utan att vattenångtrycket ändras nämnvärt [som fallet möjligen kan vara med markdimma tidiga mornar] — har T-luften blivit en t-luft: DAGGBILDNING inträder: vattenångans innehåll via RH-värdet har nu I PRINCIP övergått till återbildning av vatten [också en process som i etablerade meningar är MYCKET komplicerad att beskriva/förklara UTAN hjälp av ANDRA element: pollenkorn o-dyl. som anses krävas för vattendroppsbildning. Se utförlig genomgång i H2Odata]; enskilda vattenmolekyler som förenas till större enheter, bestående, utan att strax separera igen.

— Den andra sidan av saken är samma fason men på högre höjd: vattenbildningar inom olika hydrostatiska regioner — varierande omgivande atmosfäriskt tryck: processen då den givna markens T-luft med RH% stiger uppåt mot kallare områden, och på den vägen avkyls mot daggbildande = molnbildande t-luft.

Markens primära luftfuktighet RH beror på solvärmens lokala intensitet och markens beskaffenhet [Vinter/Sommar]. Generellt typiskt varierande relativa luftfuktighetsvärden under sommarperioden hos oss [Sverige/Norden] är grovt 50-80% vid runt 20—30°C — vi kan enkelt avläsa RH-värden direkt i % via en mekanisk luftfuktighetsmätare.

VATTENiMOLNbildningsHÖJDEN

Med hjälp av översiktliga allmänna samband [inom troposfären] kan vi beräkna vid vilken höjd (h) över marken som den givna uppvärmda markluften, från T med RH%, kommer att tangera motsvarande molnbildande t-luft [EXEMPEL MED VARIERANDE HÖJD].

— Beräkningen utgår från ett initiellt förhållande mellan lufttrycket p(h) (utan inslag av vattenånga) vid h och [mark-]vattenångtrycket p(SVP) vid T; följande sammanfattning grundas på ett Studieexempel där sambandsformerna redovisas mera konkret med aktuellt exempel:

— Tillsammans med RH%-värdet leder dessa — p(h) och p(SVP) — till ett t-värde [SambandDaggpunkten]: Det erhållna t-värdet tillämpas sedan på p(SVP)-sambandet som via det lägre t-värdet från föregående T-värde kommer att ge ett högre RH%-värde för den högre belägna ursprungliga markTluftens RH%-värde [på grund av avkylningen uppåt]:

— h-värdet [som vi måste iterera fram med hjälp av ett kalkylkort, från givet T och RH%: Se ITERATIONSEXEMPEL] som SÅ ger slutRH%-värdet=100, blir den t-aktuella [absolut lägsta] VATTENiMOLNbildningsHÖJDEN vid vilken en synlig atmosfärisk molnbas kommer att visa sig.

— Med ytterligare en LITEN avkylning = stigning [som överlappar en liten övergångströskel] kommer vattenmolekylerna helt säkert att börja förenas [H2Odata] till vattendroppar. Typexempel [DAGGPUNKTEN Tabell5|5A i Blixt2014.ods]:

— Med T=10°C och RH%=70 visas VattenImolnBildning från lägst h=1100 M vid t=2,86°C;

— Med T=15°C och RH%=70 visas VattenImolnBildning från lägst h=1150 M vid t=7,48°C;

— Med T=20°C och RH%=70 visas VattenImolnBildning från lägst h=1220 M vid t=12,04°C;

— Med T=10°C och RH%=50 visas VattenImolnBildning från lägst h=2060 M vid t=–3,43°C;

Höga moln för låga RH%-värden; Sommarens åskvädersmoln är lågstrykande vattentunga kolosser.

— Med en motsvarande grov approximationsform börjar VATTENiMOLN lägst vid markhöjden h=125(T–t) [Lifted condensation level].

— Områden med ett system av mindre molntappar eller »vackertVädermoln» är ett av flera tecken på primär molnbildning.

— Ju mera vatten som fortsätter avdunsta från marken, desto större blir ansamlingen vatten i molnets basdel. På den vägen kan molnet tydligen förstås utvecklas från de välbekanta s.k. stackmolnen till större och tyngre komplex.

— Utvecklingen kulminerar då vattendroppsbildningen i molnet ger så stora (tunga) vattendroppar att deras tyngdkraft överväger molnets inre gastryck (vindstilla) och molnvattnet börjar falla tillbaka till marken som regn.

— Sambandet för daggpunkten via SVP-sambandet gäller med tillämpning på, för och i alla möjliga atmosfäriskt avgränsade skikt där vi på samma sätt som vi här i marknivån kan räkna med ett stort omfattande omgivande RUM med bestämt atmosfäriskt tryck inom en viss tidsgräns. Se vidare utförligt från SVP-integralen [SVP-sambandet] om ej redan bekant.

VW, VattenWebben

2014III23

Webbens klargörande beskrivningar?

UTRYMME BORDE I N T E FINNAS FÖR DEN HÄR TYPEN AV DOKUMENT om naturvetenskapen vore välformulerad i ämnet

EXEMPELREFERENS SOM BEVISAR ÄMNETS NÄRMAST HUTLÖST SVÅRA NAVIGERING —

när man inte känner sambandsgrunderna

· vattenångtrycket [SVP-sambandet] beror INTE — är inte beroende — av lufttrycket:
Vattenångtrycket [SVP-sambandet] för given mängd vattenånga i luften, beror enbart på temperaturen;

· specifika luftfuktigheten — massandelen vattenånga i luft med given volym — ändras inte med temperaturen förutsatt inget vatten fälls ut, medan däremot relativa luftfuktigheten (RH-värdet) varierar med temperaturen:
— Denna detalj är kanske den allra svåraste grundformen av alla att förstå — och som ställer till mest oreda tills detaljerna faller på plats — för den som kommer in i ämnet som nybörjare enbart hänvisad till nuvarande etablerad nomenklatur. Se särskilt (till viss vägledning) utförligt i sammanställning med exempel i DaggpunktenGraferVänster.
— Ett utförligt exempel som behandlar samtliga parametrar ges i StudieExempel.

LiftedCon

Kondensationsnivån

— Wikipedia skriver för sin del, upplysande:

@INTERNET Wikipedia Lifted condensation level [2014-03-23]

http://en.wikipedia.org/wiki/Lifted_condensation_level

”The lifted condensation level or lifting condensation level (LCL) is formally defined as the height at which the relative humidity (RH) of an air parcel will reach 100% when it is cooled by dry adiabatic lifting. The RH of air increases when it is cooled, since the amount of water vapor in the air (i.e., its specific humidity) remains constant, while the saturation vapor pressure decreases almost exponentially with decreasing temperature. If the air parcel is lifting further beyond the LCL, water vapor in the air parcel will begin condensing, forming cloud droplets.”.

— ”The RH of air increases when it is cooled” är precis vad DaggpunktenGrafer, vänstra grafen, samt det som DaggpunktenSambandet beskriver särskilt: ekvivalensen mellan det högre T-värdets RH%-värde och det lägre t-värdets RH%-värde=100:

Vattenångtrycket vid T[färg] med relativa luftfuktigheten RH% är lika med vattenångtrycket vid t med RH%=100

Notera att luftvattenmängden som sådan (Se Specifika Luftfuktigheten) — och förutsatt inget vatten utfälls, och ångtrycket bevaras — INTE ändras: andelen luftvattenmassa i viktsprocent berörs inte.

Den andra delen i Wikipediacitatet

— ”the saturation vapor pressure decreases exponentially with decreasing temperature”, överensstämmer också med det som visas i pSVPgrafen.

— Se även i Procentuella VattenÅngMättnaden.

— Notera återigen att RH-värdet INTE är vattenångans viktsprocent (eng. specific humidity) i luften.

— RH-värdet varierar med temperaturen (T) för en viss fast viktsmängd vattenånga i luften DÄRFÖR att vattenångtrycket (SVP) gör det.

AKTUELLA VATTENÅNGTRYCKET MED HÄNSYN TILL RELATIVA LUFTFUKTIGHETEN:

— Normalt sett kan vi inte (enkelt) mäta vattenångans vattenångtryck i luften (pH2Oactual);

— Vi mäter istället (via enklare instrument, som inte sällan (förr) finns på typen köksklockor) RH-värdet i %.

— På den vägen via SVP-sambandet och känd temperatur får vi fram vattenångans aktuella deltryck i luften.

HYGROMETER

Foto: PHP aEXP 6Maj2014 Humid2;3 · Nikon D90 · BellDharma UNIVERSUMS HISTORIA

Luftfuktighetsmätare på en av den billigare typen köksur som vi [förr — OK-sortiment runt 2000] kunde hitta på olika marknader — CosmoTime.

— Wikipedias artikel på Dew point [2014-03-23] innehåller emellertid inte (än) den avgörande klargörande Daggpunkten t [DaggpunktenGrafer, vänstra grafen] — från variabla RH via bestämda T — endast (högra grafen) Daggpunkten t från variabla T med bestämda RH — och dessutom inte heller den (möjligen, mycket) klargörande sambandsbilden i Samband.

— AVSAKNADEN av den överblicken leder (möjligen, också) till en del onödiga sammanblandningar som nämnda bidrag enklare undviker. I varje fall har deras framställningen i den här presentationen bevisat en rejäl städning i ämnet: från början mer eller mindre rena kaoset, till ren befriande ORDNING.

Daggpunkten, def.

DAGGPUNKTEN [‡]:

— Daggpunkten är den temperatur t vid vilken luft är vattenångsmättad.

— Vattenångsmättad luft som bringas (ytterst) litet under t fäller ut flytande vatten.

Daggpunkten är (konventionellt) tillståndet — temperatur och fuktighet — där vattenångans enskilda vattenmolekyler kan övergå i vatten i samma takt som vattnet kan övergå i vattenångans enskilda vattenmolekyler.

— Balansen i tillståndet är tydligen liktydigt med en GRÄNSFORM:

under gränsformDAGGPUNKTEN bildas vatten entydigt: ångmängden avtar;

över gränsformDAGGPUNKTEN bildas vattenånga entydigt: vattenmängden avtar.

Ref. Wikipediaartikeln om Dew point:

DAGGPUNKTEN är vatten-i-luft-mättnads-temperatur.

Svenska Wikipediaversionen [Moln, Utveckling [2014-03-23]]:

”Molndroppar bildas ur fuktig luft. Principiellt gäller att när den relativa fuktigheten är över 100 % övergår fler vattenmolekyler från gas till vätska än vice versa och blir därför en förutsättning för att kondensation skall inträffa.”.

Annan webbkälla skriver: Dew point

”the temperature to which air must be cooled, at a given pressure and water-vapor content, for it to reach saturation;

the temperature at which dew begins to form.”, Dictionary.com @INTERNET [2014-03-19]

Formuleringarna man finner i etablerad litteratur har genomgåtts (grundligt, sett från TNED) och har befunnits konsistenta — men här enbart med hjälp av klarläggandena främst i DaggpunktenSamband och DaggpunktenGraferVänster, dessa har eftersöks på webben men inte påträffats — med den relaterbara genomgången av sambandsformerna. Se utförligt från Daggpunkten.

— Tyvärr visar sig inte samma fina resultat i samband med genomgången av molnbildningens elementära grunder [PascoCitat].

InledningH2Odata, H2Odata

Vattenånga formar vattendroppar

— DIREKT FRÅN VATTENÅNGA?

Ångdimman från pipen på vattenkokande kaffepanna.

Foto PHP aEXP WaterVapor — 19Maj2014 Bild93 · Nikon D90 — ISO 3200 — 1/500S — F/10 —

Kontrasterad, uppljusad, Konturförstärkt, Inverterad.

— Bilden tagen med ångan som tränger ut ur pipen på en svagt vattenkokande kaffekanna mot svart bakgrundspannå — i ljuset av en 500 W bygglampa.

— Inslaget med delvis linjärt avgränsade [heta] slöjor framgår tydligt.

Modern akademi (Maj2014):

— Jamen [NoDrop], det är BARA DÄRFÖR ATT DET FINNS aerosoler i köket. Alltså, dammpartiklar som vattenångan kan fästa sig på, och FÖRST därifrån bilda den synliga ångdimman som mikrosmå vattendroppar.

— Så: Du menar att MAC har kollat med absolut renad luft i absolut renat vatten: kokande vatten i ett kliniskt rent KÖK, ren damm- och pollenfri köksluft:

— Man VET att i ett sådant kliniskt rent kök kokande vatten INTE visar ångdimma, INGA mikroskopiska vattendroppar syns ovanför koket, man ser ingenting alls: nollKoll:

— VET man det?

— Har sådana experiment genomförts?

— Nej.

I modern akademi (2014) är man tydligen av den allmänna uppfattningen [NoDrop] att ångdimman vi ser från kökets kastruller med kokande vatten

på samma grundfysik (Daggpunkten): morgondimmorna (över speciellt sjöar och vattendrag), samt vidare molnbildningen (StudieExempel), det som vi vanliga dödliga TROR NATURLIGT sammanhänger med vattnets fysik och inget annat

INTE ALLS grundas på vattenfysiken, utan är HELT beroende av förekomsten av mikroskopiska (vattenlösliga) partiklar i luften, s.k. aerosoler.

MAC-företrädarna i föreningen NoDrop stödjer sig på (den numera berömda) Kelvins ekvation (»vattendroppens förångningsekvation»):

— Då droppradien understiger Ø120nM »blir Kelvinångövertrycket så stort att ingen naturlig miljö existerar som kan förhindra att droppen förångas (snabbt och »explosivt», ju mindre den är)». MAX Naturliga VattenÅngövertryck är runt RH=102%, analogt ett Kelvinångövertryck på 2%, medan typ den allra första vattendroppen med 2(H2O) med r=2,43Å enligt Kelvinekvationen vid 0°C markluft kräver p/p₀=140 — motsvarande RH=14000% för att droppen inte ska förångas.

— Det är hela historiens bakgrund — + uppgifter (KelvinWebben), synpunkter (Katz2007) och en del motsättningar [URDM2007] i ljuset av experimentella test;

— Kelvinekvationen (KE) har VISST testats, och den stämmer också I VISSA FALL OCH OMRÅDEN utomordentligt väl med experimentella observationer, men inte alltid, och då också tillsammans med tydliga inre motsättningar inom vetenskapssamfundet.

I H2Odata genomgås speciellt en del uppenbara brister i Kelvinekvationen som alldeles tveklöst — väl relaterbart — sammanhänger med oklarheterna, och som också ser ut att innehålla en del väsentligen klargörande information enbart från sambandsformen som sådan. Men trots Kelvinekvationens egna självservering på den punkten, tycks dess glänsande inre inte alls tilldra sig den etablerade författarskarans intresse.

Tillsammans med den delen, och under den här författningens gång, har ett speciellt experimentellt — banbrytande, som det får förstås — resultat upphittats genom omfattande webbsökningar och som daterar sig till Maj2013:

Från Maj2013 (Tretyakov2013) finns nu (2014) i varje fall ett experimentellt resultat som påstår sig ha avgjort den långt utdragna djupkonflikten i vetenskapssamfundet i frågan om vattnets fysik (eng. water dimer problemet):

— 2(H2O) — den allra minsta vattendroppen (Kelvinövertrycket 140) — existerar i rumstempererad luft.

Kan 2, kan alla. Kan inte 2, kan inga.

— Det betyder tydligen trubbel för aerosolteorin — och föreningen NoDrop som Atmosfäriska Vattnets Regering.

Se vidare utförligt från H2Odata.

H2Odata, 10Maj2014, Se även i InledningH2Odata och Grundbegreppen

FRÅGAN OM NATURLIG VATTENBILDNING enbart FRÅN ren VATTENÅNGA I ATMOSFÄREN

— Resultatet från Tretyakov2013 — 2(H2O) existerar — har ställt den (»urgamla, av MAC-etablissemanget redan avfärdade») frågan i nytt ljus.

——————————————————————————————————————————————————————————————————————

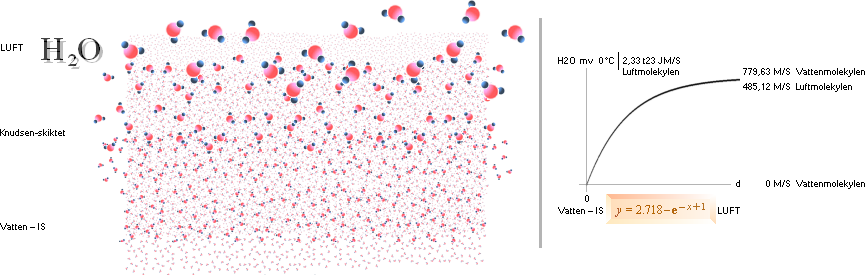
Vid 0°C markluft (och RH=100%) är förångningen — inom KNUDSENskiktet — från en vatten- eller isyta lika med noll: ingen enda vattenmolekyl H2O lämnar vatten- eller isytan i netto: alla stannar kvar. Bilden, höger ovan, illustrerar hur de vatten- eller isbundna vattenmolekylernas rörelsemängd mv ändras successivt från i princip NOLL vid ytan till luftmolekylernas maximerade medelvärden i den omgivande luften. Det illustrerar samtidigt graden av en motsvarande FÖRÅNGNINGSPOTENTIAL som bör finnas av princip då omgivningstemperaturen sakta växer och därmed energi existerar som KAN verkställa en förångning. Ju närmare 0°C desto längre TID behöver N st H2O för att förångas. VID exakta 0°C är den tiden uppenbarligen obegränsad.

— I Kelvinekvationens form p/p₀=2Ŝ(U/ρ)/r(R)T finns emellertid ingen motsvarande DÄMPNING, främst nära och strax över 0°C som motsvarar den fysikaliska processen: Kelvins ekvation beskriver en obetingad — tydligen otillåten — förångning ÄVEN VID vattnets 0°C.

— Förutsättningen för förångning är under alla omständigheter närvaron av en verkställande energi. Och den energin måste naturligtvis också besitta en nollform vid 0°C. Och alltså måste ovillkorligen också Kelvins ekvation, i naturbeskrivningen, innefatta en sådan form, men vilket alltså inte är fallet.

— Se vidare utförligt i KOF.

Bakgrund:

Avgörande i hela frågan om s.k. homogen atmosfärisk vattenbildning (vattenbildning utan annan hjälp än vattenmolekylerna själva; se allmän förklaring i RoWest2008 Homogen/Heterogen nukleation)

alltså minst en 2(H2O)

från atmosfärisk vattenånga

enskilda H2O

är (den berömda) Kelvins ekvation — med Wikipedias beteckningar ln[p/p₀]=2γVm/rRT:

— Kelvins ekvation — till vissa men inte alla delar »allmänt experimentellt bekräftad» [Katz2007] [KelvinH2Owebben] — beskriver förångning (p/p₀>1) »hos vatten med radien r». Kärnan i sambandet — och som vi ofta hittar igen i den etablerade beskrivningen där Kelvinekvationen finns med — är av typen i NoDrop:

Man framhåller generellt att:

— Vattendroppar < r=60nM »är omöjliga» på grund av att »droppen avdunstar» via p/p₀=1,02 motsvarande relativa fuktigheten RH=102% — de möjliga 2% överfuktighet som Jordtroposfären kan uppvisa, max. Det är förklaringen varför det anses allmänt att regn och snö inte kan bildas utan hjälp av s.k. aerosoler (luftburna vattenlösliga partiklar i nano och mikrostorlek — damm, pollen, föroreningar — som vattenmolekylerna kan fästa sig på).

KEB

Kelvinekvationens brister:

Dokumenten vittnar om (långvariga [URDM2007]) konflikter och motsättningar i vetenskapssamfundet i ämnet vatten och vattenånga, ända fram tills helt nyligen:

— 2(H2O) existerar i fysiken [Tretyakov2013].

— Påvisandet har än så länge gjorts i laboratoriemiljö vid rumstemperatur (22,85°C) 296°K och 0,017 atm (1733 Pa = 13 torr).

Kelvinekvationen (KE) innehåller också här — eftersökta på webben men ännu inte upphittade — flera uppmärksammade begränsningar som ansluter till sammanhanget. Det är i deras ljus — med omfattande och ihärdiga webbsökningar — som det experimentella 2(H2O)-påvisandet från Tretyakov et al. från 2013 (här) uppmärksammats, och som därmed grundlagt en mera solid bas i framställningens detaljer:

· Kelvinekvationens avsaknad av förångningspotential vid ämnets övergång till fast; vattnets 0°C (KOF);

· Kelvinekvationens avsaknad av övergångsområde genom KNUDSEN-skiktet mellan fast, flytande och gas (KOFappl);

· Kelvinekvationens avsaknad av energitäckning för de allra minsta vattendropparnas förångning (SEA);

· Kelvinekvationens obefintliga roll i vattendropparnas molekylära uppvärmning från 0°K via PARBILDNING (H2Opar);

· Kelvinekvationens obefintliga roll i resultaten från Tretyakov2013: 2(H2O) — den allra minsta vattendroppen av alla — existerar i rumstempererad luft, tydligen DÄRFÖR att förångningspotential (EkinEs) inte existerar vid den nivån;

— Att Kelvinekvation i sig (i makrosammanhang) är väl experimentellt bekräftad på observationer av givna vattendroppar över 0°C i given konstant lufttemperatur och som får förångas fritt finns här ingen anledning att betvivla [KEexp].

Däremot — speciellt för vattnets fysik — på nanometernivån:

— Alla de ovan nämnda punkterna pekar på att Kelvinekvationen — av rena energitekniska skäl — INTE kan eliminera de allra minsta vattendropparna, att det finns gränsformer i Kelvinekvationen som visar att denna INTE gäller med början från 2(H2O), och inte heller under en viss minimigräns (SEA) som dessutom är temperaturberoende. Komplikationerna verkar dessutom ha den omfattningen (H2Opar) att detaljerna inte ens omnämns i det mest synliga utbudet av InternetWebbens gratisvaror (Maj2014).

Vi studerar det.

Inledande belysande exempel:

Vatten VID, eller obetydligt nära, 0°C uppvisar ingen förångning av H2O: vattenmolekylerna H2O stannar kvar i netto inom vattenvolymen (inkluderat KNUDSEN-skiktet).

— Kelvinekvationen [KE] preparerad för vatten vid 0°C har den enkla formen

p/p₀ = e^ 1,2 t9 M/r ; Kelvinövertrycket för vattendroppar med radien r vid T = 273,15°K = 0°C [‡]

Men resultatet av den matematiska operationen tar alls ingen hänsyn till det faktum att, som nyligen påpekades, ingen förångning existerar vid 0°C för vatten.

Jämför fallet med den allra minsta vattendroppen 2(H2O) med radien r=2,464 t10 M ~ 2,43 Å = 0,243 t9 M:

p/p₀ = e^ 1,2 t9 M/(0,243 t9 M)

= 139,52888

~ 140 ; Det motsvarar en relativ fuktighet på RH = 14.000%.

Jämför de etablerade uppfattningarna i ljuset av det resultatet i NoDrop:

— »En sådan minsta möjlig vattendroppe kan följaktligen omöjligen existera».

Men:

— Tretyakov2013: 2(H2O) existerar i fysiken.

Och, alltså?

bStyret

Spärr mot förångning saknas:

Den allra första och främsta angelägenheten med Kelvinekvationen är att dess FORM — i typbeskrivningen, som ovan, av vatten VID dess fasta gräns, is — BORDE innehålla en p/p₀-spärr för vattnets del vid 0°C av formen (utförligt i KOF)

p/p₀ = e^ [([1,2 t9 M/r]^ [1 – 1/(aT°C + 1)]) – 1/(bT°C + 1)]

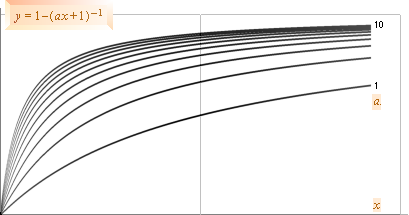
Grafexempel. Brantheten i STYRET för relevant Kelvinfunktion i Kelvinekvationen,

a-koefficientens olika värden 1-10.

Nämligen med T°C=0 ges då — korrekt fysikaliskt — p/p₀=1 oberoende av vattendroppens radie.

p/p₀ = e^ [([1,2 t9 M/r]^ [1 – 1/(a0°C + 1)]) – 1/(b0°C + 1)]

= e^ [([1,2 t9 M/r]^ 0) – 1]

= e^ [0]

= 1

b-koefficienten kan sättas godtyckligt högt för att resultatet inte ska påverkas med T°C>0.

a-koefficienten däremot KAN — och bör — ha direkt fysisk koppling till HUR det närmaste molekylskiktet mellan vattenkroppen och den omgivande luften genomgås (speciellt från nära 0°C och närmast uppåt). Dvs., hus snabbt Kelvinekvationen når sin normalform enligt

p/p₀ = e^ [1,2 t9 M/r]

Grafen till höger i vinjettfiguren [‡] illustrerar den delen.

— Se mera utförligt i KOF (KELVINEKVATIONENS OFULLSTÄNDIGA FÖRÅNGNINGSPOTENTIAL).

— Se även komplementet till KOF i KOFappl.

Kunden tar ut mer än kontot innehåller:

Men den allra största och mest anmärkningsvärda avvikelsen från uppenbar grundfysik i Kelvinekvationens form visar sig ändå i energiräkningen (SEA) — för de allra minsta teoretiska Kelvindropparna. Övriga berörs inte.

Sammanställningarna i SEA med graferna EkinES och EkinESlimes visar hur Kelvinekvationens ytspänningskoefficient tar ut större kredit på »vattendroppens förångning» än vad kontoinnehavaren är god för:

— Från en viss undre gräns beroende på temperatur och droppradie blir vattendroppens inneslutande ytspänningsenergi större än de inneslutna motsvarande fria — förångade — vattenmolekylernas rörelseenergier ute i luften omkring. Det betyder uppenbarligen en rent energitekniskt ohållbar situation: vattenmolekylernas samlade rörelseenergi i luft måste under alla omständigheter vara större än den energi — ytspänningsenergin i vattendroppen — som omsluter dem i vattendroppen. I annat fall finns ingen energiförklaring till HUR vattenmolekylerna kommer ur greppet från den samanhållande vattendroppens ytspänning.

— Gränsen vid 0°C markluft går vid N=58 vattenmolekyler, och avtar sedan med växande omgivningstemperatur (N=40 vid 20°C).

TROUBLE:

Emellertid finns via uppgifterna på ångbildningsvärmet (eng. latent heat) L(W) för vatten ytterligare en HÖGRE tröskel för dessa basvärden. Nämligen — det synbara faktum — att den rena råa rörelseenergin (mvv/2) för den enskilda H2O-molekylen bara är en mild fläkt i förhållande till den mera praktiska energi som krävs — i varje fall sett makroskopiskt — för att få vattenmolekylerna UR vattenkroppen.

Per H2O-molekyl:

0°C:

9,09 t21 J ; Vattenmolekylens rörelseenergi E=mv²/2 vid 0°C markluft [RH=100%] :

7,48027 t20 J ; ångbildningsvärmet per H2O-molekyl i vatten vid 0°C ; 74,8/9,1 = 8,228803 ;

Används istället den betydligt tuffare ångbildningsvärmeenergin som värdemätare, kan ytspänningsenergin i motsvarande grad sänkas:

— Resultatet blir: ingen — noll — förekomst. EkinESlimes-kurvan hamnar så långt ner mot x-axeln att ytspänningsenergin i EkinES aldrig överstiger ångbildningsenergin.

TroubleCancelled:

Men då befinner vi oss å den andra sidan i den trängda situationen att vatten vid 0°C och samma luft inte besitter någon sådan förångningspotential: den är noll: ingen enda vattenmolekyl kan förångas, oberoende av vattendroppens storlek.

— För att PER enskild H2O komma upp i ångbildningsvärmets energinivå 7,5 t20 J vid 0°C måste — märkligt som det är — en enskild omgivande medelluftmolekyl med motsvarande Ekin=mv²/2=7,5 t20 J ligga i området T = 3350 °C [TMref].

— Motsvarande luftekvivalent för kemiska bindningsenergin (MinstaVatten) Ekem=2,2 t20 J blir T = 790 °C.

— Varifrån, i den situation då luftens omgivande temperatur är 0°C — eller till och med 100°C — ska energin komma ifrån till ”ångbildningsvärmet 7,5 t20 J/H2O”? Finns inte i omgivande 0°C luft.

— RÄKNINGEN — i den hemliga skattjakten på vad som gäller — blir alltså INTE så enkel som att jämföra rena basvärden.

— ÄNNU VÄRRE blir det om vi försöker »härleda omvändningen»: från befintlig vattenånga TILL vattendroppe. Då, nämligen, ingen enda vattendroppe ännu existerar, bara enkla fria H2O, och därför strängt taget heller ingen Kelvinekvation (KE) existerar:

— enskilda H2O omfattas inte av Kelvinekvationen. Första minsta vattendroppen — r-faktorn i Kelvinekvationen — är 2(H2O): r=0,243nM.

Används alternativt uppgiften från (kemiska) bindningsenergin mellan 2 stycken förenade H2O, den s.k. dissociationsenergin (MinstaVatten)

2,19495 t20 J ; dissociationsenergin — delningsenergin — för att separera två förenade vattenmolekyler

sänks Kelvinribban med motsvarande 2,4145934 (nära 1+√2=2,4142135): gränsen går då vid strax över N=4 stycken H2O vid 0°C, N=3 vid 20°C.

Så: Hur är det då?

DEN ALLRA MEST PLAUSIBLA »lösningen» till hela problematiken är att räkna energitekniskt i reda TILLGÄNGLIGA rörelseenergier per fri H2O — vid 0°C Ekin=9,09 t21 J/H2O — och summera deras motsvarande NOLLNING då de omsluts av en gemensam vattenkropp: totalt frigjorda värmemängden är summan av H2O-kollektivets fria rörelseenergier.

— DÄRFÖR nämligen att MED 2(H2O) följer en elektrisk/kemisk bindningspotential som INTE den fria H2O omfattar, men som måste tillföras en vattendroppes bundna H2O för deras frigörelse. Alltså: ångbildningsvärmet får INTE förstås samma som kondensationsvärmet (»parbildningsvärmet»), i varje fall inte på molekylär nivå (de bägge sammanstrålar då mängden H2O blir stor).

Därmed skulle hela dramatiken gå ut på grafbilden i EkinES: det är de fria H2O-molekylernas rörelseenergier hela saken handlar om med bildningen av vatten från vattenånga. Ångbildningsvärmet hör inte dit, och heller inte kemiska bindningsenergierna — frånsett deras helt avgörande inneslutande roll i ytspänningskoefficienten: styrkan med vilken de vattenhinneinneslutna vattenmolekylerna kvarhålls.

Svaret:

I varje fall med referens till resultatet från Tretyakov2013 — 2(H2O) existerar i rumsvarm luft (22,85°C=296°K) — är det tydligt att ångbildningsvärmets data INTE omfattar de allra minsta möjliga vattendropparna. Om 2(H2O) överlever, finns ytterligare möjligheter.

Vi studerar det.

— Uppvärmningen tar TID:

— När rena enskilda H2O sammanträffar i vattenångan (H2Ounited) kittas de samman av (par-)dissociationsenergin (MinstaVatten)

2,19495 t20 J ; dissociationsenergin — delningsenergin — för att separera två förenade vattenmolekyler

OM — vilket är tydligt enligt Tretyakov2013 — 2(H2O)-föreningen är permanent, KAN vi se sammanträffandet som att de fria H2O-rörelseenergierna praktiskt taget reduceras till noll. Därifrån — i princip 0°K — behöver sedan paret 2(H2O) bara en eller annan putt från omgivande luftmolekylers mv(0°C)=2,33t23JM/S för att överta deras medelimpuls (mv) och därmed motsvarande temperaturrelaterad rörelseenergi.

— Fortsätter vi på samma fason — två 2(H2O) sammanträffar till 2(2(H2O)) — gäller samma princip. Men denna gång kommer det att ta (betydligt) längre TID för den omgivande luftens medelmolekyler att stöta och knuffa fram den större vattendroppens motsvarande homogena medeltemperatur, och med motsvarande lägre medelhastighet för den större bildade vattendroppen.

tWARM, tWATER

Vi kan grovräkna TIDEN det tar för luftmolekylerna i 0°C markluft att värma upp en vattendroppe med given diameter från 0°K till 0°C eller 273,15°K (inverkan av luftfuktigheten bortses här ifrån då denna i vilket fall är max 4% i luft och därmed inte kritisk för grovräkningen):

m = ρV = ρ(4πr³/3);

E/mT = 4190 J/KG°K ; Vattnets specifikka värme [värmekapacitiviteten för vatten]:

ref. Karlebo HANDBOK s76 Tabell 4.2 Utg.12 Esselte 1977

E = (4190 J/KG°K)mT

= (4190 J/KG°K)m(273,15°K)

= (1 144 498,5 J/KG)m

= (1, 144 4985 T6 J/KG)ρ(4πr³/3)

= (1, 144 4985 T6 J/KG)(1000 KG/M³)(4πr³/3)

= (1, 144 4985 T9 J)(1/M³)(4πr³/3) ;

E = (4,79406 T9 J)(1/M³)r³

d(0)_L ~ 2 t7 M = 200nM ; Medelfrivägen för luftmolekyler i 0°C markluft [med eller utan vattenånga]

v(0)_L ~ 485 M/S ; Medelhastigheten för luftmolekyler, som ovan:

f (0)_L = (485 M/S)/(2 t7 M)/2

= 1,2125 T9 Hz ; Repeterande stötfrekvens över medelfrivägarna:

t(0)_L = 8,24742 t10 S ; Tidsintervallet för repeterande stötar inom medelfrivägens medelvolym för 1 LM

Antalet LuftMolekyler LM som står i kontakt med VattenDroppen VD kan beräknas från medelavståndet d(LM) mellan LMolekylerna: π(d_LM/2)² fördelat över VD-ytan med

d_LM = (V_LM)^1/3 = (U_Lu/ρ_L)^1/3

— Den räkningen måste emellertid också innefatta motsvarande återuppvärmning av kontaktagenterna från LM längre ut från vattenytan, och den matematiken kräver därför ytterligare genomgång:

— Om vi förutsätter ett LED av nLM som kopplar varandras temperaturåterställande in mot vattendroppen som håller på att värmas upp från LM-stötarna, kan vi grovräkna på vilket ungefärligt sådant antal vi måste räkna med, tillsammans med ovanstående:

— För att TESTA PRAKTISKT DIREKT och få en ungefärligt matchande praktik med vad vi kan observera i uppvärmningstid — med exempel från frysboxen (–18°C) till rumstemperatur (20°C) — kan vi plocka ut några små frostbitar 1-5mM från frysen och lägga dem direkt på köksbänken — direkt på bänkplåten — och mäta tiden tills bara vatten återstår:

— Vi får ungefär och grovt omkring 1 minut eller runt 40-60 sekunder [för en vattendroppe med diametern 2mM].

— Prövar vi motsvarande i Kalkylkortet [Tabell 5A] i jämförelsen mellan 0°C och 20°C på en Ø2mM droppe [skillnaden ungefär 40 sekunder] finner vi grovt nLM=3000 tillsammans med ovanstående justering för antalet LM omkring vattendroppens yta. Med medelavståndet 3.33nM mellan LM betyder det en molekylär temperaturåterställningsdistans på 10µM.

— Det betyder samtidigt att UPPVÄRMNINGSTIDEN via omgivande luft för de allra minsta vattendropparna tar VÄLDIGT relativt LÅNG TID — typ 0,589 mS för en Ø1nM droppe,

— Kalkylen visar då att det skulle ta drygt 19 minuter [1180 sekunder] för luft med rumstemperaturen 0°C att värma upp en vattendroppe med diametern Ø2mM från 0°K till 0°C. Det förefaller rimligt, men vi vet inte det här.

— Motsvarande tWARM=tWATER ges då via en vattendroppe med diametern 130nM på t=0,153 sekunder.

E(L) = 5,66 t21 J ; Medelrörelseenergin från medelluftmolekylen, som ovan

För r = 60 nM ges:

E = 1,03551 t12 J ;

E/E(L) = 1,82953 T8 ; Antalet luftmolekylstötar som krävs IDEALT för uppvärmningen:

t = t(0)_L E/E(L) ; tWARM

= 0,1508894 S ; Tiden för uppvärmningen till 0°C av en r=60nM vattendroppe.

— Räkningen förutsätter IDEALT att varje luftmolekylträff överför HELA sin rörelseenergi på vattendroppens vattenmolekyler — vilket i netto betyder att andra luftmolekylgrannar måste kompensera stötbortfallet med sina stötar och knuffar för att få upp agenthastigheten igen, och vilket i praktiken sänker den enskilda luftmolekylens stötkapacitet på den områdeslokala, nära stillastående Ø120nM-vattendroppen.

— Tidsvärdet man får ovan blir alltså ett SNABBASTE FALLETS ORIMLIGT KORTASTE värde.

— GROVRÄKNINGEN kan därför HOFTAS mera praktiskt orienterande genom att dubblera ovanstående tWARM.

I slutänden får vi för fallen vid (allt mer över) den kritiska gränsen 0°C där i vilket fall ingen förångningspotential existerar en TÄVLING mellan tiden för uppvärmning och tiden för bildning. Något förenklat:

t_WARM/t_WATER = t(0)_LE/E(L) / r⁴(K)

= t(0)_LE / E(L)r⁴(K)

= [2d(0)_L/v_L]E / E(L)r⁴(K)

= [2[(√2)πr_L²ρ_L/U_Lu]^–1/v_L]E / E(L)r⁴(K)

= [2[(√2)πr_L²ρ_L/U_Lu]^–1]E / v_LE(L)r⁴(K)

= [2U_Lu[(√2)πr_L²ρ_L]^–1]E / v_LE(L)r⁴(K)

= [2U_Lu[(√2)πr_L²ρ_L]^–1]E / v_L[U_Luv_L²/2]r⁴(K)

= 2[2[(√2)πr_L²ρ_L]^–1]E / [v_L³]r⁴(K)

= 4[[(√2)πr_L²ρ_L]^–1](4,79406 T9 J)(1/M³)r³ / [v_L³]r⁴(K)

= 4[(√2)πr_L²ρ_L]^–1(4,79406 T9 J)(1/M³) / [v_L³]r(K)

= 4[(√2)πr_L²ρ_L]^–1(4,79406 T9 J)(1/M³) / [v_L³]r[16,11992(ρ_V)^–1/3/[3(mv)_LUFT/4πρ_W]]

= 4[(√2)πr_L²ρ_L]^–1(4,79406 T9 J)(1/M³) / [v_L³]r[16,11992(ρ_V)^–1/3/[3(mv)_LUFT/4π1000KG/M³]]

= 4[(√2)πr_L²ρ_L]^–1(4,79406 T9 J)(1/M³) / [v_L³]r[16,11992(ρ_V)^–1/34π1000KG/M³/[3(mv)_LUFT]]

= 4[(√2)πr_L²ρ_L]^–1(4,79406 T9 J)(1/M³)[3(mv)_LUFT](ρ_V)^1/3 / [v_L³]r[16,11992·4π1000KG/M³]

= 4[(√2)πr_L²ρ_L]^–1(4,79406 T9 J)(1/M³)[3(m)_LUFT](ρ_V)^1/3 / [v_L²]r[16,11992·4π1000KG/M³]

= 4[(√2)πr_L²ρ_L]^–1(4,79406 T9 J)(1/M³)[3(m)_LUFT](ρ_V)^1/3 / [v_L²]r[202.568,88 KG/M³]

= 4[(√2)πr_L²ρ_L]^–1(4,79406 T9 J)(1/M³)[3U_Lu](ρ_V)^1/3 / [v_L²]r[202.568,88 KG/M³]

= 4(4,79406 T9 J)(1/M³)[3U_Lu](ρ_V)^1/3/[(√2)πr_L²ρ_L][v_L²]r[202.568,88 KG/M³]

= (63921,522 J)[U_Lu](ρ_V)^1/3/[r_L²ρ_L][v_L²]r[KG]

= (63921,522 J/KG)[U_Lu](ρ_V)^1/3/[r_L²ρ_L][3bT/U_Lu]r

= (63921,522 J/KG)[U_Lu]²(ρ_V)^1/3/[r_L²ρ_L][3bT]r

= [(ρ_V)^1/3/ρ_LTr](63921,522 J/KG)[U_Lu]²/[r_L²][3b] ;

t_WARM/t_WATER = [(ρ_V)^1/3/ρ_LTr](2,2292867 t4 J/KG) ; Förhållandet mellan tWARM och tWATER

E-formen ovan är för 0°C=273,15°K. För T-anpassning ska tWARM, analogt E, divideras med (273,15°K) och sedan multipliceras med aktuell temperatur T=(T°C + 273,15°K). Därmed bortfaller T i sista högerledet ovan (men ett T-beroende finns integrerat i tätheterna för luft och vattenånga, se TMekv i TillämpningM).

Variablerna (ρ_V)^1/3/ρ_LTr ger i slutänden [ρ_L har en inverterad T som relaterar till atmosfäriskt temperaturprefix] i Kalkylkortet [Tabell 5A] i netto att växande lokal temperatur T ökar — inte minskar — uppvärmningstiden tWARM relativt bildningstiden tWATER: ju högre T med allt mindre r desto större tidsskillnad mellan tWARM och tWATER.

— Dvs., allt större vattendroppar kan bildas under allt längre tider med allt högre omgivningstemperatur innan uppvärmningstiden hinner ikapp.

— tWATER-värdet bygger på ena delen av föreningsmassorna som vilande. Praktiska motsvarigheten i massföreningarna blir därför dubbla medelhastigheterna och därmed praktiskt approximativt halva tWATER-tiderna.

— Det betyder totalt en faktor gånger 4 för ovanstående kvot tWARM / tWATER.

— I modern akademi räknar man på HELT annorlunda sätt (NoDrop): utgångspunkten är en REDAN existerande, tempererad aerosol (dammpartikel) på vilken fria vattenångsmolekyler samlas på viss tid (konv. nucleation).

Det är en kondensationfysik, en helt annan matematik.

Droppbildningen överrider Kelvinekvationen

— Och SÅ vidare.

— Det har heller i princip ingen betydelse från vilken temperaturnivå processen börjar (egentligen sämre läge för Kelvinekvationen ju högre starttemperaturen är).

— Förutsatt att processen med vattendroppar som förenas är snabbare än tiden som krävs för luftmolekylerna att värma upp »nollKelvinDropparna», är det tydligt att Kelvinekvationen blir överspelad. Den hinner aldrig träda i kraft under den snabbaste delen av vattendroppsbildningsprocessen: Vattendropparna hinner passera »KelvingÅngtröskeln» vid ca 2% övertryck via droppdiametern ca Ø120nM (tWATER=0,113S; 0°C) INNAN dropparna ens hunnit bli uppvärmda (tWARM=0,141S; 0°C) och kan tillämpas på Kelvinekvationens temperaturhomogena förutsättningar (samma temperatur >0°C hos droppen som i den omgivande luften).

Med andra ord:

Kelvinekvationen (KE) gäller bara för vattendroppar i Jordatmosfären som redan finns, som har den i Kelvinekvationen föreskrivna temperaturen (T), och som ligger över 0°C. Under droppbildningen (H2Opar | MultiH2O) från rena vattenångan tar det TID (tWARM) att nå dit via luftmolekylernas uppvärmning på förenade droppar (som alltid börjar idealt från 0°K efter förening: noll rörelsemängd genom vattenkroppens successivt växande inre kemiska bindningar: nolltemperatur). Så, när väl Kelvinekvationen kommer in i bilden, finns redan dropparna där, och »Kelvintåget» har så att säga redan gått. Den beskrivningsformen uppenbarligen varken omnämns eller ingår i MAC.

— Vattenånga via fria H2O kan på så sätt (H2Opar) förstås bilda vattendroppar genom att Kelvinekvationen (KE) överspelas. Kelvinekvationen hinner helt enkelt inte med.

— Inte ens om vattenånga sprutar ut ur kaffepannans pip (H2OdataInledning) i T=120°C har Kelvinekvationen någon roll att spela: H2O-Parföreningarna kan tydligen förstås tvinga den omgivande luften att börja uppvärmningen i princip från 0°K, från de första 2(H2O) till större vattendroppar. Den uppvärmningsprocessen tar (mycket) längre tid (tWARM) än tiden (tWATER) för droppbildningen, och Kelvinekvationens förutsättningar (att försöka hindra processen genom förångning) kommer aldrig i dagen: Kelvinekvationen kan inte tillämpas på vattendroppar vars temperatur är lika med eller mindre än 0°C: ingen potential för förångning existerar.

När dropparna väl når 0°C-nivån, har »Kelvintåget» med andra ord redan gått (för länge sedan).

— Notera att i en kondensationsprocess finns ingenting av den fysiken närvarande.

— KONDENSATION ser vi praktiskt på toalettstolens kalla (8-12°C) emaljerade vattenbehållare under varma fuktiga sommardagar då den svala behållaren drar till sig den varma luftens vattenmolekyler som samlas där och fäller ut drällande vatten.

— Vattenbildningen i moln, de mikroskopiska vattendropparna som bildas ur pipen på den kokande kaffekannan och ovanför den varma tekoppen, har tydligen inte kondensationens fysikgrund som främsta turistattraktion om beskrivningen i H2Opar och MultiH2O håller streck.

— Av det som syns främst på webben i ämnet finns inget spår av ovanstående typräkning i etablerade led. Inget omnämnande verkar heller finnas.

Om inga felaktigheter finns i framställningssättet, skulle det vara hela historien om vattendroppens bildning enbart från vattenånga: parföreningar, inte kondensation. Den delen verkar dessutom helt obefintlig i omnämnande i etablerad litteratur.

— Se vidare i MultiH2O där matematiken för parbildningarna genomgås på det allra enklaste sättet.

OM grovvärdena ovan stämmer någorlunda praktiskt, skulle droppgränsen med tWARM/tWATER=1 vid 0°C markluft och RH=100% gå vid droppdiametern Ø=250nM, på samma tider ca 2,1 S och motsvarande Kelvinövertryck p/p0=1,0096459.

— Motsvarande vid 100°C visar värdena Ø=1,575µM med t=522S (8,7min) och p/p0=1,0008682 [TMkalkyl].

MinstaVatten, KonÅng

2014V17

MINSTA MÖJLIGA VATTENDROPPEN — 2(H₂O)[‡]

— Kan 2, kan flera. Kan inte 2, kan inga.

Enbart med hjälp av tillgängliga uppgifter på molekylära bindningskrafter framgår omedelbart följande:

Scenario:

7,48027 t20 J ; ångbildningsvärmet per H2O-molekyl i vatten vid 0°C:

N/KG = 1/[18,0154·u] = 3,34319 T25 H2O/KG; [2,5008 T6 J/KG]/[N/KG] = 7,48027 t20 J/H2O:

”Latent heat is the energy released or absorbed by a body or a thermodynamic system during a constant-temperature process.”

”The latent heat of condensation of water in the temperature range from −25 °C to 40 °C is approximated by the following empirical cubic function:

L_water(T) = (2500.8 – 2.36T + 0.0016T ² – 0,00006T ³) J/g.^[10]

where the temperature T is takern to be the numerical value in °C.”

@INTERNET Wikipedia Latent heat [2014-05-14]

http://en.wikipedia.org/wiki/Latent_heat

L_W(T°C) = (2,5008 T6 – 2360·T + 1,6·T² – 0,06·T³) J/KG ; vattnets ångbildningsvärme

2,19495 t20 J ; dissociationsenergin — delningsenergin — för att separera två förenade vattenmolekyler

se WIKIPEDIA Water dimer, Structure and properties [2014-05-14], ”13,22 kJ/mol ”;

0°C:

9,09 t21 J ; Vattenmolekylens rörelseenergi E=mv²/2 vid 0°C markluft [RH=100%] ; 22/9,1 = 2,4 ;

5,66 t21 J ; medelLuftmolekylens rörelseenergi E=mv²/2 vid 0°C markluft ; 22/5,7 = 3,9 ;

20°C:

9,76 t21 J ; Vattenmolekylens rörelseenergi E=mv²/2 vid 0°C markluft [RH=100%] ; 22/9,8 = 2,2 ;

6,07 t21 J ; medelLuftmolekylens rörelseenergi E=mv²/2 vid 0°C markluft ; 22/6,1 = 3,6 ;

— Frånsett datat för ångbildningsvärmet (>3ggr dissociationsenergin):

— Det finns med ovanstående grunddata tydligen ingen normal Jordatmosfärisk fysik som förmår sönderdela en förening 2(H₂O) — konv. eng. water dimer — då den väl har verkställts: den allra minsta möjliga vattendroppen; Ø0,485nM (0°C STP markluft).

— Även om två fria vattenmolekyler (största individuella rörelseenergierna) försöker störta in mot en 2(H2O) för att försöka splittra upp denna i ett totalt gemensamt frontalangrepp (20°C) på (2×9,8t21=1,96t20)J räcker ändå inte den stötenergin till, grunduppgifterna ovan:

— 2(H2O)-föreningen låter sig inte delas upp på den vägen.

— Och alltså: Enbart den helt enkla räkningen visar att Jordatmosfären bör innehålla absolut minsta möjliga vattendroppar. 2(H2O) existerar i luften. Vissa webbkällor (Maj2014) tycks också intyga det.

”Water dimer

Much effort has been expended on the structure of small isolated water clusters. Typically, in the ambient atmosphere there is over one water dimer for every thousand free water molecules rising to about one in twenty in steam.”;

Water structure and science — WATER MOLECULE STRUCTURE May2014

http://www1.lsbu.ac.uk/water/molecule.html

Fram till 2013 [WD2013] [Tretyakov2013] (verkar det som) skulle INGEN etablerad meteorologisk inrättning skriva under på det.

— Den främsta anledningen framgår. som det ser ut, i ljuset av den decenniumlånga, djupgående kontrovers som tydligen bitit sig fast i de akademiska korridorerna i ämnet:

URDM2007

University of Reading — Departement of Meteorology CAVIAR

WATER VAPOUR CONTINUUM (2007) datumuppgift saknas

http://www.met.reading.ac.uk/caviar/water_continuum.html

”Thus, a deep controversy on the nature of the water vapour continuum still remains unresolved.”.

— de rent teoretiska möjligheterna. Tillsammans med den tillhörande, fram tills helt nyligen, experimentella forskningen där ingen lyckades påvisa några naturliga förekomster, har tydligen någon form av »stark spärr» etablerats i den moderna akademins kvarter. Nu [Tretyakov2013] vet man bättre: 2(H2O) finns rent fysiskt — ännu så länge direkt påvisat i laboratoriets ”pressure chamber”.

— Vi har med den grunden mera fria tyglar att skissa upp ett möjligt scenario i den naturliga Jordatmosfäriska vardagsluften:

Förutsättningarna

Förutsättning i vattenbildning:

Vattenmolekylen (H2O) har svag dipolkaraktär [ref. bl.a. Wikipedia — Properties of water, Physics and chemistry].

Blandningen 1:6 motsvarar grovsituationen generellt inom Jordtroposfären och 0°C, proportionerna med luftens molekyltäthet kontra vattenångans täthet. Den situationen bildar (här) ramen för uppgiften att härleda vattendroppsbildning ENBART via den befintliga vattenångan [H2Opar | MultiH2O] genom parbildning.

Notera att den konventionellt benämnda s.k. homogena vattenbildningen, se exv. RoWest2008 — vattenånga som sägs KONDENSERA till vattendroppar enbart på vattenmolekylernas närvaro — INTE ansluter till den uppgift som behandlas här: parföreningar enligt H2Opar.

Den delen har ingen koppling till kondensationsfysiken. Vi förutsätter här bekantskapen i H2Opar och H2Oparam.

— I MAC har den uppgiften ansetts OMÖJLIG [NoDrop] fram till resultaten från Tretyakov2013: fria 2(H2O) — de allra minsta vattendropparna — existerar i rumstempererad luft. Se särskilda sammanställningar i KEB i H2Odata.

Fria vattenmolekyler i vattenånga i ett område med hög markvärme relativt ett område i luften strax ovanför — centimeter — med något lägre luftvärme TAR värme (KonÅng) från den avdunstande regionens materialdel, t.ex. Jordytans markdelar, och GER den delen åter vid rekombination [kondensation eller parbildning — 2(H2O) Tretyakov2013]. För att bryta upp den rekombinerade föreningen — vattenkroppen — krävs alltså en viss minsta motsvarande delningsenergi (MinstaVatten).

— Så länge vi håller oss strax över 0°C

— som garanterar minimal avdunstning från redan bildat vatten, och samtidigt garanterar ett flytande tillstånd för det vatten som finns

— finns i varje fall med ovanstående noterade egenskaper hos två teoretiskt förenade H2O (H2Opar) en viss BINDNINGSENERGI motsvarande just värmeavgivningen från den enskilda H2O-molekylens tidigare avdunstning.

H2OKontakt, H2Ounited

De två möjliga extremsituationerna ab mellan ett par vattenmolekyler i luften: antingen inbördes rörelse med max kollision rakt på, eller maximalt fjärmande parallellt med nollkontakt.

— I praktiken gäller också alla möjliga grader och vinklingar mellan dessa.

Ser vi till hur fristående H2O-molekyler fungerar tillsammans med luftmolekylerna generellt finns (figuren ovan) bara två extremlägen att välja på i molekylernas inbördes frekventa sammanstötningar med alla mellanliggande gradskillnader:

— Antingen rätt på med full impuls, eller diametralt åt skilda håll. För kontaktfallen finns extremfallen nedan illustrerade:

H2Ounited, MinstaVatten

Figuren illustrerar två vattenmolekyler som sammanträffar under olika betingelser. Elektronmassornas osymmetriska fördelning — H-O-H — i H2O-molekylen garanterar maximal flexibilitet och anpassning då två individer närmar sig varandras atom- eller molekylsfärer [Ø3,86Å]. Närkontakt kan då förstås innebära en ökad aktivitet mot ’organiserad maximal elektrisk attraktion’: molekylerna saktar in inför mötet, och börjar förbereda sig för förening. Vi vet inte exakt närmare hur det ser ut i den praktiska fysiken, bara att förutsättningarna finns och, som ovan, att viss experimentell forskning bekräftar såväl en direkt existerande 2(H2O)-fysik [Tretyakov2013] som en [i varje fall i vatten] dokumenterad ”omfamningsdans” [Roncaratti2014].

— OM figursättet skulle vara representativt för fria H2O i luften, alla idealt samma medelhastighet [0°C markluft, v=779,63 M/S från luftmolekylernas medelimpulser, vattenmolekylerna förutsatt i minoritet: max 4% i de varmaste mest fuktiga regionerna på Jordytan], är det tydligt att 1. sammanträffande H2O ger ut HELA sin rörelseenergi mv²/2 vid föreningen till omgivningen i form av värme och därmed 2. [frånsett aktuella Planckstrålningens omedelbara inverkan] börjar från NOLL grader Kelvin via uppvärmning från omgivande knuffande och påstötande luftmolekyler [0°C markluft, vLUFT=485,12 M/S], och vilken uppvärmningstakt på denna molekylnivå kan ske ytterst snabbt: Det behövs bara en enda knuff [inom picosekunder] ifrån någon närliggande luftmolekyl som kan överföra sin impuls till det förenade paret.

— DÄREMOT finns knappast i det förenade paret någon INRE kraft som kan åstadkomma en separation [Kelvinekvationens övertryck p/p0 för 2(H2O) med Ø4,85Å är 140]. En separation måste i så fall ske på kredit från någon yttre impuls. Det innebär ytterligare en svårighet för oss i teorin: att försöka luska ut hur en sådan detalj påverkar teorin för den vidare möjliga vattendroppsbildningen — speciellt med början från en omgivningstemperatur av typen 0°C [där verkställandet av Kelvinekvationens övertryck bör — vilket vi ville veta mer om [KOF] — vara starkt tidsreducerat inom det kritiska s.k. Knudsenskiktet: molekylgränsområdet till makrofysikens temperaturreferenser], eller mycket nära strax över.

— För varje ytterligare tillkommen möjlig H2O-molekyl avges motsvarande EXAKT lika stor värmemängd till omgivningen som den MED vilken H2O-molekylen STANNAR KVAR i »avgivningszonen». Vilket här skulle vara

1. den påträffade H2O-makens molekylyta om bindningen är primär (2[H2O]) eller

2. den kontakterande ytan mellan två sammanträffande redan bildade vattendroppar (2+2=4, osv.).

— Med andra ord: UTFLÖDET av H2O — förångning, avdunstning via enskilda vattenmolekyler — kan omöjligen göras på någon ANNAN energigrund än den på vilken aktuell vattendroppe bildats.

— Anledningen bakom dessa till synes triviala anmärkningar är Kelvinekvationens obetingade resultat vid typ 0°C markluft med RH=100%: absolut förångning även för vatten vid 0°C: Kelvinekvationen ger alltid p/p₀>1, oberoende av vattendroppens radie. Punkterna ovan understryker att den obetingade resultatformen inte är fysikaliskt relevant; Kelvinekvationen har ingen förångningspotenial alls för vatten vid 0°C — dessutom helt oberoende av vattendroppens radie: p/p₀=1 där.

Varje H2O

1. avger viss värme till omgivningen VID förening 2(H2O) och

2. binder viss energi (motsv. dissociationsenergin) VID förening 2(H2O) genom den elektriska kopplingen, vilket betyder att

3. varje vattendroppes tillväxt bildar en motsvarande ENERGISPÄRR, en viss medelbaserad bindningsenergi per H2O.

Eftersom bundna vattenmolekyler besitter praktisk taget nollhastigheter inom vattenkroppen, men som förångade omgivande (max RH=100%) luftblandade fria H2O-molekyler besitter höga hastigheter (780 M/S vid 0°C), kan vi med viss rätt postulera en fundamentalsats i sammanhanget:

inhastigheten hos en inkommande H2O eller vattendroppe är ALLTID — energitekniskt — större än uthastigheten. Nettoskillnaden består just i FORMEN för vattendroppen, dess samlade bildnings- och bindningsenergi. Vattendroppen garanterar — i bevarad temperaturhomogen miljö — att intakten > uttakten.

Se PRAKTISKT REFERENSEXEMPEL i KOFappl.

— Så: Kelvinekvationen »ser inte det». Kelvinekvationen ser bara till tillståndet i netto. Inte huruvida det rådande tillståndets normalisering går fort (omgivningstemperatur upp mot 100°C) eller långsamt (omgivningstemperatur ner mot 0°C).

En vattenmolekyl som lämnar en vattenyta måste tvunget, under alla omständigheter, besitta en viss minsta rörelseenergi för utarbetet: värme.

— Är vämegraden inifrån vattenkroppen större än värmegraden utifrån kan H2O-molekylen lämna området. Annars inte. Kelvinekvationen gäller då fortfarande, nämligen som en ren tillståndsekvation — ett exempel SKULLE KUNNA VARA för den första primära 2(H2O)-vattendroppen med idealt sfäriska diametern Ø=4,85 t10 M på Kelvinövertrycket p/p0=140. Dess utpekade, latent liggande potentiella ytavdunstningar har bara ännu inte letts i verkställande.

— Det finns emellertid ytterligare spärrar i Kelvinekvationen — ytspänningsfaktorn, utförligt i SEA — som visar följande:

— De allra minsta vattendropparnas (ca 60[H2O] vid 0°C; ca 40[H2O] vid 20°C) samlade rörelseenergier för motsvarande antal fria H2O är inte större än den aktuella vattendroppens inneslutande ytspänningsenergi — att de fria H2O är större är den rimliga energiräkningens blotta förutsättning för att H2O-molekylerna ska kunna komma ut ur vattenkroppen. Kelvinekvationens form besitter därför heller ingen energiteknisk förutsättning för att verkställa förångning på den nivån: det finns minimala vattendroppar i luften omkring oss som aldrig låter sig förångas (frånsett en och annan kontakt med någon kosmiskt inkommande höghastighetspartikel).

Se även artikelsammanställningar från H2Odata.

KOF, KELVINEKVATIONENS OFULLSTÄNDIGA FÖRÅNGNINGSPOTENTIAL

Se även i MinstaVatten | SEA | H2Odata

För att få KELVINEKVATIONEN att uttrycka exakt noll förångningspotential vid ämnets stelning, måste i princip följande matematik infogas — här med exempel från vattnets fryspunkt 0°C:

p/p₀ =e^ ([1,2 t9 M/r]^ [1 – 1/(a0°C + 1)] – 1) =e^ 0 = 1 ;

Vid stelningspunkten (=0°C för vatten):

p/p₀ =e^ [([1,2 t9 M/r]^ [1 – 1/(a0°C + 1)]) – 1/(b0°C + 1)]

=e^ 0

= 1 ;

Över stelningspunkten (>0°C för vatten):

p/p₀ =e^ [([1,2 t9 M/r]^ [1 – 1/(aT°C + 1)]) – 1/(bT°C + 1)]

=e^ [([1,2 t9 M/r]^ [1 – 1/(1001°C + 1)]) – 1/(100001°C + 1)]

=e^ [([1,2 t9 M/r]^ [0,990099]) – 0,00009999...]

~e^ [1,2 t9 M/r] ; Kelvinekvationens normalform för 0°C markluft RH=100%

b-koefficienten är inte kritisk och kan sättas »hur högt som helst»:

a-koefficienten beror på hur snabbt förångningspotentialen genomgår KNUDSEN-skiktet — vid viss temperatur.

2014V16

KELVINEKVATIONENS OFULLSTÄNDIGA FÖRÅNGNINGSPOTENTIAL

————————————————————————————————————————————————————————

konv. Knudsenskiktet, ref. Wikipedia Knudsen layer: d=bT/pπr_H2O² är gränsområdet mellan ett fast ämne och omgivande luft eller vakuum.

————————————————————————————————————————————————————————

Illustrationen förtydligar vad Kelvinekvationen p/p₀ = e^ 2Ŝ(U_W/ρ_W)/r(R)T tycks sakna:

— Vatten obetydligt nära fryspunkten 273,15°K=0°C vid STP uppvisar obetydlig H2O-förångning: ingen potential existerar för förångning. Men Kelvinekvationen beskriver ett påtvingat övertryck [här för 0°C markluft med RH=100%] p/p₀=e^ 1,2 t9 M/r >1 på vattendroppen oberoende av fastillstånd — här i det närmaste is — och som »leder till vattendroppens upplösning genom förångning». De Etablerade Författarleden på webben (Maj2014) som framhäver de minsta vattendropparnas hopplöst dömda upplösning på den fasonen tycks f.ö. aldrig sina [NoDrop].

— Kelvinekvationen BORDE för fallet med fast ämne — is — istället uppvisa p/p₀=1 — oberoende av vattendroppens storlek: ingen energi existerar inom ett fast ämnes ramar som SJÄLVMANT kan åstadkomma ämnets upplösning. I vattenfallet: ingen energimässig potential existerar vid 0°C [och under våra Jordmarksnormala förhållanden] för H2O-förångning.

— Ett sätt att rent principiellt STYRA ut Kelvinekvationen så att den stämmer på den punkten är enligt [här särskilt för 0°C markluft med RH=100%]

p/p₀=e^ [([1,2 t9 M/r]^ [1 – 1/(aT°C + 1)]) – 1/(bT°C + 1)]

— b-koefficienten kan sättas hur högt som helst för att garantera att 0°C ger 1/(bT°C + 1) = 1 — e^(1–1=0)=1 — och att varje värmegrad över 0°C ger 1/(bT°C + 1) = 0,000000...9999, som garanterar försumbar inverkan på den normala Kelvinexponentens kvantitet.

— Vid T=0°C [och mycket nära] blir p/p0=1. Beroende på snävheten i funktionen från 0°C och uppåt, a-koefficienten, kommer sedan (a=1) Kelvinekvationens normalform snabbt att uppnås redan vid T=9°C; potensformens exponent blir då ^0,9. Snabbare åtkomst med typ a=2 ger motsvarande ^0,947, osv. Negativa T-värden gäller naturligtvis likvärdigt med T=0.

— Se även ytterligare »magiska friheter som Kelvinekvationen tar sig» i SEA: Vid RH=100% 0°C markluft visar Kelvinekvationen större innesluten ytspänningsenergi [J/M²] för vattendroppar lika med och mindre än 58 stycken H2O än vad dessa som fristående H2O-molekyler i fria luften omkring summerar i total rörelseenergi. Den räkningen går definitivt inte ihop: Kelvinekvationen innefattar gränsformer som tar ut mer än vad kontot innehåller.

Katz2007 antyder — men tyvärr inte närmare beskriver — den detaljen. Uppenbart är det i vilket fall att Kelvinekvationen för typ vattnets 0°C gör anspråk på att innefatta mystiska och magiska extrakrafter — extraenergier — som tar sig friheten att förånga det som saknar förångningspotential.

Kelvinekvationen innehåller med andra ord och tydligen inget STYRE för fasövergången till FAST ämne:

— Speciellt för de små vattendropparna från Ø120nM och mindre

här särskilt för 0°C markluft med RH=100% [KEis]

p/p₀ = e^ [1,2 t9 M/r]

som uppvisar p/p0-värden från omkring 1,02 — motsvarande max naturlig överfuktighet RH=102%, och sedan växande — betyder omständigheten illustrerad och belyst ovan att ingen förutsättningen existerar i Kelvinekvationens ljus för dess uppvisade höga p/p0-värden med avtagande droppdiameter. För 2(H2O)-droppen Ø0,485nM ges p/p0=140, analogt RH=14000%.

— Det finns uppenbarligen i fallet 0°C vatten i omgivande 0°C luft ingen sådan närvarande förångningsenergi som kan verkställa den utpekade ordningen.

Dokument eller skrift på webben som omnämner eller vidrör detaljen har eftersökts (Maj2014) men ännu inte påträffats (området är milt sagt omfattande, komplicerat, delvis svårtillgängligt — jämför KelvinH2Owebben: ett mer eller mindre uttalat kaos). Den enda möjliga antydan, i den vaga beskrivningen, ges från Katz2007:

”Unfortunately, we all also know that the predictions of ... the Kelvin equation .. do not agree with the measured temperature dependence ...”

Se även vidare i SEA.

Vi noterar att de här påpekade ogynnsamheterna i Kelvinekvationen BARA — endast — berör temperaturer nära och lika med fasta tillståndet (is), samt (SEA) de allra minsta vattendropparna (räknat vid RH=100% 0°C markluft) från Ø1,5nM och neråt (från p/p0=5).

— Övrigt berörs inte.

— Om det inte framkommer något som träder in och dementerar dessa här påpekade resultat, är det tydligt att den allmänt etablerade uppfattningen (NoDrop) att det krävs främmande mikropartiklar (konv. aerosoler) i luften för att vattendroppar (och snökristaller) ska kunna bildas, har stött på trubbel.

— Tillkomsten av Tretyakov2013 intygar det särskilt: 2(H2O) existerar i fysiken.

— Det faktum ATT närvaron av mikropartiklar HAR katalyserande verkan på vattendroppsbildningen råder (här) inget som helst tvivel om. Det är alldeles säkert så. Men att också naturboken av princip skulle föreskriva det, obetingat, helt vid sidan av vattenfysiken självt, FÖREFALLER mindre troligt (»självständighetsprincipen»). Ovanstående är — möjligen — ett bidrag i det klargörandet.

— Upptäckten (här, Maj2014) med tillkomsten av Tretyakov2013 intygar det särskilt: 2(H2O) existerar i fysiken;

— Natur och Modern akademi visar sig — återigen — INTE kunna musicera tillsammans [TNED], ehuru experimentalfysiken ständigt tjusar utsikterna (experimenterande är av naturen teoretiskt oberoende, eller ska i varje fall vara det: experimenten klargör dynamiken, förklarar sammanhangen, påvisar grunderna, belyser Logiken). Det är tydligen inte ekvationerna, den algebraiska genialiteten, det hänger på. Problemet är alldeles tydligt attityden.

— Se även vidare i H2Odata.

— Se även komplementet till KOF i KOFappl som ansluter ytterligare till ovan.

KOFappl, KOF

Ang. Kelvinekvationen och TAKTEN i vattenmolekylernas kondensation och avdunstning:

Vid 0°C besitter vattenbundna H2O ingen nämnvärd rörelsemängd: mv=0. Utanför vattenytan däremot bestäms rörelsemängden av luftmolekylernas genomsnitt med molekylhastigheter hos vattenmolekylerna på runt 780 M/S (0°C markluft med RH=100%).

— Med en liten temperaturhöjning över 0°C finns fortfarande en teoretiskt nära obetydlig förångning, samtidigt som de höga molekylhastigheterna utanför vattenytan kvarstår.

— Med hänsyn till den SAMMANSTÖTNINGSFREKVENS som de fria H2O-molekylerna besitter, och den LÅNGSAMHET som förångningen så verkställs igenom, synes uppenbara möjligheter finnas för de fria H2O att förenas innan de hinner förångas.

— Exempelformen gäller bara speciellt nära 0°C (och RH=100%).

PRAKTISKT REFERENSEXEMPEL:

— Vi använder förnämligt den 0°C markluft (RH=100%) preparerade Kelvinekvationen [KEis] för vatten enligt

p/p₀ = e^ 1,2 t9 M/r

Vi exemplifierar med en rent TEORETISK minsta möjliga vattendroppe bestående av 2(H2O) med r=2,43Å som ger

p/p₀ = e^ 1,2 t9 M/(0,243 t9 M)

~ 140

»De flesta författare på webben» ansluter den matematiken till frasövningarna i NoDrop: ’den vattendroppen är omöjlig’.

— Frånsett tillkomsten av resultatet i Tretyakov2013 — 2(H2O) existerar i fysiken:

— VID 0°C existerar ingen energi som KAN verkställa Kelvinekvationens ”p/p₀=140”. Den potentialen är noll — helt oberoende av r-värdet. Det är den främsta uppenbarligheten.

— Ökar vi omgivningstemperaturen bara SÅ litet över 0°C, ATT det fortfarande finns en SÅ liten förångningspotential ATT mängden omgivande fria vattenmolekyler i lufthavet som har betydligt större rörelsefrihet än de vattenbundna HINNER sammanträffa många gånger om — har vi nått fram till MÅLET i beskrivningen:

— De fria H2O hinner i princip TEORETISKT bilda föreningar INNAN någon verkställighet ALLS i förångning HUNNIT inträda: möjligheten för H2O-sammanslagningar (förutsatt inga interna krafter bryter föreningarna) att ackumuleras INNAN någon nämnvärd ”p/p₀=140”-förångning ALLS hunnit visa sig — just på grund av den mycket nära 0°C aktuella omgivningstemperaturen, eller så nära noll som en motsvarande praktisk fysik kan tillåta.

EXEMPELFORMEN belyser tydligen Kelvinekvationens inneboende begränsning i beskrivningen av aktuell vattenfysik.

Kelvinekvationen »påstår» generellt att vattendroppar <60nM »är omöjliga» på grund av att »droppen avdunstar»: droppen besitter ett Kelvinövertryck (p/p₀=1,02 motsv. RH=102%) som kräver mera H2O-utvandring än invandring: droppen avdunstar. Men Kelvinekvationen säger ingenting om TAKTEN i den avdunstningen. Är takten långsam nämligen — T°C nära 0 — finns fortfarande visst teoretiskt utrymme för singulära H2O att förenas och därmed bilda vattendroppar.

— Citatet nedan är på visst sätt välkommet i upplysningen om var man står i ämnet (2007), och som delvis ansluter:

Katz2007

NUCLEATION AND ATMOSPHERIC AEROSOLS: 17th International Conference, Galway, Ireland, 2007

Colin D. O'Dowd, Paul E. Wagner —

HOMOGENEOUS NUCLEATION: What I Understand, What I Somewhat Understand, What I do not Understand,

Professor Joseph L. Katz

”For gas to liquid nucleation one can use the Kelvin equation as our evaporation rate model. However, the Kelvin equation is derived using equilibrium thermodynamics. In a supersaturated gas there is equilibrium only for the clusters of critical size. In principle, using it for all other sizes is incorrect. Evidence that doing so indeed is incorrect is provided by the comparison of predictions with collection of experimentally measured nucleation rates. The Kelvin equation version of theory results in an equation for the self-consistent version of the Classical Theory of Nucleation. The fully measured fluids the self-consistent version of classical theory fairly accurately predicts rates of nucleation rate differ negligibly. We all know that for all, carefully measured fluids the self-consistent version of classical theory fairly accurately predicts the measured supersaturation dependence of the nucleation rate. (The Kelvin equation makes predictions which are identical to well within the accuracy of this statement.) Unfortunately, we all also know that the predictions of this equation (and also of the Kelvin equation) do not agree with the measured temperature dependence of the nucleation rate.

Farkas (who credits Szilard) created a scheme for obtaining these evaporation rates by equating them to evaporation rates of identically sized cluster in a supersaturated vapor constrained to be in ”equilibrium”. I have created one which equates the evaporation rates to the evaporation rates from identically sized clusters, but in a truly equilibrium vapor, the saturated vapor at the same temperature. To obtain these evaporation rates one then assumes that the clusters are identical to small droplets of liquid density with liquid surface tension, etc. Improvements have consisted of using a variety of thermodynamic or statistical mechanics models, models which try to correct for percieved differences such as entropy effects, a better estimate of the relationship of droplets to clusters, attributing a size dependence to the surface tension, etc. I know these well; my name is on several such papers. Nontheless, I remain uncertain about the relevance of any of these models to a quantitative description the rate at which molecules leave clusters.”, s132.

GoogleBOOKS från »vaporization rate, kelvin equation»

— Speciellt omkring 0°C — eller generellt i den naturliga Jordatmosfäriska molnbildningen inom 1-2 KM med temperaturer grovt 0-1°C — är det tydligt att i varje fall IS inte uppvisar någon överdriven tendens i materialytan att förångas. Den förångning som sker där är tydligen att förstå som liten.

— Med uppfattningen att en vattenmolekyl H2O infångad av isytan besitter i det närmaste noll rörelsemängd (vH2O=0)

— endast minimala atomsvängningar i iskristallen finns, liknande atomgittersvängningar i andra fasta ämnen

— och det faktum att rörelsemängden (mv) hos fria vattenmolekyler utanför iskroppen i luften ovanför bestäms just av majoriteten luftmolekyler och deras genomsnittliga rörelsemängd

mv_LUFT = 2,33 t23 JM/S vid T=0°C med medelhastigheten 485,12 M/S, medelavstånd 3,34nM

är det tydligt att det bör finnas en gradient — en kurva (vinjettbilden i H2Odata höger, bStyret) — som börjar på is-vattenmolekylens NOLL rörelsemängd, analogt NOLLHASTIGHET och slutar vid någon viss molekylmultipels distans från iskroppen på de omgivande luftmolekylernas genomsnittliga rörelsemängd — vid 0°C markluft betyder det för en fri H2O molekyl i luften vH2O=779,63 M/S.

Vad säger Kelvinekvationen i det sammanhanget?

— Uppenbarligen intet: Kelvinekvationen besitter ingen sådan beskrivande fysik. Kelvinekvationen beskriver endast formen för ett vattenångövertryck, ett faktiskt tillstånd som beskriver att utflödet H2O från vattendroppen är större än inflödet — inte hur fort utflödet verkställs.

Och alltså:

Är omgivningstemperaturen alldeles sublimt strax över 0°C, långsamt i avtagande i ett molnområde med mättad RH=100% vattenånga, (med en motsvarande nyligen uppnådd daggpunkt) och alltså strängt läge finns för vattendroppsbildning, då utsäger Kelvinekvationen (0°C) ett övertryck p/p0=140 på den första möjliga 2(H2O)-föreningen, den första minsta möjliga vattendroppen med ideala sfärradien 0,243nM. Kelvinövertrycket 141 motsvarar i den vattendroppens idealt sfäriska yta en relativ fuktighet på RH=14000%, och vilket normalt sett i makroskopiska sammanhang skulle innebära rena ångexplosionen: »vattendroppen ångtrycksexploderar». Man säger därför [NoDrop]: en sådan minimal vattendroppsbildning är därför omöjlig.

— Här kommer alltså aspekten in med »Kelvinövertryckets temperaturberoende». Citatet ovan (Katz2007) delvis understryker att kunskaper i ämnet (fortfarande) saknas.

— Det är nämligen uppenbart att OM »Kelvindroppförångningen» sker i långsam takt — mycket mera långsamt än takten med vilken omgivande H2O kan komma i kontakt med primären 2(H2O) för påbyggnad — kan visserligen Kelvinekvationen fortsätta fungera som den vill. Men då nu flera utifrån inströmmande »höghastighets-H2O» hinner komma med på den maximalt långsamt rullande bussen än de »maximalt låghastighets-H2O» som droppar av från isen, blir resan aldrig inställd på grund av för låg anslutning.

— Den primära 2(H2O)-individen hinner i så fall samla på sig flera H2O än de som förångas och därmed samtidigt sänka Kelvinövertrycket, och därmed allt mera gynnsamma förutsättningar för fortsatt tillväxt.

— Var finns den aspekten genomgången i etablerad litteratur? På visst sätt berörs den i citatet från Katz2007: ’man vet inte’. Det bör alltså (ännu 2014) inte finnas mycket att hämta i etablerad litteratur i ämnet.

— Situationen ändra(de)s (drastiskt — under den här författningens gång [Maj2014]) med uppmärksammandet från Tretyakov2013:

2(H2O) existerar redan i fysiken. Det understryker bara (ytterligare) exempelbeskrivningen.

— Beskrivningen föregående den detaljen:

Wang2013

PHYSICS AND DYNAMICS OF CLOUDS AND PRECIPITATION — Pao K. Wang 2013

”There are numerous experiments that have been carried out to check the validity of the Kelvin equation. Sambles et al. (1970) used an electron microscope and tested the evaporation rate of small lead and silver droplets of radii less than 0.1 µm before evaporation and found that the Kelvin equation predicts evaporation rates agreeing with experiments down to a few nanometers (10^–9 m).”, s120.

GoogleBOOKS från »vaporization rate, kelvin equation»

Wang refererar till det som J. R. Sambles beskriver (1971) i

AN ELECTRON MICROSCOPE STUDY OF EVAPORATING GOLD PARTICLES:

The Kelvin equation for liquid gold and the lowering of the melting point of solid gold particles

”Secondly. Sambles, Skinner & Lisgarten (1970) have confirmed, using a less direct technique, the exact exponential, form of Kelvin’s theory by observation of the evaporation of small particles in thje electron microscope. Liquid lead and solid silver particles less than 50 nm in radius were studied. The present work is a continuation of their study using a similar technique with liquid and solid gold particles. These observations, as well as being a further confirmation of Kelvin’s theory, yielded a new type of evaporation curve. Sudden changes in the rate of evaporation of solid gold particles have been interpreted as being due to melting of the particles from an initially solid phase with an evaporation coefficient less than unity, to a liquid phase with an evaporation coefficient of unity (Blackman & Sambles 1970).”,

Med begränsad åtkomst från (BiblioteksCertifieradInternetDokumentAccess)

JSTOR — NÅGON FORM AV INTERNETJOURNALARKIV SOM KRÄVER SÄRSKILD REGISTRERING [2014-05-06]

http://www.jstor.org/discover/10.2307/78060?uid=3738984&uid=2129&uid=2&uid=70&uid=4&sid=21103762749391

Resultatbilden som antyds ovan är inte alls så entydig som Wang påstår. Beskrivningen i citat ovan från Sambles själv antyder snarare meningar som ansluter till Katz2007: ”Unfortunately, we all also know that the predictions of this equation (and also of the Kelvin equation) do not agree with the measured temperature dependence of the nucleation rate.”.

Ho1997

— Koll på liknande dokument visar att ”evaporation rate” (som möjligen avses i Wang2013) visar innebörden: Vid 20°C mäts avdunstningen i milligram per sekund vid olika luftfuktighetsintervall [EVAPORATION OF PENDANT WATER DROPLETS IN FRACTURES Clifford K. Ho 1997 http://onlinelibrary.wiley.com/doi/10.1029/97WR02489/pdf]. Det är uppenbarligen inte vårt bord. Uppgiften här är att försöka klarlägga det molekylära tillväxtförhållandet mellan hastigheterna hos utgående och inkommande H2O-molekyler. (Sambles-citatet antyder att tydliga differenser existerar, mer visas inte från webbkällan).

— Kelvinekvationen utsäger att »förångningstakten» ökar med avtagande droppradie. Vi VET det redan.

— Molekylhastigheterna utanför en vattendroppe behärskas av luftmolekylernas rörelsemängder (mv=28,95u·485,12M/S = 2,33 t23 JM/S vid 0°C markluft), medan rörelsemängden hos en H2O-molekyl på ytan av en vattendroppe eller isbit (v=0) är praktiskt taget noll. Vartefter omgivningstemperaturen ökar, blir också ytaktiviteten på droppytan eller isytan motsvarande mera utpräglad. Det är nog inte den analysen som författaren Wang2013 avser.

Kelvinekvationen [KE] innehåller inga fysikaliska parametrar som innefattar förångningstakt i samtidigt beroende av omgivningstemperaturens olika värden, explicit för vattnet från fryspunkten och uppåt. Föregående citats författare förefaller också ansluta till det ämnesområdet (men vi vet inte säkert, än, vad som menas),

”Unfortunately, we all also know that the predictions of this equation (and also of the Kelvin equation) do not agree with the measured temperature dependence of the nucleation rate.”, Katz2007.

— Sambandsformen (Se även i Wikipedia Kelvin equation: ln[p/p₀]=2γVm/rRT) uttrycker en gränsform för droppradien (r) via ångtryck (p/p₀>1), ytspänning (γ) och molekylvolym (konv. V_m , rel. U_Wu/ρ_W) på allmänna gaskonstanten (konv. R, rel. Ru) och temperaturen (T): Temperaturfaktorn kopplar till omgivningstemperaturen, och säger ingenting om hur Kelvinekvationen uppför sig i molekylskiktet (Knudsenskiktet) mellan vattendroppens yta (v=0M/S) och luften (v=500 M/S) i en omgivningstemperatur typ 0,001°C; hastigheten med vilken H2O-molekyler förångas, lämnar vattendroppen, i den miljön. Det finns ingen sådana parameter med i Kelvinekvationen.

Författaren Wang avslöjar också (den tydligt ytliga) nivån på sitt inlägg (relativt det här ämnets avsikter) i meningen

”Otherwise they could not remain but would have to evaporate as soon as they were produced as required by the Kelvin equation.”, Wang2013 s120m.

— ”as soon as”. Så snart som.

Det är uppenbarligen ingen molekylär inblick författaren avhandlar.

— Jämför de två möjliga fallen med två fria H2O-molekyler:

De två möjliga extremsituationerna mellan ett par nära vattenmolekyler i luften: antingen inbördes rörelse med max kollision rakt på, eller samåkning parallellt med ingen trängande kontakt alls. I praktiken gäller också alla möjliga grader mellan dessa.

— Två skilda H2O i fri luft är för tillfället på väg att sammanträffa.

— Vattenmolekyler har f.ö. svag dipolkaraktär och besitter därför viss tendens att förenas om mötet sker lätt. Vid föreningen avges respektive molekyls rotationsenergi som värme (Planckstrålning), och den energin håller sedan paret tillsammans i en motsvarande bindningsenergi.

— Vattenmolekylernas svaga dipolkaraktär gör det möjligt för dem att förenas.

Illustrationen närmast ovan visar principen.

— ”evaporate as soon as they were produced”?

— Med vilken KRAFT då, herr Wang? Visa.

— Vad vi VET i fysiken, existerar inga sådana mystiska magiska explosionskrafter mellan molekylerna ”så snart de förenas”.

Som (nog) redan framskymtat från citatet Katz2007 finns (nog) inga direkta forskningsresultat att studera så länge man inte finner en (optisk) experimentell metod att studera typ vattendroppsbildning i naturliga molnförekomster.

— Vi har för det ändamålet följande scenario att undersöka närmare:

Kelvinövertryck p/p0=140:

OM omgivningstemperaturen ligger kring fryspunkten (0°C) OCH en H2O kommer i kontakt med en annan H2O i den fria luften, existerar ingen omedelbar SEPARATIONSKRAFT utöver en eventuellt återlämnad föreningskraft (fullständigt elastisk stöt). Tvärtom finns vattenmolekylernas dipolkaraktärer som kan garantera en varaktig förening: 2(H2O), Ø=4,85 t10 M [MinstaVatten].

Kelvinövertryck p/p0=51:

— OM också ytterligare en sådan 2(H2O) kommer i mjuk kontakt med den förra, och förutsatt att förångningstakten INTE sker med den omgivande luftens kollisionsfrekvenser [medelfrivägen för luft runt 0,3µM med medelhastigheten grovt 500 M/S ger stötfrekvensen 3,3 GHz med perioden 0,3nS] kan också dessa förenas. 4H2O, Ø=4,85 t10 M.

Kelvinövertryck p/p0=1,02:

— Förutsatt att det håller på så — H2O-molekyler lämnar droppytan i betydligt långsammare takt än mängderna som förenas, fortfarande i Kelvinekvationens fulla giltighet — kommer »Kelvinspärren» att passeras (i en normal molnbank med max 2% överfuktighet) via antalet fördubblingar vid 2²⁵H2O, Ø=120 t9 M = 0,12µM, se sammanställda kalkylceller till Kalkylkortet i TillämpningM | H2O Tabell5A i Blixt2014.ods. Därifrån är det sedan i princip fritt fram utan hinder.

— Problemet är att vi inte VET om den »molekylräkningen» — låga H2O-utflyktshastigheter — stämmer.

Vi kan något »vända på resonemanget» och anställa ett mera upplysande energiresonemang:

— Vattenmolekyler som förenas förlorar hela eller en del av molekylens rotationsenergi, och som avges som värme (Planckstrålning). OM, vilket vi inte vet här, vattenmolekyler som träffas med frontalhastigheterna 700 M/S i fri luft verkligen KUNDE sluta i förening, SKULLE det häftiga mötet resultera i att bägge skulle förlora HELA sitt rörelseenergikapital som värme till omgivningen, och, så att säga, sedan börja historien tillsammans från exakta 0°K. Vi behöver inte explicit förutsätta den möjligheten här [Tretyakov2013], men kan ändå räkna med den om inget finns som hindrar.

Roncaratti2014

»colliding water molecules»

AIP — THE SPONTANEOUS SYNCHRONIZED DANCE OF PAIRS OF WATER MOLECULES,

Roncaratti et al., (2014)

http://scitation.aip.org/content/aip/journal/jcp/140/12/10.1063/1.4869595

”The experimental findings and the theoretical treatment developed to shed light on the details of the process suggest that the transformation from free rotations to pendular states depends on the rotational level of both molecules, on the impact parameter, on the relative collision velocity, on the dipole moment product and occurs in the time scale of picoseconds.”

pendular state, kräng-vipp-vrid-rörelser hos inbördes förenade molekyler — asymmetriska elektronmassfördelningar i molekylkopplingarna (induktiva, elektriska, magnetiska elektronmasseffekter):

— OBSERVERA DEN KNAPPHÄNDIGA INFORMATIONEN I WEBBKÄLLAN OVAN (API-forskningsrapport som måste köpas): vi vet inte om saken gäller H2O-molekyler som studerats i FLYTANDE vatten, eller om man (ev. också) avser beskrivningar av fria H2O-molekyler.

Harvard University — PENDULAR STATES, Dudley Herschbach [2014-05-06]

http://faculty.chemistry.harvard.edu/dudley-herschbach/pages/pendular-states

”Molecules can be aligned by exploiting the interaction between their permanent or induced dipole moment and an external electric, magnetic, or laser field”.

CITATEN NÄRMAST OVAN — speciellt AIP-citatet — får (nog) INTE tolkas som »bekräftelser» på föreningar mellan fria vattenmolekyler. AIP-artikelns sammanfattning är alldeles för knapphändig, och det går explicit inte att utläsa vad sammanhanget, riktigt, går ut på.

MEN:

— För att få veta det måste man köpa rapporten. Det är inte vårt bord:

— Vi tar (här) inte betalt av barnen för att de tycker det är roligt — kul — med Kunskap.

— Vi tycker (här) tvärtom bara det är roligt om vi får bidra med något intresseväckande.

Vilka Stater är det som ännu inte har fattat galoppen med Det Sociala Ansvaret? Det heter Infrastruktur. Allmänna skattemedel. Fria läromedel. Fri undervisning. Alla som jobbar hjälps åt, allt efter förmåga, motivation och intresse.

SEA

EkinEs, EkinEsLimes

2014V14

Kelvinekvationens ytspänningskoefficient [‡]

BEGRÄNSAR KELVINEKVATIONENS ENERGIRÄKNING FÖR ANTALET H2O

Ŝ = E/A — [Ŝ, »s-flex»]: Vid [RH=100%] 0°C passerar Kelvinekvationens ytspänningsenergi samma vattendroppes samlade rörelseenergier från samma antal N=58 stycken fria H2O i luften omkring som droppen består av, eller kan förstås vara sammansatt av. Den energiräkningen går uppenbarligen inte ihop:

— Kelvinekvationen innehåller Ŝ-faktorn med den avgörande vattendroppsradien.

— Generellt i MAC är man av uppfattningen att, typ, »Kelvinekvationen utsäger att vattendroppar mindre än ca Ø120nM enbart bestående av vattenmolekyler inte kan förekomma» [NoDrop]: Kelvinövertrycket är p/p0=1,02 vid den droppdiametern [0°C RH=100%], vilket motsvarar en maximalt naturlig luftfuktighet RH=102%.

— Resultatet nedan ger viss inblick.

Från en viss undre gräns förutsätter Kelvinekvationen tydligen MERA ytspänningsenergi (J/M²) i vattendroppens yta än vad hela vattendroppens samlade rörelseenergi på komponenterna har att visa upp.

NEWinvestigation (2014V14):

— Förutsatt att luftmolekylerna befinner sig i majoritet

— vilket också är fallet i Jordatmosfärens klimatskikt (troposfären) med som mest max ca 4% vattenmängd på 96% luftmängd (SVPgrafen), vilket garanterar att luftmolekylernas medelimpulser (mv) bestämmer medelimpulserna också för de fria vattenmolekylerna i luften

— kan följande upplysande energibalansräkning anställas:

E_kin = N · m_Vv²/2 = N(U_Vu)[j_LUFT/(U_Vu)]²/2 ; j=mv:

= N[j_LUFT]²/2(U_Vu)

= N[m_L√ 3bT/m_L]²/2(U_Vu)

= N[√ 3bTm_L]²/2(U_Vu)

= N3bTm_L/2(U_Vu)

= N3bT(U_Lu)/2(U_Vu)

= N3bT(U_L)/2(U_V)

= N3(1,38055 t23 J/°K)T(28,952127)/2(18,0154)

= N·T(3,32797 t23 J/°K) ; VerifiedOK. T = 273,15°K = 0°C:

E_kin = N·(9,09035 t21 J) ;

E₀ = (9,09035 t21 J) ; E₀ = T°K(3,32797 t23 J/°K)

E_kin = N·E₀ ; summan av N Fria H2O i [max RH=100%] T°K luft

Ytspänningen:

Ŝ = E/A ; J/M² ; Ŝ_W = 0,07564 J/M² – (0,0001679 J/M²°C)·T°C | 0-100°C

E_Ŝ = AŜ = 4πr²Ŝ ; J

r = [N3(U_Vu)/4πρ_W]^1/3

= N^1/3[3(U_Vu)/4πρ_W]^1/3

= N^1/3[3(18,0154[1,66033 t27 KG])/4π(1000 KG/M³)]^1/3

= N^1/3(1,92567 t10 M) ;

E_Ŝ = 4πr²Ŝ

= 4π[N^1/3(1,92567 t10 M)]²Ŝ

= N^2/34π(3,7082 t20 M²)Ŝ

= N^2/3(4,65986 t19 M²)Ŝ ; Ŝ[0°C] = 0,07564 J/M²:

E_Ŝ = N^2/3(3,52471 t20 J) ; E_Ŝ = N^2/3(4,65986 t19 M²)(0,07564 – 0,0001679 ·T°C)J/M²

E_Ŝ = N^2/3(3,8774194)E₀ ; Droppytans inre ytspänningsenergi för N inneslutna H2O

: Med det mera avancerade ytspänningssambandet från Vargaftik1983 ges N=59:

E_kin = E_Ŝ ;

N·E₀ = N^2/3(3,8774194)E₀ ;

N^1/3 = (3,8774194) ;

N = (3,8774194)³

= 58,294603

~ 58 H2O ; Ytspänningsenergin än större än fria komponentenergin upp till N = 62 H2O.

— Den matematiken går uppenbarligen INTE ihop:

— agenten tar ut mer pengar från banken än vad kontot innehåller.

EkinEs, EkinEsLimes

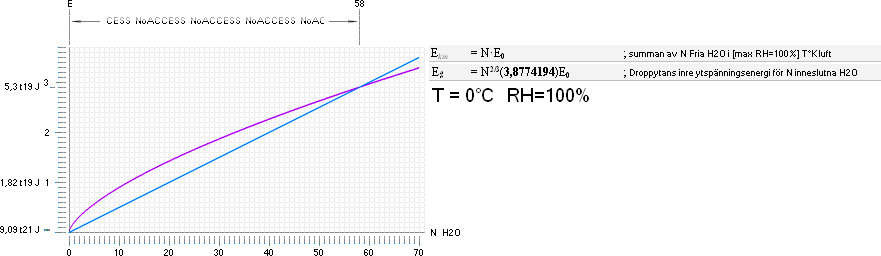
Energiräkningen visar att en gräns existerar där Kelvinekvationens ytspänningsenergi [Ŝ=E/A] — den i vattendroppsytan inneslutna ytspänningsenergin — för en vattendroppe med bestämd radie som är bildad från N stycken H2O-molekyler blir STÖRRE än den totalt samlade rörelseenergin från lika många N stycken fria H2O-molekyler i luften omkring. Gränsen vid T=0°C [RH=100%] ligger vid N=58. Räkningen visar att — vattnets ytspänningsenergi per M² avtar något med växande temperatur — N-gränsen sjunker från N=58 med växande temperatur via en kubisk funktion. Vid 20 | 100°C är gränsen N=41 | 11, se sambandet för N nedan.

Graf y = 0.5(1([x])+0(3.88x'2/3))

ER, EnergiResonemanget

Så länge de N förångade vattenmolekylerna summerar större samlad rörelseenergi (E_kin) än ytspänningsenergin (E_Ŝ) i den omslutande N(H2O)-vattendroppens yta, finns i varje fall en teoretiskt balanserande energiräkning som kan skriva under på och attestera arbetsavtalet: De N molekylerna har tillräcklig samlad energi för att kunna förångas ut igenom och bryta spärrytan. Är däremot ytspänningsenergin (E_Ŝ) den större parten, till vänster om kurvskärningen i figuren ovan (EkinEs), finns inte längre någon balanserande energiräkning som garanterar utträdet, och därmed heller ingen säker teoretisk bas för vattenmolekylernas förångning. En gränsform har i så fall uppnåtts där förångningen inte längre är teoretiskt säkrad.

— Grafbilden ovan i den raka blå grafen visar de N förångade vattenmolekylernas samlade rörelseenergi (E_kin) vid 0°C markluft med RH=100%, den violetta kurvan visar den motsvarande N(H2O)-vattendroppens omslutande ytspänningsenergi (E_Ŝ).

— Skärningspunkten mellan graferna markerar E_kin=E_Ŝ. Ovanför den gränspunkten, och endast där, finns tydligen de rent energitekniska garantierna för vattenmolekylernas förångning, ut ur vattendroppsytans ytspänningsgrepp.

Sammanställda kalkylceller för alla beräkningar finns i Kalkylkortet TillämpningM Tabell5A i Blixt2014.ods.

Grafbilden nedan är en utvidgning av EkinEs-grafen och definierar gränsområdet med E_kin=E_Ŝ i antalet N vattenmolekyler med varierande lufttemperatur. Energiresonemanget betyder att förångning av vattenmolekyler ur en vattendroppe i området under kurvorna inte besitter någon säker teoretisk bas för vattenmolekylernas energigrundade förångning. Vattendroppens omslutande ytspänningsenergi (E_Ŝ) är i dessa fall större än den samlade rörelseenergin (E_kin) hos antalet N förångade vattenmolekyler, och frågan hur vattenmolekylerna då ska kunna ta sig ut, förbi ytspänningsenergispärren, förblir obesvarad rent energitekniskt: »vattendroppen är självspärrad» för dessa fall.

Se även i — Vattenmolekylernas parbindningsenergi (eng. The Water Dimer) spärrar ytterligare för förångning.

E_kin = E_Ŝ ;

N·T°K(3,32797 t23 J/°K) = N^2/3(4,65986 t19 M²)(0,07564J/M² – 0,0001679J/M²°C ·T°C) ;

N^1/3·T°K(3,32797 t23 J/°K) = (4,65986 t19 M²)(0,07564J/M² – 0,0001679J/M²°C ·T°C) ;

N^1/3 = (T°K)^–1(14002,109 M²°K/J)(0,07564J/M² – 0,0001679J/M²°C ·T°C) ;

limes(E_kin=E_Ŝ):

N = [(273,15+T)^–1(14002,109)(0,07564 – 0,0001679 ·T)]³ ;

Graf y = ([(273.15+x)'–1](14002.109)[0.07564–0.0001679x])'3

— linjärt Ŝ via T från Wikipedia.

Graf y = ([(273.15+x)'–1](14002.109)[(0.2358)[(1–(273.15+x)/647.15)'1.256](1–0.625[1–(273.15+x)/647.15])])'3

— samband Ŝ via T från Vargaftik1983.

EkinEsLimes

Kelvinekvationen omfattar tydligen inte de allra första H2O-molekylernas möjliga vattenföreningsfysik

— området under kurvorna:

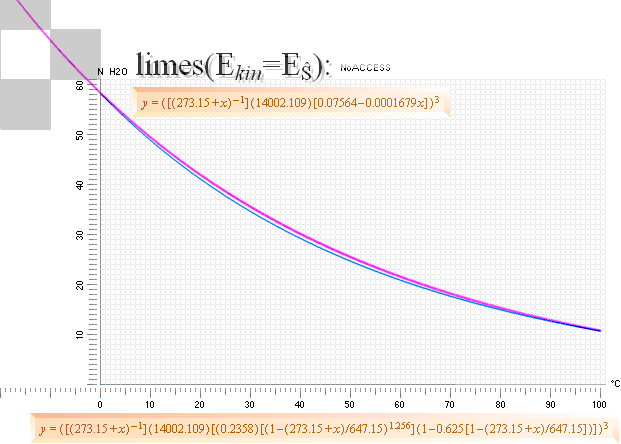
Grafen visar gränsantalet för N [vertikala] stycken H2O vid [horisontella] temperaturen T°C där Ŝ = E. Ŝ-värdena i blå-violetta:

Blå: linjärt via Wikipedias enklare tabelldata [0.07564–0.0001679x]; Violetta: via sambandet i Vargaftik1983 (0.2358)[(1–(273.15+x)/647.15)'1.256](1–0.625[1–(273.15+x)/647.15]).

Ŝ: Kelvinekvationens ytspänningsenergi [Ŝ=E/A] — Ŝ i p/p₀ = e^ 2Ŝ(U_W/ρ_W)/r(R)T, den i vattendroppsytan inneslutna ytspänningsenergin — för en vattendroppe med bestämd radie som är bildad från N stycken H2O-molekyler.

E: Den totalt samlade rörelseenergin från lika många N stycken fria H2O-molekyler i luften omkring, samma temperatur.

— För mindre N-antal — hela området i figuren ovan under kurvorna — blir Ŝ-värdet större [GrafEkinEs]: Ŝ utpekar mera energi än vad som finns tillgängligt från de fria komponenterna:

— Kelvinekvationen har uppenbarligen inte access till det området. I andra ord: Vattendroppar med N under E=Ŝ-gränsen omfattas tydligen INTE av Kelvinekvationens tillgängliga energiform. Vattendroppens gränsdiameter med N=58|59 vid T=0°C [RH=100%] är f.ö. Ø1,5 nM.

KE, KelvinsEkvation,

H2Odata

Kelvinekvationen — »vattendroppsekvationen»

KELVINS EKVATION BESKRIVER VATTENDROPPENS FÖRÅNGNING — p/p₀ > 1

— Egentligen: vattendroppens förångningsekvation

ETABLERADE KÄLLOR brukar anföra den s.k. (”well-known”) Kelvins Ekvation (Niessner2010 s15mn) som grund för påpekandet att

”nanoparticles would never be incorporated into condensing water”.

— Sambandsformen figurerar generellt i alla (matematiskt orienterade) ämnesdokument som beskriver vattendroppsbildning i samband med olika klimattekniska avhandlingar (Se även i Wikipedia Kelvin equation: ln[p/p₀]=2γVm/rRT).

— Sambandsformen uttrycker en gränsform för droppradien (r) via ångtryck (p/p₀>1), ytspänning (γ) och molekylvolym (konv. V_m , rel. U_Wu/ρ_W) på allmänna gaskonstanten (konv. R, rel. Ru) och temperaturen (T):

p/p₀ = 2Ŝ(Uu/ρ)/r(Ru)T = 2Ŝ(U/ρ)/r(R)T ;

KEis, KE

Kelvins VATTENDROPPSEkvation — analys efter insättning: Alla värden vid 0°C markluft med RH=100%:

p/p₀ = e^ 2(0,07564)(18,0154u/1000)/r(8314,9148u)T

= e^ 2(0,07564)(18,0154/1000)/r(8314,9148)T

= e^ (3,27768 t7)/rT ; T= 273,15°K=0°C :

p/p₀ = e^ 1,19995 t9 M/r ;

~ e^{1,2 t9 M/r} ;

— Är r=1,2 nM blir p/p0 lika med 2,718, samma som RH = 217,8%:

— Resultatet från högerledet blir alltså i MULTIPLER av RH=100%:

— Multiplicerat med 100 således RH-värdet direkt i %.

— Uppgiften på Surface Tension Wikipedia Water visar en [nära] linjär variation 0-100°C

[7564t5—5885t5]/100°C = 16,79t5/°C;

— Den variabeln kan läggas in i ett samband på formen SurfaceTension = 0,0754 — T°C·0,0001679 för att få heltäckande värden.

— Totalresultatet blir att p/p0-värdet relativt 0°C-sättningen ovan avtar [drastiskt] med högre temperaturer.

— Vi ser att: Sambandsformen medger ALDRIG något exakt p/p₀=1 → RH=100%, vilket istället blir ett gränsvärde då r→∞, analogt PLAN vattenyta DÅ.

Kelvinekvationens speciellt MAKROSKOPISKA aspekt:

MAKROTOLKNINGEN — väl representerad i MAC

— Notera också Kelvinekvationens »Akilleshäl» i ekvationens MAKROTOLKNING — på omgivande makroskopiska (RH=100%)-ångtrycksmultipler:

· En vattenmolekyl är INTE en vattendroppe: idealt sfäriska radien för en H2O är
1,93 t10 M, som ger p/p₀=501,4000469; den ingår alltså egentligen INTE i Kelvinekvationen;

· Närmast större — första egentliga vattendroppen — blir två H2O med ideala sfärradien
2,43 t10M som ger p/p₀=139,5053549 — och som skulle komma varifrån då, herr Kelvin?
— Kelvinekvationen räknar inte med droppbildning på molekylnivå, utan förutsätter makrodroppar som förångas.

· Slutsats: Kelvinekvationen innehåller flera molekyltekniska oklarheter i ett tydligt diffust gränsland som här helt saknar klara innebörder, främst den att ekvationen förutsätter vattendroppar <60nM (p/p₀=1,0202006) den strängt taget förutsätter inte kan bildas i atmosfären enbart med vattenmolekylernas egen hjälp: max tillgängligt naturligt molnvattenångövertryck p/p₀ är runt 1,02 som motsvarar max RH=102%.

Aktuella H2O-hastigheten vid 0°C och enbart sådana molekyler är (Momentekvationen) med molekylmassan

m=NUu=(1)(18,02)(1,66033 t27 KG)=2,99191 t26 KG ~ 3 t26 KG

v = √ 3bT/m = √ 3(1,38055 t23 J/°K)(273,15 °K)/(3 t26 KG)

= 614,08243 M/S ;

Värdet något högre [780 M/S] om luftmolekylerna är i majoritet och deras rörelsemängder [2,33 K·M/S] bestämmer takten i medelvärdena.

Kelvinekvationens sambandsform utpekar, precis som det påstås i MAC

(»sfärvattenytans ångtryck är större än planvattenytans»),

RoWest2008

MODELLING CLOUD DROPLET FORMATION — Rosalind West 2008

http://www.atm.ox.ac.uk/group/eodg/1st_year_reports/rosalind_west.pdf

”Initially, ΔG increases with increasing r, inhibiting the growth of very small particles in supersaturated conditions.”

RoWest2008 s7m.

; Kelvinekvationens villkor för vattendroppar:

”It is apparent from the Kelvin equation that the vapour pressure over a curved surface of a substance

is always greater than the vapour pressure over a plane surface of the same substance [42, 50].

Ultimately, because of this Kelvin effect, the larger a droplet, the faster it will grow, as described in

section 2.2.3.”

RoWest2008 s7n.

; Homogen nukleation:

”In supersaturated air, cloud droplets may form by either of two microphysical processes. Homogeneous

nucleation is the nucleation of water vapour onto embryonic droplets themselves consisting

only of water [42]. This requires the initial formation of tiny embryonic droplets (clusters of water

molecules) with a very tightly curved surface. The effect of this curvature is that the saturated

vapour pressure over the embryo is much higher than that over a plane surface of water, as described

by the Kelvin effect (section 2.2.1). As a result, the saturation ratio (actual vapour pressure divided

by saturated vapour pressure over a plane surface) required for droplets to form on these clusters is

predicted to be of the order 3.5 to 8. Experimentally, relative humidities of over 800% have been

reached, in air free of all impurities and ions, before cloud droplets will form spontaneously in an

expansion chamber [37].”

RoWest2008 s5n.

;Heterogen nukleation:

”The abundance of aerosols in the atmosphere provides an alternative mechanism for droplet formation

at far lower supersaturations. As a result, levels of supersaturation required for homogeneous

nucleation are never reached [7]. Heterogeneous nucleation, the condensation of water on a foreign

substance or surface, is favourable because of the reduction in saturation vapour pressure over the

droplet either due to the presence of a solute (discussed in section 2.2.2) or due to the opposition of

the Kelvin effect provided by the presence of an insoluble core which increases the radius of curvature

of the droplet.”, RoWest2008 s6ö.

NoDrop

Samt därmed det avgörande

(»nanodroppar kan omöjligen bildas från fristående H2O»),

NeverHappens:

”This

would mean that nanoparticles would never be incorporated into condensing water,

since the required water supersaturation for acting as condensation nuclei would be

tremendously high, by far exceeding the available 1 or 2% within a cloud or fog

situation.”,

;

”The only route to lowering the required supersaturation is described by

Roault’s law, where dissolvable compounds increase the surface tension (as surface

tension is directly proportional to the number of ionized molecules).”,

Niessner2010 s15mn.

UnlikelyToForm:

University of Washington — DROPLET FORMATION [2014-05-06]

http://www.atmos.washington.edu/~dennis/501/HomogeneousNucleationNotes.pdf

”Since the RH of clouds is usually not greater than 101% then a_d must be greater than

0.1 microns. A droplet of this size is unlikely to form via collisions and sticking of many

smaller droplets so in real life, a condensation nucleus (ice, dirt, pollution, etc) really needs

to exist”, sist.

CannotHappen:

@INTERNET WIKIPEDIA Cloud physics [2014-05-14]

http://en.wikipedia.org/wiki/Cloud_physics

”Cloud condensation nuclei are necessary for cloud drop formation because of the Kelvin effect, which describes the change in saturation vapor pressure due to a curved surface. At small radii, the supersaturation needed for condensation to occur is so large that it does not happen naturally.”.

HighlyUnlikely:

ETH — Institute for Atmospheric and Climate Science (Zürich, Schweiz) — ingen datumuppgift [2014-05-14]

http://www.iac.ethz.ch/edu/courses/bachelor/vertiefung/atmospheric_physics/Script-2013/Script-Koehler-revised.pdf

”However,

under typical atmospheric conditions, the saturation ratio seldom exceeds 1.01 due

to the presence of CCN. This renders homogeneous nucleation of water droplets

directly from the vapor phase highly unlikely. Instead cloud droplet formation in

the atmosphere occurs via activation where cloud droplets form in the presence of

a foreign substance, i.e. CCN.”.

NOTERING: Vad betyder ”CCN”? Källan ger ingen upplysning: man får söka på annat håll — vilket också illustrerar EXPERTÄMNERTS ytterst ytliga (extremt snåla) och snäva horisont. Läs »vi vill inte ha någon publik här».

— CCN, mest troligt, ”Cloud Condensation Nuclei” [Wikipedia CCN]. Dvs, konv. aerosoler.

Närmare bestämt för grundmolekylen H2O, idealt sfäriskt tagen r=1,93 t10 M, och med ovanstående insatta värden för 0°C markluft

p/p₀ = e^ 1,2 t9 M/(1,93 t10 M) ; Gäller vid RH=100% och 0°C markluft

~ 500 ggr (RH=100%)=(p/p₀=1)

”Tremendously” var just ordet.

— Gränsformen för »acceptabel» i makrotolkningen — max ett par procent övermättnad typ RH=102% med p/p₀=1,02 i den vanliga klimatluften — betyder en minsta tillåten »Kelvinvattendroppe» med diametern ca Ø60nM: lika med 30 240 791 st H2O-molekyler.

— Det är alltså självaste grunden (äntligen framkommen i klartext) för den allmänt etablerade uppfattningen som entydigt framhäver att:

— Det krävs typ pollenkorn, dammpartiklar eller annat SKIT I LUFTEN för att det ska kunna REGNA och SNÖA — någon redan beväxt luftburen DecaNanopartikel som vattenmolekylerna kan söka trösten hos och klänga sig fast vid, växa till sig på, i sorgen över den uteblivna privatföreningen. (Man har sedan i samma MAC-korridorer ett h-e att förklara duggregn [”warm rain initiation problem”, Malinowski2007]).

Snökristaller:

Samma förutsättningar beskrivs för bildning av snökristaller:

Institute Of Physics Publishing — THE PHYSICS OF SNOW CRYSTALS, Kenneth G Libbrecht 2005

http://www.its.caltech.edu/~atomic/publist/rpp5_4_R03.pdf

”The story begins inside a cloud, which typically consists of a large number of liquid water droplets

nucleated on minute dust particles.”, s861.

Webbkällan innehåller f.ö. fina bilder på snökristallernas olika typer och former.

Även källan nedan från 1959ansluter till samma som ovan, samt ger f.ö. värdefulla uppslag i snökristallernas bildning,

Geophysical Monograph Series — THE NUCLEATION AND GROWTH OF ICE CRYSTALS, B. J. Mason

datumuppgift saknas (1959)

http://www.agu.org/books/gm/v005/GM005p0226/GM005p0226.pdf

KEexp, KelvinH2Owebben

Förutsatt Kelvins Ekvation verkligen beskriver fysiken på H2O-nivån:

Dokument intygar Kelvinekvationens experimentella förankring

Flera gratis tillgängliga dokument finns (Maj2014) på Webben i ämnet »Kelvin equation, experimental test». De verkar samstämmiga i intygandet att sambandsformen överensstämmer med experiment (ända ner i området enstaka nM). Nedanstående citat används tills vidare för att styrka vissheten:

Wagner2013

NUCLEATION OF VAPOURS - MOLECULAR CONTENT OF CRITICAL CLUSTERS AND ACTIVATION OF NANOPARTICLES — Wagner et al. (2013) datumuppgift salnas

http://eac2013.cz/EAC abstracta/Fundamentals/Wagner-Paul_Fundamentals_20130221-174207_0471182412.pdf

”Homogeneous nucleation experiments (Strey et al. 1994) have provided information on the sizes of critical clusters down to diameters of about 2nm in satisfactory agreement with the Kelvin equation.”, s1sp1n.

Se allmänt artiklarna i sammanställning om Kelvinekvationen och 2(H2O) från H2Odata.

— Se även KelvinH2OWebben.

YV, YtspänningenVatten — Ŝ = E / A

VATTNETS YTSPÄNNING — Ŝ = E /A ; J/M²=N/M

”Ytspänning och adsorption

De intermolekylära krafterna ger sig till känna på ett speciellt iögonenfallande sätt i en vätskeyta. Ytskiktet bildar liksom ett skinn på vätskan, och den kraft som skapar detta kallas ytspänning. Kraften verkar på ytan och parallellt med denna. Ytspänningen är ett mått på ytans tendens att förminskas.”,

[FMs205sp1n].

Allmänt:

Begreppet YTSPÄNNING hos vatten grundas (vad man vet) på vattenmolekylernas dipolkaraktär: vattenmolekyler (H2O) strävar att förena sig: vattenytor strävar att dra ihop sig.

— Inuti vattnet betyder det — »i allmänhet» — att »krafterna tar ut varandra»; egentligen att varje vilande avgränsad (svävande) vattenvolym eftersträvar sfärisk form genom den totalt sammanlagda kontraktiva egenskapen (vatten är »elektriskt graviterande»).

— Om vi kommer underifrån, och vill tränga upp till, eller IGENOM, vattenytan, måste vi »dra isär» de inbördes föreningsbenägna vattenmolekylerna med en viss kraft — ytspänningskraften, riktad parallellt (cirkulärt expansivt) utmed vattenytan (vilket betyder att ytspänningsvektorn egentligen, på samma sätt som impulsmomentet för ett snurrande hjul, på visst sätt får tolkas som en kraft riktad rätvinkligt [uppåt], rakt motsatt »det inåt roterande» vattendjupet; Konventionellt anges den dock ”parallellt med vattenytan”).

Är vattenytan konvex — som delformen på en vattendroppe — måste den utträngande separationskraften i ytans tangent också till viss del dra ut vattenmolekyler från själva vattenkroppens form, alltså ut från konvexytan, och vilket kräver extra kraft:

ytspänningen för en konvex vattenyta är proportionsvis större än för en plan vattenyta;

Är vattenytan konkav kommer den utträngande separationskraften i ytans tangent till viss del också att pressa in vattenmolekyler inåt vattenkroppen där ytspänningskrafterna är noll, och därmed mindre kraft i netto:

ytspänningen för en konkav vattenyta är proportionsvis mindre än för en plan vattenyta.

— Kraften över vägen ger energin = arbetet, och energin fördelad över ytan ger ytspänningsenergin eller YTSPÄNNINGEN (konv. ofta sigma σ,här s-flex) Ŝ = E/A = Fd/A. Ju större yta, desto större energiinnehåll E=ŜA.

— Vattnets ytspänning vid 0°C är (enligt tabell) 0,07564 J/M². Värdet avtar med högre temperatur [0,5885 vid 100°C].

— Villkoret för relevant energiräkning är: energiinnehållet i en vattenyta i ett rum med T°C kan aldrig överstiga den samlade rörelseenergin hos de vattenmolekyler med samma temperaturprofil T°C som sammansätter vattenkroppen. KomponentSumman från bildningen besitter alltid högsta energivärdet.

Graf y = 100(0.2358)[(1–(273.15+10x)/647.15)'1.256](1–0.625[1–(273.15+10x)/647.15])

Webbreferensen nedan ger tabellvärden i 5°C-intervall tillsammans med en allmän ekvationsform 0-374°C.

Varga1983

INTERNATIONAL TABLES OF THE SURFACE TENSION OF WATER, Vargaftik et al., 1983

http://www.nist.gov/data/PDFfiles/jpcrd231.pdf

”The values in the table are well represented by Eq. (1) with T_c = 647.15 K and this eqiation is recommended for use as an interpolating equation

σ = B[(T_c – T)/T_c]^µ[1 + b(T_c – T)/T_c], (1)

where B = 235.8 × 10^–3 N/m, b = – 0.625, and µ = 1.256.”,

s820sp1ö.

Grafen nedan efter sambandet ovan.

VSEA

Vattnets ytspänning med varierande temperatur — Vargaftik-sambandet här teoretiskt utvidgat till –100°C

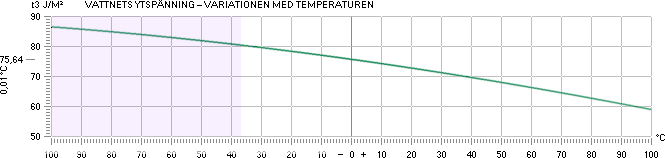
GrafUnit30p y = 100(0.2358)[(1–(273.15+10x)/647.15)'1.256](1–0.625[1–(273.15+10x)/647.15])

Samband enligt Vargaftik1983:

Ŝ = (0,2358)[(1 – T/647,15)]^1,256[1 – 0,625(1 – T/647,15)]

= E/A ; Vattnets ytspänning [0-100°C]

Enligt uppgift kan speciellt små vattendroppar i Jordatmosfären fortsätta i flytande tillstånd ner till ca –37°C.

Tabellen nedan visar värdena i Wikipedia (Surface tension) i jämförelse med värdena i TABLE 1 s810 i Vargaftik1983.

JmfS

Jämförande ytspänningsvärden för vatten i t3 J/M² sammanställt 15Maj2014

——————————————————————————————

0	25	50	100	°C
75,64	71,97	67,91	58,85	Wikipedia
75,64	71,99	67,94	58,91	Vargaftik

——————————————————————————————

Uppgifterna från Wikipedia i WIKIPEDIA Surface tension, Data table [Lange's Handbook of Chemistry (1967)] [2014-05-14].

Differenserna ligger omkring 0,1%.

KelvinH2Owebben, -Maj2014

KELVINEKVATIONEN PÅ WEBBEN

Angående H2Odata (Kelvinekvationens brister):

— Man frågar sig närmast:

— Varför syns ingen etablerad redovisning av de milt sagt remarkabla gränsformerna?

— Varför undanhålls publiken informationen?

— Varför beskrivs inte ämnets kritiska punkter?

Kanske ett av svaren på dessa frågor framskymtar i nedanstående citat som tillsammans med föregående påpekanden i H2Odata (Kelvinekvationens brister, KEB) visar ett vetenskapssamfund i mer eller mindre (total) upplösning.

Kelvins ekvation från Gibbs Energy:

University of Washington — DROPLET FORMATION [2014-05-06]

http://www.atmos.washington.edu/~dennis/501/HomogeneousNucleationNotes.pdf

Källan härleder sambandsformen för Kelvins ekvation från konv. eng. Gibbs free energy och beskriver den konventionella uppfattningen i slutet varför de minsta vattendropparna inte får vara med.

— Notera begränsningarna som Kelvinekvationen uppvisar i KEB. Konventionsbegreppet Gibbs free energy (G) är f.ö. INTE tillämpligt på vatten i omgivande luft vid 0°C: G=0 där eftersom ingen förångningspotential existerar: vattendroppen kvarstår, oberoende av storlek. Se även en möjlig motsvarande anmärkning i citatet från Katz2007, ”Unfortunately, we all also know that the predictions of ... the Kelvin equation ... do not agree with the measured temperature dependence”.

SmallMayNotApply:

CORRELATIONS FOR VAPOR NUCLEATING CRITICAL EMBRYO PARAMETERS,

Magnusson et al., 2003

”However, it was found at the same time that the situation is different for water, so that the Kelvin equation may not be applicable for lownanometer sized water droplets.”, s1391sp2ö.

Öppnas särskilt separat, URL-saknas.

KelvinEquationLacksVerification!:

PHYSICOCHEMICAL PERTURBATIONS OF PHASE EQUILIBRIUMS,

Vladimir Kh. Dobruskin (2002)

”The most famous attempts to verify the Kelvin equation were undertaken by Shereshefsky and co-worker in the course of 44 years (1928-1972).^46-50 They studied equilibrium in conical capillaries and found that the equilibrium radii of liquid columns in the capillaries were always greater then the values calculated from the Kelvin equation. Adamson²⁵ points out that the situation with the experimental verification of the Kelvin equation is still conflicting; whereas Everett, Haynes, and McElroy⁵¹ in their conclusion remark draw attention to the fact that the Kelvin equation still lacks experimental verification! The data of Shereshefsky raised hot debate and have remained unexplained for decades and only the main equation proved to be in agreement with the Shereshefsky experiments.³³”, (nära slutet, siduppgift saknas).

Datumuppgift saknas.

Det finns en uppsjö av författare på webben (Maj2014) som beskriver Kelvins ekvation [KE]. Men alla, utan undantag, tycks göra det »som i kör»: ingen omnämner ens ett närmande till någon UNDERSÖKNING, inte ens en elementär teoretisk dito på Kelvinekvationens egna villkor och med H2O-molekylernas hjälp [typ i H2Odata, Kelvinekvationens brister] och allmänna (elementära) hydro-termofysiska basdata. Man tycks i etablerade led läsa Kelvinekvationen rakt av, utan att närmare undersöka innehållet. Exempel på fraser som tycks upprepas av samtliga etablerade författare ges i NoDrop (”Highly unlikely”).

Webbkällan nedan (från 1953) påstår experimentella resultat (”may be cooled”) som verkar sakna referenser, samt förklaringar (”is inherently improbable”) som i vår tid (Tretyakov2013) stött på tydlig patrull: 2(H2O) existerar i rumsvarm luft. Kan 2 kan flera. Kan inte 2, kan inga. Det sänker definitivt nedanstående typ av källa till kategorin opålitlig.

Journal of Meteorology —

HOMOGENEOUS NUCLEATION OF SUPERCOOLED WATER DROPS, James E. McDonald 1953

http://puhep1.princeton.edu/~mcdonald/JEMcDonald/mcdonald_jm_10_416_53.pdf

”In this latter case, one observes that a vapor which contains no intermixed foreign particles and which is not in contact with a liquid water surface of any kind may be cooled far below its nominal dew point without any appearance of water drops. The fundamental reason for this possibility of supersaturation of pure vapor is that the only way in which liquid drops can be formed under such homogeneous conditions is for a chance succession of collisions to build up embryonic water droplets one molecule at a time. But this mode of formation of drops is inherently improbable, even at temperatures well below the nominal dew point of the vapor because (to describe it in simplified terms) the total binding force exerted by very small aggregates of molecules upon one of their surface members is too low to overcome the disgregative action of thermal motions of the individual members. Only by cooling the system far below its normal dew point can one suppress this thermal disgregating effect on randomly forming embryos sufficiently to permit the embryos to gain member molecules faster by bombardment from the vapor phase than the embryos lose them to the vapor phase by evaporation.”, s417sp1n

Kan inte kopieras.

Vi kan ju fråga oss:

— Är det någon som har testat med att koka upp kemiskt rent vatten i ett kök med luft ”which contains no intermixed foreign particles”?

— I våra vanliga kök ser vi en ”dimma” — man intygar allmänt att vattenånga INTE är synlig — som också, etablerat, sägs bero på att ångan ovanför koket kondenserar (MAC: CondensationCitat) till små vattendroppar (TNED: H2Opar) , det är vad vi ser. Enligt citatkällan ovan skulle den vattendroppsbildningen bero på kondensation på ”aerosoler” i köket.

— Men Enligt citatkällan ovan skulle OCKSÅ den visuella tydligheten HELT försvinna om vi bara kunde rensa bort allt eller det mesta ur luften som kan hänföras till typen ”aerosoler” och använda destillerat vatten.

— Har man gjort sådana, avgörande, experiment för att SÄKRA de påstådda »slutsatserna»?

— Nej.

— Inte enligt det som syns främst på webben i varje fall.

— SPECIELLT resultatet från Tretyakov2013 utpekar också — direkt: 2(H2O), den minsta vattendroppen, existerar i rumsvarm luft — att sådana experiment, om de genomförs, INTE kommer att verifieras på ovanstående webbkällas kredit.

— Se även i InledningH2Odata.

McDonald 1953 ovan antyder att SÄTTET som fria sammanträffande H2O-molekyler möts på »är alldeles för HÄFTIGT» för att tillåta typ stadigvarande 2(H2O), ”But this mode of formation of drops is inherently improbable”.

— Det var just DEN AVGÖRANDE grundaspekten vi ville veta närmare om.

— Jämför, som sagt, Tretyakov2013. Tillämpning: Se MinstaVatten och H2Opar.

— 2(H2O) existerar i rumsvarm luft. McDonald 1953 talar tydligen mot bättre naturvetande.

Se även liknande, mera nutidsenliga:

Physics — FOCUS: WATER MOLECULES, UNITE! Jun2007

http://physics.aps.org/story/v19/st19

”.. bigger than for water vapor, where the molecules don’t interact”.

— Typ: »2(H2O) fungerar inte fritt i fysiken — Jordatmosfären — eftersom ”the total binding force ... is too low to overcome the disgregative action of thermal motions”».

Tretyakov et al., 2013: 2(H2O) finns i 22,85°C luft.

— Bägge citatkällorna McDonald 1953 och Physics 2007 talar tydligen mot bättre vetande: 2(H2O) existerar i luften, dessutom påvisat i vanlig rumstemperatur. Jämför återigen de högst elementära punkterna i Kelvinekvationens brister som redan där belyser den principiella anledningen.

Genomsökning på webben (-16Maj2014) »har hela tiden», med jämna mellanrum, resulterat i (»en ständig ström av») NYA TIDIGARE DOLDA för sammanhangets allmänna begripande avgörande FUNDAMENTALBEGREPP som i den allmänna ämnespresentationen inte syns generellt, och som är svåra att hitta, men som när de väl hittas, leder till en uppsjö av klargöranden.

— Ett sådant, avgörande (förlösande för ämnessökningarna) expertbegrepp är termen water dimer:

water dimer

Wikipedia ger en introduktion i

@INTERNET Wikipedia Water dimer [2014-05-14]

http://en.wikipedia.org/wiki/Water_dimer

— Med upptäckten av den förlösande termen »börjar det plötsligt »spöregna» — vi tar om det igen, för säkerhets skull:

— 2(H2O)molekyler finns VISST — ännu så länge bara påvisat i ett ryskt laboratoriums ”pressure controlled chamber”, dessutom vid rumstemperatur 22,85°C och (för det experimentella påvisandets spektralt begränsade möjligheter endast) vid 1733 Pa (0,017 atm; 13 Torr) [Tretyakov2013]:

WD2013

ChemistryWorld — ELUSIVE WATER DIMER DETECTED AT LAST, 7Mar2013

http://www.rsc.org/chemistryworld/2013/03/water-dimer-detected-atmosphere-climate

”Scientists have long debated the presence of water dimers - two water molecules held together with a hydrogen bond - in this vapour. Such dimers would have a considerable effect on the vapour’s behaviour and therefore our understanding of the earth’s climate. But for decades scientists have been unable to find evidence of dimers under atmospheric conditions.”,

;

”The group has spent over a decade developing a high sensitivity spectrometer, which they have now used to detect the rotational spectrum of the dimer in water vapour at 296K and 0.017atm.”,

;

”It’s the first time anyone has been able to observe transitions of the water dimer under equilibrium room temperature conditions,’ says Richard Saykally at the University of California, Berkeley, US. ‘People would love to be able to detect them but it is extremely difficult - that’s why this particular paper is an important step forward.’ However, Saykally also points to a loose end in the research – the observed dimer peaks are four times broader than predicted.”

— Detaljerna (utom ”pressure controlled chamber”) beskrivs i

Tretyakov2013, WD2013

Fria 2(H2O)-enheter existerar i VANLIG aerosolren RUMSTEMPERERAD men till 1,7% uttunnad LUFT

2(H2O) existerar i fysiken:

WATER DIMER ROTATIONALLY RESOLVED MILLIMETER-WAVE SPECTRUM OBSERVATION AT ROOM TEMPERATURE, Tretyakov et al., Mar2013

http://physics.aps.org/featured-article-pdf/10.1103/PhysRevLett.110.093001

”Water dimers (H₂O)₂ are believed to affect Earth’s radiation balance and climate, homogeneous

condensation, and atmospheric chemistry. Moreover, the pairwise interaction which binds the dimer

appears to be of paramount importance for expounding a complete molecular description of the liquid and

solid phases of water. However, there have been no secure, direct observations of water dimers at

environmentally relevant temperatures despite decades of studies. We report the first unambiguous

observation of the dimer spectrum recorded in equilibrium water vapor at room temperature.”,

”The pairwise interaction that binds the dimer appears to be of paramount importance for expounding a complete molecular description of the liquid and solid phases of water [34].”, s093001—3sp2m.

— Författarna anger att observationerna avser ”vid 13 Torr och 296°K”; ~ 13·(101325/760) = 1733 Pa = 0,017 atm (»vanlig luft uttunnad till 1,7%») och 22,85°C — var eller hur anges emellertid inte. Vilken miss.

— Förklaringen antyds i förbigående i slutet: ”We thank V. F. Vdovin for his help modifying the spectrometer temperature and pressure controlled chamber”.

— Artificiell laboratoriemiljö (vanlig rumstempererad luft, men uttunnad till 1,7%).

— Artikelns abstraktionsnivå är SÅ beklämmande påtaglig att man undrar om författarna ALLS vill att någon vanlig trottoarbefolkning ska få kännedom om framsteget. Det finns inte en enda mening i artikeln som beskriver vad, exakt, det är man har mätt på — och vilken kopplingen skulle vara till luften vi andas och går omkring i. Ordet ”chamber” förekommer bara på ett (1) enda ställe i artikeln, det ovan citerade.

Vilken innebörd har det experimentella resultatets laboratoriemiljö med det låga trycket 1733 Pa (13 Torr)?

— Artikelförfattarna varken klargör ämnet på den punkten, eller ens, utom i förbigående i slutet, omtalar att observationerna endast berört en specifik laboratoriemiljö, ”pressure controlled chamber”.

— Det är (verkligen, min mening) på gränsen till en acceptabel redovisning.

— Experimentets låga tryck KAN vara förklarligt med att man sökt reducera partikelförekomsterna så långt möjligt (till 1,7% av den normala markluften) för att reducera felkällor i den ytterst krävande mätuppgiften.

— Det reducerade trycket bör (i så fall) inte ha någon inverkan på själva den påvisade förekomsten: finns enheten i någon atmosfär, finns den i alla möjliga normala Jordatmosfäriska sammanhang.

— Den meningen behöver dock explicit framhållas av de som har direkt anknytning till den aktuella forskningen — och antas här tills vidare föregripande.

Vi behöver uppenbarligen inget mera i rent experimentella referenser för att komma vidare i ämnet:

— Den minsta vattendroppen existerar i luften.

— Se även i syntes från H2Odata, och mera i grundteorin för den möjliga parbildningens vattenfysik i H2Opar.

Applikation, Mar2014 — Vattenångans luftandel — Vattenånga i luft

Vattenångans luftandel — H2O i luft

—————————————————————————————————————————

Förberedande datauppgifter till beräkningar för vattendroppsbildning enligt H2Odata

Webbreferens MAX 4% H2O i luften

THE ULTIMATE WEATHER EDUCATION WEBSITE [2014-03-19]

http://www.theweatherprediction.com/habyhints/40/

UluftRef

Ungefärliga medelatomvikten för luft — inte alla beståndsdelar medtagna

[(0,7809)(2·14,0067)_N + (0,2095)(2·15,9994)_O + (0,00933)(39,948)_Ar ]u = 28,952127u ;

Atomvikterna från HOP-tabellen, se Tabell2—TabellHOP i RF_HOP.ods.

ρ_LUFT = U(ρ₀=0,0446126 KG/M³ vid STP) = 1,2916296 KG/M³ frånräknat inslaget av koldioxid.

Sammansättningar vid STP:

LUFT:

U_LUFT = 28,24u = (0,78)(28)u + (0,2)(32)u ; Luftmolekylens atomvikt

Här används det mera ambitiöst beräknade värdet ovan 28,952127:

ρ_LUFT = 1,2922 KG/M³ ; Luftens täthet vid STP

DELVIS KAOTISKA UPPGIFTER på Webben @INTERNET — en skur av olika ENHETSSTANDARDER tävlar numera (2014) om Bästa Utsikten:

— Under hela 1900-talet användes STANDARDISERADE enheter typ MKSA-systemet MeterKiloGramSekundAmpere och som också används genomgående i UniversumsHistoria. Men Wikipedias InternationellaTalGrupper vill Helst Framhålla Sin Privata Landsdels Särskilda RyggsäcksMetrik typ lbvc/pkl³ [Det gäller att utveckla flerspråkigheten]. Resultat: Att försöka luska ut VAD SOM EGENTLIGEN GÄLLER ENLIGT VEDERTAGEN VETENSKAPLIG STANDARd kan bli en rätt frustrerande uppgift. Som här.

— Vad är EGENTLIGEN luftens täthet vid STP?

— Webbkällan About.com Chemistry anger 1,29 gram per liter —samma som KG/M³ — vid STP, samt vid 20°C 1,2041 motsv KG/M³ med bibehållet STP-tryck = 1 atm = 101325 Pa. I LuftBasic har STP-värdet för luft antagits som 1,2922 KG/M³ [på visst kaotiskt sätt från den angivna Wikipediaartikeln]. Men det värdet är (enligt Wikipediaartikel) ett NIST-data (gäller vid 100 000 Pa).

— Tills vidare används det antagna värdet 1,2922 KG/M³ för luft vid STP.

Medelkubavståndet vid STP:

V = m/ρ = d³; Vi använder m=Uu: ρ=U·ρ0; m/ρ=Uu/Uρ0=u/ρ0;

d = (m/ρ)^1/3 ; = [(28,952127·1,66033t23)/1,2922]^1/3

= 3,33822 t9 M

~ 3,339 nM ; = (u/ρ0)^1/3 = [(1,66033t27)/(0,0446126)]^1/3=3,33871t9

Molekyldiameter 2r — efter förhållandet mellan flytande och gas, se dDIVr: flytande luftens densitet [Wikipedia] 870 KG/M³:

d/r = (4πρ_flytandeLUFT/3ρ_LUFT)^1/3

= 14,128391

~ 14,13 ;

d/2r = 7,064 ;

VATTEN:

U_H2O = 18,02u = 2(1,0080)u + 1(15,9994)u = 18,0154 ; Vattenmolekylens atomvikt; UH2O=UV=UW

ρ_H2O = Uρ₀ = 0,803919 KG/M³ ; Vattenångans täthet vid STP

ρ_W = 1000 KG/M³ ; Vattnets täthet

[999,8395 vid 0°C; ref. Wikipedia Properties of water]

Medelkubavståndet vid STP:

V = m/ρ = d³; Vi använder m=Uu: ρ=U·ρ0; m/ρ=Uu/Uρ0=u/ρ0;

d = (m/ρ)^1/3 ; = [(18,0154·1,66033t23)/0,803919]^1/3

= 3,33871 t9 M

~ 3,339 nM ; (u/ρ0)^1/3 = [(1,66033t27)/(0,0446126)]^1/3=3,33871t9

Molekyldiameter 2r — efter förhållandet mellan flytande och gas, se dDIVr: vattnets densitet 1000 KG/M³.

Vattenmolekylens volym enligt vattnets täthet 1000 KG/M³ : N/M³ = ρ/Uu ; 1/N = V = 2,99115 t29 M³:

Vattenmolekylens kubsida s = V^1/3 = 3,10417 t10 M; »H2O-KUBsidan»

Vattenmolekylens sfärradie r = (3V/4π)^1/3 = 1,92567 t10 M; »H2O-SFÄRradien»

d/r = (4πρ_W/3ρ_H2O)^1/3

= 17,336394

~ 17,34 ;

d/2r = 8,67 ;

Bakgrund

Mellan 0°C och 100°C övergår vatten SUCCESSIVT till vattenånga. Det är i det diffusa gränslandet som den vardagliga atmosfärens MATEMATISKA LUFT- OCH VATTENFYSIK utspelas, och som vi här ska försöka penetrera närmare.

— Vattenångans täthet som ovan 0,8 KG/M³ betyder enbart vattenånga vid STP — med andra ord praktiskt taget helt utan närvaro av luft: bara vattenånga.

— För beräkningen av de praktiska fallen i blandluft, se grundbegreppen i AGLV, sambanden i syntes från TillämpningM.

— Se även vidare i MKA [MEDELKUBAVSTÅNDEN] som fortsätter genomgången via resultaten ovan.

MKA, medelkubavstånden

MEDELKUBAVSTÅNDEN MELLAN LUFTMOLEKYLERNA OCH VATTENMOLEKYLERNA

EXEMPLET klargör mera ingående HUR fördelningsbilden mellan H2O-molekylerna och luftmolekylerna ser ut:

Grundläget (Se AppH2Oluft) med ganska precis lika stora medelavstånd via egentäthetsvärdena

Kubiska molekylmedelavståndet för egentätheterna hos luft och vattenånga vid STP är i bägge fallen 3,34 nM.

— I den Jordtroposfäriska praktiken är emellertid andelen vattenånga i luft — även vid maxvärden — ytterst blygsam [Max 4%, se SVP-grafen].

— Nedanstående visuella jämförelser försöker ge en bild av hur den vardagen ser ut.

Täthetsdistributionen, bilden nedan, för ideal vattenånga för sig (ρ_V=0,8 KG/M³) och ideal luft för sig (ρ_L=1,3 KG/M³) visar ganska precis lika stora molekylmedelavstånd (samband i AppH2Oluft):

KMAex

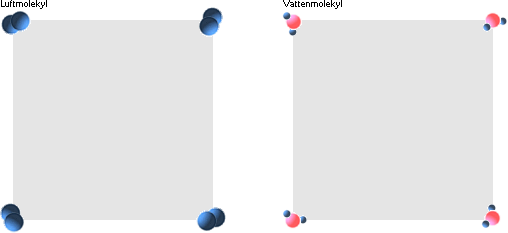
Med resultatbilden från H2OmaxLuft — praktiska viktsmängden vattenånga relativt luftens viktsmängd är i vilket fall bara max runt 4% — får vi en första mera praktisk översikt av hur det ser ut i luften vid absolut maximalt mättad mängd vattenånga (4% vid 38°C [SVPgrafen]).

— I figuren nedan är ovanstående kvadrater förminskade 10ggr (höger) för att visa proportionerna, därifrån (vänster) H2O-kvadraten förstorad 25ggr (1/0,04), vilket motsvarar respektive tätheter med 4% andel vattenånga.

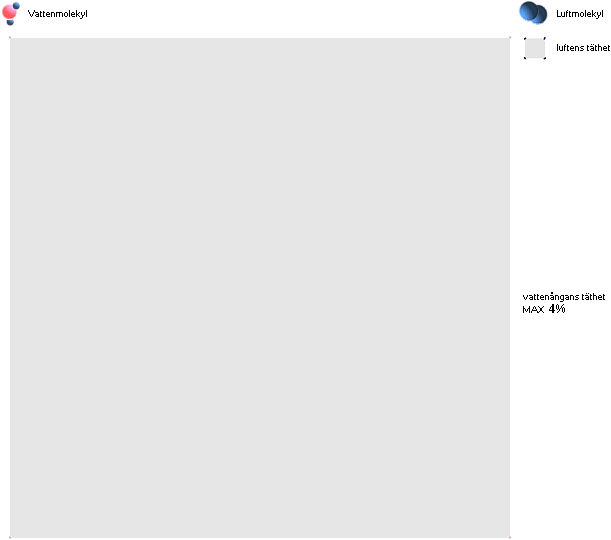
Notera hörnen på den stora H2O-kvadraten: där ligger nu motsvarande vattenmolekyler i täthetsbilden fördelade relativt »den 25ggr tätare» normalluften (vid STP), bildens övre högra del.

— Det är ett alldeles förfärligt chockerande STORT vattenmolekylmedelavstånd relativt det betydligt tätare omgivande luftmolekylhavet — speciellt om huvuduppgiften (som här) skulle vara att försöka HÄRLEDA HUR vattendroppsbildning går till i vanlig vardaglig atmosfärisk luft.

— HUR (i himmelens namn) bär sig vattenmolekylerna i vattenångan åt för att UR den hopplösa mönsterbilden

(nästan löjligt löjeväckande uppgift — publiken reser sig upp och börjar skratta spontant)

bilda konkreta vattendroppar? Hela det mellanliggande området är proppat med luftmolekyler.

— PROPORTIONERNA i den grovräkningen är dock INTE riktigt rättvisa, men »orienterar för samtliga värden»: i själva verket sämsta fallets största differenser.

Vi studerar det.

För gasens egentäthet räknas (här) kubmedelavståndet från atomvikten (U) via ideala fundamentalgasens masstäthet ρ₀=0,0446126 KG/M³ enligt

d = (m/ρ=Uu/ρ=Uu/Uρ₀=u/ρ₀)^1/3 = 3,33871 t9 M:

alla gaser får en och densamma atomära massenhetens ideala kubmedelavstånd 3,34 nM.

Gasernas egentätheter upplöser sig i en praktisk blandluft i olika proportioner [AGLV] och det gäller då istället för förhållandet mellan medelkubavstånden i de bägge gaserna d_L/d_V=1

— givetvis med hänsyn till tryck och temperatur

— att

d_L/d_V = ([lm/Uρ₀]_L/[vm/Uρ₀]_V)^1/3 = ([lUu/Uρ₀]_L/[vUu/Uρ₀]_V)^1/3

= (l_L/v_V)^1/3 ;

Är proportionerna 1/25 blir förhållandet mellan molekylavstånden d_V/d_L bara 1/(25)^1/3~1/2,924.

— Bildexemplet [KMAex] ovan (25:1) skulle kräva ett massförhållande på l_L/v_V=(25)³=15.625.

— Sammanställningen i TillämpningM Tabell5A i Blixt2014.ods visar ungefär den storleksordningen med skärmdumpen nedan från aktuella parametrar i ett allra sämsta fall — BarGrafen med strecken ||||| visar d-relationerna vid sämsta fallets RH=1% luftfuktighet vid Jordytan (h=0) och fryspunkten (T°C=0) [Sambandsformen TMekv i TillämpningM]:

Se Kalkylkortet TillämpningM Tabell5A i Blixt2014.ods — grafStripen ||||||||||||||||||||| . . visar proportionerna i molekylmedelavstånden hos markluft L med och vattenånga V, sämsta fallet

Parametervärdena från TMekv med resultatbilden för en sämsta fallets Jordtroposfäriska situation med minsta möjliga vattenånga i luften för teoretisk prövning och undersökning av vattendroppsbildning. Vertikalstecksindikatorerna vid d(V | L) visar respektive kubmedelavstånd mellan gasmolekylerna med hänsyn till aktuell medeltäthet.

Uppgiften här kommer snarare främst att fokusera på temperaturer över fryspunkten (0-30°C) och luftfuktigheter över 1% (1-100%), motsvarande en teoretisk bild av vad som händer i »typiska sommarmoln» och som kopplar förhistorien till blixturladdningar.

— Ovanstående fall blir då det allra mest maximalt SÄMSTA utgångsläget för TEORETISKT PRÖVANDE TEST av vattendroppsbildning för blixturladdning.

— Som sagt: HUR kan vattendroppar bildas ur den mönsterbilden?

— Vi måste först ha koll på vattenångans aktuella lokala täthet innan vidare. Se RhoVmålet och RHbasic.

— Vi kan pröva en räkning på genomsnittlig rörelsemängd (mv) för alla möjliga delpartiklar (som inte får uppta allt för stora områden relativt luftmolekylerna) i luften och som bestäms (enväldigt) av luftmolekylernas värmemekanik via allmänna gaslagen, och på den vägen se om det ev. finns gynnsamma resultat.

— Det är nog BÄST att det finns sådana, resultat, om vi inte ska hamna i trubbel med regnförklaringen.

— Se vidare från H2Odata och MultiH2O (aktuella vattendroppsbildningen i exempel).

RhoVmålet, Vattenånga i luft

MED FORTSÄTTNING FRÅN Vattenångans luftandel

Det hägrande målet: Vattendroppsbildningen — hur?

— Parametervärdena vi måste känna till behöver relateras (frekvent).

— I RHbasic finns en syntes som kopplar en del av nedanstående detaljer för vattenångans aktuella täthet samt efterföljande räkneexempel.

— Hur får vi koll på den aktuella vattenångans täthet (ρ_V) — om vi nu vill försöka genomföra en del beräkningar i den avgörande vattendroppsbildningen (fundamentet i blixturladdningens fysik, se MultiH2O)?

— Vi hade nyligen kommit fram till en allmän formulering för vattenångans täthet, här fortsättningsvis ρH2O=ρ_V:

MEN:

— ρ_H2O är INTE vattenångans aktuella, praktiska täthet i luften.

— FÖRST [GVK] måste vi använda en värmekapacitetskonstant (Ř) för att få lokal egentäthet: vattenångans täthet varierar med den omgivande hydrostatiska atmosfärens tryck-temperatur-profil.

— SEDAN tillkommer blandningen med luften [AGLV].

Sambanden för vattenångans täthet ρ_V i syntes i RHbasic.

Vattenångans aktuella täthet i aktuell atmosfärisk lokal — gäller endast inom troposfären (max 10 KM, PDASdata)

Sammanställningen nedan med räkneexempel sammanfattar de användbara sambanden till beräkningen av vattenångans aktuella lokala täthet — före vattendroppsbildningen. I RHbasic ges en syntes.

Känner vi [GVK] lokalt tryck (p[h]) och temperatur (T[h]) i en specifik atmosfärisk region (h) kan vattenångans aktuella egentäthet (specifika vikten) (ρ[h]) bestämmas där enligt

ρ = (p/T)/(461,42711 J/KG°K) ; KG/M³, GVK ; Lokala vattenångans egentäthet [specifika vikten]

Den vattenångan kommer sedan att fördelas i luften på en betydligt snävare LuftÅNGtäthet som kopplar förhållandet mellan vattenångtrycket och [torra] lufttrycket. Se grundbegrepp i GVK och AGLV.

Enbart med kännedom om temperaturen (T[h]) får vi [TillämpningM] vattenångans maximala viktsandel i luft med RH=100% [SVP-grafen] enligt

M_STP = (3,75086 t3) · e^{17,2694/(1+238,3/T°C)} ; Viktsandelen vattenånga vid STP i luft vid RH=100%

M-formen ovan gäller vid STP :s p=101325 Pa. För aktuella hydrostatiska skikt på höjden h över Jordytan inom troposfären med p[h] fås motsvarande

M(h) = M(STP) · (101325 Pa)/p[h]

Därmed kan den aktuellt lokala viktsandelen vattenånga vid samma T-värde erhållas ur M-värdet som en bråkdel via det lokalt aktuella RH-värdet.

Mex

EXEMPEL — med hjälp av ovanstående samband

[Kalkylkort TillämpningM Tabell5A i Blixt2014.ods]:

Vid h=1KM är p=89747 Pa och T=8,5°C=281,65°K [från 15°C vid h=0].

Bestäm vattenångans aktuella egentäthet ρ_V och aktuella viktsandel m_V av luftens viktsandel m_L vid h om relativa luftfuktigheten är RH=60%.

Lösning:

— Vattenångans aktuella egentäthet (specifika vikten) vid h är

ρ = ([89747 Pa]/[281,65°K])/(461,42711 J/KG°K)

= 0,691 KG/M³ ;

Maximala viktsandelen vattenånga [gäller vid RH=100%] i förhållande till viktsandelen luft vid T=8,5°C är vid h

M(h) = [(101325 Pa)/(89747 Pa)](3,75086 t3) · e^{17,2694/(1+238,3/8,5°C)}

= [1,129007]· 0,007

= 0,008517

= (m_V/m_L)_MAX ;

Är RH%=60 blir aktuella viktsandelen vattenånga i luften vid (p | T)[h] tydligen

m_V/m_L = 0,6 · M

= 0,005110

Bonus:

Sambandsformen för M innefattar också en koppling till motsvarande förhållande mellan vattenångtryck och lufttryck för givet lufttryck (p[h]) enligt

p_V/p_L = (1,6070767)m_V/m_L = (1,6070767)M

: p[h] = 89747 Pa (8974,7 mbar) summerar p_V + p_L ;

Vi kan därför också här få de direkt lokala värdeformerna för respektive vattenångans (p_V) och luftens (p_L) tryckvärden:

p_V/p_L = (1,6070767)0,005110

= 0,008212 ;

p_V + p_L = p = 89747 Pa ;

p_V/p_L = p_V/(p – p_V)

(p_V/p_L)^–1 = p/p_V – 1 ;

(p_V/p_L)^–1 + 1 = p/p_V ;

p_V = p/[(p_V/p_L)^–1 + 1] ;

= (89747 Pa)/[(0,008212)^–1 + 1]

= 731,007 Pa ; Vattenångans deltryck i p:

p_L = p – p_V

= (89747 – 731,007)Pa

= 89015,540 Pa ; Luftens deltryck i p.

Man kan också med alternativt kända grundvärden gå omvända vägen via exemplet ovan — samma funktion som en reguljär kontrollräkning av ovanstående resultat:

— Med lufttrycket p=89747 Pa och m_V/m_L=M=0,00474182 kända, via ett RH=60%, bestäm p_V/p_L och därur p_V. Lösning:

m_V/m_L = 0,005110 ;

p_V/p_L = (1,6070767)0,005110

= 0,008212 ;

p_V = p/[(p_V/p_L)^–1 + 1]

= (89747 Pa)/[(0,008212)^–1 + 1]

= 731,007 Pa ; Vattenångans deltryck i p:

p_L = p – p_V

= (89747 – 731,007)Pa

= 89015,540 Pa ; Luftens deltryck i p.

Svar: Se ovan.

RESULTAT:

— Vi ser att det, i vilket fall, handlar om oerhört små mängder vattenånga i luften som grundlägger molnbildningen, under alla normala väderleksförhållanden (efter våra förhållanden i Norden).

Se även vidare i RHbasic — vattenångans aktuella täthet.

— För den atmosfäriska vattenbildningen särskilt, se från H2Odata och MultiH2O (aktuella vattendroppsbildningen i exempel).

KonÅng. MinstaVatten

VATTENFÖRÅNGNINGENS TVÅ OLIKA SÄTT — och vattendroppens uppvärmning från 0°K

När vattenmolekyler förångas ur den tajtare bindningen i vatten eller is, GES — eller rättare erhåller på grund av formens specifika fysik — H2O-molekylerna rotation — extra energi som lagras som rotationsmoment — i det fria luftutrymmets gastillstånd via energin i förångningsprocessen.

— Samma mängd energi frigörs sedan då samma vattenmolekyler återgår till vatten (eller is).

Två olika förångningssätt:

Den omgivande luftens temperatur är den högre:

Är temperaturen strax utanför vatten eller isytan bara ett uns större än 0°C, kan värmegradsskillnaden via luftens molekyler överföras till vattenkroppens molekyler (successivt, ner genom Knudsenskiktet till vattenkroppen): Då dessa — först inom Knudsenskiktet, räknat utifrån luften och inåt mot vattenkroppen — upptar överskottet som rotationsenergi, frigör de sig alltmer från bindningen till vattenkroppen, och kan strax lämna denna.

Det är den ena sidan av saken — vattnets förångning via luftens rörelseenergier och allmänna Planckstrålning.

— I den delen finns ingen form för någon direkt temperaturminskning hos vattenkroppen som följd av förångningen, eftersom förångningen helt styrs av en uppvärmning av vattenkroppens yta utifrån.

Vattendroppens temperatur är den högre:

Den andra sidan av saken visar sig då vattenkroppen besitter en initiellt högre värmegrad än det omgivande rummets.

— För varje vattenmolekyl som lämnar vattenkroppen kommer vattenkroppens egen värmegrad att minska. Minskningen bör vara direkt proportionell mot styrkan i förångningen, alltså temperaturskillnaden mellan vattenkroppen och omgivande luft.

— Även här får den förångade vattenmolekylen »extra spinn» då den frikopplas från den tajtare vattenbindningen. Vartefter vattenmolekylerna förångas, sjunker vattenkroppsytans temperatur.

I de allmänna problemställningar som i denna framställning specifikt berör homogen VATTENDROPPSBILDNING I ATMOSFÄRISKA MOLN finns av dessa två beskrivna enda möjliga sätt INGET alternativ. I modern akademi (RoWest2008 Homogeneous/Heterogeneous) använder man en KONDENSATIONSMODELL — vattendroppsbildning genom successiv vattenmolekylanslutning: vattenånga som fäller ut vatten på en given, svalare, materialyta — medan den modell som genomgås här bygger på vattendroppsbildning genom successiv parförening (forts.):

I DEN HOMOGENA VATTENDROPPSBILDNINGEN (jmfr., RoWest2008 Homogeneous) — vattenbildning enbart via rena H2O, här via parföreningar — måste alla successivt bildade n(H2O)+n(H2O)-enheter värmas upp principiellt ända nerifrån bottenläget 0°K:

— Enhetsföreningarna bygger på att de enskilda komponenterna ger upp sina individuella rörelseenergier för att förenas på en gemensam vattenbindningsenergi. Den avgivna energin måste sedan omgivande luftmolekyler återinföra till enheten för att få upp denna i lufttemperaturens värmegrad.

— Den processen tar TID. Grovräkningarna visar att:

— Under uppvärmningstiden (tWARM) hinner vattendropparna förenas (tWATER) SÅ mycket att de överspelar Kelvinekvationen och dess övertrycksformer.

— Det är i varje fall den grundfysik som framträder mest spontant och synligt i ämnets granskning — men som inte verkar vara värt ett endaste omnämnande i det som syns främst i ämnets etablerade litteratur (Maj2014).

Vi studerar det.

H2Opar, KonÅng

PARFÖRENINGAR — MultiH2O

H2O-föreningen från 0°K:

Två frispinnande H2O som förenas på sin gemensamma kemiska bindningsenergi (2,2 t20 J dissociationsenergi MinstaVatten) tvingas — av den dipolelektriskt förenande kraften — släppa ifrån sig sina individuella frispinn. Figuren ovan illustrerar den möjliga principen i den föreningen: bägge H2O tappar såväl sina ordinarie fria rörelseenergier (Ekin=mvv/2) som sina rotationsmoment (J=mvr). Föreningstillfället betyder att energin som paret förlorar individuellt överförs på motsvarande induktiva kopplingar på omgivande luftmolekylers elektronbesättningar som får överta 2(H2O)-parets tidigare värmenivåer i formen av motsvarande Planckstrålning (E=hf=J/t).

— I den situationen befinner sig 2(H2O)-paret i princip på nivån 0°K. Endast efter en viss TID av stötar och knuffar från omgivande luftmolekyler, kan 2(H2O)-paret komma in till och helt eller delvis återta medelformen för luftmolekylernas medelvärmegrad.

Parföreningar — INTE KONDESATION:

I en vattenångas kondensation — vattenmolekyler som attraheras av = strömmar in till en materialyta med marginellt lägre temperatur och där fäller ut gemensamt vatten — finns inte den fysiken. Parföreningar visar en helt annan fysik.

— Efter parföreningen (H2O)+(H2O) i en vattenånga med homogen täthet finns inte längre någon vattenånga kvar, endast 2(H2O) — osv. med ytterligare parföreningar med allt växande droppstorlek. Se processen med parförening vidare från MultiH2O.

— Webbdokument som omnämner den principen har eftersöks men ännu inte upphittats.

— Citatutdragen nedan understryker HUR och ATT man i etablerade kvarter inte alls ens tycks ha uppfattat principen, utan istället ensidigt talar om condensation:

Condensation

SCIENCE FORUMS — Are Steam & Water Vapor Visible? May2011 [2014-05-14]

http://www.scienceforums.net/topic/56904-are-steam-water-vapor-visible/

”However, as it moves farther away from the source of heat, the vapor starts to cool and condense into liquid drops.”

@INTERNET Wikipedia Steam [2014-05-14]

http://en.wikipedia.org/wiki/Steam

”Technically speaking, in terms of the chemistry and physics, steam is invisible and cannot be seen; however, in common language it is often used to refer to the visible mist of water droplets formed as this water vapor condenses in the presence of (cooler) air.”

Princeton University — STEAM, datumuppgift saknas [2014-05-14]

https://www.princeton.edu/~achaney/tmve/wiki100k/docs/Steam.html

”In common speech, steam most often refers to the visible white mist that condenses above boiling water as the hot vapor mixes with the cooler air. This mist consists of tiny droplets of liquid water.”:

”This content of this page is taken from Wikipedia, and may not be up-to-date.”

Med föreningen av 2(H2O)-par till ett större 2(2(H2O))-par inträffar i princip samma sak: den större enheten binds på kredit av att individerna ger upp sina individuella energier, och alltså i princip — eller för vår grovräkning, i varje fall idealt — kommer att börja från absolut lägst möjliga energinivå. Därifrån kan sedan luftmolekylerna omkring träda in i arbetet med att stöta och knuffa in värmegrader i enheten och så åstadkomma dess successiva uppvärmning. Föreningsprincipen kan fortsätta på den formen så länge de förenade enheterna har tillräckliga hastigheter för att nå varandra inom rimliga tidrymder som blir allt längre ju större enheterna blir och deras medelhastigheter allt lägre.

— KELVINEKVATIONEN (KE) har för vattendroppens del ingenting att säga till om VID exakta 0°C: ingen förångningspotential existerar VID 0°C: ingen energi existerar som kan verkställa vattendroppens förångning vid 0°C. För att Kelvinekvationen ALLS ska komma ifråga för vattenmolekyler att LÄMNA en vattendroppe med egentemperatur 0°C måste under alla omständigheter, under alla förhållanden i den naturliga Jordatmosfärens fysik, den omgivande luftens temperatur vara större än 0°C.

— Betraktar vi således AV PRINCIP ett naturligt molnområde omkring 0°C (h=2300M, T=0,05°C, ref. Kalkylkortet PDAS Tabell6) med mättad vattenånga (RH=100%) tillsammans med befintliga vattendroppar, oberoende av vattendropparnas litenhet, har Kelvinekvationen i den miljön uppenbarligen ingen som helst ställning: ingen potential för förångning existerar.

— Lägger vi TILL den situationen — ”For gas to liquid nucleation one can use the Kelvin equation as our evaporation rate model”, Katz2007 — vattenångans övergång till vattendroppar genom PARFÖRENINGAR (H2Opar), den ovan skisserade möjliga processen som tvingar paren att börja principiellt nerifrån 0°K men som inte har ett enda omnämnande i den mest synliga etablerade litteraturen i ämnet, har Kelvinekvationen HELLER ingen betydelse för den processen eftersom fortfarande ingen energi existerar för förångning så länge temperaturen ligger under eller vid 0°C. Citatmeningen är alltså inte tillämplig i det fallet — men ingen etablerad, gratis tillgänglig mest synlig skrift verkar ens omnämna den detaljen.

DET kan också bero på ämnets milt sagt omfattande natur: det är LÄTT att falla in i tankemönster som REDAN omfattas av mainStream, men betydligt svårare att försöka se sammanhangen bakom: det finns avgörande aspekter i naturboken som ingen etablerad inrättning har brytt sig i att kolla upp, på grund av en djupgående föreställning om speciellt intelligensens hemvist: man tror sig veta vad man i grunden inte förstår, eller/och framhärdar i föreställningen att det inte är troligt att mängden missar grundfysiken.

— Så kan med andra ord parbildningarna ske i lugn och ro utan risk för Kelvinekvationens intrång ända upp till 0°C.

— Men FRÅN 0°C finns ytterligare »Kelvinrestriktioner» (KEB) som berör själva förångningsenergin som sådan i matchning med aktuella vattendroppens ytspänningsenergi (SEA), och som visar (EkinES) att de allra minsta vattendropparna (upp till runt 60stH2O vid 0°C markluft och RHG=100%) har egenspärrar mot förångning, och vilka spärrar sedan avtar med ökande omgivningstemperatur.

— Så: ÄVEN om vattenånga, fria H2O, vräker sig upp över ytan på kokande vatten hinner aldrig Kelvinekvationen med förrän vattendroppar genom parbildning REDAN hunnit bildas i uppvärmningsprocessen som alltså i princip kan förstås börja molekylärt för de successiva parföreningarna från 0°K och upp mot, främst 0°C (vilket kan ske inom en tiondels sekund, se tWARM).

— KONVEKTIONSPRINCIPEN (Wkon)

— FlaskExperimentet som visar hur svalnande fuktig varmluft uppvisar volymminskning

— kan sedan göra resten: De redan bildade nära stillastående mikrovattendropparna (vattendropparnas medelhastigheter i den idealt stillastående vattenångsmättade luften avtar proportionellt med föreningarna via växande droppstorlek) påförs en kollektiv hastighet (typ centimeter i sekunden) in mot molnets centrum och som oundvikligen leder till att vattendropparna kommer att förenas till större, med oåterkalleligt resultat i drypande regn. Hela den processbilden finns tydligen inte omnämnd i etablerad mening — eller om den anses icke giltig, skälen heller inte redovisas.

H2Oparam

Figuren ovan illustrerar exemplifierat de olika detaljer som tydligen (främst) måste beaktas i processen med de omgivande luftmolekylernas uppvärmning av den nyligen (varje) bildade vattendroppen enligt PARBILDNING (H2Opar). De angivna värdena ansluter till beskrivningen i tWARM.

— Den främsta aspekten är »värmetappet» som varje närliggande luftmolekyl till vattendroppen tvingas genomgå vid stötkontakten. Eftersom den kontakten tvunget innebär att luftmolekylen tappar rörelseenergi,

enda sättet att återfå denna är via ett visst LED av bakomvarande grannar som kan hjälpa till med en successiv överföring (i kraft av hela luftkollektivets samlade idealt konstanta värmegradspotential, om luftrummet hålls vid konstant temperatur)

måste motsvarande tillföras via någon djupkoppling (MOTHERS, här Molecular Thermal Recovery Space, MolekylTermiska ÅterhämtningsRymden, MOTÅR) i molekylhavet och på principen »handräckningslag».

— Antalet närliggande molekyler som för tillfället utövar stötar på vattendroppens yta kan beräknas via tvärsnittsytan för fria medelvägen hos luftmolekylerna, analogt deras motsvarande stötfrekventa medelvägar (ca 200nM i 0°C markluft med RH=100%). Den tvärsnittsytan jämförs sedan med aktuell vattendroppsyta, och man får då antalet aktiva stötande luftmolekyler för den aktuella vattendroppens uppvärmning. Se aktuella samband i tWARM.

— Effektförlusten hos dessa närmast aktiva stötagenter kopplar sedan via ett visst distansdjup (dM) i termiska återhämtningen, som innebär en motsvarande tidsfördröjning.

— Antalet (50st) medelvärdesdistanser (10µM) i figuren kopplar till en grovmätning som gjordes från små frostbitar 2-5mM som togs ur frysen (–18°C) och fritinades upp i rumstemperatur (20°C direkt på diskbänkens plåt) till vatten med tidmätningen 40-60 sekunder. Den antalsformen har sedan utnyttjats för att avstämma sambandsformen (i grovräkningen) för tWARM.

— Den tidsfördröjningen garanterar — eller har i varje fall förutsättningar för att göra det — att vattendropparnas uppvärmning till lufttemperaturen, speciellt för de mindre dropparna från början, kommer att ta betydligt längre TID i anspråk än tiden för själva droppbildningen. Det betyder — analogt — att KELVINEKVATIONEN uppenbarligen inte har något alls att hämta i vattendroppsbildningens skeden (H2Odata | KOFappl) fram tills dess att uppvärmningstider och bildningstider blir lika stora; Kelvinekvationens form förutsätter att vattendroppar existerar på den bestämda Kelvintemperaturen i sambandet. Den temperaturen existerar alltså inte omedelbart med den rena vattendroppsbildningen från enbart fria H2O, utan blott så småningom.

(forts.)

— Jämför »sommarläget» med markuppvärmd fuktig luft som stiger mot kallare regioner:

— Frånsett förekomsterna av redan existerande 2(H2O)Tretyakov2013, alltså enbart med förutsättningen i fria singulära H2O, finns ingen redan existerande vattenkropp att relatera till.

— Vi SKULLE säga med utgångspunkt från en redan existerande vattenkropp, och med etablerade termer:

Omvänd förångning genom vattenmolekylernas kondensation:

— Alltså: från fria H2O i varmare luft till vattenbundna H2O i kallare luft med samtidigt frigörande av vattenmolekylernas tidigare upplagrade rotationsenergier.

— Emellertid har parbildningen (H2Opar) ingenting med kondensation att göra. Kondensation är en helt annan fysikprocess som bygger på att vattenångans fria H2O-molekyler dras till en redan etablerat något kallare materieyta vars temperatur inte nämnvärt ändras och där ansamlas som i princip omedelbart temperaturanpassat utfällt vatten. Parbildningen (tWATER) — H2O-grupper som förenas på individuellt avyttrade rörelseenergier och därför måste börja sin uppvärmning mot omgivningstemperaturen från i princip 0°K — har uppenbarligen ingenting med den processen att göra (MultiH2O).

— Då vattenmolekylerna ingår förening i den tajtare vattenkroppens bindning, förloras samtidigt (det mesta av) rotationerna. Då dessa förloras, ges motsvarande lokala temperaturhöjningar (som omsätts främst inom Knudsenskiktet): först ytan, sedan längre in.

— Aspekten med lokal uppvärmning vid vattenångans vattenbildning är emellertid ingen springande kärnfråga eftersom molnbildningen i allmänhet handlar om områden med stadigt avtagande temperaturer (Wkon) för uppåtstigande uppvärmda markluftpelare. Därmed, i vilket fall, kompenseras varje tillskott i lokal uppvärmning via vattenmolekylernas vattenbildningar av processen med stadigt sjunkande omgivningstermperatur — vilket för övrigt också garanterar att bildat vatten inte strax förångas igen, och förutsatt att inte Solen bryter igenom och tittar fram på just det stället (vilket i så fall garanterar snabb förångning).

DE HÄR BESKRIVNA GRUNDASPEKTERNA PÅ OCH I DEN HOMOGENA VATTENDROPPSBILDNINGEN har (tydligen, att döma av det mest synliga webbutbudet) aldrig tilldragit sig den moderna akademins intresse. I MAC utgår man istället ifrån s.k. aerosoler (vattenlösliga mikropartiklar som vattenmolekyler kan fästa sig vid och på den vägen växa till genom eng. heterogeneous nucleation). Grundprinciperna beskrivs utförligt i RoWest2008.

— Den tillväxtmatematiken är av en helt annan art än den som beskrivs här (grovt och förenklat).

— I modern akademi (RoWest2008 Hetereogeneous) favoriseras istället den s.k. heterogena nukleationen: på en redan lufttempererad typ mikroskopisk vattenlöslig pollenkärna kondenserar vattenmolekyler i en viss takt (eng. Köhler theory, Gibbs free energy, RoWest2008 s6). Det är en helt annan modell för vattendroppsbildning. ATT den delen också finns med råder inget tvivel om. Men att den skulle vara obetingat avgörande för vattenbildningen har i ovanstående menings ljus (här) mindre kredit.

— Speciellt tillkomsten av resultaten från Tretyakov2013 — 2(H2O) existerar i rumstempererad luft — endast understryker det faktum att, främst, den minsta av alla vattendroppar REDAN finns i naturboken. Se även sammanhangen i KelvinH2OWebben.

— Se även artiklarna i sammanfattning och syntes från H2Odata, om ej redan bekant.

Wkon

KONVERGENSHASTIGHETER I KALLNANDE MOLNOMRÅDEN

I FLASKEXPERIMENTET tydliggjordes HUR uppvärmd fuktig luft krymper ihop — volymreducerar — då den kallnar fritt till omgivningens temperaturnivå. Förutsatt att också liknande fenomen är att räkna med högre upp i atmosfären — inte enbart i det enkla kökets anspråkslösa miljö — kan vi räkna med i varje fall en extra liten men avgörande effekt som kan återföras på den möjliga vattendroppsbildningens fysik, här idealt sett i en helt vindstilla lokal. Nämligen att sammandragningen påtvingar en liten sammanstrålande hastighet (några centimeter eller millimeter per sekund eller så) på redan existerande mikrosmå vattendroppar. Då den processen väl en gång satts i funktion, finns inga makter i universum som kan hindra vattendropparnas sammanstrålande och därmed åtföljande händelse: oåterkalleligt drypande regn.

— Möjligen är det också så den naturliga vattendroppsbildningen fungerar i molnbaserna där den största anhopningen finns. Vi får därför, tydligen mer av regel än undantag, förutsätta att den mer eller mindre svagt konvergerande processen är verksam i alla former av atmosfärisk vattendroppsbildning, och så länge som inget argument framkommer som visar att den ståndpunkten är ohållbar.

Figuren nedan visar principen.

Bonus — långsam avsvalning (Flaskexperimentet):

OM den vattenformande molndelen (FlaskExperimentet, JAVKbasic) befinner sig i (långsamt) avsvalnande, vilket i allmänhet bör vara fallet — det är just på den formen droppbildningen kan initieras via daggpunkten — får vi tydligen förstå att molndelen också genomgår en volymminskning: rörelseenergierna mellan molekylerna som håller volymen uppspänd avtar, och molndelen sammandras motsvarande långsamt (typ centimeter per sekund):Vattendropparna erhåller en motsvarande långsamt kontraherande hastighetskomponent — som sedan INTE enkelt låter sig avstyras: vattendroppens mekaniska tröghet mot rörelseändring,

Med luftmolekylerna som impulsbestämmare har en Ø1µM vattendroppe i 15°C markluft med RHG=100% en medelhastighet på

ca 4 t8 M/S = 0,00004 mM/S: i princip stillastående i lufthavet.

värre ju större droppe. Har en sådan kontraktion väl en gång startats — vindstilla förutsatt och förutsatt att Solen inte tittar fram och värmer upp området igen — finns ingen fysisk möjlighet att undvika droppkontakter med obönhörligt resultat i (drypande) regnbildning.

MultiH2O, H2Odata | KonÅng | MKA

Från vattenånga till vattendroppe —

baserat på vattenfysiken (KEB) i H2Odata och parbildningsprincipen i H2Opar

————————————————————————————————————————————————————————

Från enskilda vattenmolekyler i ett atmosfäriskt moln, till de enskilda tyngre vattendroppar som kan börja falla ner som regn — enbart via allmänna gaslagens samband

— Vi frånser all avdunstning från bildade vattendroppar — vilket betyder att vårt exempel har parkerat (strax under) VID daggpunkten (från en något högre punkt): ingen mer vattenånga får plats i luften vid det trycket och den temperaturen.

— Vi börjar från vattenångans enskilda vattenmolekyler H2O och tillämpar sedan PARBILDNING (H2Opar). Vi ska testa och undersöka hur en ideal förening mellan varje par H2O ger en gemensam minsta möjlig vattendroppe: första parföreningen betyder större avstånd mellan paren. Föreningen mellan dessa i sin tur ger ännu något större medelavstånd mellan återstående, och så vidare, och så långt upp vi kan komma i droppstorlek med hänsyn till en rimlig TID (tWATER) som vattendropparna kan spendera i ett atmosfäriskt moln. Vi förutsätter att luftmolekylerna är i majoritet från början och använder deras huvudsakliga impulser (mv) som referens: rörelsemängden fördelas då lika mellan samtliga luftpartiklar oberoende av storlek, och så länge luftmolekylernas normala rörelsemängder inte hämmas avsevärt, och de fortsätter att vara i majoritet. Eftersom vattenmängden i den normala luften aldrig överstiger ens några få procent [AppH2Oluft | SVPgrafen], och därmed grovt bibehållen luftmolekyldynamik, bör felet heller inte bli större än just max några få procent i grovberäkningarna.

— En ytterligare förutsättning finns — som i slutänden visar sig sammanhänga med det möjliga bildandet av de slutligt större vattendroppar som kan övergå i regn: Wkon. Vartefter de fria H2O-molekylerna försvinner från lokalen och ersätts av växande vattendroppar i ideala parföreningar, försvinner samtidigt den ursprungliga tillståndsbilden med mättad vattenånga och temperatur. Bara om temperaturen, således, fortsätter att långsamt avta, och därmed daggpunkten reduceras, kan processen med parföreningar fortsätta utan risk för förångning av redan bildat vatten — och förutsatt att aktuella temperaturer och fuktigheter inte överrids av Kelvinekvationens speciella villkor. Se särskilt genomgången för dessa fall i KEB. Se även i RegnDroppen.

WaterBegin

Två vattendroppar som närmas varandra, hängande i spetsen på varsin tandpetare, »förenas omedelbart» till en större vid minsta närkontakt. Principen bakom den följande undersökningen grundas på samma egenskap (H2Opar) [Tretyakov2013]. Vi studerar den möjliga allra enklaste och mest direkta matematiken för hur ett område med enskilda H2O-molekyler kan försvinna genom att bilda 2(H2O), hur dessa kan upphöra genom att bilda 2(2(H2O)) och hur dessa kan förstås övergå i 2(2(2(H2O))) osv., och så långt vi kan komma med hänsyn till den TID ett moln har på sig. Figuren ovan illustrerar en syntes av tillvägagångssättet.

— Liknande uppslag har eftersökts på webben (nu löpande under framställningen, 19Mar | 22Maj 2014) men ännu inte påträffats.

d/r

Förhållandet mellan medeldroppsavstånd (d) och droppdiameter (Ø) är för given andel vattenånga och temperatur konstant — oberoende av droppdiameter

m_W vattendroppens massa: suffix W | V för Water | Vattenånga:

d = [m_W/ρ_V]^1/3 ; Se d-referensen i RegnDroppen: vattendropparnas medelkubavstånd i 1 M³.

d₀ = [U_VWu/ρ_V]^1/3 ; H2O-molekylernas kubiska medelavstånd i alktuell vattenånghaltig luft:

r = [3m_W/4πρ_W]^1/3 ; vattendroppsradien

d/r = ([m_W/ρ_V]/[3m_W/4πρ_W])^1/3

= (m_W4πρ_W/3m_Wρ_V)^1/3

= (4πρ_W/3ρ_V)^1/3 = (4π·[1000 KG/M³]/3ρ_V)^1/3 = (4188,7902/ρ_V)^1/3

= 16,11992(ρ_V)^–1/3 ; Förhållandet mellan droppmedelavstånd och droppradie

= k₁ ;

d = rk₁ ;

MFP

Medelfrivägen från början

— för stationära målpartiklar relativt mobila källprojektiler d_F ~ 1/(σn) = 1/(π[r_H2O]²N/M³); för molekylerna i gaser typ luft d_F ~ 1/([√2]σn)

— ref. Wikipedia Mean free path, Derivation

— är inverterade produkten av antalet målpartiklar per M³ (n) och målpartikelns träffyta (σ) (gånger 0,7 för homogena gaser): ca 200nM från start för H2O-molekylerna (eller luftmolekylerna); Medelavståndet (d0) från början mellan de fria vattenmolekylerna (RH=100%) är vid 0°C markluft 19nM (ca 6ggr större än luftmolekylernas drygt 3nM):

— Medelfrivägen (dF) är alltid större än partikulära (gasmolekyl-)medelavståndet (d0), här minst 200/20=5 gånger större än medelavståndet mellan H2O-molekylerna från start. Det garanterar att friväg existerar för vattenmolekylerna att nå varandra för en första förening enligt den antydda principen i vinjettfiguren [‡]:

— Vi räknar enklast sämsta fallet med målpunkterna vilande och källpunkterna på aktuell hastighet (v). Vartefter vattendropparna växer till sig och blir de största partiklarna kommer deras medelfriväg — via konstant medelhastighet från medelimpulserna — bara att begränsas av tillfället fram till att två eller flera droppar sammanträffar. Dvs., »bara en tidsfråga».

— I den följande utvecklingen räknar vi idealt med att ett sådant sammanträffande sker EXAKT på den tid som utpekas av medelavståndets vägform.

Vattenmolekylernas initiellt höga medelhastigheter i gasmolnet — v(V[0°C])~780 M/S; v(V[20°C])~800 M/S — avtar i takt med att vattenmolekylerna förenas till större vattendroppar med allt lägre medelhastigheter: v(V[T°C])=(mv)_LUFT/m_V ;

— Lika vattendroppar som möts idealt rakt på (icke-splashande), tappar direkt hela varandras ursprungliga rörelsemängder och fortsätter tillsammans i tiden som EN enda sammanhängande större droppe — eller kontaktsplashar i en skur av smådroppar om hastigheten i mötet är kritisk.

— Från ett sådant antaget läge med EN förening utan splash kommer sedan luftmolekylernas medelmässiga rörelsemängder att antingen

1. dela med sig på föreningsdroppen och efter viss tid ge denna en motsvarande ekvivalent rörelsemängd om droppmassan inte är för stor, eller

2. låta större vattendroppars föreningsimpulser själva bestämma utfallet — luftmolekylerna är då så små relativt vattendroppen att dess rörelsemängd knappast kan påverkas av enskilda stötar från omgivande luftmolekyler.

Därmed kan vi enkelt förstå i grovräkningen hur alla ojämnheter i vilket fall med början från de allra minsta vattendropparna sprids ut över en viss (rimlig) tid.

— Växande droppstorlek med allt avtagande rörelseförmåga, kan alltså i vilket fall förstås lika med avtagande medelhastighet per vattendroppe. I den enklaste av alla räkningar som görs här, antar vi den enklaste modellen att alla partiklars rörelsemängder bestäms entydigt av majoriteten luftmolekyler (vattenandelen är som mest i vilket fall i Jordtroposfären bara max 4%) och deras genomsnittliga rörelsemängd j=(mv)_LUFT beroende på luftens temperatur.

— OM räkningen går ut på att de allt större vattendropparnas medelhastigheter (v) i gasmolnet SÅ går obegränsat mot noll, kommer tydligen enbart TIDSASPEKTEN som sådan (tWATER) till slut att garantera en slutprodukt med växande vattendroppar som hålls svävande (om de inte hinner avancera till Regndroppen) i gasmolnet i garanti av gastryckets inverkan.

— Inbördes hastighet mellan dropparna avtar snabbt med dropparnas växande omfång.

— Inga droppar HINNER till slut förenas mera i par då deras medelhastighet i molnet blir så låg att medelavstånden tar längre tid att avverka än tiden molnet finns till.

— EVENTUELLT, vilket resultaten kommer att visa, fortgår processen ända tills vattendroppstyngden från de senast bildade större dropparna tar överhanden och dessa börja falla till marken som regn. Vi förutsätter då i allt att inga yttre extra vindkrafter spelar in, och heller inga andra variationer som kan störa själva den droppbildande föreställningens lugna faser. Exakt vad som gäller på den punkten kommer att avslöjas dels på matematiken i slutänden av undersökningen, och dels via en separat beräkning som beskriver storleken hos en vattendroppe som precis bildar regndroppe med hänsyn till den lokala tyngdkraften och luftens inre partikeluppbärande medeltryck, se Regndroppen.

Beräkningarna görs från sammanställningarna i TMekv i TillämpningM tillsammans med grundparametrarna för luftfuktighet (RH) höjd över marken (h) och aktuell lokal temperatur (T), se Kalkylkortet Tabell 5A — sambanden bestämmer ramarna för vattendropparnas del i deras bildning optimalt i atmosfäriska förhållanden med RH=100%

Genom den relativt (max 4%) ringa förekomsten vatten i atmosfären/molnen, synes tillräcklig provisorisk prövande exempelgrund finnas för luftmolekylernas genomsnittliga rörelsemängder (j=mv) att bestämma takten i energiomsättningen (pV=kT=E) där också vattenånga finns närvarande.

— Olika »gästpartiklar» [m(PAR)] som införs i luften kommer därmed (olika snabbt) att få sina specifika medelhastigheter v=j/m

— och förutsatt att mellanrummet mellan gästpartiklarna fortfarande är »tillräckligt stort» för att luftmolekylernas rörelseenergier (enligt allmänna gaslagen) ska få bestämma tillståndstakten (j).

— Slutmedelhastigheten i gastillståndet för gästpartikeln — i vårt fall vattendropparna i luftrummet — kan då skrivas enkelt

v_PAR = (mv)_LUFT/m_PAR

med partikelparametrarna (PAR)

m = ρV

= ρ·4πr³/3 ;

v_PAR = (mv)_LUFT/m_PAR

= (mv)_LUFT/(ρ4πr³/3)_PAR

= 3(mv)_LUFT/(ρ4πr³)_PAR ;

K = 3(mv)_LUFT = konstant ; ingen temperatur- eller tryckändring under processen

v_PAR = K/(ρ4πr³)_PAR

= ([K/ρ_PAR]/4π)/(r³)_PAR ;

k = (K/4πρ_PAR)

= 3(mv)_LUFT/4πρ_PAR ; T=20°C: ca: 3(2,4 t23)/4π(ρ_W)

v_PAR = k(r^–3)_PAR

Den avgörande impulsen j=mv som kommer att reglera hela processen beror på den lokala temperaturen (T°K). Genom MOMENTEKVATIONEN i allmänna gaslagen kan luftmolekylernas medelhastighet (v) bestämmas enligt

v_LUFT = √ 3bT/U_Vu

= √ 3(1,3805502 t23 J/°K)T/(28,952127)(1,66033 t27 KG) ; Vid 0°C =T=273,15°K:

= 485,12 M/S

och motsvarande för de fria vattenmolekylerna

v_LUFT = √ 3bT/U_Vu

= √ 3(1,3805502 t23 J/°K)T/(18,0154)(1,66033 t27 KG) ; Vid 0°C =T=273,15°K, [ ±4%]:

= 779,63 M/S

Förhållandet ger vH2O / vLUFT = 1,2677052 ~ 1,27

Vattenångans aktuella praktiska täthet (ρ_V) i luften beror på tryck (p), temperatur (T) och luftfuktighet (RH) — RH-värdet bör väljas nära 100% och T-värdet förstås som ett t-daggpunktsvärde [‡] i samband med aktuell vattendroppsbildning. Sambandet TMekv i TillämpningM sammanfattar dessa parametrar. Det är den sambandsformen som kommer att fastställa TpRH-värdena på resultatformen för varje motsvarande praktisk aktuell vattenångstäthet (ρ_V) inom Jordtroposfären.

tWATER, tWARM

PRAKTISKA RESULTATVÄRDEN — se närmast nedan:

Grovvärdena (direkta, icke-summerande t-formen, se t nedan) med t och r ger vid 0°C markluft med RH=100% och (K)=1,74 T28 M²/S droppbildningstider

t = r⁴(K) med r = [t/(K)]^1/4:

Ø_VATTEN = 1 | 10 | 100 | 1000 nM-droppar på t = 1,09 {t9 | t5 | t1 | T3 } S:

Från grovt 1000 S (16,7 minuter) tar det sedan allt längre tider för att få ytterligare större vattendroppar.

— Vi kan testa (med tidur, eller med direkt grov uppskattning) genom att se på molnbildningar:

Vi väljer företrädesvis tidiga HETA försommardagar då Solmarkvärmen stiger uppåt till kallare avsnitt (som ännu inte uppnått dagsvärmen och därför är utmärkta — ytterst snabbverkande — molnbildningsskikt). I sällsynta fall, kan vi då få se molnbildningar i de allra lägst liggande atmosfäriska skikten (kanske upp till 1-2KM) som TYDLIGT avancerar inom tiotal sekunder. Den räkningen med grovt t=10 S skulle, om ovanstående har någon praktisk förankring

och förutsatt absolut vindstilla och absolut konstant temperatur under hela processen (vilket vi vet INTE gäller i praktiken: temperaturen vid naturlig molnbildning är ALLTID i något avtagande genom att den markuppvärmda luftpelaren just är föremål för temperaturminskning), i annat fall kan tiderna (drastiskt) förkortas,

motsvara droppar med diametern runt 2r=Ø=0,3µM. Högre lufttemperatur (20°C) ger något snabbare bildningstid med marginellt större vattendroppe (nära 0,4µM).

— Olika webbkällor (Maj2014) tycks hålla sig inbördes ungefärligt till samma basområde (ännu ingen direkt upphittad webbkälla som säger det rakt ut):

— omkring Ø1µM skulle vara (lägsta) syngränsen för vattendroppar då dimma eller dis börjar visa sig.

— Det betyder, sett i väldigt grova drag, att räkningen ovan, och observationen, (ännu så länge) håller sig inom det rimligas ramar.

TIDEN (t) för vattendroppen Ø=2r att avverka sin medelkubdistans (d) i gasrummet kan tydligen skrivas

t = d/v

= d/k(r^–3) ; k = 3(mv)_LUFT/4πρ_PAR, KG·M/S / (KG/M³) = M²/S

= r³d/k

= r³rk₁/k ; k₁ = d/r = 16,11992(ρ_V)^–1/3

(K) = k₁/k ; (K) = d/rk

t = r⁴(K) ; tWATER

— Vi snabbtestar första resultatbilden:

— (K)-värdet kan vi grovberäkna från luftmolekylernas mkedelhastighet grovt runt 500 M/S — »gäller i stort» 0-50°C — med luftmolekylens massa m = Uu = 28,95·1,66033t27KG = 4,81 t26 KG med mv= 2,41 t23 KG·M/S; k-värdet blir då med max 4% av ρV=0,8 lika med

k = 2,41t23 / [4π · 0,04 · 0,8] = 6 t23 M²/S; Därmed också

(K) = 0,64/k = 1,1 T22;

— r-värdet [här grovt förenklat i helheten] blir då från föregående [2:an för 2st H2O motsvarande »första vattendroppen»]

r = 2(3U_Vu/4πρ_V)^1/3 = 2[3·18,02·1,66033t27/(4π·0,04·0,8)]^1/3 ~ 1,21 t8 M

Om vi sätter tidsgränsen till 10 minuter = 600 sekunder blir motsvarande droppstorlek på den medeldistanstiden lika med

r = (600/1,1T22)^1/4 ~ 15,3µM; — Ytterligare tid tillkommer för alla föregående sammansmältningar.

— Vi BÖR vara EXPERTER på den här grovräkningen: Mulna grå dagar, molntäcket glider fram i lugn takt, timme in och timme ut. Över en natt — 43200 sekunder eller 12 timmar med optimalt LÅG temperatur, ingen Sol — har molnmassorna god tid på sig att FORMA mikrodroppar, och som sedan, beroende på lokalt gynnsamma förhållanden — lugna glidvindar, smärre tryckändringar via mindre temperaturfluktuationer — har möjlighet att förenas till ännu större, ända upp till gränsen för regndroppe. Mot morgontimmarna kommer det strilande regnet: minimala regndroppar, helt vindstilla. Jubel utbryter på marken bland alla Blommor.

— Värdena i slutänden [RESULTATBILDEN], grovt över alla möjliga fall och inom dygnets timmar, visar runt 1/3 av grovresultatet ovan.

— Tidssummorna totalt blir:

t_SUM = (K)(r₁⁴ + r₂⁴ + r₃⁴ ... + r_n⁴)

— Går vi bakåt från r=15,3µM till närmast föregående ges r mindre med 2^1/3=1,26 som ger r=12,1µM; tiden blir nu betydligt kortare:

t = 238 S. Ytterligare ett steg bakåt ger r = 9,6µM som ger

t = 94 S. Och på samma sätt i fortsatta led: r = 7,6µM — t reduceras med drygt 1,259921^4=ca2,52 per steg, se HTK nedan:

t = 37 S ...

t = 15 S

t = 6 S

... ;

t₀ = r₀⁴(K) = d₀/v_0V = 2,7 t11 S vid 0°C markluft RH=100%:

t₁ = [r₀2^1/3]⁴(K)

t₂ = [r₀2^2/3]⁴(K)

t₃ = [r₀2^3/3]⁴(K)

...

Tillväxten ska emellertid börja från de två första vattenmolekylernas förening (r₀) och sedan deras successiva fördubblingar med tillhörande matchande rörelsemängder (j=mv)_W för den successivt tillväxande vattendroppen:

t_SUM = (K)[[r₀2^0/3]⁴ + [r₀2^1/3]⁴ + [r₀2^2/3]⁴ + ... + [r₀2ⁿ^/3]⁴]

= (K)r₀⁴[[2^0/3]⁴ + [2^1/3]⁴ + [2^2/3]⁴ + ... + [2ⁿ^/3]⁴]

= (K)r₀⁴[[2^4/3]⁰ + [2^4/3]¹ + [2^4/3]² + ... + [2^4/3]ⁿ]

= (K)r₀⁴[1 + [2^4/3]¹ + [2^4/3]² + ... + [2^4/3]ⁿ] ; Geometriska Serien [Se RECIPROKA GS]

a = [2^4/3] = 2,5198421 ;

t_SUM = (K)r₀⁴[1 + (aⁿ⁺¹ – a)(a – 1)^–1] ; VerifOK — Tabell4 Blixt2014.ods

n+1 = ln(a + (a – 1)[t_SUM/(K)r₀⁴ – 1])/ln(a) ; VerifOK

OM i medeltal två mindre idealt lika stora sfäriska vattendroppar (r) möter varandra och förenas till en idealt större sfär (R), gäller tydligen

V = V(r) + V(r) = 4πr³/3 + 4πr³/3

= 8πr³/3

= 4πR³/3 ;

4πR³/3 = 8πr³/3 ;

R³ = 2r³ ;

R/r = 2^1/3 ; =1,259921

R = r2^1/3 ;

HalveringsTidsKvoten, MultiH2O

Med förhållandet mellan två konsekutiva R(TILL)r som avr. 1,26 blir förhållandet mellan två konsekutiva t-värden dubbla det värdet:

t_a/t_b = r_a⁴(K)/r_b⁴(K)

= (r_a/r_b)⁴

= (R/r)⁴

= (2^1/3)⁴

= 2^{4/3 = 3/3 + 1/3} = 2·2^1/3

= 2,5198421 ;

~ 2,52 ; Konstanta tidsdifferenskvoten mellan två konsekutiva föreningsfaser

Med processen av successiva sammansmältningar 2r till R inom en (begränsad) del av luftrummet i molnet således

Rsum = (r₀2^1/3)2^1/32^1/32^1/32^1/3... 2^1/3

= r_FINAL ; Sista droppens slutradie

r_FINAL = r₀2^1/32^1/32^1/32^1/32^1/3... 2^1/3

= r₀[2^1/3]ⁿ

= r₀[1,259921]ⁿ ; Vi räknar r0 från de två första vattenmolekylernas förening:

r_H2O = (3U_Vu/4πρ_W)^1/3

= (3[2·18,02u]/4π[1000 KG/M³])^1/3

r_H2O = 2,4264 t10 M ; Minsta Vattendroppens radie: 2st H2O

Vattenmolekylens radie som hela processen baseras på:

r₀ = (3U_Vu/4πρ_W)^1/3

= (3[1·18,02u]/4π[1000 KG/M³])^1/3

r₀ = 1,92584 t10 M ; Vattenmolekylens radie: 1st H2O

Därmed kan antalet sammansmältningar (n) fram till den kritiska falldroppsstorleken (r_FINAL) beräknas alternativt enligt

n = [ln(r_FINAL/r₀)]/[ln(1,259921)] ; VerifOK

RB, MultiH2O

RESULTATBILD:

| t_SUM = (K)r₀⁴[1 + ([2^4/3]ⁿ⁺¹ – [2^4/3])([2^4/3] – 1)^–1] | n = [ln(r_FINAL/r₀)]/[ln(2^1/3)] = ln([2^4/3] + ([2^4/3] – 1)[t_SUM/(K)r₀⁴ – 1])/ln([2^4/3]) – 1

— Det visar sig i slutänden [TillämpningM | H2O Tabell5A i Blixt2014.ods] med RH=100% att såväl lokala temperaturvärden (T) som avstånd över Jordytan (h) har helt marginell inverkan:

— EXEMPELVÄRDEN med tSUM=12h=43200S — ett halvt dygn för att matcha bilden av vad molnen kan åstadkomma »under en typiskt helmulen dag» — visar 2rFINALvärden runt 3µM (2,79 t6 M till 3,23 t6 M) i intervallen T=0-25°C med h=0-10KM marginellt oförändrat;

— Inom timmen (tSUM=3600S) ges grovt halva det värdet eller ca Ø=1,5µM vattendroppar — droppmedelhastigheten i det omgivande 0°C marklufthavet med omkringputtande luftmolekyler med medelhastigheter runt 485,12 M/S är då runt 1,3 t8 M/S; Inom sekunden ges grovt Ø=0,2µM droppar (Ø0,193 t7 M).

— Vi måste erinra här direkt att medelhastigheterna i beräkningarna ovan har utgått ifrån droppföreningarna på enbart ENA droppens medelhastighet. I praktiken gäller bägge tillsammans, vilket förkortar reella bildningen på halverad tid. Halva tidsvärdena ovan således (Ø1µM-droppen nås då efter 730/2=365 S ~ 6 min).

Vattenånga, i luft — 19Mar2014 — Vattenångans luftandel

Vattenånga i luft — när blir vattendroppe regndroppe?

RegnDroppen

När vattendroppen blir regndroppe

Allmänna Gaslagen pV=kT=p(m/ρ) med fundamentala gaskonstanten k=370,95002 J/°K har gastrycket (p) på ekvivalenten p=F/A: kraft (F) över tryckyta (A).

— Med sambandet för gasernas och ångornas täthet (ρ = Uρ₀; ρ₀=0,0446126 KG/M³ vid STP [Standard Temperature and Pressure — havsnivån T=0°C med p=1 atm = 101325 Pa=N/M²], se mera utförligt i Allmänna Gaslagen) kan vi då idealt beräkna hur stor (sfärisk diameter) en vattendroppe ska vara för att precis uppväga tyngdkraften (F=ma) från Jordytan via gastryckets kraft (F=pA);

— Förutsättningar: Vi förutsätter ett harmoniskt jämviktsläge i rörelsemängder (mv) mellan vattenånga OCH luft »i samma molnvolym» — som betyder att alla luftmolekyler för sig och alla vattendroppar för sig tillsammans besitter en och samma medelbaserade rörelsemängd baserad på tryck och temperatur enligt gaslagen. Genom att (i allmänhet) andelen vatten i luften bara är maximalt enstaka procent, kan felet i beräkningarna också bli max av samma storleksordning (max 4% fel).

— Kan vi någotsånär (med allmänna gaslagens hjälp) bestämma hur stor en vattendroppe i ett moln måste vara för att precis bli SÅ tung att tyngdkraften överväger gastryckskraften, och droppen börjar falla mot marken?

— Den här typen av försök att besvara en grundfråga har eftersökts på webben (Mar2014) men ännu inte påträffats.

Vi studerar det.

NATURLIGA ATMOSFÄRISKA MOLNETS FÖRUTSÄTTNINGAR:

u atomära massenheten: 1,66033 t27 KG

ρ₀ rhåNoll: ideala fundamentalgasens masstäthet vid STP: 0,0446126 KG/M³ Se utförligt i Allmänna gaslagen

U(H₂O) vattenmolekylens atomvikt: 18,02154 u konv. tabellvärde från sammansättningen 2 st Väte + 1st Syre

ρ(H₂O) vattenångans täthet vid STP via ρ₀ : = Uρ₀ = 0,803919 KG/M³

ρ_W vattnets täthet: 1000 KG/M³ konv. tabellvärde

m_W vattendroppens massa U_Vu = m_V även vattenångmolekylens [halva] massa

V_m vattendroppens volym: ρ_W = m_W/V_m ; V_m = m_W/ρ_W = 4πr³/3

r vattendroppens idealt sfäriska radie: r = (3m_W/4πρ_W)^1/3

2r vattendroppens idealt cirkulära tvärsnittsdiameter

πr²=A vattendroppens idealt gastrycksexponerade gastrycksyta [tvärsnittets medelyta]

N(H₂O) antalet vattendroppar per 1 M³ vattenånga: N/M³ = ρ(H₂O)/m_W :

Totala massan är m_V, enhetens massa är m_W; m_V/m_W ger antalet m_W i m_V:

d medelkubavståndet mellan vattendropparna i 1 M³: [1M³/N]^1/3 = [m_W/ρ(H₂O)]^1/3

N(SQR) droppantalet per 1 kvadratmeter total gasyta: 1M²/d²

p_W gastrycket på varje droppes idealt cirkulära tvärsnittsyta: p/N(SQR)

p aktuella atrmosfäriska gastrycket per 1 kubikmeter: p = kT/1M³ T i °K och k = 370,95002 J/°K

Ekvivalenterna p=F/A=(ma)/A ger (OBS vid ideala STP)

p_W = p/N(SQR)

= p/[1M²/d²]

= pd²/1M²

= p[(1M³/N)^1/3]²/1M²

= p[(1/N)^1/3M]²/1M²

= p[(1/N)^1/3]²

= p(1/N)^2/3

= p(1/[ρ(H₂O)/m(W)])^2/3

= p[m(W)/ρ(H₂O)]^2/3

= m_Wa/A ;

m_Wa/A = p[m(W)/ρ(H₂O)]^2/3 ;

m_W[m(W)]^–2/3a/A = p[1/ρ(H₂O)]^2/3 ;

[m(W)]^1/3a/A = p[1/ρ(H₂O)]^2/3 ;

[m(W)]^1/3/A = p[1/ρ(H₂O)]^2/3/a ;

[m(W)]^1/3/A = p[ρ(H₂O)]^–2/3/a ;

[m_W]^1/3/A = p[ρ(H₂O)]^–2/3/a ;

[ρ_W4πr³/3]^1/3/A = p[ρ(H₂O)]^–2/3/a ;

[ρ_W4π/3]^1/3r/(πr²) = p[ρ(H₂O)]^–2/3/a ;

[ρ_W4π/3]^1/3/πr = p[ρ(H₂O)]^–2/3/a ;

r^–1 = πp[ρ_W4π/3]^–1/3[ρ(H₂O)]^–2/3/a ; Vattendroppens storlek för att bli regndroppe — vindstilla

Ø = 2a[ρ_W4π/3]^1/3[ρ(H₂O)]^2/3/πp = 2r ; a=9,81 M/S²

= p^–1(87,0402631667 N/M)

= 0,8590206259 mM vid STP-ideala T = 0°C = 273,15 °K

Ø ~ 0,00086 M

Svar: Vattendroppen i molnet blir regndroppe

— falldroppe

— först från diametern Ø = 0,86 millimeter vid STP (havsytan 0°C, 1 atm).

— Se även noteringarna nedan.

— Mindre droppar hänger alltså kvar i molnen, förutsatt noll inverkan från extra vindtryck.

— Högre temperaturer ger ytterst marginella skillnader

— 20°C ger Ø=0,800 mM grovräknat på enklaste sättet: diametern avtar med högre gastryck = högre temperatur, given volym.

— Notera också att vattendroppen avger vattenmolekyler i form av avdunstning på vägen ner mot marken, mer eller mindre beroende på omgivande temperatur och inverkan på vindtryck, vilket ytterligare reducerar droppens storlek då den kommer ner, förutsatt inte förstorad genom sammanslagning med andra på nerfärden (man räknar med att droppar större än Ø4mM byts upp av luftmotståndet i flera mindre).

— Notera också LABORATORIEEXPERIMENT MED enskilda DROPPAR:

— Enskilda vattendroppar i laboratorieexperiment har INTE ovanstående molnnaturliga vattenångans täthet att falla tillbaka på, typ flera miljoner 1mM-droppar per M³ som i räkneexemplet ovan. Med enbart EN enda droppe (tillsammans med laboratorielokalens normalluft) blir täthetsfaktorn ρ(H₂O) för vattenångan i sådana experimentfall

[ρ(H₂O)]^2/3

betydligt lägre — och därmed mindre droppdiameter — på enstaka experimentdroppar utspridda över stora (torra) laboratorielokaler.

— Jämför en (upphittad webb-) källa som beskriver just sådana fallexperiment med vattendroppar från Ø0,1mM och uppåt,

NUMERICAL MODEL FOR THE FALL SPEED OF RAINDROPS IN A RAINFALL SIMULATOR,

John H. van Boxel, 1997

http://staff.science.uva.nl/~jboxel/Publications/PDFs/Gent_98.pdf?iframe=true&width=900&height=450

Se särskilt s83 Figure 4 — texten kan kopieras men är krypterad.

Jämför även till synes någorlunda samstämmiga uppgifter på annat håll:

”According to the team’s new calculations, these clusters appear to be about a millimeter in size–just the size needed for raindrops to begin falling.”,

Källa: American Physical Society 2001

Det verkar f.ö. inte finnas några webbkällor ALLS som ens (försöker) närma sig ovanstående (»enkla elementära») räkneuppgift med alla basdata för vanlig atmosfärisk luft innefattade. Man menar generellt, som det ser ut, att vattendroppar i moln hålls kvar där på grund av UPPVINDAR (eng. ofta updrafts, ”Raindrops must be heavy enough to overcome the upward lift of air.”, http://www.education.com/science-fair/article/rainy/). Inte på grund av det naturliga molnets inre atmosfäriska gastryck. Den senare delen har särskilt eftersökts i omnämnande, men har inte påträffats (19Mar2014).

BUF, Blixturladdningens fysik, huvudavsnitt Maj2014 — LU

BlixtTGF2014a ........ Part 1 GRUNDBEGREPPEN I MOLNBILDNINGENS TEKNISKA FYSIK — basbegreppen till

BlixtTGF2014b ........ Part 2 BLIXTURLADDNINGENS FYSIK — Jordströmmar och Molnbildning

En mera utvidgad detaljbeskrivning av blixturladdningens fysik från Blixturladdningens Fysik 2008 — Editor2014II18|V5|V22

——————————————————————————————————————————————————

BLIXTURLADDNINGENS FYSIK

MED JORDSTRÖMMAR OCH MOLNBILDNING


BlixtDetaljerCAT	Jordatmosfären	SVP	MultiH2O	H2Odata	H2Opar	Jordströmmen	Naturblixt

Lägsta Molnpunkten	Laddningsbildens Uppkomst	StegFronten	FörstaSteget	ElvesBildningen	Molbegreppet	KosmiskaStrålningenÄrOrsaken

BD, Blixtdetaljer

BLIXTDETALJER

Luftblixtkanalens övergång i markkanalen för CAT enligt TNED

Miljontals enskilda atomtrådar förklarar blixtkanalens tvärsnitt i luftdelen. Men bara om den mångtrådiga kanalen kopplas ihop med några ytterst få atomtrådar (4 för Syre, 5 för Kväve) i slutänden kan urladdningen enligt TNED bilda en TGF med positronbildning.

18Feb2014:

Positronbildningen i Zambiafallet

Genomgång med efterkoll (Zambia-TGF:en) visar att villkoret med MAGNETISKA SPEGELPUNKTEN tunnar ut kandidaturen betydligt för scenariot till fenomenformen.

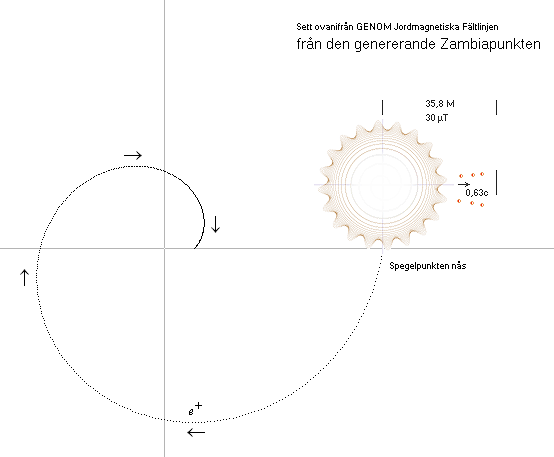
POSITRONENS EXPANSIONSHASTIGHET 0,63c bestämmer gränsformen.

— Om, som det ser ut (illustrationen ovan sammanfattar detaljerna), positronerna måste komma nerifrån marken och avancera upp mot spegelpunkten, Zambialokalen — alternativet att positronerna skulle komma in i fältspåret ovanifrån är uteslutet på grund av energibristen den vägen — är det tydligt att fenomenet med den infångade positronbanan i Jordmagnetiska fältspåret bara har en enda ingång i den fenomenformen att välja på:

— Positronerna måste DELS ha tillräcklig hastighet (v||) PARALLELLT med Jordmagnetfältlinjen på väg upp till magnetiska spegelpunkten, och DELS EXPANDERA (rätvinkligt ut från fältlinjen från bildningslokalen) MED TILLRÄCKLIG HASTIGHET (v|_=0,63c):

— Just rätvinkelexpansionshastigheten AVGÖR positronernas inneslutning i fältspåret mellan de bägge magnetiska spegelpunkterna: totala hastigheten pendlar mellan (kvadraterna på) v|| (med v|_=0) och v|_ (med v||=0), vilket är förutsättningen för partikelpendlingen mellan spegelpunkterna.

Med andra ord:

— v|_=0,63c måste under alla omständigheter uppnås INTE BARA EXPANSIVT (eller partikulärt translativt) utan TYDLIGEN även så att den expansiva delen skjuts upp (via en separat v||-del) mot spegelpunkten och där har dämpats ut till praktisk taget 0. Den återstående v|_=0,63c kan då förklara Fermisatellitens observation.

Ännu (18Feb2014) har vi inte sett tillstymmelse till någon precis förklaring i MAC hur positronbildningen MED ERFORDERLIGA riktningar och hastigheter skulle gå till.

(MAC har bara sin kosmiska strålning att lita till som Avalache-triggare, och då fortfarande med flera frågetecken än någon (vanlig dödlig) klarar av. Se även i Wilsonströmmen).

— TNED ser ut att klara den biten galant som ovan.

PARTIKELBEVISET i sig utesluter allt annat än att positronbildningen kommer från atomkärnor.

(Positronbildningen — kärnsönderfallet — föregår gammastrålningen. Gammastrålningen kommer [tydligen] senare från parannihilationerna ±e).

MAC/TNED

BETINGELSER FÖR POSITRONOBSERVATIONER

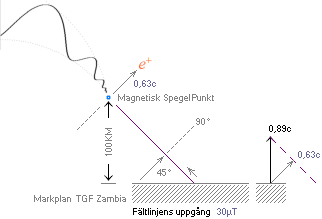
— Med observationsdatat (grovberäknat) v|_=0,63c som måste uppfyllas för positronernas expansion rätvinkligt fältlinjen vid magnetiska spegelpunkten och som garanterar den fortsatta pendlande partikelrörelsen mellan de bägge magnetiska spegelpunkterna (Zambia-Egypten i Fermiexemplet), måste i vilket fall för varje teori en motsvarande partikelacceleration garanteras i något bildningstillfälle, samt att tillräckligt mycket av varan bildas för att någon del ska visa sig från magnetiska spegelpunkten ca 100KM över marken och därmed Fermisatellitens observation.

— Figuren ovan höger ger grovvärdena v|_=0,63c; v↑=0,89C (i Zambiafallet) för motsvarande bashastigheter som måste finnas för att förklara Fermisatellitens observation.

— Uppenbart är det att partikelbildningen måste ske UNDERIFRÅN och UPPÅT mot magnetiska spegelpunkten — alternativet att partikelbildningen skulle ske ovanifrån och (snett) ner mot magnetiska spegelpunkten är allmänt utesluten på grund av att energitätheten i de regionerna (100 KM ovan Jordytan) är på tok för låga — och därmed motsvarande villkor för själva partikelaccelerationen.

Positronaccelerationerna

I modern akademi (MAC) har man ingen annan MEKANISM att stödja sig på än principen »partikelacceleration över avstånd», analogt »klassisk kondensatorspänning»: moln-moln eller moln-mark.

Accelerationen av positronerna enligt MAC har bara distanserna moln-mark eller moln-moln till förfogande.

— Vad alla verkar vara överens om är att den fysikgrunden INTE är tillräcklig: elektrontätheten moln-moln eller moln-mark vid atmosfärsiska fenomen är på tok för låg för att få fram den resulterande, observerade, typen (Se utförlig genomgång i Den Mystiska Coulombtätheten).

— Teorierna för den fortfarande helt gåtfulla blixtbildningens kanalstam i modern akademi (2014) går (bl.a.) ut på KOSMISK STRÅLNING (inkommande partiklar med enorma energier) som triggar en sensationell elektronisk Jordatmosfärisk lavineffekt med garanterat magiska mönsteregenskaper, och som garanterat ingen person på den här planeten (ännu) förstår ett enda dugg av: MAC-teorierna är ännu (2014) resultat av ett ihopplock av delvis ofullständiga teorier + genomförda mätningar och observationer + avancerade datorsimuleringar. Såvitt jag vet har behovet av naturkunskap aldrig varit större.

— Centrala Svårigheten i modern akademi (MAC):

— Från molnlokalens medelbaserade laddningstäthet på runt 20C/KM³ till den smala blixtstammens mer än tio miljarder gånger högre laddningstäthet — strömbanans urladdningsväg — 2,5 T11 C/M³ blir i modern akademi inte bara en veritabel händelsegåta, utan ett fundamentalt fysikaliskt olösbart fenomenproblem — om man inte får använda TNED som förklaringsgrund (Blixturladdningens Fysik).

— 1. Töm FÖRST blixtkanalen på elektroner (e^–) — sedan den väl bildats enligt TNED (Stegcellens Bildning; Urladdningen);

— 2. Låt SEDAN den omgivande molnlokalen i lugn och ro överlämna sitt elektronöverskott till den centraltäta plasmatiska jonstammens så elektronutarmade atombesättningar (vilket ger ljusfenomenet). Det är i kort mening kärnan i den relaterade fysikens förklaring till blixturladdningens fenomenordning.

I relaterad fysik (TNED) är situationen helt annorlunda:

— Blixturladdningens väsentliga PRIMÄRA fysik handlar uppenbarligen om repulsion inifrån ytterst korta distanser, inte om attraktion utifrån kilometerlånga avstånd:

Sökning på Webben (2013-14) efter liknande fotografiska dokument (eller beskrivningar över huvud taget) som visar nanopartiklar (här från elektrisk urladdning via aluminiumfolie) i kollision med luftens molekyler, bilden ovan, verkar helt sakna representation utom i UniversumsHistoria. Tills vi får djupare kunskap om fenomenet är det tydligt att meningen får stå kvar.

Teorin för positronbildningen vid (de extrema) atmosfäriska urladdningarna är i TNED alldeles densamma som i teorin för »vanlig gnisturladdning», fotografiet ovan (Se Figur 3 med utförlig beskrivning och referenser i Blixturladdningens Fysik 2012).

— Positronbildningen ur (endast extremt starka) blixturladdningar enligt TNED åstadkoms inte av acceleration utifrån, utan av repulsion inifrån.

— Men som vi redan vet från TNED-beskrivningarna ingår inte den möjligheten i modern akademi: ATA med CAT: atomkärnans härledning. Därmed kan vi heller inte strängt taget jämföra TNED/MAC. Endast en av dessa kommer — tydligen, följdriktigt — att gå ur den här historien som (utomordentlig) FENOMENFÖRKLARARE (med den andra i säkert koppel som mera primitiv underordnad).

Fotografiet ovan från en urladdning genom aluminiumfolie visar principen enligt TNED: partiklar kastas ut med initiellt (mycket) höga hastigheter i urladdningsområdet av den Coulombrepulsion som hela fenomenformen omsätter (ytterst sammansatt i flera avgörande delsteg).

— TYPEN av energiräkning blir också av en helt annan karaktär än den motsvarande »acceleration över avstånd» som folket i MAC brottas med — och som vi redan tror oss ha förstått ÄR omöjlig för att förklara fenomenformen.

KosmiskaStrålningen

ANGÅENDE ”NYA TEORIN” (2013) ATT

Blixturladdning orsakas av KOSMISK STRÅLNING

Urladdningsbilden i luft från Laboratorieexperiment

BILDKÄLLA [20Feb2014]: Wikipedia ImageFile — from Wikipedia Article Tesla coil http://en.wikipedia.org/wiki/Tesla_coil

File:Lightning simulator questacon02.jpg

http://en.wikipedia.org/wiki/File:Lightning_simulator_questacon02.jpg

Urladdningsbilden i luft från naturlig blixturladdning

UTOMORDENTLIGT I ÖVERENSSTÄMMELSE MED FÖREGÅENDE

BILDKÄLLA [20Feb2014]: Wikipedia ImageFile — from Wikipedia Article Lightning http://en.wikipedia.org/wiki/Lightning

File:File:Blitze IMGP6376 wp.jpg

http://upload.wikimedia.org/wikipedia/commons/a/a0/Blitze_IMGP6376_wp.jpg

De bägge MÖNSTERFORMERNA är tydligt analoga — samma typ av förgrenande trådstruktur:

— Laboratorieformens tydliga basexempel visar och bevisar att mönsterformen följer och bestäms av MINSTA MOTSTÅNDETS URLADDNINGSVÄG genom urladdningsmediet (här luft)

— inte partikelvägarna från DEN KOSMISKA STRÅLNINGEN.

Föreställningen om kosmisk strålning som PRIMÄR FÖRORSAKANDE AGENT i urladdningsmönstret typ atmosfärisk blixturladdning blir intressant som TEORI FÖRST när man kan visa att den kosmiska strålningens MÖNSTERVÄGAR verkligen är analoga med de laboratioremässiga urladdningsvägarna: samma mönsterbilder.

— Att enbart komma med KVANTITATIVT JÄMFÖRANDE ENERGIVÄRDEN räcker (uppenbarligen) inte. Det avgörande är ett STRUKTURBEVIS: naturbilden.

Visa det, så vill jag vara den första att konvertera. Please.

Nämligen så (det efterfrågade kosmostrålbeviset ska m.a.o. vara OMÖJLIGT — men för all del: visa gärna):

— Då det är uppenbart att laboratorieförsökets urladdningsbild INTE har någon VÄSENTLIG koppling till kosmiska strålningens inverkan, HAR DEN NATURLIGA DET INTE HELLER.

— Visa gärna att den enkla meningen saknar relevans. Tills dess alldeles uppenbart: no way.

Med andra ord:

— Urladdningsmönstret i atmosfären föreligger i ett motsvarande MATERIELLT AVGRÄNSAT INNESLUTET ELEKTRISKT SYSTEM; Inverkan från yttre faktorer

(som t.ex. att flertalet åskväder inträffar under dagens senare del i årets varma period, över land, samt visar små variationer med Solvindens sammansättning och magnitud)

har för själva fenomenformens fysikgrund INGEN SOM HELST BETYDELSE.

För MAC-teorins grunder till elektrisk urladdning, se Wikipediaartiklar generellt orienterande

Avalanche breakdown

http://en.wikipedia.org/wiki/Avalanche_breakdown

Electron avalanche

http://en.wikipedia.org/wiki/Electron_avalanche

Electrical breakdown, Mechanism

http://en.wikipedia.org/wiki/Dielectric_breakdown

LU, Laddningsbildens uppkomst, med exempel på dess praktiska effekter — BUF

BlixtTGF2014a ........ GRUNDBEGREPPEN I MOLNBILDNINGENS TEKNISKA FYSIK — basbegreppen till

BlixtTGF2014b ........ BLIXTURLADDNINGENS FYSIK — Jordströmmar och Molnbildning

2014II

BlixturLADDNINGSBILDENS UPPKOMST Del I

Om UPPHOVET TILL Potentialerna som åstadkommer urladdning

————————————————————————————————————————————————————————

Se även i Del II — hur elektronelementen överförs från marken till molnen enligt relaterad fysik

TrädBlixt | InduceratMAC | Induktion och Influens |

AntaletPerSekund, Globala urladdningsfrekvensen

Totala antalet blixturladdningen över hela Jordytan anges med siffror typ 50 per sekund.

”; on Earth, the lightning frequency is approximately 40–50 times a second or nearly 1.4 billion flashes per year.[1]”.

@INTERNET Wikipedia LIGHTNING [26Feb2014]

http://en.wikipedia.org/wiki/Lightning

25% av urladdningarna (webbkällan ovan) är av typen Moln-Mark (uppgifter finns som säger att den fördelningen beror på geografi [annan källa: Norge påstås ha upp emot 50% Moln-Markurladdningar]), samt att huvuddelen (70%) av alla urladdningar sker i tropikerna (land).

Orsaken bakom den laddningsdynamik som förorsakar urladdningarna är (ännu 2014) oklara.

”Mechanisms that cause the charges to build up to lightning are still a matter of scientific investigation.[67][68”,

@INTERNET Wikipedia LIGHTNING — Scientific study, Properties [26Feb2014]

http://en.wikipedia.org/wiki/Lightning

En webbsida som (särskilt väl) illustrerar detaljerna i den nu (-2014) etablerat antagna teorin bakom åskväder finns på

NWS

NATIONAL WEATHER SERVICE — Lightning Safety (datum saknas) [26Feb2014]

http://www.lightningsafety.noaa.gov/science/science-overview.htm

Genomgående: Laddningsbilden påstås uppkomma genom att vatten/luft/is-partiklar inuti moln uppvisar inbördes olika strömningar, ”Air movements and collisions between the various types of precipitation in the middle of the cloud cause the precipitation particles to become charged.”, källan ovan; ”These collisions and air movements cause the top of the thunderstorm cloud to become positively charged and the middle and lower part of the storm to become negatively charged.”.

— Vi vet inte om källan TEORETISERAR eller citerar från någon belagd forskning (källan ger inga referenser till de olika påståendena).

Den bild som NWS-källan målar upp av urladdningens upptakt är tydlig: det är MOLNET som »SKAPAR» laddningsregioner genom »intern partikelturbulens»: Den omgivande luften »utanför molnet» fungerar som ISOLATOR, tills överslag sker;

”Lightning is a giant spark of electricity in the atmosphere or between the atmosphere and the ground. In the initial stages of development, air acts as an insulator between the positive and negative charges in the cloud and between the cloud and the ground”, NWS.

Alltså i klartext:

— Den omgivande luften utanför molnet har ingen del i laddningsfördelningen (den omgivande luften fungerar som mellanrummet mellan två elektroder [Moln|Mark] i en elektrisk gastub).

— Men källan ger samtidigt INTE någon beskrivning till eller förklaring av markdelens motsvarande positiva laddning relativt molnets negativa laddning. Och ingen annan etablerad källa verkar göra det heller.

— Omfattande webbsökning har gjorts, men ännu har inget påträffats som beskriver markens del i det hela (i fallen Moln|Markurladdningar).

InduceratMAC

Jämför (källan refererar till Umans berömda bok [1971]):

”When the stepped leader approaches the ground, carrying some five coulombs of charge, a large positive charge is induced below it and an upward-moving discharge some 30-50 meters long comes up to meet it.”,

HYPERPHYSICS — Cloud Charge Transfer, The Stepped Leader (datumuppgift saknas [2014-02-26])

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/ligseq.html

Praktiska jämförelser...

— INDUKTIONEN från en negativt laddad kropp som accelererar (stegledarens stötvisa framryckning mot marken) strävar att ATTRAHERA lika laddningar — och REPELLERA, inte attrahera, motsatta laddningar. Citatkällan ovan ger ingen ytterligare information i saken, och det förefaller därför som att man lämnat ORSAKSKOPPLINGEN i den påstådda men tydligt oklara induktionsdetaljen utan vidare förklaring;

”a large positive charge is induced below it and an upward-moving discharge ... comes up to meet it”.

— Vad vi vet finns ingen direkt motsvarande grundfysik att studera exempel på: urladdning genom induktion.

— Vad vi vet, krävs två distinkt skilda områden, domäner, med distinkt motsatta elektriska laddningar, för att en elektrisk urladdning ska komma ifråga.

— Elektriska laddningar som accelererar har som sådana ingen urladdningsfysik att visa upp: det måste finnas två STATISKT motsatta elektriska områden.

— Det är det främsta relaterade argumentet varför »förklaringen» i MAC inte är fysiskt relevant.

Markdelens uppåtstigande mötande positiva del måste i relaterad mening grundas på en reguljärt befintlig motsatt elektrisk laddning, ingen inducerad sådan.

— Vi vet med andra ord inte närmare hur man resonerar i modern akademi för att detaljförklara den påstådda ”large positive charge below”.

Enligt TNED finns den positiva Q-maken redan i marken (se utförligt i Jordströmmen), långt innan någon blixturladdning ens är påtänkt. Den omständigheten ansluter därmed direkt till grundfysiken i förklaringen av blixturladdningens detaljer. HUR den positiva Q-maken sedan utvecklas från själva urladdningstillfället, tillsammans med den nedkommande stegledarfronten, BLIR alldeles tydligt en särskild historia för sig (Se från FörstaSteget).

Bilderna nedan visar i vilket fall exempel på hur markdelen (möjligen) uppfört sig i en del fall.

TrädBlixt

Jämför naturfallet — starka statiskt motsatta laddningar åstadkommer (grym) delning:

BILDKÄLLA: Författarens arkiv · 9Sep2011 E17 Bild Blixt1_7 · Nikon D90 — Naturblixt i Granträd

Bilderna ovan/nedan visar ett möjligt exempel på effekten efter blixtnedslag i ett granträd:

— Vid pass 1 M över marken är granstammen i princip TYDLIGT AVANCERAT delad: Sättet som restträdet ligger vid sidan av ASSOCIERAR till att HELA trädet har lyfts uppåt, förflyttats något sidledes och sedan fallit av egen tyngd. Bilden visar tydliga partier där en AVANCERAD uppdelning av trädets inre struktur skett — »höghusformerna» — utan avslitning. Partierna med tydliga flisstrukturer däremot tyder på avslitning: Om avslitning sker genom samtidig böjning/brytning bör fiberresterna också uppvisa motsvarande krökningar i efterhand. Här finns bara riktningsrester på principen RAKT UPP. Händelseförloppet FÖREFALLER således utpeka:

— Blixtnedslaget har ca 1 M ovan marken delat trädet MOLEKYLÄRT (»höghusformerna») med sådan kraft, rakt uppåt/nedåt, att resterade sammanhängande trädfibrer DRAGITS av och fått hela trädet att kastas upp — hela det ovanförvarande trädet — någon sträcka, delvis i sidled. Resterande händelseförlopp har sedan överlämnats åt gravitationen. Flera liknande trädexempel finns i samma område (även bara några meter ifrån objektet i bild men de är tydligt gamla [10-tal år] och detaljspåren är delvis borta). Miljö: Fuktig skogssänka med ett eller annat synligt tunt vattendrag (ofta under kraftig vegetation).

— Delning på molekylär nivå kan veterligt bara ske om det på ömse sidor delningsområdet finns en positiv (marken) och negativ (blixtkanalen) elektrisk laddning med tillräckig strömstyrka som kan separera respektive atomregioner.

BILDKÄLLA: Författarens arkiv · 9Sep2011 E17 Bild Blixt: ÖvVä 1_15: Mitt 1_19; ÖvHö1_3; NedHö 1_21 · Nikon D90

Jämför principen »Rail Gun»:

— En på en rörlig elektriskt strömförande ramp fast monterad projektil (Granens övre del) skjuts iväg med (ofattbar) MAGNETISK kraft då strömvägen skär genom projektilvagnen: strömpulsen (från + till –) kommer från marken, går upp till projektilvagnen som strömmen går in i vinkelrätt mot markströmmen (blixttrådens möte med markledartråden), och återvänder sedan på andra sidan (motsatta stamsidan) ner i marken (alternativt ström upp i centrum, åter perifert efter snittskärning vinkelrätt mot ursprungliga strömriktningen, krafteffekten i netto blir densamma):

— magnetiska kraften på projektilvagnen skjuter iväg projektilen uppåt. Kraftigt.

— Figuren nedan visar en sammanställning över hur B-krafterna kan samverka för att DRA AV granstammen.

Hur magnetiska krafter kan samverka för att »såga» ett träd

Från molnsidan (uppifrån) kan vi relativt enkelt först förstå hur blixttrådarnas elektronbanor (e–) drar ner över Granstammen (i princip runt om) i samlad kraft — före själva urladdningstillfället.

Vid urladdningstillfällets kritiska punkt — mötet med markens positiva laddningspotential — kan vi förutsätta att blixttrådarna från det tunnare luftrummet från molndelen med stor och plötslig hast viker av rätvinkligt (↓_ _↓) inåt centrum mot det tätare markrummets material, i detta fall ett Granträd i bildfallet ovan ca 1 M ovanför marken.

Urladdningstillfället består tydligen av just strömriktningens ändring från ett tunnare medium (luftrummet) till ett tätare (markmaterialet), just då molndel möter markdel.

— Från högerhandsregeln, de blått utritade magnetiska fältriktningarna (B) bilden vänster, ser vi att B-fälten mellan de olika riktade blixtkanalströmvägarna är samriktade i rätvinkelrummen:

— Den samlade B-verkan utpekar tydligen att blixtvägens ändring med tvärriktningen in mot Grancentrum (→←) bildar en KRAFTBASERAD SEPARERINGSSKIVA (vi tänker oss skivan idealt cirkulär med illustrationen som ett vertikalsnitt genom skivan).

— Samriktade B-fält betyder att strömlederna ovanför och under mittskivan strävar att SKILJA sig från varandra.

Då blixtkanalen från molnsidan träffar positiva ledartråden från marksidan kan vi med andra ord förstå att föreningsskivan i mitten söker avlägsna molndelen från markdelen (vilket inte går).

Kraftutvecklingen blir som antytts i beskrivningen till bilderna ovan att HELA TRÄDET ovanför mittströmskivan, som mer eller mindre direkt molekylärt nu har separerat delarna topp/stam via ett mer eller mindre idealt SNITT, KASTAS upp i luften.

InduktionOchInfluens, InduceratMAC

Stegade ledaren avancerar SNABBT nedåt marken — och är därmed ingen fixerad STATISK laddningspelare utan en högeligen STATISKT BASERAD INDUKTIV — accelerationsrekylsinducerande — anordning.

Induktion och influens i MAC

Den enda rimliga förklaringsbilden till den moderna akademins ståndpunkt (InduceratMAC, ”a large positive charge is induced below it”), här, skulle vara av rent STATISK natur: negativa laddningar skapar — påtvingar — ALLTID (genom influens) motsvarande positiva delar i närliggande material: elektronmassornas elektriska fält påverkar varandra: en negativ stav stöter bort negativa laddningar från omgivande material och frilägger därmed en motsvarande positiv potential mot den negativa staven.

— Det är redan välbekanta fenomen från Köket [om inte annat: använd isolerande skyddshandskar: stryk upprepat papper åt ett och samma håll mot en liten bit på ett hörn av ett plexiglas för att bilda elektrostatisk laddning: lägg ut några riskorn på ett papper, och för den tidigare bestrukna laddade plexiytan mot: ett eller annat riskorn reser sig och följer med].

— Men den effekten är INFLUERANDE (elektroSTATIK), inte inducerande (elektroDYNAMIK).

— OM influensargumentet är det enda modern akademi har för att »få fram» markdelens positiva respons på den negativa inkommande blixtkanalens syn på saken, finns det i så fall en betydligt mer raffinerad förklaring (TNED) till hur marken REDAN besitter positiv potential [nämligen Jordströmmen], och som därmed automatiskt förklarar VARFÖR de negativt laddade blixttrådarna i Moln|Mark-urladdningar söker sig JUST mot marken.

— Nämligen (just) URSPRUNGET till hela historien, själva MOTORN BAKOM:

— Markytans kontinuerliga (ytterst svaga) elektronemission till atmosfären — Jordströmmen: friktionens inverkan (vind+värme) HAR förutsättningar för att frigöra ELEKTRONELEMENT (e/n), men vilken fysikräkning INTE ingår i modern akademi sedan den berömda uteslutningen från år 1927 [Citat: för ändamålet att framhäva relativitetsteorin (se även denna från vic-felet)].

RELATERAD FYSIK — elektronelementen spelar avgörande roll

[Jämför SPEKTRUM OCH KVANTTALEN]

ACCELERERAT FRAMRUSANDE negativa laddningsmassor FÖRORSAKAR (Induktionslagen) negativa elektriska laddningar som finns framför de framrusande minusladdningarna (»accelerenterna») att ATTRAHERAS mot »accelerenterna».

— OM en stegad ledare för minusladdningar (elektronmassor i stor mängd) ner mot marken i successiva STÖTANDE steg, måste TVUNGET (induktionslagen) en INDUKTIVT rekylerande aktion ske i den fasta markdelens elektronlandskap (elektronkomponenterna, tau-ringarna i TNED): negativa laddningselement från marken strävar att dras upp mot molndelens nedströmmande minusaccelerent. Därmed KAN i motsvarande mening förstås att markdelen blottläggs på motsvarande positiv potential. DET är en direkt INDUCERANDE effekt.

— Men, eftersom elektronelementen garanterat INTE finns med i modern akademi, kan det heller inte vara på DERAS kredit som modern akademi framställer sin inducerande mening (InduceratMAC, ”a large positive charge is induced below it”).

— INDUCERANDE Meningen är — i relaterad fysik — riktig. Men den saknar (här, i brist på exakta referenser) uppenbarligen referenser i MAC.

— OM det verkligen förhåller sig på det sättet

— stegledarens nedstigande mot marken drar ut (en del) motsvarande elektronelement ur markytans BIOMASSYTA (som kan variera stort, se BioYtmassKoefficienten)

— KAN därmed i varje fall i induktiv princip stegledarens framstötningar frilägga en passande och matchande positiv STATISK markpotential LIKT en »elektrisk grävskopa» [StegledarenIdealt]:

Då stegledarfronten närmar sig markytan på Stegledarens E=UQ, snöps samtidigt motsvarande bioyta (A) av i minskande via Q/(A→0) med stegledarfrontens Q på konstant och bevarad U (elektronmassans nollresistiva koppling till atomkärnan [‡] [Kraftekvationen]). Illustrationen Stegledaren nedan i Induktion&Influens antyder funktionssättet.

Flera liknande exempel på blixtnedslag i träd: här ytterligare främst två björkar med delning ca 1-1,5M från marken:

Foto: 25Apr2014 E4 Bild 75;87 · Nikon D90

Foto: 25Apr2014 E4 Bild 24;12 · Nikon D90

Alla hittills observerade exemplar (Gran, Björk) uppvisar samma typiska AVANCERADE delningsstruktur: en blandning mellan »höghusformering» och raka (avdragna) fibertoppar påminnande om »bergsformationer»:

Foto: 25Apr2014 E4 Bild 54 · Nikon D90

— Till jämförelse: Träets dragbrotthållfasthet i fiberriktningen ligger i storleksordningen som STÅL.

— Ingen lätt match med lårtjocka trädstammar.

Allmänt

— Hur VET man att objekten bakom bilderna ovan INTE grundas på träd som har knäckts av stormar?

— Stormfällda träd finns också i området. Men dessa håller ihop med stam och rot: Vid stormfällning tar (tydligen) trädet med sig hela rotverket vid fallet.

— Att träd skulle kunna bytas av på någon meters höjd över marken enbart på grund av stormstyrkor på våra breddgrader, och dessutom i relativt inbördes täta trädbestånd där träden inbördes hjälps åt att dämpa verkningarna av vindkrafter, finns här inga som helst referenser för.

— Främst det aktuella mest tydliga exemplet i Trädblixt FÖREFALLER visa oss HUR överdelen har LYFTS UPPÅT — trädet har delats via ett mer eller mindre decimetertjockt »horisontellt plansnitt» — och sedan fallit ner av egen tyngd. Vi ser inga spår som tyder på BRYTNING — som dessutom i så fall skulle kräva brytkrafter som, veterligt, inte existerar i naturvindarna på Jordytan på våra breddgrader: fiberresterna är tydligt VERTIKALA och RAKA i växtriktningen. Alla här liknande (hittills upphittade) exempel visar samma typ av delningskaraktär.

InduktionInfluens, Induktion och Influens i TNED — Induktion OCH influens i MAC — Se även i Q-fördelningen med fältstyrkans växande.

Schematisk illustration Stegledaren av stegade ledarens induktiva infångning av markpotentialens Streamer — enligt relaterad fysik.

Från första stegets bildningspunkt i »molnets lägsta del» — molnladdningens elektriska tyngdpunkt med Q — kommer (den nedre, längre fram urladdningsutlösande) Stegledar-Q-mängden att tvingas avta i takt med att blixtkanalen uppvisar förgreningar — inte utritat i Stegledaren.

— Men samtidigt med den Q-minskningen, minskar också motsvarande andel elektrisk fältsammanhörande markyta (BIOytan) associerad med aktuellt avdelat Q. BILDEN TOTALT endast understryker elektriska fältets elementära fysikgrunder [Elektriska Fältets Fysik] att mot den aktuella stegledarens reducerade Q en motsvarande reducerad markfältstyrka finns. IDEALT betyder det att kvoten Q/A kan förstås bibehållas KONSTANT enligt [vi förutsätter att elektriska konstanten Rc inte ändras under förloppet]

(Q/n)/(A/n) = Q/A med A→0 då stegledarens avstånd från marken går mot noll

Se särskild illustrerad beskrivning i QdAk (QdivAkonstant).

QAlternativet

Björkens grenverk får här illustrera

blixtträdets utveckling från

en basstam: elektriska fältet

Moln/Mark styr grenmorfologin.

— MarkYtladdningsfältstyrkan Ξ=Rc(Q/A) [Ξ grek, Xsi, ”e-f”] tvingas, således, i vilket fall mot oändligt av konstantspänningen i stegledarfronten relativt markdelen med den således proportionellt framträdande kvoten Q/A.

— IDEALISERAT — men inte praktiskt — kan vi på den krediten illustrera hela förloppet som nedan i StegledarenIdealiserat, just på HELA Q — inga sidoförgreningar förekommer då, och blixtkanalen betraktad som utvecklad bara på EN enda stegledarfront.

— I praktiken med flera Q-förgreningar, kommer bara en del av hela den ursprungliga Q-mängden att ladda ur — beroende på omständigheterna — då stegledaren möten markdelen.

— Samma blixtkanal kan, då, också förstås leda ner ev. kvarvarande överskottsladdning om första urladdningen inte leder ner alltsammans direkt: flera Q-tömningar kan förstås ske i samband med en enda bildad blixtkanal.

Men det finns också ett annat alternativ, mera harmoniskt, sätt att se utvecklingen med stegledaren som närmar sig marken, och som kan förstås behålla den ursprungliga, första, stegledarfrontens Q-mängd orörd — vi förutsätter Moln(MINUS)|Mark-urladdning:

— Sedan första steget bildats på hela molnets/markens ömsesidigt uppbyggda Q-kapital,

avståndet till marken minskar via stegledarfrontens initierande accelererande framryckning; en INDUKTIV rekylverkan — markytans omskrivna fältområde minskar — framtvingar motsvarande markelektronmassa in till luften i respons till stegledarens nedåtgående accelererade elektronfront, och berikar därmed molnområdet med motsvarande extra Qminus

sker motsvarande elektronmassatillströmning till luftdelen från markytan (biomassYTAN):

— ENDAST om en SÅDAN extra tillkommen Qminus-mängd finns tillgänglig i anslutning till den REDAN först bildade första stegledarens intervall — och ENDAST då — KAN en ny motsvarande partiell Q-gren bildas: Varje delgren i blixtträdet som INTE tillhör huvudgrenen, bildas på kredit av inkommande EXAKT BALANSERAD motladdning från marken — eller så inte alls — i följd av den redan utlösta första stegledarfrontens INDUKTIVA härjningar i lokalen. Därmed kan den initierande stegledaren utvecklas GENOMGÅENDE på HELA molnets aktuella Q-mängd, och alla övriga blixtförgreningar på den utvecklingsbasens markINDUKTION.

— Ingenting säger att inkommande Qminus måste komma från marken, den delen kan komma också från molnområden; huvudsaken är den elektriska Q-balansen, och att det är på dess räkning som hela utvecklingen verkställs.

Stegledaren, ideala utvecklingen

InduktionInfluens

NOTERA OVANSTÅENDE FÄLTELEKTRISKA GEOMETRI. INKRÖKNINGEN av e-fältet i en ICKE-RÄTVINKLIGT IDEALT PLANA MARKYTA kan bara vara förbehållet en utpräglad BiomassYTA (eller en bergstopp). Mängder med markvegetation, och träd kan forma multipla motsvarande idealt plana markytor, och därmed idealt likna illustrationsformen ovan. Blixturladdningar över plana markytor (öken, is, hav) blir med ovanstående fältbild delvis annorlunda.

Med det — enligt relaterad fysik i ovan beskrivna schematiska tappning — konstanta UQ som medföljer stegledaren ända fram till urladdningsögonblicket, går samtidigt blixtkanalens förmedlade elektriska fältstyrka U/h mot oändligt som stegledarfrontens h avancerar mot noll från bildningshöjden h.

— Med också stegledarens front som förmedlare av det moln-Q-värde som — via gränsspänningen U — bär ansvaret för stegledarens inledande bildning, måste den motsvarande ”infångade” markytan — biomassans ytdel: löv, barr, grenar, stammar, grässtrån, blombildningar, över huvud taget allt som uppvisar YTA och som KAN frigöra ELEKTRONELEMENT — minska i fältomfånget: Q/markA går mot oändligt med givet Q och ständigt avtagande markA: Styrningen ges på kredit av potentialbalansen med stegledarens förmedlade (idealt) konstanta molnQ — ända tills ”blixten går” och urladdningen inträffar.

— I andra ord, illustrationerna ovan i StegledarenIdealt: Stegledaren som UQ-chaufför kan förstås ”gräva upp” eller gräva IN en motsvarande UQ-potential [så småningom en uppåtgående s.k. Streamer] markvägen — via den markBIOMASSyta som alltid [mest sommartid] står till förfogande — enligt TNED. [Processen över hav, is och slätmark BÖR därför också bli något annorlunda — möjligen mycket häftigare urladdningar].

— MAC har av de egna portförbjudna skälen som nyligen omnämnts [‡] ingen möjlighet att verkställa DEN (galant enkla) matematiska fysiken. För biomassmarkytan, se exemplet med Dubbelbjörken (Sjörs, 1954).

Stegledarens medelsteg (50M, olika källor ger något olika värden) skvallrar om en viss gränsspänning som måste finnas — oberoende av de enskilda stegen i molnladdningen Q mot marken — och som matar stegledaren mot marken, sedan första steget väl en gång bildats.

UmU, Utvecklingen mot Urladdningspunkten

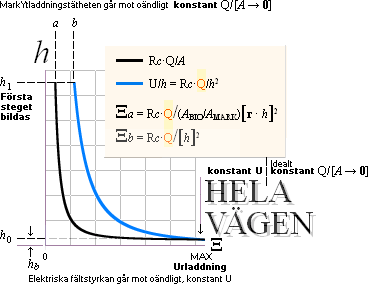
Sedan första steget i stegledaren bildats — som tvingar h att minska, och därmed obönhörligt växande [Ξ] elektrisk fältstyrka — sannolikhet — för stegledarens front att koppla ytterligare steg — följer obönhörligt en urladdning längre fram enligt kurvformerna skisserade ovan [y= f (1/x²)]. Speciellt med markens närmast enorma BIOMASSYTA (ABIO) som står till förfogande för stegledarens UQ att bilda motsvarande Q-del — elektriska fältstyrkans U/h ständigt avtagande fältform i marksnittet, via stegledarens minskande avstånd mot marken, och som därmed framtvingar en allt avtagande motsvarande innesluten markytsdel (BioMarkYtan ABIO) — tvingas MARKytladdningstätheten också öka: (ABIO→0) med konstant Q [StegledarenIdealt].

— Genom att (ABIO→0) tvingas upp mot stegledaren [elektriskt omskrivna fältkraftens minskande tvärsnittsyta med avtagande h], kommer en ofrånkomlig OFFSET att tilldelas Q/A-kurvan just beroende på en markuppstigande del. Det innebär och garanterar att de bägge fältstyrkskurvorna kommer att skära varandra i någon urladdningspunkt.

— Slutpunkten blir alltså ofrånkomligt och obönhörligt att stegledarens MINUS — blå kurvan — måste möta markdelens PLUS — svarta kurvan — via en av stegledarens framryckning på en separat Q/A-räkning upptvingad motsvarande markledare, det vi nu kan förstå som en s.k. Streamer.

— Principen blir densamma oberoende av stegledarens mål: Moln|Mark-urladdningar eller Moln|Moln-urladdningar måste i vilket fall fungera efter samma genomgående princip.

Elektronunderskottet på marken (markdelen påtvingas POSITIV POTENTIAL via Q/[A→0]) och elektronöverskottet i atmosfären (molnens underdelar blir [i allmänhet] NEGATIVA) KAN på den vägen förstås underhålla alla Jordens Moln|Mark-urladdningar:

— Grovt räknat (etablerade värden) ges en konstant Jordytström på 1000 Ampere fördelat på genomsnittsurladdningen 20 Coulomb och 50 urladdningar per sekund totalt sett för hela Jordklotet (ca 1/4 är av typen Moln|Mark). Se Allmänna Moln|Mark-exemplet.

Att den molnupptagna laddningen kan förorsaka interna laddningsfördelningar (partikelfriktioner luft/vattenånga/is) inuti molnen som föranleder motsvarande urladdningar Moln|Moln är en (given) sak för sig — och som helt säkert ansluter till den allmänna teorin om molnbaserad laddningsbildning.

— Men tar man ENBART molninterna partikelfriktioner som grund OCKSÅ för typen Moln|Mark-urladdningar, blir det (tydligen) svårt att förklara fenomendynamiken på djupet (markladdningens dynamik). Nämligen HUR urladdningen Moln|Mark går till i detalj.

— Se utförligt exemplifierat i jämförelsen MAC/TNED i Jordströmmen.

Ursprunget till laddningsfördelningen (Moln|Mark) bakom atmosfärens blixturladdningar har i UniversumsHistoria (före denna genomgång Feb2014) inte tidigare varit föremål för särskilt intresse.

— Framställningen har enbart koncentrerat sig på själva urladdningsfenomenet (Blixturladdningens Fysik) — med Moln|Mark som Negativ|Positiv laddningskropp (som generaliserat exempel) och med den mellanliggande luften som »urladdningskammare»

Vänster: Som urladdningen A|C har illustrerats i BlixturladdningensFysik: mellanliggande »isolerad» luft.

Höger: DEN MERA PRAKTISKA omständigheten, som det MÖJLIGEN har visat sig. Se även funktionskurvan nedan för laddningsfördelningen:

— Den mellanliggande luften KAN I SJÄLVA VERKET FÖRSTÅS DELTA i laddningsfördelningens utjämning mellan moln och mark, själva blixten — inte sällan med (tydligt synliga) täta ridåer av spöregn [emellanåt, vilket i sig inte är väsentligt men tydligen ofta förekommande]. Men var omtalas den fördelningen i forskningen? Inget hittat (Feb2014).

— och därmed (som det har visat sig, mer och mer ..) en viss oklarhet i vad som EGENTLIGEN gäller — mera i detalj.

SUNDA FÖRNUFTET säger (»mig») nämligen att från Överskott på Negativt (Molnets underdel) till Underskott på Negativt (Marken) — blixtbanans väg, tydligen — bör det finnas en helt neutral zon där varken överskott eller underskott finns (vertikal|y-axeln nedan). Figuren nedan visar principen.

Funktionskurvan, LADDNINGSFÖRDELNINGEN MOLN-MARK

Laddningsfördelningen Moln | Mark strax före blixturladdningen

——————————————————————

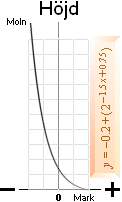
Blixtbanans urladdningsväg följer (SOM VI FÅR FÖRMODA) laddningstäthetens avtagande — från »molnets nedre del» [MINUS] till markpunkten [PLUS] — med motsvarande mellan stegledare och markpunkt.

— Laddningen slutar inte vid molnets nedre del [Lägsta punkten], utan fortsätter NATURLIGTVIS i avtagande ner mot marken för att övergå i dennas positiva del. Men ingen etablerad beskrivning verkar finnas som ens omnämner eller berör den detaljen.

— Etablerat (SOM DET FÖREFALLER — klargörande källor saknas som sagt) tänker man sig ett ELEKTRISKT FÄLT (luftrummet mellan moln|mark) medan relaterad fysik kräver AKTIV ELEKTRISK LADDNING över HELA spänningsvägen, grafbilden ovan. Molnladdningen har ingen elektrod (bara en inre elektrisk tyngdpunkt som blixtbanan utgår ifrån), utan ligger utspridd över hela molnmassan och luften mellan moln|mark. Vidare i Lägsta punkten.

DET FÖREFALLER OMÖJLIGT att funktionstypen ovan INTE skulle finnas närvarande i den redan framställda (men som det nu har visat sig vid en närmare genomgång delvis oklara, eller rättare ofullständiga) beskrivningens NATURFYSIK enligt TNED: hur blixturladdningen fungerar i detalj.

— Se vidare från Jordfältets Upphov.

QdAk, QdivAkonstant — (Q/n)/(A/n) = Q/A med A→0 då stegledarens avstånd från marken går mot noll

LADDNINGENS AVTAGANDE —

med avtagande markkopplande fältyta, och fältstyrkan som växer obegränsat

——————————————————————————————————————————————————————————

HUR STEGADE LEDARENS FRAMRYCKNING MOT MARKPUNKTENS URLADDNINGSPUNKT FUNGERAR i relaterad fysik

Från första steget avancerar blixtkanalens utbildning via (främsta) stegledarens väg mot markens motsvarande elektriska potential.

— Med HELA den primärt utlösande påtriggande gränsspänningens belopp, avancerar stegledarens nedre framände sedan via ett motsvarande avtagande Q-värde i laddningsbilden — MELLAN stegledaren och motsvarande markfältskopplande potential;

(Q/n)/(A/n) = Q/A med A→0 då stegledarens avstånd från marken går mot noll

Se särskild beskrivning i InduktionInfluens samt i Q-fördelningen med fältstyrkans växande.

Alltså, så:

— Som stegledarens framände (S) avancerar mot markens fältmake (M), uttunnas mellanrummet S|M alltmer på Q-massa. Samtidigt avtar också den markkopplande fältyta (A) som svarar mot Q-mängden. Vi kan förstå den detaljen som att förhållandet mellan Q och A hålls konstant (som om det vore fråga om ett statiskt tillstånd). Men samtidigt förmedlar — för neråt mot marken — också S hela den ursprungliga primära gränsspänningens påtriggande spänningspotential (UG) via atomtrådens nollresistiva taxibana. Och det blir den delen som kommer att bestämma själva urladdningsögonblickets KRAFT: U/h med h→0 betyder att spänningen växer obegränsat.

— Stegledaren kan inte avancera fortare än den gör, och ljushastigheten kan heller inte skynda på förloppet mer än den gör. Så: »U/h-syndromet» bara förutsäger den oundvikliga kommande händelsen att en oåterkallelig urladdning kommer.

Qförd, Q-fördelningen med fältstyrkans växande — 7Mar2014-03-07 — förtydligande, blixturladdningens fysik enligt TNED — se även i Induktion&Influens hur UQ avancerar från början.

Q-fördelningen med fältstyrkans växande

Beteckningen Ξ (grek. Xsi) ”e-f” används här som bekväm akronym för ELEKTRISK FÄLTSTYRKA U/d = F/Q = Ξ

strax före första stegets bildning	data	(Q/n)/[(A→0)/n]	ekvivalenter	kurvornas skärning ger urladdningen

a	b	c	d	e

Illustrationerna ovan ska föreställa en möjlig förklaring till hur de bägge fältstyrkornas funktioner sammanhänger och utvecklas: Stegledarens Q-front med ursprungets U-värde och ständigt minskade markavstånd (h) å ena sidan, och Stegledar-Q-värdets koppling till BioMarkYtan — som kan variera (stort) beroende på om den är helt slät (vatten, öken, is) eller maximalt växtbesutten (mest sommartid, våra regioner) [BioYtmassKoefficienten].

Hur dynamiken kan förklaras och förstås enligt relaterad fysik:

a: Oberoende av urladdning, finns alltid en RELATION [Funktionskurvan] mellan ett molns laddningsmängd Q (centrerad i molnets elektriska tyngdpunkt) och motsvarande motsatta laddningsmängd i marken (eller på motsvarande sätt mellan olika molndelar). Mellan Moln-Q och Mark-Q finns ett utbildat elektriskt fält (vita linjer i a). Hur stor markdelen är beror på den tillgängliga ytan: helt plan mark kräver ett större markområde för att uppväga Moln-Q (vi förutsätter här förenklat att andelen elektronelement per ytenhet är konstant oberoende av marktyp), en växtbesutten mark (BioYtan) kan ge betydligt större totalyta räknat per plan markyta beroende på säsong (våra nordliga breddgrader) och typ av växtlighet (markvegetation, träd).

c: Sedan första steget bildats från toppen (molnets elektriska tyngdpunkt, a) avdelas i allmänhet (som vi numera kan se flera videoexempel på via webbens utbud, testa GoogleSök @INTERNET på Lightning med Stepped Leader) flera stegledare i en karaktäristiskt förgrenad blixtkanal. Det betyder (QAlternativet frånsett) att den ledande stegledarens Q-front i motsvarande grad tappar Q-andelar på de övriga bildades bekostnad. Samtidigt reduceras motsvarande MarkYt-kopplande del för att matcha den mindre Q-mängden. Resultatbilden i netto kan tydligen, då, förstås bli som visades i Stegledaren i InduktionInfluens att

(Q/n)/(A/n) = Q/A med A→0 då stegledarens avstånd från marken går mot noll

Sambanden i kolumn d

stegledarens reducerade Q (i princip) kommer att förhålla sig konstant till den reducerade MarkYt-kopplande delen. Därmed (i princip) KONSTANT Q/(A→0) för den markkopplande Q-delen och som ansvarar för att positiv laddning friläggs genom [Jordströmmen] elektronelementens stötvisa — som vi får förstå — framryckning på stegledarens accelererande bekostnad (markelektronmassan frigörs INDUKTIVT):

— Elektronmassa avdelas från (Bio)MarkYtan och gör denna i motsvarande mening STATISKT POSITIV för att matcha den nedkommande (statiskt) NEGATIVA Stegledarens fältstyrka.

— Genom att den markkopplande Q-delen Q/(A→0) just ÄR markkopplad [maximalt mark-BOTTEN-avkännande], och Stegledaren (i slutänden) kopplar marken via en UPPÅTLEDARE (»mark-Streamern») tvingas den markkopplande Q-delen Q/(A→0) i slutänden upp mot stegledaren någon bit ovanför marken (på en motsvarande framtvingad luftledare), och därmed en högre slutpunkt för den markkopplande Q-delen Q/(A→0) än Stegledarens U/h-del. Vilket vill säga: den markkopplande Q-delen Q/(A→0) tvingas SKÄRA U/h-funktionskurvan, precis där urladdningen inträffar.

e: Ovanstående genomgång är (grovt förenklat) sammanfattad i de bägge fältstyrkekurvorna i e.

— Första stegbilden vid h1 betyder att fältstyrkorna för U/h och Q/(A→0) ligger värdemässigt förskjutna i förhållande till varandra — mer ju större biomarkyta som kopplar Moln-Q med Mark-Q. De bägge fältstyrkekurvorna tvingas alltså börja från olika utgångsvärden — förutsatt homogen laddningsfördelning [vi måste idealisera förenklat — i praktiken finns alltid skillnader] är det Q/(A→0)-värdet som alltid blir det lägre värdet — i allmänhet på grund av den större markytan [och den markytans givna elektronavgivningskapacitet (som också bör variera med DYGNSVÄRMEN)].

— Är markytan helt plan är [med dessa förutsättningar] Q/(A→0) mindre än U/h med minst (cirkulär markyta)

r/h=√π=1,7724538.

Jordatmosfären — Sammanställning Feb2014 JORDATMOSFÄREN I ÖVERSIKT FRÅN OLIKA ETABLERADE KÄLLVERK med Jordytans elektriska fältstyrka U/h

— HUVUDGRAFEN i sammanställningen ovan är (naturligtvis, den grova grå) Jordelektriska fältstyrkans allmänna BILD i Jordatmosfären: blixturladdningens fysikgrund.

Uppgifterna i sammanställningen ovan har kontrollerats generellt (olika stickprov, här utan redovisning) mot tillgängliga etablerade webbkällor Feb|Mar2014, alla med inbördes samstämmiga resultat — med vissa smärre differenser, och beroende på epok. En del av dessa differenser framgår i jämförelserna ovan mellan typ FOCUS MATERIEN 1975 och Wikipedia 2014 — och beroende på vilken PREFERERANDE TERMINOLOGI som de olika skikten avgränsas via (Termiskt[VÄRMEGRADER], Kemiskt[SAMMANSÄTTNING] eller Kinetiskt[TÄTHET, tryck]).

— Sammanställningen ovan har visat sig generellt användbar i orientering inte bara av de olika begrepp och fenomen som berör Jordens Blixturladdningar, utan generellt i alla Jordatmosfäriska sammanhang där viss orientering behövs. Speciellt är det grafiskt markerade/hoftade Jordelektriska fältet av särskilt intresse — de grovt gråmarkerade kurvdelarna med brytningen omkring 10KM [tropopausen] över marken. Notera speciellt att dessa kurvdelar är NORMALISERADE MEDELVÄRDEN; [MYCKET] Stora variationer sker dagligen dels genom Solens inverkan och typ av väderlek [och även säsongsvis och region], speciellt vid åskväder.

— Se särskilda webbreferenser i Jordelektriska fältvariationer.

— Se även särskilda webbreferenser i Whitaker2006, WHO, Bhattacharya2013, Oregon1999 och Paghis1966.

Jordfältet, upphov [Se även i konv. JORDFÄLTET] — Jordströmmen — Induktion&Influens — Feb | Mar2014

Jordens elektriska fält får sin naturliga förklaring i TNED — e-massans komponenter + Sol&Vind

— Minusladdningar lämnar Jordytan kontinuerligt med luftens uppströmning via Solvärmen: e^— associerar sig med luftens vattenånga [TauH2O]: molnbildning framtvingar urladdning.

— Ett nära formidabelt KAOS av tillsynes »virriga uppgifter» i etablerad litteratur gör att man LÄTT tappar geisten — tills man kommer på Diamantådern:

Se mera detaljerat i Jordströmmen — BLIXTGRUNDERNA I RELATERAD FYSIK — Så fungerar Jordytans elektriska balans enligt TNED:

Markytan avger kontinuerligt — med stora variationer (säsong, dagtid, marktyp) — elektronmassa till luften genom uppströmning via Solvärme + Vindar + Friktion. Laddningsmängden som krävs, även räknat per elektronmassa och kvadratmeter tillgänglig markyta, för att underhålla hela Jordytans samtliga åskväder året runt [Globala urladdningsfrekvensen] är oerhört [GRYMT] liten. Se utförligt [TD] med samband från Markytans globala elektronström. Elektronmassan associeras med Vattenångan [TauH2O] som ackumuleras i allt tätare molnsamlingar, analogt växande elektronladdning. Molnladdningens negativa del, elektronmassan, har hela tiden en motsvarande elektriskt balanserande fältkontakt [Globalsatserna] med en motsvarande positiv markdel. När laddningsmassan i Moln|Mark-laddningen passerar det kritiska gränsvärdet [elektriska spänningsisolationen Moln|Mark, eller Moln|Moln], sker elektrisk urladdning efter en stegvis process [Stegbildningen] där molnet lämnar tillbaka sin elektronmassa till marken. Därmed är balansen återställd, och en ny cykel kan börja.

— Ingenting hindrar interna laddningsfördelningar inuti molnen, vilket kan resultera i blixturladdningar mellan olika molnpartier. Även omvända fallen kan inträffa: tillfälliga negativa överladdningar på marken med motsvarande molnunderskott ger urladdningsriktningar med elektronflöden från mark till moln.

— Nettoeffekten totalt ger att Jordmarkytan fluktuerar mellan ± med en medelvärdesform som gör Jordmarkytan elektriskt neutral. Drivkraften bakom hela underhållningen blir alltså i grunden bara Solen.

Uppströmningen eller omsättningen av uppströmmande elektronmassa till luften bildar det kända Jordmarkselektriska fältet på (nominellt — stora variationer finns) ca 100V/M. Se mera utförligt illustrerat i Jordströmmen, Markytans globala elektronström och Jordatmosfären.

— I modern akademi finns inte den relaterade fysikens ELEKTRONKOMPONENTER [de förkastades 1927, se Citat], vilket gör det omöjligt i modern akademi att härleda Jordelektriska fältet på ovan beskrivna elektronKOMPONENTemitterande Sol+Vind+Friktion-fason.

— Man tvingas i modern akademi istället anta en helt annorlunda modell [WilsonMAC], och med sådana inre förvecklingar att ännu (Mar2014) ingen etablerad källa finns som kan beskriva blixtfysikens detaljer — främst den HUR molnen samlar på sig elektronmassa, och hur denna resulterar i blixturladdning. Generellt anser man i MAC att drivkraften bakom hela laddningscykeln är partikelfriktioner i molnen, se Citat i Jordytsladdningens Orsak.

— Men den främsta och mest anmärkningsvärda skillnaden i synsätt är att man i MAC anser att Jordytsfältet beror på att Jordmarken i själva verket har en fast negativ elektrisk laddning, exakt samma kvantitativa mätdata — som i sin tur kopplar till Jonosfären, med vidare resonemang och ännu obesvarade detaljfrågor med blixten i fokus. Se utförligt illustrerat i WilsonMAC.

Första samlade genomgången i UniversumsHistoria finns (2008) i Blixturladdningens Fysik. Den framställningen behandlar själva den centralt relaterbara urladdningsfysiken med blixtbanans bildning och karaktär. Här, i detta dokuments framställning, görs kompletteringar med fördjupade beskrivningar, och ett försök till en mera heltäckande framställning (Jordströmmen): GRUNDBEGREPPEN i Molnbildningens Tekniska Fysik genomgås i separat dokument. Här beskrivs ingående Laddningsbildens uppkomst (Del 1 | Del 2) tillsammans med exempel i markdelens elektronmassabidrag från avsnittet om Dubbelbjörken (BIOytan), samt vattenångans alla grundsamband (SVP) och de förgreningar (H2Opar | MultiH2O) som krävs för en kvantitativ resultatprövning — tillsammans med jämförelser med modern akademi (Kelvinekvationen | H2Odata). Se även fortsättningen på illustrationen ovan, hur själva urladdningen går till enligt TNED från Första Steget Bildas.

— Flera centrala sammanhang framkommer, men som inte framgår i etablerad litteratur. Se särskilt i Jordströmmen, H2Opar och Kelvinekvationens begränsningar, samt ytterligare i genomgången från GRUNDBEGREPPEN.

Bakgrund, Jordfältets centrala roll

GENERELLT INOM ELEKTROFYSIKEN (man antog felaktigt från elektricitetsvetenskapens början att laddningsbärarna i strömledare var positiva) gäller STRÖMRIKTNINGEN PLUS→MINUS: strömmen (av positiva laddningsbärare går från P till M: i praktiken gäller naturligtvis samma potentialbild i och med att laddningsbärarna i själva verket är elektronmassor (eMINUS): eMINUS vandrar från M till P. Nettoverkan är densamma.

— På samma sätt med Jordytans påvisade elektriska fält; Man har uppmätt (hållvärde — variationerna är stundtals stora beroende på väder och vind) runt 100 V/M i elektrisk fältstyrka (Gerden-cylinder) med riktningen ±(↓): från luft mot mark.

— Man har då bara TVÅ möjliga dynamiska (strömningsmässiga) sätt att välja på:

1. det ena berör förflyttningen av elektronmassa (eMINUS) som strömmar från marken och uppåt i luften, och

2. det andra berör förflyttningen av jonmassa (Joniserade atomer/Molekyler, ePLUS) som strömmar från luften till marken

(konv. Wilsonströmmen, Whitaker, 2006 s24).

— Bägge ger samma nettoresultat: elektriska fältstyrkan (F/Q=U/h) ± mellan elektroderna.

I modern akademi förkastade man redan år 1927 (Citat) elektronmassans komponenter, trots att man med deras hjälp nått så glänsande resultat (Heisenberg och Schrödingers matris- och vågekvationer för atomernas spektrum). Jämför f.ö. relaterad fysik i SPEKTRUM OCH KVANTTALEN. Det betyder att man i MAC bara har ett enda alternativ att välja på: nr2.

— Som vi redan (kanske) vet har samtidigt med den problematiken uppstått frågor som inte verkar enkla att besvara. Se vidare illustrerat till jämförelse med relaterad fysik i WilsonMAC.

— Relaterad fysik har alltså ytterligare ett sätt att TESTA matematiken på: nr1:

— Bioväxtmassans YTA (Jämför exemplet med Dubbelbjörken, Sjörs 1954) som står till förfogande på markytan för att »hjälpa till med den högeligen observerat variabla laddningstransporten» är närmast ENORM: en fullvuxen sommarbjörk har runt (minst) 500 M² bioytmassa (nära en halv miljon femkronorsstora löv) att exponera för värme, vind, sol — elektronMASSAtransport i ytterst ofattbart små mängder. Och då räknar vi inte sommargräset (och den varierande topologin) runt omkring. Med den vyn i bagaget öppnar sig en helt ny syn på ämnet och som mig veterligt aldrig tidigare har sett något omnämnande i vår kända del av historien. Det har givit uppslaget till (och utformningen av) hela den här presentationen (Feb|Mar|Maj||Jun2014).

Frågan (Feb2014) kan ställas på sin spets:

— EFTERSOM vi kan visa per enkla experiment ATT elektronmassa frigörs mellan olika material ALLTID där MEKANISK FRIKTION föreligger — akvarellpenseldraget 1cM över plexiskivans ena hörn, se JFET-sensorn — finns INGENTING som HINDRAR oss att förstå att VIND tillsammans med SOL — speciellt i växtlighetens enorma ytmaterialiserade biosfär — FAKTISKT med det enkla experimentets förebild KAN förstås frigöra elektronmassa FRÅN markens isolerade material, speciellt organiskt, TILL luften. Resten sköter Solen: den uppvärmda luften stiger uppåt, och laddningarna kan så överföras till atmosfärens huvudagent: vattenånga (TauH2O).

Vattenbindningen, Jordfältet

2014III14

Med medelglobala åskmolnets blixtfärdiga 20 Coulomb per 1(KM)³ = 1 T9 M³ och Jordglobala medelvärdet 50 Hz för antalet 20C-urladdningar per sekund, omsätts per sekund (673026τ=e):

EN tau-ring [τ] på 4T8 H20 definierar 20 C-molnet

(20 C = 20e·1/[1,602 t19 C)(50 Hz=1/S) = 1 T12 CM³/S = 6,24219 T30 eM³/S = 4,20116 T27 τM³/S

Vattnets atomvikt: 18,02u. u=1,66033 t27 KG;

— Med 1KG_H2O/M³ är antalet luftvattenmolekyler per M³ lika med 1KG/18,02u = N = 3,34234 T25 ~ 3,34 T25.

— Med 0,8KG_H2O/M³ är antalet luftvattenmolekyler per M³ lika med 0,8KG/18,02u = N = 2,67387 T25 ~ 2,67 T25.

— Med max 4% vattenånga i luften är antalet luftvattenmolekyler per M³ lika med 0,04·2,67 T25 ~ 1 T24.

— 1(KM)³ luftvatten är 1 T9 M³; antalet luftvattenmolekyler per 1(KM)³ blir då 3,34 T34.

— Med max 4% vattenånga 0,8KG/M³ är antalet luftvattenmolekyler per KM³ lika med 0,04·0,8·3,34 T34 ~ 1 T33

— 50 KM³ ger 5,34 T34 H2O.

— 50 (KM)³ luftvatten är 50 T9 M³; antalet luftvattenmolekyler per 50(KM)³ blir då 1,67 T36.

1(KM)³ (åsk-)moln innefattar i genomsnitt

20 Coulomb = 1,24843 T20 e ~ 1,25 T20 elektronmassor = 8,41282 T25 tau-ringar,

50(KM)³ (åsk-)moln innefattar i genomsnitt

50·20 Coulomb = 6,24219 T21 e ~ 6,242 T21 elektronmassor = 4,20116 T27 tau-ringmassor

varje elektron fördelas då på antalet vattenmolekyler lika med

(3,34 T34 H2O)/(1,25 T20 e) = 2,672 T14 H2O/e, =

(1,67 T36 H2O)/(4,2 T27 τ) = 3,97509 T8 H2O/τ.

— Praktiskt med 0,8·0,04·(RH=60%)=0,02ggr lägre: ~ 8 T6 H2O/τ

— Det finns alltså betydligt flera (1,67 T36) luftvattenmolekyler än tau-ringar (4,2 T27): totalt 50Hz.

— Det finns alltså betydligt flera (3,34 T34) luftvattenmolekyler än tau-ringar (8,4 T25): per 20C-moln.

— Det finns alltså betydligt flera (1,00 T33) luftvattenmolekyler än tau-ringar (8,4 T25): per 20C-moln.

— Vi har ingen teori som per vattenavdunstningsfysik kan koppla EN tauring till 4T8 | 8T6 vattenmolekyler: En ring per H2O KUNDE gå an, eller FLERA ringar per H2O vore också OK. Däremot, om vi utgår ifrån att varje elektronring avges vid sidan av JUST vattenavdunstningens fysik, separat på fast markmassa, KAN en ring associera sig med en liten vattendroppe från avdunstningen, och på den vägen ge en mera begriplig dynamik.

— Men »en liten droppe från avdunstningen» är också problematisk: i markområdet där vattenavdunstningen sker finns knappast ANNAT än fria H2O.

GV, GlobalaVattenomsättningen, Vattenbindningen

— Dessutom enligt

http://earthobservatory.nasa.gov/Features/Water/page2.php

”The amount of water in the atmosphere at any moment in time is only 12,900 cubic kilometers, a minute fraction of Earth’s total water supply: if it were to completely rain out, atmospheric moisture would cover the Earth’s surface to a depth of only 2.5 centimeters. However, far more water—in fact, some 495,000 cubic kilometers of it—are cycled through the atmosphere every year. It is as if the entire amount of water in the air were removed and replenished nearly 40 times a year.”

omsätts bara runt 5 T35 H2O per sekund total globalt i vattenatmosfärisk medelcirkulation UppNer:

4,95 T5 (KM)³/år = 4,95 T14 M³/(86400S·365,25) = 1,5685603 T7 M³/S = 1,5685603 T10 KG/S;

1KG vatten = 3,34234 T25 H₂O; N/S = 5,24266 T35 H₂O/S;

— Det gör bara 31% av totala vattenluftmolekylmängden associerad med tau för blixturladdning;

Resultatbild:

— Omsättningen i tau-ringsassocierade H₂O-molekyler i globala medelblixturladdningar är 3ggr större än omsättningen H₂O-molekyler i globala vattenomloppet mark-atmosfär.

— Den resultaträkningen bara understryker att elektronringarnas markemissioner troligtvis INTE har med själva vattenavdunstningens processer att göra:

— Jordelektriska markladdningens emissionsupphov [‡] kan då snarare förstås ske på den omgivande uppvärmda (brisaktiga, uppvärmda) luftens räkning. På dess väg, längre fram, kan en successiv överföring ske till vattenångans molekyler (TauH2O), och sedan dessa i sin tur till mikroskopiska vattendroppar i molnbaserna — OM det nu är den förklaringsgrunden som gäller, vilket vi ska försöka reda ut i den här framställningen.

— Med justeringen (0,8·0,04=0,032)·(1,67 T36 H2O per 50 KM³)=5,344 T34 ges den ovannämnda globala vattenomsättningen 5,24266 T35 H2O/S som 9,8103667 (!) ggr större än totala vattenluftmolekylmängden associerad med tau för blixturladdning:

— Blixturladdningsassocierade vattenmängden — den som, här ev. tänks förmedla laddningsbilden — skulle därmed vara runt 10ggr lägre än aktuella atmosfäriska sköljningen: NEDERBÖRD associerad med blixturladdningar utgör bara ca 1/10 av all nederbörd.

— Det var ju upplysande.

— Med den upplysningen FÖREFALLER det ännu mera problematiskt för vattenavdunstningen generellt att vara den eftersökta AGENTEN bakom laddningstransporten mark-moln — OM nu TNED-teorin för blixturladdningens fysik verkligen fungerar så som har skisserats i UniversumsHistoria;

— Om vattenavdunstningen skulle vara TrafikAB för 10 laddningar mark-moln och bara 1 av dessa är associerad med aktuella blixturladdningar (Jordströmmen), borde också Jordelektriska fältet uppvisa 9ggr större elektrisk fältstyrka än den aktuella.

— Den matematiken går uppenbarligen inte ihop:

laddningstransporten mark-moln sker inte på kredit av vattenavdunstningen, utan JUST via luftfriktionen från Solvärmen: vind+värme.

Laddningarna förs till luften från de långt flera luftmolekylerna, och sporadiskt — en elektronring från en markdel på en luftmolekyl med långa tidsmellanrum:

Enda chansen är sedan att luftmolekylerna för över tau-ringarna på motsvarande JUST åskmolnsvattenånga (TauH2O).

— Kan vi inte härleda en sådan mekanik, är TNED-teorin för hur laddningarna kommer till molnen i blixturladdningens fysik körd.

(Så: Tau-ringemissionerna kan INTE enkelt hänföras generellt till globala vattenavdunstningen).

TD, TauDroppen, GV

— På varje tau-ring (τ; tau, grek. t) ryms då antalet vatten(H2O)-Mole(c)kyler (H2O-Mlc) i genomsnitt i globala omsättningsflödet per sekund

Mlc/τ ~ (0,032)4 T8 H₂O/τ ;

Gäller för globala medelvärden i åskmoln med laddningstätheten 20C/KM³

τ/Mlc = (8,4 T25 τ)/(3,34 T34 H2O) = 2,51497 t9 τ/H₂O

τ/Mlc ~ 2,5 t9 τ/H₂O ;

Det krävs alltså 1/(2,51497 t9 τ/H₂O) = 3,97619 T8 ~ 4 T8 H₂O på varje tau-ring:

— Den vattendroppens diameter blir Ø=2,8 µM.

— OM tau-emission sker, måste den i så fall tydligen ha någon annan överförande materiebas än vattenavdunstningen till atmosfären;

Kandidaten (den enda återstående) är sporadisk tau-emission från fasta markmaterial: från särskilt heta/varma områden;

— HUR en emitterad tau-ring slutligen kan associera sig med en lämplig vattendroppe finns här f.n. ingen räkning på (avdunstningen från Jordytan uppvisar störst andel vattenhalt närmast avdunstningskällan, alltså marken, och därmed störst chans för tau-ringen att »komma med» på en större vattendroppe: största adhesionskraften [Casimireffekten]).

— Svaret på gåtan ges sammanställt i TauH2O: luftmolekylerna tar Tauringar från markens fasta material, som sedan efter viss tid kan upptas av H2O i luften: vattenmolekylens utpräglade dipolkaraktär garanterar mottagande av överskottsladdningar.

— 3,97619 T8 H₂O ger idealt en samlad vattendroppe med radien (D=1KG/M³=m/V; V=m/D=4πr³/3);

r = (3m/4πD)^1/3

= (3[18,02u](3,97619 T8)/4π[1KG/M³])^1/3

= 1,41615 t6 M

~ 1,42 µM ;

= Ø2,84µM ; minsta molnTauELEKTRISKA vattendroppens diameter

— En hel elektronmassas motsvarande vattendroppsdiameter skulle bli (2,67607 T14 H2O) Ø = 0,248208 mM.

TauH2O, TD, Jordfältet

Möjlig laddningsöverföringsmekanism luft-vattenånga

Hur kommer tau-ringen dit?

— Hur kommer tauringarna till molnens vattendroppar?

— VARFÖR ska de dit?

— Därför att molnen — luftens tydliga vattensamlingar — är den lokal som — vanligtvis — blixturladdningar sammanhänger med.

— Vi måste utgå ifrån att elektrisk laddning kommer DIT. Exakt HUR det går till är, som sagt, ett STORT problem för etablerad naturvetenskap.

2014V24 — hittills mest samlade förklaringen

Figuren ovan illustrerar grovt det allmänna medeltäthetsförhållandet 1:6 i ett kubiskt snitt mellan vattenånga (endast en enda H2O-molekyl, mitten) med RH=100% och luftmolekyler (alla övriga i hela kuben) i 0°C luft, vid marknivå ända upp till h=2KM. Högre upp minskar andelen luftmolekyler.

— På annat ställe (GlobalaVattenomsättningen) har resultatbilden redan fastställt genom uppgifter från den globala vattenomsättningen i atmosfären att vattenavdunstningen som sådan från Jordytan INTE kan bära ansvaret för den avgörande laddningstransporten av elektronelement till blixturladdningens lokaler (TNED). Den primärt transporterande agenten måste istället och tydligen vara luftmolekylerna. Luftmolekylernas markfriktion med solvärme och vind har den allra största potentialen för att kunna ta med sig de glest utspridda och enstaka elektronelement som laddningsräkningen kräver (Jordfältet).

— Figuren ovan illustrerar sedan resten: H2O-molekyler är också utpräglade dipolmolekyler (MinstaVatten). Genom att varje vattenmolekyl omges av i medeltal runt 280 luftmolekyler på sin färd upp mot molnbaserna och den övre atmosfären, finns riktigt med tillfällen för H2O-individen att träffa på en stor mängd luftmolekyler under resan. Därmed finns också de rent naturliga betingelserna för den aktuella överföringen: H2O-molekylens dipolkaraktär har betydligt större potential att ta emot eventuella laddningsöverskott i lufthavet än enskilda luftmolekyler vars bindningar är betydligt mindre dipolbetingade: OM en luftmolekyl som lyckats ta med sig en elektronring från markmaterialet träffar på en vattenmolekyl, kan vi räkna med att luftmolekylen lämnar över paketet till den mera receptibla vattenagenten. Därmed är eltransporten verkställd.

— Resten av historien kommer sedan att bestämmas av ansamlingen vatten/vattenånga i molnbaserna, och därmed koncentrationen av elektrisk laddning som kan trigga en blixturladdning.

TEORETISK KONSEKVENS TILL PRÖVNING (har inte visat sig tidigare):

Hela extra elektronmassor per åskmolnvattendroppe förekommer inte för mindre vattendroppar än Ø0,25 mM (Vattenbindningen):

Genom möjligen ÖMSESIDIG ELEKTROSTATISK INFLUENS:

Flera Ø2,84µM-droppar (e/673026) kan bilda »en INBÖRDES elektriskt neutral vattendroppe» OM HELA föreningen strävar att putta ut överskottsladdningen förutsatt mindre än e till droppens periferi* (detaljer i vattenfysiken vi här inte närmare känner till):

— Dropparna förenas via ett dem omgivande bidragande elektronöverskott så länge detta är mindre än en hel elektronladdning: dropparna som förenas bibehåller totala samlade negativa laddningarna i den resulterande större droppens periferi. Hela droppen framstår motsvarande negativ UTÅT; Molnets aktuellt ACKUMULERADE negativa laddning som från början associerats med enskilda luft/vattenmolekyler från Jordströmmen puttas SÅLEDES ut (genom »elektrisk självstyrning») MELLAN vattendropparna (i princip på deras yta).

— Molnets blixturladdningsfas inträder: molnet förbereder sig för elektrisk urladdning genom att isolera elektronöverskottet — placerar överskottet mellan de successivt växande vattendropparna — och förbereda detta för maximalt snabb transport (elektronmassan som ska strömma in till den kommande blixtkanalens högeligen positiva plasmastam).

— Motsägelser eftersöks.

———— ‡*

Det skulle i så fall ske spontant genom centralverkan:

— En samlad massa, en liten mängd vatten, med utspridda enskilda smådroppar, var och en med en liten (negativ) överskottsladdning, bildar ALLTID i gemensamma gravitella centrum en gemensam elektrisk tyngdpunkt (Superpositionsprincipen):

— FÖRUTSATT att överskottsladdningen [–] drivs bort, utåt, mellan två centralt närliggande smådroppar

— – + – + – (förenade atomer delar alltid på gemensam elektronmassa – Mellan sig)

— kan dessa i motsvarande MOMENT förenas (Casimireffekten: områden µM till nM) då ingen hindrande mellanliggande extra avskärmande elektronmassa hindrar:

...– – – – – – + – + – – – – – – ...

Och sedan »på samma sätt» med successivt närliggande; Överskottsladdningen [–] puttas ut i takt med att centraldroppen växer i storlek.

Se även undersökningen från Vattenångans luftandel — H2O i luft.

E-ringarnasBindning — TAU-ringens Energibindning

Elektriska kraftlagen (F) ger formella sambandet för attraktions- eller repulsionskrafter mellan två elektronelement idealt i ringplanen ±e/n med n antalet element i elektronmassan.

F = k(Q/d)²

Med Q= [e=1,602 t19 C]/n och d typisk medelavståndet mellan luftmolekyler (d=3nM=3t9M) ges med elektriska konstanten

k = 9 T9 VM/C

F = (9 T9 VM/C)([[e=1,602 t19 C]/n]/3t9M)²

= (9 T9 VM/C)([[e=1,602 t19 C]]/3t9M)²/n²

= (2,5664 t11 N)/n² ; Kraften mellan två elektronringar

Attraktionskraften idealt mellan atomkärnan med laddningen +Z och elektronelementet (MINUSe/n) är på samma form

F = k(Ze(e/n)/d²

= kZ(e/d)²/n ; Kraften mellan atomkärna och elektronring utan hänsyn till mellanliggande skärmning

Medelavståndet mellan atomerna i fasta ämnen är grovt 2,5 Å (2,5 t10 M). För en Jordytsmedelatom (Kisel) med Z=14 och n=673026 fås

F = (9 T9 VM/C)(14)[(1,602 t19 C)/(2,5 t10 M)]²/(673026)

= 7,68747 t14 N ; Oskärmade kraften mellan en Kiselatomkärna och en elektronring över 2,5 t10 M

Räknas mera realistiskt den aktuellt praktiska kraften i Kiselfallet, kan vi utnyttja värdet för Kiselatomens yttersta elektrons jonisationsenergi [Wikipedia, Ionization energies (data page)] 786,5 KJ/mol (multiplicera med 1T6u),

E = Fr = 1,30584 t18 J eller (dividera med e=1,602 t19 C) 8,1513704 eV. Över HALVA fasta atommedelavståndet 2,5 t10 M ger det bindningskraften mellan hela elektronmassan och Kiselatomen

F = E/(0,5·2,5 t10 M)

= 1,04467 t8 N ; Kraften mellan en Kiselatomkärna och dess yttersta elektronmassa över halva 2,5 t10 M

För en elektronring ges motsvarande

F = (1,04467 t8 N)/673026

= 1,5522 t14 N ; Kraften mellan en Kiselatomkärna och dess yttersta elektronring över halva 2,5 t10 M

När CASIMIREFFEKTEN in träder — två materialytor som närmas varandra inom atomavstånden — kommer elektronringarna in i ett INGENMANSLAND där i princip mellanliggande elektronringar kan associera sig fritt med vilken som helst närliggande passande minsta möjliga närmast attraherande atomvärd. Det betyder att också FRIKTIONSKRAFTER på en materialyta — typ från omgivande LUFT — besitter direkta möjligheter att kunna avdela ytterst små mängder elektronringar från typ mark mot luft.

För elektriska kraftverkan mellan marken och en enskild elektronring på nominella molnhöjden h=1 KM ges kraftverkan

F = k(e/nh)²

= (9 T9 VM/C)[(1,602 t19 C)/(673026)(1000 M)]²

= 5,09922 t46 N ; CoulombKraften mellan marken och en elektronring 1KM över marken

ENERGIN — fria mekaniska arbetet — för att föra/HÅLLA ringen upp/uppe 1 KM blir (idealt konst lokal tyngskraftsacceleration 10 M/S²)

E = Fh = mah

= [(m[e] = 9,11 t31 KG)/673026](10 M/S²)(1000 M)

= 1,35358 t32 J

= 1,35358 t32 J ; Energin för att föra ut en elektronring från marken till höjden 1 KM

PLANCKFREKVENSEN — E=hf [h=6,626 t34 JS] — för den energin blir

f = E/(6,626 t34 JS)

= 20,428312 Hz

Det motsvarar en Planckljusvåglängd — c = λf —

λ = c/f

= (2,99792458 T8 M/S)/(20,428312 Hz)

= 14 675 340 M

Värdena understryker den LÄTTHET med vilken elektronringar KAN frigöras och DELAS mellan materiens olika former.

Är också separationsavståndet samma medelavstånd mellan luftmolekylerna d ges elektromekaniska bindningsenergin idealt

E = Fd

= (7,6992 t20 J)/n²

~ (7,7 t20 J)/n²

= (0,4806491 eV)/n²: ideala bindningsenergin mellan två elektronringar ±e/n åtskilda av 3nM

Sämsta fallets beräkningar i TNED av n-värdet visar 177062 (Elektronmassans komponenter). Men det värdet är samtidigt ett absolut omöjligt värde (från toroidmatematiken med minsta möjliga dimensioner). Med Casimireffektens matematik öppnade sig ett tillfälle i TNED att söka ett mera praktiskt n-värde Exakta n-värdet: n=673026, vilket är det som hittills (Feb2014) förefaller vara det mest korrekta. n-värdet 673026 insatt ger då

F = 5,66579 t23 N ;

~ 5,7 t23 N ; separationskraften i idealt stillastående luft mellan två ±elektronringar åtskilda av 3nM

E = 1,69973 t31 J ;

~ 1,7 t31 J ; separationsenergin i idealt stillastående luft mellan två ±elektronringar åtskilda av 3nM

Planckenergin E=hf ger då lägsta möjliga frekvensen (f) för motsvarande separation:

f = [1,7 t31 J]/[h=6,626 t24 JS]

= 256,56504 Hz

~ 256 Hz ; Planckfrekvensen som krävs för att separera två elektronringar åtskilda av 3nM

Växande temperatur medför att kraftbilderna också ändras

[kemiska bindningsenergierna avtar: energin för att åstadkomma kemisk bindning ökar].

— Elektronringarnas praktisk naturliga ömsesidiga repulsionskraft gör att räkningen ovan delvis blir redundant (överflödig): Varje elektronring är bunden till sin atom via atomkärnans bägge huvudsamband (Atomfysikens två kungsekvationer). I turbulensen med gränsytorna mellan två material [Casimireffekten] finns ett ingenmansland för elektronringarna, och ingen bestämd tillhörighet finns att relatera till. Se från Casimireffekten i Distansparametern.

— Därmed kan man i princip för gränsområdet mellan olika material — t.ex. luft och mark generellt — förstå en relativt stor men begränsad potentiell möjlighet för elektronringar att ge sig iväg ENBART på aktuella materialströmningar: i princip ingen kraft alls behövs frånsett själva strömningsRÖRELSEN.

Med successiv utarmning av elektronringar växer motsvarande positiva potentialer som återkräver underskottet.

Exakt hur dessa detaljer fungerar i samtliga materiella fall finns f.n. (Feb2014) ingen framställd matematik på i TNED.

— Med Casimireffekten på elektronringarnas kredit som giltig enligt TNED, kan en ständig tillförsel av elektronringar till luften från marken via inverkan från SolVindFriktionen alldeles tydligt förklara hela det globala urladdningssystemet [Jordströmmen].

— Den elektronmassa som krävs för att underhålla hela Jordens åskväder visar sig bli nära ofattbart liten med hänsyn till den Solbestrålade Jordytan och speciellt dess biomassa [Exemplet Dubbelbjörken] med dess närmast enorma YTA (två sidor på varje löv + grenverk + stam; gräs, mossa, barr ..).

Jordströmmen — Jordfältet — Elektronelementets energibindning — Huvudtexten i FemtioPerSekund — Inledande beskrivande illustrationer nedan jämför WilsonMAC/RelateradFysikTNED

Så fungerar Jordströmmen 1000A som underhåller Blixurladdningarna på Jorden — enligt relaterad fysik:

Ett »bio-fysiskt» samband har visat sig [Planetströmmen] som visar att hela vädersystemet kan HÄRLEDAS ur basdata om antalet helaJordenBlixtar per sekund [50] och varje blixts medelladdning [20C].

Elektronmassa (se Casimireffekten) KAN enligt TNED frigöras genom friktion (Sol=värme + vind) i ytterst små mängder via elektronmassans element. Principen bör vara densamma som i experimentet med JFET-sensorn: ytterst små friktionskrafter visar hur frigjorda elektronmassor kan påvisas. Elektronelementen (bilden ovan röda pilvägen) förs ut i atmosfären av luftens atomer och tas så småningom upp av luftens vattenånga (TauH2O). Med molnens tillväxt garanteras växande mängd negativ laddning. Frånsett interna molnurladdningar, återlämnas markens elektronelement till Jordytan igen genom Moln|Mark-urladdningar. Det är basen i hela TNED-teorin för Blixturladdningens Fysik. Se även separat beskrivning för fenomentypen ELVES i ELVESbeskrivning.

— Hållvärdet som försörjer hela verksamheten är tydligen en konstant global medelbaserad Jordström om ca 1000 Ampere (som kan variera med stora marginaler) fördelad på genomsnittet ca 20 Coulomb per genomsittsurladdning Moln|Mark och i genomsitt 50 sådana per sekund taget över hela Jorden (av dessa är bara ca 1/4 av typen Moln|Mark).

— Uppströmningen av elektronelement från Jordytan till luften (TauH2O) garanterar det experimentellt uppmätta elektriska Jordytsfältets fältstyrka på grovt 100 V/M (Jordens atmosfär, med stora variationer sommar/vinter, natt/dag, och även under/på sidan om aktuella åskmoln):

— Friktionen från solvärme och vind mellan fast markmassa och luft kan förstås överföra enskilda elektronelement (i oerhört låga mängder, TD) från markytans materialtoppatomer (Casimireffekten) till omgivande luftmolekyler via molekylgränsen mellan fasta marken och omgivande luft (Kundsenskiktet).

— Med den bilden av allmän laddningstransport finns sedan, här veterligt, inget spår av alla de etablerade gåtfullheter och ouppklarade frågetecken som emellertid framträder i samband med den moderna akademins föreställningar om grunderna i blixturladdningens fysik: ”den Jordiska Jonosfäriska Strömgåtan” och som tydligen ingen förstår funktionen för, se WilsonMAC nedan.

— Resterande del av hela historien, hur elektronelementen återvänder till Jorden, beskrivs relaterat från Stegledaren.

— Se även hela genomgången från Laddningsbildningen.

Se även grundbegreppen i

Elektronringarnas energibindning | TauH2O | Jordfältet | Jordatmosfären |

Q-fördelningen med fältstyrkans växande | QdivAkonstant | Induktion och Influens i TNED | Induktion och Influens i MAC | TrädBlixt

om ej redan bekant.

Referenser till källupgifterna: Molekylsammansättningen, Jonosfärens nedre gräns, Dissocierat Kväve, Dissocierade molekyler, Ozon, Troposfärens gräns från FOCUS MATERIEN 1975 s497, Jonosfärens nedre elektrontäthetsgräns (60 KM) från FOCUS MATERIEN 1975 s512sp2mö, Mixing Layer, Fairweather Field från Whitaker 2006 s21.Fig.12; s30.Fig.17.

Ovan relaterad fysik (TNED) — se utförligt för sambanden nedan med värden i Planetströmmen

i = (Â/t)·[K=(N/M²)(e/n) = 3,81 t6 C] | Elektriska Jordströmstyrkan = 1000 Ampere nominellt [med STORA möjliga inre variationer]

Blixturladdningarnas slutna energiräkning i jämförelse TNED/MAC (Feb2014)

WilsonMAC — TNED

Nedan modern akademi (MAC) [»Wilsonströmmen», efter Whitaker 2006, s30 Fig.17]:

— Ingen motsvarande räkning kan göras i modern akademi eftersom elektronmassans komponenter inte accepteras i modern akademi.

— Varifrån kommer negativa laddningen i molnet? Perfekt frågat. Det är just den moderna akademins centrala svårighet: ingen vet. Man brottas med teorier som söker förklara den negativa laddningens uppkomst genom partikelfriktioner från luft/is/vatten i olika strömingsvägar. Men ingen har ännu lyckats få fram någon HELT tillfredsställande varken beskrivning eller förklaring. Ännu en annan detalj, om möjligt ännu mera problematisk: hur bildas en oerhört elektrontät smal blixtkanal av nedströmmande elektroner från ett negativt laddat moln med samma laddning UTSPRIDD. Det är den moderna akademins verkliga huvudvärk i försöken att förklara blixturladdningens fysik.

I modern akademi finns inte elektronelementens friktionsavdelningar med, varken från marken i samband med blixturladdningarnas energiräkningar i synnerhet eller alls inom fysiken i allmänhet.

— Bilden ovan visar hur modern akademi skiljer sig i betraktelsesättet från relaterad fysik (och förutsatt att här inga fel har begåtts och förutsatt att jag som författare inte håller på att lura i dig som läsare rena soporna), se föregående vy.

— Med föreställningen om en FAST negativ elektrisk Jordytsladdning (ingen känner till något annat: Solens inverkan nere på Jordytan har ingen direkt elektronseparerande kraft, och därmed ingen teori som kan matcha elektronmassa som avges kontinuerligt till atmosfären: ytterst litet i taget) blir ENDA ÅTERSTÅENDE MÖJLIGHETEN att ”uppfinna kredit” på den överliggande Jonosfärens fysik: Positiva joner strömmar NERÅT Jordytan i balans med Jordytans FASTA negativa laddningsöverskott. Blixturladdningarna för tillbaka jonerna uppåt (eng. return stroke) till molnet, och vidare den vägen längre upp tillbaka till Jonosfären.

— Vi behöver bara FÖRSÖKA förstå, och hänga med i, den moderna akademins olika forskningsrapporter för att strax få veta att INGEN EGENTLIG SAMMANHÄNGANDE TEORI existerar, främst på grund av STORA KUNSKAPSREVOR i den experimentellt observerbara delen av de atmosfäriska rummen: man MISSTÄNKER laddningszoner som ingen (ännu) har sett, samt en del andra (kufiska) detaljer som gör att helheten försvinner i fler frågetecken än NÅGON klarar av: ingen vettig förklaring finns.

— Vi ser att NETTOKVANTITETERNA i MAC/TNED- framställningarna är DESAMMA, och ”till viss del” ÄVEN flödesformerna.

— I TNED kan man emellertid till skillnad från MAC HELT koppla bort Jonosfären: den har UPPENBARLIGEN ingen EGENTLIGT AVGÖRANDE roll att spela i det FÖRKLARANDE sammanhanget. Hela historien handlar i stället om just molnens närområden — marken, avdunstningen, luften, molnen, den ofrånkomliga urladdning som måste komma — knappast högre höjder än runt 3KM.

FemtioPerSekund, Globala urladdningsfrekvensen — Jordströmmen — Härledningen till Markytans Globala Elektronström

Elektronmassans komponenter [‡]

E-ringarnas bindning

50 urladdningar per sekund á 20C över hela Jorden

Totala medelladdningsmängden för alla blixturladdningar över hela Jorden

i = (50Hz×20C=1000)C/S = (1000 C)/(e=1,602 t19 C)/S = (6,24219 T21 e)/S

1000C/S = 1000 Ampere

Med den konventionellt medelbaserade uppgiften om ca 50st atmosfäriska blixturladdningar per sekund över hela Jordytan året runt [Citat Wikipedia 2014] med medelströmmen ca 20.000 Ampere per medelblixt [Citat FocusMaterien 1975] och en medelurladdningsmängd på ca 20 Coulomb [Allmänna grunddata, Uman 1987] blir medelbildningstiden per medelblixt

I = Q/T ; allmänna sambandet för elektrisk strömstyrka, A = C/S

T = Q/I

= (20 C)/(20 000 A)

= 0,001 S ; medelbildningstiden för medelblixten

= 1 t3 S

Per sekund för hela Jordytans alla blixturladdningar med frekvensen 50Hz=1/t året runt blir totala kontinuerliga globala strömstyrkan som försörjer Jordens samtliga atmosfäriska blixturladdningar

I = Q/t

= (20 C)/(1/50 S)

= (20 C)(50 Hz)

= 1000 C/S

= 1000 A ; konstanta medelglobala Jordytsströmmen som försörjer alla Jordens åskväder, året runt

Etablerade källor (i olika epoker) ger något olika motsvarande globala medelvärden: 1800 A [Citat GF Liber 1980], 2000 A [Whitaker 2006 s26ö] ”From direct current measurements it is possible to estimate the total fairweather current over the whole earth to be nearly 2000 amperes”.

Variationerna är påtagligt stora mellan land och hav [Citat AMS2012, se även särskilt i WilsonMAC] och även periodiskt beroende på dagtid (AMS-källan s3n. Figure 4). Se även liknande uppgifter från andra webbkällor i Jordelektriska fältvariationer. I denna presentation används värdet ovan (1000A) genomgående som nominellt referensexempel. Se även sammanställningen i Exempel MolnMark.

I den moderna akademins lärosystem ingår inte (sedan 1927, se Citat) elektronmassans element. Därmed finns heller inte ENS möjligheten i modern akademisk matematisk-fysikalisk teori att elektronmassans element kan frigöras kontinuerligt genom den ständiga friktion (Casimireffekten) mellan luft och mark som garanteras genom Solens inverkan (värme+vind, se jämförande översikt MAC/TNED i Jordströmmen).

Med nominellt globala medelladningen Q=1000 C per sekund som försörjer Jordens alla åskväder kan vi ENLIGT RELATERAD FYSIK anställa en Jordytsrelaterad Q-ekvivalent;

Q = AN · e/n

Q anger laddningsaktuella Jordmaterieytan (A) med medelantalet (N) ytatomer per M² via varje elektronladdnings (e) minsta möjliga enskilda element (e/n).

Bindningsenergin [lägst för 55Cesium 3,7 eV = 6,23785 t19 J, se Wikipedia Ionization energies (data page)] mellan en atom och dess yttersta elektron ligger (nämligen, mycket) högre än effektiva arbetet (energin) som utförs av »minsta lilla vindpust» (jämför e-ringarnas bindning); Det är inte rimligt att ens försöka sig på någon räkning med frigörande av en hel elektronmassa på den fysikräkningen. Kraften är alldeles på tok för liten på Jordytan. I Jordatmosfärens övre skikt exemplifieras saken av Solstrålningen som bara där kan jonisera atomer via den ultravioletta strålningen (λMAX=400nM), alltså förmå en atmosfärisk atom att avyttra en hel elektronmassa;

E=hf, λMAX=400nM, h=6,626 t34 JS, c=3 T8 M/S, f=c/λ; för λ=400nM ges E=hc/λ ~5 t19 J = 3,1 eV

— 3,1 eV — Solstrålningens energi vid synliga ljusets kortaste våglängd (violett) på Jordytan — är för litet att ens avlägsna den yttersta elektronen på grundämnet Cesium som har lägsta bindningsenergin av alla. Jordatmosfären filtrerar bort våglängder i Solljuset med högre energi. Frånsett vissa möjliga ”hotSpots” [ozonhål] finns ingen reguljär möjlighet för Solljuset på Jordytan att jonisera markatomer på enskilda elektronkvanta.

— Däremot ställer sig saken annorlunda i den täta materierymden nära markytan (se e-ringarnas bindning) för elektronmassans komponenter enligt relaterad fysik; Solvärmen+Vinden sveper kontinuerligt luftmolekyler strykande över markens fasta massformers molekylytor — och därmed (Casimireffekten, relaterad fysik) läge för en absolut oerhört minimal elektronELEMENTemission.

— Det enda rimliga sättet att söka en fysiklösning blir alltså i relaterad mening (TNED) att pröva DELAR AV elektronmassans frigörelse på kredit av ELEKTRONMASSANS KOMPONENTER (samma fenomengrund som i Casimireffekten enligt TNED): Enstaka Elektronringar KAN associeras med vilkensom av närliggande materierum (fasta, flytande eller gasiska) och därmed svepas (med minimal kraftverkan) med i aktuell strömning.

— Exakta n-värdet (673026) för antalet elektronelement (τ [tau]) i elektronmassan i relaterad fysik ger oss en viss möjlighet att grovräkna på motsvarande nominellt globala värdeformer, och därmed pröva en allmän global lösning.

Sambandsformen ger oss en nominell medelform för »globala åskväderströmmen» till prövning enligt relaterad fysik (TNED)

i = Â(N/M²)(e/n)/t | Elektriska Jordströmstyrkan, 1000 Ampere

Antalet ytatomer N = 1,6 T19 per medelkvadratmeter i Â [1/ kvadraten på medelavståndet grovt 2,5 Å mellan fasta materiens atomer]:

i = (Â/t)·[K=(N/M²)(e/n) = 3,81 t6 C] | Elektriska Jordströmstyrkan

;

i = (A/tM²)(3,81 t6 C) ; t = 1S, i = 1000 [A = C/S]:

A = (1000 AM²)/(3,81 t6 C)(1S)

= 2,63 T8 M² ; globala laddningsytan som krävs för att försörja globala åskväderströmmen

Q = (A/M²)(3,81 t6 C)

= 1000 C

Var och en av de A kvadratmetrarna lämnar sitt Q-bidrag på tiden

t = (A/iM²)(3,81 t6 C)

= 4326,304 S ; laddningsemissionstiden per M² i A som försörjer globala åskväderströmmen

= 72,1 min ; Totalt bidragande laddningsytan per sekund blir At = 1,14 T12 M²: 1/224 av Jordhalvan

= 1h 12m 6s

Antalet ekvivalenta elektronmassor n(e) med e-laddningen 1,602 t19 C på t=4326,304S över A=2,63 T8 M² blir n(e) = Q(1M²)/etA = (5,48611 T9 elektroner)/S för varje kvadratmeter i A.

Markytladdningstätheten, nominella globalmedelvärdet

i = e(5,5 T9 elektroner)·(4326,304 S)·(2,63 T8 M²) = 1002,5313 A = 1002,5313 C/S

Markytladdningstäthetens globala medelvärde blir per M² lika med

Q/A = C/M² = (5,5 T9 · 1,602 t19 C = 8,811 t10 C)/M²

— Eller räknat i elektronelement (×673026): 3,7 T15 elektronringar per sekund per aktuellt bidragande Jordmarkbaserad laddningskvadratmeter.

— Bidragande Jordmarkens laddningsyta At/M²=(2,63 T8 M²)(4326,304 S)=1,14 T12 M² blir avrundat 1/224 av den solbelysta Jordhalvan: [(5,11 T14 M²)/2]/(1,14 T12 M²) = 224, eller 0,44%.

— Genom att olika markområden — tveklöst — bidrar med den möjliga laddningsemissionen på olika sätt — inverkan av värme+vind+säsong med variationer i bioytmassa och planmark — kan regionalt, dygnsmässigt och säsongsvis MYCKET stora variationer förekomma — och vilket också stämmer med de aktuellt rapporterade fallen (Jordelektriska fältvariationer).

— Med N=1,6 T19 tillgängliga ytatomer per fast medelkvadratmeter avgränsad Jordladdningsyta A=1,14 T12 M² som krävs för att underhålla Jordens alla åskväder med totala globala medelströmstyrkan 1000 A, blir antalet elektronringar som avdelas från marken till luften på totala laddningsytan A lika många som antalet ytatomer 1,6 T19 i varje ytkvadratmeter om tidsintervallet för elektronringarnas avyttring utsträcks över hela ytkvadratmetern till

i = A(N/M²)(e/n)/t ;

t = A(N/M²)(e/n)/i

= (1,14 T12 M²)(1,6 T19 M^–2)·(1,602 t19 C)/(1000 A)(673026)

~ 4341 S ;

= 1h 12m 21s

laddningsemissionstiden per hel mark-M² med bidrag från varje markytatom i A som försörjer globala åskväderströmmen

(N=1,6 T19)/(t=4326,304 S) = 3,7 T15 elektronringar per sekund per kvadratmeter

Vi kan INTE meningsfullt (här) tala om ett »antalet ekvivalent emitterade elektronkvanta» eftersom utförseln ALDRIG fungerar efter den modellen: enskilda hela elektronmassor berörs aldrig sett i avdelningen från marken, enbart deras bråkdelar (e/n), dessutom tydligen under relativt långa tidsperioder.

Resultat:

Om enligt TNED varje dryg timme (1h 12m 20s) varje avgränsad (0,44% av den Solbelysta idealt materialsläta Jordhalvan: A=1,14 T12 M² — en markcirkel med radien 107 mil) Jordytskvadratmeters fasta materialtoppsytsatom avger EN — endast en enda — elektronring, 1/673026 av en hel elektronmassa — då matchar den totala laddningsmängden i=(6,24219 T21 e)/S via alla ytatomers bidrag i A alla 50 blixturladdningar per sekund med medelurladdningsmängden 20C över hela Jorden; Summa 1000 Ampere konstant.

— Mindre landdel, kortare avdelningstid, flera elektronringar per aktuell landdelskvadratmeter.

— Andelen är ofantligt (komiskt) liten.

i = (1,13597 T12 M²)(1,6 T19)·[(1,602 t19 C)/(673026)]/(4326,303994 S) = 1000 Coulomb/S

En elektronring (e/673026) per varje toppytsatom (medeltäthet på idealt släta Jordlandytan nära Kisel 2330 KG/M³), N=1,6 T19 per kvadratmeter Jordlandyta (0,44% av Jordhalvan) 1,14 T12 M² per 4326,304 S (1h 12m 6,304s):

Planetströmmen — Jordfältet — Markytans globala elektronström — HÄRLEDNING — Jordströmmen — konv. Global Electric Circuit [GEC]

Markytans globala elektronström

»Planetströmmen» eller GLOBALA PRIMÄRSTRÖMMEN som försörjer Jordens alla åskväder

i = (1,13597 T12 M²)(1,6 T19)·[(1,602 t19 C)/(673026)]/(4326,303994 S) = 1000 Coulomb/S

INGA SOM HELST hinder FINNS ATT MÄNGDEN KAN FLUKTUERA INOM MULTIPLA STRÖMVÄRDEN

I medeltal, hela Jorden, 50 blixturladdningar per sekund med medelurladdningsmängden 20 Coulomb.

Tas även biomassans stora utvecklade växtyta med kan tidsfaktorn per M² förlängas/fluktuera upp mot (MINST) 10ggr beroende på säsong och region, alternativt häftigare åskväder (10ggr större medelurladdningar).

i = 1000 Ampere konstant oupphörligt — med variationer

— Minskar landdelens elektronemissionsyta KAN också avdelningstiden per elektronring per ytatom i varje aktuellt tillgänglig landkvadratmeter minska och med bibehållet samma slutresultat 1000 Ampere. Här finns alltså flera (biokemiska) faktorer som kan inverka och styra verksamheten.

— Men vi vet redan (på våra breddgrader) att åskvädren följer värmen (årstiderna), och därmed markvegetationens (starkt) varierande materialyta. Referensvärdet 1000 A bör därför variera både regionalt och med årstiderna (och med dagtiden — flest åskväder mellan middag [efter max Solvärme] och kväll).

i = Â(N/M²)(e/n)/t | Elektriska Jordströmstyrkan : nom1000 A

Q(J) = [n(Bolt)·C(mean)/ASOL]A₀/2 | Laddningen vid Jordytan : nom450 000 C

Â/A₀ = 2·n(Bolt)·C(mean)/Q(J) = 0,00444444 ... = 1/225 ;

Ξ(J) = Q(J)/ε₀A₀ | Elektriska fältstyrkan vid Jordytan : nom100 V/M

Â, a-flex [Alt+0194]; landdelens SOLBELYSTA DELYTA som deltar i elektronmassans friktionsbaserade avgivning till atmosfären — varierar starkt med dagtid, säsong, väderlek, marktyp

A₀, Totalt släta sfäriska Jordytan: 5,11 T14 M² via ekvatorialradien 6,378 T6 M

N, Antalet ytatomer N=1,6 T19 per medelkvadratmeter i A [1/ kvadraten på medelavståndet grovt 2,5 Å mellan fasta materiens atomer]

e, elektronladdningen 1,602 t19 C

n, antalet elektronelement [tau-ringar] i elektronmassan [673026]

t, tidsintervallet för varje elektronrings avdelning från sin ytatom i medelkvadratmetern

i = (Â/t)·[K=(N/M²)(e/n) = 3,81 t6 C] | Elektriska Jordströmstyrkan

— Högre värme förkortar t; Högre vindhastighet = högre friktion = högre impuls förkortar t;

— Lövträden med löv från våren över sommaren bidrar med stora variationer i A, liksom växtlighetens säsongsvariationer generellt på norra halvklotet. Se BIOytan.

— Sommartid norra halvklotet således: Maximalt stora A- värden, maximalt små t-värden: hög åskfrekvens [på land], stor markfältstyrka [vid »vackert väder»] I=Q/T.

I modern akademi förkastade man som bekant »elektronmassans komponenter» redan 1927 [Citat], och man har inte ovanstående grundverktyg i problemets lösning.

Wilsonströmmen

ETABLERADE omnämnanden — alls — beträffande möjligheten att åskvädren handlar om ett kontinuerligt utbyte — STRÖMSTYRKA — mark/atmosfär är — beroende på referenser — SVÅRA att hitta på webben.

— Man talar i modern akademi MEST och FRÄMST — beroende på referenser — ensidigt om att laddningar som triggar åskvädren byggs upp INOM molnen, alltså i atmosfären (via partikelfriktion luft/is/vattenånga).

— En upplysande webbkälla som innehåller många förlösande beskrivningar (nyckelbegrepp som normalt verkar utelämnas av de andra flesta webbkällor) finns hos Whitaker 2006. Speciellt »Wilsonströmmen» (se motsvarande figurbild WilsonMAC i Jordströmmen) klargör hur man menar i modern akademi för totala energiräkningens balans [”THE GLOBAL THUNDERSTORM CIRCUIT”].

Emellertid. Eftersom bara runt 1/4 av alla blixturladdningen är av typen Moln|Mark [FM1975]

övrigaMoln|Moln beror på laddningsfördelningar internt i moln och återför därför ingen laddning i netto till marken, och kräver därför heller inget i retur därifrån

är det också bara 1/4 av värdet ovan som krävs för underhållet.

Biomassans yta (BIOytan)

Huvudpunkten — land- och biomassans enorma ytvariabilitet

— Tas dessutom med i beräkningen den närmast enorma (variabla) biomassans stora materialyta, se exempelbeskrivning i Dubbelbjörken (Sjörs 1954), betyder det att den tillgängliga laddningsemissionsMARKytan kan sättas MÅNGA gånger större — beroende på marktyp, säsong, värme- väderbild — och därmed tidsbilden lika många gånger längre per M² (med bibehållen åskstyrka).

Vartefter den här författningen framskrider (nu 3Mar2014), ges alltmer preciserade sambandsformer. Och det visar sig, veterligt i slutänden, att STORA variationer kan — och faktiskt kan förstås — förkomma. Biomassans närmast enorma ytkapacitet för elektronmassans koppling till blixturladdningens fysik [Se exemplet från Dubbelbjörken, Sjörs 1954] har mer eller mindre vänt upp och ner på alla föregående begrepp: här finns närmast lika enorma förklaringskällor att ösa ur. Inverkan från biomassans variationer i materialyta igenkänns direkt från redan etablerade källbeskrivningar: åskväder följer säsonger och [mest] land med max värme [och vegetation; tropikerna mest], samt Solens dagliga inverkan [flest åskväder mellan middag och kväll].

— Vad vi vet finns ingen DIREKT mätutrustning som kan avkänna en sådan oerhört liten laddningsmängd. JFET-sensorn i vårt särskilt upplysande test — som bevisar att elektronmassa frigörs genom även den allra [häpnadsväckande] minsta möjliga friktion — klarar själva elektronmängden runt 2 T8 e (enligt grovberäkningar) men då på den övre (ca 1cM) delen av ett plexiglas via EN lugn och lätt strykning med toppen på en akvarellpensels fina hårkropp. Till jämförelse skulle vi här ha 5,5 T9 hela elektronkvanta per hel kvadratmeter (och sekund), motsvarande 2 T8 elektroner på ca 1/27 M² eller en kvadrat med sidan 2 dM, eller i jämförelse med det experimentella penseldraget (ca 1 cM²), grovt och runt 1/400 av mätutslaget. En sådan mätuppgift blir tydligen och tvunget en (betydligt) svårare uppgift om det gäller att få syn på något mätutslag. Inverkan av minimala luftvirvlar gör att en sådan uppgift måste bli ytterst krävande, om alls möjlig.

Fortsättning i Molnladdningen.

Molnladdningen

Laddningen mellan Moln|Mark

MolnSpänningen

Det har SÅLEDES inte tidigare omnämnts i UniversumsHistoria — underligt som det verkar, centralt som det är:

— Tittar man efter på webben på bilder/illustrationer/figurer av LADDNINGEN I MOLN ser man (genomgående) olika laddningsfördelningar utritade INOM molnet — men ingenting MELLAN Moln|Mark. Jämför Funktionskurvan Moln|Mark.

”Although there is still some debate in the scientific community about how the electrification of clouds actually occurs, it is agreed that the separation of positive and negative charges must occur within a cloud for lightning to take place. It is also generally agreed that ice must be present within a developing storm for it to eventually form lightning.

The turbulent wind environment of a thunderstorm with its updrafts and downdrafts is an ideal environment to separate electric charges: negative charges generally gather near the base of the cloud, while positive charges build in the upper reaches of the cloud. This allows electric fields to form and grow between the cloud and the ground and within the cloud itself - all necessary conditions for lightning to occur. ”,

Government of Canada | Environment Canada — HOW LIGHTNING WORKS (28Jun2013) [24Feb2014]

http://ec.gc.ca/foudre-lightning/default.asp?lang=En&n=9353715C-1

Se även instruktiva (flera fina bilder finns) ”cloud bottom ground surface”-figuren (nära slutet) i

SCIENTIFIC EXPLORER — Lightning Part 3: The Lightning Bolt (25Jan2013) [24Feb2014]

http://sciexplorer.blogspot.se/2013/01/lightning-part-3-lightning-bolt.html

— Man SER (tydligen) KONVENTIONELLT generellt INTE laddningsmassan fördelad över mellanrummet, utan ser mellanrummet — elektriska fältstyrkan — som luft eller vakuum mellan två kondensatorplattor.

— Atmosfäriska urladdningar FÖREFALLER inte riktigt fungera så (enligt relaterad fysik): Det finns (nämligen) inga utpräglade elektroder i kopplingen Moln|Mark: laddningsmassan i Molnet som sådan ÄR elektrodmaterialet, medan elektrodmassan i markfallet kan uppfattas som fast. Se delvis mera utförligt i InduktionInfluens.

Se även en superb höghastighetsserie i 5 bilder av en blixturladdning (får inte visas utan tillstånd) på

LIGHTNING — Steven A. Cummer, Duke University (2012) [24Feb2014]

http://people.ee.duke.edu/~cummer/Lightning.html

— MestaLjuset från fronterna i stegledarna i blixtförgreningarna framgår tydligt.

— CC-urladdningar (Cloud to Cloud; även IC, Intra Cloud) KRÄVER en laddningsfördelning HELA urladdningsvägen. Vi studerar det.

— Att laddningsmassan plötsligt skulle upphöra från »Molnets Nedre Område» och sedan vara helt orepresenterad resten av vägen ner mot marken FÖREFALLER (av urladdningsförloppet i CC) inte troligt. Å andra sidan: Var finns tekniska observationer?

— Eftersökt på webben, inte upphittat.

Den övervägande delen forskningsrapporter i ämnet VERKAR dessutom INTE vara gratis tillgängliga.

— Så: Resten får vi räkna ut själva.

(Vi är inte inbjudna till Nobelfestligheterna — för låg inkomst [”Above your paygrade”]).

Situationen före urladdning:

— Det naturligt rimliga antagandet med förebild från CC-urladdningar [Funktionskurvan Moln|Mark] är att (den negativa) laddningsmassan avtar från lägsta molnpunkten (samma som molnets elektriska tyngdpunkt där [den synliga] blixtbanan börjar utbildas via stegledaren) mot markens omvända (positiva) laddningsmassa

vilket betyder att en neutral mellanliggande region måste finnas [strax över markytan];

Om inte på annat sätt, finns i vilket fall en sådan laddningsfördelning genom elektrisk influens mellan de olika laddningsdelarna.

— Det ger en mera preciserad BILD av förutsättningarna till (och fysiken i) urladdningsförloppen.

— MOLNETS ÖVRE LADDNINGSDEL (»blåmarkerade laddningsträdet i illustrationerna» i Blixturladdningens Fysik) markerar den här FÖRMODADE övre (negativa) laddningsmassa som BÖR finnas ovanför startpunkten (A) i »lägsta molnpunkten» [ref. BlåTrädet].

BIOytan, DubbelBjörken, från SVENSKA VÄXTGEOGRAFISKA SÄLLSKAPET, Sjörs 1954 — Referensstudieexempel med vars hjälp markens växtyta kan grovberäknas

BIOytan hos Gran

Hur markytans biomassa (möjligen) kan påverka vädret

(50år gamla) Dubbelbjörkens totala bladyta, 461 500 löv, bägge sidor, full sommartid: 580M².

— Grenverket (en fullvuxen [30år] björk) grovräknat: 200 M². Detaljer i huvudtexten.

Biomassytan besitter närmast enorma variationsmöjligheter beroende på region, säsong, dagtid och väder — om uppgiften gäller att hjälpa till med att lösgöra en (nära ofattbart ringa) minimal mängd elektronelement som ska frigöras till luften i samband med den allmänna vattenavdunstningen: Lövytan, bägge sidor, hos en fullvuxen SommarDubbelBjörk ligger runt (minst) 500 M².

— Ämnet här gäller att pröva källformen för den allmänna globala vädermatematiken med ansamlingen av elektrisk (negativ) basladdning i molnens domäner: säkringen av den allmänna globala balansräkning som underhåller Jordens alla åskväder året runt. Se även jämförande basteorier i MAC/TNED i Jordströmmen.

Sjörs1954

— En (50 år gammal [PDF-forskningsdokument [‡] från 1954]) dubbelbjörk har runt 336000/(1400/M²) = 250 M² lövyta PÅ ENA SIDAN (ett fullvuxet björklöv har ungefär samma toppyta som en femkrona), totalt runt 500 M² lövyta + grenverk (säkert upp mot 100 M²), men mäter sett ovanifrån bara en upptagande markyta (max 3 meter grenlängd) på grovt 30 M²; Ungefär samma värden gäller för andra (fullvuxna) träd (källan nämner Lind som nära lika i resultat som björken), även barrträd; Till den bilden kommer TYP allt GRÄS — strån, den enorma mängden (små, välutvecklade) blombildningar (kolla Ljungen till jämförelse — direkta räkneexempel saknas här)

BILDKÄLLA: Författarens arkiv ·

12Jun2013 E13 Bild64 ·Nikon D90

————— ‡

SVENSKA VÄXTGEOGRAFISKA SÄLLSKAPET —

SLÅTTERÄNGAR I GRANGÄRDE FINNMARK, Hugo Sjörs 1954

http://www.diva-portal.org/smash/get/diva2:565424/FULLTEXT01.pdf

s96:

”Stora dubbelbjörken. .. Björken, som

tillhör Betula pubescens, är dubbelstammig, vardera

stammen har ca 25 cm diameter i brösthöjd, och

den gemensamma stubbens diameter är ca 60 cm.

Kronan börjar ca 4 m över marken, ehuru enstaka

kvistar hänger ner till ca 3 m, och når en höjd

av 16 m och en diameter av 8-10 m (kronprojektionens

yta 56 m²).”, s96sp2ö;

”Totala lövmängden är alltså ca 461 500 st, med

en medelvikt i lufttorrt tillstånd av 0,046 g, utgörande

21,2 kg totalt. Lövmängden utanför

kurvan för 10 löv/m² utgör härav något mindre

än 2 %.”.

DBres

(50år gamla) Dubbelbjörkens totala bladyta, bägge sidor, full sommartid:

— 580M².

— Dubbelbjörken i jämförelse med motsvarande enkelbjörk betyder att MINST halva dubbelbjörkens värden återfinns på enkelbjörkens (Ø25cMBröstHöjd): Enkelbjörken:

— 290 M².

— Ett fullvuxet björklöv i sommartid har ungefär och grovt (taget väl i underkant) ytan av en femkrona

(A=πr²=π[0,0285/2]²) ~ 6,38 t4 M². Femkronans diameter Ø=28,5mM. Björkbladets (torkat) bladstjälksyta (stjälken ca 25mM lång med Ø0,5mM) är grovt ca 6% av hela bladytan (bägge sidorna, se grovräkningen nedan).

BILDKÄLLA: Författarens arkiv · 27Maj2014 Bild 49 E7; 2Mar20134 Bild Björklöv [torkat, från hösten 2013, ytterst toppen avbruten] ·Nikon D90

Värdena i resultatbilden nedan från högerbildens torkade lövexemplar. Vårens nyutslagna fullvuxna björklöv, vänsterbilden, visar betydligt större bladyta.

Per kvadratmeter krävs (i underkant) 1567 fullvuxna björklöv räknat enbart på bladets ena toppyta. Bägge bladytorna (plus bladstjälken som vi inte räknar [typiskt torkat 0,025×2π(0,0005 M) ~ 7,8 t5 M²: ger extra 36 M²: 461500×7,8t5]) ger då MAX 784 fullvuxna björklöv per M². Med uppgiften (biomassan) 461500 fullvuxna björklöv på en (förmodligen runt 50-70 år gammal dubbel-) björk ges totala bladytorna (461500)/(784) ~ 588 M².

— Lägger vi till det omfattande grenverket

— stammen (mycket grovt förenklat): 2×(2π[0,2 M])×16M ~ 20 M²;

— grovgrenarna (grovt 7st L3MØ5cM-grenar per höjdmeter [16M]), ~ 53 M²;

— mängden mindre grenar ner till lövstjälkarna (samma faktor53/20=2,65), grovt ~ 140 M²;

— totalt grenverket mycket grovt räknat ~ 20+53+140=213 M²:

— ges för hela Dubbelbjörken grovt lägst i full sommartid (588 + 213 = 801) M².

— Biomassans fördelning på andra träd (här utan referenser webben ger vissa antydningar) ger ungefär lika yta för såväl andra lövträd som barrträd. Källan ovan omnämner (s99spn) ”Linden och björken skulle alltså lämna nära nog lika stor lövmassa”. Källan omnämner endast barrträden generellt (s109sp1n) ”Den gröna barrmassan hos ett växtligt äldre granbestånd består av ungefär sju barrårgångar och innehåller därför ett många gånger större näringsförråd än lövmassan hos ett motsvarande björkbestånd”. Vi behöver (alltså) genomföra en mera omfattande kontrollräkning för typen barrträd (en fullvuxen skogsgran) för att få bättre besked [Jag misstänker att granen med sin till synes utomordentligt rika barrbank möjligen uppvisar större bioyta än björken [40st encentimeters Ø1mM granbarr täcker ett fullvuxet björklövs bägge bladytor], men det är rimligt för en lekman till att börja med att anta att alla träd i stort är jämförliga].

SSSe, BioYtmassKoefficienten via SkogsSverigeSe

Dubbelbjörken 800/10=80, grenverket inkluderat:

80M² naturlig bioyta per 1M² plan trädbesutten markyta, full sommartid (bottenvegetationen oräknad).

Enkelbjörken 400/10=40, grenverket inkluderat:

40M² naturlig bioyta per 1M² plan trädbesutten markyta, full sommartid (bottenvegetationen oräknad).

— I gallrad skog [http://skogssverige.se/node/34784] finns ca 1 träd per 20 M² plan markyta. Ogallrad (naturskog) har ca 1 träd per 10 M².

— Om vi tills vidare använder forskningsbasen citerad ovan (Sjörs, 1954) och utgår ifrån att varje fullvuxet (från 30-50år och uppåt) barr- eller lövträd vilketsom under sommartid har en bioyta åtkomlig för värme och vind om grovt reducerat med möjliga marginaler 2/3 av ovanstående dubbelbjörksexempel FÖR MINSTA MÖJLIGA BLADYTA, eller avrundat neråt 800·2/3 = 500 M² för Dubbelbjörken och för Enkelbjörken 250 M², och för MAXIMAL BLADYTA en faktor ×1,5 (Se DBres, jämförelsen med fullt utvecklade blad) som ger 800·3/2 = 1200 M² för Dubbelbjörken och för Enkelbjörken 600 M², ges i naturlig skog med uppgiften ovan — och då oräknat markens egen (säkerligen anmärkningsvärda underliggande) bioyta med stora mängder gräs, blommor, sten, grus och sand — en EnkelbjörkenAbsolutMINSTA 250M² bioyta per 10M² markyta, eller grovt 25M² bioyta per 1M² plan markyta, och en DubbelbjörkenAbsolutSTÖRSTA 1200 M² bioyta per 10M² markyta, eller grovt 120M² bioyta per 1M² plan markyta:

Räknar vi direkt oberoende av citatkällan på den praktiska trädradien — för dubbelbjörken (minst) r=4M som ger projektionsMARKcirkelytan ~ 50,27 M² (Sjörs1954 anger för Dubbelbjörkens del ”kronprojektionens

yta 56 m²”) — ges alternativt typ ~ 500/50=10.

— I naturskogen går EMELLERTID OFTA trädindividernas grenar in i varandras motsvarande ideala individuella markytcirkelprojektioner, och uppgiften från webbkällan skogssverige.se kan därför ända vara den mera praktiskt korrekta.

— Lägger vi dessutom till stam- och grenverkets andel (totalt ca 800/50 = 16, alt. 800/10=80) ges ännu högre referensvärden.

Bioytmasskoefficienten — Dubbelbjörken i Exempel

A(BIO)

——— = 25-120 M²/1M² = 25-120 = B ; BioYtmassKoefficienten BYK förk. B — full sommartid FÖR BJÖRK

A(GND)

A(GND) = A(BIO)/B

Dubbla bladytan plus uppskattat bidrag från totala grenverket

— Uppgiften används i utvärderingen av blixturladdningens elektriska fältfysik i de möjliga markkopplingarna, särskilt sommartid.

— Se efterföljande exempel.

En markcirkel (BYK=50) med radien drygt 12 KM över naturskog sommartid räcker för att trigga en medelblixt (20C)

— Det kan inte (ännu) visas här. Men det FÖREFALLER ligga i sakens natur att biomassytan KAN uppvisa en betydligt HÖGRE initierande elektronmassmobilitet [högre markytladdningstäthet] än ovan antagna globala medelvärde [och därmed betydligt trängre R-värde än exemplet nedan]. På grund av svårigheten att veta exakta vad som gäller från fall till fall — man vet redan att variationerna är stora (se etablerade Referenser) — kan det bli äventyrligt att (här) (ens) försöka »exemplifiera närmare». Vi nöjer oss tills vidare med att fortsätta betrakta grovexempel via de här framräknande globala nominella medelvärdesformerna [Utförligt från Markytans Globala Elektronström].

— Med markytladdningstätheten från (5,5 T9)(1,602 t19 C)/M² = 8,811 t10 C/M², analogt den medelbaserade markladdningsyta 1,13494 T9 M²/C (=1M²/8,8t10C) som Jordströmmen försörjer hela Jordens medelbaserade blixturladdningar på (1000 Ampere nominellt, utförligt från Markytans Globala Elektronström) krävs idealt för en enskild 20Coulombs blixturladdning en under alla förhållanden maximalt effektiv Sol-Vind-åtkomlig elektronmassavgivningsyta på

A(BIO) = (20 C)·(1,135 T9 M²)

= 2,268 T10 M² ;

Ekvivalenta globala medelvärdesbaserade PLANA markladdningsytan för en 20 C molnladdning

Division med ovanstående grovt framräknade sommartidensBjörk A(BIO)/A(GND)=50M²/1M²=50 bioytmasskoefficient ger då resterande idealt plan markyttäckning

A(GND) = (2,268 T10 M²)/50

= 4,536 T8 M²

Det blir en markprojicerad laddningscirkel med radien

R = √[A(GND)/π]

= 12016,046 M

~ 12 KM ; Med BYK=120 ges R = 7,7546142 KM.

Eller, förgrovat ganska precis en plan kartmarkytcirkel med diametern 2,5 mil (25 KM). Det blir — sommartid — medelformen för den underliggande COULOMBISKA koppling I ELEKTRISK JÄMVIKT som en medelbaserad global 20C blixtkanal behöver mot (biomassa-)marken för att INITIERA elektriska fältets styrka på marken mot 20C-balansen i Molnet, och som ska leda fram till en framgångsrik blixturladdning. Är bioytmasskoefficienten lägre blir R motsvarande större.

— Som ett initierande grovexempel på praktisk tillämpning FÖREFALLER R-värdet 12 KM marktäckning för en 20C molnladdnings medelblixt inte helt taget ur fantasin.

Se vidare hur blixturladdningen och markfältkopplingen utvecklas enligt TNED i Laddningsbildningen och från gränsspänningens genombrott i Första Steget.

— Allmän sammanfattande genomgång hur laddningsbilden mark|moln utvecklas i relaterad mening ges i JORDFÄLTET.

Sammanställning 27Maj2014

GRANENS BIOYTA

Undersökningar och grovmätningar våren 2014

Foto: 27Maj2014 Bild1 E7; PHP aEXP Granbarr 19Maj2014 Bild 1;5 · Nikon D90

1. 35cM delkvist: En 35 cM delkvist togs från en nedfallen yngre gran, DBHØ15cM~20-30år (DBH=50cM/π; h=13M; antal grenar 115-120 > Ø2cM); Delkvistens orientering: Granstam, bilden ovan vänster, första huvudgrenen, en av dess delförgreningar i sin tur som aktuella testobjektet;

2. 40GB/20mM: Från 20mM-toppen på en av delkvistens förgreningar plockades först alla granbarr (GB) av för hand och räknades till 40; Det ger i ett grovt medeltal 2000 GB/M;

3. 15mM/GB: De avplockade granbarren lades ut sida vid sida och mättes i längd till ca 15mM — men det finns både mindre och större som avviker, ingen ytterligare räkning har gjorts på den delen, utan vi utgår i denna framställning ifrån grundmåttet 15mM för ett typiskt (idealt) granbarr och kommer längre fram att anpassa all räkning efter VIKTSMÄNGDEN motsvarande barr, vare sig barren är längre eller kortare;

4. 15×0,55×1,2 LBH i mM: Ett 15mM granbarr mättes sedan ungefärligt i rektangulärt tvärsnitt via skjutmått med måtten 0,55×1,2 mM: omkretsen summerar 3,5mM, men barrformens hörn är rundade och räkningen görs här via en medelrektangel med omkretsen respektive (3+3,5)/2=3,25mM; Ytan för 1 GB blir då (15·3,25=48,75)mM² = 4,875 t5 M²;

5. 4,875 t5 M²/GB; Ytan för ett granbarr av typen i (4);

6. 1,54M/0,35M: Den uttagna 35cM-kvistens olika barrbekädda delkvistar mättes upp separat och summerades tillsammans med delkvistens centralstam vilket gav 1,54 M totalt. Med grovmedelvärdet i (1) ovan, 2000 GB/M, skulle 35cM.kvistens totala 1,54M hålla 1,54·2000 = 3080 GB. Vi kan jämföra den uppgiften med efterföljande (2033 GB) mera noggranna vägning på, obs, motsvarande idealt utplockade 100st granbarr av typen (4) som vågekvivalent (ca 1/3 av det verkliga antalet bortfaller för att få idealbarret i nr4);

Foto: PHP aEXP Granbarr A 19Maj2014 Bild 4;7;8;10 · Nikon D90

7. 2033 (15mM)GB: 100 stycken granbarr valdes ut med motsvarande ungefärliga barrlängd 15mM. En enklare men ytterst känslig anordning med balanssticka SHINWA 30cM stålskala, på mitten en 2mM rak kopparstång som balanscentrum och en tändsticksask konstruerades för ändamålet: Kopparstången läggs på en bit dubbelhäftande tejp som lagts över ett A4-ark som underlag; Över kopparstången placeras sedan balansstickan; Asken får fungera som hållare för granbarren i ena änden och askhöljet som motvikt i andra änden: Man justerar asken med de 100 granbarren i ena änden (i mitt fall precis med synlig kant mot 30cM-stecket) i exakt balans med askhöljet på andra sidan (i mitt fall precis med synlig kant mot 37mM-stecket); Den ytterst enkla balansvågen visade sig vara känslig på ett granbarr när (0,00522978 Gram, se vidare nedan). Faktiskt.

— Sedan 35cM-kvisten torkat ca en vecka och alla granbarr kunde samlas, vägdes granbarren mot de hundra avplockade i 15mM-gruppen. Totalt visade sig då 20 grupper med en rest på 33 granbarr. Totalt och idealt således 2033 stycken 15×0,55×1,2 granbarr;

— Notera som ovan, att en del barr är mindre, en del större, förmodligen med övervikten åt större antal mindre. Det betyder att det verkliga antalet granbarr är större än det uppvägda via referensbarret i (4), kanske upp till 2500 men den uppgiften är här osäker.

8. 10,63 Gram: Alla (2033) granbarren vägdes slutligen på brevvåg; Min brevvåg kontrollerades mot 80 Grams vanligt kontorspapper; Ett A4-ark väger (80 Gram/M²)·(0,297×0,21)M² = 4,9896 Gram; 10 ark väger 49,896 Gram; Min brevvåg visade 48 Gram efter mesta möjliga noggranna kalibrering; avvikelsen som ska adderas ger 1,9896 Gram per 48 Gram eller addera 0,04145 Gram per vägt gram:

— En låda viktes från ett A4-ark där alla granbarren hälldes i utom de hundra i det särskilda referensblocket, vilka lades löst på brevvågens vägplatta: Vågen visade då tämligen precis 15 Gram; Justeringen ger 15+15·0,04145 = 15,62175 Gram, minus A4-arkets 4,9896 Gram som ger 10,63215 Gram

— Utslaget på 2033 stycken barr av typen i (4) därmed per sådant granbarr 5,22978 t3 Gram.

9. 0,0991087 M²/0,35M: Totala barrytan för 35cM-kvisten därmed från (4) och (5): 2033·4,875 t5 M² = 0,0991087 ~ 0,1 M²;

Grovräkning, runt 600 M²:

Den ytterligare grovräkning som krävs för att få en bild av vilken den totala BARR-bioytan är för en typisk svensk/nordisk skogsgran kräver att den ovan redovisade (typiska) 35cM-kvistens del relateras till helheten.

— En snabb grovhoftning (med en tillagd nivå huvudgren från aktuella objektet): 6st35cM-kvistar på delgrenen; 5 sådana på ena sidan huvudgrenen, totalt per gren som utgår från granstammen 6·5·2 = 60 stycken 0,1M² eller 6 M² per huvudgren; Vi räknar med 5 sådana per 1-meters höjdnivå och granhöjden 20 meter, vilket ger 5·20 = 100 grenar med 6 M² i varje, totalt 600 M². Till den räkningen kommer sedan själva grenverkets yta (uppsk. ca +20%).

— Jämför resultatet från Dubbelbjörken: total bladyta bägge sidor 580 M²;

— Den vidare undersökningen (RESULTAT) visade att — inkluderat möjliga stora variationer — en GammelGran (DBH~Ø40cM) kan ha mycket större BIObarryta (~1400 M²) än en motsvarande EnkelBjörks totala bladyta (250-600 M²).

— På grund av möjligen STORA variationer — främst växtsätt för granens del, dess ljuskänsliga områden — finns här ingen alternativ undersökning som kan bekräfta räkningen. Se vidare nedan.

Utvärdering:

Det aktuella granexemplet FÖREFALLER till en början inte representativ för beståndet: Den aktuella 35cM-delkvisten kan i direkt visuell mening hänföras till typen »glesare bestånd», dessutom på yngre granar. I jämförelse nämligen med närstående äldre granar — upp till 5 meter långa markhuvudgrenar med första delgrenar i en del fall som meterlånga hängen (GranPK) och oerhört rikt besuttna med granbarr — betraktar vi närmast »en helt annan art». Den vidare undersökningen har emellertid lett till att 35cM-kvisten — genom sitt växtsätt — förefaller VÄL kunna beskriva granträdet generellt i avseende på barrbesättningen. Den delen visade sig på följande sätt:

— För att få ut någon begriplig överensstämmelse med ovanstående räkning, måste vi på ett eller annat sätt mäta exempelgrenens representation i aktuella granobjekt.

— Det finns flera olika sätt att genomföra den räkningen på — alla med sina brister.

Foto: 26Maj2014 Bild4 Granbarr A · Nikon D90

Den aktuella 35cM exempelGranDelgrenen, bilden ovan med alla (2033 15mM) barr uppsamlade, visar grovt 7 stycken mellanrum om vardera i genomsnitt ca 5cM mellan parförgreningar från centralstammen;

— Förhållandet mellan första delgrenens längd och hela 35cM-grenlängden är då ca 3/7 med sista minsta 1/7.

— Under DEN förutsättningen, att 35cM-delgrenen kan förstås representativ för HELA granträdet kan följande approximerade matematik användas i en översiktlig utvärdering av mängden granbarr för en hel gran TILLSAMMANS med en viss allmän uppskattning av Antalet Huvudgrenar som (generellt) finns på en fullvuxen gran — från h=20 meter och större:

GranBasic:

1. — Vi utgår ifrån granstammens huvudgren som enheten 1;

2. — Vi indelar huvudgrenen i utskottsintervall (parförgreningar) om 5cM; Varje gren och varje dess delgren avspeglar alltid ett 5cM-intervall, vare sig Granen är ung eller gammal; 5cM-intervallet är en tillväxtkonstant, karaktäristisk för (just den) arten;

3. — Vi bestämmer att huvudgrenens första = längsta = innersta delgren mäter 3/7 av huvudgrenlängden (d) — d visar f.ö. närmast enorma avsnitt, upp mot 5-6 meter, för »Gammelgranar» med basstammar (DBH) runt 40cM (alla dessa är uppskattningsvis minst 100 år gamla träd);

4. — Vi summerar sedan huvudgrenens alla delgrenar i parutväxterna fram till huvudgrenens ände, tillsammans med d-värdet; Vi får då totala barrväxtstamlängden för en hel basgren; Vi använder sedan exempelgrenens basdata med medelbarrets antal per barrväxtstamlängd (3080 barr per meter, alla barr; 2033 standard 15mM-barr med 48,75 mM² totalyta; vilket ger idealbarren som ca 2/3 av hela barrbeståndet 10-15mM) och dess medelyta och räknar så ut motsvarande total barryta för hela huvudgrenen;

Vi SKULLE konsekvent genomföra »samma fraktaldelning» för alla delgrenar av givna. En enklare undersökning visar EMELLERTID att den typen FÖREFALLER utöva SJÄLVKVÄVNING:

GranFORM1

Figuren överst ovan ansluter till 5cM-delningsintervallet [... / / / / ...] på en HuvudGranGren, aktuella barrbeståndet inte utritat, endast första delgrenarna;

— Tar man den FORMEN som fraktalindex — mittfiguren — och förminskar den för passning på första delgrenen, ser man (LÄTT) att OM Granträdet, verkligen, försöker VÄXA på den fasonen, är det tydligt att Granen sysslar med självmord:

— Mängden barrutväxter kommer att bli närmast enorm och risken är överhängande att mängden tätt liggande barr utestänger kompisarna från det viktiga ljuset. Jämför f.ö. längst in mot basen på en äldre granstam: i princip heltorrt, mörkt, inte ett levande barr, för övrigt ingen växlighet alls.

— Den undre figuren visar första steget i en sådan, tänkt och förmodad, situation. Fortsätter vi på samma fason, är det tydligt att vi håller på att kväva ihjäl i stort sett hela trädet.

Bilden nedan visar en mera växttekniskt rimlig situation: alla utväxta barr ges absolut rimlig chans att få vara med och dela på ljusytorna:

GranFORM2

Figuren ovan samma typ som föregående övre, men här beklädd med motsvarande idealbarret (längd 15cM, yta 48,75 mM²).

— I praktiken — inre tonade delen — måste vi (ändå) räkna bort en viss procent på grund av det ringa ljus som når in till själva trädstammen och då i allt högre grad för allt äldre granträd.

Praktisk kontrolltest:

Jag testade »algoritmens växtförutsägande styrka» genom att (1Jun2014) besöka en Gammelgran (DBH=126cM/π~Ø40cM) och testräkna på ett avsnitt:

Foto: 1Jun2014 Bild 22;25 E9 · Nikon D90

På en drygt 5 meter lång basgren (höger ovan) från trädstammen — grenen lutar neråt 45° med markprojektionens längd ca 3,5 M — mättes längst ut upp TOTALT 25 stycken grenutväxter från huvudgrenen över ca 50 cM av huvudgrenens yttre del.

— Vissa av dessa tunga grenbarrhängen är nära meterlånga.

— OM vi »kompenserar» — i grova approximerande uppskattande hoftningar — den egentliga (men som nyligen påpekades ljusotillåtna) fraktaldelningen med motsvarande LÄNGRE nerhängen DÄR LJUSINSLÄPPET SÅ MEDGER, som på bilden ovan vänster, KAN vi se att Gammelgranen uppvisar en VISS »kompensation» för det medelmässiga 5cM-intervallet från testgrenen genom att förlägga motsvarande intervall som 25grenar/50cM=1gren/2cM, och där fördela motsvarande balansräkning på en LJUSMATEMATIK som i stort sett — med »försumbara förluster» — tillåter ALLA BARR ATT FÅ VARA MED i sommarfröjderna.

— Till viss del, men som det här INTE finns någon ytterligare kontrollräkning på, kan möjligen den tätare delen innefatta en kompensation som annars bortfaller mot den inre granstammens regioner där barrförekomsten i praktiken är noll (bilden ovan höger).

Antal huvudgrenar:

Antalet huvudgrenar på (fullvuxna) Granträd kan vi försöka huvudräkna i de otaliga landskapsvyerna med grangestalterna på våra breddgrader — tillsammans med viss vidare uppskattning:

Foto: 1Jun2014 Bild26 E9 · Nikon D90

Bilden ovan, Granträdet i mitten, förstorat höger med siffran 20, visar ungefär en halv fullvuxen (20 meter eller högre) Granträdsindivid.

— Genom att FÖRST räkna alla synliga huvudgrenar — alla grenar som utgår från trädstammen — genom att försöka urskilja DERAS Avslutande Karaktäristiska Spets — och på den kvartshalva av Granträdet som vätter mot observationsfältet — har jag i detta fall räknat till ca 20 stycken tydligt urskiljbara grenindivider — på ungefär halva trädet (kameran riktad snett uppåt).

— OM den matematiken är HOMOGEN (vilken den INTE är i praktiken: grangrenar växer riktligast mot Söder, minst [noll] mot Norr) skulle det betyda totalt (2·20)_HELA×4=160 huvudgrenar.

— Räknas norrdelen bort kan vi hofta den bortfallande delen som ~ 1/3;

— Slutresultatet skulle vara: grovt sett 100 grenar per Gran.

Foto: 29Maj2014 Bild10 E8 · Nikon D90

— Liknande försök (bilden ovan en DBH=127cM/π Gammelgran) visar ungefärligen samma förekomster:

— Grovt sett 100 grenar per vuxen Gran.

I JÄMFÖRELSE MED GRENANTALET på Exempelgrenens Granträd — 115-120 > Ø2cM — förefaller grenantalet rimligt — samt knappast föränderligt (för huvudresultatdelen) med växande ålder.

— Det blir i vilket fall huvudgrenens längd som avgör slutvärdet — här utan vidare hänsyn till Granträdets konicitet, vi endast utnyttjar ett generaliserat grovt »rakmedelvärde».

Med den totalbilden i slutresultatet kan vi nu ställa upp kalkylceller (i gratisprogrammet OpenOffice.Kalkyl) med vars hjälp alla granträd (upp till någon max grenlängd typ 5 meter) kan bestämmas en approximerad total barrBIOyta.

— Algoritmen är av samma natur som i figurerna GranFORM1 och GranFORM2: successiv summering med begränsade begynnelse (3/7)- och slutvillkor(1/7) i 5cM-intervall.

RESULTAT:

GranFORM1 och GranFORM2

Se Kalkylkortet i Blixt2014Gran.ods Tabell1:

— För vår 35cM Testgren blir dess totala barrBIOyta 0,10595 M², mot grundvärdet (de 2033 15mM barren) 0,991087 M²; Totala motsvarande 100-grenars granträdets barrBIOyta skulle bli 10,595 M²;

— För Gammelgranen med basgrenlängden 500 centimeter blir totala barrBIOytan per huvudgren 14,3637 M², med hela trädets barrBIOyta 1436,37 M² — det omfattande grenverket frånsett (i varje fall runt +20%).

— OM den siffran har någon naturförankring är det tydligt att Granen är MYCKET mera bioYTtät än den fullvuxna Sommarutslagna EnkelBjörken med sina ca (MINST) 250 M² fullvuxna sommarblad — frånsett räkningen på grenverket.

— Det skulle alltså vara en betydande skillnad i BladBioYTA mellan SommarBjörk och Gran, närmare bestämt ca 1440/250~5,7ggr.

— Det vore KUL om det fanns något oberoende, klargörande, sätt att kvittera den räkningen på.

(Min gissning att alla träd, fullt utvecklade, visar ungefär samma bioyta håller inte).

LAI, Leaf Area Index — etablerad term för ENSIDIGA totala bladytornas förhållande till trädets projicerade markupptagande yta

Allometri — kroppsmorfologi, studiet av förhållandet mellan kroppars storlek och deras form

Först — som vanligt: Svårt att hitta kvantitativa referensdata i webbdokument i ämnet: GoogleSökning ”birch leaf area index” 31Maj2014 ger EN (1) träff — och den webbsidan kan inte visas (kräver särskild behörighet).

EC2003

ALLOMETRIC RELATIONSHIPS OF SELECTED EUROPEAN TREE SPECIES, European Comission 2003

http://publications.jrc.ec.europa.eu/repository/bitstream/111111111/874/1/EUR 20855 EN.pdf

Dokumentet kan inte kopieras

Källan ger standardiserade grundbegrepp, rikliga referenser och en hel del allmänna samband.

— 30% av Jordytan täcks av skog. Europa är 8:e största skogsytsområdet (Ryssland störst).

— Centralterm i sambanden är DBH, Diameter-at-Breast-Height och (för vår del) och LAI, Leaf Area Index, ”It is defined as the one-sided green leaf area per unit ground surface area (LAI = leaf area / ground area, m² / m²) in broadleaf canopies.[1]”, Wikipedia Leaf Area Index [2014-05-28]; ’ensida lövyta per enhet markytarea i bredbladiga skogsvalv’.

— Webbkällan EC2003 skriver för sin del om LAI s5m ”The meaning of LAI that is used within this document relaters to the ratio of the ’one sided area of foliage element of a single tree’ and the ’vertically projected crown area of that tree’.”. Alltså (totala) lövytans uppsida i förhållande till trädets projicerade planmarkyta.

Samband EC2003:

Sambanden nedan med DBH i cM, Al-värdet i M² per aktuellt träd:

”The (one sided) leaf area (A_l) of young Birch stands can be described to the information appendic 4 of Bugmann (1994)

A_l = 0.028 DBH ^1.43 [m² tree^–1] (4)

Martin et al. (1998) descibes a leaf area - DBH relationship for Betula lenta [vanlig björksort] as (dasched line in the left hand panel of Figure 6):

A_l = 0.148252 DBH ^2.008 [m² tree^–1] (5)

”, EC2003 s13ö.

— Men källan redovisar underliga uppgifter: ”Figure 6” visar för DBH=25cM samma värde ca 50 M² ”Leaf area / tree” för bägge kurvorna Bugmann och Martin, gemensam skärningspunkt. Men respektive värden från sambanden ovan ger

A_l = 0.028 25 ^1.430 [m² tree^–1] = 2,7939089 Bugmann

A_l = 0.148252 25 ^2.008 [m² tree^–1] = 95,074510 Martin

— Det finns tydligen ingen överensstämmelse i den presentationen. (Författarna BORDE ge enkla räkneexempel i samband med formelvisningar, främst för att försäkra sig själva om att korrekta samband används. Det har man uppenbarligen missat här).

— Den tydligt slarvigt framställda webbkällan EC2003 redovisar en allmän LAI-ekvation (s13m)

LAI = 0.65 DBH ^0.43 [tree^–1] ; Björk endast

som för exempelfallet DBH=25cM ger LAI=2,5943439 — 5,1886879 för bägge lövsidorna.

— Jämför BYK-värdet för Dubbelbjörken: ca 10 med uppgiften från Sjörs kronprojektionsyta (56M²) och lövytan 500M², till max 50 med uppgiften (SSSe) 1 träd per 10M² ogallrad skogsmarkyta. Det är långt ifrån någon naturvetenskaplig överensstämmelse.

— ÖVERENSSTÄMMELSERNA ÄR TYDLIGT URUSLA.

— Den mest pålitliga utvärderingen är FÖRMODLIGEN lövräkningen från Sjörs 1954 i Dubbelbjörkens exempel (461 500 löv, Ø25cM per stam i brösthöjd) med markprojicerade trädkronytan (basgrenlängd ca 4,22 M) 56 M², varje bladtoppyta (minst, DBres) som femkronans 6,38 t4 M², och som ger totala enkelsidiga bladytan (461.500·6,38t4M²=) 294,437 M²; Bägge bladytorna 588,874 M²; eller max största [‡] bladytan (minst 1.5ggr): 883,311 M².

— En motsvarande Ø25cM enkelbjörk visar (minst) halva det värdet eller ca 440 M² — vilket i vilket fall med basgrenradien 4,2 M leder oss till ett LAI-värde (enkelsidiga bladytan, ytterligare en halvering) på runt MAX LAI(Ø25cMBjörkSommartid)=220/55=4.

— Jämfört med EC2003-källans LAI(Ø25cMBjörkSommartid)-värde 2,6 är det fortfarande en oanständigt stor differens, och långt ifrån något som ens liknar någon naturvetenskapligt belagd forskning (manuell hoftning till närmaste stjärnor).

— Urdåligt.

— Vi kommer därför här tills vidare att HELT försöka hålla oss till Sjörs1954-exempel för Björkens del.

— EC2003-källan beskriver i stort sett samtliga Europeiska förekomster med alla parametrar. Men som i exemplet ovan, då det är tydligt att ingen resonabel koppling finns i värdegrunderna: EC2003-källan är komplett värdelös som praktisk referens.

— Författarna måste redovisa sambandens KORREKTA giltighet MED TYDLIGA EXEMPEL. Tills dess: ZeroCredibility.

— EC2003-ger f.ö. en LAI-ekvation för GRAN av typen LAI=3,52+ 2,3·10log(DBH) [tree^–1] s35n;

— För en Ø40cM gran (DBH=127cM/π) ger det ett LAI-värde på ca 7,2 — med totala barrets yta således 14,4.

— INDIKERINGEN (om EC-källan alls är användbar) antyder att Granens bioyta (barren) är avsevärt större än Björkens (löven).

EC2003-källan om granbarrens yta

Källans avsnitt om barrträden ( sekt. 5, s30: Norway Spruce, Picea Abies):

”5.9 Foliage and Biomass

Johansson (1999) reports an average needle length of 17.5 (11.6 – 21.0) mm. This corresponds to a total surface area of 52 mm² (or 58 mm² according to the formula of Kerner et al. (1977) who state that the total needle area ranges between 40 – 60 mm² depending on the origin of the needle in the crown).”, EC2003 s36.

Särskilt det yngre (h=ca13M) granobjektet i avsnittet om BIOytanGran visade granbarr i längder om 10 – 15 mM. Men bara ett tiotal meter från platsen för den nedfallna unggranen står en grupp Ø40cM gammelgranar. Stickprov (29Maj2014) på deras — bitvis — tydligt kraftiga barr visade avsnitt med d=24mM.

Foto: 1Jun2014 E9 Bild 115 — Gammelgranens 24mM barr · Nikon D90

Med medelbarret (punkt 4) LBH = 15×0,55×1,2 mM med ytan 48,75 mM² blir motsvarande (relativt medelbarrets yta)

Jämförande tabell för olika granbarrlängder L med motsvarande ungefärliga granbarryta A

——————————————————————————————————————

L mM	A mM²
10	32,50
15	48,75
24	78,00

Wikipedia Picea Abies [2014-05-28] ger mer MED DE HÄR PRESENTERADE FÄLTVÄRDENA relevanta data: 12-24mM.

Snarare än EC2003-källans uppgift ”total needle area ranges between 40 – 60 mm²” visar ovanstående tydligen ’30-80’ mM².

— Det jämförande exemplet bara understryker (åter igen) att ALLMÄNNA uppgifter på förekomsterna uppvisar LOKALT STORA inbördes variationer — i princip upp till dubbla eller ner till halva; dessutom beroende på säsong, lokal näring, växtsätt.

LägstaMolnpunkten, — Illustrerat särskilt i LägstaPunkten — Feb2014

»MOLNETS LÄGSTA SPÄNNINGSPUNKT»

LÄGSTA MOLNPUNKTEN

2014II22

LägstaPunkten — Molnets LÄGSTA punkt —

MolnLADDNINGENS elektriska tyngdpunkt

I BlixturladdningensFysik finns utöver Allmänna Grunddata ingen egentligt klargörande (tydlig, illustrerad) BILD av HUR laddningskroppen i den atmosfäriska blixturladdningen ser ut eller fungerar. Den antas underförstått — dels efter »våra vardagliga vanliga observationer» och dels efter etablerade källors referenser i deras omnämnande (och bemötande). I samband med denna uteblivna laddningsbild finns flera ställen i framställningen som förefaller oklara. Efterhandsgranskningar (-Feb2014) har visat hur ämnet (möjligen) kan klargöras, illustrationerna nedan.

molnkroppens laddningsmassa

urladdningsvägen

Är INTE lika med

en konventionell elektronisk kondensator

PASCHENSAMBANDET [samband för urladdning mellan massiva elektroder, se Isolationsspänningen för luft] ÄR INTE TILLÄMPLIGT I ATMOSFÄREN: molnmassan ÄR elektroderna.

MOLNKROPPEN (a) utgör EN motsvarande elektronisk kondensatorelektrod utspridd — med någon elektrisk Q-tyngdpunkt —

—————

över HELA urladdningsvägen: spänningsbilden kan INTE (c) liknas vid någon samlad elektronisk komponent (d) typ plattkondensator eller liknelser med spänning mellan TVÅ elektriskt strömförande kopparledare EFTERSOM HELA LADDNINGEN INKLUDERAT MOTSVARANDE IDEALA MOLNELEKTROD ligger utspridd IN TILL den fasta markelektroden.

— Den blotta nödvändigheten med JUST Molnelektrodens UTSMETNING över urladdningsvägen betyder uppenbarligen att molnladdningen INTE kan UTVECKLAS i meningen frikopplad från markdelen: molnladdningen måste kunna avancera, fluktuera, ändras, öka, med kopplingen mark-luft obruten: enda påfyllande kandidaten blir fasta markelektrodens fysik [Utförligt från Jordfältets Upphov med Jordströmmen].

— Enbart av det skälet är det uteslutet rent teoretiskt att molnladdningen skulle kunna byggs upp ENBART på den allmänna MAC-teorins grund: isolerade partikelfriktioner luft/is/vatten INUTI molnet »skapar» en molnladdning fristående från markkontakt och som sedan antas »ladda ur» mot marken på ännu mystiska vis som ingen [ännu Mar2014] tycks kunna beskriva i detalj.

— Enda rationella sättet är ENLIGT relaterad fysik: molnladdningen byggs upp FRÅN markelektroden via Jordströmmen. Det bevarar dynamiken. Funktionskurvan Moln|Mark stadfäster sammanhanget.

Med ett medelbaserat globalt konstant blixtlängdsmedelvärde (h=1KM Norra Halvklotet Moln|MarkExemplet) växer spänningen (U=kQ/h=E/Q) Moln|Mark med växande ackumulerande molnladdning (Q, gröna grafen nedan). Q-massan tillförs (Casimireffekten) luften|molnen via markytans ytterst sublima elektronmassaavgivning (E-ringens energibindning, Jordfältet, Primärströmmen) på SolvärmeVindFriktionens kredit:

Laddningsbildningen, från första Elektronringen — RELATERAD FYSIK — Se även i Del I om UPPHOVET TILL Potentialerna som åstadkommer urladdning

LADDNINGSBILDENS UPPKOMST Del II

FRÅN FÖRSTA ELEKTRONRINGEN

Grafen (gröna linjärt, blå exponentiellt) visar hur molnladdningen kan förstås öka med bidrag från markavgivningens elektronelement (TauH2O). Både elektriska fältstyrkan och spänningen Moln|Mark tillväxer entydigt: Fältstyrkan börjar från obegränsat litet med första elektronringen på maximalt utbredd associerad Jordmarksfältyta, och växer sedan med växande laddning; Med en fast höjdreferens (h=1 KM, Moln|MarkExemplet) växer likaledes spänningen Moln|Mark entydigt. När elektriska genombrytningsgränsen nås för atommassan i laddningsrummet mellan Moln|Mark sker överslaget, och molnet lämnar tillbaka elektronelementen till marken. Därmed är balansen återställd (Jordens elektriska neutralitet), och strömcykeln (Jordströmmen) kan börja om igen på Solens kredit. På grund av inre molnströmningar kan olika laddningsfördelningar ske internt. Därmed kan vi förstå hur separata urladdningar blir möjliga mellan olika molnlokaler som fristående separata fenomen. Även omvända urladdningar Mark|Moln är möjliga om en sådan tillfällig laddningsfördelning finns.

Det enskilda elektronelementets (Tau[τ]Ringen, se Elektronmassans Komponenter) atomtillhörighet (från Casimireffekten, se Distansparametern) tappar helt kontakten [E-ringarnas bindning] med sin SPECIFIKA ursprungsmoderatom i Knudsenskiktet på kredit av den friktionskraft som råder mellan mark och luft via solvärme och vind då TauRingen frigörs från marken till luften och associeras med någon av luftatomerna (senare, vattenångan via TauH2O).

Från det att TauRingen lämnar Knudsenskiktet (molekylmaterialgränsen mellan två olika materierum typ Mark|Luft) kommer den i princip att associera sin MATERIALFASTA LADDNINGSTILLHÖRIGHET med HELA Jordklotet, närmast (elektriska fältets utbildning på gravitationens kredit, se Superpositionsprincipen).

Globalsatserna, molnladdningarnas uppbyggnad, QbildnTau

Den globalbilden medför tydligen en allmän satsbild, »primärströmmens agentur» [TAU-ringens energibindning]:

minsta möjliga molnladdning [Tau[τ]Ringen] söker koppla ihop sig med största — vidast — möjliga mark[mass]fältyta, vilket medför:

PREFIXxSIN

molnladdningens uppbyggnad börjar från minsta möjliga elektriska fältstyrka

(1) F/Q = Ξ → ∞ = Rc·(Q → ∞)/A_GND ;

i markfältytans A_GND ideala snittplan: minsta Q=[Tau[τ]Ringen] börjar på största möjliga A_GND, vilket medför:

(2) E/Q = U → ∞ = Rc·(Q → ∞)/h ;

molnladdningens uppbyggnad på en fast referenshöjd (h) börjar från minsta möjliga elektriska spänning, vilket medför:

största möjliga MOBILITET för minsta molnladdningselementet, minsta Q=[Tau[τ]Ringen], i dess ASSOCIATION med andra element, typ »MAX Luftfrihet»: sättet som moln/molnladdningar ansamlas på.

I varje momentan tidpunkt — varje fast situationsbild med en viss utbildad molnladdning enligt Primärströmmen beskriven ovan, kan då följande förstås gälla:

— Laddningsfördelningen mellan molnladdningens elektriska tyngdpunkt (QMINUS) och marken (QPLUS) följer tvunget den principiella Funktionskurvan för laddningsfördelningen Moln|Mark;

Laddningsfördelningen Moln | Mark strax före blixturladdningen

——————————————————————

— Elektriska fältstyrkan (1) i fältsnittet – – – – – på olika markparallella höjdsnitt på distansen d över marken, mellan molnladdningens elektriska tyngdpunkt (QMINUS) på fasta höjden h över marken (illustrationen nedan vänster) och marken (QPLUS), följer konsekvent, entydigt och uteslutande ett avtagande delQ (inte utritat) som fältkopplar marken via ett motsvarande avtagande delA_GND, så att IDEALT KONSTANT ELEKTRISK FÄLTSTYRKA råder hela laddningsvägen för varje delladdning i Q som bidrar till molnets totalt samlade elektriska tyngdpunkt Q på h över marken och i varje tidpunkt fram till urladdningsögonblicket;

(3) F/Q = Ξ = Rc·(Q)/A_GND = Rc·(Q/n)/[A_GND/n] = konstant = E/Qd = U/d ;

KRAFTEN över laddningen är konstant för alla avsnitt mellan laddningens potentialdomäner:

ENERGIN i varje sådant avsnitt varierar direkt proportionellt mot höjdsnittets markdistans: större d, större E.

SOLVÄRMEN underhåller hela verksamheten.

För A_GND, se Biomassytkoefficienten.

— Elektriska fältstyrkans konstans i (3) följer därmed precis samma SPÄNNINGSMÄSSIGA ideala elektrofysik som idealt mellan elektroderna på en plattkondensator med mellanliggande vakuum: Ξ = U/d överallt i mellanrummet.

Spänningen U=Ξd=E/Q, från marken upp mot den samlade molnladdningens elektriska tyngdpunkt (Q) på höjden h över marken

— och för varje momentan situationsbild med given ansamlad molnladdning Q på h över marken, sambandet i (2) ovan

— växer därmed entydigt med distansen d: Från marken, upp mot molnladdningens elektriska tyngdpunkt QMINUS, eller motsvarande omvända vägen räknat uppifrån och ner, mot markens utspridda QPLUS.

— Vi kan INTE på något SÄKERT ALLMÄNGILTIGT SÄTT påstå något (ytterligare) om spänningsbilden mellan godtyckliga referenspunkter MELLAN markens QPLUS och molnets QMINUS EFTERSOM den delen är ägnad alla möjliga FLUKTUATIONER med olika täthetsändringar, kontinuerligt fortsatt laddningsackumulation och atmosfäriska strömningsfenomen fram till urladdningstillfället. Dessa variabler, i stort sett, punkterar varje försök till någon homogeniserad totalbild. Däremot kan vi tydligen behålla extrempunkterna med markens QPLUS och molnets QMINUS som ovan.

— Historiens ögonblick då den växande elektriska fältstyrkan och därmed Moln|Markspänningen genom fortsatt laddningsackumulation når gränsvärdet för överslag, kommer drastiskt att ändra situationsbilden.

— Enligt TNED: Uppladdningen följer en utpräglad materiefysik eller makrofysik på spänningsgrunderna [Elektriska Fältets Fysik], medan massfysiken träder in från urladdningsögonblicket.

Genom att mellanliggande laddningsmängd Q

mellan mark och nederänden på den blixtbana som håller på att utbildas (»stegad ledare») före själva urladdningstillfället

avtar med minskat avstånd MELLAN Mark|Blixtkanalpunkt måste också tvunget PÅ VISST SÄTT den elektriska spänningen avta (U=E/Q=kQ/d; observera underförståddheterna och vanan att »blanda in egna illustrationer från elektroniken» som bara förvillar):

Elektriska fältstyrkan mellan molnets elektriska tyngdpunkt (Q) och fältets markYTkopplande tvärsnitt (A) är (idealt) KONSTANT för alla Q/n proportionellt mot alla A/n, så att (idealt) samma förhållande (Q/A) gäller för alla (isolerade) delLADDNINGSpunkter i mellanrummet Moln|Mark, hela vägen från marken upp till molnets elektriska tyngdpunkt Q. Det betyder att:

— Spänningen INUTI laddningsmolnets fasta Q mellan två fasta ISOLERADE (elektriska Q-tyngd-) punkter som ändrar avstånd inbördes

. . . . .

VÄXER med växande punktavstånd (s) — U=(Ξ=konstant)s=E/Q=kQ/s— och AVTAR med avtagande punktavstånd (s) EFTERSOM den mellanliggande laddningsmängden gör det. (Q växer mera än s).

Jämför motsvarande för plattkondensatorn: ingen laddning finns explicit mellan plattorna: laddningen ligger koncentrerad, utspridd i, inuti, plattorna: en fast Q-mängd mellan två parallella plattor med ett fast plattavstånd (h), utverkar en bestämd elektrisk fältstyrka (Ξ=U/h=F/Q=kQ/h²) mellan plattorna på den fasta platt-tvärsnittsytans bekostnad. Går man från endera plattan mot den andra, växer spänningen med avståndet s från 0 till h enligt U=Ξs.

Termen »lägsta molnpunkten» [‡] har tidigare i UniversumsHistoria (BlixturladdningensFysik, Sibiriska Exemplet) använts för att markera BLIXTBANANS TOPP: stället där blixtbanan börjar bildas UR molnmassan (ner mot markdelen).

— I resonemanget användes två strömförande parallella kopparledare som exempel för att illustrera omöjligheten i — enligt relaterad fysik, som saken skulle framställas — att tillämpa »vanligt elektronik» på urladdningsfenomenet:

— Försöker man närma spetsen (S) på en tunn tråd (motsvarande blixtkanalens utbildning) som är kopplad till den ena (övre, Ö) — av två parallellt strömförande ledare — mot en undre (U), flyttar S samtidigt Ö-potentialen mot U — i princip detsamma som att minska avståndet mellan ÖU — med följd i att ett överslag sker då avståndet SU underskrider ett visst gränsvärde:

— elektriska fältstyrkan (F/Q = E/Qs = Ξ = U/s) växer med avtagande avstånd (s).

— Spänningen mellan ledardelarna SU (»=ÖU»: avståndet s mellan ledarna ändras inte i U=E/Q=kQ/s) är konstant, oberoende av var någonstans man placerar »proben» S mellan ledarna; mellanrummet med luft eller vakuum är egalt; Laddningsmängden som bildar spänningen mellan ledarna åtskilda av avståndet s, befinner sig INTE — är inte utsmetad som i molnfallet — (»på visst sätt» S frånsett) i mellanrummet mellan ÖU.

— I laddningsmolnet är det annorlunda: det finns ingen SÄRSKILD »ledare» eftersom hela molnet är »ledare»:

Molnfysikens del kan alltså förstås så:

— Spänningen mellan två referenspunkter i laddningsmolnet (idealt homogen laddningstäthet Q/M³) växer med växande punktavstånd och avtar med avtagande punktavstånd, proportionellt mot den växande/avtagande mellanliggande laddningsmängden.

Analogt: ett fast punktavstånd (s) får spänningen (U) mellan punkterna att avta med mellanliggande avtagande Q och spänningen att öka med mellanliggande växande Q: U=E/Q=kQ/s.

DET HELT ANMÄRKNINGSVÄRDA i liknelsen eller jämförelsen med de parallellt strömförande kopparledarna och laddningsmolnet — och som bara framkommit just här i denna framställning (22Feb2014) — är just i molnfallet (Blixtbanans bildning i syntes) stegledarens kontinuerligt steppande flashande och lysande FRAMFLYTTADE toppspänningspunkt (från Lägsta Molnpunkten [A]) motsvarande (spetsen på) den nyligen omnämnda tunna S-trådens funktion i kopparledarfallet:

UTAN just funktionen att Stegledarens nedre lysande topp (S) förmedlar den nollresistiva blixtbanans toppspänningspunkt, och vilket är HELT reserverat för TNED, SKULLE spänningsförhållandet (Molntoppen|Stegledarframänden) A|S bara bli det just påpekade: Spänningen mellan två laddningsmolnpunkter som rycker allt närmare varandra AVTAR: ingen urladdning kan ske mellan två sådana närliggande molnladdningspunkter.

MED blixtbanans nollresistiva funktion, nämligen, FLYTTAS just A-punktens HELA MELLANLIGGANDE mark-molnladdningspotential ALLT NÄRMARE MARKDELEN (med »kaotiska förgreningar» i luftmolekylernas turbulens som hela molnet söker markpotentialen) — samtidigt som LOKALA (bara sett till den avgränsade S-delen) MOLNLADDNINGSPOTENTIALEN Mark|S avtar med allt mindre mellanliggande molnladdningsmängd.

— Och alltså — lik förbaskat — KAN i slutänden liknelsen (»på visst sätt») med de parallella kopparledarna användas: NÄR S-spetsen når ett visst minsta kritiskt avstånd till U-ledaren SKER överslaget.

I MODERN AKADEMI har man inte den avgörande relaterade (TNED) fysikens nollresistiva taxibana: kemikopplingens basfysik: ström- och kemiekvationen. Man har bara MELLANRUMMET MELLAN ATOMKÄRNORNA. Det räcker — uppenbarligen — inte för att förklara fenomenformen.

Magnetisk eller elektrisk fältstyrka garanterar den slutliga omfamningen?

— Magnetisk som det ser ut (magnetiska »suger», elektriska »stöter»):

Som redan noterats i Arbetet

kommer molntråd och marktråd enligt TNED att förenas på samma kärnspinn — förutsättningen för fullständigt slutligt utvecklad sammanhängande elektrontömning moln|mark.

— Föreningstillfället kräver alltså i vilket fall en HARMONISK magnetisk förening typ två elektriska makrospolar (atomkärnornas samriktade spinn) som förenas på gemensamt centralflöde (elektronströmmen).

Som också tidigare noterats (B-styrkan från stegänden) FÖREFALLER hela räkningen kräva den slutliga föreningen på en MAGNETISK kraft, inte en elektrisk. Därför nämligen som det resonerades, att blixtbanans successiva bildning via den flashande lysande spetsen (S) frammanar INDUKTIONSEFFEKTER (Induktionslagen) i det att S successivt kopplar upp elektronströmmar till varje nytt steg i blixtbanan:

Elektroner som strömmar ner genom hela blixtkanalen och UT ur en S-punkt, accelererat vid varje nytt steg, tvingar (InduceratMAC) omgivande elektronmassor IN mot accelerationsområdet, och som möjligen föranleder lokal jonisation med tillhörande ljusglöd efter fältlinjerna från Stegledarspetsen med avtagande ljusstyrka utåt.

StegFronten — Stegade ledarens lysande front [Feb2014], relaterad fysik

Se även motsvarande konventionella figurbeskrivningar i Lalande1996.

Det FRAMSKYMTAR verkliga fotografier på webben av spetsen på stegledare (Feb2014) som LIKNAR den ovan vänster illustrerade figurens schematiska fältbild.

Men källförfattarna verkar inte överdrivet intresserade att dela med sig av bilderna.

En del typ PPT-dokument på webben kan man visserligen få titta i, men ingen URL anges (en kopia lagras på datorn). FINNS ingen annan vägledande källuppgift i själva dokumentet än den typen av referens, är den källtypen tydligen värdelös.

Illustrationen ovan höger visar motsvarande LJUSBÅGSSTRÖM enligt TNED med principen hur ljuseffekten underhålls i stegledare och blixtkanalerna generellt, och till viss del i avsnittet framför en stegledares (lysande) topp (mitten — med ett möjligt nästa steg som håller på att utbildas i »sökningen» av lämpliga spänningskandidater i luftrummet).

— Modern akademi har inte den relaterade fysikens CENTRALA plasmastam att referera till [BlixturladdningensFysik]: elektronbanan GENOM atomkärnorna.

— Modern akademi har bara sitt »klassiska mellanrum mellan atomerna». Därmed Kampen (med »lavineffekter som triggas av kosmisk strålning») HUR en sådan LADDNINGSTÄT bana ALLS kan bildas.

— Enligt TNED finns bara ett och endast ett enda fysiskt möjligt sätt. Se även i ARBETET i Blixturladdningens Fysik (TNED) — hur atomtrådarna delas och kan förstås sammanhänga i blixtkanalens utbildning.

— En upphittad webbkälla illustrerar stegledaren i teori till etablerad jämförelse i Lalande et al., 1996.

Relaterad fysik:

— De nämnda stötvis utströmmande elektronerna i stegledarens nederände tvingar samtidigt via induktionseffekten närvarande positivt laddade atomer (luftjoner; lika attraheras, olika repelleras) BORT från accelerationsområdet. Jämför InduceratMAC.

Hela utströmningen ur stegledarens öppning sker också MÖJLIGEN med HELA DET REDAN UPPLAGRADE ELEKTRONSTRÖMNINGSTRYCK som den aktuella blixtkanalen REDAN utbildat (vilket kräver ytterligare motsvarande INDUKTIOSREKYLARBETE lika med »flashande kanaler» i de omgivande luftatomernas elektronrekombinationer, se Grunddata Stegande Ledaren).

Med den blotta förutsättningen — S-punktens framstötande utströmmande elektronmassor (MINUS) stöter (ur-STARKT) bort marktrådens joniserade toppunkt (PLUS) — blir det svårt att förklara en förening mellan ledarändarna S|Mark(Streamer). Räkningen (B-styrkan från stegänden) på magnetiska fältstyrkan FÖREFALLER ha löst den gåtan: föreningen sker inte på bas av elektrisk fältstyrka, utan på bas av magnetisk fältstyrka.

— Elektriska fältstyrkan (Ξ[grek. xsi (»e-f»)] = U/d) S|Mark(Streamer) — i takt med att blixtkanalens nedre punkt S rycker allt närmare marken (Sibiriska Exemplet) — medför VISST att Ξ måste öka med »KONSTANT U i S» (vilket »förklarar» varför S »i medeltal» dras ENTYDIGT mot urladdningspunkten via minsta motståndets tillgängliga väg). Men induktionseffekten från HELA den redan etablerade elektronmassan i det att S-punkten avancerar STÖTVIS motverkar YTTERST STARKT (med HELA den utbildade elektronNEDströmmens styrka i blixtkanalen och vars elektroner strömmar ut ur S-toppen) varje NÄRA förening: induktionseffekten strävar att stöta bort +— från varandra. Däremot (från ett visst minsta näravstånd) harmonierar magnetiska fältstyrkorna (B-styrkan från stegänden), och det blir naturligt att lägga föreningen på deras kredit.

— Laddningsbildens uppkomst och utveckling beskrivs detaljerat från LADDNINGSBILDENS UPPKOMST Del 1.

Stegbildningen, Första steget bildas — Från Laddningsbildningen Del 2

2014V25

STEGBILDNINGEN — första steget

BLIXTURLADDNINGENS relaterad FYSIK

Vi studerar det enklaste fallet med urladdning moln-mark: molndelen tömmer elektronmassa i markdelen

I Laddningsbildningen Del II finns sammanställt hela processen med den avgörande primära laddningstransport mark-moln som bildar förutsättningen för blixturladdningens fysik.

— Här detaljstuderas första steget i blixtbanans bildning, och föregående själva urladdningstillfället (TrädExempel) då molndel och markdel möts.

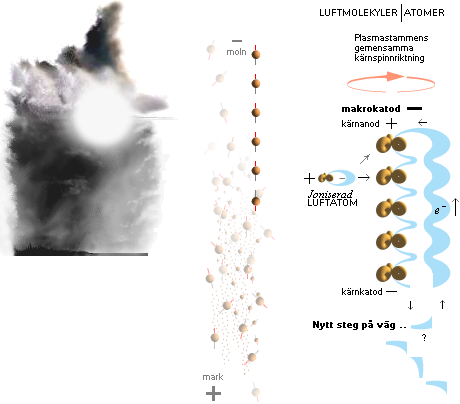
När gränsspänningen (UG) uppnås i det redan väl utbildade elektriska fältet mellan moln och mark, söker sig en minsta möjliga motståndets elektriska utjämningsväg utbildas mellan molndelens elektriska tyngdpunkt — stället där blixtbanan mot marken börjar utbildas — och genom vars taxibana den elektriska spänningens domäner kan uttömma sig i varandra och därmed normaliseras.

— HELA urladdningsvägen moln-mark tar emellertid TID att iordningställa på den begränsade elektriskt återkopplande ljushastighetens räkning (2,99792458 T8 M/S), och det sker (uppenbarligen) genom att hela blixtbanan delas upp sekventiellt och successivt adderande i enskilda s.k. steg (eng. stepped leader).

— Eftersom inte hela blixtbanan omedelbart bildas med en gång, utan endast så småningom genom de enskilda stegen, kan vi (illustrationen ovan mitten) se hur första stegets atomtråd (höger ovan) kopplar sin spänningsdel på den vidare resan mot markdelen. Hela processen anställs av den utlösande gränsspänningen moln-mark som garanterar att en urladdningsväg är möjlig, hela vägen.

— InternetWebben är numera (2014) representerad av flera videodokument som visar olika detaljer i blixturladdningar. Vi kan förmoda, men här inte bevisa, att första stegets utbildning föregås av ett visst ljusskensfenomen (ovan vänster) som ansluter till den omsättning i elektronmassaomfördelning som första atomtrådens plasmakoppling otvetydigt måste bygga på.

Steglängden motsvarar kraften i den spänningsbild som över stegavståndet orkar koppla motsvarande mängd atomer till den sammanhängande atomtråden: NÄR den gränsen uppnås, som vi får förstå saken, sker HELA trådkopplingen »omedelbart»: alla ingående atomer kopplas ihop synkroniserat i en och samma sekvens.

Step1, Stegbildningens första steg

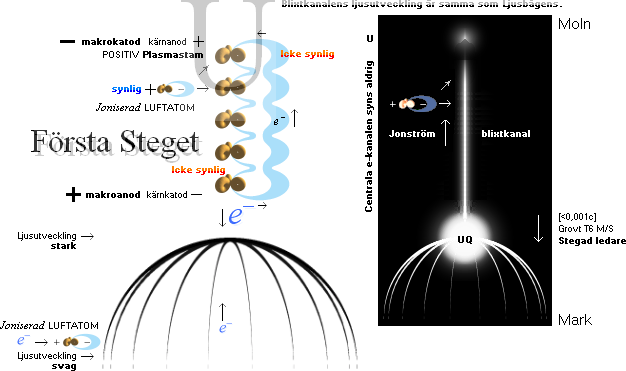
· Centralstammen döljs effektivt av ljuset från Jonströmmen.

· Plasmastammen stjäl elektroner = Joniserar omgivningen;

· De bestulna moderatomerna återfår sina fråntagna elektronbesättningar vid makrokatoden.

· Samtidigt dras de bestulna moderatomerna — via sina ev. kvarvarande elektroner — in mot plasmastammen.

· Stegledarens framryckande stötar +Joniserar luftatomerna i framriktningen
— och tvingar INDUKTIVT elektronmassa in mot stegledarens framdel.

· Då de +Joniserade atomerna återtar elektroner från andra (längre bort) kringliggande luftatomer utsänds ljus.

Illustrationen med huvudpunkterna ovan beskriver sammanhanget kortfattat.

— Så länge den primärt utlösande gränsspänningens fysik bevaras — förhållandet moln|mark i elektriska fältets form och styrka — kommer stegledarens framände att fortsätta leta efter minsta elektriska motståendets väg för att hitta ner till och fullborda föreningen med markpotentialens molnmake. Som vi kan se genom en del webbvideodokument eller fotografier, pågår den stegledarsökningen mot markpotentialen via flera olika stråk och som tillsammans bildar den aktuella blixtkanalens karaktäristiska trädgrensstruktur.

— I slutänden (frånsett vissa sällsynta fall) kommer bara en enda stegledares front att hitta sin slutliga uppstigande markmake, där urladdningen verkställs.

— Själva blixturladdningsförloppet, mötet moln|mark där molnets elektronladdning återlämnas till markdelen, beskrivs och behandlas utförligt i Urladdningen i BlixturladdningensFysik2008.

— Se även i Stegfronten.

MolnSpänningen, Globala medelvärden — Mar2014

Ekvivalenta värden — med praktiskt ELMEK-exempel, Elvesbildningen i översikt

ELVES [snabba 1mS ringformigt expanderande ljussvaga, h=80-90KM],

HALOS [långsammare, flera mS, ljusstarkare ELVES-typer på lägre höjd, h=75KM] and

SPRITES [vertikala ljuskvistar [vertikala »HAVREKÄRVAR»] under ovanstående]

Se webbreferens som beskriver de olika fenomenformerna i

IMAGING OF ELVES, HALOS AND SPRITE INITIATION AT 1MS TIME RESOLUTION, Moudry et al., 2003

http://www.atmo.arizona.edu/students/courselinks/spring07/atmo589/articles/Elves_Etc_JASTP_2003.pdf

”In the high speed

imager, there is a definite delay between elves and halos,

suggesting halos and their variations are not due to EMP.”, s516sp1ö.

Den korta skissartade och summariskt inledande beskrivningen i den möjliga TNED-förklaringen till uppkomsten av de s.k. ELVES (eng. sing. Elve, pl. Elves) i ELMEK-artikeln (från2008) ges här en något vidare beskrivning tillsammans med jämförande etablerade referenser i utvärderingen av fenomengrunderna. Sammanställningen nedan [i relaterad fysik] ger typiska referensvärden som kan användas i allmänna grova utvärderingar inom de olika översiktliga grovberäkningarna i samband med blixturladdningar vid Jordytan.

SOM REDAN har framskymtat, är svårigheterna STORA om uppgiften gäller att få fram »exakta spänningsvärden vid blixtbildning». Det tycks man även vara rörande eniga om i den moderna akademins korridorer (Citat Winderberg2000 nedan).

Vad vi kan göra är i vilket fall att använda grundsambanden (elektriska kraftlagen; integrala energiformen) för att få fram grund- och grovvärden till jämförelse.

UGref

U(G), gränsspänningen enligt TNED idealt med vilande atomer: T(°K) = 0;

Notera att UG-värdet i TNED beror av antalet elektronelement i elektronmassan. Absolut minsta värdet n=177062 är det som använts generellt i grundbeskrivningarna i Blixturladdningens Fysik [2008]. Genom resultaten [Exakta n-värdet] i CASIMIREFFEKTEN har en — möjligen — mera praktisk värdeform visat sig n=673026 — ca 3,8ggr absoluta grundvärdet. Vad vi f.n. vet [Mar2014] är det detta värde man bör räkna med i en mer realistisk prövning.

U(B), urladdningsgränsspänningen som föranleder inledande Blixtkanal (eng. Bolt) i första stegledarens utveckling;

U(G) = 475 V per 1M via 3nM medelavstånd luftmolekylerna idealt vilande;

U(G) = k_e·e/n([3 t9 M]/2) ;

= (8,98744 T9 VM/C)(1,602 t19 C)/[(673026)([3 t9 M]/2)]

= 1,4261832 t6 V/3nM ; U(G) via molekylmedelavståndet 3nM i luft

U(G) = 475,3944 V/M

~ 457 V/M ; U(G) i normalluft per meter

Temperaturberoendet, U(B) grundsamband

EFTERSOM temperaturen (enligt allmänna gaslagen) GENERELLT följer energin (E=pV=kT) LINJÄRT via fundamentala gaskonstanten (k), kan vi till prövning försöka skriva blixtbildningsspänningen på en motsvarande T-beroende form via TNED-härledningens allmänna gränsspänningen [U(G)] för kemisk bindning = sammankoppling av flera atomer i samma »atomtråd» — blixtbildens grunder enligt relaterad fysik. Sambanden nedan visar resultatbilden.

U_B = U_G + U_G(kT/°K) ; k numerisk konstant

= U_G(1 + kT/°K) ; Med E=kT, T=E/k=E·°K/J, blir k en energikoefficient

1 + kT/°K = U_B/U_G ;

kT/°K = (U_B/U_G)–1 ;

k = T^–1(°K)[(U_B/U_G) – 1] ;

EX: T = 12°C = 12°C+273,15°K = 285,15°K ;

Medelladdning 20C per medelblixt 1KM via elektriska kraftlagen

U_B = k(Q/d) = (9T9 VM/C)(20C/1000M)

= 1,8 T8 V ; Medelspänningen för globala medelblixten Moln|Mark h=1KM Q=20C

k = T^–1(°K)[(U_B/U_G) – 1] ; U[B(G)] = U(G)d/M = 475×(d=1000 M) V

= (285,15°K)^–1(°K)[([1,8 T8 V]/475×1000 V) – 1]

= 1,3254335 ; Gränsspänningens medelglobala Temperaturkoefficient k_B

;

k = T^–1(°K)[([k(Q/d)]/[U(G)d/M]) – 1]

= T^–1(°K)[([k(Q)]/[U(G)d²]) – 1]

= T^–1(°K)[(kQ/d²U_G) – 1]

= T^–1(°K)[(k/U_G)(Q/d²) – 1]

= (285,15°K)^–1(°K)[(k/U_G)(Q/d²) – 1]

ExempelMolnMark — Molnspänningen

OM en blixturladdning via ett Moln/Markförhållande på 20 Coulomb över 1KM initieras på spänningsvärdet som ovan 1,8 T8 V (1,8 T5 V/M), ges en motsvarande idealt homogenfördelad 50 M stegledarspänning på

(50M)(1,8T8V/1000M) = (5M)(1,8T6V/1M) = 9T6V = 9 MV.

· Energin: Energiutvecklingen över den 1KM långa 20C blixtbanan, E = LI²/2 = (U/2)Q = (1,8T8V/2)(20C), blir 1,8 T9 J.

· Strömmen: Sker 20C-urladdningen totalt på tiden 1mS (1 t3 S) blir totala strömstyrkan I=Q/T=20.000 A.

— Genom att den initierande blixtbildningsspänningen U(B) i vilket fall enligt TNED bibehålls hela vägen för stegledaren [Induktion&Influens, StegledarenIdealt; elektronmassans nollresistiva koppling till atomkärnan i relaterad fysik], stämmer räkningen så långt med stegledarens konstanta urladdningsfysik.

· Induktansen (L, elektriska accelerationsmotståndet, E=LI²/2; L=2E/I²) blir 2(1,8T9J)/(2T4A)²= 9 Henry.

· Strömderivatan (di/dt): Om själva huvudströmrusningen omfattar hela molnladdningen 20C över hela blixtbanans längd 1KM som kopplas slutligt vid marken över den sista stegledarens längd 50 M via idealt maximala kopplingshastigheten v=c (vi intresserar oss bara för kortaste, snabbaste transientresponsen), kan vi räkna med att HELA strömtrycket på 2 T4 A ligger över transienttiden t=d/v=(50 M)/(3 T8 M/S)=1,67 t7 S = 0,17 µS. Momentana strömderivatan (di/dt) blir då
(di/dt) = (2 T4 A)/(1,7 t7 S) = 1,17647 T11 A/S.

·          Induktionsspännngen [û=L(di/dt)] tagen idealt rakt vertikalt uppåt på höjden h (allt vidare) över marken kan vi räkna på via avtagande strömbidrag med växande höjd från energiekvivalenterna E=UQ=UIt=Pt=Fh=kQ²/h. Dvs, vi kan räkna med att energin (E) i proportion till strömstyrkan (I) med given källspänning (U) avtar med höjden (h), vilket leder oss till
û        = L(di/dt)(1M)/h           ; di/dt strömderivatan vid källan som ovan
Men också induktansen (L) beror av mellanliggande massformer (täthet, temperatur). Vi skulle egentligen behöva specificera partikeltäthetens avtagande med växande h, men kan förenkla den delen (grovt) genom att anta att också L avtar proportionellt med växande h. Därmed
û        = L(di/dt)(1M²)/h²        ; di/dt strömderivatan vid källan som ovan
          = (9 H)(1,17647 T11 A/S)(1M²)/(h²)
          = (1,05882 T12 HA/S)(1M²)/(h²)          ; H = VS/A; HA/S = (VS/A)A/S = V;
          ~ (1 T12 V)(1M²)/(h²)

Praktiskt ELMEK

ELMEK (eng. pl. ELVES, sing. ELVE [eller elf]), planvågsexpanderande rekylljusfenomen (80KM, 1mS, 60KA) ovanför blixturladdningar;

— Viss sammanblandning med SPRITES. Enligt Wikipedia Upper-atmospheric lightning | Sprite (lightning) [2014-03-03] är 80KM-halon att hänföra till SPRITES-fenomen [50-90KM], medan ELVES uppträder betydligt högre upp [400KM]. Delvis oklara uppgifter.

”They are sometimes mistaken for ELVES, due to their visual similarity and short duration.[10][11]”, Wikipedia Sprite (lightning), Sprite halo [2014-03-03].

— NOT: WikiLänkarna [10][11] leder ingenvart, ”Webbsidan kan inte visas”.

Ex: Med h= 80 KM (8 T4 M) — området för ELVE-bildningar — ges i vår typiska medelblixt induktionsspänningen grovräknat

û = (1 T12 V)(1M²)/(8 T4 M)²

= 156,25 V

Den motsvarande vertikalt påverkande induktivt verkande accelerationsspänningens (û=U) inverkan på en fri elektron Q(e)=1,602 t19C med vilomassan m(e)=9,11 t31 KG blir då med c=3 T8 M/S (sambandet för elektronens hastighet genom elektrisk acceleration i vakuum) hastigheten (u)

—————————

u = c√ 1 – 1/[(UQ/m₀c²) + 1]² ; laddningshastigheten u från accelerationsspänningen U, idealt vakuum (övre Jordatmosfären)

= c · 0,0247045 ; M/S

~ 0,02c

Tiden att ta elektronen 1 KM vertikalt via û=156,25 V blir t=d/v ~ 1,7 t4 S (0,17 mS).

— I Zambiaexemplet (Jordmagnetiska Spegelpunkterna, 100 KM över marken) framgick att de Jordmagnetiska spegelpunkterna som infångar elektroner-positroner i deras aktuella repeterande Jordmagnetiskt infångade banformer kräver (Horisontellt, parallellt med Jordytan) v=0,63c (Positronens expansionshastighet). I Jordmagnetiska partikelbanformernas övre atmosfäriska mönster får vi (tydligen) förstå dessa banor i olika etablerade mönsterstråk, ytterst känsliga för störningar typ inkommande stötpartikelströmmar från Soleruptioner som förorsakar Norrsken då de inkommande Solvindspartiklarna växelverkar med de redan Jordmagnetiskt etablerade partikeltrafikanternas vägbanor — och åstadkommer lokala atomjonisationer hos de tunt utspridda normalt neutrala kväve och syreatomerna som delar plats med de banbundna laddare partiklarnas Jordmagnetiska banmönster.

— Explicita bekräftelser i klartext som utpekar just den här beskrivna ANISOTROPA mönstersammansättningen i etablerad litteratur (blandningen laddade + neutrala + etablerade geomagnetiska trafikmönster) »finns delvis» på Webben @INTERNET. Se t.ex. anisotropin i Citat Wikipedia, och särskilt Citat NeutralKollisioner.

— Sammansättningarna Kväve-Syre-friaElektroner-friaVätejoner beskrivs väl etablerat i området (80 KM, Jonosfärens och Magnetosfärens nedre delar generellt), se särskilt Citat Heavner2000. Uppfattningen att ljusemissionerna i den övre Jordatmosfären i samband med blixturladdningar nära Jordytan (ELVES, SPRITES, HALOS) handlar om en växelverkan JUST mellan de elektrisk laddade banpartiklarna och de — av allt att döma integrerat närvarande — neutrala uttunnade Kväve-Syreatomerna verkar därmed allmänt utbredd (även i MAC).

Elvesbildningen, översikt

Den möjliga Elve(s)bildningen enligt TNED

MED ANDRA ORD via maximal motverkan: två mer eller mindre diametralt kolliderande geomagnetiska elektrontrafikleder — trafikmönstret ← e → stört av ovan grovt framräknade lokala induktionsspänning û — i 80 KM-skiktet (rätvinkligt skärande över ekvatorn) med medelhastigheten relativt Jordytans fasta g-fält v=0,63c betyder enligt relaterad fysik (Beviset för multipla c; Ljusets friställning från kinetiken) uppenbarligen en summerande (relativt endera elektronmassan) hastighet på runt 1,2c.

Det blir enligt TNED med en sådan kolliderande situation OMÖJLIGT att undvika en lokalt cirkulär (speciellt i kollisionsriktningen) CIRKULÄRT EXPANDERANDE induktiv stötELEKTROMAGNETISK PLANVÅG SOM UTBREDER SIG radiellt från kollisionsområdet MED max LJUSHASTIGHETEN. Med andra ord: diametralt max dubbla c.

Genom att exakt c-utbredning i relaterad fysik reducerar MAGNETISKA FÖNSTRET till också exakt noll — ingen elektromagnetisk effekt hinner utbildas: nollverkan — är en massbaserad c-utbredning från ett expansionscentrum inte praktiskt möjligt (utom möjligen över ytterst snäva områden typ inom atomkärnornas begränsade volymer). Mekanisk-Elektriska sambandet visar att elektromagnetiska verkan (inverkan av magnetismen) avtar (drastiskt) över v=c/2. Med den föresatsen kan vi räkna med att maximalt DIAMETRALA utbredningshastigheten för en »kollisionsvåg» mycket väl kan överstiga c — som ovan typ v=0,63c radiellt.

I modern akademi finns inte den matematiken (Se från vic-felet). Källcitaten (Stanford1999) exemplifierar hur vetenskapsetablissemanget ser på fenomenformen (ELVES) som påstås utbreda sig cirkulärt diametralt snabbare än c. Orsaksgrunden är i bägge fallen TNED/MAC densamma: induktionsverkan (di/dt), men teorierna är väsensskilda.

—————————————————————————

Figurerna vänster i delvis extrakt från Jordatmosfären. Uppgifter om ELVES, HALOS och SPRITES är i stort samstämmiga oberoende av webbkällor (Mar2014), se särskilda webbkällor i ELVES. Beteckningen MP vid 100KM och 0,63c avser uppgiften om Magnetiska spegelPunkten i Zambiaexemplet.

Induktionsrekylerna är i vilket fall de enda fysiska baskällor som finns till förklaringen av de olika fenomenobservationerna (Elves, Halos, Sprites, Jets) i samband med atmosfäriska blixturladdningar vid Jordytan. Speciellt är de s.k. HALO-formerna i association med Sprites delvis formlika Elve-byggnaderna, men (betydligt) långsammare (och senare i utveckling) och mera långvariga.

För Elve-energierna anges etablerat (Rakov et al., 2003)

”For a typical negative first-stroke current of 30 kA, elves would be produced only if the return stroke speed were greater than about 2.5×10⁸ m/s.”,

Rakov2003 s8-6sp1mö.

— Man är generellt av den uppfattningen att Elve-fenomenen kräver speciellt häftiga urladdningar — knappast av den vanligare typen.

I TNED skulle den begränsningen (di/dt) hänsyfta snarare på strömstyrkan (i) än transientintervallet (t). Medan själva blixtkopplingen (t) torde vara en mer eller mindre utpräglat »blixtkonstant» för samtliga fall, har däremot strömstyrkan (i) avgörande inflytande på totala strömderivatan. Exakt vilka gränser som gäller i TNED explicit (med avseende på övre Jordatmosfären) finns här f.n. ingen räkning på.

Notera också den avgörande TEORETISKA SKILLNADEN ModernAkademi(MAC)/RelateradFysik(TNED) i föreställningen om orsaksgrunden vid TILLFÄLLET (eng. konv. discharge) för maximala strömtrycket (20 KA i vårt typiska räkneexempel), själva blixturladdningens höjdpunkt.

@INTERNET Wikipedia Lightning, Attachment, Discharge [2014-03-10]

http://en.wikipedia.org/wiki/Lightning - Attachment

”An enormous current of positive charges races up the ionic channel towards the thundercloud. This is the 'return stroke' and it is the most luminous and noticeable part of the lightning discharge.”,

;

”The electrical current of the return stroke averages 30 kiloamperes for a typical negative CG flash, often referred to as "negative CG" lightning.”.

I modern akademi (Se jämförelsen MAC/TNED i Blixturladdningens fysik) finns ingen ”atomtrådskanal” (och därmed heller ingen begriplig förklaring till blixtkanalens blotta bildning, se Citat ElectronSeed). TILLFÄLLET för Blixturladdningens Huvudström anses i MAC just vara som i citatet ovan: den upprusande JONSTRÖMMEN som i relaterad fysik OMGER blixtstammens centrala osynliga plasmatiska atomtrådsstam i vars centrum enligt relaterad fysik FÖREGÅENDE HUVUDSTRÖM elektronmassa redan har passerat, vårt studieexempel MolnNEGATIVT|Mark (konv. eng. negative CG lightning).

— Så: Medan man i MAC förlägger induktiva orsaken till typ ELVES på »returpumpen», ligger induktiva orsaken i TNED omedelbart före MAC: i DET att blixtkanalens koppling fullbordas med kopplingen stegledarens front mot marken och MarkStreamerns uppdel — tillfället då elektronkanalen fullständigas och full ATA-koppling (med möjlig CAT) verkställs.

Notera att induktiva RIKTNINGSFORMEN inte påverkas:

— TNED: elektronströmmen NERÅT MARKEN.

— MAC: jonströmmen UPPÅT molnet.

— Induktionslagen ger i bägge fallen en och samma RIKTNING i induktionsrekyleffekt på omgivande laddningsmassor. Enda skillnaden är att STRÖMTÄTHETEN i den mycket trängre elektronkanalen i TNED-fallet är betydligt högre än i den längre ut liggande jonströmmens periferi. Samt att TNED innefattar BÄGGE förekomsterna (först elektronrusningen, sedan jonrusningen), medan MAC i varje fall ansluter till Jonströmningsdelen men, som sagt, har svårt med det övriga.

”Return Strike”, »returpumpen», som fyller på elektronunderskottet i atomtrådarna i blixtkanalen, kommer enligt TNED först DÄREFTER (och i lugnare takt). Men den primära inre smala tunna elektronströmningen syns aldrig utåt. Det enda vi (fysikaliska mätinstrument) kan se i det yttre är just den uppåtströmmande returdelen, samma typ som i ljusbågsfenomenet enligt TNED.

— Men hur beskrivs då sammankopplingen moln/mark detaljerat i modern akademi, just på strömaspekten?

— Det är just Problemet i MAC: ingen vet. Ingen etablerad begriplig sammanhängande beskrivning finns (ännu Mar2014).

@INTERNET Wikipedia — Lightning Downward leader formation for negative CG lightning [2014-03-10]

http://en.wikipedia.org/wiki/Lightning

”In a process not well understood, a channel of ionized air, called a "leader", is initiated from a negatively charged region in the thundercloud.”

Winterberg2000Ref

BREAKDOWN VOLTAGE:

Lightning

ATTAINMENT OF GIGAVOLT POTENTIALS BY FLUID DYNAMIC SUPPRESSION OF THE STEPPED LEADER – ITS SIGNIFICANCE FOR THERMONUCLEAR IGNITION — F. Winterberg, University of Nevada (2000) datumuppgift saknas

http://arxiv.org/ftp/arxiv/papers/0804/0804.1764.pdf

”According to Paschen’s law the breakdown voltage between two plane

parallel conductors is only a function of the product pd, where p is the gas pressure and d the distance between the conductors. For dry air the breakdown voltage is 3×10⁶ V/m, such that for a distance of 300m the breakdown voltage would be 10Volt. This is the voltage which under ideal condition is reached in a lightning discharge. In reality the breakdown voltage is much smaller. The reason is that by a small initial inhomogeneity in the electric field, more negative charge is accumulated within the inhomogeneity, further increasing the inhomogeneity and eventually forming a “leader”, a small luminous discharge of electrons bridging part of the distance between the electrodes with a large potential difference. As a result a much larger electric field inhomogeneity is created at the head of the “leader”, which upon repetition of the same process leads to a second “leader”, followed by a third “leader”, and so on, resulting in a breakdown between the electrodes by a “stepped leader”, even though the electric field strength is less than the field strength for breakdown by Paschen’s law. What one has here is a growing electrostatic instability, triggered by a small initial electric field inhomogeneity.”

Se även andra kompletterande citat i Blixtspänningen.

Kalkylkorten — GranData, BlixtData

Kalkylkorten

GranData:

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN Blixt2014Gran.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/Blixt2014Gran.ods

Blixt2014Gran.ods — Tabell 1

Tabell1 — GranData

Tabell1 — Blixt2014Gran.ods: Summerar GROVRÄKNAT totala delgrenlängderna hos granträd med totalt 100 medelhuvudgrenar som utgår från själva trädstammen (grovt från granträd med höjden 12 meter och vidare uppåt; ref., Punkt1), samt beräknar totala BIObarrMedelytan för alla 100 grenar på TestKvistens basmatematik. Se utförligt från BIOytan.

BlixtData:

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN Blixt2014.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/Blixt2014.ods

Blixt2014.ods — Tabell 1-7

Tabell1 — Konstanter

Tabell2 — UtvecklingsTabell — Blixtkanalen — basdata — 25Feb2014

Tabell3 — UtvecklingsTabell forts. frn. Tabell2

Tabell4 — Utvecklings- och TestTabell, forts. frn. Tabell3

Tabell5 — DAGGPUNKTEN med KONSTANT LapseRate

Tabell5A — DAGGPUNKTEN med variabel LapseRate + TillämpningM med H2O

Tabell6 — Aktuella kalkylceller till jämförelse med PDASdata — SlutgrafernaPDAS

Tabell7 — Jämförelser | Noteringar — SlutgrafernaPDAS

Webbreferenser — Feb | Mar2014

PPT-doument kan (ofta) inte kopieras, saknar (ofta) källreferens

— men innehåller en del väsentlig information om HUVUDTRENDER.

WEBBKÄLLOR SOM VIDRÖR JORDYTANS LADDNING:

FÖREGÅENDE angiven WEBBKÄLLA (Experimenten i Sibirien Blixturladdningens Fysik 2008)

[http://205.243.100.155/frames/longarc.htm]

verkar inte längre (Feb2014) finnas tillgänglig.

— Återfunnen (2Mar2014) på

More Arcs 'n Sparks! (Updated 06/24/13)

http://teslamania.delete.org/frames/longarc.htm - Longspark

KÄLLA MED TYDLIG ILLUSTRATION HUR MODERN AKADEMI TÄNKER SIG BLIXTURLADDNINGENS INITIERING:

florica vlad — LIGHTNING (datumuppgift saknas) [8Mar2014-03-07]

http://florica.files.wordpress.com/2008/02/image004.gif

http://www.floricavlad.com/category/uncategorized?page=45

BESKRIVNING FRÅN 1966 — UTVECKLINGEN DE JORDATMOSFÄRISKA VETENSKAPSBEGREPPEN 1900-1965 — texten kan inte kopieras,

Defense Research Telecommunications Establishment, Ottawa —

THE EARTH OUTERMOST ATMOSPHERE, Irvine Paghis, 1966

http://adsabs.harvard.edu/full/1966JRASC..60..261P

”IN recent years our model of the earth’s upper atmosphere has changes almost beyond recognition.”, s261.

;

”Until about 1925 a division of the atmosphere into three spherically symmetric regions — the troposphere, stratosphere and exosphere — provided a reasonably consistent interpretation of the experimental data.”, s263mö.

— Ännu runt 1965 hade man inga mera säkra kunskaper om DE MERA PRECISA sammansättningarna i Jonosfären.

EN SAMTIDA PÅ SAMMA TEMA,

—Maskinskriven boktext — Stundtals så svag svärta att det är svårt att läsa (kan kopieras) — men (historiskt) intressant:

University of Illinois — AERONOMY REPORT NO. 5 |

AN INVESTIGATION OF IONOSPHERE- PROTONOSPHERE COUPLING

Geisler et al., 1965

https://archive.org/details/investigationofi05geis

”Above about 15 km the density of water vapor is so low that condensation

rarely occurs.”,

”The atmosphere is still characterized by winds and

vertical currents, however, and this continual stirring keeps the atmosphere

well mixed. Thus, water vapor is still found as high as 80 km, and the atmosphere

here can still be described as air, however rarilied, in the sense that

the relative abundance of the constituents is very nearly the same as that

near the surface of the earth”, s1m,

;

”Some ionization is found at all altitudes above

about 55 km, the level of the transient C-layer. Originally, it was thought that

this ionization existed in the form of discrete layers, separated by regions

of negligible ion content. It is now known that these "layers," (distinguished

by the prefix D, E and F) are little more than slight enhancements in an

electron density that increases montonically with altitude up to the F2-layer

maximum.”, s5m;

— Källan visar tydlig diagramfigur s6: elektrontäthetens variation 0-600KM, regionerna DEF markerade.

”The plasma of the F2-layer is one of oxygen ions and electrons.”, s7n.

;

”In addition to ions of atomic oxygen, the topside ionosphere is composed

of helium and hydrogen ions.”, s8mö.

;

”The whole of the topside ionosphere may be rather accurately described

as a region of three ionic constituents (O⁺ , He⁺ , H⁺) and electrons in a state

of diffusive equilibrium.”, s9n.

;

”Such

a situation cannot occur in the highly conducting ionospheric plasma and is

prevented by the presence of a vertically directed electric field of magnitude

sufficient to overcome the separative power of gravity and maintain charge

neutrality.”, s11ö.

;

”The altitude at which hydrogen first becomes the dominant

ion is highly variable in time and in latitude. Generally, it occurs between

about 1000 and 2000 km. The 1000 km level has been adopted as the base of the

protonosphere in this investigation.”, s11m.

BlixtSpänningen

ALLMÄNNA LABBDATA med enkla samband för utpräglade massiva elektroder PÅ LUFTENS GENOMSLAGSSPÄNNING

Wiley Online Library — SPARK-OVER VOLTAGES

Electrostatic Discharge: Understand, Simulate, and Fix ESD Problems, Third EditionPublished Online: 22 SEP 2009

http://onlinelibrary.wiley.com/doi/10.1002/9780470495070.app3/pdf

”The voltage at which a given air gap will arc depends on the shape of

the electrodes, the micrometric roughness of their surfaces, the air pressure and

temperature, and eventually their speed of approach if one electrode is mobile.

Provided that (a) the voltage is dc or at a frequency low enough to allow a

complete deionization of the channel between two consecutive arcs and (b) the

gap itself is dry and dust free, spark-over voltages are given by the law established

by Paschen in 1889, from which the curves in Figures C.1 and C.2 are derived.

They show that in the range of 0.3–3 atmosphere (1 atm = 1016 mbar, or 15 psi),

the breakdown voltage is about proportional to the exact pressure and gap length.

Little more accurate than the gross 10-kV/cm rule-of-thumb for sharp edges, a

coarse approximation for millimeter to few centimeter gaps can be used: (1)

• For flat, or large radii spherical electrodes:

V (kV) = 3pd + 1.3√d

• For sharp, needle electrodes:

V (kV) = pd + 0.7

where

d = gap length, mm

p = atmospheric pressure, atm

”.

Se även

@INTERNET Wikipedia High voltage — Sparks in air [2014-03-02]

http://en.wikipedia.org/wiki/High_voltage

”The dielectric breakdown strength of dry air, at Standard Temperature and Pressure (STP), between spherical electrodes is approximately 33 kV/cm.[2] This is only as a rough guide, since the actual breakdown voltage is highly dependent upon the electrode shape and size.”; 33KV/cM = 3,3 T6 V/M.

;

”For air at STP, the minimum sparkover voltage is around 327 volts, as noted by Friedrich Paschen.[3].

While lower voltages don't, in general, jump a gap that is present before the voltage is applied, interrupting an existing current flow often produces a low-voltage spark or arc.”.

— Notera återigen inverkan av elektrodernas form: ”etablerade experiment” använder (ofta) sfäriska kulelektroder i basförsöken.

UPPHITTAT REFERENS TILL JORDLADDNINGEN:

LIGHTNING — PHENOMENOLOGY (ytterst långsam uppladdning typ 0,02 MB/S, totalt 9,41 MB)

— webbkällan saknar dessutom namn och datum

http://www.tau.ac.il/~colin/courses/AtmosElec/LightningFlash.pdf

”Upper atmosphere/ionosphere is positively charged. Ground is negatively charged.”

— Separat sökning (”http://english.tau.ac.il/”) visar att källan är Israelisk. TEL AVIV UNIVERSITY

JordElektriskaFältvariationer

Jordladdningens variationer, tydliga diagram

FIRST RESULTS OF THE NEW TYPE OF MEASUREMENTS OF ATMOSPHERIC ELECTRIC FIELD IN MEXICO —

Pulinets et al., 2006

http://www.geociencias.unam.mx/~bole/eboletin/EF_Pulinets_4_BOL-E.pdf

POWER SPECTRUM FEATURES OF THE NEAR-EARTH ATMOSPHERIC ELECTRIC FIELD IN KAMCHATKA —

Mikhailov et al., 2004

http://www.earth-prints.org/bitstream/2122/759/1/25Mikhailov.pdf?origin=publication_detail

AMS, variationer land hav dygn

American Meteorological Society —

RELATING ELECTRIFIED CLOUD PROPERTIES TO WILSON CURRENTS: AN OCEANIC AND CONTINENTAL CASE STUDY, Sarah Al-Momar 2012

https://ams.confex.com/ams/93Annual/webprogram/Paper218670.html

”They measured continental thunderstorms to have mean Wilson currents of approximately 1.0 kA while oceanic thunderstorms contributed 1.6 kA. In contrast, continental ESCs produced only 0.13 kA while oceanic ESCs produced 0.39 kA (Mach et al. 2011).”, s3n,

;

”Land thunderstorms had an average flash rate of 2.2 flashes/minute while oceanic storms had an average rate of only 0.8 flashes/minute.” s4ö,

— VAD VI VET: Solvinden står för både positivt laddade partiklar (mest protoner, en del tyngre joniserade atomer) och negativt laddade partiklar, elektroner, som når Jorden kontinuerligt/variabelt med Solaktiviteterna.

FOCUS MATERIEN 1975:

Blixt, Jonosfär

”De elektriska urladdningarna, blixtarna, sker i regel mellan olika delar av ett och samma moln eller mellan närliggande moln eller mellan den nedre negativa laddningen och jorden. Blixtar inom molnen är ca 4 gånger vanligare än blixtnedslag.”, s507sp1mö.

;

”Genomsnittliga längden på en blixt vid nedslag är i Europa 1–2 km och i tropikerna 2–3 km. Spänningsfallet längs en blixtbana är ca 20–50 miljoner volt och strömstyrkan rör sig omkring 20 000 ampere.”, s507sp1mn.

;

”Jonosfären

Ju högre upp i atmosfären man kommer, desto större inverkan får solens ultravioletta strålning och långvågiga röntgenstrålning. När denna strålning träffar en syre- eller kväveatom, lösgörs en elektron och återstoden blir då en molekylär eller atomär positivt laddad jon. En del av elektronerna förenar sig med atomer eller molekyler av syre och bildar negativa joner. Även flera andra rekombinationer förekommer. Den partikelstrålning från solen, som orsakar norrsken, medverkar till sådana processer.”, s512sp2mö.

;

”Det finns ingen bestämd gräns mellan jordens atmosfär och solens, de övergår kontinuerligt i varandra. I det yttersta skiktet av det som kallas jordatmosfären är vätet helt joniserat. Det kallas protosfären.”, s513sp1m.

FOCUS MATERIEN 1975 (s486sp1mö) anger att 70,8% av Jordytan upptas av haven. Grovt räknat ger det en effektiv fast landyta på ca 29% (71% oceaner).

JONOSFÄREN:

— kopplingen Jordmagnetiska fältet

@INTERNET Wikipedia — Ionosphere[2014-03-07]

http://en.wikipedia.org/wiki/Ionosphere

”The ionosphere is a region of the upper atmosphere, from about 85 km (53 mi) to 600 km (370 mi) altitude, and includes the thermosphere and parts of the mesosphere and exosphere. It is distinguished because it is ionized by solar radiation. It plays an important part in atmospheric electricity and forms the inner edge of the magnetosphere.”.

;

@INTERNET Wikipedia — Ionospheric dynamo region, Atmospheric Electric Conductivity [2014-03-07]

http://en.wikipedia.org/wiki/Ionospheric_dynamo_region

”At heights between about 85 and 200 km however -the dynamo region-, solar X- and extreme ultraviolet radiation (XUV) is almost completely absorbed generating the ionospheric D-, E-, and F-layers. Here, the electrons are already bound to the geomagnetic field gyrating several times about these lines before they collide with the neutrals, while the positive ions still essentially move with the neutral gas. Thus, the electric conductivity becomes anisotropic. The conductivity parallel to an electric field E is called Pedersen conductivity. The conductivity orthogonal to E and the geomagnetic field Bo is the Hall conductivity. Ohmic losses and thus Joule heating occur when Pedersen currents flow. The component parallel to Bo still increases with altitude. Near the geomagnetic dip equator, a west-east directed electric field generates vertical Hall currents which cannot close. Therefore, a vertical polarization field builts up generating a horizontal Hall current which adds to the Pedersen current. Such enhancement is described by the Cowling conductivity. Pedersen and Hall conductivities reach maximum values near 120 to 140 km altitudes with numbers of about 1 mS/m during sunlit conditions. During the night, these numbers may decrease by a facor of ten or more. The values of these conductivities depend on local time, latitude, season and solar 11- year cycle. The height integrated conductivities become of the order of 50 S, or a total resistance of the dynamo region of about 1/50 = 0.02 Ohm during day time conditions.[5]”.

JORDFÄLTET:

Fältladdningen

TROPOSPHERIC-IONOSPHERIC COUPLING BY ELECTRICAL PROCESSES OF THE ATMOSPHERE

— Bhattacharya et al., May2013

http://ijaiem.org/Volume2Issue5/IJAIEM-2013-05-30-086.pdf

”Integrating the vertical electric field profile derived from aircraft or balloon measurements up to the troposphere one can determines the ionospheric potential. As reported at 12 UT this has the value 230 kV and it rises to 310 kV at 16 and 20 UT which then falls to 200 kV at 24 UT. The curve closely resembles the Carnegie Curve [117] and is considered as one of the “confirming ideas” [119] supporting the behaviour of the Earth-atmosphere global circuit system. A significant generator of the conduction currents up to the ionosphere, also known as Wilson currents, is owing to the action of thunderstorms which serve as batteries.”, page331top CURRENT FLOW AND IONOSPHERIC POTENTIAL;

”The electrodynamics coupling between the Earth’s atmosphere and the ionosphere is very complex and described by the

global electric circuit. Currently, many aspects are not well understood.”, page331bot CONCLUSIONS.

PDF-dokument som presenterar elektrontätheten i atmosfären (jonosfären, »ionosphere, charge density») finns. Men diagramuppgifterna (Feb2014) omfattar bara exceptionellt höga altituder: inte lägre än (vid en första grov genomläsning av det som kommer fram först) 50-60 KM. Jämför ett av citaten nedan: övre gränsen för Jordytans elektriska fältstyrka (konstant) ligger vid runt 3 KM. Stort glapp.

— Wikipedias artikeldiagram för elektrontätheten (Ionosphere 28Feb2014) anger värden från 600 KM till 85 KM.

— Se tilljämförelse en »hittills mest upphittad» diagramkarta:

EAS 4360/6360 — bildsida 29:19 (datum/namn saknas)

http://shadow.eas.gatech.edu/~cpaty/courses/SpacePhysics2013/SpacePhysics2013/Lectures_files/Lecture29_2013.pdf

— Källverket verkar vilja framhäva att elektrontätheten vid en viss nivå helt upphör. (Säg det då — se FM1975 nedan).

— Källverket illustrerar Birkeland Currents bildsida 29:32 (”Pedersen currents”).

FOCUS MATERIEN 1975 säger det:

Elektrontäthet, Jonosfären

”Den del av atmosfären inom vilken förekomsten av joner och elektroner är tillräcklig för att påverka utbredningen av radiovågor, kallas jonosfären. Den har ingen utpräglad vare sig undre eller övre gräns. Av mätningar framgår, att hög elektrontäthet inte förekommer under ca 60 km höjd och rent definitionsmässigt låter man jonosfärens undre gräns sammanfalla med mesopausen i 75 km-nivån. Därifrån sträcker sig jonosfären upp till mycket stor höjd.”, FOCUS MATERIEN 1975 s512sp2mö.

PDF-DOKUMENT SOM VISAR ELEKTRONTÄTHETEN jonosfären EXPLICIT I DIAGRAM (s7352; s7356)

— störst omkring 300 KM över Jordytan, mellan 200KM/450KM,

JOURNAL OF GEOPHYSICAL RESEARC —

TWO-COMPONENT MODEL OF TOPSIDE IONOSPHERE ELECTRON DENSITY PROFILES

RETRIEVED FROM GLOBAL NAVIGATION SATELLITE SYSTEMS RADIO OCCULTATIONS,

González-Casado et al., 2013

http://gage6.upc.es/gAGE_WEB/papers/2013/10.1002_2013JA019099.pdf

—OBS: Akta IE(9); AkrobatReader slutar fungera med ovanstående URL-öppning; Mozilla-webbläsaren fungerar OK.

PLAG

Positiva lagrets atmosfäriska gåta

JordFältstyrkan mäts med en s.k. Gerdien-cylinder [Whitaker2006, s17n]. Stora variationer förekommer via inverkan från Solen, väderleken generellt (vind, temperatur), speciellt vid åska och nederbörd.

WILSONSTRÖMMEN:

THE ATMOSPHERIC GLOBAL ELECTRIC CIRCUIT: AN OVERVIEW, Siing et al., (2006) datumuppgift saknas

http://arxiv.org/ftp/arxiv/papers/0906/0906.1280.pdf

”The global electric circuit (GEC) links the electric field and current flowing in the lower

atmosphere, ionosphere and magnetosphere forming a giant spherical condenser

(Lakhina, 1993; Bering III, 1995; Bering III et al., 1998; Rycroft et al., 2000; Siingh et

al., 2005), which is charged by the thunderstorms to a potential of several hundred

thousand volts (Roble and Tzur, 1986) and drives vertical current through the

atmosphere’s columnar resistance. The current causes weak electrification of stratified

clouds (Harrison and Carslaw, 2003) and produces a vertical potential gradient in

atmospheric layers near the surface. Horizontal current flows freely along the highly

conducting earth’s surface and in the ionosphere, which is closed by the current flowing

from the ground in to the thunderstorm and from the top of the thunderstorm to the

ionosphere and back from the ionosphere to the ground through the global fair-weather

load resistance (~ 100 Ω).”, s2ö.

;

”In an active thunderstorm the upward current flows from thunderstorm to the

ionosphere, which is known as Wilson current.”, s2m.

HISTORICAL REVIEW Wilsonströmmen

THE EARTH’S ELECTRICAL SURFACE POTENTIAL —

A summary of present understanding, Gaetan Chavalier Jan2007

http://74.63.154.231/here/wp-content/uploads/2013/06/Chevalier_electrical_surface_potential-2007.pdf

Whitaker2006

— En av de bästa referenserna, absolut (Centralen Upphittad Feb2014):

THE EFFECT OF IONS ON THE CONDUCTIVITY OF EARTH’S ATMOSPHERE — Jerry C. Whitaker, 2006

http://chemtrailsplanet.net/2012/12/09/the-effect-of-ions-on-the-conductivity-of-earths-atmosphere/

http://saive.com/WXMOD/Atmospheric_Electrostatics.pdf

”Cosmic rays originate from solar flares and other galactic objects such as supernovas and

exploding stars.”, s16.

;

”The result is that one cosmic particle could be responsible for the creation of as many as one

billion ion pairs.”,

”The average production rate at sea level is about ten million ion pairs per cubic metre per

second. However, the average ion population at any given time is nearly

one hundred times more, and ion mobility with altitude as air gets

thinner has a drastic effect on the electric structure of the atmosphere.”, s17.

;

”The average field strength at the earth’s surface is on the average 100 volts per metre and

decreases to less than 10 volts per metre at an altitude of 3 km.”, s23.

— Källan beskriver Mixing Layer vid 3 KM, s21, ”less than 10 volts per metre at an altitude of 3 km.”, s23ö.

s24:

”One crucial question still remains to be answered. What causes the

positive space charge in the atmosphere and how is the opposite

negative charge maintained on the earth's surface?”.

s29:

”THE ELECTRIC BUDGET

Where does the energy of nearly 200 million watts come from that is

required to maintain the earth-atmosphere electric fairweather field?

Are thunderstorms generating the fairweather field by leaking off

positive charge from cloud tops to the conducting ionosphere and by

bringing negative charge to earth in the form of negative ground strokes

and point discharge currents?”,

”Or is the electric charge on the earth's surface maintained by the electrochemical charging mechanism in close

collaboration with convection and eddy diffusion? These are some of the

basic questions that are still in need of answers.”.

s30:

Wilson-strömmen.

Forskingsfakta

— eller ren teoretisk spekulation?:

s25:

”As already mentioned, the atmosphere is conducting and the earth's

electric potential or field must cause a current to flow in the

atmosphere. Since there is an excess of positive ions residing in the

atmosphere and an opposite negative charge bound on the earth's

surface, charge must flow to earth in the form of a positive ion current.”

;

s32:

”recent satellite

data show that thunderstorms are mainly active over continental land

masses rather than over oceans (Turman, 1978, Turman and Edgar,

1982).”

GYMNASIETS FYSIK åk2 Liber 1980 s26:

— Källan beskriver korrekt enligt TNED — men hurså? Andra MAC-källor?

”Jordens elektriska cykel

Den kraftiga elektromagnetiska strålning som utsänds från solen ger upphov till variabla elektriska fält. Dessa fält växelverkar med jordens magnetfält och skapar kraftiga elektriska strömmar i jordens innandöme.

Negativa laddningar av storleksordningen 1800 C lämnar per sekund jordens yta och går ut i atmosfären. Detta motsvarar som du vet en ström av 1800 A. I jonosfären där norrsken uppträder kan man påträffa tillfälliga maximiströmmar på upp till 500 000 A! Dessa strömmar är dock obetydliga jämfört med dem som flyter fram i jordens kärna. Man uppskattar storleken av dessa strömmar till omkring 10⁹ A.

Man vet inte i detalj hur jorden kompenseras för sin förlust av negativ laddning. Dock tror man sig veta att ständigt mellan

3 000 och 6 000 åskväder är aktiva över hela jorden (100 blixtar/s) för att föra tillbaka denna laddning.

Urladdningarna vid ett åskväder äger rum på de ställen, där den elektriska fältstyrkan är som störst, t ex vid torn och höga träd. I bilden nedan ser vi ett åskmoln som passerar över en kyrka. Det huvudsakliga elektronförrådet vid molnets bas repellerar elektroner i markytan omedelbart under molnet. Dessa elektroner ger sig iväg och skapar potentialdifferenser ända upp till storleksordningen 10⁸ volt. När luftens elektriska hållfasthet överskrids sker en spontan jonisation och urladdning, varvid negativ laddning tillförs jorden.”.

WHO (World Health Organisation):

Jordfältet, styrka

WHO — NATURAL BACKGROUND AND HUMAN-MADE SOURCES AND EXPOSURE — (datum saknas) [28Feb2014]

— texten kan inte kopieras

http://www.who.int/peh-emf/publications/3_EHC_232_Sources_and_Exposure.pdf

”Natural electric fields

The natural electric field encountered above the surface of the Earth varies greatly with time and location. The primary cause of the field is the charge separation that occurs between the Earth and the ionosphere, which acts as a perfect conductor separated by air of negligible conductivity (König et al., 1981). The field near the surface typically has a fair weather strength of about 130 V m^–1 (Dolezalek, 1979). The field strength decreases with height, with values of about 100 V m^–1 att 100 m elevation, 45 V m^–1 at 1 km, and less than 1V m^–1 at 20 km. Actual values vary widely, depending upon the local temperature, the humidity profile and the presence of ionized contaminants. Large field variations occur att ground level beneath thunderclouds ..”.

— Källan ger typvärden i tabell (Table 3; sidnummer saknas).

;

Annan version samma källa som kan textkopieras (men med modifierat innehåll),

WHO — EXTREMELY LOW FREQUENCY FIELDS (2007) [28Feb2014], frn.s25

http://apps.who.int/iris/bitstream/10665/43646/1/9789241572385_eng.pdf?ua=1

”Variations of up to 40 kV m^–1 occur near thunderstorms, although

even in the absence of local lightning, fields can reach up to 3 kV m^–1.

Because the dominant component usually changes very slowly, the phenomenon

is often described as “electrostatic”.”

Jordladdningen

EARTH’S CHARGE AND THE CHARGES OF THE VAN ALLEN BELTS — Jacob Biemond (2010)

http://vixra.org/pdf/1008.0071v1.pdf

”It is generally assumed that the naked Earth bears a large negative charge Q_s of

about – 4.5×10⁵ C (see e.g., Uman [1])..”.

Jordfältet, styrka

CHARGE OF THE EARTH — 1999 Oregon State University

http://www.physics.oregonstate.edu/~mcintyre/COURSES/ph431_F12/examples/EarthCharge.pdf

”The electric field strength in the atmosphere near the surface of the earth is

about 100 volts/meter and points downward. The potential increases with

increasing height, up to about 300 kV = 300 000 volts. This field is

maintained by thunderstorms, which deposit negative charge on the earth

at the rate of about 10³ amperes.”.

JORDYTSLADDNINGEN, ORSAK:

ORIGIN OF THE EARTH’S OVERALL ELECTRICAL NEGATIVE CHARGE — (10Jul2013)

http://fgservices1947.wordpress.com/2013/07/10/origin-of-the-earths-overall-electrical-negative-charge/

”It’s generally accepted that the earth’s surface is, from an electrical sense, charged negatively and that this negative charge is caused by the charge separation observed in thunderclouds in the earth’s atmosphere. That charge separation is thought to be due to the collision between ice and/or water particles inside clouds, with the subsequent lightning redistributing those charges to the surface”.

BIRKELAND CURRENT — Wikipedia [2014-02-27]

http://en.wikipedia.org/wiki/Birkeland_current

”A Birkeland current is a set of currents which flow along geomagnetic field lines connecting the Earth’s magnetosphere to the Earth's high latitude ionosphere”,

;

”Auroral Birkeland currents carry about 100,000 amperes during quiet times[7] and more than 1 million amperes during geomagnetically disturbed times.[8] Birkeland had estimated currents "at heights of several hundred kilometres, and strengths of up to a million amperes" in 1908.[3] The ionospheric currents which connect the field-aligned currents heat up the upper atmosphere due to the finite conductivity of the ionosphere”.

YAHOO ANSWERS — Does the earth have a net positive/negative electrical charge? (datumuppgift saknas, ”3 years ago”);

man får själv [2014-02-27] räkna ut sifferresultatet, så att det TYDLIGT kan anges på enklare form, men det är ingenting som källan står för typ GodtyckligMånadOchDagFårDuSjälvGissa.

http://answers.yahoo.com/question/index?qid=20100929082548AA6zwU8

”The Earth is negatively charged, carrying 500, 000 C of electric charge, and is at 300, 000 V of voltage difference from the positively charged ionosphere. There is a constant flow of electricity, at around 1350 A, and resistance of the Earth atmosphere is around 220 Ohms. This gives a power output of around 400 MW, which is ultimately regenerated by the power of the Sun that affects ionosphere, as well as troposphere, causing thunderstorms. The electrical energy stored in atmosphere is around 150 GJ.

The Earth-ionosphere system acts as a giant capacitor, of capacity 1.8 Farads.

The earth surface carries around -1 nC of electric charge per square meter of surface.

The global atmospheric electrical circuit produces the Earth's natural DC electric field. The natural field can be visualized as a spherical capacitor system: the outer shell is formed by a conductive layer of positive charge, the electrosphere, balanced by a layer of negative charge distributed over the surface of the Earth. The electric field close to the ground is maintained by continual transfer of charge to the ground through global thunderstorm activity. The electrosphere is at elevations above the clouds forming a continuous and distinct element”. Källan refererar till artiklar från Wikipedia.

FORUM:

PHYSICS FORUMS — Earth's charge (5Feb2005)

http://www.physicsforums.com/showthread.php?t=62780

”How come the Earth is negatively charged?”;

;

”Where did you hear or read that?”;

”Electrons are much more easily removed from molecules in the air and clouds. Rain can carry the electrons to the earth where the negative charge is distributed. At some point, a lighting discharge occurs and some of the electrons travel up the arc back to the positive ions.”.

— Artikeln som sådan kan inte läsas gratis, här endast kommentarerna.

SCIENTIFIC AMERICAN — Detecting the Earth's Electricity (9May2009)

http://www.scientificamerican.com/article/detecting-the-earths-elec/

”The article states that we stand on top of a massive negative charge. It is my understanding that the earth maintains a massive positive charge. Is this an error in reasoning or do my facts conflict with actuality?”;

;

”If the earth has a massive negative charge, the Cumulo Nimbus clouds must have a positive charge. This does not make sense to me. Does someone have an answer to this question?”;

;

”Not sure, but I have always thought that the leading lightning stroke is from Earth to sky. Since real current (not the electronic circuit convention) is carried by electrons, with negative charges, the Earth must be negative with respect to sky and clouds. After the first stroke, the current oscillates until neutrality is reached, at least for a while. That's the way I have always thought of it. Let me know if I'm wrong; I'd really like to know.”

BlåTrädet

Se även ELMEK (eng. Elves)

Webbkällor med fotografier (och videosekvenser) finns som visar eller ANTYDER att blixturladdningar Moln|Mark FÖREFALLER ske med en samtidig utsträckning av blixtträd UPPÅT inåt i molnet.

— Det är också svårt att bevisa enbart via synintryck på videosekvenser, då åskväder i allmänhet innehåller en skur av blixttivolin på många olika ställen.

— OM det ändå är så, KAN det i sig förstås vara en ren jämviktskonsekvens av den nedåtgående laddningsbilden. Men det verkar inte finnas någon direkt (gratis tillgänglig) etablerad webbreferens som omnämner saken.

ELVES — Elves, Halos, Sprites, Jets — Mar2014

GOOGLE BOOKS:

Elves fenomengrunder — Obs begränsad åtkomst

BALL LIGHTNING: AN UNSOLVED PROBLEM IN ATMOSPHERIC PHYSICS, Mark Stenhoff 1999

books.google.se/books?isbn=0306461501

”A group at Stanford University detected a third form of stratospheric lightning in December 1994. These were named ”elves” in the same vein as the name ”sprite.” These are halos of red light that are formed above a CG flash at altitudes of about 90 km and spread into rings up to 300 km across in less than 1 ms.””, s36m.

NYARE SAMMANFATTNING:

OBSERVATION OF ELVES AT THE PIERRE AUGER OBSERVATORY — 33RD INTERNATIONAL COSMIC RAY CONFERENCE,

RIO DE JANEIRO 2013

http://143.107.180.38/indico/getFile.py/access?contribId=676&sessionId=4&resId=1&materialId=paper&confId=0

”Transient luminous events (TLEs) like elves, sprites, halos

and jets are luminous emissions detectable well above

thunderstorms. Lightning discharges generate electromagnetic

pulses (EMPs) which accelerate free electrons.”.

NYARE SPRITETEORI:

Aspekter på Lightning ingår (s799)

SURVEYS IN GEOPHYSICS — Toward Better Understanding of Sprite Streamers: Initiation, Morphology, and Polarity Asymmetry,

Pasko et al., 2013

http://www.ee.psu.edu/Directory/FacultyInfo/Pasko/Publications/PaskoSG2013.pdf

”As the thundercloud charges slowly build up before a lightning discharge, high-altitude regions are shielded from the quasi-electrostatic fields of the thundercloud charges by the space charge induced in the conducting atmosphere at the lower altitudes.”, s799ö.

TIDIGA 3D-SIMULERINGAR:

THREE DIMENSIONAL SIMULATIONS OF SPRITES AND ELVES, H.L. Rowland (1998|9) datumuppgift saknas

http://www.agu.org/webcast/rowland/web1wp.html

— Se källans länkar i Animations.

— Ingen grundteori diskuteras.

Heavner2000

BRA REFERENSVERK

— Viss teori diskuteras:

SPRITES, BLUE JETS, AND ELVES: OPTICAL EVIDENCE OF ENERGY TRANSPORT ACROSS THE STRATOPAUSE,

Heavner et al., (2000|1) datumuppgift saknas

http://www.uas.alaska.edu/artssciences/naturalsciences/envs/faculty_staff/pubs/chapman.pdf

”The common sources of energy driving these processes in the stratosphere and mesosphere are tropospheric thunderstorms and lightning.

The electric field generated by these storms heats ambient electrons which result in electron impact excitation of the ambient N₂ leading to the observed optical emissions.”, s1sp2n.

;

”Since initial documentation in 1989, three types of phenomena occurring above thunderstorms have been documented: sprites, blue jets, and elves”, s3sp2n

;

”Sprites are associated with the Quasi-Electrostatic (QE) fields of lightning, as first suggested by Wilson [1925]. Their sources are the electrostatic fields from

the charges in thundercloud.”, s4sp1ö.

;

”Sprites span the altitude between ~40-95 km and last ~10-100 ms.”, s3sp2n.

;

”Sprites generally occur in association with large positive cloud-to-ground (CG) lightning”, s3sp2mö.

;

”Elves, while not currently triangulated for accurate altitude determination, are estimated to occur between 75-95 km altitudes, lasting less than 1 ms.”, s3sp2n.

;

”The EMP fields are associated with the generation of elves.”, s2sp1ö.

— ElvesEnergier är svåra att hitta på webben (Mar2014), se upphittat i Rakov et al.,

NeutralCol

Orsaken till ljusemissionerna;

”The optical emissions observed in sprites, blue jets, and elves are caused by collisions of energetic (heated) electrons with neutrals.”, s3sp1ö.

Källan beskriver saken mera utförligt s7sp2n.sek3.2.

;

”Negative cloud-to-ground discharges remove negative charge from the thunderstorm to ground and constitute approximately 90% of

lightning activity”, s3sp2ö.

CG%

— Uppgiften ovan kan (möjligen) vara ett feltryck (samma uppgift användes av mig i Blixturladdnings Fysik): Senare källor (Wikipedia Lightning, General properties Mar2014) ger ca 1/4 MolnMark-urladdningar. Men redan FOCUS MATERIEN 1975 [‡] håller sig till just ca 1/4 för MolnMark-urladdningar.

”Great progress has been made in the theoretical understanding of sprites, elves, blue jets and blue starters since the first video recordings.”, s3sp2m.

;

”In a thunderstorm, electrical charges are accumulated in a number of charge centers by a slow process, typically minutes or 10's of minutes [MacGorman and Rust, 1998].”,

;

”A lightning discharge is a rapid rearrangement of these charges and consequently intense electric fields are generated. These fields have two primary sources, one electromagnetic and one electrostatic.”, s3sp2mn.

Orsaken till radiella spridningen;

”The current change (di/dt) in a lightning stroke radiates a large electromagnetic pulse (EMP). The EMP fields propagate upward, with amplitude decreasing inversely with distance 1/r (like the far field of an antenna) until reaching the bottom of the ionosphere. These fields are not large enough to cause breakdown in the atmosphere at low altitudes, but the atmospheric density and, thus, the field required for breakdown decreases exponentially with altitude (the scale height in the middle atmosphere is ~7 km).”, s3sp2n.

;

”The theoretical studies discussed below (originating with work by Inan et al. [1991]) show that breakdown from the EMP field will occur in the region between the bottom of the iono sphere at about 95 km and about 75 km,”, s3sp2n.

;

”The EMP fields are associated with the generation of elves.”, s4sp1ö.

;

”The 100 µs duration of elves is close to the 10-100 µs duration of the high current portions of typical lightning strokes. Elves also have a large horizontal extent (100's of km) matching expectations from the 1/r drop in field strength.”, s4sp1ö.

ElectronSeed

Källan om »ElektronFröet» som triggar blixturladdningar:

”The runaway electron model postulates a high energy seed electron (possibly a cosmic ray secondary) accelerated by the electric field above a thunderstorm [Roussel-Dupré et al., 1998; Taranenko and Roussel-Dupré, 1996; Lehtinen et al., 1996]. If the seed electron has enough

kinetic energy, a collision between the seed electron and a low energy (ambient) electron can result in two relativistic electrons. This process is predicted to produce a beam of avalanching runaway electrons. Optical emissions produced from this mechanism would have a much higher characteristic energy than the quasi-electrostatic heating model predicts.”, s8sp1mn.

SCIAM:

Elves, radiella spridningen

SCIENTIFIC AMERICAN — SPRITES AND ELVES LIGHTNING'S STRANGE COUSINS FLICKER FASTER THAN LIGHT ITSELF

(1999) datumuppgift saknas

http://nova.stanford.edu/~vlf/optical/press/elves97sciam/

”The Stanford researchers managed to get a good look at 10 elves. All started just above a groundstroke of normal lightning but expanded into rings up to 300 kilometers (200 miles) across in less than a thousandth of a second. Although the elves appear to spread faster than light, analysis of the physics behind elves demonstrates that no particles actually move that fast, so Einsteinian relativity is not violated. The faster-than-light illusion seems to be caused by successively distant air molecules lighting up in rapid-fire sequence, like the strobe lights running along an airport runway.”.

— Ingen av MOVIE-länkarna i artikelns slut leder någonvart [Mar2014].

Rakov2003

ELVES ENERGIER:

kolla sökfiltret (som visar hur besvärligt det KAN vara att få fram varan):

energy transmission in elves :pdf -elf -elven -customer -christmas -prince -festival

LIGHTNING ELECTRIC FIELD INTENSITY AT HIGH ALTITUDES: INFERENCES FOR PRODUCTION OF ELVES,

Rakov et al., 2003

http://www.lightning.ece.ufl.edu/PDF/Rakov%26Tuni.pdf

”[10] Electromagnetic field pulses produced by lightning return strokes can cause breakdown of the neutral atmosphere at altitudes ranging from about 70 to 95 km where the gas density is considerably reduced (so that the electron mean free path is considerably increased) relative to that at ground level [e.g., Inan et al., 1991; Krider, 1994; Rowland et al., 1996]. This breakdown (heating of the electrons by the lightning electromagnetic pulse) is thought to be responsible for the transient optical emissions (enhanced airglow) observed at those altitudes and termed elves [Fuknunishi et al., 1996]. According to Fernsler and Rowland [1996], the breakdown first occurs at about 95 km, where the gas density is about 4×10¹³ cm^–3 (the electron mean free path is of the order of 1 m) and the minimum field needed to increase the electron density by more than two e-folds (their definition of breakdown) is about 15 V/m, with the field pulse duration being about 100 ms. Using the critical value of field, 15 V/m, and integrating the corresponding Poynting vector for the TL model over the first 100 ms, we obtained the value of energy density of 60 µJ/m² needed for the production of elves.”, s8-3sp2n.

— Det är dock fortfarande oklart VAD källan REFERERAR det värdet till: produktionen i blixtkanalen som GER, eller själva ELVEN som TAR. Olyckligt. Källan beskriver f.ö. exempel med ELVE-bildningar från ReturnStrokes på 30-300 KA.

”For a typical negative first-stroke current of 30 kA, elves would be produced only if the return stroke speed were greater than about 2.5×10⁸ m/s.”,

s8-6sp1mö.

NSTA

WEBBKÄLLA SOM VIDRÖR JORDYTANS LADDNING:

NATIONAL SCIENCE TEACHERS ASSOCIATION — Books & Resources | NSTA WebNews Digest | Science and Children : Science 101 | What causes lightning and thunder? | 6/14/2006

http://www.nsta.org/publications/news/story.aspx?id=52177

”Charge Separation on Earth

It might surprise you that there is a more-or-less constant charge separation between the Earth and the atmosphere, no matter what the weather. The Earth is negatively charged, and there is a gradual move toward a more positive charge as you move up in the atmosphere.

Scientists believe that cosmic rays (subatomic particles traveling the universe) are largely responsible for creating this charge separation between the Earth and the atmosphere; they ionize molecules in the atmosphere through collisions.”,

;

”Well, if everything in the universe tends toward electric neutrality, why then don’t electrons move around until the atmosphere “discharges” itself? Turns out they do. Scientists have measured the rate of this discharge, and if this discharge were the only motion of charges in the atmosphere, the Earth and the atmosphere would neutralize each other in a very short time.

Of course, I already told you that the charge separation between the Earth and the atmosphere is more-or-less constant. This means that there must be something that keeps “charging up” this system and maintaining the initial charge separation. That something is lightning, which acts like a battery keeping the Earth-atmosphere system charged up.”,

”Because cosmic rays interacting with the atmosphere create a charge separation [referens saknas], there is a steady current flowing from the atmosphere to Earth.

Lightrning strikes create an electric current that counteracts the current from Earth to the atmosphere.”, Figure 1.

;

”There are competing theories as to how this charge separation happens, but the result is well documented. The clouds end up with an overall negative charge at the bottom, an overall positive charge at the top, and a concentration of positive charges towards the center. The negative charge buildup at the bottom of the cloud is much more concentrated than the normal negative charge of the Earth, so the bottom of the cloud is more negative than the Earth. Because electric forces get stronger the closer things are, the electric forces between the bottom of the cloud and the Earth are very strong—much stronger than the electric forces between the Earth and the positive charges in the upper part of the cloud. It looks something like Figure 2.”,

”The large negative charge at the bottom of the cloud means Earth just below the cloud is positive with respect to the cloud.”, Figure 2.

;

”This charge separation between the bottom of the cloud and the Earth ionizes the air between the cloud and the Earth and does so in steps. Something called a “step leader,” which is nothing more than ionized air, begins to stretch from the cloud to the Earth. It progresses in steps of about 50 m (hence the name step leader) and brings excess negative charges from the cloud toward the Earth.”,

;

”The step leader itself consists of moving charges and constitutes a small electric current, but the return electric current from the Earth is much larger and thus the current we associate with the major lightning flash. So, lightning actually moves from the Earth upward.”,

;

”To revisit where we started, note that each lightning bolt results in negative charges flowing to the Earth (because the bottom layer of the cloud is more negative than the Earth). This maintains that constant charge separation between the Earth and the atmosphere that I discussed earlier”.

”Acts like a battery”.

— Det var något nytt.

ÄNTLIGEN — DÅ — EN ETABLERAD WEBBKÄLLA SOM BESKRIVER DETALJERNA I DET STORA HELA.

LalandeRef

PDF-DOKUMENT SOM VISAR FRONTEN på Stegade ledaren

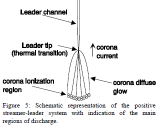
MODELLING OF THE LIGHTNING CONNECTION PROCESS TO A GROUND STRUCTURE, Lalande et al., (datumuppgift saknas [1996]) [28Feb2014]

http://www.irsweb.it/en/PDF/Modelling_of_the_lightning_connection_process_to_a_ground_structure.pdf

Texten kan kopieras men är KRYPTERAD — omöjlig att få ut något begripligt ur. Sidnumrering saknas dessutom.

Molbegreppet — JAGVH — Språkförbistringen i mol inom modern akademi

Se även från tidigare i

KJ/mol — ElektronenVdW

Molbegreppet — Allmänna gaslagen

MOLBEGREPPET — mol

2014III17

WIKIPEDIA med många andra är EXPERTER på att INTE I enkel KLARTEXT KUNNA förklara vad ENHETEN typ ”KJ/mol” betyder.

— KJ — kilojoule till att börja med — vet vi betyder 1000Joule. Men:

Per mol?

— Vad betyder PERmol?

Kolla läsarens utdragna lidande — inget svar ges:

@INTERNET Wikipedia Joule per mole [2014-05-14]

http://en.wikipedia.org/wiki/Joule_per_mole

Per Amount of Material:

1: inget svar:

”The joule per mole (symbol: J·mol⁻¹) is an SI derived unit of energy per amount of material. Energy is measured in joules, and the amount of material is measured in moles.”;

.. quantities .. context-depemdent ..:

2: fortfarande intet svar:

”Physical quantities measured in J·mol⁻¹ usually describe quantities of energy transferred during phase transformations or chemical reactions. Division by the number of moles facilitates comparison between processes involving different quantities of material and between similar processes involving different types of materials. The meaning of such a quantity is always context-dependent and, particularly for chemical reactions, is dependent on the (possibly arbitrary) definition of a 'mole' for a particular process.”;

.. these quantities .. usually ..:

3: fortfarande noll respons: — SNÄLLA: FÖRSÖK KOMMA TILL SAKEN NÅGON GÅNG (!, please):

”For convenience and due to the range of magnitudes involved these quantities are almost always reported in kJ·mol⁻¹ rather than in J·mol⁻¹. For example, heats of fusion and vaporization are usually of the order of 10 kJ·mol⁻¹, bond energies are of the order of 100 kJ·mol⁻¹, and ionization energies of the order of 1000 kJ·mol⁻¹.”;

1KJ/mol = 1,04 t2 eV per partikel:

4: viss ledtråd:

”1 kJ·mol⁻¹ is equal to 0.239 kcal·mol⁻¹ or 1.04×10^-2 eV per particle. At room temperature (25 °C, 77 °F, or 298.15 K) 1 kJ·mol⁻¹ is equal to 0.4034 k_BT.”, ”k_BT” ingen förklaring; artikeln slutar där.

SVAR —

se även vidare RELATERAT i efterföljande huvudtext:

— PER 1000u/KG.

Enhetsnormaliseringen med ”1/KG” är för att få numeriska kvantiteter;

— Samma som PER 1000 · 1,66033 t27 KG/KG = GÅNGER 1,66033 t24;

— Samma som PER Avogadros tal: Avogadros tal = 1KG/1000u = PER 6,02289 T23.

PRÖVNINGSEXEMPEL MOT WIKIPEDIAARTIKELNs PÅSTÅENDE

för att styrka samhörigheterna:

— 1KJ/mol = 1000J·1000u/KG = 1,66033 t21 J; 1,66033 t21 (J=V·C)/(e=1,602 t19 C) = 0,0103641 eV ~ 1,04 t2 eV.

— Enda ”problemet” är: enheten (1,66033 t21 J). Enheten (1,66033 t21 J) gäller

1. per atom om, och endast då, den materiella enheten också är en atom och

2. per molekyl om, och endast då, den materiella enheten också är en molekyl: en molekyl är samma som flera atomer som förenats (elektroKemisk bindning) till en enda materiell enhet.

— Enkelt uttryckt: per MOL betyder »per Avogadros tal för de materiella enheterna, whatever».

— Men AKTA, se vidare nedan i MAC-fasonerna (Molbegreppet, språkförbistringen i MAC).

Utförligt — relaterat:

RELATERAD FYSIK (TNED):

— Atomvikten (U) för ett atomslag är medelvärdet för de experimentellt uppmätta atomernas medelmassor i det atomslaget (m_ATOM) dividerat med atomära massenheten (u = 1,66033 t27 KG i denna framställning), vilket ger U som en dimensionslös numerisk kvantitet:

m_ATOM/u = U ; atomviktens definition med bestämd dimensionslös numerisk beteckning U

Svar på frågan VARFÖR SEPARAT BETECKNING FÖR ATOMVIKTEN INTE INGÅR I ETABLERADE VERK har eftersökts men ännu [Mar2014] inte påträffats. Däremot anges U-värdena frekvent i olika etablerade tabellverk. Exempel nedan.

— Atomvikterna anges i internationellt standardiserade atomviktstabeller (eng. atomic weight, eller relative atomic mass), men (ännu utan upphittat undantag) utan separat beteckning; Man använder istället — med kaotiskt resultat — identiteten typ ”Atomic weight, u” med u korrekt som ”Atomic mass unit”, men vilket sammanhang INTE varken är tydligt, entydigt eller förklarande. Se refererande exempel nedan från Wikipedias tabell List of elements.

Notera i engelsk litteratur (numera):

— ENGELSKA Webbkällor verkar ha YTTERST SVÅRT för att relatera det ytterst enkla begreppet atomvikt — ANTALET ATOMÄRA MASSENHETER (u=1,66033 t27 KG), värdebokstaven U, för en specifik atom — till det lika ytterst enkla begreppet atomär massa, samma som produkten av U och u i MKSA-enheter — eng. atomic mass.

— Tabellexempel finns [http://www.lenntech.com/periodic/mass/atomic-mass.htm] [2014-03-26] som använder den engelska termen Atomic Mass för motsvarande (vars beteckning INTE skrivs ut) atomvikten U [webbkällan anger heller ingen motsvarande term för Uu].

WikipediaList

— Wikipedia (Relative atomic mass) använder beteckningen A(r) för den relaterade fysikens U=m(ATOM)/u (U, själva den numeriskt ENHETSASSOCIERADE atomviktsbeteckningen) och benämner denna korrekt [traditionellt] ”atomic weight”.

— MEN på ett annat ställe — LIST OF ELEMENTS [http://en.wikipedia.org/wiki/List_of_elements][2014-04-01] — anges i kolumnen för ”Atomic weight” [Relaterat U=m(ATOM)/u] beteckningen ”u [Atomic mass unit]”:

— DEN UPPENBARA OFÖRMÅGAN ATT ANVÄNDA EN BETECKNING FÖR atomic weight [Relaterat U=m(ATOM)/u] fördunklar BARA YTTERLIGARE den helt enkla presentationsformen: Vad, exakt, menar tabellförfattaren? Ingen beskrivning finns.

— Så här skulle kolumnen i Wikipediatabellen List of elements ha betecknats KORREKT med motsvarande upplysande, fullständigt relaterbar, text:

Atomic weight

U — med Hinten [peka på U:et, en liten ledtext kommer fram]: ”Atomic weight U in units of The Atomic Mass Unit u”:

U = m[ATOM]/u ; m[ATOM] experimentally measured ; u = 1/12 of mass of Carbon12-atom [= 1,66033 t27 KG]

Inte med mindre.

— U anger atomviktens numeriska värde i u-enheter. Så enkelt — men TYDLIGEN helt orepresenterat i MAC.

— Och det är samma visa i stort sett överallt i etablissemangets atomära festligheter: numerisk [U] beteckning för atomvikt saknas.

— Man kan [stillsamt] undra varför typ etablissemanget generellt INTE KAN FÖRMÅ SIG ATT ANTA ENTYDIGA BETECKNINGSSÄTT FÖR redan väl [under 1900-talet] etablerade begrepp — t.ex. beteckningar U för atomvikt — utan envisas att [ständigt] införa en flora av RETORISKA ersättare.

— Dessa detaljer bidrar ytterligare till att ämnet försvåras: floran »standardbeteckningar».

— Mer eller mindre måste man genomgå en LISTA för VARJE tillämpningsområde för HITTA igen någon ENHET som begripligt passar till MKSA-systemet.

Molbegreppet:

Varför sysslar (typ) Wikipedia (vetenskapsetablissemanget generellt -2014) med den här typen,

”Mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as the amount of any substance that contains as many elementary entities (e.g., atoms, molecules, ions, electrons) as there are atoms in 12 grams of pure carbon-12 (12C), the isotope of carbon with relative atomic mass 12. This corresponds to the Avogadro constant, which has a value of 6.02214129(27)×10²³ elementary entities of the substance.”

utan att klargöra exakt samma kvantitet enligt standardiserade universella enheten i MeterKilogramSekundAmpere;

1 mol = U·1KG/1000Uu ; u atomära massenheten 1,660[33] t27 KG

= 1KG/1000u

= 6,022[89] T23 ; Avogadros tal; Se Webbkällan ovan i citat

”amount of any substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12”

= Avogadros tal ; ρ = m/V

Wikipediaförfattningens RETORISKA anda — att ALDRIG FÖRST OCH FRÄMST klargöra genom kvantitativa beräkningsbara matematiska samband, utan istället försöka ARTIKELPRATA SIG FRAM — gör ämnesbeskrivningen svårfattlig, klumpig, tvetydig: ”Amount”? Endast med ledning av talvärdet hittar vi [i detta fall] rätt lösning. Så fungerar INTE en naturvetenskaplig encyklopedi.

— Varför inte?

— Varför måste man (ofta i Wikipedia) läsa hela noveller, försöka lirka och lista ut vad som menas kvantitativt i klartext i fysikbeskrivningen, vad det är som gäller? Därför att författarna är teoretiker som inte sysslar med praktiskt naturvetenskapligt arbete (utan har Wikipedia som Egen Glänsande PinkExpertDomän), och därför inte förstår värdet av upplysningen. Please. Det är i och för sig inget fel på framställningen. Den är bara väldigt mycket TRÄAKTIG.

— ÄNNU VÄRRE blir det (i Wikipediaartikeln, sektionen The mole as a unit) när författarskaran börjar med den här utläggningen — efter att har upplyst om att det framförts viss kritik även från EN DEL ETABLERADE vetenskapsled angående molbegreppets status:

”In chemistry, it has been known since Proust's law of definite proportions (1794) that knowledge of the mass of each of the components in a chemical system is not sufficient to define the system.”

— Och VEM ATOM har nu påstått något sådant att ”massan enbart skulle räcka”?

GaslagenEkv

— Allmänna gaslagen [E=pV=kT; energi (E), tryck (p), volym (V), OBS hydrostatisk konstant (k) typ vid STP, temperatur (T)]

pV = kT ; k fundamentala gaskonstanten = 370,95002 J/°K vid STP

= bN·T ; b Boltsmanns konstant = 1,38[055] t23 J/°K vid alla möjliga tillstånf

= b(m_ρ/Uu)·T ; N Loschmidts tal = 2,68697[22T25] antalet ideala gasbollar i 1 M³ vid STP

= b(ρV/Uu)·T ; ρ gasens täthet KG/M³; U gasens atomvikt i antal u; u atomära massenheten 1,660[33] t27 KG

= NuR·T ; R allmänna [konv. universella] gaskonstanten = 8314,9148 (J/°K)/KG = k/Nu

; R anges R i originalförfattningen, fetstilen här enbart för att underlätta den visuella navigeringen:

= (m_ρ/Uu)uR·T ; Notera också R-formen mot den i modern akademi, se R* — samt den förhärskande språkförbistringen i mol

= (m_ρ/U)R·T ; = kT ; m_ρ/k = U/R :

= (ρV/U)R·T

Notera att allmänna gaslagen bara gäller specifikt INOM ett bestämt HYDROSTATISKT [av Jordgravitationen bestämt] område: fundamentala gaskonstanten k är specifik för en bestämd volym [1M³] där alla 1M³p/T=konstant. Vid havsytan [STP] gäller k=370,95002 J/°K [Se Beräkningen av k från hydrostatiska trycket], medan lägre k-värden gäller med växande höjd över markytan [alla Tpρ avtar med växande höjd — upp till grovt ca 10 KM, troposfären]. Se vidare från Allmänna gaslagen, om ej redan bekant.

innehåller SOM VI SER ALLDELES TYDLIGT OCH KLART redan alla fullständiga — kemiska — parametrar i det internationella MKSA-systemet. Så vadan invändningen?

Mitt förslag endast baserat på denna skrifts ytterst trånga framställning, och inget annat — jämför WikipediaStilen nedan med ”molar mass unit” som definitivt bevisar angelägenheten året 2014 — författarna kan inte hantera begreppen:

— Ta bort molbegreppet — HELT; anpassa det FÖRST till MKSA-systemet med enheten Kmol (se nedan) och ersätt det sedan med DET FULLSTÄNDIGT DIREKT BEGRIPLIGA

1Kmol = 1KG/u ; u atomära massenheten 1,660[33] t27 KG: mol är numeriskt:

1 mol = 1KG/1000u

DÄRFÖR ATT DET ÄR I VILKET FALL SÅ VI MÅSTE RÄKNA I DET PRAKTISKA FALLET FÖR ATT KUNNA UTFÖRA BERÄKNINGAR i reda kvantiteter.

— Människor som läser »nuvarande mol-standard» i typ Wikipedia (-2014) har ett h-e att komma någonvart i grundstudierna, ENBART på grund av den allmänt klassiskt kemiskt etablerade latheten att INTE specificera ovanstående.

— Men det kanske (också) finns en annan anledning: atomära massenheten (u) är INTE väldefinierad i MAC. Dvs.: Man hänger kvar vid en definitionsbas som i grunden är överflödig, men som inte förstås vara det på grund av brist på härledande preferenser.

EXEMPEL — Wikipedia (Barometric formula)

”M = Molar mass of Earth's air (0.0289644 kg/mol)”;

— I MKSA-enheter skriver vi istället DIREKT

»M = Atomvikten hos luft vid Jordytan är 28,9644u», u=atomära massenheten [konv. (2014) 1,66053 t27 KG].

I UniversumsHistoria har antagits u = 1,66033 t27 KG genomgående för samtliga kvantitativa beräkningsgrunder, för att kunna ge allmänna konkreta exempel [med början FÖRE anknytning till Internet].

Molbegreppet, språkförbistringen i MAC:

Wikipediaexemplets formbutik SKULLE alltså också KUNNA skrivas (citatet nedan) kvantitativt:

molar mass unit = KG/mol

= KG/(1KG/1000u)

= 1000u ; u = 1KG/(1000·AvogadroNumber)

= 1KG/AvogadroNumber

Wikipedia — MOLAR MASS [2014-03-26]

http://en.wikipedia.org/wiki/Molar_mass

”In chemistry, the molar mass M is a physical property. It is defined as the mass of a given substance (chemical element or chemical compound) divided by its amount of substance.[1] The base SI unit for molar mass is kg/mol.”,

— Försök sedan slå upp vad »amount of substance» betyder, och man hamnar definitivt i trubbel: ”size of an ensemble of elementary entities”.

— Vad ska det föreställa för något? Är det CircusGuitar som har anlänt?

Size?

— ”The base SI unit for molar mass is kg/mol”.

— Nej. SI-enheten för molar mass är U/1000 · KG/mol.

— Ett konkret exempel klargör:

molar mass unit = (U/1000) · 1KG/AvogadroNumber

med exemplet för luften vid Jordytan

M = 0,0289644 KG/mol

= 0,0289644 KG/(6,02289 T23)

= 4,80905 t26 KG

= (U[luft]=28,9644)·(u=1,66033 t27 KG)

= Uu

Och alltså: Generellt för godtyckliga atomärt sammansatta material med bestämda atomvikter U;

molar mass unit = U · 1KG/1000AvogadroNumber

= (U/1000) · 1KG/AvogadroNumber

= (U/1000) · 1KG/mol ; Konv. »molar mass unit» sv. »molMassEnheten»

= (U/1000) · 1KG/(6,02289 T23)

= U · 1KG/1000mol

= U · 1KG/Kmol

= AtomicWeight · 1KG/Kmol

= AtomicWeight · 1KG/1000AvogadroNumber

= AtomicWeight · 1KG/1000(6,02289 T23)

= AtomicWeight · 1KG/(6,02289 T26)

= AtomicWeight · u

NOT — svenska INTE (ej, icke, nopp, osv.) — ”kg/mol”. Utan »ATOMVIKTEN dividerat med 1000 GÅNGER» ”kg/mol”.

— Då stämmer det perfekt i kassaräkningen.

— Föregående uttryckta ståndpunkt upprepas därför bestämt : ta bort mol-begreppet ur standardformerna: molbegreppet har inte där att göra.

— Molbegreppet, som i exemplet ovan, bara förkrångligar, missleder, skapar oklarheter och är oändligt knöligt, rent träaktigt att använda — utom för inbitna experter: de som redan etablerat sin privata domäns tempelcirkel, på väl upptrampade stigar.

Molbegreppet kan tydligen inte klargöras — relateras — i den etablerade samlingens regi.

— Vari, egentligen, består haken?

Sett från relaterad fysik, TNED:

— Alldeles tvärsäkert består haken i det här: atomära massenheten (u), den som modern akademi har VELAT med under hela kemins vetenskapshistoria (först från Väte1, sedan Syre16, sist rätt träff på Kol12): man förstår inte preferenserna; ingen kan relatera grunderna; fattas MOTIVET, försvinner också intresset: ingen kan förklara. Se utförlig relaterad härledning i Atomära Massenheten.

FOCUS MATERIEN 1975, s156sp1m

”En mol av ett ämne är så många gram av ämnet som den samanlagda atomvikten anger.”

— Påståendet i citatet ovan är bara delvis korrekt formulerat.

Vi studerar hur och varför.

— Enda konsekventa MATEMATISKA innebörden i termen och begreppet 1 mol är Avogadros tal — 6,02289 T23 — om resultatenheten är i gram, eller Avogadros tal gånger 1000 — 6,02289 T26 — om resultatenheten är i KG. Belysande exempel nedan.

— Begreppet mol används i samband med Avogadros tal (gram-mol) eller Avogadros tal gånger 1000 (kilogram-mol) efter följande matematiska grundform:

totala massan

(1) N = —————— = antalet enheter i totala massan

enhetsmassan

— Enhetsmassan beskrivs i atomfysiken som produkten av enhetens atomvikt U och atomära massenheten

u = 1,66033 t27 KG (1/12 av Kolatomens massa).

— Med beteckningen m för totalmassan därmed

(2) N = m/Uu ; antalet Uu-enheter i m, numerisk kvantitet

— U-värdet för en viss enhet

— en atomtyp (atom) eller flera atomtyper tillsammans (molekyl) då dessa föreningsKemiskt formar ett materiellt ämne

— ges experimentellt från tabellvärden med uppmätta atomvikter (U) för alla grundämnesatomer.

— Är ett ämne, t.ex. vatten (H2O) sammansatt av flera olika atomer (2st Väte H och 1st Syre O) — en molekyl — beräknas U som summan av de enskilda atomära atomvikterna (se etablerade atomviktstabeller). I fallet vatten får man avrundat U=18,02;

— Massan (m) hos en vattenmolekyl beräknas då

(3) m = NUu = 1·18,02·u = 2,99191 t26 KG ; Massan hos 1 vattenmolekyl

RD, Relaterat dubbelexempel

— Betrakta nu följande »grepp» — grunden bakom »poängen» med DET FLERTYDIGA (hopplöst virriga) BEGREPPET mol:

— Vi använder FOCUS-citatets meningsform ovan för att belysa sammanhanget med den retoriskt förvirrande sammanblandningen mellan numeriska och fysikaliska enheter:

— Och vi sätter sedan som ovan

N = m/Uu

Använder vi här genomgående — konsekvent — ett fast bestämt N-värde lika med 1KG/u=6,02289 T26 = Avogadros tal gånger 1000 ger det i vattenexemplet

m = NUu

= (1KG/u)(18,02)u

= 18,02 KG ;

N = m/Uu

= (18,02 KG)/[18,02u]

= 1/(1,66033 t27)

= 6,02289 T26 för samtliga U-fall, oberoende av U-sammansättning; jämför Focus-citatet ovan;

En KILOmol av ett ämne är så många KILOGRAM av ämnet som sammanlagda atomvikten anger.

— Alltså i klartext: Avogadros tal gånger 1000 av ämnet.

Med massenheten för totalmassan istället i gram (här förenklat g) ges motsvarande:

Använder vi här genomgående — konsekvent — ett fast bestämt N-värde lika med 1g/u=6,02289 T23 = Avogadros tal ger det i vattenexemplet

m = NUu

= (1g/u)(18,02)u

= 18,02 g ;

N = m/Uu

= (18,02 g)/[18,02u] = (0,01802 KG = [18,02/1000] KG)/[18,02u]

= 1/(1000·1,66033 t27 = 1,66033 t24)

= 6,02289 T23 för samtliga U-fall, oberoende av U-sammansättning; jämför Focus-citatet ovan;

En mol av ett ämne är så många gram av ämnet som sammanlagda atomvikten anger.

— Alltså i klartext: Avogadros tal av ämnet.

— De bägge färgmarkerade avsnitten visar motsvarande FOCUS-mening omsatt i praktiskt exempel — men dessa meningar är INTE korrekta mot fysiken.

— Det finns, veterligt HELLER, inget RETORISKT JUSTERANDE SÄTT att rätta till Focuscitatets mening så att den delen STÄMMER med matematiken.

No way.

Nämligen därför, som exemplet ovan entydigt visar, att molbegreppet används synonymt MATEMATISKT med inverterade värdet av atomära massenheten (u) — dessutom i gram eller kilogram beroende på preferens.

PER 1 mol är PER Avogadros tal 6,02289 T23: antalet enheter (molekyler eller atomer) i ämnesmassan:

m = U; »1 mol är ämnets molekylAvogadros tal» (det är vid dessa tillfällen man funderar på att börja riva biblioteket)

— m är i KG, medan U är numerisk kvantitet. Korrekt sätt är m=Uu; U = m/u.

Rekommendationer:

Egna beräkningar: UNDVIK SAMTLIGA HELT ONÖDIGA OKLARHETER i »molbegreppets vetenskapsklassiska turbulens» genom att ALLTID använda den enkla, rena och RAKA massformen i sambandet nr(2) ovan.

Olika Påståenden i Etablerad litteratur: Exemplen ovan kan användas för att, jämförelsevis, försöka klara ut vad någon viss påstådd mening försöker berätta.

EXEMPEL:

— TYP Wikipediaartiklar KAN kasta fram den helt meningsmässigt LOGISKT VIRRIGA (helt omöjliga att klara ut i mening, innebörd och sammanhang, eftersom en sådan historia inte existerar i matematiken, se MAC-exemplen ovan) men väl etablerat klassiska typen ”molvikten för vatten är 18,02 g/mol”.

”The molar mass of water is 18.02 g/mol”,

@INTERNET Wikipedia — Water vapor [2014-03-18]

http://en.wikipedia.org/wiki/Water_vapor

— Vad betyder det?

— Det betyder (uppenbarligen) inget annat än 18,02 gram per 6,02289 T23 stycken vattenmolekyler; Vi testar det genom att räkna enligt nr(3):

m = NUu

= (6,02289 T23)(18,02)(1,66033 t27 KG)

= 0,0180199 KG

= 18,0199 g ; Stämmer tydligen utomordentligt.

Jämför det BETYDLIGT mer upplysande:

— Atomvikten för vatten är 18,02u.

— Direkt. Exakt. Rakt på sak. Inga omvägar. Jättesvårt i MAC.

Molndata, 14Mar2013 — begreppen i Modern Akademi

MAC: En SNÖFLINGA kräver ett — typ — pollenkorn för att bildas PÅ [http://www.noaa.gov/features/02_monitoring/snowflakes_2013.html] [2014-03-19].

— Lever vi i året 723? Snöflingor kan inte bildas ENBART från vatten? VAR finns DEN referenten? Det vore underbart att få beskåda. Jämför H2Odata.

— MAC: Snöflingans iskristaller växer till SOM flingan faller genom (det kalla) molnet och träffar på allt flera vattenmolekyler.

— Så: Varför är inte snöflingor i så fall ALLTID kubiska, varför flata? Därför att snöflingor inte utvecklas enligt MAC.

— Se sammanställning i bild på alla olika snöflingetyper i http://www.nasa.gov/pdf/183517main_snowcrystals.pdf.

@INTERNET Wikipedia — Snow, Snowflakes [2014-03-19]

http://en.wikipedia.org/wiki/Snow

”In warmer clouds an aerosol particle or "ice nucleus" must be present in (or in contact with) the droplet to act as a nucleus.”.

Ingen referens ges.

Från vattenånga till vattendroppe

— Ingen vet, riktigt. Vetenskapsetablissemanget (-2014) anser generellt (webbsökningar @INTERNET) att droppbildning från utspridda vattenmolekyler KRÄVER en separat fast central katalyserande kondenskärna — typ mikroISpartikel (som i sin tur har bildats genom ..) eller pollenkorn — för att begreppet vattendroppe i moln ska bli av.

Arnott1997

Molndroppar 1-14µM, optisk mätning:

Optical Society of America —

DROPLET SIZE SPECTRA AND WATER-VAPOR CONCENTRATION OF LABORATORY WATER CLOUDS:

INVERSION OF FOURIER TRANSFORM INFRARED (500–5000 CM^–1) OPTICAL-DEPTH MEASUREMENT —

Arnott et al., 1997

http://www.patarnott.com/pdf/dropletSizeRetrieval.pdf

”Direct measurement of the cloud droplet

size spectra agree with size spectra retrieved from inversion of the extinction measurements. Both

indicate that the range of droplet sizes is 1–14 µm.”

Kondensationen börjar ..

@INTERNET Wikipedia — Atmospheric electricity [2014-03-18]

http://en.wikipedia.org/wiki/Atmospheric_electricity

”Most authorities agree that whatever may be the origin of free electricity and the net unbound positive charge in the atmosphere, the generation of enormous currents (flow of electrons, negative charges), that flow between clouds and ground during a lightning discharge, begins with condensation of water vapor within the clouds; each minute water droplet moving through the air collects upon its surface a certain amount of negative charge by collecting 'free' electrons. As these tiny drops coalesce into larger drops, and still larger drops, there is a corresponding decrease in the total exposed surface upon which the collected electronic charges can be carried, raising the negative voltage as droplets combine. The combined negative electric potential of all the coalescing water drops rises until it overcomes the resistance of the, usually non-conductive, air, and jumps to earth in a flash, moving negative electrons against the electric field gradient. In effect, the lightning, acting as a charge pump, restores the positive charge of the lower atmosphere.”

SkjuusMe:

”.. begins with condensation”?

— Det här är en underlig Passage: EN vattenmolekyls massa (m) är m=NUu=(1)(18,02)(1,66033 t27 KG)=2,99191 t26 KG ~ 3 t26 KG; Sambandet [Momentekvationen] för gasers — även ångors — medelhastighet i 12°C luft

v = √ 3bT/m = √ 3(1,38055 t23 J/°K)(285,15 °K)/m

= √ (1,18099 t20 J)/m

ger med m=1H2O

v = √ (1,18099 t20 J)/(3 t26 KG)

= 627,42635 M/S

Hastigheten avtar sedan med växande ångpartikelmassa. En Ø2,8µM vattendroppe har motsvarande v ca 3 cM/S.

— Vadå ”begins with condensation”? Vattenmolekylerna STÖTER HELA TIDEN IHOP (H2Opar | Tretyakov2013), precis som luftmolekyler, och det blir omöjligt att — i varje fall under någon tidrymd — INTE åstadkomma större H2O-föreningar på den vägen (MultiH2O): Beroende på tillgång och tryck, formas tydligen på viss argumentkraft vattendroppar AUTOMATISKT av värmegraden i aktuellt luftrum. (Begreppet condensation blir irrelevant ...).

Vattendroppar bildas omedelbart från molekylär avdunstning genom värmerörelser som tvingar vattenmolekyler att förenas kontinuerligt i proportion till medelmässig väglängd i gastrycket.

— UPPGIFTEN HÄR skulle bl.a. vara att visa att det argumentet är FEL. Ännu inget upphittat: Jämför Tretyakov2013.

Met Office — WHAT ARE CLOUDS AND HOW DO THEY FORM? (28Oct2013) [18Mar2014-03-18]

http://www.metoffice.gov.uk/learning/clouds/what-are-clouds

”How do clouds form?

Clouds form when the invisible water vapour in the air condenses into visible water droplets or ice crystals. There is water around us all the time in the form of tiny gas particles, also known as water vapour. There are also tiny particles floating around in the air - such as salt and dust - these are called aerosols.

The water vapour and the aerosols are constantly bumping into each other. When the air is cooled, some of the water vapour sticks to the aerosols when they collide - this is condensation. Eventually, bigger water droplets form around the aerosol particles, and these water droplets start sticking together with other droplets, forming clouds.”

(Väl Fjuttig argumentering).

— Om det bara är BUMPNINGEN det kommer an på, varför blanda in aerosoler (luftpollen o dyl.)?

— Därför att dessa katalyserande agenter rättfärdigar AVKYLNINGSMEKANISMEN — allmänna kondensationsdynamiken:

— I ett varmt rum med hög luftfuktighet, INGA synliga MOLN, faller synligt vatten direkt ut VIA en införd KALL materialyta.

— Generellt i MAC tycks man vara av den allmänna uppfattningen att vattendroppar — moln, se även i NoDrop — bildas på typ pollen:

@INTERNET Wikipedia — Cloud condensation nuclei [2014-03-18]

http://en.wikipedia.org/wiki/Cloud_condensation_nuclei

”Water requires a non-gaseous surface to make the transition from a vapour to a liquid”.

Referens saknas.

Please DO show. Wikiartikelns högst avgörande påstående saknar referens.

— Jag vill för min egen del på intet sätt motsätta mig det faktum ATT vatten KAN och faktiskt kondenserar på SEPARATA material med lägre temperatur än luftens.

— Men det var inte dagens rätt. För att hoppa över alla mellanliggande led: på menyn står det 2H2O existerar:

— Kan 2, kan alla. Kan inte 2, kan inga. Vidare i H2Opar, EkinEs och H2Odata.

— Alltså: Det finns ingen anledning att ifrågasätta inverkan av luftpartiklar som katalysatorer för vattendroppsbildning ur en närvarande vattenånga. Det är INTE sakens uppgift:

— Sakens uppgift är att vattendroppar — från minsta vattendroppen 2H2O och större — förenas om de möts, vilket leder oss till slutsatsen att bara någon minsta föreningshastighet existerar, kommer vattendroppar att bildas ur vattenånga.

— Närmaste köksexemplet är dimman — mikroskopiska vattendroppar — över kokande vatten. Vattenånga är osynlig.

— Man skulle också — utan stöd av typ Tretyakov2013 — vara benägen att säga i konsekvens, vilket kan prövas: en vattenånga bildar genom vattenmolekylernas föreningsbenägna dipolkaraktär en viss minsta droppstorlek (i området nanometer, H2Opar) beroende på temperatur och tryck.

Niessner2010

Springer — Chapter 2

NANOPARTICLES ACTING AS CONDENSATION NUCLEI — WATER DROPLET FORMATION AND INCORPORATION, Reinhard Niessner, 2010

”Cloud or fog formation is not possible without the existence of submicron-sized particles.”, s13

PDF-dokument som måste öppnas separat

Författaren ger inget annat än exempel från typen aerosoler.

”från vattenånga till vattendroppe” — noll sakvetenskapliga artiklar 2014-03-19 GoogleSök

”from water vapor to water droplet” — noll sakvetenskapliga artiklar 2014-03-19 GoogleSök

Niessner2010 s15mn [10Maj2014]:

”This

would mean that nanoparticles would never be incorporated into condensing water,

since the required water supersaturation for acting as condensation nuclei would be

tremendously high, by far exceeding the available 1 or 2% within a cloud or fog

situation.”.

Endast Vatten i Vatten: Ø1,72 nM:

Flytande vattendata — och synpunkten med vattenmolekylens elektriska dipolkaraktär

THE MOLECULE OF WATER 2014 [2014-03-18]

http://www.chem1.com/acad/sci/aboutwater.html

”Theoretical models suggest that the average cluster may encompass as many as 90 H2O molecules at 0°C”,

”At 70° C, the average cluster size is probably no greater than about 25.”.

En upphittad äldre (1940) källa verkar vara den enda som till viss del berör sakdetaljerna (HUR vattendroppar formas i moln):

AN EVALUATION OF THE BERGERON-FINDEISEN PRECIPITATION THEORY, A. R. STICKLEY 1940

http://docs.lib.noaa.gov/rescue/mwr/068/mwr-068-10-0272.pdf

”As then formulated, it asserted that, disregarding

some rather exceptional cases, the necessary condition

for the formation of drops large enough to produce rain

of any considerable intensity is that subfreezing temperatures

exist in the cloud layer from which the rain

descends.”, s272sp1ö

;

”When

the mean value together with the assumed initial radius is

used in Schmidt’s equation, it is found that it requires over

7 days for drops with a radius of 100µ to form and over

75 days are required for the formation of drops with a

radius of 1,000µ.”, s273sp1m

The National Center for Atmospheric Research — CLOUDS AND HOW THEY FORM, 2011

https://spark.ucar.edu/shortcontent/how-clouds-form

”It’s easier for water vapor to condense into water droplets when it has a particle to condense upon. These particles, such as dust and pollen, are called condensation nuclei. Eventually, enough water vapor condenses upon pieces of dust, pollen or other condensation nuclei to form a cloud.”

Scientific American — HOW DO WATER DROPLETS IN CLOUDS COHERE? , 25Jun2001 [2014-03-18]

http://www.scientificamerican.com/article/how-do-water-droplets-in/

”The number and size of the droplets depend on the degree to which the atmosphere is oversaturated, and the number and characteristics of tiny particles, called cloud condensation nuclei, on which the water condenses. When enough droplets of at least a few tenths of a micron form, they become visible as a cloud.”

APSref

FÖRSTA RELEVANTA DATA:

American Physical Society | Physics — FOCUS: HOW RAINDROPS FORM, 22Mar2001 [18Mar2014]

http://physics.aps.org/story/v7/st14

”Theorists have suspected for nearly forty years that wind was a catalyst helping the raindrops form more quickly. The wind, it was believed, increased the relative velocities of the micrometer-sized droplets and caused them to collide and stick together until they became large enough to begin falling. But even after theorists included wind velocities in their models, they could not make their predictions match observation.”,

;

”According to the team’s new calculations, these clusters appear to be about a millimeter in size–just the size needed for raindrops to begin falling.”

Malinowski2007

Ingen URL finns, datumuppgift saknas (2006) [18Mar2014]

CLOUD-CLEAR AIR INTERFACIAL MIXING:

ANISOTROPY OF TURBULENCE GENERATED BY EVAPORATION OF LIQUID WATER.

LABORATORY OBSERVATIONS AND NUMERICAL MODELLING, Malinowski et al., (2007)

”The so called “warm rain initiation problem” attracts

attention of cloud physicists, turbulence researchers,

engineers and meteorologists. It is still uncertain which

mechanism is responsible for the formation of drizzle

and rain (precipitation) drops.”,

;

”Unfortunately, properties of cloud turbulence at

scales relevant for the interactions between droplets and

the air flow have never been documented. In a recent

paper by Siebert et al. (2006) the authors were able to

study turbulent velocities at scales down to 20 cm. Such

a scale is still about two orders of magnitude larger than

a typical distance between cloud droplets, which,

coincidentally, is also the Kolmogorov microscale for

typical levels of cloud turbulence. It follows that farreaching

assumptions have to be made in order to study

interaction between cloud dynamics, thermodynamics,

and microphysics.”

As expected.

Se även i sammanhanget (laddningen och vattnet i molnen)

@INTERNET Wikipedia — Water vapor [2014-03-18]

http://en.wikipedia.org/wiki/Water_vapor

”Water vapor plays a key role in lightning production in the atmosphere. From cloud physics, usually, clouds are the real generators of static charge as found in Earth's atmosphere. But the ability, or capability of clouds to hold massive amounts of electrical energy is directly related to the amount of water vapor present in the local system.”

VMJAM, Vattenmängden i Jordytans atmosfäriska moln

Ingen verkar kunna ge besked Hur mycket vatten ett åskmoln innehåller, eller släpper ifrån sig:

ScienceNordic — THUNDERCLOUDS CHALLENGE LAWS OF NATURE, 25Feb2013 [2014-03-12]

http://sciencenordic.com/thunderclouds-challenge-laws-nature

” ”But the big question is: how much of this water falls down to Earth as rain and at which intensity?” asks Härter.”

On the Science of Lightning: An Overview

URL-saknas, laddas ner genom separat Öppna-REMSA

ROYAL METEOROLOGICAL INSTITUTE OF BELGIUM —

On the Science of Lightning: An Overview, Dieter R. Poelman 2010

— PDF-dokumentet beskriver MAC-teorin för elektrifieringen i åskmoln.

”Lets focus for this moment on the downward negative lightning discharge to the Earth’s surface,

as this type accounts for about 90 percent of all the CG discharges.”, s11m.

Flera tidigare eftersökta diagramformer generellt som inte hittats på Webben återfinns här.

”Because the leader develops in virgin air it follows ..”, s11n

Se även på samma tema

Atmospheric Research | ELSEVIER —

A POSSIBLE NEW MOLECULAR MECHANISM OF THUNDERCLOUD ELECTRIFICATION — Jungwirt et al., 2005

URL saknas.

”Thunderclouds are electrified when charge is transferred between small and large ice particles

colliding in a cloud that contains strong updrafts.”

The USGS Water Science School —

THE WATER CYCLE: WATER STORAGE IN THE ATMOSPHERE (6Mar2014) [2014-03-12]

http://water.usgs.gov/edu/watercycleatmosphere.html

”The National Oceanic and Atmospheric Administration (NOAA) provides some estimates of air and cloud density and weight. NOAA found that dry air has a density of about 1.007 kilograms/cubic meter (kg/m³) and the density of the actual cloud droplets is about 1.003 kg/m³.”.

— Den uppgiften stämmer väl med en grovräkning på ett häftigt skyfall:

— På en kvadratmeter markyta (plan asfalt) dräller en hel 10-litershink ner på en sekund, om varje kubikmeter »drällmoln» innehåller/släpper 1 KG = 1 liter vatten i sekunden som ramlar ner med hastigheten 10 M/S (36 km/h) — 10 drällande liter vatten per 10 M³ drällmoln, per sekund, eller 1 liter per M³: kvdratmeterytan 10 meter upp — och på en drällmolnstapel med höjden 1 KM som, då, kan drälla i drygt 16 minuter (1000 S): [(1KG)/(1M³)]/(1S).

END.

— Björken i förgrunden nu nersågad 2014 av Kommunen — helt utan synbar eller annan praktisk anledning. Befolkningen förstår — möjligen — INTE Naturvärdena.

Bildkälla: Författarens arkiv · 11Jun2013 E12 Bild 105 · Nikon D90

— Always a New Beginning.

— Det är INTE heller det ENDA stället NATURVANDALERNA har varit och sågat på — nu igen 2014. I andra sammanhang — Naturen lappar ihop, »Patienten» river upp — kallas det cancer.

— Vore det inte bättre att göra slag i saken direkt? Testa BOSÄTTNING på MÅNEN om Utsikten här Stör. Trevlig Sommar.

Universums Historia — TGF2014b —

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

TGF2014

ämnesrubriker

innehåll

BLIXTURLADDNINGENS FYSIK II — TGF2014b

JORDSTRÖMMARNAS VATTENBILDNING

PART 2: BLIXTURLADDNINGENS FYSIK MED JORDSTRÖMMARNA OCH MOLNENS VATTENBILDNING

Atmosfäriska vattenbildningens fysik — vattenånga, daggpunkt och vattenbildning

GRUNDBEGREPPEN

GasVärmeKapacitivitetsKonstanten

Relativa gastätheten via T

Lufttryckets variation med höjden

Jordatmosfärisk översikt

MinLokalaTekopp, Exempel

ISNAP citat

ALLMÄNNA GRUNDBEGREPP FÖR LUFT OCH VATTENÅNGA — relaterad matematisk fysik

Fuktighetsnivån eller VÅM, VattenÅNGAmassAndelen

Jämförande tabell DIFFERENSEN AKTUELL VIKTSANDEL VATTENÅNGA M OCH SPECIFIK LUFTFUKTIGHET q

Relativa Luftfuktigheten — RHbegin

ArizonaUniversity RH

RHbasic — vattenångans aktuella täthet

Visuellt Exempel — visuella referensvolymer

SVP:

SVP — Vattenångans utövande EGENTRYCK

VLM — VattenångaLuftMASSandelsFÖRHÅLLANDET

GasUrel — Förhållandet mellan gaselementens atomvikter

RH-värdet

H2OmaxLuft — VattenÅNGAviktsmängden, max H2O i luft

TillämpningM

TMekv

SVP-grafen — 4%-gränsen

INTEGRALFORMEN TILL SVP

pSVPgrafen — Vattnets mättnadsångtryck

RH-komplementet i SVP

Daggpunkten:

VattenWebben

LiftedCondensationLevel

HYGROMETER

Daggpunkten, definition

H2Odata:

H2Odata — Inledning

H2Odata

Bakgrund

Kelvinekvationens brister

bStyret

tWARM

MinstaVatten — minsta möjliga vattendroppen

URDM2007

Förutsättningarna — 1:6

H2O-kontakt

H2O-united

KOF — KELVINEKVATIONENS OFULLSTÄNDIGA FÖRÅNGNINGSPOTENTIAL

KOFappl. — TAKTEN i vattenmolekylernas kondensation och avdunstning

SEA- Kelvinekvationens ytspänningskoefficient

KEis — isKelvinVattenEkvationen

WikiSlin

Kelvinekvationens speciellt MAKROSKOPISKA aspekt

RoWest2008

NoDrop

Kelvinekvationen experimentellt

Wagner2013

Vattnets Ytspänning

Varga1983

VSEA — Ytspänningsgrafen för vatten

Jämförande ytspänningsvärden för vatten

KELVINEKVATIONEN PÅ WEBBEN

WD2013

Tretyakov2013

H2O-applikation — Vattenångans luftandel — H2O i luft

Webbreferens 4%

Luftens medelatomvikt

LUFT

VATTEN

MKA — Medelkubavstånden, luftmolekyler och vattenmolekyler

KMAex

RhoVmålet — hur målet med vattendroppsbildningen kan förverkligas

Mex

MrelRef

KonÅng — VATTENFÖRÅNGNINGENS TVÅ OLIKA SÄTT

H2Opar

Condensation

H2Oparam

Wkon — KONVERGENSHASTIGHETER I KALLNANDE MOLNOMRÅDEN

MultiH2O — Från vattenånga till vattendroppe

Regndroppen — Vattenånga i luft — när blir vattendroppe regndroppe?

Regndroppen

uREF atomära massenheten

RhoNoll fundamentalgasens masstäthet vid STP

UV vattenmolekylens atomvikt

RhoV vattenångans täthet

RhoW vattnets täthet

dMKA medelkubavstånd mellan vattendroppar — från ideala parbildningar ur vattenånga

Regndroppen — Svaret

Vi befinner oss nu ungefär på hälften i hela dokumentet:

Blixturladdningens fysik 2014

BlixtDetaljer — förtydliganden i TGF

Luftblixtkanalens övergång i markkanalen för CAT

Positronbildningen i Zambiafallet

MAC/TNED — BETINGELSER FÖR POSITRONOBSERVATIONER

Positronaccelerationerna

KosmiskaStrålningen

LADDNINGSBILDENS UPPKOMST Del I:

LADDNINGSBILDENS UPPKOMST Del I

Globala urladdningsfrekvensen

TrädBlixt

INDUKTION OCH INFLUENS I MODERN AKADEMI

INDUKTION OCH INFLUENS I RELATERAD FYSIK

Q-alternativet

Stegledarens ideala utveckling

Utvecklingen mot Urladdningspunkten

Funktionskurvan, LADDNINGSFÖRDELNINGEN MOLN-MARK

LADDNINGENS AVTAGANDE

Q-fördelningen med fältstyrkans växande

Jordatmosfären — illustrerad sammanställning

Jordfältets upphov

Vattenbindningen

GlobalaVattenomsättningen

TauDroppen

TauH2O

TAU-ringens Energibindning

Jordströmmen

WilsonMAC

Globala urladdningsfrekvensen

Markytladdningstätheten, nominella globalmedelvärdet

Planetströmmen — Jordfältet — Markytans globala elektronström

Dubbelbjörken

Resultatbild DubbelBjörken

BioYtmassKoefficienten via SkogsSverigeSe

BYK — Bioytmasskoefficienten

Granens bioyta

GranBasic

Gran — Praktisk Kontrolltest

Gran — Antal Huvudgrenar

Gran — RESULTATBILD

LÄGSTA MOLNPUNKTEN

Lägsta punkten

LADDNINGSBILDENS UPPKOMST Del II:

LADDNINGSBILDENS UPPKOMST Del II

Atmosfäriska laddningens uppkomst från elektronmassans element

Globalsatserna, molnladdningarnas uppbyggnad

GlobalMolnSats1 — börjar från minsta laddningen

GlobalMolnSats2 — från minsta spänningen

StegFronten — Stegade ledarens lysande front

Stegbildningen — Första steget

Step1

MolnSpänningen, Globala medelvärden

nUG — gränsspänningen

ExempelMolnMark

Elvesbildningen, översikt

Kalkylkort:

Webbreferenser:

JordElektriskaFältvariationer

FM CC — CG

Jonosfären Wikipedia

Jordfältet — Bhattacharya2013

Positiva lagrets atmosfäriska gåta

NSTA — WEBBKÄLLA SOM VIDRÖR JORDYTANS LADDNING

Lalande1996 — Stegledarens front

Molbegreppet:

Molbegreppet, språkförbistringen i MAC

Relaterat dubbelexempel

Molndata:

Molndata — begreppen i Modern Akademi 14Mar2013

Arnott1997

Niessner2010

APS2001 — uppgifter om droppstorlek för regn

Malinowski2007 — duggregn oförklarat

Vattenmängden i Jordytans atmosfäriska moln

referenser

[BKL] BONNIERS KONVERSATIONS LEXIKON, 12 band A(1922)-Ö(1928) med SUPPLEMENT A-Ö(1929)

[BA] BONNIERS ASTRONOMI 1978 — Det internationella standardverket om universum sammanställt vid universitetet i Cambridge

[FM] FOCUS MATERIEN 1975, Focus uppslagsböcker Stockholm, Almqvist & Wiksell förlag AB Stockholm; tryckår 1979 Uppsala

[HOP] HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i UniversumsHistoria, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1,602 t19 C ...................... [ref. FOCUS MATERIEN 1975 s666]

ε₀ = 8,8543 t12 C/VM ............. [ref. FOCUS MATERIEN 1975 s666]

MKSA-systemet:

MeterKilogramSekundAmpere, det (en gång) internationellt standardiserade enhetssystem; det är alla enheter som krävs för fysikbeskrivningen.

— M, KG, S och A motsvarar också de enhetliga universella fysikaliska storheter distans (d). massa (m). tid (T|t), och elektrisk strömstyrka (I|i) som definierar hela fysikens fält av möjliga samband.

— MKSA-enheterna används genomgående i UniversumsHistoria, om inget annat anges särskilt.

— Men notera också (den nära ofattbart, komiskt) STORA SVÅRIGHETEN att hitta webbreferenser (Mar2014):

— Sökning på ”MKSA-system” resulterar i träffar överst med rubriken MKS-system (Wikipedia MKS system of units): Ampere fattas för att fullständiga fysikbeskrivningen.

— INTERNATIONELL STANDARD (2014: SI, eng. Standard International, eg. International System of Units, http://en.wikipedia.org/wiki/International_System_of_Units) har INTE enhetliga normer för enheternas FORM; Väl finns MKS och A-enheterna i SI-systemet. Men de SKRIVS ofta godtyckligt (se Wikipediaartikelns tabell) i teckenformen och med kaotiska resultat [jämför PREFIXEN nedan]:

— Vi ser numera ofta i etablerade beskrivningar beteckningar som (vad vi mestadels kan förstå) avser typen meter (M) som massa (m), kilogram (KG) som någon konstant·gravitationskonstanten (kg), sekund (S) som spatium (s) — annan term för distans, d — och så vidare.

— Det är heller inte att förvänta annat i ett lärosystem (MAC generellt) där det förväntas av eleven och studenten att det viktigaste i undervisningen är att göra som den lokalt begåvade och akademiskt meriterade läraren säger, inte förstå innehållet — definitivt inte ifrågasätta det: Läroplanen har inte TID med det.

— Notering [31Mar2014] specifikt för Wikipedia @INTERNET: Skriver man in MKSA i Wikipedia sökbox med Enter, omdirigeras man till, just, artikeln om International System of Units.

PREFIXEN FÖR bråkdelar och potenser av FYSIKALISKA STORHETER — alla med stor bokstav MeterKiloGramSekundAmpere

Här används genomgående och konsekvent beteckningarna

förkortning för förenklad potensbeteckning

d deci t1

c centi t2

m milli t3

µ mikro t6

n nano t9

p pico t12

f femto t15

Alla Enheter anges här i MKSA-systemet [Se International System of Units] (M meter, KG kilo[gram], S sekund, A ampere), alla med stor bokstav, liksom följande successiva tusenprefix:

K kilo T3

M mega T6

G giga T9

T tera T12

Exempel: Medan många skriver cm för centimeter skrivs här konsekvent cM (centiMeter).

— I förekommande fall (ytterst sällsynt här) då enheten gram används — för att undvika onödig sammanblandning med Giga-prefixet — används enhetsbenämningen gram; 1 gram = 1KG/1000.

tT t för 10^–, T för 10⁺, förenklade exponentbeteckningar

MAC ofta använd förkortning för modern akademi i Universums Historia (eng. Modern ACademy)

TNED — Related PHYSICS And MATHEMATICS

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också

RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

SHORT ENGLISH — TNED in general is not found @INTERNET except under this domain

(Universe[s]History, introduced @INTERNET 2008VII3).

TNED or Toroid Nuclear Electromechanical Dynamics is the dynamically equivalent resulting description following the deductions in THE PLANCK RING, analogous AtomNucleus’ Deduction. The description according to TNED is related, meaning: all, each, details claim to be fully logically explainable and understandable, or not at all. With TNED is (hence) also understood RELATED PHYSICS AND MATHEMATICS. See also the emergence of the term TNED in AtomNucleus’ Deduction.

Senast uppdaterade version: 2021-06-11

*END.

Stavningskontrollerat 2014-06-07.

rester

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

∫ ∫ √ τ π ħ ε →∞ UNICODE — ofta använda tecken i matematiska-tekniska-naturvetenskapliga beskrivningar

σ ρ ν ν π τ γ λ η ≠ √ ħ ω → ∞ ≡

Ω Φ Ψ Σ Π Ξ Λ Θ Δ Γ Ŧ ŧ

α β γ δ ε λ θ κ π ρ τ φ ϕ σ ω ϖ ∏ √ ∑ ∂ »stiliserat d» ∆ ∫ ≤ ≈ ≥ ˂ ˃ ˂ ˃ ← ↑ → ∞ ↓

ϑ ζ ξ

Pilsymboler, direkt via tangentbordet: Alt+24 ↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬

Alt+23 ↨ — även Alt+18 ↕; Alt+29 ↔

åter till portalsidan · portalsidan är www.UniversumsHistoria.se