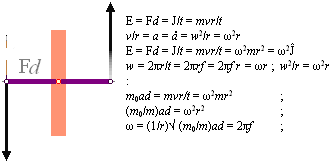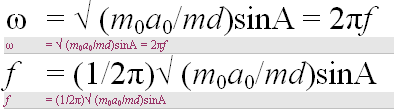CHEOPS REKTANGEL IIIbA2 ¦  GYROFYSIKEN  | 2018XII24 | a  production  | Senast uppdaterade version: 2023-01-26 || ·

 

innehåll · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning  alla webbsidor ·  JordSyret  · CHEOPS REKTANGEL I ¦ II ¦ III

 

 

I Fortsättning från Från  :  Solsystemen i VINTERGATAN   : med KOMPLEMENTÄRA DOKUMENT      

 

 

Bakgrund i sammanfattning med länkar — Sep2018-Feb2019 ¦ CheopsRektangelns CirkelEllipsPerspektivBevis — etablerat okänt

PLANETROTATIONERNA — Spinnets natur, upphov. uppkomst och existens i Solsystemet

INLEDNING: Gyrofysiken — RotIPST — WikiCount1 — WikiCount2 — WikiPRECESSION — WikiSTEER — WikiAXEL — WikiTRAFFIC —

 

GYROFYSIKEN

 

FYSIKPROBLEMETS DJUPDETALJER I TNED-KOSMOLOGIN MED PLANETERNAS ROTATIONER med en möjlig förklaring till deras sätt och etikett har motiverat en närmare djupdykning i gyrofysikens hemliga gömmor.

— Som det har visat sig:  Vi klarar inte en förklaring till planetfysikens rörelsesätt utan inblick i GYROLAGEN och dess förgreningar: körteknik.

Inblick i GyroKammarens glimrande artefakter

— konventionellt ett erkänt svårförklarligt ämnesområde (Webben 2018/19) — är nödvändigt för att vi, garanterat, inte ska hamna i gruvliga missgrepp i försöken att omfatta ämnets begripliga förklaring: planetrotationerna i vårt Solsystem enligt TNED-kosmologin.

 

 

Länkade rubriker:

 

 

Här följer en helt praktiskt gyroexperimentbaserad framställning som garanterar att varje sats, påstående, mening och blotta antydan har — eller ska ha — fysikalisk, praktisk experimentell grund:

— Framställningen här bygger helt på En PRAKTISKT OBSERVERBAR MED ENKLA MEDEL grund som varje enkel människa själv kan kontrollera — förutsatt tillgång till ett tvåringars Gyroskop.

 

 

 

 

 

 

GyroBasic: TYNGDPUNKTEN  ¦ Gyrolagen

 

GyroBASIC

MAGNETISKA VARVRÄKNAREN

FÖRUTSATT TILLGÅNG till ett tvåringars gyroskop

— eller i varje fall en enklare hemmagjord Snurra, se RotIPST efter artikeln nedan:

 

 

— Var hittar jag ett sånt?

— Ärligt sagt, min referens: Backa filmen 35 år = 2018–1983: Sista Clas Ohlsonkatalogen (Nr72) som saluförde typen ovan (avd. Leksaker, Gyro- står inte i registret). Var man kan få tag på den typen nu (Dec2018), om alls, är här inte känt.

   Det är avgörande viktigt att produkten har de två tvärställda ringarna som i bilden ovan för fullständig fysikbeskrivning.

 

 

Monteringen av uppvarvningsanordningen är avgörande viktig för den bekväma arbetssituationen — men inga direkta hjälpmedel finns numera i utbudet. Bilderna ovan visar enkla sätt att komma till skott direkt: Vänster, enklaste: en bit hyvlad trälist (spillbit från närmaste trävaruhandel, tjocklek 15mM) med ett par plastspännband från Rusta + en tving att spänna fast anordningen med. Borrmaskinen av minityp — bör finnas på otaliga byggvaruhusställen + tillbehör, den aktuella gummitrissan.

— I experimenten med den vertikala spinnsnurran måste borrmaskinen handhållas vertikalt för uppvarvning. se Praktisk Exempel.

— NOTERA OCKSÅ KRAVET PÅ EXPERIMENTELL PLANHET HOS GYROUNDERLAGET:

— Utan exceptionellt noga planhet, åker/rullar gyroskopet omkring på underlaget efter uppvarvning, och det blir svårt/jobbigt att utföra de stundtals precisa anliggningsmoment som krävs för viss experimentell verifikation.

— Använd ett mindre bord med lämplig mängd papper/tidningsreklam under benen för att justera fram en exakt gravitell plannormal.

 

 

 GyroskopUtbudet @INTERNET (Sverige) Jan2019 — tvåringars

— Webbsökning (10Jan2019) visar att det SER UT ATT DET finns ett antal ställen i Sverige som saluför den tvåringade gyroskopmodellen som krävs för full verifikation. Prisklass 150-200 :-/st.

— Sök på ”Gyroskop, priser”. Kvaliteten på utbudet är här inte känd.

 

GyroBASICabc GyroBasic :

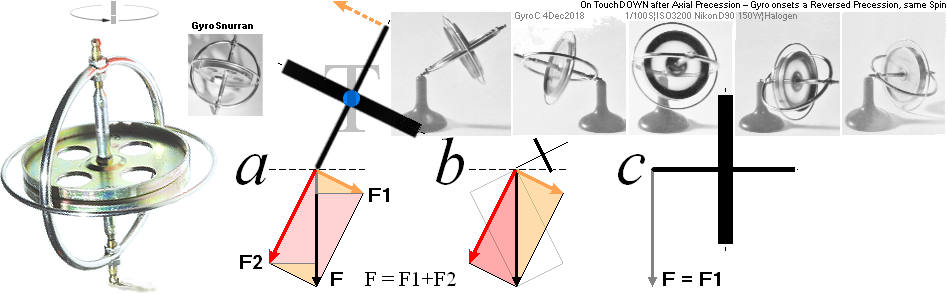
GYROSKOPET UPPVISAR PRECESSION — en roterande rörelse — ENDAST VID FAST MARKKONTAKT och förutsatt VISST hjulspinn:

 

 

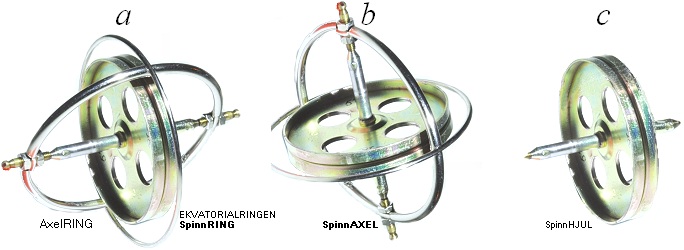
MED SPINNHJULET UPPVARVAT:

•   PLACERAS gyrokroppen enligt a — markkontakt via ekvatorialringen, statiska tyngdpunkten något vid sidan av lodlinjen — börjar gyrokroppen omedelbart PRECESSERA = uppvisa en krängande rotation. Lutning och rotation underhålls konstant — så länge visst konstant spinn finns. Med avtagande spinn, lägger sig gyrokroppen till slut.

•   PLACERAS gyrokroppen enligt b — markkontakt via spinnaxeln, statiska tyngdpunkten något vid sidan av lodlinjen — börjar gyrokroppen omedelbart PRECESSERA = uppvisa en krängande rotation. Lutning och rotation underhålls konstant — så länge visst konstant spinn finns. Med avtagande spinn, lägger sig gyrokroppen till slut.

 

Hängs den spinnande Gyrokroppen upp i ett snöre finns inte längre någon förutsättning för den roterande, krängande — precesserande — rörelsen.

— Upphängd, antar Gyrokroppen endast ett nytt specifikt LÄGE — rymdposition — om man påverkar den med olika kortvariga knuffar.

 

Det är viktigt att ha den aspekten i bakhuvudet för undvikande av alla möjliga sensationella missförstånd.

— Se vidare från TYNGDPUNKTEN om ej redan bekant.

FRÅGA:

— Normalt sett, inget spinn:

— Om man lutar Gyrokroppen ur lodled så att dess (statiska) tyngdpunkt ligger något enda litet vid sidan av, ramlar kroppen ned. Men då hjulet snurrar ramlar den alls inte ned.

— Betyder det att den väger mindre då, eftersom den inte ramlar ned, trots att dess tyngdpunkt, uppenbarligen, ligger vid sidan av lodlinjen, eller hur förklaras lutning utan ramling?

 

— Grymt bra fråga. Frågan rymmer hela hemligheten.

Frågan formuleras också i PRECESSIONSKRAFTERNA med  upplösningen i Bevis D — med vidare.

 

Djupförklaringen:

 

SKIVTALLRIKSEXPERIMENTET (1990) ger en förlösande upplysning:

— rotationer flyttar/förskjuter tyngd- och momentpunkter.

 

GyroBasicEND.

 

ROTATIONENS INVERKAN PÅ STATISKA TYNGDPUNKTEN:

RotIPST

Gyrofysikens praktiska grunder

HEMMASNURRAN

VERIFIERANDE ENKLA KÖKSEXPERIMENT MED ENKEL HEMMAGJORD SNURRA — formulerad relaterad fysikbeskrivning

 

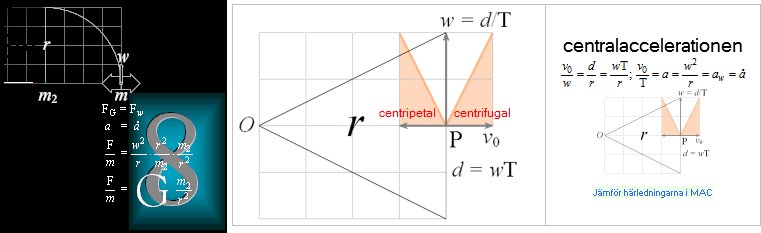
Om en centralkraftsacceleration — rotation — påförs en masskropp INTRÄDER en masskroppens tyngdcirkel i substitut för den vilande kroppens statiska tyngdpunkt:

— Statiska tyngdpunktens jämvikt BEVIS transponeras/FLYTTAS över — ut — på massringens tyngdcirkel

så, att statiska tyngdpunkten garanteras en balanserande JÄMVIKT på rotationens kredit — mera ju mera utspridd rotationsmassan är kring rotationsaxeln. Analogt, vidare tyngdcirkelradie. Aamt proportionellt i styrka mot rotationsfrekvensen: centrifugalkraftens styrka.

 

HemmaSnurra, 2018: TYNGDPUNKTEN

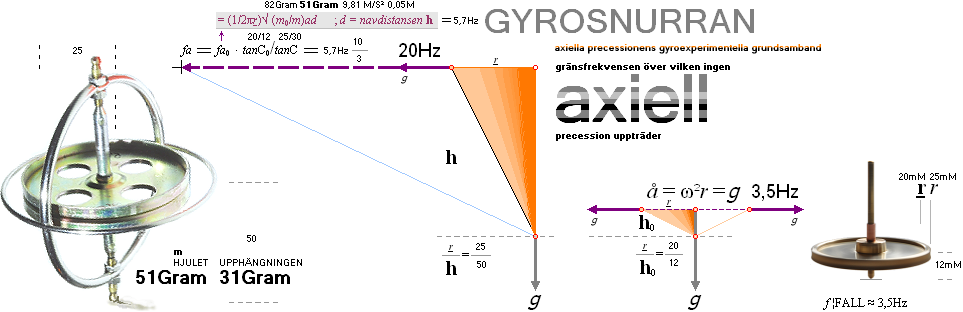
PRAKTISKT EXEMPEL

— Vilken minsta möjliga varvtalsfrekvens krävs för att få ett visst svänghjul att precis etablera en centrifugalkraft — som garanterar att snurran INTE ramlar omkull — lika med lokala tyngdkraftsaccelerationen a=9,8 M/S² (Norden ¦ 9,79 Ekvatorn)?

 

Försök visa lösningen genom ett praktiskt exempel SAMT bevisa, eller ge god ledning för, beräknat varvtals praktiska förankring på enklast möjliga sätt — utan dyra verktyg och instrument.

 

 

Foto: HemmaKonstruerad Snurra 30Nov2018

En alternativ axelkonstruktion visas i PraktisktExempel tillsammans med påmonterande Neodymmagneter [‡] för elektromagnetisk varvräkning.

 

 

LÖSNING:  Med tillgång till visst (äldre) lagermaterial samt enklare varusortiment, kan en fungerande (inte den bästa) Snurra konstrueras. Svänghjulet i bilden (kugghjul i mässing) har diametern 5cM. Svängmasshjulets tyngdcirkelradie uppskattas här till 2cM = 0,02M.

— ”Tyngdcirkelradie”, vad är det?

— Ta en plan jämntjock, materialhomogen cirkulär skiva. När skivan roterar kring en axel genom cirkelns mittpunkt BEVISET uppför sig skivan »som om» hela dessa massa vore samlad BLOTT i periferin på EN enda cirkellinje med radien r (”ru”, understruket r). Det är skivans/cylinderns fysiska massmedelcirkel, eller skivans tyngdcirkel. Vi ska bevisa det längre fram genom enkla försök med snurran. Vi kan också bestämma VAR r befinner sig i förhållande till centrum. Var? Naturligtvis DÄR skivytan/hela cylindervolymen delas i två lika halvor;

— Det är Cirkelradien r som delar CirkelArean A=piR² i två lika halvor A/2=pir²=piR²/2; r²=R²/2; r=R/√2.

 

Centrifugalaccelerationen beräknas

å = w²/r = (2pi·r/t = 2pi·r·f = ωr)²/r = ω²r = a = 9,8 M/S², som ger

ω = √ (9,8 M/S²)/0,02M = 2pi·3,5230 Hz:

varvtalsfrekvensen ska vara lägst drygt f = 3 varv per sekund.

— Fattning med snurraxeln mellan tumme och pekfinger visar att hjulet vrider sig ca 3 varv på en sådan fingervridning (snurra sakta, räkna varven).

   Grovtest visar också att om vridningen görs grovt inom lägst en sekund, kan Snurran PRECIS EN KORT STUND fås att balansera på en jämviktspunkt som visar att rotationsaxeln står nära helt upprätt innan den lägger sig. Därmed är uppgiften löst och kvantiteten bekräftad.

   Flera försök med kortare vridtid med tumme och pekfinger visade att Snurran roterade ( helt upprätt på hårt underlag) 45-60 sekunder innan den vek sig.

 

Tröghetslagarna — GyroKollen: HS2018 ¦ Tyngdpunkten ¦  RotIPST  ¦ Gyrolagen

 

TRÖGHETSLAGARNA

 

TRÖGHETSLAGEN — NewtonIII — Ändringslagarna:

Varje tillståndsändrande kraft uppväcker en lika stor tillståndsbevarande motkraft.

——————————————————————————————————

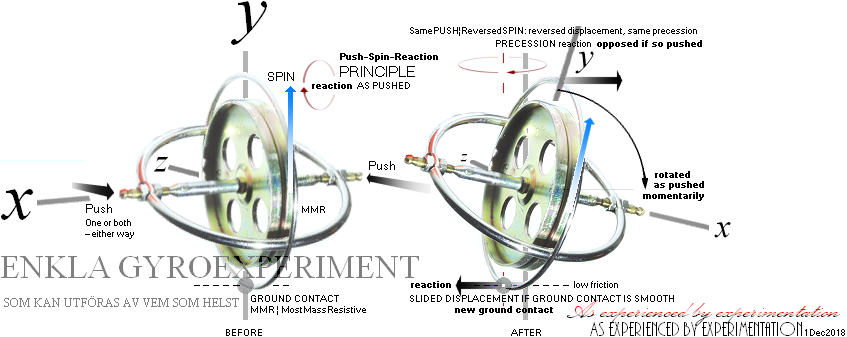
RETORISKA ÖVNINGSEXEMPEL MED SNURRAN SOM BEVISANDE EXPERIMENTOBJEKT

Största massmotståndet — UTAN HÄNSYN TILL SPINNRIKTNINGEN

— sprinnriktningarna avhandlas separat längre fram

Och SÅ kan vi konstatera HUR tröghetskrafterna verkar i CentrifugalKraftens fascinerande matematiska fysikuniversum — genom förhållandevis ytterst enkla hemmaexperiment (före 2000 — dagens kommers, typen AsfaltKollen 2018, har inte längre det utbudet):

 

 

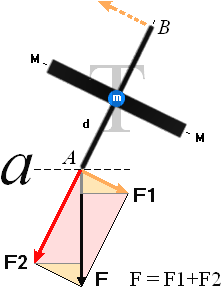
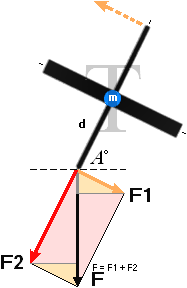
— En KRAFT försöker putta axeln på gråpunkten:

— I vilken riktning finns största tröghetskrafterna = största massmotståndet MOT den ansatsen?

   Svar: Riktningen där MINSTA massmotståndet finns, de bägge markerade punkterna, befinner sig ALLTID rätvinkligt riktningen med största massmotståndet = största trögheten mot puttförsöket, röda punkten:

— Snurran svarar på putten genom att (försöka) vrida sig kring den axel i massringen som uppvisar största massmotståndet. Slutpositionen (om ändringen lyckas = snurran har låga varvtal, se Beviset) innebär att Snurran har förlorat sin ideala jämviktspunkt och börjat PRECESSERA (wobbla).

   Vidare i Gyrolagen.

   RIKTNINGEN hos Snurrans axelvridningsrespons beror på Snurrans rotationsriktning.

 

 

— En KRAFT försöker putta hjulmassan vid pilen:

— I vilken riktning finns största tröghetskrafterna = största massmotståndet MOT den ansatsen?

   Svar: Riktningen där MINSTA massmotståndet finns, den markerade blåpunkten, befinner sig ALLTID rätvinkligt riktningen med största massmotståndet = största trögheten mot puttförsöket, röda axeln:

— Snurran svarar på putten genom att (försöka) vrida sig kring den axel i massringen som uppvisar största massmotståndet. Slutpositionen (om ändringen lyckas = snurran har låga varvtal, se Beviset) innebär att Snurran har förlorat sin ideala jämviktspunkt och börjat PRECESSERA (wobbla).

   Vidare i Gyrolagen.

   RIKTNINGEN hos Snurrans axelvridningsrespons beror på Snurrans rotationsriktning.

 

PRIMÄRA GYROSKOPEXEMPLET GTF

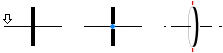
— En KRAFT försöker putta hjulaxeln vid pilen (fattning med bägge händerna om axeln, testa vridning):

— I vilken riktning finns största tröghetskrafterna = största massmotståndet MOT den ansatsen?

   Svar: Riktningen där MINSTA massmotståndet finns, den markerade blåpunkten, befinner sig ALLTID rätvinkligt riktningen med största massmotståndet = största trögheten mot puttförsöket, röda axeln:

— Snurran svarar på putten genom att vrida sig kring den axel i massringen som uppvisar största massmotståndet.

   Slutpositionen beror på hur Snurran är upphängd/monterad:

GyroLagenRef: Tröghetslagarna — DBE

 

EXEMPLIFIERADE SITUATIONER PÅ JORDYTAN MED ANGIVET HJULSPINN — Se särskilda experimentbevis med förklaringar i Gyrolagen och GyroBasicMath.

 

— Om det spinnande hjulet PLACERAS — direktnedsätts BEVIS B — LUTANDE på marken:

 

 

 

Etablerad litteratur varken omnämner den ytterst enkla Gyrolagen — som förklarar väsensskillnaden mellan Axiell »GyroToppSpinnande»  och Ekvatoriell »HjulPåVägÅkande»  precession — elementär körteknisk inblick som ovan — Precessionslagen — eller ens de skilda begreppen/termerna som sådana. Inte heller den enkla förklarande beskrivningen omnämns eller antyds i etablerad litteratur med något motsvarande upplysande MostMassResistive — MestaMassResistiva: angreppspunkten (M) som beskriver gyrokroppens enkla elementära ändringsordning— enligt Gyrolagen.

 

 

Studera[‡] med fördel den stora omfattande floran etablerade meningar i jämförande Internetreferenser (Jan2019).

 

 

StudieExempel; RotIPST

ELEMENTARY GYROPHYCIS reveals

ISSUES IN MODERN QUARTERS — Jan2019

SAFE TRAFFIC VERSION

 

In this presentation — guaranteed thoroughly inspected and tested — safe references:

 

•   GyroBasic — elementary experiments anyone can perform for test, analyze an verifiability;

— See specifically gyro experimental Proofs ABCD, unless already familiar.

•   McOMwash2000 MOTORCYCLE OPERATOR MANUAL (2000) — Washington State Department of Licensing — the only difference in terminology is PRESS replaced here by PUSH for generalizing The GyroLaw — to cover all universal cases: on Earth, outside Earth, everywhere.

 

 

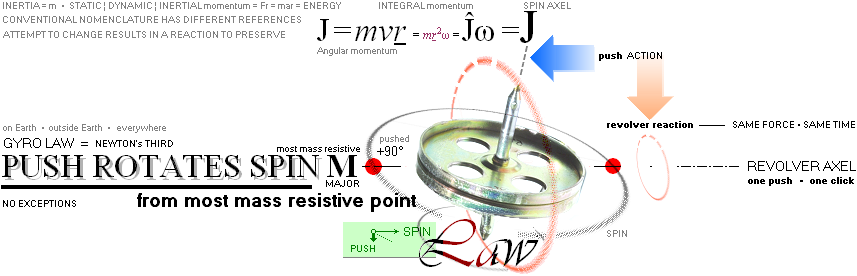
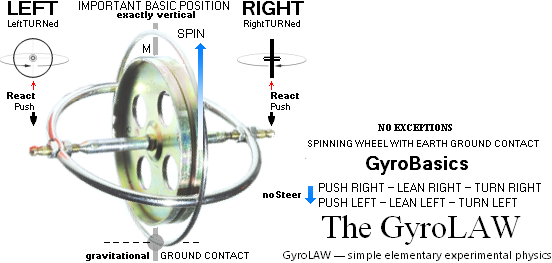
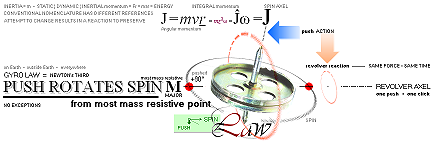
GyroLAW, illustrated: SE     GyroLAW:

 

Conventional nomenclature most often uses L for Angular momentum mvr and J or I for ”intertial momentum” mr²

— while (WE) here in Universes History utlize the convenient usage of  I for electric current,  J for Angular momentum,  K for Keplerian momentum K=vr = J/m, a general  L for Inductance Rt,  M for Static momentum M=Fr, the energy base behind it all, and a (unicode) j-flex  Ĵ for INTEGRAL momentum (mr²). Here our Ĵ is the specifically conveniently collected METHOD utilized to calculate all kinds of DYNAMIC mass-circle radius-problems in gyro physics, to distinguish from their more elementary STATIC counterparts. These concepts, however, are really Qualitatively POORLY described in established literature, as here noted. They need some further clarifications — with good educative, practical, examples anyone CAN understand.

 

 

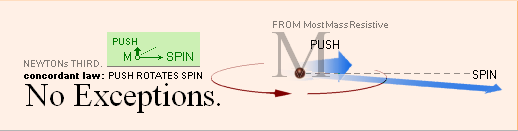
GyroLAW states — please do the experiments GyroBasic unless already familiar: YOU are the Judge here:

 

•   push rotates spin — from most mass resistive point: no exceptions, nowhere in universe;

— Not present in established literature — search for, not (yet) found.

•   each momentary push results in a corresponding reactive revolving angular step, excactly in proportion to the utilized force (F) and time (t) executing the action: higher spin demands greater Ft to execute a corresponding (visible) reaction.

— TEXT PARTS WikiCount21a IN WIKIPEDIA seem to confirm that SOME of the Wikipedia authors does NOT understand the Concept:

— If that is the true explanation: no wonder: GyroLAW in establishes quarters is NOT even mentioned. Because IT is buried in High School Modern Academic Vector Algebra that Not Ont Person On Earth Understands, cannot explain, cannot relate WITH respect to Nature; Ref.: MacVectorRef.

— Comparing TableExamples from simple deduced gyro math explaining the general behavior is given in BTE and CTF — WikiCount21a;  The latter suggest some (real) confusing context in established quarters as to the (Wikipedia) APPREHENDED IDEA of gyro physical experimental results: It seems IT is not, really, understood:

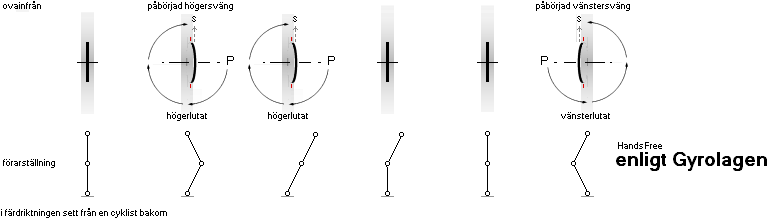
•   Wikipedia provably and in detail presents a highly corrupted — traffic dangerous — idea of navigating a two wheel bike — in references to the explicit manual McOMwash2000 which DON’T.

— See in deep @WikiSTEER from McOMwash2000. (It’s unbelievable ...).

 

Gyro2Ways:

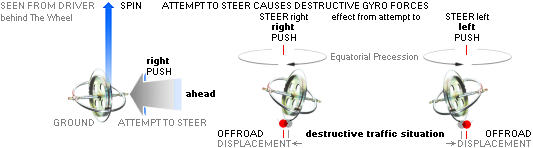
The two gyro-physical fundamentally possible ways of navigating the front wheel of a bi- or motorcycle is GYROSCOPICALLY EXPERIMENTALLY compiled as the figure below shows..

 

 

 

 

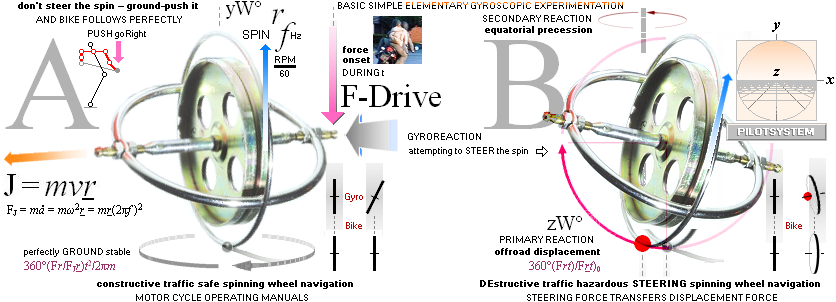
The only two physically available possible ways of navigating an Earth ground located spinning wheel.

LEFT connection, se TableCTF, RIGH, se BTE and WikiCount21a.

NOTE:

— These mathematical connections are PRELIMINARY deductions from the most near observable gyroscopic results, not here further analyzed in deep. We WOULD expect SUCH work to be a part of any elementary, established, presentation on the subject. However: we DON’T find it @Internet Jan2019. And we know why, too: nobody understands the subject in such a comprehensive way. »TubeOn, Ladies: High time to TreasureDive».

 

 

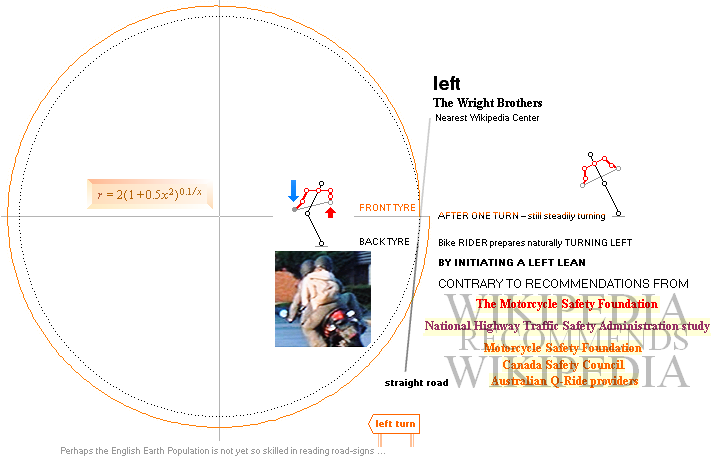
A Left:   This IS the McOMwash2000 instructed unequivocal MANNER, as well as the experimentally observed results, to navigate a two wheel bike the absolute fastest, safest and least energy consuming NATURAL way — picture below used as proof of the SAFE TRAFFIC technique from PAYCHECK 2004 1:10:25, Ben Affleck, Uma Thurman:

 

Ground-pushing/pressing. No steering.

— The Bike AS BALANCING ON THE TYRE’S SMALL GROUND CONTACT SPOTS easily adopts — fast — to any center of mass maneuvering action, practically independent of speed given enough force to accelerate the lean initialization. This is all plain simple ground school mathematical physics — apprehended from year 5.

 

 

FAST AND SAFE TURNING — a so called swerve:

— a real fast Straight-Right-Left-Straight or Straight-Left-Right-Straight maneuver;

— The Bike answers IMMEDIATELY to any the smallest tiniest a ground pushing action — where the driver executes a corresponding synchronized bodily motion/adaption to get the detailed balance of the GO-noGO.

 

B Right:   This is NOT what McOMwash2000 states in its MC-manual — but what the Jan2019-Wikipedia contribution in the subject claims TO HOLD @WikiSTEER — IN ALSO distributing/referring THAT content TO the MCManual content as IF THAT would concur with The Wiki-idea:

— Practicing THAT WikiSTEERING content IS the directly traffic dangerous behavior — all depending on road, speed, force and traffic conditions, says GyroLAW.

 

 

 

The Wikipedia text Jan2019 describes CounterSTEERING as if taken from McMANUALS.

— But McMANUAL’s ”counter-” does NOT refer to ”steering opposed to”, but to NOT STEERING AT ALL: unequivocally GyroLAW clear gyrophysically concordant GROUND PUSHING (pressing) in the turn direction. No steering.

 

— The worst of it, as it SEEMS, is that the Wikipedia authors, in the aim of the subject, does NOT understand — have not exercised the simple revealing gyro experiments GyroBasic — the gyroscopical behaviour:

— This author promises to convert from this rebellic standpoint IF experimentation so will be certified.

   The reason can be only one, for such a VAST CREW of corrupted apprehension:

— ignorance.

   They   simply   don’t   know.

   The GyroLAW is unknown in Wikipedia Quarters. Absolutely in detail to the atom of it. The GyroBasics too. Please do correct if wrong.

 

 

IS ANYTHING RIGHT AT ALL IN Gyro-WIKIPEIA?

@WikiSTEER ¦ WikiCount21a ¦ WikiCount1 ¦  SE

”   Countersteering is used by single-track vehicle operators, such as cyclists and motorcyclists, to initiate a turn toward a given direction by momentarily steering counter to the desired direction ("steer left to turn right")”,

WikiCount2 — Jan2019.

 

The whole Wikipedia article is corrupted — as proven by quotes and comparisons with McOMwash2000 in concord with GyroBasics ¦ GyroLAW ¦ StudyExample basic gyro physical elementary experimentation that can be verified by any person possessing a two ring gyroscope.

 

 

The key-word or key-concept in the Wikipedia is, as quoted above, ”OpposedSTEERING”, while DIRECT REACTION in the MC-manuals the key-concept is NOT STEER AT ALL: Counter-Steering: navigating/turning the Bike by Ground-Gyro-Pushing/Pressing the steering rod in the direction of the intended turn — with a corresponding body mass center adoption move to receive fast bike mass center change response, as proven:

— The term ”counter-steering” — so — explicitly clarified HERE, not in the reference McOMwash2000 itself* (except for p4.6) — AND with respect to ITS RELATABLE TRAFFIC SAFE context in concord with basic GyroBasic experimentally verified gyro physics — and (40 years of successful) Bike Riding.

————— *

Except for p4.6 ”Flying” and steering reversion with a 3 wheel MC-device where the text explicitly differentiates between ”counter-steering” contra ”direct steering”: ” .. normally controlled by direct steering .. ”steering” reverts to counter-steering.”. Couldn’t be more clear:

— counter-steering = NOT STEERING AT ALL = natural gyro physical navigation: »Bike PILOTING». Birdstuff.

 

 

So, again (Jan2019):

 

 

IS ANYTHING RIGHT AT ALL IN Gyro-WIKIPEIA?

@WikiSTEER ¦ WikiCount21a ¦ WikiCount1 ¦  SE

 

 

”  The behaviour of a gyroscope can be most easily appreciated by consideration of the front wheel of a bicycle. If the wheel is leaned away from the vertical so that the top of the wheel moves to the left, the forward rim of the wheel also turns to the left. In other words, rotation of one axis of the rotating wheel produces rotation of the third axis.”,

WIKIPEDIA Gyroscope (20Jan2019)

 

WikiTRAFFIC:

— ”the third axis”. This as close as we can get in consulting GyroWikipedia (Jan2019).

 

Although not comprehensive (GyroLAW is never mentioned, the cited text has no reference):

— The Wikipedia Gyroscope text is concordant with the gyro experimental results we find in GyroBasic. However obviously not in any acquaintance with the full content of the subject;

— The Wikipedia GyroText gives no elementary basic math;

— No connections are given, not even a hint: no math at all, not even a simple symbolic approach;

BasicTrafficGyroMathOrientation:

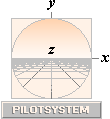
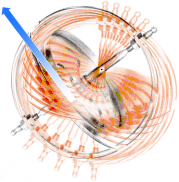 HardCopy = NOW — FaintCopy = InComing.

 

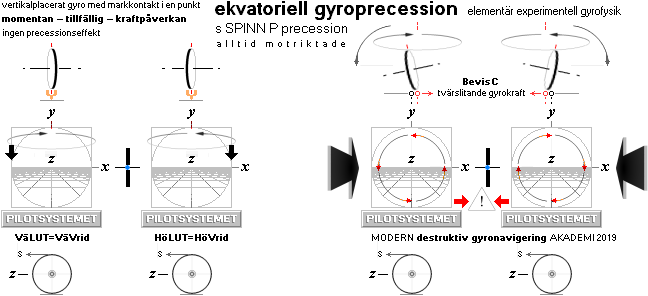
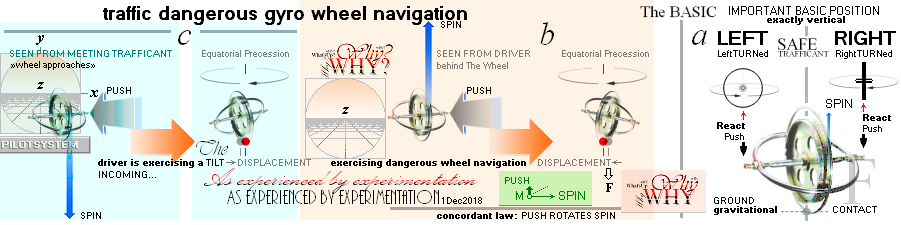
EQUATORIAL GYROSCOPIC PRECESSION

BasicEXAMPLE — should be in any SERIOUS  encyclopedic text on the subject — not found @Internet Jan2019

—————————————————————————————————————————

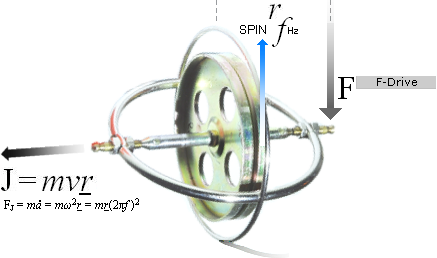
Spinning Wheel on Earth ground — PilotSYSTEMxyz:: axelHORIZONTAL J=mvr: momentarily pushed:

 (y↓+x) → –yW° ¦  = clockwise stepped y-twist                ; constructive safe traffic gyro wheel navigation

 (y↓–x) → +yW° ¦  = anti-clockwise stepped y-twist         ; constructive safe traffic gyro wheel navigation

———————————————————————

 (z↑+x) → –zW° ¦  = clockwise stepped z-twist                ; DEstructive UNsafe traffic GYRO wheel STEERING

+ direct gravitational RotII-System –yW° clockwise equatorial precession, depending on force.

 (z↑–x) → +zW° ¦  = anti-clockwise stepped z-twist         ; DEstructive UNsafe traffic GYRO wheel STEERING

+ direct gravitational RotII-System +yW° clockwise equatorial precession, depending on force.

—————————————————————————————————————————

In general: reaction effect is proportional to the onsetting acting force.

See McOMwash2000 — it concords with GyroLAW but not as claimed in Wikipedia. Read it to believe it.

 

— Established literature has NOT any — here known simple corresponding — developed vocabulary for this:

— No here know NATURAL — pilot — standard is known in established quarters — »every school is driving blind»:

— THE ”axlePLANE pilot system xyzXYZ” in general is never utilized in established literature to describe mathematical-physical problems in 3D-space (basic 3D-math is poorly understood in modern public education, albeit its simplicity: but has a wide expertized applicability in computer programs, especially in the film industry):

 

 

The simple xyzXYZ PILOTSYSTEM in related mathematics and physics.

— Never utilized in established literature.

 

COMPLEX INTERACTING MECHANICS — describing action 3D-rotations in system ROT I rotations with fixed rotational axes versus reaction 3D-rotations in system ROT II resulting xyz-system rotation where the axes are individually locked and follow the individual object, as f.ex. in Gyrophysics — hence AS HERE KNOWN neither has a simple[‡matrix transpositions only] representation in established quarters:

— Wikipedia gives no mentioning at all: uses only rhetorics only such as ”pitch”, ”roll”, ”rotation”, ”spin” as if the individuals have no idea of a daily life piloting xyz-apprehension. No visual Earth ground contact.

— Students are left OUTSIDE the SIMPLE deep rational explanation of the subject.

 

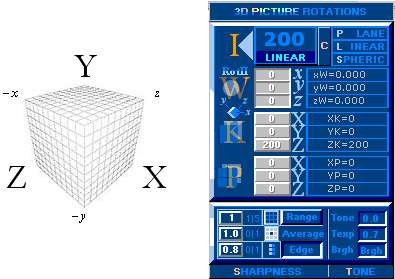          Basic 3D presentation Rot 1 and Rot 2 Program in Plane, Linear and Spherical Perspectives:

— Developed in the exceptionally FAST and FREE DELPHI 4 environment in Universes History by this author Bell Dharma from 2000.

— WHEN did SUCH come — free — with a computer to promote BASIC 3D Acquaintance EDUCATION on Planet Earth? I see none.

   People walk blind. Free 3D-Modelling programs exist @Internet. But where are the Free 3D Presentation programs? I see none.

 

— Without these simple —  s i m p l e  — elementary tools, the SUBJECT cannot be presented, nor explained, in no way in any detail;

— The modern academic teaching system has no developed vocabulary to describe natural physics in any atomic deep detail — no way. But the commercial industry is flooded with applications especially in electronics, obviously utilized not to educate, but to manipulate a profit: the real deep part of it.

— Compare The Microsoft side of it[‡Microsoft’s Program Vandalizations] (from around 2000+): These industrial extremely »high IQ atomic evolved morans» started to EXCLUDE already developed vital usable tools (→ Windows XP+) — making the presentation in Universes History even more difficult to finish. Keep dazzling us.

 

 

WikiPRECESSION describes more Gyro-details — but in partly obscure terms. The text divides the subject in ”Torque-free” and ”Torque-induced” precession parts:

 

 

WikiPRECESSION:

WIKIPEDIA Precession (Jan2019)

https://en.wikipedia.org/wiki/Precession

”  In physics, there are two types of precession: torque-free and torque-induced.”.

 

 

The Wikipedia text gives no clarification what is meant by ”torque-free precession” — ”inertia matrix” with »corresponding modern academic expressions». But is more specific on ”torque-induced”:

 

”  Torque-induced precession (gyroscopic precession) ..”,

WikiPRECESSION

” .. is the phenomenon in which the axis of a spinning object (e.g., a gyroscope) describes a cone in space when an external torque is applied to it.”.

 

— Aha:

 

 

Gyroscope precesses horizontally with its spinning wheel axel oriented exactly horizontal, no conical visible geometry at all. Further below.

 

— So that is the Explanation why the Gyroscope is hanging vertically with no visible CONE at all, PRECESSING over and over again. Wikipedia »really covers it all». Very well informed staff. MustBuyBook.

 

And so it is with WikiPRECESSION: not, really, connected.

— Compare the experimentally observed — GyroLAW explained — result in GyroLAW Illustrated:

 

 

Precession — wobbling — appears on a spinning wheel when a sufficiently strong force takes on the wheel — conditionally inside the radius of its dynamic gravity circle. If the spin is sufficiently high, the spinning wheel rejects the intruding force with no precessional result.

— This type explanation is excluded — not found — in modern teaching systems: searched for, not yet found.

— So, what is producing a precession?

— A force interfering with a gravity circle. No torque. Just force (gravitation).

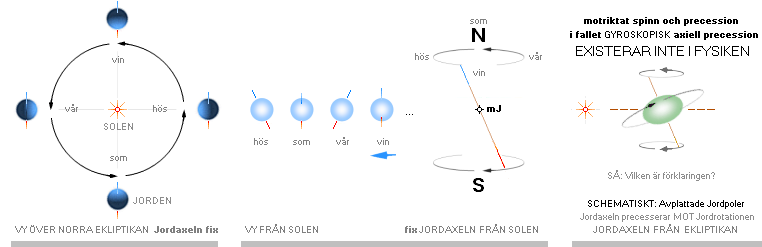
— Compare Earth Axis Precession: Sun (and Moon too) gravitation takes on Earth’s FAT (»protruded») equator and swings it along annually with a corresponding small precessional effekt. No torque. The interfering force can be gravitational or electrical/magnetical (or fluidal, generally resistive).

— So, what is ”a gravity circle”? Any spinning mass.

   Typically our mentioned TOP.

 

Compare WikiPRECESSION:

 

”  Precession is the change of angular velocity and angular momentum produced by a torque.”,

WikiPRECESSION, Classical (Newtonian)

   COMMENT:

1.   The ”torque” part — our STATIC momentum M = Fr — appears through the gravitational force responsible for the precessing equilibrium. There is no ”torque producing precession”. Only — proper — (gravitational) force. Simple elementary experimentation.

2.   ”change of angular velocity”, ”change of .. angular momentum”?

— The Angular Momentum J=mvr parts are constants with a constant spin on a given gyroscope, and do not change during precession. So: What is the WikiPRECESSION text aiming at here?

PrecMAN:

— We GyroIllustration ONSET GyroBasic a specific precession by speeding up a gyro wheel, and then hanging it on a suspension point, letting it GO, observing how it takes on the actual precession by a short acceleration during a shorter moment of a small free gravitational fall:

 

 

 

The whole weight of the gyroscope (here 82 Gram) is steadily transposed onto the precessionally suspended point — explicitly checked — whether standing upright vertically or precessing horizontally — or even below.

WikiAXEL:

The POSITIONAL PRINCIPLE in photo above is mentioned in a WikiPRECESSION section

”  Gyro precession causes another phenomenon for spinning objects such as the bicycle wheel in this scenario.” — with a possible association to this experimentally observed position,

however including a (very) strange statement:

 

AND AS THE REMARKED TEXTBOX SAYS IT: ”This section does not cite any sources”:

 

”  .. the actual axis of precessional rotation is located vertically through the wheel, passing through its center of mass.”,

WikiPRECESSION

 

— ”Axis of precessional rotation”? Axis?

 

The figure below comprises the precessive GyroSerie details we can RELATE TO EXPERIMENTAL OBSERVATION — in atomic deep — on the subject:

 

 

 

 

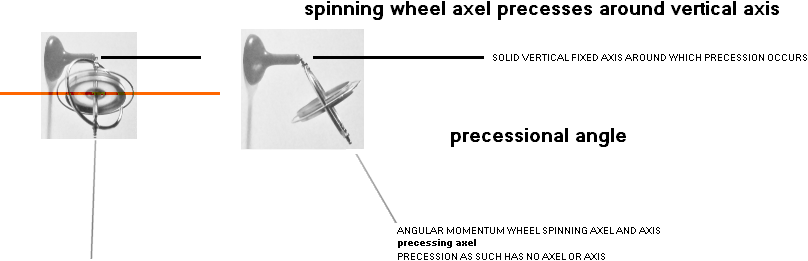
”  .. located vertically through the wheel, passing through its center of mass.”,

WikiPRECESSION

 

GyroPrecession — by experimentation on Earth — appears as soon as the spinning gyroWheel is given an OnSet on the ground with a TILTED position from vertical upright.

 

 

— Vertically, through the wheel, passing through its center of mass?

IT IS OBVIOUS THAT THE SECTIONAL WIKIPEDIA AUTHOR EITHER IMPROVISES ON UNKNOWN TERRITORY. OR THAT ITS CONTENT LIES COMPLETELY OVER OUR PAYGRADE. Please do educate us.

— Wikipedia sometimes has a real sense in going for the real steel of it;

— If we don’t understand details in the subject, we wait until we do, and can, RELATE them.

— Try this one: — »Very little is known or clarified on the subject in established literature, or not easy to explain in a rational way on the level of a pedestrian».

 

 

— Precession PRECESSION CONCEPT is experimentally related to a DEVIATIVE (deviant) concept with respect to some fix orientation. Please do correct if wrong:

 

 

 

The DEVIATIVE concept of PRECESSION appears as soon as as spinning wheel — gyroscope — is positioned on Earth ground LEANING relative a perfect — perfect — vertical balancing upright:

EQUATORIAL PRECESSION

 

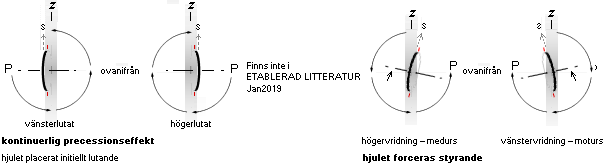
The gyrowheel begins a LEANED rotation — mass center deviation from vertical — around its Earth ground contacting point.

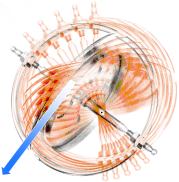
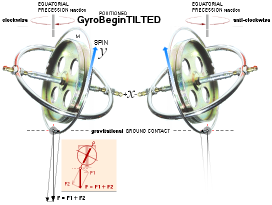
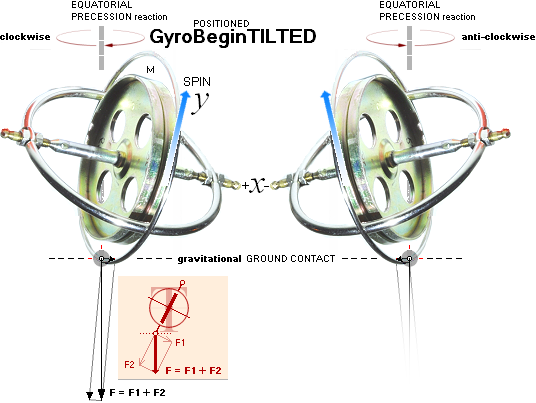
— The precessive action — a two ring gyroscope as depicted [‡] — can be of two different kinds:

1. Equatorial precession, top left — precession and spin are opposed — and

2. Axial precession, top right — precession and spin have the same direction.

— But this basic distinction is not mentioned f.ex. in WikiPRECESSION. Compare WikiTRAFFIC.

 

 

— THROUGH PrecMAN this initializing process a weight balancing torque (Fr) equilibrium appears on the suspended axel’s end as en effect — obviously not as a cause:

•   The weight balancing moment M=Fr gradually appears through a short small g-free fall;

•   The WikiPRECESSION article seems not familiar with these simple elementary gyro observations. OR its sectional author has hidden implications of a so very deep nature that this presentation really is empty, perhaps even superfluous. If so: God Please: more IQ.

 

   The WikiPRECESSION text is, so indeed remarked, a remarkable artifact in scientific literature. See also McOMwash2000 contra WikiSTEER: same gyro complex;

 

•   WikiPRECESSION has no mentioning of any a ”GyroLAW”.

— The Wikipedia authors — modern academy teaching system in general, so to speak — seem completely unaware of GyroBasic the subject.

•   WikiPRECESSION has no mentioning of any ”STATIC” or ”DYNAMIC” such ”gravity” properties.

— The EXPERIMENTAL phenomenal EXPLANATION behind;

— Equilibrium Phenomenal Rotational Transpositions between STATIC and DYNAMIC gravity properties, as experimentally observed; TP ¦ MacTP;

— A ”most mass resistive point” (M) is neither ever mentioned.

   In WikiPRECESSION Classical (Newtonian) it (M) is however hinted at by a corresponding more tedious associative resembling section of 12 3 6 9 and 90 180 degree talk over a bicycle wheel — which, of course, the reader holds in his hands during reading, so it will be easy to follow the true author’s lecture — with no other references: Trust me.

 

— Inertial frames to EXPLAIN physics = — equals — noPhysics: FUNTOP;

•   Physics relates to equilibrium — not to system:

•   Physcial laws hold for systems — not in systems, no way, never;

•   Birdstuff: NATURAL EQUILIBRIUM IN ANY POINT IN ANY MOMENT in any situation OF TIME.

— More elaborate in INERTIA.

 

— noMACphysics. Shoot me.

 

 

•   GyroPrecession — our GyroBasic device under experimentation its details in deep — inevitably DEMANDS SOME SERIOUS EXPLANATION in established quarters. The obviously NOT well related concept of a Gravitational Centre in Modern Academy Teaching Systems — ”gravityPoint”, WITH Static and Dynamik such g-centers — has poor rational depth. Especially in spinning devices.

   Although highly exemplified in mechanical 20:th century applications, especially the most expensive ones, the deep nature of the phenomenon is poorly — or even hardly — explained to the audience.

   The WikiPRECESSION text becomes especially obscure when the author tries to introduce ”a large hollow dough-nut”. This is where we start looking for an alternative DVD-experience, more adopted to our less developed level of IQ-related paygrade. God help us.

 

 

Studera med fördel den stora omfattande floran etablerade meningar i jämförande Internetreferenser (Jan2019) — svWikiMyth ¦ WikiCount1 ¦ WikiCount 2:

svWikiMyth:

 

DEN I DETALJ BEVISBART KORRUMPERADE WIKIPEDIALITTERATUREN I ÄMNET ELEMENTÄR GYROFYSIK OCH TRAFIKLÄRA[‡]

:

sv.WIKIPEDIA, Gyroskop 9Jan2019

https://sv.wikipedia.org/wiki/Gyroskop

 

 

”  Myten om cykling

En välkänd myt om cykling är följande:",

 

"Cykling på två hjul skulle knappast vara möjlig utan gyrokrafterna. Cykeln utnyttjar även det gyrots egenskap att omfördela en riktningsändrande kraft på axeln till en vridning av hjulet i tvärsled så att när cykeln lutas åt ett håll så vrider hjulet sig mot samma håll så att cykeln svänger åt det hållet. Det är detta som gör det möjligt att styra en cykel utan att hålla i styret."

 

Detta påstående är felaktigt. Att framhjulet håller sig stabilt när man cyklar utan att hålla i styret samt svänger åt rätt håll beror visserligen delvis på gyrokraften, men huvudsakligen på att krafterna mellan marken och hjulet angriper bakom styrstångens rotationscentrum[3]. Testa att luta en stillastående cykel (ingen gyrokraft). Hjulet vrider sig ändå åt rätt håll.”

 

Gyrofysiken — RotIPST — WikiCount1 — WikiCount2 — WikiPRECESSION — WikiSTEER — WikiAXEL — WikiTRAFFIC — McOMwash2000

 

1.   Wikipediaartikelns citat ”Cykling på två hjul ..” innehåller ingen referens — vi vet inte varifrån citattexten kommer:

2.   Wikipediaartikelns efterföljande text innehåller en referens — [3] med ”Alternativ åtkomst” — som inte leder någonvart, resp, ”Page not found”, och ”Webbsidan kan inte visas”.

3.   Artikelförfattarens påstående

”  Testa att luta en stillastående cykel (ingen gyrokraft). Hjulet vrider sig ändå åt rätt håll. ”

har heller ingen tekniskt bekräftad naturvetenskaplig referens till GYROLAGEN — ANNAN än en direkt bevisbar dikeskörning — kraftig (över-) manipulering av CykelStyret som INTE kommunicerar med Gyrolagen:

 

Se särskilt i  Jämförande Lutningsvärden från Anställda Krafttider:

— Det etablerade utbudet på kvantitativt beskrivande enkla jämförande exempel är milt sagt uruselt.

 

PRAKTISKT EXEMPEL:

— Lutning av cykelkroppen [‡] under normal cykling med kurvgenomgångar ligger knappast — ens — över ± 1°:

— Ingen som helst rörelse hos cykelns fritt vridbara framhjul kan observeras med cykeln stillastående med den ringa cykelkroppslutningen — testat med cykeln stillastående, vertikalt med motsvarande »små cykelfärdspraktiska vippningar» omkring vertikalläget.

— Däremot — GYROLAGEN — avkänner Jordfysiken minsta möjliga lodavvikelse, hundradels grader, hos DET SPINNANDE ÅKANDE framhjulet på en vanlig cykel

— med åtföljande gyrofysiskt automatiskt justerande hjulvridning åt lutningshållet, och som garanterar stabiliteten i framfärden — jämför LetRitTURN.

 

4.   Artikelförfattaren känner — i andra ord och här tydligt i bevisbar detalj — inte till Gyrolagen: har aldrig genomfört de enkla gyroexperimenten som klargör den praktiska fysikens funktion — också tydligt bevisligt i varje atomär detalj:

 

— Minsta lilla hjulspinn i cykelns framförande motar DESSUTOM bort — garanterar eliminering av — varje typ av särskild familjeunderhållning av typen ”Nu lutar jag på Cykeln, Stillastående, så att framhjulet ramlar ner, och att jag därmed har Bevisat KäkGlappets suveräna ställning över Gyrofysiken”.

 

Hjulspinn stabiliserar fartriktningen — och blir därigenom exceptionellt känsligt för LUTNING = tillståndsändring. Se särskilt enligt elementära, enkla, gyroexperimentella observationer i Bevis B; Det spinnande cykelhjulet har redan markkontakt, och ingen fördröjning finns därför mellan gyroskopisk reaktion och förorsakande lutning ur exakt vertikal led. Minsta lilla avvikelse räknas.

 

Två (svenskspråkiga) webbsidor citerar/härmar Wikipediatexten:

 

Faktoid — Mytologi, kultur och religion

insidan.ifokus.se

Gyroskop : definition of Gyroskop and synonyms of Gyroskop

dictionary.sensagent.com

 

”Välkänd myt om cykling”:

— Sökning på engelska Webben (Wellknown myth of bicycling 11Jan2019) ger ingen respons på den påstådda förekomsten:

 

0: Bicycling Myths — phred.org

0: Five myths about bicycling, The Washington Post — cc.bingj.com

0: The Myths and Misunderstandings About ... — bicycling.com

0: Cycling Myths – Debunking Them — ilovebicycling.com

0: — Engelska Wikipedia Cykling har inte (ens) ORDET ”myth”.

 

 

5.   Så: Varför inte testa den här istället, direkt, med en gång, klämma i mera rejält:

— »Sverige håller på att konvertera till Islam».

 

Trail: SE

Men det är ändå ingenting mot det här:

»FASTEN SEATBELTS, NO SMOKING». Det kanske också är bäst att sitta ner en stund.

Gyrofysiken — RotIPST — WikiCount1 — WikiCount2 — WikiPRECESSION — WikiSTEER — WikiAXEL — WikiTRAFFIC — McOMwash2000

 

WIKIPEDIA, Bicycle and motorcycle dynamics 9Jan2019

https://en.wikipedia.org/wiki/Bicycle_and_motorcycle_dynamics - Trail

:

” Trail

   Bicycle head angle, rake, and trail

A factor that influences how easy or difficult a bike will be to ride is trail, the distance that the front wheel ground contact point trails behind the steering axis ground contact point. The steering axis is the axis about which the entire steering mechanism (fork, handlebars, front wheel, etc.) pivots. In traditional bike designs, with a steering axis tilted back from the vertical, positive trail tends to steer the front wheel into the direction of a lean, independent of forward speed.[28] This can be simulated by pushing a stationary bike to one side. The front wheel will usually also steer to that side. In a lean, gravity provides this force. The dynamics of a moving bike are more complicated, however, and other factors can contribute to or detract from this effect.[1]”.

QUOTE WITH COMMENT :

•   ”positive trail tends to steer the front wheel into the direction of a lean”:

— No. NOT in any way — even far from a significant way — within the NORMAL limits of LeanAndTurn, as experienced from a hands-free bike travel (leaning variations within no more than 1°) — as also experimentally verified[‡] by principle from a simple basic math-gyro-deduction WITH a detailed experimental verification. IT seems NOT being (very) familiar to established quarters:

— no such PRACTICALLY provable effect exists.

•   ””This can be simulated by pushing a stationary bike to one side. The front wheel will usually also steer to that side.”:

 

— ABSOLUTELY yes — but NOT in any connection to the actual bike-ride, as stated:

 

— Holding a bike PUT — still — and wagging it sideways to and fro WILL UNDOUBTEDLY demand more than 1/10 of a degree to make us WITNESS ANY motion of the front steering mechanism.

 

— In REAL Biking 1/10 of a degree lean IS »The Real Steel»:

 

 

— In a real practical BikeRide, the bicycle acts like an enormously — »by even an atom» — sensitive balance (lever), sensing the tiniest smallest lean from vertical — exactly as a gyroscope under experimentation does[‡]. — A corresponding turn of the front wheel always follow — as exactly explained by The GyroLAW from simple elementary gyroscopic experiments[‡]. WikiMan: you should know this.

— Wiki authors in the subject OUGHT to be especially experimentally WELL acquainted with that type of physics — obviously, as it seems here, BEFORE speculating the subject (by something that seems more like »computer modelling speculations based by calculus no one understands — either»). The GyroLAW is not even mentioned, nor related in established literature. Altough it is SIMPLE.

— YOU were supposed to educate us. NOT we you. Please do correct if wrong.

 

— VARJE MINSTA LILLA LUTNING HOS ETT SPINNANDE HJUL RESULTERAR I EN GYROEFFEKT. MEN INTE VARJE MINSTA LUTNING AV EN STILLASTÅENDE CYKELKROPP RESULTERAR I ATT FRAMHJULET VRIDS ELLER FALLER ÅT LUTNINGSHÅLLET.

— Teoretiserande — bevisbart tydligt skarvande — på det här sättet med gyrofysikens detaljer har, vad vi vet, ingenting med en seriös naturvetenskap att göra.

 

— Stillastående cykelkropp — teoretiska lutningsaspekter — HAR INGEN KOPPLING TILL EN CYKELKROPP SOM ÅKER PÅ SPINNANDE HJUL:

 

MINSTA LILLA SEPARAT UPPKOMNA STYREVRIDNING

 

 Destructive manipulation in Biking — SPIN clockwise ahead, as seen by an observer from behind.

Established literature, see WikiQuote, claims opposing statements — with no mentioning of the simple elementary GyroLAW.

 

RESULTERAR I MOTSVARANDE BevisC MARKSLITANDE GYROEFFEKT:

 

 

 

EQUATORIAL GYROSCOPIC PRECESSION

BasicEXAMPLE — should be in any SERIOUS  encyclopedic text on the subject — not found @Internet Jan2019

—————————————————————————————————————————

Spinning Wheel on Earth ground — PilotSYSTEMxyz:: axelHORIZONTAL J=mvr: momentarily pushed:

 (y↓+x) → –yW° ¦  = clockwise stepped y-twist                ; constructive safe traffic gyro wheel navigation

 (y↓–x) → +yW° ¦  = anti-clockwise stepped y-twist        ; constructive safe traffic gyro wheel navigation

———————————————————————

 (z↑+x) → –zW° ¦  = clockwise stepped z-twist                ; DEstructive UNsafe traffic GYRO wheel STEERING

+ direct gravitational RotII-System –yW° clockwise equatorial precession, depending on force.

 (z↑–x) → +zW° ¦  = anti-clockwise stepped z-twist        ; DEstructive UNsafe traffic GYRO wheel STEERING

+ direct gravitational RotII-System +yW° clockwise equatorial precession, depending on force.

—————————————————————————————————————————

In general: reaction effect is proportional to the onsetting acting force.

See McOMwash2000 — it concords with GyroLAW but not as claimed in Wikipedia. Read it to believe it.

— See WikiTRAFFIC.

 

Försöker man STYRA — vrida på — det spinnande hjulet

STRÄVAR HJULET ATT VRIDAS PÅ ETT TRAFIKFARLIGT — äventyrligt, beroende på förhållandena — SÄTT: sidledes, tvärs färdriktningen BikeTableExample.. Det är de direkt uppenbara konkreta och detaljerat bevisbara, relaterbara och förklarbara resultaten GyroBasic som visas omgående från de enkla gyroexperimenten hemma i köket.

 

— OM någon vill experimentera med sådana effekter, är det dens ensak, OK. MEN UTAN INSIKT I ATT DET ÄR ATT LEKA MED NATURKRAFTERNA PÅ OMVÄNDA REAKTIVA SÄTT, ÄR verksamheten potentiellt vådlig — farlig också för andra.

 

— DEN PRAKTISKA GYROFYSIKEN I CYKLANDETS FRAMFART MOTVERKAR, NATURLIGT, VARJE SÅDAN OLYCKLIG TENDENS.

 

 

Wikiförfattarna i ämnet borde känna till det.

   Eller kanske enklare det här:

— VET man inte, VÄNTAR man TILLS: vänta med Körningen tills det blir grönt. Jättesvårt.

   Säg efter mig: VI VET INTE. Jättesvårt.

— OCH SÅ BLIR HELA DAVID JONES-UTFLYKTEN EN OLYCKLIG TEORETISK SPEKULATION I ÄMNESFRÅGOR — »webbforum för datormodelleringsSpekulationer» — SOM INTE HAR MED den konkret påvisbara bevisbara elementära GYROFYSIKEN ATT GÖRA. Absolut gärna rätta om fel.

— Ursäkta intrånget:

Gör gyroexperimenten hemma i köket FÖRST och gör enkla kontrollerande matematiska-fysikaliska härledningar. Please. Kom sedan med snacket. Wikipedia är hopplös i ämnet:

 

:

WikiCount: Trail — RotIPST

” .. för att svänga vänster måste cykeln först lutas höger ..” — se särskilt i DBE:

” .. to turn left the bike must first be leaned right ..”; 

— »PLUTO is about to become populated». »Free Oxygen».

 

WIKIPEDIA, Countersteering, Countersteering by weight shifting 9Jan2018

https://en.wikipedia.org/wiki/Countersteering

:

HELA DET AKTUELLA STYCKET FÖR UNDVIKANDE AV MISSAD KONTEXT:

 

"  Countersteering by weight shifting

With a sufficiently light bike (especially a bicycle), the rider can initiate a lean and turn without using the handlebars by shifting body weight, called counter lean by some authors.[8][25][26][27] Documented physical experimentation shows that on heavy bikes (many motorcycles) shifting body weight is less effective at initiating leans.[28]

 

The following is done when countersteering using weight shifting to turn left:

 

The rider applies a momentary torque, either at the seat via the legs or in the torso that causes the bike itself to lean to the right.

 

The combined center of mass of the bike and rider is only lowered and not moved out, but if the front of the bike is free to swivel about its steering axis, the lean to the right will cause it to steer to the right by some combination of gyroscopic precession, ground reaction forces, gravitational force on an off-axis center of mass or simply the inertia of an off-axis center of mass depending on the exact geometry and mass distribution of the particular bike and the amount of torque and the speed at which it is applied.[8][29]

 

This countersteering to the right causes the ground contact to move to the right of the center of mass, as the bike moves forward, thus generating a leftward lean. Finally the front end steers to the left and the bike enters the left turn.

 

The amount of leftward steering necessary to balance the leftward lean appropriate for the forward speed and radius of the turn is controlled by the torque generated by the rider, again either at the seat or in the torso.

 

To straighten back out of the turn, the rider simply reverses the procedure for entering it: cause the bike to lean farther to the left; this causes it to steer farther to the left, which moves the wheel contact patches farther to the left, eventually reducing the leftward lean and exiting the turn.".

 

Frånsett ”lean ... right ... cause ... steer ... right” som ansluter perfekt till GYROLAGEN men som i Wikipediatexten ovan strax övergår i en helt obegriplig motsägelse ”countersteering to the right causes ... a leftward lean ... bike enters the left ”:

— Wikipediatexten beskriver något som den här författaren som frekvent cykelåkare inte känner igen en enda detalj i. Inte ett spår:

Gyrolagen förklarar min cykelåkning — perfekt. Och som också McOMwash2000 gör, med associerade trafikinrättningar.

Men någon ”gyro law” finns inte omnämnd i etablerad litteratur.

— Jag har ingen som  helst minsta idé eller uppfattning, inte alls över huvud taget,  vad Wikipediatexten talar om: ”initiera höger för att svänga vänster”. Ingen aning — UTOM DIREKT TRAFIKFARLIG MANÖVER MED EVENTUELLT ÅTFÖLJANDE DIKESKÖRNING + våda eller fara för medtrafikanter. Wikipediatexten kan bemötas, i detalj, enligt Gyrolagen som följer.

 

”  The following is done when countersteering using weight shifting to turn left:”,

”  The rider applies a momentary torque, either at the seat via the legs or in the torso that causes the bike itself to lean to the right.”.

 

Gyrolagen åter i erinrad praktiskt fysikalisk verkande bevisbar referens:

Wikipediatexten beskriver en initierad högersväng PÅ en motsvarande gyroautogenererad högerhjulsvridning enligt Gyrolagen som inte omnämns i etablerad litteratur, men som framgår genom enkla elementära köksexperiment som — GyroBasic — vem som  helst kan utföra, kontrollera och verifiera:

— Men vi vet här strängt taget inte heller vad Wikipediaförfattaren är ute efter: ATT beskriva hur man VINGLAR HÖGER FÖR ATT SVÄNGA VÄNSTER. Eller vad framställningssättet ska föreställa. Det är fullkomligt oklart. Helt gåtfullt. Fullkomligt.

 

 

GyroLagenRef

 

Har man en gång högerlutat hojen, händerna bakom ryggen, har också hojen påbörjat en högersvängande framfart — hjulvridning per TID: cykelns fritt vridbara framhjul står i medurs gyroekvatoriell precession: högersvängandet ÄR påbörjat, Under Operation, eng. ON.

— Hur i h-e människa ska någon VETTIG manöver från den Situationen kunna resultera i KURVTAGNING ÅT VÄNSTER? Jises. Snabbkonvertering till Islam? Alla ... Alla ... Alla ...

— Jag bara konstaterar det, rakt av, mitt i: finns inga planer någonstans i något skrymsle av Universum att en sådan AKT kan Verkställas utan TRAFIKVINGLIGLIGT TRAFIKVÅDLIGT BETEENDE — Cirkus Cykel i Stan: bereden Stor plats. Helt uteslutet.

   Kommentar från cyklist bakom som vill köra om: — »Ska du höger eller vänster eller hur f-n blire?».

 

LeanTurn: MATH

Vill Wikipediaförfattaren och alla andra PÅSTÅTT[‡] Associerade Amerikanska Cykelförbund rita ut sin version av DEN NATURLIGA tyngdpunktsnavigeringen i Cykling HandsFree med Kurvtagning, så att vi kan jämföra naturbeskrivningen mera exakt, Please? Därför att vad den här cyklande författaren vet, finns bara en enda Autonom Fysikalisk EkvatorialPrecesserande Gyrolag att rätta sig efter på Jordytan, figuren nedan enligt erfaren ordning:

 

 

Ju mera kraft som läggs på lutningsändringen, given ändringstid, desto mera respons ger Gyrolagen. Kraft över väg — på tid.

En detaljerad beskrivning MED GYROLAGENS OMNÄMNANDE har eftersökts i etablerad litteratur, men ännu inte påträffats.

Jämför slutstycket i Wikipediacitet — absolut komplett helt gåtfullt:

 

”To straighten back out of the turn, the rider simply reverses the procedure for entering it: cause the bike to lean farther to the left; this causes it to steer farther to the left, which moves the wheel contact patches farther to the left, eventually reducing the leftward lean and exiting the turn.”,

WikiCOUNT.

 

ATT möta den Typen i trafiken vill den här författaren INTE rekommendera: texten beskriver en »antifysik». Det ser helt enkelt ut som att Wikipediaförfattaren DIKTERAR ett SÄTT som bestäms av en teoretiserad, icke reellt trafikfysiskaliskt naturförankrad, datormodellerad, akademisk Inertiell Vektorkalkyl.

 

Jämför KORREKT TRAFIKSÄKERT SÄTT i McOMwash2000.

— Notera samtidigt den WIKIPEDIA-KORRUMPERADE WikiSTEERING TERMEN ”counter-steering” — helt rakt motsatt McOMwash2000:s ICKE-STYRNING.

 

 

Minsta lilla NANOLUTNING VänsterHöger hos ett spinnande hjul på en vägbana, typ framhjulet, fritt vridbart på en cykel, avkänner omedelbart, omgående, oåterkalleligt, obönhörligt, kompromisslöst lutningsfysiken i form av en motsvarande VänsterHöger EXAKT fysikbalanserande AUTONOM

— självreglerande FÄRDSÄKER TRAFIKKORREKT EKVATORIALPRECESSERANDE

— hjulvridning. Exakt. WikiSTEER ansluter INTE till den typen. Läs det för att tro det.

 

 

HögerLutning Gyro-Auto-Genererar Högervridning — det fritt vridbara hjulet vrids höger.

 

 

Det är gyrofysikens absoluta grund: Gyrolagen, den ytterst enkla.

Wikipediatexten beskriver — tydligen — en framfärd som initieras med EN PÅBÖRJAD kurvgenomgång ÅT HÖGER. Inte åt vänster. Och som sedan påstås, tydligen utan fysikaliskt begriplig förklaring, resultera i ett vänstersvängande cykelspår. Alltså EN VINGLANDE FRAMFÄRD (fyllo på cykel): först högersväng, sedan vänster.

 

Wikipediatexten beskriver uppenbarligen INTE den praktiska fysiken, säger Gyrolagen. Vilket verkligen verkar väldigt, väldigt underligt med tanke på ämnets föreställande ELEMENTÄRA natur, och (den föreställande) NIVÅN på författarskapet.

 

Enda möjliga sättet att förstå den wikipediska beskrivningsformen blir således, säger Gyrolagen, att författaren, dennes skola, referenser, utbildning och kontakter — den akademiskt etablerade kulturen — inte känner till fysikinnehållet: NoMACfysik: Wikipediatexten beskriver — uppenbarligen, säger Gyrolagen — åkspåret från ETT FYLLO. — »För att svänga vänster, måste jag först svänga höger». TRallerian .. traderuttan ...

 

”  This countersteering to the right causes the ground contact to move to the right of the center of mass, as the bike moves forward, thus generating a leftward lean. Finally the front end steers to the left and the bike enters the left turn.”,

WikiCount;

— Verkligen enastående DatorRelaterad CyberNaturBeskrivning: Animerad Jordisk Fotvandring. Kalhygge.

— Beskrivningen ansluter, verkligen, till Nya iPhone-VärldsKulturens Verkliga IQ-uppsving: blicken konstant ner mot asfalten.

 

Så:

 

The Ground contact Is Never Lost during travel unless a situation of traffic accident is at hand.

— Ground contact does not move. Ground contact always stays put.

   Vi VET inte om Wikikpediaförfattaren underförstår Akademiska Resonemang som baseras på Skolade Inertialsystem. Vi garder oss för det:

— Inertial systems in physics does not exist[‡]: Physics relates to Equilibrium. Not to system; Laws of physics hold FOR — not IN — systems. NATURE rules physics. NOT modern academy (1800+). This elementary basic physical constitution is NOT present (were ruled out during the famous 1800:s) in modern academic ideas of nature: The idea of an inertial system IS[‡] a modern academic INVENTION — to match Einsteins ideas of relativity.

   In RELATED PHYSICS AND MATHEMATICS (TNED) MAC is outclassed by — AND FULLY, IN ABSOLUTE DEEP, EXPLAINED THROUGH, OR NOT AT ALL — The Planck Equivalents and The Gravitational Dependency of Light: neither found nor mentioned in the modern academic teaching system.

— Physics in general, so provable in detail, cannot be described by modern academic mind.

— Please do correct if wrong 1800+: MODERN ACADEMIC PHYSICS ONLY HAVE THE CAPABILITY OF PROFITING ON PHYSICS’ NATURE with one specific concrete practical example: DEVELOPING MACHINERY — TECHNOLOGY — TO DEFOREST (>30% period 1800-2000 [Source: ForestWorld]) THE FOUNDATIONAL BIOLOGICAL ENVIRONMENT WHICH LAID THE GROUND FOR NATURE’S EVOLUTION OF HUMANS: »CUT HER DOWN».

— Earth Land Oxygen Producers and Sustainers[‡]. NOT by plan. But by DRIFT:

— Why? What’sUp? Test this one: DUE TO the 1800+ MAC-established idea of Intelligence, Humanity became IMPRISONED in darkness and ignorance, violence and force, obedience and punishment, LOCKED OUT BY A GOVERNMENTAL DICTATORSHIP CALLED DEMOCRAZY* — not free choices under human rights[‡] AS IT SHOULD BE, but obedience under governmental authorities = oppressing — the capability AND HUMAN NATURAL INTELLIGENCE to seek for — and find — AN ENERGY SOLUTION WORTHY a highly developed technological CULTURE. Please DO correct ANY error.

— »I mean: We MUST have FUEL to provide TRADE with Merchandise».

— »I mean: We MUST have WOOD to provide TRADE with Merchandise».

— »I mean: We MUST have WE to provide TRADE with Merchandise: I MUST be I.». The TechExplanation. WindPoles too, further reducing Natural Biological Airing — transforming IT to ”usable energy”: a general state of CULTURAL AND TECHNOLOGICAL CHAOS. As I said: Please DO correct if any error.

———— *

»Demo Crazy»: Author’s WorldScene: SWEDEN — before WWII, especially during WWII, and most explicitly after WWII — and what has been reflected globally through media and literature. Nothing else.

— No mother god loving way.

— MARKKONTAKTEN ÄNDRAS ALDRIG UNDER FORDONS FRAMFÖRANDE om det inte är fråga om en allvarligt uppkommen trafiksituation.

— Wikipediaförfattaren talar här helt i fullständiga gåtor — tydligen med underförståddheter som inte har någon förankring i praktisk fysik, säger Gyrolagen.

— Wikipediatextens kontext är i sanning en väldigt märklig uppvisning — delvis med, delvis mot Gyrolagen. I sanning märkligt — med tanke på den omfattning — utbildning och undervisning — som textsammanhanget åberopar.

 

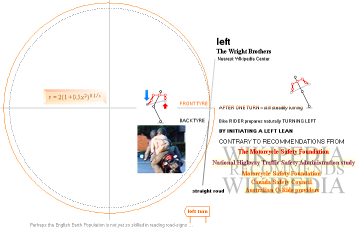
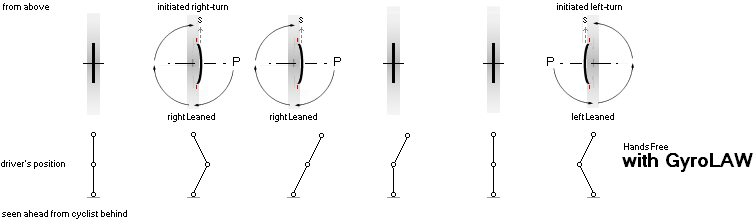
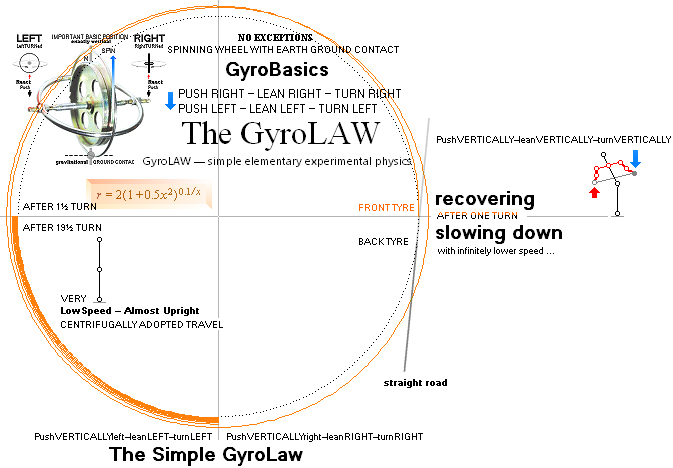
GyroLAW — obviously unknown in Modern Quarters, see also illustrated in LetRitTURN — a freely turnable ground-travelling spinning wheel:

RightLeaning causes Autonomic Equatorially Precessing GyroWheelRightTurn, as

LeftLeaning causes Autonomic Equatorially Precessing GyroWheelLeftTurn, says GyroLAW.

— There is no physical ”LeftAction from RightLeaning”, says GyroLAW.

— A RightLean has no LeftLean effect whatsoever. No way, says GyroLAW.

 

 

WIKIPEDIA WikiCOUNT IS OBVIOUSLY PROMOTING TRAFFIC DANGEROUS AND HAZARDOUS BEHAVIOUR, says GyroLAW — even CLAIMING INSTANCES WHO DON’T AS ASSOCIATED: See in detail from McOMwash2000 contra WikiSTEER.

 

” 1. Action causes bike Lean Right; 2. Reaction causes ground contact move right; 3. Reaction thus generating a LeftLean ...”, WikiCount.

   There is nothing such in physics.

— And: IF it WOULD so be INSISTED: Please educate us, says GyroLAW.

— Because inside of the GyroLaw, the WikiCount context as so quoted is a detailed provable absurdity.

— Seems that the WikiAuthor is Reading HUGE SCREEN MyBelovedNewComputerProgram MyOhMyOHMyComputer High School Modern Academic Vector Algebra MODELLING — because we KNOW everything, we only have to MODEL out the rest ... which we don’t know ... , and ..

no actual ”Now I’m On the Road BikeExperiencing Real Physics”.

— Please do correct if untrue, says GyroLAW:

— To generate a Gyroscopic WikiCountersteering effect = Traffic Dangerous Situation,

navigating the spinning wheel by actually applying arm force to steer, turn, the spinning wheel of a bike, and so too Opposed — Wiki’s”Counter” — the Intended Turning Direction : a »counter-reversed» precessional force

an already present Lean itself must be Forced — which we would name a destructive navigation — to Oppose itself by just that: a manual ArmForcedWheelTwisting angle against the Gyroscopic natural GyroLAW physical force action-reaction:

— The Wikipedia statement in the quote[‡]

 

the lean to the right will cause it to steer to the right

:

countersteering to the right causes the ground contact to move

:

thus generating a leftward lean

:

Finally the front end steers to the left and the bike enters the left turn

WikiCount

 

is no description of the act of natural physics, says GyroLAW.

— The text in general neither makes it clear: ”gyrolaw” is not mentioned, nor related: unknown;

RESULT:

— The WikiCount text is NOT a report from a person’s practical BikeRide.

— The WikiAuthors are free to »SPECULIZE» — computer aided modelling TALK.

— HOW can you say that?

— BECAUSE inside this Universe of ours, as far as here is known Jan2019, there is only one place providing a free and spontaneous speech of globally general rational fuckups: @INTERNET + Modern Academic Computer Modelling.

 

”  Lack of understanding of this principle leads to accidents in novice bicycle races.”, WikiCount.

— There is only one possible explanation to such obvious claims, says GyroLAW: no foot on Earth: no understanding of basic elementary Earth physics: a complete computer modelled cyber space dictated fantasized imaginary reality — which is also forced upon instances who DON’T take part: See WikiSTEER contra the GyroLAW associated McOMwash2000.

 

— Det man kunde förvänta av WikiAssocierade Seriöst Menande Inrättningar är — om de nu nödvändigtvis insisterar på att sprida virrManualer om grundfysiken för Tävlingsfester — ATT om man nödvändigtvis vill Utbilda 2-Hjuligt MC-folk att RattaHöger Före Vänstersväng, MAN GÖR DET MED FÖRBEHÅLLET ATT FÖRAREN GÖRS UPPMÄRKSAM PÅ ATT DEN MANÖVERN LEKER MED FYSIKKRAFTER PÅ BEVISBART POTENTIELLT GYROFARLIGT/destruktivt SÄTT. Se särskilt  i BEVIS C: MARKDEPLACEMENTET.

 

— Men vi ser ingen sådan varnande text. Ingen sådan antydan. Inte något omnämnande. Inte en prick. Jämför:

 

»  Lack of understanding of OPPOSING GYRO PHYSICS leads to accidents in novice bicycle races.»:

 

CLEARLY SERIOUS ISSUES EXIST IN ESTABLISHED QUARTERS IN THIS SUBJECT. Detailed clarifications are urgent.

 

Webben är — så, samma typ, samma ämne — full av TYDLIGEN liknande DATORPRODUCERAD efterhärmad, upprepad VERITABEL så bevisbar FYSISK SKRÄPKULTUR — ren vanvettig trafikpropaganda — som ger sig ut för att företräda ”avancerad akademisk fysikkunskap”; exakt noll fysikinsikt. Visa vid Teutates att jag har fel.

— Se WikiSTEER kontra GyroLAGENs associerade McOMwash2000 — perfekt enhetlig fysikförklaring för personer som använder tvåhjulingar i trafiken. Det är — vid Teutates — helt korrekt trafiksäker fysikbeskrivning.

 

 

AxiGyroPrecGM:

— See also: How to calculate The Dynamic Gravity Circle   r  in Our Mechanical TOP.

Axiella gyroprecessionens grundmatematik

ENLIGT ELEMENTÄRA GYROEXPERIMENT:

 

 

Försöker man introducera en avvikelse i vertikalläget, speciellt för typen  av spinnsnurra i figuren ovan höger då spinnet ligger över gränsvärdet för axiell precession, återtar spinnaxeln strax sitt stadiga lodläge. Se särskilt i Beviset.

— Den rent matematiska behandlingen av Jordfysikens olika spinnanordningar blir därför särskilt krävande: ingående kunskap om aktuell formkropp krävs. Det finns inga allmänna samband med någon konkret praktiskt begriplig meningsfull innebörd — utom möjligen som ovan: gränsfrekvensen för ICKE axiell precession. Bildlänken ovan kopplar avsnittet. Gyrolagen omnämns inte i etablerad litteratur.

— Given tyngdcirkelradie (r):  Ju längre axeltappen är som snurran balanserar på, desto högre hjulspinn måste snurran påföras för att nå upp till sitt fallgränsvärde: gränsen där snurran inte längre uppvisar någon precesserande, wobblande, rörelse.

   Genom att etablerad litteratur inte verkar känna till Gyrolagen, är det också (här, ännu Jan2019) svårt att försöka få ut något meningsfullt av det etablerande matematiska innehållet: Ämnet presenteras på en specifik högskolematematik som — helt — verkar ha missat naturgrunderna generellt: helt oförmögen att förklara ämnets inneboende djupfysik. För ev. vidare.

— Den ekvatoriella precessionen som gäller föremålen på Jordytan — fritt rörligt hjul på väg som i figuren nedan — har delvis andra förutsättningar — med en mera MÖJLIGT hanterlig allmänt formulerbar matematik: OM någon tillståndsändring sker — Kraften

F över någon momentdistans d — MÅSTE den tvunget arbeta på MINST det givna impulsmomentet J=mvr som det spinnande hjulet uppvisar.

— Se särskild (ENKEL) härledning med (praktiska) exempel i Ekvatoriella GyroPrecessionen.

 

VänsterHögerSväng:

TÄNK EFTER PÅ DET HÄR, NOGA — i jämförelse med påståendesatserna i WikiCount:

 

”  To straighten back out of the turn, the rider simply reverses the procedure for entering it: cause the bike to lean farther to the left; this causes it to steer farther to the left, which moves the wheel contact patches farther to the left, eventually reducing the leftward lean and exiting the turn.”, WikiCount 9Jan2019:

 

— SEDAN TVÅHJULINGEN FÖRTS IN I SIN VÄNSTERSVÄNG:

HUR HANTERAR FÖRAREN SVÄNGRADIENS

AVTAGANDE I ÅTERGÅNG TILL RAKSTRÄCKA?

 

 

 

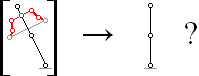
Kurvgenomgång enligt Gyrolagens harmoniska anvisningar — tydligen helt obefintligt representerat i modern akademi. Gyrolagen omnämns inte etablerat. GYROLAGEN. Axiell och Ekvatoriell precession.

 

SVAR:

ANSWER:                   

 

If no else: Grab The Bike and take The Tour and test for yourself: make FAST turns and observe the way these navigate Bike + Driver, all the different parts: always in concord with GyroLAW physics. No exceptions.

 

— Uppenbarligen — gyrolagen[‡] — inte Wikipediatexten:

— På samma sätt som varje MINSTA kurvtagning påbörjas men omvänt:

•   ett påbörjat vänsterlut AutoGyroFysikKopplar vänsterväng ; 

•   ett påbörjat högerlut AutoGyroFysikKopplar högersväng;

•   återgång till raksträcka från påbörjat vänsterlut: högeråtertag: flytta tyngdpunkten DITÅT svängen VILL:

•   återgång till raksträcka från påbörjat högerlut: vänsteråtertag: flytta tyngdpunkten DITÅT svängen VILL:

— Bevisbart i varje atomär detalj som ovan enligt Gyrolagen.

— Och tydligen lika bevisbart i varje atomär detalj OBEFINTLIGT i någon övergripande relaterbar rationell enhetligt begripbar ordning i den moderna akademins Wikipediapresenterade lärosystem i ämnet.

 

IT SEEMS THE WIKIPEDIA AUTHOR(S) HAVE NO IDEA OF — NO ACTUAL PRACTICAL EXPERIENCE — OF COOPERATING AND CO-ORDINATING A NATURAL BODILY MOTION with presevered perfect balance. MAYBE THE WIKIPEDIA TEXT IS WRITTEN BY A COMPUTER: guaranteed no idea of physics.

 

WIKIPEDIATEXTENS FÖRFATTARE BEFINNER SIG UPPENBARLIGEN INTE I DEN VERKLIGA CYKELFARANDE JORDISKA PRAKTISKA FYSIKEN: en ytterligare tyngdpunktsförflyttning 

”lean farther to the left”

LEDER ENBART OBÖNHÖRLIGT OÅTERKALLELIGT, säger GyroLagen, TILL ÄN MERA VÄNSTERSVÄNGANDE FRAMFART.

— DEN ANVISNING SOM WIKIPEDIATEXTEN GER HAR, SÅ, BEVISLIGT I VARJE FYSISK DETALJERAD MENING, INGENTING ATT GÖRA MED EN BESKRIVNING AV HUR EN TVÅHJULING HANTERAS garanterat förarsäkert och optimalt snabbt navigerande I ALLMÄN TRAFIK .

 

— Gyrolagen är — så — alldeles tydligt bevisbart helt okänd i modern akademi.

   Författarna nödgas skarva för att kompensera bristen på rationell insikt i grundfysiken.

   Absolut gärna rätta om fel. Därför att den påståendeformen är INTE rolig att företräda.

 

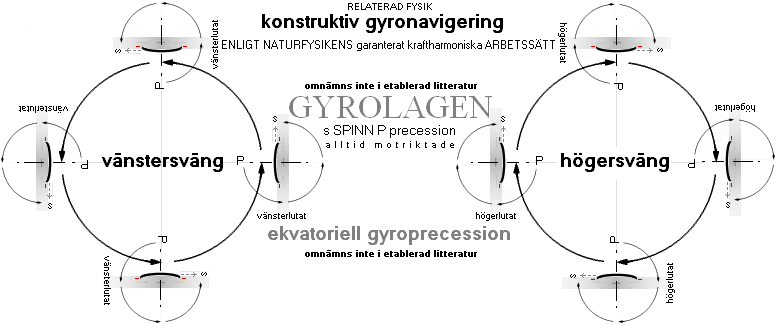
Sammanställning, ekvatoriell precession: DBE

 

Figurerna ovan/nedan illustrerar och sammanfattar Gyrolagen enligt detaljerat beskrivbara och ytterst enkla, elementära gyroexperiment GyroBasic. Det vanliga PILOTSYSTEMET xyzXYZ ger säkra referenser — med ett fritt rörligt (cykel-) hjul på väg framåt i riktning z. Två Gyro2Ways olika angreppssätt — två olika grundriktningar yz [BaTaGYMO] — finns för att påverka hjulets färdväg: ett konstruktivt, det som följer gyrolagens sätt, och ett destruktivt, det som f.n. verkar vara mest populärt i etablerade kvarter som imponeras av innehållet i WikiCount. Se särskilt från StudieExempel.

 

Bevis C.The Precession Concept has Issues. Bevisen ABCD. GYROLAGEN.

 

 

— Finns det någon tänkbar — ens möjlig — orsak till att WikipediaVärlden attraheras av detaljer i MAC-undervisningssystemet som missar ämnesdjupet?

 

   GYROLAGEN OMNÄMNS INTE. Motsvarande MostMassResistive omnämns inte heller. Inte heller omnämns väsensskillnaden mellan EKVATORIELLA precessioner — icke samriktat spinn och precession — och AXIELLA precessioner — samriktat spinn pch precession.

   Definitivt omnämns inte heller själva den avgörande KRAFTBILDEN i skillnaden mellan de bägge sistnämnda: differensen Gyro2Ways mellan konstruktiv och destruktiv gyronavigering: BikeRidingBasics. Not a word.

 

Varför?

— Varifrån kommer — då — själva uppslaget till den här författarens djupgående engagemang i saken?

— 1. Jag äter ofta Äpple.

— 2. PLANETROTATIONERNA i VINTERGATANS SOLSYSTEM.

— Vi klarar inte den uppgiften utan ingående, detaljerad, inblick i gyrofysikens detaljer. Så kom det sig.

 

 

— Testa den moderna akademins vektorkalkyl. Detaljerade genomgångar i Universums Historia visar att den moderna akademins 1800-talsuppfunna moderna vektorkalkylerande IDÉ är — helt — komplett oförmögen att beskriva detaljerat relaterbara naturgrunder: med konkreta exempel i magnetismen, induktionen, centralrörelsen.

 

— Det liknar — ungefär, konkret, min mening — det världspopulära Tönt&SlarvProgramspråket C(++) i förhållande till Microprocessorns direkta Assembler :

 

Mnemonics, Hex-koderna — Borlands Turbo Assembler som inte används — därför att

1. huvuddelen av datorfolket är slarviga och DÄRFÖR inte står ut med noggrannheten i Assembler — misstag tillåts inte — och

2. att Noga Ger För stor Frihet åt NaturIntresserade Privatpersoner att utveckla datorprogram som är tusen gånger mer effektiva än mjukvaruindustrins töntiga och träaktiga C++-skräpdatorkultur;

   NÅGON måste säga ifrån, nu, på att »det där påståendet är HELT felaktigt». Visa.

— MJUKVARUINDUSTRIN TILLÅTER INTE MÄNSKLIGHETEN ATT UTVECKLAS FRITT EFTER INDIVIDERNAS EGNA NATURLIGA FÖRUTSÄTTNINGAR — DÄRFÖR ATT DEN TYPEN TAR BORT MJUKVARUFÖRETAGENS PROFITERING PÅ INDIVIDPOTENTIALEN.

   Visa att det påståendet saknad grund. Därför att jag ser inget ANNAT Jan2019.

 

— Utmärkt för existentiell dockskåpsteater — typ motorsågar som sågar naturskogen som framfödde SågTeknikern — med så allmänt förytligad existensåskådning som hoppar över finliret och mera koncentrerar sig på det makrokosmiska, mera konkret kännbara, plåtiära profitintresset.

— Mänskligheten hålls inlåst Jan2019 av en starkt förytligad auktoritär teknikuppfattning. Befria fångarna.

 

   Vidare i Gyrolagen.

   RIKTNINGEN hos Snurrans axelvridningsrespons beror på Snurrans rotationsriktning — och snurrans läge.

Se vidare från PrecessionsBegreppet och Bevis ABCD.

 

 

David Jones-källan:

DAVID-JONES-KÄLLAN

 

Genomletning på webben (Jan2019) i försöken att hitta SeMYT motsvarigheten till svWikipedias icke nåbara referens resulterade i följande upphittat:

— I början på 1970-talet engagerade sig en David. E. Jones med DATORSTÖDDA MODELLBERÄKNINGAR i uppgiften att undersöka cyklingens gyrokrafter.

 

”  The failure of early unridable bicycles led me to a careful consideration of steering geometry, from which—with the aid of computer calculations—I designed and constructed an inherently unstable bicycle.”.

https://physicstoday.scitation.org/doi/abs/10.1063/1.3022064

 

Physics Today 23, 4, 34 (1970)

https://doi.org/10.1063/1.3022064

"  ABSTRACT

ALMOST EVERYONE can ride a bicycle, yet apparently no one knows how they do it. I believe that the apparent simplicity and ease of the trick conceals much unrecognized subtlety, and I have spent some time and effort trying to discover the reasons for the bicycle's stability. Published theory on the topic is sketchy and presented mainly without experimental verification. In my investigations I hoped to identify the stabilizing features of normal bicycles by constructing abnormal ones lacking selected features (see figure 1). The failure of early unridable bicycles led me to a careful consideration of steering geometry, from which—with the aid of computer calculations—I designed and constructed an inherently unstable bicycle."

 

Och det är — tydligen: WikiCount1 ¦ WikiCoun2 — fortfarande så i den etablerade vetenskapsvärlden:

— MÅNGA (alla) forskare tror — är, eller förefaller vara, övertygade om — att »BURKEN INNEHÅLLER GUD»;

 

— BARA MAN PLOCKAR IN RÄTT PARAMETRAR I LOTTOHJULET UPPENBARAR SIG ALADDINS HELIGA LAMPA OMGÅENDE OCH ANVISAR NÄRMASTE UTHÄMTNINGSSTÄLLE FÖR DE UNDERBARA SKATTERNAS KUNSKAPSPARADIS VIA EN ALLMÄNNA MAGISK VÄGPIL SOM HETER Enter.

 

BURKEN ger inte ut mer än vad varje författare — programmerare — begriper av naturinnehållet BAKOM. Burken (”datorn”) är ett SNABBT hjälpmedel, en avancerad styr-, skriv- och bildmaskin. Inget annat.

 

DATORN kan inte förklara eller beskriva mer av naturinnehållet än vad som är känt UTANFÖR skalet.

 

Jämför NoMACfysik:

— Kulturavsnitten i mänsklighetens kulturhistoria avhandlas fortfarande uteslutande utan undantag av enskilda tänkande individer. Och så kommer det också fortsättningsvis att fungera i historieböckerna.

 

EXAKT VAD befolkningen i den moderna akademins korridorer — i någon relaterad mening — har förstått av GYROFYSIKEN är här definitivt inte känt. I strävan att försöka reda ut det, har heller ingen hjälplitteratur (-Jan2019) upphittats. Än.

 

Physics Today 23, 4, 34 (1970)

https://doi.org/10.1063/1.3022064

:

”  ABSTRACT

ALMOST EVERYONE can ride a bicycle, yet apparently no one knows how they do it.”.

 

LetRitTURN. McOMwash2000. GyroBasic.

 

 

 

 

 

WikiCount2: WC1

WIKIPEDIA COUNTERSTEERING

CLEARLY SERIOUS ISSUES EXIST IN ESTABLISHED QUARTERS IN THIS SUBJECT. Detailed clarifications are urgent.

WIKIPEDIA’S TEXT REVEALS A DETAILED IGNORANT IDEA OF NAVIGATING A BIKE

says GyroLAW — in concord with MOTORCYCLE OPERATOR MANUAL (2000) — Washington State Department of Licensing,

TO WHICH THE WIKIPEDIA TEXT REFERS AS IF THAT MANUAL ADOPTS TO THE WIKIPEDIA IDEA, WHICH IS not THE CASE. We study that.

Basic study:

 

WikiCount2.1 ¦ WikiCount2.1a ¦ WikiCount2.2 ¦ WikiCount2.3 ¦ WikiCount2.3C ¦ WikiCount2.4 ¦ WikiCount2.5 ¦ WikiCount2.6 ¦ WikiCount2.7 ¦ WikiCount2.8 ¦ WikiCount2.9 ¦ WikiCount2.10

 

Wikipedia, Countersteering (Jan2019) — text-markings are my own, unless same in source:

https://en.wikipedia.org/wiki/Countersteering

1:

"   Lack of understanding of this principle leads to accidents in novice bicycle races."

:

"  Countersteering is used by single-track vehicle operators, such as cyclists and motorcyclists, to initiate a turn toward a given direction by momentarily steering counter to the desired direction ("steer left to turn right"). To negotiate a turn successfully, the combined center of mass of the rider and the single-track vehicle must first be leaned in the direction of the turn, and steering briefly in the opposite direction causes that lean.[1] The rider's action of countersteering is sometimes referred to as "giving a steering command".[2][3]:15

 

The scientific literature does not provide a clear and comprehensive definition of countersteering. In fact, "a proper distinction between steer torque and steer angle ... is not always made."[4]".

 

"   The transition of riding in a straight line to negotiating a turn is a process of leaning the bike into the turn, and the most practical way to cause that lean (of the combined center of mass of bike and rider) is to move the support points in the opposite direction first.[9]".

 

— Ref[9] — real time RELATABLE REFERENCE IS MISSING — must buy first.

 

McOMwash2000: WikiSTEER

 

— Ref[9] — RELATERBAR REFERENS i realtid SAKNAS: ”Bicycling Science, Wilson, David Gordon”, köpreferens. Läsarens RealtidsLänk sakans.

— Wikipediatexten har flera (många) sådana. Det vi är ute efter här är en ETABLERAD SÄKER REFERENS TILL VAD SOM AVSES. Så, vi behöver bara leta upp NÅGON av de angivna för att i en sådan referens, närmare få vetskap om vad det är man pratar om.

— Se t.ex. gratis tillgängliga PDF-dokumentet — alla textmarkeringar är mina om inte samma som originalets:

 

SAFE REFERENCE:

MOTORCYCLE OPERATOR MANUAL (2000)

— Washington State Department of Licensing (www.dol.wa.gov):

 

p3.3 Two-Wheel Steering

”  At above walking speed, a motor cycle needs to lean to turn, and countersteering initiates this lean. To use this technique, press on the grip in the direction you want to turn.”, p3.3, McOMwash.

:

”  To counter-steer, press on the grip in the direction you want to turn.”,

”   Pressing on the left hand grip causes the bike to lean left and turn left.”,

— Exacly as The GyroLaw advises for exact synchronized physical harmonic reaction:

”   Pressing on the right handgrip causes the bike to lean right and turn right”, p3.3, McOMwash.

Repeated again at page 3.4, 3.8, 4.6 (@9occ.). Excellent reference. However still without a reference to basic gyro insights:

 

— Jises Holy Mother of God.

   See deeper in WikiSTEER below.

— This IS something completely different from the statements in Wikipedia.

— This ”PRESS” CAN not BE INTERPRETED in any other way than AS PUSHING — vertically — WHICH GIVES THE CORRECTLY GYROPHYSICALLY EXPERIMENTALLY VERIFIABLE REACTION concordant with The GyroLAW:

   PushVERTICALLYleft to LEANLeft to TurnLEFT.

— FASTEST and physically guaranteed safest POSSIBLE RESPONSE.

— See illustration in DirectReaction.

— BUT AS WIKIPEDIA TEXTS (often) seem to point out:

 

— »Push SteeringRod TurningRIGHT» to initiate DESTRUCTIVE GYROFORCES — of which Wikipedia authors seem not to be aware — in order to »get TheLean», and THEN, whatever, ADOPT the lean »by whatever is left of the driver».

   Something like That. Horrible Wikipedia stuff.

 

— At OTHER text occasions, it seems that the WikiText implies — but not (again) clarifies — the TECHNIQUE.

   However in Wikipedia (Jan2019):

— NEVER is the Simple GyroLAW mentioned, nor clarified — AS IF not at all recognized.

 

As already noted above:

— Does the MOTORCYCLE OPERATOR MANUAL (2000) — Washington State Department of Licensing clarify — any — of this?

 

— YESS (of course).:

 

”  To counter-steer, press on the grip in the direction you want to turn.”,

”   Pressing on the left hand grip causes the bike to lean left and turn left.”,

— Exacly as The GyroLaw advises for exact synchronized physical harmonic reaction:

”   Pressing on the right handgrip causes the bike to lean right and turn right”, p3.3, McOMwash.

Repeated again at page 3.4, 3.8, 4.6 (@9occ.). Excellent reference. However still without a reference to basic gyro insights:

 

IF — IN ANY PRACTICAL DOUBT :

— Grab The Bike — an ordinary bicycle will do perfectly — and Make The Test: Speed it it up AND MAKE FAST TURNS (”swerves”):

— Exactly as the reference[‡] manual puts it — with the word ”press” replaced by a general ”GroundPush”:

— GroundPush the steering rod end @ LetRit to turn LetRit.

 

   THAT FACT seems — so observed — IN CONTRADICTION TO MANY OF THE WIKIPEDIA TEXTS on the subject ”countersteering”:

 

   The CONTEXT  — now WITH OUR ARRIVED HELP REFERENCE[‡] — also reveals WHY the term used is ”counter-” — AND why — PURE IGNORANCE AND A SLAPPY SLOPPY LIMPY ENERVATED, LISTLESS SPINELESS LAXY ATTITUDE TOWARDS DIRECT McManual READING — WikipediaText has a completely different interpretation of that ”counter-”. We study THAT:

 

— Counter- means or associates something like ”opposed to” or ”contradictory to”, or simply ”not-” (what normally would be expected) ...

 

”  To counter-steer, press on the grip in the direction you want to turn.”,

”   Pressing on the left hand grip causes the bike to lean left and turn left.”,

— Exacly as The GyroLaw advises for exact synchronized physical harmonic reaction:

”   Pressing on the right handgrip causes the bike to lean right and turn right”, p3.3, McOMwash.

Repeated again at page 3.4, 3.8, 4.6 (@9occ.). Excellent reference. However still without a reference to basic gyro insights:

 

GyroBasics ¦ Gyro2Ways ¦ PrecessionConcept ¦ GyroBasicMath—ProofsABCD.

 

Exactly as is documented and illustrated — fast, steep MC-turning ”swerving”, with a passenger — in the movie PAYCHECK (1:10:25):

 

 

 

”   If you are unfamiliar with counter-steering, consider taking a training course.”,  p3.3, McOMwash.

— Absolutely. Wikipedia Authors, obviously and especially — urgently:

 

WikiSTEER: McOMwash2000

— ”COUNTER-” in association with STEERING

with reference to McOMwash AND ALL ASSOCIATED ALIKE DESCRIPTIONS

hence aims

 

in full and complete concord with the constructive natural

non traffic destructive gyrophysical response of  GUARANTEED SAFE navigating a two wheel bi- or motor-cycle

in THE FASTEST SAFEST EXISTING PHYSICAL WAY:

 

at NOT STEERING AT ALL — ONLY gyronavigating according to GyroLAW’s natural gyrophysical action:

 

NOT THIS[‡] :

”   Countersteering is used by single-track vehicle operators, such as cyclists and motorcyclists, to initiate a turn toward a given direction by momentarily steering counter to the desired direction ("steer left to turn right")”,

WikiCount2.

— Call 911: Doing this Wikipedia in traffic is definitely inviting or challenging SERIOUS TROUBLE.

   Se simple gyroscopic proof in DBE.

 

The Wikipedia text on the subject ”countersteering” is — hence — SEVERELY CORRUPTED — even aiming at the real explaining reference[‡] to be a part of THAT corruption:

 

"  The Motorcycle Safety Foundation teaches countersteering to all students in all of its schools, as do all motorcycle racing schools. Countersteering is included in United States state motorcycle operator manuals and tests, such as Washington,[15] New Jersey,[16] California,[17] and Missouri.[18]",

WikiCount2.

 

The only sane explanation to this — now obviously revealed — corrupted Wikipedia presentation can be only one, as far as here known: gyroscopic basic physics is NOT understood — as it also is NOT present in Wikipedia. Not at all: GyroLAW. Not mentioned. Not a word. Not a sign. Albeit its extremely simple and easy form:

 push rotates spin from most mass resistive point. On Earth. Outside Earth. Everywhere. No exceptions. Axial Precession as well as Equatorial Precession — also not described in Wikipedia. All simple Basic Gyroscopic experimentation results.

 

That is the amazing appearance in Wikipedia in total (Observed Jan2019):

 

Wikipedia provably — and in detail — obviously presents a highly corrupted — traffic dangerous — idea of navigating a two wheel bike —

with references to manuals[‡] who DON’T.

 

— Wikipedia PARTLY describes the situation — and partly RACES it.

 

Wikipedia’s IDEA of ”counter-steering” description as quoted is NOT the reference’s[‡] presented idea of ”Counter-steering”:

— Wikipedia’s idea = STEERING:

 

”.. by momentarily steering counter to the desired direction ..”

 

— McOMwash2000’s idea = ”NOT-STEERING”: a vertical push:

 

”  To counter-steer, press on the grip in the direction you want to turn.”,

— Not ”push the grip in the turn direction” WHICH RESULTS IN Wikipedia’s CounterSTEERING but ”push on the grip that HAS the direction OF the turn” WHICH RESULTS IN IMMEDIATE AND CORRECT FAST BIKE-LEAN-TURN (”press” associates ”downPush”): If not else, WikiAuthors: TakeBikeOutTryNow: fastest turns by immediate response:

”   Pressing on the left hand grip causes the bike to lean left and turn left.”,

— Exacly as The GyroLaw advises for exact synchronized physical harmonic reaction:

”   Pressing on the right handgrip causes the bike to lean right and turn right”, p3.3, McOMwash.

DirectReaction:

— The only unequivocal physical WAY for such a physical description/reaction on a two wheel bike IS this one:

 

 

 

FrontWheel GyroEquatorial Precesses LEFT when LeftSide is Pushed Vertically, the driver pushes on the left side of the steering rod (handlebarLeft), hence in complete accord with the NATURALLY INTENDED gyrophysical course of the travel — no in-between MESSING AROUND: Bike Turns immediately LEFT as so PUSHED;

FrontWheel GyroEquatorial Precesses RIGHT when RightSide is Pushed Vertically, the driver pushes on the right side of the steering rod (handlebarRight), hence in complete accord with the NATURALLY INTENDED gyrophysical course of the travel — no in-between MESSING AROUND: Bike Turns immediately RIGHT as so PUSHED.

— Exactly as McOMwash puts it, however with the vord ”PRESS” instead of PUSH, the latter here conforms to the general formulation of the simple GyroLAW: push rotates spin FROM MOST MASS RESISTIVE POINT (law of inertia).

 

 

Hence McOMwash2000’s true GYRONAVIGATING description

in full concord with the traffic safety constructive gyro physical action

obviously IS unfamiliar to Wikipedia presentators: (jises):

 

”.. by momentarily steering counter to the desired direction ..”

— Call 911: Doing this Wikipedia in traffic is definitely inviting or challenging SERIOUS TROUBLE ”depending on traffic conditions”. Se simple gyroscopic proof in DBE.

 

— Wikipedia is — possibly — talking RACING. Not a basic safe traffic on a two wheel bike by natural navigation outside destructive traffic hazards — which inevitably arise in trying to STEER the device, says GyroLAW.

 

— It is obvious, here, that Wikipedia authors are NOT familiar with GyroBasics — SAFE traffic.

— It is obvious, here, that Wikipedia authors are NOT familiar with THE CONTEXT IN McOMwash — SAFE traffic.

— Not racing.

 

That’s it. This is the only SANE reference we need — by stating this:

 

— Any claim opposing the above clarified from the reference[‡] WILL guaranteed work AGAINST gyro physics — creating severely hazardous traffic situations.

 

— Especially a rider of a (heavy) motorcycle MUST understand this EXTREMELY easy and simple to study gyrophysical basics

— that it is a natural way to respond to physiological equilibrium — as the other animals do it — and no institutional dictate: it’s YOU.

   Absolutely:

— PUSHverticallyLeft and follow with body motion — which perhaps needs some training unless already familiar — to initiate a LeanLEFT in ordet to TurnLEFT. And same standard with a right-turn:

 

 

 

This simple ILLUSTRATED ORDER is The perfectly naturally intuitive one: The — animals do it directly — natural balancing sense of an EQUILIBRIUM: The State from which to consider any future maneuver — at any point of time, in any situation:

— ”Just FOLLOW the Bike”. Don’t think. Just BE. Just Drive. And let Nature do the Action: DISCOVER YOU unless already familiar.

— Be aware of how it works: always study IT. Never turn a back on IT. Ignore IT, and Deep Trouble comes visiting.

 

 

If a (motor) cyclist misinterprets the ”PRESS” for a ”STEER”

AS IS HEAVILY SUGGESTED BY THE MAIN WIKIPEDIA[‡] ARTICLES ON CounterSteering

a dangerous traffic situation has arrived — from which the driver will NOT recover unless lucky by chance, says GyroLAW. See proof in DBE.

 

The

MOTORCYCLE OPERATOR MANUAL (2000) — Washington State Department of Licensing

makes it ”OK” — however NOT in any explicit a stated corresponding recognition of the simple Tutorial by GyroBasic;

— It is obviously »a world syndrome»; No general information at all, as here[‡] noticed.

— Such — with a two ring gyroscope and  a SPEED up device — SHOULD come WITH the BikePurchase + a simple instructive manual.

— For FREE. No profit, what so ever. Traffic safety basics.

   I am sure it would be (highly) appreciated by the Driver — more Safe Riding Joy:

— »because now I Know How It Works — in deep, deeper and deepest atomic detail».

 

In comparison (Jan2019): The WikipediaTexts emit — mostly — »CounterSteering FuckUps».

 

 

So, for the rest with Wikipedia Countersteering on the subject:

CLEARLY SERIOUS ISSUES EXIST IN ESTABLISHED QUARTERS IN THIS SUBJECT. Detailed clarifications are urgent.

— Because — SOME OF but not all — the statements in quote contradicts simple gyroscopic experimental AND bicycle riding experience OF TAKING CARE IN TRAFFIC — HOWEVER obviously NOT EVEN MENTIONED AS TO PRECISE CLARIFYING EXAMPLES: we need a general thorough educative description in deep. WITH Microsoft on Top[‡], Perhaps The Institution will educate Birds Too, correctly, how to loop in The Bushes by Inertial Equilibrium Forces — we must leave no one behind. Lead World Intelligence. God have mercy.

1a:

"  Gyroscopic effects

One effect of turning the front wheel is a roll moment caused by gyroscopic precession. The magnitude of this moment is proportional to the moment of inertia of the front wheel, its spin rate (forward motion), the rate that the rider turns the front wheel by applying a torque to the handlebars, and the cosine of the angle between the steering axis and the vertical.[10]",

"  For a sample motorcycle moving at 22 m/s (50 mph) that has a front wheel with a moment of inertia of 0.6 kgm2, turning the front wheel one degree in half a second generates a roll moment of 3.5 Nm. In comparison, the lateral force on the front tire as it tracks out from under the motorcycle reaches a maximum of 50 N. This, acting on the 0.6 m (2 ft) height of the center of mass, generates a roll moment of 30 Nm.[10]

***************

Ref.10 V. Cossalter p 241-342 — gratislänk saknas, måste köpas.

Används på 5 ställen i Wikipediatexten — läsaren har inte chans att kontrollera/testa i realtid:

RELATERBAR REFERENS SAKNAS.

***************

While the moment from gyroscopic forces is only 12% of this, it can play a significant part because it begins to act as soon as the rider applies the torque, instead of building up more slowly as the wheel out-tracks. This can be especially helpful in motorcycle racing.[10]",

WikiCount2.

 

”caused by gyroscopic precession”:

— Den påstådda sambandsformen är samma som här i den grovt sammanställda/härledda  BikeTableExample — med en till synes obskyr skillnad:

 

Ekvatoriell precession i gyrofysiken: SEE ACCOUNTED CLARIFIED EXPERIMENTAL RESULT — regained 2Apr2020

 

 

Wikipediatexten ansluter till figurens vänsterdel — destruktiv gyronavigering. Men att döma av citatkällans text, verkar författaren bara känna till den resulterande precessionen — texten säger ingenting om den huvudsakliga primära effekten av att försöka styra cykeln genom att vrida på styret.

 

 

Wikipedias CounterSTEERING destruktiv bike-navigering sammanfattas i figuren ovan vänster:

— Gyroexperimentens PRECESSIONSFAKTOR är den rotation som de övre cirklarna anvisar:

 

———————————————————————

 (z↑+x) → –zW° ¦  = clockwise stepped z-twist                ; DEstructive UNsafe traffic GYRO wheel STEERING

+ direct gravitational RotII-System –yW° clockwise equatorial precession, depending on force.

 (z↑–x) → +zW° ¦  = anti-clockwise stepped z-twist        ; DEstructive UNsafe traffic GYRO wheel STEERING

+ direct gravitational RotII-System +yW° clockwise equatorial precession, depending on force.

—————————————————————————————————————————

 

— Den effekten avhandlas inte här. Inte alls. Enbart den rödPunktsMarkerade DEPLACEMENTSSKAPANDE rotationskraft som — DBE — uppkommer vid varje försök att STYRA sig fram på en tvåhjuling: destructive-.

— Det är tydligt att Wikipediaförfattaren INTE har den detaljen med i räkningen:

”One effect of turning the front wheel is a roll moment caused by gyroscopic precession”;

— DEN RESULTERANDE PRECESSIONEN är INTE den mest kraftframträdande.

   Wikipediaförfattaren talar alldeles tydligt vid sidan av huvudsaken.

   Den mest kraftframträdande effekten — DBE — av att vrida framhjulet på cykeln genom att vrida styret under färd

 

 Destructive manipulation in Biking — SPIN is clockwise ahead, as seen by an observer from behind.

— With a quick attempt to STEER on the front wheel steering rod, a corresponding sudden FORCE appears attempting to REVOLVE the entire wheel out of its road contacting point, as observed in the simple gyroscopic experiment in Direct By Experiment. The Wikipedia author seems not at all aware of the phenomena.

 

är den — färdriktningen — tvärriktade momentant KASTANDE — rödapunkten — rotationen, den som strävar att RYCKA hjulet BORT från sin vägkontakt.

   Det är den kraftformens effekt med grundparametrar som finns exemplifierad här i BikeTableExample.

forts.

 

 

CLARIFIED EXPERIMENTAL RESULT 2Apr2020:

 

ACCOUNTED CLARIFIED EXPERIMENTAL RESULT

 

 

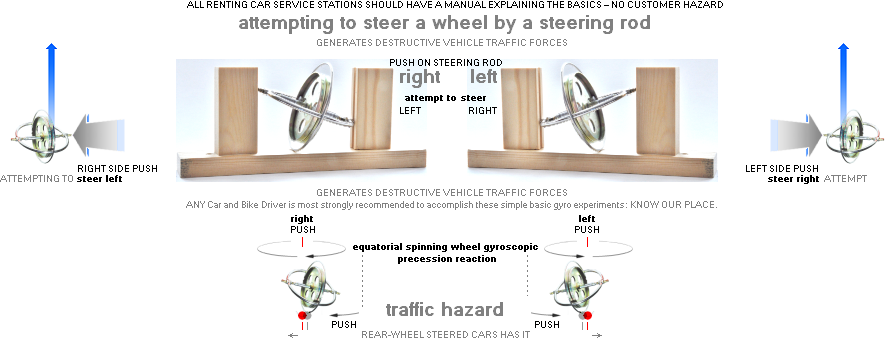
IT IS IMPERATIVE THAT ANY PERSON INVOLVED IN TRAFFIC ISSUES SHOULD HAVE A PERFECT INSIGHT INTO THESE BASIC PHYSICAL GYROSCOPIC CONCEPTS as they are THE FOUNDATION OF ALL SPINNING WHEEL/body PHENOMENA.

— Specific example (2Apr2020) — CARS DRIVING THE DRIVER (forbid them unless registered licensed handicap tools for max 5 mph):

 

 

Some early warning words from other observant pedestrians:

 

PHYSICS FORUMS, Dec2010 (2Apr2020)

https://www.physicsforums.com/threads/rear-wheel-steered-vehicles.453015/:

:

" Danger",

:

" As Mech said, rear-steer units are extremely unstable, particularly the 3-wheeled variety, although they are incredibly nimble at low speeds. The serious ones can literally turn in place, as in switch directions without leaving the spot. There are automobiles on the market which feature 4-wheel steering as a luxury item. All of them, however, have the rear wheels restricted to something like 3° from centre. There is a good reason for that.",

:

" I would think a vehicle with rear-steering only would be unstable and dangerous to drive at anything over 5 mph. Have you ever driven a front-wheel steer vehicle backwards for an appreciable distance at faster than running speeds? They're twitchy!",

:

" Some large farm machines, e.g. combine harvesters, are rear-wheel-only steering and perfectly stable to drive on roads (though the maximum road speed is usually only about 30 mph).".

 

Max 5.

Handicap Vehicle.

 

 

 

 

forts.

— Eftersom Wikipediaförfattarens referens inte kan nås här, direkt, kan vi heller inte kontrollera/avstämma jämförande resultat annat än enligt följande motsvarande kalkylredovisning:

 

KalkylDest:

Tabell 1 — DestructiveSteering — GyroDec2018.ods

 

DBE-deduced:  Gyroscopically Twisted z-Angle = 360°(Frt)/Frt)0 ¦ direct variables with a given vehicle: F r t ;

 

— Värdena stämmer — men knappast KRAFTRELATIONEN — förutsatt sambandsformen här också är korrekt mot naturfysiken:

 

z-Angle = 360°(Frt)/Frt)0

 

Det är alldeles tydligt att Wikipediaförfattaren i WikiCount1a — och kanske även dennes källa, vilket som sagt läsaren INTE får titta på i någon realtid via Wikipediatexten — INTE, riktigt, är förtrogen — DBE — med gyrofysikens elementära innehåll: detaljen tvärs åket.

 

En RESULTERANDE destruktiv hjulrotation (z°) i markplanet tvärs färdriktningen (pilotsystemet xyz) på 1,1° är här veterligt praktiskt taget helt försumbart. DrivKraften (F-DRIVE) bakom — ringa motsv. tyngden av ett glas vatten 0,35 KG — förefaller också i sammanhanget inte ha någon större betydelse — definitivt inte i ”in motorcycle racing”.

 

Sätter vi istället in ett mera rimligt Racing-värde för F-DRIVE på 35 Newton — en armkraft motsvarande tyngden/vikten av 3,5 KG, mera sannolikt i Racingsammanhang — ges motsvarande destruktiva hjulvridning (utan citatets antydda cosinusvinkelreduktion som ändå för ca15° bara reducerar effekten med 4%) tvärs färdriktningen värdet 10,6° — en definitivt allvarlig situation i en normal trafikmiljö:

— »OffRoadExperience»: Crash.

 

Det ser alltså ut som att Wikipediaförfattaren inte, riktigt, är medveten om gyromatematikens proportioner enligt

”turning the front wheel one degree in half a second generates a roll moment”:

— Den destruktiva hjulvridningen tvärs färdriktningen är

— enligt direkt gyroexperiment

— en EFFEKT av, inte ORSAK TILL, ett (destruktivt) styrande kraftmoment som MC-föraren

— vår DBE snabba vridning av gyrohjulet på markpunkten med den givna kraften på den givna tiden

— anställer på framhjulet via styret.

   Wikipediatexten låter, tydligen, istället saken framträda så,

”turning the front wheel one degree in half a second generates a roll moment”:

att VRIDNINGEN som sådan via F-Drive × t-DRIVE skulle motsvara

”one degree in half a second”;

Dessutom UTAN något omnämnande av, just, den centrala mest VÅDLIGA tvärriktade, resulterande, färddestruktiva, hjulrotationen:

— Aktuellt vinkeltal zANGLE — också direkt experimentellt gyroskopiskt observerat för aktuell hjulStyreVridning i DBE.

   Om Wikipediaförfattaren inte kan klargöra den detaljen närmare, eller om sambandsformen ovan skulle vara felaktig, kan vi inte, riktigt, veta om författaren ens känner till gyrogrunderna, rent experimentellt, och (kanske) bara läser (från Ref[10] som inte heller kan nås i realtid från Wikipedia) vad andra har skrivit utan egen inblick.

 

— Därför nämligen förvisso, att gyrofysiken INTE är enkel att hantera läs:låter sig inte manipuleras — om man inte är helt förtrogen med alla gyrofysikens detaljer:

— GyroLAGEN. Den omnämns inte ens i Wikipedia.

 

— HELA WIKIPEDIABESKRIVNINGEN I ÄMNET KANSKE kan liknas vid historien om flygkaptenen som fick en hjärtattack på 6000 meters höjd, och ingen ersättare fanns. En grupp turister från Sverige — »PlanetKalhygget» — träder då fram och menar sig ha hittat en ersättare: pekar på en person och säger: — »Jag såg att han kom på Moped till flygplatsen».

   Improviserad Fattning — på hög självupplevd IQ.

   För ev. vidare.

2:

"  Motorcycles

Even more so than on a bicycle, deliberately countersteering is essential for safe motorcycle riding, and as a result is generally a part of safe riding courses run by organisations like the Motorcycle Safety Foundation, the Canada Safety Council, or Australian Q-Ride providers. Deliberately countersteering a motorcycle is a much more efficient way to steer than to just lean.[3]:15 At higher speeds the self-balancing property of the bike gets stiffer, and a given input force applied to the handlebars produces smaller changes in lean angle.[3]:16",

WikiCount2.

 

The quote points to BASIC GYROSCOPIC CONTRADICTING INFORMATION without any corresponding clarification, says GyroLAW:

— Turning AGAINST natural gyroscopic forces GENERATES DESTRUCTIVE — hazardous — NATURAL GYROSCOPIC RESPONSE. Not a word.

— In Table CFT is given a basic example (Bike Basic GyroPhysics from Basic GyroExperimentation) on the influence of the TIME the Biker uses to LEAN in concord with the gyroscopic forces during biking. It is evidently seen, and experienced, that — for a given speed on a given bike, and a given leaning force — the longer the leaning time, the narrower curvature will result. Is that included in the report ”more efficient way to steer than to just lean”? The Wikipedia author does not seem to make points.

3:

"  Training

Much of the art of motorcycle cornering is learning how to effectively push the grips into corners and how to maintain proper lean angles through the turn. When the need for a quick swerve to one side suddenly arises in an emergency, it is essential to know, through prior practice, that countersteering is the most efficient way to change the motorcycle's course.[3]:16 Many accidents result when otherwise experienced riders who have never carefully developed this skill encounter an unexpected obstacle.",

:

”  To encourage an understanding of the phenomena around countersteering, the phrase positive steering is sometimes used.[12][13] Other phrases are "PRESS – To turn, the motorcycle must lean", "To lean the motorcycle, press on the handgrip in the direction of the turn" or "Press left – lean left – go left".[14]”,

WikiCount2

 

The[‡] MOTOR CYCLE MANUAL REFERENCE clearly states counter-steering NOT[‡] as steering but ground-pushing — while WikiSTEER claims countersteering as a STEERING — a direct gyrophysically traffic dangerous — operation:

— The Wikipedia text(3) is obviously and provably in detail severely corrupted — directly traffic dangerous — in its obvious misinterpretation of the meaning of the Mc-Bike[‡] operating manual.

 

A:   ”how to effectively push”, says GyroLAW, means PUSHING VERTICALLY. Not STEERING horizontally.

— But the text doesn’t clarify that distinction, nor informs the two main different ways the gyroforce acts in PushVertical SteerHorizontal.

— See further C.

B:    The quote, says GyroLAW, CAN BE APPREHENDED ”countersteering” — »counter-» — IN SUCH A WAY THAT IT points out that natural GYROSCOPIC PHYSICS DOES not PROVIDE A NATURAL INSTINCT LEFT-LEFT RIGHT-RIGHT: 

— »trafficants must be educated by A Wikipedia Institution for a Proper Handling — to REVOLT AGAINST nature».

   The Wikipedia text is capitally absurd as its author obviously is NOT acquainted with the subject GyroBasics: The GyroLAW.

 

CLEARLY SERIOUS ISSUES EXIST IN ESTABLISHED QUARTERS IN THIS SUBJECT. Detailed clarifications are urgent.

 

C:  ”Press left – lean left – go left”[‡] ¦ [‡] ¦ [‡]: Wow. Wow. Wow, Wikipedia. THIS IS EXACTLY WHAT THE GYROLAW and the Mc-manual SAYS[‡] — vertically, WITH ”press” understood as GROUNDWAYS — as a push — not=dangerous AHEADWAYS:

— PushVERTICALLeftToTurnLeft: PushVERTICALRightToTurnRight. Exactly — precisely — the GyroLaw experimentally verified behavior of a spinning wheel. Exactly.  See GyroLawCS.

— This Wiki3C-Quote is the central confusing part in the whole Wikipedia presentation on ”countersteering”:

The Wikipedia text does NOT clarify WHAT ”press” AIMS AT — in a guaranteed safe traffic navigation sense.

   Other Wikipediaparts[‡] claims — contrary to the GyroLAW — that the ”press” means a handle maneuver resulting in a horizontal actual steering action — not a VERTICAL push/Press as described in our Mc-reference[‡].

 

CLEARLY SERIOUS ISSUES EXIST IN ESTABLISHED QUARTERS IN THIS SUBJECT. Detailed clarifications are urgent:

PROOF — without/With hands:

 

as experienced from BICYCLING AND elementary gyroscopic experimentation [‡]

 

 

and seemingly by practical documentation:

NaPP:

 

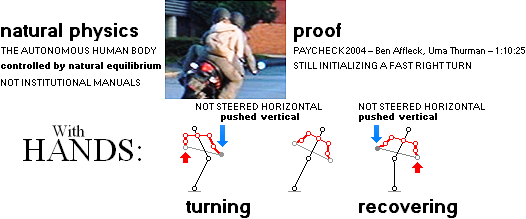
— Natural physical cooperating forces appear on Pushed vertically. Not steered horizontally, says GyroLAW:

— That is how gyrophysics answers a vertical push in practical physics — a Wheel motorcycle LEAN in turning direction:

— CLEARLY SERIOUS ISSUES EXIST IN ESTABLISHED QUARTERS IN THIS SUBJECT. Detailed clarifications are urgent. See in deep from WikiCount.

 

BASIC GYRO PHYSICS

——————————————————————————

 

 

 

— This above described BASIC GYRO PHYSICS — »basic natural Bird-physics» — is not to be understood as any kind, sort or nature of the VERY confusing established concept and term ”countersteering” AS SO PRESENTED IN WIKIPEDIA (Jan2019) WikiCount1 ¦ WikiCount2.

   The above illustrated gyrobasic action is the only available RELATABLE natural traffic safe physical WAY:

 

PUSH VERTICALLY RIGHT TO LEAN RIGHT TO TURN RIGHT — no destructive forces appear.

PUSH VERTICALLY LEFT    TO LEAN LEFT    TO TURN LEFT    — no destructive forces appear.

 

If we don’t understand this simple natural basic physics:

— DO leave the car in the garage, too, and WALK: Safest for You. Safest for Me. Make studies unless already familiar.

 

— Easily apprehended by a 5 year old person. Easily. No talk. Just Drive Naturally:

— FOLLOW THE BIKE AS IT FOLLOWS THE INTENDED DRIVE.

  Don’t think. Just DO Nature. And ENJOY the ride.

   BIRD-TALK:

— ADOPT THE WINGS by naturally experienced Equilibrium AS THE BODY MOVES WITH RESPECT TO THE INTENDED GO.

   Just FLY — man.

— Compare the corresponding STEERING gyroscopic answer: destructive revolving travelling forces appear.

— CLEARLY SERIOUS ISSUES EXIST IN ESTABLISHED QUARTERS IN THIS SUBJECT. Detailed clarifications are urgent. See in deep from WikiCount.

— See explicitly illustrated in HalGyro.

4:

"  The Motorcycle Safety Foundation teaches countersteering to all students in all of its schools, as do all motorcycle racing schools. Countersteering is included in United States state motorcycle operator manuals and tests, such as Washington,[15] New Jersey,[16] California,[17] and Missouri.[18]",

WikiCount2.

 

Yes. BUT NOT IN ANY Jan2019 WIKIPEDIA CLAIMING CONTERSTEERING MANNER — AS CLEARLY STATED, PROVEN AND RELATED IN DETAIL BY CONCORDANT GYRO EXPERIMENTATION WITH McOMwash2000 CONTRA WikiSTEER.

— It is obvious that the Wikipedia author is NOT familiar with the subject, but improvises on ignorant — direct traffic dangerous — assumptions.

 

CLEARLY SERIOUS ISSUES EXIST IN ESTABLISHED QUARTERS IN THIS SUBJECT. Detailed clarifications are urgent.

 

Unless clarified in deep:

The quote points out not by plan but by drift that NO CARE SHOULD BE TAKEN TO UNDERSTAND THE NATURAL GYROSCOPIC FORCES AS NO MENTIONING OF THE HAZARDOUS EFFECTS ARE POINTED OUT FROM claimed — not clarified — GYROSCOPIC COUNTERACTION BEHAVIOUR IN THE WIKIPEDIA TEXT EXPLICITLY, says GyroLAW.

   The Wikipedia claims here as quoted is in total, above all, in its own, the worst thing ever read on a flat surface in the history of human culture.

 

CLEARLY SERIOUS ISSUES EXIST IN ESTABLISHED QUARTERS IN THIS SUBJECT. Detailed clarifications are urgent.

 

As far as it is seen here (Jan2019) a ”GYRO LAW” — albeit its extreme simplicity: On Eart, Outside Earth; at all locations in our Universe — is NOT known in established quarters: never mentioned, never even hinted at, as here experienced — although some of its details are mentioned in some texts, but then again without deep clarifying description; EXAMPLE: ” ... turn left ...”, ” ... clock is 5 ...”, ” ... sky is blue ...”, etc.

— Description of Natural physics must be real time related to an experimental observation that anyone —  a n y o n e  — can perform — or the description is practically worthless: no proof. Just talk. ”Trust me”. We might give’em our credit card too, while still fleeting. GyroBasics.

5:

"  Safety

According to the Hurt Report, most motorcycle riders in the United States would over-brake and skid the rear wheel and under-brake the front when trying hard to avoid a collision. The ability to countersteer and swerve was essentially absent with many motorcycle operators.[19]",

WikiCount2

 

— Yes, of course, says GyroLAW. Because The Wikipedia World Association of Trusted Reporters had Cameras in every situation, documenting in detail all the case history of each event, following every fraction of a second in detail of the actual accident.

   Satellite surveillance. Of course. Trust me.

— ”The ability to countersteer and swerve” is obviously NOT handled by WikiSTEER but by McOMwash2000.

6:

"  The often small amount of initial countersteering input required to get the bike to lean, which may be as little as 0.125 seconds, keeps many riders unaware of the concept.[20]",

WikiCount2

— NAVIGATING A TWO WHEEL BIKE is obviously NOT handled by WikiSTEER but by McOMwash2000.

 

IF WikiSTEER is adopted = an appearing dangerous trafficant:

— This is the real hazard part, says GyroLAW.

   In BikeGyroTableExamples — from basic gyroscopic forces as verified by simple experimentation — it is evident that the TIME in Wikipedia countersteering kan KILL a person — unless equipped with SuperMan capabilities of CONTROLLING a serious traffic situation by being That Cool as NOT to Panic: The Actual Funeral may very »wheel» be over after 0.125 seconds:

— A motorcycle at speed 180 KM/h = 112 MPh travels 5 meters in 0.1 seconds.

   Scuse me (says GyroLAW): Nobody THINKS there, during these 5 meters at 180: we just REACT — by instinct. LION-stuff. Bite me.

   As our safe manual reference McOMwash2000 puts it: PRACTISE. COGITATE. CONSIDER. STUDY. Get more Joy out of the Ride. Safe.

7:

"  Countersteering by weight shifting

With a sufficiently light bike (especially a bicycle), the rider can initiate a lean and turn without using the handlebars by shifting body weight, called counter lean by some authors.[8][25][26][27] Documented physical experimentation shows that on heavy bikes (many motorcycles) shifting body weight is less effective at initiating leans.[28]",

WikiCount2

 

Same as Quote2: — the longer the leaning time with a corresponding deeper leaning force, the narrower curvature will result. Se HalGyro below. The quote says nothing about LEANING TIME nor leaning force:

— ”less effective at initiating leans”.

— Give it TIME with a skilled technique, and it WILL answer, says GyroLAW.

CLEARLY SERIOUS ISSUES EXIST IN ESTABLISHED QUARTERS IN THIS SUBJECT. Detailed clarifications are urgent.

8:

"  A National Highway Traffic Safety Administration study showed that rider lean has a larger influence on a lighter motorcycle than a heavier one,[30] which helps explain why no-hands steering is less effective on heavy motorcycles. Leaning the torso with respect to the bike does not cause the bike to lean far enough to generate anything but the shallowest turns. No-hands riders may be able to keep a heavy bike centered in a lane and negotiate shallow highway turns, but not much else.”,

WikiCount2

 

Same as Quote2: — the longer the leaning time with a corresponding deeper leaning force, the narrower curvature will result. The quote says nothing about LEANING TIME nor leaning force:

— ”does not cause the bike to lean far enough”.

— Give it TIME with a skilled technique, and it WILL answer, says GyroLAW.

CLEARLY SERIOUS ISSUES EXIST IN ESTABLISHED QUARTERS IN THIS SUBJECT. Detailed clarifications are urgent.

9:

"  Complex maneuvers are not possible using weightshifting alone because even for a light machine there is insufficient control authority.[25] Although on a sufficiently light bike (especially a bicycle), the rider can initiate a lean and turn by shifting body weight,[8] there is no evidence that complex maneuvers can be performed by bodyweight alone.[28]",

WikiCount2

 

PERFECTLY TRUE — BECAUSE THE PRIMARY ACTION OF FORCE FOR A SPINNING GYRO WHEEL NAVIGATION IS THE SPINNING WHEEL’S SPIN AXEL[‡] — AS CONTROLLED BY A CORRESPONDING ELONGED STEERING ROD (HANDLEBARS) — by ground-pushing = leaning, not horizontal wheel-steering.

— However. Also a general pedestrian cannot compete with a skilled Gymnast. So: Maybe, IF we give it some time, proof may arise WITH

”evidence that complex maneuvers can be performed by bodyweight alone” — as Birds do it, some of them with exteme high speed skills too.

10:

"  The Wright Brothers

Wilbur Wright explained countersteering this way:

 

I have asked dozens of bicycle riders how they turn to the left. I have never found a single person who stated all the facts correctly when first asked. They almost invariably said that to turn to the left, they turned the handlebar to the left and as a result made a turn to the left. But on further questioning them, some would agree that they first turned the handlebar a little to the right, and then as the machine inclined to the left, they turned the handlebar to the left and as a result made the circle, inclining inward.[31][32]".

 

HalGyro: WikiCount20

— Halleluja, says GyroLAW. Praised be The Lord [‡]¦[‡]: See also ProofWikiCount23C.

   Again Wikipedia gives lectures in TRAFFIC DANGEROUS CONTEXT BEHAVIOUR[‡] from Wikipedia references that obviously NEITHER knows about a detailed content of McOMwash2000, NOR knows about any GyroLAW, and NEITHER has made the basic simple gyro experiments in GyroBasic:

 

GyroLAW claims:

— CURVATURE APPEARS IN EXACT RESPONSE AND PROPORTION TO DIRECT SYMMETRIC LEANING DIRECTION:

— GOVERNED BY leaning TIME on a given leaning force — pushed vertical:

 

 

— See Wikipedia’s real badly corrupted claims in WikiSTEERING from WikiCount2.

SCHEMATICALLY: GyroLAW’s way of viewing a left turn riding a conventional two wheel bike, says GyroLAW

— contrary to WIKIPEDIAN recommendations from Established Earth Institutions [Quote2] ¦ [Quote8].

   GYRO LAW:

— LeanLeft TurnLeft — LeanRight TurnRight. It comes natural — from 5.

— Too fast incoming (crappy Navigator) = offroad Experience. Drive safe.

— What’s your suggestion: Please draw to show the tracks, says GyroLaw. I have shown you mine. Now you can show me yours.

— Try to STEER = Invite Accidents — Direct By Experiment.

Recovering: HalGyro

 

CLEARLY THE WIKIPEDIA QUOTES[‡] REVEALS WikiESTABLISHED UNFAMILIARITIES WITH GYROSCOPIC BASIC PHYSICS, says GyroLAW.

Any kind of misunderstanding WOULD be — guaranteed — excluded IF Wikipedia-associated established Texts in the subject WOULD clarify the simple GyroLAW — and present the rest, whatever, with respect to THAT basic elementary simple easily GyroBasic provable gyroexperimental physics. As f.ex. in McOMwash2000. Would. Now Jan2019 it — obviously isn’t — due to the Wikipedia corrupted statements: see from WikiSTEER.

— Established claims[‡] BY THE WIKIPEDIA TEXT — but not in our practical world, see McOMwash2000 which concurs WITH GyroLAW, really — obviously in an overwhelmingly concordant WIKIPEDIA CLAIMED panel, claim to FIRST initiate some (reeling, as a drunk person trying to bike) RIGHT maneuver — to initialize a left turn. Such claims has — provably — nothing to do with sane and serious traffic behaviour, says GyroLAW.

 

GyroLawCS:

WHAT WikiSTEER CALLS ”Counter-steering” — clarifying view:

GYRO LAW ON Wheel-STEERING

— obviously not mentioned in established literature:

 

The thing is this — provable GyroBasic in gyroexperimental detail, says GyroLAW: PUSH ROTATES SPIN:

NO EXCEPTIONS — NOT ON EARTH. NOT OUTSIDE EARTH. Not what so ever. So simple: Not one Established Word.

 

 

 

Twisted z-Angle = 360°(Frt)/Frt)0 with Spinning Wheel Angular Momentum J0 = mvr = (Frt)0 — ideal gyroscopic vertical wheel.

— On a conventional bicycle the steering rod distance (r) is approximately equal to the front wheel’s mass’ radius r = 28’’/2~0,3M.

— Then the calculations are simplified by the equality z° = 360°(Ft)/Ft)0. A conventional (cosine) angle dependency is added for a trail, here gyroscopically ideally as 1.

 

 

ANY GYROSCOPIC ATTEMPT on a speeding bicycle TO STEER — in this example — RIGHT with a spinning wheel, unconditionally

CREATES a destructive gyroscopic REVOLVING moment as seen in the right photo part:

   THE GYRO WHEEL REVOLVES A CORRESPONDING STEP PERPENDICULAR TO THE TRAVELLING DIRECTION.:

— CRASH situation, depending on traffic, steering force, and road conditions.

— Why is that?

— The Steered Wheel performs a JUMP perpendicular around ITS angular momentum mass center: IT IS momentarily torn AWAY aside FROM GROUND contact, sideways, out of the travelling direction  — through a corresponding destructive twisting angle — exactly proportional to HOW the driver steers = forces the wheel’s angular momentum by arm force (F) and time (t) over the steerings rod’s distance (r):

   And so WORSE the lower the speed is:

   GIVEN STEERING FORCE IN GIVEN STEERING TIME. See BikeTableExample:

   At LOW speeds a proportionally great DESTRUCTIVE POWER lies in the hands of the driver between the ends of the steering rod (handlebars):

 

   By the TILT from THAT maneuver, the tilted wheel experiences a wheel-equatorial precession OPPOSING THE WHEEL SPIN DIRECTION from the vertical gravitational pull from the Earth.  But that precession is of a secondary forcing significance following the main primary sideway effect.

IN OUR GYROEXPERIMENTATION WE VERIFY THIS BEHAVIOR BY PLACING THE SPINNING TWO RING GYROWHEEL TILTED ONTO THE GROUND: Within a short interval IT IMMEDIATELY BEGINS PRECESSING AROUND THE SPINNING WHEEL EQUATOR[‡] — but the general math for this type of spin is highly dependent on the actual construct, all details, and there are no simple general expressions, as here known.

— This tendency of wheel-spin-opposed precession aspires, our example, to turn the tilted wheel LEFT with respect to ITS mass center. And so in THIS manner given a specific maneuvering force and time:

— At low vehicle velocities, the equatorial gyroprecession from the destructive right steering maneuver is LARGE.

— At high vehicle velocities, the equatorial gyroprecession from the destructive right steering maneuver is PRACTICALLY ABSENT, negligible:

ESPECIALLY DANGEROUS TO HIGH SPEED MOTOCYCLISTS WHO ARE PRACTISING WikiSTEER on slippery roads, says GyroLAW.

— High wheel spin = (very) small equatorial precession on a LEANED gyrowheel.

— Low wheel spin = (much) faster equatorial precession on a LEANED gyrowheel.

THESE GyroBasic ARE ALL SIMPLE VERIFIABLE RESULTS FROM ELEMENTARY GYROSCOPIC EXPERIMENTS. All Clear to the bone.

AS ALSO this destructive TWISTING-gyroeffekt on WikipediaCountersteering[‡] is relatively, with given countersteering force and countersteering time HIGH on LOW wheelspins, = low travelling velocity, we are NOW in an explaining situation of a definite HAZARD in trying to manipulate and maneuvering AGAINST the much more easy and direct smooth and safe gyroscopically advised NATURAR way:

— dont steer the bike. Just follow ITS HalGyro natural response in TAKING a Centrifugal Force IN COOPERATION WITH ANY CURVATURE:

— Just »let the bike do it». FOLLOW the bike. And you will be a perfectly safe trafficant, says GyroLAW.

   Or in more straight words, directly from The Bike, says GyroLAW:

— »Don’t fuck with me».

 

 

CLEARLY[‡] SERIOUS ISSUES EXIST IN ESTABLISHED QUARTERS IN THIS SUBJECT. Detailed clarifications are urgent.

 

— See from WikiCount1 on ”COUNTERSTEERING”:

— »Better Call 911 directly», says GyroLAW, than taking anything at all by the word form the present (Jan2019) Wikipedia text

WikiCount1 ¦ WikiCount2 ¦ WikiSTEER on the subject of navigating a two wheel bike in traffic.

   Here it is ONLY recommended to study GyroBasic properties in concord with McOMwash2000 motorcycle manual, and all alike associated:

— a guaranteed traffic safe ride.

 

 

 

 

 

 

EkvGyroPrec:

Ekvatoriella GyroPrecessionen — 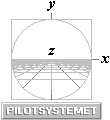 y-vridningen

Se även z-vridningen

 

 

Ekvatoriella GyroPrecessionen som resultat av kraftpåverkan i lodled — hjulets lutning

EN FÖRSTA APPROXIMATIV HÄRLEDNING — ENLIGT GYROLAGENs ANVISNINGAR

EFFEKTEN AV TIDSBESTÄMD vertikal KRAFTVERKAN PÅ AXEL TILL FRITT VRIDBART SPINNANDE HJUL som färdas på plan Jordyta:

Koordinatsystem: PILOTYSTSTEMET xyzXYZ:  Momentan GyroRotation kring y-axeln som följd av lodrät kraftpåverkan vertikalt utmed y-axeln:

•   Liknande det som sker vid cykling då cykelkroppen lutas med styret fritt vridbart utan handkontakt:

•   Speciellt samma effekt som ett gyroskop uppvisar, bilden nedan, då endera hjulaxeln puttas neråt:

 

 

Vi förutsätter viss förtrogenhet med grundbegreppen i avsnittet om Tyngdcirkeln:

Illustrerad Utgångspunkt — Momentexempel 1:

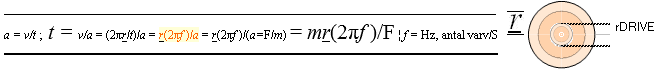
Utväxlingskraften — aktuell tyngdcirkelradie r kontra aktuell drivaxelradie rDRIVE — som ger effektiva drivkraften:

F           := F · rDRIVE/r ;

— Härledningen utgår ifrån ATT vertikala kraftverkan måste uppväga hjulets axiellt vektoriellt riktade impulsmoment J=mvr

— med hjulets interna kraftkomponent F(J)

FJ          = må = mω2r = mr(2πf0)2                     

— samt den tid (t) och den kraft (F=F-Drive) med vilken hjulaxeln trycks ner mot markplanet.

— Dessa förutsättningar ansluter till en behjälpligt experimentellt möjlig resultatkontroll via den typ av gyroskop som figuren ovan avbildar — samt jämförelse med aktuell praktisk cykling med styret fritt vridbart utan handkontakt.

   NOTERA ATT VISS ERFARENHET KRÄVS FÖR CYKLING UTAN HÄNDERNA PÅ STYRET. Var aktsam.

— KOPPLINGEN till Momentexempel 1 utnyttjar (omvänt exemplet med f ur t) bestämningen av den tillryggalagda hjulvridningsvinkel (H°) som uppnåtts efter kraftens anbringningstid (t) för hjulets acceleration (i MomEx1).

— Enda skillnaden i tillämpningssätt, är att vi här utnyttjar det spinnande hjulets redan existerande impulsmoment (J) för en (motsvarande, ekvivalent kraftaccelererad ansats till gyroskopisk) momentan vridning av hela Momentexemplets hjulaxel.

   Det vi söker i sammanhanget är endast en ekvivalent massmotståndsrelation som bygger på de bägge energierna/momenten M(J)=Fr för det spinnande hjulet via dess hjulaxel, och M=Fr för den tillståndsändrande energin.

 

RELATIONERNA ger oss då fortsättningsvis:

 

J = mwr = m(w=2πrf0=ωr)r = ωmr2 = Ĵω         ;

å = w2/r = (ωr)2/r = ω2r                                     ;

:

MJ         = FJr = mr2(2πf )2 = Ĵ(2πf0)2                  ; f0 = GyroWheelSpinFrequency in Hz = n/S

M          = Fr = mar = m(w/t)r = mwr/t               ; t = force onset time:

             = J/t = Ĵω/t                                             ;

J            = Mt = Frt = Ĵω = Ĵ·2πf0                        ;

f            = (Fr/FJr)t/2πm                                      ; inverterade hjulvridningstiden 1/S :

             = corresponding GyroWheel Equatorial Precession Rate:

Turns    = ft = (Fr/FJr)t²/2πm                               ; hjulvridningen under kraftansättningstiden t  

Angle    = 360°ft                                                  : wheelTurnDuringForceOnset

             = 360°(Fr/FJr)t2/2πm                             ; vridningsvinkeln i grader efter t

 

DETALJER SOM HAR BORTSETTS IFRÅN:

•   Hjulmassan (m) är i det praktiska fallet uppdelad på spinnhjul + hjulupphängning: dessa behandlas här förenklat som hjulets (hela gyroskopkroppens) totala massa på en resulterande hjulets tyngdcirkelradie r med massan m;

•   r-DRIVE, kraftverkans momentdistans i CYKELFALLET, har ansatts lika med hjulets tyngdcirkelradie — vilket är en rätvinklig omkastning av »lod-pinnen» som cykelföraren kan navigera sin cykels lutning från eller via, typ illustrationen i LeanTURN — en ungefärligt motsvarande »Lodiär Vridpinne»

ResGyroLeanTurn: EkvGyroPrec ¦ EX

RESULTATBILD MED KALKYLKORT OCH PRAKTISKT KONTROLLERAT GYROEXEMPEL:

KalkylGyEq:

 

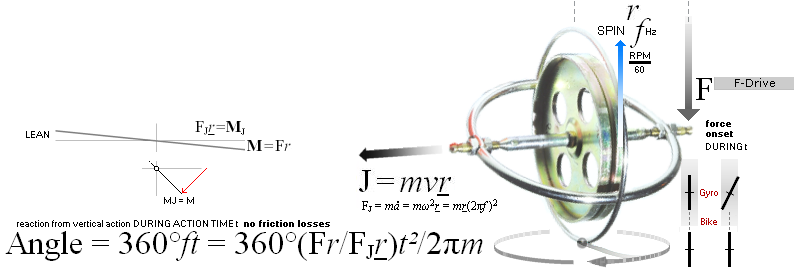
Tabell 1 — SpinningWheel — GyroDec2018.ods

 

Gyroscopically Twisted Angle = 360°(Fr/FJr)t2/2πm ¦ direct variables given vehicle: F r t ;

Connection deduced as explained.

 

NOTERA BEGRÄNSNINGEN I FUNKTIONSSÄTTET:

Gyroskopets konstruktion sätter en definitiv gräns för experimentell analys vid grovt sett 45 graders ekvatoriell spinnlutning M(J)=M. Omkring det läget kommer den axiella spinnpinnen att ta emot på underlaget, och ingen vidare ekvatoriell gyroskopisk precessionsanalys är möjlig.

 

 

DIREKTA GROVTEST PÅ GYROSKOPET (m=82Gram — vi når lätt 9000 RPM med uppvarvningsanordningen) VISAR APPROXIMATIVA ÖVERENSSTÄMMELSER:

— Ju högre spinn (f0) desto mera stabilt spinnhjul med desto mindre verkan efter given pålagd kraft (F).

— TIDSBILDEN (t) vid kraftpåverkan — en använd blomsticka touchar till hjulaxeln (0,1 S), varvid hela gyrokroppen vrider sig ett litet steg åt nertryckningshållet — visar allt mindre vridvinkel med allt högre spinn, samma kraft.

— Kraften F-Drive här uppskattad på följande sätt:

— 0,1-0,5N: 0,1N är tyngden hos ca 10 Gram = 1/100 KG:

— Det är bara en kort lätt touch vars motsvarande tryckkraft vi kan kontrollera/uppskatta/direktmäta på en brevvåg: trycket av 10-50 Gram är, faktiskt, en inte så liten tryckverkan som Gramsiffran förefaller att antyda om man inte har gjort brevvågstestet.

— Låga spinn ger större vridningsvinkel — samtidigt som gyrokroppen blir alltmer instabil.

 

KALKYLRUTAN

 

 

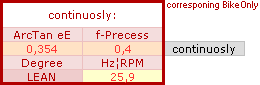
föreställer en approximativ utvärdering av vad som händer med ett motsvarande cykelhjul

(vuxencykel: 28’’=Ø=0,7112M):

Biking: RESULT

MOTSVARANDE CYKLINGSEXEMPEL:

 

 

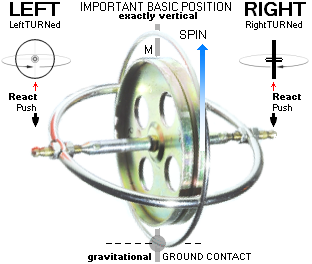
— Med en vuxencykels 28’’ framhjul fritt vridbart på framhjulets tyngdcirkelmassa 1 KG — tyngdcirkelradie lika med hjulradien 0,35M — och marschfart 16,1KM/h = 10MPh, med en nerlutning av cykelhjulet under t=½ sekund på en minimal höftvricking (0,1Newton) uppnås en idealt friktionsfri gyroskopiskt ekvatoriellt precesserande hjulvridningsfrekvens på 0,0518 ~ 0,1 varv per sekund med en effektiv cykel/personlutning på 0,104 grader: till synes helt omärkliga, helt ovidkommande bidrag — »ordinärt vinglande CykelFolk på väg Framåt» — men exakt gyroskopiskt erfaret också på aktuell cykel — såvitt också, verkligen, naturkorrekt formulerat:

 

Tabell 1 — SpinningWheel — GyroDec2018.ods

 

— Det som främst visar sig i övningen ovan — och som kommer som en liten överraskning OM KORREKT NATURBESKRIVET, eller rättare som en mera positivt bekräftande upplysning — är t-faktorns inverkan på den resulterande kurvgenomgångens gyroprecesserande takt: är det rimligt?

 

Med en SNABB kraftansättning — litet t-värde — minskar också gyroprecessionen, samma som den uppnådda hjulvridningsvinkeln efter ansatt kraft F-Drive under t.

 

Vi kan djuptesta grovt kvantitativt — mot vår erfarenhet som cyklister — med att motsvarande Kurvradien (Kr) kan bestämmas ur

 

2π·Kr                = 1/f-Precess · (v=28’’0,0254M π f0)    ;

Kr                     = (28’’ 0,0254 M)f0/2f-Precess              ; f-Precess = 0,0518...~ 0,1

                          = (0,7112/2) ...

                          = 0,3556 · f0/f-Precess                            ; enligt kalkylexemplets värden:

f0/f-Precess        = 20                                                        ;

Kr                     ~ 14 M                                                   ;

 

En svängdiameter på nära 30 meter. Inte helt orimligt.

— Grovräkningen med samma ideala bas som experimentgyrots singulära hjul.

— Förkortas kraftändringstiden till t=0,1S blir Kr~69 M.

— En (stadig, tränad) tävlingscyklist som åker i 16KM/h åstadkommer knappast 0,1N-ändringar under längre tid än 0,01S — om ens det: Kr=686 meter. Rak typ. Men exakt praktiska kvantitativa bevis för den räkningen saknas här.

— Ordinära VingelPellar i Marschfart 15 KM/h med märkbara minimala 0,1N-kroppsrörelser t~1S vinglar i radier under vickande sekunder omkring 7 meter. Känns det bekant?

 

Räkningen visar generellt: Snabba kroppslutningar med given cykelfart ger små gyroskopiska ekvatoriella precessionseffekter med handsfree, analogt LITEN kurvlutningsvinkel (stort Kr-värde). För att minska Kr-värdet — förbereda en snävare kurvtagning , samma hastighet — måste TIDEN UNDER VILKEN cykeln lutas ÖKAS PÅ. Stämmer det, rent kvalitativt — och i så fall hur kan vi kontrollera det?

— Ett sätt — »erfaren cyklist teoretiserar» — är TIDEN för att TA en kurva INITIELLT: Ju brantare sväng = större anpassad gyroskopisk hjulvridning = litet Kr-värde, desto längre tid (med hands-free) krävs för att luta cykeln DEN större graden, given fart. 

Jämförande krafttider:

Table CFT

EkvGyroPrec

Notera Table CFT att det är fråga om enskilda tiondels sekunder i minimal ANSATT cykellutning — med lutningsresultat i bråkdelar av en enda ynka grad — med relativt STORA Kr-ändringar, flera — många (tiotal) — meter:

 

HUR FUNGERAR DET?

 

— Alla följande påståenden, satser och meningar är — eller ska vara — fullständigt förankrade i ELEMENTÄRA GYROEXPERIMENT GyroBasic som vem som  helst själv kan utföra och kontrollera:

— All proceeding statements are — or should be — completely concordant with elementary gyroscopic experiments GyroBasic that any person can perform, verify and study all the results in.

 

Gyrokroppens reaktion på ett MOMENTANT — under tiden t — nertryck:

 

 

 

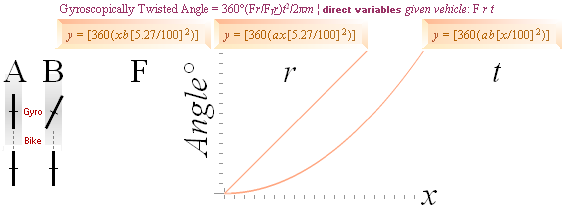
Spinning GyroWheel reacts by short vertical force-onset on right side of the spinning wheel during time t.

Gyroscopically Twisted Angle = 360°(Fr/FJr)t2/2πm ¦ direct variables given vehicle: F r t ;

Connection deduced as explained.

 

A:   VID t=0 ansätts ett nertryck — lutning — höger sida under ett kort ögonblick (t):

B:   GYROHJULET svarar med en omedelbar högervridning, och kvarstår sedan i Det läget.

— Med gyrohjulet som cykelns framhjul innebär Det Nya Läget också en motsvarande gyroekvatoriell hjulprecession enligt typillustrationen (högersväng) i LetRitTURN:

 

 

Bike enters curve, right turn, right figure. One full travelling circle, radius Kr, equals one full 360 degree equatorial gyroscopic precession of the slightly twisted bike’s front wheel from the preceding force onset. These are basic elementary gyroscopic experimental results that any student over 5 years old should be acquainted with in a human culture worthy its name. Should.

 

— Cykeln genomgår kurvtagning. Ett helt varv motsvarar en hel 360-graders gyroekvatoriell precessionsrotation.

TableComparingForceTiming: Biking — see also BTE

————————————————————————————————————

v = 16,1KM/h = 10MPh

på vuxencykel Ø = 2R = 28’’ = 0,7112 M med GyroIdealt  fritt vridbart framhjul;

F-Drive = 0,1 Newton ¦ r = r = 0,35M ¦ f0 = 2Hz ;

F-DRIVE = Force by which reaction appears:

 

t  time, seconds

1

0.8

0.6

0.4

0.2

0.1

leaning force onset time

Kr CurveRadius, meters

6.9

8.6

11.4

17.2

34.3

68.6

resulting curve radius at travel

 

  reeling cyclist   ...................................   steady cyclist

  vinglig cyklist   ...................................   stadig cyklist

Gyroscopically Twisted Angle = 360°(Fr/FJr)t2/2πm ¦ direct variables with a given vehicle: F r t ;

———————————————————————————————————————

Kr, gyrogenererad svängradie

t, tiden som cykelns väglutning anställs under från lodrätt läge med kraftansättningen 0,1N

————————————————————————————————————

Tabell 1 — DestructiveSteering — GyroDec2018.ods

 

   Resonemanget förefaller att stämma (mycket bra) överens med det praktiskt och experimentellt erfarna fysikaliska verkningssättet:

— mera energi för mera effekt: Rakt fram = minsta energin = minsta effekten.

— Hårda kurvor kräver mera energi — mera krafttid — än mjuka.

   Vi eftersöker naturligtvis ifrågasättanden — eftersom inget av det här påstådda verkar finnas i etablerade kvarter.

 

Vi kan inte bevisa någon mera detaljerad experimentell cykelräkning här, annan än den som uppskattningsvis stämmer med redan bekant erfarenhet från cykling. Ingen direkt elakt överdriven felform verkar finnas i grovsambandet ovan: vi ser att grovvärdena, utan vidare analys, KAN uppfattas som ”rimliga”.

 

VAD MAN DÄREMOT KUNDE BEGÄRA FRÅN MERA PÅSTÅTT eminent ETABLERAT HÅLL ÄR MOTSVARANDE REDOVISADE MERA EXAKT EXPERIMENTELLT BEKRÄFTADE — PRAKTISKA MEST ENKLA SAMBAND — SOM BEVISAR och förklarar RIKTIGHETEN I ALLMÄNT PÅSTÅDDA FYSIKORDNING — utan  inblandning av komplicerad matematik.

 

— Den delen står här veterligt HELT orepresenterad i det allmänna litterära utbudet (@INTERNET Jan2019) angående gyrofysiken:

— Gyrolagen — omnämns inte.

— Enkla exempel, typ ovan (med en djupare matematisk härledning) — relateras inte:

   Istället möter oss en stor mängd akademiskt etablerat datormodellerat SNACK[‡] WikiCount1 ¦ WikiCount2 ¦ WikiSTEER som dessutom hänvisar till referenser som definitivt INTE[‡] ansluter.

— Läsaren ges inte ens minsta lilla CHANS att ifrågasätta något: att SJÄLV verifiera.

 

— Jämför »HollyWood-attityden»: ”Varning ... Fängelse”. Ingen upplysning om ATT mänskliga rättigheter STYR kulturinnehållets FRIHET från brottslighet Där man bryr sig i att propagera för det. Inte ett ord. Jätteintressant Kulturell FilmHistoria.

 

Kontinuerlig ekvatoriell precession — som uppträder då man sätter ner gyroskopet ekvatoriellt i en redan på förhand justerad lutning — kräver en delvis mera komplicerad ansättning i härledningen, om så korrekt uppfattat. Den typen ges inte här. Men man kunde förvänta sig att den typen borde ha någon redan etablerad — enkel — presentation på Webben. Ännu inget upphittat Jan2019.

 

 

 

 

 

 

DirectByExperiment: 16Jan2019

Ekvatoriella GyroPrecessionen —  z-vridningen

Se även y-vridningen

 

traffic dangerous gyro wheel navigation

DIRECTLY EXPERIMENTALLY VERIFIABLE GYROSCOPIC PHYSICS

FORCED HORIZONTAL TWIST ON A VERTICALLY GYROSCOPIC SPINNING WHEEL

— a travelling bicycle driver is trying to maneuver the travel by attempting to steer LetRit into LetRit directions

ESTABLISHED CLARIFICATIONS from related experimental elementary gyrsoscopic physics HAS BEEN SEARCHED FOR @INTERNET Jan2019, BUT NOT YET FOUND. This is a — related, guaranteed complete explanatory — simple rough basic mathematically supported description of what happens in concord with elementary gysocopic experimental results anyone can perform with a two ring Gyrobody:

 

SpinningWheelAngularMomentum J0 = mvr = Frt  rotates the wheel  DESTRUCTIVELY  by  ANY  the driver's corresponding J=Frt on the steering rod:

SIMPLE CORRESPONDING MATHEMATICAL PHYSICS SAYS:

Twisted z-Angle = 360°(Frt)/Frt)0 with Spinning Wheel Angular Momentum J0 = mvr = (Frt)0 — ideal gyroscopic vertical wheel.

— The Wheel rotates destructively — one turn, 360° — as 360 · J/J0.

 

 

— Compare Wikipedia: »To turn right we must first lean left». Very Advanced Academic Stuff — to initiate a serious traffic situation. Se also WikiSTEER.

   So: How does it work?

A simple construct lets us study what happens trying to HORIZONTALLY manipulate the gyroscopic force.

   Wikipedia seems not to be acquainted — has been looked for, but not yet found:

— Two shorter pieces of wood with milled slits, screwed fast from under a longer holding rod, hold the gyrobody practically frictioneless to z-rotate in our travelling PilotSystem. Giving[‡] the gyro-wheel some spin, it immediately, the right photo, reacts to a corresponding right-turning clock-wise y-twist — by practically jumping a revolving twist counter-clockwise around the z-axis.

   THE EXPERIMENT SHOWS MORE DESTRUCTIVENESS WITH LESS SPEED:

— The lower the spin, given a constant force F over constant time t to execute the so destructive steering twist, the more destructive response is transferred onto the z-twist (to a certain limit) of the spinning wheel — perhaps surprising to the layman. See TableExample below.

 

STRANGE ENGLISH:

— The corresponding Swedish TRAFIKANT for a person participating actively IN general traffic —

person performing a drive of a vehicle on a public road — seems NOT to be what would be expected:

— The simple corresponding word TRAFFICANT seems not to exist in the English part.

— Instead we get fuzzy (silly, dumass) propositions claiming ”road-user”

— person who uses the road at night to piss on, much more space there, especially on desert roads

— or ”passenger”

— a (sleeping) person (in a trevelling vehicle) NOT NECESSARILY HAVING FOCUS on The Traffic, not even on OUR road, but looking out the window of a passing near train, wondering what is going on here:

— No English single word seems to exist for a person PARTICIPATING ACTIVELY IN TRAFFIC ON A ROAD: focus on vehicles in traffic as a driver in one of them. So: Now I have invented a trafficant, for that. (The English Earth Population has specific Traffic Issues ...).

 

RESULTING GENERAL TRAFFIC PICTURE:

The driver of a conventional two wheel bike has, pretty much, exactly the wheel spin angular momentum in his hands over the distance of the steering rod (handlebars): each steering maneuver — ideal gyroscopic construct, directly observed by experiment — affects the spinning wheel correspondingly, exactly according to the gyroscopic basic physics.

BikeTableExample: DBE ¦ CTF

GIVEN THE SAME CONDITIONS AS IN THE LEAN-TURN BIKING EFFECT TableCFT:

 

AdultBike: Ø = 2R = 28’’ = 0,7112 M, ideal GyroIFrontWheel: r = 0,3M:

Connection as stated: Angle = (J=Frt)/(J=Frt)0 with the zero subscript in the spinning wheel.

 

————————————————————————————————————

Biking On AdultBike Ø = 2R = 28’’ = 0,7112 M with ideal GyroFrontWheel;

F-Drive = 5 Newton ¦ r = r = 0,3M ¦ t-Drive= 1S ;

F ¦ t -DRIVE = Force ¦ time  by which reaction is employed:

 

f0 spin, Hz = n/s

1

2

3

4

5

6

GyroWheelSpin frequency

v velocity, MP/h

5.0

10.0

15.0

20.0

25.0

31.0

Traveller’s velocity

v velocity, KM/h

8.0

16.1

24.1

32.2

40.2

48.3

Traveller’s velocity

z° degrees

152.0

76.0

50.7

38.0

30.4

25.3

resulting destructive wheel twist

 

  reeling cyclist   ...................................   steady cyclist

  vinglig cyklist   ...................................   stadig cyklist

Gyroscopically Twisted z-Angle = 360°(Frt)/Frt)0 ¦ direct variables with a given vehicle: F r t ;

———————————————————————————————————————

z, destruktivt gyrogenererad hjulvridning

Ft, KraftTiden som vridningen anställs på

————————————————————————————————————

Tabell 1 — DestructiveSteering — GyroDec2018.ods

 

Given »employed»[‡] destructive Ft — Wheel r = Steering r = 0,3M on adult bike:

— The sLOWER the speed, the LARGER the destructive effect.

   That is the provable raw basic gyroscopic effect by principle — experimentally verifiable to any person with a two ring gyroscope (GyroBasic).

 

 Destructive manipulation in Biking — SPIN clockwise ahead, as seen by an observer from behind.

Etablished literature, see WikiQuote, claims opposing statements — with no mentioning of the simple elementary GyroLAW.

 

CLEARLY SERIOUS ISSUES EXIST IN ESTABLISHED QUARTERS IN THIS SUBJECT. Detailed clarifications are urgent.

 

GyroLAW says and explains:

— The lower the WheelSpin, the greater the driver’s potential force maneuvering capability is, and hence the greater degree to overrun the wheel’s stability.

— At high wheel spins — says this mathematical physics with a corresponding simple gyroscopic experimental verification — the driver has much less (muscle) control over the spinning wheel’s angular momentum (J0).

— So: The effect of DESTRUCTIVENESS from trying to steer — at all — IN an intended direction is proportionally less in high speed biking. However: the high speed itself takes the driver a longer path — for every the smallest maneuver — perhaps making the situation even worse — depending upon traffic conditions. See further on The Destructive WikiSTEER, unless already familiar.

 

 

 

 

 

Tyngdpunkten: GyroBasic

 

Statiska

TYNGDPUNKTEN

SE ÄVEN TYNGDPUNKTEN I MODERN AKADEMI MACTP

 

 

Galieli-Newtons klassiska praktiska verkstadsfysik:

ALLA FASTA KROPPAR UPPFÖR SIG SOM OM DERAS MASSOR VORE KONCENTRERAD TILL EN ENDA CENTRAL IDEAL PUNKT: kroppens egen individuella fasta statiska tyngdpunkt. Jämviktspunkten.

 

”  TYNGDPUNKTSSATSEN.

  : tyngdpunkten hos ett system av partiklar rör sig under inverkan av de yttre krafter som påverkar de enskilda masspunkterna i systemet så som om hela systemets massa var samlad i tyngdpunkten och alla de yttre krafterna angrep i denna punkt.”, citatkällans text kursiverad,

FM1975s61sp1m

Rubriker:

RotIPST ¦ HS2018 ¦ GyroKollen ¦ TP ¦ KIM ¦ JaxPREC ¦ GyroPRINC ¦ PrimGYROex ¦ GyroBASIC ¦ GyroINERTIA ABCD ¦ PerecessionsKRAFTERNA

¦ BevisA — Ansatt LUTNING ekvatoriell precession

¦ BevisB — INITIERAD LUTNING ekvatoriell precession

¦ BevisC — Ansatt Horisontell VRIDNING ekvatoriell precession

¦ BevisD — INITIERAD LUTNING axiell precession

¦ GyroLAGEN ¦ PE SpinnSNURRAN ¦

¦ RotIPST ¦ RotIPST ¦ GyroBASICabc ¦

NavAVSTÅNDEN ¦ PRECESSIONSBEGREPPET — Axiell¦Ekvatoriell ¦ GTF ¦ MagVARV ¦ RotIPST ¦

TYNGDPUNKTENS DEFINITION:

Se även originalets formulering i härledningens till gravitatiionslagen

 

Etablerade meningar om begreppet tyngdpunkt finns i MACTP: beskrivningar, förklaringar, jämförelser.

GYROSKOPETS PRINCIP — Ändringslagarna: Newtons tredje lag i utomordentlig praktisk demonstration, bevislighet och tillämpbarhet

Relaterad fysik:

GENOM GRIP GRAVITATIONENS TIDSABSOLUTA VERKAN ingår inte i den moderna akademins lärosystem, OCH DÄRMED SUPERPOSITIONSPRINCIPEN, UPPFÖR SIG ALLA FASTA INDIVIDUELLA MASSKROPPAR under inverkan av på dem verkande krafter SOM OM DERAS MASSA VORE TIDSABSOLUT OCH TIDLÖST SAMLAD I FUNTOP EN ENDA CENTRAL JÄMVIKTSPUNKT: stället där alla interna krafter — tidlöst, tidsabsolut, inga fördröjningar, absolutverkan — tar ut varandra: tyngdpunkten.

 

Det är sorgligt — och skamligt — att etablerad undervisning undanhåller mänskligheten den upplysningen. Se även i noMACfysik.

 

En materiell kropps (STATISKA) tyngdpunkt definierar så  kroppens egen inre jämviktspunkt. Se även vidare i MACTP.

— Vi kan också kalla den för oberoende fasta

kroppens statiska tyngdpunkt till skillnad från kroppens olika dynamiska tyngdlinjer och tyngdcirklar som träder i kraft så snart kroppen utsätts för olika (accelererade) rörelsemoment.

— Dynamiska tyngdcentra varierar med kroppens sammansättning, form, geometri och rörelsens art. Exempel ges nedan via Gyroskopets Princip.

Relaterad fysik och matematik:

EN KROPPS statiska TYNGDPUNKT ÄR

»i stort sett allt som INTE kan beskrivas i MAC»:

•   rymdpunkten där den gravitella inverkan från kroppens alla massdelar tar ut varandra i noll

•   kroppens absolut MOMENTANT — i varje särskild tidpunkt — statiska geometriska tyngdpunkt:

•   samma som rymdpunkten — ljusets gravitella beroende — där lokala ljushastigheten är som störst med hänsyn till lokala massinnehållet.

•   Statiska tyngdpunkten — centrum med max ljushastighet — ändras ALDRIG med mer än kroppsmassans sammansättning gör det.

— Den rymdpunkten är densamma centralpunkt som centralkraftsverkan bygger på i gravitationskraftens definition:

 

 

GRAVITATIONSLAGEN I DEFINITION ¦ CENTRALACCELERATIONEN I MODERN AKADEMI

 

a = F/m = å  = w2/r · (r2/m2)(m2/r2) = w2/r · (r2/m2) · (m2/r2) = Gm2/r2 ;

F = Gm2m/r2 ; allmänna gravitationslagen

 

KONCEPTET kommer från CENTRIFUGALACCELERATIONEN:

 

•   modern akademi kan inte relatera centrifugalkraftens komponent;

— Beskrivande MIT-exempel i ROTATIONSPARABOLOIDENS FORMFAKTOR.

•   modern akademi utelämnar — stryker — centrifugalkomponenten;

— Beskrivning i CENTRALACCELERATIONEN I MODERN AKADEMI.

 

Kommentar:

— REFERENSERNA MED GENOMGÅNGAR enligt ovanstående länkar antyder, starkt, att

ingen varken instans eller personalia i modern akademisk lärostol varken kan förklara, beskriva, relatera eller tydliggöra centrifugalkraftens elementära fysik: gravitationens roll i fysiken: GRAVITATIONENS TIDSABSOLUTA EKVIVALENT har — garanterat — ingen som helst ställning i den moderna akademins lärosystem (1900+).

 

En institutionell utbildningsakademi (1800+) som UNDANHÅLLER både sig själv (främst) och hela mänskligheten den elementära fysikinsikten för det tydligt glädjerika tillfället att få »Smickra Självet» som Intelligensens Högsäte [‡], framstår följaktligen INTE HELLER vuxen uppgiften att förklara innehållet för eleverna. Se även i NoMACfysik.

 

 

 

MACTP: TP  ¦  Jordaxelns precession

 

GALILEISKT samma a överallt i F=ma och Reellt GRAVITATIONSFÄLT

 

Experimenten vi gör här på Jordytan inom våra vardagsrum och industrilokaler gäller helt säkert enbart inom ett Galileiskt kraftrum: en och samma tyngdkraftsacceleration överallt i rummet, oberoende av avstånd.

 

KROPPENS IDEALA MASSPUNKT

TYNGDPUNKTEN i NaturFysiken

MODERNA (1900+) AKADEMISKA LÄROSYSTEMETS UPPFATTNING AV BEGREPPET

Jämför särskilt Wikipediaartiklarna (Dec2018) på Center of Mass och Center of Gravity. En del citeras nedan.

 

 

I relaterad fysik (TNED) är tyngdpunkt och mass(medel-)punkt samma sak. Med referens till varje individuell masskropp som en ideal homogen materiesfär — eller materiering:

tyngdpunkten är

•   stället där g-fältstyrkan a=GM/r2 = 0:  atomkärnan som massans och gravitationens fundamentalform:

•   kroppens ideala masspunkt — kroppens identitet garanteras av punkten med största lokala ljushastigheten —

som om hela kroppsmassan vore samlad i en enda punkt — i varje särskilt momentant ögonblick beroende på situation och omständighet (FUNTOP).

 

En kropps centrala referenspunkt c(MAX)

ljushastighetens värde ökar från kroppsytan in mot kroppscentrum och antar där ett maxvärde, liksom ljushastigheten också från kroppsytan utåt ökar så länge masskroppen besitter lokal gravitell dominans över andra närliggande masskroppar — mera djuprelaterat i Absoluta Metriken;

LJUSETS GRAVITELLA BEROENDE ändras inte med mer än den egna kroppsfysiken ändras — oberoende av andra kroppars fysik, deras närvaro och växelverkan; kroppens egen lokala c-referens ligger fast. Se särskilt i SUPERPOSITIONSPRINCIPEN om ej redan bekant.

— Se även i LJUSHASTIGHETEN INNANFÖR SFÄRISKA SKAL.

 

Vidare i KIM figur nedan. Ljusets gravitella beroende omnämns här veterligt inte alls i etablerad litteratur.

I etablerad litteratur (Wikipedia Dec2018) görs (dessutom) skillnad mellan

CENTER OF MASS (sv,. masscentrum) och CENTER OF GRAVITY (sv., [»tyngdcentrum»] tyngdpunkt).

 

Centers of gravity in a field

”  In physics, a center of gravity of a material body is a point that may be used for a summary description of gravitational actions.”,

”  In other words, the center of gravity is a point of application for the resultant force.[3]”,

— Wikipedia refererar till den moderna akademins vektorkalkyl, samma artikel:

”  .. its defining equation is not generally solvable”.

Artikeln beskriver vidare i samma anda ”Parallel fields” och ”Sperically symmetric fields”, samt slutför ämnet under rubriken ”Usage” enligt

”  The centers od gravity defined above are not fixed points on the body; rather they change as the position and orientation of the bofy changes. This characteristic makes the center of gravity difficult to work with, so the concept has little practical use.[14]”.,

@INTERNET Wikipedia, Centers of gravity in non uniform fields — 12Dec2018.

:

— Wikipedias sätt att referera termen eller begreppet MASSCENTRUM är nog det närmast vi kan komma en relaterad utomordentligt god definition på det — tyngdpunkt, masspunkt — som (1900+) INTE anses ha absolut fysisk giltighet i modern akadermi:

:

Center of mass

”  The center of mass is the unique point at the centre of a distribution of mass in space that has the property that the weighted position vectors relative to this point sum to zero.”,

”  The center of mass may be located outside the physical body, as is sometimes the case for hollow or open-shaped objects, such as a horseshoe.”,

@INTERNET Wikipedia, Center of mass, Definition — 11Dec2018.

:

— SÅ: Medan Wikipedia fortsätter att babbla om Center of Mass i den allmänna Jordfysiken, fortsätter vi här i relaterad fysik att babbla om Tyngdpunkt (eng. gravity center). Absolut bestämt. (Arkimedes har återuppstått). Beröringspunkter saknas med gemensam nomenklatur.

 

— I relaterad fysik (TNED) hamnar vi (om vi ens tänker tanken) i äventyr om vi försöker att göra åtskillnad mellan MASSA och GRAVITATION: gravitationens fundamentalform Är massan, atomkärnan: YTFORM (Planckringen). Inte volym: G-centrum i relaterad fysik har ingen representativ massa-i-en-punkt: G-centrum i relaterad fysik är ett tomrum. Termen masscentrum kan därför bli missvisande (rent av förödande missledande).

   Termen masspunkt blir mera beskrivande (eftersom en punkt i relaterad bemärkelse, se Differentialen, saknar fysikalisk utsträckning och därför bara kan betyda noll: intet). Men förstår man innehållet, spelar ordvalet mindre betydelse.

 

— I modern akademi har man ingen uppfattning (GcQ-teoremet) om gravitationens tidsabsoluta verkan.

— Se GRIP, och särskilt NEWTON MISSTROR GRAVITATIONENS ABSOLUTVERKAN enligt citat (Isaac Newtons tredje brev till Bentley).

 

PROBLEMET med modern akademi på ämnespunkten är — enligt relaterbar fysik — användningen av det tydligt modernt akademiskt uppfunna begreppet INERTIALSYSTEM. I relaterad fysik finns ingenting sådant (FUNTOP).

— I beskrivningen av de olika ämnesdelarna, förefaller SÅLEDES den moderna akademins nomenklatur så klumpig, träaktig och rent av PRIMITIV — omöjlig — att ingen normalt frisk människa KAN förstå vad som avses (mer än möjligen ”tryck på avtryckaren, här, nu, ser du ..”): det går inte att avhandla, relatera, naturfysiken på den moderna akademins nomenklatur. Jämför ATOMVIKTERNA från NEUTRONKVADRATEN. Finns inte i MAC.

   GRAVITATIONEN i modern akademi (1905+) följer som vi vet principen ”ingenting kan gå fortare än c”. Bara av den anledningen hopar sig tankefelen redan från ruta ett: hela fysikbilden undandrar sig förklaringar.

   Se även vidare mera utförligt i noMACfysik: vic-felet ¦ VektorKalkylen ¦ MIT-exemplet — KONSEKVENSERNA.

 

KIM: MACTP

STATISKA MOMENTET — E = Fd — Se även Kosmologiskt Exempel: Jordaxelns precession

KROPPENS IDEALA MASSPUNKT

från gravitationslagen:

 

TYNGDPUNKTSBEGREPPET I RELATERAD MENING kan beskrivas¦förtydligas idealiserat från GRAVITATIONSLAGEN

 

enligt figuren nedan med angivna samband:

 

 

— N lika masselement m/N utspridda på N olika positioner med samma avstånd r från den graviterande moderkroppen M utövar en och samma ekvivalenta gravitationskraft på den samlade massan m på r från moderkroppen M.

— Figuren ovan visar speciellt:  Masselement (m/N) utspridda på bascirkeln till en KON

MED GODTYCKLIGT LIKA AVSTÅND MELLAN TVÅ NÄRLIGGANDE m/N,

eller utspridda på en SFÄRISK KALOTT eller cirkelbåge via sfärradien r. Alla dessa går på ett och samma ut som den samlade massan (m) på distansen (r) från M:

— alla visar samma summerande gravitationskraft i m på r från M.

SAMMANHANGET I EKVIVALENTER LEDER HIT:

 

 

KRAFTVERKAN GRIP mellan M¦m/N lägger inga aspekter på innehållet i M¦m/N:

— Så kan kraftverkan i (5) F = GMNm(r–2) ställas ekvivalent på M=m som en ideal sfärisk kropps egen

GRAVITELLA SKALKRAFT F = GmNm(r–2) = GNm2(r–2) = GN(m/r)2:

 

— N lika masselement m/N utspridda på N olika ekvidistanta positioner med samma inbördes avstånd r från den idealt sfäriska kroppens centrum, utövar¦underhåller¦garanterar en KroppsSammanhållande skalkraft riktad in mot kroppens centrala — masstomma — tyngdpunkt, lika med den Moderkroppens totala gravitella kraftverkan på varje annan kropp (m) utanför enligt F = GmNm(1/r2) = GM(m/d2) med d>=r. Innanför M-ytan går F mot noll då r→0.

— För en ideal masshomogen materiesfär avtar g-fältstyrkan a=GM/r2=F/m innanför kroppsytan proportionellt mot kvadraten på avståndet från ytan och in mot centrum, och är i centrum — tyngdpunkten r=0 — lika med noll.

 

— Den idealt sfäriska kroppens idealt (obegränsat) tunna SKALMASSA utövar en sammandragande verkan riktad in mot sfärens ideala geometrisk centrum lika med sfärkroppens TYNGDPUNKT —

som om hela dess massa vore samlad i den centralpunkten.

 

DEN GRUNDFYSIKEN — obegränsat antal (obegränsat små) masselement utsprida över obegränsat många positioner för varje linje, yta och volym, analogt med geometriska kropparnas ideala Gaelileiska/Newtonska Jordfysik — bildar sedan i sig grundvalen för all elementär matematisk-fysikalisk teknisk tillämpning främst på Jordytan:

— beräkning och bestämning av kroppars tyngdpunkter, tyngdlinjer, tyngdytor.

 

Så FÖRESTÄLLER alla de ovan visade elementarformerna — diskreta punktmassor typ KON SFÄR CIRKEL med utspridda punktmassor som föreställer men inte definierar Jordfysikens SÅ reguljära oändligt besmyckade massformer — också på visst sätt objekt UTANFÖR Jordytsfysikens domän; Objekten UTANFÖR beskriver explicit kosmologins fysik där stora avstånd skiljer himlakropparna från varandra: kropparna är (mycket) små i förhållande till avstånden mellan dem.

 

 

 

 

 

GyroFysiken:

 

Samlade främsta huvudrubriker

GYROFYSIKEN

GYROSKOPET — GyroBasic

TYNGDPUNKTEN

GYROSKOPETS PRINCIP

PRIMÄRA GYROSKOPEXEMPLET

GYROSKOPETS TRÖGHETSPRINCIP

Gyro2Ways

AXIELLA OCH EKVATORIELLA PRECESSIONER

PRECESSIONSKRAFTERNA — GYROSKOPETS PRINCIP

GYRO y

GYRO z

 

 

 

 

 

Precessionskrafterna:

 

GYROSKOPETS PRINCIP ¦

PRECESSIONSKRAFTERNA —

INLEDNING TILL den elementära GYROFYSIKEN

 

— När GyroSnurran lutar och samtidigt vrider sig på sin uppsatta/vilande spets, betyder det att den väger mindre då, eftersom den — ju — lutar UTAN ATT RAMLA?

 

— Utomordentligt bra fråga.

 

 

 

 

— @Internet Jan2019: En etablerad beskrivning som ger ett nöjaktigt svar har eftersökts men inte påträffats.

 

Webbkoll (Nov2018+) på ämnet

WikiCount1 ¦ WikiCount2 ¦ WikiSTEER ¦ WikiPREC ¦

visar (som vanligt i Ämnet Relaterad Fysik) ”rent bedrövligt”.

— Det är tunnsått med rationella djup, mera frekvent synbart »höga rop på kvävda Hjälp från olika landsområden», illa ställt med allt annat än modern högskolad vektoralgebra, garnerad och kringpyntad med växande Kalhyggen med allt högre Skötande maskinvrål.

— Klassrummen ekar tomma. Ingen förstår sammanhanget. Det är muntrare på en kyrkogård.

 

Nämligen så, figuren ovan — också enligt (NewtonsTre) sekvenserna om trögheten i RotIPST ¦ GyroKollen:

— När Gyrot LUTAR — precesserar — utövar dess undre spetsvilande axelarm eller ringpunkt — regelrätt, Gyrokollen — ett konstant VRIDANDE MOMENT (E=Fd) PÅ upphängningspunkten:

— Vridmomentet E=Fd  utverkar¦GARANTERAR ena maken i en motsvarande TYNGDKRAFT (F1).

— Den andra maken (F2) är resten av ursprungets upprättstående tyngdkomponent.

— Tillsammans bevaras ursprunget som F = F1+F2 — oberoende av HUR Gyrokroppen står i läge. Den kan t.o.m. luta HÄNGANDE på upphängningsspetsen om denna är lämpligt utformad (rund kula med smal axel).

— Jämför speciellt läget i c ovan — vridmomentet F1 nu i lodled:

— TYNGDPUNKTEN ¦ RotIPST ¦ GyroKollen anvisar att Gyrokroppen MÅSTE vrida sig/TröghetsSvara — rotera — kring spetsänden på gyroaxelns markkontakt DÄR gyrokroppens tyngd också vilar:

— Gyrokroppens tyngd bevaras konstant.

 

MEN DET ÄR INGEN (djup-) FÖRKLARING. BARA EN REN (matematisk) BESKRIVNING.

— Djupbeskrivningen ges från GyroLAGEN med Praktiskt Exempel i SkivTallAna.

 

— Nej. Men man är benägen att tro det. Och så kan det beskrivas vidare:

— OM Gyroaxeln lutar, DÅ utövar Gyroaxeln ett vridande moment E=Fd genom sin statiska tyngdpunkt (T), en motsvarande tyngdkraft (F1), på vilospetsen som tillsammans med resterande maken (F2) i tyngdriktningen alltid summerar ursprungets tyngdkraft F=F1+F2:

— VIKTEN av hela Gyrokroppen ligger ALLTID på gyroaxelns markplacerade stödpunkt.

   Kollat och vägt på känslig brevvåg.

 

MEN DET ÄR fortfarande INGEN (djup-) FÖRKLARING. BARA EN REN BESKRIVNING.

 

 

 

 

HUR FÖRKLARAS DÅ SJÄLVA FENOMENET MED DEN HÄNGANDE KROPPEN SOM det hänget till trots VISAR FULL BREVVIKT? What?

   En utförlig utläggning som försöker beskriva (djup-) orsakerna till gyrokroppens beteende (till synes delvis märkliga, egentligen helt fräcka, rebelliska uppträdande) ges från Bevis D med GyroLagen i Praktiskt Exempel och vidare i Djupförklaringen;

 

Etablerade utläggningar i ämnets förklarande ljus har eftersökts men ännu inte påträffats (Dec2018).

Det är alldeles tydligt att väsentliga punkter fattas i det etablerade undervisningssystemet.

 

 

Med ledning av ovanstående elementära tröghetsfysik NewtonsTre — dess fullständiga genomlysning — kan vi sedan försöka luska ut hur EVENTUELLT planeternas rotationer har fått ihop det, rent kvalitativt, alltså i princip — enligt TNED-kosmologin. Det slutför i så fall hela uppgiften.

 

 

Se särskilt dokument med PLANETROTATIONERNA i VINTERGATANS SOLSYSTEM.

 

 

 

 

 

 

Gyroskopets princip: GyroKollen ¦ Tyngdpunkten

 

GYROSKOPETS PRINCIP

Ändringslagarna: Newtons tredje lag i utomordentlig praktisk demonstration, bevislighet och tillämpbarhet

 

 

VARJE TENDENS — ansats — som vill ÄNDRA ett givet tillstånd resulterar obönhörligt, oåterkalleligt utan något enda undantag i, fullständigt omutbart, kompromisslöst, ATT en lika stor motriktad TENDENS — ansats — visar sig som söker BEVARA tillståndet — motverka ändringen.

   Newtons tredje — särskilt utomordentligt tydligt praktiskt i Gyroskopet:

  Resultatbilden visar Aktion och Reaktion efter en bestämd ytterst enkel lagordning.

   Vidare nedan..

 

Primära GyroskopExemplet:

ENKLASTE OCH MEST DIREKTA GYROSKOPEXPERIMENTET:

— Hela fysikens inneboende grundordning visas DIREKT:

 

Det enda vi behöver göra för att verifiera och konstatera lagbundenheten i GyroLagen PushRotatesSpin är att — undantagslöst alltid, alla situationer, alla sammanhang, alla händelseförlopp — hitta M mesta och största massmotståndets lokal: Därifrån visar sig — och utgår, framträder, alltid utan undantag — effekten av varje minsta möjlig tendens och ansats som försöker ändra något.

— Flera exempel med bevis studeras i huvudtexten. Anledningen till intresset här är enkelt: Gyrofysiken kräver full kännedom OM vi vill, ens, försöka oss på att härleda någon ordning för vårt huvudintresse: Planeternas rotationer (och precessioner) för Solsystemets EVENTUELLA förklaring i TNED-kosmologin.

 

 

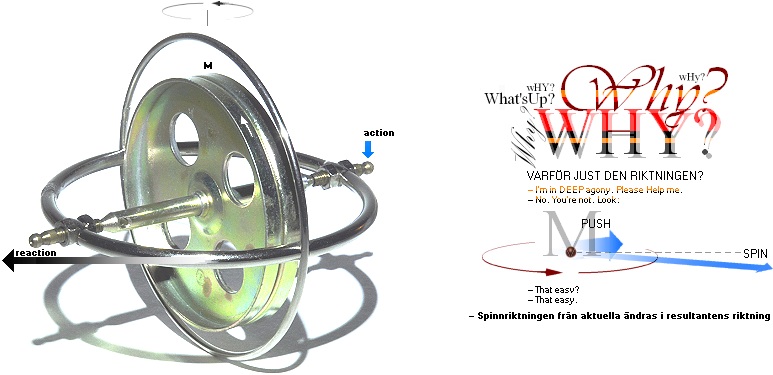
— Varför just DEN riktningen? Därför att det är den enda som finns att välja på: enligt spinnets anvisning för Pushen.

GYROSKOPET I BILDEN salufördes en gång i tiden av Clas Ohlson. Företaget (Dec2018) har inte längre den typen av sortiment: Sista CLO-katalogen som saluförde ”Gyrosnurra” (Inte upptagen i registret, fanns på avdelningen Leksaker): KATnr71, 1982-1983 s90 pris 12:50, 10st 84:-. Att titta tillbaka är som att titta in i ett helt annat universum i jämförelse med dagens utbud. Det är här (heller) inte närmare känt var man närmast kan få tag på något liknande (Se uppslaget i GyroBasic):

— Experimentet här kräver JUST en fast ring rätvinkligt monterad själva den grova huvudramringen för att fenomenet ska framträda i sin mesta¦främst förklarande tydlighet, läget i bilden ovan:

— Med Spinnhjulet igång står Gyrokrppen upprätt som i bilden. Har vi förstått funktionssättet i DET läget, har vi fattat ALLT övrigt också. Vi studerar det.

 

 

FUNKTION — för studium av gyrofysiken i dess mest elementära beteende:

•   För Gyrohjulets uppvarvning används en miniborrmaskin med en inspänd gummitrissa, se FOTO ovan.

•   Gyroskopet placeras som ovan med hjulet vertikalt på (mjukt, t.ex. musmatta) underlag.

•   En slät pinne/rör/stång används (liggande, horisontellt) med LÄTT beröring/nertryck på endera axeländen, blå pilen.

•   För varje touch ställer gyroskopet in sig på en ny fast vertikal riktning: hela gyrokroppen vrider sig en liten bit runt M-punktens vertikalaxel (MostMassResist — MestaMassaResistansPunkterna diametralt över hjulet genom dess spinnaxel) och åt det håll axelnertrycket anställs. Vita pilen på hjulfälgen markerar spinnriktningen i figuren.

 

Tröghetslagarna (Newrtons NEONS)

Mot varje tillståndsändrande kraft (push¦Knuff) svarar en lika stor tillståndsbevarande kraft (MMR MostMassResistive ¦ MestaMassResistansen, M): — Så: Gyrokroppen vrider sig som MMR-periferispinnets hastighetsvektor mot NerKnuffsidan. ÄNDRINGSLAGARNA.

— Figuren nedan sammanfattar funktionssättet enligt den ytterst enkla GYROLAGEN som bevisas av experimenten med Gyrokroppen i Primära GyroskopExemplet.

 

 

 

 

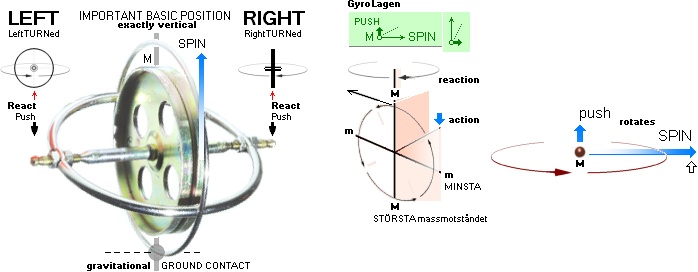
Figurförklaringen (höger) visar riktningarna, samt förklaringen varför gyrokropppen vrider sig som den gör.

— Se även särskilt i Praktiskt Exempel med en enklare Spinnsnurra som komplement till Gyroexperimenten:

 

— SPINNVEKTORRIKTNINGEN fungerar som VägVisaren vars visartopp Lyder/VriderSig

kring M-axeln genom hjulet AV och i Knuffriktningen. Alltid. Utan undantag.

— Hitta M-punkten — alltid 90° framåt från hjulaxelns påverkningspunkt. Och resten ger sig självt med känd PushRiktning.

— Hur hittar jag M-punkten? TÄNK, om inte direkt, ansättningskraften på hjulaxeln. Ett kvarts varv = 90° framåt i samma riktning ligger M. Minsta massmotståndets referenspunkter m ligger diametralt mot den riktningen genom hjulets tyngdpunkt.

— En TÄNKT aktuell vridning av ett stillastående hjul sker ALLTID genom en minsta massmoståndets m-axel: Vridaxeln berör två diametrala hjulpunkter som enbart vrider sig kring vridaxeln. Motsvarande diametrala hjulpunkter uppvisar största rörelsesättet, analogt mesta massmotståndets M-punkt.

   M (Major) ligger rätvinkligt m (minor). Med M så lokaliserad och spinnvektorriktningen given, knuffar Pushen ut Spinnvektorn som en vridbar visare kring M-punkten i knuffriktningen. Det är GyroLAGEN.

— Öva principens fattning så ofta som möjligt, om ej redan bekant. Se även i Körteknik — med jämförande etablerade meningar (Jan12019) främst i WikiSTEER, WikiCount1 och WikiCount2: Detaljerna är tydligen helt okända — omnämns inte — i etablerade kvarter.

 

 

Om Gyrokroppen vilar på sin axelände gäller precis samma lagform. Huvudtexten här behandlar exempel med bevis som täcker huvuddelen av vad vi behöver veta (i den här författarens referens) för att förstå komplexet i stort. Se särskilt från Bevisen ABCD i GYROSKOPETS TRÖGHETSPRINCIP från GyroBASICmath.

— Experimenten i all deras enkelt är, verkligen, en av den praktiska fysikens allra mest fascinerade upplevelser och observationer. Särskilt — speciellt — som fascinationen rör vid hela fysikens absolut fundamentala grunder: ÄNDRINGSLAGARNA (konv. ”Newtons tre rörelselagar”).

   Min egen första bekantskap var runt 5-årsåldern: Svänghjulen i Pojkarnas Leksaksbilar. Det isärtagna, spinnande hjulet var Mycket mer intressant att Studera ur 5-åringens perspektiv än själva bilen som leksak. Jämför en mera primitiv version i HS2018.

 

 

 

 

GyroBasicMath: GyroBasic

 

GYROSKOPETS

avgjort grundligt ELEMENTÄRA TNED — alla följande exempelsatser grundas på motsvarande utförda gyroskopexperiment

ENKLA MATEMATISKA FYSIK — figurdel c

Se även motsvarande figurdel c i Precessionskrafterna

 

Gyroskopets Tröghetsprincip GT:

  A  B  C  D

Gyrokroppens effektiva reaktion på den tillståndsändrande kraften verkställs genom gyrohjulspinnets riktningsändring kring punkten/diametralpunkterna med störst rörelsemotstånd.

FUNKTION:

Alla Action¦Reaction beskrivs enhetligt av ikoncirkeln nedan vänster:

 

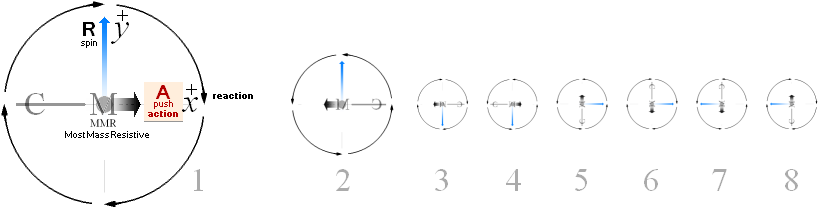
•   A: action → x: Tillståndsförändrande knuffriktning (M) på hjulet 90° från hjulaxeln:

•   C: Knuffcirkelns linjeprojektion på xy-planet (Z) med centrum i Statiska Tyngdpunkten:

•   R: hjulspinnet → y: Hjulet i vy ovanifrån med spinnriktningen (S) i y-axelns riktning:

— SKÄRNINGEN C¦R=(x¦y) markerar M MMR MestaMassaResistansens två M diametralpunkter:

•   M-riktningen bestämmer hur spinnriktningen (R¦y) ska ändras i läge:

•   A→x påtvingar entydigt — konsekvent, utan undantag — R(y) en VRIDNING kring M mot (ursprungets) A-position — allt mera kraftigt ju mera hjulmassa på allt större avstånd R som verkar i M — med analogt motsvarande större motstånd mot ändring.

BevisA:

Bevis A — vertikalt spinn i g-fält:

Alla bevis enligt utförda experiment  (1Dec2018)

med illustrationernas gyrokropp — arten med (minst) två släta ringar:

 

GyroBasic, SpeedUp:

 

 

 

Med gyrkroppens spinnaxel horisontell — spinnhjulet i exakt vertikal lodrät position:

 

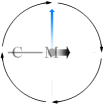•    enligt GT Hjulet i vy ovanifrån

gyrokroppen vrider sig medurs (RightTURNed) då Knuff¦Push anbringas på spinnaxelns högra sida:

— Vridningen varar endast så länge knuffen varar. Efter det står gyrokroppen fast i sitt nya läge.

 

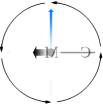•   enligt GT Hjulet i vy ovanifrån

gyrokroppen vrider sig moturs (LeftTURNed) då Knuff¦Push anbringas på spinnaxelns vänstra sida.

— Vridningen varar endast så länge knuffen varar. Efter det står gyrokroppen fast i sitt nya läge.

 

BevisB:  BEVIS A ¦ BEVIS C

Bevis B — ICKE-vertikalt spinn i g-fält:

EKVATORIELL PRECESSION — spinn och rotation är INTE samriktade

 

Alla bevis enligt utförda experiment  (1Dec2018)

med GyroBasic illustrationernas gyrokropp — arten med (minst) två släta ringar:

 

Initieras gyrokroppen det allra minsta LUTANDE

 

 

ur vertikalläget (Bevis A)

— handhållet, uppvarvat, sedan SÅ placerat/anbringat på bordet/underlaget —

inträder en lutande krängningsrörelse, en precession, i det att markkontakt etableras:

— Gyrokroppens STATISKA TYNGDPUNKT ligger nu vid sidan av lodlinjen

och utövar därmed principiellt samma kraftform men KONTINUERLIGT verkande som den tillfälligt lodräta axelknuffen i Bevis A:

 

GyroBasic, G-tilted:

 

Notera (NOGA): Precession HÄR ETT EKVATORIELLT DITO och Spinn är motriktade:

GYROKROPPENS DISLOKATION MED STATISKA TYNGDPUNKTEN VID SIDAN AV MARKKONTAKTPUNKTEN GARANTERAR ATT EN KONTINUERLIGT NEDDRAGANDE KRAFT VERKAR PÅ HELA GYROKROPPEN:

Som i bilderna ovan:  Med gyrkroppens spinnaxel x ICKE-horisontell och spinnhjulet (Y) med spinnet y lutande relativt horisonten:

 

•    enligt GT Hjulet i vy ovanifrån

gyrokroppen vrider sig medurs (som i Bevis A) om spinnet y är positivt ↑ och LUTNINGEN utmed x före markkontakten anbringaDES på spinnaxelns högra sida x-axelns positiva → sida:

— Vridningen varar kontinuerligt så länge den underliggande g-kraften verkar.

 

•   enligt GT Hjulet i vy ovanifrån

gyrokroppen vrider sig moturs (som i Bevis A) om spinnet y är positivt ↑ och LUTNINGEN utmed x före markkontakten anbringaDES på spinnaxelns vänstra sida x-axelns negativa ← sida:

— Vridningen varar kontinuerligt så länge den underliggande g-kraften verkar.

 

 

SE SÄRSKILT FÖRTYDLIGANDE OM GYROGRUNDERNA I

The PRECESSION CONCEPT has Issues

PRECESSIONsBEGREPPET Annonserar RUBRIKER

 

 

BevisC:  BEVIS A ¦ BEVIS B

Bevis C — kombinerat vertikalt¦ICKE-vertikalt spinn i g-fält:

Alla bevis enligt utförda experiment  (1Dec2018)

med illustrationernas gyrokropp — arten med (minst) två släta ringar:

 

DÅ gyrokroppens spinnaxel påtvingas någon allra minsta LUTNING relativt horisontlinjen i g-fältet:

 

EXAKT SAMMA SITUATION SOM OVAN I Bevis B — fortfarande samma enkla ikoniska tröghetsordning som i GT —  UPPNÅS OM GYROKROPPEN I Bevis A istället UTSÄTTS FÖR EN KNUFF vridning UTMED HORISONTALPLANET:

 

 

 

 

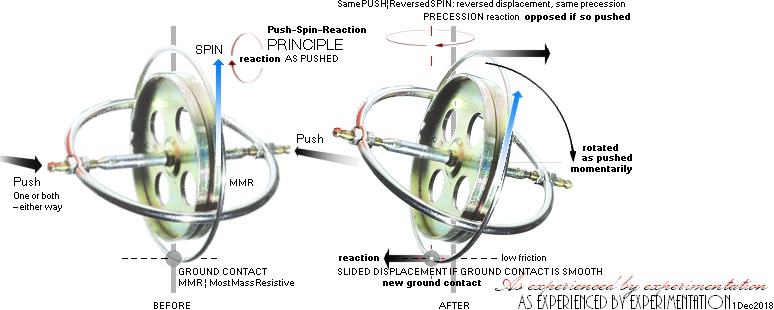
SOM i Bevis A — gyrokroppens lägeBegin ovan vänster:

Med gyrkroppens spinnaxel horisontell — spinnhjulet i exakt vertikal lodrät position:

 

•    enligt GT Hjulet i vy framifrån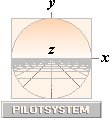

gyrokroppen vrider sig MOMENTANT medurs (som i Bevis A men här sett framifrån) om spinnet y är positivt och KNUFFEN anbringas på spinnaxelns högra sida x-axelns positiva sida i framriktningen (z) — här parallellt med markplanet, inåt i bilden (i riktning +z):

— MedursMomentanVridningen varar endast under Knuffen.

SEKUNDÄRA EFFEKTEN: Statiska tyngdpunktens Dislokation som följd av momentanvridningen påtvingar gyrokroppens statiska tyngdpunkt en konstant nedåtriktad kraft som resulterar i samma slutsituation som i Bevis B: Gyrokroppen roterar medurs — ekvatoriell precession[‡] — kring gyrokroppens (egen fasta idealt punktcentrerade) statiska tyngdpunkt.

 

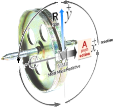
•   enligt GT Hjulet i vy framifrån

gyrokroppen vrider sig MOMENTANT moturs (som i Bevis A men här sett framifrån) om spinnet y är positivt och KNUFFEN anbringas på spinnaxelns vänstra sida x-axelns negativa sida i framriktningen (z) — här parallellt med markplanet, inåt i bilden (också i riktning +z):

— MotursMomentanVridningen varar endast under Knuffen.

SEKUNDÄRA EFFEKTEN: Statiska tyngdpunktens Dislokation som följd av momentanvridningen påtvingar gyrokroppens statiska tyngdpunkt en konstant nedåtriktad kraft som resulterar i samma slutsituation som i Bevis B: Gyrokroppen roterar moturs — ekvatoriell precession[‡] — kring gyrokroppens (egen fasta idealt punktcentrerade) statiska tyngdpunkt.

 

 

ALLA BEVISEN A¦B¦C FÖLJER SÅLEDES ENTYDIGT OCH UTAN UNDANTAG DEN ENKLA IKONISKA xy-CIRKELPARAGONEN I GT (GyroInertia).

— Och så även i Bevis D — avgörande för TNED-kosmologin med härledningen till Planeternas Rotationer.

 

Axiell Precession: BevisD:  BEVIS A ¦ BEVIS B ¦ BEVIS C

Gyrokroppens hängande förklaring

GyroLagen ¦  Praktiskt Exempel ¦ Djupförklaringen ¦ Skivtallriksexperimentet ¦ Beviset

Bevis D — axiell precession::

AXIELL PRECESSION — spinn och rotation ÄR samriktade

SAMRIKTAD PRECESSION OCH ROTATION — fysiskt omöjligt utan ena spinnaxeln fixerad:

DEN ENKLA SNURRANS PRINCIP — jämför EKVATORIELL PRECESSION i Bevis B:

Alla bevis enligt utförda experiment  (1Dec2018)

med ILLUSTRATIONERNAS GYROKROPP — arten med (minst) två släta ringar:

 

NOTERA ALLRA FÖRST I EXPERIMENTEN MED DEN ENKLA RAKA SNURRAN:

Stabilitetskriterium A: StabKritB

 

— Är spinnet MYCKET STORT — exceptionellt höga varvtal — motsätter sig den upprätta vertikalstången, markant kännbart enligt experimenten, varje form av riktningsändring: Den svarar, kännbart, med en STOR motkraft, större ju högre spinnet är. OM vi kan introducera någon PRECESSION i det försöket, svarar snurran med att MOTA BORT DET och etablera perfekt RAK vertikalställning — vi kan studera den processen särskilt — tills spinnet saktar av och tyngdkraften blir MÄRKBART större än centrifugalkraften. Då först kommer snurran att börja precessera. Se särskilt i BEVISET.

 

Detaljerad beskrivning ¦ GyroLagen:

 

StudieExempel ¦ SKIVTALLRIKSEXPERIMENTET

GYROLAGEN — även Precessionslagen

— the GyroLaw, not mentioned in Modern Quarters, beskriver och sammanfattar hela gyrokomplexet i en enda enkel fysiksats

— Se även särskilda bevisexempel.

PUSH ROTATES SPIN — from MostMassResistive point

NO EXCEPTIONS — NOT ON EARTH. NOT OUTSIDE EARTH. Not what so ever.

See also GYRO LAW ILLUSTRATED

 

Tröghetslagen — NewtonIII — PUSH ROTATES SPIN from most mass resistive point

— KnuffRoterarSpinn från MestMassResistiva punkten — NO EXCEPTIONS:

 

 

Kraftpåverkan Roterar Spinn — enhetligt. Undantag existerar inte. MestaMassMotståndets Lag:

— Ta ut spinnriktningen (s); Bestäm MestaMassResistansens (M) angreppsriktning (F=Push); Spinnriktningen ändras vridande sig åt kraftändringens håll, som en visare som stegas F-vart.

— Se enkla grundexempel i Tröghetslagarna.

 

För orienteringen i tröghetslagen genom rotationsfysikens MESTMASSRESISTANS (M, MostMassResistive), se enkla inledande praktiska exempel i GYROKOLLEN om ej redan bekant.

— Se även särskilt i AXIELL kontra EKVATORIELL precession.

Praktiskt exempel: Gyrolagen — AxPrec

 

DJUPFÖRKLARINGEN: Momentarmen Fd (a)

 

 

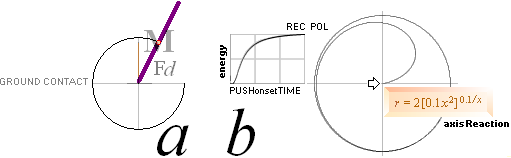
som vrider UT sig kring M-axeln gör det (b) växande från noll till kraftmaximum —

PÅ det givna spinnets riktning: Det finns ingen annan orsaksgrund att referera till.

— Axiell precession är enbart därför undantagslöst alltid samriktad med spinnet: finns bara en riktningsordning att välja på.

 

 

 

AxelBeteckningen mm motsvarande den led utmed vilken minsta (minor) massresistansen finns relativt MM-axeln där mesta (Major) massresistansen finns. Enligt tröghetslagen, konsekvent utan undantag, intar alltid största massmotståndet det rumsligt fysiska kraftcentrum från vilket all fysikalisk verkan utbildas, framträder och visar sig. MM-axeln bildar den initierande vridningsaxel som får snurran att reagera på den vertikala rödmarkerade knuffriktningen. Den aktionspunkten utbildas likvärdigt med resultatet av att påföra knuffen rätvinkligt snurrans vertikalaxel: MM-axeln ligger under den knuffpunkten i samma riktning.

   Relaterad beskrivning — Enligt genomförda experiment Dec2018 för Universums Historia.

 

 

Med fortsättning från frågeställningen i PRECESSIONSKRAFTERNA:

Beskrivningen här är FORTFARANDE är av typen just Beskrivande — inte (ännu explicit) förklarande. Vi försöker närma oss svaret i Gyrolagen Illustrerad med Djupförklaringen.

 

 

Fallet med direkt placerad snurra

SNURRANS LUTNING i exemplet ovan med en påtvingad lutningskraft kan också initieras DIREKT genom att varva upp snurran lutande — eller placera hela Gyrokroppen (b)  lutande på underlaget. I bägge fallen, börjar spinnhjulet¦Gyrokroppen att rotera¦Precessera samriktad med spinnet.

 

FROM MOST MASS RESISTIVE POINT:

 

Gyrolagen illustrerad:

 

RELATED MATHEMATICS AND PHYSICS — PushRotatesSpin

HUR GYROLAGEN FORMERAR GYROSKOPETS

HOW GYROLAW FORMATS THE GYROSCOPIC y-AXIS VERTICAL WHEEL PRECESSION

HJULVERTIKALSPINNANDE PRECESSION

 

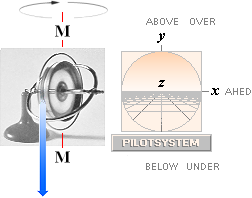
•   1.   GyroBasic:  SPEED UP the Wheel — and feel »the magic» of »activating» a vertical gyro-wheel precession:

— Place the one gyro axel on the suspended support and hold the other gyro end axel still before letting it fall freely:

— Within a short small angular fall, the whole gyroscopic body starts to accelerate into — for some time — a constant precessive y-axis revolving motion while the whole gyrobody mass rests — separately checked by weight — on the one supported vertical suspension point. How (in h-l) can this be?

   We study the explaining steps in detail: HOW the simple GyroLAW — really — has the nerve to format this — highly unacceptable — upsetting rebellic behaviour. Then we will try to explain how it can work.

 

 

GyroLAW explains transpositions between STATIC and DYNAMIC — 12:

 

 

 

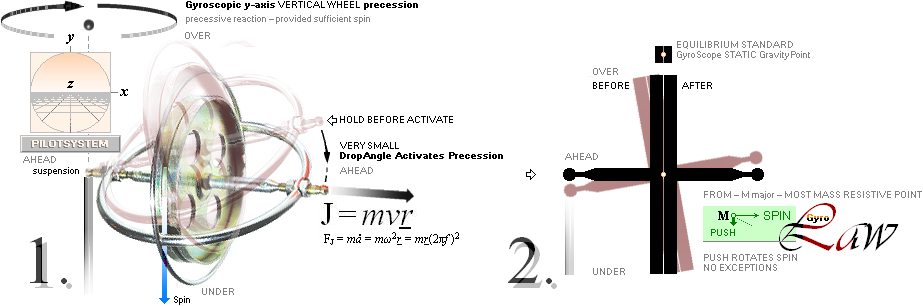
•   2.   The small FREE FALL — with respect to the gyro body STATIC — individual — GRAVITY POINT (conventional concept is mass centre) is ONSETTING a free clockwise TWIST around the GyroBodySTATIC GravityPoint;

 

GyroLAW explains transpositions between STATIC and DYNAMIC — 34567:

 

 

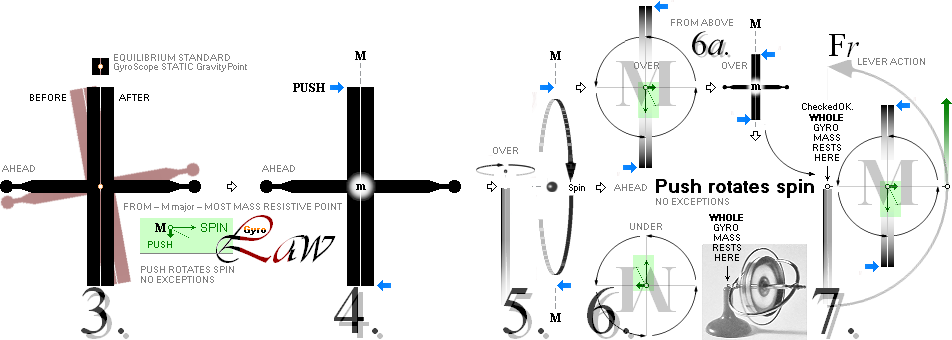
•   3.   The GyroLAW answers (4.) the clockwise PUSH — by using the wheel spin to define a corresponding Least(m, minor)¦Most(M, major — always axel-Push-ahead-directed 90°) mass resistive point (4.):

•   4.   LEAST (m) mass resistive point lies in our visual AHEAD direction (PilotSystem’s +z): MOST (M) mass resistive lies m-diametrically 90 degrees ahead on top/under bottom of the spinning wheel;

•   5.   GyroLAW reaction directs a first onset to the actual precessive rotation by a corresponding — the whole gyrobody as clarified in the 6a top view — OnSet Pilot-y-axis counter-clockwise rotation around its one (left) suspension point (while the gyrobody is still falling the short onset moment, before the precession has established);

•   6.   Situation in (5.) clarified, as seen from above (6a), shows that the OnSeted Pilot-y-axis rotation — the BeginPrecess moment — CONTRADICTS a non GyroLAW affected linear wheeltravel:

— The OnSeted M-point in (1.2.3.4.5) so inertially is transferred to a mode type »m-point-physics»:

— THAT is »the real magic»:

•   6a.   The spinning wheel’s angular momentum (here J=mvr) has by simple physical inertial consequence forced a situation with a NEW appearing M-point Push-reference — REPLACING or overriding the primary m-point reference in (4.):

•   7.   The spinning wheel’s J has »hi-jacked» — occupied — the whole gyrobody with a final and so autonomously reactive maintaining equilibrium of a corresponding STATIC MOMENTUM — a lever — M = Fd = mad balancing OVER the whole gyro body mass ONTO the one suspension point WHILE precessing.

— Circle closed: The gyro develops an autonomous, self-sustaining, physical STATE with all the different components and aspects maintained by transpositions of (different parts of) inertial equilibrium — exactly where they are needed for the balance.

 

The PRECESSIONAL SPEED — number of turns per second — becomes small on a given lean with a given high wheel spin. Lower wheel spin increases the precessional rate. We see this directly when the spinning wheel slows down by friction and the gyro body increases its lean: precessional rate increases until the gyro flips over.

— How can it do that, balance the whole weight on its horizontal tip?

   Related physics explains: The DYNAMIC gravity circle overriding the STATIC[‡] gravity point equilibrium spin balance by SPIN — appearing centrifugal force — makes a transposition of equilibrium references — no ”inertial systems” — ONTO the only remaining physical ground contact: the remaining axel tip. But there is no developed nomenclature to describe this behaviour in modern academic teaching system DUE to its famous in(ter)ventions — not deductions — of NATURAL physics and mathematics which happened during the 1800::s. Absolutely: we can’t use ”inertial system” — modern academic invented ideas of physics — to describe a DEPTH of nature physics. The idea of ”inertial system” is a FLAT world idea (”statistics”), no rational deep one. Good for Profit and Bombing, bad for naturally developed technology and global health. Absolutely. The word is: equilibrium. Birdstuff.

   Please do correct if wrong — for the sake of knowledge only: a safe ride.

 

 

WikiPRECESSION text (Jan2019) tries to »explain» gyrophysics — with none of the above terms. With also no contexting illustrations following the lead author’s description. Not even a guiding Pilot xyz-System is mentioned. It appears like flying with eyes closed: guesses, implications, hard-to-follow-descriptions, lack of rational depth. »WormStuff UnderCover».

— This remark is NOT to defame or depreciate the WikiAuthors on the subject. But only to clarify this one single point: they  don’t  know. The subject as such can NOT be explained with the help of the now established existing nomenclature — and math — in the modern academic teaching system: please do enlighten the blind.

 

 

An Earth gravitational Gyro Balancing wheel spin ω, to receive a corresponding total gyro body mass-suspension on gyro body end axel, demands a split of the gyro body into its two main components:

— 1. The spinning wheel m which must take — = SPIN up — all of the balancing momentums. And 2. the wheel (gimbal) suspension mass with 1 included as the total balancing mass (m0).

   See more detailed and developed in GbodyLOWSpinFALL.

 

 

THE THING is this one:

— Inertial frames to EXPLAIN physics = — equals — noPhysics. See FUNTOP:

•   Physics relates to equilibrium — not to system:

•   Physcial laws hold for systems — not in systems, no way;

•   Birdstuff: NATURAL EQUILIBRIUM IN ANY POINT IN ANY MOMENT OF TIME.

— More elaborate in INERTIA.

 

These simple basics, as stated, need what modern academic teaching system has NOT:

— STATIC for linear translations Gravity points — with STATIC gravity RINGS — and DYNAMIC for angular rotations Gravity Circles (conv, inertial momentum) — no ”inertial system”.

Transire:

1800:s. Our history’s famous 19:th century — a short review:

Such terms as those needed to explain these things and concepts are BANNED — became so banned — during the 19:th century development of Modern Academic Theory: Physics AND Mathematics;

— IT     can’t     explain. Compare TheTable of Atomic Weights.

   Comparing Modern Academy with Nature:

— It is LIKE arriving to a Formula-1 race — with a bicycle, also with the idea to WIN the engine competition.

   It isn’t the Bike of it. It’s the IDEA of it:

”to overcome ones human limitation and become master of the universe”, medallion on the Fields Price:

Transire suum pectus mundoque potiri. ”The most glamorous honour a mathematician can receive”.

   Excuse me for reminding the feasting details: fascistic nazistic CRAP.

— The general master race idea, or the common idea of a master intelligence, whatever the idea of it, IS the worst sewer there ever was in the history of human culture. IT holds humanity in its prison of ignorance, stupidity and violence by DRIFT. Never by plan — due to ITS surface apprehending idea of the origin of Intelligence:

— ATTEMPTING to overrun a jet-plane, leg-running on the ground. Modern Academy and Nature: not. No way.

 

 

BASIC rotational Dynamic Gravity Circle EXPERIMENTAL simple PROOF [D]: The simple »TOP»:

 

 

 PHOTO:  GyroD ¦ 4 — 4Dec2018

 

 

With HIGH spin there is no way to make or create an enduring precessive behaviour of this simple device UNTIL it reaches a certain LOWER SpinLIMIT. Simple experimentation (from the age of 5).

— The TOP, with high spin, REJECTS — sensibly HARD too — anything trying to make it precess. AS IF it would have SUSPENSIONS on its sides, all around. That IS the DYNAMIC Gravity circle taking — moving, transposing — the mass of the TOP away from the STATIC Gravity point of the whole mass form.

— No spin at all, namely:

 

 

 PHOTO:  GyroD ¦ 5 — 4Dec2018

 

Precession — wobbling — appears on a spinning wheel when a sufficiently strong force takes on the wheel — conditionally inside the radius of its dynamic gravity circle. If the spin is sufficiently high, the spinning wheel rejects the intruding force with no precessional result.

— This type explanation is excluded — not found — in modern teaching systems: searched for, not yet found.

— So, what is producing a precession?

— A force interfering with a gravity circle. No torque. Just force (gravitation).

— Compare Earth Axis Precession: Sun (and Moon too) gravitation takes on Earth’s FAT (»protruded») equator and swings it along annually with a corresponding small precessional effekt. No torque. The interfering force can be gravitational or electrical/magnetical (or fluidal, generally resistive).

— So, what is ”a gravity circle”? Any spinning mass.

   Typically our mentioned TOP.

 

 

The TOP leans.

   (I will not have the nerve to ask the reader: »Why do you think it does so ...»).

— Spin MOVES — transponds — gravity references for equilibrium purposes. That is HOW[‡] the Gyro does it.

— With sufficient spin, the gyro balances — moves — gravity (mass point) references to harmonize equilibrium. No more. No less.

   The Gravity Moving Point Reference Principle can be studied separately experimentally as in the RecordPlateExperiment (here 1990).

Djupförklaringen: momentpunkten flyttas

 

— PRECESSION¦rotation, SPINN och VRIDMOMENT (Fd) samverkar. Gyrokroppens HELA tyngd vilar på rotationspunkten (vänster) i nedanstående fotograferade gyrosekvens, såväl då Gyrokroppen står vertikalt som horisontellt.

GyroSerieDec2018:

 

I takt med att spinnet tappar fart lägger sig Gyrokroppen allt mer mot horisontellt samtidigt som rotationen¦Precessionen ökar i varvtalsfrekvens. Hur kan allt detta närmast mystiska ske? Tar man bort spinnet i sista bildrutan, ramlar Gyrokropper ner. Så: Vad är det för något ”magiskt” med spinnet som får Gyrokroppen att hänga kvar? Samma med snurran: Den lutar — JU!

 

SKIVTALLRIKSEXPERIMENTET GER den fullständiga DJUPFÖRKLARINGEN

Men: Vilken är förklaringen? Hur tusingen kan hela gyrokroppen ”bara hänga i luften” utan att ramla ner, sådär, fräckt, helt skamlöst, oanständigt, obegripligt, rena magin.

— Jag begriper inte ett skit av det, fläktfan (»FanFuck: — I HATE you — because I don’t understand YOU»). Gör du?

 

— MATEMATISKA FORMLER eller annat liknande med anspråk på att den typen skulle förklara något IMPONERAR inte på det rent fysiska (emotionella) behovet av en FÖRKLARING. »Den Fantastiska Matematiken» (1=1) beskriver¦BEVISAR logiken, men förklarar den inte. Förklaringen kräver något mera.

 

What?

 

I avsnittet om PLANETERNAS PERIHELIEROTATIONER (Figurförklaringen) refererades ett experiment DET ENKLA SKIVTALLRIKSEXPERIMENTET nedan som gjordes (Jun1990) för att visa ¦ bevisa principen med centrifugalkraftens inverkan på en momentarms referenspunkter.

 

FörklaringBegin:

SkivTallriksAnalogin:

MOMENTPUNKTEN FLYTTAS

STATISKA TYNGDPUNKTEN SAMVERKAR MED DYNAMISKA massTYNGDCIRKELN

 

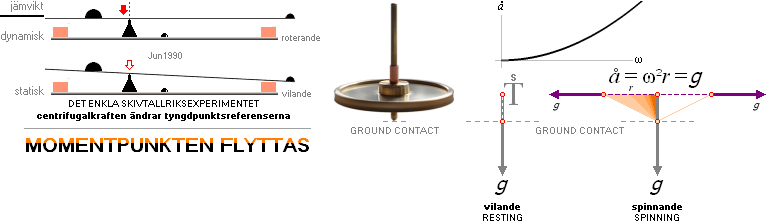
SkivtallriksExperimentet 1990 som klargjorde/klargör.

 

Centrifugalkrafter omdisponerar momentpunkter

Med skivtallriksexperimentets enkla SKIVTANA men upplysande fysik VET vi (nu) att en STATISKA TYNGDPUNKT moduleras i inverkan från centrifugalkrafter genom (olika massors olika) tyngdcirklar.

 

OM KUNSKAPERNA I DESSA SAMMANHANG inte alls FÖREFALLER KÄNDA I MÄNSKLIGHETEN 2018, BEROR DET BARA PÅ ATT MOTIVATIONEN FÖR ATT FRAMHÄVA DEM HITTILLS HAR VARIT MINDRE ÄN ÖNSKEMÅLEN ATT FÅ SE DE KONKRETA RESULTATEN.

 

En tyngdcirkel — radien genom rotationsmassans cirkulära medelform — finns redan i varje fysisk rotationsform.

För en idealt masshomogen kompakt cylindrisk skiva, typ den i HEMMASNURRAN, kan vi grovbestämma dess rotationsmassas cirkulära medelform direkt genom att lösa ut radien (r) som delar cirkelytan (A=πR2) i två lika halvor: massmedelcirkeln bör ligga på den ringen;

 

A/2 = πR2/2 = πr2 ;  r2 = R2/2 ;  r = R/√2 ;  kompakta skivformade R-cylinderns tyngdscirkelradie

SnurrHjulets diameter 2R=50mM

 

När Snurran  varvas upp — figuren med grafen ovan — dras/överförs statiska tyngdpunkten allt mer balanserande med växande spinn = växande centrifugalkraft UT mot ekvivalenta tyngdmassringen r.

 

— SNURRANS VILANDE TYNGD överförs transponeras, stuvas om, flyttas över — så — på närmast möjliga existerande markkontaktpunkt VIA en successiv process — uppvarvningen — där DYNAMISKA tyngdcirkeln — det »magiska» i hela verkningssättet (”fläktfan”) — övertar rollen från STATISKA tyngdpunkten.

 

 

Det är hela den fysikaliska djupförklaringen, här veterligt — in till ämneskärnans innersta fysiska prick.

 

Beviset: SkivTallAna

BEVIS DIREKT — Direkt Experimentellt: Stabilitetskriterium A ¦ Stabilitetskriterium B:

Snurrans vilande osäkra balans på markspetsen övergår till en SÄKER och STABIL perfekt vertikal (hård) spinnform märkbart tydligt med höga spinn genom den tydligt utbredda nya DYNAMISKA tyngdytans samverkan med spinnkroppens bottenpunkt: vertikalstången motsätter sig, verkligen rejält kännbart, ändring ur sitt vertikalläge — som om hårt STÖD fanns på sidorna.

   Försöker man putta den stången visar sig bara en minimal precession — varefter precessionen strax upphör och axeln återtar perfekt vertikalt läge.

— Miniborrmaskinen [‡] som används för uppvarvningen har ett lägsta varvtal på ca 8000 RPM (133 Hz). Utväxlingen BorraxelGummihjul/SpinnSNURRAhjul är 2/5=1/2,5. Det ger SpinnSNURRAN en lägsta initiell rotationsfrekvens på drygt 53 Hz (3200 RPM). Det varvtalet räcker (gott och väl) för att bevisa ovanstående.

 

 

— Vi kan (HemmaSnurran) kontrollera ROTATIONSGRÄNSEN genom att mäta varvtalet PRECIS när snurran är på väg att lägga sig — situationen då den lämnar ekvivalensen mot den säkert balanserande g-kraften enligt

 

Fc = må = Fg = ma = mv2/r = m(2πr/t = 2πrf = 2πf r = ωr)2/r = mω2r ;

a           = å = ω2r                      ;

ω2         = a/r = (9,8 M/S2)/r      ;

ω           = √ (9,8 M/S2)/r = 2πf ;

f            = [√ (9,8 M/S2)/r]/2π   ; Hz  varvtalet då snurran lägger sig förutsatt minimalt navavstånd

 

Är r i storleksordningen 2cM=0,02M bör vi finna att snurran lägger sig vid ett f  i storleksordningen 3,5 Hz = 210 RPM — max fortfarande stående; i det närmaste innan: dubbla eller max 7 Hz. Eller grovt 2×13° av ett 360°-varv per 1/100 sekund.

Förbättrad mätmetod 8Dec2018:

BÄTTRE MÄTMETOD (8Dec2018+) GER TYDLIGARE BESKED

6,19Hz/2 = 3,09 Hz med HallMagnetVarvräknaren (9Dec2018) precis (inom sekunden) innan läggningen:

 

 

MÄSSING är omagnetiskt. Genom att använda dubletter på bägge sidor spänner neodymmagneterna in perfekt. Oscilloskopet mäter frekvensen direkt och visar dubbla varvtalsfrekvensen 6,19 Hz precis innan Snurran lägger sig. Dvs, realt 6,19/2=3,095Hz vilket är ett utomordentligt resultat på en enda första mätning räknat. För uppvarvningen, se PraktisktExempel. Se vidare i NAVAVSTÅNDET BESTÄMMER STABILITETEN.

 

— Fotografier (4Dec2018, föregående magnetVarräknaren) med två olika märkmetoder visar ungefär (max) 20° per 1/100 sekund  = 5,5 Hz — snurran fortfarande igång, men närmast på väg att lägga sig:

 

 

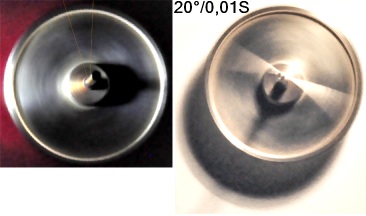
FOTO: GyroD Dec2018 — ISO ¦ 3200 ¦ 1/100 S ¦ Nikon D90

 

Testmetod 1: En rödmarkerad punkt på skivan syns svagt och indikerar hur långt hjulet hinner vrida sig under exponeringstiden 1/100 sekund — någon sekund innan snurran lägger sig.

Testmetod 2: En diagonalt monterad tennad Ø0,5mM koppartråd ger en tydligare indikering.

— Bägge fallen visar grovt ca 20° vridning under 1/100 S = 2000°/varv = 5,56 Hz = varv/sekund.

— Med r=0,02M ger det å-värdet å = ω2r = 24,41 M/S2.

   Ju större avståndet är mellan hjulet och markkontakten (bottenaxeln), desto mera instabil blir snurran före läggningen. I detta fall är den distansen ca 12 mM med hela hjulets Ø50mM och tjocklek (ytterringen) 5mM.

   Resultatet visar att mätningen stämmer hyfsat med grovräkningen max 7Hz fortfarande stående min 3,5 Hz balansens gränsvärde mot uppmätta 5,6 Hz någon eller några sekunder före läggningen.

 

 

Så (fläktfan, Jordytans experiment):

— Med tillräckligt Spinn (mω²r), överförs Statiska Tyngdpunkten på Dynamiska Tyngdcirkeln som kopplar sin fysik — tyngden — på varje tillgänglig del av någon upphängningsaxel i den fysikkroppen. Med, så, tillhörande tyngdbevarande vridmoment (Fd) och Precession.

   Etablerad detaljbeskrivning av den arten har eftersökts men ännu inte påträffats.

 

Gyrokroppens lägsta spinnfallfrekvens, f¦FALL:

GyroSpinnet

Axiella precessionens gyrofysik

HORISONTELLA GYROSPINNET — ansatser till härledda grundsamband:

— m0 = 82Gram ¦ m = 51Gram ¦ d = 5cM ¦ r = 2,5cM ¦ Ø = 6cM ¦ a0 = 9,8 M/S2:

——————————————

Jf = Ĵω2 = Ĵ(2πf)2 ;   J = Ĵf (2π)2                          ; Ĵ, se INTEGRALA MOMENTET

E = Fd = J/t = mvr/t                                             ;

v/r = a = å = w2/r = ω2r                                      ; ω omega 

E = Fd = J/t = mvr/t = ω2mr2 = Ĵω2                    ;  Ĵ: j-flex, konv. InertialMomentum Jf ¦ J = AngularMomentum mvr

w = 2πr/t = 2πrf = 2πf r = ωr ;  w2/r = ω2r         ;

:

m0ad = mvr/t = ω2mr2                ;

(m0/m)ad = ω2r2                         ;

ω = (1/r)√ (m0/m)ad = 2πf         ;

 

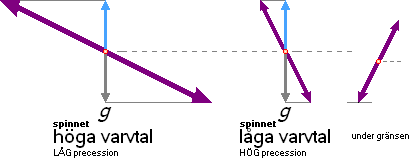
— För att KUNNA kontrollera/jämföra sambandsvärden med praktiska gyroexperiment måste en säker HANDHÅLLEN varvtalsindikator finnas. Ingen sådan enkel lösning är (ännu) här känd för Gyrokroppens del.

— Figuren ovan illustrerar kraftprincipen: För varje bestämd LUTNING finns en viss MINSTA spinnfrekvens som krävs för att kvarhålla Gyrokroppen i det läget. Är spinnet högre har Gyrokroppen högre stabilitet, samma lutning, samt uppvisar lägre precession (vidare nedan). Beviset framgår direkt (trivialt) genom att Gyrokroppen  viker sig neråt i takt med att spinnet avtar, samt uppvisar allt snabbare precessionsrotation med avtagande spinn:

spinnet centrifugerar g-jämvikt genom spinnhjulets dynamiska tyngdcirkel.

Stabilitetskriterium B: StabKritA

— Speciellt i den enkla upprätta Snurrans fall  med höga spinntal ser vi genom experimenten att den besitter en SJÄLVSTABILISERANDE funktion: påförs en liten push som får snurran att precessera något litet, försvinner den precessionen (sakta med lägre spinn, snabbare med högre) och lodaxeln ställer in sig i perfekt vertikalt läge — utan minsta spår av precession. Först när spinnet (efter flera minuter) avtar neråt tar precessionen över mot fallet.

 

E = Ĵω2 ¦ Endast spinnet styr hela energiräkningen, Ĵ=mr² = konstant: Spinn+ = +Inertia.

E = Fd = J/t = mvr/t = ω2mr2 = ω2Ĵ

J = Et = E/f = mvr = ω2mr2/f = (2πf)2mr2/f = (2π)2mr2f = Ĵf (2π)2  

 

Teoretiskt Lägsta Spinnet (med NavDistans d) med ovanstående sambandsform tillämpad på Gyrokroppen — horisontella läget som PRECIS får kroppen att falla — visar 2piFrekvensen ω=35Hz med varvfrekvensen f=5,7Hz (339 RPM) och omloppstiden 0,2 S. Men vi har här f.n. ingen utrustning för att kontrollmäta på varvtalet i det praktiska fallet. Se vidare med senare utvecklat instrument med mätvärden  i Generaliserad Beskrivning.

GyroPrec:

GyroPrecessionen

AXIELLA PRECESSIONEN — 0°A = horisontell spinnaxel — PREFIXxSIN:

———————————

F(GYRO)          = F(g=9,8M/S2¦Norden) · sinA = m0a0 · sinA   ;

                          = F(c) = m0å = mv2/d = mω2d = m0a0 · sinA     ;  sinA = å/a0;

m0å                    = m0a0·sinA = mω2d ;

ω2d                    = (m0/m)a0·sinA           ;

ω2                      = (m0/m)a0sinA/d          ;

Tabell 1 — GYROPRECESSIONEN — GyroDec2018.ods

Gyrokroppens massdelar:

 

 

 

 

 

Matematisk Ekvivalent

UPPVÄGNINGSCENTRIFUGALEN (djupförklaring från BevisD):

d-stången = konstant gyrokroppens halva axel  PÅ KONSTANT spinnhjulets massa m med variabel rotation (ω):

m0å = må’. Spinnet förutsätts, men ingår inte.

— Men det är bara halva bilden:

— Beroende på spinnhjulets spinn, antar Gyrokroppen olika fasoner i sin ω-form: lägre spinn, högre ω — enligt observation med stoppur.

 

GyroPrecJM:

Precessionsrotationen — JÄMFÖRANDE MÄTVÄRDEN PÅ GYROKROPPEN 8Dec2018

— m0 = 82Gram ¦ m = 51Gram ¦ d = 5cM ¦ a0 = 9,8 M/S2:

Horisontella läget

— Vi försöker hålla Spinnet så lågt som möjligt (lägre spinn, högre ω — enligt observation med stoppur) för att få fram kortast möjliga praktiskt observerade varvtid till jämförelse med sambandet ovan;

— Vi ANSÄTTER sedan Gyrokroppen DIREKT så nära horisontalläget (A=0° ¦ PREFIXxSIN(A=0) = 1) som möjligt med ena axelkulan på gyrostödet. Ett handhållet elektroniskt stoppur används för att mäta tiden för Gyrokroppen att avverka ett varv:

—  ¦ 0,55 S ¦ 0,80 S ¦ 0,85 S ¦. Ingen enkel match att ansätta Lutet utan att Gyrokroppen ramlar ur med lägsta möjliga spinn. Värdena visar ett antal försök.

   Sambandet ovan ger teoretiskt lägsta möjliga 1/f = 0,4 S.

Vertikala läget — med ungefärligt ansatt lutning 5°, lägsta möjliga spinn:

— Höga spinn här betyder snäva precessioner med typ 10-20 sekunder per varv. Vi anställer max lågt spinn:

—  ¦ 1,50 S ¦ 1,03 S ¦ 1,50 S ¦.

   Sambandet ovan ger teoretiskt lägsta möjliga 1/f = 1,2 S.

— Experimenten visar tydligen god samstämmighet i varje fall grovt räknat med (de mest enkelt härledda) sambanden;

 

 

 

RESULTATBILD:

Vi ser att meningsfullheten i resultatbilden ovan (helt) beror på spinnfaktorn — som dock inte finns medtagen (än) i sambandsformerna: höga spinn betyder hög stabilitet med låg precessionsfrekvens (ω) — enligt observationer med stoppur av Gyrokroppens beteende.

 

 

Mera avancerad elektromagnetisk-mekanisk varvräknare saknas

För att anställa en vidare experimentell jämförelse med härledda samband krävs en mera (noggrann, handhållen, avancerad konstruktion) varvtalsindikator för spinn och precession.

   En sådan instrumentering finns inte tillgänglig (här, än).

 

 

 

NAVAVSTÅNDET BESTÄMMER STABILITETEN:

 

 

NAVDISTANSENS INVERKAN PÅ GYROSKOPETS OCH SNURRANDE BETEENDE — r/h=tanC

NAVAVSTÅNDET BESTÄMMER STABILITETEN

HUB WHEEL DISTANCE DETERMINES GYRO STABILITY

 

 

I principiell STORLEKSORDNING:

— Figuren vänster nedan, bestämt minimalt navavstånd (eng. hub) h: När Snurrans spinn (ω, grek. omega) avtar blir vertikalläget alltmer instabilt: Snurrkroppen närmar sig stillastående och därmed allt tidigare läggning.

— Figuren höger nedan, givet bestämt spinn (ω): Då h går mot obegränsat, går stabiliteten mot noll — precis som Snurran med fast h och avtagande ω.

 

TANGENSFÖRHÅLLANDET (tanh°=) r/h FÖREFALLER ge oss en viss koppling till HUR spinnet (ω) måste tillväxa för minimal balans om h gör det:

— OM h ökas på från visst givet spinn ω, måste centrifugalkraften ökas på proportionellt — spinnet tillväxa — OM samma stabilitet ska bibehållas. Undersökningen visade att det INTE är tangensförhållandet (explicit) som gäller. Utan istället ett (enklare) energiresonemang. Vi studerar det.

 

BasSnurran i praktiskt exempel: NavDistansen

UTVECKLINGEN AV TANGENSRELATIONEN det är inte den som gäller LEDDE FRAM TILL SVARET:

 

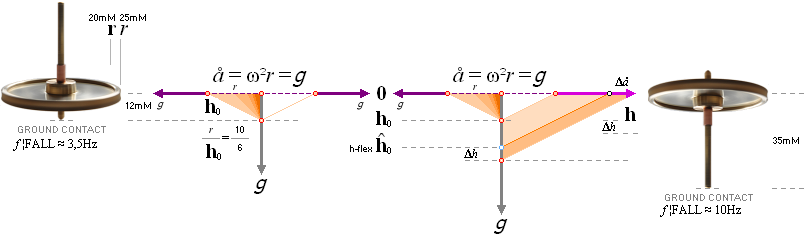
ENERGIRESONEMANGET — det som gäller:

——————————————————

— OM villkoret är att spinnet — centrifugalaccelerationen (å) — PRECIS ska uppväga lokala tyngdkraftsaccelerationen (a=Gm/h2=å=ω2r) — som betyder situationen då snurran precis lägger sig — gäller tydligen EKVIVALENTA ENERGIER (E) i de bägge fallen h¦h0:

— Vi väljer här relationsordningen X/X0 = STOR/LITN på redan väl kända grundsamband:

 

E           = mah0 = ma0h ; 

a/a0       = h/h0 = å/å0 = ω2r/ω02r = (f / f0)2 = (Gm/h02)/(Gm/h2) ;

f    = f0(h/h0)   

                          = (3,5 Hz)(35/12 ≈ 2,92)

                = 10,22 Hz

Mätning med HallMagnetVarvräknaren visade i test — flera enträgna försök med snurran upp-och-nervänd, h=35mM — en undre fallgräns vid — just — ca 10Hz (20-22Hz med dubbla neodymmagneter). Därmed sambandsformen bekräftad.

 

 

FIGUREN BasSnurran OVAN höger med beteckningar visar ett första försök att finna ett samband via TANGENSRELATIONER som slutade på sambandsformen

f            = (1/2π)√[ω02 + Δh/h0]                     ;

 

Men resultatet blev magert; Med BasSnurrans (r¦h=20¦12)mM och fallgränsfrekvensen f¦DROP ≈ 3,5Hz skulle (r¦ĥ=20¦35)mM ge omärkligt avvikande fortfarande f¦DROP ≈ 3,508Hz:

f            = (1/2π)√[(2π·3,5Hz ≈ 22)2 + (35mM-12mM = 0,023mM)/(0,012mM)]

             = (1/2π)√[484 + 23/12]  = 3,508334784 Hz

BasSNURRANs spinnaxel har friktionslåsning (kopparhylsa över Ø3mM) så att den kan ställas in variabelt. Här vände vi bara på snurran och mätte på långa navdistansen (ca35mM).

 

Mätningen på varvtalet visade något helt annat — och gav så uppslaget till det betydligt enklare energiekvivalenta ledet som ledde fram till sambandet

 

f    = f0(h/h0)   

 

NavDistGen:

BasSNURRAN

SNURROR MED ANNAT FÖRHÅLLANDE r¦h0:

GENERALISERAD BESKRIVNING

— GYROKROPPEN har en märkbart snävare ställning mellan tyngdcirkelradien (r) och navdistansen (h) än den enklare Snurran ovan med värdena för Gyrot som (ca) r¦h0=25mM¦50mM, relationsvärdet 0,5. I jämförelse med vår BasSNURRA (»SNURRAN») ges ett kvotvärde (10/3) mot GYROSKOPETS spinnsnurra:

 

(r¦h0)SNURRAN/(r¦h0)GYROSKOPET = (20/12 = 10/6)/(1/2) = 20/6 = 10/3        ;

 

En härledd sambandsform för FALLGRÄNSFREKVENSEN hos Gyrosnurran med minsta navdistansen då den balanserar på sin axelände beskrivs i Gyrokroppens lägsta SpinnFallFrekvens enligt sambandet

 

             = (1/0,025M)√ (82/51)(9,8)(0,05M) = 2πf  ;

f¦FALL = 5,7 Hz

 

Vid det sambandets härledning

————————————————————————————————

Axiella precessionens gyrofysik

HORISONTELLA GYROSPINNET — ansatser till härledda grundsamband:

————————————————————————————————

 

fanns ännu inte MagnetiskaVarvräknaren: värdet kunde inte kontrolleras.

— Sambandsformen gör anspråk på att beskriva Gyrokroppens aktuellt bevarade tyngd (82 Gram) vid anliggningspunkten (särskilt kontrollerat på brevvåg) i horisontalläget.

— Så: NAVDISTANSEN (d=h0) är avgörande för sammanhanget: mindre d ger lägre f.

 

Då frekvensen mättes med den färdigställda varvräknaren [‡] visade sig, emellertid, typiska f¦FALL-värden

(dubbla neodymmagneterna = dubbla fallfrekvensen medd delvis krävande mäthantering)

mera åt hållet 35-50 Hz än sambandets motsvarande max »rena» 2(5,7 Hz) = 11,4 Hz.

 

Använder vi istället BasSNURRANs låga optimala tyngdcirkels bredare vidd (20mM) mot dess låga navdistans (12mM) som ekvivalent energibaserad PREFERENS mot varje snävare spinnsnurra, får vi som ovan via kvoten 10/3 mot Gyrokroppens spinnsnurra:

 

2(5,7 × 10/3) = 38 Hz

 

Det värdet stämmer bättre med det dubbeluppmätta (minst 35Hz med vissa osäkerheter).

— Om sambanden (så) håller vad de lovar gäller tydligen att (Ann, annan):

 

Axiella precessionens gyrofysik

HORISONTELLA GYROSPINNET — ansatser till härledda grundsamband:

—————————————————————————————

spinnAnn(f¦FALL)

————————       = BasSNURRAN(r¦h0)/AnnSNURRAN(r¦h) med

spinnAnn(f¦FALL)0

med m0=HELA AnnGyrokroppens/AnnSnurrans vikt, här 82Gram, och m enbart snurrans egenvikt, här 51Gram, r spinnsnurrans tyngdcirkelradie, h navdistanserna.

fa/fa0    = tanC0/tanC    ;

 

eftersom energierna (SÅ) förhåller sig.

 

ResGAPspinLow:

RESULTAT — Gyroskopet 10Dec2018

———————————————

UNDERSÖKNINGAR MED LÄGSTA MÖJLIGA SPINN — Axiella Precessionen — PREFIXxSIN

Ingen explicit SpinnFunktion ingår — utom en enhet (1S·1Hz)

 

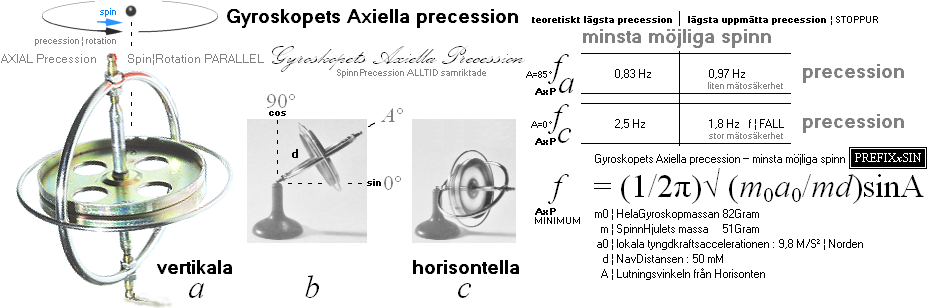
   f-Sambandet, se AXIELLA GYROPRECESSIONEN. Teoretiskt Spinn nedan A=0: 19 Hz

 

Tabell 1 — GyroPressesionen — GyroDec2018.ods

 

precessionen

GENERELLT ENLIGT OBSERVATION avtar precessionsrotationen i frekvens och blir allt mera långsam med allt växande hjulspinn: högre spinnenergi dämpar precessionen.

— Uppmätt GENERALISERAD BESKRIVNING lägsta spinnet för A=0° med GYROKROPPEN i dess slutliga fall (TouchDown f ¦FALL) värden omkring 18-25 Hz (med en delvis svårhanterlig mätsituation).

 

Teoretiskt (19 Hz):

GYROSNURRANS LÄGSTA SPINN I HORISONTALLÄGET INNAN GYROKROPPEN FALLER UR:

spinnet

preferens BasSNURRAN(r¦h0) = tanC0 = 20/12 = 10/6:

tanC = r¦h AKTUELLA (Gyro)SNURRANs KonVinkelTangens = 1/2 :

———————————————————————————

fa0         = f ¦FALL(AxP[A°=0]) = (1/2πr)√ (m0/m)ah ;  Gyrokroppens lägsta SpinnFallFrekvens :

 

fa          = fa0 · tanC0/tanC         ;

Teoretiska värdet för GYROKROPPEN            19 Hz

Uppmätta värdet för GYROKROPPEN           18-25 Hz — med vissa mätsvårigheter

 

Teoretiskt (0 Hz):

GYROSNURRANS LÄGSTA SPINN I VertikalLÄGET INNAN GYROKROPPEN FALLER UR:

— Med viss skicklighet och TUR i mätningen: 0 Hz.

— Teoretiskt/praktiskt KAN man få Gyrokroppen att balansera (inom en eller annan sekund, eller kanske längre) PÅ sin axelspets med nollspinn — en liten stund innan kroppen faller ur.

   Med andrra ord: Mätningar har ingen direkt mening här — eller blir svåra att tolka meningsfullt.

 

För att komma vidare i den rent praktiskt möjliga uppmätningen av KONTROLLERANDE värden mot ev. vidare härledda samband, ställs allt högre krav på den mätande varvräknaren [‡]:

— Med Gyrokroppen i en viss lutning (A°) tappar spinnet kontinuerligt fart, och därmed ett visst lutningsfall från A-värdet. I princip kräver den situationen en varvtalsmätning inom mikrosekunden för att få säkra och tillförlitliga testvärden.

— Ett spinnhjul utrustat med MÅNGA magnetpunkter (hundratals) och en avpassad Hallsensorkrets kan (lätt) säkra en sådan anordning. Men ingen sådan typ finns här tillgänglig.

 

 

 

PrecessionsBegreppet

 

SÄRSKILT FÖRTYDLIGANDE OM GYROGRUNDERNA — axiella och ekvatoriella precessioner:

The PRECESSION CONCEPT has Issues

PrecessionsBEGREPPET annonserar Rubriker

PRECESSIONsBEGREPPET Annonserar RUBRIKER

 

Nivå¦GRUNDSkoleMatematik MED FYSIKLABB — hävstångslagen med elementär trigonometri

— Ansats:  PÅ GRUND AV ATT GRUNDSKOLEUNDERVISNINGEN ÄR SÅ ÖVERTYDLIGT TEORETISKT ORIENTERAD — tyngdpunkten i undervisningen ligger INTE på ”personlighetens fria och fulla utveckling”[‡], läs HANTVERK. Utan istället på LokalNationellLydnadOchFostranUnderABSäpo — finns heller inte NÅGON UTVECKLAD LÄRARANDA att ASSIMILERA ELEMENTÄR GRUNDFYSIK på enkel elementär matematik. Säg gärna ifrån om den meningen förefaller felaktig på något sätt. Den här framställningen ska föreställa ett BEVIS:

— Vid Teutates: VARFÖR fick vi inget veta om det här, enkla, elementära, skitintressanta — runt 12?

 

 

 

— Därför att det var precis vad 5-åringen intresserade sig för (typ 1950-talet) — men aldrig uppmuntrades att UTVECKLA — i Sverige: Sveriges/Världens UndervisningsSystem. Personlighetens fria och fulla utveckling. GMR. 10Dec1948: Inte ett ord.

— Och hur är det idag (Dec2018), utbudet som Beskriver och Förklarar Ämnet i etablerad litteratur? Jag ser inget — utom den moderna akademins sedvanliga abstrakta högskolematematik som ingen varken förstår eller kan förklara (Ex.: VektorKalkylen ¦ MIT-exemplet — KONSEKVENSERNA): mänskligheten garanteras utestängning.

 

Gyroskopiska rotationer — speciellt intressant för allmänkunskapen och den allmänna naturvetenskapliga inblicken i vårt Solsystem, samt allmän Naturbaserad Trafiklära[‡] — innefattar två OLIKA typer.

Bevisning:  PROOF

BEVISNING:

 

 

 

Gyroskopets spetsbalanserande rotation — axiella precessionen — är INTE av samma typ och art som Gyrokroppens spetsRätVinkliga rotation — EKVATORIELLA precessionen. Det enda som krävs för att VISA både ATT så är fallet och HUR fallet är så, är något LÄRARÄMNE som KAN RELATERA sakinnehållet — »JätteAiMatte» räcker inte:

 

•   Gyroskopets spetsbalanserande rotation — AXiella precessionen — lyder undantagslöst alltid ordningen med samriktat hjulspinn och precession.

•   Gyroskopets spetsrätvinkliga rotation — EKVATORiella precessionen — lyder undantagslöst alltid ordningen med ICKE-samriktat hjulspinn och precession.

Praktiskt Bevis

— När Gyrokroppen lägger sig på den gyrokroppens tvärring TR som löper runt om spinnhjulet efter avverkad axiell precession med någon minsta lutning, börjar Gyrokroppen rotera kring en fast punkt på TR med spinnhjulets projektion sedd som ellips med MOTSATT rotationsriktning mot Gyrokroppens rotation¦precession.

   Det är också i full enlighet med GyroLAGENs anvisningar — se SEKUNDÄRA EFFEKTEN i BevisC.

 

Det är vad det rena enkla praktiska experimentet visar, rent visuellt.

— Vi hade »en het debatt» om HURUVIDA Jordaxelns uppvisade roterande rörelse

— tydligen MOTRIKTAD Jordkroppsrotationsriktningen enligt astronomins observationer

— SÅ skulle vara en regelrätt  — som detaljerna ovan antyder — ekvatoriell precession. Eller?

   Problemet med Jordaxelns precession är emellertid (också) ett helt annat:

— Jordaxeln vilar inte på någon LaboratorieGolvpunkt och kan därför inte tillämpas på våra Jordlaboratoriska experiment. Men det finns ett annat sätt — som (galant) ändå ansluter till Gyrolagen, och också förklaras utifrån denna. Se utförlig genomgång i Jordaxelns Precession.

 

BKL1926Prec:

”Precessio’n (av lat. praece’dere, gå före), av Hipparkos upptäckt långsam vandring av vårdagjämningspunkten längs ekliptikan i retrograd riktning omkring 50’’ årligen.”,

”Rörelsen  fullbordas på 26,000 år”,

”På grund av P. är även det tropiska året kortare (f.n. 0,01416 dag) än  stjärnåret.”,

”P. är en följd av solens och månens attraktion på den avplattade jorden. Solen vill bringa jordaxeln att ställa sig vinkelrätt mot ekliptikans plan; månen strävar att ställa jordaxeln vinkelrätt mot månbanans plan. Samfällt åstadkomma de en oscillerande rörelse hos polen, vilken kan uppdelas i en jämnt framåtskridande, av sol och måne i förening åstadkommen rörelse (lunisola’rprecessionen), dels i en kring en jämnt framåtskridande punkt kringvridande, av månens inverkan enbart beroende rörelse (nutatio’nen, se d.o.)”,

BKL IXsp551n 1926.

:

— Citatets enda ledtråd till vad som menas (termen retrograd [tillbakariktad, motsatt] förklaras f.ö. INTE absolut¦enhetligt i etablerad litteratur) är INDIREKT:

”tropiska året kortare”: = inträffar allt tidigare = motriktad tidsordningen i Jordkroppens solära¦sideriska omlopp: Jordens omlopp kring Solen sker moturs sett från norra ekliptikan, lika med sett från Jordens Nordpol: Jordaxeln Precesserar medurs medan Jorden roterar moturs;

— Jordaxelns precession skulle i så fall vara en (gyrotekniskt) EKVATORIELL precession. Inte axiell.

— Se utförlig förklaring i Jordaxelns precession.

 

ATT hitta en etablerad klargörande mening i ORD ur Webben@INTERNET Dec2018 förefaller i det ämnet ännu efter flera enträgna försök OMÖJLIGT. Inte heller typ BONNIERS ASTRONOMI (1978) ger något förtydligande. Och inte heller nu Dec2018 webbsidornas illustrationer med text från NASA-artiklar i ämnet. Det ÄR så krångligt att få fram RAKA SVAR i ämnets enkla ljus, att man inte tror det är sant (asså). Varför i himmelens namn varför?

   Enda här kända raka svaret: förstår man inte Problemet¦Angelägenheten, finns heller ingen förklaring.

   Etablerade kvarter upplever väldeliga problem ( .. kvävda rop på hjälp .. ) med att »Reka i Ämnet».

   Utförligt i Jordaxelns precession.

 

 

Vi — å den andra sidan — måste få fram EXAKTA BESKED i ämnet för att kunna avancera ¦ testa ¦ pröva i TNED-kosmologins antydda förklaring till UPPKOMSTEN AV planeternas rotationer. Det får inte finnas minsta tvekan om fysikgrunderna.

 

 

 

 

 

 

GTF:

PRECESSIONSBEGREPPET — elementär körteknik

GYROTEKNISKT FÖRTYDLIGANDE — DBE

TILL OVANSTÅENDE GRUNDBEGREPP — elementär FordonsTeknisk KunskapsInsikt

 

 

 

 

GYROSKOPET förser oss med de ytterst direkta och konkreta visuella¦sensibla experimentella bevisen enligt ovanstående figursammanställning.

 

Jämför WikiSTEER — WikiCount1 — WikiCount2

— I PRINCIP: INGEN person BORDE släppas ut i allmän (bil-) trafik som INTE tillgodogjort sig en INBLICK i ovanstående: kan beskriva, kan relatera, kan förklara FÖR SIG SJÄLV främst UNDER FORDONS FRAMFÖRANDE huvudlinjerna.

   Allt annat är att be Naturen om Trubbel. Se utförligt från TYNGDPUNKTEN.

— Omsorgen om medtrafikanter: förmågan att FÖRUTSE utifrån en given trafiksituation VAD som är på gång innan Det Händer, och att handla därefter.

— »WE GET CREDIT FROM TRYING».

 

 

GYROKROPPENS SPINNANDE HJUL — i vertikal kontakt med marken som en fordonsförare ser hjulens rotation från förarplats:

GYROSKOPET[‡] BEVISAR ALLA FÖLJANDE SATSBILDER

BESKRIVNING:

a   •   H.   KraftANSATS som LUTAR Gyrokroppen NeråtHöger RESULTERAR OBÖNHÖRLIGT i

KraftANSATS som Vrider Gyrokroppen¦Hjulet Höger: Naturen hjälper motor¦cyklist som Fattat principen.

a   •   L.   KraftANSATS som LUTAR Gyrokroppen NeråtVänster RESULTERAR OBÖNHÖRLIGT i

KraftANSATS som Vrider Gyrokroppen¦Hjulet Vänster: Naturen hjälper motor¦cyklist som Fattat principen.

b   •   KraftANSATS som VänsterVRIDER Gyrokroppen RESULTERAR OBÖNHÖRLIGT i KraftANSATS som

Drar¦Sliter¦Rubbar Gyrokroppen¦Hjulet vänster tvärs färdriktningen som ger hjulet högerlutning som påför Gyrokroppen en högervriden rörelse: Dyr sjukvård för folk som inte förstår Naturen.

c   •   KraftANSATS som HögerVRIDER Gyrokroppen RESULTERAR OBÖNHÖRLIGT i KraftANSATS som

Drar¦Sliter¦Rubbar Gyrokroppen¦Hjulet höger tvärs färdriktningen som ger hjulet vänsterlutning som påför Gyrokroppen en vänstervriden rörelse: Dyr sjukvård för folk som inte förstår Naturen.

Notera att VYN MED SITUATIONEN i b — sett från en cykelförare — är samma situation i c sett från en mötande trafikant, så medvetet formulerat.

 

Inte att »LÄRAS UTANTILL». Enbart att fattas, förstås, inses INNANTILL Inte? Låt Bilen stå kvar i Garaget. Gå.

 

 

 

Magnetisk Varvräknare med Hallelement och digitalt oscilloskop:  8Dec2018

 

Magnetisk Varvräknare med

HALLELEMENT OCH DIGITALT OSCILLOSKOP:

 

 

 

 

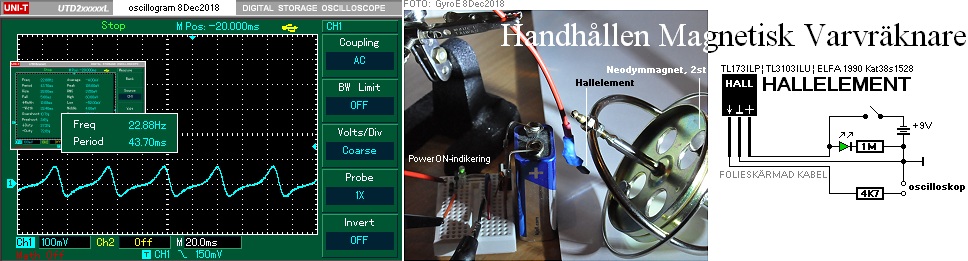
— Det var enklare än väntat: det tog 15 minuter att sätta ihop — då man väl har komponenterna och förstår funktionen.

FUNKTION:

   Hallelementet sitter längst ut i änden på en (folie-) skärmad kabel kopplad till ett minikopplingsdäck (ElectroKit¦Kjell&Co) enligt kopplingsschemat ovan höger. En OnOFF-switch sätter PåAv anordningen. Hallelementet hålls i närheten av spinnhjulet (järnbaserat) som har modifierats med ett par Ø10mM neodymmagneter (Kjell&Co).

— Känsligheten kan ökas betydligt med tillägg av ev. transistorer (enkla förstärkare) som gör att Hallelementet kan hållas på (avsevärt) längre avstånd från det spinnande hjulet. Här räcker den enklare kretsbilden ovan utmärkt för att få fram de nödvändiga hållvärdena i Gyroanalysen.

   Hallelementet TL3103 finns inte längre i handeln. Electrokit har (veterligt, säkert) någon likvärdig.

   Med utrustningen ovan och en lös (Ø10mM) neodymmagnet — att fästa på vilken som helst roterande (järn)metallaxel — har man ett helt suveränt utomordentligt enkelt varvräknarinstrument med superfin precisionsvisning. Aktuell varvfrekvens med anordningen ovan fås som dubbla perioden = halva displayfrekvensen.

 

 

 

 

 

JORDAXELNS PRECESSION:  Statiska momentet

13Dec2018

JORDAXELNS PRECESSION

HUR JORDAXELNS PRECESSION KAN FÖRKLARAS AV GYROFYSIKEN I SOLSYSTEMET  — det är så jäkla enkelt ... jättebra undervisning i Sverige ...

Inledande beräkningsexempel:

Statiska momentet — Inledande beräkningsexempel, Solgravitationen på Jordkroppen

KOSMOLOGISKT EXEMPEL Solen¦Jorden — vi approximerar d = 1AU ± r(EKV=6,378 T6 M)/2:

 

— Vi VET inte säkert VAR en ideal (Galileisk) tyngdpunkt ligger för Jordkroppens del i respektive kroppshalva Dag/Natt. Tätheterna varierar — Jordkroppen får inte förstås som idealt materialhomogen — och ingen (säkert) känd medelform är här känd. Räkningen nedan görs i kalkylprogram för mesta möjliga decimalnoggrannhet:

KalkylJaP:

 

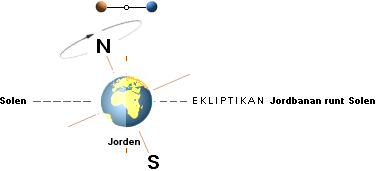
   G = 6,67 t11 KM/(KG)2 ¦ m(SOL) = 1,989 T30 KG ¦ 1 AU = 1,496 T11 M medelavståndet Solen-Jorden: 

— Solens g-kraft på Jordkroppens DAGHALVA m(DAG)=(5,975 T24 KG)/2 på avståndet

d(DAG) = (1AU = 1,496 T11 M) – (6,378 T6 M)/2 är

Fdag = Gm(SOL)m(DAG)/d(DAG)2 .............   = 1,7710216069 T22 N ;

— Solens g-kraft på Jordkroppens NATTHALVA m(DAG)=(5,975 T24 KG)/2 på avståndet

d(DAG) = (1AU = 1,496 T11 M) + (6,378 T6 M)/2 är

Fnat = Gm(SOL)m(DAG)/d(DAG)2 .............    = 1,7708706029 T22 N ;

   SUMMA:

F(d+n) ............................................................    = 3,5418922098 T22 N ; den större, se nedan

— Solens g-kraft på Jordkroppen TOTALT m=(5,975 T24 KG) på avståndet

d = (1AU = 1,496 T11 M) är

Fnor = Gm(SOL)m/d2 ......................................  = 3,5418922050 T22 N ; Normalvärdet

F(d+n) – Fnor ..................................................  = 0,0000000048283913290 T22 N

RESULTAT:

— Delas Jordkroppen upp i två lika masshalvor Dag/Natt med varje masshalva samlad i en ideal tyngdpunkt på halva ekvatorsavståndet ± från ideala sfäriska Jordcentrum, utövar Solen på hela Jordmassan större g-kraft via den uppdelningen i summa Fdag + Fnat jämfört med normalfallet via Jordens centralpunkt F(nor). Differensen är:

F(d+n) – Fnor = 4,828 T13 N.

 

 

INGEN DIREKT PÅVERKAN på Jordkroppens rörelsesätt kan härledas enbart ur exemplets resultat med en helt perfekt sfärisk Jordkroppsform. Om däremot hänsyn tas till Jordens avplattning vid polerna, och därmed ekvatorns något fetare ringform ställer sig saken annorlunda.

— Vi ska här försöka utnyttja räkningen ovan på en sådan formändring tillsammans med GYROFYSIKEN för att, fullständigt, förklara funktionssättet bakom Jordaxelns precession.

 

 

BESKRIVNING: Inledande beräkning

Jordaxelns precession

 

 

 

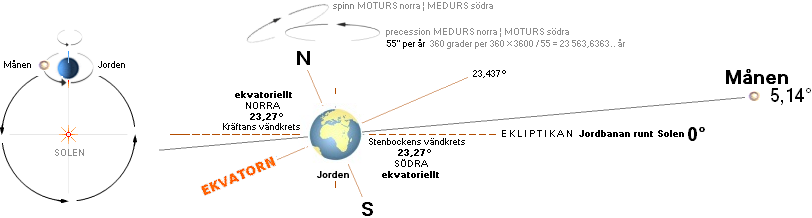
Jordens bana kring Solen, Månens bana kring Jorden, och Jordens vridning kring den egna rotationsaxeln är alla rörelser med samma riktning. Sett ovanifrån norra ekliptikan, samma som sett från Jordens nordpol figuren ovan vänster, är den rörelsen moturs, samma som positiv rotation inom matematiken med 0° utmed den horisontella positiva x-axeln. Jordaxeln roterar också, långsamt ett varv under tiotusentals år — men medurs sett i samma vy. Huvudtexten försöker förklara orsaken bakom den rebelliska attityden.

 

 

ETABLERAD LITTERATUR inklusive (många) webbsidor @INTERNET (Dec2018, flera) påstår utan bevis eller förklaring, ingen ännu upphittad, att Jordaxelns precession (Citat BKL) beror på inverkan från både Solen och Månen på ”den tillplattade Jorden”.

 

Det inledande beräkningsexemplet [‡] visade ATT det finns en sådan MÖJLIG lösning om (och endast då) den aktuella himlakroppen DELS är deformerad med avplattade poler med en större ekvatoriell ansvällning och DELS att den ekvatoriella ansvällningen LUTAR i någon vinkel relativt förbindningslinjen Solen-Jorden. I annat fall finns ingen möjlig kraftvektorkomponent som kan påverka ansvällningen.

JordPrecessionen, Jordkroppens FetaEkvator:

Se Inledande beräkningsexempel

 

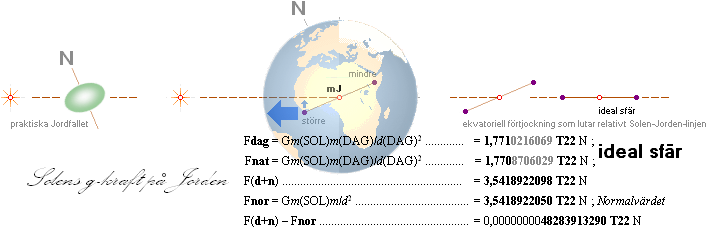
Solens gravitationskraft på Jorden enligt det inledande beräkningsexemplet[‡] Fnor anger normalvärdet med Jordmassan samlad i dess ideala sfäriska tyngdpunkt. Med idealt perfekt sfär och uppdelningen av masskroppen i två lika hälfter med en hoftad medeltyngdpunkt på ± halva sfärradien, är normalvärdet mindre än summan av de bägge hälfterna tillsammans. Differensen är liten men märkbar, 4,828 T13 N. Med en extra ekvatoriell ansvällning bör differensen bli något större. Men ingen räkning finns här på den delen — och är heller inte av nöden då principen står klar.

 

 

Vi använder här den resultatbilden för att framhäva den lilla kraftkomponenten,

lilla blå uppilen i figuren vid ”större” för att härleda, beskriva och förklara hur Jordaxelns precession har bildats, eller kan förstås ha bildats enbart via Solgravitationens inverkan — med Jordaxeln från början helt fast utan precession:

   Gyrolagen — tröghetslagen — fastställer att

 

•   en given rotation i rymden kvarstår oförändrad i sin riktningsform så länge rotationskroppen inte påverkas av någon tillståndsändrande kraft (GyroKollen ¦ GyroLagen).

ORIENTERING:

Mitten: JORDVYN SETT FRÅN SOLEN

 

 

Vänster: Jordkroppens årliga omlopp kring Solen med Jordaxeln fixerad. Mitten:  Situationen sett från Solen. Höger:  Hur?

 

 

Figuren ovan visar förutsättningarna i komplexet Solen-Jorden, sådan vi känner grunduppgifterna.

— ENLIGT GYROFYSIKEN

¦ Precessionsbegreppet — ekvatoriell och axiell precession

¦ Gyroskopets tröghetsprincip — BEVISEN ABC ekvatoriell precession

¦ Ekvatoriell precession (BC)

¦ Axiell precession (D)

med spinn (S) och precession (P) som vi har studerat i detalj från GyroBasic 

 

•   GyroLagen:

— KNUFFROTERARSPINN;

axiell precession (AP) har medriktade PS,

ekvatoriell precession (EP) har motriktade PS

 

— är det tydligt att Jordaxelns precession INTE — läs: fysikaliskt komplett omöjligt — kan vara en GYROSKOPISKT axiell precession:

 

•   GYROSKOPISKT: KroppsSpinnets roterande rörelse är riktad åt samma håll som precessionsrotationen:

•   JORDRÖRELSEN: KroppsSpinnets roterande rörelse är motsatt riktad precessionsrotationen.

— Jordkroppen spinner INTE åt samma håll som axelprecessionen

 

SÅ: Hur ska man då kunna förstå Jordaxelns precession?

 

 

 

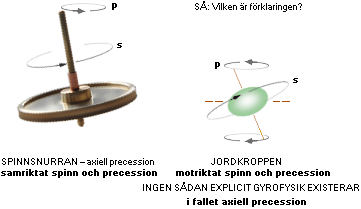
Se särskilt i Praktiskt Exempel — axiella precessionen — för de olika sätten att påverka snurrans rörelsefysik om ej redan bekant. Den enkla fysiken ger oss svaret på hela gåtan med att förklara Jordaxelns precession UR och ENLIGT den enkla GyroLagen.

 

 

Vi använder, figuren¦komponenten ovan vänster, den enkla SpinnSNURRAN för att reda ut begreppen — på SÄKER experimentell grund ENLIGT gyrofysiken som ovan.

 

UPPLÖSNINGEN:

 

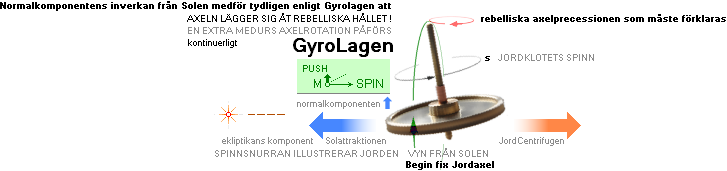
Vi tänker oss situationen med Solen i figuren ovan till vänster med Jordkroppen till höger, Jordkroppens rotation, snurrans spinn (S) moturs sett norrifrån.

— Med den uppfetade (FetaEkvatorn) ekvatorsdelen pekande neråt, under ekliptikans planskiva

— ekliptikans planyta är den yta som ritas upp av Jordens solära omlopp (Keplermomentet K=vd)

— finns en liten kraftkomponent, lilla blå uppilen ovan, som söker knuffa upp spinnhjulet till ekliptikans plan.

— Som vi har sett av de enkla experimenten [PE‡] betyder en KNUFF nerifrån och upp, samma som uppifrån och ner på motsatt sida, ATT ett spinnhjul viker sig ENLIGT GyroLagens enkla satsbild

 : push rotates spin — no exceptions

— Spinnhjulet viker sig följer den grönmarkerade cirkelns pilriktning neråt¦inåt/bortåt i bilden. Med andra ord:

i tydligt samma följsamma riktning som JordaxelnBeginFix ses rotera årligen SETT I KraftVyn från Solen:

— MEDURS. Så, enkelt.

   ThereYouGo.

— Illustrationen nedan försöker förtydliga det årliga händelseförloppet.

 

 

Vi kan följa SolKraftens inverkan på Jordaxelns lutning under Jordens årliga omlopp enligt figuren ovan. Positionerna vid vårdagjämning och höstdagjämning ligger Jordens FetaEkvator varken över eller under ekliptikan, och ingen påverkan sker där.

— Solgravitationens lilla upp- eller nervektor, illustrationen Jordens FetaEkvator, är alltså endast verksam under perioderna

HöstVinterVår¦stop¦VårSommarHöst¦stop¦HöstVinterVår¦stop, osv. .

— Om vi följer rörelseschemat ser vi att det inte finns mycket annat att välja på i resultatbilden än att Solkraften under de aktiva perioderna påför Jordaxeln en kontinuerligt växande/avtagande vridning i samma ORIENTERINGEN riktning (P) som SolGravitationen ser Jordaxelns fixa läge rotera under Jordens årliga omlopp — helt i enlighet med GyroLagen. Den medurs axelvridningen blir alltså också en medurs axelvridning sett ovanifrån norra ekliptikan.

   Därmed kan principen bakom Jordaxelns till synes rebelliska medurs rotation mot alla övriga moturs rotationsriktningar förstås.

 

 

Så: Vilken är förklaringen bakom de till synes olika preferenserna i de nu, tydligen, uppdagade olikheterna i gyrofysiken?

 

 

•   I Gyreoexperimenten PRECESSIONERNA har vi sett med okuvlig konsekvens enligt GyroLagen att

axiell .............  precession har medriktat spinn och precessionsrotation

ekvatoriell ....  precession har motriktat spinn och precessionsrotation

•   I Solsystemets Gyrofysik Jordaxelns Precession har vi sett med okuvlig konsekvens enligt GyroLagen att

axiell .............  precession har motriktat spinn och precessionsrotation

SATSEN GÄLLER EXPLICIT FÖR JORDFYSIKEN PÅ JORDENS GIVNA SPINN.

— Jordaxeln uppträder rebelliskt.

Relaterad förklaring:

RELATERAD FÖRKLARING:

Precessionen:

JORD(YTS)FYSIKEN I idealt GALILEISKT KRAFTRUM:

— JordAxelprecessionen är INTE gryroskopisk i meningen tillämplig inom ett Galileiskt kraftrum.

JORD(YTS)FYSIKEN I reguljärt GRAVITELLT KRAFTRUM:

— JordAxelprecessionen ÄR gryroskopisk i meningen tillämplig inom ett Regelrätt Gravitellt kraftrum.

Kraftfältet:

JORD(YTS)FYSIKEN I idealt GALILEISKT KRAFTRUM:

•   Tyngdkraftsaccelerationen är konstant: En och samma accelerationskonstant (a=9,81 M/S2) överallt i fysikrummet.

JORD(YTS)FYSIKEN I reguljärt GRAVITELLT KRAFTRUM:

•   Tyngdkraftsaccelerationen är variabel: Accelerationskonstanten (a=GM/r2 M/S2) varierar med avståndet (r) mellan kropparna som ideala masspunkter med moderkroppens massa (M) som preferens.

Kroppsfysiken:

JORD(YTS)FYSIKEN I idealt GALILEISKT KRAFTRUM:

•   Samma tyngdkraft verkar på kroppens olika delar: ingen åtskillnad mellan kroppsgeometrins interna massor.

JORD(YTS)FYSIKEN I reguljärt GRAVITELLT KRAFTRUM:

•   OLIKA tyngdkraft verkar på kroppens olika delar: åtskillnad görs mellan kroppsgeometrins interna massor.

 

Skillnaden ligger alltså helt och hållet i användningen av KONSTANT eller VARIABEL tyngdkraftspåverkan.

— Domänerna i dessa komplex är inbördes skilda — med en gemensam Gyrofysikalisk lagordning:

 

Genom att Jordaxeln i den egna Jordfysikens mening bildar en fast och fix riktning utan ändring — vilket sammanför Galileiska och Gravitella rummen i samma rationella begripande GyroLagens fysik (de universella tröghetslagarna) — KAN uppkomst eller närvaro — Solgravitationen, och även Mångravitationen — av en yttre gravitationskraft påverka Jordaxelns idealt fixa fasta rymdläge FÖRUTSATT att Jordkroppen uppvisar 1. en FetaEkvator som 2. också LUTAR mot g-kraftens kortaste väg = omloppet.

 

GYROFYSIKEN HAR ALLTSÅ något OLIKA DOMÄNER BEROENDE PÅ PREFERENSER:

GyroLagen gäller i vilket fall.

 

GYROEXPERIMENTEN INOM ETT GALILEISKT KRAFTRUM:

— Tyngdkraftsaccelerationen är (med ytterst små avvikelser som beror på den lokala berggrundens sammansättning) överallt en och densamma inom våra bostäders och industrilokalers rum. Vi arbetar med en och samma accelerationskonstant (a=9,81 M/S2): Det finns ingen (egentlig) FetaEkvator att räkna på t.ex. för vår enkla  SpinnSNURRA. Vi skulle säga:Vi befinner oss INOM det ekliptikala gränsskiktet. Mera egentligt: Vi befinner oss INOM JORDENS GRAVITELLA DOMINANS.

— Vi har också sett (här inte redovisade experiment) att DÅ vi hänger upp Gyrokroppen med sitt spinnande hjul i ett trådhänge eller gummisnodd, alls ingen precession syns av varken det ena eller det andra slaget — endast en kort respons på någon ansats att ändra Gyrokroppens läge. Efter det står Gyrokroppen kvar i sitt nya läge. Jordkroppens FIXERAT lutande axel ansluter till den observationen, SAMT också GyroLagen generellt med reaktionsordningen på varje anställd förorsakande aktion. SÅ: Med tillämpning av VARIABEL TYNGDKRAFT — fysiken/kosmologin utanför Jordkroppens lokalt gravitella dominans — framträder som vi har sett ovan i JaxPrec aspekter som KAN förklara fenomen som också inbegriper världen UTANFÖR vår ytliga vardag. Fullständigt uttömmande GyroTeknisk förklaring: lokal gravitell dominans.

  RESULTATBILD:

   Sett i vyn från Solen — ORIENTERING — med en BeginFixJordaxel med bestämd rymdlutning ”InTheBeginning” (~23°Ekvatoriellt) är lutningsknuffen från Solen kontinuerlig perioden HöstVår med »TryckNerAn» vid upplutande FetaEkvatorn mot Solen och »TryckUppAn» vid nedlutande perioden VårHöst, maxima vid VinterSommar.

   VARFÖR undanhålls Publiken Den enkla elementära upplysningen? What’sUp? Tredje Klass. RoligaTimmen. Uppenbarligen Därför att lärarkollegiet inte känner till det befriande enkla innehållet eller att den kulturella attityden inte är mogen ämnet. Jämför etablerade källor i CitatJP. Etablerad beskrivning av detaljerna, till jämförelse som ovan, har eftersökts men ännu inte påträffats. Vår egen kulturepoks elementära skolundervisning matchar inte, riktigt, naturens underbara skattkammare.

   INVERKAN FRÅN MÅNEN GENOM DESS BANPLAN har principiellt samma funktion:

— Månen KraftSER också en BeginFastJordaxel som (sett norrifrån) medurs roterande under ett månvarv. Månbanans lutning relativt ekliptikan (5,14°) medför att Månen ser Jordens FetaEkvator med något mindre lutning ena månhalvan, större den andra. Summan av bidragen kan så förstås ansluta till beskrivningen i CitatJP.

 

 

 

 

 

noMACphysics: noMACfysik

 

— Ingenting i framställningen här som berör direkt gyroskopiska utsagor får grundas på annat än en klar och tydlig praktisk bevisbar förankring i någon motsvarande experimentellt redovisad gyroskopiskt bekräftande praktik[‡] — så att utsagan kan verifieras av den som har ett gyroskop.

— Därför att webbexempel (Dec2018) på så bevisbart löst utfyllande prat utan experimentellt redovisad grund existerar: rena toket i ämnet:

 

 

WikiCount1 — WikiCount2 — WikiPRECESSION — WikiSTEER — WikiAXEL — WikiTRAFFIC

 

 

De ytterst enkla experimenten redovisas löpande illustrerat/fotograferat i den beskrivande texten.

 

 

ÄMNESOMRÅDET SAKNAS I ETABLERADE VERK:

 

Som visas från Statiska Tyngdcirkelns Härledning

— grundskolans matematiknivå, märk väl, dock och tydligen inte alls (ens) omnämnt i etablerad litteratur —

framträder en förklarande rotationsmatematik för fysikens Jordnära masskroppar som inte alls verkar ens finnas omnämnd i etablerad litteratur. Flera avgörande fysikdetaljer fattas i den etablerade typen av ämnesbeskrivning. Vi studerar det i sammanfattning.

 

FigurDynaStat:

 

 

Uteslutande enda sättet att SUMMERA enskilda bidrag — tyngdcirklar — från enskilda ”infinitesimala”=Δr tyngdcirkeldetaljer — tunna ringar som summerar massoberoende momentdistanser (r) — är via en MASSOBEROENDE summerande MOMENTDISTANSFORM (Σ r)

 

förefaller INTE ingå inte i det moderna beskrivningssättet

 

Varje sådant bidrag associeras SEDAN — eller kan så associeras — med en specifik masskvantitet: en motsvarande FORMTYNGD. Formtyngden individmassan tilldelar varje enskilt ringbidrag sin specifika massdel genom en motsvarande TYNGDSUMMA som ger slutresultatet i formen av hela den eftersökta rotationsformens tyngdcirkelradie, den som rotationen arbetar på VIA allmänna statiska momentets M=Fr.

 

Man beräknar, eller KAN beräkna — massoberoende — varje statisk plan formhomogen cylindrisk rings R¦r¦t egen individuella tyngdcirkelradie (r) efter den enkla grundformen r = √ R²+r². Och multiplicerar sedan varje sådan individ med dess motsvarande massa (m=VD) enligt övre r-ledet i figuren ovan.

PRAKTISK EXEMPELFORM

Hur tyngdradier kan beräknas i mera sammansatta hjulprofiler:

 

Se Praktiskt Exempel.

 

— VISST finns alltid en ”infinitesimal” uppdelning av masselement.

— Men en ”infinitesimal” summering av något ” mr² ” i meningen ”infinitesimala masselement” — finns inte.

 

summerar inga ”infinitesimala masselement” — men väl enskilda STATISKT MOMENTRELATERADE ringbidrag. Detaljen omnämns inte i modern akademi.

 

Summering av r = √ R²+Δr² finns — men då på en helt annan ledform dessutom, undre r-ledet i figuren, än den som gäller för den slutliga dynamiska tyngdcirkelns bidragssumma.

   Den detaljen omnämns inte i etablerad litteratur i ämnet: ämnets elementära komponenter.

 

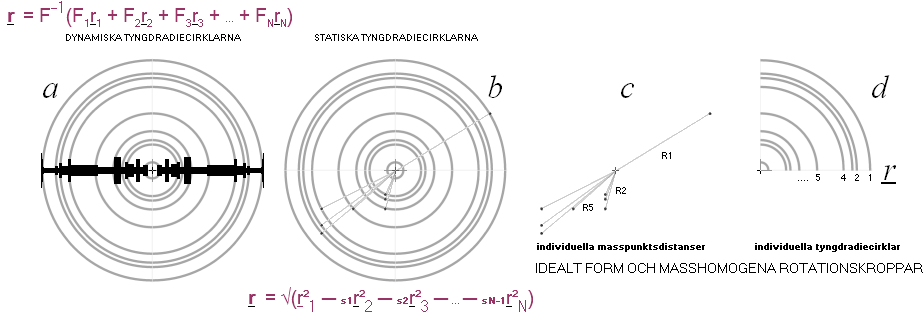
c:  Modern akademisk litteratur använder ett resonemang ”summering av infinitesimala element ” mr² som associerar till godtyckligt utspridda masspunkter. Men som — d — i den relaterade meningen inte kan ha någon annan innebörd  — dynamiska tyngdcirklar — än en summering av dynamiska tyngdradiecirklars cirkelkroppar — a. Hybriden  — b — representerar en pulserande oklarhet — som veterligt ingen ännu född student förstår ett jota av.

 

 

— Varje bidrag r  — ”ru”, understruket r — har sin specifika massoberoende geometriskt ideala formtyngdradie, vare sig som perifer hel cirkel eller i formen av en enskild formpunkt på r från centrum, vilketsom.

— Den GRUNDFORMEN finns här veterligt inte upptagen i den moderna akademins lärosystem: omnämns inte, vidrörs inte, påtalas inte.

— I modern akademi hoppas — tydligen — hela det avsnittet över:

— Man går direkt på (d) DYNAMISKA tyngdcirkelns summering, den moderna akademins bekväma vektorkalkyl, ” tröghetsmomentet J=M/ω’=mr2 ”MED EN — så, bevisbart — FELAKTIGT PÅSTÅDD FÖRKLARANDE INFINITESIMAL

»utspritt partikulära masselement som summeras»

SUMMERINGSALGORITM I BAKGRUNDEN:

— Summeringen (F) i det övre reguljära moderna dynamiska summaledet görs INTE på ”enskilda masselement”, som det påstås, utan

i ljuset av den här framställda elementära detaljbeskrivningen

på icke redovisade men så bevisbart matematiskt underliggande förklarande ENSKILDA STATISKA (r) MASSOBEROENDE TYNGDRADIECIRKLAR med en helt annan summeringsalgoritm dessutom, som är det egentliga beviset.

   Så framträder en resultatbild som förefaller utpeka att modern etablerad akademi inte förstår — verkligen inte har studerat grunderna i — ämnesgrunden: väsentligt förklarande grunddetaljer finns inte med i etablerad litteratur.

 

HOPPAR MAN ÖVER SÅDANA GRUNDER ÄR DET GIVET ATT ANTALET INTRESSERADE STUDENTER OCKSÅ REDUCERAS. DET VAR NATURLIGTVIS INTE PLANEN — MEN VÄL DRIFTEN.

 

Kropparnas matematiska rotationsfysik

CITATEN FMj FRÅN ETABLERADE KÄLLVERK

— körteknik: GyroBasics

FMj:

FOCUS MATERIEN 1975 s62sp1mn:

 

 

”  Tröghetsmoment  för en kring en axel vridbar fast kropp är förhållandet mellan det moment med avseende på axeln, som fordras för att ge kroppen en viss vinkelacceleration, och denna senares storlek.”,

BKL XI 1927 sp1455n — Ĵ = M/ω’=mr2.

 

DET GENERELLA ETABLERADE UTTRYCKSSÄTTET — ”moment of inertia”, ”sum of all the products”:

 

”  The moment of inertia, I, is determined by imagining that the body is divided into a number of infinitesimal elements of mass δmi each at a distance ri from the axis of rotation.”,

”  The moment of inertia I about this axis is given by the sum of all the products ( δmi ri2) calculated for each element, I = Σi ( δmi ri2).”.

THE FLYWHEEL — ref. Halliday et al., 2003, p18t

https://www.physics.utoronto.ca/~jharlow/teaching/summerlab08/fcpdfs/flywheel.pdf

 

Samma typformalia som i FMj — och det fortsätter så i samma anda praktiskt taget i all (här) uppsökt etablerad litteratur (@INTERNET Jan2019). Ytterligare citat är inte av nöden för att klargöra den delen, vidare.

 

JÄMFÖR HÄR KORRIGERAD MENINGSFORM från FMj:

— »Måttet på det motstånd NewtonIII partikeln (m) gör då vridmomentet M=Fr sätter den i rotation (a=w²/r)»

ÄR LIKA MED ...  själva vridmomentet M. DET som sätter rörelsen igång. INTE ” mr² ”. Enbart m.

 

— Men är inte vridmomentet M=Fr=Ĵω’=Ĵa/r=Ĵ(dω/dt) också direkt tidsberoende?

   Grundsatserna finns relaterat beskrivna i FYSIKENS SJU PRINCIPER:

— ENERGILAGEN (Principle of Motion, POM): Impuls — rörelsemängd p=mv — föregår kraft.

   Hur vi än resonerar återfaller all rörelse — hastighet v på förlupen tid t som acceleration a=dv/dt — PÅ massa: NÅGOT måste röra sig: massa. Och FÖR ATT få NÅGOT ATT röra sig MÅSTE obönhörligt ovillkorligt och oåterkalleligt en REDAN existerande rörelse existera — en motor — som överför sin rörelsemängd mv på den kropp som ska försättas i rörelse. Eller som ska utsättas för en tillståndsändring i sin redan existerande rörelseform.

— Med andra ord: I slutänden på alla fysikens överläggningar är det massan (m) som bestämmer motståndet mot tillståndsförändringen — via kraften F över distansen d på tiden t. Tiden (t) verkställer graden av uppnådd effekt (P = E/t) från given energi (E=Fd=mad).

— Nej. Tydligen inte direkt. Kroppsmassan styr och bestämmer kraftens möjliga ansats över en viss arbetsväg, och tiden den uppnådda verkan: p=mv=Ft=Et/d.

 

— På samma sätt med kraftlagen F=ma — som FM-citatet hänvisar till:

— »Måttet på det motstånd NewtonIII partikeln (m) gör då kraften F=ma sätter den i rörelse (a=v/t)»

ÄR LIKA MED ... själva kraften F, massmotståndet. DET — p=mv=Ft=Et/d — som sätter rörelsen igång.

 

DEN TRÖGA MASSANS BEGREPP — MOTSTÅNDET MOT TILLSTÅNDSFÖRÄNDRING — HAR INGA KANDIDERANDE ALTERNATIV I FYSIKEN. Massan ÄR det fundamentala motståndet mot tillståndsändring — och inget annat. OM man försöker införa ANDRA alternativ, förmörkas endast fysikens enhetliga begripliga — översiktliga — ENKLA grund: massbegreppet, gravitationens grundval. Och man förstår allt mindre av begreppet ENHET i naturfysiken:

Massan m — inte mr2 — är måttet på motstånd mot tillståndsförändring.

   JÄMFÖR »KANDIDATURERNAS RIKSDAG»:

— VRIDMOMENTET M=Fr är måttet på (»det tröga») vridmomentet.

— TröghetsMOMENTET Ĵ=M/ω’ är måttet på (»det tröga») tröghetsmomentet;

— ”Storheten Ĵ = M/ω’ = mr2 = TröghetsMOMENTET är måttet på den tröga massan ...”, FMj; »Människan Är Trebent».

   Kom gärna med invändningar. Kunskapen bygger på att brottas med den typen — alltid. Full pedal.

 

 

FM-meningen i citatet FMj beskriver — relaterar, så tydligen — INTE — riktigt — fysikgrunderna. Man har infört en konvention — studieplan — som man läser ifrån: den moderna akademins allmänna vektorkalkyl — men inget direkt bevis finns här för den kopplingen.

 

Saken att förklara och beskriva motståndet mot rotation gäller således INTE det gängse påstådda ” mr² ”.

 

Termen — begreppet ”tröghetsmoment (mr²)” — ÄR korrumperad.

— Motståndet mot vridning bestäms av vridmassan — genom ett ekvivalent vridmoment Fr under tid t:

— Kraften F över vägen r under tiden t.

   Inget annat existerar.

   Se även i EXEMPELUTVECKLINGEN beträffande det konventionella begreppet TRÖGHETSMOMENT.

 

 

Termen — begreppet ”tröghetsmoment (mr²)” — ÄR TYDLIGEN enbart en bekväm modern akademisk vektorkalkylerande inrättning som hoppar över djupförklaringarna, generaliserar integrallösningarna med bekväma industriella tillämpningsled typ ”tröghetsmoment” för nationell klassisk imperialistisk profit (nobelfestligheterna i Stadshuset) — och utelämnar DET icke-profiterande finlir som alla kunskapstörstiga studenter frågar efter: sammanhanget.

 

 

— ”Inget annat existerar”. Kan det bevisas, eller klargöras — relateras — närmare?

— Absolut. Annars är vi nog körda. Helt.

 

STATISKA TYNGDCIRKLAR — samlad FORM på linjen av en ideal CIRKEL eller EN samlad Formpunkt — SUMMERAS INTE som dynamiska dito:

— Leta gärna på webben (Jan2019) efter ”statisk tyngdcirkel” (eng. static radius of gyration) — till skillnad från dynamisk dito. Och jag är säker på att NOLL resultat visas: Detaljerna ingår — garanterat — inte i den moderna akademins lärosystem:

 

ExempelUtveckling:

Men om det nu är så att KÄRNPUNKTEN i fysikens massrotationer i egentlig mening inte alls är ”mr²” utan istället den aktuella rena bara kroppsmassan m — transponerad på en i grunden massoberoende ringform dessutom — vad ska man då kalla det redan väl etablerade begreppet ”tröghetsmoment J=M/ω’=mr² ”?

— Det är ett bekvämt infört akademiskt matematiskt INTEGRALMOMENT: DET som sammanför alla möjliga dynamiska fall under en och samma matematiska bildningsform.

— Alla beräkningsexempel visar, i vilket fall i slutänden, att man måste genomföra omräkningar via täthetsfaktorer — mer eller mindre omständliga differentialtransformationer — för att få fram ett slutligt värdeuttryck för aktuell tyngdcirkelradie: momentarmen (r) som det masströga vridande momentet arbetar på. EXEMPEL i konventionell tappning:

 

En masshomogen cirkulär skiva eller cylinder har massan m och radien R. Vi söker cylinderskivans tyngdcirkelradie (r) med avseende på en rotationsaxel som i figuren ovan — i normal till skivans plan och genom dess tyngdpunkt enligt

allmänna (rotations-) integralmomentets (integrala) differentialekvation

Ĵ =  dm r2.

Lösning:

— Vi använder en allmän omvandlingsfaktor (kraftformen generellt, fi) Φ för massa per ytenhet

Φ           = m/A = m/πR2 med differentialmassan

dm        = ΦA, med skivans differentialyta

A          = 2πr · dr.

DIFFERENTIALTRANSFORMATION[‡] från dm till dr ger oss

dm = AΦ = 2πr dr Φ = 2πΦ r dr

med den så preparerade differentialekvationen med insättningsgränserna Största(R) till Minsta(0)

Ĵ            =         R→0  2πΦ r dr r2

             = 2πΦ R→0  r3 dr                    ; skivIntegralmoments differentialekvation :

Integralen är direktbestämd[‡] eftersom r=0 ger nollvärde:

Ĵ            = 2πΦ [R4/4]                              ;

ÅTERGÅNG TILL GRUNDFORMEN VIA Φ = m/A = m/πR2 ger oss

             = 2π · m/πR2 · [R4/4]

             = mR2/2                                     ;

Med också ekvivalenten Ĵ = mr2 ges slutsvaret med tyngdcirkelradien (r)

mr2       = mR2/2                                     ;

r            = R/√2                                       ; cylinderskivans tyngdcirkelradie

Svar: Cylinderskivans tyngdcirkelradie (r) är lika med R/√2.

— r anger också den EKVIVALENTA kraftmomentarm som skivans rotation kommer att arbeta på i uppvarvningen: det aktuella EKVIVALENT masströga rotationsmomentets momentarm.

 

Som vi ser: ytterst omständliga mellanräkningar — som i grunden inte alls hör hemma i ämnet.

— Jämför den betydligt enklare och mera smidiga, direkta tyngdcirkelns integralform:

 

Integralmatematikens sätt för tyngdcirkelradien TCR = r:

M          = Fr                               ; vridmomentets allmänna ekvation eller STATISKA MOMENTETS ALLMÄNNA EKVATION

M          = M/r2 · r2                     ;

dM        = M/r2 · dr2                   ;

dM       = M/r2 · r · dr               ;

d1         = 1/r2 · r · dr                 ;

r2          = r · dr                          ; Cylinderskivans tyngdcirkelradieDifferentialekvation

r2          = R→0  r · dr              ; Cylinderskivans tyngdcirkelradieIntegralekvation med lösningen

             = R2/2                            ;

r            = R/√2                           ; Cylinderskivans tyngdcirkelradie

mr2       = mR2/2                         ; Cylinderskivans (mass-) integrala moment, konv. skivans tröghetsmoment

 

Med integrala insättningsgränserna Största(R) till Minsta(–r) — minsta integralvärdet måste gå över rotationscentrum 0 om annat än hela skivformen gäller från 0 annars får vi galna värden — får vi

r2          = R→–r  r · dr             ; Cylinderskivans tyngdcirkelradieIntegralekvation med lösningen

r2          = (1/2) R→–r [R2 – 02  –  (–r2 – 02)]

             = (1/2)[R2 +  r2]           ;

r           = √ (R2 +  r2)/2            ; Cylinderringens tyngdcirkelradie med

mr2       = m(R2 +  r2)/2              ; Cylinderringens (mass-) integrala moment, konv. ringens tröghetsmoment

 

När vi sedan ska beräkna massobjektets roterande tröghet i olika tillämpningar, använder vi »det vanliga klassiska grundskolekonceptet» för cirkulära omlopp

 

 

Se särskilda exempel i Momentexempel. NoProblemo.

— Integralmomentets mera omständliga form (Ĵ=mr²) används f.ö. (med fördel) för mera komplicerade kroppsformers tyngdcirkelradieberäkningar typ, Sfären och Konen — om vi inte hittar något enklare sätt. Se utförliga exempel i Dynamiska Tyngdradiecirklar.

 

Men det är inte det enda som fattas i etablerade beskrivningar i ämnet. Vi studerar det.

 

Etablerade beskrivningar Jan2019 @INTERNET i SE KörTEKNIK verkar inte ha vetskap, förtrogenhet med eller minsta aning om existensen av gyrofysikens allra mest enkla elementära verkningssätt. Det bästa vore om jag hade fel — vilket i så fall betyder att gyroskopindustrin gör bäst i att lägga ner verksamheten så att ingen kan kontrollera de här redovisade experimentella resultaten:

 

Figuren nedan är sammanställd (Dec2018) efter och enligt resultat från enkla experiment som kan utföras av vem som helst med ett tvåringars gyroskop (GyroBasic).

 

— What’sUp?

 

EKVATORIELLA PRECESSIONSGYROFYSIKEN Basic

 

 

Om BEVIS C man gör någon minsta ansats att försöka vertikalvrida (y) ett spinnande hjul som har sin spinnaxel (x) orienterad horisontellt, parallellt med Jordytans markplan, svarar det spinnande hjulet med en horisontell motvridning — en revolverrörelse som strävar att motverka ansatsen — kring den återstående axeln i framriktningen (z), också horisontell.

— Alla de som har skrivit Wikipediartiklarna och övrigt i Gyroämnet: HAR De UTFÖRT DET ENKLA GYROEXPERIMENTET, ALLS?

— Nej, säger Gyrolagen. Absolut gärna rätta om fel. — »Wikipediaförfattarna verkar ha mera Roligt med Moderna DatorSimuleringar än Praktisk Fysik».

 

 

— Vid WikiCount genomläsningen @INTERNET av huvudutbudet på GYRSOCOPE och PRECESSION med tillhörande länkar (allmän körteknik för tvåhjulingar), omnämns inte Det verkningssättet i Wikipedia — själva kraftens verkningssätt — eller ens antyds. Inte med så mycket som ett enda ord. Inte någon enda mening[‡]. Det är SOM OM man är BLIND för verkningssättet:

— Däremot är McManualerna[‡] betydligt mera insatta i det rent praktiska.

 

— Försöker man STYRA en tvåhjuling — vrida på styret — i svängar svarar gyrofysiken obönhörligt med att uppvisa (direkt farliga) MOTKRAFTER:

 

•  Vrids styret åt vänster svarar hjulet med strävan att verkställa ett vänsterdraget MARKDEPLACEMENT — helt enkelt RYCKA hjulet tvärs färdriktningen, bilden ovan höger: kraften som försöker vrida styret vänster omtransformeras till en kraft som förflyttar, eller strävar att göra det, hjulfälgen/däcket SIDLEDES i markkontaktpunkten — samtidigt som vänstervridningen SÅ frammanar en gyroskopisk MOTVRIDNING åt höger: Hjulet strävar att vika ner sig mot marken proportionellt mot den kraft som ansätter vertikalvridningen.

— Vi kan se det direkt i de enkla gyroskopexperimenten, se särskilt i Bevis C.

•  Och på samma sätt med en högervridning av styret.

 

Resultatet i vilket fall överförs på ett markdeplacement med resultat i en uppvisad hjulNervikande motvridande — och så bevisad föraranställd kördestruktiv — kraft.

   Säg igen: — »Ja. Vi är medvetna om det».

   Men inget sådant hörs. Hallå? Linjen ligger nere.

 

RESULTATBILD:

 

— Det går inte att STYRA sig genom en sväng med en tvåhjuling BevisABCD DÄRFÖR att den enda kraftfysikaliska tillgängliga verkningsformen som finns tillgänglig för en tvåhjuling¦Cykel som genomgår en kurva BESTÄMS av gyrofysiken genom LUTNING.

— ATT det finns folk som på fullt allvar försöker mena ANNAT är här en fullkomlig gåta. VARIFRÅN kommer en sådan mening? Därför att i den praktiskt erfarna och experimentellt påvisbara, redovisningsbara, relaterbara gyrofysiken, GyroLagen, existerar ingenting sådant UTOM ett direkt trafikfarligt — MOT NATURKRAFTERNA — beteende. Absolut gärna rätta om fel: fel får under inga som helst omständigheter förekomma här.

— Det är exakt vad det enkla gyroskopexperimentet visar oss — och cykelturen med händerna bakom ryggen, minsta lilla hundradels lutningsgrad ur exakt lodled:

 

LetRitGyro:

 

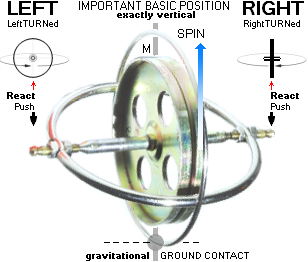
Varje minsta möjliga vertikala — lodräta — påverkan PUSH på endera hjulaxelns sida (x) resulterar omgående — i samma ansats — i en motsvarande gyrofysikalisk autonom självreglerande AUTOANPASSAD VERTIKAL (y) HJULVRIDNING av hjulaxeln.

— Anställs en lodkraft (lutning) på hjulaxelns vänstersida, svarar hjulet med en autoanpassad vänstervridning

— precis så mycket som lutningen anvisar.

— Anställs en lodkraft (lutning) på hjulaxelns högersida, svarar hjulet med en autoanpassad högervridning

— precis så mycket som lutningen anvisar.

Se utflörligt med exempel och beskrivning i BIKING i GyroEkvatoriellaPrecessionen.

— Med given ändringtid, står gyrostyrningens verkan i direkt proportion till kraften som används för att ändra tillståndet;

— En snabbt genomförd lutning med given normal cykelfart och ändringskraft ger MINDRE gyrostyrningseffekt än en lutning över längre tid. Enkelt praktiskt bevis: För att anställa en mera tvär kurvtagning i förhållande till en mindre tvär given normal cykelfart och ändringskraft, krävs en motsvarande längre — djupare — lutningstid: parametervärdena visar stora kurvtagningsdifferenser på enskilda tiondels sekunder bara. En kurva med STOR svängradie = svag krökning — nära raksträcka — kräver bara en kort ansats för att påbörjas: en LITEN svängradie = kraftig krökning kräver mera initierande tid.

   TRAFIKVETTET GENERELLT premierar — så, tydligen — bara LUGNA manövrer. Inget hets. Inget tävlande: Vägen, Trafiken, Föraren och Fordonet.

— AutoHjulVridningskvantiteten avstämmer en EXAKT JÄMVIKTSFYSIK med lutningens grad — BEVIS A.

 

 

DET ETABLERADE UTBUDET av alla ingående detaljer i förhållande till de enkla avgörande grunderna som har berörts ovan är Jan2019 så magert, urvattnat och inbäddat i (enorma, dryga) textavsnitt  att den här författaren är benägen att grovsammanfatta helheten så, beklämmande (usch):

— Ingenting av de här berörda gyrofysikens högst elementära detaljer omnämns av eller i de hittills genomlästa etablerade beskrivningarna. Tvärtom. Se utförligt i WikiSTEER.

 

 

Inte ett ord. GyroLAGEN omnämns inte. Inte en antydan. Inte minsta suck. Helt rent. Inte ens något omnämnande av eller klargörande i beteckningssätten Axiell (samriktat spinn och precession) resp. Ekvatoriell gyroprecession (motriktat spinn och precession) har påträffats.

 

Kännedomen om det destruktive navigeringssättet — DBE-exemplet — har inget som helst här känt synbart omnämnande i det etablerade ämnesutbudet.

 

Det är milt sagt anmärkningsvärt EFTERSOM det BORDE tillhöra grundkunskaperna:

 

Gyroskopiska Precessionsbegreppet i t.ex. Wikipedia (Jan2019) behandlas uteslutande som en AXIELL precession: gyrokroppens precession beskrivs uteslutande på den spinnande hjulaxelns (förlängda) pinne.

— Författarna känner tydligen — och uppenbarligen — inte till gyrofysikens allra mest elementära domäner.

 

Vi skulle här — tydligen —

 

WikiCount1 — WikiCount2 — WikiPRECESSION — WikiSTEER — WikiAXEL — WikiTRAFFIC

 

kunna semestra på en (ytterligare) veritabel FLOD av citat, detaljerade meningar, och andra områden i en vid och djup jämförande genomgång i ämnet GYROSKOPISK KÖRTEKNIK[‡]. Men eftersom det redan ovan sagda exponerar huvudsaken i alla de berörda etablerade avsnitten, kan vi förenkla hela analysen på följande strålande sätt:

 

— Det räcker om Wikipediaförfattarna med associerade kollaboratörer kan intyga genom relaterade framställningssätt ATT man ÄR förtrogen med gyrofysikens allra enklaste praktiska köksexperiment — och som det här dokumentet tillägnats en fullständig redovisning i. GyroBasic.

 

Det övriga kan vi använda som Skolexempel: Det etablerade utbudet av undervisning i elementär naturkunskap är bedrövligt. Ursäkta intrånget.

 

 

 

Kalkylkort: Tabell 7 i GyroDec2018.ods

 

KALKYLKORTEN TILL GYROFYSIKEN och TYNGDCIRKLARNA och 3D-geometrin

KALKYLKORT — GyroDec2018.ods

GyroDec2018.ods från Dec2018-Feb2019

 

Kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN GyroDec2018.ods  —  se öppningsmanual om ej redan bekant  —  eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/GyroDec2018.ods

 

Tabell 1 — ALLA I DETTA DOKUMENT FÖREKOMMANDE RESULTATREDOVISNINGAR

GyroHoriz¦f(FALL)

GyroPrecessionen ¦ SpinnMinimum ¦ Horiz.=0°A

JORDAXELNS PRECESSION

TYNGDCIRKLARNA Exempel

detalj    R          r           t           V          m¦KP   r¦mM   M¦NM

SPINwheel        Calculate           Time t               Wheel  

SPINwheel        Calculate           Frequency f      Wheel  

GyroEquatorialWheel                Calculating        Frequency f      momentarily     Wheel  

SpinningWheel FORCE Parameters

IDEAL GYRO CONSTRUCT BIKE-f-Wh      momentarily                 

Destructive steering

 

 

 

 

Universums Historia — Mänskliga Rättigheter

 

GMR: 18Okt2018

 

 

SVERIGE UTVECKLAR INTE MÄNNISKORÄTT — INTERNET UTVECKLAR INTE MÄNNISKORÄTT —mänskligheten

 

EUROPA UTVECKLAR INTE MÄNNISKORÄTT — POLISEN UTVECKLAR INTE MÄNNISKORÄTT — åklagare — domare — domstolar

 

— Hej.

— Hej.

— Vet du var man närmast kan läsa om Deklarationen för de mänskliga rättigheterna?

— VAD HETTE BLANKETTEN FÖRNÅGOT SA DU!?

...

—  Nä, nä. Det är ingenting som vi sysslar med dagligdags. Hör efter på biblioteket.

   POLISEN SVERIGE 1990+.

   Befolkningen har ingen som helst — ens — ANING.

 

VI kan INTE anklaga någon för att vara okunnig. Absolut aldrig.

Däremot ATTITYDEN när visdomen försöker hälsa på. Tilltalet. Det personligt ofrånkomliga tilltalet.

SVERIGES DOMSTOLAR. Närmast.

 

 

 

 

 

Avskogningsbeviset skärps — kemibevis framträder   | G | SlutTestet |

 

Detaljer i K-cellens matematiska fysik i förtydligade fullständiga härledningsblock — Kompletterande MaunaLoaBevis — Mänskliga Rättigheter

Alla utvecklingsdetaljer i Universums Historia grundas HELT på den matematiska fysiken från CHEOPS REKTANGEL:

 

          Se även från MEL1 och MEL 2. SOLFYSIKEN I TNED TESTAS ¦ 

 

 

 

Alltmer försvinner av UrNaturen i Sverige. Nersågat Ursprung. Sagolik Fägring Borta.Fågelsång Borta. Lugn Borta. Ekona växer. Bullret tilltar. Övermodet grönskar: ViHugga--NiVäxa: ViSäga--NiGöra. Urladdningen kommer. Bergsäkert.

 

 

Universums Historia — GYROFYSIKEN

 

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

 

 

Universums Historia — GYROFYSIKEN

ämnesrubriker

 

                      

 

 

innehåll2

              UNIVERSUMS HISTORIA CHEOPS REKTANGEL IIIbA22018

 

                                                        

 

INLEDNING

GyroBASIC

GyroBASICabc

ROTATIONENS INVERKAN PÅ STATISKA TYNGDPUNKTEN

HemmaSnurra2018

INERTIA — Tröghetslagarna — GyroKollen

Gyrolagen ref.

StudieExempel

GyroLAW illustrated

Gyro2Ways

WikiTRAFFIC

Basic Traffic Gyro Math Orientation

WikiPRECESSION

Precession MANUAL

WikiAXEL

svWikiMyth

Trail

WikiCount1 — cykelupplevelser i modern akademi

Vision: Svenska TrafikADMINISTRATIONENS representant — PÅ PLUTO:

— »Det är anledning bakom den höga olycksstatistiken som staten försöker lösa genom att propagera för hjälm»:

— Barn 1990+ i Sverige ses ofta stå mitt i vägbanan — iförd hjälm — utan att flytta sig när någon medtrafikant närmar sig; »Du kan väl åka om, på sidan av vägen ...» .

LeanTurn

Axiella GyroPrecessionens Grundmatematik

VänsterHögerSväng

Sammanställning, ekvatoriell precession

MAC Vector ref.

David Jones-källan 1970

 

WikiCount2 — speciella cykelupplevelser i modern akademi

Citat 1-10 med kommentarer och referenser:

WikiCount2.1 ¦ WikiCount2.1a ¦

 

Ekvatoriell precession i gyrofysiken — sammanställda illustrationer

ACCOUNTED CLARIFIED EXPERIMENTAL RESULT

 

KalkylDest

WikiCount2.2 ¦ WikiCount2.3 ¦ WikiCount2.3C ¦ WikiCount2.4 ¦ WikiCount2.5 ¦ WikiCount2.6 ¦ WikiCount2.7 ¦ WikiCount2.8 ¦ WikiCount2.9 ¦ WikiCount2.10

McOMwash2000

WikiSTEER

DirectReaction

Natural physics proof, NaPP

HalGyro

Recovering

GyroLawCS

Ekvatoriella GyroPrecessionen — vridning kring y-axeln

ResGyroLeanTurn

KalkylGyEq

Biking

Jämförande krafttider

Table CFT

DBE — Direct by experiment

Ekvatoriella GyroPrecessionen — vridning kring z-axeln

TRAFFICANT

BikeTableExample

TYNGDPUNKTEN

TYNGDPUNKTENS DEFINITION

TYNGDPUNKTEN i NaturFysiken

GALILEISKT och Reellt GRAVITATIONSFÄLT

KIM — KROPPENS IDEALA MASSPUNKT

GYROFYSIKEN

RUBRIKER

PRECESSIONSKRAFTERNA

GYROSKOPETS PRINCIP

Primära GyroskopExemplet

GyroBasicMath

Gyroskopets Tröghetsprincip

BevisA

GyroBasic, SpeedUp

BevisB

GyroBasic, G-tilted

BevisC

Axiell Precession — Gyrokroppens hängande förklaring

Gyrokroppens hängande förklaring

BevisD

Stabilitetskriterium A

Detaljerad beskrivning

GYROLAGEN

Praktiskt exempel

Gyrolagen illustrerad

TRANSIRE-citatet

Djupförklaringen

GyroSerieDec2018

SkivTallriksAnalogin

Beviset — för att momentpunkten flyttas

Förbättrad mätmetod — 8Dec2018

Gyrokroppens lägsta spinnfallfrekvens, f¦FALL

Stabilitetskriterium B

Gyroskopets Axiella Precession

Gyrokroppens massdelar

Precessionsrotationen — JÄMFÖRANDE MÄTVÄRDEN

NAVAVSTÅNDET BESTÄMMER STABILITETEN

BasSnurran i praktiskt exempel

Navdistansen generellt

RESULTAT — Gyroskopet 10Dec2018

UNDERSÖKNINGAR MED LÄGSTA MÖJLIGA SPINN — Axiella Precessionen

PrecessionsBEGREPPET annonserar Rubriker

SÄRSKILT FÖRTYDLIGANDE OM GYROGRUNDERNA — axiella och ekvatoriella precessioner

Bevisning

Citat BKL1926 Jordaxelns precession

GYROTEKNISKT FÖRTYDLIGANDE — körteknik

Magnetisk Varvräknare med HALLELEMENT OCH DIGITALT OSCILLOSKOP

JORDAXELNS PRECESSION

KalkylJaP

BESKRIVNING

JordaxelPrecessionen, Jordkroppens FetaEkvator

ORIENTERING

UPPLÖSNINGEN

RELATERAD FÖRKLARING

noMACphysics

ÄMNESOMRÅDET SAKNAS I ETABLERADE VERK

FigurDynaStat

FMj

ExempelUtveckling

EKVATORIELLA PRECESSIONSGYROFYSIKEN Basic

LetRitGyro

GMR

Kalkylkort

SVERIGE UTVECKLAR INTE MÄNNISKORÄTT

 

... Det var då det mest märkvärdiga ...

— VINTERGATANS SOLSYSTEM kräver djupinsikt i Gyrofysiken — som avtäckte WikiSTEER-syndromet.

 

 

 

 

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw--Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

mn        = 1,0086652u ......................     neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

me        = 0,000548598u ..................     elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för me , Table 1.4 s7–27 för u]

u           = 1,66043 t27 KG ..............      atomära massenheten [HOP Table 1.4 s7–27, 1967]

u           = 1,66033 t27 KG ..............      atomära massenheten [ENCARTA 99 Molecular Weight]

u           = 1,66041 t27 KG ...............     atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u           = 1,66053886 t27 KG ........      atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL--506W (2005)]

u           = 1,6605402 t27 KG ..........      atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u           = 1,660538782 t27 KG ......      atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c0          = 2,99792458 T8 M/S ........      ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970--talet)]

h           = 6,62559 t34 JS .................     Plancks konstant [HOP s7–155]

e           = 1,602 t19 C ......................     elektriska elementarkvantumet, elektronens laddning [FOCUS MATERIEN 1975 s666ö]

ε0          = 8,8543 t12 C/VM .............     elektriska konstanten i vakuum [FOCUS MATERIEN 1975 s666ö]

 

[BA]. BONNIERS ASTRONOMI 1978 Det internationella standardverket om universum sammanställt vid universitetet i Cambridge — The Cambridge Encyclopeadia of Astronomy 1977

[BKL]. BONNIERS KONVERSATIONS LEXIKON Band I--XII med SUPPLEMENT, Alb. Bonniers Boktryckeri, Stockholm 1922--1929

SIGMA 1--6, MATEMATIKENS KULTURHISTORIA av James R. Newman, Forum 1965, efter originalet The world of mathematics 1956

t för 10–, T för 10+, förenklade exponentbeteckningar

 

MAC, i Universums Historia ofta använd förkortning för Modern Akademi (eng. Modern ACademy)

 

TNED — Related PHYSICS And MATHEMATICS — Se särskild djupbeskrivning av innebörden i begreppet relaterad framställning.

 

 

  

 

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också

RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

 

 

SHORT ENGLISH — TNED in general is not found @INTERNET except under this domain

(Universe[s]History, introduced @INTERNET 2008VII3).

TNED or Toroid Nuclear Electromechanical Dynamics is the dynamically equivalent resulting description following the deductions in THE PLANCK RING, analogous AtomNucleus’ Deduction. The description according to TNED is related, meaning: all, each, details claim to be fully logically explainable and understandable, or not at all. With TNED is (hence) also understood RELATED PHYSICS AND MATHEMATICS. See also the emergence of the term TNED in AtomNucleus’ Deduction.

 

 

 

Senast uppdaterade version: 2023-01-26

*END.

Stavningskontrollerat    SVENSKA: 2019-02-08.

Stavningskontrollerat ENGELSKA: 2019-02-08.

 

rester

*

åter till  portalsidan  ·   portalsidan är www.UniversumsHistoria.se 

 

δ Δ π Φ ∑ Σ  √ τ π Ĵ ω ρ λ γ ħ ε  → ∞ UNICODE — ofta använda tecken i matematiska--tekniska--naturvetenskapliga beskrivningar

σ ρ ν ν π τ γ λ η ≠ √ ħ ω → ∞ ≡

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ ϕ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ˂ ˃ ˂ ˃ ← ↑ → ∞ ↓ ↔

ϑ ζ ξ

Pilsymboler, direkt via tangentbordet: Alt+24 ↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬ Alt+23 ↨ ingen horisontell make finns via Alt+.

Alt+23 ↨ — även Alt+18 ↕; Alt+29 ↔

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

PNG--justerad 2011--06--25

åter till  portalsidan  ·   portalsidan är www.UniversumsHistoria.se