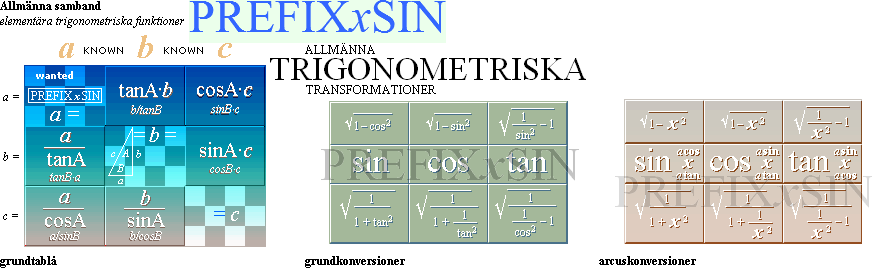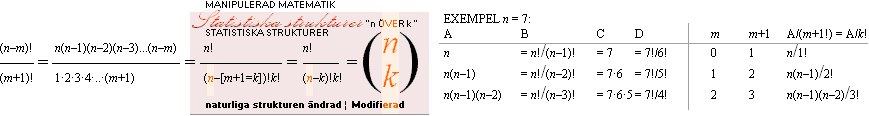CHEOPS
REKTANGEL IIIbA1 ¦ TYNGDCIRKELN | 2018XII24 | a ![]() production
| Senast uppdaterade version: 2025-02-23
|| ·
production
| Senast uppdaterade version: 2025-02-23
|| ·
innehåll · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning alla webbsidor · JordSyret · CHEOPS REKTANGEL I ¦ II ¦ III
|
I Fortsättning från Från |
Nov2018-Jan2019: INTEGRALREFERENSER ¦ Si1 — Första Systemintegralen ¦ Si1-Exemplen
Bakgrund
i sammanfattning med länkar — Sep2018-Feb2019 ¦ CheopsRektangelns
CirkelEllipsPerspektivBevis — etablerat okänt
Tyngdcirkeln: STATISKA
TYNGDCIRKELNS HÄRLEDNING
TYNGDCIRKLARNAS FYSIK I MODERN AKADEMI
TYNGDCIRKLARNAS INTEGRALA MATEMATIK
HUR MODERN AKADEMI FÖRSTÅR ÄMNETS NATUR. Vi studerar det. Noga.
• Genombrott i
Solsystemets detaljerade förklaring i Vintergatan — impulsmomentets matematik
förklarar
• Gyrofysiken får en
heltäckande utförlig förklaring — stundtals rena villervallan i MAC
• Tyngdcirkelns
matematiska fysik klarläggs ingående — MAC missar förklaringen
Länkade rubriker:
Speciella avsnitt i
matematiken framträder som förtydligar och klargör elementära kopplingar till
fysiken: Hur och varför matematiken visar sig som den gör. Ett centralt Exempel
visas här i inledningen till EXEMPLEN: Varför den moderna
akademins lärosystem har så svårt att verkligen FÖRKLARA för naturbarnen varför
och hur saker och ting fungerar som de gör i matematikens underbara värld.
STATISKA TYNGDCIRKELN — HÄR GENOMGÅENDE ANVÄND BETECKNING FÖR TYNGDRADIE: r, ”ru”
Elementära
fysikbegrepp i Universums Historia
—————————————————————————————————————————————————————————
TYNGDCIRKELN 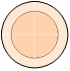 R
= R/√2 ¦ R¦r, ”ru”,
eng. »ArEYOu».
R
= R/√2 ¦ R¦r, ”ru”,
eng. »ArEYOu».
Detaljer vi bör känna till: Matematiken från början med FORMLAGARNA och NOLLFORMSALGEBRAN med elementära INTEGRALA EXEMPEL
STATISKA TYNGDCIRKELN FRÅN STATISKA MOMENTET M = Fr:
—————————————————————————————————————————————————————————
r = √ (R2
+ r2)/2:
Reella fysiska motståndet mot
rotation:
M = Fr roterande ¦
polära ringens vridmotstånd
KRAFTEN ÖVER VÄGEN — tiden för att accelerera upp m-ringen med given kraft F:
—————————————————————————————————————————
a = v/t ; t = v/a = (2πr/t)/a = r(2πf )/a = r(2πf )/(a=F/m) = mr(2πf )/F ¦ f = Hz, antal varv/S
——————————————————————————————————————
Jmfr. konv.: ”tröghetsmoment” — se BETECKNINGAR:
——————————————————————————————————————
Ĵ = mr2 ¦ M = Fr ¦ M/Ĵ = mar/mr2 = a/r = α ¦ t = ω/α = (2π·RPM/60)/(M/Ĵ) = r(2πf )/a
—————————————————————————————————————————
Jämför WikipediaCitatet
Ämnets elementära klargörande har tydligen undgått
den moderna akademins skarpsinnen.
MODERN AKADEMI FÖRSTÅR UPPENBARLIGEN INTE kan inte relatera och klargöra ÄMNET — om inget främsta synligt litterärt har missats.
— Notera det för undvikande av alla möjliga missförstånd: Det är ALDRIG fel på matematiken. NoWay. Problemet är att fattningen på naturinnehållet 1800+ har ockuperats av typen ”människan har skapat matematiken” = Automatiska Merit&Betygssystem = garanterat noll utrymme för NaturStudium = fängelse:
— Omfattande miljömord. — »Städpersonal sökes», förefaller det som att Naturen vill uttrycka saken.
ÄMNET GÄLLER uppenbarligen INTE — ej, icke, neh, Nej, NEJ, Nopp, osv. — r2-integreringar eller dito summeringar — de etablerade textböckernas manualer till trots — vänta bara ska du få se;
INTE Ĵ = mr2. Utan istället mr — Via M = Fr = mar:
— Kraften F över radien r — energierna i momenten M=Fr med deras momentarmar (r). Inte r-kvadraterna.
Vi studerar det — se särskilt beviset genom WikipediaCitatet.
STATISKA MOMENTETS REDAN ETABLERADE NOMENKLATUR
BEVISEXEMPEL — det allra enklaste med anknytning till redan väl kända applikationer under minst 100 år:
— Vi
skiljer här på beteckningarna M (fetstil,
Statiska Momentet) = Fr och M (meterEnhetsbeteckningen) och låter resten
förklaras av sammanhanget.
— En jämntjock PLÅT har massan per ytenhet 1KG/M2. Dess kantform begränsas av kurvan y=f (x) och vertikallinjerna x=a (minsta) och x=b (största), samt horisontlinjen y=0.
— Bestäm plåtens statiska moment M med avseende på y-axeln. Använd standard MKSA-enheter.
Lösning:
Φ = F/x¦y¦z ; allmän beteckning för Kraftfaktorns
olika dimensionsreferenser
för integrallösningar
Φ = F/xy = F/A = ma/M2 ;
Φ = F/A ;
F = ΦA ;
dF = Φ dA = Φ · y · dx ;
MY = Fx ;
dMY = dFx = Φ · y · dx · x ;
dMY = Φ · xy · dx ;
Vi sätter y=f (x) = konstant k=1M :
dMY = Φ · x · 1M · dx ;

Plåtlösningen —
x=a¦b:
— Insättningsgränserna b→a
från största till minsta: största=b minsta=a:
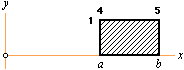
MY = ΦM · b→a![]() x dx ; [EXP7] direkt bestämd integral via M=0 om x=0:
x dx ; [EXP7] direkt bestämd integral via M=0 om x=0:
= ΦM · (b2 –
a2)/ 2 ; Φ = (N=KG·M/S2)/M2
= KP/M2 ; 1KP=1KG·9,81M/S2 ;
= ΦM · (25 – 16 = 9)/2
= ΦM · 4,5 M2 = 4,5
NM
Ringlösningen
— x=R¦r; b=R, a:=–a=–r:
— Insättningsgränserna b→a från största till minsta: största=b minsta=–a:

MY = ΦM · b→–a![]() x dx ; Integralens lösning [EXP7]
x dx ; Integralens lösning [EXP7]
= ΦM · (b2 +
a2)/ 2 = Fr ;
NM = NM/r2 ...
1 = 1/r2 ...
r2 = (52 + 42 =
41)/
2 ;
STATISKA MOMENTETS planringens
tyngdcirkelradie
r =
√ (R2 + r2)/2
= 4,52
769 25 69 M ; STATISKA
TYNGDCIRKELN vidare
nedan.
Saken gäller — tydligen som det får förstås — ett DISTANSMOMENT:
— Kraften öven vägen: F över (gånger) r. Inget annat. Motståndet mot Det: Fr. Inget annat.
— Rotationscirkeln som samlar/definierar hela kroppsformens ROTERANDE massekvivalent.
»PLÅTSEKTIONEN» ovan i figuren — symmetriskt omkring
y-axeln som rotationsaxel — beskriver i vilket fall EXAKT SAMMA diametralt
jämviktande TVÄRSNITTSMOMENT GENOM EN RING MED innerYTTERradierna ab
— MASSOBEROENDE.
— What’sUp, ”tröghetsmomentet mr2”? Här finns inget ”mr2 måste summeras/integreras”. r. Inte r2.
MY = ΦM · R→–r![]() r dr ;
r dr ;
Nämligen så: I moderna kvarter GENERALISERAR man behandlingssättet genom
(FM-källan i citatet nedan använder J, här används j-flexet)
vridmoment M = Fr = m(a=w2/r=[2πr/t]2/r=rω’)r = mr2ω’ = Ĵω’
SEDAN integrerar MAN genom kraftfaktorn (Φ) med mr2 som leder till en integrand r3 dr som ger lösningen r4/4 — VAREFTER man GÅR TILLBAKA TILL kraftfaktorn (Φ) och LÖSER TILLBAKA GENERALISERINGEN med resultat i ett r2. Jätteintressant.
— Jag har det: Varför inte, istället, ta fram en kortlek, dela ut korten, och spela poker, istället, med matteeleverna?
— Rent matematiskt-integralt FÅS
EXAKTA SAMMA SLUTRESULTAT. Exakt. Men förklaringen via generaliseringen blir
helt galen:
” .. blir definitionsekvationen
J = ∫ r2 dm
Summeringen måste utföras med en integral eftersom antalet masselement är oändligt.”,
” Storheten mr2 måste därför motsvara den tröga massan m i ekvation (16) [F=ma];
den måste vara ett mått på det motstånd partikeln gör då vridmomentet sätter den i rotation. Denna storhet kallas partikelns tröghetsmoment med avseende på den givna rotationsaxeln.”,
— Masströgheten är och förblir det RENA m:et: Kraften (F) över vägen (r). Bevisbart i detalj.
STATISKA TYNGDCIRKELNS ENKLA GRUND bevisar det också vidare. Se WikiCit särskilt jämförande citat från Wikipedia: vi jämför ekvationssätten och bevisar sammanhanget i detalj.
Modern akademi kan — heller — inte hantera differential, derivata och integralkalkylen. Se utförligt med exempel och jämförelser i NOLLFORMSALGEBRAN om ej redan bekant.
Ovan motsvarande klargörande i etablerade kvarter har eftersökts men ännu inte påträffats, Dec2018.
Genomgången visar att den etablerade synen på saken, milt sagt, lämnar en del övrigt att önska: Folket i moderna korridorer har uppenbarligen INTE förstått grunden till konceptet — med största sannolikhet beroende på det hängivna moderna akademiska beundrandet för den moderna akademins egenhändigt ihopsnickrade s.k. vektorkalkyl[‡]. Den, som vi ockå i andra sammanhang har sett vränger det mesta av DJUPFÖRKLARINGARNA. Ungefär som C-språket i datorsammanhang i förhållande till Assembler: C-programmering kan INTE specificera logiken i atomistisk detalj, medan Assembler — direkt CPU-kommunikation med HEX-kod — gör det med enorm pace. Varför då C, alls? Därför att SLARVPELLARNA inte gillar — blir överkörda av — NOGA. ”Assembler är jobbigt” = ”NOGA är besvärligt”.
Absolut gärna rätta om fel.
EXEMPEL: magnetismen ¦ induktionen ¦ centralrörelsen.
Se vidare med integrala exempel i RingenStångenSfärenKonen.
GRUNDREFERENSER TILL GYROFYSIKENS
ELEMENTÄRA MATEMATIK — enligt relaterad fysik och matematik i Universums
Historia
BETECKNINGAR MED INTEGRALA EXEMPEL
JÄMFÖRANDE FRAMSTÄLLNING
BETECKNINGAR I RELATERAD FYSIK (TNED)
associativa beteckningar om möjligt
KONTRA ETABLERAD LITTERATUR (Wikipedia Dec2018, List of physical quantities ¦ physical constants)
NEDANSTÅENDE TABELLERADE BETECKNINGAR ANVÄNDS
INTE GENOMGÅENDE — OLIKA KÄLLOR ANVÄNDER OLIKA.
——————————————————————————————————————
storhet beteckning enhet
————————— ————— —————
omloppshastighet w M/S ¦ 1/t = f , Hz
= 2πr/t = ωr
vinkelrotation ω 2piVarvtalet¦1Hz=2πrad/S
= 2π/t = 2πf
acceleration a M/S2 ¦ α
= a/r = ω’
=
dw/dt =
r(dω/dt) = rω’ ¦ rad/S2 ¦ = w/t
= 2πr/t2 = (2π/t2)r
= α · r
Boltzmanns konstant b J/°K
impuls [impetus] p NS
= mv = Ft
rörelsemängd, linjemoment, eng., (linear) momentum.
impulsmoment J ¦ konv. L JS
= mvr = mr2ω = Ĵω
rörelsemängdsmoment, vinkelmoment, eng., angular momentum.
konv. tröghetsmoment I ¦ J M2KG
= mr2
konv. eng., inertial momentum, moment of inertia, rotational inertia,
angular mass
integralmoment Ĵ M2KG
¦ Ĵ j-flex
j-flex ingår explicit inte i den moderna akademins
vokabulär
dĴ = dm r2 — kräver differentialtransformation för lösning till fysikens olika problemområden:
Relaterat: KROPPARS
ROTATIONSTRÖGHET: Egentliga fysiska tröghetsmomentet är vridmomentet M:
MEN
GENOM ATT ETT massoberoende INTEGRALMOMENT SAMMANFÖR STATISK OCH
DYNAMISK
via
praktiskt fysikaliska massformer — Konv. J, här j-flex Ĵ — som blir en
allmän bekväm matematiskt integral metod för praktiskt taget samtliga fall —
har begreppet (sv.) tröghetsmoment (OEGENTLIGT) etablerats som »kroppars
rotationströghet» — ehuru kropparnas rotationströghet entydigt emellertid
definieras av M=Fr:
vridmoment M NM
=Fr = mar = mr2ω’ = Ĵω’
statiskt moment, hävstångsmoment, eng., torque, enhet samma som Joule J
SE
VIDARE UTFÖRLIG GENOMGÅNG VIA WIKIPEDIACITATET. Utförliga Exempel följer.
energi E Joule
= mw2/2 = (1/2) · mr2ω2 = Ĵω2/2
induktans L VS/A, Henry
= Rt
luminositet ¦ effekt P ¦ konv.L ¦ Watt
——————————————————————————————————————
röelsemängdsmoment J = Ĵω = mvr, JS
vridmoment M = Ĵω’ = Fr, J
rörelseenergi E = Ĵω2/2 = mw2/2, J
——————————————————————————————————————
Ĵ = mr2 ¦ M = Fr ¦ M/Ĵ = mar/mr2 = a/r = α ¦ t = ω/α = (2π·RPM/60)/(M/Ĵ) = r(2πf )/a
—————————————————————————————————————————
Enheter (internationalMKSA ¦ 1961+):
—————————————————————————————————————————
J Joule ¦ N Newton ¦ M Meter ¦ S Sekund ¦ KG KiloGram ¦ A Ampere ¦
SÄRSKILD BETECKNING Ĵ I TNED FÖR TRÖGHETSMOMENT M2KG från J=mvr: SAMBAND:
E = Fd = J/t = mvr/t
;
vridmoment, statiskt moment
v/r = a = å = w2/r = ω2r ; ω, vinkelfrekvens omega
E = Fd = J/t = mvr/t = ω2mr2 = ω2Ĵ = Jf ; Ĵ: j-flex:
Ĵ = mr2
= J f ω–2 = Fd/ω2 ; tröghetsmoment
Ĵω¦ω’¦ω²
innefattar
STATISKA MOMENT tyngdlinjer, tyngdytor,
tyngdcirklar,
yttröghetsmoment (»hängstyvhet» för typ balkar, stora fartygsplåtar, etc.):
Ĵ
förekommer enbart med vinkelfrekvens ω
i olika sammanhang enbart med
2piFrekvenser = NÅGON vridande rörelse,
hur än liten vinkelfrekvens, ω med avseende på typ xyz-axlar (axiella eller polära tröghetsmoment).
—————————————————————————————————————————
w = 2πr/t
= 2πrf = 2πf r = ωr ; w2/r = ω2r
; w rotationshastighet M/S ; ω vinkelfrekvens = 2pi-varvtalet
m0ad = mvr/t
= ω2mr2 ;
(m0/m)ad = ω2r2 ; vinkelfrekvensen:
ω = (1/r)√ (m0/m)ad = 2πf ; f = ω/2π, Hz antal varv per sekund
tyngdcirklar eng. Radius of Gyration r här ”ru” — Kraften F över radien r:
r = rotationsmassans tyngdcirkelradie — tyngdcirkeln; M statisktMoment = Fd ;
:
F/r = Fr/r2 = M/A = M/r2 = Φ, grek. Fi associativt vald beteckning — Φ = F/x¦y¦z kraftfaktorn:
F/r = Φ ;
M = Fr ;
dM = d(Fr) = dF · r ;
dM = dF · r ;
F = Φr ;
dF = d(Φr) = Φ ·(dr=dr) ;
dF
= Φ · dr ;
dM = Φ · dr · r ;
dM = Φ r dr ; statiska momentets ENDIMENSIONELLA differentialekvation : Φ = F/x
TyngdCirkelRadieBegreppet relaterat: ideala geometriska/matematiska orten
för en roterande kropps idealt samlade kropps(mass)form: tyngdcirkeln r »ru».
— Momentarmen r
med pålagd kraft F bestämmer momentenergin M=Fr i kroppens
reaktion på — trögheten mot — rotation.
— Grundformen är cirkelskivans tyngdradie som
delar/definierar skivytan A=piR² i två lika halvor 2pii²=A=piR²: r²
= R²/2; r = R/√2 = R.
— Den roterande cirkelskivan reagerar på rotation som om
hela dess kroppsmassa är koncentrerad i cirkeln med radien R:
M = Fr = mar = m(w/t = 2pir/t² = rω’)r =
mr²ω’ = Ĵω’; Ĵ
= mr² = r²(m/N)N
= m(r²/N)N = (mr²/N)N ≠ m(r1²+r2²+...+rN²).
Notera
etablerade referenser: ytterst svårgenomträngligt ämne i etablerade kvarter.
Här görs ett
försök att bryta isen genom att relatera ENKLA grunder — i jämförande
etablerade utdrag. Vi fortsätter först på ovan inledda led:
Integralmatematikens
sätt för TCR = r:
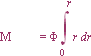 : Bildoriginal — webbläsarna
kan inte hantera den typen: FÖRENKLAT — integraltecknet i
ArialBlackSize25;
: Bildoriginal — webbläsarna
kan inte hantera den typen: FÖRENKLAT — integraltecknet i
ArialBlackSize25;
Insättningsgränserna MÅSTE BEAKTAS SÄRSKILT
FÖR TYNGDCIRKLARNAS INTEGRALER — se särskild beskrivning:
M = Φ R→–r![]() r dr ; KONV. statiska
momentets integralform
¦ Φ = (F=ma)/x¦y¦z
r dr ; KONV. statiska
momentets integralform
¦ Φ = (F=ma)/x¦y¦z
dM = (M/r2)
r dr ; r2 =
R2/2 ; dr2 = d(R2/2
) = dr2 = r dr ;
d1 = (1/r2)
r dr ; dr2 = dr2
= r2/∞ = r2/∞ = r
r/∞ = r r/∞ = r dr;
dr2 =
r dr ; STATISKA tyngdcirkelns
differentialekvation
r2 = R→–r![]() r dr ; RINGSUMMAN förklarar insättningsgränserna
r dr ; RINGSUMMAN förklarar insättningsgränserna
r = √ R→–r![]() r dr ; [EXP7] STATISKA tyngdcirkelns integral: [R²—0 — (—r²—0)] = R²+r²
:
r dr ; [EXP7] STATISKA tyngdcirkelns integral: [R²—0 — (—r²—0)] = R²+r²
:
= √ (R2 + r2)/ 2 ; R största, r minsta = 0 om hel skiva
utan hål.
INTEGRALEN ÄR DIREKT BERÄKNINGSBAR eftersom r=0 om
R=0.
— Se Bestämda
och Obestämda Integraler om ej redan bekant.
M = Fr ;
F=ma
KAN anges direkt i materialets TYNGD = KiloPond: 1 KP = 1KG × 9,18 M/S² = 9,81 Newton.
= M1 + M2 + M3 + ... + MN
= (Fr)1 + (Fr)2 + (Fr)3 + ... + (Fr)N
= (F√ [R2+r2]/2)1 + (F√ [R2+r2]/2)2 + (F√ [R2+r2]/2)3 + ... + (F√ [R2+r2]/2)N
Noggrant klargörande exempel genomgås i huvudtexten.
KLARGÖRANDEN SAKNAS I ETABLERAD
LITTERATUR
RELATERAD FYSIK — integralmomentet:
INTEGRALA MOMENTET Ĵ — kropparnas
tyngdrelaterade integralmoment
statiska
och dynamisk är inte samma — modern akademi kan inte klargöra naturdomänerna
— Genom att DYNAMISKA tyngdcirkelbegreppet kräver MASSA (m) måste, tvunget, någon massa (F=ma) eller tyngd multipliceras¦associeras med varje STATISKA tyngdcirkel r2 som i ledet närmast ovan: mr2 om vi extraherar den gemensamma tyngdkraftsaccelerationen (a). Den formen — mr2 — blir det generella uttrycket för varje särskild rotationskropps BIDRAG till en total tyngdcirkelradie som sedan erhålls som i ledet ovan; r = M/F. SÅ: faktorformen mr2=Ĵ (j-flex) MetodFORMERAR — inte definierar — samtliga möjliga dynamiska tyngdcirkelradiefalls LÖSNINGAR där varje särskilt fall UTLÖSES enligt
Ĵ
= mr2
; Ĵ/m = r2
; IntegralTCR
r = √ Ĵ/m;
Konventionellt kallas (konv.bet. ofta J) j-flex-faktorn (Ĵ) tröghetsmoment: dynamiska (m) tyngdradiekvadraten:
mr2 = (F/a)r2 = (1/a)Fr · r = (1/a)Mr ; JM · S2/M = JS · S = J/f : impulsmoment mvr per varvtal:
— En
mellanfaktor som representerar en METOD (»integralmomentet») för samtliga falls lösning:
GENERALISERINGEN för samtliga fall betyder att mr2-formen måste uttryckas på en allmän differentialekvation:
dĴ = dmr2
;
Ĵ
= ![]() dmr2 ; integralmomentet i relaterad fysik
dmr2 ; integralmomentet i relaterad fysik
där integrationskonstanten dm tvunget måste genomgå en differentialtransformation i vart särskilt problemkomplex för att få anpasslighet till aktuella storheter och dimensioner. Därmed kan integralen lösas och DYNAMISKA tyngdradien r bestämmas.
— SÅ: OM vi vill hoppa över alla FORMALITETER och gå direkt PÅ dynamiska målet, bör vi — alltid — koncentrera hemmaartilleriet till att befria dm-formen ur våndorna för r-anpassning, och sedan integrallösa.
Se fullständiga utvecklingsexempel i IntExRTC
med ringens
tyngdcirkel via Jflexets IntegralMoment Ĵ = ∫ dm
r2 — även Sfären och Konen härleds.
STATISKA TYNGDCIRKELN
Enkla
övningsexempel — Grundskolematematikens sätt:
— uppgifterna kan lösas med Grundskolans matematik — med bara litet vind i ryggen:
EXEMPEL 1 — ![]() — cirkelskivans tyngdcirkel:
— cirkelskivans tyngdcirkel:
Uppgift:
— Försök TÄNK UT — bestämma »formmitten» — en tyngdcirkelns radie för en cirkelrund masshomogen skiva eller cylinder med radien R. — ANVÄND INTE INTEGRALKALKYLEN. Enbart grundskolans enkla samband är tillåtet här.
Lösning:
— Cirkelradien r som delar cirkelytan A=πR2 i två lika halvor kan skrivas

A = 2(πr2)
= πR2 ; 2r2
= R2 ; r2
= R2/ 2 ; r =
R/√2 = R
SVAR: r = R/√2
— Medelcirkeln med radien r
som delar skivan i de bägge lika cirkulära ythalvorna kan förstås som en
skivans rent geometriska — massoberoende, statisk
— tyngdcirkel i skivtjocklekens mittplan — som om hela skivmaterialet
vore samlat i den ringcirkeln.
EXEMPEL 2 —  — cylindriska ringens tyngdcirkel
— cylindriska ringens tyngdcirkel
Uppgift:
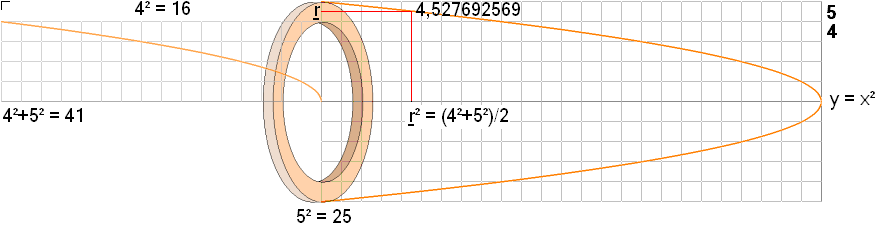
— En masshomogen cylindrisk ring med ytterradien R=5 enheter och innerradien r=4 enheter bör ha sin tyngdcirkel r någonstans mellan r¦R. Försök bestämma r.
— INTEGRALKALKYLENS LÖSNING ovan ger oss direkt
r = √ (R2 + r2)/ 2 = √ (25+16)/2 = √ 20,5/2
= 4,527692569 enheter.
SVAR: r = √ 20,5/2 = 4,53 enheter.
— Vi studerar »Grundskolans lösning» alternativt nedan (läs: mycket mera innehållsrik):
CIRKELSKIVANS VILLKORADE MEDELGRÄNSFORM R=R/√2 FÖR VÄXANDE-AVTAGANDE r MOT ORIGO
FRÅGA:
CIRKELSKIVANS VILLKORADE MEDELGRÄNSFORM R=R/√2 FÖR VÄXANDE-AVTAGANDE r MOT ORIGO
— Varför står det ett PLUS i integrallösningen? Normalt sker integrationen (insättningsgränserna) från största till minsta enligt regeln som här skulle vara
[R2 – 0 — (r2 — 0)] = R2 — r2 . Inte plus.
— What’sUp?
FÖRSTA DELSVARET:
— Kolla exemplet: √ (25 — 16)/2 = √ 9/2 = 2,12...
— 2,12 enheter ligger uppenbarligen långt utanför massringen, in mot centrum. Integrationen ska, i så fall, istället tydligen utföras på formen
[R2 – 0 — (–r2 — 0)] = R2 + r2 . Inte minus. Vidare nedan (interna villkor framträder).
ANDRA DELSVARET:
RINGSUMMANS VILLKOR
Tyngdcirklarnas elementära
grunder —
r , ”ru”, understruket r, betecknar tyngdcirkelradien
CIRKELSKIVANS VILLKORADE  MEDELGRÄNSFORM R=R/√2:
MEDELGRÄNSFORM R=R/√2:
— Med ett visst antal ringar N¦Rr kan vi först kontrollera hur varje r(N¦Rr) förhåller till en helt fylld cirkelskiva r(R→0) = R=R/√2.
— Om tilläggsringens r i en summering av två ringar — nämligen — ligger UTANFÖR R måste r-summeringen göras omvänt fallet då tilläggsringens r ligger INNANFÖR R:
— Ligger maxRr-ringens r (=No1¦Rr) utanför R, kommer varje tilläggsring innanför No1 att MINSKA r1-värdet:
— r2-värdet
måste i så fall subtraheras från r1-värdet,
så, att resulterande r3 hamnar längre in mot centrum. Omvänt:
— Ligger maxRr-ringens r (=No1¦Rr) — eller ett föregående resultat — innanför R, kommer varje ytterligare tilläggsring innanför No1 att ÖKA PÅ senast erhållna r-värdet för att åter driva det mot R för fylld skiva,:
— r2-värdet
måste i så fall adderas till
senaste r-värdet, så, att resulterande r3 hamnar
närmare R.
Totalt för samtliga fall med summerande Rr-ringar kan alltså följande villkor formuleras:
— Vi använder en SIGNAL faktor (s) med möjliga värden ±1 i association till varje successivt framräknad resulterande statisk tyngdcirkel rN:
— FÖREGÅENDE EN RINGSUMMERING testas sedan varje rN enligt en allmän
VILLKORSFORM för statiska tyngdcirkeln
endast: Från ett största R in mot Origo:
OM r1<R: s1=—1; annars +1; OM r2<R: s2=—1; annars +1; ... : rN=R = helt fylld skiva.
Ringsummeringen görs sedan enhetligt enligt sambandsformen
r¦statiskaTCR = √ [1(R2 + r2)/2 — s12(R2 + r2)/2 — s23(R2 + r2)/2 — ... — sN–1N(R2 + r2)/2 ]
r =
√(r1² – s1r2² – s2r3² – ... – sN–1rN²)
Vi kan kontrollera resultatet genom ett jämförande
exempel med resultaten ovan: Grundskolans Matematik:
r¦R→0 = √ 25/2 = 5/√2 = 3,54... ; R=5
r¦ r→0 = √ 16/2 = 4/√2 = 2,83... ; r= 4
——————————————————————————
r¦R→r ≠ √25/2 + √16/2 = 9/√2 = 6,37... ;
notOK: tyngdradier
kan inte
DIREKT summeras
(r¦R→r)² = 25/2 + 16/2 = 41/2 ;
OK: men
deras kvadrater kan det:
PLUS betyder: tyngdradien
PÅ VÄG UTÅT bort från origo.
(r¦R→r) = √ 41/2 = 4,527692569 ;
MINUS betyder: tyngdradien
PÅ VÄG INÅT mot centrum.
(r¦R→0)² = (r¦R→r)² — (r¦r→0)² = 41/2 – 16/2 = 25/2 :
(r¦R→0) = √ 25/2 = 3,54...
— 25/2-Rcirkeln är den som har sin r längst in mot centrum/origo.
— Tas en inre skivdel bort — 25/2 + 16/2 = 41/2 — flyttas r obönhörligt UTÅT.
— Läggs en inre skivdel till — 41/2 – 16/2 = 25/2 — flyttas r obönhörligt INÅT.
SÅ: OM vi börjar längst ut med en ring — normala vanliga största integralgränsen, analogt största tyngdcirkelradien — och avancerar inåt mot centrum genom att lägga till andra skivdelar, måste vi
SUBTRAHERA, inte addera, de olika bidragen SÅ LÄNGE r-resultatet > R:
r dras in mot R = fylld skiva med tilläggen av växande mellanliggande massa:
ADDERA, inte subtrahera, de olika bidragen SÅ LÄNGE r-resultatet < R:
r flyttas mot R = fylld skiva med fortsatt växande mellanliggande massa:
REFLEXION:
— Säg den ämnesintresserade människa som INTE från början frågar just efter dessa grundläggande, mest enkelt matematiskt upplysande detaljer. Det är barnets enkla första fråga: Hur.
Möjligen finns detaljerna ovan någonstans (kanske i äldre) etablerad litteratur — men tydligen helt osynligt i nuvarande utbud.
SÅ: I slutänden ser det ut som att Grundskolematematiken klarar biffen, trots allt.
Se även i MATEMATIKEN FRÅN BÖRJAN om inte redan bekant.
Vi fortsätter grundhärledningen:
DYNAMISKA TYNGDCIRKELN
Dynamiska tyngdcirkeln — den
enda representerade i etablerad litteratur, här veterligt;
OM SKIVDELARNA HAR OLIKA TJOCKLEK:
— en delrings tjocklek påverkar INTE r-värdet, enbart r-värdets STYRKA: massmotståndet endast:

— Så: Tyngdcirkeln för ... Jahadu: ![]()
Studentens ARGUMENT i resonemanget:
— Svänghjulet eller
»Snurren» i Figurdel¦a ovan är klar: ytterringen (Rr) + hela skivan (r) innanför
har tyngdcirkeln (med nyligen omnämnda
exempelräknings repetition):
r = √[(R² + r²)/2 — (r² + 0²)/2] = R/√2: »tyngdcirkeln har en och samma styrka».
— Men kolla alternativet
i b:
— OM ytterringens (grått)
r² = R²/2 + r²/2 ÖKAS PÅ I SAMMA MASSÄMNE
är det tydligt ATT den
extra massan tvunget måste DRIVA tyngdcirkeln mot det masstillskottets region —
snarare än att »den geometriska tyngdcirkeln» behåller sin rent matematiska
status.
— HUR löser man en sådan uppgift, rent fysiskt
tekniskt: Hur ändras STATISKT GIVNA r med olika PÅLAGDA masstyrkor?
![]()
— Uppenbarligen ingen
rent geometrisk/matematisk lösning kan användas för den uppgiften.
RESONEMANG — summan av alla energibidrag
Fr=E=M:
— Alla massbidrags MOMENT
— eg. vridmomentet E=Fd = kraften över vägen — uttrycker en ENERGI (E) som inte har några
»medelvärdesformer», endast effektiva dito: inget läggs till, inget tas bort.
Alla bidrag räknas, absolut:
M = Fr = (Fr)1 + (Fr)2
+ (Fr)3 + ... + (Fr)N
= 1→NΣ (Fr) = mad = Energin
Kroppens delar
summerar hela massformen.
SLUTSATS: Enda tillägget som behöver göras
— för våra vardagliga
Jordiska experiment inom den medelmässiga gravitella fältstyrkan på Jordytan a
= 9,81 M/S²
— blir alltså att
multiplicera varje geometriskt/matematiskt given tyngdcirkel (r) med
dess TYNGD
(F=ma:
m×9,81M/S²=m(KiloPond¦KP):
FN = Cirkelsegmentets/Ringens VIKT i KG ger
enheten KP med integrerat a=9,81M/S²
Fr = F · √(R²/2 + r²/2) ;
M = (Fr)1 + (Fr)2 + (Fr)3
+ ... + (Fr)N = mar ;
= (F√(R²/2 + r²/2))1 + (F√(R²/2 + r²/2))2 + (F√(R²/2 + r²/2))3 + ... + (F√(R²/2 + r²/2))N
= a[(mr)1 + (mr)2 + (mr)3 + ... + (mr)N]
= Fr ;
mar = a[(mr)1 + (mr)2 + (mr)3 + ... + (mr)N] ;
mr = [(mr)1 + (mr)2 + (mr)3 + ... + (mr)N] ;
Och sedan helt enkelt
LÖSA UT motsvarande resultant ur det givna:
r = M/(F = totalmassan i KP) ;
Vi
behöver — nödvändigtvis Praktiskt Exempel —
ingen specifik integralmatematik för den uppgiften.
Resultatbild:
GRUNDEN FÖR DYNAMISKA
TYNGDCIRKLAR
—
totala momentenergin är summan av de enskilda energimomenten enligt
Fr
= M = M1+M2+M3+ ... +MN = (Fr)1+(Fr)2+(Fr)3+...+(Fr)N
— ÄR statiska TYNGDCIRKLAR: De idealt homogena mass- och kroppsformernas
massoberoende tyngdcirklar PÅ VILKAS FORMKROPPAR SEDAN PÅLÄGGS OLIKA
MASSOR/tyngder. Se Praktiskt Exempel.
— MEN DEN
GRUNDMATEMATIKEN TYCKS INTE ALLS FINNAS I ETABLERADE KVARTER;
Sagt i andra ord: en
(TCR, förk. [efter summering resulterande] tyngdcirkelradie)
DYNAMISK
(TCR) TYNGDcirkelRADIE i en RING r ≠ √(R²/2 + r²/2)
r = F–1(F1r1 + F2r2 + F3r3 + ... + FNrN)
kontra
ingår tydligen INTE i modern akademi
r = √(r²1
— s1r²2 — s2r²3 — ... — sN–1r²N)
enSTATISK
(TCR) TYNGDcirkelRADIE i en
RING r = √(R²/2 +
r²/2) är INTE samma sak.
— Termen el.motsv. har
eftersöks i etablerade kvarter (Dec20018) men ännu inte påträffats. Se PRAKTISKT
Jämförande EXEMPEL.
— Varifrån kommer
Uppslaget, här?[‡]. Svar:
— En plan cirkulär
jämntjock skiva delas i två lika ythalvor A/2=pir²=piR²/2 av
(geometriska¦ här Statiska) tyngdradien r=R/√2.
— Vi kan, tydligen,
beräkna, analysera och bestämma elementära gyroskopiska värden på helt enkel
grundskolematematik (Pythagoras
Sats). Men (Dec2018) ingen
här ännu upphittad etablerad källa verkar ha uppmärksammat den möjligheten —
ämnets annars väl svårfattliga grunder. Etablerade verk i ämnet (eng. radius of gyration — ingen avvikande ännu
upphittad) uppehåller sig uteslutande vid integral matematik och modern
akademisk vektoralgebra — Ingen varken förstår eller kan förklara innehållet.
Citat nedan.
— En Statisk (TCR) r =
√(R²/2 + r²/2) är helt oberoende av höjd;
RingSummans Villkor — gäller endast summerande statiska
tyngdcirklar:
r ÖverUnder R=R/√2 reglerar ±summeringen av ringbidragen.
SATSEN har eftersökts i
etablerade kvarter men ännu inte påträffats.
— Dynamisk (TCR) r ≠ √(R²/2 + r²/2) VÄGER sin (höjd) form mot aktuell VIKT (KP), vilket påverkar
tyngdlinjens förskjutning mot aktuell maximal massdel då svänghjulet INTE är en
enkel rak skiva.
En
dynamisk med F tyngdcirkel har ingen sådan 1-cirkelskiva- singulär uttryckbar
form:
— En DYNAMISK TYNGDCIRKEL kan bara FORMAS — beskrivas, förklaras, uttryckas, definieras —
EFTER minst två olika RINGARS olika MASSBIDRAG PÅ GIVNA MASSOBEROENDE STATISKA
TYNGDCIRKELVÄRDEN.
— Snabbkoll @INTERNET
23Dec2018 visar att etablerad litteratur (Wikipedia+) INTE klargör DET —
omnämns inte ens.
Statisk
kontra Dynamisk. Enkla skolexempel — Med inledande exempel från RINGSUMMAN :
— Se PRAKTISKT
EXEMPEL.
Dynamiska tyngdcirkelns värde (r) fås summerande ur totala momentenergin M=Fr enligt summeringen
r = F–1(F1r1 + F2r2 + F3r3 + ... + FNrN)
F¦N varje bidragande dels egen individuella
vikt i KP, F hela svänghjulets vikt i KP
Statiska tyngdcirkelns värde (r) däremot fås summerande
r = √(r²1
— s1r²2 — s2r²3 — ... — sN–1r²N)
som en — tyngdcirkelbegreppets elementära grundval — massoberoende
sambandsform på en helt annan summerande fason än dynamiska tyngdcirkelns r-resultant.
— Den verkar helt ha
tappats bort i det främst synliga utbudet i etablerad litteratur: inget hittat.
— Den sambandsformen
gäller enbart — uteslutande — för raka oprofilerade cirkulära
geometriska-matematiska planskivor — EGENTLIGEN: HELT MASSLÖSA
HJULFORMER MED GODTYCKLIG FORMSAMMANSÄTTNING EFTERSOM CYLINDERHÖJDEN I EN RING
INTE PÅVERKAR STATISKA TYNGDCIRKELNS VÄRDE — med en förklarande vidhängande VILLKORSFORM R=R/√2 för (signal) s-faktorerna EFTER successiv summering: Med inledande exempel från RINGSUMMAN :
r¦sTCR = √ [(52 + 42)/2 — (42 + 02)/2 = √ [(52 + 02)/2 = 5/√2 =
3,54... :
— Föregående EN RINGSUMMERING testas varje ny tillagd beräknad rN enligt en allmän
VILLKORSFORM för statiska tyngdcirkeln
endast: Från ett största R in mot Origo:
OM r1<R: s1=—1; annars +1; OM r2<R: s2=—1; annars +1; ... : rN=R = helt fylld skiva.
— Summeringen av Ringarnas olika tyngdcirklar görs sedan enhetligt enligt sambandsformen
r¦statiskaTCR = √ [1(R2 + r2)/2 — s12(R2 + r2)/2 — s23(R2 + r2)/2 — ... — sN–1N(R2 + r2)/2 ]
= √ ( r12 — s1r22 — s2r32 — ... — sN–1rN2 )
—
En dynamisk tyngdcirkel kräver ett massberoende, medan statiska tyngdcirklar är
helt massoberoende. Så skrivs statiska tyngdcirklarnas summering via
individuella ringar som.
r = √[((R²/2 + r²/2))1 — s1((R²/2 + r²/2))2 — s2((R²/2 + r²/2))3 — ... — sN–1((R²/2 + r²/2))N]
=
√(r²1 — s1r²2 — s2r²3 — ... — sN–1r²N)
— Den resulterande
tyngdcirkeln r gäller sedan för en godtycklig (oberoende) PLAN massform.
— Förekommer olika
rektangulära sektioner gäller dynamiska tyngdcirkelns samband.
Etablerad
litteratur verkar inte — alls — vidröra den ämnesgrenen:
— Därmed inte sagt att
ämnesbeskrivningen INTE existerar i MAC. Om den gör det, finns
den i så fall i väl undangömda gamla arkiv.
Exempelbeskrivningarna
uppehåller sig (samtliga här upphittade) uteslutande kring dynamiska
tyngdcirklar i uteslutande integral matematisk tappning via begreppet
tröghetsmoment (här Beteckningar Ĵ=mr²).
WIKIPEDIACITATET
Statiska tyngdcirkelns
sambandsform DynaStatFörkl UTTRYCKER uppenbarligen och bevisligen INTE — ej, icke, NEJ,
osv. — ANNAT än en plan rak homogen idealt geometriskt cirkulär skiva, ring
eller cylinder i olika omfång, alla i samma skivplan.
Hittills upphittade,
inkl. Wikipedia Dec2018:
Det
verkar som att etablerad litteratur INTE noterar den detaljen.
—
Kaos råder — tydligt — om inget har missats:
”
Formula of moment of inertia if all the particles are of same mass m,
then
I = m1r1² + m2r2²
+ ... + mnrn²
If all the masses are the same, then
the moment of inertia is:
I = mn(r1² + r2²
+ ... + rn²”)/n since mn = M, total mass of the body,
I = M(r1² + r2² +
... + rn²”)/n
From the above equations we have
MRg² = M(r1² + r2²
+ ... + rn²”)/n
Radius
of gyration is the root mean square distance of particles from axis formula
Rg² = (r1² + r2²
+ ... + rn²)/n
Therefore the radius of gyration about
a given axis may also be defined as the root mean square distance of the various particles of the
body from the axis of rotation.”,
@INTERNET — Wikipedia,
Radius of gyration, 23Dec2018
— Eng. Radius of
Gyration, sv. tyngdcirkeln.
JÄMFÖR ENDA TILLGÄNGLIGA
SAMBANDSFORMERNA FÖR motsv. BEGREPPET TRÖGHETSMOMENT via StatiskaDynamiska FRÅN
M = Fr = mar = m(w/t = 2pir/t² = rω’)r = mr²ω’ =
Ĵω’ ENLIGT: Ĵ =
mr² = r²(m/N)N = m(r²/N)N =
(mr²/N)N ≠ m(r1²+r2²+...+rN²).
— Andra ekvivalenta typled finns inte. Det finns inget ”I = mr²
= m1r1² + m2r2² + ...”: Inte i Statiska. Inte i Dynamiska.
Wikipedias text talar visserligen om
PARTIKLAR, beståndsdelar, medan sambanden här berör enbart summerande
tyngdcirklar eller dito ringar.
— MEN VI HAR HELLER INGET ANNAT ATT JÄMFÖRA
MED EFTERSOM STATISKA TYNGDCIRKELNS BEGREPP[‡] INTE AVHANDLAR NÅGRA
PARTIKLAR, ENBART FÄRDIGA ENHETER. DET ÄR DET FRÄMSTA BEVISET: Modern akademi
verkar ha missat det;
— Varför göra besvärliga (integrala)
utläggningar om ”partiklar”[‡] när Enheten redan står där?
Det sammanhanget antyder att själva sättet
med ”summera partiklar via olika
r” INTE fungerar som förklaring. Det är galet sätt.
Att saken gäller ett ”r²” är tydligt. Men
begreppet ”partiklarnas
rotmedeldistans från rotationsaxeln” är tydligt galet — som
ovan.
SÅ:
Begreppet tyngdradie, tyngdcirkel,
masscirkel, ”radius of gyration” kan TYDLIGEN[‡] FÖR DET ENKLA RELATERBARA FÖRNUFTETS RÄKNING INTE beskrivas
genom någon ”summering av delar” — på samma sätt som inte heller GRAVITATIONEN
— från centralverkan: cirkelrörelsen,
centrifugalkraften — kan det. Så, återigen:
— sTCR Masscirkeln eller tyngdcirkeln kan bara förklaras — djupförstås
— genom statiska tyngdcirkelns STATISKA MOMENTETS elementära form: cirkelradien som delar cirkelytan i två lika
halvor — enhet utan delar — och som leder direkt på
ringens enkla tyngdekvation r = √ (R² + r²)/2;
A/2 = piR²/2 = pir²
; r² = R²/2 ; r = R/√2 = R —- med dess vidare differentialekvation d(r²)=d(R/√2)=r·dr, se IntegralTCR — BLIR tvunget tyngdcirkelns absolut MASSOBEROENDE definition: statiska tyngdcirkeln.
På dess elementära, helt
massoberoende form Praktiskt Exempel
kan sedan TYNGD och MASSA användas i olika partier och sektioner för att
utveckla praktiska tyngdcirklar och/eller masscirklar. Så, återigen i
resultatbildens tydligt relaterbara ljus:
Den moderna akademins lärosystem har
uppenbarligen inget begrepp om tyngdcirkelns ”radius of gyration” rent logiska,
förklarbara, relaterbara, elementärt FÖRKLARANDE definition och innehåll.
Det är också en jäkla mening att sätta på
pränt i den närmast enorma tekniska applikation som ämnet intar i vår närmast
200-åriga kulturepok.
Wikipediatexten bygger
tydligen på — en djup okunskap med konsekvenser — att försöka framhäva en
HYBRID mellan StatiskaDynamiska.
OM vi inte har missat avgörande förklarande litteratur i Modern Akademi, är det
tydligt att samma instans verkligen har förstått ämnet illa: huvuddelarna STATISKA TYNGDCIRKELN utelämnas — stryks. Och man
uppfinner, i vanlig klassisk 1800+-ordning egna, helt obegripliga saker.
Undervisningssystemet sköter sedan resten:
upprepningar, efterhärmningar. Produkten matas ut till mänskligheten typ
”Meddelanden På Wikipedia”.
Beskrivningssättet ÄR »Helt obegripligt».
Stora tvärhål gapar öppna i Logiken.
—
Använder man SÅLEDES generellt för alla möjliga fall den mera sammansatta
differentialformen dĴ=r²dm — som kan utvecklas på en mängd olika sätt —
berörs ALDRIG grundformen med Statiska Tyngdcirklar: Integrationerna leder
ALLTID direkt på slutmålet med (dynamiska) tyngdcirklar, tyngdytor och
tyngdlinjer: Ingen BEHÖVER bryr sig i något mellanliggande.
— Och så kom det sig ”i
senaste släktens år” att Kunskapen sjönk ner, allt mer i glömska ... .
Verkligen fascinerande KulturHistoria.
— Fyll i här nu.
InteTänkaSjälv. ViTänka—DuGöra. Såga här nu. Jättebra för miljön.
WIKIPEDIA WikiCit GER INGET KLARGÖRANDE MELLAN STATISK OCH DYNAMISK — ATT
DYNAMISKA GES FRÅN STATISKA: WIKIPEDIAS UTVECKLINGSLED OVAN ÄR OMÖJLIGA UR DEN
STATISKA TYNGDCIRKELNS PERSPEKTIV, OCH OCKSÅ UR DEN DYNAMISKA: INGET AV
SAMBANDSFORMERNA ÄR RELEVANTA I NÅGON FÖRKLARANDE MENING.
Masslösa tyngdcirkelformen är reserverad för
statiska tyngdcirkelns samband endast. Och den känner man tydligen inte till i
etablerade kvarter:
Bedrövligt. Urdåligt.
— SAMBANDSFORMERNA SOM
WIKIPEDIA ANGER HAR INGEN KOPPLING TILL VARKEN STATISKA ELLER DYNAMISKA
TYNGDCIRKLARNAS SAMBANDSFORMER.
— Det går inte att
uttryca dessa på Wikipedias ovan exemplifierade former:
— Wikipediaförfattarna
känner uppenbarligen INTE till det.
Eller så har den här författaren förirrat
sig till baksidan på någon krater på Pluto.
(Jag glömde ta med mig bränsle för
återresan — syret börjar ta slut ...).
Wikipedias masslösa
samband har bara en möjlig formkoppling till StatiskaDynamiska sambandsformerna
för tyngdcirklarnas relaterbara förklaring: statiska tyngdcirkelns summaform —
frånsett tecken, divisionen med N, samt villkoret mot R=R/√2 —
r² = r²1 — s1r²2 — s2r²3 — ... — sN–1r²N
Och vi ser att det är
INTE den som gäller i Wikipediafallet;
StatiskaDynamiska har
ingen motsvarande möjligt typ ”mr²”-summaform.
Det enda PRAKTISKT EXEMPEL närliggande som finns är formtypen
mr = (mr)1+(mr)2+(mr)3+
... +(mr)N
enligt dynamiska
tyngdcirklarnas summerande individer
r = F–1[(F√(R²/2 + r²/2))1 + (F√(R²/2 + r²/2))2 + (F√(R²/2 + r²/2))3 + ... + (F√(R²/2 + r²/2))N]
= F–1(F1r1 + F2r2 + F3r3 + ... + FNrN)
= aF–1(m1r1 + m2r2 + m3r3 + ... + mNrN)
WIKIPEDIAS ARTIKEL —
etablerade referenskällorna — ÄR VERKLIGEN DJUPT KAOTISKT MISSVISANDE OCH
SÄRSKILT FÖRVIRRANDE SETT FRÅN STATISKA TYNGDCIRKELNS ELEMENTÄRA DEFINITION.
—
GENERELLT: Vad gör MAC-folket
för fel, egentligen?
Mitt svar:
—
MAC-korridorerna befolkas av genuint skickliga algebraiker, oerhört vassa
naturintellekt — med noll utvecklad förmåga att förklara/förstå innehållet: ”människan har skapat matematiken” [‡]. Verkligen fascinerande undervisning. Det är aldrig fel på matematiken. Men: Inblicken blir mera
knepig om man envisas med att försöka leka ”herre över universum” [‡]: trångsynt, ytligt,
tarvligt — BEVISLIGT I VARJE DETALJ — djupt ointelligent:
—
Individerna får inte utvecklas längre. Eleverna nödgas rätta sig efter ett
fastställt meritsystem: DET ÄR INGET FEL I SIG —
FÖRUTSATT ATT »Den Akademiska ÖVERHETEN» HARMONIERAR MED NATURINNEHÅLLET —
VILKET TYVÄRR OCH BEVISLIGT noMACfysik INTE ÄR FALLET I VÅR TID.
Principerna är givna. Tillämpningarna däremot — iakttagandet av INTE
BESLUT ÖVER Naturlagarna — uppvisar global huggsexa: miljömord, naturmord.
— Enda sättet blir alltså: GÅ PÅ VIKTEN (tyngden, massan) — genom att summera alla enskilda skivmoment (M=Fr) och därifrån lösa ut summaresultanten (r).
— Om vi har en skiva med olika (rektangulära) sektioner, alltså olika massor¦tyngder (F) i olika partier, ska regelverket ovan fungera om summeringen görs TOTALT via M:
Momentsumman
M = Fr totala
tyngdcirkelmomentet — tyngdCirkelEnergin från »KRAFTEN ÖVER RADIEN» —
= (F√ [R2+r2]/2)1 + (F√ [R2+r2]/2)2 + (F√ [R2+r2]/2)3 + ... + (F√ [R2+r2]/2)N
= Fr ;
r = M/(F¦totalvikten i KP) ;
Det enda som behöver göras är att bestämma materialets masstäthet för att, via måtten tjocklek t gånger cirkulär ringyta A, få respektive M-dels aktuella F-tyngd (i KiloPond: F=ma = 1KP = 1KG · 9,81 M/S2 = 9,81 Newton):
(m→F) = DensityVolume = D(thickness×Area)
Praktiskt exempel, Statisk Dynamisk
Tyngdcirkel:
EXEMPEL
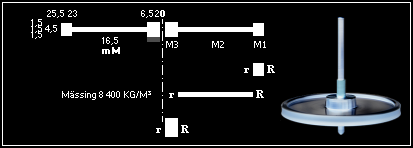
Tätheten för mässing (KH1977s97) varierar 8 100 - 8 600 KG/M3 beroende på legering (mer/mindre koppar 8 930 KG/M3). Standardvärdet för tyngdkraftsaccelerationen vid Jordytan är 9,81 M/S2.
— Ett SVÄNGHJUL av Mässing med tätheten 8 400 KG/M3 har följande profil med mått i mM:
— Bestäm hjulets totalt resulterande dynamiska tyngdcirkel;
— Använd om möjligt KalkylProgram (GratisOpenOffice) för att säkra räknefel och presentera resultatet i dess kalkylceller som ett separat Kalkylkort.
Lösning:
Tabell 1 — TYNGDCIRKLARNA — GyroDec2018.ods
SVAR: Med de angivna dimensionerna är Svänghjulets dynamiska tyngdcirkelradie r = 18,2448 mM räknat från origo/centrum.
STATISKA tyngdcirkeln sTCR = r = 18,0866 mM har
beräknats RINGSUMMAN enligt cirkelskivans
villkorade medelgränsform R=R/√2 för växande-avtagande r mot origo
r¦sTCR = √ [(25,52 + 23,02)/2 — s1(23,02 + 6,52)/2 — s2(6,52 + 2,02)/2]
=
√ [(25,52 +
23,02)/2
— (23,02
+ 6,52)/2
+ (6,52 + 2,02)/2] = 18,0866 mM
VILLKORSFORMEN statiska
tyngdcirkeln endast: Från största R in mot Origo:
OM r1<R: s1=—1; annars +1; OM r2<R: s2=—1; annars +1; ... : rN=R = helt fylld skiva.
Kommentar:
— Genom att mata in VÄXANDE t-värde (ringhöjden) för resp. M-del kan vi kontrollera att dynamiska r-värdet verkligen närmar sig masstillskottets aktuella region.
IntExtRTC: IntegralTCR
Dynamiska tyngdradiecirklar
EXEMPEL 3 —IntegralExempel
— Dynamiska tyngdradiecirklar
Ringen 1
RINGENS TYNGDCIRKELRADIE FRÅN INTEGRALMOMENTET Ĵ = ∫ dmr2:
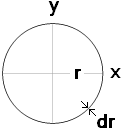
DIFFERENTIALTRANSFORMATION: dm ska anpassas till r:
— Vi anställer k = massa/ytenhet = m/A = m/πr2:
m = k · A ;
dm = k dA ;
— Cirkelns/ringens differentialyta kan skrivas alternativt som omkretsen 2πr gånger omkretsens differentiella bredd dr:
dA = 2πr · dr ;
dm = k dA = k · 2πr · dr ;
Ĵ = ![]() dmr2
;
dmr2
;
Ĵ = ![]() k · 2πr
· dr ·r2
k · 2πr
· dr ·r2
= k · 2π
∫ r3dr ;
Integralens
lösning: EXP7
= k · 2π [r4/4] ;
= π [r4/2] k ; integralens insättningsgränser från största till minsta, se nedan:
= π [r4/2] m/πr2
=
m · [r2/2] ; INTEGRALEN ÄR DIREKTBESTÄMD eftersom Ĵ=0 då r=0:
INSÄTTNINGSGRÄNSERNA GÖRS tvunget MED
STÖRSTA = R OCH MINSTA = — r:

LÖSNINGEN FÖR KOMPAKTA CYLINDERN: R=R, — r = 0;
Ĵ/m = R→–r[r2/2] = [R2/2 – (–02/2)] = R2/2 ;
Ĵ/m = R2/2 = r2 ;
Ĵ = mr2/2 ; kompakta cylinderns integralmoment
r = R/√2 ; Kompakta Cylinderns tyngdcirkelradie.
LÖSNINGEN IntegralTCR FÖR RINGEN: R=R, — r = — r;
Ĵ/m = R→–r[r2/2] = [R2/2 – (–r2/2)] = (R2 + r2)/2 ;
Ĵ/m = (R2 + r2)/2 = r2 ;
r = √ (R2 + r2)/2 ; Ringens tyngdcirkelradie. [‡]
EXEMPEL 4 —IntegralExempel
— Dynamiska tyngdradiecirklar
Ringen 2
RINGENS TYNGDCIRKELRADIE FRÅN momentintegralen M = ∫ dFx:
— Vi får alldeles samma resultat som i EX3
genom den (betydligt enklare) momentintegralen:
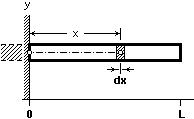
En rak masshomogen balk med längden L är infäst i en vägg (y-axeln). Balkens tvärsnittsyta är konstant och balkens tyngd i KiloPond (1 KP = 9,81 N) är F. Hur stort är balkens statiska moment M=Fx med avseende på balkens ideala infästningspunkt?
Lösning:
F/x = Φ = ma/Meter ;
F = Φx ;
dF = Φ (dL=dx) ;
dMY = dF·x = Φ dx·x ;
MY = Φ ![]() x dx ;
Integralens lösning: [EXP7]
x dx ;
Integralens lösning: [EXP7]
SVAR: M = Φ L→0[x2/2] ; vidare:
= (F/x) [x2/2] = Fx ;
Fx = (F/x) [x2/2] ;
x2 = L→–l[x2/2] ;
:
— Ser vi balksnittet som just en balk med insättningsgränserna L→0 blir dess statiska moment M med avseende på infästningspunkten lika med MY = ΦL2/2 KpM (KiloPondMeter).
— Ser vi balksnittet som snittet
genom ena halvan i en cirkulär cylindrisk skiva får vi hela skivans
tyngdcirkelradie r via insättningsgränserna L→0 med L=R som
x2 = r2 = R→0[x2/2] = R2/2; r = R/√2.
— Med insättningsgränserna för hela cirkelskivan R→–r[x2/2] får vi den cylindriska ringens tyngdcirkelradie r
x2 = r2 = R→–r[(R2/2) – (–r2/2)] = (R2 + r2)/2; r = √ (R2 + r2)/2, vilket vi ser är samma som i EX3.
— Härifrån kan vi lösa ut respektive kropps INTEGRALMOMENT (Ĵ, j-flex)
Ĵ¦CYL = mr2 = mR2/2 ;
Ĵ¦RIN = mr2 = m(R2 + r2)/2 ;
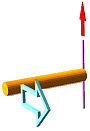
— Hur gör man för att bestämma en motsvarande tyngdcirkelradie för balk- eller stångobjektet i EX4 i fallet då balken roterar kring en axel i änden — eller kring en axel på mitten?
— Har man inget annat roligt för sig kan man alltid försöka befria fångarna med Allmänna MetodIntegralens Vägform:
TYNGDRADIER FRÅN INTEGRALMOMENTET Ĵ = ∫ dmr2. Vi gör ett försök:
EXEMPEL 5 — Integralmoment för en frisvängande rak homogen stång eller balk:
Stången
TYNGDRADIECIRKEL FÖR ROTERANDE STÅNG
Den raka masshomogena stångens massa m per längdenhet x¦L är konstant:
k = m/L ;
k = dm/dx ;
dm = k · dx ;
Ĵ = ![]() dmx2 ;
Integralmomentet
[‡] — konv. tröghetsmomentet
dmx2 ;
Integralmomentet
[‡] — konv. tröghetsmomentet
=
![]() k · dx x2
k · dx x2
= (m/L) ∫ x2 dx ; Integralens lösning: [EXP7]
= L→–l[x3/3] (m/L) ;

LÖSNINGEN MED MITTROTATIONEN :
L/2→–L/2[x3/3] = [(L/2)3/3 + (L/2)3/3] = 2(L/2)3/3 = 2L3/24 ;
Ĵ = (m/L)L3/12 = ;
=
mL2/12 ;
Integralmomentet
med rotationsaxel mitt på rak homogen stång
Ĵ/m = r2 = L2/12 ;
r = L/√12 ; Tyngdradien
LÖSNINGEN MED ÄNDROTATIONEN :
L→0[x3/3] = L3/3 ;
Ĵ = (m/L)L3/3 = ;
=
mL2/3 ;
Integralmomentet
med rotationsaxeln i stångens ände
Ĵ/m = r2 = L2/3 ;
r = L/√3 ; Tyngdradien
Sfären
SFÄRENS TYNGDCIRKEL r
OCH INTEGRALA MOMENT Ĵ, j-flex, konv. tröghetsmomentet:
Med uppslag från
http://www.hyperphysics.phy-astr.gsu.edu/hbase/isph.html
- sph2
HYPERPHYSICS
Dec2018
— Sfärens tyngdcirkel kan bestämmas genom användning av cylinderns tyngdcirkel[‡] r=R/√2 med hjälp av allmänna integralmomentet[‡] (här j-flex, konv. J) Ĵ=mr2 som nedan.
y2 = R2 – x2 ;
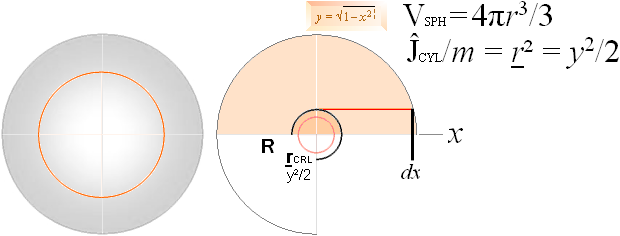
Vi använder
blandprojektioner för att förtydliga xy-systemets hantering av uppgiften: r-Cirkeln
i mitten är vyn sedd från positiva x-axeln då cylinderns tyngdcirkelradie
integreras motsv. sfäriskt som tunna cylinderskikt från maxX=R till minX=0.
Referenskällan ovan visar ett annat sätt — ingen detaljerad information.
GENOM CIRKELNS REKTANGULÄRA EKVATION y = √ (R2 – x2) omfattas enbart halva cirkeln;
— xy-systemet i detta fall kan bara uttrycka positiva y-värden.
Tyngdradiens utbredning/integration sett från x-axelns sida kan heller (meningsfullt) inte föras mer än till max ±y = R.
SÅ: I vilket fall måste tyngdradien r integreras över halva sfären med en dubblering i slutet.
— Webbkällan i referensen ovan (har annat koordinatsätt) ger ingen antydan i den detaljen — utom genom att ange insättningsgränserna som ”R→–R”: slutformen skrivs bara ut utan kommentarer. Genomför man — reguljärt — insättningarna ”R→–R” i integrallösningen får man något annat än nedan:
— Vi följer utvecklingsprocessen i detalj:
ySPH = √(R2 – x2) ; Sfären
i xy-systemet:
VSPH = 4πr3/3 ;
k = m/V = 3m/4πr3 ;
ĴCYL/m = r2 = y2/2 = (R2 – x2)/2 ;
k = dm/d(V=πy2x)
= dm/πy2dx ;
dm = kπy2dx ;
dĴ = (y2/2)dm
= (y2/2)kπy2dx
= (kπ/2)(y2)²dx
= (kπ/2)(R2 – x2)²dx
=
(kπ/2)(R4
– 2R2x2 + x4)dx ; integralmomentets
differentialekvation
=
(kπ/2)(R4dx
– 2R2x2dx + x4dx) ; Lösningen [EXP7] för halva sfären som ovan:
Ĵ/2 = (kπ/2)(R→0![]() R4dx – R→0
R4dx – R→0![]() 2R2x2dx + R→0
2R2x2dx + R→0![]() x4dx)
x4dx)
INTEGRALERNA ÄR AV BESTÄMD FORM [‡] EFTERSOM R=0 0M x=0 och därmed direkt
beräkningsbara:
= (kπ/2)(R5 – 2R2R3/3 + R5/5)
= (kπ/2)(R5 – 2R5/3 + R5/5)
= (kπ/2)(15R5/15 – 10R5/15 + 3R5/15)
= (kπ/2)(15R5 – 10R5 + 3R5)/15
= k(π/2)(8R5)/15
= k(π/2)(8R5)/15
= (1/2)k(πR5)8/15
= (1/2)(3m/4πr3)(πR5)8/15
= (1/2)(m)(R2)2/5
=
(1/2)mR2(2/5) ;
Ĵ = mR2(2/5) ; Hela
Sfärens integrala moment.
Ĵ/m = r2 = R2(4/10) ; Hela Sfärens tyngdradiekvadrat:
r = R√ 4/10 ; Hela Sfärens tyngdradie.
Konen
KONENS TYNGDCIRKEL r
OCH INTEGRALA MOMENT Ĵ, j-flex, konv. tröghetsmomentet:
y2 = x2 ;
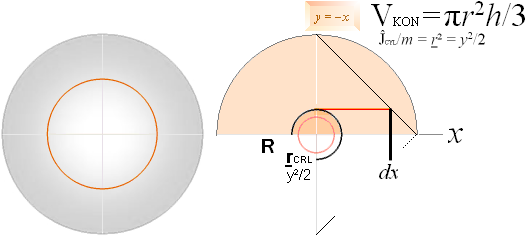
Vi använder
blandprojektioner för att förtydliga xy-systemets hantering av uppgiften: r-Cirkeln
i mitten är vyn sedd från positiva x-axeln då cylinderns tyngdcirkelradie
integreras motsv. sfäriskt som tunna cylinderskikt från maxX=R till minX=0.
— För KONKROPPEN med given täthet k=m/(V=πr2h/3)=3m/πr2h och given basyta (πr2) bevaras k om m och h varierar omvänt proportionellt: För en masshomogen konkropp med en fast given basyta (πr2) är konhöjd (h) och massa (m) proportionella. I detta fall kan vi alltså skriva konvolymen förenklat med h=r som V=πr3/3;
— Vi får samma utvecklingstyp som för Sfären EX6 men med Konens karaktär:
yKON = –x ;
Konen
i xy-systemet:
VKON = πr3/3 ;
k = m/V = 3m/πr3 ;
ĴCYL/m = r2 = y2/2 = (x2)/2 ;
k = dm/d(V=πy2x)
= dm/πy2dx ;
dm = kπy2dx ;
dĴ = (y2/2)dm
= (y2/2)kπy2dx
= (kπ/2)(y2)²dx
= (kπ/2)(x2)²dx
=
(kπ/2)(x4)dx ; integralmomentets
differentialekvation
Ĵ = (kπ/2)(h=R→0![]() R4dx) ; Lösningen: [EXP7]
R4dx) ; Lösningen: [EXP7]
= (kπ/2)(R5/5)
= (1/2)kπ(R5/5)
= (1/2)(3m/πR3)π(R5/5)
= (1/2)(3m)R2(1/5)
= mR2(3/10) ; Konens integrala moment.
Ĵ/m = r2 = R2(3/10) ; Konens tyngdradiekvadrat:
r = R√ 3/10 ; Konens tyngdradie.
SAMMANSTÄLLNING Konen Sfären Cylindern:
———————————————————
————————————————————
Kon mR2 3/10 R√ 3/10
Sfär mR2 4/10 R√ 4/10
Cylinder mR2 5/10 R√ 5/10
———————————————————
MOMENTEXEMPLEN
ROTERANDE KROPPARS VARVTALSACCELERATIONER
Teoretiskt
EXEMPEL
1
En trumma med tyngdradien
r = 0,8M på massan m = 200 KG drivs av en konstant kraft F = 120 N via
en kedja kopplad till ett kugghjul med effektiv drivradie r = 0,15M.
— Bestäm tiden som åtgår
för att accelerera trumman upp till varvtalet per sekund f = 1/3 Hz (20RPM).
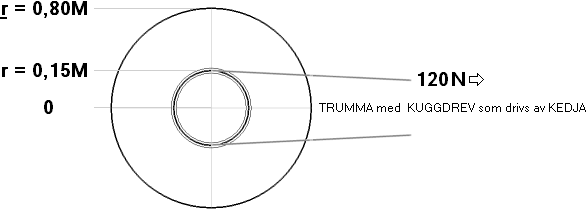
Hämtat WEBBEXEMPEL från
Worked example No.6, D.J. DUNN — SOLID MECHANICS DYNAMICS
TUTORIAL — MOMENT OF INERTIA ¦ 2016
http://www.freestudy.co.uk/dynamics/moment of%inertia.pdf
— Orsaken till
Webbreferenserna är att använda redan (väl) genomräknande exempel från andra
författare — vilket säkrar minimala räkne- och utvecklingsfel då exemplen SÅ
blir särskilt felkontrollerade, och samtidigt breddar perspektivet för en redan
befintlig — säker — referenslitteratur.
Lösning:
— Vi använder den enkla
grundformen som angavs i INLEDNINGEN enligt
—————————————————————————————————————————
a = v/t ; t = v/a = (2πr/t)/a = r(2πf )/a = r(2πf )/(a=F/m) = mr(2πf )/F ¦ f = Hz, antal varv/S
——————————————————————————————————————
t = 200KG · 0,8M · 2pi(1/3S)/(120N · 0,15M/0,8M)
= 200KG · 0,8M · 2pi(1/3S)/(22,5N)
= 320KG · 1M · pi(1/S)/(67,5N)
= (320/67,5)pi S
= 14,893476628 S
SVAR: Tiden som åtgår för att accelerera trumman
till 20RPM med kraften 120N och kraftutväxlingen 0,15/0,8=1,5/8 är 14,89 S.
KOMMENTAR:
—
KRAFTUTVÄXLINGSFÖRHÅLLANDET 1.5/8 används INTE i webbkällans exempel. Där
används istället drevmomentet M = Fr = 120N · 0,15M = 18
NM — tillsammans med den vanliga konventionella typen
——————————————————————————————————————
Ĵ = mr2 ¦ M = Fr ¦ M/Ĵ = mar/mr2 = a/r = α ¦ t = ω/α = (2π·RPM/60)/(M/Ĵ) = r(2πf )/a
—————————————————————————————————————————
t = 2pi(20/60S)/(120N·0,15M/200KG[0,8M]²)
= pi(2/3S)·200KG·0,64M²/(120N·0,15M)
= pi(2/3S)·128KG·M²/(18 NM)
= pi(1/S)·256KG·M²/(54 NM=KG·M²/S²)
= 14,893476628 S
— Webbkällan använder
INTE DIREKT den enklaste sambandsformen.
Teoretiskt
EXEMPEL
2 — en klassiker

Svänghjul med axel och uppvindad lodlina med
lodmassa i änden
— Ett svänghjul av
figurens formtyp med massan m = 1KG och tyngdradien r = 1M sitter friktionsfritt
uppmonterat på en smal genomgående stålaxel (med försumbar inverkan) i ett
Jordlaboratorium med lokal tyngdkraftsacceleration a = 9,81 M/S².
På en cylindrisk mellanaxel med radien r = 0,6M finns en uppvindad lina med försumbar tyngd med en frihängande
lodmassa på m(L) = 1 KG i änden.
— Bestäm svänghjulets
varvfrekvens per sekund sedan lodmassan fått falla fritt under 10 sekunder.
Lösning:
— Vi använder också här
den enkla grundformen som angavs i INLEDNINGEN enligt
—————————————————————————————————————————
a = v/t ; t = v/a = (2πr/t)/a = r(2πf )/a = r(2πf )/(a=F/m) = mr(2πf )/F ¦ f = Hz, antal varv/S
——————————————————————————————————————
KRAFTUTVÄXLINGEN: F := F
· 0,6/1 = 6/10;
KONSTANT PÅLIGGANDE
DRIVKRAFT: F = ma = m(L)·9,81 M/S² = 9,81 N;
Vi söker frekvensen f
efter t = 10S:
t = 1KG · 0,6M · 2pi · f / (9,81N · 0,6) = 10 S ;
f = 10S · 9,81N · 0,6/(1KG · 0,6M · 2pi)
= 98,10NS/(1KG · 2piM)
= 49,05NS/(1KG · 1piM)
= 15,61309992 Hz = avr. 937 RPM
SVAR: Varvtalet per sekund som uppnås efter 10
sekunder är avr. 15,61 Hz.
KOMMENTAR:
— Våndan att (ens)
försöka lösa problemet ovan med den etablerade ”Ĵ=mr²”-metoden leder här
till så stora utsvävningar att vi (här) helt hoppar över den delen. Vi använder
istället tiden vi fick till övers att minnas (och ära) alla de studenter som,
utan framgång en gång i tiden, förtvivlade över liknande problem. Det får inte
fungera så i en anständig kunskapskultur. Kunskapen ska lysa upp, inte mörka
ner.
Praktiskt
EXEMPEL
3 — gyrofysiken
Från SKIVTALLRIKSANALOGIN
2009
Svänghjul (Snurra) av mässing med massan
40Gram = 0,04 KG och tyngdradien 18,25 mM = 0,01825 M, undre navdistans ca 12
mM = 0,012 M,
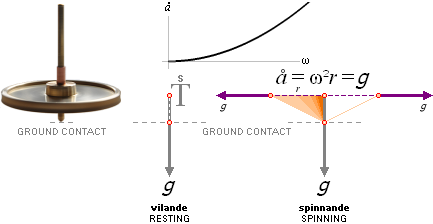
Ett svänghjul av typen ovan vägrar resolut
ANNAT än att LUTA mot underlaget så länge varvtalet (f) genom sin utvecklade
centrifugalkraft F=må=mw²/r inte kan uppväga den nedåtriktande
tyngdkraftens inverkan F=ma. r (”ru”) anger tyngdcirkelradien.
UPPGIFT:
— Vilket minsta möjliga varvtal
i vårt Jordiska laboratorium med a=9,81M/S² krävs för att snurran med r=0,01825M
ska hålla sitt svänghjul rakt horisontellt innan den uppvisar tendenser att
lägga sig?
Lösning:
— Med minsta möjliga undre navavstånd ger
ma=må=mw²/r villkoret
a=å=w²/r = (2pir/t)²/r = (2pi ·
f)²r = 9,81 M/S² med lösningen
f = (1/2pi)√ 9,81M/S²/r
= (1/2pi)√ 9,81M/S²/0,01825M
= 3,689973107 Hz = avr. 238 RPM.
SVAR: För en snurra med r=0,01825M
krävs en minsta varvtalsfrekvens lika med avr. 3,69 Hz för att dess svänghjul
inte ska börja precessera. Under den gränser precesserar snurran allt mera och
lägger sig strax.
KOMMENTAR:
Större navavstånd (d)
kräver högre varvtal genom att kvoten r/d avtar, = sämre stabilitet.
— Vid ett försök med
snurran ovan — 4st extra Ø10mM påmonterade neodymmagneter för noggrann mätning
av varvtalet via en Hallsensor med oscilloskop — noterades (med en mindre mätosäkerhet, ett mättillfälle) frekvensen 3,06 Hz precis innan snurran vek ner sig.
I
ALL ENKELHET tänkte man sig, så: Med SÅ enkla praktiska exempel skulle webben
@INTERNET året 2018 vara proppad med tillämpade praktiska exempel med EXAKT
verifierbar matematik — och snygga lösningar på trådlösa elektroniska
varvräknare.
Inte ett liv Dec2018.
— Håller Marknaden på med
att LÅSA IN MÄNSKLIGHETENS ELEKTRONIKBEROENDE i ett PRIMITIVT INTELLEKTUELLT
SKRÄPSKAL?
Jag vill mena det: Ytlighet, Offentlig
Gapighet; Offentlig Störighet: Ingen Märkbart Kulturell Intellektuell
Produktion Annan än NuÄräJaHärNuSöddö. Andefattigheten breder ut sig över
asfalten.
— ENORMT AVANCERAD
ELEKTRONIK. Noll datorbaserade
produktionsverktyg för vanliga privatpersoner.
MAN MÅSTE KÖPA MERA ÄN DET SOM REDAN FINNS. TROTS ATT DET SOM FANNS TIDIGARE —
20 år bakåt — GOTT OCH VÄL RÄCKTE TILL. Vad gjorde man med Det? Skippade Det.
Kasserade Det. Och Ersatte Det med ”hundra gånger långsammare” till ”tiodubbla
priset” med ”halv funktionalitet”. Stämmer det, är det så?
Folk, vanliga trottoarfotgängare som
utvecklats i de två decennierna ”VetaIntet”? Offer för en elak, girig, tarv fan
som uppträder, mer och mer, som ExistensÄgare: ”Vi Hyr Ut Alfabetet Per Månad”.
Regionala inlåsningar. Är det så? Marknaden har tagit över. Uppträder som
bestämmare. Härskare. En elak, girig, tarv fan. Hur kan den trenden ändras, eller
kan den inte? ”Här är det vi som bestämmer”. Atomerna bockar och bugar.
— Electronic Tools for
PRIVATE Productivity? Det FANNS en gång i tiden — runt 2000. Bergis.
— »Dagens marknadskrafter
2018+ är INTE ute efter Kunskap»?. Herravälde. Fascismens Klassiska Ansikte.
Slavägare. Okunnighetens DRIFT.
— Integralmatematikens olika detaljer kräver (ständig) träning och erinran. Här ges de främsta referenserna i Universums Historia för den (författaren själv inkluderat, från och till) som vill friska upp minnet med baskunskaper.
— @INTERNET innehåller också (värdefulla) referenser. Men det är (ännu 2018 ofta) svårt att hitta annat än ”meddelanden”: Integrala härledningar är (ofta) komplicerade och litteraturen är inte direkt lättåtkomlig (än).
Se även samlat i DOKUMENTÖVERSIK FÖR MATEMATIKEN i Universums Historia
INTEGRALREFERENSER — Integrallista
Alla integrala utvecklingsexempel som beskrivs i detta dokument har särskilda noteringsmärken [i‡] som leder hit:
RÄKNELAGARNA FÖR OÄNDLIGT — differentialbegreppets absoluta grunder
Skillnaden mellan Integral och Gränsvärde
Eulers Ekvivalenter
— exponentialekvivalenterna
FORMLAGARNA
— tabell med (engelska) härledda
referenser till grundintegralerna
Formlagarna —
översikt
DIFFERENTIALBEGREPPET — derivata, differential och integral
Integralbegreppet
— alla grundbegreppen
INSÄTTNINGSGRÄNSER — hur integralens lösning används
Differentialekvation — termen finns inte etablerat —
Integralkonstanten
— termen finns inte etablerat, betecknas
konventionellt C
Integrationskonstanten — termen finns inte etablerat, betecknas konventionellt dx
Se även differentialbegreppet
mera historiskt i modern akademi:
VARFÖR MISSADE NEWTON DIFFERENTIALEN? — se även etablerade begreppet
Differentialelementet i modern akademi — jämförande analys
DIFFERENTIALTRANSFORMATIONER — några exempel visar hur TYP dm omvandlas till TYP dx
INTEGRALKALKYL — metoder och exempel med lösningar:
Integrala Exempel
— atomtriangeln grunderna utan integraler
Integralbegreppet i den högre analysen — mera avancerat
INTEGRALBEVISET — beviset för enhet utan delar
Integralen genom Derivatan — basic
INTEGRALEN I NUMERISKA BERÄKNINGAR — konv. Simpsons Formel: komplicerade integraler
Vissa elementära integralexempel ger i ELEMENTARYTORNA tillsammans med jämförande mera klassiska lösningsmetoder (Sfären, Konen).
I ANALYSENexempel härleds några centralt integrala sambandsformer inom matematik och fysik:
Globala vattenflödets
allmänna ekvation — kapacitans och induktans
Ljusets ändring genom
materien
Fritt fall med luftmotstånd
Den Logistiska
tillväxtekvationen
Allmänna Svängningsekvationen
————————————————————————————————
Välj passande artikel — där
beskrivs detaljerna vidare om ej redan bekant
———————————————————————————————————
NOTERA ATT BESKRIVNINGARNA HÄR ANSLUTER TILL relaterad MATEMATIK:
— Fullständigt beskrivbara och härledningsbara grunder i detalj, eller så inte alls.
— Avsnitten innehåller, eller ska i varje fall göra det, särskilda jämförande exempel och genomgångar av etablerade (motsvarande, om alls) begrepp och termer.
Integrallista UHDec2018
FÖLJANDE LISTADE INTEGRALER FINNS UPPTAGNA exempel, härledningar I UNIVERSUMS HISTORIA t.o.m. 27Dec2018:
— Listan har ordnats efter typ (art och sort) för bekväm åtkomst och referens.
NEDAN: ALLA direkt integralt uttryckta
FÖREKOMSTER i de 129 UH-dokumenten 28Dec2018:
![]()
MOTSVARANDE ![]() UNICODETECKEN — olika för varje teckensnitt —
visas av webbläsarna FULA KLUMPIGA, KLADDIGA:
UNICODETECKEN — olika för varje teckensnitt —
visas av webbläsarna FULA KLUMPIGA, KLADDIGA:
— WebbVärlden (2015+) behärskas
av — bevisbart tydligt — ostädade typer. Titanic. Här används bildkopia
av hemmagjort:
MJUKVARUINDUSTRINS OERHÖRT AVANCERADE
UTVECKLING 1980+.
Integral ![]() INTEGRAND integrationskonstant
(dx) — anges om annan el. sammansatt:
INTEGRAND integrationskonstant
(dx) — anges om annan el. sammansatt:
UPPTAGNA INTEGRALER, Alla Webbsidor
Löpande UH-dokumenten: DEL 1
|
|
|
|
|
|
|
|
1 |
t(AGW) dx |
6[1– (1+[x/10]4)–1] |
AGW-komplexet |
1 |
|
|
2 |
6(1 – [1+(x/10)4]–1) dx |
saknas ännu |
energiintegralen |
2 |
|
|
3 |
(a4 + x4)–1 |
saknas ännu |
energiintegralen |
3 |
|
|
4 |
dA |
A |
räknelagarna för oändligt |
4 |
|
|
5 |
0dx |
0x |
nollintegralen |
5 |
|
|
6 |
dx |
x |
atomtriangeln |
6 |
|
|
7 |
y’ |
y |
atomtriangeln |
7 |
|
|
8 |
dy |
y |
atomtriangeln |
8 |
|
|
9 |
2x |
x2 |
atomtriangeln |
9 |
|
|
0 |
f (x) |
b→a[F(x)] |
atomtriangeln |
0 |
|
|
1 |
kx |
kx2/2 |
atomtriangeln |
1 |
|
|
2 |
|
|
|
|
2 |
|
3 |
x2/2Z |
x3/6Z |
atomtriangeln |
3 |
|
|
4 |
πx3/Z |
πx4/4Z |
atomtriangeln |
4 |
|
|
5 |
2·2πx2 |
4πx3/3 |
atomtriangeln |
5 |
|
|
6 |
ds=vdt |
vt=s |
atomtriangeln |
6 |
|
|
7 |
|
|
|
|
7 |
|
8 |
PI–2 dI |
PI–1 |
ljusbågsfysiken |
8 |
|
|
9 |
mv dv |
mv2/2 |
integrala analogierna |
9 |
|
|
0 |
LI di |
LI2/2 |
integrala analogierna |
0 |
|
|
1 |
dp/p |
p/p0 |
en.gaslag. |
1 |
|
|
2 |
|
|
|
|
2 |
|
3 |
aU/RT dh |
p0e–hUa/RT = –h(0,0341579)/T |
tryckvarianten |
3 |
|
|
4 |
(1 + T/b)–2 dT |
b/(1 + b/T) |
SVPintegralen |
4 |
|
|
5 |
f (x)(A – y) |
A + C e–F(x) |
strålintegral |
5 |
|
|
6 |
(a/cn) vn dv |
(a/cn) vn+1/(n+1) |
elektriska förskjutningen |
6 |
|
|
7 |
v dv |
v2/2 |
accelerationsbegreppet |
7 |
|
|
8 |
|
|
|
|
8 |
|
9 |
dBPx |
µ0(I/4πx) cosb |
magn. exp. integralen |
9 |
|
|
0 |
sinb db |
b→90[cosb] |
rakledaren, induktionen |
0 |
|
|
1 |
(cscb – csc2b) db |
0→90[ln tan(b/2) + cotb] |
rakledaren, induktionen |
1 |
|
|
2 |
r–2 dr |
–r–1 |
dipolfältstyrkan |
2 |
|
|
3 |
µ0(I/4πx) dbs |
µ0(I/2x) |
ringen, magnetismen |
3 |
|
|
4 |
µ0(r2)(I/4πm3) d(2π)s |
µ0Ir2/2m3 |
konen, magnetismen |
4 |
|
|
5 |
|
|
|
|
5 |
|
6 |
sina da |
cosa |
till sfärytan |
6 |
|
|
7 |
(r2 – x2) dx |
r2x – x3/3 |
till sfärvolymen |
7 |
GRUNDINTEGRALER: REF:
|
|
trigonometriska : |
|
|
|
|
|
1 |
–cos |
sin |
1 |
||
|
2 |
sin |
cos |
2 |
||
|
3 |
–n(cos nx) |
sin nx |
3 |
||
|
4 |
n(sin nx) |
cos nx |
4 |
||
|
1/sin2 |
tan |
5 |
|||
|
6 |
–1/cos2 |
cot |
6 |
||
|
7 |
–1/√1–x2 |
asinx |
7 |
||
|
1/√1–x2 |
acosx |
8 |
|||
|
1/(1+x2) |
atanx |
9 |
|||
|
0 |
–1/(1+x2) |
acotx |
0 |
||
|
|
|
|
|
|
|
|
|
exponentiella : |
|
|
|
|
|
a(P)a–1Dn(P) |
(P)a |
1 |
|||
|
2 |
axa–1 |
xa |
2 |
||
|
3 |
(P)nDn(P) |
(P)n+1/(n+1) |
3 |
||
|
4 |
xa |
(xa+1)/(a+1) |
4 |
||
|
5 |
A(DnB) + B(DnA) |
AB |
5 |
||
|
6 |
[B(DnA) – A(DnB)]B–2 |
A/B |
6 |
||
|
|
logaritmiska : |
|
|
|
|
|
e(P)Dn(P) |
e(P) |
1 |
|||
|
2 |
zezx |
ezx |
2 |
||
|
3 |
ex |
ex |
3 |
||
|
4 |
B(P)Dn(P)lnB |
B(P) |
källförklaring: |
4 |
|
|
5 |
BxlnB |
Bx |
källförklaring: |
5 |
|
|
Dn(P)/(P) |
ln(P) |
6 |
|||
|
1/x |
ln x |
7 |
NOTERA ÅterDeriveringen:
Derivatan (Dn) till integralen = integranden åter.
Del 2: Del 1
|
|
|
|
|
|
|
|
1 |
dI/I |
lnI |
Ljusflödet |
1 |
|
|
2 |
dU/(U0 – U) |
–ln(U0 – U) |
GlobalaVattenflödet |
2 |
|
|
3 |
(1/RC)dT |
T/RC |
kondensatorn |
3 |
|
|
4 |
(R/L)dT |
RT/L |
spolen |
4 |
|
|
5 |
ω sinωT dT |
cosωT |
reaktanserna |
5 |
|
|
6 |
xne(P) |
metod med helt avsnitt ...................................... |
................................... |
6 |
|
|
√1–x2 dx |
(1/2)(acosx+x√1–x2) |
cirkelns integral |
7 |
||
|
√a–x2 dx |
a(1/2)[acos(x√a) + (x√a)(√1–(x√a)2]] |
Variabelsubstitution 1 |
8 |
||
|
1/√a–x2 dx |
acos (x√a) |
Variabelsubstitution 2 |
9 |
||
|
0 |
xex dx |
ex(x–1) |
Partiell Integration 2 |
0 |
|
|
1/√a+x2 dx |
ln(x + √a+x2) |
Hyperbelinversens integral |
1 |
||
|
2 |
ρ0(1+r/R)–4 dr |
ρ0R/3[1 – (1+r/R)–3] |
Solfysiken |
2 |
|
|
3 |
rR–2 drR |
–rR–1 |
Solfysiken |
3 |
|
|
4 |
Q(4πr2ε0)–1 dr |
–Q(r · 4πε0)–1 |
Solens kapacitans |
4 |
|
|
5 |
0→2π∫ d(2π) |
2π |
Solmagnetismen |
5 |
|
|
6 |
–2(3/2πG)T–3 dT + k dT |
(3/2πG)T–2 + kT |
Pulsarerna |
6 |
|
|
7 |
k1T·1dTx2dTy3dTz |
k1T4 |
Stef.Boltzm. str.lag |
7 |
|
|
8 |
x(a+x 2)–2 dx |
(1/2)[a–1 – (a+x2)–1] |
K-cellens effektfunktion |
8 |
|
|
9 |
c0–1(√ 1 – x2b)–1 dx |
c0–1(1/√b)acos(x√b) |
Ljuvägens integral |
9 |
|
|
0 |
dr/r2 |
–1/r |
Fria g-fallets hastighet |
0 |
|
|
1 |
T dt |
T2/2 |
Fria g-fallets tid |
1 |
|
|
2 |
(x2 ± a)–1/2 dx |
ln[x + (x2 ± a)1/2] |
Ljuvägens integral |
2 |
|
|
3 |
[b]–1/2(k – x2)–1/2
dx |
[b]–1/2(acos[x/k1/2]) |
Ljuvägens integral |
3 |
|
|
4 |
[b]–1/2(x2 – k)–1/2
dx |
[b]–1/2(ln[x+k1/2
+ ((x+k1/2)2 – k)1/2] – ln[k1/2]) |
Ljuvägens integral |
4 |
|
|
5 |
T–1/3 dT |
T–1/3 + 1/(–1/3 + 1) |
Exp.v-formen,
K-cellen |
5 |
|
|
6 |
(Gρ24π/3) r dr |
(Gρ24π/3)r2/2 |
HydroBasic |
6 |
|
|
7 |
τ–1dτ |
ln τ/K |
Jkropparnas
värmefysik |
7 |
|
|
8 |
dW/W = d(S/b) |
lnW = S/b |
EntropiIntegralen |
8 |
|
|
9 |
y’ dx |
y |
Differentialbegr.i
MAC |
9 |
|
|
0 |
p dp |
(1/2)p2 |
Halvertingstiden,
radiofys. |
0 |
Till Dec2018 Upptagna REGULJÄRA ROTINTEGRALER UiDel2 i PREFIXxSIN:
———————————————————————————————————
(7) ![]() √1–x2
dx = (1/2)(acosx+x√1–x2)
; .................................. cirkelns
integral
√1–x2
dx = (1/2)(acosx+x√1–x2)
; .................................. cirkelns
integral
(8) ![]() √a–x2
dx = a(1/2)[acos(x√a)
+ (x√a)(√1–(x√a)2]] ; ..... cirkelns generaliserade integral
√a–x2
dx = a(1/2)[acos(x√a)
+ (x√a)(√1–(x√a)2]] ; ..... cirkelns generaliserade integral
(9) ![]() 1/√a–x2
dx = acos (x√a)
; ................................................. generaliserad acos-integral (TRIG7)
1/√a–x2
dx = acos (x√a)
; ................................................. generaliserad acos-integral (TRIG7)
(11) ![]() 1/√a+x2
dx = ln(x +
√a+x2) ;
............................................. hyperbelinversens
integral [‡]
1/√a+x2
dx = ln(x +
√a+x2) ;
............................................. hyperbelinversens
integral [‡]
Jämför den reguljära METODISKA LÖSNINGEN här i IRa — ytterst krävande.
Hyperboliska
produktintegraler:
Kompletterande i detta dokument (1Jan2019):
HPi: HYPERBOLISKA PRODUKTINTEGRALENS INTEGRALER:
![]() √x2±a dx = x(√x2±a)/2 ± (a/2)ln(x
+ √x2±a) ; HYPERBELNS INTEGRAL
√x2±a dx = x(√x2±a)/2 ± (a/2)ln(x
+ √x2±a) ; HYPERBELNS INTEGRAL
![]() 1/√x2±a dx = ln(x + √x2±a) ; IRa ¦ (11)
1/√x2±a dx = ln(x + √x2±a) ; IRa ¦ (11)
![]() x2/√x2±a dx = (1/2)[x√x2±a
x2/√x2±a dx = (1/2)[x√x2±a
![]() a ln(x + √x2±a)] ;
Hyperboliska
Produktintegralen
a ln(x + √x2±a)] ;
Hyperboliska
Produktintegralen
Länkar — särskilda referenser som krävs vid utveckling och lösning av integraler:
—————————————————————————————————
SAMBANDSKARTOR TILL TRIGONOMETRIN
KOMPLETTERANDE GRUNDINTEGRALER
29Dec2018
GRUNDTABLÅERNA ¦ secans integral ¦ cosecans integral ¦ IRa ¦ Hyperboliska Produktintegralen ¦
———————————————————————————————————————————
1/sin = sec; 1/cos = cosec; 1/tan = cotan ; cos/sin=tan=y/x: 1=x2+y2=sin2+cos2.
sin cos tan —
sec cosec cot — PREFIXxSIN
— nomenklaturen genomgående i Relaterad
Matematik; rakt, enkelt.
——————————————————————————————————————————————
cos
sin tan — cosec sec cot — PREFIXxCOS — nomenklaturen
i modern akademi; krånglig, omständlig.
1/cos = sec; 1/sin = cosec; 1/tan = cotan — »taskig koordinering».
———————————————————————————————————————————
ENDA SKILLNAD: etiketterna sin ¦ cos byter plats. Inget annat: »Håll Eggen Skarp,
Alltid (KangFuMath)».
MÄNGDEN GRUNDSAMBAND:
— Det är helt uteslutet för den som vill lösa integraler
framgångsrikt att INTE ha hela biblioteket med referenser och grundsamband
framför sig — antingen uppradade per skrifter på ett separat — långt — bord.
Eller genom övning och färdighet per direkt ihågkomst. Referensmaterialet ÄR
omfattande. Det finns inga genvägar.
Vi måste — i vilket
fall — erinra grundsambanden så att vi, säkert, kan återföra hela
lösningsprocessen, detaljerat, på grundformerna. Och det arbetet är väldigt —
mycket — stimulerande OCH arbetskrävande. OCH (mycket) rent intellektuellt
energiGIVANDE. Absolut.
För trigonometrins del
som nedan — grundtablå,
grundkonversioner, arcuskonversioner —
Grundtablån — grundkonversionerna —
arcuskonversionerna ¦ PREFIX xSIN ¦ TrigBasic ¦ Sambandstablåerna:
med grundsambanden från VINKELSUMMATEOREMET ¦ Sin nA ¦ BastablånFormLagarna ¦;
VST: Vinkelsummateoremet ¦ Sin nA
:
sVST: VST SÄRSKILDA
TRIGONOMETRISKA RELATIONER från ovanstående — delvis upprepningar
för sammanhanget
— se särskilt sammanställd mera utförlig ekvationskarta i SekVST;
1. cos2A = 2cosAsinA ¦ VST13
2. cos2A = √ (1 – sin4A)/2
3. cos(A+90)/2 = √ (1 – cosA)/2
4. sin2A = 2/(1 + [tanA]2) – 1 ¦ VST2
5. sin2A = 1 – 2(cosA)2
6. sin2A = 2(sinA)2 – 1
7. sin2A = √ (1 + sin4A)/2
8. tan2A = √ 2/(1 + sin4A) – 1
Kännedomen här grundas på härledningarna till alla samband från GRUNDMATEMATIKEN, med den vidare derivata, differential och
integralkalkylens detaljer. NOLLFORMSALGEBRAN är grunden.
— Se vidare här från början i INTEGRALREFERENSER i Universums Historia.
Utöver de grunderna
krävs också — vid mera avancerad lösning — kännedom om EKVATIONSLÄRAN (partialbråksuppdelningar särskilt).
Länkarna
här i UH till de olika avsnitten ska föreställa SÄKRA repetitionsgrunder för
den som har varit borta ett tag från ämnet, och vill ha en SNABB minnesrefresh
(PilotTräning).
Vi försöker lägga in sådana länkar i härledningarna (här, på
lämpliga ställen) för att förenkla för den läsare att hänga med som inte
erövrat tungviktstiteln — än.
GENERELLT: MED ett
(genuint) LÄNKAT, detaljerat, läromedel, datoriserat noggranna genomgångar,
blir det så ofantligt mycket lättare för i princip vem som vill och har TID att
plöja (relativt) komplicerade manualer i matematik (och fysik). Det är ett av syftena med UH: att studera, lära,
och begrunda, från platsen vi står på för tillfället — med maximal direkt
villkorslös åtkomst. Jorden är — och förblir — rund.
Generellt i UH används beteckningssättet Dn för Derivatan alternativt till det mera normalt etablerade enkla primet (’) efter derivatans objekt (»derivanden»), typ
Dn y = dy/dx = y’. Se f.ö. grunderna i Differentialbegreppet, om ej redan bekant.
— Många integralproblem innefattar nödvändigheten att utföra en DIFFERENTIALTRANSFORMATION (ofta analogt med eller kombination av en s.k. konv. variabelsubstitution). Den delen KAN vara knepig för den som inte riktigt kommer ihåg grunderna. Utöver exemplen som ges här, finns ett särskilt sammanställt avsnitt DialTransEX som visar några olika praktiska UH-exempel.
KOMPLETTERANDE GRUNDINTEGRALER:
cosecans integral ¦ secans integral ¦
Secans Integral — ![]() 1/sinx
dx = ln[tan (π/2 + x)/2]
1/sinx
dx = ln[tan (π/2 + x)/2]
SECANS 1/sin = secans (sec) INTEGRAL — PREFIXxSIN — Integralen för 1/sinx
INTEGRAND: 1/sinx
UPPGIFT: Bestäm integralen för den angivna trigonometriska integranden
1/sinx.
GRUNDSAMBAND: sinA =
cos(90–A=B) = cos(π/2 – x) = cosa
= cosB;
Differentialtransformationer: a = (π/2)–x ; radianvinkeln generellt ¦ SINUSKURVAN
¦ Radianer:
Dn a dx = –dx
sina = cosx ; sin (π/2 – x) = cos x ;
sinx =
cosa ;
da = Dn a dx = –dx ;
dx = –da ;
a/2 = b ;
dx = –da = –2db ;
db = –(1/2)dx ;
b = – x/2 ;
a = 2b ;
Lösning:
dx = –da = –2·d(a/2) = –2db ...................................... TÄLJAREN
–db –db sinb –db 1 d(tanb)
↓↑ = —————— = ————— = ————— , [—— = Dn tan = ———— ] ;
cosb sinb cosb sin2b tanb sin2a sin2 db
sinx = cosa = 2cos(a/2)sin(a/2) = 2cosbsinb ............ NÄMNAREN = cos2b ; STS(1)
RESULTAT:
dx/sinx = –d(tanb)/tanb
![]() 1/sinx
dx = –
1/sinx
dx = –![]() 1/tanb
d(tanb) = – ln tanb = – ln[tan
(π/2 – x)/2] = ln 1/tan b
1/tanb
d(tanb) = – ln tanb = – ln[tan
(π/2 – x)/2] = ln 1/tan b
Tvivlar vi på resultatet genomförs en oberoende prövning;
ÅterDERIVERING Ger : LOG5 :
(x/2) – x = a ; da/dx = Dn(a) = –1 ; da = –dx
Dn –ln(tan b) = –Dn(tan b)/(tan b) ;
Dn(tan b) = d(tan b)/db = –2d(tan b)/dx = 1/sin2b ; TRIG4
d(tan b)/dx = –/2sin2b = Dn(tan –x/2) = Dn(tan b) ;
Dn(tan b)/(tan b) = –1/2(sin2b)(tanb)
= –1/[2(sin2b)(tanb = √(1/sin2b – 1))
= –1/2(sinb)√(1 – sinb2) = –1/2(sin)cos = –1/2(sinacosa) ;
Dn –ln(tan b) = – [–1/2(sinb cosb)] = 1/(2sinb cosb = cos2b [TF13, B=0]) = 1/cos2b ;
; cosA + cosB =
2cos[(A+B)/2] · sin[(A–B)/2] ¦ B=0; A=2b; VST13, B=0 ;
; cos2b =
2cos[b] · sin[b] = 2sinb cosb ;
; cosb =
2cos(b/2)sin(b/2) ;
; cos2b = cosa = sinx enligt
förutsättningarna, se ovan.
= 1/cos2b = 1/sinx ;
Således INTEGRANDEN ÅTER.
Svar: ![]() 1/sinx dx = – ln[tan (π/2 – x)/2]
¦ = ln[tan (π/2 +
x)/2]
1/sinx dx = – ln[tan (π/2 – x)/2]
¦ = ln[tan (π/2 +
x)/2]
Cosecans Integral — ![]() 1/cosx
dx = ln(tan x/2)
1/cosx
dx = ln(tan x/2)
COSECANS 1/cos = cosecans (cosec¦csc) INTEGRAL — PREFIXxSIN — Integralen för 1/cosx
På samma sätt som i fallet med secans integral utnyttjar vi trigonometriska grundformer för att försöka åstadkomma en upplösning av integranden i grundintegrander. Utvecklingen blir här enklare då vi direkt utan mellanled kan utnyttja att
cosx = 2cos(x/2)sin(x/2) ¦ VST13 ¦ STS(1).
INTEGRAND: 1/cosx
UPPGIFT: Bestäm integralen för den angivna trigonometriska integranden
1/cosx.
GRUNDSAMBAND: cosx
= 2cos(x/2)sin(x/2) ;
Differentialtransformationer: Variabelsubstitution — enskild faktorterm
ersätter mera sammansatt uttryck för enklare mellanräkningar:
Variabelsubstitutionen ges här som den mera sammansatta typen
t = tan x/2 = tana ;
1/cosx dx ; a = (x/2) ; radianvinkeln generellt ¦ SINUSKURVAN ¦ Radianer:
da = Dn a dx = (1/2) dx ;
Lösning:
dx = 2da ..................................................................... TÄLJAREN
da da sina da 1 d(tana)
↓↑ = —————— = ————— = ————— , [—— = Dn tan = ———— ] ;
cosa sina cosa sin2a tana sin2a sin2 da
cosx = 2cos(x/2)sin(x/2) = 2cosa sina ....................... NÄMNAREN
Resultat:
dx/cosx = d(tana)/tana
![]() 1/cosx
dx =
1/cosx
dx = ![]() 1/tana
d(tana) = ln
tana ;
1/tana
d(tana) = ln
tana ;
Tvivlar vi på resultatet genomförs en oberoende prövning;
ÅterDERIVERING Ger : LOG5 :
(x/2) = a ; da/dx = Dn(x/2) = 1/2 ; da = dx/2
Dn ln(tan a) = Dn(tan a)/(tan a) ;
Dn(tan a) = d(tan a)/da = 2d(tan a)/dx = 1/sin2a ;
d(tan a)/dx = 1/2sin2a = Dn(tan x/2) = Dn(tan a) ;
Dn(tan a)/(tan a) = 1/2(sin2a)(tana)
= (1/2)[1/(sin2a)(tana = √(1/sin2a – 1))
= 1/(sina)√(1 – sina2) = 1/(sin)cos = 1/(sinacosa)] ;
Dn ln(tan a) = (1/2)/(sina cosa) = 1/(2sina cosa = cos2a ¦ VST13]) = 1/cosx
Således INTEGRANDEN ÅTER.
Svar: ![]() 1/cosx dx = ln(tan x/2)
1/cosx dx = ln(tan x/2)
Integralt Rotkomplement (a) —
![]() 1/√1+x2
dx = ln(x+√1+x2) ¦
1/√1+x2
dx = ln(x+√1+x2) ¦
![]() 1/√x2±a dx = ln(x+√x2±a)
1/√x2±a dx = ln(x+√x2±a)
— Vi använder (här) omväxlande beteckningssätten ”Dn” och ” ’ ” för ”derivatan (till)” typ Dn x = x’:
HYPERBELINVERSENS INTEGRAL — PREFIXxSIN — Integralen för 1/√1+x2:
DEN YTTERST ENKLA LÖSNINGEN genom substitution och bekantskapen med Formlagarna — R = √1+x2:
; 1/R = (R+x)/R(R+x) = [1/(R+x)](R+x)/R = [1/(R+x)](1+x/R) ;
; 1+x/R = Dn(x+R) = Dnx + DnR = x’ + R’ ¦ EXP4 ¦ EXP7 ;
; 1/R = (x+R)’/(R+x) = Dn ln(x+R) ¦ LOG5 .................................. ;
; ![]() 1/R dx = ln(x+R)
1/R dx = ln(x+R)
DEN YTTERST KOMPLICERADE LÖSNINGEN:
I grundintegralerna
ser vi att typen 1/√(1+x2) inte alls har någon representation. Uttrycket ARCUSBEGREPPET finns emellertid i Arcuskonversionerna ¦ Trigonometrins tangensformer som
1/√(1+x2) = sin atan x. Det ger en möjligt ansats:
INTEGRAND: 1/√(1+x2)
UPPGIFT: Bestäm integralen för den angivna trigonometriskt associerade integranden
1/√(1+x2).
GRUNDSAMBAND: 1/√(1+x2)
= sin atan x ;
Differentialtransformationer: Variabelsubstitution — enskild faktorterm
ersätter mera sammansatt uttryck för enklare mellanräkningar:
Vi söker en passande omformning:
tan x = t ;
x = atan t ;
sin x = sin atan t ;
= 1/√(1+ t2) ;
Integration på dt kräver en reguljär differentialtransformation. Vi får
dt = d(tan x) = Dn tan x dx = (sin x)–2 dx ; sammanställning ger ;
sin atan t dt = sin x dt
=
sin x (sin x)–2 dx ;
= (sin x)–1 dx
= 1/√(1+ t2) dt ;
dx/sinx = dt/√(1+ t2) ;
Med återställningen t = tan x har fått två likvärdiga integraler
![]() dx/sinx =
dx/sinx = ![]() dt/√(1+x2) :
dt/√(1+x2) :
Lösningen till integralen ò1/Ö(1+ t2) dt återfaller på en lösning till integralen ò (sin x)–1 dx med t = tan x.
Vi återkommer till den delen senare.
— Härledningen till integralen för 1/(R=√(1+x2)) blir fortsättningsvis:
SÄRSKILDA TRIGONOMETRISKA SAMBANDET STS(8)![]() inom trigonometrin, ekvivalenterna
inom trigonometrin, ekvivalenterna
tan(a/2) = √ (2/[1 + sina]) – 1) hjälper oss vidare:
[tan(a/2)]2 = 2/(1 + sina) – 1 ;
• Vi utnyttjar differentialtransformationen från secans integral
a = (π/2)–x ;
b = – x/2 ;
a/2 = b = (π/2 – x)/2 ;
• Konvertering från a till x genom a = π/2 – x ¦ A° = 90° – B° ¦ x = π/2 – a :
2/(1+sina) – 1 = (2 – [1 + sina])/(1 + sina) = (1–sina)/(1 + sina) ;
; sin a = cos x ; sinA = cos(90-B); 1 = sin2 + cos2 = x2+y2:
= (1–cosx)/(1+cosx) = (1–cosx)[1+cosx]/[1+cosx](1+cosx) = [1 – (cosx)2]/[(1 + cosx)2] → Konjugatlagen;
= (sinx)2/(1+ cosx)2 = [tan (a/2)]2 ;
tan (a/2) = (sinx)/(1+ cosx) ;
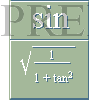 Grundkonversionerna 1/sin = √ 1+
tan2 ;
Grundkonversionerna 1/sin = √ 1+
tan2 ;
Förenkling — vi utnyttjar grundsambanden från trigonometrin i slutleden: cos/sin=tan=y/x:
1/tan(a/2) = (1+ cosx)/(sinx) = secx + tanx = tanx + √ 1+ (tanx)2 ;
Resultat:
1/tan(a/2) =
tanx + √
1 + tan2x ;
ln 1/tan(a/2) = ln(tanx + √ 1 + tan2x)
= –ln tan(a/2) ; Logaritmlagarna (9.1) : ln(A)=–ln(1/A); ln(1/A)=–ln(A);
–ln tan(a/2) = –ln tan b = –ln[tan (π/2 – x)/2]
Enligt secans integral föregående resultat hade vi
–ln tan b = ![]() 1/sinx
dx
1/sinx
dx
Insättning av ekvivalenten till –ln tanb i ovanstående led ger oss alltså
![]() 1/sinx dx
= – ln tan b =
ln(tanx + √ 1 + tan2x)
1/sinx dx
= – ln tan b =
ln(tanx + √ 1 + tan2x)
Med tan x=t hade vi RIaMR från början de likvärdiga integralerna
![]() 1/sinx dx =
1/sinx dx = ![]() 1/√
1+ t2 dt
1/√
1+ t2 dt
Insättning av ovanstående ekvivalent ger oss
![]() 1/sinx
dx = ln (tanx +
√ 1 + tan2x)
1/sinx
dx = ln (tanx +
√ 1 + tan2x)
=
ln (t + √1+ t2) = ![]() 1/√1+
t2 dt ;
1/√1+
t2 dt ;
![]() 1/√1+
t2 dt = ln
(t + √1+ t2)
1/√1+
t2 dt = ln
(t + √1+ t2)
De bägge sista leden har så visat svaret:
— Vi kan direkt ersätta t med x i leden ovan vilket ger oss
![]() 1/R
dx = ln (x+R); R = √1 + x2 ;
1/R
dx = ln (x+R); R = √1 + x2 ;
![]() 1/√1+x2
dx = ln (x+√1+x2)
1/√1+x2
dx = ln (x+√1+x2)
:
Tvivlar vi på resultatet genomförs en oberoende prövning;
ÅterDERIVERING Ger : LOG5 :
Dn ln(x+R) = (1+xR–1)/(x+R) = R–1(x+R)/(x+R) = R–1
Således INTEGRANDEN ÅTER.
Svar: ![]() 1/√1+x2
dx = ln(x+√1+x2)
1/√1+x2
dx = ln(x+√1+x2)
BONUS:
Återderiveringen via R = √1+x2 visar oss att koefficienten (1) är egal: rotinnehållet 1+x2 eller ±a+x2 går på ett ut;
Svar: ![]() 1/√x2±a+
dx = ln(x+√x2±a)
1/√x2±a+
dx = ln(x+√x2±a)
Se även det betydligt enklare integrala utvecklingssättet för integranden ovan i ROTUPPDELNING—Exempel1:
— Den enkla kraftfulla PEFECD-METODEN som finns — men inte existerar (!) — i modern akademi.
Hyperboliska Produktintegralen — ![]() x2/R
dx = (1/2)[xR
x2/R
dx = (1/2)[xR ![]() a ln(x + R)] ; R
= √x2±a
a ln(x + R)] ; R
= √x2±a
PARTIELLA INTEGRATIONENS KRAFTFULLA METOD — Hyperbelns integral från biprodukter genom Partiell Integration Metod 2:
Utvecklingsexempel som — i jämförelse med samma
resultat via andra, mera omständliga metoder, länkar ges nedan — visar
kraftfullheten i
PARTIELL INTEGRATION Metod 2:
:
INTEGRAND: x2/√x2±a
UPPGIFT: Bestäm via Metod 2 Partiell Integration integralen för den sammansatta integranden
x2/√x2±a.
GRUNDSAMBAND: ![]() AdB
= AB –
AdB
= AB – ![]() BdA
; PARTINT Metod 2: Vi
använder EXP7 ¦ LOG5:
BdA
; PARTINT Metod 2: Vi
använder EXP7 ¦ LOG5:
Lösning:
B = R = √x2±a = (x2±a)1/2 ; R = (P)1/2 · P/P = (P)–1/2 · P = (x2±a)/√x2±a = x2/√x2±a ± a/√x2±a = x2/R ± a/R ;
Dn R = d(R=B)/dx = Dn (P)1/2 = (1/2)(P)1/2–1=–1/2 · [(P)’ = 2x] = (1/2)(x2±a)–1/22x = x/R ; EXP7
dB = x/R dx ............................................................................................................ ;
A = x ;
![]() x2/R
dx = xR –
x2/R
dx = xR – ![]() Rdx
..................................................................................................... ; (1)
Rdx
..................................................................................................... ; (1)
= xR – ![]() (x2/R ± a/R)dx
(x2/R ± a/R)dx
= xR – ![]() x2/R dx
x2/R dx ![]() a
a![]() 1/R dx
;
1/R dx
;
2 ![]() x2/R
dx = xR
x2/R
dx = xR ![]() a
a![]() 1/R dx
1/R dx
; 1/R = (R+x)/R(R+x) = [1/(R+x)](R+x)/R = [1/(R+x)](1+x/R) ;
; (1+x/R) = Dn(x+R) = Dnx + DnR = x’ + R’ ;
; 1/R = (x+R)’/(R+x) = Dn ln(x+R) ¦ LOG5 .................................. ; (2)
; ![]() 1/R dx = ln(x+R) ¦ Jämför
metodiska lösningen i IRa:
1/R dx = ln(x+R) ¦ Jämför
metodiska lösningen i IRa: ![]() 1/R dx = ln(x+R)
1/R dx = ln(x+R)
=
xR ![]() a ln(x+R) ;
a ln(x+R) ;
Resultat:
![]() x2/√x2±a dx = (1/2)[x√x2±a
x2/√x2±a dx = (1/2)[x√x2±a ![]() a ln(x + √x2±a)] =
a ln(x + √x2±a)] = ![]() x2/R
dx = (1/2)[xR
x2/R
dx = (1/2)[xR ![]() a ln(x + R)] ; R
= √x2±a.
a ln(x + R)] ; R
= √x2±a.
BONUS (1) — Hyperbelns integral (automatiskt generaliserad):
![]() Rdx = xR –
Rdx = xR – ![]() x2/R
dx
x2/R
dx
=
xR – [xR/2
![]() (a/2)ln(x + R)] = xR – xR/2
± (a/2)ln(x + R)
(a/2)ln(x + R)] = xR – xR/2
± (a/2)ln(x + R)
= xR/2 ± (a/2)ln(x + R) ;
BONUS (2) — Integrala Rotkomplementet a IRa på mycket enklare sätt:
![]() 1/R dx = ln(x+R)
; R = √x2±a
1/R dx = ln(x+R)
; R = √x2±a
:
Tvivlar vi på resultatet genomförs en oberoende prövning;
ÅTERDERIVERINGEN av (1/2)[x√x2±a ![]() a ln(x + √x2±a)] Ger ;
a ln(x + √x2±a)] Ger ;
Dn x√x2±a =
x[ (1/2)[1/(√x2±a)](2x) ] +
[√x2±a]
= x2/R + R ;
Dn a·ln(x+√x2±a) = a[ Dn(x+R)/(x+R) ]
= a[ (1+[x/R]
)/(x+R) ]
= a[ 1/R
] ;
summering: =
(1/2)[x2/R + R ![]() a/R]
a/R]
= (1/2)[x2/R + R2/R (–+) a/R]
= (1/2)[x2/R + [R2 (–+)
a]/R]
= (1/2)[x2/R + [x2±a (–+) a]/R]
= (1/2)[x2/R + [x2]/R]
= (1/2)[2x2/R]
= x2/R
Således INTEGRANDEN ÅTER
Svar: ![]() x2/√x2±a dx = (1/2)[x√x2±a
x2/√x2±a dx = (1/2)[x√x2±a
![]() a ln(x + √x2±a)] ;
Hyperboliska
Produktintegralen
a ln(x + √x2±a)] ;
Hyperboliska
Produktintegralen
![]() √x2±a dx = x(√x2±a)/2 ± (a/2)ln(x
+ √x2±a) ; HYPERBELNS INTEGRAL
√x2±a dx = x(√x2±a)/2 ± (a/2)ln(x
+ √x2±a) ; HYPERBELNS INTEGRAL
![]() 1/√x2±a dx = ln(x + √x2±a) ; IRa ¦ (11)
1/√x2±a dx = ln(x + √x2±a) ; IRa ¦ (11)
Uppslaget till produktintegranden x2/R
från PI Metod 1 från RotHyperbeln (R):
:
Bestäm ![]() √ x2+a dx.
Förenkla med R = √ x2+a.
√ x2+a dx.
Förenkla med R = √ x2+a.
Lösning:
![]() f (x) d[·]
= f (x)[·] –
f (x) d[·]
= f (x)[·] – ![]() [·]d[f
(x)] ............ Partiell integration, Metod 1
[·]d[f
(x)] ............ Partiell integration, Metod 1
f (x) ................................................................ = R = √ x2+a
[·] .................................................................. = x
![]() R dx = xR –
R dx = xR – ![]() x dR
x dR
Differentialtransformation, högerintegralen:
dR = Dn R dx = x/R dx ; insättning ger
![]() R dx = xR –
R dx = xR – ![]() x2/R dx
.............................. ;
→ x2/R :
x2/R dx
.............................. ;
→ x2/R :
— Se vidare i Hyperboliska Produktintegralen — hela lösningen visar sig genom PARTINT Metod 2.
Första Systemintegralen Si1 ELLER »matematikens grundläggande maskinlära» enligt
INTEGRALERNAS ARITMETIK — ![]() xc(Axa + Bxb)n
dx
xc(Axa + Bxb)n
dx
1997IX27 · 2001III — Binomialteoremets BT Integralaritmetik — numerisk och algebraisk djupanalys till matematikens praktiska användbarhet.
De raka enkla integranderna av formen xc(Axa + Bxb)n har — här veterligt 2018+ — ingen direkt konventionell representation. Wikipedia (Jan2019, Lists of integrals) har en enda närmaste representant ”Absolute value-functions” av formen ”(ax+b)n”. Det är allt.
Det finns (säkert, kanske) mera kött på benen i andra delar, typ
MATHEMATICAL HANDBOOK FOR SCIENTISTS AND EGINEERS Appendix E Integral Tables p925-,
McGraw-Hill Second Edition 1968 — sektioner E-1 till E-9 (Summor och serier från E-4).
Men inget är här känt om dessa ev. förekomster (Biblioteken har för länge sedan magasinerat de klassiska »tegelstensböckerna» från 1900-talets typografiska guldålder — om de alls finns kvar).
Första systemintegralen är — emellertid — relativt lätt att härleda med hjälp av Binomialteoremet. Se Si1-Härledningen.
—
Enda skillnaden i att x^c finns med/utesluts är högerledets respektive an+c+1
eller an+1:
![]()
SummaINDEXERINGEN har innebörden FRÅN undre
m=0 TILL övre n — i rak form: m=0→n.
— Med
n<1 ges oändliga serier. Se tillämpade exempel nedan..
Webbläsarna klarar
inte naturvetenskapen:
KOLLA SVÅRIGHETERNA ATT PRESENTERA ÄMNET @INTERNET :
Bildoriginalet från MsWorks 4.0 importerat till htm-dokumentet i WORD 2000:
![]()
MOTSVARANDE I WEBBLÄSAREN — IE9 — fram till 2015 — Även
GoogleCHROME 2015+ bortsett från Chromes suddiga text:
![]()
KORRIGERINGEN SOM MÅSTE GÖRAS i WORD-htm-dokumentet för
korrekt läsbarhet — författarens trevliga dokumentvy:
![]()
MOTSVARANDE SLUTLIGT UTSEENDE I WEBBLÄSAREN (i varje fall
t.o.m. Dec2018):
![]()
Jämför aktuell webbläsare, htm-originalet här:
= An([(xan+c+1)/(an+c+1)] + m=0→nΣ [[(B/A)(n–m)]m!x(b–a)(m+1)+an+c+1]/[[(b–a)(m+1) + an + c + 1] (m+1)!])
EN HEL DEL AV ORIGINALARBETENA i MsWorks 4.0 har på detta sätt mer eller mindre spolierats av Internetvärldens olika tydligt IMPERIALISTISKT FÖRETRÄDDA KöpListaLäsare (klarar — knappt — 0123456789): Matematiken GRATIS är urdåligt representerad: klumpig, rent ut sagt FUL. Det FINNS enkla typsnitt — Times New Roman + Symbol. Men webbläsare i allmänhet är inte utformade för att ta med fingraderna utan skalar bort det mesta i nivåpresentationer och storlekar — för att mera prioritera det verkliga glädjeämnet: allmänna globala slaveriets utbredning: mera vinst, mera makt. SAMT att en del webbläsare (FIREFOX särskilt) INTE läser Symbol, alls — vad exakt Firefox läser är här inte känt (De bevisligt överlägset rent kulturellt utbildade programmakarna funderar på att utesluta Times New Roman också, eller?). Det är i vilket fall — så bevisat — INTE en webbläsare anpassad och utformad för naturvetenskapliga presentationer som kan produceras av vem som helst med internetabonnemang.
— För att undvika GLIDNINGAR, TABBFÖRSKJUTNINGAR och andra olika olägenheter som en del webbläsare envisas med i deras glada köptävlingar med att — SÅ — förstöra så mycket som möjligt av kunskapsinnehållet, har här bildkopior lagts in från originalen (de flesta perioden 1994-2006: Windows 3.1, Windows 95, Windows XP) — ev. tillsammans med raka kopierbara textversioner där så är påkallat.
S1 ¦ S2 ¦ S3
¦ S4
¦ S5
¦ Se även sammanställning i kalkylprogram
FÖRSTA SYSTEMINTEGRALEN i Tillämpade
EXEMPEL
— kraftfulla verktyg i
matematikanalysen:
• ALLA INTEGRALA LÖSNINGAR HÄR BLIR DIREKT BESTÄMDA EFTERSOM SERIELEDET ÄR FAKTORISERAT x-BEROENDE: integralen=noll om x=0.
• Fallen an+c+1=0 och (b–a)(m+1)=0 ger division med 0 — systemintegralen är inte (direkt) tillämplig för dessa fall.
• Systemintegralen kan INTE ge formen för ln x direkt eftersom den integralen är obestämd — däremot är integranden 1/(1+x) OK. Se exempel.
• x-värden större än 1 får seriesumman att växa över alla gränser. Se följande exempel.
• n-värden mindre än 1 garanterar oändliga seriesummor.
I modern akademi — BinomialTeoremets strukturkomponent stryks [‡] — kan systemintegralen inte utvecklas. Sättet
man skriver BT på komprimerat i den moderna akademins lärosystem utelämnar —
stryker, korrumperar, punkterar — kärnan: den fristående avgörande separata
strukturkomponenten (m+1)!. Formen kan inte användas — utom SÅ för formerad-dikterad statistik och kombinatorik. Jämför:
relaterad matematik — EULERS EKVIVALENTER — NOLLFORMSALGEBRAN:
(a+b)n = an[1 + m=0→nΣ [(b/a)(n–m)]m!/(m+1)!] ; a¦b¦n ; (1+1/∞)∞ = 1 + m=0→∞Σ [(1/∞)(∞)]m!/(m+1)! = 1 + m=0→∞Σ [1]m!/(m+1)!
= 1 + 1 + 1/2! + 1/3! + 1/4! + 1/5! + ... + 1/m! = e = 2,718 ...
modern akademi — MATEMATIKLEXIKON W&W 1991 s45-47
— Ordet BINOMIALTEOREM ingår f. ö. inte alls i källans boktext:
(a+b)n = an[1 + m=0→nΣ (b/a)mn!)/[(n–m)m!]] ; a¦b¦n ; (1+1/∞)∞ = 1 + m=0→∞Σ (1/∞)m∞!)/[(∞–m=∞)m!] = 1 + m=0→∞Σ 1/∞
= 1 + 1/∞ + 1/∞ + 1/∞ + 1/∞ + 1/∞ + ... +1/∞ = 1+ 0 = 1:
Punkter — dx = x/∞ = x · 1/∞ = A/∞ ≠ Δx = x/(n→∞) — kan inte adderas; det existerar inga oändliga mängder: MÄSTARLOGIKENS HUVUDSATS i relaterad matematik och fysik. Existerar inte i den moderna akademins lärosystem. I princip: grundligt bannlyst. Se även i ALLA TAL.
RESULTATBILD — MED BEVIS:
— Den moderna akademins matematiska idé STÄNGER VÄGEN FÖR människans fulla och fria INTELLEKTUELLA UTVECKLING [‡].
Det är en bevisbart trångsynt, inskränkt, träaktig, smalspårig, enögd, enbent existensföreteelse vars främsta bevisliga landvinning är omfattande naturmord.
— Kommunikationerna 1800+ ställdes in. Den korresponderande gemenskapen avlivades. Mänskligheten inträdde i den mänskliga kulturhistoriens allra mörkaste period. Jämför det moderna sättet att härleda e i Citat. Se även vidare i HÄRLEDNINGEN TILL FÖRSTA SYSTEMINTEGRALEN.
Vad gör Modern Akademi för fel i BT-ledet? Uttryckssättet med typen ”n över k” beskrivs f.ö. i bokkällan ovan på s45 (”binomialkoefficienter”);
binomialteoremets ekvivalenta
strukturform:
(b/a)m+1(n–m)!/(m+1)!; Exponent-Koefficientformen T/N = (n–m)!/(m+1)!;
BinomExponenten n insatt
i nämnarledet eliminerar naturliga strukturkriteriet: naturprocessernas
e-logaritmiska differentialekvationer. Se Den
Högre Analysen.
— SVAR: [‡] ”Att övervinna sin mänskliga begränsning och bli herre över universum”, ”Transire suum pectus mundoque potiri”: Fascistattityd. Relaterat.
Det är inte formalian som sådan; Matematiken är aldrig fel. Problemet gäller ATTITYDEN bakom: Den moderna akademins lärosystem 1800+:
Det är inget FEL i att formulera algebra och aritmetik som en typ ”Manipulerad Matematik” — om man klart och tydligt ANGER ATT SÅ ÄR FALLET. Att däremot upphöja tilltaget såsom kriterium på Speciellt Glänsande mänsklig Intelligens är något helt annat — och att också påtvinga studenter, mänskligheten, och elever att MERITERA I BETYG på sådant bevisligt fascistinspirerat kulturellt kloakutflöde: hävden i manipulerande överhet. Kulturmord: naturvandalisering.
Hur så? Den
uppenbara, här direkt bevisliga, avsaknaden av inblick i naturläran i den
moderna akademins lärosystem, med motsvarande kaxhävder.
— STRUKTURKOMPONENTEN — den fundamentala naturliga icke-manipulerade strukturella ordningen — i BT-ledet är ENTYDIGT RESERVERAD FÖR NUMERISKA KOEFFICIENTER i nämnaren (m+1) — inte täljardelar exponentiella (n). Införs täljarfaktorer (n) i nämnardelen, spolieras grundordningen.
— Varfördå?
— Därför — relaterad matematik och fysik TNED, Eulers Ekvivalenter — att BT-ledet innefattar naturliga logaritmens — talet e:s — fundamentala struktur såsom grundläggande fundamental för alla fysikaliska naturliga processer — naturliga strukturer — genom ett TIDSBEROENDE (t):
— dF/dt
leder till e-logaritmiska DIFFERENTIALEKVATIONER — varianter
och universaler BT-ledets grundval — som beskriver hela
floran av alla möjliga naturprocesser. Och därmed deras STRUKTUR — efter den
enda (förbannade) härledbara matematiska grundordning som alls existerar i
universum:
BT-ledet, Eulers Ekvivalenter.
— Genom att en exponentfaktor (n) införs i nämnarledet,
spolieras den naturligt strukturella ordningen. Och e framträder inte
längre: naturstrukturen är raderad. Det S5 är beviset.
Resultatbild:
NATURSTRUKTURERNA PREMIERAR INTE modern akademi: lärosystemet som utesluter naturstrukturerna för att hävda egen natursuveränitet på statistikens bevisligt manipulerande grunder. Naturen premierar Inte Kalhyggen: människans och djurens utveckling genom en Naturskog — icke modernAkademiskt Manipulerad Existensgrund — bevisar Det: Modern Akademisk Intelligens främjar NaturTeknikFientlig Marknad&Produktion — inte naturharmoni. Naturen premierar Inte Uppfunna Akademiska Strukturbegrepp såsom intelligensens mest högtstående. Säg igen. Lägg fram bevisen.
Naturordningen är Rättslära. Matematikgrunderna. UDHR10Dec1948. Rätten att få utvecklas som människa. Inte någon (förbannad) skyldighet att påtvingas utveckling som privat världsakademisk nationell ägodel: STATSFÖRVALTNINGENS FÖRBANNADE SKYLDIGHET ATT FRÄMJA PERSONLIGHETSUTVECKLINGEN men som åsidosätts för andra intressen: noll iakttagen naturrespekt. Dödspsykningar mot våldsvägrare under 150 år.
Säg igen. Visa. Lägg fram bevisen. Den moderna akademin — dess påstådda meningar om speciellt intelligensens hemvist — är så KÖRD den alls kan bli: Naturliga strukturer STRYKS och ersätts med Akademiskt Uppfunna Egna — som Statsförvaltningarna sedan också anser att Befolkningen ska Lära Sig; fascismens klassiskt historiska äresäten: absolut oinskränkt besluts- och bestämmanderätt. Tala sedan om omfattande kunskapsmörker, vidskepelser och djupgående vanföreställningar.
Jämför särskilt HÄRLEDNINGEN TILL PLANCKS STRÅLNINGSLAG från PLANCKS ENTROPISAMBAND I RELATERAD FYSIK OCH MATEMATIK: helt — intrinsiskt — rent från statistik. Naturordningen innehåller — garanterat — inga statistiska inslag.
Vi vill ytterst gärna se någon ynka minsta TENDENS till ett motbevis. Jätteintressant. Det räcker med ett, enda. Please.
Den nu Jan2019 världsetablerade statsorganiserade moderna akademins
allmänt påstådda intresse för naturvetenskap är härmed, och tydligen — starkt —
ifrågasatt: Inrättningens etablerade NaturTeknikFientliga Verksamhet — eng.
Enterprise — är uppenbar: Akt1800.
DRIFT[‡]— inte plan. ”Systemets egenrörelse”[‡] — inte planering. Människorättsliga Konsekvenslagen[‡] — eller Mänsklighetens Kulturutvecklingslag[‡]: Samhällen, kulturer, människor, föreningar som INTE utvecklar mänskliga rättigheter, utvecklar obönhörligt, oeftergivligt, oåterkalleligt ICKE mänskliga rättigheter. Det finns inga undantag, inga »halvfall», inga gränsfall, inga oklara detaljer eller händelseförlopp att gömma sig bakom och spela oskyldig, ingen dunkel historia att åberopa som ursäkt.
Rättsutövningen i Sverige, Europa generellt (och övriga världen) är — speciellt — sedan 1800-talet i den meningen inne på en totalt destruktiv väg som garanterat INTE leder framåt utan bakåt — som vi redan har sett åtskilliga naturbevis på, och i fortsatt växande. Maktbegär och auktoritär beslutstarvhet lägger grunden till utbrett efterapat våld, intrång och övergrepp mot allt och alla.
Den trenden kommer — garanterat i ljuset av nyligen antydda naturordning — inte att upphöra förrän statsförvaltningsfolket, samhällskraften som underhåller utvecklingen, lägger band på sig och inser att samhällsarbetet handlar om IAKTTAGANDE AV REDAN EXISTERANDE NATURLAGAR, aldrig om BESLUT — precis som BYGGNADSNÄMNDEN: hänsyn till HÅLLFASTHETSDETALJER: gravitation, elektricitet. INTE egna personliga önskemål.
Mänskliga rättigheter. INTE ”rikets säkerhet”: INTE fascism. Jorden ÄR rund. FÖRSVAR för rätten att utvecklas efter ”grundvalen för frihet, rättvisa och fred i världen”[‡] — Allt annat är, således, utövande förtryck: fascism, satanism, djävulsdyrkan, naturangrepp, intrång, jävulskap. Absolut gärna rätta om fel.
Har man — för tillfället
— ingen direkt lösning till en specifik (mera sammansatt) integrand, kan man i
vilket fall försöka med någon alternativ direkt numerisk lösning. Det ger
(oftast, vidare) ledtrådar som kan jämföras med uppnådda resultat på andra
vägar. Första Systemintegralen är ett sådant utmärkt verktyg. Genom att sätta
in alternativa koefficientvärden för cAaBbn formeras — framträder — specifika
integrander med integrala lösningar. Serieformerna har dock (relativa)
begränsningar som kräver viss förtrogenhet. Vi studerar några exempel.
Si1Ex1 ¦ Arcusintegranden för tangens x:
— Vi studerar TRIG8 hur en av integrandformerna i grundtablån, 1/(1 + x2) framträder ur systemintegralen:
S1 ¦ SYSTEMBAS: ![]() xc(Axa + Bxb)n dx
;
xc(Axa + Bxb)n dx
;
integrandOBJEKT: (1 + x2)–1 :
![]() xc(Axa + Bxb)n dx = xdAn[(1/d) + m=0→nΣ [xb–a(B/A)(n–m)]m!/(d+k)(m+1)!]
xc(Axa + Bxb)n dx = xdAn[(1/d) + m=0→nΣ [xb–a(B/A)(n–m)]m!/(d+k)(m+1)!]

KOEFFICIENTformat: c=0 ¦ A=B=1 ¦ a=0 ¦ b=2 ¦ n=–1 → xc(Axa + Bxb)n = (1 + x2)–1 ;
————————————
d = 1 ; k = 2(m+1) = 2m+2 ; d+k = 2m+3 ;
![]() (1
+ x2)–1 dx =
x[ 1 + m=0→∞Σ [xb–a(1)(–1–m)]m!/(2m+3)(m+1)!]
(1
+ x2)–1 dx =
x[ 1 + m=0→∞Σ [xb–a(1)(–1–m)]m!/(2m+3)(m+1)!]
INDEXERINGEN m=0→n med n=–1 betyder att serien saknar slut: m(=0)→∞:
Sista termen (binomialteoremets b^n) utgår, serien saknar slut;
— Vi noterar att (–1–m)m! = (–[1+m])m! ; (–1–m)]m!/(m+1)! = (–1)0(–1)1(–1)2... = (–1)m+1 ;
Ledformen efter insättningar som ovan:
—————————————
c=0 ¦ A=B=1 ¦ a=0 ¦ b=2 ¦ n=–1
= x[ 1 + m=0→∞Σ
[x2(–1)m+1]m!/(2m+3)]
= x[ 1 + m=0→∞Σ (–1)m+1x2(m+1)/(2m+3)]
Lösning — integralens numeriskt approximerade
summaform:
=
x( 1 – x2/3 + x4/5
– x6/7 + x8/9 – x10/11 +
… ) = m→∞limes atan
x : TestatOK
med insättningar i kalkylkort.
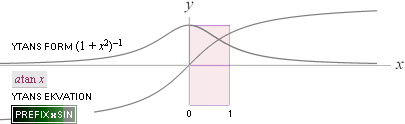
Med x=1 ges serien för
pi/4 = 0,785398163.. — serien konvergerar ytterst långsamt med x= eller nära 1:
— Vi ser (direkt,
exponenterna) att x>1 (tan>45°) medför att seriesumman växer över alla
gränser (x^n>>1/n då n→∞ om x>1).
— För att få ut värden
även för fallen x>1 kan inversen (arc)cotangensvärdet
användas tillsammans med en justerande subtraktion,
grader: ......... arctan3 =
90° — arctan1/3 ¦
radianer: ..... arctan3 = pi/2
— arctan1/3.
Med x<1 ges snabbare seriekonvergens:
Med x=0,5 behövs bara 13 delsummor för att få resultatet
atan 0,5 = 0,463647609 radianer = 26,565051177 grader = rad·180/pi .
Binomialteoremet är, i vilket fall, just
grunden för hela den praktiskt tillämpade matematiska aritmetiken. Så, vi har
stor nytta av serieformen ovan om det gäller att få inblick i GRUNDINTEGRALERNA maskineriet som hjälper oss förstå innehållet i tillvaron:
Universums Historia: relaterad matematik och fysik.
KALKYLKORT (Tabell3-6 ¦
GyroDec2018.ods): Systemintegralen SI1 har överförts till ett kalkylprogram (GratisOpenOffice) med
detaljerna inskrivna i (100st radsummerande) separata kalkylceller. Det
garanterar maximalt felfri presentation med detaljerad inblick, helt grundad på
ledformens algebraiska detaljer: fel får inte förekomma här.
Si1Ex2 ¦ Alternativ med en rotform:
hyperbelekvationens integrand:
— (HPi) ![]() x2/R
dx = (1/2)[xR
x2/R
dx = (1/2)[xR ![]() a ln(x + R)] ; R
= √x2±a — på den bestämda formen R = √1+x2
:
a ln(x + R)] ; R
= √x2±a — på den bestämda formen R = √1+x2
:
:
S2 ¦ SYSTEMBAS: ![]() xc(Axa + Bxb)n dx
;
xc(Axa + Bxb)n dx
;
integrandOBJEKT: √1+x2 = (1+x)1/2 :
![]() xc(Axa + Bxb)n dx = xdAn[(1/d) + m=0→nΣ [xb–a(B/A)(n–m)]m!/(d+k)(m+1)!]
xc(Axa + Bxb)n dx = xdAn[(1/d) + m=0→nΣ [xb–a(B/A)(n–m)]m!/(d+k)(m+1)!]

KOEFFICIENTformat: c=0 ¦ A=B=1 ¦ a=0 ¦ b=2 ¦ n=1/2 : → xc(Axa + Bxb)n = (1+x)1/2 ;
————————————
d = 1 ; k = 2(m+1) = 2m+2 ; d+k = 2m+3 ;
![]() (1
+ x)1/2 dx = x[ 1
+ m=0→∞Σ
[xb–a(1)(1/2
– m)]m!/(2m+3)(m+1)!]
(1
+ x)1/2 dx = x[ 1
+ m=0→∞Σ
[xb–a(1)(1/2
– m)]m!/(2m+3)(m+1)!]
INDEXERINGEN m=0→n med n=1/2 betyder att serien saknar slut: m(=0)→∞:
Sista termen utgår, serien saknar slut;
Ledformen efter insättningar som ovan:
—————————————
c=0 ¦ A=B=1 ¦ a=0 ¦ b=2 ¦ n=1/2
= x[ 1 + m=0→∞Σ [x2(1/2 – m)]m!/(2m+3)(m+1)!]
; (1/2 – m)]m! = x2(1/2)0x2(1/2–1)1x2(1/2–2)2x2(1/2–3)3x2(1/2–4)4x2(1/2–5)5
... TÄLJAREN:
; = x2(1/2)0x4(1/2–2/2)1x6(1/2–4/2)2x8(1/2–6/2)3x10(1/2–8/2)4x12(1/2–10/2)5
...
; = x2(1/2)0 x4(–1/2)1 x6(–3/2)2 x8(–5/2)3 x10(–7/2)4 x12(–9/2)5
...
; = x2(1/2)0
¦ x4(1/2)(–1/2)1 ¦ x6(1/2)(–1/2)(–3/2)2
¦ x8(1/2)(–1/2)(–3/2)(–5/2)3 ¦ x10(1/2)(–1/2)(–3/2)(–5/2)(–7/2)4
...
; = x2(1/2)0
¦ x4(–1/4)1
¦ x6(+3/8)2
¦ x8(–15/16)3
¦ x10(+105/32)4
...
; = x2(1!!/21)0
¦ x4(–1!!/22)1 ¦ x6(+3!!/23)2
¦ x8(–5!!/24)3
¦ (+7!!/25)4
...
[2m+3](m+1)! = [3]0(1!) [5]1(2!) [7]2(3!)
[9]3(4!) [11]4(5!) [13]5(6!) ... NÄMNAREN:
T/N = x2(1!!/21)0/[3]0(1!) ¦ x4(–1!!/22)1/[5]1(2!) ¦ x6(+3!!/23)2/[7]2(3!) ¦ x8(–5!!/24)3/[9]3(4!) ...
= x( 1 +
1!!x2/21·3·1!
– 1!!x4/22·5·2
+ 3!!x6/23·7·3!
– 5!!x8/24·9·4!
+ ... ) =
Udda SemiFakulteten: 1!! = 1; 3!! = 1·3; 5!! = 1·3·5; 7!! = 1·3·5·7; ...
= m→∞limes
(1/2)[ln(x+R) +
xR] ; R = √1+x2
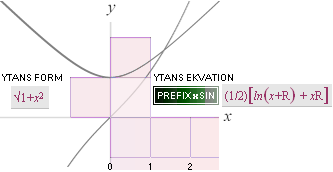
Från x=1 och större blir
seriesumman divergent, också i detta fall, och värdena blir missvisande.
— Med x=1 ger 100
delsummor integralvärdet
1,1477928048 medan den reguljära
integrallösningens samband ger värdet
1,1477935747. Seriesummor
med x-värden över 1 ger växande fel.
— Ingen arcusfunktion
(automatiska stopp och referensvärden) som i föregående fall finns här (direkt)
som kan hjälpa till med en inverterad anpassning. Och det blir också
systemintegralens allmänna praktiska begränsning:
— Systemintegralens
summaserier lämpar sig INTE (direkt) som verktyg för allmänna integrala
lösningar — ytberäkningar — över godtyckliga x-intervall genom godtyckligt
sammansatta funktioner.
Lösningens aritmetik återfaller, här,
istället på de reguljära logaritmiska serierna.
Se utförligt i FUNKTIONSKLASSERNA
I RELATERAD MATEMATIK.
Ytterligare Si1-exempel nedan.
Si1Ex3 ¦ Alternativ med en integrand med integral
logaritmisk lösning:
— Vi använder Si1-integranden (1 + x)–1 — dess integral finns inte med i grundintegralerna, men ansluter närmast till en obestämd make LOG6, Vi får den direkt ur LOG5 genom (P)=(1+x): Dn ln(P) = Dn(P)/P = 1/(1+x).
S3 ¦ SYSTEMBAS: ![]() xc(Axa + Bxb)n dx
;
xc(Axa + Bxb)n dx
;
integrandOBJEKT: 1/(1+x) = (1 + x)–1 :
![]() xc(Axa + Bxb)n dx = xdAn[(1/d) + m=0→nΣ [xb–a(B/A)(n–m)]m!/(d+k)(m+1)!]
xc(Axa + Bxb)n dx = xdAn[(1/d) + m=0→nΣ [xb–a(B/A)(n–m)]m!/(d+k)(m+1)!]

KOEFFICIENTformat: c=0 ¦ A=B=1 ¦ a=0 ¦ b=1 ¦ n=–1 : → xc(Axa + Bxb)n = (1 + x)–1 ;
————————————
d = 1 ; k = m+1 ; d+k = m+2 ;
![]() (1
+ x)–1 dx = x[ 1
+ m=0→∞Σ
[xb–a(1)(–1–m)]m!/(m+2)(m+1)!]
(1
+ x)–1 dx = x[ 1
+ m=0→∞Σ
[xb–a(1)(–1–m)]m!/(m+2)(m+1)!]
INDEXERINGEN m=0→n med n=–1 betyder att serien saknar slut: m(=0)→∞:
Sista termen utgår, serien saknar slut;
— Vi noterar att (–1–m)m! = (–[1+m])m! ; (–1–m)]m!/(m+1)! = (–1)0(–1)1(–1)2... = (–1)m+1 ;
Ledformen efter insättningar som ovan:
—————————————
c=0 ¦ A=B=1 ¦ a=0 ¦ b=1 ¦ n=–1 :
= x[ 1 + m=0→∞Σ [x(–1)m+1]m!/(m+2)(m+1)!]
= x[ 1 + m=0→∞Σ (–1)m+1xm+1/(m+2)]
= x(
1 –
x1/2 + x2/3 – x3/4
+ x4/5 – ... ) =
= m→∞limes ln(1 + x)
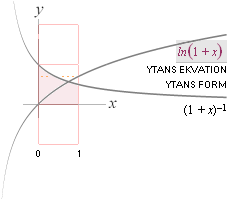
Från x=e-1=1,718 och
större blir seriesumman divergent och värdena blir alltmer missvisande.
— Men redan med x=1
konvergerar serien (mycket) långsamt: 100 delsummeringar ger
0,6982752508 mot reguljära aritmetiska
värdet ln(1+x)
0,6931471806.
Ju mera sammansatt Si1 är i speciellt
nämnaren, desto snabbare konvergens = många korrekta decimaler med få
delsummor.
I vilket fall är systemintegralen användbar
för att kontrollera basvärden — och visa det inre maskineriet. TIDEN (nämligen)
har en viss tendens att ämnen faller i glömska. Och utan NÅGON referens som kan
hjälpa till att damma av urtidens guldgruvor är det kört.
Si1Ex4 ¦ Alternativ med en produktintegrand — PREFIXxSIN:
— Vi använder Si1-integranden x2√(1–x2) = x2(1–x2)1/2 — dess integrala lösning finns inte upptagen i grundintegralerna. Integrallösningen här är hämtad från ett mera omfattande avsnitt med lösning av olika typer av systemintegraler (arbeten i MsWorks 4.0 perioden 1994-2006). Se lösningen i IntxN-lösningstablån 2001IX1.
S4 ¦ SYSTEMBAS: ![]() xc(Axa + Bxb)n dx
;
xc(Axa + Bxb)n dx
;
integrandOBJEKT: x2√(1–x2) = x2(1–x2)1/2 :
![]() xc(Axa + Bxb)n dx = xdAn[(1/d) + m=0→nΣ [xb–a(B/A)(n–m)]m!/(d+k)(m+1)!]
xc(Axa + Bxb)n dx = xdAn[(1/d) + m=0→nΣ [xb–a(B/A)(n–m)]m!/(d+k)(m+1)!]

KOEFFICIENTformat: c=2 ¦ A=1 ¦ a=0 ¦ B=–1 ¦ b=2 ¦ n=1/2 : → xc(Axa + Bxb)n = x2(1–x2)1/2 ;
————————————
d = 3 ; k = 2(m+1) = 2m+2 ; d+k = 2m+5 ;
![]() x2(1 – x2)1/2 dx = x3[ 1/3 + m=0→∞Σ
[x2(–1)(1/2
– m)]m!/(2m+5)(m+1)!]
x2(1 – x2)1/2 dx = x3[ 1/3 + m=0→∞Σ
[x2(–1)(1/2
– m)]m!/(2m+5)(m+1)!]
INDEXERINGEN m=0→n med n=–1 betyder att serien saknar slut: m(=0)→∞:
Sista termen utgår, serien saknar slut;
Ledformen efter insättningar som ovan:
—————————————
c=2 ¦ A=1 ¦ a=0 ¦ B=–1 ¦ b=2 ¦ n=1/2 :
= x3[ 1/3 + m=0→∞Σ
[x2(–1/2
– m)]m!/(2m+5)(m+1)!]
= x3[ 1/3 + m=0→∞Σ [(–[1/2 + m])x2]m+1/(2m+5)(m+1)!]
= x3( 1/3 – (1/2)1x2/5·1! + (3/2)2x4/7·2!
– (3/2)3x6/9·3! + (5/2)4x8/11·4!
– ... ) =
= x3/3 – (1/2)1x5/5·1! + (3/2)2x7/7·2!
– (5/2)3x9/9·3! + (7/2)4x11/11·4!
– ... =
= m→∞limes (1/4)[
(1/2)(acos x – xR) + x3R] ; R = √(1–x2)

Värden större än x=1 för
integrallösningen — ytans ekvation — ger inre negativt rotvärde: Normala
elektroniska kalkylatorer och kalkylprogram ställer inte upp på den typen:
visar FEL!, Overflow!, #VÄRDE! eller annat ”NowI’mFucked”. I grafritningen kan
vi hoppa över den spärren och rita ut positiva rotvärden som visar PRINCIPEN i
hela funktionsfönstret.
— Seriesumman med x=1 för
100 delsummeringar visar värdet
0,1964480473 att jämföra med
kalkylprogrammets
0,1963495408.
— Med x=0,5
uppnås tio decimaler redan efter 8 delsummor:
0,0383865531 seriesumman
0,0383865531
kalkylprogrammet
Si1Ex5 ¦ MatematikBasen:
SE ÄVEN I Integralreferenser RÄKNELAGARNA FÖR OÄNDLIGT
om ej redan bekant:
— Vi använder här här Eulers tal naturliga logaritmbasen e = (1+1/∞)∞ för att se efter hur första systemintegralen behandlar e integralt.
S5 ¦ SYSTEMBAS: ![]() xc(Axa + Bxb)n dx
;
xc(Axa + Bxb)n dx
;
integrandOBJEKT: (1+1/∞)∞ = e — Eulers tal, eller naturliga logaritmbasen :
![]() xc(Axa + Bxb)n dx = xdAn[(1/d) + m=0→nΣ [xb–a(B/A)(n–m)]m!/(d+k)(m+1)!]
xc(Axa + Bxb)n dx = xdAn[(1/d) + m=0→nΣ [xb–a(B/A)(n–m)]m!/(d+k)(m+1)!]

KOEFFICIENTformat: c=0 ¦ A=1 ¦ a=0 ¦ B=1/∞ ¦ b=0 ¦ n=∞ : → xc(Axa + Bxb)n = (1 + 1/∞)∞ ;
————————————
d = 1 ; k = 0 ; d+k = 1 ;
![]() (1 + 1/∞)∞ dx = x[ 1 + m=0→∞Σ
[1(1/∞)(∞)]m!/1(m+1)!] bannlyst
i den moderna akademins lärosystem
(1 + 1/∞)∞ dx = x[ 1 + m=0→∞Σ
[1(1/∞)(∞)]m!/1(m+1)!] bannlyst
i den moderna akademins lärosystem
Ledformen efter insättningar som ovan:
—————————————
d = 1 ; k = 0 ; d+k = 1 ;
= x ( 1 + m=0→∞Σ [1]m!/1(m+1)!)
= x ( 1
+ 1/1! + 1/2! + 1/3! + 1/4! +
1/5! + ... + 1/m!)
= x (e = 2,718...)
KALKYLKORTETS VÄRDE Si1Kalkyl ger också resultatet ovan:
— Med x=1 och
insättningen (t.ex) B=t15= 1×10^-15 och n=1/B=T15 ges värdet
2,718 281 8285 att
jämföra med direktvärdet EXP(1) = e^1
2,718 281 8285. Dvs.,
samma.
LÄNKEN i (1 + 1/∞)∞ VISAR EN ETABLERAD CITATKÄLLA SOM GARANTERAR HELA ÄMNESOMRÅDETS Eulers Ekvivalenter FULLKOMLIGA UTESLUTNING I DEN MODERNA AKADEMINS LÄROSYSTEM: finns inte. Existerar inte. ”Fel”.
Se även jämförelsen i INLEDNINGEN till Si1-exemplen:
— Den moderna akademins matematiska blotta idé STÄNGER VÄGEN FÖR människans fulla och fria INTELLEKTUELLA UTVECKLING [‡].
Så Bevisat.
BEKLÄMMANDE RESULTATBILD som
ingen vettig människa någonsin skulle önska se i text:
Eleverna tvingas underordna sig en märkbart fascistisk — uppfunnen på DRIFT, inte PLAN, regelbestämd av en Beslutande Majoritet — tankeordning. Absolut gärna rätta om fel. 1800+.
Naturordningen — härledda, inte uppfunna — grundbegrepp körs över: kalhyggen framträder ANALOGT. Absolut gärna rätta om fel. 1800+.
Naturordningen gynnar INTE profit, INTE fascism, INTE Bestämmande. ENBART samarbete, IAKTTAGANDE (Exempel: standardiserade byggnormer, industristandard för bygghållfasthet, etc. som främsta exempel: elementär maskinlära). Jorden ÄR rund.
Så: VAD, exakt på Jorden (nu Jan2019) är det som är så förskräckligt INTRESSANT i — eller med — PekApparaten?
What’sUp?
VARFÖR ANVÄNDER 2010+ en växande mängd FOLK
I MÄNGD PEKAPPARATER UNDER ÖPPEN HIMMEL? ÄR DET HANDIKAPPADE MÄNNISKOR? Är det
människor som har förlorat väsentliga hjärnfunktioner, som, nu, plötsligt, uppträder
i sådan enorm mängd? Beskurna Sinnesförnimmelser? Är det människor som måste ha
elektroniska stöd för att ta sig fram? Vart Tog Mänskligheten vägen? Vart tog
Människan vägen? 90KM/h betyder 25 M/S. 180KM/h betyder 50M/S — En hel BilLängd
varje 1/10 Sekund. Varje minsta avvikande FOKUS på ANNAT än bilkörningen i den
pacen, betyder — helt säkert — en antågande begravning, för den som kör, eller
andra. Elektroniska hjälpmedel? Lägg av.
Varför tilldrar sig INTE Naturen runt omkring STÖRRE fokus än Peken, MERA intresse, DJUPARE engagemang?
What’sUp?
INTE LEVER VÄL Mänskligheten i ett formidabelt, detaljerat bevisbart, kunskapsmörker, ett FÄNGELSE av vanföreställningar, vidskepelser — av en sort, slag och natur som ingen tidigare kultur skådat maken till?
— ”Såå många kan ju inte ha fel heller”.
Visa oss. Blända oss med Kunskapen. Undervisa oss.
Återigen: DET FINNS INGEN KORKAD KNÄPPGÖK SOM HAR TÄNKT UT SÅDANT som »konsekvensgenererat kollektivt kulturmord». DET, om det alls förekommer, är en DRIFT: Konsekvensen av att INTE iaktta ordningen i Naturen. Utan istället försöka [‡] ”övervinna sin mänskliga begränsning och bli herre över universum”: fascism. Satanism. Djävulsdyrkan.
Men det finns ingen sådan proklamation eller någon sådan erkänd bevekelsegrund.
DET är enbart resultatet av en naturordningens minutiöst bevisligt tankerättsliga autonomi. Jämför HÄVDEN, och SYSTER ”systemets egenrörelse”.
Jämför SVERIGES DOMSTOLAR — frihetens närmast bevisligt lokala högsäte: ”Vi kan inte underordna oss mänskliga rättigheter”.
Galileo Galilei 1632. ”Sluta med dom där dumheterna!”. Kinas behandling av Tibet, tibetanska buddhister: Sveriges behandling av våldsvägrare. Europas Diktatur.
— Stöd SÄPO [‡]: Personlighetens fria och fulla utveckling: RÅ, JK, JO, ... Banemännen för lösningen till mänsklighetens akuta energiproblem. Jättebra.
OM VI INTE FÅR TILLFÄLLE
ATT ÖVA OSS I ÄMNET — se vad som finns, hur det ser ut, hur det TER sig, hur
det ändras, hur det växlar, hur det formas — vad nytta har vi då av ... VAD för
något sa du gumman?
Matematiken — BLOMMORNA — är vårt liv —
liksom Kärleken är det. Slutar vi bry oss, slutar vi leva. Slutar vi engagera
oss i kärleksdjupen, är det döskallarnas riksdag som gäller.
— Ibland blir jag
fullständigt utmattad — sju veckor i sträck, inte en blund i ögonen: ingen
lösning i sikte. Alls. Jag vill inte se dig längre. I HATE you. Jag funderar på
att montera upp en artilleripjäs, längs med bokhyllan, och skjuta stora tvärhål
i alla Böcker, befria mig från Eländet. Hämnas. Rejält. Men eftersom Kärleken
är odödlig, segrar vettet alltid i slutänden. Och OM man får vila en stund, ger
det med sig. Alltid.
IntxN-lösningstablån 2001IX1
REFERENS till integrallösningsexemplet S4 — bildkopia från originalet SAMLING.wps i MsWorks 4.0 Windows 95:
Lösningen är
![]() x2√(1–x2)
dx = (1/4)[ (1/2)(acos x – xR) + x3R] med R=√(1–x2) enligt (bildkopia
av) IntxN-lösningstablån 2001IX1 för alla
integranden av typen xN(√a±x2)±1.
x2√(1–x2)
dx = (1/4)[ (1/2)(acos x – xR) + x3R] med R=√(1–x2) enligt (bildkopia
av) IntxN-lösningstablån 2001IX1 för alla
integranden av typen xN(√a±x2)±1.
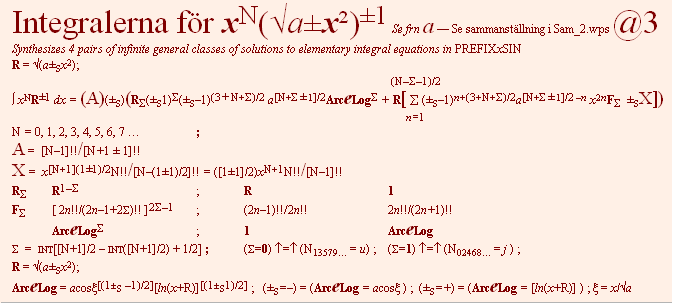
Förklaring:
FRÅN BÖRJAN — ruta ett
med Windows 3.1 (min historia från 1994) — fanns ambitionen att presentera
material av typen ovan på @INTERNET. Men som vi har sett genom historien 1994+
(idag Jan2019) har »mjukvaruindustrin» INTE haft naturvetenskapen som främsta
drivande äktenskapskonsult — tydligen som det får förstås och kan (be)visas i
detalj :
— Utomordentligt väl
fungerande HJÄLPMEDEL/verktyg som en gång tagits fram
— typ
MsWorks 4.0 (t.o.m. Hemköp sålde manualer) och därmed renderade tecken på
papper i mängd
— kasserades — definitiv
under perioden Windows Vista (2007). Världsledande Företagsamhet: kasserar
VERBALT användbara verktyg. Och därmed omöjliggör EN REDAN LÅNGT GÅNGEN
fortsatt NATURVETENSKAPLIG PRODUKTION PÅ REDAN VÄL FUNGERANDE VERKTYG.
Produktionen kördes bara över — med tendens att lägga i backen och backa över
också.
Får man göra så?
»Varför får jag inte SLUTFÖRA MITT
ARBETE?».
»Varför avbryts jag — ständigt — med
INTRÅNG UTIFRÅN?».
»Varför får jag inte ARBETA IFRED?».
— Varför då?
Uppenbarligen FÖR ATT inte — icke —
BEREDA MAXIMAL UTVECKLINGSPOTENTIAL ÅT ENSKILDA PRIVATPERSONER — »vi är
inte här för att hjälpa till med att UTVECKLA naturinsikterna, utan för att
profitera på dem» — UTAN ISTÄLLET FÖRSÖKA LÄGGA BESLAG PÅ SÅ MYCKET
EGENPROFITERANDE KRAFT SOM MÖJLIGT FÖR ATT — så, profiterande, utnyttjande —
TVINGA TROTTOARFOLKET som redan hunnit bli beroende av verktygen ATT KÖPA NYTT.
Profiteringsintressets löjligt uppenbara
främsta styrelseargument.
Jämför filmen The Company Men (Ben Affleck,
Tommy Lee Jones, Kevin Costner, 2010: konsekvenserna av, och upprördheten över,
att företagsamhet — historisk profit som oundvikligt leder till krasch:
uppsägningar, familjetragedier — demolerar människors engagemang).
Tillvaron för en del människor i vår tid
TER sig så: Företagsvärlden har övergått i utövande förnedrande, ett (jävla)
kloakHål.
Det
är som EFTER att ha köpt en ny bil ProduktionsÄgarFöretaget avvecklar
Hjulfunktionen och erbjuder nyinköp till extrapris.
Det finns inget ädelt i en sådan
företagshistoria, ingenting som har med naturvetenskap att göra.
Vad säger du? OM det finns ett särskilt
folk som anser att KAPITAL — pengar — styr naturvetenskapens utveckling VORE
det kul att få se ett enda praktiskt exempel på det. Hur så? Därför att vad vi
vet, förs naturvetenskapen framåt av engagerade arbetare på verkstadsgolven: Städerskor. Diskare. Tvättare.
Restaurangpersonal. Kockar. Servicefolk. Maskinoperatörer. Instrumentmakare.
Hantverkare. Artister. Engagemang — stil, klass, attityd — kan inte köpas för
pengar. Inte kunskapen heller: Produkter uppkommer ur material, kunskap och
engagemang. Inget annat. Jorden är rund.
Därför är och förblir tanken om VINST FÖR
PROFIT — inte för kulturell mångfald — en parasit på mänskligheten: driften att
ständigt vilja ha MER (Microsoft, Google, ...), att ALDRIG låta nöja sig med
LAGOM, att INTE utveckla företaget SÅ att alla andra människor också kan få
vara med och leva i livet UTAN TRAGEDIER, utan intrång. Det är ett ansvar som —
tydligen i global världsekonomisk mening — ännu väntar på föredömliga exempel:
iakttagande av en redan given naturordning: Jorden ÄR rund.
Vad vi vet idag Jan2019: Inte ett steg tas av människor som lever
under företagsvärldens inflytande på Jorden utan att MER miljöförstöring sker:
utarmning, förödelse, intellektuellt degenererande tänkande: teknik som
utnyttjas för naturmord I MENINGEN AV RAKT MOTSATT EFFEKT. Det vore underbart
om den meningen vore felaktig bara ytterst litet — så att resten rasar
självmant.
Se särskilda miljöbevis i sammanställning
från SYREFRÅGAN. NATTLYSANDE
MOLN och MAUNA LOA VARIATIONERNA om ej redan bekant.
Si1-Härledningen
Från 1997IX27 · Enhanced 2001III
Si1-Exemplen SiEx1 ¦ SiEx2 ¦ SiEx3 ¦ SiEx4 ¦ SiEx5
Det finns en
utpräglad bestämd [definit] aritmetisk integral som gäller för en
stor mängd av alla typer och klasser av integraler. Vi finner den genom att
tillämpa exponentialderivatan EXP7 i dess integrala form direkt på
binomialteoremet genom att integrera term för term. Med grund i
binomialteoremets enkla potensform (A+B)n framträder en generell struktur eller systemintegral.
FÖRSTA SYSTEMINTEGRALEN
Integralen till xc(Axa + Bxb)n
Utvecklingen och härledning till denna första systemintegralen är elementär då den arbetar direkt på BT binomialteoremets komprimerade summaform. Den kan härledas i olika enklare sammansättningar. Men vi genomför här den mest fullständiga. Vi studerar i detalj hur härledningen förlöper.
— Vi erinrar skrivsätten högerledHL vänsterledVL samt — relaterad matematik enligt BT — summaalgebrans
m=0\m[xa]m! = m=0→m[xa]m! = [xa]0[xa]1[xa]2 … [xa]m = xa(m+1). Se även i Potenslagarna och Logaritmlagarna.
Resultatbilden:

Härledningen:
UTGÅNGSPUNKT BT:
(A+B)n = An(1+ m=0→nΣ [(B/A)(n–m)]m!/(m+1)!) ;
binomialteoremets positiva form
Vi studerar nu hur HL ändras med tillagda termer i VL:
Steg
1:
(A+Bx)n = An(1+ m=0→nΣ [(Bx/A)(n–m)]m!/(m+1)!)
= An(1+ m=0→nΣ [(B/A)(n–m)]m!xm+1/(m+1)!) ;
Steg
2:
(A+Bxb)n = An(1+ m=0→nΣ [(B/A)(n–m)]m!xb(m+1)/(m+1)!)
Steg
3:
(Axa+Bxb)n = Anxan(1+ m=0→nΣ [(B/Axa)(n–m)]m!xb(m+1)/(m+1)!)
Tillagda A-faktorer formeras som A: egenExponent
Och ParentesExponent.
= Anxan(1+ m=0→nΣ [(B/A)(n–m)]m!x(b–a)(m+1)/(m+1)!)
= An( xan + xan m=0→nΣ [(B/A)(n–m)]m!x(b–a)(m+1)/(m+1)!)
= An( xan + m=0→nΣ [(B/A)(n–m)]m!x(b–a)(m+1)+an/(m+1)!)
— Men var kommer själva integralkonceptet in i bilden?
Integrationen sker i binomialteoremet på varje enskild term;
![]() (Axa+Bxb)n dx =
(Axa+Bxb)n dx = ![]() f(x1) dx +
f(x1) dx + ![]() f(x2) dx +
f(x2) dx + ![]() f(x3) dx +
f(x3) dx + ![]() f(x4) dx +
f(x4) dx + ![]() f(x5) dx + ...+
f(x5) dx + ...+![]() f(xN) dx
f(xN) dx
Summaledet syntetiserar dem ELEMENTÄRA GRÄNSSNITTETS FUNKTIONSRANGER i två basrangtermer,
den ena genom integralen ......... xan+ 1/[an+1]¦ EXP7 som addend till summadelen, och
den andra genom integralen ...... x(b–a)(m+1)+an + 1 = q/q i summadelen:
![]() (Axa+Bxb)n dx =
(Axa+Bxb)n dx =
An(xan+1/[an+1] + m=0→nΣ [(B/A)(n–m)]m!x(b–a)(m+1)+an + 1 = q/q(m+1)!)
![]()
Vi ser att den nu formerade systemintegralen blir bestämd direkt: x=0 ger nollvärde.
Prövningen för återderiveringen ges direkt av EXP7 exponentialderivatan; följ ovanstående baklänges.
Steg
4:
Utan större dramatik kan binomiala systemintegralen från Steg3 utvidgas med en potensbaserad variabel x framför integrandparentesen:
xc(Axa+Bxb)n = (xc/n[Axa + Bxb])n
= (Axa+c/n + Bxb+c/n)n
Vi insätter respektive a+c/n och b+c/n i seriens a och b:
![]()
= (b+c/n–a–c/n)(m+1) + an+cn/n
+ 1
= (b–a)(m+1) + an+c
+ 1
= k + d
![]()
— Det ger oss från Steg3 den slutliga, mera sammansatta, binomiala (första) systememintegralen enligt

ALLMÄNNA EGENSKAPER
FÖRSTA SYSTEMINTEGRALEN Si1 är baserad på integration
av enskilda x-potenser i binomialserien och är därför inte (direkt)
tillämplig på de goniometriska
relationsformerna sin, cos och tan. Se särskilt i SERIERNA FÖR SINUS OCH
COSINUS MEDi ¦ UTANi. Trigonometrins funktioner följer emellertid
själva också ur binomialserien varför vi likväl kan återfinna integralerna till
en del av trigonometrins funktionsuttryck. SPECIELLT finner vi en
representation av cyklometriska
funktioner — alltså arcusfunktioner som
vi har sett i SiEx1 och SiEx4.
Endast bestämda
integraler framträder
— Se förklaring i Bestämda
och Obestämda Integraler om ej redan bekant
Systemintegralen
Si1 kan i sin integrandform inte uttrycka formen för ln x direkt eftersom den
typintegralen är obestämd. Och på samma sätt beträffande alla övriga obestämda
[indefinita] integraler. Däremot kan Si1 ge integrala lösningar SiEx2 och SiEx3
som just ger e-logaritmens integraler
på bestämd form.
Reguljära integrala
exponentlösningar
INTEGRANDEN
xc(Axa + Bxb)n till Systemintegralen Si1 kan också skrivas I
PRINCIP på formen
(xb)n,
hela tal för b och n, om man sätter cAaBbn = 0 t10 0 1 b n:
—
Normalt sett kan A inte sättas 0 — ger division med 0. Men vi får ett gott
närmevärde genom att sätta A NÄRA noll, typ
A
= t10 = 0,0000000001.
—
Så visar Si1 t.ex. via integranden (x2)2 med x=0,5 integrala lösningsvärdet 0,0625 = x5/5
— vilket vi vet är integrala lösningen enligt EXP7. Med x=10 ges lösningsvärdet
20000,0000000667. Användbarheten är tydligt utmärkt.
—
I KALKYLKORTET till Si1 kan vi även, direkt, testa t.ex. typen (1+xb)n
cAaBbn
= 0101bn, bn bägge tal större än 1 för test
med
insättning av olika x-värden >1. EXEMPEL:
Integralen för (1+x²)² visar värdet 20676,6666666667 med x=10 korrekt
enligt integrallösningen EXP7:
![]() (1+x²)² dx =
(1+x²)² dx = ![]() (1+x²)(1+x²)dx =
(1+x²)(1+x²)dx = ![]() (1 + 2x² + x4)dx =
(1 + 2x² + x4)dx = ![]() 1dx +
1dx + ![]() 2x²dx +
2x²dx + ![]() x4dx = x + 2x3/3 + x5/5
x4dx = x + 2x3/3 + x5/5
=
10 + 2000/3 + 100.000/5 = 676 + 2/3 + 20.000 = 20.676 + 2/3.
SPECIELLA NOTERINGAR
Som vi har sett från Si1-Exemplen SiEx1 ¦ SiEx2
¦ SiEx3
¦ SiEx4
är summaseriens numeriska värden divergenta för oändliga serier (växer
över alla gränser) med (generellt) x>1.
Ur den rent allmänt
praktiska synvinkeln, är alltså
Si1-verktyget mindre lämpligt för allmänna integrala (numeriska)
lösningar. Emellertid som noterats ovan, är det en regel med undantag: Det
FINNS möjligheter att få fram integrala lösningar med x-inmatningar >1.
Allt beror på DEN INTEGRALA STRUKTUREN.
Däremot som allmänt verktyg för att kontrollera
DE OFTA MYCKET
ARBETSKRÄVANDE och tålamodspåfrestande SYSTEMINTEGRALA UTVECKLINGARNA, eller
andra integrala resultat
resultat från separata oberoende arbeten, blir Si1 ett självskrivet,
helt utomordentligt användbart testverktyg.
Se även de olika ARITMETISKA SUMMASTRUKTURERNA i FUNKTIONSBEGREPPET Funktionsklasserna i relaterad matematik för matematikens olika funktionsgrupper exponentiella, logaritmiska och trigonometriska.
Si1-representationen i kalkylkort
— GyroDec2018.ods Tab3-6
FÖRSTA
SYSTEMINTEGRALEN
![]()
För att säkra alla möjliga misstag, felskrivningar, överföringsfel, och annat traditionellt känt litterärt sull som verkar omöjligt att bli av med i någon första författning, har Si1-ledet insatts i (GratisOpenOffice) ett kalkylprogram som garanterar test på varje särskilt uttryck för sig via inmatning av de sex koefficienterna i d och k som ovan. Samt ett lämpligt x-värde (generellt <=1 för oändliga serier).
— Följande fyra separata kalkylkort har testats med alternativa utbrytningar som ger något olika algebraiska Si1-teckningar.
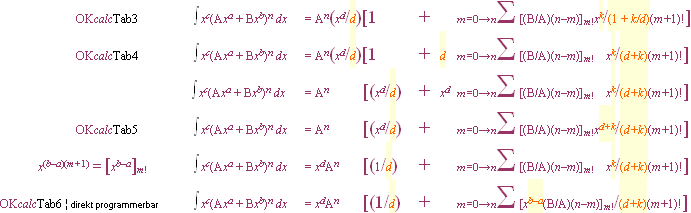
Notera
BT binomialteoremets n<1: Sista termen utgår och
serien blir ändlös: m=0→∞.
Ledformen närmast (Tab6) ovan är den som är den mest (direkt) enkla att programmera.
PROGRAMEXEMPEL I Borlands Turbo Pascal (DELPHI 4), Si1Ex4:
programform Test ![]()
integrandOBJEKT: x2√(1–x2) = x2(1–x2)1/2 :
x:=
0.5; y:= 1/3; R:= 1;
for I:= 0 to 5 do begin R:= -R*x*x*(1/2 - I)/(I+1); y:= y
+ R/(2*I+5); end;
y:=
y*x*x*x;
ClipBoard.AsText:=
FloatToStr(y); {0,038386561935016}
[x i acos x (PREFIXxSIN) i radianer]. Vi noterar i dessa sammanhang att ju mera sammansatt systemintegralen är, desto mera sannolikt uttrycker serien en mycket snabb konvergens. I exemplet ovan behövs endast 5 delsummeringar för att få minst motsvarande antal korrekta decimaler. Det är emellertid en regel med vassa kanter; i vissa lägen kan man få en serie med extremt långsam konvergens (jämför serien för atan med x nära 1). Som vi ser av exemplen, bestäms ( i allmänhet) seriens konvergens av x-värdet — litet x, snabb lösning med många decimaler — men även av seriens egen struktur.
DIALtransEX
DIFFERENTIALTRANSFORMATIONER I EXEMPEL — ofta kärnan i en integrals aktuella praktiska lösning, enligt exempel
Listade tillämpningsexempel i
Universums Historia (-2018):
EXEMPEL (Jan2019) I UNIVERSUMS HISTORIA SOM VISAR HUR DIFFERENTIALTRANSFORMATIONER KAN UTFÖRAS:
Exemplen erinrar
tillvägagångssättet i praktiska tillämpningar
ALLA EXEMPEL OCH UTVECKLINGAR I PREFIXxSIN

IndMag_Magnetismen:
[‡] ¦ [‡] ......... ds till db: x/s = tanb. s= x/tanb; ds/db = Dn s = s’ ger ds = Dn s db = Dn (x/tanb) db = (–x/cos2b) db
[‡] ................. db = d(s/x) = ds/x
[‡] ................. DIFFERENTIALTRANSFORMATION referens med
några exempel
IndMagAppendix2:
[‡] ................. dB/ds = sinbP/r²; dB/db = sinbP/x
InduktionenOchMagnetismen:
[‡] ................. ds/db=–x/cos²b=–x/(x²/r²)=–r²/x; db=–x/r²ds
MatElementarytorna:
[‡] ................. da/ds = Dn a = Dn s/r = 1/r ; ds = r da
MatematikenAnalys:
[‡] ................. LÄNKAR
MatematikenAnalysEXPINT:
[‡] ................. dR = Dn R dx = (1/2)(–2x)/R dx = –x/R dx
[‡] ................. dξ = Dn ξ dx = (1/√a) dx;
dx = dξ √a
MatematikenAnalysPALM:
[‡] ................. d(eF(x))/dx = Dn eF(x) = eF(x) Dn F(x) = eF(x) f (x) ; dx = d(eF(x)) / eF(x) f (x)
[‡] ................. dx²/dx = Dn x² = 2x ; dx² = 2x dx
[‡] ................. dR = Dn R dx = (1/2)(–2x)/R dx = –x/R dx ; insättning ger x dR = x(–x/R dx)=–x²/R dx
Solfysiken:
[‡] ................. dV till drR: dV/dr=V’=(4π/3) Dn r³=(4π/3) · 3r²=4πr² som ger dV=4πr²dr med r=rR
STS — SÄRSKILDA TRIGONOMETRISKA SAMBAND från VST i PREFIXxSIN —
Sammanställda (inte tidigare presenterade i Universums Historia) från föregående arbeten (Jun1984)
En del av sambanden är speciellt användbara vid lösning och utveckling av integraler. Se (STS¦1) exempel i Secans och Cosecans integraler och IRa (STS¦8).
— Sambanden nedan från kalkylprogram som visar och bevisar att samhörigheter och samband är konsistenta, numeriskt kontrollerade och så tillförlitliga.
GyroDec2018.ods Tab2
Sambanden
[N] utvecklade efter VST
Vinkelsummateoremets numrerade (N) samband enligt följande noteringar:
—————————————————————————————————————————————
1. Följer av (13) genom B=0.
2. Följer av (11) genom B=0 (sin0=1: sinA
– 1 = – 2(cos A/2)2 .
3. Följer av (13) genom B=90 (cos90=1)
som ger cosA + 1 = 2cos(A+90)/2 · sin(A+90)/2
— där
vi (analys) finner att sin(A–90)/2 = cos(A+90)/2, se figuren nedan:
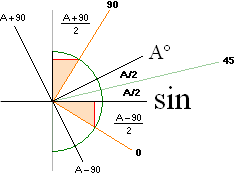
4. Följer av (2) genom B=A som ger sin2A = (sinA)2 – (cosA)2 där
(r=1): [y/r = cosA]2 = 1 – [x/r = sinA]2.
Dvs., sin2A = 2(sinA)2 – 1,
[6] .
Med
konversionen (sinA)2 = 1/(1 + [tanA]2) — GRUNDKONVERSIONERNA — ges så [4].
5. Se omvändningen av [2]: cosA.
6. Se [4].
7. Se omvändningen av [6]: sinA. Följer
även direkt ur VST12 genom
B=0; 1 + sinA = 2(sin A/2)2.
KALKYLKORTEN TILL GYROFYSIKEN och
TYNGDCIRKLARNA och 3D-geometrin
KALKYLKORT — GyroDec2018.ods
GyroDec2018.ods från Dec2018-Feb2019
Kalkylkortet nedan DIREKT FRÅN DEN
HÄR WEBBLÄSAREN GyroDec2018.ods — se
öppningsmanual
om ej redan bekant — eller kopiera
URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att
SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på
datorn)
http://www.universumshistoria.se/AaKort/GyroDec2018.ods
Tabell 1-6¦+7Matematiken3D— 3D-Cirklarnas Ellipser i Linjärperspektiv
Tabell 1 — ALLA I GYRODOKUMENTET FÖREKOMMANDE RESULTATREDOVISNINGAR

GyroHoriz¦f(FALL)
GyroPrecessionen ¦ SpinnMinimum ¦ Horiz.=0°A
detalj R r t V m¦KP r¦mM M¦NM
SPINwheel Calculate Time t Wheel
SPINwheel Calculate Frequency f Wheel
GyroEquatorialWheel Calculating Frequency f momentarily Wheel
SpinningWheel FORCE Parameters
IDEAL GYRO CONSTRUCT BIKE-f-Wh momentarily
Tabell 2 — KOMPLETTERANDE TRIGONOMETRITABELL i detta dokument
Tabell 3-6 — FÖRSTA SYSTEMINTEGRALEN I KALKYLCELLER i detta dokument — Se BESKRIVNING

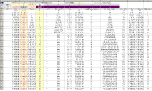
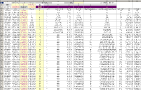
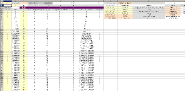
Tabell 7 — Cirklarnas ELLIPSER I LINJÄRA PERSPEKTIV i detta dokument — Se ExempelBESKRIVNING

Universums Historia — Mänskliga Rättigheter
SVERIGE UTVECKLAR INTE MÄNNISKORÄTT — INTERNET UTVECKLAR INTE MÄNNISKORÄTT —mänskligheten
EUROPA UTVECKLAR INTE MÄNNISKORÄTT — POLISEN UTVECKLAR INTE MÄNNISKORÄTT — åklagare — domare — domstolar
— Hej.
— Hej.
— Vet du var man närmast
kan läsa om Deklarationen för de mänskliga rättigheterna?
— VAD HETTE BLANKETTEN FÖRNÅGOT
SA DU!?
...
— Nä, nä. Det är ingenting som vi sysslar med
dagligdags. Hör efter på biblioteket.
POLISEN SVERIGE 1990+.
Befolkningen har ingen som helst — ens —
ANING.
VI kan INTE anklaga någon
för att vara okunnig. Absolut aldrig.
Däremot ATTITYDEN när
visdomen försöker hälsa på. Tilltalet. Det personligt ofrånkomliga tilltalet.
SVERIGES
DOMSTOLAR. Närmast.
Avskogningsbeviset skärps — kemibevis framträder | G | SlutTestet |
Detaljer i
K-cellens matematiska fysik i förtydligade fullständiga härledningsblock — Kompletterande
MaunaLoaBevis — Mänskliga Rättigheter
Alla utvecklingsdetaljer
i Universums Historia grundas HELT på den matematiska fysiken från CHEOPS
REKTANGEL:
Se även från MEL1 och MEL 2. SOLFYSIKEN I TNED TESTAS ¦

Alltmer försvinner av UrNaturen i Sverige. Nersågat Ursprung. Sagolik Fägring Borta.Fågelsång Borta. Lugn Borta.
Ekona växer. Bullret tilltar. Övermodet grönskar: ViHugga--NiVäxa:
ViSäga--NiGöra. Urladdningen kommer. Bergsäkert.
Universums Historia — TYNGDCIRKLARNAS
INTEGRALA MATEMATIK
innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER
Universums Historia — TYNGDCIRKLARNAS INTEGRALA MATEMATIK
ämnesrubriker
innehåll
INLEDNING MED RUBRIKER
TYNGDCIRKLARNAS
INTEGRALA MATEMATIK
STATISKA MOMENTETS ETABLERADE
NOMENKLATUR
BETECKNINGAR MED INTEGRALA
EXEMPEL
TYNGDCIRKELRADIENS INTEGRALFORM
INTEGRALA MOMENTET Ĵ — j-flex: — konv. ofta ” J
”: tröghetsmoment
Statiska och Dynamiska
Tyngdcirkelradierna
Praktiskt exempel — Statisk och
Dynamisk Tyngdcirkel
Integrala moment och tyngdradier
INTEGRALA EXEMPEL MED DYNAMISKA
TYNGDRADIECIRKLAR
Sammanställning Kon Sfär Cylinder
ROTERANDE KROPPARS VARVTALSACCELERATIONER — och deras praktiska rotationsstabila funktion (Ex3)
MomEx1 — Webbexempel: Kedja som
accelererar Hjul
MomEx2 — En Klassiker:
Industricylinder med repkopplat lod
MomEx3 — Gyrofysiken:
Köksexperiment med mässingssnurra
INTEGRALREFERENSER — Integrallista
i Universums Historia
UPPTAGNA
INTEGRALER, Alla Webbsidor — Löpande UH-dokumenten: DEL 1
UPPTAGNA
INTEGRALER, Alla Webbsidor — Löpande UH-dokumenten: DEL 2
HYPERBOLISKA
PRODUKTINTEGRALENS INTEGRALER
KOMPLETTERANDE
GRUNDINTEGRALER
SÄRSKILDA
TRIGONOMETRISKA RELATIONER
KOMPLETTERANDE
GRUNDINTEGRALER
Hyperboliska Produktintegralen
INTEGRALERNAS ARITMETIK — ![]() xc(Axa + Bxb)n
dx
xc(Axa + Bxb)n
dx
Webbläsarna
klarar inte naturvetenskapen
FÖRSTA
SYSTEMINTEGRALEN — exemplen Si1-Si5
BT-ledet — EULERS EKVIVALENTER
INGÅR INTE I MODERN AKADEMI
Si1Ex1 ¦
Arcusintegranden för tangens x
Si1Ex2 ¦
Hyperbelekvationens integrand
Si1Ex3 ¦ Integral
logaritmisk lösning
Si1Ex4 ¦ Integral
med produktintegrand
Si1Ex5 ¦
MatematikBasen: e-integralen
HÄRLEDNINGEN TILL FÖRSTA SYSTEMINTEGRALEN
Si1-representationen
i kalkylkort
DIFFERENTIALTRANSFORMATIONER
I EXEMPEL — Listade förekomster i Universums Historia -2018
SÄRSKILDA
TRIGONOMETRISKA SAMBAND från VST i PREFIXxSIN
SVERIGE
UTVECKLAR INTE MÄNNISKORÄTT
referenser
[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw--Hill 1967
Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.
mn = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]
me = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för me , Table 1.4 s7–27 för u]
u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]
u = 1,66033
t27 KG .............. atomära
massenheten [ENCARTA 99 Molecular Weight]
u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]
u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL--506W (2005)]
u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]
u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],
CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]
c0 = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970--talet)]
h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]
e = 1,602 t19 C ...................... elektriska elementarkvantumet, elektronens laddning [FOCUS MATERIEN 1975 s666ö]
ε0 = 8,8543 t12 C/VM ............. elektriska konstanten i vakuum [FOCUS MATERIEN 1975 s666ö]
[FM]. FOCUS MATERIEN 1975, FOCUS UPPSLAGSBÖCKER · STOCKHOLM — Andra
reviderade upplagan 1975 — ALMQVIST & WIKSELL FÖRLAG AB, STOCKHOLM
1965,
Fysikens, kemins och astronomins
historia — Allt från atomen till universum — fysik, kemi, jordvetenskap och
astronomi — Register med appendix.
[BA]. BONNIERS ASTRONOMI 1978 Det internationella standardverket om universum sammanställt vid universitetet i Cambridge — The Cambridge Encyclopeadia of Astronomy 1977
[BKL]. BONNIERS KONVERSATIONS LEXIKON Band I--XII med SUPPLEMENT, Alb. Bonniers Boktryckeri, Stockholm 1922--1929
SIGMA 1--6, MATEMATIKENS KULTURHISTORIA av James R. Newman, Forum 1965, efter originalet The world of mathematics 1956
t för 10–, T för 10+, förenklade exponentbeteckningar
MAC, i Universums Historia ofta använd förkortning för Modern Akademi (eng. Modern ACademy)
TNED — Related PHYSICS And MATHEMATICS — Se särskild djupbeskrivning av innebörden i begreppet relaterad framställning.
(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också
RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.
SHORT ENGLISH —
TNED in general is not found @INTERNET except under this domain
(Universe[s]History, introduced @INTERNET 2008VII3).
TNED or Toroid
Nuclear Electromechanical Dynamics is the dynamically equivalent resulting
description following the deductions in THE PLANCK RING, analogous AtomNucleus’
Deduction. The description according to TNED is related,
meaning: all, each, details claim to be fully logically explainable and
understandable, or not at all. With TNED is (hence) also understood RELATED
PHYSICS AND MATHEMATICS. See also the emergence of the term TNED in AtomNucleus’
Deduction.
Senast uppdaterade version: 2025-02-23
*END.
Stavningskontrollerat 2019-02-09.
rester
*
åter till
portalsidan
· portalsidan är
www.UniversumsHistoria.se
√
ω τ π ρ λ γ ħ ε Δ →
∞ UNICODE — ofta använda tecken i matematiska--tekniska--naturvetenskapliga
beskrivningar
σ
ρ ν ν π τ γ λ η ≠ √ ħ
ω → ∞ ≡
Ω
Φ Ψ Σ Π Ξ Λ Θ Δ
α
β γ δ ε λ θ κ π ρ τ φ
ϕ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫
≤ ≈ ≥ ˂ ˃ ˂ ˃ ← ↑
↨ → ∞ ↓ ↔
ϑ
ζ ξ
Pilsymboler, direkt via tangentbordet: Alt+24 ↑; Alt+25
↓; Alt+26 →; Alt+27 ←; Alt+22 ▬ Alt+23 ↨ ingen
horisontell make finns via Alt+.
Alt+23
↨ — även Alt+18 ↕; Alt+29 ↔
PNG--justerad 2011--06--25
åter till
portalsidan
· portalsidan är
www.UniversumsHistoria.se