NEUTRINOBEGREPPET I SOLFYSIKEN ENLIGT RELATERAD FYSIK | 2010V|VII | en BellDHARMA produktion | Senast uppdaterade version: 2012-02-17 · Universums Historia · relaterad fysik och matematik

 

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER  ·  förteckning över alla webbsidor

 

 · Moderna Akademins Solära Neutrinoproblem · Solära Neutrinoproblemet ·  Tabellmatematiken · Vilka säkra slutsatser kan dras av resultaten? · NEUTRINOBEGREPPET I RELATERAD FYSIK ·

 

 

·          OPERA-projekt bekräftar TNED

·          Neutrinoandelen från Solen — 1967: 3%; 2010: 1% ...

 

 

 

Neutrinostrålningen från Solen — Resultatredovisning · Grovberäkning · Neutrinobegreppet i TNED · Neutrinotvärsnittet · Strålningstvärsnittet · Kalkylkortet · 

 

 

a-b 1,6% av Solmassan

 

SSM i TNED

Standardiserade Solmodellen i TNED

Databaserna för neutrinoberäkningarna i TNED

 

 

Bahcalls neutrinotoleranser

σ grafer

 

 

neutrinotvärsnittet σ som funktion av neutrinoenergin

σ tabeller

tabelldata Bahcall 1997

 

 

 

Observerat tillfälligt avbrott i http://www.sns.ias.edu/-källan 2010-05-23 ”webbsidan kan inte visas”; sedan åter OK (testat dagen efter). Två av dessa webbreferenser används här.

 

 

 

Solära neutrinoproblemet i modern akademi

 

Se även direkt Kort snabbgenomgång — om inte redan bekant i detaljerna

FÖR KONVENTIONELL BESKRIVNING AV NEUTRINOBEGREPPET se senaste sammanställning i

@INTERNET Wikipedia Neutrino 2010-05-23

 

Solära neutrinoproblemet i Modern Akademi

PROBLEMET ÄR FÖLJANDE:

 

SOLEN ENLIGT TNED — men inte enligt modern akademi — är tillräckligt tät i kärnan (8,13444 T16 KG/M³) för att verkställa COMPTONDÄMPNING av den neutrinostrålning som frigörs genom fusionsfasen: strålningens ljusenergi överförs till mekanisk rörelseenergi för Solmassans atomer.

 

Nedanstående inledande resultatredovisning visar hur två något olika KONVENTIONELLA databaskällor med grundsamband för neutrinotvärsnittet har använts för att få fram resultaten enligt TNED (Peltoniemi 1999 och Bahcall 1997, referenser nedan). En sammanställd graf med Bahcall-Peltoniemis databaser finns på Bahcalls toleranser. Den inbördes skillnaden Bahcall-Peltoniemi är (som vi ser) mycket liten relativt Bahcalls egna interna osäkerhetsmarginaler. Men den inbördes skillnaden i nettovärden (nedan) är ändå SÅ katastrofalt stor för varje preciserad analys att BÄGGE uppenbarligen inte kan gälla. Man får i respektive fall slutresultaten (ungefärligt) med andelen neutrinoenergi som lämnar Solen i förhållande till hela Solenergin:

Inledande resultatredovisning

 

 

 

(databas: Peltoniemi99) med x=0,0013:

ANDEL NEUTRINOENERGI FRÅN SOLEN [3,12201% med x=0,0013] [26,73 MeV; 3,36077%; 0,89833 MeV; / (28,774); = 3,12201%]

3,12%

Delandel i de 3,36077%:en — hur värdena beräknas, se i Fördelningen

0,9MeV            70%

27MeV             3%

1-27MeV          27%

—————————

summa              100%

 

(databas: Bahcall97TableIIBestFit) med x=0,0013:

ANDEL NEUTRINOENERGI FRÅN SOLEN [1,04757% med x=0,0013] [26,73 MeV; 1,12769%; 0,30143 MeV; / (28,774); = 1,04757%]

1,05%

Delandel i de 1,12769%:en — hur värdena beräknas, se i Fördelningen

0,3MeV            81%

27MeV             1%

1-27MeV          18%

—————————

summa              100%

 

 

 

Den inbördes skillnaden mellan Peltoniemi och Bahcall är nära 3:1 vilket helt utesluter att bägge är giltiga. Men det betyder också att motsvarande krav på precision ställs i varje mätande anordning för att kunna avgöra vad som gäller i praktiken.

 

Nedan beskrivs (vidare) kortfattat hur Solära neutrinoproblemet framträder i MAC (modern akademi).

 

 

 

Kort snabbgenomgång — Solära neutrinoproblemet i modern vetenskap

 

Kort snabbgenomgång — med anknytning till

SOLÄRA NEUTRINOPROBLEMET I MODERN AKADEMI OCH VETENSKAP

Solära Neutrinoproblemets uppsegling · Neutrinoproblemet ·

 

 

 

Solära Neutrinoproblemets uppsegling

 

Med en kort hållen essens; Man hade (runt 1960) räknat fram följande teoretiska värdetabell i fallet Solen:

 

 

 

 

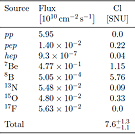
Källa:

s12, Table 1.3 (teoretiska värden enligt SSM)

PRINCETON BOREXINO GROUP - ANALYSIS CLUSTER — Chapter 1: The Physics of Low Energy Solar Neutrinos (2003)

http://borex.princeton.edu/public-docs/theses/pocar_phd_by_chapter/pocar_phd_chapter1.pdf

 

 

 

Tabellkolumnen markerad Cl motsvarar uppställningen i den först experimentellt förväntade neutrinoförekomsten i Solflödet från slutet av 1960-talet (från 1967) — man använde flytande KLOR-baserad neutrinoreagens som mätbas. Som vi ser står det ”0,0” för kollisionsfusionstypen pp. Typen pp betyder proton-proton, och utgör första länken i den totala kolliderande kedja av förenande atomkärnor som enligt SSM leder till slutprodukten med en Helium-4-kärna från fyra Vätekärnor — och som IN TILL 99% UTGÖR HUVUDDELEN AV KOLLISIONSFUSIONERNA.

 

Men varför står det då ”0,0” — just där det som mest behöver stå något alls?

— Därför att experimentanordning saknade DEN känsligheten: man mätte runt sagt — som ovanstående källförfattare målande beskriver saken (citatet nedan)

 

Den uppmätta neutrinoandelen

s24n:

”The Sun has proven to be a powerful natural neutrino source, but most of what we have understood from solar neutrinos has been obtained from only the neutrinos at the high end of the energy spectrum, which make up about 1 part in 104 of the total solar neutrino flux.”,

 

 

— på 1/10 000 av hela besättningen; Långt ifrån den HELHET som (nog) de allra flesta som (ytligt) läser typ POPULÄRA WEBBKÄLLOR ”ser” i presentationen (kvantiteterna 1/3 och 2/3 är ofta förekommande med ”expected” och ”measured”). Nämligen själva det experimentellt framhållna MÄTRESULTATET från den FORTFARANDE ENLIGT SSM helt ringa observerade andelen en tiotusendel av hela Solflödet [se citatreferensen ovan]:

Neutrinoproblemet

Därmed Solära Neutrinoproblemets uppsegling:

 

2,56/7,6Cl-KOLUMNEN i Tabellen  = 0,3368421 ~ 1/3

 

s11n:

”The experiment successfully detected solar neutrinos (mainly 7Be, 8B and CNO ones, see tables 1.1 and 1.2); the average neutrino capture rate after 25 years of data taking is [25]

 

             RHomestake = 2.56 ± 0.16 (stat.) ± 0.16 (syst.) SNU              (1.15)

 

where 1 SNU (Standard Neutrino Unit) is defined as 10−36 captures per target atom per second (i.e. one argon atom every few days!). Solar neutrino fluxes predicted by the SSM are presented in table 1.3. According to this table, the Homestake result (a Chlorine experiment) is only one-third of the predicted value. This discrepancy was noted (with much bigger uncertainties) from the early days of the Homestake experiment and represented the so-called solar neutrino problem [26].”

 

 

Bara en tredjedel infann sig — men, och alltså, ingalunda kopplat till HELA Solflödet, bara till den del som kvarstår sedan man skalat bort huvuddelen (Se ovanstående citat) med kollisionsfusionstypen (pp) — och som man ännu (Maj2010) inte har instrumentella resurser för att penetrera.

 

MED VIDARE EXPERIMENT — på samma typ av strängt avgränsade neutrinoenergier, just med hänsyn till den mätande anordningens begränsade känslighet — infann sig så ett ANDRA Solära Neutrinoproblemet — och sedan också ett TREDJE Solära Neutrinoproblemet.

 

Andra och tredje Solära neutrinoproblemen

 

Detaljerna beskrivs ingående i ovan nämnda källförfattning (PRINCETON BOREXINO GROUP; s13, ”This neutrino deficit, completely independent of the solar model, became known as the second solar neutrino problem”, s14, ”Hence, the third solar neutrino problem.”).

 

— En tredjedel av 1/10 000.

Inte 1/3 av 1.

 

— ANDELEN av den övervägande andelen pp-fusioner i hela Solomsättningen beräknas enligt SSM (»enkelt» för den som känner grunderna) enligt [se även särskilda citatreferenser i Konventionella Neutrinoandelen i Solen]

 

1H11,518              +          1H11,518              =          1H22,917              1,442 exoMeV

 

Ett par elektronmassor bortfaller (±e, 1,02 MeV) för varje pp-fusion [en positron bildas ur pp-fusionen, och positronen annihileras tillsammans med en elektron], vilket ger återstoden (utan extra rörelseenergi)

neutrinoenergin från pp-fusionen = 1,442 – 1,02 = 0,422 MeV

Med 2 pp på varje bildad Helium-4 bortfaller totalt 2,04 MeV från totala exotermiska bildningsenergin 26,7 MeV för Helium-4. Relationen ger alltså

(neutrinoandel)/(hela Soldelen) = (0,844)/(26,7) ~ 3%

 

 

 

Solmodellen i TNED

 

I TNED finns ingen motsvarande problemställning:

 

 

 

 

 

 

Solfusionerna enligt TNED baseras på g-tryck via ett 11µM tjockt fusionsskal som omsluter en centralt högtät masskärna, Solstädet. Fusionsvågen utgår från Solpolerna och sprids ner mot Solekvatorn — EN gång vart elfte år. Inte på kollisioner.

 

Den frigjorda neutrinomängden enligt TNED i Solstädets fusionsmantel — 26,73 MeV — innefattar, utan extra moment, alla motsvarande diskreta kollisionsfusionssteg i en och samma fusionsring. Det finns därför inga EXPLICIT diskreta neutrinoenergier att räkna på från Solkärnan sett — men väl en neutrinodämpningsfaktor från den högtäta centralkärnan (8,13444 T16 KG/M³). Neutrinodämpningsfaktorn visar ENLIGT TNED hur mycket neutrinostrålning som Solkroppen släpper ifrån sig. För att kunna använda den faktorn i mera preciserad mening (TABELLMATEMATIKEN) måste man använda någon form av en EXAKT funktion för neutrinotvärsnittet som funktion av neutrinoenergin (databaserna från Bahcall och Peltoniemi);

 

 

 

‡ särskild förklaring till huvudtexten — Solstädets produktion av reguljär neutrinostrålning enligt TNED

 

 

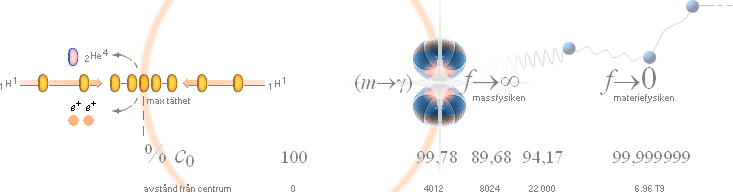
41H11,518            – (m®g)26,73MeV            = 2He414,483   .............    Solkärnan, frigjord exotermisk energi per Helium-4: 26,73 MeV

 

Solkärnan enligt TNED [Se även i Solens energiräkning] levererar E(He4)=26,73 MeV via 4 Väte-1 till 1 Helium-4; 100% E(He4) dämpas sedan (tabellmatematiken, x=0,0013) till 3,36% för Peltoniemi till motsvarande 0,89833 MeV och 1,13% för Bahcalls motsvarande 0,30143 MeV;

Men med varje bildad Helium-4 följer också 2 positroner (en per diskret bildad deuteron), dessa förs ENLIGT TNED (Se Solfläcksbildningen) upp till Solytan där de annihileras (massförintas) tillsamman med ett motsvarande par elektroner med totalenergin 4×0,511MeV=2,044 MeV. Totalt för varje bildad Helium-4 ges då 26,73+2,044=28,774 MeV. Tas respektive dämpvärden för detta fall fås totalt motsvarande delar av Solens totala energiomsättning med referens till 100% för den samlade potten exotermiska energibidrag i samband med bildningen av en Helium-4

 

Peltoniemi      (0,89833)/(28,774) = 0,0312201     = 3,12%  ................     totalt rel. hela Solenergin

Bahcall            (0,30143)/(28,774) = 0,0104757     = 1,05%  ................     totalt rel. hela Solenergin

 

Se även mera utförligt i RESULTATREDOVISNING.

 

 

 

Solens energiproduktion enligt TNED grundas helt på grundämnesbildningen — fusionsringar — genom EXOTERMISKA KÄRNREAKTIONSLAGEN med typexemplet från 4 Väte-1 till en Helium-4 enligt energiräkningen

 

Solkärnan

41H11,518            – (m®g)26,73MeV            = 2He414,483   .............    frigjord exotermisk energi per Helium-4: 26,73 MeV

 

I den räkningen finns inga som helst aspekter på enskilda neutrinoenergier från enskilda diskreta fusionssteg därför att sådana inte ingår explicit i fusionsringens matematik, endast ingångskomponenterna, slutprodukten och den mellanliggande atomära massdefekten i formen av massdestruktion för bildning av ljuset och värmen, (m→γ), analogt Planckstrålningens uppbyggnad från noll våglängd med högsta frekvenserna och lägsta energierna via Plancks Strukturkonstant.

   Dvs., i den energiräkningen — från Solstädets energibank — finns ingen särskild form för någon särskild neutrinoenergi, utan alla neutrinonivåer med atomkärnans alla ekvivalent möjliga fraktalnivåer blir tvunget representerade genom det motsvarande kärninduktivt utvecklade strålningstrycket från de 26,73 megaelektronvolten.

   Och alltså, i motsvarande grad, kan vi heller inte tala specifikt om några särskilda »neutrinotvärsnitt» med grund i strålningsflödet från den centrala Solkärnan.

 

Det finns inga diskreta neutrinoenergier från Solkärnan enligt TNED

 

— För att få exakta besked i fallet TNED SKULLE DET ALLTSÅ KRÄVAS någon EXAKT neutrinoenergi med EXAKT uppgift på neutrinotvärsnitt (som funktion av neutrinoenergin). Men som vidrörts ovan, finns tydligen inga sådana förutsättningar i Solfysiken sett från Solkärnan enligt TNED. Det enda vi, tydligen, kan få ut enligt TNED av Solfysikens neutrinomatematik är en allmän MEDELVÄRDESBILDNING typ från ett IDEALT TOPPVÄRDE med neutrinoenergin 26,73 MeV och som kan anställas på någon (rimlig, experimentellt förankrad) uppgift om neutrinotvärsnitt (med ev. funktion av neutrinoenergin) och på den vägen få ut motsvarande (dämpade) medelvärden.

   Det är med den förutsättningen som TABELLMATEMATIKEN utformats till prövning med grund i de bägge databaserna för Peltoniemi 1999 och Bahcall 1997. Exakt VILKEN INNEBÖRD en sådan »dämpad neutrinomedelvärdesform» skulle ha för innebörd i (någon) jämförelse med diskreta neutrinoenergier från diskreta kollisionsfusioner, det är här en helt öppen fråga som det (ännu, veterligt) inte finns någon framställning på.

   Eller med andra ord: Jämförelser med beräkningar från diskreta neutrinoenergier baserade på konventionella kollisionsfusioner för syftet att anställa jämförelse med Solfysiken enligt TNED är helt uteslutet. Det finns inga diskreta neutrinoenergier från Solkärnan enligt TNED. Se även i SSM i TNED.

 

 

 

 

Solära Neutrinoproblemet

 

Solära neutrinoproblemet

 

[Ref. @INTERNET Wikipedia Solar neutrino problem 2010-05-06].

För konventionell beskrivning av Solära Neutrinoproblemet, se referensen ovan (med flera på webben).

 

 

 

 

Neutrinostrålningen från Solen enligt TNED

 

förenklad tabell från Inledande resultatredovisning

 

 

ANDEL NEUTRINOENERGI FRÅN SOLEN (databas: Peltoniemi99):

3,12%

                          Delandel

0,9MeV            70%

27MeV             3%

1-27MeV          27%

—————————

summa              100%

 

ANDEL NEUTRINOENERGI FRÅN SOLEN (databas: Bahcall97TableIIBestFit):

1,05%

                          Delandel

0,3MeV            81%

27MeV             1%

1-27MeV          18%

—————————

summa              100%

 

 

 

Ett resultat som uppvisar en förekomst 3% i förhållande till en annan uppgift på samma materiella databas som visar 1% är utesluten som PRECISIONSDATABAS. Det spelar ingen roll hur vi räknar i ett sådant läge: felet är 3 gånger. Precisionen i Solfysikens neutrinoutbud utpekar med andra ord och tydligen att det är ANTINGEN Peltoniemi ELLER Bahcall som gäller. Bägge kan uppenbarligen inte fungera i samma fysik.

 

För resultatet enbart från TNED, se Grovberäkningen i TNED.

 

 

 

Fördelningen

2010V18 från Webb2010.htm

TEORI — fördelningen

 

Med maxenergin Emax i Solstädet dämpad till Eout vid utträdet från Solkroppen bör det också finnas en medföljande, omgivande, spridning av både högre och lägre E-värden men med allt lägre förekomster. Uppgiften här är att i varje fall försöka få någon första grovt approximativ bild av hur den fördelningen (möjligen) kan se ut — för ev. jämförelse med experimentellt uppmätta delar (i den mån en sådan, genomgripande, allt-i-ett-mätanordning finns: alla möjliga neutrinoenergier från Solen uppmätta; I dagens läge Maj2010 VET vi att en sådan avancerad anordning ännu väntar på sin praktik).

 

Ju kraftigare dämpning från Emax till Eout, desto större andel bör Eout uppta av den totala återstående utgående andelen. Dvs., allt mindre delar blir kvar åt övriga, spridda, energier om Eout domineras av ett lågt värde. Motsvarande ges större utrymme för högre omgivande E-värden med högre Eout.

 

EoutHIGH med lägre andel än Eout

Eftersom neutrinostrålningens utträngning också beror av vilka Solatomkärnor som för tillfället befinner sig precis mitt i strålvägen för den idealt radiella neutrinostrålen — på samma sätt som ett inställt sikte tvärs en vältrafikerad gatukorsning pekar på de inbördes mötande fordonen — finns en viss statistisk möjlighet att en MED DEN LOKALT DÄMPADE URSPRUNGSENERGIN  BEVARAD allt mindre andel neutrinostrålning slinker igenom och når ut. Om vi börjar vid utträdeslokalen för Eout och går baklänges, har vi med nämnda modell och således och i andra ord en viss rätt att förvänta oss att vi vid Eout även återfinner allt högre E-värden men med allt lägre andel: minst sannolikt är att finna E-värden vid Eout lika med Emax.

 

EoutLOW med lägre andel än Eout

Men neutrinostrålningen uppvisar också en SPRIDNINGSEFFEKT, motsvarande inre reflektivitet: Med utträdet av Eout bör det också följa med en »konisk svans» av neutrinovåglängder vars energier har dämpats via omgivande (upprepade) reflexioner — och därmed energidämpningar via Comptoneffekten. Ju längre ut mot Eout som dessa reflexioner tränger, desto större andel samlar de, tydligen, på E-värden som ansluter till just Eout — och därmed en motsvarande spridning med avtagande E-värden från just Eout och med allt mindre andel. I slutänden, vid Eout, betyder det tydligen att lägre E-värden från Eout också bör finnas representerade men i allt lägre andel med allt lägre E-värden.

 

Hur värdena beräknas

Eftersom neutrinodämpningen i princip är spektralt (våglängdsmässigt) kontinuerlig — från ett Emax=26,73 MeV och sedan neråt via kontinuerlig dämpning — finns varken bestämda diskreta eller individuellt beräkningsbara särskilda neutrinoenergier att räkna med.

 

Om ovanstående ordning tillämpas på den framräknade utgående neutrinoenergin (här grovt för enkelhetens skull via Peltoniemis databas, se RESULTATREDOVISNINGEN) Eout=1MeV (eg. 0,9 MeV) med andelen (avr.) 3% av Solenergins totala 100%, blir motsvarande genomgångsandel (separat insättning i tabellkalkylen) för 1MeV-energin lika med ca 67%:

— Vi skriver bara in typ 1 (MeV) i inmatningsrutan (Peltoniemis databas här som exempel) med intervallprecisionen 0,001, trycker Enter och får svaret 66,69768% (här förenklat 67%).

— Med (avr.) Emax=27MeV (eg. 26,73 MeV) vid Eout lika med (avr.) 1 MeV (eg. 0,89923 MeV) — kan vi alltså använda 3%-resultatet enligt räkningen

Eout/Emax = EoutHIGH/Eout = 3%

— och därmed också få (approximativt) högenergiandelen 27 MeV av de 3 procenten som, tagna som 100%, likaledes 3%.

På grund av avrundningseffekterna ges enklare nedanstående grovexempel med 4%:

 

Exempel (avr.):

(1MeV)/(27MeV) = 0,04 ; 27MeV finns i 4% av Eout — dvs., med 1 del på 625=1/(0,04)²:

;

0,04 = 27/x; x=625; 25/625 = 0,04

Sammanställt (databas: Peltoniemi99) med x=0,001 således i (grovt) approximativ fördelning:

 

1MeV               66%

27MeV             4%

1-27MeV          30%

—————————

summa              100%

 

Återstående delen 100–(66+4=70) kan då grovt klassificeras som neutrinoenergier 1-27MeV med andelen ca 30% av hela neutrinoenergins pott.

 

 

Vi kan inte sträcka oss längre i TNED: det finns inga specifikt diskreta neutrinoenergier varken att räkna på eller att eftersöka från Solkärnan enligt TNED — ingen explicit statistisk fördelning relativt typ »olika individer» — eftersom neutrinostrålningens dämpning från Solstädet enligt TNED sker kontinuerligt från toppvärdet Emax=26,73 MeV.

 

 

Och alltså på motsvarande sätt: Att eftersöka en motsvarande experimentell matchning ÄR MENINGSLÖS SYSSELSÄTTNING: det finns SETT FRÅN SOLKÄRNANS FUSIONSHÄRD ingenting sådant i Solfysiken enligt TNED. Alla möjliga neutrinoenergivärden mellan lägsta (0) och Emax 26,73 MeV finns representerade.

 

 

Om istället — till jämförelse för att visa den (extrema) känsligheten — Bahcalls databas tillämpas (Bahcall 1997 Table II, BestFit) ges motsvarande sammanställning (med x=0,0013):

 

0,3MeV            81%

27MeV             1%

1-27MeV          18%

—————————

summa              100%

 

NOTERA att olika neutrinoenergier — den givna beräkningsgrunden med tabellintervallen och med ansats från Solstädets fusionsmantel än just Emax=26,73 — rymmer ur Solen på delvis MYCKET olika lokaler;

Med Peltoniemis datas bas (x=0,001) ges följande tabellresultat till jämförande exempel:

 

MeV     KM

———————

1           7449                

10         10928

;

1,1        476802

10,1      32197

 

TABELLRESULTATEN ger alltså inte några direkt sammanhängande distansgränser.

Anledningen är det slumpvisa urvalet av exponentiellt växande fria medelvägsdistanser som slutar på närmast mindre värde än Solradien.

 

Gradskillnaden mellan databaserna från Peltoniemi och Bahcall är i sammanhanget MYCKET LITEN I FÖRHÅLLANDE TILL BAHCALLS EGNA INRE OSÄKERHETSMARGINALER — men ändå SÅ stor att ovanstående jämförelser UTESLUTER varje möjlig preciserad analys. Jämför ovan: en osäkerhet på 1–18/30=30% för att exemplifiera är UTESLUTEN som grundval för naturvetenskaplig experimentalism.

 

 

 

Neutrinoenergins avtagande

 

Neutrinoenergins avtagande i Solen enligt TNED

 

                y=e–x

 

 

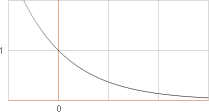
Neutrinostrålning i TNED är entydigt detsamma som masslös em-strålning (ljus) från massdestruktion (m→γ) med våglängder som ansluter till atomkärnans fraktala kraftstruktur enligt TNED. Se utförligt från ATOMKÄRNANS HÄRLEDNING, om ej redan bekant.

 

Därmed kan neutrinostrålningen i TNED bara utvecklas på Comptoneffekten i materiell växelverkan:

 

RENT KVALITATIVT, grafen ovan (samma typ som allmänna ljusintensitetsfunktionen), finns ingenting annat att välja på för neutrinokapitalets grundstock på 26,73 MeV från Solstädet än ett konsekvent avtagande mot noll — samtidigt med strålningens utträngande ur den centralt högtäta Solkärnan. Därmed reduceras neutrinovåglängderna i takt med att de uttränger ur Solkroppen. TNED har ingen annan HUVUDSAKLIG grund för neutrinostrålningen att presentera.

 

Det finns f.ö. inga diskreta neutrinonivåer i Solens huvudsakliga neutrinoproduktion enligt TNED, bara Solkärnans grundstock på 26,73 MeV och som innehåller alla möjliga mellangrader. Se även i SSM i TNED.

 

Hur neutrinostrålningens avtagande beräknas i TNED beskrivs utförligt i TABELLMATEMATIKEN.

 

 

 

Grovberäkningen i TNED

 

2010-05-10:

Grovberäkning av andelen neutrinostrålning som (möjligen) kommer från Solen enligt TNED — värderesultat helt oberoende av neutrinotvärsnitt

 

Vi väljer att studera Solmassan i skiktet räknat från städkärnans fusionsmantel r(4KM) till yttergränsen r(18KM) för Coulombtätheten som närmast tar emot den bildade neutrinostrålningen vid städmanteln från massdestruktionerna (m®g) i fusionsfasen. Det är i detta skikt som den mest centrala dynamiken verkställs enligt TNED, och som också innefattar huvuddelen (82%) av hela Solmassan. På denna dellokal kan vi sedan göra enkla grovberäkningar på den kvarvarande neutrinostrålningen och dess andel från ursprunget i städmanteln, dess dämpning och därmed vidare för att få någon jämförande uppfattning om vilka värden det är fråga om.

 

Ytterkanten

På avståndet 18 KM från Solcentrum är i TNED-modellen för Solens fysik den inneslutna sfärmassan lika med m(18KM);

Omslutna tätheten ρ(18KM) är nära samma som Coulombtätheten (ρC=8,13444 T16);

Nuklidbaserade strålningstrycket (ej att beblanda med elektrokinetiska strålningstrycket) är p(18KM);

 

m(18KM)         = 81,88% av hela Solmassan 1,989 T30 KG

 

ρ(18KM)          = 8,14 T16 KG/M³

 

p(18KM)          = 2 T32 Pa

Städmanteln

Motsvarande vid städradien (4012 M) — neutrinokällan — visar enligt TNED

 

m(4KM)           = 50,23% av hela Solmassan 1,989 T30 KG

 

ρ(4KM)            = 7,42 T18 KG/M³  ..............            dynamisk maxtäthet vid Städmanteln

 

p(4KM)            = 8,2 T34 Pa

 

Förhållandet

TÄTHETSFÖRHÅLLANDET eller »sållbreddningen» — DYNAMIKEN som bestämmer takten (styrkan) i neutrinostrålningens energireduktion vid dess energiöverföring på Solmassan — blir via de bägge avstånden lika med

 

(8,14 T16)/(7,42 T18) = 1,097%

 

Vi har knappast några andra fasta referenser att välja på i Solkroppen:

städradien och Coulombtäthetsradien.

 

 

Resultatet

 

Relativt ett idealt täthetshomogent material (som uppvisar en exponentiell reduktion för intensiteten hos ljus som genomtränger materialet, grundsambandet nedan, se även i Strålningstvärsnittet)

 

                y=e–x

 

 

betyder relationen (1,097% ~1,1%) TYDLIGEN (omvänt) KVALITATIVT att:

neutrinoflödet vid utflödets vidare mynning vid r(18KM) BÖR ha motsvarande 98,9% större bevarande än vid ingången vid r(4KM) (resonemanget går ut på att knappast mera dämpning sker än de redan resterande 1,1 procenten):

 

Neutrinostrålningen dämpas = omsätts mest effektivt i den mest högtäta delen, och tar sig sedan allt lättare utåt med avtagande täthet. Är tätheten 98,9% lägre, bör också »flyktfriheten» (alltså, neutrinodivergensen) vara motsvarande större.

   Notera dock att denna uppskattning också är och förblir en approximation som inte har andra parametrar än de här nämnda.

 

Vilket vill säga:

— I förhållande till Solstädet vid r(4KM) kan lokalen vid Coulombtäthetens yttergräns r(18KM) betraktas som (nära, frånsett 1%) PRAKTISKT TAGET HELT transparent — för den därifrån vidare utträngande neutrinostrålningen.

   Denna ytterst grova uppskattade beräkning säger TYDLIGEN ENLIGT TNED att:

(SÄKERT, med tydligtvis liten marginal att döma av täthetsrelationen)

 

1,097% av Solenergin från Solstädet

 

(från den aktuella domänen mellan referensdistanserna 4-18KM)

 

KAN FÖRSTÅS bestå av centraldämpad neutrinostrålning

från den centrala städkärnans fusionsmantel — och som, från r(18KM)-punkten vidare ut genom Solkroppen, kommer att energidämpas mera marginellt med allt minskad materietäthet.

 

Den energidämpningen behöver inte innebära att hela neutrinokaraktären (våglängder kortare än största utsträckningen hos elektronmassans komponenter) »försvinner» på energidämpningens kreditnota — men nödvändigtvis att neutrinoenergin reduceras i den vidare växelverkan med Solmaterien, på samma sätt som sker med början från städmanteln, men utanför r(18KM)-gränsen i allt mindre omfattning. Erinra dock att neutrinodämpningsdynamiken ENLIGT TNED är mera avancerad — med grund i Plancks strukturkonstant. Se utförlig grundbeskrivning i Neutrinostrålningens växande tvärsnitt.

[Se även generellt COMPTONEFFEKTEN, VÄRMEBILDNINGENS GRUNDER].

 

Med totala energidelen

(Solkärnans 26,73 MeV + Solytans 2,044 MeV = 28,774 MeV per bildad Helium-4)

enligt

[(26,73 MeV)(0,01097)=0,2932281 MeV]/(28,774 MeV) = 1,01907%

kan man därmed säga att neutrinodelen av hela Solenergin uppgår till max 1,02%.

Med andra ord:

 

Grovberäkningen i TNED enbart på täthetsändringens bas utpekar alltså att andelen neutrinostrålning som lämnar Solklotet utan ytterligare dämpning skulle vara ganska precis 1% (1,0191%) av hela Solenergin.

 

Till jämförelse visar »mera exakta beräkningar» via neutrinotvärsnittet som funktion av neutrinoenergin — med användning av databasen från Bahcall (1997, BestFitTabII) — värdet 1,13%,

 

— Men då MED BAHCALLS EGEN ANVISNING

 

”I recommend the most conservative procedure: Assume all errors are fully correlated and add the uncertainties linearly not quadratically. This is the procedure that I have followed in calculating Table III and Table IV.”, Bahcall s3406sp2m

 

Alltså: utan några som helst garantier för att databasens värden är ABSOLUT tillförlitliga (Bahcalls osäkerhetstoleranser är i själva verket i sig så stora att hela värdeberäkningen urartar om toleransgränserna antas. Toleransen måste (alltså) t.o.m. vara MYCKET mindre än skillnaden i resultat mellan databaserna för Bahcall och Peltoniemi). Se vidare i RESULTATREDOVISNING och INLEDANDE RESULTATREDOVISNING.

 

 

SOLENS NEUTRINODÄMPNING END.

 

 

Neutrino cross section — neutrinotvärsnitt (webbreferens)

 

neutrino cross section

Answers.com — neutrino mean free path

HYPERPHYSICS — Neutrino Cross Section

http://hyperphysics.phy-astr.gsu.edu/hbase/particles/neutrino3.html

 

Webbkällan ovan beskriver ”neutrino mean free path”, sv. »neutrinomedelfrivägen», enligt d

 

             u

d = ————

           σ ρ

 

Med insatta värden

 

u           = 1,66033 t27 KG

σ           = 1 t47 M² konstant värde från Hyperphysics

ρ           = KG/M3 materialtätheten

 

ges

 

d           = (1/ρ)(1,66033 T20 M·M³/KG)

 

Se även Fria Medelväglängden i Strålningstvärsnittet, där härleds sambandet för d. Se även Neutrinotvärsnittet i TNED.

 

 

 

Neutrinomängd

Neutrino flux

 

Några webbkällor som syns främst på »neutrino flux»:

http://www.cosmicrays.org/muon-solar-neutrinos.php

”Calculation of the solar neutrino flux …”

 

http://en.wikipedia.org/wiki/Solar_neutrino

”The highest flux of solar neutrinos …”

 

http://hyperphysics.phy-astr.gsu.edu/hbase/particles/neutrino.html

”Bahcall's modeling of the solar neutrino flux …”

…

 

I MODERN AKADEMI räknar man med ANTALET NEUTRINOEMISSIONER (eng. neutrino flux) baserat på Solmodellens termonukleära fusionsfysik med fusioner baserade på hastighet (kollisionsfusioner): man räknar med ett visst ANTAL neutriobildningar per sekund i en viss termonukleär lokal med en viss sammansättning.

 

Solfusionerna enligt TNED

 

 I TNED FINNS INGEN MOTSVARIGHET. G-tryckets fusionsfas bildar ALLA NEUTRINOFÖREKOMSTER som finns representerade i Solen under en 11-årsperiod. Se utförligt från SOLFYSIKEN, SOLENS ENERGIPRODUKTION.

 

En kortare sammanfattning finns i Solstädets produktion av reguljär neutrinostrålning enligt TNED.

 

Eftersom neutrinostrålningen i Solkärnan enligt TNED bildas i ett enda tag för hela Helium-4-bildningen 26,73 MeV

— de bägge paren elektroner-positroner (4×0,511MeV=2,044MeV) tillkommer för energiräkningen totalt sett, men anställs separat på Solytan via explicit (konventionell) gammastrålning

— finns ingen SPECIFIK fusionsbaserad singulär neutrinoenergi att referera till — sett från Solkärnan enbart: neutrinospektrum är — genom atomkärnans härledda PlanckFraktala struktur — kontinuerligt enligt TNED. En sådan specifik nuklidräkning är alltså helt meningslös i sakens beskrivande ljus — men den enda som tillämpas i moderna kvarter.

 

Den konventionellt brukade termen ’neutrinoflux’ har därmed ingen (entydig) innebörd i Solmodellen enligt TNED.

 

 

 

Neutrinoandelen i MAC

 

Konventionella neutrinoenergins andel från Solen

 

OM HELA SOLMASSAN fusionsverkställer på (i huvudsak) diskreta Väte-1-föreningar, har vi exemplifierat för föreningen mellan två Väteatomer

(utan räkning för extra kinetisk energi) först

 

1H11,518              +          1H11,518              =          1H22,917              1,442 exoMeV

 

Med Deuteronbildningen 1H2 (den specifika atomkärnan eller nukliden till deuteriumatomen 1H22,917) frigörs samtidigt en positron (e+);

Låter vi positronen annihileras via massdestruktion (m®g) tillsammans med den enda elektronen från Deuteriumatomen

— vilket inte innefattar någon neutrinostrålning explicit utan enbart (konventionell) gammastrålning, totalt (2×0,511MeV=1,022 MeV)

— återstår endast restDeuteronens massdefekt lika med rena neutrinoenergin

 

1,442 – 1,022 = 0,42 MeV

 

— effektivt lika med en fusion (i neutrinoenergi) mellan två rena vätekärnor eller två protoner (p), en s.k. p-p-fusion.

 

Totalt för varje Helium-4 ges 26,7 MeV, som totalt innefattar bildning av 2 positroner genom 2 diskreta pp-fusioner som ovan, och därmed motsvarande separat gammamassdestruktion av 2 par ±e (2,044 MeV);

Med två pp-fusioner därmed

totala neutrinobidraget 2×0,42=0,84MeV för hela Helium-4-bildningen;

(0,84)/(26,7) = 0,0314606 ~3%;

 

Ungefär 3% av Solenergin är att förvänta sig i form av (0,84MeV) neutrinoenergi från en Solmodell som förutsätter fusioner baserade på konventionell laboratoriestödd partikelkollision, neutrinoenergin förutsatt odämpad.

 

Se även nedanstående citat.

 

1969:

SCIENTIFIC AMERICAN, VOLUME 221, NUMBER 1, JULY 1969, PP. 28-37

http://www.sns.ias.edu/~jnb/Papers/Popular/Scientificamerican69/scientificamerican69.html

Observerat tillfälligt avbrott i ovanstående http://www.sns.ias.edu/-källa 2010-05-23 ”webbsidan kan inte visas”; sedan åter OK (testat dagen efter).

”About 3 percent of the total energy radiated by the sun is in the form of neutrinos.”.

 

(2×0,4 MeV Se nedan)/(26,7 MeV) = 0,0299625 ~3%

 

1995:

THE NATIONAL ACADEMIES PRESS — Why Neutrino Astrophysics?

http://www.nap.edu/openbook.php?record_id=9185&page=1

”While most of this energy ends up as electromagnetic radiation from the surface, approximately 3 percent is believed to be emitted directly from the center of the sun in the form of neutrinos [2].”.

 

2008:

PRINCETON BOREXINO GROUP - ANALYSIS CLUSTER — Chapter 1: The Physics of Low Energy Solar Neutrinos (Aug2008)

http://borex.princeton.edu/public-docs/theses/pocar_phd_by_chapter/pocar_phd_chapter1.pdf

”Most of the energy produced by the Sun is released as photons, while approximately 3% is believed to be carried out by neutrinos, all with energies < 20 MeV [22] (see table 1.3 and fig. 1.3).”, s10.

 

 

NEUTRINOANDELEN FRÅN SOLEN — inledande räkneexempel:

 

 

Inledande räkneexempel

 

En första approximativ grovberäkning som visar hur man kan beräkna andelen neutrinoenergi som läcker ut ur Solen enligt TNED med hjälp av ett etablerat konstant standardgrovvärde för neutrinotvärsnitttet (σ, i området låg neutrinoenergi 1-25 MeV).

   För grundbegreppen och deras matematik, se Fria medelväglängden i Strålningstvärsnittet samt Neutrinotvärsnittet i TNED, om ej redan bekant.

 

SOLEN:

 

(1)        Ta         = (4pG/akP)1/4 r–3/2 (r0R4/3)1/2  ......................    värmegradens radiella. variation, °K

             = r–3/2(1,13035 T17 °K[M]3/2)

 

Med hjälp av ett bestämt (approximerat) konstant värde på neutrinotvärsnittet (σ, Grek. sigma, s) kan man göra en första grov approximation med känd täthetsändring för Solen enligt TNED — beräkningen grundas på att använda hela sträckan d med den återstående delen

1/e = 0,3678794 efter dämpningen via d — se utförligt från härledningen till d i Fria medelväglängden i Strålningstvärsnittet; Summan av R+d1 ger sedan nästa bas för beräkningen av nästföljande d som d2 och som på samma sätt leder till R+d1+d2 och så vidare;

 

R                       = 4012 M  ........................................     Solstädets mantelradie enligt TNED

ρ0                      = 8,13444 T16 KG/M3 ....................     Coulombtätheten

akP                    = 2,53387 t16 (N/M2)°K–4 ...............     konstanten i Stefan-Boltzmanns strålningslag

(4πG/akP)1/4      = 42,646936 = √ 1818,7612

(ρ0R4/3)1/2         = 2,65048 T15

 

u           = 1,66033 t27 KG

σ           = 1 t47 M2 [HyperPhysics]

ρ           = ρC(R/r)4 = ρCR4 r–4

             = r–4(2,10751 T31 KG·M)  ..........................            Se täthetens radiella variation

d           = u/σρ = u/σ[ρCR4 r–4] = r4u/σρCR4 = r4(7,87812 t12 M–3)

 

r M                   T °K                 ρ KG/M3          d M = u/σρ med σ = t47 M2 se HyperPhysicsKällan ovan;

—————      ————         ————         ———

4012                  4,45 T11           8,13 T16           2041                 1/e1       = 0,3678794

+2041               2,40 T11           1,57 T16           10576               1/e2       = 0,1353352

+10576             5,27 T10           2,76 T14           602404             1/e3       = 0,0497870     »sista hållplatsen»

+602472           2,32 T8             1,44 T8             1,16 T12           1/e4       = 0,0183156     nås aldrig i Solens fall

 

Tätheten i varje trappsteg beräknad efter tillryggalagda fria medelväglängden med idealt samma täthet; den väglängden blir i verkligheten kortare eftersom tätheten avtar med avståndet, vilket i slutänden (i det verkliga fallet) ger ett lägre max%-värde

4012+1*2041+1*10576+1*602404

4012+2040,97+10573,86+602104,47

 

Ovanstående grovt approximerat beräknade fall inträffar (med växande mening) allt tidigare med växande täthet: Sämsta fallet, räkningen ovan, ger att den andel av neutrinostrålningen ENLIGT TNED som lämnar Solen blir MAX 4,9% av Solens totala energi/effekt, LÄGST 1,8%.

 

Men det betyder också KVALITATIVT detsamma som att NEUTRINOENERGINIVÅN likaledes följer samma mönster:

 

max 5% av max(26,7) MeV ger 1,335 MeV

min 2% av max(26,7) MeV ger 0,534 MeV

 

Värdena motsvarar STÖRSTA FÖREKOMSTEN MED LÄGSTA neutrinoenergin. Sedan därifrån allt högre med mindre förekomst.

 

Se vidare i TABELLMATEMATIKEN och FÖRDELNINGEN. Där ges samma typräkning som ovan men i betydligt flera trappsteg och med referens till mera omfattande (etablerade) databaser för neutrinotvärsnittet — med variabla värden som funktion av varierande neutrinoenergi. Dock skiljer sig inte de resultatet så VÄRST mycket från ovanstående enklare approximation. Man får i ett fall (Peltoniemis databas från 1999) 3,36% och i ett annat fall (Bahcalls databas från 1997) 1,13%, samt direkt ett annat approximerat värde via Solmodellen enligt TNED i Grovberäkningen som visar 1,02%.

   Se även hur konventionella neutrinoandelen (~3%) beräknas från kollisionsfusionerna i Konventionella neutrinoandelen.

 

 

 

 

TABELLMATEMATIKEN:

Tabellmatematiken

 

  Tabellräkningens matematiska samband

Tabellmatematiken

  HUR RESULTATBERÄKNINGARNA HAR GJORTS

  Se även Inledande räkneexempel som visar en exemplifierad snabbgenomgång av beräkningsprincipen

 

MATEMATIKEN TILL RESULTATREDOVISNINGEN grundas på följande allmänna samband och förhållanden:

 

 

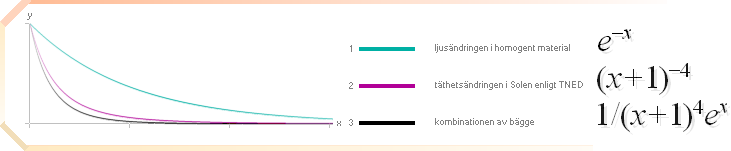
Den övre formen — ljusdämpningen i homogena material — SKULLE kunna användas DIREKT via x=d/dMAX om det inte vore för att dMAX innehåller en parameter (neutrinotvärsnittet σ) vars funktion beror av resultatvärdet. Det betyder att ingen exakt formulerbar kontinuerlig matematisk funktion existerar i fallet då materialtätheten ändras kontinuerligt. Komplikationen är (rent matematiskt-tekniskt) den följande — termerna förklaras mera utförligt längre ner i Beskrivning om ej redan bekanta:

 

— Med ljusdämpningen i homogena material

 

I/I0                     = e–d/dMAX = e–x

                          = a

där

dMAX              = u/σρ = u/σ[ρCR4 r–4]

                          = r4u/σρCR4

                          = σ–1r4(7,87812 t59 M–3)

SKULLE man kunna beräkna a DIREKT med r=d [d/dMAX=r/dMAX] via

d/dMAX           = r/σ–1r4(7,87812 t59 M–3)

                          = σ/r3(7,87812 t59 M–3)

 

 

 

med modifikationen (annars omvänt procentvärde)

a        = 1–EXP[–σ/r3(7,87812 t59 M–3)]

          = 1–EXP[–σ(1,26933 T58 M3)/r3]

                          [EXP = e^];

som med växande r alltmer övergår i motsvarande praktiska värdefunktion

~ σ(1,26933 T58 M3)/r3

Med (MAX) σ = 6 t45 M² vid r=42,295359 KM ges a=1–1/e = 0,6321205; a=1–EXP[–(7,61598 T13)/r^3]

Med (MAX) σ = 6 t45 M² vid r=100 KM ges a=1–1/e = 0,0733691;

Med (MAX) σ = 6 t45 M² vid r=200 KM ges a=1–1/e = 0,00947978;

 

Med (MAX) σ = 1 t47 M² vid r=6,463304 KM ges a=1–1/e = 0,6321205; a=1–EXP[–(1,26933 T11)/r^3]

Med (MAX) σ = 1 t47 M² vid r=100 KM ges a=1–1/e = 0,00012699;

 

EXP-Funktionen har formen

 

y

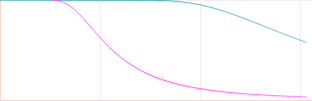 x

 

ÖVRE: y = 1– EXP[–25/x^3]; unit100

UNRE: y = 1– EXP[–  1/x^3]; unit100

Funktionen är relevant enligt följande: Dämpningen börjar från den övre typen (största tvärsnittet σ) och avtar sedan mot den (i det praktiska fallet betydligt) brantare undre typen (tillsammans med anpassade offsetvärden).

   [Rent tekniskt matematiskt är det inte lika enkelt att åstadkomma en motsvarande kurva om man börjar från den brantare delen som ska sluta på den flackare].

   ETT SÄTT ATT HOFTA MELLANLÄGET skulle vara att laborera med en något högre (r)x-exponent. Med x^3,35 via σ = 6 t45 M² ges (för den inre delen) mera hyfsade värden — men helhetsformen urartar i vilket fall mot slutet: Solradien för x ger första decimalen (i storleksordningen) i sextonde positionen. Korrekt funktion skulle (i så fall) betyda ytterligare »mixtrande» med exponenten som en separat funktion av x i sig: komplicerat.

Editor2010V21

 

 

 

— OM det inte vore för neutrinotvärsnittet σ som funktion av neutrinoenergin:

d/dMAX           = σ/r3(7,87812 t59 M–3)

 

Förklaring

Neutrinoenergin (Ev) som funktion av växande strålväg r är just föremålet för huvudfunktionen: Vi måste i varje r veta värdet för neutrinoenergin Ev. Men eftersom Ev påverkas av den avtagande tätheten kommer vi inte åt Ev-värdet oberoende.

— Ev som funktion av utsträckningen r har ingen entydig sambandsform: vi kan inte beräkna Ev från σ via r — därför att varje r förutsätter att varje givet Ev REDAN genomgår dämpning. Den fasta referensen saknas.

— Enda möjligheten är alltså att ITERERA. Eller rättare sagt, göra beräkningar i små steg med varje i formen av konstant täthet. Därmed fås Ev och därmed σ och därmed den aktuella dämpkvoten. Det finns alltså ingen entydig sambandsform — och därmed i princip heller ingen entydig differentialekvation att formulera. DET VARIABLA NEUTRINOTVÄRSNITTET σ har ingen explicit DIREKT koppling till begreppet distans (r). Därför går det inte.

   Översikten nedan visar hur beräkningarna kan göras.

 

BERÄKNINGSALGORITMEN

Algoritmen för beräkningen av neutrinodämpningen i Solen

 

 

 

 

 

 

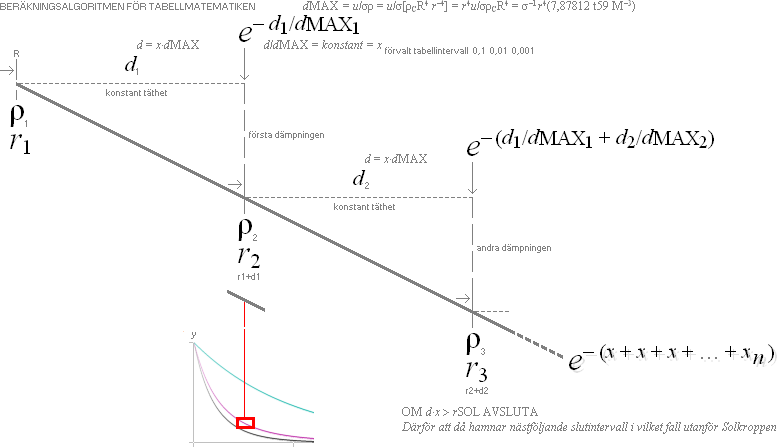
Sammanställningen ovan visar hur tabellresultaten framräknats. Se även den ovan infällda kurvformens matematik i inledningen. Principen är att beräkna dämpningen via den linjära materialhomogena funktionen (EXP[–x]) i så små steg som möjligt (i det praktiska Solfallet in till millimeter från början), räkna fram ett lägre täthetsvärde för varje nytt trappsteg tillsammans med ett nytt neutrinotvärsnittsvärde från en särskild databas (se Databas), och sedan summera de resulterande individuella dämpningarna genom successiv ackumulation

(EXP[–(x+x+x+…+x]). För neutrinotvärsnittets energifunktion har använts två något olika databaser för det jämförande syftet (se resp. Peltoniemi och Bahcall). Resultatet redovisas i RESULTATREDOVISNING.

Beskrivning

 

DEN KVANTITATIVT MATEMATISKT IDEALA NEUTRINOPARTIKELNS FRIA MEDELVÄGLÄNGD innebär i konventionella ekvivalenter den väg (dMAX) en ideal neutrinostråle ska passera/genomtränga för att dess INTENSITET (även energi) ska reduceras från 100% till 100×1/e=36,8%avr.

Med summan av antalet n tillryggalagda (dMAX) i det givna materialet kommer neutrinostrålningen då att reduceras/dämpas med

1/(e^[1+1+1+1+…+n]) = e–n

Är masskiktet mindre än (dMAX) — x=d/(dMAX) — gäller motsvarande [alla x lika med samma bråkdel av ett givet (dMAX), varje (dMAX) nödvändigtvis inte samma],

1/(e^[x+x+x+x+…+nx]) = e–nx

 

I konventionell litteratur beräknas (dMAX) enligt

dMAX = u/σρ

med

u           = 1,66033 t27 KG atomära massenheten

σ           = 1 t47 M2 [HyperPhysics] neutrinostrålens sannolikhetstvärsnitt; eller alternativt

σ           = 9,3 t48 M2 (E/1MeV)2 mera noggrant via THE ULTIMATE NEUTRINO PAGE (se sep. ref.)

ρ           = ρC(R/r)4 ; R(Solen) = 4012 M;  ρC = 8,13444 T16 KG/M³

             = ρCR4 r–4

             = r–4(2,10751 T31 KG·M)

 

Tätheten ρ gäller för Solen enligt TNED (Se täthetens radiella variation) med

dMAX = u/σρ = u/σ[ρCR4 r–4] = r4u/σρCR4 = r4(7,87812 t12 M–3)  = σ –1 r4(7,87812 t59 M–3)

 

Med Hyperphysicsvärdet t47 M² kan dMAX också skrivas särskilt

dMAX = u/σρ = u/(σ)[t47 M²][ρCR4 r–4] = r4u/σρCR4 = (σ)–1r4(7,87812 t12 M–3)

med (σ) = f (σ); sigma (σ) kan vara en konstant (linjär neutrinoenergi som i HyperPhysicsFallet) eller en funktion (typ NEUTRINOENERGIN²).

Särskilt för sambandsformen (Peltoniemi) (E/1MeV)² gäller då också tydligen

d           = u/σρ

             = u/σ[ρCR4 r–4]

             = r4u/[a t47 M2 · (E/MeV)2]ρCR4

             = r4u/[a t47 M2]ρCR4 · (E/MeV)–2

             = r4u/[a t47 M2][2,10751 T31 KG·M] · (E/MeV)–2

             = r4u[4,74491 T15]/[a M3KG] · (E/MeV)–2

             = r4[7,87812 t12 M–3]/[a([E:=E·e–nx]/MeV)2]

             = r4[7,87812 t12 M–3]/[a(E/MeV)2(e–nx)2 ]

 

Den införda bråkdelen E:=E·e–nx blir den successivt utdämpade neutrinoenergi som återstår att fortsätta på efter varje fullbordad passage av ett givet täthetsskikt enligt serien

1/(e^[x+x+x+x+…+nx]) = e–nx

E-värdet (E) blir fast värde, lika med hela energin för Helium-4-bildningen, och som reduceras successivt med växande nx.

Faktorn a är optimal för prövning av olika närliggande sigma-värden (optimal precision), nominella värdet är a=1 (eller a=0,93 [Peltoniemi] beroende på källtest).

 

Med givet delintervall x=d/(dMAX) kan Solen indelas i smala skikt med inbördes konstant täthet för en approximativt prövande grovberäkning av neutrinostrålningens totala dämpning via ovanstående sigma-värde. Utgångsvärdet för Solens del enligt TNED är städkärnans mantel på avståndet R=4012 M från centrum. Där bildas 100% neutrinostrålning enligt TNED genom stjärnornas allmänna tryckekvation via nominella lokala Coulombtätheten (kärna vidrör kärna) 8,13444 T16 KG/M3. Därifrån dämpas sedan neutrinostrålningen ut successivt med uppvärmningen av den omgivande Solmassan. Den neutrinostrålning som lämnar Solen blir alltså ENLIGT TNED en (avsevärt) dämpad rest av den ursprungliga primära neutrinokraften som bildades i Solkärnan.

 

Med given bråkdelsprecision [x=d/(dMAX)] bestäms varje avverkad deldistans (d) enligt sambandet för d ovan.

Föregående summa av ackumulerade d-värdena, med start från R=4012 M, används som bas i r-värdet (d-sambandet ovan) för att bestämma det nya d-värdet (analogt, för att bestämma det nya d-skiktets lokala täthet).

 

Tabellen får då typformen (i exemplet nedan börjar deldistanserna på intervallet ca 3 cM; med x=0,001 ges motsvarande 3 mM)

 

——————————————————————

TABELL 1 | a=1                       precision

                                                   x=0,01              n

dAMAX           ∑d                   e–nx

4012                  4012,00            0,99005            1

0,03                   4012,03            0,98020            2

0,03                   4012,05            0,97045            3

…

                                                   0,03112            347

——————————————————————

TABELL 2 | a=1,09                  precision

                                                   x=0,001            n

dAMAX           ∑d                   e–nx

4012                  4012,00            0,99900            1

0,003                 4012,00            0,99800            2

0,003                 4012,01            0,99700            3

…

                                                   0,03112            3470

——————————————————————

 

Resultaten finns vidare grafiskt sammanställda i RESULTATREDOVISNING.

 

 

Tillägg:

(26)Maj2010:

TABELLMATEMATIKEN

Två fall kan inträffa som passerar Solradien (tabellutdrag som konkret exempel):

1. OM(A2561*$C$13>697000000;0;B2560+A2561); aktuellt d·C13 är större än rSol

2. (B2560+A2561) är större än rSol

Det senare alternativet missat till hit. Kalkylkortet justerat och anpassat som ovan tillsammans med motsv. ändringar i huvudtexten.

Editor2010V26

 

 

Granskning — med värdegaranti

 

— Är verkligen beräkningsgrunden i Tabellmatematiken korrekt formulerad?

 

Distanserna som avverkas växer hela tiden med varje nytt beräknat värde för fria medelväglängden (vilket skulle vara felet).

— Prövar man (nämligen) med en ordinär (exponentiell) funktion får man VISSERLIGEN överensstämmande värden OMKRING de första nR-intervallen (samstämmigt med prövningen från täthetsrelationen som ger utläckande 1,097% neutrinoenergi från Solen), men sedan i vilket fall i slutänden NOLL bara efter typ n=5, sambandet (EXP=e^, a=[ln2]^–1/4 = 1,0959573...)

–1 + EXP[(x+a)–4]

— Jo. Det är nog alldeles riktigt. Men man kan också vända på resonemanget och säga så här:

VARJE beräknad täthet som beräknas för en given delsträcka, se BERÄKNINGSALGORITMEN, medför ALLTID EN HÖGRE TÄTHET vid målsnöret är den verkliga tätheten som alltid är lägre: från målsnöret till nästa start hoppas sedan ett helt minskningsintervall över; Varje ny delsträcka börjar alltid på en täthet som alltid gäller exakt bara i just den startpunkten; vartefter neutrinostrålningen dämpas ENLIGT LINJÄRA SAMBANDET e^(d/dMAX) utmed d ges alltid en KRAFTIGARE dämpning via den konstanta högre tätheten än det verkliga praktiska fallet eftersom tätheten där i realiteten avtar men som aldrig kommer med.

— Det betyder att Tabellmatematiken i exemplet arbetar (förnämligt) efter SÄMSTA FALLETS FÖRUTSÄTTNINGAR — som här betyder att den verkliga strålningsdämpningen BÖR, helt säkert, vara (något, marginellt) mindre: (marginellt) mera % återstår i slutänden än Tabellmatematiken anger (Här finns ingen exakt specifikation, men jämförelsen mellan de olika x-intervallen antyder att skillnaden ligger i fjärde eller femte decimalen 0,000nn..., alltså som mest i tiondels procent).

— Men vi ser (det) också spåren i jämförelsen mellan de olika intervallparametrarna (x={0,1; 0,01; 0,001}): slutresultaten är samstämmiga (2,47%; 3,24%; 3,36%, resultatdelen för Peltoniemi i RESULTATREDOVISNING).

— SÅ: Ingen behöver, tydligen, befara att Tabellmatematiken i exemplet SKULLE ta ut mer kapital från kontot än vad innehavaren är god för; Det finns tydligen ALLTID — helt säkert NÅGOT — mer kvar i slutänden i det verkliga fallet än det beräknade värdet anger.

Editor2010V21

 

 

 

Säkra slutsatser

 

Vilka säkra slutsatser kan dras av resultaten?

ANGÅENDE ANDELEN NEUTRINOENERGI FRÅN SOLENS TOTALA ENERGIOMSÄTTNING

 

·          På grund av att endast (max) 1,6% av hela Solmassan enligt TNED kan försörja de kollisionsfusioner som enligt SSM karaktäriserar Solens energiomsättning blir, enligt TNED, varje Solär neutrinoförklaring enligt SSM utesluten. Se även särskild beskrivning i Solära neutrinoproblemet i modern akademi.

·          Neutrinofenoment som sådant — med referens till neutronens sönderfall — är enligt TNED alldeles bestämt masslös induktiv elektromagnetisk (em-) strålning (Se särskilt i COEI, Conservation of energy by induction); Energilagen med massdestruktionen och den primära massförstöraren E=mc² klargör distinktionerna i KOMMUTATIVITETEN (den inbördes kopplingen och korrespondensen) för ekvivalenserna i massans kvantitet
E = (m→γ)cc = (γ→m)cc
och kvalitet
E = (m→γ)cc ≠ (γ→m)cc = E
vilket enbart i sig helt — bergsäkert i TNED — utesluter varje möjlig fysikaliskt grundad uppfattning att neutrinostrålningen skulle bestå av partiklar med vägbar g-massa. Se även särskilt från Neutrinobegreppet i TNED. Se även i Värmefysikens grunder: värme är inte vägbar g-massa.

 

 

STANDARDSOLMODELLEN (SSM, den moderna akademins Solmodell) — den grundläggande teoretiska UPPFATTNINGEN OM neutrinoflödet från Solen — bygger på KOLLISIONSFUSIONER (Nuklidbarriären passeras per rörelseenergi). Solmodellen enligt TNED bygger istället på g-tryck (Stjärnornas allmänna tryckekvation, se även den illustrerade jämförelsen TNED/MAC för stjärnfysiken generellt). Kollisionsfusioner (analoga med SSM) måste också, tvunget, finnas i Solen enligt TNED, men då

(främst med hänsyn till det konventionellt Solärt angivna fusionstemperaturområdet från ca 1,5 T7 °K)

tydligen i ett mycket smalt band; Bandet uppvisar (max) 1,6% av Solmassan (utförligt i SSM i TNED)— men då också med betydlig större tryckdynamik och även temperatur som varierar märkbart i området. Den smala remsan saknar uppenbarligen kraft att förklara hela Solens neutrinoproduktion. Av det skälet utesluts den här helt som primär Solär neutrinokälla. Därmed försvinner, analogt automatiskt, hela SSM från varje potentiell lista med kandidater över tänkbara, fysikaliskt relaterbara möjliga förklaringar i fallet Solen och stjärnorna generellt. Se även i Helioseismologiska argumentet. Det främsta exemplet från TNED med atomvikterna och den därmed följande utvidgade fysikbeskrivningen inkluderat behandlingen av Solens grundläggande fenomenformer (Koronafysiken, Solfläckarna, Solperioden, Solmagnetismen) utesluter fö.ö. i särskild tydlighet SSM från kandidaturen som teoretisk grund för Solfysiken i reell, naturvetenskaplig mening — generellt överhuvudtaget. TNED och MAC representerar två helt skilda kärnfysikaliska modeller. MAC framstår i TNED tydligen som en primitiv resurs. Se särskilt från Atomkärnans härledning. Därmed skulle endast återstå resultaten från TNED i sammanställning som nedan:

 

NEUTRINOSTRÅLNINGENS ANDEL AV SOLENS TOTALA ENERGI

Grovberäkning enligt TNED oberoende av neutrinotvärsnitt:

1,02%

Resultat (x=0,0013) med databas från Peltoniemi:

3,12%

Resultat (x=0,0013) med databas från Bahcall:

1,05%

 

 

 

SSM i TNED:

 

 

SSM i TNED

 

RESULTATEN i modern akademi går — i vilket fall, tydligen — ut på att BEVARA DEN TRADITIONELLA SOLMODELLEN (SSM, Standard Solar Model). SSM beskriver Solens energicentrum i formen av kollisionsfusioner inom en sfär med ca 1/4 Solradie och en maxtäthet på ca 1,5 T5 KG/M³ [ref. @INTERNET Wikipedia Sun 2010-05-14]. I den modellen ingår en stor flora av olika kollisionsfusioner fördelade på en stor mängd olika energinivåer.

 

 

SSM i TNED representeras av ett smalt band i Solens inre — med bara 1,6% av totala Solmassan — dessutom med lokala tillägg nära referenspunkten på betydligt högre temperatur och tryck

 

 

 

 

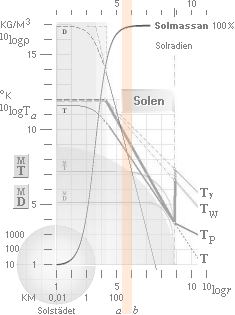
Området a-b motsvarar det teoretiska området i Solkroppen enligt TNED för den moderna akademins Solmodell (SSM Standard Solar Model). Gränserna går vid b 1,5 T7 °K (0,003 MeV) och approximativt (MAX för kollisionsfusioner) vid a T10 °K (3 MeV). Motsvarande massinneslutningar enligt TNED räknat utifrån och inåt är vid a 2% och vid b 0,4% av Solmassan, totalt för ab-bandets sfäriska skal ca 1,6% av Solmassan. Av rena proportionsskäl är det uteslutet att HELA den uppmätta neutrinostrålningen från Solen skulle komma ENBART ifrån det skiktet. Grundräkningen i den etablerade Solmodellen (SSM) visar att ca 3% av Solenergin återfaller på den neutrinostrålning som lämnar Solen — men den räkningen grundas på teorin att Solenergin verkställs på kollisionsfusioner. Någon direkt experimentell uppmätning av TOTALA andelen neutrinostrålning från Solen finns (veterligt) ännu inte (Maj2010) [‡].

   Prövning med olika databaser (Peltoniemi 1999 och Bahcall 1997) i TNED ger motsvarande värden mellan 3% och 1% återstående neutrinoenergi via neutrinostrålningens dämpning från Solstädet, vidare i huvudtexten. Grovberäkningen enligt TNED enbart via täthetsvariationen ger 1,097% med snäva marginaler.

   RESULTATREDOVISNINGEN visar att den neutrinostrålning som lämnar Solen till största delen (Peltoniemis databas) består av energin ca 1 MeV med högre/lägre energier i mindre andelar [Bahcalls databas liksom grovräkningen från TNED ger motsvarande 0,3 MeV]. Frånsett det markerade bandet, är diskreta fusionsenergier i Solen enligt TNED helt uteslutna.

   För Solfysiken enligt TNED, se utförligt från STJÄRNORNAS ALLMÄNNA TRYCKEKVATION.

   De horisontella kurvdelarna märkta MöverT (temperaturen) och MöverD (densiteten) motsvarar SSM-data och beskrivs utförligt bl.a. i BONNIERS ASTRONOMI 1978 s129.

 

 

 

Stjärnmassans radiella variation [Se utförligt i Solfysiken]:

m = kSTAR(1 – [1+r/R]–1) + mSLIM  ................    stjärnmassans radiella variation

OBS r räknas från städradien R.

graf:

a[1–1/(1+x/b)+c]

10-LOGARITMISKA massan från Solorigo:

graf unit15:

1–1/(1+[10'(x+1)]/4012)

 

 

Det betyder att varje PRECISERAD fusionsanalogi med TNED som grund för Solfysiken är UTESLUTEN — i betydelsen olika kollisionsfusioner som grund för Solens övergripande neutrinoproduktion — redan av principen.

 

Helioseismologiska argument

NOTERA OCKSÅ FÖLJANDE »bevisföring» — faran i att alltför hastigt favorisera sin egen favorit; Helioseismologi och allmän kärnfysik

 

”Meanwhile, solar models have become more detailed and precise. They have had independent experimental confirmation, in particular from helioseismological studies that helped trim down uncertainties to the point where the inconsistencies between solar models and solar neutrino experiments have become increasingly reduced. One such study is a comparison of the measured and calculated sound speeds in the Sun as a function of the distance from the center and is represented in fig. 1.5.”, s16n,

”Figure 1.5: One of the most convincing tests of the validity of the SSM is the measurement of the sound speed as a function of distance from the Sun’s core. The agreement with the theoretical expectations is astonishingly good and seems to leave no room for an explanation of the solar neutrino problem that relies on poor understanding of the Sun [22].”,

PRINCETON BOREXINO GROUP - ANALYSIS CLUSTER — Chapter 1: The Physics of Low Energy Solar Neutrinos (2003)

http://borex.princeton.edu/public-docs/theses/pocar_phd_by_chapter/pocar_phd_chapter1.pdf

 

 

Temperatur OCH tryck HÖR IHOP FÖR EN GIVEN KÄRNFYSIKALISK TEORI. Ovannämnda »helioseismologiska bevis» för att man tillämpar »korrekt fysikuppfattning» i Solens fall är helt korrekt — i den KÄRNMODELL man har av fysiken. Någon direkt OBEROENDE MODELLTEST kan aldrig genomföras därför att studier av fenomenets ena sida (t.ex. tryckanalogier) beror av grundsamband i den andra änden (temperaturanalogier, kärnfysik), och omvänt. Den ena delen beror av den andra och bara bekräftar den därmed — ett spel för gallerierna (som få tänker på, jämför nedan).

 

SÅ ÄR DET OCKSÅ I TNED. Men TNED och modern akademi (MAC) representerar helt skilda — olika — kärnmodeller [Se från ATOMKÄRNANS HÄRLEDNING om ej redan bekant]. Därför är den ovannämnda citatets bevisföring i GRUNDEN värdelös. Den säger inget annat än : jag är bäst, därför att jag alltid röstar på mig själv. Temperatur och tryck hjälper varandra i varje bestämd kärnfysikalisk teori. Endast i jämförelse mellan två skilda sådana teorier — MAC och TNED — kan en verklig slutsats visa sig: Vem av de bägge som bäst, klarast och tydligast innefattar, förklarar och beskriver den andras inneboende matematiska fysik är tydligen också den mest naturvetenskapliga.

 

 

 

Referenser

 

CROSS SECTION

Tvärsnitt

 

referenser på webben (2010-05-16 som ger upplysande beskrivningar)

@INTERNET Wikipedia Cross section (physics), Nuclear physics

@INTERNET Wikipedia Mean free path, Derivation

 

Neutrino Cross Section ENERGY DEPENDECE

Neutrinotvärsnittets energiberoende

 

Bahcall

XI. ABSORPTION CROSS SECTIONS AT SPECIFIC ENERGIES — John N. Bahcall Dec1997

http://www.sns.ias.edu/~jnb/Papers/Preprints/Gallium/paper.pdf

 

[σ = t50 M² × tabellvärden], s3400n

(OBS införd WEBBändring under de senaste tre dagarna) — dokumentet kan inte åtkommas (2010-05-23), gäller tydligen samtliga av typen

http://www.sns.ias.edu/

OK igen 2010-05-24 04:24 — möjligen tillfälligt webbfel …

Alternativ webbkälla (samma som ovan men annan disposition [spalterna borttagna, annan sidnumrering], tabellerna sist, samt att datum saknas)

http://cdsweb.cern.ch/record/337233/files/9710491.pdf

Flera olika Bahcall-exemplar finns dock (i varje fall en med datum 28 Oct 1997) på

http://cdsweb.cern.ch/

genom särskild sökning på den webbsidan typ ”ABSORPTION CROSS SECTIONS AT SPECIFIC ENERGIES”.

 

”For energies above 25 MeV, the uncertainties become so large as to make the calculated cross sections not very useful.”.

Bahcall s3391 (fösta PDF-sidan) sp1ö:

”Gallium solar neutrino experiments are, at present, the only detectors capable of detecting the fundamental pp neutrinos, which constitute about 90% of the neutrinos predicted by standard solar models to come from the Sun.”,

s3391sp1n:

”The theoretical uncertainties in the capture cross sections, which are a function of neutrino energy, limit the ultimate interpretation of the observed results. Therefore, I devote a large part of the present paper to evaluating quantitatively the uncertainties that exist in the calculations of neutrino absorption cross sections.”.

 

Tabelldata Bahcall

Jämförande data — Se även Jämförande Databas PeltoniemiBahcall

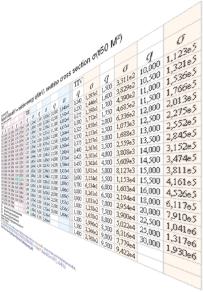
Table II-IV Bahcall97 — neutrino energy q(MeV), neutrino cross section σ(t50 M²)

Alla tre tabellerna sammanförda

 

TII

 

 

 

 

 

 

TIII

 

 

 

 

 

 

TIV

 

 

 

 

 

q

σ

q

σ

q

σ

 

q

σ

q

σ

q

σ

 

q

σ

q

σ

q

σ

0,240

1,310e1

1,500

2,243e2

10,000

5,710e4

 

0,240

1,224e1

1,500

1,882e2

10,000

3,040e4

 

0,240

1,395e1

1,500

3,311e2

10,000

1,123e5

0,250

1,357e1

1,600

2,553e2

10,500

6,705e4

 

0,250

1,268e1

1,600

2,122e2

10,500

3,541e4

 

0,250

1,446e1

1,600

3,829e2

10,500

1,321e5

0,275

1,499e1

1,700

2,886e2

11,000

7,781e4

 

0,275

1,400e1

1,700

2,378e2

11,000

4,082e4

 

0,275

1,598e1

1,700

4,390e2

11,000

1,536e5

0,300

1,662e1

1,750

3,061e2

11,500

8,937e4

 

0,300

1,551e1

1,750

2,511e2

11,500

4,657e4

 

0,300

1,772e1

1,750

4,685e2

11,500

1,766e5

0,325

1,836e1

2,000

3,972e2

12,000

1,017e5

 

0,325

1,714e1

2,000

3,162e2

12,000

5,264e4

 

0,325

1,958e1

2,000

6,336e2

12,000

2,013e5

0,350

2,018e1

2,500

6,493e2

12,500

1,148e5

 

0,350

1,884e1

2,500

4,971e2

12,500

5,902e4

 

0,350

2,153e1

2,500

1,073e3

12,500

2,275e5

0,375

2,208e1

3,000

9,905e2

13,000

1,287e5

 

0,375

2,060e1

3,000

7,318e2

13,000

6,568e4

 

0,375

2,357e1

3,000

1,688e3

13,000

2,552e5

0,400

2,406e1

3,500

1,464e3

13,500

1,432e5

 

0,400

2,244e1

3,500

1,041e3

13,500

7,260e4

 

0,400

2,567e1

3,500

2,559e3

13,500

2,845e5

0,425

2,648e1

4,000

2,129e3

14,000

1,585e5

 

0,425

2,465e1

4,000

1,456e3

14,000

7,973e4

 

0,425

3,101e1

4,000

3,808e3

14,000

3,152e5

0,450

2,862e1

4,500

3,074e3

14,500

1,745e5

 

0,450

2,664e1

4,500

2,017e3

14,500

8,706e4

 

0,450

3,362e1

4,500

5,609e3

14,500

3,474e5

0,500

3,314e1

5,000

4,380e3

15,000

1,912e5

 

0,500

3,083e1

5,000

2,766e3

15,000

9,455e4

 

0,500

3,921e1

5,000

8,127e3

15,000

3,811e5

0,600

4,300e1

5,500

6,133e3

15,500

2,085e5

 

0,600

3,996e1

5,500

3,744e3

15,500

1,022e5

 

0,600

5,154e1

5,500

1,153e4

15,500

4,161e5

0,700

5,397e1

6,000

8,434e3

16,000

2,264e4

 

0,700

5,011e1

6,000

5,001e3

16,000

1,098e5

 

0,700

6,534e1

6,000

1,603e4

16,000

4,526e5

0,800

6,848e1

6,500

1,144e4

18,000

3,040e5

 

0,800

6,245e1

6,500

6,615e3

18,000

1,406e5

 

0,800

8,261e1

6,500

2,194e4

18,000

6,117e5

0,900

8,276e1

7,000

1,530e4

20,000

3,899e5

 

0,900

7,505e1

7,000

8,658e3

20,000

1,689e5

 

0,900

1,031e2

7,000

2,954e4

20,000

7,910e5

1,000

9,830e1

7,500

2,009e4

22,500

5,064e5

 

1,000

8,868e1

7,500

1,117e4

22,500

1,955e5

 

1,000

1,258e2

7,500

3,900e4

22,500

1,041e6

1,100

1,226e2

8,000

2,576e4

25,000

6,296e5

 

1,100

1,076e2

8,000

1,412e4

25,000

2,056e5

 

1,100

1,658e2

8,000

5,022e4

25,000

1,317e6

1,200

1,440e2

8,500

3,230e4

30,000

8,789e5

 

1,200

1,251e2

8,500

1,752e4

30,000

1,484e5

 

1,200

1,996e2

8,500

6,316e4

30,000

1,930e6

1,300

1,672e2

9,000

3,968e4

 

 

 

1,300

1,439e2

9,000

2,136e4

 

 

 

1,300

2,366e2

9,000

7,779e4

 

 

1,400

1,921e2

9,500

4,797e4

 

 

 

1,400

1,640e2

9,500

2,566e4

 

 

 

1,400

2,768e2

9,500

9,422e4

 

 

 

TII:       Table2—BAHCALLDec1997p3401tBestEstimated

TIII:     Table3—BAHCALLDec1997p3401t3σMIN

TIV:     Table4—BAHCALLDec1997p3402t3σMAX

Originalets ×10 ersatt med e — kalkylprogrammets form för 10^

Originalets . ersatt med ,

OBS: Cellmarkeringen ovan i TII q16,000 med sigma 2,264e4 förmodligen felskriven: ska vara e5 — annars irrelevant fördelningsresultat.

Bahcall Dec1997, frn. s3401ö:

—————————————

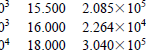 Bildkopia

—————————————

I den alternativa webbkällan nedan är felet rättat (not. 2010-05-23).

http://cdsweb.cern.ch/record/337233/files/9710491.pdf

MatchKurva till Bahcall97TabIIBestEstimate

Graf unit1200:

(x'3.35)(0.505+x'2)'–4

MathJusterad:

(1200/31)[0.9([15,4x/1200]'3.35)(0.505+[15,4x/1200]'2)'–4]

 

5 –: ökar amplituden och vänsterdrar

5 –; ökar amplituden

2 +; ökar amplituden

4 +; ökar amplituden och vänsterdrar

 

Typformens variation för neutrinotvärsnittet från neutrinoenergin

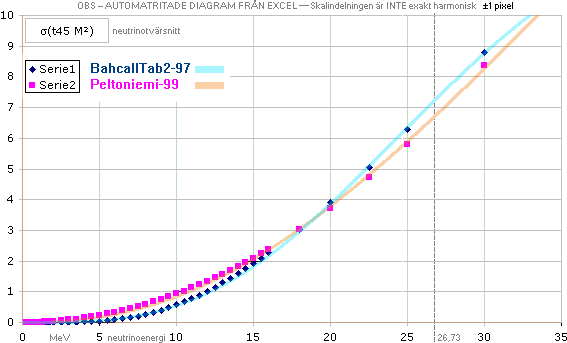
— databas Bahcall 1997 BestFit (”Best estimated”). PunktDiagrammet nedan Automatritat i EXCEL från databaserna för Bahcall och Peltoniemi

 

 

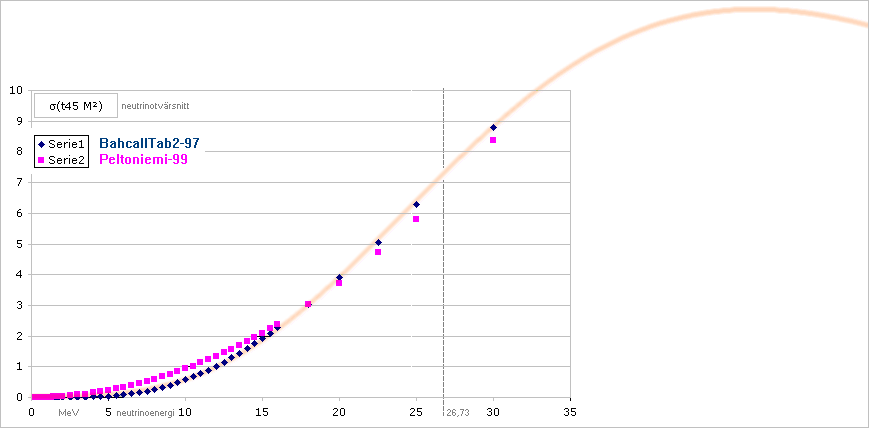
Kurvformen för variabla neutrinoenergier enligt Bahcalls databas (MÖRKBLÅ PUNKTER) följer approximativt typformen för den grova heldragna ljusorangea kurvan. Kurvans ekvation (de blå punkterna från Bahcall 1997) är approximativt

 

σ           = bc[aEv]3,35(d+[aEv]2)–4 ..............................      t45 M2, neutrinotvärsnittet från neutrinoenergin Ev i MeV

a           = 15,4/1200      ~ 0,0128

b           = 1200/31         ~ 38,71

c           = T5 · t50 M2 = t45 M2

d           = 0,505

 

Peltoniemi (1999, ljusvioletta punkter) motsvarar en ideal (begränsad) parabel

σ           = 1000(9,3 t48 M2)[Ev]2 ...............................     t45 M2, neutrinotvärsnittet från neutrinoenergin Ev i MeV

 

THE ULTIMATE NEUTRINO PAGE — Juha Peltoniemi 1999, Cross sections  (2003)

http://cupp.oulu.fi/neutrino/nd-cross.html

 

Peltoniemi ger utförliga sambandsteckningar, men ger (till skillnad från Bahcall 1997) ingen (vidare) referens till sambandens (explicita) härledning (parabelformen urartar, förr eller senare; Peltoniemi anger vissa gränser för sambanden, men väldigt löst — ingen vet ännu i grunden hur det fungerar).

Webbkällans Appendix-länk leder ingenvart.

 

 

 

Databas PeltoniemiBahcall

Neutrinotvärsnittet från neutrinoenergin

————————————————————————————————————————————————

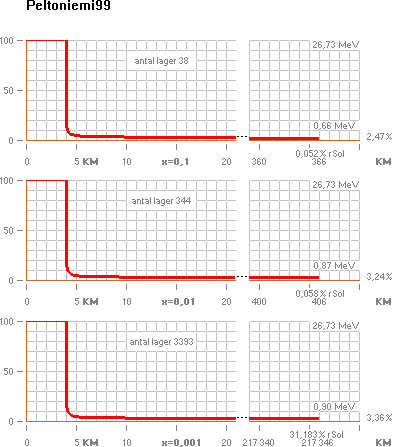
Peltoniemi99 kurvapproximation (beige heldragen unit1200):

y = (x'2.35)(0.25+x'2)'–0.75

Bahcall97 kurvapproximation (indigo heldragen unit1200):

y = (x'3.35)(0.505+x'2)'–4

————————————————————————————————————————————————

 

 

————————————————————————————————————————————————

---------------- vertikal gräns för Solstädets neutrinoproduktionsnivå max 26,73 MeV enligt TNED

 

Bahcalls tabelldata saknar ekvationsform: För att kunna utföra täthetsberäkningarna för Neutrinodämpningen från Solen ENLIGT TNED krävs en motsvarande kontinuerlig funktion som (RÄTTVIST) avspeglar originalets grundform (intervallen måste kunna beräknas in till millimetern för prövning av neutrinodämpningen). Ovanstående hoftning (heldragen indigo, se sambandsformen ovan) för Bahcalls tabellvärden (mörkblå fyrkantpunkter) motsvarar den åsyftningen och har använts i utvärderingen. Motsvarande för Peltoniemi finns redan från hans parabelform (E²) — men har här kompletterats på motsvarande Bahcallpulsgrafens form (för ordningens skull) — och därmed i (vidare) jämförelse med samma grafiska grund (Peltoniemis parabel urartar annars då den växer obegränsat [Denna senare detalj har dock mindre betydelse eftersom Solvärdet i vilket fall i TNED börjar från max 26,73 MeV]).

 

Resultatredovisning TNED

Resultat — med databaser för neutrinotvärsnittes funktion av neutrinoenergin från Peltoniemi och Bahcall

Se även beräkningsgrunderna i TABELLMATEMATIKEN med FÖRDELNINGEN.

 

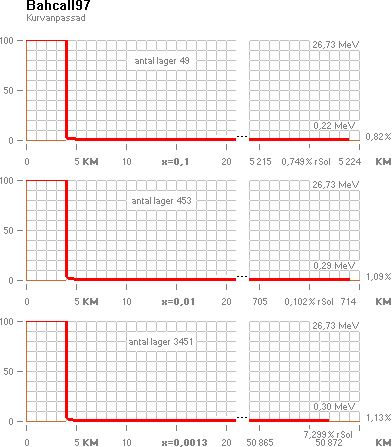
NEUTRINODÄMPNINGEN sker praktiskt taget omedelbart från Solstädet (R=4012 M); Redan efter 4012M + 1 KM är huvudsaken redan avklarad. Men kolla känsligheten: Den till synes ringa skillnaden mellan Peltoniemi och Bahcall bildar rena katastrofen i precision; en säger 1,13%, den andra 3,36%. Det är en inbördes avvikelse på nära 1:3. Neutrinostrålningen från Solkärnan enligt TNED dämpas i fallet Peltoniemi från max 26,73 MeV till utgående (3,36413%) 0,89923 MeV, eller i fallet Bahcall (1,12769%) till 0,30143 MeV. Övriga nivåer (både högre och lägre) bör också finnas med, men i mindre andelar.

 

Utgående neutrinostrålning från Solen enligt TNED — max 4% (Peltoniemi) min 1% (Bahcall)

———————————————————————————————————————————————————————————————————

 

 

———————————————————————————————————————————————————————————————————

ANTAL LAGER: För att genomföra beräkningarna måste Solkärnan indelas i bestämda skikt eller lager med konstant täthet: neutrinostrålen får gå en liten bit (bara millimeter i fallet x=0,001). Därefter beräknas ett nytt täthetsvärde som från det dämpade neutrinoenergivärdet ger ett nytt värde på neutrinostrålningens fria medelväglängd med ytterligare ett intervall, osv. Antal lager ger totala antalet sådana intervall i beräkningarna — som bara anställs fram tills fria medelväglängden tar strålvägen ut ur Solkroppen. Successionerna med x från 0,1 till 0,001 visar samhörigheten i resultatvärdena. I Bahcalls fall har x=0,0013 använts då x=0,0010 inte räcker för de använda max 10 000 cellberäkningarna. Skillnaden är i vilket fall helt marginell.

Den röda grafens baslängd slutar där nästföljande beräknade fria medelväglängd tar strålen ut ur Solklotet. Denna är i fallet Peltoniemi resp. för x = { 0,1;  0,01;  0,0013} lika med  avr. i KM {366;  406;  217 346}.

Tätheten i dessa fall för Solen enligt TNED beräknas ρ = (1/r^4)·(2,10751 T19 KG·M) med r i KM, med resp. värden 1,17 T9; 7,76 T8; 94,4 KG/M³.

(Homogena Tätheten måste vara minst T9 för att resultatet ska bli minst 1%).

 

 

OM det klassiska KVANTITATIVT konventionellt grundade påståendet vore riktigt att ca 3% av Solenergin återfinns i formen av utläckande neutrinostrålning (med huvuddelen samlad omkring strax under 1 MeV), och förutsatt antagen Solmodell enligt TNED, samt att också neutrinostrålningens tvärsnitt följer den energiberoende funktionens kontinuerliga matematik, då är det tydligt att Peltoniemis parabelform ligger närmare svaret på Solfrågan än Bahcalls tabellberäkningar. De sistnämnda visar snarare drygt 1%.

Bahcalls toleranser

——————————————————————————————————————————————

 

 

——————————————————————————————————————————————

 

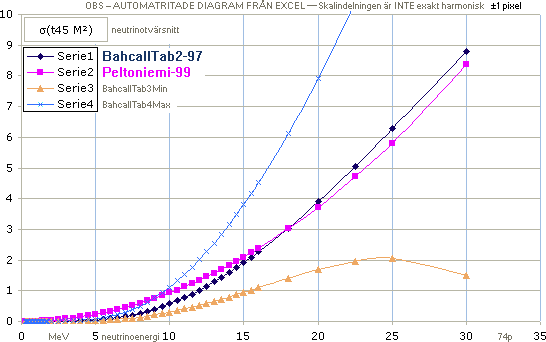
Bahcalls toleransgränser MAX — övre ljusblå — och MIN — undre beige — med centralkurvan BestFit mörkblå fyrkanter. Databasen ljusviolett tillhör parabelformen för Peltoniemis neutrinotvärsnitt som funktion av neutrinoenergin enligt

σ = 9,3·t48 M² ·(E/1MeV)².

 

Vi kan i ljuset av ovanstående resultat (dessutom) DIREKT avfärda Bahcalls OSÄKERHETSMARGINALER (ljusblått-beige ovan): dessa medför, tydligen, så galna värden att de helt saknar ställning i den här analysen. Precisionen måste, tydligen för att matcha den påstådda huvudandelen återstående neutrinoenergiandel på ca 3% av Solens totala omsättning — OM nu den kvantiteten verkligen ÄR hållbar och relevant angiven — ligga inom samma principmarginal som skillnaden Peltoniemi-Bahcall. Peltoniemi beskriver f.ö. inte sin sambandskälla närmare.

 

 

 

Strålningstvärsnittet

2010-05-18

Strålningstvärsnittet — med ljusets fria medelväglängd

Vi studerar grundbegreppen med härledning till grundsamband för beräkning av neutrinostrålningen från Solen enligt TNED

 

Från härledningen till LJUSETS ÄNDRING GENOM MATERIEN gäller

 

                y=e–x

 

 

I/I0 = e–µx ....................  stråldämpningen som funktion av vägen x

Webbreferenser

För motsvarande utförliga webbreferenser (per 2010-05-18), se t.ex.

@INTERNET Wikipedia Cross section (physics), Nuclear physics

@INTERNET Wikipedia Mean free path, Derivation

 

”In physics the mean free path of a particle is the average distance covered by a particle (photon, atom or molecule) between successive impacts.[1]. Alternatively, it is the distance at which the intensity of particles drops by 1/e”,

@INTERNET Wikipedia Mean free path 2010-05-12

 

Samband

Genom konventionell standard gäller generellt

d = 1/µ = x ...........................     M

som strålningens fria medelväglängd (eng. radiation mean free path). Då gäller

I/I0        = e–1

             = 0,3678794

             ~37% ........................    återstående strålning efter fria medelväglängden

OM strålningen sammanhänger med någon motsvarande identifierbar METRIK — till exempel i TNED en viss fraktal nivå i atomkärnan med en viss största utsträckning och därmed en viss VÄXELVERKANDE återkoppling på motsvarande våglängd i den växelverkande elektromagnetiskt induktiva dynamiken (vidare nedan) — kan vi IDEALT betrakta den våglängdens »längsrotation» utmed strålvägen som skuggbilden — tvärsnittet — av en cirkelskiva, samma som SKUGGBILDEN av ljusvåglängdens idealt matematiskt sfäriska kvantitativa E=hf-partikel.

Fria medelväglängden

Tvärsnittet

 

Med beteckningen σ (Grek. sigma, s), konventionellt benämnt det s.k. tvärsnittet

σ = πr² ..................................     M², ideala ljustransportens tvärsnitt

bildas då (idealt) via strålvägen x en cylinder med volymen V=σd.

OM vi — utan hänsyn till material — sprider ut varje godtyckligt närvarande massa över hela det lokala tomrummet genom att utnyttja ATOMÄRA MASSENHETEN u=1,66033 t27 KG, får vi en rättvis medelform som gäller varje upptänklig masslokal (förutsatt idealt masshomogen) med en viss given MASSTÄTHET (ρ, Grek. rhå, r)

ρ = u/V ................................      lokala masstätheten

Vi kan då, tydligen, för varje möjlig (idealt homogen) masslokal i universum, var som helst, hur som helst, bilda den formella ekvivalensen V=u/ρ=σd med avseende på den del av massrymden som ses från ljusstrålens sida sett. Likheterna ger oss, tydligen

σd         = u/ρ    ;

d           = u/σρ  ....................     M, fria medelväglängden

Vilket vill säga: fria medelväglängden kan bestämmas ur materialets lokala täthet och ljusformens idealt motsvarande partikulära tvärsnitt.

 

Stavningskontrollerat 2010-05-18

 

 

Neutrinotvärsnittet i TNED, σ

Se även utförligt inledande samband från Strålningstvärsnittet — om ej redan bekant

2010-05-18

 

TNED ger grovt approximativa grunddata i tvärsnitt (σ) för gamma (γ) och neutrino (ν) — men måste korreleras med experimentell observation

 

(Det finns, här veterligt, inget direkt teoretiskt sätt att härleda grundvärdena mera exakt numeriskt — men det är bara min egen mening)

 

Grunddata i TNED på toroidaggregatet N3m20 ger vissa grundläggande uppgifter om första och andra fraktalnivåernas inre formfaktorer (Se utförligt i PLANCKRINGENS DIMENSIONER och ELEKTRONMASSANS KOMPONENTER).

 

τ-ringen

 

 

max r0 · 0,000 000 8

max r0/50

 

 

GAMMASTRÅLNINGENS GRÄNSVÅGLÄNGD bör ligga i storleksordningen elektronelementets (τ-ringens) största utsträckning — främst med referens till parannihilationsstrålningen, den anses konventionellt utpräglad gammastrålning (i TNED övre gränsområdet för neutrinostrålningen [strålning associerad med massdestruktion]). Sämsta fallets (minsta) värde från ELEKTRONMASSANS KOMPONENTER ger

r           = r0/50 = (1,37 t15 M)/50 = 2,74 t17 M;          r0 = 1,37 t15 M

πr2        = 2,35858 t33 M²

             = 0,0236 mb ........................     skulle motsvara lägsta gammaenergins tvärsnitt

Enheten b används konventionellt för ”Barn”, 1b= t28 M², beteckning mb lika med milliBarn (t31 M²). Webbkällan nedan ger ett exempel (för övrigt ytterst svårt att få fram basdata: många skrifter finns i ämnet, men i stort sett alla kräver antingen betalning eller särskild behörighet) som visar att storleksordningen (i grov mening) är relevant.

 

Tabell över viss Gamma Cross Section (i olika material) — ca 1-7 MeV,

http://meco.ps.uci.edu/old/internal/memos/meco146.pdf

Figur 6 ger sigmavärden för gammastrålningen i mb, milliBarn, 1b=t28M², 1mb=t31M² (0,5-40 mb, Aluminium).

 

PÅ LIKNANDE SÄTT skulle man kunna approximera NEUTRINOSTRÅLNINGENS tvärsnitt — som en generell medelvärdesbildare för samtliga fall — på τ-ringens (största, sämsta fallet) inre tvärsnitt (elektronmassans komponenter ingår gemensamt för alla atomkärnors balansräkningar, se Atomfysikens två kungsekvationer i TNED, och bör därför kunna användas generaliserande);

Från ELEKTRONMASSANS KOMPONENTER gäller (nämligen) för τ-ringen som ovan

 

tτ           = 0,15r0/177062 = r0(8,4716 t7) = 1,16061 t21 M (approximering med tjockleken som tvärsnittsradien:)

πr2        = 4,23177 t42 M²  ...........................     TNED-modellens grovt minsta neutrinoenergins tvärsnitt

Eftersom ovanstående mäter sämsta fallets värden — som i princip inte medger någon toroidfaktor alls för den resulterande ringformen — bör värdet ovan öppna upp en sådan på (här uppskattningsvis) minst 10ggr lägre värde, alltså med r reguljärt

r= (1,16061 t21 M)/2/10 = 5,80305 t23. Det ger tvärsnittet 1,0579 t44 M².

 

PRAKTISK MÄTNING visar (se Bahcall nedan) att neutrinostrålningens tvärsnitt från Solflödet (i området kring 10 MeV neutrinoenergi) snarare ligger i storleksordningen t45 M². Alltså runt tusen gånger mindre — eller runt grovt 30 ggr mindre omslutning.

Källan Hyperphysics

— Källan HYPERPHYSICS

 

HYPERPHYSICS — Neutrino Cross Section

http://hyperphysics.phy-astr.gsu.edu/hbase/particles/neutrino3.html

 

berättar hur olika pionjärer — från 1960-talet — räknat fram och korrelerat experimentellt ikring neutrinostrålningens tvärsnitt: Cowan & Reines uppmätte ca t48 M², hyperphysicskällan själv refererar till ett diagram (Rohlf) med uppgiften t45 M², samt via en referens Krane som anger t47 M². Det skiljer alltså även på flera tiopotenser mellan de olika konventionella grundversionerna.

— Eftersom ovanstående rådata från TNED gäller sämsta fallets beräkningar (absolut trängsta möjliga formfaktorer [som betyder att reella fallet TVUNGET skiljer sig (markant) från detta (flera tiopotenser är fullt rimligt i fraktalmatematikens ljus)] är den experimentellt korrelerade delen också rimlig i teorin.

   Man har kommit fram till nuvarande kvantiteter genom just samkörning experiment-teori — men ännu (Maj2010) fortfarande utan djupare kunskaper i ämnet, alla insatta tycks medge den delen öppet.

 

John Bahcall (1934-2005) framstår som en förgrundsfigur i neutrinosammanhangen (en av banemännen för de första neutrinomätningarna från Solen i slutet på 1960-talet). Särskilt hans resultaträkningar från 1997 finns i webbkällan Bahcall.

 

——————————————————————————————————————————————

 

 

Kurvorna ovan automatritade i EXCEL (vars förfärligt fula diagrammall här bearbetats i efterhand till ovanstående) efter sammanställda tabelldata från Bahcall 1997 och Peltoniemi 1999, se nedan. Bahcalls tre kurvor (ljusblå-mörkblå-beige) visar resp. MAX BestFit MIN, Peltoniemis kurvdata (ljusviolett) baseras på en parabelform. Ovanstående tabelldata beskrivs vidare i huvudtexten.

 

Observera att ovanstående datavärden (här veterligt) INTE representerar någon allmän vetenskaplig konsensus — området är svårforcerat och litet är ännu känt. Man tycks istället allmänt vara av uppfattningen (genom olika webbkällor) att det ännu återstår mycket innan något mera säkert kan fastställas. (Intresset för Neutrinoforskningen verkar närmast Enormt [2010] — vilket också avspeglas i mängden till synes kaotiska data som, ännu, ingen tycks kunna få ut något begripligt av ...).

 

——————————————————————————————————————————————

 

Bahcalls resultat ger en utgångspunkt för vidare prövande grund. Liknande resultat till jämförelse finns även genom Peltoniemi (1999, THE ULTIMATE NEUTRINO PAGE).

 

John Bahcalls EXTENSIVA beräkningsarbeten från 1997 (med samtidig koll på experimentella resultat), exemplifierar just och tydligen samverkan mellan experimentalfysik och matematisk resultaträkning — utan att vi här (i vinkling från TNED) behöver lägga några aspekter på TYP av metod, teori eller annat tillvägagångssätt (TNED har t.ex. ingenting ANNAT gemensamt med den moderna kärnfysikens QCD-teori [kvarkteorin] än talet 3, se utförligt från härledningen till N3m20-aggregatet). Det är i vilket fall och uppenbarligen alltid endast slutresultatet som räknas — tillsammans med experimentalfysiken.

 

Det väsentliga i sammanhanget är att neutrinotvärsnittet (och alla andra) är beroende av energin. Utan den förutsättningen kan vi inte använda grundsambanden.

 

Stavningskontrollerat 2010-05-18

 

 

                       Neutrinobegreppet i TNED | Moderna Akademins Solära Neutrinoproblem | Solära neutrinoproblemet |

 

 

Citatreferenser, allmänna och särskilda

 

SÄRSKILDA CITATREFERENSER

                                         

[‡]1:      Konventionella Soldata — kärnans temperatur

”Temperature of core ~15.7×106 K [1]”,

@INTERNET Wikipedia Sun 2010-05-25

[‡]1.1:  

”Fig. 8.1 och 8.2 redovisar hur solens temperatur och densitet förändras med avståndet från dess centrum. Temperaturen är i centrum ca 1,5 × 107 K, och sjunker sedan kontinuerligt, för att ute vid ytan vara ca 5800 K.”,

BONNIERS ASTRONOMI 1978 s129sp1ö

[‡]1.2:   Konventionella Soldata — Max inre täthet

”The core of the Sun is considered to extend from the center to about 0.2 to 0.25 solar radii.[31] It has a density of up to 150 g/cm3[32][33] (150 times the density of water at standard temperature and pressure)”,

@INTERNET Wikipedia Sun,Core 2010-05-25

NOT.: [(1KG=1000G)/(1M=100cM)³=(KG/M³)/1000 G/cM³]; 150 000 KG/M³ = 150 G/cM³.

 

[‡]2:      SSM, Standard Solar Model

@INTERNET Wikipedia Standard Solar Model 2010-05-25

[‡]2.1:   Energibas

”The sun produces energy through nuclear reactions in which nuclei collide and stick together.”,

UNIVERSITY OF LIVERPOOL — (2006)

http://www.vias.org/physics/example_2_4_4.html

 

[‡]3:      Särskilda Samband i Solfysiken enligt TNED som används i beräkningarna med resultat som omnämns i huvudtexten:

 

Värmegradens radiella variation (T)

Ta         = (4pG/akP)1/4 r–3/2 (r0R4/3)1/2  ......................    Se värmegradens radiella variation, °K

             = r–3/2(1,13035 T17 °K[M]3/2)

 

Stjärnmassans radiella variation [Se utförligt i Solfysiken]:

m          = kSTAR(1 – [1+r/R]–1) + mSLIM  ..................      Se stjärnmassans radiella variation, KG

OBS r räknas från städradien R.

 

Täthetens radiella variation

ρ           = ρC(R/r)4 = ρCR4 r–4  ...................................     Se täthetens radiella variation, KG/M³

= r–4(2,10751 T31 KG·M)

 

Vätekärnans medelhastighet per temperatur

v           = √ 3bT/m  ..................................................      Se MOMENTEKVATIONEN i Allmänna Gaslagen, M/S

Med Boltzmanns konstant 1,38 t23 J/°K och Vätekärnans massa (protonmassan 1,0072766u = 1,67241 t27 KG) ges

= (157,33624 M/S)(√[T · 1/°K])

;

mv²/2    = 3bT = (4,14 t23)T  ...................................      J

 

Sambanden ovan har använts i speciellt sammansatta KALKYLKORT (Speciella avsnitt i Kalkylprogram avsedda för speciella beräkningsändamål [här sammanställda i OpenOfficeKalkyl för allmän tillgänglighet]) för att få fram de referensvärden som anges i huvudtexten.

 

[‡]4:      Neutronens sönderfall

”Equation (7.3) implies an instability of the free neutron. It decays [5] with a mean life of about 12 min”,

HOP 1967, s9–195.sp1n

;

”… neutronen sönderfaller som redan tidigare omtalats till proton + elektron (+ neutrino) med en medellivstid av omkring 13 minuter”,

FOCUS MATERIAN 1975 s138sp2n

;

”Neutronen är en neutral elementarpartikel, som är instabil och sönderfaller i en proton, en elektron och en antineutrino med en halveringstid på 12 minuter.”,

BONNIERS ASTRONOMI 1978, s478sp2n

;

”The neutron has a negative magnetic moment of -1.913141 nuclear magnetons or approximately a thousandth of a Bohr magneton. The currently accepted value of its half-life is 615 s +/- 1.4 s [10,25min]. The corresponding value of the mean life, which is now more commonly used, is 887 s +/- 2s [14,78min].”,

ENCARTA 99 Neutron

;

”While bound neutrons in stable nuclei are stable, free neutrons are unstable; they undergo beta decay with a mean lifetime of just under 15 minutes (885.7±0.8 s [14,7617min]).[2]”,

@INTERNET Wikipedia Neutron 2010-05-25

 

 

 

 

OPERA -projektet, referenser

 

   En presentationsfilm som beskriver OPERA-projektet konventionellt finns på YouTube,

http://www.youtube.com/watch?v=ufCyDHSAvLE&feature=youtu.be&a

 

   En av vetenskapsmagasinens artiklar beskriver nyheten från 10 Maj 2010 i webbkällan

ETHlife — TAU NEUTRINO LIKELY OBSERVED IN OPERA DETECTOR — 1 Juni 2010

http://www.ethlife.ethz.ch/archive_articles/100601_Neutrino_oszillation_su/index_EN

 

   Kompletterande beskrivningar på själva anordningarna i OPERA-projektet finns i

The OPERA long baseline neutrino oscillation experiment — G Wilquet (2008)

http://iopscience.iop.org/1742-6596/110/8/082022/pdf/jpconf8_110_082022.pdf

 

Se även i OPERA BEKRÄFTAR TNED.

 

 

Steven Hardy ref.

Se särskilt (omfattande redovisning)

Separat länk till det omfattande PDF-dokumentet (PhD-thesis, ca 15 MB)

 

MEASURING THE 7BE NEUTRINO FLUX FROM THE SUN:

Calibration of the Borexino Solar Neutrino Detector — Steven E. Hardy, Mar2010

http://scholar.lib.vt.edu/theses/available/etd-04092010-132651/unrestricted/Hardy_SE_D_2010.pdf

finns på

http://scholar.lib.vt.edu/theses/available/etd-04092010-132651/

 

 

 

s7mn; viss grundbeskrivning av hur neutrinooscillationen fungerar; beror på massegentillstånden (inducerade av relativa masskvadratsskillnaderna)

s17; pp-diagram

s18ö; hur elektronneutrinon ändras med Solpassagen, äv. s19ö.ill.

s18m; sannolikhetsvärdet 1/3

s24; varför 2(1H2) inte fusionerar direkt till en 2He4 (nuklidkoncentrationen)

 

 

OPERA bekräftar TNED

 

Uppmärksammat 15Jun2010

OPERA-projekt bekräftar TNED

 

Enligt TNED (se från GRUNDÄMNESBILDNINGEN) avancerar nuklidbildningarna via exotermiska fusioner (Se Exotermiska Kärnreaktionslagen) från lättare till tyngre atomer genom motsvarande massdestruktioner (m→γ). Avancemanget sker med neutrinonivåer från de allra högsta frekvenserna med de allra kortaste våglängderna för de allra lättaste nukliderna analogt med Planckstrålningens uppbyggnad (Plancks strålningslag med Plancks strukturkonstant i TNED). Se även separat artikel i Neutrinosignaturen.

   Med Comptoneffektens inverkan (Se Comptoneffekten) på TNED-neutrinostrålningens färd genom materia skulle motsvarande effekt bli den att en viss bildad neutrinokaraktär via en viss nuklidmassa, säg en lättare typ, dämpas ner mot motsvarande neutrinoprofiler som hör till de tyngre nivåerna, analogt motsvarande längre våglängder med lägre frekvenser.

   Eftersom MyonNeutrinostrålningen enligt TNED tillhör den lättare partikeltypen (Myonen 105,66 MeV med MIC-våglängden 0,67r, se MIC-EKVIVALENTERNA) relativt TauonNeutrinotypen som tillhör den tyngre partikeltypen (Tauonen 1777 MeV med MIC-våglängden 0,07r) bör Comptondämpningen gå från MyonNeutrino (högfrekvens) till TauonNeutrino (lågfrekvens) — OM övergången följer samma schema som gäller för de ordinära nuklidbildningarna enligt TNED.

 

Det är också precis det som OPERA-projektet [‡] är byggt för att försöka detektera: från νμ– till ντ.

 

   Rent experimentellt kan alltså ett positivt resultat bara gynna TNED; neutrinostrålning är masslös em-strålning som följer Comptoneffekten. Citatet nedan visar bekräftelsen.

 

 

”Geneva 31 May 2010.

Researchers on the OPERA experiment at the INFN1’s Gran Sasso laboratory in Italy today announced the first direct observation of a tau particle in a muon neutrino beam sent through the Earth from CERN2, 730km away.”,

CERN Press Release — Particle Chameleon Caught in the act of Changing, 31Maj2010

http://public.web.cern.ch/press/pressreleases/Releases2010/PR08.10E.html

 

 

Ytterligare bekräftelse

 

ATT neutrinostrålning verkligen är masslös em-strålning som följer Comptoneffekten — netrinostrålningens hf-energi dämpas speciellt starkt vid utträdet från höga tätheter — understryks bara ytterligare av resultaten från TNED i jämförelse med MAC angående andelen (noga) neutrinostrålning (%) från Solen av Solens totala energiproduktion, samt toppnivån (MeV) på den dämpade rest som når Jorden.

   Den här framställningen behandlar den resultatredovisningen.

   Se vidare närmast nedan.

 

 

NEUTRINOANDELEN FRÅN SOLEN:

 

 

 

 

Sammanställning 2010VI5

Neutrinoandelen från Solen — 1967: 3%; 2010; 1%

 

Efter flera (korsrefererande) genomgångar av tillgängligt webbmaterial SER DET UT SOM

— men inte helt säkert eftersom citatförfattarna verkar ha bara LITET svårt för att föra ner resultatmatematiken på en elementär, begriplig nivå, vi väntar ännu på en enda röst ur den högen, vidare exempel nedan

— att hela ämnet neutrinostrålning från Solen kan sammanfattas (till hit, Jun2010) på följande ENKLA sätt.

 

 

KONVENTIONELLT utgår man ifrån att huvuddelen in till 99% av neutrinostrålningen från Solen sammanhänger med typen positronneutrino (ve+) i typen pp-fusionen

 

p + p     →         2H + e+ + ve+  ................................       konventionellt skrivsätt med atomkärnor, masstalNAMN

;

1H1 + 1H1 – (m®g) = 1H2 + e+  ................................      skrivsätt med hela atomer, atomnummerNAMNmasstal

;

(p + e–) + (p + e–) – (m®g)  = (d  + e–) + e+

; elektronerna e– tas bort från fysiken i modern akademi, enbart atomkärnorna räknas (atomen|kärnans tyngdcirkelmatematik [TNED] står nämligen orepresenterad):

(m®g) = p + p – d – e+

;

2p(1,0072766) – d(2,0135536) – e+       = 0,000999598u            – e+

                                                                = (9,99598 t4)u             – e+

                                                                = 0,931105 MeV          – e+

                                                                = 0,42 MeV

 

Dock räknar vissa författare [se exv. GOOGLEBÖCKER, Nuclear physics of stars — Christian Iliadis · 2007 · s381] med samma totala energiräkning som i TNED, 1,442 MeV

 

1H11,518 + 1H11,518 – (m®g)1,442 MeV        = 1H22,917  +  e+

1H11,518 .......................................................................      skrivsätt med hela atomer, atomnummerNAMNmasstalATOMÄR MASSDEFEKT

Men återigen (vissa författare) uppdelat enligt typen [Hardy 2010, s22], 2.2.1 PP chain

 

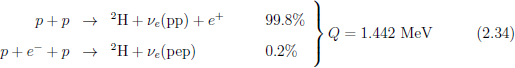
Bildkopia

 

med vidare;

 

Förklaring

 

Man räknar (som ovan [Hardy 2010, s22]) med »ett kontinuum» för typen pp-neutrinos

(reguljära konventionella neutrinotypen ve+, samma som positronemissionsassocierad neutrino, positronneutrino, till skillnad från reguljära konventionella antineutrinotypen ve– [här även v], elektronemissionsassocierad neutrino, elektronneutrino).

 

   I kvantiteter »säger man» att positronneutrinon som bildas i Solen som mest kan ha energin 1,442 MeV (pep-typen [0,2%], men »egentligen» 0,42 MeV, pp-typen [99,8%]) och som minst noll MeV med ett medelvärde på grovt 0,3 MeV (0,265 MeV, Bahcall 1989 [GOOGLEBÖCKER, Nuclear physics of stars — Christian Iliadis · 2007 · s381]).

 

————————————

 

EN OFTA FÖREKOMMANDE ILLUSTRATION man möter i Solneutrinoavhandlingar är typen nedan:

 

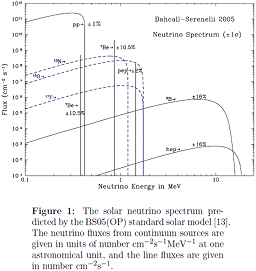
s6;

SOLAR NEUTRINOS REVIEW — Revised December 2007 by K. Nakamura · KEK, High Energy Accelerator Research Organization, Japan

http://pdg.lbl.gov/2009/reviews/rpp2009-rev-solar-neutrinos.pdf

En av de webbkällor som förbarmar sig med i varje fall ett minimum av fugurbeskrivning.

;

BESKRIVNING

pp-typen (ve+, vänster, högsta kurvan) upptar huvuddelen (99%) med sina drygt T11 förekomster (T för 10^+);

Kurvan

— som är en förutsagd beskrivning av HUR den Solproducerade neutrinobesättningen (det sägs inte explicit) framträder i sammanhang som EMELLERTID inte närmare framgår av källan, inte den citerade, och tydligen inte heller andra som använder samma typillustration

— sammanfattar huvuddelen av pp-neutrinoenergitoppen vid ca 0,3 MeV (med ett gränsvärde på 0,42 MeV). Det verkar f.ö. ytterst svårt att få klarhet i vilken detaljerad HISTOGRAFISK innebörd som tillskrivs ovanstående typgrafs betydelse.

   OM resultatvärdena avser Förväntade/Beräknade/Uppmätta förekomster på JORDYTAN (eller ev. dito vid Solranden, eller möjligen i Solkärnan), sägs det i så fall här veterligt varken av ovanstående citatkälla, eller andra genomsökta som använder samma typfigur. Kort sagt finns tydligen ingen webbkälla som klart och tydligt talar om vad figuren avser; Institutionerna hänvisar till varandra. Ingen kan förklara.

 

Genom visst detektivarbete ”… at earth …”

 

NUCLEAR PHYSICS IN ASTROPHYSICS IV — Understanding the Sun: Borexino, Aldo Ianni 2010, s1, Figure 1, s2

http://iopscience.iop.org/1742-6596/202/1/012028/pdf

 

framgår »vissa sammanhang» — men om dessa inte uttryckligen utsägs av källförfattarna själva, är varje påpekande HÄR helt värdelöst källmaterial.

 

Kort sagt: så dåligt, virrigt och kaotiskt som det alls kan bli.

————————————

 

MED EN SENARE UTVECKLAD (delvis förnyad, delvis påbyggd) NEUTRINOTEORI menar man nu (exemplifierat 2010 [Hardy 2010, frn. s17] Adiabatic Flavor Conversion) att pp-neutrinon »i stort sett bevaras» genom passagen ut från Solen — men i gengäld genomgår »transformationer genom olika egentillstånd». Hardy skriver (alla textmarkeringar är mina egna, om inte analoga med dem i originalet)

 

”Thus, an electron neutrino produced at the center of the sun is born predominantly in the

|v2m¦ eigenstate. Now, as the neutrino propagates outwards through the sun, the density

reduces approximately monotonically with a shallow slope, and meets the condition for an

adiabatic density change. This slow density change means that the neutrino stays in the |v2m¦

mass eigenstate and upon exiting the sun, the density (and the |v2m¦ eigenstate) transitions

smoothly and the neutrino now exists predominantly in the |v2 vacuum eigenstate.”,

”Once the neutrino reaches the earth it is observed as ve with probability:

... ~1/3”,

[Hardy 2010, s18] Mar2010

 

BESKRIVNING

Den ursprungliga positronneutrinon (ve+) som bildades i Solen med medelenergin 0,3 MeV bibehåller i stort sin energi då den försvinner ut ur Solkroppen. Men genom en speciell typ av massväxelverkan (egenvärdestransformationer enligt konv. MSW-effekten) förändras sannolikheten FÖR ATT TRÄFFA PÅ 0,3MeV(ve+)-OriginalSolNeutrinon på Jorden;

 

Istället för att uppvisa 100% förekomst, uppvisas istället (typiskt) 33% förekomst.

 

Hardy sammanfattar (med andra ord):

Återstoden 1%

”Produced in the solar center, the initial electron neutrino is predominantly in the heavier mass eigenstate, and if the density changes slowly, it stays in the heavier mass eigenstate all the way until it exits the sun. If the neutrino is in the heavier mass eigenstate

when it arrives at the earth, it has only a 33% probability to be observed as an electron neutrino”,

[Hardy 2010, s20] Mar2010, Figure 2.5

Min översättning:

Producerad i Solcentrum, befinner sig den ursprungliga elektronneutrinon huvudsakligen i det tyngre massegentillståndet, och om tätheten ändras sakta, stannar den i det tyngre massegentillståndet hela vägen tills den utträder Solen. Om neutrinon befinner sig i det tyngre massegentillståndet när den anländer till Jorden, har den bara en 33% sannolikhet att observeras som en elektronneutrino.

 

Med åter andra ord: 33%=1/3 av ursprunget 3% blir 1%.

 

Endast ca 1% av Solens totala energi (förväntas) visas i formen av Jorddetekterad neutrinostrålning

 

Ovanstående syntes representerar alltså DEN NYA FÖRUTSÄGELSEN (urspr. utarbetad fram till ca 2007, men exakta uppgifter finns ännu inte på den delen) till skillnad från den gamla förutsägelsen (från slutet av 1960-talet) som menade att av Solens 100% energi produceras ca 3% i form av (99%) neutrinostrålning (av typen positronassocierad, ve+). I den gamla beskrivningens motsvarande termer (justering med 1/3) betyder med andra ord den nya förutsägelsen (som ovan) att endast ca 1% (33% av 3%) av Solens totala energi kan observeras i formen av JORDDETEKTERAD NEUTRINOSTRÅLNING av den ursprungliga typen (SolOriginalBildad) positronassocierad neutrino (ve+) med medelenergin runt 0,3 MeV.

 

Fråga:

— Vad menas med det? Om neutrinon inte kan iakttas som »elektronneutrino» vad kan den då iakttas som?

— EXEMPEL: Typen elektronassocierad neutrino (ve–) uppvisar en annan »reaktionsnyckel» (strukturprofil) än typen positronassocierad neutrino (ve+); Givet bägge samma energi, kan t.ex. inte typen ve– verkställa en nukleär omvandling som däremot typen ve+ kan. Se särskild beskrivning med tidiga experiment som klargjorde denna skillnad. Dvs., med varje massdestruktion (m→γ) associerad med atomkärnan och olika typer av (konventionella) betaemissioner eller dito absorptioner finns en viss strukturprofil, en slags NYCKEL av en viss typ och form och som bara passar ihop med just den byggnaden (resonansvillkor); Min nyckel passar bara till min lägenhet, trots att alla nycklar i hela byn i stort sett ser likadana ut (Det står ASSA på alla). OM alltså en viss neutrinotyp omvandlas till en annan typ, kan den heller inte längre låsa upp sin gamla värds lägenhet; den fungerar inte längre i sina tidigare kärnprocesser, utan har istället antagit en annan profils roll.

 

   Observera dock att den beskrivningen/förklaringen DELVIS enbart ansluter till Relaterad Fysik (TNED), neutrinostrålningens nuklidindividuella karaktär genomgående i TNED, se från PLANCKS STRUKTURKONSTANT, och DELS inte enligt TNED alls eftersom SÅDAN neutrinostrålning knappast kan »omvandlas», bara genomgå konventionellt motsvarande Comptondämpning (se Comptoneffekten) — motsvarande den massbaserade värmefysikens uppbyggnad från kortare till längre våglängder med ändstation i materiefysiken (Se särskilt Plancks strålningslag).

 

— Svaret på frågan vad den då kan iakttas som blir alltså: något annat. Exakt vad är just Problemet i modern akademi: det finns inte något direkt experimentellt klargörande i den frågan:

 

The OPERA long baseline neutrino oscillation experiment — G Wilquet (2008)

http://iopscience.iop.org/1742-6596/110/8/082022/pdf/jpconf8_110_082022.pdf

”The strong energy dependent deficit in the solar νe flux observed since several decades is well

understood in terms of νe disappearance into an undetermined superposition of the other two active

neutrino flavours”.

 

Det finns ännu (Jun2010) ingen utvecklad teknik för att direkt kunna mäta alla möjliga typer av neutrinopåverkan:

 

”The theory for beta-decay, with some extension, allows the calculation of the basic pp→d+e+νe cross-section, which at 1 MeV is around 10–47 cm2. Measuring such a small value is beyond the reach of current technology, so the cross-section for this important process – which drives the evolution of the Sun – can only be determined theoretically. A check of the flux predicted by the SMM for pp neutrinos is therefore important.”,

CERN COURIER — Borexino homes in on neutrino oscillations (Gianpaolo Bellini, Aldo Ianni report), Jun2009

http://cerncourier.com/cws/article/cern/39162

 

Ingen vet, ännu.

   NOVA-projektet är planerat att börja mätningar från 2013 med syfte att försöka få fatt på just en experimentellt observerad övergång från MyonNeutrinos till ElektronNeutrinos. Referens, se webbkällan

 

NOVA NEUTRINO EXPERIMENT — 12Maj2010

http://www-nova.fnal.gov/

 

   Beträffande de bägge andra neutrinoNycklarna (MyonNeutrino, TauonNeutrino) verkar det dock som att man nära den skrivande stunden (här uppmärksammat 15 Juni 2010) har nått vissa experimentella framgångar (31 Maj 2010), se särskild artikel i Opera bekräftar TNED:

Man har till 98% fastslagit säkert att en TauonNeutrinoförekomst har visat sig i OPERA-detektorn 73 mil från CERN-anläggningens MyonNeutrinoStråleAlstrare; En viss del MyonNeutrinos ändras under den 73 mil långa färden genom Jordskorpan till TauonNeutrinos.

   ElektronNeutrinoSortens eventuella förehavanden med materien i koppling till typen Myon och Tauon är dock fortfarande oklar då elektronNeutrinon ännu tycks undandra sig en närmare inspektion.

   Enligt TNED är Myon och TauonNeutrinonycklarna nuklidassocierade typer via kärnaggregatets 1818e-massa medan elektronNeutrinos är associerade med 18e-delen (Det betyder att det blir svårt att hitta en rent experimentell övergång om det är TNED som gäller). Se mera utförligt från MIC-EKVIVALENTERNA.

 

 

 

Vad utsäger TNED?

 

 FRÅN 26,73 MeV TILL 0,3 MeV

Vad utsäger TNED?

 Se även via länkarna från början av dokumentet

 

Enbart genom täthetsändringen i Solkärnan:

1,097 % med toppenergin 0,2932281 MeV.

Med Peltoniemis databas (Neutrinotvärsnittet som funktion av neutrinoenergin, parabolisk funktion, x=0,0013):

3,36 % med toppenergin 0,89833 MeV.

Med Bahcalls databas (Neutrinotvärsnittet som funktion av neutrinoenergin, särskild funktion, x=0,0013):

1,13 % med toppenergin 0,30143 MeV.

Bägge de sistnämnda kan inte gälla samtidigt (297,3% skillnad).

Se utförligt från RESULTATREDOVISNINGEN.

 

 

 

Neutrino Antineutrino

 

 SKILLNADEN MELLAN

NEUTRINO OCH ANTINEUTRINO

 

Citatet nedan ger en tidig referens (1955) till den experimentellt påvisade skillnaden mellan neutrino och antineutrino.

 

Citat Davis 1955

”The equality of the neutrino and antineutrino could be tested by studying the inverse reaction of electroncapture

 

37Ar + e–           →         37Cl + ve

 

that is

 

37Cl + ve            →         37Ar + e–

 

but, using antineutrinos. It should be noted that the neutrinos are emitted in the fission process where neutron rich nuclei lower their neutron number through the β–-decay process

n → p + e– + ve. The experiment of Davis (1955) gave a negative result pointing towards an experimental way of distinguishing between the neutrino and antineutrino.”, s159m

GOOGLEBÖCKER

Basic ideas and concepts in nuclear physics, Kris L. G. Heyde, (1994|1999|2004)

 

 

TNED:

— Solkärnan producerar bara neutrinostrålning associerad med positronemission.

— Produktion av neutrinostrålning associerad med elektronemission förekommer inte i Solkärnan.

 

 

 

Kalkylkortet

 

Kalkylkortet — Neutrinostrålningen från Solen enligt TNED

 

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN SolNeutrino.ods  —  se öppningsmanual om ej redan bekant  —  eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/SolNeutrino.ods

 

 

Flik1    Solmassans radiella variation — grundsamband enligt TNED för basvärden från Solen; täthet, värmegrad, inneslutna massan

Flik2    databas Hyperphysics — inledande prövningsformer, se Inledande räkneexempel — hur tabellmatematiken fungerar

Flik3    databas Peltoniemi 1999 — tabellvärden från Peltoniemis kvadratsamband — inkluderat jämförelser med nedan

Flik4    databas Bahcall 1997 — tabellvärden från Bahcall

 

Flikarna navigeras med Ctrl+PageUp|Down.

Kalkylkortet ligger helt öppet och kan fritt ändras och modifieras. Generellt: Mörkviolett anger inmatning, rött resultat.

Kortet öppnas med OpenOffice, se Öppningsmanualen om ej redan bekant.

 

 

 

 

 

 

Allmänna samband

 

 

 

 

innehåll: SÖK på denna sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER  ·  förteckning över alla webbsidor

 

 

 

Neutrinobegreppet I Solfysiken Enligt Relaterad Fysik

ämnesrubriker

 

                                     

 

 

innehåll

              NEUTRINOBEGREPPET I SOLFYSIKEN

 

                                                         Vinjettlänkar

 

 

                       Solära neutrinoproblemet i modern akademi

 

                                                         Inledande resultatredovisning

 

                                                         Kort snabbgenomgång — Solära neutrinoproblemet i modern vetenskap

 

                                                                            Solära Neutrinoproblemets uppsegling

 

                                                                            Den uppmätta neutrinoandelen

 

                                                                            Andra och tredje Solära neutrinoproblemen

 

                       Solmodellen i TNED

 

                                                         Solfusionerna enligt TNED

 

                                                         Solstädets produktion av reguljär neutrinostrålning enligt TNED

 

                       Solära Neutrinoproblemet

 

                                                         Neutrinostrålningen från Solen enligt TNED

 

                                                                            Fördelningen

 

                                                                            Hur värdena beräknas

 

                                                                            Neutrinoenergins avtagande

 

                                                         Grovberäkningen i TNED

 

                                                                            Ytterkanten

 

                                                                            Städmanteln                                                 

 

                                                                            Förhållandet

 

                                                                            Resultatet

 

                                                         Neutrino cross section — neutrinotvärsnitt (webbreferens)

 

                                                         Neutrinomängd — Neutrinoflux MAC

 

                                                         Solfusionerna enligt TNED

 

                                                         Neutrinoandelen i MAC

 

                                                         NEUTRINOANDELEN FRÅN SOLEN  — inledande räkneexempel:

 

                       Tabellmatematiken

 

                                                         Tabellräkningens matematiska samband

 

                                                         BERÄKNINGSALGORITMEN

 

                                                         Beskrivning

 

                                                         Granskning — med värdegaranti

 

                                                         Säkra slutsatser

 

                       SSM i TNED — SSM för Standard Solar Model

 

                                                         Helioseismologiska argument

 

                       Referenser

 

                                                         Tvärsnitt — Neutrinotvärsnittets energiberoende

 

                                                         Bahcall 1997

 

                                                                            Tabelldata Bahcall

 

                                                         Peltoniemi

 

                                                         Databas PeltoniemiBahcall

 

                                                                            Neutrinotvärsnittet från neutrinoenergin

 

                                                         Resultatredovisning TNED

 

                                                                            Bahcalls toleranser

 

                                                         Strålningstvärsnittet

 

                                                                            Webbreferenser

 

                                                                            Samband

 

                                                                            Fria medelväglängden

 

                                                                                               Tvärsnittet

 

                                                         Neutrinotvärsnittet i TNED, σ

 

                                                                            Källan Hyperphysics

 

                                                         Citatreferenser, allmänna och särskilda

 

                                                                            OPERA -projektet, referenser

 

                                                                            Steven Hardy ref.

 

                                                         OPERA-projekt bekräftar TNED

 

                       Neutrinoandelen från Solen — sammanställning Jun2010

 

                                                         Vad utsäger TNED?

 

                                                         Neutrino och Antineutrino

 

                                                                            Citat Davis 1955

 

                       Kalkylkortet

 

                                                         Beskrivning

 

referenser

 

[FM]. FOCUS MATERIEN 1975

 

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

mn        = 1,0086652u  ......................    neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

me        = 0,000548598u  ..................    elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för me , Table 1.4 s7–27 för u]

u           = 1,66043 t27 KG  ..............     atomära massenheten [HOP Table 1.4 s7–27, 1967]

u           = 1,66033 t27 KG  ..............     atomära massenheten [ENCARTA 99 Molecular Weight]

u           = 1,66041 t27 KG ...............     atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u           = 1,66053886 t27 KG  ........     atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u           = 1,6605402 t27 KG  ..........     atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u           = 1,660538782 t27 KG  ......     atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c0          = 2,99792458 T8 M/S  ........     ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h           = 6,62559 t34 JS  .................    Plancks konstant [HOP s7–155]

 

EXP     allmän förkortning för e^;För e, se NATURLIGA LOGARITMBASEN (Härledningen till e)

 

PREFIXEN FÖR bråkdelar och potenser av FYSIKALISKA STORHETER

Här används genomgående och konsekvent beteckningarna

 

förkortning       för        förenklad potensbeteckning

 

d                       deci      t1

c                        centi     t2

m                      milli      t3

µ                       mikro   t6

n                       nano     t9

p                       pico      t12

f                        femto   t15

 

Alla Enheter anges här i MKSA-systemet [Se International System of Units] (M meter, KG kilo[gram], S sekund, A ampere), alla med stor bokstav, liksom följande successiva tusenprefix:

 

K                      kilo       T3

M                     mega     T6

G                      giga       T9

T                       tera       T12

 

Exempel: Medan många skriver cm för centimeter skrivs här konsekvent cM (centiMeter).

 

 

TNED

  

 

 

TNED (Toroid Nuclear Electromechanical Dynamics), eller

Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

 

γ                    Grek. gamma, g, är i TNED (ofta) en generaliserad beteckning för massdestruktionsstrålning som [via Plancks strålningslag] byggs upp från kortare till längre våglängder med representation först vid gammanivån i materiefysiken.
Skrivsättet (m→γ), »m till gamma», betyder här ’massa som omvandlas till ljus och värme i materiefysiken’, från lägst gammanivån vilket generaliserat inbegriper värmefysiken överförd på materiefysikens atomkärnor och elektronmassor. Se även utförligt från Energilagen. Mera allmänt betyder (m→γ) massdestruktionsstrålning från primära massförstöraren E=mc².

 

 

Senast uppdaterade version: 2012-02-17

*END.

Stavningskontrollerat 2010-07-15.

 

rester

*

UPPDATERAD VERSION FRÅN 2010-05-29 — Totala Soleffekten räknas med kärndelen för sig (26,7 MeV) och skaldelen för sig (2,04 MeV) per bildad Helium4.

 

åter till portalsidan   ·   portalsidan är www.UniversumsHistoria.se 

 

UNICODE ofta använda Symboltecken i naturvetenskapliga sammanhang

σ ρ ν ν π τ γ λ η ≠

Ω Φ Σ Π Ξ Λ Θ Δ   α β γ δ ε λ θ κ π ρ τ φ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ← ↑ → ∞  ↓

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

PNG-justerad 2011-10-10

åter till portalsidan   ·   portalsidan är www.UniversumsHistoria.se