NEUTRONENS FRAGMENT | Komplement Del I | 2010VII5 | Senast uppdaterade version: 2017-08-13 | en BellDharma produktion |

innehåll · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Partikelbildning med masschokning · ·

NEUTRONFRAGMENTEN i relaterad fysik

Skapelse eller delning?

Modern akademi säger skapelse. Relaterad fysik (TNED) säger delning.

Vi studerar hur.

BILDKÄLLA: Författarens arkiv · Drop16iso3200Bild218 · Mar2009 · NikonD90 — se även fristående textdel separat, detaljen nedan endast i bild

Se f.ö. om Teorin för rotationens uppkomst enligt TNED i samband med K-cellens avyttringar (GALAXBILDNINGARNA med kropparnas primära rotation).

Se även i Vattenrekylens spinn. Vattendropparna på bilderna är i storleksordningen en eller annan millimeter i diameter.

BILDKÄLLA: Författarens arkiv · Drop19iso3200Bild131 · Apr2009 · NikonD90

Fem kortvarigt [1-5S] friliggande vattendroppar — efter rekyl från EN [1] droppe som träffade vattenytan.

— Naturfysiken innehåller, tydligen, inga EXPLICIT GÖMDA PRINCIPDELAR: Allt som finns återspeglas i allt befintligt.

— Nämligen så, att UNIVERSUMS HISTORIA även kan härledas av specifikt fattigt folk: utan stora dyra kikare, förutsatt tid och intresse.

Neutronfragmenten.htm ......................... originalförfattningen från 2008 — bubbelkammarbilden från FOCUS MATERIEN 1975 med inledande exempelbeskrivning NeutronfgmKompl1.htm .................. partikeldelningens principer i TNED med Exempel NeutronfgmKompl2.htm ......................... Massunderskottet, MIC-ekvivalenterna — ovanstående mera ingående med samband SolNeutrino.htm .................................... neutrinostrålningen från Solen enligt TNED

För att fullständiga den påbörjade beskrivningen i NEUTRONFRAGMENTEN (2008) har närmast vidstående kompletterande htm-dokument utformats (våren-sommaren 2010).

Toroid Nuclear Electromechanical Dynamics — ToroidNukleära Elektromekaniska Dynamiken

—————————————————————————————————————————————————————————————————————————————————————————

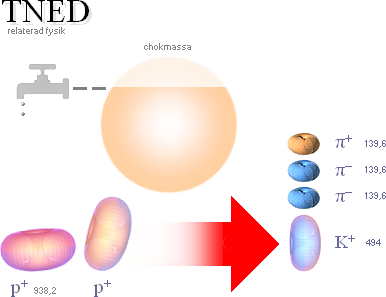
Partikelbildning från partikelkollision — skapelse eller delning? MAC säger skapelse. TNED säger delning.

NEUTRONFRAGMENTEN i relaterad fysik

Utvidgad BESKRIVNING

NEUTRONFRAGMENTEN i Originalförfattningen

Fullständig matematikbeskrivning med PARTIKELACCELERATORNS ENERGI för att bilda partikeln x ur proton-proton-kollision enligt MIC-ekvivalenterna

En mera fullständig kompletterande översikt av NEUTRONENS FRAGMENT i Partikelnomenklaturen

PROBLEMKOMPLEXET SKÄRPS: TNED uppdagar Oförklarade — obemärkt — massunderskott i partikelfysiken

Spårbilden

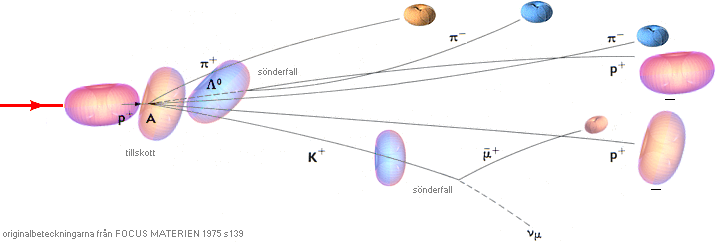
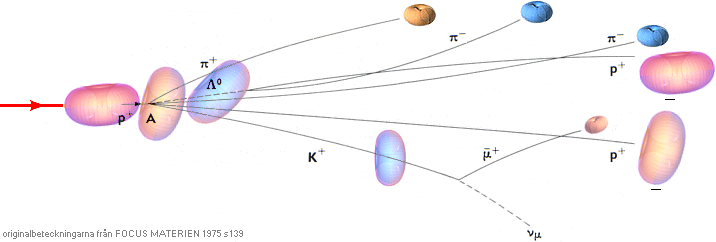
Bubbelkammarfotografi från FOCUS MATERIEN 1975 s139

Strålknippet i bilden nedan med beteckningar (men inte ikonerna) från källan ovan samma sida.

Partikelacceleratorns

ekvivalenter

Hur det fungerar:

Grundbegreppen förklaras och beskrivs utförligt via länkar i de olika avsnitten. Formellt: Vi förutsätter förtrogenhet med härledningen till massökningseffekten inom elektrofysiken med Chokmassan [m(U)=m–m0=UQ/c²] enligt PLANCKEKVIVALENTERNA och MAFEM, samt MIC-ekvivalenterna som beskriver partikelacceleratorenergin för att få en viss partikel (x) att framträda ur proton-protonkollisioner med tillhörande våglängdsekvivalenter.

Chokmassan [UQ/c²] bildas genom energin (E=UQ) i det slutna elektriska accelerationssystem som ger projektilprotonen rörelseenergi och som garanterar systemets bevarade energi via Planckekvivalenterna enligt E=m₀c²=mc_uc=konstant: ingen massa skapas, ingen massa försvinner.

Chokmassan måste därför återlämnas till systemet då projektilmassan återgår till viloläget. Se utförligt från PLANCKEKVIVALENTERNA om ej redan bekant.

Figurerna nedan med beskrivning ger huvudsaken i kort sammandrag.

Ikonstorlekarna här anpassade efter neutron-protonmassan enligt (r/R)³=(m/M).

Chokmassans fysik bestäms induktivt via induktionsmotståndet R i det slutna elektriska system som garanterar bevarandet av Q för den berörda elektriska laddningen Q=√(m/R)(A/dT): m och R varierar exakt proportionellt. Utförligt från MAFEM.

TNED/MAC,

se även Spårbilden

Vi frånser mellanläget med den neutrala Lambdapartikeln (Λ) och ser enbart till partiklarna som framträder tillsammans (tidsanalogt) med protonerna. Den mera utförliga genomgången ges i Exempelframställningen och Massunderskottet.

TNED: De tre Pionerna (π) med Kaonen (K) avdelas ur de bägge givna protonernas kärnstruktur (±e) som garanterar bevarande av laddning och kärnspinn enligt Atomkärnans härledning. För de avdelade miniatyratomkärnorna betyder det att de måste sönderfalla längre fram genom massdestruktion (i TNED samma som neutrinostrålning) ytterst till elektroner (eller positroner) eftersom, vad vi vet, inga stabila minikärnformer existerar. Massunderskottet i protonerna fylls på — ersätts — av chokmassan från partikelacceleratorn så att protonerna framstår som massintakta (chokmassans impuls garanterar spårbilden).

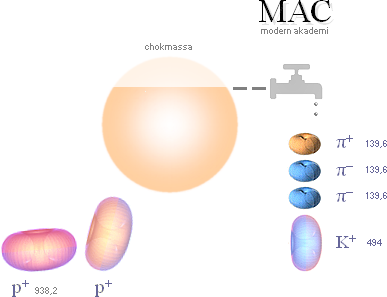
MAC: De tre Pionerna med Kaonen »skapas direkt ur chokmassan». Protonmassorna lämnas intakta — det förefaller i varje fall så enligt spårbilden. I MAC finns inte atomkärnans härledning med ±e-strukturerna, och därmed heller ingen fraktal kärndelningsstruktur som kan definiera nollsumma för laddningar och spinn i atomkärnan (en bild av atomkärnan i MAC kan f.ö. inte förekomma [‡]), vilket gör att delningen inte kan härledas (Kvarkteorin hindrar); OM ±e-strukturer föreligger påstår man att »massa skapas» [‡] ur den kvantitativa ekvivalensen mellan massa och energi E=mc². I TNED finns ingenting sådant. Se även Spinnbegreppet i MAC. Där görs vidare jämförelser. Se även spinnbegreppet TNED/MAC i Jämförande Tabell.

Spårbilden i kvantitativa massimpulsekvivalenter blir i bägge fallen TNED/MAC densamma — i fallet partikelkollisioner grundade på artificiell partikelacceleration. Men det betyder enligt TNED att chokmassan döljer ett massunderskott i protonmassorna genom spårbildens massimpulser — och som aldrig har kommit fram i MAC till kännedom; Då protonerna återgår till viloläget måste chokmassan lämnas tillbaka till accelerationssystemet enligt MAFEM. m₀c²=mc_uc=konstant.

(Se härledningen till massökningseffekten genom elektriska acceleration i PLANCKEKVIVALENTERNA; det slutna elektriska systemets energi bevaras enligt E=m₀c²=mc_uc=konstant: ingen massa skapas, ingen massa försvinner).

Men då är experimentbilden redan förverkad:

— Ingenting syns av slutformen i spårbilden som sådan:

— Protonernas massdeficit passerar obemärkt i MAC.

Anledning: Elektriska laddningens härledning ingår inte i MAC och heller inte PLANCKEKVIVALENTERNA som helt ersätter r-teorins matematik — och förklarar den som primitiv. Se utförligt från vic-felet.

I DET NATURLIGA KOSMISKA STRÅLNINGSFALLET, motsvarande ovanstående spårbild, finns enligt TNED inte chokmassan eftersom denna bara kan ges via elektrisk acceleration genom resistansfaktorn R; R garanterar att Q=√(m/R)(A/dT) bevaras i exakt proportion till variationer i m. Men R finns inte i mekaniken; Enligt TNED finns bara mekaniska orsaker som kan förklara hur kosmiska protoner och andra atomkärnor kan accelereras till höga hastigheter: Elektrisk acceleration — chokmassa — i det naturligt kosmiska fallet är helt uteslutet enligt TNED [‡].

I det naturkosmiska partikelstrålningsfallet måste alltså enligt TNED protonerna (eller kollisionskärnorna) uppvisa motsvarande massunderskott för de partiklar som bildas (PiMesoner och andra).

Svårigheterna i jämförelser mellan den artificiella partikelacceleratorns fall och det naturkosmiska fallet är emellertid avsevärda.

Den främsta skillnaden enligt TNED finns belyst i BEVISET FÖR MULTIPLA c: den naturliga spårbilden kan aldrig erhållas artificiellt eftersom den artificiella bilden alltid begränsas av det slutna elektriska systemets vMAX=c medan ingen sådan gräns finns i naturfallet enligt TNED och förutsatt v på mekanisk väg. Det går inte att jämföra de olika domänerna i någon direkt mening. Med givna impulser måste spårbilderna hur som helst bli olika eftersom energierna INTE är lika medan impulserna ÄR det (Se ENERGIERNA i sambandsredovisningen i MIC-ekvivalenterna).

Emellertid är hela den kosmiska partikeldetekteringsteorin helt uppbyggd på motsvarande artificiella partikelacceleratormatematik (Matematiken i ämnet ENLIGT TNED beskrivs utförligt i PLANCKEKVIVALENTERNA — som inte ingår i MAC). Ingen känner till något annat — i MAC.

I försöken att hitta avgörande bevis, enbart med hjälp av allmänt tillgängliga webbkällor, som kan upplysa oss i det så — enligt TNED som ovan — uppmärksammade massunderskottet från den kosmiska partikelbildningen, tycks ingenting annat framkomma än INDICIER som enbart stärker TNED-alternativet: Det är ytterst svårt att ens försöka få fram avgörande bevis, främst därför att den teknik man använder (fotografiska emulsioner, utvecklades först 1932-1937 av Blau-Wambacher [‡] med den avgörande upptäckten 1937 av nämnda, sedan vidare från 1938 av Powell [‡]) inte DIREKT kan avslöja en viss partikels massa [‡], enbart dess förmåga att jonisera (energiomsätta) emulsionsmaterialet (silverbromid): för att tolka emulsionsspåren har man använt experimentella resultat från partikelacceleratorer som spårmallar [‡].

ATT spårbilder erhållna från partikelacceleratorer INTE stämmer med spårbilder erhållna från kosmisk strålning finns f.ö. å ena sidan redan omvittnat i särskilda delar för sig [‡] och är å andra sidan redan ett välkänt faktum på grund av den kosmiska partikelstrålningens allmänt mycket högre energier [‡] — och följaktligen med (helt) andra spårfenomen än vad som någonsin kan bildas på artificiell väg.

Detaljerna blir (just därför) obskyra då varje ANALOG jämförelse undandrar sig direkt experimentell observation (energin i partikelacceleratorfallet är som redan påpekats avsevärt lägre än i naturfallet) och ingen direkt klar slutsatsform finns därför (ännu) att presentera.

Den rent teoretiska sidan av saken enligt TNED är dock redan utomordentligt klar: massa kan inte skapas av energi därför att massa kan upplösas till energi. Se från ENERGILAGEN, och särskilt Kommutativa ekvivalenten i Massvärmet : massa är inte värme, och värme är inte massa. Med den förutsättningen (resultatet av kollisionerna via kosmiska partikelstrålningen, partikelbildningen) är det klart att partiklarna avdelas från befintliga kärnmassor (som därmed kommer i massunderskott); Masslös energi kan inte bilda en separat, fristående, vägbar massa: Lokal gravitation (massa) kan inte skapas, endast förintas.

Ett av skolexemplen skulle vara Rutherfords experiment från 1919: Kväve-14 bestrålades med Helium-4 som resulterade i Syre-17 och Väte-1 — på kredit av Heliumkärnans rörelseenergi (min0,0012u=1,12MeV): materia skapas ur rörelseenergi. Se särskilt EXEMPEL.

PARTIKELBEVIS som visar att protonen KAN lämna ifrån sig massa i UTBYTE mot energi finns redan i det s.k. INVERTERADE BETASÖNDERFALLET (eng. inverse beta decay). Där framgår också, mera grundligt — om än något omständligt — TNED-beviset för att energi INTE kan skapa massa kvalitativt, endast ge en kvantitativ ekvivalent i utbyte.

Helheten visar att TNED tycks ge en (helt) perfekt fysikförklaring överlag — men på grunder som fortfarande kräver mera tydliga experimentella bevis.

BEVISBARHETEN I PARTIKELACCELERATORERNAS BEGRÄNSADE FYSIKBESKRIVNING:

2010VI25

Partikelacceleratorns begränsade fysikhorisont

Följande framställning utgår från bevisen för att massa inte kan skapas av energi därför att massa kan upplösas i energi enligt primära massförstöraren E=mc² — samt från enda fysiska möjligheten i relaterad fysik (TNED) att kosmiska partikelstrålningens impulser har mekaniska orsaker [R finns inte med i Q=√(m/R)(A/dT)], inte elektriska (R finns med i Q, se särskilt från PLANCKEKVIVALENTERNA om ej redan bekant):

Starka elektriska spänningsfält finns visserligen enligt TNED för alla aktiva stjärnor mellan centrum och hölje, se från Solens Kapacitans. Men det är en inre polarisation med en intern balans som upprätthålls av det kärninduktiva strålningstrycket. Då stjärnan slocknar, upphör strålningstrycket och stjärnan sjunker ihop som en gummiballong som töms på luft. Förutsättningen för att partiklar ska kastas ut med höga hastigheter finns enligt relaterad fysik först sedan stjärnan slocknat och stjärnmaterialet når maximal täthet genom gravitell sammandragning på den högtäta centralkroppen, dvs., då stjärnan »novar». Se utförligt från PULSARMATEMATIKEN. Men den dynamiken utesluter samtidigt varje möjlig elektrisk acceleration. Enda möjligheten enligt TNED är alltså på rent mekanisk väg, antingen från speciellt tunga stjärnor som bildar nova, eller från aktiva områden i centrum av tunga materiesamlingar typ galaxcentrum (mera intensiva novaområden), eller som rester från primära divergenständningar — eller mera exotiskt från den infallande påfyllnaden av neutroner-protoner från c0-kroppen, men ingen analys finns ännu framställd på den punkten. Till jämförelse detonerar K-cellen som sådan i ytterskiktet på runt 25 miljoner c (som dock snabbt dämpas på grund av den starka centralgravitationen). Se från K-cellens Detonation. Se även i GcQ-teoremet som garanterar korrekta grundpremisser.

Den mekaniska ekvivalenten till den experimentellt observerade högsta kosmiska partikelenergi som uppmätts (ca T11 GeV eller runt T20 eV) motsvarar med protonens vilomassa en mekanisk hastighetskomponent på runt en halv miljon c. Huvuddelen som omsätts i Jordatmosfären ligger dock ekvivalent omkring ca 10c. Se även i BEVISET FÖR MULTIPLA c. Ingenting av dessa detaljer ingår emellertid i modern akademi eftersom K-cellens värmefysik — såväl divergenständningsfysiken som pulsarmatematiken enligt TNED — står helt orepresenterad i modern akademi, just på grund av atomkärnans härledning.

Inledande beskrivning

MIC-ekvivalenterna beskriver partikelacceleratorns energi med tillhörande brytningsvåglängd (MIC, λ=h/mv, alltid mindre är atomkärnans yttre spinnradie) som kan uppvisa (»syntetisera») en partikel x med känd vilomassa genom kärndelning via proton-protonkollision.

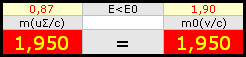
Resultatruta för x=494MeV — Från Kalkylkortet till MIC-ekvivalenterna.

MIC-EKVIVALENTERNA innefattar sambandsbeskrivningen med motsvarande impuls (mv) och energi (mv²/2) för det naturligt kosmiska fallet — med förutsättningen att projektilprotonen får sin impuls på rent mekanisk väg. Se även i BEVISET FÖR MULTIPLA c.

I TNED bildas kärndelarna genom reguljära avdelningar från de bägge kolliderande protonerna. I modern akademi (MAC) menar man istället att kärndelarna SKAPAS ur de kolliderande protonernas rörelseenergier.

Bilden ovan (förminskad från större originalbild) från partikelacceleratorns ekvivalenter.

I MODERN AKADEMI DÄREMOT finns enbart partikelacceleratorfysiken — i TNED representerad av PLANCKEKVIVALENTERNA med härledningen till elektronens massökning (chokmassan) i elektriska accelerationsfält.

När därför den kosmiska strålningen först uppmärksammades (Wulf 1910, Hess 1912) [‡] kläddes den omedelbart i relativitetsteorins teoretiska matematik — och har sedan dess så behållit den klädnaden i de etablerade korridorerna.

Som resultatrutan ovan visar för MIC-ekvivalenterna (här från x=494 MeV), är impulserna (mu=m₀v) alltid ekvivalenta i jämförelsen partikelacceleratorfallet och naturkosmiska fallet, medan rörelseenergierna inte är det (mu²/2≠m₀c²/2). Se även i ENERGIERNA.

Kosmiska partikelstrålningen ofullständigt beskriven

————————————————————————

Kosmisk strålning och artificiell partikelacceleration utgör olika fysikfenomen enligt TNED

Vilket vill säga: Med den kosmiska strålningens orsaksfysik

— sådan den förmodas vara till naturen av TNED, dvs bildad på rent mekanisk väg, vilket utesluter det elektriska fallets massökningseffekter via Q=√(m/R)(A/dT) eftersom elektriska motståndets parameter R inte finns i mekaniken

— existerar ingen exakt analogi till motsvarande partikelacceleratorfall. Det finns ingen direkt analogi. Den kända kosmiska partikelstrålningens fysik är med andra ord i ovannämnda förutsättningar tydligen ofullständigt beskriven — om TNED gäller.

Hur MAC blandar ihop naturfallet med artificiella fallet

————————————————————————

Flera tillgängliga webbkällor intygar samma detaljsammanhang:

KONSULTATION AV TILLGÄNGLIGA WEBBKÄLLOR (Jun2010) visar:

I analysen av de partikelspår från den kosmiska strålningen som grundas på den nukleära fotografiska emulsionstekniken som utvecklades av Blau-Wambacher perioden 1932-1937 och sedan vidare bl.a. av Powell (från 1938, eng. nuclear photographic emulsions, sv. [förenklat] kärnemulsionsplåtar eller kärnspårsplåtar) används SPÅRMALLAR av främst Vätekärnor (protoner) och Heliumkärnor (alfapartiklar) som preparerats via olika partikelacceleratorer för att få fram jämförelsedata; Acceleratorn får producera kända partikelenergier som sedan studeras i givna emulsioner. Datat tabellförs som spårmallar och som sedan används i motsvarande kosmiska emulsionsanalyser. Om den beskrivningen är korrekt, har man alltså med andra ord byggt upp hela analysen, ända in till våra dagar, på en förmodad ekvivalent partikelacceleratorfysik.

Det faktum att emulsionstekniken bygger på en delvis komplicerad »materiell algoritm»

— (också med erkända brister [‡] som varit föremål för förbättringar — med en vidare, alltmer avancerad analys) som grundas på jonisation — energiomsättning — i emulsionsatomernas silver(bromid)korn

— betyder att olika ingångsenergier bildar olika förutsättningar. Även om impulserna är desamma (se även r-teorins matematik) i jämförelsen partikelacceleratorfallet och naturfallet enligt TNED, kan slutprodukten aldrig bli samma eftersom energierna är strängt olika — värre ju större impulser det handlar om [‡].

Jämför exemplet ovan med x-partikeln på 494 MeV (konv. en Kaon): Naturvägens energi är 2,18 ggr större än partikelacceleratorns (1,90/0,87=2,183908). OM emulsionstekniken bygger på energikänslighet, och så sägs det (se citatet närmast nedan), är det alltså tydligt att varje jämförande spåranalogi är helt utesluten. Det är fråga om olika fenomenvärldar.

s1828sp1m:

”The silver halide grains in the emulsion are made developable by the ionization produced by a charged particle. Since the same process is responsible for the energy loss of the particle in its passage through matter, the grain density, like the specific energy loss, will increase with increasing charge and decreasing velocity of the particle and will be independent of its mass.”,

Physical review — kan inte textkopieras, kan inte sökas i

INVESTIGATION OF THE PRIMARY COSMIC RADIATION WITH NUCLEAR PHOTOGRAPHIC EMULSIONS — H. L. Bradt, B. Peters, 1948

http://cos.cumt.edu.cn/jpkc/dxwl/zl/zl1/Physical%20Review%20Classics/cosmic/019.pdf

Med E=UQ=accelerationsspänning×laddning och accelerationsspänningen direkt kopplad till partikelacceleratorns projektilhastighet (u) blir ovanstående redovisning bara en bekräftelse på att partikelacceleratorns partikelenergi avgör spårbildningen i spårmallen: laddning, hastighet (dessutom på delvis omvänt sätt).

Det finns också etablerade beskrivningsexempel som påtalar observerade skillnader i jämförelsen mellan plåtar från kosmisk strålning och motsvarande partikelaccelererade analyser — men det är här ingalunda någon enkel sak att få fram en mera preciserad beskrivning på vad, exakt, som avses. Se exv.,

WIDTH OF HEAVY-ION TRACKS IN EMULSION — E. J. Kobetich, Robert Katz, University of Nebraska 1968

http://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1008&context=physicskatz

s406sp2m:

”Comparison of the widths of cosmic-ray tracks with those produced by known ions in G-5 emulsion at the Berkeley HILAC yielded inconsistent and inconclusive results. Machine-accelerated ions at 10 MeV/amu have a range less than 150 µ and, when suitably oriented for photography, lie in the top 15 µ of emulsion, while the cosmic-ray tracks used here were selected so as to lie

near the middle of a 400-µ or a 600-µ pellicle. Similar discrepancies in photometrically measured track width have been observed by Hall and Zaffarano⁴ in the outer 15 µ of emulsion.”,

Berkeley HILAC, Berkeley Heavy Ion Linear Accelerator. Ref.,

http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=4325364

Om den naturkosmiska strålningen gäller enligt TNED betyder det att den etablerade bild som växt fram av partikelfragmenten (deras kvantiteter) inte är välgrundad — om än tvivelslöst utomordentligt väldokumenterad som fenomengrund. Dvs., vi vet nog helt säkert att detaljerna finns, men vi har ingen (direkt) koll på deras motsvarande naturliga förekomst och innebörd utom i referens till den tydligt begränsade beskrivningen via Planckekvivalenternas matematiska fysik, analogt partikelacceleratorns fullständiga fysikbild.

— INTE på sätt och vis DIREKT FEL, skulle man alltså kunna säga, MEN DEFINITIVT PRIMITIVT.

[FEL kan man bara säga om en detalj där någon gör anspråk på att den primitiva framställningen är den fullständiga. Det övriga kallas (oftast) ’ofullständig beskrivning’].

Skillnaden

Vari består skillnaden?

————————————————————————

Partikelacceleratorfysiken ser inte massdeficiten

Helhetsbeskrivningen enligt TNED går i vilket fall enbart ut på följande:

— Partikelbildning ur partikelkollision skapar ingen materia, ingen massa, endast uppdelar en redan befintlig massa i delar (genom bevarande av spinn, J=mvr) och med den uppbrytande kraften i den kolliderande rörelseenergin (eg. impulsen via MIC) — precis som deldropparna i en vattensplash.

På samma sätt som rörelseenergin m(Ekin) hos den fallande vattendroppen är oförmögen att SKAPA någon extra massa utan bara förmå en given underliggande vattenmängd att uppvisa DELNING i smådroppar, så måste samma relaterade fysik gälla för en accelererad källpartikel som träffar en stationär målpartikel och därigenom åstadkommer en skur av delpartiklar. Rörelseenergin som sådan har ingen kapacitet att skapa materia, den bara verkställer arbetskraften i uppbrytningen. Annars kan vi lika gärna med en gång sätta igång att knäppa med fingrarna i luften för att skapa hundrakronorssedlar

(med ’jag är alltid bäst’, med flera).

Frånsett eventuellt ingående massdestruktioner som sammanhänger med delarnas eventuella sönderfall:

— Summan av massorna före kollisionen är exakt samma som summan efter kollisionen (vilket man inte anser i modern akademi: man menar att kollisionsenergin Skapar materia). Ingen massa skapas. Ingen massan försvinner.

— Om delning i flera kärnfragment förekommer i en proton-proton-kollision (pp-kollision), kan omöjligen p-massorna före kollisionen vara desamma som p-massorna efter kollisionen — men ingenting av det syns direkt i partikelacceleratorns fall eftersom massdeficiten göms av chokmassan m(U) från den elektriska accelerationen. Därför undgår den detaljen upptäckt: den finns fysiskt, men den syns inte (direkt). Genom att den detaljen heller inte ingår i den moderna akademins teori (Jämför BEVISET FÖR MULTIPLA c), är det heller ingen som saknar en förklaring.

Vidare följer.

Restprotonernas öde

Nästa scen:

————————————————————————

Vart tar de massdeficita restprotonerna vägen?

BILDKÄLLA: Författarens arkiv · Drop19iso3200Bild131 · Apr2009 · NikonD90

Fyra friliggande vattendroppar — efter rekyl från EN [1] droppe som träffade vattenytan.

I moderna kvarter är den frågan i ljuset av ovanstående uppmärksammande — och förutsatt att natursaken är korrekt uppfattad enligt TNED — helt säkert representerad av noll litteratur. Om vi försöker göra en syntes av ämnet med hjälp av TNED och vad som kan utläsas av den tillgängliga matematiska fysiken, finner vi en möjlig HÄR TILL ATT BÖRJA MED HELT TEORETISERAD HYPOTETISK men energiekvivalent lösning.

Elektronmassans delning

— Restprotonernas bevarade enhetskärnladdning (+e) [Se från Kärnladdningens bevarande genom h och E] — men massunderskott — gör att de inte kan bilda ordinära stabila atomkärnor med motsvarande omgivande HEL elektronmassa (–e). Restprotonen är joniserad i samband med (eller redan före) kollisionen och uppför sig därför som en normal proton i spårbilden i det artificiella fallet.

Chokmassan fyller ut massdeficiten så att ingen skillnad är direkt synlig. Då restprotonen sedan saktar av och förenar sig med det omgivande materialet och återlämnar chokmassan till vilosystemets induktiva referenser

— (samma som det slutna elektriska system som gav protonen chokmassan i accelerationen), vilket sker induktivt via induktionsresistansen R i Q=√(m/R)(A/dT) på omgivande laddningsbesättningar enligt MAFEM

— har den emellertid inte den vanliga protonens förmåga att bilda en harmonisk atom: Restprotonen har med proportionaliteten mellan massa och laddning för kärnformen (atomkärnan är massans fundamentalform) enligt TNED bara koppling till lika stor e-mängd som dess restmassa i förhållande till hela protonmassan. Den e-massan kan alltså bara delvis fylla ut hela kärnladdningen e. Därmed bildas tvunget en motsvarande återstående kärnladdningsrest — SOM FÖLJAKTLIGEN tvunget GÖMMER RESTPROTONEN: delar av e kan inte avkännas av fysiska system eftersom fysikens atomärt materiella system bygger på resonanser (hela tal) i de enskilda atomerna med endast hela e-massor i atombesättningarna [Se även utförligt från Spektrum och Kvanttalen]. Med andra ord: Restprotonen »försvinner från radarn». Den blir elektriskt osynlig.

OM — endast under förutsättning — att den osynliga positiva kärnladdningsresten fylls igen med lån från omgivande atomers elektronmassor så att restprotonens kärnladdning neutraliseras, finns möjligheten att restprotonen kan förenas med andra atomkärnor, utan yttre extra moment precis som i det vanliga neutronfallet. Värdatomen kommer då tydligen att erhålla ett masstillskott m(E) som den kan disponera hur den vill.

Restprotonens öde kan alltså helt enkelt förstås analogt med bildsituationen ovan med vattendropparna: restprotonerna absorberas (efter viss elektroninfångning för kärnneutralisering) av atomkärnorna i det allmänna atomkollektivet.

Enklaste exemplen skulle vara med direkt återuppdelning från vilken tyngre värdatom som helst till enskilda Väte-1-atomer, eller andra;

; X till Väte

_ZX^A + m(E) = A₁H¹

U 0,nnn U+m(E)

EXEMPEL:

sammansättning extra för kärna/hölje* totalt u

—————————————————————————— ———————— ———

; Kväve till Väte

₇N¹⁴ + m(E) = 14₁H¹ 7e=+0,0039u 0,107

14,003 0,107 14,110

———————————

* extra för kärna/hölje — ingår i kärnmassan i m(E) enligt TNED [Utförligt från ATOMKÄRNANS HÄRLEDNING]

Om ytterligare restprotonmassa finns kvar, kan förloppet upprepas — resten tas upp av åter en annan värdatom osv. — tills slutresten hamnar på typen elektron (eller positron). Därmed har hela restprotonen upplösts — eller återanvänts.

Partikeldelningen i TNED

Med energiekvivalent och bevarad enhetsladdning

————————————————————————

Hur går partikeldelningen till enligt TNED?

Mass Interactive Connection (MIC), massinteraktiva sambandet i TNED för neutron-protonaggregatet N3m20

_PLANCKRINGENh = m₀cr

———————— < r_FORMENN3m20

mv_{KOLLISIONSIMPULS}

BILDKÄLLA: Ur författarens arkiv

Vattendroppar i rekyl från vattenyta efter en infallande vattendroppe ·

Nikon D90 · Mar2009 · Drop1Bild 113,124 ,140 ·

Se även Droppanordningen. Se även Vattenrekylens spinn.

På liknande sätt som två (eller flera) vattendroppar avdelas ur en gemensam volym

— om och om igen, åter och åter, samma typavdelningar för samma typimpuls (mv), jämför bilderna ovan av vattendroppar som bildas ur en rekyl från en anordning som med jämna intervall avger en vattendroppe med nära samma återkommande massa och hastighet via en bestämd fallhöjd och som därför träffar vattenytan med nära samma återkommande impuls och som därför uppvisar nära samma rekyltyp om och om igen

— måste protonen uppföra sig på principiellt samma sätt: spinndelning — med resultat i ett massunderskott. Vi hade redan kommit fram till den delen längre upp [‡].

OM våglängden (λ) i MIC-sambandet (λ=h/mv) kan tolkas som hela verkningslängden (slaglängden fram och åter) av den påverkande kraft som läggs stötande på målobjektet från projektilens MIC-impuls (p=mv) enligt λ=h/mv, då är det också tydligt att λ definierar ett avsnitt eller en utsträckning i målobjektet som bör vara föremål för en störning eller brytning i målobjektets formbyggnad.

Om vi antar den satsbilden som förenlig med en elementär kärnfysikalisk vågmekanik (vilket explicita avsnitt i TNED inte finns formulerat utom här) kan tydligen ringformen

i neutron-protonformen given som PLANCKRINGEN h=m_Nc₀r_N

brytas rent teoriskt från den punkt där en yttre infallande impuls (p=mv) är max lika med Planckringens egenimpuls (p₀=m_Nc₀). Det skulle i så fall ge en ekvivalent impulsstörning med verkningslängden, eller den massinteraktiva våglängden (MIC-våglängden)

m_Nc₀r_N

———— = r_N = λ

mv

För att bryta den sammanhållande spinnformen (r_N) måste kvoten

p₀=m_Nc₀

———— = k

p=mv

tydligen vara säkert mindre än 1 så att den massinteraktiva våglängden λ säkert blir mindre än spinnradien. Annars påverkas bara hela kärnformen (spinnradien och mera) av impulsens verkningslängd och inget annat händer (jämför även konv. neutrondiffraktion [modesta kollisionsimpulser utnyttjas för att få elektromagnetiska interferensbilder av olika ämnens atomgitter]): kärnan delas inte, den bara stötvibrerar.

Vi kan då teckna sambanden totalt för den massinteraktiva våglängden enligt

λ = h/mv = (m_Nc₀r_N)/mv = k·r_N = (p₀/p)·r_N ; med relationerna

λ/r_N = h/r_Nmv = (m_Nc₀r_N)/r_Nmv = k = (p₀/p)

Planckringens radie (r_N) är emellertid generellt i TNED dynamiskt relaterad till atomkärnans tyngdcirkel [utförligt i ATOMKÄRNANS HÄRLEDNING]. Som visas i KÄRNRADIERNA Del II kan den yttre formradien för N3m20-aggregatet förstås inte exakt men praktiskt taget lika med dubbla tyngdradien (eg. 1,9926606~2; se Planckringens dimensioner för A=1), analogt

r_F = 2r_N ..................... formradien kontra tyngdcirkelradien för neutronen-protonen

Den praktiskt (vågmekaniskt) formbrytande spinnradien enligt TNED ska därför mera korrekt skrivas in i sambandet som gäller för max formbrytande våglängd (λ) enligt r_F =2r_N.

För neutronradien gäller r_N=1,32 t15 M och protonradien r_P=1,37 t15 M. Utförligt i KÄRNRADIERNA Del I och NEUTRONKVADRATEN.

I det praktiska fallet måste alltså λ vara kortare än r_F för att en teoretisk delning ens ska komma på fråga.

Motsvarande för massinteraktiva våglängden i praktiken blir alltså från föregående

λ = h/mv = (m_Nc₀r_N)/mv = k·r_N = (p₀/p)·r_N

lika med nedanstående med relationerna via r_F =2r_N innefattade enligt

λ/2r_N = h/2r_Nmv = (m_Nc₀r_N)/2r_Nmv = k·r_N/2r_N = (p₀/p)·r_N/2r_N = k = h/2r_Nmv

λ/r_F = h/r_Fmv = (m_Nc₀r_N)/r_Fmv = k·r_N/r_F = (p₀/p)/2 = k = h/2r_Nmv

ENDAST OM λ<r_F finns alltså en teoretisk/praktisk förutsättning för att λ kan distordera (störa) spinnformen och därmed framtvinga en spinnbaserad formdelning: atomkärnan kan dela upp sig utan associerad massdestruktion — därför att ingen nukleär, kärnstrukturell, instabilitet föreligger, endast en mekanisk formstörning.

Potentialbarriärens energiekvivalent c_z=c₀/2

Som vi ser av sambandet ovan

h/2r_Nmv = m_Nc₀r_N/2r_Nmv = λ/r_F

blir kvoten λ/r_F lika med c₀/2v=(c₀/2=c_z)/v med m=m_N. Det är alldeles uppenbarligen en ekvivalent till följande utsaga:

neutronens kärnbyggnad m=m_N kan endast avdelas i mindre delar om kärnstrukturens elektriskt kopplande energizondivergens (cz) undertrycks, dvs. begränsas — därmed avdelas en kärndel på den cz-överskjutande neutronens verkansfysik

Vilket vill säga: kärndelen som avdelas, avdelas på en del som »stryper» den normala cz-funktionen. Förhållandet skulle då generellt i Obs mekaniska ekvivalenter ge

λ/r_F = (c₀/2v) = 1/1 för v=c₀/2 ; λ = r_F /1

λ/r_F = (c₀/2v) = 1/2 för v=c₀/1 ; λ = r_F /2

λ/r_F = (c₀/2v) = 1/3 för v=c₀/(2/3) ; λ = r_F /3

…

λ/r_F = (c₀/2v) = 1/n för v=c₀/(n/2) ; λ = r_F /n ;

λ/r_F = (c₀/2v) = 1/n för v=2c₀/(n) ; λ = r_F /n

OM vi söker en PLAUSIBEL elektromekanisk djupförklaring till dynamiken i MIC-formen, är det tydligt att ovanstående energikoppling har betydelse; Kärndelning är möjlig endast om MIC-våglängdens förhållande till formrelaterade kärnspinnradien (r_F ) är mindre än 1.

Se även i POTENTIALBARRIÄREN om ej redan bekant.

Resultat:

Figuren nedan visar MIC-våglängder för konventionellt angivna s.k. vilomassor hos de delpartiklar som bildas ur proton-protonkollisioner via partikelacceleratorer med typexempel från Focuskällan, dvs., med analog matematisk fysik enligt PLANCKEKVIVALENTERNA i TNED. [Samband och kvantiteter som berör partikelacceleratorns parameterfysik är alltså formellt samma som vi hittar i konventionell litteratur, se från MIC-ekvivalenterna].

Partikeldelningen i TNED

För samband och härledningar, se MIC-ekvivalenterna

MIC-våglängderna för proton-protonkollisioner i illustrerad sammanställning med beräknade värden från PLANCKEKVIVALENTERNA, se utförligt från MIC-ekvivalenterna. Basvärdena till partiklarnas vilomassor har använts från särskild tabell i Partikelnomenklaturen.

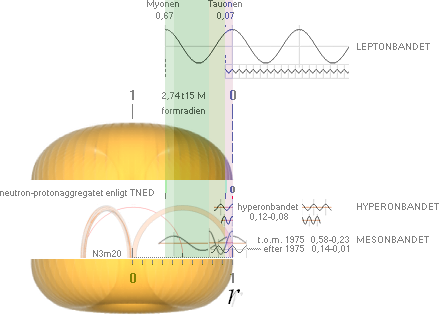
Den angivna våglängden kräver en viss motsvarande kollisionsimpuls (mv, MIC-impulsen) för att den aktuella partikeln ska visa sig — som en viss deldroppe framträder ur en större (vattenvolym) vid droppexperiment med vatten. MIC, från Mass Interactive Connection (massinteraktiva sambandet).

Neutron-Protonvåglängden ligger vid ca 0,14r.

pp-kollisioner: Med allt kortare MIC-våglängder bildas allt tyngre delpartiklar. I partikelacceleratorfallet (spårfönstret) betyder det aldrig några problem eftersom chokmassan alltid finns som utfyllnad: ju högre partikelenergi, desto större delpartikelmassa (den konventionella analysen omfattar inte vad som händer med partiklarna efter spårbilden). Däremot i det naturliga kosmiska partikelinfallets fall enligt TNED där chokmassan inte finns kan inte samma partikelomfång påvisas: delpartiklar av partikelaccelererad typ lika med eller större än protonmassan (938,2 MeV/c²) har ingen möjlighet att komma fram.

Naturkosmiska kollisioner: I detta fall används konventionellt fotografiska emulsioner [‡] som bygger på tunga grundämnesatomer (typ Silver, masstal 107;109). Där kan betydligt tyngre delpartiklar än protonmassans visa sig genom att massunderskottet kan fördelas på hela grundämnesatomens nuklid.

OM experimentell grund finns för att avfärda TNED, skulle alltså en sådan möjligen kunna anställas på just ovannämnda fenomen.

För kritiken av TNED är det viktigt att den aspekten är särskilt uppmärksammad.

I varje fall om de konventionellt angivna s.k. vilomassorna för delpartiklarna har någon naturlig motsvarighet [Se Partikelnomenklaturen], är det tydligt av ovanstående värdesammanställning för MIC-våglängderna att TNED väl beskriver den rent vågmekaniska delningsdynamiska ekvivalensprincipen för hur dessa delpartiklar kan avdelas ur protonen (eller neutronen): inom kärnformens spinnradie.

Myonen med lägsta delmassan (105,66 MeV)/c² har största MIC-våglängden på 0,67r_F. Ju kortare MIC-våglängd, desto högre MIC-impuls krävs för att få fram den delpartikeln.

Notera att det enligt TNED bör finnas en obegränsad mängd djupare liggande leptontyper än Tauonen enligt atomkärnans fraktalstruktur, men energierna för att få fram dessa går också mot oändligt; Med ju högre energier man bombarderar protonen (eller neutronen) desto flera delpartiklar visar sig och med allt högre bildningsenergier.

Det finns (följaktligen) ingen slut på den fysiken enligt TNED. Därmed endast understryks atomkärnans fraktalstruktur enligt atomkärnans härledning.

I härledningen till MIC-ekvivalenterna ingår en del av ovanstående med delvis utförligare beskrivning. Möjligheten med flera neutrinotyper än Myon och TauonNeutrino har också föreslagits konventionellt. Se citat.

Notera dock som tidigare, att TNED inte lämnar någon direkt upplysning på fraktalnivåernas positioner frånsett de två första enligt N3m20-aggregatet.

EN MOTSVARANDE BILD I MODERN AKADEMI kan NATURLIGTVIS inte framställas — N3m20-aggregatet från Planckringen enligt Atomkärnans härledning i TNED ingår av princip inte i modern akademi. Föreningspunkter saknas. Jämför ATOMVIKTERNA.

En mera Exakt fysikbeskrivning än ovanstående finns alltså inte — enligt TNED.

Regelverket

Enligt vilket regelverk sker partikeldelning från proton-protonkollision — med experimentella observationer inkluderade —?

————————————————————————

Partikeldelningens ytterst enkla regelverk enligt TNED

Från Partikeldelningen i TNED

1. Bevara kärnladdningsenheterna;

2. Tillåt ±e=0 så långt restmassorna medger.

Utöver ovanstående två enkla satsbilder finns (tydligen) inga andra som bestämmer partikeldelningens fysik. Bägge baseras på energilagen (nedan) där ±e=0 bildar de enda möjliga laddningsdelar som kan påvisas i den detekterbara materiefysiken.

Vi studerar innehållet — om inte redan bekant.

Elektronmassan i atomkärnan

Tillgången på ±e är naturligt given i TNED eftersom neutronmassan bygger på direkt proportionalitet mellan massa och laddning — atomkärnan som massans fundamentalform. Se från ATOMKÄRNANS HÄRLEDNING.

Kärnladdningens bevarande

genom h och E

Bevarandet av kärnladdningsenheten (e) återfaller på den kvantitativa massa-energiekvivalentens giltighet E=(m→γ)c² från atomkärnans grundform enligt Planckringen eller NEUTRONEN (h=m_Nc₀r_N); E certifierar den omvända byggnaden: ursprungskomponenterna måste energimässigt kunna återfås från delarna:

;

PLANCKRINGEN h=mcr definierar i TNED fundamentala nukleonindividen N3m20, samma som neutronen (n); Efter sitt naturliga sönderfall blottlägger neutronen den stabila protonen (p) med enhetsladdningen +e som definieras i Spektrum och Kvanttalen. Endast ett entydigt sätt, och ingenting annat än endast ett entydigt sätt, finns för p att delas i mindre delar;

— p kan inte delas i två instabila delar. Energiekvivalentens kvantitativa giltighet för massa-energi E=(m→γ)c², som kräver att p ska kunna fås tillbaka, kan inte erhållas om inget stabilitetsvillkor finns: två instabila komponenter har inget kriterium för stabilitet.

— p kan inte heller delas i två stabila delar. Protonkärnans enhetsladdning (e) kan inte delas så att också varje del får e. Nukleonindividens detekterbara fysik (Spektrum och Kvanttalen) bygger f.ö. på en hel elektronladdning. Enhetsladdningens centralkoppling kan tydligen bara ges åt den ena delen.

— Enda återstående alternativet för energiekvivalentens giltighet och kärnenhetsladdningens bevarande via Plancks konstant h blir alltså att p (eller n) bara kan delas i en kärnstabil och en kärninstabil del. Den instabila delen kan sedan i princip delas upp i så många ±e-par som massdelen tillåter.

;

Energivillkoret att t.ex. protonformen måste kunna återfås ur delarna betyder att delningen av protonen kräver en garanterad +-del med protonens ytkärnladdning intakt. Det betyder att den andra delen måste vara neutral — som sedan i sig kan delas i godtyckliga ±-par (så länge ±e finns tillgängligt i restmassan).

Partikeldelningen är alltså garanterad att INTE kunna uppdelas i godtyckliga e/n, det är bara hela ±e som gäller.

;

Med exemplet proton-proton-kollision (pp-kollision) finns KONTINUERLIGT, utan tomma mellanrum, hela tiden en stadigvarande kärnladdningssumma lika med kollisionskomponenternas (här 2+): laddningssumman kan flyttas över i princip på godtyckliga delar men inte försvinna för att sedan återkomma därför att tillfället då laddningen inte är synlig också raderar principen med kärnladdningens bevarande, analogt energiekvivalentens garanterade giltighet för ombyggnad.

Om den ena + flyttas över på den andra så att en proton bär 2+ måste den andra bära 0 (elektriskt neutral), denna kan sedan delas i ett ±-par (proton åter, tillsammans med en –e-komponent). Är laddningssumman 2+ före kollisionen, är den också 2+ efter.

Delningsprincipen för en pp-kollision uppvisar alltså (i allmänhet) för varje p en restproton (+e) tillsammans med minst två ytterligare som summerar ±e=0.

— Det betyder också (eller i sammanfattning) att

· för varje p-delning måste summa av alla delarnas laddningar sluta på samma som p, dvs., på plus en enhetsladdning, helt oberoende av antalet delar;

· p-delningen i en stabil och en instabil kan inte vara förknippad med någon massdestruktion (m→γ) eftersom en sådan enligt TNED (Se CENTRALKONTAKTERNA) endast sammanhänger med en övergång från en instabil till en stabil form; stabila former utverkar ingen massdestruktion; inget inre arbete utförs;

· p-delningen kan alltså bara initieras av en rent mekaniskt ekvivalent formbrytningsimpuls ([h=m₀cr]/mv=r, r måste vara mindre än spinnradien);

· massdestruktion (m→γ) kan följaktligen bara komma ifråga för den instabila delen genom dess delningar;

· varje instabil del sönderfaller (likt en radionuklid) i minst en lättare komponent tillsammans med massdestruktionsstrålning (m→γ); den avdelade komponenten sönderfaller sedan på samma princip i sin tur, och vilken process fortsätter tills en stabil slutstation nås; elektronen (eller positronen).

Partikeldelmassor större än protonmassan

Ur föregående beskrivning framgår:

Partikeldelmassor godtyckligt större än protonmassan kan bildas

· genom pp-kollisioner i partikelacceleratorfallet om delpartikeln bygger på ett protonsubstrat som erhåller chokmassa från projektilpartikeln; endast partikelacceleratorns energitak bestämmer gränserna;

· i det naturliga partikelkosmiska fallet om projektilprotonen kolliderar med en atomkärna med tillräcklig nuklidmassa för att avdela massekvivalenten till delpartikelns (konv. ideala) vilomassa; målkärnans kärnmassa bestämmer gränserna; målkärnans restmassa efter kollisionen motsvarar restprotonen i det enkla pp-fallet, inkluderat med samma kärnladdningsvillkor; Z = Z₁+Z₂+Z₃+…+Z_n; restkärnan bevarar sin ursprungliga enhetskärnladdning;

NOTERA i det enkla partikelaccelererande pp-fallet att en tyngre, neutral, partikel alltid i princip kan bildas via en protonkärna tillsammans med extra chokmassa — som i Focusexemplet med LambdaNoll-partikeln (E₀=1116 MeV) — och som sedan längre fram ENLIGT TNED delas i en restproton (+e, E₁=938,2 MeV) och en negativt laddad partikel (–e [som i Focusexemplet, oftast en Pion–], E₂=139,6 MeV);

E₀–E₁=177,8; originalprotonen tappar max Pionmassan 139,6 MeV — eller någon annan delpartikel som avdelats från protonkärnan.

Dvs.: Ur en neutralt masspumpad kollisionspartikel från en pp-kollision kan alltid en restproton framträda tillsammans med någon negativt laddad delpartikel (P);

P kan i princip ha större (konv. ideal) vilomassa än protonen genom att mellanskillnaden alltid kan tas från chokmassan.

Jämför en P i formen av en masschokad kärndel som längre fram sönderfaller till en elektron, alltså i princip en masschokad elektronmassa: enbart partikelacceleratorns eget energitak sätter gränsen för hur stor den karaktäristiska P-massan kan vara. Då P sönderfallit och lämnat tillbaka chokmassadelen till det fasta accelerationssystemets materialdel [enligt MAFEM], återstår bara den vanliga elektronmassan. I ett motsvarande naturkosmiskt partikelkollisionsfall måste en motsvarande målatomkärna finnas som kan försörja den aktuella massdelen — i allt enligt TNED.

StudieEXEMPEL:

Man har i ett naturkosmiskt partikelkollisionsfall i en fotografisk emulsion [‡] funnit partikelspår med följande upplösning:

HYPERON AND HYPERON RESONANCE PROPERTIES FROM CHARM BARYON DECAYS AT BABAR — Veronique Ziegler 2007, s5

http://www.slac.stanford.edu/cgi-wrap/getdoc/slac-r-868.pdf

Källan ger tyvärr ingen detaljerad beskrivning utöver nedanstående, tillsammans med en kryptisk emulsionsbild

Bildkopia s5 Figure 1.2

NOTERA att »restProtonen» här är en Silveratomkärna (atomnummer 47, masstal 107;109)

Ω^– 1673 MeV/c² ~ 1,796u

Ξ⁰ 1315 MeV/c² ~ 1,412u

K^– 494 MeV/c² ~ 0,530u

Ag (107,87u – 47×0,000548598u) = 107,84421u ~ 100 455 MeV/c²

Omegapartikeln (Ω) beskrivs bl.a. i webbkällan

@INTERNET Wikipedia Omega baryon 2010-07-03

Se även tabellen i Partikelnomenklaturen — sönderfall sker nerifrån och uppåt i tabellen.

Partiklar och antipartiklar

Som redan påpekats tidigare på flera ställen i TNED garanterar neutronens positiva laddningsdeplacement från c₀-kroppen i K-cellens värmefysik att stationär nukleärbaserad materia med omvänt deplacement

— omvänt kärnmagnetiskt moment med omvända kärnytsladdningar, s.k. antimateria

— inte existerar. Universum innehåller ingen stationär antimateria — enligt TNED.

Deplacementet kan därför endast TILLFÄLLIGT — inom bråkdelar av sekunder — växla polaritet av princip med tillförande av viss energi som kan störa den ordinära nuklidbalansen och därmed, kortvarigt, uppvisa en nukleär »antimake». För det krävs alltså en sammansatt ±e-struktur, det som i TNED definieras som en atomkärna (eller dess avdelade miniatyrer).

Termen antipartikel i TNED

Termen »anti-» bör alltså förstås med viss försiktighet i TNED: ±e i meningen ett elektron-positronpar är i TNED inget partikel-antipartikelpar. Elektronen i TNED är i sträng mening ingen enskild partikel alls, ingen kärnform, utan en hop, en komponentmängd, en kvantitet. Se från ELEKTRONMASSANS KOMPONENTER.

Vi relaterar dessa grunder nedan mera ingående, om ej redan bekant.

Hela kärnfysiken från ATOMKÄRNANS HÄRLEDNING enligt TNED bygger på en ekvivalent kraftväv av ±e-massor som bildar den oskapade neutronens kärnform (se från c₀-kroppen: Om energin till sin natur varken kan skapas eller förintas utan måste förutsättas, gäller samma principer för massan; massan är av princip oskapad, föregiven, vår uppgift blir tydligen endast att härleda, och tillämpa, dess byggnad). Kärnformen som sådan kan f.ö. bara upplösas med speciella villkor [Se även från CAT].

Neutronens naturliga sönderfall inom 12-14 minuter frigör en elektronmassa (–e). Och som vi vet från betasönderfallen [Se Nuklidstrukturen] kan atomkärnan även avge positronmassa (+e) för att reglera atombalansen.

±e bildar med andra ord enligt TNED byggelementen i kärnstrukturens laddningsdeplacement och kan därför som sådana, i varje fall enligt TNED, inte direkt klassificeras som partikel-antipartikel. Man använder dock den nomenklaturen konventionellt (bekvämt) i samtliga fall, och ingenting hindrar att man använder den i TNED heller då inga missförstånd kan uppkomma. Massdestruktion (m→γ) kan f.ö. bara verkställas genom att ±e (eller deras fraktala ekvivalenter) förintar varandra på motsatta ringspinn. Det är den primära energiutvinningens grund i relaterad fysik (TNED). Se även från Solfysiken.

GRUNDEN till partikel-antipartikelfysiken i relaterad fysik kan bara vara den allmänna symmetriprincipen (flödesbegreppen med +–) inom matematiken — och därmed via den matematiska fysiken [massan tillsammans med Keplermomentet K=vr, kinematiken, som ger impulsmomentet mvr, kinetiken] med motsvarande dynamik som tillåter kommutativa (ömsesidigt korresponderande) omkastningar mellan ±. Tillsammans med energilagen och dess inneboende giltighet för massa-energiekvivalensen E=(m→γ)c² har (således) med experimentalfysikens hjälp — inte minst via studier av den kosmiska strålningen med hjälp av kärnemulsioner [‡] — visats att just ±-omkastningar — antipartiklar — verkligen KAN existera (men, som sagt, endast kortvarigt). Exempel nedan enligt TNED.

Vilken partikelacceleratorenergi krävs för att bilda en antiproton från en pp-kollision?

————————————————————————

Exempel med konventionell referens

MIC-ekvivalenterna beskriver generellt

— ENLIGT TNED MED OVANNÄMNDA VILLKOR i partikelacceleratorfallet med ena protonen som projektil som bär hela acceleratorenergin m(U) och den andra protonen som målkärna, och med x som den partikel som ska avdelas som kärnsubstratmassa från protonen

— transiteringen

m(U) + p + p → [p – m(x₁) + m(U)₁] + [p – m(x₂) + m(U)₂]

Med föregående partikeldelningsvillkor (kärnladdningens bevarande, ±e=0) kan en antipartikel bara bildas ur en ±e=0-ekvivalent. För x som en antiproton (–e)

m(U) + p + p → p + p – 2m(x) + 2m(U^±)

krävs alltså också en extra normal protonmassa (+e). Mycket förenklat (jämför det konventionella sättet längre ner [‡1]) skulle vi kunna skriva transiteringen »karikerat» som

m(U) + p + p → p + p + X⁰

X-partikeln måste vara neutral (±e=0) för att ett partikel-antipartikelpar ska kunna framträda enligt partikeldelningens allmänna villkor (kärnladdningens bevarande, ±e=0).

Teckningen mera utförligt enligt TNED skulle då bli motsvarande (vi förutsätter symmetri mellan de bägge ±e-substraten)

m(U) + p + p → p – m(x⁺) + m(U⁺) + p – m(x^–) + m(U^–) ;

m(U) + p + p → m(U^±) + p – m(x⁺) + p – m(x^–) ;

m(U) + p + p → p – m(x⁺) + p – m(x^–) + m(U⁺) + m(U^–) ;

De bägge m(U⁺) + m(U^–) bildar respektive (extra) proton och antiproton — de förintas »omgående» via (m→γ) och kvarlämnar — Obs enligt TNED — de bägge restprotonerna

p – m(x).

Accelerationsenergin som krävs E(MeV) för pp-bildningen beräknas direkt ur MIC-ekvivalenterna och man finner

Svar:

E(MeV)pp = 6 567,400 (6,5674 GeV) eller 7 protonmassor (nära lika [6,582 protonmassor] som krävs för att bilda Tauonvilomassan [1777 MeV]). Jämför även samma konventionella resultat i referenskällan nedan [‡1].

Sambandet för E(MeV) i protonmassor (m₀) är (se MIC-ekvivalenterna)

m/m₀ = 1/√1 – (2/[a+1/a])² med

a = √ 1 – [m(p)/(m(p) + m(x)/2)]² med exemplets m(x)=2m(p) ; m(p)=1;

a = √ 1 – [1/(1 + 2/2)]²

= √ 1 – 1/4

= √ 3/4

m/m₀ = 7 protonmassor

I konventionell litteratur (räkneexemplet ovan, men med andra beteckningar, ingår i referensen nedan) skrivs motsvarande ovanstående transitled enligt (typiskt [‡1])

p + p → p + p + p + p’

[‡1] ——————————————

Particle production threshold energies

http://galileo.phys.virginia.edu/classes/252/particle_creation.html

Kärnkollisioner bildar inte elektron-positronpar enbart — enligt TNED

EFTERSOM ELEKTRONEN ENLIGT TNED inte är någon kärnpartikel kan den heller inte — enligt TNED — explicit avdelas som sådan i samband med kärnkollisioner. Elektron-positronpar kan emellertid ändå ’slinka igenom’ via »restvibrationer»; Om kärnkollisionen innefattar energi som omsätts i gammastrålning av den våglängd som sammanhänger med motsvarande parannihilation, kan en atomkärna lämna ifrån sig ett par ±e i utbyte. Utöver denna rent gammarelaterade energikälla finns här veterligt ingen annan som per direkt fysik kan få en atomkärna att utväxla ±e mot em-strålning (minst 2×0,511=1,022 MeV).

[TNED Toroid Nuclear Electromechanical Dynamics uppvisar inget överdrivet intresse för »nukleära vattensplashar», det är (som mest, naturtillfällena frånsett) ett ämne förbehållet den konventionella partikelfysikens allra mest avancerade instrumentbyggen. Tonvikten i TNED ligger istället på att söka svaret på frågan huruvida ett sätt alls finns att upplösa atomkärnan, fullständigt, för energiutvinning utan restprodukter — alltså verkligen noll skräp. Det är hela anledningen, i varje fall i min författarreferens, varför UNIVERSUMS HISTORIA alls kommit till. Enligt TNED ska det, tydligen, finnas ett sådant sätt om allt är korrekt uppfattat (atomkärnan innefattar en inneboende strömfälla). Men inte utan tekniska problemnötter. Se utförligt från CAT och ATA].

Historia Kosmiska Partikelstrålningen

Photographic Emulsion Technique

Nukleära Fotografiska Emulsionstekniken, eng Nuclear Photographic Emulsion Technique

KORT HISTORIK — upptäckten av den kosmiska strålningen och dess producerade kärnfragment:

1896 Henri Becquerel upptäcker radioaktiviteten; Man ansåg att den observerade jonisationen av luftpartiklar berodde på radioaktiv strålning från den underliggande Jordkroppen. [Ref. Wikipedia Cosmic ray, History 2010-06-23].

1910 Theodor Wulf konstruerar en elektrometer med vars hjälp han visar att strålningen uppe på Eiffeltornet är högre än nere på marken. [Ref. Wikipedia Cosmic ray, History 2010-06-23].

1912 Victor Hess förfinar Wulfs elektrometer och bevisar genom en uppskickad ballong (5,3 KM ö.h.) att strålningen fyrfaldigas relativt markvärdena. [Ref. Wikipedia Cosmic ray, History 2010-06-23].

1936 Carl Anderson och Seth Neddermeyer genomför mätningar av kosmisk strålning vid Pike’s Peak (Klippiga Bergen, Colorado) på 4,3KM ö.h. Man använde konventionell fotografering tillsammans med en (ca Ø12 cM) dimkammare bestyckad med en omgivande elektrisk spolanordning som levererade en magnetisk fältstyrka till dimkammaren på (upp till) 7900 Gauss (0,79 Tesla). Det är f.ö. det enda dokumenterade reguljära magnetfältsbestyckade bildbaserade experiment som verkar finns gratis tillgängligt på webben (Jun2010).
[Ref. THE PHYSICAL REVIEW — A Journal of Experimental and Theoretical Physics Established E. L. Nichols in 1893 — Cloud Chamber Observations of Cosmic rays at 4300 Meters Elevation and near Sea-Level — C. D. Anderson, S. H. Neddermeyer 1936].

Upptäckten av Myonen (även benämnd MyMeson) tillskrivs olika personer vid olika årtal via olika referenskällor:
Carl Anderson 1936:
;
@INTERNET Wikipedia Carl David Anderson 2010-06-23
”Carl David Anderson (3 September 1905 – 11 January 1991) was an American physicist. He is best known for his discovery of the positron in 1932, an achievement for which he received the 1936 Nobel Prize in Physics, and of the muon in 1936.”.
;
@INTERNET Wikipedia Muon 2010-06-23
”Muons were discovered by Carl D. Anderson in 1936 while he studied cosmic radiation. He had noticed particles that curved in a manner distinct from that of electrons and other known particles, when passed through a magnetic field. In particular …”.

Street-Stevenson 1937
;
DISCOVERY OF THE MUON 2010-06-23
http://hyperphysics.phy-astr.gsu.edu/hbase/particles/muonhist.html
”The muon was discovered in 1937 by J. C. Street and E. C. Stevenson in a cloud chamber. The discovery was published in "New Evidence for the Existence of a Particle Intermediate Between the Proton and Electron", Phys. Rev. 52, 1003 (1937).”.

1937 Marietta Blau och Hertha Wambacher upptäcker (2,3 KM ö.h.) det karaktäristiska ’explosionsmönster’ (eng. star, stjärna) som framträder på fotografiska plåtar från kosmisk strålning som följd av partikelkollision (eng. spallation events, spjälknings- eller fragmenteringshändelser). De bägge kvinnorna hade tidigare (från 1932) under ett antal år (Prisbelönat 1937 av Österrikiska vetenskapsakademin) utvecklat den fotografiska grundmetoden för detektering av joniserade partiklar [Wikipedia Hertha Wambacher 2010-06-23].

1938 Cecil Powell utvecklade metoden från pionjärerna Blau-Wambacher (se ovan) för mera reguljär mätning av kosmisk strålning. Mätningarna började år 1938 vid olika högt belägna geografiska platser, samt även med hjälp av högtflygande ballonger. [Ref. Wikipedia Cecil Frank Powell 2010-06-23]. Se även Powells nobelföreläsning från år 1950 i separat PDF-dokument, där beskriver han grunderna och ger bildexempel. samt vissa beskrivningar till de olika partikelfragmenten (men ingen djupare utläggning om spåranalysen),
THE COSMIC RADIATION — Cecil F. Powell, Nobel Lecture, December 11, 1950
http://nobelprize.org/nobel_prizes/physics/laureates/1950/powell-lecture.pdf
Powells metod bygger i korthet på att använda silver(bromidkorn) som grundsubstans: en elektriskt laddad partikel som genomfar emulsionen påverkar omgivande atomers elektronmassor genom att söka dra elektronerna till sig, dvs., att åstadkomma lokal jonisation. Ju snabbare den inträngande laddade partikeln rör sig desto längre blir avståndet mellan de påverkade silverkornen, analogt svagare jonisation. Långsamma, starkt laddade partiklar, ger korta avstånd mellan de påverkade silverdomänerna och åstadkommer därmed kraftiga spår medan snabba partiklar med enkla laddningar blir knappt skönjbara.
[Ref. GOOGLEBÖCKER Radioactivity: introduction and history, Michael F. L'Annunziata, 2007 s375mö].
Partiklar med speciellt hög ingångsenergi (hög hastighet, minimal laddning) syns inte alls, om de inte kolliderar med en stationär atomkärna. Metoden kan inte på något direkt sätt avgöra partikelmassan: en given partikel med viss laddning och given hastighet kan i princip ha godtycklig massa. För att avgöra de aktuella fallen krävs speciell analys med en föregiven grundteori.
Ref. Se nedanstående referens Bradt-Peters 1948 s1828, s1830, s1835.

1947 Upptäckten av Pionen tillskrivs Powell (1947). Ref.,
DISCOVERY OF THE PION 1947 — Reprinted from the CERN Courier, June 1997
http://fafnir.phyast.pitt.edu/particles/pion.html

1948 Webben (Jun2010) uppvisar en stor flora av (PDF-) dokument som behandlar grundforskningen kring den kosmiska strålningen perioden 1940-1970 — men tyvärr är de allra flesta belagda med särskild behörighet, eller man måste betala 30 dollar PER för att läsa dem. De PDF-dokument som finns gratis tillgängliga verkar dock uteslutande vara av typen ’kan inte textkopiera, kan inte textsöka’. En av dessa, den hittills mest beskrivande i termer av underliggande metodredovisning och matematiska grundsamband, är den nedanstående
Physical review — kan inte textkopieras, kan inte sökas i
INVESTIGATION OF THE PRIMARY COSMIC RADIATION WITH NUCLEAR PHOTOGRAPHIC EMULSIONS — H. L. Bradt, B. Peters, 1948
http://cos.cumt.edu.cn/jpkc/dxwl/zl/zl1/Physical%20Review%20Classics/cosmic/019.pdf

-1975 Perioden 1947-1975 händer i stort sett ingenting nytt på området detektering av kosmisk strålning utöver en vidare förfinad utveckling av emulsionsmaterialet och metoderna för att få fram data. De obemannade ballongexpeditionerna intar ännu 1975 den övervägande grunden för kosmiska strålningsdata baserat på medsända nukleära fotografiska emulsionsplåtar. Ämnet beskrivs allmänt i FOCUS MATERIEN 1975 s545.
Det finns en närmast enorm uppsjö av webbdokument (de flesta tyvärr, vad det verkar ännu Jun2010 inte gratis tillgängliga) som beskriver forskning och resultat från den kosmiska strålningens fenomen ända in i våra dagar. Tyvärr framkommer emellertid inte så mycket mera i sak i ämnet fotografiska emulsioner än det redan ovan framkomna; Ingen skickar upp dimkammare eller bubbelkammare med obemannade ballonger 2-3 mil över marken för att mäta kosmisk strålning, i varje fall inte så det framgår i den här författarens webbsökande. Så, någon direkt jämförelse med artificiella partikelacceleratorer (konventionella bubbelkammarspår) finns inte utöver ovannämnda bidrag från Anderson-Neddermeyer (1936).

-2010 Med »den kommersiella elektronikrevolutionen» från början av 1980-talet (Intels första 8-bitars mikroprocessor 8080, släpptes först 1974), samt de stora framstegen som följde under 1990-talet med planartekniken (snabba CMOS-kretsar, utvecklingen av högpresterande MOSFET-transistorer m.m.), har numera (2010) i stort sett all analog elektronik ersatts av digital teknik. Datorerans första analoga CRT-bildskärmar är numera helt utspelade och ersatta av en digitaliserad LCD-teknik. Inga elektronstrålar lyser längre upp bildskärmarna utan vi ser istället bilden genom små enskilda bildpixels som matas via ett sinnrikt elektroniskt nätverk av pulserande signaler genom olika system av elektriskt ledande mikrokanaler.
Så har även den digitala tekniken med »de gamla kosmiska emulsionerna» ersatts av integrerade kretsar och specialpreparerade material — med exempel från den satellitburna Fermi LAT (invigdes 2008) som bl.a. mäter den kosmiska strålningens elektronspektrum — utan att ens kunna skilja mellan positiv och negativ elektricitet;
Ref. s53n, Ingen URL-adress finns på nedanstående PDF-dokument
THE COSMIC RAY ELECTRON SPECTRUM MEASURED BY THE FERMI LAT — Melissa Pesce Rollins, Università Degli Studi di Siena (2009)
”Throughout this work the term electrons will be used to refer to the sum of electrons and positrons due to the fact that the Fermi-LAT does not distinguish the charge of the particle.”.
Ordningen endast understryker att det inte längre finns något »enkelt» traditionellt sätt att varken studera eller analysera resultat genom »experimentell observation», allra minst beträffande den kosmiska partikelstrålningens spårbilder.
Den klassiska experimentalobservationen är numera, mer eller mindre helt, dränkt i datoriserade algoritmer och specialkomponenter som i stort omöjliggör varje preciserad direkt inspektion.

Spårmallar citat

Se även Kort sammanställning av Vetenskapshistorien till den kosmiska partikelstrålningen

SPÅRMALLARNA FRÅN PARTIKELACCELERATORER

s485 — kan inte textkopieras, kan inte sökas i

COSMIC RADIATION MEASUREMENTS USING NUCLEAR EMULSIONS ONBOARD THE ZOND-5 AND 7 AUTOMATIC STATIONS

V. A. Blashkovsky et al.— (1969)

http://cdsweb.cern.ch/record/864491/files/p484.pdf

Bildkopia

Dvs.; Man använder partikelacceleratorer (här en synkrotoncyklotron) för att generera olika SPÅRTOLKAR med givna karaktäristiska.

Det utsägs tydligen knappast vanligen explicit i de beskrivande delarna, utom i ovanstående raritet.

Källan från Bradt-Peters 1948

Physical review — kan inte textkopieras, kan inte sökas i

INVESTIGATION OF THE PRIMARY COSMIC RADIATION WITH NUCLEAR PHOTOGRAPHIC EMULSIONS — H. L. Bradt, B. Peters, 1948

http://cos.cumt.edu.cn/jpkc/dxwl/zl/zl1/Physical%20Review%20Classics/cosmic/019.pdf

skriver t.ex. s1828sp2n, fetstilen min markering,

”If some portion of the track consists of a series of resolved, developed silver grains, we can obtain the specific energy loss K of the particle by comparison with a track of equal grain density produced by a known particle of known energy or residual range (proton or α-particle).”

Enda sättet att få fram en sådan mall är genom en artificiell partikelaccelerator.

Här finns ett kopierbart, sökbart PDF-dokument som delvis beskriver ämnet mera ingående, s406sp2m:

SpårAnomalier

WIDTH OF HEAVY-ION TRACKS IN EMULSION — E. J. Kobetich, Robert Katz, University of Nebraska 1968

http://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1008&context=physicskatz

”Comparison of the widths of cosmic-ray tracks with those produced by known ions in G-5 emulsion at the Berkeley HILAC yielded inconsistent and inconclusive results. Machine-accelerated ions at 10 MeV/amu have a range less than 150 µ and, when suitably oriented for photography, lie in the top 15 µ of emulsion, while the cosmic-ray tracks used here were selected so as to lie

near the middle of a 400-µ or a 600-µ pellicle. Similar discrepancies in photometrically measured track width have been observed by Hall and Zaffarano⁴ in the outer 15 µ of emulsion.”,

; s407sp2m,

”The track-width theory is based on the computation of the spatial distribution of ionization energy, from empirical relations describing the dissipation of the energy of normally incident beams of electrons onto films of material, and on the δ-ray distribution formula, empirically modified to take electron binding into account.”.

Berkeley HILAC, Berkeley Heavy Ion Linear Accelerator. Ref.,

http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=4325364

I bland undrar man — man får LETA innan man hittar en webbkälla som löser upp akronymen HILAC.

Ytterligare en webbkälla som beskriver resultat från en partikelaccelerator i samband med fotografiska emulsioner, här från Berkeley Bevatron-anläggningen:

GOOGLEBÖCKER, s35n

NUCLEAR PHYSICS — Luke C. L. Yuan, Chien-Shiung Wu, Academic Press, 1961

Bildkopia

Emulsionstekniken, massoberoende

Physical review — kan inte textkopieras, kan inte sökas i

INVESTIGATION OF THE PRIMARY COSMIC RADIATION WITH NUCLEAR PHOTOGRAPHIC EMULSIONS — H. L. Bradt, B. Peters, 1948

http://cos.cumt.edu.cn/jpkc/dxwl/zl/zl1/Physical%20Review%20Classics/cosmic/019.pdf

Bildkopia s1828 | s1

mass independence

s1828sp1m:

”The silver halide grains in the emulsion are made developable by the ionization produced by a charged particle. Since the same process is responsible for the energy loss of the particle in its passage through matter, the grain density, like the specific energy loss, will increase with increasing charge and decreasing velocity of the particle and will be independent of its mass.”,

;

· Källan redovisar att protoner med hög ingångsenergi (1 GeV per nukleon) inte lämnar några spår i emulsionen (de omgivande ämneselektronmassorna hinner aldrig reagera, och det bildas aldrig något jonisationsspår). Ref. s1830sp2mö, s1835sp1nö.

· Vissa data korrelerades mot cyklotrondata (men inget mera fördjupat är här känt om den ev. betydelsen av den detaljen), s1832sp1m;

Bildkopia s1832sp1m

Emulsionstekniken, brister, metodens utveckling

Här finns visst material med en delvis fördjupad beskrivning av GrainDensityTech, kan inte textkopieras, kan inte sökas i

THE CHARACTERISTICS OF TRACKS IN NUCLEAR RESEARCH EMULSIONS — A. J. Herz & G. Davis, 1955

http://adsabs.harvard.edu/full/1955AuJPh...8..129H

Bildkopia

Magnituderna

@INTERNET Wikipedia Cosmic ray 2010-06-27

”Cosmic rays can have energies of over 10²⁰ eV, far higher than the 10¹² to 10¹³ eV that man-made particle accelerators can produce.”.

Atomkärnan,

åskådning i MAC

Bilder av atomkärnan i MAC kan inte förekomma:

Sättet att beskriva nutidens (2007-2010) etablerat åskådliga uppfattning av atomkärnan och dess avdelningar framgår av följande citat:

”2.2 Matter Particles

The fundamental particles that make up the matter of the world can be organized in two groups, the quarks and the leptons. These are both fermions¹ of spin 1/2 and, as far as we know point-like.”,

; s3n,

ON ANTIHYPERON-HYPERON PRODUCTION IN ANTIPROTON-PROTON COLLISIONS WITH THE PANDA EXPERIMENT,

A Thesis submitted for the degree of Master of Science in Engineering Physics,

NUCLEAR AND PARTICLE PHYSICS, UPPSALA UNIVERSITY — Catarina E. Sahlberg, March 2007

http://www5.tsl.uu.se/panda/pub/2007/CatharinaSahlberg.pdf

Min översättning:

De fundamentala partiklar som utgör materievärlden kan ordnas i två grupper, kvarkar och leptoner. Dessa är bägge fermioner [partiklar med halvheltaliga spinn] med spin 1/2 och, såvitt vi vet punktlika.

SYNBARHETSKRITERIET I MODERN AKADEMI utgår ifrån ljusets fysiskt möjliga våglängder. Eftersom information om all möjlig em-aktivitet i materiefysiken ombesörjs av atomernas elektronhöljen och därmed elektronmassans begränsade dynamik, finns definitiva gränser för begreppet ÅSKÅDLIGHET i kärnfysikalisk mening — om åskådningskriteriet är det nämnda. Då objekten närmar sig det fysikaliskt detekterbara ljusets egen våglängd [flytande från ca t12 M atomens maxfrekvens genom elektronmassan], se Comptongränsen, är det inte längre meningsfullt att tala om åskådlighet eftersom specifika formegenskaper inte kan avgöras på enskilda ljusvåglängder utan kräver en stor mängd sådana inom ett större intervall.

I TNED avgörs INTE synbarhetskriteriet av ljusets fysik, utan av människans möjligheter att FÖRSTÅ SAKINNEHÅLLET (enligt relaterad fysik kan således fysiken även förstås av människor som av olika anledningar saknar fysisk synförmåga). Skolexemplet är DEN MATEMATISKA KRISTALLEN vars hörn och kanter ansluter till den rent ideala geometriska åskådningen — som innebär att hur små områden som helst är CERTIFIERADE som åskådliga domäner i den praktiska fysikens matematik. Med HÄRLEDNINGEN TILL ATOMKÄRNAN via Plackringen ges därför åskådligheten full skärpa med den frakta strukturens principiella giltighet genom ekvivalenterna för impulsmoment (J) och kraftverkan (F) enligt Atomfysikens två huvudekvationer. Se även från PLANKRINGENS DIMENSIONER.

SAMBANDSBEVISET FÖR KÄRNDELNING UTAN MASSDESTRUKTION:

ENERGILAGEN i relaterad fysik (TNED) innefattar redan en bevislig beskrivning som klargör skillnaden mellan massa-energiekvivalenternas kvantitativa och kvalitativa betydelser: massa kan förintas därför att massa inte kan skapas. Här följer ett mera partikelorienterat beviskomplement som grund för den vidare framställningen.

Det formella beviset i relaterad fysik för att partikeldelning kan existera av princip utan att någon massa skapas eller försvinner

Genom EXOTERMISKA KÄRNREAKTIONSLAGEN

K1 + K2 – (m→γ) = K ;

täcks samtliga reaktiva fall som inbegriper massdestruktioner (m→γ), inkluderat delningar av typen

K + (m→γ) = K1 + K2

Med den kvantitativa ekvivalensen (m→γ)=(m←γ) — värme (rörelseenergi, Ekin) kan energimässigt ersätta massa som m(Ekin), även genom elektrisk acceleration som m(U), se från Planckekvivalenterna — gäller även

Ekin = (m→γ)v²/2 = (m←γ)v²/2. Därmed verkställs tydligen också

ett K-samband generellt för fall med enbart delning utan massdestruktion:

K1 + K2 – m(Ekin) = K ;

K + m(Ekin) = K1 + K2 ; delning utan massdestruktion

K kan vara en godtyckligt sammansatt nuklidsumma [typ inkommande källproton som via m(Ekin) eller m(U) kolliderar med en annan atomkärna och därmed åstadkommer delning i åter andra kärnor].

;

Blotta sambandets existens bevisar att

delning kan förekomma utan att någon massa skapas eller någon massa försvinner;

m(Ekin) är massa-energiekvivalentens rörelseenergi som krävs för att bryta upp massformen så att den uppvisar delning;

summan av massorna före delning = summan av massorna efter delning

Se vidare i Praktiskt bevis (Beviset för att masslös energi inte kan skapa massa | INVERTERADE BETASÖNDERFALLETS BEVIS).

OBSERVERA att i en partikelaccelerator där m(Ekin) är utbytbar mot chokmassan m(U) fördelas också m(U) på delarna så att de uppför sig som om massorna efter delningen via det extra m(U) verkligen vore större än före — så länge partiklarna besitter impuls. Genom det elektriskt slutna systemets bevarande av laddning måste chokmassan lämnas tillbaka till vilosystemet, men den delen syns aldrig i experimenten som berör de accelererade delarna. Se utförligt från PLANCKEKVIVALENTERNA.

Det går därför explicit inte att genomföra någon avgörande mätning med hjälp av elektriskt accelererade partiklar eftersom chokmassan döljer resultatet. När partiklarna sedan återgår till vila och chokmassan lämnas tillbaka till det fasta accelerationssystemet, och som därmed kräver energi-massaräkningen E=m₀c²=mc_uc=konstant [Planckekvivalenterna], är varje mätbart spår igensopat.

PARTIKELBEVISET FÖR ATT ENERGI INTE KAN SKAPA MASSA:

Se även formella beviset för Kärndelning utan massdestruktion

2010VI25

INVERTERADE BETASÖNDERFALLETS BEVIS enligt TNED FÖR MASSANS KVALITATIVA FRISTÄLLNING FRÅN ENERGIN

Praktiskt bevis

Partikelbeviset för att energi inte kan skapa massa

— masslös energi kan bilda en massdeficit (energiexciterad) kvantitativ energiekvivalent som gör att protonen kan emittera massa i utbyte mot masslös energi

Även beviset (integrerat) för att protonen, och neutronen, utgör en ekvivalent väv av ±e.

Lemma (inledande påståendeBeskrivningsSats):

Neutronsönderfallet i relaterad fysik (TNED)

₀n¹₀ – (m→γ)_0,782 = ₁H¹_1,518 med massdestruktionen (lägst) enligt TNED (m→γ) = 0,782 MeV = v eller här ve– (elektronneutrino) samma som konv. antineutrino (eg. strecket över v, Grek. n, ny)

skrivs konventionellt [Jämför samma typ men med positron och konventionell neutrino] i termer av endast atomkärnor (n neutronen, p protonen, e– elektronen, e+ positronen) enligt

(1) n – ν_{e– 0,782 MeV} → p + e^–

med (minimum) ve– = (m→γ) = 0,782 MeV.

Adderas en positron (e+) till bägge leden

(2) n + e⁺ – ν_e– → p + e^– + e⁺

annihileras — massförintas — högerdelens bägge elektron-positronmassor,

(3) n + e⁺ – ν_{e– + E(±e)} → p + 0

och för att få KVANTITATIV balans mellan leden enligt den kvantitativa massa-energiekvivalensen E = (m→γ)c² = (m←γ)c² påtvingas en ekvivalent annihilationsenergi 2×0,511=1,022 MeV till vänsterledets elektronNeutrinoEkvivalent

(4) ν_{e– 1,804 MeV} + p → e⁺ + n

så att den får totalsumman (minst) 0,782 + 1,022 = 1,804 MeV; Reaktionsledet är f.ö. samma som används i KamLAND. Se citat.

Postulat:

M.a.o.: Exciteras en Vätekärna (p) med ENLIGT TNED masslös OBS ElektronNeutrinoStrålning [positronNeutrino går inte, det måste vara elektronNeutrino] [‡] på (lägst) 1,804 MeV tvingas protonen av massa-energi-ekvivalensens balansräkning att emittera en positron med resultat i en »neutronproton» (n).

Medan energibalansen är exakt, finns ingen motsvarande uppvägande g-massa; Den (1,804 MeV)-exciterade protonen som emitterat en positron är uppenbarligen ingen riktig massneutron, utan en massreducerad energiexciterad neutron (n). [Den förenas (längre fram) med en proton till en deuteron, se Deuteriumbildningen].

Bevis:

Massförintelsen ±e i högerledet i (2) kan kompenseras med motsvarande strålningsenergiekvivalent (m→γ) i vänsterledet: Massdestruktionen (m→γ) från typ ±e [reguljär gammastrålning eller s.k. parannihilationsstrålning, se Parannihilation] bevisar att energiekvivalenten, alldeles helt säkert INTE är massa, eftersom massekvivalenten i ±e förintas (med närmast konkreta exempel från Solen) för att kunna bilda just (m→γ). Är nu ekvivalenten en förintad massa — icke-massa — i formen av masslös em-strålning — värme och ljus — då kan den ju uppenbarligen inte vara vägbar, konkret g-massa; Inte materia; Inte fysikalisk substans.

Resultat:

Alltså är uppfattningen att materia kan skapas ur energi en vanföreställning. Det finns naturligtvis ingenting sådant i fysiken. Massa kan utbytas mot, inte skapas av, energi enligt kvantitativa massa-energiekvivalensen E = (m→γ)c² = (m←γ)c². Se även enligt relaterad fysik från Energilagen.

Med andra ord: Bestrålningen av p med massenergiekvivalenten (m→γ)=1,804 MeV=E/c²=m ger tvunget en massreducerad energiexciterad neutronekvivalent (n).

Den förhärskande föreställningen att materia skulle kunna skapas ur masslös energi motsäger alltså faktum: att massa kan upplösas till värme och ljus (Solen): masslös em-strålning. I relaterad fysik (TNED, Energilagen) gäller alltså och således i varje begriplig mening: massan kan förintas därför att den inte kan skapas.

Beviset ovan ansluter helt till och harmonierar fullständigt med Kommutativa ekvivalenten i TNED — värme är inte massa, massa är inte värme. Se Massvärmet, Kommutativa Energiekvivalenten.

Att vägbar massa därför skulle kunna bildas ur typ värme eller med samma principiella innebörd projektil rörelseenergi (bildad på rent mekanisk väg) är enligt TNED entydigt grundligt alldeles säkert helt uteslutet.

Neutrinobegreppet i MAC

Invändning:

— Neutrinon har massa.

— Vi är nog här allihopa helt övertygade om (Jul2010) att inspicienten också kan relatera det påståendet ingående — med speciellt utförliga referenser.

Neutrinooscillationerna i modern akademi

Jämför:

NEUTRINON I MODERN AKADEMI infördes som en PARTIKEL för att få den redan etablerade spinnomenklaturen att gå ihop [Se Införandet av neutrinopartikeln genom spinnbegreppet i modern akademi]; I relaterad fysik (TNED) har varje nuklidform sin neutrinonyckel (uppsättning våglängder och frekvenser, se från Plancks strukturkonstant, särskilt i Neutrinosignaturen) och som fungerar på samma sätt som »vanlig em-strålning» i växelverkan med materien, dvs., enligt Comptoneffekten [som biljardbollar som stöter emot varandra och successivt tappar energi]; neutrino i TNED är bara ett annat ord för massdestruktionsstrålning, analogt med sådana våglängder som (vida) understiger atomkärnans yttre dimensioner och därför inte direkt kan avkännas av elektronmassan som enhetligt laddningskvantum.

— För att neutrinofenomenet tolkat på motsvarande sätt i modern akademi ska kunna genomgå motsvarande Comptonändringar [konv. Comptonspridning] — eftersom man redan bundit upp sig för att se neutrinon som en spinnande partikel — blir Närmaste Greppet att associera neutrinopartikelns TEORI med en massparameter — annars går man bet med den teoretiska grund man redan bundit upp sig för.

Först då kan man »härleda» att en viss neutrinotyp kan »omvandlas» (’oscillera’) — och som visas experimentellt i typ

KamLAND-projektet (reduktion av elektronNeutrinos som funktion av neutrinostrålningens växelverkan med materia) och

OPERA-projektet (övergång från MyonNeutrino till TauonNeutrino som funktion av neutrinostrålningens växelverkan med materia).

Denna (enligt relaterad fysik som ovan Comptonrelaterade) omvandling mellan de olika strålnycklarna är det som i modern akademi kallas för neutrinooscillation.

Notera dock att neutrinooscillationerna i modern akademi inte baseras på någon associerad Comptoneffekt, även om den typen ligger närmast till hands i jämförelsen med TNED. Se vidare Webbreferenser nedan.

— Därför säger man i konventionell mening att »neutrinon har massa».

— Inte därför att neutrinon har massa utan för att den moderna teorin kräver det (neutrinooscillationerna) för att kunna förklara neutrinostrålningens ändring med (speciellt, en) materiell genomgång.

I TNED är alla sådana matematiska resonemang helt överflödiga. Neutrinobegreppet i TNED är helt säkert identiskt med det helt masslösa värme och ljus som (beroende på nuklid) ges från massförintelsestrålning (m→γ) och som utgör arbetskraften (eller strukturbindningsenergin som måste upplösas) i samband med kärnändringar.

Webbreferens

FÖR ATT I VARJE FALL OMNÄMNA ETT FÄRSKT KONVENTIONELLT gratis tillgängligt referensverk i neutrinoämnet: Se Hardy 2010.

Där beskrivs de flesta termbegreppen i samband med den konventionella neutrinofysikens problem (men framställningen är en PhD-tes och kräver därför [stundtals] en del av läsaren).

Artikelkällan

@INTERNET Wikipedia Neutrino oscillation 2010-07-15

ger också en tämligen utförligt illustrerad och (ännu delvis) välrefererad genomgång av det etablerade begreppet neutrinooscillation (som grundas på den s.k. MSW-effekten).

I TNED har neutrinooscillationsbegreppet ingen som helst koppling.

Se utförligt från NEUTRINOBEGREPPET I SOLFYSIKEN ENLIGT RELATERAD FYSIK.

Notering angående Wikiartikelns liknelse med sammankopplade mekaniska pendlar

Liknelsen som används i wikiartikeln

@INTERNET Wikipedia Neutrino oscillation, Theory, Classical analogue of neutrino oscillation 2010-07-15

är helt utomordentlig — för mekaniken.

För att en motsvarande analogi skulle gälla i praktiken skulle den moderna akademins neutrinobyggnad tvunget innefatta motsvarande två (eller tre) distinkt mekaniska komponenter (liknande den modellbyggnad som används i den moderna akademins kvarkmodell i ämnet allmän kärnfysik).

Frånsett den moderna akademins åskådningsproblem — som betyder att i grunden existerar ingen motsvarande åskådlig formbild, den gäller inte — har ovannämnda pendelanalogi ingen som helst motsvarighet i TNED — just på grund av atomkärnans fraktala strukturbyggnad: det finns hur många neutrinonycklar som helst i TNED.

Även i moderna kvarter har man räknat med att det utöver de nuvarande tre neutrinoassocierade leptonerna (elektronen, myonen och tauonen) skulle kunna finnas (minst) ytterligare en, se citat.

I TNED garanterar atomkärnans fraktalstruktur enligt ATOMKÄRNANS HÄRLEDNING och MIC-ekvivalenterna att antalet neutrinoprofiler är obegränsat. Därför kan heller inte den mekaniska analogi som används i wikiartikeln ges någon naturvetenskaplig koppling i TNED.

Steven Hardy ref.

Se särskilt (omfattande redovisning)

Separat länk till det omfattande PDF-dokumentet (PhD-thesis, ca 15 MB)

MEASURING THE 7BE NEUTRINO FLUX FROM THE SUN:

Calibration of the Borexino Solar Neutrino Detector — Steven E. Hardy, Mar2010

http://scholar.lib.vt.edu/theses/available/etd-04092010-132651/unrestricted/Hardy_SE_D_2010.pdf

finns på

http://scholar.lib.vt.edu/theses/available/etd-04092010-132651/

s7mn; viss grundbeskrivning av hur neutrinooscillationen fungerar; beror på massegentillstånden (inducerade av relativa masskvadratsskillnaderna)

s17; pp-diagram

s18ö; hur elektronneutrinon ändras med Solpassagen, äv. s19ö.ill.

s18m; sannolikhetsvärdet 1/3

s24; varför 2(1H2) inte fusionerar direkt till en 2He4 (nuklidkoncentrationen)

EXEMPELSAMLING — massa-energi

EXEMPEL enligt TNED

med grundsamband från

SAMBANDSBEVISET FÖR KÄRNDELNING UTAN MASSDESTRUKTION

PARTIKELBEVISET FÖR ATT ENERGI INTE KAN SKAPA MASSA

Rutherford 1919

Exempel:

År 1919 observerade Ernest Rutherford [‡] hur Helium-4-kärnor från ett radioaktivt preparat efter kollision med Kväve-14-kärnor hade bildat Syre-17 och Väte-1.

Rutherfords experiment 1919 — Från Helium4 (He4) och Kväve14 (N14) till Syre17 (O17) och Väte1 (H1):

UPPGIFT 1: Beräkna vilken rörelseenergi som Helium-4-kärnan minst måste besitta för att kärnreaktionen K + Ekin = K1 + K2 ska verkställas med värdena

bet. atom med atomvikten i antal u=1,66033 t27 KG

—— —— —————————————————

K = ( ₂He⁴ 4,0026

+ ₇N¹⁴) 14,0031

K1 = ₈O¹⁷ 16,9991

K2 = ₁H¹ 1,0078

Notera att K alltid kan ha godtycklig sammansättning.

UPPGIFT 2: Beräkna motsvarande idealt mekaniska hastighet för Heliumkärnan från den beräknande rörelseenergin i uppgift 1.

Lösning UPPGIFT 1:

K-summan blir 18,0057u, K12-summan blir 18,0069u, differensen blir 0,0012u.

Uttryckt i MeV:

E(u) = (1,66033 t27 KG)(2,99792458 T8 M/S)² ; = (m=u)c²

= 1,49223 t10 J = UQ = Ve, e=1,602 t19 C ;

E(uMeV) = (E(u)/e)/(T6) = E(u)/(e T6)

= E(u)/(1,602 t13 C)

= 931,47946 MeV

~ 931,48 MeV ; atomära massenhetens energiekvivalent

0,0012u = 1,12 MeV

Lösning UPPGIFT 2:

Ekin = mv²/2 ger

v² = 2Ekin/m ;

Massan m=Uu i MeV beräknas via sambanden i Uppgift 1 från E=mc² via m=E/c² med c= 2,99792458 T8 M/S enligt

m(MeV) = m(u)(931,48 MeV)/c²

= (4,0026)(931,48 MeV)/c²

= (3728,3418 MeV)/c² ;

v² = 2Ekin/[m(u)(931,48 MeV)/c²]

= 2Ekin·c²/[m(u)(931,48 MeV)]

= 2Ekin·[9,64868 T13 (M/S)²]/m(u)(MeV)

= Ekin·[1,92973 T14 (M/S)²]/m(u)(MeV)

= (1,12 MeV)[1,92973 T14 (M/S)²]/(4,0026)(MeV)

= 5,39975 T13 (M/S)² ;

v = 7 348 301,4 M/S = 0,0245112c

Svar:

UPPGIFT 1: Minsta rörelseenergin är 1,12 MeV = 0,0012uc².

UPPGIFT 2: Hastigheten är 7,348 T7 M/S eller 0,0245c.

MAC säger Skapelse

Jämför föreställningen i modern akademi: GYMNASIETS FYSIK Liber 1979 åk3s251-252ex.29:

”Detta betyder att vid kollisionen har 0,0012·1,66·10^–27 kg materia skapats.”.

Läroboksexemplet beskriver och beräknar med samma kvantitativa resultat som ovan hur Rutherford (1919) bestrålade Kväve med Helium och fick Syre+Väte.

Se mera utförligt i TNED från Kommutativa ekvivalenten — värme är inte massa, massa är inte värme. Se Massvärmet, Kommutativa Energiekvivalenten.

I korthet (utdrag från Kommutativa ekvivalenten)(erinra att med förintelsen av ±Q sker tvunget en induktansökning för att energin ska kunna bevaras: Minskande antal strömelement betyder ökande induktans om energin är konstant):

m i Q måste förintas för att Induktansen L i E=LQ²/t² (energins bevarande genom induktansens och laddningens proportionalitet) ska kunna agera och därmed mass-energin från den förintade massan kunna överföras induktivt, masslöst, på andra mQ-system i form av värme och ljus. M.a.o.: Modern akademi motsäger induktionsfysikens fenomengrund med hävden ”värme är massa”. Det finns ingenting sådant i fysiken enligt TNED. Energilagen förklarar/sammanför dessa detaljer utomordentligt klart.

EXEMPELSAMLING — massa-energi END.

Partikelbildning med masschokning

PARTIKELBILDNING MED MASSCHOKNING — Exempelframställning

Partikelbildning med masschokning

2010VI16

Hur ska man förstå »partikelbildning» med masschokning?

Se även resultatbeskrivning direkt från Inledningen till Observerade massunderskott i partikelfysiken enligt TNED

— Förmodligen inget annat fenomenområde i fysiken är mera svårbegripligt än typexemplet med elektronmassan som ökar genom en elektriskt styrd accelerationsspänning (MAFEM). Fenomenet kopplar direkt till motsvarande problem i samband med de »partikelskurar» som uppstår vid typ kosmisk strålning; inkommande höghastighetsprotoner kolliderar med atomkärnor i Jordens övre atmosfär och ger upphov till en skur av partikelfragment. Motsvarande fenomen kan studeras genom artificiella partikelacceleratorer i de traditionella bubbelkammarfotografierna.

I TNED ger PLANCKEKVIVALENTERNA det formella matematiska svaret och uttömmande förklaringen till fenomenet med den elektriskt laddade partikelns massökning (»masschokning» i TNED). Men den delen förklarar inte motsvarande — synbarligt betydligt mera svårfattliga — fenomen med hur massökningar från partikelaccelerationer fungerar på stationära målpartiklar. Funktionen innefattar också svårigheten att skilja mellan partikeluppdelningar med associerad massdestruktion (i TNED samma som neutrinostrålning) — sönderfall — och partikeluppdelning utan massdestruktion — delning — vilket med andra ord framtvingar en grundlig genomgång av, exakt, vilka fenomengrenar som också innefattar och inte innefattar massdestruktioner (m→γ), i TNED detsamma som neutrinostrålning.

Inte förrän nu (Våren-Sommaren2010) har dessa problemavsnitt kunnat föras vidare i min författarreferens och enligt de grunder som TNED framvisar.

Följande avsnitt gör anspråk på att ge en fullständigt uttömmande kvalitativ förklaring och beskrivning — tillsammans med redan kända, etablerade grundbegrepp.

ARGUMENTERINGEN FÖR ELLER MOT föreställningen att ’massa kan skapas ur energi’ kräver en avancerad genomgång med tydliga exempelbeskrivningar — helst INKLUDERAT noggrant beskrivna »ELEMENTÄRA NYBÖRJARFEL» (som man lätt kan känna igen) för tillfället att därmed få understryka den relaterbara, rent praktiska sidan av fysiken i ämnet.

FOCUS MATERIEN 1975 s139 (nedan) erbjuder ett excellent exempel med bubbelkammarfotografiet från en proton-protonkollision med spåren efter de resulterande partikelfragmenten. Vi bör i dagens läge vara, väl, i stånd att kunna lösa ut alla väsentliga detaljer ur källbilden med hjälp av tillgängliga webbkällor där redan etablerade data kan kontrolleras och jämföras. Källor anges löpande i huvudtexten.

Argument

ENLIGT TNED kan inte vägande (kvalitativ) massa skapas ur masslös (kvantitativ) energi enligt ENERGILAGEN; massan kan förintas (primära massförstöraren E=mc²) DÄRFÖR att den inte kan skapas (POM2).

[För att ge en vulgär liknelse till efterföljande jämförelse: Det är ingen idé att familjen Svensson är ute och åker bil med barnen för tillfället att få bilavgaserna att bilda nya leksaksbilar åt traktens ungar med hjul och karossfjädringar och baklucka och grejer bara därför att familjen är ute och åker BIL heller].

Men bubbelkammarfotografiet

magnetiska B-vektorn upp genom bildytan

Bubbelkammarfotografi från FOCUS MATERIEN 1975 s139

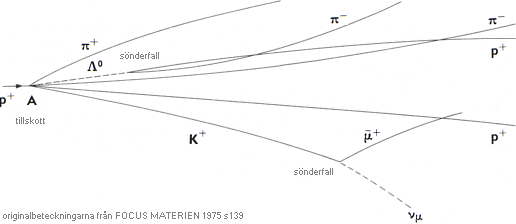
FOCUSKällans renritade partikelspår, sidan 139, här med större bokstäver inlagda samt bilden lagd horisontellt. NOTERING: Beteckningen med strecket över µ förmodligen feltecknat i Focuskällan (andra källor inklusive FM i beskrivningen s138sp) anger konsekvent µ+ som antipartikeln till Myonen µ–.

TYCKS VISA JUST DET:

ikon	part.	MeV
	π^+	139,6
	π^–	139,6
	π^–	139,6
	p^+	938,2
	Λ^0	1116
	p^+	938,2
	K^+	494
	µ^+	105,66
ikon	part.	vilom.

Från vänster kommer en källproton från en partikelaccelerator in i mellanrummet mellan ett par Helmholtzspolar i en bubbelkammare. Riktningen på magnetfältet i bubbelkammarfotografierna är konventionellt upp mot betraktaren (e– böjer av uppåt, e+ neråt, se Högerhandsregeln). Vid incidenspunkten (A) träffar källprotonen på en målproton. Kollisionen är våldsam, och resultatet syns i bubbelkammaren som ett antal karaktäristiska spår av olika partiklar med olika egenskaper och som fotograferas med speciellt inmonterade kameror för senare analys. Partikelikonerna i figuren har enligt TNED gjorts ungefär proportionella mot protonens masstäthet som enhet. Alla värden i MeV avser motsvarande (konventionella) ekvivalenta vilomassor.

Myonen (µ) sönderfaller längre fram till en positron, Pionerna (π) längre fram till Myoner [‡].

Övre sönderfallet motsvarar differensenergin 1116–(139,6+938,2)=38,2 MeV och undre sönderfallet 494–105,66=388,34 MeV.

π⁺ + π^– + π^– + K⁺ = 3×139,6 + 494 = 912,8 < 938,2; diff = 25,4

UTÖVER de bägge ursprungsprotonerna, projektilprotonen från partikelacceleratorn (pa) och målprotonen i bubbelkammarvätskan (pm), FRAMTRÄDER alldeles särskilt TYDLIGT vägbara tröghetsmassor som lyder avböjningarna via det uppåtriktade magnetfältet: tre Pioner (π^±) med vardera vilomassan 139,6 MeV, en Kaon (K⁺) med vilomassan 494 MeV och en antiMyon (µ⁺) med vilomassan 105,66 MeV — samt föregående den senare övre »återuppväckta protonen», en osynlig Lambda (Λ⁰) med vilomassan 1 116 MeV.

TNED lämnar ingen möjlighet öppen för dessa massor (x) att förstås som självständiga masspartiklar bildade utöver de givna protonmassorna och vilkas kollision uppenbarligen frammanar mängden x. Kärnpartiklar med en egen kraftstruktur i kvalitén TNED-väv med ±e-laddningar enligt ATOMKÄRNANS HÄRLEDNING kan inte skapas ur masslös kvantitativ energi [ENERGILAGEN]. Så, hur förklaras då de tydligt bildade partiklarna enligt TNED?

Resonemanget från början

Resonemanget från början

Se Originalförfattningen till NEUTRONFRAGMENTEN

Utan en fördjupad inblick med ett vidare perspektiv (precis det som en nybörjare börjar med, första erfarenheten, den viktigaste av alla), blir den allra första ansatsen den att försöka härleda en alternativ men EKVIVALENT partikelform för de bägge ändprotonerna.

— Varför då?

Därför nämligen, att enda möjliga synbara möjligheten för TNED att få fortsätta avhandlingen om UNIVERSUMS HISTORIA — och INTE kasseras som värdelöst skräp — är uppenbarligen att ursprungsprotonerna måste »sönderfalla» till andra partiklar; Massa, enligt TNED [se ENERGILAGEN], kan inte skapas kvalitativt av den inkommande pa-protonens blotta rörelseenergi (Ekin). De bildade partiklarna måste därför, tydligen, bildas av sönderfallande ursprungsprotoner, deras g-vägande kraftspinnstruktur. Alla vet, nämligen redan, att bara för att jag viftar med händerna i luften (rörelseenergin från den inkommande källprotonen pa), regnar det INTE alls ner några guldmynt (Kaoner och Pioner) över nejden.

RESULTATET som (nybörjaren i mitt exempel) man kommer fram till blir (till exempel) det här — obetingat, utan vidare kännedom:

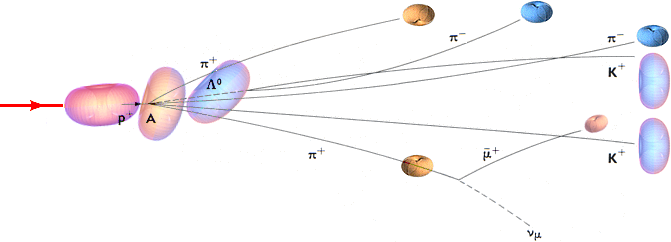
Se Resonemanget med härledning till partikelekvivalenterna i Originalförfattningen till NEUTRONFRAGMENTEN

Referenstabell med uppställningar till

TNED-resonemanget — Neutronens fragment, se Neutronfragmenten.htm

ikon

part.

MeV

ikon

part.

MeV

ikon

part.

MeV

ikon

part.

typ

MeV

+Ekin

FM

MeV

→

π^+

139,6

→

π^–

139,6

→

π^–

139,6

U

→

p

938,2

Ekin

p

938,2

→

Λ^0

1 116

→

K^+

494

+ 444,2

p^+

938,2

→

K^+

494

+ 444,2

p^+

938,2

→

π^+

139,6

+ 354,4

K^+

494

µ^+

105,66

—

—

388,34

ΣMeV↓

ΣMeV↓

912,8

- 482,4 =

633,6

951

+ 773,2 =

1 711,4

+ 177,8

- 38,2 =

1 077,8

;

Ekin = mv²/2; v² = 2Ekin/m = 2(951 MeV)/(938,2 MeV/c²) = c²(2,0272862) ; v/c = √[2(Ekin)_eV/(938,2 T6 eV)=(2,0272862)] = 1,423828

TABELLFÖRKLARINGAR:

—————————————————————————————————————————

GULFÄRGADE CELLER anger Focuskällans originalpartiklar med deras summerande värden.

KRITISK GRANSKNING AV RESULTATET 2010VII5

2010VI7

Kritisk granskning av resultatet

— Hur stämmer resultatet med möjliga basdata?

Från RESULTATET i NEUTRONFRAGMENTEN Originalet

Se även mera ingående från inledningen i Partikelbildning med masschokning, om ej redan bekant.

1. FÖRSTA INVÄNDNINGEN

— Är sönderfallet från Kaon till Myon verkligen praktiskt möjligt att ersätta med ett sönderfall Pion till Myon?

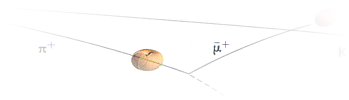
— Tydligen, ja.

Sönderfallet π⁺ till µ⁺ är OK (eftersom Kaonen K+ och Pionen π+ bägge är av samma typ), se exv. Feynmandiagram i Wikipedia Pion 2010-06-07,

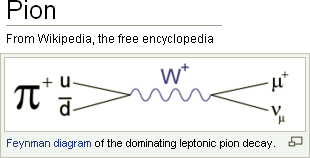
KLARLÄGGANDE OM FOCUSKÄLLANS UNDERLIGA µ-beteckning. Beträffande Focuskällans Myonteckning (µ+) finns här en viss osäkerhet om vad källan menar; På ena stället, dels (s138sp2), och dels i tabellen på samma form (s140sp1n), beskrivs utförligt de olika partikeltyperna respektive normala och anti-, med Myonbeteckningarna respektive µ– och µ+ — men i spårteckningen (som ovan) med ett antistreck över µ (här motsv. µ). Focuskällan skulle därmed antyda två olika beteckningssätt för anti-; dels det textbeskrivna µ+, och dels det bildtecknade µ+.

Om vi söker efter någon eventuell koppling Kaon+ till typen µ+ på webben finns i varje fall enligt Wikipedia Kaon · Properties of kaons 2010-06-09 ingen antydan om att K+ skulle sönderfalla till annat än just en µ+. Focuskällan skulle med andra ord möjligen vara felskriven i bilddelen (illustratören var möjligen inte lika insatt i nomenklaturen som författaren). Vi håller oss här konsekvent till µ+.

Sönderfallstiderna

— Sönderfallstiderna matchar också ungefärligt — både Pion (π⁺) och Kaon (K⁺) har grovt och runt t8 S som medellivslängd;

@INTERNET Wikipedia (Kaon, Pion, 2010-06-07) anger

Pion π⁺ Kaon K⁺

———————————————————————————

(halflife) medellivslängd 2,6033 t8 S 1,238 t8 S

— Om det enskilda fallet dessutom beror på energiinnehållet (högre energi, snabbare sönderfall) blir de redan snäva gränserna mellan de olika typerna (tydligen) nära flytande enbart sett till tidpunkten för sönderfallet.

— Det finns i varje fall med de uppgifter som framkommit här ingen (direkt) tydlig grund för att avfärda möjligheten att den konventionellt angivna Kaonen i det nedre partikelspåret i själva verket är den Pion som TNED kräver.

2. ANDRA INVÄNDNINGEN

— Däremot finns (veterligt) ingen motsvarande koppling med Lambdapartikeln (Λ⁰) till Kaonen (K⁺),

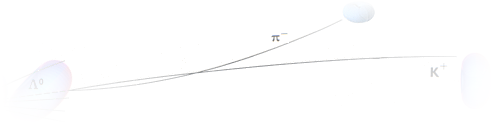
Lambdapartikel ska istället (enligt experimentalfysikens observerade praktik [Ref. @INTERNET Wikipedia Hyperon · List of hyperons 2010-06-08]) sönderfalla till Pion (π^–) och proton (p⁺).

3. TREDJE INVÄNDNINGEN

— Enligt det ursprungliga Resonemanget med härledning till partikelekvivalenterna är nettoskillnaden mellan den bildade Lambda0 (Λ⁰)[1116 MeV] och sönderfallskomponenterna Kaon (K⁺)[464 MeV] och Pion (π^–)[139,6 MeV] lika med 512,4 MeV (explicit inte angivet i den ursprungliga författningen). Det skulle innebära att Lambdapartikelns sönderfall (som i figuren ovan) till Pion (i originalet en Kaon, K+) innefattar en verkligt kraftig emission på just (minst) 512,4 MeV — och som i det ursprungliga resonemangets ljus underförstod en sönderdelning genom fission via massdestruktion (m→γ): neutrinostrålning.

(Det var den inre kärnpunkten i det ursprungliga resonemanget. Det visas i den här presentationen att den föreställningen [av allt att döma] inte är hållbar; Den förmodade fissionen, kärnsönderfallet, ska tydligen istället förstås som en delning med samtidig utgivning av kärnrelaterad gammastrålning, inte massdestruktionsstrålning [neutrinostrålning i TNED]. Men vi återkommer till den aspekten senare, se Övre Protonen).

Om vi söker på webben efter någon etablerad referenskälla som omnämner/relaterar någon typisk utgivningsenergi i samband med Lambdapartikelns observerade sönderfall, finns i varje fall en sådan enligt följande:

”The free Λ-hyperon undergoes almost with 100% probability the mesonic decay, i.e. Λ → π^– + p or Λ → π⁰ + n.

The energy release (≈ 40 MeV) and its sharing among pion and nucleon implies …”,

NONMESONIC DECAY OF THE Λ-HYPERON IN HYPERNUCLEI PRODUCED BY P+AU COLLISIONS — B. Kamys et al. Nov2000

http://arxiv.org/PS_cache/hep-ex/pdf/0011/0011063v1.pdf

Med Focuskällans komponenter blir motsvarande energiutgivning

Lambdapartikeln (Λ⁰)[1116 MeV] – proton (p⁺)[938,2 MeV] – Pion (π^–)[139,6 MeV] = 38,2 MeV.

— Det stämmer uppenbarligen ganska precis med det som påstås i beskrivningen ovan från Kamys (~40 MeV).

DISKUSSION

DISKUSSION — protonsönderfallen (andra invändningen)

— Tillsammans med invändningen i (2) betyder invändningen i (3) att resonemanget med protonen ersatt av Kaonen uppenbarligen inte håller.

— Men ingenting säger väl emot att EN AV originalprotonerna KAN sönderfalla?

— BÄGGE de konventionellt angivna protonerna (p⁺) i Focuskällan kan inte — helt omöjligt enligt TNED — vara verkliga protoner. Skulle någon på något sätt kunna, verkligen, bevisa att bägge ÄR verkliga protoner, har UNIVERSUMS HISTORIA ingen som helst mening. Rena skräpet. Framställningen bygger (nämligen) helt på ENERGILAGEN (POM), och den medger ingen KVALITATIV (strukturbaserad, g-vägande) skapelse av massa ur kvantitativt ekvivalent energi. CHOKMASSA är (å andra sidan) på sitt sätt vägande g-massa. Men den är det bara i kraft av att vara just en KRAFTCHOKNING på en redan befintlig masstruktur, i varje fall enligt den beskrivande matematiska fysiken (se utförligt från MAFEM): inget nytt skapas, den aktuella formen blir bara kraftigare genom accelerationsfältets elektriska energi på bekostnad av att en annan del får motsvarande mindre massinnehåll.

En stabil atomkärna kan enligt relaterad fysik (TNED) utöver sin egen masstruktur naturligtvis inte bilda elektriskt strukturerade kärnfragment, vägbar massa, och DÄRMED samtidigt behålla sin status som stabil — vilket i så fall, just, skulle betyda att massans kvalitativa struktur kan uppkomma genom någon slags magisk, mystisk kraft (skepnader som tar vägande fysisk form — finns bara på bio) och att masslös elektromotorisk induktion skulle kunna formas till konkret vägbar massa. Bubbelkammarfotografiets experimentella realitet med de ovan uppmärksammade obesvarade sammanhangen ställer alltså upp ett tydligt påvisande av att det måste finnas en verklig fördjupning i ämnet, och som förtjänar extra uppmärksamhet.

— Originalprotonen (övre spåret) kan »MASSPUMPAS» av den inkommande kollisionsprotonen — upp till en neutral Lambda⁰ (Λ⁰), för att sedan återgå till proton⁺ för sin del och släppa masspumpningens motsvarande pion (π^–). Det är i varje fall en möjlighet — och tydligen den enda som SKULLE KUNNA rädda hela framställningen.

Till prövning för TNED

Den övre angivna protonen (p⁺) KAN ENLIGT TNED vara en av de ursprungliga protonerna vid kollisionsstället (A) — OM den får överta en viss massdel från den inkommande protonen och som (minst) motsvarar antiPionen (π^–) 139,6 MeV — vilket därmed ENLIGT TNED tvingar resten i kollisionsprotonen att delas upp på strängt sönderfallande delpartiklar.

— Den konventionellt angivna bottenKaonen (K⁺) skulle ENLIGT TNED i originalförfattningen vara en Pion (π⁺) (med Focuskällans partikeltabell som referens).

— Den konventionellt betecknade komplementprotonen (undre spåret) från kollisionsstället (A) skulle enligt TNED i samma originalförfattning själva verket vara en kraftchokad Kaon (K⁺).

— Men haken i det resonemanget är att den Kaonen (normalt, möjligen) i så fall borde ha uppvisat ett sönderfall i spårfönstret eftersom Kaonens sönderfall (tabellen) bör inträffa tidigare än Pionens, inte som ovan en lång nära rak (opåverkad) spårbana. Det undre p⁺-spåret kräver i originalförfattningen enligt TNED i vilket fall allt annat än en av protonerna från kollisionsplatsen (A); Ursprungsprotonen krävs för att ge strukturmassa åt de omgivande tre tydligt bildade partiklarna två Pioner (π^–, π⁺) och en Kaon (K⁺).

Det övre p⁺-spåret kan f.ö. och som redan påpekats tydligen inte vara från en Kaon eftersom Lambda (Λ⁰) (veterligt) inte uppvisar sönderfall till Kaon, endast (vad man vet) till typen p (och n) och π.

För konventionella referenser till ovannämnda partikelfragment, se t.ex. eng. Wikipedia; Kaon, Pion, Lambda baryon.

— Det verkar pyrt.

— Finns det ingen annan lösning?

Frånsett att den enligt TNED förmodade Kaonen (1,2 t8 S) i undre p⁺-spåret ovan INTE uppvisar något rimligt liknande sönderfall som den enligt TNED undre Pionen (2,6 t8 S):

— Det verkar väl magstarkt att det undre p⁺-spåret — hela svitens minst ändrade riktning, vilket antyder en speciellt tung partikel (med särskilt hög hastighet) — skulle vara från en betydligt (2,0219827ggr) lättare partikel?

— Vi vet strängt taget inte det heller, eftersom chokmassan m(U) KAN spela in på sätt som tydligen ligger utanför den här presentationens analysram; Vi har varken uppgifter på det aktuella exemplets energi- eller fältdata eller uppgifter på hur man menar att chokmassan fördelas, så vi har i vilket fall ingenting att jämföra med.

— Men vi kanske heller inte behöver bry oss i den delen: Den vidare genomgången visar att det finns en möjlig alternativ helhetsbeskrivning — som bevarar Focusoriginalets beteckningar men i kraft av den här dynamiken: Protonens massdeficit passerar obemärkt. Vi studerar hur.

— Kolla:

Upplösningen

© Adam-Hart Davis, Natural Science 2008.

http://gallery.hd.org/_c/natural-science/_more2006/_more03/splash-crown-water-drop-on-blue-crazed-cracked-surface-frozen-2-AJHD.jpg.html

UPPLÖSNINGEN

— Men varför skulle inte den accelererade protonen (pa) — den har ett tillskott på minst 951 MeV med exakt summaräkning på de ingående partikelmassorna enligt Focuskällans tabell s140sp2n — kunna avdela någon del av sin egen normala vilomassa vid kollisionstillfället (A), vilket (frånsett den aktuella kollisionsimpulsen) skulle ge

1. målprotonen plus

2. den återställda källprotonen (accelerationsprotonen) plus

3. chokmassan som en ytterligare — från accelerationsprotonen — LÅNAD MASSTRUKTURERAD KRAFTCHOKAD (virtuell men dock g-vägande) kärnMASSmängd på (minst) 951 MeV:

— Tre Pioner på vardera 139,6 MeV, plus en Kaon på 464 MeV, totalt 912,8 MeV, resten på 38,2 MeV tillhör sönderfallsenergin (eller delningsenergin) för Lambdapartikeln.

— Dessa överskottsvålnader skulle då vara DÖMDA TILL MER ELLER MINDRE SNABBA SÖNDERFALL — som måste, tvunget enligt TNED för den totala energiräkningens del, hela anordningen, sluta på motsvarande elektronaccelerationsmassor (accelerationsspänningens elektriskt slutna system) så att balansen kan återställas.

— Exakt. (Nu börjar det likna något).

Därför att OM chokmassan kan »liera» sig med källprotonen då den accelereras av partikelacceleratorn och därmed anta värdpartikelns elektriska och mekaniska signatur, KAN man (likväl) förstå den påförda CHOKMASSAN (konv., den s.k. relativistiska massan, se utförligt från PLANCKEKVIVALENTERNA) som en slags tillfällig likvärdig »strukturövervikt»; Om källprotonen plötsligt stoppas upp och övergår till sin normala form, är det tydligt att övermassan, in till någon viss tid, tvingas fortsätta som en associerad masskomponent med den föregående värdens sigill.

— Det skulle förklara hela tillställningen. Men i gengäld också göra hela partikelfysiken så mycket mera komplicerad (eller möjligen enklare ...).

— Vad vi, enligt min mening, skulle behöva här, till klargörande, är en motsvarande bubbelkammarbild från (motsvarande) proton-protonreaktion FRÅN ÖVRE JORDATMOSFÄREN; enligt TNED är INTE inkommande kosmiska protoner hastighetsdrivna via elektriska accelerationsfält, utan istället av rent mekaniska orsaker (divergenständningarnas häftiga utkastningar). Vilket vill säga: enligt TNED skulle en (helt) annan partikelspårbild uppvisas där.

Förmodligen får vi aldrig se något sådant. Bubbelkammartekniken är (numera) föråldrad och ersatt av mera sofistikerade, datorberäknande anordningar.

— Men om man då ställer den avgörande frågan:

— OM det skulle vara som antyds ovan, vad gör det åt ev. VERKLIGA delfragment från en (typisk) »protonsplittring»?

— Alltså, precis så som exempelframställningen visar i Focuskällan: Är dessa partikelfragment (verkligen) verkliga?

— Kan man se t.ex. Pioner eller Myoner som resultat av kosmiskt inkommande höghastighetsprotoner (vilket TNED vill göra gällande)?

— Ja. Tydligen är det så. Se Beviset för multipla c.

— Myoner är, tydligen för att exemplifiera, subnukleära partikelfragment som bildas ur den ekvivalenta impuls (mv) som en kosmisk proton verkställer i kollision med Jordatmosfärens atomkärnor — i analogi med ett artificiellt partikelacceleratorprov. Myoner finns tydligen ända in till deras sönderfall, som alltid slutar på elektroner.

— Men skulle sådana partikelfragment kunna bildas UTOM masschokning?

— Isåfall, från vad?

Den frågans exakta formulering bildar den verkliga ingången till hela problemets lösning — och därmed en betydande utvidgning av beskrivningsreferenserna i TNED, speciellt beträffande svårigheten att förstå masschokningens natur [Se utförligt från PLANCKEKVIVALENTERNA och MAFEM].

© Adam-Hart Davis, Natural Science 2008.

http://gallery.hd.org/_c/natural-science/_more2006/_more03/splash-crown-water-drop-on-blue-crazed-cracked-surface-frozen-2-AJHD.jpg.html

Om protonen verkligen delas upp, som en vattensplash, i mindre delar och därmed tvunget uppvisar en massdeficit (ett massunderskott) på de bildade delarnas kredit kommer partikelacceleratorns chokmassa m(U) i vilket fall att effektivt DÖLJA det massunderskottet; Massunderskottet kan kompenseras av chokmassan m(U) så att den massdeficita protonen uppför sig på chokmassans kredit som en ordinär proton: ingenting anmärkningsvärt syns i partikelspåren. Massdeficiten visar sig först med partiklarnas avstannande, då chokmassan lämnas tillbaka till det elektriskt slutna accelerationssystemet. Men då är experimentet (för protonens del) sedan länge redan avslutat — alla har gått hem för dagen. Laboratorielokalerna ligger tysta och nersläckta. Ingen bryr sig om den delen. Se utförligt från MAFEM.

Protonens massdeficit passerar obemärkt: r =mv/BQ, spårets krökningsradie i magnetfältet med fältstyrkan B; Med givet BQ kan v vara högt med litet m eller lägre v med högre m: spårböjningen blir i vilket fall densamma. Ingen kan avgöra vad som är vad (mv-faktorerna kan dock inte varieras omvänt godtyckligt eftersom vMAX=c sätter en gräns i partikelacceleratorfallet);

Summan av alla partikelmassor, med chokmassorna inkluderat, bildar summan av alla spårens partikelmoment (mv) med tillhörande magnetfältsavböjningar (r=mv/BQ):

För att bilda de tre Pionerna och Kaonen (Σ 912,8 MeV) krävs en minsta accelerationsenergi på 3,419 m(p) [1m(p)~938,2 MeV] eller 3207,84 MeV (från MIC-ekvivalenterna).

Det finns alltså en EXCESS på 3207,84 – (912,8) = 2295,04 MeV (2,446 protonmassor) tillgängligt som chokmassa att fördela på de ingående komponenterna.

Med MÖJLIGHETEN i ekvivalenta impulser [Mv=mV] finns följaktligen ingen som helst matematisk möjlighet att utesluta att endera (eller bägge) protonen uppvisar ett massunderskott: Protonens massdeficit KAN passera obemärkt.

Observera f.ö. att impulserna i det slutna elektriska systemet är samma som i den vanliga mekaniken, se f.ö. r-teorins grundmatematik.

Notering. Vi kan (här) inte genomföra någon exakt redovisande jämförelse med referens till Focuskällans bubbelkammarbild eftersom vi inte vet exakta instrument- och bilddata (T.ex. accelerationsenergin, vi vet inte den här, men den måste vara minst det ovan angivna värdet (den s.k. tröskelenergin, eng. threshold energy). Av samma skäl begränsas också exaktheten i den här framställningen.

KRÖKNINGSRADIEN (r) beräknas f.ö. direkt från en given båglängd (sekanten eller kordan med längden k och höjden h) enligt r =(h²+[k/2]²)/2h. Vi känner dock inte magnetiska fältstyrkan i anordningen (r =mv/BQ).

Att en proton verkligen av princip KAN avdela massa i utbyte mot masslös energi finns redan experimentellt klarlagt genom det s.k. INVERTERADE BETASÖNDERFALLET (eng. inverse beta decay) och som (bl.a.) används i KamLAND-projektet (nutida avancerade experiment för att klarlägga den sublima neutrinofysiken). Reaktionen skrivs (här i TNED-ekvivalenter)

(m←γ)_e– + (m←γ)_v + (m←γ)_e+ + p = ₀n¹ + e⁺

0,511MeV + 0,782MeV + 0,511MeV = 1,804 MeV minimum

Sedan den energiexciterade protonen bildat en energiekvivalent »neutronproton» förenas den med en ordinär Väte-1-kärna och bildar en deuteron: nettoenergiräkningen blir i slutänden densamma som för deuteriumbildning via två Väte-1 [‡].

Övre protonen

Den övre protonen — lösningen enligt TNED

På liknande sätt SKULLE, t.ex., målprotonen vid A

Till prövning för TNED

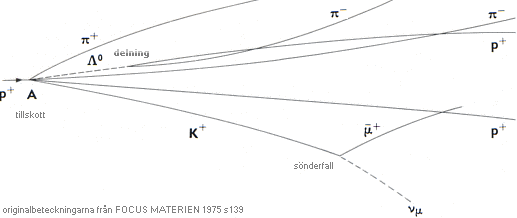
kunna exciteras (med minst 38,2 + Pion 139,6 = 177,8 MeV) — för att tillfälligt bygga om (»pumpa upp») kärnstrukturen och så bilda en »energipumpad neutral proton» i formen av en Lambdapartikel (Λ⁰, 1 116 MeV) — som strax delas (inte explicit sönderfaller)

Λ⁰ = p⁺ + Ekin = [Ekin1 + (p⁺ – m)] + [Ekin2 + (m=π^–)] … ............... vi vet (ännu) inte hur överföringen går till (ser ut)

till den ursprungligt ENERGIEKVIVALENTA men nu massdeficita protonen — PÅ GRUND AV ATT DEN i sitt exciterade tillstånd TVINGAS LÄMNA IFRÅN SIG en Negativt laddad Pion och därmed själv, likt »neutronprotonen» har blivit en energiekvivalent, en massdeficit proton (med ett negativt kärnstrukturunderskott som uppvägs av den mekaniskt tillförda energin vid kollisionen), och som fortsätter att behålla sin signatur i kraft av energiekvivalenten — utan att sönderfalla.

Det vi ser i partikelspåren i Focuskällans bubbelkammarbild skulle alltså kunna förstås inte som spåren efter splittrade (med massdestruktionsstrålning associerade) kärnfragment, utan snarare som spåren efter en motsvarande hydrodynamisk vattendroppsdelning: En »höghastighetsSplash» (med vissa inre förvecklingar).

© Adam-Hart Davis, Natural Science 2008.

http://gallery.hd.org/_c/natural-science/_more2006/_more03/splash-crown-water-drop-on-blue-crazed-cracked-surface-frozen-2-AJHD.jpg.html

Snarare än det ursprungliga resonemangets samband

Λ⁰ = p⁺ + π^– …

skulle det vara det mera förklarande

Λ⁰ = p⁺ + Ekin = [Ekin1 + (p⁺ – m)] + [Ekin2 + (m=π^–)] …

som tecknar det praktiska fallet; Ekin1 kompenserar/tvingar massutgivningen som sammanhänger med Ekin2, dessa delas strax och kan därmed, tydligen, förstås liknande två vattendroppar som lösgör sig ur en gemensam sträng som effekt av ytrekylen. I slutänden sönderfaller +m till en elektron- (eller positron-) massa; Pionen– sönderfaller till en Myon– (genom massdestruktion), och Myonen– i sin tur sönderfaller till en elektron. Frånsett neutrinoförlusterna (m→γ) i sönderfallen, återstår därmed minst en elektron (eller positron) från den ursprungliga moderkärnan som gav sitt substrat för bildning till (här) en negativt laddad PiMeson från en hyperon (Lambda0) och som strax delades utan massdestruktion i Pimesonen (π–) och moderkärnan med massdeficit (massunderskott), (p⁺ – m).

Undre protonen

Den undre protonen — lösningen enligt TNED

I varje fall om förloppet sker snabbt, skulle i princip samma omvandling kunna ske nära omedelbart efter incidenspunkten i A för den nedre protonen; Vi sätter som tidigare accelerationsprotonen pa, målprotonen pm:

När pa överför sin impuls på pm sker en snabb ändring i pa då den plötsligt förlorar en del av sin höga impuls till pm;

Ändringen kvarlämnar en energiexciterad originalproton (p⁺, den undre protonen i partikelspåren ovan, och den som uppvisar största impulsen, analogt minsta avvikelsen); EXCESSEN (överskottet) som blir kvar utöver normalprotonens massekvivalent tvingar p⁺ att lämna ifrån sig massdelar som — likt en bestämd RESONANS med vattendroppar som försörjer deras specifika form och massa i det atomära fallet — formar partikelfragmentens massbaserade strukturformer med 2 Pioner (±π)[2×139,6=279,2 MeV] och en Kaon (K⁺)[494 MeV], totalt 773,2 MeV energiekvivalenta partikelfragment (med bibehållen kärnstruktur) och som sönderfaller i slutänden (efter mellanformer [Myoner]) till elektroner (genom massdestruktion av själva kärnstrukturen så att elektronmassan kan friläggas). Den kvarvarande energiexciterade undre protonen i partikelspåren får därmed, i princip, samma status som den övre.

BILDKÄLLA: Författarens arkiv · 2009

Bild4Drop15iso3200

På samma sätt som olika droppformationer lösgör sig ur vattenytan då den påverkas av en (snäv) impuls, kan (tydligen) också atomkärnans ytform beskrivas genom att olika rekylformer bildas ur kärnytan i kraft av en inkommande kolliderande partikel och som tvingar kärnformen att uppdelas på olika avsnitt. Det som avdelas i atomkärnans fall är tydligen enbart (uteslutande) en motsvarande bevarad kärnstruktur (±e) som konserverar partikelfragmentens massform på moderkärnans bevarade spinnform (bevarande av massa, laddning och spinn). I kraft av kärndroppens instabila natur som just en atomkärna i slutänden — sådana miniversioner vet vi finns inte i någon stabil version i fysiken — tvingas den avdelade strukturen sönderfalla med associerad massdestruktion (m→γ) till den enda möjliga stabila slutprodukten som vi vet finns närmast under vätekärnan: en elektron (eller positron).

Motsatserna

MAC utsäger att chokmassan på 3,419 protonmassor skapar de tre Pionerna och Kaonen på totalt 912,8 MeV och kvarlämnar en chokmassaexcess på 2,446 protonmassor med de ursprungliga två protonmassorna intakta.

TNED utsäger att de tre Pionerna och Kaonen på totalt 912,8 MeV istället avdelas ur protonmassorna via kärnstrukturernas samlade bevarande av massa, laddning och spinn

— så att dessa miniatyratomkärnor senare, längre fram, kan sönderfalla ytterst till elektroner (eller positroner); massunderskottet i protonmassorna fylls ut av chokmassan på 3,419 protonmassor, resten med chokmassaexcessen på 2,446 protonmassor fördelas på partiklarnas spårimpulser.

Nettoräkningen med massor och impulser och därmed den magnetiska spårbilden blir i bägge fallen exakt densamma.

I ena fallet associeras chokmassan rent kvantitativt med de nybildade partiklarna, originalprotonmassorna intakta.

I andra fallet framträder de nybildade partiklarna ur originalprotonernas kärnmassor där chokmassan fyller ut massunderskottet i originalprotonerna så att dessa, i vilket fall i bubbelkammarbilden, fungerar som de ordinära protonmassorna i det andra alternativet.

Det finns alltså i grunden — i bubbelkammarbilden — ingen KVANTITATIV skillnad mellan de två sätten.

DET FINNS INGEN KVANTITATIV MOTSÄGELSE.

Den kvalitativa skillnaden är dock betydande:

MAC säger att de nybildade partiklarna skapas ur chokmassan.

TNED säger att de nybildade partiklarna avdelas (spinnkorrekt) ur protonernas kärnmassor — som vattendroppar i en vattensplash; kärnmassans struktur med laddning (±e) och kärnspinn är avgörande för att dessa partiklar längre fram kan och måste sönderfalla (genom massdestruktionsstrålning), ytterst till elektroner (eller positroner).

I MAC finns (vad vi vet) ingen liknande djupbild.

OM denna beskrivning håller streck, utverkas, i princip men på ett komplicerat sätt, samma partikelstrukturer från värdpartikeln (protonen) i fallet reguljär masschokning från partikelacceleratorer som i det naturliga fallet med den kosmiska strålningen (höghastighetsprotoner från den yttre rymden alstrade på mekanisk väg). Den vägande g-massans centrifugalkraft bildar en avgörande skillnad i de bägge fallen, samt att någon egentlig exakt jämförelse ALDRIG kan ske eftersom impulskomponenten (mv) i det kosmiska fallet inte kan observeras för komponenter med hastigheter större än c — man missar första träffen. Då sådana blir synliga, har redan huvudimpulsen dämpats ut, och det man KAN se måste med fysikens nödvändighet skilja sig (avsevärt) från partikelacceleratorns fall.

— Dessa ovan påtalade aspekter fanns inte klart uppmärksammade i min referens då NEUTRONFRAGMENTEN först författades.

Därmed skulle gåtan vara löst — om inga ytterligare oklarheter framkommer.

SAMMANFATTNING

NEUTRONFRAGMENTEN

SAMMANFATTNING

De FÖRMODAT SKAPADE PARTIKLARNA i proton-protonkollisioner från artificiella partikelacceleratorer kan tydligen enligt TNED förstås som bildade genom avdelningar från endera moderkärnans ordinära spinnstruktur (±e). Avdelningarna verkställs genom svängningsenergin som överförs från rörelsemängden (mv) hos kollisionspartikeln genom ett massinteraktivt samband (MIC) λ = h/mv konventionellt benämnd de Broglies vågekvation. Villkoret är att våglängden (λ) måste vara mindre än den avdelande atomkärnans spinnradie så att svängningen via λ garanteras tillträde till spinnstrukturens underavdelningar som därmed kan åtkommas för uppdelning. De substratmassor (±e) som moderkärnan avdelar via λ sönderfaller ytterst till elektroner (e–) och positroner (e+) genom massdestruktionsstrålning (m→γ), samma som neutrinostrålning i TNED. Därmed, frånsett neutrinoförlusterna, garanteras att den massdeficita moderkärnan i princip ges möjlighet att återta sin avdelade substratmassa genom att alla atomer delar på alla elektronmassor gemensamt (med utbyten och växelverkan). Energin som omsätts i partikelaccelerationen bildar enligt TNED den chokmassa (se från PLANCKEKVIVALENTERNA) som påtvingar de avdelade partiklarna extramassa utöver deras vilomassor. Jämför det enklare skolexperimentet med TRÅDSTRÅLERÖRET som visar effekten av elektronernas massökning genom elektrisk partikelacceleration (r=mv/BQ; radien ökar märkbart genom att de mera massiva elektronmassorna utverkar större centrifugalkraft med given hastighet från accelerationsfältet, BQ givna, f.ö. kanske det bästa experimentella sättet att klargöra ämnet).

Särskilt i sammanfattning beträffande chokmassan från den elektriska partikelaccelerationen

DET FINNS EN UTMANING I TNED beträffande chokmassan. Med referens till avsnittet i Beviset för multipla c och därmed ursprunget till den (typiskt) kosmiska protonens hastighet på rent MEKANISK väg — vi minns att R i Q=√(m/R)(A/dT) inte ingår i mekaniken, se utförligt från PLANCKEKVIVALENTERNA om ej redan bekant — finns inte möjligheten med partikelacceleratorns chokmassa. Med ekvivalenta impulser [r=mv/BQ, den Q-laddade m-partikelns avböjningsradie i det pålagda magnetfältet B] ges istället en motsvarande högre partikelhastighet i det mekaniska fallet — och därmed elimineras motsvarande partikelspårsegenskaper i jämförelse med ett typiskt bubbelkammarfotografi som grundas på partikelaccelererade källprotoner; I det mekaniska fallet skalas alla förlopp bort med v>c. I det mekaniska fallet kan alltså enligt TNED omöjligen de motsvarande avdelade kärndroppspartiklarna uppvisa den aktuella stora massimpulsen från det elektriskt accelererade fallet [Se särskilt i Massunderskotten]. Dvs., från den tidpunkt då de laddade partiklarna väl framträder (sedan de i det mekaniska fallet dämpats ut från initiellt högre hastigheter än c och kommer in i området för c) kan de väl uppvisa analoga hastigheter med det artificiellt partikelacceleratorgrundade bubbelkammarfotografiets partikelspår — men knappast i fråga om massan. I motsvarande grad med den (betydligt) lägre partikelmassan (ordinära elektroner med ett minimum av extra ±e-struktur typ Myonpartikel) tvingas centrifugalkrafterna avta i växelverkan med det pålagda magnetfältet (r=mv/BQ). Resultatet måste följaktligen, tvunget, uppvisa (betydligt) större avböjningar med mindre radier — mera liknande reguljära elektronspår (större eller mindre cirkulära spiraler) än långa svagt krökta raksträckor av motsvarande tyngre partiklar. Men detta är bara, här och rent teoretiskt, en högst privat uppskattning (som t.ex. lätt skulle köras över av höga partikelhastigheter, analogt rakt motsatt verkan: betydligt rakare spår).

MIC-ekvivalenterna beskrivs utförligt i särskilt avsnitt.

———————————————————————

Från magnetiska kraftlagen F=BQv och centralkraften F=ma=m(v²/r) ges BQv=m(v²/r) som ger BQ=m(v/r) och därmed r=mv/BQ.

EXEMPELFRAMSTÄLLNINGEN originalförfattningen END.

NEUTRONPROTONEN

Neutronprotonen

En Proton kan AVDELA kärnsubstrat — utan att sönderfalla

— EXEMPLET är samma som används i KamioKAN-DEdektorn;

Se även i Partikelbeviset för att energi inte kan skapa massa;

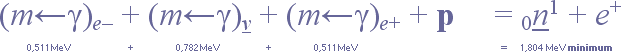
(m←γ)_e– + (m←γ)_v + (m←γ)_e+ + p = ₀n¹ + e⁺

0,511MeV + 0,782MeV + 0,511MeV = 1,804 MeV minimum, jämför den konventionella teckningen i nedanstående citat.

Protonen avger en positron (och blir en »neutronproton») om den matas med en OBS antineutrinoenergi [‡] på (minst) 1,804 meV.

Den protonen har då (tydligen på visst originellt sätt) blivit instabil — den är ENLIGT TNED INTE massekvivalent med neutronen, men väl energiekvivalent.

I KamLAND-fallet förenas »neutronprotonen» med en närliggande fri proton till en deuteron (se Deuteriumbildningen nedan). Föreningen ger en elektrisk signal som tillsammans med 1,804 MeV-initieringen ger en karaktäristisk signatur, och som kan användas för att (tämligen säkert) mäta neutrinoförekomsterna. Nettoresultatet av den ovan beskrivna originella deuteronbildningen är precis densamma som i »det ordinära fallet» med en pp-fusion.

En mera utförlig beskrivning på Hur och Vad i KamLANDfallet finns i KamLAN-Detektorns NeutrinoOscillationsbevis.

Se även (inledningsvis, om ej redan bekant) Neutrinobegreppet i MAC.

PROTONSÖNDERFALL MED ENERGIMATNING VIA ANTINEUTRINO — Beskrivning:

NEUTRONENS SÖNDERFALL TILL VÄTEATOM innehåller redan en uppbunden Atomär MASSDEFEKT med lägst

₀n¹ – ₁H¹ = 0,782 MeV = v ............. samma som konv. antineutrino, här v

Vilket betyder: För att rent kärntekniskt kunna påverka (typ) vätekärnan (protonen, p) — med samma verksamhet som försiggår »inuti» vid deuteriumbildning

2[1H1] = 1H2 + e⁺ + (m→γ)

måste FÖRST massdefektsenergin (v, v fungerar inte [‡]) påföras vätekärnan (Väteatomen) så att den kommer tillbaka till det ENERGIMÄSSIGT EKVIVALENTA utgångsläget

(m←γ)_e– + (m←γ)_v + p = ₀n¹ = p + e^– + (m→γ)_v ;

(m¬g)_e– + (m←γ)_v + ₁H¹ = ₀n¹ = ₁H¹ + (m→γ)_v ; energiexciterad e⁺ neutronekvivalent, avger INTE (återigen) en e–

Minst 1,804 MeV krävs

Först då blir det meningsfullt att påföra (samma energityp) ytterligare den ENERGIEKVIVALENT [(m←γ)_e+] — energimängden som normalt frigörs i deuteriumbildningen motsvarande positronmassan (e⁺) — vilket ger en »neutronproton» [₀n¹]

(m←γ)_e– + (m←γ)_v + (m←γ)_e+ + p = ₀n¹ + e⁺

0,511MeV + 0,782MeV + 0,511MeV = 1,804 MeV minimum

Observera att den praktiska energiekvivalenten helt baseras på elekteronneutrinostrålningen (»grundnyckeln» motsvarande neutronsönderfallets neutrinonyckel) ve– (konv. ve). Det krävs tydligen inte (Neutrinoidentiteterna) att den avgörande energimängden måste vara en »blandtyp» med inslag av positronneutrino (ve+, konv. ve).

Konventionell teckning

Ovanstående totalt skrivs konventionellt enligt

”Electron antineutrinos (νe) are detected via the inverse beta decay reaction (νe + p → e+ + n ) which has a 1.8 MeV νe energy threshold.”, [v i originalet med strecket över]

@INTERNET Wikipedia KamLAND, The KamLAND detector 2010-05-23

ν_e + p → e⁺ + n

Den energiexciterade protonen avger en positron och bildar därmed själv en »neutronproton»

Deuteriumbildningen

Tillsammans med en ordinär vätekärna (proton, p) kan sedan neutronprotonen slutföra samma nettoresultat som två ursprungliga väteatomer; föreningen till en Deuteriumatom. Nettoresultatet blir energimässigt detsamma (ideala yttre nollmoment som alltid i exotermiska kärnreaktionslagen);

₀n¹₀ + ₁H¹_1,518 – (m→γ)_{2,225 MeV} = ₁H²_2,917 ; positronen redan utgiven innan fusionen

₁H¹_1,518 + ₁H¹_1,518 – (m→γ)_{1,442 MeV} = ₁H²_2,917 ; positronen ges ut i samband med fusionen

I bägge fallen tillkommer alltså en positronmassa [+ e⁺], men på olika sätt.

Neutrinoidentiteterna

Notera neutrinoidentiteterna

Jämför citat.

Som redan påpekats i TNED (Se Plancks strukturkonstant) avspeglar ARBETET — energin — till alla kärnombyggnader genom massdestruktioner (m→γ) en karaktäristisk PROFIL (en slags nyckel eller »röst») för varje nuklidform, analogt neutrinostrukturens speciella uppsättning av våglängder och frekvenser och som inte kan ersättas av någon annan profil (Se Neutrinosignaturen). Experimentalfysiken, speciellt från de första mätningarna (Davis 1955) tydligen endast understryker den neutrinoprincipen enligt TNED.

Se även mera utförligt från NEUTRINOBEGREPPET I TNED om ej redan bekant.

KamiokaReferenser

KamioKAN-DEtektorn, KamLAN-Detektorn [eng. KamLAND], KamiokaNDE, KamLAND

För KamLAND-projektet, se särskild beskrivning nedan i KamLAN-Detektorns NeutrinoOscillationsbevis.

KamioKAN-DEtektorn här en ekvivalent (försvenskad) akronym till KamLAND, se referenserna sist nedan;
KamiokaNDE-projektet:

KamLAN-Detektorn [eng. KamLAND], här en försvenskad omskrivning för Kamioka Liquid Scintillator Antineutrino Detector, se referensen nedan sist

KamiokaNDE efter Kamioka Nucleon Decay Experiment, se referensen nedan

KamLAND invigdes 2002, se @INTERNET Wikipedia KamLAND (Kamioka Liquid Scintillator Antineutrino Detector) 2010-05-23.
KamLAND-projektet: Neutrinostrålning från 53 kärnreaktorer får passera visst material varefter mängden kontrolleras genom inverterade betasönderfallets neutrinospridningsreaktion (se Snabbgenomgång KAMLAND). Påvisad differens styrker teorin om neutrinotypens ändring i materiell växelverkan.
OPERA-projektet: Av samma typ som ovan, fast mera avancerat genom MyonNeutrinostrålare;
Från CERN (Genève, Schweiz) riktas (genom sekundära partikelreaktioner) en MyonNeutrinostråle mot en detektor 73 mil längre bort genom Jordskorpan (OPERA-detektorn i Gran Sasso, Italien).
Genom (teoretiskt:) växelverkan med det mellanliggande materialet ändras MyonNeutrinostrålarens profil till en TauonNeutrinostrålare som, om teorin håller, kan frigöra en Tauon från någon atomkärna i ett målobjekt (här i formen av tunna Blyblad) och därmed lämna ett detekterbart partikelspår.
Den förutsagda förekomsten skulle vara ca 5 tillfällen på ca 10,4 år.
Den 31 Maj 2010 meddelade OPERA-projektets ansvariga ledning att man med 98% säkerhet funnit en sådan positiv indikation [‡].
[Den här artikelserien påbörjades i början av 2010, utan vetskap om OPERA (framkom här, först, till kännedom 15 Juni) — och fick, tydligen oväntat, lämplig assistans som ovan: Vi är, tydligen, många som åker på samma våg — upprinnelsen till TNED ligger f.ö. som mest (i min referens) 39 år bakåt i tiden].

KamLAN-Detektorns NeutrinoOscillationsbevis

KamLAN-Detektorns NeutrinoOscillationsbevis

för Kam-Kamiok-akronymerna, se även KamiokaReferenser

Se även inledningsvis i Neutrinobegreppet i MAC om ej redan bekant.

SNABBGENOMGÅNG KAMLAND — bevisen för neutrinooscillationer

KORT SNABBGENOMGÅNG:

KamLAN-Detektorn får sin neutrinotrafik från betryggande 53 st omgivande kärnreaktorer (som producerar s.k. antineutrinos, ve–). När en neutrinofoton med lägst 1,804 MeV träffar på en vätekärna i KamLAN-Detektorn bildas — energiekvivalent — en neutron plus en positron. Reaktionen skrivs konventionellt (se citat med utförlig beskrivning i Neutronprotonen)

Inverse Beta Decay

Inverterade betasönderfallet

ν_e + p → e⁺ + n

NOTERING — ur protonen framkommer en neutron och en positron:

Kärnreaktionens produkt

neutrino + vätekärna = neutron + positron

uppvisar samma principiella kärnladdningsstruktur enligt TNED som i neutronsönderfallets

neutron = vätekärna + elektron + neutrino

och som bevisar atomkärnans (neutronens dolda) kärnstruktur av ±e, se från laddningsdeplacementet — men som knappast tilldrar sig något intresse i modern akademi, trots mängden (numera vardagliga) experimentella bekräftelser;

Ingen I MODERN AKADEMI tycks »se=förstå» framträdandet av den elektriska laddningen (elektron-positron) från atomkärnan (neutron-proton) som ett bevis för en regelrätt UTGIVNING av ±e — trots att man kan SE den beskrivningen framför sig på bordet i energiekvivalenter som ovan.

Ytterligare ett exempel på distinktionen TNED/MAC.

När sedan (den virtuella) neutronen (”~200mS senare”) krockar (förenas till Deuterium) med en vätekärna uppkommer en elektrisk stöttransient. Den helt säkra elektriska tidssignaturen säkerställer (elegant) att bara reaktorneutrinos kommer med i mätningarna (minimalt eller ingenting från Jordens inre, Solen eller övriga kosmiska källor).

Ett händelsediagram som visar hur hela detekteringsförloppet går till finns på

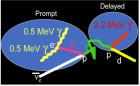
”Online Trigger Data Analyzer”,

KAMLAND CAPABILITIES AS A SUPERNOVA NEUTRINO DETECTOR — Petr Vogel, CalTech 2007

http://sn1987a-20th.physics.uci.edu/0855-Vogel.pdf

(neutrinostrålning träffar en vätekärna i det flytande materialet [mineraloljor och bensen med höga halter av väte tillsammans med fluorescerande kemikalier], vätekärnan emitterar en positron som strax annihileras tillsammans med en elektron, samtidigt har vätekärnan transformerats till en energimässigt ekvivalent neutron, då denna stöter ihop med en vätekärna, som medför ev. förening till Deuterium, ger vätekärnan/Deuteriumkärnan ifrån sig en elektrisk signal). Källan använder explicit beteckningarna npd för neutron, proton, deuteron.

En utförlig beskrivning på atomkonfigurationen i de kemikalier som ingår i KamLAN-Detektorn (i stort sett enbart kol-väte-föreningar) finns på

AN OVERVIEW OF THE KAMLAND 1-KILOTON LIQUID SCINTILLATOR — F. Suekane et al. (2003)

http://arxiv.org/ftp/physics/papers/0404/0404071.pdf

Ett annat, liknande diagram, finns på (s6)

KAMLAND: MEASURING TERRESTRIAL AND SOLAR NEUTRINOS — Patrick Dekowski (2006)

http://www.aps.org/meetings/multimedia/april2007/upload/H2_3.pdf

Man påvisade att av en viss förväntad mängd neutrinos (86,8) av den vissa energi som förknippas med neutrinotrafiken från de 53 omgivande kärnreaktorerna i själva verket bara en mindre mängd återfanns (54) med en lägre energi. Ändringen (den s.k. neutrinooscillationen) sammankopplas med en masskvadrat (∆m²) enligt källuppgiften

∆m² = 7,9 ±0,5 t5 eV².

KOMMENTAR:

Beviset grundas alltså på en DISKREPANS — ingen regelrätt observation som visar att neutrinos av den ena sorten skulle uppvisa en förvandling till den andra sorten [För detta senare fall, se OPERA-projektet]. Diskrepansen KAN med andra ord förstås vara av alldeles samma kvalitativa typ som »vanlig högenergetisk em-strålning» som genomgår dämpning via Comptoneffekten (ljusets växelverkan med materien gör att ljusenergin hf tappar frekvens f — kvantitativt precis som biljardbollar som stöter emot varandra och tappar fart/energi). Effekten beskrivs emellertid inte (riktigt) så i modern akademi.

Se även Neutrinobegreppet i MAC för jämförelsen med Neutrinobegreppet i TNED.

I TNED är neutrinostrålning masslös em-strålning och lyder därför också under Comptoneffekten. Se utförligt från Neutrinobegreppet i TNED, om ej redan bekant.

De rent experimentella resultaten således endast bara gynnar TNED kvalitativt.

Jämför även med Partikeldelningen i TNED: Myonen (105,66 MeV) är lättare än Tauonen (1777 MeV); Enligt TNED [Se Neutrinospektrum och Plancks strukturkonstant] är den lättare kärnformen associerad med den högre frekvensen: MyonNeutrinostrålning KAN följaktligen genomgå spontan dämpning då den växelverkar med materia — och därmed möjligen transponeras till TauonNeutrino som enligt TNED besitter en lägre neutrinostrålningsfrekvens. Den rent kvalitativa delen i detta förhållande är också precis vad som påvisats i OPERA-projektet (31Maj2010). Se mera utförligt i OPERA-projektet.

Det enda I PRINCIP som skiljer TNED från MAC i dessa avseenden är kvaliteten att MAC tvunget måste använda ett massbegrepp (∆m²) för att kunna förklara den experimentellt observerade neutrinostrålningens ÄNDRING med (speciellt) materiell växelverkan men vars massfaktor inte finns i TNED eftersom neutrinoändringen enligt TNED följer Comptoneffektens matematiska fysik som en ordinär (men [betydligt] mera högfrekvent) helt masslös em-strålning i materiell växelverkan. Se f.ö. Neutrinobegreppet i TNED, om ej redan bekant.

ATT en dämpverkan förekommer enligt TNED i materiell växelverkan visas speciellt tydligt i Neutrinostrålningen från Solen — även här tycks TNED hålla sig väl framme (Nästan så ruskigt väl att man med en viss mindre överdrift ryser. Inväntan av en uppseglande aspekt, något minsta lilla korn, som kan sänka TNED ens ett minsta snäpp väntar ännu på sin rapport. AutoSkanningen är inställd på läget Letar alltid).

Se även i OPERA-projektet.

MAC och experimentalfysiken

Notera också följande:

NEUTRINOPROBLEMET I MAC har (med början från slutet av 1960-talet [‡] in till våra dagar 2010) — om inte annat — visat oss hur den moderna akademins teori genomgår modifieringar i takt med nya experimentella rön. I TNED — däremot till noggrann jämförelse — avtäcks istället mer och mer av en redan befintlig fast grund: Grunden ändras inte. Den är visserligen helt beroende av experimenten i sakernas uppdagande men likväl oberoende av experimenten genom att dessa inte ändrar något i grunden, endast skapar flera belysningspunkter på en redan uppritad karta. Det är i varje fall så som TNED tycks uppvisa sitt sakinnehåll in till skrivande stund — som en redan arbetande motor vars detaljer uppdagas mer och mer i takt med växande insikt. Men det kanske finns personer som uppfattar också den moderna akademins historia på samma sätt. Se även i ATOMVIKTERNA.

Se även mera utförligt från Solära neutrinoproblemet i modern akademi, Solära Neutrinoproblemets uppsegling.

SNABBGENOMGÅNG KAMLAND END.

Fristående text till Vinjettbilden

På samma sätt som en vattendroppe kan »slira» PÅ vattenytan — ibland upp emot sekunden eller mera innan den dras in — så kan också ENLIGT TNED en atomkärna (vattenytan) avdela en del av sig själv ENDAST UNDER FÖRUTSÄTTNINGEN att den avdelade droppen får SPINN (J=mvr): den självständiga droppen kan bara bildas som en del av en utskjutande kraft som innefattar en roterande rörelse. Annars inte.

Men spinn — massa — kan inte skapas utan en redan befintlig massform: spinn kan inte skapas av ljusenergi, endast ur en redan befintlig spinnande massform — enligt TNED. Mycket starkt argument.

En vattendroppe kan glida, slira, rotera och ÅKA på vattenytan endast under den förutsättningen att vattendroppen besitter ett inneboende SPINN som hindrar den normala ytspänningens formomslutande funktion.

Utan spinnet dras droppen in direkt av vattenytan.

Neutronens Fragment | Komplement Del I · Universums Historia

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

NEUTRONENS FRAGMENT | Komplement Del I

ämnesrubriker

innehåll

NEUTRONFRAGMENTEN i relaterad fysik

Skapelse eller delning?

Spårbilden

Partikelacceleratorns ekvivalenter

TNED/MAC

Partikelacceleratorns Begränsade Fysikhorisont

BEVISBARHETEN I PARTIKELACCELERATORERNAS BEGRÄNSADE FYSIKBESKRIVNING:

Varför TNED utesluter elektriska källor som orsaken till den kosmiska partikelstrålningen

Inledande beskrivning

Restprotonernas öde

Elektronmassans delning

Partikeldelningen i TNED — Hur går den till?

Partikeldelningen i TNED

Regelverket

Kärnladdningens bevarande genom h och E

Termen antipartikel i TNED

Historia Kosmiska Partikelstrålningen

Spårmallar citat

SpårAnomalier

Emulsionstekniken, massoberoende

Emulsionstekniken, brister, metodens utveckling

Magnituderna

Atomkärnans åskådning i MAC

Sambandsbeviset för Kärndelning utan Massdestruktion

Partikeldelning utan massomsättning

Partikelbeviset för att Energi inte kan skapa Massa

INVERTERADE BETASÖNDERFALLETS BEVIS enligt TNED

Neutrinobegreppet i MAC

Webbreferens

Steven Hardy ref.

EXEMPELSAMLING — massa-energi

Rutherford 1919

MAC säger Skapelse

Partikelbildning med Masschokning

Hur ska man förstå »partikelbildning» med masschokning?

Resonemanget från början

Referenstabell

Kritisk granskning av resultatet

Sönderfallstiderna

Upplösningen

Övre protonen

Undre protonen

Motsatserna

SAMMANFATTNING

Neutronprotonen

PROTONSÖNDERFALL MED ENERGIMATNING VIA ANTINEUTRINO

Konventionell teckning

Deuteriumbildningen

Neutrinoidentiteterna

KamiokaReferenser

KamLAN-Detektorns NeutrinoOscillationsbevis

Fristående text till Vinjettbilden

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

[BA]. BONNIERS ASTRONOMI 1978

SIGMA 1-6, MATEMATIKENS KULTURHISTORIA av James R. Newman, Forum 1965, efter originalet The world of mathematics 1956

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

TNED

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också

RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

MAC — I UNIVERSUMS HISTORIA ofta använd allmän förkortning för Modern ACademy, modern akademi.

em — I UNIVERSUMS HISTORIA ofta använd allmän förkortning för elektromagnetisk-

MeV — Mega elektron Volt. Från energin E=mc²=UQ används U=1Volt och Q=e=1,602 t19 Coulomb; E/Q=eV=elektronVolt = E/(1,602 t19 C);
eV/T6 = MeV = E(Joule)/(e·T6) = E(MeV);
E(MeV) = E(Joule)/(e·T6)
E(J) = E(MeV)(T6)/(e=1,602 t19 C).
EXEMPEL: Elektronmassan m(e)=0,000548598(u=1,66033 t27 KG) motsvarar energin
E = m(e)·c² = (0,000548598u)(2,99792458 T8 M/S) = 8,18634 t14 J. Utryckt i MeV:
E(MeV/)c² = m(e) = (8,18634 t14 J)/(e·T6) = 0,511077 ............... elektronmassan i MeV(1/c²)

γ Grek. gamma, g, är i TNED (ofta) en generaliserad beteckning för massdestruktionsstrålning som [via Plancks strålningslag] byggs upp från kortare till längre våglängder med representation först vid gammanivån i materiefysiken.
Skrivsättet (m→γ), »m till gamma», betyder här ’massa som omvandlas till ljus och värme i materiefysiken’, från lägst gammanivån vilket generaliserat inbegriper värmefysiken överförd på materiefysikens atomkärnor och elektronmassor. Se även utförligt från Energilagen. Mera allmänt betyder (m→γ) massdestruktionsstrålning från primära massförstöraren E=mc².

Senast uppdaterade version: 2017-08-13

*END.

Stavningskontrollerat 2010-07-15.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

UnicodeStandard: TYPOGRAFIN I DETTA HTM-DOKUMENT HAR I DE FLESTA (MÖJLIGA) FALL UTNYTTJAT DEN TILLGÄNGLIGA (men krångliga) TECKENSNITTSSTANDARDEN FÖR UNICODE — SOM FINNS KOMPLEMENTÄRT TILL SYMBOL-TECKENSNITTET FÖR DET KLASSISKA GREKISKA ALFABETET SOM NORMALT ANVÄNDS I NATURVETENSKAPLIG LITTERATUR I OLIKA MATEMATISKT-FYSIKALISKT BESKRIVANDE SAMMANHANG med typexempel Ω Φ Σ Π Ξ Λ Θ Δ α β γ δ ε λ θ κ π ρ τ φ σ ν ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ← ↑ → ↓ ∞ . DET ÄR FÖR ÖVRIGT BARA WEBBLÄSARNA INTERNET EXPLORER OCH GOOGLE CHROME SOM LÄSER SYMBOLTECKENSNITTET (MOZILLA VISAR t.ex. Ö för rottecknet, etc.).

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se