UNIVERSUMS HISTORIA ENLIGT RELATERAD FYSIK OCH MATEMATIK · JORDENS ÅLDER | 2009IV25 | en BellDHARMA produktion | Senast uppdaterade version: 2017-09-19 · Universums Historia

J-KROPPARNAS VÄRMEFYSIK | JORDENS ÅLDER | Betingelser för det organiska livets uppkomst enligt TNED |

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor ·

UNIVERSUMS HISTORIA en BellDHARMA produktion Betingelser för det organiska livets uppkomst enligt TNED J-KROPPARNAS VÄRMEFYSIK JORDENS ÅLDER Enligt relaterad fysik och matematik — se optimala fusionsgränsmassan — är tydligen Jorden som himlakropp som det får förstås ENLIGT TNED en referenskropp i fysiken — likt en Pythagoras sats i matematiken — och som (följaktligen) återbildas periodiskt med K-cellens periodiska pulsning — naturligtvis med unika exemplar. I följande presentation studeras dessa detaljer mera ingående tillsammans med frågan om vår Jordkropps explicita individålder i vårt specifika universum — tillsammans med redan kända basfakta från geologin.

Betingelser

2009III11

Betingelserna för det organiska livets uppkomst enligt TNED

—————————————————————————————————

JORDYTANS MÖJLIGA ÄMNESSAMMANSÄTTNING med JORDENS URTIDSATMOSFÄR ENLIGT TNED

Den unika nuklidagenten ₆C¹⁶

Den häftiga energiutvecklingen under den korta fusionsfasen i himlakroppens bildning enligt TNED garanterar att betainstabila nuklider (här också benämnda betaagenter, nedan) som normalt har mycket korta sönderfallstider exciteras och väntar med sina sönderfall tills nivån på den lokala energigenomströmningen sjunker under hållvärdet: den häftiga lokala energin skjuter tillfälligt upp betasönderfallet via massa-energiekvivalenter tills den lokala energin sjunker under (det normala) betasönderfallets energitröskelvärde. Därmed är det — helt säkert — fritt fram för den mycket viktiga och centrala fusionsagenten 6C16 under den korta men viktiga fusionsfasen i himlakroppsbildningen. Fusionsfasen är emellertid så kort (max t20 sekunder, vidare nedan) att den i fallet 6C16 (0,747 S) knappast har någon betydelse. Vi bör emellertid känna till detaljen med »väntnukliderna» för ev. undvikande av missförstånd (i mera komplicerade verkstäder).

I den mån vi kan förstå att divergenständningen sker homogent över hela J-kroppen, sönderfaller också neutronerna homogent i respektive regioner med hänsyn till de fördröjningar som ges av den aktuella J-kroppens egengravitation. Om vi frånser denna period (tIGN) där fusionsringarna alltså byggs upp, är hela J-kroppens fusionsbildning överstökad på en ringa bråkdel av en sekund. Därefter är loppet kört och J-kroppen har då fått sin slutliga grundämnessammansättning med hänsyn till neutronfördelningen och de därmed sammanhängande olika fusionsringarnas neutronkvoter. Efter fusionsbildningen återstår en stor mängd restnuklider som efter normala förhållanden kommer att betasönderfalla till stabila atomer.

Ström-, Kraft- och Kemiekvationen i TNED

Ström-, kraft- och kemiekvationen i TNED i godtyckliga steg — Se ATOMFYSIKENS TVÅ KUNGSEKVATIONER —

(F_BT+F_eZ)₁+(F_BT+F_eZ)₁+(F_BT+F_eZ)₁+…+(F_BT+F_eZ)_n = 0 ........................... atomens kemiekvation

garanterar fusionsringarna i den maximalt täta J-kroppen: alla möjliga kombinationer är OK så länge atomkärnorna kopplar inom varandras nuklidbarriärer. Instabila, kortvariga nuklider som i normalt artificiella Jordiska laboratorier sönderfaller snabbt kan tillfälligt hindras i sönderfallet om energigenomströmningen lokalt uppväger den nuklidens sönderfallsenergi, och endast då.

Betaagenterna som krävs för fullständig materiebildning är, som tidigare omnämnts i nuklidbildningarna, nukliderna

2He6 (0,82 S), 3Li8 (0,86 S) och 6C16 (0,75 S).

Vi kan emellertid redan här observera att deras sönderfallstider ligger långt högre upp i tidsskalan än den aktuella fusionsfasen för en J-kropp (idealt) från divergenständningens ögonblick (max 300 fusionssteg med max ett per t22 sekunder ger att fusionsfasen för hela den J-kroppen är »överstökad», idealt, inom 5 t20 sekunder).

Den typiska mönsterkopplingen för fusionsringarna kan då, enligt kraftekvationen, tydligen illustreras som nedan;

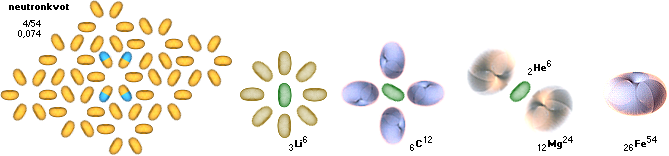
Neutronkvoten kan variera för en och samma slutnuklid, vilket garanterar att grundämnet får spridning inom kroppen redan från bildningstillfället. Neutronkvoten i J-kroppens centrum blir tvunget noll relativt J-kroppens rand med maximala neutronkvoten 1, enligt förutsättningen med max c i J-kroppens centrum. Mönsterkopplingarna för en fusionsring behöver (som här) nödvändigtvis inte vara plan utan kan lika gärna vindla sig i t.ex. en sfäriskt tätt sluten form, eller andra typer, beroende på. Kärnorna bestämmer själva allt eftersom de fysikaliska omständigheterna medger. Se även i Udda och Jämna Nuklidserierna som garanterar J-kroppens centrala järnkärna.

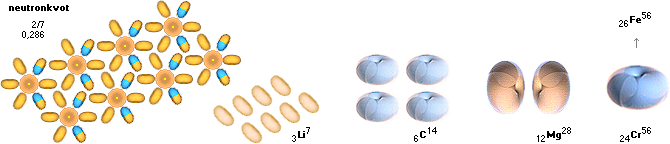
Från divergenständningen börjar de maximalt tätt liggande neutronerna (blågult) sönderfalla till väteatomer (vätekärnan, gul). Eftersom J-kroppens centrum håller lägsta g-värdet, analogt högsta c-värdet (se från ljusets g-beroende), sker sönderfallet där snabbast, sedan långsammare utåt kroppsranden. Då neutronerna således »vaknar» i positiv divergens och därmed Coulombkrafterna (elektriska krafterna som mäts i Coulomb, se från elektriska kraftlagen) utanför atomkärnorna börjar agera, kan kärnorna nu synkronisera sig för den fusionsfas som uppenbarligen alldeles strax är i antågande. Kärnkopplingarna bygger på att atomkärnorna redan befinner sig innanför varandras nuklidbarriärer (se nuklidbarriären), och de behöver därmed bara sluta en bestämd fusionsring enligt kraftekvationen, typ exempelformen illustrerad ovan. Kärnorna har bara EN chans i varandras primära maximala närhet att genomföra denna koppling, sedan är det kört i och med att Coulombrepulsionerna mellan atomkärnorna och omedelbart efter fusionsfasen (som ökar medelavstånden mellan de primärt maximalt tättliggande atomkärnorna) omöjliggör exotermiska fusioner (som ger energi): Påföljande fusionsfas (max 300 steg för en ring, analogt grovt max t20 sekunder) bildar en tyngre produktkärna av ringkomponenterna och lämnar motsvarande tomrum öppet, vilket (i allmänhet) betyder att betingelsen för fusionskoppling upphör mot närliggande bildade nuklider. Separationen garanterar därmed Coulombisk repulsion, analogt J-kroppens expansion omedelbart efter fusionsfasen.

Syreförekomsten

Med (tabellen nedan) den översiktliga bilden av ämnessammansättningen i Jordskorpan [BONNIERS ASTRONOMI 1978 Tabell 10.2 s174] framgår de möjliga nuklidagenterna.

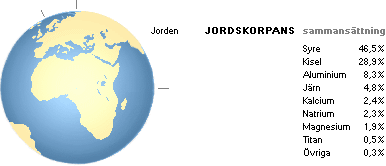
Betaagenterna som krävs för den fullständiga exotermiska materiebildningen, ända in till de allra högsta masstalen (max 317 enligt TNED) blir då som tidigare omnämnts nukliderna

2He6 (0,82 S), 3Li8 (0,86 S) och 6C16 (0,75 S).

Agenten 6C16 är utöver sin koppling till Syret (8O16) speciellt användbar på grund av sin låga massdefekt (14e), vilket gör att den kan användas för att bilda exotermiska nuklider långt in i den tunga gruppen (upp till masstal runt 160).

EXEMPEL atomnummerNUKLIDmasstal(atomärMassdefekt) EXOTERMISK ENERGI:

24Cr54(17,705) + 2·6C16(14) = 36Kr86(17,54) 24,602 MeV

Se även mera utförligt i maximalringen.

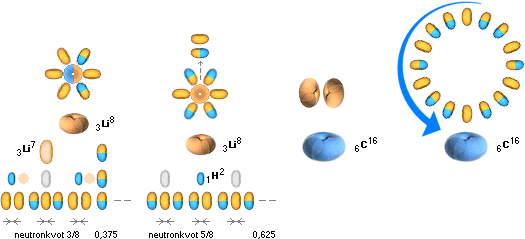
Bildningen av 6C16 omspänner neutronkvoterna 0,375 till 0,625. Om vi studerar det intervallet i Diakvadratens referens nedan, ser vi att »bandbredden» för 6C16 blir tämligen stor i Jordkroppen — vilket garanterar en allmän spridning av oxidföreningar i hela materialkroppen då 6C16 efter fusionsfasen slutligen sönderfaller till 8O16 (halveringstid 0,75 S [ref. Wikipedia Carbon isotopes]).

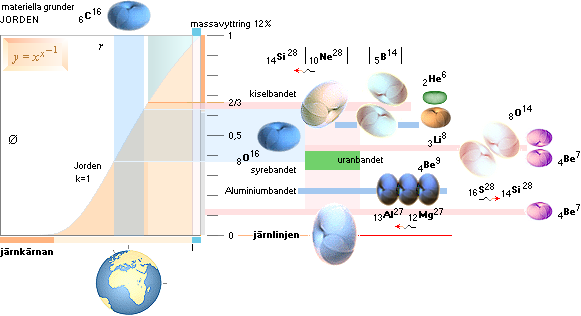
Diakvadraten med neutronkvoterna 0-1 och grundämnesfördelningens baskarta enligt TNED

Bildningen av Kisel och Aluminium kan bl.a. återföras på agenterna 4Be7 och 4Be9; Med dessa givna kan de nämnda grundämnena (till exempel) bildas enligt de illustrerade sekvenser som visas mera utförligt i Basnuklider med olika neutronkvoter. Järnkärnan i Jorden — utförligt i Grundämnesbildningens Två Basgrupper Järnkärnans absolut största gränsradie (från i princip allt över Ø=0,01) blir med vidstående modell 0,285r. I BONNIERS ASTRONOMI 1978 s172 visas en graf över seismiska mätningar på Jorden som anger den inre kärnans utsträckning till 0,27r (den fyllda rektangeln). ENCARTA 99 (Earth) ger uppgiften 1275 KM för kärnans radie, vilket med ekvatorialradien 6,378 T6 M ger ca 0,2r. Eftersom neutronkvoten noll är helt förbehållen JÄRNGRUPPEN [Se Grundämnesbildningens Två Basgrupper] har vi en viss rätt att förvänta oss att denna del också isoleras där neutronkvotens gradient mot 1 växer markant. Som visas t.v. i Diakvadraten (Ø-kvadraten) för Jordkurvan, är det precis fallet i referens till ovannämnda källuppgifter: Järnkärnan sträcker sig precis till fotlängden av Jordkurvan. Det finns emellertid en stor mängd ytterligare sätt för Järnet att bildas på med växande neutronkvot, vilket garanterar Järnet stor spridning i hela den övriga J-lokalen. Men dessa bildningar är mera komplexa och inte lika enkla som i den utpräglade Järnlinjen med neutronkvoten exakt noll.

Förekomsten 2×4Be7 med max Ø=0,43 ger en unik ändnuklid 8O14 som ENLIGT TABELLVERKET [HOP] saknar både binär och triplär egennuklid (vilket inte innebär att sådana är omöjliga, men de är inte experimentellt kända eller upptagna i referenstabellen). Den sönderfaller till stabila kvävenukliden 7N14, men kan också ingå i fusionen med 4Be9 som ger 12Mg23 som sedan sönderfaller till stabila 11Na23. Natrium är nämligen relativt väl representerad (2,3%) i Jordskorpans ämnessammansättning, enligt ovanstående sammanställda gängse uppgifter.

UTANFÖRNUKLIDEN (nuklid som [ännu] inte finns upptagen i tabellverket) 2×8O14=|16S28| kan emellertid realiseras ekvivalent med avyttring av en positron till 15P28 som sedan sönderfaller (inom 0,28 sek) till stabila Kisel 14Si28. På samma sätt kan UTANFÖRNUKLIDEN 3×8O14=|24Cr42| avyttra 3e+ till Skandiumindividen 21Sc42 som sedan sönderfaller (efter 0,62 sek) till stabila Kalcium 20Ca42.

2×2He6 (principgrafens högsta neutronkvot 0,67, samma för tritium) kan i princip bilda 6C12 genom UTANFÖRNUKLIDEN |4Be12|5B12 (som i sin tur kan bilda stabila Magnesium24 över Natrium24). Därmed kan teoretiskt också bildas UTANFÖRNUKLIDEN 2He6+5B12=|7N18|8O18.

YTTERLIGARE MÖJLIGHETER öppnas upp om 2He6 kan förenas via utanförnuklidprincipen med en neutron och bilda 3Li7. I sådana fall ligger max neutronkvot vid 5/7=0,71.

Frånsett möjligheten i periferidelen, kan 6C16 bidra till den tunga nuklidgruppens uppkomst dock bara in till en viss maxgräns som bestäms av massdefekterna. För att komma över (runt approximerat) masstalet 170 måste en fusionsagent med lägre massdefekt användas (2He6), samt slutligen en ännu lägre (1H2-3) för att få fram de allra högsta masstalen. Se mera utförligt i maximalringen, där ges direkta nuklidexempel ända upp till masstal 257 (Lw).

Speciellt genom neutronkvotens försorg och dess allmänna skala enligt diakvadraten ovan, kommer tvunget vissa tyngre nuklider att få vissa självskrivna »zoner», motsvarande vissa bildningsskikt i Jordkroppen. Uranbandet är ett exempel — och som garanterar att det Uran(Oxid) som finns i Jordskorpan bara kan komma dit genom konvektion.

För Järnets del observerar vi att det finns flera (många) olika sätt genom flera olika neutronkvoter så att Järnet också får stor spridning generellt i Jordkroppen. Detta gäller också generellt för ämnena överlag, även om vissa stråk gynnas mera för vissa avsnitt.

En mera exakt genomgång kräver ett mera omfattande räknearbete, och en sammanställning som täcker en mera övergripande analys finns för närvarande ännu inte (Mar2009|Jan2010).

;

Med bildningen av den stora mängden 6C16 förutsatt, utarmas samtidigt en del vidare möjliga påbyggnader med grundTYPnukliderna 2He6, 3Li7, 3Li8 och 4Be9. Uppställningen nedan ger en viss orientering i vilka agenter som krävs för att säkerställa Jordytans grundförekomster av främst Kol(C)-Kväve(N)-Syre(O) och som är avgörande viktiga för att säkerställa Jordkroppens primära ytgeologi; även om Jordkroppens inre genomgår mineralblandningar, kvarstår atmosfären som en friliggande del, och påverkas inte mycket av den underliggande kroppsfysiken, frånsett ändringen i ytans lokala accelerationskonstant (Jorden sväller betydligt under förhistorien) som kan påverka gasernas kvarhållning om den minskar avsevärt.

[ref.: VNS, Wikipedia Carbon isotopes]

Orienterande nuklidbildningar sönderfallstid (halveringstid)

1H3 + 1H3 = 2He6 ; ® 3Li6 (0,82 S)

1H2 + 2He6 = 3Li8 ; ® 4Be8 ® 2×2He4 (0,86 S)

1H1 + 2He6 = 3Li7 ; stabil

1H2 + 2He4 = 3Li6 ; stabil

;

1H1 + 1H2 = 2He3 ; stabil

2He3 + 2He6 = 4Be9 ; stabil

;

4Be9 + 3Li6 = 7N15 ; stabil

4Be9 + 3Li7 = 7N16 ; ® 8O16 (7,36 S)

4Be9 + 3Li8 = 7N17 ; ® 8O17 (4,14 S)

;

3Li8 + 3Li6 = 6C14 ; ® 7N14 (5,57 år)

3Li8 + 3Li7 = 6C15 ; ® 7N15 (2,3 S)

3Li8 + 3Li8 = 6C16 ; ® 7N16 ® 8O16 (0,747 S)

;

3Li6 + 3Li6 = 6C12 ; stabil

Det 6C16 som kvarstår singulärt (Ø=0,375 till 0,625) sönderfaller till stabila syrenukliden 8O16. Med hänsyn till det breda området i nuklidkvoten för 6C16 (0,375-0,625) finns därmed direkta förutsättningar för förklaringen till den mycket stora förekomsten av syre (också) i Jordskorpan — generellt för alla motsvarande fasta himlakroppar (typ stenmaterial generellt).

Omedelbart efter fusionsfasen, bildas genom den naturliga blandning som uppkommer då J-kroppen expanderar direkta kemiska föreningar mellan O och alla övriga närvarande, vilket garanterar att Jordatmosfären från början blir syrefri — men att den samtidigt får en hög koncentration av vattenånga, kväve (kol) och väte.

Genom att Jordkroppen först så småningom sväller till sin nuvarande storlek, garanteras för övrigt under hela den primära utvecklingen en maximal ytaccelerationskonstant vid Jordytan som kan kvarhålla speciellt den lätta vätgasen under den viktiga förhistorien.

Kväveförekomsten

STABILA KVÄVEBASEN (7N14-15, huvudnukliden är 7N14) använder (främst) betainstabila 6C14 från stabila 2×3Li7 med neutronkvoten (största) 0,57 vilket garanterar de yttersta perifera delarna, analogt J-kroppens yttre del.

Väteförekomsten

VÄTEBASEN är redan given genom att alla J-kroppar i vilket fall får en ytterdel med maximalt hög neutronkvot i bildningsfasen och som garanterar väteförkomst i samtliga fall.

J-kroppens minimala storlek, som blott successivt inträder sin slutliga (nuvarande) formradie genom successiv expansion, garanterar genom motsvarande maximal tyngdkraft vid ytan att vätet kvarhålls under huvuddelen av kroppens utsvällning (Se även J-kropparnas expansion).

Bekräftelser: Webbkällan nedan talar om forskning i stöd för uppfattningen om en väteatmosfär i Jordens urtid,

[http://www.theallineed.com/science/05042506.htm] 2009-03-09, 2005, The All I need (Lexur) PWHM Networks, Published in the April 7 issue of Science Express.

Även källan nedan refererar till samma artikel,

[http://www.colorado.edu/news/releases/2005/156.html] 2009-03-09, 6 April 2005,

News Center, University of Colorado

Vattenförekomsten

— Se även separat avsnitt i JORDENS VATTENBANK.

Genom ytdelens (uppenbart) initiellt stora mängd 6C16, dess garanterat breda neutronkvotsband, fås en garanterad syrebas vid fusionsfasens slut då hållvärdet för 6C16-agentens betaenergi underskrids och den börjar sönderfalla till 8O16. Med denna komponent i förening med övriga grundämnen, ges direkt kemiska O-föreningar; Det blir här lätt att »förstå» att praktiskt taget allt syre binds till andra grundämnen. Vätebanken, ytterst, garanterar för sin del att den syreföreningen bildar vatten (HOH). Emellertid är J-kroppen (synnerligen) het i det skedet (Se J-kropparnas värmefysik, se även en kortare illustrerad sammanställning nedan i Jordens ålder), och kommer att fortsätta vara det åtskillig tid framöver, vilket innebär att J-kroppens atmosfär bör betingas (starkt) av vattenånga tillsammans med främst väte och kvävebaser (samt koldioxid, COO). Först när J-kroppen svalnat så mycket att fritt vatten kan fällas ut (områden under kokpunkten) kommer det förmodligen ytterst täta atmosfäriska lagret av vattenånga att tunnas ut. Samtidigt har också J-kroppen svällt ut och fått en allt lägre accelerationskonstant vid sin kroppsyta, vilket medför att det tidigare kvarhållna lätta vätet i den primitiva J-atmosfären nu kan börja ge sig iväg.

Under den långa avsvalningsperioden bör Solens inverkan på J-kroppens yttre atmosfär ha haft god tid på sig att sönderdela de övre gasiska skikten, och därmed hunnit bilda det viktiga ozonet (O₃). Det skyddar, som vi vet, från Solens annars vådliga ultravioletta strålning och vilket är en förutsättning för det organiska livets harmoniska utveckling. En konsekvens av hela den processen är, och som vi redan känner till, att den organiska livsflorans utveckling bär ansvaret för den kontinuerliga produktionen av fritt atmosfäriskt syre.

Därmed har den huvudsakliga grunden berörts — till det till synes svåraste grundproblemet i spårningen av det organiska livets grunder i Jordhistorien:

— den viktiga syrefria primära men kväve och väterika atmosfären, tillsammans med det avgörande vattnet,

— samt villkoret att huvuddelen av Solstrålningen (initiellt, under lång tid) måste vara direkt utestängd (den kraftiga ångbildningen, samt den atmosfäriska vätebasen i garanti av en Jordkropp med trängre radie och därmed högre lokal ytacceleration), för att inte äventyra de känsliga molekylära bindningarna (aminosyrebaserna), samt att denna fas veterligt måste ha ytterst lång tid på sig.

Därmed är alla grundproblem röjda ur vägen.

Bekräftelser: Webbkällan nedan ger geologiska belägg för tidig COO i Jordatmosfären.

[http://news-service.stanford.edu/news/2004/june2/lowegeo-62.html]

Stanford news Service — Rocks tell tale of warm early atmosphere, Stanford Report, June 2, 2004

Jordens ålder

Den Urgamla Jorden

Enligt relaterad fysik och matematik — se optimala fusionsgränsmassan — som det får förstås ENLIGT TNED, är tydligen Jorden som himlakropp en referenskropp i fysiken — likt en Pythagoras sats i matematiken. Nedan studeras den delen tillsammans med frågan om vår Jordkropps explicita individålder i vårt specifika universum, tillsammans med basfakta från geologin.

— ENLIGT TNED återbildas, tydligen, himlakropparna periodiskt med K-cellens expansion — en gång per 2×336 miljarder år

— från en föregående kontraktion och vilken fysik helt återfaller på optimala fusionsgränsmassan, Jorden:

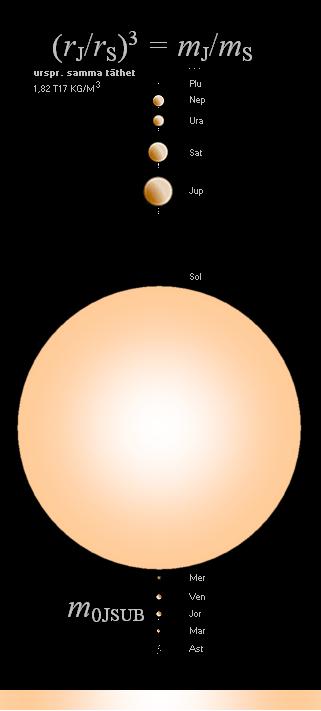
— Med kännedom om Solsystemets kroppsmassor, utpekas utan tvivel Jordkroppen som individen för den optimala fusionsgränsmassan. Grundmatematiken ges från den kosmiska c0-kroppens energiräkning, se utförligt från K-cellens värmefysik.

— Jorden som optimal fysikalisk kropp innehåller tydligen alla grunddata som bestämmer grundämnenas bildning och fördelning i alla typer av himlakroppar, se Diakvadraten i Jordens fjärde ekvation.

Med ÅterbildningsPrincipen given och förutsatt praktiskt giltig, upprepas alltså Jordbildningen, om och om igen — evigt — dock naturligtvis inte exakt lika för varje ny period;

— Varje period lämnar i vilket fall sitt energispår i den tillgängliga materien för varje kommande generation och som därmed garanteras sin unika gestalt: två exakt lika universum existerar inte.

— Genom K-cellens periodiska pulsning (se vidare länkar i illustrationen närmast nedan) återbildas tydligen Jorden, evigt, alltid, men periodiskt genom en ytterst välordnad matematisk fysik

— PER TID, som det tydligen får förstås enligt resultaten i K-cellens värmefysik, se även Jordens Andra Ekvation.

— Vi får (av allt att döma, heller) inte tro att bara EN Jord bildas åt gången: bildningsmatematiken (se Jordens tredje ekvation) bygger på ett resonansvillkor, och sådana uppträder tvunget på flera olika ställen i expansionen av universums olika materieöar (typ spiralgalaxer som vår egen).

— Med allra största sannolikhet befolkas därför även vår egen galax Vintergatan av FLERA (många) Jordar liknande vår egen — men med mycket stora avstånd emellan. Allt annat vore verkligen underligt i ljuset av de strukturer som universum uppvisar enligt TNED. Å andra sidan kan vi inte VETA det säkert (på annat sätt än det faktum att vår Jord kom till SÅ [också]).

Universums utveckling visas komprimerat illustrerat närmast nedan med inlagda länkar till mera utförliga beskrivningar.

K-cellen STJÄRNFYSIKEN Galaxbildningen

kontraktion detonation expansion himlakroppsbildningen grundämnesbildningen K-cellens värmefysik strukturkriteriet materieöarnas form

Vi studerar de rent naturvetenskapliga detaljerna.

A BellDHARMA production 1988

ILLUSTRERAD ÖVERSIKT MED JORDSKALETS BILDNING FRÅN INITIELL SMÄLTA ENLIGT TNED

JORDENS ÅLDER

2009III8 Sammanställning EARTH6.BMP

J-kroppens expansion J-kroppens värmefysik J-kroppens ytbildning

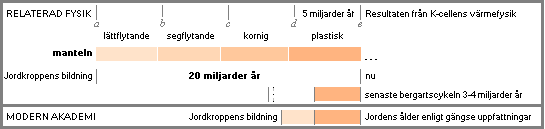
I modern akademi hoppar man över historien a-d på grund av den allmänna kosmologiska teorin med himlakroppsbildningen genom gravitationell sammandragning efter Big-Bang.

Figurerna visar i sammanställning Jordkroppens möjliga utveckling ENLIGT TNED från J-kropparnas expansion genom J-kropparnas värmefysik.

I modern akademi [‡1] hoppar man över historien a-d, den delen finns inte med; Man utgår istället DIREKT (inom hundratals miljoner år) från typ (d) ”tjärliknande geggamoja” för Jordens primärtillstånd [‡2]; Detta primärtillstånd skulle ha bildats via de s.k. planetesimalerna [‡3] med material från den urplanetariska nebularhypotesen [‡4] som (katastrofteorier) stötte ihop sig till Jorden och övriga planeter genom differentiellt roterande materieringar kring Ursolen som den lokala urnebulosans centrala rest, liknande ringarna kring Saturnus.

I ett (eller flera) av dessa ringstråk menar man att meteorider av en viss typ skulle ha samlats (eller bildats) och som inte haft grundämnet Uran från början men väl grundämnet Bly [‡5]. Dessa meteoritämnen används numera som korrelationsbaser mot Jordsammansättningens Blyförekomster [‡6]; I meningen att skillnaderna avspeglar Jordytans successiva ändring i blysammansättningen som följd av det naturliga uransönderfallet och därmed Urbergens ålder (Se Bergartscykeln), visar resultatet av dessa radiometriska Uran-Bly-dateringar en period på ca 4,51 miljarder år [‡6], och som allmänt beskrivs i termer av ”jordens ålder”.

— TNED: Proportionerna Bly-Uran i Jordens fall hinner aldrig byggas upp med några större värden förrän en gammal berggrund är helt ersatt av en ny, med underliggande omsmältningar med tillhörande diffusion av föregående cykels producerade Bly in i Jordkroppens mantel (jämför bläck som droppas ner på en vattenyta och som strax blandas upp med vattnet så att knappt något spår alls syns av den ursprungliga kraftiga färgmättningen) och därmed reduktionen av dess relativa andel i Jordskorpan — och därmed nollställning av uranklockan för en ny bergartscykel: alla spår av föregående cykel sopas effektivt igen. I en fast, stel, meteoridkropp däremot finns inga omsmältningsprocesser som kan hindra, och blymängden kan därför fritt ackumuleras in till sista uranatomen.

— Därmed bevisas, emellertid, bara den senast aktuella bergartscykelns period — vilken enligt TNED tydligen har föregåtts av flera tidigare — inte Jordkroppens egenålder.

GENERELLT SETT finns (således) ingen absolut direkt oberoende mätmetod med vars hjälp Jordkroppens ålder (flera, konsekutiva bergartscykler) skulle kunna avslöjas

— därför att preferenserna (Jordytans fasta bergmassiv) försvinner/förnyas över längre perioder.

— Man kan (alltså) bara få helt säkra rådata på en enda (den senaste) bergartscykels motsvarande livslängd, såvitt korrekt uppfattat.

I TNED grundas värdet för Jordens ålder (i stort samma som hela Vintergatans ålder, 20,82 T9 år) på resultaten från K-cellens värmefysik som utgår ifrån »de allra enklast tänkbara» kosmologiska observationsdata: Planckstrålningen på 2,7 °K, den medelmässiga rödförskjutningen (K=1,5), den synliga materiens medeltäthet (1 H-atom per 10 M³ rymd). Genom energitransientens allmänna matematik som grundlägger K-cellens värmefysik ges, tillsammans med grundvärden för kärnfysikaliska parametrar ENLIGT TNED, direkta tidsvärden. Se utförligt från K-cellens värmefysik.

Se även vidare för Jordens ålder i Månens recession.

[‡]1 @INTERNET sv.Wikipedia Planetesimal 2009-03-08)); @INTERNET Wikipedia Crust (geology) 2009-03-07

[‡]2 FOCUS MATERIEN 1975 s412sp2m

[‡]3 @INTERNET sv.Wikipedia Planetesimal 2009-03-08

[‡]4 @INTERNET Wikipedia Nebular hypothesis 2009-03-08

[‡]5 :

”Because the original abundances of lead on the planet cannot be measured, scientists use meteorites to get at the Earth's original lead composition. Some meteorites contain the four lead isotopes but no uranium or thorium parents. This means that the lead composition in these meteorites has not changed since their formation, and scientists believe this is a reasonable approximation of the composition of the Earth's original lead, the so-called primordial lead.”;

[‡]6 :

”Comparing the amounts of the four lead isotopes in primordial lead to their present amounts, scientists can determine how much lead has been added by radioactive decay since the Earth was formed. They can then calculate, using the half-life of each parent, how long it took to create the differences between the amount of present-day lead and primordial lead for each of the three isotopes. These calculations also yield an age of about 4.6 billion years for the Earth, which is consistent with the ages determined from meteorites and lunar rocks.”,

[http://www.kgs.ku.edu/Extension/geotopics/earth_age.html], 2009-03-07,

Age of the Earth May 2005 GEOKANSAS

Månrecessionen

Framställningen nedan beskriver inte Månens recession fullständigt, men ger en första avgörande bakgrund. Det som fattas är senare upphittade kompletterande — avgörande — uppgifter som fullständigar helhetsbilden.

— Se fullständigt beskrivning i MÅNENS RECESSION (Jul2017).

2009III9

Månens recession certifierar Jordens ålder enligt TNED

”Lunar laser ranging establishes the current rate of retreat of the moon from Earth at 3.82±0.07 cm/year (Dickey et al., 1994).”,

THE RECESSION OF THE MOON AND THE AGE OF THE EARTH-MOON SYSTEM, Tim Thompson, 2000

http://www.talkorigins.org/faqs/moonrec.html

Allt originalmaterial i Universums Historia får användas fritt förutsatt källan anges — BellDHARMA 2009

På samma sätt som i fallet med vattendropparnas bildning genom rekylverkan

— vår enkla men exakt experimentella motsvarighet till den primära himlakroppsbildningen ENLIGT TNED genom den plötsliga expansion som bildas från divergenständningen

— måste vi för samtliga J-kroppar förutsätta en primär fas där avståndet mellan TYP en centralkropp och dess kommande månkropp snabbt ökar till ett maximum. Denna initiella fas stabiliseras sedan när den tyngre kroppens g-fält infångat den mindre i en fast (cirkulär) bana (se Planetbanornas summamatematik) — förutsatt ett initiellt impulsmoment hos moderkroppen som ger hela systemet det nödvändiga primära spinnet, se utförligt från Hur delkropparna avdelas — uppkomsten av roterande moment.

Denna primära synkroniseringsfas är emellertid helt kort och kan för den vidare historien helt bortses ifrån. Vi kan därmed betrakta BEGYNNELSEN med de vidare (egentliga, vår historia) himlakroppsrelationerna med TYP Jorden-Månen från exakt noll distansökning mellan kropparna.

— När (nämligen) TYP Jordkroppen börjar uppvisa YTVATTEN, analogt från en tidpunkt då Jorden uppvisar ett ytskal (5-10 miljarder år bakåt enligt TNED, se föregående artikel), sker samtidigt en momentdislokation (uppkomsten av extra vridmoment) som gör att TYP Månkroppen, mycket marginellt, börjar avlägsna sig från Jordkroppen.

— Fenomenet kallas Månens recession (eng. Moon recession); Man har uppmätt den till 0,0382 M per år — vilket betyder att Månen avlägsnar sig från Jorden med 3,82 centimeter per år [‡].

— Tas Månrecessionen helt linjärt bakåt med nuvarande medelavståndet Månen-Jorden 3,844 T8 M, fås tiden

T = d/v

= (3,844 T8 M)/(0,0382 M/år)

= 10,0628 T9 år » 10 miljarder år

Resultatet återfaller på en absolut kontakt mellan Jorden-Månen för (allra minst) 10 T9 år sedan. Om, däremot, Jordåldern enligt konventionella teorier används (4,65 T9 år) blir begynnelseavståndet Jorden-Månen

d = vT = 1,7763 T8 M

vilket bara är knappt halva vägen (»Månen började på halva»). För att Månen ska ha haft kontakt med Jorden från början är det, således, uppenbart att man får stora teoretiska problem att brottas med om man bara har en tidsmarginal på runt 5 miljarder år — det måste vara minst 10 enligt ovanstående resultat. TNED klarar det, men inte modern akademi.

Med förutsättningen att Månrecessionen är noll från början och fortsätter vara det fram till perioden för Jordens mera reguljära skalbildning (möjligen från runt 5-10 miljarder år bakåt), analogt möjligheten för stationärt ytvatten, se föregående Illustrerad översikt, blir perioden (T) tydligen en mer eller mindre fullträff i Jordens Urhistoria. Vi vet dock inte exakt hur kurvan ser ut, men det finns vissa geologiska indikationer som kan vägleda, se vidare nedan.

TNED kräver, se från K-cellens värmefysik, att Jordens ålder ska vara 20,82 T9 år, alltså dubbla det beräknade T ovan.

Med den rimliga offsetperioden före T i hänsyn till Jordkroppens primära avsvalning, alltså grovt sett lika lång tid, verkar med andra ord den faktiska Månrecessionen inte helt orimlig att inpassa i Jordkronologin med de givna förutsättningarna. Därmed och så långt har Månrecessionens fenomenform alldeles tydligt certifierat ett stöd för den allmänna kronologi som Jordåldern kräver — enligt TNED.

Att Månrecessionen också, verkligen, har varit lägre i det förflutna, finns omvittnat i observationer av s.k. tidala sedimentära avlagringar (tidala rytmiter, eng. tidal rythmites, se citat nedan), alltså geologiska avlagringar som kopplar till tidvattenseffekterna. Medelvärdet i Månrecessionen perioden 650 miljoner år bakåt anges ca 2,16 cM/år, samt ännu lägre (1,27 cM/år) ännu längre tillbaka (perioden 0,65-2,5 miljarder år bakåt).

Källuppgifter på Månrecessionen och rytmiterna, samt en (översiktlig) grundbeskrivning av recessionens mekanismer ges i webbkällan nedan. Se även efterföljande kortare sammanställning i Basdata för Månen.

Månrecessionen i cM/år

The Recession of the Moon and the Age of the Earth-Moon System, Tim Thompson 2000 [2009-03-09]

http://www.talkorigins.org/faqs/moonrec.html

Författaren anger referenskällor i texten.

”Lunar laser ranging establishes the current rate of retreat of the moon from Earth at 3.82±0.07 cm/year (Dickey et al., 1994).”,

Min översättning:

»Månlaserområdning» [friare, Månlasermätning] etablerar nuvarande hastighet i månens avlägsnande från Jorden till 3,82±0,07 cM/år.

;

”This paleontological evidence comes in the form of tidal rhythmites, also known as tidally laminated sediments. Rhythmites have been subjected to intense scrutiny over the last decade or so, and have returned strong results. Williams (1990) reports that 650 million years ago, the lunar rate of retreat was 1.95±0.29 cm/year, and that over the period from 2.5 billion to 650 million years ago, the mean recession rate was 1.27 cm/year. ”;

”Williams reanalyzed the same data set later (Williams, 1997), showing a mean recession rate of 2.16 cm/year in the period between now and 650 million years ago. That these kinds of data are reliable is demonstrated by Archer (1996). There is also a very good review of the earlier paleontological evidence by Lambeck (1980, chapter 11, paleorotation)”,

Min översättning:

Detta paleontologiska bevis kommer från tidala rytmiter, också kända som tidalt laminerade sediment. Rytmiterna har varit föremål för intensiv detaljgranskning över det senaste decenniet eller så, och har framburit starka resultat. Willams (1990) rapporterar att för 650 miljoner år sedan var Månrecessionen 1,95±0,29 cM/år, och att över perioden från 2,5 miljarder till 650 miljoner år sedan recessionstakten var 1,27 cM/år.

Williams återanalyserade samma datamängd senare (Williams, 1997), som visar en medelrecessionstakt på 2,16 cM/år i perioden nu och 650 miljoner år bakåt. Att dessa typdata är tillförlitliga demonstrerades av Archer (1996). Det finns också en mycket bra återblick på de tidigare paleontologiska bevisen av Lambeck (1980, kapitel 11, paleorotation).

Basdata Månen

2009III11

Basdata Månen

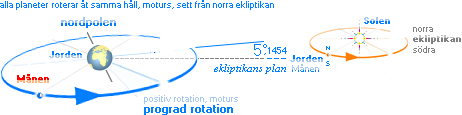
Figuren ovan vänster övre visar Månbanans orientering sett från normalstället norra ekliptikan.

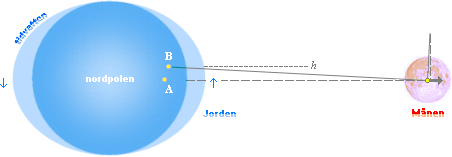
Figuren ovan vänster undre visar detaljerna till Månrecessionen, vidare nedan.

Figuren ovan underst visar skalenligt storleken Jorden-Månen och medelavståndet mellan dem 3,844(4) T8 M.

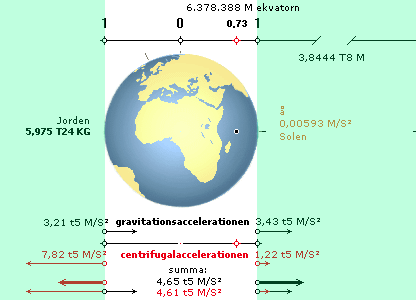
Figuren ovan höger visar uträkningarna för accelerationskrafterna Jorden-Månen med referens till tidvattenseffekten och de enkla elementära grundsambanden: resultaten visar att centrifugalkrafterna är nära lika stora på motsatta sidor Jorden genom linjen Månen-Jorden. Det betyder att nära två lika men diametralt riktade tidvattensbulor uppträder på Jordklotet (figuren ovan vänster undre, starkt överdrivet för den schematiska visningen).

Månrecessionens fysik, figuren ovan vänster undre; Gemensamma tyngdpunkten Jorden-Månen är — då vi bortser ifrån den effekt som ges av Jordens egenrotation tillsammans med Jordens ytvatten — idealt i den markerade punkten A. När Jorden roterar, och förutsatt ett bromsande ytvatten finns, släpar Jordkroppen med sig Månsidans vattenbula något litet i Jordrotationens riktning. Med den starkare gravitationen på Månsidan i en liten favör, blir nettoresultatet av den lilla dislokationen att tyngdpunkten vid A klättrar uppåt mot B. Resultatet yttrar sig i en motsvarande horisontell förskjutning av tyngdpunkten betecknad h i figuren. Därmed är det ideala, rent gravitella, statiska, tillståndet brutet. En ny, extra kraftväg (F·rMånen) har uppkommit, dock med mycket liten skillnad mot den stela, ideala. Vinkelskillnaden i Månänden resulterar i en liten extrahastighet (erinra centralaccelerationens härledning) vars dynamik söker motverka orsaken till ändringen och som därmed yttrar sig i att Månen, ytterst långsamt, börjar drivas längre bort (recessera) från Jordkroppen (experimentellt uppmätt till 3,82 centimeter per år, se även webbreferenserna nedan): Orsaken till Månrecessionen är alltså och tydligen ytvattensförekomsten på Jorden tillsammans med Jordklotets egenrotation. Med en enklare relationsform kan Månrecessionens storlek förstås översiktligt i termer enligt nedan. Se även efterföljande webbreferenser, där ges mera ingående matematiska beskrivningar (baserat på elementära grunder) som dock inte är av nöden i denna korta presentation.

h, tidala deplacementet på Jordytan (i havsvattnet) rätvinkligt linjen Jorden-Månen

rJ, Jordradien vid ekvatorn 6,378 T6 M

vM, Månens sideriska (relativt fixstjärnorna) omloppsrotationshastighet,

d/T = (2p·3,844 T6 M)/([27+0,3216608796]86400 S) = 1035,3465 M/S

v, Månrecessionen, experimentellt uppmätt 0,0382 M/år = 1,21048 t9 M/S

En enklare men gott orienterande relation (»ekvivalenta Jordära sekundtidala tryckhöjden») som ansluter till figurens beteckning, (horisontella förskjutningen) h, blir

h/rJ = v/vM som via v = 0,0382 M/år = 1,21048 t9 M/S ger

h = rJ(v/vM) = 7,45686 t6 M eller 0,0075 mM;

Tas den per år blir h (»tryckhöjdens fasta årsekvivalent») lika med 235,3206 Meter motsvarande Månrecessionens 0,0382 Meter.

Uppgifter finns som omnämner Jordrotationens avsaktning med värdet

8,836 mS/år = 2,79995 t10 S/S (ref. eng. Wiki Moon recession); Med Jordrotationshastigheten (grovt) vid ekvatorn

vJekv=(2p·rJ)/86400 = 463,82124 M/S ges på ändringstiden

t = 2,8 t10 S ett motsvarande värde på h enligt

(h) = v(Jekv=6,378 T6 M)·t = 1,29869 t7 M » 0,13 t6 M

Månrecessionens matematik på webben

På Googles Boksökning finns (bl.a.) källverket nedan som beskriver Månrecessionens matematik utifrån mera noggranna (avancerade) mekaniska grunder (boksidorna 387-389)[2009-03-11],

Notera att förhandsgranskningen i GoogleBoksök är begränsad: sidvisningen är INTE ALLTID exakt samma: gör man en paus och går tillbaka till samma bok senare, kan de avsnitt man nyss tittade på vara utestängda från granskning.

Planetbanorna

Planetbanornas primära inrättning

— i analogi med Månbanans Primära Matematik

Se ovan med inledning från Månrecessionen

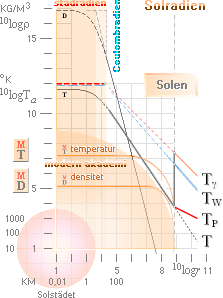
Solkärnan enligt TNED, se täthetskurvan (D) i figuren ovan, uppvisar ett relativt skarpt övergångsområde i intervallet 1-10 KM. Medan den inre delen motsvarar ett högtätt område, motsvarar den yttre delen en mera utpräglad gasisk representation. Därmed bildar också Solstädet (R=4012 M) en motsvarande brytande yta mellan ett inre tätare och ett yttre tunnare materierum. Genom att Solen också roterar, föreligger med andra ord i princip samma situation som i fallet Jorden-Månen; Solklotet utanför Solstädet är ”vattnet” och Solklotet innanför städet är den motsvarande fasta kroppen. Genom samma typ av gyromoment som i fallet Jorden-Månen, bildas följaktligen motsvarande moment mellan Solen och varje befintlig omloppskropp. Vilket vill säga: Också planeterna uppvisar tvunget en recession från Solen så att planeterna (ytterst långsamt) spiralerar allt längre utåt. Denna detalj blir, tvunget, speciellt märkbar i Solens fall eftersom energin bakom Solrotationen inte är passiv utan aktiv: Den energi som frigörs genom fusionsfaserna i Solen används till en mindre del för att öka rotationen av den inre städkärnan relativt det yttre gashöljet och som, enligt TNED, är förklaringen till storleken hos Solens nuvarande rotation: rotationen växer under hela Solens livstid. I fallet Jorden-Månen saktar Jordrotationen av då ingen underhållande energi driver upp den, och därmed minskar Månrecessionen i takt med tiden. I Solens fall finns alltså inte den avsaktningen, varför istället planetrecessionerna antingen och möjligen är konstanta eller i långsamt växande. Också detta borde i princip vara utläsbart ur de geologiska formationerna.

Men — som det här kan förstås — torde de här antydda variationerna vara ytterst sublima och därmed (otroligt) svåra att spåra — utöver det faktum att solstrålningens intensitet på bergavlagringarna måste vara (ytterst marginellt) större i det förflutna motsvarande ett kortare avstånd till Solen. I det sammanhanget vet vi redan att eftersom Solen hela tiden tappar massa genom energiomsättningen, dock ytterst blygsamt, minskar dess attraktionskraft och därmed försvinner planeterna iväg utåt bara av det skälet, även om den recessionen är mycket mycket liten. Att skilja ut den delen från en reguljär rotationsrecession torde därmed inte höra till den allra enklaste geologiska uppgiften.

Ingenting är heller här känt om något omnämnande i saken från etablerat håll (det är ingen enkel sak ens att formulera vad man ska fråga efter).

I etablerade kretsar talar man (på sin höjd, Mars 2009) om ”The Faint Young Sun Paradox”; I modern akademisk stjärnteori menar man att en stjärna av Solens typ bör tillväxa i intensitet med tiden (30% starkare nu än i början), vilket lett till (teoretiska) motställningar mot praktiska observationer (som istället tyder på en tämligen jämn Solstrålning). Därutöver finns veterligt ingenting omnämnt i saken.

Planetbanornas matematik i summa skulle därmed i stort sett följa samma polära funktionsform som i fallet med Solens allmänna vågekvation,

r = [A + a(x^3,5)cos nx^w]^{–1/(x+0,01)} ....................... Solens vågekvation i PREFIXxSIN

med enda skillnaden att vi ersätter den inre svängningsformen (cos-delen) med 1 så att vi får

r = [A + a(x^3,5)]^{–1/(x+0,01)} ................................... Planetbanornas primära tillväxt och bildning i PREFIXxSIN

med det illustrerade exemplet

r = [1 + (10¹) + 0,01(x^3,5)]^{–1/(x+0,01)}

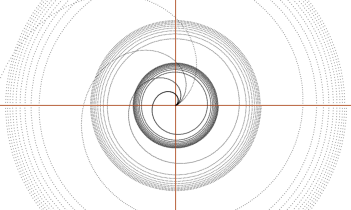
Spiralfiguren ovan exemplifierar r-funktionen i 10 varv i olika förstoringsgrader med varje ändcirkel motsvarande en (typiskt) given planets primära bildningscirkel. Hela Solsystemet börjar initiellt på sitt givna impulsmoment från moderkroppen (se från Uppkomsten av roterande moment), tillsammans med den utskjutande avyttringskraften analogt med droppbildningen i vattenfallet och som får till följd att delkropparna driver isär på den spiralformiga kurvans båge, figuren ovan. Vartefter den centralt belägna Solkroppen fångar in den aktuella planeten genom att g-kraften avtar i successiv balans mot centrifugalkraften och endast den rätvinkliga banhastigheten återstår, etableras en alltmer idealt cirkulär grundbana. I detta tidiga skede är emellertid Solrotationen helt försumbar för inverkan på recessionsprincipen då Solkroppen ännu inte hunnit utbilda någon utpräglad rotation utöver sin ytterst marginellt primära rotation (se från Rotationerna i Stjärnfysiken). Recessionsverkan i planeternas fall bör alltså byggas upp successivt först efter långa tidrymder genom Solens energiproduktion. Därmed kan den egentliga recessionen för planeternas del börja vid ett (långt) senare tillfälle, eller rättare sagt, tillväxa gradvis från ett minsta (noll-) värde i Solsystemets allra första tid.

Eftersom hela Solsystemet, tydligen, kan återföras på en resonansserie (d = F3a₀2^n–1+d₀), Se Jordens tredje ekvation (SOLSYSTEMETS BILDNING), där avståndsskalan framträder tydligt (Samma som den s.k. TITIUS TALSERIE {[3,6,12,24,48,96,…]+4}/10 = 0,4; 0,7; 1; 1,6; 2,8; …), innefattas tydligen också de olika motsvarande sluthastigheterna för de olika planetkropparna i samma matematik, idealt genom Keplers tredje lag. Därmed innefattas också centralkrafterna, och därmed massorna. Vilket vill säga:

— Hela spiralmatematiken

— typ illustrationen ovan, med planetavstånden, deras relativa banhastigheter, massorna och deras idealt utgångsmässiga helt cirkulära banformer med Solen som centralkropp och Jordkroppens som preferenskropp från Jordens andra ekvation via fusionsgränsmassans definition

— ingår tydligen i resonansserien.

Bergartscykeln

BERGARTSCYKELN — Jordytans ålder

Se även sammanfattad översikt i JORDENS ÅLDER

Jordskalets ålder — en cyklisk process

Varje absolut tidmätning

kräver en fast kristallin struktur som inte ändras genom kemiska, termiska eller mekaniska processer. Begreppet »Jordens ålder» har därför ingen annan absolut referens än den senaste geologiska bergartscykeln med bildningen av de äldsta (prekambriska) bergarterna. Det gängse begreppet ”jordens ålder” med grund i geologiska radiometriska mätningar betyder alltså jordskorpans ålder, inte Jordkroppens. ENCARTA 99- (Earth) använder värdet 4,65 miljarder år för Jordkroppens ålder enligt ”age of the Earth”.

Om i ett mineral AB, A sönderfaller till B och man inte känner AB från start är varje absolut tidmätning utesluten. Ekvationen a+b=c kan inte lösas entydigt för c om inte bägge ab är kända eller givna. Vartefter bergartscykeln utvecklas, ändras mineralsammansättningen tillsammans med de radioaktiva nuklidernas förekomster. De nya bergmassiv som bildas uppdateras på detta sätt kontinuerligt av den aktuella ämnessammansättningen, och därmed försvinner dess äldsta spår med de gamla bergens borteroderande och nersjunkade i manteln — där de delvis ombakas och delvis omsmälts till förmån för nya formationer. Enbart med hjälp av Jordskorpans mineral finns alltså inget direkt sätt att fastställa en absolut tidsskala för Jordkroppens ålder. Vad som däremot avspeglas absolut i varje bergcykel är temperaturstrålningen från Jordens inre.

”Genom att mäta de nuvarande utåtriktade värmeströmmarna i jordskorpan har man kommit till den slutsatsen att temperaturen i jordens inre knappast kan ha fallit mer än några tiotal grader sedan den tidpunkt då jordskorpan bildades.”

FOCUS MATERIEN 1975 s439sp2ö

; (20°C)/(3 miljarder år)

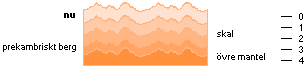
Bergartscykeln. Den genomsnittliga erosionstakten på Jordytan är [BONNIERS ASTRONOMI 1978 s192sp2mn] 0,086 M per 1000 år: Kemiska reaktioner, frostsprängningar, vattendragen, glaciärerna, vågorna, strömmarna, vinden, nederbörden. Områden med hög terräng och stor nederbörd eroderar snabbast. Inom »bara» 100 miljoner (0,1 T9 år) år har Mount Everest nära nio kilometer höga bergmassiv jämnats till i stort sett havsytan — enbart genom erosionens inverkan. Erosionen tillsammans med den naturliga nybildningen av bergarter sätter alltså vissa gränser för begreppet ålder i geologiska tidmätningar. Bergartscykeln producerar kontinuerligt nya områden, delvis och direkt med material inifrån Jordens mantel och delvis genom veckning, tryckande, vridande, pressande och dragande processer. Äldre formationer pressas successivt och sekventiellt ner under nyare bildningar tillsammans med erosionsprodukter. Efter en period av runt 4 miljarder år (senaste bergartscykelns längd), har bergarterna förändrats i sin sammansättning av mekaniska, kemiska och radioaktiva processer och också direkt genom omsmältande aktiviteter, och alla spår av den föregående cykeln har gått förlorade.

Men bergartscykeln har också en växande aspekt som gör att cykeltiden inte kan vara helt linjärt periodisk. Vartefter materialet i Jordens inre stelnar från ett initiellt smält tillstånd, allt mera med tiden, bildas naturligtvis allt större och tjockare fasta ytdelar och som alltså därmed befinner sig i växande. Ju flera bergcykler som passerar, desto hårdare blir hela kroppen i takt med dess successiva avsvalning — och desto mindre ändras de större redan bildade bergartsformationerna med sin växande tröghet, medan erosionen fortsätter med oförminskad styrka. En cyklisk bergartsformering på ytan av en himlakropp som genomgår avsvalning måste därför och rimligen få ett exponentiellt förlopp med korta initierande cykler som blir allt längre ju mera kroppen svalnar och stelnar. När väl stora och tunga djupbergryggar en gång har bildats, är det rimligt att också förmoda att de knappast kommer att genomgå andra förändringar i den fortsatta historien än att de tillväxer tills hela kroppens stelnat. Om erosionen får härska till slutet, slutar tydligen Jordkroppen som en nederoderad fullkomligt slät sfär, möjligen vattentäckt, med noll vulkanisk aktivitet.

Ur föregående beskrivna delar framgår alltså att den nu använda termen ”jordens ålder” torde referera till den senaste bergcykelns längd, en Jordens senaste geo-biologiska ålder, att denna period ENLIGT TNED av allt att döma haft flera cykler och att tvunget föregående cykler varit kortare på en allt hetare Jordkropp. Därmed, och sett på beskrivet sätt, finns inget absolut, egentligt tidsvärde för Jordskorpans ålder eftersom den periodvis försvinner och periodvis återbildas.

Webbreferenser till jämförelse:

En utmärkt svensk animerad illustration finns (2009-03-08) på

[http://www-vaxten.slu.se/ekologi/bergarter_cykel.htm],

Geologiska cyklar, Växten & Marken

Se motsvarande engelska webbkällor på »Rock Cycle», flera videos och (bra) filmer finns att se, t.ex.,

[http://videos.howstuffworks.com/hsw/17356-basics-of-geology-the-rock-cycle-three-types-of-rock-video.htm],

Basics of Geology: The Rock Cycle

Oceanskorpan förnyas snabbt

” - Oceanskorpan är endast 5-10 km tjock och består av tunga basaltiska bergarter. Genom att den ständigt nybildas vid oceanryggarna och sjunker tillbaka ner i manteln i s.k. subduktions-zoner vid oceanernas kanter finns idag ingen oceanskorpa äldre än ca 200 miljoner år.”,

[http://www.nrm.se/sv/meny/faktaomnaturen/geologi/jordklotetochjordskorpan/jordklotetsbyggnad.1068.html] 2008-12-05,

Naturhistoriska Riksmuseet — Jordklotets byggnad

Vattenbanken

Periferidelens Neutronbank

————————————————————————————

JORDENS VATTENBANK

Periferidelens neutronbank i association med J-kroppens inre delar

VATTENBANKEN

Från UniversumsHistoria.doc 2004

JORDENS VATTENBANK OCH UPPKOMSTEN AV URBERGEN 2004XI24

Bildkälla Bilder.AlltingGratis.se

GEMENSAMT FÖR SAMTLIGA PLANETKROPPAR är att de i sin yta uppvisar olika gas- och ångkoncentrationer — med väte som huvudaktör. De större planeterna (inkluderat Solen) har utpräglade väteatmosfärer medan Jorden — som enda positiva temperaturagent i termogravitella jämviktstrycket [Se JORDENS FÖRSTA EKVATION] — utmärker sig för en vattenbaserad toppyta.

Omedelbart efterföljande fusionsfasen

Eftersom neutronen saknar Coulombbarriär (men har en nuklidbarriär som alla andra) och därför har stor fusionsbenägenhet under alla förhållanden (men inte lika stor som i det optimala fusionsläget och bara med andra än sig själv), kan den i stort sett fritt förena sig med och komplettera isotoperna (atomer med samma kärnladdning men olika kärnmassa) i de primära grundämneskärnor som bildats under fusionsfasen. Vi frånser då den del av neutronstocken som av olika skäl och omständigheter innefattas i den primära massavyttringen.

Fritt syre förekommer inte direkt efter J-kroppens bildning

Neutronerna deltar inte i Coulombrepulsionen som efterföljer fusionsfasen, och kan därför på sätt och vis sägas ”stå stilla” i J-kroppen medan övriga passerar förbi under expansionen. På detta sätt uppkommer på sätt och vis (och in till en viss gräns) förutsättningen för en naturlig blandning — DELS mellan fria neutroner från neutronbanken och befintliga färdigbildade primärnuklider i formen av FUSIONER, DELS mellan befintligt ytväte och befintliga färdigbildade primärnuklider i formen av KEMISKA FÖRENINGAR. Därmed kan DELS nuklidkartan kompletteras naturligt, och DELS J-kroppens kemiska ytmineralogi erhålla en grundform.

Det som återstår efter J-kroppens bildning är alltså en färdigbildad mineralkropp. Frånsett den mer eller mindre kompakta järn-nickelkärnan som gäller i Jordens fall, blir J-kroppen på detta sätt TVUNGET fullständigt fri ifrån rena grundämnesförekomster — frånsett periferidelens väteförekomst.

Den springande punkten i sammanhanget är just den för Jordens del avgörande förekomsten av vatten (HOH). Den förekomsten bör, via grundämnet väte (H) i J-ytan som ovan, i varje fall initiellt vara begränsad också just till J-ytan.

Om vi tittar på baskartan över Jordens grundämnesfördelning enligt neutronkvoterna i DIA-kvadratens samband, ser vi att grundämnet Väte i fri grundform efter fusionsfasen i stort sett bara kan förekomma från maximala neutronkvotens övre referensgräns (2/3) och upp till J-kroppens yta. I stort sett NOLL förekomst av väte bör därmed föreligga inuti den fusionsbildade J-kroppen, alltså vid den tidpunkt då expansionsfasen inträder. Då J-kroppen expanderar, kan en stor del av det ytliggande fria vätet, tillsammans med neutronbanken, diffundera in till en viss gräns i J-kroppens redan färdigbildade nuklidmassa — och därmed följdriktigt bilda och komplettera kemiska föreningar. Det relativt breda syrebandet i DIA-kvadraten [Se baskartan] garanterar på detta sätt alltid en viss initiell förekomst av vatten tillsammans med de så indiffunderade väteföreningarna och som blandas med övriga grundämnen i toppskiktet.

Generellt för alla färdigbildade fasta J-kroppar, vare sig små eller stora, gäller alltså följande enkla egenskap: både fritt förekommande och mineralogiskt bundet vatten i ytdelarna med utanförliggande vätgas. Beroende på J-kroppens massa (och storlek), kan den lätta vätgasen kvarhållas i större eller mindre utsträckning. Om vi rent allmänt ser till de olika planeternas sammansättningar är detta, för övrigt, också just det praktiska fallet.

Jämför (fetstilen min markering):

”Dessutom skulle närvaron av signifikanta mängder fritt syre allvarligt ha hämmat bildandet av de organiska molelyler som är nödvändiga för jordiskt liv. Vi har direkta bevis för frånvaron av syre för två miljarder år sedan: vi har funnit att bergarter av den åldern vittrade utan att oxideras. Ett indicium för frånvaron av syre före den tidpunkten utgörs av observationen att flytande vatten har förekommit på jorden sedan 3,3 – 3,6 miljarder år tillbaka. (De äldsta bergarterna visar tecken på att ha stelnat under vatten.)”

BONNIERS ASTRONOMI 1978 s391sp2mö

Mer eller mindre en fullträff alltså.

Bildkälla

http://www.pryroda.gov.ua/en/index.php?newsid=5001030

NATIONAL SPACE AGENCY OF UKRAINE 15 July 2008

Vattenbanken

Allt vatten som nu finns synligt på Jorden har ursprungligen antingen/och legat bundet i rena hälleberget (eller i motsvarande bergsmälta) i formen av olika H-O-föreningar, eller som ovan omnämnts förekommit direkt från mineraljordens bildning i form av het vattenånga som inte kunnat fällas ut förrän Jordytan bildat ett fast skal med temperaturer under kokpunkten. Trots sin väldighet är den nu blottlagda totala vattenmassa över hela Jordklotet bara 0,053 delar (se nedan) av den fortfarande — i hälleberget — kemiskt bundna vattenmassan (vilket visar vilken enorm potential Jorden har). Det är inte slut på långa vägar för den delen.

För att frigöra en sådan bindning ur berggrunderna krävs, vad vi vet, tidsmässigt långa processer med en relativt hög temperatur som bakgrund, alltså en »långsam urkokning».

Om man känner avgivningsparametrarna (vilket vi tyvärr inte gör här) bör man kunna beräkna minimitiden för den nu blottlagda vattenmassan — vilket borde kunna ge avgörande bidrag till fastställandet av de olika skedena i Jordens fornhistoria.

Emellertid, om Jordatmosfären redan från början innehöll betydande mängder vattenånga, vilket föregående utläggning antyder, kan den räkningen till viss del bli irrelevant. Möjligen kan mera speciella geologiska data vägleda oss på den punkten, men ingenting är (här) ännu känt i den saken.

Bildkälla

http://www.pryroda.gov.ua/en/index.php?newsid=5001030

NATIONAL SPACE AGENCY OF UKRAINE 15 July 2008

Allmänt om Jordens Vattenbank

Huvuddelen av allt vatten som nu finns på Jorden ligger fortfarande bundet i mineralytan (litosfären). FOCUS MATERIEN 1975 (S483sp1m) ger uppgiften 25 900 miljoner KM³, analogt 2,59 T19 M³ eller (förenklat med 1KG vatten per liter) ca 2,6 T22 KG. Det är 0,00433472 delar (0,4%) av hela Jordmassan.

Oceanerna står »bara» för ”1 370 000 tusen KM³” eller 1,37 T18 M³ motsvarande 1,37 T21 KG (1KG » 1 liter vatten; 1000KG = 1 M³). Det är trots sin väldighet bara 0,0526923 delar av den kemiskt bundna vattenmassan (5,3%). Dessa tal visar endast att frigörandet av vattnet ur Jordytan inte på långa vägar uttömt vattenmängden och att tempot i detta frigörande därmed heller inte torde vara överdrivet hetsigt. Om vi rent hypotetiskt räknar oceanernas vattenmassa (tillsammans med atmosfärens mera blygsamma 14 T12 KG [14000 KM³], runt en hundramiljondel av oceanvattenbanken) som grovt sett 1,4 T21 KG bildat på en period om 4 miljarder år (1,2623 T17 sekunder) får vi ett globalt sekundtempo på 11090,83 liter (eller litet drygt 11 ton) i sekunden av vatten som frigörs ur rena hälleberget — Jorden runt totalt. Det blir inte mycket det räknat per kvadratmeter, ens per dygn. Genom geologin vet man emellertid att flytande vatten förekom redan för grovt sagt minst 3 miljarder år sedan, se citat. Innan så stora mängder kommit fram att det bildas pölar eller pussar måste (i varje fall i en medelvärdesform) hela atmosfären ha en motsvarande koncentration som kan fälla något synligt vatten. Redan för 3 T9 år sedan bör alltså vattenmängden bara av den anledningen ha varit betydande. Det indikerar att vattenbildningen antingen pågått långt tillbaka — eller att den kan förklaras med den samtidiga förekomsten av atmosfärisk vattenånga och som efter vissa (geologiska) omständigheter kan uppvisa utfällningar. Exakt hur långt tillbaka är vad vi skulle vilja veta. Utgår vi nämligen ifrån en ytsmälta som innehåller mineralogiskt bundet vatten är det uppenbart att vattenavgivningen pågår fortlöpande (konstant) ända fram tills dess ytan börjar kristallisera eller stelna. Därefter är enda möjligheten för vattenavgivning vad som kan komma från vulkanisk verksamhet då stelnat berg, vad vi vet, inte släpper ifrån sig sitt mineralbundna vatten i någon översvallande bemärkelse. Om vi vet vattenavgivningstakten ur en mineralsmälta med given vattenhalt, kan tiden beräknas.

Citatet ovan antyder att bergbildningen sammanhänger med förekomsten av vatten. Det finns dock (explicit) ingenting som säger att en sådan fornjordisk bergbildning skulle vara den enda i sitt slag. Exempel på berg som stelnar under vatten finns ännu i vår tid genom vulkanisk aktivitet under havsytan. Ön som bildades utanför Island 1963 (Surtsey, FOCUS MATERIEN 1975 s410) är ett exempel. Den prekambriska bergbildning man har observerat behöver (alltså) inte vara den första i en bergbildningscykel, den kan vara den andra eller den tredje eller ännu senare bildningar efterföljande föregående cykler.

Se även i J-kropparnas värmefysik, där beskrivs ENLIGT TNED (relativt) enkla ekvationer för TYP den fasta Jordytans bildning, samt hur temperaturen generellt sett kan ha vuxit fram från J-kroppens primära bildning.

För termen ”J-kropp”, se särskild beskrivning från Himlakropparnas Primärbildning (GALAXBILDNINGARNA).

Förtydligande av Universums ålder — se Särskild beräkningsgrund

2012II13

Förtydligande om Universums ålder 20,82 T9 år enligt TNED

Strålsfärens | K-cellens utveckling via Stefan-Boltzmanns strålningslag i TNED — Förtydligande av Universums ålder 20,82 T9 år i TNED — från K-cellens värmefysik

T_nu = (16,3 + 4,52 = 20,82) T9 år — UNIVERSUMS ÅLDER NU (2000)

16,3 T9 år effektmaximum inträder i K-cellens expansion på K-cellens centralparametrar [medelbaserad rödförskjutning, bakgrundsstrålning, synlig medeltäthet, genomsnittlig heliumhalt]

4,52 T9 år ljustiden som krävs för den PERIFERA primärinformationen att nå HIT IN TILL OSS I ELLER NÄRA K-CELLENS CENTRUM [området med max ljusets topphastighet]

— En viss svårighet finns

— (möjligen, för den som kanske inte genomgått K-cellens matematik [K-cellens värmefysik])

— att relatera/förstå TNED-uppgiften på universums ålder (20,82 miljarder år).

— Värdet grundas på en SAMMANSÄTTNING av tiden vid K-cellens effektmaximum (16,3 T9 år) och de från vår nutids sida sett avgörande parametervärdena (medelbaserad rödförskjutning, bakgrundsstrålning, synlig medeltäthet, genomsnittlig heliumhalt, utförligt i Kalkylkortet) PLUS ljustiden (4,52 T9 år) för den informationen att nå hit till oss, in till K-cellens centrum där ljushastighetens toppvärde råder [Universums Form] [Ljusets Gravitella Beroende].

— Följande förtydligar uppgiften om Universums ålder 20,82 T9 enligt TNED:

Vid T=16,3 miljarder (T9) år utvecklas K-cellens effektmaximum — enligt kalkylkortets beräkningar från TNED-teorin (Se utförligt från K-cellens värmefysik) — med fördelningen 25% Helium 75% Väte, samt Kosmiska Bakgrundsstrålningen (»Planckstrålningen») på ca 2,7 °K.

K-cellens ålder

Enligt K-cellens värmefysik i TNED är Solsystemet 20,82 miljarder år gammalt sett till hela K-cellens nuvarande utsträckning, se särskilt tidsskalan med de olika enheterna i illustrationen nedan från avsnittet i K-cellens värmefysik.

— Men: INFORMATIONEN om den fördelningen, inkluderat den aktuella bakgrundsstrålningen, innefattar K-cellens hela sfär vid det tillfället — eller mera exakt uttryckt, räknat från K-radien via rödförskjutningens antagna medelvärde K=1,5, se utförligt i K-radien om ej redan bekant.

— Med effekträkningen från Stefan-Boltzmanns strålningslag är det alltså K-radien som används i TNED för att få fram INFORMATIONEN OM bakgrundsstrålningens aktuella temperaturvärde — VID T=16,3 miljarder (T9) år;

— Då det — från K-radien (x) som var aktuell vid strålsfärens T=16,3 T9 år — tar ljustiden T(x)=4,52 T9 år att nå hit till oss i de av allt att döma EKVIVALENT centrala delarna av K-cellen [Se UNIVERSUMS ISOTROPI] där de avgörande observationsvärdena 25% He; 75% H; 2,7 °K; K=1,5 kan iakttas, måste vi följaktligen se K-cellens ålder TOTALT från just den observerade utgångspunkten:

T₀ = T+T_x= (16,3+4,52=20,82) T9 år — UNIVERSUMS ÅLDER NU (2000)

NOTERA ATT VISSA MARGINALER FINNS — som inte ger precisionen mindre utrymme än max några få procent:

— Jämför de olika värdena för K-cellens totala massa beroende på de något olika parametrarnas precision: Minst 4,08, högst 4,18 T53 KG, vilket ger en inbördes precision på max 4,08/4,18=97,6%, eller grovt avrundat en felmarginal på max 3%: inte mera än max två decimaler.

— K-cellens effektmaximum har då på motsvarande tidrymd passerats med T(x)=4,52 T9 år;

— Vår tid, T+T(x), ligger alltså alldeles i början på effektgrafens nedförsbacke (ungefär vid pilen under illustrationen).

Med hänsyn till bakgrundsstrålningens observerade temperaturvärde (nu ca 2,7 °K för vår del) kan människor för sin specifika tid, i godtyckliga tidsavsnitt och så länge Jorden finns beboelig (Se Solens livslängd [idealt totalt 121 T9 år med fullständig väteförbränning — alltså 100 miljarder år kvar, samma konstanta effekt]) och tekniken finns, på samma sätt pricka in sin specifika position.

— K-cellens ålder NU ska alltså (med en marginal på max 10 miljoner år för Solsystemets ålder, se Härledningen till Solsystemets ålder) förstås som 20,82 T9 år — i princip tiden som solar, stjärnor och galaxer funnits från startpunkten: från tillfället för K-cellens detonation.

J-kropparnas värmefysik

UNIVERSUMS HISTORIA 2004X10 | ref c0.wps · TNED167A.BMP |

J-KROPPARNAS VÄRMEFYSIK

JORDVÄRMETS TERMISKA GRUNDER

J-kropparnas temperaturfysik

J-KROPPARNAS ALLMÄNNA VÄRMEBILDNING

Den upplagrade Coulombrepulsionen från kontraktionsfasen återlämnas till formbildningens fysiska rum: Energiräkningen tappar ingen punkt. Det sker i expansionsfasen i försorg av g-delenergin E genom kallplasmats bildning enligt E=b^1/T=pV=kt; E avtar — återförs eller frigörs — med växande T så att E^T=konstant=b.

Beteckningen T används normalt både för tid och temperatur. I samband där bägge förekommer, har här valts grekiskans lilla t — t — (tau) för temperaturen med bibehållet T och t för tiden.

Saken kan också formuleras på följande sätt.

RÖRELSEENERGIN MELLAN ATOMERNA i kallplasmat är i termisk mening noll. Den är också i princip noll under fusionsfasen (egentligen negativ eftersom fusionsnukliderna är attraherande) med referens till nuklidseparationen efter divergenständning k=1 för fusionsgränsmassan. I expansionsfasen skjuts atomerna ifrån varandra via Coulombrepulsionen, vilket genererar rörelseenergin (E_kin) som ger temperaturekvivalenten (t). Denna återfaller alltså ytterst på den i J-kroppen upplagrade g-energin (E) som under K-cellens kontraktion åstadkom kallplasmat. Då blir (idealt och utan förluster) tiden T g-energins (logaritmiska) multiplikator

E·E·E·…·E=E^T så att E^T=konstant=b. Dvs., E avtar (återförs eller frigörs) med växande T enligt

E=b^1/T=pV=kt. Funktionens optimala form tecknas då bestämt

(b=1/B=1/eⁿ) enligt t=AB^–1/T=Ae^–n/T med AB som konstanter.

A anger temperaturens gränsvärde och kopplar alltså till avståndet från J-centrum. n-koefficienten kopplar till tidsskalan.

t = Ae^–n/T .................................... temperaturens förlustfria grundform

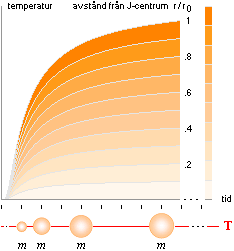
Allmänna gaslagens användning (se Allmänna Gaslagen). Så länge atomkärnor i kollektiv inte utvecklar kemiska bindningar uppför de sig som kolliderande kulor i en ask som utsätts för skakningar. För alla sådana situationer gäller allmänna gaslagen pV=kt med excellent noggrannhet i den praktiska fysiken, inte enbart för gaser utan även för ångor. Innan J-kroppens atomkollektiv kan bilda kemiska bindningar, måste J-kroppen först expandera. Därmed kan dess expansionsfas tillämpas på allmänna gaslagen — till större delen, men självklart med vissa reservationer. I vilket fall är syftet med denna framställning uteslutande enbart att försöka få fram en första grovt orienterande bild av hur detaljerna fungerar. Sambandsformerna som härleds ur de enkla elementära grundbegreppen, blir därför också preliminära vägvisare. Ingenting annat.

Den analytiska härledningen. J-kroppens termiska expansion med t som temperaturen, T tiden, n i sekunder och K i grader Kelvin (°K), svarar mot varianten

dt/dT=t/n med differentialekvationen

dT/n=t^–1dt som har lösningen (första integralen)

òdT/n=T/n, (andra integralen)

òt^–1dt=ln t/K enligt deriveringarna (förkortat Dn, se derivatan),

Dn (ln t/K) = d(ln t/K)/dt = (1/K)(°K)/(t/K)=°K/t. Termen K (°K) kan sättas på den fysiska enheten (J/°K)/J med koefficienterna k/a så att lösningen kan skrivas

T/n=ln kt/a, eller omvänt

n/T=ln aE^–1=–ln E/a=–ln kt/a från kopplingen till allmänna gaslagen enligt

E=pV=kt=ae^–n/T=b^1/T med t=(a/k)e^–n/T=Ae^–n/T och n=Tln A/t där E^T=b=konstant.

VARIATIONSMAXIMUM fås ur andraderivatan som 0=(Ae^–n/T)’’ enligt T=1/2. Som T är en allmän metodIdentifierare för variabeln (mIx_=T) i beroende av n, blir variationsmaximum totalt T=n/2.

Värmebildningen. När J-kroppen börjar expandera från sin maximala täthet efter fusionsfasen, introduceras en acceleration på dess atomer från Coulombrepulsionen. När accelerationen når sitt maximum har atomerna fått en bestämd rörelsemängd, en kinetisk energi (E_kin). Med inträdet i decelerationsfasen mot r_final, se J-kropparnas Expansion, börjar magnituderna från E_kin bidra till den allmänna temperaturstrålningen från J-kroppen. Någon egentlig temperaturstrålning förekommer alltså, idealt, inte i J-kropparna förrän huvuddelen av expansionen avverkats.

Expansionen sker kallt. Eftersom J-kroppen fortsätter att retardera i expansionen, fortlöpande mot sitt r_final, kommer det initiella E_kin-bidraget från accelerationsfasen idealt att fortsätta ge termiska bidrag så länge J-kroppen fortsätter att retardera, dock allt svagare med växande tid, i enlighet med den ovan härledda enkla termiska förlustfria temperaturfunktionen t=Ae^–n/T.

Den komplexa Coulombiska expansionen genererar alltså temperatur.

En primär dynamisk temperaturgivare har på detta sätt bildats ur den termo-gravitella expansionen. Den bygger alltså helt på en initiellt maximal täthet med tillhörande maximalt fysiskt tryck som bara successivt tillåts avta i kraft av den inåttryckande gravitationen:

Gravitationen blir en termisk »konservatris».

VÄRMETS DYNAMISKA ROT I JORDENS INRE ÄR ALLTSÅ INGET FYSIKALISKT PROBLEM (längre).

Frånsett förlusterna, visar t-funktionen Ae^–n/T att temperaturen växer stadigt men gradvis långsammare mot ett övre gränsvärde (A) medan bidraget från det initiella E_kin avtar.

Som i alla fysiska kroppar, läcker strålning ut också från J-kroppen, vilket tar bort delar ur den termiska Planckstrålningskurvan. Därmed bildas en effektförlust. Det betyder att den ideala temperaturstegringen kommer att tappa gradient. Om ingen separat värmegivande energikälla introduceras, kommer därför J-kroppen att börja svalna. Uppenbart, med en redan installerad primär värmegivare, skulle en separat sekundär värmegivare bara behöva bidra med ett minimum av energi, bara precis tillräckligt för att hålla J-kroppens temperatur på en jämn och stadig nivå, dessutom under extremt långa tider.

I Solens fall är den separata värmegivaren självskriven som den termonukleärt bildade energin från H-H-fusionerna. I Jordfallet finns ingenting annat att välja på än alla de bidrag som ges av instabila nuklider, både betaaktiva och de mera tungt radioaktiva, kärninstabila nukliderna, främst (i huvudsak) Uran (och Thorium, även sv. Torium).

UNIVERSUMS HISTORIA

Värmeförlustens bidrag kan skrivas på samma form som den primära värmegivaren med enda skillnaden att dess T-skala ges utdragen, samt att kvantiteten är negativ.

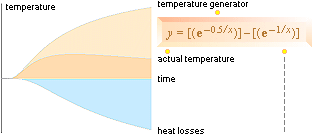
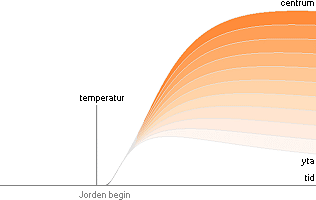
Nettot från dessa bägge med n_P som värmegivaren och n_N som avsvalaren blir då med ekvivalenta temperaturkoefficienter A (som betyder att t går mot noll med växande tid)

t=Ae^–nP^/T–Ae^–nN^/T

Illustrationen ovan visar principen. För bidraget från den separata eller sekundära värmebildaren gäller följande allmänna delar.

Den sekundära värmegivaren

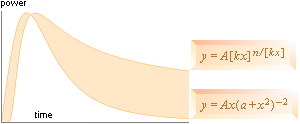
Livstiden för VARJE VÄRMEBILDARE följer typiskt endera av ovanstående två illustrerade kurvtyper. Vi studerar hur.

AKTIVERINGEN av det positiva bidraget från den sekundära värmegivaren börjar från noll, stiger till ett maximum, för att sedan avta antingen 1. direkt kontinuerligt mot noll i takt med värmegivarens kontinuerliga avklingande, eller 2. först mot ett nedre gränsvärde, en platå, som funktion av ackumulerande effekter i de radioaktiva sönderfallsserierna (i Solens fall som följd av att Solen förbrukar massa med exakt funktion av värmebildningen), och först därefter vidare mot noll. En funktion i fall 2 är (typiskt, fram till nedre gränsvärdet, övre slutkurvan) en potensfunktion av formen

t_g = AT^n/T °K/S

med A som nedre gränsvärdet. Högre n-värde förskjuter maximum längre ut från T-nollpunkten, A-värdet reglerar toppvärdet. I respekt till följande vägledande riktmärken extraherade från geologiska undersökningar, är också denna typfunktion det aktuella celesta fallet.

”Genom att mäta de nuvarande utåtriktade värmeströmmarna i jordskorpan har man kommit till den slutsatsen att temperaturen i jordens inre knappast kan ha fallit mer än några tiotal grader sedan den tidpunkt då jordskorpan bildades.”

FOCUS MATERIEN 1975 s439sp2ö

”Fossila fynd på jorden ger vi handen att solen har strålat ut energi i ungefär samma takt som nu i ca 4 × 10⁹ år.”

BONNIERS ASTRONOMI 1978 s50sp2ö

”Vi har som ovan nämnts säkra geologiska indicier för att den mängd solstrålning som jorden per tidsenhet tagit emot förändrats mycket litet på de 4,5 × 10⁹ år som jorden existerat.”

BONNIERS ASTRONOMI 1978 s55sp1ö

Citaten utpekar en utomordentlig temperaturstabilitet, de säger att inte mycket har hänt under de senaste 3-5 miljarderna åren i utvecklingen av de temperaturändringar från Solen och Jorden som uppmätts geologiskt. Bägge dessa kroppar uppvisar alltså en rent häpnadsväckande exceptionellt jämn temperaturhållning över en lika exceptionellt lång tidrymd.

I Solens fall arbetar värmebildarna från centrum genom termonukleära reaktioner (väte till helium), medan de i Jordfallet (initiellt, enligt Ø-kvadraten) ligger i manteln som radioaktiva nuklider. Man får alltså något olika kurvskaror för olika J-kroppar där de olika parametrarna ändras efter olika betingelser.

UNIVERSUMS HISTORIA

J-kroppens allmänna temperaturfunktion

I EN GROVT SAMMANFATTANDE ÖVERSIKT för samtliga J-kroppar (vilken bild naturligtvis är en praktisk omöjlighet) skulle man därmed kunna beskriva temperaturfördelningen i J-kroppen enligt funktionsformen med kurvskaran (B från 1 till 0)

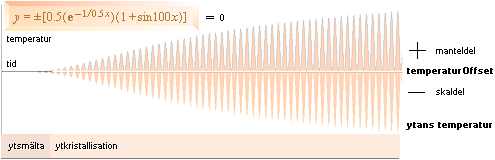
t = Ae^–nP^/T – Ae^–nN^/T + (BTⁿg^/T °K/S)

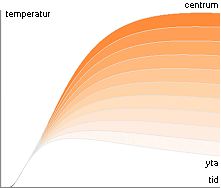GRAFISKA FUNKTIONEN (DELPHI4Test2002) [2(è'–0.5/x)]–[2(è'–1/x)]+{0-1}x'1/x unit200

limes t_T®¥ = B °K .................... gränsvärdet då T®¥

Termen BTⁿg^/T är densamma som i föregående illustration t_g=AT^n/T, här med separerade suffix mot de andra termerna.

Koefficienten A (gemensam för den primära värmegivaren och avsvalaren) får här innebörden av en temperaturgradient som kan tolkas olika för olika kroppar. Större A innebär en initiellt hetare kropp. Med A=B=1 ges toppvärdet för centrumdelen vid avrundat 1,6B °K enligt

t = e^–0,5/T – e^–1/T + T^1/T ................................. °K

Koefficienten n_P i den positiva värmegivaren ger ett allt lägre toppvärde med en allt mer utdragen formgraf med större n_P.

Koefficienten n_N i den negativa värmegivaren (avsvalaren) ökar toppvärdet med större n_N.

För att funktionen ska vara termiskt (kausalt) meningsfull måste avsvalaren (n_N) ligga förskjuten eller utdragen relativt n_P, vilket framtvingar villkoret att n_N>n_P.

Sambandet ovan ansluter till föregående grundsamband i värmeförlustens bidrag.

Exakt hur koefficienterna ska formuleras tillhör möjlighen en ytterst komplicerad — eller enkel — överläggning. Tills vidare används formen ovan som grundreferens.

Om den kurvformen också kan tolkas som representativ för Jordlokalen innebär det att centrumdelens initiella temperatur, från nuvarande ca B=6.500 °C=6.770 °K, blir 10.832 °K.

[I vilket fall ges typformen, även för centrumdelen, enligt den i Resultat nedan].

Det tillförda inre värmet från den sekundära värmegivaren innebär i princip, med ledning av resultaten från de geologiska värmestrålningsmätningarna för Jorden och Solen, att ytavsvalningen (under en period) avstannar innan den slutligen går mot noll. Ytans temperaturfunktion kommer då (typiskt) att följa värmebildarens potensfunktion enligt

t_Y = B(aT)ⁿg^/(aT) °K/S

med a typiskt som 2 och B=0,4 och n_g=2,4 som en rättvis matchning mot föregående kurvskaras nedre graf, den aktuella ytgrafen.

Yttemperaturen stiger från noll till ett maximum, därefter i långsamt avtagande mot ett undre gränsvärde (B), slutligen (exponentiellt) mot noll vilken del inte ingår i sambandet.

Toppvärdet ges vid aT=e enligt Be^n/e=B(e^1/e)ⁿ=B(1,444668)ⁿ.

Resultat

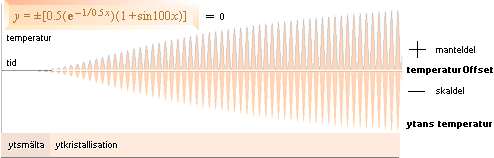
Ytgrafens temperaturfunktion — med den korta branta stigtiden i J-kroppens initiella expansionsfas och den efterföljande utplaningen mot gränsvärdet B — tecknar i slutänden följande odramatiska originella transientform:

Gränsvärdet för yttemperaturen motsvarar referensvärdet 0,4 med maxtemperaturen vid 0,967. Tidpunkten för temperaturtoppvärdet blir med referens till sambandet för expansionshastigheten (se från J-kropparnas Expansion) i stort sett och för samtliga fall ett dagvärde (inom 24 timmar). Det gör att hela funktionsformen, i princip, blir en enda rät linje med en initierande extremt kort transient i förhållande till den efterföljande historien typ

_|_______________ …

SOM VI SER återstår det ännu mycket innan vi kan få fram något samband som kan beskriva en rättvis ytformering av J-kroppen. Ytavsvalningen medför förr eller senare en begynnande ytkristallisation från den initierande smältan, vilket innebär en samling komplicerade periodiska funktioner överlagrade på t-funktionens enkla form. Frågan hur gränsvärdet B för den slutliga yttemperaturen ska definieras måste därför antingen bli en medelvärdesform inom ett visst skalskikt, eller en reguljär ytekvivalent som sammanhänger med balansen mellan den sammandragande gravitationen och det lokala elektriska (kemiska) gastrycket.

En kropp med hård yta och ett successivt mjukare inre tyder på en kropp som har utlämnats åt avsvalning under LÅNG tid.

En kropp med hård yta och en inre, underliggande smälta tyder på en het kropp som har avkylts snabbt.

Den nu kända sega Jordmanteln under det hårda skalet vittnar om att avsvalningen har skett under lång tid och med liten gradient.

UNIVERSUMS HISTORIA

Jordskorpans bildning

Jordskorpans bildning

Matematiken på den här nivån övergår (lätt) till ren (grafisk) formlära. Sambanden nedan i PREFIXxSIN.

SVÄNGNINGSFORMERNA sinnx återfinns inom och utgår elementärt från atomkärnornas ringstrukturer genom impulsmomentets bevarande enligt TNED J_0K+3J_1K=0.

Genom de kemiska bindningarna och temperaturens successiva avtagande generellt för J-kroppen bildas otvivelaktigt cykliska ekvivalenter som balanserar tryck och temperatur. Balansen kan återföras på nettosumman noll. Kemiska föreningar som bildar högre termisk isolation och därmed ytkristalliserar, åstadkommer ett motsvarande djuptryck med tillhörande relativ temperaturökning. I ytdelen bildas motsvarande temperatursänkning. På detta sätt kan man ur de givna svängningsformerna och en given temperaturoffset t_Y från grundformen

t_Y=B(aT)ⁿg^/(aT) °K/S härleda en överlagrad cyklisk eller periodisk funktion som indelar eller separerar ytoffseten i två motvända skikt, ett djupgående (manteldelen) som intränger i manteln och ett ytgående (ytdelen) som bildar det fasta skalet. Sambandets enklaste form ges av funktionen

t=±Ae^–b/T(1+sincT). Delen Ae^–b/T ger konturkurvan som avgränsar den periodiska sincT, gränsvärdet är 2A. +A ger övre manteldelen och –A ger undre skaldelen. Gränsen mellan dessa skikt blir alltså och av princip flytande, periodisk, med en stor intern flora av liknande och möjliga överlagrade cykliska ekvivalenter. Bergformationerna i ytdelen får i stort motsvarande omvända formationer i djupdelen så att nettovärdet i vilket fall blir noll.

Temperaturfunktionen i stort och grovt för en J-kropp som bildar fast yta kan därmed återföras på typformen enligt illustrationen nedan.

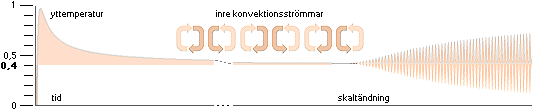
Funktionen för ytans temperaturutveckling — enbart –A-delen tillsammans med t_Y — kan då skrivas totalt i PREFIXxSIN

t = t_Ybas – t_skal = B(aT)ⁿg^/(aT)(°K/S) – Ae^–b/T(1+sincT)

med typformen

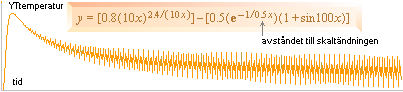
b-värdet (b=2) i grafillustrationen har satts lågt för att förtydliga principen.

Avståndet till skaltändningen (där A-delen, analogt ytkristall[is]eringen visar sig) regleras av b-faktorn (inverterad i illustrationen).

Högre värde förlägger skaltändningen längre bort från yttemperaturens toppvärde.

De överlagrade kurvmönstren i kurvformen är resonanseffekter från den begränsade pixelupplösningen och ingår explicit inte i sambandet. Men de illustrerar på ett utomordentligt sätt hur ytterligare sammansättningar kan bildas.

UTANFÖRNUKLIDPRINCIPEN

UTANFÖRNUKLIDPRINCIPEN

Vad händer OM K1+K2=K (se exotermiska fusionslagen) väl har ett motsvarande atomnummer för resultanten K, men inget matchande masstal I TABELLREFERENSEN?

Betrakta exemplet

₁₀Ne²⁰_16,343 +₂₀Ca⁴⁰_17,35 =₃₀Zn⁶⁰ FINNS INTE (i HOP-tabellen)

Använd nuklidkartan (nedan, se även utförligt från NUKLIDKARTAN AZ) för orientering. I detta fall är K (30Zn60) en Jumboproton (b+). Den är alltså alldeles för lätt för sitt atomnummer och måste därför släppa av e-massa för att avancera uppåt (mot noll) för att få lägre atomnummer med bibehållet masstal. Närmaste tabellmatchningen (HOP) är ₂₉Cu⁶⁰. Den positron som måste avdelas från ₃₀Zn⁶⁰FINNS INTE för att komma till ₂₉Cu⁶⁰ får inte associeras med massdefekten i fusionsfasen. Det betyder att vi måste utgå ifrån ett något lägre massdefektsvärde än det som normalt gäller för K. Slå alltså ut överskottspositronen på hela masstalet 60 (som ger en subtrahend på e/60) och dra bort detta ifrån massdefekten för ₂₉Cu⁶⁰_17,546. Sätt sedan in komponenterna i exotermiska fusionslagen. Uppfylls villkoret är fusionen exotermiskt OK, annars inte.

Är däremot K-FINNS INTE en Jumboneutron kan den avyttra en elektron till höljet som därmed ökar kärnladdningen med 1 enhet och därmed puttar ner nukliden längre ner i kartan. Även denna elektronmassa måste exkluderas från kärnkomponenterna och slås ut på masstalet, samt subtraheras från massdefekten i befintlig K.

Exempel

Vi studerar några exempel med en allmän sammanfattning av nuklidkartan.

Nuklidkartan — Allmän orientering i grundämneskartan

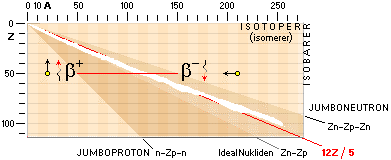
Det är enkelt att orientera sig i nuklidkartan ENLIGT TNED.

Kärnstrukturen ENLIGT TNED utpekar bestämda gränslägen för sammansättningen n-p (neutron-proton) i bevarandet av kärnans allmänna positiva laddningsdeplacement — som f.ö. galant förklarar varför det ENLIGT ENERGILAGEN inte kan finnas någon stationär antimateria i universum.

Nuklidstatiska medelvärdeslinjen A=12Z/5 (medelvärdet av idealnuklidens gränslinje Z=A/2 och Jumboneutronens Z=A/3) utpekar den enkla linjära men inte helt exakt teoretiska baslinje efter vilken man finner grundämnesnukliderna. Fältet i vitt anger de verkliga nuklidernas förekomst enligt gängse tabelldata. Termen JUMBOPROTON (b+) betyder att nukliden är för lätt för sitt atomnummer, den sönderfaller mjukt (utan kärnklyvning) uppåt (lägre Z) till lämplig stabil nuklid. Termen JUMBONEUTRON (b–) betyder att nukliden är för tung för sitt Z, den sönderfaller mjukt neråt till högre Z. Bägge dessa s.k. betainstabila nuklidtyper har i allmänhet längre sönderfallstider om jumbonukliden ligger nära sin grupps stabila nuklid (approximativt utmed 12Z/5-linjen).

Jumboprotonens sönderfall sker antingen genom att kärnan avyttrar en positron — som därmed ”omedelbart” annihileras tillsammans med en yttre elektron — eller med samma resultat netto att kärnan plockar upp en yttre elektron (eng. electron capture). Jumboneutronens sönderfall innebär att kärnan avyttrar en elektronmassa till höljet. I bägge fallen avges alltid en viss mängd arbetsenergi (neutrinostrålning) som åtgår för ombyggnaden (m®g).

Ovanstående exempel fullständigt, med några ytterligare:

12Mg23 kan t.ex. bildas ur 2He4+2He3+2He4=6C11 tillsammans med 6C12 från 3(2He4). Alla kan återföras på neutronkvoten noll.

Exempel med K som Jumboneutron:

Den/de avgivna elektronen ingår inte i den avgivna fusionsenergin utan tillhör hela atomens fasta massystem. Annihileras emellertid ett par ±e utanför kärnan ges naturligtvis ett separat exotermiskt bidrag. Observera att resultaten förutsätter noll tillförda moment i fusionslokalen, enligt kärnreaktionslagens exakta form, vilket utesluter både partikelacceleratorer och strålkällor som experimentbas.

Reservation

I många men inte alla fall visar tabelldata en tendens att Jumbonukliderna har allt kortare sönderfallstider ju mer deras masstal skiljer sig från den stabila gruppens nuklider.

Man skulle därmed kunna förmoda att utanförnukliden i ovanstående exempel snabbt växlar in på den närmaste i tabellverket.

Det finns emellertid (här) inget direkt samband att stödja sig på och antagandet av Jumbonuklider som ligger utanför tabelldata kan därför innebära en viss äventyrlighet.

Att tabellerna inte tar upp en sådan nuklid behöver inte innebära att den inte finns, och vi bör därför iaktta en viss reservation i antagandet av de ovan exemplifierande och andra liknande beräkningar. Vi kan räkna med dem, men inte bevisa att de är praktiskt genomförbara på annat sätt än att kärnreaktionslagen accepterar dem.

En ledtråd beträffande elektron och positronavyttring från atomkärnan i allmänhet är ENLIGT TNED att avyttring (och infångning) av e-massa är en successionsprocess. Det innebär att e-massan avges litet i taget, snabbare eller långsammare beroende på hur atomen beräknar sin balans via impuls och kraftekvationerna. Fusioner som är helt fria från separata e-avyttringar bör därför (tvunget) bli de allra snabbaste.

Jordens ålder

innehåll: SÖK äMNESORD på denna sida Ctrl+F ·

Jordens ålder

ämnesrubriker

innehåll

JORDENS ÅLDER

Betingelserna för det organiska livets uppkomst enligt TNED

JORDYTANS MÖJLIGA ÄMNESSAMMANSÄTTNING

Den unika nuklidagenten 6C16

Ström-, Kraft- och Kemiekvationen i TNED

Syreförekomsten

Kväveförekomsten

Väteförekomsten

Vattenförekomsten

Den uråldriga Jorden

Jordens ålder

ILLUSTRERAD ÖVERSIKT MED JORDSKALETS BILDNING FRÅN INITIELL SMÄLTA ENLIGT TNED

Månens recession

Månrecessionen i cM/år

Basdata Månen

Månrecessionens matematik på webben

Planetbanorna

Bergartscykeln

Vattenbanken

ALLMÄNT OM JORDENS VATTENBANK

Förtydligande av Universums ålder

J-kropparnas värmefysik

JORDVÄRMETS TERMISKA GRUNDER

Allmänna gaslagens användning

Värmebildningen

Värmeförlustens bidrag

Sekundära värmegivaren

J-kroppens allmänna temperaturfunktion

Jordskorpans bildning

Utanförnukliderna

Exempel

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

[BA]. BONNIERS ASTRONOMI 1978, Det internationella standardverket om universum sammanställt vid universitetet i Cambridge

[EST]. Encyclopedia of Science & Technology · McGraw-Hill 1992

[FM]. FOCUS MATERIEN 1975

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

et al, allmän förkorting (i engelskan) som används för att ange typ X et al, X med medarbetare, eller X med kolleger

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

Senast uppdaterade version: 2017-09-19

*END.

Stavningskontrollerat 2009-04-26

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

PNG-justerad 2011-10-10

åter till portalsidan · portalsidan är www.UniversumsHistoria.se