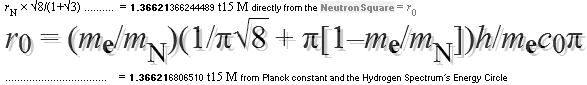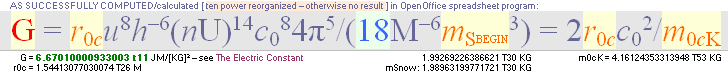THE ATOMIC NUCLEUS II 2023IX10 | a production · | Senast uppdaterade version: 2023-12-21 · Universums Historia ♦ HumanRight is a knowledge domain

content — innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i indexREGISTER · förteckning över allUHwebbsites

PO4 ¦ ATOMIC MASS EQUATION — mATOM = Uu ¦ ATOMIC WEIGHT — U [ »relative atomic mass» ] ¦ ATOMIC MASS UNIT — u [ Dalton] = m[ 6C12 ]/12 ¦ ATOMIC MASS defect EQUATION ¦ ComparingNUCLEAR ¦NScredit

Atomic masses — AtomicNucleus — INTRODUCTION, nuclear radii, basic nuclides, comparing early Weizsäcker solutions ¦ STANDARD UNIVERSAL — divergence c0 = 2.99792458 T8 M/S is preserved independent of gravitation.

TheAtomicNucleus I Jun2023 — DeducingTHErZ ¦ TAN II Sep2023 — comparing nuclear physics ¦ TAN III Nov2023 — relating Earth crust isotopic compositions ¦ TAN IV Dec2023 — FusionLimitMass FULIMA

EXPERIMENTALconfirmations: Atomic masses

The Atomic Nucleus

mDweiz ¦ NSsolutions ¦ CONOR ¦ NSUunit ¦ PO4

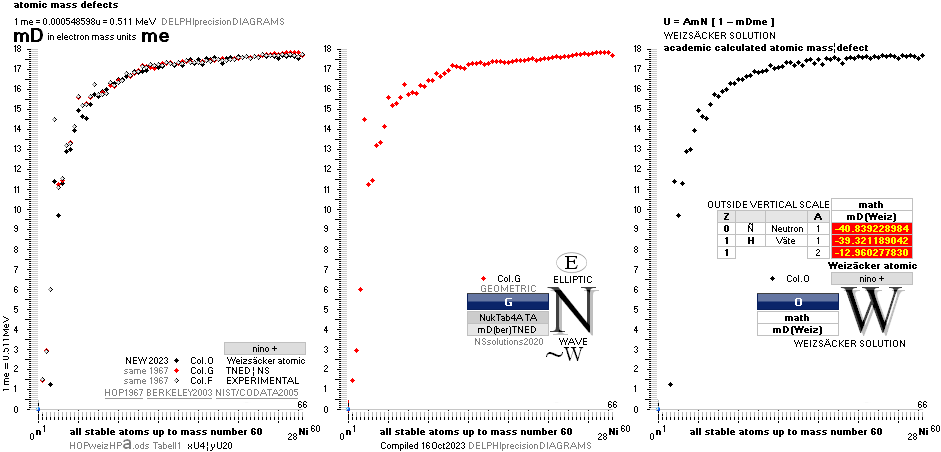
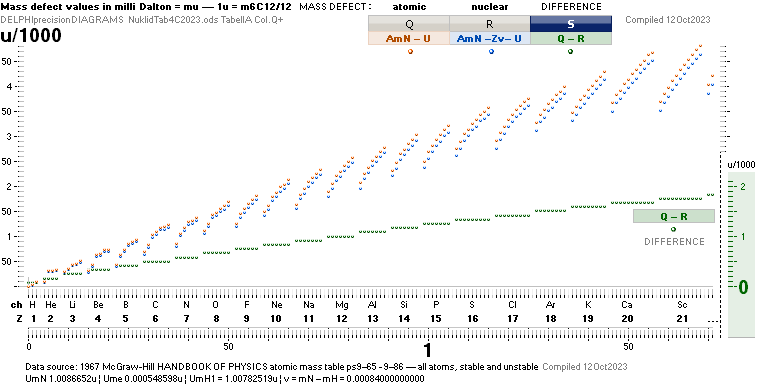
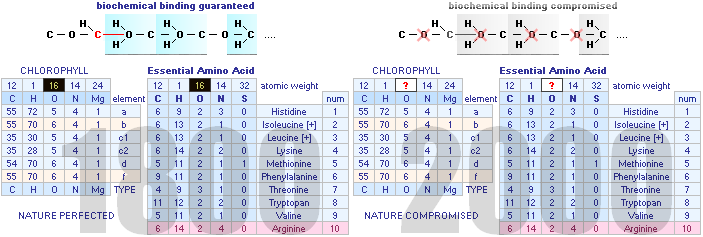
ATOMIC MASS, ATOMIC WEIGHT, ATOMIC MASS DEFECT, NUCLEAR MASS DEFECT, NUCLEAR BINDING ENERGY, AND THE ATOMIC MASS UNIT

——————————————————————————————————————————————————————————————————————

comparing fundamental atomic-nuclear physics: related-established

See Different Ways in comparing data between theory and experimentally measured

Differences in atomic mass defect electron masses — per mass number

MODERN ACADEMY IS OUTCLASSED BY TNED — related physics and mathematics

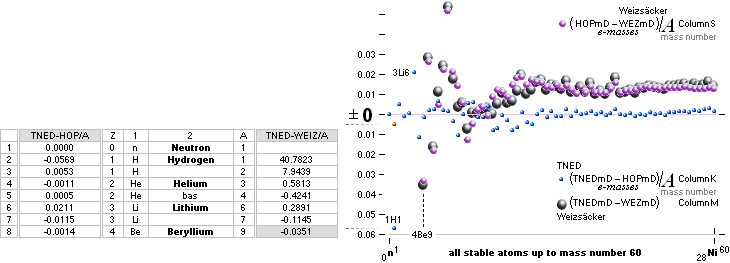
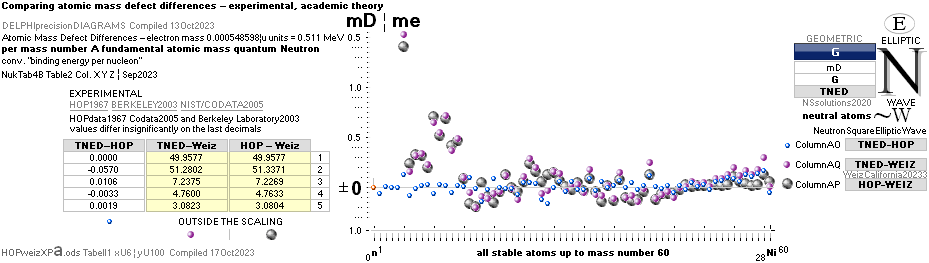
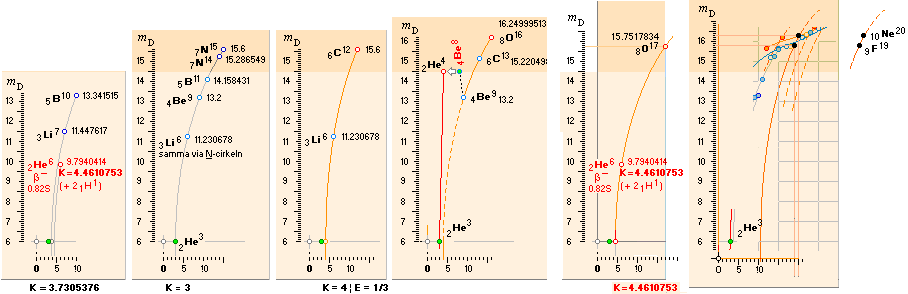
NuklidTab4A2023.ods Table4 — Columns KMS

Left table: The 7 left out Weizsäcker solution posts are far outside the vertical scale. While the NS-solution have a more tight experimental connection.

The diagram above is of the same kind as the Comparing diagram. Only difference: diagram above is Comp/A ( yielding .. »per A-square» .. more tight Show).

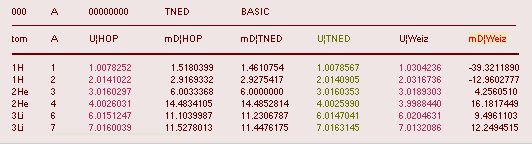
HOP¦WEZ mD = ( 1 — [HOP¦WEZ U]/AmN)/me ¦ me = 0.000548598¦u, mN = 1.0086652¦u, HOP¦WEIZSÄCKER U = element’s atomic mass in Dalton units u = 1.66033 t27 KG, A = mass number

HOPweizXP.ods Table1 ¦ NuklidTab4A2023.ods Table4 — HOPtable1967, Weizsäcker values¦ WEIZSÄCKER EQUATION DETAILS ¦ ComparingTable ¦ WeizsäckerCALC

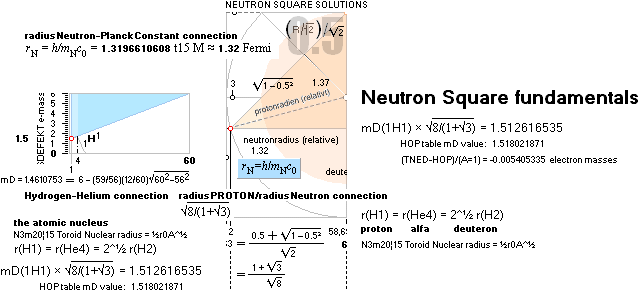
1H1-details: IN GENERAL: THE NEUTRON SQUARE SOLUTIONS OFFERER SEVERAL 3 WAYS TO CALCULATE ATOMIC MASSES THROUGH ATOMIC MASS DEFECTS mD. This is an example:

mD ¦ NeutronSquare = 6 — (59/56)(1/5)√ 60² — 56² = 1.461075377, HOPmD = 1.518021871, (TNED–HOP)/(A=1) = -0.056946494 basic

mD ¦ NeutronSquare = mD × (ProtonRadius/NeutronRadius = [√8]/[1+√3]) = 1.512616535, (TNED–HOP)/(A=1) = -0.005405335 precision

NOTE THAT EXPERIMENTAL VALUES USE SPECTROSCOPIC IONIZATION TECHNIQUES, [WHERE THE ATOMS ARE ACCELERATED] AND HENCE reflect SLIGHT DIFFERENT MASSES.

No explicit specific data on these spectroscopic ionization [»mass affection»] data differences are known here.

The large 7 first Weizsäcker differences. The Element isotopes from 1H1 to 3Li7 are left out in the diagram above as the Weizsäcker values anyway lie far beyond the vertical scale. TNED says — very close to experimentally measured values — the reason is because the idea behind the Weizsäcker solutions — charged liquid drop mathematics — have no corresponding atomic nuclear connection. Only when the atom grows larger and heavier, that difference decreases. See further definite proofs [Jun2023] in THE ATOMIC NUCLEUS.

EXCON: ExpCon

EXPERIMENTAL CONFIRMATIONS

So much credit in present scientific literature is given to Albert Einstein (1905) on the formula E = mc² — when in fact it is just a ride on (Max Planck 1900) the Planck constant h=mcr: E = hf = mcr/t = mc². But the form also shows a (differentials ¦ x = yz : x/∞ = x/∞ⁿ = dx = dy · dz) more simple deducible nature (not mentioned: divergence energy):

dE = dF·dd = dma·dd = dm(c/t)dd = (m/∞)(c/t)(d/∞) = (m/∞)(c·d/t)(1/∞) = m(c²)(1/∞²) = m(c²)(1/∞) = dmc²: E = mc².

dE = d(Fd) = d(mad) = d[m(c/t)d] = d[m(c·d/t)] = d(mc²); E = mc². Or just: E=Fd=mad=m(c/t)d=mc². No big deal.

• light does not connect kinetics Solar eclipse expeditions 1919+ — experimental confirmations:

c and v are not additive in physics — the vic-error — Michelson and Morley experiments 1881+

• Curved light paths does not develop centrifugal — kinetics — properties:

• light is massless — light is not gravitation — gravitation is not light — gravitation is NOT a particle:

• Max Planck was right, Albert Einstein was wrong:

The photoelectric effect reflects properties of the atoms (THE PERIODIC SYSTEM — resonance matrices) — not properties of light. Light propagates massless through electromagnetic Planck E=hf quanta named photons — also (inductively COEI conservation of energy by induction) interacting (Compton effect) with (±e nuclear structured) matter (atomic particles) where the Planck energy E=hf=mc² always is conserved (ENERGY LAW ¦ POM):

EnergyLaw: energy cannot be created, nor destroyed, only converted. (±e nuclear structured) mass can be destroyed (COEI) because it cannot be created: light is massless. Particle proof that energy cannot create mass.

While the scientific community has the idea in particle physics, that energy and mass are substantial equivalents, related physics (Planck equivalents) explains mass-energy exchange properties: the Planck energy E=hf=mc² is always conserved, under all circumstances. The scientific community introduced the idea of a spin property on the Einstein’s proposed massive photon — ”to make the chart complete”. In related physics, no such invention exist: the sum of all spins and moments in the atom is zero. When (Star physics) mass is destroyed E = (m→γ)c², COEI certifies that the Planck energy E=hf=mc² always is conserved.

The difference is excited (±e nuclear structured) gravitational mass, while modern corridors claim real steel gravitational mass creation — although also these aces know that mass cannot be created out of no mass.

The atomic nucleus compresses all these aspects in also verifying that all collected (Angeli2004) world data merges with the TNED deduced atomic and nuclear properties [The (rZ)²/r complex] — as verified from the coherent RevisitedHofstadter1956 electron scattering experiments: it all exposes the general charge-density distribution characteristics of the atomic nuclei — as so TNED confirmed.

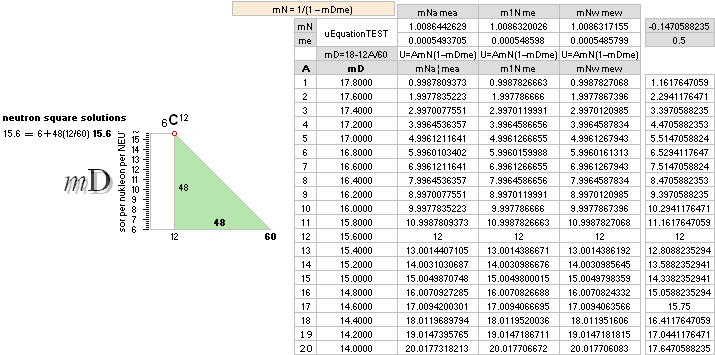
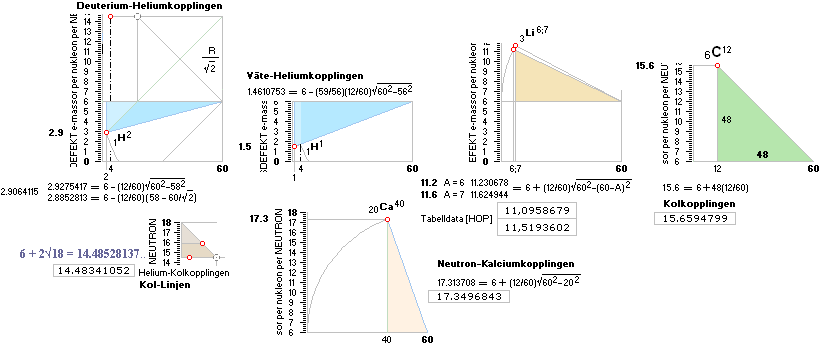
— And so we can return to The Neutron Square — its Planck constant accounted confirmed deduced nuclear size properties — and their following connection to atomic mass properties for comparison on experimentally measured.

— Shorter: »we are just warming up».

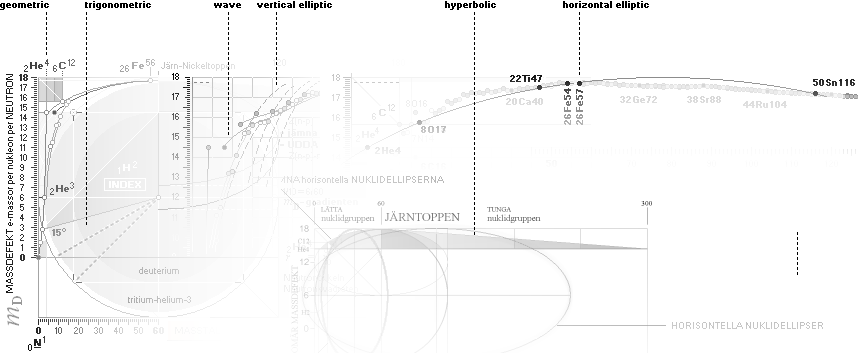
NeutronSquareFundamentals: THE NEUTRAL ATOM — PROVISIONS

EXPERIMENTALconfirmations

CosmicMATHrevelation ¦ Geometric

NeutronSquareSOLUTIONS ¦ VerticalELLIPTIC

For ToroRADIUS, see the Deduction. Basics from ProtonRADIUS.

Neutron Square atomic nuclear solutions has no physical or experimental foundational reference at all, not a single point in space —

except beginning from the Planck constant h = mcr: The Planck Ring: the fundamental atom: the Neutron

(0°K, c=c₀=2.99792458 T8 M/S: c0 is preserved as a natural constant independent of gravitation’s influence DGD on local divergence = local light propagation).

All mD(atomic mass defect)-values emanate out of the Neutron Square and its deduced, related and fully explained elliptic-trigonometric (wave)-hyperbolic (CompCALu2023) mathematics equations — with so basic geometric solutions to the first basic light atomic masses on their atomic mass defects, mD. See FIBAPO Comparing Table.

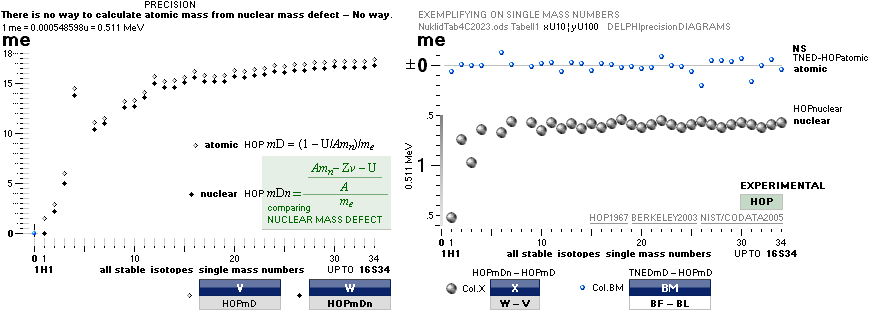
NOTE: (ErrorTransferElectronMass) The 1967 HOP-table uncertainty value for 1H1 in mD electron masses is specified as 0.02277 me (0.08 µu NuklidTab4B2023.ods TableA 4G) — see graph and diagram in ExperimentalErrors. The Neutron square 1H1 mD value difference on 0.0054 to the HOP-table’s is more than four times less (and the HOP error and NS-difference cannot readily be compared). If appropriate, that is an unprecedented precision in pinpointing an experimental result.

charge does not connect mass — Never18 ¦ NSsolutions

THE PIN POINTING QUESTION — no yet found academic answer:

— In what way is the Measured Object’s Electric Charge involved in the object’s Measured mass?

Because the Neutron Square Solution has

♦ no explicit nuclear charge (Z) connectivity to atomic mass:

mD = (1 — U/AmN)/me — no Z.

THE ATOMIC NUCLEUS ¦ CompareQm ¦ Discovery

♦ nuclear charge does not connect atomic mass, nor nuclear size (rZ)²/r. No way.

ALTHOUGH HOWEVER THESE [±e nuclear structure] ARE INTEGRATED IN THE ATOM

♦ charge DIVERGENCE — electric field — does not connect mass CONVERGENCE Physics756

EXPERIMENTAL nuclear-atomic PHYSICS [±e nuclear structure] CANNOT SEPARATE THESE: BOTH NEEDED.

Modern academy educated freely available papers seem not to get to the chase on relating the quest .. recycling .. NS .. in the beginning ..

TNED — concentric atomic production

Related physics and mathematics:

———————————————

NUCLEAR FRAGMENTATION — How The K-cell Dmax is regained ¦ Exothermal nuclear reaction law ¦ NUCLEAR REACTION LAW ¦ GeneralCosmicStateLaw ¦ FusionRINGS

Odd and Even Nuclide Groups — why the core fusion body ends on IRON ¦ CWON from CAP ¦ The IRON CORE ¦ MilkyWay SolarSystems

REGAINING — from the deduction of the exothermal nuclear reaction/fusion law

————————————————————————————————————

According to K1+K2–(m→γ)=K the Nuclear Reaction Law — related physics deduction — each composed atom and its nucleus from the point (light propagation c in space; see Comparing mathematics between related physics, Schwarzchild, and Einstein) and moment where the enveloping dominant gravitation has reduced divergence to c=0, a reversed situation is born. K+(m→γ₌₀)=K1+K2. If the atom and its nucleus finds exactly the g-mass corresponding to the energy emission (atomic mass defect) when that atom was formed, K apparently decays back to K1+K2. Further increasing gravitation pulls the net resulting fundamentally rebuilt Neutron (Planck constant h=mcr) masses into a state of Dmax until (COLLECTIVE bounce recoil when contacting on a max gravitation) a following Detonation occurs (The Incompressibility of the atomic nucleus). So it is all governed by gravitation. See further details from CosmoBasics (gravitational redshift, K-cell mathematics) unless already familiar (details in how the expansion and contraction works by related mathematics and physics — modern academic confusion »dark energy» on motion and general cosmological gravitational redshift, no motion: no »dark energy»).

EXPERIMENTALconfirmations

ComAtNu: Comparing Atomic and Nuclear mass defect concepts and values — clarifying the terminology

Comparing Atomic and Nuclear

CLARIFYING THE TERMINOLOGY — by experimentally measured examples

Explaining ¦ EXAMPLIFYING

THE DIFFERENCE BETWEEN ATOMIC AND NUCLEAR MASS DEFECT

ATOMIC AmN – U

the work mass-energy WASTE needed to build the atom [Sw., arbetets massa-till- energi bortfall: gravitell svinn-massa; g-mass-svinn].

NUCLEAR AmN – U – Zv ¦ v = mN – m1H1 = 0.00084u ¦ U = mATOM/u ¦ u = m(6C12)/12 = 1 Dalton

mN = neutron mass 1.0086652u, A = mass number = number of FAMQ fundamental atomic mass Quanta mN

that built the atom ¦ u = 1.66033 t27 KG ¦ Z = atomic number = the atom’s nuclear electric +charge, same as

the atom’s electron mass electric -charge.

the work mass-energy WASTE needed to build the atom — minus the Zv mass energy work waste:

v is the NEUTRONIC n nuclear structural mass energy WASTE equivalent 0.00084u in

becoming [electric displacement rearranging work] the PROTONIC p nuclear structural property

integrating the fundamental PROTONIC p nuclear structure with the fundamental NEUTRONIC n nuclear structure into the fundamental atomic NUCLEAR — in related physics NOT the academic nucleonic — structure.

While the academic idea is that of »separately inside the nucleus spinning neutrons and protons», related physics is dealing with a fundamental nuclear electric displacement ±e structure (Planck fractal structural ring constant): no inside spinning particles — as verified in the (rZ)²/r complex (The Atomic Nucleus).

EXCONdetails:

Weizsäcker nuclear binding energy form: (AmN – U – Zv)

nuclear mass defect.

Weizsäcker atomic binding energy form: (AmN – U)

atomic mass defect; Weiz + Zv.

WeizCalifornia

Related physics — particle and unity

AS IT IS WITH MERGING WATERS

———————————————

CREATION OR DIVISION — nuclear fragments¦ SPIN SYNCHRONIZATION ¦ The 3Li8 Nuclide ¦ The Water Surface Spinning GIF water drop ¦ UNIT WITHOUT PARTS — nature illustrates the principles

EXCON details: While the scientific community (1905+) has adopted the idea in particle physics, that energy and mass are substantial equivalents — real physical substantial gravitational particle mass creation — related physics (Planck equivalents) explains the Planck constant h=mcr energy-mass equivalence E=hf=mcr/t=mc² on a principle of exchange properties: the Planck energy E=hf=mc² is always conserved, under all circumstances. Meaning: When (±e nuclear structured) matter (atomic particles) merge from lighter to heavier atoms/elements — where the Planck energy E=hf=mc² always is conserved — the general RULE in mathematical physics becomes that the reverse also holds — however with a resulting excited fission product (atomic and nuclear mass defect concepts). In modern quarters, this energy split product is — with no exception — always implied as a fully substantial gravitational spouse. In related physics that is a grave delusion, and a most honest deep and real steel fundamental physical impossibility;

ENERGY LAW ¦ POM ¦ EnergyLaw: energy cannot be created, nor destroyed, only converted. (±e nuclear structured) mass can be destroyed (inductively COEI conservation of energy by induction) because it (substantial gravitational ±e nuclear structured) cannot be created: light is massless — Particle proof that energy cannot create mass. When (Star physics) mass is destroyed E = (m→γ)c², COEI certifies that the Planck energy E=hf=mc² always is conserved: light and heat.

Max Planck was right. Albert Einstein was wrong. No doubt (EXCON): light is massless. No gravitation. No developed centrifugal property in curved light paths. No way.

— See more comparing academic related details in EXPERIMENTAL CONFIRMATIONS, unless already familiar.

The most interesting aspect (not explained):

— The experimental measure of the neutron mass:

— Its precision.

It cannot be directly measured (yet).

ComAtNu

NeutralToExperimental:

NS fundamentals

We should not be overly enthusiastic on raising the experimentally measured atomic masses values to the heavens, without certifying that the influence of the experimental ”mass-to charge” complex not significantly affects the actual neutral atomic mass. How do we know?

neutral to experimental

We can put it this way — testing how the NS solutions conform on the true physical ones:

— HOW DO WE GET RID OF THE EXPERIMENTAL CHARGE electric magnetic FROM THE EXPERIMENTAL RESULTS — in REFINING THE WHOLE PICTURE TO INCLUDE ONLY THE NET mass VALUES?

The neutral atom. The NS — for comparing purposes.

— We can’t (says the present scientific PhD community as one man, do correct) — unless we have a Gauge — a preference Index — by which to perform explicit advanced experimental tests:

— Telling us what to look for. At present, no other is known here than The NS solutions.

HowardUniversity:

” Because atoms are much to small to measure individually and do not have a charge, there is no convenient way to accurately measure absolute atomic masses.”,

” Scientists can measure relative atomic masses very accurately, however, using an instrument called a mass spectrometer.”,

” The technique is conceptually similar to the one Thomson used to determine the mass-to-charge ratio of the electron.”,

” First, electrons are removed from or added to atoms or molecules, thus producing charged particles called ions. When an electric field is applied, the ions are accelerated into a separate chamber where they are deflected from their initial trajectory by a magnetic field, like the electrons in Thomson’s experiment.”,

” The extent of the deflection depends on the mass-to-charge ratio of the ion.”,

CHAPTER 1.6: ISOTOPES AND ATOMIC MASSES, Howard University

Libre texts — Chemistry — No date reference ( .. perhaps 1634 .. they were psychic .. ),

sampled @Internet 7Sep2023

THE INTRODUCED ELECTRIC CHARGE ADDS EXTRA MASS SPECTROSCOPIC DEFLECTING POWER

related physics: mass and charge — massless electric field: light c property — does not connect

What we know: the experimental charge dependency cannot be separated from the actual mass spectroscopic experiment — by no other means than through a (thorough) theoretical insight: some real steel knowledge of the actual mechanism. To trap it, also experimentally, a first encouraging insight must exist that IT is missing.

What we do know is that nuclear charge (Z) and nuclear mass (m) frequently is used in established works on nuclear (rms) charge radii determinations: nuclear mass and nuclear charge are implied physical cooperators — while (rZ)²/r related physics (Angeli2004data) proves that the charge dependent idea as such to be more of an experimental necessity than a true real physical property: nuclear charge has no volumetric physical reality: Z is a nuclear surface structure extension (NuclearStructure), and has no connectivity to nuclear size — other than the fact that electric charge cannot be removed from atomic/nuclear experimental investigation.

—»It is included in the general computer modeling mathematics».

— It is taken for granted — but has no physical correspondence — related physics TNED NeutronSquare solutions says.

So: how is it?

The tight Neutron Square solutions NSdeDIA1 compared to the experimental values strongly suggests — still here with no other proofs — that there really is »an experimental charge issue» in the complex of experimentally measuring atomic masses. Namely also so: Outside the NS solutions (unknown in modern corridors) nothing reflects even such a possibility: it lies hidden, dormant. The experimental charge »issue» becomes apparent first when the NS complex becomes uncovered: mass and charge does not interact, although intrinsically integrated: the atom, the fundamental form of gravitation.

Continue on

THE UNIVERSAL NATURE OF THE NEUTRON SQUARE — how reliable is it?

and

CosmicMATHrevelation — proving the real steel essence of nature ..

EXPERIMENTALconfirmations

NS8Oct2023: NSUunit: Provisions¦ NScredit ¦ CAUSE ¦ Normalization

TheQuest of

THE ATOMIC MASS UNIT u=m(6C12)/12 PREFERENCE

— IN THE NEUTRON SQUARE mD Exacting The A=12

IS THE NEUTRON SQUARE SOLUTIONS COMPLEX VALID EVERYWHERE, UNDER ALL POSSIBLE CONDITIONS, NO EXCEPTIONS?

QUESTIONING A UNIVERSAL NATURE of THE NS

Neutron Square Solutions

NEUTRON SQUARE SOLUTIONS

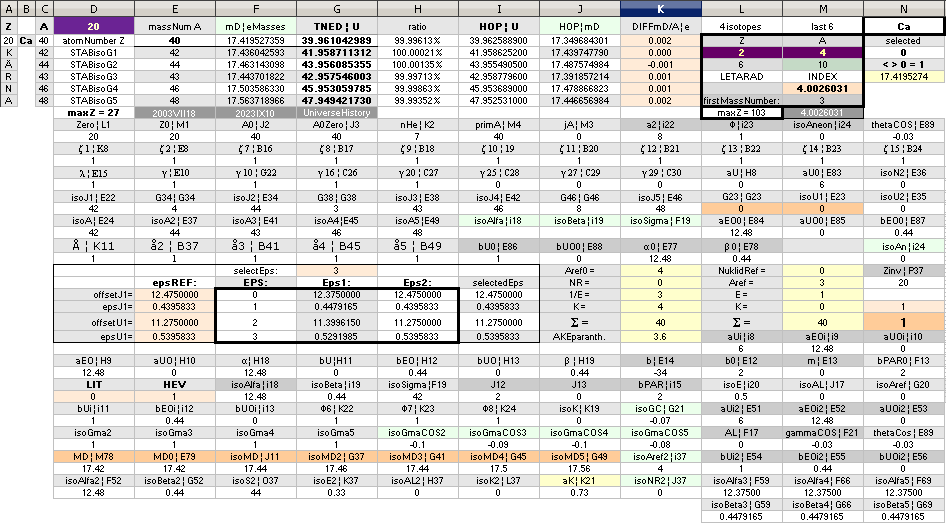
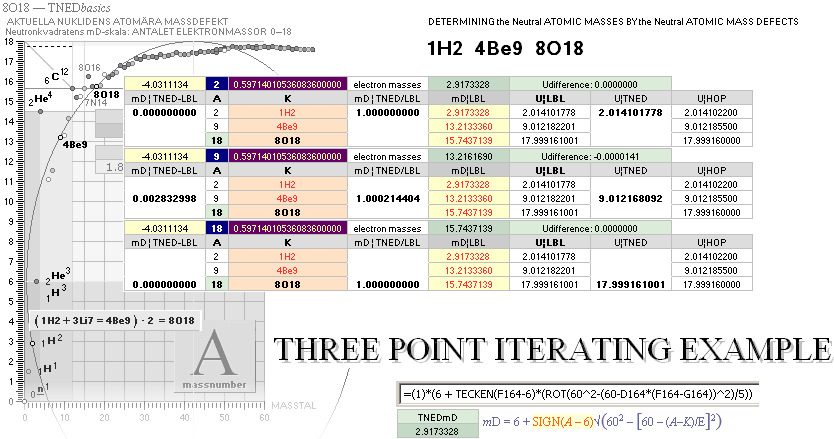
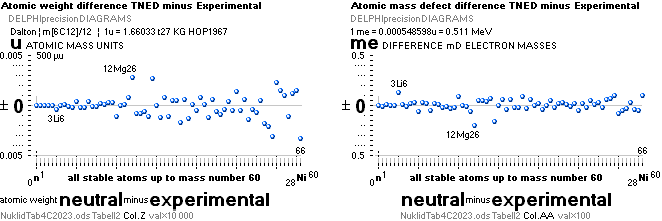
NuklidTab4C2023.ods Tabell 2A Col.M ¦ TheActualDifferences

CAUSE:

The basic apparently highly experimentally matching NEUTRAL ATOMIC NEUTRON SQUARE SOLUTIONS NS solutions ¦ TheActualDifferences has introduced a QUESTIONING central atomic mass defect equation

mD = (1 – U/AmN)/me. THROUGH ITS U FORM U = m/u ¦ m = Uu

U = AmN(1 – mDme) ¦ THE neutral atom’s atomic weight U = m/u CAN BE SPECIFIED FROM A UNIVERSAL

u = m(6C12)/12 = 1 Dalton = 1 cosmological atomic mass unit. The proof below. Original Swedish deduction 2008.

Universal atomic mass unit

Giving any a universal credit to such a suggested atomic cosmologically valid m(6C12)/12 mass unit u, its NS suggested atomic mass defect (total atomic binding energy) mD value is exactly 15.6 electron masses. NS solutions Proof (NScredit ¦ Discovery) :

Only WHERE — and IF — a single unique m/u = U = A exists will define a corresponding 1 = mN(1—mDme), mN = 1/(1—mDme); mN/me = 1/(me — mDme²). Only one, otherwise no solid preference. mD = (1 — 1/mN)/me = Neutron Square order geometrical mathematics = 6 + (60—A)(12/60) = 6 + 12 — 12A/60 = 18 — A/5 = 6 + 12(1 — A/60) — 12/60 = 1/5 is a scale transfer

NuklidTab4C2023.ods Tabell1 A260+ — exemplifying different me and mN (Wikipedia mNw mew), clarifying the above validity test for a single U=A.

In modern quarters, no such explicit occurrence is known (CU). And the academic choice of m6C12/12 (1961 ¦ 1993 coined: one Dalton ¦ 2005 IUPAP) therefore appears arbitrary on »a best fit» (preferred in chemistry) basis (earlier 8O16, first 1H1).

Normalization:

NS8Oct2023

Normalization — see end comparing results in CONOR

The u-condition — U = A only one — not several, under no conditions ever — single unique occasion: it defines the proof:

mN = 1/(1 – mDme)

WE ONLY HAVE TO FIND ONE ANY THE FIRST mD SOLUTION — ANY. Just a first. Any — if at all:

GEOMETRIC ¦ NuklidTab4C2023.ods Tabell1 A260+

The mNw and mew are the present (Oct2023) Wikipedia reported values for neutron and electron mass in Dalton units.

In calculating mD =18–12A/60 all the mD:s for all the mass numbers A, then calculating/seeking U = AmN(1–mDme) a corresponding integer U=A will always return the same answer 12 — provided (CAUSE) the used mN amd me follow the Neutron square suggested general solution’s u-equation provision

mN = 1/(1 — 15.6me) OR me = (1 — 1/mN)15.6. The precision of the me or mN is insignificant;

— A test column (above right) with an me=0.5 giving an mN=-0.1470588235 still returns a single U=A=12, all other have decimal tails. 6C12 it is. A17, 17Clorine35.

The approximated solution: mN/me = 1836minimum; U = (1836/2[15.6])(1 — √ 1 — 4(15.6)/1836) = mN = 1.008644262901; me = mN/1836 = 0.0005493705; mD = 15.6 = 18 — A/5 ; A = 5(18 — 15.6) = 12.

FROM THIS RESULT, IT DOES NO LONGER MATTER WHICH SPECIFIC mD or me — institution, laboratory, region, epoch — WE USE, BECAUSE THE UNIQUE

u-CONNECTION mN = 1/(1 — 15.6me) OR me = (1 — 1/mN)15.6 WILL AUTOMATICALLY ALWAYS CORRECT ON THE SAME END STATION RESULT: m(6C12)/12=u.

BUT THIS mD15.6me NS PREFERENCE ALSO BREACHES ON THE ESTABLISHED EXPERIMENTAL mN¦me PROVISIONS. Type

HOPmN 1.0086652u from the HOPme 0.000548598u: 1/(1 – 15.6me) = 1.0086320026u IS NOT THE SAME AS the HOPmN 1.0086652u. NS SUGGESTING: The experimentally measured masses involves electric and magnetic — not neutral — provisions, and have — therefore — no exact corresponding experimentally proven neutral quantities matching the Neutron Square guaranteed neutral atomic mass defect (atomic binding energy) suggested values.

WHEN IT COMES TO THE QUOTE mN/me THESE DIFFERENCES ARE MINOR (not directly significant);

HOP mN/me = 1838.6235458387. 1818 + 18 + 2.624.

HOP mN’/me = 1838.5630326577. 1818 + 18 + 2.563. There is a 0.00329% deviation in the relation. We know not here how plausible such is experimentally in measuring mN.

THESE RESULTS MIGHT ALERT A CHALLENGE. NAMELY IN COMPARING THE EXPERIMENTALLY MEASURED ATOMIC MASSES/WEIGHTS WITH THE CORRESPONDING NEUTRON SQUARE VALUES, A NORMALIZATION MUST BE MADE ON THE EXPERIMENTAL [mN’ = 1/(1 – 15.6me)] TO SECURE THE NS REFERENCE ON THE UNIVERSAL ATOMIC MASS UNIT m(6C12)/12=u AS STATED.

Normally — no adjustments — we just would translate the experimental U values to NS mD values by the given

Uexp → mD = (1 — Uexp/AmN)/me — given the laboratory or institutional mN and me values.

However in sequring the NS named m(6C12)/12=u transfer, the translation must respect an atomic mass unit normalization

Uexp → mD = (1 — Uexp/AmN’)/me, = (1 — Uexp/A[1/(1—15.6me)])/me, = (1 — (1—15.6me)Uexp/A)/me.

THE EXPERIMENTAL U IS FORCED MODIFIED THEN. AND THERE IS NOTHING WE CAN DO ABOUT THAT IF AN EXACT NS ATOMIC MASS UNIT REFERENCE COMPARISON IS ON THE TABLE. If it isn’t, the NS values have no true and fair comparing meaning, and only the experimentally values count.

That is an especially sensitive task when comparing on the new (WeizCalifornia) Weizsäcker solution quantities — which we already know is aiming at a persistent academic chase on the (new popular academic computer modeling) experimental (NScredit). The NS solution values will breach that dependence: The Weizsäcker quantities (uniformly charged liquid drop nucleonic model) have absolutely no connection to the (TNED toroid Planck constant) NS complex. No way. The comparing diagrams will underline that position (CONOR ¦ ComNorm).

QUESTIONING A UNIVERSAL NATURE of

THE NS NEUTRON SQUARE SOLUTIONS

———————————————

Absolute metrics ¦ The Absolut METRIC ¦ The ATOMIC NUCLEUS ¦ NEUTRON SQUARE SOLUTIONS ¦ NSdeDIA1 ¦ Geometric

AllKeplerMATH

—————————————————————————————————————————————————————————————

9Oct2023:

U = AmN(1 – mDme) ; AtomicMassDefectEquation

12 = 12X(1 – 15.6me) ;

1 = X(1 – 15.6me) ;

X = 1/(1 – 15.6me) ;

me = 0.000548598 u ; Wikipedia Oct2023: 0.000548579909065

X = 1.008632002589970 ; »NSexMatchTractor»:

= mXN UNIVERSAL neutron square Experimental Mass-to-Charge Transfer Corrector

—————————————————————————————————————————————————————————————

THE NEUTRON SQUARE SOLUTIONS EXPLANATION

Normalized comparison

NSdeDIA0:

NuklidTab4C2023.ods Tabell2A Col.K ¦ M

———————————————

AtomicMassDefectEquation

Discovery:

THE DISCOVERY — TNED Universe History

The original ideas (2003) leading to the NS atomic mass defect (mD) chart:

♦ NuclearSTRUCTURE: (HOP values) mN/me = 1838.6235458387.

PRIME NUMBERS: 1836 + 2.6235458387 = 1818 + 18 + k (BASICmN):

1818 + 18

———————— = 606 + 6 = 3 × (»±101» + »±1»)

3

A prime number certifies a basic barrier on whole number divisibility (Periodic system matrix basics — it is all about structure: resonances: basic whole number solutions): ±e NuclearSTRUCTURE.

♦ Scrutinizing (2003) the 1967 HOP table on atomic masses, comparing on a first drafted nuclide chart (TheoryExperiment) immediately revealed a possible apparent elliptic (Paintbrush, Windows 3.1) morphological complex — taken on (exothermal) fusion paths (Nuclide/FusionRING ¦ mDmethod ¦ Geometric ¦ VerticalElliptic).

♦ Attempting to deduce a connection on elliptic equations (EllipticEquation ¦ Deduction), immediately gave response:

♦ The Neutron Square discovery (2003) was a fact (Comparing Experimental/NS).

— Never mentioned in modern quarters.

On Aug2008 this UH UniverseHistory domain was introduced @Internet — on the NS discovery credit alone (»a new model of the universe»).

———————————————

ProtonRADIUS ¦ NuclearSTRUCTURE ¦ Atomic Mass Defect — ATOMIC MASS UNIT — deducing the atomic mass unit

See also — mass-to-charge dependency issue:

NeutralToExperimental.

The elementary mass-charge independence (Planck equivalents deductions)

NOTE the related deduction to the electric charge (Q), not mentioned in modern quarters:

———————————————

EXPERIMENTAL CONFIRMATIONS

No matter the electric and magnetic influence on the electron mass (e) — independent of any type of experimentation — under all conditions, no exceptions:

Q is preserved — unless ±e annihilated (COEI conservation of energy by induction).

The proportionality between affected mass (m) over (space electric) resistance (R) guarantees that electric (particle) acceleration (Planck equivalents as deduced) leaves the electric charge (Q) intact.

Assuming, or implying, any idea of ”mass-to-charge ratio” without proper specification and definition, will no doubt expose hazard to the reader.

As we know: Atomic Particle experimentation is dependent on charge properties. But the academic (Wikipedia Windows) insight into these physical domains seems less developed than the ambition to present modeling data on their nature: the atomic nucleus.

See further in

Provisions

• the neutral and optimal unaffected conditions under which the Neutron Square Solution NS neutral atomic mass defect (mD) values can be understood to apply.

Compare:

The GPS example

— precision (signal) measuring under significantly different gravitational conditions.

NS8Oct2023

ClarifyingTheUequation: 17Oct2023

It belongs to a common understanding that the energy needed to complete an assembly is the same energy reversed to restore the original — ideally »the movie backwards».

See Wikipedia quote in Not represented.

But the present common science set of terms and concepts apparently exposes some lack of a developed and well related, explainable and understandable vocabulary. The reader will be the judge on that in the following.

aMAD: CTU

Necessary clarifying concepts from established literature — related, compared and exemplified

ATOMIC MASS DEFECT AND NUCLEAR MASS DEFECT — MATHEMATICAL EXPRESSIONS AND CONCEPTS

The number (A) of Fundamental Atom Quanta (FAMQ) — the neutron mass mN — that made the atom (a), minus the actually (experimentally) measured atomic mass U=mATOM/(u=m[6C12]/12=1Dalton), defines the total mass-energy waste Work MDa needed to complete (a), taken from the masses of AmN through the Planck mass energy equivalent E = hf = mcr/t = mc².

atomic mass defect MDa = AmN – U ¦ U = mATOM/u ¦ u = m(6C12)/6 = 1 Dalton

U = AmN – MDa

nuclear mass defect MDn = AmN – U – Zv ¦ v = nino = mN – (mP + me) = mN – m1H1 (= 0.00084u)

MDn – Zv = MDa MDn = MDa + Zv.

v: the work mass energy waste that built the first atom — 1H1 Hydrogen — from the fundamental atom: The Neutron [ FAMQ ]

SEE ILLUSTRATED FROM EXPERIMENTAL VALUES IN Comparing nuclear AND AtomDiffNuc.

— As above: When there is vocabulary lack of terms in an established corridor, still attempting to handle the different domains, inevitable confusions will most certainly arise: we have to find safe and clear examples in closing out such traps in the descriptions. Compare Examples.

NUCELAR mass defect general expression: — WikiWEIZnuclearMass exemplifying by quote

E(MeV)/A = (AmN – U – Zv) × uc₀²/(A × T6 × e) nuclear

T6 = 10⁶ — in UH we use the simplification Tt for 10^± ¦ E = UQ = mc² ¦ U(eVOLT) = mc²/(Q=e) ¦ U(MEGAeVOLT) = mc²/(T6 e)

ATOMIC mass defect general expression:

E(MeV)/A = (AmN – U) × uc₀²/(A × T6 × e) atomic

COMPARING EQUALITIES — provided gravitational masses only — me electron mass

mNUC = U – Zme ¦ related: nucleus gravitating mass + electrons gravitating mass = atom gravitating mass; Rest: 0.

= AmN – MDa – Zme ; WikiWeizNuclearMASS

— On a RELATED basis — to Check and say:

There is no way to express this equality OTHER than INCLUDING these factors; Rest: 0:

The mNUC nuclear mass comes first after the mATOM has been assembled. So, it relates to U, not to AmN;

= AmN – (MDn – Zv) – Zme

= AmN – MDn + Zv – Zme . No way.

When n neutrons decay, lying inside of each others nuclear barriers (the nuclear delimiting sphere), and so performs a fast phase of spontaneous fusions, the resulting atom’s binding energy can not bring these original neutrons back on their original masses. These were partly wasted by working mass-energy during the fusion phase, the actual atomic mass defect.

Compare: the Planck equivalent mass-energy EXCHANGE term in EXCON: related physics.

See also NUCLEAR REACTION LAW.

MDa: ATOMIC MASS DEFECT —

aMAD ¦ CTU ¦ UnequivocalAmD

CLARIFYING attempt on THE TERMINOLOGY AND ITS RELATED MEANING

MDa = AmN – U

———————————————————————————————

(1) U = AmN – mDme ¦ simplified —— when we know the meaning of the parameters:

U = atomic mass m per atomic mass unit u = atomic weight — ”relative atomic mass”

mN fundamental atomic mass quantity QUANTUM — the neutron, enveloping the Hydrogen Atom

A number of mN that built the A atom also called MASS NUMBER — ”number of protons Z plus neutrons n”

mD IN RELATED PHYSICS: atomic mass defect —

the Planck energy E = hf = mcr/t = mc² working energy wasted on building the A atom;

me electron mass — 0.000548598 u here in UH, = 0.511 MeV:

♦ atomic mass is the raw A neutron quanta mass minus the energy building work

Related (1):

Left side of the (1) rank is the (U) atomic mass expressed in Dalton units (u).

Right side of the rank’s first term AmN is the Fundamental Atomic Mass Quantum (FAMQ) the neutron mass (mN = 1.0086652) times the atom’s mass number (A) from which the U atom was built. The second term is the per mass number (A) atomic mass defect mD (Planck work hf-energy E=mc² equivalent) in number of electron mass units, times the electron mass (me, 0.000548598) in Dalton units.

The complete left side U value of the whole atomic mass on the right side is

(2) U = AmN – mDme × AmN

completing the third term also for the whole atomic mass. Hence

the AtomicMassDefectEquation

(3) U = AmN(1 – mDme), = AmN – MDa .

There is no dependency on electric charge in this mutual equality equation.

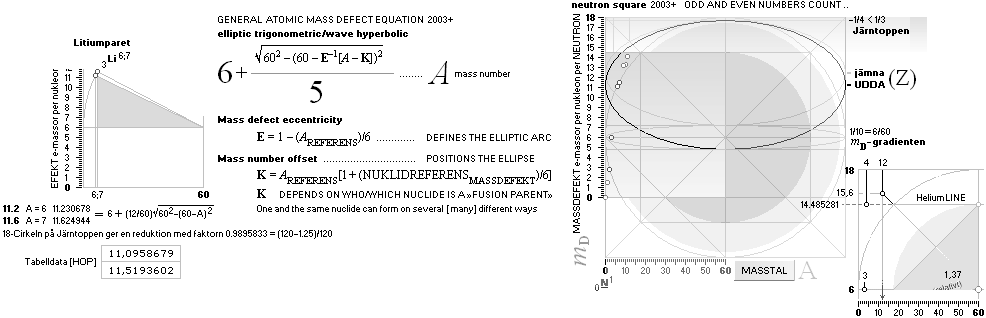
Through the deduced Neutron Square general elliptic equation

mD = 6 + (1/5)√ 60² — (60 — [ A–K]²)/E see NSsolutions

mD values are not entirely dependent on the mass number (A).

— The (EllipticEquation) KE factors connect FUSION PATHS (connecting elliptic arcs) defining (VerticalElliptic) the end atom — still no charge (Z) dependency.

Or so automatically integrated with no direct need for a separate analysis.

So (conclusion):

THE (UnequivocalAmD) ASSUMPTION IN NS SOLUTIONS THAT ISOBARIC ATOMS (same A, different U) IN PHYSICAL PRACTICE WOULD HAVE A MEAN AVERAGE ATOMIC MASS WILL NOT HOLD — except as a simplified violation on the true masses.

• Atoms with same mD can have different U from different A.

• Atoms with same mD can have different A.

• Atoms with same A can have different U from different mD.

— In NS solutions it is the mD Elliptic equation (KE) that secures also different U from same A, depending on how the end atom product becomes assembled on its A fusion production path. There is still no parametric electric (nuclear) charge dependency in these expressions.

See specific comparing isobars between experimental values and NS in

ComparingIsobaric

— there is a suggested (systematic) significant difference.

ClarifyingTheUequation

CosmicMATHrevelation: 25Sep2023 — Never18 ¦ Geometric

Modern academy teaching system with its merits and general moral and educative standards, a short review:

We do NOT intend to be rude — just fair and just. Have your say. EXAMPLE: A student who cannot »keep up» with the competition, commits suicide. Real world situation. Unfortunately, a not very seldom happening inside modern quarters educational institutions history. There are several examples — through several disciplines.

— The AIM of science and knowledge — HumanRight recognition standards; decency, respect, honour — was NOT to kill. It was to teach and educate: to share. As life has evolved with cooperating organs to a single admirable individual. The aim was NOT to profit, not to push or stress — individual care. The natural aim was a respectful cooperation. HumanRight recognition. ”.. every individual and every organ in society ..”. 24/7.

— And how is it, what’s up? Not a word. Not a spell. Not a sound. Modern academic teaching system cannot handle that quest. Most certainly not. It is — appears — a complete abstract to present academic thinking. Not existent. No say.

— 2023: Humanity continues to be brought into the biological dark:

GUARANTEED PRESERVED BIODIVERSITY —— on a never disturbed natural root fungi — TRDWS: biodiversity suffocates with the kill of alive trees — THE WORLD DEMOCRACY CRISIS PHENOMENA. RespondingNature.

HEALTH.

” Människan har skapat matematiken. Därom är alla lärde överens”,

Vetandets Värld 25Mar1988, Sveriges Radio.

English:

”Man has created mathematics. Thereof are all the educated in agreement.”,

SWEDISH RADIO, the weekly Knowledge World radio program 25Mar1988

— The Swedish definition of Education: »you are not welcome here». Very high IQ. MustBuyBook.

Delar Svenska Vetenskapsakademin ut någon annan behörighet än den som innefattar kalhyggen, förstörd natur? Det ligger ingen medveten illasinnad tanke bakom. Men det är vad ögat ser och hjärtat känner.

Naturfientligt utvecklad teknik. Var finns ett deklarerat bestämt avståndstagande, en erinran om respekterad människorätt? ”.. varje individ och varje organ i samhället ..”.

” matematik Enligt etablerad uppfattning är matematiken läran om tal, om rummet, och de många generaliseringar av dessa begrepp, som skapats av det mänskliga intellejtet,”,

MATEMATIKLEXIKON W&W 1991 s278sp2ö

English:

”mathematics According to established ideas mathematics is the teaching of numbers, of space, and the many generalizations of these concepts, having been created by the human intellect.”,

Swedish version of THE CRESCENT DICTIONARY OF MATHEMATICS (1962), W. Karush

— Test »formulated» for »created». Then we can talk.

Summing:

By a natural DRIFT of ignorance, not deliberately or by any such planning: Modern 1800+ academic ideas of our origin is holding mankind in a mental prison.

— Disclaim that, and we will surrender immediately.

Mankind 1800+ became locked up by [ apparently in many ways on Natural Destructive ] authoritative merits and ideas about moral and educational standards. These still prevent the individual from developing a natural insight: not one word HumanRight recognition. The below stuff is part of the proof: modern academic thinking is intrinsically continuing to present proofs that works against any idea of intelligence other that itself. Again: by Drift. Not plan. Against nature. Not with her. It holds its own present established academic teaching system to be a product of type »absolute intelligence» — on a not seldom favorized foremost example (”nothing lasts forever”, popular academic entropy study): Our universe was created in the past out of nothing, and it will die when the stars run out of fuel, and there is nothing any one can do about that. Cutting out every nerve and tissue out of the human child mind. Very high IQ stuff. MustBuyBook. — ».. but if there is a deep meaning, why don’t we see it?». TEST STOP DENYING IT.

COMPARE THE REAL STEEL WORLD OF NATURE, AS EXPERIENCED:

Man discovers mathematics: The paragons from natural observations give us hints in how to develop a formulating language. Man creates no math at all — except provably faulty statements. The LIST. Say.

— What was never created, timeless, perfectly solid, no exception.

Shorter: perfect flawless joy. Say.

— We are not here to weaken Defense. We are here to make it stronger, deeper, more fundamental.

THE GUARD OF CIVILIZATION

CosmicMATHrevelation ¦ Resurrection11Sep2023 ¦ AtomicMassDefectEquation

Geometric: NeutronSquareSolutions ¦ VerticalELLIPTIC ¦ NeutronSquareFundamentals ¦

CosmicMATHrevelation

neutral to experimental —— U = mATOM/uC12÷12 — traditional Atomic Weight, present as Relative Atomic Mass, u = 1.66033 t27 KG, 1 Dalton — beginning from the neutron Planck ring h = mcr

CONCURRENT ATOMIC MASSES: U = Am_N(1–mDm_e) ¦ mD = 6 ± k(1/5)√ 60²–(60–A)² ¦ Never18

Neutron Square Solutions — atomic nuclear physics — as testified by experimental results — absolute neutral atom preference — NEUTRAL ATOMIC Weights/MASSES

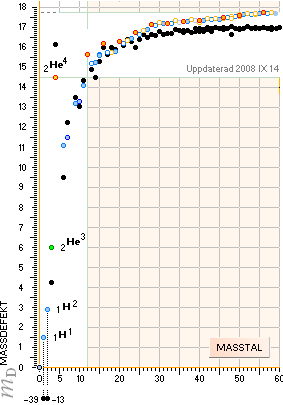
NuklidTab4B2023.ods Table1 Col.AI+ — The simple amazing astounding coherences that, apparently, nobody can deny — never noticed in modern quarters. No way.

The 7 exemplified Neutron Square paragonic parts below are tabled above in comparing experimentally measured results.

HOP, experimentally measured, NS, NeutronSquare solutions — in this UniverseHistory beginning from 2003+ on a Windows XP machine [with Windows 3.1 Paintbrush] and the HOP table data.

The experimental coherence NSdeDIA1 is no doubt astounding (EXPERIMENTALconfirmations).

Compare modern academic standard (Entropy Quote), the observed and noted1800+ central instance of denial of the cosmic nature: »nothing lasts forever» — the apparent modern academic 1800+invention or more fairly expressed, a modern academic dictated delusion to keep the timeless truth of nature on a safe distance — with zero physical solidity. Compare the rhetoric response: If you say so, that nothing lasts forever, when does that cease? Wake up to reality.

These paragon »matrix formations» apparently have no origin in time: time never began — realize it, read it and weep. As the Pythagorean Theorem, it can be forgotten but never destroyed — and rediscovered, any amount of times — without changing the least or the smallest, not at all. The atomic mass defect values from the geometric neutron square solutions have no physical or experimental foundation — except the Planck constant: the neutron, the fundamental atom: h=mcr. Testing the experimentally found values on the basic Planck ring principle, made the neutron square solutions appear immediately — concurrent in values (2003 in this history).

— There is apparently no way to undo these discovered results — never known, and never asked for, in modern corridors. Shorter:

— Why was the above never presented from the academic aces — What’sUp — why is it unknown in there?

— Educate us.

Modern academic cosmological idea is so occupied by its own supreme standard, that it has forgotten how it came that it locked humanity into a dark box.

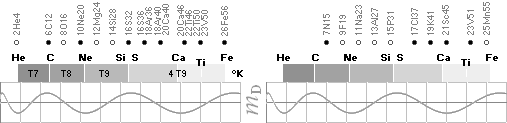
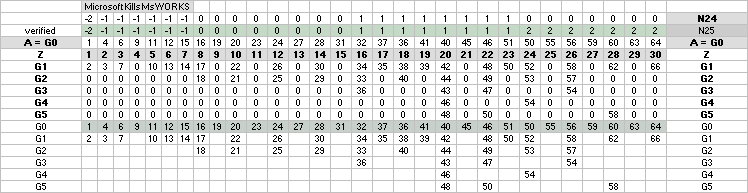
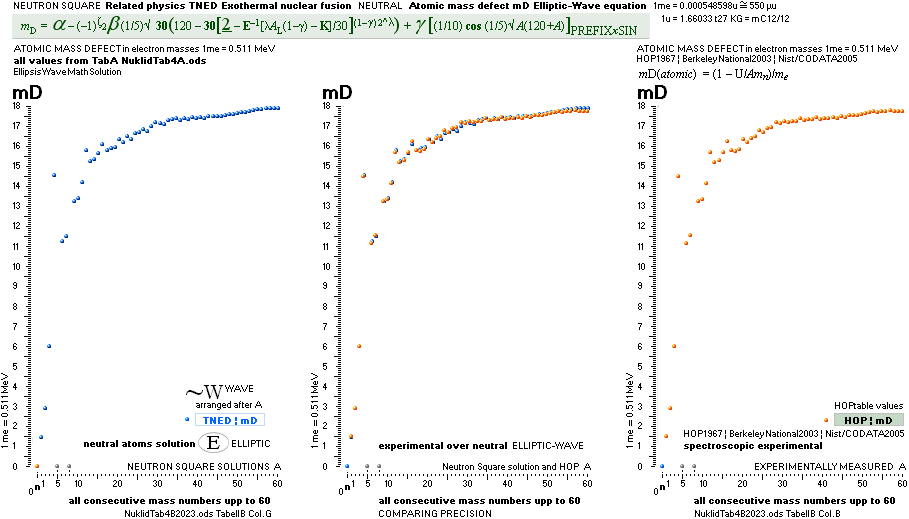
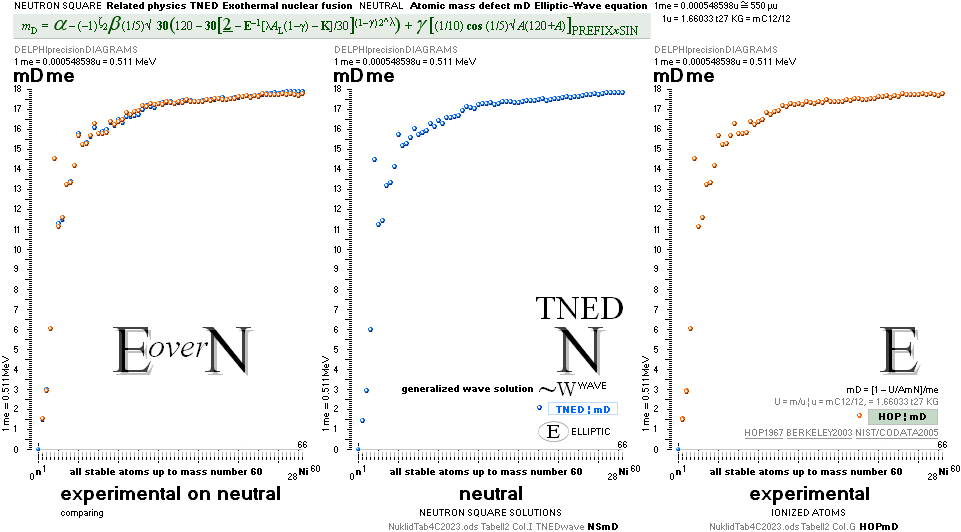
NuklidTab4A2023TableA: NuklidTab4A2023.ods ¦ EC ¦ BaseGroupMassNumbersEquation

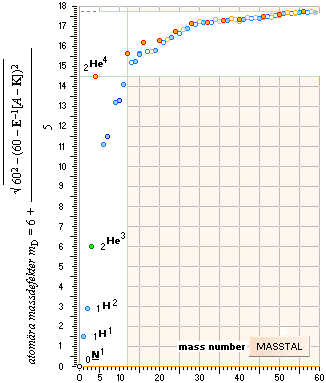
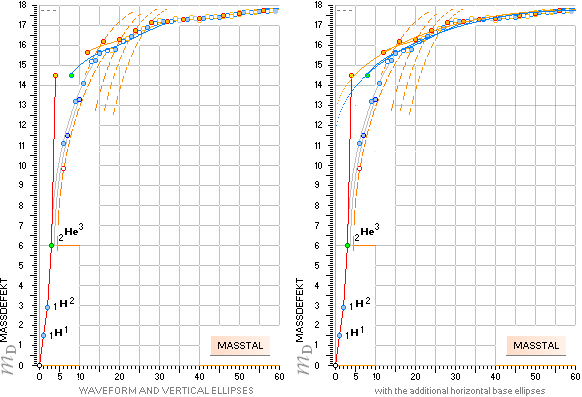
THE NEUTRON SQUARE ATOMIC MASSES UPP TO A=60 —

from MproblemSolved the original MsWORKS 4.0 that Microsoft suddenly blocked from computer usage 2008 — see

ExcelOpenOfficeCALCULUSprograms, TheMicrosoftLIST.

The precision increases with increasing mass number:

THE TNED DEDUCED ATOMIC MASS DEFECT mD IN ELECTRON MASSES PER ORIGINAL NEUTRON same as total mD divided with mass number BETWEEN EXPERIMENTAL AND TNED CALCULATED TAKES A LARGEST VALUE

ON THE HYDROGEN ATOM WITH —0.057 e-MASSES and a U-ratio 100.00313%. 20Ca42 HAS THE LOWEST DIFFERENCE WITH —0.0001 e-MASSES, and a U-ratio 100.00021%.

NOTE: ₁₉K⁴⁰ — not stable — Kalium-40 är betaMinusAktiv

Mass number 40 for the Potassium element 19K40 has in the HOP table no remark suggesting otherwise than a stable nuclide — abundance 0.0001181.

However other contemporary sources Van Nostrand’s Encyclopedia claim beta-activity with a half life of 1.3 billion years. Not included here as a stable atom.

Masstal 40 för Kaliumindividen 19K40(17.27) har i HOP-källan ingen anmärkning i tabellen som antyder annat än att nukliden är stabil. Tre sådana anges.

I avdelningen Nuclear Physics i HOP, första kapitlet General Principles of Nuclear Structure (s9-7sp2n) påstås emellertid att ”For odd Z there are never more than two stable isotopes”. Man skulle då kunna misstänka att HOP-tabellen längre fram i verket är felaktig på den punkten, eller att författaren är fel ute. Emellertid, kontroll i en annan källa, Van Nostrand´s Scientific Encyclopedia (Ed5 1976 s491-515) anger i en liknande tabell att Kaliumindividen 19K40 är –betaaktiv med en livslängd på 1.3 miljarder år.

Innan denna detalj uppmärksammades togs HOP-tabellens specifikationer för givna varför individen 19K40 också finns medtagen i tabellreferenserna här som en icke instabil markerad isotop. Den är dock inte upptagen i nedanstående gruppredovisning av alla stabila isotoper upp till masstal 60. Om vi tittar efter på masstal 40 ser vi den också, tydligt. Den avviker något från övriga i en liten dipp som därmed avslöjar att ovanstående citerade referens tycks ha visst fog för sig. Vi får därmed frånräkna individen 19K40 för vidare, men låter den stå kvar i tablåerna som ett exempel på precisionen för de stabila nuklidernas del.

Editor2003VII15

THE GENERAL COLLECTED NEUTRON SQUARE SOLUTION on elliptic and trigonometric-wave equations — from [2003] the MsWORKS original NuklidTab4.wks ¦ Windows 95, Windows XP, Windows Vista

NuklidTab4A2023.ods TableA From NuklidTab4.wks 2008 — finally solved for OpenOffice and Microsoft EXCEL. Explicitly designed for ZERO interrupts: no errors allowed.

ALL STABLE ISOTOPES UP TO ATOMIC NUMBER 27 — max mass number 60 — the NeutronSquare horizontal square side scale

— From A=60 and up the precision — elliptic equations — becomes more demanding. See FusionEllipsesCompleteExplanationInTNED. There is however (CompCALu2023) a simpler »general hyperbolic» solution for all the 60+ atomic masses (TheWaveFunction ¦ WAFO). In TNED from the NeutronSquare it exposes a »still excellent fit» to the experimentally measured values. We can study these for a first rough comparison, and then test the further more precise determined values. Largest-Smallest mD e-mass per A neutron difference for this hyperbolic case is +0.00173 -0.00459 — taken for all the (NuklidTab4A2023.ods) HOP table listed nuclides — including the unstable ones from mass number A=60 to A=257.

The details behind the above illustrated content is specified in

BaseGroupMassNumbers.

Geometric ¦ AtomicMassDefectEquation

Resurrection11Sep2023:

2003: The NeutronSquare — nuclear mass connects definite nuclear size.

With the advent of the atomic mass defect equation in (TNED) related physics and mathematics

mD in number of electron masses me

U atomic weight in Dalton — u = 1.66033 t27 KG — units: 1u = m[6C12]/12

A mass number — number of originally primary neutrons — conventionally »number of neutrons n and protons p»

mN neutron mass in Dalton 1.0086652

me electron mass in Dalton 0.000548598

mN/me = 1838.623545838670 = 1818 + 18 + 2.623545838670..

conventional atomic weight in UniverseHistory denoted U in u units

the extensive 1967 available (HANDBOOK OF PHYSICS,McGraw-Hill, ed. 1967) HOP table

NuklidTab4A2023.ods

on experimentally measured atomic masses did expose

TheoryExperiment:

ELLIPTIC EQUATION

Uncertainty: ±1 pixel, or ca 1 electron mass (±½) me = 0.000548598u = 0.511 MeV per mass number A ¦ 1 u = 1 Dalton = mC12/12 = 1.66033 t27 KG

definite regular connections to elliptic equations of the form

explaining the coherences as exposed:

— In this scale [6 pixel colored dots, MAX 18 electron masses Atomic Mass Defect Equation per mass number A on equation (5) ¦ DiffREF] no direct difference is visible between the HOP table experimentally measured and the TNED atomic mass defect equation wave form (WAFO) and its elliptic equated values

(see TheActualDifferencesHOP/TNED ¦ ExperimentalErrors):

WaveElliptic:

Beginning from The Cosmological Fundamental Neutron 0;0 (Planck constant h = mcr):

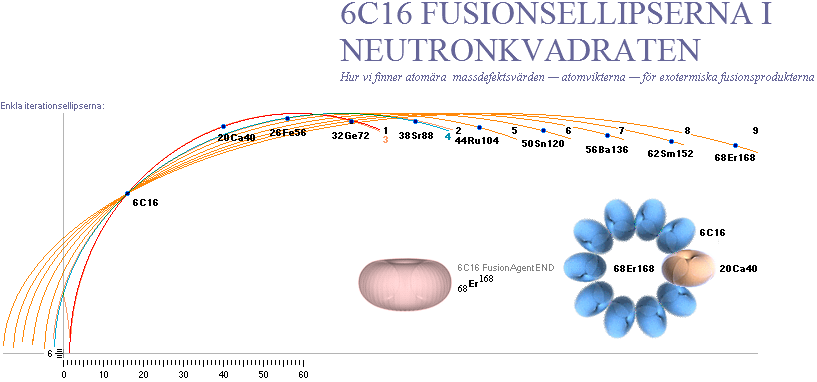
Left: The ordered (exothermal, beginning from Dmax) fusion paths for the stable nuclide formation according to the TNED discovered Neutron Square paragonic geometric mathematics. The (dotted) vertical ellipsis arcs point to (exemplified) a corresponding nuclide’s atomic mass defect for a given mass number through the neutron square’s special elliptic functions.

Right: Uppermost are included the two fundamental mean ellipses along with their modification in the form of a general in explicit connecting and containing also A hyperbolic expression (CompCALu2023) connecting the nuclide chart also to the heavy part of the chart further from mass number 60 Wave Equation (WAFO)

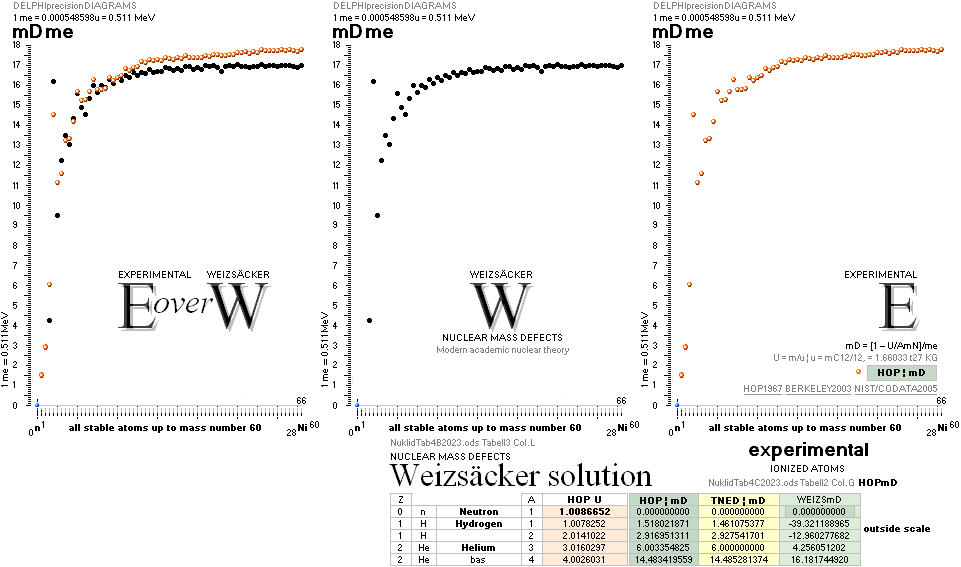
TNEDComparingMAC: TheoryExperiment

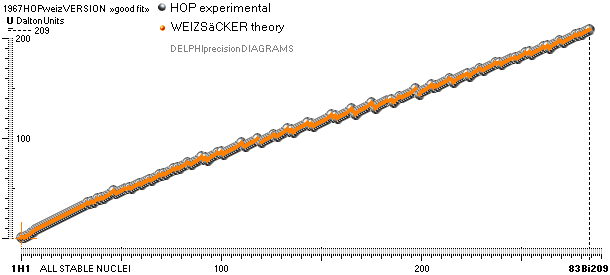
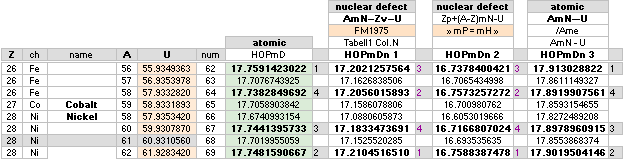
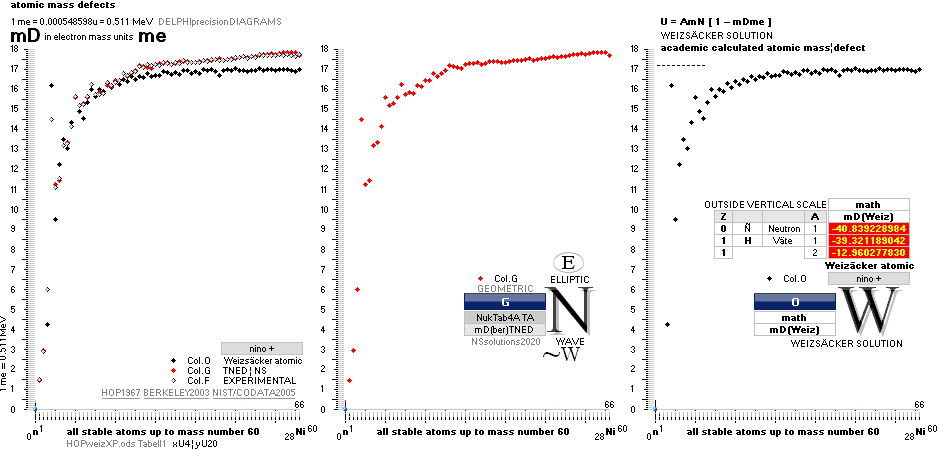
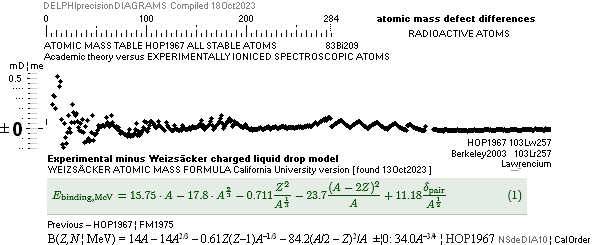
COMPARING TNED RESULTS WITH WEIZSÄCKER VERSION HOP1967¦FM1975

heavy differences in established corridors

See also the comparing modern academic MAC theory values in Comparing TNED/MAC:

Black dots: Values from the Weizsäcker equation solution transformed to the TNED mD value form through the general (colored dots) experimental transfer equation

— The U value is the atomic (”molecular”) weight value in Dalton units (1Dalton = 1u = 1.66033 t27 KG) in the different available tables on atomic masses.

— The Weizsäcker solution is the modern academic concept of nuclear physics based on nuclear — not atomic — mass defect. It uses the idea of the atomic nucleus as a uniformly charged liquid drop consisting of discrete neutron n and proton p smaller drops. See the Weizsäcker equation more detailed in THE WEIZSÄCKER EQUATION DETAILS.

Colored dots: The experimentally measured values. Especially in the first part of the chart, the Weizsäcker values differ vastly — apparently exposing a direct inaccurate chosen idea of the atomic nucleus. The Neutron Square calculated TNED values in this scale have no visual difference from the colored dots.

— In our era of experimental physics, the neutron was first discovered 1932 by James Chadwick (ordinary atomic physics fact book information).

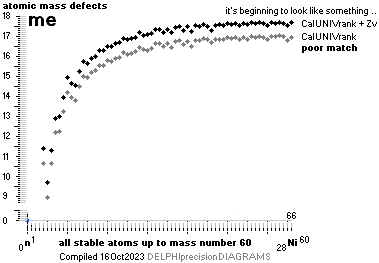
— The above divulging vast Weizsäcker values show no such divulging visibility if viewed in comparing U-values, the graph below. And because the mD solution never was searched for in modern corridors — never represented — also what we know the above mD divulging chart was lost in modern quarters.

Uweiz: »the ideal perfect match» — TNEDcomparingMAC

One way of viewing the Weizsäcker theoretical comparing experimental (THE WEIZSÄCKER EQUATION DETAILS). Comparing experimental with theoretical on the Weizsäcker form in U values, no essential difference is seen, the diagram above. Viewed on the established term ”nuclear binding energy” the differences exposes more visibility. See for example TheTakadaDiagram2006. That figure has the following text, recited here:

The above figure is not the Takada reference — see the actual Takada figure in TheTakadaDiagram2006:

“ As seen in the above figure, the Weizsaecker-Bethe mass formula can reproduce well the experimental data for a wide range of nuclei. We can therefore conclude that the liquid drop model is enough valid in nuclei.”,

Internet Seminar MICROSCOPIC WORLD –3– The World of the Atomic Nucleus, Dr. Kenjiro Takada 2006.

The following Takada consenting HOPweizQuote ”good approximation” certifies the educated established scientific community merits:

” A number of fairly good semiempirical binding-energy or mass functions have been constructed which give a good approximation to the true masses over the wide range of both stable and unstable nuclei in terms of relatively few empirical constants. Perhaps the most simplest such formula is that of Weizsäcker: .. (2.1)”, HOP1967, p.9—8.

With no further references — unknown NS solutions — also no objections could be made on the quoted and established sentences. We just had to conceive them as »provably accurate».

See further contextual in FIBAPO ¦ NScredit: an explaining inclusive overview.

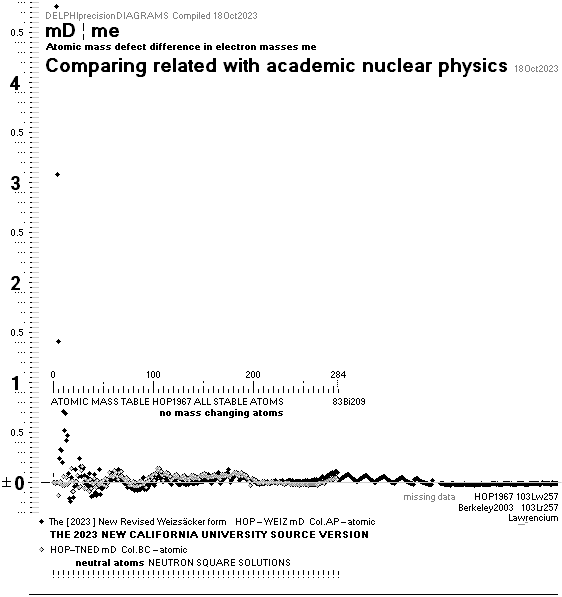
mDweiz: EC

Differences in atomic mass defect electron masses per mass number

MODERN ACADEMY IS OUTCLASSED BY TNED — related physics and mathematics

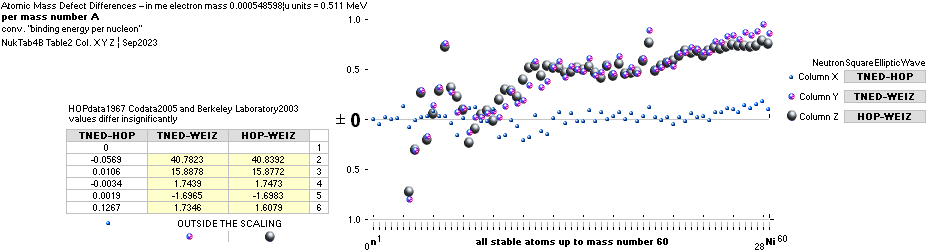
NuklidTab4A2023.ods Table4 — Columns KMS ¦ 1.00 e-mass = 0.511MeV

The large first 1967¦1975 Weizsäcker differences. The Element isotopes from 1H1 to 4Be9 are left out in the diagram above as the Weizsäcker values anyway lie far beyond the vertical scale. The reason: The idea behind the Weizsäcker solutions — charged liquid drop mathematics — have no corresponding atomic nuclear connection — says TNED on its near and close contact to the experimentally measured values, directly from the neutron and up. Only when the atom grows larger and heavier, that difference decreases. See further definite proofs [Jun2023] in THE ATOMIC NUCLEUS.

The Weizsäcker value equative calculations are accounted for in the separate spread sheet HOPweizXP.ods Table1. Its equative details are exposed as quoted in The Weizsäcker details.

Resurrection11Sep2023 ¦ AtomicMassDefectEquation

AtomicMassDefect: Equation

• mD = (1 — U/AmN)/me

• U = AmN(1 — mDme)

THE ATOMIC MASS DEFECT

Related physics and mathematics: not represented in the modern academic teaching system.

And it can never be.

No way.

— IF the reader believes that this production is some kind of ATTEMPT to be welcomed into modern quarters, the reader has perfectly lost control of the reading capability. It will never happen. We could equally hope to have an aquarium at home with gold fishes in it, on the level of all the Pacific Ocean’s water. It will guaranteed never happen.

— So what is your aim?

— Live and see. Don’t die.

— That’s easy for you to say, not living in the middle of an ongoing war; ”don’t die”.

— I hear you. But I’m not talking to the body, only the mind: it can never die. No way.

TNED — related physics

The atomic mass defect ..

• Each atom is built of — weighed (U) on — a (mass) number of A neutrons, each with mass mN = 1.0086652 ¦ u: 1u = 1.66033 t27 KG, the atomic mass unit;

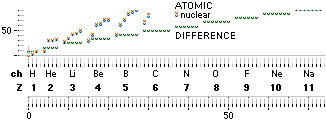
The TNED related A-Z chart. White: all stable atoms.

See related deduction from DeducingTheAZ.

• The atomic weight (U=m/u) of an atom will always be smaller than AmN = A · mN, because

• building an atom from lighter units needs work = energy, and

• it is the atom self that must offer some of its mass for a (an exothermal, giving out) mass-energy emission during the work.

• This energy work for building a physical atom never exceeds or even touches 18 electron masses (Never18);

• It is (see further below in The 18e capital) the mN/me structure

mN/me= 1818(»Central Massif») + 18(»Work Capital»: TheNeutronSquare that (2003) revealed the whole story) + (mN/me — 1836 = 2.624 =»lubricant») electron masses which is responsible for that mathematics;

See further on

DeducingTheAZ chart.

AtomicMassDefect

AtomicMassDefectEquation: Explaining the U equation

mD ¦ AtomicMassUnit

Deduction:

THE IMPORTANCE OF relating the mass defect quantity to the fundamental ATOMIC MASS QUANTITY (FAMQ)

The Neutron mass mN:

Atomic mass defect is the Planck energy E=hf=mcr/t=mc² mass-energy Waste Work needed to build the atom from its number A mass number neutron masses — as related. MDa = (m[WASTE]=E/c²)/u in Dalton units: 1u=1Dalton = m(6C12)/12, = 1.66033 t27 KG

MDa=mD(u) = AmN — U, atomic mass defect in U Dalton units, 1u = m(6C12)/12 = 1.66033 t27 KG

mD(AmN) = (AmN — U)/AmN, atomic mass defect

per mass number A neutron masses mN

mD(me) = [(AmN — U)/AmN]/me, atomic mass defect

in electron mass units me per mass number A neutron [ fundamental atomic mass quantum ] mass mN

= AmN[(1 — U/AmN)/meAmN]

mD = (1 — U/AmN)/me, atomic mass defect

in electron mass units me per mass number A neutron masses mN; 1 me = 0.511 MeV = me·c²/[e=1.602 t19C · T6]

mDATOMIC = (1 — U/AmN)/Ame, atomic mass defect PER MASS NUMBER ¦ sometimes used in UH for comparison

Neutron Square solutions

EXAMPLE:

mD(u¦6C12) = 12·1.0086652 — 12.0000000 = 12(1.0086652 — 1 = 0.0086652)

mD(AmN) = (0.0086652)/(AmN) = 0.008590759

mD(me) = (0.0086652)/(meAmN)

mD = (0.0086652)/(0,000548598·1·1,0086652)

= 15.659479896 — establishedNominal¦experimentalHOP

NOTE THAT DIFFERENT PRECISION VALUES ON THE DIFFERENT CONSTANTS GIVE DIFFERENT END QUANTITIES. AS THERE YET IS NO COMMON HIGH PRECISION DEFINITION OF NUCLEAR MASSES PER KILO GRAM — STANDARD UNIT KG — WE ARE STILL FIGHTING A PRECISION BATTLE LOOKING FOR »BETTER CONFIRMATIONS».

= (1 — U/AmN)/me

• mD = (1 — U/AmN)/me

• U = AmN(1 — mDme)

The NeutronSquare gives (directly trigonometric)

15.6

The NeutronSquare general[‡] elliptic-Wave (from NuklidTab4A2023.ods TableA) gives

15.739439592 (NuklidTab4A2023.ods Table5 A6): NeutronSquare average

(15.739439592 + 15.6)/2 =

15.669719796.

As an average:

That is a good precision average original neutron mass defect score for the 6C12 atomic mass relative the experimental

15.659479896

The rounded difference in electron masses: 0.01.

The mD average gives a corresponding comparing experimental

U = AmN(1 — mDme) =

11.999932005.

Highest score

The atom with the highest building atomic mass defect work score is represented by Iron (experimentally) 26Fe58 with mD = 17.759142302 electron masses

(1me = 0.000548598u = 9.1085 t31 KG = 0.511 MeV);

18me → max 9.198 MeV.

Atomic and nuclear mass defect concept — what modern academy missed: onsetting the deduction to the periodic system: the (deduction) cube analogy, with further ..

WHEREAS the neutron in any case is a compressed or »sequestered» version of the hydrogen atom, so containing the proton, the hydrogen nucleus, one can relate any atom on a sum of neutrons alone. That the atom — then — consists of a nucleus detailing electron masses to the surrounding cover makes nothing to the point in the internal charge distribution. It is the same. The only difference consists of the mass defect (beta transfers) associated with the atomic rebuild on its fitness to the actual atomic harmony. It was precisely this detail (here in UH) which showed up its importance for the (TNED) discovery of (the hidden and forgotten) electron resonances in (the astoundingly simple) deduction of the elements periodic system via the Kepler momentum. See THE KEPLER RESONANCES.

Reason for choice of e-mass units — atomic mass defect mathematics — related physics

ATOM DYNAMICS — matter in general (The ATOMIC CHEMISTRY RANK) — entirely is built on the electron resonances in the Periodic System. It is the related, deduced and described resonant areas 2-8-18-32-50- .. -2n² with the related resolution 2-6-10-14-18-… that are the featuring Commander DoIt. When the atom switches building, these resonant conditions must be preserved, if we are talking stable tables. That preservation apparently involves that the resonances — also, in deep — must be related to the basic fundamental atomic nucleus. That is: The neutron — which contains the proton-hydrogen atom — as the most elementary UNSTABLE nuclide — with a mass defect zero. Shorter:

— The resonant conditions (basic nuclear STRUCTURE) must be — also dynamically beginning from the neutron — related to the hydrogen atom with its atomic mass defect (mD) when the neutron decays and becomes stable (THE NUCLEAR CHARGE BASICS 2).

— If hence the mass defect is uniformly expressed in e-masses of the neutron mass, one receives directly a quantified measure on ”distance to resonant stability” with the neutron-proton-hydrogen atom as a foundational basic reference. The higher mass defect, the more stable building, analogously more work to build the construct and thereby harder to break it up. Consequence, related physics (HIGHESTmD):

— Iron ₂₆Fe⁵⁶ ¦ U = 55.9349363 ¦ m_D =17.759142 has the highest mass defect score in the max18 scale related physics atomic masses.

— Compare the different modern academic related highest score elements in (Swedish original) TWO DIFFERENT MASS DEFECT REFERENCES: And more related, here in English from HIGHESTmD.

— There is no correspondence between the two different domains. The academic highest (nuclear mass defect) is 28Ni62 with 17.176463 — with the 26Fe56 in a third place on 17.168214. The term atomic mass defect has no representation in the academic society.

Capital18e:

Decay, fusion and fission — in preserved resonant orders: basic related nuclear surface n-p-structure.

The top spinning atomic nucleus’ inherent spin cannot be removed or stopped. No way.

Any attempt to do so will promptly result in either a complete ±e structural annihilation. Or a corresponding (water splash) split on lighter nuclide elements, of shorter or longer lifetimes.

— But (intelligent) experimentation can divulge (such impossible) inner structural properties (Collisions between spin polarized protons 1979 ¦ 1987), helping us to pinpoint the essentials. This story has exactly that type of credit to thank for.

Preserved electron resonances — demands a defined characteristic nuclear n-structure and a characteristic defined p-structure: nuclear structure:

nuclear surface charge electric displacement — decays, fusions and fissions

ON BUILDING ATOMS in preserving the electron resonances for all the elements nuclides, in accordance with the ordered deduction of the elements periodic system, the nucleus always must preserve a definite basic configuration related to the neutron-proton basic aggregate. Such a condition guarantees that the nucleus always is exacting distributions of separate n-p-individuals in their preserved properties. As this, primary through the neutron decay, basic configuration is determined by the resonant numbers in the corresponding integer electron area numbers (2-8-18-32-50- .. -2n²), with groups and sub-groups, there is apparently a definite whole number order by which THE NUCLEAR DYNAMICS adjusts in all possible decays, fusions and fissions.

The 18e capital ..

The MAXmD = 18e capital — basic np-structure

mN/me = 1.0086652/0,000548598 = 1838.623545838670 = 1818 + 18 + 2.623545838670..

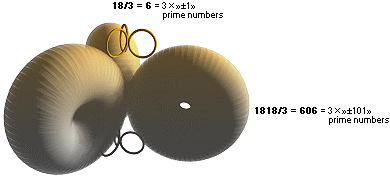
THE EIGHTEEN BODIES —— 3 × 606 + 3 × 6 + k = 3 × »±303» + 3 × »±3» + k = 3 × 3 × »± 101» + 3 × 3 × »± 1» + k ¦ prime numbers

WHOLE NUMBER PRESERVED RESONANT SOLUTIONS

mK = 1818, MAXmD = 18 ¦ MPcKärnteorin.doc 28Jun2003 Author’s reference

Mass is taken from the atom for rebuilding energy

The atom’s performance in the rebuilding work (m→γ) of producing other atoms needs an available marginal working mass-energy expendable waste capital (MAXmD). That capital secures that no causing havoc happens on the central preserved and protected nuclear massif (mK) on its inherent status of maintaining a stable nuclear and atomic dynamic function. The expendable (MAXmD) mass must have the capability in preserving the basic neutron deduced Planck ring (h=mcr) structural symmetry. That symmetry optimizes a greatest possible symmetric deadlock, a safe guard, on the entire ring structure of ±β-charges, certifying the structure does not collapse (PRIME).

— WHEREAS this deduced Planck ring structure in TNED is founded on a ±β pairwise (fractal hollow ring) symmetry (NuclearStructure ¦ NuclearMassprinciple ¦ TheFractal TNEDPlanck RingStructure), it is obvious that the fix nuclear mass (mK, total mass m minus MAXmD) must be whole number based (PeriodicSYSTEM) with respect to this pairwise symmetry — if a guaranteed exact balance is to be certified.

— The expendable mass must be based on an INTEGER nuclear ring symmetry.

— By further divisible consequence the integer part in the fix nuclear mass (mK, so) must be based on an odd integer — a prime number. A prime number blocks any further split. The prime number thereby determines the limit for the nuclear symmetry (type 1818 ÷ 18 = 101, prime number; can only divide by itself for a resulting integer — nuclear divisions, fragmentation).

The expendable MAXmD mass thereby becomes a function of the named pairwise ±β electric charge symmetry on the topmost rings structure’s 3- number (HOW3), so that one receives MAXmD = x(2[±β]×3)=6x: 6 · N=3 = 18: there never was not much to chose on.

See also THE simple BASIC NEUTRON MASS PROVISION MATHEMATICS.

npSTRUCTURE: CAPITAL18e

Basic related nuclear physics n-p surface charge structure

the neutron and its decay

———————————————

TNED NUCLEAR CHARGE BASICS ¦ TNEDbacisPlanckRingStructure ¦ TNED nuclear charge basics 2

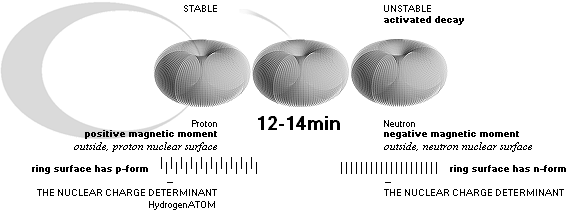
The neutron has by consequence a certain negative nuclear surface prominent electric displacement (The Neutron Decay) which by consequential known theory through the nuclear top spin gives the neutron a corresponding known negative magnetic moment. When the neutron undergoes decay the displacement is changed, ending on the proton characteristic positive electric displacement with a positive magnetic moment. These moments are well empirical documented, and mark one of the TNED nuclear toroid morphology’s most important confirmations (Toroid Nuclear Electromechanical Dynamics, TNED).

See more related nuclear structure details in

Deducing the AZ chart.

AtomicMassDefectEquation

DeducingTheAZ:

TNED RELATED NUCLEAR ATOMIC PROPERTIES

npSTRUCTURE

NuclearSTRUCTURE ¦

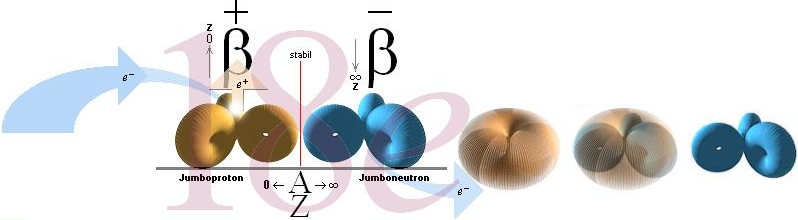
If a p-nucleus ( ¦ ) grows optional with enclosing n-masses ( | ) on each p-ring, ideally a Zn-p-Zn nuclide (a »JumboNeutron» .. | | | ¦ | | | ..), we can directly see why the resulting edifice sooner or later must lose its characteristic original p nuclear type charge property: The neutron masses forces the edifice to withdraw (»bury») the (±e structural) positive β-displacement.

The same (with slower destructive force) would hold for a »JumboProton» (Z=[A=»n+p+n»]/3) of the form type Zn-Zp-Zn = .. | ¦ | | ¦ | | ¦ | | ¦ | .. = Z(n-p-n): the p-type gradually loses impact over the n-type, and the nuclear structural balance is again compromised — IF we are talking »overall uniformly distributed charge». If not, this alternative would apparently suit the best fit in preserving a given Zp (on still larger nuclei), type nX-Zp-nX.

If the p-nucleus on the other hand grows evenly with a minimum of enclosing n-mass type (»A=Z»),

n¦..1111111111..¦n .. ideally a n-Zp-n nuclide (a »JumboProton»), we see equally easy that the nuclear surface charge — n-p-p-p..p-n = n-Zp-n — is forced to grow in magnitude with the integer number Z>1; The original p-nucleus also here loses its original hydrogen atom harmonics.

An ideal (Z=[A=»n+p»]/2) p-type nucleus Zn-Zp = Z(n-p) = .. | ¦ | ¦ | ¦ | .. would be the theoretically preferred natural choice on building heavier atoms from lighter atoms for a preserved exact balance — provided the nuclear ring structure did have a »uniformly distributed electric displacement» all over the nuclear surface.

— It hasn’t.

NScredit:

— For the most low atomic nuclear charge atomic number Z-values, the ideal Z(n-p) type »is The Man». In the empirical table values, it holds practically up to the stable Calcium 20Ca40. After that, further on the stable Calcium isotopes, the Z(n-p) type is definitely done; On the following nearest stable Scandium atom 21Sc45, the threshold has already been passed: more n:s than p:s. And so the more n:s than p: s continues to grow with still heavier atoms — remember we talk Structure here. A balanced growth on heavier atoms apparently (in some way) favors the named type nX-Zp-nX.

NuclideStaticAverage:

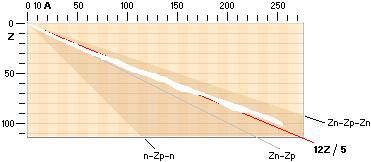
The NUCLIDE MAP (AZ) IN TNED

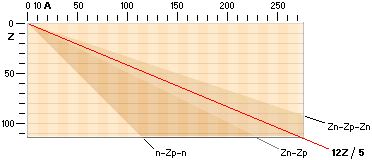
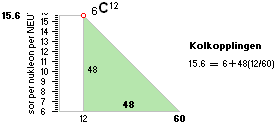
Nuclide static average value line A=12Z/5 crosses with good approximation the nuclide field (white in the AZ-map below). In that region we find the natural element’s stable atoms. While the n-p structure demands certain structural padding with growing atomic number Z, some of the atomic elements will expose isotopes. That is, atoms with same Z (same chemical properties) but different masses (different n-p structural paddings on their mass number A).

Atoms with same mass number (A) but different atomic numbers (Z) are called isobars.

TheNEUTRON ¦ TheNeutron

Beta decay emission mechanism

The term beta relates to both polarities of the electron mass — the normal negative electron mass and its positive spouse, the positive electron: the positron

Jumboneutrons at right and Jumboprotons at left. The Jumboneutron is to heavy for its atomic number Z. It strives to get rid of one or several electron in order to switch down to a more stable position further down in the chart via a higher Z padding. The Jumboproton is to light for its Z. By burning off +β rings, or alternatively pull in one (or several) electron, it can reduce its Z and there by emigrate further up for a more correct balance. The AZ-chart also includes limits for atoms of a hard (nuclear) instability (their mass number A changes during the decays — in general from 83Bismut209). The description of the hard unstable atoms are (what we know) more demanding and will apart from the short description below on Radioactive mathematical physics not be mentioned further in this presentation (it needs a whole document, not to say several — see article links Swedish edition in Radioactive Decay’s Physics).

Atoms classified apart from the stable atoms are unstable atoms. These are either soft or hand unstable. The soft unstable are classified as beta (Greek b, β) unstable atoms. They become stable by electron transactions, give or take: their mass number (A) is preserved. The hard unstable are classified as the alpha unstable atoms (often emitting a Helium-4 nucleus — and more). They become stable by nuclear decay, nuclear emission or nuclear split. In the AZ map below only the beta unstable atoms are addressed.

AZchart: NuclideStaticAverage ¦ DeducingTheAZ

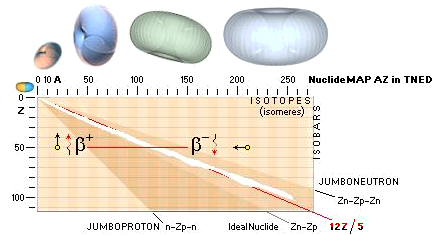
THE related RADIOACTIVITY MATHEMATICAL PHYSICS IN TNED

Short description

According to TNED all unstable atoms change towards a stable and balanced state and condition is described by the two type ranks below:

(K) – E_hf18 = K = (K1 + K2 – (m→γ) + _β0_γm ) – E_hf18 ................ beta decay, beta unstable atoms, beta nuclides

(K) – E_hf1818 = K = (K1 + K2 – (m→γ) + _T0_γm ) – E_hf1818 ............. nuclear decay, nuclear unstable atoms, radio nuclides

the cryptic are explained further through the link Radioactive Decay’s Physics — these factors explain necessary energy-mass transactions

Is the E_hf1818 neutrino regulated radio component removed out of the nuclear reaction law, one receives only the expression of a stable nuclide, which not is the radio case. By that reason we safely know that the neutrino influences play an important role for the decay of the radio nuclides. But the related TNED theory — it is extensive — is not found in modern quarters: TNED is not welcome there. No way (npStructure).

— Each radionuclide has its own specific neutrino spectrum. And different radio types therefore does not interfere in their specific decays. Beta decays on the contrary have mutual influences because the neutrino emissions are of the same electron-positron type for all beta decaying atoms. Their corresponding energies can therefore also be generated by electron oscillations. In the radio nuclide case on the contrary, the neutrino levels are isolated from electron generating effects (Planck’s structural constant).

NuclearStructure:

Understanding the world we live in: We get credit for trying.

DEDUCING THE ATOMIC A-Z NUCLEAR CHART

A = n + p A = mass number — number of original fundamental neutron = whole fundamental atomic masses

= n + Z

n = A – Z the actual practically atomic physical case in any way — Z = the nuclear charge = the atomic electron charge

With the three named nuclear compositions as delimited by the Jumbo Proton n-Zp-n ¦ »A=Z» nuclide, the ideal Z(n-p) ¦ Z=A/2 nuclide, and the Jumbo Neutron Z(n-p-n) ¦ Z=A/3 nuclide, the theoretical region for all possible nuclides is identified by its absolute limits and borders — with respect to the discussed ring structure in the TNED toroid nuclear complex:

Theoretical limits of atomic nuclide spectra as related by nuclear n-p-structure

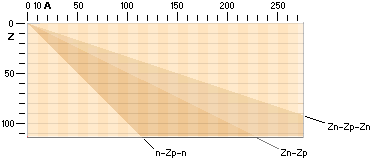
The theoretical limits for all possible atomic nuclei in a general A-Z nuclide chart, related physics (Deducing the AZ).

The diagram summarizes the extreme limits for the Jumbo Proton (n-Zp-n) left bottom and the Jumbo Neutron Z(n-p-n) right limit in the theoretical nuclide spectrum, as related. Z denotes atomic number or nuclear charge, A denotes mass number, n denotes neutron nuclear surface structure type and p denotes proton nuclear surface structure type, as explained in related nuclear physics (TNED — see Nuclear STRUCTURE).

DEDUCING THE A-Z CHART

The connection for the Nuclide static average value line A=12Z/5 is the average mean of the coefficients for the ideal Z(n-p) nuclides via k=1/2 with Z=A/2, and the Jumboneutron’s Z(n-p-n) nuclides via k=1/3 with Z=A/3. The average mean becomes [(1/2)+(1/3)]/2=5/12 with Z=5A/12, or A=12Z/5.

Author’sRef: MPcKärnMatIIIa.doc ¦ MPcKärnMat.doc ¦ MPcKärnMatII.doc

And that is also the stretch where we find the stable atoms and their surrounding unstable.

LighterToHeavier:

TNED BASIC RELATED ATOMIC NUCLEAR PHYSICS AND ITS MATHEMATICS

THE PLANCK STRUCTURE CONSTANT, THE ATOMIC MASSES, CAP and CWON

Building heavier from lighter —

basic related atomic nuclear principles (Neutrino Spectrum ¦ The Plateaus)

Because electron spectrum is the same for all atoms (beta decays) but not the neutrino radiation (the high frequency radiation associated with the building up of the atomic nuclear structures by fusions from lighter to heavier, our Sun the nearest source) mass equivalent electron energies CAN decompose all atomic nuclei according to the qualitative connection

E = hf = (m→γ)c² = (m←γ)c²

The same quantitatively decomposing energies namely

E = hf = (m→γ)c² ≠ (m←γ)c²

gravitation, the atomic nucleus, is not a particle — BackGROUND ¦ Atomkärnan ¦ CompareQm

gravitation cannot be compressed, it is already standing on a zero

gravitation is not light — ENERGY related physics LAW

light is not a particle, but its matter generated induction quanta makes it convenient to express as »traveling photons»:

MAX PLANCK WAS RIGHT, ALBERT EINSTEIN with associated WAS WRONG

mass is not light — EXPERIMENTAL CONFIRMATIONS

mass cannot be created, only destructed, and has hence quality light energy equivalents

ENERGY EXCHANGE — NO MASS CREATION. See also The Particle Proof , Swedish edition.

formed by the fusions guarantee that the released (exothermal) energies in building heavier from lighter does not break or destroy the already built lighter atomic nuclei structures. The neutrino energies connecting the atomic nuclei buildings, so constrainedly form different fractal (Planck structural constant) levels (see from Planck Ring 1). These so safely built levels become inwardly secured in that the highest neutrino frequencies belong to the lightest atomic nuclei, attesting that these in no way are compromised on credit of the heavier built structures.

— So in deducing the atomic masses, we must properly find the different exothermal fusion paths to each single individual atom and its nucleus, its actual atomic mass defect, and do the end experimental testing theory mass calculations from there, for any further heavier building: the Neutron Square, Neutron Squatre solutions as noted, is our only reference.

• The only possible spontaneously exothermally energetic way for the basic fundamental atomic nucleus the neutron to build heavier atoms, unequivocally must begin from a maximum closed packed neutron nuclei state, a Dmax (certifying the nuclei lie inside each others nuclear barriers, leading to direct fusion): A compact high gravitating neutron mass spherical body. Thereby a process begins of a gravitational (light’s gravitational dependency) managing concentric atomic production (CAP). The gravitational potential is the least in the center, analogously the local divergence c the highest, and thereby the fastest decaying neutrons: the atomic building process begins at the centre, ends on the surface (CWON). It is fast and releases humongous amounts of exothermal energy (Element formation’s two basic nuclide groups).

See a basic complementary basic description in

The Plateaus.

DeducingTheAZ

WAFO: Neutron Square solutions ¦ BaseGroupMassNumbers

Neutron Square solutions

THE MEAN ELLIPTIC WAVE FUNCTION

TNED NEUTRON SQUARE SOLUTIONS ATOMIC AND NUCLEAR RELATED MATHEMATICAL PHYSICS

Excerpts from the original Swedish edition (2003 — Toroid Nuclear Electromechanical Dynamics)

———————————————

Atomic Weights ¦ THE NEUTRON SQUARE PARAGONIC BODY ¦ Mean Ellipsis for Even and Odd ¦ THE WAVE FUNCTION ¦ The wave function’s explanation ¦ WaveFunction Description

Explain:

The (EE) neutron square horizontal elliptic basic equation

y = 0.2[5x(120 + 5x)]^½

has a simple (PREFIXxSIN) associated damped cosine wave functional form:

y = cos 0.2[5x(120 + 5x)]^½

A = 5x accounts for the graphical scale adoption.

This PREFIXxSIN neutron square elliptic associated damped cosine wave functional form has the followingt close general first provisional connection to the experimentally measued atomic masses:

—————————————————————————————————————

mATOM = Uu ¦ atomic weight U = mATOM/u, u atomic mass unit m(6C12)/12 named 1 Dalton (1.66033 t27 KG)

—————————————————————————————————————

The plateaus: THE ORIGIN OF THE GENERAL NEUTRON SQUARE WAVE EQUATION 2003

WAFO ¦ PREFIXxSIN

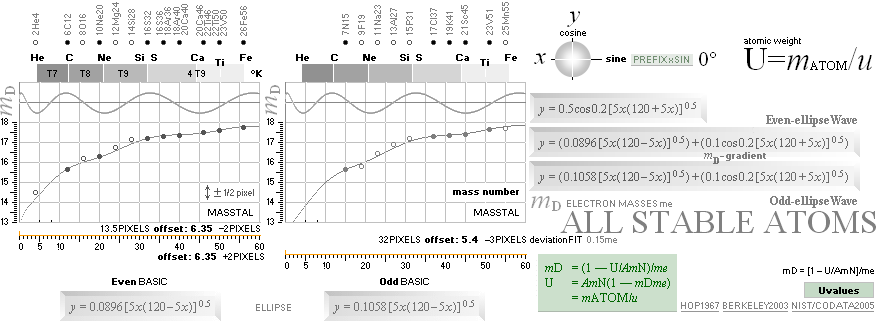
The open rings apart from the curved elliptic wave line follow (VerticalElliptic) specific fusion paths by vertical elliptic arcs with specific mass defect equations. See further (Sw., ed original) in Wave function’s Explanation.

The Plateaus:

DeducisngTheAZ ¦ PLATÅERNA — The plateaus¦ NuclearSTRUCTURE ¦ IronTOP ¦ HIGESTmD

Transdlated 22Oct2023 from the original 2003:

Helium plateau to Carbon plateau

From the Helium Reference the nucleus captivates a stable state (ideal nuclear). We then conceive the nucleus on (the previously described) nuclear line for the Z(n-p) type — the nuclide chart’s angled space, right below the static mean value line (12/5-line). As the nucleus grows with n-p pair nuclear structures, it however approaches the Jumbo Proton — which gives instability. Already at the Carbon plateau, a phase shift appears where stable nuclides can form with the addition of one neutron. Then nuclear fusions can proceed toward stable nuclides with growing mass defect — more atomic binding energy — in a slower phase where the additional neutron gives a certain margin ahead.

Neon plateau to Silicon plateau

When further neutrons must be added to fend off the divergence toward a Jumbo Proton condition, the nucleus enters into the state phase three, the Neon plateau. From this point — the n-Z(n-p)-n nuclide type — the mass defects growth can occupy an even larger interval before the nucleus enters stage phase four, the Silicon-Sulfur plateau. From that point more nuclear neutron structure addition is demanded to bring (Planck) ring stability to the nucleus

— the 2n-Z(n-p)-2n type nuclides. And as earlier, this fill promotes an even longer stage and with even lower mass defect increase before the nucleus enters the final Calcium plateau.

Calcium plateau

From here the nucleus receives a further neutron dilutive fill in guaranteeing a stable nuclide. We now see the 3n-Z(n-p)-3n nuclide type appear mixed with the 2n-Z(n-p)-2n type from the previous plateau, and with certain neutron additions. This phase then continues finally up to the iron top where the 18 limit is reached by the nuclide individual 26Fe56 (HIGESTmD) — composition 15n-26p-15n, analogously 2n-26(n-p)-2n. That finalizes the basic nuclear synthesis.

HeavyGroup:

The heavy nuclide group’s Certification

The heavy nuclide group

Continuing the atomic production — exothermal (heat and light emission of the work mass-energy waste in building heavier from lighter) — from the basic ideal top mass number 60 highest atomic mass defect point, demands a presence of specifically neutron rich low mass beta active nuclides, type:

₂He⁶, ₃Li⁸ and ₆C¹⁶.

Such exothermal provisions are only possible in a — TNED deduced (CAP) — situation where atomic production begins from a maximum dense celestial body of neutrons. With their decay — fastest where the gravitational potential is the lowest, that is in the body center — close an tight fusion rings are asserted to bring out heavier atoms from the lighter. Beginning from a celestial core with a such iron end atomic produced center (no significant net neutron quote in the center), heavier atoms beginning from neutron decay need a farther distance (slower decay) from the center, securing a higher rate of neutron quote — and thereby a much more diverse possible set of also the most heavy atomic products. However, the fusions agents into the heavier nuclides (A>60) depend on momentarily produced beta active atoms of the above suggested type: neutron structure rich nuclei who can complete the near fusion processes in building the most heavy possible atoms.

This is readily physically energetically impossible unless all those atoms — during the very short moment of time in the celestial body’s fusion phase — far less than a second — are collected in one and the same massive (primary neutron) body. Sharing the (enormous) massive energy release during the (short) collective fusion phase, guarantees that the momentarily (normally fast) decaying beta active nuclides will WAIT on their decays — momentarily FED by the environmental exothermally fusion emitting mass-energy equivalents. This high surge energy throughput delay will provides the necessary standard relatable energy calculable support in building the heavier atoms. The fusion processes as such, are guaranteed as long as the involved fusion ring agents are situated inside each others nuclear potential barriers (meaning: inside each others circumscribed spheres) — where the close nuclear ±e structure sucks and takes care of the spontaneous fusions.

See further from

Lighter to Heavier.

WAFO

BaseGroupMassNumbers: EllipticWaveEquation: — up to mass number 60 — WAFO

NeutronSquareSolutions

THE GENERALIZED WAVE-ELLIPTIC FORMULA

The originally 2003 compiled Elliptic-Wave equation for the light atomic nuclide chart up to mass number 60 — see NuklidTab4A2023.ods TabellA

THE BASE GROUP MASS NUMBERS NEUTRAL ATOMIC MASS DEFECTS

— from the original works in MsWorks ¦ which Microsoft suddenly and abruptly denied computer access to after a rude Microsoft update on a Windows Vista computer (Aug2008) — supported by bought jurisdiction.

” .. the foundation of freedom, justice and peace in the world”. World Jurisdiction Enterprise. Mississippi 1820.

Unless there are other here unknown candidates:

ONLY WAY TO DEDUCE EXPERIMENTALLY CONCORDANT ATOMIC MASS VALUES IS TO TRACE THE ATOM’S ACTUAL FUSION TRACK FROM ITS SET OF ORIGINAL NEUTRONS and the two different nuclear structural types of ±e electric displacement:

the neutron nuclear structural n type and the proton nuclear structural p type

| | | | | | | | | | | | | | | | | | | | | | .. | ¦ | ¦ | ¦ | ¦ | ¦ | ¦ | ¦ | ¦ | ¦ | ¦ | ¦ ..

with all their possibly relatable combinations, see Nuclear STRUCTURE in related physics

— its trace of atomic mass defects, forming the foundation in building heavier from lighter

Mintrusion2008: Base

With the Microsoft 2008 intrusion into the pending work, also followed a blockade of a possible transfer code to other spread sheet programs (Microsoft EXCEL and its imitating OpenOfficeCalc). The Microsoft MsWORKS inhibited corresponding mod/REST operators had been compromised: Microsoft EXCEL has other routines. See describing example in EOOK — and some additional ”Microsoft EXCEL features” in the following text and cell code examples. Through these ”Microsoft modification” the MsWORKS original was blocked. Until the recent attempts (Aug2023) to find a solution, the work made no progress. This is the solution.

THE LIGHT atomic NUCLIDES

FROM A=1 TO A=60¦64

G0—isoA0 — BaseGroupMassNumbers — from Z

Basic Group — the group base mass number A for the given atomic number Z — valid up to Z=30, light nuclide chart only (Amax=64):

The role of Z here is only of an organizing manner, according to the basic observations on the Elliptic and wave coherences on the HOP experimental values

A = [2Z+Zmod2 + (Zdiv[17+ 5(1–Zmod2)])(2×round[(Z–8+Zmod2 )/ 2(6–Zmod2)])]=A’

+ (1–ζ6)(–1)Zmod2(A’–Z)mod3 [1–(Zmod3)div2]

ζ 6 = INT[1–(abs[Z0/6–1] – [Z0/6–1])/2] ................................... Zζ = .. ,111,101,91,81,71,60,50,40,30,20,10,00,–1–1,–2–1,–3–1, ..

OPEN OFFICE CALC SwedishVersion:

= HELTAL(1-(ABS(Z/6-1)-(Z/6-1))/2)

A’ OPEN OFFICE CALC SwedishVersion = R3:

= 2*Z + REST(Z;2) + (HELTAL(Z/(17 + 5*(1-REST(Z;2)))))*(2*AVRUNDA((Z-8+REST(Z;2))/(2*(6-REST(Z;2)))))

+(1-HELTAL(1-(ABS(Z/6-1)-(Z/6-1))/2))(–1)^(REST(R2;2))*(REST(R3 - R2;3) * (1 - HELTAL(REST(R2;3)/2) ))

ALL IN ONE CELL ONLY:

= 2*Z+REST(Z;2)+(HELTAL(Z/(17+5*(1-REST(Z;2)))))*(2*AVRUNDA((Z-8+REST(Z;2))/(2*(6-REST(Z;2)))))

+((1-HELTAL(1-(ABS(Z/7-1)-(Z/7-1))/2)))*(-1)^(REST(Z;2))*(REST((2*Z + REST(Z;2)+(HELTAL(Z/(17+5*

(1-REST(Z;2)))))*(2*AVRUNDA((Z-8+REST(Z;2))/(2*(6-REST(Z;2))))))-Z;3)*(1-HELTAL(REST(Z;3)/2)))

Proof:

NuklidTab4A2023.ods Table4 —— verified ¦ Author’sREF: MPcKärnMatIIIa.doc 9Aug2003 —— algorithm: just the atomic number Z plus »integer selector algebra»

APART FROM THE BASE GROUP, THERE ARE FIVE MORE ISOTOPIC GROUPS:

NuklidTab4A2023.ods TableA

How it did develop —

all based on and from the (2003) sudden discovery of the Neutron Square apparently universal paragon geometrical mathematics

on comparing atomic masses from known tables: elliptic equations, simple wave form adoptions — whole numbers selector algebra

(Swedish original ..)

Analysen visar att bestämningen av en nuklids massdefekt helt och hållet betingas av dess underliggande sammansättning, dess fusionsväg. Känner man denna och kan återföra nukliden på mera elementära grundnuklider får man en specifik massdefektsekvation.

..

Det innebär att hela nuklidkartan byggs upp som en händelse (som en organism som breder ut sig): varje nytt steg beror av sammansättningarna i föregående och kan beräknas om man känner nämnda. Av den anledningen, speciellt med tanke på grundnukliderna upp till Helium (första fasen) finns inte den typ av ”kärnekvation” som den moderna akademin försöker uppställa.

..

Man måste dela in nukliderna i olika grupper, en huvudgrupp med underliggande isotopgrupper som följer händelsevägen via växande massdefekt upp till Järntoppen. Därefter, från Järntoppen mot nuklidkartans slut, följer en annan typ av analys med avtagande massdefekt. Man måste emellertid också känna samtliga instabila (betaaktiva) nukliders massdefekter och hur de bildas innan en fullständig beskrivning kan ges. De betaaktiva nukliderna spelar nämligen en (delvis) stor roll i bildningen av de tyngre nukliderna.

Men ingen sådan övergripande (betaaktiv) analys har ännu utförts i UniversumsHistoria (Okt2023).

Hela nuklidkartan blir (alltså) en karta över hela den kosmiska händelsehistorien.

..

Mass number A generally for all basic nuclides (from the Helium reference) up to the Iron group (part of the original draft):

A = A0

+ AEvenFromCarboOddFromNitro

+ AcorrectionBelowCarboNitroPreference

A = [2Z+Zmod2

+ (Zdiv[17+ 5(1–Zmod2)])(2×round[(Z–8+Zmod2 )/ 2(6–Zmod2)])]=A’

+ (1–z 6)(–1)Zmod2(A’–Z)mod3 [1–(Zmod3)div2]

Author’sRef: MPcKärnMatIIIa.doc ¦ MPcKärnMat.doc ¦ MPcKärnMatII.doc

isoGROUP 1

G1— isoA

The actual isoA¦1-5 cell equations are written out as follows.

— What we know (related physics, NS solutions):

— There is no ”overload version” possibly defining the isotope mass numbers in a given atom — before, prior, that specific atom base nucleus has been made/specified.

So, when the math to this analyze was first projected (from 2003), it had to be on »all the tabled stable isotopes together», in order for the author to have any the smallest chance in »luring out the hidden matrix». That is: all based on already existent atomic mass tables. Below is an illustrating extract of the actual providing data needed (the neutron square content) in order to succeed on the exercising quest.

isoGROUP 1

G1— isoA

A = isoAJ

+ isoAU

+ isoAneon

:

A_isoA1 = isoJ1

+ isoU1

+ isoAneon

isoJ1 = (A+2)g10(1–Z0mod2)

isoU1 = A(Zmod2) – b[round([(Z–7)/2]mod8/8) – 1]

isoAneon = ζ1(1– γ10)(Φ[(1+λ)Z + λ(1–Amod2)] + (1–λ))

b = (Zmod2)nollarViaJämna(round[(nHe+1)/4] – 1)mod2 (INT[(nHemod7)/7+7/8])

nHE = (Z – 6 – Z0mod2)/2

Φ = INT[1–(|a2–1| – [a2–1])/2] ......................................................... A|Φ= 11,41,61,90,101,121,151,161,190

a2 = (Amod9)(Zmod9) ......................................................................... A|a2= 11,48,618,90,105,1218,1542,1656,190

λ = INT[1–(abs[Z0/03–1] – [Z0/03–1])/2] ........................................ Zλ = .. ,51,41,31,20,10,00,–10,–20, ..

ζ1 = INT[1–(abs[Z0/01–1] – [Z0/01–1])/2] ........................................ Zζ = .. ,51,41,31,21,11,00,–10,–20, ..

γ10 = INT[1–(abs[Z0/10–1] – [Z0/10–1])/2] ......................................... Zγ = .. ,111,101,90,80, .. ,20,10,00, ..

OpenOfficeCalc:

isoJ1 = (A+2)*Gma10*(1-REST(Z0;2))

isoU1 = (A*REST(Z0;2)-AVRUNDA(REST(((REST(Z0;2)*(N24+0*REST((AVRUNDA((nHe+1)/4;0)-1);2))*HELTAL(OM(nHe<0;nHe;REST(nHe;7))/7+7/8))*(Z0-7)/2);8)/8;0)-1)*(REST(Z0;2)*(N24+0*REST((AVRUNDA((nHe+1)/4;0)-1);2))*HELTAL(OM(nHe<0;nHe;REST(nHe;7))/7+7/8))

N24 = OM(N25<0;N25; REST(N25;2)) ¦ the tricky MicrosoftEXCEL-OpenOffice cell code removal of the original MsMORKS mod operator consequence

N25 = (AVRUNDA((nHe+1)/4;0)-1)

= (AVRUNDA((((Z0-6-REST(Z0;2))/2)+1)/4;0)-1)

IT MEANS THAT VERY WELL IN MsWORKS 4.0 — BLOCKED FOR FURTHER WINDOWS USE BY MICROSOFT 2008 IN WINDOWS VISTA — WE CAN CALCULATE THE G1 A-VALUES from the Z inputs IF WE STILL HAVE A TYPE WINDOWS XP COMPUTER ALIVE accepting MsWORKS. — BUT HOWEVER NO SO DIRECTLY in Microsoft Excel and OpenOffice — »the Excel imitator». To do so also in these latter programs, we need to add the above N25 and N24 in two demanding separate cell rows. See the complete — but very lengthy — solution in last rank 5 below. See NuklidTab4A2023.ods Table4, Rows 2 and 3.

isoAneon = Theta1*(1-Gma10)*(L10*((1+Lda)*Z0+Lda*(1-REST(A;2)))+1-Lda)

L10 = HELTAL(1-(ABS(K10-1)-(K10-1))/2)

K10 = REST(A;9)*REST(Z0;9)

isoAneon = Theta1*(1-Gma10)*(HELTAL(1-(ABS(REST(A;9)*REST(Z0;9)-1)-(REST(A;9)*REST(Z0;9)-1))/2)*((1+Lda)*Z0+Lda*(1-REST(A;2)))+1-Lda)

= (HELTAL(1-(ABS(Z/01-1)-(Z/01-1))/2))*(1-(HELTAL(1-(ABS(Z/10-1)-(Z/10-1))/2)))*(HELTAL(1-(ABS(REST(A;9)*REST(Z0;9)-1)-(REST(A;9)*REST(Z0;9)-1))/2)*((1+(HELTAL(1-(ABS(Z0/3-1)-(Z0/3-1))/2)))*Z0+(HELTAL(1-(ABS(Z0/3-1)-(Z0/3-1))/2))*(1-REST(A;2)))+1-(HELTAL(1-(ABS(Z0/3-1)-(Z0/3-1))/2)))

b = 6-A

nHE = (Z0-6-REST(Z0;2))/2

ΦFi = HELTAL(1-(ABS((REST(A;9)*REST(Z0;9))-1)-((REST(A;9)*REST(Z0;9))-1))/2)

λLda = HELTAL(1-(ABS(Z0/3-1)-(Z0/3-1))/2)

ζ₁ = HELTAL(1-(ABS(Z/01-1)-(Z/01-1))/2) ¦ Theta1, i.e., Tzeta (ϑ not explicitly available 2003 in this production)

γ₁₀ = HELTAL(1-(ABS(Z/10-1)-(Z/10-1))/2) ¦ Gma10

OpenOfficeCalc ¦ Tabell4 G1:

G1.1:

(A+2)*Gma10*(1-REST(Z0;2))+

(A*REST(Z0;2)-AVRUNDA(REST(((REST(Z0;2)*(N24)*HELTAL(OM(nHe<0;nHe;REST(nHe;7))/7+7/8))*(Z0-7)/2);8)/8;0)-1)*(REST(Z0;2)*(N24)*HELTAL(OM(nHe<0;nHe;REST(nHe;7))/7+7/8))+

Theta1*(1-Gma10)*(HELTAL(1-(ABS(REST(A;9)*REST(Z0;9)-1)-(REST(A;9)*REST(Z0;9)-1))/2)*((1+Lda)*Z0+Lda*(1-REST(A;2)))+1-Lda)

G1.2:

(A+2)*(HELTAL(1-(ABS(Z/10-1)-(Z/10-1))/2))*(1-REST(Z0;2))+

(A*REST(Z0;2)-AVRUNDA(REST(((REST(Z0;2)*(N24)*HELTAL(OM(((Z0-6-REST(Z0;2))/2)<0;((Z0-6-REST(Z0;2))/2);REST(((Z0-6-REST(Z0;2))/2);7))/7+7/8))*(Z0-7)/2);8)/8;0)-1)*(REST(Z0;2)*(N24)*HELTAL(OM(((Z0-6-REST(Z0;2))/2)<0;((Z0-6-REST(Z0;2))/2);REST(((Z0-6-REST(Z0;2))/2);7))/7+7/8))+

(HELTAL(1-(ABS(Z/01-1)-(Z/01-1))/2))*(1-(HELTAL(1-(ABS(Z/10-1)-(Z/10-1))/2)))*(HELTAL(1-(ABS(REST(A;9)*REST(Z0;9)-1)-(REST(A;9)*REST(Z0;9)-1))/2)*((1+(HELTAL(1-(ABS(Z0/3-1)-(Z0/3-1))/2)))*Z0+(HELTAL(1-(ABS(Z0/3-1)-(Z0/3-1))/2))*(1-REST(A;2)))+1-(HELTAL(1-(ABS(Z0/3-1)-(Z0/3-1))/2)))

G1.3:

(A+2)*(HELTAL(1-(ABS(Z/10-1)-(Z/10-1))/2))*(1-REST(Z;2))+

(A*REST(Z;2)-AVRUNDA(REST(((REST(Z;2)*(N24)*HELTAL(OM(((Z-6-REST(Z;2))/2)<0;((Z-6-REST(Z;2))/2);REST(((Z-6-REST(Z;2))/2);7))/7+7/8))*(Z-7)/2);8)/8;0)-1)*(REST(Z;2)*(N24)*HELTAL(OM(((Z-6-REST(Z;2))/2)<0;((Z-6-REST(Z;2))/2);REST(((Z-6-REST(Z;2))/2);7))/7+7/8))+

(HELTAL(1-(ABS(Z/01-1)-(Z/01-1))/2))*(1-(HELTAL(1-(ABS(Z/10-1)-(Z/10-1))/2)))*(HELTAL(1-(ABS(REST(A;9)*REST(Z;9)-1)-(REST(A;9)*REST(Z;9)-1))/2)*((1+(HELTAL(1-(ABS(Z/3-1)-(Z/3-1))/2)))*Z+(HELTAL(1-(ABS(Z/3-1)-(Z/3-1))/2))*(1-REST(A;2)))+1-(HELTAL(1-(ABS(Z/3-1)-(Z/3-1))/2)))

G1.4:

(A+2)*(HELTAL(1-(ABS(B5/10-1)-(B5/10-1))/2))*(1-REST(B5;2))+

(A*REST(B5;2)-AVRUNDA(REST(((REST(B5;2)*(N24)*HELTAL(OM(((B5-6-REST(B5;2))/2)<0;((B5-6-REST(B5;2))/2);REST(((B5-6-REST(B5;2))/2);7))/7+7/8))*(B5-7)/2);8)/8;0)-1)*(REST(B5;2)*(N24)*HELTAL(OM(((B5-6-REST(B5;2))/2)<0;((B5-6-REST(B5;2))/2);REST(((B5-6-REST(B5;2))/2);7))/7+7/8))+

(HELTAL(1-(ABS(B5/01-1)-(B5/01-1))/2))*(1-(HELTAL(1-(ABS(B5/10-1)-(B5/10-1))/2)))*(HELTAL(1-(ABS(REST(A;9)*REST(B5;9)-1)-(REST(A;9)*REST(B5;9)-1))/2)*((1+(HELTAL(1-(ABS(B5/3-1)-(B5/3-1))/2)))*B5+(HELTAL(1-(ABS(B5/3-1)-(B5/3-1))/2))*(1-REST(A;2)))+1-(HELTAL(1-(ABS(B5/3-1)-(B5/3-1))/2)))

G1.5: only variables: B5=Z and B2

(B4+2)*(HELTAL(1-(ABS(B5/10-1)-(B5/10-1))/2))*(1-REST(B5;2))+

(B4*REST(B5;2)-AVRUNDA(REST(((REST(B5;2)*(B2)*HELTAL(OM(((B5-6-REST(B5;2))/2)<0;((B5-6-REST(B5;2))/2);REST(((B5-6-REST(B5;2))/2);7))/7+7/8))*(B5-7)/2);8)/8;0)-1)*(REST(B5;2)*(B2)*HELTAL(OM(((B5-6-REST(B5;2))/2)<0;((B5-6-REST(B5;2))/2);REST(((B5-6-REST(B5;2))/2);7))/7+7/8))+

(HELTAL(1-(ABS(B5/01-1)-(B5/01-1))/2))*(1-(HELTAL(1-(ABS(B5/10-1)-(B5/10-1))/2)))*(HELTAL(1-(ABS(REST(B4;9)*REST(B5;9)-1)-(REST(B4;9)*REST(B5;9)-1))/2)*((1+(HELTAL(1-(ABS(B5/3-1)-(B5/3-1))/2)))*B5+(HELTAL(1-(ABS(B5/3-1)-(B5/3-1))/2))*(1-REST(B4;2)))+1-(HELTAL(1-(ABS(B5/3-1)-(B5/3-1))/2)))

It works.

ALL THE ABOVE IN THE FIRST ATOMIC NUMBER CELL. THEN COPIED FOR EACH NEW CELL WITH EXTENDING COLUMN PREFERENCE UP TO Z=28, MASS NUMBER 60.

— It is amazing that OpenOffice can handle this — because OpenOffice in other tracks is sometimes readily horrible. .. cannot write in capitals .. program insists on converting to literals, or vice versa, in forming constant names .. suggests .. cannot leave the user alone STOP SURVEILLING SPYING AND MAKING CHANGES TO MY WRIT .. shut the fuck up .. .. we are trembling on the brink .. cannot select last color .. cannot read bookmarks backwards .. looses text caret position in text documents .. why was I born .. COPYING an OpenOfficeCalc to a new document it is IMPOSSIBLE to get rid of the Original’s 178 Constants by erasing That Table, these must be erased manually, one by one, through repeated several button clickings .. why not let us die directly .. and when pressing Ctrl+F3 in finding out what Constants are there, no key shortcut exists to get into the actual Box: must Click to get there .. no single keyboard operations, no sir .. but the Design is OK .. don’t touch me .. so in time we learn how to escape the OpenOffice Orcs .. taking care not to be too creative ..

— On the other hand:

THE OpenOffice FREEWARE AT PRESENT 2023 IS APPARENTLY THE BEST HUMANITY CAN OFFER.

Yes, we CAN get things done .. but OpenOfficeProgram Man .. you’ve got to fix the engine .. jises ..

The other 4 groups are somewhat simpler.

The70: BGMN

70 stable isotopes

NuklidTab4A2023.ods Table4 —— verified mapping ¦ the five atomic group finalized with their corresponding atomic and mass numbers

OPEN OFFICE HAS NO HERE KNOWN FUNCTION BY WHICH TO LEAVE A CELL BLANK IF ITS RESULT IS IRRELEVANT to the author: OPEN OFFICE DEMANDS A VALUE 0. SO TO SHOW THE RESULTS IN ONLY VALID POSITIONS, NO OTHER WRITS, WE MUST MAKE A NEW TABLE USING THE CELL CODE FOR EACH POSITION: if B2 = 0 then ShowNothing: Sw.: Om(B2=0;””).

AND THE MOST STRANGE OF ALL IN OPEN OFFICE: IF ANOTHER OPEN OFFICE DOCUMENTS IS OPENED with the first showing its cell code in the inbox THAT TEXT DISAPPEARS ON OPENING THE NEW OPEN OFFICE DOCUMENT.

It just proves on the many examples in OpenOffice, that IT is a more or less MicrosoftOffice2000 Imitation — with SOMETIMES extremely careless and left out functionality. Microsoft Office (2000) has no such.

— The OpenOffice case: Most likely poor partial functionality because the programming personnel cannot solve the programming functions: If they could, there would be no problems. Meaning: it is the programming language — or the programming person not understanding what a computer is for: the functionality is anyway incomplete. Say I’m wrong.

— But the design is OK.

A = isoJ1

+ isoU1

+ isoAneon

A_isoA1 = (A+2)γ10(1–Z0mod2)

+ A(Zmod2) – b[round([(Z–7)/2]mod8/8) – 1]

+ ζ1(1– γ10)(F[(1+λ)Z + λ(1–Amod2)] + (1–λ)) ¦ A = mass number in group isoA0, the base group — the structure extends from there:

NuklidTab4A2023.ods TableA

isoGROUP 2

G2— isoA2

A = isoJ2

+ isoU2

+ isoN2

— IT LOOKS LIKE A RAIL YARD WITH SETS, CARTS, SWITCHES, longer or shorter trails, SIMPLE WHOLE NUMBER ORGANIZATIONS ..

isoJ2 = γ16(1 – γ27)(1 – Z0mod2)(2Z0 + round[(2Z0 + 1)/10] – abs(1 – 2Z0mod32) + [1 – 2Z0mod32])

isoU2 = Z0(18/8)ζ8(1 – ζ9)

isoN2 = ζ10(1 – ζ15)(1 – Z0mod2)(2Z0 + 1)

γ16 = INT[1–(abs[Z0/16–1] – [Z0/16–1])/2] ................................... Zζ = .. ,191,181,171,161,150,140, .. ,20,10,00, ..

γ27 = INT[1–(abs[Z0/27–1] – [Z0/27–1])/2] ................................... Zζ = .. ,291,281,271,260,250,240, .. ,20,10,00, ..

ζ 8 = INT[1–(abs[Z0/08–1] – [Z0/08–1])/2] ................................... Zζ = .. ,111,101,91,81,70,60,50,40,30,20,10,00, ..

ζ 9 = INT[1–(abs[Z0/09–1] – [Z0/09–1])/2] ................................... Zζ = .. ,111,101,91,80,70,60,50,40,30,20,10,00, ..

ζ 10 = INT[1–(abs[Z0/10–1] – [Z0/10–1])/2] ................................... Zζ = .. ,111,101,90,80,70,60,50,40,30,20,10,00, ..

ζ 15 = INT[1–(abs[Z0/15–1] – [Z0/15–1])/2] ................................... Zζ = .. ,171,161,151,140,130,120, .. ,20,10,00, ..

OpenOfficeCalc:

isoJ2 = Gma16*(1-Gma27)*(1-REST(Z;2))*(2*Z + AVRUNDA((2*Z+1)/10;0)-(ABS(1-REST(2*Z;32))+(1-REST(2*Z;32))))

isoU2 = Z0*(18/8)*(Theta8*(1-Theta9))

isoN2 = Theta10*(1-Theta15)*(1-REST(Z;2))*(2*Z+1)

γ₁₆ = HELTAL(1-(ABS(Z/16-1)-(Z/16-1))/2)

γ₂₇ = HELTAL(1-(ABS(Z/27-1)-(Z/27-1))/2)

ζ8 = HELTAL(1-(ABS(Z/08-1)-(Z/08-1))/2) ¦ Theta8, i.e., Tzeta (ϑ not explicitly available 2003 in this production)

ζ9 = HELTAL(1-(ABS(Z/09-1)-(Z/09-1))/2)

ζ10 = HELTAL(1-(ABS(Z/10-1)-(Z/10-1))/2)

ζ15 = HELTAL(1-(ABS(Z/15-1)-(Z/15-1))/2)

OpenOfficeCalc ¦ Tabell4 G2:

(HELTAL(1-(ABS(B5/16-1)-(B5/16-1))/2))*(1-(HELTAL(1-(ABS(B5/27-1)-(B5/27-1))/2)))*(1-REST(B5;2))*(2*B5 + AVRUNDA((2*B5+1)/10;0)-(ABS(1-REST(2*B5;32))+(1-REST(2*B5;32))))+B5*(18/8)*((HELTAL(1-(ABS(B5/8-1)-(B5/8-1))/2))*(1-(HELTAL(1-(ABS(B5/9-1)-(B5/9-1))/2))))+(HELTAL(1-(ABS(B5/10-1)-(B5/10-1))/2))*(1-(HELTAL(1-(ABS(B5/15-1)-(B5/15-1))/2)))*(1-REST(B5;2))*(2*B5+1)

isoGROUP 3

G3— isoA3

A = isoJ3

isoJ3 = g16(1 – g27)(round([Z0mod2]/4)(2Z0 + abs[round(2Z0/10) – 7])(1 – Z0mod2)

γ16 = INT[1–(abs[Z0/16–1] – [Z0/16–1])/2] ............................. Zγ = ,191,181,171,161,150, .. ,50,40,30,20,10,00 ..

γ27 = INT[1–(abs[Z0/27–1] – [Z0/27–1])/2] ............................. Zγ = ,291,281,271,260,250, .. ,50,40,30,20,10,00 ..

OpenOfficeCalc:

isoJ3 = Gma16*(1-Gma27)*(AVRUNDA(REST(Z;6)/4;0)*(2*Z+ABS(AVRUNDA(2*Z/10;0)-7)))*(1-REST(Z;2))

γ₁₆ = HELTAL(1-(ABS(Z/16-1)-(Z/16-1))/2)

γ₂₇ = HELTAL(1-(ABS(Z/27-1)-(Z/27-1))/2)

OpenOfficeCalc ¦ Tabell4 G3:

(HELTAL(1-(ABS(B5/16-1)-(B5/16-1))/2))*(1-(HELTAL(1-(ABS(B5/27-1)-(B5/27-1)/2)))*(AVRUNDA(REST(B5;6)/4;0)*(2*B5+ABS(AVRUNDA(2*B5/10;0)-7)))*(1-REST(B5;2))

isoGROUP 4

G4— isoA4

A = isoJ4

isoJ4 = g20(1 – g25)(1 – Z0/2mod2)(2Z0 + 6)(1 – Z0mod2)

γ20 = INT[1–(abs[Z0/20–1] – [Z0/20–1])/2] ................................... Zζ = .. ,231,221,211,201,190,180, .. ,20,10,00, ..

γ25 = INT[1–(abs[Z0/25–1] – [Z0/25–1])/2] ................................... Zζ = .. ,281,271,261,251,240,230, .. ,20,10,00, ..

OpenOfficeCalc:

isoJ4 = Gma20*(1-Gma25)*((1-REST(Z/2;2))*(2*Z+6))*(1-REST(Z;2))

γ₂₀ = HELTAL(1-(ABS(Z/20-1)-(Z/20-1))/2)

γ₂₅ = HELTAL(1-(ABS(Z/25-1)-(Z/25-1))/2)

OpenOfficeCalc ¦ Tabell4 G4:

(HELTAL(1-(ABS(Z/20-1)-(Z/20-1))/2))*(1-(HELTAL(1-(ABS(Z/25-1)-(Z/25-1))/2)))*((1-REST(Z/2;2))*(2*Z+6))*(1-REST(Z;2))

isoGROUP 5

G5— isoA5

A = isoJ5

isoJ5 = g20(1 – g29)round(INT[(Z0mod12)/4]/2)(2B50 + 2[1 + abs(HELTAL[2Z0/7] – 8)])(1 – Z0mod2)

γ20 = INT[1–(abs[Z0/20–1] – [Z0/20–1])/2] ................................... Zζ = .. ,231,221,211,201,190,180, .. ,20,10,00, ..

γ29 = INT[1–(abs[Z0/29–1] – [Z0/29–1])/2] ................................... Zζ = .. ,321,311,301,291,280,270, .. ,20,10,00, ..

OpenOfficeCalc:

isoJ5 = Gma20*(1-Gma29)*AVRUNDA(HELTAL(REST(Z;12)/4)/2;0)*(2*Z + (2*(1+ABS(HELTAL(2*Z/7)-8))))*(1-REST(Z;2))

γ₂₀ = HELTAL(1-(ABS(Z/20-1)-(Z/20-1))/2)

γ₂₉ = HELTAL(1-(ABS(Z/29-1)-(Z/29-1))/2)

OpenOfficeCalc ¦ Tabell4 G5:

(HELTAL(1-(ABS(B5/20-1)-(B5/20-1))/2))*(1-(HELTAL(1-(ABS(B5/29-1)-(B5/29-1))/2)))*AVRUNDA(HELTAL(REST(B5;12)/4)/2;0)*(2*B5 + (2*(1+ABS(HELTAL(2*B5/7)-8))))*(1-REST(B5;2))

MintrusionArt:

THE MICROSOFT INTRUSION (Aug2008) led to so much (sad and weary) trouble. And it was such a release when (at last Aug2023) the light came through,. The solution here deserves all thorough attention on that dramatic history’s compressed content:

— »Fuck you Microsoft2008», the galactic leading prohibiter of a perfectly functioning MsWorks spread sheet program Aug2008 on Windows Vista: Microsoft2008, destroyer of MsWORKS mod operator, vandalized in Microsoft EXCEL and so apparently imitated equally by the free OpenOfficeCalc.

— As it so seems, the aim was and is to promote a deeper insight into the world business inducement of appearing to be the best of the best in the world of computer programming science:

REST(-A;B) ¦ -A mod B

MsWORKS ¦ Division algorithm ¦ Windows Calculator latest W7 ¦ Borland’s Pascal:

–A

Microsoft (prohibiting further Windows use of MsWORKS from 2008)EXCEL¦OpenOfficeCalc:

+A

----------------------------------------------

HELTAL(-0.99)

MsWORKS ¦ Division algorithm ¦ Windows Calculator latest W7 ¦ Borland’s Pascal

–0

Microsoft (prohibiting further Windows use of MsWORKS from 2008)EXCEL¦OpenOfficeCalc:

–1

----------------------------------------------

Microsoft Enterprise:

— If you cannot handle mathematics on the computer level:

— What can you handle?

”Restart your computer or we will do it for you”.

• Where is world jurisdiction

— allowing such raging human right intrusion partying and feasting?

Not one word human right recognition.

TNED.

WE, the customers, bough the Windows HUMANITY DEVELOPING products during a period of several decades, BROUGHT the company UP, buying merchandise for tens of thousands of dollars PER PERSON. How were we met? A spit in the face, a foot in the back, vandalized text, dictating, overriding, private computer settings, a controlling and demanding authority of We-Own-You attitudes — and We have the Deciding power over your computer.

”Pick a time”.

”Fuck you asshole”.

Muzzled. Handcuffed. Bandaged.

”Let’s kick off ..”.

”Was this helpful?”.

”Like us”.

Toying humanity. Openly. Freely.

Muzzled. Handcuffed. Bandaged.

Tagged Cattle.

— Why, and how, in the world do humans take such shit?

— Or.. They don’t. But no one is allowed — deeply afraid — to say it.

.. the foundation of freedom, justice and peace in the world

— Where is world jurisdiction — other than bought bitches to serve Microsoft Enterprise human right intrusions?

Not one word human right recognition.

Talk about lawlessness and anarchy. It is gushing.

Microsoft:

— Offer fully freeware Microsoft OFFICE fully detailed to every single born human being on Earth, from here to eternity, at no cost,

to be used freely as Pen, Rubber and Paper. Remove the brakes, and let humanity DEVELOP on humanity’s provisions and conditions, not Microsoft’s.

Stop killing humanity.

Stop Human Trafficking.

IT IS NOT ALLOWED TO USE HUMANITY FOR PROFITING PURPOSES, NOT BY BODY, NOT BY MIND, INTENTIONALLY OR NOT, NOT AT ALL. ALL FORMS AND TYPES OF SLAVERY SHALL BE FORBIDDEN.

Where is world jurisdiction? Where is United Nations?

United Nations explicit formulation in UDHR10Dec1948 — and present Trafficking.

Slavery (Swedish classic encyclopedic) definition, five words:

— A state of personal noFree.

(Sw., ett tillstånd av personlig ofrihet).

Human right recognition. Microsoft. GOOGLE. Police. Prosecutor. Court. World Business Enterprise. Not one word. Not a sound. Not a hint.

Where not heard: violence is gushing.

.. the foundation of freedom, justice and peace in the world

BaseGroupMassNumbers

modREST2008: 10Sep2023

Regaining the mod and Rest operators in Microsoft’s New EXCEL and — the imitating — Open Office Calc

— NOTE: MICROSOFT Windows Calculator still existed on Windows 7 y2015, same as the old MsWORKS mathematical division algorithm mod operator:

— Not in Windows 10 — several reports on failed calculator in W10 — many cookies blocking web sites inhibits further free information on the W10 calculator subject: Still not one word human right recognition. No mentioning. Not a sound. Not a hint. Just interrupting. Blocking. Demanding cookies consent.

AFTER THE 2008 MICROSOFT REMOVAL/banning OF FURTHER WINDOWS COMPUTER USE OF MsWORKS

CRUSHING THE CONTINUED COMPILATION WORKS ON THE NEUTRON SQUARE SOLUTIONS RESULTS IN ATOMIC MASSES DETERMINATION

2003—10Sep2023 REVISITING THE NEUTRON SQUARE MATHEMATICS

The deuced mathematics to the Light Nuclide Group — up to mass number 60

——————————————————————————————————————

This following was the simple spread sheet calculus code we failed (TNEDa0EOOK) to create a corresponding transfer expression for in OpenOfficeCalc (and MicrosoftEXCEL):

The original (2008) in MsWORKS NuklidTab4.wps:

Rest(A;B)

BORLAND’S DELPHI PASCAL: A mod B

for the case of A less than zero (nHe)

Rest(-1;2)

IN MsWORKS (blocked 2008+ by Microsoft Windows Vista from further computer use)

— AND IN BORLAND’S PASCAL DELPHI CODE, the mod operator

as derived in basic mathematics from the DIVISION ALGORITHM

it reads

= -1

In OPEN OFFICE and MICROSOFT EXCEL it presents the result:

= 1

— Why?. Because in Microsoft’s standard Windows Calculator — latest Windows 7 — the mod operator has the same status as the above mentioned MsWORKS, Borland Pascal, General Mathematics, basic deduced division algorithm.

AND WE SHOULD TAKE ADVANTAGE OF THIS OPPORTUNITY TO ALSO UNDERLINE FURTHER IN OPEN OFFICE Swedish Version Here THE STRANGEST OF ALL mathematics CALCULUS PROGRAMMING FEATURE:

OPEN OFFICE ¦ MICROSOFT EXCEL:

Heltal( 0.99) ¦ = 0 INT( 0.99) = 0 ¦ correct

Heltal(-0.99) ¦ = -1 INT(-0.99) = -1 ¦ incorrect

ONLY PERSONNEL THAT is occupied by DO NOT CARE MUCH ABOUT ELSE THAN PROFIT CAN DO THAT. Say. Do correct. No serious scientific. Intelligence is still OK. Problem is: low on moral.

— » Please Refill. Follow Instructions .. ».

No PHYSICS — AND MATHEMATICS — DEVELOPS ON SUCH PROGRAMMING SKILLS- RESULTS.

(It smells rotting brains all over the place ..).

The reason why Microsoft — apparently after MsWORKS ¦ after Windows 95 — did lose its nerve and fell into other inducements, is not known here, except for the apparent possibility of leaving the company to less educated.

correctly related mathematics — for developing physics purposes in explicit:

Heltal(±0.99) ¦ = 0 INT(±0.99) = 0

The INT integer operator takes the integer part of the argument

— an: makes no operation or modification on the argument,

♦ independent of sign = direction.

IN 2008 MICROSOFT EXCLUDED ALL USE OF MsWORKS — WINDOWS VISTA — AFTER AN UNANNOUNCED UPDATE, WHICH THE COMPANY REFUSED TO HELP REMOVE SO THAT WE COULD CONTINUE TO USE MsWORKS SPREAD SHEET PROGRAM.

Microsoft blocked further use. An abrupt interference in and a direct attack on our work.

— See also The Microsoft LIST. The great interest 2008+ from Microsoft to educate humanity.

NuklidTab4A2023.ods TableA From NuklidTab4.wks 2008 — finally solved for OpenOffice and Microsoft EXCEL

So .. what has all this to do with presenting details in nuclear physics? Explain.

THIS WAS THE BOTTLENECK WE COULD NOT SOLVE BEFORE — in translating the excellent MsWORKS NuklidTab4.wks to a corresponding OpenOffice — and Microsoft Excel — spread sheet code:

The MsWORKScalc original — during the actual work around 2008:

SwedishVersion

REST((AVRUNDA((nHe+1)/4;0)-1);2)

English:

REST((ROUND ((nHe+1)/4;0)-1);2)

Namely for the case where nHe becomes = –2;

See BaseGroupMassNumbers:

— if not properly handled according to the deduced mathematics

the division algorithm —1mod2 = —1 which Microsoft removed from use 2008 and replaced as exemplified above with a +1, then also apparently adopted by other (OpenOffice) impressed programmers —

the overall result crashes (like the ”Error41” in the movie PayCheck, Ben Affleck 2003: perfect machine — blocked from use).

The solution .. finally:

SOLUTION IN OPEN OFFICE (English) — as tested and verified:

IF(nHe<0 ; nHe ; Rest(nHe;2))

.. a separate context breaching type of explaing atomic physics language ..

Explain ..

PART OF the WHOLE INTENTION BEHIND THE DEDUCED NUCLEAR/ATOMIC PHYSICS WAS TO USE ONLY WHOLE NUMBERS — PROVING THAT ATOMIC MASSES THROUGH THE NEUTRON SQUARE INDEED CAN BE DEDUCED LIKE A RAIL YARD WITH POINTS AND SWITCHES DELIMITING NUMBERS OF ALLOWED CARTS, VACANCIES, WHEN AND HOW TO SWITCH FROM ONE PART TO ANOTHER, BASED ON THE ADVISED NEUTRON SQUARE BASIC GEOMETRY AND ITS INHERITED ELLIPTIC/wave EQUATIONS.

Now detailed in BaseGroupMassNumbers.

Type (the Division Algorithm deduced mod operator: A mod B = subtract B from A until rest is <B:

— if A<0 and B>0 the operation is locked on rest = A<0)

Rest(-A;2) = -A

-A mod 2 = -A

THE APPENDING WINDOWS 7 OPERATING SYSTEM CALCULATOR HAS A mod OPERATOR:

• it works perfectly the same as the concordant division algorithm,

• but not in Microsoft EXCEL —

• and not its imitating OpenOfficeCalc.

a STRICT NUMERICAL solution in OpenOfficeCalc looks like this (detailed ex: MproblemSolved):

INT(√1+nHe/|nHe|) → +nHe = 0 ¦ –nHe = 1

THE SQUARE ROOT OPERATOR ALWAYS TAKES THE SQUARE DIAGONAL,

AND THE INTEGER OF THE SQUARE DIAGONAL IS ALWAYS THE SQUARE SIDE 1

INTEGER(ROOT(1+nHe/ABS(nHe))

[HELTAL (ROT (1+nHe/ABS(nHe))] → +nHe = 0 ¦ –nHe = 1

(1 – [HELTAL (ROT (1+nHe/ABS(nHe))]) → +nHe = 1 ¦ –nHe = 0

MsWORKS — Borland’sDelphi

Rest(nHe;2)

=

continue ..

SWrSep2023:

SWEDISH REFLECTED — steady growing interest in preserving biodiversity and caring for universal animal rights: It is such a joy;

Tala om att stänga vägen för mänsklighetens naturliga naturvetenskapliga utveckling:

• För ändamålet och tillfället: Att få bedriva affärer — som tillvarons allra högsta enda mål

• av DRIFT. Inte plan. Inte avsiktligt.

— Enbart genom ett girighetsfall. Egobegär. Dess euforiska domäner leder sinnet in på vägar som täcker för allt annat.

Mänskligheten får inte tillgång till Resurserna — copyrightägda juridiskt köpta kärringar skyddar hela verksamheten: lag. Den mänskliga historiens i särklass värsta huggsexa.

— H. Ugga:

— Vad har du för utbildning?

— The foundation of freedom, justice and peace in the world.

— DE BLIR SKITFÖRBANNADE. NÄR DERAS VÄRDERINGSLUSTA AVTÄCKS FÖR DEN SKITIGA AVGRUND DEN ÄR, UPPRESER SIG PÖBELN OCH KRÄVER KORSFÄSTELSE.

— I sinnlig bemärkelse. Inte ett enda vettigt ord. Inget människorättsligt igenkännande. Inte ett pip. Tvärt om. Hugg och slag, lydnad och bestraffning. Ingen utbildning.

— OCH MAN UNDRAR: VILKEN SKITAKTIGHET ÄR DET EGENTLIGEN SOM STÅR ALLRA HÖGST?

— Är det att avliva en obekväm, rent fysiskt? Eller är det att häva ur sig sådana elakheter mot offret, rent verbalt, att offret begår självmord —— enbart för att slippa vidare se utseendet på kräket?

Inte ett ord MänniskoRätt. Inte ett pip. ”.. varje individ och varje organ i samhället ..”. Befolkningen undanhålls kunskaperna.

Det är inget fel på intelligensen. Problemet: låg moralisk nivå: Lydnad och bestraffning. Ingen utbildning. Ingen undervisning.

Urlåg ordning — allt avgörs genom flest gillapoäng. Ingen resonerande, relaterande, beskrivande och förklarande förmåga. Lydnad och bestraffning.

continued;

[HELTAL(ROT (1+nHe/ABS(nHe))] *nHe + (1 – [HELTAL(ROT (1+nHe/ABS(nHe))])*Rest(nHe;2)

MicrosoftEXCEL — OpenOfficeCALC.

IF(nHe<0 ; nHe ; Rest(nHe;2))

MicrosoftEXCEL — OpenOfficeCALC.

— Microsoft — after MsWORKS 2008 — is definitely not mathematically educated. No way. But, please: do disclaim: show examples.

— Breaking, Hacking, Chopping.

— ”Restart your computer, or we will do it for you”. Free open jurisdictional certified experimentation enterprise on humanity mind manipulation and decision.

NuklidTab4A2023.ods TableA From NuklidTab4.wks 2008 — finally solved for OpenOffice and Microsoft EXCEL

BaseGroupMassNumbers

ALL STABLE ISOTOPES UP TO ATOMIC NUMBER 27 — max mass number 60 — the NeutronSquare horizontal square side scale

The population is stranded on a culture where it is only allowed to use 1% of the brains capacity ..

Microsoft Enterprise alternative (C++) HighIQ solutions?

Who in this universe would understand a STRUCTURE of

IF A>B AND C .. while K AND not D in .. where IF L=E AND ..

instead of THE MUCH MORE VIEWABLE AND GRASPABLE TYPE

λ = INT[1–(abs[Z0/03–1] – [Z0/03–1])/2] ........................................ Zλ = .. ,51,41,31,20,10,00,–10,–20, ..

ζ1 = INT[1–(abs[Z0/01–1] – [Z0/01–1])/2] ........................................ Zζ = .. ,51,41,31,21,11,00,–10,–20, ..

γ10 = INT[1–(abs[Z0/10–1] – [Z0/10–1])/2] ......................................... Zγ = .. ,111,101,90,80, .. ,20,10,00, ..

Meaning:

— A regular rail-yard system with (many trains, ranks, of) whole numbers and defined flipping and flopping relays has (supreme) a more explaining overviewing power than any other (here) known method.

See all the details in

BaseGroupMassNumbers.

modREST2008

HIGHESTmD:

Related physics meets established physics on atomic nuclear presentations

HIGHEST SCORED MASS DEFECT CONTEST

THE PREFERENCES ARE SWITCHED true 1432 against untrue 3241 unless a more thorough explanation exists:

— What we know: atomic mass and its properties cannot be described solely from the point of view of nuclear properties. The electron mass must be included.

HIGHEST SCORED MASS DEFECT — COMPARING ATOMIC WITH NUCLEAR: ATOMIC IS THE CLEAR WINNER

— The Table1 exerpt below compares mass defect values in electron masses (1me = 0.511 MeV) between

atomic mass defect mD(atomic) = (1 – U/Am_n)/m_e and

nuclear mass defect mD(nuclear) = (Am_n – Zv – U)/m_e ¦ FM1975 s124sp2ö ”ΔM = ZMp + NMn – Mnuc” where

U = m(ATOMexperimentallyMeasured)/u(m[6C12/12]=1.66033 t27 KG) ¦ HOP1967 ¦ BerkeleyNational 2003 ¦ Nist/Codata 2005

A mass number

Z atomic number — nuclear charge, atom’s electron mass charge

m_n = 1.0086652000u

m_e = 0.0005485982u

v = m_n – m(1H1=1.007825200u) = 0.00084000000000u

mD(atomic) = (1 – U/Am_n)/m_e

apparently COMPARING NUCLEAR completely unknown in modern corridors

Never18: HIGHESTmD

Captial18e

Never @18

Highest mass defect atoms — COMPARING ESTABLISHED AND RELATED ATOMIC AND NUCLEAR PHYSICS

18Sep2023 — enhanced and more detailed version from Nov2007 — exact values depends on chosen constants

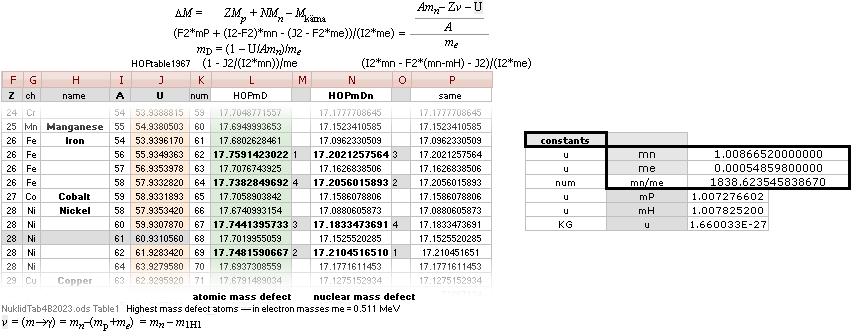
NuklidTab4B2023.ods Table1

The difference: Nuclear mass defect (Am_n – Zv – U)/m_e uses A Z U. Atomic mass defect (1 – U/Am_n)/m_e uses only A U.

THE ATOMIC MASS DEFECT SOLUTION IN NEUTRON SQUARE HAS ONLY ONE BASIC EllipticTrigonometricHyperbolic form: mD = 6 + (1/5)√ 60² — (60 — [ A–K]²)/E see NSsolutions

Compare The rZ results from Atomic Nucleus in related physics:

♦ atomic/nuclear mass and nuclear radius have no space metric connection to nuclear charge —

neutron basics: the neutron decays to an atom; the neutron has no (significant) nuclear charge.

♦ mass — gravitation — and charge — heat and light, electricity and magnetism — does not connect.

COMPARE The Related Physics Deduction of The Electric Charge Q —— no direct mass connection: Q² = (m/R)(A/dT); Q²/m = A/RdT; m = Q²RdT/A = mA/RdT × RdT/A = m. No light E=hf connection.

♦ light does not connect kinetics [Light’s Liberty Clause].

See explaining details in Proton Radius and Atomic Nucleus.

U = m(atom — from mass spectroscopic experimental measures)/u —

older (1960+) ”atomic weight”, present (2023) ”relative atomic mass”.

In UniverseHistory: just U you [ = Real Weighable Mass/u].

u = 1.66033 t27 KG (the Dalton unit), = m(6C12)/12 — different sources in different epochs have different u.

COMPARE WIKIPEDIA, (Atomic mass):

” At the peak of binding energy, nickel-62 is the most tightly bound nucleus (per nucleon), followed by iron-58 and iron-56.[19]”,

WIKIPEDIA Nuclear binding energy curve (19Sep2023)

The present science community is not aware of any other preference than the already present established:

— ”Atomic mass defect” is not a scientific community established term — no such article in Wikipedia.

———————————————

ORIGINAL Nov2007: IronTOP ¦ ComparingMAC ¦ Formula ¦ Atomic Nucleus — Jul2023¦ ProtonRADIUS

CompHmD: HIGHESTmD

Further comparing examples and sections

COMPARE again THE CONCEPTUAL DESCRIPTION on atomic mass defect, the table above:

IRON 26Fe56_17.759 is the strongest built atom that needed the highest working energy waste to build, correspondingly the hardest most energetically demanding atom to restore on its original bricks, followed by Nickel 28Ni62_17.748, 28Ni60_17.744 and again Iron 26Fe58_17.738.

The population is apparently a related victim of a too meager developed terminology in atomic and nuclear physics. We find the exact same order of business in comparing from the more regular equations

atomic (AmN – U)/A

nuclear (AmN – U – Zv)/A

NuklidTab4C2023.ods TabellB A1+

Introducing ”Z” transfers values to nuclear mass defects — A LOWER ORDER OF STRONGEST most wasted mass energy work on its building BINDING ATOMIC ENERGY.

Iron it is.

See also (Sw) the Odd and Even Nuclide Groups — ending on IRON (from zero neutron quote, related), the (CAP) reason why all primary celestial bodies develop an iron core center.

See also further in

FAMQ ¦ FIBAPO ¦ DIFFERENCE BETWEEN ATOMIC AND NUCLEAR ¦ Clarifying the U equation

unless already familiar — related.

:

Introducing ”Z” in the calculations only decreases the maximum atomic strength.

— »Well .. I give a shit about atomic. I’m just interested in nuclear».

Further exemplifying the different concepts

THE COMPARING NUCLEAR — DIFFERENCE BETWEEN ATOMIC AND NUCLEAR

The comparing nuclear diagrams examples (internally calculated comparing values from experimentally measured atomic masses) further underlines the hazard and adventure in — generalizing and favoring — the idea and concept of ”nuclear binding energy”:

(FIBAPO): Unaware of the Neutron Square solutions, it was impossible to foresee any a coming conflict. Humanity was so involved in the industrial progress from the technical revolution. And it just evolved and grew. The wealth of the world ..

As developed during the 1900s, present (2023) academic quarters still uses a concept of type ”binding energy potential to the number of nucleons” (HOPweizQuote1967 below) as connected to our complex describing ”a good approximation to the true masses”.

’good approximation to true masses’

HOPweizQuote1967

That is the whole story point in this presentation: the accurateness in presenting the (2003) discovered NS natural neutral atomic mass quantities. And the tools, the theories and their difficulties (compared) involved to reach a related explanation.

The present scientific community

The ’binding energy per nucleon’ concept relates to the classic modern academic idea of the atomic nucleus as enveloping freely inner (spinning) existent neutrons and protons. As commonly termed nucleons, these relates to a The present established explanation of the atomic nucleus and its physics.

The terminology ”Binding energy per nucleon” (Wikipedia, Atomic mass¦Nuclear binding energy¦Nuclear binding energy curve, Sep2023) is also the present (2023) only apparent (freely available) concept in our highly beloved Earth science community when discussing and presenting associated atomic mass subjects on a theoretical (calculable) basis.

In the atomic mass defect preference, table above HIGHESTmD,

” At the peak of binding energy, nickel-62 is the most tightly bound nucleus (per nucleon), followed by iron-58 and iron-56.[19]”,

WIKIPEDIA Nuclear binding energy curve (19Sep2023)

— The present science community is not aware of any other preference than the already present established.

— You know, the one type »We know everything»-standard. MustBuyBook.

”.. most tightly bound nucleus ..”

— »When we have removed all the Zv electrons from the atom, the most tight bound atomic nucleus is ..».

— There is no atomic nuclear physics understandable relatable reason in the statement.

Never18 IN RELATED ATOMIC NUCLEAR PHYSICS:

the leading maximum atomic tight binding energy top is reserved for iron-56 followed by nickel-62 and nickel-60: In concern of a general presentation of an Atomic species and its property, other preferences than an Atomic one will cause confusion. Nuclear binding energy always exposes a lower quantitative value.

DIFFERENCE BETWEEN ATOMIC AND NUCLEAR ¦ Clarifying the U equation

— THE »Take» in modern corridors is understandable — other top rated atomic individuals — WHERE academic theory lacks terminology:

NotRepresented:

” The page ”Atomic mass defect” does not exist”.

Wikipedia 9Oct2023.

A search on ”mass defect” on the other hand is redirected in Wikipedia to the article on

Nuclear binding energy.

nuclear mass defect

atomic mass defect MDa = AmN – U ¦ U = mATOM/u ¦ u = m(6C12)/6 = 1 Dalton

nuclear mass defect MDn = AmN – U – Zv ¦ v = nino = mN – (mP + me) = mN – m1H1 (= 0.00084u)

MDn – Zv = MDa MDn = MDa + Zv.

v: the work mass energy waste that built the first atom — 1H1 Hydrogen — from the fundamental atom: The Neutron [ FAMQ ]

THE DIFFERENCE BETWEEN ATOMIC AND NUCLEAR (binding energy, mass defect) can apparently not be clearly explained and related without understanding the concept of atomic mass defect (Clarifying the U equation):

The choice of »explaining everything by nuclear preferences» is the only one available in established corridors. With the introduction of the Neutron Square paragon solutions (NSsolutions) in related physics (TNED), the present scientific idea is (partly, or perhaps completely) overrun: no direct comparing is possible (other than: two different property domains).

———————————————

HIGHESTmD ¦ Comp ¦ ComparingNuclear

HIGHESTmD

ComparingNuclear: Comp — Compiled 9Oct2023 ¦ Difference between atomic and nuclear — illustrated on experimentally measured values

In modern standard academic quarters — atomic and nuclear physics — there is only one single basic preference: experimentation.

Neutron Square Solutions has no such. It is a PLATE: neutral atomic mass defect values for comparison. No electric or magnetic experimentation details or other involved — other than the computer (Windows 3.1, Paintbrush) on which the discovery was made (2003) in studying the (HOP1967) atomic mass tables. The reader might himself lure out the rest, as also this author is an equal standard tourist on the page.

PURPOSE (NSsolutions):

COMPARING ATOMIC MASS DETERMINATION

Main Weizäcker liquid drop model equation — nuclear mass defect type

B(Z,N ¦ MeV) = 15.75A – 0.711000Z²A^–1/3 – 17.8A^2/3 – 23.7(A – 2Z)²/A ±¦0: 11.18A^–1/2 + Zv ¦ WeizCalifornia 2023 NSdeDIA13

B(Z,N ¦ MeV) = 14.00A – 0.61Z(Z–1)A^–1/3 – 14.0A^2/3 – 84.2(A/2 – Z)²/A ±¦0: 34.0A^–3/4 adjust. ¦ HOP1967 NSdeDIA10

General attitude:

ANY COMPARING CONTEST

between nuclear mass defect and atomic mass defect on any quest of precise ATOMIC masses

WILL BE OUT OF THE QUESTION

Statement:

On observation of established claims connecting atomic mass to nuclear binding energy

———————————————————————————————————

There is no available cosmic way, path, or other known universal opening to calculate a precision atomic mass from nuclear mass defect — No way.

Oct2023:

But it seems like the scientific community is claiming exactly that, unless we here in UH are victims of even worse misunderstandings.

— This author would be happy if that also had been explained from the beginning.

— Well then, NeutronSquare Solutions suggests — in clarifying the issue:

♦ Let us compare: Weiz1:1967¦1975 — Weiz2: WeizCalifornia2023 — Weiz3 u=m(6C12)/12 ¦ CONOR.

NSdeDIA5: CoNu ¦ DIFFERENCE BETWEEN ATOMIC AND NUCLEAR

INTERNAL EXPERIMENTAL MEASURED VALUES WITH DIFFERENCE BETWEEN ATOMIC AND NUCLEAR

NuklidTab4C2023.ods Tabell1 Col. V W X BM

Proof:

WEIZSÄCKER EQUATION DETAILS AND PARAMETRIC CONSTANTS SOURCES:

HOP 1967 — HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967, section 9, p.9—8 — HOPweizQuote

The Swedish FOCUS MATERIEN 1975 s125sp2n

GENERAL ATOMIC MASSES DATA — concurrent [ except marginal on last decimals on later measures ]

HOP1967 BerkeleyNATIONAL2003 NIST/CoDATA2005+

NSdeDIA8: — THE 1967 ¦ 1975 COMPARING WEIZSÄCKER VERSION — NSde5

— See the present Wikipedia ¦ California University Weizsäcker versions in WeCALu

Revisting

FIRST (2003+) OBSERVED DIFFERENCES BETWEEN EXPERIMENTAL AND TNED-ACADEMIC(MAC)

HOPweizXP.ods Tabell1 Col. F G O

———————————————

Neutron Square Solutions — NSsolutions ¦ The Atomic Nucleus ¦ THE DIAGRAM DIFFERENCES — NSdeDIA9 ¦ THE here used WEIZÄCKER EQUATION PROGRAM — WeizPRO

1. The precision aspect (N) is already occupied by Neutron Square solutions — directly beginning from the neutron (Neutron Square Fundamentals — BasicCHART ¦ FIBAPO).

2. The established claims connecting atomic mass with nuclear binding energy uses the (foremost) so called semi-empirical mass formula (WIKIPEDIA, 15Oct2023 — WikiWEIZ) — most known as the Weizsäcker liquid drop model atomic nuclear equation. As so recognized (WikiWEIZ quote):

B(Z,N ¦ MeV) = 14A – 0.61Z(Z–1)A^–1/3 – 14A^2/3 – 84.2(A/2 – Z)²/A ±¦0: 34.0A^–3/4 ¦ HOP1967 example

” The semi-empirical mass formula therefore provides a good fit to heavier nuclei, and a poor fit to very light nuclei, especially ⁴He.”,

WIKIPEDIA, Semi-empirical mass formula (as quoted 15Oct2023).

The poor part is visually obvious as further clarified below in NSdeDIA9. But the ”good fit” part — where is it except on the intersecting regions @6Carbon12 and @10Neon20¦21¦22? Wikipedia (15Oct2023) gives no quantitative example.

However further ahead here, we will come back to that.

NSdeDIA9: The NSdeDIA8 comparing DIFFERENCES: — THE 1967 ¦ 1975 COMPARING WEIZSÄCKER VERSION

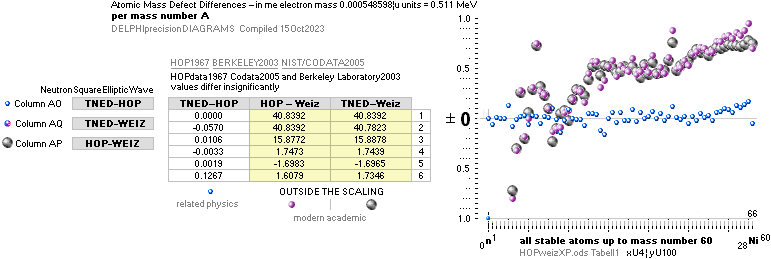
HOPweizXP.ods Tabell1 Col. AO AP AQ

A possible lead (» .. they don’t know it ..»):

See Wikipedia quote in Not represented — Clarifying the U equation.

— They the general scientific community apparently don’t know It.

Say it: THAT IS COMPLETELY WRONG — Further [» .. they don’t know it .. »] Clarifying Examples will follow.

NSdeDIA10: The Weizäcker PROGRAM — THE 1967 ¦ 1975 COMPARING WEIZSÄCKER VERSION

the parameters — different sources — vary depending on application — and epoch —

here assumed [ as proven ] not really deviating much from the presented:

NSdeDIA9

B(Z,N ¦ MeV) = Zv+ 14A – 0.61Z(Z–1)A^–1/3 – 14A^2/3 – 84.2(A/2 – Z)²/A ±¦0: 34.0A^–3/4 ¦ HOP1967

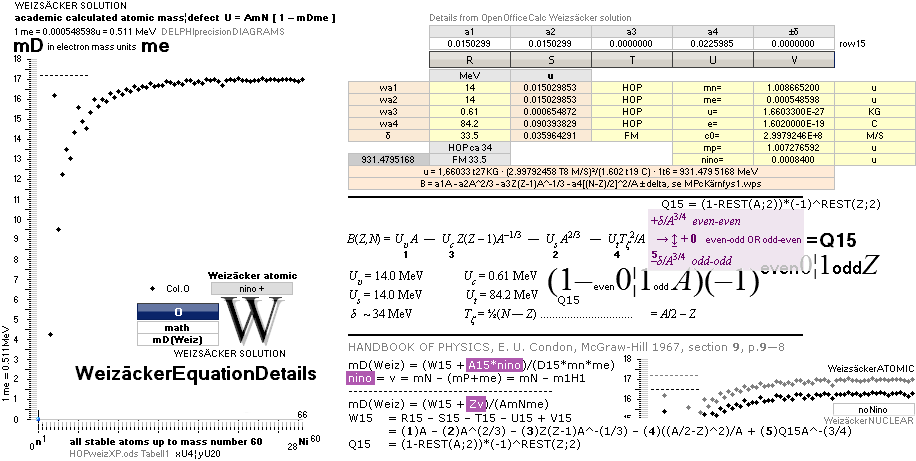
HOPweizXP.ods Tabell1 Col.O

B(Z,N ¦ MeV) = 14A – 0.61Z(Z–1)A^–1/3 – 14A^2/3 – 84.2(A/2 – Z)²/A ±¦0: 34.0A^–3/4 ¦ HOP1967

B(Z,N ¦ MeV) = 14A – 0.61Z(Z–1)A^–1/3 – 14A^2/3 – 84.2(A – 2Z)²/A ±¦0: 33.5A^–3/4 ¦ FM 1975 ¦ N–Z=A–Z–Z=A–2Z

MeV → m(ATOM): e(MeV)T6/c₀² ;

MeV → U = mATOM/u(Dalton):

MeV → U: e(MeV)T6/c₀²u ¦ U = mATOM/u ¦ 1u = m(6C12)/12 = 1.66033 t27 KG

———————————————

HOPweizQuote1967 ¦ WeizsäckerCALC ¦ WeizsäckerEquationDETAILS ¦ WeizäckerEVENoddCriteria — the Q15 solution

WhatZv: Zv

What’sUp?

— The thing is this:

atomic mass defect MDa = AmN – U ¦ U = mATOM/u ¦ u = m(6C12)/6 = 1 Dalton

nuclear mass defect MDn = AmN – U – Zv ¦ v = nino = mN – (mP + me) = mN – m1H1 (= 0.00084u)

The (HOP1967) Weizsäcker »nuclear binding enery»

”binding energy potential to the number of nucleons” equation

B(Z,N ¦ MeV) = 14A – 0.61Z(Z–1)A^–1/3 – 14A^2/3 – 84.2(A/2 – Z)²/A ±¦0: 34.0A^–3/4 ¦ HOP1967

is apparently — related — of the type nuclear mass defect (nuclear binding energy).

♦ But NSdeDIA10 lower right of the illustration

• the Weizsäcker equation formula as such has no inside referring »–Zv»

HOPweizXP.ods Tabell1 Col.O — Weizsäcker ATOMIC-mD HasA+Nino=Zv ¦ Col. AN — Weizsäcker NUCLEAR-mD HasNoNino=Zv

so that the end station exhibits this building:

the experimental nuclear matches the Weizsäcker atomic on its + 1Zv

or/and

the experimental atomic matches the Weizsäcker atomic on its + 2Zv

right below:

♦ The HOP1967 ¦ FM1975 Weizsäcker equation formula as such has no inside referring term »–Zv I am A Nuclear concept» or factor:explicitly declaring it is a nuclear mass defect expression.: it lies below the experimental nuclear MDa = AmN – U.

For it to reach the experimental nuclear for comparison, an extra additional +Zv must be added:

NSdeDIA11: NSdeDIA10

Comparing results on THE 1967 ¦ 1975 COMPARING WEIZSÄCKER VERSION

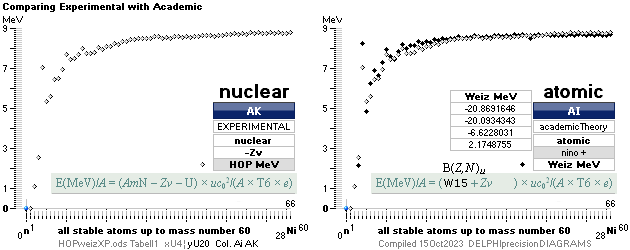
HOPweizXP.ods Tabell1

B(Z,N ¦ MeV) = 14A – 0.61Z(Z–1)A^–1/3 – 14A^2/3 – 84.2(A/2 – Z)²/A ±¦0: 34.0A^–3/4 + 1Zv ¦ nuclear-atomic HOP1967

So: In »fixing a most close match» between the two agents, the Weizsäcker form must either add one Zv to its original to reach the experimental NUCLEAR level — right part above:

— »ExperimentalNuclearMatchesWeizsäckerAtomic»;

Or add one extra Zv, in all 2Zv, to reach the fairly good matching experimental ATOMIC level:

— »ExperimentalAtomicMatchesWeizsäckerDoubleNuclear», right below:

NSdeDIA12: NSdeDIA11

Comparing results on THE 1967 ¦ 1975 COMPARING WEIZSÄCKER VERSION

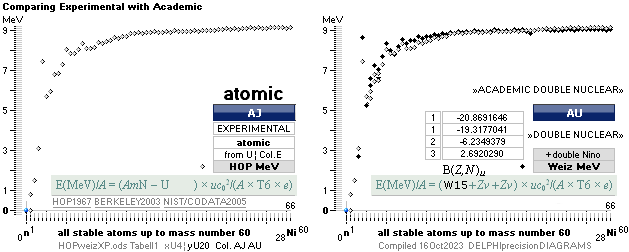
HOPweizXP.ods Tabell1

B(Z,N ¦ MeV) = 14A – 0.61Z(Z–1)A^–1/3 – 14A^2/3 – 84.2(A/2 – Z)²/A ±¦0: 34.0A^–3/4 + 2Zv ¦ atomic-DoubleNuclear

Besides these minor points:

♦ The Weizsäcker general solution is a horrible nightmare for the first light atoms — always outside the vertical scale.

• The basic idea (charged liquid drop model) apparently does not apply at all to the atomic nucleus as a corresponding fair model. Not even close to (FIBAPO).

Or as already stated (ComparingNuclear — proof continued):

There is no available cosmic way, path, or other known universal opening to calculate precision atomic mass from nuclear mass defect — No way.

— Why? Because it apparently already is occupied by the Neutron Square solution complex: geometric, trigonometric, elliptic, hyperbolic ¦ CompCALu2023.

— On the other hand, as deduced: The only difference between atomic mass defect MDa and nuclear mass defect MDn hangs on one single factor term: Zv. If no objective argument is visible, the simple way to make adjustments between the two is by adding or removing the factor Zv term.

See the comparing Weizsäcker diagrams in ComparingNUCLEAR.

See Wikipedia quote in Not represented.

Missing vocabulary: It seems like the modern academic idea has pushed Nuclear and Atomic into one more or less arbitrary useful Hollywood popular computer modeling galactic houseboat, traveling around the neighborhood, collecting near space data for further popular academic enlightenments.

ANY COMPARING CONTEST

between nuclear mass defect and atomic mass defect on any quest of precise ATOMIC masses

WILL BE OUT OF THE QUESTION

The present versions (16Oct2023) as collected @Internet on available sources:

There is (Oct2023) a COOKIES BLOCKED SCIENTIFIC FORUM

physics.stackexchange.com ¦ COMPARISON BETWEEN BETHE-WEIZSÄCKER-MODEL FOR NUCLEAR BINDING ENERGY AND MEASUREMENTS ¦ posted 2017

mentioning »The Weizsäcker mass equation syndrom».

— At first, in the Internet younger days, it was open for any Earth inhabitant to read and fetch inspiration from, now sadly partly blocked. A Weizsäcker equation diagram draft has been programmaticly exposedby a person — very extensive and visually educative — however not fully completed (or so recognized):

— The point to show was: ”the claimed precision does not seem to fit”.

The contributor refers to a German source (”Handbuch der Physik”) claiming ”the model should match the data with an error of 1 percent for large A”.

— The right end part above in NSdeDIA12 A=60 ends on a 4% deviated match (assumed to decrease further with growing A — stable atoms exemplified).

— So: where precision?

Try Comp2023.

Further explained an related below in NewWeiz2023,

NewWeiz2023: NSdeDIA12

THE NEWER WEIZSÄCKER SOLUTION VALUES

— The 1967¦1975 Zv issue removed ..

The development of electronics and the advent of powerful computers and new measuring techniques on all science branches — especially from the 1980s (Intel’s first microprocessor 8080) — made way for the Weizsäcker equation to reach new precision levels: chasing the nuclear origins behind the experimental results. We know that and also in part how by comparing the early (1967¦1975 — Comp) use of the Weizsäcker form with the present: 2023 Wikipedia sourcing articles, California university Comp2023 and other free document contributors.

The WeCALu (2023) diagrams below in NSdeDIA13 are the same as in NSdeDIA8 the 1967¦1975 version type, but now with modified constants, and some apparently significant and important changes on the actual algebraic structure (a clear adoptive change as seen in the comparing):

CHANGES:

Former [ 1967¦1975 ] most tight Weizsäcker match HOP1967 NSdeDIA10 :

B(Z,N ¦ MeV) = 14A – 0.61Z(Z–1)A^–1/3 – 14A^2/3 – 84.2(A/2 – Z)²/A ±¦0: 34.0A^–3/4 + 1Zv ¦ nuclear-atomic

B(Z,N ¦ MeV) = 14A – 0.61Z(Z–1)A^–1/3 – 14A^2/3 – 84.2(A/2 – Z)²/A ±¦0: 34.0A^–3/4 + 2Zv ¦ atomic-DoubleNuclear

The California University version

B(Z,N ¦ MeV) = 15.75A – 17.8A^2/3 – 0.711Z²A^–1/3 – 23.7(A – 2Z)²/A ±¦0: 11.18A^–1/2 ¦ WeizCalifornia

has automatically adjusted the earlier 1967¦1975 literature »nuclear-atomic» level issue

Col.O: The additional 2Zv 1967¦1975 NSdeDIA8 Weizsäcker NSdeDIA11 ”double nuclear” has disappeared completely, leaving only (the now corrected) single +Zv correction. But it is still not so mentioned in the actual PDF source (California University):

♦ IF the WeizCalifornia expression is taken as is

B(Z,N ¦ MeV) = 14A – 0.61Z(Z–1)A^–1/3 – 14A^2/3 – 84.2(A/2 – Z)²/A ±¦0: 34.0A^–3/4

— no included Zv = nino — the level of the right below Weizsäcker diagram receives the NSdeDIA14 same flaw as the earlier exposed — in this new costume a corresponding »ExperimentalAtomic matches Academic Nuclear»:

The California Match:

B(Z,N ¦ MeV) = 15.75A – 17.8A^2/3 – 0.711Z²A^–1/3 – 23.7(A – 2Z)²/A ±¦0: 11.18A^–1/2 + Zv ¦ atomic-atomic

is the diagram below right, and its experimental matching below left.

— The change in parameters between the old and new epoch has — apparently — automatically removed one Zv from the old standard, »at the same time» raised that lower level to the former included Zv end result. With so only one »still integrated» Zv, the Weizsäcker has reached »atomic mass defect standard».

By striving to approach the experimental results, the theoretical reasoning is forced to approach the Neutron Square Solution complex: neutral atoms. No involving electric or magnetic. No charge math. Guaranteed intrinsically electric clean.

THE READ CURVE BELOW [ latest 2020 results — BAGMAN ] IS THOUGH NOT OPTIONAL— WE STILL HAVE MUCH WORK TO DO ON DERIVING THE MORE PRECISE ELLIPTIC ATOMIC MASS SOLUTIONS, ATOM BY ATOM.

See also further comparison in

ComNorm

from

CONOR.

ComparingNuclear ¦ NewWeiz2023

NSdeDIA13: WeCALu: NSdeDIA8

NSdeDImA12

B(Z,N ¦ MeV) = 15.75A – 17.8A^2/3 – 0.711Z²A^–1/3 – 23.7(A – 2Z)²/A ±¦0: 11.18A^–1/2 ¦ WeizCalifornia

See the below left Weizsäcker diffference to the Experimental and TNED in Comp2023.

THE 2023 COMPARING California University VERSION ¦ and other associated similar

HOPweizXPa.ods Tabell1

NSdeDIA14: WhatZv

B(Z,N ¦ MeV) → mD¦me: e(MeV)T6/mec₀²u — Why the 18 scale? Never 18 — Captial18e.

— But the point is still: our included Zv — the left match above — is NOT the California University formula result, the here representative present 2023 Weizsäcker form. That one

B(Z,N ¦ MeV) = 15.75A – 17.8A^2/3 – 0.711Z²A^–1/3 – 23.7(A – 2Z)²/A ±¦0: 11.18A^–1/2 ¦ WeizCalifornia

lies lower [ Col.AN ]:

THE PURE WEIZSÄCKER EQUATION RESULTS REFLECT ..

— Just compare on the HOP nuclear alternative ..

— Do not lose the objective:

— Aim: atomic masses comparison (NS).

Not nuclear.

HOPweizXPa.ods Tabell1 Col.AN

It is mildly spoken confusing

— So: What’sUp?

There is apparently something the institution does not tell the visitor .. if the visitor did not forgot his shoes at home .. or the teacher has some holes in his universe ..

WeizCalifornia: ThePureWeizsäcker ¦ WeCALu

THE found 13Oct2023 UNIVERSITY OF CALIFORNIA free PDF has a detailed presented comparing picture with given and explained Weizsäcker parametric vales — not easy at all to find @Internet as a comparing source:

———————————————————————————————————————

E(binding, MeV) = B(Z,N ¦ MeV):

B(Z,N ¦ MeV) = 15.75A – 17.8A^2/3 – 0.711Z²A^–1/3 – 23.7(A – 2Z)²/A ±¦0: 11.18A^–1/2

NUCLEAR PHYSICS ¦ University of California ¦ Phys 239 Quantitative Physics Lecture 18

NUCLEAR PHYSICS free PDF, p2.Eq.(1)

MeV → m(ATOM): e(MeV)T6/c₀² ;

MeV → U = mATOM/u(Dalton):

MeV → U: e(MeV)T6/c₀²u ¦ U = mATOM/u ¦ 1u = m(6C12)/12 = 1.66033 t27 KG

B(Z,N ¦ MeV) = 14A – 14A^2/3 – 0.61Z(Z–1)A^–1/3 – 84.2(A/2 – Z)²/A ±¦0: 34.0A^–3/4 ¦ HOP1967 NSdeDIA10 ¦ CalOrder

B(Z,N ¦ MeV) = 14A – 0.61Z(Z–1)A^–1/3 – 14A^2/3 – 84.2(A/2 – Z)²/A ±¦0: 34.0A^–3/4 ¦ HOP1967 NSdeDIA10

B(Z,N ¦ MeV) = 14A – 0.61Z(Z–1)A^–1/3 – 14A^2/3 – 84.2(A – 2Z)²/A ±¦0: 33.5A^–3/4 ¦ FM 1975 ¦ N–Z=A–Z–Z=A–2Z

B(Z,N ¦ MeV) = a_VA – a_CZ(Z–1)A^–1/3 – a_SA^2/3 – a_A(N – Z)²/A + δ(N,Z)A^–3/4 ¦ Wikipedia, Semi-empirical mass formula, 15Oct2023,

no specified composition example: ”.. can again be derived by modeling ..”, ”.. not easily explained ..”.

— So: WHAT IS THE DIFFERENCE?

Again:

See Wikipedia quote in Not represented.

Is the present scientific community in a deep lack of explaining terms, or have we missed something?

THE DIAGRAMMATIC EXPERIMENTALLY

measured DIFFERENCE BETWEEN

atomic MASS DEFECT AND

nuclear MASS DEFECT as equated

atomic mass defect MDa = AmN – U ¦ U = mATOM/u ¦ u = m(6C12)/6 = 1 Dalton

nuclear mass defect MDn = AmN – U – Zv ¦ v = nino = mN – (mP + me) = mN – m1H1 (= 0.00084u)

is as illustrated below from experimentally measured atomic mass values

— but no established literature seems to describe or explain the terminology.

WeCALu ¦ ComparingNuclear

NSdeDIA7: AtomDiffNuc: FAMQ

The mass defect concept

DIFFERENCE BETWEEN ATOMIC AND NUCLEAR

The chart below is a partial extraction from the more generally extensive atomic nuclide chart (free available tables @Internet).

ORANGE dots: MDa = AmM – U ....... atomic mass defects

SkyBLUE dots: MDn = AmM – U – Zv nuclear mass defects

part of the atomic chart exemplifying the concepts

JUST CLARIFYING THE MANY SEEMINGLY CONFUSING basic and elementary TERMS AND CONCEPTS IN ATOMIC AND NUCLEAR PHYSICS

A mass number [ FAMQ], mN = 1.0086652u neutron mass, U = mATOM/u = atomic weight, u = m(6C12)/12 = 1.66033 t27 KG = 1 Dalton, Z atomic number = nuclear charge, atom’s number of electron masses

DIAGRAM: Atomic mass defect, Nuclear mass defect — often ”nuclear binding energy” in modern corridors — and their difference by quantity

Data source: part of 1967 HOP table on atomic masses — with minor end decimal differences, same values as in the tables from BERKELEY2003 and NIST/Codata2005 — the latter have more isotopic posts

The atomic mass defect

demands more WASTE energy input to become U than the available

minimum nuclear mass defect. The difference is:

= Zv = Z(mN — mH1) ¦ mH1 = 1.00782519u difference between atomic and nuclear

THE MORE WASTE MASS-ENERGY INPUT FOR ASSEMBLING THE END PRODUCT, THE HARDER TO REGAIN: the ”binding energy” concept:

— »My motivation to withhold information for you, is stronger than your attempt to get such info». »Binding energy».

FAMQ: RELATED PHYSICS

ComparingNuclear ¦ aMAD

All atoms are built from a number (A) of (FAMQ) fundamental atomic mass quanta called a NEUTRON (Chadwick 1932) with mass mN. AtomOrigin = A × mN. The neutron itself so also contains the first atom (1H1, Hydrogen). It shows on the (ca 12 to14 minutes) neutron decay in credit of its natural atomic unstable property, ending on the first stable atom, hydrogen mH: proton nucleus (mP) + 1 electron mass (me).

RELATED MDa:

All relations of the form

(AmN — U)/A or

(AmN — U)/AmN or

(AmN — U)/AMnme

belong to the same basic general ATOMIC (total) mass defect concept (MDa).

It is a value for the mass working energy needed to complete the entire atomic assembly. Entirely, or an averaged over the original number of A masses mN — or further expressed in electron masses (me).

RELATED MDn:

All relations of the form

(AmN — U — Zv)/A or

(AmN — U — Zv)/AmN or

(AmN — U — Zv)/AMnme

belong to the NUCLEAR mass defect concept (MDn) — often ”binding energy per nucleon” in established literature.

It exposes a lower quantity than MDa — another type of mathematics — never including the entire atomic energy (building) concept:

v = mN — mH1 ¦ the actual neutron decaying mass working energy waste in raising the building of the hydrogen atom:

— The atom’s nuclear charge Z balances the actual atom’s electron mass envelope.

The atomic mass defect (MDa)

AmN — U demands more WASTE energy input to become U than (MDn)

AmN — U – Zv the minimum nuclear mass defect. Difference is:

= Zv = Z(mN — mH1) ¦ mH1 = 1.00782519u ¦ v = 0.00084u

THE MORE WASTE MASS-ENERGY INPUT FOR ASSEMBLING THE END PRODUCT, THE HARDER TO REGAIN: the ”binding energy” concept:

— »My motivation to withhold information for you, is stronger than your attempt to get such info». »Binding energy».

— »What’s the difference?».

— »Love me or leave me». [ ITERATION PRINCIPLE ].

AtomDiffNuc ¦ ComparingNuclear

NuclearBindingEnergy:

COMPARE THE FOLLOWING:

Wikipedia, Nuclear binding energy (Oct2023)

” Nuclear binding energy in experimental physics is the minimum energy that is required to disassemble the nucleus of an atom into its constituent protons and neutrons, known collectively as nucleons.”.

THE REFERRED TABLE IN THE Wikipedia ARTICLE REFERS ONLY SINGLE ATOMIC MASSES, THERE IS NO CALCULATING COMPARING EXAMPLE between two different masses on releasing an example-neutron ALIKE THE BELOW NSdeDIA6:

NSdeDIA6: WikiQuote

EXPOSING THE BINDING ENERGY CONCEPT exemplified

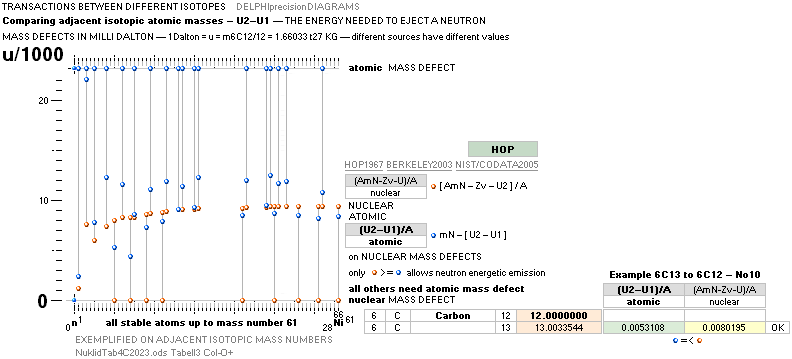
Explain:

IN The 18 cases of the exemplified extracted 27

the minimum energy that is required to disassemble the nucleus of an atom into

releasing energetically the equivalent Planck energy E=hf=mcr/t=mc² one neutron from a heavier atom U2 resulting in a lighter isotopic atom U1

is defined by the atomic mass defect

(AmN — U)/A.

Only in 9 cases of the exemplified extracted 27

the minimum energy that is required to disassemble the nucleus of an atom into

releasing one neutron from a heavier atom U2 resulting in a lighter atom U1

is sufficiently provided by the lower existing nuclear mass defect

(AmN — U — Zv)/A, or ”the nuclear binding energy” quantity.

Compare:

Wikipedia, Nuclear binding energy (Oct2023)

” Nuclear binding energy in experimental physics is the minimum energy that is required to disassemble the nucleus of an atom into its constituent protons and neutrons, known collectively as nucleons.”.

APPARENTLY SOMETIMES. Yes.

But definitely not always.

As the exemplifying extracted experimental values NSdeDIA6 diagram shows.

See also comparing diagram AtomDiffNuc:

Atomic lies always above nuclear in total maximum BINDING energy.

What means ”binding”?

THE MORE WASTE MASS-ENERGY INPUT FOR ASSEMBLING THE END PRODUCT, THE HARDER TO REGAIN: the ”binding energy” concept:

— »My motivation to withhold information for you, is stronger than your attempt to get such info». »Binding energy».

— »What’s the difference?».

— The natural »Love me or leave me» principle. [ ITERATION PRINCIPLE ¦ IterationTheorem ]:

— »I might get looser on you if you show me some kindness ..».

COMPARE (vulgarized):

— I give a shit about more or less, if it is the least, it covers any quantity over.

— Yes. OK. So if you are asked of an investor How much money do you have in the bank? .. you would expect a reasonable response in answering .. At least one dollar : it fucking covers any quantity over. Yes? I didn’t think so. We have to get educated — related answers only.

THE VOCABULARY HAS MISSING PARTS

We cannot blame or critizise the Wikipedia authors or other sources on this noted and observed issue. Because, the problem apparently is this: A central explaining term is missing — in the established teaching and educating system;

See Wikipedia quote in Not represented.

NScredit:

— All these revealing facts have only the Neutron Square solutions as a source. And that source was never observed in modern quarters.

— So that the reader will understand, know and be able to relate that these ”new statements” are in no way any mumbo-jambo hocus-pocus gravel.

Examples: InternetExample

NSdeDIA6

Further EXAMPLIFYING THE CONFUSING CONCEPTS —

that must be understood by thorough examplifying and comparing examples:

A direct quote from the same Wikipedia article Nuclear binding energy just underlines »the confusion of tongues»:

Provision:

The Wikipedia article does not say

Mnuc = U – Zme ¦ nucleus gravitating mass + electrons gravitating mass = atom gravitating mass:

Mnuc = U – Zme ¦ nucleus gravitating mass = atom gravitating mass — electrons gravitating mass.

”total binding energy”

” If we assume the reference nucleon has the mass of a neutron (so that all ”total” binding energies calculated are maximal) we could define the total binding energy as the difference from the mass of the nucleus, and the mass of a collection of A free neutrons. In other words it would be

(Z + N )m_n — m_nuclide.

The ”total binding energy per nucleon” would be this value divided by A.”,

WIKIPEDIA, Nuclear binding energy, Example values deduced from experimentally measured atom masses (12Oct2023).

(Z + N )m_n — m_nuclide ”the total binding energy”, Wikipedia article says

— No.

(Z + N )m_n — m_atom the total binding energy, related physics and mathematics says

(Oh please .. Someone has to cut the oxygen from this rebellious intruder .. questioning everything ..)

Explain:

See Wikipedia quote in Not represented.

(Z + N )m_n — m_nuclide ; the Wikipedia quote [ Z + N = A ] ;

AmN — (U — Zme) is not a ”total binding energy” ¦ WikiWEIZnuclearMass quoted comparison:

SHORT: The Wikipedia article postulates a more demanding expression for ”the mass of an atomic nucleus” :

We test that part with a related provision of a gravitationally related nuclear mass concept, U – Zme, and find that the Wikipedia stated expression is verified. Then, the continuing:

AmN — (U — 0.00) is. RelatedNUCLEAR

MDa = AmN — U atomic mass defect = total atomic FULLY RELATED binding energy:

MDn = AmN — U—Zv nuclear mass defect = nuclear binding energy — ClarifyingTheUequation — always less

APPARENTLY related unless we lost some vital parts of our mother ship when entering the on ramp IT IS THE GENERAL ATOMIC MASS DEFECT — fundamental atomic mass Quantum binding power MDa — that ON ITS MINIMUM determines weather or not a neutron release is possible, our 18 U2 minus U1 examples NSdeDIA6.

— So ..IF the article had written ”(Z + N )m_n — m_atom” we would be safe:

We would be in a perfect agreement with the results:

total binding energy relates to all the wasted working mass-energy needed to reach the end atomic mass (atomic weight U = m/u) U station.

— If other understatements hold, confusions arise unless explicitly specified.

♦ Atomic — in most cases, exemplified NSdeDIA6 the least binding energy to allow a neutron emission.

♦ Not nuclear.

Related physics TNED ¦ NScredit

The atomic nucleus U = m(ATOM)/u has no inner np-constituents. No way. It has a fundamental np nuclear structure. No np particles. We only use these n (neutron) and p (proton) in addressing (AZchart) their fundamental nuclear structural type morphological properties. Not any kind or nature of »their particle forms». We talk: ±e structure.

Nuclear charge (Z) in related physics has no volumetric substance. No way. Z is a well relatable ±e nuclear surface electric displacement (with a corresponding nuclear magnetic moment), stretching (rZ) no further out from the nuclear center than the gravity radius of the nuclear space extension (r). See the finally collected (already existent before our eyes) experimental proofs in The Atomic Nucleus.

— What is this author trying to say?

Provably :

THE present academic IDEA OF NUCLEAR MASS DEFECT

”BINDING ENERGY PER NUCLEON”

COMPROMISES ANY THEORETICAL CALCULATION OF ATOMIC MASSES FOR COMPARING on EXPERIMENTALLY MEASURED.

— Why? CompareQm: The NSdeDIA5 Diagram exhibits the relatively huge corruption between atomic and nuclear:

Because gravitation the fundamental atomic nucleus/atom The NEUTRON has no particle constituents inside of it:

Gravitation is not a particle.

Its fundamental physical Form, the basic atomic nucleus, the Neutron h=mcr is NOT a particle, has no particle constituents. See Nuclear STRUCTURE. It is proving that the Atomic Nucleus experimental results, no way sir, can be successfully modeled by any macroscopic physical idea type uniformly charged liquid drops as in the Weizsäcker equations. And it — gravitation, the atomic nucleus, the neutron — definitely cannot be compressed: it is already standing on a zero [Spin and Moment, Background].

— There is nothing wrong with the experiments, the experimental results. No way. These are accurate.

— Problem is The Aces behind the keyboards pushing in new parameters to make the design more adopted to Hollywood Experimental Enterprise. Experiments are fine. The Aces have been collected into a constantly leaking Boat, left in the middle of The Pacific.

— How do we explain the later (WeizCalifornia ¦ CompCALu2023) more precise Weizsäcker nuclear binding energy solutions precision with the experimental results?

♦ Always CHASING THE EXPERIMENTAL WITH FILLING IN COMPUTER MODELING:

• Because that is the only provisional preference the present scientific community has: it has no NS.

• And so, seen from the NS-position: The Weizsäcker rank mathematics solution or any other liquid drop nucleonic model, no matter the computing power fails the target : neutral (TNED) atomic masses. NS solutions. Weizsäcker solutions and associated is guaranteed locked out, no matter the experimental precision or the computing power.

— Or, if these statements will fail: NS solutions has no value, not at all. Dodge that one, anyone who can:

FIBAPO: Never18 ¦ Comp

FIRST BASIC PROOF — Geometric

———————————————

ComparingTable ¦ WeizsäckerEquationDetails

Any comparison between NS solutions and any theoretical mathematical idea of calculating atomic masses from an idea of uniformly charged liquid drops directly becomes out of the question. The present academic scientific community idea of the atomic nucleus as inhabited by ”nucleons inside the nucleus” is apparently (very, and deeply, and fundamentally — related) cosmologically and universally definitely incorrect.

— But it is the only one available in a referring past science history, all beginning from around 1900. We grew up with it. Everywhere. Merits.

— »Good dog».

Unaware of the Neutron Square solutions, it was impossible to foresee the coming conflict. On the other hand: Without that science history development, this (or any other existing, what we know) author would definitely never had come upon the Neutron Square discovery (2003 — from studying the experimental values on atomic masses). So .. the established unawareness made way for the discovery — while the unaware was collecting the answers: the imperative mass tables. The instrumental lead.

— See further from HIGHESTmD.

NuclearBindingEnergy ¦ ComparingNuclear

NSconditions: FIBAPO — first proof

NeutronSquareFundamentals

Provisions

NEUTRON SQUARE CONDITIONS (NScredit)

Related physics and mathematics — Neutron Square solutions — NSsolutions

———————————————————————————————

The atomic mass defect (mD) mathematics is founded on the Neutron Square and its deduced general elliptic equations (A K E). It generates — exposes — unique neutral as in experimentally independent atomic mass calculated values. As compared to the experimentally tabled results, the NS values apparently have close kinship (Actual differences):

♦ The NS solutions have no dependency on the physical property of nuclear charge Z (DeducingTHErZ).

Modern academic scientific community atomic and nuclear physics

———————————————————————————————

The nuclear mass defect traditional modern academic science theory [WeizCalifornia2023] uses different modeled macroscopic concepts (uniformly Z charged liquid drops) to describe the variations in atomic masses (A Z).

♦ Present academic solutions use of nuclear charge (Z):

— The (materialistic) idea is that the atomic nucleus consists of sub atomic inner freely spinning proton and neutron particles (A=n+p = n+Z): Z reflects determining significance on the nuclear size (and its mass).

Summing:

———————————————————————————————

♦ In Comp and ComparingNuclear (HOP167¦FM1975 Weizsäcker solution) it is readily apparent that the present academic idea of sphericity, drop modeling and uniformly distributed charge does not reflect the natural morphology of the atomic nucleus and its physical properties. That is explicitly obvious on the basic first light atoms. As a representative of explaining nature (science), we had expected something more alike the compared NS solutions results: tight, right from the beginning (FIBAPO).

See the basic (HOP1967¦FM1975) comparing examples in

NSsolutions ¦ FIBAPO ¦ EXPERIMENTALconfirmations ¦ CosmicMATHrevelation ¦ HIGHESTmD ¦ Comp ¦ ComparingNuclear

NSconditions

NSsolutions: INTRODUCED 2003 in UH —

NScredit ¦ VerticalElliptic

NSconditions ¦ NeutronSquareFundamentals ¦ CosmicMATHrevelation ¦ AboutTheMETHOD ¦ Geometric

NEUTRON SQUARE SOLUTIONS

See the (related) basics in how the Planck constant (h=mcr) connects to (i.e., defines — verifies) the neutron square solutions, connecting the (related physics) Hydrogen Spectrum to a consistent derivation of the neutronic atom’s space basic metrics:

The radius of the proton and the neutron. Never included in modern quarters.

NEUTRAL ATOMS — charge-experimentally independent

electric and magnetic experimentally independent atomic mass defect values

The Neutron Square Solutions complex contains

trigonometric, direct geometric, vertical elliptic, wave, horizontal elliptic, and hyperbolic solutions to NEUTRAL atomic mass defects mD. From mD a direct transfer

U = AmN(1 – mDme) gives the atomic mass (U=m/u) in Dalton units

(u = mC12/12) for direct experimental comparison (NScredit).

NEUTRON SQUARE FUNDAMENTALS

———————————————

TRIGONOMETRIC — basic¦ Trigonometric — geometry¦ Geometric ¦ Wave ¦ VerticalELLIPTIC ¦ Hyperbolic — basic ¦ HYPERBOLIC — detailed — Principle ¦ HorizontalELLIPTIC — SameAonDifferentU? ¦

What the reader should know, first ..

Neutron Square solutions:

U = AmN(1 — mDme): atomic mass m/u = U = [older] atomic weight [ newer ] ”relative atomic mass”

A mass number, mN 1.0086652 me 0.000548598 neutron electron mass in Dalton u=1.66033 t27 KG units = mC12/12.

mD atomic mass defect NEUTRON SQUARE SOLUTIONS in electron masses, 1me = 0.511 MeV = 0.000548598u.

Nuclear Mass related physics NSsolutions

mNUC = U — Zme: Z nuclear charge as atomic number as the atom’s electron mass charge

has no connection to nuclear charge in NSsolutions, related physics — AtomicNucleus ¦ NScredit :

ELECTRIC CHARGE divergence AND GRAVITATIONAL MASS convergence ARE TWO DIFFERENT PHYSICAL PROPERTIES — Never18.

In MAC mNUC is associated with nuclear charge: mNUC = ZmP + (A–Z=N)mN – B,

B nuclear/nucleon binding energy between the idea of the nucleus as composed of inner freely spinning Z mP and N mN particles:

all established academic experimental data are collected, ordered and compiled in accordance with that program.

IN NS SOLUTIONS, IT HAS NO CONNECTION, as proved in AtomicNucleus: all Angeli2004 collected experimental data.

The NS solution is EXPERIMENTALLY INDEPENDENT: neutral atoms

no charge dependency — NScredit.

— Either it is. Or it isn’t.

It is our job to clarify which it is.

SO, WE ONLY HAVE TO FIND ONE SINGLE ITTY BITTY THE SMALLEST TINIEST PROOF, whatever:

— Either it is, or it isn’t.

It is not about a contest. It is about knowledge of the world we are born to: science. No consensus. Just pure true natural knowledge — what can be proven, related, explained and understood, inclusively. Or not at all.

Wang2020:

” Nowadays, several mass measurements are conducted with fully or almost fully ionized atoms. In such cases, a correction must be made for the total binding energy of all the removed electrons B_e(Z).”,

” Unfortunately, the precision of the calculated B_e(Z) values is not well established, since this quantity (approximately 760 keV for ₉₂U) cannot be easily measured.”,

THE AME2020 ATOMIC MASS EVALUATION, Wang et al., Chinese physics C 2021 ¦ free PDF, p1

The Wang table has specified uncertainties: 1H1(1.007825 03190) → 0.00001 µu

THE DISPERSING BINDING ENERGY COMPROMISING AND CORRUPTING NATURE ¦ see ComparingNuclear

— The Neutron Square atomic mass defects have revealed the details in this complex — completely unknown in modern quarters. Electric and magnetic features are imperative in experimentation on atomic and nuclear matters. Yes.. But — as proven (ReHofstadter1956) through NS — nuclear charge and nuclear extension — volume, radius — does NOT connect. No way. Charge and mass have no common physical ground, although integrated in the atom (TheQ). So — rhetorically: how do modern academic experimentation rinse the results from such »experimental infection»?

Test Answer: »The PhD does not understand the question». Not one person inside present scientific community really knows what nuclear and atomic physics in reality is all about (NScredit). The community just jumped on The Train, and followed the lead to the cafeteria.

” Modern mass-spectroscopic measurements employ the ”mass doublet” technique. One determines the differences in mass between ions of the same mass number having slightly different masses. Because there is only a small mass difference between the two kinds of ions, the instrument dispersion need not be known as accurately as would be the case if the masses differ widely ..”,

HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967, Nuclear physics p.9—64 col.2b

The HOP table has specified uncertainties: 1H1(1.007825 19) → 0.08 µu ¦

See ExperimentalErrors and ISOBARIC COMPARISONS.

PROVISIONS:

PROVISIONS

THERMALLY INDEPENDENT ¦ ZERO GRAVITATIONAL POTENTIAL c0 environment — TNED K-cell physics : zero gravitational redshift

NSUnit

Neutron Square Fundamentals — one Unequivocal atomic mass for one specific mass number A : — no. BACKGROUND:

The bare clean fact ComparingIsobaric that both the experimentally measured and the NS solutions UnequivocalAmD same A have values lying VERY close in U values:

CHECK OUT THE GENERAL very small experimentally tabled DIFFERENCES in electron masses me BETWEEN stable ISOTOPIC PARTS FROM DIFFERENT ATOMIC FAMILIES [ isobaric]:

NuklidTab4B2023.ods Tabell1 Col.Y+

— At most: 0.086 me; At least: 0.001 me — isobaric occasions for all stable isotopes from 1H1 to 83Bi209. HOWEVER:

— THE MDa CONCLUSION on Neutron Square solutions STATES and proves by principle THAT

THESE NARROW DIFFERENCES no longer FAVORS A FURTHER AND DEEPER NS INSPECTION ON THE isobaric EXPERIMENTAL RESULTS

THE NEUTRON SQUARE SOLUTIONS

— UNDER WHICH PHYSICAL CONDITIONS?

♦ apparently not EXACTLY the established scientific community experimental ones for starters:

WE — APPARENTLY — MUST ASSUME THE CORRESPONDING NS CONDITIONS

1. • no gravitational potential (ideal mass center) — highest possible divergence = max c₀ =2.99792458 T8 M/S space (NSUunit)

2. • no heat — no specific [ heat ] energy fluxes in that g-free ideal dark space: 0°K — different regions have different conditions

3. ♦ experimentally gravitationally c₀ dependent — where light propagation c in space is maximized, same as the natural divergence constant c₀ ¦ K-cell mass center;

we have no other independent — GEOMETRIC — neutral maximized atomic mass quantity to refer to.

4. ♦ HEAT charge electricity and magnetism IS NOT MASS (NScredit) —

and the NS solution neutral atomic mass complex is therefore, or can so therefore be understood as, absolutely independent of thermal regions.

The geometric neutral atomic NS provisions complex apparently just compare — or states — the actual gravitational conditions with those from any possible theoretical statement. It is our job to secure a certified interpretation of such comparisons, on whatever scale that relates to a scientific explanation.

See further precise examples from

Comparing Normalized (CONOR).

Universal example: h = mcr

Planck constant h = mcr — conservation of angular momentum (the neutron mNc₀rN) should be equally determinable — independent of experimentally measuring region.

Caring for LGD-basics (the TNED deduced universal K-cell mass center gravitational redshift, modern academy’s ”dark energy” related to ”extra expansion”, in related physics a standing still with corresponding Doppler red shift instrumental readouts), the two factors mN and c can have inverse proportionality without breaking the conservation of angular momentum.

Where (significant) gravitational redshift affects electric and magnetic experimental measurements, the locally lower divergence c then demands a proportionally higher resulting quantity mN if h is to remain a universal constant.

As the experimentalists however — the absolute metrics — uses not the local c divergence, but the universal (absolute metric) c=c₀ quantity in all experimentation, the actual higher mN value will reflect an experimental position in an actual such c=c₀ region. In other words: with a slightly received higher mass value for mN than the actual where c=c₀. Again: the true c=c₀ region mass mN value will be slightly lower.

As suggested in NSUnit — universal atomic mass unit u = m(6C12)/12 = 1 Dalton — given a (c₀ experimental laboratory based) measured electron mass me, a comparing normalized (CONOR) neutron mas mN = 1/(1 – 15.6me) will — with no exceptions — be less than that specific laboratory’s correspondingly measured neutron mass (mNc).

WikipediaStandard:

By Wikipedia (finding U=A exemplified) reported standard values, example:

mew = 0.0005485799u Wikipedia original electron mass

mNw = 1/(1 – 15.6mew) = 1.0086317155u; u-normalized

mN(W) = 1.00866491588u Wikipedia original

mNw/mN(W) = 0.9999670848 — Planck constant local c-divergence u-correction:

h = mcr = universally constant, no exception; h/r = independent universally constant = mc

— lower local c = consequential but not real mass higher m, LGD-basics

The farther away from the ideal g-center (TNED K-cell related physics only), the greater the difference. At the universal c-rim (c approaches zero) the experimental mN mass would display an experimental approach to infinity — on the laboratory’s c₀ use;

— »In for a penny, in for a pound».

LGDbasics: RELATED PHYSICS ONLY — Provisions ¦ NSUnit

———————————————

FOREMOST PRACTICAL APPLICATION: GPS-example ¦ CWON from CAP — concentric atomic production ¦ light’s gravitational dependency ¦ NScredit

While light’s gravitational dependency (LGD) is recognized in modern corridors experimentally as the so called Mössbauer effect, its corresponding reversed spouse from the gravitational center with increasing enveloping mass — universal gravitational redshift, related physics — is, more or less, heavily denied (See modern academics ”dark energy”, Sw., Mörk energi).

In related physics and mathematics (Sw., K-cell heat physics) the universally cosmic LGD explaining core is a central pulsating K-cell (half period: 336Gy).

It is maintained, and mathematically explained, by a gravitational energy balance between a central and a surrounding mass complex. This complex is governed by LGD light’s gravitational dependency (General cosmic state law). And as such, it is founded on the universal Planck constant h=mcr and the energy law: energy cannot be created, nor be destroyed (Physics first principle ¦ ExperimentalConfirmations), only converted.

The quest of the origin of mass

(modern academy 1800+ postulated a limited existential mass, perhaps by reasons more relating to the Bible’s ”In the beginning” literary interpretation, than the alive eye of a child — and it has so become a mission for the academy to preserve that delusion)

has no logic or reasonable resolution, because the origin of energy¦mass has none:

— Everywhere we look, there is always more behind. Incontestably experimental fact.

(Modern academy 1800+ always had deep existential problems).

It is all related mathematics.

See further exemplified in

CONOR

(comparing normalized).

NSsolutions

CONOR: comparing normalized — 25Oct2023

INTRODUCING EXAMPLE IN Provisions ¦ ComNorm

COMPARING NORMALIZED

NSUnit ¦ LGD-basics — CONNECTING CONTEXT — defining a universal atomic mass unit u = m(6C12)/12 = 1 Dalton

———————————————————————————————————————

RELATED TNED MATHEMATICAL K-CELL´PHYSICS

The (2021) Andromeda Test result on partly not easily nor precisely reliable data however suggested that the TNED K-cell universal gravitational center — where c=c0 resides — possibly would have this overviewing orientation:

The modern academic consensus is that the measured Doppler values are proving a future collision course between our Milky Way galaxy and the Andromeda galaxy. However, related physics suggests, taking that Doppler shift on a gravitational red shift scale, a mathematical complex apparently not known inside modern corridors, the explanation is: No. Not at all. The galaxies are suggested to have a very close standing still status, possibly with some very minor rotational feature involved. They are not going to penetrate each others discs, at any future — ever.

A gravitational Doppler red shift suggested for our position a most 0.999633079 as corresponding to a local c-correction against the top divergence c0 = 2.99792458 T8 M/S. As these data are more or less highly uncertain, a certain possibility exists that — if at all — »the true» positional deviating value would be some

”0.9999670848” — »WikipediaStandard»

Much closer to our position.

Believe it or not. Even though the different epoch standard values (1960-1999 instrumental ¦ 2000+ data computerized) have relatively large inside differences (the TNED 2018 IAU Sun photometric effect test revealed that both will not do, as far as yet tested), in taking these different standards on the comparing Normalization Neutron Square u-testing preference, they render practically the same end station result:

WikipediaStandard

mew = 0.0005485799u Wikipedia original electron mass

mNw = 1/(1 – 15.6mew) = 1.0086317155u; u-normalized

mN(W) = 1.00866491588u Wikipedia original

mNw/mN(W) = 0.9999670848 — Planck constant local c-divergence u-correction:

h = mcr = universally constant, no exception; h/r = independent universally constant = mc

— lower local c = consequential but not real mass higher m, LGD-basics

HOP1967Standard

meh = 0.000548598u HOP1967

mNh = 1/(1 – 15.6meh) = 1.0086320026u; u-normalized

mN(H) = 1.0086652u HOP1967

mNh/mN(H) = 0.9999670878 — Planck constant local c-divergence u-correction:

h = mcr = universally constant, no exception; h/r = independent universally constant = mc

— lower local c = consequential but not real mass higher m, LGD-basics

On testing this Neutron Square Solutions suggestion

— our Earth Solar system experimentally provision in the universe has a

0.99996708 true c0 diversion, covering (atomic, nuclear) mass measuring in a slight deviation from universally true mass quantities

— the already given GPS-example will serve as a first Testing Guard:

— Is the GPS system satellite signaling technology mathematics results in any the slightest possible way, even mathematically theoretically, affected on this NS suggested minor true c0 diversion?

Apparently: no. Not at all.

In our GPS test — proving the validity of the TNED deduced results to be in accord with the present GPS technology and its reported quantities — we had this compiled resulting table on all the used and comparing variables (Deduced connections):

GPSexComp: CONOR

Deduced connections ¦ Compiled TNED GPS-test results — no relativity theory involved

NOW we take the exact same table — with only one single difference:

We replace the Laboratory Standard Earth Academic c= c0 2.99792458 T8 M/S used in the equative solution, with the u-NS-comparing-Normalized suggested

c = c0 × 0.99996708

c = 2.99 782 591.164946 M/S

Then we take the two tables, the original GPS test table and the suggested cNSComparingNormalized, ANDING them through each other picture-wise, looking for any deviation in figures. And this is what appeared:

NuklidTab4C2023.ods Tabell5 D1+

No — what we know — significant change.

Same daily route.

No disturbance.

And that is apparently exactly what the Neutron Square Solutions u-defining provisions demand for a fair and correct universal comparison on neutral atomic masses m=Uu.

The above GPS oriented test proof, does not mean that the above suggested universal c0 deviating possibility IS the explanation to the Normalization level shift, as illustrated below. The effect of the mN normalization level shift MIGHT — not known here — as well be caused by a (mass-to-charge experimental) issue in measuring the experimentally unaffected NS neutron mass preference (Normalization). The NS solution suggest an error of 100(1/0.99996708 –1) = 0.00329%.

In any case it is clear that the Weizsäcker general ”uniformed charged liquid drop model” has nothing to do with the NS solution complex. The Weizsäcker model in the NS light clearly appears as a sophisticated academic game in chasing experimentally perfected computer animations: exactly zero explaining power. Or the reverse: »the NS solution complex is a complete heap of ancient rocky gravel crap». Please do share the revelations.

ComNorm: CONOR

Comparing differences in me:

THE GENERALIZED TNED NS SOLUTIONS from A=60 up to 83Bi209 HERE REPRESENTED BY THE GENERAL SIMPLE NS HYPERBOLC EQUATION The Gold Hyperbola [ Sw. orig. 10Oct2004 ]:

HOPweixXPa.ods ¦ NuklidTab4C2023.ods

General first atomic chart part rough band Neutron Square solutions (NS) deviation: 0.45 me = 0.00025u. The NS independent neutral atomic solutions suggest that the experimental values have systematic — »variational» — mass-to-charge issues locked on habituated computer modeling adopted to match experimental results. The Normalization as such have, apparently, only two available explanations. 1. The 0.99996708 c0 dislocation possibility, or: 2. A corresponding misapprehended interpretation of an experimental evaluation of the neutron mass on a 0.00329% basis. Or, at worst, a combination.

— Which it is, any way, will be our job to find out. Or, perhaps the most academic imperative: to get rid of this presentation, as it threatens modern academic ideas to distinction: »so many cannot be wrong», and the like. Type: »you don’t have enough amount of pals to get in here». HighSciIQ.

The first light atoms in the Weizsäcker solutions lie far outside the vertical scale.

— No way the modern academic idea of the atomic universe reflects a just and fair model of the atomic nucleus. Not even on my best day.

— The »modern PhD aces» are apparently more interested in chasing the experimental values by using computer modeling parametric algorithms, than studying the basics of our universe. Say that : that is completely wrong. Say it.

NScredit.

Weizsäcker solution is chasing the experimental

and the experimental is chasing the neutral — the NS neutral atomic masses:

the experimental cannot dispense with electric and magnetic field strengths:

The Neutron Square solutions has nothing of the kind.

NS solutions it is, suggesting:

Experimental deviations from true atomic masses exist — possibly but not settled partly due to a less understood universal laboratory position.

Dodge that one, anyone who can.

— We surrender immediately on any related disclaimer.

NScredit and Discovery.

Modern academic ideas of atomic and nuclear physics is not just outclassed and overrun: It is buried.

But please, anyone: do disclaim on any related argumentation.

We will surrender immediately.

CONOR

EllipticEquation: Neutron Square solutions ¦ Geometric ¦ Vertical Elliptic

The neutron square and

THE ELLIPTIC EQUATION —

neutron square solutions

The ELLIPTIC EQUATIONS ¦ NeutronSquareBasic for NeutronSquare solutions — NSconditions ¦ Neutron Square Fundamentals

The Neutron Square sophisticated paragon system — as deduced, departing from The Neutron as Planck constant h = mcr

E = 1 → 0 ¦

K = A_REF (1 + mD’/6), see OFFSETfactor positions the exothermal fusion path ellipse

If mD’ relates to the Neutron, mD’ = 0, one receives K = A = AREF

A_REF = 6(1–E)

K = (1–E)(6 + mD’) ¦ E=0 → K=(6 + mD’) ¦ E=1 → K=0

Exothermal fusion paths from lighter atoms with already determined mD as mD’ to heavier is the foundation:

mDmethod: Geometric

Generally one must first realize a thorough — related, deduced — evaluation for a certain atom and its nuclide in certifying it is accountable as an exothermally valid formed atom. That is, the nuclear fusion path (see FusionRING) must ascertain a giving-out-energy process at its formation, the actual mD end value. That evaluation gives basic data on the factors Aref and mD’ (nuclide reference’s atomic mass defect). These are imperative for realizing the calculation, leading to the end station mD value. All such calculations depart from the BASIC NUCLIDES (FIBAPO), themselves, on the NeutronSquare geometry only: basic values appear directly/geometrically in the Neutron Square. See basic illustrated examples in Geometric, unless already familiar. From these, all heavier atoms are formed.

UnequivocalAmD: mDmethod ¦ MDa

Atomic mass defects on Neutral atoms — NeutronSquare solutions

THE ELLIPTIC EQUATION

mD = 6 ± (1/5)√ 60² – (60 – [A – K]/E)²

different A can have same mD:

U = AmN(1 — mDme) ¦ :

same mD on different A give different atomic masses m=Uu.

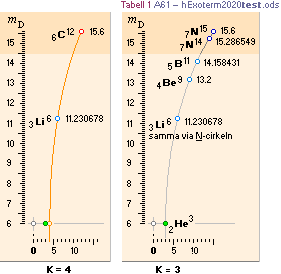The 3Li6Group

A = K + E(60 – √ 60² – [5(6 ± mD)]²)

different mD can have same A —— provided that

A = K + Ek ; K = A — Ek ; E = (A — K)/k

A = (1–E)(6 + mD’) + Ek .. investigating the possible mathematical solutions may be extensive ..

— What we know: As far as we can come from »all combinations have been examined»

— here at present Sep2023 in UniverseHistory: We can only, at present, state what has been found on the examined cases.

— More related arguments and precision examples are needed before any regular general atomic chart will appear (all stable atoms up to 83Bi209).

Provided an exothermal fusion path (FusionRing) can be related and deduced, the above basic elliptic atomic mass defect equation apparently allows different mD on same mass number A. Unless we can prove that it does not exist, we cannot say.

♦ What we can say (AtomicNUCLEUS):

♦ Nuclear charge (Z) has no part in the NS solutions atomic mass determinations.

♦ No Z dependency exist on atomic mass: mass and charge does not connect in physics (NScredit).

Further resolution in MDa (conclusion).

ISOBARIC ATOMS

The general NS solutions by the commonly compiled elliptic and wave equations (EllipticWave) show several different mD on same A :

♦ The NS calculated isobaric (same A) value differences on the light chart part up to A=60 (see also IsobaricMEAN ¦ ComparingIsobaric ¦ ExperimentalErrors) are small: at most 0.011 me, at least 0.001 me (averaged minus actual), 1me = 0,00055u;

NuklidTab4B2023.ods TableB — all stable up to A=60 :

A36:Z16,18 ¦ A40:Z18,20 ¦ A48:Z20,22 ¦ A50:Z22,23,24 ¦ A54:Z24,26.

Averaging these mD calculated differences, will render no visual difference in the scales used here to present the resulting graphical and diagrammatic picture. The differences decrease with increasing A.

However, where the solution is of the wave type[‡], there should be a more precise regular elliptic value. At present (Sep2023) not all occasions have been precisely analyzed.

Some parts in this (demanding — vast) analysis are exposed below.

The first iteration — before the enhanced method — took three hours. Enhanced: ten minutes.

It is still deterrent.

CheckTabAElliptic: mDmethod

CHECKING NuklidTab4A2023.ods TabellA for hExoElliptic

UP to A=60, all stable:

16S36 17.311533460 HOP

16S36 17.367203106 NuklidTab4A2023.ods TabellA wave

18Ar36 17.375553421 NuklidTab4A2023.ods TabellA wave

18Ar36 17.288717952 HOP

18Ar40 17.358932488 HOP

18Ar40 17.419527359 NuklidTab4A2023.ods TabellA wave

20Ca40 17.419527359 NuklidTab4A2023.ods TabellA wave

20Ca40 17.3137085 hExoterm.2020test.ods Tabell1 17R elliptic

20Ca40 17.349684301 HOP

20Ca46 17.478866823 HOP

20Ca46 17.503586330 NuklidTab4A2023.ods TabellA wave

22Ti46 17.506348590 NuklidTab4A2023.ods TabellA wave

22Ti46 17.520408136 HOP

20Ca48 17.446656984 HOP

20Ca48 17.4795692 hExoterm.2020test.ods Tabell1 173R elliptic

20Ca48 17.563718966 NuklidTab4A2023.ods TabellA wave

22Ti48 17.565741332 NuklidTab4A2023.ods TabellA wave

24Cr54 17.704877156 HOP

24Cr54 17.774214752 NuklidTab4A2023.ods TabellA wave

26Fe54 17.774214752 NuklidTab4A2023.ods TabellA wave

26Fe54 17.680262846 HOP

ExplicitElliptic: hExoterm.2020test.ods Table1 — Excerpt, iterative results

Who did ever think of that in modern academic corridors?

— »There is A neutral gauging ATOMIC NUCLEAR PHYSICS PARAGON the neutron square — explaining the detailed nature of nuclear and atomic physics (at c₀).

— And mathematics (apparently very much).

— Concordant with experimental results.

— Including a further, separate section, deduction of the periodic system of the elements from »simple Kepler (momentum) Resonances». Basically »the same principle mathematics» (nuclear matrix algorithm).

No.

Modern academic inducements had other ideas during its birth 1800+:

• The mission was — became — to Invent rather than Deduce.

As prosperous as that voyage went on, the merits became established (experimental physics on the underlying theories): university, high school, all kinds of established institutions: education. No time for scrutinizing the basics. We adopt, or go bye-bye.

So .. this author chose to find another, more appropriate, tourist bus ..

See further in

NeutronSquareFundamentals.

EllipticEquation

AboutTheMETHOD: NSsolutions

The fundamental lead is the Neutron Square deduced Elliptic Equations and their possibly deducible exothermal fusions paths (VerticalElliptic), with some guidance from the average simple wave equations (BaseGroupMassNumbers):

(the analysis may be demanding .. always interesting .. only the end result will tell ..)

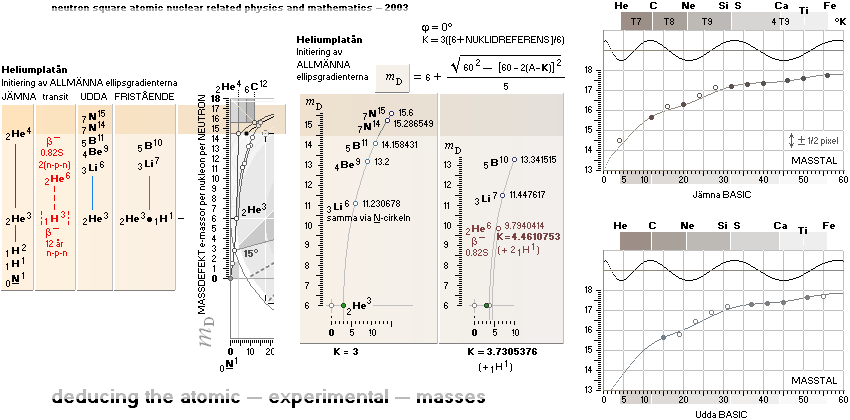
How nucleus and its communicating electron mass cooperate in the atom — explaining the TNED neutron square atomic masses deductions, the foundations ¦

basics connecting the periodic system — excerpt MPcKärnMatIIIb.wps 8Feb2008 — the nuclear n-p structural electric displacements through resonances:

— See detailed in THE RELATED PHYSICS DEDUCTION OF THE PERIODIC SYSTEM THROUGH KEPLER RESONANCES.

central force dynamics

J = m(K=2A/T=2A f =2n²f )KEPLER AREA resonance MOMENTUM, Jf ^–1=2n²

SWEDISH EXCERPT:

J arbetar på elektronmassans beståndsdelar; det bildas stående, fasta vågmönster kring kärnan och som grundlägger, beskriver och definierar hela atomens elektromekaniska jämviktssystem.

Kommunikationen mellan kärna och hölje sker genom ovanstående avbildade kärnmatrisiska algoritm, från kärnnivåerna (underst) till resonansnivåerna (överst), från lägre till högre, och som ges av Keplermomenten. Den kärnmatrisiska algoritmen definierar varje grundämne genom en bestämd uppsättning Z omgivande elektronmassor som bildar ett helt resonanssystem. Den matrisiska algoritmens successiva Z-bildningar definierar på det sättet grundämnenas periodiska system enligt ordningen (i utdrag från utvecklingarna, typexempel, period 4)

… 2-8-8-1, 2-8-8-2, got it: 2-8-9-2, 2-8-10-2, … 2-8-18-2, I’m on: 2-8-18-3, 2-8-18-4, …

₁₂3₉4₁₀5₁₁6₁₂7₁₃8₁₄8₁₅8₁₆1₁₇2₁₈345670 .... 2-8-18-8 ...... period4

Vi använder här 0 som en periodisk avdelare genom en binär-hexal [oktal] avdelningsordning när vi räknar successivt i matrisen, den allmänna 2-6-formen framgår inte direkt här utan först när vi studerar upplösningen i Keplerresonanserna mera ingående.

AboutTheMETHOD

ExperimentalErrors: TheActualDifferencesHOP/TNED ¦ IsobaricMEAN ¦ CompCALu2023

HOPuncertainty

A GOOD START IN DETERMINING THE UNCERTAINTY STATUS OF THE NeitronSquare COMPLEX WOULD BE TO HAVE ACCESS TO THE EXPERIMENTALLY STATED UNCERTAINTIES — and so we have through the early 1967 collected HOPtable

EXPERIMENTAL VALUES UNCERTAINTY —

IN NEUTRON SQUARE ATOMIC MASS DEFECT

ELECTRON MASSES REFERENCE

— Comparing NS with Experimental needs a transformation from the HOP-table’s m/u=U (atomic weight) units to the electron mass unit in atomic mass defect (mD)

Atomic mass defect equation (1 – U/Am_n)/m_e ¦ U=m/u HOP-table values, A mass number, mn me neutron electron mass in u = 1.66033 t27 KG selected value in UH.

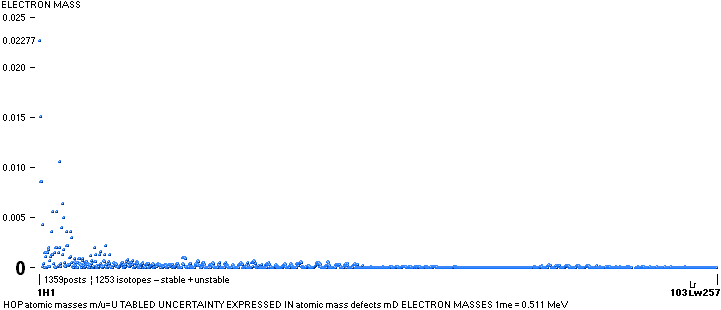
Atomic mass uncertainty (positive value) in electron masses 1me = 0.511 MeV for the 1967 HOP TABLE 2.1. MASS TABLE p.9—65+, HANDBOOK OF PHYSICS, McGraw-Hill 1967. Transfer Equation explained below.

— Later table references (developed methods) have (or claim so to have other (much more precise) error specifications (WANG2021, see quoted description). The above would represent the first scientific available during the 1900:s (ref. HOP on spectroscopic method of atomic mass determination. The HOP-table values source: from the 1964 ”least-squares reduction of data by Mattauch et al.”).

— In itself, this electron mass info has poor significance, unless compared to some atomic mass calculating competitor, as the NS calculated values. Their difference here to the experimentally measured, given in electron masses is related at first up to mass number A=60 — here only the stable nuclei extracted (as also calculated from the NS paragon).

HOPuncertainty: ExperimentalError

HOPtable uncertainty (ΔU) expressed (”Error in µu”) in a separate column for each atom as a positive integer value on

the t6:th (10^–6) decimal of the m/u=U atomic weight (relative atomic mass) value

uncertainty = m(U) — lowest for the lightest (ΔU1H1 = 0.08), highest for the heaviest (ΔU103Lw257 = 1070).

EX:

(ΔU103Lw257=1070) × t6 = 0.001070

DifferenceMAX:

(U103Lw257=257.09894) – ΔU = 257.09787

By atomic mass defect mD —

corresponding tabled experimental uncertainty in electron masses (positive value):

DIFFERENCE Expressed in atomic mass defect electron masses:

Atomic mass defect equation (1 – U/Am_n)/m_e;

U(103Lw257) = 257.09894

V(103Lw257) = 257.09787

ErrorTransferElectronMass: HopUncertainty

mD(U) – mD(V) = (1 – U/Am_n)/m_e – (1 – V/Am_n)/m_e ¦ A mass number, mn me neutron electron mass in u:

= [(1 – U/Am_n) – (1 – V/Am_n)]/m_e

= [ 1 – U/Am_n – 1 + V/Am_n)]/m_e

= [ – U/Am_n + V/Am_n)]/m_e

= [ V/Am_n – U/Am_n)]/m_e

= [V – U]/Am_nm_e

= [(U – ΔU) – U]/Am_nm_e

= ΔU/Am_nm_e

= (HOPtableError in µu)t6/Am_nm_e

= (HOPtableError in µu)/(T6 · Am_nm_e)

mDdiff =

(±)DIFFERENCE/uncertaintyExperimentalTabledHOP1967 in atomic mass defect

electron masses: = 0.0000016896 electron masses

uncertainty for

U(103Lw257) = 257.09894

mD = 14.9637550311 ¦ (±) 0.0000016896

ExperimentalErrors

Comp: Comp2023 ¦ HOP1967 —1975 EE¦ ComparingNuclear

TNED/MAC ¦ WeizSOURCES ¦ WeizCalifornia

COMPARING DIFFERENCES

MAC 1967¦1975 version:

NukTab4B2023.ods Tabell2

Comparing precision in calculated atomic masses — TNED trough Neutron Square solutions and Weizsäcker equations — with the 1967 HOP-table presented experimentally measured — the horizontal zero line »exact value». While the Weizsäcker solution shows vulgar differences on the first light atoms, TNED/NS solutions appear readily »excellent» — especially on the first light atoms. See in explicit the reason for the precision NS details from the Proton/NeutronRADIUS, unless already familiar (basic Planck constant math h=mcr).

Comp2023: Comp — 1967¦1975 ¦ Orientation, see NewWeiz2023 ¦ CompCALu2023

MAC [ 2023 ] version:

HOPweizXPa.ods Tabell1 — WEIZSÄCKER EQUATION California University — NSsolutions — BaseGroupMassNumbers, general wave solution up to mass number 60 — further calculated precision values are pending ..

The diagram above reflects the new (Oct2023) enhanced Weizsäcker solution from a recently found Weizsäcker California university (WeizCalifornia) PDF document.

Related:

Difference to above — exact comparing below should flip the above TNED—HOP to HOP—TNED

——————————————————————————————————

The (13Oct2023) recently found California university source (WeizCalifornia) shows »a new Weizsäcker equation» form — never previously observed here in UH.

All (Comp) Weizsäcker data had so far (until now) been based on the HOP1967 ¦ FM1975 book sources on the Weizsäcker details.

The diagram above (Oct2023) exposes the striking difference compared with the HOP1967 version difference (Comp). A prominent advancement in precision has apparently been made.

See details in NewWeiz2023.

The diagram below — now, finally, for the first time — shows the (California source credited) overall TNED¦NSsolutions status on the comparing scale between TNED related physics and present Weizsäcker academic scientific community. That is (for the first time) on the level of present academic theoretical atomic and nuclear physics versus the neutral atomic Neutron Square solution values.

See also the original (2008) Comparing TNED/MAC, and the accompanying »modern academic Weizsäcker nuclear-atomic» in NSdeDIA10: WhatZv.

CompCALu2023: NSdeDIA15: Comp2023

————————————————————————————————————

18Oct2023 — HOPweizXPa.ods Tabell1 :

Col.AP ¦ Col.F — Col.O HOP — WEIZ THE WEIZSÄCKER ATOMIC MASS EQUATION WeizCalifornia

NuklidTab4C2023.ods Tabell2A Col.V-AA :

Col.AA ¦ Col.G — Col.Z HOP — TNED THE Neutron Square GENERAL Solutions version [ discovered 2003 ] — the precision solution not yet available

The TNED form explained by sources in NuklidTab4C2023.ods Tabell2A Col.V-AA optional— see further short description below.

HOP EXPERIMENTALLY MEASURED COMPARING PREFERENCE, Atomic masses table

NEUTRON SQUARE SOLUTIONS.

For the moment, we leave the comments to the reader.

Previous difference comparison (the 1967¦1975 Weizsäcker version): Comp.

See details in NewWeiz2023 on the (13Oct2023 found) California version.

More will follow.

TNED — short:

A mass number — from A=60: on the simple hyperbolic equation ¦ NuklidTab4C2023.ods T2A Col.V-AA.

— When the hyperbolic part was first discovered as part of the neutron square solutions, it was coined: The Gold Hyperbola [ Swedish original 10Oct2004 ].

Up to 2022 (TNEDa0.htm):

Neutron Square precision mD values (Elliptic Equation) demand a defined deduced fusion path from lighter to heavier — on the lighter already known mD values: Basic mD values ¦ FIBAPO (tool; exothermal nuclear reaction law, on confirming experimentally measured atomic masses/weights) Exothermal nuclear reaction law ¦ NUCLEAR REACTION LAW : it features a regular building, from bottom to top. Finding such an exothermal fusion path alerts elliptic candidates. An elliptic candidate binds the possible atomic products together on its path from lighter to heavier — but it must be so proven: Finding a suggested elliptic agent, it must satisfy (12-20 decimals, at least) a net difference (on known comparing agents) of type 0.00000000000000000000. Or at least 12 for starters. Then that solution has earned the status of preliminary Neutron Square precise solution. These solutions (at present) have only a (time consuming and demanding) manually iterative procedure to offer (TheExample), and far from all atoms have been tested.

The general Neutron Square solutions has, however, some more (fairly elegant, very) close simpler mathematical approximation provisions (geometric/trigonometric, wave and hyperbolic, see here most detailed the wave form in BaseGroupMassNumbers).

Up to latest 2020 it is those values with some precision elliptic that are presented here (Oct2023). Further work will attempt to make that picture more clear (provided the author will live say 514 years more, give or take ±12: the first manual iteration took over three hours)(and it must be checked, rechecked .. and double checked ..).

WEIZ — short:

The above (»Latest California World News») Weizsäcker expression now (Oct2023, WeizCalifornia) takes the lead in the continuing exciting story:

Chasing the fundamentals of our constitutional parts — the atom- and nuclear physics atomic masses.

How they exist, and on what related precision.

The Weizsäcker equation form (from Weizsäcker 1935) is based on a regular charged liquid drop model (George Gamow) with thorough material physics properties, at least its original.

The Neutron Square solution has nothing of the kind. And that will apparently be our future challenge to explore the content of. For further.

Continue on

NeutralToExperimental.

ExperimentalErrors

IsobaricMean: ExperimentalErrors

NSsolutions Related physics TNED Neutron Square Atomic mass defect mD calculations — entirely builds upon :

♦ comparing on Experimentally tabled atomic masses from U=m/u atomic weight tables — HOP1967, Berkeley2003, Nist-Codata2005

♦ no nuclear charge Z dependency — Z in NSsolutions is never used other than as an order number from lighter to heavier atomic families.

EXPLAINING THE NEUTRON SQUARE SOLUTIONS

There is no known experimental method to measure atomic masses without removing their neutral property. Neutron Square solutions have perfectly neutral atoms, no Z math.

Mass spectroscopic methods excludes neutral — introduces parametric dependence — while their physical nature still is not understood.

Comparing

ISOBARIC MEAN DIFFERENCE

———————————————

Atomic Mass Defect equation ¦

The striking (coherence NSdeDIA1 and) differences between the static-geometric Neutron Square solution values (N) and the experimentally measured (E) apparently tugs (tows) some (heavy, urgent need of) clarification.

— Unless, possibly: » .. that is a natural .. spray in differences .. ».

Explaining example:

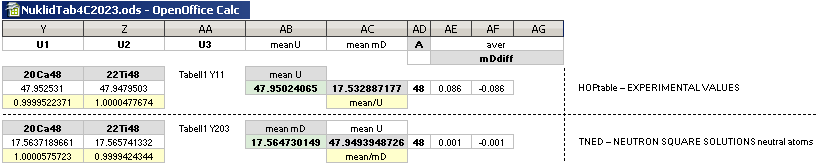
NuklidTab4C2023.ods Table1 Col.Y+

The (Tabell1 Y11) experimentally measured (HOP1967) isobaric (A=48) atomic mass defect mean value difference between 20Ca48 and 22Ti48 is: 0.086 electron masses.

The (Tabell1 Y203) TNED Neutron Square solutions (A=48) isobaric atomic mass defect

mean value difference between 20Ca48 and 22Ti48 is: 0.001 electron masses. Same object.

ComparingIsobaric:

IsobaricMEAN

IF — as it is suggested — the neutral atomic Neutron Square solution atomic mass complex is supreme[‡NScredit] to the experimentally charge dependent atomic mass determination procedure, the relatively large difference between the two isobaric agencies advices this explanation:

— Disturbing the neutral atom’s properties by introducing charge dependent (mass spectroscopic electric and magnetic features) into the mass determining procedure, adds a (difficult to determine, small) skewing property — impossible to detect if only the experimental — not neutral atomic — values have representation.

Further (or present) experimentation should have capacity to resolve that issue.

Data source:HOP167 table — all stable isobaric atoms 16S36 to 82Pb204

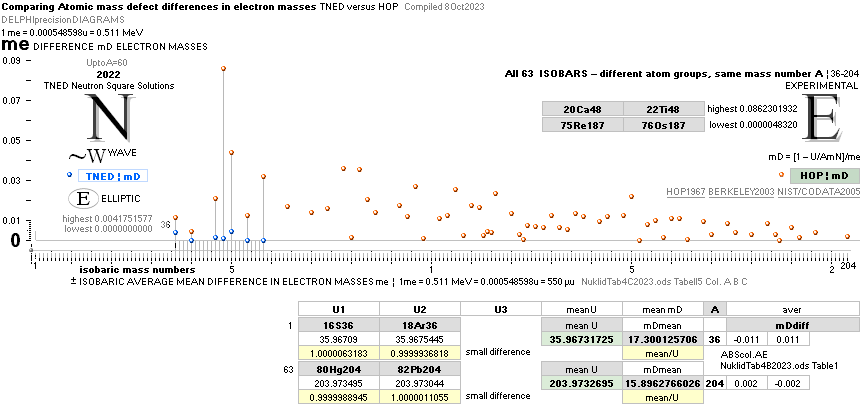
NuklidTab4B2023.ods Table1 Col.Y+

NuklidTab4C2023.ods Table5 Col.A B C

Neutron Square Solutions up to Apr2020 — these isobaric data are the present compiled results on atoms up to mass number 60 as given from the generalized wave-elliptic Base Group Mass Numbers equation (2008). NSdeDIA1.

— We still have much work to do here in UH on completing the basic stable atoms in the nuclide chart on the Neutron Square solutions. These data now 8Oct2023 are the present available for comparing purposes.

Based on the 1967 HOP table atomic masses data:

— Taking the average mean from any isobaric occurrences over the 63 different atomic families, and expressing the tabled U value difference to the averaged U in the Neutron Square atomic mass defect mD electron masses, gives the above diagram: the differences are generally small.

— The overall comparing picture exposes differences between Experimental and NeutronSquare solutions — large enough for a further, deeper investigation.

Shorter: Unless we have missed some vital parts of the mother ship in coming up on the on ramp, we are just warming up.

The isobaric difference and mean average was calculated

NuklidTab4C2023.ods Table5 Col.A B C — Table1 Col. Y+

isoAVER = (isoU1 + isoU2 + .. + isoUn)/n ¦ nMAX = 3

mDisoA = (1 — isoAVER/AmN)/me

mDisoDiff = mDisoA — (1 — isoUn/AmN)/me ¦ the (pair) difference is ± symmetric

See also further from

ExperimentalCONFIRMATIONS.

ExperimentalErrors

TheActualDifferencesHOP/TNED: ExperimentalErrrors ¦ IsobaricMEAN ¦ HIGHESTmD ¦ Comp ¦ Comp2023 ¦ CompareNUCLEAR ¦ CompCALu2023

NSsolutions

The Actual Differences TNED/HOP

The TNED atomic nucleus, inner structure N3m20¦15 — Originally 3D modeled in Simply 3D in Windows 3.1¦95 1994+

THE [‡Table][‡Equation] neutral atom NEUTRON SQUARE ATOMIC MASSES all stable isobaric mean isotopes UP TO A=60

THE DIAGRAMS BUT NOT THE SCALES FROM the free OPEN OFFICE CALCULUS — extremely difficult and tedious to reach an end result: the OOcalc program has no exact pixel representation — and changes frequently the precise positional conditions arbitrarily — however still useful where no other is available. Compare the more guaranteed exact DELPHIpreciseDiagrams version.

———————————————

u = 1.66033 t25 KG ¦ me = 0.000548598 u ¦ HOP-Berkeley-Nist-Codata ¦ NeutronSquareFundamentals — Geometric

Left: TNED/NS solutions Difference to HOP — also the established Weizsäcker nuclear mass defect solution in COMP and ComparingNUCLEAR ¦ ExperimentalErrors.

— The different TNED/NeutronSquare solution types described in NS solutions ¦ Geometric.

— The above left chart results came through a (first deduced [‡Original2003][‡Deduction][‡Table], ordered mathematical) MIX between the basic Elliptic-Wave solutions.

— These values are transferred from the actual original NuklidTab4.wks — after tedious attempts, Microsoft’s 2008 banning of the MsWORKS: the removal of its cell coding on the imperative mod operator and the REST command. It was finally (this production) successfully translated to OpenOfficeCalc cell commands (NuklidTab4A2023TableA) in NuklidTab4B 2023 Table2 Col.J, along with its explaining elliptic-wave mathematics in BaseGroupMassNumbers. How the Code finally after fifteen years came in to OpenOfficeCalc.

— The wave parts [‡NKwaveFunction] reflect generalized values, not elliptic precise. So, there is room for further precision in the left above chart — however on the more demanding (and time consuming — yet only manually solvable in this presentation) elliptic equations credit (EllipticITERATIVEmDSolutions).

NOTE 1: THERE ARE NO STABLE NUCLIDES FOR MASS NUMBERS A=5 AND A=8.

NOTE 2: NS solutions have only neutral atoms. There are no experimental properties at all — no experimental charge dependency.

— The experimentally presented stable nuclides (for starters) have several same mass number A over several different U atomic families. If this offers a conflict between experimental and neutral NS solutions — as it would appear — we have at the present no developed argumentation to settle what is what.

— However again, the differences (IsobaricMEAN) between these same A but different experimental U [and mD = (1 – U/AmN)/me] are relatively small. It is at most (all stable isotopes up to 83Bi209) 0.08623 me = 0.000047305 u = 47.305 µu — which has no visual representation in the above chart scale. Meaning:

— For comparing NS/TNED with HOP on the above given scale, it makes no difference if we use the original HOP table experimental U value — or even »a generalized mean» U value for one and the same mass number A over the actual occasions.

The difference as such has — though — other interesting features, worthy of a separate investigation: Clarifying the significance of the subject — possibly divulging flaws and errors.

NOTE 3: Also compare on the corresponding established Weizsäcker solution on NUCLEAR mass defects in FIBAPO: We must exclude (Comp) the first light atoms from the Weizsäcker results as these are way outside the vertical scale: any idea of a regular comparison becomes out of the question: the present academic idea of the atomic nucleus is badly incorrect — in any precision manner.

— Further Weizsäcker solution comparisons in Comp, WeizCalifornia, WeCALu, Comp2023 and CompCALu2023.

VerticalElliptic: NSsolutions ¦ Geometric

VERTICAL ELLIPTIC

TNEDexperimental ¦ TheActualDifferencesHOP

NeutronSquareFundamentals

We are investigating the NS (Neutron Square) solutions (»carved in the rock») CITER (Carved In ThE Rock) status against the experimental results — and any academic or other theoretical idea of solving the mathematics of true atomic masses.

VerticalElliptic

TheExample:

THE AMAZING H2 Be9 O18 EXAMPLE

LBL — Lawrence Berkeley Laboratory

LBL — LAWRENCE BERKELEY NATIONAL LABORATORY — Atomic masses, Audi et al., 2003 — was used for comparing basics.

The HOP table 1967 shows similar LBL values [ later values have more claimed precision ], not really significant in difference to this present analysis.

ITERATING NEUTRON SQUARE SOLUTIONS BY a simple DETAILED EXAMPLE

——————————————————————————————————————

The iterating aim is to reach a (12 decimal) comparing 1.000000000000 and 0.000000000000

As the effort to iterate further extends, there is always the possibility that there is a more precise decimal representation — if the agent has got more time, and can stand the stress

Nuk8O18

Having a first clue on a fusion path (separate analysis) connecting 1H2, 4Be9 and 8O18, A=18

——————————————————————————————————————

On the TNED given/deduced general Neutron Square atomic mass defect (mD) equation

mD = 6 ± √ 60² – (60 – [ A – K]/E)²

we ITERATE (the Iteration Theorem — studying examples) om K and E until we find a closest possible match with a given or proposed experimental value.

The mission is to find — and prove — that the Neutron Square Solutions elliptic atomic mass equations do connect very close paths — close corresponding quantitative physically related values — with the already experimentally observed.

Nuk8O18 — here rearranged cells for more overview. Original table — CalCard — in hExoTerm2020.ods Table1 B163.

LBL — LAWRENCE BERKELEY NATIONAL LABORATORY — Atomic masses, Audi et al., 2003 — was used for comparing basics.

The HOP table 1967 shows similar LBL values [ later values have more claimed precision ], not really significant in difference to this present analysis.

The above example:

Before a further method was developed on the above (three point iterative) complex, the above result did arrive after an intense three hour expedition: manually flipping, flopping and seeking between the K and E entrance decimals, slowly (the paycheck) observing a growing precision of decimals. The search aim: show us that

T / L = 1.000000000 and T – L = 0.000000000

Or as many decimals we can buy us time for to find — provided undisturbed. Intense interest and concentration is demanded — under absolute natural authority.

— »I am now in the center of the Galaxy, and I do not accept to be disturbed».

Result:

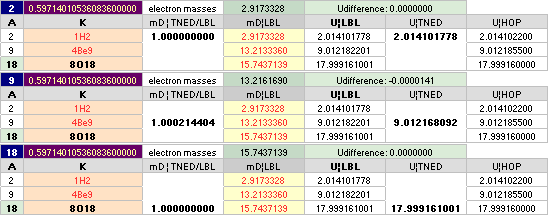
With both 1H2 and 8O18 matching exact the LBL data, a third 4Be9 atomic mass defect shows the T–L U-difference 9.012168092 – 9.012182201 = –0.0000141u = 14.1 µu or -0.02572 me.

— The Neutron Square solution preferences have no ionization connection or other possible impact from other sources. So, the precision should be of type astounding unless we have missed something. It only proves that the Neutron Square solutions mathematics hold the test.

ThePOINT: ».. we are just warming up ..»

THE POINT — finding the Neutron Square O18 atomic mass solution defect ..

————————————————————————————————

WHEREAS the basic 1H2 and 4Be9 already have defined GroundNuclide atomic mass definitions (About the method ¦ UnequivocalAmD ¦ FIBAPO) — and the elliptic iterative job is to use these for testing experimental results on the higher elements mass defect determination, the next step on the 1H2-4Be9-8O18 expedition was to investigate IF SUCH a defining three point ellipse also exists where — exactly — the differences to 1H2 AND 4Be9 are zero, respectively one in relation. It is exposed in hExoterm2020test.ods Tabell1 Q53:

In this case the 8O18 atom is captured by almost the same ellipse E = 0.696711778, but more precisely an E-vaule of exactly 0.700000000. The mD(O18) = 15.7262112 (LBL15.7437139 and HOP15.743814445), ended on the mD difference of a rounded –0.02 me. About the same as the above 4Be9 difference (–0.026 me).

As a first standard, presenting the general (HOP+) atomic weight/mass table data on a visual computer based pixel precision diagram, we can use the ± 1 pixel tolerance on the 18 me mD scale as a lower least accepted difference:

HOPfirst66: TheEX

mD = (1 – U/AmN)me —

U tabled experimental atomic weights in u = Dalton units = m(6C12)/12,

here: u = 1.660033 t27 KG

—————————————————————————

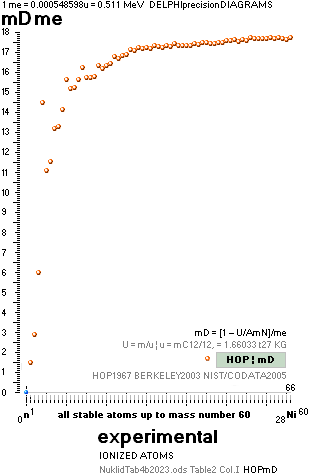
The 66 stable atoms in the HOP 1967 atomic mass/weight table, as expressed in atomic mass defect electron masses mD = (1 – U/Am_n)m_e with U = mATOM/u with u = mC12/12 = 1.66033 t27 KG, and A the atom’s mass number, m_n and m_e the neutron and electron mass in u (Dalton units).

ComparingToleranceStandard: HOPfirst66

If the type TNED–LBL data mD is equal to 0.05 me, a difference of one pixel (standard computer LCD screen) is touched. Below that limit, there is no visual difference between TNED results and HOP/LBL experimental values. The result above on 4Be9 with -0.02572 me lies below that limit. And we would not know, at the present, any method in disregarding such a result as incorrect.

— Accepted first equality limit: ± 1 pixel (±0.05 me: anything below will not be visible in the above scale). So we can use the most exact and sharp visual available tools to present exact (mathematically rounded) data.

On further iterative tests, we would anyway have to set up a form of basic standard, informing us on an iterated result IF it is acceptable as a standard of basic overviewing comparison — or if further precision is needed.

Suggested connection and explanation:

The Neutron Square NEUTRAL Atomic

no experimental encroachment BUILDING HEAVIER FROM LIGHTER

mass defects (mD) versus the experimentally measured results:

TNED¦NS ← (HOP¦Berkeley¦NistCodata)EXPERIMENTAL ← (WEIZ)AcademicTHEORY

See further resolution from

NScredit and CONOR.

TheEXAMPLE

NeutronNIST2009: 3Sep2023

Short science history

THE NEUTRON

Quotes from a Free PDF @Internet 3Sep2023

THE FUNDAMENTAL PROPERTIES OF THE NEUTRON ¦ NIST 2009

Fundamental Neutron Physics Summer School, NIST June 2009

1932:

” Chadwick replaced the paraffin with a variety of other targets and, by measuring the recoil energies of the ejected particles, was able to determine the mass of the neutral particle

Chadwick claimed this was Rutherford’s Neutron ”,

1933:

” Bainbridge makes precision measurements of the atomic masses of the proton and the deuteron using the mass spectrograph ”,

1934:

” Chadwick and Goldhaber make the first ”precision” measurement of the neutron mass by looking at the photo-dissociation of the deuteron

hv + d → p + n

Using 2.62 MeV gammas from Thorium and determining the recoil energy of the protons they were able to determine*:

M_n = 1.0080 ± 0.0005

”,

NeutronNIST2009.

See also The Neutron Decay as explained by TNED in related physics:

— The Neutron gradually loses mass rebuildWORKenergy as it decays

(ca 12-14 minutes, np-Structure).

BASICmN: NeutronNIST

Related physics deductions

COMPARING THE NEUTRON SQUARE INTERNAL APPROXIMATED NEUTRON MASS VALUE: 1.008644262901 .. u

U = (mN/2mDme)(1 — √ 1 — 1/[mN/4mDme]) ; as deduced in Neutron’s AtomicWeight Value

U = (mN/2[15.6]me)(1 — √ 1 — 1/[mN/4(15.6)me]) ;

U = ([mN/me]/2[15.6])(1 — √ 1 — 1/[(mN/me)/4(15.6)]) ;

U = ([mN/me]/2[15.6])(1 — √ 1 — 4(15.6)/[(mN/me)]) ; mN/me minimum = 1836 :

1818 + 18

———————— = 606 + 6 = 3 × (»±101» + »±1») ; Discovery — nuclear structure, the neutron

3

U = (1836/2[15.6])(1 — √ 1 — 4[15.6]/1836) ;

U = (918/15.6)(1 — √ 1 — 15.6/459) ;

U = 1.008644263 ; mN approximated

Ume = mN/1836minimum = 0.0005493705 ; me approximated

HOP source: mN = 1.0086652 ¦ me = 0.000548598 ¦ mN/me = 1838.6235458387

Neutron’s AtomicWeight Value — the first minimum approximation

mNminimum = (1836/[2·15.6=31.2])(1 — √ 1 — 1/[1836/[4·15.6=62.4]]) = (1836/31.2)(1 — √ 1 — 1/[1836/62.4]) = 1.008644262901 ..

That is one decimal position better than the above quoted 1934 James Chadwick measured approximation 1.008.

— However note: This TNED/NS deduction, the equation (11), builds upon — is totally promoted by — already existent known experimental data (1900+). What we know (at the present) it cannot be inferred outside those premises — unless some (ancient, long forgotten) genius FIRST discovered the Neutron Square Fundamentals »as carved in the rock» — and from there made further conclusions, theoretical and/or practical. In any way, that is not our present era of the related scientific way.

(Children have a [strong natural] tendency of exposing such breakthroughs .. anyway ..).

NuklidTab4C2023.ods Tabell1 A20

Explain:

The NS solutions mD value in electron masses (me) for mass number A=12 is exactly 15.6 — mass numbers 5 and 8 have no stable atomic nuclear isotopes.

As observed (The atomic mass unit — u):

— The natural choice of an atomic mass unit

(u, Dalton, here 1.66033 t27 KG = m[6C12]/12)

ends (1960+) on the stable carbon atom 6C12.

— In our science history one first adopted 1H1 for u, then 8O16, and finally 6C12 [1960+].

— A correlated corresponding real experimental physics u-value would then match the equation 11 above (The Neutron’s Atomic Weight Value).

PRIME: BASICmN

Taking the TNED (mathematical) structural provisions

(prime number base: the nuclear stability ends on not whole number divisible quantities)

based on the general top quantum number 3 (TNED’s first N3m20 — HOW), there is apparently not much to chose on:

— With a ±e nuclear (from The Neutron) structure — with a possible Electric Displacement (defining a net nuclear charge [Z] and magnetic moment) — the choice, as based on the neutron atom (enclosing the hydrogen atom), is

1818 central massif ¦ Central Contacts

18 expendable for mass defects mD in building heavier from lighter — Nuclide AZ map

These whole numbers (connecting The Periodic System by whole number solutions: the Nuclear matrix algorithm: Kepler resonances) ends on the prime numbers: 1 3 101. That certainly locks up a certificate for the atomic/nuclear stability, as noted

1818 + 18

———————— = 606 + 6 = 3 × (»±101» + »±1»)

3

So the theoretical end station — after (Nov2007) some in between reckoning (Explaining The atomic mass unit — the atomic, not nuclear, mass defect principle) — ended on the deduced equation (11) — giving us directly a first simple approximation of the neutron atomic weight/mass value mN = 1.0086.. u.

AtomicMASS:

NeutronNIST

Planck constant h = mcr = The Neutron = mN × c₀ × rN —

See The Proton Radius in related physics

ATOMIC MASS — AND THE NEUTRON SQUARE

As hinted at above (NeutronMass):

— Atomic mass, beginning from the Neutron — concealing the Hydrogen atom — can in no way be measured experimentally without affecting the subject of measure by changing its neutral unaffected conditions.

While the precision of the measuring method, technically, can be extended to »unlimited numbers of decimals», the practical part of the quest — the actually unaffected mass — needs additional calculating work — uncertainties over the time of change — before any end value arrives on the table.

Meaning:

The experimental way on atomic mass determination has inside of itself no precise or exact parametric preference. The resulting values can and will differ, more or less, depending on experimental method — and its time consuming length: the amount of affection.

GETTING TO THE POINT:

So:

— How do we know that the NS Neutron Square solution connects to any experimental results at all?

First Bold:

— By proving it is supreme to any theoretical mathematical attempt on explaining a corresponding true atomic result.

Because if it isn’t: — what is the use of it? Answer. Apparently none. Completely worthless.

Answer:

Transfers:

— We know so by comparing (THE ATOMIC NUCLEUS) — inspecting by the eye on any resolvable scale — the neutral atom’s Neutron Square internal solutions — the values — with the experimental and theorecial whatever results on these two atomic mass defect transfer expressions:

mD = (1 — U/AmN)/me :

U = AmN(1 — mDme)

————————————————————————————————————————————

mD atomic mass defect i electron masses me ¦ ClarifyingTheUequation ¦ AtomicMassDefectEquation

the actual wasted mass-energy difference in building a heavier atom K from lighter K1 + K2:

— these mD values are calculated in the Neutron Square solutions, then compared with [ freely available ] experimentally tabled values on atomic weight values U: The NS solution has internal mD:s, resulting in calculable U:s, then comparable to the experimentally available tabled U values from different laboratories.

me electron mass 1me = 0.000548598u = 0.511 MeV

mN neutron mass 1mN = 1.0086652u

U = m(ATOM)/u

u = m(6C12)/12

= 1 Dalton unit (u) [”Da”]

= 1.66033 t27 KG

A mass number

the number of original neutrons making up the actual atom —

in related physics through exothermal nuclear fusion reactions only:

— in modern corridors: A = n + p = A—Z + Z, Z atomic number or nuclear-electronic charge

TNEDexperimental: NSdeDIA1: EnhancedPrecision

———————————————

The Generalized WaveElliptic Equation ¦ NeutronSquareSolutions

E experimental U-values transfered to mD values by mD = (1 — U/AmN)/me

generally based on instrumentally activating changes in the atomic neutral and unaffected condition

N the TNED Neutron Square internal solutions — here by The generalized WaveElliptic formula

GENERAL VERTICAL ELLIPTIC and WAVE-elliptic — The ELLIPTIC EQUATION ¦ GEOMETRIC ¦ WaveMETHOD

entirely based on geometric/paragonic structure provisions, based on Planck constant h=mcr=Neutron.

See TheAtomicNucleus, The ProtonRADIUS, The PlanckRING unless already familiar.

The different methods here are overviewed in NeutronSquareFundamentals.

By the same mD equation, the NS values can transfer on U values, and thereby directly to atomic weights/masses, U = m(ATOM)/u = AmN(1 — mDme).

The fact that, the left diagram above, the experimental (E) over the neutron square values (N) differ (1pixel = 0.05 me = ————) only marginally proves beyond any doubt in the very first place:

the NS solution complex apparently has a real steel solid not possible to destroy natural nuclear physical connectivity. If the reader can discalim: please do share.

In the second place — if the reader has no objections — the coherence proves that nature — not human academy — rules science:

apparently and so provably by internal (eternal) indestructible paragon structures — »carved in the rock» — like a flower in the field

(mathematical matrices: nuclear structure, the periodic system: all basic mathematical concepts: Mathematics5: what we humans find if willing to dig).

More Weizsäcker comparing details will follow on the (13Oct2023) in a way very new and different California University Weizsäcker recently found Weizsäcker equation. See from WeizCalifornia. It has (in most parts) superseded the below comparing results.

In the third place — the academic way of consenting (beginning from around 1900), not deducing, ideas on atomic and nuclear physics has a comparable diagram to the above: the Weizsäcker equation solutions (WeizsäckerDetails):

WAcademicExperimental: NSdeDIA2:

B(Z,N ¦ MeV) = 14A – 0.61Z(Z–1)A^–1/3 – 14A^2/3 – 84.2(A/2 – Z)²/A ±¦0: 34.0A^–3/4 ¦ HOP1967 NSdeDIA10

The WEIZSÄCKER SOLUTION ON ITS FIRST 1967¦1975 TESTED FORM

———————————————

WeizsäckerDetails ¦ HOPweizQuote1967

NuklidTab4B2023.ods Tabell3 — WEIZSmD Col.L

HOPweizXP.ods Tabell1 — has the table construct [ somewhat extensive ] from which the Weizsäcker values have been extracted as above.

E experimental U-values transfered to mD values by mD = (1 — U/AmN)/me

generally based on instrumentally activating changes in the atomic neutral and unaffected condition

W the Weizsäcker nuclear mass defect solution.

B(Z,N ¦ MeV) = 14A – 0.61Z(Z–1)A^–1/3 – 14A^2/3 – 84.2(A/2 – Z)²/A ±¦0: 34.0A^–3/4 ¦ HOP1967 NSdeDIA10

See HOPweizQuote1967 and WeizsäckerDetails.

See also the original comparing Experimental/TNED/Weizsäcker diagram in

ComparingTNED/MAC (UH Nov2007): TNEDcomparingMAC.

The first two Weizsäcker atoms lie outside the vertical scale.

See also the diagrams on the actual differences between the combatants in

Comp and ComparingNUCLEAR.

— While the TNED/NS solution (TEX) exposes an apparent minimum of differences, the academic theoretical solution exposes: not really a succesful idea of the atom and its nucleus. No way. Not even close.

NeutronNIST2009

TAP0solutions2020: EnhancedPrecision:

The latest 2020 results from enhancing the General wave solution by Geometric and precise Elliptic iterations — as of 6Oct2023

PRECISION ELLIPTIC OVER WAVE GENERAL

NS solutions

TNED History

Up to May2020 (TNEDatomPhysics0 — TAP0) the NS precision elliptic solutions (Geometric ¦ NSsolutions ¦ EllipticVertical) only had a provision of the light atomic chart up to mass number 60.

Enhancing the (VerticalElliptic) elliptic method by introducing a first manual iteration procedure (FEfullTNED ¦ TheEXAMPLE ¦ The Iteration Theorem)

the generalized regular wave-elliptic solution could be superseeded by a more precise actual atomic mass number Neutron Square regular elliptic (»exact») solution (CheckTabAElliptic — Extracted examples).

It should be noted here (4Sep2023) that no further Neutron Square Solutions work has been done since May2020 on examining the entire stable atomic chart up to (at first) mass number 60. The iterated elliptic equation results presented here only rely on those past represented results in TAP0. (And, at present; working with the solutions by a manual iteration Example on each atom is, still, a demanding and time consuming enterprise).

The most NS solution favorable compared to the experimental

——————————————————————————————————————————

In selecting the more exact solutions — exposing a possible closer match

(NuklidTab4C2023.ods Tabell2 Col.G i L V) — the following (6Oct2023) compiled picture holds:

NSdeDIA3:

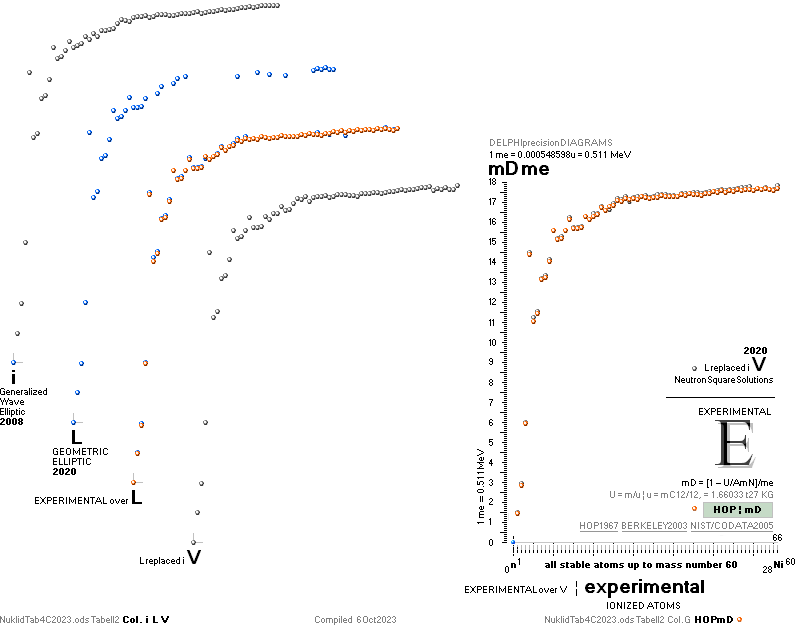
NuklidTab4C2023.ods Tabell2 Col. i ¦ L ¦ V ¦ G

———————————————

GeneralizedWave ¦

The marginal differences NSdeDIA1 between Experimental and NS solutions just underlines the essential:

— Unless a deeper natural connection does exist in atomic and nuclear physics between actual experimentally collected values and the static geometric paragonic NS results, the pictured coherence would — by logic — never have shown. And now that it does show: It is apparently systematically of the type: tight. Real steel stuff, »carved in the rock» so to speak.

We can use the Carved In The Rock specification (NS CITER) for a further test on its credibility in comparing all available data on the atomic and nuclear masses complex.

The above presented, derived from TNED¦N NSdeDIA1, is just a first preliminary overviewing picture on the results from May2020 (TNEDa0). We are (here in UH) far from finished on these deeper (hopefully more precise) elliptic iterative solutions.

As these are of the more demanding and time consuming nature, time is not really on the side of a single individual to carry out a more extensive investigation — unless healthy enough to carry on for some further 514 years, give or take ±12.

The present available results are sufficient enough to stress the central point:

• the coherences between TNED and Experimental have an apparent provable common nature;

• the small differences are small enough to urge a deeper inspection of the experimental nature (laboratory details, not normally exposed freely @Internet) and its parametric composition, comparing on the NS solution results.

The end picture above to the right shows that the TNED deduced nuclear and atomic complex definitely connects to the experimental complex. However on smaller differences here not yet clarified.

Taking the NSdeDIA3 TNED/Experimentally values on differences in atomic weight values (U) and atomic mass defect (mD) on the end Experimental over V diagram renders the following view :

NSdeDIA4:

ATOMIC WEIGHT AND ATOMIC MASS

NuklidTab4C2023.ods Tabell2 Col. Z ¦ AA

HOP u

NeutralToExperimental

Apparently the first basic Question:

WHAT IS THE REASON FOR THE DIFFERENCES

— especially the increasing aspect, growing from lighter to heavier:

♦ The NS solution is apparently a static/geometric/VerticalElliptic —

not much we can do about it, what we know, especially so in concern of the first five posts: 0n1, 1H1, 1H2, 2H3 and 2He4

— while the experimental is a dynamic: entailing many (complicated) parametric/instrumental involved parties on the most technically sophisticated developed level (1932+).

We have no (explicit) answer to that question here (yet).

(We refuse to speculate here: proof is needed).

Especially because of the tight first light elements — greater difference on heavier — there is a growing urgent reason to investigate a rational explanation:

The NS solutions have only neutral atoms — no charge dependency

• The NS solutions describe neutral atoms: no affection: should be »linear».

• The Experimental results uses ionizing (hf-quanta), plus relativistic ideas on conversion between mass and energy (E=hf=mcr/t=mc²), introducing a complex of other conditions than the neutral aspects.

Exactly which is this further aim to penetrate.

— Compare: AllKeplerMath

— present scientific academic community appears to be in deep cosmological theoretical trouble (the death of modern academic ideation).

See also SPECIFIC NOTES

— details on the above complex-comparing NSdeDIA3.

NeutronNIST2009

SPECIFICnotes: 6Sep2023

SPECIFIC NOTE TO THE NSdeDIA3 COMPARING DIAGRAM

NSsolutionsTNEDmD 1H1: 1.512616535

The Neutron Square’s special transfer expression

— rP/rN = (√8)/(1 + √3) = 1.0352761804 involving the two basic atomic and nuclear agents: the neutron and the proton radius

— offers an option of averaging.

———————————————

The ProtonRADIUS ¦ Geometric

Given the exact geometric (Geometric) NS solution to the 1H1 atomic mass defect mD(1H1) = 1.461075377, there is the option

mD(1H1) = mD(1H1GEO) × rP/rN

= 1.512616535 ;

HOPmD = 1.518021871 ;

mDdiff = -0.0054 ..

Compared to the pure geometric mD difference (-0.0569), the rP/rN option in absolute is more than a ten times precision improvement.

It has been used in the NSdeDIA3 enhanced comparing diagram in the replacing L Geometric-Elliptic.

NeutronNIST2009

CLAIR: 17Oct2023 — The WikipediaWeizsäckerQuote ¦ ClarifyingTheU

THERE IS NO ESTABLISHED ARTICLE IN THE SCIENTIFIC COMMUNITY ON ATOMIC MASS DEFECT

The different concepts of atomic and nuclear mass defect — exemplified

CLARIFYING EXAMPLES IN PRESENT LITERATURE

ATOMIC AND NUCLEAR

There are some (several) flourishing misconceptions and delusions — (almost) impossible to resolve with the present established set of scientific community vocabulary — (as proven for starters by this example, Oct2023):

” The page ”Atomic mass defect” does not exist”.

Wikipedia 9Oct2023.

A search on ”mass defect” on the other hand is redirected in Wikipedia to the article on

Nuclear binding energy.

nuclear mass defect

atomic mass defect MDa = AmN – U ¦ U = mATOM/u ¦ u = m(6C12)/6 = 1 Dalton

nuclear mass defect MDn = AmN – U – Zv ¦ v = nino = mN – (mP + me) = mN – m1H1 (= 0.00084u)

MDn – Zv = MDa MDn = MDa + Zv.

v: the work mass energy waste that built the first atom — 1H1 Hydrogen — from the fundamental atom: The Neutron [ FAMQ ]

WEB@INTERNET EXAMPLE:

Confusions arise on the idea that ”mass defect” is a unitive concept. It is not.

It is necessary to specify weather ”mass defect” relates to atomic or nuclear.

— But that was also a hell of a way to put it, in light of the above sampled:

— The term for clarification is not even represented.

InternetExample:

The Internet example

(many domains have this typical formulation, none mentioned):

” A mass defect is the difference between an atom’s mass and the sum of the masses of its protons, neutrons and electrons.”

@INTERNET search 10Oct2023

As interpreted on atomic mass defect:

MDa = ZmP + (A–Z)mN + Zme – U

= ZmP + AmN – ZmN + Zme – U

= AmN + Z[mP – mN] + Zme – U

= AmN – Z[mN – mP] + Zme – U

= AmN – Z[mN – (mH1 – me)] + Zme – U

= AmN – Z[mN – mH1 + me] + Zme – U

= AmN – Z[v + me] + Zme – U

= AmN – Z[v + me – me] – U

= AmN – Zv – U ¦ the NUCLEAR MASS DEFECT quantity related definition. Not the atomic.

Unless so clarified, grave misunderstanding may arise — »impossible to sort out: .. I hate you ..».

No.

MDa = AmN – U.

As interpreted on nuclear mass defect:

Yes.

MDn = AmN – Zv – U

We take the quote on the word by an example and see how it works:

HOP table Example on Iron ¦ _ZATOM^A_{mD ¦ U}

——————————————————

₂₆Fe⁵⁶_{17.759142302 ¦ 55.9349363 u} :

——————————————————

mP 1.00727660200000u

mN 1.00866520000000u

me 0.00054859800000u

——————————————————

NUCLEAR MASS DEFECT:

protons + neutrons + electrons – atom’s actually (measured) mass ¦ per number A of neutrons mN that built the atom

26mP + (56–26)mN + 26me – 55.9349363 ¦ ÷ AmN ¦ ÷ me mass defect expressed in units of electron masses

= 0.5284749 ÷ 56mN = 0.009355980 ¦ ÷ me = 17.0543464337

——————————————————

ATOMIC MASS DEFECT:

56mN – 55.9349363 = AmN – U ¦ ÷ Amn / me

= 0.5503149 ÷ 56mN = 0.009742630 ¦ ÷ me = 17.7591423022

See Wikipedia quote in Not represented.

See further

The mass defect concept

DIFFERENCE BETWEEN ATOMIC AND NUCLEAR.

See also similar comparing (confusing unless related)

HighestScore.

WikiWEIZ: WikiWeisNUCm

Checking on Academically established atomic and nuclear — exemplified and related WikiWEIZnuclearMass

THERE IS NO ESTABLISHED ARTICLE IN THE SCIENTIFIC COMMUNITY ON ATOMIC MASS DEFECT

THE WIKIPEDIA WEIZSÄCKER QUOTE ON THE BINDING ENERGY CONCEPT AND EXPRESSION

See Wikipedia quote in Not represented.

As quoted,

” The semi-empirical mass formula therefore provides a good fit to heavier nuclei, and a poor fit to very light nuclei, especially ⁴He.”,

WIKIPEDIA, Semi-empirical mass formula (as quoted 15Oct2023).

The Wikipedia article leaves no comparing diagrams or other comparing quantitative results on the differences between calculated and experimentally measured. Here we (only until recently) have the HOP 1967 source (and the Swedish FOCUS MATERIEN 1975) concurrent values.

Wikipedia on the Weizsäcker nuclear binding energy equation

—————————————————————————

WIKIPEDIA, Semi-empirical mass formula (14Oct2023)

” It was first formulated in 1935 by German physicist Carl Friedrich von Weizsäcker,^[2] and although refinements have been made to the coefficients over the years, the structure of the formula remains the same today.”,

” The formula gives a good approximaltion for atomic masses and thereby other effects. However, it fails to explain the existence of lines of greater binding energy at certain numbers of protons and neutrons. These numbers, known as magic numbers, are the foundation of the nuclear shell model.”.,

” The formula represents the liquid-drop model proposed by George Gamow,[1] ..”,

WikiWEIZnuclearMass: WikiWEIZquote ¦ RelatedNUCLEAR

” The formula The mass of an atomic nucleus, for N neutrons, Z protons, and therefore

A = N + Z nucleons, is given by

m = Zm_p + Nm_n – E_B(N,Z)/c²

where m_p and m_n are the rest mass of a proton and a neutron respectively, and E_B is the binding energy of the nucleus.”,

WIKIPEDIA, Semi-empirical mass formula (as quoted 15Oct2023).

Clarifying the rank

INTERPRETING THE WikipediaQUOTE — here, our UH designations unless misunderstood (no direct quote exists, so there is a certain margin of hazard here):

m = Zm_p + Nm_n – E_B(N,Z)/c²

”The mass of an atomic nucleus”:

Mnuc = ZmP + (A–Z)mN – B ¦ ”The mass of an atomic nucleus”; B = E_B(N,Z)/c² ;

= ZmP + AmN – ZmN – B

= AmN + ZmP – ZmN – B

= AmN + Z(mP – mN) – B

= AmN – Z(mN – mP) – B ¦ mN = mP + me + Zv

gravitating proton mass + gravitating electron mass

= AmN – Z(me + v) – B ¦ m, the Wikipedia proposed nuclear mass

B, ”the binding energy of the nucleus” ;

AmN – B = Mnuc+ Z(me+v)

AmN = Mnuc+ Z(me+v) + B

------------------------------------------------

Checking — related — the Wikipedia rank

RELATED NUCLEAR MASS CONCEPT:

—————————————————

Checking — related — the Wikipedia rank

—————————————————

Mnuc = U – Zme ¦ nucleus gravitating mass + electrons gravitating mass = atom gravitating mass:

: Wiki:

AmN – B = Mnuc+ Z(me+v)

AmN = Mnuc+ Zme + Zv + B ;

AmN = U – Zme+ Zme + Zv + B ;

AmN = U + Zv + B

B = AmN – U – Zv

B ”the binding energy of the nucleus” ; verified

nuclear mass defect — related physics

MDn = AmN – U – Zv

AmN – U – Zv = nuclear mass defect ¦ MDn

AmN – U = atomic mass defect ¦ MDa = total atomic binding energy = absolute max binding energy

Summing

The Wikipedia RANKING Quote (certainly) certifies that the underlying implied conceptual idea behind the Weizsäcker equation on ”binding energy” connects to the NUCLEAR — not atomic — mass defect concept.

That is comforting — comparing the (erlier 1967¦1975) different Weizsäcker equation results.

See NSdeDIA14 and NSdeDIA11.

CLAIR

PO4:

Health and care issues on planet Earth — outside modern academic quarters

WHY PLANTS¦LIFE PREFER O16 BEFORE O18

Connecting the DOLE1965 observations

————————————————

Oct2023 — a final (strong) possible proof and resolution (quoted) on the respiratory disease phosphorylation oxygen (O18¦16) molecular connection to deforestation, as suggested by several earlier articles[‡] in the UniverseHistory productions: the general global biochemical connected deforestation complex (investigating basic life matrix chemistry).

————————————————

———————————————

CWON from CAP

Related physics and mathematics

——————————————

In CWON from CAP

there is already an atomic/nuclear proven connection to a preorganic »chemical matrix» system. It has a provided proof on already known samples from meteorites NOT TO SAY how THE ALREADY EXISTING EARTH LIFE BIOLOGY here came on (Primary Neutron Nuclear Carbon Matrices): principally and deeply verified.

All (CAP) primary surface celestial bodies develop an organic surface nuclear-atomic matrix structure from the K-cell expansion, and further.

The reason, as noted, lies or can be related so to lie in the concept of STRUCTURE — beginning from the fundamental atom: the neutron: Planck constant h=mcr. Normally within 12-14 minutes, a regular stable Hydrogen atom appears out of the unstable neutron atom/nucleus. FastForward: Each celestial body develops its own specific surface structural combinations, depending on the body’s mass (Surface synthesis — CWON).

Phosphorylation: PO4

So the central Quest in this article was: The PO₄ molecule:

phosphorylation

a Phosphorus atom15P31 no isotope with 4 Oxygen atoms O16 isotopes O17¦18 hooks up — or triggers other events — with a larger biochemical structure

@INTERNET ¦ WIKIPEDIA Phosphorylation (28Sep2023)

” In biochemistry, phosphorylation is the attachment of a phosphate group to a molecule or an ion. This process and its inverse, dephosphorylation, are common in biology.”.

Cell division, mitosis PO4 agent:

The PO4 component is, as testified in many texts, the (finally 1970-1980) discovered agent — biochemical mechanics — responsible for most (not to say all) biological events connected to cell division (mitosis): DNA-RNA, general amino acid and (glucose) protein structure input-output organization and maintenance. The »Commander DoIt».

— What about PO4 — what are you trying to say?

Specifically unknown in modern corridors:

The PO4 CAP atomic/nuclear primary chemical matrix — proven in CWON — only allows or at a first glance appears so to allow a regular (biochemical) matrix with O16. That is: In precise concurring observation with DOLE1965 (deforestation already during 150 years beginning from 1800, see MLN):

(»PO4-mechanics») organic plants »prefer» O16 over O18.

At first, as noted: There is an eleven percent gain in mass/energy: 1—16/18=0.11 ..: Using O16 is the most effective and biological economic.: fastest, least losses.

At second, the real steel argument — however not apparent in modern corridors, the CWON (proof) from CAP complex, responsible for organic structure — is this:

As preliminary tested: P with O18 offers no direct primary regular biochemical structure (here known — no direct proof: we are talking origin of Earth life here). It is readily obvious NOT appropriate for a primary natural repetitive chemical molecular chain construct (with smallest amount of blanks: the effective covering primary volume structure, exemplified and illustrated below).

The hint is:

PO4 with O18 is (definitely) not suited for life biochemistry. No way. O16 it is.

StrongHINTEDproof: Phosphorylation

———————————————

CWON from CAP

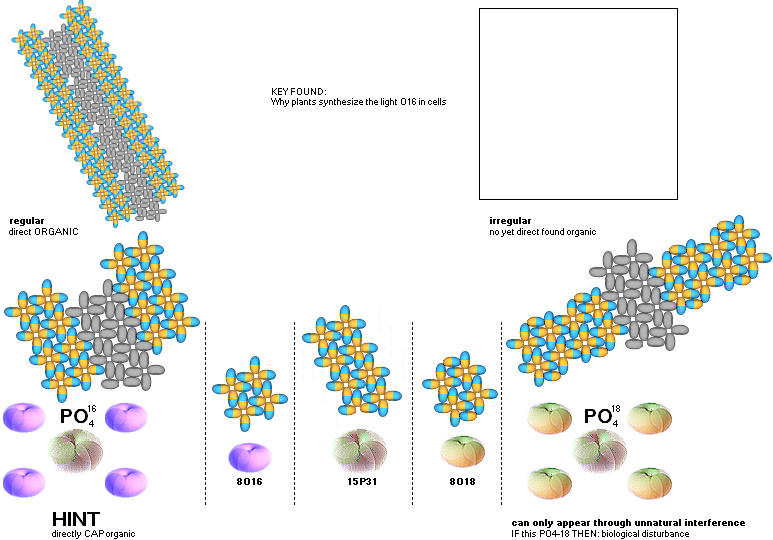
The O16 is the (CWON) natural component in the biological CO2 cycles. Deforestation breaks that state, dumping normally ground based cyclic natural O16 into excessive atmospheric CO2 — where the nearest ground (air gases after atomic weight ¦ OxygenFilter: CO2 the heaviest followed by) replacement is: O18. Result: impoverishment of the natural life sustaining biological health foundation. That was the original reflection here in UH (BioEK1 ¦ Present state atmospheric lies way below: 1254 ¦ TheTEN): Deforestation kills — suffocates — life. A statement to be biochemically proven. Now the PO4 suggests a serious link to such a (final) proof: life power decrease. Pandemic situations. Affecting both plants and animals.

No direct obvious primary atomic/nuclear chemical matrix for 1(P) + 4(O18).

— Possibly PO2. No more.

So, IF O18 associates chemically with P, no natural such biochemistry ever existed ..

— says — or strongly suggests — CWON from CAP.

1(P) + 4(O16) on the other hand, seems to reflect excellent biochemical primary matrix systematics — as too the other exemplified parts (amino acids, chlorophyll and hematin exemplified in KemBlockEX).

The DOLE1965 preferred O16

There is an eleven percent gain in kinetic (mv) mass/energy: 1—16/18=0.11 ..: Using O16 is the most effective and biological economic.: fastest, least losses.

is primarily not because of the 11% mechanic-electric argument.

Percent11

The primary reason (CWON from CAP) is: THAT IS HOW LIFE HAS BEEN ASSEMBLED. During its rough 3 billion years on earth, organic life began by an already inherited atomic/nuclear ordered STRUCTURE (periodic system) — all from the birth of the Earth as a celestial body (VoJ). TNED and its related physics strongly suggests so — based on atomic/nuclear structure. Not random and chance. No pharmaceutical industry. No unintelligent Mother Nature. No bald cuts.

— These arguments and aspects lie totally outside the horizons of present academic cosmological ideas. No way. Intelligence is under question.

HintedConsequences: HntedProof

So (SAN1), on assumed relevant proceedings:

AIR GASES BY ATOMIC WEIGHT

What happens IF natural biology is FORCED to replace O16 with O18 — because a huge amount of the original natural cyclic O16-C12 has been dumped in the atmosphere because of industrial exploration on alive forests, not allowing them to live and die naturally (the root system guaranteeing biodiversity, Simard2012). A created growing amount of bald cuts on Earth compromises life sustainability:

— What happens to Life biochemistry?

———————————————

SDandCWON ¦ MLF ¦ MaunaLoaProof ¦ MLN1812IPCC2013Graph284ppmvCO2 ¦ WHAT PUSHES THE TREND RISE?

BioEK1 (heavily compromised by deforestation 1812+) with the naturally normal forest preference MLN1812IPCC2023Graph284ppmvCO2 as proven in CWON guarantees the primary difference between biological CO2 cyclic O16 and general atmospheric O16 — these have (VoJ) a well related separate geological history explanation (not in present established corridors) — and do not mix on credit of a preserved natural biology. A definite (heavy, natural, scientific) dispute is so lying on our table.

Shorter — on the presumed relevant quest:

What happens (Phosphorylation) with a Life, educated during some 3Gy on (15P31)(8O16)₄ if it suddenly is forced by human PhD interests from some 1812+ and further pharmaceutical industry 1850+, now during a rough 150y, to develop on a »life alien species» of the form (15P31)(8O18)₄ ?

.. slower .. demanding more effort .. problematic connection ..

QUOTES: Con ¦ Phosphorylation

Quotes ...

” All organisms produce a phosphate compound, ATP, which is the universal energy currency of life.”,

WIKIPEDIA , Photophosphorylation (27Sep2023)

:

” During respiration and photosynthesis

Phosphorylation is essential to the processes of both anaerobic and aerobic respiration, which involve the production of adenosine triphosphate (ATP), the "high-energy" exchange medium in the cell. During aerobic respiration, ATP is synthesized in the mitochondrion by addition of a third phosphate group to adenosine diphosphate (ADP) in a process referred to as oxidative phosphorylation. ATP is also synthesized by substrate-level phosphorylation during glycolysis. ATP is synthesized at the expense of solar energy by photophosphorylation in the chloroplasts of plant cells.",

WIKIPEDIA , Phosphorylation (27Sep2023)

:

” The phosphorylation serves two purposes: to activate each already-assembled pre-replication complex, and to prevent new complexes from forming. This ensures that every portion of the cell's genome will be replicated once and only once. The reason for prevention of gaps in replication is fairly clear, because daughter cells that are missing all or part of crucial genes will die. However, for reasons related to gene copy number effects, possession of extra copies of certain genes is also deleterious to the daughter cells.”,

WIKIPEDIA, Cell cycle (27Sep2023)

:

” Protein phosphorylation is an important cellular regulatory mechanism as many enzymes and receptors are activated/deactivated by phosphorylation and dephosphorylation events, by means of kinases and phosphatases. In particular, the protein kinases are responsible for cellular transduction signaling and their hyperactivity, malfunction or overexpression can be found in several diseases, mostly tumors.”,

” This reversible mechanism occurs through protein kinases and consists of the addition of a phosphate group (PO4) to the polar group R of various amino acids. Consequently, this addition modifies the protein from hydrophobic apolar to hydrophilic polar, allowing the protein to change conformation when interacting with other molecules.”,

THE CRUCIAL ROLE OF PROTEIN PHOSPHORYLATION IN CELL SIGNALING AND ITS USE AS TARGETED THERAPY

Ardito et al., Published online 2017 Jun 22 (25Sep2023)

INTERNET SEARCH

»Phosphorylation and Covid» 28Sep2023:

phosphorylation shown in coronavirus

” Glycogen Synthase Kinase-3 Regulates the Phosphorylation of Severe ...

https://www.ncbi.nlm.nih.gov › pmc › articles › PMC8011290

The involvement of GSK-3 in N phosphorylation has also been shown in another coronavirus, JHMV. Finally, we found that inhibition of GSK-3 could suppress the replication of both coronaviruses. The results not only indicate that GSK-3 is critical for N phosphorylation but also suggest its involvement in regulating viral replication.

”.

coronavirus proteins predicted be phosphorylated

” Role of phosphorylation clusters in the biology of the coronavirus ...

https://www.ncbi.nlm.nih.gov › pmc › articles › PMC7103301

Although coronavirus N proteins were predicted to be phosphorylated at multiple serine residues, mass spectroscopic analyses identified two regions of phosphorylation on the IBV N protein (when over-expressed) which are located at two conserved amino acid clusters, Ser 190 and Ser 192 and Thr 378 and Ser 379 (Chen et al., 2005).

”.

phosphorylation sites

conserved in coronavirus proteins

” The Global Phosphorylation Landscape of SARS-CoV-2 Infection

https://www.sciencedirect.com › science › article › pii › S0092867420308114

The cluster of phosphorylation sites within an arginine/serine (RS)-dipeptide rich region, C-terminal to the RNA binding region (Figure 2 A), is conserved in other coronavirus N proteins. This region is phosphorylated in SARS-CoV by serine-arginine (SR) protein kinases, modulating the role of SARS-CoV N protein in host translation inhibition ( Peng et al., 2008 ).

”.

Eighty-seven compounds identified

global phosphorylation profiles

representing potential COVID-19 therapies

” The Global Phosphorylation Landscape of SARS-CoV-2 Infection

https://pubmed.ncbi.nlm.nih.gov › 32645325

Eighty-seven drugs and compounds were identified by mapping global phosphorylation profiles to dysregulated kinases and pathways. We found pharmacologic inhibition of the p38, CK2, CDK, AXL, and PIKFYVE kinases to possess antiviral efficacy, representing potential COVID-19 therapies.

”.

systematic study of phosphorylation

and phosphoproteins help find

suitable therapeutics of COVID-19

” Frontiers | SARS-CoV-2 Infection Triggers Phosphorylation: Potential ...

https://www.frontiersin.org › articles › 10.3389 › fimmu.2022.829474 › full

17 feb. 2022A systematic study of the dynamic change in phosphorylation site and phosphoproteins will help to find suitable therapeutics of COVID-19, especially suitable kinase inhibitors. SARS-CoV-2 affects various kinases including CMGC, CK2, CDK, and PKC, and also regulates important signaling pathways including MAPK cascade, GFR signaling ...

”.

phosphorylation of STAT1 enhanced

in severe COVID-19 cases

” Altered increase in STAT1 expression and phosphorylation in severe COVID-19

https://pubmed.ncbi.nlm.nih.gov › 34676541

Contrary to the baseline STAT1 expression, the phosphorylation of STAT1 was enhanced in severe COVID-19 cases, indicating a dysbalanced JAK/STAT signaling that fails to induce transcription of interferon stimulated response elements (ISRE). This abnormality persisted after IFN-α and IFN-γ stimulation of PBMCs from patients with severe COVID-19.

”.

current study aimed understanding

SARS-CoV-2 protein

influenced by phosphorylation

” Phosphorylation of SARS-CoV-2 N protein affects its function

https://www.news-medical.net › news › 20200701 › Phosphorylation-of-SARS-CoV-2-N-protein-affects-its-function.aspx

The current study is aimed at understanding how the N protein is influenced by phosphorylation. Characterization of N protein condensates. an SDS-PAGE analysis of all N protein mutants used in...

”.

Phosphorylation of disordered region

underlying mechanism is not known

” Phosphoregulation of Phase Separation by the SARS-CoV-2 N ... - PubMed

https://pubmed.ncbi.nlm.nih.gov › 33248025

Phosphorylation of the central disordered region promotes the protein's transcriptional function, but the underlying mechanism is not known. Here, we show that the N protein of SARS-CoV-2, together with viral RNA, forms biomolecular condensates.

”.

modulation of phosphorylation

” Nucleocapsid mutations in SARS-CoV-2 augment replication and ... - PLOS

https://journals.plos.org › plospathogens › article?id=10.1371 › journal.ppat.1010627

21 juni 2022Our results indicate that changes in N phosphorylation correlate with differences in virus replication; thus, we sought to modulate N phosphorylation using kinase inhibitors. Prior work has identified two consensus sites for GSK-3 phosphorylation within the SR domain and inhibition of GSK-3 has been shown to reduce SARS-CoV-2 replication ( Fig ...

”.

And many others.

SumPhosphorylation:

Phosphorylation

SUMMING Internet articles on PO4 versus Covid:

The advertising headlines — having identified the phosphorylation PO4 as an active agent — reflect an underlying pharmaceutical effort to control its PO4 agency of biochemical mechanics — by pharmaceutically testing disease inhibiting molecular compositions at least not directly (½-2 year tests) having any negative effects on the patient.

SHORTER — unless disclaimed

Present pharmaceutical industry is playing with fire. No doubt.

Modern academic ideas of highly manipulative medicine have a max 70 years experience (1950+), compared with Mother Nature’s roughly 3Gy — on a PO4 assembling life maintaining credit (still 2 eyes, not 3).

No way.

Other Quotes:

” Early cell cycle studies established that phosphorylation was important for cell division. ",

p2Col1t —

DISSECTING THE MECHANISMS OF CELL DIVISION, Ong et al.,

JBC Papers in Press. Published on June 7, 2019 ¦ Free PDF (28Sep2023)

:

” This is because protein phosphorylation has gradually become an integral part of all the systems they are studying themselves. Indeed it would be difficult to find anyone today who

would disagree with the statement that “the reversible phosphorylation of proteins regulates nearly every aspect of cell life.”,

” Phosphorylation and dephosphorylation, catalysed by protein kinases and protein

phosphatases, can modify the function of a protein in almost every conceivable way; for

example by increasing or decreasing its biological activity, by stabilizing it or marking it

for destruction, by facilitating or inhibiting movement between subcellular compartments, or by initiating or disrupting protein–protein interactions.”,

” The simplicity, flexibility and reversibility of phosphorylation, coupled with the ready availability of

ATP as a phosphoryl donor, explains its selection as the most general regulatory device adopted by eukaryotic cells.”,

THE ORIGINS OF PROTEIN PHOSPHORYLATION, Philip Cohen , 2002

Free PDF (28Sep2023) — [eukarotic-, which have a nucleus]

IF NOT ALREADY PART OF A FUNDAMENTAL PROOF ..

These quotes, at this stage, does not prove anything else than a strong hint. The needed proof is: A thorough — mass — spectroscopic analysis of the (PO4 associated biochemical) molecular content. At first clarifying IF the (general) O in the PO4 is of type O16 — or what is feared here: of type O18.

[ beginning at 1812: dumping the recycling natural CO2 by deforestation, creating a corresponding biochemical biological disturbance, gradually evolving through many forms of disease ]

— Possibly: We are just looking at the top of the iceberg. Deforestation continues.

While State administration should alert a global alarm, nothing of the kind is seen.

Perhaps such mass spectroscopic O16-O18 analysis already has been made. But none of it is seen at the free non-cookies established Internet now September 2023.

Many (especially medical) sites are — also — blocked to the visitor, demanding a prioritizing cookies consent for site access — blocking, interrupting, the actual serious scientific interest. It reflects treating the visitor as an infant, really, in deep need of support for further life from a more acquainted instance than the individual scientific interest : no access.

Nature, and other medical associated:

Declare it, then: »This website is NOT for any average human to access on serious scientific interests».

— »The Visitor will be interrupted, asked to bow, and consent, before other inducements».

— Not one word HumanRight recognition. Not a sound. Not a spell. Not a hint.

”.. every individual and every organ in society ..”, ”.. of the greatest importance ..”. No sound.

Wickedness — evil — continues to beat up Violence, intrusion, rape .. spanking .. domination ..

— Again: by DRIFT. Not plan. With zero teaching and education on basic care and responsibility — UDHR10Dec1948: no sound — humanity is caught in a daily expanding trap of impossible intercoursing solutions other than .. violence, despair, desperation .. explored by the police, prosecutor, court — and the screaming public — to practice punishment and obedience. No sound. Not one word. Evil — no care — knocks on Violence’s door. No moral.

Short:

Around 1800 a type enters Europe forcing the populations to cooperate under laws of violence by threat of punishment.

The authoritative pressure has since forced the populations to adopt with solidarity and loyalty: obedience and punishment on a general scale of most popular conduct: spanking. Rape.

— So: When did that cease?

No teaching. No education.

Just obedience and punishment. A deep yearn for domination.

— »Here, you do as you are told. And that is the end of it».

Phosphorylation

NuclearReactionLaw: Exothermal nuclear reaction law — SWEDISH EDITION, full deduction and explanation¦ NUCLEAR REACTION LAW — connecting expression to general cosmic state law — related energy equivalents

NUCLEAR REACTION LAW

———————————————

Exothermal nuclear reaction law ¦ NUCLEAR REACTION LAW ¦ FusionRINGS

GIVEN THE RELATED DEDUCED EXPRESSION, the nuclear reaction law uses already established tables of atomic masses/weights for evaluation — and determination of the basic involved parameters. The nuclear reaction law mathematics tests IF two (or three) given atomic nuclei can form a heavier atom and its nucleus by exothermally emitting Planck energy (m→γ) E=hf taken from the involved fusing masses [K1 + K2 – (m→γ) = K].

Example (hExoterm2020.ods Tabell1 — autoFormat):

NOTE: the free OpenOffice spread sheet cell program here has been

ADOPTED FOR USE WITH LAWRENCE BERKELEY NATIONAL LABORATORY ATOMIC MASS TABLE 2003

LBL — LAWRENCE BERKELEY NATIONAL LABORATORY — Atomic masses, Audi et al., 2003

NOT ENOUGH fusion mass to generate exothermal energy:

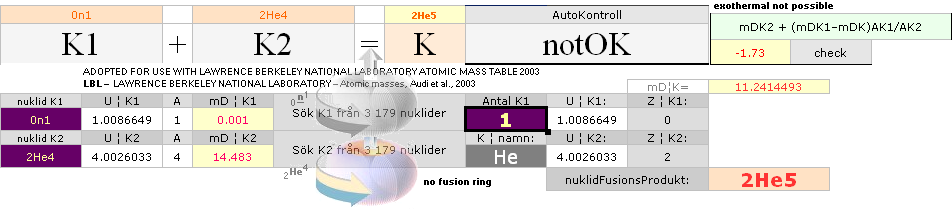
SUFFICIENT fusion mass to generate exothermal energy:

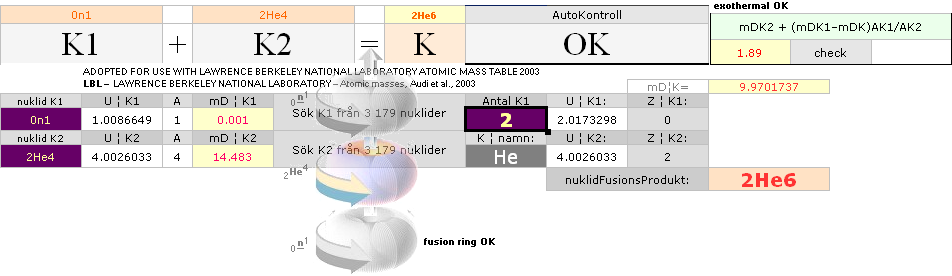
The result generates the LBL table parameters — and the corresponding Neutron Square values (the actual view of parameters here are reduced for clarity).

Based on the results, further analysis continues on NeutronSquareSolutions.

NOTE: In modern corridors — no TNED theory — the above may very well exist by mathematical principle. But given the basics of the TNED complex, it is not likely that we ever will see any of the above kind in type Wikipedia or other established encyclopedia. Wikipedia is reserved for the modern academy history alone: ”related sources — not truth”. Safely separated.

NuclearReactionLaw

NScredit: 20Oct2023 — LGDbasics ¦ NSUnit

Weizsäcker solution is chasing the experimental

and the experimental is chasing the neutral — the NS neutral atomic masses:

the experimental cannot dispense with electric and magnetic field strengths:

The Neutron Square solutions has nothing of the kind.

WHAT IS THE ENIGMATIC AND STRANGE STATUS OF THIS REMARKABLE NEUTRON SQUARE SOLUTION PARAGONIC »CARVED IN THE ROCK» EDIFICE? AND HOW DID IT COME HERE? AND WHY WAS IT NOT DISCOVERED BEFORE?

Short review:

THE ORDERS AFTER WHICH THE NEUTRON SQUARE WAS DISCOVERED AND REVEALED ¦ Discovery

Planck constant the universal efficacy quantum (Max Planck 1900) ¦ TheNEUTRON

h = mcr

= 6.62559 t34 JS

= mN · c₀ · rN ¦ mass charge spin ANGULAR MOMENTUM — mvr, Kepler momentum vr

= 1.0086652u · 2.99792458 T8 M/S · rN ¦ u = 1.66033 t27 KG = m(6C12)/12

rN = h/mNc₀ ¦ neutron gravity circle radius ¦ the fundamental PlanckRING radius

= 1.319897164124040 t15 M

NUCLEAR STRUCTURE mass charge spin: electric displacement

±e — secured indivisible on a specific basic prime number:

1818 ÷ 18 =101 cannot be further divided — »carved in the universal rock»:

(1818+18)/3 = 606 + 6 = 3 × (»±101» + »±1») › See HOW3.

Total number of electron-positron masses in the neutron: 1818+18+k: (k=2.624..¦ mN/me=1836 + 2.623545838670)

1818 central massif

18 maximum (never touched) mass-energy waste per neutron in building heavier atoms

26Fe56 HighestmD 17.7591423022 electron masses [ the discovery 2003 ]

NS the neutron square with square side mass number 60 ¦ Elliptic Equation

rP ProtonRADIUS r₀ = 1.37 Fermi — Planck constant on Hydrogen spectrum’s energy circle:

The Neutron Square solution outclasses/challenges present scientific community idea on the nature of nuclear physics

EXPERIMENTALLY MEASURED ATOMIC WEIGHTS/MASSES VERIFIES NEUTRON SQUARE SOLUTIONS

THE ATOMIC NUCLEUS

as so observed:

— »carved in the universal rock»:

— GRAVITATION — the neutron atom, the fundamental form of gravitational mass, the Planck Ring — is not a particle.

— CHARGE (Z) is not mass, does not interact with mass, although integrated with mass in the atom.

— Gravitation is not light (charge: electric and magnetic properties).

— Light is not gravitation.

— Light is not a particle.

— Curved light paths does not develop centrifugation: light is massless.

— Max Planck was right. Albert Einstein was wrong.

.. normalized on u = m(6C12)/12: U = 12 = m/u

TNED ← EXPE ← WEIZ

NORMALIZED

Weizsäcker solution is chasing the experimental

and the experimental is chasing the neutral — the NS neutral atomic masses:

the experimental cannot dispense with electric and magnetic field strengths:

The Neutron Square solutions has nothing of the kind.

StandardUniversal: Discovery

PO4 ¦ ATOMIC MASS defect EQUATION ¦ ComparingNUCLEAR ¦NScredit

EXPERIMENTALconfirmations: Atomic masses

THE MACHINE THAT RUNS THE WHOLE SHOW:

Light’s Top Divergence c₀ is preserved independent of gravitation’s influence on light’s propagation in space:

HRB w² – c² = c₀² ¦ CRL w² + c² = c₀² ¦

c = (c₀/2)(1 ± √| 1 – (2w/c₀)² |) light’s gravitational dependency LGD ¦ w = √Gm₂/r = c ¦ 2c² = cc₀ ¦ c = c₀/2 = c_z energyZone: ¦ c₀ = 2√G[m₂/(n→∞)]/[r/(n→∞)]:

c0 is preserved independent of any possible [m/(n→)]/[r/(n→∞)] fractal nuclear construct: the fundamental atom, the neutron,

the fundamental form of gravitation: gravitation is not a particle. No way.:

local gravitational dominance has the strongest stand in the atom, the atomic nucleus, the neutron — its Planck fractal hollow ring toroid structure, not its volume

G = (c₀/2)²(r/m₂) = c₀²(r/4m₂) = c₀²([r/(n→∞)]/4[m₂/(n→∞)]) ; c₀ = √4G[m₂/(n→∞)])/[r/(n→∞)] — it is dynamic, not static. It comes with the ±e structure of the atom.

NO BEGINNING— it was never created ¦ NEVER CREATED, NEVER DESTROYED — c₀ ¦

Relating mass — physical existence — to atoms, the fundamental neutron, and the neutron to a fundamental (Planck Ring hollow TNED toroidal fractal) ±e nuclear structure (EXPERIMENTAL CONFIRMATIONS), the (Newton) universal law of gravitation exposes a forcing rank expression leading to the deduction of Light’s Gravitational Dependency (Fig.1: Related and comparing · Einstein · Schwarzschild). Its related and comparing mathematical connection to the fundamental neutron (The origin of energy = mass ¦ EnergyLaw) becomes as stated above. This Universe History (UH) knows of no other sources (EXCON).

THE ONLY KNOWN UNIVERSALLY DIRECT EXPLAINABLE PROOF SHOWING THAT THE NATURE OF DIVERGENCE (light: electric, magnetic and thermal) c HAS A TOP HIGHEST VALUE c0 = 2.99792458 T8 M/S AbsoluteMetrics INDEPENDENT OF THE INFLUENCE OF GRAVITATION — while at the same time the actual propagation of light in space IS highly determined by the presence of gravitational potential (GPS-example ¦ Swedish Original GPS) IS: Light’s macroscopic cosmic universal gravitational dependency LGD.

Divergence c₀ is preserved independent of gravitation’s influence on light’s propagation in space

See also (Sw. version original) Negative divergence.

BackGround — all the necessary introductory concepts

The microscopic gravitation property — the atom, the atomic nucleus (the fundamental neutron) — has not the macroscopic gravitation property. These apparently reflect two different realms of the aspect and idea of reality: gravitation is not a particle. No way.

ANC2023:

AS YET (Gtest) FOUND and related ABSOLUTE NATURAL CONSTANTS (in UH universe history):

c₀ 2.99 792 458 T8 M/S light’s divergence ¦ AbsoluteMetrics ¦ G, universal gravitational constant:

G fundamental but not absolute determined — tested on the IAU P_SUN in TNED ¦ 6.670 t11 JS/(KG)²

h mN c₀ rN, not absolute determined ¦ 6.62559 t34 JS Planck constant — the neutron ¦ mass ±e-charge spin

e fundamental but not absolute determined ¦ 1.602 t19 C electron’s electric charge

u m(6C12)/12, not absolute determined ¦ 1.66033 t27 KG universal atomic mass unit

rN fundamental but not absolute determined ¦ 1.32 Fermi neutron g-circle spin radius

rP = r₀ = (m_e/m_N)(1/π√8 + π[1–m_e/m_N])h/m_ec₀π = (rN = h/mNc₀) × (√8)/(1 + √3) ¦ 1.37 Fermi proton g-circle spin radius

mN fundamental but not absolute determined ¦1.0086652u neutron mass

me fundamental but not absolute determined ¦ 0.000548598u electron mass

ε₀ 1/(4π t7 AM/VS · c₀²) = 8.8541878176 t12 C/VM ¦ IAUtest electric constant

P_SUN IAU value, 3.8275 T26 W ± 0.0014, TNED tested in K-cell heat physics on all the above Sun’s photometric effect

m_EARTH 5.975 T24 KG (CWON from CAP) Earth’s mass — suggested a natural constant

m_0cK K-CELL MASS at the moment of its detonation 4.161432507433896 T53 KG

r_0c K-CELL RADIUS at the moment of its contraction 1.544177741 T26 M

NScredit

CalCards: Kalkylkort: NOTE. OpenOffice SpreadSheet. Swedish EditionOnly

PART OF THE AIM behind these open (author’s working original) available CalCards is of course

• first the availability of the proving mathematics on exact basics

• with the possibility for any interested reader to make own tests, or further, whatever

• offering a complete open access index to the complete work behind the main text :

• we leave no one behind in related physics and mathematics, as far as we can.

HOPweizXP.ods ¦ HOPweizXPa.ods ¦ NuklidTab4A2023.ods ¦ NuklidTab4A2023.ods ¦ NuklidTab4A2023.ods

——————————————————————————————————————

1967HOP atomic mass table —

HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967 ¦ Atomviktstabellen i HOP

allmän referens i denna presentation, Table 2.1 MASS TABLE ¦ s9–65—9–86

——————————————————————————————————————

THE SWEDISH OPEN OFFICE CELL CODED VERSION —

we do not know how the cell code looks if opened in an English version — if at all ;

— We should have thought about that from the start [ 2008 ] — which we didn’t.

HOPweizXP.ods

kalkylkorten nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN HOPweizXP.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/HOPweizXP.ods

T1 The 1967HOP¦1975FM here in UH first observed Weizsäcker equation solution ”nuclear binding energy” parametric matrix and values

T2 The 2008 original UH collected CODATA/NIST values up to 83Bi209, all stable atoms

T3 The corresponding 1967HOP original data

HOPweizXPa.ods

kalkylkorten nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN HOPweizXPa.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/HOPweizXPa.ods

T1 The markedly enhanced (13Oct2023) found California university New Weizsäcker equation — with drafts and results as in the main text

T2-T3 same as in the above XP.ods

NuklidTab4A2023.ods

kalkylkorten nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN NuklidTab4A2023.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/NuklidTab4A2023.ods

TA BaseGroupMassNumbers General elliptic wave atomic mass defect Neutron Square solutions up to mass number 60

TB 1967HOP table index for comparing

T1 constants

T2 1967HOP data up to 103Lw257 ¦ results and drafts to TA

T3 the original (2008) MsWORKS NuklidTab4.wks constants — used for the final OpenOffice transitions

T4 The70 isotope resulting/proving cell coding A-Z chart from TA

T5 General drafts and results up to 83Bi209.

NuklidTab4B2023.ods — Contined and enhanced works from NuklidTab4A2023.ods

kalkylkorten nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN NuklidTab4B2023.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/NuklidTab4B2023.ods

T1 constants with drafts and results as specified in the main text

T2 1967HOP table data for further drafts with results as specified in the main text

T2A 1967HOP table data for further drafts and results as specified in the main text

T3-T5 1967HOP table data for further drafts and results as specified in the main text

TA the original 1967HOP table data — manually transferred (2000) from the library book

TB all stable 1967HOP table isobaric

NuklidTab4C2023.ods — THE MOST/latest UPDATED AND COLLECTED DATA from the above AB spouses

kalkylkorten nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN NuklidTab4C2023.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/NuklidTab4C2023.ods

T1 constants — with drafts and results as specified in the main text

T2 1967HOP table data — with drafts and further results as specified in the main text

T2A 1967HOP table data — with drafts and further results as specified in the main text

T3-T4 1967HOP table data — with drafts and further results as specified in the main text

T5 isobaric 1967HOP table data ¦ the GPS table comparison on two different c-preferences

T2A The 1967HOP table data with further drafts and results

TB comparing HIGHESTmD

ALL AS LISTED: HOPweizXP.ods ¦ HOPweizXPa.ods ¦ NuklidTab4A2023.ods ¦ NuklidTab4A2023.ods ¦ NuklidTab4A2023.ods

kalkylkorten nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN HOPweizXP.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/HOPweizXP.ods

kalkylkorten nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN HOPweizXPa.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/HOPweizXPa.ods

kalkylkorten nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN NuklidTab4A2023.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/NuklidTab4A2023.ods

kalkylkorten nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN NuklidTab4B2023.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/NuklidTab4B2023.ods

kalkylkorten nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN NuklidTab4C2023.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/NuklidTab4C2023.ods

CalCards

content:

Atomic Nucleus II 2023VII15

innehåll: SÖK äMNESORD på denna sida Ctrl+F ·

The Atomic Nucleus

innehåll — content

2008VIII6 ¦ 2023IX10

The Atomic Nucleus II — NeutronSquareMATH 2003-2023

EXPERIMENTALconfirmations

mDdiffEx1H1

EXCON

NeutronSquareFundamentals

ComAtNu

EXCONdetails

NeutralToExperimental

HowardUniversity

NS8Oct2023

NS U unit

CAUSE

Normalization

NSdeDIA0

Discovery

ClarifyingTheUequation

aMAD

MDa

CosmicMATHrevelation

Geometric

NuklidTab4A2023TableA

DiffREF

Resurrection11Sep2023

TheoryExperiment

WaveElliptic

TNEDComparingMAC

Uweiz

mDweiz

AtomicMassDefect

AtomicMassDefectEquation

Capital18e

npSTRUCTURE

DeducingThe AZ

NuclideStaticAverage

AZchart

NuclearStructure

LighterToHeavier

WAFO

Plateaus

HeavyGroup

BaseGroupMassNumbers

EllipticWaveEquation

Mintrusion2008

G0

G1

MproblemSolved

The70

G2

G3

G4

G5

MintrusionArt

modREST2008

CONTout

SWrSep2023

CONTin

HIGHESTmD

Never18

CompareQm

CompHmD

NotRepresented

ComparingNuclear

NSdeDIA5

WeizSOURCE

NSdeDIA8

WEIZref

NSdeDIA9

NSdeDIA10

WhatZv

NSdeDIA11

NSdeDIA12

NewWeiz2023

NSdeDIA13

WeCALu

NSdeDIA14

WeizCalifornia

NSdeDIA7

AtomDiffNuc

FAMQ

NuclearBindingEnergy

NSdeDIA6

Examples

FIBAPO

NSconditions

NSsolutions

Wang2020

PROVISIONS

WikipediaStandard

LGDbasics

CONOR

GPSexComp

ComNorm

EllipticEquation

mDmethod

UnequivocalAmD

CheckTabAElliptic

AboutTheMETHOD

ExperimentalErrors

HOPuncertainty

ErrorTransferElectronMass

Comp

Comp2023

CompCALu2023

NSdeDIA15

IsobaricMean

ComparingIsobaric

TheActualDifferences

VerticalElliptic

TheExample

ThePOINT

HOPfirst66

ComparingToleranceStandard

NeutronNIST2009

BASICmN

PRIME

AtomicMASS

Transfers

TNEDexperimental

NSdeDIA1

WAcademicExperimental

NSdeDIA2

TAP0solutions2020

EnhancedPrecision

NSdeDIA3

NSdeDIA4

SPECIFICnotes

CLAIR

WikiWEIZ

WikiWEIZnuclearMass

PO4

Phosphorylation

StrongHINTEDproof

HintedConsequences

QUOTES

SumPhosphorylation

NuclearReactionLaw

NScredit

StandardUniversal

ANC2023

CalCards

Kalkylkort

content

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 MASS TABLE ¦ s9–65—9–86 ¦

concurrent — with such minor end decimal differences with Berkeley National 2003 and Nist/Codata 2005 — having no significance in this presentation

Comparing CODATA2005-HOP1967 ¦

———————————————————————————————————————————————————————

m_n = 1.0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0.000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

m(1H1) = 1.007825200u .................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

u = 1.66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1.66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1.66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1.66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1.6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1.66053906660 t27 KG .... atomära massenheten [@INTERNET (2023) en. Wikipedia, Atomic mass]

u = 1.660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2.99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6.62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1.602 · t19 C .................... FOCUS MATERIEN 1975s666

[BA]. BONNIERS ASTRONOMI 1978

— Det internationella standardverket om universum sammanställt vid universitetet i Cambridge, The Cambridge Encyclopaedia of Astronomy, London 1977.

[FM]. FOCUS MATERIEN 1975 — Fysikens, kemins och astronomins historia. Allt från atomen till universum — fysik, kemi, jordvetenskap och astronomi

[BKL]. BONNIERS KONVERSATIONS LEXIKON, 12 band A(1922)-Ö(1928) med SUPPLEMENT A-Ö(1929)

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

PREFIXEN FÖR bråkdelar och potenser av FYSIKALISKA STORHETER

Här används genomgående och konsekvent beteckningarna

förkortning för förenklad potensbeteckning

d deci t1

c centi t2

m milli t3

µ mikro t6

n nano t9

p pico t12

f femto t15

Alla Enheter anges här i MKSA-systemet (M meter, KG kilo[gram], S sekund, A ampere), alla med stor bokstav, liksom följande successiva tusenprefix:

K kilo T3

M mega T6

G giga T9

T tera T12

Exempel: Medan många skriver cm för centimeter skrivs här konsekvent cM (centiMeter).

MAC, här ofta använd förkortning för Modern ACademy — etablerad vetenskap sedan början av 1800-talet

In UH often used abbreviation for modern academy — explicitly from the beginning of the 1800s

MAC — often used abbreviation in TNED for Modern ACademy

TNED — Related PHYSICS And MATHEMATICS — Se särskild djupbeskrivning av innebörden i begreppet relaterad framställning.

Toroid Nukleära Elektro MEKANISKA Dynamiken

(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också

RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.

SHORT ENGLISH — TNED in general is not found @INTERNET except under this domain

(Universe[s]History, introduced @INTERNET 2008VII3).

TNED or Toroid Nuclear Electromechanical Dynamics is the dynamically equivalent resulting description following the deductions in THE PLANCK RING, analogous AtomNucleus’ Deduction. The description according to TNED is related, meaning: all, each, details claim to be fully logically explainable and understandable, or not at all. With TNED is (hence) also understood RELATED PHYSICS AND MATHEMATICS. See also the emergence of the term TNED in AtomNucleus’ Deduction.

Senast uppdaterade version: 2023-12-21.

*END.

Stavningskontrollerat-SpellChecked up to: .. 10Sep2023 ¦ 27Oct2023.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

Unicode:

∫ ∫ Δ √ Δ ≠ → ∞ γ √ ω π τ ε ħ UNICODE — ofta använda tecken i matematiska-tekniska-naturvetenskapliga beskrivningar

— Ctrl+Shift+Q i Microsoft WORD direkt till SYMBOL

σ ρ ν ν υ π τ γ λ η ≠ √ ħ ω →∞ →γ ≡ ¦ Alt+ 1..9 ☺☻♥☺♦♣♠•◘○ υ Ψ

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ ϕ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ˂ ˃ ← ↑ → ∞ ↓

ϑ ζ γ λ ξ

Pilsymboler, direkt via tangentbordet:

Alt+24 ↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬

Alt+23 ↨ — även Alt+18 ↕; Alt+29 ↔

Senast uppdaterade version: 21 december 2023 | 00:20:31 | 2023-12-21. [GMT+1]Solar [GMT+2]Industry

*

BILDKÄLLA: Författarens arkiv · 3Jul2012 E12 Bild 198;293 · Nikon D90 · Fria Teckningar — Angående Statens och Kommunernas uppmärksammade UPPENBART SJUKA NATURUPPFATTNING — civilisationens återerövring.

Denna webbsidas ansvariga författare kan nås med e-mail på Webbadressen

¦belldharma¦SNABELA¦universumshistoria¦PUNKT¦se¦ MEN SKICKA INTE MED LÄNKAR — utom överenskommelse kasseras sådan e-post omgående

åter till portalsidan · portalsidan är www.UniversumsHistoria.se