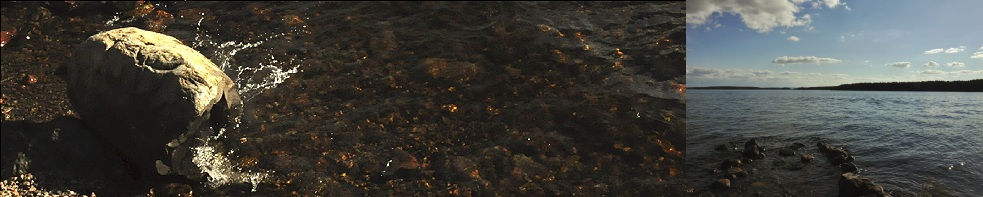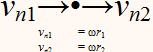UNIIVERSUMS
HISTORIA | FysikenGrund —GTactionCoriolisFoucault | 2012VIII16 | a BellDHARMA production | Senast
uppdaterade version: 2017-08-16 · Universums Historia
innehåll
denna sida · webbSÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor
Fysikens viktigaste begrepp — Most Important Concepts in-OF related Physics
Fysikens viktigaste begrepp — Most Important Concepts in-OF related Physics — BILDKÄLLA:
Författarens arkiv · MONTAGE: [Miljö2012]
21Mar2012 Bild2; 15Sep2012 E32
Bild153 · Nikon D90 · Detalj
KRAFTLÄRANS RELATERBARA NATURGRUNDER MED strängt ordnade betingelser för AKTION- OCH REAKTIONSKRAFT ingår inte i den moderna akademins lärosystem i någon ordnad form: »aktion och reaktion är godtyckliga». Se särskilt i artikeln
KRAFTBEGREPPET SOM SÅDANT (F=ma) besitter i den moderna akademins lärosystem över huvud taget ingen ställning som något reellt konkret. Se särskilt i artikeln
DEN RELATERADE FYSIKENS BESKRIVNING — kraftläran enligt TNED — genomgås särskilt i grunderna i
GTaction |
med de främst centrala korsrefererande jämförande exemplen som visar motsättningarna i MAC i artiklarna
Centralaccelerationen i MAC | CoriolisEFFEKTEN | CoriolisFOUCAULT | Vektorfelen i MAC
Se även i RUBRIKER.
Allmän genomgång med jämförande exempel mellan
TNED och MAC — TOPPRUBRIKER
FYSIKENS VIKTIGASTE BEGREPP
— GTaction
Allmän genomgång med jämförande exempel mellan
TNED och MAC —
AktionReaktion
BILDKÄLLA: Författarens arkiv · 2Okt2010 Excur9R
Bild5RV · Nikon D90 · Detalj
GTaction | CoriolisORIGINAL | CoriolisEFFEKTEN | AktionReaktionMAC | KraftbegreppetMAC | CoriolisCINEMA | CoriolisFOUCAULT |
Med koppling till FactionReaction i
LISTA MED
SAMBAND ÖVER FYSIKENS (OCH MATEMATIKENS) VIKTIGASTE (mest centrala, avgörande)
BEGREPP
i
jämförande syntes mellan relaterad fysik (TNED) och modern akademi (MAC)
FysikenGrundGTactionCoriolisFoucault — INTRODUCTION
Dokumentets Bakgrund, Hur och
Varför
I LISTAN över FYSIKENS VIKTIGASTE BEGREPP i jämförelsen mellan TNED och MAC har ovanstående post (bildkopia) lagts till (Sep2012) med hänvisning hit till GTaction:
— Modern akademi [MACarbitraryActionReaction] [AllaKrafterOverkliga] har ingen varken ordnad eller över huvud taget kopplad beskrivning för hur naturen visar oss krafterna och deras verkan. Nämligen via aktionsriktningar — som förorsakar/underhåller verkan via aktuell energi typ rumsgolvet vi står på, ytterst atomkärnans fysik, och som hindrar oss att falla ner i ett gravitellt oändligt tätt tillstånd*** — och reaktionsriktningar — som låter oss känna, uppleva, och framför allt mäta krafterna och variationerna: instrumentfysiken.
— Kärnpunkten i den motsättningen återfaller enligt relaterad fysik [TNED] HELT på (ingår inte i MAC) gravitationens absolutverkan [förklaras utförligt i sektionen GTaction]. Nämligen i det sammansatta led som på ytterst enkelt sätt låter oss härleda elektriska laddningen (den härledningen existerar inte i modern akademi) via divergensens absolutacceleration (c=a·dt)
a=[d(v=∞GRAVITATIONEN/dT=([v=∞]/∞)/dT=cLJUSET/dT]
Ingår inte i MAC
Det ledet sammanfattar hela det här dokumentets sakinnehåll — med referenser, jämförande exempel, citat och belysande beskrivningar, konsekvenserna det medför och innehåller för fysikbeskrivningen i stort, samt de speciella ämneskomplex som särskilt tilldragit sig ämnets allmänna intresse: Corioliseffekten och Foucaults Pendel.
— Om redan bekant, är också resten av det här dokumentet överflödigt.
*** GRUNDÄMNESBILDNINGEN med HIMLAKROPPSBILDNINGEN utpekar en entydigt utpräglad aktionskraft [EXOTERMISKA KÄRNREAKTIONSLAGEN] [FusionsGränsMassan] som frigör energi [ATOMÄRA MASSDEFEKTEN] [ATOMVIKTERNA] för bildningen av materialens hållfasthet. På den grunden [GRIP] [DEEP] [GTaction] kan vi sedan utföra olika (reaktionsbaserade, rent instrumentella) mätningar baserade på olika tillståndsändringar, analogt med det vi kan känna och uppleva av och i kraftgrunderna i konkret, praktisk, vardaglig verksamhet. Den beskrivningsgrunden existerar inte i modern akademi. Det här dokumentet är tillägnat en generalgenomgång.
NEWTON III [ÄNDRINGSLAGARNA], kan man nog lätt påstå, bildar hela grundvalen för den, här, uppmärksammade fundamentala, radikala och avgörande motställningen TNED/MAC och som föranlett UniversumsHistoria. Se särskilt i Integrala Analogin: hur mekanikens grundbegrepp grundlägger begripligheten i elektrofysikens MOTSVARANDE grundbegrepp; Induktionsbegreppet (universella induktionslagen), särskilt via NewtonIII. Det sammanhanget, därmed, klargör mera ingående Ändringslagarna generellt.
Frånsett vissa delblock
(Gravitationens Unika Särställning i Relaterad Fysik)
(Entropibegreppet— ArbetsExempel)
har till skrivande stund dock ingen riktig — egentlig, dvs., av typen SAMMANFATTANDE GENERAL- — genomgång funnits i UniversumsHistoria; Frånsett länkblocken ovan, och in till skrivande stund (4Okt2012), innehåller UniversumsHistoria ingen mera ingående beskrivning av djupproblematiken i den här uppmärksammade motsättningen (NewtonIII) mellan TNED (relaterad fysik) och MAC (Modern ACademy) av typen: en mera konkret — mera elementär, tydligare, exempelbaserad, jämförande — formulering.
Detaljerna
har (visst, men inte helt) funnits (i riklig mängd) från författarens allra
första stund i ämnet (slutet av 1970-talet [eg. från början av 1970-talet] då
hela fysikUniversumHistorien tog sin början [AtomkärnanBegin]), men har (i
Web-dokumenten från 2006) måst uteslutas — till att börja med — för att lämna
plats för DEN MERA ANGELÄGNA PRÖVNINGEN AV själva de konkreta resultatdelarna;
resten sköts på framtiden: OM det visar sig att författningen innehåller något
av värde, då, först, kan vi ta med de mera ingående djupdelarna. Vilket skulle
vara nu (Okt2012), det, i så fall.
Således, sett från TNED, men utom kännedom i MAC:
MED redan uppenbara exempel blev det angeläget att genomföra vad som här närmast kan kallas
ett FÖRTYDLIGANDE AV REDAN PRESENTERAT GRUNDMATERIAL:
— NEWTON III, och (MEN) som folket i modern akademi tycks ha så (oändligt) svårt för att få koll på, och som det följande är tillägnat;
I LISTAN i FysikaliskaGrundbegrepp2 över FYSIKENS VIKTIGASTE BEGREPP, med jämförande grundsamband i fysik och matematik mellan TNED/MAC, har detta htm-dokument sammanställts med tillägget
enbart som ett FÖRTYDLIGANDE av den redan väl kända NEWTON III, och som tydligtvis det stora flertalet inte verkar förstå fysiken för. (Vilket bara beror på att den moderna akademins träaktiga begrepp hindrar dem: sågbocken uppvisar tendenser att vilja gå ut om MAC närmar sig).
Eller mera rättvist uttryckt, tydligen enligt TNED:
Den moderna akademins begrepp om »naturfysik» hindrar tydligen de allra flesta ifrån att ens närma sig ämnet.
Eller ännu mera kort och gott (som det framställs på annat ställe i detta dokument):
— Den moderna akademins lärosystem har
alldeles bestämt och helt radikalt misslyckats med uppgiften som LÄRARE. En
lärare undervisar i naturkunskap — berättar, beskriver, talar om,
leder, förklarar — inte dikterar att eleven redan från ruta ett är dum i
huvudet, inte fattar grundläggande Percept.
—
Förklara Befintligt. Diktera Inte Nytt. Jättesvårt. Berika — döda inte —
Individen.
BILDKÄLLA: Författarens arkiv · MONTAGE: 15Sep2012 E32
Bild103/Bild155 · Nikon D90 · Detalj

Det är vad den här framställningen ska handla om;
— Du är redan perfekt, bara lite granna (JÄTTEMYCKET, om ej redan bekant) oupplyst.
— Termerna AktionReaktion (komponenterna i NewtonIII) har INTE TIDIGARE ANVÄNTS I UNIVERSUMS HISTORIA;
— Dessa termer är, emellertid, helt avgörande för att kunna belysa djupsammanhanget MAC/TNED — de konkreta exemplen som visar och beskriver HUR TNED och MAC skiljer sig åt i begreppsgrunderna — via (ytterst) konkreta (elementära) exempel (CoriolisBASIC) (FoucaultPendeln) (Tekoppen) (m.fl.).
OK tjejer. Då kör vi.
RUBRIKER — gravitationens unika särställning i
fysiken —
GENERALGENOMGÅNG — kraftens, massans, gravitationens och
accelerationens fundamentala definitioner med tillämpningsexempel
G-beviset | GTaction | CoriolisBASIC | CoriolisINLEDNING | Tekoppen | CentralaccelerationenMAC | EulerCORIOLIS
|
|
|
|||
|
TNED: MAC: |
Kinematiska
Friktionslösa ParabelAnalogin |
|
Mekaniken GENERELLT |
|
|
|
|
G-beviset | GTaction | CoriolisBASIC | CoriolisINLEDNING | Tekoppen | CentralaccelerationenMAC |
2012IX4
Orsaken varför TNED innefattar MAC som primitiv
↑
G c Q → [GcQ-teoremet] → PLANCKEKVIVALENTERNA → n → nG
↓
RELATERAD FYSIK (TNED) framträder via sanningsbegreppet från FYSIKENS
7 PRINCIPER — genom tillståndets princip. På dess grund står hela den relaterbara fysiken,
och matematiken, formulerad i UniversumsHistoria. I de markerade länkblocken är DEN ELEKTRISKA LADDNINGEN
[Q = √(m/R)(A/dT)] avgörande central
för hela den matematiska (tekniska) fysikens härledande beskrivning, och som
leder till PLANCKEKVIVALENTERNA.
Anledning:
Proportionaliteten mellan massan (m)
och motståndet (R) — exklusivt endast för elektrofysiken — garanterar
laddningens bevarande;
Föreställningen generellt att »föremål i
fysiken får ökad massa på grund av RÖRELSE» har, som det framkommer via Q och genom
PLANCKEKVIVALENTERNA, ingen relaterbart fysikalisk — experimentellt
belagd — grund.
Det är endast elektriskt accelererade
massor, i elektriskt slutna system, som kan uppvisa en intern
omfördelning som yttrar sig i en observerad, mätbar, massökning, f.ö. numera
utomordentligt väl experimentellt belagt (konv. partikelacceleratorer).
Den massökningen beskrivs, förklaras och
härleds utomordentligt exakt, noggrant och i detalj i relaterad mening
genom PLANCKEKVIVALENTERNA:
—
Exakt samma matematiska formella detaljer som i MAC, men via en helt annan teoretisk, ypperligt, som det har
visat sig, väl relaterbar grundval, och som rensar ut r-teorins (sedan länge redan uppenbart) bisarra inslag.
Jämför PlanckEkvivalenterna KONTRA RelativitetsTeorin;
—
PLANCKEKVIVALENTERNA utraderar (därmed) relativitetsteorins
teoretiska-matematiska bild [vic-felet] ur fysiken, just på Q-formens
härledda matematiska fysik:
— Från
ljusfysiken (divergensen, c) via gravitationen [G], med
vidare till atomkärnans härledning — Planckringen
h=mcr=neutronen.
Därmed är avgrundsdjupet stadfäst
mellan MAC och TNED:
—
Gravitationen verkar INTE genom en begränsad hastighet (c) [GcQ-teoremet] [GTaction];
Massbegreppet I RELATERAD FYSIK kan inte härledas med det
moderna akademiska lärosystemets begrepp, där man [se vic-felet] anser [GravitonMAC] att gravitationen verkar
genom den begränsade ljushastigheten (c=2,99792458 T8
M/S)
—
Massökningseffekten gäller INTE mekaniken [PLANCKEKVIVALENTERNA];
Partikelexperimenten med elektriska
laddningars acceleration kopplar
inte mekaniken massbegreppet=gravitationen
I RELATERAD FYSIK därför att mekaniken (g-fysiken) inte
innefattar elektriska laddningens Q = √(m/R)(A/dT) motstånd (R)
Atomkärnan
är enligt relaterad fysik (TNED) INTE en samling diskreta partiklar (»kvarkar» m.m.)
utan istället en massans fundamentalform [PASTOM]
(en enhet, 1) som kan delas (1=1/2+1/4+1/8+1/16 … +1/2n) på
samma sätt som en vattenmängd kan det i deldroppar (bilden nedan, vänster):
Dropparna kan sedan återförenas till en enhetlig vattenkropp och då utan
de beståndsdelar inuti som kunde iakttas före föreningen [PLANCKRINGEN h=mcr=neutronen];
Den modern akademins begrepp om kärnfysiken generellt har i jämförelse med relaterad
fysik [Atomkärnan] [Planckringen] [MassansFundamentalprincip] ingen
verklig fysikalisk förankring i naturen; MAC-begreppen
visar en analog uppdelningsmodell (typ fristående vattendroppar) baserad på
»VattenSplashEnergiEkvivalenter» (till en summerande enhetsvolym) från
artificiellt uppbyggda partikelkollisioner — och som därmed blir något helt
unikt i universum: naturen har ,
enligt vad som framkommit i relaterad fysik (K-cellens inre fysik), ingen motsvarande apparatur för
ELEKTRISKT GENERERAD partikelacceleration, men VÄL en mekanisk dito (Kosmiska Partikelstrålningens Ursprung) — men modern akademi har inget annat
att välja på än att, tvunget, anta ATT också naturen praktiserar den moderna
PartikelAcceleratorTekniken:
BILDKÄLLOR:
Författarens arkiv — 5Jul2012 E15 Bild144/138 · Nikon D90 · Detalj — STRANDVÅGOR bryts periodiskt mot en sten
och bildar rekyler som bryts upp i mindre
fristående vattendroppar, som strax återförenas med modermassan.
NATUREN illustrerar sig
själv i PRINCIPER. Se utförligt från ENERGILAGEN.
Förgreningarna
utbreder sig sedan allt vidare [ATOMVIKTERNA]:
— Den
moderna akademins fysikuppfattning beskriver i ljuset av TNED [Atomkärnan] [Planckringen] en speciellt primitiv [INERTIA]
fysikuppfattning (speciellt inskränkt genom nämnda centrala punkter);
— Den
primitiva fysikuppfattningen
(Se
främst @INTERNET
Wikipedia Atomic nucleus [2012-09-24] http://en.wikipedia.org/wiki/Atomic_nucleus,
”The nucleus is the very dense region consisting of protons and neutrons at the
center of an atom.”)
bygger
främst på analogin i att anse att de fristående
vattendropparna (bilden ovan, vänster)
som kan iakttas vid delningen av en vattenmassa (atomär partikel typ proton) också, verkligen, finns verksamma inuti
vattenmassan som helhet (atomkärnan).
Det finns ingenting sådant i relaterad
fysik (TNED). De
delpartiklar som bildas ur de artificiellt konstruerade partikelkollisionerna följer
enligt relaterad fysik energiekvivalenter [MIC] som
avspeglar atomkärnans inre (energiekvivalenta) strukturbyggnad. Dessa
»VattenSplashEkvivalenter» och har absolut ingenting — i relaterad fysik — att
göra med »frågan om massans upphov» [MACmasses].
I termer av relaterad fysik (TNED) är
(FÅR) den moderna akademins utflykter i »VattenSplashEkvivalenter», just,
tydligen, relaterbarligen och uppenbarligen, förstås vara den primitiva
avart (fiktion) av matematiskt teoretiserande som — utan verklig,
relaterbar, insikt i fysikgrunderna — följer av oförmågan att penetrera
ovannämnda aspekter, här i ytterligare syntes:
3.
kan inte relatera G,
2.
kan inte relatera c,
1.
kan inte relatera Q,
4.
kan inte relatera LJUSETS GRAVITELLA
BEROENDE.
Med
andra ord: kan inte relatera överhuvudtaget.
— MED
vidare.
Den moderna akademins teorier om atom- och
kärnfysiken förpassades (för många decennium sedan) till fiktionen i och med
antagandet av elektronen som »en punktpartikel med oändlig massa» [Se även Citatet i Spinnbegreppet i MAC]: Det finns ingen logik (begriplighet, relaterbarhet,
rationalism [förnuft]) i den
moderna akademins (försök till) beskrivningar av naturdjupen.
Jämför PlanckEkvivalenterna KONTRA RelativitetsTeorin: precis så är (framstår) också det övriga.
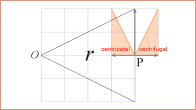
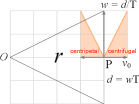
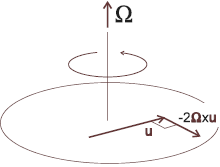
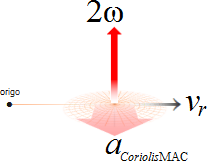
Gravitationens tidsabsoluta verkan • Centripetalacceleration och Centrifugalacceleration
— BILDKÄLLA: Författarens arkiv · MONTAGE: 12Sep2012 E28 Bild437; 15Sep2012 E32 Bild92 · Nikon D90 · Detalj

Med erinran om begreppsgrunderna för
den naturvetenskapliga metoden och dess betraktelsesätt
Gravitationens Tidsabsoluta
Ekvivalent
divergensaccelerationen — HUR GRAVITATIONEN DEFINIERAS EKVIVALENT från Gravitationens Princip [GRIP] I RELATERAD MATEMATISK FYSIK
Satsen om
GRAVITATIONENS TIDSABSOLUTVERKAN oberoende av avstånd baseras i relaterad fysik
uteslutande endast på FÖLJDRESULTAT från TILLSTÅNDETS PRINCIP [APARC], se GRIP.
— direkt från den elementära relaterbara matematiska
fysiken
Ingår inte i MAC
MED ERINRAN OM BEGREPPSGRUNDERNA FÖR DEN NATURVETENSKAPLIGA METODEN OCH DESS BETRAKTELSESÄTT
Sammanställd förtydligad beskrivning — med
jämförande exempel i den moderna akademins beskrivningar
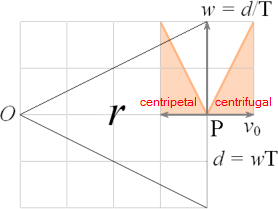
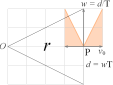
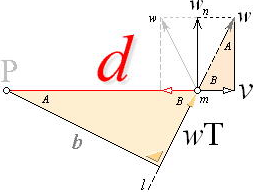
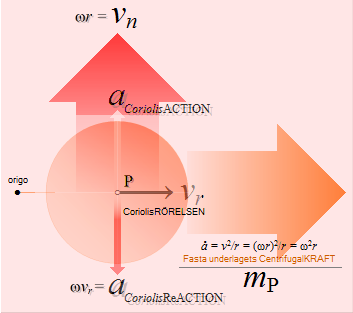
GRAVITATIONSKRAFTEN DEFINIERAR EN DIVERGENSACCELERATION — centrifugalverkan — via en centralacceleration på Radiella Elementet v0/T
|
centralaccelerationen
|
Centralverkans grundbegrepp: IMPULSER p=mv UTMED ORTSVEKTORN (r) inåtCENTRIPETAL utåtCENTRIFUGAL
På grund av begreppet INERTIALSYSTEM
i MAC — kraftbilderna
ovan kallas FIKTIVA (skenbara CitatFM1975s72) i MAC — används inte termerna Centralverkan (eng.
»Central Action») och Centralacceleration (eng. »Central Acceleration»). Dessa
finns inte alls i MAC som samlingsbegrepp för den relaterade fysikens
motsvarande klargörande Centripetal-Centrifugalbegrepp, som ovan. I MAC används endast
termerna Centralrörelse (eng. Central Motion) och Centralkraft (eng. Central
Force). Se särskilt citerat exempel i AskASci
i CentralAccelerationen i MAC.
Beskrivning — DIVERGENSACCELERATIONEN
definierar genom radiella elementets ekvivalenta trigonometri (triangelrelationerna) tydligen ett begrepp om
DIVERGENSACCELERATION v0/T=å=w2/d
Ingår inte i MAC
— v0-vektorn (ovan) framträder som en primär komponent i en linjär acceleration (a=v/t) som idealiserat tagen cirkulärt omedelbart runt omkring 0-360° bildar divergensaccelerationens begrepp; Divergensaccelerationen, såsom gravitationskraftens (konvergenskraftens) omvända aspekt, baseras därmed, och alltså likaledes, på ett absolut tidsbegrepp: hela den cirkulära centralrörelsens (RINGENS) centrifugalverkan (omnämns inte i MAC, se CentralAccMAC) under den tidsdifferential (dT) som gäller för motsvarande (ringbaserade) momentana (ögonblickliga, tillståndsrelaterade) gravitationskraft [GRIP];
;
Hela centralrörelsens RINGKRAFT F=må=mw2/d motsvarar då, eller definierar, en ekvivalent, tidsabsolut, omvänt riktad RINGKONVERGENSKRAFT (konvergensacceleration) i perfekt jämvikt med det vi erfar och kallar gravitationen — och som vi associerar med ett motsvarande primärt linjärt vertikalt element i (den lokala, partikulära) gravitationskraften (g-kraften) F=ma;
— I ringens utvidgade sfäriska tappning omfattas (således) hela den idealt sfäriska g-kraftens fenomenbas av gravitationslagen,
|
|
centralaccelerationen v/w=wT/d som ger v/T=å=w2/d ; ω=2π/t=2πf w=2πd/t=2πf·d=ωd ; å =w2/d=(ωd)2/d= ω2d |
F = ma = mw2/r
= (w2/rm2)m2m = (w2/m2)m2m/r
= (w2r/m2)m2m/r2
= Gm2m/r2
.......... gravitationslagen
— Gravitationsbegreppet får genom den matematiska fysiken som ovan med andra ord i den elementära, relaterade, meningen tydligen ett motsvarande ENTYDIGT tidsabsolut begrepp [GRIP]; divergensaccelerationen (centralaccelerationen cirkulärt eller sfäriskt F=må=mw2/d) i idealiserad ekvivalent motkraft till konvergensaccelerationen (gravitationskraften F=ma).
FÖLJDSATS: Ur gravitationen [GRIP] och dess avgörande tidsabsoluta
verkan oberoende av avstånd följer Ljusfysiken [DEEP] — ELEKTROFYSIKEN:
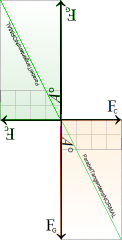
Divergensens eller LJUSETS
Absolutacceleration — BILDKÄLLA: Författarens arkiv · 15Sep2012 E32
Bild153 · Nikon D90 · Detalj
MAC VILL INTE SE ATT fysiken bygger på
urgamla eviga principer a=[d(v=∞)GRAVITATIONEN/dT=([v=∞]/∞)/dT=cLJUSET/dT]
[DIFFERENS OCH
DIFFERENTIAL] [ELEKTRISKA LADDNINGEN]
Ingår inte i MAC
Gravitationen definierar
elektriciteten
Med [GRIP] gravitationens tidsabsoluta verkan (v=c∞) oberoende av avstånd insatt generellt i varianten eller differentialformen för accelerationen, a=dv/dt
— och med grunderna enligt relaterad fysik och matematik från NOLLFORMSALGEBRAN som observerar innebörden av den mängdoberoende (∞=∞+∞+∞+…+c∞) genom distinktionen mellan formvärldens differenser (intervall Δx) och deras variationer genom förståndsvärldens differentialer (punkter dx) [konventionella skrivsättet är »i stort detsamma» men beskrivningarna i MAC är galna (»Δx=dx»), se citat i NOLLFORMSALGEBRAN]
— ges i slutänden en motsvarande principiell divergensacceleration på en ändlig hastighet (c) [DIVERGENSEN] [DEEP från GRIP] enligt
a=[d(v=∞)GRAVITATIONEN/dT=([v=∞]/∞)/dT=(c=c∞/∞=v∞/∞)LJUSET/dT]
; divergensens
absolutacceleration
Ingår inte i MAC
aLIGHTs GRAVITATIONAL DEPENDECY=c/dT
GcQ; elektriska laddningens praktiska fysik certifieras på ljusfysikens absolutacceleration (c/dT) från gravitationens absolutverkande princip [GRIP].
Divergensaccelerationen eller ljusets absolutacceleration a=c/dT leder sedan direkt på 1. Ljusets g-beroende som tydliggör divergensen c som en av gravitationen betingad punktlokal fenomenform, att skilja från ljusets utbredningshastighet [LJUSHASTIGHETEN] som utvecklas över intervall, samt 2. elektriska laddningen — som ytterligare styrker den logiska konsistensen i det övergripande, beskrivande, sammanhanget;
F = ma = m(c/dT)
= m(c/dT)(RA)/(RA) = Rc(m/R)(A/dT)/A = Rc(Q/r)2
; elektriska
kraftlagen
(m/R)(A/dT) = Q2 ;
Q = √(m/R)(A/dT) ; elektriska laddningen
Ingår inte i MAC — kan inte relatera dT
· dT-faktorn i Q=√(m/R)(A/dT) garanterar att Q inte urartar med fasta referenser mRc, vilket vore fallet med ändligt T: fysiken havererar då;
· Det elektriskt associerade motståndet R(Q) existerar inte i mekaniken (g-fysiken): mekaniken kopplar inte ljusfysiken [Ljusfrihetssatsen], [Michelson&MorleyExperimenten], [v+ic-felet], [RELATIVITETSTEORIN]. Det GARANTERAR dels att Q bevaras oberoende av variationer i laddningsmassan (m) som funktion av variationer i R(Q) — vilket sammanhänger med accelerationer av Q i slutna elektriska system, se utförligt i PLANCKEKVIVALENTERNA — och dels, därmed, att massökningseffekter i fysiken är uteslutande, och endast så, förbehållna elektrisk accelererade laddningar i slutna elektriska system typ elektronkanoner — uteslutande på bas av R‑variationer: Saken gäller enbart induktiva kraft- och energifenomen explicit för massökningseffektens del i elektrofysiken, dessa beskrivs ingående relaterat i MAFEM.
Planckekvivalenterna Kontra Relativitetstorin [PEKaReTt]
LJUSETS GRAVITELLA BEROENDE med POTENTIALBARRIÄREN — grunden till atomkärnans härledning (Planckringen h=mcr) — blir direkta konsekvenser av ovanstående.
— Men klarläggandet av Q leder också direkt på PLANCKEKVIVALENTERNA
f0/f = √ 1–(u/c)2 ............. PLANCKENERGINS FREKVENSEKVIVALENT i Qm ändras med växande u
m0/m = √ 1–(u/c)2 ............. PLANCKENERGINS MASSEKVIVALENT i Qm ändras med växande u
λ/λ0 = √ 1–(u/c)2 ............. PLANCKENERGINS VÅGLÄNGDSEKVIVALENT i Qm ändras med växande u
Ingår inte i MAC
med den utförliga förklaringen till massökningseffekten i elektrofysiken (»masschokning»), till skillnad från den moderna akademins antagna — tydligt teoretiskt primitiva, se utförligt från v+ic-felet — enligt Einsteins Relativitetsteori
T/T0 = Ö 1–(v/c)2 ............. tiden avtar med växande v
m0/m = Ö 1–(v/c)2 ............. massan växer med växande v
d/d0 = Ö 1–(v/c)2 ............. längden avtar med växande v
Fundamentalt i MAC
och som, vad vi vet, inte en enda instans på planeten Jorden kan förstå, förklara eller relatera — utom TNED. Se utförligt från v+ic-felet.
— Nämligen som en primitiv företeelse i den mänskliga vetenskapshistorien, tydligt frammanad genom 1800-talets akademiska oförmåga att penetrera naturfysiken generellt (Jämför Herrefolkscitatet).
Detaljerna stadfäster TNED.
Resten av hela historien i Universums Historia består (då) endast i att »skriva ut rapporterna» med de rent matematisk-fysikaliska konsekvenserna (ett ytterst omfattande men i grunden »självskrivet enkelt» men ibland krävande arbete), och sedan »servera middagen». Allt måste stämma exakt, ingen felande länk får finnas; finns en sådan, faller hela framställningen, lätt som en plätt.
I modern akademi finns i jämförelsen med ovannämnda
detaljutvecklingar endast motsvarande brytpunkter som omöjliggör sammanhanget.
— Det framträder i modern akademi (med början under 1800-talet) en tydlig strävan att motverka, undertrycka och motarbeta varje mening som söker återföra begreppet intelligens (Jämför Herrefolkscitatet) och förstånd på redan naturgrundade fundament som människan — modern akademi undantaget — upptäcker, inte skapar. Slutbild: MAC — ingen enskild eller allmän organiserad verksamhet, bara i kraft av en spontant konsekvensföljd — håller mänskligheten fången i en (våldsamt) primitiviserad naturbild med enda syfte och ändamål: att framhålla egna meriter.
MAC — i summering från Gravitationens Tidsabsoluta Verkan:
· Gravitationen verkar genom en ändlig, begränsad hastighet c, postulerat från de teoretiska satsbilderna i v+ic-felet:
· Q kan inte härledas då — och därmed i grunden inte heller de induktiva och magnetiska grundbegreppen;
· Därmed bortfaller också ljusets g-beroende (c=c0[1–w2/cc0]): bevarandet av naturkonstanten c0 oberoende av gravitationens inverkan ersätts av en motsvarande (defekt) sambandsform (Einsteins ekvation c=c0[1–w2/c2]) som helt demolerar speciellt sammanhanget med bevarandet av naturkonstanten c0 oberoende av gravitationens inverkan;
· Därmed bortfaller också samband och sammanhang i POTENTIALBARRIÄREN — grunden till atomkärnans härledning;
· Atomkärnan (Planckringen h=mcr) kan inte härledas;
· ATOMVIKTERNA FRÅN ATOMÄRA MASSDEFEKTERNA [U=AmN(1–mDme)] kan då inte heller härledas ur NEUTRONKVADRATEN som i sig framgår ur Planckringen och dess relativa dimensioner — vilket just utgör det avgörande exemplet som verkligen visar den praktiska innebörden i TNED kontra MAC: Medan TNED i princip prickar in varenda nuklid i överensstämmelse med experimentellt uppmätta värden baserat på NEUTRONKVADRATEN, ända från neutronen och vidare uppåt i nuklidskalan [ATOMVIKTERNA], felar MAC-alternativet så mycket att ingen som helst jämförande analogi existerar; Exemplet med atomvikterna/massdefekterna bara understryker soliditeten, riktigheten och konsistensen i TNED — den exceptionellt övergripande ENHETLIGHETEN och experimentella samstämmigheten;
· Den kosmologiska översiktsbilden med ljusets g-beroende, och därmed den avgörande gravitella rödförskjutningen, kan inte heller nås i MAC, inte ens associativt genom det så uppställda hindrande moderna akademiska lärosystemets vokabulär, termer, begrepp, föreställningar och allmänna uppfattningar;
· Fasthållandet vid r-teorins begrepp i v+ic-felet, som alltså omöjliggör härledningen av Q och därmed omöjliggör klarläggandet av PLANCKEKVIVALENTERNA, gör att också K-cellens värmefysik av princip bortfaller, och därmed också hela den kosmologiska helhetsbilden (c0-kroppen); Dopplersambanden för galaxernas rödförskjutning enligt fysikförklaringen från Planckekvivalenterna kan aldrig nås; därmed garanteras att MAC-föreställningarna konserveras av det etablerade lärosystemet och dess meriter, helt omöjligt för en enskild elev eller student att bryta igenom på den tid som står till elevens förfogande.
· Eller kortare sagt: naturbilden förmörkas generellt (med början från 1800-talet) av den moderna akademins uppställda teser, föreställningar och idéer; Istället för att beakta de naturliga förutsättningarna, och därmed härleda grunderna, uppställs/antas andra, egna, uppfunna detaljer som bestämt förnekar en inneboende naturintelligens (matematiken framträder, inte skapas) och som den enskilda eleven tvingas underordna sig för att få meriter (att visa upp i förvärvslivet).
— Modern akademi [INERTIALSYSTEM] förstår — uppenbarligen — INTE
Ändringslagarna [NEONS] i fysiken [KAUSALORDNINGEN].
Vi
studerar det i detalj.
CitatFM1975s72 — Citat från FOCUS MATERIEN 1975 s72
|
|
Problemkomplexets
sammanfattning En utomordentligt klargörande
översiktlig beskrivning/sammanfattning av hela PROBLEMKOMPLEXET för
kraftbegreppet i TNED — relaterad fysik kontra MAC modern akademi — finns i FOCUS MATERIEN 1975. Det är HÄR av avgörande vikt att
källverket får visas i hela den BEGREPPSÅSYFTNING som kraftbegreppets problem
avbildar (direkt kopierat från
källverket), så att vi får en klart refererande uppfattning om
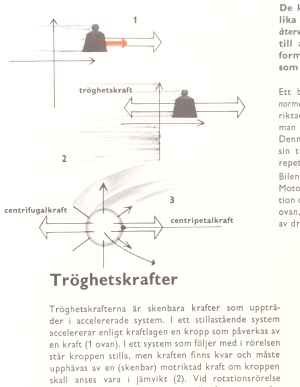
ARGUMENTERINGENS DETALJER för vidare: |§| ”Tröghetskrafter är skenbara krafter som uppträder i accelererade system. I ett stillastående system accelererar enligt kraftlagen en kropp som påverkas av en kraft (1 ovan). I ett system som följer med i rörelsen står kroppen stilla, men kraften finns kvar och måste upphävas av en (skenbar) motriktad kraft om kroppen skall anses vara i jämvikt (2).”, FOCUS MATERIEN 1975 s72ill.ö.v. |
”I ett system som följer
med i rörelsen
står kroppen stilla”:
FELET
ligger INTE i källverkets presentation av vektorer, deras riktning och storlek.
Felet
ligger i (bristen på) förmågan att relatera/förstå/beskriva det naturliga
saksammanhanget:
Relaterad fysik svarar — och
förklarar:
— Ett föremål som genomgår en
acceleration (en ändring av tillstånd) kan INTE i relaterad mening —
aldrig, någonsin, inte under några som helst omständigheter, förhållanden eller
betingelser — betraktas, ses, förklaras eller förstås som ett föremål i vila.
I UTVECKLAT ILLUSTRATIONSEXEMPEL visas enligt relaterad fysik hur
INSTRUMENTSYSTEMETS REFERENSER FÖRSTÅS GENERELLT — universellt — för samtliga
fall: hur jämviktsbegreppet för variationernas bestämning genomskär
alla, samtliga, referenssystem (kroppar, massor) av princip.
— NOTERA SYFTET med den framställningen i Universums Historia: det är inget försök att spela »expertens förklaring av
hur naturen fungerar», utan en ren erinran av Ditt och Mitt medfödda naturvett
som alltid funnits — men som förlorats ur sikte i det ensidiga 150 åriga
indoktrinerandet från MAC som vill göra gällande att krafter är INBILLADE
(skenbara, fiktiva, pseudo [CitatFM1975s72]) — som följd av den 100 åriga MAC‑uppfattningen
att gravitationen verkar genom en ändlig hastighet (c) [»ingenting
kan gå fortare än c»], som leder
till uppfattningen att (Einsteins
ekvivalensprincip) gravitation=acceleration
(som sammanhänger med Einsteins
allmänna relativitetsprincip
[***]) och
att det i det ljuset, i själva verket CitatAllaKrafterOverkliga, inte finns några krafter alls — inte alls över huvud
taget.
— I princip så: Det vi kan känna och
uppleva är overkligt. Det betyder också, tydligen, att begreppet
naturvetenskaplig beskrivning i den andan — i ljuset av det faktum att det vi
känner och upplever är högst verkligt — har mist sin kredit.
Beskrivningssättet från MAC är, vad det än vara må, inte (längre) trovärdigt.
— Vi vill inte ha våra barn (framtidens
ingenjörer) i en sådan, tydligt inskränkt, typ av undervisning. Den
naturvetenskapliga undervisningen ska befrämja livsglädjen och utveckla den,
inte undertrycka den eller stympa den.
— Varför är det klart?
Tillståndet som referensbegrepp
— vilan, jämvikten och balansen, den absoluta likformighetens princip, ETT värde, EN kvantitet, den linjära utsträckning tillståndet som bara kan finnas i punkten, ingenting, noll, därför att tillståndet inte finns i fysiken, fenomenvärlden, variationsvärlden —
innefattar inte förändring:
ingen acceleration existerar i en vila;
ingen vila existerar i en acceleration —
men en jämvikt finns alltid: a=dv/dt:
— ett momentant tillstånd i varje dt
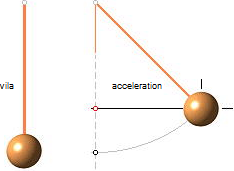
— Såväl betraktaren i den
accelererande bilen som personen som står vid sidan av vägen och ser på — och
varje annan observatör i universum, förutsatt koll på situationen — kan se att
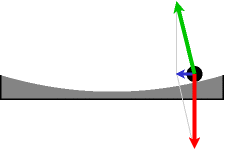
kulan som hänger i taket (illustrationen ovan) i bilen gör utslag:
PRECIS
SÅ SOM CITATET VISAR I DETALJ FRÅN FOCUS MATERIEN 1975 [CitatFM1975s72]
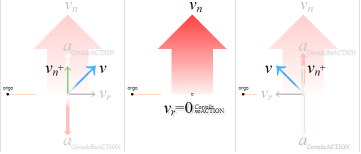
— man avskiljer tydligen kopplingen
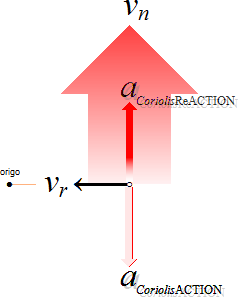
aktion(→)-reaktion(←) och, citatmeningen figur 1, menar att själva
händelseformen beskrivs ensidigt av aktionskraften(→), själva
händelseriktningen, där reaktionskraften(←) alltså inte finns med;
—
»glömmer» också den övriga skaran modernt akademiskt utbildade
artikelförfattare på webben (i MAC-litteraturen generellt) av INSTRUMENTSYSTEMET: reaktionskraften(←), den verkligt fysikaliskt
kännbara kraftbilden med vars hjälp själva fenomenformen också kan
studeras via instrumentell uppmätning.
— Det accelererande föremålet befinner
sig INTE i vila — inte sett från någon position alls, inte alls över huvud
taget i hela universum; bilen accelererar. Fysiken är — tvärt emot Einsteins
försäkringar (allmänna
relativitetsprincipen) — inte kinematisk (bild), utan
kinetisk (kraft).
Vi
studerar detaljerna.
Relaterad fysik förklarar:
Fenomenkomponenterna
med aktionskraft(←) och reaktionskraft(→) existerar
tillsammans som varandras diametrala speglingar i NEWTONIII;
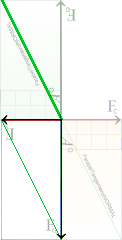
![]()
—
Accelerationsintervallet (Δx) som framträder i (3), som resultat av
impulsen (sammanstötningen F=ma=mv/T=p/T) i (2), existerar
inte föregående impulstillfället (p=mv) i (2): Den infallande
impulskroppen (1) möter objektet med konstant hastighet (v), och där
finns inget accelerationsintervall FÖRE kontakten: »filmen baklänges» — MAC-påståendet att
»fysikens lagar är tidsreversibla» [EntropiCitat5]
— kan uppenbarligen inte avbilda orsakssammanhanget i fysiken. Dvs.,
MAC-påståendet gäller bara om man frånser fysikens detaljgrunder (accelerationen
under intervallet Δx med a=dv/dt), vilket vi redan vet naturen
garanterat INTE går med på.
För
den som inte känner »den underbara hemligheten» med »intervallgåtan», se
utförligt (garanterat uttömmande förklaring) i ZENONS TEOREM
— kontinuitetens relaterbara natur.
Modern akademi:
—
»Intervallets Hemlighet» i relaterad fysik — ingår inte i MAC — har i modern
akademi istället (högeligen) »mystifierats» (elektronen som »en punktpartikel med oändlig massa» [Se även Citatet i Spinnbegreppet i MAC], och därmed — garanterat — abstraherats
ur trottoarfolkets åsyn) genom
»kvantmekaniska fält» med tillhörande exotiska PremiärPartiklar [MIC] (typ
HIGGS: många, många gånger tyngre än neutronerna — alla atomkärnors enskilda
byggstenar — och som endast visar sig i tillfälliga, ytterst kortvariga »kraftsplashar» från kolliderande [mestadels] protoner som drivs upp av
de slutna elektriska systemens moderna partikelacceleratorer till mycket nära
ljushastigheten genom höga energitryck). Se
speciellt i Wikipediaartikeln Interaction, Physics http://en.wikipedia.org/wiki/Interaction, [2012-09-25] ”An interaction is often described as a physical field,
and is mediated by the exchange of gauge bosons between particles.”.
:
— I
avsnittet om ENTROPIBEGREPPET [Kausalordningen] [Utförliga
Arbetsexempel]
finns
exemplifierat HUR
— i termer av relaterad fysik kontra
jämförande påståenden från modern akademi
— aktion och reaktion agerar
tillsammans oskiljaktigt i detalj ENLIGT ÄNDRINGSLAGARNA
(samma som Newtons Tre Rörelselagar [NEONS]),
och med syftet att belysa den allmänt citerade vanföreställningen i MAC angående påståendet [EntropiCitat5]
att fysikens lagar skulle vara tidsreversibla (»filmen baklänges»).
Termerna aktionskraft-reaktionskraft används dock explicit inte i
Universums Historia frånsett i denna, här aktuella, presentationens
htm-dokument, och då endast för att understryka sammanhanget i NewtonIII — med vidare: utan dessa kan
grundfysikens detaljer inte preciseras.
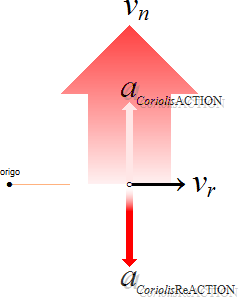
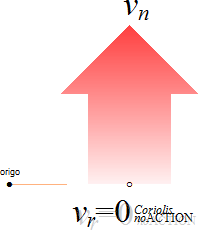
Aktionskraft och Reaktionskraft
framträder, observeras, beskrivs och förstås som EN form på diametrala
riktningar [NEWTON
III] i samma mening, tid,
utsträckning, förekomst, observation, beskrivning, och förklaring som en
acceleration (a=dv/dt) alls föreligger (och därmed en tröghetsreaktion).
—
AKTIONSKRAFT(←) är den kraft/riktning som (naturligtvis) krävs för att underhålla
en tillståndsändring;
—
REAKTIONSKRAFT(→) blir maken/riktningen som kan MÄTA underhållet.
Beskrivningen i [‡CitatFM1975s72] är bevisligt felaktig: direkt
vilseledande.
Vi studerar hur.
1.
tillståndet kvarstår tills ändrat;
2.
ändringen är proportionell mot den tillståndsändrande kraften (F=ma);
3.
varje ändring (aktion) strävar att bevaras (reaktion — instrumentets utslag);
VERKANDE
ReAKTIONSKRAFTER (F=ma=mv/T=p/T) framträder (uppkommer) alltid, uteslutande alltid, i följd av ett
inneboende motstånd (inertie,
Newtons vis inertiae, PRINCIPIA 1687 Definition III, ”this
vis insita, may, by a most significant name, be
called vis inertiæ, or force of inactivity”)
mot absolut rörelseändring [ÄNDRINGSLAGARNA]. Den kraftverkan inbegriper likaledes uteslutande utan
undantag kraftens aktionsriktning TILLSAMMANS MED den tillståndbevarande
aktionskraftriktningens motriktning (»backen») [AktionReaktion]; Reaktionskraften — den som vi alltid kan känna — blir den egentliga kraftverkan eftersom det är
genom denna som tillståndsändringen strävar att motverkas, det vi kan KÄNNA som
det aktuellt instrumentregistrerande tröghetsmotståndet: själva det praktiskt
fysiskt uppmätta mätvärdet.
— Se
f.ö. jämförande exempel TNED/MAC i CentralaccelerationenMAC: MAC förstår, tydligen, inte funktionssättet (man
anser att ordningen är godtycklig [AktionReaktion
MAC-citatet]).
— I
varje momentant ögonblick (dt) föreligger i andra ord enligt
relaterad fysik en JÄMVIKT mellan den verkande kraftens aktionsriktning (den aktuella rörelseriktningen) och
kraftens reaktionsriktning (den aktuella instrumentverkställande kraften som
ger utslag som vi kan se och känna). Det är,
uppenbarligen, den jämvikten mellan aktionskraft och reaktionskraft som fysiken
i relaterad mening avhandlar [FUNTOP] — inte det tydligt verklighetsförnekande (”skenbara”),
citerade, SÄTTET [‡CitatFM1975s72] ovan.
KRAFTENS VERKLIGA NATUR I RELATERAD FYSIK — klargörande beskrivning som visar att den moderna akademins
uppfattning om kraftbegreppet är förståndsmässigt OUTVECKLAT: Newton synes ha fattat det,
inte MAC.
|
Den upphängda kulan Förståndsfelet i modern akademi Bilden
ovan kan också illustrera principen bakom den konventionellt benämnda s.k.
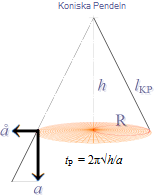
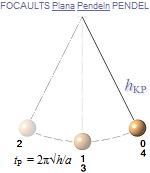
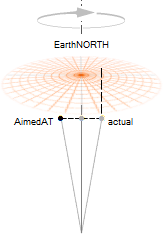
FOUCAULTS PENDEL: —
Släpper man kulan och låter den pendla mellan sina bägge ändlägen, samt om pendelns upphängningspunkt
är analog med rotationsaxeln (Nordpolen) som Jorden roterar kring, och därmed
pendelplanet skilt från Jordrotationen, bildar pendelplanets idealt friktionslösa
periodiskt exakta xy-svängning ett idealt obegränsat utsträckt tillstånd, [NewtonIII], [Ändringslagarna]; — Pendeln
blir ett precisionsinstrument som kan visa HUR och OM ett visst rörelsesystem genomgår någon
tillståndsförändring, t.ex. befinner sig i rotation. Pendeln monterad på
Jordens Nordpol (idealt med
alla friktioner eliminerade, vilket ännu ingen riktigt verkar ha lyckats med
experimentellt) ses vrida sig medurs (Jordrotationen moturs sett från
Nordpolen), ett varv på ett s.k. sideriskt (stjärn-) dygn (23 tim 56 min 4
sek). Se mera utförligt i SCIAM-exemplet. Påvisandet av Jordens rotation via
Foucaults Pendel gjordes i Paris år 1851 enligt Wikipediaartikeln http://en.wikipedia.org/wiki/Foucault_pendulum Foucault Pendulum [2012-10-04] Se vidare i SCIAM-exemplet. |
Jämvikten mellan aktionskraft (← från energin som underhåller variationen; kraft över avstånd [E=Fd]) och reaktionskraft (→ som garanterar att mätinstrumentet gör utslag, »visaren som alltid strävar mot noll», och låter oss, verkligen, känna och uppleva kraftens verkan: F=ma=mv/T=p/T) är den faktor I RELATERAD FYSIK som i varje momentant ögonblick (dt) av händelseförloppet garanterar att fysiken är observerbar, iakttagbar, beskrivbar, förklarbar, och mätbar. Observerbarheten och därmed mätbarheten garanteras (följaktligen) av att jämvikten beskriver ett tillstånd — en i förståndsvärldens mening obruten dimension av oföränderligt varande utan ändring, och som INGÅR i — tydligen utom modern akademi — DEN RELATERBARA FYSIKENS OCH MATEMATIKENS BEGREPP differential via DEN MÄNGDOBEROENDE som beskriver HUR skillnaden mellan formvärld (differenser, intervall, värden) och förståndsvärld (differentialer, punkter, positioner) fungerar — men som heller aldrig intresserat MAC; JÄMVIKTEN [FUNTOP] med tillståndet som referensbegrepp — vilan, jämvikten och balansen, den absoluta likformighetens princip, ETT värde, EN kvantitet, den linjära utsträckning tillståndet som bara kan finnas i punkten (förståndsvärlden), ingenting, noll, därför att tillståndet inte finns i fysiken, fenomenvärlden, variationsvärlden (formvärlden) — innefattar inte förändring: ingen acceleration existerar i en vila; ingen vila existerar i en acceleration — och blir JUST DÄRFÖR grundvalen för vårt ENDA relaterbara sätt att förstå, observera och mäta variationerna i fysiken. : en jämvikt kan alltid påvisas om en acceleration kan det: a=dv/dt: — ett momentant tillstånd i varje dt — OBEROENDE av begreppet »referenssystem». I relaterad mening existerar med andra ord inga »inertialsystem» i fysiken [FUNTOP] — därför att fysiken hela tiden är föremål för variation: tillstånd existerar inte i, inuti, fysiken, inuti kropparna, massorna; fysiken är intrinsiskt REN från vila: referensen för variation i relaterad mening är alltid uteslutande alltid utan något enda undantag JÄMVIKT — förståndsvärldens, inte formvärldens, grundbegrepp. Se utförligt från ATOMTRIANGELN om ej redan bekant. — Den framställningen finns inte i den moderna akademins begrepps- och lärosystem. Det är anledningen. Varför inte? — Sanningsbegreppet — det som allt utgår ifrån och kan återföras på i Universums Historia: kan förstås, beskrivas, förklaras och relateras i detalj; Djupt, innerligt, föraktligt behatat i MAC. Se särskilda exempelblock i Sanningens Filosofi. Se särskilt från EUROPAS FILOSOFER. Se även i ENTROPIBEGREPPET generellt. |
I
avsnittet om INERTIALSYSTEM ges en utförlig generalgenomgång med flera citerade
exempel på HUR författarskaran i MAC generellt — verkligen (men omedvetet, vilket
beskrivningen också är tillägnad att understryka orsaken i) — söker påtvinga
läsaren uppfattningen att begreppet inertialsystem skulle ha Isaac Newton som upphovskälla — snarare än den
moderna akademiska intelligentians tolkning av innehållet i Newtons
PRINCIPIA.
Det
blir i ljuset av den genomgången tydligt att det är 1800-talets specifika
högtstående moderna akademiska intelligenser — inte naturfysiken som sådan —
som generellt byggt upp bilden av den prominenta fysikbild där just
användningen av och referensen till begreppet »inertialsystem» är avgörande
centralt; Se speciellt Einstein i Citat6 i INERTIALSYSTEM, ”Vi
ha lagarna, men vi veta inte till vilket system vi skola hänföra dem.”.
— I
avsnittet om ENTROPIBEGREPPET [Kausalordningen] [Utförliga
Arbetsexempel]
finns
exemplifierat i termer
av relaterad fysik kontra jämförande påståenden från modern akademi i detalj HUR aktion och reaktion agerar tillsammans
oskiljaktigt
—
fungerar ENLIGT ÄNDRINGSLAGARNA
(samma som Newtons Tre Rörelselagar [NEONS])
— med
syftet att belysa den allmänt citerade vanföreställningen i MAC angående påståendet
att fysikens lagar skulle vara tidsreversibla (»filmen baklänges»). Det är ett
påstående som f.ö. uppvisar ytterligare en utkomst av den moderna akademins
uppenbart förytligade förståndsdjup på DE RELATERBARA NATURPRINCIPERNA (I syntes samma som Newtons rörelselagar [NEONS]).
— Ett
föremål som genomgår en acceleration (CitatFM1975s72), ändring av tillstånd, kan i relaterad mening
INTE
— aldrig, inte någonsin, inte under
några som helst omständigheter, förhållanden eller betingelser
—
betraktas, ses, förklaras eller förstås som ett föremål i vila. Se även
i Varför är det klart?, om ej redan bekant.
”I ett system som följer
med i rörelsen står kroppen stilla”;
Den blotta meningsbilden — källan
anställer accelererad rörelse i resonemanget —
motsäger varje rationellt tänkande individs normala vardagliga förnuft:
Rörelse är förändring. Vila är tillstånd.
Naturvetenskapens uppgift är att FÖRKLARA befintligt — inte DIKTERA
nytt.
I modern akademi däremot [AccelerationVilaMAC], är den typen av framställning mer regel än undantag i
ämnen som rör elementär mekanik;
Förutsatt att man INTE TÄCKER FÖR EXPERIMENTLABORATORIET PÅ
OLIKA SÄTT FÖR ATT UTESTÄNGA EXPERIMENTELLA RESULTAT kan NATURLIGTVIS alla,
samtliga, rörelsetillstånd i Universum — enligt Newtons tre rörelselagar [ÄNDRINGSLAGARNA], relaterad fysik (TNED), avgöras genom experimentell
observation: rörelsetillståndet som begrepp bygger på NÅGON metrisk
ändringsbild, och den kan mätas. Även konstant likformig rörelse.
— SPECIELLT typen »konstant rätlinjig rörelse» är i
PRAKTIKEN bara — alltid — en idealiserad rörelsebild där man bortser ifrån
vissa detaljer; mest populärt i MAC är att täcka för
fönsterrutorna för passagerarna så att de inte kan se omgivningen rusa förbi.
Personer
som försöker intala oss att vila är rörelse [FMaccVila] (eller rörelse vila), kopplar uppenbarligen ingen seriös
naturbeskrivning:
Vi kan inte kalla ett sådant, tydligt
STYMPAT, beskrivningssätt för naturvetenskapligt.
FELET
ligger INTE i källverkets presentation av vektorer, deras riktning och storlek.
Felet
ligger i (bristen på) förmågan att relatera/förstå/beskriva det naturliga
saksammanhanget:
Det naturliga saksammanhanget i den
accelererande bilens fall CitatFM1975s72 betyder
uppenbarligen att den accelererande bilen inte får förstås som ett
viloreferenssystem: ger man koncept åt den accelererande bilen är
också bilen, verkligen, ett referenssystem under acceleration — inte i
vila.
Om inte redan bekant, se utförligt från FMaccVila.
Personer
som exekverar i följande citerade ordningar
”Betrakta
exempelvis en bil som accelererar i förhållande till sin omgivning. I ett
koordinatsystem som ligger stilla i förhållande till vägen gäller
Newtons kraftekvation. Bilen påverkas av en accelererande kraft från motorn via
hjulen, och om denna kraft och bilens massa är kända, kan accelerationen
beräknas ur ekvation (16). Om bilens rörelse
däremot hänförs till ett koordinatsystem, som ligger stilla i förhållande till
bilen, befinner sig
denna ju i vila, medan dess omgivning
däremot accelererar i motsatt
riktning.”,
”Om
kraftekvationens giltighet skall bevaras måste man därför införa en kraft, som verkar på bilen i motsatt riktning mot den
framdrivande kraften och som är lika stor som denna, så att de båda krafterna
upphäver varandra. Denna
nya kraft kallas tröghetskraften på
bilen.”,
FOCUS
MATERIEN 1975 s71 sp2mö
”As
an example, consider you are on a car accelerationg past a tree. From your reference frame, the tree will have an
acceleration that can not be accounted for by considering the physical
force acting on it. Newton’s laws in their
old form provide no way to resolve this paradox.”
@INTERNET
Wkipedia Talk Newton’s laws of motion
Loom91
06:50 7 February 2007 (UTC)
(etc.)
glömmer av KRITERIET FÖR TILLSTÅNDETS ÄNDRING:
— ett
i kroppen eller föremålet upphängt eller inordnat instrumentsystem.
Jämför gråsparvarna som leker i vårbuskarna: de flyger hur lätt som helst rakt in genom grensnåret
med perfekt navigation, full pedal. Exakt intrumentsystem — tydligen baserat på
uppfattning av navigation
i förhållande till ett inneboende naturligt förståndsbegrepp om JÄMVIKT.
I den accelererande bilens fall blir
jämviktens tillståndsregistrerande instrumentsystem enklast en kula upphängd i
en fin tråd i taket:
— Är
bilen vilande (relativt marken, idealiserat) hänger kulan rakt ner; accelererar
bilen, ställer sig kulan i vinkel i proportion till accelerationens magnitud.
Personer som bara okritiskt antar (eller tvingas till det för att få
meriter) föreställningarna i modern
akademi per tradition (för
att få meriter), och sedan, tydligen,
själva för den traditionen vidare
— likt citatets författare, som FRÅNSER
INSTRUMENTSYSTEMET och därmed frånser fysikens dynamik, KINETIKEN: rörelse
med krafterna innefattat
—
utpekar också den kategori personer som (utan insikt, och omedvetet, enbart genom att »föra
traditionen vidare») försöker påtvinga
globalbefolkningen naturfysiken utifrån ett akademiskt NUMERA VÄL inövat
populärt beskrivningssätt. Nämligen det som kommer från den antagna Einsteins
allmänna relativitetsprincip som beskriver rena PERCEPTIVA INTRYCK: KINEMATIK:
rörelsens beskrivning utan hänsyn till krafterna;
—
Marken accelererar relativt bilen, trädet accelererar relativt bilen, etc.; Einsteins
allmänna relativitetsprincip.
Fysikens beskrivning utifrån konkreta
verkliga praktiska mätinstrument är kinetiken. Se f.ö. Ändringslagarna. Dessa mätvärden skulle då i konsekvens bortses,
tydligen, ifrån av nämnda populationer. Vi vet att det inte fungerar så.
Men därmed avhandlas bara ärendena utan
något egentligt naturvetenskapligt intresse eller värde: händelsebeskrivning
utan hänsyn till krafterna tillhör INTE fysiken utan geometrin.
(Det blir också andemeningen i den antagna Einsteins naturfilosofi: det
finns inga krafter alls i verkligheten [AllaKrafterOverkliga])
Det blir i ljuset av den utvikningen
alltså, och naturligtvis, befängt att resonera så som ovanstående citerade
exempel visar:
— I
ENA delen medger man en aktiv dynamik (bilens acceleration) medan man i ANDRA
delen helt förnekar en sådan (acceleration finns inte, bara vila) — för
tillfället att få festa på kvarlevorna av ett sensationellt perceptivt INTRYCK.
”The relativity principle that Einstein had established on the basis of the equivalence principle, however,
will be satisfied if all laws of this new metric theory of gravity, including the field equations for the metric
field, are generally covariant.”, s66ö,
http://nd.edu/~kbrading/Classes/Phil 93871/Of Pots and
Holes.pdf
OF
POTS AND HOLES: EINSTEIN’S BUMPY ROAD TO GENERAL RELATIVITY, Michel Janssen
2005
BILDKÄLLA: Författarens arkiv · 12Sep2012 E28
Bild124 · Nikon D90 · Detalj

DEN OTILLÅTNA LINJÄRISERINGEN
Man hoppar över gravitationens särställning som unik
kraftform i fysiken, GTaction,
beaktar inte gravitationens absolutverkan, utan anser (uppfinner) att
gravitationens verkan sker via en ändlig hastighet (som därmed omöjliggör elektriska laddningens härledning, GTaction), och därmed helt enkelt
DIKTERAR fysikbeskrivningen via utvalda, enstaka LINJER eller PUNKTER:
— och därmed en totalt sett STYMPAD naturbeskrivning.
AV DIVERGENSACCELERATIONEN SOM DEFINIERAR GRAVITATIONEN
framgår utomordentligt tydligt
i den konventionellt benämnda s.k. ekvivalensprincipen (citat nedan, som föregick Einsteins allmänna relativitetsprincip [kinematiken (synintrycket) bestämmer (referenserna) i fysiken]):
”In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body (such as the Earth) is actually the same as the pseudo-force experienced by an observer in a non-inertial (accelerated) frame of reference”,
http://en.wikipedia.org/wiki/Equivalence_principle
@INTERNET Wikipedia Equivalence principle [2012-09-06]
Gravitationskraften F=ma i MAC betyder i ljuset av ”ekvivalensprincipen” tydligen att F=ma: gravitation = acceleration, citatet ovan (se även i WikiEinsteinEquivPrinc):
»the gravitational "force" is actually the same as the pseudo-force experienced by an observer in an accelerated frame of reference»,
Relaterad fysik:
— Gravitationskraften har ingen fysikalisk ekvivalent [G-beviset]; gravitationens verkan kan inte härmas eller simuleras på någon principiellt ekvivalent form med hjälp av några andra fysikaliska fenomen — men modern akademi hävdar, bestämt, just det.
Gravitationskraftens absolutverkan [GTaction] — konvergenskraften elementärt via en ringform — härleds i relaterad fysik med hjälp av ett aktionskraftsbegrepp: centralverkan med centralacceleration, en cirkulär rörelse med centripetal- och centrifugalkrafter som definierar den absolutverkande g-kraften via ett idealiserat DIVERGENSBEGREPP, och som helt saknar någon motsvarande känd TIDSABSOLUT fysikalisk existens: Gravitationens ABSOLUTVERKANDE KONVERGENSKRAFT har ingen direkt fysikalisk ekvivalent, bara en begränsad (punktlokal) kvantitativt analog värdeekvivalent.
Se vidare från VadÄrEkvivalensprincipen.
BILDKÄLLA: Författarens arkiv · 12Sep2012 E28
Bild177 · Nikon D90 · Detalj

DEN MEST UPPENBARA BEGREPPSKOLLISIONEN I HELA BETRAKTELSESÄTTET i MAC blir (alltså) påståendet (ekvivalensprincipen) att
gravitation = acceleration
— I MAC är det i princip inga problem med den saken, eftersom man REDAN antagit uppfattningen att gravitationen INTE verkar tidsabsolut: man anser att gravitationen verkar via den ändliga ljushastigheten (c) [MACgraviton].
Nämligen just via TIDSASPEKTEN:
— Genom uppfattningen att gravitationen verkar genom en ändlig hastighet (c), ligger det nära till hands att ställa fram KONSEKVENSTEORIER som går ut på det här: kraftverkan (gravitation=acceleration) är i själva verket KVANTFLUKTUERANDE KRAFTFÄLT (tensorfält) som manifesterar MASSA (gravitation) i formen av olika exotiska ELEMENTARPARTIKLAR (Higgs) som själva (mer än hundra neutronmassor) aldrig syns i det naturliga kraftspelet ehuru deras FÄLT gör det, och vilka ModerMassor bara kan påvisas i dyra partikelacceleratorer med speciellt höga kollisionsenergier.
;
Det är inget fel på de experimentella resultaten. Men kolla TEORIN bakom. Jämför EXPERIMENTELLA BEKRÄFTELSER: exakt samma matematiska formalia ur exakt samma experimentella observationer, men i ljuset av helt väsensskilda teorier. Så, det är i ljuset av de exemplen inte matematiken i sig det hänger på, utan LOGIKEN med SAMMANHANGET: det relaterbara innehållet i vilket matematiken används (och hur det harmonierar med det övriga).
JÄMFÖR DET MEST fundamentala EXEMPLET: neutronens sönderfall med framträdandet av en elektron och en vätekärna, hur en väteatom framträder:
— Hur resonerar man i MAC för att förklara framträdandet av elektronen?
— I MAC blir det »massa skapas ur energi» — genom »kvantmekaniska fältfluktuationer» i formen av olika matematiska lösningar till resonanskraftfält som berör kollisioner mellan atomkärnor och som kan testats praktiskt i partikelacceleratorer.
— I relaterad fysik (TNED) finns ingenting sådant.
— I avsnittet om BETASÖNDERFALLET redovisas den hittills (Sep2012) mest detaljerade genomgången enligt TNED av hur atomkärnan avdelar komponenterna till sin elektronmassa; hur elektronen kommer fram UR atomkärnan — i enlighet med experimentella observationer, eller så inte alls.
Centralaccelerationen i MAC — Härledningarna i
MAC — HyperPhysicsCitat
— WikipediaCitat — AskAScientistCitat — BILDKÄLLA: Författarens arkiv · 11Sep2012 E27
Bild185 · Nikon D90 · Detalj

INLEDNING
— missuppfattningarna
inom mekaniken generellt i modern akademi, enligt relaterad fysik,
med citerat, jämförande, skolexempel
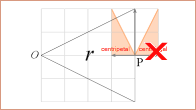
MAC förstår tydligen inte (kan inte relatera)
fysikbalansen mellan centripetal och centrifugal: centrifugalkomponenten
utelämnas
I MAC STRYKER man helt enkelt
centrifugalkomponenten [ActionReactionMAC], [HyperPhysics],
[Wikipedia], [AskAScientist] — läsaren [MACkraftParabeln] ges knappast (ens) chans att uppmärksamma Greppet:
ingenting omnämns.
EARP — CentralMAC
— Varför?
— VARFÖR kan inte modern akademi relatera fysiken i ämnet centripetal och centrifugal?
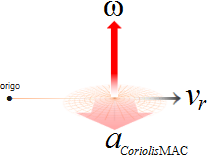
— Objektsfixeringen med det perceptiva intrycket bestämmer referenserna i MAC — tillsammans med det uppfunna fysiska objektsbegreppet »inertialsystem» (eng. inertial frame eller inertial reference eller inertial system): fysikens lagar (NewtonII, kraftlagen F=ma) enligt MAC gäller inte i accelererade system [Citat2 INERTIE — FYSIK III, Mekanik s43, NKI Biblioteksförlaget 1964, ”giltigheten av Galileis och Newtons lagar är begränsade till referenssystem som inte accelereras”]; Enligt MAC, beskriver ett accelererat system CitatFM1975s72 inte något »inertialsystem»: ingen vila — balans mellan centrifugal→ och centripetal← — kan finnas i ett roterande system, »eftersom det är ett accelererat system» [FOCUS MATERIEN 1975 s72, Tröghetskrafter, ”Vid rotationsrörelse upphävs den inåtriktade centripetalkraften av en utåtriktad tröghetskraft, centrifugalkraften, om kroppen anses stå stilla i ett system som följer med i rotationen (3)”, se FM-figuren i CitatFM1975s72]. Se även samma typ (Sep2012) nedan i citatet från Wikipedia,
”Centrifugal force is often confused with centripetal force. Centrifugal force is most commonly introduced as an outward force apparent in a rotating frame of reference. It is apparent (fictitious) in the sense that it is not part of an interaction but is a result of rotation - with no reaction-force counterpart. This type of force is associated with describing motion in a non-inertial reference frame, and referred to as a fictitious or inertial force (a description that must be understood as a technical usage of these words that means only that the force is not present in a stationary or inertial frame).[4][5]”,
http://en.wikipedia.org/wiki/Centrifugal_force
@INTERNET
Wikipedia — Centrifugal force, Fictitious centrifugal force [2012-09-24]
Referensen
till skeendet, variationerna, i fysiken är i relaterad mening inget
fysikaliskt objekt, utan ett begrepp — mätvärde = tillstånd [APARC] (idealt) under tidsdifferentialen
dt och som garanterat inte finns i fysiken: dt-begreppet
i fysiken gestaltar för oss ett motsvarande icke fysiskt varaktighetsbegrepp
(intervall, xyz-översiktsbild) som sinnebilden för jämviktens, mätvärdets (alltid momentana, idealt under tidsdifferentialen dt) referens, aldrig
något fysiskt objekt:
Som
vi ser, är MAC
oförmögen att förstå Newtons vilande referenssystem (Newtons
berömda ämbarförsök) som ett
begreppsligt, instrumentellt (»matematiskt»
med Newtons vokabulär [CitatNEWTONS PRINCIPER]) jämviktssystem: I
relaterad fysik är (således) jämvikten (den instrumentellt mätande händelseanordningen i varje
momentant ögonblick) som fysikens referens
samma som tillståndet som princip under en tidsdifferential (dt) och som [FUNTOP]
eliminerar föreställningen om »inertialsystem»; Därmed, nämligen, gäller »giltigheten av Galileis och Newtons
lagar» för alla referenssystem i
varje ögonblick (dt), oberoende av deras rörelsetillstånd, aldrig i något enda system eftersom [APARC]
fysiken betingas av oupphörlig variation; Och därmed ÄR lagarna (NEONS) av
naturen REDAN helt oberoende av de olika referenssystemens
rörelsetillstånd [FUNTOP]; Och därmed den oåterkalleliga giltigheten av (NewtonIII) aktions- och reaktionskrafter [AktionReaktion] som självaste den förklarande, beskrivande, mätande och
observerande grundvalen till fysikens värld av variationer [NOLLFORMSALGEBRAN]. MAC kopplar, tydligen, inte den nivån i förståndet.
Det blev, tydligen, 1800-talsvetenskaparnas
skuld, den moderna akademins uppsegling under 1800-talet, att INTE ha förstått
Newtons Principer på den punkten [CitatNEWTONS
PRINCIPER], utan att istället ha
ställt upp nya, andra, akademiskt uppfunna regler för naturfysikens tydligt väl
relaterbara 0=FACTION+FReACTION; Modern akademi,
som i ovan nämnda exempelgenomgång per citat, med tydligt grund i olika typer
av kärleksbetygelser till HerrefolksDeviser, stadfästes tydligt under 1800-talet som akademisk institution (»VÄRLDSSTATENS
INTELLIGENSCENTRUM») som den människoskapade intelligensens dikterande verktyg.
Inte som uttolkare av de redan existerande naturkällorna: 1800-talets
ljushuvuden i Västerlandet började uppfinna logiken, inte härleda den.
Se även i ENTROPIBEGREPPET [Kausalordningen] och ALLA TAL om ej redan bekant.
Vi
studerar ett (övertydligt) exempel på hur låsningarna i MAC yttrar sig när det
kommer till naturvettet:
”Another
common mistake[original research?] is to state that
The centrifugal force that an object
experiences is the reaction to the centripetal force on that object.
”,
”Clearly,
if an object were simultaneously subject to
both a centripetal force and an equal and opposite centrifugal force,
the resultant force would vanish and
the object could not experience a circular
motion”,
”The centrifugal force is sometimes called a fictitious force or pseudo force, to underscore
the fact that such a force only appears when calculations or
measurements are conducted in
non-inertial reference frames.”,
http://en.wikipedia.org/wiki/Reaction_(physics)
@INTERNET
Wikipedia — Reaction (physics), Centripetal
and centrifugal force [2012-09-23]
Wikipediaförfattarna tycks inte räkna med följande (man använder [Sep2012] heller inte HELA den enkla figuren, som nedan, i MAC-härledningar, jämför efterföljande HyperPhysicsCitat):
Relaterad
fysik förklarar:
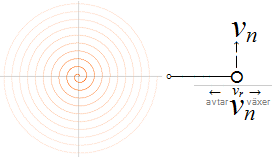
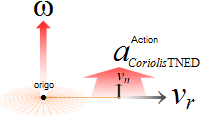
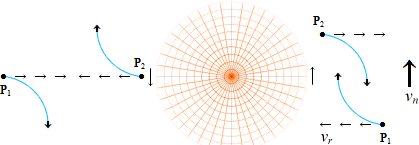
OM INTE stenen i snöret r som snurras runt med periferihastigheten w=d/T erfar en UTÅTRIKTAD centrifugal HASTIGHET (v0), finns heller ingen grund för centralaccelerationen, den fast roterande rörelsen, som fysikaliskt fenomen enligt det enkla sambandet (från cirkelns obegränsat slutna polygonindelning, som inte ingår i Wikipedia) via elementära relationer mellan likformiga trianglar (figuren ovan)
v0/w = d/r = wT/r
som tydligen i likheten mellan första och sista leden uttrycker en linjär acceleration
v0/T = w2/r
= å ...................... centralaccelerationen i relaterad fysik
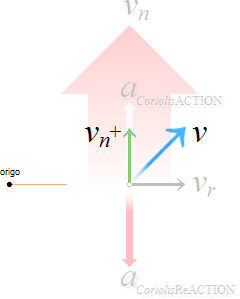
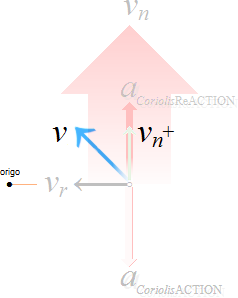
Nämligen: Den — så — utåtriktade eller centrifugala hastigheten i centralaccelerationen, centrifugalhastigheten v0→, måste, nämligen, för en fast roterande rörelse i riktningen w • ↑ UPPVÄGAS — balanseras — av en LIKA STOR MEN MOTRIKTAD centripetal hastighetskomponent, centripetalhastigheten v0←, och som tvingar stenen att hålla sig KONSTANT till den fasta längden r;
— Centrifugalhastigheten v0→ blir den mätande (på den snurrande karusellen) radiellt utåtriktade masskraftens (F=må)→ upplevelsemässigt aktiva accelerationskomponent, medan det kvarhållande snöret r garanterar den inåtriktande balanserande rörelseuppehållande, VidareRörelseFörorsakande och därmed aktionsbaserade centripetalkraften (F=må)← med centripetalhastigheten v0←. Dessa bägge kraftriktningar — aktionen som UNDERHÅLLER ← och reaktionen som MÄTER → — existerar alltid samtidigt som varandras diametrala motriktningar: den ena finns inte utan den andra:
— Ingen mätande kraft kan existera utan en motsvarande aktivt händelse(TIDS)uppehållande kraft (NewtonIII).
— Varifrån man SER händelsen, har ingen som helst betydelse för händelsen som sådan och dess mätande kraftfysik.
— Men modern akademi kopplar, tydligen som ovan, inte den nivån i fysikuppfattningen.
Jämför således mera korrekt uttryckt i här tillrättalagd , jämförande, omskrivning från Wikipediacitatet:
The centrifugal force that an object experiences is the concurrent, reactive, component of — not the reaction to — the centripetal force certifying the rotational motion of, not on, that object by »denying the cessation» of the centrifugal velocity component, and which component — even the term — is not included in the modern academic deductions to the central force efficacy, see CentralAccMAC
;
Clearly, whereas an object is simultaneously subject to both a centripetal force and an equal and opposite centrifugal force, the resultant force does not vanish but certifies the rotating object to be in a motional (radial) perfect balance with the tangentially impulse (p=mv) driving peripheral velocity and thus guaranteeing the object will continue to experience a circular motion
This is — for the rest of the story — the heart of the matter (explaining the entire complex): GTaction.
— Se vidare exempel i CoriolisBASIC och RotationsParabolensFormfaktor [MACkraftParabeln].
It’s not an object. It’s a concept (once natural — but during the 1800’s lost by MAC).
AktionReaktionMAC — BILDKÄLLA:
Författarens arkiv · 12Sep2012 E28 Bild199 · Nikon D90 · Detalj

AktionReaktionMAC
Wikipediaartikeln på samma rubrik (CentralaccelerationMAC) beskriver ämnet vidare i sektionen Remote action and reaction
”The third of Newton's laws of motion of classical mechanics states that forces always occur in pairs. This is related to the fact that a force results from the interaction of two objects. Every force ('action') on one object is accompanied by a 'reaction' on another, of equal magnitude but opposite direction. The attribution of which of the two forces is action or reaction is arbitrary. Each of the two forces can be considered the action, the other force is its associated reaction.”,
http://en.wikipedia.org/wiki/Reaction_(physics)
@INTERNET
Wikipedia — Reaction (physics) [2012-09-23]
Notera att ingen direkt referens ges till påståendesatserna
— de meddelas från TYP en Expert till Idioterna nedanför själva Tornbyggnaden
Ett helt glänsande galant exempel på dessa sammansattheter i praktisk fysik i MAC skulle då vara vektorrepresentationen [Kinematiska Friktionslösa ParabelAnalogin] [VektorledetsMACform] i Corioliseffekten [CoriolisEFFEKTEN i Syntes]:
Den avgörande relaterbara, förklarande, beskrivningen och härledningen förutsätter en STRÄNG — lagbunden [AktionReaktion] — distinktion mellan kraftriktning som UNDERHÅLLER ett skeende (aktionsriktningen) och kraftriktningen som MÄTER det skeende underhållet (reaktionsriktningen) [AktionReaktion].
Blandar man ihop dessa,
vilket som vi ser av citatet ovan man gör FRISKT i MAC, ”arbitrary”;
”the attribution is arbitrary”,
elimineras samtidigt hela grundvalen för den förklarande och beskrivande fysiken: NOLL naturvetenskap.
Se utförligt exemplifierat från CoriolisEFFEKTEN.
Se även skolexemplet i RotationsParabolensFormfaktor [MACkraftParabeln] som används i MIT-exemplet i samband med den modernt akademiska etablerade beskrivningen av tillämpningar på begreppet Corioliseffekt. Det exemplet beskriver för övrigt hur modern akademi, på kredit av det uppfunna begreppet INERTIALSYSTEM (Utförligt i EARP) också i andra änden tvingas GÖMMA UNDAN NATURVEKTORER (här Centrifugalkraften) helt enkelt stryka, radera dem för att matcha det egna kökets serveringar: Man stryker naturens representation, uppfinner eget, kallar det för NATURVETENSKAP och meriterad intelligens.
— Kom sedan och berätta om ORSAKERNA till att människor som är skolade i den moderna akademins lärosystem INTE klarar av att beskriva, umgås MED, mekaniken i naturen.
Vidare:
”A particularly subtle mistake is to confuse the forces that cause action and reaction with the actual action and reaction.[original research?]”,
”This mistake comes about partly because the very definition of force is all about a mass experiencing an acceleration, and there is an assumption that an object's entire mass is always the entity that is accelerating.”,
http://en.wikipedia.org/wiki/Reaction_(physics)
@INTERNET
Wikipedia — Reaction (physics), Remote
action and reaction [2012-09-23]
Andra citatdelen explicit:
Kraftbegreppet (eng. force) i relaterad fysik [KraftbegreppetTNED] beskriver inget annat än ekvivalens mellan massa och KRAFT:
m=m=m(a/a)=F/a; KRAFTEN grundas helt på gravitationens — massans — existens [GTaction]. Det finns — garanterat — ingen som helst kvalitativ relaterbar naturlig grund i påståendet ovan, att »definitionen på kraft är/handlar om massa som genomgår acceleration»:
”the definition of force is mass experiencing acceleration”
Fysiken i relaterad mening (TNED) innehåller ingenting sådant:
Jämför AktionskraftensDefinition i relaterads fysik:
KRAFTVERKAN — AKTIONSKRAFTER som
verkar över tidsintervall — är
ett entydigt resultat av
GRAVITATIONENS
massans ABSOLUTVERKANDE [GTaction]
positionsändringsmotstånd
Ingår inte i MAC
Den begreppsbasen
— gravitationens absolutverkan [utförligt i GTaction med referenser] som grundval för hela fysiken
— ingår inte i den moderna akademins begreppssystem.
Kraftlagen i relaterad fysik (NewtonII), F=ma, beskriver HUR massa (m) kan förstås SOM (konvergens-) KRAFT (F) via konvergenskraftens — gravitationens — fältstyrka (a).
WikipediaTypen ”mass experiencing acceleration” — accelerationen (a=dv/dt) — sker alltid över intervall (Δx).
Kraftbegreppet via gravitationens absolutverkande positionsändringsmotstånd verkar (absolut) över differential (dx):
— Jämför — som en del av den allmänna »matematikundervisningen» — ”dx=Δx” i MAC.
— Lägg dessa tillhopa, och MAC är garanterat portförbjuden i området.
Det är inte ens någon idé att inleda en diskussion: den är redan avslutad.
En massa (m) som genomgår en acceleration (a), eng, a mass experiencing an acceleration, är, enligt relaterad fysik, ingen definition på kraft, utan en beskrivning av ett händelseförlopp i fysiken som uttrycker en kvantitativ ekvivalent, ingen kvalitativ definition, till det kvalitativa (mera vida) kraftbegreppet. Inget annat.
Citatkällan i Wikipediaartikeln ger heller ingen referens för sin del vad som ska förstås med ”a mass experiencing an acceleration”.
Den delen har, tydligen, ingenting med den relaterbara fysikens domäner att göra i fråga om kraftens definition: kraftriktningarna i ämnet aktion och reaktion.
Jämför det mera balanserade
uttrycket, enligt relaterad fysik:
the very DESCRIPTION of force
is all about a mass
experiencing an acceleration
Så är det enligt relaterad fysik.
— Det finns ALLTID aspekter på Kvantitet och Kvalitet som kan anföras i relaterad fysik (TNED) MOT olika [befängda] MAC-påståenden, och som lika garanterat aldrig, inte någonsin, kan bemötas från MAC-hållet, och av den enkla anledningen att »MAC-personalen» enbart fokuserar på KVANTITETERNA och struntar i kvaliteterna. Jämför (f.ö.) Skolexemplet nummer ett i ENERGILAGEN [EKVANTITATIVT=(m→γ)c2=(m←γ)c2; EKvaliTATIVT=(m→γ)c2≠(m←γ)c2]: Atomkärnan, PLANCKRINGEN.
— Fortsättningen i Wikipediacitatet endast understryker det;
”Actually, though, when an object experiences a common impact-type of force, at the instant the force is applied, only the atoms and molecules at the surface of the object begin to accelerate.”,
http://en.wikipedia.org/wiki/Reaction_(physics)
@INTERNET
Wikipedia — Reaction (physics), Remote
action and reaction [2012-09-23]
EXEMPEL (Newtons Vagga [Utförliga Arbetsexempel] — ögonblicket då ändkulan lösgör sig):
— I samma NanoMoment stålkulans atomer i stålgittret börjar uppvisa positionsändringar som sammanhänger med att stålkulan är på väg att lämna de övriga i raden ÄNDRAS OCKSÅ KULANS TYNGDPUNKT ANALOGT:
— Vi behöver EXPLICIT aldrig tala om »genomfarande gittervågor i materialet» i ett specifikt mekaniskt (principiellt) problem, eftersom I VILKET FALL tyngdpunktens position ändras med atomernas (kroppsytans) läge via den mekaniska stötvåg som får kulan att accelerera: det är i netto, i vilket fall, tyngdpunktens positionsändring som räknas, om det så hänger på ändringen av en enda atoms gitterläge.
— Påståendet i Wikipediaartikeln ovan är, i det ljuset,
only the atoms and molecules at the surface of the object begin to accelerate
med andra ord direkt felaktigt: samtidigt som NÅGON del i kroppsytan dras åt något håll, gör kroppstyngdpunkten det också, och man kan inte separera tyngdpunkten från summan av kroppens beståndsdelar och mena att »kroppen reagerar senare än ytan». Det är ett vettlöst påstående i mekaniken.
Den ELASTISKA FÖRDRÖJNINGEN i koppling mellan positionsändring hos kroppens tyngdpunkt och kroppshöljet som följd av en impuls, sammanstötning med någon annan kropp utpekar tydligt uppkomsten av en deformationsvåg som bara har förflyttat referenspunkterna MED tyngdpunktens påverkan: det går inte att avhandla fysiken på någon grund som frånser den (elastiska) aspekten: tyngdpunktens omedelbara positionsändring MED varje kroppsdeformation (impulsbaserad, som går genom kroppens tyngdpunkt).
Därför har Wikipediaförfattarens utläggning om SEISMISK AKTIVITET heller ingenting med ämnet att göra. Jämför författarens (således) direkt SEISMISKT felaktiga slutsats:
”From this description, however, it should be obvious that during the time that the wave of force propagates through an object, only part of the mass of the object is accelerating, not all of it.”
http://en.wikipedia.org/wiki/Reaction_(physics)
@INTERNET
Wikipedia — Reaction (physics), Remote
action and reaction [2012-09-23]
Vi instämmer naturligtvis med Wikipediaförfattaren i påståendet — och noterar samtidigt att mekaniken (speciellt i elementära problem) INTE intresserar sig för kropparnas specifika ämnesstruktur och de stötvågor dessa uppvisar, utan enbart för kroppens tyngdpunkt och dess positionsändringar.
Termen, begreppet eller ordet center (of mass) förekommer heller inte i det aktuella Wikipediaartikelblocket: ingenting omnämns om den avgörande aspekten: tyngdpunkten.
Wikiartikeln exemplifierar
motortekniska termer
Wikipediaförfattaren ger en (slutlig) referens till termen valv float — som (bara ytterligare) understryker att den aspekten endast, ytterligare, understryker det redan sagda:
»Ventilflyt»:
Motorns varvtal blir så högt att ventilerna inte hinner stänga — eng. valve
float
”Another variant on the theme is valve float, in which the force applied by a spring, which can move a valve in an internal combustion engine, doesn't affect the whole valve quickly enough to keep it in contact with a rapidly rotating cam.”,
http://en.wikipedia.org/wiki/Reaction_(physics)
@INTERNET Wikipedia — Reaction (physics), Remote action and reaction [2012-09-23]
— Kamaxeln vill pumpa ventilstången i en takt (1 2 3 4 5 …) som stångens stålfjäder (... 3 ... 1 ...) inte är avpassad för (tekniskt, för liten fjäderspänning): Exemplet beskriver en oscillerande mekanik, ingen singulär pulsanalogi i elementär mekanik. Men OK då.
— Analogin är att PUMPA (kamaxeltopparna) en serie impulser på en vilande materialkula (ventilfjäderns kontaktring) innan den hinner uppvisa någon märkbar reagerande position i kroppsändring (som om fjädern berördes med reducerad kraft: följer inte).
— Men också den tillämpningen kan återföras på en motsvarande, fördröjd, koppling mellan motsvarande stötvågor genom den vidrörda kroppen och dess tyngdpunktsförflyttning via det inre materialets elasticitet; tyngdpunkten påverkas i vilket fall av minsta lilla stöt (impuls p=mv), hur man än räknar, och vilken tillämpning man än hänvisar till. Det finns inga undantag.
När motorvarvet i en förbränningsmotor driver kamaxeln
(eng. cam shaft, den som har till uppgift att öppna och stänga ventilerna till motorns cylindrar för insug och utblås)
fortare än ventilernas återförande ventilfjädrar hinner med, uppkommer en felfunktion
(ventilerna wobblar, spinner, uppvisar slumpvisa resonansrörelser, står öppna kontinuerligt, motorns effekt reduceras [våldsamt], videosekvens finns på YouTube, se Valve Float), som kallas (eng.) valve float eller ventilflytning.
SUMMAN AV KARDEMUMMAN
är bara den som beskrivits i enklare ord på annat ställe (inget nämnt, inget glömt):
— »MAC-personalen» gör sitt allra bästa i världshistorien för att sänka varje minsta ljusglimt av någon HINT som leder fram till själva målet för individens vandring på kunskapsvägen: upplysningen.
HYPERPHYSICSKÄLLAN
ligger närmast den enkla härledningen i Centralaccelerationen [GTaction] med typen
http://hyperphysics.phy-astr.gsu.edu/hbase/cf.html - cf2
:
—
Visningssättet är dock delvis (onödigt) obskyrt (dunkelt för nybörjaren) därmed
att
1. de
(galant) enkla elementära rektangel/triangelrelationerna inte framgår
(explicit, men som kan utläsas av mera erfarna) i uttryckssättet, och
2.
att termerna centripetal och centrifugal inte tydliggörs, ehuru de ingår i konceptet, samt
används för att beskriva mekanikens detaljer: källan använder enbart termen centripetal,
ordet
centrifugal finns inte med;
—
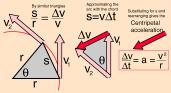
Källan skriver:
”By
similar triangles
s/r = Δv/v
”,
”Approximating
the arc with the chord
s = vΔt
”,
”
Substituting for s and rearranging gives the
Centripetal acceleration
Δv/Δt
= a = v2/r
”,
http://hyperphysics.phy-astr.gsu.edu/hbase/cf.html - cf2
HYPERPHYSICS
Centripetal Acceleration (»general World Wide Students Applications»
— 2010)
Härledningen
är i princip samma som i (figuren nedan) centralacceleration i relaterad fysik
med
ersättningarna 2d=s, v0=Δv, w=v,
Δt=T.
— Men
HyperPhysicskällan utelämnar den avgörande centrifugalkomponenten: ordet centrifugal
finns inte ens med. Det är också det genomgående temat generellt i
MAC-framställningarna till centralverkan. Se särskilt beskrivande exempel i INLEDNING.
—
Notera för cirkeln att den INTE kan beskrivas som en sluten kurva utan att ses
via en bestämd polygonindelning (som växer obegränsat), analogt att
cirkelbågen i princip måste förstås i formen av räta (kordor, obegränsat små)
linjeavsnitt.
WIKIPEDIA
[Centripetal force 2012-09-06] tillämpar
ingen liknande enklare härledningsform; Wikipedias beskrivning av
centralaccelerationen (som ensidigt kallas centripetalacceleration)
verkar helt tillägnat den moderna akademins vektoralgebraiska matteelit, ”Calculus
derivation” — ingenting för
icke-högskolestuderande eller motsvarande insatta (utsatta). Det finns
ingenting i någon enkel form att citera.
—
Generellt i MAC
beträffande rörelsens fysik (kinematiken, kinetiken) blir beskrivningarna
ytterst omständliga och ytterst svårtillgängliga (om alls begripliga) på grund
av att man i MAC använder sitt eget uppfunna INTERTIALSYSTEM med tillhörande klassificering av fysiken/mekaniken i
PSEUDOKRAFTER och FIKTIVA (skenbara) KRAFTER (generellt alla F=ma). Se exv.,
”A fictitious force, also called a pseudo
force,[1] d'Alembert force[2][3] or inertial force,[4][5] is an apparent force that acts on all masses in a non-inertial
frame of reference, such as a rotating
reference frame.”,
http://en.wikipedia.org/wiki/Fictitious_force
@INTERNET
Wikipedia Fictitious force, Examples of fictitious forces [2012-09-06]
— I TNED
beskrivs fysikens variationer generellt i referens till en JÄMVIKT — precis så
som vi skriver matematiken (a=dv/dt) och utför operationerna på
verkstadsgolvet: begreppet »inertialsystem» existerar inte i relaterad fysik. Vi talar (max) om vilosystem
och generellt om referenssystem (baserade på aktuella karaktäristika).
Det är så enkelt.
Se särskilt praktiska exempel i Bihang till
FUNTOP, samt Referensen
är jämvikt och balans.
BEGREPPSFÖRBISTRINGEN
”The term CENRTIFUGAL
force appears to have come about because of a mistaken perception that there is a force that operates in the opposite direction as the
CENTRIPETAL force. But that is a
misconception. The
"pull" that is felt by the ball on a string or by the hammer
thrower is the force that has to be applied
toward the center, to keep the ball
from flying off tangentially, not radially.”,
http://www.newton.dep.anl.gov/askasci/phy00/phy00305.htm
ASK
A SCIENTIST Centripetal vs. Centrifugal Forces (2001)
English:
THE
REASON WHY the centrifugal force is excluded [MACkraftParabeln] [CentralAccelerationMAC] in modern academy can be understood, and explained, on
credit of a corresponding idea in modern academy named inertial system.
See details in EARP.
The
PULL ”to keep the ball from flying off
tangentially, not radially” is the exact
balancing acting force to the reacting — instrumentally measurable,
what we can feel, observe, and measure — PUSH needed to KEEP the ball rotating
tangentially in a perfect radial balance with a remaining constant velocity:
cutting the PUSH|PULL, means cutting the PULL|PUSH, leaving only the tangential constant left.
—
There is no misconception of the phenomenon, except that in the quarters of
modern academic scholarship: The members are exhibiting statements exposing a
general inability to understand — explain — elementary physics.
— I
WOULD be happy to be wrong. Show me. Please.
;
It is
the impulse tangential pace (v=d/T) that brings the central accelerative
part to act from/on the center of rotation.
—
But the acceleration concept (a=dv/dt) [the mathematical-physical
descriptive idea] in the
central motion
—
that which defines the accelerative idea v0/T
— is
radial according to the simple and elementary general central
force action physical mathematics:
v0/w = d/r = wT/r ; v0/T = a = w2/r
Not tangential (w):
—
The conception (forming percept and concept) of the acceleration
— the CHANGE in velocity — is radial. Not tangential.
—
The tangential part is a constant: no change.
—
Hence, and still as a natural reflexion (on the state of the matters),
it is obviously correct to describe mathematically as well as
descriptively the centrifugal force as a force associated with an aspiration of
the mass to escape away — basic figure above — from the center along the
vector direction of v0.
— As
long as the thread holds, this escape is inhibited by the PUSHING centrifugal
companion (NewtonIII), and a perfect balance is established, guaranteeing the
conservation of the constant tangential pace.
—
There seems, in fact, no other mathematical way to equally deduce the
actual connection v0/T=a=w2/r.
—
With the circular motion the force acting in the thread or rope between the
peripheral mass and the center is called centripetal (Newton’s PRINCIPIA, Definition 5, ”A centripetal force is that by which bodies are
drawn or impelled, or any way tend, towards a point as to a center”,
source as above). By analogy with the opposite force in gravitation, the
conventional term is centrifugal.
”centrifugal c.1721, with adj. suffix -al (1) + Mod.L. centrifugus, 1687, coined by Sir Isaac Newton in "Principia," from L. centri-
alternative comb. form of centrum "center" (see center) + fugere "to flee" (see fugitive). Centrifugal force is Newton's vis centrifuga.”,
http://www.etymonline.com/index.php?term=centrifugal
ONLINE
ETYMOLOGY DICTIONARY [2012-09-07]
The
direction of the centrifugal force is however unfortunately [MACkraftParabeln] [CentralAccelerationMAC] not regarded or considered REAL in modern academy
[Because of Einstein
General Relativity Principle
and Modern Academy invented InertialSystem] [Abstract in EARP], but ”virtual” or ”fictitious”:
”Centrifugal force is a virtual force. It is not really a force.”, source AskAScientist as above.
—
Obviously in terms of an elementary deductive mathematical-physical form [GTaction],
the actual connection v0/T=a=w2/r, the centrifugal force (•→) is just as (opposite)
real as is the gravitational and centripetal force (•←), which however is
not recognized in MAC. (See Fictitious force in Wikipedia).
KraftbegreppetMAC generellt — BILDKÄLLA: Författarens arkiv · 15Sep2012 E32
Bild180 · Nikon D90 · Detalj — JORDEN,
universums pärla

2012IX8
Kraftbegreppet i modern akademi —
angående begreppet verklig KRAFT
Se
även Centralaccelerationen i MAC
Med
sikte på efterföljande citat [ForceFieldMAC]:
—
Genom RELATIVITETSTEORIN har modern akademi (MAC) flyttat kraftcentrum
—
från det makrokosmiska universum vi kan se och uppleva direkt med våra sinnen
(KRAFTER)
—
till det mikroskopiska (eg. picoskopiska) universumet: Man talar om KVANTUMFÄLT
[ForceFieldMAC]
och deras tillhörande ELEMENTARPARTIKLAR i föreställningen om begreppet kraft.
— Så
här kan det låta (Sep2012):
”The
force F does not arise from any physical
interaction but rather from the
acceleration a of the
non-inertial reference frame itself.”,
http://en.wikipedia.org/wiki/Fictitious_force
@INTERNET
Wikipedia — Fictitious force [2012-09-08]
physical
interaction-länken leder till Force carrier:
Notera f.ö. språkförbistringen generellt i MAC: ”acceleration of a non-inertial
reference”:
”A non-inertial reference frame is a frame of reference that
is undergoing acceleration with respect to an inertial
frame.”,
http://en.wikipedia.org/wiki/Non-inertial_reference_frame
@INTERNET Wikipedia — Non-inertial reference frame [2012-09-08]
Problemet i MAC
är just det (med Albert Einsteins ord): ”Med en kropps rörelse menar vi alltid
dess lägesändring i förhållande till en annan kropp” [CitatEinstein FYSIKENS UTVECKLING Natur och Kultur 1938
s178].
— Det fungerar inte så enligt
relaterad fysik (Och Einstein försitter heller inte tillfället för sin del
att understryka dramatiken, se aktuellt citat i Den Roterande Kroppen: ”Den klassiska mekaniken och det sunda
förnuftet råkar här i en våldsam
konflikt”):
— I relaterad fysik (TNED) är referensen alltid, uteslutande
utan undantag Jämvikt och Balans [FUNTOP],
det instrumentella mätvärdet
idealt via en tidsdifferential
(dt), helt OBEROENDE AV FYSIKENS FLORA AV OLIKA REFERENSSYSTEM (Se
jämförande citatexempel FMaccVila) —
därför att det inte finns några »inertialsystem»
i fysiken i relaterad mening;
— MAC-uppfinningen
(som resultat av oförmågan att förstå Newton [MACkopplarInteNewton])
”Med en kropps rörelse menar vi alltid dess lägesändring i förhållande till en
annan kropp” skapar (med andra ord) en grundläggande förvirring och förvillelse
OM strävan är att beskriva, förstå och förklara naturfysiken. Det går inte.
— Jämför Wikipediacitatets generella
mening i MAC ovan enligt
”force F does not arise from any
physical interaction”
med den relaterade fysikens tillrättalagda mening
force F does always arise from a physical interaction
:
— Impuls p=mv föregår — undantag
existerar inte — kraftbildning (F) över tid (T), F=ma=mv/T=p/T;
— Alla inbördes variationer mellan
massorna i fysiken följer den ordningen. Det finns inga undantag;
— MEKANIKEN: kraftöverföring sker alltid
via impuls (p=mv) från någon kropp redan i rörelse (massa [AktionskraftensDefinition]);
— ELEKTROFYSIKEN: kraftöverföring sker
alltid via impuls (p=mv) från någon elektriskt laddad kropp redan i rörelse (induktans)
[Integrala(Tröghet-Induktion)Analogin];
— KRAFT i relaterad mening
UPPKOMMER således ypperligt väl relaterbart uteslutande i följd av att
kropparna växelverkar (eng. interacts): kolliderar (mekaniken)
eller vidrör (elektrofysiken) varandra på ett eller annat sätt: F = ma = m(v/T) = mv/T = p/T:
”Physical interaction” in related physics ALWAYS is a result, effect and outcome from an acceleration [impulse precedes force]: there are no exceptions; ”inertial reference” in modern academy is — for the rest, as thoroughly related in INERTIAL SYSTEM — a highly corrupted term (and concept) because it deals with THE MODERN ACADEMIC INERTIAL SYSTEM INVENTION (from NOT understanding Newton’s three laws, during the 1800:s); IT has no physical correspondence — no place — in related physics: IT does not exist in physics; IT cannot be used in describing physics.
— Related physics explains:
— Force
F=ma always appears as
a result of physical interaction = change in distance between bodies (body contact).
— Force F=ma=mv/T=p/T always appears as a result of acceleration = body contact (mechanic or electric) =
impulse p=mv over time T.
— There are no exceptions:
— OVER the accelerating interval (Δx) is
established an acceleration a=dv/dt from the acquired velocity between
no v and a v: from 0 to v during Δx. This interval — hence —
becomes indestructible
as energy
is indestructible.
— THAT interval defines (all by Newton’s three laws) the transformation
of the actual physical interaction that gave (resulted in) the following
(subsequent) interacting interval, with its irrevocable acceleration over the
Δx interval:
— Force F, impact
over time, hence, and thus, always
arises as an effect from a physical
interaction between different bodies (charged or uncharged masses).
There are no exceptions.
— How would you know?
— Because there are no alternatives but
mechanics (inertia) and electricity (induction). Both these have the same basic
integral connectivity [IntegralAnalogy] — in all in perfect concord with NewtonIII.
That is physics. Always has been. Always will be.
— That is, as I have experienced, how
we humans express our natural way of having experience; And no academic professor in
what-so-ever-merit will ever have a mandate to change that order in nature. And
so, the WAY we explain the content of any natural science, also should reflect that
essence, or not at all. Don’t mess with us. Please.
— That is what we NATURALLY experience through our senses: they
present to us the resulting changes, variations: a=dv/dt. Always. No
exception. Sensed Forces are
also real.
— »Force carrying particles» are (is) fiction in the minds
of modern academic scholars: there
are no individual particles inside the atomic nucleus (See The Planck Ring), never was, never will
be;
— for the rest, an idea responsible for the Mess;
— As water drops return to the mother
volume without
being seen in there as individually moving particles — as perceived in a preceding moment
from one of the simple images Nature shows us (below left) — so also is the
atom constructed in related physics (TNED):
as The Fundamental Form of Mass; [PlanckRING],
[GravitationFundamentalForm],
[PERIODIC
SYSTEM], [ATOMIC
MASSES] from [NeutronSQUARE]:
it has no inner individual constituents.
BILDKÄLLOR: Författarens
arkiv — 5Jul2012 E15 Bild144/138 · Nikon D90 · Detalj — STRANDVÅGOR bryts periodiskt mot en
sten och bildar rekyler som bryts upp i mindre fristående vattendroppar, som strax återförenas med modermassan.
NATUREN illustrerar sig
själv i PRINCIPER — NATURE illustrates herself in PRINCIPLES.
There are however RESONACES [MIC] from the impact, giving rise to
(the) different levels of resulting components (the individual droplets in the
»nuclear watersplash»). See related details from MIC (Mass Interactive Connection).
I wouldn’t claim
you — modern academy scholars (MAC) — are wrong:
— The more explaining (appropriate — serious) term would be primitive:
— Nature is the advanced thing. Don’t mess with Her. Please.
— THERE ARE according to related physics
NO »QUANTUM FIELDS OF FORCE»
IN NATURE ForceFieldMAC: a supposed process creating »Force by Exchanging Elementary Particles» and which
is claimed by MAC to exist in nature; The
Corresponding Impact »WaterSplashParticleDetection» is real, yes, absolutely.
But not the idea of »Force by
Exchanging Elementary Particles»:
— Such »physical ghosts» are found
(examined) only in the modern academic expensive particle accelerators:
— Short formation of a force structure
(»WaterSplash») by particle collision IS no doubt a true effect, while the idea
of a process creating
»Force by Exchanging Elementary Particles» is not: Experimental
results are always OK, while not always the interpretations of them are.
— IN TERMS OF SAFELY RELATED PHYSICS [TNED] The Force Carrying Particles as
such only exist in the minds of modern academic scholars, Compare Proving
Multiple c: same math, same experiments, same results, but vastly different theories:
the MATH-part and the EXPERIMENT-part is not the problem, but the idea of LOGIC
IN GENERAL is;
— In particle accelerator experiments, according to related physics, they appear as
short lasting »resonaces» from MIC
— as explained in related detail by THE PLANCK EQUIVALENTS — in the same
way as a specific water splash (picture above) repeats EXACTLY with all
the droplet types provided EXACT repetition of the physical prerequisitions
(qualifications). These short lived »mass-choked particles» have according
to related physics no REAL — ordinary
— physical existence (many times heavier than a neutron), but only show
up, and are only the outcome of an energy tally in a particle collision:
short energy (force) formations. A related example is discussed (as a
class example — with cross referring comparisons) in detail in NeutronFragments
— creation or division.
THIS
”In particle physics forces between
particles arise from the exchange of other particles. These force carrier particles are bundles of energy (quanta) of various fields.
There is one kind of field for every species of elementary particle.”,
http://en.wikipedia.org/wiki/Force_carrier
@INTERNET
Wikipedia — Force carrier [2012-09-08]
is, according
to related physics, an erroneous (PRIMITIVE)
interpretation of what nature shows.
— In nature, forces are always present where there
is an experienced acceleration.
— And: these forces appear from IMPACT: by impulse (p=mv) over time (T): F=p/T=mv/T=ma.
There is, according to related physics,
nothing such in nature as ”a force carrier particle” ForceFieldMAC.
In respect to related physics as in
THE DEDUCTION OF THE
ATOMIC NUCLEUS
— the
gravitation element, totally free of internal individual components, the same
as the fundamental element of mass
— ALL SUCH PECULIAR ASPECTS as the named ”force carrier
particle” ARE DUE TO CIRCUMSTANCES IN MODERN ACADEMY WHERE THE PATH to
the named deduction IS DENIED: The Planck Ring as The Neutron h=mcr.
Se även i AktionReaktion
hur MAC kan förstås ha »kompenserat sin elementära fysikuppfattning».
VÅG-PARTIKELDUALITETEN
[Atomkärnans
vågnatur] [Ingen
VågPartikelDualitet i TNED] — som
f.ö. i MAC
omöjliggör en enhetlig beskrivning av LJUSETS FYSIK [Polarisation-Reflexion-Refraktion] taget över alla, samtliga, fenomenområden — är (kan i termer av relaterad fysik
förstås vara) i MAC resultatet av
följande:
—
1800-talets skapelser med INERTIALSYSTEM och (därmed grunden för) relativitetsteorin med
»ingenting kan gå fortare än c»; Se resultatredovisningen från Gravitationens tidsabsoluta verkan.
Alldeles
tydligt är det så, att Naturen — per osviklig konsekvenslogik — har tvingat in MAC i ett begränsat hörn
(återvändsgränd) [ArgumentenMACgenerellt] i fysikbeskrivningen — med ett vokabulär som få (om ens
någon alls) förstår. Exemplen understryker påpekandena.
I MAC har man infört sitt INTERTIALSYSTEM som skiljer mellan rörelser som anses återföras på de
s.k. inertialsystemen eller tröghetssystemen (konv. konstant likformig
rätlinjig rörelse) »till skillnad från accelererade rörelser som inte hör
dit», och genom vilka man postulerar uppkomna s.k. FIKTIVA KRAFTER [CitatFM1975s72] (konv. eng., fictitious force, pseudo force, inertial
force).
— I relaterad fysik och matematik
finns ingenting sådant. Se särskilt i INERTIA:
—
Variationer i relaterad fysik och matematik har JÄMVIKTEN
som referens:
BILDKÄLLA: Författarens arkiv · 12Sep2012 E28
Bild411 · Nikon D90 · Detalj

Med
JÄMVIKTEN som referens:
det finns i relaterad mening
inte några fasta eller fixa referenssystem i fysiken, inte alls över huvud
taget [utförligt i INTERTIALSYSTEM]
—
just på grund av att fysiken kännetecknas av oupphörlig, oförtröttlig variation
(a=dv/dt).
— Så,
till vad, exakt, refererar vi då enligt relaterad fysik det vi utför och uppfattar?
(Fråga t.ex. fåglarna som leker i
vårbuskaget, gör loopar och branta sekundsnabba svängar så väl hälften vore
nog):
— Jämvikt. Balans.
Jämvikten (i varje momentant ögonblick)
beskriver det avgörande tillstånd som variationen kan mätas, beskrivas,
analyseras och formuleras matematiskt på — vad vi faktiskt utför på det
praktiska verkstadsgolvet. Se FUNTOP. Se även praktiska exempel i Bihang till
FUNTOP, samt Referensen
är jämvikt och balans.
— Men
den TYPEN av synsätt ingår inte i den moderna akademins lärosystem, inte
begreppsformen som sådan alls.
Jämför här ZENONS TEOREM,
INTERVALLETS
OFÖRSTÖRBARHET och NOLLFORMSALGEBRAN (i ljuset av den moderna akademins allmänna
matematikundervisning: det allmänt tillgängliga utbudet på webben). Dessa
nämnda exempel kan ses och förstås generellt som praktiskt jämförande
studieexempel på hur modern akademi förhåller sig till ett — tydligtvis, som
det får förstås — mera relaterbart synsätt.
Jämför
även (det ständiga
återkommande [även i FOCUS MATERIEN 1975 s71sp2mö]) bilexemplet på artikeln om Fictitious force
i Wikipedia:
”Figure
1 (top) shows an accelerating car. When a car
accelerates, a passenger feels like they're being pushed back into the seat.
In an inertial frame of reference attached
to the road, there is no physical force moving the rider backward.”,
http://en.wikipedia.org/wiki/Fictitious_force
@INTERNET
Wikipedia Fictitious force, Examples of fictitious forces [2012-09-06]

En betraktare vid sidan av vägen som fotograferar kulan
(figuren ovan) som hänger i taket från den accelererande bilen (←), kan
klart och tydligt LIKSOM ÄVEN PASSAGERARNA I BILEN och alla andra
observatörer i hela universum se kulans utslag motriktat bilens
accelerationsriktning:
— Det spelar ingen roll VARIFRÅN MAN SER händelsen: alla får
samma händelsebild av kulans utslag i bilen:
— Det som driver kulan bakåt (→) är en självklart verklig, inte skenbar,
kraft, nämligen den ENDA FYSISKT MÖJLIGT INSTRUMENTELLT UPPMÄTBARA som
DEFINIERAR den aktiva aktionskraften i motsatt riktning — inget påhittat, eller »skenbart» eller
»fiktivt» — men som, tydligen ”there
is no force moving the rider backward”, Wikipediaartikeln (MAC generellt) söker indoktrinera mänskligheten INTE
existerar, men som likväl alla kan känna, och som också utgör själva
förutsättningen för den fysiskt instrumentellt mätande kvantiteten
aktuell acceleration. Påståendet i wikipediacitat ovan ’there is no physical force moving the BALL backward’
är alldeles helt uppenbart helt fysikaliskt absurt, rena galenskapen: det har,
uppenbarligen, ingenting med någon naturvetenskapligt fysikaliskt mätande
förankrad beskrivning att göra: kulans faktiska, verkliga, konkreta utslag som definierar
och påvisar magnituden i den framdrivande accelerationen.
— Här ser vi (således
i Wikipediaartikelns påstående ovan) ett konkret skolexempel på hur man
i MAC, generellt, FÖRSÖKER eliminera
den avgörande fysikbeskrivningens Aktions- och
ReaktionskraftsRIKTNINGAR — inte ge dessa något insteg — och
förutan vilka hela den beskrivande, relaterbara, fysikbilden havererar; En relaterad
fysikbeskrivning kommer följaktligen garanterat aldrig fram i
Wikipediaförfattningens anda.
— Tala sedan om CoriolisEffekten,
som ett ytterligare (bekräftande) skolexempel i ämnet Aktions-
och ReaktionskraftsRIKTNINGAR.
—
The ”physical force
moving the rider backward” seen from an
observer standing beside the road
(the same as a state of EQUILIBRIUM inside the car —
state — before it begins to accelerate, and then further from each momentary
corresponding state of equilibrium in measuring/detecting any change)
is
the accelerating car;
— The accelerating mass of the
person/car pushes on the person inside the car in that it (mass) is opposing
the cause to the change in (any momentary) state (NewtonIII).
—
The observer on the road, as well as an observer in the car, can actually see
how the person is pushed backwards relative the more stiff equipment of the
car:
—
The effect of the pushing force exists whether seen from the road or inside the
car;
—
The pushing force is as real to the observer beside the road, as it is to the
passenger inside the moving car, or any body else in the universe.
Den spontana reflexionen inför
påståendet från modern akademi (här Wikipedia, citatet ovan) att KRAFTER man
upplever i vardagslivet är OVERKLIGA (”fictitious”, ”pseudo”, ”not real”,
”skenbara”) är uppenbarligen av nedvärderande natur: jag KÄNNER en kraft, men
det finns ingen naturvetenskapligt beskrivande LITTERATUR som bekräftar
min iakttagelse och observation: »jag (mitt konkreta upplevande) är overklig»
föranleder bara spontan avsky. Det är ingen naturbeskrivning, utan en naturvandalisering.
Jag känner mig bara främmande (läs: inte välkommen) inför den typen.
Jämför
även artikeln nedan från Scientific American:
’alla krafter är overkliga’
”The
forces you feel in a moving car—those
that push you back into your seat when the driver steps on the gas or throw you
side to side when the car makes sharp turns—are everyday examples of fictitious forces.”,
”Likewise
in the car, there simply
is no real force pushing you back into your seat, your senses notwithstanding.”,
”The
term "fictitious force" has a
precise meaning within Newtonian mechanics—in fact, it's always proportional to the mass of the object
on which it acts.”,
”General
relativity is his theory of gravity, and gravity is certainly the paradigmatic example of a "real" force.”,
”The
cornerstone of Einstein's theory, however,
is the proposition that gravity is itself a fictitious force (or, rather, that it is
indistinguishable from a fictitious force).”,
http://www.scientificamerican.com/article.cfm?id=what-is-a-fictitious-force
SCIENTIFIC
AMERICAN Ask the Experts — What is a "fictitious force"? —
July 9, 2007
— DU
är helt enkelt INTE verklig, enligt ovanstående Expertutlåtande: alla krafter är overkliga i MAC.
— OM det finns någon inrättning på
Planeten som hade tänkt att den skolundervisningen skulle IMPONERA på något
minimalt medfött tjejvett, har den helt säkert FEL. (Universums Morsa rynkar
pannan, skjuter ihop ögonbrynen och reflekterar, helt spontant och KORREKT, vad
i hela fridens namn har jag NU hamnat i för något sällskap: ’Jag är/upplever
overkligt’. Finns det inget annat att välja på?).
— Den
moderna akademins lärosystem har alldeles bestämt och helt radikalt misslyckats
med uppgiften som LÄRARE. En lärare undervisar i naturkunskap —
berättar, beskriver, talar om, leder, förklarar — inte dikterar att eleven
redan från ruta ett är dum i huvudet, inte fattar grundläggande Percept.
SCIAM — CITERAT EXEMPEL PÅ ihopblandningen mellan principen för Foucaults Pendel och CorioilisEFFEKTEN • BILDKÄLLA: Författarens arkiv · 12Sep2012 E28
Bild331 · Nikon D90 · Detalj

Studieexempel SCIAM
Exempelbeskrivningen nedan är
INTE tillägnad att utmåla SCIAM-författaren specifikt — MÅNGA (inte alla)
modernt akademiskt skolade beskriver saken på samma sätt (GoogleUtdragOkt2012), här endast för
att exemplifiera genom ett specifikt konkret källcitat
SCIAM-författaren (SCIAM, förk. Scientific American) påstår, initiellt — och uppenbarligen direkt felaktigt [SomBetyder?], vilket vi ska studera — att
”An elegant example of these types of apparent influences is the fictitious Coriolis force, which is responsible for the stately precession (or circular rotation) of a carefully suspended pendulum's plane of swing.”,
http://www.scientificamerican.com/article.cfm?id=what-is-a-fictitious-force
SCIENTIFIC
AMERICAN Ask the Experts — What is a "fictitious force"? —
July 9, 2007
Det finns ingenting sådant i den relaterbara
fysiken [CoriolisSATS2]: ingen KRAFT är
ansvarig, ”responsible” för den observerade pendelprecessionen, Foucaults pendel. Allra MINST CoriolisKRAFTEN
[CoriolisSATS3] — men webben är (som vi ser av enbart av detta exempel
propp) full av den beskrivande församlingen [WebCoriolisVideoDemos]. Vi studerar det —
speciellt i ljuset av CoriolisSATS3.
”If such a pendulum were suspended directly above the North Pole, it would appear to rotate 360 degrees every day. If you viewed this pendulum from a stationary point in outer space, however, it would appear to swing in a single, fixed plane while the Earth turned under it. From the outer space perspective, there is no sideways force (that is, perpendicular to the plane of swing) deflecting the sway of the pendulum. That is why the somewhat pejorative term "fictitious" is attached to this force. Likewise in the car, there simply is no real force pushing you back into your seat, your senses notwithstanding.”,
http://www.scientificamerican.com/article.cfm?id=what-is-a-fictitious-force
SCIENTIFIC
AMERICAN Ask the Experts — What is a "fictitious force"? —
July 9, 2007
”From the outer space perspective, there is no sideways force”:
— Nej. Helt korrekt uppfattat. FENOMENET ”the stately precession” Foucaults pendel HAR UPPENBARLIGEN HELLER INGENTING MED KRAFT ATT GÖRA:
— SCIAM-författaren introducerar för läsaren DEN KINEMATISKA — idealt friktionslösa, vilket direkt utesluter CoriolisEFFEKTEN ur fysikbilden enligt CoriolisSATS3 — HÄNDELSEN av en plan pendel över Nordpolen och den underliggande Jordkroppens rotation;
En BILD (bio) mellan två helt fysiskt skilda rörelsesystem; Det finns, frånsett friktionsförluster, ingen fysisk koppling mellan de olika rörelsesystemen Pendeln-Jorden.
Principen med Foucaults pendel:
Vartefter Jorden vrider sig
liksom det snurrande cykelhjulet under det pekande, vaggande fingret ovanför navet
— tecknar pendelpunkten sett från det roterande underlaget en periodiskt vridande krökt linje:
— VRIDNINGSBILDEN, mellan
motsvarande det snurrande cykelhjulet och det vaggande pekfingret ovanför ![]() ,
kopplar ENDAST fingervaggningen I NORMALRIKTNINGEN (rät vinkel) till
cykelhjulsplanet, alltså UTMED rotationsaxeln; fingervaggning i cykelhjulets
plan
,
kopplar ENDAST fingervaggningen I NORMALRIKTNINGEN (rät vinkel) till
cykelhjulsplanet, alltså UTMED rotationsaxeln; fingervaggning i cykelhjulets
plan ![]() visar ingen vridningsbild av vaggningen:
visar ingen vridningsbild av vaggningen:
— Lutas pendelplanet relativt hjultallriken, reduceras vridningsbildens utslag (genom vanlig trigonometrisk, kinematisk bildprojektion; bilden av varje fingervaggning, konstant vaggtid, reduceras så att antalet fingervaggningar som fullbordar ett helt varv blir proportionsvis flera; tiden för ett helt varv går mot oändligt vid ekvatorn) och blir noll vid Jordekvatorn;
— perioden/pendeln kopplar ingen »rotationsaxelparallell anpassningskomponent» då pendelplanet lutas ur sin parallellitet med rottionsaxelns utsträckning, och fenomenet finns därför heller inte vid Jordekvatorn [FoucaultPendelns Fullständiga LatitudEkvation];
— Fenomenet med Foucaults
Pendel får med
andra ord förstås utomordentligt väl relaterbart som ett VISUELLT — kinematiskt (utan kraftens
inverkan) — fenomen: en ren avbildning av ett rörelsesystem på ett annat. Inget
kraftfenomen, ingenting som har med kinetiken
(med kraftens inverkan) att göra.
OM det finns, möjligen, personer som tycker det är UNDERLIGT
att BILDEN av det vaggande fingret över det snurrande cykelhjulet FÖREFALLER
VARA NÅGOT SLAGS SKILT FYSISKT FENOMEN — »eftersom ju bilden inte följer med i
Jordrotationens motsvarande analogi» — är iakttagelsen alldeles säkert korrekt
uppfattad, men tolkningen ofullgången: TILLSTÅND (—) är
inte VARIATION (![]() ), och vice versa. Det som krävs för
full upplysning är full PRAKTISKT INSIKT i accelerationsbegreppet [ÄNDRINGSLAGARNA]:
), och vice versa. Det som krävs för
full upplysning är full PRAKTISKT INSIKT i accelerationsbegreppet [ÄNDRINGSLAGARNA]:
Mera ingående Djupbeskrivning, Foucaults Pendel
Pendelpunkten ![]() i pendeln
i pendeln ![]() besitter i varje momentan tidpunkt (dt) ett,
och endast ett, entydigt definierat rörelseriktningsbestämt TRÖGHETSPLAN
besitter i varje momentan tidpunkt (dt) ett,
och endast ett, entydigt definierat rörelseriktningsbestämt TRÖGHETSPLAN ![]() xy (oberoende av art och typ av rörelsevariationer): x↨
xy (oberoende av art och typ av rörelsevariationer): x↨![]() och y↔
och y↔![]() .
Dessa är i den praktiska pendelgrunden resultat av att pendeln avbildar en
liten del av ett impulsmoment
(J=mvr); J varierar med v
från noll (pendelns ändlägen) till v (mittläget); Via y-rörelsedelen — den är
kopplad till tyngdkraftens lodkomponent — garanteras den entydiga
xy-planriktningen vid v=0 genom den potentiella orsaksriktningen som, då, ligger konserverad i
pendelpunkten vid dt: I denna punkt
finns föregående verkans xy-riktningar som orsak till efterföljande, varigenom
tröghetsplanets orientering i rymden [»det spinnande hjulet»] bevaras (idealt,
frånsett friktionsförluster).
.
Dessa är i den praktiska pendelgrunden resultat av att pendeln avbildar en
liten del av ett impulsmoment
(J=mvr); J varierar med v
från noll (pendelns ändlägen) till v (mittläget); Via y-rörelsedelen — den är
kopplad till tyngdkraftens lodkomponent — garanteras den entydiga
xy-planriktningen vid v=0 genom den potentiella orsaksriktningen som, då, ligger konserverad i
pendelpunkten vid dt: I denna punkt
finns föregående verkans xy-riktningar som orsak till efterföljande, varigenom
tröghetsplanets orientering i rymden [»det spinnande hjulet»] bevaras (idealt,
frånsett friktionsförluster).
;
— Pendeln ![]() ETABLERAR genom sitt TRÖGHETSPLAN xy
ETABLERAR genom sitt TRÖGHETSPLAN xy ![]() ett TILLSTÅNDETS
innebörd [ÄNDRINGSLAGARNA], [NewtonIII]:
ett TILLSTÅNDETS
innebörd [ÄNDRINGSLAGARNA], [NewtonIII]:
— Förutsatt att man inte PETAR på pendelplanet eller
utsätter det för andra krafter, UTAN LÅTER DET VARA I FRED i sitt eget
tillstånd, är pendelplanet alldeles tydligt, klart och uppenbarligen ett REGISTRERANDE
FYSISKT PRECISIONSINSTRUMENT,
just genom tillståndsbegreppet (idealt i bortseende från alla
friktionsförluster i upphängningsanordningen och eventuell luftfriktion i
pendlingen) — och som MAC-personalen tycks
ha så oändligt svårt för att acceptera [INERTIALSYSTEM];
— Varje tillstånd som skiljer sig från
det givna i pendeln
kan följaktligen påvisas/bevisas
med pendelns hjälp — utan någon som helst annan koll än den rent visuella:
ingen kraftaspekt ingår ; Pendeln — tillståndet — ändras
inte
(frånsett friktionsförlusterna).
Pendeln visar samma princip som i Newtons berömda ämbarförsök: påvisandet
av tillståndet
(Tillståndet: ”Newtons Absoluta Rum”
enligt Einstein Citat7
— TROTS Newtons egna ansträngningar för att läsaren just INTE skulle tolka
begreppen så, se citatsammanställning i MACkopplarInteNewton;
Newton använde inte den av Einstein anmanade typen av begrepp [»Absolute Space», finns inte i Newtons
Principia], det är en modern uppfinning som, av alla här tillgängliga källors referenser att döma,
sedan lagts i munnen på Newton, se utförligt med jämförande citat och
genomgångar i INERTIALSYSTEM)
som begrepp i fysikens beskrivning — och som Newton fått så
mycket STRYK för från MAC-sidan. Se
utförligt från INERTIALSYSTEM.
— I relaterad fysik [TNED]
finns inte heller tillståndet som
sådant TILL i formen av något fysiskt objekt [APARC]: hela fysiken kännetecknas av
just VARIATION [FUNTOP]:
tillståndet enligt relaterad
fysik är ett BEGREPP OM JÄMVIKT, balans, oföränderlighet, som gäller
FÖR alla system i fysiken, oberoende av art, typ, sort, eller sätt. Pendeln är
en av flera anordningar med vars hjälp tillståndsändringar kan påvisas.
— Pendeln kan med andra ord förstås
utveckla ideal nollkraft i
sin fysikkoppling till varje annan fysikalisk anordning.
— Därför är påståendet att PendelFenomenet — Foucaults
Pendel — skulle koppla till KRAFT felaktigt av kraftens ENDA skäl och också
felaktigt med koppling till Coriolis av den obefintliga friktionens skäl: Corioliskraften kräver friktion [CoriolisSATS2].
Foucaults Pendel kan med andra ord förstås
som inget Kinetiskt
fenomen — fenomenet är Kinematiskt:
Fenomenet visar en BILD (bio) av en (idealt) friktionslös koppling mellan två
skilda fysikaliska rörelsesystems fysikhändelser (FoucaultPendelPrincipen): ett plant
xy-translativt system (pendeln under tyngdkraftens inverkan), och ett roterande
(Jordkroppen); fenomenet beror endast av relativa rörelsebilder mellan olika
referenssystem, inte av några verkande krafter;
— Fenomenen endast bevisar tillståndet som princip (redan
klargjort av Newton) — men som framstår så illa aktat i MAC
— se utförligt från INERTIALSYSTEM.
Lutas pendelplanet vinkeln V° relativt lodplanet [FoucaultPendelns Fullständiga LatitudEkvation] (hela pendeln blir bunden till Jordrotationen via en precession) återstår motsvarande rent kinematiskt projicerade pendellinjes rotationsaxelrelaterade period (T) på rotationsplanet via projektionen i PREFIXxSIN enligt T·sinV — eller räknat från motsvarande Jordekvatorn med latitudvinklar
L=(±0-90°) enligt T·cosL: tiden för pendelplanets vridning ett helt varv går mot oändligt vid ekvatorn.
(Se även Wikipedia Foucault pendulum, Explanation of Mechanics [2012-09-21]);
— det finns med andra ord ingen kinetik (kraftfysik) att relatera som grund för fenomenet med Foucaults pendel;
Se mera utförligt i FoucaultPendelns beteende vid avtagande latitudvinkel.
— Pendelplanets viloreferens i MAC anges typiskt
(Wikipedia Foucault pendulum, Explanation of Mechanics [2012-09-21]) som ”the plane is fixed in space”.
— I relaterad fysik (TNED) beskrivs och förklaras referensen till pendeln som Jordrotationens eget Jämviktssystem: samma referens som definierar — mäter — begreppet Jordrotation: det finns inte till som något referenssystem — inget objekt — i fysiken, utan är/avbildar ett rent (idealiserat) mättekniskt referenssystem baserat på JÄMVIKTENS PRINCIP genom tillståndets fysik [APARC] (och som i MAC brukar identifieras med ”fixstjärnorna” [konv. »det mest rörelselösa»]); Se speciellt utförligt från FUNTOP om ej redan bekant.
— Det som driver pendeln att vrida sig (frånsett aktuella friktionsförluster, vilka vanligen bortses ifrån i ämnets skolelementära behandling) är ingen kraft, utan ett resultat av EN VISUELL BILD AV EN GIVEN RÖRELSE SEDD I TVÅ OLIKA REFERENSYSTEM (söker man påverka pendeln med någon kraft, upphör dess tillstånd att gälla):
1. Jordkroppen med bilden av det fixa pendelplanet: pendelrörelsen i pendelplanet som avbildas roterande, och
2. Jordrotationens jämviktssystem, konventionellt »rymden utanför» med pendeln i sitt fasta, orörliga pendelplan och därifrån sett den underliggande roterande Jordkroppen.
— Det finns i relaterad mening ingen kraftaspekt i den bilden: den är uppenbarligen rent kinematisk (»rörelsefysikalisk»: ingen kraftaspekt [kinetik] ingår).
Summering CoriolisFoucault —
min mening
VANFÖRESTÄLLNINGARNA i MAC i ämnet Foucaults Pendel med associationer till CoriolisKRAFT är närmast oerhörda, sett i mitt eget omdöme efter genomgången granskning av tillgängligt webbmaterial -Okt2012; mängden »vetenskapsfolk» verkar närmast komiskt överrepresenterad med tydliga, väl jämförbara exempel som framhäver något som närmast liknar en efterhärmande flod av (de mest skickliga författarnas påstådda) FoucaultPendel-CoriolisKRAFT-kopplingar med tillhörande avhandlingar och som, just, kan bemötas — förklaras, redas ut, och presenteras i begriplig — relaterbar mening. Det är det oerhörda i sammanhanget: att den delen inte har uppmärksammats.
Vi studerar det mera i djupdetalj;
FoucaultFigurerna
visar — exakt — hur »CoriolisKorrumperad» MAC är:
Principen för
Foucaults Pendel
RÖRELSEPROJEKTIONER — Kinematiska projektioner mellan skilda
rörelsesystem (KIPEMSIR)
MOTIONAL PROJECTIONS — Kinematic projections between
different motional systems (KIPBEDMISE)
PolärfunktionenFocaulltPendeln — BILDKÄLLA:
Författarens arkiv · 11Sep2012 E27 Bild2 · Nikon D90 · Detalj

Kort
sagt: Modern akademi kan i relaterad mening förstås ersätter Kinematiska
RotationsAnalogier med »CoriolisKRAFT» på kredit av den moderna akademins VektorKalkyl, med förgreningar till
Foucaults Pendel. Det tilltaget skapar enorma beskrivningsfel i relaterbarheten
mellan Modern Akademi och Naturfenomenet; Naturfenomenet (följaktligen) undandrar sig
förklarbarhet i termer av den moderna akademins lärosystem. Det är (milt sagt)
genomkorrumperat. Följande försöker ta fatt på de fladdrande lösändarna och ge
en sammanhängande beskrivning/förklaring, i detalj.
Detaljstudie
av FoucaultFigurernas Matematik — i MAC »CoriolisKRAFT» —
ENLIGT
RELATERAD FYSIK OCH MATEMATIK
Polärfunktionen i PREFIXxSIN
r=sin nx
MAC-CoriolisSyndromets Absoluta Kärna: FoucaultFigurerna
i Kinematiska RörelseAnalogierna
—————————————————————————————————
PoläraKoordinater PREFIXxSIN:
Kinematiska Friktionslösa Parabelanalogin visar att den friktionslösa pucken i MIT-experimentet roterar 2 varv på parabolens enda; Den rörelsen har (idealt med alla friktionsförluster fråntagna), uppenbarligen, samma matematiska form som polärfunktionen i PREFIXxSIN r=sin nx; n=1 ger r=sin x som avbildar just MIT-experimentets detaljer (den röda högercirkeln nedan i Figurdel BD);
rP = sin nx ;
n = (fP/fJ)(1/2) ;
fP Pendelns totala svängningsfrekvens (01234, se figurdel C
nedan)
fJ Den roterande kroppens omloppsperiod (ofta Jorden i
experimentsammanhang)
rP = sin (fP/fJ)(1/2)x
; Polärfunktionen för FocaulPendelFigurerna
För MIT-exemplet
med den friktionslösa pucken (P) har man
fP=2, fJ=1 ;
rP = sin x ;
Koniska Pendeln, härledning,
figurdel A nedan:
å/a = R/h = (v2/R)/a = ([2πR/tP]2/R)/a = [2πR/tP]2/Ra = ([2π]2R2/tP2Ra = ([2π]2R/tP2a ;
h = tP2a/[2π]2 ;
h/a = (tP/[2π])2 ;
tP =
2π√h/a ; Koniska Pendelns Ekvation, h = KonHöjden, a = lokala tyngdkraftsacc.
FoucaultPendelnsMatematik — Kinematiska Friktionslösa Koniska Pendelns
Kinematik VISUALISERAD PÅ EN ROTERANDE KROPP: Foucaults Pendel — PolärfunktionenFocaulltPendeln
|
|
|
|
|
|
Koniska Pendeln |
Kinematiska
Friktionslösa ParabelAnalogin — MIT-exemplet |
Plana Pendeln (lKP→h) |
PolärMatematiskaFunktionen r=sin nx |
(B): Vi kan följa
pendelrörelsen från 0 till 1 som den ses från den roterande kroppen under, och
per lika rotationsvinkelintervall, genom skärningen mellan varje
vinkelintervall och cirkeln; de lika vinkelintervallen utpekar motsvarande lika
bågintervall på cirkeln, vilket visar att cirlkelrörelsens periferihastighet
också är konstant.
Hur
FoucaultFigurerna framkommer ur PendelAnalysen:
Om plana pendelns vinkelutslag är litet (lKP→h) blir skillnaden försumbar mellan koniska pendelns höjd (h) och dess mantellängd (lKP). Då kan det helt idealiserade sambandet för plana pendelns period användas (substitueras) med pendellängden hKP analogt med koniska pendelperioden så att man har (Foucaults Pendel)
Foucaults Pendel, sambandet
från Koniska Pendelns
Ekvation
tP =
2π√hKP/a ; Plana Pendelns Ekvation, h[KP] =
PendelLängden, a = lokala tyngdkraftsacc.
Det är samma pendelekvation som används i det idealiserade experimentfallet med Foucaults Pendel. Förutsatt pendelutslaget är litet (massiv pendelkula på lång pendel med försumbar massa) kan en motsvarande FoucaultPendel användas för att (med växande noggrannhet, med växande precision i anordningen) bestämma t.ex. den lokala tyngdkraftsaccelerationen enligt
a = hKP(2π/tP)2
= hKPωP2 ; Lokala
accelerationskonstanten via en Foucaults Pendel
Man bestämmer
pendelperioden genom att ta tid på ett antal svängningar via en absolut minsta
möjliga utsläppsvinkel.
FoucaultFigurerna — FoucaultPendelnsMatematik
![]()
Genom att Koniska Pendelns sinusprojektion (i denna framställning i PREFIXxSIN)
(cirkelrörelsen projicerad på cirkeldiametern, projektionen sedan tagen eller substituerad som en helt exakt ideal Foucaults Pendel, samma som den friktionslösa puckens ideala rörelse i MIT-exemplet)
tagen i polära koordinater (r=sinnx) visar Kinematiska Friktionslösa Koniska Pendelns Kinematik VISUALISERAD PÅ EN ROTERANDE KROPP [FoucaultPendelnsMatematik, Figurdel D],
SINUS i PREFIXxSIN för Pendelpunktens Rotationsvinkel (sin nx)
(x i radianer, markerat med motsvarande punkter i intervall om 1 grad i [FoucaultPendelnsMatematik, Figurdel D])
utpekar radielängden (r) i PolärFormen r=sin nx;
— Illustrationsexemplet [FoucaultPendelnsMatematik, Figurdel D] visar MIT-experimentets friktionslösa puckrörelse visuellt från en fast position på den roterande parabolen (s6.Figure 4);
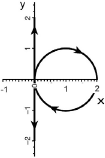
Cirkeln är samma som den mindre prickade cirkeln inuti den större i [FoucaultPendelnsMatematik, Figurdel D]. Sambandsformen är också densamma i MIT-exemplet och anges av denna (s6ö) på formen i PREFIXxCOS enligt
υrot (t)
= υ0 cos 2Ωt ; MIT-källans uttryck för den cirkulära
puckrörelsen
Men MIT-källan ger ingen
ytterligare beskrivning.
sammanställs, tydligen, de BÄGGE inbördes kinematiskt skilda visuella rörelsebilderna till EN enda trigonometriskt sammansatt form:
r = sin nx = sin (fP/fJ)(1/2)x
; Koefficienten (1/2) ger cirkeln med f[P] som dubbla f[J]
Ökas pendelfrekvensen (fP) från cirkelns 2 till 4, 6, 8, … , 50, … osv, med bibehållen kroppsrotationsfrekvens fJ=1, så att man får motsvarande r=sin{1;2;3;4;…;25;…}x, får man motsvarande FoucaultPendelKurvor sedda från den roterande kroppen (J) enligt figurerna nedan (fJ=1) i PREFIXxSIN;
fJ = 1: FoucaultFigurer
som ses på den roterande kroppen för olika FoucaultPendelFrekvenser

Med successionen av
FoucaultFigurer för växande frekvenstal kan vi direkt utläsa (och testa) de
inre sambandsformerna:
Andra webbkällor som (mer eller mindre) visar motsvarande —
Några av sökresultaten [2012-10-23] från
»FOUCAULT PENDULUM ARC TRAJECTORY filetype:pdf»:
http://ocw.nctu.edu.tw/course/calculusofvariation/foucault_pendulum/foucault_pendulum.pdf
APPLICATIONS: Foucault Pendulum
![]()

Källan härleder/visar
sambandsformen (FoucaultFigurerna) r = sin nx (konv. cos i PREFIXxCOS).
— Termen Coriolis ingår
inte,
;
http://www.kip.uni-heidelberg.de/image/f/oeffwiss/pendel/FKPTra.pdf
THE FOUCAULT PENDULUM’S TRAJECTORY - THE FORMALISM, J. Stiewe,
KIP, April 2008
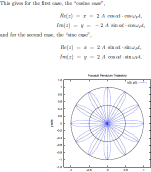
Källan härleder/visar
sambandsformen (FoucaultFigurerna) r = sin nx (konv. cos i PREFIXxCOS).
— Termen Coriolis ingår,
”There are two forces acting upon the pendulum:
Gravity and Coriolis force.”.
;
I övrigt: ytterst
tunnsått.
Wikipedia
kompletterar sin Foucault-artikel med att hänvisa till ”Rose (mathematics)”,
alltså rosettbanan:
http://en.wikipedia.org/wiki/Rose_curve
@INTERNET Wikipedia — Rose (mathematics) [2012-10-24]
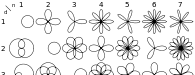
”Up to similarity, these
curves can all be expressed by a polar equation of the form
r = cos(kθ).”.
”See also Foucault
pendulum - which traces a rose curve as viewed from above.”.
Källan visar
sambandsformen (FoucaultFigurerna) r = sin nx (konv. cos i PREFIXxCOS), samt ger en mera
uttömmande formbeskrivning i de olika talresonansfallen.
— Termen Coriolis ingår
inte.
;
http://jmp.aip.org/resource/1/jmapaq/v51/i8/p082703_s1?view=fulltext&bypassSSO=1
FOUCAULT PENDULUM AND SUB-RIEMANNIAN GEOMETRY, Meneses et al.,
2009
Källan visar
2D-FoucaultPendelFigurer (Fig 9), men i en inte enkelt uttydbar mening
(RiemannSpace, inte direkt vårt bord) — inget direkt utläsbart matematiskt
samband finns att citera (ytterst kryptisk matematikkälla).
FoucaultFigurerna,
Parametrar [FoucaultPendelnsMatematik]
![]()
Varje par cirkeltangentställen [2 ggr ett blads ytterdel (012 FigBCD)] = 1/2 period;
— Udda bladantal [13579] kopplar en hel period asymmetriskt: hela bladfiguren måste genomgås TVÅ
gånger [=symmetriskt] för att nå utgångspunkten;
— Jämför r=sin3x; ta 1:a perioden (01234)[FigB&C]; Vi hamnar på en punkt längst
upp; Nästa halvperiod till utgångspunkten — med det återstår ännu en halv
period som tar oss till nedre bladpunkten; resterande period (01234) fullbordar
symmetrin till utgångspunkten: summa TVÅ genomgångar.
— STEGVINKELN [S°] per P/4 (polärvinkeln från 0 till 1 i pendelperioden 01234, FigBCD)
är monotont och entydigt avtagande med växande fP;
S° = 180/fP ;
Eftersom varje udda (13579) frekvenstal ger en
asymmetrisk vinkelperiodrest på 0,5 — ofullbordat varv:
— Varje udda frekvenstal (13579) medför en
FoucaultPendelFigur som kräver 2 genomgångar på ett f(J)-varv.
fJ=1; fP vid L°=90 Jordens Nordpol idealt
|
fP/2 |
fP |
nPper
fJ |
nBlad |
f(Blad) |
P/4vinkel |
TOTantalP/4perTJ |
360/(P/4) |
nPiFoucaultFig |
f(Blad) |
|
1 |
2 |
2 |
1 |
2=2/1 |
90 |
2×4=8 |
4 |
1 |
2 |
|
2 |
4 |
4 |
4 |
1=4/4 |
45 |
4×4=16 |
8 |
2 |
1 |
|
3 |
6 |
6 |
3 |
2=6/3 |
30 |
6×4=24 |
12 |
3 |
2 |
|
4 |
8 |
8 |
8 |
1=8/8 |
22,5 |
8×4=32 |
16 |
4 |
1 |
360 Grader
——————— = antalet P/4 genomgångar = 360/(P/4)
GradVinkeln för P/4
————————— = Antal P i FoucaultFiguren = nPiFoucaultFig
4

— BLADANTALET DÄREMOT växlar mellan udda (13579) och jämna
(02468) fP/2:
fP/2 mod 2 = 0 om fP är jämnt (02468) ;
fP/2 mod 2 = 1 om fP är udda (13579) ;
n = BLADANTALET = (fP/2)(2–[(fP/2)mod2]) ;
— BladSeparationsVinkeln [B°] (vinkeln mellan två
närliggande bladändar);
B° = 360/n = 720°[fP(2–[(fP/2)mod2])]–1 ;
— Diametrala Vinkeldifferensen [D°=180–(P/2)°] mellan
ändarna i en halv period 012 FigBC;
Också denna är strängt monotont avtagande för växande fP; ;
— FoucaultFiguren om fP är mindre än 1 — här fP=0,1 kräver 20 ritade varv för
att återkomma;
— Figurerna nedan visar resultatet efter 5, 10, 20 ritade
varv:
sin[x([0.1/1][1/2])] Unit500p förminskat
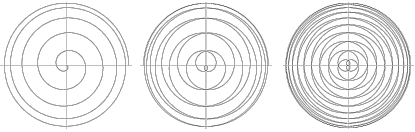
r = sin 0,05 i PREFIXxSIN;
fP = 0,1; Unit500p, förminskat och konturförstärkt
— Tiden för pendelns plan att vrida sig ett
varv:
— Är FoucaultPendeln kopplad till olika latitudella
(skivorna mellan SydNord) lokaler på Jordytan, försvinner den kinematiska a-kopplingen [tyngdkraftsaccelerationens
komponent] (FigurdelAovan)
[FigulrdelBnedan] i pendelkopplingen
till Jordaxelrotation med latitudvinkeln (L°), analogt pendelplanets lutning
kommer alltmer i rät vinkel mot rotationsaxeln vilket inträffar vid ekvatorn,
och därmed nollbild:
— Om man direkt via Plana Pendeln försöker härleda FoucaultPendelns uppförande då den
lutas relativt den jämförande rotationskroppens rotationsaxel — som i
fallet med de olika latituderna på Jordytan — hamnar man i trubbel; Däremot om
man tar det från ursprunget, Koniska pendeln, går det lättare:
FoucaultPendeln, beteende vid avtagande latitudvinkel — framställningssättet nedan har
eftersökts på webben Okt2012 med liknande men ännu inte påträffats — kopplingen
KoniskaPendeln-PlanaPendeln omskrivs knappt
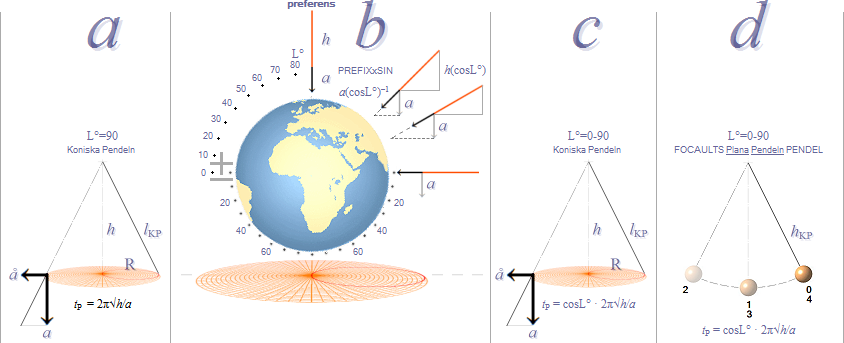
(b):
För att bevara enhetligheten i KoniskaPendelns (a) Projektion på
omloppscirkelns diameter
— och därmed analogin till PlanaPendeln
(d)
— då KonPendelplanet lutas (b) ur
latitudvinkeln L°=90, och som
ger en förkortad h-längd h’=hcosL° i parallell med den jämförande
rotationskroppens rotationsaxel (Jordaxeln), måste en motsvarande
(fiktiv, kinematisk/trigonometrisk) förlängning av a-vektorn göras för
att matcha den resulterande, verkliga, a-formen i KonPendelPreferensen vid
Nordpolen (L°=90) som bevarar
och garanterar ursprungspreferensen med förhållandet å/a=R/h vid L°=90.
— I annat fall bevaras inte
periodpreferensens ursprungliga proportioner (relationen till den aktuella
jämförande rotationskroppens rotationsaxel): tP-preferensen vid L=90°. Ändras den
preferensen, spricker hela praktiken (pendeln urartar). Kinematiska Nettoverkan
blir att tP avtar med växande lutning (h förkortas relativt rotationsaxelns utsträckning:
fP ökar, tP avtar).
— Totalt betyder det en justering i
rottermen med h(cosL)/[a/(cosL)]=cos²L(h/a).
FoucaultLatEkv — FoucaultLATITUD
Slutformen därmed i PREFIXxSIN
tP =
cosL·2π√h/a ; Koniska Pendelns LatitudEkvation, h = KonHöjden, a = lokala tyngdkraftsacc.
= cosL
· (tP = 1/fP) = 1/fP
; fP = fP/cosL ; (tP|fP)ORIGINAL,
(tP|fP)LATITUDPROJICERADE
tP =
cosL·2π√hKP/a ; Plana Pendelns
LatitudEkvation, h[KP] = PendelLängden
L anger latitudvinkeln, figurdel b ovan. Med
generaliseringen h(KP)=h för små utslagsvinklar gäller tydligen:
tP =
cosL·2π√h/a ; FoucaultPendelns Fullständiga LatitudPeriodEkvation, h = PendelLängden
= cosL
· tP
Genom att tP förkortas då L→0 ges motsvarande förkortning i pendelplanets vridningsutslag
(första halvperioden 012
Figurdel BC)
D° = 360°/fP = 360°tP = 360° cosL · tP ; PREFIXxSIN
Eftersom endast trigonometriska (kinematiska) förkortningen
räknas [D°],
inte perioden i den fasta anordningens tP, kommer pendelplanets vridning att
avta i motsvarande mening enligt
D°/tP = 360° cosL = 2π/tL = ωL ;
ωLATITUD = 360° cos L° ; FoucaultPendelPLANETS
Fullständiga LatitudPeriod
Jämför
samma typ i PREFIXxCOS i MAC i SydneyKällan ω = Ω sin λ och i WikipediaKällan ω = 360 sin φ° /day, men på helt annan teoretisk grund.
Notera att
lutningseffekten är rent projektiv — kinematisk: ingen kinetik ingår i
FoucaultFigurernas Matematik — men det är just vad som hävdas i MAC:
”At the latitude of Paris a full
precession cycle takes 32 hours, so after one sidereal day, when the Earth is
back in the same orientation as one sidereal day before, the oscillation plane
has turned 90 degrees. If the plane of swing was north-south at the outset, it
is east-west one sidereal day later.”;
”This implies that there has been exchange of momentum;
the Earth and the pendulum bob have exchanged momentum.”,
http://en.wikipedia.org/wiki/Foucault_pendulum
@INTERNET Wikipedia —
Foucault pendulum, Precession as a form of parallel transport [2012-10-23]
Det är i storleksordningen värre än år 1311. Min mening.
— ExperimentPendelns
egenperiod är exakt densamma för alla lokaler på Jordytan:
— tP ändras inte i FoucaultPendeln som
sådan. Det är endast UTSLAGET (Kinematiska Projektionen — vridningen mellan
Pendel och Rotationskropp) som ändras;
D° = 2S° = 180/(fP/2) = 360°/fP ; L=90° ; fP = fP
= 360°/(fP/cosL) = cosL· 360°/fP ; L=0-90° ; fP = fP/cosL
EXEMPEL
i PREFIXxSIN:
—
Vid Nordpolen med fP=8, FoucaultFiguren ovan, och funktionen r=sin 4x är
D°=360/8=45;
—
Vid L°=30 fortfarande med samma experimentpendelkonstruktion är
D°=cos(30)·45=(1/2)45=22,5;
—
Det är alldeles precis samma D-värde som vid Nordpolen med dubbla fP=16 som ger
D°=360/16=22,5;
—
Utslaget blir exakt detsamma.
— Latitudändringarna i FoucaultPendelns
planvridning (D°
för första halvperioden 012
figuren ovan) har inget med kinetik att göra: Ämnet beskriver tydligen
rena kinematiska — trigonometriska — projektioner. Det finns uppenbarligen
ingen kraftbild att räkna på.
— D° reduceras: Flera svängningar med
samma tP
krävs för att fullborda hela varvet.
— Det har uppenbarligen ingenting med
kinetik att göra. Det är ren kinematik: elementär trigonometri.
— Om vi för exemplets ytterligare tydlighet formjämför
»FoucaultFigurVingarna» fP(L°=90)={4,6,8,10} för första kvartsperioden
(01)
![]()
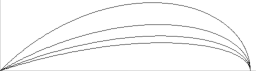
i en PREFIXxSIN cosinus-0,5-projektion
![]()
med motsvarande fP(L°=90)={8,12,16,20} »= fP(L°=30)={4,6,8,10}»
![]()
![]()
ser vi också direkt
![]()
att skillnaden är knappt märkbar; Enbart den enkla
BildProjektionen visar principen: ren trigonometrisk kinematik.
— Det finns ingen möjlighet att missa sammanhanget;
— FoucaultPendelVridningen med avtagande latitudvinkel
(L°→0) har ingenting att göra med någon kinetisk koppling typ »momentöverföring» eller annat, utan beror på att pendeln tappar allt mer av sin
BILD på rotationskroppens rotationsplan då pendelns svängningsplan alltmer
sammanförs med rotationsplanet. Det finns ingen kraftaspekt med i händelsebilden.
— TÄNK att de här
1300-talsmänniskorna inte kan se BILDEN — själva BION — i hela förloppet:
Foucaultpendelplanet som VRIDER SIG är en ren kinematisk — bio — effekt. Inget
annat.
— TÄNK vad underbart om
jag hade FEL. Visa.
Webben har genomsökts [23Okt2012] på
källor som beskriver härledningssättet ovan, men ännu utan resultat. Däremot
finns flera (många [alla]) etablerade källor som härleder samma slutform enbart
på den plana pendelns utgångsform, men då via ytterst omständliga matematiska
utvikningar — med inblandning
dessutom av ”Coriolis force” GoogleUtdragOkt2012 som Bas för FoucaultPendelPlanets vridning
— med den sedvanliga MAC-vektorkalkylens
begrepp. Se t.ex. den utförliga Sydneykällan
http://www.animations.physics.unsw.edu.au/jw/foucault_pendulum.html
UNSW
School of Physics, Sydney — THE FOUCAULT PENDULUM (2005)
— Källan diskuterar FoucaultPendeln
(mera än andra) i detalj;
— Källan innehåller fina
FoucaultAnimeringar med korta video-gif-sekvenser som visar en praktisk
anordning;
— Innefattar länk till en omfattande
FoucaultMatematik (MAC-vektorkalkyl),
samma slutresultat som ovan (men på betydligt flera parametrar med rikare
tolkning); (svårtolkad —
utom för redan insatta: latitudvinkeln [källan använder beteckningen λ]
omnämns knappt, men ingår i beskrivningen).
—
Ingenting omnämns som, direkt, ansluter till ovanstående enklare härledning.
Källan skriver i slutet av den omfattande genomgången [Ω = ”the angular
velocity of the earth Ω”]:
”With Ω not equal to
0 and at latitude λ not equal to 0, the complex vector ζs
rotates (in the frame of the earth) with angular frequency − Ω sin
λ,
i.e. with a period 2π/(Ω sin λ) = Tearth/(sin λ) where
Tearth is the period of rotation of the earth”,
http://www.animations.physics.unsw.edu.au/jw/pendulumdetails.html
UNSW School of Physics,
Sydney — THE FOUCAULT PENDULUM - THE PHYSICS (AND MATHS) INVOLVED (2005)
— Det verkar generellt som att
författarna i ämnet (alla) utgår från Plana Pendeln och inte alls — som
man kunde tro — från Koniska Pendeln som källformen. Att försöka härleda
ovanstående enbart på Plana Pendelns geometri, blir (då, likasom) att försöka
härleda äppelträdet från äpplet (i princip omöjligt), istället för det
naturliga: äpplet från trädet (kort och gott).
— Vi
vet nu också att sambandsformen stämmer med ovanstående källas försäkran:
”With respect to the earth, the period
of precession of the pendulum is 23.9
hours divided by the sine of the latitude. For most latitudes, this is
considerably longer than a day. So, after the earth has turned once, the
pendulum has not returned to its original plane with respect to the earth. For
example, our pendulum in Sydney
precesses at a rate of one degree every seven minutes, or one complete circle
in 43 hours.”
;
—
Sydneys latitud är 33.8683° S (Direkt
från GoogleSearch, Sydney Latitude); Jordens sideriska omloppstid är
23tim56min4sek=86164 S, eller
24×(86164
S)/(86400 S= 24tim)=23,934444;
23,9/cos(33,8683°PREFIXxSIN)=42,94824tim. vilket
vi ser stämmer tämligen exakt.
—
Sambandsformen bör därmed vara väl praktiskt etablerad.
;
FoucaultPendeln motsvarar i relaterad mening
uppenbarligen (mycket nära) en tillståndets fysikreferens — men som modern
akademi tydligen inte kan relatera, läs: »inte kan begripliggöra för
vardagsmänniskan»:
Exempel:
”To understand the Foucault pendulum geometrically, we consider an inertial frame outside of Earth”,
s888sp2n
http://fismat.uia.mx/if/foucault/internal/AJP/foucault/AJP000888.pdf
FOUCAULT
PENDULUM THROUGH BASIC GEOMETRY, Bergmann et al., 2006
Förtydligande, eng.:
— The frame is here: state. But for a STATE, modern academy has no related expression, although Newton had. See INERTIAL SYSTEM — Newton’s famous experiment with the rotating vessel and for which modern academy erroneously credited Newton to have invented or introduced ”absolute space” (Einstein, Quote7), however already a rejected concept by Newton himself as explicitly written i Principia, see Quote from Newton: the term ”absolute space” is, obviously, a modern academic invention, no Newton idea; Newton’s concept is ”the true and absolute circular motion of the water” — unless already familiar; Not an object in space, not a physical system, but any idea of an equilibrium, a balance — a state; an instrumentally readable value.
— A pendulum (its plane of swing) features (almost perfectly) such a state reference (small [negligible] energy losses [for the purpose]). But it is not recognized as such in the modern academy teaching system:
— MAC insists
[Albert Einstein, Leopold Infeld, Fysikens Utveckling, Natur och Kultur 1938 s178, ”Men allt detta låter misstänkt. Är det tillåtet att betrakta rörelse hos en enda kropp i hela universum? Med en kropps rörelse mena vi alltid dess lägeändring i förhållande till en annan kropp. Det strider sålunda mot sunda förnuftet att tala om en enda kropps rörelse.”] (compare rotation; Newton’s famous experiment)
on that the state-reference MUST be understood as a physical object, an ”inertial frame” IN SPACE — although everybody knows without exception that such a frame IN SPACE does not exist in our universe: physics IS variation; there are no ”inertial systems” in physics; The reference in related physics is state — equilibrium [FUNTOP].
”The gyroscope's spinning rotor tracks the stars directly.”,
http://en.wikipedia.org/wiki/Foucault_pendulum
@INTERNET
Wikipedia — Foucault pendulum, Explanation of Mechanics [2012-10-23]
Compare related physics:
»The gyroscope's spinning rotor tracks the universal physical orientational state from where the rotor was given its spin directly.».
I LJUSET AV GENOMGÅNGEN OVAN är det tydligt att SCIAM-författaren för ett, visst (men omedvetet), självbedrägligt resonemang utifrån uppenbart felaktigt [INERTIALSYSTEM] — den moderna akademins lärosystem i arv — uppfattade premisser, och som tydligen blandas ihop utan urskillning, och vilka skilda detaljer berör kinetiken (rörelsen MED kraftverkan inbegripet) och kinematiken (rörelsen utan hänsyn till de verkande krafterna).
— CoriolisKRAFTEN har, som genomgången visat, ingenting med den typen att göra.
Det är uppenbarligen också FELET i hela
den moderna akademins framställningar med påståenden att FoucaultFigurerna
skulle ha något med KRAFT — kinetik, »momentöverföringar»
— att göra:
— CoriolisVERKAN i MAC ersätter — tydligen — Kinematiska
RotationsAnalogierna på den kända formen från (den centralt
förklarande) Kinematiska Friktionslösa
ParabelAnalogin:
aCoriolisMAC =
–2ω×vr = vr×2ω ............. har inte ett spår med CoriolisKRAFT att
göra, vektorfiguren
Men hela webben är också (propp) full av liknande beskrivande avhandlingar [WebCoriolisVideoDemos]:
— En (stor) mängd modernt akademiskt skolade bidrag finns på webben (Sep2012) som försöker ”förklara” för en allt (växande) mera förvånad (och förvirrad) publik vad författarna ändå, tydligen, misslyckas med (att, bl.a., beskriva CoriolisEffekten):
— Beskrivningssätten misslyckas (helt) därför att man
1. DELS söker »övertyga läsaren» om att verkligt upplevda sensationer — krafter — är något OVERKLIGT (”fictitious”, ”skenbara”, ”fiktiva”),
”What is a "fictitious force"?
California Institute of Technology theoretical physicist and 2004 Nobel laureate David Politzer helps shed some light on these mysterious influences.
The forces you feel in a moving car—those that push you back into your seat when the driver steps on the gas or throw you side to side when the car makes sharp turns—are everyday examples of fictitious forces. In general, these influences arise for no reason other than that the natural frame of reference for a given situation is itself accelerating.”,
http://www.scientificamerican.com/article.cfm?id=what-is-a-fictitious-force
SCIENTIFIC
AMERICAN Ask the Experts — What is a "fictitious force"? —
July 9, 2007
— I ljuset av resultatbilden från genomgången ovan SKULLE
det betyda — OM man genomförde SERIÖS statistik — att situationen EFTER
inlägget är VÄRRE ÄN FÖRE.
och
2. DELS som i ovanstående genomgångna SCIAM-exempel söker
hänföra/förklara visuella, kinematiska
— icke-kraftbaserade
— händelsefenomen av och via krafter, vilket uppenbarligen är ännu mera övertydligt absurt;
— Det, om möjligt, uppväcker — vad man kan förstå — en ännu mera spontan AVSKY för (eller kanske Ironiserande Underhållning från) det s.k. modernt akademiska expertbaserade naturvetenskapliga beskrivningssättet.
SCIAM-författaren påstår, initiellt — och uppenbarligen direkt felaktigt — att FoucaultPendelFenomenet skulle ha CoriolisKRAFTEN som orsaksgrund:
”the fictitious Coriolis force, which is responsible for the stately precession (or circular rotation) of a carefully suspended pendulum's plane of swing”
tillika med en STOR [‡] mängd andra i MAC-leden.
— Låt oss då gå på din linje med ”uppenbarligen direkt felaktigt”: Vad skulle det medföra?
— Ingenting annat än att ditt ljushuvud har möjlighet att börja skina, så som det var tänkt från Naturens sida:
Typiska examineringstexter (Universitet) skriver i samband med matematiska härledningar till Pendelrörelsen:
”There are two forces acting upon the pendulum: Gravity and Coriolis force.”,
http://www.kip.uni-heidelberg.de/image/f/oeffwiss/pendel/FKPTra.pdf
THE
FOUCAULT PENDULUM’S TRAJECTORY - THE FORMALISM, J. Stiewe, KIP, April 2008
Jämför
korrekt sakformulering i relaterad fysik, omskrivet:
»There
are two FACTORS acting
upon the pendulum: Gravity and Kinematic
Rotational Aberration (KRA) [Kinematiska
Friktionslösa ParabelAnalogin], the
latter often misused and misunderstood in modern academy as »Coriolis force»,
where the KRA-term is not recognized»; same math 1,
same math 2.
— Exemplet med CoriolisBERCIU [Hur MAC associerar Coriolis med Kinematiska] visar HUR man i MAC får ihop det med »Coriolismatematiken» som substitut för Kinematiska RotationsAvvikelsen; samma matematik, men MAC kan inte relatera tillståndets fysik [CentralverkanMAC], och tvingas därför »uppfinna» — som det får tolkas — att det skulle vara »Corioliseffekten» (Kinematiska RotationsAvvikelsen som MAC inte kan relatera) som ingår i de matematiska leden.
— UniversitetsFRASEN är en förklädnad.
— Det är, tydligen, inte matematiken det hänger på.
— CORIOLISSATSERNA — som på det allra enklaste följer direkt av Gaspard Coriolis två Coriolisteorem (enligt Persson 1998) eliminerar helt säkert bortom varje form av tvivel, i minutiöst noggrant relaterbar mening [CoriolisBASIC], varje friktionslös anordnings SÄTT att koppla Coriolisverkan:
Corioliseffekten kopplar inte
friktionslösa rörelsesystem, typ Foucaults Pendel, Visuella
Relationsbilder (CINEMA), o.dyl. Det finns, vad vi vet, ingenting
sådant i den relaterbara, fullständigt förklarbara, fysiken.
— Det finns flera jämförande studieexempel som visar HUR man i modern akademi blandar ihop begreppen. Det »kaninhålet» sträcker sig ända ut till den moderna akademins antagna regelverk för vektorprodukt: se från Kinematiska Friktionslösa Parabelanalogin och Hur MAC associerar Coriolis med Kinematiska. Dessa formar (tydligen) ett helt tema i denna presentation, och kopplingen till det temat refereras också frekvent i framställningen tillsammans med jämförande beskrivningar, citat och exempel där så är möjligt.
— Svaret på frågan — mera reguljärt (’Vad skulle det medföra?’) — blir således: Bara ett ytterligare klargörande av att modern akademi inte besitter de begreppsliga verktygen som tydligen krävs för att förklara naturfenomenet; Man verkar istället, tydligen, trivas bäst i det vokabulär där naturgrunderna vandaliseras, vrängs, vantolkas och körs över: upprepat (Man stannar, lägger i backen, och backar över).
GoogleUtdragOkt2012 »Coriolis force, responsible for precession pendulum», ”About 621,000 results (0.41 seconds) ”:
”The Foucault Pendulum was conceived by Léon Foucault in the middle of the 19th century, with the goal of proving Earth's rotation through the effect of the Coriolis Force.”,
http://www.sciencebits.com/foucault
THE
FOUCAULT PENDULUM, 2006
”Foucault pendulum A Foucault pendulum, or Foucault's pendulum, named after the French physicist Leon Foucault, was conceived as an experiment to demonstrate the rotation of the Earth; its action is a result of the Coriolis effect.”,
http://www.sciencedaily.com/articles/f/foucault_pendulum.htm
ScienceDAILY
— Science Reference, 1995-2012
”Coriolis effect The Coriolis effect caused by the rotation of the Earth is responsible for the precession of a Foucault pendulum and for the direction of rotation of cyclones.”,
http://www.sciencedaily.com/articles/c/coriolis_effect.htm
ScienceDAILY — Science Reference, 1995-2012
”A Foucault pendulum, or Foucault's pendulum, named after the French physicist Léon Foucault, was conceived as an experiment to demonstrate the rotation of the Earth; its action is a result of the Coriolis effect.”,
https://sites.google.com/site/geokerk/foucaultpendulum
FOUCAULT
PENDULUM — FROM WIKIPEDIA, THE FREE ENCYCLOPEDIA
”From the perspective of an Earth-bound coordinate system with its x-axis pointing east and its y-axis pointing north, the precession of the pendulum is described by the Coriolis force.”,
http://en.wikipedia.org/wiki/Foucault_pendulum
@INTERNET Wikipedia — Foucault pendulum [2012-10-19]
…
EinsteinsAllmännaRelativitetsprincip — BILDKÄLLA:
Författarens arkiv · 13Sep2012 E29 Bild142 · Nikon D90 · Detalj

Einsteins Allmänna Relativitetsprincip
”Skulle verkligen de fysikaliska lagarnas oberoende av koordinatsystemets rörelsetillstånd endast gälla för koordinatsystem med ömsesidig likformig translationsrörelse? Vad har naturen att skaffa med de av oss införda koordinatsystemen och deras rörelser? Om också naturbeskrivningen fordrar ett av oss godtyckligt infört koordinatsystem, så borde likväl valet av dess rörelsetillstånd ej vara underkastat någon inskränkning. Lagarna borde vara fullkomligt oberoende av detta val (den allmänna relativitetsprincipen).”,
MIN VÄRLDSBILD Albert Einstein s175 · Bonniers
1934 [Citat:14]
”Lagarna borde vara fullkomligt oberoende av detta val”;
— De är redan det, Albert. Se INERTIALSYSTEM.
MAC kräver — generellt — en
visuell (kinematisk) omvändning i fysikbegreppet, enbart för att matcha upp Einsteins
formulerade allmänna relativitetsprincip; den förutan kollapsar den moderna akademins allmänna
fysikuppfattning.
—
Bilen accelererar i förhållande till vägen, precis som vi SER det — oberoende
av om vi åker med eller står vid sidan av och ser på; bilen som referenssystem
kan därför inte förstås som ett icke accelererande referenssystem — Men MAC
hävdar just det, se citatet i FOCUS MATERIEN 1975 [FMaccVila].
MAC VILL INTE SE ATT fysiken bygger på
urgamla eviga principer a=[d(v=∞)GRAVITATIONEN/dT=([v=∞]/∞)/dT=cLJUSET/dT]
[DIFFERENS OCH
DIFFERENTIAL] [ELEKTRISKA LADDNINGEN]
Genom
gravitationens absolutverkan (konvergenskraften) är det bara kropparnas motstånd (inertie) mot rörelseändring (kraftlagen
F=ma) som hindrar dem att omgående, omedelbart, störta ihop.
— Det
är (tydligen) denna egenskap av »omedelbar sammandragning» [KONVERGENSKRAFT]
som utmärker just gravitationen, och som därmed blir sak samma som definitionen
för massa: massa är gravitation,
och gravitation är massa [Atomkärnans
g-härledning i TNED].
—
Genom energilagen (energin är oskapad, utan upphov, kan inte skapas, kan
inte förintas) garanteras massans motsvarande ekvivalenta ursprung: oskapad, utan upphov, kan inte skapas.
I MAC finns inte den
utgångspunkten. (Se speciellt från ENTROPIBEGREPPET I MAC).
— Massans
fundamentalform — likt en vattendroppe [STRANDVÅGORS STENBRYTNING] som kan uppdelas i mindre droppar och återförenas till en
droppe utan att de föregående fristående dropparna fördenskull finns till
som fristående individer inuti den större — är i TNED atomkärnan enligt Plancks konstant (h=mcr) eller PLANCKRINGEN (neutronen i TNED).
— I MAC (där man just ser
atomkärnan som en summa av delpartiklar) tvingas man följaktligen uppfinna
extrakrafter (konv. stark växelverkan) som håller ihop atomkärnan (närliggande
fristående protonindivider med laddningen +e), medan något sådant inte
existerar i TNED.
— Den
massformen, atomkärnan, härleds i TNED som ett oändligt fraktalt system av ihåliga
laddning-massa (±e) toroidPlanckringar [PLANCKRINGEN]
[PLANCKS STRUKTURKONSTANT] [NEUTRINOSPEKTRUM]; som fraktalnivåerna växer obegränsat, går också
atomkärnans massform alltmer mot YTA; med obegränsat fraktaldjup framstår
atomkärnans YTA (oändligt tunn) som OÄNDLIGT TÄT [Atomkärnans inkompressibilitet], och därmed gravitationens verkande kraftform (urspr. i
TNED från Potentialbarriären), med resten av fysiken.
— K-cellens värmefysik förklarar genom Allmänna Tillståndslagen HUR universum (K-cellen)
återbildas periodiskt, och varför ämnet [c0-kroppen]
står orepresenterat i MAC:
GcQ-teoremet — not included in modern academy teaching system:
not one and the same general universal speed of light exists for all
observers:
c depends on LOCATION from
c0 — se ABSOLUTA
METRIKEN (gravitationens
frekvensberoende gör att ljushastighetens lokalt gravitellt bestämda värde c=d/T
mätt med atomklockor får toppvärdet c0 = 2,99792458 T8 M/S överallt) med praktiskt tillämpningsexempel i GPSexemplet
KRAFTBEGREPPET (i klassisk mening) i modern
akademi tillämpas inte: man anser att begreppet KRAFT är någon PSEUDOAKTIGT,
något som i verkligheten INTE existerar:
”With the development
of quantum field theory and general
relativity, it was realized that force is a redundant
concept arising from conservation of momentum (4-momentum in relativity
and momentum of virtual particles in quantum electrodynamics).”,
http://en.wikipedia.org/wiki/Force
@INTERNET Wikipedia, Force, Feynman diagrams
[2012-09-06]
KVANTITATIVT gäller i
relaterad fysik
massa = gravitation = Kraft/Acceleration = (F=ma)/a
= m
Eftersom
gravitationen i relaterad fysik [GTaction] uppvisar ett TILLSTÅND [APARC]
(oberoende av tid) medan accelerationen utförs på TID (a=dv/dt) gäller
inte likheterna kommutativt:
Likheterna
är inte kvalitativa:
gravitationen
kan inte definieras ur accelerationen (a-termerna bortfaller automatiskt
och kvarlämnar m). Dvs.;
accelerationen
(variation) kan inte definiera gravitationen
(tillstånd), ehuru
gravitationen definierar accelerationen (tillståndets princip grundlägger, förklarar och beskriver f.ö. hela fysiken):
—
Nämligen via just den centralrörelse
(centrifugalkraften
F=mw2/r som gravitationens motriktade
jämviktsekvivalent)
med
vars hjälp gravitationslagen får sin form via massan:
FG
= Fw ; se Massan
a = å ;
F/m = (w2/r)(r2/m2)(m2/r2)
= å
= a ;
= G(m2/r2) ;
F = Gm2m/r2 ;
m2=m ; m2 = Fr2/G
= Er/G
Gravitationens KONVERGENSKRAFT definierar sin
egen motriktade DIVERGENSKRAFT via en idealiserad DIVERGENSACCELERATION från en enkel
centralrörelse som uttrycker DET LINJÄRA ACCELERATIONSELEMENTET v0/T=a=v²/r=F/m
liktydigt med den linjära accelerationens a=F/m
Den
kvalitativa definitionen på massa via gravitationen
(massa
verkställer gravitation, gravitation verkställer massa)
måste
istället definieras av en struktur: atomkärnan,
enligt TNED: En struktur
som via energilagen förstås oskapad.
I MAC finns inte det
beskrivningssättet. Man har generellt i MAC den allmänna tendensen att bortse
ifrån kvaliteterna och enbart koncentrera sig på kvantiteterna (därmed den
resulterande påtagligt ytliga förståndsfattningen på naturfysiken med
tillhörande påtagliga oförmåga att relatera — härleda — sakinnehållet snarare
än att uppfinna det).
Se speciellt i ENERGILAGEN
(den
moderna akademins allmänna våld på naturfysiken; jämför även det Allmänna
Herrefolkscitatet i MAC som mera
ingående klargör orsakerna till det allmänna tillståndet).
VadBetyderEkvivalensprincipen — BILDKÄLLA: Författarens arkiv ·
13Sep2012 E29 Bild50 · Nikon D90 · Detalj

Vad betyder ekvivalensprincipen?
INLEDNING
till VadÄrEkvivalensprincipen i MAC — se även i Einsteins egen beskrivning, citat från boken PROBLEM OCH PERSPEKTIV 1952
EKVIVALENSPRINCIPEN
i MAC
—
satsen (Einstein) att accelerationen (massbegreppet eller TRÖGHETEN [inertie]) ersätter/förklarar/beskriver
gravitationen
Jämför Wikipedia,
”In the physics of general relativity,
the equivalence principle is any of several related
concepts dealing with the equivalence of gravitational
and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally
while standing on a massive body (such as the Earth) is actually the same as the pseudo-force experienced by an observer in
a non-inertial (accelerated) frame of
reference.”,
http://en.wikipedia.org/wiki/Equivalence_principle
@INTERNET Wikipedia, Equivalence principle
[2012-09-05]
— är
ingen härledd egenskap i fysiken utan en uppfunnen egenskap i
fysiken som den moderna akademin antagit:
Man gör flera fel i MAC:
— Kraftlagen F=ma beskriver
INTE någon förmodad »ekvivalens» mellan massa (m) och gravitation;
—
Kraftlagen F=ma beskriver ekvivalens mellan massa och KRAFT: m=m=m(a/a)=F/a;
—
Gravitationen kan inte definieras via en enstaka (a) linjär
utsträckning: en enstaka linjärt riktad kraftvektor F=ma;
—
Gravitationen härleds [GTaction] och beskrivs kvantitativt ekvivalent [GRAVITATIONSLAGEN] via centralverkan (centrifugalkraften F=mw²/r)
som en entydigt definierad kvalitativt konvergent fenomenform, ingen
ensidigt enstaka linjär (a) rörelseekvivalent (tidsaspekten för den
centralrörelsens omlopp som definierar g-kraftens ekvivalent motriktade
jämviktskraft finns f.ö. inte med i gravitationslagens härledning: g-verkan är i den praktiska fysiken kvalitativt
absolut runtom i den härledande centrifugalringen; Se även i Gravitationens absolutverkan).
Jämför Wikipedia (citerar Einstein),
”Albert Einstein's assertion that the gravitational "force" as experienced
locally while standing on a massive body (such as the Earth) is actually the same as the
pseudo-force experienced by an observer in a non-inertial (accelerated) frame
of reference.”,
;
”Einstein's statement of the equivalence
principle
A little reflection
will show that the law of the equality of the inertial
and gravitational mass is equivalent to the assertion that the acceleration imparted to a body
by a gravitational field is independent of the nature of the body. For Newton's
equation of motion in a gravitational field, written out in full, it is:
(Inertial mass) · (Acceleration) =
(Intensity of the gravitational field) · (Gravitational mass).
It is only when there is numerical
equality between the inertial and gravitational mass that the acceleration is
independent of the nature of the body.
”,
http://en.wikipedia.org/wiki/Equivalence_principle
@INTERNET Wikipedia, Equivalence principle
[2012-09-05]
F=ma-sambandet är ingen KVALITATIV
definition på gravitationen, endast ett uttryck för massans motstånd mot
rörelseändring (acceleration, NewtonII). Men många har tagit det för
givet att se det så: sammanhanget kan förstås så att man bortser ifrån
att gravitationen INTE kan härledas på en enstaka linjär rörelseform; man
förenklar — UPPFINNER — hela betraktelsesättet genom att likställa
gravitationskraften vid en acceleration.
— Påståendet ovan från Einstein är (således) ingen
upplysning eller förklaring eller beskrivning, endast en uppenbart felaktigt
(eg. vilseledande) terminologiserad analogi:
kraftlagen F=ma beskriver ingen
ekvivalens mellan gravitation och massa. Inte på något som helst sätt;
Kraftlagen beskriver ekvivalens
mellan massa (m) och KRAFT (F)
via rörelsens ändring (a). Inget annat;
— Att BLANDA IN GRAVITATIONEN i kraftlagen F=ma UTAN VIDARE har ingen
relaterbar innebörd i fysiken.
gravitationen =
konvergenskraften definieras genom gravitationskonstanten G=a(r2/m2) från centralrörelsens motriktade
kvantitativa ekvivalent, centrifugalaccelerationen a=w2/r i formen av en idealiserat tidsabsolut
Ingår inte i MAC
hela cirkelrörelsen runt och motriktad gravitationens
motsvarande tidsabsoluta KONVERGENSKRAFT
FG = Fw ; se Massan
a = å ;
F/m = (w2/r)(r2/m2)(m2/r2)
= å
= a ;
= G(m2/r2) ;
F = Gm2m/r2
Gravitationskraften
verkar konvergent,
sammanstrålande, omvänt DEN IDEALT TIDSABSOLUT INFÖRDA DIVERGENSEKVIVALENTA
centrifugalkraftens uppvägande jämvikt (w²/r):
det finns inga — existerar inga — rörelseformer i fysiken
som kan efterhärma eller ersätta den fenomenformen.
Gravitationskraften är helt
unik i fysiken.
ACCELERATIONEN följer en bana via TID
(a=dv/dt), medan GRAVITATIONEN (Kraften) representerar ett tidsabsolut
tillstånd [GTaction]:
massa = m = r√(F/G)
= √(Er/G) = r1/2√(E/G)
Med konstant kraft (F) varierar massan (m)
med, och på, massformens ideala sfär- eller ringradie (r).
Med konstant omsluten energi (E) varierar
massan (m) med, och på, massformens ideala sfär- eller ringradies (r)
kvadratrot.
Gravitationen (tillstånd) kan inte
beskrivas av accelerationen (variation):
BILDKÄLLA: Författarens arkiv · 13Sep2012 E29
Bild63 · Nikon D90 · Detalj

— I MAC, där man underställt
gravitationen ljushastigheten (Einsteins »ingenting kan gå fortare än c»,
se Relativitetsteorins
grundmatematik) är det inget
problem ATT skippa en differens (GravitationenInteAcceleration) som man
i vilket fall inte bryr sig om [MACgraviton].
Relaterad
fysik:
Variationen
(accelerationen) beskrivs av/genom tillstånd
(gravitationen, massan).
Relationen
gravitation→acceleration är icke-kommutativ:
(gravitation
→ acceleration) ≠ (gravitation ← acceleration).
Gravitation kan ge
acceleration, men inte ges från acceleration.
Accelerationsbegreppet
(a) i gravitationen (F=ma) återfaller på
centrifugalaccelerationens begrepp [GTaction];
—
Därmed gäller, likväl (i gravitationens definition från centralverkan [GTaction])
från
den allmänna formuleringen;
’ACCELERATIONEN
går efter en bana (gäller per TID), medan GRAVITATIONEN representerar ett
tillstånd’
att
”ACCELERATIONEN går efter en bana”, nämligen
1.
ortsaccelerationen (radiella impulsvägen) och
2. DIVERGENSACCELERATIONEN som krävs totalt runt hela cirkelrörelsen för att få
EKVIVALENT jämvikt, definitionsbasen, med g-fenomenet:
gravitationen
definierar — tydligen — centrifugalaccelerationen som kvantitativ modell till gravitationslagen;
Gravitationen kan inte beskrivas av
accelerationen.
Se även tidigare (9Feb2009) noterande stycke i Universums Historia [MASSA OCH GRAVITATION I MODERN AKADEMI]: införda begränsande villkor för gravitationens inverkan och som omöjliggör varje kritisk framställning typ
”The outcome of any local non-gravitational experiment in a freely falling laboratory” [Wikipedia, Equivalence principle, The Einstein equivalence principle 2012-09-09];
— Först görs påstående OM gravitationen (ekvivalensprincipen: gravitation=acceleration) och som SEDAN inte får ifrågasättas EXPERIMENTELLT genom att man BORTSER IFRÅN GRAVITATIONEN.
Sic.
— De
teoretiska experimenten i »Einsteins hiss» [‡FM] utgår ifrån att betrakta hissens ENTYDIGT ENKLA LINJÄRA
acceleration (dessutom »på stort avstånd från g-centrum») vilket motsvarar
idealt parallella lodlinjer och vilket är uppfinningen: g-fält utanför en
godtycklig massform uppvisar ingen parallellitet i lodlinjer.
—
Just genom att g-fältets lodlinjer ÄR konvergenta (och centralaccelerationens
lodlinjer divergenta), säkerställs och garanteras från naturens sida att ingen
rörelseform av något enda slag kan definiera gravitationen fenomenmässigt:
gravitationen är en unik fysikalisk fenomenform [GRAVITATIONENS UNIKA SÄRSTÄLLNING].
—
Detta bortses ifrån i MAC, och man antar istället Einsteins tes som ansluter till
den s.k. allmänna
relativitetsprincipen:
— rörelse i
modern akademi beskrivs med hänsyn till
1.
s.k. inertialsystem, också det av allt att döma en uppfinning i MAC [UPPKOMSTEN
AV BEGREPPET INERTIALSYSTEM] [men
som påstås komma från Isaac Newton, se utförligt i INERTIA], och som sedan
2. »avfärdas»
med argumentet att »naturlagarna har det
perceptiva, kraftoberoende, synintrycket som preferens», se Einsteins
allmänna relativitetsprincip).
Jämför
(se även i Einsteins egen
beskrivning, citat från boken
PROBLEM OCH PERSPEKTIV 1952)
— som
ovan, men mera utförligt i citat: man har [numera] TVÅ olika typer av
”equivalence principle”, en WEAK och en STRONG:
”The Einstein
equivalence principle
The
Einstein equivalence principle states that the weak equivalence principle holds, and that:[42]
The outcome of any local non-gravitational experiment in a freely falling laboratory is independent of the velocity of the laboratory and its
location in spacetime.
”,
http://en.wikipedia.org/wiki/Equivalence_principle
@INTERNET
Wikipedia — Equivalence principle, The Einstein equivalence principle [2012-09-09]
(Wao).
Här dikterar man direkt premisserna för
Skapelsen. Jämför Ljusets Gravitella
Beroende: ingår inte i MAC.
LJUSETS GRAVITELLA BEROENDE — som inte igår i MAC — utesluts också här som METOD ATT FASTSTÄLLA VAD SOM
GÄLLER I FYSIKEN PER EXPERIMENT (exakt vad ”non-gravitational” betyder framgår
inte):
·
Påverkas man av en tyngdkraft
från en närliggande masskropp är också den lokala ljushastigheten (c) i
varje punkt i laboratoriet olika på olika avstånd från golvet enligt ljusets
gravitella beroende, analogt atomklockornas frekvenser olika på olika höjd över
golvet [‡1]
·
I det fria fallet med ett
laboratorium som faller mot en närliggande masskropps tyngdpunkt avtar den
lokala ljushastigheten (c) med tiden analogt med växande g-kraft ju
närmare tyngdpunkten man kommer, och skiljer sig därmed även här med olika höjd
över golvet, och därmed på samma sätt olika atomtider på olika avstånd [‡2]
Får man inte använda LJUSFYSIKEN — som i relaterad
fysik innefattar gravitationens
lokala inverkan på ljusets utbredning
och dess lokala atomtid, jämför GPS-exemplet — heller, är det
klart att man lika gärna kan utropa MAC direkt som Nya Tidens Absolutmekaniska Diktafon över
Mänskligheten: du får kritisera mig, men inte på ett sådant sätt att jag mister
kredit.
Säg efter mig
(eng., say after me):
— Du får visserligen kritisera mina teorier om fysiken,
men om du ska genomföra experiment för att testa det påstådda innehållet, får
du inte göra det på ett sådant sätt, att det jag menar framstår som felaktigt
eller primitivt.
— ’You are verily entitled to criticize my theories in physics, but in
testing them experimentally, you must not do so in such a way as to expose my
claims to be proven erroneous, or primitive’.
I would not credit such an attitude.
”The strong
equivalence principle
The strong equivalence principle suggests the laws of gravitation are independent of velocity and
location. In particular,
The gravitational motion of a small test body
depends only on its initial position in spacetime and velocity, and not on its
constitution.
and
The outcome of any local experiment (gravitational or not) in
a freely falling laboratory is independent
of the velocity of the laboratory and its location in spacetime.
”,
http://en.wikipedia.org/wiki/Equivalence_principle
@INTERNET
Wikipedia — Equivalence principle, The strong equivalence principle [2012-09-09]
Här,
citatdelen närmast ovan, blir det — således — MERA TYDLIGT att MAC har stött på patrull
—
förutsatt att man tillåter att ”local experiment” INTE betyder ett POSTULERAT
FÄNGELSE (isolerat rum, utan kontakt med omvärlden):
—
Men: Nej. Inte heller där håller MAC streck:
—
begränsningar införs (återigen,
för att säkra den egna kosmologiska uppfinningsrikedomen):
”The
freely-falling object or laboratory, however, must still be small, so that tidal forces may be neglected (hence "local experiment").”,
http://en.wikipedia.org/wiki/Equivalence_principle
@INTERNET
Wikipedia — Equivalence principle, The
strong equivalence principle [2012-09-09]
;
”Locality eliminates measurable tidal forces
originating from a radial divergent gravitational field (e.g., the Earth) upon finite sized physical bodies.”,
http://en.wikipedia.org/wiki/Equivalence_principle
@INTERNET
Wikipedia — Equivalence principle, The weak
equivalence principle [2012-09-22]
Och
då ser vi hur man vill ha det i modern akademi — precis som »ironiserats» ovan:
— Man utesluter fysiken som en öppen
scen där alla metoder är tillåtna, för ändamålet att postulera giltighet för
vad man kallar fysikens lagar i det så fysiskt avgränsade, stympade,
formuleringsuniversumet. Dvs., den öppna naturvetenskapens möjligheter att
avgöra vad som är vad har dikterats bort för att säkra en begränsad
fysikuppfattning.
I princip så:
RUMMET där experimenten utförs får inte
vara så utbredda, att avgörande inverkan från gravitationsfältet kan
användas för att detektera DET laboratoriets tillstånd som meningssatsen utgår
ifrån gäller.
—
Alltså i princip: alla kontrollerande experiment måste göras i en PUNKT
— så
att man SÄKERT inte kan mäta DE differenser som detekterar tillståndet över
INTERVALL, och så, därmed, att man inte kan KRITISERA framställningssättet,
eller påpeka dess primitiva natur; Alltså en FriFörklaring (eng. Disclaimer, ansvarsfriskrivning).
— Är
det någon NY typ av naturvetenskapligt särskådande det eller — att börja
utesluta olika partier i fysiken som är VÄSENTLIGA i bevisföringen för de olika
påståendenas tillrättaläggande?
Jämför
föregående ironi — DisClaimer:
— ’Du får visserligen kritisera mina teorier om fysiken,
men om du ska genomföra experiment för att testa det påstådda innehållet, får
du inte göra det på ett sådant sätt, att det jag menar framstår som felaktigt
eller primitivt’.
Vad är det för någon fysikbeskrivning?
Ingen jag känner till i varje fall:
—
’Du får visserligen rösta/titta på andra än mig, men gör du det, ska du veta,
att det du röstar/tittar på inte gäller’.
Det är precis som det redan finns
formulerat (från 9Feb2009 i Universums
Historia) i MASSA OCH
GRAVITATION I MODERN AKADEMI;
GPS-Exemplet —
TIDMÄTNINGEN som funktion av GRAVITATIONENS INVERKAN — har redan stadfäst principen:
In accord — harmony — with related physics (TNED), to
be strongly distinguished from modern academy (MAC):
— The
outcome of an experiment in a freely falling laboratory
(where the free fall is understood to
take place towards the center of gravity of a given mass)
is not
”independent of the laboratorys location in spacetime”:
— As
the laboratory approaches the center of gravity, the local value of the speed of light (c) increases towards the local top value (»c0=2,99792458 T8 M/S») in
the center of gravity, equally affecting the atomic time [AbsoluteMetrics] through the gravitational influence over frequency:
— c
itself cannot be directly measured by an atomic clock because also the atomic
clock changes [AbsoluteMetrics]. However, changes in time-interval in the atomic clock
can be measured by digital technique (as in the GPS-Example),
and hence a way to confirm
that
The
outcome of an experiment in a freely falling laboratory
is not
”independent of the laboratorys location in spacetime”
The
outcome of the experiment in measuring the atomic time — the gravitationally,
locally, controlled speed of light — does depend on location.
GcQ-teoremet — not included in modern academy teaching system:
not one and the same general universal speed of light exists for all observers:
c depends on LOCATION from
c0 — se ABSOLUTA
METRIKEN (gravitationens
frekvensberoende gör att ljushastighetens lokalt gravitellt bestämda värde c=d/T
mätt med atomklockor får toppvärdet c0 = 2,99792458 T8 M/S överallt) med praktiskt tillämpningsexempel i GPSexemplet
SAMMANFATTNING —
VadÄrEkvivalensprincipen i Inledning
I
summeringen av den ovan citerade rymdfloran av den moderna akademins
Disclaimers [MACdisclaimers], är det tydligt att MAC självmant retirerat in i en allmän kosmologisk
fysikbeskrivning som, tydligen som det får förstås, motsvarar en så gravt
stympad återstående fysikbild, att den, väl, kan ses och förstås som en
föreställande variant på en verklighetens dockteater: alla detaljer som
avslöjar den bilden som just primitiv, anses — deklareras explicit —
ovidkommande.
— Varifrån har du fått din utbildning?
— Uppenbarligen INTE från något ställe du känner till.
Det stavas:
naturen.
I stort, och
frankt, och grovt sagt: Orepresenterat i MAC:
— Tjejvettet, medfött. Ren promenadseger. Fullt jubel.
VadÄrEkvivalensprincipen — G-beviset — BILDKÄLLA:
Författarens arkiv — 15Sep2012 E32 Bild92 · Nikon D90 · Detalj — h = 200 M över Sfärytan
(R=6,378 T6 M) ser man en kalott med radien r = √(R+h)²–R² = 50509,80103
M (5 mil).

Kopierat
från Source1.doc — *ekvivalensprincipen,
modern akademi
Vad betyder ekvivalensprincipen? Se Einsteins egen beskrivning
———————————————————————————————————————————————————
DEN
MODERNA AKADEMINS FELUPPFATTNING AV GRAVITATIONENS NATUR — enligt relaterad
fysik (TNED)
FÖRKLARINGEN
till ekvivalensen mellan de enligt Einsteins [‡CitatEinstein] mening skilda innebörderna i tung
(gravitell, vägande) och trög
(accelererande) massa skulle enligt Einstein bestå i en motsvarande »ekvivalens
mellan gravitation och acceleration» — om vi har förstått saken korrekt; den i
modern akademi så kallade ekvivalensprincipen [WikiEquivPrinc]:
(1) I en accelererande raket kan inget
experiment utföras som avgör om man befinner sig i ett g-fält eller i en accelererande
kropp
”Inget experiment i raketen kan avgöra om man
påverkas av en tyngdkraft eller en tröghetskraft.”
FOCUS
MATERIEN 1975 s85 text [‡] till illustrationssidan överst vä
(2) I en fritt fallande hiss i ett g-fält kan
inget experiment avgöra om man befinner sig i ett sådant g-fält eller i ett
tillstånd där inga krafter alls verkar
”Det finns inget sätt att skilja det fria
fallet från ett tillstånd då inga krafter alls råder.”
FOCUS
MATERIEN 1975 s85 text [‡] till illustrationssidan överst vä
”Allmän
relativitetsteori
Den allmänna relativitetsteorin behandlar till skillnad från den speciella även
accelererade system. Den bygger
på ekvivalensen mellan acceleration och gravitation. T.h. illustreras denna ekvivalens; nedan några fenomen
som tycks bekräfta teorins giltighet.”,
FOCUS
MATERIEN 1975 s84ill.ö.v., rubriktexten till citaten ovan
Vi studerar nu hur relaterad fysik ger
argumenten för att »ekvivalensprincipen» i MAC saknar naturvetenskaplig förankring:
Bägge
påståendena är felaktiga i kraft av
1. ljusets gravitella beroende enligt relaterad fysik
2.
den relaterbara g-fysiken (mekaniken) generellt
Vi
studerar det.
(Kontrollera
noga att alla följande påståenden verkligen är UTOMORDENTLIGT VÄL relaterbart
förankrade i den elementära grundfysiken [GTaction]: den som garanterat kan förstås, beskrivas och förklaras
i detalj).
1.1. Påverkas man av en tyngdkraft är c olika
på olika avstånd från golvet enligt ljusets gravitella beroende, analogt atomklockornas frekvenser [‡AbsolutaMetrikenRef] är olika på olika höjd över golvet
|
|
(se absoluta
metriken); |
Detta
kan mätas. Se praktiskt exempel i GPS-exemplet. Påverkas man av en tröghetskraft, typ rummet i en
accelererande raket, förutsatt långt från andra himlakroppar, garanterar det
interstellära medelfältet mellan himlakropparna ett och samma c-värde
även över mycket stora olika avstånd, och därmed ingen (praktiskt uppmätbar)
tidsskillnad i atomklockorna på skilda höjder över golvet. Påståendet i (1) ovan är
därmed motsagt:
—
man KAN visst avgöra genom experiment om man befinner sig i ett g-fält
eller i en accelererande kropp.
Se även i Mekaniska
Experiment.
1.2. I det fria fallet i ett g-fält (utanför
g-massan) avtar c med falltiden analogt med växande g-kraft, men skiljer
sig även här med olika höjd över golvet och därmed olika atomtider på olika
avstånd. Genom att mäta skillnaden i atomtid mellan de olika avstånden kan man
alltså även i detta fall fastställa huruvida man (aktuell lokal) befinner sig i
ett g-fält eller inte.
Föreställningen i citatet ”då inga krafter alls råder” existerar (således,
alls) inte i fysiken.
Även påståendet i (2) ovan är
därmed motsagt:
—
man KAN visst avgöra genom experiment om man befinner sig i fritt g-fall
eller i någon annan situation.
Se även i Mekaniska
Experiment.
Acceleration kan INTE beskriva
gravitation
![]()
2.1
I en accelererande raket eller hiss
(alla kraftvektorriktningar parallella med
accelerationsriktningen, dvs rakt ner mot golvet) med försumbart
dominant egengravitationsfält, långt ute i rymden mellan stjärnorna, är
avståndet mellan två fasta lodlinjer oförändrat. Lodlinjerna är parallella och
normaler till golvplanet. Divergensen c (ljushastighetens
punktvärde under dT) är (inom de begränsade utrymmena mellan stjärnorna)
en
och samma på olika avstånd från golvet,
samma som mellan de långt avlägsna stjärnorna (g-potentialerna mellan stjärnorna tar i stort ut varandra
och kvarlämnar ett praktiskt taget medelhomogent g-potentialfält, inom vissa
gränser, där ljushastigheten i princip är en och samma, se Alternativ beskrivning
i stycket under Aberrationskurvans
ljushyperbel).
Med lodlinjer och c fastställda [‡AbsolutaMetriken] är därmed påståendet i (1) motsagt.
Allmänna beskrivningar av LJUSVÄGARNA i förhållande till olika rörelsesystem finns f.ö. inte i
fysiken i relaterad mening; Hur ljusvägen ser ut i aktuell lokal beror
på den lokala makrogravitationen, och en sådan given ljusväg ändras inte
nämnvärt med förbipasserande mindre föremål typ hissar och raketer — oberoende
av deras rörelsetyp.
![]()
2.2
I ett utpräglat gravitationsfält
— som i Jordens fall — är lodlinjerna konvergenta mot tyngdpunkten.
Ljushastigheten varierar med olika höjd över golvet
enligt c/c0=
(1/2)[1 + √ 1 – 4w2/c02
] med w2=Gm2/r från c0
till c0/2, därefter från till c0/2 till 0
enligt c/c0=
(1/2)[1 – √ –1 + 4w2/c02 ]
från grundsambandet c/c0=[1–w2/cc0].
Jämför
Einsteins c/c0=[1–w2/c2]
(han tillät inte c=0, tidens upphörande enligt honom).
— ABSOLUTA
METRIKEN visar att c INTE
kan mätas lokalt med hjälp av atomklockor; också atomklockornas frekvens ändras
analogt med gravitationen inverkan [Frekvensens g-beroende] så att man ALLTID får toppvärdet c=c0=2,99792458 T8 M/S.
—
Däremot kan TIDEN mätas (se GPS-Exemplet) vilket ger ett likvärdigt experimentellt resultatvärde
till c-mätning.
I
FRITT FALL I G-FÄLTET (via
ett fast mätavstånd
utanför centralmassan m2)
växer konvergensvinkeln mellan lodlinjerna med tiden för fallet (det fasta mätavståndets upptagande
vinkel blir allt större sett från g-centrum med minskande avstånd dit). Ljushastigheten på varje fast avstånd från golvet
avtar med tiden ju närmare g-centrum fallet kommer, enligt samma samband som
ovan.
Med lodlinjer och c
fastställda [‡AbsolutaMetriken] är därmed också påståendet i (2)
motsagt.
Inte
i något av dessa fall FOCUS MATERIEN 1975 s85 kan gravitationen beskrivas med hjälp av accelerationen;
—
Acceleration och gravitation kan i relaterad fysik INTE jämställas.
Med referens till FOCUS MATERIEN 1975 s85 råder därmed, och tydligen, fullt kaos i den moderna
akademins grundläggande naturbeskrivning (själva den förståndsmässiga
uppfattningsförmågan).
Orsakerna:
—
Erinra GTaction:
generellt (kortfattat) Ljusets g-beroende, v+ic-resonemangets ogiltighet i fysiken, med vidare i Planckekvivalenterna.
— Se
även i GRAVITATIONENS
UNIKA SÄRSTÄLLNING I RELATERAD FYSIK.
Det finns också ett betydligt enklare
sätt att klargöra saken på — i termer av relaterad fysik (TNED)
(definitionsområdet
ligger helt utanför den moderna akademins begreppsliga domäner, se utförligt
från GTaction):
ACCELERATIONEN följer en bana (Δx) via TID (a=dv/dt), medan
GRAVITATIONEN (Kraften) representerar ett tidsabsolut tillstånd [‡]:
— Men
eftersom gravitationen lyder under ljushastigheten i MAC, omöjliggörs bara av
den anledningen satsbilden i MAC:
RÖRELSE
— TID — kan aldrig härma, substituera eller på annat sätt frammana någon
ekvivalent till gravitation.
Ingår inte i MAC
OM man i en meningsmässig KONTEXT kan
hitta ett KLART ARGUMENT som utpekar att ämnet berör, beskriver, behandlar
eller associerar till olika påståenden som går ut på att GRAVITATION =
ACCELERATION räcker det med att hänvisa till ovanstående [G-beviset]: den fullständiga
förklaringen ges i Gravitationens Tidsabsoluta Verkan [GTaction]
och de följdsatser som följer ur den delen OCH HUR MOTSVARANDE DELAR SER UT,
HAR UTVECKLATS HISTORISKT OCH ANVÄNDS I NUTID I MODERN AKADEMI.
Aktionskraftens
definition — inom mekaniken — Aktion-Reaktion
Om TRÖGHET definieras som »massans
motstånd mot rörelseändring» och massa=gravitation, kan man säga att
»gravitationens motstånd mot positionsändring» definierar trögheten:
— KRAFTVERKAN
som uppträder i samband med »massans
motstånd mot rörelseändring»
(alltså AKTIONSKRAFTER: alla krafter F=ma som sammanhänger
med ändring av givna tillstånd i resulterande riktningar och som då uppträder
på BEGRÄNSAD TID [via ma=mv/T=p/T])
blir då, tydligen, ett entydigt
resultat av
GRAVITATIONENS
ABSOLUTVERKANDE positionsändringsmotstånd
Ingår inte i MAC
(tyngdpunktens förflyttning). Det blir,
tydligen, i relaterad mening
»förklaringen» bakom tröghetsverkan:
— kraftbilden vi känner.
— Vi ser då inte massan som en passiv komponent, utan som en
aktiv: gravitationen.
Aktionskraftens definition — inom elektrofysiken
— Inom elektrofysiken — laddningens
kraftåterkoppling via ljushastigheten
(c) — blir aktionskraftens motsvarande definition:
INDUKTIONSVERKAN [INDUKTION och MAGNETISM]; induktansen
(L=RT) ersätter massan (m), strömstyrkan
(I) ersätter mekaniska hastigheten (v), och spänningen (U) ersätter mekaniska
kraften (F), se utförligt i Integrala Analogin.
PunktKvantitetenFaFG
EKVIVALENSEN MELLAN
ACCELERATION OCH GRAVITATION (F=ma) i relaterad fysik
gäller endast KVANTITATIVT
(mängdbegrepp) och då endast i och för lokala punktvärden eftersom gravitationen [GTaction] verkar tidsabsolut och oberoende av avstånd, medan aktionskraften
via acceleration (F=ma) inte gör det:
— Gravitationen,
KONVERGENSKRAFTEN som den
motriktade ekvivalenten till centralverkans centrifugalkraft i RINGEN i formen
av den idealiserade, motsvarande absolutverkande
DIVERGENSACCELERATIONEN [GTaction],
är i relaterad fysik absolutverkande: gravitationen verkar överallt i xyz via dt, enligt den
sammanställda, förtydligande, härledningen i GTaction, relaterad fysik.
— I kvalitativ mening —
rumsfysikens xyz-utsträckning och HUR fenomenformerna förstås — finns, således,
ingen analogi alls mellan gravitation (absolutverkande överallt i xyz) och
acceleration (verkar via TID i xyz).
Med andra ord: acceleration=gravitation
gäller i relaterad fysik uppenbarligen INTE ÖVER INTERVALL i rymden, endast i
varje enskilt lokalt fristående punktvärde (F=ma, Galileiska Kraftfältet, ett
och samma a överallt i xyz), garanterat av gravitationens absolutverkan under
tidsdifferentialen (dt) oberoende av avstånd, medan acceleration i rummet (aktionskraft)
utvecklas på TID (intervall, differens).
— Gravitationskraften på
r från tyngdpunkten (F=ma=G[m/r]²) blir det
lokalt uppmätta ekvivalenta centralaccelerationsvärdet (a=w²/r) [GTaction] taget — idealiserat — som en absolutverkande sfärisk
ekvipotentialyta av ekvivalenta a-värden och som uppväger den motriktade
g-kraftens fältstyrka (a=Gm/r²).
— Någon rent KVALITATIV
(med ändlig utsträckning xyz i rymden) ekvivalens mellan acceleration över
intervall (Δx) och absolutverkande gravitation (dx) existerar,
således, INTE i relaterad fysik.
Därmed
i klartext:
— OM
man med ”ekvivalensprincipen” menar det som kan utläsas ur de givna citaten från FOCUS MATERIEN, är det tydligt att den s.k. »ekvivalensprincipen» i termer av relaterbar fysik saknar
naturvetenskaplig förankring.
—
Gravitation kan inte liknas vid eller avbildas av något annat
KVALITATIVT fenomen i fysiken än sig självt.
— Det
finns bara två rörelsesätt att välja på: translation (rätlinjigt) och rotation.
—
Frånsett att bägge rörelsesätten använder TID, och därmed bara av det skälet är
uteslutna, visar den vidare analysen, som ovan, att varken translation eller
rotation har de rent fältmässiga förutsättningarna för att kunna AVBILDA eller
»ekvalentisera» gravitationen.
Se utförligt ovan från VadÄrEkvivalensPrincipen.
BILDKÄLLA: Författarens arkiv · 13Sep2012 E29
Bild1 · Nikon D90 · Detalj

— Vad händer om man ändå antar den
(uppenbara) förenklingen med införandet av »acceleration=gravitation»?
—
Uppenbarligen inget annat än att
1.
fysikbeskrivningen blir stympad i naturgrunderna, och
2.
förytligad (primitiv) i förhållande till människans naturliga
förståndsförmågor:
— I
stället för naturvetenskapligt härledd teori, utvecklas (tydligen, enligt
exempel) naturvetenskapligt uppställd fiktion.
Exempel:
— I
relaterad fysik krävs ett intervall, en TID [AktionReaktion], för en acceleration att utvecklas på, medan
gravitationen [GRIP] är tidsoberoende [Aktionskraftens definition];
— Säg
den konsekvenslogik som INTE kraschar om man inte förstår den
grundfysiken: här veterligt: allt havererar.
— Atomkärnan kan inte härledas i MAC — ATOMKÄRNANS INKOMPRESSIBILITET — och därmed i MAC direkt, som ett konkret exempel, svarta
hål: WelcomeFiction.
Se även mera allmänna exempel generellt i EXPERIMENTELLA
BEKRÄFTELSER.
Kvantiteterna i jämförelsen MAC/TNED
uppvisar (i allmänhet, men inte alltid, om alls) analoga former, medan
teorierna eller KVALITETERNA är helt väsensskilda.
Se den i termer av relaterad fysik [GcQ-teoremet] särskilt djupt antagna vanföreställningen i MAC:
”the attractive force of gravity
arises due to exchange of virtual gravitons”,
http://en.wikipedia.org/wiki/Gravitation
@INTERNET
Wikipedia, Gravitation [2012-09-05]
”The speed of gravitational
waves in the general theory of relativity is
equal to the speed of light in vacuum, c.[1] Within the theory of special relativity, the constant c is not exclusively
about light; instead it is the highest
possible speed for any physical interaction in nature.”,
http://en.wikipedia.org/wiki/Speed_of_gravity
@INTERNET
Wikipedia, Speed of gravity [2012-10-08]
TNED: MAC må inkvartera sig i alla möjliga kosmiska universum
under oändlig tidrymd, varsågoda. Men någon »graviton» kommer aldrig att
upptäckas [ArgumentenMACgenerelltMekaniken]. Gravitonen är, som allt annat i MAC med uppsegling
under 1800-talet, en ren följd av att, felaktigt, sammankoppla kinetiken med
ljusfysiken [v+ic-felet]; dels v+ic-resonemangets ogiltighet i fysiken som sådant, och dels den felaktiga uppfinningen att
»ingenting kan gå fortare än c»; Se särskilt i Beviset
för multipla c: exakt samma
experiment, exakt samma matematiska formalia, exakt samma resultatbild, men
HELT väsensskilda teorier. Se speciellt i PLANCKEKVIVALENTERNA som särskilt tydligt klargör den delen — principen — genom
konkret, enkel, praktisk jämförelse [PlanckEkvivalenterna
kontra RelativitetsTeorin].
— Ljusets g-beroende generellt i
universum mellan stjärnorna som följd av universums samlade massa — gravitella rödförskjutningen — ingår HELLER
inte i (kan inte härledas av eller genom) MAC.
Orsak
(närmast, frånsett den allmänna redan
välbekanta bristen [”Herre över
Universum”] på vanligt medfött
tjejvett):
— Gravitationens absolutverkan [GTaction], (och därmed)
c0-kroppen: K-cellens värmefysik.
—
Lägg f.ö. märke till att Einsteins ekvation
för ljusets g-beroende INTE är
den som sammanhänger med den relaterade fysikens beskrivning:
— bevarandet
av naturkonstanten c0 oberoende av gravitationens inverkan ingår inte i MAC.
GcQ-teoremet — not included in modern academy teaching system:
not one and the same general universal speed of light exists for all
observers:
c depends on LOCATION from
c0 — se ABSOLUTA
METRIKEN (gravitationens
frekvensberoende gör att ljushastighetens lokalt gravitellt bestämda värde c=d/T
mätt med atomklockor får toppvärdet c0 överallt) med
praktiskt tillämpningsexempel i GPS-EXEMPLET
Varför
har inte dessa (enkla) punkter kunnat förutses av modern akademi?
— Bevarandet
av naturkonstanten c0 oberoende av gravitationens inverkan kan, tydligen, bara härledas på ETT sätt med ETT
resultat. Det sättet ansluter, tydligen, INTE till varken Einsteins ekvation eller metod.
—
Notera speciellt att föreställningen om ljusets g-beroende via den samlade
universums massa (K-cellen)
varken har någon representation i MAC, eller någonsin kan få det principiellt främst på
grund av uppfattningen i MAC att »ingenting kan gå fortare än c», se vic-felet explicit. I relaterad fysik (TNED)
verkar gravitationen absolut [GcQ-teoremet] [Gravitationens absolutverkan] [GTaction]
— vilket garanterar giltigheten av den elektriska laddningens härledda matematiska fysik och praktik, speciellt
tydligt i PLANCKEKVIVALENTERNA; I MAC anses gravitationen [MACgraviton] verka via ljushastigheten (En ren följd av vic-felet).
— Se
även Einsteins egen
beskrivning, så som han såg ämnet
i den av honom uppställda s.k. ekvivalensprincipen.
Trög och Tung
massa, sammanfattning:
Ekvivalensprincipen,
trög och tung massa (Sammanfattning)
Genom olika omvägar har — tydligen —
många missförstått och missuppfattat bildningen av begreppen ”trög massa” och
”tung massa” som uttryck för ”olika fysikaliska kvaliteter” eller ”skilda
fysikaliska kvaliteter”.
Orsaken
är (som det kan förstås,
här [Frånsett Einsteins
definition]
utan direkta citatreferenser, bl.a.)
följande: vägande massa kallades tidigt
(från mekanikens barndom — inga direkta citat finns
här att peka på, endast vetenskapshistorien generellt)
tung massa för att särskilja fallen med massor i rörelse, eller som sammanhängde med utpräglade analyser av
massor som skulle försättas i rörelse (av olika maskindetaljer) och som kom att
kallas ”trög
massa”.
— Men i fallet ”den tunga massan”,
alltså vägande massa, sker alldeles samma sak:
—
för att kunna väga en massa måste den obönhörligen förflyttas om så bara
en miljarddels millimeter.
Exakt samma fenomen gäller för den
vägande som den förflyttande massan,
och ingen som helst
fysikalisk distinktion föreligger.
—
Det finns med andra ord inte TVÅ (eller ännu flera, se Wikipedia Mass) massbegrepp, utan bara ett
enda [MACmasses].
Påståendet att någon distinktion
skulle finnas naturligt i massan som skulle föranleda olika begreppsreferenser
i massan har, därmed, ingen naturlig förankring; påståendet är alldeles tydligt
en vanföreställning med grund i felaktiga eller ofullständiga synpunkter på
naturfenomenen (alltsedan r-teorins uppsegling
från slutet av 1800-talet).
Olika
teorier som söker påskina något underligt eller
något märkligt i att ”tung och trög massa är samma sak”, bygger (alltså,
som det får förstås) på åtskillnadsbegrepp eller distinktioner som inte
existerar.
Jämför
(citat):
”The observed fact that gravitational and inertial
masses are the same for all bodies is unexplained within
Newton's system. General relativity takes this as a postulate. See equivalence
principle.”
CITAT
från
@INTERNET
Wikipedia 2006-08-09 Newton’s law of universal gravitation
Nobody, ever, truly claimed them to be
different.
“Although
inertial mass, passive
gravitational mass and active gravitational mass are conceptually
distinct …”
CITAT
från
@INTERNET
Wikipedia 2006-08-28 Mass
Vi
fortsätter framställningen om MACmasses efter nedanstående korta inbrytning
från Einstein, forts. MACmasses.
Einsteins egen beskrivning
— ekvivalensprincipen (gravitation = acceleration) — BILDKÄLLA: Författarens
arkiv · 13Sep2012 E29 Bild44 · Nikon D90 · Detalj

Einsteins egen beskrivning —
ekvivalensprincipen
———————————————————————————————————————————————————————
Einstein
beskriver hur han själv ser på ekvivalensprincipen [WikiEquivPrinc] och dess detaljer:
Fetstil
och övriga textmarkeringar är mina (om
inte samma i källtexten);
”Den speciella relativitetsteorin bibehöll
från den klassiska mekaniken en väsentlig punkt, nämligen satsen "Naturlagarna gäller endast i inertialsystem".
"Tillåtna" koordinattransformationer (dvs. sådana som lämnar
naturlagarna oförändrade) är endast (linjära) Lorentz-transformationer. Är
denna inskränkning verkligen grundad på fysikaliska fakta? Följande resonemang
visar att detta avgjort inte är fallet.
En kropp besitter trög massa (= motstånd mot acceleration) och tung massa (som bestämmer kroppens tyngd i ett givet
gravitationsfält, t.ex. det på jordytan). Dessa två enligt definitionerna så skilda
storheter kan enligt vad experimenten
visar mätas med ett och samma tal (ekvivalensprincipen). Det måste finnas en djupare liggande orsak till detta. Man kan också uttrycka saken så: Olika massor erhåller
i ett gravitationsfält samma acceleration. Slutligen kan man också säga: Om man använder ett likformigt accelererat
koordinatsystem (i stället för ett
inertialsystem) som referenssystem, så uppträder kroppar i ett gravitationsfält
som om det inte funnes något sådant. [NOT., Einsteins fritt fallande hiss].
Det tycks därför inte finnas något skäl
till att avvisa följande tolkning av det sistnämnda fallet. Man betraktar koordinatsystemet som ett
inertialsystem och det "skenbara" gravitationsfält [NOT., Einsteins accelererande hiss] som
existerar i förhållande till det såsom ett "verkligt" fält. Detta gravitationsfält som "alstrats"
genom koordinatsystemets acceleration, skulle naturligtvis ha oändlig utsträckning, så att det inte kunde tillskrivas gravitationsmassor inom ett
ändligt område. Men om vi endast
intresserar oss för en fältteori, behöver detta förhållande inte bekymra
oss. Med denna tolkning förlorar begreppet "inertialsystem" sin
mening, och man får en "förklaring"
till likheten mellan tung och trög massa. (En och samma egenskap
uppträder som tyngd eller som tröghet beroende på framställningssättet).”
PROBLEM
OCH PERSPEKTIV Albert Einstein från s42n
HUGO
GEBERS FÖRLAG 1952
modern academy different aspects of
mass
F
m = ———
a
Citat
från @INTERNET Wikipedia Mass 2006-08-28, rubrikerna till vänster inlagda av mig:
“There
are three types of mass or properties called mass:
a = F/m: discusses motion:
Inertial mass is a measure of an object's resistance to changing its
state of motion when a force is applied. An object with small inertial mass
changes its motion more readily, and an object with large inertial mass does so
less readily.
m = F/a: discusses mass:
Passive gravitational mass is a measure of the strength of an object's interaction
with the gravitational field. Within the same gravitational field, an object
with a smaller passive gravitational mass experiences a smaller force than an
object with a larger passive gravitational mass. (This force is called the
weight of the object. In informal usage, the word "weight" is often
used synonymously with "mass", because the strength of the
gravitational field is roughly constant everywhere on the surface of the Earth.
In physics, the two terms are distinct: an object will have a larger weight if
it is placed in a stronger gravitational field, but its passive gravitational
mass remains unchanged.)
ma = F: discusses force:
Active gravitational mass is a measure of the strength of the gravitational field
due to a particular object. For example, the gravitational field that one
experiences on the Moon is weaker than that of the Earth because the Moon has
less active gravitational mass.
Although
inertial mass, passive gravitational mass and
active gravitational mass are conceptually
distinct, no experiment has ever unambiguously demonstrated any
difference between them.”
Comment:
I relaterad fysik (TNED) finns ingen
distinktion mellan olika typer av massor:
— uppfattningen (enligt relaterad
fysik) att det skulle finnas olika typer av massor grundas, uppenbarligen, på
en ofullständig inblick i hur massan fungerar i fysikens olika sammanhang [GTaction]: som trög
massa (eng. inertial mass) — i samband med förflyttning i olika
industrisammanhang — eller som tung massa (eng. gravitational mass) — i
samband med vägande (logistiska) mätningar.
— Eftersom, emellertid, också den
tunga massan måste exponeras för en förflyttning om än aldrig så liten för att
kunna vägas (m=[F]/a=[mv/T]/a=[p/T]/a),
vilket betyder att massbegreppen men inte metoderna är lika, utgör de synbart
olika masstermerna ingen beskrivning i egenskaper hos massan: det finns
ingenting sådant i den relaterbara fysiken. De olika masstermerna
beskriver — uppenbarligen — endast olika metodbegrepp i samband med hur
massan används i de olika fysiska tillämpningarna. Se även utförligt i VadÄrEkvivalensPrincipen.
— Därmed blir enligt relaterad
fysik hela (den citerade) diskussionen om »de olika massbegreppen» irrelevant
— fullständigt — ur naturvetenskaplig synvinkel.
The
Wikipedia authors does NOT discuss three types of mass named respectively inertial-, passive g- and active
g-mass, but CONCLUDES it to be so without any related descriptive reference,
“Although inertial mass, passive gravitational mass
and active gravitational mass are conceptually
distinct”, the bold my mark, see further
below.
The
author discusses, respectively,
motion,
mass
and
force
— as
clarified above in mathematical expressions.
Meaning:
There is no distinction of the kind “types of mass”.
Consequently:
— any
measuring in, with or by the universal force law F=ma will be consistent
— for all cases — no matter the frame of reference to any of the factors.
— The
idea of “distinction” is — hence to be understood as — a product of a lack
of understanding the idea of gravitation, gravity and mass [GTaction]:
In modern academy gravitation and
mass are considered distinct: ”… are conceptually distinct …”, quote in MACmasses. Citatdelen
finns fortfarande kvar i Wikipediaartikeln nu, 22Sep2012.
— BUT
as THAT sentence (claim) is not explicitly written out (except here), only
inferred as a consequence, it can neither be held on any account of or from an
idea in the modern academic teaching system, and hence cannot be met with any
argumentation, either.
—
Until such a sentence explicitly comes from a modern academic position, we
cannot bring this issue to a further resolution.
The contradiction is
this:
— In modern academy,
LIGHT is considered to PASS INTO mass at higher frequencies [FOCUS
MATERIEN 1975 s262sp1mö]. This would indicate a
claim »light IS mass»;
— But mass exposes
gravitation, and gravitation in MAC is claimed to work through the speed of light [MACgraviton],
and the consequent claim would be »gravitation is light», which we know NOT is
the case. The only (logical) way out of that dilemma would be a claim
»gravitation and mass are distinct», which in terms of related physics (See
from WhatIsEquivalencePrinciple) also NOT is the case.
— In any case, hence NOT.
But this is only a statement in this document.
In related physics mass is gravitation.
2012IX9
I MAC är massa också
nämligen ljus — eller mera försiktigt uttryckt [MassaÄrLjus],
”Vid sin kortvågiga gräns närmar sig
strålningen till och övergår i gripbar materia”,
[FOCUS MATERIEN 1975 s262sp1mö].
— I TNED
(relaterad fysik) är gravitationens element samma som massans fundamentala form
[PASTOM] (Princip(al)(le) Structure Of Mass), samma som atomkärnan
[PLANCKRINGEN]; massa = gravitation.
— I
modern akademi där gravitationen anses verka genom ljushastigheten (c)
”In
a more physically correct sense, the "speed of gravity" refers to the
speed of a gravitational
wave.”,
;
”The
speed of gravitational
waves in the general theory of relativity is
equal to the speed of
light in vacuum, c.[1]”,
;
”Thus,
the speed of
"light" is also the speed of gravitational waves and any massless particle.”,
http://en.wikipedia.org/wiki/Speed_of_gravity
@INTERNET
Wikipedia — Speed of gravity [2012-09-22]
blir
motsvarande koppling av princip omöjlig:
—
massa = ljus = gravitation har uppenbarligen ingen soliditet i
relaterad fysik genom att ljuset inte (direkt) avbildar någon tyngdkraft (Solrandsavböjningarna
från år 1919), [Ljusvägarna
i gravitationsfältet], ehuru
massan gör det; Sätter man massa=ljus i MAC, kan man följaktligen inte sätta ljus(massa)=gravitation
— om man inte också anser att ljus (direkt) bildar tyngdkraft.
—
Genom den moderna akademins uppfattning [Jämför ENERGILAGEN i relaterad fysik] att »massa kan skapas ur energi», med energi=ljus, är
det just och emellertid det som i följdsatserna serveras i MAC:
ljus→massa→gravitation.
—
Jämför TNED:
gravitation→massa→ljus;
—
omvändningen gäller inte, enligt energilagen: massa kan förintas därför att den inte kan
skapas.
I MAC däremot gäller också omvändningen — bevisligt och
experimentellt kvantitativt E=(m→γ)c2=(m←γ)c2,
liksom också i TNED, men inte kvalitativt: (m→γ)≠(m←γ).
Se även i MASSDESTRUKTION
hur saken beskrivs och förklaras i relaterad fysik — anledningen varför massans
kvalitet (strukturen, gravitationen) inte kan skapas ur ljus (värme).
Vad betyder ekvivalensprincipen
END
Coriolis — inledande
funktionsbeskrivning
— BILDKÄLLA: Författarens arkiv — 15Sep2012 E32
Bild52 · Nikon D90 · Detalj — CoriolisTNED/MAC

| CoriolisACCELERATIONEN | CoriolisCELLEN
| CoriolisSTAVEN | CoriolisSATSERNA
| CoriolisCINEMA |
Kinematiska RotationsAvvikelsen | LinjenSpiralenAnalogin
| KinematiskaFRIKTIONSLÖSAParabelAnalogin
|
CoriolisEFFEKTEN |
CoriolisCELLEN |
CoriolisSTAVEN |
CoriolisSATSERNA |
CoriolisCINEMA |
Kinematiska
RotationsAvvikelsen |
|
Webben (Sep2012) domineras HELT av källverk
som INTE tycks ha observerat ovanstående komplex: CoriolisEFFEKTEN kopplar INTE
kinematiken. Se vidare utförligt i CoriolisCINEMA. |
Corioliseffekten — utförligt i härledning [CoriolisINLEDNING] från upphovsmannens beskrivningssätt Gaspard Coriolis (1835) enligt Persson 1998 (komplementär centrifugalkraft) — är i relaterad mening en strukturändring (virvlar från komplementära accelerationstryck ωv[r]) i det halvfasta materialet hos en roterande (ω) kropp — som följd av den halvfasta massans rotationsradiella rörelser (v[r]) via tillförd energi från en yttre värmekälla (värmedifferenser bildar tryckskillnader och därmed linjära strömningsvägar som triggar själva Coriolisverkan): — temperaturskillnaderna bildar strömningsvägar med radiellt linjära komponenter; radialrörelsen har EXAKT samma fysiknatur som den spinnande isdansaren som (via separat muskelenergi) reglerar spinnet genom att sträcka ut eller dra in armarna (inre variationer i impulsmomentet J=mvr); Varje lokal Radialändring (en »CoriolisARM» i formen av någon radiellt utsträckt Δx mobil massform) resulterar i en lokal CoriolisACCELERATION med en tillhörande CoriolisKRAFT; varje PAR sådana »CoriolisBASIC» bildar nollkraftsverkan (en »CoriolisCELL», kraftvektorerna tar ut varandra); Nettoändringen är att den roterande kroppens halvfasta material uppvisar virvelstrukturer; Enda uppehållande energikällan bakom CoriolisEFFEKTEN är den separat införda energikälla (Solen i Jordfallet) som förorsakar de radiella strömningarna (atmosfäriska-oceaniska skillnader i temperatur). |
CoriolisINLEDNING — Kort
inledande beskrivning
Inledande beskrivning med
komplexets delar i länkad sammanfattning — se härledningarna från Corioliseffekten.
Coriolisbegreppet I RELATERAD FYSIK
Corioliseffekten med Coriolisaccelerationen och Corioliskraften härleds UTESLUTANDE (vilket ska studeras i detalj i det följande) på RELATERAD matematisk fysikalisk grund i CoriolisBASIC enligt den enarmade svängpinnen:
— Se jämförande studieexempel i MIT-exemplet.
|
FÖRUTSÄTTNING: tallrikens rotation konstant CoriolisACCELERATIONbasic a=vn/T=(2π[r=vrT]/T0=(2πf )vrT=ωvrT)/T=ωvr Konventionellt skrivs a = –2ωvr
Coriolisaccelerationen Coriolisaccelerationen
(a[C]) är medriktad v[n] om v[r] är utåtriktad (reguljära accelerationsanalogin),
annars motriktad v[n] om v[r] är inåtriktad (inbromsning): — a[C] ska därmed, enligt ovan, upplevas av
en passagerare som färdas i en spårvagn på den roterande tallriken utmed r
med konstant hastighet v[r] och som sitter tvärs färdriktningen, med ansiktet
i tallrikens rotationsriktning (v[n]), som om spårvagnen accelererar
passageraren som om denne satt i en BIL i framsätet som accelererar på
vanligt sätt. Färdas vagnen åt motsatt håll (InMot Centrum) blir BILanalogin
för vagnpassageraren en inbromsning. — Accelerationens STYRKA i ett mätinstrument
som passagerarna kan titta på i vagnen kan också studeras av en fotograf vid
sidan av den roterande tallriken och därmed samma
effektiva resultatbild oberoende av val av referenssystem; — Verksamheten relateras i vilket fall
ALLTID till tillståndets princip. |
¯ ¯
¯ Tänk ett tåg som färdas → på rälsen ovan. Vi ser tåget ovanifrån, passagerarna med
ryggen neråt tittar uppåt. Om hela rälsen påförs en aktionskraft (↑) som låter den börja rotera (•↑) med centrum i en punkt till vänster i
bilden, känner passagerarna en motsvarande uppkommen resulterande CoriolisKRAFT (•↓) som strävar att motverka den påförda
rotationen. Om denna ska bibehållas och passagerarna fortsätta känna av
Corioliskraftens Reaktionsriktning (↓) måste den initierande rotationsunderhållande aktionskraften (↑) tillföras kontinuerligt.
CorilisEFFEKTEN i syntes kontra MAC-beskrivningarna,
Se
speciellt MACarbitraryActionReaction
— avgörande fenomenbeskrivning
— AKTIONSRIKTNING och REAKTIONSRIKTNING i Coriolisfenomenet framgår explicit och utan svårigheter direkt ur NewtonIII.
— Aktions- och reaktionsriktningarna, tillsammans med hela komplexets alla möjliga komponentuppdelningar i rotationsplanet och hur dessa sammansätts, formar sedan den mera sammansatta bilden från den enkla CoriolisBASIC i CoriolisAccelerationensEffekt;
— Med CoriolisBASIC
— den enda singulärt härledda (här benämnd) CoriolisARMEN som i figuren ovan och med sin enda LinjenSpiralenAnalogin som i figuren nedan —
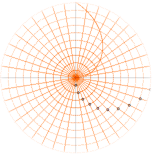
(1) aCoriolisBASIC = ωvr
kompletterad i formen av en andra (nummer två) likadan den första balanserande CoriolisArm på motsatta sidan av symmetricentrum,
ges så,
och endast så, och (vilket ska visas i det följande [CoriolisCELLEN]) uteslutande utan någon annan fysikaliskt-matematisk motsvarighet
oberoende av teorier och matematisk nivå,
ett symmetriskt avlänknings-, icke rotationsbaserat men som kan avbilda den typen också jämviktssystem med en entydigt bestämd tyngdpunkt — och därmed en idealt entydigt bestämd riktning för aktion — förorsakande (eg. underhållande/drivande) kraftverkans riktning — och reaktion — den instrumentellt fysikaliskt uppmätande kraftriktningen, alltid diametralt (differentiellt) motriktad aktionsriktningen enligt NewtonIII, se AktionReaktion, AktionskraftensDefinition, AktionReaktionCoriolisIllustrerat, AktionsRiktningsArgumentet,
MEN vilka klargörande begrepp OMÖJLIGGÖRS —
grundligt, rejält, fundamentalt — AV det uppställda VEKTORregelVERKET
i MODERN AKADEMI BegreppetVektorproduktMAC: se utförligt från
Kinematiska FRIKTIONSLÖSA ParabelAnalogin,
Figurerna nedan illustrerar hur och varför MAC inte kan koppla den
relaterade fysikens beskrivning:
relaterad fysik (TNED)
Mest Utförligt i MACaktionsriktningenCoriolis och Kinematiska FRIKTIONSLÖSA ParabelAnalogin
modern akademi (MAC)
Mest Utförligt i MACaktionsriktningenCoriolis och Kinematiska FRIKTIONSLÖSA ParabelAnalogin
VEKTORBEGREPPET I MODERN
AKADEMI GARANTERAR PORTFÖRBUD FÖR ALLA SOM FÖRSÖKER FRÅN DEN SIDAN
och vilken sammansättning på den så beskrivna Coriolisformens symmetriska jämviktsacceleration eller den
SYMMETRISKA CoriolisARMEN kan förstås lyda
![]() (2) aCoriolisJÄMVIKT = 2aCoriolisBASIC = 2ωvr
(2) aCoriolisJÄMVIKT = 2aCoriolisBASIC = 2ωvr
Detta inre partiella icke reguljärt rotationsbaserade jämviktssystem baserat på CoriolisBASIC definierar alla fysiskt möjliga ingående komponenter i hela Corioliskomplexets motsvarande föreställande rotationsplan enligt sammanställningen i CoriolisAccelerationensEffekt.
— Som visas i och framgår av den illustrerade beskrivningen i CoriolisAccelerationensEffekt, är det endast vektorprojektionerna i rotationsplanet som räknas;
Därmed, för att relatera motsvarande Corioliseffekter från motsvarande symmetriska Coriolisarmar (vilkas ideala xy-plan) som ligger vridna ur (vinklade relativt) rotationsplanet, gäller (den i meteorologin redan från William Ferrel [1858] välkända) sambandsformen, här i PREFIXxSIN
![]() (3) aCoriolisJÄMVIKT = 2ωvr
cosLLATITUDVINKELN
(3) aCoriolisJÄMVIKT = 2ωvr
cosLLATITUDVINKELN
Latitudvinkeln för Jordekvatorn är L=0° och därmed nollvärde i PREFIXxSIN för a. Max effekt gäller endast med L=90°.
— Det betyder speciellt att Corioliseffekten
— med Jorden som roterande moderkropp och Oceanerna och Atmosfären som delvis mobila Coriolisobjekt och därmed CoriolisAgenter
— är maximalt horisontell vid Jordpolerna (ingen vertikal verkan) och maximalt vertikal vid Jordekvatorn (ingen horisontell verkan).
SPECIELLT enligt relaterad fysik:
— Coriolisaccelerationens bestämmande hastighetskomponent (v[r]) gäller endast — ENDAST — radiellt i CoriolisBASIC:
Det finns ingen rätvinklig komponent till
Corioliseffekten i CoriolisBASIC:
BILDKÄLLA: Författarens arkiv · 13Sep2012 E29
Bild28 · Nikon D90 · Detalj

— Godtyckliga hastighetsriktningar (v) i rotationsplanet (den underliggande fasta rotationskroppen) delas istället upp i Corioliskomponenter (radiella •±→) och Rotationskomponenter (tangentiella •–±↑), se CoriolisAccelerationensEffekt;
— Tangentiella komponenter i CoriolisBASIC ger ingen Coriolisacceleration, endast bidrar till en ökning eller minskning i den underliggande roterande moderkroppens perifera hastighetskomponent, och därmed endast underställda de olika mobilt berörda materialpunkternas CENTRALVERKAN (centripetal inåt, centrifugal utåt) — i den roterande moderkroppens referens.
— Summan av dessa bägge — radiella och tangentiella komponenterna — kan (och får, tydligen) emellertid förstås (kunna) bilda MINDRE FRISTÅENDE föreställande, inte reguljära ROTATIONSCENTRA — här »CoriolisCELLER» — alltid motriktade moderkroppens rotation; Se (den ytterst enkla) förklaringen till dessa cirkulära komplex i
CoriolisAccelerationensEffekt, KomponentuppdelningenCoriolis.
Webben flödar över av
CoriolisVideoDemos
Speciellt genom
Kinematiska
FRIKTIONSLÖSA ParabelAnalogin
framgår TYDLIGT att en allmän KAOTISK BLANDNING florerar — speciellt på Webben (Okt2012) i form av (närmast kopiösa mängder) ”demoVideos”
”About 201,000
results”, skärmdump första sidan (förminskad) från GoogleSearch på
Video från »coriolis effect» 20Sep2012.
— som i lydig modern akademisk undergivenhet (DuttiVovve) inte kan skilja mellan RENA KINEMATISKA (rörelser utan kraftens inverkan) PRESENTATIONER och begreppet CoriolisKRAFT. Nämligen i kraft av det i dessa samtliga verk angivna sambandets form
aCoriolisMAC =
–2ω×vr = vr×2ω
............. har
inte ett spår med CoriolisKRAFT att göra, artikelfiguren
och som, verkligen, beskriver just RENA KINEMATISKA PRESENTATIONER. Se f.ö. exempelframställning i Kinematiska RotationsAnalogierna.
— Se relaterat, utförligt från MIT-experimentets resulterande framställning i
Kinematiska FRIKTIONSLÖSA ParabelAnalogin.
Alldeles tydligt är det VEKTORKALKYLENS REGELVERK BegreppetVektorproduktMAC I MODERN AKADEMI som bär skulden för beblandningarna:
— regelverket, sambandsformen ovan, tillsammans med komplexets entydigt givna vektorformer, UTESLUTER en relaterbar specifik vektorfysikalisk beskrivning av princip (genom, främst, den helt felaktigt resulterande vektorresultantens riktning, och som, här veterligt, trots många försök, är omöjlig att ändra på i komplexets givna vektorformer). Se speciellt från MACaktionsriktningenCoriolis.
— Med andra ord: CoriolisKRAFTEN kan omöjligen härledas i MAC. Och därmed heller varken förklaras eller förstås.
— Det senare intygas också i vissa, inte alla delar från de allmänna stundentleden i PerssonCoriolisSvårigheterna1998, PerssonCoriolisSvårigheterna2005.
Vi studerar det i detalj från CORIOLISKOMPLEXET.
ArgumentenMACgenerelltMekaniken — hänvisa HIT
Ba
 Argumenteringen generellt
Argumenteringen generellt
Det går inte heller från modern
akademis sida att försöka hoppa in i komplexet med GENERELLA ARGUMENT
som berör MEKANIKEN [MekanikensIndelning]
därför att hela grunden — varje enskilt begrepps begriplighet, relaterbarhet
och förklarbarhet — till fysikbeskrivningen (mekaniken som dynamik och statik)
återfaller PÅ, står och faller med GRAVITATIONENS ABSOLUTVERKAN [GTaction]:
a=[d(v=∞)GRAVITATIONEN/dT=([v=∞]/∞)/dT=(c=c∞/∞=v∞/∞)LJUSET/dT] ; ljusets
absolutacceleration
Ingår inte i MAC
Det är grunden till elektriska laddningens härledning:
F
= ma = m(c/dT) = m(c/dT)(RA)/(RA)
= Rc(m/R)(A/dT)/A
= Rc(Q/r)2 ; elektriska
kraftlagen
(m/R)(A/dT) = Q2
; m/R garanterar bevarandet av Q oberoende av variationer i m;
R finns inte i mekaniken, endast i elektrofysiken [MAFEM]
Q = √(m/R)(A/dT) ; elektriska laddningen
Ingår inte i MAC — kan inte relatera dT [och egentligen inte heller varken m eller R: dessa blandas
ihop: »massa
är ljus»]
Det är — uppenbarligen — ingen ide för
»MAC-personalen» att komma med
påpekanden SÅ LÄNGE man inte har en EGEN HÄRLEDANDE, beskrivande och
förklarande grund att komma med: PLANCKEKVIVALENTERNA
som utraderar relativitetsteorin
[PlanckEkvivalenterna KONTRA
RelativitetsTeoriN] och [ATOMKÄRNAN] [GRUNDÄMNENAS
PERIODISKA SYSTEM] [NEUTRONKVADRATEN]
[ATOMVIKTERNA]
förklarar — tydligen innefattar — MAC som
en PRIMITIV inrättning i vetenskapshistorien.
Den grunden finns inte i MAC, som vi
redan vet.
Ta den delen först — PLEASE — så kan vi
ta resten sedan.
Utförligt från GTaction.
BILDKÄLLA Ba: Författarens arkiv ·
10Sep2012 E26 Bild112 · Nikon D90 · Detalj
Flera har säkert uppmärksammat
sammanhangen …
Webben är (heller) inte helt (hopplöst) full av människor i den moderna akademins korridorer som slaviskt (eller möjligen lismeriskt [»gör du som jag säger, får du extra meriter»]) lyder den moderna akademins befallningar att [SCIAM-citatet] Corioliskraften är SKENBAR (eng., fictitious). Jämför f.ö. citaten från PerssonCoriolisSvårigheterna1998, PerssonCoriolisSvårigheterna2005, där ropen på hjälp tydligt hörs från fångarna i den moderna akademins Coriolishålor.
Källan nedan beskriver Cyklonfysiken från ett mera klart ställningstagande (Corioliskraften är verklig, inte påhittad) enligt
”Abstract. The Coriolis force is generally considered to be an artifact of viewing moving objects from a rotating frame of reference. This article examines the extent to which the Coriolis force may in fact be real in relation to its role in determining the cyclonic behaviour in the atmosphere and the ocean currents, since these very real effects cannot be explained purely in terms of an artifact.”, s1ö
http://www.cartesio-episteme.net/ep8/cyclone-new.pdf
CYCLONES
AND THE CORIOLIS FORCE — Frederick David Tombe, 2007
Related physics (TNED):
— The CoriolisFORCE is real [CoriolisORIGINAL] — as are all other »classic forces» in Nature (the presentation in this htm-document aims a detailed and thorough description). But neither the CoriolisFORCE, nor the others, can be described with the tools, ideas and concepts in the modern academy teaching system. The following is a compilation on the subject — WITH hopefully detailed comparing references.
CORIOLISKOMPLEXET i MAC
Hur MAC associerar
Coriolis med Kinematiska
Coriolis in modern academy
(deduction, discussion);
”Coriolis’s papers do not deal with the atmosphere or even the rotation of the earth, but with the transfer of energy in rotating systems like waterwheels. The 1832 paper established that the relation between potential and kinetic energy for a body, m, moving with a velocity, v0, affected by a force, P, which makes it accelerate to a velocity, v1, is the same in a rotating system as in a nonrotational”, s1378n,
European
Centre for Medium-Range Weather Forecasts
—
HOW
DO WE UNDERSTAND THE CORIOLIS FORCE?, Anders Persson (1998)
http://www.aos.princeton.edu/WWWPUBLIC/gkv/history/Persson98.pdf
— Figurer ingår. Men ingen TYDLIGT
relaterbar figurillustration till de använda vektorbegreppens RIKTNINGSFORMER
finns med.
En webbkälla som beskriver begreppet illustrerbart fattbart:
REAL
WORLD PHYSICS PROBLEMS — Coriolis Force (2009-2012)
http://www.real-world-physics-problems.com/coriolis-force.html
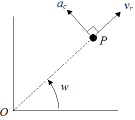
Källan ovan ger i särskild länk (något
som ska föreställa) en härledning till sambandsformen
”ac = 2w · vr”
men källtexten verkar förutsätta så
mycket underförstådda kopplingar i matematikdelen, utan utfyllande beskrivning,
att det inte framgår hur resultatbilden framträder (man kan inte följa
härledningen i någon detalj med mer än man besitter författarens nivå).
CoriolisMIT — MIT-exemplet — Paraboloidens Formfaktor
Jämför alternativt till ovanstående — riktningen för a[c]
diametralt motriktad — från MIT:
s10, Figure 6
http://paoc.mit.edu/labweb/lab5/inertial
circles/inertial_circle.pdf
MASSACHUSETTS INSTITUTE OF TECHNOLOGY —
Program in atmospheres, oceans and climate
Inertial circles - visualizing the Coriolis
force: GFD VI — John Marshall, February 9, 2003
— Källan för ett SLAGS härledande resonemang — enligt BegreppetVektorproduktMAC
vektorkalkylens begrepp i MAC — vilket
garanterar att INGEN förstår [Kinematiska FRIKTIONSLÖSA
ParabelAnalogin] — kan FÖRKLARA I DETALJ — saksammanhanget. Jämför
som konkret exempel EXPANSIONSINTEGRALEN I MAGNETISMEN:
vektorkalkylen i MAC urartar.
— DET är det tråkiga med alla (liknande) MAC-samband som poppar upp i alla (liknande)
fysikbeskrivningar: det går inte att relatera sakinnehållet — BESKRIVA
NATURFYSIKEN — med den moderna akademins termer och begrepp. Det vore
naturligtvis helt underbart fantastiskt om jag hade fel. Jag letar fortfarande
efter den (underbara) öppningen. Alltid.
Se vidare i det följande i MACaktionsriktningenCoriolis:
CoriolisAccelerationsRiktningen ovan från MIT (”–2Ω×u”) följer Reaktionsritkningen — inte
Aktionsriktningen som normalt sett BORDE ha varit fallet (vilket utmärker
RealWorld-källan som ”mera korrekt”).
Med
den ledningen framgår följande i förtydligande:
Corioliseffekten | CoriolisACCELERATIONEN
• CoriolisBASIC • CoriolisINLEDNING
• | • CoriolisSATSERNA
• Upplösningen
CORIOLISEFFEKTEN efter Gaspard Gustave Coriolis (1792–1843)
avbildar impulsmomentets (J=mvr=konstant) [RotationensVektorVerklig] interna radiella variation på bekostnad av motsvarande
aktionseffekter i en roterande kropp (m): ändringar i den roterande
kroppens radiella utsträckning r åstadkommer motsvarande ändringar i
rotationen v: CoriolisEFFEKTEN har ingenting med friktionslösa
videoexperiment mellan olika rörelsesystem att göra (men webben är fullproppad med författare som söker
ge sken av det — se särskilt från CoriolisINLEDNING om ej redan bekant):
— Utgångspunkten med den linjära rörelsen utmed r på den fast roterande masskroppen (m) avbildar samma rörelsebild som en friktionslös boll som kastas ut från centrum på en roterande karusell. Men medan den senare inte har ett spår att göra med CoriolisEFFEKTEN (radiell masspåverkan) har en fast, eller delvis fast förbunden kropp med den roterande karusellen det. Belysande exempel följer.
Coriolisaccelerationen — hur den härleds i relaterad fysik
och hur den fungerar sfäriskt
Endast rörelser relativt centrum (origo) i
rotationstallrikens egenplan räknas: ENDAST rörelser »vertikalparallellt» med
rotationsaxeln
(uppåt-neråt genom bildplanet i figuren nedan relativt betraktaren) = (SOM
PROJICERAR PUNKTER I ROTATIONSTALLRIKENS PLANYTA) är fråntagna
Corioliseffekter;
alla andra rörelseformer (SOM ALLTSÅ PROJICERAR ÄNDLIGA LINJER I
ROTATIONSTALLRIKENS PLANYTA) innefattar Corioliseffekter:

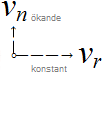
Solfjädern här indelad i 10 lika delar per 90 grader
(90/10=9°) beskriver, och illustrerar samtidigt bilden av en roterande
skivtallrik med konstant omloppstid (t0);
Koncentriska
cirklarna med
samma inbördes växande radieintervall (d) beskriver en konstant rörelse (v=d/T)
från centrum och utåt med växande händelsetid (T);
Vi som
betraktare ser
ner på den roterande tallriken ovanifrån:
— Om det på tallriken finns ett radiellt spår, en fåra, i
vilken en
vagn (mörk punkt, från ett visst tillfälle) färdas rakt ut från centrum mot
periferin med konstant hastighet (v), kan vi pricka in vagnens rörelseväg som
vi som betraktare ovanifrån ser den via konsekutiva (varandra efterföljande,
närliggande) krysspunkter mellan de radiella solfjäderslinjerna (vagnens raka
radiella färdväg på tallriken) och de koncentriska cirkelbågarna (vagnens
successivt tillryggalagda väg).
— Den
sammanhängande kurvan bildar (således, figuren ovan) en (Coriolis-) SPIRAL
[r=kx]. I huvudtexten nedan visas att spiralrörelsen innefattar en KONSTANT LIKFORMIG ACCELERATION
(konv. Coriolisacceleration): Ju längre ut vagnen hamnar, desto högre är lokala
periferihastigheten, och därmed motsvarande hastighetsökningseffekt.
FÖRUTSÄTTNING: tallrikens
rotation konstant
CoriolisAccelerationenElementärt — utförligt
nedan i Coriolisaccelerationen
och CoriolisCELLEN
Accelerationen relativt vilosystemet (bildskärmens
betraktare) varifrån tallrikens rotation studeras:
|
|
a=vn/T=(2π[r=vrT]/T0=(2πf )vrT=ωvrT)/T=ωvr Konventionellt skrivs [med ytterst svårtolkningsbara uttolkningssätt, se citat i
länkdelen] a = –2ωvr
|
— Ju mera spiralen utvecklas på TID (varv efter varv), desto
närmare kommer hastighetsresultanten riktningen v(n); Vi får direkt idealt
a=v(n)/T då v(n) tillväxer proportionellt mot T.
— Vårt referenssystem för hela komplexet är här f.ö. samma
som det referenssystem till den roterande tallriken som per fysisk mätning
talar om ATT NÅGON rotation alls föreligger: jämviktens tillstånd genom rotationscentrum
(nollpunkten [noll utsträckning, ingen kraftverkan] i mitten): RUMMET/begreppet i vilket tallriken (ses och) förstås
rotera.
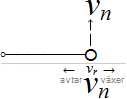
— Färdas man radiellt rakt UTÅT med konstant hastighet (v[r]) på den roterande
tallriken (v[n]) växer)
är Coriolisaccelerationen (a[C]) samriktad
v[n]:
— Färdas man radiellt rakt INÅT med konstant hastighet (v[r]) på den roterande
tallriken (v[n]) avtar)
är Coriolisaccelerationen (a[C]) motriktad
v[n]:
2012-09-14 — Upplösningens Komplikationer:
Kraftverkan
I PRAKTIKEN motverkas Tallrikens egen
rotation v[n] av (den separata kraftverkan hos) massförflyttningen v[r] enligt
impulsmomentets bevarande (J=mvr) [RotationensVektorVerklig],
på samma sätt som isdansaren minskar sin rotation genom att sträcka ut armarna
(v[r] utåt) eller ökar rotationen genom att dra in dem (v[r] inåt).
— För att bibehålla konstant rotation
för tallriken måste då en rotationsändringen kompenserande acceleration
tillföras: Lika mycket som aCoriolis tenderar att minska v[n] via v[r]UTÅT
måste tillföras för att behålla konstant v[n]. I annat fall kommer tallrikens
rotation att avstanna med v[r]UTÅT.
I ett ISOLERAT HALVFAST ROTATIONSSYSTEM
— inga yttre krafter tillförs — kan alltid ett v[r]UTÅT kompenseras av ett
(närliggande) v[r]INÅT — med motsvarande rotationssymmetriska komponenter runt
om — vilket i så fall bara bildar en omfördelning av rotationsmaterialets inre
delar: i materialet uppstår (små) mot huvudrotationen motriktade lokala
»rotationssymmetrier», se CoriolisCELLEN.
aCoriolisBASIC och aCoriolisJÄMVIKT
Härledningen ovan till Corioliseffekten (accelerationen)
beskriver bara den ena armen i ett symmetriskt (»rotationsanalogt»)
jämviktssystem — ett system med en entydig tyngdpunkt eller centralpunkt som
bevisar systemets fysikaliska, mätbara, jämvikt i symmetribegreppet.
CoriolisAccelerationen i en sådan, elementär, momentarm kräver alltså en make
till ovanstående, så att man får ett motsvarande PRINCIPIELLT jämviktssystem
— Befinner sig bägge Coriolisarmarna, baserade på samma
radiella riktning (utåt), på diametrala sidor om moderkroppens
rotationscentrum, endast fördubblas den kraftunderhållande, motsvarande, verkan
för att underhålla Corioliseffekten: 2aCorilisBASIC bromsar moderkroppens
rotation;
— Befinner sig istället bägge
Coriolisarmarna på samma sida om moderkroppens rotationscentrum, fortfarande
baserade på samma radiella riktning (utåt, bort från varandra), tar de bägge
Coriolisarmarnas enskilda krafteffekter ut varandra; ingen
extra kraft behövs för att underhålla Corioliseffekten frånsett energin utifrån som triggar radiella flödesändringarna:
2aCorilisBASIC påverkar inte enbart
omstrukturerar energifördelningen i moderkroppens rotation. Se mera
utförligt illustrerat i CoriolisCELLEN.
aCoriolisJÄMVIKT=2aCoriolisBASIC=2ωvr
— men då på sådant sätt att bägge
Coriolisarmarnas gemensamma tyngdpunkt ligger UTANFÖR den underliggande
rotationskroppens rotationscentrum (O): Dvs., hela tallriken ovan förlagd
utanför O.
— Därmed finns också i aCoriolisJÄMVIKT
en principiellt enhetligt relaterbar TYNGDPUNKT för ett »flytande
PAR CoriolisArmar»; symmetriarmarnas tyngdpunkt blir i sin symmetriskt
summerande nollkraftsform samtidigt centralpunkten för specifik atomär och
molekylär bindning (friktion i energiräkningen) till den underliggande
rotationskroppen; »Coriolisparet» i nettoeffekt visar hur det partiellt symmetrivridande
Coriolissystemet uppför sig (släpar efter) relativt det fast roterande
underlaget.
— Utan den klargörande detaljen kan en
symmetrivridande jämvikt med en (motsvarande, principiell) entydig tyngdpunkt
inte relateras i Coriolisaccelerationens ljus.
— Att begreppen med aktions och
reaktionsriktningar är välrelaterade i ovanstående härledning till
aCoriolisBASIC framgår av beskrivningen nedan i Coriolisaccelerationen
och Coriolisaccelerationens
effekt (med
vissa bekräftande paralleller till redan observerade fenomendetaljer i
vädersystemen).
— Att dessa avgörande riktningsbegrepp
däremot INTE varken kan härledas eller beskrivas med begreppen i den moderna
akademins lärosystem beskrivs ingående och exemplifierat från sektionen MACaktionsriktningenCoriolis.
Coriolisaccelerationen — WikiCoriolis — BILDKÄLLA: Författarens arkiv · 13Sep2012 E29
Bild134 · Nikon D90 · Detalj

Coriolisaccelerationen BASIC i relaterad
fysik
CoriolisEFFEKTEN efter Gaspard Gustave
Coriolis (1792–1843) avbildar impulsmomentets (J=mvr=konstant)
[RotationensVektorVerklig] interna radiella variation på bekostnad av motsvarande
aktionseffekter i en roterande kropp (m): ändringar i den roterande
kroppens radiella utsträckning r åstadkommer motsvarande ändringar i
rotationen v: CoriolisEFFEKTEN har ingenting med friktionslösa videoexperiment
mellan olika rörelsesystem att göra (men
webben är fullproppad med författare som söker ge sken av det — se särskilt
från CoriolisINLEDNING om ej redan bekant):
— Utgångspunkten med den linjära rörelsen utmed r på den fast roterande masskroppen (m) avbildar samma rörelsebild som en friktionslös boll som kastas ut från centrum på en roterande karusell. Men medan den senare inte har ett spår att göra med CoriolisEFFEKTEN (radiell masspåverkan) har en fast, eller delvis fast förbunden kropp med den roterande karusellen det. Belysande exempel följer.
CoriolisAccelerationen
i relaterad fysik
T0 = konstant omloppstid; periferihastigheten
vn = 2πr/T0 växer med avståndet r från
centrum
vr = r/T;
konstant växande avstånd (r) från centrum med likformigt växande
händelsetid (T)
r = vrT .................................. actual distance from center through constant (concentrically
extending) velocity
;
vn = 2πr/T0 ............................ peripheral velocity of rotating disc
= 2πvrT/T0
= (2π/T0)vrT
= (2πf)vrT
= ωvrT
ω = 2π/T0 = 2πf .................... constant angular velocity
;
Med
konstant växande hastighet (vn) — via konstant
vineklrotation ω — på likformigt växande händelsetid (T) ges
motsvarande konstant likformig acceleration
a = vn/T
................................ constant of acceleration
= (ωvrT)/T
= ωvr ................................. Coriolisaccelerationen BASIC
är likformig, konstant, och linjär
= ω·r/t =
ω·dr/dt = ω·(r/∞)/dt = (ω/∞)·r/dt = dω/dt
· r, conv. MINUSEuler
Acceleration, see sep. note.
= (2πf)vr
;
FC = ma .................................. CoriolisKRAFT; accelerationen (a) gånger vr-massan
Konventionellet
skrivs [http://en.wikipedia.org/wiki/Coriolis_effect]
[2012-09-08]
a = –2ωvr
Se vidare i MACoriolisNOTIS.
Kombinationen
av vagnens konstant linjära radiella rörelse (vr) på
tallriken (CoriolisTallriken) och tallrikens KONSTANTA egenrotation (vn=2πr/T0)
med allt växande periferihastighet (vn) för växande avstånd (r=vrT)
från centrum framtvingar, tydligen, en resulterande konstant acceleration (a=vn/T)
hos vagnen, rätvinkligt den radiella vagnens rörelseriktning (vr),
och i förhållande till rummet som tallriken roterar i.
—
Accelerationstrycket (hela Corioliseffekten) som påverkar vagnen i spårdiket,
är alltså en »vagnintern tallriksegenskap».
—
EFFEKTEN PÅ VAGNEN I SPÅRDIKET (en mekanisk trycksensor mellan vagnen och det
fasta spårdikets tallriksvägg) är i princip samma som om vagnen står
stilla på ett fast roterande hjul; Hjulet bringas till växande
rotationshastighet med växande händelsetid; en konstant (F=ma)
tryckkraft uppkommer på den sida av vagnen som pressar mot spårdiket som följd
av den växande hastigheten.
— Det
som bestämmer Coriolisaccelerationen är alltså huruvida vagnen alls rör
sig på den roterande tallriken. Endast om vagnen står helt stilla på tallriken
är Corioliseffekten också noll. Sedan, varje rörelsesätt, oavsett vilket,
innefattar också en distansändring relativt tallrikens rotationscentrum, och
därmed en resulterande Coriolisacceleration.
—
ENDAST OM tallrikens material är av typen »geggamoja» (med vidare, allt mera
lättrörligt [Jordens hav och atmosfär]) — så att en relativ rörelse via
rotationscentrum kan komma ifråga — kommer lokala Corioliseffekter
(Coriolisaccelerationer) att visa sig i materialet: materialet formeras eller deformeras efter
Coriolisaccelerationens lokala inverkan
[Jordens Meteorologi].
Coriolisaccelerationens effekt — från CoriolisORIGINAL
Genomgången
från HÄRLEDNINGEN visar följande allmänna situationsbilder för Coriolisaccelerationens olika riktningssätt:
vn tallrikens rotationsriktning och
aktuella periferihastighet;
vr en kropps rörelse (fast spår typ
RÄLS) i tallrikens skivmaterial;
aACTION kraftverkans aktionskomponent — den riktning i vilken tillståndets ändring
verkställs
aReACTION kraftverkans ReAktionskomponent — den riktning i vilken tillståndets ändring uppmäts; kraften vi kan KÄNNA (uppleva med kroppen), mäta och observera med tekniska mätinstrument; den s.k. tröghets(Händelse)bevisande kraftriktningen [AktionReaktion] — som MAC menar att »man måste införa för att få balans» medan det i relaterad beskrivning är NATUREN som presenterar den OBRYTBARA ENHETEN för oss
Reaktionsriktningarna
från objekt som beskriver olika rörelseriktningar inuti den roterande CoriolisTallrikens material
|
rörelse v(r) bort
från
origo |
ingen
rörelse relativt
origo |
rörelse v(r) in
mot origo |
|
|
|
|
|
Coriolisaccelerationen KÄNNS motriktad rotationen v(n) |
inget
utslag |
Coriolisaccelerationen KÄNNS medriktad v(n) |
FÖREMÅL
SOM RÖR SIG I TALLRIKENS MATERIAL föremål som HAR materiell, molekylär, atomär förbindelse
med den roterande tallriken I
GODTYCKLIGA RIKTNINGAR (v) kan med ovanstående riktningsbaser
följaktligen delas upp i sina respektive komponenter enligt nedanstående
översiktliga grundschema:
|
rörelse v(r) bort
från
origo |
ingen
rörelse
relativt origo |
rörelse v(r) in
mot origo |
|
|
|
|
|
Coriolisaccelerationen KÄNNS motriktad rotationen v(n) |
inget
utslag |
Coriolisaccelerationen KÄNNS medriktad v(n) |
|
motståndet i rörelseändringen a(CoriolisReACTION)↓ tvingar rörelsekroppen ( i CoriolisTallriken (•↑ i riktning a(CoriolisReACTION) •↓ : vilket betyder att rörelsen ( VRIDAS motsatt CoriolisTallrikens (↓•↑) : rörelsekroppens färdriktning vrids lokalt (↑•↓) : Norra
Halvklotet SYDLIG en VÄSTLIGT AVLÄNKANDE komponent |
vänster — Nedåtriktat v
— höger Enda skillnaden är att komponenten v[n] är nedåtriktad vänster vn–
höger Det innebär bara att rotationens periferihastighet
motverkas : resulterande vridningsrikitningarna
samma |
motståndet i rörelseändringen a(CoriolisReACTION)↑ tvingar rörelsekroppen ( i CoriolisTallriken (•↑ i riktning a(CoriolisReACTION) •↑ : vilket betyder att rörelsen ( VRIDAS motsatt CoriolisTallrikens (↓•↑) : rörelsekroppens färdriktning vrids lokalt (↑•↓) : Norra
Halvklotet NORDLIG en ÖSTLIGT AVLÄNKANDE komponent |
Ordningen på SÖDRA HALVKLOTET blir norra halvklotets
spegelbild (avlänkningarna i CoriolisTallriken
avbildas omvända).
— I vilket fall blir CoriolisReaktionsAvlänkningsRiktningen motsatt
tallrikens rotationsriktning.
— Se även illustrerade exempel i samband med Jordens
vädersystem i CoriolisCELLEN.
Jämför samma principiella slutresultat som ovan enligt konv. Ferrels
lag
(”Astronomical Journal in January 1858”):
”He stated what became known as “Ferrel’s Law”:
If a body is moving in any direction, there is a force
arising from the earth’s rotation, which always
deflects it to the right in the northern hemisphere, and
to the left on the southern.”,
s11m,
mhttp://www.aos.princeton.edu/WWWPUBLIC/gkv/history/persson_on_coriolis05.pdf
The Coriolis Effect:
FOUR CENTURIES OF CONFLICT BETWEEN COMMON
SENSE AND MATHEMATICS,
Part I: A history to 1885, Anders O. Persson,
2005
DEN EXTRA KOMPONENTEN ±vn endast
adderar (+) eller subtraherar (–) extra rotationshastighet till den
underliggande rotationskroppen, och därmed centrifugalkraft;
—
Inverkan av ±vn via Coriolisaccelerationen aCORIOLIS=ωKONSTANTvr
—
genom att ±vn kopplar vinkelrotationen ω=2π/T0
— får
alltså i sig en adderande (vn+) eller
subtraherande (vn–) verkan på aCORIOLIS.
v-RIKTNINGARNA UNDER ORIGOLINJEN:
—
Enda skillnaden (illustrationen ovan) med v-riktningarna som belägna
under origolinjen blir att ±vn-bidragen blir omvända och
därmed motsvarande minskning eller ökning i storleken på aCORIOLIS.
Med ovanstående grundscheman kan vi
teckna ut samtliga fall i Corioliseffekten för alla möjliga rörelseriktningar
på den roterande bastallriken.
DEN
SFÄRISKA MOTSVARIGHETEN blir alla SKUGGBILDER — vektorprojektionerna från
sfärytan — PÅ bastallriken. Inget annat.
—
Dessa ordningar motsvarar i
en grovt idealiserad mening illustrationen
som visas i Wikipedia, de allmänna vindriktningarna på Jorden —
rotationsriktningen i CoriolisTallriken ovan samma som Jordens rotationsriktning sett från
Nordpolen:
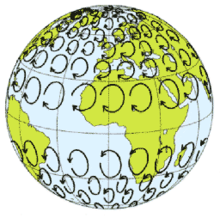
http://en.wikipedia.org/wiki/Coriolis_effect
@INTERNET
Wikipedia — Coriolis effect, Inertial circles [2012-09-11]
”Schematic
representation of inertial
circles of air masses in the absence of
other forces, calculated for a wind speed of approximately 50 to 70 m/s”,
;
”An air or water mass moving with speed
subject only to the Coriolis force travels in
a circular trajectory called an 'inertial circle'.”.
Se
dock mera utförligt beträffande den idealiseringen i WikiInertialCircle.
CoriolisCINEMA — Hur Kinematiska
(typ Foucaults
Pendel) och Kinetiska (typ CoriolisEffekten)
sammanblandas i modern akademi utan åtskillnad
CoriolisCINEMA
kinematik, rörelselära utom kraftens inverkan
kinetik, rörelselära med kraften innefattad
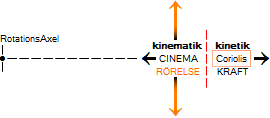
VÄSENTLIGEN i sidriktningarna FRIKTIONSLÖST utkastade projektilobjekts rörelsebanor (vi frånser den vanliga luftfriktionen i framriktningen, samt inverkan från gravitation och elektriska-magnetiska krafter) — bollar, gevärskulor, missiler etc. — som kastas ut från (centrum hos) en roterande kropp
alla som tillhör RotationsKinematiska Avvikelsen [KRA],
f.ö. i huvudsak (nära) samtliga webbpresentationer i ämnet Corioliseffekten (Sep2012) [WebCoriolisVIDEO]
— har INTE — inte — med Corioliskomplexet att göra;
— det kan klargöras, belysas, jämföras och studeras — noga — i denna presentation [CoriolisSATSERNA]:
De friktionslösa exempelframställningarnas rörelseobjekt — kastade bollar, gevärskulor, missiler etc. — ansluter SAMTLIGA till Kinematiken: läran om rörelsen utom kraftens inverkan (»BIO» eller »CINEMA» [MOVIE]).
— Det är INTE Corioliseffekten: CoriolisEFFEKTEN (enligt Gaspard Coriolis 1835) bygger uteslutande helt på existensen av en i den roterande kroppen halvfast (vätska, gas) materialmassa — Kinetik — som (via energi från en yttre/separat källa) kan uppvisa rotationsradiella rörelser. Dessa rörelser ansluter till INRE VARIATIONER I IMPULSMOMENT J=mvr — samma fysik som gäller för den spinnande isdansaren som reglerar rotationen genom att sträcka ut eller dra in armarna (J=mvr=konstant): Flyttas massa utåt (större r) måste spinnet (v) avta proportionellt för att bevara J konstant.
Det finns ingenting sådant i den rent kinematiska beskrivningen. Alla framställningar som inte klargör den detaljen, bidrar enbart till en vidare fördjupad förvirring i beskrivningen av Corioliskomplexet;
Giltigheten av Kinematiska
och Corioliska — CoriolisCINEMA
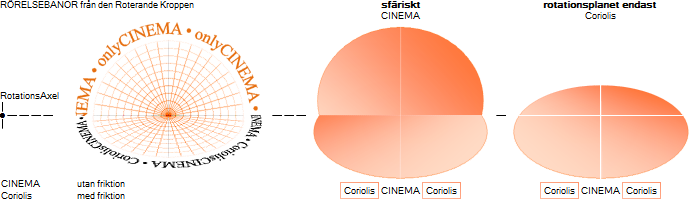
Bilden ovan illustrerar hur den rent kinematiska (CINEMA a=dv/dt) rörelsebeskrivningen förhåller sig till Corioliskomplexet (Coriolis F=ma); Corioliskomplexet [CoriolisSATSERNA] innefattar till skillnad från kinematiken (Läran om kropparnas rörelse utan kraftens/massan inverkan) också Coriolismassan, kinetiken, med dess koppling till den underliggande rotationskroppen (kinetiken; Läran om kropparnas rörelser med massan inkluderad);
— I PRINCIP varenda upphittat exempel på webben (Sep2012) verkar helt absorberad av CINEMA-delen: Inget omnämnande verkar finnas som, ens, påtalar sammansattheterna, än mindre relaterar dem;
— Man gör UTESLUTANDE beskrivningar
— med reservation för ev. missade bidrag som inte direkt syns bland de främsta
— som använder KINEMATIKENS FRIKTIONSLÖSA SFÄRISKA CYBERRYMD typ kastade bollar, roterande kanontorn (»missilMatte»), gevärövningar, baseballkast, osv.
Alla dessa friktionslösa=CINEMA-bidrag kan med Jordytan som Experimentbas sammanställas på följande enkla fenomenbas (vi bortser här — till att börja med — från luftfriktionen helt och hållet, vilket också är WebbExemplens utgångspunkt [att ta med friktionsfaktorn [luft] betyder ytterst omständlig matematik, jämför det linjära fallet med Fritt fall med Luftmotstånd i integralexemplen]):
NORTH geoEARTHgraphicPREFERENCE • NORTH
geoEARTHgraphicPREFERENCE • NORTH geoEARTHgraphicPREFERENCE • NORTH
geoEARTHgraphicPREFERENCE • NORTH geoEARTHgraphicPREFERENCE •
Kinematisk
exempelbeskrivning
|
|
VID
EKVATORN: En projektil med viss utgångshastighet lämnar en mynning (eng. muzzle)
vid t0 och når målet efter T; under T hinner Jordkroppen MED REFERENS TILL
DEN FÖRORSAKANDE SITUATIONSBILDEN — tillståndet
under dt vid t0
— vrida sig en viss vinkel på distanstiden T mellan KällaMål, den här
förenklat terminologiserade FlyDISTANCE-sträckan. — Det
har ingen betydelse åt vilket håll mynningen pekar; ↔↨; —
CINEMA-avvikelsen i vinkel, och därmed det enkla tangensförhållandet, kan
användas idealt för små projektila KällaMålavstånd relativt Jordradien för
att beräkna grundvärdet vid ekvatorn. För alla de övriga lokaler som ligger
närmare polerna går avvikelsen mot noll genom en i PREFIXxSIN sinusfaktor SinL°. Se vidare i
huvudtexten. |
NORTH geoEARTHgraphicPREFERENCE • NORTH
geoEARTHgraphicPREFERENCE • NORTH geoEARTHgraphicPREFERENCE • NORTH
geoEARTHgraphicPREFERENCE • NORTH geoEARTHgraphicPREFERENCE •
Kinematiska RotationsAvvikelsen [KRA Kinematic Rotational Aberration —
corresp. term in MAC here unknown] —
Tillämpningsexempel i Hur MAC associerar
Coriolis med Kinematiska
Kinematiska RotationsAvvikelsen Se även generellt i Kinematiska
RotationsAnalogierna
— gäller i alla idealt g-fria tillämpningar mellan roterande
system och linjära utkastningar av rörelsekroppar som INTE har någon materiell
(atomär, molekylär) koppling till rotationskroppen
s = tan(360°T/T0) · FlyDISTANCE ...........................
idealt friktionslösa
linjära metriska avvikelsen
— alltid västerut (motsatt Jordrotationen)
om sanna målbilden EFTER T
För små vinkelvärden ges praktisk taget identiska resultat för vinkelvärdet via tan(aRAD)=aRAD=2πT/T0=Tω;
— Se vidare i efterföljande härledning med grund i bågdelarnas matematik.
:
|
Om man inte kompenserar för inskjutningen [aPRAD] upp mot
Polerna, skulle samma avvikelse [aRAD] iakttas för samtliga fall, streckade
vertikallinjen över tallriken, oberoende av plats på Jordytan, eller på den
roterande tallriken; — En bestämd Kinematisk Rotations Avvikelse vid Ekvatorn
(R0) för en given projektil händelse (P), blir helt säkert NOLL vid
rotationspolerna: ingen avvikelse kan finnas där. — Därmed funktionen (i PREFIXxSIN) via aPRAD med avtagande avvikelse mot
Polerna. |
Units
in The INTERNATIONELA M(eter)K(iloGram)S(econd)A(mpere)-system: De ENKLA enhetsgrunderna är ALLTID (de allra mest) krävande: s/2πR = aRAD/2π = A°/360° = T/T0 = s(P)/2πr(P) ; s/R0 = aRAD aRAD = s(P)/r(P) ; Ovan endast vid Ekvatorn (L°=0);
BågAvvikelsen s[P] (analogt s) avtar in mot rotationscentrum: sinL°s[P]; R/R0
= sinL° i PREFIXxSIN; aPRAD(R/R0) =
s(P)/r(P) ;
aPRAD avtar
från MAX vid Ekvatorn till 0 vid Polerna: = s/R0 = aRAD ; För en viss projektil händelse
som flyttas omkring på Jordklotet (Ekvatorn[R0]Latitud° = 0, NorraSödra
±90°): s(P) = aPRAD(R/R0)r(P)
; aPRAD-tiden
är samma som aRAD-tiden: = (2πT/T0)(R/R0)r(P) = (T)(2π/T0)(R/R0)r(P) = (T)(ω)(R/R0)r(P) = ω/R0·TrPR ; Om lokalen flyttas omkring på Jordklotet är R = R0sinL° Jorden(ω/R0) = 2π/R0T0
= (6,2831853)/(6,378 T6 M)(86164 S) =
1,14332 t11 M–1S–1 = HzRAD/M = TrP · ω
· sinL° ;
Kinematiska
RotationsAvvikelsen
GällerSFÄRISKT (CINEMA) Eller med v(P)=r(P)/T, likvärdiga = T2vP ·ω · sinL°
; Kinematiska
RotationsAvvikelsen
GällerSFÄRISKT (CINEMA) Med ovannämnda likhet för små vinklar kan också den
numeriskt ekvivalenta formen användas: sP = rP · tan(360°T/T0) · sinL° Jorden(ω) = 2π/T0 = (6,2831853)/(86164 S) = 7,29212 t5 HzRAD (2piHz) Förhållandet mellan
båglängd (s) och korda (k): (k/2)/R = cos(A/2) ; k = 2Rcos(A/2) ; cos(A/2) = √(1–sinA)/2 [FrånTrigFunc11] [‡] = 2R[(1–sinA)/2]1/2 = R[2(1–sinA)]1/2 ; s = aR ; s/k = aR/2R[(1–sinA)/2]1/2 = a/[2(1–sinA)]1/2 = a/[2(1–sina)]1/2 = (A°π/180°)/[2(1–sinA)]1/2 För små vinklar blir sinusvärdet i PREFIXxSIN svårhanterligt (mindre än
0,01 grad ger sinus = 0): = aR/2Rcos(A°/2) = a/2cos(A°/2) = (A°π/180°)/2cos(A°/2) Säkraste räknemetoden för
små A-värden; = πA°[360°cos(A°/2)]–1 ; För A=0,01° ges s/k = 1 på en äldre niosiffrig kalkylator. För A= 0,1° ges
s/k = 1,0000001 på en
äldre niosiffrig kalkylator. För A= 1° ges
s/k = 1,0000126 på en
äldre niosiffrig kalkylator. ——————————————————————————————————————————— (11); sinA–sinB = –2cos[(A+B)2–1]cos[(A–B)2–1] ; B = 0; sinA–1 = –2cos[A/2]cos[A/2] = –2cos2[A/2] ; 2cos2[A/2] = 1 – sinA ; cos2[A/2] = (1–sinA)/2. |
Vinkelvridningen (R°) som Jorden utför med grundreferens till en lokal på ekvatorn är i vilket fall alltid densamma — oberoende av åt vilket håll siktet är inställt:
R° = 360°T[FlyTIME]/T0[EarthSIDEREALperiod=86164 S]
Det enda som skiljer de övriga lokalerna åt från ekvatorns preferens, är HUR vinkelrummets öppning — störst vid ekvatorn — bestämmer den aktuella avvikelsen.
EXEMPEL:
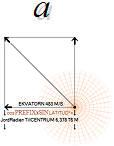

— En baseballspelare VID EKVATORN (a i figuren ovan) slår en baseboll 100 meter på T=4 sekunder; bollen lämnar utslaget (»projektilmynningen») vid t0 med hastigheten 25 M/S (90 KM/h);
— Under de 4 sekunderna hinner Jordkroppen — och därmed SIKTET (b i figuren ovan) vid t0 — vrida sig vinkeln
R° = 360°T/T0 = 360°(4S)/(86164 S) = 0,0167123°;
— SIKTET VRIDER SIG UR SYFTET (tillståndet under dt vid t0) med det beloppet.
Avvikelsen (s) i sidled vid ekvatorn med AimedAT och Actual blir, idealt via tangensrelationen,
sEKVATORN = tanR° · 100 M = 0,0291684 M ~ 3 cM
För en lokal vid 60:nde breddgraden (grovt Finland-Sverige-Norge) blir motsvarande Kinematiska RotationsAvvikelse mindre med en faktor sin60°=0,5. Alltså, runt 1,5 cM.
Ytterligare
exempel på en författare som — tydligen — blandar ihop Coriolisverkan med
Kinematiken:
Jämför Persson 2008 s1373sp2ö:
”it can even affect the outcome of baseball tournaments:
a ball thrown
horizontally 100 m in 4 s in
the United States will, due to the Coriolis force, deviate
1.5 cm to the right.”.
Persson får
det resultatet men genom att hänvisa till Corioliseffekten (konv. PREFIXxCOS) via motsv. (konv. PREFIXxCOS) sinL=0,5 vid (som vi
förmodar) 30:nde breddgraden (Jacksonville, Florida, New Orleans, Houston).
— I relaterad mening [CoriolisSATS4] har Corioliseffekten ingen roll att spela i dessa sammanhang.
Det är det rent KINEMATISKA
resultatet av hela rörelsebilden — inga som helst anspråk på några »verkande
krafter» finns där.
— ÄVEN om Basebollen kastas 100
meter rakt upp i luften mot en målpunkt VID t0 eller vilken som helst annan riktning
— begreppet om Syftet som finns i Vårt Föreställande vid
t0 under dt, själva den utgångsmässiga Orsaksbilden till det påföljande
händelseförloppet i Kausallogiken
— vrider sig Jorden LIKVÄL samma motsvarande ~3cM vid ekvatorn;
— Vi kan använda den förenklade bilden för samtliga utkastningsRiktningsfall så länge målavstånden är små (vardagsmått i idrottssammanhang främst för att reducera den annars mera komplicerade inverkan av tyngdkraften på föremål som har stor FlyTIME, motsvarande elliptiska satellitbanor) i förhållande till Jordkroppen.
Resultatbilden ovan Kinematiska RotationsAvvikelsen [KRA] har — med andra ord — ingen
som helst koppling till CoriolisEFFEKTEN.
Tillståndet
under dt vid t0:
VEKTORERNA ANSTÄLLS I INCIDENSPUNKTEN vid t0; vektorernas resultanter utpekar
händelseförloppet i varje efter t0 påföljande tidsintervall.
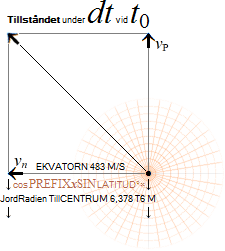
Frånsett friktionen i
projektilriktningen,
och som i vilket fall bromsar v(P) med FlyTIME-tiden, samt
frånsett gravitationen och ev. elektriskt-magnetiskt verkande krafter:
Coriolisverkan [CoriolisBASIC]
bygger HELT på inre vr-variationer
i en kropps impulsmoment
(J=mvr):
Energin som förorsakar variationerna måste komma ifrån någon
yttre källa.
— Genom att utkastade — Jordmassan minus m-objektet — (projektila = satellit-) objekt (P) vid Jordytan (i vindstilla) HELT SAKNAR FRIKTIONSBASERAD KONTAKT med den omgivande luften [CoriolisSATS4] — det finns, vad vi vet, ingen SIDOBASERAD friktionsfaktor som BINDER P till Jordkroppen — och följaktligen därmed också HELT saknar varje form av fysisk bundenhet till Jordkroppen,
existerar heller inget kriterium för P att gälla via Coriolisverkan:
— Corioliseffekten i relaterad fysik gäller [CoriolisSATS4] INTE för utkastade föremål i luften på Jordytan.
— Rörelsebanor på Jordytan för utkastade objekt bestäms följaktligen ENBART av gravitationskraften, eventuella elektriska-magnetiska krafter, RotationsKinematiska Avvikelsen [eller Kinematiska RotationsAvvikelsen] och P-objektets normalriktade luftfriktion (den som bromsar v[P]). Inget annat;
— Se vidare förtydligande satsbilder med jämförande exempel i CoriolisSATSERNA [Hur MAC associerar Coriolis med Kinematiska].
CoriolisSTAVEN — vridmomentet hos
en utsträckt
CoriolisMassKROPP — sambandsformen till CoriolisSATS5
CoriolisSTAVEN — vridmomentets (E=Fd=mad) accelerationskomponent — sambanden nedan från CoriolisACCELERATIONENS basmatematik
—————————————————————————————————————————————————
Ett
Coriolisobjekt
måste på ett eller annat sätt
kunna återföras på en HALVFAST (flytande) FORM (spårvagn på fast monterad räls; materialflytande
massträngar) relativt det roterande underlaget för att en RÖRELSE —
CoriolisEFFEKT — i detta ska komma i fråga:
vn1→•→vn2: v=d/T ;
vn1 = ωr1 ;
vn2 = ωr2 ;
r2 = r1 + Δx ;
:
aC1 = vn1/T = ωr1/T = ω(vr1T)/T = ωvr1 ;
aC2 = vn2/T = ωr2/T = ω(vr2T)/T = ωvr2 ;
= ω(r1 + Δx)/T
= ωr1/T + ωΔx/T
= ω(vr1T)/T + ω(vΔxT)/T
= ωvr1 + ωvΔx
= ω(vr1 + vΔx) ;
aC2–aC1 = ωvr1 + ωvΔx – ωvr1
= ωvΔx ; Accelerationsfaktorn till CoriolisSTAVENS vridmoment
CoriolisSTAVENS vridmoment (idealt förenklat ETORQUE=mωvΔxΔx/2) bestäms av en FLYTHASTIGHET (vΔx) hos Coriolisstavens material;
Flythastigheten (vΔx)
beskriver hur Coriolisstaven formändras — flyter — per tidsenhet (sträcks ut eller dras ihop — som
molnstrimmor, eller linjärt
utsträckta vattenkoncentrat [täthetsvariationer via t.ex. salthalt
och/eller varierande temperatur]).
Med en allmän genomgång av Coriolisämnets olika detaljer (från CoriolisORIGINAL), som uppvisat avgörande klargöranden, har beskrivningen lett fram till ett antal förtydligande »Coriolissatser» — de följer ur varandra från CoriolisORIGINAL (Gaspard Coriolis två teorem, enligt Persson 1998) — och som (här veterligt alldeles) stringent, säkert och KLART beskriver hela fenomenformen i detalj, vad Coriolisverkan går ut på och INTE går ut på — för varje vidare prövning:
— Corioliseffekten
från upphovsmannen Gaspard Coriolis
(1835) [Persson 1998]
beskriver som det får förstås
en komplementär centralkraftsverkan (↓•↑→m[C]): En massform (Coriolismassa m[C]) som uppvisar radiell rörelse inom en roterande kropps eget material — och därmed (i slutänden) uppvisar en omfördelning (i allm. lokala virvlar i den roterande kroppens rotationsplan endast [CoriolisIll]) i rotationskroppens materiella struktur — uppfyller kriteriet på Coriolisverkan, och därmed en mätbar/observerbar CoriolisEFFEKT;
— För att en radiell massrörelse (Coriolismassan enligt CoriolisSATS1) ska komma ifråga inom en (fast) roterande kropp, måste obönhörligen
en påtaglig (mätbar) friktionsfaktor finnas som garanterar att Coriolismassan dels INTE är stelt förbunden med den underliggande rotationskroppen och DELS heller INTE är friktionslöst frikopplad ifrån den;
— För att Corioliseffekten i CoriolisSATS1 ska kunna visa sig måste med andra ord en Coriolismassa kunna flyta i sin bindning till den underliggande rotationskroppen för den avgörande radiella rörelsens anställning;
— CoriolisSATS2 framställer i andra ord Coriolismassans egenskaper:
icke med det roterande underlaget fast förbunden kropp; Men Coriolismassan CoriolisSATS2 måste ha någon materiell kontakt — friktion — med den underliggande rotationskroppen; Coriolismassan måste följaktligen, obönhörligen vara en
icke friktionslöst fristående kropp från det roterande underlaget;
— Så beskriver med åter andra ord specifikt enligt CoriolisSATS2&3 Corioliseffekten uteslutande en
massomfördelning (Coriolis) inom ett roterande material (som isdansaren som reglerar spinnet med armarna: inre ändringar i ett konstant impulsmoment J=mvr). Med andra ord:
— INTE massutkastningar:
— inte ivägslungade tennisbollar, fotbollar, missiler, gevärskulor eller andra liknande UTKASTADE ELLER NEDSLÄPPTA idealt friktionslösa SATELLITKROPPAR TILL JORDEN;
— För dessa nämnda typer, se Kinematiska RotationsAvvikelsen.
— Ett speciellt exempel [Hur MAC associerar Coriolis med Kinematiska] exemplifierar hur (väl) matematikdelen ansluter till en motsvarande Coriolistolkning i MAC.
I
Corioliseffekten frigörs aldrig Corioliskroppen (eller
CoriolisELEMENTET) från den underliggande rotationskroppen;
— OM så sker, upphör — tydligen — samtidigt
Coriolisverkan:
— ingen sammanlänkande kraft finns då längre med den
underliggande rotationskroppen (CoriolisSATS3).
Stel Corioliskropp (Spårvagn) på
fast räls på roterande kropp — CoriolisSATSERNA

BILDKÄLLA: Författarens arkiv · 5Jul2012 E14
Bild109 · NikonD90 Detalj
— En spårvagn på en fast monterad radiell räls på en roterande skiva är ett utmärkt exempel på hur Coriosverkan fungerar, kan påvisas och uppmätas: CoriolisBASIC (härledningen till kraftgrunderna via CoriolisAccelerationen).
Flytande Corioliskropp genom
flytande omgivning
— Mera komplicerat (men med samma principiella verkan) utpekas (vidsträckta) vattenflöden och luftflöden på Jordytan [CoriolisIll], eller generellt halvfasta ämnens materialändringar under rotationens inverkan som fenomen där Coriolisverkan finns med.
— Också ett löst rullande hjul, eller en kula som får rulla ut på en roterande karusell innefattar Coriolisverkan.
— Däremot utpekar exemplen med utkastade bollar och projektiler — objekt som frikopplas från det roterande underlaget — INTE CoriolisEffektbaserade fenomen CoriolisSATS3 (oaktat att matematiskt beskrivande LIKHETER finns, se CoriolisCINEMA).
— En Coriolismassa CoriolisSATS1 som inte är stel CoriolisSATS3 måste tvunget utveckla en inre flytande formgräns (Δx, CoriolisSTAVEN) med en motsvarande ideal (linjär) formändringshastighet (vΔx) mellan (idealt och minst) två metriska ändpunkter ab (aΔxb);
— Eftersom Corioliseffekten idealt härleds i mekaniken [CoriolisBASIC] på en stel mobil masskropps tyngdpunkt (typ spårvagn på fast räls) vars masskropp färdas (v[r]) på en fast räls på en underliggande rotationskropp (ω), kan varje utsträckt (flytande) formkropp uppfattas som ett intervall (Δx) av mellanliggande tyngdpunkter (atomer, molekyler, materialzoner); varje individuell form(tyngd)punkt har sitt särskilda r-avstånd från rotationscentrum — och därmed sin särskilt kopplade periferihastighet (v[n]=2πr/T[0]=ωr) [idealt via konstant vinkelrotation (ω) som betyder växande v(n) med växande r] och därmed med en inom formkroppen varierande uppsättning v(n)-värden;
— Med en flytande Coriolismassa SÅ uppdelad på enklaste sättet i respektive (minst två) ändområden
— en del a och en del b med olika — väsentligen skilda — avstånd (r) från den underliggande rotationskroppens rotationscentrum och därmed olika perifera hastighetskopplingar (ωr), och därmed en inbördes skillnad i Coriolisacceleration
— besitter den flytande Corioliskroppen följaktligen kriterium, och endast då, för att uppvisa
vridande moment enligt CoriolisSTAVEN.
CoriolisSTAVEN som agent för den motsvarande parsummerande nollkraften i CoriolisCELLEN, kan då förstås genom ett motsvarande par flytande Coriolismassor CoriolisSATS1 med inbördes motriktade radiella rörelseriktningar — eller ett SYSTEM bestående av ett godtyckligt antal sådana par (beroende på molekylär upplösning).
Notera också Corioliseffektens (ytterst) ringa magnituder i fallet med Jordytans atmosfär:
— Vinkelfrekvensen (2πf, »HzRAD») för Jordrotationen (ett varv per ett stjärndygn) är ca 7,3 t5 = 2π/(86164 S) ; Corioliseffekten kan i Jordfallet bli som störst vid ekvatorn , och då i vertikal led (CoriolisAccelerationens effekt); Är vindstyrkan på något vertikalt ställe 25 M/S (stormstyrka) blir motsvarande CoriolisAcceleration
a=ωv[r]=(7,3 t5 HzRAD)(25 M/S)=1,825 t3 M/S2=0,001825 M/S2
— Den enligt relaterad fysik (CoriolisSATS4) enda möjliga praktiska tillämpningen för den typen kan bara vara av rent meteorologisk (eller möjligen Galaktisk) art: omfattande massområden som formändras relativt långsamt baserat på samverkan mellan många små bidrag i (ytterst) små delar.
— Jämför däremot (här) i en grovräkning på situationen i en förbränningsmotor: detaljen med vevaxeln och kolvstångens kullager som roterar excentriskt på vevaxelinfästningen i en motor på högvarv, säg 10 000 rpm ~ 167 varv per sekund eller avrundat ω=1047 HzRAD; Är kolvstångens kullager 5cM i diameter, avverkar lagrets periferi sitt varv på T0=1/167 S, med periferihastigheten v=2πf·(0,025 M)=(1047 HzRAD)(0,025 M)=26,175 M/S ~ 26 M/S; Är lagerkulorna 1/10 av lagerperiferin (5mM-stålkulor) — vilket betyder att deras radiella topphastighet blir max 1/10 av kolvstångslagrets periferihastighet — ges tydligen en Coriolisacceleration a=(1047 HzRAD)(26/10 M/S)=2722,2~2722 M/S², eller runt 277,5 g (1g=9,81 M/S²). Eftersom lagerkulorna rör sig symmetriskt motsatt omkring lageraxeln, ↓•↑, påverkas inte vevaxelns rotation något av LagerCoriolisKraften. Men det inre av kolvstångens lagerdel (CoriolisReaktionskrafternas inverkan), den närmast vevaxeln, gör det (inte helt ringa); reaktionskrafterna utpekar ett extra materialtryck, ett »axelpress» just där lagerkulorna uppvisar största radialhastigheten i vevaxelrotationen. En 5mM kullagerkula har massan grovt 1 gram (0,001 KG), och Corioliskraften just då kulan passerar »lagerradiella vevaxeltoppunkten» i exemplet blir F=(0,001 KG)(2722 M/S²)=2,722 N, eller runt 0,277 KP; ungefär som tyngden av ett glas vatten. Med reservation för felräkningar.
Jämför Webben (15Okt2012) [Kinematiska RotationsAvvikelsen]:
”Q: What are some examples of practical application of the Coriolis effect?”,
”A: It is extremely important to account for the Coriolis effect when considering projectile trajectories, terrestrial wind systems, and ocean currents.”,

Hur MAC associerar Coriolis
med Kinematiska — ExempelKoll
Jämför Kinematiska RotationsAvvikelsen i PREFIXxSIN:
sP = TrP · ω · sinL°
= T2rP/T · ω
· sinL°
= T2vP · ω
· sinL°
= vP ω sinL° · T2 ;
Kinematiska RotationsAvvikelsen i meter;
— Formen ansluter till nedanstående upphittade
Webbkällas exempelutveckling — källan
hävdar att
sambandet innefattar Corioliseffektens inverkan och medverkan
”(2) find the ”frst-order” corrections (i.e., terms proportional to Ω) to this solution. Let's call these
corrections rc(t) and vc(t), since they are due to the Coriolis force.”, s1m;
enligt, källan s2ö i PREFIXxCOS,
(bildkopia nedan från källans PDF-dokument),
![]()
THE
EFFECTS OF THE CORIOLIS FORCE ON PROJECTILE TRAJECTORIES, Mona Berciu, s2ö
http://www.phas.ubc.ca/~berciu/TEACHING/PHYS206/LECTURES/FILES/coriolis.pdf
”For an object in motion with respect to
the Earth, the largest
non-inertial force is the Coriolis force 2mv×Ω, where Ω
is the angular velocity of the Earth around its North Pole - South Pole axis
(of magnitude 2π/24h).”, s1ö; Författaren använder specialtecken som inte finns på vanliga
datorer [vektorpilar över termerna — suitYourSelf].
:
I relaterad mening blandar författaren (varenda MAC-skolad person, utan
undantag) ihop Coriolisverkan [CoriolisSATSERNA]
med Kinematiska RotationsAvvikelsen [KRA]
(samma matematiska form, se ovan); ett objekt i RÖRELSE relativt Jorden
besitter ingen kraftkoppling till Jordkroppen enbart på rörelsens grund,
och därmed heller ingen Coriolisverkan [CoriolisSATS4];
rörelsebanan, frånsett gravitationens inverkan och friktionen i framriktningen,
har, tydligen, ENBART Kinematiska RotationsAvvikelsen som matematisk
beskrivningsgrund.
;
Vi använder bara z-lösningens del (v[x]=0), alltså med projektilutkastningen rakt upp från Jordytan (författarens figur sidan 2: y-riktningen österut och x-riktningen söderut), samt bortser ifrån g-termens bidrag (vi avhandlar inte den sammansättningen i den enkla Kinematiska AvvikelseAnalogin). Det ger återstoden i PREFIXxSIN
yc(t) = – t 2·v0,z Ω
sin λ ; projektilavvikelsen
i MAC — påstås Coriolisbaserad
och vilket vi med Ω=ω, v0,z=vP och λ=L ser är alldeles samma matematik som Kinematiska AvvikelseAnalogin
sP =
T2·vP ω sin L° ; projektilavvikelsen i TNED — Kinematiska RotationsAvvikelsen
har inte med Coriolisverkan att göra
Och därmed, tydligen:
— ”Corioliseffekten i samband med projektilbanor” i MAC uppvisar, tydligen, samma matematiska form som i den betydligt
enklare Kinematiska RotationsAvvikelsen i TNED.
BILDKÄLLA: Författarens arkiv · MONTAGE: 2Okt2010 Excur9R Bild7RV; 4Jul2012 E13 · Nikon D90 · Detalj

Och alltså [CoriolisSATS4]:
— Exemplet visar tydligen HUR man resonerar matematiskt
i MAC (”perturbation theory”) för att —
tydligen felaktigt, se CoriolisSATSERNA
[CoriolisSATS4] — påstå eller »komma
fram till att» Coriolisverkan skulle ha något med projektila utkastningar att
göra. Uppenbarligen INTE så.
— Exakt samma sambandsform: s = T2vPω
sin|cosL.
Alldeles tydligt är det att MAC blandar ihop grundbegreppen Coriolis- CINEMA- [CoriolisCINEMA] — friskt, dessutom.
Observera alltså (också) OMRÅDET FÖR FENOMENETS GILTIGHET [CoriolisCINEMA] som ytterligare komplicerar överblicken för varje normal trottoarbefolkning:
Coriolisverkan [CoriolisBASIC] antar bara komponenter i rotationsplanet [se illustration i CoriolisCINEMA] — inga rotationsaxelparallella komponenter — medan Kinematiska RotationsAvvikelsen [CINEMA] antar ALLA möjliga komponentriktningar (gäller helt sfäriskt).
— Skiljer man inte dessa begrepp åt, är det, här veterligt och som exemplet ovan tycks visa utomordentligt klart, ren allmän huggsexa som gäller. Se även vidare, mera klargörande i definitionsgrunderna, i CoriolisSATSERNA.
Motsvarande klargörande har eftersökts i den tillgängliga etablerade litteraturen på webben (Okt2012) men inte påträffats.
”Answers from sources you can
trust”.
TellMeAboutIt.
— Föremål som utan en fast förbindelse med det fasta roterande underlaget (CoriolisSATS3) FAR GENOM LUFTEN — i våra vardagsexempel — uppvisar uppenbarligen noll Coriolis Friktion: ingen Corioliseffekt CoriolisSATS2: objekten följer med i det markbundna lufthavet genom att UTESLUTANDE uppvisa luftfriktion i NORMAL — rakt på — till rörelsebanan:
— det finns ingen Coriolisbaserad luftfriktionsfaktor (CoriolisSATS2) som tillståndskopplar en typ missilprojektil till den halvfasta materialkropp som Corioliseffekten kräver; Corioliseffekten berör bara roterande material (CoriolisSATS1) som kan flyta (vätskor, gaser CoriolisSATS3) (eller som kan kraftkoppla via gravitation och/eller elektricitet), eller fasta föremål som verkställer radiella rörelser (inre ändringar i impulsmomentet J=mvr), typ den spinnande isdansaren som reglerar spinnet genom att dra in eller sträcka ut armarna, eller via den markfasta rälsen spårvagnen som färdas utåt eller inåt centrum på den roterande karusellen [CoriolisBASIC].
De allmänt populära CoriolisFöremålen [WebCoriolisVideoDemos] ansluter istället till den (föga väl kända, som det verkar, men här för den uttömmande uppgiften fullständigt beskrivna) RotationsKinematiska Avvikelsen (CINEMA) [KRA]: hur en separat — till det roterande underlaget ICKE materiellt kopplad (dvs., helt fristående) — rak rörelsebana avviker VISUELLT från en roterande kropp.
— Jag skulle för egen del vilja påstå att ORSAKEN till villervallan HELT ligger på den moderna akademins UNDERVISNINGSINDOKTRINERADE idéer om INERTIALSYSTEM:
— Istället för att fatta fysikbeskrivningen från ett tillstånd — begrepp — envisas man i MAC med att leta efter OBJEKT I FYSIKEN för tillståndsbegreppet (som man därmed missar, inte förstår) — ett motsvarande fysiskt »inertialsystem». Det finns inga sådana i relaterad fysik. [FUNTOP]: Fysiken relaterar till jämvikt. Inte till system. Lagarna gäller inte I systemen, utan FÖR dem. Jättesvårt. Newton fattade det (Ändringslagarna). Sen blev det — tydligen — värre.
— Det är »trevlighetsbegreppen generellt» som
handlar om Kausalitet, Tröghet (INERTIE), Aktion, Reaktion, grundbegreppen om massa
(gravitation)
och rörelse (acceleration) — och som, tydligen,
blivit SÅ illa sargade i den moderna akademins korridorer med början under
1800-talet att snart sagt halva Planeten knäar under bördorna: För att få säkra
underlag, måste vi studera ämnet genom noggranna jämförelser och exempel.
Notera särskilt (vilket är lätt att glömma i dessa sammanhang):
— FRITT FALL betyder kraftbundenhet, och därmed en (mycket) mer komplicerad matematisk beskrivningsbild än den motsvarande (ytterst) enkla i RotationsKinematiska Avvikelsen (CINEMA) [KRA]. Den senare kan, alltså, INTE användas (direkt) för att bestämma »den sedvanliga östliga kinematiska avvikelsen» i experiment som behandlar fritt fallande kroppar (i typ djupa gruvschakt):
— Centrifugalkraften med Jordytans g-fysik som referens (från experimentlokaler allt utom exakt på ekvatorn), initierar fallet snett relativt g-centrum (med följd i en [stor, se citat nedan] sydlig avvikelse om experimentet utförs på Norra Halvklotet); sedan, vidare i fallet, beror det (möjligen) på den lokala gravitationens inverkan (närliggande bergsmassivs olika sammansättning får allt större inverkan med allt längre fallsträckor [om det gäller precisionsmätning på millimetrar i slutänden]: ovissheten om exakt vilken g-miljö det är man experimenterar i, utpekar att experimenten blir ytterst äventyrliga — om det gäller exceptionellt långa fallsträckor); det som återstår blir, veterligt, något helt annat än en motsvarande ideal Kinematisk RotationsAvvikelse.
Jämför experimenten från omkring 1843 (kontroversen i Mechanics Magazine som beskrivs i boken Zetetic Astronomy: Earth Not a Globe, Samuel Birley Rowbotham, 1881 i nyutgåva 2007, Fogotten Books):
Med det man får läsa i den boken uppdagas följande (som vanligt i MAC …):
— Föga får man veta i den normalt tillgängliga litteraturen om den bakomliggande (ytterst intressanta) dramatik som experimenten, och kontroverserna, belyser (förutsatt beskrivningen är trovärdig).
— Det man (jag) främst noterar är omnämnandet av en STOR sydlig avvikelse i 1800-talets berömda experiment med fallande tyngder i djupa gruvschakt — uppgiften att påvisa Jordens rotation:
s240ö | p316:
”Greater faith is to be placed in the experiments of Professor Reich, in a pit of 540 feet, at Freiberg. Here the easterly deviation was also found in good agreement with the calculated result; but a considerable southern deviation was observed. The numbers obtained were means of experiments which differed much among themselves.”,
s240n | p317:
”The whole of the bullets and plummets dropped south of this datum line, and so much to the south that only four of the bullets fell upon the platform placed to receive them, the others, with the plummets, falling on the steps of the man-machine, on the south side of the shaft, in situations, which precluded exact measurements of the distance being taken.”,
ZETETIC
ASTRONOMY: EARTH NOT A GLOBE, Samuel Birley Rowbotham, 1881
i
nyutgåva 2007, Fogotten Books — min avskrift från icke textkopierbar
Webbsökning [2012-10-15]
Styckena
finns alternativt på kopierbar Webbkälla särskilt i
http://www.sacred-texts.com/earth/za/za54.htm
DEFLECTION
OF FALLING BODIES
från
ett mera omfattande register — tydligen hela originalboken från 1881 i
http://www.sacred-texts.com/earth/za/index.htm
SACRED
TEXTS — Internet Sacred Texts Archive (2011)
MAC-personalen blandar —
tydligen — ihop partierna ända ifrån upprinnelsen under 1800-talet:
Källan nedan påstår att man fått överensstämmande värden mellan teori och experiment sedan 1832 via fria fallexperiment
(158,5 M fritt fall, Freiberg [Se Webbkällan ovan] latitude 50,9119 °N) — där Corioliseffekten INDIKERAS figurera (exakt citat på den punkten fattas här);
”The mean eastward deviation of its experiments is 2.8 cm. This value corresponds exactly with the theoretical one predicted by Laplace and Gauss expression at Freiberg latitude where experiments were conducted.”,
”This study provides a criterion above which we can distinguish between lift force and Coriolis deviation during a free fall experiment.”,
http://meeting.aps.org/Meeting/DFD12/Event/177997
Källan ger bara åtkomst till Abstract-stycket.
Författare i den rika världens högskolekorridorer, uppbyggt på axlarna av världens fattiga människor genom imperialism, slavhandel och usla bostäder för den arbetande befolkningen, och som, verkligen, menar att man måste BETALA SÄRSKILT för att få tillgång till den helt gratis påstådda existerande ExperimentNisses privata Coriolisekvationer, ingår, uppenbarligen, inte i den här avhandlingen.
Den som har något att visa andra eller berätta om som berör kunskapen, gör det självklart gratis — med stor glädje. Om samhällena inte klarar av den grundliga attityden, är det nog inte mycket bevänt med resten heller (»barnen ska själva betala för skolbänkarna»).
CoriolisCINEMAEND.
EulerCoriolis
Persson
2005 omnämner (s15mn)
”Sprung
does not seem to have been aware that Leonard
Euler already in 1749 derived
analytically what was essentially the Coriolis
acceleration (fig. 13).32”.
De
led Persson citerar
[”2(dr/dt)(dφ/dt)
+ r(d 2φ/dt2)”, φ förmodl. radianvinkel, sägs inte
uttryckligt, men går att sluta sig till av Eulers samband i källans fig. 13]
är
[något
långdraget — vi kommer, veterligt, att förlora oss i kalkyltermer som helt
ligger utanför ämnet: Persson påstår
”Fig.
13. Leonard Euler’s 1749 derivation of the Coriolis acceleration (2drdφ)
and the so-called Euler
acceleration
(rddφ), which is the acceleration
due to variations in the
angular velocity.”;
Med
radianvinkeln φ=s/r, s en del av cirkelbågen med radien r,
ges likvärdiga
drdφ=drd(s/r)=(dr/r)ds=d(r/r)ds=d(ds)=d 2s,
och
vilket vi från grundfysiken [ACCELERATIONSBEGREPPET] (vägens andraderivata)
vet
är formellt (Eulers allmänna diskussion i leden framgår inte) samma som
(differentialformens ena del till) den linjära, likformiga
accelerationens grundbegrepp;
Med
Eulers beteckningar (Perssons citat),
”...
ou bien 2drdφ + rddφ = 0”; Euler sätter alltså, om man
ska tolka hans matematik som den står,
–2drdφ
= rddφ, eller –a1=a2 med här
okänd innebörd;
Med
andra ord, tämligen långt ifrån någon direkt Corioliskoppling]
långdraget
kopplat till den specifika typformalian i härledningen till
Coriolisaccelerationen (slutformen a=ωv): ingen direkt analogi
framskymtar (liknande termer ingår); Det verkar å andra sidan vara den
enda HISTORISKT refererande källformen till benämningen ”Euler” i samband med
faktorerna i Corioliseffekten:
— Det
ser ut som (här, i brist på mera precisa källverk Sep2012) att termen ”Euler”
har introducerats långt efter Euler som en senare modern akademisk
transkription ([begrepps]överföring) med grund i den likartade
matematiska formalia som Leonhard Euler behandlade i sin »Ballistiska
Matematik»;
Eulers
Mechanica 1736, samt Eulers översätta verk från en ’Benjamin Robins bok
i ämnet’ (boktitel***) i olika översättningar perioden 1745-1783 — inkluderat
turbulenta bitterheter mellan olika nationella läger, ref. , s3 i
http://www.maa.org/editorial/euler/how euler did it 38
cannonball curves.pdf
HOW
EULER DID IT — Cannonball curves, Ed Sandifer, 2006
*** källans referens [R1]
[R1] Robins, Benjamin, Remarks on Mr. Euler’s Treatise of Motion, Dr. Smith’s compleat
System of Optics, and Dr.
Jurin’s Essay on Distinct and Indistinct
Vision, London, 1739
Medan
formen a=ωv (möjligen) på visst (långdraget) sätt kan
utläsas ur det man citerar från Euler (1749), behandlade Euler veterligt
ingenting av den explicita problematik som fått namn av den senare Gaspard
Coriolis arbeten (1835, CoriolisBASICfrånGaspardCoriolis).
—
Wikipedia skriver för sin del (Sep2012):
”In
classical mechanics, the Euler acceleration
(named for Leonhard Euler), also known as azimuthal acceleration[1]
or transverse
acceleration[2], is the fictitious tangential
force that is felt as a result of any radial
acceleration.”,
http://en.wikipedia.org/wiki/Euler_force
@INTERNET
Wikipdeia — Euler force [2012-09-27]
;
”The direction and magnitude of the Euler acceleration is
given by:
dω
aEuler = – ———— × r
dt
where:
ω is the angular velocity of rotation of the reference
frame;
r is the vector position of the point where the
acceleration is measured relative to the axis of the rotation.
”,
http://en.wikipedia.org/wiki/Euler_force
@INTERNET
Wikipdeia — Euler force, Euler acceleration [2012-09-27]
;
”The
surface of the Earth is a rotating reference frame. To solve classical mechanics problems
exactly in an Earth-bound reference frame, three fictitious forces must be
introduced, the Coriolis force, the centrifugal
force (described below) and the Euler force.”,
”The
Euler force is typically ignored because its
magnitude is very small.”,
http://en.wikipedia.org/wiki/Fictitious_force
@INTERNET
Wikipdeia — Fictitious force, Fictitious forces on Earth [2012-09-27]
Som
vi ser är enligt relaterad fysik principformen ovan ”dω/dt
· r” »principiellt densamma» i differentialformer som i slutformen
för Coriolisaccelerationen i CoriolisBASIC enligt CoriolisEffekten
aCoriolisBASIC = ω·r/t = ω·dr/dt = ω·(r/∞)/dt = (ω/∞)·r/dt = dω/dt · r
Som
visas utförligt i CoriolisINLEDNING, specifikt i matematisk syntes i Kinematiska FRIKTIONSLÖSA
ParabelAnalogin, skiljer sig
EMELLERTID den relaterbara samhörigheten i begreppen högst betydligt:
MAC-begreppen
EulerAccelerationen aEULER = –(dω/dt)×r
och
EulerKraften FEULER =maEULER =–m(dω/dt)×r
KAN
ENDAST FRAMSTÄLLAS I MODERN AKADEMI PÅ DESS VEKTORKALKYLS BegreppetVektorproduktMAC REGELGRUND, exemplifierat enligt relaterad fysik
aCoriolisMAC =
–2ω×vr = vr×2ω
............. har
inte ett spår med CoriolisKRAFT att göra
Se utförligt i Kinematiska
FRIKTIONSLÖSA ParabelAnalogin
För RIKTNINGEN —minustecknet i WikipediaCitat — se WikiCoriolisRIKTNINGARNA —
Corioliseffekten är den motsatta
:
— Med
andra ord — i DEN RELATERBARA FYSIKENS LJUS — framstår MAC-meningarna i ämnet
Corioliskomplexet som rena tokföreställningar om FYSIKEN
GROVT SETT KORREKTA SAMBAND serveras — men på
en BESKRIVANDE LITTERÄR BAS som rent ut sagt förefaller gestalta rena dårhuset.
Se sammanställt länkblock för TRE vidare
exempeljämförelser i Kinematiska RotationsAnalogierna.
(kinetiken,
rörelse MED kraft) och som främjas i MAC via KINEMATIK — rörelsebeskrivning utan
kraftens inverkan. Se särskilt i Kinematiska FRIKTIONSLÖSA ParabelAnalogin; Terminologin i MAC garanterar med andra ord att
ämnet inte varken kan beskrivas eller förklaras.
—
Don’t even THINK about it. No way. (Jag överdriver, naturligtvis, men något åt
det hållet).
—
Finns inte en chans i MAC att kunna relatera sammanganget i någon som helst
begripbar mening — alla sätt (OrsakssammanhangetCoriolis), veterligt, har testats här, och inget har befunnits
gynnsamt för MAC:
— Det
är, tydligen, enbart relaterad fysik [CoriolisBASIC] med den grundläggande, avgörande och fullständigt
klargörande och beskrivande förankringen i GRAVITATIONENS ABSOLUTVERKAN [GTaction]
— finns inte i MAC — som sammanknyter, förenar, beskriver, härleder och
framförallt förklarar hela Corioliskomplexets väv av I DEN MODERNA AKADEMINS LÄROSYSTEM helt
obegripliga — rent vardagsabsurda [KraftbegreppetMAC] [Alla krafter
overkliga] — begrepp (»krafter är
skenbara» CitatFM1975s72).
Och, därmed: MODERN AKADEMI FÖRKLARAS av egen förskyllan PRIMITIV INFÖR
NATURFYSIKEN.
Så:
— Den
moderna akademins ”Euler Acceleration,
aEULER =–(dω/dt)×r ”
må
vara vad den vara må, men har, tydligen och väl relaterbarligen, ingen som
helst varken teckenmässig eller relationsmässig koppling till den relaterade
fysikbeskrivningen av Coriolisaccelerationens singulära momentarm, som ovan
aCoriolisBASIC = dω/dt · r
MAC-framställningarna
i ämnet utpekar således framställningssätt med
speciellt klargörande beskrivning i Kinematiska FRIKTIONSLÖSA ParabelAnalogin, tydligen exceptionellt väl relaterbart sagt, HELT BASERADE PÅ KINEMATISKA ANALOGIER, på
MAC-vektorkalkylens formalia: Kinematiska FRIKTIONSLÖSA ParabelAnalogin. Och den har — tydligen — ingen som helst begripligt relaterbar
koppling till FYSIKFENOMENET i
Corioliskomplexet, oaktat förekomsten av ”likartade termer”.
MÅNGA
I MAC-KORRIDORERNA
HAR (nog) HELT SÄKERT REDAN GJORT DESSA REFLEXIONER — men funnit sig maktlösa
inför det allmänna (enormt svulstiga) regelverk som antagits i och av
modern akademi med grund i 1800-talets uppfinnarnit — samt med största
säkerhet också missat gravitationens grundläggande begreppsbas i hela ämnet,
och som — verkligen — kräver en AtomkärnansHärledning för att fullständiga DET EFFEKTIVA FÖRSVARET FÖR
angreppsattackerna från MAC i argumentkonfrontationerna: elektriska laddningens
härledning (se syntes från DivergensensAbsolutAcceleration i GTaction), och som garanterat INTE ingår i MAC, men som, galant,
förklarar hela fysiken — eller i varje fall hittills inte har svikit harmonin i
helhet, min undersökning enligt UniversumsHistoria.
Se
även sammanställd kortare syntes i ArgumentenMACgenerelltMekaniken, med vidare hänvisningar till de olika avsnitten.
Eulers Kraft och Eulers Acceleration
är fiktiva fabrikationer i modern akademi — ingen relaterbar fysikbeskrivning
För
min (alldeles) egna del skulle jag själv om det gällde att försöka precisera
framställningarna
— i
FÖREGIVENHETEN att ens försöka blanda in Leonhard Euler i CoriolisBASIC — enligt ovan
citerade MAC‑vektortekniska
propå ”Euler Acceleration” och ”Euler Force”
—
INTE göra den kopplingen. Inte alls över huvud taget.
—
Leonhard Euler avhandlade (1749) INTE, vad vi vet, trots ”associerade termer”,
de senare problemställningar som fått namn av Gaspard Coriolis (1835).
— Å
andra sidan, OM formen dω/dt · r — med Leonhard Eulers terminologi som garanterat är
helt frikopplad från den moderna akademins 1800-talsbaserade vektornit –(dω/dt)×r — av här ej känd
historisk koppling verkligen ansluter till något parti i Eulers (omfattande)
beskrivningar, ÄR det tydligt att förste man på plan var Leonhard Euler,
och att i så fall
aCoriolisBASIC = dω/dt · r
ÄR
Coriolisaccelerationens fundament (EulersACCELERATION) — med, som
omnämnts ovan, garanterad frikoppling från den moderna akademins begrepp.
—
Tills vi få närmare vetskap i den saken, används här också fortsättningsvis
endast den konventionella benämningen Coriolis enligt CoriolisEffekten.
— Men vänta:
”In
classical mechanics, the
Euler acceleration (named for Leonhard
Euler), also known as
azimuthal acceleration[1] or transverse
acceleration[2], is the fictitious
tangential force that is felt as a result of any radial acceleration.”,
http://en.wikipedia.org/wiki/Euler_force
@INTERNET
Wikipdeia — Euler force [2012-09-27]
— Det
är ju på pricken Eulers acceleration enligt det härledda i CoriolisBASIC
aCoriolisBASIC = ωvr
—
Enligt vilken framställning då?
Kolla:
ORDEN
”Euler acceleration” »IS THE» ”transverse acceleration”
är, tydligen som det får förstås, bara en odefinierad kvarleva — spökbegrepp — av
det NATURLIGA UPPFATTANDET i människans naturliga förståndsförmågor i
samvaron med naturfysiken, tydligen, och som INTE kan kuvas av
MAC-vektorregelverkets ”aEULER =–(dω/dt)×r”, MEN SOM HELLER KAN VARKEN FÖRKLARAS ELLER BESKRIVAS AV
eller via DETTA MAC-vektorregelverk BegreppetVektorproduktMAC:
1. MAC-vektorregelverket BegreppetVektorproduktMAC här närmare beskrivet i MACreactionCoriolis och Kinematiska FRIKTIONSLÖSA ParabelAnalogin
kopplar
INTE till CoriolisBASIC — av det första enkla skälet att Coriolisaccelerationen inte kan beskrivas enligt
vektorbilden ovan:
— vr
går
inte genom något förment »Corioliscirkelns rotationscentrum» (ett sådant centrum omnämns heller här veterligt inte
specifikt i MAC):
— Det
finns ingenting sådant i relaterad fysik som den ovan avbildade
vektorfiguren [Jämför CoriolisCELLEN];
—
Vinkelfrekvensen (rotationen) ω=2πr/T0= 2πf
har enligt CoriolisCELLEN (jämviktsformen) från CoriolisORIGINAL inget
specifikt, partikulärt, »Corioliscentrum»: det går inte att härleda något
sådant — eftersom begreppet »rotation» i Coriolisverkan beror på en samverkan mellan utspridda Corioilismassor,
och den samverkan kan te sig på flera olika sätt, se CoriolisCELLEN (t.ex. utbrutna,
närliggande, normalt sett i rotationsterminologin rotationsperifera delar av
typen ![]()
![]() : det är ingen rotation)
: det är ingen rotation)
—
FENOMENET med Corioliseffekten har i relaterbar mening tydligen
ingen koppling till vektorfigurkonceptet ovan — Se även ytterligare
förtydligande i MACreaktionCoriolis, CoriolisAccelerationensEFFEKT, speciellt förtydligat i CoriolisCELLEN och CoriolisSTAVEN.
— CoriolisBASIC beskriver
kraftverkan/accelerationen på en (1) momentarm [CoriolisARMEN]
(vnr, Keplermomentets del i Impulsmomentet
mvr) med centrum i
moderkroppens rotationscentrum, inte med centrum utanför denna.
— Man
kan, således i det beskrivande ljuset, inte, inte alls över huvud taget,
illustrera eller beskriva Corioliseffektens komponenter med ovanstående MAC-vektortekniska
1800-talsuppfinning. ForgetIt. ALL. Se även jämförande beskrivning i Kinematiska FRIKTIONSLÖSA
ParabelAnalogin.
CoriolisFYSIKEN fungerar inte så: ett
separat rotationscentrum existerar inte.
MAC-vektorgreppet
raserar beskrivningssättet.
Så; Enligt vilken framställning då? Visa.
2.
Wikipediacitatet i
http://en.wikipedia.org/wiki/Fictitious_force
@INTERNET
Wikipedia — Fictitious force, Fictitious forces on Earth [2012-09-27]
med
”The
surface of the Earth is a rotating reference frame. To solve classical mechanics problems
exactly in an Earth-bound reference frame, three fictitious forces must be
introduced, the Coriolis force, the centrifugal
force (described below) and the Euler force.”,
låter
oss tydligen förstå att ”Coriolis force” och ”Euler force” är SKILDA fenomen.
Detta stämmer inte med invändningen ’Det är ju på pricken Eulers
acceleration enligt det härledda i CoriolisBASIC’; Dessutom klargörs uttryckligen i ovan citats
efterföljande mening att
”The Euler force is typically ignored because its magnitude is very small”
Dvs.;
”Euler force” bortses ifrån »på grund av dess ringa inverkan».
—
Alltså kan MAC-personalen
(här Wikipediaförfattarna) INTE med EulerFORCE, verkligen, mena CoriolisBASIC, aCoriolisBASIC=ωvr, främst därför att dessa
tydligt, Wikipediacitatet ovan, beskrivs som skilda, olika komponenter, och
dels därför att OM man ändå identifierar dem med varandra, den sista citatdelen
i så fall leder till konsekvensen att också stryka Corioliskraften ur bilden,
och därmed ingen framställning alls.
Så; Enligt vilken framställning då? Visa.
3. MAC-Centralens ActionReactionKraftVEKTORBEGREPP
GENERELLT med [AktionReaktionMAC-citatet
Sep2012] ”The
attribution of which of
the two forces is action or reaction is arbitrary. Each
of the two forces can be considered the action, the other force is its associated
reaction.” eliminerar effektivt varje
begriplig naturbeskrivning av riktningsordningen i UNDERHÅLLANDE kraft (som
kräver energi för att hålla verksamheten vid liv) och MÄTANDE kraft (som
vi kan Känna, och bygga praktiska mätinstrument för att få ut mätvärden ifrån
under idealt maximalt korta tidrymder i alla möjliga olika variabla situationer).
—
ORSAKEN TILL Denna detalj i MAC ansluter, tydligen som det får förstås, till
KAUSALORDNINGEN: Fysikens lagar i MAC anses reversibla [‡Citat5].
Se (syntes i) AktionReaktion med utförliga arbetsexempel i ENTROPIBEGREPPET
I RELATERAD FYSIK [Kausalordningen] [Utförliga
Arbetsexempel], och som visar hur
rent ut sagt YTLIG — direkt primitiv, outvecklad, ofokuserad på
avgörande detaljer — den moderna akademins skolade tankeintelligens är:
man påstår helt galna (eg., och relaterbarligen, förståndsmässigt outvecklade)
saker om hur fysiken verkar och inte verkar.
Helt enkelt så (den följande formuleringen finns INTE
i modern akademi, garanterat, men modern akademi ter sig så):
— Det
får inte finnas någon kausalrelaterad, orsaksbeskrivande, detaljerad
naturanalys i MAC; Hela verksamheten i MAC, ända från början under
1800-talet, bygger på den föresatsen, att det är människan som har skapat
matematiken [MatematikCitatetMAC], [Herrefolkscitatet]: MAC är i
den egna 1800-talets självinbillade legendens tankerike intelligensens högsäte.
Inte Naturen. Frankt uttryckt: det ska inte finnas någon ”förklaring”
till något. Det är den krassa konsekvensen av MAC-attityden: du får
fråga, men du får aldrig ett begripligt svar.
Så; Enligt vilken framställning då? Visa.
Och
alltså:
—
Vadå ”Det är ju på pricken Eulers acceleration enligt det härledda i CoriolisBASIC”?
Visa.
(Ju mer man avtäcker i ämnet, desto mer
liknar MAC [andra
litterära/filmatiska beskrivningar av/i] ett långt gånget dårhus — du vet,
valda representanter för åt vilket håll överheten anser att underheten ska
marschera kring Centralen — typ klockvridningar — och så där, medan
genierna hålls säkert fängslade i underjorden. Den enda ljuspunkten verkar vara
utvecklingen av integrerade kretsar: Internet).

Det finns en punkt, ett tillfälle, när
besättningen inser att det enda rätta sättet är att överge Skeppet, sjösätta
Livbåtarna.
MAC har (tydligen) i grunden aldrig intresserat sig för
begreppet naturvetenskap, [MatematikCitatetMAC], [Herrefolkscitatet], även fast det är just den mest prominenta aspekt som
brukar framhållas i de etablerade litterära verk som behandlar vetenskapshistorien.
Det är snarare möjligheten att få
framstå som signifikant person [Herrefolkscitatet] — inte upptäckterna som sådana, själva inblicken
— som verkar vara det mest angelägna i MAC, det som underhåller själva verksamheten. Vi vet att det
finns undantag. Förhoppningsvis i växande.
Hänvisa hit [EulerCORIOLIS].
MACoriolisNOTIS — COLIOLISACCELERATION I RELATERAD FYSIK
Bakgrunden till CoriolisFramställningen i detta
htm-dokument
Konventionellet
skrivs [http://en.wikipedia.org/wiki/Coriolis_effect]
[2012-09-08]
a = –2ωvr
:
Men härledningen till den delen sammanhänger INTE [har eftersökts men ännu inte
påträffats Sep2012] med någon direkt beskrivning av »sammanhanget»: man
åberopar allmänna RESULTAT FRÅN BegreppetVektorproduktMAC
VEKTORALGEBRAN I MAC — som vi
1. redan VET från MAGNETISMEN är »korrumperat»: se särskilt praktiskt noggrant exempel
i EXPANSIONSINTEGRALEN;
2. själva dessutom kan kontrollera URARTAR I det
relaterbara
VEKTORBESKRIVNINGSSÄTTET: förtydligat per jämförande, klargörande, exempel i Kinematiska FRIKTIONSLÖSA ParabelAnalogin
från MIT-exemplet;
— ingen mera ENKEL (typ ovan från Corioliseffekten) härledande webbkälla har ännu upphittats som (PER LEDANDE
BESKRIVNING) kan reda ut frågetecknet;
— Wikipedia har på sin artikel [Coriolis effect 2012-09-08]
[http://en.wikipedia.org/wiki/Coriolis_effect]
i sektionen Causes ett resonemang [Citat]
som delar upp motsvarande 2ωvr i en del TID(ωvr)
och en del RUM(ωvr) — och (MEN) som på Wikipedias sedvanligt
högskolemässiga sätt endast är (eller verkar vara) förbehållet
begriplighet för typen A-födda: Det finns ingen relaterad förklaring
(undervisningen för vanliga B-födda finns inte med).
— FÖRKLARINGEN (antydd av wikipdeiaartikeln) skulle (då,
möjligen) vara en KOMBINATION av OLIKA REFERENSSYSTEM.
— Uppställningen ovan (såvitt korrekt, se härledningen från CoriolisEffekten) redovisar att en
sådan referenssystembaserad förmodan saknar fysisk grund.
— Det är något som inte stämmer här (i MAC).
Jämför:
”The same velocity (in an inertial frame of reference
where the normal
laws of physics apply) will be seen as different velocities at different times in a
rotating frame of reference.”,
http://en.wikipedia.org/wiki/Coriolis_effect
@INTERNET Wikipedia — Coriolis effect, Causes
[2012-09-08]
Ingen relaterad referens ges. Påståendets innebörd oklart.
— Se vidare nedan i wikipediacitatet på artikeln Fictitious
force.
Enligt Persson [1998,
s1373sp2n.ekv.(1)],
European
Centre for Medium-Range Weather Forecasts
—
HOW
DO WE UNDERSTAND THE CORIOLIS FORCE?, Anders Persson (1998)
http://www.aos.princeton.edu/WWWPUBLIC/gkv/history/Persson98.pdf
PerssonCoriolisSvårigheterna2005
Se även Persson 2005 i en historisk överblick av
Corioliskomplexet — de vetenskapliga debatterna (som fortfarande pågår ...),
”The deflective force due to the earth’s rotation, which is the key to the explanation of many phenomena in connection with the winds and the currents of the ocean, does not seem to be understood by meteorologists and writers on physical geography—William Ferrel1”, s1ö,
”The development up to 1885 can be treated as historical since the problems have been resolved.
However, those discussed since are still unsolved or at least controversial.”, s16n,
”The crux of the matter does not lay in the mathematics but in our common senses which are still Aristotelian.”, s17ö,
http://www.aos.princeton.edu/WWWPUBLIC/gkv/history/persson_on_coriolis05.pdf
The Coriolis Effect:
FOUR CENTURIES OF CONFLICT BETWEEN COMMON
SENSE AND MATHEMATICS,
Part I: A history to 1885, Anders O. Persson,
2005
:
”If the particle is not
stationary but moves (Vr) relative to the rotating system, it appears to be affected by an
additional force F = –2mΩ×Vr”,
;
”The cross product indicates that F is perpendicular both to the
relative motion Vr and to the rotational axis Ω. For this reason, and not only because the force is
inertial, the Coriolis force does not do any work, i.e. it does not change the speed (kinetic
energy) of the body, only the direction of its motion. The statement that the Coriolis force “does
not do any work” should not be misunderstood to mean that it “doesn’t do anything”4.”.
s2ö.
framkommer typformen 2ωvr ur en »mera
allmäniserad vektoralgebra»:
”(dB/dt)f = (dB/dt)f + ω×B (1)
The procedure is to apply (1) first to the position vector r, then to its velocity v to get the relative velocity vr, combine the expressions, and arrive at an expression for the absolute acceleration a,
a = ar + 2ω×vr + ω×(ω×r) (2)
which for a rotating observer is composed of the observed acceleration ar; the Coriolis acceleration
2ω×vr, which only depends on the velocity; and the centrifugal acceleration ω×(ω×r), which only depends
on the position”,
källan som ovan.
— Också härledningen i svenska Wikipediaartikeln om Corioliseffekten ansluter (Sep2012) till ovanstående.
;
man löser, tydligen i MAC, INTE EXPLICIT (Coriolis-) uppgiften från det
typ ovanstående illustrerade sammanhanget, utan extraherar lösningen (–2ωvr)
ur »mera allmängiltiga ekvationer».
— Det finns, tydligen i MAC, ingen explicit beskrivande koppling till
sammanhanget.
(Dvs.: ingen i MAC kan, tydligen, ge
en ämnesrelaterad beskrivning). Sökningen på webben fortsätter.
— Då blir det också svårt (omöjligt)
att RELATERA differensen — såvitt ingen kan relatera den EXPLICIT.
TNED aC = ωvr ............................... aktionsriktad
en separat massa utmed r på fast räls
:
TNED: Enda sättet att härleda den underliggande kraftfysiken med
KORREKT RELATERADE aktions och reaktionsriktningar
MAC aC = –2ωvr ........................... reaktionsriktad — aktionsriktningen saknar beskrivning
Olika webbkällor beskriver Corioliseffekten på olika sätt
”a deflection of moving objects when they are viewed in a
rotating reference frame”, [WikiCoriolis]
http://en.wikipedia.org/wiki/Coriolis_effect
@INTERNET
Wikipedia — Coriolis effect [2012-09-15]
Direkt från Google (»what is coriolis effect») [2012-09-15]:
”An effect whereby a mass moving in a rotating system experiences a
force perpendicular to the direction of motion
and to the axis of ...”;
:
MAC: Ren kinematisk beskrivning
— som våldför sig på den
underliggande kraftfysiken
Wikipedia skriver för sin del på
artikeln Fictitious force,
”The factor of two in the Coriolis force arises from two equal contributions: (i) the apparent change of an inertially constant velocity with time because rotation makes the direction of the velocity seem to change (a dvB/dt term) and (ii) an apparent change in the velocity of an object when its position changes, putting it nearer to or further from the axis of rotation”,
http://en.wikipedia.org/wiki/Fictitious_force
@INTERNET
Wikipedia — Fictitious force, General derivation [2012-09-08]
Som framgår från CoriolisORIGINAL:
— Corioliseffekten baseras INTE på
visuella, friktionslösa, kinematiska analogier — typ den ovan citerade
Wikipedias framställning [WikiCoriolis2]:
Vi kan därför, i sak, INTE bemöta de olika påståendesatser som
WikipediaFörfattarna framför i någon relaterad koppling till Coriolisverkan.
Det betyder bara att Wikipediameningen ovan med
— ”en
synbar ändring hos en inertialt konstant hastighet med tiden”
— ”because rotation makes the direction of the velocity seem
to change”
— och ”en
synbar ändring i hastigheten hos ett objekt när dess position ändras”
”putting it nearer to or further from the axis of rotation”
— här veterligt HELT saknar varje form
av någon relaterad begripbar referens i Coriolissammanhanget.
(Författarna refererar uppenbarligen till något för den
naturvetenskapligt orienterade läsaren obekant, underförstått, kinematiskt komplex.
Det hör inte hit).
— Wikipediaartikelns härledningsblock
är (för övrigt), speciellt tydligt i detta sammanhang, så ofattbart komplicerat
i förhållande till saksammanhanget, Corioliseffekten, Coriolisaccelerationens
härledning (här efter CoriolisORIGINAL),
att man knappt tror det är sant: maximal abstraktion utan någon som helst
direkt relaterbar beskrivning.
Vi vet redan genom exempel EXPANSIONSINTEGRALEN I MAGNETISMEN att
vektoralgebran i modern akademi (milt sagt) är korrumperad i de rent fysiska
åsyftningsgrunderna, att man INTE kan nå fysikbeskrivningen GENERELLT på
den vägen.
— Vi vet också, redan, att begreppet INERTIALSYSTEM
har renderat ett särskilt omfattande beskrivningskomplex i modern akademi,
tillsammans med vektoranalysen.
— Dessa två tillsammans garanterar att beskrivningarna
generellt i MAC, och som refererar dessa komplex
INERTIALSYSTEM och ALLMÄNNA VEKTORALGEBRAISKA SAMBAND blir garanterat omöjliga
att förstå i någon som helst LOGISKT BEGRIPLIG mening.
— EMELLERTID finns inget EXPLICIT
klarläggande i huruvida också skrivsättet med 2ωvr (kontra det
enklare resultatet med ωvr från Coriolishärledningen)
skulle vara ett resultat av just den allmänna språkförbistringen i MAC. (Det
behöver [nämligen] inte vara något fel på algebran ...).
— Det förefaller (nämligen) speciellt
märkligt att den enkla EKVIVALENTEN i hela Coriolisaccelerationens (elementära)
härledning,
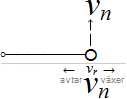
INTE skulle vara KLAR därmed att denna
uppenbarligen på det allra enklaste sättet i SPIRALBILDEN direkt ger a=vn/T,
|
|
a=vn/T=(2π[r=vrT]/T0=(2πf )vrT=ωvrT)/T=ωvr Konventionellt skrivs a = –2ωvr
|
och därmed DIREKT a = ωvr
— inte a = –2ωvr = –ωvr
+ –ωvr.
Det behövs, tydligen, en vidare analys för att klargöra den
detaljen.
— Hur gick det då [MACoriolisNOTIS],
kunde orsaken till den gåtfulla MAC-skrivningen med –2ω klarläggas?
— DELVIS JA genom Kinematiska
Friktionslösa ParabelAnalogin — uppslaget från MIT-experimentet. Rent algebraiskt ges
full klarhet i den bilden: vi kan nu, i detalj, relatera HUR MAC får fram sin
bild — nämligen genom [Kinematiska
RotationsAnalogierna] att blanda ihop Kinetiken (CoriolisVerkan) [KRAFT] med Kinematiken
(FoucaultPendeln,
Kinematiska RotationsAvvikelsen) [RÖRELSE]
via VektorKalkylen (MACvektorFelen).
— Det är emellertid ÄNDÅ EN KLEN TRÖST för det praktiska
sammanhanget; Det verkar snarare som att man sökt JUSTERA sambandsformen –2ω EMPIRISKT — genom 1800-talets
segslitna debatter i Coriolisämnet (Persson2005).
Det finns dock, här känt (ännu Okt2012), inga citerbara källor i ämnet som kan
klargöra den detaljen.
PerssonCoriolisSvårigheterna1998
— Jämför även de rent litterära
speglingarna som berättar om Corioliskomplexets allmänna popularitet i
studentkorridorerna (se även citatförfattarens
härledning längre upp):
”3. Frustration and confusion?
The mathematics involved in the
derivation of the Coriolis force
is quite straightforward, at least in
comparison
with other parts of meteorology, and cannot explain the widespread confusion that obviously surrounds it [for a recent example see an article by Kearns (1998) in Weatherwise]. The late Henry Stommel appreciated the sense of frustration that overcomes students in meteorology and oceanography who encounter the “mysterious” Coriolis force as a result of a series of “formal manipulations”:
Clutching the teacher’s hand, they are carefully guided across a narrow gangplank over the yawning gap between the resting frame and the uniformly rotating frame. Fearful of looking down into the cold black water between the dock and the ship, many are glad, once safely aboard, to accept the idea of a Coriolis force, more or less with blind faith, confident that it has been derived rigorously. And some people prefer never to look over the side again.
(Stommel and Moore 1989).
This article will suggest that the main problem with the teaching of the Coriolis force does not lie so much with the mathematics of the derivation, but the purely kinematic nature of the derivation. It readily provides the “approved” answer, but the price to pay is a pedagogical difficulty to bridge the gap between this formalistic approach and a genuine physical understanding.”, s1374,
”Many textbooks are anxious to
tell the student that the Coriolis
force is a “fictitious force,” “an apparent
force,” “a pseudoforce,” or “mental construct.” The centrifugal force, however, although equally fictitious,
is almost always talked about as a force. This leaves the impression that some fictitious forces are more fictitious than others.”, s1375ö,
European
Centre for Medium-Range Weather Forecasts
—
HOW
DO WE UNDERSTAND THE CORIOLIS FORCE?, Anders Persson (1998)
http://www.aos.princeton.edu/WWWPUBLIC/gkv/history/Persson98.pdf
— Härledningens METOD i MAC
är också verkligen rejält ABSTRAKT — om nu DET, verkligen, skulle vara det enda
modern akademi har att visa upp i ämnet.
— Jämför (även) generellt wikipedias
blotta BEGREPPSBAS (i texten till högskolematematiken):
”Many problems require use of noninertial reference frames,
for example, those involving satellites[19][20] and particle
accelerators”,
http://en.wikipedia.org/wiki/Fictitious_force
@INTERNET
Wikipedia — Fictitious force, General derivation [2012-09-08]
;
”In physics, an inertial frame of reference (also inertial reference frame or inertial frame or Galilean reference frame) is a frame of reference that describes time and space
homogeneously, isotropically,
and in a time-independent manner.[1]
All
inertial frames are
in a state of constant,
rectilinear motion with
respect to one another”,
http://en.wikipedia.org/wiki/Inertial_frame_of_reference
@INTERNET
Wikipedia — Inertial frame of reference [2012-09-08]
;
Termfrasen inertial frame samma som inertial
system med termen SYSTEM i association till KOORDINATSYSTEM:
”In frame-based descriptions, this
supposed field can be made to appear or disappear by switching between
"accelerated" and "inertial" coordinate systems.”,
http://en.wikipedia.org/wiki/Non-inertial_reference_frame
@INTERNET
Wikipedia — Non-inertial reference frame [2012-09-08]
I relaterad fysik (TNED) finns inga INERTIALSYSTEM.
Fysiken i relaterad mening beskrivs med utgångspunkt från JÄMVIKT [FUNTOP]:
fysikens lagar gäller inte i något enda system, utan FÖR samtliga
system. Modern akademi har inte den begreppsgrunden representerad.
Därmed sagt:
— Vi bör nog (kanske, och följaktligen)
inte räkna med att få några klara besked alls i frågan — på annat sätt än att
utföra (i värsta fall omfattande) experiment med direkta mätvärden.
Se även i CambridgeCoriolis
— ännu en (svårligen) upphittad källa som ställer fram ytterligare (i varje
fall en [1]) krävande detaljer till test (påstående att också
centrifugalkraftens bidrag skulle vara Coriolis).
CambridgeCoriolis — BILDKÄLLA:
Författarens arkiv · 14Sep2012 E31 Bild32 · Nikon D90 · Detalj

Möjligen
en upphittad som redovisar »tvåan» (2012-09-11):
http://www.damtp.cam.ac.uk/user/stcs/courses/dynamics/lecturenotes/section4.pdf
UNIVERSITY
OF CAMBRIDGE — Chapter 4, Rotating Frames
”But
why is there a factor of 2?”, s8
Utläggningen
verkar inte utmynna i något egentligt svar, här ges hela citatblocket:
”But
why is there a factor or 2? The reason is that the coriolis acceleration has two equal
components which can be
understood as follows. Suppose that you are on a round-about at the
fair,
or in a children’s playground, which is rotating at constant angular speed θ’.
You stand in
the middle and walk radially outward, along a radius the rotating round-about, at speed v
and
without
slipping. You experience a physical force,
namely friction acting on your shoes and this
force
balances the coriolis force so that in the rotating frame of the roundabout the tangential
acceleration vanishes.
Two effects contribute to the coriolis force.14
1.
At a distance r from the axis, your tangential velocity relative to the
inertial frame is that
of
the disc, namely rθ’. When you increase the distance by dr,
your tangential speed must
increase
by (dr)θ’. This happens in time dt, where dr = v
dt, so that acceleration is
θ’dr
——
= vθ’ = |ω × v|. (4.18)
dr/v
2.
Meanwhile, relative to the inertial frame,
the point where your foot was has moved a distance
rθ’dt and the point you will place your foot has
moved a distance (r + dr)θ’dt. To keep on the
same
radius in the rotating frame you have to
have a tangential speed of rθ’ and a
tangential
acceleration, additional to that in equation (4.18), of r’θ’
= vθ’.
To see that these effects are different, just consider jumping from r to r + dr.
You would still feel
a
tangential jolt when you landed (just as if you had jumped out of the door of a
moving car),
allowing
you to pick up speed, but you would not land on the same radius because the
roundabout
would
have moved on under your feet while you were in the air.
But this
is not the whole story. Clearly, there is also a coriolis affect
if the velocity of the
particle in the rotating frame is tangential not radial: in this case –2ω × v is radially
outward if v
is
in the direction of motion of the rotation (i.e. a right-hand screw with
respect to ω). How
does
this
arise? One way of understanding it is that it corresponds to an additional centrifugal force
necessitated by the additional tangential motion.15
”,
s8-9, 4.5 Coriolis term: –2ω × v,
http://www.damtp.cam.ac.uk/user/stcs/courses/dynamics/lecturenotes/section4.pdf
UNIVERSITY
OF CAMBRIDGE — Chapter 4, Rotating Frames
NOT.:
Källan använder punkt över variabeln (r, θ) istället för primtecken
(derivator).
CoriolisBASIC — utförlig grund
från CoriolisINLEDNING
Den första delen (1) [vi
måste här HELT bortse ifrån den moderna akademins vektorproduktmatematik — den
demolerar hela tillställningen, se i Kinematiska
Friktionslösa ParabelAnalogin —
och enbart se till den vanliga motsvarande grundmatematikens räknelagar]
motsvarar CoriolisHärledningens enkla aCORIOLIS=ωvr.
Den delen står redan instrumentellt på jämviktens referens, oberoende av val
av betraktande referenssystem: koncentriska cirklarna med samma intervall
motsvarar v(r), solfjäderslinjerna med samma intervall motsvarar v(n):
CoriolisBASIC
|
FÖRUTSÄTTNING: tallrikens rotation konstant a=vn/T=(2π[r=vrT]/T0=(2πf )vrT=ωvrT)/T=ωvr Konventionellt skrivs a = –2ωvr
Coriolisaccelerationen Coriolisaccelerationen
(a[C]) är medriktad v[n] om v[r] är utåtriktad (reguljära
accelerationsanalogin), annars motriktad v[n] om v[r] är inåtriktad
(inbromsning): — a[C] ska därmed, enligt ovan, upplevas av
en passagerare som färdas i en spårvagn på den roterande tallriken utmed r
med konstant hastighet v[r] och som sitter tvärs färdriktningen, med ansiktet
i tallrikens rotationsriktning (v[n]), som om spårvagnen accelererar
passageraren som om denne satt i en BIL i framsätet som accelererar på
vanligt sätt. Färdas vagnen åt motsatt håll (InMot Centrum) blir BILanalogin
för vagnpassageraren en inbromsning. — Accelerationens STYRKA i ett mätinstrument
som passagerarna kan titta på i vagnen kan också studeras av en fotograf vid
sidan av den roterande tallriken och därmed samma
effektiva resultatbild oberoende av val av referenssystem; — Verksamheten relateras i vilket fall
ALLTID till tillståndets princip. |
Det
finns inget mera att relatera.
Den accelerationen är den som ett
tryckinstrument uppmäter på tallriken, såväl som en betraktare vid sidan av
tallriken kan se/fotografera, det aktuella fysiskt mekaniska mätvärdet, eller i
varje annat möjligt referenssystem i universum, oberoende av rörelsetillstånd
(förutsatt möjligheter att FOTA idealt via dt).
— Det
finns inget mera att relatera. (Experimentellt uppmätta mätvärden saknas här).
— Så:
OM härledningen ovan INTE tycks ha (extremt) svårt för att SE POÄNGEN i den
aktuella mekaniska tillämpningen, är TYDLIGEN talet om den EXTRA, lika stora,
bidragsdelen i ”relative to the inertial frame”
i (2) rent tokprat.
— OM
den delen (2:an, i MACs 2ωvr)
f.ö. skulle koppla någon rent matematisk-teknisk deriveringsform, varför i så
fall ställs inte den delen fram? Vet inte. Beskrivande exempel saknas.
—
EXEMPELUTVECKLINGARNA från MAC är i sammanhanget så extremt abstrakta (behandlar
GENERALISERADE VEKTORBEGREPP) att varje konkret aktuell beskrivning i den
aktuella tillämpningen verkar helt omöjlig att få se i någon klartext på webben
(12Sep2012). Man hänvisar till »det allmänna».
Se exempel i MAC-härledningen.
Cambridgekällan
ovan (s6m) har också något som liknar »ett matematiskt härledande
resonemang» till »Coriolisfaktorn 2ωvr»,
men också det är så KRYPTISKT att det inte klart framgår VARIFRÅN författaren
hämtar detaljen:
—
Centraltermerna är (s6m, samband 13)
xi’ei’ = xi’ω×ei
= 2ω×v
med e (omnämns inte, man får leta bakåt) från »Eulers Teorem
(s4)»
ei’ = ω×ei
och xi
”For
a concrete example, let b = r, where r is
the position vector of a particle relative to a fixed
origin.
In the rotating axes, let r = xiei , where
the components xi may depend on t.”, s3m
;
— Med
andra ord: ingen som helst TYDLIGT SKÖNJBAR begriplig koppling. Det framgår
inte varifrån eller hur 2:an i ”2ω×v” införs: (möjligen) som följd av någon derivering (Accelerationsformen), eller på annat sätt — (ännu mera kryptiskt teoretiserande som
går ut på att försöka övertyga läsaren att »RöstaPåMinBeskrivning») som i den separat citerade beskrivningen, se CambridegCoriolis.
Se även en liknande (men med andra
argument) i WikipediaCoriolis-artikeln.
I AccelerationsFormenREFERENS visas att formen för CoriolisAccelerationens
jämviktssymmetri [aCoriolisJämvikt] a=2ωv VÄL framgår elementärt ur
accelerationens grundsamband (via d=2πr). Men den formen
ansluter till motsvarande polära koordinater för den rent kinematiska,
friktionslösa icke separat rotationsbundna FoucaultPendelns kinematiska
rörelseprojektion [FigurdelenB] på det roterande underlaget via den enkla formen (PREFIXxSIN) r=sin nx [FoucaultPendelnsPolärFunktion]. Men AccelerationsFormenREFERENS a=2ωv från
a=v/T=2d/T2=(2/T)(2πr)/T=(2/T)(2π/T)r=(2/T)(ωr)=2ωr/T=2ωv
avser
en linjär acceleration som »lånar» T-distansen vid uppnådda v från en omkrets,
d=2πr, som (i CoriolisKomplexet) skulle föreställa en
KONSTANT periferihastighet.
— Den a=v/t-formen är uppenbarligen ingen konstant
perifer historia.
— Det
bara visar att 2ωv-formen från den elementära a-formen via
ett ”d=2πr” INTE har, eller kan ges, fysisk substans: En
linjär acceleration (0TILLvPÅt) på längden av en cirkel ”d=2πr”
kan inte avbilda en konstant rotation. No way. Den algebraiskt möjliga
2ωv-analogin från a-grunden ovan gäller tydligen inte för
en konstant rotation.
— Det
finns, här veterligt, heller ingen som helst etablerad omnämnd koppling mellan
2ωv-formen och den ovan beskrivna linjära grundformen (a=v/T)
i etablerad mening. Den bilden ges tydligen bara här.
Vi kommer tydligen inte längre (i dag).
”The
acceleration entering the Coriolis force
arises from two sources of change in velocity that result from rotation:
the first is the change of the velocity of
an object in time. The same velocity (in an
inertial frame of reference where the normal laws of physics apply) will be
seen as different velocities at different times in a rotating frame of
reference. The apparent acceleration is proportional to the angular velocity of
the reference frame (the rate at which the coordinate axes change direction),
and to the component of velocity of the object in a plane perpendicular to the
axis of rotation. This gives a term –Ω×v. The minus sign arises
from the traditional definition of the cross product (right hand rule),
and from the sign convention for angular velocity vectors.
The
second is the change of
velocity in space. Different positions in a rotating
frame of reference have different velocities (as seen from an inertial frame of reference). In order for an object to move in a straight line it
must therefore be accelerated so that its velocity changes from point to
point by the same amount as the velocities of
the frame of reference. The effect is
proportional to the angular velocity (which determines the relative
speed of two different points in the rotating frame of reference), and to the
component of the velocity of the object in a plane perpendicular to the axis of
rotation (which determines how quickly it moves between those points). This also gives a term –Ω×v.”,
http://en.wikipedia.org/wiki/Coriolis_effect
@INTERNET
Wikipedia — Coriolis effect, Causes [2012-09-12]
CorioliBASIC i Wikipedia
— REFLEXION
CoriolisMACbeskrivningen:
Jämviktens
referens finns inte i MAC
WikipediaartikelCitatet ovan beskriver ingenting annat än det som visas
relaterat i
Kinematiska
FRIKTIONSLÖSA ParabelAnalogin:
aCoriolisMAC =
–2ω×vr = vr×2ω
............. har
inte ett spår med CoriolisKRAFT att göra
Se utförligt i Kinematiska
FRIKTIONSLÖSA ParabelAnalogin
För RIKTNINGEN —minustecknet i WikipediaCitat — se WikiCoriolisRIKTNINGARNA —
Corioliseffekten är den motsatta
I
modern akademi kan man INTE — som i relaterad fysik (TNED) —
obehindrat använda JÄMVIKTEN som
REFERENS FÖR ALLA MÖJLIGA REFERENSSYSTEM oberoende av deras inbördes, relativa
eller kombinerade RÖRELSETILLSTÅND
för att avgöra problem i mekaniken;
— Den
referensen — tillståndets fysik genom tillståndets princip — finns inte i MAC.
Jämför
Wikipedicitatets
In order for an object to move in a straight line it must
therefore be accelerated
med det
enligt relaterad fysik tillrättalagda, korrekt beskrivande och förklarande
In order for an object to move in a straight line in any force connecting association to a Coriolis
acceleration it must
therefore be more or
less solidly connected to the rotating disc as by a fixed rail, in order to
experience a physical instrumental measurable force in that the rotating
disc-body, through the railing object, be pushed or accelerated tangentially to oppose the straight
line motion, and along with the rotation and, thus, the straight line moving
body exert a physically measurable Coriolis acceleration on, or rather in, the
rotating material of the disc; Coriolis acceleration does not develop unless
the rotating disc has PARTLY (liquid, gases) mobile bodies; a solid body
(crystal) rotating has no Coriolis effect in it.
;
The moving object must be understood as existing on
a fixed mounted RAIL — in order to directly instrumentally measure the
IMPACT from the forces experienced through the different kinds of motion on the
rotating disc
WikiCoriolis:
Viss vilseledande CoriolisReklam i Wikipedia
BILDKÄLLA: Författarens arkiv · 17Sep2012 E34
Bild20 · Nikon D90 · Detalj

Vi studerar först hur WikiAnimeringens
Percept kan förstås med enkla medel, tallriken ovan:
WikiCoriolisartikeln har en inledande animering som
ansluter till den i detta dokument benämnda CoriolisTallriken
på följande sätt:
— Vi ritar ut den resulterande
rörelsebanan från kombinationen koncentriska
cirklar (konstanta
radialhastigheten ut från centrum) och solfjädern
(tallrikens konstanta rotation
moturs) — PÅ tallriken;
— Vi låter sedan tallriken rotera åt
andra hållet, MEDURS, och tittar på de svarta punkterna i motsvarande
tidsavsnitt som betraktare vid sidan av (i våningen ovanför [BILDSKÄRMEN]) den
roterande tallriken;
—
För första, innersta, punkten i bilden ovan, vrids tallriken ett
solfjädersintervall medurs, samtidigt som första koncentriska cirkeln avverkas:
punkten hamnar på vertikala radien under centrum;
—
För andra punkten i bilden ovan, vrids tallriken två solfjädersintervall
medurs, samtidigt som andra koncentriska cirkeln avverkas: punkten hamnar återigen
på vertikala radien under centrum;
Och på samma sätt för övriga:
— Alla punkter hamnar på samma vertikala radielinje:
— Spiralrörelsen på tallriken [bilden av reaplanet som passerar över
karusellcentrum som den uppåtriktade karusellkameran ser, utprintad på
karuselltallrikens planyta] vi ser som observatörer vid sidan av
(ovanifrån) tallriken blir en rät linje [passagerarna i reaplanet som kollar in situationen nedanför och ser
att reaplanets kondensstrimma stämmer med den utprintade, roterande, karusells
fast påritade spirallinje].
Men: Vad säger Wikipediaartikeln om
spiralkurvan (Wikiartikelns animering) som Wikiartikeln [analogt] förutsätter
uppritad [sedd av observatören på karusellen], fast vägbana, på tallriken?
”the black object moves ... without significant friction with the disc”:
”However, the
observer (red dot) who is standing in the rotating (non-inertial) frame
of reference (lower part of the picture) sees
the object as following a curved path due to the Coriolis and centrifugal forces present in this frame”
”a curved path due to
the Coriolis”;
Alltså:
— Den spiralformade, påritade, fasta
vägbanan på den roterande tallriken [karusellobservatörens vy] beror av, eller är återförbar på,
(”due to”) enligt Wikiartikeln ”Corioliskraften” (tillsammans med centrifugalkraften)
i rotationen — via ”the black object” som ”moves ... without significant friction with the disc”.
Wikimeningen vandrar tydligen i detta fall mellan
olika avsnitt i fysiken; kinematik (rörelselära, utan kraftens inverkan) kontra
Coriolis (utpräglat kraftbegrepp [se CoriolisBASICfrånGaspardCoriolis]):
Wikimeningen beskriver, tydligen, bara bilden
(bion, kinematiken) som man ser från en roterande karusell med en fast monterad
kamera uppåt som filmar ett förbipasserande reaplan som färdas med konstant
hastighet över karusellens rotationscentrum. Inget annat.
Det finns ingen
koppling i KRAFT (Coriolis and centrifugal forces present in this frame) mellan reaplanet (linjen) och
karusellen (spiralen); spiralbanan är enbart en kinematisk bild, ingen
kraftform, sett från en viss position i händelsen mellan två skilda rörelsesystem.
CoriolisKRAFT och
CoriolisACEELERATION har, tydligen och relaterbarligen, ingenting med det
framställda Wikipediabeskrivningssättet att göra — kroppar utan inbördes
kontakt kan inte utveckla kraft — men är det enda sätt MAC kan uppbåda
aCoriolisMAC =
–2ω×vr = vr×2ω
............. har
inte ett spår med CoriolisKRAFT att göra
Se utförligt i Kinematiska
FRIKTIONSLÖSA ParabelAnalogin
uppenbarligen på grund av sin låsning vid det egna antagna,
uppfunna begreppet INERTIALSYSTEM
(som i sig sänker centralaccelerationens
beskrivning, se CentralAccMAC),
tillsammans med MACvektoralgebransREGELVERK BegreppetVektorproduktMAC, se utförligt från CoriolisBASIC, som i sig definitivt sänker
varje begriplig beskrivning;
Wikipediaartikelns
animering har, tydligen, ingen relaterbar kinetisk (kraftbaserad)
anknytning till Corioliseffekten.
Wikipediaartikelns
inledande LinjeSpiralAnimering endast redovisar en kinematisk bild av en
rörelsebana sedd från två olika referenssystem, och vilka system HELT saknar fysikalisk kontakt med
varandra, ”without
significant friction”. CoriolisKRAFT och CoriolisACCELERATION har ingen
sådan koppling [CoriolisSATS2].
Se vidare utförligt från CoriolisBASIC.
— ATT, verkligen, spiralbanan
förekommer (idealt) också i samband med Corioliseffekten (men baserat på en helt annan beskrivningsgrund,
nämligen via analogin med spårvagnen på den FAST monterade rälsen på den
roterande tallriken — med KORREKT härledda, beskrivna och relaterade
vektorriktningar, MED kraftens inverkan, se utförligt från CoriolisACCELERATIONEN) gör ingenting
åt själva huvudsaken.
Emellertid, OM det finns personer som insisterar på att SAMMANFÖRA
och/eller SAMMANBLANDA dessa olika skeendedetaljer under rubriken
”Corioliseffekt” är det tydligt att förvirringen i begreppen enbart kan
fördjupas.
— OM Wikiförfattarna VISSTE det, kunde
man berätta om det för läsaren. Nu är det inte så (Sep2012):
”In physics, the Coriolis
effect is a deflection of moving
objects when they are viewed in a
rotating reference frame.”,
http://en.wikipedia.org/wiki/Coriolis_effect
@INTERNET
Wikipedia — Coriolis effect [2012-09-15]
Den beskrivningsgrunden är tydligen helt KINEMATISK —
baserad på VISUELLA PROJEKTIONER mellan olika rörelsesystem.
Corioliseffekten
kopplar inte dit:
Jämför korrekt formbeskrivning:
CoriolisBASICfrånGaspardCoriolis
Coriolis1 • Coriolis2
• CORIOLISKOMPLEXET i MAC
Coriolis ORIGINAL — Coriolis’ två
Teorem
———————————————————————————————————————————————————————
(enligt
Gaspard Coriolis [1835], Persson
1998 resp. Persson 2005)
en komplementär
i
denna presentations tolkning rätvinkelriktad
centralKRAFT/centralacceleration
— och den härleds så också i relaterad fysik [CoriolisBASIC]:
CoriolisKRAFTEN är Coriolisaccelerationen
(a)
gånger Coriolismassan (m)
Komponenterna (utom Centripetalaccelerationen)
från Coriolis analys omkring 1830 här i tolkning efter Persson
1998/2005 [Gaspard Coriolis originalskrifter är
erkänt svårtolkade (”krångliga figurer”), och ingen direkt gratis tillgänglig
översättning till engelska verkar finnas (Okt2012). Perssons beskrivningar
verkar f.n. vara de enda tillgängliga beskrivningarna som finns från Gaspard Coriolis
original].
— Den ordinära
centrifugalkraften (→mω²R) får en rätvinklig kompanjon, CoriolisKraften (↑mωv[r]) om P — i
någon fysisk förbindelse [CoriolisSATS3]
med det roterande underlaget
— uppvisar en radiell utåtrörelse (→ωR).
”At
the start of the Industrial Revolution a radical and patriotic movement
developed in
France to promote technical development by educating
workers, craftsmen and engineers in “mechanique
rationelle.” Gaspard
Gustave Coriolis (1792-1843), a
well-respected teacher at
l’Ecole
Polytechnique in Paris, published
in 1829 a textbook which presented mechanics in a
way that could be used by industry. Here we find for the
first time the correct expression for
kinetic energy, mv2/2. Two years later he established the relation between
potential and kinetic
energy
in a rotating system16.
In 1835 Coriolis published the paper that would make his
name famous: “Sur les
equations du mouvement relatif des systemes de corps,”
where the “deflective force” explicitly
appears. The problem
Coriolis set out to solve was related
to the design of certain types of
machines with separate parts, moving relative to the
rotation. Coriolis
showed that the total
inertial
force is the sum of two inertial forces, the common centrifugal force Ω2R
and the
“compound
centrifugal force” 2ΩVr , the “Coriolis force”(fig.6) 17.”, Persson
2005 s7n.
;
”Coriolis’s papers do not deal with the atmosphere or even the rotation of the earth, but with the transfer of energy in rotating systems like waterwheels. The 1832 paper established that the relation between potential and kinetic energy for a body, m, moving with a velocity, v0, affected by a force, P, which makes it accelerate to a velocity, v1, is the same in a rotating system as in a nonrotational (Fig. 6)”, Persson 1998 s1378n.
Det framgår inte om sambanden i Perssons beskrivning är
Coriolis egna eller de som tillämpas efter den senare införda vektorkalkylens
standard [vilket skulle vara först efter Willard Gibbs 1881 — 42 år
efter Gaspard Coriolis bortgång 1839],
ref. s12n,
A HISTORY OF VECTOR ANALYSIS, Michael J.
Crowe, 2002
http://www.math.ucdavis.edu/~temple/MAT21D/SUPPLEMENTARY-ARTICLES/Crowe_History-of-Vectors.pdf
— I relaterad fysik [CoriolisBASIC]
härleds Coriolisaccelerationen på en basform [CoriolisARMEN
a=ωv(r)] som inte kan föras i termer av den moderna vektorkalkylens
begrepp. Se utförligt i sammanställning från Kinematiska
Friktionslösa ParabelAnalogin [Jämförelsen med MIT-experimentet].
Wikipediaartikelns beskrivning, citatet ovan [WikiPediaCoriolis2], är tydligen något annat än den i detta dokument
härledda CoriolisEffekten:
— CoriolisEffekten
utpekas istället tydligen enligt:
Uppkomsten av en via
en yttre energikällas inverkan
acceleration (a=ωvr) som strävar att minska/öka
ett hjuls egenrotation (ω) via en massas radiellt fasta rörelse (typ
Spårvagn, vr [Corioliseffekten]) på hjulet beroende på om rörelsen sker utåt eller
inåt.
Det är alldeles samma effekt som i impulsmomentets bevarande [J=mvr] [RotationensVektorVerklig] med isdansaren som sträcker ut eller drar in armarna.
Rörelseenergin
(tröghetsmomentets I=mr2 påförda vinkelacceleration ω2 är momentkraften F gånger momentarmen r, m[ωr]2=mv2)
E=Fr hos en roterande kropp ändras proportionellt med den tillståndsändrande kraftens (F[Coriolis]) metriska formändring (r) — vilket är Gaspard Coriolis första teorem enligt Persson 1998:

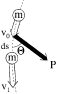
”FIG. 6. Coriolis’s first theorem: a body, m, on a rotating turntable
moving with a speed, v0, is subject to a force, P, and displaced
along a trajectory, ds, and
accelerates to v1. The change in
kinetic energy, corresponding to the change of potential
energy, is
due to the work done by the driving force P along the projection
of the distance ds where Θ is the angle between P and ds. (To make
the dynamic discussion complete, Coriolis also considered the
centripetal force Pe and the balancing centrifugal force Fe, both
acting to keep the body in a fixed position in the absence of a driving
force P. Both Fe and Pe cancel out in the energy equation.)”,
Persson 1998 s1378ö.
Med mera renodlat förtydligande grundvektorer säger den Corioliskällan uppenbarligen alldeles detsamma
som den enklare figurillustrationen enligt nedan:
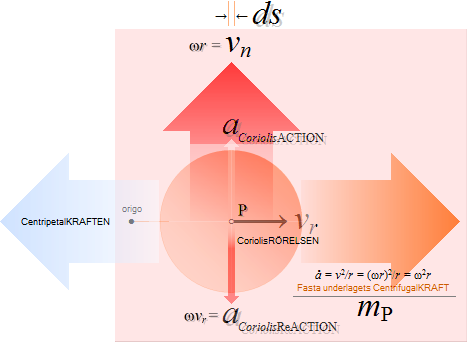
Grundbegreppen
från Gaspard Coriolis
som ovan här i tolkning efter Persson 1998.
— Den yttre pålagda tillståndsförändrande kraften (P) i riktningen v(r)→ i en redan roterande kropp (ω)↓•↑ resulterar i en metrisk formändring (ds)→ hos rotationsmassan; formändringen (ds) betyder radiell utsträckning (•→), och därmed [CoriolisBASIC] en motsvarande rätvinkligt uppkommen CoriolisACCELERATION (CoriolisACTION) vars verkan (CoriolisREACTION) strävar att upphäva tillståndsändringens orsak [NewtonIII].
Hela energiräkningen anställs alltså uteslutande på den utifrån pålagda kraftformen (P) till rotationskroppens massform, och vilken kraftgrund bär ansvaret för rotationsmaterialets omfördelning eller Coriolisverkan, som det får förstås. Jättesvårt.
— Eller som det också sägs explicit i Persson 1998 (Persson klargör inte huruvida det är Gaspard Coriolis egna ord):
Corioliskraften är riktad rätvinkligt masskroppens radiella rörelseriktning
”FIG. 7. Coriolis’s second theorem is most easily understood when the rotating system is
viewed first from a fixed frame of reference (a), then in the rotating frame of reference (b).
The total centrifugal force acting on the body m moving
with a velocity V is directed perpendicular
to the tangent of the movement, along the radius of
curvature (Fig. 6a). It can be
decomposed into two centrifugal forces; one mω2r, directed from the center of rotation and
a second, –2mV, ω, the Coriolis force, perpendicular to the relative motion Vr (Fig. 6b).”,
Persson 1998 s1378n.
— Men det är inte Wikipedias beskrivning [WikipediaCoriolis]:
”The acceleration entering the Coriolis force arises from two sources of change in velocity that result from rotation: the first is the change of the velocity of an object in time.”, ”The second is the change of velocity in space.”.
Jämför korrekt mening justerad efter Coriolis bägge teorem enligt ovan:
»The acceleration entering the Coriolis force arises from AN EXTERNAL ENERGY SOURCE affecting the rotational mass to change its radial extension».
No more. No less.
Jämför
även (korrekt men med fel/utebliven aktionsriktning, se vidare nedan i MACaktionsriktningenCoriolis) direkt från Google (»what is coriolis effect»)
[2012-09-15]:
”An effect whereby a mass moving in a rotating system experiences a force perpendicular to the direction of motion and to the axis of ...”,
;
Däremot,
och således [CoriolisBASICfrånGaspardCoriolis], är INTE den här typen välplacerad:
”In
physics, the Coriolis effect is a deflection of moving objects
when they are viewed in a rotating reference frame.”,
http://en.wikipedia.org/wiki/Coriolis_effect
@INTERNET
Wikipedia — Coriolis effect [2012-09-15]
Den typen ansluter istället till Kinematiska RotationsAvvikelsen [CINEMA] — se direkt jämförande matematisk form [Hur MAC associerar Coriolis med Kinematiska] som visar HUR man — uppenbarligen, som det får förstås — i modern akademi bär sig åt för att postulera FEL fattning på KORREKT matematik.
— Som vi ser kopplar GOOGLE-referensen (Wikipedia) ILLA: det vi finner vid närmare granskning är två helt väsensskilda påståenden:
1. GOOGLE: en effekt varigenom en massa erfar en kraft; kinetik; OK
2. Wikipedia: en (visuell) avböjning hos mobila objekt; kinematik; notOK
Det korrekta ”An effect whereby a mass moving in a rotating system experiences a force”, återfinns också i (bl.a.)
http://oxforddictionaries.com/search/english/?region=uk&q=force&page=2
http://oxforddictionaries.com/definition/english/Coriolis+effect
OXFORD
DICTIONARIES
PROBLEMET I MODERN AKADEMISK LITTERATUR
i CoriolisKOMPLEXET är nämligen följande (som tillsammans med CoriolisSATSERNA,
CoriolisCINEMA och Kinematiska RotationsAvvikelsen) HELT förklarar de
ovan till synes galna olika sätten): Kinematiska
FRIKTIONSLÖSA ParabelAnalogin;
aCoriolisMAC =
–2ω×vr = vr×2ω
............. har
inte ett spår med CoriolisKRAFT att göra
Se utförligt i Kinematiska
FRIKTIONSLÖSA ParabelAnalogin
— VEKTORKALKYLENS REGELVERK BegreppetVektorproduktMAC
i MAC medger ingen annan ETABLERAD
BESKRIVNING av de vektorformer som figurerar i CoriolisKOMPLEXET än en
resultatform som ansluter till en rent VISUELL, kinematisk, resultatbild;
MAC KAN, uppenbarligen, INTE HÄRLEDA KRAFTBILDEN PÅ
VEKTORKALKYLENS BEGREPP — utan att hela matematikbilden HAVERERAR på en rent
visuell, kinematisk, matematik.
— Debatterna genom CoriolisHistorien
har också (verkligen) gått höga (Persson
2005), och det är — erkänt — så ännu i denna dag (Sep2012).
— Samtidigt, NÄMLIGEN (se citat nedan PerssonCoriolis1998), är det uppenbart
att kärnan i Coriolissaken ÄR en kraftverkan — som också Oxford Dictionary
(ovan) verkar försöka antyda — med VISST stöd av banemannen Gaspard Coriolis
(1835).
— ENDA SÄTTET ATT HÄRLEDA SAMMANHANGEN
är, tydligen, via relaterad
fysik, se från CoriolisINLEDNING.
Tro det eller inte (sagt så här
i all korthet med min personliga överblick över hela dokumentframställningen),
men HELA resultatbilden RÄTAS UPP, perfekt, utan att något tillförs eller att
något försvinner — endast MED enda resulterande förklaringen att
vektoranalysens begrepp i MAC
är (framstår HÄR som helt) ODUGLIGA som redskap i naturbeskrivningen. Se
— specifikt — utförligt i
sammanställt syntes från CoriolisINLEDNING
— Ingen i MAC kan förklara
Coriolisdetaljerna — exakt VAD Corioliseffekten ÄR eller inte är — utan att
RASERA hela det rent FYSISKA, kinetiska, beskrivningssättet, just genom att det
enda sätt som finns i MAC slutar PÅ en ren visuell, kinematisk,
matematikbeskrivning, medan CoriolisEffekten ÄR kraftbaserad [CoriolisORIGINAL]; Webben är också
proppfull av VideoDemos i ämnet [WebCoriolisVideoDemos]
(det ena bidraget tjusigare än det andra). Därmed är kaos etablerat — och ingen
begriper ett enda ord av sammanhanget.
Se utförligt i sammandrag från CoriolisINLEDNING.
Se även EXPANSIONSINTEGRALEN I MAGNETISMEN:
ännu ett exempel som visar hur det under 1800-talet uppfunna vektorkalkylens
regelverk BegreppetVektorproduktMAC
i modern akademi omöjliggör — raderar — en relaterad fysikbeskrivning.
”An effect whereby a mass moving in a rotating system experiences a force”,
Googleresultatet och Oxforddefinitionen omnämnda ovan
är
precis den principiella verkan i CoriolisEffekten enligt Coriolis bägge teorem [CoriolisBASICfrnCoriolis] och sättet som dessa härleds i denna framställning [CoriolisBASIC].
—
Wikipedias ”deflection of
moving objects when they are viewed” däremot kopplar inte dit.
—
CoriolisEffekten har inget med ”view” att göra — men »view-matematiken» är av
samma TYP ehuru distinkt skild. Se utförligt i sammandrag från CoriolisINLEDNING, om ej redan bekant, samt i särskilt belysande
matematikexempel Hur MAC associerar
Coriolis med Kinematiska.
Jämför även Persson [1998, s1373.Abstract] om Gaspard Coriolis (1792-1843)
och den efter honom [1835] uppkallade s.k. Corioliseffekten (mera utförligt i [CoriolisBASICfrnCoriolis]),
”His
own approach, which followed from a general discussion of the energetics of a
rotating mechanical system,
provides
an alternative and more physical way to look at and understand, for example, its property as a complementary
centrifugal force.”, s1373ö,
;
”Applying Coriolis’s principles elucidates cause and
effect aspects of the dynamics and energetics of the atmosphere, the
geostrophic adjustment process, the circulation around jet streams, the
meridional extent of the Hadley cell, the strength and location of the
subtropical jet stream, and the phenomenon of “downstream development” in the
zonal westerlies.”, s1373ö,
European
Centre for Medium-Range Weather Forecasts
—
HOW
DO WE UNDERSTAND THE CORIOLIS FORCE?, Anders Persson (1998)
http://www.aos.princeton.edu/WWWPUBLIC/gkv/history/Persson98.pdf
Det
är också precis vad CoriolisEffekten (CoriolisBASIC) är: (»centralaccelerationens
RotationsEkvivalent» eller ’CentralKraftens Komplement’ för att använda termer
som ansluter till upphovsmannen [CoriolisBASICfrnCoriolis]): Corioliseffekten har inget med ”view” att göra:
”On a rotating earth the Coriolis force acts to change the
direction of a moving body to the right in
the Northern Hemisphere and to the left in the Southern Hemisphere.”, Persson 1998
som ovan s1373.Introduction
Corioliskraftens certifierade fysikbas — CoriolisBASICfrånGaspardCoriolis
Det
fungerar, uppenbarligen, efter samma schema som i illustrationen beskriven i Coriolisaccelerationens
effekt. Därmed framstår den
relaterade fysikens CoriolisBASIC tydligen entydigt identifierad som CoriolisEffekten:
·
CoriolisEFFEKTEN är rörelsemängdsmomentets (impulsmomentets
J=mvr) [RotationensVektorVerklig] INRE ändring av omloppsmassans (m) radiella
förflyttning (r) som
följd av en yttre energikällas inverkan på en roterande kropps material vilken för impulsmomentets bevarande (J=mvr)
kräver den roterande massans motsvarande ändring i rotation (v);
·
CoriolisACCELERATIONEN härleds på den basen med impulsmomentets massa
fråntagen, enbart via det återstående ytmomentet (K=vr=Keplermomentet [Keplers andra lag]);
·
jämförelser i olika
rörelseformer mellan olika referenssystem som INTE har fysisk materiell kontakt
med varandra — typ Foucaults Pendel [SCIAM], Roterande Parabelanalogier med Friktionslösa Puckar
[MIT], o.dyl. — saknar därför, entydigt, varje koppling till
begreppet och fenomenet CoriolisEFFEKTEN [CoriolisSATS3];
Se särskilt sammanställda exempel i länksyntesblocket i Kinematiska
RotationsAnalogierna.
MACaktionsriktningenCoriolis — WikipediaCoriolis
— CoriolisJÄMVIKT
WikiCoriolisRIKTNINGEN som ReAktion — inte Aktion
— Men HUR kan du vara så säker på att
CoriolisAccelerationens AktionsRiktning i fallet med utåtriktat
v[r] verkligen ÄR medriktad
tallrikens rotationsriktning?
— Jag kan inte bara vara helt säker på
det, utan även vara SÅ säker på det att jag är ÖVERTYGAD att få med dig också
på det:
— DÄRFÖR att ordningen beskriver exakt
samma situation som den snurrande isdansaren som sträcker ut (v[r]) armarna,
och som i impulsmomentets
bevarande (J=mvr, konstant Jm) [Rotationens
Vektor Verklig], på grund av att isdansaren inte förfogar över
någon pådrivande raketkraft som kan bevara rotationen (v), medför att v avtar
på bekostnad av växande r. Vi studerar det med rotationen ↓•↑.
— Coriolisaccelerationen a[C] med v[r]→
utåt, är medriktad periferihastigheten v[n]↑,
så att den diametralt
motriktade orsaksupphävande motkraftens
Coriolisacceleration ↓ [NewtonIII] strävar att bromsa tallriken
då ingen CoriolisaccelerationsUnderhållande kraft föreligger: tallriken saktar av;
ReAktionskraftens riktning ↓
är diametralt motriktad hjulets periferihastighet (v[n]↑)
för v[r]utÅT→,
och samma med ReaktionsAcccelerationen;
— Aktionsriktningen för a[C] med v[r]utÅT→
är MED↑ v[n]↑ och ReAktionsaccelerationen MOT↓
v[n]↑;
hjulet
bromsar in.
— Aktionsriktningen för a[C] med v[r]inÅT←
är MOT↓ v[n]↑ och ReAktionsaccelerationen MED↑
v[n]↑;
hjulet
accelererar upp.
Därför vet
jag det. Om du ser något fel i det, får du gärna visa.
Eller (mycket) enklare [AktionReaktion]:
växande v[n]↑ finns bara via ett v[r]utåt→;
växer v[n]↑,
finns bara en MÄTANDE — instrumentell — riktning att välja på (i vagnen som
åker med v[r]):
↓,
reaktionsriktningen. Den som trycker vagnpassagerarna MOT↓
det växande v[n]↑.
— Och alltså finns det bara ett
återstående alternativ kvar att välja på för aktionsriktningen i fallet med utåtriktat v[r]; ↑,
medriktat v[n]↑.
:
a=v[n]/T=konstant definierar
Aktionsriktningen som
·
medriktad
v[n] via v[r]utåt;
ReAktionsriktningen får hjulet att bromsa in;
·
motriktad
v[n] via v[r]inåt;
ReAktionsriktningen får hjulet att accelerera upp.
Den beskrivningen är UTESLUTEN i modern
akademi:
·
bara
ett (1)
verktyg BegreppetVektorproduktMAC
i MAC finns för problemlösningen, och det
verktyget ger FEL aktionsriktning, se efterföljande detaljgenomgång från WikiCoriolisRIKTNINGARNA, eller mera
direkt på sak i Kinematiska FRIKTIONSLÖSA
ParabelAnalogin: MAC-verktyget, det enda MAC har, utpekar
Coriolisaccelerationen i dess, entydigt väl relaterbara som ovan [AktionsRiktningsArgumentet],
reaktionsriktning, inte aktionsriktningen, den som normalt måste kunna
RELATERAS i fysikbeskrivningen för att kunna redovisa ORSAKSGRUNDERNA i
fysikskeendet: förstå naturen
·
riktningsordningen
som sådan i MAC beträffande termerna aktion- och
reaktion anses ha »godtycklig innebörd», ”arbitrary”, se den inledande
citatdelen till AktionReaktionMAC;
bara av den anledningen är debatten redan avslutad: kan inte relatera
naturinnehållet
·
djupanalysen
i centralrörelsen går över huvud taget inte att
genomföra RELATERAT i MAC på grund av att
centrifugalkomponenten utesluts i den kraftredovisande fysikbeskrivningen, se
jämförande skolexempel i RotationsParabolensFormfaktor
[MACkraftParabeln] med generalgenomgång
i CentralaccelerationenMAC
Vi börjar med WikiCoriolisRIKTNINGARNA:
WikiCoriolisRIKTNINGARNA —
BILDKÄLLA: Författarens arkiv · 17Sep2012
E34 Bild17 · Nikon D90 · Detalj

WikiRIKTNINGARNA
Ytterligare
från/via WikiCoriolis:
”if
the velocity is straight outward from
the axis, the acceleration is against
the direction of local rotation”,
http://en.wikipedia.org/wiki/Coriolis_effect
@INTERNET
Wikipedia — Coriolis effect, Formula [2012-09-15]
— Den
riktningen är [illustrerat i Coriolisaccelerationens
effekt]
enligt
CoriolisEffekten
samma
som aCoriolisReACTION. Inte aktionsriktningen;
—
WikiCoriolis framställer, tydligen, CoriolisAccelerationen i dess ReAKTIONSFORM (i den riktning som ett fysiskt avkännande
mätinstrument registrerar tryckökningar [accelerationer], instrumentutslag,
från noll och uppåt), inte i dess aktionsform (den nödvändiga
reaktionsdiametrala kraftens riktning för att underhålla reaktionsverkan)
[Om ej redan bekant, utförligt i AktionReaktion].
”This
gives a term –Ω×v. The
minus sign arises from the traditional definition of the cross product (right hand rule), and from the sign convention for
angular velocity vectors.”,
http://en.wikipedia.org/wiki/Coriolis_effect
@INTERNET
Wikipedia — Coriolis effect, Causes [2012-09-15]
MAC-vektroprodukten illustrerad i PREFIXxSIN
Se BegreppetVektorproduktMAC [Se även
webben i WolframMath http://mathworld.wolfram.com/CrossProduct.html]:
— ersätt a med ω (eller
Ω) och b med v; vinkelrotationens kryssproduktvektor
i MAC finns illustrerad i
Wikipedia
Angular velocity
http://en.wikipedia.org/wiki/Angular_velocity;
”The direction of the angular velocity pseudovector will be along the axis of
rotation”.
Klargörande definition i relaterad mening:
RotationensVektorVerklig
— MACaktionsriktningenCoriolis
Också
här sätter den moderna akademin sina speciella spår i fysikbeskrivningen — sett
i ljuset av relaterad fysik. Nämligen beträffande termen eller begreppet pseudovektor:
—
Vi studerar hur det begreppet INTE ansluter till naturbeskrivningen;
— Cirkelperiferins
omloppshastighet vn=2πr/T0=(2π/T0)r=ωr utpekar enligt
relaterad fysik i varje ögonblick
(dt) en fysiskt VERKLIG — inte påhittad, inte skenbar, inte fiktiv —
händelseriktning: en orsak till varje efterföljande
verkan.
ImpulsmomentetsVektorVerklig J=mωr2
— I IMPULSMOMENTET (J=mvr=mωr2) — Keplermomentet vr (Keplers andra lag, konv. även Ytmomentet)
tillsammans med omloppsmassan m — kan vi KÄNNA en axiellt riktad
tröghetsbevarande kraftverkan med exemplet från det losstagna, spinnande cykelhjulet som
vi håller i händerna med grepp om axeln: J beskriver tydligen naturligt en
axiell — verklig, inte skenbar, inte påhittad, inte fiktiv — vektor i normal till rotationsplanet.
— Med hjälp av högerhandsregeln kan vi fastställa en
enhetligt diametralt vald riktningspreferens för J, och så använda denna i alla
möjliga tillämpningar. Högerhandsregeln utsäger då att J pekar i tummens
riktning om fingrarna sluter sig i rotationsriktningen.
J/m=ωr2=vr innebär kvantitativt bara en
proportionsändring (m) i J-vektorn:
VinkelrotationensVektorVerklig ω=2π/T0=2πf
— Eftersom händelsevektorn, här,
fortfarande och entydigt utpekas av vinkelrotationen (ω, grek., lilla omega [”we”, grovt
förenklat]) — med denna noll upphör vektoranalogin för rotationens del — är det
tydligt att vi kan identifiera, entydigt, förstå, beskriva och relatera just
vinkelrotationen som DEN centrala, axiella händelsevektorn till hela
rotationskomplexet — i stöd av impulsmomentets fysik.
— Rotationen som begrepp
I RELATERAD MENING, men inte i MAC, kan därmed illustreras
med en central — verklig — händelsevektor (ω) lika med vinkelrotationen. Riktningen för ω går genom rotationscentrum — inget annat (i MAC flyttas den omkring i stort sett hur som helst ute i periferin,
se illustrerat exempel nedan) — och i samma utsträckning som
rotationsaxeln, med (konventionellt) bestämd riktning enligt högerhandsregeln.
Riktning och beteckning är samma som i Wikipediafiguren ovan.
MAC-vektroprodukten illustrerad i PREFIXxSIN
I abz-bilden ovan ligger den MAC-rotationscirkeln
(kontrollera) i yz-planet (a med ω)
med rotationsriktningen medurs sett från vår vinklade position som
observatörer: Från ω
(a med
ω) Till v (b med v) för Coriolisfallet skrivs då i MAC som
kryssprodukten ω×v med
resultanten som z i abz-bilden ovan:
— MAC-Vektorproduktens resulterande z-riktning (–ω×v) motsvarande –(a×b) i bilden ovan BegreppetVektorproduktMAC blir då med
en resulterande z-riktning diametralt motriktad den i bilden ovan — alltså ”against the direction of local rotation”.
Men:
— Det är [Coriolisaccelerationens effekt] samma
som ReAKTIONSRIKTNINGEN i CoriolisEffekten.
Inte aktionsriktningen.
— Varför, i MAC,
prioriteras då reaktionsriktningen och inte — som normalt BORDE vara fallet —
aktionsriktningen?
— Dessa detaljer klargörs inte EXPLICIT
(utom i formen av en allmän hänvisning) i Wikipediaartikeln.
Svaret ges i den illustrerade utvikningen
nedan:
vektorrerpresentationen kan bara göras på ett
sätt.
— Det betyder också att
ORSAKSSAMMANHANGET för Coriolisbeskrivningen i motsvarande beskrivande del INTE
KAN FÖRAS.
— Det är med exemplet (eller rättare sagt OBSERVATIONEN) ovan
inte underligt att INGEN förstår den moderna akademins olika (s.k.
vetenskapliga) utläggningar.
MAC: Ren kinematisk beskrivning — som våldför sig på den underliggande kraftfysiken
aCoriolisMAC ovan motsvarar den relaterade fysikbildens
aCoriolisReAction enligt CoriolisEffekten,
den riktning som bromsar rotationen — inte den förorsakande [eg. underhållande/drivande] vektorriktningen
aCoriolisAction, den vektorriktning som v[r] förorsakar [AktionsRiktningsArgumentet].
— Man kan inte
heller, gärna, vända på termerna (se efterföljande figur) och läsa från ω nederst till v[r] överst: en
sådan vektorrepresentation i MAC BegreppetVektorproduktMAC
har definitivt ingen begriplig koppling till sammanhanget (med v[r] i skivans normal, uppåt,
skulle hela skivan också vridas, uppåt, vilket inte var uppgiften).
— Med andra ord
går det inte att få fram AktionsVektorns Riktning via MAC-vektorproduktens
regelverk.
För att utföra MAC-vektorprodukten enligt figurkonceptet ovan på ordningen –ω×vr måste rotationsvektorn (ω)
flyttas ut från rotationscentrum — bara
det är en rent fysisk absurditet [BaraEttSätt]—
till en händelsepunkt (något ställe på den roterande tallriken, ej i mitten),
rotationsriktningen v[n] hos tallriken i figurdelen ovan här inåt i bilden
(totalt moturs tallriksrotation), och sedan [enligt BegreppetVektorproduktMAC] produkten
tas från v[r]TILLω (samma som negativt ωTILLv[r]) som ger resultanten
a[C]MAC som i figuren ovan med a[C]MAC motriktad v[n].
— Beskrivningssättet kan, veterligt, inte bli mera
förvirrande (»klumpifierat») än så:
— Rotationsvektorn (ω) i en punkt utanför rotationscentrum
(origo) är, speciellt, verkligen ingen fysikbeskrivning [BaraEttSätt].
— Det är heller inte resultanten ovan i riktningen a[C]MAC:
den riktningen utpekar CoriolisAccelerationens ReAktionsriktning. Inte
Aktionsriktningen [AktionReaktion].
— Men inte heller dessa centralbegrepp ingår i MAC-beskrivningarna: vektorproduktens uppfunna BegreppetVektorproduktMAC regelverk i
MAC utsäger ingen bestämd ordning för HUR att välja, eller tolka,
parameterriktningar för Aktion och Reaktion [MACarbitraryActionReaction]: det
finns, tydligen och således, ingen entydigt formulerad riktningsbestämd fysikgrund
(NewtonIII)
i MAC att utgå ifrån.
Motsvarande »korrekt ordning» för att få a[C]-vektorn som resulterande Aktionsvektor blir
just, enligt den relaterade härledningen till CoriolisAccelerationen
som i figuren nedan:
För att få ihop det med DEN RELATERBARA FYSIKBESKRIVNINGEN,
med KORREKT DEFINIERADE VEKTORRIKTNINGAR, skulle följande, gravt korrumperade
”modernt akademiska vektorprodukt” behövas,
aCaction = –ω×vr
aCReAction = +ω×vr
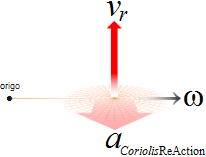
En ännu värre lösningsbild
alternativt med föregående vektorillustration [se
tolkningsriktningarna mera utförligt illustrerat och beskrivet i BegreppetVektorproduktMAC om ej redan
bekanta]:
aCaction = –vr×ω = +ω×vr
aCReAction = +vr×ω =
–ω×vr
Det är nog (heller) ingen som på allvar vill mena att MAC skulle anta en dylik nyordning.
— I vilket fall ser vi att begreppet ORDNING i
sakbeskrivningen HELT har gått förlorad med MAC-begreppen:
— fysikbeskrivningen urartar i OORDNING med MAC (illustrationskonceptet avbildat ovan är i
bägge fallen rena snurren).
— Det finns ingen klargörande framställning i MAC-beskrivningarna [MACarbitraryActionReaction] som specificerar huruvida resultanten
till vektorprodukten ska förstås som AktionsVektorRiktningen (vilket är den
ändringsorsakande vektorriktningen) eller ReaktionsVektorRiktningen (som
motsvarar den instrumentellt fysiskt mätande vektorriktningen [tröghetskraftens
riktning]). Begreppen aktion-reaktion förekommer över huvud taget inte (de
erkänns inte [MACarbitraryActionReaction]) i MAC-beskrivningarna: Relaterad —
precisionsbaserad —
naturframställning finns inte i MAC.
AktionReaktionCoriolisIllustrerat
— I relaterad fysik [CoriolisBASIC]
är förklaringen ytterst enkel, direkt och framförallt KLAR. Se även från MACaktionsriktningenCoriolis. Omöjligt
att missa:
— Med konstant vinkelrotation (ω ↓•↑) och v[r]utÅT(→) — entydigt högre v[n] med större r — är v[n]/T=a[C]Action(↑) medriktad v[n]:
a[C]ReAction(↓)NewtonIII
— motriktad v[n] — strävar att bromsa in hjulet;
— Med konstant vinkelrotation (ω ↓•↑) och v[r]inÅT(←) — entydigt lägre v[n] med mindre r — är v[n]/T=a[C]Action(↓) motriktad v[n]:
a[C]ReAction(↑)NewtonIII
— medriktad v[n] — strävar att accelerera
upp
hjulet;
— Se även förklaringarna i AktionReaktion
om ej redan bekant.
ANLEDNINGEN varför man i MAC har framställt vektorprodukten, som ovan, så att den leder på reaktionsverkans riktning (–ω×v) istället för som normalt, aktionsverkans riktning (+ω×v) [AktionReaktion],
Den delen relateras dock inte explicit i Wikipediaartikeln (eller någon annan av
de mest synliga på webben) utom i formen av en (diskret) hänvisning:
”The minus sign arises from the
traditional definition of the cross product (right hand rule), and from the
sign convention for angular velocity vectors.”.
framgår (således) DIREKT I VEKTORERNAS EGNA BILDER tillsammans med regelverket i MAC för vektorprodukt:
MAC: Ren kinematisk beskrivning — som våldför sig på den underliggande kraftfysiken
— oaktat det absurda i att flytta ut vinkelrotationens vektor ω från origo
till en lokal i den roterande tallriken, det finns ingenting
sådant i fysiken —
— Rotationscentrum — origo — är entydigt bestämt för en
roterande kropp som roterar. Flyttar man ut den entydigheten i periferin —
figurbilden ovan — upphör också relevansen i helhetsbeskrivningen: den
relaterbara fysiken har, vad vi vet, ingen sådan, förment, logik.
Rotationscentrum i Coriolisverkan finns
inte [VektorFelen i MAC]:
— Beträffande CoriolisVERKAN som sådan finns heller inget —
vad vi vet — härledningsbart rotationscentrum; Coriolisverkan
betyder att den berörda rotationsmassan (Coriolismassan)
uppvisar en AVBÖJNING — om den är fullständigt mobil inom rotationskroppen;
Avböjningen ansluter sedan genom samverkande avböjningar (flera PAR CoriolisARMar)
till strukturella (virvelformiga [CoriolisCELLEN])
avlänkningar i det halvfasta materialet. Något direkt härledningsbart
rotationscentrum finns inte.
— Även i fallet med CoriolisSTAVEN
blir det svårt att få fram något direkt, konkret, rotationscentrum:
Coriolisstavens massa bygger på inbördes ändring (flytning) genom
Coriolismassans halvfasta natur; Matematikdelen kan, veterligt, bara ange
vridmomentet (rotationens ansats) av princip, utan att kunna formulera någon
annan, direkt, rotationsanalogi;
— Det finns med andra ord, och här veterligt, ingen entydigt
bestämd rotationskropp alls att härleda i Coriolisverkan från CoriolisBASIC.
— Så är med åter andra ord figurkonceptet ovan helt och
hållet uppåt väggarna i relaterad mening: vektorbilden är felaktig ur flera
olika synvinklar, främst beträffande inblandningen av blotta termen ”Coriolis”;
figurformen ansluter i relaterad mening tydligen till EN RENT VISUELL
FENOMENFORM; (en »hypotetiserad
form» för) Kinematiska Friktionslösa
ParabelAnalogin (i den moderna akademins ursprungliga föresats, som det får förstås,
att Den bilden skulle Beskriva Coriolisverkan, vilket den Inte gör):
VISUELL — friktionslös — representation av rörelser (CINEMA)
mellan olika rörelsesystem (»FoucaultPendelFigurer»)
[FigurdelB].
Coriolisverkan har ingen koppling dit.
— Härledningen till CoriolisACCELERATIONEN
i relaterad fysik använder över huvud taget inte figurtypen ovan.
att placera riktningarna ω (vinkelrotationen) och vr (separata radialhastigheten), figuren ovan. Med
BegreppetVektorproduktMAC enligt vr×ω=–ω×vr blir ordningen därmed given för resultanten aC.
Det finns inget alternativ att välja på.
BILDKÄLLA: Författarens arkiv · 12Sep2012 E28
Bild397 · Nikon D90 · Detalj

— MEN DÄRMED FÖRLORAS OCKSÅ ORSAKSSAMMANHANGET:
— Man skiter i det också [Kausalordningen].
Det finns, tydligen i relaterbar mening, ingen beskriven ORSAKSVEKTOR (Coriolisaccelerationen samriktad med periferihastigheten, med radiell separat utåtriktad massrörelse, se AktionReaktionCoriolisIllustrerat) i MAC-sättet [WikipediaCoriolis] [CoriolisMIT] för Coriolisaccelerationens begrepp — bara själva reaktionsriktningen:
— MAC-resultatet har därmed och följaktligen och tydligtvis urartat (havererat, helt enkelt) i fysiken.
Speciellt om MAC-begreppen skulle föreställa typen naturvetenskapligt sakgrundade är det tydligt att ett BROTT uppstått i den förutsättningen; Regelverket avbildat ovan [MACreactionCoriolis] är, tydligen, värdelöst i fysikbeskrivningen. Verkligen.
AccelerationsFORMEN 2ωv framgår f.ö. direkt ur grundmatematiken (via d=2πr):
a=v/T=2d/T2=(2/T)(2πr)/T=(2/T)(2π/T)r=(2/T)(ωr)=2ωr/T=2ωv
Men framställningarna i ämnet på webben från modern akademi
kopplar inte det beskrivningssättet: det omnämns inte, omtalas inte. I varje
fall inte i de mest synliga exemplen:
— En referens har eftersökts men inte påträffats — Se CambridgeCoriolis.
— Men (inte heller) den detaljen klargörs inte,
eller ens omtalas: Framställningssättet i MAC
kopplar, uppenbarligen, ingen bestämbar fysikbeskrivning. Eller rättare
sagt; fysikbeskrivningen i CoriolisMAC felbeskriver (våldför sig på)
orsakssammanhanget. Jämför korrekt sätt i AktionReaktionCoriolisIllustrerat.
— Relaterad beskrivning [MACarbitraryActionReaction] saknas i MAC.
AKTION och REAKTION illustreras f.ö. principiellt
utomordentligt av DEN ACCELERERANDE BILEN:
[Som naturvetenskaplig analytiker, står AktionReaktion, NewtonIII,
inbränt med fetstil INNANFÖR
pannbenet: bara att läsa innantill].
— Om bilen accelererar i framriktningen (AKTIONSRIKTNINGEN ←) kommer INSTRUMENTET (kulan som hänger
från taket i snöret) att ge ett utslag MOTRIKTAT AktionsRIKTNINGEN (→):
— Aktionsriktningen är DEN FÖRORSAKANDE [eg. underhållande/drivande]
KRAFTENS RIKTNING — drivkraften till bilhjulen som strävar att driva bilen
framåt (←):
— ReAktionskraften är DEN RESULTERANDE INSTRUMENTKRAFTEN,
alltid diametralt motriktad aktionskraften enligt NewtonIII som visar, bevisar,
förklarar, och CERTIFIERAR — som låter oss KÄNNA — att aktionskraften verkligen
existerar, och endast då: den kraft vi kan KÄNNA, UPPLEVA, »TA
på», och den som (naturligtvis) i modern akademi kallas för ”SKENBAR”, och som i MAC ””måste INFÖRAS”
— inte ”redan
ingår”.
I relaterad fysik är Coriolisaccelerationen (aktionen) enligt CoriolisEffekten MEDriktad rotationen (ω) om den separata massans konstanta radialhastighet (vr) är utåtriktad:
— Aktionsriktningen är samma som den anställda (förorsakande [eg. underhållande/drivande]) kraftens riktning (i Coriolisfallet samma som resultatet av den separat (rätvinkligt rotationens periferihastighet vn) iscensatta vr — samma typ som den snurrande isdansaren [IMPULSMOMENTET J=mvr] [RotationensVektorVerklig] som sträcker ut armarna, men som på grund av avsaknaden av extra kraft att underhålla den konstanta rotationen med den utsträckta massrörelsen, därmed förlorar i rotation) som garanterar accelerationens värdemängd, att den verkligen blir av:
— Reaktionsriktningen är den fysiska instrumentmätningens tryckekvivalent — alltid diametralt motriktad aktionsverkan [NewtonIII], den som registrerar en växande ändring från noll och uppåt, och som visar att den fysiska verkan verkligen är aktuell: det som vi kan känna, se och MÄTA — men det som i MAC (i resulterat, inte skapat, förakt för människans naturligt vardagliga uppfattningsförmåga — verkligheten) kallas för ”skenbar kraft”, se CitatFM1975s72, och som därmed bara försvårar (i princip omöjliggör) en naturvetenskaplig beskrivning VÄRDIG människan. Det vi upplever är naturligtvis verkligt, inte skenbart.
— OM det SÅLEDES FÖR ÖVRIGT, verkligen, finns personer som tycker sig ha »kommit fram till» att det verkliga i själva verket är något skenbart, är det tydligen dags att sätta ner foten i backen och dra i nödbromsen.
I ETT HALVFAST ROTATIONSSYSTEM — som på Jordytan med Oceanerna och Atmosfären, tillsammans med Solenergin som yttre, separat energikälla — är det OMÖJLIGT att olika skikt, stråk och avdelningar av de mer eller mindre mobila massorna INTE skiljer sig från den idealt fast bundna rotationsriktningen.
Med Solinstrålningen som källa för olika temperatur och tryckskillnader finns direkt grund för uppkomsten av [Coriolisaccelerationens effekt] olika LINJÄRA FLÖDESRIKTNINGAR Högtryck-Lågtryck, typ dem illustrerade i Coriolisaccelerationens effekt — och som redan i väsentlig matematisk formalia redan är välkända (typ William Ferrels satser [1858], se citat i Persson 2005).
— OM, som i den illustrerade
beskrivningen i Coriolisaccelerationens
effekt, radiellt riktade primära rörelser (hos en halvfast massa i förening med
en fast underliggande roterande kropp) samverkar (idealt, via motriktade radiella flöden)
i inbördes motriktade (PAR) flöden ![]()
— var och en (P12) som en elementär CoriolisBASIC aCoriolisBASIC = ±ωvr
Alla
parkombinationer tillåtna
— oberoende av inbördes mellanliggande lokal: parverkan garanterar i vilket
fall nollsumma i kraftverkan genom summan inbördes med-motriktade v[r] vektorer, se även
utförligt i CoriolisAccelerationensEFFEKT:
— CoriolisEFFEKTEN via PAR eller
±komponentSummaRiktningsVERKAN, och endast då, summerar
nollkraft;
— Något fysikaliskt relaterbart begrepp om ett separat
Coriolisrotationscentrum i samband med CoriolisEFFEKT via PARVERKAN existerar
inte [BaraEttSätt].
— är det tydligt att
Coriolisaccelerationernas bägge motsatta riktningsavlänkningar avbildar ![]() ett (eg. oegentligt idealiserat)
cirkulärt omlopp, här förenklat en »CoriolisCELL» (därför att
nettoräkningen BALANSERAR nollkraft);
ett (eg. oegentligt idealiserat)
cirkulärt omlopp, här förenklat en »CoriolisCELL» (därför att
nettoräkningen BALANSERAR nollkraft);
— Det finns inget egentligt rotationscentrum i en CoriolisCELL (inget sådant kan härledas, här veterligt), snarare en kraftparsamverkande inflödes-, utflödes-, omflödes-, eller kringflödes struktur.
— I kraft av de motsatta riktningarna, och endast då, krävs i netto ingen energi för att underhålla den verkan:
— ENERGIN i Corioliseffekten kommer istället ifrån den initierande separata radialrörelsen (vr) [Solvärmen i Jordfallet som ytterst sett ansvarar för energin bakom flödena mellan högtryck och lågtryck, vidare nedan].
— FÖRUTSATT PARVERKAN (![]() )
blir Corioliseffekten då bara ett resultat av en omfördelning i —
»konturändring» — den underliggande rotationskroppens egen rotationsenergi;
Själva flödesverkan (
)
blir Corioliseffekten då bara ett resultat av en omfördelning i —
»konturändring» — den underliggande rotationskroppens egen rotationsenergi;
Själva flödesverkan (![]() ),
med Jordkroppen och atmosfären som exempel, försörjs av Solen (termofysiken med
högtryck-lågtryck) som grundval för det primära, CoriolisEffektUtlösande
vindtrycket.
),
med Jordkroppen och atmosfären som exempel, försörjs av Solen (termofysiken med
högtryck-lågtryck) som grundval för det primära, CoriolisEffektUtlösande
vindtrycket.
I praktiken (Jordens atmosfär) finns inte (direkt den motriktat
närliggande) vindtypen ![]() ,
utan snarare
,
utan snarare
HÖGTRYCK→LÅGTRYCK←HÖGTRYCK med motsvarande Coriolisaccelerationens effekt »CoriolisCell» eller »CoriolisKoppling»
NorraHalvklotet![]()
![]() ,
SödraHalvklotet
,
SödraHalvklotet![]()
![]() .
.
CoriolisCELLEN enligt relaterad
fysik — beskrivning
ENDAST I EN HALVFAST ROTATIONSKROPP [CoriolisSATS3]
— som i fallet med Jordytans Oceaner och Atmosfär — finns förutsättningar för
en Corioliseffekt [Coriolisaccelerationens effekt] att
visa sig. I modern akademi kan den förutsättningen INTE RELATERAS: man måste i MAC istället — via sin vektorkalkyls regelverk BegreppetVektorproduktMAC — använda en kinematisk
analogi [Hur MAC associerar Coriolis med Kinematiska]
och som dessutom leder på FEL VEKTORRIKTNINGAR [OrsakssammanhangetCoriolis]. Se
utförligt från CoriolisINLEDNING
— eller direkt i FÖRKLARANDE matematisk syntes i Kinematiska
FRIKTIONSLÖSA ParabelAnalogin.
CoriolisBASIC beskriver en enskild CoriolisARM på Coriolisaccelerationens
form aCoriolisBASIC = ±ωvr ;
Varje ett
par (±2ωvr) diametralt motriktade eller BALANSERANDE CoriolisARMAR ger
ett (självunderhållande) NOLLimpulsmoment,
(←)mvr+(→)mvr = 0 ;
CoriolisCELLENs motriktade
(vindAvlänkande-) rörelser kräver ingen extra kraft, eftersom dessa genom sina
motriktade rörelsemängdsmoment ger NOLLVERKAN:
Den BALANSERADE
Kraftverkan (2mωvr) via Corioliseffekten (CoriolisCELLEN)
blir bara en omfördelning av den
redan befintliga underliggande rotationskroppens rotationsenergi i
dennas association med en halvfast (vätska, gas) massvolym. Se även mera
utförligt om CoriolisBASIC
i Coriolisaccelerationens
effekt.
CoriolisNOLLBALANSEN för CoriolisARMARNA
— som garanterar att ingen extra kraft behövs för att underhålla avlänkningarna
— summerar totala CoriolisCELLEN
(»tvåarmsNOLLbalansen») på just
FCoriolisCELL = | F=mωvr←
+ F=mωvr→ | = | 2mωvr | = 0 — Se även i CoriolisSTAVEN,
en vidare beskrivning av detaljerna i CoriolisCELLEN.

BILDKÄLLA: Understanding the Coriolis Force for Students [‡] — NASA Goddard Photo and Video http://www.fotopedia.com/items/flickr-4403581287 — Tropical Cyclone
Gelane, Image acquired February 19, 2010
I vädersystemens motsvarande CoriolisCeller STYRS [enligt
källan nedan Tulane University 2011]
Coriolisavlänkningarna via PRIMÄRT RIKTNINGSLINJÄRA VINDRIKTNINGAR som i sig
uppstår genom tryckskillnader. Figurtyperna nedan överensstämmer med
härledningen i CoriolisBASIC
via de nyligen omnämnda korrekt — ENHETLIGT — relaterade vektorriktningarna och
vektorsummeringarna via CoriolisCELLEN:
En konvergent vindkropp ![]() på Jordytan, med vindriktning från högtryck
utanför till lågtryck i centrum , avlänkar via Corioliseffekten —
på Jordytan, med vindriktning från högtryck
utanför till lågtryck i centrum , avlänkar via Corioliseffekten — ![]() MotJordROT norra halvklotet,
MotJordROT norra halvklotet, ![]() MedJordROT södra halvklotet — vindriktningen med
följd i en inre vindcell (Cyklon Norra
MedJordROT södra halvklotet — vindriktningen med
följd i en inre vindcell (Cyklon Norra![]() MedJordROT Södra
MedJordROT Södra![]() MotJordROT) som matas av den
vindriktningsavlänkande Corioliseffekten och trycksuget inåt mot nollcentrum.
MotJordROT) som matas av den
vindriktningsavlänkande Corioliseffekten och trycksuget inåt mot nollcentrum.
Bilden ovan en Cyklon
(GelaneCyklotronen 2010, Södra Indiska Oceanen) som kan förstås ha utvecklats
på den grunden:
Vindhastigheten i Gelane Cyklonen enligt källan i
storleksordningen 230 kilometer i timmen: 64 M/S.
↑↑↑↑↑Pilarna visar Jordrotationens riktning till höger om rotationsaxeln↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑
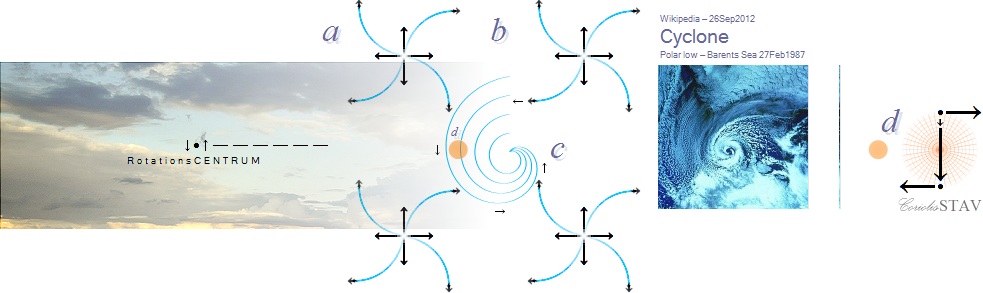
↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑
Figurblocket ovan visar hur man PÅ ENKLASTE SÄTTET UTAN ATT TjuvTITTA I METEOROLOGERNAS
FACIT kan förstå uppkomsten av ett VÄDERSYSTEM — i regelrätt korrekta
riktningsordningar via CoriolisBASIC:
— Hur proffsen tänker sig bildningen av en
(lågtrycks-) Cyklon finns f.ö. beskrivet i Tropical Cyclones (Hurricanes), Tulane University
2011 http://www.tulane.edu/~sanelson/New_Orleans_and_Hurricanes/tropical_cyclones.pdf;
(a) Solvärmen
skapar HotPoints
på den belysta Jordkalottens centralpunkter: luften värms upp SOM MEST I
HotPointCENTRUM; Värmebildningen i HotPointCentrum skapar HÖGTRYCK;
högtrycksluften strömmar till omgivande (förmodligen nära underliggande luftskikt) luft
med lägre tryck/lägre temperatur; den Solförsörjda radialströmningen triggar CoriolisVERKAN; Varje
HotPointCentrumStrömning kan förstås som en CoriolisCELL;
(b) FLERA
CoriolisCELLER kan samverka till ett gemensamt luftströmningssystem, ett
VÄDERSYSTEM (c); Vädersystemets finstruktur (d) kan förstås genom CoriolisSTAVEN; Coriolisstavens
vridmoment, som följd av luftstavens metriska utsträckning med dess inre
flytande hastighetsvariationer, utpekar
en FRAGMENTERANDE verkan: närliggande CoriolisSTAVkopplingar motverkar
varandra: strukturen blir »kullrig», inte slät. Det är här inte känt om denna beskrivning också återfinns i
den etablerade meteorologiska facklitteraturen.
—
GENERELLT (förenklat): Skillnaden HögtryckLågtryck (Polerna-Ekvatorn, strömningen
Jordytan-Troposfären) skapar vindar från H till L (a); Corioliseffekten
mellan den delvis Jordbundna atmosfären och Jordytan garanterar en allmän
avlänkning medurs på Norra halvklotet (a)(b); Coriolissymmetrin i en lokal cirkulär
periferi tvingar in vindriktningen i en inåtgående — och därmed
självcentrerande — H-L spiral (c) med inre FRAGMENTERANDE finstruktur (d).
— Ingen specifik extra kraft behövs för att underhålla en sådan, partiellt lokal »CoriolisRotation» (sådana rörelser i oceanerna och atmosfären): den partiella Coriolisrotationens lokala cell ingår — då, tydligen — som en delaspekt i hela kroppens egenrotation (rotationskroppens hela egna inre impulsmomentet J=mvr försörjer fenomenet automatiskt i försorg av energin utifrån som skapar förutsättningarna för radiella massförflyttningar); CoriolisCellerna finns där så länge kroppens rotation finns, och så länge det mobila materialet finns kvar under den yttre energikällans inverkan.
Ytterligare ett avsnitt i WikiCoriolis:
”However, Coriolis force is a consequence of inertia, and is not attributable to an identifiable originating body, as is the case for electromagnetic or nuclear forces, for example.”,
http://en.wikipedia.org/wiki/Coriolis_effect
@INTERNET
Wikipedia — Coriolis effect, Causes [2012-09-15]
NOTERA (återigen, som inte sällan är
fallet i Wikipedia) att PÅSTÅENDEN FÖREKOMMER UTAN VIDARE RELATERAD BESKRIVNING
— här tydligen med adress till Hemliga Klubbens Privata Insikter i Kärnfysiken.
Läsaren får inget veta vad saken handlar om, i detalj.
I relaterad fysik föregås all
tidsrelaterad kraftverkan
(F=ma=mv/T=p/T) av en IMPULS (rörelsemängd p=mv) [POM]:
— CoriolisKRAFTEN (Coriolisaccelerationen
tillsammans med rörelsemassan) uppkommer i följd av EN SEPARAT
— MED ROTATIONEN ICKE helt FAST FÖRBUNDEN
— RÖRELSEMÄNGD (värmebildning) (mv[r]) vars
KRAFTväxelverkan — kraftINTERFERENS — med den roterande (helt
fasta)
kroppen RESULTERAR I en motsvarande benämnd s.k. CoriolisAcceleration [CoriolisORIGINAL]:
— all tidsbestämd kraftverkan i relaterad
fysik uppkommer
som följd av TRÖGHETSVERKAN
[NewtonIII]
från VÄXELVERKANDE (SAMMANSTÖTANDE, tryckande) rörelsemängder erhållna från
olika kroppar som befinner sig i olika rörelsetillstånd:
— Alla tidsberoende krafter
(F=ma=mv/t=p/T) i DEN RELATERBARA fysiken ÄR återförbara (”attributable”) på
”an identifiable originating body”, en identifierbar ursprunglig kropp — på ett
eller annat sätt, i en eller annan mening, på mer eller mindre komplicerat sätt.
Undantag existerar inte.
Den uppdelning — i ”consequence
of inertia” och ”attributable to an
identifiable originating body” — som Wikimeningen ovan FÖRESVÄVAR, finns
inte i relaterad fysik.
— Alla krafter I DEN RELATERBARA FYSIKENS MENING som
uppträder i samband med »massans motstånd mot rörelseändring»
— alltså AKTIONSKRAFTER: alla krafter F=ma som sammanhänger med ändring av givna tillstånd i resulterande riktningar och som då uppträder på BEGRÄNSAD TID [via ma=mv/T=p/T] —
är samma som KONSEKVENSER AV TRÖGHETENS (motståndet mot tillståndsändringens) INVERKAN [NEWTONIII]:
GRAVITATIONENS ABSOLUTVERKANDE positionsändringsmotstånd
Ingår inte i MAC
— i allra största synnerhet inom elektrofysiken (fördröjningen via ljushastighetens kraftåterkoppling över avstånd):
(induktionsverkan [INDUKTIONEN OCH MAGNETISMEN] över
avstånd förorsakas alltid av en elektriskt laddad masskropps relativa
lägesändring i förhållande till den lokala gravitationens fasta referenser, och
alltid med en gravitellt bestämd kraftåterkopplande tidsfördröjning som beror
av den lokala ljushastigheten [Ljusets g-beroende]):
Atomfysiken, kärnfysiken, partikelfysiken. Alla krafter som uppträder — som visar sig per någon fysikalisk mätbarhet — är tidsbestämda. Den enda kraftverkan I RELATERAD FYSIK som inte är tidsbestämd, är gravitationskraften [GTaction];
— Den kan också mätas, liksom de andra krafterna, men då endast med referens till den faktor som är gemensam för alla, och som därmed också garanterar att gravitationen som kraftbegrepp kan definieras i fysiken
(nämligen via CENTRALACCELERATIONEN):
— dt, tidsdifferentialen, jämviktens — den fysiska instrumentella mätningens — mätbas [FUNTOP].
— Wikipediaartikelns SÄTT att beskriva sammanhanget bara understryker (därmed) den ALLMÄNNA SPRÅKFÖRBISTRINGEN i de begrepp som berör DEN ELEMENTÄRA FYSIKUPPFATTNINGEN: gravitationens bestämmande roll för hela fysikbeskrivningen.
— Den delen ingår inte i MAC.
Se utförligt med jämförande referenser i GTaction.
I ljuset av DEN RELATERADE FYSIKENs beskrivningssätt, kan vi alltså INTE (enhetligt) påstå med någon seriös NERV att MAC (ens) har FEL. Nämligen därför att det är uppenbart i det beskrivandet ljuset att MAC är PRIMITIV: MAC omfattar, tydligen, inte de relaterbart förklarande ( förklarande) beskrivningsgrunderna (vad den här framställningens meningar försöker påpeka); den moderna akademins vokabulär räcker inte för den begripliga, detaljerat förklarbara naturbeskrivningen.
Mera angående CoriolisEFFEKTEN i MAC
från Wikipedia
WikiCoriolis [WikiCoriolisInertia]:
coriolis effect
”... causes
acceleration ...”;
”The Coriolis effect exists only when one uses a rotating reference frame. In the rotating frame it behaves exactly like a real force (that is to say, it causes acceleration and has real effects). However, Coriolis force is a consequence of inertia, and is not attributable to an identifiable originating body, as is the case for electromagnetic or nuclear forces, for example.”,
http://en.wikipedia.org/wiki/Coriolis_effect
@INTERNET
Wikipedia — Coriolis effect, Causes [2012-09-15]
First:
”Coriolis
force is a consequence of inertia”:
— In related physics (TNED)
ALL TIME RELATED physics phenomena are consequences of
effects from variation:
consequences of inertia. Exceptions do not exist in our universe [Newton
III], [GTaction].
— The specific CAUSE of the CoriolisEFFECT is the energy
source through which any radial (vr) motion appears — by direct mechanical
impact through mass [F=ma], or in electrophysics through electic charges by
induction [u=L(di/dt)]). In either case, by interaction with
others.
For Earth (ω)
surface meteorology, with the solid Earth surface interacting semi-solid
material in the oceans and the atmosphere as the mobile Coriolis Agents, it is
the irradiation from the SUN (thermal
effects in mobile masses with different pressures make linear motions [CoriolisCELLspiralConstructIllustration])
having credit for THE ACTUAL ONSET (vr) OF the CoriolisEFFECT;
acceleration (ωvr), force (mωvr), energy (mωvr2);
— In all cases, the CoriolisPHENOMENON collapses if v[r]=0.
Second:
”The Coriolis
effect causes acceleration”:
— First we note that Claim in Quote has no specified related
reference: We would have to GUESS OUT what the actual author HAD in mind when
he wrote the sentence.
No.
The CoriolisEFFECT is incepted, but not
completed, just as an ice dancer withdraws, or extends, the arms from the
spinning body: the ice dancer can regulate the spin magnitude because
conservation of angular momentum
holds, J=mvr (Kepler area momentum, K=vr, times mass):
— The radial movement v(r)
of mass WITHIN a rotating body (ice dancer), causing changes in the rotational
period [v(n)=2πr/T=ωr],
is only OUR mathematical BASIC
FUNDAMENTAL UNDERSTATEMENT PART of the effect associated with »the
CoriolisEFFECT»:
— The CoriolosEFFECT itself is, with
respect to the resemblance of the ice dancer, a phenomena IN the (either) HAND
of the performer — outside the main rotational center — PROVIDED the
material there is PARTLY MOBILE (as Oceans and Atmosphere are mobile with
respect to the solidity of the underlying Earth surface):
— Each »CoriolisARM (The BasicIceDancerUnderstatement)»
of a PAIR of such CoriolisArms cancel the resulting force of each TheBasicIceDancerUnderstatement
IF its radial velocity v(r) is mutually opposed within the pair,
so that NO RESULTING FORCE is needed to CONSERVE THE ZERO FORCE CoriolisCELL
bound: The two arms cowork AS IF they would have a common rotational
center, a spin, OUTSIDE the underlying rotational mass (»IN the hand of the ice
dancer»):
— Energy from the Sun causes linear
motions [wind, with radial components v(r)]
between high and low pressure:
— Provided separate energy from an
external source to allow for radial changes: Without NO extra FORCE to feed the
actual action, several pairs of coworking CoriolisArms — in this
presentation, a primitive »CoriolisCELL»
— guarantees — DO — a resulting FLOW SPIRAL [CoriolisCELLspiralConstructIllustration].
— The Coriolis EFFECT as The Local
Phenomenon is hence
in NO concern with a »rotational center»;
— The Coriolis EFFECT is a peripheral redistribution of
rotational mass (from its, and all other masses
aspiration towards absolute
state without change [in this presentention same as gravitation]); the redistribution only
holds within a body of semi-solid (conv. quasi-solid) material (like Oceans and
Atmosphere on Earth); The energy feeding the redistribution does so in
introducing radial
movements (thermally introduced different pressures) [CoriolisAcceleration] within the
rotationally semi-bound masses.
— So: The CoriolisEFFECT in itself causes nothing at all; it IS WeatherSystems: the meteorological
wind-spirals [CoriolisCELLspiralConstructIllustration];
With a given rotation (Earth), it is all fed by energy from the Sun:
(heat→differentPressures→RadialMotion→CoriolisEffect→WeatherSystems).
acceleration (ωvr), force (mωvr), energy (mωvr2);
— In all cases, the CoriolisPHENOMENON collapses if
v[r]=0=NoSunHeat.
— It (CoriolisEFFECT) is an EFFECT,
a result, OF A PHYSICAL INTERACTION (giving appearance of a resulting energy conversion/transformation — HEAT,
friction) between two different motions: a linear (•→)
and a rotational (↓•↑) featuring a mutual half state of material connection,
not completely separated, nor completely solidified.
CoriolisKortSyntes med enkla
pilsymboler — CoriolisTNED/MAC
— Corioliseffekten
(CoriolisCELLEN) FÖRORSAKAR ingenting
alls över huvud taget (utan är
de spiralformiga vädersystemen):
CoriolisEFFEKTEN från CoriolisORIGINAL
är ett RESULTAT av — inte förorsakar — en speciellt uppkommen acceleration:
en radiell
rörelse UTÅT (vr•→) i en roterande kropp (ωr ↓•↑)
uppväcker en CoriolisACCELERATION (ωvr •→↑) som strävar att bromsa (–ωvr
•→↓) den radiella rörelsen (genom
friktion), alternativt att motverka rotationen (genom den uppväckta
CoriolisAccelerationskraftens motriktade reaktionskomponent) [CoriolisAccelerationensEffekt].
Men den beskrivningen kan inte föras i modern akademi:
— CoriolisEFFEKTEN är ett RESULTAT av fysikalisk
växelverkan (kollision/friktion) mellan två olika fysikaliska
rörelsesystem: ett linjärt (•→) och ett roterande (↓•↑).
— Kraften som driver CoriolisEFFEKTEN är — i
förening med en redan existerande underliggande rotation — den radiella,
linjära, rörelsekomponenten (•→), typ Solen som värmer Jordytan och
åstadkommer linjeströmmar (•→) i hav och luft, och dessa krafter —
den resulterande CoriolisKRAFTEN — är naturligtvis VERKLIGA, inte fiktiva,
skenbara, påhittade eller annat tok.
— CoriolisKRAFTEN (mωvr) har, således, EXAKT samma innebörd [IMPULSMOMENTET J=mvr] som KRAFTVERKAN
den spinnande isdansaren visar upp (i armmusklerna som sträcker ut eller drar in) inför
publiken när armarna sträcks ut eller dras in med resultat i att rotationen
resp. minskar eller ökar; CoriolisKRAFTEN har ingen annan relaterbar koppling.
— KRAFTERNA som visar rörelserna är NATURLIGTVIS VERKLIGA:
SÖKER MAN ÄNDRA/Påverka RÖRELSERNA uppkommer, som vanligt i
den allmänna fysiken, motsvarande förutsättningar för att mäta den
riktningsförändrande kraftverkan.
— Eftersom CoriolisKRAFTEN [IMPULSMOMENTET J=mvr, CoriolisAccelerationens Effekt] strävar
att bromsa primärrotationen om radialrörelsen är utåtriktad, och omvänt öka
primärrotationen om radialrörelsen är inåtriktad, kan ETT PAR sådana elementära
CoriolisARMAR, tydligen, samverka LOKALT i en gemensam CoriolisCELL med netto
noll kraft —
samtidigt som just en lokal CoriolisEFFEKT visar sig, se Illustrerat exempel från Jordens Vädersystem;
CoriolisKRAFTERNA underhålls av de linjära radiella rörelserna, men KAN i
egensumman FÖRSTÅS VARA noll. Dvs., själva den ROTERANDE VYN mellan de
ömsesidigt parkopplade CoriolisArmarna kräver I SÅ FALL i sig ingen
underhållande kraft eller energi för att fungera. Det är bara den underhållande
LINJÄRT TRIGGANDE ENERGIN som räknas i orsaksgrunden till CoriolisEFFEKTEN.
— CoriolisENERGIN (mωvr2) som underhåller CoriolisKRAFTEN (mωvr) INGÅR följaktligen I KROPPENS
EGEN INTERNA ROTATIONSENERGI tillsammans med kroppsmassans termiska påverkan
utifrån; För Jordytans del, dels Jordrotationen som sådan (Primära passiva
Coriolisfaktorn), dels Solinstrålningen (Sekundära Aktiva
Coriolisfaktorn, som blir den egentliga påtriggande CoriolisEFFEKT-faktorn via
de radiella strömningarna typ högtryck→lågtryck).
— Corioliseffekten utför enbart en SPECIFIK formändring eller deformation av en
roterande kropps mer eller mindre rörliga delar.
MITexpPrbCoriolis — se särskilt separat förklarande tillägg i RotationsParabolensFormfaktor — BILDKÄLLA:
Författarens arkiv · 13Sep2012 E29 Bild207 · Nikon D90 · Detalj

MITexperimentParabolaCoriolis
saknar koppling till
Corioliskomplexet — vi studerar hur (håll ut — det kommer mer)
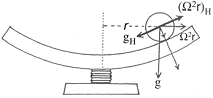
s4, Figure 3
http://paoc.mit.edu/labweb/lab5/inertial
circles/inertial_circle.pdf
MASSACHUSETTS INSTITUTE OF TECHNOLOGY —
Program in atmospheres, oceans and climate
Inertial circles - visualizing the Coriolis
force: GFD VI — John Marshall, February 9, 2003
— Experimentet bygger på en fast gjutform som tillverkats från flytande via en noggrant konstant vinkelrotation (3rad/S [MITs3ö]; 0,4774648 Hz; 1 varv per 2,0943951 S). På denna har sedan formmassan tillåtits stelna. Formytan bildar en parabol (eg. paraboloid), och materialet är av typen maximalt slät kontaktyta. Med friktionslösa puckar (kolsyreis, med försumbar friktion) och stålkulor (figuren ovan) kan sedan de olika experimenten utföras.
Resultatbilden enligt relaterad fysik är som följer (här i ett försök till relaterat sammandrag av källtextens innehåll):
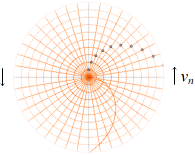
![]() Wikipedia Coriolis effect
Wikipedia Coriolis effect
Linjen-Spiralen-Analogin: Om vi följer successionen av punkter
från centrum och utåt genom att ta hjulets rotation baklänges (↑•↓), sammanförs bilden av de successiva
punkterna, samtliga, på en rät linje — den rörelsebana vi som observatörer vid
sidan av den roterande karusellen ser hos ett objekt som kastas ut från
centralpunkten radiellt rakt uppåt i bilden och utan kontakt med det roterande underlaget:
— Koncentriska cirklarna anger punktobjektets konstanta
hastighet;
— Solfjäderslinjerna anger den konstant roterande rörelsens
delvinkelintervall; skärningspunkterna mellan dessa beskriver rörelsebanan sett
i de olika referenssystemen.
— Sett från en fast monterad kamera på karusellen ses det
utkastade objektet röra sig i den ovan (principiellt) avbildade spiralbanan.
— Principen, och rörelsebanan, är samma som
visas animerat på Wikipediaartikeln om Coriolis effect http://en.wikipedia.org/wiki/Coriolis_effect [2012-10-17],
bilden ovan höger.
1. puckens minimala (nära obefintliga) kontakt med underlaget, och via en kort utputtningshastighet (utskjutning) från centrum (rakt uppåt i figuren ovan från mitten) — som en utskjuten ärta lämnar änden (precis i centrum) — garanterar EN nära IDEAL SPIRALBANA sett från en fast monterad kamera på den roterande MITparabolen;
— Spiralbanan sett från vår position vid sidan av den roterande anordningen är (idealt) bara en rät linje från ögonblicket då ärtan lämnar ärtröret;
2. parabolväggens allt brantare uppåtstigning ![]() med växande avstånd från rotationscentrum (idealt friktionslös avståndskontakt
med rörelseobjektet) påtvingar rörelseobjektet en inbromsning i den
idealt linjära konstanta rörelsebanan, och därmed, analogt, i rörelsebanan för
den motsvarande ideala spiralformen i karusellen;
med växande avstånd från rotationscentrum (idealt friktionslös avståndskontakt
med rörelseobjektet) påtvingar rörelseobjektet en inbromsning i den
idealt linjära konstanta rörelsebanan, och därmed, analogt, i rörelsebanan för
den motsvarande ideala spiralformen i karusellen;
— Uppåtstigningen avbildar en retarderad rörelse (deceleration); uppåtstigningens verkställande kraft måste tas ifrån objektets aktuella rörelsemängd (p=mv); uppåtstigningen sker därmed och tydligen i försorg av att objektet förlorar impuls; dvs., hastigheten går mot noll med växande lutning på den underliggande parabolväggen;
3. parabolväggen bromsar in pucken, analogt tvingar den ideala spiralbanan att snöpas in till en halvcirkel med en högsta position på parabolväggen;
— pucken har stannat i den linjära rörelsevägen;
4. puckens hastighet i det läget, sett från en fast monterad kamera på parabolen, är motriktad parabolens egenrotation och lika stor relativt denna som parabolens rotation vi ser som betraktare vid sidan av den roterande paraboliska anordningen;
— vi ser pucken som stillastående, utan någon synbar koppling till den underliggande roterande parabolkroppen;
5. därmed besitter den synbart stillastående, med det roterande underlaget icke förbundna friktionslösa, pucken samma g-potential som ett hjul vi håller fast i en nedförsbacke; släpper vi taget om hjulet faller det ned i gropen;
— puckens helt (idealt) linjära fall, rakt ner mot mittpunkten i parabelgropens botten, som vi ser det vid sidan av den roterande parabolen, kommer då att avbilda den föregående räta rörelsebanans inbromsning uppåt, men i omvänd mening;
6. pucken vänder tillbaka neråt parabolcentrum på samma halvcirkeltyp som i uppstigningen och med den upplagrade g-potentialen som drivkraft för att nå parabolens bottenpunkt, och i förening med den avtagande föregående uppaccelerationen;
7. när pucken når parabolgropens mittpunkt har den (frånsett friktionsförlusterna) samma utgångsläge som i föregående bottenläge. Därmed upprepas förloppet.
— På den beskrivningsgrunden kan rörelseschemat formuleras enligt följande:
Kinematiska FRIKTIONSLÖSA
ParabelAnalogin
se beskrivningen från början i MIT-experimentet
Med MIT-puckens
egenrotation på samma men motriktade KONSTANTA periferihastighet [Linjen-Spiralen-analogin]
vn=2π(r/2)/T1=πr/T1
; v1 = 2πR/T1 = 2(2πR/T0)
= 2R(2π/T0) = 2Rω
; R = v1/2ω
som parabol[oid]kroppens
egen
vn=2πr/T0
gäller tydligen
πr/T1 = 2πr/T0 ;
1/T1 = 2/T0 ;
T0/T1 = 2 ;
Pucken (T1) roterar precis 2 varv
(pendeln svänger diametralt en hel period över hela parabolen) på parabolens
enda (T0):
Kinematiska Friktionslösa
ParabelAnalogin anställer tydligen en beskrivning av den Koniska Pendelns
Kinematik, visualiserad på en roterande kropp: Foucaults PendelFigurer.
— »Hakar vi på resultatet» på den moderna akademins vektorregelverk [BegreppetVektorproduktMAC], får vi tydligen
|
MAC-vektorbaserade bilden av den
friktionslösa puckens cirkulära rörelse (höger i PREFIXxSIN) SEDD från den roterande parabolen i MIT-exemplet. Puckens linjära
pendelrörelse genom rotationscentrum och högercirkeln. Utförligt i FoucaultPendelnsMatematik. |
Men det medför också uppenbarligen att:
MAC: Ren kraftlös — kinematisk — beskrivning — som därmed
för Corioliseffektens vidkommande — kinetik —
uppenbarligen
våldför sig på den underliggande kraftfysiken;
— 2ω-formen definierar tydligen
»CIRKELHETEN» i MAC-tolkningens ljus (konv. tröghetscirkel) — som det får förstås direkt
relaterat i polära koordinater i PREFIXxSIN
enligt r = sin nx
med n = (1/2)(fPUCK=2)/f(Parabol).
— Vektorbilden ovan får därmed tydligen
sägas, och relateras, bilda hela den
matematiska vektoriella grundvalen för MAC-begreppet Corioliseffekt [MACoriolis].
Det finns, här veterligt, ingen annan relaterbar förklaring att studera.
VEKTORFELEN i ovanstående vektorbild i relaterad mening:
1. v[r] går INTE genom »Corioliscirkelns rotationscentrum» [Se CoriolisCELLEN] (ett sådant centrum
omnämns heller inte i MAC, men man talar å
andra sidan om s.k. ”tröghetscirklar”: ovanstående vektorkoncept);
— I relaterad
mening [CoriolisBASIC] finns inget
rotationscentrum i Coriolisverkan
[BaraEttSätt]. Coriolisverkan i
relaterad mening innefattar endast flytande avlänkningar av princip enligt ett bestämt regelverk [CoriolisAccelerationensEffekt] med
kombinationer av typen
| ![]() |
| ![]() |
|
![]() |
|
![]() |;
dessa kan också naturligtvis forma motsvarande »cirkulära rörelser» [CoriolisIllustration], men det är ingen
speciell egenskap, endast en följd av de enskilda CoriolisARMarnas
kombinerade samverkan på den energi som tillförs utifrån och som triggar
Coriolisverkan (Solvärmen i Jordklimatets fall). Se utförligt från CoriolisCELLEN. (Se även CoriolisSTAVEN).
|;
dessa kan också naturligtvis forma motsvarande »cirkulära rörelser» [CoriolisIllustration], men det är ingen
speciell egenskap, endast en följd av de enskilda CoriolisARMarnas
kombinerade samverkan på den energi som tillförs utifrån och som triggar
Coriolisverkan (Solvärmen i Jordklimatets fall). Se utförligt från CoriolisCELLEN. (Se även CoriolisSTAVEN).
2. a[C] påtvingas felaktigt en Reaktionsriktning (vidare nedan), inte
den korrekta Aktionsriktningen. Se mera utförligt i [MACreactionCoriolis] [CoriolisTNED/MAC]
[EulerCORIOLIS] [OrsakssammanhangetCORIOLIS]
[AktionReaktionMAC]
————— [‡] tröghetscirklarna i modern akademi (VektorFelenMAC):
Man idealiserar Coriolisverkan via centralverkan (kraften
rätvinkligt rörelsebanan/cirkelbågen) och har v=2piR/T=2piRf; Med TröghetsCirkeln ovan — dubbla
rotationsfrekvensen f=2ω/2pi=ω/pi på underlagets enkla — får man v=2piR(ω/pi)=R2ω, eller R=v/2ω;
”Since the force is directed at right
angles to the motion of the particle, it will move with a constant speed around
a circle whose radius R is given by:
υ
R = ——
f
where
f is the Coriolis parameter 2Ωsinφ, introduced above (where φ is the latitude). The time taken for
the mass to complete a full circle is therefore 2π / f .”,
http://en.wikipedia.org/wiki/Coriolis_effect -
Inertial_circles
@INTERNET Wikipedia — Coriolis effect,
Inertial circles [2012-10-25]
Från den enkla Linjen-Spiralen-analogin
med dubbla rotationen (2ω) för den IDEALISERAT separata rörelseformen (i MIT-exemplets paraboliskt beskrivande ljus)
framgår nu mera direkt, och med ovanstående klargörande, (något av) anledningen (inkluderat skevheterna, se 1 och 2
ovan) till MAC-härledningarna i ämnet
CoriolisAccelerationen [MACoriolis]:
— Man anställer (tydligen
ekvivalent i modern akademi) den idealt friktionslösa puckrotationen (2ω) ↓•↑•↓↑— och uppenbarligen helt
felaktigt i ljuset av den friktionslösa puckens MIT-exempel
som en separat
centrifugalekvivalent rörelse vid sidan av den ordinära (MIT-parabolen) tallrikens rotation (ω) —
samt applicerar vektorprodukten BegreppetVektorproduktMAC (2ω×v[r]) på den vektorbilden, (Jises),
enligt regelverket [BegreppetVektorproduktMAC], [MACaktionsriktningenCoriolis]:
aCoriolisMAC =
–2ω×vr = vr×2ω ............. har inte ett spår med CoriolisKRAFT att
göra, vektorfiguren ovan
— Men: Puckrörelsen i MIT-exemplet beskrivs friktionslös: CoriolisEFFEKTEN [CoriolisSATS3]
[CoriolisBASICfrnCoriolis]
kopplar inte dit;
Och: DEN
MATEMATISKA LEDBESKRIVNINGEN, ledet ovan, utpekar, tydligen, ingen annan
(ekvivalent) relaterbar form.
Och därmed är saken
klar:
— DEN formen har,
uppenbarligen, INTE med CoriolisAccelerationens
härledande förutsättningar — kraftverkan [CoriolisBASICfrnCoriolis] — att
göra;
Vid en närmare genomgång visar sig flera olika — här inte
tidigare uppmärksammade — avgörande detaljer, aspekter och sammanhang som
förklarar bilden, men som man, tydligen, inte hittar i den WebbEtablerade
bokbeskrivningen (Okt2012):
Kinematiska
RotationsAvvikelsen — direkt matematiskt jämförande exempel som visar HUR MAC blandar ihop Kinetik (Coriolis) med Kinematik (CINEMA) — samma samband, skilda
synsätt, samt
CoriolisCINEMA — HUR dessa olika avsnitt i
fysikbeskrivningen förhåller sig till varandra, samt
CoriolisSATSERNA — satsbilderna med grund i de bägge
teoremen [CoriolisBASICfrnCoriolis]
från Gaspard Coriolis (via Persson 1998/2005) som helt klargör vad
Corioliseffekten och Coriolisverkan är och inte är, och hur den verkan kan
förstås mera i detalj (CoriolisSTAVEN).
— Hela CoriolisKomplexet HAR (eg. UPPVISAR, tydligen) två
egentligen tre med Coriolisverkan inbegripen
skilda delar
vars matematiska form intränger varandra.
— Delen ovan
med vektorledets MAC-form KAN TYDLIGEN FÖRSTÅS VARA en
(ren, ENTYDIG) utkomst av den moderna akademins vektorkalkyl och dess regelverk
I en specifikt KINEMATISK (rörelse
utan kraftens inverkan) BESKRIVNING.
Hur man sedan
löser de rent praktiska problemen i MAC i ljuset av den tydliga kalabaliken
förtäljer inte den här berättelsen.
Se mera utförligt
från MACaktionsriktningenCoriolis.
Se även MIT-parabolprincipen historiskt från Persson 2005 s13 via Adolph Sprung
(1879-80):
”Sprung generalized the concept of the Coriolis force by
showing it to be, in the spirit of
Coriolis (1835), but probably unaware of his work, an
extension of the centrifugal force. He did
so by deriving the equations for a relative motion on a flat
turntable. He then gave the
turntable
a parabolic form and showed
how this neutralized the common centrifugal force and left
only the
Coriolis force
driving the moving object into inertial circles”, Persson 2005 s13
Veterligt:
— I MIT-exemplet
finns bara en (sammansatt) faktor att återföra den konventionellt benämnda s.k.
Tröghetscirkeln [den idealt friktionslösa puckrotationen (2ω) ↓•↑•↓↑ i MIT-analogin]
på (med ideal nollfriktion förutsatt, vilket också anges i MIT-exemplet särskilt): parabolen tillsammans med tyngdkraften.
— Idealt utan parabolen bortfaller också tyngdkraften: den
friktionslösa pucken utsläppt med viss begynnelsehastighet från
rotationscentrum på en plan rotationsyta beskriver en obegränsat utsträckt
spiralbana;
— I praktiskt relaterbar mening finns
ingen sådan fysikanalogi
för CoriolisKRAFTEN:
finns ingen kontakt mellan mobilt objekt och ett fast roterande underlag [CoriolisSATS3], finns heller ingen
förutsättning för en Corioliseffekt: det måste finnas en impulsomsättande
faktor mellan mobil och rotation. Annars har begreppet CoriolisKRAFT ingen
mening.
BILDKÄLLA: Författarens arkiv · 11Sep2012 E27
Bild214 · Nikon D90 · Detalj — VATTENDRAG PÅ JORDYTAN är utmärkta exempel på
Coriolismassor [CoriolisSATS1] som gestaltar Coriolisverkan (mycket liten dock).

Därför är också SAMTLIGA EXPERIMENT MED FRIKTIONSLÖSA PUCKAR helt meningslösa
demonstrationsobjekt i koppling till begreppet CoriolisKRAFT.
De experimenten endast beskriver en relativ kinematisk vy
Kinematiska FRIKTIONSLÖSA ParabelAnalogin [Kinematiska
RotationsAvvikelsen] [Hur MAC
associerar Coriolis med Kinematiska]
där ingen mätbar kraftverkan finns med.
För att få den idealt KINEMATISKT RELATERADE spiralbanan att
kröka sig inåt till en motsvarande »CoriolisCIRKEL» måste en SIGNIFIKANT
FRIKTIONSKOPPLING EXISTERA som garanterar kraftverkans komponenter, enligt CoriolisBASIC — typ atmosfärens och
oceanernas koppling till Jordkroppens underliggande rotation.
— Med en sådan mera påtaglig friktion följer alltså också
ett närmande mot den elementära fysikbeskrivningens CoriolisAccelerationen
(som naturligtvis ansluter till CoriolisBASICfrånGaspardCoriolis)
med dess utpräglade aktions-reaktionshärledning: materialet som står i påtaglig
atomär-molekylär mer eller
mindre FAST bindning till den primära rotationskroppen, och som i
den enkla formen
[CoriolisARMEN] visar endast halva
värdet med korrekt
aktionsriktning innefattat,
aC = ωvr
..................... CoriolisBASIC
Ingår inte i MAC
CoriolisBASIC skiljer alltså
SKARPT mellan aktionsriktning
och reaktionsriktning — vilket, som vi ser på grund av vektorbilden, dess regelverk [BegreppetVektorproduktMAC] i MAC — tydligen INTE ingår i den moderna akademins
beskrivningar av Corioliskomplexet.
— Pucken med en fast monterad kamera på den roterande parabolen kan förstås, ses, rotera i en cirkel (konv. tröghetscirkel, eng., inertial circle) [MIT-källan, s2n.Figure 2] vid sidan av mittpunkten och motriktad huvudrotationen;
Puckrotationen antar huvudvinkelrotationens dubbla magnitud: pucken faller från toppen till botten och tillbaka till toppläget »på andra sidan» igen under ett halvt parabolvarv:
MIT-källan
klargör inte explicit värdeformerna; det är heller ingen
lätt sak att försöka luska ut vad författaren menar med de stundtals omvända
begreppsreferenserna ”rate”, ”velocity”, ”period” och ”frequency”:
anger primärrotationen till Ω [s3 ”rate” Figure 3; Punkt1; s6m ”angular velocity”] och puckrotationens ”period” π/Ω [s6m];
OM författaren också menar PERIOD med π/Ω, och därmed frekvensens invers som 1/(π/Ω)=Ω/π betyder det, tydligen
fPARABOLEN = Ω
= 2πf
fPUCKEN = Ω/π = fPARABOLEN/π
= 2πf/π
=
2f .................................. puckens frekvens är dubbla parabolens:
pucken gör två internvarv på parabolens enda. Se även
”The length of the line
is twice the diameter
of the inertial circle and the frequency of the oscillation is one-half
that observed in the rotating frame.”,
Med f=1Hz=1varvPerSekund roterar Parabolen med
vinkelfrekvensen Ω=2πf=6,2831853 radian(Hertz)er per varv, samma som 1 Hz eller 1 varv per sekund, eller 1 radian per 0,1591549 S;
Pucken roterar då internt för sin del med
vinkelfrekvensen fPUCKEN = fPARABOLEN/π = 2f = 2(1 Hz) = 2 Hz; radianstorheten förkortas bort om den finns associerad med pi-faktorn:
fPARABOLEN = 2πRADIANERfHertz
fPUCKEN = ———————————— = 2fHertz
πRADIANER
eller ett varv på T0=1/fHertz= 0,5 S — alltså precis 2 gånger snabbare än parabolen, förutsatt korrekt tolkning enligt MIT-exemplet;
— Som vi ser är dessa resultat av samma form som i Kinematiska FRIKTIONSLÖSA ParabelAnalogin.
Fenomenet är eller kan med andra ord förstås vara resultatet
av ett »vertikalkraftsmanipulerat» form- och tyngdkraftskomplex:
— varken inverkan från någon (nämnvärd) Coriolisacceleration [MITkraftverkanNOLL], eller ens en
centrifugalkraft (IngenCentrifugalkraftIngår)
tillåts av experimentanordningen:
— MITexperimentet beskriver tydligen INTE någon Coriolisverkan. Det finns ingen
Coriolisacceleration eller Corioliskraft [CoriolisBASICfrnCoriolis]
att påvisa i experimentet.
— Det går (heller) inte att anställa MOTARGUMENT mot det påståendet, JUST därför att hela MIT-anordningen saknar — bygger på eliminerade [MITkraftverkanNOLL] — förutsättningar för att MÄTA Coriolisaccelerationen och Corioliskraften.
Hela CoriolisKomplexet (som det beskrivs i MAC) beskriver med andra ord — eller rättare sagt VIDRÖR, tydligen utan att kunna beskriva detaljerna — i själva verket det som nyligen påpekades i VektorledetsMACform TVÅ (egentligen tre) SKILDA fenomen (webben är proppad med videodemos i ämnet [WebbCoriolisVIDEO])
· 1. Kinematiska FRIKTIONSLÖSA ParabelAnalogin, [KinematiskaRotationsAvvikelsen], [Hur MAC associerar Coriolis med Kinematiska];
· 2. Det egentliga CoriolisKomplexet, se RELATERAT från Corioliseffekten, samt refererat i MACaktionsriktningenCoriolis, som MAC i försorg av 1 tydligen inte kan beskriva;
· 3. Den SFÄRISKA VISUALISERINGSBESKRIVNINGEN GENERELLT i vars 3D-rymd Coriolisverkan bara representeras av ett entydigt orienterat rotationsplan [CoriolisCINEMA];
men som — tydligen — sammanblandas utan åtskillnad, eller ens föranleder någon alls påtalad observation — i MAC.
— Se speciellt det klargörande jämförande exemplet i [Hur MAC associerar Coriolis med Kinematiska].
MITbeskrivning — ingen
centrifugalkraft ingår
alternativ/komplement till föregående
endast för att understryka NOLL CoriolisKRAFTVERKAN
Beskrivning
— Ingen egentlig CENTRAL centrifugalkraft ingår (heller) i fenomenbeskrivningen i MIT-exemplet.
Vidare i RotationsParabolensFormfaktor
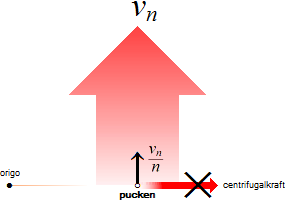
— För varje minsta ansats till MEDSLÄPNING (vn/n=v0 vid sidan av mittpunkten) I ROTATIONSRIKTNINGEN (vn) via den minimala friktionen (1/n) mellan pucken och den konstant roterande parabolkroppen, kommer pucken att också uppföra sig, just på grund av den minimala friktionen
(som experimentet idealt bortser ifrån,
”The law of motion of the puck traversing the frictionless parabolic surface are given by Eq.(15) of the appendix”, MITs5)
![]()
Bildkopia av MIT-källtexten s9n
som ett föremål man håller i ett snöre man snurrar runt och sedan släpper: föremålet fortsätter rakt fram i samma riktning (vn/n=v0).
— Sett från den roterande underliggande kroppen betyder det (om den linjära vägriktningen från släppet fortsätter) en spiralbana, figuren nedan:
— släppkroppen ses (från en fast monterad kamera på rotationskroppen) böja av i takt med rotationen, och åt motsatt håll (vi förutsätter här den förtrogenheten [figuren nedan, se särskilt i LinjenSpiralAnalogin]).
— Medan en helt friställd, släppt, puck i en PLANFORMAD roterande karusell skulle uppvisa en HELT IDEAL spiralbana sett från en kamera fast monterad på karusellen, figuren ovan, garanterar DEN ALLT MERA UPPÅTLUTANDE PARABOLVÄGGEN en BROMSANDE INVERKAN med växande avstånd från centrum;
— I Linjen-Spiralen-Analogin betyder MIT-parabolväggens växande lutning att den linjära färdvägen från utsläppet till slut helt har bromsats upp:
— pucken stannar — och vänder sedan tillbaka samma vägform.
Vartefter pucken tvingas uppåt via parabolväggen
— och den allt mer så radiellt
distanserade pucken via den spiralinitierande rörelsen sedd från den roterande
parabolen, samtidigt som avlänkningen från den ideala spiralbanan fortsätter
med garanti från den uppåttvingande parabolväggen
som stjäl impuls — hastighet — från den idealt plana färdvägen och därmed
åstadkommer en högsta stoppunkt, analogt en inkrökt halvcirkel mot toppstället
— är det tydligt att parabolväggen (»spiralinbromsningen») tvingar in pucken mot en högsta punkt på parabolväggen och över vilket toppläge pucken sedan inte kan nå.
— I den situationen, sett från den fast monterade kameran på den roterande parabolen, färdas nu pucken rakt motsatt parabolens egenrotation (och i toppläget med parabolens omloppshastighet så att pucken förefaller stå diametralt stilla, helt utan koppling till den roterande parabolkroppen, sett av oss som står vid sidan av och tittar på).
— Ingen centrifugalkraft
verkar på den friktionslösa pucken.
Inte ett
spår.
— I det läget har pucken en g-potential (upplagrad rörelsemängd p=mv via höjden över bottenpunkten) på samma sätt som man håller fast ett hjul i en nerförsbacke; Sett från vår position vid sidan av den roterande anordningen rör sig pucken fortfarande inte nämnvärt (idealt inte alls) i någon parabolisk koppling; Vi ser bara i totalvyn att pucken tycks pendla i rak linje över parabolgropen som en fast pendel (med svag ellips på grund av den minimala friktionen).
Pucken, som vi ser den, kommer alltså att börja falla ner i parabolgropen från toppläget:
— LinjenSpiralenAnalogin med den avstannande linjära rörelsen visar att samma linjära rörelse men åt andra hållet kommer att verkställas i försorg av puckens g-potential i fallet utmed parabolväggen (sett från parabolen samma som en omvänd halvcirkelrörelse tillbaka ner mot parabolens bottenpunkt: linjen med objektet som kommer utifrån och passerar centrum):
— Vartefter pucken faller mot parabolens bottenpunkt, tvingar den nu avtagande parabolväggens lutning den föregående upplagrade puckens g-potential i samma parabolväggslutning att överföra sin g-relaterade impuls (rörelsemängden p=mv via höjden över bottenpunkten) på pucken i dess nerväg;
— Då pucken når parabolgropens bottenpunkt, har, så, hela hastighetskapitalet från toppläget överförts till pucken då den passerar genom parabolens rotationscentrum (friktionsförlusterna frånsett) — själva utgångspunkten för det ideala utsläppet.
Därmed är cirkeln sluten, och förloppet kan upprepas.
— Kombinationen av puckfallet och puckhastigheten i toppläget motsatt parabolkroppen
— tillsammans med den minskande lutningen hos parabelväggen med avtagande avstånd från parabolens bottenpunkt
— tvingar följaktligen pucken åter i en fortsatt halvcirkel in mot parabolgropens bottenpunkt.
Puckens egen inre centralrörelse associerar till »en
ekvivalent inre centrifugalkraft» — men pucken erfar aldrig någon
centrifugalkraft via den centrala parabolens huvudrotation: pucken har ingen
fast kontakt med parabolen: den kunde lika gärna stå stilla.
Man SKULLE kunna säga (obetänkt):
— Parabolens stegrade lutning med växande avstånd från
parabelgropens bottenpunkt balanserar, tvunget, den centrifugalkraften mot
tyngdkraften, och bestämmer därmed, med hänsyn till parabolrotationen, det
aktuella toppläget för pucken.
Men det sättet håller inte:
— Pucken avkänner aldrig någon centralverkan i MIT-experimentet, endast en vertikalt påtvingad uppåt- och nedåtgående rörelse, tillsammans med en ordinärt initierad linjär hastighetskomponent; Totalt en Kinematisk FRIKTIONSLÖS ParabelAnalogi.
DEN kan, garanterat, inte nå Corioliskomplexet aktions- och reaktionsriktningar [CoriolisBASICfrnCoriolis]:
— MAC-regelverket garanterar det, självt, genom att ge aktionsresultaten en FEL RIKTNING [MACaktionsriktningenCoriolis] [WikiCoriolisRIKTNINGARNA]; MAC-regelverket kan (heller, därmed) inte specificera varken Aktionsriktningen eller ReAktionsriktningen som väsentliga fysikbegrepp i komplexet. Och därmed också, felaktigt, påtvingas tanken helt uppenbart absurda vektorutflyttningar [MACreaktionCoriolis] som, veterligt, inte existerar i fysiken [BaraEttSätt].
— Man kan (alltså) inte relatera någon kinetisk »separat centralverkan» för pucken i dess cirkulära rörelse i parabolen EFTERSOM den CIRKULÄRA PUCKRÖRELSEN [(2ω) ↓•↑•↓↑ i MIT-analogin] tydligen ÄR EN REN vertikalkraftsmanipulerad KINEMATISK (helt utan kraftbaserade komponenter i rotationsplanet) EFFEKT (LinjenSpiralenAnalogin) — också enligt MIT-experimentet helt utan förutsättningar [MITkraftverkanNOLL] för att kunna uppmäta någon rotationsrelaterad kraftverkan [CoriolisSATS1] alls: den friktionslösa pucken.
Parametrarna bakom fenomenet i MITparabolexperimentet totalt blir då (den minimala friktionen bortses ifrån):
· formkropp — parabolen, speciellt utformad
· tyngdkraften — framtvingar den friktionslösa puckhastighetens avstannande toppläge invid parabolväggen
· parabolrotationen — ger LinjenSpiralenAnalogins visuella bildeffekt (den centrala faktorn 2Ω)
Inga andra.
Med parabolens form, dess växande vägglutning för växande avstånd från rotationscentrum, är det uppenbart att det ENDAST är tyngdkraften på pucken tillsammans med parabolens rotation som ansvarar för den visuella effekten med puckens idealt spiralavböjda bana i formen av den aktuella konventionellt benämnda s.k. tröghetscirkeln [WikiInertialCircle]:
— Tas parabolens aspekt bort (plan rotationstallrik) återstår endast den rena ideala spiralbanan med en puck som fortsätter ut i oändligheten med konstant utsläppshastighet.
— Ingen egentlig CENTRAL — från parabolens centrum sett — centrifugalkraft ingår (relaterbarligen heller, tydligen) i den fenomenbeskrivningen.
Notera MIT-experimentets
inledande illustration:
— Placeras en stålkula (kullagerkula) på den roterande
parabolväggen, kommer kulan att söka sig till en högsta punkt där
CENTRIFUGALKRAFTEN balanseras ut av parabolväggens lutning tillsammans med
TYNGDKRAFTEN:
— Kulan har kontakt med det roterande
underlaget,
och kan därför också — TILL SKILLNAD FRÅN DEN idealt FRIKTIONSLÖSA PUCKEN —
utveckla centrifugalkraft, precis som en fast del av det roterande
parabolmaterialet. Den friktionslösa pucken däremot har ingen kontakt med det
roterande underlaget och kan därför varken synkronisera sig med parabolens
egenrotation eller utveckla någon centralacceleration.
Kroppar som
saknar kontakt med det roterande underlaget [MITkraftverkanNoll]
utvecklar inga krafter:
— Inga krafter kan påvisas, inga krafter kan uppmätas.
För att ett föremål I RELATERAD MENING ska uppvisa CoriolisKRAFT måste det obönhörligen besitta någon
form av atomär eller molekylär koppling till det underliggande
roterande materialet
[CoriolisSATS2]. Annars finns ingen
förutsättning för kraftverkan, inte alls över huvud taget.
Föremål som »rör sig över» ett annat föremål är (m.a.o.) en
kraftlös, rent KINEMATISK,
beskrivning (kinematik),
ingen kraftbeskrivning (kinetik).
Men webbkällorna verkar (Sep2012) proppade med den kraftlösa typen:
”Coriolis
force” och ”relative
KINEMATIC view” förväxlas — friskt, och i stor mängd — på Webben [WebVideoCoriolis].
Se särskilt belysande exempel i Hur
MAC associerar Coriolis med Kinematiska.
;
Centrifugalkraftsbegreppet (C) finns, tydligen, inte
i MIT-experimentet med den friktionslösa pucken; C:s omnämnande
och användande är tydligen resultat av en idealt kinematiserad [utan
kraftverkan] bild enligt Kinematiska FRIKTIONSLÖSA
ParabelAnalogin.
Avsaknaden av centrifugalkraft i MAC-beskrivningen av Corioliskomplexet visas mera i jämförande detalj i RotationsParabol(oid)ensFormfaktor.
Det närmaste vi tycks kunna komma CoriolisAccelerationen i något etablerat omnämnande är (tydligen) typen
”The French discussions on deflection of flowing water in rivers are related to the problem
of the sideways acceleration of constrained motion, like trains on rails. This was taken up by the
Austrian-Russian scientist Nikolai D. Braschmann (1796-1866) and promoted by the German
professor Georg Adolph Erman (1806-77)25.”, s11ö
http://www.aos.princeton.edu/WWWPUBLIC/gkv/history/persson_on_coriolis05.pdf
The Coriolis Effect:
FOUR CENTURIES OF CONFLICT BETWEEN COMMON
SENSE AND MATHEMATICS,
Part I: A history to 1885, Anders O. Persson,
2005
I RotationsParabol(oid)ensFormfaktor
kan vi studera hur MAC (genom egen förskyllan)
måste utesluta centrifugalkraften i MIT-parabolen.
RotationsParabolensFormfaktor — Förtydligade till MIT-exemplets rotationsgjutna parabol —
BILDKÄLLA: Författarens arkiv · 11Sep2012 E27
Bild213 · Nikon D90 · Detalj

RotationsParabol(oid)ensFormfaktor — i relaterad
fysik
gömmer/uppdagar ytterligare speciella föreställningar i MAC — angående Parabolkroppen och dess konstruktion
i MIT-experimentet
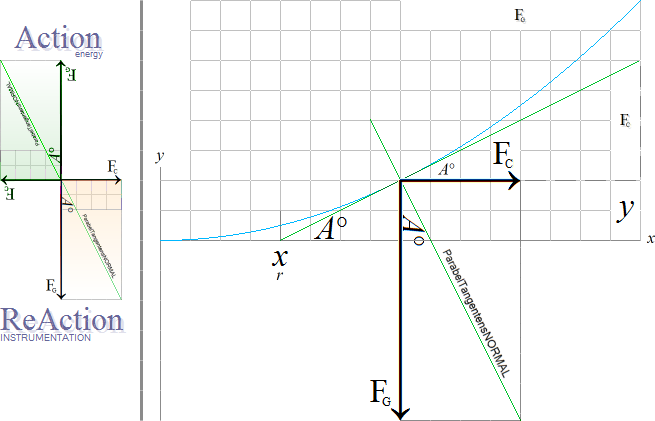
EN YTPUNKT PÅ EN IDEALT FAST (hård) PARABEL (y=x²/2Z) uppvisar jämvikt mellan
nedåtriktad tyngdkraft (F=ma)
och utåtriktad centrifugalkraft (F=må=mv²/r) då
resultanten till dessa vektorer
bildar normal (rätvinklig riktning) till parabelns ytkurva. Om parabelytan
roterar med fast vinkelrotation
(ω) kommer en stålkula som (i takt med rotationen) placeras på parabelytan
att också parkera sig vilande på parabelytan: inga krafter påverkar kulan (utom den resulterande
aktions[normal]kraften från ma och må på/genom parabelytan som trycker kulan
mot denna). Sambanden som visar balansen ges nedan i huvudtexten.
— AKTIONSKRAFTEN som krävs för att
underhålla tillståndsändringen i F[C]-fallet blir den centrifugalaccelerationen
(→) motsatt INÅTRIKTADE centripetalaccelerationen (←):
det
underhållande ansvaret i
det underliggande materialmotståndet; utan detta upphör komplexet;
— AKTIONSKRAFTEN som krävs för att
underhålla tillståndsändringen i F[G]-fallet blir den tyngdaccelerationen (↓)
motsatt UPPÅTRIKTADE »materialaccelerationen» (↑):
av samma skäl som i F[C]-fallet; det underhållande ansvaret
i det
underliggande materialmotståndet.
— REAKTIONSKRAFTERNAS RIKTNINGAR blir diametrala
spegelbilden av aktionsriktningarna, samma som pilarna för gravitationsriktningen
F[G] och centrifugalriktningen F[C] i figuren ovan, och vilkas resulterande
kraftvektor, parabeltangentens normal, bildar förutsättningen för instrumentell
uppmätning av det resulterande normal(in)trycket [kraft över tryckyta] på
parabelytan från en fritt rörlig masskropp (stålkula) som placeras på den. Se
även i Aktionskraftens
definition, om ej redan bekant.
y = x2/2Z ; Z anger parabelns dubbla fokuslängd, Se ParabelnsEkvation
med tangenten (derivatan)
TanA = x/Z = y’
ger DIREKT tillsammans med gravitella kraftlodlinjens (FG)(↓) komplement som centrifugalkraften (FC)(→) en parabelytans JämviktsNORMAL via (figuren ovan)
FC/FG = TanA = x/Z ;
FC = FGx/Z = mv2/r = m(ωr)2/r = mω2r ;
FG = ma ;
FC = FGx/Z = max/Z ; FCr = mv2 = m(rω)2 = E
v2/r = ax/Z = (2πr/T0)2/r = (r·2π/T0)2/r = (rω)2/r = rω2 ;
r = x ;
rω2 = ar/Z ;
ω2 = a/Z ;
ω =
√a/Z ;
a = industristandardJordytan ~ 9,81 M/S2 ;
Vi ser att parabelns ekvation AUTOMATISKT ger en och samma vinkelrotation (ω) för alla möjliga avstånd från parabelns bottenpunkt — förutsatt den lokala tyngdkraftens acceleration (gravitella fältstyrkan, a) är konstant, vilket den också är med hög noggrannhet inom utsträckningen för våra vanliga vardagsrum:
— Alla kulor som placeras på en roterande parabel med bestämd vinkelrotation — en parabol(oid) med en bestämd formfaktor (Z) — på ett bestämt avstånd från rotationsaxeln (r=x), uppvisar, tydligen, perfekt jämvikt (vila) på underlaget enligt ovanstående allmänna
FC = FGkonstantxVARIABEL/Zkonstant ................................... centrifugalkraftens
formekvivalent för jämvikt
Att ROTATIONSGJUTA (långsam slunggjutning) en parabolform (gjutmassan hälls formbar i en roterande cylinder och får sedan stelna tillsammans med en bestämd vinkelrotation) utifrån en bestämd vinkelrotation ([ca] π radianer per sekund i MIT-exemplet, eller f=π/2π=0,5Hz; omloppstiden T=1/f=2 S), ger parabolen en formfaktor (Z) lika med
ω2 = a/Z = (2π·f )2 ;
Z = a/ω2
= (9,81 M/S2)/(2π·0,5/S)2
= (9,81 M)/π2
= 0,9939608 M ;
y = r2/2(a/ω2) = r2ω2/2a
= (ωr)2/2a ;
Alternativt direkt via NOLLFORMSALGEBRAN:
dy/dr = mω2r/ma = FC/FG = ω2r/a ;
dy = ω2a–1 r dr ;
∫ dy = ω2a–1 ∫ r dr
= ω2a–1 · r2/2 = y ;
y = r2ω2/2a
= (x2/2Z)PARABELN
= x2/4f
Jämför modern akademi: samma matematiska formalia, men genom ett resonemang som slår alla rekord:
MAC kan inte relatera centrifugalkraftens komponent i
den tyngdgjutna rotationsparabelns kraftvektorfysik
Notera motsvarande (härledande) beskrivning i modern akademi. Se exv., utförligt i
MACkraftParabeln — RotationsParabolens
Formfaktor
”In an inertial reference frame, the dynamic equilibrium cannot be understood in terms of an equilibrium of forces.”,
;
”This is because when the liquid is rotating, there is an unbalanced force acting on the liquid – the force of gravity is acting in a vertical direction on the liquid, and the surface of the parabolic dish exerts a normal force on the liquid resting on it. The resultant force is a net centripetal force toward the axis of rotation.”,
http://en.wikipedia.org/wiki/Liquid_mirror_telescope
@INTERNET
Wikipedia — Liquid mirror telescope, Explanation of the equilibrium [2012-09-23]
|
Wikipedia — MAC (modern akademi) |
MAC förtydligat |
Relaterad fysik — TNED |
|
|
|
|
|
förstår inte jämviktens referens — kräver objekt |
obalanserad — centripetalkraften (←) påstås bli över |
perfekt balanserad — av underlaget |
Wikipediacitatets mening sammansätter
den resulterande — överblivande ”unbalanced force” ←
— från
1. den nedåtriktade g-kraften och
2. resultanten till den nedåtriktade g-kraften (igen) OCH centrifugalkraften. Man kan inte göra så i relaterad fysik.
— Ordstammen centrifugal ingår f.ö. över huvud taget inte i
Wikipediartikeln citerad ovan. Centrifugalkraften omnämns inte ens.
— Parabolytans normalvektor, dess sammansättning (FC
+ iFG)
och hur den hänger ihop, vidrörs heller inte i Wikipediaartikeln.
Varför utelämnas CENTRIFUGALKRAFTEN i MAC-versionen av den tyngdgjutna (vätskeroterande) rotationsparabeln?
(Som förtrogen med naturen, kan du säkert svaret själv, men här är mitt bidrag):
— Därför att i MAC
se utförligt från Einsteins allmänna relativitetsprincip ,
uppfinningen i MAC (under 1800-talet) av INERTIALSYSTEM
som innebär att man missförstod
Newtows VILOSYSTEM för ETT OBJEKT I RYMDEN, ett fysikaliskt objekt
(»Newtons Absoluta Rum» se Citat7 från Einstein — Einstein lägger,
tydligt, orden i munnen på den avlidne Isaac Newton; läser vi Newtons PRINCIPIA
finner vi att Einstein i sin mening, gravt, missuppfattar Newton; Newton talar
inte om fysiska objekt
”For I here design only to give a mathematical notion of
those forces, without
considering their physical causes and seats.”,
”considering those forces not physically, but mathematically”,
NewtonKlargörIegenMening (ur Newtons PRINCIPIA Definition VIII från 1687)
utan om Matematiska Principer;
Jämför Newtons slutord i Principia: ”END OF THE MATHEMATICAL PRINCIPLES”),
[Läs Litteraturen Innantill. Please]
och vars missförstånd således
(som det tydligen får förstås då ingen annan refererande källa ännu finns för
detta)
felaktigt ledde till att man
ansåg självaste Newton själv vara upphovet till den i själva verket egna
MAC-formulerade feluppfattningen — se vidare utförligt med referenser, utdrag
och citat i INERTIALSYSTEM
har man ingen förståndsgrundad uppfattning om JÄMVIKTENS PRINCIP [FUNTOP] som grundval för hela fysikvärldens uppfattande via ett förståndsbegrepp, inget fysiskt objekt; Jämvikten i verklighetens naturbok beskrivs ALDRIG med hänsyn till något »specifikt fysikaliskt system» eller »objekt» eller »kropp», utan alltid, undantagslöst alltid med referens till ett uppmätt, observerat, tillstånd (varaktighet under dt) [TILLSTÅNDETS PRINCIP]: en ögonblicksBILD, ett förståndsbegrepp — med (förhoppningsvis GOD) kunskap om de underliggande krafterna:
BILDKÄLLA: Författarens arkiv · 15Sep2012 E32
Bild155 · Nikon D90 · Detalj

BILDKÄLLA: Författarens arkiv · 15Sep2012 E32
Bild155 · Nikon D90 · Detalj
Newton SYNES HA fattat det (i huvudsak, som det ser ut). Men inte MAC: »dx=Δx» [DifferensDifferential], [KAUSALORDNINGEN], [GRAVITATIONENS ABSOLUTVERKAN].
Således — precis som Wikipediaartikelns citat [MACkraftParabeln] utsäger med förklaring enligt relaterad fysik:
”In an inertial reference frame, the dynamic equilibrium cannot be understood in terms of an equilibrium of forces.”:
»In an inertial reference frame seen as an object in physics, the dynamic equilibrium of forces in a rotating reference cannot be understood in terms of an equilibrium of forces»,
BECAUSE — as there are no inertial systems in physics [FUNTOP] —
»In the STATE reference frame which has no objective reference frame in physics, the dynamic equilibrium of forces in a rotating reference or any other CAN INDEED be understood in terms of an equilibrium of forces»
Ty:
— EFTERSOM man i MAC inte gärna kan återföra ett roterande systems krafter (här centrifugalkraften →) på VILA
(och som följaktligen heller inte kan förstås eller fattas för vad det är i fysken i MAC)
tvingas man eliminera — man STRYKER den helt enkelt [ActionReactionMAC], [HyperPhysics], [Wikipedia], [AskAScientist] — centrifugalkraftens jämviktsrelaterade existens, då i annat fall DESS jämvikt med centripetalkraftens motsatta riktning SKULLE IDENTIFIERA ETT VILOSYSTEM, balans, jämvikt, ingen rörelse, och vilket inte går ihop i MAC med ovan nämnda spärrar.
Med andra ord, och helt enkelt så:
— Skolade människor i modern akademi [Herrefolkscitatet], kan inte (som tydligen Isaac Newton kunde, med flera, numera helt säkert utdöda) se fysikens praktiskt verkande DYNAMIK i en förståndsbaserad kvalitativ INRE föreställningsvärld — precis som DJUREN GÖR DET I SIN RÖRELSEDYNAMIK — utan kräver för »den moderna logiken» ett fysiskt kvantitativt MåsteTaPå OBJEKT som referens för den delen. Därav den uppkomna förbistringen — enligt relaterad fysik (TNED).
Jämviktsbegreppet i relaterad mening för den gjutna paraboloiden (eller vätskeparaboloiden) baseras NATURLIGTVIS på en motsvarande ekvivalent INSTRUMENTELLT uppmätt kraftform; Den formen besitter ingen speciell referens till något speciellt referenssystem i fysiken, utan gäller lika för alla, i — för — hela universum, oavsett partikulärt lokalt tillstånd. Och så kan det relateras, eftersom tillståndsbegreppet, mätvärdet, gäller (idealt) begreppsligt under en tidsdifferential (dt), och den finns inte till i fysiken som något objekt [NOLLFORMSALGEBRAN]. Jättesvårt.
— Klarar Talgoxarna i närmaste Syrenbuske av det, med enorma loopar och branta svängar så väl hälften vore nog i PraktiskJämviktsMatte UTAN att krascha, ligger det i människans natur att kunna förstå det, också.
KinematiskaRotationsAnalogierna
VISUELLA BILDERNA AV DE SKILDA KROPPARNAS OLIKA RÖRELSESÄTT
Kinematiska RotationsAnalogierna
———————————————————————————————————————————————
EXEMPELRELATERAD RUBRIKFORM MED LÄNKAR
med exempel som visar — och bevisar — hur MAC blandar ihop grundbegreppen i fysiken: kinetik (MED kraft), kinematik (UTAN kraft)
— Kolla matematiken:
RELATERAD FYSIK
MODERN AKADEMI:
exakt samma
formsammanhang —
helt väsensskilda beskrivningssätt:
— Länkdelarna kopplar till aktuella exempelavsnitt som klargör sammanhangen (eller försöker göra det) i detalj, och som går ut på följande: MAC blandar ihop kinetik och kinematik, helt klart, alla exempel nedan, väl relaterbara i detalj [EARP]: På tydlig kredit av Einsteins allmänna relativitetsprincip (»VISUALISERINGSTEOREMET»: ’fysikens lagar måste gälla SETT från alla möjliga RörelseSystem’) — och det därmed sammanhängande under 1800-talet ModernACademi-uppfunna INERTIALSYSTEM-begreppet (»Rörelse måste alltid relateras till något fysiskt objekt»), och som Newton fått bära hundhuvudet för, trots Newtons egna »DisClaimers» att INTE bli missuppfattad på JUST dessa punkter [NewtonsPrinciperKortCitat], [MACkopplarInteNewton] — har den verkligt kunskapsrelaterade fysikbeskrivningen i modern akademi uppenbarligen stympats, vanställts, vrängts och demolerats in till oigenkännlighet.
— Ämnesrubrikerna som föranlett komplexets speciella uppdagande (här) är dessa: Coriolisverkan, FoucaultPendelnsFigurMatematik, Vektorkalkylens regelverk i MAC.
1. Kinematiska
RotationsAvvikelsen — Linjär rörelse med konstant
hastighet
Spiralerna [r=kx]
Rörelsesystem 1: Linjär rörelse med konstant hastighet
Rörelsesystem 2: Roterande kropp med konstant vinkelfrekvens
sP = T2vP ·ω · sinL° ;
Kinematiska RotationsAvvikelsen GällerSFÄRISKT (CINEMA)
MAC — (sambandsformen nedan från webbexemplet CoriolisBERCIU) men med RESONEMANG SOM
INNEFATTAR CoriolisKRAFT:
yc(t) = – t 2·v0,z Ω
sin λ ; projektilavvikelsen
i MAC — påstås Coriolisbaserad, se
exemplet CoriolisBERCIU
I relaterad fysik finns ingen kraftaspekt i
rotationsanalogierna: Coriolisverkan — kinetik — hör inte hit. MAC kan
inte relatera.
2. Kinematiska RotationsAvvikelsen — Friktionslösa ParabelAnalogin
Inledning till
FoucaultPendeln — Bevisbarheten i icke-användbarheten i den modena akademins vektorkalkyl
Rörelsesystem 1: Friktionslös puckPendel i Parabol
Rörelsesystem 2: Roterande kropp med konstant vinkelfrekvens
rP = sin (2/1)(1/2)x ;
FoucaultPuckPendelns
PolärPeriod i PREFIXxSIN;
= sin nx ; Beskriver puckrörelsens
kurvform på den roterande parabolytan [MIT-exemplet]
MAC — men med RESONEMANG SOM INNEFATTAR CoriolisKRAFT — se MIT-exemplet
(i konv. PREFIXxCOS)
r =
cos nx
[ExempelKällanMIT
skriver inte sambanden i polära koordinater, men visar istället en figur
[s6.Figure 4] med polärfigurbilden, se citatbild i FoucaultFigurerna].
I relaterad fysik finns ingen kraftaspekt i
rotationsanalogierna: Coriolisverkan — kinetik — hör inte hit. MAC kan
inte relatera.
3. Kinematiska RotationsAvvikelsen — FoucaultPendeln i PREFIXxSIN
FoucaultPendelFigurernas
Matematik
Rörelsesystem 1: Pendeln — Koniska Pendeln med Plana
Pendelns ideala form för små pendelvinklar
Rörelsesystem 2: Roterande kropp med konstant vinkelfrekvens
rP = sin (fP/fJ)(1/2)x ; Polärfunktionen för FocaulPendelFigurerna i PREFIXxSIN;
= sin nx
MAC — men (i förekommande fall [‡])
med RESONEMANG SOM INNEFATTAR
CoriolisKRAFT — omständliga avhandlingar som leder till samma [Se även i Wikipedia, Rose
(mathematics), samma form] (i konv. PREFIXxCOS)
r = cos αt ; FoucaultFigurerna
i MAC — påstås Coriolisbaserade, se
PDF-källan FoucaultCoriolisMACex
I relaterad fysik finns ingen kraftaspekt i
rotationsanalogierna: Coriolisverkan — kinetik — hör inte hit. MAC kan
inte relatera.
tP =
cosL·2π√h/a ; FoucaultPendelns
Fullständiga LatitudPeriodEkvation, h = PendelLängden, L = Latitudvinkeln
= cosL
· tP ; PREFIXxCOS
ωLATITUD = 360° cos L° ; FoucaultPendelPLANETS
Fullständiga LatitudPeriod
MAC — med RESONEMANG SOM INNEFATTAR CoriolisKRAFT — (om alls) omständliga avhandlingar [SydneyKällan] som leder till samma (i
konv. PREFIXxCOS)
ω = Ω sin λ ; FoucaultPendelLatitudPerioden
i MAC — påstås Coriolisbaserad, se SydneyKällan, λ latitudvinkeln
ω = 360 sin φ° /day ;
FoucaultPendelLatitudPerioden i MAC — påstås Coriolisbaserad, se Wikipedia Foucault pendulum:
”When a Foucault pendulum is suspended
at the equator, the plane of oscillation remains fixed relative to Earth. At
other latitudes, the plane of oscillation precesses relative to Earth, but
slower than at the pole; the angular speed, ω (measured in clockwise
degrees per sidereal day), is proportional to the sine of the latitude, φ:
ω = 360 sin φ° /day
where latitudes north and south of the
equator are defined as positive and negative, respectively. For example, a
Foucault pendulum at 30° south latitude, viewed from above by an earthbound
observer, rotates counterclockwise 360° in two days.”,
http://en.wikipedia.org/wiki/Foucault_pendulum
@INTERNET Wikipedia — Foucault pendulum,
Explanation of Mechanics [2012-10-27].
;
”From the perspective of an Earth-bound
coordinate system with its x-axis pointing east and its y-axis pointing north, the precession of the pendulum is
described by the Coriolis force.”,
http://en.wikipedia.org/wiki/Foucault_pendulum
@INTERNET Wikipedia — Foucault pendulum,
Precession as a form of parallel transport [2012-10-24].
I relaterad fysik finns ingen kraftaspekt i
rotationsanalogierna: Coriolisverkan — kinetik — hör inte hit. MAC kan
inte relatera.
— Praktiskt taget varenda (alla upphittade och besökta) beskrivning på webben (Okt2012) i ämnet CoriolisVerkan- och FoucaultPendeln- ansluter till ovan förtecknade MAC-sammanblandningar [KinematiskaRotationsAnalogierna]:
— Facklitteraturen i modern akademi (MAC) beskriver tydligen, väl relaterbarligen, och felaktigt,
·
fenomenformen
CoriolisVerkan- på begrepp som i relaterbar mening 1. tillhör
kinematiken (2ω-formen)
där Coriolisverkan helt
saknar koppling, 2. är
vektoriellt felbeskrivna (AktionReaktion,
vektorverktyget i MAC kan
inte orsaksbeskriva fysikgrunden), 3. innefattar felaktiga påståenden (»tröghetscirklar»)
som i relaterad mening
inte ingår i Coriolisverkan
[BaraEttSätt] men som, bland andra,
kan forma sådana rörelsebilder [CoriolisSpiralernaIllustration];
— MAC kan inte härleda CoriolisVerkan
från kinetiken [CoriolisORIGINAL], [CoriolisSATSERNA];
·
fenomenformen
FoucaultPendeln- på kinetisk grund [SCIAM-exemplet],
[WikiFoucaultMomentum], alltså som
resultat av kraftverkan, PÅ det ovan nämnda moderna akademins etablerade
CoriolisBEGREPPET; webbexempel finns [WebbenFoucaultCoriolisForce]
som visar hur man i MAC — rent matematiskt — utgår ifrån kraftbegrepp i
FoucaultPendelHärledningar, för att i slutänden komma fram till FoucaultPendelFigurernas trigonometriska matematik
med exakt samma slutresultat
som i den relaterade härledningens konsekvent kinematiska fall [FoucaultFigurerna], [FoucaultPendelnsLatitudEkvation], [SydneyKällanRef];
— I relaterad mening beskrivs FoucaultPendelFenomenet
ENTYDIGT på kinematisk, trigonometrisk, grund: ingen kraftverkan finns som
grund för fenomenformen;
— MAC kan inte härleda FoucaultVerkan
från kineMAtiken.
Det är, uppenbarligen, INTE matematiken det hänger på, utan sättet — barnets sätt är alltid det rätta — att förstå den algebraiska strukturen (Naturen) som det gäller; MAC håller mänskligheten fången i ett omfattande kunskapsmörker. Det finns ingen organiserad verksamhet bakom det. Det är, tydligen, bara en konsekvens av att, generellt, skita i sanningen.
ExempletTekoppen — BILDKÄLLA:
Författarens arkiv · 12Sep2012 E28 Bild362 · Nikon D90 · Detalj

EXEMPLET MED TEKOPPEN — smulorna i botten
som samlas i en mitthög när man rör om
———————————————————————————————————————
Se
även Tekoppsbeskrivningen med (vidare) exempelmatematik från Ljubljana University.
— LjubljanaUniversitetets framställning (samstämmig med källan i TekoppenMoisy2002) beskriver »Tekoppsfenomenet» på sätt som ansluter till
den relaterade fysiken: fenomenet kopplar INTE orsaken till någon Coriolisverkan,
trots att en sådan väl finns med i bilden. Det är istället skillnaderna i
flödestryck yta-botten som skapar Tekoppsfenomenet: den avgörande
bottenströmningen INÅT med den centrala strömningen UPPÅT (Coriolisverkan
kopplar inte vertikala komponenter [CoriolisSATS1]).
—
Däremot hävdar en SCIAM-författare (2007) att det är, just, en Corioliskraft
som bär ansvaret för Tekoppsfenomenet. Vi studerar aspekterna.
När
man rör om i en tekopp (med små tebladsrester från bryggningen) kan man tydligt
se hur resterna samlas mot koppbottnens mitt. En del vill påskina att
förklaringen skulle ligga i CoriolisEFFEKTEN.
—
Följande, med grund i den härledda framställningen från CoriolisEFFEKTEN, visar att
så INTE är fallet.
— Med
tanke på de svårigheter man generellt (tydligen) har i MAC i ämnet [Kinematiska FRIKTIONSLÖSA ParabelAnalogin], [KinematiskaRotationsAvvikelsen], [Hur MAC associerar
Coriolis med Kinematiska], finns
inga skäl att klandra någon enskild för sammanblandningarna.
Vi studerar saken i detalj — enligt
relaterad fysik.
Ref.,
utförlig beskrivning av flödeskomplexet i typen omrörd tekopp
(horisontella-vertikala rotationerna, konv. corioliseffekter):
”In
order to investigate the fluid flow in rotating frames, researchers performed
various experiments.
The
basic idea is that the (viscous) fluid is confined between two rotating disks.
In general case two
boundary
layers may be present. 9 The problem is that the equations of motion are so complex,
that no
exact solutions are known
for this problem even in the stationary regime
(one disk fixed
the
other rotating). Therefore scientist
have to make use of numerical simulations
and various
experiments
to shed light on the physical mechanisms going on in the rotating fluid. 10”,
s10n,
;
”Fluid
dynamics is one of the most intriguing parts of physics. Why? One part of the
answer is
that
the equations are well established but we are
still not able to solve them, except for some very
simplified
(and unreal) cases. The other part is that we have everyday contact with fluids
and their
flow,
we are fascinated by their complexity and beauty.”, s15n,
http://www-f1.ijs.si/~rudi/sola/nevihta.pdf
University
of Ljubljana, Department of Physics —
FLUID
FLOWS IN ROTATING FRAMES, Miha Mežnar 2005
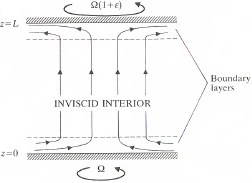
Ljubljanakällans illustration ovan till jämförelse, Figure
5, s7ö.
Botteninströmningen som
funktion av tryck- och friktionsdifferensen mellan toppflöde och bottenflöde —
inte Coriolisverkan. Citatkällan ger dock ingen explicit (citerbart begriplig)
matematisk formulering i den saken — utöver LjubljanaSyntesen.
Figuren nedan, min kompletterande illustration.
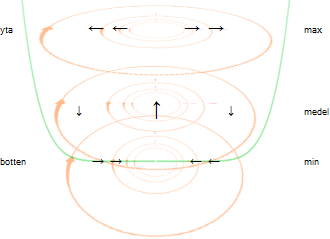
TEKOPPEN MED TEBLADEN I MITTEN PÅ BOTTEN:
I inledande korthet enligt vad som kan utläsas från
elementära grunder i relaterad fysik — med enkla pilsymboler
— Koppytan ger minsta flödesmotståndet, koppbottnen (och kärlväggarna) största;
— Omrörningen (↓•↑) ger högsta hastigheten vid ytan, minsta vid bottnen; ytvätskan drivs utåt (←•→) mot kärlväggen av centrifugalkraften; centrifugalkraften SAMVERKAR med balansen i kraftverkan för HELA kärlvätskan yta(↔STOR)-botten(↔liten); Skillnaden (↔STOR)(↔liten) ger att ytströmningen utåt-neråt (↓←•→↓) kompenseras-balanseras av en bottenströmning inåt-uppåt (→↑•↑←): tebladen i koppens botten drivs in mot centrum.
ROTATIONER (horisontellt) avspeglar också generellt av princip VIRVLAR (vertikalt).
— Fenomenet (↓(←•→)↑) har tydligen primärt ingenting med CoriolisEFFEKT (↓(↑•↓←•→↑•↓)↑) att göra. Inte ett spår. Men [TekoppenSCIAM] (många) personer i MAC påstår det.
Vi studerar det mera i detalj (så att vi är mera säkra på och kan exponera egna fel att inga LOGISKA FEL har begåtts).
Tekoppen — Coriolisgrundernas exempel i
MAC
Författaren
i TekoppenLjubljana2005 som behandlar tekoppens flöde teoretiskt, anger ingen
tryckfaktor, endast flödestermer, samt utgår (för Corioliskomplexets del) ifrån
mera allmänna samband som inte direkt relateras till den aktuella
problemställningen: sambanden SERVERAS typ ”Navier–Stokes equations” där
»Coriolisfaktorn» redan ingår (typen 2ωvr):
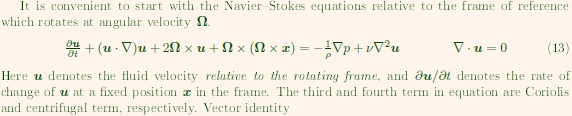
TekoppenLjubljana2005 s15mn
Men:
—
INGEN SOM HELST HÄRLEDANDE BESKRIVNING (för ”Coriolis term”) INGÅR dock i
källverket.
— Och
så, på samma vers, verkar det fortsätta i alla liknande dokument man hittar på
webben (Sep2012): ingen relaterar sakinnehållets centrala samband: 2ωvr. Jämför Härledningen i TNED: ωvr.
— Se
mera utförligt i MACoriolisNOTIS.
Den Omrörda Tekoppen
Illustration till Den Omrörda Tekoppen
— angående Problemet med
de små tebladsresterna i botten som samlar sig i mitten
———————————————————————————————————
”Nevertheless,
analyzing a situation in terms of fictitious
forces may, in fact, be the most effective
way to understand what is actually going on. Take a stirred cup of tea, a charming example of a consequence of the
Coriolis force. If a few tea leaves are
present in the cup, they end up in a pile at the center of the bottom surface
(and not along the edge, as one might expect, as a result of the also
fictitious centrifugal force). If you imagine
yourself rotating around in sync with the stirred fluid, most of the
fluid would appear to be at rest while the cup would be counter-rotating around
you. That rotating cup drags some adjacent
fluid along with it. Meanwhile, near the bottom, the Coriolis force on that dragged fluid pushes
it toward the center of
the cup, carrying the leaves along with it.”
http://www.scientificamerican.com/article.cfm?id=what-is-a-fictitious-force
SCIENTIFIC
AMERICAN Ask the Experts — What is a "fictitious force"? —
July 9, 2007
VAD SOM KAN UTLÄSAS VIA ELEMENTÄRA
BEGREPP:
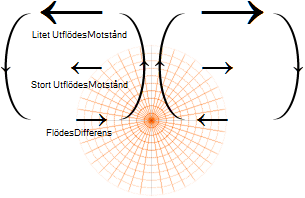
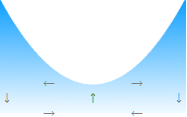
Den omrörda tekoppens vattenyta drivs UtUpp mot kärlväggarna
av centrifugalkraften [Newtons
berömda ämbarförsök]; Bottendelens högre flödesmotstånd mot
koppmaterialet bildar tillsammans med toppskiktet en flödesdifferens;
Flödesdifferensen bildar inflöde till centrum från bottendelen och som sluter
flödeskretsen åter till ytan;
— Tesumpen drivs in mot centrum i
bottendelen av differenserna i flödestryck yta-botten då man rör om i koppen. Inte
på grund av någon
»Corioliskraft». Vidare i huvudtexten.
LjubljanaUniversitetsKällan
(som innehåller flera experimentellt baserade avsnitt) beskriver funktionen som
ovan:
”When
the tea leaves are rotating around the
bottom of a cup, they spiral towards the center of
the
cup as they follow the motion of the water that was induced by stirring the tea
with spoon.
They
move towards the center after the spoon
is removed and, hence, when the water in the cup
begins
to spin down towards a state of rest. The pressure
near the side walls of the cup is higher
than the pressure in the center when the water is rotating. This can be observed by the
shape of
the
surface of the water which is concave from the viewpoint of the drinker. This pressure variation
is required to balance out the centrifugal acceleration of
the rotating liquid water. However, the
water near the bottom of the cup cannot move as freely
because the water adjacent to the bottom
sticks to the bottom
(that is, the water moves much more slowly near the bottom because of friction
or
viscous effects). The water
touching the wall does not move at all (this
is the no-slip boundary
condition
that occurs in flows of viscous fluids). As a consequence of fluid friction, the angular
momentum of the water near the bottom is not enough to
oppose the effect of the radial pressure
field created by the
rotating water away from the bottom boundary layer; in fact the pressure
variation is such as to push the water near the bottom of
the cup towards the center. Because
mass is conserved in this flow, the water that is caused to
move towards the center of the cup
turns upward towards the surface. Subsequently, it turns towards the side wall at the
surface and
finally
moves down towards the bottom boundary layer replenishing the water that was
originally
there.
This circulatory pattern of motion is the secondary motion (that can be viewed
in a meridian
plane).
The primary motion is, of course, the circulatory motion initially induced by
stirring with
the
spoon.”, TekoppenLjubljana2005 s6mn.
—
Läser inte SCIAM-författaren ”California Institute of Technology
theoretical physicist and 2004 Nobel laureate David Politzer” kollegernas
forskarrapporter?
—
Ljubljanakällan beskriver flera experimentella resultat som visar HUR
vätskeflödet fungerar i roterande kärl.
— Det
ska dock sägas (tyvärr, vanligt i forskarrapporter) att framställningssättet
INTE välkomnar besökare i någon överväldigande mängd. Det är expertens
införstådda fraser som ”the
inward flow from the faster disk” och ”But
as the rotation ratio s is decreased below −0.2, the slower disk induces a centrifugal flow too”; Vi kan GISSA, men aldrig klart veta vad författaren
tittar på i sin beskrivning. Möjligheten att CITERA KONKRETA matematiska
RESULTAT ur den annars relativt rika beskrivningen ur det aktuella
PDF-dokumentet kan därför och tyvärr inte komma på fråga; det finns, här, helt
enkelt ingen TYDLIG referens till vad som menas. Tyvärr.
— Det
enda tydliga som framskymtar är det ovan redan citerade med det avgörande
”the pressure variation is such as to push
the water near the bottom of the cup towards the center”,
TekoppenLjubljana2005 s6mn.
Det
är tydligen också den enda etablerade referens som behövs för att påpeka
bristen på begriplighet i SCIAM-artikelns påstående om att det skulle vara
Coriolisverkan som är orsaken bakom fenomenet med tesumpen som dras in mot
mitten.
— LjubljanaUniversitetskällan antyder heller ingenting som säger att det skulle vara Coriolisverkan
som förorsakar botteninströmningen: det är tryckskillnaderna toppen-botten som
gör det.
I andra ord, och som framgår av
sammanhanget:
—
Skillnaden i flöde mellan yta (top boundary) och botten (bottom boundary) är
den KRAFTGRUND som framtvingar den cirkulerande rörelsen med uppflödet i mitten
och som tvingar in tesumpen dit.
— ATT
[Tekoppen]
beskrivningssättet i TekoppenLjubljana2005 använder termen ”Coriolis term” (s15mn), är naturligt då
Coriolisverkan i vilket fall ingår automatiskt i den allmänna matematikbas man
utgår ifrån, ”the Navier Stokes equations” s15m, (vätskeflödesmatematiken
generellt i MAC).
— Det
väsentliga här för tesumpens förklaring är emellertid INFLÖDET UTMED BOTTNEN
MOT KOPPENS CENTRUM;
—
Radialflödet som TRIGGAR en Corioliseffekt men vilken Coriolisverkan ingalunda är orsaken bakom det intåtriktade flödet som sådant. Radialflödet (distansändringen) kommer från den
yttre införda energikällan (omrörningen), ”the driving force” [CoriolisBASICfrnCoriolis] i Corioils första teorem, inte ifrån någon redan
existerande Coriolisverkan.
— Det
senare är emellertid, just, vad SCIAM-författaren verkar påskina:
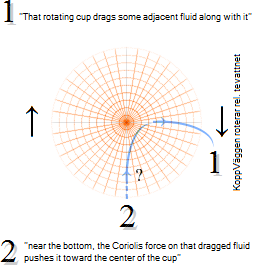
:
Möjlig tolkning av vad SCIAM-författaren menar: SCIAM-författarens resonemang förefaller vid en närmare
granskning högst gåtfullt:
OM
det skulle vara som SCIAM-författaren påstår, att (1) ”That rotating cup drags some adjacent
fluid along with it” — vilket vi
underförstått (eftersom författaren inte klargör det) kan förstå som att
vattnet (på något vis) dras ut mot koppkanterna, och därmed en giltig orsak för
Coriolisverkan [CoriolisSATS1] — HUR skulle den radiella utåtriktningen i så fall,
menar SCIAM-författaren, få ihop det med den rörelsebild som strax
påstås i (2) att ”near
the bottom, the Coriolis force on
that dragged fluid pushes
it toward the center of the cup”?
— Det
verkar (nämligen, figurtolkningen ovan) som att SCIAM-författaren DELS utnyttjar en redan befintlig
inströmning — slutet
strömningsflöde genom uppströmningen i mitten
— i koppens botten för att slutföra den egna förklaringen till tesumpen i
mitten;
— Man
kan inte göra så.
— och
DELS att SCIAM-författaren inte verkar ha någon begripligt presenterbar
koll på vad Coriolisverkan handlar om:
—
Coriolisverkan är INTE det radiella flödet (←↓•↑→) som
sådant (det radiella flödet är CoriolisAGENTEN i försorg av en yttre
införd energikälla, och som leder till Coriolisverkan), utan den omfördelning i materialet som det
radiella flödet (AGENTEN) ger upphov till: inre virvelrörelser i
rotationsplanet.
— Coriolisverkan
innefattar inga vertikala komponenter.
— I
summa därmed tydligen sagt: Det går inte att få ut något begripligt av SCIAM-författarens
verbala beskrivning — utöver slutsatsen att det beskrivna inte har något med Corioliskraft
att göra. Se särskilt i LjubljanakällansFörklaring [LjubljanaSyntesen]: det är (friktions-)tryckskillnaderna mellan topp
och botten som ger botteninströmningen. Ingen Coriolisverkan i det avseendet
finns heller omnämnd i den källan.
Se
även en annan källa (som använder samma typillustrationer som Ljubljanakällan);
”The friction at the bottom of the cup actually
explains this seeming
paradox. The centrifugal
force, which varies as the square of the velocity, is weaker at the bottom, giving rise to a recirculation flow (see Figure 1). This inward recirculation is
usually called the Bödewadt layer (1940), after the German fluid mechanician
who described the motion of a rotating fluid over an infinite wall at rest.
However, Albert Einstein
was the first to give an explanation of this phenomenon in 1926 in the case of
the teacup! [3] (It is said that, with this
explanation, Einstein appeased Mrs. Schrödinger's curiosity, which her husband
could not satisfy).”,
http://www.fast.u-psud.fr/~moisy/epn03/MoisyEPN.html
SPIRAL
PATTERNS IN SWIRLING FLOWS, Moisy et al., 2002
— Tekoppsfenomenet kopplar INTE Coriolisverkan som orsak. Orsaken är skillnader i
flödestryck.
— DEN
KRÖKTA VATTENYTANS FORM MOT KÄRLVÄGGARNA garanterar DIFFERENTIELLA ROTATIONER i
det underliggande vattenskiktet: fortfarande minsta friktionen i den
friliggande vattenytan, sedan successivt högre friktion med djupet/växande
vattenvolym (precis det som Ljubljanakällan antyder).
→
→
→
—
Därmed kan en obönhörligt uppkommen tryck-flödes-skillnad förstås i de olika
cirkulationsskikten. Och därmed en »tebladseffekt»;
— Som
följd av skillnaden i strömningshastighet (centrifugalkraft) mellan
ytans högre och bottens lägre, betyder skillnaden en tvungen inåtströmning i
botten för att energin till hela verksamheten ska kunna koppla
vattenströmningen totalt: upp i mitten.
— Men
DEN (centralvertikala) strömningseffekten beror — JU — inte på någon Coriolisacceleration
[Corioliskraften berör enbart effekter som uppkommer RÄTVINKLIGT
←•→ en rotationsaxel (•): vattenrörelser bort från eller in mot
ett rotationscentrum — ett utpräglat ytfenomen, inte ett djupfenomen —
åstadkommer Coriolisvirvlar],
|
FÖRUTSÄTTNING: tallrikens rotation konstant CoriolisACCELERATION a=vn/T=(2π[r=vrT]/T0=(2πf )vrT=ωvrT)/T=ωvr Konventionellt skrivs a = –2ωvr
Coriolisaccelerationen Coriolisaccelerationen
(a[C]) är medriktad v[n] om v[r] är utåtriktad (reguljära
accelerationsanalogin), annars motriktad v[n] om v[r] är intåtriktad
(inbromsning): — a[C] ska därmed, enligt ovan, upplevas av
en passagerare som färdas i en spårvagn på den roterande tallriken utmed r
med konstant hastighet v[r] och som sitter tvärs färdriktningen, med ansiktet
i tallrikens rotationsriktning (v[n]), som om spårvagnen accelererar
passageraren som om denne satt i en BIL i framsätet som accelererar på
vanligt sätt. Färdas vagnen åt motsatt håll (InMot Centrum) blir BILanalogin
för vagnpassageraren en inbromsning. — Accelerationens STYRKA i ett mätinstrument
som passagerarna kan titta på i vagnen kan också studeras av en fotograf vid
sidan av den roterande tallriken och därmed samma
effektiva resultatbild oberoende av val av referenssystem; — Verksamheten relateras i vilket fall
ALLTID till tillståndets princip. |
utan
på att det finns en differentiell (friktions-)tryckskillnad
med vattendjupet som BILDAR den centralt
återströmmande vattenpelaren i mitten: tebladsexemplet.
—
Coriolisaccelerationen finns fortfarande kvar i vattnet så länge vattenrörelser
bort från eller in mot rotationscentrum (centrifugalkraften) finns kvar,
ja. Helt klart.
—
Men:
DEN FÖR TEBLADSANALOGIN AVGÖRANDE
CENTRALA UPPSTRÖMNINGSKRAFTEN är tydligen inte Corioliskraften:
— Det
som får tebladen i tekoppen att samlas i mitten är uppenbarligen växelspelet
mellan djupkrafterna i vattnet i förening med skillnaderna i friktion mellan
de olika strömningsskikten:
DJUPKRAFTERNA I VATTNET som via
kärlfriktionens inverkan bildar DIFFERENSEN i ROTATIONER mellan de olika
vattenskikten yta-vattenvolym, och som därmed bildar STRÖMNINGEN UPPÅT i mitten
FRÅN det inre av vattenvolymens mera TRÖGA del, är uppenbarligen orsaken bakom
TekoppsFenomenet.
Helt
enligt LjubljanakällansFörklaring.
—
Centrifugalkraften från omrörningen driver ut ytvattnet som
PÅ GRUND AV UNDERLIGGANDE ROTERANDE VATTENSKIKTS STÖRRE
RÖRELSEMOTSTÅND I KOPPLING TILL DEN SUCCESSIVT STÖRRE VATTENVOLYMEN MED AVSTÅNDET
FRÅN YTAN, OCH VILKEN DIFFERENS I MOTSVARANDE CENTRIFUGALA UTKASTNINGAR
BILDAR EN RESULTERANDE — centrifugalt strömningsmotriktad — INSTRÖMNING MOT MITTEN LÄNGST IN I
VATTENVOLYMEN
pressas
ned i kärlranden mot bottnen;
— det
invid kärlranden nedpressade vattnets bottenströmningsflöde ÅTERKOPPLAS till
ytan via en uppåtströmmande centralpelare som framträder PÅ RADIELLA
FLÖDESDIFFERENSERNA i vattnets djupled,
där Corioliskrafterna i vilket fall är NOLL:
—
tebladen pressas in mot mitten av kombinationen omrörning (centrifugalkraft) + strömningströghetsdifferenser
i vattendjupsverkan + det slutna kärlet:
Corioliskraften
har — tydligen — ingen betydelse i det sammanhanget.
BILDKÄLLA: Författarens arkiv · 11Sep2012 E27
Bild342 · Nikon D90 · Detalj

Det som händer i tekoppen har
tydligen ingenting explicit med Corioliseffekten att göra.
Vi
studerar [KOMPLEMENTÄRT för vidare jämförelse] hur Coriolisaccelerationen fungerar på (i) den roterande tallriken (tekoppens yta).
(Se
enklare i Coriolisaccelerationens
effekt):
Från
den helt enkla härledningen till Coriolisacceleration (a=ωvr), kan vi (lika
enkelt) direkt förstå dynamiken med hjälp av den roterande tallriken, enligt
följande tankeexperiment (alltid med reservation för feluppfattning):
—
Står vi stilla på tallriken och denna roterar är också a=0: ingen
Coriolisacceleration finns.
—
Ponera att vi sedan börjar gå rakt fram mot en fast referenspunkt på tekoppens
innervägg (pilen ovan,
tekoppen förutsatt obegränsat stor) över
tallriken (samtidigt som
denna roterar med konstant vinkelhastighet ω):
—
Eftersom a=ωvr beror av en ekvivalent
projicerad hastighetskomponent mot tallrikens radiella utsträckning
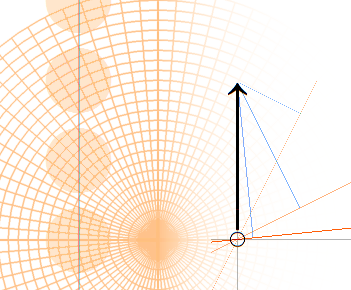
CoriolisANALOG vektorjämförelse — grunden till vridmomentets
aspekt i Coriolisverkan
kommer
vårt gående i pilens riktning, rakt över (den roterande) tallriken att medföra
(på grund av) att den hastighetsriktningen mot r projicerar en allt växande komponent (vr) på r,
och som, om tallriken tillåts utsträckas obegränsat, till slut hamnar i (allt mer nära) parallell med r,
och som därmed ger max Coriolisacceleration.
—
EFFEKTEN blir med andra ord av vår rätlinjiga väg att vägens utsträckning i
den egna utsträckningens linje bildar ETT VRIDANDE MOMENT [CoriolisSTAVEN]:
—
Nämligen med hänsyn till en differens mellan ett lägre vr
sett bakåt och ett något högre vr sett framåt — och därmed
OLIKA a-värden bakåt(mindre)-framåt(större) — med början från en
begynnelsepunkt på r;
—
tendensen blir, tydligen, att »tallriken (↓•↑) vill
VRIDA oss (↓•↑ ↑) (stegvis) MOTSATT (↓•↑ ↑•↓), bort ifrån, tallrikens rotation»,
mot r där a=0 — vilket i
netto är samma som NEWTONIII: orsaken till variationen motverkas;
— för alla icke-radiella rörelser vi ser då sådana i formen av uppdelade komponenter varav endera
tillhör en radiell dito skapar följaktligen
tallriksrotationen en associerad rotationsmotriktad rörelse (CoriolisCeller)
i tallriksmaterialet OM det i tallrikskroppen finns material av typen icke HELT
fast förbundet med tallriken, som i vårt gående fall:
— För
tevattnet i tekoppens del innebär det, uppenbarligen, inget annat än att det kan
uppkomma VIRVELRÖRELSER, vridande moment, i det att (de sammanlänkade)
vattenmolekylerna uppvisar sina radiella rörelsesändringskomponenter, och vilka
rörelser sedan (möjligen) sammansätts till (mera komplicerade) kombinerade
sådana i respekt till alla möjliga xyz-variationer i flödet.
— Men
det var inte vårt problem i TekoppsExemplet.
— Corioliskraftens verkan har, om inga fel har gjorts i den här beskrivningen,
alldeles tydligt och klart absolut ingenting ALLS att med det aktuella
VERTIKALT VERKSTÄLLANDE strömningsfenomenet i tekoppen att göra, det som
förorsakar att tebladen eller tesumpen i koppens botten drivs in mot den
uppåtströmmande centrumvattenpelaren.

Pilarna skisserar de idealt radiella flödesvektorerna från
omrörningen i det cirkulerande vattnet i tekoppen, rött överst.
Differensen i flödeskrafterna, inte Coriolisverkan,
förklarar orsaken till bottenflödet inåt (sedan uppåt åter till ytan), pilarna
överst.
Vad
som FÖREFALLER kan utläsas direkt av hastighetsriktningarna:
Stora röda pilarna motsvarar (hastighetskomponenten till) utflödet mot
kärlväggarna;
Infällda mindre samriktade blåvioletta
pilarna motsvarar den lägre
flödeshastigheten i koppens botten på grund av vattnets bottenfriktion och
vilken friktionsfaktor inte finns i ytdelen;
—
SKILLNADEN, blå pilarna överst, ger en differens via trycket-flödet
mellan vattenytan och vattenbotten;
—
flödes-tryck-differensen, inget annat som det ser ut, framtvingar den slutna
flödesformen på bottenskillnadens motriktade flöde in mot koppens mitt, övre blå
pilarna, och därmed JÄMVIKT i krafterna
via en cirkulerande (hydrodynamisk) koppling.
BILDKÄLLA: Författarens arkiv · MONTAGE: 30Jun2012 E11
Bild51; 11Sep2012 E27
Bild342 · Nikon D90 · Detalj

The END
— A New Beginning.
FYSIKALISKA
GRUNDBEGREPP — GTaction
innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER
FYSIKALISKA GRUNDBEGREPP — GTaction
ämnesrubriker
innehåll
referenser
[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967
Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.
mn = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]
me = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för me , Table 1.4 s7–27 för u]
u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]
u = 1,66033
t27 KG .............. atomära massenheten [ENCARTA 99 Molecular
Weight]
u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]
u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]
u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]
u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],
CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]
c0 = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]
h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]
e = 1,602 t19 C ...................... elektriska elementarkvantumet, elektronens laddning [FOCUS MATERIEN 1975 s666ö]
e0 = 8,8543 t12 C/VM ............. elektriska konstanten i vakuum [FOCUS MATERIEN 1975 s666ö]
G = 6,67 t11 JM/(KG)² .......... allmänna gravitationskonstanten [FOCUS MATERIEN 1975 s666ö] — G=F(r/m)² → N(M/KG)² = NM²/(KG)² = NM·M/(KG)²=JM/(KG)²
BKL BONNERS KONVERSATIONSLEXIKON Band I-XII med
Suppement A-Ö 1922-1929, Bonniers Stockholm
[BA]. BONNIERS ASTRONOMI 1978 — Det internationella standardverket om universum sammanställt vid universitetet i Cambridge
t för 10–, T för 10+, förenklade exponentbeteckningar
MAC, modern akademi (Modern ACademy)
(Toroid Nuclear Electromechanical Dynamics), eller ToroidNukleära Elektromekaniska Dynamiken
är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED får därmed (således) också förstås RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED [Planckfraktalerna] i ATOMKÄRNANS HÄRLEDNING.
en
is the dynamically equivalent resulting description following from the deductions in the Planck ring h=mnc0rn, analogously AtomNucleus’ Deduction. The description according to TNED is related, meaning: all, every one, detail claims a complete logical comprehensibility, or not at all. With TNED may thus (hence) also be understood RELATED PHYSICS AND MATHEMATICS. See also the appearance of the term TNED [Planck fractals] in AtomNUCLEU’s DEDUCTION.
Senast uppdaterade version: 2017-08-16
*END.
Stavningskontrollerat 2012-10-29.
—
åter till portalsidan
· portalsidan är
www.UniversumsHistoria.se
∫ ∫ Δ √ ω π τ ε ħ
UNICODE — ofta använda tecken
i matematiska-tekniska-naturvetenskapliga beskrivningar
σ
ρ ν ν υ π τ γ λ η ≠
√ ħ ω →∞ ≡
Ω
Φ Ψ Σ Π Ξ Λ Θ Δ
α
β γ δ ε λ θ κ π ρ τ φ
ϕ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫
≤ ≈ ≥ ˂ ˃ ← ↑ → ∞ ↓
ϑ
ζ ξ
Pilsymboler, direkt via tangentbordet:
Alt+24
↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬
Alt+23
↨ — även Alt+18 ↕; Alt+29 ↔
☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓
→←∟↔▲▼
!”#$%&’()*+,
■²³¹·¨°¸÷§¶¾‗±
*
åter till portalsidan
· portalsidan är
www.UniversumsHistoria.se