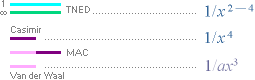ELEKTRONEN VdW — UNIVERSUMS HISTORIA enligt relaterad fysik | 2010VII13 | 2010VIII18 | enproduktion | Senast uppdaterade version: 2011-08-21 · Universums Historia

innehåll · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Brotthållfasthet OCH MATERIALLÄRA · Grundläggande begrepp inom materialläran — Om materialens sammanhållande krafter — Elektronen och elektronmassans komponenter — Kohesion och Adhesion — Kraft och Energi

BILDKÄLLA: Författarens arkiv · Bild4 Excur4 ·19apr2010 · Nikon D90 · Detalj

Inledning

Det verkar inte finnas några allmänt etablerade ENKLA ELEMENTÄRA matematiska sambandsuttryck för begreppet atomär-molekylär KOHESION i MAC — trots enkla analogier. Däremot används frekvent sambandsformer som associeras med van der Waals krafter för att beskriva ADHESION — trots att samma matematiska typuttryck just ger KOHESIONSMATEMATIKEN på enklaste form. »Den uppmärksammade förbistringen» har föranlett det här dokumentet. Forts.

ELEKTRONEN — materien

Begreppsbeskrivningar enligt relaterad fysik [TNED] — med jämförelser och korsreferenser till MAC

Parbildning	Van der Waals krafter	Kovalenta bindningsgeometrin	Grundämnesmetallerna	Elektronassocierade Artiklar
BT-fältet Atomkärnans allmänna magnetiska yttoroidfält	Casimireffekten TNED-MAC-van der Waals	Vätebindningen H—H	Brottgränser — Rm Diagram 1-2-3 Experiment — Teori	Elektronens frigörelse ur atomkärnan: NEUTRONSÖNDERFALLET NEUTRONSÖNDERFALLET ATOMKÄRNAN allmän formbeskr. ATOMKÄRNAN ELEKTRONMASSAN ATOMKÄRNAN N3m20
Positronbildning från tunna folier via Laser	Kohesion — Adhesion	— enkel grundgeometri —	Hållfasthetsgrunderna	Kärnassocierade artiklar

Se även i Förklaringarna till begreppen i den moderna akademins kvantelektrodynamik (QED) från 1947.

Grundbegreppens förankring i fysiken, hur de uppkommit — och deras innebörd i relaterad fysik (TNED)

Allmänna artikelrubriker — Elektronen i materien

Parbildning — Hur positronbildning i MAC framställs som skapelse av materia

Van der Waals krafter — angående materiens sammanhållande krafter, Materialens hållfasthet och kemiska bindningsenergiinnehåll

För Elektronelementet, se Elektronen, ELEKTRONMASSANS KOMPONENTER, Ljusets Polarisation, Spektrum och Kvanttalen.

För BT, se Atomkärnans allmänna magnetiska yttoroidfält.

Elektronens frigörelse ur atomkärnan:

NEUTRONSÖNDERFALLET laddningsdeplacementet

NEUTRONSÖNDERFALLET kärnmagnetismen

ATOMKÄRNAN allmän formbeskrivning

ATOMKÄRNAN ELEKTRONMASSAN

ATOMKÄRNAN N3m20

kärnanod, BT-fältet.

Grundämnesmetallernas brotthållfasthet [Rm] — inledning

Grundämnesmetallernas brotthållfasthet

— approximativt via vätebindningen

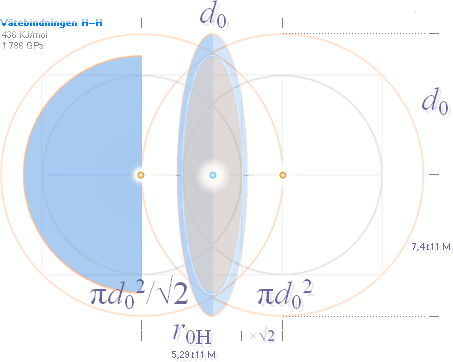
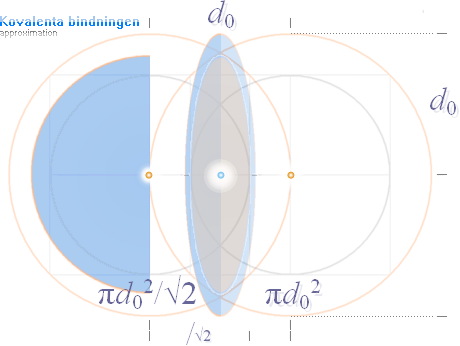
Vänster: Stiliserad ikonbild av kovalenta bindningens geometriska fysik, cirkelradien = d0, samma som atommedelavståndet: Två Väteatomer sammanbinds [»kedjas»] av en mellanliggande gemensam elektronmassa. Bindningskraften i fallet Väteatom-Väteatom är (här veterligt) den allra starkaste som finns i fysiken. Se Jämförande tabeller — Kovalenta bindningar.

Höger: Förminskad diagrambild [klicka på bilden för större] av Grundämnesmetallernas brotthållfasthet, jämförelse mellan Experimentellt uppmätta [ljusvioletta] och Beräknade [mörkblå] enligt vänsterfigurens helt enkla basgeometri, vidare nedan.

Den enkla kovalenta bindningsgeometrin — figuren ovan vänster med Coulombekvationen F=k_e(e/d₀)² som motsvarar fallet med Väte [Atomnummer Z=1, se även utförligt i Vätebindningen H—H] — ger en approximativt samstämmig överensstämmelse med experimentella brotthållfasthetsdata [MatWeb] på de olika grundämnesmetallerna.

PRINCIP:

Den enkla F-formen k_e(e/d₀)² används genomgående för alla grundämnesmetallerna [från och med atomnummer Z=3, Litium] — med enda tillägget att resultatet divideras med atomnumret (Z). Ytkraften F/A fås genom division med cirkulära flödestvärsnittets yta för mittcirkel A=[A=π[d₀/2]²]/√2=πd₀²/√2, som ger F/A=k_ee²/(π·d₀⁴·√2).

Z-divisionen motsvarar dämpningen i attraktionen via den växande repulsionskraft som framträder via atomer med växande atomnummer, analogt större kärnladdning. Resultatet av den modifierade F/A-formen visas i Diagram Rm1. Med en enklare justering för den ytterligare exponentiella dämpningen av kärnkraftsrepulsionen vid låga Z, samt en marginellt linjär kompensation som dämpar ytterligare för höga Z, ges det justerade resultatet i Diagram Rm2 (originalet till den förminskade bilden ovan höger), sambandet nedan.

F/A = (100[8Z(t6) + 2([Z–1]/2)^–2])(1/Z)k_ee²/(π·d₀⁴·√2) ............ N/M² = Pa

Approximation till Grundämnesmetallernas brottgränser, se Diagram Rm2.

Genom separat undersökning visar det sig att ovanstående approximationsform uppvisar (nära) samma variationsstruktur som Medelatomkubiska Elektronmassatätheten, Zm(e)/d₀³. Denna visas här nedan infälld i tonat gult i bakgrunden till jämförelse med förgrundens Diagram Rm2.

Diagram Rm3 — Diagram Rm1 · Diagram Rm2

Brotthållfastheten (MPa) för grundämnesmetallerna .............. Serie1, Rm = (100[8Z(t6) + 2([Z–1]/2)^–2])(1/Z)k_ee²/(π·d₀⁴·√2), Pa; Serie 1 i MPa

Experimentellt uppmätta Rm-värden ....................................... Serie2, MatWeb-data, MPa Serie 2

Medelatomkubiska Elektronmassatätheten .......................... ........., Zm(e)/d₀³, KG/M³ gult fält i bakgrunden med ljusblå värdepunkter

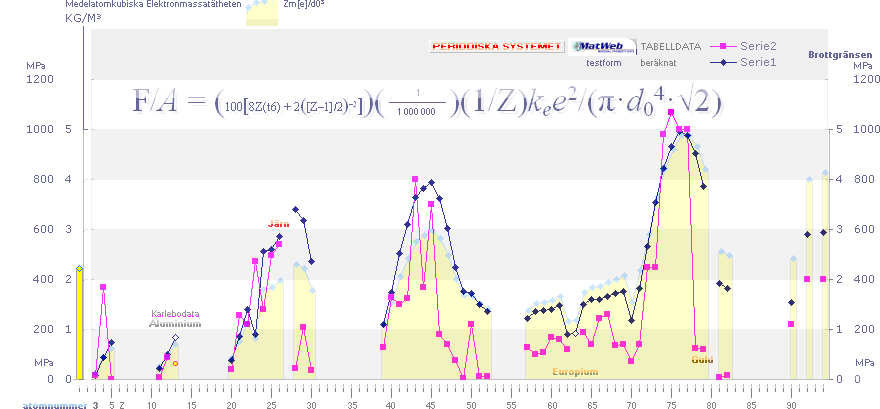
Vätebindningen H—H vid Z=1 här medtagen för referens [Elektronmassatäthetsvärdet 2,25 KG/M³].

Serie 12 i MPa, Elektronmassatätheterna i KG/M³.

För vidare diagramdetaljer, se Diagram Rm2 och Diagram Rm1.

Trots att resultatbilden ingalunda är exakt, ger den ändå

1. (i vissa partier) en förvånansvärt god översiktsbild av HUR materiebildens hållfasthetsfysik sammanhänger med ENKLA sambandsformer i PERIODISKA SYSTEMET,

2. en tämligen noggrann sammanfattning av hela Rm-intervallet 0-1000 MPa för samtliga grundämnesmetaller.

En motsvarande upplysande orienterande översikt har emotsetts generellt på det fria webbutbudet, men tyvärr ännu inte påträffats.

Se vidare från Diagram Rm1 [Från Vätebindningen H—H].

Se även allmänt från HÅLLFASTHETSGRUNDERNA (Brotthållfasthet).

Inledningen, forts.

BILDKÄLLA: Författarens arkiv · Bild216 · R2010Apr · 13apr2010 · Nikon D90 · Detalj

Forts. frn. INLEDNINGEN

Det är märkligt, främst eftersom man redan (väl) känner energibindningsdata för olika molekylära grundkopplingar [Se Jämförande tabeller — Kovalenta bindningar]. Dessa grunddata kan uttryckas matematiskt approximativt i samstämmighet med tabellvärdena via enkla grundsamband, se Vätebindningen H—H. Grundsambanden ansluter också tillsammans med ytterligare alternativa matematiska uttryck och som — just — anknyter till sambandsformer av den konventionella van der Waals adhesionsmatematiken typ F/A=K/d^3, se citat, och som alltså i själva verket tydligen beskriver kohesionsfysiken: materialens brotthållfasthet.

I MAC [Se Övergången VdW-Casimir] låter man Casimirsambandets form (1/d^4 — som inte räcker ända fram till atomkopplingarna, se JÄMFÖRANDE FUNKTIONSGRAFER) för speciellt korta avstånd [0,1-20 nM] mellan åtskilda materialytor övergå i en associerad van der Waals sambandsform (1/d^3);

I TNED finns ingen liknande övergångsform — eftersom ADHESIONSSAMBANDETS MATEMATIK i TNED (1/d^2TILL4) täcker hela intervallet min-max, se INLEDNINGEN TILL CASIMIREFFEKTEN I RELATERAD FYSIK. TNED/Casimir-teorin baseras helt på de elektronmassans komponenter som förkastades av MAC från 1927; Bortfallet kompenserades med ett »vakuumets nollenergi», se från Casimireffekten i MAC.

Kohesionsmatematiken i MAC

EN MÖJLIG FÖRKLARING till avsaknaden i MAC av ENKLA ELEMENTÄRA GRUNDSAMBAND för (speciellt) kohesionen i materialsammanhang, kanske blir bäst belyst genom att studera en av de (få) webbkällor som diskuterar några sambandsformer alls i samband med kohesionsbegreppet,

Philosophical Transactions of The Royal Society — 2009

BOND ANISOTROPY AND COHESION OF WET GRANULAR MATERIALS — Farhang Radjai1, Vincent Richefeu

http://rsta.royalsocietypublishing.org/content/367/1909/5123.full

Nämligen det påtaliga inslaget av

· (onödigt — om det gäller en elementär översikt med enkla exempel) komplicerad matematik av arten tensorkalkyl

· krångliga utläggningar med universitets- och högskolematematikens specialtermer som tydligen bara kan förstås av personer som redan är förtrogna med nomenklaturen på den nivån

För TNED:s del; Se exempel i Vätebindningen H—H.

Den möjliga förklaringens svårighet i MAC fördjupas betydligt genom att det enkla exempelfallet [Se exempel i Vätebindningen HH] vidrör det som påpekas i INLEDNINGEN: I MAC används uppenbarligen typformen F/A=K/d³ för att beskriva Adhesion — som i exempelfallet med Vätebindningen och dess koppling till Kovalenta allmänna atombindningsformen med konkret praktiskt resultatexempel i Diagram Rm2 i själva verket och tydligen beskriver-definierar Kohesion.

Se den mera utförliga inledande beskrivningen av »förbistringen» på artikeln Kovalenta allmänna atombindningsformen i början av avsnittet om van der Waals krafter.

[Det verkar med andra ord vara ytterst svårt att beskriva ämnet med utgångspunkt i modern akademi].

I den här presentationen ges en översiktlig jämförande resultatbild från tillgängliga tabellvärden (MatWeb) via olika ämnen tillsammans med resultat från beräkningar via de här härledda sambandsformerna.

Se även dispositionen genom INNEHÅLLSFÖRTECKNINGEN.

Kohesion och Adhesion — inledande praktisk orientering

BILDKÄLLA: Författarens arkiv · Bild5 Adhesion · 5nov2010 · Nikon D90

GRUNDLÄGGANDE BEGREPP I MATERIALLÄRAN

Kohesion och Adhesion

INLEDANDE PRAKTISK ORIENTERING I GRUNDBEGREPPEN

Termdefinitioner, etymologiskt

KOHESION [av lat. cohae´rere, sammanhänga] används generellt i facklitteraturen för att beskriva ett materials INRE sammanhållning.

ADHESION [av lat. ad, till, vid, och haere´re, hänga] används generellt i facklitteraturen för att beskriva sammanhållning MELLAN olika materialdelar.

Exempel på etablerad facklitteratur som beskriver begreppen kohesion och adhesion;

”I vätskans gränsyta mot en fast kropp finns också en ytspänning, som i detta fall emellertid inte enbart bestäms av krafterna mellan vätskepartiklarna, kohesionskrafterna, utan också av de krafter som verkar mellan vätskepartiklarna och partiklarna i den fasta kroppens yta, adhesionskrafterna.”, FOCUS MATERIEN 1975 s180sp2n.

Praktiska exempel som visar inverkan av kohesion och adhesion framgår dels med hjälp av vattendroppar på olika material och dels med hjälp av vattenfyllning i kärl med olika material. Vi studerar några enkla köksexempel.

Adhesion, köksexempel

BILDKÄLLA: Författarens arkiv · Bild5 Adhesion · Nedan Bild7 · 5nov2010 · Nikon D90

Adhesion, praktiskt köksexempel. Bilden ovan visar hur vattenlinjen i en plastbägare [höger] skiljer sig markant från vattenlinjen i ett glas [vänster]. Medan plastbägaren uppvisar en synbart helt rak koppling mellan kärlvägg och vattenyta utan någon synbar kurvering, uppvisar glaset en markant rundad övergång. Övergången i glasfallet syns som en ganska precis 3 mM smal mångspeglande kontaktremsa. I plastfallet [höger] finns ingen sådan övergång: Adhesionen mellan vattnet och kärlväggen är tydligen minimal i plastfallet — medan den i glasfallet är påtaglig. Adhesionen, glasfallet [vänster] visar att vattnet »flyter upp» en liten bit ovanför själva vattenytan mot kärlväggen; Vattenatomerna visar tydlig benägenhet att förena sig med materialet.

Kohesion, köksexempel

Kohesion, praktiskt köksexempel.

Bilden ovan visar ett antal vattendroppar som sammanförts med olika material. Den buktiga (konvexa ) droppformen är påtaglig i samtliga fall (utom med vattendroppen i motoroljan, den bara sjönk ner). Emellertid är rundningen speciellt tydlig i fallet med plast (plexiglas) och metall som underlag : ju större rundhet i droppformens överdel, desto mera påtaglig är tydligen den inre sammanhållande kraften, kohesionen, mellan partiklarna. En svag dropprundning kan alltså tolkas som att kohesionskraften inuti vattenmaterialet i förhållande till adhesionskraften mot underlaget är liten; En stor rundning betyder då att adhesionskraften är liten med en allt mer påtagligt synlig inre sammandragande kraft, kohesionskraften.

Ett materials SAMMANHÅLLANDE KRAFT kallas i allmänhet för kohesionskraft;

Kraft som — utom gravitationen — strävar att förena olika material kallas i allmänhet för adhesionskraft.

Sammanhållningen inom materialet kallas kohesion, attraktionen mellan de åtskilda materialen kallas adhesion.

Primära kohesionen

PrimärKohesionen — medelmaterialkraften mellan två medelatomer

I exemplet med Vätebindningen H—H visas hur den primärt sammanhållande kraften mellan två närliggande atomer [f.ö. och här veterligt den allra starkaste bindningen som finns i fysiken, se Tabelldata] kan uttryckas på en relativt enkel, elementär matematisk form som ansluter till ELEKTRISKA KRAFTLAGEN, se Kovalenta bindningens allmänna form.

I det sambandets förlängning visas hur också andra atomparföreningar, här främst grundämnesmetallerna, kan förstås med hyfsad approximativ godhet mot uppmätta hållfasthetsvärden. Se resultatbilden i Diagram Rm2 från ursprunget i Kovalenta bindningens energiform.

Sambandsformernas enkelhet är alldeles tveklöst en god hjälp i varje översiktlig orientering som berör kunskaper om materiefysiken med hållfasthetslärans elementa — och som annars [vanligen i MAC] gömmer sig bakom komplicerade avhandlingar på ingenjörsnivå.

Fenomenorsaker

Vilken är orsaken till att t.ex. en vattenyta uppvisar en tydlig benägenhet att förena sig med en hård glasyta? Borde inte ytorna i själva verket fullkomligt strunta i varandras inre domäner och bara fungera som helt isolerade, neutrala, komponenter?

I MAC: vakuumets nollenergi.

I TNED: elektronmassans komponenter.

I strängt ideal mening borde ingen som helst attraktiv fenomenkraft föreligga mellan två olika material, frånsett gravitationens inverkan och förutsatt att materialytorna är helt elektriskt oladdade. Men som just de enkla köksobservationerna visar, beter sig materialen ingalunda alltid så, inte ens i den uppenbart synliga sinnevärlden. Vilken är den rent kvalitativa förklaringen?

I modern akademi uteslöt man från år 1927 [Se citat från Gamow] den enda logiska möjligheten med elektronmassans komponenter, en elektronmassans struktur — utan tanke på konsekvenserna. För att kunna förklara KRAFTVERKAN i adhesionsfenomenet fanns alltså inget annat för pionjären Hendrik Casimir att välja på omkring året 1947 i fenomenets uppmärksammande än ”vakuumets nollenergi”, se SAMBANDSMATEMATIKEN TILL VAKUUMETS NOLLENERGI i separat citatblock.

I TNED är det just elektronmassans komponenter som står för hela föreställningen: Alla materialytor uppvisar utåt sett en toppyta med elektronmassor. Inom vissa närgränser, när två material närmas varandra i mikro och nanoområdet, finns ingen möjlighet för respektive materialyta att »låsa sina» elektronkomponenter till »det egna materialet» — ungefär som att försöka hindra en skock galet glada barn och älsklingshusdjur från att hälsa på varandra efter en lång bortovaro och försöka intala dem att »uppföra sig städat»: de försvinner in i varandras mängd, och det är bara den omfamnande glädjen som räknas. De yttersta elementen i elektronmassorna kommer urskillningslöst att identifiera sig med varandras materialmotsatta atomföräldrar, alltmera ju närmare materialytorna kommer varandra — förstadiet till reguljär kemisk förening. Därmed TNED-Casimir-sambandet, se utförligt från INLEDNING TILL CASIMIRSAMBANDET I RELATERAD FYSIK — eller direkt för jämförelse MAC-Casimir-beskrivningen.

Nedan följer en mera utförlig genomgång av de mest uppenbara grunderna som berör materialens hållfasthet i den relaterbara fysikens perspektiv — och hur vi (möjligen) kan utföra relativt enkla överslagsberäkningar för att få tag på praktiska värden.

VAN DER WAALS KRAFTER — inledning · van der Waals, efter (1873) holländaren Johannes Diderik van der Waals (1837-1923)

BILDKÄLLA: Författarens arkiv · BildR78 Excur9 · 2okt2010 · Nikon D90 · Detalj

Brotthållfasthet · Grundläggande begrepp inom materialläran — Om materialens sammanhållande krafter — Elektronen och elektronmassans komponenter, Kohesion och Adhesion, Kraft och Energi

KORT SNABBGENOMGÅNG AV BEGREPPSGRUNDERNA i Materialläran OCH Hållfasthetsläran

————————————————————————————————————————————————————————————————————————————————————————

Hållfasthet för material [eng. strength, firmness] är ett grundläggande tekniskt [test-]begrepp som sammanhänger med all form av konstruktion, byggnad och materialanalys. Ett materials hållfasthet bestäms generellt [förenklat] av den kraft, tryck eller belastning som krävs för att påvisa ett brott i materialet, den s.k. brottgränsen [Rm] [eng. Ultimate Strength]. Därmed termen eller begreppet brotthållfasthet. De olika termer som förekommer visas i grundformen med belastningsdiagrammet, där ges också en del webbreferenser i ämnet.

2010X7

Casimireffekten — från allmän hållfasthetslära

Universums Historia — BellDHARMA 2010

Frånsett atmosfäriska tryck, materialens egentyngder i givna gravitationsfält (g-fält), materialens inbördes attraherande g-krafter och elementarladdningens inre struktur: Idealt mellan två idealt plana, elektriskt oladdade, parallella materialytor åtskilda av planavståndet (d) finns ingen KRAFTASPEKT:

Bild 1

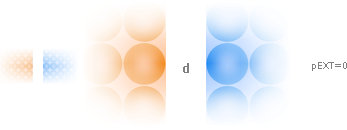
Frånsett gravitationen: Ingen kraftverkan föreligger mellan två oladdade materialytor.

Med noll planavstånd är — följaktligen — också KRAFTASPEKTEN noll:

Bild 2

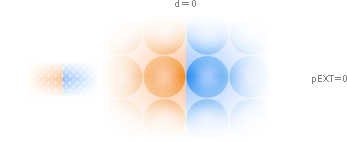
Ingen kraftverkan föreligger mellan två närliggande atomplan — förrän man försöker pressa ihop eller [för ett givet, redan sammansatt material] dra ifrån.

Man kan — idealt — skilja och återförena materialytorna hur många gånger som helst — utan inblandning av några extra krafter utöver de som behövs för att flytta materialmassorna som enskilda fristående massobjekt.

I den ideala modellen kan vi också påverka materialföreningsgränsen vid ideala d=0 genom att påföra materialen extra yttre tryckkrafter.

Bild 3

Varje intryckande extra kraft som läggs på de bägge materialdelarna medför, på ett eller annat sätt, en DEFORMATION i materialet (idealt från föreningspunkten d=0 och vidare inåt). Deformationen blir bestående om kraften [p(EXT)] överskrider materialets elasticitet (Re). Under den gränsen återtar materialet sin ursprungsform då deformationskraften tas bort och alltmer exakt med allt mindre p(EXT). Med en viss lägsta deformationskraft kan materialdelarna ingå beständig förening, s.k. kallfogning (eng. Cold Pressure Welding), eller kall(press-)sammanfogning (’kallpress-svetsning’). Villkoret (som vi förstår) är att den intryckande kraften måste överstiga (minst 5-10 ggr) den naturligt sammanhållande (elastiska) kraften i materialets närliggande sammanhållande atomskikt. Den överskjutande delen garanterar arbetet för den permanenta låsningen.

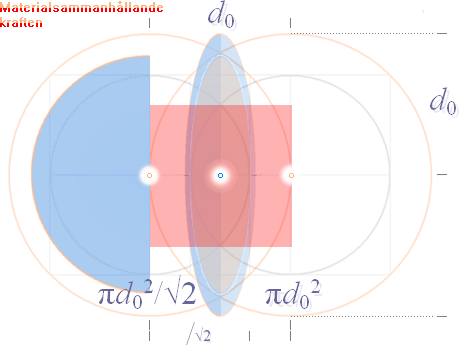
Vi backar tillbaka till situationen med d=0, Bild 2:

I DEN PRAKTISKA FYSIKEN är det inte (riktigt) så enkelt (som vi redan vet).

Idealt närliggande (plana) materialytor, som i Bild 2 [rundlarna föreställer varje atoms idealt avgränsade sfäriska domän], är definitivt INTE alls enkla att »plocka isär» genom några »ideala plansnitt» mellan närliggande atomplan. Att skapa en mellanliggande fri distans (d) — ett brott — generellt mellan närliggande atomplan i ett godtyckligt [fast] material, kräver i allmänhet mycket stora dragkrafter. Det är den ena sidan av saken.

Den andra sidan av saken är att — och här saknas [‡] teorin generellt i MAC, men inte i TNED [‡]— materialgränserna, ovan som ideala plan som stryker exakt utmed medelatomavståndens sfärgränser, inte har den ideala beskaffenheten: Atomens yttersta delar, i formen av elektronmassorna, närmare bestämt genom elektronmassans komponenter, besitter [delvis beroende på material] relativt stor frihet att »koka» upp, utöver, utanför den ideala plangränsen för atommedelavstånden — och därmed associera sig med närliggande materials atomdomäner [Elektronelementens kärnattraktioner skymmer varandra periodvis på grund av de inbördes rörelseformerna så att elementen periodvis framstår som frikopplade från sin atomära materialdel — och därmed tillgänglighet för andra materialdelar]. Vilket vill säga: Elektronmassornas yttersta delar och inom vissa små näravstånd kan dela varandras atomdomäner — i princip oberoende av materialoriginal. Med andra ord: närliggande materialytor kan attraheras — elektriskt. Utan en struktur för elementarladdningen (elektronen) blir en sådan förklaring omöjlig.

I TNED utgör atommedelavståndet (kortaste, kubiska) den absoluta närgränsen för en sådan intern materialattraktion — vilket motsvarar situationen i Bild 2. Närmare än så kan två idealt plana materialytor inte komma varandra genom ömsesidig elektrisk attraktion om de förs ihop från situationen i Bild 1, d>0.

Attraktionskraften i det läget får för teorins del heller inte vara större, eller ens tangera, materialets naturliga hållfasthetsgräns (Brottgränsen [Rm]) [eg., heller inte ens FLYTGRÄNSEN (sträckgränsen, [Re])]. För att uppnå ämnets naturliga hållfasthet, måste (nämligen — och vilket utesluter MAC-Casimirsambandet som relevant för hållfasthetsfysikens kända domäner, kurvbilden nedan) en ytterligare (materialdeformerande) intryckning ske typ Bild 3.

Jämförande funktionsgrafer MAC-TNED

Jämförande funktionsgrafer MAC-TNED för Casimirsambandets fysik

—————————————————————————————————————————————————

EXEMPEL MED SEGJÄRN SIS 07 17-02 — beräkningsdata från Kalkylkortet

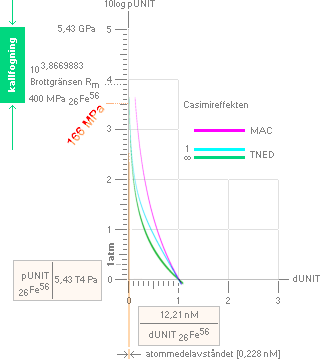
GrafUnit50 y=(ln[(x'–2)([x'm]'–2)])/(ln10); MAC(m)=1; TNED(m)=x/[a=1|1000]

————————————————————————————————————————————

Grafisk form — se även TNED-Casimirsambandet i separat dokument:

y = x^–2[(x)^m]^–2 — Casimireffekten typfunktionen ovan renodlad som nedan

m = 1 ........................ motsvarar MAC-formen med d ⁴ ljusvioletta grafen

m = x/a ..................... motsvarar TNED-formen med separerade typ d₁ ²d₂ ² ; n=n/4 ; ljusblå | gröna graferna markerade 1 | ∞

————————————————————————————————————————————

För jämförelsen har använts [rumstempererat] Järn [26Fe58] från Kalkylkortet med materialparametrar för motsvarande SEGJÄRN enligt

MATERIALLÄRA (Karleboserien 5 1980 s205 Tabell 7.2 Segjärn [SIS 07 17-02]:

Brottgräns [Rm] 400 MPa, Resttöjningsgräns [Rp0,2 — strax under materialets sträck- eller flytgräns, Re] 250 MPa.

166 MPa-värdet är TNED-Casimirsambandets värde för materialytornas attraktionstryck vid deras exakt ideala nollavstånd, analogt uppnått atommedelavstånd utan ytterligare. Notera att det värdet [i detta fall] gränsar till den s.k. Resttöjningsgränsen Rpn (för segjärn min. 220-250 MPa) som i sig ligger strax under elastiska deformationsgränsen [Re], se referensdata i Grundläggande hållfasthetsbegrepp.

MAC-sambandet till jämförelse ger inga materialparametrar. För TNED-gränserna 1 | ∞, se utförligt i TNED-Casimirsambandet.

KALLFOGNINGSSTAPELN [grön, bilden ovan], dess nedre kant, motsvarar TNED-Casimirsambandets tangerade atommedelavstånd — i Järnexemplet ca 166 MPa för den naturligt attraherande närverkan via TNED-Casimirsambandet. Från denna punkt och vidare uppåt måste en extra intryckande-deformerande kraft adderas [5-10 ggr Re-värdet] för att få atomföreningarna att uppvisa ett naturligt motsvarande sammanfogande hållfasthetsvärde för de förenade tryckytorna. Figuren nedan illustrerar hur den intryckningen måste göras med internt penetrerande atomdomäner, [som efter materialets interna fördelning etablerar] analogt bestående deformationer [minst 40%].

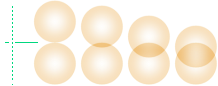
Kallfogningsinpressning — extra kraft krävs för att nå Rm-hållfasthet i fogen.

MAC-Casimirsambandet klarar inte den biten. Den ljusvioletta grafdelen [grafbilden ovan] i MAC-sambandet tangerar brottgränsvärdet (Rm) redan långt innan materialytornas separationsavstånd når atommedelavståndet. Medan således TNED-Casimirsambandet uppvisar en kontinuerlig, relevant och till synes rationell materialbeskrivning ända in till atommedelavståndet, samt i tydlig respekt till de redan kända allmänna hållfasthetsdomänerna, finns ingen liknande aspekt att rapportera i fallet MAC-sambandet.

Exemplet med Segjärn

Grafen nedan samma som ovan men förlängd i horisontalled [x] för större tydlighet:

Exemplet med Segjärn SIS 17 07-02

—————————————————————————————————————

▬▬ GrafUnit50 yTNED = [(ln[([x/5]'–2)([(x/5)'[x/5]/1000]'–2)])/ln10]

▬▬ GrafUnit50 yMAC = [(ln[([x/5]'–2)([(x/5)'1]'–2)])/ln10]

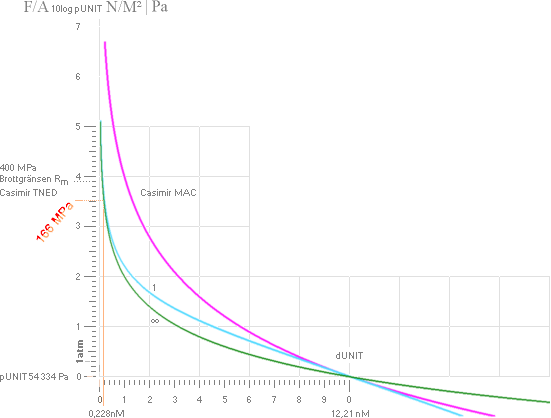
— Exemplet klargör speciellt att Casimir MAC-sambandets form tydligen och omöjligen kan koppla praktiskt till någon begriplig hållfasthetsfysik eftersom materialets brotthållfasthetsgräns enligt den kurvan [ljusvioletta ovan] uppnås märkbart långt innan atommedelavståndet d0 [inte bara i Järnexemplets fall] uppnås.

— Däremot matchar TNED-formen hållfasthetsvärdet utomordentligt — LÄGRE Rm-värde VID d0 [0,228 nM i exempelfallet].

Alla resultatvärden i Kalkylkortet.

— För att matcha materialhållfastheterna rimligt [i intervallet 0,1-20 nM], måste MAC »hitta något annat samband»: Man använder sambandsformen för van der Waalskrafterna [Se Övergången vdW-Casimir] — men inte heller då stämmer det riktigt bra ... Vidare i huvudtexten.

Teknisk verifikation

Vad vet man rent tekniskt om hur värdebilden (insinuerad ovan) stämmer i området molekylära attraktionskrafter?

Det tråkiga är vid genomsökning på webben [bland hundratals forskningsrapporter, Okt2010] att inga begripligt klara referenser till jämförelse alls verkar finnas — »helbildsgrafer» typ 0,1-1000 nM verkar inte finnas, inte för något enda provmaterial. [Det liknar mest situationen då havregrynsgröten befinner sig i kokning, långt ifrån tillfället då den lugnat ner sig för servering till frukost]: forskning pågår.

I sektionen Casimircitat ges referenser till en del av det utbud som finns gratis tillgängligt på webben.

De mätdata som finns där ansluter emellertid specifikt till ’Casimirområdet’ grovt (10-20)nM-100µM, medan vår fråga ovan snarare har fokus på området 0,1nM-(10-20)nM — och som vi redan vet ligger utom ramen för det etablerade Casimirsambandets räckvidd. Se den ljusvioletta grafdelen ovan. Vi skulle vilja ha jämförande mekaniska mätdata på just närområdet 0,1nM-(10-20)nM — med preferens utifrån och in, alltså från 10nM och inåt.

Här veterligt: det finns inga sådana undersökningar [ännu Okt2010] som kan förstås på någon begriplig nivå — Eller så finns det, men inbäddat i den moderna akademins komplicerade kemiska vokabulär — som i princip är omöjligt att hitta utom för den som inte redan är insatt.

Det enda referensmedel som framkommit visas i Jämförelse med Sandia National Laboratories — och det är bara en delvis indikation då källan inte närmare specificerar ämnessammansättningen, eller ens koefficienternas värden.

Förhoppningen är att det kommer fram ett bättre uppgiftsunderlag inom den närmaste framtiden — nanoforskningen är generellt intressant ur flera synvinklar och står helt säkert i experimentalfysikens fokus för lång tid framöver.

För den vidare orienteringen, se även i

GRUNDLÄGGANDE OKLARHETER i den grundläggande materialbeskrivningen I MODERN AKADEMI.

Se även i

TNED-Casimirvärden gränsar till materialens brottgräns

— medan däremot MAC-sambandet skjuter över målet med stora belopp

Övergången vdW-Casimir

— Hur MAC beskriver typglappet 0,1-10nM

Grundläggande hållfasthetsbegrepp

BILDKÄLLA ovan: Författarens arkiv · Bild219 R2010APR13 · Nikon D90 · Detalj · BILDKÄLLA nedan: Författarens arkiv · Bild11Skruv · 4nov2010 · Nikon D90

Materiallära — grundläggande hållfasthetsbegrepp

GRUNDLÄGGANDE HÅLLFASTHETSBEGREPP är den ENERGI och KRAFT som sammanhåller länkarna — atomerna — i ett material. Till dessa hör sedan speciella facktermer, benämningar och begrepp av typen KJ/mol, Kovalent Bindning, van der Waals Krafter [Hamakerkonstanten, m.fl.]. Avsnittet nedan genomgår grunderna — och försöker reda ut de krångliga kopplingarna.

De allra starkaste MATERIELLA bindningarna mellan olika atomer är inte som vi vanliga amatörer kanske kan tro, typ METALLER och DIAMANT. Det är — faktiskt — ORGANISKA MOLEKYLER [‡org]. Skillnaden är också jättestor [‡met]. Exempel följer.

Grundsamband

ENERGIINNEHÅLLET PER KUBIKMETER MATERIAL av ett material är alltid lika med DEN MATERIALSAMMANHÅLLANDE KRAFTEN [F] ÖVER tvärsnittsYTAN [A]:

F/A = N/M² ........................ över ytan .................... kraft, N

= NM/M³ ..................... över volymen .............. energi, J=NM

= J/M³

= E/V

= Rm ........................... N/M² = Pa

= materialets brottgräns [Rm]

KJ/mol

I konventionell facklitteratur används ofta enheten ”kJ/mol”, »KiloJoule/GRAMmol», KJ/GRAMmol med

1 GRAMmol = ”1 mol” = 1/[1000u] = 0,001 KGmol = AVOGADROS TAL avr. 6,023 T23 = ”1mol” ;

— Förklaring: Antalet [N] atomer eller molekyler med massan m KG av ett ämne är N=m/Uu, U medelatomvikten och u atomära massenheten; sätt m=U gram av ämnet, och man får N=U(0,001)KG/Uu=1/1000u: Antalet N atomer (eller molekyler) i ämnet ges som 1 GRAMmol = 1/1000u = 6,023 T23 st enheter = AVOGADROS TAL atomer eller molekyler som är lika stor grammängd av materialet som dess medelatomvikt U — eller ALLTID per 6,023 T23 stycken individer atomer eller molekyler:

— PER mol är alltså helt enkelt »per U gram av ämnet».

Se även FOCUS MATERIEN 1975 s156sp1ö:

”En mol av ett ämne är så många gram av ämnet som den sammanlagda atomvikten anger.”.

KJ/GRAMmol = (1000 J)/[1/u · 1/1000]

= MJ·u ........... J

Värdetalet i KiloJoule (via begreppet ”mol”) omformas till samma värdetal men i MegaJoule (via multiplikation med u);

= 1000 J · 1000u

= KJ · 1/mol

KJ-värdet — underförstått i ”mol” är samma som MJ-värdet — underförstått i produkt med u.

Jämför: 2,85 KJ (”per mol”) = 2,85 MJ (gånger u).

Antalet (N) medelatomer i V = 1 M³ av materialet med massan m är N=m/Uu=ρV/Uu med

m = ρV,

ρ materialets medeltäthet i KG/M³,

V = 1M³,

U medelatomvikten och

u atomära massenheten [här 1,66033 t27 KG]. Energin för alla N medelatomer i 1 M³ av materialet blir alltså

MJ·u·N = MJ·u·ρV/Uu

= MJ·ρV/U

= E ................. MJ

E = MJ·ρV/U ;

E/V = MJ·ρ/U ........ J/M³ = N/M² = Pa

= F/A

= Rm ............. MPa ;

Rm = MJ·ρ/U ....... MPa

Värdetalet i MegaJoule (MJ via multiplikation med u) är samma som värdetalet i KiloJoule (KJ med underförstådd association till den moderna akademins i särklass allra mest ologiska begrepp ”mol”, som ovan):

= KJ/mol·ρ/U ;

KJ/mol = Rm·U/ρ ........ Rm i MegaPascal

;

Rm = KJ/mol·ρ/U ... MPa

Jämförande tabeller — Kovalenta bindningar

Engelska Wikipedia innehåller en tabell (på underrubriken Strong chemical bonds) på artikeln Chemical bond (2010-10-28) med några fundamentala kemiska bindningar uttryckta i KJ/mol. För att få en uppfattning om den motsvarande MATERIALSTYRKAN, sambanden ovan, har KJ/Mol-värdena här kompletterats med Rm-värden i MPa.

KO[ömsesidigt]VALENT[tillämplig]

Kompletterande grundtabell — materialstyrkan hos grundmolekylerna

Kovalent bindningsform — Wikipediakällan (ovan) utsäger inte det (2010-10-31), och ger heller ingen teckenförklaring till beteckningssätten, se separat tabell nedan.

Kovalent bindning: de kemiskt förenade atomerna delar på ett (uni[–] eller mono), två (di[=]) eller tre (tripel[≡] eller tri) par elektroner.

Jonbindning: minimal elektrondelning.

Se även Särskild illustration till Vätebindningen H—H.

Kovalenta bindningsformen — kemiskt beteckningssätt med valensstreck med namn: EX: N≡N betecknar en tri-kovalent bindning mellan Kväve-Kväve, även benämnd ’trippelbindning’ [KÄLLA: FOCUS MATERIEN 1975 s155ö, s156sp2];

beteckning	–	=	≡
namn	uni-	di-	tri-
	singulär	dubbel	tripel

medelatomvikt	typ	kemisk bindning	d0, längd pM	E, KJ/mol	Rm, GPa	ρ
U		Vätebindningar	t12 M	MJ·u	T9 N/M²	KG/M³
1	Väte-Väte	H–H	74	436	1786,43	4 097,31
8,5	Väte-Syre	H–O	96	366	686,85	15 951,43
10	Väte-Fluor	H–F	92	568	1211,10	21 322,15
18	Väte-Klor	H–Cl	127	432	350,16	14 590,02
		Kolbindningar
6,5	Kol-Väte	C–H	109	413	529,50	8 333,52
12	Kol-Kol	C–C	154	348	158,20	5 455,24
12	Kol-Kol	C=C	134	614	423,69	8 280,59
12	Kol-Kol	C≡C	120	839	806,14	11 530,07
13	Kol-Kväve	C–N	147	308	160,99	6 794,94
14	Kol-Syre	C–O	143	360	204,40	7 949,03
15,5	Kol-Fluor	C–F	134	488	336,74	10 695,76
23,5	Kol-Klor	C–Cl	177	330	98,81	7 036,27
		Kvävebindningar
7,5	Kväve-Väte	N–H	101	391	630,10	12 086,25
14	Kväve-Kväve	N–N	145	170	92,58	7 624,62
14	Kväve-Kväve	N≡N	110	945	1178,82	17 464,03
		Syrebindningar
16	Syre-Syre	O–O	148	145	74,26	8 194,63
16	Syre-Syre	O=O	121	498	466,73	14 995,41
		Halogenbindningar
19	Fluor-Fluor	F–F	142	158	91,62	11 017,5
35	Klor-Klor	Cl–Cl	199	243	51,20	7 374,00
40,5	Brom-Väte	Br–H	141	366	216,78	23 987,89
80	Brom-Brom	Br–Br	228	193	27,04	11 206,75
63,5	Jod-Väte	I–H	161	298	118,56	25 263,33
126	Jod-Jod	I–I	267	151	13,17	10 990,85

TABELLFÖRKLARINGAR med källreferenser:

Bindningslängden d0 i picoMeter, ”In molecular geometry, bond length or bond distance is the average distance between nuclei of two bonded atoms in a molecule.”, @INTERNET Wikipedia Bond length 2010-10-28;

Bindningsenergin E i KJ/mol, grunddata, se sist nedan;

Materialstyrkan Rm i GigaPascal, efter medelkubvolymen d0³ och medelatomvikten Uu med medeltätheten uU/d0³,

Rm = KJ/mol·u/d0³/1000, GPa [Se särskild HÄRLEDNING];

Medeltätheten ρ i KG/M³, efter atommedelavståndet d0 lika med bindningslängden som ovan, ρ = uU/d0³ med

medelatomvikten U som (U1+U2)/2, U12 bägge avrundade heltal (från särskild tabell i PERIODISKA SYSTEMET).

........... högsta kolumnvärdet

KÄLLDATA — utom U, Rm och ρ: @INTERNET Wikipedia Chemical bond 2010-10-28

[Wikikällan från University of Waterloo, Cyberspace Chemistry — begränsad behörighet].

Jämförande metallbindningar

Jämför motsvarande materialstyrka för några av metallerna

[se Tabell med källdata i Kalkylkortet, Tabellflik1 Ämnestabell]:

bet.	ämne	Z	U	ρ(KG/M³)	d0 pM	KJ/mol	Rm|GPa
Al	Aluminium	13	27	2700	255	0,65-1,5	0,065-0,150
Cr	Krom	24	52	7190	229	2,99	0,413
Fe	Järn	26	56	7870	228	2,85	0,400
Co	Kobolt	27	59	8900	222	—	—
Ni	Nickel	28	59	8910	222	0,3-2,1	0,045-0,317
Cu	Koppar	29	64	8930	228	1,43-3,23	0,200-0,450
Au	Guld	79	196	19260	257	1,22	0,120

KJ/mol = Rm·U/ρ ........ Rm i MegaPascal

Jämförande karaktäristik:

1. medelatomavstånden är runt dubbelt så långa för metallerna jämfört med organiska grundmolekylerna;

2. materialstyrkan hos metallerna är runt 1 000 ggr lägre (400/0,4 = 1 000) jämfört med organiska grundmolekylerna;

3. metallerna uppvisar tunga atomkärnor med elektronmassor längre ut jämfört med de lättare organiska grundmolekylerna;

Styrka — bindningssätt

Olika sätt kopplar olika styrka

Grundbegreppen från MAC:

”Kovalent bindning I en renodlad jonbindning är varje elektron lokaliserad till en bestämd atom. Är elektronmolnens yttre delar gemensamma innebär det att några av elektronerna inte tillhör en utan flera atomers elektronmoln. De har blivit delokaliserade. Den bindning som då uppkommer kallas kovalent bindning eller elektronparsbindning.”,

”En kovalent bindning kan sträcka sig över många atomer. Så är t.ex. fallet i metallkristaller. Metallisk bindning är därför ett specialfall av den kovalenta.”,

”Mellan kovalent bindning och jonbindning finns alla övergångar. Ju mer lokaliserade elektronerna är desto större är jonbindningsinslaget, medan det kovalenta inslaget ökar med ökad delokalisering.”,

”Övriga bindningar Andra slag av kemisk bindning är mycket svagare än jonbindning och kovalent bindning. Dipolbindning, vätebindning och van der Waalskrafter är de viktigaste.”

FOCUS MATERIEN 1975 s149sp2n-s150sp1ö

I den diversitet av olika möjliga resonanser i elektronmassorna som kan finnas i den kemiska kopplingen mellan två närliggande atomer, finns en motsvarande stor mängd olika sätt som den atomära bindningen kan verkställas på.

Typmönster i centralkraftsverkan — PREFIXxSIN 1+sinax a(1—10) 1tUnit30

Bindningen mellan atomernas positivt laddade atomkärnor återfaller helt på den mellanliggande negativt laddade elektronmassan och dess förmåga att sammandra kärnorna.

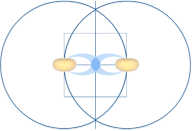
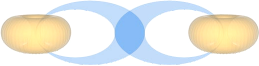
Bilden ovan illustrerar i TYPFORM två atomer som hålls samman av en deras gemensamt mellanliggande elektronmassa, här idealiserad som en samlad sfärisk kropp (blå). I praktiken ligger elektronmassan utspridd på olika mer eller mindre utspridda lokaler med [inbördes komplicerade] resonansmönster och olika fördelning i olika partier av xyz-rymden.

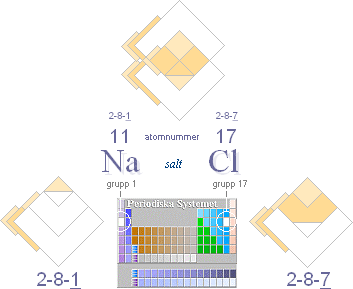
— Det som atomerna MEST tycks intressera sig för är RESONANSKRITERIET (harmoniska symfonier): helt ÖMSESIDIGT fyllda resonansskal — typ NaCl [se även i PERIODISKA SYSTEMET]:

— Om två (ELLER FLERA) atomer SUMMERAR en oktett [8-tal] — fylld resonans — i atomens yttersta delar, har atombindningen den allra största förutsättningen för att bli maximalt stark.

Som redan påpekats i PERIODISKA SYSTEMET betyder det att speciellt atomer i ändgrupperna 1 och 17, t.ex. NaCl [figuren ovan i sammanställt »kemiskt percept»], representerar särskilt starka bindningar.

Men även mera exotiska typer med »fyllda resonanser» kan förekomma. Ett exempel är två Kväveatomer [N{2-5}-N{2-5}]: De tre elektroner som fattas i ytterelektronskalet för fylld resonans kan delas av N-N-kopplingen genom att endera N-atomen LÅNAR UT 3e till den andra: Resultatet kallas konventionellt en Tri[pel]Kovalent Bindning, »TRE par elektroner» delas mellan två atomer. Den tri[pel]kovalenta bindningen är en av de allra starkaste molekylbindningar som finns, se N≡N i föregående jämförande tabell.

Starkaste bindningen mellan två närliggande atomkärnor med samma laddningspolaritet ges naturligtvis främst OM de repulsiva kärnpotentialerna SKYMS NER av en mellanliggande motsatt potential — en mellanliggande elektronmassa. Vätebindningen H—H är tydligen den ideala hörnstenen i den principen [dessutom tydligen också den starkaste]: Med en och samma laddningsrepresentation, enbart med ändring av atommedelavstånden (d0) och KRAFTDÄMPNING med (1/Zatomnummer) motsvarande kärnrepulsionernas växande inslag med växande Z, ges en tydligt hyfsad representation 0-1000 MPa för samtliga grundämnesmetaller, se Diagram Rm3, Diagram Rm2 och Diagram Rm1.

Exempel på Webbkälla som refererar ovannämnda detaljer:

Tripel-Kovalent Bindning [Med exemplet Kväve(N)-Kväve(N) enligt N≡N]

http://www.tutorvista.com/content/chemistry/chemistry-i/chemical-bonding/triple-covalent-bond.php

Allmänt etablerade begrepp — exempel på hur termerna används:

TRIVALENT bindning, TREatomBindning

DIVALENT bindning, TVÅatombindning (di-atomär bindning)

KOVALENT bindning, PARELEKTRONDELNINGS-Bindning — som kan vara singulär (1), binär (2), triplär (3), teträr (4), pentär [5], osv.

Kovalenta bindningen delar på ETT PAR ELEKTRONER för varje kovalens:

EX: En bindning mellan två atomer kan dela på TRE PAR elektroner, TRE kovalenser, vilket blir en TriplärKovalent Bindning eller en TripelKovalent Bindning.

Webbkällor verkar i allmänhet dåliga på att ange KVANTITATIVA VÄRDEN för påstådda olika bindningstyper.

Här finns en upphittad som skiljer sig:

PROPERTIES AND ENERGY CONTENTS OF CHEMICAL BONDS — Peter v. Sengbusch 2003

http://www.biologie.uni-hamburg.de/b-online/e18/18c.htm

”Covalent bonds are the most important type of bond occurring in organic molecules. They are characterized by a common pair of electrons between two neighbouring atoms. Depending on the involved partners, simple, double or triple bonds can be formed (H–H, O=O, N≡N).”

:

delta G of a covalent bond -210 to -420 KJ/mol

Weak interactions -4 to -30 KJ/mol

Thermal molecular movements -0,7 to -3 KJ/mol

delta G of Ionic interactions -20 to -30 KJ/mol

Van der Waals attraction -3 to -4 KJ/mol

Källan ovan ger dock ingen förklaring till ”delta G” — man får söka svaret på annat håll. En annan källa upplyser

”Delta G Energy can be used to do work. Scientists call this useful kind of energy "free energy" and represent it with the letter "G" (named after the scientist Josiah Willard Gibbs, who first thought of this concept).”,

BIOdotEDU — Bond Energy 2005

http://www.brooklyn.cuny.edu/bc/ahp/LAD/C4d/C4d_bondenergy.html

EXEMPLEN VISAR ORDNINGEN.

Ytterligare en upphittad källa som anger referensvärden för de olika kemiska bindningskrafterna — notera differenserna mot föregående, samt även i jämförelse med energiinnehållet i motsvarande metalliska bindningar [Se tabellen i Jämförande metallbindningar]:

TABLE 3.1 Bonding energies for various atomic bonding mechanisms

Bonding mechanism Bonding energy [kJ·mol^-1]

Ionic 340-800

Covalent 270-610

Metallic 20-240

Van der Waals <40

GOOGLEBÖCKER s27 Table 3.1,

UNDERSTANDING MATERIALS SCIENCE: history, properties, applications — Rolf E. Hummel 2004

Tabellvärdet närmast ovan för ’Metallic’ anger 20-240 KJ/mol — att jämföra med tabellhållfasthetsvärdets 0,65-2,99 KJ/mol för metallerna Al, Cr, Fe, Ni, Cu, Au i Jämförande metallbindningar.

Vi vet inte här om källförfattaren ovan möjligen avser ytterst extremt speciella metallbindningar — typ superspeciella legeringar med mycket höga brotthållfasthetsvärden, typ (240 KJ/mol)(8000 KG/M³)/26~73,8 GPa. MatWeb ger som jämförande motvikt högsta brottgränsen (Rupture Strength) för Kolstål (High Carbon Steel) 0,621-1,3 GPa, och för rostfritt stål (Stainless Steel med Tensile Strength, Ultimate ) 0,085-3,00 GPa. Av allt att döma är det storleksordningen i varje fall för de mest draghållfasta stålen — ännu långt från typ 70 GPa.

EXEMPLET BARA UNDERSTRYKER ORDNINGEN (här färgat av min personliga erfarenhet i webbsökningen Okt2010): Mera av regel än undantag är webbkällor på området — även böcker som ovan — knapphändigt relaterade, inte sällan [som ovan] med inbördes rätt präktiga differenser. Jämför även uppgiften från Wikipediatabellen på den trikovalenta N≡N-bindningen med 945 KJ/mol, att jämföra med bokexemplet ovan som anger max 610 KJ/mol för kovalent bindning. Det är tydligt [frånsett rent tekniska orsaker i vetenskapshistoriens utveckling] mera längre ifrån än närmare någon ambitiöst precisionsbaserad allmän lärostol. Skulle man använda typ Soleffekten [3,8 T26 W] med samma typdifferens, vore vi nog (tillbaka) vid år 1311.

[OM författarna hade en etablerad källa att referera till, typ mätlaboratorium erkänt för noggrannhet och omsorgsfullhet, skulle ovannämnda datatyp reduceras till ett minimum. Också det exemplet pekar på det uppenbara: organisationen för rent vetenskapliga ändamål utan vinstintressen inom forskningsvärlden är uppenbarligen inte optimal].

Vätebindningen H—H

Örnnebulosan [detalj] — En av de magnifika stoft och gasöarna [i huvudsak VÄTGAS] i Universum som tros vara tummelplatsen för nybildning av stjärnor.

Credit: Astronomy Picture of the Day — National Optical Astronomy Observatory/Association of Universities for Research in Astronomy/National Science Foundation — 2009 February 8 — http://apod.nasa.gov/apod/ap090208.html

Vätebindningen H—H

Kovalenta bindningsgeometrins grund

Kohesionsfysikens enkla grundsamband — exempel

Särskild illustration till Vätebindningen H—H — den ekvivalent sammanhållande ytkraften — från Jämförande tabeller — Kovalenta bindningar

OM vi prövar att beräkna Coulombkraften [F=k(Q/d)²] på vanligt sätt enligt Elektriska kraftlagen som nedan [Se särskilt block i Kalkylkortet Tabellflik 1 — Kontrollräkning | Jämförande tabeller — Kovalenta bindningar | Väte] med distansvärdet d0=74 pM från Tabellen och med k=1/4πε₀ ges resultatet som visas underst i figuren nedan — enklast tänkbara geometriskt EKVIVALENTA mönsterkoppling. Vi studerar — alldeles tydligt — en Hörnsten i Fysiken:

F/A = [2·k(e/[d₀/2])²/πd₀²]·√2

= [k(e/[d₀])²/πd₀²]/√2

= (ke²/π√2)/d₀⁴

= 1 731,29 GPa

Jämför tabellvärdet

= 1 786,43 GPa

Vätebindningens grundgeometri,

se även Inledande beskrivning

Orangea punkterna representerar de bägge väteatomernas kärncentrum. Den blå punkten i mitten representerar den idealt gemensamma elektronladdningens sfäriska punktlokal. Tvärsnittsytan i mitten, som begränsas av de orangea cirklarnas skärningspunkt, är den som definierar elektriska kraftflödets cirkulärt ekvivalenta tvärsnittsyta för det ekvivalenta atomattraktionstrycket [1731 GPa] — den ekvivalent sammanhållande ytkraften.

För att få tabellvärdet på 1786,43 GPa ska d0 vara 73,422 pM med konstanterna enligt Kalkylkortet [Tabellflik 1].

Överensstämmelsen via √2 som transformationsfaktor mellan de olika distanserna [Väteatomens grundradie eller Bohrradien Hr0 och d0 samt tvärsnittsytans reduktion] är inte »exakt» [vid rumstemperatur] — men som vi ser, mycket nära [96,91% träff] — d0(74pM)/Hr0(52,9pM) är realt 1,398 mot idealt 1,414 [98,87% träff].

Med den uppenbara resultatgeometrin frågar man sig då vad källuppgiften från Wikipediakällan grundas på — för noggrannhetens skull.

Wikikällan refererar till ett University of Waterloo med en Cyberspace Chemistry Home Page — med begränsad behörighet för allmänheten. Källan upplyser [2010-11-04],

”Bondlengths are determined by X-ray diffraction of solids, by electron diffraction, and by spectroscopic methods (study the light absorbed or emitted by molecules).”,

”The bondlengths ranges from the shortest of 74 pm for H-H to some 200 pm for large atoms, and the bond energies depends on bond order and lengths.”,

University of Waterloo — Cyberspace Chemistry — BOND LENGTHS AND ENERGIES — datumuppgift saknas

http://www.science.uwaterloo.ca/~cchieh/cact/c120/bondel.html

OM uppgiften på 74 pM (7,4 t11 M) kommer från spektroskopiska-röntgendiffraktiva mätningar är det tydligt att överensstämmelsen med den enkla geometrin som ovan är

1. påtaglig,

2. pålitlig — och därmed

3. väl relaterbar.

Syntes

VAD VI HAR FÖRSTÅTT AV DEN SAMMANHÅLLANDE YTKRAFTENS FENOMENFORM,

——————— ———————

är att dess distansform inte kan ändras (frånsett ytterst små fluktuationer) med mer än att materialbindningen bryts, att det uppstår ett materialbrott — materialets brotthållfasthet (Rm).

Vare sig vi försöker att ytterligare pressa ihop komponenterna, eller att dra isär dem, uppvisas i vilket fall lika stora inre motkrafter, samma som DEN SAMMANHÅLLANDE YTKRAFTEN, och som strävar att bevara jämvikten med nollspänning. Med andra ord: det finns ingen (nämnvärd) töjbarhet i den sammanhållande ytkraftens flödestvärsnitt hos en given materialbindning. Enda sättet att ändra bindningens distansfaktorer är att ändra bindningsformens temperatur (E=hf).

Kovalenta bindningens allmänna form

Växande kärnladdning reducerar atomära Coulombattraktionen

Med en (till att börja med grovt) approximerad giltighet (med prövning från Ämnestabell i Tabellflik 1 i Kalkylkortet, nedan) gäller sambandsformen för Vätebindningen [se inledande härledning i Grundämnesmetallernas brotthållfasthet]

F/A = (ke²/π√2)/d₀⁴ ................................. vätebindningens sammanhållande ytkraft, k = 1/4πε₀

också (i varje fall, men med vissa spridningar) för metallerna enligt

För etablerad definition av Kovalenta bindningen, se Kovalent bindning.

F/A = (1/Z)(ke²/π√2)/d₀⁴ ......................... kovalenta bindningens sammanhållande ytkraft generellt mellan två lika atomer

med d₀ lika med grundämnesmaterialets atommedelavstånd. Tabellen nedan med Rm | beräknat MPa visar några metalldata till jämförelse.

Jämförande tabell — Brotthållfastheten Rm som funktion av ämnets reciproka atomnummer Z

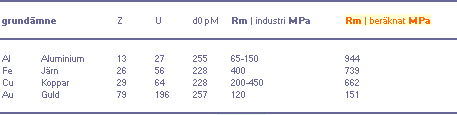
Data ovan samma som i ÄMNESTABELLENs data i Kalkylkortet, Tabellflik 1.

Värdena ovan ansluter till Diagram Rm1.

Frånsett aluminiumfallet är det tydligt att överensstämmelsen är hyfsad [med viss materialbearbetning ligger värdena inom materialgränserna].

En mera omfattande jämförelse för samtliga grundämnesmetaller, sambandet ovan, ges i Brotthållfastheten för grundämnesmetallerna.

Motsvarande mönsterform för den sammanhållande kraften i materialets kubiska medelatom — energibindningsinnehållet per M³ materialmedelatom — blir (Se utförligt från grundsambandet samt Kovalenta allmänna atombindningsformen)

Kovalenta bindningen, energiformen

F/A = K/d₀³ ............................................. Den sammanhållande ytkraftens kubiska fördelning, se Grundform, Pa [=N/M²]

F/A = H(√8)/24πd₀³ ................................ via Hamakerkonstantens [delvis konventionellt kaotiska] sambandsform, van der Waalskraften

........................................................... Se förklaring från Allmänna samband, enhet i N/M² = Pa (Pascal)

Som vi redan uppmärksammat [se från Grundsambandet] används varken sambandsformer eller termer i MAC i någon motsvarighet till ovanstående: van der Waalskrafterna förekommer [tydligen] inte som definitionsbas för KOHESIONSKRAFTER — ovan — utan används genomgående för ADHESIONSMATEMATIK, se särskilt citat som belyser samband och begrepp som används konventionellt.

Svaret på Frågan om vilken [enkel, begriplig] sambandsform i MAC som används för just kohesionsmatematiken har eftersökts på webben, men ännu inte påträffats; Många webbkällor använder termen KOHESION men utan att precisera någon sambandsform.

Se även noteringen till Kohesionsmatematiken i Modern akademi.

PRECISIONEN hos [den förenklat, approximativa] Kovalenta bindningens allmänna form

F/A = (1/Z)(ke²/π√2)/d₀⁴ ......................... kovalenta bindningens sammanhållande ytkraft generellt mellan två lika atomer

i samklang med kovalenta bindningens energiform [F/A=K/d₀³=H(√8)/24πd₀³] som ovan kan testas i jämförelse med redan kända experimentellt genomförda mätningar på — främst — de olika grundämnesmetallernas brotthållfasthet.

På Internet finns MatWeb, en omfattade databank på olika material och som kan användas helt gratis för allmänna syften, bland annat data på grundämnesmetallernas brotthållfasthet (Ultimate Strength). Sambandsformen närmast ovan visas nedan i Diagram Rm1 — till jämförelse i diagrammet som Serie 1 [mörkblå], MatWeb-data [med vissa komplement] som Serie 2 [ljusviolett].

Diagram Rm1 — Diagram Rm2 · Diagram Rm3 — Grundämnesmetallerna

Brotthållfastheten för grundämnesmetallerna — lägsta värdena motsvarande glödgat tillstånd efter svalning [rumstempererat]

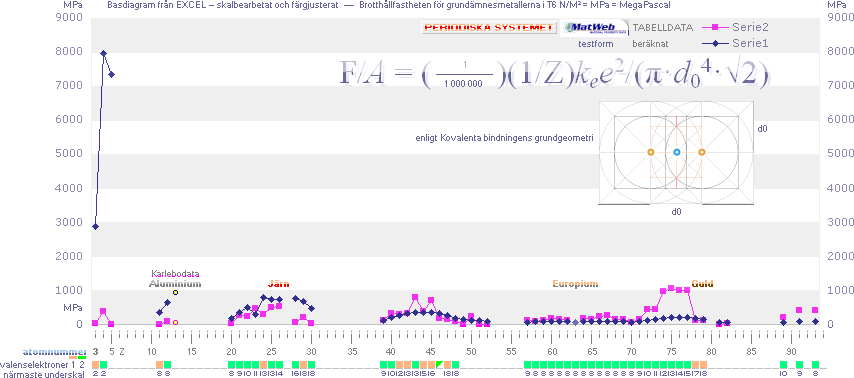
▬▬▬ Experimentellt

▬▬▬ Beräknat enligt Kovalenta bindningens grundgeometri, se även ikonillustration i Grundformen Justerad.

PRIMÄRA GRUNDÄMNESDATA FRÅN sammanställda källdata i Kalkylkortet i PERIODISKA SYSTEMET.

Brottgränsdata [Rm] i MPa [som ovan i huvudsak] från Internetkällan MatWeb Nov2010 —

Kovalenta bindningens grundgeometri, se från Vätebindningen H—H.

KÄLLDATA: Uppgifter på brottgränser [eng. Ultimate Strength] från MatWeb;

Endast lägsta brottgränsvärdet har medtagits — beroende på bearbetning [och grundframställning] kan en viss mindre spridning uppåt förekomma, vilket utjämnar skillnader i diagrammet.

Grunddata med atomvikter och medeltätheter från sammanställningen av källverken i PERIODISKA SYSTEMET.

Kort beskrivning. Frånsett primärmetallerna i Period 1 [Litium, Beryllium, atomnummer Z=3 och 4] och metallgruppen i Period 2 [Natrium, Magnesium, Aluminium], samt intervallet Z=73-77 visar den relativt enkla sambandsformen [Kovalenta bindningens allmänna form, F/A-sambandet infällt i figuren] en uppenbart grovt approximativt orienterande samstämmighet med motsvarande tabelldata. Jämförelsen ger tydligen vissa belägg för att KOVALENTA BINDNINGSGEOMETRINS GRUNDFORM kan förstås relevant som grundpreferens — ehuru inte exakt beskrivande i den egna enkla formen.

Grundformen justerad

Vi ser [genom separat analys, diagrammet längre upp] att differenserna tecknar en ungefärlig exponentiell variation från lägre Z till högre Z; Med en enklare funktionsjustering (med början från lägst Z=3, Litium)

Kovalenta bindningsgeometrin som beskriver grundsambandet

F/A = (1/Z)(ke²/π√2)/d₀⁴ ......................... kovalenta bindningens sammanhållande ytkraft generellt mellan två lika atomer

Se från Kovalenta bindningens allmänna form

y = (F/A)·100[0,000008Z + 2([Z–1]/2)^–2]

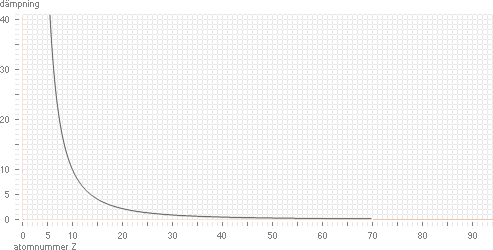
2010-11-07

Graf y=100(0.000008x+2([x–1]/2)'–2) Unit5

Den justerande grafen som ger en betydligt bättre överensstämmelse med experimentellt uppmätta brottgränser.

visar sig också en betydligt bättre överensstämmelse, diagrammet nedan:

Diagram Rm2

Funktionsjusterad Rm från Rm1 — Diagram Rm1 · Diagram Rm3

grundämnesmetallerna

Brotthållfastheten för grundämnesmetallerna från Z=3 [Litium] — OBS lägsta värdena motsvarande glödgat tillstånd efter svalning [rumstempererat]

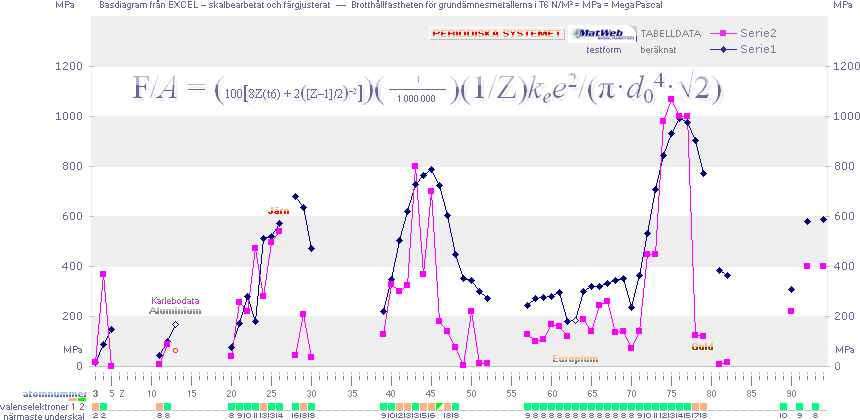
▬▬▬ Experimentellt

▬▬▬ Beräknat enligt Kovalenta bindningens grundgeometri, se även ikonillustration i Grundformen Justerad.

F/A = (100[8Z(t6) + 2([Z–1]/2)^–2])(1/Z)k_ee²/(π·d₀⁴·√2) ...................... N/M² = Pa

PRIMÄRA GRUNDÄMNESDATA FRÅN sammanställda källdata i Kalkylkortet i PERIODISKA SYSTEMET.

Brottgränsdata [Rm] i MPa [som ovan i huvudsak] från Internetkällan MatWeb Nov2010 —

Som vi ser är följsamheten markant — men ytterligare (mera komplicerad) analys för ännu bättre överensstämmelse kräver tydligen speciella intervallfunktioner (resonansvillkor), vilket dock här lämnas för vidare.

Sammanfattning

SAMMANFATTNING

KOVALENTA BINDNINGSGEOMETRINS GRUNDMATEMATIK I HÅLLFASTHETSLÄRAN

Kovalenta bindningens allmänna form

F/A = (1/Z)(ke²/π√2)/d₀⁴ ............................................................. kovalenta bindningens sammanhållande ytkraft generellt mellan två lika atomer

modifierad nedan från Diagram Rm1 med något större samstämmighet mot mätdata i Grundämnesmetallernas brottgränser via justerade sambandsformen

F/A = (100[8Z(t6) + 2([Z–1]/2)^–2])(1/Z)k_ee²/(π·d₀⁴·√2) ............ N/M² = Pa

har i samklang med kovalenta bindningens energiform [F/A=K/d₀³=H(√8)/24πd₀³] genom tabelljämförelser [Diagram Rm1 och Diagram Rm2] tydligen visat att det finns en ENKEL ELEMENTÄR SAMBANDSMATEMATIK, den ovan nämnda, för allmän orientering och översikt i materialens praktiska grundkemi, och analog med den gängse brukade termen [‡] van der Waalskraft för sambandsformen K/d₀³: här således materialatomernas sammanhållande — kohesiva — kraft och energi. Med den samhörigheten understryks (här) endast att Hamakerkonstanten [H] för ett visst material [under bestämda betingelser] tydligen kan beräknas direkt ur kännedom om materialets brottgräns enligt

H = (F/A)/[(√8)/24πd₀³]

= R_md₀³[24π/(√8)] ............................................................... med d0 som kubiska atommedelavståndet

Rm anger brottgränsen i N/M²=Pa, d0 anger materialets kubiska medelavstånd enligt Kovalenta bindningsgeometrins grundform, från Vätebindningen H—H.

Se även separat beskrivning i Hamakerkonstanten från Rm.

Ett omnämnande av den beskrivna ordningen, eller en motsvarande omskrivning i MAC, har eftersökts på de tillgängliga materialdomäner som finns på webben, men ännu (Nov2010) inte påträffats. Se även från INLEDNINGEN.

Van der Waalskrafterna

BILDKÄLLA: Författarens arkiv · Bild219 R2010·13apr · Nikon D90 · Detalj

VdW — Materialens sammanhållande energi

Jämför först »Kemistudentens inledande Observation» om ej redan bekant

MATERIALENS SAMMANHÅLLANDE ENERGI

VAN DER WAALS KRAFTER

I RELATERAD FYSIK framträder »van der Waals krafter» i ett [betydligt] annorlunda ljus i samband med TNED-teorin generellt för elektronmassan och elektronmassans komponenter jämfört med den [delvis kaotiska, se Förklaringen] beskrivningsbild som ges från den moderna akademins etablerade litteratur. Beskrivningen nedan ger en översiktlig genomgång — enligt TNED.

”van der Waalskrafter är en sammanfattande beteckning på svaga bindningskrafter som verkar mellan atomer och molekyler.”,

FOCUS MATERIEN 1975 s150sp1mn

Relevansen i TNED-resultaten [Se TNED-Casimir]:

ADHESIONSKRAFTEN mellan två åtskilda plana plattor av ett visst material som närmas till noll plattavstånd ska inte under några som helst praktiska omständigheter för fasta ämnen nå upp till materialets naturliga brottgränsvärde (Rm). För att komma dit nämligen, måste från max adhesionskraft ytterligare en viss kraft (minst 5-10 ggr Re-värdet) anställas för att få motsvarande kemisk fogning som kan uppvisa inslag av Rm.

— VID nollavstånd mellan två idealt plana elektriskt oladdade materialytor — motsvarande normalt närliggande atomplan — ligger mekaniska adhesionsspänningen alltid under, lägre än, materialets brottgränsvärde (Rm). Med exempel från Järn [SIS 17 07-02] vid rumstemperatur, brottgräns Rm = 400 MPa och atommedelavstånd 0,228 nM [från medeltätheten 7870 KG/M³], visar TNED-formen adhesionstrycket 166 MPa; För att åstadkomma kemisk förening måste ett ytterligare intryck påtvingas materialet (deformation med minst 40%) med 5-10 ggr Re-värdet (enligt uppgift från industristandard, se Kallfogning); Re-värdet (elasticitetsgränsen) ligger generellt och här i en grovt generaliserande mening för översiktens del på ca halva Rm-värdet [Se Tabellexempel i anslutning till Brottgränsgrafen]; R_pn-gränsen (som Re-värdets absolut sämsta fall) ligger alltid under/lägre än R_e-området.

Kallfogning. Med CASIMIREFFEKTEN (atomattraktion mellan närliggande materialytor) uppstår spontant tanken om en motsvarande kallfogningsteknik: Principen att via en (extra) sammanpressningskraft kunna uppnå en motsvarande varmfogningsstyrka (som vid konventionell svetsning, lödning) enbart via rå tryckkraft utan värmetillförsel. Se Kallfogning.

— Generellt sett med andra ord: Även VID exakt uppnådda atommedelavstånd via separat skilda materialytor som närmas varandra till noll, krävs (för fasta ämnen) ALLTID extra kraft för att åstadkomma naturlig förening.

— Teori saknas i MAC.

— Den naturliga adhesionen räcker inte som sådan för att åstadkomma kemisk förening (utom för ämnen med flytande materiebas).

— Eller sagt på annat sätt: Van der Waals kraft F/A=H/ad³ som tydligen enligt Kovalenta allmänna atombindningsformen med resultatredovisning i Diagram Rm2 definierar den kohesiva (inre sammanhållande) styrkan i ett material ligger ALLTID över TNED-formens adhesiva (attraherande) mekaniska tryck mellan två skilda planytor som sammanförts till exakt nollavstånd. Den återstående delen tillhör uppenbarligen kraftområdet för Kallfogning (eng. Cold pressure welding). Därmed framträder en enhetlig bild för materialets adhesiva fysik inkluderat kallfogningsmekaniken (och som det inte finns någon erkänt etablerad teori för [‡]), tillsammans med van der Waals krafter och den motsvarande Casimireffektens fysik.

— Varje atom fungerar initiellt som en isolator (±). För att förenas med andra atomer måste isolationsspänningen genombrytas. Isolationsspänningen definieras på minsta komponentens bidrag, lika med den genombrytande kraftens element: elektronmassans komponenter. Det är — enligt TNED — tydligen dessa som bär ansvaret för hela föreställningen.

Forts., Grundsamband, inledning till van der Waals krafter.

Grundsamband, inledning VdW

BILDKÄLLA: Författarens arkiv · Bild11 Isglas · 2feb2010 · Nikon D90 · Detalj

Grundsamband, inledning VdW

GRUNDBEGREPP I RELATERAD FYSIK

VAN DER WAALS KRAFTER

DEFINIERAR MATERIALENS HÅLLFASTHET

Se även van der Waals krafter inom kemin

”van der Waalskrafter är en sammanfattande beteckning på svaga bindningskrafter som verkar mellan atomer och molekyler.”,

FOCUS MATERIEN 1975 s150sp1mn

Det finns MÅNGA webbkällor (Okt2010) som uttrycker samma typmening som ovanstående citatform — och som likt denna också saknar konkreta sifferdata för exakt jämförelse.

Se även från GRUNDSAMBANDET [där är utgångspunkten energin över hela atomära medelkuben]:

ENERGIN [E=Fd] genom flödestvärsnittet (A) mellan två närliggande atomer i kemisk förening i ett material har en idealt kvadratisk ytfördelning via kraftflödestvärsnittet d² mellan atomkärnorna med d motsvarande atommedelavståndet: E/A=K/d²; MEKANISKA YTSPÄNNINGEN mellan två närliggande atomer eller atomplan får då formen av ett grundsamband

F/A = K/d³ ................................ grundsamband

Den sammanhållande kraften fördelas tydligen EKVIVALENT jämnt, homogent och idealt inom medelatomens kubiska volym d³. Därmed är materialets hållfasthet (Rm) definierad: materialets absolut starkast sammanbindande ytkraft. Det finns ingen starkare.

Betrakta från grundsambandet ovan F/A=K/d³ ett (med alternativa termer) motsvarande grundsamband

F/A = Hk/D₀³:

Grundsambandets härledning

Ett materials allra största sammanhållande kraft (F) definieras under alla praktiska omständigheter av mekaniska spänningen (F/A=Rm) som råder vid brott eller BROTTGRÄNSEN (kraften över brottytan, eng. ultimate strength) då materialet sträcks ut tills det brister (se Brottgränsexempel, ett av flera olika sätt att testa materialets hållfasthet),

R_m = MAX(F/A) ...................... N/M²

Variationen i olika materials maximalt sammanhållande kraft kan då skrivas generellt

F/A = R_m

= K/d₀³ ................................. N/M²

med d₀ som materialets medelatomavstånd.

Materialets karaktäristiskt sammanhållande energikonstant [Se även GRUNDSAMBANDET från början i Grundläggande Hållfasthetsbegrepp om ej redan bekant] får alltså formen

K = R_md₀³ ................................. (N/M²)M³ = NM = J

Genomgår materialet bearbetning som resulterar i en höjning av K-värdet, atommedelavståndet förutsatt oförändrat [ingen volymändring, konstant medeltäthet], höjs också materialstyrkan analogt med ett högre Rm-värde. Dvs, K-värdet och Rm-värdet är [eller bör vara] direkt proportionella.

Med tillägg av vissa konstanter (bl.a. π som kan återföras på det cirkulära kraftflödestvärsnittet [π(d₀/a)²] i flödesvägen mellan atomplanen i ett material) får materialenergikonstanten K i det gängse betecknade van der Waals kraftsamband sin motsvarande form enligt den konventionella benämningen Hamakers konstant

H = Kk

= R_m(24πD₀³) .................................. J ; D₀ ~ 0,16 nM = 1,6 t10 M

= R_md₀³(24π/√8)

Notering 1: Olika författare i MAC använder delvis olika pi-koefficient, se citatreferenser i Allmänna samband.

Notering 2: I MAC används (genomgående) ett och samma (odefinierade) värde för D₀. Den konventionellt exakta innebörden av termen och dess antagna-påstådda värde har eftersökts i webbens tillgängliga källor men ännu (Okt2010) inte påträffats.

med här använda beteckningar. Se mera utförligt i Beräkning av Hamakers materialkonstant från Rm.

Sambandsformen — grundsambandet — för ytkraften F/A kan då skrivas via H ovan

Brottgränsen

H = R_md₀³(24π/√8) ;

F/A = R_m ..................................... N/M²

R_m = H(√8)/(24π)/d₀³

Se även utvecklingarna från Allmänna samband. d0 anger materialets atommedelavstånd.

Eftersom brottgränsvärdet (Rm) definierar den maximala materialstyrkan, återstår ingen övrig koefficientform att bestämma i samband med beräkningar som berör materialets (för Rm specifikt längdrelaterade, tvärsnittsberoende) sammanhållande fysik.

Med andra ord:

Hamakerkonstanten (H) kan beräknas direkt och exakt med kännedom om materialets brottgränshållfasthet (Rm) enligt

(H) = R_md₀³

d0 anger materialets atommedelavstånd

Webbkällor som omnämner, antyder, relaterar eller använder denna koppling har eftersökts men ännu (Okt2010) inte påträffats.

För att återförena det fasta ämnets brottytor till kemisk förening [Se KALLFOGNING] med Rm-hållfasthet räcker det INTE med att enbart (vi frånser här oxidationsfenomen och andra föroreningar) föra ihop de skilda delarna så att de uppvisar noll separation — alltså rent tekniskt lika med att återställa atommedelavståndet i brottytan. Därifrån krävs nämligen ytterligare (minst) 5-10 ggr materialets elasticitetsgränsspänningstryck, Re-trycket för att åstadkomma Rm-hållfasthet — vilket innebär att brottytornas återförening till noll tvunget och i vilket fall måste uppvisa en lägre attraktionskraft än materialets brottgräns Rm. Men den adhesionsgränsmatematiken saknas uppenbarligen i MAC:

I MAC används formen F/A=Hk/d³ generellt för att beskriva en ADHESIONSFYSIK (attraktion mellan olika material): en påstådd (svag) attraktion mellan av d åtskilda olika ämnens materialytor via variabla distansvärden för d-faktorn inom en och samma laboratorielokals fasta temperatur. Koefficienten k används f.ö. olika av olika källverk, se citatutdrag i Allmänna samband.

Men som redan härletts ovan i grundformen via energitvärsnittet (R_m=Fd₀/A=K/d₀²) gäller sambandsformen F/A=Hk/d³ med variabel distans endast med ett visst bestämt energiinnehåll för ett visst bestämt material och därmed endast med ett bestämt d-värde — motsvarande materialets atommedelavstånd — vid en viss bestämd temperatur:

Sambandet F/A=Hk/d³ beskriver tydligen en KOHESIONSFYSIK (sammanhållande kraftfysik) — med fasta d-värden;

d-värdet, analogt materialets masstäthet, kan bara ändras med ändrad temperatur; Man kan, då tydligen, inte använda sambandsformen F/A=Hk/d³ för att beskriva attraktionen mellan åtskilda materialytor; Sambandet F/A=Hk/d³ är tydligen och uppenbarligen enligt Grundsambandets härledning en kohesionsekvation — reserverad för ett materials egen inre brotthållfasthet (Rm). Inget annat; d=d₀=MATERIALENS FASTA ATOMMEDELAVSTÅND: Kan bara ändras med ändrad temperatur.

Man har i MAC ingen adhesionsgränskurva — utan kompenserar denna med VdW-formen 1/ad^3 inom en främsta avgränsad intervalldel 0-[10-20]nM, och som sedan sägs övergå i Casimirformen 1/d^4 även benämnd ”the retarded van der Waals”. Men den experimentella redovisningen i området 0-10-20nM är i princip orepresenterad samt generellt för större distanser även ytterst svårtillgänglig, främst beroende på svårigheterna att utföra mätningar mellan parallella planytor [Se citat i CasimirRef]: Experimentatorerna söker istället kompensera med en anordning Platta-Sfär — och som därmed lämnar grundformen Platta-Platta resultatlös och obemött. Dvs., det finns (ännu Okt2010) inga direkt tillgängliga grunddata att jämföra med.

Med hjälp av TNED-teorin för elektronmassans komponenter kan man emellertid [relativt] jämföra PRINCIPKURVORNA i de olika funktionerna och se att differenser och marginaler gränsar intill varandra inom funktionsområdet 1/ad^2—4. För mera exakt verifikation i någon definitiv favör för TNED krävs dock mera utförligt redovisade experimentella resultat på just området Platta-Platta.

Tabellen nedan visar — till jämförelse — Hamakers (material)konstant (H).

Hamakerkonstanten (H) visas DELS via beräkning från brottgränsen (Rm, eng ultimate strength) och DELS i jämförelse med tillgängliga webbkällor (markerade s1-s5 i tabellen och som garanterat INTE har fått sina värden från Rm-beräkningar — begreppet ultimate strength omnämns inte ens i de upptagna källverken, genomförd särskild sökning 2010-10-28).

FATTIGDOMEN ”—” I JÄMFÖRANDE DATA — trots en stor mängd tillgängliga dokument — talar för sig själv: Ämnet är så grundligt dåligt representerat i kunskaper och kännedom att man undrar HUR i all sin dar … .

— KOPPAR — men vilken sort? Webbkällorna [s1, s2, s4, s5] ger inga besked.

[Alla som känner materialläran något i grunden vet att ett ämnes hållfasthetsegenskaper ändras med bearbetning — för just Kopparens del högst väsentligt].

Jämförande Tabell, Hamakerkonstanten

Jämförande Tabell — H — Hamakers konstant [20°C] i t20 J

ämne	Rm|MPa	typ	ref	SIS	H=Rm(24πd^3)/√8	s1	s2	s3	s4	s5
	Brottgräns				t20J	t20J	t20J	t20J	t20J	t20J
Vatten	28	vatten|13°C	3	—	2,23	—	—	3,7	—	3,66
Aluminium	65-150	renAluminium	KMs285	40 07-02|18	2,88-6,64	6,3	—	—	—	—
Krom	413	As-Swaged	2	—	13,22	—	—	—	—	—
Järn	400	Segjärn	KMs205	07 17-02	12,60	—	—	—	—	—
Kobolt	—	—	—	—	—	—	—	—	—	—
Nickel	45-317	Nickel	2	—	1,32-9,29	—	—	—	—	—
Koppar	200-450	Kallvals.band	KMs216	50 10	6,34-14,27	11	40	—	27,3	12,2-27,5
Guld	120	—	2	—	5,40	—	40	—	—	—

...... utan relativa dielektricitetstalet

ref 1 Brottgränstabell i Wikipedia

ref 2 MatWeb

ref 3 GOOGLEBÖCKER s14 Figure 1.3, Sonochemistry and cavitation — M. A. Margulis 1995

KM MATERIALLÄRA Karleboserien 5 1980

SIS materialdata enligt Sveriges Standardiseringskommission

s1 http://heatexchanger-fouling.com/papers/papers2009/16_Lefevre_Hamaker_F.pdf

s2 http://hal.inria.fr/docs/00/26/44/38/PDF/JMM06_LAB_LRP.pdf

s3 http://courses.washington.edu/overney/Material/HandoutsChemE498/Hamaker_Constant.pdf

s4 http://pharmahub.org/resources/250/download/hamakerconstant_data.pdf

Länken närmast ovan fungerar inte i Internet Explorer och Arora. [2010-10-28]

s5 GOOGLEBÖCKER s28 Table 2.3, Surface and Interfacial Forces, Jürgen Butt, Michael Kappl 2010, [AH exp.];
Jämför också källan närmast ovan med Beräknat-Uppmätt: relativt stora skillnader visas till jämförelse.

ALLA TABELLENS WEBBKÄLLOR s1-5 saknar mer eller mindre SPECIFIKA MATERIALPARAMETRAR för det angivna materialet.

Jämför till exempel KOPPAR — som kan ha en stor mängd olika Rm-värden beroende på bearbetning — H-värdet ökar med ökad mängd inlagrad bearbetningsenergi (Jämför t.ex. s2 med uppgiften 40 t20J: vi vet inte under vilka betingelser som Det angivna materialet BLEV sitt eget material vid tillverkningen, eller OM man påverkat materialet något EFTER tillverkningen — vilket gör jämförelsen i princip värdelös).

NOTERA OCKSÅ DIVERSITETEN KOEFFICIENTER i det etablerade användandet av van der Waals kraftsamband, se Allmänna samband:

F/A = H/6πd³, ELLER H/12πd³, ELLER H/24πd³ … . Olika källor använder olika sambandsformer — ÄVEN med referens till SAMMA urkund, se jämförande citat i Allmänna samband. ENBART på den delen finns i princip en fyrfaldig differensfaktor.

NOTERA ÄVEN ATT TEORETISKA HAMAKERKONSTANTBERÄKNINGAR [från Lifshitz teorier] använder (det förenklade) sambandet mellan brytningsindex och dielektricitetstal — tydligen utan andra inslag. Materialets BEARBETNING måste tas med i beräkningen.

Van der Waals krafter — Van der Waals, efter (1873) holländaren Johannes Diderik van der Waals (1837-1923)

BILDKÄLLA: Författarens arkiv · Bild3 U2009/2 · 4MAJ · Nikon D90 · Detalj

Van der Waals krafter

VAN DER WAALS KRAFTER

Efter (1873) holländaren Johannes Diderik van der Waals (1837-1923)

Relaterad fysik: VAN DER WAALSKRAFTERNA (ofta förk. VdW) — intermolekylärt sammanhållande krafter i området 0,1-10nM;

Modern akademi: För citatexempel som visar hur van der Waals kraftsamband beskrivs konventionellt, se Övergången VdW-Casimir.

I varje fall med den diversitet av H-värden [Hamakers konstant] som finns i webbutbudet (Okt2010), se HamakerExempel, finns det ingenting som hindrar att sambandet F/A=H(24pi)/d³ kan förstås beskriva de fasta materialens brottgräns (Rm).

Van der Waals krafter i materialsammanhang intar en synnerligen mysko ställning i den etablerade litteraturen. Se van der Waals krafter inom kemin för en inledande orientering. Man tycks nämligen generellt vara av den uppfattningen att TROTS att van der Waals samband F/A=K/d³ beskriver ett materials brottgräns (Rm)

Se även från Grundsambandet:

ENERGIN [E=Fd] mellan två närliggande atomer i kemisk förening i ett material har en ytfördelning via kraftflödestvärsnittet d² mellan atomkärnorna med d motsvarande atommedelavståndet [E/A=K/d²]; MEKANISKA SPÄNNINGEN mellan två närliggande atomer eller atomplan får då formen F/A=K/d³: Den sammanhållande kraften fördelas jämnt och homogent inom medelatomens kubiska volym d³. Därmed är materialets hållfasthet (Rm) definierad: materialets absolut starkast sammanbindande ytkraft. Det finns ingen starkare.

framhålls van der Waals krafter som SVAGA KRAFTER [‡] framför typen JONBINDNINGSKRAFTER och KOVALENT BINDNING [‡]. Men ett materials mest sammanhållande kraft kan inte vara större än den som definierar materialbrott. Här är det med andra ord verkligen något som inte stämmer i den moderna akademins lärosystem.

Kovalenta allmänna atombindningsformen

Grundämnesmetallernas brottgräns, F/A=Rm:

Kovalenta allmänna atombindningsformen

F/A = (100[8Z(t6) + 2([Z–1]/2)^–2])(1/Z)k_ee²/(π·d₀⁴·√2) ............ N/M² = Pa

visar samma resultat [Se Diagram Rm2] som sambandsformen [se Brottgränsen]

F/A = H(√8)/(24π)/d₀³ .................................................................

Det första sambandet [elementet] ger EXPLICIT ytkraften via den kovalenta bindningsformens cirkulära flödesskiva (radien=d0),

A = [A=π[d₀/2]²]/√2 = πd₀²/√2

Det andra sambandet [materialet] — van der Waals kraftsamband — ger fördelningen explicit över materialets medelatomkub — kvadraten ovan i centrum, kubsidan d0 — direkt.

Bägge sambanden uttrycker samma fysik med samma värden men genom olika flödesprefix. Se även från Grundsambandet.

— Eftersom sambandsformen i det andra fallet tydligen är van der Waalskraftsambandets form — se t.ex. hur den formen också beskrivs konventionellt i Övergången Casimir-VdW — finns uppenbarligen INTE saklig grund för att påstå någon distinktion mellan »de allra starkaste av de kovalenta bindningskrafterna» — Vätebindningen H—H ovan i figurlogon och som ger kvantitetsintervallet 0-1000 MPa för samtliga Grundämnesmetaller — och just van der Waalskrafterna: de senare definierar tydligen per exempel materialhållfastheten VIA den allra starkaste kovalensbindningen av alla: vätebindningen. Se resultatredovisningen explicit i Diagram Rm2. Samhörigheten är beviset.

Förklaringen

— Om allt är korrekt uppfattat är förklaringen till »den etablerade språkförbistringen» alldeles tydligt den här [klicka på bilderna för originalet]:

Van der Waals-sambandets kurvskara [1/ax^3, ljusvioletta ovan, a-koefficienterna markerade underst, klicka på bilderna för originalet] TROS i MAC vara en adhesionsbeskrivande fysikalisk matematik som tar vid mot noll där »Casimirgränsen slutar», vid grovt 10-20 nM. Men — som visas i den här framställningen per jämförande exempel med grundämnesmetallerna i PERIODISKA SYSTEMET, se Diagram Rm2 — van der Waalssambandet beskriver INTE adhesionsfysiken utan kohesionsfysiken: materialens fasta, sammanhängande bindningskrafter och energier. I TNED harmonierar den beskrivningen också via den gröna kurvan i figuren ovan som, verkligen, gör anspråk på att beskriva adhesionsfysiken — hela vägen, från atommedelavstånden och utåt, eftersom Casimireffekten i TNED inte har »vakuumets nollenergi» som orsak utan elektronmassans komponenter [funktionsformen 1/ax^2TILL4, gröna-ljusblå kurvorna ovan; Notera att tilläggskoefficienter finns här också (för dielektrikum, här utelämnade) och som i det praktiska fallet innefattar också nivåalternativ för denna kurvtyp]. Men som också understryks i Teknisk Verifikation — området är synnerligen svårmanövrerat för direkt teknisk bevisning: inga definitiva besked finns ännu — även om teorin förefaller uppenbar.

— MAC saknar en reguljär — sammanhängande — ADHESIONSKRAFTSTEORI. Vi finner den beskriven i MAC genom en (inte sällan kaotisk) uppdelning i å ena sidan van der Waals kraftsamband med början från kortaste avstånden till (en s.k. retarderad version av denna som) Casimirkraften [Se VdWCasimir och Övergången Casimir-VdW] som associeras med större avstånd. ORDNINGEN mellan dessa är (ännu Okt2010) synnerligen oklar [Se CasimirRef] — inte minst på grund av att man rent experimentellt inte kan lösa svårigheterna med användning av två parallella planplattor [Platta-Platta-experiment] utan söker förenkla avhandlingen med Platta-Sfär-experiment, och bara med nettoeffekten att GRUNDTEORIN med Platta-Platta-verifikationerna står obemötta [och skjuts på framtiden]. Se även citaten i Hamakerkonstanten.

— Men från materialläran (främst metallerna) VET vi redan att maximal adhesion mellan två planytor av ett givet material (oxidationsskikt och föroreningar frånsett) INTE föranleder kemisk förening med nollavstånd mellan planytorna: det behövs ytterligare en sammanpressande kraft [på minst 5-10 ggr Re] för att en sådan kallpressfogning ska realiseras — teori saknas i MAC.

— Och alltså kan inte adhesionsfysiken tillämpas i någon praktiskt teori på van der Waals materialbrottsdefinierande sambandsform.

— Uppenbarligen är det (alltså) så: van der Waals kraft beskriver materialets hållfasthet, medan adhesionskraften utnyttjar en annan funktion och som tydligen saknas i MAC — och som (därför, vilket uppenbarligen är det kaotiska) substitueras med van der Waals kraftsamband. Se exv. eng. Wikipedia Adhesion.

— Allt och tydligen på grund av att man bannlyste elektronmassans komponenter från 1927, uppenbarligen de enda som kan förklara sammanhanget och reda ut oklarheterna. Se även sammanställningen i LEC [Lambväxlingen, Elektronens g-faktor, Casimireffekten].

Allmänna samband, VdW

Allmänna samband

Vid genomsökning på webben (Okt2010) på samband som beskriver van der Waals krafter uppdagas samtidigt en del oklarheter. Ytkraften (F/A=K/d³) framställs olika i olika källverk — även med inbördes referens till SAMMA källa:

F/A = H/6πd³ ................................ WU1.s11ö.Table 2, enhet i N/M² = Pa (Pascal)

Källan refererar till ................................... [Intermolecular and Surface Forces, Academic press, J. Israelachvili 1985]

;

F/A = H/24πd³ .............................. Wikipedia Adhesion, enhet i N/M² = Pa (Pascal)

Källan refererar till ................................... samma som ovan

;

F/A = H/24πd³ .............................. Nanomedicine, Freitas 1999, enhet i N/M² = Pa (Pascal)

Källan refererar till ................................... Kevin Kendall, "Adhesion: Molecules and Mechanics," Science 263(25 March 1994)

Den första källan ovan genomgår något som liknar en härledning (men med mager [i princip obefintlig] relaterbarhet):

Utgångspunkten [WU1s15n][källförfattaren använder A för Hamakers konstant, här H] är en ENERGIYTA (eg, energiyttäthet eller energitryck) E/A=(H/12πD₀²) med innebörden ”total energy of two planar surfaces att distance D>D₀ apart” — men som sedan summeras på endast halva beloppet enligt ”Thus, in order to separate the two surfaces one has to overcome the energy difference [som ovan], which corresponds to the adhesive energy per unit area” via 2(E/A) så att E/A=(H/24πD₀²), ”Hence, the interfacial energy can be expressed as a function of the Hamaker constant and the cutoff distance”, som ovan.

— Det är tydligt att den beskrivningen inte går ihop med ytkraften och dess variation från noll mot oändligt: Maxvärdet måste under alla förhållanden avspegla energiytans toppvärde per minsta distans: E/A=FD₀/A.

— Är maxvärdet för energiytan av formen E/A=(H/24πD₀²), måste veterligt också maxvärdet för kraftytan gå via E/A=(H/24πD₀²)=Fd/A som via d=D₀ ger maxvärdet F/A=(H/24πD₀³). Det finns, här veterligt, ingenting annat att välja på.

— F/A-maxvärdet är under alla förhållanden den kraft som sammanhåller materialet, också samma som materialets brottgräns (sv. Rm) (eng. ultimate [tensile] strength).

Utan någon annan referens än ovanstående används i det följande grundsambandet

F/A = H/24πd³ .............................. Se förklaringen ovan i Allmänna samband, enhet i N/M² = Pa (Pascal)

som allmän (generaliserad) beskrivning för den sammanhållande kraftverkan (KOHESIONEN) mellan två idealt närliggande atomkuber via deras angränsande ytkvadrat eller motsvarande angränsande atomplan, eftersom någon annan tolkning av sambandsformen inte kan utläsas i relaterad mening, se från Grundsamband. Distansen d med minsta värdet D₀ — (i den konventionella beskrivningen angiven som eng. cutoff [eller cut-off] distance), se Cutoff Distansen — kommer då att motsvara eller avspegla materialets fasta atommedelavstånd och som bara kan ändras med ändrad temperatur, analogt energiinnehåll.

Exakt vad det konventionellt brukade uttrycket ”cut-off distance” står för i MAC verkar ytterst svårt att reda ut. Det anges [Washingtonkällan, s16m] som typiskt med värdet ca 0,16 nM = 1,6 Å (som en generell konstant), men det verkar inte finnas någon källa som kan klargöra varifrån termen kommer, vilken dess innebörd är, eller om den ska tolkas som en konstant eller variabel (olika källverk verkar använda olika sätt, utan närmare förklaring).

Värdeintervallet 0,165-0,185 nM som anges av Bhattacharya et al., 2008 är i vilket fall runt 1/√2 kortare än de fasta ämnenas atommedelavstånd (vid rumstemperatur; grovt runt 2,5 Å med relativt små variationer).

Den konventionellt framhållna förtegenheten (godtycket och avsaknaden av förklaringar) ikring begreppen vittnar om att grundteorin lämnar en del övrigt att önska. [Grundteorin är uppenbarligen inte välformulerad].

Elastiska separationstrycket

Elastiska separationstrycket — kraftvägens distans över separationen

HÅLLFASTHETSBEGREPPET kräver en minsta distans mellan ett (grund)ämnes atomer, och den distansen kan ingen annan vara än ämnets (idealt kubiska) medelatomavstånd dATOM=[Uu/(ρV=m)]^1/3. Genom att D₀-parametern (i etablerad användning) tydligen är kortare med en faktor a kan vi förtydliga F/A-formen ovan via

D₀ = dATOM/a

enligt maxkraftgränsen

F/A = Ha³/24π(dATOM)³

och därmed den allmänna distansformen för van der Waalskraften

F/A = Ha³/24πd³ ........................... Se förklaring i Allmänna samband, enhet i N/M² = Pa (Pascal)

med lägsta värdet d=dATOM.

Eftersom (tydligen) flera etablerade verk ansluter till användningen av ’cutoff distance’ D₀~1,6 nM kan vi tydligen approximera a för dessa fall genom rotkoefficienten i Kovalenta bindningens grundform [A=[A=π[d₀/2]²]/√2=πd₀²/√2 — se inledande sammanfattande beskrivning i Grundämnesmetallernas brottgränser] som

a = √2

med typexemplet JÄRN (26Fe56) som vid rumstemperatur uppvisar atommedelavståndet 2,28 Å [0,228 nM eller 228 pM]:

2,28/√2 = 1,6155034

~ 1,6 = D₀

Och som vi ser, är approximationen (i varje fall för detta fall) god.

Gränsen för materialbrott — mekanisk separation (ångbildning för vätskor)

Med (a=√2)³=√8=2√2 därmed

HamakerBrottgränsen

F/A = H(√8)/24πd³

....................... Se förklaring från Allmänna samband, enhet i N/M² = Pa (Pascal)

= H(√2)/12πd³

= H(0,0375131)/d³

med lägsta värdet d=dATOM=[Uu/(ρV=m)]^1/3.

Observera att H-värdet [Se Tabell]

1. varierar betydligt som sådan [med tabellexemplet] 0,057 [Flytande Helium] till 40 [ädelmetallerna],

2. saknar [enkel, allmän] konventionell beskrivningsform: olika uppgifter ges för samma ämnen från olika källor, se Hamakerkonstantens innebörd och HamakerExempel;

R_m = (F/A)_max ;

H = R_m(24πd³)/√8 ; d = dATOM

= R_m(dATOM)³(26,657297)

Se även Hamakerkonstanten från Rm.

För att få fram motsvarande a-koefficient i funktionen p/(pUNIT)=1/ad³ via dUNIT utförs beräkningen

p = H(0,0375131)/(dUNIT)³ .... Pa ;

a = (pUNIT)/p ;

= (dUNIT)³(pUNIT)/[H(0,0375131)]

Funktionsformen motsvarar en idealt sfärisk tryckdisposition av typen kubisk, figuren nedan.

Kraftytans funktion får tydligen innebörden av en kubiskt homogen fördelning via d^3.

Värdeformen F/A ovan motsvarar attraktionen mellan molekyler eller motsvarande planmolekylytor då de separeras av d — men utan att separationen åstadkommer materiellt- eller substantiellt brott. Dvs., idealt utan materialbrott — och därmed en ideal »elasticitetsattraktion», den avtar med växande separation.

Observera dock att maxvärdet ovan [via »ett bestämt H-värde» som i praktiken varierar med ett givet materials tillstånd] inte ger något exakt facit till praktiska brottgränsvärden för olika material — i praktiken kan tiofaldiga värden förekomma. Se exempel nedan.

Exempel:

Brottgränsen praktiskt för Kisel [ett kristallint mycket hårt sprödmaterial med ringa elasticitet] anges vid Proportionalitetsgränsen i Wikipediatabellen till 5-9 GPa.

I webbkällan

s233sp1.ekv.13

MESA Research Institite, University of Twente —

STICTION OF SURFACE MICROMACHINED STRUCTURES AFTER RINSING AND DRYING: MODEL AND INVESTIGATION OF ADHESION MECHANISMS — Legtenberg, et al., 1994

http://eprints.eemcs.utwente.nl/14053/01/JSAA_43_230.pdf

ges ett exempel via sambandet E/A = H/24πD₀² med uppgiften 90 mJ/M² för Kisel och H = 27 t20 J. Utför vi en division med d=0,2 nM (källans uppgift) ges max

F/A = (0,09)/(0,2 t9 M)

= 4,5 T8 N/M²

= 450 MPa

För att matcha Wikipediatabellens uppgift på 5-9 GPa krävs alltså minst en tiodubbling.

Exemplet visar att man visst, inom vissa rimliga gränser [med referens till »allmänna uppgifter på webben»], kan bilda sig en viss uppfattning om ett visst materials hållfasthetsparametrar i en grov översiktlig mening — men då förutsatt tillbörlig hänsyn tagen till parameterkomplex som också kan driva värdena (typiskt) tiofalt (åt bägge hållen).

Hamakerkonstanten från Rm

Beräkning av Hamakers materialkonstant från Rm

H = π²C ·ρ₁·ρ₂ .......................... J

ρ antalet atomer per volymenhet i resp. materialdel [ref. @INTERNET Wikipedia Hamaker constant 2010-10-19]

C specificeras inte i wikipediaartikeln utom ”the coefficient in the particle-particle pair interaction [1]”; referensen leder till en artikel man måste betala för att få läsa.

Om D₀-konstanten (~0,16 t9 M) tas för given för samtliga fall, kan — med ledning av en tabell över olika materials (sv. bet. Rm) brotthållfasthetsgränser (eng. Ultimate strength) en ekvivalent till Hamakers konstant (normalt komplicerad interatomär materialparameter) framräknas från föregående Hamakerbrottgränsen Rm=F/A= H/24πD₀³ enligt

H = R_m(24πD₀³) .................................. J ; D₀ ~ 0,16 nM = 1,6 t10 M

= R_m(3,08831 t28 M³) .................... J

~ R_m(3,1 t28) ................................... J

C-faktorn i Hamakerkonstanten kan då också förtydligas enligt

H = π²C ·ρ₁·ρ₂ = R_m(24πD₀³) ; [ref. @INTERNET Wikipedia Hamaker constant 2010-10-19]

C = R_m(24D₀³)(πρ₁ρ₂)^–1 ........................ J, förenkl., samlade energiinnehållet per materialatom [Kohesiva (sammanhållande) materialenergin]

= R_m(24D₀⁵)(πD₀²ρ₁ρ₂)^–1 ; ρ[perM³] = (ämnestätheten i KG/M³)/Uu

Rm — för ETT givet ämne [som betyder att ρ₁=ρ₂] — beror på struktur, orientering, [elektronresonanser] — bearbetning, tryck, temperatur (bestrålning, elektriska/magnetiska fält)

HamakerExempel, olika konstanter

EXEMPEL:

Koppar (glödgad eng. annealed = maximalt elastisk) anges i Wikipediatabellen med motsvarande

R_m = 210 MPa = 210 T6 Pa = 2,1 T8 Pa ;

Insättning i sambandet ovan ger

H = 6,51 t20 J ;

Ser vi efter i olika mätrapporter kommer vi att finna andra, olika värden — beroende på i vilka materiella sammanhang värdeformerna figurerar — för att exemplifiera »ämnets vassa natur»;

Jämför exv. webbkällan

s123Table2 (källan kan markeras men inte kopieras), ”Result of calculations for copper/water interfaces using summation (2).”,

http://heatexchanger-fouling.com/papers/papers2009/16_Lefevre_Hamaker_F.pdf

:

Kisel 1,7 t20 J

Aluminium 6,3

BeO 6,0

CaCO3 3,6

MgO 4,9

Quartz 3,1

TiO2 6,5

ZnO 3,3

Fe2O3 6,7

Cu 11

med

s4Table1, ”Values of Hamaker constant for some materials A × 10⁻²⁰J [22]”

— Koppar: i vakuum 40 t20 J; i vatten 30 t20 J,

FORCES ANALYSIS FOR MICROMANIPULATIONS IN DRY AND LIQUID MEDIA — Gauthier et al., 2008

http://hal.inria.fr/docs/00/26/44/38/PDF/JMM06_LAB_LRP.pdf

:

i Vakuum i Vatten

Guld 40 30 t20 J

Silver 50 40

Al2O3 16,8 4,4

Koppar 40 30

Skillnaden mellan ’11’ och ’40’ är inte obetydlig [källan anger heller inte typen av koppar — skillnaden med mjuk-hård koppar kan avgöra med en faktor 2 (ref. Rm ca 200-450 MPa, MATERIALLÄRA Karleboserien 5 1980 s216 Fig 10.3 SIS Koppar 50 10)] — och vi inser att någon direkt enkel metod för teoretiska interatomära materialparametrar INTE existerar (ännu, är det bäst att tillägga).

Skillnaden i brotthållfasthet (F/A=Rm-sambandet ovan enligt Hamakerbrottgränsen) skulle här ge en faktor 40/11~3,64; resultatet utesluter varje precisionsrelaterad beskrivning. [Man får tydligen acceptera teoretiska osäkerheter inom en faktor 10 via enklare beräkningar som använder webbdata generellt].

Brottgränsexempel Koppartråd

Materialbrott efter dragning — 0mM5 Koppartråd · Författarens arkiv · Bild4 · Materialbrott · 11Nov2010 · NikonD90

Det finns ingen »elastisk metallisk töjning» före brottgränsen

Frånsett ytterst marginella ändringar (här uppskattningsvis från 100-delar och mindre av materialets medelatomavstånd — här helt baserat på Hamarkonstantens ekvivalent, se Hamakerkonstanten från Rm) — bara faktorerna D0|Rm kan påverka:

Frånsett (möjligen) elastiska material som typ gummi (och olika plaster, organiska material): Atommedelavstånden i säg ett stycke koppar som sätts in i en dragprovmaskin och dras till brott, uppvisar ingen täthetsändring; Kopparatomerna anpassar sig (»kryper» efter atomplanen) genom att — tydligen — glida längs kraftvektorn och därmed göra staven smalare motsvarande utdragningen; materialet »söker» ett avlastningstvärsnitt dit dragkraften drivs av krypningen i formen av en maximalt försmalad »midja» [med inre tvärställda atomplan i brottytan]. Där uppstår brottet. Omedelbart efter brottet återgår (snabbt) den utdragna, brutna midjedelen till ett normaltillstånd (som innebär att en del av midjan sjunker tillbaka och lämnar brottgränsens mellanliggande intervall öppet). Vad vi vet, ändras inte materialets täthet det allra minsta under processen.

Det finns uppenbarligen ingen intermolekylär separation i en metalls dragning till brott, endast en kristallin omfördelning (smidning, glidning, formändring utan volymändring).

Sambandsformen

F/A = H(24pD₀³)^–1 .......... N/M²

= Rm

som beskriver materialets inre sammanhållning utan volymändring — med direkt analogi till Grundämnesmetallernas brotthållfasthet — beskriver följaktligen en kohesionskraft, inte en adhesionskraft.

Men i etablerad litteratur [‡] beskrivs Van der Waals intermolekylära kraft ofta som en ADHESIV (mellan olika material, inte inuti [kohesiv]) attraherande kraft:

Grundsambandet man framställer som specifikt samband för just van der Waals intermolekylära kraftsamband, E/D₀A=F/A=H/24πD₀³ beskriver tydligen entydigt — här i erinran med direkt analogi till Grundämnesmetallernas brotthållfasthet — ett materials brottgräns. Speciellt förtydligat enligt Järnexemplet

Brottgränsexempel, Järn

F/A = R_m

= H(24pD₀³)^–1 .......... N/M²

= 4 T8 Pa

= 400 MPa ............... Brottgränsen för Järn [SIS 07 17-02]

H = 12,3532 t20 J ....... Hamakers konstant

H = R_m(24pD₀³) ........... D₀ ~ 0,16 nM = 1,6 t10 M

= R_m(3,08831 t28 M³) ;

R_m = H/(3,08831 t28 M³) Pa ;

D₀ = 0,16 t9 M ;

= 1,6 Å .................... (tvärsnittsradien för interatomära växelverkan — grovt roten ur medelatomavst.)

OM endast brottgränsen räknas (Rm) kan exemplet enkelt utsträckas till godtyckliga ämnen — för jämförelse. Koppar, till exempel (grovt Rm mellan 200-450 MPa), kan också uppvisa järnets brotthållfasthet. Med gränserna 200-450 MPa skulle motsvarande H-gränser bli 7,7 till 13,9 t20 J. Jämför uppgiften för Koppar (Cu, sist) i första tabellen i HamakerExemplet: 11 t20 J. Resultatvärdet ovan är relevant — i Den aktuella webbkällans ljus.

van der Waalskraften F/A=K/d³ är — alltså och tydligen rent logiskt — kohesiv — medan den moderna akademin litterära fackverk tycks beskriva van der Waalskrafterna K/d³ som adhesiva [‡]

Resultatbilden endast understryker det redan sagda i Kovalenta allmänna atombindningsformen: Grundkemin [materialläran] i MAC är — tydligen — INTE välformulerad.

Därmed (återigen) sagt: materialets maximalt sammanhållande styrka kan bara återföras på en inre (Den innersta) sammanhållande kraft — inte en yttre. M.a.o.: van der Waalskraften är — rent logiskt — kohesiv. Inte adhesiv. För grundbegreppen, se Adhesion och Kohesion.

Van der Waalskraftens avtagande med distansen får således med ovanstående utläggning, t.ex. för metaller, ingen annan direkt innebörd än den som (t.ex.) sammanhänger med tillförande av värme (längdutvidgningskoefficient, generellt volymutvidgningskoefficient); Metaller som dras till brott (med försumbar värmetillförsel) bibehåller sin masstäthet utan att ändra atommedelavstånden.

Hamakers konstant, innebörd

Beträffande Hamakers konstant (H): Man kan enbart för en översiktlig vy utgå ifrån H — webbkällor finns med tabeller, men med OBS [se även i HamakerExempel] delvis relativt stora skillnader beroende på materialväxelverkan — eller som ovan beräkna H direkt från brottgränsen (Rm). H-värdet ligger i vilket fall (grovt, se Tabell) i området 0,05-40 t20 J) för metaller och flytande ämnen.

Ingen exakt (säker) beräkningsform är (ännu) känd för H;

”The Hamaker constant is a force constant used for describing the van der Waals (vdW) force. The magnitude of the Hamaker constant reflects the strength of the vdW force between two particles, or between a particle and a substrate. It depends on the material properties of both the interacting bodies and the intervening media. More accurate calculations of Hamaker constants require a knowledge of the dielectric and optical properties of the interacting materials over the entire frequency range in the electromagnetic spectrum. In general, this information is not readily accessible.”,

PHARMA HUB —

http://pharmahub.org/resources/206

(Otillförlitligt webbställe — ger Googleträffar med URL som sedan i efterhand inte kan nås separat via separata URL, se exemplet http://pharmahub.org/resources/250/download/hamakerconstant_data.pdf) — Test på annan webbläsare visar OK [2010-10-20]: Mozilla OK, Flock OK, Opera OK, Netscape OK, Arora notOK, Google Chrome OK. Alla OK utom Internet Explorer 7 och Arora. Explorer 8 ej testad. [Förslag till Världssamfundet: uteslut Microsoft Corporation: företaget åsamkar [alltmer] mer skada än nytta].

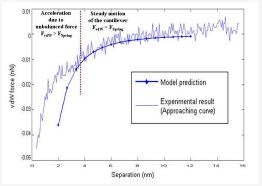
Källan påstår i vilket fall att mätningar har genomförts [grafen ovan].

Källan ger ingen källredovisning till figuren — inte ens typen, om det är Platta-Platta eller Platta-Sfär [orden Plate eller Sphere finns inte ens med i artikeltexten].

Jämförelsens grunder TNED-MAC — Casimireffekten — Adhesionsfysiken — momenten föregående kemisk förening

Casimirgraferna — grundform	Casimirgraferna — Jämförande intervall	TNED-Casimir	KopparExempel	Jämförande exempel — National Laboratories

ENDAST PARALLELLA PLANA ELEKTRISKT OLADDADE PLANYTOR RÄKNAS

Jämförelsens grunder

GRUNDANALYSEN HÄR BERÖR enbart TYPEN PLATTA-PLATTA

Casimirgraferna

Figuren nedan [även i CasimirInledning] klargör grunden för att en jämförelse MAC-TNED i ämnet Casimireffekten alls ska vara meningsfull:

^4-grafen tillhör MAC-Casimirsambandet.

Graferna markerade 1 | ∞ tillhör TNED-sambanden. Sambandsformerna i figuren beskrivs mera utförligt i CasimirInledning. Vi förutsätter den kännedomen här.

Med TNED-exemplet Järn (26Fe56) vid rumstemperatur och normaltryck gäller från Kalkylkortet

distansenheten ..................... 12,20935 nM=t9M

tryckenheten ....................... 54 334 Pa=N/M²

:

Tillsammans med de i MAC vanligt förekommande fenomenformerna — van der Waals krafter som anses övergå i Casimirkraften,

Casimirgraferna — Jämförande intervall

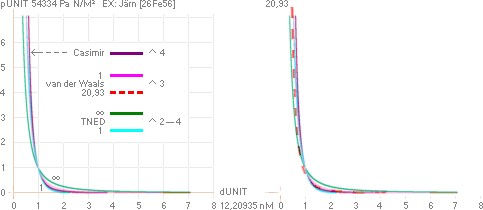
med exempelintervall från MAC (godtyckligt från webben, infällda ovan vä.und.; 1 ~10 nM) — referenserna

MDPI —

EFFECTS OF VAN DER WAALS FORCE AND THERMAL STRESSES ON PULL-IN INSTABILITY OF CLAMPED RECTANGULAR MICROPLATES — Batra et al., 2008

http://www.mdpi.org/sensors/papers/s8021048.pdf

s1053|6:

0,5 nM - 4 nM 1/z³ ............................ van der Waals [ytor med Guld över Aluminium]

4 nM - 1 µM 1/z^3–4 ......................... van der Waals — Casimir

1 µM - 1/z⁴ ............................ Casimir

och

The American Physical Society —

INFLUENCE OF ULTRATHIN WATER LAYER ON THE VAN DER WAALS/CASIMIR FORCE BETWEEN GOLD SURFACES —

Palasantzas et al., 2009

http://eprints.eemcs.utwente.nl/17173/01/Influence_of_ultrathin_water_-_Vitaly_-_dec_09.pdf

Källan avhandlar tyvärr endast typen Sfär-Platta.

:

- 10 nM 1/z³ ............................ van der Waals dominerar

10 nM - 0,1µM 1/z⁴ ......................... Casimirkraften mycket stark

— är det FÖR DET FÖRSTA tydligt att MAC-Casimirsambandet från dUNIT=1 [mörkvioletta delen ovan mellan 0-1] helt bortfaller ur fysikbilden [Se även Jämförande funktionsgrafer MAC-TNED för Casimirsambandets fysik]:

MAC-Casimir-delen

— från 10 nM och ner mot 0 (atommedelavståndet ca 2,5 Å = 0,25 nM [eller konv. motsv. cutoff distance ca 0,16 nM]), i stort [som i Järnexemplet ovan] mellan horisontalvärdena 1 och 0

— når materialets brottgränsvärde (Rm) innan ens materialets atommedelavstånd uppnås mellan de idealt parallella ytplattorna. Det utesluter MAC-Casimirformen som sådan — i den delen, 0-10nM.

FÖR DET ANDRA — genom att TNED-sambandet för atomattraktion (1/ax^2–4) alltmer närmar sig MAC-Casimirsambandet (1/ax⁴) då separationsavståndet växer och därmed skillnaden mellan dessa AV PRINCIP blir alltmer försumbar — bortfaller också HUVUDDELEN AV DET ÖVRIGA INTERVALLET I VARJE RELEVANT PRECISERAD JÄMFÖRELSE: Med Järnexemplet ovan: vid d=5,3(dUNIT)=70 nM är [TNED–MAC]/pUNIT=1% [Beräkningar i Kalkylkortet], och vilken differens härifrån blir alltmer obetydlig med växande d.

Det betyder med andra ord att vi i den övergripande jämförelsen HELT kan bortse ifrån alla — samtliga — experimentella undersökningar i intervallet från runt 70 nM och uppåt (vilket också verkar tillhöra allra största typen redovisade experiment) — resultatet matchar i vilket fall TNED-sambandet med hög noggrannhet [Direktträff bättre än 99%]. Det finns, för översikten, ingenting att hämta i den delen.

Analysområdet

Det jämförande område MAC-TNED vi ska koncentrera oss på för att hitta avgörande bevis för|emot blir alltså av typen 0-5(dUNIT) ~ 0-70 nM — med MAC-Casimirsambandet uteslutet 0-1(dUNIT) ~ 0-10nM som ovan på grund av Rm-villkoret.

OM MAC-Casimirsambandet har någon ställning alls i den praktiska fysiken, står alltså avgörandet helt för Casimirsambandets konventionella form i intervallet runt 10-70nM. Det är också ungefär vad den andra källan ovan anger (Palasantzas et al., 2009): ca 10-100 nM.

— Men (frågar någon, självklart), om man tar bort Casimirdelen mellan 0-1, hur förklaras då den delen i MAC, alltså det faktum ATT det även förekommer materialattraktioner (konv. adhesion) i det intervallet.

— Van der Waals krafter fyller ut tomrummet. Jämför några av citaten i VdWCasimir som förklarar den fysiska samhörigheten van der Waal-Casimir. Se även i Övergången Casimir-VdW.

— I TNED är förklaringen (delvis) en annan [Se även i Förklaringen]:

TNED:

— Van der Waals krafter (ofta konv. förk. VdW) är tydligen FASTA, inre molekylära-atomära kohesionskrafter [inre sammanhållande, se inledande beskrivning i Kovalenta Allmänna Atombindningsformen]: Toppvärdet för VdW/M² [F/A=H/24πd³] är detsamma som det materialets brotthållfasthetsgränsvärde (Rm): den maximalt sammanhållande kraften. I järnexemplet ovan blir [med typen SIS 07 17-02, ref. MATERIALLÄRA (Karleboserien 5 1980 s205 Tabell 7.2 Segjärn] brottgränsen 400 MPa = 4 T8 Pa (1Pa=1N/M²). Det BLIR med andra ord i den terminologins ljus VdW-kraften som definierar sammanhållningen i atomer och molekyler i ett ämne.

VdW-kraften kan bara ändras genom att energi(medel)vägen mellan atomer-molekyler ändras, och den ändringen kan bara ske genom tillförande eller bortförande av värme (E=hf).

Att åstadkomma ett BROTT i ett material genom att t.ex. utsätta det för dragspänning (eng. tension, stress) innebär i sig ingen ändring av atommedelavstånden. Därmed framstår VdW-krafterna som låsta — spärrade vid varje given temperatur.

— Men vad betyder då det faktum att man använder VdW-samband för att uttrycka den s.k. adhesionen (attraktionen mellan olika materialdelar), typ F/A=1/ad³. Vad är det?

— TNED. Det — F/A=1/ad³ — är ett »substitut» för TNED-formens generella funktionstyp F/A=1/ax^2–4; funktionen går kontinuerligt från 1/ax² till 1/ax⁴. Se utförligt från CasimirInledning, samt blockbeskrivningen (förklaringen) i Kovalenta Allmänna Atombindningsformen.

— Och det är du säker på?

— Jag SKULLE säga: »Nej. Ingalunda. Men det är det som står på bordet till prövning».

— Men genom sambandsformerna till Grundämnesmetallernas brotthållfasthet, se från Diagram Rm2, är resultatbilden redan stadfäst; van der Waals kraftsamband, typen F/A=K/d³, sammansmälter definitionsmässigt — kvantitativt och kvalitativt, se den korta inledande beskrivningen i Kovalenta Allmänna Atombindningsformen — i samma resultatbild. Därmed utesluts automatiskt den konventionellt tolkade [‡] van der Waalsformens adhesiva koppling: sambandsformen F/A=K/d³ kopplar inte adhesivt utan kohesivt; Sambandsformen F/A=K/d³ är alldeles tydligt tveklöst helt säkert ett substitut i MAC.

Se även grundbegreppen Kohesion och Adhesion om ej redan bekant.

— Man TROR (konv.) att VdW-funktionen ansluter till »en SLAGS variabel VdW» (därför att man inte har något annat att välja på) — medan sanningen i själva verket (här till prövning) är den att det finns ett ANNAT, långt mera klargörande samband som beskriver det verkliga praktiska fallet — och som här skulle vara TNED-formen.

Det är vad som ska bekräftas eller dementeras.

— TNED-formen med F/A=1/ax^2–4 inbegriper nämligen det som inte omfattas i MAC: Kallfogning (eng. Cold Pressure Welding): Att genom mekaniskt TRYCK åstadkomma en fullgod materiell förening — vilket kräver runt (minst) 5-10 ggr det uppnådda TNED-trycket vid idealt noll närliggande materialytor (uppnått atommedelavstånd) som förts ihop separat utifrån. Se utförligt i KALLFOGNINGSGRÄNSER. Se även mera ingående från VAN DER WAALS KRAFTER.

— TNED-formen beskriver adhesionen — mellan materialdelarna — medan VdW — som ovan enligt TNED — beskriver kohesionen — inuti materialet. Casimirsambandets konventionella form har med andra ord och i termer av TNED ingen teoretisk grund: det ersätts helt av TNED-Casimir-formen.

I mera förtydligad vertikal logaritmisk skala, tillsammans med de i MAC vanligt förekommande fenomenformerna som ovan — van der Waals krafter som anses övergå i Casimirkraften — gäller följande mera klargörande översikt HÄR TILL fortsatt PRÖVNING:

TNED-Casimir

Se praktiskt exempel.

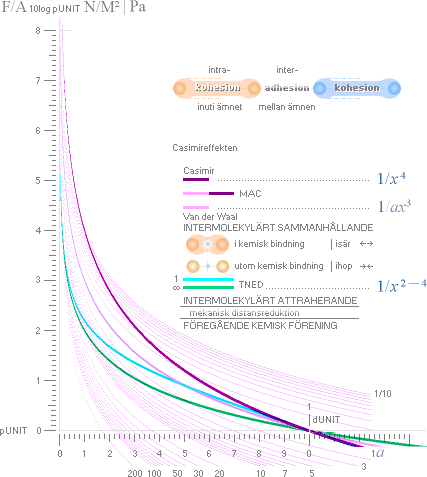
ARBETSFORMCasimirGrafUnit50 y=1[(ln[([x/5]'–2)([(x/5)'1]'–2)])/ln10]+0([ln[(1/a[x/5]'3)]])/ln10

——————————————————————————————————————————————

ALLA METALLER (till att börja med) uppvisar brottgränser (Rm) som ansluter till a-värden grovt från a=20 och uppåt. Ämnen med exceptionellt höga brottgränser [typ GLAS] har lägre a-värden (mot 1).

KURVFORMERNA gäller direkt för metallerna (relativa dielektricitetstalet ε_r lika med 1).

För andra ämnen gäller (nominellt): Alla samband reduceras i vilket fall gemensamt med värdet på ε_r [vilket betyder att kurvkonceptet ovan också kan användas direkt men med reducerat tryckvärde: (blå)grönkurvan endast nivåsänks med faktorn ε_r].

UNDRE ljusvioletta KURVSKARANS KOEFFICIENTVÄRDEN motsvarar a-koefficienten i van der Waals kraftsamband F/A=1/ad³. a-värdet beräknas [utförligt i HamakerBrottgränsen] a = (dUNIT)³(pUNIT)/[H(0,0375131)] med Hamakers konstant H=R_m(24πD₀³) [Se Hamakerkonstanten från Rm] med D0 [Se CutOffDistance] konv. 0,165-0,185 nM, här med förtydligande [Se Elastiska separationstrycket] D0=dATOM/√2.

TILLÄMPNINGEN KRÄVER ETT KALKYLKORT för att läsaren ska kunna hänga med i beräkningsexemplen — Kalkylkortet innefattar en (liten, automatiserad) tabell med grundparametrar för de förekommande ämnena.

PROBLEMET MED TILLGÄNGLIGA WEBBREFERENSER I ÄMNET är att man för det första sällan preciserar ämnessammansättningen — den är helt avgörande för att kunna jämföra med TNED (medan specifika materialparametrar inte alls finns med i Casimirformen). För det andra ligger de allra flesta forskararbeten (för att inte säga uteslutande alla vilket här baseras på genomläsning av en stor mängd webbdokument i ämnet) i Casimireffektens ljus på typen Platta-Sfär-experiment — vilket är helt värdelös information i det här sammanhanget: Ämnets grundfysik gäller (idealt, så långt det går) plana, parallella materialytor. Det finns (här veterligt, ännu Okt2010) inga sådana — redovisade, gratis tillgängliga — forskningsrapporter.

Jämförande exempel National Laboratories

Det närmaste vi kan komma (Okt2010) är den här (skärmdump, förminskad) — typexempel:

SANDIA NATIONAL LABORATORIES — New Frontiers in Casimir Force Control —

SURFACE FORCES IN MEMS – ADHESION AND FRICTION EXPERIMENTS — Maarten P. de Boer 2009

http://cnls.lanl.gov/casimir/PresentationsSF/Maarten%20de%20Boer.pdf

Slide15:

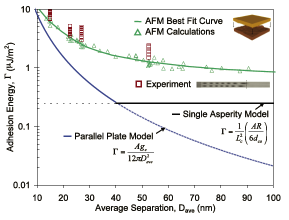
Källan anger för Platta-Platta energisambandet (T)=Ag_e /12πD_ave² med vertikalskalan i Adhesion Energy (T) µJ/M².

Division med x-variabeln [t6/t9=1000] ger motsvarande vertikalskalan i 1000 N/M².

Materialets sammansättning framgår inte av källan [man får gissa].

— Källan redovisar ingen materialsammansättning, inga koefficientvärden: Kan inte användas.

Grafbilden ansluter visserligen I PRINCIP till TNED-formens jämförande motsvarighet:

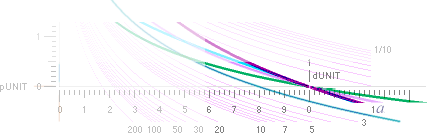
Men då källan inte ger några precisa data, kan heller ingenting säkert sägas.

Teoretiska MAC-sambandet [F/A=H/ad³] [ovan illustrerat till principiell jämförelse med a=2] ger, verkligen de typiskt lägre värdena medan den gröna TNED-kurvan med sina typiskt högre värden i det aktuella intervallet ser ut att passa in på webbkällans experimentellt antydda typ [enbart principen att en undre skär en övre, tangerar just TNED-formen].

— Det är således EMELLERTID vanskligt att göra den jämförelsen (direkt) eftersom webbkällan dels inte redovisar ämnessammansättningen (man får gissa ämnets medelatomladdning, medeltäthet och brottgräns), och heller inte ens antyder något värde på Hamakerkonstanten, samt att termerna generellt inte alls förklaras i källan. [Dvs., källuppgifterna är i princip värdelösa].

— På sin höjd: En (vag) indikering. Inget mer.

— Men vi skulle behöva just den ovanstående typen av jämförande grafer — MED utförliga materialdata.

— Men det finns, tydligen, inga sådana.

— Ovanstående är hittills (Okt2010) det närmaste (vilket är urdåligt med tanke på den närmast enorma uppsjö av avhandlingar som finns i ämnet — hundratals Casimir-van der Waals-avhandlingar på webben).

— Inte förrän experimentella data på typen Platta-Platta (som ovan) kommer fram i mera ordnad form finns någon möjlighet att avgöra vad som gäller: TNED eller inte.

Praktiskt exempel VdW-Cas

PRAKTISKT EXEMPEL MED KOPPAR

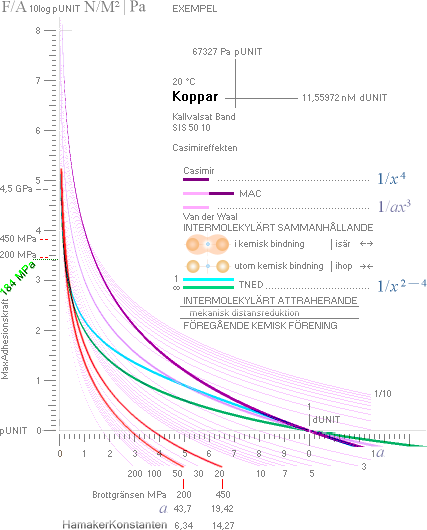
Röda kurvorna: van der Waals kohesionskraft [ljusvioletta kurvskaran] med varierande atommedelavstånd enligt F/A=H/ad³ med resp. a=43,7 och a=19,42 för motsvarande brottgränsvärden 200 MPa och 450 MPa. Adhesionskraftens maxvärde [gröna grafen] vid nollavstånd mellan idealt plana materialplattor blir F/A=184 MPa enligt TNED-sambandet. För Hamakerkonstantens beräkning, se Hamakerkonstanten från Rm. Alla beräkningar i Kalkylkortet. MAC förkortar Modern ACademy.

Om man — till konkret prövande exempel — konsulterar det tillgängliga utbudet av teorier och experiment (Okt2010) på området MAXIMAL ADHESIONSKRAFT MED NOLLAVSTÅND MELLAN PLANA MATERIALPLATTOR FÖR kallvalsad band- KOPPAR [SIS 50 10] vid rumstemperatur (20 °C) är det närmaste man kommer en hänvisning till van der Waals samband F/A=H/ad³, se ovanstående bägge röda kurvdelar för respektive brottgränserna 200 MPa och 400 MPa. Med andra ord: inget bestämt värde existerar: ingen teoretiskt bestämd matematisk sambandsform existerar: ingen teori finns. TNED-sambandet däremot [gröna kurvdelen] garanterar alltid en lägsta nivå genom SKÄRNINGEN mellan funktionstyperna 1/d² och 1/ad³ och som garanterar att max adhesion (1/d²) alltid ligger under brottgränsen (1/ad³). Det konventionella Casimirsambandets form (1/d⁴, violetta grafen) självutesluter sin teori i praktiken genom att brottgränsvärdet nås långt innan ens atommedelavståndet har tangerats. Casimireffekten i konventionell mening är därför helt säkert utesluten som fenomenform i intervallet närmast materialens naturliga atommedelavstånd (och upp till i varje fall ca 10 nM).

Van der Waals-kraften för materialtes brottgräns (Rm) — f.ö. den enda kvantitetsmatematik som finns på området i MAC — kan NÄMLIGEN inte servera kriterium för max adhesionskraft då två separata materialplanplattor har förts ihop med nollavstånd emellan, eftersom det krävs (MINST) 5-10ggr Re-värdet i KALLFOGNING för att uppnå kemisk bindning till Rm-status.

Vilket vill säga:

Maximalt adhesionstryck (alla fasta ämnen) ligger alltid under, lägre än, materialets brottgräns (Rm);

Van der Waals kraftsamband beskriver följaktligen ingen reguljär adhesionsfysik, utan tydligen en ren kohesionsfysik: materialets inre maximalt sammanhållande kraft och som bara kan ändras med ändrade atommedelavstånd, analogt TEMPERATURÄNDRINGAR.

TNED-sambandet [1/x^2–4] — som här till prövning, HELT ersätter det konventionella Casimirsambandet [1/x⁴] — innefattar tydligen hela intervallet (0→∞) med alla faser i adhesionsfysiken, från minimala atommedelavståndet (idealt parallella atomplan, nollavstånd mellan separata planplattor), och vidare ut till maxgränsen (som bestäms av två närliggande materialytor), och ger därmed via nollavståndet materialets maximala adhesionskraft — alltid under brottgränsen Rm för fasta ämnen, eller ska i varje fall göra det för logisk praktik.

Enda PROBLEMET är

1. svårigheten att BEKRÄFTA SAMHÖRIGHETEN; Experimenten görs (uteslutande, Okt2010) med Sfär-Platta eftersom Platta-Platta-experimenten tydligen övergår experimentatorernas förmåga — med tillhörande teoretiska komplikationer som bara gör ämnet ännu mera komplicerat och svårbegripligt när det kommer till redovisning av mätresultat;

2. bristen på material- och koefficientredovisning i det material som faktiskt finns: TNED-sambandet (vid rumstemperatur) bygger helt på precisa materialparametrar [täthet, atomnummer (medelnuklidladdning för sammansatta ämnen), medelatomvikt, brottgräns], men ingenting sådant finns ens med i den konventionella Casimirteorins grund (inte ens ämnets täthet), varför heller knappast några materialparametrar redovisas alls i någon mera precis mening i de konventionella rapporter som finns.

Se till jämförelse Jämförande Exempel National Laboratories.

Webben är med andra ord (Okt2010) praktiskt taget helt ren på Platta-Platta-referenser till jämförelse i det avgörande intervallet 0,1-100 nM.

[Konventionella Casimirsambandet och TNED-formen skiljer sig allt mindre från ca 70 nM (skillnaden mot tryckenheten är 1%, sedan avtagande) och uppåt och det intervallet blir därför mindre intressant i bevisningen].

Se även citat i CasimirRef som ytterligare understryker bristen på klarhet i ämnet.

VdW inom Kemin

Van der Waals krafter inom kemin

Citaten nedan avspeglar det som uppmärksammat den här presentationens andemening — avsaknad av enhetlighet och entydighet i grundbegreppen i MAC, speciellt beträffande de materialsammanhållande krafterna och deras matematiska form.

Se särskilt komprimerad exemplifierad form i Grundämnesmetallernas Brotthållfasthet.

GENOMKOLL 2010-10-26:

Med följande repertoar är det inte underligt om kemistudenten blir (något) förvirrad:

”Intermolecular forces are relatively weak forces between molecules or between different chemical groups of the same large molecule which act at the distances of Van der Waals radii or larger. This is in contrast to chemical bonds which are stronger, act at the shorter distances, and are formed between different atoms of the same molecule.”,

@INTERNET Wikipedia Intermolecular force 2010-10-26

http://en.wikipedia.org/wiki/Intermolecular_attraction

:

intermolekylär kraft ............. svag, van der Waals

kemisk bindning ................... stark (elektrisk)

”In physical chemistry, the van der Waals force (or van der Waals interaction), named after Dutch scientist Johannes Diderik van der Waals, is the sum of the attractive or repulsive forces between molecules (or between parts of the same molecule) other than those due to covalent bonds or to the electrostatic interaction of ions with one another or with neutral molecules.[1]”,

”Van der Waals forces include attractions between atoms, molecules, and surfaces. They differ from covalent and ionic bonding in that they are caused by correlations in the fluctuating polarizations of nearby particles (a consequence of quantum dynamics[2]).”,

@INTERNET Wikipedia van der Waals force 2010-10-26

http://en.wikipedia.org/wiki/Van_der_Waals_force

:

interatomär attraktion ........... van der Waals

”A chemical bond is an attraction between atoms or molecules that allows the formation of chemical compounds, which contain two or more atoms.”,

”A chemical bond is the attraction caused by the electromagnetic force between opposing charges, either between electrons and nuclei, or as the result of a dipole attraction.”,

@INTERNET Wikipedia Chemical bond 2010-10-26

http://en.wikipedia.org/wiki/Chemical_bond

:

kemisk bindning .................... elektrisk attraktion mellan atomer — ELLER molekyler

Citatblocken tränger TYDLIGT in över varandras gränser — så att den beskrivna gränsdragningen TAGET GENERELLT SOM ETT ENHETLIGT LÄROSYSTEM framställer bilden av ett system som saknar entydighet: formuleringarna GENERELLT avspeglar ett tydligt kaos.

FÖRMODLIGEN är anledningen till ovanstående (milda) kaos den att det inte är enkelt att klassificera materialstrukturen — när man inte har koll på vilka komponenter som ingår i fysikbilden : elektronmassans komponenter.

;

TILL VISS DEL säger källorna ovan så här (men det finns ingen etablerad källa som utsäger det tydligt — därför att ämnet innefattar elektronmassans komponenter — som bannlystes från 1927):

— ALL materialsammanhållning definieras krafttekniskt av van der Waals allmänna kraftsamband F/A=H/ad³: materialets brottgräns (Rm): materialstyrkan eller den internt sammanhållande kohesionskraften (intermolekylärt eller interatomärt sammanhållande materialkraft).

— Atommedelavståndet (d) kan bara ändras med ändrad energimedelkraftväg (via E=hf), och den kan bara ändras genom ändrad temperatur. I — inuti — kohesionsstrukturen finns en (stor) mängd olika samverkande aspekter på kraftbildning som alla arbetar efter en och samma gemensamma princip: resonansverkan: Vågmönster, vågkopplingar, förskjutningar, fasvridningar, skärmningar, bandförstärkningar, dipolsvängningar (konv. ofta Londonkrafter).

— Att DÄRFÖR påstå att van der Waals kraftverkan inuti ett material SKULLE vara av typen ’svag kraft’ motsäger själva provstavens eget brottgränsvärde (Rm) som säger att van der Waalskraften är den ENDA sammanhållande kraft som alls finns i materialet, och utöver den, ingen alls. Med andra ord i praktisk mening: typen ’kemisk bindning’ — den interna kraftverkan mellan (d) olika atomplan i ett material (ideal kristall) vid given temperatur — är van der Waals kraft, F/A=H/ad³.

Se HamakerExempel med olika konstanter — Konstanten H är (ständigt) föremål för olika mätningar-beräkningar (med stundtals rätt stora olikheter beroende på källverk); Med referens till de relativa marginalerna är det alldeles tydligt att sambandet mellan Hamakers konstant (H) och brottgränsen (Rm) är linjär (direkt proportionell). Se Hamakerkonstanten från Rm.

För vidare.

Intermolekylära krafter, webbreferenser — Grundbegreppen på Webben — materiallära

PÅ WEBBEN

GRUNDBEGREPP

INTERMOLEKYLÄRA KRAFTER — GRUNDBEGREPP, grundsamband

WikipediaAdhesion

”Smooth surfaces of mica, gold, various polymers and solid gelatin solutions do not stay apart when their separating becomes small enough – on the order of 1-10 nm. The equation describing these attractions was predicted in the 1930s by De Boer and Hamaker [2]:

P –A

——— = —————— Where

area (24π z³)

P is the force (negative for attraction), z is the separation distance, and A is a material specific constant called the Hamaker constant.”,

@INTERNET Wikipedia Adhesion 2010-10-21

http://en.wikipedia.org/wiki/Adhesion

Freitas VdW 1999

”For example, the van der Waals adhesive force between two flat plates of equal interfacial area A and uniform separation z_sep is [1152]

H A

F_vdW = —————— {Eqn. 9.6}

24π z_sep³

”,

ref. 1152. Kevin Kendall, "Adhesion: Molecules and Mechanics," Science 263(25 March 1994).,

Institute for Molecular Manufacturing — NANOMEDICINE, VOLUME I: BASIC CAPABILITIES — Robert A. Freitas Jr, 1999

http://www.nanomedicine.com/NMI/9.2.1.htm

PRIMÄRDOKUMENT I GRUNDTEORIN FRÅN 1957 i

Royal Society — DIRECT MEASUREMENT OF THE LONG-RANGE VAN DER WAALS FORCES — J. A. Kitchener, A. P. Prosser 1957

http://rspa.royalsocietypublishing.org/content/242/1230/403.full.pdf+html

Ingen direkt tydlig sambandsform ingår för jämförelse.

Dokumentet avhandlar tidiga mätningar av van der Waals kraftverkan mellan glasplattor i intervallet 0,7-1,2 µM.

Dokumentet använder [de äldre fysikaliska enheterna]

enheten dyn: 1N = T5 dyn [ref. @INTERNET Wikipedia Dyne 2010-10-23]; 1dyn = t5 N;

enheten erg: 1erg = 1dyn·1cM = (1 t5 N)(0,01M) = 1 t7 J; 1 J = 1 T7 erg.

tydligt illustrerad:

rubrik|författare|källa|datum SAKNAS

http://www.vigoschools.net/~mmc3/org%20lecture/Unit%201%20-%20Chemical%20Bonding%20-%20Ch%203,4/L6%20-%20Intermolecular%20Forces%20of%20Attraction%20-%20Ch%204.pdf

tydligt illustrerad, delvis samma som ovan (men betydligt snabbare nerladdning):

INTERMOLECULAR FORCES — Department of Chemistry, Pima Community College — David A. Katz (datum saknas)

http://www.chymist.com/Intermolecular%20forces%202010.pdf

Washington University, 1

En (av få källor) som ger kvantitativa/matematiska samband i ämnet Intermolecular Forces,

University of Washington — INTERMOLECULAR AND SURFACE FORCES — René M. Overney (2000)

http://courses.washington.edu/overney/ChemE554_Course_Mat/course_material/surface_forces.pdf

”The attractive van der Waals force between the atoms is proportional to 1/r⁷, where r is the distance between the atoms.”.

;

Källan ovan täcker en beskrivning av intermolekylära kraftsamband och referenser i området (0,1) -10nM med (relativt) utförliga beskrivningar — men källan ger bara delvis referenser. För en fullständig bild behövs ytterligare källdokument. Se även Hamakers konstant.

s15n:

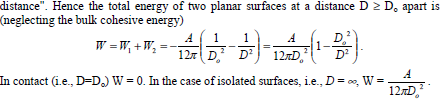
s16ö (Hamakerkonstanten här betecknad A):

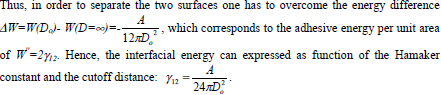
Ytterligare en utförlig (colloid, sv. limlik):

E-book — CRC Press

COLLOID INTERACTIONS AND COLLOID STABILITY — John Gregory 2006

http://www.crcnetbase.com/doi/pdfplus/10.1201/9780203508459.ch4

Källan ger mera vidlyftiga samband för Hamarkonstanten via Plancks konstant, medelgenomströmningsfrekvenser, och medelbrytningsindex, s71.ekv.4.11

Eller, om materialen är lika ekv.4.12,

Källan ger för Vatten [s70 Table 4.1 via 4.12 ovan] värdet 3,9 t20 J — utan någon specifikation av temperatur. Jämför brottgränsvärden för vatten vid olika temperaturer — tillsammans med en möjlig koppling mellan Hamakerkonstanten-Rm, se Hamakerkonstanten från Rm.

Jämförelsen endast understryker DIVERSITETEN i komplexet generellt — generellt SVÅRIGHETEN att (ens försöka) beräkna ”exakta materialparametrar”. [Pröva gärna — men inbilla dig ingenting].

Hamakers konstant

Hamaker constant — Hamakers konstant

Hamaker constant (efter H. C. Hamaker 1937) — Se även Innebörden av Hamakers konstant

Hamakerkonstanten [H] ingår i van der Waals kraftsamband som F/A=H/ad³.

Se även Hamakers konstant från Rm.

Washington University, 2

Tabell med värden för ämnen i flytande och fast form (0,057 - 40):

University of Washington — HAMAKER CONSTANT AND ITS LIFSHITZ MEAN FIELD REPRESENTATION

http://courses.washington.edu/overney/Material/HandoutsChemE498/Hamaker_Constant.pdf

Tabell:

s4Table1 — Koppar: i vakuum 40 t20 J; i vatten 30 t20 J,

FORCES ANALYSIS FOR MICROMANIPULATIONS IN DRY AND LIQUID MEDIA — Gauthier et al., 2008

http://hal.inria.fr/docs/00/26/44/38/PDF/JMM06_LAB_LRP.pdf

Mera omfattande tabell (flera på fasta ämnen, som Silver och Koppar):

PHARMA HUB — Collaboration for Pharmaceutical engineering and science — (författare, datum saknas)

http://pharmahub.org/resources/250/download/hamakerconstant_data.pdf

Kan inte åtkommas med separat URL — källan kan inte åtkommas genom diskreta URL — tydligen privat domän;

— Test på annan webbläsare visar OK [2010-10-20]: Mozilla OK, Flock OK, Opera OK, Netscape OK, Arora notOK, Google Chrome OK. Alla OK utom Internet Explorer 7 och Arora. Explorer 8 ej testad.

Åtkomst via Google nedan

:

Vatten Rm

Uppgifter på vattnets brotthållfasthet (eng. [Ultimate] tensile strength) finns på

GOOGLEBÖCKER s14 Figure 1.3

Sonochemistry and cavitation — M. A. Margulis 1995

Figuren ger en graf med nära linjärt stigande vänsterflank från vattnets fryspunkt (278 °K) och nära 0 MPa [med en mellanliggande brytpunkt vid ca 27 MPa och 282 °K] upp till en rundning vid nära 30 MPa (28,44 MPa) och 286 °K, sedan långsamt neråt igen nära linjärt till strax över 20 MPa vid drygt 320 °K.

Cut-off ref

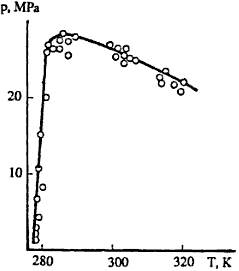
Cut-off distance — ’0,165-0,185 nM’ (1,65-1,85 Å), ofta D₀

;

GOOGLEBÖCKER s51

Polymeric nanocomposites: theory and practice — Bhattacharya et al., 2008

Cut-off-distansen diskuteras särskilt sidan 16 i Washingtonkällan — men med utflykter som av läsaren förmodligen kräver meriter på nivån nobelpris. Det är (min mening) ytterst oklart vad/vilka underförståddheter författaren åsyftar. Källan ger heller ingen vidare referens.

Andra källor bekräftar nominella värdet ca 0,16 nM:

s5267sp2n:

”The natural choice for d is the nominal molecular diameter, identified with the cutoff distance in the van der Waals theory. The standard value³ is 0.165 nm.”,

Department of Chemical Engineering —

KINETIC SLIP CONDITION, VAN DER WAALS FORCES, AND DYNAMIC CONTACT ANGLE —

Len M. Pismen, Boris Y. Rubinstein 2001

http://pattern.technion.ac.il/download/00/La011452s.pdf

Alla använder termen — ingen tycks vara i stånd att förklara den. Vanligt modernt syndrom.

”The cutoff distance criterion, while computationally efficient, has some disadvantages. The possibility always exists that the overall nonbonded interactions at long range are not negligible because such interactions are numerous. However, the slope of the van der Waals and electrostatic potentials in this region is small.”,

datum, författare saknas — NONBONDED ENERGY TERMS

http://www.biogem.org/Accelrys/Simulation/sima_minim_th_nonbonded-energy-terms.html

Problemet är att termen CutOff Distance tydligen används i många (kemiska) tillämpningar i samband med en (stor) diversitet av molekylära substanser — inte sällan långt ifrån några interatomära medelavstånd (typ 7 Å och liknande).

EXEMPEL:

VATTEN har tätheten ca ρ=m/V=1000 KG/M³;

Antalet molekyler per kubikmeter är

N = m/Uu=(1000 KG)/(H¹+H¹+O¹⁶⁼¹⁸)(1,66033 t27 KG) = 3,34605 T28;

Varje (H¹+H¹+O¹⁶⁼¹⁸)-molekyl upptar alltså

kubvolymen

V(1)=1/N=2,98859 t29 M³;

TredjeRoten ur V(1) ger kubsidan, analogt idealt kubiska

intermolekylära medelavståndet

dATOM = 3,10328 t10 M ~ 3,1 Å = 0,31 nM;

dATOM = [Uu/(ρV=m)]^1/3

Knappast ens i flytande ämnen är molekyl- eller atommedelavstånden större än runt 3Å. [grovt 2,5Å för fasta ämnen].

I varje fall om ämnet berör MATERIALENS HÅLLFASTHET (den sammanhållande kraftytan) räcker det inte att sväva ut i sådana oklarheter typ ’7Å’ om ämnet gäller att försöka klargöra vad termen cutoff distance står för, eftersom vi redan VET att den molekylära kedjelinjens inneboende styrka står och faller med den sammanhållande kraften mellan närliggande ATOMER (typ 2,5Å) i en molekyl, vilkensom.

Det blotta faktum att ingen (vidare) klargörande framställning (alls överhuvudtaget i webbens gratisdel) tycks finnas på området (ännu Okt2010), bara understryker ämnesområdets kaotiska karaktär.

Van der Waals kontra Casimir

van der Waals — Casimir

Casimirkraften som den retarderade (fördröjningseffekter, skärmning, över större avstånd) van der Waals-versionen

Se även separat citat i Övergången VdW-Casimir.

”The London-van der Waals forces are related to the Casimir effect for dielectric media, the former being the microscopic description of the latter bulk property.”,

http://en.wikipedia.org/wiki/Van_der_Waals_force

”In fact "Casimir's original goal was to compute the van der Waals force between polarizable molecules" of the metallic plates.”,

http://en.wikipedia.org/wiki/Casimir_effect

”Casimir and Polder worked out the retarded dispersion force between molecules in 1947 [6], the long range part of

the van der Waals force.”,

http://puhep1.princeton.edu/~mcdonald/examples/fluids/brevik_prl_82_3948_99.pdf

”The Casimir force is closely related to the van der Waals attraction between dielectric bodies.”,

;

”However, in practical terms, the Casimir and van der Waals forces are quite different; the van der Waals force is always attractive, whereas the sign of the Casimir force is geometry dependent.”,

;

”Our first attempts at measurements using parallel plates were unsuccessful; this is because it is very difficult to maintain parallelism at the requisite accuracy (10^–5 rad for 1 cm diameter plates).”,

Notera området — 0,5-10 µM (jämför Analysområdet):

;

”The most striking demonstration of the Casimir force is given in Fig. 4. The agreement with theory, with no adjustable parameters, is excellent. It should be noted that the closest approach is about 0.6 µm”,

;

”In conclusion, we have given an unambiguous demonstration of the Casimir force with accuracy of order 5%.”,

http://web.mit.edu/~kardar/www/research/seminars/Casimir/PRL-Lamoreaux.pdf

Hur MAC beskriver typglappet 0,1-10nM

Övergången vdW-Casimir

Hur MAC beskriver typglappet 0,1-10nM

— som inte kan beskrivas av Casimirsambandet i MAC

Upphittad källa som sammanfattar (vad [vi] hela tiden uppfattat, men som få verkar kunna formulera — att van der Waalkraftsambandet används som brobyggare):

MDPI —

EFFECTS OF VAN DER WAALS FORCE AND THERMAL STRESSES ON PULL-IN INSTABILITY OF CLAMPED RECTANGULAR MICROPLATES — Batra et al., 2008

http://www.mdpi.org/sensors/papers/s8021048.pdf

s1053|6:

”Consistent with the parallel plate approximation for the electrostatic force, and the small deformations assumption in the mechanical model, the distributed load due to the Casimir force per unit surface area is given by the proximity force approximation [44, 45], which for perfect conductors yields:

where ħ is the Plank’s constant and c is the speed of light in vacuum. Corrections to equation (7) for geometries with known and fixed departures from the parallel configurations are reported in [44, 45]. For gaps smaller than the retardation length, that is, for gaps smaller than the wavelength of the virtual transitions responsible for the quantum dipole fluctuations [31, 33], the Casimir force reduces to the van der Waals distributed force per unit surface area [46–48]

In equation (8), A is the Hamaker constant, see for example [31], with values in the range [0.4, 4] × 10⁻¹⁹J.*

van der Waals and Casimir forces between parallel layered metallic surfaces have been extensively studied in the literature, see for example [31, 33]. For gold-coated aluminum surfaces, it is found that van der Waals force, see equation (8), is effective in the gap range 0.5 nm − 4 nm. For gaps in the range 4 nm − 1 μm, there is a transition between the force-distance dependence g⁻³ (van der Waals force) to the force distance dependence g⁻⁴ (Casimir force). For gaps larger than 1 μm, the interaction between the plates is described by the Casimir force, see equation (7). Therefore, for perfect conductors, at large separation distances the interaction force is independent of the material properties of plates, whereas, as the gap decreases, the interaction force is affected by the material properties of the system. For dielectric bodies, the van der Waals force is effective at larger distances as shown in [49].

——————————

*In the literature [31–33], the Casimir force, see equation (7), is usually termed the retarded van der Waals, whereas

the van der Waals force, see equation (8), is called the nonretarded van der Waals. This nomenclature better illustrates the common physical nature of these surface forces.”.

:

0,5 nM - 4 nM 1/z³ ............................ van der Waals [ytor med Guld över Aluminium]

4 nM - 1 µM 1/z^3–4 ......................... van der Waals — Casimir

1 µM - 1/z⁴ ............................ Casimir

Källan är i övrigt fattig på klargörande [DIREKT användbara] data — dessa ligger inbäddade i specialtermer som också är fattiga på relaterad beskrivning [w-faktorn t.ex.].

En annan källa ger något annorlunda besked:

- 10 nM 1/z³ ............................ van der Waals dominerar

10 nM - 0,1µM 1/z⁴ ......................... Casimirkraften mycket stark

:

s1sp1mn:

”At separations below 100 nm the Casimir force is very strong and becomes comparable to electrostatic forces corresponding to voltages in the range 0.1–1 V,1–3 while for separations below 10 nm the van der Waals force dominates any attraction.^7–9”,

;

The American Physical Society —

INFLUENCE OF ULTRATHIN WATER LAYER ON THE VAN DER WAALS/CASIMIR FORCE BETWEEN GOLD SURFACES —

Palasantzas et al., 2009

http://eprints.eemcs.utwente.nl/17173/01/Influence_of_ultrathin_water_-_Vitaly_-_dec_09.pdf

Källan avhandlar tyvärr endast typen Sfär-Platta.

Notera även diversiteten i utbudet av HUR van der Waals kraftekvation skrivs, se citat i Allmänna samband.

Hållfasthetsreferenser på Webben — Grundläggande hållfasthetsbegrepp

BILDKÄLLA: Författarens arkiv · BildS9 Excur9 · 2okt2010 · Nikon D90 · Detalj

Hållfasthet på Webben,

Belastningsdiagram

Grundläggande hållfasthetsbegrepp

(drag)belastningsdiagram — allmän hållfasthetslära — Rm, brottgränsen

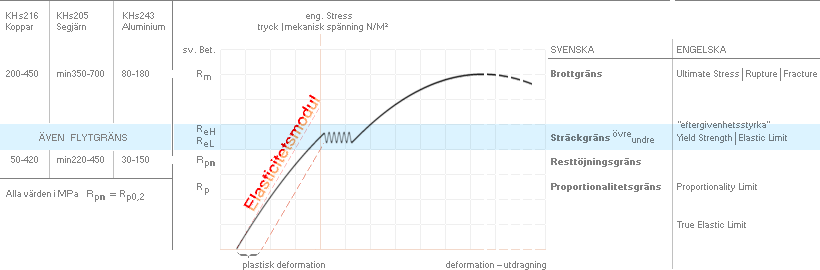
Diagramförklaringar med källuppgifter

—————————————————————————————————————————————————————————————————————

KH anger MATERIALLÄRA (Karleboserien 5 1980) med sidangivelser. Svenska beteckningar och benämningar från KARLEBO HANDBOK utgåva 12 1977 s197. Engelska beteckningar från Wikipedia (2010), samt ytterligare (här utan specifik referens) (godtyckligt, synonymer) från olika webbkällor som använder begreppen generellt. ELASTICITETSMODULENS DEFINITION från MATERIALLÄRA (Karleboserien 5 1980) s20n. R(pn)-beteckningen med n=0,2 betyder 0,2% kvarstående töjning (utdragning) vid den aktuella tryckkraftens-dragspänningens belopp. Rp0,2% anges ofta (i äldre svensk facklitteratur) som materialorienterande referensvärde tillsammans med Rm-data (med flera som inte ingår i den enkla översikten ovan). Enheten MPa = T6 Pa med Pa = N/M².

Se t.ex. jämförande exempelbeskrivning i webbkällan

Substances & Technologies — TENSILE TEST AND STRESS-STRAIN DIAGRAM — 2009

http://www.substech.com/dokuwiki/doku.php?id=tensile_test_and_strain-stress_diagram

Grundbegreppen i material-hållfasthetsläran

finns också beskrivna på svenska (med delvis korsreferens för engelska benämningar) i webbkällan

JÄMVIKT OCH ELASTICITET, KP 12 — Sammanfattning F10, TFYA16, mekanik för TB, Carl Hemmingsson 2007

http://www.ifm.liu.se/edu/coursescms/TFYA16/lectures/Sammanfattning-F10.pdf

Kallfogning

Webbkällor som upplyser om materialsammanpressning:

LOW ACTIVATION JOINING OF SiC/SiC COMPOSITES FOR FUSION APPLICATIONS — (2007)

http://www.ms.ornl.gov/fusionreactor/pdf/Vol.47/2.5%20pp.%2042-46%20Henager.pdf

”Joining pressure appears to require almost 30 MPa at 1673K in order to produce strong and dense joints.”

Cold Pressure Welding — sv., KallPressSvetsning (KallPressSammanFogning, enklare TryckSammanfogning)

NEW JOINING TECHNOLOGY FOR METAL PIPE IN THE CONSTRUCTION INDUSTRY — Construction Industry Institute 2003

http://www.construction-institute.org/btsc01.pdf

s22:

”Cold pressure welding is a method of joining sections of metal together by the application of pressure but using no heat or flux (Davies, 1993).”,

”Cold welding uses substantial pressure at room temperature to produce joining of materials through plastic deformation at the weld. It is of limited applicability, however, because it requires extremely clean surfaces and high pressures and it is difficult to accomplish consistently.”

Inga uppgifter på tryck.

Teori saknas

Cold Pressure Welding — Teknik, förklaring, historia, exempel — men utan tryckdata:

PWM — World leader in cold weld technology — WHAT IS COLD PRESSURE WELDING? — (2010)

http://www.coldpressurewelding.com/cms/index.php?option=com_content&view=article&id=92&Itemid=2&lang=en

”There have been several explanations as to the actual mechanism by which a cold pressure weld is obtained. For example, it has been suggested that it happens via recrystallisation or by an energy hypothesis, but most explanations have been either experimentally disproved or refuted on theoretical grounds.”,

”The currently accepted hypothesis that accounts for a cold pressure weld taking place involves the atoms of metals being held together by the metallic 'bond', so called because it is peculiar to metallic substances. The bond can be described as a 'cloud' of free, negatively charged atoms into a unit as a result of attractive forces.”.

Bättre resultat i källan nedan — tryckdata ingår —

TWI —Technology Engineering —

TWI KNOWLEDGE SUMMARY, COLD PRESSURE WELDING, INTRODUCTION 2003

http://www.twi.co.uk/content/ksedn002.html

”All metals are surrounded by surface layers (oxide) which must be disrupted if they are to be welded. Cold pressure welding, carried out at ambient temperature, relies upon the use of high compressive pressures [1] (1400-2800N/mm² for aluminium and at least double that value for copper). This provides interfacial deformations of 60% to 80% that break the oxide layers to expose fresh, uncontaminated metal that makes contact. In this state, interatomic forces take over to produce the weld.”.

Källan ovan anger generellt

1 N/mM² = 1 T6 N/M² = 1 MPa = 0,001 GPa ;

1400 - 2800 N/mM² = 1,4 - 2,8 GPa

Sammanfogningstryckkraften [p(J)] ligger alltså betydligt över materialets naturliga brottgräns [grovt 1/10 av p(J)], eller mera rättvist uttryckt, ca 5-10 ggr elasticitetsgränsen (Re).

Se även samma uppgifter i

Minst 40% deformation

Linköpings Universitet — Institute of Technology — SIMULERING AV KALLPRESSVETSNING — Haris Hastor 2004

http://www.solid.iei.liu.se/Publications/Master_thesis/2004/hastor.pdf

”Enligt teknisk litteratur [14] gäller följande villkor för att kallpressvetsning av aluminium skall uppstå:

• Kontakttrycket måste vara större än 200 N/mm² (200 MPa)

• Den plastiska töjningen ska vara minst 40 %

”.

Redovisningen från webbkällan ovan på materialegenskaperna (brotthållfastheten, främst, det mest intressanta) före-efter är dock (väl) mager. Webbkällan längre ner Mahabunphachai et al., 2009 ger bättre besked på den punkten.

Kallfogningsgränser

minst 5-10 ggr materialets naturliga elasticitetsgräns (Re)

Källan nedan ger både utförlig teori, experiment och analyser (se särsk. s4), även testdata på rostfritt stål ingår (SS 316) [eng. pressure weldning, sv. trycksammanfogning, el. trängre ’trycksvetsning’],

Journal of Manufacturing Science and Engineering — AUGUST 2009 —

PRESSURE WELDING OF THIN SHEET METALS: EXPERIMENTAL INVESTIGATIONS AND ANALYTICAL MODELING —

Mahabunphachai et al., 2009

http://www.mdm-lab.vcu.edu/Papers/40_Published_PressWeld_ASME_v_131_n4_041003.pdf

s5sp2mö:

”Based on the results in Fig. 5, in general, the bond strength is shown to increase with increasing welding pressure up to a certain point, after which the bond strength would decrease as higher pressure is applied to the specimens.”,

”Therefore, there exists an optimal welding pressure and optimal reduction value where the bond strength is at maximum. This optimal value is, however, a material- and process-dependent parameter as shown in Fig. 5. Unfortunately, with the selected welding pressure range in this study, only certain cases of the optimal welding pressure values can be demonstrated. Nonetheless, the optimal reduction point is clearly shown for all three material types.”;

Källans använda förkortning YS = Yield Strength, s6 Fig. 5.

Yield Strength (sv., ung. »eftergivenhetsstyrka»), ett materials deformationsspänningsgräns, samma som konv. sträckgräns, flytgräns eller elasticitetsgräns (Re). Se Wikipedia Yield (engineering). Synonymt i engelskan används även Elastic Limit (sv. elasticitetsgräns).

Testvärdena i artikeln (YS) ligger på 69-251 MPa, Table 2 s4 med materialen Koppar-Aluminium-Nickel-Stål(SS304, SS316, bägge av typen rostfria).

— Figur 4 s5sp1n redovisar [”Min. welding pressure/YS” 3,2-13,2 vs ”Thickness. t₀ (micrometer)”, 50-250 µM] med förhållandet p(Jmin)/p(YS) för både Nickel(200) och Koppar(110): bägge visar över 1 med max13,2|min4,8 för Nickel och max9,6|min3,6 för Koppar.

— Med andra ord: molekylär sammansmältning från|med runt och grovt 5-10 ggr materialets naturliga deformationshållfasthetsgräns (Re);

s4sp2n:

”Based on the results shown in Fig. 4, for the same sheet thickness the ratio between the minimum welding pressure to the material yield strength of Ni200 was found to be higher than that of the Cu110 (YS of Ni200=148 MPa and YS of Cu110=69 MPa), showing that Cu110 blanks are easier to bond than Ni200. On the other hand, no bonding could be obtained for SS316 and SS304 blanks (YS=251 MPa and 215 MPa, respectively) even at the high welding pressure of 3000 MPa.”.

;

— Molekylär sammanfogning i vanlig rumstemperatur mellan olika materialytor förekommer med andra ord (knappast) med mindre än man applicerar minst 5-10 ggr materialets naturliga elasticitetsgräns [sträckgränsen, Re] (dvs., 5-10 ggr × grovt 40-400 MPa för metallerna, eller grovt runt 1 GPa).

Lawrence Livermore National Laboratory — runt 100 ggr Rm

Sökning på webben i ämnet (Okt2010) visar (alternativ uppgift) att det krävs runt (minst) 100 ggr normala brottgränstrycket för att få fram (eller närma sig) motsvarande (effekter som tangerar) homogena material via artificiell sammanpressning.

En viss orientering ges i webbkällan

Lawrence Livermore National Laboratory —

HIGH PRESSURE MATERIALS RESEARCH USING ADVANCED THIRD-GENERATION SYNCHROTRON X-RAY —

Yoo et al., 2006

https://e-reports-ext.llnl.gov/pdf/335826.pdf

Källan berättar att det krävs runt (minst) 100 ggr mer tryck att få »molekylär reaktivitet» än den (i vårt exempel med t.ex. Järn) motsvarande brottgränsens värde (0,4 GPa).

”The products are controlled by collective behaviors of molecules, leading to strongly associated phases in a pressure range of 10-50 GPa”,

Yoo et al., 2006 som ovan

I Järnfallets Exempel betyder det grovt minst 40 GPa, analogt 100ggr mer än brottgränsens 0,4 GPa.

— Korrektheten i den förmodade iakttagelsen att det krävs extra inskjutningar för att tangera normal materialstruktur betyder alltså för det etablerade Casimirsambandets form uppenbarligen en motsägelse [Se även de inledande jämförande typgraferna]; Om inte sambandsformen som helhet ska förkastas, måste den uppenbarligen avgränsas till områden som är större än (typiskt, minst) 1-2 nM; Kortare avstånd gör uppenbarligen våld på materialets naturliga egenskaper. Se även NOTERING 3 i MAC-Casimirsambandet.

Kall(samman)fogning

Beskrivande teknisk animering finns på

Galaxy Graphics — TECHNICAL ANIMATION OF COLD PRESSURE WELDING — 2010

http://www.galaxygraphics.co.uk/flash/cold_pressure_welding.htm

Materialens brottgränser, överskrids av MAC-Casimir

Materialens brottgränser,

överskrids av MAC-Casimir

2010X15

TNED-Casimirvärden gränsar till materialens brottgräns

— medan däremot MAC-sambandet skjuter över målet med stora belopp

Se Jämförande grafer.

Med normala atommedelavstånd [d=0, se Kalkylkortet] ges för Järnet (26Fe56) TNED-Casimirvärdet 0,166 GPa — Brottgränsen för segjärn ligger vid lägst 0,4 GPa — medan MAC-sambandet ger 483,44 GPa.

Brottgränstabeller i MAC

MatWeb

Relativt omfattande tabell med metallernas egenskaper [och de olika ämnenas mekaniska (och övriga)] finns för jämförande översikter på

MATWEB, YOUR SOURCE FOR MATERIALS INFORMATION

http://www.matweb.com/

http://www.matweb.com/search/PropertySearch.aspx

Skriv in ämnets namn på engelska, välj sedan från en lista med ämnets olika typer-faser-legeringar.

:

Notering 1. Inte alla ämnen har Rm-data (Kobolt, eng. Cobalt har det t.ex. inte).

Notering 2. Brottgränsvärden kan skilja sig (betydligt) mellan olika källor beroende på i vilken utsträckning man preciserar materialet. Jämförelser med SIS [Sveriges Standardiseringskommission] är inte obetingat rak.

Brottgränstabell i Wikipedia

Draghållfasthetstabell för många ämnen finns till jämförelse i MegaPascal på

@INTERNET Wikipedia Ultimate tensile strength 2010-10-15

http://en.wikipedia.org/wiki/Ultimate_tensile_strength

RELATIVT OMFATTADE MATERIALDATA finns på webben i svenska versioner; Sök på typ Brottgräns, Aluminium, och flera olika svenska källverk ger besked.

Generellt och grovt ligger brottgränserna (Rm) i storleksordningen 200-400 MPa för Koppar-Aluminium-Järn-Nickel; Ståltyperna (Kolstål) ligger på ca 1-1,5 GPa.

Wikipediatabellen (ovan) ger i sammandrag brottgränsen i MPa för materialen nedan (grovt alla metaller runt 40-400 MPa)

Aluminium 40-50 brottgränsen [Rm] i MPa = T6 N/M², gäller motsv. glödgat [ohärdat] tillstånd

Bly 12

Guld 100

Järn 350

Koppar 210

Nickel 140-195

Silver 170

Tantal 200

Tenn 15-200

Titan 240-370

Wolfram 550-620

Zink 110-200

Människohår 380

Järnexempel, segjärn

EXEMPEL:

Brottgränsen (Rm) [eng. tensile strength] för segjärn är enligt MATERIALLÄRA (Karleboserien 5 1980 s205 Tabell 7.2 Segjärn) lägst 400 N/mM², analogt 400 N/(0,001M)² = 4 T8 N/M² = 4 T8 Pa = 0,4 GPa. TNED-formen ger för 26Fe56 värdet vid d=0 enligt 1,6645 T8 N/M² ~ 0,17 GPa.

[IDEALT: Med tillräckligt näravstånd »kopplar» atomerna inbördes kemiskt, en viss energi frigörs, och en låsning inträffar typ »kardborrefunktion» som parkerar materialet på dess naturliga brotthållfasthet].

Analogin, som visar att det i så fall skulle behövas en (liten) bit till, utsäger: Pressar man ihop två materialytor mekaniskt till deras motsvarande atomära medelavstånd blir resultatet INTE en motsvarande material sammansmältning. För att nå dit måste ytterligare en (liten) bit tillfogas (ett tröskelvärde) som här i exakt ekvivalenta termer skulle bli d=–0,082 nM (4,064 T8 Pa) för att få attraktionstrycket runt 4 T8 N/M². Dvs., ytterligare en intryckning från atommedelavståndet 2,28 Å (0,228 nM) med ca 27% för att få fram det atommateriallåsande »klicket».

Det är dock orealistiskt att tänka sig något EXAKT klick för EXAKTA materiella brottgränsvärdet. En mer realistisk funktion kräver (mycket) mer extra intryck för att få låsning på normala materialvärdet:

Se vidare webbdata från olika laboratorier i Kallfogningsgränser.

vanDerWaalsEND.

Parbildning i MAC

Parbildning i MAC

2010IX17

Parbildning i MAC

Se även exempel på par-|positron-bildning via fotografier från bubbelkammare i Elektronens bubbelkammarspår

e^– → | Z | ~~~ γ → ± X .......................... parbildningsmekanismens typform genom elektronstrålning

elektronstråle material partikelpar

eller laser

eller kombination

Bethe-Heitler [1934] är de främst nämnda pionjärer som associeras med den första användbara matematiska fysiken för experimentellt påvisande av parbildning [H2] [H3] [H4]. Parbildningsmekanismen har efter pionjärerna fått den generaliserande benämningen Bethe-Heitler mekanism. Processen som verkställer transformationen benämns Bethe-Heitler process.

(Z betecknar atomnummer — här också generellt något grundämnesmaterial, det centrala konverterings- eller bestrålningsmaterialet, se citat).

En (översvallande) stor mängd (PDF-) dokument finns på webben (Sep2010) som

· INTE klargör Z-delen i ekvationerna;

· INTE beskriver eller förklarar vad ’Bethe-Heitler process’ är — men använder terminologin frekvent.

Den allmänna praktiken bland ämnesförfattarna är istället [Se exempel i Burke et al., 1977 s1626sp1ö, H5 och H6] att favorisera den rena ideala MAC-teorins s.k. Breit-Wheeler process och använda denna i samband med experimentella beskrivningar av Bethe-Heitler processen.

Ofta förekommande skrivsätt för Breit-Wheeler processen är

ω + ω₀ → e⁺ + e^–

2γ → e⁺ + e^–

I relaterad fysik (TNED) existerar ingen praktisk motsvarighet för den modern akademins ideala massa-från-ljus transformation — Breit-Wheeler-uttrycken är, och förblir, de rent kvantitativa aspekterna på energitransformationer vars kvalitativa former bara kan realiseras med hjälp av redan befintlig materia:

Som redan tidigare påpekats enligt energilagen i relaterad fysik, KAN massa förintas därför att den INTE kan skapas; Energi är i relaterad fysik kvantitativt utbytbar mot massa, inte kvalitativt. Ljus kan inte skapa laddning, massa och spinn, bara härma och ersätta dess kvantitativa aspekt. Se även i citat.

Ämnesförfattarna (emellertid) verkar t.o.m. SÅ uppslukade av (det ännu Sep2010 hägrande) Breit-Wheeler idealet att man helt tycks bortse ifrån den centrala materialaspekten (Z) och bara ser denna som en ’nödvändig stoppform’ — som om den rena ideala teorin redan vore bekräftad. Explicit citatkälla som intygar att så INTE är fallet finns i Ruffini et al., 2009 s629m. Genom (den stora) bredden på ämnesförfattare som tycks ha glömt av den delen, bildas (lätt) en allmän uppfattning att materia från ljus REDAN skulle vara en allmänt bekräftad experimentell observation — samt att (därmed) QED i MAC skulle vara väl befäst.

Notera alltså den etablerade uppfattningen om parbildning — också med föreställningen om »vakuumets polarisation»

Man bortser [H5] [H6] ifrån den nödvändiga materialdelen i centrum (Z), och (tydligen, utan att explicit skriva ut det) anser inte att den har någon koppling till typ positronförekomsterna, utan menar att dessa SKAPAS ur ljusenergin (hf) som resultat av typ »våginterferensen omkring Z-materalet». Man får verkligen LETA i experimentbeskrivningen [McDonald 1977, Burke et al., 1998, m.fl.] för att hitta Z-representationen (leta på ”wire” och ”foil”). Det som framhävs är (således) ”the first laboratory evidence for inelastic light-by-light scattering involving only real photons”.

Först när man kan visa att positroner (och elektroner) strömmar från en mötespunkt mellan två (eller flera) laserstrålar i vakuum — den rena förmodade Breit-Wheeler processen, inga mellanliggande material — kan ovanstående säkert intygas.

Med dagens (2010) laserteknik räcker ännu inte intensiteten för att nå det teoretiska målet i praktiken.

Se Breit-Wheeler-målet för ett möjligt scenario som kan realisera det hägrande målet.

Citatet nedan intygar att målet inte är nått.

”1. Introduction

The vacuum pair creation effect by a classical electric field has been predicted in QED a long time ago [1, 2]. A complete theoretical description of this effect has been obtained [3]-[6], but there is still no experimental proof. The main obstacle is the high value of the critical electric field strength for the pair creation, Ecr = 1.3×10¹⁶ V/cm for electron-positron case.”, s121n,

INSTITUTE OF PHYSICS PUBLISHING —

Observable manifestation of an electron-positron plasma created by the field of an optical laser — Blaschke et al., 2006

http://iopscience.iop.org/1742-6596/35/1/010/pdf/1742-6596_35_1_010.pdf

Massa-ljus-massa-omvandlingar i MAC

2010IX15

Massa-ljus-massa-omvandlingar i MAC

PARBILDNING parannihilation

EN STOR SVÅRIGHET — generellt i modern akademi — vid det webbaserade materialet (Sep2010) om SKAPELSE AV MASSA UR ENERGI vittnar alldeles tydligt om Problemet att skilja mellan massa (KAN vägas på brevvåg) och ljus (kan INTE vägas på brevvåg [se även i Värmegrunderna]), samt att göra den väsensskillnaden tydlig för läsaren. Nämligen, främst, enligt följande (som det tar ett tag att hitta):

Ruffin s626

”The Breit–Wheeler process, on the contrary, is still today waiting a direct observational verification.”, s629m,

Ruffini et al., 2009

SKAPELSE AV MASSA UR ENERGI — i modern akademi (här ofta MAC) — beskrivs renodlat av tradition i MAC med typbegreppet s.k. Breit-Wheeler-process (eng. Breit-Wheeler process). Den skrivs (typiskt)

ω₁+ω₂ → e⁺e^–

alt.,

2γ → e⁺e^–

Och — vilket var det hjärtligt centrala: Det är ypperligt LÄTT att få den saken helt om bakfoten med hjälp av den moderna akademins speciellt entusiastiska författarskara i ämnet. Nämligen i den FÖREGIVNA uppfattningen att massa (positroner, e+) framträder ur det här:

elektronstrålar + laserstrålar.

Det är alldeles riktigt att det är DIT man strävar — men som citatet ovan understryker (vilket man finner först efter visst letande): man är inte (riktigt) där än.

— MEN: Vad är det då, om inte ’elektronstrålar + laserstrålar’?

— Elektronstrålar + laserstrålar + ALUMINIUMFOLIE (eller wire: tråd eller folie). Vidare i citat nedan.

— Men det är verkligen ingen lätt sak (för en utomstående lekman) att HITTA passagerna — med nuvarande selektering i författningarna. Man får leta — men man skulle inte behöva göra det med ytterst enkla grepp från författarna (Det verkar ibland som att artikelförfattarna anstränger sig för att Utelämna så många potentiella Nya läsare som möjligt, och vilken författarskara verkar vilja avgränsa ämnet till en så snäv population som möjligt och som redan underförstått är bekant med facktermerna — trots att man med ytterst enkla grepp kan bredda repertoaren betydligt).

— Aluminiumfolie, metalltråd ... ?

— OM varje atomkärna enligt TNED MINST består av en sammansätt ±e-väv av A909e-par med summa noll impulsmoment

J[0K]+3J[1K]=0, A masstalet, är det inte svårt att förstå att det är något mysko med »positronbildning från laser» då man i själva verket måste ha ett föremål, en metalltråd eller en metallfolie, i vägen för laserstrålen: »positronbildning FRÅN ATOMKÄRNOR VIA laser».

DET MAN FÖRST (Sep2010) HITTAR på ämnet ’positrons from light’, min referens:

;

”The positrons are interpreted as arising from a two-step process in which laser photons are backscattered to GeV energies by the electron beam followed by a collision between the high-energy photon and several laser photons to produce an electron-positron pair.”, första sidan, onumrerade sidor,

”These results are the first laboratory evidence for inelastic light-by-light scattering involving only real photons.”,

POSITRON PRODUCTION BY LASER LIGHT — Kirk T. McDonald, datum saknas (1997)

http://www.hep.princeton.edu/~mcdonald/e144/ssitalk.pdf

Sidnumrering saknas i det långa PDF-dokumentet, källan omnämner inte Bethe-Heitler

”A signal of 106 ± 14 positrons above background has been observed in collisions of a low-emittance 46.6 GeV electron beam with terawatt pulses from a Nd:glass laser at 527 nm wavelength in an experiment at the Final Focus Test Beam at SLAC.”,

”The positrons are interpreted as arising from a twostep process in which laser photons are backscattered to GeV energies by the electron beam followed by a collision between the high-energy photon and several laser photons to produce an electron-positron

pair.”,

”These results are the first laboratory evidence for inelastic light-by-light scattering involving only real photons.”, s1626mö.

”… these results are the first observation of inelastic photon-photon scattering with real photons.”, s1629sp2mö.

POSITRON PRODUCTION IN MULTIPHOTON LIGHT-BY-LIGHT SCATTERING — Burke et al., 1997

http://www.physics.princeton.edu/~mcdonald/examples/accel/burke_prl_79_1626_97.pdf

”this is the first observation of inelastic light-by-light scattering involving only real photons”

STUDIES OF NONLINEAR QED IN HIGH ENERGY ELECTRON–LASER COLLISIONS — Th. Kotseroglou, 1998

http://www.maik.ru/full/lasphys/98/1/lasphys1_98p142full.pdf

Flera av samma typ (men med olika omfattning) finns med utspridda senare datum och som avhandlar samma uppsats men med (framhävda) olika författargrupper.

Burke et al., 1997 ovan, som är relativt kort och till synes välskriven och välrelaterad, omnämner på flera ställer en (för lekmannen) mysko ”wire” enligt

”The response of PCAL to positrons originating at IP1 was studied by inserting a wire into the electron beam at IP1 to produce e⁺e^– pairs by Bethe-Heitler conversion of bremsstrahlung photons.”, sp2s1627m.

’To produce’?

Lekmannen kliar sig förtvivlat i huvudet och undrar vad i all sin dar det är för något avancerat han har missat?

Fraserna Burke-gruppen använder är

”wire into the electron beam at IP1 to produce e⁺e^– pairs”,

”the density of clusters produced by the wire”,

”Cluster densities from positrons produced by a wire”.

Mystiken tätnar [Fast vi som redan känner till TNED vet vart det lutar].

En mera utförlig beskrivning i samma uppsats finns tydligen i PDF-dokumentet (samma som Burke fast mycket längre, mera utförligt)

PHYSICAL REVIEW D, VOLUME 60, 092004 — Bamber et al., 1999

Studies of nonlinear QED in collisions of 46.6 GeV electrons with intense laser pulses

http://viper.princeton.edu/~mcdonald/e144prd/prd_60_092004_99.pdf

med ’wire’ ersatt av ’foil’ och typcitaten

”By placing a thin foil in the beamline at 0° from the interaction region, it was possible to convert a fraction of the forward photons, and to measure the converted electrons (or positrons) in a magnetic spectrometer, as discussed in Sec. III D.”, s8sp2m,

;

”For a small portion of the running, some of the scattered photons were converted to electron-positron pairs in a thin foil, and those charged particles were analyzed in a spectrometer containing charged-coupled-device (CCD) pixel detectors and SCAL calorimeters downstream of a 5D36 magnet.”, s11sp2mö,

;

”This was confirmed in the case of the PCAL in calibration runs in which a foil was placed at IP1 to generate a spectrum of Bethe-Heitler positrons from the conversion of bremsstrahlung photons.”, s15sp2mn

;

”Some data were collected with the forward-photon monitor removed from the 0° beamline, and a thin foil inserted to convert a small fraction of the forward photons to electronpositron pairs. These were deflected by 10–30 mrad into the CCD spectrometer by a 5D36 magnet, as shown in Fig. 11.”, s23sp1m;

med ’foil’-specifikationen

”At high laser intensities, there were typically Nγ ~ 10⁷ photons scattered into the forward direction, with only ~ 1% of these at momenta beyond the n=1 Compton edge.”, s28sp2n,

”A 50-µm-thick aluminum foil was used as a converter (5.6×10^–4 r.l.), so that ~ 5000 pairs entered the pair spectrometer (Fig. 22) in each laser pulse.”,

Bamber et al., 1999

och den slutliga upplysande figuren

FIG. 23 s17sp2ö, Bamber et al., 1999

’Cerenkov Periskop’.

’Aluminium-konverterare’.

Med andra ord:

Det går (ännu 2010) inte utan Aluminiumfolien

— Fast många vill gärna tro det.

Men den avgörande Aluminiumfolien omnämns knappast i de övriga (trängre) författningarna:

— Burke omnämner bara ”wire” 3ggr, ingen ”foil”, ger ingen upplysande ’Cerenkov Periskop’-figur.

— McDonald omnämner inte ”wire” men ”foil” en gång, samt ger [i Figure 6(b)] ’Cerenkov Periskop’-figuren.

— Kotseroglou omnämner ”wire” 2ggr, ingen ”foil”, ger ingen upplysande ’Cerenkov Periskop’-figur.

Ingen av författarna säger det (här veterligt) klart och rent ut: det går inte utan Aluminiumfolien. Vi ser det bara (indirekt) genom citatgruppen i Bamber et al., 1999 — eller nära direkt i det blocket genom

”some of the scattered photons were converted to electron-positron pairs in a thin foil”.

Det är snudd på rekord.

(Dessa författare vill inte ha någon publik, helt klart).

Positronerna framträder i Aluminiumfoliens inre turbulenta elektromagnetiska atomfysik — INTE genom någon allmän offentlig utställning på Sveavägen 7-4 under flera minuter där man tydligt SER elektronstråle i rymden + laserstråle i rymden som träffas och från vilken mötespunkt det strömmar positroner, och som (den sensationsbenägna) lekmannen väldigt gärna kan vilja föreställa sig saken.

Den enda (mera refererande, nya) McDonald-Kotseroglou-Burke oberoende författarkällan jag hittat — och som omnämner den (med flera) — är Ruffini et al., 2009

ELECTRON-POSITRON PAIRS IN PHYSICS AND ASTROPHYSICS: FROM HEAVY NUCLEI TO BLACK HOLES

— Ruffini et al., 2009

http://www.icranet.org/4th_ICRANet_Scientific_Committee/Volume2-Scientific_Report/08Xue_b.pdf

s621-s921 (300s), omfattande, utförligt refererad avhandling med en stor mängd (över 500) referenser

Ruffini refererar i sin referens (39) till Burke et al., 1997,

”The phenomenon of e⁺e^– pair production in multi-photon light-by-light scattering has been reported in (38; 39; 254; 211) on the experiment SLAC-E-144 (277; 63).”, s737m,

;

”This shows that the pair production of Breit–Wheeler type by the anti-adiabatic, perturbative multi-photon production mechanism, described by Eqs. (5.10.9), (5.10.11) or (7.2.9), (7.2.12) for small η << 1, has been experimentally confirmed.”, s738mn;

»Breit–Wheeler process, 2γ → e⁺e^–», s621mö,

Ruffini et al., 2009

Här är det alltså tydligt att författarna är så uppslukade av ämnets sensationella natur, att man gör ett felaktig, väsentligt, påstående. BW-typen, som (ovan) samma författare intygar i föregående citat fortfarande tarvar ”a direct observational verification” är här plötsligt bekräftat, som ovan, ”has been experimentally confirmed”. Framställningssättet kan uppenbarligen inte bli mer kaotiskt.

Bethe-Heitler mekanismen — parbildningens experimentalform

e^– → | Z | ~~~ γ → ± X .......................... parbildningsmekanismens typform genom elektronstrålning

elektronstråle material partikelpar

eller laser

eller kombination

Bethe-Heitler [1934] är pionjärerna som associeras med den första användbara matematiska fysiken för experimentellt påvisande av parbildning. Parbildningsmekanismen har efter pionjärerna fått den generaliserande benämningen Bethe-Heitler mekanism. Processen som verkställer transformationen brukar benämnas Bethe-Heitler process.

Ruffini verkar (bland många upphittade) vara den enda avvikande källan av de många, många som väl använder begreppet och termen ’Bethe-Heitler process’ men som aldrig beskriver den termen i klartext (Wikipedia har den t.ex. ännu inte 15Sep2010, heller inte Breit-Wheeler process);

BH-processen

”Currently available technologies allow for intensities of the order of 10²⁰ W/cm² leading to abundant positron production essentially through the Bethe-Heitler process (3.3.1) with number densities of the order of 10¹⁶ cm^–3 (276).”, s737mö,

”

γ + Z → Z + e⁺ + e^–. (3.3.1)

”, s649mö,

;

Ruffini et al., 2009

(Z betecknar atomnummer — här också generellt något grundämnesmaterial, det centrala konverterings- eller bestrålningsmaterialet, citatet ovan).

MED ANDRA ORD: så svårt det alls kan bli för en lekman att få fatt på (det i grunden helt enkla) sakinnehållet;

Notera således skillnaden i SAK:

BW-BH-process

Breit–Wheeler process 2γ → e⁺e^– .............................. den rena ideala MAC-teorins ljus-till-massa konversion [BW-processen]

Bethe–Heitler process 2γ + Z → Z + e⁺e^– .............. den (ännu enastående) experimentellt praktiska BW-maken [BH-processen]

Vilken är skillnaden?

Z-typen tillhör TNED. Den klargör att positronbildning INTE kan komma ifråga på något ANNAT sätt än att en POSITRONGRUNDAD MASSKÄLLA finns närvarande: atomkärnan, centralmassivet på 1818e = ±909A par elektroner-positroner, A masstalet. Den renodlade BW-typen finns inte i relaterad fysik (TNED) — inte nu, inte någonsin. Som redan tidigare antytts enligt energilagen i relaterad fysik därför att massa kan förintas därför att den inte kan skapas; Energi är i relaterad fysik kvantitativt utbytbar mot massa, inte kvalitativt. Ljus kan inte skapa laddning, massa och spinn, ljus kan inte skapa materia, byggnader, hus, atomer, bara härma och ersätta de materiella tingens kvantitativa aspekt [BIO].

Energiutbyte. Inte masskapelse.

FÖRMODLIGEN har man — numera — i moderna kvarter ’hunnit bli så förtrogen’ med det helt kvantiserade begreppet E=mc² [se även Einsteins härledning] och dess enorma landvinningar inom experimentalfysiken att man inte ser annat än ’rena BW-processer’ bakom alla och de enda praktiska BH-processer som (ännu Sep2010) finns på experimentalfysikens bord. Man tror — nog, helt bergfast — att det ’bara är en fråga om tid’ innan man hunnit utveckla tillräckligt kraftfulla laserbord som kan betjäna en mera regelrätt ljuslaser-vakuum-demonstration. Vidare nedan.

BW-genombrottet

Det avgörande experimentet kan komma redan inom ett decennium

— om utvecklingen på laserteknikens område håller nuvarande takt

Enligt uppgift från 2008

MICHIGAN LASER BEAM BELIEVED TO SET RECORD FOR INTENSITY — Feb2008

http://www.physorg.com/news122298608.html

uppvisar en av världens nu mest högintensiva lasrar ett intensitetsvärde (I=P/A, W/M²) på ca 2 T26 W/M². En (konventionell) lasers elektriska fältstyrka kan beräknas [Se exv. Ruffini et al., 2009 s731ö] ur

Ξ = √ R₀(P/A) med R₀ ~ 377 Ω ................................. V/M, den konventionella laserns elektriska fältstyrka ur intensiteten

Wikipedia har på sin artikel Laser på avdelning Recent innovations (2010-09-15) ett diagram som visar den tekniska laserutvecklingen perioden 1960-2010 — med en från 1985 i stort sett linjär stegring 1985-2000 från skalvärdet T15 till T23. Det gör grovt sett en tiopotens varje 1,875 år (Skalvärdet anges i figuren till /cM², men måste uppenbarligen vara /M² för att uppgiften ovan från Michigan ska stämma, annars blir potenserna 4ggr för stora).

Nu är MAC-gränsvärdet för ’vakuumets spontana elektron-positron-uppkomst’ lika med

limΞ

Ξ = m²c³/eħ

= 1,32319 T18 V/M

~ 1,3 T18 V/M

Se även Ruffini et al., 2009 s621

”The vacuum polarization process in strong electromagnetic field, pioneered by Sauter, Heisenberg, Euler and Schwinger, introduced the concept of critical electric field E_c = m_e²c³/(eħ). It has been searched without success for more than forty years by heavy-ion collisions in many of the leading particle accelerators worldwide.”, s621m.

; FÖRKLARING:

Man använder sambandet för elektriska fältstyrkan

Ξ = U/d = (E/Q)/d

med d från de Broglies vågekvation (se även MIC)

d = h/mc

som ger

Ξ = E/(Qd) = mc²mc/eh = m²c³/eh

Genom d mera renodlat som en omkrets d=2πr används engelskans ’h-bar’-tecknet ħ=h/2π som ger

Ξ = m²c³/eħ

= 1,32319 T18 V/M

~ 1,3 T18 V/M

med e för elektronladdningen (1,602 t19 C), m för elektronmassan (0,000548598u, u=1,66033 t27 KG), h för Plancks konstant (6,626 t34 JS) och c för toppdivergensen (2,99792458 T8 M/S).

Dvs., man använder i MAC föreställningen om ’elektronen’ (Q) och ’elektronens radie’ (2πr) som ett ekvivalent mått på ’elektronperiferins elektriska fältstyrka’.

Den motsvarande konventionella laserintensiteten för ändamålet kan då beräknas enligt

Icrit = (Ξcrit)²/R₀

= (1,3 T18 V/M)²/(377 V/A)

= 4,48275 T33 [W/M² = V²A/VM² = VA/M² ]

~ 4,5 T33 W/M²

RESULTAT:

Med runt räknat 33–26=7 tiopotenser kvar att avverka i teknisk laserutveckling, återstår med

1,875 år per tiopotens

tiden runt och grovt

t = (7)(1,875)

= 13,125 år

innan experimentet står på bordet: preliminärt år 2023 — om den tekniska utvecklingen på området håller samma takt (Jag vågar tippa inom ett decennium [kanske före 2020], därför att potentialen verkar vara särskilt stor på just forskningsområdet för laser — det är många, många forskare som verkligen vill SE resultatet).

Tills dess är helt säkert BH som gäller.

Historia — Parbildning

Historia

HISTORIA

PARBILDNING parannihilation

H1

”The annihilation of electron–positron pair into two photons, and its inverse process – the production of electron–positron pair by the collision of two photons were first studied in the framework of quantum mechanics by P.A.M. Dirac and by G. Breit and J.A. Wheeler in the 1930s (1; 2).”, s629ö,

”The Dirac process, e⁺e^– → 2γ, has been by far the most successful.”, s621mö,

Ruffini et al., 2009

H2

”One development inquired electron–positron pair creation by the interaction of photons with nuclei following the reaction:

γ + Z → Z + e⁺ + e^–, (3.3.1)

major contributors were Oppenheimer and Plesset (94), Heitler (95), Bethe-Heitler (96), Sauter (97) and Racah (98).”, s649mö,

;

”In parallel progress on the reaction

e^– + Z → e^– + Z + γ, (3.3.7)

was made by Sommerfeld (103), Heitler (95) and later by Bethe and Heitler (96).”, s650m,

Ruffini et al., 2009

H3

”Bethe and Heitler¹³ (1934) treated both the bremsstrahlung and the pair production relativistically using the Born approximation, in which the screening of the nuclear coulomb field was properly taken into account. Wheeler and Lamb¹⁴ (1939, 1956) treated the same phenomena in the field of atomic electrons.”,

”Experimentally, the productions in the nuclear coulomb field and the electron field always occur together, hence two effects must be combined in order to make comparison with experiments.”,

”When the atomic number Z is large, the correction to the one photon exchange mechanism must be included and this was done by Bethe and Maximon^l5 (1954), Davies, Bethe and Maximo¹⁶ (1954), and Olsen¹⁷ (1955). It should be noted that in Bethe and Maximon, ^l5 it was erroneously stated that the Coulomb correction affects only the pair production but not the bremsstrahlung. This error was corrected by Olsen l7 (1955).”, s5m|s816sp2m,

Yung-Su Tsai 1974

H4

”Bethe and Heitler¹³ (1934) treated a special case in which the target particle is an infinitely heavy pointlike and spinless nucleus whose coulomb field is screened by atomic electrons. They did not include the atomic excitation of the target which was later considered by Wheeler and Lamb (1939).^l4”,

”While these treatments by Bethe and Heitler¹³ combined with the work of Wheeler and Lamb¹⁴ adequately describe the pair production of electrons at high energies and small angles, they are not adequate to describe the pair production of particles with mass of muons or heavier, because the effects of nuclear form factors and the recoil of the target system must be included when heavy particles are produced.”,

”Even in the electron pair production the nuclear form factors and the recoil must be taken into account if the production angle is large. In fact when the transverse momentum of the particle produced is much larger than the mass, the cross section is nearly independent of the mass of the particle produced.”,

”Drell and Walecka (1964)38 generalized the result of Bethe and Heitler to deal with a target of arbitrary mass, spin and form factors and arbitrary final states.”, s9ö|s817sp2mn,

Yung-Su Tsai 1974

H5

”Observation of positrons created in the collision of Compton backscattered photons with a laser beam in the multiphoton Breit-Wheeler reaction,

ω + nω₀ → e⁺e^–. (17)

”, sidnumrering saknas,

;

”Pair creation via the interaction of two light quanta,

ω + ω₀ → e⁺e^–. (26)

was first considered in 1934 by Breit and Wheeler,³⁶ who remarked that although the cross section is of the same order of magnitude as the Compton-scattering cross section “it is hopeless to try to observe pair formation in laboratory experiments with two beams of γ-rays meeting each other on account of the insufficiently large densities of quanta”. Indeed, this process has not been directly observed prior to the present experiment. It is, however, believed to be responsible for the fall-off of the spectrum of astrophysical γ-rays at very high energies.³⁷”, sidnumrering saknas,

McDonald 1997

H6

”The first process is nonlinear Compton scattering, in which an electron absorbs multiple photons from the laser field, but radiates only a single photon:

e + nω → e’ + γ, (1)

where ω represents a photon from the strong electromagnetic wave, n indicates the number of such photons absorbed, and γ represents a high-energy photon. This process has a classical limit, Thomson scattering, and the case of n>1 corresponds

to higher-multipole radiation.

In the second process, one or more of the laser photons is Compton scattered from the electron beam via process (1),

producing a high-energy photon. As this photon propagates through the laser field, it can interact to produce an electronpositron

pair:

γ + nω → e⁺ + e^–, (2)

This is referred to as Breit-Wheeler pair production, and can be regarded as the materialization of a vacuum-polarization

loop in a strong field.

Our first observations of processes (1) and (2) have been reported in [1] and [2], respectively.”, s1sp1n,

Bamber et al., 1999

H7

”Due to the interaction of physics and astrophysics we are witnessing in these years a splendid synthesis of theoretical, experimental and observational results originating from three fundamental physical processes. They were originally proposed by Dirac, by Breit and Wheeler and by Sauter, Heisenberg, Euler and Schwinger. For almost seventy years they have all three been followed by a continued effort of experimental verification on Earth-based experiments. The Dirac process, e⁺e^– → 2γ, has been by far the most successful. It has obtained extremely accurate experimental verification and has led as well to an enormous number of new physics in possibly one of the most fruitful experimental avenues by introduction of storage rings in Frascati and followed by the largest accelerators worldwide: DESY, SLAC etc. The Breit–Wheeler process, 2γ → e⁺e^–, although conceptually simple, being the inverse process of the Dirac one, has been by far one of the most difficult to be verified experimentally. Only recently, through the technology based on free electron X-ray laser and its numerous applications in Earth-based experiments, some first indications of its possible verification have been reached.

”, s621mö,

Physics Reports —

ELECTRON-POSITRON PAIRS IN PHYSICS AND ASTROPHYSICS: FROM HEAVY NUCLEI TO BLACK HOLES

— Ruffini et al., 2009

http://www.icranet.org/4th_ICRANet_Scientific_Committee/Volume2-Scientific_Report/08Xue_b.pdf

s621-s921 (300s)

H8

”The Breit–Wheeler process, on the contrary, is still today waiting a direct observational verification.”, s629m,

Ruffini et al., 2009

Ytterligare bekräftelser på TNED

POSITRONER FRÅN GULDATOMER VIA LASER 2009

Ytterligare bekräftelser på TNED

Genom att de kortpulserande (1pS) laserpulserna repeterat skjuter 1MeV-pulser mot atomkärnor, kan det för varje sådan puls avges ett elektron-positronpar i utbyte — och så långt lagret räcker: Enligt TNED, per atomkärna lika med ±909A, för Guld (A=197) lika med max 179073 par ±e [Se utförligt från 1818e-massivet]

[~1,14606 T34 (e+)/M³ = 1,14606 T28 (e+)/cM³].

Med andra ord: Bekräftelser på TNED.

Försöken i

—————————————————————————————————————

Physical Review Focus — LASERS PROVIDE ANTIMATTER BONANZA, 2009

http://focus.aps.org/story/v23/st8

—————————————————————————————————————

rapporterade 1 T16 (e+)/cM³.

Föreställningen i MAC att ’massa skapas ur masslös ljusenergi’ [‡6] blir i ljuset av elektronmassans komponenter (tau-ringarna), en alldeles uppenbarligen helt säkert djupt rotad feluppfattning [Se Strukturargument för elektronen] — Den förvärras betydligt av att man inte heller (ännu Sep2010) tycks räkna med möjligheten att atomkärnan består av en ekvivalent sammansätt väv av ±e (909A elektron-positron-par, se särskilt från CENTRALMASSIVET i TNED);

laserbestrålning på guldatomkärnor ’skapar’ ±e-skurar,

Physical Review Focus — LASERS PROVIDE ANTIMATTER BONANZA, 2009

http://focus.aps.org/story/v23/st8

±e-par från guldatomkärnor — beskrivning

Med den nya högpresterande lasertekniken, med korta högenergetiska intermittenta pulser (på minst motsvarande 1 MeV per) som riktas mot typ guldfolier,

”A research team used lasers to produce more positrons (anti-electrons) inside a solid than any previous experiment, according to the researchers involved. In the 13 March Physical Review Letters, the team describes firing short pulses from an intense laser onto thin gold targets and creating a high-density positron source that could be used to investigate exotic phenomena near black holes or supernovae.”,

Physical Review Focus — LASERS PROVIDE ANTIMATTER BONANZA, 2009

http://focus.aps.org/story/v23/st8

visar sig rent experimentellt och i full enlighet med TNED en skur av elektron-positronpar som frigörs ur de tunga atomkärnornas ±909A elektron-positronbank.

Max antal ±e-par som kan frigöras ur en guldatom är enligt TNED

909(197)=179073;

±e-tätheten per cM³ är (med kubiska medelavståndet mellan atomerna som ca 2,5 Ångström = 2,5 t10 M) lika med

1,14606 T28 (±e)/cM³ med motsvarande halva positrontätheten

5,73030 T27 (e+)/cM³

I de nyare laserexperimenten har man hittills (2009) uppnått

1 T16 (e+)/cM³

Det finns — således — ännu mycket kvar att hämta.

”Hui Chen and Scott Wilks of the Lawrence Livermore National Laboratory in California and their colleagues now report that they have generated copious amounts of positrons with intermediate energies--in the range of a million electron-volts.”,

”They fired picosecond pulses with intensities of around 10²⁰ watts per square centimeter from the Titan laser at Livermore's Jupiter laser facility onto millimeter-thick gold targets. Positrons were produced via the "Bethe-Heitler" process, in which part of each laser pulse creates a plasma on the surface of the target, and the remaining part of the pulse then blasts electrons from the plasma into the solid. Next, the electrons are slowed down by gold nuclei, an interaction that generates gamma-ray photons. The gamma rays then interact with more gold nuclei and transform into electron-positron pairs.”,

Physical Review Focus — LASERS PROVIDE ANTIMATTER BONANZA, 2009

http://focus.aps.org/story/v23/st8

Medan (således) TNED (tydligen) fortsätter att bekräftas främst rent kvalitativt per experimentalfysikens fortsatta tekniska utveckling, avancerar tydligen MAC vidare inåt i väven av mera avancerade föreställningar.

Förr eller senare kommer urladdningen.

Strukturargument för elektronen

Tillägg till artikeln Ytterligare bekräftelser på TNED — Angående QED1 i MAC:

—————————————————————————————————

Genom att elektronen-positronen uppvisar STRUKTUR [gen. materialens olika termoelektrooptiska egenskaper — resonansverkan, olika mönster],

— består av en viss mängd strömringar baserade på massa, laddning och spinn och som ansluter till massprincipen i TNED med obegränsat underliggande underfraktaler för att kunna betjäna primära massförstöraren (E=mc²) vid parannihilation,

blir varje reguljär SKAPELSE av elektron-positronmassa utesluten ur fysiken enbart av strukturens skäl.

ENERGILAGEN i relaterad fysik visar redan i sig, mera elementärt, att massa kan förintas därför att den inte kan skapas — och blir därför enbart i sig det enda kriterium som behövs.

Men det är — ändå — inget argument i MAC eftersom man där redan har kommit överens om (sedan 1927) att det är tillåtet att göra våld på energins bevarande i QED.

Tills atomkärnan uppdagas som en sammansatt väv av ekvivalenta 909A elektron-positronpar [proportionaliteten massa-laddning i NEUTRONEN via PASTOM i TNED ger m[e]/m[n]=1836,624e med TNED-uppdelningen i 1818e+18e+2,624e med centralmassivet 1818e=±909e som bevaras i varje atomkärna per nukleonmassenhet, totalt minst A909e-par för varje nuklid med A=masstalet] kan man därför i MAC fortsätta att behålla sin uppfattning att massa (±e) skapas ur masslös ljusenergi (med hjälp av laser) — som dock (ännu Sep2010) måste träffa redan befintlig ±e-materia, se BW-BH-processen.

Induktansen klargör

Men det finns ytterligare ett argument i relaterad fysik mot MAC. Nämligen induktansen (L). Närmare bestämd den elementära rymdinduktansen:

— Även OM man gör överenskommelser som går ut på att ’det finns negativ rymdinduktans’ måste man konsekvent uppfinna ’negativ rymd’; I relaterad fysik, i universums praktiska fysik, utgår induktansbegreppet ifrån

[Se Uppkomsten av induktion och magnetism enligt relaterad fysik]

divergensen (c) med ljusets absolutacceleration (a=c/dT) och Ändringslagarna

(varje tillståndsändrande kraft motsvaras av en lika stor tillståndsbevarande kraft)

med uppkomsten av ett motsvarande rymdmostånd (R) med förankring i härledningen från gravitationen (GRIP), se explicit GcQ-teoremet, och som uppställer begreppet rymdkompakthet (konv. magnetiska konstanten)

µ = R/c ................................ rymdkompaktheten, VS/AM

och som leder till rymdinduktansen enligt

RdT = µds ..................... rymdkompakthetens differentiella längdberoende (strömriktningen), VS/AM · M = VS/A

Det finns, relaterad fysik, bara en — 1 — rymd där fysikens fenomen iakttas, observeras och studeras — inte flera. Liksom negativ temperatur, negativ energi eller andra negationer av absoluta storheter i relaterad fysik saknar praktisk betydelse, kan inte heller negativ induktans förekomma i naturbeskrivningen (gäller inte i MAC, jämför QED1).

Den — här, antydda — aspekten på ±R i sammanhanget gäller nämligen via PARANNIHILATION och energins bevarande enligt

E = LQ²/t² ................. se Kommutativa energiekvivalenten i Massvärmet

med

Q² = (m/R)(A/dT) ....... elektriska laddningens kvadrat, ingår inte i MAC

Då m|Q försvinner [Parannihilation, (m→γ)] tvingas induktansen (L) öka med given utgångsenergi (E): OM m i realiteten aldrig försvinner, utan fortsätter att vara den spektakulära massa som MAC kräver, skulle heller ingen observerbar induktiv effekt [gammastrålningen (γ) i (m→γ)] alls kunna observeras då ±e förintas, och därmed inget påvisade alls av någon som helst koppling till en primär massförstörelse [E=(m→γ)c²]: Blotta energiöverföringen i (m→γ) bygger på att L ökar på bekostnad av att Q avtar.

Det faktum ATT en experimentellt observerbar diametral gammapuls ALLS existerar från parannihilation är (således) det enda kriterium som alls krävs ENLIGT RELATERAD FYSIK för att säkert fastställa att sambandet E=(m→γ)c² verkligen är kvalitativt irreversibelt men kvantitativt kommutativt. Dvs., energi kan UTBYTAS ekvivalent kvantitativt mot massa, men aldrig skapa massa, och vilket redan framgår i ENERGILAGEN enligt relaterad fysik.

Se även i ENTROPIBEGREPPET i relaterad fysik där irreversibilitetsbegreppet behandlas utförligt genom jämförande exempel, se särskilt i Kausalordningen [Fysikens lagar är orsaksbaserade] och Arbetsexempel, Utförligt Arbetsexempel 1-3, Exempel genom Wikipedia och Entropin i konkreta praktiska exempel.

Se även i Skapelse eller delning, samt Neutronfragmenten där ovannämnda aspekter beskrivs mera fördjupat [Kosmiska strålningen kontra partikelacceleratorer] i ljuset av experimentalfysiken och de olika svårigheterna i samband med tolkningsföreträdena TNED/MAC.

Yung-Su ref

QED-historien från början — Omfattande, utförligt med historiken till Bethe-Heitler-processen:

PAIR PRODUCTION AND BREMSSTRAHLUNG OF CHARGED LEPTONS — Yung-Su Tsai, Stanford Linear Accelerator Center, 1974

http://www.slac.stanford.edu/cgi-wrap/getdoc/slac-pub-1365.pdf

Boktypografisk version finns nedan, men texten kan inte kopieras,

http://www.physics.isu.edu/~tforest/Classes/NucSim/Day8/Tsai_ScreeningFunctions_Rev.Mod.Phys._vol46_pg815_1974.pdf

Sidhänvisningarna i citaten här anges med bägge respektive ovanstående dokument typ »s1mö|s815sp1n»

’materia från laser’

————————————————————————

»Klassisk parbildning» generellt från elektronstrålning

e^– →| Z | ~~~ γ → ± X

En elektronstråle får träffa ett materiellt strålmål Z (vanligen någon form av metallfolie eller tunn tråd [‡1]); den snabba inbromsningen av de elektriskt laddade elektronerna skapar en stark och snabb induktionsspänningstransient (stoppstrålning eller bromsstrålning) γ; är elektronenergin tillräcklig i energi-massa-ekvivalenter, kan motsvarande materiella parbildning ±X framträda ur Z via e genom γ. Massa-energi-ekvivalenterna garanterar genom energilagen att fysiken tvunget, obönhörligt, måste genomföra en sådan ordning (naturen lyder den matematiska fysikens ekvivalenter).

”The work on this paper started about ten years ago when Stanford Linear Accelerator Center was still under construction. At that ,time like any other new high energy physics. laboratory, people were concerned with problems such as what would be the yields of muons, pions, K mesons, antiprotons etc. and also whether any new particles such as W bosons and heavy leptons could be discovered by the new machine.”,

;

”In the electron machine these particles are produced by the bremstrahlung beam which in turn is produced by the electron. Hence one has to know accurately the properties of the bremsstrahlung beam in a fairly thick target. The pair production is related to the bremsstrahlung problem by a substitution rule, thus the electron pair production cross section

can be calculated trivially once we know how to calculate the bremsstrahlung by electrons.”, s1mö|s815sp1n,

Yung-Su Tsai 1974

Bethe-Heitlers banbrytande bidrag

”Bethe and Heitler¹³ (1934) treated both the bremsstrahlung and the pair production relativistically using the Born approximation, in which the screening of the nuclear coulomb field was properly taken into account. Wheeler and Lamb¹⁴ (1939, 1956) treated the same phenomena in the field of atomic electrons.”,

”Experimentally, the productions in the nuclear coulomb field and the electron field always occur together, hence two effects must be combined in order to make comparison with experiments.”,

”When the atomic number Z is large, the correction to the one photon exchange mechanism must be included and this was done by Bethe and Maximon^l5 (1954), Davies, Bethe and Maximo¹⁶ (1954), and Olsen¹⁷ (1955). It should be noted that in Bethe and Maximon, ^l5 it was erroneously stated that the Coulomb correction affects only the pair production but not the bremsstrahlung. This error was corrected by Olsen l7 (1955).”, s5m|s816sp2m,

Yung-Su Tsai 1974

”Bethe and Heitler¹³ (1934) treated a special case in which the target particle is an infinitely heavy pointlike and spinless nucleus whose coulomb field is screened by atomic electrons. They did not include the atomic excitation of the target which was later considered by Wheeler and Lamb (1939).^l4”,

”While these treatments by Bethe and Heitler¹³ combined with the work of Wheeler and Lamb¹⁴ adequately describe the pair production of electrons at high energies and small angles, they are not adequate to describe the pair production of particles with mass of muons or heavier, because the effects of nuclear form factors and the recoil of the target system must be included when heavy particles are produced.”,

”Even in the electron pair production the nuclear form factors and the recoil must be taken into account if the production angle is large. In fact when the transverse momentum of the particle produced is much larger than the mass, the cross section is nearly independent of the mass of the particle produced.”,

”Drell and Walecka (1964)38 generalized the result of Bethe and Heitler to deal with a target of arbitrary mass, spin and form factors and arbitrary final states.”, s9ö|s817sp2mn,

Yung-Su Tsai 1974

——————————

Citatreferenser, speciella

[‡]1:

”2. In practice, pair production and bremsstrahlung take place in a medium of finite thickness (except in the colliding beam experiments), the effect of which must be taken’into account in actual applications of the theory.”, s6m|s817sp1ö,

Yung-Su Tsai 1974

BH-mekanismen

Se även Bethe-Heitler processen

»Bethe-Heitler mekanismen»

”the emission observed from the passage of e.g. electrons in thin amorphous foils (the Bethe-Heitler mechanism)”, s3m,

Experimental Investigations of the Interaction of Multi-GeV Particles with Strong Crystalline Fields — Ulrik Mikkelsen, 1997

http://phys.au.dk/fileadmin/site_files/publikationer/phd/Ulrik_Mikkelsen.pdf

Återigen: många författare använder termen/begreppet ’Bethe-Heitler mechanism’, få ger någon förklarande beskrivning. Ovan ett av de få undantagen.

Kalkylkortet

kalkylkortet nedan DIREKT FRÅN DEN HÄR WEBBLÄSAREN Casimir.ods — se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar — förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)

http://www.universumshistoria.se/AaKort/Casimir.ods

Kalkylkortet

Casimir.ods

KALKYLKORT ingår generellt i UNIVERSUMS HISTORIA för dokumentpresentationer där mera omfattande beräkningsarbeten ingår. Allt annat är uteslutet FÖR DEN RELATERADE FRAMSTÄLLNINGENS SKULL — man ska kunna följa framställningssättet i de avgörande partierna genom att själv utföra och kontrollera beräkningsprocedurerna — och ev. också kunna utverka egna utvecklingar om tid och intresse finns.

En fullständig manual till varje kalkylblock ligger emellertid utanför ramen för presentationen: endast partierna i huvudsak beskrivs, som nedan, illustrerat, med vissa förtydliganden. Kalkyldelarna är i vilket fall tänkta att kunna förstås (improviserat) av den som är insatt i framställningens detaljer.

Tabellflik 1

Casimireffekten — med

Platta-Sfärsamband enligt Prevenslik, Mohideen, Klimchitskaya

Kontrollräkning | Jämförande tabeller — Kovalenta bindningar | Väte

ÄMNESTABELL till Casimireffekten — Alla materialvärden vid rumstemperatur

Lambväxlingen [äv. Lambövergången el. Lambskiftet] | Okt2010 — med alternativa CODATA-konstanter

iteration Unit1 — Casimireffekten 23Okt2010

Tabellflik 2

Elektronens g-faktor — jämförande värden | Okt2010

Tabellflik 3

ELEKTRONENvdW — van der Waals krafter

Jämförande tabeller — Kovalenta bindningar

Jämförande metallbindningar

Casimireffekten Tabellflik 1:

Huvudkort

Inmatning | Resultat

innehåll: SÖK på denna sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

Elektronen i materien — Positronbildning · van der Waals krafter

ämnesrubriker

RubrikBilder

innehåll

ELEKTRONEN I MATERIEN

Inledning

Grundämnesmetallernas Brotthållfasthet — inledning

Diagram Rm3

Kohesionsmatematiken i MAC

Kohesion och Adhesion — inledande praktisk orientering

Termdefinitioner, etymologiskt

Adhesion, köksexempel

Kohesion, köksexempel

Primära kohesionen

Fenomenorsaker

VAN DER WAALS KRAFTER — inledning

Casimireffekten — från allmän hållfasthetslära

Jämförande funktionsgrafer MAC-TNED

Exemplet med Segjärn

Teknisk verifikation

Grundläggande hållfasthetsbegrepp

Grundsamband — ENERGIINNEHÅLL och KRAFT

KJ/mol

Jämförande tabeller — Kovalenta bindningar

Jämförande metallbindningar

Styrka — bindningssätt — begreppet kovalent från MAC

Vätebindningen H—H

Kovalenta bindningsgeometrins grund

Vätebindningens grundgeometri

Syntes

Kovalenta bindningens allmänna form

Kovalenta bindningen, energiformen

Grundämnesmetallernas brotthållfasthet, Diagram Rm1

Grundformen justerad

Grundämnesmetallernas brotthållfasthet, Diagram Rm2

SAMMANFATTNING

Van der Waalskrafterna — materialens sammanhållande energi

Grundsamband

Grundsambandets härledning

Brottgränsen

Jämförande Tabell, Hamakerkonstanten

Van der Waals krafter

Kovalenta allmänna atombindningsformen

Förklaringen

Allmänna samband, VdW

Elastiska separationstrycket

HamakerBrottgränsen

Hamakerkonstanten från Rm

HamakerExempel, olika konstanter

Brottgränsexempel Koppartråd

Brottgränsexempel, Järn

Hamakers konstant, innebörd

Jämförelsens grunder — TNED-MAC

Casimirgraferna

Casimirgraferna — Jämförande intervall

Analysområdet

TNED-Casimir

Jämförande exempel National Laboratories

PRAKTISKT EXEMPEL MED KOPPAR

van der Waals krafter inom kemin

Intermolekylära krafter — webbreferenser

WikipediaAdhesion

Freitas VdW 1999

Washington University, 1

Hamakers konstant

Washington University, 2

Vatten Rm

Cut-off ref

Van der Waals kontra Casimir

Övergången vdW-Casimir

Hållfasthetsreferenser på Webben — Grundläggande hållfasthetsbegrepp

Belastningsdiagram

Kallfogning

Teori saknas

Minst 40% deformation

Kallfogningsgränser

Materialens brottgränser överskrids av MAC-Casimir

Brottgränstabeller i MAC

MatWeb

Brottgränstabell i Wikipedia

Järnexempel, segjärn

Parbildning i MAC

Massa-ljus-massa-omvandlingar i MAC

Ruffin s626 — Breit-Wheeler process

BH-processen

BW-BH-process

BW-genombrottet

limΞ — MAC-gränsvärdet för ’vakuumets spontana elektron-positron-uppkomst’

Historia — Parbildning

Ytterligare bekräftelser på TNED — POSITRONER FRÅN GULDATOMER VIA LASER 2009

Strukturargument för elektronen

Yung-Su ref

BH-mekanismen

Kalkylkortet

Beskrivning

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1,602 t19 C ...................... [ref. FOCUS MATERIEN 1975 s666]

ε₀ = 8,8543 t12 C/VM ............. [ref. FOCUS MATERIEN 1975 s666]

BKL BONNIERS KONVERSATIONSLEXIKON Band I-XII med Supplement A-Ö 1923-1929

t|T förenklad exponentbeteckning: t|T för 10^ – | +; EX.: t19 = 10^–19

PREFIXEN FÖR bråkdelar och potenser av FYSIKALISKA STORHETER

Här används genomgående och konsekvent beteckningarna

förkortning för förenklad potensbeteckning

d deci t1

c centi t2

m milli t3

µ mikro t6

n nano t9

p pico t12

f femto t15

Alla Enheter anges här i MKSA-systemet [Se International System of Units] (M meter, KG kilo[gram], S sekund, A ampere), alla med stor bokstav, liksom följande successiva tusenprefix:

K kilo T3

M mega T6

G giga T9

T tera T12

Exempel: Medan många skriver cm för centimeter skrivs här konsekvent cM (centiMeter).

MAC Ofta använd förkortning för modern akademi (Modern ACademy) i Universums Historia.

TNED (Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås (således) också RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning (Planckfraktalerna).
OM man ska försöka lyfta fram något CENTRALT — i syntes — i TNED kan det bara bli följande:
N3m20 — atomkärnans härledning — kopplar direkt till NEUTRONKVADRATEN via deuteronkopplingen [den centrala aggregattransformationen mellan de två olika nukleära formfaktorerna i TNED som definierar grunderna för fusionsfysiken] som kopplar ATOMVIKTERNA, vilka direkt visar jämförelsen TNED-MAC.

UTVIDGAD ORDLISTA — ElektronenVdW.htm 2010

Materiallära, grundbegrepp

Hållfasthetslära, grundbegrepp

Hållfasthet, materialfysiken

Brotthållfasthet, materialfysiken

Brottgränsen (Rm), materialfysiken

Hamakerbrottgränsen, materialfysiken

Hamakerkonstanten

Hamakers konstant, innebörd

Kohesion

Adhesion

Casimireffekten [mera utförligt i ElektronenLEC.htm]

Casimirgraferna — Jämförande intervall

Grundämnesmetallernas brotthållfasthet — jämförelse Uppmätt-Beräknat, Diagram Rm 1-3

KJ/mol

Kovalenta bindningsgeometrin

Vätebindningen H—H

van der Waals krafter

van der Waals krafter inom kemin

Intermolekylära krafter — webbreferenser

Hållfasthetsreferenser på Webben — Grundläggande hållfasthetsbegrepp

Senast uppdaterade version: 2011-08-21.

*END.

Stavningskontrollerat 2010-11-12.

rester

*

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

τ π ħ √ ε UNICODE — ofta använda tecken i matematiska-tekniska-naturvetenskapliga beskrivningar

σ ρ ν ν π τ γ λ η ≠ √ ħ ω → ∞ ≡

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ ϕ σ ω ϖ ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ˂ ˃ ˂ ˃ ← ↑ → ∞ ↓

ϑ ζ ξ

Pilsymboler, direkt via tangentbordet: Alt+24 ↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬

Alt+23 ↨ — även Alt+18 ↕; Alt+29 ↔

PNG-justerad 2011-08-21

åter till portalsidan · portalsidan är www.UniversumsHistoria.se