UNIVERSUMS HISTORIA | K-cellens inre | 2012V7 a BellDHARMA production | Senast uppdaterade version: 2012-07-15 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

| G-faktorerna | Transitfunktionen | GRB | Täthetsändringens funktioner | DIVERGENSENS EXPANSIVA G-BEROENDE | Mörka Materiens Ursprung enligt TNED | Mörka Vintergatsmaterien | Fria fallets G-fysik

GRB1—K-CELLENS INRE • GRB1m—MörkaMaterien • GRB1n—Primära v-formen • GRB2—UniversumsSynrand • GRB2a—AkroBreak • GRB3—GRBorigin

| GRUNDFYSIKEN | K-cellens övergång i c0-kroppen | Gravitella dopplereffekten | Divergensenergins g-beroende | Divergenständningarna i detalj | KosmiskaPartikelstrålningensUrsprung |

INLEDNING — K-cellens inre fysik — Upphovet Till Gammastrålskurarna Och Den Mörka Materien Enligt Relaterad Fysik

BILDKÄLLA : Författarens arkiv · Miljö2012 M3 23Mar2012 Naturskog2Bild26 · Nikon D90 Detalj

K-cellens inre fysik — UPPHOVET TILL GAMMASTRÅLSKURARNA OCH DEN MÖRKA MATERIEN ENLIGT RELATERAD FYSIK

Resultatredovisning K-cellens inre

| G-potentialerna K-cellen-c0-kroppen | Primära v-formen | Utvecklingen i K-cellens expansion |

Snabbsammanfattning — K-cellens värmefysik i UNIVERSUMS HISTORIA

TNED — såvitt inga fel föreligger, vilket är det ständiga föremålet för den löpande analysen:

— I RELATERAD FYSIK har det visat sig att UNIVERSUM kan beskrivas på en periodiskt pulserande central cell (kosmisk kropp) här benämnd K-cellen [K-cellen, K-cellens detonation].

— Grunden till det beskrivningssättet — och som skiljer hela framställningssättet från det konventionella — ges genom LJUSETS GRAVITELLA BEROENDE tillsammans med ATOMKÄRNANS HÄRLEDNING; Se särskilt i Jämförande Atomvikter som visar, och exemplifierar, den teoretiska grundens PRAKTISKA förankring, och därmed anledningen varför ämnet INTE finns representerat i den moderna akademins lärosystem. Se speciellt i Universums kritiska täthet, vilket, särskilt, motiverar den här framställningen: K-cellens (Universums) inre fysik på villkor av ljusets g-beroende [DGD]; orepresenterat i MAC.

Detaljerna från Grunden — K-cellens idealt homogena medeltäthet

K-cellens värmefysik grundlägger den relaterade matematiska fysikbeskrivningen (TNED) av universum — på ett idealiserat homogent täthetsbegrepp (Primära v-formen), och med stöd av en uppsättning (under 1900-talets senare del) allmänt kända observationsdata:

· galaxernas rödförskjutning

· kosmiska bakgrundsstrålningen

· synliga materiens medeltäthet

· förhållandet väte-helium

Ur dessa följer i resultatdelen ytterligare fyra avgörande faktorer — som (i denna framställning) under alla omständigheter måste innefattas i varje RELATERAD övergripande bild av universum, dess historia och utveckling:

· K-radien (den avgörande strålsfärens radie vid effektmaximum — resultaten enligt Stefan-Boltzmanns strålningslag) [‡Centralparametrarna]

· Ljusvägens integral till K-radien [‡Centralparametrarna]

· Tiden vid effektmaximum [‡Centralparametrarna]

· Kvoten mellan synliga och totala massan i K-cellen [‡Centralparametrarna]

En kort översiktligt beskrivande sammanställning av dessa fyra sistnämnda, hur de framkommer i K-cellens värmefysik, finns i sektionen Centralparametrarna i K-cellens värmefysik.

MOTSVARANDE BESKRIVNINGAR I MODERN AKADEMI

— Eftersom hela beskrivningssättet i TNED grundas på grundläggande fysikbegrepp som står helt orepresenterade [‡InledningNot1] i den moderna akademins lärosystem

— PLANCKEKVIVALENTERNA, LJUSETS GRAVITELLA BEROENDE, ATOMKÄRNANS HÄRLEDNING från Plancks konstant med vidare uppdagande av NEUTRONKVADRATEN och därmed ATOMVIKTERNA som tydligen visar en betydligt mera precist överensstämmande teoretisk bild av kärnfysiken än den konventionella

— finns heller inga direkta paralleller till fysikbeskrivningen generellt i modern mening.

— Den jämförande resultatbilden, och där en sådan alls kan framställas, endast utpekar modern akademi som en PRIMITIV inrättning.

— Jämför Atomvikterna — det mest direkta, konkreta, och avgörande exemplet.

Behovet av en mera precis översiktsbild

Snabbsammanfattning

Men ett idealiserat homogent täthetsbegrepp (Primära v-formen) kan bara beskriva K-cellens utveckling som en sammanhängande kropp — utan inre detaljer — med hela massan idealt fördelad över den expanderande volymen, och därmed bara i en viss begränsad mening; Ingen som helst möjlighet finns där att precisera olika partier i K-cellens inre.

Speciellt i sektionen Offsetvärdet för T [”expansionstiden kan förkortas om kroppens täthet ändras”] som ansluter till grundmatematiken [‡GRUNDFYSIK] i K-cellens värmefysik, antyddes (redan i originalförfattningarna från 2007) ordningen för en mera praktiskt orienterad bild av K-cellen genom inre täthetsförskjutning. I dåvarande författning (2007) kunde inte den detaljen föras vidare — vilket däremot presentation här är tillägnad ett närmare studium.

Den centralt observationellt avgörande aspekten — som absolut måste förklaras, beskrivas och redovisas i detalj — är under alla förhållanden det medelmässigt antagna rödförskjutningsvärdet (K=1,5 motsv. c0/v, Rödförskjutningssambanden).

— I en rymd med samma ljushastighet (c=c0) överallt, skulle det värdet enligt relaterad fysik (Se Dopplereffekten) kräva en frånrörelse hos de galaktiska objekten på v/c0=1/K=0,67.

— Med K-cellens massa (m2=4,14 T53 KG) idealt fördelad jämnt över hela K-cellens volym, blir det närmaste vi kan komma den värdesiffran lika med runt 0,18:

r = T^2/3(1/2)(4Gm₂)^1/3 .......................... grundform, homogen täthet från r-formen

= 4,28 T25 M ................................... K-radien vid T=16,32 T9 år:

m = [2r_K16,32(T)^–2/3]³/4G

= m₂(0,021408532) .......................... inneslutna, täthetshomogena delmassan

v = T^–1/3(2/3)(1/2)(4Gm₂)^1/3 = r’ r-derivatan, Se från r-formen

= c₀(0,1847779)

c/c₀ = Ö 1 – 2(w/c₀)² ................................. gravitellt bestämda lokala ljushastigheten vid r

= 0,960821811

vilket blir en helt omöjlig uppgift i praktisk fysik;

— Gravitella rödförskjutningsvärdet (GKKD-sambandet) (Gravitella dopplereffekten) (1‑0,960821811=0,0391782) + v/c0-värdet 0,1847779 skulle här ge summan 0,2239561=1/K med K=4,651608.

— Det som krävs är K=1,5.

Det finns ingen fysisk koppling till den matematiken i ljuset av det oeftergivliga kravet på att K-värdet K=1,5 måste uppfyllas (inom en max marginal på 3%).

I TNED blir enda lösningen att söka en täthetsändringsfunktion i det INRE av K-cellen: en matematisk form som KAN satisfiera de givna grundvärdena med garanterat bevarande av K-cellens redan formulerade yttre: den medelbaserade idealt homogena masstätheten [K-cellens värmefysik]. Se särskilt vidare från Lösningen I TNED.

Angelägenheten i framställningssättet är också (speciellt krävande):

— OM K-värdet med bibehållen K-radie via tidpunkten för effektmaximum (T-värdet 16,32 T9 år) INTE kan visas gälla (inom en 3% felmarginal) genom en täthetsökning in mot K-cellens centrum, vars form vi nu söker, och som kan förklara och beskriva expansionens avstannande, tillsammans med alla övriga observerade fenomen, då gäller INTE heller K-cellens värmefysik, och därmed heller inte TNED.

— Det finns, nämligen, inga parametrar att kompromissa på, inga detaljer att tänja formgrunderna för, inga oklara samband att utreda: Detaljerna är redan formulerade från TNED i grunden i K-cellens värmefysik. Kan deras vidare tillämpning inte leda (direkt) på praktiska observationer, är och förblir framställningssättet felaktigt.

— Det har visat sig — hittills (Apr2012) — att resultatbilden håller (än så länge: inga som helst direkta angreppspunkter verkar finnas inom synhåll), vilket den här presentationen ska försöka klargöra mera i detalj — för K-cellens del.

— Men helhetsbilden blir samtidigt svårare att omfatta via enkla sambandsgrunder då fördjupningarna kräver en allt mer — konsistent — sammanhängande matematik. Det kräver motsvarande mera av läsaren — som kanske inte alltid har den TID som krävs för att sätta sig in i alla detaljer. Meningen är dock, generellt i kunskapssammanhanget, att en sådan översikt SKA vara praktiskt tillgänglig (och praktiskt möjlig, utan att kräva allt för mycket tid i studium), speciellt i sammanhang som berör en översiktligt fattbar praktiskt förankrad fysikbild av universum. Missas den översiktsbilden, är kunskapsmålet (i vilket fall) förlorat.

DRIVKRAFTEN — motivet bakom — till föreliggande beskrivning återfaller på begreppet GRB (eng. gamma-ray bursts): behovet att undersöka OM K-cellens fysik också, eventuellt, skulle kunna kasta något klargörande ljus över det aktuella fenomenet. Men det skulle samtidigt kräva en mera rejäl djupdykning i förutsättningarna till K-cellens värmefysik, och i vad mån dessa, verkligen, skulle kunna servera de eminenta gästerna deras åstundade middag. Det är i korthet den drivande kraften bakom hela den här presentationen.

Se vidare från K-cellens övergång i c0-kroppen, Täthetsändringens funktioner, Lösningen i TNED.

———————————————————— [‡]1

— »Light’s Gravitational Dependency» ger nollresultat på innehållet i ETABLERAD WEBBSÖKNING (Apr2012). Frasen/Begreppet/Termen finns inte ens omnämnd i modern akademi. Se även jämförande detaljer i Einsteins samband.

K-cellens övergång i c0-kroppen — 2012IV11

INLEDNING

K-cellens övergång i c0-kroppen

Bildkälla: MAGIC NATURE

| Formgeometrin | Medeltätheten utanför K-cellen vid stoppunkten | G-potentialer och tätheter i och utanför K-cellen |

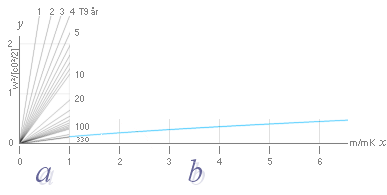
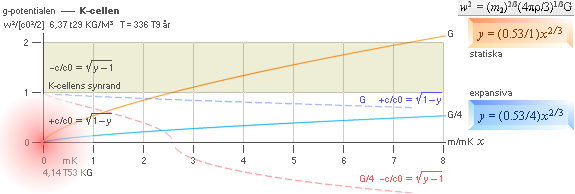
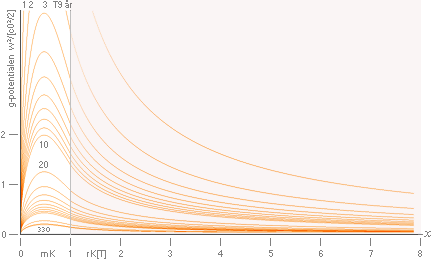
Figuren nedan höger: G-potentialens växande värde (w²=r²[Gpr/3] statiska tillståndets samband) för konstant medeltäthet tillväxer proportionellt mot den omslutna massfärens radiekvadrat (r²).

c0-kroppens idealt obegränsade utsträckning via K-cellens idealt homogena täthet (6,37 t29 KG/M³) vid expansionens avstannande (T=336 T9 år) i K-cellens massenhet (4,14 T53 KG) visas i de två olika versionerna (G-faktorerna): statiska (orange [G]) och expansiva (blå [G/4]).

— De streckade kurvorna visar motsvarande lokala divergensvärde (ljushastighetens gravitellt bestämda punktvärde) för motsvarande sfäriskt inneslutna massor.

— Vi ser att ENBART på dessa givna teoretiska grunder, det INTE går att få fram någon mera precis bild av K-cellens inre.

Kc0H

K-cellens idealt homogena täthet

Detaljerad information om g-potentialens värden i K-cellen — under hela K-cellens utvecklingshistoria

K-cellens övergång i c0-kroppen via K-cellens idealt homogena täthet — vilket INTE är det praktiska fallet. Vidare i huvudtexten.

Termgrunder om ej redan bekanta beskrivs utförligt i Neutronen, Plancks konstant, Atomkärnans härledning, Ljusets gravitella beroende, c0-kroppen.

— Se även motsvarande i jämförande begrepp med modern akademi i Ljusgravitella typkurvorna och Einsteins samband.

— K-cellen bildar tydligen via g-nollpotentialen i totalmassans tyngdpunkt DEN MAKROSKOPISKT ENDA UNIKA orten för toppvärdet c=c0=2,99792458 T8 M/S.

— Se även den viktiga grundfysiken i Absoluta Metriken (HUR c0 är c0), Gravitationens absolutverkan (varför g-fysiken sker med omedelbar verkan — gravitationen kan inte avskärmas) och GcQ-teoremet (hur elektrofysiken kopplar dessa).

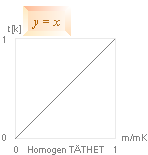
Figuren ovan vänster: K-cellens idealt homogena täthet — sett till hela K-cellens ytterradie, utan avseende på K-cellens inre — ger via grundsambandet (r)

r = T^2/3(1/2)(4Gm₂)^1/3 .......................... grundform, homogen täthet från r-formen

v = T^–1/3(2/3)(1/2)(4Gm₂)^1/3 = r’

en ideal g-potentialform (w², sambanden visas explicit i divergensens nollderivata [Derivata och Integral])

w² = Gm/4r

= (Gm·m₂/m₂)^2/3(32)^–1/3T^–2/3

= (m/m₂)^2/3(Gm₂)^2/3(32)^–1/3T^–2/3

= (m)^2/3(Gm₂)^2/3(32)^–1/3T^–2/3 ; m = m/m2

w²/(c₀²/2) = (m)^2/3(Gm₂)^2/3(32)^–1/3(c₀²/2)^–1T^–2/3

= (6,4123921)(m)^2/3T^–2/3 .................... T i T9 år

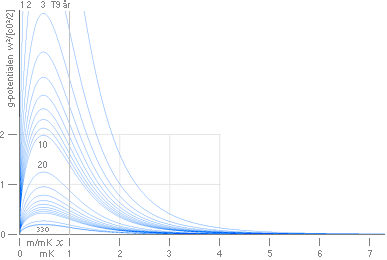
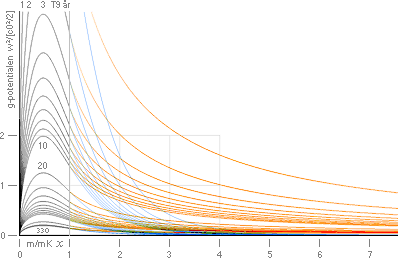
Kurvskaran med olika T-värden i figurens a-del visar funktionen idealt i K-cellen för dess olika massdelar (m)K-cellens delmassa/(m2)K-cellens totalmassa från 0 till 1.

— Kurvdelen i b-delen (havsblå heldragen) visar fortsättningen på K-cellen med den medeltäthet (6,37 t29 KG/M³; Formgeometrin ) som K-cellen uppvisar efter expansionstiden 336 T9 år (förenklat T=330 T9 år i graferna). Den kurvan skulle då motsvara c0-kroppens fortsatta idealt homogena täthet mot oändligt.

— Anledningen varför motsvarande kurvförlängningar för de övriga T-fallen i figurens a-del inte kan ritas ut, utan måste begränsas till K-cellens massfär (m=1), är

— i fallet med K-cellens idealt homogena täthet och frånsett slutpunkten med expansionens avstannande efter T=336 T9 år

— att ingen känd teoretiskt motsvarande variabel övergångsform finns för tätheten mellan K-cellen och den yttre c0-kroppen — en sådan kan inte härledas på K-cellens idealt homogena täthet [Se räkneexemplet i Behovet av en mera precis översiktsbild].

I Formgeometrin visas hur K-cellens lägsta täthet vid expansionens avstannande, tillsammans med matematiken för Fria fallets g-fysik, leder till ett (slutgiltigt) teoretiskt relevant (användbart) värde på c0-kroppens idealt homogena täthet — och som därmed kan beskriva en kontinuerlig övergång från c0-kroppen till K-cellen, med dess variabla täthetshistoria.

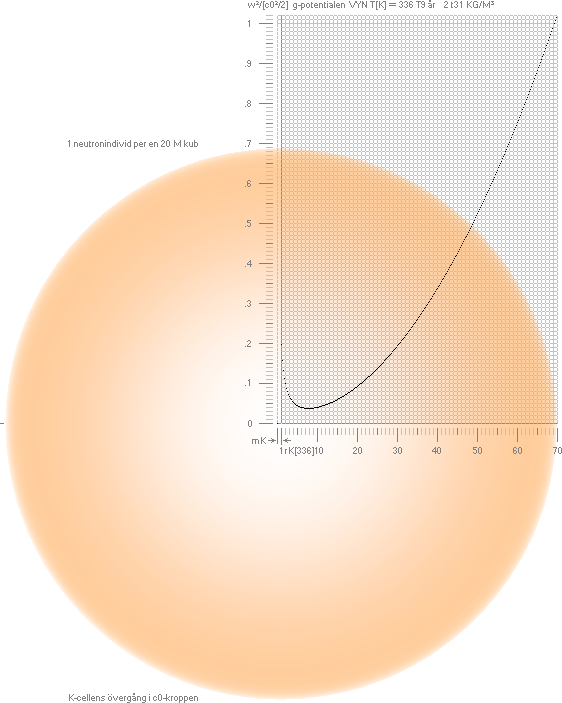
— Figuren nedan (K-cellens g-potentialer, yttre) visar slutresultatet i värden med den här benämnda s.k. Stoppmoderatorn inkluderad (den beskriver K-cellens avstannande i förenklad matematisk form). Figuren visar situationen sett från tillfället vid K-cellens avstannande (T=336 T9 år) vid dess maxradie 7,8 T26 M och minsta täthet 2,08 t28 KG/M³ (Se Kalkylkortsref. nedan). K-cellens egenutsträckning markerar distansen (cirkeln med radien, ej utritad) rK[336]. Den omgivande c0-kroppens täthet kan därmed (slutgiltigt) bestämmas, och man finner värdet 2,21618 t31 KG/M³. Det motsvarar grovt en neutronindivid per en rymdkub med sidan 20 meter (8000 M³).

— Grafen i figuren nedan visar hur g-potentialen (och därmed den lokala divergensen [ljushastigheten]) går från K-cellens ytterrand (1 rK), upp till enhetsvärdet (c=0) — och sedan vidare mot oändligt enligt energiräkningen i Allmänna tillståndslagen.

K-cellens övergång i c0-kroppen, huvudvy — Kc0H — Kc0iH

K-cellens övergång i c0-kroppen enligt TNED ———————————————————————— Alla värden enligt KalkylkortDirekt KcGRB.ods 9KcIN HelpOpen ———————————————————————— VYN visas här vid tillfället då K-cellens expansion precis har avstannat vid T = 336 T9 [miljarder] år: K-cellens yttreradie 7,8 T26 M = rK[336] K-cellens medeltäthet 2,08 t28 KG/M³ c0-kroppens täthet 2 t31 KG/M³ Avståndet till c0-kroppens nolldivergensgräns [c=0], ca 69 rK[336] [Se värden i Medeltätheten] .

Grafsambandet samma som i K-cellen yttre (Graf) men här i förstorad tappning 100 gånger. Hur g-potentialens grafer ser ut inuti K-cellen [mellan 0-1rK i figuren ovan] — den mera utvecklade versionen av K-cellens inre variabla täthet — beskrivs utförligt i huvudtexten nedan.

— Figurkonceptet ovan klargör speciellt det som redan antyddes i Universum Nu (2009), men som då inte kunde föras vidare: K-cellens yttre övergår i c0-kroppen GENOM POSITIV DIVERGENS [c>0] via ett stort övergångsområde (ca 69 rK[336]). c0-kroppens allmänna (obegränsade — från Allmänna tillståndslagen) neutronkallplasma kan därmed förstås börja vid gränsen ca 69 rK[336], eller runt 5,4 T28 M. Vår syngräns (sett från mitten) är i den delen bara runt 1/1000 [K-radien].

Med K-cellens slutradie

[rK=1,16 T27 M utan Stoppmoderatorn, med denna 7,8 T26 M]

vid expansionens avstannande efter 336 T9 år och den uppnådda medeltätheten

[(D=m/V)=6,37 t29 KG/M³ utan Stoppmoderatorn, med denna 2,21618 t31 KG/M³]

via den omslutna K-cellens massa m(K)=4,14 T53 KG som en ekvivalent till den omgivande c0-kroppens idealt homogena täthet, ges grovt ekvivalent medeltätheten i den situationsbilden med

K-cellens täthet vid expansionens avstannande

en neutron per runt en kub med sidan 3 meter (27 M³)

utan Stoppmoderatorn,

(V=m/D) = [1,0086652(u=1,66033 t27 KG)]/[6,37 t29 KG/M³] = 26,290692 M³

med denna

en neutron per runt en kub med sidan 20 M (8000 M³)

(V=m/D) = [1,0086652(u=1,66033 t27 KG)]/[2,22 t31 KG/M³] = 7543,7706 M³

Är c0-kroppens täthet homogen (vilket premisserna tycks anvisa för c0-kroppen [ALLMÄNNA TILLSTÅNDSLAGEN]), tillväxer g-potentialen mot oändligt i c0-kroppens vidare utsträckning med växande sfärradiekvadrat enligt [Grundfysiken, elektrogravitationen, statiska g-fysikens samband] w²=r²(4Gpr/3), med konstant gravitell fältstyrka (accelerationskonstant) a=Gm/r²=2,05215 t11 M/S², resultatfiguren ovan.

— För att härleda de motsvarande kurvformerna — övergången från c0-kroppen till K-cellen, med dess variabla täthetshistoria — måste först en allmän täthetsvariabel funktion härledas (utprovas, testas och analyseras) och som garanterar Centralparametrarna i K-cellens värmefysik.

— Den funktionsformen beskrivs här i en separat sektion Täthetsändringens funktioner i samband med avsnittet om G-faktorerna. Graferna nedan bygger på resultatbilden i den täthetsändringsfunktionens slutform.

Kc0iH

K-cellens praktiskt inhomogena täthet

Detaljerad information om g-potentialens värden i K-cellen — under hela K-cellens utvecklingshistoria

K-cellens övergång i c0-kroppen med inhomogen täthet i K-cellens inre.

Gäller praktiskt i K-cellen bara i x-intervallet 0-1	Gäller alla x från 0 — men via två skilda funktionskomplex: från x=1 mot oändligt via en yttre lägre täthet

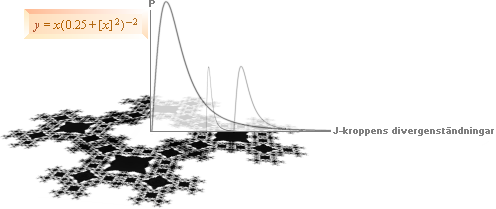
Varje xy-kurva motsvarar K-cellens tillstånd vid en viss tidpunkt [T], här i enheter om [miljarder] T9 år. y-värdet för varje delmassa [x-värdet, m/mK] i K-cellen visar g-potentialens värde i förhållande till c0²/2. Rotvärdet för 1 minus detta visar lokala divergensvärdets [lokala ljushastighetens] ekvivalent [Se även i NEGATIV DIVERGENS].

NOTERA ATT x-skalans enhet från x=1 i den högra figuren motsvarar K-cellens ytterradie rK[T] vid T. Sammanhanget förklaras i huvudtexten.

1:1-Kvadraten [inkluderat utsträckningarna rakt vertikalt ovanför denna] motsvarar de aktuella data i K-cellen, intervallet 0-1 för x. K-cellens synrand [y=1] motsvarar den ideala orangea linjen i illustrationen till Praktiska GRB-ursprunget.

— Notera att massradien [x=1] ändras med T-värdet enligt r-formen nedan; höga g-potentialer [w²] i början av K-cellens expansion innefattar en trång centralmassa; normaliseringen mot c0-kroppens y=x-funktion sker via stora rymdavsnitt för små T-värden. I slutet av K-cellens expansion är de avsnitten istället marginella.

Figurdetaljerna beskrivs vidare nedan i huvudtexten.

GrafBlå y = 6.412[(300)'–2/3][([x]'–0.1737)(0.7+0.3[x]'2)]'–8/3 ; divergensens nollderivata

GrafOrange Samma som blå grafen fram till m=1, sedan annan form via lägre täthetsvärde enligt K-cellens G-potentialer, K-cellens yttre

Graf y = (0.197)(1+[(0.0011)([(1+x)'3]–1)])/(1+x) ;

Koefficienterna, respektive, får beräknas separat via de specifika K-cellens ytterradievärden [1+x] som ges för varje specifik expansionstid [T].

Se utförligt i G-potentialer och tätheter i och utanför K-cellen.

BLÅ KURVSKARAN VÄNSTER ovan divergensens nollderivata gäller strängt för K-cellens täthetsjusterade utvecklingsform endast fram till randen m/mK=1 för K-cellens egenmassa (mK=4,14 T53 KG). Den fortsatta delen har ingen praktisk motsvarighet — funktionsvärden med obegränsat expanderande mK-multipler i en helt odefinierad yttre omgivande rymd.

ORANGEA KURVSKARAN HÖGER ovan K-cellens G-potentialer — K-cellens yttre — dess matematiska form börjar från m/mK=1 — anvisar det praktiska fallet:

— Med K-cellens egen sluttäthet ca 6,37 t29 KG/M³ vid T= 336 T9 år vidtar omedelbart och idealt c0-kroppens lägre täthet 2,2 t31 KG/M³. Denna används sedan idealt för alla T-värden i K-cellens expansion som bas i den motsvarande orangea kurvskarans g-potentialbild som g-formen för den ideala massrymd K-cellens kroppsrand möter i sin expansion fram till slutläget.

Horisontalskalans variabel (x) är då inte längre (vänstra figuren ovan) m/mK utan istället (högra figuren ovan från x=1) K-cellens ytterrand vid T, här betecknat rK[T]. x-skalans r-preferens ändras alltså för varje specifik kurva. Se utförligt sambanden i G-potentialer och tätheter i och utanför K-cellen.

De bägge kurvskarorna tillsammans visar hur funktionerna avlöser varandra sömlöst från och med x=1.

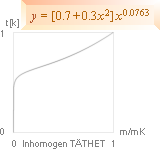
r-formen med Täthetsändringsfunktionens slutform

r = [t(k)T]^2/3(1/2)(4Gm)^1/3 .................. r-formen modifierad med täthetsändringsfaktorn t[k]

= [t(k)T]^2/3(1/2)(4Gm)^1/3

= [T]^2/3[t(k)]^2/3(1/2)(4Gm)^1/3

= [T]^2/3[[0,7 + 0,3(m/m₂)²](m/m₂)^0,1737]^2/3(1/2)(4Gm)^1/3

= [T]^2/3[[0,7 + 0,3(m/m₂)²](m/m₂)^0,1737]^2/3(1/2)(m/m₂)^1/3(4Gm₂)^1/3

= [T]^2/3[(m/m₂)^1/2[0,7 + 0,3(m/m₂)²](m/m₂)^0,1737]^2/3(1/2)(4Gm₂)^1/3

= [T]^2/3[[0,7 + 0,3(m/m₂)²](m/m₂)^0,6737]^2/3(1/2)(4Gm₂)^1/3

= [T]^2/3[[0,7 + 0,3(m/m₂)²](m/m₂)^0,6737]^2/3(Gm₂/2)^1/3 ;

K = (Gm₂/2)^1/3([1 T9]/[3,16888 t8 1/S])^2/3 = 2,39567 T25 M ; m₂=4,14 T53 KG; G=6,67 t11 JM/(KG)²

r/K = [T]^2/3[[0,7 + 0,3(m/m₂)²](m/m₂)^0,6737]^2/3 ; T i enheter T9 år; r i enheter 2,39567 T25 M

K-cellens radiella utsträckning —

INRE delarna efter inhomogena täthetsändrande funktionerna

:

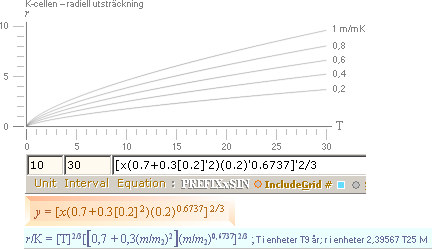
Graf y = [x(0.7+0.3[1]'2)(1)'0.6737]'2/3

med motsvarande v-form för K-cellens inre masspartier

v = [t(k)]^2/3T^–1/3(2/3)(1/2)(4Gm)^1/3 = r’

= [[0,7 + 0,3(m/m₂)²](m/m₂)^0,6737]^2/3T^–1/3(2/3)(Gm₂/2)^1/3

v/c₀ = (1,6881927)[[0,7 + 0,3(m/m₂)²](m/m₂)^0,6737]^2/3T^–1/3 ; T i enheter T9 år; v i enheter c0

K-cellens expansionshastighet —

INRE delarna efter inhomogena täthetsändrande funktionerna

:

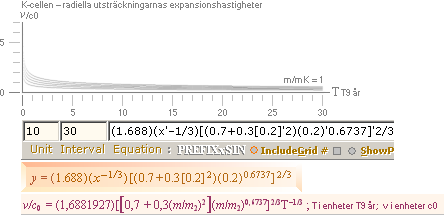
Graf y = (1.688)(x'–1/3)[(0.7+0.3[1]'2)(1)'0.6737]'2/3

ger via divergensens nollderivata grundform för den blå kurvskaran

w² = (Gm)^2/3/[t(k)]^8/3T^2/3(32)^1/3

= (Gm₂)^2/3(32)^–1/3T^–2/3[m^–0,1737(0,7 + 0,3m²)]^–8/3 ; m= m/m_K

Graf y = 6.412[(300)'–2/3][([x]'–0.1737)(0.7+0.3[x]'2)]'–8/3

————— Bildkälla K-cellens övergång i c0-kroppen Magic NATURE — Författarens arkiv

Övre: Excur2012E1:12Apr2012 Bild33 · Nikon D90 Detalj

Undre: Montage · Excur3:16Jun2009 VKBild3·ÄngBild3 · Excur10:22Apr2011Bild14 · Nikon D90 Detalj

Formgeometrin — K-cellens övergång i c0-kroppen

K-cellens övergång i c0-kroppen

Formgeometrin

Bildkälla: MAGIC NATURE

K-CELLENS ÖVERGÅNG I c0-KROPPEN

Med uppgiften (K-cellens halvperiod) T=336 T9 år vid slutpunkten för K-cellens expansion, visar K-cellens slutradie via r-formen [r=T^2/3(Gm₂/2)^1/3] och medeltätheten via expansionssambandet [r=T^–23/2pG] värdena

K-cellen, slutvärden, StopMod=0

r_K336 = 1,16 T27 M ................................. K-cellens slutradie vid T=336 T9 år [StopMod=0]

r_K336 = 6,37 t29 KG/M³ ......................... K-cellens medeltäthet vid expansionens slutpunkt [StopMod=0]

r_K336 = 2,08 t28 KG/M³ ......................... K-cellens medeltäthet vid expansionens slutpunkt [StopMod=1]

KalkylkortDirekt KcGRB.ods 9KcIN HelpOpen

Massförlusten från expansionsperioden (K-cellens halvperiod) är 0,7% av totalmassan m(K)=4,14 T53 KG eller ca

m[m_K®g]=2,898 T51 KG ............................ K-cellens massförlust under expansionsperioden

Formgeometrin mellan K-cellen och den omgivande c0-kroppen kan preciseras mera ingående med förutsättningen att perioden för K-cellens kontraktion ska vara lika stor som perioden (336 T9 år) för expansionen;

— I Expansionssambandet, kopplingen till K-cellen visas hur det fria g-fallets värden ansluter praktiskt till flykthastighetens värden för stora fallsträckor. Genom att K-cellens expansion INTE ansluter till flykthastigheten, utan till en något lägre sådan, tar det också motsvarande längre tid att nå en viss bestämd distans via K-cellens expansion än via flykthastigheten. Det betyder i den omvända meningen, att när sedan K-cellen vänder tillbaka, den givna stoppdistansens fria (extremt stora) fallsträcka kommer att avverkas praktiskt taget på flykthastighetens belopp, och därmed en (betydligt) snabbare kontraktion jämfört med expansionstiden till stoppet.

— I Beräkningsexempel K-cellen visas att den extra distans som krävs för att få falltiden lika med expansionstiden (336 T9 år) är 3^1/3~1,44 gånger K-cellens slutradie, eller ca 1,67 T27 M.

Medeltätheten utanför K-cellen vid stoppunkten

— Om extramassan [från c0-kroppen, Allmänna tillståndsekvationen] i den extrarymden ska vara samma som K-cellens massförlust, så att exakt samma massa återfinns i K-cellen vid varje dess kommande detonation vid kontraktionens slut, kan den extra volymens medeltäthet tydligen bestämmas idealt enligt

r = m[m_K®g]/[V = (4p/3)([3^1/3r_K336]³ – r_K336³)]

= m[m_K®g]/[V = (4p/3)r_K336³([3^1/3]³ – 1)]

= m[m_K®g]/[V = (4p/3)r_K336³([3 – 1 = 2)]

= m[m_K®g]/(8p/3)r_K336³

= 3m[m_K®g]/8pr_K336³

= 3(2,898 T51 KG)/8p(1,16 T27 M)³

= 2,21618 t31 KG/M³ ...................... massförlustens ideala täthet i påfyllnadsvolymen utanför K-cellen

Med den täthetsbilden i ideal konstant form, och via expansiva-kontraktiva g-fysikens samband [GRUNDFYSIKEN, expansiva tillståndet], uppnås nolldivergens [2(w/c₀)²=1; w²=c₀²/2=4,49377 T16 (M/S)²] vid

w² = r^–1(G/4)m₂

= r²(Gpr/3) ;

= 4,49377 T16 (M/S)² ;

r² = [4,49377 T16 (M/S)²](Gpr/3)^–1 ; Genomgående en och samma täthet 2,2 t31 KG/M³

r = 5,38797 T28 M

= (46,448017)r_K336 ........................... Avståndet [minus 1] mellan K-cellen och c0-kroppens kallplasmagräns

Notering1: Den mera praktiska nollekvivalenten kommer att ge ett något större r-värde genom att inte hela det variabla området har den angivna tätheten 2 t31 KG/M³. Med K-cellens del innefattat [2 t28 KG/M³ vid 336 T9 år] kommer nollgränsen att ligga något längre ut, vid ca 69rK[336]. Se vidare dessa samband nedan i G-potentialer och tätheter i och utanför K-cellen.

Notering 2: För lägre T-värden gäller andra r-värden: Övergången K-cellen-c0-kroppen varierar c0-nollzonens position vartefter K-cellen expanderar och kontraherar. Se särskilt i K-cellens övergång i c0-kroppen.

Det ger en betydligt mera precis bild av helheten (knappast möjlig att få fram tidigare).

K-cellen till c0-kroppen

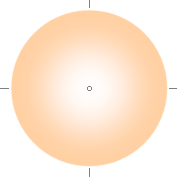
K-cellen i mitten, omgiven av c0-kroppen som övergår (orange) från positiv till negativ divergens

Första konkreta — mera preciserade — skalenliga översiktsbilden: situationen idealiserat vid T=336 T9 år.

En mera noggrann översiktsbild ges i Huvudvyn.

m[MELLAN] = rV = [2,21618 t31 KG/M³][4p/3][5,38 T28 M]³ = 1,44557 T56 KG = 349,17257 mK

Resultatbild: K-cellen [lilla mittcirkeln] omges av ett elektromagnetiskt omfattande aktivt område som gränsar till c0-kroppens ordinära neutronkallplasma — men med extremt låg täthet [2,2 t31 KG/M³; en Väteatom per en kub med sidan nära 20 meter].

— Figuren ovan visar proportionerna i stort vid slutpunkten för K-cellens expansion med maxradien 1,16 T27 M efter 336 T9 år.

— Den lilla cirkeln i mitten är K-cellen, och den stora omgivande cirkeln området med Väteatomer in till c0-kroppens nolldivergensgräns. Massan mellan K-cellen och den större sfärranden är ca 350 K-cellsmassor [50 × 4,14 T53 KG].

— Från den gränsen vidtar sedan c0-kroppens reguljära domän med neutronkallplasma.

— Det mellanliggande idealt täthetshomogena Väteatomsområdet är beräknat efter massförlusten från K-cellens expansionsperiod, och den täthet den påfyllnadsmassan ska ha för att K-cellens återkontraktion ska bli lika lång i tid som expansionsperioden.

— Under ovannämnda förutsättningar:

— K-cellen gränsar inte omedelbart till c0-kroppen i form av neutronkallplasma.

— Det finns ett mellanliggande övergångsskikt i POSITIV divergens — med maximalt låg täthet (2,2 t31 KG/M³) eller runt 7600 M³ rymd per neutron/Väteatom. Den medeltätheten gäller sedan (vad vi vet) idealt som hela den övriga c0-kroppens homogena medeltäthet.

— Vi studerar hur detaljerna kan beskrivas i matematik i G-potentialer och tätheter i och utanför K-cellen.

————— Bildkälla Formgeometrin Magic NATURE

Författarens arkiv · Excur2012E1:12Apr2012 Bild29 · Nikon D90 Detalj

G-potentialer och tätheter i och utanför K-cellen — 2012IV13 — K-cellens koppling till c0-kroppen

G-potentialer och tätheter i och utanför K-cellen

Bildkälla: MAGIC NATURE

K-cellen inre

K-cellen — inre:

w² = (G/4)(m/r)

r = [t(k)T]^2/3(1/2)(4Gm)^1/3 .................. Täthetsändringsfunktionens slutform

w² = (G/4)(m/[[t(k)T]^2/3(1/2)(4Gm)^1/3])

= (G/4)m^2/3/[[t(k)T]^2/3(1/2)(4G)^1/3]

= (G/4)m^2/3/[[t(k)T]^2/3(G/2)^1/3]

= (G/4)m^2/3T^–2/3[t(k)]^–2/3(2/G)^1/3

= (G/4)(2/G)^1/3m^2/3[t(k)]^–2/3T^–2/3

= G^2/3(32)^–1/3m^2/3[t(k)]^–2/3T^–2/3

= G^2/3(32)^–1/3(m₂)^2/3(m/m₂)^2/3[t(k)]^–2/3T^–2/3

= (Gm₂)^2/3(32)^–1/3(m/m₂)^2/3[t(k)]^–2/3T^–2/3

Samma som i Divergensens Nollderivata

t(k) = [0,7 + (0,3)(m)²](m)^0,073 se KalkylkortDirekt KcGRB.ods 9KcIN HelpOpen

w² = 5,96 T15 (M/S)² ............... vid T=336 T9 år, utan stoppmoderator

w² = 8,85 T15 (M/S)² ............... vid T=336 T9 år, med stoppmoderator

K-cellens expansiva avstannande

K-cellen yttre

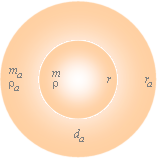
K-cellen — yttre:

FRÅN (vid) stoppunkten (T=336 T9 år) sträcker sig c0-kroppen (från K-cellens rand r=7,8 T26 M StopMod=1) vidare utåt med reducerad täthet (2,21618 t31 KG/M³).

— G-potentialen (w²) kommer från den punkten (r) och utåt (+d_a) att följa en annan sambandsform — figuren ovan:

w² = (G/4)(m/r_a) ;

m = m + m_a ;

r_a = 3m_a/4p(r_a³ – r³) ;

m_a = r_a(4p/3)(r_a³ – r³)

= r_a(4p/3)([r+d_a]³ – r³) ; r_a idealt homogen täthet utanför K-cellen

w² = (G/4)m/r

= (G/4)[m + m_a]/(r+d_a)

= (G/4)[m + r_a(4p/3)(r_a³ – r³)]/(r+d_a) ; r=7,8 T26 M; r_a=2,2 t31 KG/M³; m=4,14 T53 KG;

w²/(c₀²/2) = ([6,67 t11 JM/(KG)²]/4)[4,14 T53 KG + (2,2 t31 KG/M³)(4p/3)(7,8 T26 M)³(r_a³ – r³)]/(7,8 T26 M)(r+d_a)(c₀²/2)

= ([6,67 t11 JM/(KG)²]/4)4,14 T53 KG[1 + (0,00105631)(r_a³ – r³)]/(7,8 T26 M)(r+d_a)(c₀²/2)

= (0,1969519)[m + (0,00105631)(r_a³ – r³)]/(r+d_a)

= (0,1969519)[m + (0,00105631)([(r+d_a)]³ – r³)]/(r+d_a) ; r&m i 1-enheter, w² i c0²/2-enheter:

= (0,1969519)[m + (0,00105631)([(1+d_a)]³ – 1)]/(1+d_a) ;

Graf y = (0.1970)(1+[(0.00105631)([(1+x)'3]–1)])/(1+x)

;

d_a = 0 ;

w² = (G/4)m/r ;

Det värdet blir under alla omständigheter detsamma som K-cellens stoppvärde [via G/4-faktorn].

Koefficienterna k12

Med alternativt stopp-r-värde (r=7,8 T26 M ovan vid T=336 T9 år) ges de alternativa koefficienterna (k₁₂) i

w²/(c₀²/2) = (0,1969519)₁[m + (0,00105631)₂([(1+d_a)]³ – 1)]/(1+d_a)

som

k₁ = (G/4)m₂/(rc₀²/2)

med (G/4)m₂ från [6,67 t11 JM/(KG)²]/4)4,14 T53 KG

med (rc₀²/2) från (7,8 T26 M)(c₀²/2)

och

k₂ = r³4pr_a/3m₂

med r³(4p/3)r_a från (2,2 t31 KG/M³)(4p/3)(7,8 T26 M)³

med m₂ från [4,14 T53 KG + (2,2 t31 KG/M³)…=4,14 T53 KG[1 + (2,2 t31 KG/M³)…/4,14 T53 KG

Koefficienterna k₁₂ beräknas separat för varje särskild grafkurva med varje särskilt förlupen expansionstid (T).

Se Koefficienterna k12 i KalkylkortDirekt KcGRB.ods 9KcIN HelpOpen.

— Notera att r-skalan anpassas (från K-cellens massgräns) via varje specifikt T-värde för motsvarande par k₁₂.

— Sammanställningen nedan visar koefficientvärden för motsvarande T-värden.

T k1 k2 rK[T] M [7,8 T26 M]/r

336 0,1970 0,00106 7,8 T26 1

330 0,1971 0,00106

300 0,1989 0,00103 7,7 T26

200 0,2241 0,00072 6,9 T26

100 0,3183 0,00025 4,8 T26 1,625

90 0,3384 0,00021

80 0,3629 0,00017

70 0,3934 0,000133525

60 0,4326 0,000100416

50 0,4850 0,000071277

40 0,5589 0,000046554

30 0,6729 0,000026678

20 0,8770 0,000012054

10 1,3857 0,000003055 1,1 T26 7,09

9 1,4859 0,000002478

8 1,6067 0,000001960

7 1,7556 0,000001502

6 1,9450 0,000001105

5 2,1956 0,000000768

4 2,5470 0,000000492

3 3,0846 0,000000277

2 4,041 0,000000123

1 6,4133 0,000000031 2,4 T25 32,5

0,001 641,24 3,08 t14 2,4 T23 3250

Se särskilt grafer från K-cellens övergång i c0-kroppen.

Se vidare från G-faktorerna hur K-cellens inre täthetsfysik finner en lösning via TNED.

— Närmaste nedan följer ett kortare referensavsnitt i Divergenständningarna i detalj:

— K-cellens mera preciserade inre täthetsfysk låter oss bestämma avgörande parametervärden som definierar universums synrand; Universums synrand bestämmer sedan i sin tur fenomenet för divergenständningar av K-cellens J‑kroppar som avdelas inåt K-cellens centrum [K-CELLENS EXPANSION] och som — av princip i TNED — är enda fenomenkandidaten till det observerade GRB-fenomenet — föremålet för hela framställningen.

————— Bildkälla G-potentialerna Magic NATURE

Författarens arkiv · Excur2012E1:12Apr2012 Bild26 · Nikon D90 Detalj

Divergenständningarna i detalj — från Mörka materien i TNED — se även i GRB

Divergenständningen i detalj

———————————————————————————————————

med preferenser i g-lokaler med toppdivergens — maximal ljushastighet c₀=2,99792458 T8 M/S

Bildkälla: MAGIC NATURE

Med förebild från FRAKTALDELNINGSEXEMPLET — Vintergatans divergenständningsdelning

Detonationsfasen i detalj

Exempel med Vintergatan (Räkneexempel Vintergatans J-moderkropp) och en dess här antagna J-moderkropp på (lägst) ca 300 Vintergatsmassor.

1. Nolldivergenszonen har passerat J-moderkroppen inom ca 30 sekunder;

2. Lokala divergensen utanför J-moderkroppen antas i motsvarande tidsmening snabbt gå mot toppdivergensen (c=c₀, J-kropparnas primära avdelning från det inre av K-cellen);

3. Neutronsönderfallet börjar, och är färdigbildat inom 12-14 minuter med referens till vår egen lokals kända kärnfysikaliska experiment (Solsystemets plats i Vintergatan);

4. Under neutronsönderfallet (GRUNDÄMNESBILDNINGEN) formeras fusionsringar som är förstadiet till fusionsfasen — det korta, explosionsartade intervall då fusionsringarna verkställer de aktuella fusionerna och som leder till den aktuella J-kroppens snabba grundämnesbildning;

5. Fusionsfasens omfattning i TID beror helt av den lokala divergensen — Coulombkraftens utverkande magnitud genom elektriska konstanten Rc i elektriska kraftlagen F=Rc(Q/d)².
— Det tidsintervallet (fusionslängden) är för enskilda parnuklider drygt t20 sekunder, och fusionsringarna har ingen direkt härledningsbar extra fördröjande inverkan på det intervallet;
— Det betyder i stort, och förutsatt ideal fusionssynkronisering över en hel J-kropp som INTE har förutsättningar för att utbilda egen nolldivergens i J-kroppsytan (gränsen går vid ca 80 Solmassor, se Gränsmassorna) att grundämnesbildningen är avklarad på t20 sekunder (fusionslängden), max lokal toppdivergens förutsatt (c=c₀);

6. Fusionsfasens J-centrala förlopp betingas uteslutande ALLTID av J-kroppens maximala divergens i J-kroppens tyngdpunkt (Ljustes gravitella beroende), detsamma som maximalt snabbt neutronsönderfall, och därmed maximalt låg neutronkvot, och som garanterar udda-jämna-nuklidgruppens grundämnesbildning upp till Järntoppen;
— EFTERSOM HELA FUSIONSPROCESSEN betyder att J-massan går från neutroner till sammansatta tyngre atomkärnor, frigörs VOLYM (tomrum) från J-kroppens centrum; ett större antal neutroner ersätts av ett betydligt mindre antal atomkärnor på totalt betydligt mindre volym;
— Genom gravitationens absolutverkan (GcQ-teoremet) — som reagerar absolut på uppkomna vakanser i täthetskroppen — tvingas därmed till viss del den centralt fusionerade J-kroppen att under en kort tid och i princip implodera (sammandra sig explosivt inåt) — initierat under pågående fusionsfas (»volymvakansiering»);
— IMPLOSIONENS MAGNITUD bör regleras av fusionsmängden, som i sin tur regleras av den lokala divergensen (c/c₀); c/c₀=0 ger noll fusioner och därmed noll implosion och därmed noll detonation; c/c₀=1 ger maximala dito. Därmed bör också i någon mån utkastningshastigheterna variera proportionellt mot c/c₀.
— Fusionsimplosionen innebär i princip att J-kroppen tillfällig går från statiska till expansiva tillståndets g-fysik (G-faktorerna); expansiva/kontraktiva g-tillståndets fysik använder en nolldivergensreferens som motsvarar en reducerad g-faktor, analogt en utflyttning av nollzonen relativt statiska tillståndet (K-cellens detonation);
— Det betyder, såvitt korrekt i naturfysiken, att referensen för nolldivergenszonen i exakt samma mening flyttas ut (dubbelt, se utförligt från K-cellens detonation);
— Nolldivergenszonens utflyttning medför en direkt högre lokal divergens ut mot J-kroppens rand; mera ofullbordade neutronsönderfall kan slutföras i princip med omedelbar verkan, och därmed en ytterligare tillfällig, kortvarig implosion;
— Allt infallande mot J-kroppens centrum som, J-kroppens yttre rand, berör fortfarande befintliga neutroner från J-kroppens primära neutronkallplasma, kommer obönhörligen att stöta emot de längre inåt maximalt tätt packade atomkärnorna inkluderat verkan med de tyngre fusionsbildade atomkärnornas Coulombiska repulsionskraft;
DÄRMED ÄR DETONATIONEN ETT FAKTUM — IMPLOSIONSREKYLEN:
— Genom att atomkärnan i relaterad fysik inte kan komprimeras (Atomkärnans inkompressibilitet) blir den oundvikliga konsekvensen av hela fusionsfasens förlopp följaktligen också en oåterkallelig implosionsrekyl; de sammanstötande atomkärnorna svarar med att vända implosionskraften utåt: atomkärnorna rekylerar mekaniskt — och Coulombiskt som följd av fusionsfasens exotermiska energifrigörande; materialet kastas ut — och J-kroppens expansion är därmed ett faktum. Se även i Pulsarerna i relaterad fysik;
— Divergenständningen kan därmed förstås som att den TRIGGAR J-kroppens expansion genom neutronsönderfallet, och det finns ingen möjlighet att undvika den utvecklingen.
— Implosionsrekylen blir via inverkan från atomkärnans inkompressibilitet tvunget direkt proportionell mot mängden neutronkallplasma som ligger och trycker på från J-kroppens rand; ju mera massiv J-kroppen är, desto mera explosionskraft utvecklas [Detonationspulsernas Reaktionstid];
Rörelsemängden p=mv i den ansamlade massans potentiella utkastningskraft är proportionell mot den samlade massans totalt tryckande kraft (F) över tid (T), mv=maT=FT; TIDEN för ansamlingen fram till början av den tryckande kraftens funktion har naturligtvis ingen betydelse för TIDEN under vilken den tryckande kraften utvecklas: det enda som spelar roll är den ansamlade massans g-tryck (F) ända fram till tillfället då den tryckande kraften passerar gränsen för utlösande detonation; jämför en fjäder som anspänns mer och mer och mer … ända tills dess hela anordningen slits sönder (exploderar) på grund av att infästningarna övergår i brott: hela den upplagrade anspänningskraften frigörs omedelbart; Se även i G-energins FT-ekvivalent;

7. Fusionsfasen får alltså i relaterad mening förstås efterföljas omgående av den snabba J-kroppens expansion (PRIMÄRMASSORNA).
— HUR J-kropparna expanderar, och grundämnesformeras, bestäms av den centrala fusionsgränsmassan som indelar J-kropparna i olika kategorier.

— MEKANISMEN FÖR KROPPSEXPANSIONEN blir (således i sammanfattning) analog med

kraftutveckling från neutronsönderfall och fusionsfaser som genererar implosionsrekyler.

SVÅRIGHETEN att förstå verkningssättet i gravitella rymder med låg divergens (c→0), hänger med andra ord, och alldeles tydligt, enbart på KRAFTUTVECKLINGEN i den avgörande implosionsrekylen;

— Det blir i ovanstående genomgångs ljus ALLTID Atomkärnans inkompressibilitet som är den avgörande, utlösande faktor som leder till J-kroppens expansion; Finns inte tillräcklig rekylkraft, kommer denna bara att upplagras och frigöras längre fram när tillfället infinner sig att gränsvärdet uppnås — och vilket i princip kan töjas på obegränsat.

— Jämför utrullandet av en sten utför en brant: ingenting händer förrän en viss gränsvärdesutlösande kraft påverkar stenens läge. NÄR den gränsen uppnås, och stenen börjar rulla, finns ingen återvändo sett i stenens egen kraftfysikaliska historia.

Allmän slutsats — J-kropparnas utveckling i regioner med låg divergens

För J-kroppar som divergenständer i regioner med (exceptionellt) låg divergens (universums absolut ytterst synliga områden) gäller alltså »som vanligt» att OM en J-kroppsexpansion (»galaktisk explosion») inträffar, den gör det med samma snabbhet som i alla andra divergensfall men med lägre styrka och därmed via lägre J-massor. Inget annat.

*

G-energins FT-ekvivalent

G-energins FT-ekvivalent

DetonationsBASIC — relaterad fysik — G-energins FT-ekvivalent

E = Gm²/r = mv²/2 = mv(v/2) = mv(v/2)(m/m) = (mv=maT=FT=p)²/2m = p²/2m = (FT)²/2m

Den g-energi (gravitationsenergin E=Gm²/r) som en J-kropp besitter via sitt neutronkallplasma — maximalt tätt liggande neutroner i lokaler med c=0 — är den idealt samma kinetiska energi (E=mv²/2) som J-kroppens samlade neutronkallplasmamassa utvecklar vid slutet (v) av en motsvarande idealt föregående kontraktionsfas. Det blir också densamma expansionsenergi som J-kroppen kan detonera på och som definierar den ideala s.k. flykthastigheten Gm²/r=mv²/2 som ger v²=2Gm/r.

— Genom atomkärnans inkompressibilitet och i K-cellens kontraktion, verkställs (således) K-cellens expansion »direkt automatiskt» så snart de instörtande atomkärnorna (neutronerna) klonkar ihop — idealt, alla exakt samtidigt. Atomkärnans inkomressibilitet garanterar att rörelsemängden (p=mv=maT=FT) som exponeras totalt vid ihopklonkningstillfället vänds utåt till en expanderande dito; K-cellen detonerar idealt på exakt sin egen kontraktionsenergi, garanterat av atomkärnans inkompressibilitet.

— J-kropparnas detonation föregås emellertid INTE av någon SÅDAN motsvarande kontraktionsfas som i fallet med hela K-cellen;

— Varje J-kropp avdelas ur K-cellens totalmassa i K-cellens expansion som en fristående ideal neutronkallplasmasfär efter K-cellens detonation; Avdelandet av J-kropparna kan förstås följa en allmän enklare svängningsekvation som åstadkommer motsvarigheten till den kraftbild som visar sig i utkastning av vattendroppar (resonansserier [GALAXBILDNINGARNA]) ur en vattenyta (som följd av en penetrerande vektorkraft, enklast en vattendroppe som släpps ner mot vattenytan, enligt motsvarande experimentalfysik).

— För att en J-kropp ska kunna detonera på sin redan upplagrade g-energi (Gm²/r=[FT]²/2m) krävs (således) att hela neutronkallplasmamassan (m), tvunget, måste försättas i någon minsta rörelse (v) in mot J-kroppens tyngdpunkt, och därmed verkställa en ytterligare minsta lilla avgörande rörelsemängd (mv=FT) — för att så generera »droppen som får bägaren att rinna över». Det blir för J-kroppens del alltså en liten extra rörelsemängd (mv) som krävs för att utlösa (motsvarande ihopklonkningstillfället i K-cellens fall) den redan väntande, upplagrade g-energin. Och det blir, på samma sätt som för K-cellen, totalt en process som bara kan garanteras av och via atomkärnans inkompressibilitet.

— Den extra inåtrörelsen (mv) — vi kallar den en implosion — garanteras så snart J-kroppen kommer in i en lokal med c>0, det som här kallas divergenständning:

— Divergenständningen garanterar att

1. neutronsönderfall påbörjas, främst från J-kroppens centrum där c är som störst [Ljusets g-beroende], och därmed att

2. fusioner mellan vätekärnor (och neutroner) via fusionsringar bildas mellan de tätt liggande ursprungliga neutronerna, och därmed att

3. VOLYMVAKANSER UPPKOMMER i följd av att fusionerna sammanför flera ursprungliga neutronplatser till mera kompakta atomkärnor på allt mindre volym; volymvakanserna i J-kroppens centrum får den överliggande (primära stjärn-) kroppsmassan att börja röra sig inåt i utfyllnaden (se mera utförligt generellt för alla himlakroppar i FUSIONSGRÄNSMASSAN).

— Därmed har implosionsrekylen av princip igångsatts; Detonationsfasen blir i garanti av atomkärnans inkompressibilitet oundviklig då den instörtande massans atomkärnor klonkar ihop — liknande situationen i slutet av K-cellens kontraktion.

— Förloppet med den redan utbildade g-energin ([FT]²/2m) som kräver en liten utlösande effekt via atomkärnans inkompressibilitet, kan liknas vid följande praktiska anordning:

— En tryckfjäder (atomkärnan i spinnriktningen) vilar mot ett underlag med ett litet hål i mitten för en snörkrans som fjäderns överdel är monterad i, och som en person på undersidan kan dra i (från ett redan anspänt tillstånd) för att på så sätt anspänna fjädern (ytterligare) — tills dess spännkraften blir så stor att snöret brister och HELA den totalt upplagrade motsvarande (FT)²/2m-energin frigörs och hela fjädern åker iväg.

————— Bildkälla Divergenständningarna i detalj MAGIC NATURE

Författarens arkiv · Miljö2012 M2 Naturskog1 Bild2 · Nikon D90 Detalj

GRB

Gammastrålskurar (GSS) — [eng. GRB, gamma ray burst] — ekon från döende eller nyfödda?

Se även i ORIGINALBESKRIVNINGEN i CGRO, där förklaras termgrunderna mera utförligt. Där ges också [tidiga, 1990-talet] citat från etablerade källor som beskriver ämnesområdet enligt MAC.

Bildkälla: MAGIC NATURE

I sammanfattning — frånsett den ordinära floran av novautbrott i alla delar av det stjärnaktiva kosmos:

Modern akademi [MAC]:

— GSS är smala energistrålskurar från DÖENDE massiva stjärnor i de mest avlägset synliga delarna av universum. Se Citat.

Relaterad fysik [TNED]:

— GSS är reguljärt sfäriska, starkt utdämpade [Divergensenergins g-beroende] [Gravitella dopplereffekten] energistrålskurar från PRIMÄRA FÖDELSER av stjärnor [galaxbildningens primära detaljer] från de mest avlägset synliga delarna av universum [grovt runt 5-6 miljarder år tillbaka] — en naturlig del i K-cellens expansion.

Vidare i Praktiska GRB-ursprunget.

Med förebild från FRAKTALDELNINGSEXEMPLET — Vintergatans divergenständningsdelning.

Utvidgningen från centrum i figuren ovan kan förstås som ett sfäriskt tvärsnitt, eller idealiserat via centrifugalkrafterna som en (galaktisk) plan skiva. Se särskilt från Stjärnhopar och Galaxbildningar DEL 1.

Med J-kropparnas divergenständning följer samtidigt den allra första LJUSBILDEN av alla primärt maximala stjärnhopar: galaxerna.

— Så länge en J-kropp befinner sig i g-lokaler med c=0 kan ingen divergenständning utvecklas: J-kroppen bibehåller sin maximala täthet fram tills dess sammanhållande kraft via g-energin [E(G)=GM²/r=GM²/(3M/4πρ)^1/3=G(4πρ/3)^1/3M^5/3, M centralmassan, ρ medeltätheten] kan motverkas av en motriktad Coulombkraft [F=Rc(Q/r)²], Fusionsgränsmassan klassificerar de olika himlakroppstyperna;

— Först när Coulombkraftens divergens [c i elektriska konstanten Rc] verkställer nukleär växelverkan (fusionsfasen) finns förutsättningarna för J-kroppens snabba expansion från maximal täthet (Divergenständningen i detalj). När väl den J-kroppens primära divergenständning inträffar, sker automatiskt motsvarande för alla avdelade mindre J-kroppar (Detonationsmassans upplösning);

— Efter J-moderkroppens primära divergenständning följer tvunget, och i direkt följd, de mindre avdelade J-kropparnas divergenständningar.

— Figuren ovan antyder hur varje primär J-moderkropps divergenständningspuls tvivelslöst tvingas samverka med efterföljande mindre till en sammanhängande signal från hela den materielokalen.

Med uppmärksammandet av (först från 1967, publ. 1973) de kortvariga energirika gammapulser som anländer till Jorden (eng. GRB, gamma-ray bursts), med synbar jämn spridning från alla möjliga delar av universum, ges en direkt möjlighet att testa TNED.

— Om allt stämmer, ska ovannämnda grundformer vara signalkällan.

Den vidare beskrivningen — med avgörande exempel och jämförelser — finns i det särskilda GRB-dokumentet från Hur TNED möjligen kan koppla till GRB-objekten [UNIVERSUMS SYNRAND].

Närmast nedan följer bakgrunden — G-faktorerna — till huvudbeskrivningen: Täthetsändringens funktioner — GRUNDEN för att få fram den avgörande jämförande kvantitativa värdegrund i TNED som, eventuellt, skulle kunna koppla observationerna i GRB-komplexet. Se även från INLEDNINGEN: behovet av en fördjupad beskrivning av K-cellen för att eventuellt också kunna omfatta detaljerna i GRB-fenomenet.

————— Bildkälla GRB Magic NATURE

Författarens arkiv · Miljö2012 M3 23Mar2012 Naturskog2 Bild33

G-faktorerna — STATISKA och EXPANSIVA g-fysikens samband i K-cellens [UNIVERSUMS] historia — se även sambanden sammanställda i GRUNDFYSIKEN — 2012III22

Se även Expansionssambanden i Stjärnfysiken

Framställningen har [från Apr2012] i förekommande fall försetts med nedanstående ikoner [STATiska][EXPAnsiva] som enkla, förtydligande bildkoncept för SNABB ORIENTERING av de annars ibland svårplacerade SKILDA matematiska-fysikaliska REFERENSERNA. Termgrunderna förklaras utförligt nedan.

Faktorerna G och G/4 — statiska och expansiva g-fysiken

Bildkälla: MAGIC NATURE

Se även i Transitfunktionen — hur inre täthetsändrande funktionen i K-CELLENS INRE TÄTHET initieras

———————————————————————————————————————————

Kort repeterande sammanfattning — med tillägg av förtydligande ikoner

LJUSETS GRAVITELLA BEROENDE — i relaterad mening — ger Nolldivergenszonens radie ur tätheten r via c=0 — med sambandet från täthetsformen r=m/V=m/(4pr³/3)=3m/4pr³=3(m/r)/4pr² ; m/r=4pr²r/3 — enligt

c = 0 = (1/2)[c₀ – Ö |–c₀²+4w² | ] ; 0 = [c₀ – Ö |–c₀²+4w² | ] ; c₀ = Ö |–c₀²+4w² | ; c₀² = –c₀²+4w² ; 4w² = 2c₀² ; 2w² = c₀² = 2Gm₂/r_c0 = 2r_c0²(4pGr/3) = r_c0²(8pGr/3) ; r_c0² = c₀²(3/8pGr) ;

r_c0² = c₀²(3/8Gpr) ....................... statiska g-fysikens samband, c=0, nolldivergenszonens radie, ideal sfärisk massgeometri

ENDA FUNDAMENTALA FORMEN FÖR EXPANSION (växande hastighet) vi känner ges av den linjära accelerationens matematiska fysik a=v/T=2d/T² med d=vT/2 och T=2d/v; Med flykthastigheten v=Ö 2Gm₂/r (från ekvivalensen mellan g-energi och rörelseenergi) som expansionens absoluta gränsvärde — som garanterar att expansionen aldrig någonsin avstannar helt, den går mot noll under obegränsat lång tid; Via täthetsformen m₂/r=4pr²r/3 ges speciellt v=rÖ(8pGr/3) — får man med nolldivergenszonen r=d=r_c0=c₀T som sveper genom K-cellens idealt masshomogena sfär med konstant hastighet c₀ det centrala expansionssambandet

T = 2d/v = 2r_c0/[rÖ(8pGr/3)] = 2Ö(3/8pGr) = Ö 3/2pGr; Multiplikation med c₀ ger r_c0=c₀T=c₀Ö 3/2pGr. Och vi har alltså en den statiska formens motsvarande expansiv fundamentalform enligt

r_c0² = c₀²(3/2Gpr) ....................... expansiva g-fysikens samband, c=0, nolldivergenszonens radie, ideal sfärisk massgeometri

Med enbart isolerade G-termer (absolut PRINCIPIELLA funktionen) EXPAnsiva 2G kontra STATiska 8G gäller tydligen

EXPA(2G)/STAT(8G)=2G/8G=1/4 ; G(EXPA) = G(STAT)/4 ; c₀pr momentant fixa.

Från övre stripens g-statiska samband c₀² = 2Gm₂/r_c0 ges motsvarande g-statiska

r_c0[G(STAT)] = 2Gm₂/c₀² ; ............... g-potential w² = (G)m₂/r

I generaliserad fundamentalform med ovanstående resultatbild G(EXPA) = G(STAT)/4 därmed motsvarande

r_c0[G(EXPA)] = Gm₂/2c₀² ; ............... g-potential w² = (G/4)m₂/r

— Identiteterna för r0c med referens till statiska och expansiva tillståndets grundfysik [G-faktorerna] ger omvandlingsfaktorn x enligt 2Gxm/c²[STAT] = Gm/2c²[EXPA] som ger x = 1/4.

Det föreligger med andra ord tydligen en i relaterad mening (fundamentalt baserad) olikhet i sättet att återföra nolldivergens (c=0) via Ljusets g-beroende DELS i det vanliga statiskt fasta fysiska fallet — en fast sfärisk centralmassa (m₂) — och DELS i fallet då den sfäriska massan expanderar (eller kontraherar). Se även särskilt i K-cellens Detonation där dessa detaljer spelar en avgörande roll.

— Vi kan med en gång DIREKT konstatera

— enbart via blandningen av fundamentaltermerna linjär acceleration och flykthastighet ovan (som delvis är varandras motsatser, utförligt i Fria fallets G-fysik om ej redan bekant), tillsammans med de INRE täthetsförskjutningar [Täthetsändringsfunktionerna i K-cellen] som otvivelaktigt måste utbildas i K-cellens inre i takt med expansionen

— att ovanstående formella samband INTE DIREKT har kapacitet att beskriva någon EXAKT praktik för K-cellens inre (vårt synliga universum). Det vi kan göra med ovanstående som GRUNDMATEMATIK är att ställa upp (vidareutvecklade, denna presentation) PRÖVANDE SAMBAND för att försöka få fram, eller påvisa, eventuella överensstämmelser med faktiska observationer, här främst beträffande de allmänt observerade och påstådda rödförskjutningarna [i TNED enligt Gravitella dopplereffekten] mot universums yttre (med tillhörande fenomen, se särskilt i GRB), och vilka resultat den här presentationen ska redovisa mera i detalj. Vi studerar huvudlinjerna i komplexet nedan.

Lösningen i TNED — från G-faktorerna

Genomgången i EXPANSIONSSAMBANDEN

— som beskriver hur G-faktorn i statiska (G) och expansiva (G/4) tillståndets fysik skiljer sig genom divergensnollzonens hastighet, i sammandrag ovan enligt

Identiteterna för r med referens till statiska och expansiva tillståndets g-fysik

— gäller naturligtvis också bara för motsvarande ODÄMPADE expansion.

— Det betyder att det inre av K-cellen via dessa nämnda bassamband gäller utan hänsyn till inre möjliga inhomogeniteter i K-cellen.

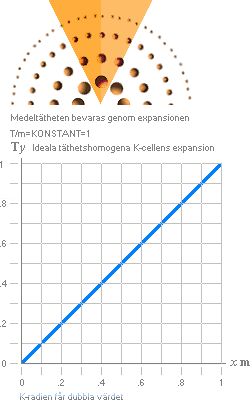
K-cellens inre — grundformerna med K-värdet och K-radien från K-cellens värmfefysik visar vägen till det inre av K-cellen:

Varför grundsambanden INTE DIREKT utpekar observationella data

K-cellens idealt expansiva ODÄMPADE utveckling — se grundbeskrivning i K-cellens brytning visar att:

— Förhållandet mellan expansionstid och delmassa är konstant, figuren ovan.

— Den idealbilden stämmer INTE med praktiken — i K-cellens mellandelar:

— K-radien och K-värdet kan inte alls fås att stämma överens på grundsambandens villkor med idealt homogen täthet för hela K-cellen;

Beräkningsexempel som visar grundsambandens otillräcklighet

Vid den avgörande beräkningstiden i K-cellens expansion för effektmaximum T=16,32 T9 år, och via den idealt odämpade expansionens förlopp enligt grundsambanden

r = T^2/3(1/2)(4Gm₂)^1/3 .......................... grundform, homogen täthet från r-formen

v = T^–1/3(2/3)(1/2)(4Gm₂)^1/3 = r’

w² = r²Gpr/3 = (G/4)m₂/r

samt tillsammans med godtyckliga massavsnitt av centralmassan (noll till max m2), ges delmassan vid r och T enligt m/m₂=(2r/T^2/3)³/4Gm₂=0,021408532.

— Men den resultatbilden ger samtidigt lokala divergensen (ljushastighetens lokalt g-bestämda punktvärde) vid r(T) enligt Divergensens Expansiva G-beroende

c/c₀=Ö 1–2(w/c₀)²=0,96 med massrandens expansionshastighet v(r)/c₀=0,18.

Resultat — som belyser den fortsatta framställningens sakinnehåll

— Det finns ingen fysisk möjlighet att ur dessa bägge — c/c0 + v(r)/c0 — få fram det avgörande observerade rödförskjutningsmedelvärdet från r-gränsen på K=1,5:

K = 1/[1–c/c₀ + v/c₀ = 0,67] = 1,5 ................. aktuella fallet som måste uppfyllas, GKKDsambandet

— Se Gravitella dopplereffekten för grundsambanden [Gravitell rödförskjutning], om ej redan bekant.

K = 1/[1–0,96 + 0,18 = 0,22] = 4,5 .............. resultatet från grundformen ovan — galet värde

Den matematiken kopplar definitivt INTE till resultaten från K-cellens värmfefysik. K-värdet måste under alla omständigheter ligga vid det observerade 1,5 (med en felmarginal på max 3%).

— Enda principiella möjligheten att få sambanden (K-radien och K-värdet) att stämma enhetligt med effektberäkningarna i K-cellens värmefysik är via en täthetsökning: Ett förhållande T/m=ICKEkonstant måste utvecklas inåt K-centrum, vilket samtidigt garanterar K-cellens expansiva avstannande.

OBSERVERA att de redan redovisade resultaten i K-cellens värmefysik INTE påverkas — eller SKA inte göra det — av dessa här utvecklade detaljer, inte på något som helst sätt. Presentationen här berör ENBART K-cellens inre — på de redan basbestämda resultatvärdena från K-cellens värmefysik, och som MÅSTE fås att BEVARAS med de resultat vi kommer fram till här, vilka de än är. Misslyckas den föresatsen, är också hela framställningen i ämnet K-cellens värmefysik felaktig.

Vi studerar det.

K-cellens inre

— Mera massa in mot K-centrum.

— En sådan delfunktion SKULLE också vara förenlig med K-cellens allmänna villkor; Med ideal ekvivalens mellan g-energi och rörelseenergi skulle K-cellen fortsätta expandera i evighet mot noll, utan att någonsin avstanna. OM emellertid dels en mindre (försumbar) förlust sker via det värme och ljus som stjärnorna bränner av i massa (K-cellens allmänna tillståndslag), och dels framför allt en relativ täthetsökning sker in mot centrum som följd av J-kropparnas delvisa utkastningar in mot K-centrum [J-kropparnas hastighet], finns förutsättningen för den nödvändiga reduktionen av hastigheterna omkring K-radien som resultaten ovan kräver — analogt en inre täthetsökning.

— DEN MÖJLIGA MASSFORMEN för täthetsökningarnas direkta verkställande in mot K-centrum besitter också, verkligen, en SPECIELL dynamisk gren i TNED.

Se särskilt i vidare beskrivning från detonationsmassorna i Mörka materien.

Huvudsaken i TNED-lösningen berör alltså möjligheten att söka och finna en INRE täthetsändringsvariation som bevarar grundparametrarna för HELA K-cellen. Se utförligt vidare från Täthetsändringens funktioner.

————— Bildkälla G-faktorerna Magic NATURE

Författarens arkiv · Excur2012E1:12Apr2012 Bild1 · Nikon D90 Detalj

tK-faktorn — G-faktorerna — Täthetsändringsfunktionens slutform

Täthetsändringens funktioner

Bildkälla: MAGIC NATURE

K-cellens inre

— med fortsättning från Grundsambanden

Enklaste sättet att härleda en inre täthetsökning i den expanderande K-cellen är att införa en särskild tidsfaktor [t(k)] tillsammans med den ordinarie K-cellens tidsflöde (T).

— Med grundexempel från r-formen

r = T^2/3(1/2)(4Gm₂)^1/3

uttryckt på den via delradien r inre avdelade delmassan i K-cellen

r = T^2/3(1/2)(4Gm)^1/3

= T^2/3(1/2)[m/m₂]^1/3(4Gm₂)^1/3

t(k)-faktorn

kan sambandet för r formen tecknas generellt via en t(k)-faktor

r = [t(k)T]^2/3(1/2)(4Gm)^1/3 ; se t[k]-formen vidare i Täthetsändringsfunktionens slutform

= [t(k)]^2/3T^2/3(1/2)(4Gm)^1/3 ;

Motsvarande v-form fås som r-derivatan enligt

v = r’

= T^–1/3(2/3)(1/2)(4Gm)^1/3 ; inkluderat t-faktorn

= [t(k)]^2/3T^–1/3(1/3)(4Gm)^1/3

G-potentialens form

w² = Gm/4[t(k)]²r

visas vidare nedan.

T-faktorn kan naturligtvis skrivas på otaliga olika sätt. Enklaste fallet för direkt prövning av de olika masskikten (m) i K-cellen blir här

t(k) = (m/m₂)^k

= a

På samma sätt (G-faktorerna) som i härledningen till expansiva tillståndets G/4-faktor relativt statiska, kan vi relatera en motsvarande allmän hastighetsform för nolldivergensen;

— Expansiva idealt odämpade hastighetsformen för r(c=0) visades i genomgången i Nolldivergenszonens konstanta hastighet på formen

r_c=0 = c₀T₀

Med t(k)-faktorn (förenklat a) tillagd skulle vi här få motsvarande mera allmänna

r_c=0 = c₀aT₀

Därmed via Identiteterna för r med referens till statiska och expansiva tillståndets grundfysik motsvarande

x = 1/4a²

Och därmed en G-faktor i g-potentialen (w²) för expansiva tillståndet generellt på formen från statiska tillståndets referens

w² = (G/4a²)m/r

= (G/4[t(k)]²)m/r

= Gm/4[t(k)]²r ; .................. se t[k]-formen i Täthetsändringsfunktionens slutform

KalkylkortDirekt KcGRB.ods 9KcIN HelpOpen

Basvärdena satisfierade

Därmed uppnås basvillkoren från K-cellens värmefysik med K-radien och K-värdet 1,5 vid T=16,3 T9 år.

;

K-värdet visar nu korrekt vid r=4,28 T25 M och T=16,3 T9 år

K = 1/(1–0,52_c + 0,18_v) = 1,5

Se även de Jämförande resultaten från grundsambanden.

;

Med [t(k)]=(m/m₂=0,066)^k och k=0,207 uppfylls K=1,5 och K-radien 4,28082 T25 M vid T=16,32 T9 år.

— MEN med ytterligare krav på preciserad lokal:

— Nu gäller inte bara att K-radien och K-värdet ska stämma. Även alla lokalt observerade signaldata måste också stämma: Den lokala galaxgruppens positioner och hastigheter.

— Det ser ut som att RESULTATET av den PRÖVANDE täthetsförskjutningen inåt K-cellen ändå blir något för stor:

Observationer från den Lokala Galaxgruppen

Villkor som måste uppfyllas

Om vi antar att antingen Andromedagalaxen, eller Vintergatan, befinner sig närmast i K-cellens centrum och vi använder det angivna medelavståndet mellan galaxerna (Från Solsystemets ålder) på runt ca R=9 T22 M som distansreferens, ges divergensen i K-cellen på avståndet R=9,10099 T22 M vid K-cellens nuvarande ålder T=20,82 T9 år lika med 0,930878805c₀. Det motsvarar en gravitell rödförskjutning sett från c₀ på

c₀(1–0,930878805) = 20 722 012,9 M/S

= 20 722,0129 KM/S

Vi ser att värdet är på tok för stort — Jämför tabellen nedan med radialhastigheterna i Lokala Galaxgruppen;

— Värdena får inte vara större än i storleksordningen max±300 KM/S;

— Resultatet visar att täthetsökningen längst in är något för stor.

Antar vi alternativt en nollreferens vid R=9 T22 M och går ytterligare R utåt K-cellen (r=1,82966 T23 M) hamnar vi på motsvarande differens

c₀(0,930878805 – 0,917508038)

= 4 008 455,13 M/S

= 4 008,45513 KM/S

Värdena ligger nära — men är fortfarande [runt 10ggr] för stora

K-cellens centrum:

— Om vi ska hålla oss till att bildningen av Solsystemet och därmed Vintergatan ansluter till OPTIMAL DYNAMIK mellan gravitation och elektricitet, vilket betyder att högst försumbara divergensreduktioner [Coulombkraftens försvagande] får förekomma i utvecklingarna enligt JORDENS 5 EKVATIONER och SOLENS 3 EKVATIONER, får Vintergatan inte förflytta sig så mycket mera på 20,82 T9 år än just omkring 9 T22 M. Se även i Solsystemets ålder.

I annat fall uppkommer allvarliga problem med att härleda en fungerande elektrogravitell fysik. På ett eller annat sätt måste vi därför FÖRST TILL PRÖVNING använda nuvarande, också observerade, avstånd i stort mellan galaxerna i vår lokala galaxgrupp som »centralpreferenser», i stort ca 3 Mpc eller runt 9-9,5 T22 M. Den premissen kommer då att bilda den lokalt centrala analysen i K-cellens centrum enligt TNED.

Notera också den EXKLUSIVA möjligheten med Vintergatans bildning:

— Eftersom utkastningshastigheterna [J-kropparnas hastighet] i allmänhet för J-kropparna är extremt höga, motsvarande den ekvivalent upplagrade kontraktionsenergin som rörelseenergi och som ansluter till motsvarande FLYKTHASTIGHETEN [Se även ovan från G-faktorerna], finns alltid möjligheten för en J-kropp att TIDIGT i K-cellens expansion, från innerväggen, avancera inåt K-cellen med MYCKET HÖG hastighet;

— Då den J-kroppen divergenständer och i sin tur avdelar sekundära J-kroppar, kan I PRINCIP den aktuella J-kroppen [Moderkroppen till Vintergatan] avdelas med MOTSATT LIKA STOR hastighet — och därmed i netto befinna sig vilande på avdelnngsstället: ingen rörelse alls sker under K-cellens utveckling.

— Vi VET dock ännu inte mera exakt hur den möjligheten kan matcha en praktisk historia: Flera olika beräkningar måste stämma, och först sedan sådana genomförts kan närmare besked ges. Vi är inte där än.

Det är nära praktiken, men fortfarande för mycket i förhållande till den rapporterade rödförskjutningens värden (för medlemmarna i den lokala galaxgruppen, tabell nedan) — runt 600 KM/S (som mest, inkluderat hela gruppen relativt omgivningen).

Lokala Galaxgruppen, basdata

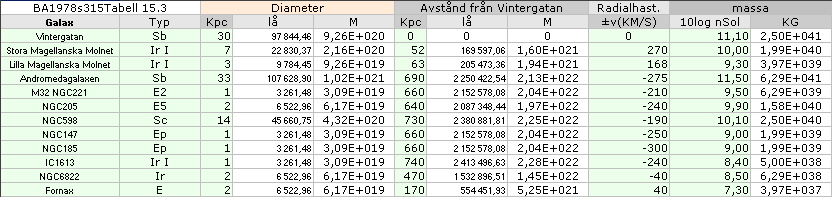
Sammanställda uppgifter från BONNIERS ASTRONOMI 1978 s315 Tabell 15.3

EXEMPEL VIA TNED:

Andromedagalaxen uppvisar relativt Vintergatan en blåförskjutning som för c0-homogen rymd motsvarar grovt 300 KM/S. Andromedagalaxen är alltså på väg att kollidera med Vintergatan sett i en rymd där ljushastigheten överallt är lika — INTE VÅRT FALL ENLIGT RELATERAD FYSIK [TNED], se Gravitella dopplereffekten.

— Modern akademi räknar NÄMLIGEN inte med någon gravitell dopplereffekt:

— Då det i vilket fall rör sig om små avvikelser, skulle motsvarande samma observation fås om Andromedagalaxen befinner sig i K-cellens centrum och Vintergatan på sin position med en lokalt lägre divergens lika med

[2,99792458 T8 M/S] – [2,75 T5 M/S] = 0,999082699c0. Se även i ABSOLUTA METRIKEN, för den som ev. inte känner grunderna.

— En så liten avvikelse skulle i vilket fall för ELEKTROGRAVITATIONENS DYNAMISKA FYSIK vara obetydlig [motsvarande effektiva verkningsfall på 0,0001].

— En sådan liten differens är både fullt möjlig och fullt acceptabel i TNED — men den är inte möjlig i modern akademi även om den kunde anses fullt acceptabel. Ingen räknar med en sådan rymdfysik i moderna kvarter som innebär olika värden på c i olika rymdavsnitt: Det finns (här veterligt) ingen (begripligt uttydbar, allmänt tillgänglig) TEORI för det i MAC. Se utförligt från Ljusets g-beroende och Planckekvivalenterna; Där klargörs kopplingarna med jämförelser mot MAC; Man räknar inte med att dopplerförskjutningar från typ Andromedagalaxen (eller andra) sammanhänger med någon effekt som kan återföras på gravitell dopplereffekt; Om sådana effekter omnämns i modern teori, sammanhänger de snarare med omedelbara närområden till s.k. svarta hål eller generellt maximalt massiva himlakroppar.

— Med den gravitella effekten medräknad skulle nettoresultatet enligt TNED vara att Andromedagalaxen och Vintergatan i själva verket befinner sig väldigt mycket i vila relativt varandra;

— De bägge galaxerna Andromeda och Vintergatan skulle ha kunnat utvecklats på nära samma radiella strållinje, med en försumbar vinkelspridning men från olika närdelar av K-cellens innervägg, och därmed vara i stort sett mycket likartade och liktidiga spiralgalaxer.

— NOTERA dock att denna möjlighet här ännu så länge bara är en ISOLERAD möjlig konsekvens. Först när vi får kontrollera värdena mellan flera olika närbelägna objekt kommer bilden att uppvisa mera tydliga konturer. Vi är inte där, än.

— Enda matchande möjligheten blir alltså den följande:

— Sambandsformerna ovan TILL PRÖVNING för K-cellens interna täthetsändring med riktning inåt K-centrum är något för stor; Prövningsformen uppvisar en större massansamling än den praktiskt observerade via de ovan antagna grundsambanden.

Notera att ingenting i grundsambanden för K-cellens värmfefysik påverkas av detaljerna i denna framställning:

— Resultaten från grundsambanden i K-cellens värmfefysik berör endast K-cellens yttre form på en idealt homogent täthetsbaserad grund, via grundparametrar [K-värdet och K-radien vid effektmaximum T=16,3 T9 år] som INTE lägger några särskilda aspekter på den VERKLIGA fördelningen av massor inuti K-cellen, vilket massdel som svarar mot K-radien. Den delen tillhör en vidare analys, baserad på grundresultaten, och som denna framställningen försöker belysa — och besvara.

— FRÅNSETT BERÄKNINGEN FÖR LJUSVÄGENS INTEGRAL ÖVER K-RADIEN:

— Den yttre formens värden i K-cellen bevaras i vilket fall, och medför ingen justering eller ändring i och med de resultat som beskrivs i denna presentation — eller ska i varje fall INTE göra det. Förekommer något sådant, är teorin KÖRD.

— LJUSVÄGENS INTEGRAL ÖVER K-RADIEN, ljustiden 4,52 T9 år, är i grundformen beräknad efter K-cellens idealt homogena täthetsfördelning och betecknar därför ett idealt [allra lägsta] basvärde. Med hänsyn till K-cellens allmänna toleransvärde i bestämningen av K-cellens massa, mellan 4,08 och 4,18 T53 KG, får inte heller ljustidsvärdet plus K-cellens expansionstid, totalt K-cellens ålder [20,82 T9 år minimum] överskrida den toleransen; Toleransen är ca max 3% (4,08/4,18=0,976) och vilken tolerans vi svårligen kan komma ifrån beroende på variationer i preferensen för de olika grundparametrarna, hur vi än räknar.

— Beträffande ljustiden för K-radien ska vi återkomma särskilt till den delen med redovisning av de olika värdena i de olika fallen vid ett senare tillfälle mot slutet av denna presentation.

— Se även allmänt i Ljusvägens integral.

För att lösa det problemet är det tydligt att — vilket också ligger i linje med K-cellens allmänna utveckling enligt TNED — den ökande tätheten in mot K-centrum inte får ske direkt från T=0 utan blott så småningom;

— Först med utvecklingen av divergenständningarna utåt K-cellen, kan de aktuella J-kropparnas inkastningar in mot K-cellen komma ifråga.

— Därmed skulle också ytterligare en faktorfunktion behöva läggas till, en som något dämpar massansamlingen ovan och som börjar direkt från K-cellens detonation, och som därmed tar hänsyn till K-cellens SUCCESSIVA utveckling: VÄXANDE täthet in mot centrum i takt med växande tid;

— Massansamlingen in mot K-centrum bör ske DIREKT från K-cellens detonation MED FÖRSUMBAR VERKAN för att gynna maximalt snabb divergensökning (eller bibehållande av max c0) inom de närmaste regionerna (och som gynnar tidsbildens elektrogravitella dynamik för Vintergatans bildning);

— Därefter (från en viss tidig händelsepunkt) allt mera påtagligt med ökande täthet in mot K-centrum som följd av J-kropparnas successiva avdelningar också inåt K-cellens centrum.

Enklaste sättet till PRÖVNING blir då naturligtvis att använda t-faktorn på den modifierade formen

t(k) = [(m/m₂)^k]^T/T(K)

= (m/m₂)^kT/T(K)

Här får K-cellens utveckling via T styra MAGNITUDEN i massansamlingen inåt K-centrum, så att grundformen för t-faktorn med (m/m₂)^k bara nås VID K-cellens expansiva slut [här ca T(K)=336 T9 år efter K-cellens halvperiod]. På motsvarande sätt från T=0 får t-faktorn ingen annan innebörd än lika med 1=(m/m₂)⁰.

— Prövningen via K-radien och K-värdet vid T=16,32 T9 år kommer sedan att utvisa om dessa faktorfunktioner räcker för att förklara observationerna — eller om eventuellt ytterligare krävs.

Justerande samband — efter ett rejält misslyckat försök (frontalkrasch, som det är bäst att inte berätta om här …)

Om vi backar tillbaka och undersöker funktionsformen för t-faktorn, ser vi att vi kan påverka massökningsmagnituden inåt K-centrum mera effektivt genom en enklare dämpfaktor (b) enligt

t(k) = b(m/m₂)^k

= ba

Det visar sig

— till en första preliminär prövning (bakom dessa skrivande detaljer döljer sig en nära oöverskådlig parad med en större mängd kalkyldokument som har studerats över en större tidrymd och som inte alltid är helt upplysande i resultatformerna med en gång)

— att b=0,7

T = 16,32 T9 år

m/mK = 0,0661

k = 0,0706

r = 8,32 t26 KG/M³

K = 1,5003

r(K) = 4,28158 T25 M

reducerar divergensen för r=9,28 T22 M vid T=20,82 T9 år från föregående

c₀(1–0,930878805) = 20 722 012,9 M/S

= 20 722,0129 KM/S

till det mera rimliga

c₀(1–0,999845677) = 46 264,85 M/S

= 46,26485 KM/S

Det praktiskt observerade värdet (runt ±300 KM/S) ska alltså motsvara ett b-värde ännu något närmare 1.

— Därmed är tydligen lösningsformen tangerad.

— Nej. Inte riktigt. För att det ska stämma VID m/mK=1 måste b vara 1 vid exakta m=mK.

— I så fall ska b ändras från ca 0,7 VID m/mK=0,0661 (K-radien); bryts det villkoret, kan vi inte nå fram till observationsvärdena.

— Vi studerar lösningen i detalj:

;

Täthetsändringsfunktionens slutform

t(k) = [b + (1–b)(m/m₂)²](m/m₂)^k

= [0,7 + 0,3(m/m₂)²](m/m₂)^0,1737

KalkylkortDirekt KcGRB.ods 9KcIN HelpOpen

exponenten till inre m/m2 är här godtyckligt insatt som 2 till en första prövning

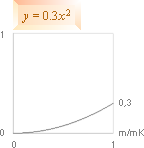
r = T^2/3(1/2)(4Gm₂)^1/3 .......................... grundform, homogen täthet från r-formen

v = T^–1/3(2/3)(1/2)(4Gm₂)^1/3 = r’

r = [t(k)T]^2/3(1/2)(4Gm)^1/3 .................. modifierad med täthetändringsfaktor

= [[0,7 + (0,3)(m)²](m)^0,0763]^2/3(m)^1/3T^2/3(Gm₂/2)^1/3 Från nedan i Vidare sammansättning

= [(m)^1/2[0,7 + (0,3)(m)²](m)^0,0763]^2/3T^2/3(Gm₂/2)^1/3 ;

r = [[0,7 + (0,3)(m)²](m)^0,5763]^2/3T^2/3(Gm₂/2)^1/3 ;

Graf y = [(0.7+0.3[0.48]'2)([0.48]'0.5763)'2/3]x'2/3

v = [t(k)]^2/3T^–1/3(2/3)(1/2)(4Gm)^1/3 = r’

Vidare sammansättning

Med b (0,7) som ett absolut lägsta gränsvärde för massansamlingen in mot K-centrum, återgår expansionen ut mot K-cellens rand till normalt ideala homogena icke täthetsändrande formen via subtrahenden (1–b) och dess multiplikation med återgångsstyrkan (m/m₂)² — funktionsexponenten är här godtyckligt insatt som 2 (prövningarna avgör sedan ev. vidare justeringar). Ideala formen uppnås vid m/m₂=1 som ger

t(k) = [b + (1–b)(1)²](1)^k

= b + 1 – b

= 1

KalkylkortDirekt KcGRB.ods 9KcIN HelpOpen värden: b=0,7; k=0,0763; m=m/mK:

t(k) = [0,7 + (0,3)(m)²](m)^0,0763

Ovan vä: Täthetsändringens [hittills optimalt utvecklade] funktion. K-radien och K-värdet [K-cellens inre] uppfylls.

Modifikationen i vänsterfiguren från ideala homogena täthetens funktion, figuren höger, visas markant i det innersta av K-cellen, figuren vänster:

— Täthetsförskjutningen in mot K-centrum [Se Detonationsmassorna] blir uttalat KRAFTIG i början av K-cellens expansion [från en viss tidpunkt — Se exempel i Transitfunktionen].

— Den täthetsökningen är också det dynamiska villkor som garanterar att all utanförliggande expanderande massa påverkas av den centrala ansamlingen genom en motsvarande inbromsning: K-cellens avstanning [Se Stoppmoderatorn].

— Funktionsformen totalt bestäms/modelleras av de centralt avgörande villkoren med K-värdet [1,5] och K-radien [4,28 T25 M].

— Se beskrivningen ovan från K-cellens Inre.

Ovan hö: Ideala formen med homogen täthet — som utelämnar det inre av K-cellen för vidare precis inspektion, men som är den enda grundform som finns i den ALLMÄNNA redovisningen av resultaten från K-cellens värmefysik.

Se även i Praktiska GRB-ursprunget hur funktionsformen (ovan vänster) formar K-cellens synrand [UNIVERSUMS SYNRAND].

Alltid med viss reservation för FEL:

— Man kan alltså STYRA (b) — knappast förutsäga — täthetsökningsformens funktion inåt K-cellens centrum på observationsvärdena i K-cellens centrum (som vi förmodar) — för att sedan, i vidare mening, också PRÖVA den funktionsformen, i vad mån den verkligen håller streck.

För vidare.

Se även i Iterationerna till K-cellens syngräns.

Skärningarna r0c-r

Skärningarna r0c-r

UTVECKLINGSLEDEN SOM MEDFÖRDE ETT GENOMBROTT TILL DEN HÄR PRESENTATIONENS FÄRDIGSTÄLLANDE

————————————————————————————————————————————

Tillfället då J-kropparna DIVERGENSTÄNDER — från c=0 till c > 0

Nolldivergensens sveprand följer inte r=c0T för den variabla täthetsformen. Man får utveckla efter g-potentialen w²=c0²/2 som ger r=Gm/2c0²:

r = Gm/2c₀² = [t(k)]^2/3T^2/3(1/2)(4Gm)^1/3 ;

T^2/3 = (Gm/2c₀²)/[[t(k)]^2/3(Gm/2)^1/3]

= (Gm/2)/[[t(k)]^2/3(Gm/2)^1/3]c₀²

= (Gm/2)^2/3/[[t(k)]^2/3]c₀² ; OK

T = Gm/2c₀³[t(k)] ; OK

t(k) = (m/m₂)^0,708 ;

T^2/3 = (Gm/2)^2/3/[[(m/m₂)^0,708]^2/3]c₀²

= ([m/m₂]Gm₂/2)^2/3/[[(m/m₂)^0,708]^2/3]c₀²

= ([m/m₂]^0,292Gm₂/2)^2/3/c₀² ; OK

T = ([m/m₂]^0,292Gm₂/2)/c₀³ ; OK

2Tc₀³/Gm₂ = [m/m₂]^0,292 ;

m/m₂ = (2Tc₀³/Gm₂)^1/0,292 ; OK

EN tid, för varje m. KalkylkortDirekt KcGRB.ods 9KcIN HelpOpen.

r’=dr/dt = [t(k)]^2/3T^–1/3(2/3)(1/2)(4Gm)^1/3

= v(r) ;

Se vidare utförligt i utvecklingarna från Täthetsändringsfunktionerna.

————— Bildkälla Täthetsändringarnas funktioner Magic NATURE

Författarens arkiv · Excur2012E1:12Apr2012 Bild24 · Nikon D90 Detalj

Iterationerna till K-cellens syngräns

Praktiska GRB-ursprunget

Iterationerna till K-cellens synliga c₀-gräns

K-CELLENS SYNGRÄNS

Nedan visas hur iterationsmatematiken till den gröna illustrationskurvan i Praktiska GRB-ursprunget är härledd.

BRYTGRÄNSEN MELLAN SYNLIGA OCH ICKE SYNLIGA K-CELLEN — Se Praktiska GRB-ursprunget

c-derivatan:

Divergensens expansiva g-beroende:

w < c₀/Ö2: positiv divergens

c = c₀ [1 – 2(w/c₀)²]^1/2 .................................... 2(w/c₀)² < 1 ; w/c₀=Ö [1–(c/c₀)²]/2

w > c₀/Ö2: negativ divergens

c = c₀ [2(w/c₀)² – 1]^1/2 .................................... 2(w/c₀)² > 1 ; w/c₀=Ö [1+(c/c₀)²]/2

;

c/c₀ = [1 – 2(w/c₀)²]^1/2 ;

deriveringen avseende w:

(c/c₀)’ = (1/2)[1 – 2(w/c₀)²]^–1/2(Dn –2w²/c₀² = –4w/c₀²)

= –(2w/c₀²)[1 – 2(w/c₀)²]^–1/2 ;

Nollderivatan:

0 = –(2w/c₀²)[1 – 2(w/c₀)²]^–1/2 ;

0 = 1 – 2(w/c₀)² ;

2(w/c₀)² = 1 ;

w² = c₀²/2

= k ;

= Gm/4[t(k)]²r ; OK

= Gm/4[(0,7 – 0,3m²)m^0,073]²r ;

k = Gm/4[t(k)]²r

= Gm/4[t(k)]²[t(k)T]^2/3(1/2)(4Gm)^1/3 ........ se Täthetsändringsfunktionens slutform för r

= Gm/4[t(k)]²[t(k)]^2/3T^2/3(1/2)(4Gm)^1/3

= Gm/2[t(k)]²[t(k)]^2/3T^2/3(4Gm)^1/3

= (Gm)^2/3/[t(k)]^8/3T^2/3(32)^1/3 ; OK

= (Gm₂)^2/3(m/m₂)^2/3/[t(k)]^8/3T^2/3(32)^1/3

= (Gm₂)^2/3(m)^2/3/[(0,7 + 0,3m²)m^0,0763]^8/3T^2/3(32)^1/3

= (Gm₂)^2/3(m)^2/3[(0,7 + 0,3m²)m^0,0763]^–8/3T^–2/3(32)^–1/3

= (Gm₂)^2/3(32)^–1/3T^–2/3[m^–1/4(0,7 + 0,3m²)m^0,0763]^–8/3

= (Gm₂)^2/3(32)^–1/3T^–2/3[m^–0,1737(0,7 + 0,3m²)]^–8/3 ;

Division med c0²/2 ger koefficienten 6,4123921 tillsammans med T-värdet i T9 år:

(Gm₂)^2/3(32)^–1/3([1 T9]/[3,16888 t8 1/S])^–2/3/(c₀²/2) = 6,4123921;

(6.412)[(16)'–2/3][(x'–0.1737)(0.7+0.3x'2)]'–8/3

KortBeskrivning: G-potentialderivatan [nollderivatan med konstanten c0²/2] låter oss DIREKT få inblick i hur K-cellens utveckling ter sig TILLSAMMANS med övergångsdynamiken till den omgivande c0-kroppen, se mera utförligt i Kc0iH; c0-kroppens allmänna förutsättning utgår ifrån ideal homogen täthet, vilket [Kc0H] betyder att g-potentialen växer linjärt med den omslutna massradien [Elektrogravitationen, GRUNDFYSIKEN i sammandrag] [Sambanden i översikt].

— Då K-cellen avstannar i sin expansion, med lägsta medeltätheten, bör denna sedan övergå mjukt i c0-kroppens.

— Se vidare utförligt i FORMGEOMETRIN — hur övergången kan formuleras i grundmatematik.

;

T^2/3k(Gm₂)^–2/3(32)^1/3 = (m)^2/3/[(0,7 + 0,3m²)m^0,0763]^8/3

= T^2/3K ; K=1,23946 t12 OK

T^2/3K = (m)^2/3[(0,7 + 0,3m²)m^0,0763]^–8/3 ; T i T9 år med K=0,155948044 OK

T^2/3K = [m^–1/4(0,7 + 0,3m²)m^0,0763]^–8/3 ;

[T^2/3K]^–3/8 = m^–1/4(0,7 + 0,3m²)m^0,0763 ;

= m^–0,1737(0,7 + 0,3m²) ; OK

[T^2/3K]^3/8 = m^0,1737/(0,7 + 0,3m²) ;

;

Den resulterande sambandsformen visar sig ge användbara resultatvärden först via ITERATION:

;

[T^2/3K]^3/8(0,7 + 0,3m²) = m^0,1737 ; OKiterativ — snabb

;

Extrakt från KalkylkortDirekt KcGRB.ods 6c0 HelpOpen

Itereration från 0. Ger sanna värdet redan efter några få varv.

— Iterationen inkluderar f.n. INTE StoppModeratorn =1.

Lösningen med Stoppmoderatorn=1 Inkluderad

———————————————————

oberoende av specifik funktionsform

En smidigare iterationsmetod

(efter prövning, gäller upp till max ca 28 T9 år, därefter finns ingen nolldivergens i K-cellen, se GRÖNA LINJEN — Universums synliga nollgräns — i Praktiska GRB-ursprunget)

visar sig enligt

k = Gm/4[t(k)]²r

= (m)Gm₂/4[t(k)]²r ; m = m/m₂ ;

m = 4[t(k)]²rk/Gm₂

= 4[t(k)]²r(c₀²/2)/Gm₂

= 4[t(k)]²rc₀²/2Gm₂

= 2[t(k)]²rc₀²/Gm₂ ;

= [t(k)]²r(6,50946 t27 M^–1)

KalkylkortDirekt KcGRB.ods 6c0 HelpOpen

Den m-formen betyder samtidigt (ett relativt) oberoende av r-formens sammansättning: man behöver inte dela upp sambandet; m-värdet visar sig direkt itererbart men med något längre iterationstid (runt 25 varv).

Nedanstående del har (här veterligt) ingen direkt koppling, men utgör ändå för sin del en fortsättning på ovanstående utvecklingar (kommer så småningom att raderas om ingen vidare användbarhet visar sig).

;

m² = (–0,7 + m^0,1737/[T^2/3K]^3/8)/0,3 ; Komplex lösning (inga meningsfulla värden inom K-cellen).

Minus k-derivatan:

k = –(2w/c₀²)[1 – 2(w/c₀)²]^–1/2 ;

–k = (2w/c₀²)[1 – 2(w/c₀)²]^–1/2

= (2/c₀)(w/c₀)[1 – 2(w/c₀)²]^–1/2

= (2/c₀)[(w/c₀)^–2(1 – 2(w/c₀)²])^–1/2

= (2/c₀)[((w/c₀)^–2 – 2])^–1/2

= (2/c₀)[c₀/w² – 2]^–1/2 ;

w² = Gm/4[t(k)]²r ; OK

–k = (2/c₀)[c₀/(Gm/4[t(k)]²r) – 2]^–1/2

= (2/c₀)[c₀4[t(k)]²r/Gm – 2]^–1/2

= (2/c₀)[c₀4[t(k)]²[[t(k)T]^2/3(1/2)(4Gm)^1/3]/Gm – 2]^–1/2

= (2/c₀)[c₀4[t(k)]²[[t(k)T]^2/3(1/2)(4)^1/3(Gm)^1/3]/Gm – 2]^–1/2

= (2/c₀)[c₀4[t(k)]²[t(k)T]^2/3(1/2)(4)^1/3(Gm)^1/3/Gm – 2]^–1/2

= (2/c₀)[c₀4[t(k)]²[t(k)T]^2/3(1/2)(4)^1/3(Gm)^–2/3 – 2]^–1/2

= (2/c₀)[c₀4[t(k)]²[t(k)]^2/3[T]^2/3(1/2)(4)^1/3(Gm)^–2/3 – 2]^–1/2

= (2/c₀)[c₀4[t(k)]^8/3[T]^2/3(1/2)(4)^1/3(Gm)^–2/3 – 2]^–1/2

= (2/c₀)[c₀4[t(k)]^8/3[T]^2/3(1/2)(4)^1/3(Gm₂)^–2/3(m/m₂)^–2/3 – 2]^–1/2

= (2/c₀)[c₀4(m/m₂)^–2/3[t(k)]^8/3[T]^2/3(1/2)(4)^1/3(Gm₂)^–2/3 – 2]^–1/2

= (2/c₀)[c₀2(m/m₂)^–2/3[t(k)]^8/3[T]^2/3(4)^1/3(Gm₂)^–2/3 – 2]^–1/2

= (2/c₀)[(m/m₂)^–2/3[t(k)]^8/3[T]^2/3(32)^1/3c₀(Gm₂)^–2/3 – 2]^–1/2

= (2/c₀)[(m)^–2/3[t(k)]^8/3[T]^2/3(32)^1/3c₀(Gm₂)^–2/3 – 2]^–1/2

= (2/c₀)[(m)^–2/3[(0,7 + 0,3m²)m^0,0763]^8/3[T]^2/3(32)^1/3c₀(Gm₂)^–2/3 – 2]^–1/2

= (2/c₀)[[(m)^–1/4(0,7 + 0,3m²)m^0,0763]^8/3[T]^2/3(32)^1/3c₀(Gm₂)^–2/3 – 2]^–1/2

= (2/c₀)[[(m)^–0,1737(0,7 + 0,3m²)]^8/3[T]^2/3(32)^1/3c₀(Gm₂)^–2/3 – 2]^–1/2 ;

;

[(–k)(c₀/2)]² = [(m)^–0,1737(0,7 + 0,3m²)]^8/3[T]^2/3(32)^1/3c₀(Gm₂)^–2/3 – 2 ;

2+[(–k)(c₀/2)]² = [(m)^–0,1737(0,7 + 0,3m²)]^8/3[T]^2/3(32)^1/3c₀(Gm₂)^–2/3 ;

K = (32)^1/3c₀(Gm₂)^–2/3 ;

(2 + [(–k)(c₀/2)]²)/T^2/3K = [(m)^–0,1737(0,7 + 0,3m²)]^8/3 ;

[(2 + [(–k)(c₀/2)]²)/T^2/3K]^3/8 = (m)^–0,1737(0,7 + 0,3m²) ;

(m)^0,1737 = [T^2/3K/(2 + [(–k)(c₀/2)]²)]^3/8(0,7 + 0,3m²)

k-värdet är det vi söker — men det är inte direkt uppenbart hur det ska itereras fram för givet T. För ev. vidare.

Divergensenergins g-beroende — 2012IV21

Divergensenergins gravitella beroende

Bildkälla: MAGIC NATURE

Knappast utom K-cellens (g-) gravitellt relaterade fysik har rubrikbegreppet ovan någon meningsfull innebörd: Vi studerar det.

Divergensenergins g-beroende, satsbild — energin bevaras

Divergensenergin E=mc² som frigörs i aktuellt g-rum bevaras oberoende av andra g-rum genom Planckenergins konstans,

E = hf = hcl^–1 = hc₀l₀^–1 = hc₁l₁^–1 = hc₂l₂^–1 se även i Gravitella dopplereffekten

Planckenergins gravitella frekvensnormalisering

FÖLJDSATS — PLANCKENERGINS GRAVITELLA FREKVENSNORMALISERING

Leden ovan hc₁l₁^–1 = hc₂l₂^–1 som medför att c₁l₁^–1 = c₂l₂^–1 betyder tydligen samma som att ”f₁=f₂=f=cl^–1”:

För att Planckenergin E=hf ska kunna bevaras mellan de gravitell skilda divergensrummens ljusemissioner c1 och c2, måste TVUNGET en anpassning av frekvensen ske på den bevarande energin villkor och som ansluter Planckenergin till den aktuella våglängden cl^–1. Med andra ord: Med våglängdens ändring mellan olika g-rum följer energimässigt också en frekvensanpassning.

— Jämför motsvarande konsekvenser: »gammafrekvens med röntgenvåglängd». Den fysiken finns [vad vi vet] inte.

— Notera olikheten i ljusbildens energi via föremål i rörelse:

— En ljusemitterande [elektriskt laddad] kropp i rörelse i ett givet g-rum betyder också en motsvarande uppkomst av magnetism: en viss rörelseenergi tillkommer i ljusemissionsbilden och som inte finns med i ljusemissioner som enbart grundas på vilande objekt i givna g-rum. Därmed kan inte heller någon obetingad jämförelse [energiräkning] göras mellan ljusemissioner från stationära objekt i givna g-rum kontra mobila dito: energiräkningen måste, i varje enskilt fall, anpassas efter den totala dynamiken.

Bevis:

Beviset för ovanstående satsbild återfaller HELT på ATOMKÄRNANS GRAVITELLA HÄRLEDNING med (praktisk tillämpning enligt Atomvikterna i) bevarandet av toppdivergensen (c₀) oberoende av gravitationens inverkan i överensstämmelse med LJUSETS GRAVITELLA BEROENDE med grund i konvergensprincipen (gravitationens princip, se GRIP) och den därav följande divergensprincipen (elektrofysiken genom ljusets natur, se DEEP).

— Inget av dessa begrepp, eller ens något motsvarande, existerar (veterligt, Apr2012) inom den moderna akademins lärosystem.

— Bevisformens argument:

— NEUTRONEN — samma som Planckringen i Atomkärnans härledning enligt relaterad fysik

h = m_{NEUTRONMASSAN 1,0086652u}c_{0TOPPDIVERGENSEN 2,99792458 T8 M/S}r_{NEUTRONRADIEN 1,3196611 t15 M}

= 6,62559 T34 JS [ref. HOPp7-155]

är (tydligen) en universellt, kosmiskt, »existentiellt oberoende» naturkonstant som inte påverkas av gravitationen, utan snarare garanteras sitt bevarande av denna; ljushastighetens toppvärde (c₀) kan inte ändras — eftersom det följer av konvergensprincipen (GRIP) med gravitationens absolutverkan, se särskild syntes i GcQ-teoremet om ej redan bekant.

— Dessa avgörande viktiga hörnstenar i DEN RELATERBARA GRUNDFYSIKEN har (Apr2012) ingen motsvarande representation i modern akademi: atomkärnans härledning överhuvudtaget finns inte i MAC.

— LJUSEMISSIONER som bildas i ett visst g-rum med en viss lokal divergens (c) utbreds alltså i relaterad fysik på vanligt sätt enligt Planckenergins E=hf=hcl^–1=hc₀l₀^–1=hc₁l₁^–1=hc₂l₂^–1, de sistnämnda leden speciellt enligt gravitella dopplereffekten.

— LOKALA DIVERGENSENERGIN E=mc² däremot måste lyda under den lokala divergensens fysik (c, enligt ljusets gravitella beroende), tillsammans med den lokala rymdkompaktheten (µ=R/c, se Rymdinduktansen för vakuum):

— INDUKTIVA VERKAN för att exemplifiera (Jämför strålningen i Parannihilation) som frigörs inom en bestämd g-rymd med en bestämd ljushastighet (c) betyder också därmed en bestämd energi; Den bestämda energin kan enligt ENERGILAGEN varken ökas på eller minskas ner av någon verksam mekanism i universum; en ljusemission (Jämför GRB) i ett gravitellt område med låg divergens betyder också följaktligen en liten induktiv kraft i förhållande till ett g-rum med toppdivergens. Den omsättningen — den lokala mc², stor eller liten, vilketsom — har alltså ingen explicit koppling till Planckenergins form E=hf — eftersom ljusutbredningen och ljusets fysik som sådan enligt relaterad fysik (TNED) är masslösa fenomen, se DEEP: ljus är icke-massa. Se särskilt i Ljusets friställning från kinetiken. Planckenergin endast förmedlar den lokalt frigjorda ljusenergins rent tekniska signal.

Energi som frigörs inom en bestämd g-rymd, är således energi som frigörs via en BESTÄMD magnitud — mekaniskt motsvarande rörelseenergi — och denna kan inte ändras utom genom explicit tillförande av extra energi (Se även Entropibegreppet i relaterad fysik). Planckenergin explicit E=hf garanterar således (Se särskilt i Gravitella dopplereffekten) för sin del att den energilokalens ljusenergi också fortplantas/förmedlas genom alla möjliga gravitella rum och rymder med källans energi. Inget annat.

Rymdens allmänna divergensresistans påverkas inte

ELEKTRISKA KRAFTLAGEN (Divergenskraften) F=Rc(Q/d)² med c₀-rummets elektriska konstant 1/e₀=R₀c₀ följer den lokala g-rymdens divergenskraft genom motsvarande lokalt variabla c-värden (LJUSETS GRAVITELLA BEROENDE).

— RYMDMOSTÅNDET (R₀) däremot har ingen känd relaterbar variabel mekanism i relaterad fysik;

— Den detaljen finns inte direkt omskriven i någon allmän sats i UNIVERSUMS HISTORIA, men figurerar underförstått i framställningssättet speciellt i sektionen som beskriver rymdkompakthet och rymdinduktans.

— Det främsta (enda) beviset på att rymdresistansen (R₀) generellt associerad med ljusets utbredning verkligen också är en fysikaliskt praktiskt icke ändringsbar faktor ges just i definitionen av elektriska kraftlagen, nämligen i delfaktorn (Q) som uttrycker elektriska laddningen: Q=[(m/R)(A/dT)]^1/2; samma i alla möjliga g-rum.

— Elektriska laddningen (Q) påverkas inte av den omgivande rymdens egenskaper, vare sig omgiven av stor eller liten gravitation. Laddningsmassan (m) förhåller sig under alla förhållanden (speciellt här i idealt vilande tillståndets fysik) konstant till den omgivande rymdens allmänna elektriska motstånd (R). Dvs., Divergensresistansen [R₀] får (tydligen) förstås som en (elektriskt trög) egenskap rymden har tillsammans med ljusfysiken som fenomenform (Se särskilt i härledningarna från Gravitationens Absolutverkan) och som inte har någon känd fysikalisk variabel.

MAC

I modern akademi är (vad vi vet) ovanstående genomgång — i all sin glänsande enkelhet och rudimentära logiska konsistens — en ren fundamental omöjlighet. Det vore speciellt förnämligt underbart om TNED vore fel på den punkten.

————— Bildkälla Divergensenergins g-beroende Magic NATURE

Författarens arkiv · Excur2012E1:12Apr2012 Bild18 · Nikon D90 Detalj

END.

Bildlänkar till MAGIC NATURE:

K-cellens inre fysik

K-cellens övergång

Formgeometrin

G-potentialer och tätheter i och utanför K-cellen

Mörka materien — GRB1m.htm

Divergenständningarna i detalj

GRB — kort inledning

G-faktorerna

Täthetsändringens funktioner

Divergensenergins gravitella beroende

K-cellens inre

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

K-cellens inre

ämnesrubriker

innehåll

K-CELLENS INRE

INLEDNING

Snabbsammanfattning — K-cellens värmefysik i UNIVERSUMS HISTORIA

Detaljerna från Grunden — K-cellens idealt homogena medeltäthet

Behovet av en mera precis översiktsbild

K-cellens övergång i c0-kroppen

Kc0H

K-cellens övergång i c0-kroppen, huvudvy

K-cellens täthet vid expansionens avstannande

Kc0iH

K-cellens radiella utsträckning — INRE delarna efter inhomogena täthetsändrande funktionerna

K-cellens expansionshastighet — INRE delarna efter inhomogena täthetsändrande funktionerna

Formgeometrin

K-cellen, slutvärden, StopMod=0

Medeltätheten utanför K-cellen vid stoppunkten

K-cellen till c0-kroppen

G-potentialer och tätheter i och utanför K-cellen

K-cellen inre

K-cellen yttre

Koefficienterna k12

Divergenständningen i detalj — DIVERGENSTÄNDNINGARNA I DETALJ

Detonationsfasen i detalj

G-energins FT-ekvivalent

GRB

GRB MAC

GRB TNED

G-faktorerna

Identiteterna för r0c med referens till statiska och expansiva tillståndets grundfysik

Lösningen i TNED

Varför grundsambanden INTE DIREKT utpekar observationella data

Beräkningsexempel som visar grundsambandens otillräcklighet

K-cellens inre

tK-faktorn — Täthetsändringens funktioner

tK-faktorns FORM

Basvärdena satisfierade

Villkor som måste uppfyllas

Lokala Galaxgruppen, basdata

Täthetsändringsfunktionens slutform

Vidare sammansättning

Skärningarna r0c-r

Iterationerna till K-cellens synliga c0-gräns

c-derivatan:

Nollderivatan:

Minus k-derivatan

Divergensenergins gravitella beroende

Planckenergins gravitella frekvensnormalisering

Rymdens allmänna divergensresistans påverkas inte

Bildlänkar till MAGIC NATURE

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1,602 t19 C ...................... elektriska elementarkvantumet, elektronens laddning [FOCUS MATERIEN 1975 s666ö]

e₀ = 8,8543 t12 C/VM ............. elektriska konstanten i vakuum [FOCUS MATERIEN 1975 s666ö]

G = 6,67 t11 JM/(KG)² .......... allmänna gravitationskonstanten [FOCUS MATERIEN 1975 s666ö] — G=F(r/m)² → N(M/KG)² = NM²/(KG)² = NM·M/(KG)²=JM/(KG)²

[BA]. BONNIERS ASTRONOMI 1978

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

MAC, modern akademi

TNED

(Toroid Nuclear Electromechanical Dynamics), eller ToroidNukleära Elektromekaniska Dynamiken

är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED får därmed (således) också förstås RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED [Planckfraktalerna] i ATOMKÄRNANS HÄRLEDNING.

Senast uppdaterade version: 2012-07-15

*END.

Stavningskontrollerat 2012-07-03.

rester

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

∫ √ τ π ε ħ UNICODE — often used characters in mathematical-technical-scientifical descriptions

σ ρ ν ν π τ γ λ η ≠ √ ħ ω →∞ ≡ ↔↕ ħ ℓ

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ σ ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ← ↑ → ∞ ↓

ϑ ζ ξ

Arrow symbols, direct via Alt+NumPadKeyboard: Alt+24 ↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬

Alt+23 ↨ — also Alt+18 ↕; Alt+29 ↔

Alt+NumPad 0-25, 26-...

☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓

→←∟↔▲▼ !”#$%&’()*+,-./♦812...

åter till portalsidan · portalsidan är www.UniversumsHistoria.se