UNIVERSUMS
HISTORIA | K-cellens
inre — AKROMATISKA
BRYTNINGEN GRB | 2012VI13 a BellDHARMA production | Senast uppdaterade version: 2017-10-27 · Universums Historia
innehåll
denna sida · webbSÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor
AKROMATISKA BRYTNINGSFENOMENET I GRB — Bildkälla, Författarens arkiv, 19Jun2012E8Bild66 NikonD90 Detalj

| Akromatiska brytningen | Light Curve Math — Ljuskurvornas matematiska fysik | GRB 980425 — SN 1998bw | Mörka materien | Kosmiska partikelstrålningens ursprung | Detonationsmassorna |
GRB1—K-CELLENS INRE • GRB1m—MörkaMaterien • GRB1n—Primära v-formen • GRB2—UniversumsSynrand • GRB2a—AkroBreak • GRB3—GRBorigin
För grunderna till ljuskurvornas matematiska fysik, se utförligt i LightCurveMath.
MAC-aspekterna på samhörigheten GRB-SN beskrivs i Akromatiska brytningen, GRB 980425 — SN 1998bw och GRB-exempel.
Akromatiska brytningen i GRB, inledning
GRB, eng. Gamma Ray Burst, se särskild
begreppsbeskrivning i NOMENKLATUR
om ej redan bekant
Akromatiska brytningsfenomenet i GRB
Primärtändningarna — se Divergenständningen
i detalj
TNED
— erinra först Planckekvivalenterna kontra Relativitetsteorin
med speciellt Beviset
för Multipla c:
— Genom K-cellens expansion i ljusets gravitella beroende inträder successivt olika partier av K-cellens massa [neutronkallplasma, c=0] i POSITIV DIVERGENS via nolldivergenszonens svep från K-cellens detonation.
— Lokaler med c>0 medför NEUTRONSÖNDERFALL [Divergenständning]. Därmed uppkommer obönhörlig detonation [GRB-utlösningen i TNED], [GRB-objektens ursprung i TNED], [Divergenständningen i detalj].
— En viss del av detonationsmassan från de större detonationskropparna [J-kroppar] kan förstås bestå av ytmassa i negativ divergens — neutroner — som kastas ut med höga hastigheter, väl jämförbara med den lokalt g-bestämda ljushastigheten (referensvärde runt 0,1c0 [Resultatreferens till GRB-källorna i TNED]), [Kosmiska partikelstrålningens ursprung i TNED]. Figuren ovan antyder funktionssättet.
— Genom detonationsmassornas primärt ytterst starka gravitation (max neutronkallplasmatäthet 1,82 T17 KG/M³) kommer förr eller senare en (stor) del av det närmast utkastade ytskiktets initialhastighet att bromsas upp:
— För att neutronsönderfall ska ske i en viss g-lokal med viss lokalt g-bestämd ljushastighet (c, lokala divergensen) måste den sönderfallande neutronens egenhastighet också befinna sig inom c. I annat fall finns ingen förutsättning för Coulombisk kraftkoppling via den lokala divergensen mellan atomkärna och elektronhölje [Kraftekvationen].
— När neutronerna bromsas upp tillräckligt mycket för att NEUTRONSÖNDERFALLET — elektronmassans koppling till den resulterande Vätekärnan — ska bli Coulombiskt fysiskt kopplande (kraftverkan under full koppling atomkärna-elektronhölje), uppkommer tydligen PLÖTSLIGT en ny materialsituation i området:
— Det ljus som tidigare OBEHINDRAT utbretts i rymden jämsides med neutronerna, kommer nu in i en situation där neutronsönderfallets Väteatomer som ett ljusabsorberande materialskikt kan ABSORBERA den tidigare odämpade ljusenergin. Då det sker, och här förutsatt efter lokalens olika betingelser, inträder en AKROMATISK LJUSBRYTNING: hela ljusbilden förändras (alla frekvenser och våglängder) inom ett relativt snävt övergångsintervall, och efterlämnar en svagare ljusbild.
— Genom att PRIMÄRENERGIN till GRB-utbrottet enligt TNED är given på känd effektform [∫ Pdt = E] [Energiintegralen och Effektderivatan], samt den inbrytande nytillkomna ljusskärmens materialbeteende är känd via ljusintensitetsfunktionen [I=I0e–bx] [Ljuskurvans intensitetsform], kan den resulterande fysikbilden sammansättas som en ÖVERGÅNG mellan dessa typfunktioner med hjälp av en TRANSITFUNKTION (den stänger av den ena funktionen för att överföra kvarvarande energi på den andra — med mellanliggande möjliga övergångsvariationer). Jämförande exempel ges i LightCurveMath med GRB-exempel.
— Det är den omedelbart mest närliggande kvalitativa förklaringen till det observerade ljusbrytningsfenomenet i GRB-objekten enligt TNED.
— I modern akademi ingår inte PRIMÄRTÄNDNINGARNA i den kosmologiska teorin — speciellt i MAC finns ingen variabel ljushastighet [Ljusets g-beroende] med universums utsträckning [Gravitella rödförskjutningen i TNED] [DET EKOLOGISKA UNIVERSUMET].
— För att kunna förklara de höga, kortvariga, GRB-energier [GRBenergiMACmaxT54erg] som i TNED utbildas från detonationsmassor i storleksordningen (tusentals) miljontals Solmassor [GRBenerginMaxTNED]
— |§| galaxbildningarna i TNED från K-cellens expansion (Primärtändningarna) [Fraktalnivåerna för GRB] [GALAXBILDNINGARNA] [Stjärnhopar och galaxbildningar Del 1]
— men som i MAC helt saknar motsvarighet, måste man i modern akademi (följdriktigt) söka en teoretisk förklaring som går ut på en REDUCERAD GRB-energimängd (från runt T47 J [T54 erg] till T44 J [T51 erg]) [Tanvir et al., 2010] [Nakamura 1999]. Nämligen i formen av en s.k. Jetstråle [JetMechMAC] [JetBreakMechMath i MAC]: bara en liten del (runt 1/100—1/1000 eller ännu mindre) av den idealt sfäriska (konv. isotropiska) strålenergin samlas i jetstrålen.
— Medan GRB-utbrottet i TNED avlöper från en primärt stor masskropps detonation i universums ytterst synliga utkanter [UNIVERSUMS SYNRAND] (primärbildningen av en hel galaxmassa med underavdelningar [GRB-förutsättningarna]), och av vilken detonationsenergi bara en ytterst liten del (bråkdelar av miljondelar) kommer ut i form av GRB-signaler [GRB-objektens ursprung i TNED] [Fraktalnivåerna för GRB] [GRB-energin i TNED], måste motsvarande energireducerade GRB-utbrottsfysik i MAC (följdriktigt) anställa en SUPERNOVA [‡Supernova] som kraftbas: Man menar att Supernovans utbrott föregår (den Jetavgränsade) GRB-förekomsten [‡Citat]. Annars går energiräkningen inte ihop.
Ytterligare en (slutligt — eg. primärt) avgörande detalj tillkommer i TNED: GRB-källan i detalj. Dess speciella aspekt via TNED ingår inte i MAC som någon direkt beräkningsbar faktor, ehuru helt avgörande i TNED: Frekvensen observerade GRBs per dygn [Antalet GRBs per dygn]. Antalet måste — ovillkorligen, obönhörligen — kunna serveras per teori MED MARGINALER av TNED i överensstämmelse med praktiska observationer. Annars är hela framställningen körd;
I korthet har följande framkommit i TNED beträffande GRB-frekvensen med referenserna [Antalet GRB‑himmelsfläckar] [Signalspridningen] [Kamouflerande g-avböjningsytan] [Frekvensen synliga pulsbilder]:
— Ljustiden i lokaler med c/c0=0,1 avverkar ett medelgalaxavstånd [Medelgalaxerna] d=1,8 T22 M på tiden T=d/c=6 T14 S eller drygt 19 miljoner år. På samma tid [TNED-sambandet J-kropparnas expansion] [Exempelreferens Vintergatans Expansion] hinner en medelgalax utveckla en medelsfärradie för den inneslutna medelgalaxmassan på 2,24 T18 M. Gravitella ljusavböjningen (Bågsekunder och Distanser) blir med d=1,8 T22 M avrundat 3,9 grader; Genom att var och en av de runt 106 miljoner medelgalaxvolymerna [Antalet randgalaxer] [Medelgalaxerna] [HUDF] avbildar en upptagande bågvinkel på ca 70 bågsekunder (70’’) på himmelsytan vid synranden — [206265](1,8 T22)/(5,25 T25 M)’’=70,719428’’ — kamouflerar g-avböjningen följaktligen som absolut maximum runt (3,9·3600)/70=200,57142 ~ 200 stycken primära galaxhimmelsfläckar; Antalet MAX DETEKTERBART förekommande GRB — spricker den siffran på praktiken gäller inte TNED — sett över hela himmelsytan totalt enligt TNED, blir då (HP, HimmelsfläcksPulsbilder)
f(P)max = (106 T6 H)/(8 T6 år [Randgalaxernas förnyelseperiod]) · (200 P) ~ 7 HP/dygn
Den angivna frekvensen detekterade/observerade är [2012] 1-3
per dygn [Antalet
GRB per dygn].
— Bara för att man NU 2012 inte har teknik för att upptäcka
mer än runt 2 GRBs per dygn, behöver inte innebära att det runt 2112 finns
kapacitet för, och upptäcks, säg 10 GRBs per dygn. Skulle så bli fallet gäller
INTE den här framställningen. Det är också ett exempel på en teoris
tidsbegränsade giltighet i förhållande till den begränsade teknik som gäller
under författarens möjliga livslängd. Akta.
Men ännu ytterligare en avgörande faktor tillkommer för TNED — och i full konsekvens av de redan ovan antydda:
— GRB-pulsernas specifika pulsbredder (som avslöjar kroppsdimensionerna via ljussignalens metriska passage):
— Alla förekomster av observerade pulsbredder i motsvarande detonationsfraktaler [Fraktalnivåerna för GRB], från kortaste (runt 1 mS eller mindre) till längsta (max 1,5 S för en hel primär medelgalaxmassa [Kärnåterkopplingens fördröjning]), måste passa in med motsvarande detonationsmassornas reaktionstid — enligt TNED. Den bild TNED anställer för sin del som förklaring till hela GRB-fenomenet måste ovillkorligen kunna ses, spåras och detaljstuderas i den observerade praktiken. Annars går det inte. Dessa värden (mS till S) FÖREFALLER också återfinnas (grovt sett) i de olika GRB-ljuskurvorna som kan studeras. Se särskilt i PrimeEnergy och DETONATIONSMASSORNAS REAKTIONSTID, samt även i VÄRDEBEVIS TNED-GRB.
Det FÖREFALLER vara »tuffa tag för TNED» (med parametrar långt utöver den moderna akademins horisonter, och som obönhörligen måste stämma överens med praktikens observationer) — och marginalerna måste också hålla om det är TNED som gäller — men är å andra sidan »bara» en ren konsekvens av att »läsa TNED-facit innantill»: det finns icke mycket annat att välja på.
Det är tydligt att inte bägge föreställningssätten, TNED-GRB resp, MAC-GRB, kan gälla samtidigt. Och alltså borde det här finnas enastående tillfällen att, via de GRB-observationer som nu finns i allt mera rik mängd, avgöra huruvida det ena eller andra sättet gäller.
Vi studerar de olika argumenten.
Inledande exempel på banbrytande PDF-dokument om huruvida JetBrytningen är akromatisk (innefattar samtliga våglängder, eg. alla optiskt synliga färger) eller inte:
”GRB990510 is the first burst to show a clearly defined achromatic break in the optical light curve (Harrison et al. 1999, Israel et al. 1999, Stanek et al. 1999) which was readily interpreted as firm evidence for beaming and a total energy release substantially less than the isotropic value of 3×1053 ergs.”, s1sp2ö;
”These results demonstrate that the decay of the afterglow is achromatic in VRI at least for the interval HDAB 0.6–8.0 and in BVRI for HDAB 0.8–3.9. We feel justified, therefore, in converting all measurements to equivalent R-magnitudes and fitting a single grand total light curve (Fig. 2. upper panel).”, s2sp2n,
AkroJet — Akromatiska brytningsfenomenet i efterglödsljuset från GRBs i MAC —
a b
Funktionsbrytningen i graf
En observerad plötslig ljusavflackning (b, figuren ovan vänster) i efterglödsljuset från vissa GRBs, en s.k. akromatisk brytning (som inbegriper alla färger), har föranlett ett fördjupande av teorier i MAC som går ut på ett fenomen benämnt JETSTRÅLAR.
— Jetstrålar [»JetMech»] anses numera i MAC (i de flesta fall) vara transportörerna bakom GRB-objektens ljusbilder. Följande beskrivning försöker ge en överblick av sammanhangen, samt [AkroGRBbreakTNED] ge en relaterad bild av fenomenet — som det får förstås enligt TNED.
Akromatiska brytningsfenomenet — och Jetstråleteorin i MAC
JETs och AKROMATISKA (som innefattar alla frekvenser)
BRYTNINGAR — i ljusbilderna från supernovor:
GRB-objekt bär visst ansvar för formeringen av Jetteorin i MAC
KOPPLINGEN mellan supernova och GRB framhålls speciellt (slutligt, 2002) genom observationerna av GRB 020813 från Chandras Röntgenobservatorium (Chandra X-ray Observatory). En artikel som beskriver detaljerna finns i webbkällan nedan;
”Scientists announced today that they have used NASA's Chandra X-ray Observatory to confirm that a gamma-ray burst was connected to the death of a massive star.”,
;
”Chandra was able to obtain an unusually long observation (approximately 21 hours) of the afterglow of GRB 020813 (so named because the High-Energy Transient Explorer, HETE, discovered it on August 13, 2002.) A grating spectrometer aboard Chandra revealed an overabundance of elements characteristically dispersed in a supernova explosion. Narrow lines, or bumps, due to silicon and sulfur ions (atoms stripped of most of their electrons) were clearly identified in the X-ray spectrum of GRB 020813.”,
http://www.spaceflightnow.com/news/n0303/24chandra/
SPACEFLIGHT
NOW — Gamma-ray burst, supernova connection confirmed
CHANDRA
X-RAY CENTER NEWS RELEASE, Posted: March 24, 2003
Att en supernova skulle ha varit inblandad i händelsen grundades på observationer med förekomst av kisel och svavel i strålningen från GRB 020813, samt övriga signaldata:
”An analysis of the data showed that the ions were moving away from the site of the gamma-ray burst at a tenth the speed of light, probably as part of a shell of matter ejected in the supernova explosion. The line features were observed to be sharply peaked, indicating that they were coming from a narrow region of the expanding shell. This implies that only a small fraction of the shell was illuminated by the gamma-ray burst, as would be expected if the burst was beamed into a narrow cone. The observed duration of the afterglow suggests a delay of about 60 days between the supernova and the gamma ray burst.”, källartikeln som ovan.
En Wikipediaartikel (2012-05-11) på GRB 020813 ger vidare data: rödförskjutning z=1,254; grundämnen som framkommit ur spektralanalyserna, ”magnesium, silicon, sulphur, argon, and calcium, which supported the theory that gamma-ray bursts are preceded by highly massive stars undergoing a supernova collapse.[5]”
Snarare än karaktäristiskt för supernovornas ljuskurvor, framträder (en del, inte alla) observationerna av GRB-objektens ljuskurvor i formen av s.k. akromatisk brytning (eng. achromatic break, akromatisk som »färglös»), eller (eng.) jet-break:
|
Förminskad
kopia av PDF-källans FIG. 2 s8n, Tanvir
et al., 2010, GRB 080319B |
I PDF-dokumentet http://arxiv.org/pdf/0812.1217v2.pdf LATE
TIME OBSERVATIONS OF GRB080319B: JET
BREAK, HOST GALAXY AND ACCOMPANYING SUPERNOVA, Tanvir et al., 2010 ges utförliga exempel på vad källan kallar ”indicating approximately achromatic behaviour, as expected for a jet break.”, s4sp1m, Jet-break and energetics. |§| Detaljerna ansluter direkt till det som i MAC anses avgörande för kopplingen GRB-supernova via pionjärobjekten (1998) GRB 980425 och SN 1998bw (Nakamura1999) — se även Wikipedia (Maj2012) Gamma-ray burst [‡], Afterglow, ”The following year, GRB 980425 was followed within a day by a coincident bright supernova (SN 1998bw), indicating a clear connection between GRBs and the deaths of very massive stars”; Källan ovan (med referens till diskussioner SN-GRB via ett senare [2008] jämförande objektet, GRB 080319B): ”Thus we find that GRB080319B was accompanied by a supernova a little fainter than the prototype SN1998bw”, s5sp1mö. |
|
a
b Funktionsbrytningen
i graf |
Samband med normala xy-enheter (Se utförligt i Transitfunktionen): y = 5 + [(1/2)(5 – x/1)(1 + [x/5]100)–1
+ (1/1)(5 – x/1)(1 – [(1
+ [x/5]100)–1])]
Graf y = 5+[(1/2)(5–x/1)[(1+[x/5]'100)'–1]]+(1/1)(5–x/1)(1–[(1+[x/5]'100)'–1]) Samband för brytningen med logaritmiska xy-enheter beskrivs med praktiska exempel i GRBexempel. |
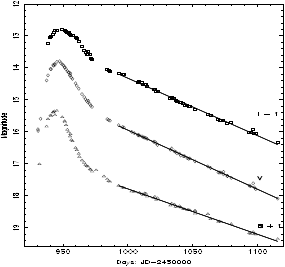
Brytintervallet i tid. Källgraferna från Tanvirgruppen ovan, de tre
vänstra, visar ljusbrytningen vid ca T6 S = 11,57
dygn; Brytningen [heldragen linje av
författarna] visas tämligen skarpt inom 2 pixels; 85p/10dekad; 10^[6+2/85]S=12,22
dygn; vilket ger ett brytintervall på grovt 0,65 dygn eller 15,6 timmar. Se
dock en mera detaljerad beskrivning i AkroBreak.
— Genom att (2012, vissa) supernovor i forskarvärlden kommit att associeras med GRBs, har också speciellt den — i ljusbilden från (många) GRBs — observerade plötsliga ljusavflackningen [AkroJetMAC] (akromatisk brytning, en plötslig nedgång i ljusintensiteten [runt ental/tiotal dygn efter effekttoppen] som berör alla frekvenser, figurerna ovan vänster) kommit att ingå som detalj i supernovornas karaktäristika.
Speciellt har den observerade plötsliga
ljusavflackningen (b, figuren ovan vänster) i efterglödsljuset från
vissa GRBs föranlett ett fördjupande av
teorier i MAC som går ut på de s.k. JETSTRÅLAR
man numera (i de flesta fall) anser är transportörerna bakom GRB-objektens
ljusbilder;
”Gamma-ray burst emission is believed to be released in jets, not spherical shells.[10]”,
http://en.wikipedia.org/wiki/Gamma-ray_burst_emission_mechanisms
@INTERNET Wikipedia, Gamma-ray burst emission mechanisms (2012-05-11)
Den helt avgörande primära anledningen bakom JETSTRÅLETEORIN (Se bl.a. Wikipediaartikeln ovan i sektionen Jet effects) kan utläsas ur följande centrala sammanhang:
”No known process in the Universe can produce this much energy in such a short time. However, gamma-ray bursts are thought to be highly focused explosions, with most of the explosion energy collimated into a narrow jet traveling at speeds exceeding 99.995% of the speed of light.[59][60]”,
http://en.wikipedia.org/wiki/Gamma-ray_burst
@INTERNET Wikipedia, Gamma-ray burst, Energetics and beaming (2012-05-11)
Det finns inom den moderna akademins lärosystem ingen känd fysikalisk process som skulle kunna uppvisa de starka energiutbrotten [Jämförande grovdiagram Novor/GRB] som associeras med GRB-förekomsterna, och under de korta tidrymder (sekunder) som de idealt (instrumentella) observationsvärdena antyder. I bilden av GRB-signalerna, så som de mätande sensorerna ser saken, framträder en smal del av en idealt sfäriskt expanderande ljusbild som träffare den mätande sensorytan (i storleksordningen kvadratcentimeter).
— Enda möjligheten blir då att söka en förklaring som bygger på att ljusbilden i sin källform i själva verket också just är en avgränsad dito: bara en smal ljuskon av hela den ideala sfäriska utstrålningen gäller — och som precis händelsevis träffar våra regioner.
— LJUSKNÄET, den akromatiska brytning som en del GRB-objekt uppvisar — inte alla
|§|[W|JetMech, ”Many GRB afterglows do not display jet breaks, especially in the X-ray, but they are more common in the optical light curves.”]
— skulle då kunna kopplas till den (starkt) reducerade effektiva jestråleenergin enligt följande skisserade figur:
Jetteorin i MAC — JetMech
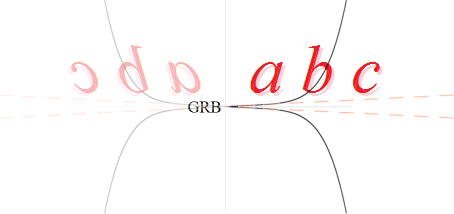

Artist’s Impression PR Image eso0828a — http://www.eso.org/public/news/eso0828/
Wikipedia GRB 080319B — hur man tänker
sig JET-strålen från ett GRB-utbrott — http://en.wikipedia.org/wiki/GRB_080319B
JetMechMAC — hur man tänker sig funktionen
Man tänker sig (figuren ovan, a) att GRB-utbrottet uttömmer sin energi i en smal (streckad) strålkon, i förlängningen som figurens c, en s.k. Relativistisk JetStråle. Utbrottet för med sig material och avancerar utåt rymden med mycket nära ljushastigheten.
— Den springande punkten handlar om situationen då farten avtar (i relaterad fysik som följd av centralmassans gravitellt bromsande dragningskraft, men den detaljen gäller inte [riktigt] i MAC eftersom också gravitationens verkan anses ske via ljushastigheten) vid ett visst kritiskt KNÄ (b):
”One of the most important open questions in gamma-ray bursts (GRBs) is whether the burst emission is isotropic or strongly beamed in our direction.”,
”According to the relativistic fireball model, the emission from a spherically expanding shell and a jet would be rather similar to each other as long as we are along the jet’s axis and the Lorentz factor γ is large compared to the inverse of the angular width of the jet θ0 (Piran 1995). When γ drops below θ0–1, the jet’s material begins to spread sideways, and we expect a break in the light curve of the afterglow at this stage.”, sL17sp1,
http://iopscience.iop.org/1538-4357/519/1/L17/pdf/1538-4357_519_1_L17.pdf
The Astrophysical Journal,
519:L17–L20, 1999 July 1 — JETS IN GAMMA-RAY BURSTS, Sari et al., 1999
Lorentzfaktorn (se exv.
Wikipedia, Lorentz factor) är samma som r-teorins γ = 1/√1–(v/c)2
— Genom att »ingenting kan gå fortare än c» i MAC hindras NORMAL SPRIDNING ’runt jetRadianten’ så att bara »RAKT UT» gäller. Det är kärnan i JetMech.
— När Relativistiska J-strålen sedan avtar i hastighet (figuren ovan, b — genom här ej närmare kända orsaker) tänker man sig nettoverkan i formen av bildningen av en karaktäristisk trumpetöppning: Jetstrålen sprider plötsligt ut sig — och »åstadkommer» då en motsvarande (sfärisk) utsmetning av den ursprungliga sfärdelkonen: ljusstyrkan, alla frekvenser, avtar plötsligt och uppvisar sedan en märkbart svagare ljusbild. Se även den mera ingående beskrivningen av förloppet i Wikipedia JetMech.
— Att MEKANISMEN bakom de antagna JETMechs inte (ännu Maj2012) är väl genomlyst framgår av följande PDF-källor:
”These jets are not continuous streams of matter, but consist of individual blobs,
or ”cannonballs”. The jets emitted by quasars must be seen to be believed: they
extend for many times the size
of a galaxy, and they are unresolvably
pencil-collimated
till their material finally loses its kinetic energy
to the intergalactic medium, stops
and expands. The mechanism producing these surprisingly energetic and collimated
emissions is not understood, but it seems to operate pervasively in nature (the mantra
here is MHD, for magneto-hydrodynamics, which is not yet solved, particularly in its
relativistic or general-relativistic versions.)”,
http://cdsweb.cern.ch/record/500958/files/0105203.pdf
Theory
Division, CERN —
HIGH-ENERGY
NEUTRINOS AND HARD γ-RAYS IN COINCIDENCE WITH GAMMA RAY BURSTS, A. De
Rújula — datumuppgift saknas (ref. 2000)
”Abstract.
Research in recent decades has seen many important advances in understanding
the role of jets and outflows in the star formation process. Although, many open issues
still remain, multi-wavelength high resolution observations have provided unprecedented
insights into these bizarre phenomena. An overview of some of the current research
is given, in which great strides have been made in addressing fundamental questions
such as: how are jets generated? what is the jet acceleration
mechanism? how are jets
collimated? what is the relationship between accretion and ejection? how does mass
accretion proceed? do jets somehow extract angular momentum? and
finally, is there
a universal mechanism for jet generation on all scales from brown dwarfs to AGNs?”,
http://arxiv.org/pdf/1112.2508.pdf
THE
ENIGMA OF JETS AND OUTFLOWS FROM YOUNG STARS, D. Coffey, 2011
Jämför även andra PDF-dokument vars författare (här tidigt 1999) ser den akromatiska brytningen som belägg för typen JetMech:
”Such a beam model is relevant now since evidence for the beaming has recently been suggested by the rapid decline of the optical afterglow of GRB 990123 after day 2 (Kulkarni et al. 1999) and by the rapid decline of GRB 980519 (Halpern et al. 1999).”,
http://iopscience.iop.org/1538-4357/522/2/L101/fulltext/995391.text.html
The Astrophysical Journal,
522:L101-L104, 1999 September 10 —
OFF-AXIS
EMISSION FROM THE BEAMED AFTERGLOW OF GAMMA-RAY BURSTS
and a Possible Interpretation of the Slowly Declining X-Ray Afterglow of GRB 980425, Takashi Nakamura 1999
Oavsett teori är alltså nettoverkan av den observerade
ändringen, den akromatiska brytningen, att hela den ursprungliga ljusbildens
intensitet plötsligt, inom ett relativt snävt tidsintervall undergår en
avskärmning: som om man vid b-tidpunkten »INFÖR» en ljusdämpande skärm mellan
sig och GRB-källan (något kommer in som inte fanns där förut).
— Notera dock, som redan påpekats [‡],
att brytningsfenomenet inte alltid verkar finnas med i ljusbilden från de
observerade gammastråleutbrotten.
PDF-dokumentet från Sari et al., 1999 påkar också (tidigt) alternativa scenarion (användningen av termen ’isotropic’ ansluter till föreställningen om idealt sfärisk ljusspridning):
”So far, with the exception of the recent GRB 990123 (Kulkarni et al. 1999), no such break was observed, even for afterglows extending for hundreds of days. More specifically, the well-studied afterglows GRB 970228 and GRB 970508 behave according to a single unbroken power law, as long as the observations continued (Zharikov, Sokolov, & Baryshev 1998; Fruchter et al. 1999), giving a strong indication that those sources were isotropic to a large extent.”, Sari1999.
Den primära anledningen bakom jetstråleteorin skulle alltså och emellertid inte vara ljusknäet som sådant, utan snarare de höga energier [Wiki|GRBenergy] som uppmätts i referens till en normal radiell (sfärisk, ofta med synonym i GRB-litteraturen »isotropisk») utstrålning:
— Eftersom ingen känner till någon process i universum som kan frigöra så stora energimängder som instrumenten registrerar, sett i deras sfäriskt upptagande del [Wiki|GRBenergy], har man alltså följriktigt tvingats utveckla »Ny Fysik».
Jetstråleteorin har — därmed — kommit att fylla flera funktioner — tydligen främst för att få ner den sfäriskt ekvivalenta (den s.k. isotropiska GRB-) energin (runt 100-tals till 1000-tals gånger genom att bara beakta den koniska stråldel som träffar mätinstrumentet) [Tanvir et al., 2010] till sådana nivåer som kan anses acceptabla för den fysikteori man har koll på.
AkroJet — Akromatiska brytningsfenomenet i efterglödsljuset från GRBs i MAC
AkroJetMech — Jetteorin i MAC
![]()
Akromatiska brytningen enligt TNED
Basic TNED:
Väsentligt material (neutronkallplasma) [Inledningen] följer med i J-kropparnas
utkastningar (v) med den lokala divergensens utbredningshastighet (c) [DETONATIONSMASSORNA]
[DETONATIONSMASSANS UPPLÖSNING].
— Kosmiska Partikelstrålningens Ursprung
intar en helt naturlig plats i det sammanhanget [RäkneexempelSi].
De värden på detonationsmassa som krävs
enligt TNED för att få fram motsvarande
observerade ungefärliga (isotropiska) GRB-energivärden (runt max T47 J eller
T54 erg), visar sig stämma överens med den relativt detaljerade bild av
K-cellens detonationsfysik [Primär Galaxbildning med Vintergatan i Fraktalexempel]
som resultatredovisningen i K-cellens värmefysik generellt bygger
på [GRB-energinMaxTNED]
[Detonationsmassorna generellt för GRB]
[VÄRDEBEVIS
TNED-GRB].
Det är här fråga om Detonationsmassor
på (tusental) miljontals Solmassor i lokaler med låg divergens i universums
allra ytterst synliga utkanter [c/c0=0,1
ResultatReferens GRB 061028 z9,7], där den utläckande
GRB-energin bara står för en försvinnande liten bråkdel.
Se även sammanfattande jämförande
beskrivning i INLEDNINGEN.
Neutronsönderfallet i dessa partier kan inte utvecklas med
full kraft förrän neutronhastigheterna (v) relativt lokala divergensen (c [DEEP] [DIVERGENSEN] [LJUSETS
G-BEROENDE])
underskrider denna (v<c). Då så sker, kan neutronsönderfallet fullbordas.
Därmed finns en relaterbar grund för att förstå HUR det kan ha BILDATS en mera
direkt ljusabsorberande SKÄRM — Vätgas, samt övrigt molekylärt material —
mellan ljuskällan och vår position — och som tidigare
inte fanns där [Resulterande Ljuskurvor i GRB-exempel].
— I termer av modern akademi kan inte
den teorin föras — (främst) på grund av att man är låst vid uppfattningen att
GRB-källorna handlar om enskilda redan primärt bildade stjärnobjekt:
— Materialet till ljusskärmen skulle inte på långa vägar
räcka — enligt TNED —
för att ge den avsedda effekten om materialkällan bara vore en enda
enstaka (eller tiotal) stjärnmassa som detonerar. Det krävs (minst) miljontals
Solmassor — ELLER att det är frågan om en smal Jetstråle med motsvarande (flera
tusen gånger) reducerad energi, vilket är vad MAC
kräver [JetMech].
— Däremot om detonationsmassan är stor
1-10
miljoner Solmassor, eller mer — i RELATERAD FYSIK i samband med de primära stjärnbildningarna
i galaxer, och som heller inte ingår som alternativ i den moderna akademins uppfattning
om universum, se
[Detonationsmassorna generellt för GRB]
finns bättre förutsättningar för den
beskrivna skärmeffekten.
— På sin höjd ger man (Samband
med exempelbeskrivning) i MAC
utrymme för detonationsmassor på runt (max) 100 Solmassor som källor till
GRB-objekt.
— Se vidare i Samband med exempelbeskrivning hur man
resonerar i MAC.
Bildkälla, Författarens arkiv, 25Maj2012E5Bild115 NikonD90
Detalj

Akromatiska brytningsfenomenet — enligt TNED
MÖJLIG FÖRKLARING
Den observerade akromatiska brytningen visar sig [AcroJetMAC] från runt 1 dygn (och mera) [‡AkroBreak] efter GRB-toppen:
— VID en viss tidpunkt [‡AkroBreak] dämpas plötsligt hela ljusbilden ned — och behåller sedan det nedtonade läget till slut.
Den närmast RATIONELLA förklaringen enligt TNED är enkel och rakt på sak:
![]()
— Det är alldeles tydligt att något mellanliggande aktiveras som en ljusabsorberande skärm — men som inte fanns där tidigare.
![]()
Materialet som J-moderkroppen enligt TNED skickar ut [PRIMÄRTÄNDNINGEN] tillsammans med den primära J-detonationen innefattar höghastighetspartiklar.
— I MAC kan inte den diskussionen föras vidare: man vidhåller Einsteins relativitetsteori framför PLANCKEKVIVALENTERNA, och missar därmed enligt TNED fenomenets rationella förklaring — i exakt bevarande av den matematiska fysikens formalia (Se även i Experimentella Bekräftelser):
![]()
— Neutroner som färdas med hastigheten v=c i ett rum med divergensen c har visserligen (Magnetiska fönstret) fortfarande en viss förmåga att sönderfalla (Neutronsönderfallet) så länge neutronerna befinner sig i ett rum med c>0. Emellertid är den Coulombkopplande kraften (Elektriska kraftlagen) mellan atomkärna och elektronhölje försvagad (jämför två tättliggande föremål — två MikroProcessorer — som rör sig med ljudhastigheten och försöker prata med varandra ändå; möjligtvis kan vissa brottstycken uppfattas om parterna pressar sig tätt, tätt tillsammans, med ett minimalt litet mellanrum) — och därmed också den LOKALT Planckenergikopplande elektromagnetiska verksamhetsbasen E=hf (Planckenergin) (Divergensenergins g-beroende):
En neutron som färdas med lika stor hastighet som den elektriskt fältåterkopplande kraften kräver — mellan atomkärna och elektron (c) och för att alls kunna utverka en aktiv svängningsfysik — har uppenbarligen och vad vi vet ingen direkt förmåga att verkställa ett neutronsönderfall med resultat i en någon direkt aktiv Väteatom:
Neutronen, som sönderfaller till en Vätekärna, drar (eftersläpar) uppenbarligen med sig det normalt elektriskt kopplande fältet utan någon möjlighet för elektronmassan att hänga på (Se Betasönderfallet generellt enligt TNED);
Elektronmassorna (om alls) som de (lokalt) relativt snabbt färdande neutronerna avdelar i neutronsönderfallet, kan därmed förstås lämnas efter — utan möjlighet att E=hf-koppla sin atomkälla.
— Det är den bild som frammanas spontant ur den vanliga vardagliga fysik vi känner (TNED).
Allt ljus, från J-detonationerna [PRIMÄRTÄNDNINGEN], som färdas tillsammans med de sönderfallande neutronerna SKULLE därmed och tydligen få en speciell karaktär:
Ljuset från J-detonationerna betingas FÖRST, intill en viss tid, av Egenheten att INTE (direkt) hindras av DET MELLANLIGGANDE MATERIALETS normala elektron-protonbindning, och som normalt skulle medföra en viss absorption (energireduktion i källjuset). En sådan effekt kommer först senare. Källjuset, som det får förstås i denna del, möter alltså initiellt maximalt (onormalt) LITET motstånd.
— Gravitationens bromsande inverkan på det material som befinner sig närmast centralmassan, analogt de neutronpartier i J-utkastningarna [PRIMÄRTÄNDNINGEN] som besitter de lägre (inte de högsta) utkastningshastigheterna, betyder att v=c-läget för de sönderfallande neutronerna (så småningom, helt säkert) saktar av. Helt säkert. Men det gör inte ljusets utbredning på vägen in mot K-centrum (c/c0=1).
— I motsvarande mening tillväxer då den normalt lokalt kopplande Coulombkraften (Elektriska kraftlagen) mellan elektronmassa och Vätekärna i den framrusande neutronens sönderfall — och därmed en mera påtaglig förmåga att också absorbera (resonansverkan) de återstående resterna av detonationsljuset (mest i det långvågiga minst energirika området, minst i det kortvågiga mest energirika området) — som nu (via sin högre hastighet) passerar de tidigare jämsides sönderfallande neutronerna.
— Genom att neutronspridningen från J-moderkroppens yta är, eller bör vara, i det närmaste idealt sfärisk, bör också allt mellanliggande »halvsönderfallet vätematerial» nå en (nära) samtidig avsaktning med motsvarande växande ljusabsorption. Ändringen kan förstås inträffa »i en hast».
Därmed SKULLE det observerade akromatiska brytningsfenomenet i samband med GRB-ljusbildens efterglöd vara förklarat i relaterad mening — i princip.
— Den resterande analys enligt TNED som kräver matchande ljuskurvor med observationerna visar sig också kunna hänga med i svängarna [GRB-exempel]:
— Förklaringen enligt TNED, som ovan, använder primärtändingens effektpuls som energibas [∫ Pdt = E] [Energiintegralen och Effektderivatan].
—Det utläckande ljuset från den primära effektdelens energi fortsätter sedan fram tills dess neutronsönderfallets avskärmningsmassa aktiveras, vilket introducerar en ljusdämpande skärm, ljusemissionen [I=I0e–bx], och förutsatt materialdistributionen verkligen är av den karaktären (en mera glest utspridd skärmmassa har inte samma förutsättningar: inte alla GRB-förekomster uppvisar fenomenet).
— Dessa bägge separata funktioner avlöser varandra genom en TRANSITFUNKTION: transitfunktionen garanterar varje separat funktions egen identitet, samt en mellanliggande, gemensam, reaktionsdel i övergången och som i sig kan uppvisa många olika fasoner beroende på omständigheterna. Sammansättningen beskrivs exemplifierat i några GRB-fall i GRB-exempel — som visar (den kraftfulla) principen.
I tidigare avsnitt [Kärnspektrum]
har detaljen med momentant hämmande neutrinoenergier omnämnts i samband med
fusionsprocessen: I TNED följer
fusionsprocessen [FUSIONSBILDNINGEN GENOM EXEMPEL]
på divergenständningarna
i himlakropparnas primärbildning:
neutrinoenergierna [NEUTRINOSPEKTRUM]
tillför tillfälligt extraenergi som tillfälligt hindrar radioaktiva sönderfall.
— Även den detaljen kan (möjligen, här
utan vidare analys) spela viss roll:
— Neutronsönderfallet SKULLE KUNNA
(utan vidare framställning) hämmas enbart av efterekot i den häftiga
energistöten från detonationstillfället, och enbart av den anledningen FÖRDRÖJA
en normalt ljusabsorberande funktion hos det omgivande (utkastade)
stoftmaterialet (Vätgas med lättare grundämnen). Det finns dock ingen räkning
på den detaljen specifikt för neutronens del (varför den heller inte ska tas
med i den här presentationen).
— Vi bör (kanske) räkna med den
möjligheten som en partiell förklaring om uppgiften gäller en (mera)
fullständig bild av speciellt de ljuskurvor som faktiskt kan uppmätas från GRB-objekten;
— UV-ljus joniserar neutral gas, samt
bryter eventuella molekylbindningar [Petitjean et al., 2011,
s11n] — samt vidare med tillgång till allt högre primära
utbrottsenergier. För ev. vidare.
Genom att divergenständningarna sker lokalt i ett område med — här till generell prövning värdet c/c0=0,1 enligt Resultatreferens till GRB-källorna i TNED, och möjligen ännu mindre i vissa fall — finns goda förutsättningar för att det ljus vi ser av den (kraftiga) gravitella rödförskjutningen drivs in mot spektrats längre våglängder [‡Se även MAC-citat]: Inte alla GRB-objekt uppvisar det karaktäristiska brytningsfenomenet; det beskrivs dessutom mest verksamt i optiska området; Den ljustäckande slöjan påverkar (tydligen) de våglängder mest som har den lägsta energin, medan de högre (ultraviolett, röntgen, gamma) slipper igenom lättare.
— HUR brytningen sker skulle därmed också bero på den lokala hastighetsfördelning som råder: utkastningshastigheten (v/c0), lokala divergensen (c/c0), materialmängden (vanligtvis närmast enorm enligt TNED, se Detonationsmassorna).
Den karaktäristiska brytningsknäcken [‡Illustrerad funktionsform] skulle därmed också få motsvarande kortare eller längre övergångsintervall.
— Som vi redan sett av visuella exempel på novor [‡V838 Monocerotis] och supernovor, har utkastat material en viss tendens att »parkera» sig (med långsam ändring) på olika karaktäristiska avstånd från detonationskällan [‡Krabbnebulosan] och med tillhörande s.k. joniationsnivåer (novastoftets/gasens olika färger beroende på stoftets art). Det skulle i vårt fall bara förtydliga att den (av gravitationen primärt) inbromsade neutronsönderfallande materialdelen (också, strax) parkerar sin inbromsningslokal utanför J-centrum — och därmed (underförstått) en relativt snabb normalisering (timmar/dagar). Se AkroBreak för exempel på några (inledande) olika GRB-objekt.
— Notera balansen mellan g-kraft och termonukleära strålningstrycket i TNED:
— Neutronen har minst förmåga av alla atomära element att svara på Planckstrålningens olika effekter (E=hf). Neutronen känner bara i princip av gravitationen så länge neutronen är en neutron. När den sönderfallit till Väteatom, påverkas den definitivt av närliggande stjärnljus [termonukleära strålningstrycket i TNED], och därmed en motriktad g-kraft; omgivande interstellära gas och stoftmoln (oftast i huvudsak Vätgas i olika former) har en tendens att Parkera sig på vissa bestämda avstånd inom och omkring olika stjärnfält.
I MAC skulle man (helt säkert) resonera på alldeles precis samma sätt — om man HADE släppt Einstein för Planck.
— Se utförligt från Relativitetsteorin, PLANCKEKVIVALENTERNA och EXPERIMENTELLA BEKRÄFTELSER om ej redan bekant.
Se vidare i GRB-exempel.
”If GRB 980425 is associated with SN 1998bw, the distance is ~40 Mpc (Galama et al. 1998), and the isotropic gamma-ray total energy is unusually low (~1048 ergs compared with the greater than 1051 ergs for other gamma-ray bursts [GRBs] for which a redshift measurement is available).”,
http://iopscience.iop.org/1538-4357/522/2/L101/fulltext/995391.text.html
The Astrophysical Journal,
522:L101-L104, 1999 September 10 —
OFF-AXIS
EMISSION FROM THE BEAMED AFTERGLOW OF GAMMA-RAY BURSTS
and a Possible Interpretation of the Slowly Declining X-Ray Afterglow of GRB 980425, Takashi Nakamura 1999
Den äldre Energienheten erg används ofta i dessa sammanhang: samma som Joule×t7; 1erg=t7 J; 1J=T7 erg; nJ=nT7erg.
http://arxiv.org/pdf/1104.0844.pdf
GAMMA RAY BURSTS AS PROBES OF THE DISTANT UNIVERSE, Petitjean et al., 2011
———————
‡ Akromatiska ljusbrytningens intervall
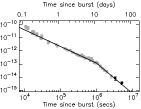
GRB 080319B-sammanställningen av Tanvirgruppens kurvor [AkroJetMAC], vänstra tre kurvorna, speciellt den översta (flest angivna datapunkter) och då enbart sett till den heldragna mörkblå linjen, visar
brytning efter 11,57 dygn, brytningsintervallet inom grovt 15,6 timmar:
Brytintervallet i tid. Källgraferna från
Tanvirgruppen ovan, de tre vänstra, visar ljusbrytningen vid ca T6 S = 11,57
dygn; Brytningen [heldragen linje av
författarna] visas tämligen skarpt inom 2 pixels; 85p/10dekad;
10^[6+2/85]S=12,22 dygn; vilket ger ett brytintervall på grovt 0,65 dygn eller
15,6 timmar. Se dock en mera detaljerad beskrivning i AkroBreak.
Den redovisningen, sett till datapunkterna, innehåller emellertid flera olika resultatbilder (vänstra tre graferna, kontra högra tre dito);
DELS (vänstra tre, översta) ett litet BUL-GUPP-intervall från ca 3 T5 S (3,47 dygn): 3,47(3T5S)→11,57(1T6S)=8,1dygn;
DELS (högra tre) — inget brytknä alls egentligen utan istället en liten BULA: 2T6S(23,15dyn)→6T6S(69,44dygn)=46,29dygn.
;
GRB990510-sammanställningen av Beuermann et al., 1999 (s4-Fig. 2) visar — mera entydigt — i grova tal (en stor rund övergång)
brytning efter 1 dygn (x=100 days After Burst), brytningsintervallet inom grovt 2 dygn.
;
GRB 011121-sammanställningen av Zeh et al., 2004 (Figure 2 s2) [‡Bildkopia] visar i runda tal
brytning efter drygt 1 dygn, brytningsintervallet inom grovt 1-2 dygn.
LightCurveMath — Bildkälla, Författarens arkiv, 27Jun2012E10Bild6
NikonD90 Detalj

De kosmologiska ljuskurvornas allmänna matematik — enligt relaterad fysik
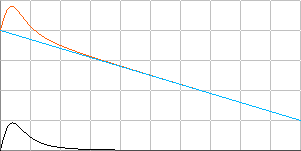
I den allmänna relaterbara fysikens funktionsbild av LJUSSTRÅLNINGSFENOMEN finns TVÅ elementärt relaterbara grundfunktioner: grundmatematik som hela fenomenformen kan förstås utvecklas och visas på:
P = E/t y = ax(b+cx2)–2 Effektfunktionen (Energifunktionens derivata)
Från härledningarna i K-cellens värmefysik, här även separat i Energiintegral och Effektderivata.
I = P/A y = e–ax Ljusintensitetsfunktionen (samma typ som Halveringssambandet)
Från härledningar i INTEGRALEXEMPEL.
De grafiska karaktärerna för dessa två huvudfunktioner visas nedan — med de olika skalalternativ som brukar användas i det allmänt tillgängliga materialet på Webben i de olika PDF-dokumenten i ämnet GRB och ljuskurvor, generellt i samband med astronomiska observationer.
I
studiet av de många PDF-dokumenten, här främst i ämnet GRB,
måste vi ha full koll på de olika grafiska presentationssätten — annars missas
poängen i framställningarna.
Uppställningen
nedan är ägnad att ge (erinra och uppfriska innebörden av och i) de olika
grundformernas detaljerade grafkaraktärer i en översiktlig sammanställning —
just de detaljer vi behöver studera (frekvent) och erinra i varje detalj i de
olika presentationerna för att förstå sammanhanget.
—
Dessa grundformer hjälper oss också att dra vissa slutsatser om HUR de olika
fenomenformerna EVENTUELLT ser ut i sin praktiska orsaksgrund (under
förutsättning att vi är kloka nog att förstå funktionssätten). Exempel följer.
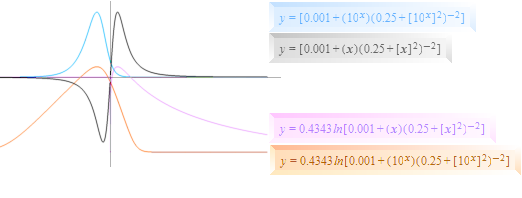
Uppställningen nedan i de fyra olika kurvsätten visar
olikheterna i skalrepresentationerna: normala enhetsskalor kontra logaritmiska
dito.
GRÅ anger normalskalor ; ORANGE anger vertikalskalan i
10-logaritmer och horisontalskalan i 10-potenser ; BLÅ anger horisontalskalan i 10-potenser ; VIOLETT anger
vertikalskalan i 10-logaritmer.
|
Ljusintensitetsfunktionen [INTEGRALEXEMPEL] Strålningens intensitet avtar med djupare inträngning i
materialmassan |
Effektfunktionen [Energiintegral
och Effektderivata] Strålningens intensitet avtar med använd energi |
|
|
|
|
Graf 10log(y) =
0.4343ln[(è'10'–x)] Unit100 |
Graf 10log(y) =
0.4343ln[0.001+(10'x)(0.25+[10'x]'2)'–2] Unit25 |
|
Graf 10log(y) =
0.4343ln[(è'–x)] |
Graf 10log(y) =
0.4343ln[0.001+(x)(0.25+[x]'2)'–2] |
|
Graf y =
[(è'10'–x)] |
Graf y =
[0.001+(10'x)(0.25+[10'x]'2)'–2] |
|
Graf y =
[(è'–x)] |
Graf y =
[0.001+(x)(0.25+[x]'2)'–2] |
x-skalan
horisontella —, y-skalan vertikala |.
Effektfunktionen. Effektfunktionen är den utlösande fysiska faktor som frigör den ENERGI som ett fysikaliskt fenomen visar sig på.
— Jämför (elementärt) effekt- och energigraferna i K-cellens värmefysik.
— Ljusbildningen (Planckstrålningen E=hf) från effektformens uppkomst strålar ut i den omgivande fria rymden precis som den använda energin under hela förloppet anvisar: Ju fortare energin används (typ omgivande absorberande material) desto brantare blir lutningen i logaritmeffektgrafens form (orangea ovan), och desto snabbare avtar effekten.
Ljusintensitetsfunktionen. Ljusintensitetsfunktionen beskriver ljuskällans kvarvarande Planckstrålning (eg. ljusintensiteten, effekten per ytenhet) i takt med att ljuset genomtränger allt mer av samma idealt homogena massrymd (typ olika material med olika absorptionsförmåga).
— Ljusintensitetsfunktionen får därmed alldeles samma typform som i fallet med det radioaktiva sönderfallet [HALVERINGSSAMBANDET]. Se även Ljusintensitetsfunktionens härledning i Integralkalkylen.
Vidare beskrivning med praktiska exempel i ENERGIINTEGRAL OCH EFFEKTDERIVATA.
Energiintegral
och Effektderivata
ENERGIINTEGRAL OCH EFFEKTDERIVATA
Utlösande effektpuls — ENERGIFRIGÖRARE:
Effekt ENERGI
Graf y =
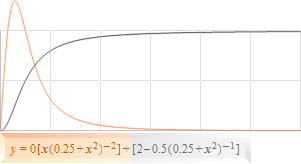
0[x(0.25+x'2)'–2]+[2–0.5(0.25+x'2)'–1]; Unit50
Dn yE = Dn [2–0.5(0.25+x2)–1] = [0–0.5(0+2x)(–1)(0.25+x2)–2] = –0.5(0+2x)(–1)(0.25+x2)–2 = 0.5(2x)(0.25+x2)–2 = x(0.25+x2)–2 ;
Dn [a–b(c+xd)–e] = 0–b(0+d·xd–1)(–e)(c+xd)–e–1 = b(d·xd–1)e(c+xd)–(e+1) = be(d·xd–1)(c+xd)–(e+1) = bed·xd–1(c+xd)–(e+1) ; Se FORMLAGARNA, Derivata och Integral.
;
INTEGRAL Energi DERIVATA
Effekt
E[a–b(c+xd)–e]’
= P[bed·xd–1(c+xd)–(e+1)]
; e ≠ 0 ;
Energiintegralen härleds utförligt i K-cellens värmefysik [HÄRLEDNINGARNA TILL K-CELLENS VÄRMEFYSIK] [EFFEKTKURVAN] [ENERGIHÄRLEDNINGEN].
∫ Pdt = E

![]()
Graf y = [2–0.5(0.25+x'2)'–1]; Unit50 e=0TILL1
Eftersom energiformens funktion (E) tydligen innehåller en funktionskomponent (e) som sammanfattar en multiplicerande faktorform,
E = a – b(c+xd)–e
= a – b(c+xd)–(e1 + e2 + e3 + ... + eN )
= a – b(c+xd)–e1(c+xd)–e2(c+xd)–e3···(c+xd)–eN
är det tydligt att varje sådan komponent (c+xd)–e(N) i sig kan anställa en motsvarande partiell deleffekt efter något aktuellt villkor som det aktuella fysiska rummet ställer upp. Till exempel en viss strålande verksamhet inom en viss energiram.
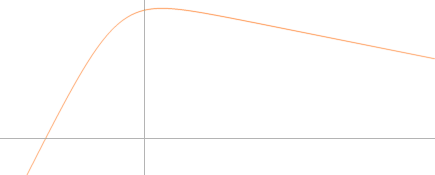
Om vi utnyttjar den möjligheten i beskrivningssättet, kan olika deleffektfunktioner beskrivas med större artrikedom. Nämligen i formen av deleffekternas varierande avsaktningar mot noll:
— Vi kan då relatera motsvarande partiella effektfunktionsformer av typen

![]()
Graf y = [(x)(0.25+[x]'2)'–1]; Unit50 p=1TILL2
P = x(c+x2)–(e+1)
Och därmed motsvarande 10-logaritmiska utsträckningspartier,
![]()
Graf y =
0.4343ln[0.001+(10'x)(0.25+[10'x]'2)'–0.5]; Unit50 t=1TILL2
y = 10log(0,001 + [10x][0,25 + (10x)2]–t)
Termen 0,001 är här
tillagd godtyckligt som ett slutvärde typ »stjärnans slutliga fasta sken» då i
annat fall logaritmkurvan sträcker sig obegränsat neråt negativa y-värden.
— i princip med t-exponenten (bilden ovan) ner till t=0,5 som (här) skulle ge effektgrafens högerdel utmed x-axeln med motsvarande gränsvärdet y=1 (ej utritat ovan).
Därmed kan vi närma oss en mera praktisk fattning på detaljfunktionerna i de olika ljuskurvornas formationer;
— Genom att partiella effektens funktion i formen y=x(c+x2)–1 som del i föregående beskrivna x(c+x2)–(e+1) i princip kan återföras på den inverterade funktionen y=(c/x+x)–1, och därmed enligt det helt enkla gränsfallet y=(0/x+x)–1=1/x, kan vi också på enklare sätt sammansätta olika deleffektpartier för att SIMULERA motsvarande observerade ljuskurvformer, och på den vägen bilda oss en viss uppfattning om vilken FUNKTION som (eventuellt) kan tänkas ligga till grund för en viss observerad variation i något visst parti, om alls.
GRB-exempel — Bildkälla, Författarens arkiv,
27Jun2012E10Bild22 NikonD90 Detalj

GRB-exempel
Basic från Energiintegral
och Effektderivata
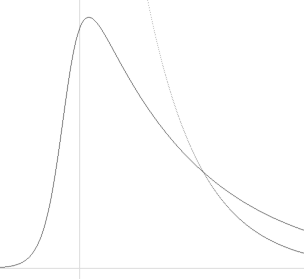
I efterglöden från en GRB-förekomst uppvisas i ett delparti närmast efter effekttoppen ett förlopp av typen nedan.
![]()
Graf y = 2(0.4343)ln[12([2(10'x)(0.25+(10'x)'1.1)'–1])]; Unit50
Strålbilden är i princip densamma som från ett (hastigt) uppvärmt föremål som sedan får svalna fritt utåt tomma rymden, och därmed efter de betingelser som effektkällans kropp bestämmer.
— Vi tänker oss sedan att man innesluter strålkällan i ett kärl: En materialvägg införs mellan oss och strålkällan som plötsligt sänker ljusstyrkan.
— Med samma mening kan vi då säga, att TAKTEN I ENERGIANVÄNDNINGEN ÖKAR: Den införda kärlväggen uppträder som en absorbator, och minskningstakten i den återstående energins utstrålande måste därför öka så att den kvarvarande energin används i snabbare takt på den energibestrålade kärlväggens energiupptagande kredit.
—Det uppstår ett BROTT, en brytning, som medför att effektkurvan når bottenläget i snabbare takt.
Frågan är då:
— Hur sammansätter vi en sådan brytfunktion? Vi vill få den att stämma överens med den praktiska fysikbilden av hela processen.
Lösningen — i princip:
— Införandet av den energiabsorberande kärlväggen innebär tydligen detsamma som införandet av en ny, absorberande effektfunktion;
x-skalan i
10-potenser; y-skalan i normala enheter;
Primära
effektfunktionen y = 12([2(10'x)(0.25+(10'x)'1.1)'–1]); Unit50;
Nya effektfunktionen,
förenklad form y =[0.00075([10'(0.2x–5)])'–1]; Unit50;
— I samma takt som kärlväggen förs in, börjar den absorbera energin från primäreffektens utstrålning;
— Absorptionen pågår ända fram till jämviktsläget då kärlväggen absorberat den energimängd som med kärlmaterialets karaktär tangerar den återstående, kvarvarande, energimängdens kapital;
— Från den händelsepunktgen kommer sedan den fortsatta utstrålningen från den nu inneslutna strålkällan att ges ut med svagare kraft, och därmed nå bottenläget snabbare.
— Figuren ovan visar primära effektens graf tillsammans med området då den nya effektgrafens infall skär primäreffekten. Den nya effektens uppåtstigande del (ej utritad) motsvarar en primär absorption av primäreffektens kvarvarande energikapital och vars kvarvarande del sedan kommer att distribueras av den nya, inbrutna effektens energifunktion (den införda kärlväggen som en ny strålkälla, med tillhörande effektförlust).
— Figuren nedan visar resultatet med skarven (det brytande ljusknäet) mellan avslutad primär effektform och den nyinsatta.
x-skalan i
10-potenser; y-skalan i normala enheter — här dämpad med 0,5 för att reducera
det illustrerade utrymmet;
Primära och Nya tillsammans
med sömlös övergång i varandras funktioner;
0.5[12([2(10'x)(0.25+(10'x)'1.1)'–1])+0[(1+[(10'[x–5])]'30)'–1]+0[([0.00075([10'(0.2x–5)])'–1])(1–(1+[(10'[x–5])]'30)'–1)]]
Via TRANSITFUNKTIONEN med jämn inpassning mellan de bägge effektfunktionerna blir slutresultatet som nedan i 10-logaritmens form:
![]()
x-skalan i
10-potenser; y-skalan i 10-logaritmer;
Primära och Nya
tillsammans med sömlös övergång i varandras funktioner;
2(0.4343)ln[12([2(10'x)(0.25+(10'x)'1.1)'–1])[(1+[(10'[x–5])]'30)'–1]+[([0.00075([10'(0.2x–5)])'–1])(1–(1+[(10'[x–5])]'30)'–1)]]; Unit50
2(0.4343)ln[12([2(10'x)(0.25+(10'x)'1.1)'–1])[(1+[(10'[x–5])]'30)'–1]+[([0.00075([10'(0.2x–5)])'–1])(1–(1+[(10'[x–5])]'30)'–1)]]; Unit50
Knälinjens
lutning Skärningspunkten
ItereradAnpassning(DOCKNINGSFAKTOR)
Primära effektfunktionen Nya Effektfunktionen
TRANSITFUNKTIONEN har bara till uppgift
att stänga av [¯_] primärfunktionen (läge Off) och initiera ersättaren (läge ON
_¯) i transitpunkten.
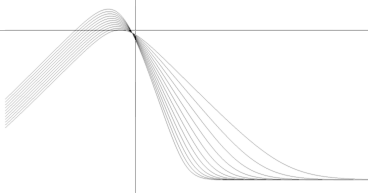
Notera de här närliggande rent GRAFISKA aspekterna på funktionsformerna av princip — och som kan laboreras med i dessa rent prövande och undersökande sammanhang:
— HAVSGRÖNA Grafbilden ovan vänster visar föregående primära effektform
y = 24(10x)(0.25+(10x)1.1)–1
12([2(10'x)(0.25+(10'x)'1.1)'–1])
SVARTA grafen ansluter mera till föregående beskriva uppdelning i faktorkomponenter från energibasen enligt
y = 24(10x)(0.25+(10x)2)–0.55
12([2(10'x)(0.25+(10'x)'2)'–0.55])
Vi ser ingen direkt skillnad, frånsett att amplituder och stigningar är något olika. Huvuddelen med funktionsövergången bibehålls.
— I den allmänna (grovt översiktliga) analysen har dessa skillnader mindre betydelse.
— Genom att energiformens funktion tvunget styr hela verksamheten, kan i princip vilka som helst möjliga kurvformer komma i fråga — beroende på omständigheterna enligt parameterbilden i de upptecknade grundsambanden i Energiintegral och Effektderivata.

Förstoring 5[Unit200pixels] av originalgrafen för att förtydliga
övergången mellan funktionerna.
De markerade partierna i ekvationsstripen [Resultatbilden 10log] förtydligar
vilka värden som ändrats respektive.
Notera även speciellt DEN idealt längst upp i bildsekvensen ovan SÖMLÖSA KNÄSKARVEN mellan funktionerna, och SÄTTET som skarven kan moduleras på.
— Detaljerna ovan (i förstoring [Unit200pixels] av originalgrafen) markerar några olika versioner med den känsliga knäskarvningen och som här införts för att illustrera principen.
— Exponentvärdena (30|28) i transitfunktionerna bestämmer övergångens branthet. Den parametern har därmed viss koppling till möjliga egenskaper i sättet som materialdelarna uppvisar under tidsintervallet då ljusskärmen införs.
— Dockningsfaktorn (D) (72|75|78) visar sig vara en amplitudfaktor i den tillkommande effektformens energibild. D bestämmer den relativa synkroniseringen i gradient (lutningspassningen i höjdled mellan de bägge funktionerna som ska avlösa varandra), och därmed funktionernas idealt optimalt mjuka övergång i varandra.
— Finns någon förskjutning i nivån mellan de avlösande effektformerna, är det tydligt att
1. (bildexemplet ovan med faktorn 0,00078) en tillväxt i amplitud kräver motsvarande energitillförsel, och att denna i så fall bara kan komma ifrån den nytillträdande effektformens materialdel, eller
2. (bildexemplet ovan med faktorn 0,00072) en reduktion i övergången motsvarar ett tillfälligt starkare upptag av primäreffektens energidel i den nytillträdande effektformen materialdel.
Den införda, nya, effektfunktionen ersätter den
primära (som väggen på ett kärl) och bildar formen för en ny strålkälla.
— Men den RATIONELLA tolkningsbilden
föreligger INTE i MAC:
Se även från AkroJetMAC
|
Förminskad
kopia av PDF-källans FIG. 2 s8n, Tanvir
et al., 2010, GRB 080319B; Bilden
överst vänster här sammanställd i separat kopia för jämförelse:
|
”It has long been thought that GRB outflows are likely to be collimated into narrow jets, and that this could reduce the total energy requirement by 1–3 (and in extreme cases perhaps more) orders of magnitude.”, ”The observational signature of such beaming is an achromatic break (hereafter referred to as a “jet-break”) in the power-law decline of afterglow light (Rhoads 1999; Sari, Piran, & Halpern 1999).”, s2sp1n, http://arxiv.org/pdf/0812.1217v2.pdf LATE
TIME OBSERVATIONS OF GRB080319B: JET
BREAK, HOST GALAXY AND ACCOMPANYING SUPERNOVA, Tanvir et al., 2010 Källan ger i FIG. 2 s8, här förminskad referens till
vänster, exempel på gammastrålobjektet GRB 080319B i formen av en
karaktäristiskt observerad brytning (vad källan kallar JetBreak analogt med
AKROMATISK BRYTNING) i ljusbilden (”the sharp break in the X-ray lightcurve”) runt 11 dagar efter
utbrottet. Notera PDF-källans x-skala (horisontalskalan —) i
10-logaritmen för resp. dagar och sekunder, samt y-skalan (vertikalskalan |)
i magnituder — som motsvarar 10-logaritmen för ljusstyrkan. |
Brytintervallet i tid. Källgraferna från Tanvirgruppen ovan, de tre
vänstra, visar brytningen vid ca T6 S = 11,57 dygn; Brytningen [heldragen linje av författarna] visas tämligen skarpt inom 2 pixels;
85p/10dekad; 10^[6+2/85]S=12,22 dygn; vilket ger ett brytintervall på grovt
0,65 dygn eller 15,6 timmar. Se dock en mera detaljerad beskrivning i AkroBreak.
Övers.:
Det har länge ansetts att GRB-utflöden sannolikt är
samlade [eg. parallelliserade strålflöden,
se eng. Collimated light] till smala
strålar, och att det skulle kunna minska den totala energin med 1-3 (och i
extrema fall kanske mer) tiopotenser.
Den observationella signaturen för sådan strålning är en
akromatisk brytning (härefter refererat till som en ”strålbrytning”) i
potenslagens avtagande för efterglödsljus.
— I MAC figurerar istället en (ännu ofullständigt känd) Jetstrålemekanism: För MAC-teorin till uppfattningen om jetstrålarna, se JetMech.
— I följande del nedan visas några typiska exempel på HUR man kopplar ihop de olika delarna — i modern akademi — med GRB-fenomenet, samt enligt TNED hur effektformen [Resultabilden 10log] stämmer med observationerna.
’evidence for supernova light in all gamma-ray burst
afterglows’
http://www.slac.stanford.edu/econf/C041213/papers/2225.PDF
EVIDENCE
FOR SUPERNOVA LIGHT IN ALL GAMMA-RAY BURST AFTERGLOWS, Zeh et al., 2004
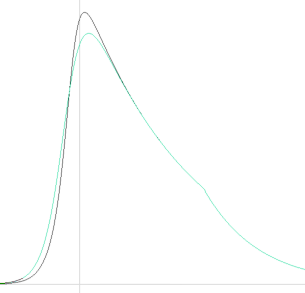
Författargruppen ovan (illustrationer nedan) har genomfört en förnämlig översiktlig genomgång — som erbjuder ett enastående tillfälle för TNED att anställa en grundlig prövning:
— Man har via 29 studerade pilotfall funnit belägg för att SAMTLIGA GRB-objekt kan förstås — ses, observeras — i association med en (liten) LJUSBULA i efterglöden från den primära starka GRB-pulsen.
— Med MAC-teorin generellt, och efter de förutsättningar som gäller in den moderna akademins lärosystem speciellt i kosmologin, har man då associerat den detaljen med en tillhörande Supernovas ljusemitterande energibidrag — typiskt enligt illustrationen nedan från Zeh et al., 2004.
— Den inlagda havsgröna kurvan är den som här har modulerats fram från TNED-teorin enligt effektformens allmänna parameterform [Resultatbilden 10log] — enbart för tillfället att undersöka OM TNED-formen alls har någon rent teknisk-grafisk förmåga att hänga med i svängarna, vilket vi (tydligen) ser är fallet. Parameterbegreppen är redan välrelaterade från grundsambanden i Energiintegral och Effektderivata, och besitter därför av princip direkt fysikalisk soliditet.
— I MAC däremot får man samhörande kurvdata genom föreställningen om en summerande Supernovaljuskurva (bilddelen nedan markerad SN). Författarna skriver i inledningen;
s1:
”These results strongly support our previous conclusion based on all afterglow data of the years 1997 to 2002 [47] that in fact all afterglows of long-duration GRBs contain light from an associated supernova.”;
s1sp2n:
”In contrast to direct spectroscopic evidence, several cases of photometric indication of extra light in GRB afterglows have been reported, starting with the pioneering work on GRB 980326 [3]. Inspired by this finding, the discovery of extra light in archived data of the afterglow of GRB 970228 [12, 33] made it clear that a search for late-time bumps in optical afterglow light curves provides a powerful tool to constrain or even reveal the nature of the underlying sources. Since then various groups successfully fit SN 1998bw templates to explain these late-time bumps (e.g., [5]), the most convincing case being that of GRB 011121 [4, 13, 15].”;
s1sp2n:
”The goal of our study is to search for supernova bumps in GRB afterglow light curves using a systematic
approach, allowing us to draw statistically founded conclusions on the physical properties of this new class of GRB-SNe in particular and on the GRB progenitors in general.”;
s3sp2n:
”Again, our key finding is photometric evidence of a late-time bump in all GRB afterglows with a redshift z <~ 0.7. We interprete this bump as light from an underlying supernova, and model this component as a redshifted version of SN 1998bw.”,
Författarna om osäkerheten i data för supernovautbrottens uppkomst:
”No correlation was found of the
deduced SN luminosities with the redshift or any afterglow parameter. Note, however, that we cannot
exclude the existence of such a correlation since in most cases when a SN was found there is a lack of early
time data in the optical light curve (resulting in an unknown break time tb
and, hence, an
unknown parameter α1; Eq. 2).”, s3sp2n, Zeh et al., 2004.
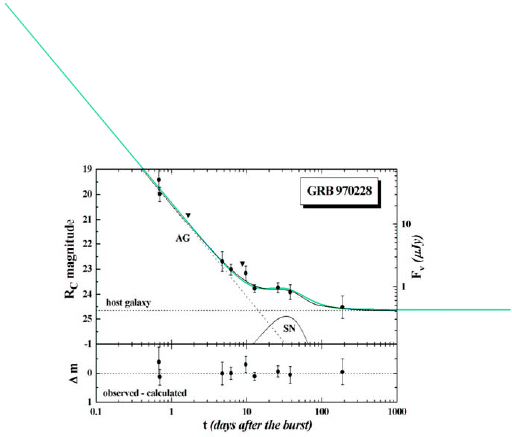
Figure 1 s1 Zeh et al., 2004. PDF-dokumentets förstoringsgrad 117% (Default).
20(0.4343)ln[2([(10'x)(0.25+(10'x)'2)'–0.53])[(1+[(10'[x–10.055])]'1.9)'–1]+[(0.525+0[0.000000005([10'(0.5x–10)])'–1])(1–(1+[(10'[x–10])]'1.9)'–1)]]
20(0.4343)ln[2([(10'x)(0.25+(10'x)'2)'–0.53])[(1+[(10'[x–10.055])]'1.9)'–1]+[(0.525)(1–(1+[(10'[x–10])]'1.9)'–1)]]
![]()
Unit70pixels
— Sammansättningen
till den havsgröna grafen och sambandsformen här via TRANSITFUNKTIONEN. Se särskild beskrivning i MODELLERINGSEXEMPEL
MED TRANSITFUNKTIONEN. Här undersöker vi endast HURUVIDA
den givna effektformens parameterkomplex i TNED alls KAN matcha observationsdata ovan — vilket vi ser verkar
fungera.
—Här har
slutoffsetvärdet för magnituden (+0,525) lagts endast på den nytillkomna
effektkurvans räkning — i annat fall fungerar inte matchningen.
50%Unit35
![]()
Som en första prövning är det tydligt att effektformen hänger med i huvuddelen av de kurvformer per exempel som visas i de etablerade resultatrapporterna, typ nedan (och föregående ovan). Jag kan i varje fall för min egen del INTE utesluta effektformen på den nedanstående redovisade resultatdelen: det stämmer inte exakt med källförfattarna modellresultat, och ska inte heller göra det — men följsamheten är påtaglig.
— Det är också TRIXIGT att försöka modulera effektformens olika parametrar: bara därför att två första försök inte träffar exakt behöver inte betyda att alla andra försök också kommer att missa målet. Resultaten nedan är emellertid tillräckliga för att visa principen: De bägge moduleringsförsöken nedan, havsgröna inlagda kurvan, visar att man når delvis olika matchresultat med olika försök, bägge i någon mån i grundformens huvudsakliga överensstämmelse.
— Det resultatet är också anmärkningsvärt, därför att TEORIN bakom effektformen [Resultatbilden 10log] [Energiintegral och Effektderivata] INTE ansluter till någon utarbetad supernovautkastningsfysik, utan ENBART koncentrerar eldgivningen på föremålet: ett INFÖRT AVSKÄRMANDE MATERIAL. Därför nämligen att GRB-objektens ursprung i TNED också har helt andra teoretiska förutsättningar.
— Därmed en berättigad fråga:
— Kan, möjligen, effektformen [Resultatbilden 10log] — verkligen — vara den del som beskriver fenomenet?
’Evidence for supernova light in all gamma-ray burst afterglows’
skulle i så fall inte betyda annat än
’evidence for inset matter in all gamma-ray burst afterglows’ — samt med en helt annat teoretisk grund.
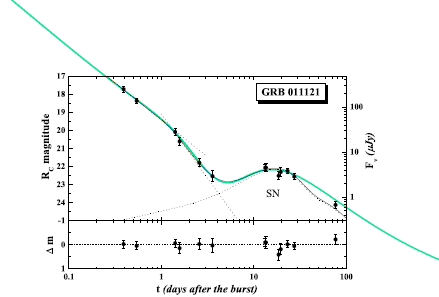
Figure 2 s2 Zeh et al., 2004.
PDF-dokumentets förstoringsgrad 117% (Default).
12(0.4343)ln[5([(10'x)(0.25+(10'x)'2)'–0.535])[(1+[(10'[x–9.6])]'1.1)'–1]+[(0.6+[0.000000007([10'([0.2x'0.98]–10)])'–1])(1–(1+[(10'[x–10])]'0.87)'–1)]]
![]()
Uit50pixels
— Sammansättningen
till de havsgröna graferna och sambandsformerna här via TRANSITFUNKTIONEN. Se särskild beskrivning i MODELLERINGSEXEMPEL
MED TRANSITFUNKTIONEN.
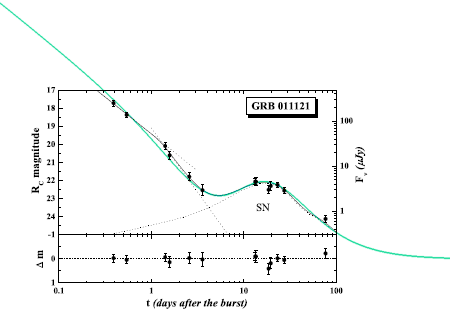
Figure 2 s2 Zeh et al., 2004. PDF-dokumentets förstoringsgrad 117% (Default).
20(0.4343)ln[2([(10'x)(0.25+(10'x)'2)'–0.52])[(1+[(10'[x–10.03])]'2)'–1]+[(0.758)(1–(1+[(10'[x–10])]'2.28)'–1)]]
1+20(0.4343)ln[2([(10'(x+7))(0.25+(10'(x+7))'2)'–0.52])[(1+[(10'[(x+7)–10.03])]'2)'–1]+[(0.758)(1–(1+[(10'[(x+7)–10])]'2.28)'–1)]]
![]()
Unit140pixels — 1+, 20· och x+7
har här tillagts för att få fokus på detaljen i grafritningen, annars utanför
bildskärmen med Unit280pixels (med efterföljande 50% förminskning).
JetBreakMechMath i MAC — Bildkälla, Författarens arkiv,
27Jun2012E10Bild39 NikonD90 Detalj

JetBreakMechMath i MAC
— två ljusskänklar (¯\) plus en
Supernovamall (SN 1998bw)
— Man har redan BESTÄMT sig för hur det SKA fungera:
I MAC använder man en s.k. bruten potensform (eng. broken power-law) av formen
M = a([t/tb]c(1)s + [t/tb]c(2)s)–1
” broken power-law model of Beuermann et al. (1999; see also Stanek et al. 2001)”,
http://iopscience.iop.org/1538-4357/626/1/L5/fulltext/19330.text.html
The
Astrophysical Journal, 626:L5-L9, 2005 June 10,
DEEP
PHOTOMETRY OF GRB 041006 AFTERGLOW: HYPERNOVA BUMP AT REDSHIFT z =
0.716,
Stanek
et al., 2005
med den grafiskt logaritmiska formen
y = 10log a([10x/tb]c(1)s + [10x/tb]c(2)s)–1
med exempel
Graf y =
2(0.4343)ln([([(10'x)/20]'1/1)+([(10'x)/20])'8/1]'–1/4)
![]()
Unit50pixels
Lutningarna kan modelleras direkt via de markerade exponentkoefficienterna resp. 1/1 och 8/1. Hela formgrafen kan tiltas (lutas) via den multiplicerande funktionsfaktorn (a).
— Ovanstående sambandsform används sedan tillsammans med en ’supernovanormalmall’, SN 1998bw: Man sammanställer JetBreak-funktionen ovan, som antas gälla för alla GRB, tillsammans med SN1998bw-typen för att pröva (ungefärligt) motsvarande ljuskurvors karaktärer för (alla) GRB-förekomster (även då inget direkt observationellt påvisande av ett JetBreak finns från en GRB-förekomst);
”We present an update of our systematic analyses of all Gamma-Ray Burst (GRB) afterglow data, now published through the end of 2004, in an attempt to detect the predicted supernova light component. We fit the observed photometric light curves as the sum of an afterglow, an underlying host galaxy, and a supernova component. The latter is modeled using published UBV RI light curves of SN 1998bw as a template.”,
s1/2225, Zeh et al., 2004.
Se även särskilt SN 1998bw.
Referensen till sambandsformen ovan, den angivna (Beuermann et al., 1999): ”We choose a function F(t)=(F1–n + F2–n)–1/n …”, sL28sp1n [Beuermann et al., 1999, VLT OBSERVATIONS OF GRB990510 AND ITS ENVIRONMENT], upplyser om den bakomliggande fysikgrunden:
”Burst models (Piran 1999,
Rhoads 1999, Sari et al. 1999) explain
the afterglow as synchrotron emission of shockaccelerated
electrons injected into an expanding medium with a power law spectrum E–p. In jet models, the time dependent spectral flux at frequencies below the cooling break varies as Fv(t)(=)v–βt–α with β=(p–1)/2 independent of time and α=3(p−1)/4 or α=p, depending on, respectively, whether the opening angle of the relativistically beamed radiation ϑ ~ 1/γ < θ early in the expansion, or ϑ > 0 at later time when the jet has been slowed down (θ = opening angle of the jet, γ = bulk Lorentz factor). We choose a function
F(t) = (F1–n + F2–n)–1/n with Fi = kit–αi , n > 0 (1)
to describe the transition
between the early and late power laws F1 and F2,
where F1 = F2 at the transition time t =
t*. Eq. (1)
was also employed by Rhoads (1999) to parameterise his numerical models and is a more general form of the expressions
used by Israel et al. (1999), Stanek et al. (1999), and by Harrison et al. (1999), who assumed n = 1 and n ~ 1.5, respectively. Of the five free parameters in Eq. (1) (k1,2, α1,2, n), the exponent n provides a measure of the relative width and the smoothness
of the transition from F1 to F2. The extrapolation of the OT brightness from HDAB < 8.0 to late times will also depend on
he choice of n.”,
http://arxiv.org/pdf/astro-ph/9909043.pdf
VLT
OBSERVATIONS OF GRB990510 AND ITS ENVIRONMENT, Beuermann et al., 1999
— Men vad gäller saken: Är JetModellMatematiken — ovan —
förbehållen GRB-objektens fysik, menar man, eller
beskriver JetMechMath-akademikerna Supernovautbrottens (SN) ljusbilder, eller
är det ev. fråga om en BäggeGäller-akademi — men INTE SN enskilt?
— ReferensCitatdelen i Jetteorin från GRB antyder att det är
GRBs som ansvarar för upphovet. Inte SN.
— Emellertid anser man att SN föregår
GRB [‡SNföreGRBCitat].
— Alltså så här:
— I MAC
FAVORISERAS (tydligen) JetTeorin — utan att man riktigt VET vad saken gäller,
och (i vanlig ordning) »hoppas att det ordnar upp sig framöver». Man har
teorin, men ingen kan visa någon SOLID grund för den.
— SN (Supernova) i MAC måste — måste — föregå GRB (Gamma Ray Burst),
därför att man inte har någon annan energiräkning att räkna på: GRB-energierna
räknade som ideala sfäriska utstrålningsutbrott (s.k. isotropisk
energifördelning) uppvisar mera energi (upp mot T47 J = T54 erg) än det finns
fattning på i moderna kvarter (runt max T45 J). Och därför har JetTeorin
framlagts: enda plausibla alternativet. Och alltså (eftersom kärleken till
naturvetenskapen är så stor) läggs det ner stora ansträngningar på att försöka
få fram en förklarande helhetsbild [‡CitatJetFrånGRB]
med just den förutsättningen.
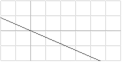
— Beuermann-Funktionerna representerar två sammansatta, olika, intensitetskurvor som avlöser varandra i en summerande funktionspunkt (t[break]). Dvs., man lägger ingen primärt styrande effektfunktion (processens energiaspekt) på förloppet, utan använder endast den essentiella ljusintensitetslinjen [I=I0e–bx] [Ljuskurvans intensitetsform], dess enklare variabelinvers y=1/x som substitut för [I=I0e–bx] för att modellera fram en motsvarande grafisk lösningsbild — enligt typformen för varje skänkel (vinkelben)
y = 0,4343ln(10x)–1
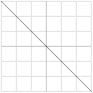
![]()
;
y = x–1
![]()
— Vart tog Fysiken vägen?
— Det är (exemplifierat) den främsta anledningen varför TNED och MAC saknar beröringspunkter.
— Se vidare utförligt från GRB-objektens ursprung i TNED: energikällan gäller inte ental eller tiotal eller ens hundratal Solmassor, utan miljontals: signalerna från universums starkt gravitellt rödförskjutna utkanter [GRAVITELLA RÖDFÖRSKJUTNINGEN] från de primära galaxbildningarna — i takt med K-cellens expansion.
Se även i GRB980425SN1998bw — jämförande exempel.
GRB
980425 — SN 1998bw — jämförande exempel —
Bildkälla, Författarens arkiv, 20Jun2012E9Bild3 NikonD90 Detalj

Förkortningar SN SuperNova GRB Gamma Ray Burst
GRB 980425 — SN 1998bw CE 1998 April 19 13:50:52.8
UT Sunday | B-band
Ljuskurvorna
nedan vänster för
GRB 980425 [25Apr1998
21:49 UTC] — vänster primärpulsen (20 S+), höger efterglöden (2500 S) .
Ljuskurvorna
nedan höger för
den associerade supernovan [26Apr1998]
SN 1998bw (180 dygn [½ år]).
— Exemplet nedan är
pionjärexemplet som anses koppla GRB (eng. Gamma Ray Burst) med SN
(Supernova).
|
Ljuskurvan för GRB
980425 |
Ljuskurvan för SN
1998bw |
|
|
|
|
Fig.
1 s15, Fig. 2 s16 http://iopscience.iop.org/1538-4357/522/2/L101/fulltext/995391.text.html The
Astrophysical Journal, 522:L101-L104, 1999
September 10 — OFF-AXIS EMISSION FROM THE
BEAMED AFTERGLOW OF GAMMA-RAY BURSTS and a Possible
Interpretation of the Slowly Declining X-Ray Afterglow of GRB 980425, Takashi Nakamura 1999 |
Fig.
1 s13 http://arxiv.org/pdf/astro-ph/9904397v2.pdf THE LATE TIME LIGHT CURVE OF
SN 1998BW ASSOCIATED WITH GRB980425, McKenzie et al., 1999 Notera att vertikalskalan ovan är angiven i
Magnituder (10logaritmisk). |
JulianDays: TIDSENHETEN i ljuskurvan för SN 1998bw är angiven i JD — Julian Days, används
stundom av astronomer — som ovan i exemplet med SN 1998bw enligt offset 2 450
000 plus x-skalans numrering;
Se Webbkällan JULIAN DATE CONVERTER http://aa.usno.navy.mil/data/docs/JulianDate.php för omvandling:
JD 2450950 — x-skalan angivna 950 —
motsvarar CE
1998 May 16 12:00:00.0 UT Saturday.
GRB980425SN1998bw — jämförande exempel
Jämförande kurvstudieexempel på kosmologisk
ljuskurva
— från supernovan SN
1998bw
Jämför ljuskurvan för SN 1998bw — TYP
fotoblixt på fosforescerande material:
En mikrosekundsnabb, stark, fotoblixt som lyser upp en viss mängd (småkornigt) fosforescerande material (som kan absorbera energin och sedan putta ut den i långsammare takt), visar ett lysande (svagt) sken — långt efter att blixtlampan slocknat.
— Om blixtlampan är primärpulsen
och det fosforescerande materialet novastoftet, kan vi (enkelt, och grovt) se
att LJUSSTYRKAN — det utstrålade ljusets intensitet — i ljuskurvan bör bli
(ungefär) en rät linje i avtagande (minus):
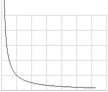
dI/dt=–kI; dI/I=–kdt; ∫dI/I=–∫kdt; ∫dI/I= lnI = –∫kdt= –kt; lnI=–kt; I=e–kt; [t=0]=[I=I0]; I=I0e–kt;
ref. Integralexempel. Det är också samma principfunktion som
för HALVERINGSSAMBANDET
i radioaktiva sönderfallet.
— I normala xy-enheter avbildas den funktionen enligt figuren nedan,
y = e–x
![]()
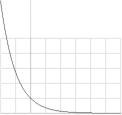
Begreppet LJUSINTENSITET (ljusstyrka, effekt per ytenhet I=P/A) relateras (visuellt) emellertid på samma sätt som LJUD: via en logaritmisk (synuppfattande) skala (konv. magnitud [M], M = –2,510log[I/I0], se exv. @INTERNET Wikipedia Apparent magnitude, Calculations [2012-06-15]):
y = 10log(e–x)
= [ln(e–x)]/[ln10
= 1/~0,4343]
= 0,4343ln(e–x) ; ex = P ; x = lnP ; ea = ea ; a = ln ea ;
=
–0,4343x
![]()
Därmed framgår ljusfunktionens linjära aspekt: Konstant (visuellt, logaritmiskt) avtagande ljusstyrka (I) med tiden.
— En sådan funktionsform är — i relaterad mening tydligen — en utpräglad funktion av en centralmassa (ljuskällan) som (under viss begränsad tid) matar ljusenergi på en redan parkerad (helt plan och homogen) utanförmassa (vidare nedan i ExempelSN1998bw).
— LJUSEMISSIONEN från en sådan fast parkerad massa är samma som Intensitetsfunktionen [I=I0e–bx] som härleddes i Integralexempel: Funktionen som sådan börjar vid en viss tidpunkt från en viss största intensitet (I0), funktionen har ingen explicit koppling till någon EFFEKTFUNKTION från någon utlösande massenergi (m→γ), utan är en utpräglad fristående helt rymdbaserad ljusemissionsfunktion.
— I takt med att ljuset från en ljuskälla genomtränger en fast, stillastående homogen materialrymd, reduceras den kvarvarande ljusenergin och intensiteten (I) avtar därför (visuellt »LinjärLogaritmiskt»).
— Om stoftmassan utanför centralmassan också expanderar (med nämnvärd hastighet) under ljusemissionen, bör ljusstyrkan (effekten per kvadratmeter) bli motsvarande mindre — och på motsvarande sätt, större om stoftmassan utanför är på väg in mot centralmassan; Den ljusemitterande »pixeltätheten» i stoftmassan varierar med stoftmassans varierande täthet, och därmed högre effekt per kvadratmeter om stoftmassan kontraherar.
— Är ljusemissionen anställd på energi som frigörs i samband med radioaktivitet [MAClightSN1998bw], finns ingen annan källa att uppväcka den verksamheten än en primär centralmassa via utlösande massenergi (m→γ); På ett eller annat sätt föregås den separata ljusemissionen [I=I0e–bx] av en primär effektform [∫ Pdt = E] (en »primär ljustopp») som frigör efterföljande ljusagentmassa.
Men:
— Vi kan (veterligt) inte (fullständigt) styra en sådan funktionsform från centralmassans utgångspunkt;
— Vi kan inte uttrycka den kurvformen på primärpulsens effektform — eftersom det finns en annan massform som kommer att överta (en del av) primärpulsens framvisade massenergi (m→γ) och utveckla den energin på sin specifika fysik.
— Det SKULLE betyda »särskilt krångliga övningar» om det gäller att få fram den motsvarande praktiska grafens naturliga motsvarighet:
— Vi måste (följaktligen, i så fall) använda TRANSITFUNKTIONER.
Kort sagt:
— Enda synbarliga möjligheten att beskriva sakämnet på FYSISKT RELATERBART KORREKT sätt — alltså ur den strikt dynamiska, orsakssammanhängande naturprocessens synvinkel, med grund i elementära samband — blir då tydligen genom att RELATERA OLIKA AVSNITT AV OLIKA CENTRALKROPPSFUNKTIONER som VID olika kritiska tidpunkter tonar UT ur och IN i varandras övergångar.
— Det finns ingen gemensam materiellt förenande summerande aspekt; Det är frågan om två skilda material, vart och ett med sin specifika fysik.
— Det finns med andra ord ingen (direkt enkelt relaterbar) amplitudsummerande fysikaliskt relaterbar funktion — även om det finns en sådan sett rent graftekniskt-matematiskt.
Fig.1
![]()
Graf y =
(4–0.3x)+0[x(0.5+x'2)'–2]
— Grafexemplet ovan visar hur man VÄL kan simulera ljuskurvan i exemplet SN 1998bw (här utan logaritmisk vertikalskala). En motsvarande naturlig funktionsform är svårare att finna;
— Jämför en överlagrad effektpuls som BÖRJAR på en viss effektnivå, +4 i grafexemplet ovan (fenomenformen har redan gått av stapeln): Det var inte vår servering;
— Fenomenformen börjar i själva verket från noll med den primära ljuskällans effektpuls. Det betyder att den motsvarande naturformen blir (betydligt) mera svårfångad.
I den följande framställningen studerar vi hur sammansättningen kan göras via TRANSITFUNKTIONER i ett (berömt) praktiskt exemplet mera i detalj.
— Se utförligt i följande ExempelSN1998bw.
Från originalet i GRB980425SN1998bw
Enkelt EXEMPEL … SN 1998bw — SN konv. förk. SuperNova — se Funktionsgrafen:
Fig.2
TIDSSKALAN med ovanstående kurvpassning
skärs av ljuskurvan vid x=923 — 4/13 × 10 = 3,076923 + 920; JulianDate för 2450920+3,077 är [‡] CE 1998 April 19
13:50:52.8 UT Sunday; MEN:
— SN
1998bw sägs ha upptäckts 26 April1998 — GRB
980425 detekterades 25 Apr1998.
— Sex dagar (och åtta timmar) efter.
— Här är det (alltså)
tydligen allmän huggsexa som gäller;
— LITET ironi finns också
här: Vilket som är vad spelar mindre roll i TNED eftersom det, enligt TNED, i vilket fall inte
finns någon koppling. Se GRB efter/före SN.
Det finns — här — heller
ingen garanti för att precisionen ovan verkligen skulle vara någon allmänt
erkänd dito: Skrivningen här baseras HELT på den ovan visade rent visuella
matchningen.
Kurvpassningen ovan — OCH FÖRUTSATT LJUSTEKNISKT TILLÄMPLIG
I DET PRAKTISKA FALLET — är knappast oprecis på runt 5 dygn=6,5pixel — halva
det markerade intervallet (10 dygn) på 13pixels. På sin höjd skiljer det på
±1pixel (±1/13·10=±0,77dygn): SN ligger tydligt (mer än fem dygn) före GRB.
— MAC: FÖRST utvecklas SN [sex
dagar före associerad GRB],
19Apr1998, SEDAN kommer en GRB 25Apr1998 [sex dagar senare], enligt gängse meningar i modern akademi.
Det var generöst. FÖRST underhållningen SEDAN betalningen (PayPerView).
— ATT GRB 980425 som primär
effektpuls enbart av det observerade
skälet INTE — enligt
relaterad fysik — hör
ihop med SN 1998bw [980419] är alldeles tydligt.
— Se citat som
förklarar varför man generellt i MAC anser att SN måste föregå GRB.
— En annan sak vore det OM GRB-förekomsten, verkligen
[OCH SOM KANSKE OCKSÅ ANDRA LÄSARE HAR UPPFATTAT SAKEN DÅ TYDLIGEN INGET ANNAT KLARGÖRANDE FINNS]
hade legat precis i RANDEN, alldeles inom sekunden vid
SN1998bw-kurans uppgång. Då skulle man med rätta ha kunnat associera
SN-förekomsten med GRB-förekomsten. Men sex dagar EFTER?
—
Rapporterna berättar också om vissa observerade osäkerheter [McKenzie1999].
— I Källan Woolsley2006 ges ytterligare referensuppgifter för SN 1998bw — av
synnerligen obskyr natur (”that the time of the SN
explosion was the same as the GRB to about one day”) och som bara (ytterligare) fördunklar ovanstående
observation: Ingen rapportkälla i det upphittade materialet verkar kunna
precisera sig på punkten NÄR, mera exakt, som SN 1998bw gick av stapeln — men
alla (de här studerade) artikelförfattarna
verkar utgå ifrån ATT en sådan TYDLIG punkt existerar. Visa. Bidraget ovan
visar uppenbarligen att viss avgörande information fattas — och såvitt
kurvpassning här är korrekt relaterad.
— I TNED finns i vilket fall ingen (sådan) förmodad koppling som
utsäger att GRB-förekomsterna skulle vara SEKUNDÄRA energiutbrott. Se mera
utförligt i GRB-objektens
ursprung i TNED.
Nedan visas vidare hur passkurvan (violetta ovan) har
framräknats:
Funktionsgrafen med
vertikalskalan i 10-logaritmer
Fig.3
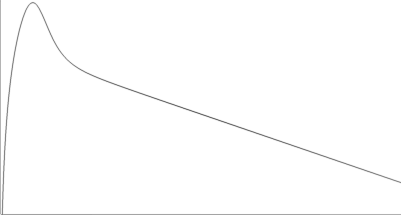
Graf y = 0.4343ln([14.5x(0.4+x'2)'–2][(1+[([x]/0.2)]'6)'–1]+(7[2.2'–x])[1–(1+[([x]/0.2)]'6)'–1])
![]()
Modulering: 0.4343ln ger vertikalskalans värden efter
10-logaritmen. Transitfunktionen 1–(1+[([x]/0.2)]'6)'–1 aktiverar [—¯] vid x=0,2 och
Transitfunktionen (1+[([x]/0.2)]'6)'–1 deaktiverar [¯—] vid samma x=0,2;
Transitfunktionens
exponent 6
modulerar HÅRDHETEN i övergången mellan de bägge funktionerna: lägre värde
betyder mjukare=rundare övergång. INTENSITETSFUNKTIONEN (7[2.2'–x])=7e–(ln2,2)x är samma som den ordinära ljusfysikens
funktion för strålning som genomtränger ett homogent
material —
och/eller kurvan för radioaktiv emission [HALVERINGSSAMBANDET] — med successivt
avtagande intensitet i proportion till genomträngd distans [Se Utvecklingsexempel
i Integralkalkylen].
Koefficienten 7
modulerar-passar övergången till huvudfunktionens effektgraf 14.5x(0.4+x'2)'–2]. Effektgrafens fysik beskrivs särskilt
i K-cellens värmefysik, samt här särskilt
i EFFEKTDERIVATA
OCH ENERGIINTEGRAL.
Komponenterna i SN 1998bw utom Transitfunktionerna (Fig.5 längre ner, de låga blå-röda som korsar varandra vid x=0,2, dessa blir obegränsat negativa mot noll i en vertikal logaritmskala och har därför inte medtagits här):
Fig.4
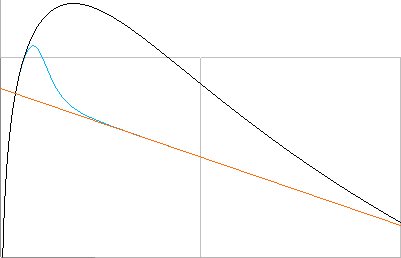
Komponenterna i SN 1998bw i normal enhetsskala, amplituderna dämpade 4ggr, samt hela bilden förminskad ytterligare 4ggr. Trots det: Notera den svarta effektgrafens höga amplitud i grafbilden ovan (med dess relativt långa tidsbas, inte alls framträdande i slutbilden; effekttoppen nås efter 51,54 dygn enligt ovanstående grafer), här avkortad:
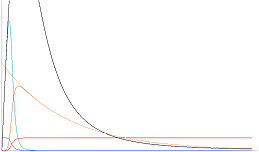
SVART, effektgrafen som tänder energin till
hela processen;
BLÅ nedre [¯—] är Transitfunktionen som deaktiverar
effektgrafen vid x=0,2;
LJUSBLÅ är resulterande grafen för
SvartaGångerTransit;
ORANGE
exponentiella —
kurvan som fortsätter mjukt uppåt höger till vänster — är
Ljusintensitetsfunktionen;
RÖDA [—¯] är Transitfunktionen som aktiverar
Ljusintensitetsfunktionen vid x=0,2;
ORANGEA brutna — kurvan som börjar från noll — är
resulterande grafen för OrangeaExponentiellaGångerRöda.
Resulterande
totala grafen i normala enhetsskalor, samma skala som ovan (amplituden dämpad 4ggr, sedan hela
bilden ytterligare förminskad 4ggr, samma som ovan men alla tillsammans):
Funktionsgrafen med
vertikalskalan i normala enheter
Fig.6
Graf y =
0.25([14.5x(0.4+x'2)'–2][(1+[([x]/0.2)]'6)'–1]+(7[2.2'–x])[1–(1+[([x]/0.2)]'6)'–1]),
Unit50
![]()
INTENSITETSFUNKTIONEN I=7e–(ln2,2)x [Se härledning i Integralexempel] är samma som den helt ideala funktion som gäller för ett fast, stationärt — eller som färdas med KONSTANT hastighet — homogent material som utsätts för strålning (ljusgenomträngning) från en fast, stationär ljuskälla; Koefficienten (7) anger startvärdet för ljuskällans intensitet sett från det mottagande materialet (x=0). Övergångsformerna (Transitformen) i samstämmighet med originalet (om det är det som gäller) endast understryker att hela fenomenformen — därmed — kan liknas vid en stationär ljusblixt, effekttoppen, vars delenergi matas in i ett utanförvarande STATIONÄRT — eller med konstant hastighet flygande — PLANT MATERIALSKIKT, där ljuset genomgår den aktuella dämpningen — hela funktionen med vertikalskalan i 10-logaritmer [‡10log], alternativt som närmast ovan i normalskala [‡Normal].
— ARTEN av RÖRELSE hos — och i — det mottagande strålningsskiktet bestämmer uttoningens form. I fallet i exemplet ovan är det tydligen fråga om ett homogent skikt som antingen finns stationärt, eller färdas med konstant hastighet, eller som uppvisar en kombinerad rörelseform som bildar en ekvivalent till nämnda.
MAC-tolkningarna av ljuset från
SN1998bw
MAC-tolkningarna till
exponentialkurvan i SN 1998bw
— Webbkällan till SN 1998bw-illustrationen ger aspekter på exponentialkurvan: Den anses bero på radioaktiv strålning från Kobolt;
”The decay rate of the tail is so close to an exponential that we suggest that this is no
coincidence.”,
”In addition, the measured decline rate corresponds
to that expected from the
decay of radio active cobalt (with a half-life of 78.5 days) as modified by the effects due
to the expansion of the shell (Colgate and McKee 1969).”, s8n, 4. Comparison with Models,
Man räknar inte med att det skulle finnas något fast, stationärt stoftskikt, utan att det (i detta fall) är frågan om ett expanderande skikt — men källan ger ingen resonerande redovisning i detaljer, utöver ovan citerade typ:
”Hence, it is reasonable to take
our light curve as strong evidence that the late time
light curve of SN 1998bw is being
powered by the decay of cobalt, with the difference in slope caused by the leakage of gamma
radiation from the shell.”, s8n, 4. Comparison with Models,
Flera basuppgifter (hastigheten hos stoftskiktet) på SN 1998bw finns f.ö. i
http://iopscience.iop.org/0004-637X/559/2/1047/pdf/0004-637X_559_2_1047.pdf
THE
NEBULAR SPECTRA OF THE HYPERNOVA SN 1998bw AND EVIDENCE FOR ASYMMETRY, Mazzali et
al., 2001
Ovanstående tolkningsbild — explicit — är tydligen också förenlig med TNED:
— För att åstadkomma en upplysande funktion — som INTE är den primära massförstörande massenergi (m→γ) [∫ Pdt = E] som hela energiomsättningen anställs på — krävs uppenbarligen DELS en separat mellanliggande »ljusmassa», mellan primäreffektkällan och oss som observatör (om det nu nödvändigtvis inte är primärkällan som emitterar hela kapitalet), något som intensitetsfunktionen [I=I0e–bx] kan använda som medium för sin specifika utstrålning (exponentkoefficienten), och DELS en från primäreffekten specifikt avgiven intensitetskälla (I0) som matar ljusmassan.
— Är den från primärkällan [∫ Pdt = E] avdelade ljusmassan ett radioaktivt material, är det tydligt att intensitetsfunktionen [I=I0e–bx] blir den radiomassans emissionsform; I-funktionens specifika Planckljus (E=hf) avlöser primäreffektens egen tillfälliga men snabbt falnande ljusemission i formen av en linjärt (ljusLogaritmisk) avtagande intensitet, och så som det avbildas i exemplet med SN 1998bw.
— Däremot finns i TNED ingen grund för att associera GRB-förekomster med SN-förekomster. Anledningen till den (ytterst bestämda) ståndpunkten är flera, och beskrivs mera detaljerat från GRB-objektens ursprung i TNED.
— I det påstådda fallet med samhörigheten GRB980425SN1998bw, se särskilt den observerade detaljen med datumuppgifterna för de olika objekten.
Citatreferenser GRB-SN:
”In their search for an optical counterpart for the gamma ray burst GRB980425, Galama et al. (1998a) detected SN 1998bw in the galactic arm of ESO 184-G82(EOP 184-82), which Tinney et al. (1998) determined to have a red shift of 0.0085 ± 0.0002. The supernova’s light curves rose sharply after the burst, and its spatial coordinates were well within the burst’s error box, strongly suggesting a connection between the two events. The probability of their independence was estimated by Galama et al. (1998a) at 1.1 × 10−4. However, BeppoSAX also detected a fading x-ray source (generally thought to be the hallmark of the burst counterpart) at a position inconsistent with SN 1998bw (Pian et al. 1998, Piro et al. 1998, Pian et al. 1999), so the relationship between SN 1998bw and GRB980425 is unclear. Further observations showed that SN 1998bw is positionally coincident with a second BeppoSAX x-ray source which has faded by a factor of two in brightness from 26 April to 10 November 1999, which is consistent with x-ray emission from a supernova plus the galaxy (Pian et al. 1999).”, 1. Introduction, s2ö,
http://arxiv.org/pdf/astro-ph/9904397v2.pdf
THE
LATE TIME LIGHT CURVE OF SN 1998BW ASSOCIATED WITH GRB980425, McKenzie et al.,
1999
”The arguments listed above in
favor of the GRB–SN association are compelling but fail to provide an
observational clue as to how a SNe can generate a burst of
gamma-rays. Theoretical
models17 have great
difficulty generating a burst of gamma-rays.”, s3ö,
;
”In this paper we show how a simple interpretation of the radio
data forces us to conclude that
SN 1998bw had a shock moving at relativistic speed,
ahead of the low velocity
ejecta which powers the optical light curve. If our interpretation is correct (and fortunately it is amenable
to observational verification) then we have identified a specific phenomenon – a relativistic shock – which
could potentially generate a burst of gamma-rays at early times in a SN.”, s3ö,
http://arxiv.org/pdf/astro-ph/9807001.pdf
THE γ-RAY BURST OF 980425 AND ITS ASSOCIATION WITH THE EXTRAORDINARY RADIO EMISSION FROM A MOST UNUSUAL SUPERNOVA, Kulkarni et al., 1998
http://arxiv.org/pdf/astro-ph/0609142v1.pdf
THE
SUPERNOVA GAMMA-RAY BURST CONNECTION, Woosley et al., 2006
:
s7,
”after a careful reanalysis of the X-ray data
(Pian et al., 2000) the association of the GRB with the supernova was confirmed:
consistent with the location of the SN was a slowly variable X-ray source.”,
;
”Almost irrespective of modeling
assumptions, the rapid
rise of radio emission from SN1998bw showed that the time of the SN explosion
was the same as the GRB to about one day.”,
;
Stämmer inte. Visa. Enligt Kurvmatchningen i McKenziefiguren ligger B-bandskurvfoten
för SN 1998bw vid 19Apr1998 13:50 UT (6
dygn, 8 timmar — inte 1 dygn) före GRB 980425 (25Apr1998 21:49 UTC). Underligt påstående med
referens till passningen nedan:
;
”SN1998bw peaked in the
V-band 16.2 days (rest frame) after the GRB with MV = −19.16±0.05+5 log h71
mag (Galama et al., 1998).”,
;
Stämmer med McKenzie-kurvorna. Kontrollerat.
APPENDIX:
APPENDIX —
SOLENS 4 VÄRMEGRADER enligt
relaterad fysik: Tgamma ¦ Twien
¦ Tsol ¦ Tplanck
¦ + TplanckWien våglängdsberoende,
övriga distansberoende
En öppen och fritt — 27Okt2017: respekteras inte av Firefox&InternetExplorer — redigerbar kopia av ett kalkylkort
kalkylkortet nedan DIREKT FRÅN DEN HÄR
WEBBLÄSAREN SolenT.ods
— se öppningsmanual om ej redan bekant — eller kopiera URL:en nedan till valfri webbläsare (vilket som fungerar —
förutsatt att SVENSKA VERSIONEN av gratisprogramvaran OPEN OFFICE finns
installerad på datorn)
http://www.universumshistoria.se/AaKort/SolemT.ods
har sammanställts Aug2017 tillsammans med avsnittet nedan med sambanden (utom TplanckWien) enligt TNED som visar de olika värmegraderna för givna avstånd från solcentrum. Tγ ¦ Tw ¦ Ts ingår inte i modern akademi, se resp. not.
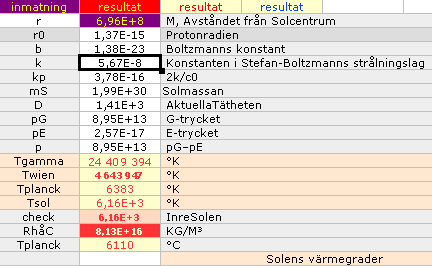
Stråltryckstemperaturens
Radiella Variation
STRÅLNINGSTRYCKETS TERMONUKLEÄRA EKVIVALENT Rekapitulation Aug2017
Strålningstryckets Värmegrad: p = a·kP·T4
:= γp i N/M²: GammaPe -- att särskilja från modern akademis teorier enligt
följande
NOTERA WEBBLÄSAREN FIREFOX
SÄRSKILT I DESSA LÄNKAR — KLAR TEXT, MEN LÄSER INTE NATURVETENSKAPENS ENHETLIGA
TECKENSNITTSBOKTRYCKSSTANDARD SYMBOL. Enda nu (Aug2017) kända webbläsarna som
fortfarande läser det klassiska naturvetenskapliga boktryckets Symbol är
GoogleChrome och Microsofts e-läsare — men dessa gör texten suddig istället
(sedan runt 2011+), ibland nära oläsbart.
Konstanten k i Stefan-Boltzmanns Strålningslag P = aAkT4:
k = 5,7 t8 WM–2°K–4 ............. experimentellt [GFåk3LIB1980s112m]
= 2π b4π4/15h3c02 ................ teoretiskt, från Plancks strålningslag (b, Boltzmanns konstant 1,3805502 t23 J/°K)
= 5,66893154148517 t8 WM–2°K–4
b = 1,3805502
t23 J/°K .......... Boltzmanns konstant
h = 6,62559 t34 JS ................. Plancks konstant -- äldre: det universella verkanskvantumet
c0 = 2,99792458 T8
M/S ......... ljushastigheten i g-fritt vakuum
kP = 2k/c0
= 3,781904041 t16 NM–2°K–4
Intet av följande ingår i den moderna akademins lärosystem.
Anledning: TNED. Se även illustrerat i SKILDA
TEORIER.
STJÄRNFYSIKENS ELEMENTÄRA GRUNDER ENLIGT RELATERAD FYSIK:
— Solen:
Om inte redan bekant: För undvikande av ev.
missuppfattningar på grund av ämnets allmänna svårighetsgrad -- Se inledande
orienteringar i
SOLENS ENERGIPRODUKTION I JÄMFÖRELSER MELLAN MODERN
AKADEMI OCH RELATERAD FYSIK, SOLENS ENERGIPRODUKTION I DETALJ.
Tγ = (γp/akP)1/4 .......................... °K: strålningstryckets värmegradsekvivalent
a absorptionskoefficienten
......... generellt 2/3
:
γp = p – pe .................................. NM–2: STJÄRNORNAS ALLMÄNNA TRYCKEKVATION enligt Relaterad Fysik
γp StrålningsTrycket .................. ingår inte i MAC : GammaPe
p Gravitations-Trycket .............. ingår inte i MAC :
Pe ................ F[G]/A = G[m2/r]² / 4πr²
pe CoulombTrycket
.................... ingår inte
i MAC
: PeE .............. F[E]/A = k[Ze/d]² / πr0²
Se även i PULSARERNA.
p = G(m2/r)2/4πr2
...................... NM–2 : Gravitations-Trycket
Pe,
Stjärnans g-kraft fördelad över omslutna rymdStrålSfärens yta -- från lägst r=R=4012 M i Solens fall
G ...... Gravitationskonstanten ... 6,67
T11 JM/[KG]²
r ........ Solstrålningens
omslutna rymdStrålSfärsRadie, minst R = 4012 M i Solens fall
R ........ Stjärnstädet:
RSTAR = rSTAR(ρr ρ0–1)1/4
................ stjärnans centrala stjärnstäd där fusionerna utvecklas
periodiskt via G-tryck
rSTAR = (3mSTAR/4πρn)1/3 .... stjärnradien (stjärnans g-rand), primärt
oroterad stjärna:
se STJÄRNORNAS OMFÅNG -- rotationens inverkan på stjärnans fysik, räkneexempel ges där med Sirius.
=
mSTAR1/3(0,0554245
KG–1/3M)
≈ mSTAR1/3/18 ............. mSTAR, stjärnans egenmassa
ρn = 1402,1847 KG/M² se härledningen i Massa-LuminositetsRelationen
ρr .................. RhåÄrr, PrimärStjärnornas allmänna yttäthetskonstant
ρr
= 8,9277145 t5 KG/M³
:
ρ0
= ρC = mA/8r3 ........ maximala
Coulombtätheten från given atombas,
kärnkuben (2r)³ = 8r³, r = r0 = Vätekärnans radie = 1,37 t15 M
ρ0 = 8,13444 T16 KG/M³
:
rG-STAR = [ρr
(8/mA)–1/3/r0]–1/4(3/4p)1/3·[(1/m0SLIM)1/3
– (1/mS)1/3]–1 : Stjärnans g-radie,
se härledningen i Solens
Gravitella Radie: Se mA
r0 m0SLIM mS
nedan
Solens g-radie ... 6,97063467
T8 M
-- större än synliga Solradien -- 6,957 T8 M
WikiSolar radius -- med ca 1000 KM
:
RSOLEN = 4012,1338 M ..................... Solens
städradie
m2 ..... stjärnmassan i KG
:
m0SLIM ........... ÄmmNollSlim,
Stjärngränsmassan, se härledningen i Solgränsmassan:
m0SLIM =
(1/mA)2(eZ)3π–7/2(288)(k/G)3/2 Z e mA k
förklaras nedan
m2
...... mS ............... ÄmmÄss,
Solmassan -- Från
Keplers 3:e Lag: mS =
1,98941 T30 KG
:
pe =
[k(Ze/πr0d)2] ............ NM–2 :
Coulomb-Trycket PeE -- Felskrivning i originalet:
täthetsfaktorn redundant : ingen skada skedd.
= [k(Ze/πr0[r–R])2] ... se städradien R = R-STAR ovan
:
r ........ godtyckligt variabla avståndet från
Solcentrum -- lägst 4013
M
d ........ ekvivalenta kärncylinderlängden, se
ill. ovan: beskrivning i STRÅLNINGSTRYCKETS RADIELLA VARIATION
k ........ = Rc0= 1/4πε0
= (8,98743 T9 ≈ 9) T9
VM/C
ε0 ....... elektriska konstanten i vakuum 8,8543 t12
C/VM egentligen KapacitivitetsKonstanten för vakuum
Se separat HÄRLEDNINGEN
TILL ELEKTRISKA KRAFTLAGEN -- RC=1/4πε0
förklaras -- och ELEKTRISKA KONSTANTEN
————————————————————————
PARAMETERFORMERNA
BESKRIVS MERA UTFÖRLIGT FRÅN BÖRJAN I SOLFYSIKEN
————————————————————————
Z ...... Kärnladdningen hos den atomtypen i stjärnans
stjärnstäd -- vad vi vet: vanligen Z=1 för primärstjärnornas
Vätebaser
e ....... elektronladdningen
.......... 1,602 t19 C
r0 ....... kärnradien hos Z-agenten .. Se Volymenergin i Stjärnfysikens Fundamentalteorem
: grovt: r0 = R·A^1/3, A atomkärnans masstal: för väte är A=1, R=1,37 t15 M: se Kärnradierna
mA ... Z-agentens atommassa ... väteatomens massa är 1,00782252 · 1,66033 t27 KG -- använd tabellvärden
![]() r0
tyngdcirkelradien
r0
tyngdcirkelradien
Toroidytan (Guldins regler) totalt AK = PaPb = (2π·r0/2=πr0) · 2πr0 = 2(πr0)2:
Exponerade Coulombiska kraftytan mot en spinnsynkroniserad inkommande eller utgående blir halva värdet:
Effektiva elektriska kraftytan: AK/2 = (πr0)2.
— F/Aeff = k(Ze/d)2/(πr0)2, Coulombtrycket som används i härledningen av Solfysiken-Stjärnfysiken.
— En mera (praktiskt) orienterad effektiv ekvivalent elektrisk tryckreaktionsyta, ovan vänster högra, framträder om vi erinrar detaljerna från avsnittet om Kärnradierna Del 2, TYNGDCIRKELN. Halva effektiva toroidytan som ovan (πr0)2 via tyngdcirkeln motsvaras av en ekvivalent toppcirkelskiva, en ideal cirkulär tvärsnittsyta lika med
tyngdcirkelradien (r0) gånger √π = 1,7724538: A = πr2 = π(r0√π)2 = (πr0)2.
— r0 är väteatomkärnans ”klassiska” 1,37 t15 M (Vätekärnans radie). Den associeras i relaterad fysik (TNED) med Neutronen = Plancks konstant h=mcr som neutronradien (h/mnc0 = r=1,32 t15 M) som genom sitt naturliga sönderfall antar den något större protonradien 1,37 t15 M. Se utförligt i PROTONRADIENS BESKRIVNING hur neutronradien och protonradien kan härledas i samband med NEUTRONKVADRATEN (atomära massdefekterna).
r0e := r0√π; A =
π(r√π)2 = πr2π =
(πr)2
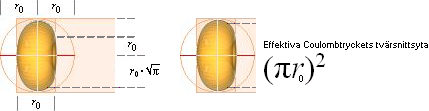
ToppToroidYtans Matematik
Detaljerna uppmärksammades redan i samband med härledningsarbetena till Jordens Första och Andra Ekvationer (Jordens5, se särskild beskrivning i FUSIONSGRÄNSMASSAN).
— Se resonemanget i detalj i Gränsmassans matematiska fysik.
Coulombtrycket (pe) har signifikant kvantitativ mening endast i det trånga området omkring själva städkärnan (R), de aktuella fusionsfaserna med primärstjärnans bildning. pe-värdet har ingen roll att fylla ens en meter över den kroppsytan — i Solens fall: r=4013 M: pe=2,43 t6 N/M² mot p=8,1 T34 N/M²)
— Den fullständiga formen för strålningstryckets radiella variation som ovan
γp = p – pe
kan därför förenklas med enbart
γp = p – (pe→0) = p
= G(m2/r)2/4πr2
r ........ avståndet från Solcentrum, lägst 4013 M
m2 ..... Solmassan -- Från Keplers 3:e Lag: mS = 1,98941 T30 KG
om uppgiften gäller Gamma-p-värden speciellt från Solranden rSTAR och utåt. Den mera korrekta formen som också medger motsvarande värden från Solytan och inåt, ner mot stjärnstädet kräver Coulombtryckets medverkan. Och man får då sambandsformen
γp = p – pe
= G(m2/r)2/4πr2 – [k(Ze/πr0[r–R])2]
= Gm22/4πr4 – [k(Ze/πr0[r–R])2]
r ........ godtyckligt variabla avståndet från
Solcentrum -- lägst 4012
M
m2 ..... Solmassan -- Från Keplers 3:e Lag: mS = 1,98941 T30 KG
r0 ..... Vätekärnans radie 1,37 t15 M för Solen
Z = 1
e ...... elektronladdningen 1,602 t19 C
RSOLEN = 4012,1338 M ..................... Solens städradie
— Värdet på pe
i Solens fall blir maximalt 6,63 T30 N/M² med r—R = vätekärnans radie 1,37
t15 M.
— Värdet på maximala p blir motsvarande vid städytan r=4012M lika med 8,11
T34
N/M².
Termonukleära Strålningstryckets Värmegrad från Solytan:
Utanför Solen -- ingår inte i MAC
Strålningstryckets
temperaturekvivalent därmed från Solytan och utåt obegränsat
Tγ = (γp/akP)1/4 .......................... °K: strålningstryckets värmegradsekvivalent
a absorptionskoefficienten
......... generellt
2/3 för
alla primärstjärnor.
Se även i Primära
Övergången.
kP = 3,781904041 t16 NM–2°K–4 som ovan.
TERMONUKLEÄRA STRÅLNINGSTRYCKETS FUNKTION enligt TNED — γp (GammaPe) såväl som Tγ (TeGamma) — bygger på en given Solens gravitella radie rG=6,67 T8 M (se härledningen i SOLENS GRAVITELLA RADIE). Genom att Solmassan avtar innanför den g-ytan mot centrum betyder det att värden Solytan heller inte blir strängt relevanta.
TeGamma bär ansvaret enligt TNED för den höga ekvivalenta värmegraden i Solkoronan (Se Koronafysiken).
— Vid SolGytan (r=6,97 T8 M) är TeGamma 24 374 373 °K.
— Vid Jordbanan (r=1,496 T11 M) är TeGamma 113 562 °K.
Sambandet ovan gäller strängt taget inte innanför Solens g-yta (6,97 T8 M) — på grund av att en aktuellt variabel täthetsfunktion inte finns integrerad: Solmassan avtar mot centrumklotet. För det ändamålet finns en särskilt härledd lokalt täthetsberoende värmegradsfunktion som gäller inom Solklotet. Se nedan i (Ts) TeÄss, Solklotets Inre Soltäthetsvariabla Temperaturvariation.
Wienekvivalentens Energigravitella värmegrad:
Utanför Solen -- ingår inte i MAC
TNED visar också en annan Solens Värmegrad — från Wiens förskjutninglag (Planckstrålningens derivata):
TW
= k2,898
t3 M°K · mAGm2/rhc0
... G-energins
ekvivalenta Wientemperatur
r ........ godtyckligt variabla avståndet från Solytan
-- lägst fotometriska radien 6,96
T8 M
mA ... atommassan hos Solkärnans atomtyp:
Väteatomens mA = 1,0078252 · 1,66033 t27 KG
h ........ Plancks
konstant 6,62559 t34 JS
c0 ..... toppdivergensen 2,99792458 T8 M/S
G ...... gravitationskonstanten 6,67 t11 JM/KG²
k ....... Wienkonstanten 2,898
t3 M°K
:
= r–1(3,23219 T15 °K)·M
TeWe baseras på g-energi fördelad på Solens fasta antal atomkärnor av typen mA och gäller därför idealt som elektromagnetisk strålkälla endast från Solytan och utåt obegränsat.
— Vid SolGytan (r=6,97 T8 M) är TeWe 4 637 284 °K.
— Vid Jordbanan (r=1,496 T11 M) är TeWe 26 606 °K.
Planckvärmegraden -- SOLEFFEKTVÄRMESTRÅLNINGEN:
Utanför Solen -- ingår i MAC
Soleffektvärmestrålningen är den ordinära allmänt kända värmegradsformen från Stefan-Boltzmanns strålningslag.
TP = (P/aAk)1/4
............................ värmeeffektgraden
P .... Soleffekten 3,84E T26 W
a ..... absorptionskoefficienten, initiellt 2/3
A ..... Solstrålningens
omslutna sfäryta
A = 4πr2
r ........ godtyckligt variabla avståndet från
Solytan -- lägst fotometriska radien 6,96 T8 M
Konstanten k i Stefan-Boltzmanns Strålningslag P = aAkT4:
k = 5,7 t8 WM–2°K–4 ............. experimentellt [GFåk3LIB1980s112m]
= 2π b4π4/15h3c02 ................ teoretiskt, från Plancks strålningslag (b, Boltzmanns konstant 1,3805502 t23 J/°K)
= 5,66893154148517 t8 WM–2°K–4
b = 1,3805502
t23 J/°K .......... Boltzmanns konstant
h = 6,62559 t34 JS ................. Plancks konstant -- äldre: det universella verkanskvantumet
c0 = 2,99792458 T8
M/S ......... ljushastigheten i g-fritt vakuum
kP = 2k/c0
= 3,781904041 t16 NM–2°K–4
:
TP = (P/4πakr2)1/4 = r1/2(P/4πak)1/4
= r–1/2(1,68397035 T8 °K)·M1/2
— Vid SolGytan (r=6,97 T8 M) är TePe 5 415 °K.
— Vid Jordbanan (r=1,496 T11 M) är TePe 435 °K.
Se även till jämförelse Solytans temperatur via fotometriska effekten, 5800 °K.
Wiens förskjutningslag: PLANCKVÄRMEGRADEN :
Utanför Solen -- ingår i MAC
Wiens förskjutninglag — Planckstrålningens TOTALA våglängdsspektrum deriverat — ger värmegraden för HELA Planckstrålningsspektrumets emissioner enligt sambandet
k = 2,898 t3 M°K
TPW = ———————— °K ................. Planckvärmegraden för Solljus i fri rymd
λ = c0/f
Solen är en sådan ideal ”Jag-Visar-Allt”-strålkälla.
— Täcks någon del för via strålningens växelverkan med materien (Comptoneffekten) gäller sambandet med allt sämre precision ju mer material som ställs i vägen.
— TePeWe-formen får därför förstås gälla utomordentligt för Jordens del endast i atmosfärens allra översta delar. Successivt under, ner mot Jordytan, sprids solljuset och allt mer av den ursprungliga (högfrekventa) Planckstrålningen suddas ut.
— TePeWe har ingen direkt radiell variation. Det är endast ljusets olika våglängder som spelar in.
— Temperaturekvivalenten vid synligt ljus »RymdRött»=7000Å är 4 140 °K, 1Ångström = 1 t10 M.
— Vi kan anställa vissa jämförande resultat med hjälp av Allmänna gaslagens form för ekvivalenta medelhastigheter hos gasmolekyler vid givna temperaturer enligt MOMENTEKVATIONEN
v2 = 3 RTU–1
................ gaspartiklarnas
medelhastighet vid
T °K, M/S
R ....... allmänna gaskonstanten 8314,9148 J/[KG°K]
T ....... temperaturen i °K = n°C + 273,15 °C
U ...... gasmolekylens atomvikt -- avrundade
värden för U används ofta som rena heltal
— För vätgasens U=1 och T=4140°K blir avrundat v = 10 162 M/S.
— Flykthastigheten i Jordens nedre s.k. Exosfär (översta delen ut mot den öppna rymden), lägst 1000 KM upp — beräknas enligt sambandet
v2 = Gm2/r ................. flykthastigheten:
en kropp med minst v ut från Jorden återvänder ALDRIG
G ...... gravitationskonstanten 6,67 t11 JM/KG²
m2 ..... Jordmassan 5,975 T24 KG
r ........ avståndet från Jordcentrum till
rymdpunkten, M
— Med Jordradien (ekvatorn) rJ = 6,378 T6 M och höjden + 1000 KM (1 T6 M) blir avrundat
v = 7 350 M/S.
— Det betyder att en väteatom 1000 KM upp över Jorden lever farligt: den tenderar att påföras den högre Planckvärmegradens 10.162 M/S, och därmed försvinna bort ur Jordatmosfären. Hade flykthastigheten varit högre, hade väteatomen stannat kvar.
— Vattenmolekylen däremot med U=18 (H+H+O: U = 1+1+16 = 18) i samma lokal stannar kvar med sitt lägre
v = 2 395 M/S via Planckvärmegraden 4140 °K från »RymdRött».
För att vattenmolekylen ska nå upp till minst 7350 M/S via gaslagens v-form — och så få möjlighet att rymma ifrån Jorden via solljusets inverkan — måste tydligen T idealt vara minst
T = 38.982 °K. Det motsvarar i TPW-formen en rymdöppen SolljusPlanckvåglängd på
λ = 767 Å = 76,7 nM — inne i det ultravioletta området.
Hur det sedan förhåller sig i praktiken är en annan fråga. Värdena ovan är bara de rena ideala grovvärdena.
Solklotets inre Temperaturvariation med lokala Soltätheten:
Solens inre -- ingår inte i MAC
— Temperaturvariationen, internt täthetsberoende mellan Solcentrum ut till Solytan, beskrivs särskilt i TNED av sambandet TeÄss
Ts = (4πG/akP)1/4r–3/2(ρCR4/3)1/2 ... värmegradens radiella variation inuti Solklotet, °K
=
r–3/2(1,13147 T17
°KM3/2) .. r > 4012 M, r < 6,97 T8
M.
Se Solens första ekvation i SOLENS VÄRMEGRADER ENLIGT TNED.
— Föreställningen om ”exakta värden” nära och invid städkärnan (R=4012 M för Solen) blir äventyrliga med de enklare sambanden ovan: Städkärnan genomgår viss åldring i tiden (avtar i radie) samt innehåller fluktuerande skalskikt som kopplar till olika faser i Solens energiproduktion. T-värden nära R får därför (här ännu) förstås med viss försiktighet:
— Med r=4012 M ges Ts = 4,45 T11 °K; r=1M ger koefficientvärdet 1,12 T17 °K.
Jämför Termiska Ekvivalenter: Fysikens praktiska gräns ligger (TNED) vid ca T12 °K, i MAC ca 100 gånger lägre.
— SolGradien r=6,97 T8 M ger Ts = 6 150 °K.
Se även till jämförelse Solytans temperatur via fotometriska effekten, 5800 °K.
———————————————————————
Solens primära magnetfält:
Noter i STJÄRNANS EGENPRODUCERADE ROTATION:
— Från början skulle Solen — enligt TNED — ha haft en LITEN primärt given
egenrotation. Den har sedan byggts på via Solkärnans fusionskomplex med strålningstryckets utträde från den högtäta
städkärnan ut mot lägre g-områden, enligt TNED-teorin. Så: Från början (Se Jordens-Solsystemets ålder) skulle Solens magnetfält ha varit knappt
märkbart.
END.
AKROMATISKA
BRYTNINGEN GRB
innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER
Akromatiska Brytningen GRB
ämnesrubriker
innehåll
referenser
[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967
Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.
mn = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]
me = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för me , Table 1.4 s7–27 för u]
u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]
u = 1,66033
t27 KG .............. atomära massenheten [ENCARTA 99 Molecular
Weight]
u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]
u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]
u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]
u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],
CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]
c0 = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]
h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]
e = 1,602 t19 C ...................... elektriska elementarkvantumet, elektronens laddning [FOCUS MATERIEN 1975 s666ö]
e0 = 8,8543 t12 C/VM ............. elektriska konstanten i vakuum [FOCUS MATERIEN 1975 s666ö]
G = 6,67 t11 JM/(KG)² .......... allmänna gravitationskonstanten [FOCUS MATERIEN 1975 s666ö] — G=F(r/m)² → N(M/KG)² = NM²/(KG)² = NM·M/(KG)²=JM/(KG)²
[BA]. BONNIERS ASTRONOMI 1978 — Det internationella standardverket om universum sammanställt vid universitetet i Cambridge
t för 10–, T för 10+, förenklade exponentbeteckningar
(Toroid Nuclear Electromechanical Dynamics), eller ToroidNukleära Elektromekaniska Dynamiken
är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=mnc0rn, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED får därmed (således) också förstås RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED [Planckfraktalerna] i ATOMKÄRNANS HÄRLEDNING.
Senast uppdaterade version: 2017-10-27
*END.
Stavningskontrollerat 2012-07-03.
åter till portalsidan ·
portalsidan är www.UniversumsHistoria.se
∫
√ τ π ε ħ UNICODE — often used
characters in mathematical-technical-scientifical descriptions
σ
ρ ν ν π τ γ λ η ≠ √ ħ
ω →∞ ≡ ↔↕ ħ ℓ
Ω
Φ Ψ Σ Π Ξ Λ Θ Δ
α
β γ δ ε λ θ κ π ρ τ φ
σ ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈
≥ ← ↑ → ∞ ↓
ζ
ξ
Arrow symbols, direct via Alt+NumPadKeyboard: Alt+24 ↑; Alt+25
↓; Alt+26 →; Alt+27 ←; Alt+22 ▬
Alt+23
↨ — also Alt+18 ↕; Alt+29 ↔
Alt+NumPad 0-25, 26-...
☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓
→←∟↔▲▼
!”#$%&’()*+,-./♦812...
åter till portalsidan ·
portalsidan är www.UniversumsHistoria.se