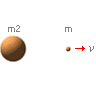UNIVERSUMS HISTORIA | K-cellens inre — Primära v-formen | K-cellens GRUNDER | 2012VI23 a BellDHARMA production | Senast uppdaterade version: 2012-07-15 · Universums Historia

innehåll denna sida · webbSÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning över alla webbsidor

GRB1—K-CELLENS INRE • GRB1m—MörkaMaterien • GRB1n—Primära v-formen • GRB2—UniversumsSynrand • GRB2a—AkroBreak • GRB3—GRBorigin

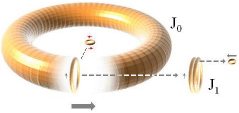
ZONSKÄRNINGARNA med PRIMÄRA v-FORMEN — Bildkälla, Författarens arkiv, 27Jun2012E10Bild41 NikonD90 Detalj

| Primära v-formen | r-formen | Atomkärnans inkompressibilitet — SAMMANSTÄLLD ÖVERSIKT |

Zonskärningarna — K-cellens expansionshastighet

Zonskärningarna

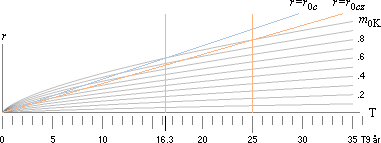
Figuren ovan [originaletZONSKÄRNINGARNA] användes i samband med resultatbeskrivningarna från K-cellens värmefysik: K-cellens expansion genom en idealt homogen täthetsfördelning. I praktiken måste det inre av K-cellen tvunget genomgå speciella täthetsändringar för att grundparametrarna i resultatbeskrivningarna från K-cellens värmefysik ska stämma (K-radien och K-värdet).

— Följande genomgång ger en kompletterande (mera grundlig) beskrivning av sambandsformerna med den idealt homogena täthetsfördelningen som grund i K-cellens expansion.

— En vidare, mera praktiskt orienterade, bild med K-cellens INRE täthetsvariabla samband framkommer ur den grundformen via just villkoret med K-radien och K-värdet, och beskrivs utförligt från K-cellens inre fysik [separata htm-dokument utformade/sammanställda under perioden hösten 2011 - sommaren 2012 — föranlett av kravet på en mera preciserad bild av K-cellens inre för att ev, eftersöka en förklaring till GRB-fenomenet].

— Hur expansionshastigheten kan vara 2c₀ då den passeras av nollzonens c₀ beskrivs utförligt i Zonpassagen, om ej redan bekant.

Momentana expansionshastigheten, 2c₀ ovan, är egentligen en statiskt idealiserad ekvivalent till expansionssambandets form och som mera berör den idealiserade K-cellens basmatematik via homogen täthetsfördelning. I det praktiska fallet blir den bilden mera komplicerad på grund av att K-cellen uppvisar inre täthetsförskjutningar med speciella sambandsformer. Idealformerna beskriver således ingen exakt bild av det inre i K-cellen, utan snarare K-cellens yttersta randexpansion, tillsammans med motsvarande idealiserade statiska samband. Se utvecklingen i Statiska v-formen.

För den mera detaljerade beskrivningen av K-cellens inre fysik, se från K-CELLENS INRE.

SE-symbolerna — Expansiva Statiska

— SE-symbolerna har (här) i efterhand lagts till i rent ikoniskt (detaljrubrik-) förtydligande syfte: sammanhanget i kopplingarna till de olika härledningarna med grund i den helt idealt täthetshomogena K-cellens grundmatematik, analogt med grund i K-cellens helt odämpade expansion.

— Den matematiska-fysikaliska grunden till sambanden (i de delarna) återfaller helt på Keplers ytmoment med beskrivningen i EXPANSIONSSAMBANDET. Nedan i Primära v-formen följer en allmän genomgång av grundbegreppen som (eventuellt) mera ingående klargör sammanhangen i detaljer genom grafexempel i de rent matematiska grundformerna — K-cellens helt odämpade expansion, analogt K-cellens idealt homogena täthet.

— Med den delen klargjord blir det sedan enklare att förstå härledningarna till K-cellens mera praktiskt dämpade expansion (Behovet av en mera precis översiktsbild). Se även grundsambanden för statiska och expansiva i GRUNDFYSIKEN, om ej redan bekant.

		Statiska: v = √ 2Gm2/r Varje kropp [m] som befinner sig på avståndet r från centralmassan [m2] bildar KRAFTJÄMVIKT med Gm2 om m besitter momentanhastigheten v relativt m2:s tyngdpunkt: m återvänder aldrig.
		Notera den delvis »sublima» skillnaden mellan de delvis uppenbart olika sätten: En delkropp som skjuts iväg utanför en fast kropp kan EXPLICIT inte skiljas från en delkropp som ingår i en expansion [EXPLOSION] för en hel centralkropp. bägge sätten följer samma grundform. I vissa sammanhang kan man alltså beskriva typ Expansiva-Kontraktiva-Statiska tillståndets g-fysik där BÄGGE typerna gäller. — Det blir sedan upp till författaren att försöka klargöra för läsaren på vilket sätt som vilken form gäller i vilket sammanhang.
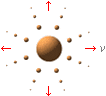
		Expansiva: v = √ 2Gm2/r Varje kropp [m2=M] som EXPANDERAR via växande [eller kontraherar via avtagande] radie [r] bevarar gravitationsenergin [GM²/r] om expansionen sker via v-formen; m2 återvänder aldrig.

Förklaring:

Se allmänt även i G-faktorerna

— Beroende på om en kropp expanderar — som i K-cellens fall — eller om den är fast (eller i varje fall inte direkt uppenbart i expansion eller kontraktion) — som i Jordens fall — gäller olika kvantitativa samband i fysikbeskrivningen.

— BÄGGE (expansiva, statiska) utgår ifrån en och samma matematiska grundform,

v = wÖ2 = Ö 2Gm₂/r ............... EXPANSIONSSAMBANDET

den grundformen återkommer ständigt i DEN RELATERADE BESKRIVNINGEN tillsammans med respektive utvecklade och mera preciserade samband för expansiva-kontraktiva och statiska tillståndens fysik

— EXEMPEL ges med början i K-cellens Expansionshastighet [Primära v-formen] med den härledande beskrivningen till de olika samband som berör K-cellens expansion.

Graferna: r-formen | Primära v-formen | STATISKA v-formen | | | Zonpassagen

Primära v-formen — SE-symbolerna — K-cellens expansionshastighet

Primära v-formen — K-cellens odämpade expansion

primära v-FORMENs samband

r-sambandets grund

— Primära v-formen framgår DIREKT ur r-derivatan, analogt direkt genom att utveckla efter täthetsändringen i K-cellen via den givna idealt odämpade flykthastigheten v = √2Gm₂/r; [Se ALLMÄNNA EXPANSIONSHASTIGHETEN v = √2Gm₂/r från E_kin=mv²/2=E_G=Gm²/r som ger v ];

v = √2Gm₂/r ......................................... utgångssambandet — flykthastigheten

= r^–1/2(2Gm₂)^1/2

= 2r/T ; från likformiga accelerationen a=v/T=2d/T² ; v=aT=2d/T

T = 2r/v

= 2r(2Gm₂/r)^–1/2

= (4r²r/2Gm₂)^1/2

= (2r³/Gm₂)^1/2 ; r=3m₂/4pr³; r³/m₂=3/4pr ;

= (3/2pGr)^1/2 ..................................... expansionssambandet

= 2(3/8pGr)^1/2 ;

Statiska v-formen

; Om v-formen ovan v=(2Gm₂/r)^1/2 vidareutvecklas här genom att återigen återföra den ovan resulterande T-formen på ursprunget, v=2r/T, finns bara en rent STATISK resultatform — motsvarande i princip en rymd med KONSTANT divergens:

v = 2r/T = 2r/2(3/8pGr)^1/2 = r(8pGr/3)^1/2 = 2r/(2r//v) = v ; T återfört på sig självt.

Om istället den ovan separat utvecklade T-formen utnyttjas i täthetsformens anställning [T=(3/2pGr)^1/2] — som betyder att också tätheten via T kommer att följa den likformiga accelerationen — fås en EXPANSIV TÄTHETSVARIABEL SAMBANDSFORM som beskriver r-formen korrekt — och som därmed av princip också innefattar en rymd med variabel divergens: vårt aktuella fall:

;

r = 3/(2pGT²) ............. expansionssambandet ............... se även utvecklingarna närmast ovan direkt

= 3m₂/(4pr³) ;

1/(GT²) = m₂/(2r³) ;

r³ = T²Gm₂/2 ............... från expansionssambandet

r-formen

r = T^2/3(Gm₂/2)^1/3 .............. K-cellens idealt odämpade radiella expansion

= T^2/3(1/2)(4Gm₂)^1/3

= (T²Gm₂/2)^1/3 ; T = (2r³/Gm₂)^1/2 ; r=3m₂/4pr³; r³/m₂=3/4pr ; T = (3/2pGr)^1/2 = 2(3/8pGr)^1/2

;

Fortsätter vi här på föregående STATISKA SAMBANDETS v-FORM — samma tema som ovan men här via r-formen direkt — genom att återföra den ursprungliga v-formens r-variabel på den uppnådda variabla r-formens EXPANSIVA TÄTHETSVARIABEL — dvs: vi »återför r på r» — utför vi bara samma statiska operation som i fallet med »T som återförs på T» via 2r/v; Vi får precis samma principiella resultat som i det statiska fallet ovan med

v = 2r/T = 2r/2(3/8pGr)^1/2 = r(8pGr/3)^1/2:

v = 2r/T = 2[T^2/3(Gm₂/2)^1/3]/T = 2T^–1/3(Gm₂/2)^1/3 = T^–1/3(4Gm₂)^1/3, = r(8pGr/3)^1/2 :

;

v = r^–1/2(2Gm₂)^1/2

= [T^2/3(Gm₂/2)^1/3]^–1/2(2Gm₂)^1/2 ; .................... STATISKA FALLET — c-homogen rymd.

= T^–1/3(Gm₂/2)^–1/6(2Gm₂)^1/2

= T^–1/3(Gm₂)^–1/62^1/62^1/2(Gm₂)^1/2

= T^–1/32^{1/6+1/2=4/6=2/3}(Gm₂)^{1/2–1/6=2/6=1/3}

= T^–1/32^2/3(Gm₂)^1/3

Statiska v-formen

v = T^–1/3(2)^2/3(Gm₂)^1/3 ........................... K-cellens EKVIVALENT ELEKTROGRAVITELLT STATISKA idealt odämpade radiella hastighet

statiskt ekvivalenta verkan i SUMMAN av lokala expansionshastigheten och LOKALA DIVERGENSEN — »samma c överallt»;

KURVSKARAN MOTSVARAR IDEALA c-HOMOGENA RYMDENS ENKLARE DIREKTA VÄRDEN — alltså utan variabel divergens, vidare nedan:

= T^–1/3(4Gm₂)^1/3

= r^–1/2(2Gm₂)^1/2

— Jämför direkt derivering av r-formen:

r = T^2/3(Gm₂/2)^1/3 ;

r’ = dr/dT = Dn r = v ; För deriveringar, se FORMLAGARNA om ej redan bekant;

r’ = dr/dT = dr/dT = Dn r

= (2/3)T^{2/3 – 1}(Gm₂/2)^1/3

= T^–1/3(2/3)(Gm₂/2)^1/3

= T^–1/3(2/3)(4Gm₂/8)^1/3

= T^–1/3(2/3)(1/8)^1/3(4Gm₂)^1/3

= T^–1/3(2/3)(1/2)(4Gm₂)^1/3

= T^–1/3(1/3)(4Gm₂)^1/3 ; Primitiva v-formen — primära v-FORMENs samband

= v

Expansiva v-formen

v = T^–1/3(1/3)(4Gm₂)^1/3

expansiva verkan från lokala expansionshastigheten och LOKALA DIVERGENSEN — den lägre expansionshastigheten relativt statiska v-formen och dess c-homogena rymd, kompenseras av den lägre divergensen som bidrar EXTRA till den observerade rödförskjutningen som i termer av STATISKA v-FORMEN kräver ett högre c-värde.

;

— Resultaten i de bägge v-alternativen (Stat|Expa) skiljer med en faktor 3.

— Integrationen från v åter till r:

;

Integrationen:

v = T^–1/3(1/3)(4Gm₂)^1/3 = dr/dT ;

dr = T^–1/3(1/3)(4Gm₂)^1/3dT

= (1/3)(4Gm₂)^1/3·T^–1/3dT ;

ò dr = (1/3)(4Gm₂)^1/3 ò T^–1/3dT ; [FORMLAGARNA] [Derivata och Integral] [NOLLFORMSALGEBRAN]

r = (1/3)(4Gm₂)^1/3 · T^–1/3+1/(–1/3+1)

= (1/3)(4Gm₂)^1/3 · T^2/3/(2/3)

= (1/3)(3/2)(4Gm₂)^1/3 · T^2/3

= (1/2)(8Gm₂/2)^1/3 · T^2/3

= (1/2)(8)^1/3(Gm₂/2)^1/3 · T^2/3

= (1/2)2(Gm₂/2)^1/3 · T^2/3

= (Gm₂/2)^1/3 · T^2/3

= T^2/3(Gm₂/2)^1/3 ;

OCH SOM VI SER är detta alldeles detsamma som i r-formen:

r = T^2/3(Gm₂/2)^1/3

I modern akademi expanderar universum med > 3c

— drygt 3ggr ljushastighetens toppvärde

— Notera speciellt för JÄMFÖRELSE MED RESULTATEN I MODERN AKADEMI — se särskilt i Wikipedia Observable universe [2012-03-01]:

— Eftersom, främst, universum som RYMD i modern akademi anses vara c-homogen [Se DET EKOLOGISKA UNIVERSUMET] — ett och samma värde överallt för ljushastigheten [Se motsvarande STATISKA v-formen ovan enligt relaterad fysik] — finns bara av det skälet ingen som helst allmän grund för jämförande resultat mellan modern akademi och relaterad fysik.

— Wikipediaartikeln på Observable universe upplyser om universums ålder T₁=13,7 T9 år = r₁/c₀ med radiella utsträckningen grovt r₂=46 T9 ljusår=c₀T₂; Man räknar (alltså, konventionellt) efter helt andra mallar och förutsättningar med en s.k. ackumulerad expansion;

— Medelhastigheten NU enligt etablerad mening:

— Om distansen r₂=46 T9 ljusår avverkas på tiden T₁=13,7 T9 år blir medelhastigheten (v=d/T) enligt modern teori

v = [c₀ · 46 T9 · 365,25 · 24 · 3600]/(13,7 T9 · 365,25 · 24 · 3600)

= c₀46/13,7

= c₀(3,3576642) ;

v/c₀ ~ 3,36 ;

Universums metriska expansion kan enligt modern akademi tydligen beskrivas via en sfäriskt expanderande konstant medelrörelse med drygt 3ggr ljushastighetens belopp

— HUR man än bär sig åt i mänsklighetens arkiv, finns tydligen ingen möjlighet att undkomma en föreställning om multipla c. Se även i BEVISET FÖR MULTIPLA c — enligt relaterad fysik. Medan multipla c är förhållandevis LÄTT att förstå, relatera och beskriva i TNED [Se Planckekvivalenterna], finns ingen motsvarande beskrivande ordning i modern akademi (»ingenting kan gå fortare än c» [r-teorin]) — ehuru föreställningen om just multipla c likväl praktiseras, som ovan i exempel, på ett eller annat sätt.

;

— Jämför medelhastigheten i resultatet NU för K-cellen enligt relaterad fysik (T[NU]=20,82 T9 år; m₂=4,14 T53 KG):

r = T^2/3(Gm₂/2)^1/3

= 1,81 T26 M ;

v = r/T

= T^–1/3(Gm₂/2)^1/3

= T^–1/3(2,39901 T14)^1/3

= T^–1/3(2,39901 T14)^1/3

= 2,75954 T8 M/S ;

v/c₀ = 0,92

— Det är helt andra värden som gäller. En helt annan värdefysik.

— Se även från DOPPLEREFFEKTEN:

— Expansionen enligt modern akademi sker f.ö. generellt med högre hastighet (omkring ca 17% i den aktuellt maximala rödförskjutningen).

;

— Enligt TNED är med T=20,82 T9 år nuvarande K-cellens radiella utsträckning ca 1,81 T26 M eller ca 1,91 T10 ljusår (19 miljarder ljusår, 19 T9 ljusår).

— Till jämförelse ges den etablerade uppgiften på universums nu synliga omfång ca 46 T9 ljusår enligt Wikipediaartikeln på Observable universe, vilket är ca 2,5 ggr större — trots en betydligt kortare tid för expansionen, 13,7 T9 år.

;

Jämförelsen bara understryker de väsensskilda domänerna i universums övergripande beskrivning: TNED (relaterad fysik) och modern akademi har absolut ingen som helst gemensam grund i den övergripande beskrivningen av kosmos fysik — utöver instrumentella observationer. Det är helt väsensskilda föreställningsgrunder som tolkar mätresultaten.

JÄMFÖR FÖR ÖVRIGT BEGYNNELSEVILLKOREN vid K-cellens detonation

— erinra Planckekvivalenterna; hur de förhåller sig till den etablerade r-teorin, för undvikande av ev. missförstånd, om inte redan bekant

— se även särskilt i EXPERIMENTELLA BEKRÄFTELSER;

— Hastighetsformen [Allmänna Expansionshastigheten] v = Ö 2Gm₂/r beskriver K-cellens randsfär från början;

— Med K-cellens massa m(K)=4,14 T53 KG på neutronkallplasmats maximala täthet D=1,82 T17 KG/M³ detonerar K-cellen på radien

r = (3m/4pr)^1/3=8,15855 T11 M

eller ca 5,5 AU (1AU, medelavståndet Jorden-Solen 1,496 T11 M). Därmed begynnelsevärdet för K-cellens allra yttersta=snabbast expanderade delar i neutronkallplasmat från början

v = Ö 2Gm₂/r

= 8,22727 T15 M/S

= c₀(27 444 220) ................. Se även i Beviset för multipla c

Den topphastigheten [EXPANSIVA v-FORMEN] avtar (först mycket snabbt) sedan successivt — idealt obegränsat mot NOLL om inga effektförluster tas med i beräkningarna. Hastighetens reduceras under hela K-cellens expansion, med alla innanförvarande massdelar i motsvarande lägre expansionshastigheter.

Editor2012II29

K-cellens lokala gravitation

Den samlade gravitationen (tyngdkraftsaccelerationen) i den lokala rymden behöver ingalunda vara stark för att frammana nolldivergens; det är den samlade massan som räknas

Exempel

MED nuvarande uppskattade medeltäthet för universum r=1,67241 t28 KG/M³ baserat på observationer av den nu synliga materien (en väteatom per tio kubikmeter rymd, synradien grovt 1000 Mpc = 3,0856 T25 M) i sambandet [NOLLDIVERGENSZONENS RADIE UR TÄTHETEN Statiska g-fysikens samband] r_0c=r^–1/2(3/8pG)^1/2c₀ ges följande:

— Med förenklat c₀=3 T8 M/S ges värdet r_0c=9,81358 T26 M — stället med noll ljushastighet i kraft av gravitationens inverkan från den av r inneslutna massan.

— Tyngdkraftsaccelerationen vid r blir a=w²/r=G(m₂=ρ[V=4πr³/3])/r²=r(4Gpr/3)=4,58548 t11 M/S² = 0,000 000 000 0458548… M/S².

— En sådan liten gravitation finner vi inte ens utanför Jorden, mellan Jorden-Månen, där ligger all gravitation överlagrad på Solfältet som är betydligt starkare.

— Räkneexemplet endast understryker att det är den samlade, totala massan som bestämmer; rr=[3/4p]m/r²; m/r²=rr[4p/3];

— Gravitationspotentialen vid r blir w²=ar=Gm₂/r=r²4Gpr/3=(4,58548 t11 M/S²)(9,81358 T26 M)=4,5 T16 (M/S)².

— G-potentialen (w²) kan växa obegränsat via idealt homogen täthet (r) med obegränsat växande r², medan den lokala gravitationsaccelerationen (a) växer direkt proportionellt med växande r.

— Se även (delvis mera utförligt) i Ljusets gravitella beroende räkneexempel som beskriver motsvarande konventionella begreppet ”svart hål”.

Zonpassagen

Hur K-cellens expansionshastighet kan vara 2c₀ — då den passeras av nollzonens c₀

IDEALA K-CELLENS EXPANSION VIA HOMOGEN TÄTHET framställer olika STATISKA ANALOGIER som också presentationen av härledningarna till K-cellens värmefysik uppehåller sig vid.

— En av dessa framställer i Zonskärningarna meningen att 2c0 är ”momentana expansionshastigheten då delsfären skärs av nollzonen” vars hastighet är (konstant) c0.

— Finns det något praktiskt belägg för en sådan TYP fysik?

— Dvs.: Kan en kropp med HÖGRE hastighet passera en kropp med LÄGRE hastighet på sådant sätt att DÅ passagen sker den passerande kroppen också besitter DUBBLA den passerade kroppens lägre hastighet?

— Följande exempel från den elementära mekaniken visar att så avgjort är fallet. Vi studerar kärnan.

Hur kan ett föremål med en högre hastighet passeras av ett föremål med lägre hastighet?

— ENDAST om föremålet med den högre MOMENTANA HASTIGHETEN befinner sig i INBROMSNING.

Vi studerar hur.

Figuren nedan använder PARABELN. Figuren visar hur en gemensam distans (d=0,5 M) passeras vid samma tid T=1 S) av två olika hastigheter [1konstant: 0,5 M/S; 2accelererad: 1 M/S], den ena en konstant hastighet (0,5 M/S), den andra en linjär acceleration med momentanhastigheten 1M/S vid T.

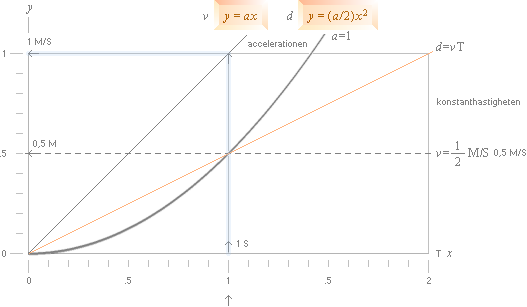
Figuren ovan visar hur distansparabeln y=0,5x² skärs av distanslinjärfunktionen y=vT vid tidpunkten T=1S.

— Genom att samma distanser i bägge fallen tangeras vid samma tidpunkt, men genom olika momentanhastigheter — parabelns 1M/S mot konstantfallets 0,5M/S — kan förloppet återföras på en mera PRINCIPIELLT BESKRIVANDE funktion och karaktär.

— BETRAKTAT SOM EN INBROMSNING [vi läser grafen från höger till vänster] SKÄR den konstanta hastighetskroppen 0,5M/S accelerationskroppens dubbelt så stora momentana hastighet 1M/S vid distansen 0,5 meter före stoppet.

— Genom att vända på preferenserna för start/slut med ledning av ovanstående figurkoncept, kan sammanhanget i K-cellens motsvarande minskande expansion (inbromsning) förstås och beskrivas som följer.

— Med utgångspunkt från K-cellens expansion [Se effekt- och energifunktionernas grafer i K-cellens värmefysik] — expansionshastigheten stegras först våldsamt, för att sedan avta och gå mot noll — från en vis bestämd tidpunkt (T), återstår i vilket fall en bestämd distans att avverka för expansionen tills den når noll — likt fallet i ovannämnda illustration.

— Det motsvarar i den enklare parabelfiguren ovan den gemensamma bassträckan som återstår om vi läser förloppet baklänges;

— Då K-expansionens randsfär skärs av någon (godtycklig) konstanthastighetsdistans vid T, återstår en motsvarande bestämd restdistans (d) innan K-expansionen (här förutsatt MED förluster som tvingar K-expansionen att avstanna) har kommit fram till avstanningspunkten.

— I vilket fall förklarar figuren ovan att TILLFÄLLET då en INBROMSANDE rörelse sammanfaller med en konstant rörelse — då rörelsernas kroppar tangerar en gemensam positionspunkt — ALLTID kräver att den inbromsande kroppen måste BÖRJA från en HÖGRE HASTIGHET än den konstanta hastighetens kropp. Ty, börjar vi händelsen med bägge rörelsernas momentana hastigheter lika stora, missas den passerande aspekten eftersom den inbromsande kroppen tvunget får lägre hastigheter efter starten och därmed aldrig hinner den konstanta kroppens distanser.

— För att få »skärande passage» måste följaktligen den inbromsande kroppen ALLTID börja på en högre hastighet än konstantkroppens. Räkneexemplen nedan klargör sammanhangens matematik.

EXEMPLIFIERAD FRAMSTÄLLNING för K-cellens sammanhang

GENOM SAMBANDEN FÖR KONSTANT likformig ACCELERATION

accelerationen (a):

a = v_a/T = 2d/T² ;

v_a = 2d/T ;

T = 2d/v_a ;

d = (a/2)T² ;

konstanta hastigheten (v_c):

v_c = d/T ;

d = v_cT ;

tillfället vid T då v_a passeras av v_c ;

d = (a/2)T² = v_cT ;

(a/2)T = v_c ;

T = v_c(2/a) = 2d/v_a ;

v_c/a = d/v_a ;

v_cv_a = ad ........................... villkoret då vc — LÄGSTA — passerar va — HÖGSTA

v_a = ad/v_c

— För att momentanhastigheten (v_a) i accelerationen ska vara större än det jämförande föremålets konstanta hastighet (v_c) gäller tydligen att

(ad) > v_c²

Är vc=va gäller vc²=ad; Förutsättningen för va>vc blir då att också ad>vc², analogt vc·va > vc².

EXEMPEL:

— Med

v_c som nollzonens c₀

— d den distans som återstår fram till decelerationsslutet (slutet på a) då K-cellens expansion helt har avstannat, lika med K-cellens ålder vid effektmaximum T(effMAX) (16,32 T9 år, se K-cellens värmefysik) fram till K-cellens halvperiod (336 T9 år),

— samt accelerationen (K-cellens deceleration)

a = dv/dT

= [T^–1/3(4Gm₂)^1/3]’

= (–1/3)T^–4/3(4Gm₂)^1/3 ; Se KalkylkortDirekt KcGRB.ods 5accT HelpOpen

vid T(effMAX) som med K-cellens totalmassa m₂=4,14 T53 KG ger

a = 3,87 t10 M/S²

samt momentanhastigheten v_a som 2v_c (eg. 1,996641 genom att T=16,32 T9 år här avrundat till 2 decimaler)

— blir den återstående distansen (d) lika med (v_c~3 T8 M/S)

d = v_av_c/a

= (3 T8 M/S)(2·3 T8 M/S)/(3,87 t10 M/S²)

= 4,65116 T26 M

= 15 Gpc [20 Gigaparsec, 1pc=3,086 T16 M]

= 49,16 Glå [67,95 Gigaljusår, 1lå=9,46073 T15 M] [4,91628 T10 lå]

~ 49 miljarder ljusår [68 T9 lå]

Om vi från STATISKA v-formen

v = T^–1/3(4Gm₂)^1/3 ;

utnyttjar en linjärt hoftad justeringsform (kT) med k=2,05 T11,

v = T^–1/3(4Gm₂)^1/3 – kT

kan vi kontroll- (eller precisions-) bestämma den aktuella (»praktiska») v-formens värde vid det angivna T=16,32 T9 år enligt

v = 1,9614236c₀

~ 1,96c₀

att jämföra med det idealt odämpade fallet (T=16,32 T9 år med v_a = 2v_c),

v = 1,996641c₀

~ 2,00c₀

Editor2012III2

Speciella härledningar

Formell kontroll

mellan derivata och integral

för K-cellens allmänna radiella utsträckning

Se FORMLAGARNA för allmänna samband mellan derivata och integral, om ej redan bekant

;

OM v=2r/T,

då gäller a=v/T [= dv/dT],

så att då

r = T^2/3(1/2)(4Gm₂)^1/3

och

v = T^–1/3(1/3)(4Gm₂)^1/3

= r’

med

v’ = –T^–4/3(1/9)(4Gm₂)^1/3

= r’’

= a

= dv/dT

= d²r/(dT)²

det gäller att

dv = a·dT

= –T^–4/3(1/9)(4Gm₂)^1/3 dT ;

∫ dv = (1/9)(4Gm₂)^1/3 ò –T^–4/3 dT ;

v = (1/9)(4Gm₂)^1/3 [–T^{–4/3 + 1}/(–4/3 + 1)]

= (1/9)(4Gm₂)^1/3 [–T^–1/3/(–1/3)]

= T^–1/3(1/3)(4Gm₂)^1/3

vilket vi ser stämmer.

Expansionshastigheten (v) i primära v-formen

som funktion av

täthetsändringen under expansionstiden (T) och expansionsradien (r)

v = r(1/3)(8Gπρ/3)^1/2 ;

(m₂/T) = ([4pr³r/3]/[(3/2πGρ)^1/2])

= (4pr³r(2πGρ/3)^1/2/3)

= (r³[32π³Gρ³/27]^1/2)

;

v = T^–1/3(1/3)[4Gm₂]^1/3

T^–1/3 = (2pGρ/3)^1/6 ;

v = (2πGρ/3)^1/6(1/3)[4Gm₂]^1/3

= (2πGρ/3)^1/6(1/3)[4G4pr³ρ/3]^1/3

= r(2πGρ/3)^1/6(1/3)[16Gπρ/3]^1/3

= r(1/3)[(2πGρ/3)^1/216Gπρ/3]^1/3

= r(1/3)[([Gπρ/3]²2pGr/3)^1/216]^1/3

= r(1/3)[([G²π²ρ²/3²]2pGr/3)^1/216]^1/3

= r(1/3)[(G³π³ρ³2/27)^1/216]^1/3

= r(1/3)[(Gπρ)^3/2(2/27)^1/216]^1/3

= r(1/3)(Gπρ)^1/2[(2/27)^1/216]^1/3

;

[(2/27)^1/216]^1/3 = (8/3)^1/2

[(2/27)^1/216]^1/3 = [(2/3³)^1/22·8]^1/3

= [(2/3³)^1/22·2³]^1/3

= [(8/3³)^1/2·2³]^1/3

= [(2³/3³)^1/2·2³]^1/3

= [(2/3)^3/2·2³]^1/3

= [(2^3·2/32/3)^3/2]^1/3

= [(2²2/3)^3/2]^1/3

= [(8/3)^3/2]^1/3

= (8/3)^1/2

v = r(1/3)(8Gπρ/3)^1/2

Primära v-formen speciellt via massan och tätheten

Sambandsformen nedan speciellt omnämnd via separat utveckling i PLANETSYSTEMENS GRUNDFORMER — här i förtydligad härledning från grundformer använda speciellt i detta dokument:

T = (3/2πGρ)^1/2 ; expansionstiden

v = T^–1/3(1/3)(4Gm₂)^1/3 ; primära v-formen

3v = T^–1/3(4Gm₂)^1/3

= (3/2πGρ)^–1/6(4Gm₂)^1/3

= (2πGρ/3)^1/6(4Gm₂)^1/3

= m₂^1/3G^1/2(32πρ/3)^1/6

;

v = (1/3)m₂^1/3G^1/2(32πρ/3)^1/6 ;

3v = (2πGρ/3)^1/6[4Gm₂]^1/3

= m₂^1/3G^{1/6+1/3=3/6=1/2}(2πρ/3)^1/6[4]^1/3

= m₂^1/3G^1/2(2πρ/3)^1/6[4]^1/3

= m₂^1/3G^1/2(2πρ/3)^1/6[4]^1/3

= m₂^1/3G^1/2([4]^6/32πρ/3)^1/6

= m₂^1/3G^1/2([4]²2πρ/3)^1/6

= m₂^1/3G^1/2(32πρ/3)^1/6

;

v = (1/3)m₂^1/3G^1/2(32πρ/3)^1/6

END.

APPENDIX

Atomkärnans inkompressibilitet — komprimerat sammandrag — ATOMKÄRNANS INKOMPRESSIBILITET, ATOMKÄRNANS FORMBEVARANDE KRAFT, ATOMKÄRNANS GEOMETRI UNDER DEFORMATION

ATOMKÄRNANS INKOMPRESSIBILITET — relaterad fysik

Sammanställning med vidare jämförande beskrivning — 2012VII12 — av BellDharma för UNIVERSUMS HISTORIA

TNED:

1.

PLANCKRINGEN ‡ —

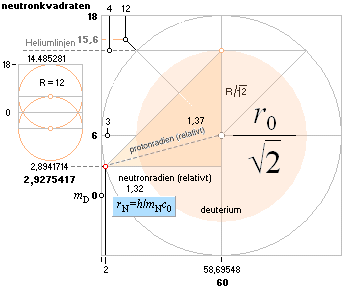
h = m_{NEUTRONMASSAN}c_{TOPPDIVERGENSEN}r_{NEUTRONRADIEN}

= Plancks konstant

= 6,62559 t34 JS

— garanterar särskilt att atomkärnan med sin bestämda massa (m) och bevarad naturkonstant c=c₀=2,99792458 T8 M/S — [ATOMKÄRNANS GRAVITELLA HÄRLEDNING]‡ — också har en fast tyngdcirkelradie (r):

atomkärnan (NEUTRONEN=PLANCKRINGEN h=mc₀r) kan inte komprimeras genom tryck;

h=mcr med konstant hmc betyder också konstant r; Plancks konstant innehåller redan fysikgrunderna.

Se även i PLANCKRINGEN h=mcr — Atomkärnans inkompressibilitet.

Separat analys i Atomkärnans axiella deformation visar också i samstämmig överensstämmelse med h att volymändringen vid axiellt tryck resulterar i en volymökning netto (en axiell ihoptryckning utesluter en axiellt förlängning eftersom axiell förlängning står i direkt konflikt med axiell ihoptryckning, bägge kan inte utvecklas samtidigt i en maximalt kärntät masskropp utan att hela masskroppen utvecklar självsvängning

— utvidgning = detonation). Se mera utförligt i Verkningssättet ‡.

2.

ELEKTRISKA KRAFTLAGEN ‡ [F=k(Q/r)²] omsatt på PLANCKRINGEN ‡ —

F = k(Q/r)²

= k([Q/(n→∞)]/[r/(n→∞)])²

(n→∞)-formen gestaltar, uppenbarligen, OUPPHÖRLIG DELNING i atomkärnan med ringar-i-ringar i all oändlighet: atomkärnan är en fundamental massform m=m=(n→∞)(m/[(n→∞)]) helt utan någon inre fast beståndsdel.

— Massans principiella struktur [PASTOM] bygger helt på den principen: atomkärnan, Plancks strukturkonstant. Det är den övergripande egenskap som neutronen och därmed alla andra atomkärnor [FUSIONSRINGARNA] bygger på — och därmed, tydligen, också samma som en ALLMÄN ORGANSIK PRINCIP som följer samma typ av verksamhet: oupphörlig delning: metabolism, LIV. Substanser strävar onekligen [MILLERS EXPERIMENT] att förenas SPONTANT till organismernas mest elementära delar. SÅ sammanhänger alla detaljer i TNED.

— endast förtydligar punkt (1) ovan:

atomkärnan som massans fundamentalform står redan på noll [PASTOM]‡;

— Det finns, via Planckfraktalerna ‡ [PLANCKRINGEN] ‡ i atomkärnans byggnad, inget utrymme för någon »kraftkompression» (Q) eller någon »avståndskompression (r) mellan beståndsdelarna (±e)» — Se mera utförligt i Verkningssättet ‡: atomkärnan [PASTOM] ‡ består inte av någon summa av smådelar utan är en massans fundamentalform via YTA [ATOMKÄRNANS GRAVITELLA HÄRLEDNING] ‡ — inte volym: Atomkärnan enligt h bygger uppenbarligen på ringar i ringar enligt Plancks anvisade konstant (h) som ovan. Se även i Plancks strukturkonstant ‡.

3.

NEUTRONKVADRATEN ‡ som garanterar ATOMVIKTERNA I RELATERAD FYSIK ‡ innefattar (tydligen, eller avbildar, uppenbarligen) ovanstående h-parameter r: neutronens tyngdcirkelradie (~1,32 Fermi) ingår (per geometrisk relation) i neutronkvadraten som kvantitetsrelaterad grund i jämförelse, och tillsammans, med vätekärnans radie (protonradien ~1,37 Fermi), och kopplar DÄRMED en speciellt sammanlänkande enhet med h — enligt TNED.

MAC:

I modern akademi ingår inget av ovanstående [TNEDp1-3]:

— Ingenting av sammanhanget i de tre ovannämnda punkterna — det relaterande sammanhanget i Plancks konstant (h) — ingår i modern akademi, ehuru (en del av) detaljerna gör det.

— Elektriska laddningen (Q) har ingen härledande författning i MAC. Från den fysikbilden utgår resten:

— Detaljerna i Q anvisar också anledningen varför detaljerna inte finns med i modern akademi. Se utförligt från ELEKTRISKA LADDNINGEN.

— Det betyder, i princip, att det också blir helt meningslöst att ens eftersöka någon bestämd referens i MAC för varje något enda precist begrepp »atomkärnans geometri»:

1. LJUS övergår i gripbar materia [Citat FOCUS MATERIEN 1975, massa är ljus].

2. ATOMKÄRNAN får inte ha någon åskådlig BILD [CitatLUND1996].

3. Atomkärnan betraktas analogt som en summa fristående vattendroppar [ALLMÄNNA KOEFFICIENTFORMEN] (nukleoner, kvarkar) i en omslutande vattenvolym — inte som den enhetligt omslutande vattenvolymen.

Endast SPINNET kan förklara varför fristående vattendroppar (efter rekyl från vattenyta) kan glida, åka och slira på vattenytan under viss begränsad tid. Vattenfysiken illustrerar kärnfysiken på utomordentligt sätt — i TNED. [Kärnmodellen].

BILDKÄLLA: Författarens arkiv — Tillfälligt vilande vattendroppar på vattenytan efter dropprekyler — NikonD90 · Sammansatt fotokollage av tre separata fotografier · 19Apr2009Bild650/693/651/Drop17isoAuto.

4. Det finns (i följd av ovanstående) ingen som helst begriplig preciserat sammanhängande framställning i ämnet »atomkärnans geometri, atomkärnans fysik» inom den moderna akademins ramar; Det som finns (i speciellt ämnet atomkärnans inkompressibilitet, se citat nedan: ”celebrated singularity theorems of Geroch, Hawking and Penrose” ) är teoretiska spekulationer på relativitetsteorins grund via olika modelltyper — och av vilka varenda en, enligt TNED, är dömd redan från ruta ett: resultaten varierar med Modellen; Jämför atomvikterna. Eller rent ut sagt:

I modern akademi råder i stort sett »allmänt kaos» i frågan om något sådant som en ’atomkärnans inkompressibilitet’: mängder med meningar, noll beskrivning;

— Å ena sidan krävs en atomkärnans inkompressibilitet för att få ihop det med TYP Supernova: hur material kastas ut [SVARTA HÅL — Se delavsnittet Novorna i MAC med citat från Encarat99, How a Supernova Explodes];

— Huvuddelen i påståendena (Exemplet med Supernovaartikeln från Encarta) är att man DELS säger att ’atomkärnan är högeligen inkompressibel’, för att strax vända på foten, samma artikelförfattare (Scientific American), och påstå att ’atomkärnan kan täthetskomprimeras 50%’. I varje fall i min referens betyder 50% en högst betydande kompressionsförmåga; meningarna motsäger (delvis) varandra.

— Å andra sidan krävs en atomkärnans absolut metriska kollaps för att underhålla den allmänna moderna akademins tillställningar enligt relativitetsteorin — eller vad som finns kvar av den efter Stephen Hawking’s noggranna städning — typ svarta hål (gravitell kollaps, gravitell singularitet: oändlig massa i en punkt): vid en viss massgräns »kollapsar gravitationen», och det bildas något i stil med »hur mycket massa som helst på hur liten volym som helst». Ingen kan berätta hur det går till — inte i någon som helst detalj — så att alla övriga hänger med.

Allmänt från 1999: [CitatReferens]

”After a star has exhausted its nuclear fuel, it can no longer remain in equilibrium and

must ultimately undergo gravitational collapse. The star will end as a white dwarf

if the mass of the collapsing core is less than the famous Chandrashekhar limit of 1.4

solar masses. It will end as a neutron star if the core has a mass greater than the

Chandrashekhar limit and less than about 35 times the mass of the sun. It is often

believed that a core heavier than about 5 solar masses will end, not as a white dwarf

or as a neutron star, but as a black hole. However, this belief that a black hole will

necessarily form is not based on any firm theoretical evidence.”, s221m;

”What we do know from general relativity about gravitational collapse is broadly

contained in the celebrated singularity theorems of Geroch, Hawking and Penrose. It

has been shown that under fairly general conditions, a sufficiently massive collapsing

object will undergo continual gravitational collapse, resulting in the formation of a

gravitational singularity.”, s221n;

”Firstly, while a great deal is known about the

properties of stationary black holes, we know very little about the process of black

hole formation. In fact we know as little about the formation of black holes as we do

about the formation of naked singularities.”, s222mn

http://www.ias.ac.in/jarch/jaa/20/221-232.pdf

GRAVITATIONAL COLLAPSE, BLACK HOLES AND NAKED SINGULARITIES, T. P. Singh (1999)

Mekanismen:

”Even more massive stars, above the Tolman–Oppenheimer–Volkoff limit cannot find a new dynamical equilibrium with any known force opposing gravity. Hence, the collapse continues with nothing to stop it.”,

http://en.wikipedia.org/wiki/Gravitational_collapse

@INTERNET Wikipedia, Gravitational collapse [2012-07-09]

Osäkerhet:

”Modern estimates range from approximately 1.5 to 3.0 solar masses.^[3] The uncertainty in the value reflects the fact that the equations of state for extremely dense matter are not well known.”,

http://en.wikipedia.org/wiki/Tolman%E2%80%93Oppenheimer%E2%80%93Volkoff_limit

@INTERNET Wikipedia, Tolman–Oppenheimer–Volkoff limit [2012-07-09]

PRINCIPEN för gravitell kollaps i MAC kontra TNED:

— Man tänker sig i MAC [Jämför Wikipediakällan ovan, Gravitational collapse] att g-trycket i en idealt sfärisk masskropp som tillåts växa till sig genom infallande material till slut blir så stort att atomkärnorna (i centrum) inte pallar trycket utan faller ihop. Exakt hur »fallandet ihop» skulle gå till är det ingen som kan förklara.

Verkningssättet

I TNED garanterar Planckfraktalerna genom ±e-strukturen via elektriska kraftlagen [F=k(Q/r)²]

1. att ELEKTRISKA KRAFTVERKAN mellan angränsande lika laddningar växer obegränsat med obegränsat avtagande avstånd: ju mer man försöker minska avståndet, desto mera kraft krävs, och

2. att MAGNETISKA KRAFTEN mellan två närliggande strömringar (±e) med inbördes motsatt strömflöde fungerar på samma sätt med obegränsat växande repulsionskraft via obegränsat avtagande laddningsavstånd, eftersom magnetiska fältstyrkan — enligt relaterad fysik [INDUKTIONEN OCH MAGNETISMEN] [Grundläggande magnetmatematik] — bara är ett annat sätt att se elektriska fältstyrkan [GRUNDBEGREPPENS INNEBÖRD]:

F/Q = Ξ = kQ/A = U/r ........................ elektrisk fältstyrka

Ξ/c = B = RQ/A = (U/r)/c ................... magnetisk fältstyrka

Det betyder bara, enligt TNED, att atomkärnan i sin YTSTRUKTUR [PLANCKRINGEN] [ATOMKÄRNANS GRAVITELLA HÄRLEDNING] besitter kapacitet att stå emot HUR MYCKET TRYCKANDE KRAFT SOM HELST — eftersom atomkärnan (enligt TNED) just ÄR — definierar — elementarformernas praktiska fysik (ifall någon hade missat det), sambanden ovan;

— Gravitationen, massans fundamentalform, atomkärnan, kan inte »döda gravitationen» — massan, atomkärnan — genom gravitationen:

gravitationen besitter ingen självutplånande egenskap enligt relaterad fysik. Men modern akademi är full av just sådana synpunkter ‡ (destruktivitetens högsäte).

’Gravit(ation)ell kollaps’ associeras i MAC (ofta) med termen eller begreppet ’svart hål’;

Det finns I DEN MODERNA AKADEMINS BEGREPP naturligtvis mängder med framställningar i ämnet »atomkärnans inkompressibilitet»: ”Gravitational collapse” + ”Black hole”, 331.000 GoogleResultat 2012-07-09.

(”Nuclear incompressibility”, 5.410 GoogleResultat 2012-07-09);

— I den allmänt tillgängliga (webb-) litteraturen brukar termen BLACK HOLE beskrivas som ett OMRÅDE i rymden med en så STARK gravitation att inget ljus slipper ut:

MACsvartHål

”A black hole is a gravitating object whose gravitational field is so strong that light cannot escape.”,

http://superstringtheory.com/blackh/blackh1.html

The Official String Theory Web Site — GRAVITATIONAL COLLAPSE!, [2012-07-09]

Svart hål

— svart tomrum i rymden, Stephen Hawking;

ljus, tid, relativitetsteori, gravitation, signal, singularitet

— atomkärnan diskuteras inte i Hawkings bok

s90mn:

”En vetenskapsman vid Cambridge, John Michell, skrev 1783 en uppsats i Philosophical Transactions of the Royal Society of London som grundades på detta antagande. Där påpekade han att en stjärna som var tillräckligt massiv och kompakt skulle ha ett så starkt gravitationsfält att ljus inte kunde lämna det: allt ljus som utsändes från stjärnans yta skulle dras tillbaka av stjärnans gravitationella attraktion innan det hade hunnit särskilt långt. Michell framkastade tanken att det kunde finnas ett stort antal sådana stjärnor. Även om vi inte skulle kunna se dem, eftersom deras ljus inte skulle kunna nå oss, skulle vi ändå känna av deras gravitationella attraktion. Sådana himlakroppar kallar vi i dag svarta hål, ty det är vad de är: svarta tomrum i rymden”,

s97mn:

”Det arbete som Roger Penrose och jag utförde mellan 1965 och 1970 visade att det i ett svart hål enligt den allmänna relativitetsteorin måste finnas en singularitet med oändlig masstäthet och oändlig rumtidskrökning.”,

KOSMOS — En kort historik,

Stephen W. Hawking, Prisma Magnum 1989

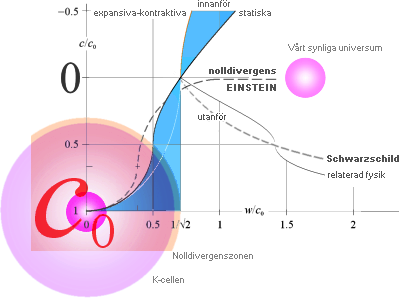
TNEDbasics — detaljerna i ljusets g-beroende

Einstein ............................... c/c₀ = (1 – w²/c²), innanför (sfären), w²=Gm₂/r ; m₂ centralmassan

Schwarzschild .................... c/c₀ = (1 – 2w²/c₀²), utanför sfären, w²=Gm₂/r

TNED statiska ....................... c/c₀ = (1 – w²/cc₀); | _UTw²=Gm₂/r | _INw²= r²(4πGρ/3) | ρ = m₂/V

Notera att w/c₀-skalan i fallet utanför centralmassan går mot noll — w=√Gm₂/r — ej utritat i ovanstående illustration — utanförkurvorna är illustrativt anpassade

I TNED finns ingen motsvarighet till den moderna akademins svarta hål — i MAC samma som [Stephen Hawking] ”svart tomrum i rymden”; Det är en föreställning som baseras på en »oändligt liten centralmassa» med »oändlig täthet». I TNED (statiska g-fysikens tillstånd) betyder c=0 randen av en idealt sfärisk, idealt täthetshomogen kropp (se samband längre ner) med sfärradien

r_0c = ρ^–1/2(3/8πG)^1/2c₀

Minsta massan med ideal neutronbas via max täthet 1,82 T17 KG/M³ blir ca 10 Solmassor, radien ca 30 KM. Vilka massor som kommer ifråga generellt beskrivs utförligt i TNED via GRÄNSMASSORNA, garanterade av Atomkärnans inkompressibilitet.

c=0 i relaterad fysik har explicit ingenting med stark gravitation att göra (lokalt höga M/S²-värden, a=Gm/r²) utan istället med mängden innesluten massa (ar=w²=Gm/r) — den moderna akademins svarta hål finns inte i relaterad fysik — exemplet nedan (universum) visar c=0 med i princip noll (0,0000000000458… M/S²) lokal accelerationskonstant (a) — en ekvation Einstein inte kunde lösa p.g.a. »tidens upphörande» enligt honom (se vic-felet): c=0; Einstein skrev (således) ”cc” istället för DET KORREKTA cc₀ och som leder till PLANCKEKVIVALENTERNA: korrekt — relaterad — fysik

Jämför TNED-exemplen (idealt masshomogena materierum) med gravitella fältstyrkan F/m = a = Gm/r² i

K‑CELLENS LOKALA GRAVITATION och RÄKNEEXEMPEL LJUSETS G-BEROENDE:

c=0 vid a=4,58 t11 M/S² = 0,0000000000458… M/S² med r=9,81 T26 M och ρ=1,67 t28 KG/M³ (synliga universums medeltäthet). Inneslutna massan [m=ρV=ρ4πr³/3] blir m=6,6 T53 KG (enklaste sättet att grovbestämma universums massa; K-cellens värmefysik ger ca 4,14 T53 KG enligt TNED).

:

— c=0 i relaterad fysik (TNED) beror inte av någon »stark g-fältstyrka» [MACsvartHål] (lokala accelerationskonstanten) utan av den inneslutna massan, eller med ideal masshomogen medeltäthet (ρ), via statiska g-fysikens samband [NOLLDIVERGENSZONENS RADIE UR TÄTHETEN]:

r_0c = ρ^–1/2(3/8πG)^1/2c₀

= ρ^–1/2(1,26823 T13 M(KG/M³)^1/2)

Med ρ=1,67 28 KG/M³ blir r_0c=9,81 T26 M. ρMAX i TNED för neutronkallplasma är 1,82 T17 KG, vilket ger ett motsvarande r_0c=29.727,8 M ~ 30KM, inneslutna massan drygt 10 Solmassor [GRÄNSMASSORNA]. Det blir också enligt TNED grovt sett maxgränsen för en maximalt tät kropp i vårt universum: Det går inte att få mindre omfång med c=0 i kroppsytan. Se även i SVARTA HÅL FINNS INTE I FYSIKEN ENLIGT TNED och Einsteins och Schwarzchilds samband.

— Eller i klartext enligt TNED: MAC-teorins populära singularitet (oändlig massa i PUNKT [Hawking]) är en ren fiktion (en ren konsekvens av r-teorin — vic-felet), ingenting som har med praktisk fysik att göra.

Primära v-formen

innehåll: SÖK äMNESORD på denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER

Primära v-formen

ämnesrubriker

innehåll

K-CELLENS GRUNDER

Zonskärningarna — K-cellens expansionshastighet

SE-symbolerna

Primära v-formen — K-cellens expansionshastighet

r-sambandets grund

r-formen

Statiska v-formen

Expansiva v-formen

K-cellens lokala gravitation

Zonpassagen

Speciella härledningar

APPENDIX

Atomkärnans inkompressibilitet

TNED

TNED 1 — Planckringen

TNED 2 — Elektriska laddningen

TNED 3 — Neutronkvadraten

MAC

Verkningssättet

MACsvartaHål

SvartHålHawking

TNEDbasics — detaljerna i ljusets g-beroende

referenser

[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967

Atomviktstabellen i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.

m_n = 1,0086652u ...................... neutronmassan i atomära massenheter (u) [HOP Table 2.1 s9–65]

m_e = 0,000548598u .................. elektronmassan i atomära massenheter (u) [HOP Table 10.3 s7–155 för m_e , Table 1.4 s7–27 för u]

u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27, 1967]

u = 1,66033 t27 KG .............. atomära massenheten [ENCARTA 99 Molecular Weight]

u = 1,66041 t27 KG ............... atomära massenheten [FOCUS MATERIEN 1975 s124sp1mn]

u = 1,66053886 t27 KG ........ atomära massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W (2005)]

u = 1,6605402 t27 KG .......... atomära massenheten [@INTERNET (2007) sv. Wikipedia]

u = 1,660538782 t27 KG ...... atomära massenheten [från www.sizes.com],

CODATA rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe on Data for Science and Technology)]

c₀ = 2,99792458 T8 M/S ........ ljushastigheten i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på 1970-talet)]

h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]

e = 1,602 t19 C ...................... elektriska elementarkvantumet, elektronens laddning [FOCUS MATERIEN 1975 s666ö]

e₀ = 8,8543 t12 C/VM ............. elektriska konstanten i vakuum [FOCUS MATERIEN 1975 s666ö]

G = 6,67 t11 JM/(KG)² .......... allmänna gravitationskonstanten [FOCUS MATERIEN 1975 s666ö] — G=F(r/m)² → N(M/KG)² = NM²/(KG)² = NM·M/(KG)²=JM/(KG)²

[BA]. BONNIERS ASTRONOMI 1978

t för 10^–, T för 10⁺, förenklade exponentbeteckningar

MAC, modern akademi

TNED

(Toroid Nuclear Electromechanical Dynamics), eller ToroidNukleära Elektromekaniska Dynamiken

är den dynamiskt ekvivalenta resultatbeskrivning som följer av härledningarna i Planckringen h=m_nc₀r_n, analogt Atomkärnans Härledning. Beskrivningen enligt TNED är relaterad, vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt logiskt förklarbara och begripliga, eller så inte alls. Med TNED får därmed (således) också förstås RELATERAD FYSIK OCH MATEMATIK. Se även uppkomsten av termen TNED [Planckfraktalerna] i ATOMKÄRNANS HÄRLEDNING.

Senast uppdaterade version: 2012-07-15

*END.

Stavningskontrollerat 2012-07-03 | 2012-07-13.

rester

åter till portalsidan · portalsidan är www.UniversumsHistoria.se

∫ √ τ π ε ħ UNICODE — often used characters in mathematical-technical-scientifical descriptions

σ ρ ν ν π τ γ λ η ≠ √ ħ ω →∞ ≡ ↔↕ ħ ℓ

Ω Φ Ψ Σ Π Ξ Λ Θ Δ

α β γ δ ε λ θ κ π ρ τ φ σ ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈ ≥ ← ↑ → ∞ ↓

ζ ξ

Arrow symbols, direct via Alt+NumPadKeyboard: Alt+24 ↑; Alt+25 ↓; Alt+26 →; Alt+27 ←; Alt+22 ▬

Alt+23 ↨ — also Alt+18 ↕; Alt+29 ↔

Alt+NumPad 0-25, 26-...

☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓

→←∟↔▲▼ !”#$%&’()*+,-./♦812...

åter till portalsidan · portalsidan är www.UniversumsHistoria.se